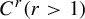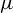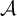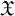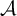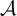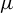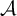1 Introduction
Let f be a
![]() $C^r(r>1)$
diffeomorphism of a compact Riemannian manifold M, preserving an ergodic hyperbolic measure
$C^r(r>1)$
diffeomorphism of a compact Riemannian manifold M, preserving an ergodic hyperbolic measure
![]() $\mu $
with positive entropy, and let
$\mu $
with positive entropy, and let
![]() $\mathcal {A}$
be a Hölder continuous cocycle of bounded linear operators acting on a Banach space
$\mathcal {A}$
be a Hölder continuous cocycle of bounded linear operators acting on a Banach space
![]() $\mathfrak {X}$
. If the cocycle satisfies the so-called quasi-compactness condition, then there is a sequence of horseshoes for f and dominated splittings for
$\mathfrak {X}$
. If the cocycle satisfies the so-called quasi-compactness condition, then there is a sequence of horseshoes for f and dominated splittings for
![]() $\mathcal {A}$
on the horseshoes, such that not only the measure theoretic entropy of f but also the Lyapunov exponents of
$\mathcal {A}$
on the horseshoes, such that not only the measure theoretic entropy of f but also the Lyapunov exponents of
![]() $\mathcal {A}$
with respect to
$\mathcal {A}$
with respect to
![]() $\mu $
can be approximated by the topological entropy of f and the Lyapunov exponents of
$\mu $
can be approximated by the topological entropy of f and the Lyapunov exponents of
![]() $\mathcal {A}$
on the horseshoes, respectively. As an application of the main result, we prove the continuity of sub-additive topological pressure of singular value potentials for Banach cocycles. For an explicit statement, see §2.
$\mathcal {A}$
on the horseshoes, respectively. As an application of the main result, we prove the continuity of sub-additive topological pressure of singular value potentials for Banach cocycles. For an explicit statement, see §2.
This paper is inspired by Katok [Reference Katok16] (or Katok and Hasselblatt [Reference Katok and Hasselblatt17, Theorem S.5.9]) and Cao, Pesin, and Zhao [Reference Cao, Pesin and Zhao7]. The approximation of an ergodic hyperbolic measure by horseshoes was first proved by Katok [Reference Katok16]. In [Reference Mendoza23], Mendoza showed that for a
![]() $C^2$
surface diffeomorphism, an ergodic hyperbolic Sinai–Ruelle–Bowen measure can be approximated by horseshoes with unstable dimensions converging to one. Avila, Crovisier, and Wilkinson [Reference Avila, Crovisier and Wilkinson1] observed that the horseshoe constructed by Katok [Reference Katok16] also has a dominated splitting (for
$C^2$
surface diffeomorphism, an ergodic hyperbolic Sinai–Ruelle–Bowen measure can be approximated by horseshoes with unstable dimensions converging to one. Avila, Crovisier, and Wilkinson [Reference Avila, Crovisier and Wilkinson1] observed that the horseshoe constructed by Katok [Reference Katok16] also has a dominated splitting (for
![]() $Df$
) and the Lyapunov exponents of the hyperbolic measure can be approximated by the exponents on the horseshoe.
$Df$
) and the Lyapunov exponents of the hyperbolic measure can be approximated by the exponents on the horseshoe.
In the
![]() $C^1$
setting, if a hyperbolic measure has positive entropy and whose support admits a dominated splitting, Gelfert [Reference Gelfert12] asserted the approximation of ergodic hyperbolic measures by horseshoes. Wang, Zou, and Cao [Reference Wang, Cao and Zou30] further studied the horseshoe approximation of Lyapunov exponents, which is used to show the arbitrarily large unstable dimension of the horseshoes.
$C^1$
setting, if a hyperbolic measure has positive entropy and whose support admits a dominated splitting, Gelfert [Reference Gelfert12] asserted the approximation of ergodic hyperbolic measures by horseshoes. Wang, Zou, and Cao [Reference Wang, Cao and Zou30] further studied the horseshoe approximation of Lyapunov exponents, which is used to show the arbitrarily large unstable dimension of the horseshoes.
The case of
![]() $C^r(r>1)$
maps was considered by Chung [Reference Chung8], Yang [Reference Yang31], and Gelfert [Reference Gelfert11]. Cao, Pesin, and Zhao [Reference Cao, Pesin and Zhao7] constructed repellers such that both the entropy and the Lyapunov exponents can be approximated on the repellers. They also used this result to show the continuity of sub-additive topological pressure for
$C^r(r>1)$
maps was considered by Chung [Reference Chung8], Yang [Reference Yang31], and Gelfert [Reference Gelfert11]. Cao, Pesin, and Zhao [Reference Cao, Pesin and Zhao7] constructed repellers such that both the entropy and the Lyapunov exponents can be approximated on the repellers. They also used this result to show the continuity of sub-additive topological pressure for
![]() $GL(d,\mathbb {R})$
cocycles, and then gave a lower bound estimate of the Hausdorff dimension of a non-conformal repeller.
$GL(d,\mathbb {R})$
cocycles, and then gave a lower bound estimate of the Hausdorff dimension of a non-conformal repeller.
For infinite-dimensional dynamical systems, Lian and Young [Reference Lian and Young20, Reference Lian and Young21] generalized Katok’s results [Reference Katok16] to mappings and semiflows of Hilbert spaces. Recently, Lian and Ma [Reference Lian and Ma19] generalized Katok’s result to mappings of Banach spaces. For a Banach cocycle
![]() $\mathcal {A}$
over a hyperbolic system f, Kalinin and Sadovskaya [Reference Kalinin and Sadovskaya14] proved that the upper and lower Lyapunov exponents of
$\mathcal {A}$
over a hyperbolic system f, Kalinin and Sadovskaya [Reference Kalinin and Sadovskaya14] proved that the upper and lower Lyapunov exponents of
![]() $\mathcal A$
with respect to an ergodic measure can be approximated in terms of the norms of the values of
$\mathcal A$
with respect to an ergodic measure can be approximated in terms of the norms of the values of
![]() $\mathcal A$
on hyperbolic periodic points of f.
$\mathcal A$
on hyperbolic periodic points of f.
The main results of this paper are stated in §2, together with some notation and preliminaries. In §3, we prove some preliminary results. The proofs of the main results are given in §§4 and 5.
2 Statement of main results
2.1 Cocycles and Lyapunov exponents for cocycles
Let f be a
![]() $C^r (r>1)$
diffeomorphism of a compact Riemannian manifold M, and
$C^r (r>1)$
diffeomorphism of a compact Riemannian manifold M, and
![]() $L(\mathfrak {X})$
be the space of bounded linear operators on a Banach space
$L(\mathfrak {X})$
be the space of bounded linear operators on a Banach space
![]() $\mathfrak {X}$
. Assume
$\mathfrak {X}$
. Assume
![]() $A:M \to L(\mathfrak {X})$
is a Hölder continuous map. The cocycle over f generated by A is a map
$A:M \to L(\mathfrak {X})$
is a Hölder continuous map. The cocycle over f generated by A is a map
![]() $\mathcal {A}:M\times \mathbb {N}\to L(\mathfrak {X})$
defined by
$\mathcal {A}:M\times \mathbb {N}\to L(\mathfrak {X})$
defined by
![]() $\mathcal {A}(x,0)=Id,$
and
$\mathcal {A}(x,0)=Id,$
and
![]() $\mathcal {A}(x,n)=A(f^{n-1}x)\ldots A(fx)A(x)$
. We also denote
$\mathcal {A}(x,n)=A(f^{n-1}x)\ldots A(fx)A(x)$
. We also denote
![]() $\mathcal {A}(x,-n):=A(f^{-n}x)^{-1}\ldots A(f^{-2}x)^{-1}A(f^{-1}x)^{-1}$
for
$\mathcal {A}(x,-n):=A(f^{-n}x)^{-1}\ldots A(f^{-2}x)^{-1}A(f^{-1}x)^{-1}$
for
![]() $n>0.$
Note that
$n>0.$
Note that
![]() $\mathcal {A}(x,-n)$
is not always defined. To be more flexible, we also denote
$\mathcal {A}(x,-n)$
is not always defined. To be more flexible, we also denote
![]() $\mathcal {A}_x^n:=\mathcal {A}(x,n).$
$\mathcal {A}_x^n:=\mathcal {A}(x,n).$
Let
![]() $\mathcal {M}_f(M)$
be the set of f-invariant probability measures. Then for a fixed dense subset
$\mathcal {M}_f(M)$
be the set of f-invariant probability measures. Then for a fixed dense subset
![]() $\{\varphi _j\}_{j= 1}^\infty $
of the unit sphere of
$\{\varphi _j\}_{j= 1}^\infty $
of the unit sphere of
![]() $C(M)$
, it induces a metric on
$C(M)$
, it induces a metric on
![]() $\mathcal {M}_f(M)$
:
$\mathcal {M}_f(M)$
:
 $$ \begin{align*}D(\mu,\nu)= \sum\limits_{j=1}^{\infty}\frac{|\int \varphi_j\,d\mu-\int \varphi_j\,d\nu|}{2^j}\quad \text{for all } \mu,\nu\in \mathcal{M}_f(M).\end{align*} $$
$$ \begin{align*}D(\mu,\nu)= \sum\limits_{j=1}^{\infty}\frac{|\int \varphi_j\,d\mu-\int \varphi_j\,d\nu|}{2^j}\quad \text{for all } \mu,\nu\in \mathcal{M}_f(M).\end{align*} $$
We now study some properties of Lyapunov exponents. The following version of multiplicative ergodic theorem was established by Froyland, LLoyd, and Quas [Reference Froyland, Lloyd and Quas10], based on the work of [Reference Lian and Lu18, Reference Oseledec24, Reference Thieullen28]. To state the multiplicative ergodic theorem, we introduce some definitions.
Denote by
![]() $B_1$
the unit ball of
$B_1$
the unit ball of
![]() $\mathfrak {X}$
. Then for any
$\mathfrak {X}$
. Then for any
![]() $T\in L(\mathfrak {X}),$
we define the Hausdorff measure of non-compactness of T by
$T\in L(\mathfrak {X}),$
we define the Hausdorff measure of non-compactness of T by
Then by the definition, we have
![]() $\|T\|_\kappa \leq \|T\|$
, and
$\|T\|_\kappa \leq \|T\|$
, and
![]() $\|\cdot \|_\kappa $
is sub-multiplicative, that is,
$\|\cdot \|_\kappa $
is sub-multiplicative, that is,
![]() $\|T_2T_1\|_\kappa \leq \|T_2\|_\kappa \cdot \|T_1\|_\kappa $
for any
$\|T_2T_1\|_\kappa \leq \|T_2\|_\kappa \cdot \|T_1\|_\kappa $
for any
![]() $T_1,T_2\in L(\mathfrak {X}).$
Let
$T_1,T_2\in L(\mathfrak {X}).$
Let
![]() $\mu $
be an ergodic f-invariant measure on
$\mu $
be an ergodic f-invariant measure on
![]() $M$
. Then by the sub-additive ergodic theorem, the limits
$M$
. Then by the sub-additive ergodic theorem, the limits
 $$ \begin{align*} \unicode{x3bb}(\mathcal{A},\mu):=\lim\limits_{n\to +\infty}\frac{1}{n}\int \log \|\mathcal{A}_x^n\|\,d\mu,\\ \kappa(\mathcal{A},\mu):=\lim\limits_{n\to +\infty}\frac{1}{n}\int \log \|\mathcal{A}_x^n\|_\kappa \,d\mu \end{align*} $$
$$ \begin{align*} \unicode{x3bb}(\mathcal{A},\mu):=\lim\limits_{n\to +\infty}\frac{1}{n}\int \log \|\mathcal{A}_x^n\|\,d\mu,\\ \kappa(\mathcal{A},\mu):=\lim\limits_{n\to +\infty}\frac{1}{n}\int \log \|\mathcal{A}_x^n\|_\kappa \,d\mu \end{align*} $$
exist. We say that the cocycle
![]() $\mathcal {A}$
is quasi-compact with respect to
$\mathcal {A}$
is quasi-compact with respect to
![]() $\mu $
, if
$\mu $
, if
![]() $\unicode{x3bb} (\mathcal {A},\mu )>\kappa (\mathcal {A},\mu )$
.
$\unicode{x3bb} (\mathcal {A},\mu )>\kappa (\mathcal {A},\mu )$
.
For a given f-invariant set
![]() $\Lambda ,$
a splitting
$\Lambda ,$
a splitting
![]() $\mathfrak {X}=E_1(x)\oplus \cdots \oplus E_i(x)\oplus F_i(x)$
on
$\mathfrak {X}=E_1(x)\oplus \cdots \oplus E_i(x)\oplus F_i(x)$
on
![]() $\Lambda $
is called an
$\Lambda $
is called an
![]() $\mathcal {A}$
-invariant splitting if
$\mathcal {A}$
-invariant splitting if
![]() $E_j(x)=A(x)^{-1}E_j(fx)$
and
$E_j(x)=A(x)^{-1}E_j(fx)$
and
![]() $F_i(x)= A(x)^{-1}F_i(fx)$
for every
$F_i(x)= A(x)^{-1}F_i(fx)$
for every
![]() $x\in \Lambda , j=1,\ldots ,i.$
$x\in \Lambda , j=1,\ldots ,i.$
Remark. In the literature ([Reference Froyland, Lloyd and Quas9, Reference Lian and Lu18, Reference Thieullen28] for instance), the splitting
![]() $\mathfrak {X}=E_1(x)\oplus \cdots \oplus E_i(x)\oplus F_i(x)$
is called
$\mathfrak {X}=E_1(x)\oplus \cdots \oplus E_i(x)\oplus F_i(x)$
is called
![]() $\mathcal {A}$
-invariant if
$\mathcal {A}$
-invariant if
![]() $A(x)E_j(x)=E_j(fx)$
and
$A(x)E_j(x)=E_j(fx)$
and
![]() $A(x)F_i(x)\subset F_i(fx)$
for every
$A(x)F_i(x)\subset F_i(fx)$
for every
![]() $x\in \Lambda , j=1,\ldots ,i.$
If
$x\in \Lambda , j=1,\ldots ,i.$
If
![]() $A(x)|_{E_1(x)\oplus \cdots \oplus E_i(x)}$
is a bijection for every
$A(x)|_{E_1(x)\oplus \cdots \oplus E_i(x)}$
is a bijection for every
![]() $x\in \Lambda ,$
then the two definitions are actually equivalent. Indeed, if
$x\in \Lambda ,$
then the two definitions are actually equivalent. Indeed, if
![]() $A(x)E_j(x)=E_j(fx)$
and
$A(x)E_j(x)=E_j(fx)$
and
![]() $A(x)F_i(x)\subset F_i(fx)$
for every
$A(x)F_i(x)\subset F_i(fx)$
for every
![]() $j=1,\ldots ,i,$
denote
$j=1,\ldots ,i,$
denote
![]() $H_i(x)=E_1(x)\oplus \cdots \oplus E_i(x).$
Then by Lemma 4.2,
$H_i(x)=E_1(x)\oplus \cdots \oplus E_i(x).$
Then by Lemma 4.2,
![]() $\mathfrak {X}=H_i(x)\oplus A(x)^{-1}F_i(fx)$
. Hence,
$\mathfrak {X}=H_i(x)\oplus A(x)^{-1}F_i(fx)$
. Hence,
![]() $\mathrm{codim}(A(x)^{-1}F_i(fx))=\dim (H_i(x))=\mathrm{codim}(F_i(x))$
. Then it follows from
$\mathrm{codim}(A(x)^{-1}F_i(fx))=\dim (H_i(x))=\mathrm{codim}(F_i(x))$
. Then it follows from
![]() $F_i(x)\subset A(x)^{-1}A(x)F_i(x)\subset A(x)^{-1} F_i(fx)$
that
$F_i(x)\subset A(x)^{-1}A(x)F_i(x)\subset A(x)^{-1} F_i(fx)$
that
![]() $F_i(x) = A(x)^{-1}F_i(fx)$
.
$F_i(x) = A(x)^{-1}F_i(fx)$
.
Given two topological spaces Y, Z and a Borel measure
![]() $\mu $
on Y, a map
$\mu $
on Y, a map
![]() $g:Y\to Z$
is called
$g:Y\to Z$
is called
![]() $\mu $
-continuous if there exists a sequence of pairwise disjoint compact subsets
$\mu $
-continuous if there exists a sequence of pairwise disjoint compact subsets
![]() $Y_n\subset Y$
, such that
$Y_n\subset Y$
, such that
![]() $\mu (\bigcup _{n\geq 1}Y_n)=1$
and
$\mu (\bigcup _{n\geq 1}Y_n)=1$
and
![]() $g|_{Y_n}$
is continuous for every
$g|_{Y_n}$
is continuous for every
![]() $n\geq 1$
.
$n\geq 1$
.
We now state a version of multiplicative ergodic theorem used in this paper. To simplify the statement, we write
![]() $\mathbb {N}_k:=\{1,2,\ldots ,k \}$
for
$\mathbb {N}_k:=\{1,2,\ldots ,k \}$
for
![]() $1\leq k <+\infty $
and
$1\leq k <+\infty $
and
![]() $\mathbb {N}_{+\infty }:=\mathbb {N}_+$
.
$\mathbb {N}_{+\infty }:=\mathbb {N}_+$
.
Theorem 2.1. [Reference Froyland, Lloyd and Quas10]
Let f be a
![]() $C^r(r>1)$
diffeomorphism of a compact Riemannian manifold M preserving an ergodic measure
$C^r(r>1)$
diffeomorphism of a compact Riemannian manifold M preserving an ergodic measure
![]() $\mu $
, and let
$\mu $
, and let
![]() $A:M\to L(\mathfrak {X})$
be a Hölder continuous map. If
$A:M\to L(\mathfrak {X})$
be a Hölder continuous map. If
![]() $\mathcal {A}$
is quasi-compact with respect to
$\mathcal {A}$
is quasi-compact with respect to
![]() $\mu $
, then there exists an f-invariant set
$\mu $
, then there exists an f-invariant set
![]() $\mathcal {R}^{\mathcal {A}}\subset M$
with
$\mathcal {R}^{\mathcal {A}}\subset M$
with
![]() $\mu (\mathcal {R}^{\mathcal {A}})=1$
such that for every
$\mu (\mathcal {R}^{\mathcal {A}})=1$
such that for every
![]() $x\in \mathcal {R}^{\mathcal {A}}$
:
$x\in \mathcal {R}^{\mathcal {A}}$
:
-
(i) there exist
 $k_0\leq +\infty $
, finite dimensional subspaces
$k_0\leq +\infty $
, finite dimensional subspaces
 $E_1(x),E_2(x),\ldots $
, and infinite dimensional closed subspaces
$E_1(x),E_2(x),\ldots $
, and infinite dimensional closed subspaces
 $F_1(x),F_2(x),\ldots $
indexed in
$F_1(x),F_2(x),\ldots $
indexed in
 $\mathbb {N}_{k_0}$
, such that for any
$\mathbb {N}_{k_0}$
, such that for any
 $i\in \mathbb {N}_{k_0}$
, there exists an
$i\in \mathbb {N}_{k_0}$
, there exists an
 $\mathcal {A}$
-invariant splitting on
$\mathcal {A}$
-invariant splitting on
 $\mathcal {R}^{\mathcal {A}}$
$\mathcal {R}^{\mathcal {A}}$
 $$ \begin{align*}\mathfrak{X}=E_1(x)\oplus\cdots\oplus E_i(x)\oplus F_i(x);\end{align*} $$
$$ \begin{align*}\mathfrak{X}=E_1(x)\oplus\cdots\oplus E_i(x)\oplus F_i(x);\end{align*} $$
-
(ii) there exist numbers
 $\unicode{x3bb} (\mathcal {A},\mu )=\unicode{x3bb} _{1}>\unicode{x3bb} _{2}>\cdots >\kappa (\mathcal {A},\mu ) $
indexed in
$\unicode{x3bb} (\mathcal {A},\mu )=\unicode{x3bb} _{1}>\unicode{x3bb} _{2}>\cdots >\kappa (\mathcal {A},\mu ) $
indexed in
 $\mathbb {N}_{k_0}$
such that for any
$\mathbb {N}_{k_0}$
such that for any
 $ i\in \mathbb {N}_{k_0}, \lim \nolimits _{n\rightarrow \pm \infty } ({1}/{n})\log {\|\mathcal {A}_x^n(u)\|} = \unicode{x3bb} _{i}, \text { for all } u\in E_{i}(x)\setminus \{0\},$
$ i\in \mathbb {N}_{k_0}, \lim \nolimits _{n\rightarrow \pm \infty } ({1}/{n})\log {\|\mathcal {A}_x^n(u)\|} = \unicode{x3bb} _{i}, \text { for all } u\in E_{i}(x)\setminus \{0\},$

where
 $\unicode{x3bb} _{{k_0}+1}:=\kappa (\mathcal {A},\mu )$
if
$\unicode{x3bb} _{{k_0}+1}:=\kappa (\mathcal {A},\mu )$
if
 $k_0<+\infty ;$
$k_0<+\infty ;$
-
(iii) for any
 $i\in \mathbb {N}_{k_0}$
,
$i\in \mathbb {N}_{k_0}$
,
 $E_i(x),F_i(x)$
are Borel measurable
$E_i(x),F_i(x)$
are Borel measurable
 $\mu $
-continuous and the norms of the projection operators
$\mu $
-continuous and the norms of the projection operators
 $\pi ^i_E(x),\pi ^i_F(x)$
associated with the splitting
$\pi ^i_E(x),\pi ^i_F(x)$
associated with the splitting
 ${\mathfrak {X}}=(E_1(x)\oplus \cdots \oplus E_i(x))\oplus F_i(x)$
are tempered, that is, (2.1)
${\mathfrak {X}}=(E_1(x)\oplus \cdots \oplus E_i(x))\oplus F_i(x)$
are tempered, that is, (2.1) $$ \begin{align} \lim\limits_{n\to \pm\infty}\frac{1}{n}\log \|\pi^i_\tau(f^nx)\|=0\quad\text{for all } \tau=E,F. \end{align} $$
$$ \begin{align} \lim\limits_{n\to \pm\infty}\frac{1}{n}\log \|\pi^i_\tau(f^nx)\|=0\quad\text{for all } \tau=E,F. \end{align} $$
The numbers
![]() $\unicode{x3bb} _{1}>\unicode{x3bb} _{2}>\cdots $
indexed in
$\unicode{x3bb} _{1}>\unicode{x3bb} _{2}>\cdots $
indexed in
![]() $\mathbb {N}_{k_0}$
are called the Lyapunov exponents of
$\mathbb {N}_{k_0}$
are called the Lyapunov exponents of
![]() $\mathcal {A}$
with respect to
$\mathcal {A}$
with respect to
![]() $\mu ,$
and the decomposition
$\mu ,$
and the decomposition
![]() ${\mathfrak {X}}=E_1(x)\oplus \cdots \oplus E_i(x)\oplus F_i(x)$
is called the Oseledets decomposition. Denote
${\mathfrak {X}}=E_1(x)\oplus \cdots \oplus E_i(x)\oplus F_i(x)$
is called the Oseledets decomposition. Denote
![]() $d_j:=\dim (E_j).$
$d_j:=\dim (E_j).$
2.2 Main result
Recall that an ergodic f-invariant measure is called a hyperbolic measure if it has no zero Lyapunov exponents for
![]() $Df$
. We now state the main result of this paper.
$Df$
. We now state the main result of this paper.
Theorem 2.2. Let f be a
![]() $C^r(r>1)$
diffeomorphism of a compact Riemannian manifold M preserving an ergodic hyperbolic measure
$C^r(r>1)$
diffeomorphism of a compact Riemannian manifold M preserving an ergodic hyperbolic measure
![]() $\mu $
with
$\mu $
with
![]() $h_{\mu }(f)>0$
, and let
$h_{\mu }(f)>0$
, and let
![]() $A:M\to L(\mathfrak {X})$
be a Hölder continuous map such that the generated cocycle
$A:M\to L(\mathfrak {X})$
be a Hölder continuous map such that the generated cocycle
![]() $\mathcal {A}$
is quasi-compact with respect to
$\mathcal {A}$
is quasi-compact with respect to
![]() $\mu $
. Then for any
$\mu $
. Then for any
![]() $i\in \mathbb {N}_{k_0},$
there exists
$i\in \mathbb {N}_{k_0},$
there exists
![]() $\varepsilon _i>0$
, such that for any
$\varepsilon _i>0$
, such that for any
![]() $0<\varepsilon <\varepsilon _i,$
there exists a hyperbolic horseshoe
$0<\varepsilon <\varepsilon _i,$
there exists a hyperbolic horseshoe
![]() $\Lambda $
satisfying the following properties:
$\Lambda $
satisfying the following properties:
-
(i)
 $|h_{\mathrm{top}}(f|_{\Lambda })-h_\mu (f)|<\varepsilon ;$
$|h_{\mathrm{top}}(f|_{\Lambda })-h_\mu (f)|<\varepsilon ;$
-
(ii)
 $\Lambda $
is
$\Lambda $
is
 $\varepsilon $
-close to
$\varepsilon $
-close to
 $\text {supp}(\mu )$
in the Hausdorff distance;
$\text {supp}(\mu )$
in the Hausdorff distance; -
(iii) for any f-invariant probability measure
 $\nu $
supported in
$\nu $
supported in
 $\Lambda $
,
$\Lambda $
,
 $D(\mu ,\nu )<\varepsilon $
;
$D(\mu ,\nu )<\varepsilon $
; -
(iv) there exist
 $m\in \mathbb {N}$
and a continuous
$m\in \mathbb {N}$
and a continuous
 $\mathcal {A}$
-invariant splitting of
$\mathcal {A}$
-invariant splitting of
 $\mathfrak {X}$
on
$\mathfrak {X}$
on
 $\Lambda $
,
$\Lambda $
,  $$ \begin{align*}\mathfrak{X}=E_1(x)\oplus\cdots\oplus E_i(x)\oplus F_i(x),\end{align*} $$
$$ \begin{align*}\mathfrak{X}=E_1(x)\oplus\cdots\oplus E_i(x)\oplus F_i(x),\end{align*} $$
with
 $\dim (E_j(x))=d_j\text { for all } 1 \leq j \leq i$
, such that for any
$\dim (E_j(x))=d_j\text { for all } 1 \leq j \leq i$
, such that for any
 $x \in \Lambda , $
we have
$x \in \Lambda , $
we have 

The main difficulty in the proof of Theorem 2.2 is to obtain the
![]() $\mathcal {A}$
-invariant splitting in property (iv) of Theorem 2.2. If
$\mathcal {A}$
-invariant splitting in property (iv) of Theorem 2.2. If
![]() $\mathfrak {X}$
is finite dimensional, there is a classical argument to obtain the linear subspaces
$\mathfrak {X}$
is finite dimensional, there is a classical argument to obtain the linear subspaces
![]() $E_i(x)$
(see [Reference Barreira and Pesin3, Theorem 6.1.2] for instance). However, this argument relies on the compactness of the unit sphere of
$E_i(x)$
(see [Reference Barreira and Pesin3, Theorem 6.1.2] for instance). However, this argument relies on the compactness of the unit sphere of
![]() $\mathfrak {X}$
, which is invalid in the infinite dimensional case. To overcome this difficulty, we obtain the invariant splitting by showing that
$\mathfrak {X}$
, which is invalid in the infinite dimensional case. To overcome this difficulty, we obtain the invariant splitting by showing that
![]() $E_i(x)$
is actually a limit of a certain Cauchy sequence in the Grassmannian of closed subspaces of
$E_i(x)$
is actually a limit of a certain Cauchy sequence in the Grassmannian of closed subspaces of
![]() $\mathfrak {X}$
.
$\mathfrak {X}$
.
2.3 Application: continuity of sub-additive topological pressure
For a given continuous map
![]() $f:M\to M$
, a sequence of continuous functions
$f:M\to M$
, a sequence of continuous functions
![]() $\Phi =\{\varphi _n\}_{n\geq 1}$
on M is called sub-additive if
$\Phi =\{\varphi _n\}_{n\geq 1}$
on M is called sub-additive if
Recall that a subset
![]() $E\subset M$
is called (n,
$E\subset M$
is called (n,
![]() $\epsilon $
)-separated if for any
$\epsilon $
)-separated if for any
![]() $x,y\in E$
, there exists
$x,y\in E$
, there exists
![]() ${0\leq i<n}$
such that
${0\leq i<n}$
such that
![]() $d(f^ix,f^iy)>\epsilon .$
Now for a given sub-additive potential
$d(f^ix,f^iy)>\epsilon .$
Now for a given sub-additive potential
![]() ${\Phi =\{\varphi _n\}_{n\geq 1}}$
, the sub-additive topological pressure of
${\Phi =\{\varphi _n\}_{n\geq 1}}$
, the sub-additive topological pressure of
![]() $\Phi $
is defined by
$\Phi $
is defined by
where
 $$ \begin{align*} P_n(\Phi,\epsilon)=\sup\bigg\{\sum\limits_{x \in E} e^{\varphi_n(x)}: E \text{ is an } (n,\epsilon)\text{-}\text{separated subset of }M\bigg\}. \end{align*} $$
$$ \begin{align*} P_n(\Phi,\epsilon)=\sup\bigg\{\sum\limits_{x \in E} e^{\varphi_n(x)}: E \text{ is an } (n,\epsilon)\text{-}\text{separated subset of }M\bigg\}. \end{align*} $$
The variational principle for sub-additive topological pressure was proved by Cao, Feng, and Huang [Reference Cao, Feng and Huang5].
Theorem 2.3. [Reference Cao, Feng and Huang5]
Let
![]() $f:M\to M$
be a continuous map on a compact metric space M, and
$f:M\to M$
be a continuous map on a compact metric space M, and
![]() $\Phi =\{\varphi _n\}_{n\ge 1}$
be a sub-additive potential on M. Then,
$\Phi =\{\varphi _n\}_{n\ge 1}$
be a sub-additive potential on M. Then,
where
![]() $h_{\mu }(f)$
is the metric entropy of f with respect to
$h_{\mu }(f)$
is the metric entropy of f with respect to
![]() $\mu $
(for details see [Reference Walters29]) and
$\mu $
(for details see [Reference Walters29]) and
Let
![]() $A:M\to L(\mathfrak {X})$
be a continuous map. We shall consider the singular value functions of A. The concept of singular values in a general Banach space is not well defined, instead, many different generalizations exist (for details, see [Reference Quas, Thieullen and Zarrabi26, §A.3]). We choose the number
$A:M\to L(\mathfrak {X})$
be a continuous map. We shall consider the singular value functions of A. The concept of singular values in a general Banach space is not well defined, instead, many different generalizations exist (for details, see [Reference Quas, Thieullen and Zarrabi26, §A.3]). We choose the number
 $$ \begin{align*}\sigma_k(T)=\sup\limits_{\dim(V)=k}\inf\limits_{v\in V\setminus\{0\}}\frac{\|Tv\|}{\|v\|} \end{align*} $$
$$ \begin{align*}\sigma_k(T)=\sup\limits_{\dim(V)=k}\inf\limits_{v\in V\setminus\{0\}}\frac{\|Tv\|}{\|v\|} \end{align*} $$
to be the singular value of index k of an operator T. Let
 $$ \begin{align*}\psi^s(x,n):= \sum_{i=1}^{[s]}\log\sigma_i(\mathcal{A}_x^n)+(s-[s])\log \sigma_{[s]+1}(\mathcal{A}_x^n), \end{align*} $$
$$ \begin{align*}\psi^s(x,n):= \sum_{i=1}^{[s]}\log\sigma_i(\mathcal{A}_x^n)+(s-[s])\log \sigma_{[s]+1}(\mathcal{A}_x^n), \end{align*} $$
and denote
![]() $P(A,s):=P(f,\Psi )$
as the topological pressure of the singular value potential
$P(A,s):=P(f,\Psi )$
as the topological pressure of the singular value potential
![]() $\Psi =\{\psi ^s(\cdot ,n)\}_{n\geq 1}$
.
$\Psi =\{\psi ^s(\cdot ,n)\}_{n\geq 1}$
.
Remark. Though
![]() $\Psi $
is not sub-additive, it is equivalent to a sub-additive potential. Indeed, we define a k-dimensional volume of vectors
$\Psi $
is not sub-additive, it is equivalent to a sub-additive potential. Indeed, we define a k-dimensional volume of vectors
![]() $(v_1,v_2,\ldots ,v_k)$
by
$(v_1,v_2,\ldots ,v_k)$
by
 $$ \begin{align*}\mathrm{Vol}_k(v_1,v_2,\ldots,v_k)=\bigg(\prod_{i=1}^{k-1} {\mathrm{dist}} (v_i,\mathrm{span}(v_{i+1},\ldots,v_k))\bigg)\|v_k\|, \end{align*} $$
$$ \begin{align*}\mathrm{Vol}_k(v_1,v_2,\ldots,v_k)=\bigg(\prod_{i=1}^{k-1} {\mathrm{dist}} (v_i,\mathrm{span}(v_{i+1},\ldots,v_k))\bigg)\|v_k\|, \end{align*} $$
where
![]() ${\mathrm{dist}} (v_i,\mathrm{span}(v_{i+1},\ldots ,v_k))=\inf \{\|v_i-v\|:v\in \mathrm{span}(v_{i+1},\ldots ,v_k)\}.$
For
${\mathrm{dist}} (v_i,\mathrm{span}(v_{i+1},\ldots ,v_k))=\inf \{\|v_i-v\|:v\in \mathrm{span}(v_{i+1},\ldots ,v_k)\}.$
For
![]() ${T\in L(\mathfrak {X}),}$
define
${T\in L(\mathfrak {X}),}$
define
 $$ \begin{align*}V_k(T)=\sup\limits_{\substack{\|v_i\|=1 \\ 1\leq i\leq k}}\mathrm{Vol}_k(Tv_1,Tv_2,\ldots,Tv_k).\end{align*} $$
$$ \begin{align*}V_k(T)=\sup\limits_{\substack{\|v_i\|=1 \\ 1\leq i\leq k}}\mathrm{Vol}_k(Tv_1,Tv_2,\ldots,Tv_k).\end{align*} $$
Then by [Reference Lian and Lu18, Lemma 4.7],
![]() $V_k$
is sub-multiplicative. Moreover, by [Reference González-Tokman and Quas13], there exists a constant
$V_k$
is sub-multiplicative. Moreover, by [Reference González-Tokman and Quas13], there exists a constant
![]() $C\geq 1$
which is independent of
$C\geq 1$
which is independent of
![]() $T\in L(\mathfrak {X})$
such that
$T\in L(\mathfrak {X})$
such that
 $$ \begin{align} C^{-1}\cdot V_k(T)\leq \prod_{i=1}^k\sigma_i(T)\leq C\cdot V_k(T). \end{align} $$
$$ \begin{align} C^{-1}\cdot V_k(T)\leq \prod_{i=1}^k\sigma_i(T)\leq C\cdot V_k(T). \end{align} $$
Let
Then it gives that
![]() $\Phi =\{\phi ^s(\cdot ,n)\}_{n\geq 1}$
is sub-additive and
$\Phi =\{\phi ^s(\cdot ,n)\}_{n\geq 1}$
is sub-additive and
![]() $|\phi ^s(x,n)-\psi ^s(x,n)|\leq \log C,$
which implies
$|\phi ^s(x,n)-\psi ^s(x,n)|\leq \log C,$
which implies
![]() $P(A,s)=P(f,\Psi )=P(f,\Phi ).$
$P(A,s)=P(f,\Psi )=P(f,\Phi ).$
We shall consider a
![]() $C^{r}(r>1)$
diffeomorphism
$C^{r}(r>1)$
diffeomorphism
![]() $f:M\to M$
which satisfies the assumptions:
$f:M\to M$
which satisfies the assumptions:
-
(A1) the entropy map
 $\mu \mapsto h_\mu (f)$
is upper semi-continuous;
$\mu \mapsto h_\mu (f)$
is upper semi-continuous; -
(A2) every f-invariant measure is hyperbolic, that is, the Lyapunov exponents of f are non-zero for every f-invariant measure.
Paradigms of diffeomorphisms which satisfy assumptions (A1) and (A2) but not are uniformly hyperbolic are given, for example, by a one-parameter family of
![]() $C^k$
maps constructed by Rios [Reference Rios27], and a family of
$C^k$
maps constructed by Rios [Reference Rios27], and a family of
![]() $C^2$
Hénon-like maps constructed by Cao, Luzzatto, and Rios [Reference Cao, Luzzatto and Rios6].
$C^2$
Hénon-like maps constructed by Cao, Luzzatto, and Rios [Reference Cao, Luzzatto and Rios6].
Theorem 2.4. Let
![]() $f:M\to M$
be a
$f:M\to M$
be a
![]() $C^{r}(r>1)$
diffeomorphism satisfying the hypothesis of assumptions (A1) and (A2), and let
$C^{r}(r>1)$
diffeomorphism satisfying the hypothesis of assumptions (A1) and (A2), and let
![]() $A:M\to L(\mathfrak {X})$
be an
$A:M\to L(\mathfrak {X})$
be an
![]() $\alpha $
-Hölder continuous map such that
$\alpha $
-Hölder continuous map such that
![]() $A(x)$
is a compact operator for every
$A(x)$
is a compact operator for every
![]() $x\in M$
. Then for any
$x\in M$
. Then for any
![]() $s<k_0$
,
$s<k_0$
,
![]() $A\mapsto P(A,s)$
is continuous at A, that is, for any
$A\mapsto P(A,s)$
is continuous at A, that is, for any
![]() $\epsilon>0$
, there exist
$\epsilon>0$
, there exist
![]() $\delta>0$
such that
$\delta>0$
such that
for every
![]() $\alpha $
-Hölder continuous map
$\alpha $
-Hölder continuous map
![]() $B: M\to L(\mathfrak {X})$
with
$B: M\to L(\mathfrak {X})$
with
![]() $\|A-B\|_0<\delta $
, where
$\|A-B\|_0<\delta $
, where
![]() $k_0$
is given by Theorem 2.1 and
$k_0$
is given by Theorem 2.1 and
![]() $\|A-B\|_0:=\max _{x\in M}\|A(x)-B(x)\|$
.
$\|A-B\|_0:=\max _{x\in M}\|A(x)-B(x)\|$
.
If the Banach space
![]() $\mathfrak {X}$
is finite dimensional, then we have the following corollary.
$\mathfrak {X}$
is finite dimensional, then we have the following corollary.
Corollary 2.5. Let
![]() $f:M\to M$
be a
$f:M\to M$
be a
![]() $C^{r}(r>1)$
diffeomorphism satisfying the hypothesis of assumptions (A1) and (A2), and let
$C^{r}(r>1)$
diffeomorphism satisfying the hypothesis of assumptions (A1) and (A2), and let
![]() $A:M\to M_d(\mathbb {R})$
be an
$A:M\to M_d(\mathbb {R})$
be an
![]() $\alpha $
-Hölder continuous map. Then
$\alpha $
-Hölder continuous map. Then
![]() $A\mapsto P(A,s)$
is continuous at A, that is, for any
$A\mapsto P(A,s)$
is continuous at A, that is, for any
![]() $\epsilon>0$
, there exist
$\epsilon>0$
, there exist
![]() $\delta>0$
such that
$\delta>0$
such that
for every
![]() $\alpha $
-Hölder continuous map
$\alpha $
-Hölder continuous map
![]() $B: M\to M_d(\mathbb {R})$
with
$B: M\to M_d(\mathbb {R})$
with
![]() $\|A-B\|_0<\delta $
, where
$\|A-B\|_0<\delta $
, where
![]() $\|A-B\|_0:=\max _{x\in M}\|A(x)-B(x)\|$
.
$\|A-B\|_0:=\max _{x\in M}\|A(x)-B(x)\|$
.
In [Reference Cao, Pesin and Zhao7, Theorem 7.1], Cao, Pesin, and Zhao proved a similar result for f being a sub-shift of finite type. This corollary relaxes the condition of f to be a totally non-uniformly hyperbolic diffeomorphism, that is, f satisfies the hypothesis of assumptions (A1) and (A2).
3 Preliminary results
This section is devoted to the preparation of technical tools which shall be used to prove the main theorem. The main result in this section is Lemma 3.5, in which the invariant cones for cocycles are established. This is a necessary step to obtain the dominated splittings in Theorem 2.2. This was also the main step in the previous work [Reference Avila, Crovisier and Wilkinson1], as well as [Reference Cao, Pesin and Zhao7]. Comparing with the previous result, the main difference in the proof of Lemma 3.5 is to obtain the invariance of the cone
![]() $V_j(x,\theta )$
in item (ii) of Lemma 3.5. This difficulty comes from the fact that
$V_j(x,\theta )$
in item (ii) of Lemma 3.5. This difficulty comes from the fact that
![]() $\mathcal {A}_x^{-n}$
is not a bounded linear operator. We begin by introducing the regular neighborhoods for non-uniformly hyperbolic systems.
$\mathcal {A}_x^{-n}$
is not a bounded linear operator. We begin by introducing the regular neighborhoods for non-uniformly hyperbolic systems.
3.1 Regular neighborhoods
Let f be a
![]() $C^r \, (r>1) \, $
diffeomorphism of a compact Riemannian d-dimensional manifold M, preserving an ergodic hyperbolic measure
$C^r \, (r>1) \, $
diffeomorphism of a compact Riemannian d-dimensional manifold M, preserving an ergodic hyperbolic measure
![]() $\mu $
. Then by Oseledets multiplicative ergodic theorem [Reference Oseledec24], there exists an f-invariant set
$\mu $
. Then by Oseledets multiplicative ergodic theorem [Reference Oseledec24], there exists an f-invariant set
![]() $\mathcal {R}^{Df}$
with
$\mathcal {R}^{Df}$
with
![]() $\mu $
-full measure, a number
$\mu $
-full measure, a number
![]() $\chi>0$
, and a
$\chi>0$
, and a
![]() $Df$
-invariant decomposition
$Df$
-invariant decomposition
![]() $TM=E^u\oplus E^s$
on
$TM=E^u\oplus E^s$
on
![]() $\mathcal {R}^{Df}$
such that for any
$\mathcal {R}^{Df}$
such that for any
![]() $x\in \mathcal {R}^{Df}$
, we have
$x\in \mathcal {R}^{Df}$
, we have
Denote
![]() $d_u=\dim (E^u), d_s=\dim (E^s)$
, and denote by
$d_u=\dim (E^u), d_s=\dim (E^s)$
, and denote by
![]() $B(0,r)$
the standard Euclidean r-ball in
$B(0,r)$
the standard Euclidean r-ball in
![]() $\mathbb {R}^d$
centered at
$\mathbb {R}^d$
centered at
![]() $0.$
We now introduce some properties of regular neighborhoods, see [Reference Pesin25] for the proofs.
$0.$
We now introduce some properties of regular neighborhoods, see [Reference Pesin25] for the proofs.
Theorem 3.1. (Pesin)
Let f be a
![]() $C^r(r>1)$
diffeomorphism of a compact Riemannian manifold M,
$C^r(r>1)$
diffeomorphism of a compact Riemannian manifold M,
![]() $\mu $
be an ergodic hyperbolic measure. Then for any
$\mu $
be an ergodic hyperbolic measure. Then for any
![]() $\varepsilon>0,$
the following properties hold.
$\varepsilon>0,$
the following properties hold.
-
(i) There exists a measurable function
 $l^\prime :\mathcal {R}^{Df}\to [1,\infty )$
and a collection of embeddings
$l^\prime :\mathcal {R}^{Df}\to [1,\infty )$
and a collection of embeddings
 $\Psi _x:B(0,l^\prime (x)^{-1})\to M$
for
$\Psi _x:B(0,l^\prime (x)^{-1})\to M$
for
 $x\in \mathcal {R}^{Df}$
such that
$x\in \mathcal {R}^{Df}$
such that
 $\Psi _x(0)=x$
,
$\Psi _x(0)=x$
,
 $l^\prime (x)e^{-\varepsilon }\leq l^\prime (fx)\leq l^\prime (x)e^{\varepsilon }$
, and the preimages
$l^\prime (x)e^{-\varepsilon }\leq l^\prime (fx)\leq l^\prime (x)e^{\varepsilon }$
, and the preimages
 $\widetilde {E}^j(x)=(D_0\Psi _x)^{-1}E^j(x)$
are orthogonal in
$\widetilde {E}^j(x)=(D_0\Psi _x)^{-1}E^j(x)$
are orthogonal in
 $\mathbb {R}^d$
, where
$\mathbb {R}^d$
, where
 $j=u,s$
.
$j=u,s$
. -
(ii) If
 $\widetilde {f_x}=\Psi _{fx}^{-1}\circ f\circ \Psi _x:B(0,l^\prime (x)^{-1})\to \mathbb {R}^d,$
then there exist
$\widetilde {f_x}=\Psi _{fx}^{-1}\circ f\circ \Psi _x:B(0,l^\prime (x)^{-1})\to \mathbb {R}^d,$
then there exist
 $A_u\in GL(d_u,\mathbb {R})$
and
$A_u\in GL(d_u,\mathbb {R})$
and
 $A_s\in GL(d_s,\mathbb {R})$
such that
$A_s\in GL(d_s,\mathbb {R})$
such that
 $D_0(\widetilde {f_x})=\mathrm{diag}(A_u,A_s)$
and
$D_0(\widetilde {f_x})=\mathrm{diag}(A_u,A_s)$
and  $$ \begin{align*} \|A_u^{-1} \|^{-1}\geq e^{\chi-\varepsilon},~\|A_s\|\leq e^{-\chi+\varepsilon}. \end{align*} $$
$$ \begin{align*} \|A_u^{-1} \|^{-1}\geq e^{\chi-\varepsilon},~\|A_s\|\leq e^{-\chi+\varepsilon}. \end{align*} $$
-
(iii) For any
 $a,b\in B(0,l^\prime (x)^{-1})$
,
$a,b\in B(0,l^\prime (x)^{-1})$
,  $$ \begin{align*}\|D_a(\widetilde{f_x})-D_b(\widetilde{f_x}) \|, \|D_a(\widetilde{f_x}^{-1})-D_b(\widetilde{f_x}^{-1}) \|\leq l^\prime(x)|a-b|^{r-1}. \end{align*} $$
$$ \begin{align*}\|D_a(\widetilde{f_x})-D_b(\widetilde{f_x}) \|, \|D_a(\widetilde{f_x}^{-1})-D_b(\widetilde{f_x}^{-1}) \|\leq l^\prime(x)|a-b|^{r-1}. \end{align*} $$
-
(iv) There exists a constant
 $0<c_1<1$
such that
$0<c_1<1$
such that  $$ \begin{align*}\|D(\Psi_x)\|\leq c_1^{-1}, \|D(\Psi_x^{-1})\|\leq l^\prime(x). \end{align*} $$
$$ \begin{align*}\|D(\Psi_x)\|\leq c_1^{-1}, \|D(\Psi_x^{-1})\|\leq l^\prime(x). \end{align*} $$
So for any
 $a,b\in B(0,l^\prime (x)^{-1})$
,
$a,b\in B(0,l^\prime (x)^{-1})$
,  $$ \begin{align*}c_1\cdot d(\Psi_x(a),\Psi_x(b))\leq |a-b|\leq l^\prime(x)\cdot d(\Psi_x(a),\Psi_x(b)). \end{align*} $$
$$ \begin{align*}c_1\cdot d(\Psi_x(a),\Psi_x(b))\leq |a-b|\leq l^\prime(x)\cdot d(\Psi_x(a),\Psi_x(b)). \end{align*} $$
The set
![]() $\mathcal {N}(x):=\Psi _x(B(0,l^\prime (x)^{-1}))$
is called a regular neighborhood of x. Let
$\mathcal {N}(x):=\Psi _x(B(0,l^\prime (x)^{-1}))$
is called a regular neighborhood of x. Let
![]() $r(x)$
be the radius of maximal ball contained in
$r(x)$
be the radius of maximal ball contained in
![]() $\mathcal {N}(x)$
. Then Theorem 3.1 implies
$\mathcal {N}(x)$
. Then Theorem 3.1 implies
![]() $r(x)\geq l^\prime (x)^{-2}.$
By Lusin’s theorem, for any
$r(x)\geq l^\prime (x)^{-2}.$
By Lusin’s theorem, for any
![]() $\delta>0,$
there exists a compact subset
$\delta>0,$
there exists a compact subset
![]() $\mathcal {R}^{Df}_{\delta }\subset \mathcal {R}^{Df}$
with
$\mathcal {R}^{Df}_{\delta }\subset \mathcal {R}^{Df}$
with
![]() $\mu (\mathcal {R}^{Df}_{\delta })>1-\delta $
such that
$\mu (\mathcal {R}^{Df}_{\delta })>1-\delta $
such that
![]() $x\mapsto \Psi _x$
,
$x\mapsto \Psi _x$
,
![]() $l^\prime (x)$
and the Oseledets splitting
$l^\prime (x)$
and the Oseledets splitting
![]() $T_xM=E_x^u\oplus E_x^s$
vary continuously on
$T_xM=E_x^u\oplus E_x^s$
vary continuously on
![]() $\mathcal {R}^{Df}_\delta $
.
$\mathcal {R}^{Df}_\delta $
.
3.2
 $(\rho ,\beta ,\gamma )$
-rectangles
$(\rho ,\beta ,\gamma )$
-rectangles
Let
![]() $M,f,\mu $
be as above and let
$M,f,\mu $
be as above and let
![]() $d_u=\dim (E^u),d_s=\dim (E^s)$
. Then
$d_u=\dim (E^u),d_s=\dim (E^s)$
. Then
![]() $d_u+d_s=d.$
Let
$d_u+d_s=d.$
Let
![]() $I=[-1,1]$
, so then we say
$I=[-1,1]$
, so then we say
![]() $R(x)\subset M$
is a rectangle in M if there exists a
$R(x)\subset M$
is a rectangle in M if there exists a
![]() $C^1$
embedding
$C^1$
embedding
![]() $\Phi _x:I^{d}\to M$
such that
$\Phi _x:I^{d}\to M$
such that
![]() $\Phi _x(I^{d})=R(x)$
and
$\Phi _x(I^{d})=R(x)$
and
![]() $\Phi _x(0)=x$
. A set
$\Phi _x(0)=x$
. A set
![]() $\widetilde {H}$
is called an admissible u-rectangle in
$\widetilde {H}$
is called an admissible u-rectangle in
![]() $R(x)$
, if there exist
$R(x)$
, if there exist
![]() $0<\unicode{x3bb} <1, C^1$
maps
$0<\unicode{x3bb} <1, C^1$
maps
![]() $\phi _1,\phi _2:I^{d_ u}\to I^{d_s}$
satisfying
$\phi _1,\phi _2:I^{d_ u}\to I^{d_s}$
satisfying
![]() $\|\phi _1(u)\|\geq \|\phi _2(u)\|$
for
$\|\phi _1(u)\|\geq \|\phi _2(u)\|$
for
![]() $u\in I^{d_u}$
and
$u\in I^{d_u}$
and
![]() $\|D\phi _i\|\leq \unicode{x3bb} $
for
$\|D\phi _i\|\leq \unicode{x3bb} $
for
![]() $i=1,2,$
such that
$i=1,2,$
such that
![]() $\widetilde {H}=\Phi _x(H)$
, where
$\widetilde {H}=\Phi _x(H)$
, where
Similarly, define an admissible s-rectangle in
![]() $R(x)$
.
$R(x)$
.
Definition 3.2. Given
![]() $f:M\to M$
and
$f:M\to M$
and
![]() $\Lambda \subset M$
compact, we say that
$\Lambda \subset M$
compact, we say that
![]() $R(x)$
is a
$R(x)$
is a
![]() $(\rho ,\beta ,\gamma )$
-rectangle of
$(\rho ,\beta ,\gamma )$
-rectangle of
![]() $\Lambda $
for
$\Lambda $
for
![]() $\rho>\beta >0,\gamma >0$
if there exists
$\rho>\beta >0,\gamma >0$
if there exists
![]() $\unicode{x3bb} =\unicode{x3bb} (\rho ,\beta ,\gamma )$
satisfying:
$\unicode{x3bb} =\unicode{x3bb} (\rho ,\beta ,\gamma )$
satisfying:
-
(i)
 $x\in \Lambda , B(x,\beta )\subset \mathrm{int}~R(x)$
and
$x\in \Lambda , B(x,\beta )\subset \mathrm{int}~R(x)$
and
 $\mathrm{diam}(R(x))\leq \rho /3$
;
$\mathrm{diam}(R(x))\leq \rho /3$
; -
(ii) if
 $z,f^mz\in \Lambda \cap B(x,\beta ) $
for some
$z,f^mz\in \Lambda \cap B(x,\beta ) $
for some
 $m>0$
, then the connected component
$m>0$
, then the connected component
 $C(z,R(x)\cap f^{-m}R(x))$
of
$C(z,R(x)\cap f^{-m}R(x))$
of
 $R(x)\cap f^{-m}R(x)$
containing z is an admissible s-rectangle in
$R(x)\cap f^{-m}R(x)$
containing z is an admissible s-rectangle in
 $R(x)$
, and
$R(x)$
, and
 $f^mC(z,R(x)\cap f^{-m}R(x))$
is an admissible u-rectangle in
$f^mC(z,R(x)\cap f^{-m}R(x))$
is an admissible u-rectangle in
 $R(x)$
;
$R(x)$
; -
(iii)
 $\mathrm{diam}~f^kC(z,R(x)\cap f^{-m}R(x))\leq \rho \cdot e^{-\gamma \min \{k,m-k\}}$
, for
$\mathrm{diam}~f^kC(z,R(x)\cap f^{-m}R(x))\leq \rho \cdot e^{-\gamma \min \{k,m-k\}}$
, for
 $0\leq k\leq m$
.
$0\leq k\leq m$
.
The following lemma is a simplified statement of [Reference Katok and Hasselblatt17, Theorem S.4.16].
Lemma 3.3. Let f be a
![]() $C^r(r>1)$
diffeomorphism of a compact Riemannian manifold M and
$C^r(r>1)$
diffeomorphism of a compact Riemannian manifold M and
![]() $\mu $
be an ergodic hyperbolic measure. Then for any
$\mu $
be an ergodic hyperbolic measure. Then for any
![]() $\rho>0, \delta >0,$
there exists a constant
$\rho>0, \delta >0,$
there exists a constant
![]() $\beta =\beta (\rho ,\delta )>0$
, such that for any
$\beta =\beta (\rho ,\delta )>0$
, such that for any
![]() $x\in \mathcal {R}_\delta ^{Df}$
, there exists a
$x\in \mathcal {R}_\delta ^{Df}$
, there exists a
![]() $(\rho ,\beta ,{\chi }/{2})$
-rectangle
$(\rho ,\beta ,{\chi }/{2})$
-rectangle
![]() $R(x)$
.
$R(x)$
.
3.3 Lyapunov norm for cocycles
We now establish some preliminary results for cocycles. Let f be a
![]() $C^r$
diffeomorphism of a compact Riemannian manifold M with
$C^r$
diffeomorphism of a compact Riemannian manifold M with
![]() $r>1$
, and
$r>1$
, and
![]() $\mu $
be an ergodic hyperbolic measure for f with
$\mu $
be an ergodic hyperbolic measure for f with
![]() $h_{\mu }(f)>0$
. Let
$h_{\mu }(f)>0$
. Let
![]() $A:M\to L(\mathfrak {X})$
be an
$A:M\to L(\mathfrak {X})$
be an
![]() $\alpha $
-Hölder continuous map such that
$\alpha $
-Hölder continuous map such that
![]() $\unicode{x3bb} (\mathcal {A},\mu )>\kappa (\mathcal {A},\mu )$
. Then by the multiplicative ergodic theorem stated in §2.1, there are Lyapunov exponents
$\unicode{x3bb} (\mathcal {A},\mu )>\kappa (\mathcal {A},\mu )$
. Then by the multiplicative ergodic theorem stated in §2.1, there are Lyapunov exponents
![]() $\unicode{x3bb} _1>\unicode{x3bb} _2>\cdots $
indexed in
$\unicode{x3bb} _1>\unicode{x3bb} _2>\cdots $
indexed in
![]() $\mathbb {N}_{k_0}$
for some
$\mathbb {N}_{k_0}$
for some
![]() $k_0\leq +\infty .$
$k_0\leq +\infty .$
Fix any
![]() $i\in \mathbb {N}_{k_0}$
,
$i\in \mathbb {N}_{k_0}$
,
![]() $\varepsilon>0$
, and
$\varepsilon>0$
, and
![]() $x\in \mathcal {R}^{\mathcal {A}}$
. We define the Lyapunov norm
$x\in \mathcal {R}^{\mathcal {A}}$
. We define the Lyapunov norm
![]() $\|\cdot \|_x=\|\cdot \|_{x,i,\varepsilon }$
on
$\|\cdot \|_x=\|\cdot \|_{x,i,\varepsilon }$
on
![]() ${\mathfrak {X}}$
as follows.
${\mathfrak {X}}$
as follows.
For any
![]() $u=u_1+\cdots +u_{i+1}\in \mathfrak {X},$
where
$u=u_1+\cdots +u_{i+1}\in \mathfrak {X},$
where
![]() $u_j\in E_j(x)~ \text { for all } j=1,\ldots ,i, $
and
$u_j\in E_j(x)~ \text { for all } j=1,\ldots ,i, $
and
![]() $ u_{i+1}\in F_i(x)$
, we define
$ u_{i+1}\in F_i(x)$
, we define
 $$ \begin{align} \|u\|_x:=\sum_{j=1}^{i+1} \|u_j\|_x, \end{align} $$
$$ \begin{align} \|u\|_x:=\sum_{j=1}^{i+1} \|u_j\|_x, \end{align} $$
where

and

Then the following lemma holds.
Lemma 3.4. Let
![]() $f, \mu $
, and A be as in Theorem 2.2. Then for any
$f, \mu $
, and A be as in Theorem 2.2. Then for any
![]() $i\in \mathbb {N}_{k_0}$
,
$i\in \mathbb {N}_{k_0}$
,
![]() $\varepsilon>0$
, the Lyapunov norm
$\varepsilon>0$
, the Lyapunov norm
![]() $\|\cdot \|_x=\|\cdot \|_{x,i,\varepsilon }$
satisfies the following properties.
$\|\cdot \|_x=\|\cdot \|_{x,i,\varepsilon }$
satisfies the following properties.
-
(i) For any
 $x\in \mathcal {R}^{\mathcal {A}},$
we have (3.3)
$x\in \mathcal {R}^{\mathcal {A}},$
we have (3.3) (3.4)
(3.4)
-
(ii) There exists an f-invariant subset of
 $\mathcal {R}^{\mathcal {A}}$
with
$\mathcal {R}^{\mathcal {A}}$
with
 $\mu $
-full measure (we may also denote it by
$\mu $
-full measure (we may also denote it by
 $\mathcal {R}^{\mathcal {A}}$
), and a measurable function
$\mathcal {R}^{\mathcal {A}}$
), and a measurable function
 $K(x)=K_{\varepsilon ,i}(x)$
defined on
$K(x)=K_{\varepsilon ,i}(x)$
defined on
 $\mathcal {R}^{\mathcal {A}}$
such that for any
$\mathcal {R}^{\mathcal {A}}$
such that for any
 $x\in \mathcal {R}^{\mathcal {A}}$
,
$x\in \mathcal {R}^{\mathcal {A}}$
,
 $u\in \mathfrak {X},$
we have (3.5)
$u\in \mathfrak {X},$
we have (3.5) $$ \begin{align} \|u\|\leq \|u\|_x\leq K(x)\|u\|, \end{align} $$
(3.6)
$$ \begin{align} \|u\|\leq \|u\|_x\leq K(x)\|u\|, \end{align} $$
(3.6) $$ \begin{align} K(x)e^{-\varepsilon}\leq K(fx)\leq K(x)e^{\varepsilon}. \end{align} $$
$$ \begin{align} K(x)e^{-\varepsilon}\leq K(fx)\leq K(x)e^{\varepsilon}. \end{align} $$
Proof. (i) We will prove the inequality
the others can be proved analogously. By the definition, we have

(ii) For any
![]() $u=u_1+\cdots +u_{i+1}\in {\mathfrak {X}}$
, by the definition,
$u=u_1+\cdots +u_{i+1}\in {\mathfrak {X}}$
, by the definition,
This estimates the lower bound. To estimate the upper bound, we define


Then,
 $$ \begin{align} \|u\|_x &\leq \sum_{j=1}^{i}\sum_{n=-\infty}^{+\infty}M_{j}(x)e^{-({1}/{2})\varepsilon |n|}\cdot \|u_j\| + \sum_{n=0}^{+\infty}M_{i+1}(x)e^{-({1}/{2})\varepsilon n}\cdot\|u_{i+1}\| \nonumber\\ & \leq c_0 \cdot \bigg(\sum_{j=1}^{i}M_{j}(x)\cdot\|\pi^{j}_{E}(x)-\pi^{j-1}_{E}(x)\|\cdot\|u\|+M_{i+1}(x)\cdot\|\pi^{i}_{F}(x)\|\cdot\|u\|\bigg)\nonumber\\ & =: M(x)\cdot\|u\|, \end{align} $$
$$ \begin{align} \|u\|_x &\leq \sum_{j=1}^{i}\sum_{n=-\infty}^{+\infty}M_{j}(x)e^{-({1}/{2})\varepsilon |n|}\cdot \|u_j\| + \sum_{n=0}^{+\infty}M_{i+1}(x)e^{-({1}/{2})\varepsilon n}\cdot\|u_{i+1}\| \nonumber\\ & \leq c_0 \cdot \bigg(\sum_{j=1}^{i}M_{j}(x)\cdot\|\pi^{j}_{E}(x)-\pi^{j-1}_{E}(x)\|\cdot\|u\|+M_{i+1}(x)\cdot\|\pi^{i}_{F}(x)\|\cdot\|u\|\bigg)\nonumber\\ & =: M(x)\cdot\|u\|, \end{align} $$
where
![]() $c_0=\sum _{n=-\infty }^{+\infty }e^{-(1/2)\varepsilon |n|}$
and
$c_0=\sum _{n=-\infty }^{+\infty }e^{-(1/2)\varepsilon |n|}$
and
![]() $\pi ^{0}_{E}(x)=0$
.
$\pi ^{0}_{E}(x)=0$
.
Claim.
![]() $M(x)$
is tempered on an f-invariant subset of
$M(x)$
is tempered on an f-invariant subset of
![]() $\mathcal {R}^{\mathcal {A}}$
with
$\mathcal {R}^{\mathcal {A}}$
with
![]() $\mu $
-full measure, that is,
$\mu $
-full measure, that is,
Proof of the claim
Since
![]() $\|\pi ^j_{E}(x)\|,\|\pi ^j_{F}(x)\|$
are tempered by equation (2.1), it is enough to prove
$\|\pi ^j_{E}(x)\|,\|\pi ^j_{F}(x)\|$
are tempered by equation (2.1), it is enough to prove
![]() $M_{j}(x)$
is tempered for any
$M_{j}(x)$
is tempered for any
![]() $ 1\leq j\leq i+1$
. Since
$ 1\leq j\leq i+1$
. Since

where
![]() $c_1=\max \nolimits _{x\in M}{\|\mathcal {A}_x\|}/{e^{\unicode{x3bb} _{i+1}-(1/2)\varepsilon }}$
, we obtain
$c_1=\max \nolimits _{x\in M}{\|\mathcal {A}_x\|}/{e^{\unicode{x3bb} _{i+1}-(1/2)\varepsilon }}$
, we obtain
 $$ \begin{align*}(\log M_{i+1}(x)-\log M_{i+1}(fx))^+ \leq \log \max\bigg\{c_1,\frac{1}{ M_{i+1}(fx)} \bigg\}\leq\log \max\{c_1,1\},\end{align*} $$
$$ \begin{align*}(\log M_{i+1}(x)-\log M_{i+1}(fx))^+ \leq \log \max\bigg\{c_1,\frac{1}{ M_{i+1}(fx)} \bigg\}\leq\log \max\{c_1,1\},\end{align*} $$
and then we conclude
![]() $M_{i+1 }(x)$
is tempered on a subset of full measure by [Reference Mañé22, Lemma III.8]. The result for
$M_{i+1 }(x)$
is tempered on a subset of full measure by [Reference Mañé22, Lemma III.8]. The result for
![]() $ 1\leq j\leq i$
is obtained similarly.
$ 1\leq j\leq i$
is obtained similarly.
Let
and then by [Reference Barreira and Pesin3, Lemma 3.5.7],
![]() $K(x)$
satisfies equations (3.5) and (3.6). This completes the proof of the lemma.
$K(x)$
satisfies equations (3.5) and (3.6). This completes the proof of the lemma.
Fix any
![]() $i\in \mathbb {N}_{k_0}$
. Then by Lusin’s theorem, for any
$i\in \mathbb {N}_{k_0}$
. Then by Lusin’s theorem, for any
![]() $\delta>0,$
there exists a compact subset
$\delta>0,$
there exists a compact subset
![]() $\mathcal {R}^{\mathcal {A}}_{\delta }\subset \mathcal {R}^{\mathcal {A}}$
such that
$\mathcal {R}^{\mathcal {A}}_{\delta }\subset \mathcal {R}^{\mathcal {A}}$
such that
![]() $\mu (\mathcal {R}^{\mathcal {A}}_{\delta })>1-\delta $
and
$\mu (\mathcal {R}^{\mathcal {A}}_{\delta })>1-\delta $
and
![]() $K(x)$
is continuous on
$K(x)$
is continuous on
![]() $\mathcal {R}^{\mathcal {A}}_\delta $
. Denote
$\mathcal {R}^{\mathcal {A}}_\delta $
. Denote
Since the Oseledets decomposition is
![]() $\mu $
-continuous, we may assume the Oseledets decomposition is continuous on
$\mu $
-continuous, we may assume the Oseledets decomposition is continuous on
![]() $\mathcal {R}^{\mathcal {A}}_{\delta }$
.
$\mathcal {R}^{\mathcal {A}}_{\delta }$
.
Let
![]() $\widetilde {\mathfrak {X}}$
be the collection of norms on
$\widetilde {\mathfrak {X}}$
be the collection of norms on
![]() $\mathfrak {X}$
which are equivalent to
$\mathfrak {X}$
which are equivalent to
![]() $\|\cdot \|$
. Then
$\|\cdot \|$
. Then
![]() $\widetilde {{\mathfrak {X}}}$
is a metric space with respect to the metric
$\widetilde {{\mathfrak {X}}}$
is a metric space with respect to the metric
 $$ \begin{align*}\widetilde{D}(\varphi,\psi)=\sup\limits_{u\in {\mathfrak{X}}\setminus\{0\}}\frac{|\varphi(u)-\psi(u)|}{\|u\|}\quad \text{for all } \varphi,\psi\in\widetilde{{\mathfrak{X}}}. \end{align*} $$
$$ \begin{align*}\widetilde{D}(\varphi,\psi)=\sup\limits_{u\in {\mathfrak{X}}\setminus\{0\}}\frac{|\varphi(u)-\psi(u)|}{\|u\|}\quad \text{for all } \varphi,\psi\in\widetilde{{\mathfrak{X}}}. \end{align*} $$
We claim that the function
![]() $x\mapsto \|\cdot \|_x$
is continuous on
$x\mapsto \|\cdot \|_x$
is continuous on
![]() $\mathcal {R}^{\mathcal {A}}_{\delta }$
, which will be used in the proof of equations (3.17), (3.18) in Lemma 3.5 and equation (4.9) in Proposition 4.1. Indeed, for any
$\mathcal {R}^{\mathcal {A}}_{\delta }$
, which will be used in the proof of equations (3.17), (3.18) in Lemma 3.5 and equation (4.9) in Proposition 4.1. Indeed, for any
![]() $x\in \mathcal {R}^{\mathcal {A}}_{\delta }, u=u_1+\cdots +u_{i+1}\in {\mathfrak {X}},$
where
$x\in \mathcal {R}^{\mathcal {A}}_{\delta }, u=u_1+\cdots +u_{i+1}\in {\mathfrak {X}},$
where
![]() $u_j\in E_j(x), \text {for all } j\,{=}\,1,\ldots ,i, $
and
$u_j\in E_j(x), \text {for all } j\,{=}\,1,\ldots ,i, $
and
![]() $ u_{i+1}\in F_i(x)$
, we define
$ u_{i+1}\in F_i(x)$
, we define

and then by equation (3.7),
 $$ \begin{align*} |\|u\|_x-\|u\|_{k,x}| & \leq \sum_{|n|>k}e^{-({1}/{2})\varepsilon |n|}\cdot M(x)\cdot\|u\| \\ & \leq \frac{2e^{-({\varepsilon}/{2})k}}{e^{({\varepsilon}/{2})}-1}\cdot K(x)\cdot\|u\| \\ & \leq \frac{2l\cdot e^{-({\varepsilon}/{2})k}}{ (e^{({\varepsilon}/{2})}-1)}\cdot\|u\|, \end{align*} $$
$$ \begin{align*} |\|u\|_x-\|u\|_{k,x}| & \leq \sum_{|n|>k}e^{-({1}/{2})\varepsilon |n|}\cdot M(x)\cdot\|u\| \\ & \leq \frac{2e^{-({\varepsilon}/{2})k}}{e^{({\varepsilon}/{2})}-1}\cdot K(x)\cdot\|u\| \\ & \leq \frac{2l\cdot e^{-({\varepsilon}/{2})k}}{ (e^{({\varepsilon}/{2})}-1)}\cdot\|u\|, \end{align*} $$
that is,
 $$ \begin{align*}\widetilde{D}(\|\cdot\|_x,~\|\cdot\|_{k,x})\leq \frac{2l\cdot e^{-({\varepsilon}/{2})k}}{ (e^{{\varepsilon}/{2}}-1)}, \end{align*} $$
$$ \begin{align*}\widetilde{D}(\|\cdot\|_x,~\|\cdot\|_{k,x})\leq \frac{2l\cdot e^{-({\varepsilon}/{2})k}}{ (e^{{\varepsilon}/{2}}-1)}, \end{align*} $$
which implies
![]() $\|\cdot \|_{k,x}\to \|\cdot \|_x$
uniformly for
$\|\cdot \|_{k,x}\to \|\cdot \|_x$
uniformly for
![]() $x\in \mathcal {R}^{\mathcal {A}}_{\delta }$
as
$x\in \mathcal {R}^{\mathcal {A}}_{\delta }$
as
![]() $k\to +\infty .$
Since
$k\to +\infty .$
Since
![]() $x\mapsto \|\cdot \|_{k,x}$
is continuous, we have
$x\mapsto \|\cdot \|_{k,x}$
is continuous, we have
![]() $x\mapsto \|\cdot \|_x$
is continuous on
$x\mapsto \|\cdot \|_x$
is continuous on
![]() $\mathcal {R}^{\mathcal {A}}_{\delta }$
. This proves the claim.
$\mathcal {R}^{\mathcal {A}}_{\delta }$
. This proves the claim.
3.4 Invariant cones for Banach cocycles
We now estimate the growth of vectors in certain invariant cones for cocycles. Let f,
![]() $\mu $
, and A be as in §3.3. Fix any
$\mu $
, and A be as in §3.3. Fix any
![]() $i\in \mathbb {N}_{k_0}$
, and let
$i\in \mathbb {N}_{k_0}$
, and let
![]() $\varepsilon _i:=\min \{\tfrac 12\chi \alpha ,{\chi }/{4},{\chi (r-1)}/{2r},({\unicode{x3bb} _1-\unicode{x3bb} _{2}})/{8},\ldots ,({\unicode{x3bb} _{i}-\unicode{x3bb} _{i+1}})/{8} \}$
, where
$\varepsilon _i:=\min \{\tfrac 12\chi \alpha ,{\chi }/{4},{\chi (r-1)}/{2r},({\unicode{x3bb} _1-\unicode{x3bb} _{2}})/{8},\ldots ,({\unicode{x3bb} _{i}-\unicode{x3bb} _{i+1}})/{8} \}$
, where
![]() $\chi $
is given in §3.1. For any
$\chi $
is given in §3.1. For any
![]() $0<\varepsilon < \varepsilon _i, x\in \mathcal {R}^{\mathcal {A}},$
let
$0<\varepsilon < \varepsilon _i, x\in \mathcal {R}^{\mathcal {A}},$
let
![]() $\|\cdot \|_x=\|\cdot \|_{x,i,\varepsilon }$
be the Lyapunov norm on
$\|\cdot \|_x=\|\cdot \|_{x,i,\varepsilon }$
be the Lyapunov norm on
![]() $\mathfrak {X}$
defined in equation (3.1). For any
$\mathfrak {X}$
defined in equation (3.1). For any
![]() $1\leq j\leq i$
, we have the Oseledets decomposition
$1\leq j\leq i$
, we have the Oseledets decomposition
![]() $\mathfrak {X}=H_j(x)\oplus F_j(x)$
, where
$\mathfrak {X}=H_j(x)\oplus F_j(x)$
, where
![]() $H_j(x)=E_1(x)\oplus \cdots \oplus E_j(x)$
. For any
$H_j(x)=E_1(x)\oplus \cdots \oplus E_j(x)$
. For any
![]() $\theta>0$
,
$\theta>0$
,
![]() $u\in \mathfrak {X},$
let
$u\in \mathfrak {X},$
let
![]() $u=u_H+u_F$
, where
$u=u_H+u_F$
, where
![]() $u_H\in H_j(x), u_F\in F_j(x)$
. We consider two cones:
$u_H\in H_j(x), u_F\in F_j(x)$
. We consider two cones:
For any
![]() $\delta>0,$
recall that a sequence
$\delta>0,$
recall that a sequence
![]() $(x_n)_{n\in \mathbb {Z}}$
is a
$(x_n)_{n\in \mathbb {Z}}$
is a
![]() $\rho $
-pseudo-orbit of
$\rho $
-pseudo-orbit of
![]() $f^m$
in
$f^m$
in
![]() $\mathcal {R}^{\mathcal {A}}_\delta $
for some
$\mathcal {R}^{\mathcal {A}}_\delta $
for some
![]() $ m \in \mathbb {N}$
, if
$ m \in \mathbb {N}$
, if
![]() $x_n,f^m(x_n)\in \mathcal {R}^{\mathcal {A}}_\delta $
and
$x_n,f^m(x_n)\in \mathcal {R}^{\mathcal {A}}_\delta $
and
![]() $d(f^mx_n,x_{n+1})\leq \rho $
for any
$d(f^mx_n,x_{n+1})\leq \rho $
for any
![]() $n\in \mathbb {Z}$
. Let
$n\in \mathbb {Z}$
. Let
![]() $l=l_\delta $
be as in equation (3.8). The following lemma is related to a horseshoe
$l=l_\delta $
be as in equation (3.8). The following lemma is related to a horseshoe
![]() $\Lambda ^*$
which is given in §4.1. The definition of
$\Lambda ^*$
which is given in §4.1. The definition of
![]() $\Lambda ^*$
using Markov rectangles. In the definition of
$\Lambda ^*$
using Markov rectangles. In the definition of
![]() $\Lambda ^*$
, the integer m is fixed once for all, and any point
$\Lambda ^*$
, the integer m is fixed once for all, and any point
![]() $y\in \Lambda ^*$
is determined by a sequence
$y\in \Lambda ^*$
is determined by a sequence
![]() $(x_n)_{n\in \mathbb {Z}}\in F_m$
, where
$(x_n)_{n\in \mathbb {Z}}\in F_m$
, where
![]() $F_m\subset \mathcal {R}^{\mathcal {A}}_\delta $
has finite cardinality. More precisely, for any
$F_m\subset \mathcal {R}^{\mathcal {A}}_\delta $
has finite cardinality. More precisely, for any
![]() $y\in \Lambda ^*$
, there exists
$y\in \Lambda ^*$
, there exists
![]() $\{x_n\}_{n\in \mathbb {Z}}\subset F_m$
such that
$\{x_n\}_{n\in \mathbb {Z}}\subset F_m$
such that
The sequence
![]() $\{x_n\}_{n\in \mathbb {Z}}\subset F_m$
is actually a
$\{x_n\}_{n\in \mathbb {Z}}\subset F_m$
is actually a
![]() $\rho $
-pseudo-orbit of
$\rho $
-pseudo-orbit of
![]() $f^m$
in
$f^m$
in
![]() $\mathcal {R}^{\mathcal {A}}_\delta $
, and the orbit of
$\mathcal {R}^{\mathcal {A}}_\delta $
, and the orbit of
![]() $y\in \Lambda ^*$
shadows
$y\in \Lambda ^*$
shadows
![]() $\{x_n\}_{n\in \mathbb {Z}}$
.
$\{x_n\}_{n\in \mathbb {Z}}$
.
Lemma 3.5. For any
![]() $0<\varepsilon <\varepsilon _i, \delta>0$
, there exist
$0<\varepsilon <\varepsilon _i, \delta>0$
, there exist
![]() $\rho _0>0, ~\theta _0>0$
such that for any
$\rho _0>0, ~\theta _0>0$
such that for any
![]() $0<\rho <\rho _0 $
,
$0<\rho <\rho _0 $
,
![]() $1\leq j \leq i$
, any
$1\leq j \leq i$
, any
![]() $\rho $
-pseudo-orbit
$\rho $
-pseudo-orbit
![]() $(x_n)_{n\in \mathbb {Z}}$
of
$(x_n)_{n\in \mathbb {Z}}$
of
![]() $f^m$
in
$f^m$
in
![]() $\mathcal {R}^{\mathcal {A}}_\delta $
with
$\mathcal {R}^{\mathcal {A}}_\delta $
with
![]() $m\geq {2\log l}/{\varepsilon }$
, and for any
$m\geq {2\log l}/{\varepsilon }$
, and for any
![]() $y\in M$
with
$y\in M$
with
![]() $d(f^kx_{n},f^{k}(f^{nm}y))\leq \rho \cdot e^{-({\chi }/{2})\min \{k,m-k\}}$
,
$d(f^kx_{n},f^{k}(f^{nm}y))\leq \rho \cdot e^{-({\chi }/{2})\min \{k,m-k\}}$
,
![]() $k=0,\ldots ,m$
, we can find
$k=0,\ldots ,m$
, we can find
![]() $\eta =\eta (\varepsilon ,\delta ,m)\in (0,1)$
such that:
$\eta =\eta (\varepsilon ,\delta ,m)\in (0,1)$
such that:
-
(i)
 $ \mathcal {A}_{f^{nm+k}y}^mU_j(f^kx_{n},\theta _0)\subset U_j(f^kx_{n+1},\eta \theta _0),$
and
$ \mathcal {A}_{f^{nm+k}y}^mU_j(f^kx_{n},\theta _0)\subset U_j(f^kx_{n+1},\eta \theta _0),$
and 
-
(ii)
 $\mathcal {A}_{f^{nm+k}y}^{-m}V_j(f^kx_{n},\theta _0)\subset V_j(f^kx_{n-1},\eta \theta _0),$
and
$\mathcal {A}_{f^{nm+k}y}^{-m}V_j(f^kx_{n},\theta _0)\subset V_j(f^kx_{n-1},\eta \theta _0),$
and 
Proof. (i) For the simplicity of notation, we prove
![]() $\mathcal {A}_y^mU_j(x_{0},\theta _0)\subset U_j(x_{1},\eta \theta _0)$
and
$\mathcal {A}_y^mU_j(x_{0},\theta _0)\subset U_j(x_{1},\eta \theta _0)$
and
![]() $ e^{(\unicode{x3bb} _{j}-4\varepsilon )m}\|u\|\leq \|\mathcal {A}_y^m(u)\|\leq e^{(\unicode{x3bb} _1+4\varepsilon )m}\|u\| \text { for all } u\in U_j(x_{0},\theta _0), 1\leq j\leq i.$
$ e^{(\unicode{x3bb} _{j}-4\varepsilon )m}\|u\|\leq \|\mathcal {A}_y^m(u)\|\leq e^{(\unicode{x3bb} _1+4\varepsilon )m}\|u\| \text { for all } u\in U_j(x_{0},\theta _0), 1\leq j\leq i.$
For any fixed
![]() $0<\varepsilon <\varepsilon _i, \delta>0$
, denote
$0<\varepsilon <\varepsilon _i, \delta>0$
, denote
![]() $\theta _0:=e^{\unicode{x3bb} _{i+1}-\unicode{x3bb} _1}(e^\varepsilon -1)<e^\varepsilon -1$
and
$\theta _0:=e^{\unicode{x3bb} _{i+1}-\unicode{x3bb} _1}(e^\varepsilon -1)<e^\varepsilon -1$
and
![]() ${{\eta }_0:=\max \{e^{\unicode{x3bb} _{j+1}-\unicode{x3bb} _j+4\varepsilon }: 1\leq j\leq i\}}$
. We have the following claim.
${{\eta }_0:=\max \{e^{\unicode{x3bb} _{j+1}-\unicode{x3bb} _j+4\varepsilon }: 1\leq j\leq i\}}$
. We have the following claim.
Claim. There exist
![]() $\widetilde {\rho }_0>0,$
such that for any
$\widetilde {\rho }_0>0,$
such that for any
![]() $x_{0},f^mx_{0}\in \mathcal {R}^{\mathcal {A}}_\delta $
,
$x_{0},f^mx_{0}\in \mathcal {R}^{\mathcal {A}}_\delta $
,
![]() $y\in M$
with
$y\in M$
with
![]() ${d(f^kx_{0},f^{k}y)\leq \rho \cdot e^{-({\chi }/{2})\min \{k,m-k\}}}$
for
${d(f^kx_{0},f^{k}y)\leq \rho \cdot e^{-({\chi }/{2})\min \{k,m-k\}}}$
for
![]() $k=0,\ldots ,m$
and
$k=0,\ldots ,m$
and
![]() $0<\rho <\widetilde {\rho }_0$
, we have
$0<\rho <\widetilde {\rho }_0$
, we have
Proof of the claim
For any
![]() $0\leq k\leq m-1, ~u=u_H+u_F\in U_j(f^{k}x_{0},\theta _0)$
, by equations (3.3) and (3.4), we have
$0\leq k\leq m-1, ~u=u_H+u_F\in U_j(f^{k}x_{0},\theta _0)$
, by equations (3.3) and (3.4), we have
Let
![]() $w\kern1.3pt{=}\kern1.3pt(A(f^{k}y)\kern1.3pt{-}\kern1.3pt A(f^kx_{0}))u\kern1.3pt{=}\kern1.3ptw_H+w_F, $
where
$w\kern1.3pt{=}\kern1.3pt(A(f^{k}y)\kern1.3pt{-}\kern1.3pt A(f^kx_{0}))u\kern1.3pt{=}\kern1.3ptw_H+w_F, $
where
![]() $w_H\kern1.3pt{\in}\kern1.3pt H_j(f^{k+1}x_{0}), w_F\kern1.3pt{\in}\kern1.3pt F_j(f^{k+1}x_{0})$
. Then
$w_H\kern1.3pt{\in}\kern1.3pt H_j(f^{k+1}x_{0}), w_F\kern1.3pt{\in}\kern1.3pt F_j(f^{k+1}x_{0})$
. Then
Since
![]() $A:M\to L(\mathfrak {X})$
is
$A:M\to L(\mathfrak {X})$
is
![]() $\alpha $
-Hölder continuous, there exists a constant
$\alpha $
-Hölder continuous, there exists a constant
![]() $c_0>0$
such that
$c_0>0$
such that
Since
![]() $x_0,f^m(x_0)\in \mathcal {R}^{\mathcal {A}}_\delta $
and
$x_0,f^m(x_0)\in \mathcal {R}^{\mathcal {A}}_\delta $
and
![]() $K(x)$
is continuous on
$K(x)$
is continuous on
![]() $\mathcal {R}^{\mathcal {A}}_\delta $
, by equations (3.5) and (3.8),
$\mathcal {R}^{\mathcal {A}}_\delta $
, by equations (3.5) and (3.8),
 $$ \begin{align*} K(f^{k+1}x_{0}) & \le \min\{e^{\varepsilon(k+1)}K(x_0),e^{\varepsilon(m-k-1)}K(f^mx_0) \}\\ & \le le^{\varepsilon\min\{k+1,m-k-1 \}}. \end{align*} $$
$$ \begin{align*} K(f^{k+1}x_{0}) & \le \min\{e^{\varepsilon(k+1)}K(x_0),e^{\varepsilon(m-k-1)}K(f^mx_0) \}\\ & \le le^{\varepsilon\min\{k+1,m-k-1 \}}. \end{align*} $$
Then by equation (3.6),
 $$ \begin{align} \|w_H\|_{f^{k+1}x_{0}}\leq \|w\|_{f^{k+1}x_{0}} & \leq K(f^{k+1}x_{0})\|A(f^{k}y)-A(f^kx_{0})\|\cdot\|u\| \nonumber\\ & \leq le^{\varepsilon\min\{k+1,m-k-1 \}}\cdot c_0\rho^\alpha e^{-({\chi}/{2})\alpha\min\{k,m-k \}}\|u\|\nonumber\\ & \leq c_0le^\varepsilon\rho^\alpha e^{(\varepsilon-({\chi}/{2})\alpha)\min\{k,m-k \}}\|u\|_{f^{k}x_{0}}\nonumber\\ & \leq (1+\theta_0)c_0le^\varepsilon\rho^\alpha \|u_H\|_{f^{k}x_{0}}, \end{align} $$
$$ \begin{align} \|w_H\|_{f^{k+1}x_{0}}\leq \|w\|_{f^{k+1}x_{0}} & \leq K(f^{k+1}x_{0})\|A(f^{k}y)-A(f^kx_{0})\|\cdot\|u\| \nonumber\\ & \leq le^{\varepsilon\min\{k+1,m-k-1 \}}\cdot c_0\rho^\alpha e^{-({\chi}/{2})\alpha\min\{k,m-k \}}\|u\|\nonumber\\ & \leq c_0le^\varepsilon\rho^\alpha e^{(\varepsilon-({\chi}/{2})\alpha)\min\{k,m-k \}}\|u\|_{f^{k}x_{0}}\nonumber\\ & \leq (1+\theta_0)c_0le^\varepsilon\rho^\alpha \|u_H\|_{f^{k}x_{0}}, \end{align} $$
as
![]() $\varepsilon -({\chi }/{2})\alpha <0.$
Similarly,
$\varepsilon -({\chi }/{2})\alpha <0.$
Similarly,
Let
where
![]() $(A(f^{k}y)u)_H\in H_j(f^{k+1}x_{0}), (A(f^{k}y)u)_F\in F_j(f^{k+1}x_{0})$
. Then by equations (3.10), (3.12), and (3.13),
$(A(f^{k}y)u)_H\in H_j(f^{k+1}x_{0}), (A(f^{k}y)u)_F\in F_j(f^{k+1}x_{0})$
. Then by equations (3.10), (3.12), and (3.13),

if
![]() $\rho $
is small enough. Similarly, by equations (3.11), (3.12), and (3.14),
$\rho $
is small enough. Similarly, by equations (3.11), (3.12), and (3.14),

if
![]() $\rho $
is small enough. Thus,
$\rho $
is small enough. Thus,
that is,
![]() $A(f^{k}y)U_j(f^{k}x_{0},\theta _0)\subset U_j(f^{k+1}x_{0},{\eta }_0\theta _0)$
.
$A(f^{k}y)U_j(f^{k}x_{0},\theta _0)\subset U_j(f^{k+1}x_{0},{\eta }_0\theta _0)$
.
The claim implies
Since, by §3.4, the Lyapunov norm and the Oseledets decomposition are uniformly continuous on the compact set
![]() $\mathcal {R}^{\mathcal {A}}_\delta $
, there exists
$\mathcal {R}^{\mathcal {A}}_\delta $
, there exists
![]() ${\eta }_0<\eta <1$
such that
${\eta }_0<\eta <1$
such that
 $$ \begin{align} V_j(x_{1},\theta_0)\subset V_j\bigg(f^mx_{0},\frac{\eta}{\eta_0}\theta_0\bigg) \quad \text{for all } d(f^mx_{0},x_{1})\leq \rho, \end{align} $$
$$ \begin{align} V_j(x_{1},\theta_0)\subset V_j\bigg(f^mx_{0},\frac{\eta}{\eta_0}\theta_0\bigg) \quad \text{for all } d(f^mx_{0},x_{1})\leq \rho, \end{align} $$
if
![]() $\rho $
is small enough. Hence, for any
$\rho $
is small enough. Hence, for any
![]() $1\leq j \leq i,$
we have
$1\leq j \leq i,$
we have
Moreover, for any
![]() $0\leq k\leq m-1$
and
$0\leq k\leq m-1$
and
![]() $u\in U_j(f^{k}x_{0},\theta _0)$
, it follows from equation (3.15) that
$u\in U_j(f^{k}x_{0},\theta _0)$
, it follows from equation (3.15) that

Therefore, for any
![]() $1\leq j\leq i$
and
$1\leq j\leq i$
and
![]() $u\in U_j(x_0,\theta _0)$
, by equations (3.9) and (3.5), we conclude
$u\in U_j(x_0,\theta _0)$
, by equations (3.9) and (3.5), we conclude
This is the first time that the estimate on l is used. Similar to equation (3.15), we can also get
Thus, we obtain by using equation (3.16) that

Hence, for any
![]() $u\in U_j(x_0,\theta _0)$
, by equations (3.9) and (3.5), we conclude
$u\in U_j(x_0,\theta _0)$
, by equations (3.9) and (3.5), we conclude
This proves the conclusion (i).
(ii) For simplicity, we only prove
![]() $\mathcal {A}_{f^my}^{-m}V_j(x_{1},\theta _0)\subset V_j(x_{0},\eta \theta _0)$
and
$\mathcal {A}_{f^my}^{-m}V_j(x_{1},\theta _0)\subset V_j(x_{0},\eta \theta _0)$
and
![]() $\|\mathcal {A}_y^m(v)\|\leq e^{(\unicode{x3bb} _{j+1}+4\varepsilon )m}\|v\| \text { for all } v\in \mathcal {A}_{f^my}^{-m}V_j(x_{1},\theta _0), 1\leq j\leq i.$
$\|\mathcal {A}_y^m(v)\|\leq e^{(\unicode{x3bb} _{j+1}+4\varepsilon )m}\|v\| \text { for all } v\in \mathcal {A}_{f^my}^{-m}V_j(x_{1},\theta _0), 1\leq j\leq i.$
Let
![]() $\theta _1=({\eta }/{\eta _0})\theta _0$
, where
$\theta _1=({\eta }/{\eta _0})\theta _0$
, where
![]() $\eta \in (\eta _0,1)$
is given by equation (3.17). We have the following claim.
$\eta \in (\eta _0,1)$
is given by equation (3.17). We have the following claim.
Claim. There exists
![]() $\bar {\rho }_0>0,$
such that for any
$\bar {\rho }_0>0,$
such that for any
![]() $x_{0},f^mx_{0}\in \mathcal {R}^{\mathcal {A}}_\delta $
,
$x_{0},f^mx_{0}\in \mathcal {R}^{\mathcal {A}}_\delta $
,
![]() $y\in M$
with
$y\in M$
with
![]() $d(f^kx_{0},f^{k}y)\leq \rho \cdot e^{-({\chi }/{2})\min \{k,m-k\}}$
for
$d(f^kx_{0},f^{k}y)\leq \rho \cdot e^{-({\chi }/{2})\min \{k,m-k\}}$
for
![]() $k=0,\ldots ,m$
and
$k=0,\ldots ,m$
and
![]() $0<\rho <\bar {\rho }_0$
, we have
$0<\rho <\bar {\rho }_0$
, we have
Proof of the claim
For any
![]() $1\le k\le m, v\in {A}({f^{k-1}y})^{-1}V_j(f^{k}x_{0},\theta _1),$
one has
$1\le k\le m, v\in {A}({f^{k-1}y})^{-1}V_j(f^{k}x_{0},\theta _1),$
one has
![]() $A(f^{k-1}y)v\in V_j(f^{k}x_{0},\theta _1).$
Let
$A(f^{k-1}y)v\in V_j(f^{k}x_{0},\theta _1).$
Let
and
Denote
![]() $w:=(A(f^{k-1}y)-A(f^{k-1}x_0) )v.$
Since
$w:=(A(f^{k-1}y)-A(f^{k-1}x_0) )v.$
Since
![]() $A(f^{k-1}y)v=A(f^{k-1}x_0)v+w,$
one has
$A(f^{k-1}y)v=A(f^{k-1}x_0)v+w,$
one has
Similar to the proof of equations (3.10), (3.11), (3.13), and (3.14), we can obtain
and
 $$ \begin{align*} \begin{split} \|w_H\|_{f^{k}x_{0}}\leq \|w\|_{f^{k}x_{0}} & \leq K(f^{k}x_{0})\|A(f^{k-1}y)-A(f^{k-1}x_{0})\|\cdot\|v\| \\ & \leq le^{\varepsilon\min\{k,m-k \}}\cdot c_0\rho^\alpha e^{-({\chi}/{2})\alpha\min\{k-1,m-k+1 \}}\|v\|\\ & \leq c_0le^\varepsilon\rho^\alpha e^{(\varepsilon-({\chi}/{2})\alpha)\min\{k-1,m-k+1 \}}\|v\|_{f^{k-1}x_{0}}\\ & \leq c_0le^\varepsilon\rho^\alpha \|v\|_{f^{k-1}x_{0}}, \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \|w_H\|_{f^{k}x_{0}}\leq \|w\|_{f^{k}x_{0}} & \leq K(f^{k}x_{0})\|A(f^{k-1}y)-A(f^{k-1}x_{0})\|\cdot\|v\| \\ & \leq le^{\varepsilon\min\{k,m-k \}}\cdot c_0\rho^\alpha e^{-({\chi}/{2})\alpha\min\{k-1,m-k+1 \}}\|v\|\\ & \leq c_0le^\varepsilon\rho^\alpha e^{(\varepsilon-({\chi}/{2})\alpha)\min\{k-1,m-k+1 \}}\|v\|_{f^{k-1}x_{0}}\\ & \leq c_0le^\varepsilon\rho^\alpha \|v\|_{f^{k-1}x_{0}}, \end{split} \end{align*} $$
Therefore,

and

Note that
![]() $A(f^{k-1}y)v\in V_j(f^{k}x_{0},\theta _1).$
It follows that
$A(f^{k-1}y)v\in V_j(f^{k}x_{0},\theta _1).$
It follows that
Hence, by equations (3.21) and (3.22),

if
![]() $\rho $
is small enough. Thus,
$\rho $
is small enough. Thus,
that is,
![]() $v\in V_j(f^{k-1}x_{0},{\eta }_0\theta _1)$
.
$v\in V_j(f^{k-1}x_{0},{\eta }_0\theta _1)$
.
This claim implies
By equation (3.18), we obtain
Now, for any
![]() $v\in \mathcal {A}_{f^my}^{-m} V_j(x_{1},\theta _0)$
, one has
$v\in \mathcal {A}_{f^my}^{-m} V_j(x_{1},\theta _0)$
, one has
Let
![]() $w=w_H+w_F,$
where
$w=w_H+w_F,$
where
![]() $w_H\in H_j(f^kx_{0}),w_F\in F_j(f^kx_{0})$
. Then,
$w_H\in H_j(f^kx_{0}),w_F\in F_j(f^kx_{0})$
. Then,
It follows that

Similar to equation (3.13), we can obtain
![]() $\|A(f^ky)w-A(f^kx_0)w\|_{f^{k+1}x_0}\leq c_0le^{\varepsilon }\rho ^\alpha \|w\|_{f^{k}x_0}$
. Therefore,
$\|A(f^ky)w-A(f^kx_0)w\|_{f^{k+1}x_0}\leq c_0le^{\varepsilon }\rho ^\alpha \|w\|_{f^{k}x_0}$
. Therefore,

if
![]() $\rho $
is small enough. It implies that for any
$\rho $
is small enough. It implies that for any
![]() $v\in \mathcal {A}_{f^my}^{-m} V_j(x_{1},\theta _0)$
,
$v\in \mathcal {A}_{f^my}^{-m} V_j(x_{1},\theta _0)$
,
This completes the proof of the lemma.
4 Proof of Theorem 2.2
4.1 Construction of hyperbolic horseshoes
The aim of this subsection is to construct a hyperbolic horseshoe
![]() $\Lambda $
satisfying the properties listed in Theorem 2.2. This construction resembles Theorem S.5.9 in [Reference Katok and Hasselblatt17].
$\Lambda $
satisfying the properties listed in Theorem 2.2. This construction resembles Theorem S.5.9 in [Reference Katok and Hasselblatt17].
We begin with producing a separated set with sufficiently large cardinality. For
![]() $n\geq 1,$
denote by
$n\geq 1,$
denote by
![]() $d_n(x,y)=\max _{0\leq k\leq n-1}d(f^kx,f^ky)$
the dynamical distance on M, and denote by
$d_n(x,y)=\max _{0\leq k\leq n-1}d(f^kx,f^ky)$
the dynamical distance on M, and denote by
![]() $B_n(x,\rho )=\{y\in M: d_n(x,y)\leq \rho \}$
the
$B_n(x,\rho )=\{y\in M: d_n(x,y)\leq \rho \}$
the
![]() $d_n$
-balls of radius
$d_n$
-balls of radius
![]() $\rho $
. Let
$\rho $
. Let
![]() $N_\mu (n,\rho ,\bar {\delta })$
be the minimal numbers of
$N_\mu (n,\rho ,\bar {\delta })$
be the minimal numbers of
![]() $d_n$
-balls of radius
$d_n$
-balls of radius
![]() $\rho $
whose union has measure at least
$\rho $
whose union has measure at least
![]() $\bar {\delta }.$
Then by [Reference Katok16, Theorem 1.1], for any
$\bar {\delta }.$
Then by [Reference Katok16, Theorem 1.1], for any
![]() $\bar {\delta }>0,$
$\bar {\delta }>0,$
Given any
![]() $0<\delta <1/2,$
let
$0<\delta <1/2,$
let
![]() $\Lambda _\delta =\mathcal {R}^{Df}_\delta \cap \mathcal {R}^{\mathcal {A}}_\delta \cap \text {~supp}(\mu ).$
Then,
$\Lambda _\delta =\mathcal {R}^{Df}_\delta \cap \mathcal {R}^{\mathcal {A}}_\delta \cap \text {~supp}(\mu ).$
Then,
![]() $\mu (\Lambda _\delta )>1-2\delta >0.$
Take
$\mu (\Lambda _\delta )>1-2\delta >0.$
Take
![]() $\bar {\delta }=({1}/{2})\mu (\Lambda _\delta ),$
and then for any given
$\bar {\delta }=({1}/{2})\mu (\Lambda _\delta ),$
and then for any given
![]() $i\in \mathbb {N}_{k_0}, 0<\varepsilon <\varepsilon _i$
, there exist
$i\in \mathbb {N}_{k_0}, 0<\varepsilon <\varepsilon _i$
, there exist
![]() $0<\rho _1<\varepsilon /2, N>1,$
such that for any
$0<\rho _1<\varepsilon /2, N>1,$
such that for any
![]() $0<\rho <\rho _1,n\geq N,$
one has
$0<\rho <\rho _1,n\geq N,$
one has
Fix a dense subset
![]() $\{\varphi _j\}_{j= 1}^\infty $
of the unit sphere of
$\{\varphi _j\}_{j= 1}^\infty $
of the unit sphere of
![]() $C(M)$
. We consider the induced metric on
$C(M)$
. We consider the induced metric on
![]() $\mathcal {M}_f(M)$
:
$\mathcal {M}_f(M)$
:
 $$ \begin{align*}D(\mu_1,\mu_2)= \sum\limits_{j=1}^{\infty}\frac{|\int \varphi_j\,d\mu_1-\int \varphi_j\,d\mu_2|}{2^j}\quad \text{for all } \mu_1,\mu_2\in \mathcal{M}_f(M).\end{align*} $$
$$ \begin{align*}D(\mu_1,\mu_2)= \sum\limits_{j=1}^{\infty}\frac{|\int \varphi_j\,d\mu_1-\int \varphi_j\,d\mu_2|}{2^j}\quad \text{for all } \mu_1,\mu_2\in \mathcal{M}_f(M).\end{align*} $$
Take J large enough such that
![]() ${1}/{2^{J}}<{\varepsilon }/{8}$
, and take
${1}/{2^{J}}<{\varepsilon }/{8}$
, and take
![]() $\rho <\min \{\rho _0,\rho _1/2\}$
small enough (where
$\rho <\min \{\rho _0,\rho _1/2\}$
small enough (where
![]() $\rho _0$
is given by Lemma 3.5) such that
$\rho _0$
is given by Lemma 3.5) such that
Since
![]() $\Lambda _\delta \subset \mathcal {R}^{Df}_\delta $
, by Lemma 3.3, there exists
$\Lambda _\delta \subset \mathcal {R}^{Df}_\delta $
, by Lemma 3.3, there exists
![]() $0<\beta <\tfrac {1}{3}\rho $
and finite
$0<\beta <\tfrac {1}{3}\rho $
and finite
![]() $(\rho , \beta ,{\chi }/{2})$
-rectangles
$(\rho , \beta ,{\chi }/{2})$
-rectangles
![]() $R(q_1),\ldots ,R(q_t)$
, such that
$R(q_1),\ldots ,R(q_t)$
, such that
![]() $\bigcup _{j=1}^tB(q_j,\beta )\supset \Lambda _\delta $
. We consider a partition
$\bigcup _{j=1}^tB(q_j,\beta )\supset \Lambda _\delta $
. We consider a partition
![]() $\mathcal {P}=\{P_1,\ldots ,P_t \}$
of
$\mathcal {P}=\{P_1,\ldots ,P_t \}$
of
![]() $\Lambda _\delta $
, where
$\Lambda _\delta $
, where
 $$ \begin{align*}P_1=B(q_1,\beta)\cap\Lambda_\delta\quad\text{and}\quad P_k=B(q_k,\beta)\cap\Lambda_\delta\setminus \bigg(\bigcup_{j=1}^{k-1}P_j\bigg) \quad\text{for all } 2\leq k\leq t.\end{align*} $$
$$ \begin{align*}P_1=B(q_1,\beta)\cap\Lambda_\delta\quad\text{and}\quad P_k=B(q_k,\beta)\cap\Lambda_\delta\setminus \bigg(\bigcup_{j=1}^{k-1}P_j\bigg) \quad\text{for all } 2\leq k\leq t.\end{align*} $$
Let
 $$ \begin{align*} \Lambda_{\delta,n} := \bigg\{ & x\in \Lambda_\delta: \text{there exists~} k\in[n, (1+\varepsilon)n]\text{~such that~} f^k(x)\in \mathcal{P}(x),\\&\text{~the collection~}\{f^k(x)\}_{1\leq k\leq n} \text{~is~} \varepsilon/2\text{-dense in supp}(\mu), \text{ and~}\\ & \bigg|\frac{1}{m}\sum\limits_{p=0}^{m-1}\varphi_j(f^px)-\int \varphi_j \,d\mu\bigg|\leq \frac{\varepsilon}{4} \text{ for all } m\geq n, 1\leq j\leq J \bigg\}. \end{align*} $$
$$ \begin{align*} \Lambda_{\delta,n} := \bigg\{ & x\in \Lambda_\delta: \text{there exists~} k\in[n, (1+\varepsilon)n]\text{~such that~} f^k(x)\in \mathcal{P}(x),\\&\text{~the collection~}\{f^k(x)\}_{1\leq k\leq n} \text{~is~} \varepsilon/2\text{-dense in supp}(\mu), \text{ and~}\\ & \bigg|\frac{1}{m}\sum\limits_{p=0}^{m-1}\varphi_j(f^px)-\int \varphi_j \,d\mu\bigg|\leq \frac{\varepsilon}{4} \text{ for all } m\geq n, 1\leq j\leq J \bigg\}. \end{align*} $$
Claim.
![]() $\lim \nolimits _{n\to \infty }\mu (\Lambda _{\delta ,n})=\mu (\Lambda _{\delta }). $
$\lim \nolimits _{n\to \infty }\mu (\Lambda _{\delta ,n})=\mu (\Lambda _{\delta }). $
Proof of the claim
Let
and
![]() $A_{n,j} =\{ x\in P_j: \text {there exists~} k\in [n, (1+\varepsilon )n]\text {~such that~} f^k(x)\in P_j\}.$
Then,
$A_{n,j} =\{ x\in P_j: \text {there exists~} k\in [n, (1+\varepsilon )n]\text {~such that~} f^k(x)\in P_j\}.$
Then,
![]() ${A_n=\bigcup _{j=1}^tA_{n,j}}$
. Considering
${A_n=\bigcup _{j=1}^tA_{n,j}}$
. Considering
![]() $P_1$
, we may assume
$P_1$
, we may assume
![]() $\mu (P_1)>0$
. For any
$\mu (P_1)>0$
. For any
![]() $\tau>0,$
let
$\tau>0,$
let
 $$ \begin{align*}A_{n,1}^{\tau}=\{x\in P_1: \mu(P_1)-\tau\leq\frac{1}{m}\sum_{j=0}^{m-1}\chi_{P_1}(f^jx)\leq \mu(P_1)+\tau \text{ for all } m\geq n \}. \end{align*} $$
$$ \begin{align*}A_{n,1}^{\tau}=\{x\in P_1: \mu(P_1)-\tau\leq\frac{1}{m}\sum_{j=0}^{m-1}\chi_{P_1}(f^jx)\leq \mu(P_1)+\tau \text{ for all } m\geq n \}. \end{align*} $$
Then the Birkhoff ergodic theorem gives
![]() $\mu (\bigcup _{n\geq 1}A_{n,1}^{\tau })=\mu (P_1)$
. Since
$\mu (\bigcup _{n\geq 1}A_{n,1}^{\tau })=\mu (P_1)$
. Since
![]() $A_{1,1}^{\tau }\subset A_{2,1}^{\tau }\subset \cdots ,$
we have
$A_{1,1}^{\tau }\subset A_{2,1}^{\tau }\subset \cdots ,$
we have
Take
![]() $\tau <{\varepsilon }/({2+\varepsilon })\mu (P_1)$
. Then for any
$\tau <{\varepsilon }/({2+\varepsilon })\mu (P_1)$
. Then for any
![]() $x\in A_{n,1}^{\tau }$
, by the definition of
$x\in A_{n,1}^{\tau }$
, by the definition of
![]() $ A_{n,1}^{\tau }$
,
$ A_{n,1}^{\tau }$
,
 $$ \begin{align*} \text{card}\{k\in [n,n+n\varepsilon]:f^k(x)\in P_1 \} & \geq (\mu(P_1)-\tau)(n+n\varepsilon)-(\mu(P_1)+\tau)n\\ & = n(\mu(P_1)\varepsilon-2\tau-\tau\varepsilon)\\ & \geq 1, \end{align*} $$
$$ \begin{align*} \text{card}\{k\in [n,n+n\varepsilon]:f^k(x)\in P_1 \} & \geq (\mu(P_1)-\tau)(n+n\varepsilon)-(\mu(P_1)+\tau)n\\ & = n(\mu(P_1)\varepsilon-2\tau-\tau\varepsilon)\\ & \geq 1, \end{align*} $$
if n is taken large enough. Thus,
![]() $x\in A_{n,1}$
, that is,
$x\in A_{n,1}$
, that is,
![]() $A_{n,1}^{\tau }\subset A_{n,1}$
. Therefore,
$A_{n,1}^{\tau }\subset A_{n,1}$
. Therefore,
![]() $\lim \nolimits _{n\to \infty } \mu (A_{n,1})=\mu (P_1).$
Reproduce the proof above for every
$\lim \nolimits _{n\to \infty } \mu (A_{n,1})=\mu (P_1).$
Reproduce the proof above for every
![]() $P_j$
. Then we conclude
$P_j$
. Then we conclude
Since, by [Reference Walters29, Theorem 1.7],
![]() $\{x\in M:\overline {\mathcal {O}^+(x)}=\text {supp}(\mu ) \}$
has
$\{x\in M:\overline {\mathcal {O}^+(x)}=\text {supp}(\mu ) \}$
has
![]() $\mu $
-full measure, letting
$\mu $
-full measure, letting
we have
![]() $\mu (B_n)\to \mu ( \Lambda _\delta )$
as
$\mu (B_n)\to \mu ( \Lambda _\delta )$
as
![]() $n\to +\infty .$
Let
$n\to +\infty .$
Let
 $$ \begin{align*}C_n=\bigg\{x\in \Lambda_\delta:\bigg|\frac{1}{m}\sum\limits_{k=0}^{m-1}\varphi_j(f^kx)-\int \varphi_j \,d\mu\bigg|\leq \frac{\varepsilon}{4} \text{ for all } m\geq n, 1\leq j\leq J \bigg \}.\end{align*} $$
$$ \begin{align*}C_n=\bigg\{x\in \Lambda_\delta:\bigg|\frac{1}{m}\sum\limits_{k=0}^{m-1}\varphi_j(f^kx)-\int \varphi_j \,d\mu\bigg|\leq \frac{\varepsilon}{4} \text{ for all } m\geq n, 1\leq j\leq J \bigg \}.\end{align*} $$
Then by Birkhoff ergodic theorem,
![]() $\mu (\bigcup _{n\geq 1}C_n)=\mu (\Lambda _{\delta })$
. Since
$\mu (\bigcup _{n\geq 1}C_n)=\mu (\Lambda _{\delta })$
. Since
![]() $C_1\subset C_2\subset \cdots ,$
one has
$C_1\subset C_2\subset \cdots ,$
one has
Together with equation (4.3),
This proves the claim.
Choose
![]() $n>\max \{ {2\log l}/{\varepsilon }, N, {1}/{\varepsilon }\log t,{1}/{4 \varepsilon } \}$
large enough such that
$n>\max \{ {2\log l}/{\varepsilon }, N, {1}/{\varepsilon }\log t,{1}/{4 \varepsilon } \}$
large enough such that
![]() $\mu (\Lambda _{\delta ,n})>\tfrac {1}{2}\mu (\Lambda _{\delta })=\bar {\delta },$
and
$\mu (\Lambda _{\delta ,n})>\tfrac {1}{2}\mu (\Lambda _{\delta })=\bar {\delta },$
and
![]() $n\varepsilon +1<e^{\varepsilon n}$
, where the constant
$n\varepsilon +1<e^{\varepsilon n}$
, where the constant
![]() $ ({2\log l}/{\varepsilon })$
comes from Lemma 3.5. Denote by E an
$ ({2\log l}/{\varepsilon })$
comes from Lemma 3.5. Denote by E an
![]() $(n,2\rho )$
-separated set of
$(n,2\rho )$
-separated set of
![]() $\Lambda _{\delta ,n}$
of maximum cardinality. Then
$\Lambda _{\delta ,n}$
of maximum cardinality. Then
![]() $\bigcup _{x\in E}B_n(x,2\rho )\supset \Lambda _{\delta ,n}.$
By equation (4.1),
$\bigcup _{x\in E}B_n(x,2\rho )\supset \Lambda _{\delta ,n}.$
By equation (4.1),
For
![]() $ k\in [n, n(1+\varepsilon )]$
, let
$ k\in [n, n(1+\varepsilon )]$
, let
![]() $F_k=\{x\in E:f^k(x)\in \mathcal {P}(x)\}$
and take
$F_k=\{x\in E:f^k(x)\in \mathcal {P}(x)\}$
and take
![]() $m\in [n, n(1+\varepsilon )]$
satisfying
$m\in [n, n(1+\varepsilon )]$
satisfying
![]() $\text {card}(F_m)=\max \{\text {card}(F_k):n\leq k\leq n(1+\varepsilon ) \}.$
Then,
$\text {card}(F_m)=\max \{\text {card}(F_k):n\leq k\leq n(1+\varepsilon ) \}.$
Then,
Choose
![]() $P\in \mathcal {P}$
satisfying
$P\in \mathcal {P}$
satisfying
![]() $\text {card}(F_m\cap P)=\max \{\text {card}(F_m\cap P_k):1\leq k\leq t\}.$
Then,
$\text {card}(F_m\cap P)=\max \{\text {card}(F_m\cap P_k):1\leq k\leq t\}.$
Then,
Without loss of generality, we may assume
Otherwise, since
![]() $e^{(h_\mu (f)+2\varepsilon )n}-({1}/{t})e^{(h_\mu (f)-2\varepsilon )n}\ge e^{(h_\mu (f)-2\varepsilon )n}(e^{4\varepsilon n}-1)>1$
, we can choose a subset of
$e^{(h_\mu (f)+2\varepsilon )n}-({1}/{t})e^{(h_\mu (f)-2\varepsilon )n}\ge e^{(h_\mu (f)-2\varepsilon )n}(e^{4\varepsilon n}-1)>1$
, we can choose a subset of
![]() $F_m\cap P$
such that equation (4.4) holds.
$F_m\cap P$
such that equation (4.4) holds.
By the definition of the partition
![]() $\mathcal {P}$
, there exists
$\mathcal {P}$
, there exists
![]() $q\in \{q_1,\ldots ,q_t\}$
, such that
$q\in \{q_1,\ldots ,q_t\}$
, such that
![]() ${P\subset B(q,\beta )\cap \Lambda _\delta }$
. Thus, for any
${P\subset B(q,\beta )\cap \Lambda _\delta }$
. Thus, for any
![]() $x\in F_m\cap P,$
since
$x\in F_m\cap P,$
since
![]() $x,f^m(x)\in B(q,\beta )\cap \Lambda _\delta ,$
by Definition 3.2, the connected component
$x,f^m(x)\in B(q,\beta )\cap \Lambda _\delta ,$
by Definition 3.2, the connected component
![]() $C(x,R(q)\cap f^{-m}R(q))$
of
$C(x,R(q)\cap f^{-m}R(q))$
of
![]() $R(q)\cap f^{-m}R(q)$
containing x is an admissible s-rectangle in
$R(q)\cap f^{-m}R(q)$
containing x is an admissible s-rectangle in
![]() $R(q)$
, and
$R(q)$
, and
![]() $f^mC(x,R(q)\cap f^{-m}R(q))$
is an admissible u-rectangle in
$f^mC(x,R(q)\cap f^{-m}R(q))$
is an admissible u-rectangle in
![]() $R(q)$
.
$R(q)$
.
We claim that if
![]() $x_1,x_2\in F_m\cap P$
with
$x_1,x_2\in F_m\cap P$
with
![]() $x_1\neq x_2,$
then
$x_1\neq x_2,$
then
![]() $C(x_1,R(q)\cap f^{-m}R(q))\cap C(x_2,R(q)\cap f^{-m}R(q))=\varnothing $
. Indeed, if there is
$C(x_1,R(q)\cap f^{-m}R(q))\cap C(x_2,R(q)\cap f^{-m}R(q))=\varnothing $
. Indeed, if there is
![]() $y\in C(x_1,R(q)\cap f^{-m}R(q))\cap C(x_2, R(q)\cap f^{-m}R(q)),$
by Definition 3.2, one sees
$y\in C(x_1,R(q)\cap f^{-m}R(q))\cap C(x_2, R(q)\cap f^{-m}R(q)),$
by Definition 3.2, one sees
![]() $d(f^kx_j,f^ky)\leq \rho $
for any
$d(f^kx_j,f^ky)\leq \rho $
for any
![]() ${0\leq k\leq m}$
and
${0\leq k\leq m}$
and
![]() $j=1,2$
. Thus,
$j=1,2$
. Thus,
![]() $d_m(x_1,x_2)\leq 2\rho $
. However, since
$d_m(x_1,x_2)\leq 2\rho $
. However, since
![]() $F_m\cap P$
is an
$F_m\cap P$
is an
![]() $(n,2\rho )$
-separated set, we obtain
$(n,2\rho )$
-separated set, we obtain
![]() $d_m(x_1,x_2)\geq d_n(x_1,x_2)>2\rho $
, which is a contradiction. Therefore, there are at least
$d_m(x_1,x_2)\geq d_n(x_1,x_2)>2\rho $
, which is a contradiction. Therefore, there are at least
![]() $\text {card}( F_m\cap P)$
disjoint s-rectangles in
$\text {card}( F_m\cap P)$
disjoint s-rectangles in
![]() $R(q)$
, mapped by
$R(q)$
, mapped by
![]() $f^m$
to
$f^m$
to
![]() $\text {card}(F_m\cap P)$
disjoint admissible u-rectangles in
$\text {card}(F_m\cap P)$
disjoint admissible u-rectangles in
![]() $R(q)$
.
$R(q)$
.
Let
 $$ \begin{align*}\Lambda^*=\bigcap\limits_{n\in\mathbb{Z}}f^{-mn}\bigg(\bigcup\limits_{x\in F_m\cap P}C(x,R(q)\cap f^{-m}R(q)) \bigg).\end{align*} $$
$$ \begin{align*}\Lambda^*=\bigcap\limits_{n\in\mathbb{Z}}f^{-mn}\bigg(\bigcup\limits_{x\in F_m\cap P}C(x,R(q)\cap f^{-m}R(q)) \bigg).\end{align*} $$
Then
![]() $f^m|_{\Lambda ^*}$
is conjugate to a full shift in
$f^m|_{\Lambda ^*}$
is conjugate to a full shift in
![]() $\text {card}(F_m\cap P)$
-symbols. Moreover, for any
$\text {card}(F_m\cap P)$
-symbols. Moreover, for any
![]() ${y\in \Lambda ^*,}$
any
${y\in \Lambda ^*,}$
any
![]() $n\in \mathbb {Z}$
, there exists
$n\in \mathbb {Z}$
, there exists
![]() $x_n\in F_m\cap P$
such that
$x_n\in F_m\cap P$
such that
![]() $f^{mn}(y)\in C(x_n,R(q)\cap f^{-m}R(q)).$
Note that the orbit of
$f^{mn}(y)\in C(x_n,R(q)\cap f^{-m}R(q)).$
Note that the orbit of
![]() $y\in \Lambda ^*$
remains in the union of
$y\in \Lambda ^*$
remains in the union of
![]() $R(q),\ldots ,R(f^m(q))$
. Let
$R(q),\ldots ,R(f^m(q))$
. Let
Then
![]() $\Lambda $
is a hyperbolic horseshoe.
$\Lambda $
is a hyperbolic horseshoe.
It remains to show the conclusions (i)–(iv) of Theorem 2.2 hold for this
![]() $\Lambda $
.
$\Lambda $
.
(i) Since
by equation (4.4),
![]() $h_{\mathrm{top}}(f|_{\Lambda })\geq -{1}/{m}\log t + {n}/{m}(h_\mu (f)-2\varepsilon ).$
Since
$h_{\mathrm{top}}(f|_{\Lambda })\geq -{1}/{m}\log t + {n}/{m}(h_\mu (f)-2\varepsilon ).$
Since
![]() $({1}/{\varepsilon })\log t< n\leq m\leq n(1+\varepsilon )$
,
$({1}/{\varepsilon })\log t< n\leq m\leq n(1+\varepsilon )$
,
By equation (4.4), we also have
(ii) By the construction of
![]() $\Lambda $
and the definition of
$\Lambda $
and the definition of
![]() $R(q)$
, for any
$R(q)$
, for any
![]() $y\in \Lambda ,$
there exist
$y\in \Lambda ,$
there exist
![]() $x\in F_m\cap P, 0\leq k\leq m-1$
such that
$x\in F_m\cap P, 0\leq k\leq m-1$
such that
![]() $d(y,f^kx)\leq \rho <\varepsilon /2.$
Since
$d(y,f^kx)\leq \rho <\varepsilon /2.$
Since
![]() $x\in \Lambda _\delta \subset \text {~supp}(\mu ),$
we conclude
$x\in \Lambda _\delta \subset \text {~supp}(\mu ),$
we conclude
![]() $\Lambda $
is contained in an
$\Lambda $
is contained in an
![]() $\varepsilon /2$
-neighborhood of supp
$\varepsilon /2$
-neighborhood of supp
![]() $(\mu )$
. However, fix any
$(\mu )$
. However, fix any
![]() $x_0\in F_m\cap P\subset \Lambda _{\delta ,m}$
. By the construction of
$x_0\in F_m\cap P\subset \Lambda _{\delta ,m}$
. By the construction of
![]() $\Lambda _{\delta ,m}$
, for any
$\Lambda _{\delta ,m}$
, for any
![]() $z\in \text {~supp}(\mu )$
, there exists
$z\in \text {~supp}(\mu )$
, there exists
![]() $1\leq k\leq m$
, such that
$1\leq k\leq m$
, such that
![]() $d(z,f^kx_0)\leq \varepsilon /2$
. Take
$d(z,f^kx_0)\leq \varepsilon /2$
. Take
![]() $y\in \Lambda ^*$
such that
$y\in \Lambda ^*$
such that
![]() $y\in C(x_0,R(q)\cap f^{-m}R(q))$
, so then
$y\in C(x_0,R(q)\cap f^{-m}R(q))$
, so then
![]() $d(f^kx_0,f^ky)\leq \rho <\varepsilon /2$
. Therefore, supp
$d(f^kx_0,f^ky)\leq \rho <\varepsilon /2$
. Therefore, supp
![]() $(\mu )$
is contained in an
$(\mu )$
is contained in an
![]() $\varepsilon $
-neighborhood of
$\varepsilon $
-neighborhood of
![]() $\Lambda $
. Hence,
$\Lambda $
. Hence,
![]() $d_H(\Lambda ,\text {~supp}(\mu ))\leq \varepsilon .$
$d_H(\Lambda ,\text {~supp}(\mu ))\leq \varepsilon .$
(iii) For any f-invariant measure
![]() $\nu $
supported on
$\nu $
supported on
![]() $\Lambda $
, we may assume
$\Lambda $
, we may assume
![]() $\nu $
is ergodic first. Since
$\nu $
is ergodic first. Since
 $$ \begin{align*}D(\mu,\nu)\leq \sum\limits_{j=1}^{J}\frac{|\int \varphi_j\,d\mu-\int \varphi_j\,d\nu|}{2^j}+\frac{1}{2^{J-1}}\leq \sum\limits_{j=1}^{J}\frac{|\int \varphi_j\,d\mu-\int \varphi_j\,d\nu|}{2^j}+\frac{\varepsilon}{4},\end{align*} $$
$$ \begin{align*}D(\mu,\nu)\leq \sum\limits_{j=1}^{J}\frac{|\int \varphi_j\,d\mu-\int \varphi_j\,d\nu|}{2^j}+\frac{1}{2^{J-1}}\leq \sum\limits_{j=1}^{J}\frac{|\int \varphi_j\,d\mu-\int \varphi_j\,d\nu|}{2^j}+\frac{\varepsilon}{4},\end{align*} $$
it is enough to show:
![]() $|\int \varphi _j\,d\mu -\int \varphi _j\,d\nu |\leq \tfrac {3}{4}\varepsilon \text { for all } 1\leq j\leq J.$
Take
$|\int \varphi _j\,d\mu -\int \varphi _j\,d\nu |\leq \tfrac {3}{4}\varepsilon \text { for all } 1\leq j\leq J.$
Take
![]() $y\in \Lambda ^*$
and
$y\in \Lambda ^*$
and
![]() $s{\in \mathbb {N}}$
large enough such that
$s{\in \mathbb {N}}$
large enough such that
 $$ \begin{align*}\bigg|\frac{1}{ms}\sum\limits_{k=0}^{ms-1}\varphi_j(f^ky)-\int \varphi_j \,d\nu\bigg|\leq \frac{\varepsilon}{4},\quad 1\leq j\leq J.\end{align*} $$
$$ \begin{align*}\bigg|\frac{1}{ms}\sum\limits_{k=0}^{ms-1}\varphi_j(f^ky)-\int \varphi_j \,d\nu\bigg|\leq \frac{\varepsilon}{4},\quad 1\leq j\leq J.\end{align*} $$
Then there exist
![]() $x_0,x_1,\ldots ,x_{s-1}\in F_m\cap P$
such that
$x_0,x_1,\ldots ,x_{s-1}\in F_m\cap P$
such that
By equation (4.2) and the construction of
![]() $\Lambda _{\delta ,m}$
, we obtain
$\Lambda _{\delta ,m}$
, we obtain
![]() $|\int \varphi _jd\mu -\int \varphi _jd\nu |\leq \tfrac {3}{4}\varepsilon $
,
$|\int \varphi _jd\mu -\int \varphi _jd\nu |\leq \tfrac {3}{4}\varepsilon $
,
![]() $1\leq j\leq J,$
which implies
$1\leq j\leq J,$
which implies
![]() $D(\mu ,\nu )\leq \varepsilon $
.
$D(\mu ,\nu )\leq \varepsilon $
.
If
![]() $\nu $
is not ergodic, by the ergodic decomposition theorem,
$\nu $
is not ergodic, by the ergodic decomposition theorem,
![]() $\nu $
-a.e. ergodic component is supported on
$\nu $
-a.e. ergodic component is supported on
![]() $\Lambda $
. Hence,
$\Lambda $
. Hence,
 $$ \begin{align*} D(\mu,\nu) = \sum\limits_{j=1}^{\infty}\frac{|\int \varphi_j\,d\mu-\int \varphi_j\,d\nu|}{2^j} & = \sum\limits_{j=1}^{\infty}\frac{|\int(\int \varphi_j\,d\mu-\int \varphi_j\,d\nu_x)\,d\nu(x)|}{2^j} \\ &\leq \int D(\mu,\nu_x) \,d\nu(x) \\ & \leq \varepsilon. \end{align*} $$
$$ \begin{align*} D(\mu,\nu) = \sum\limits_{j=1}^{\infty}\frac{|\int \varphi_j\,d\mu-\int \varphi_j\,d\nu|}{2^j} & = \sum\limits_{j=1}^{\infty}\frac{|\int(\int \varphi_j\,d\mu-\int \varphi_j\,d\nu_x)\,d\nu(x)|}{2^j} \\ &\leq \int D(\mu,\nu_x) \,d\nu(x) \\ & \leq \varepsilon. \end{align*} $$
4.2 Dominated splitting for cocycles
The conclusion ![]() of Theorem 2.2 is contained in the following proposition.
of Theorem 2.2 is contained in the following proposition.
Proposition 4.1. Under the condition of Theorem 2.2, for any
![]() $i\in \mathbb {N}_{k_0}$
and any
$i\in \mathbb {N}_{k_0}$
and any
![]() $0<\varepsilon <\varepsilon _i$
, let
$0<\varepsilon <\varepsilon _i$
, let
![]() $\Lambda $
be constructed as above. Then there exists a continuous
$\Lambda $
be constructed as above. Then there exists a continuous
![]() $\mathcal {A}$
-invariant splitting on
$\mathcal {A}$
-invariant splitting on
![]() $\Lambda $
$\Lambda $
with
![]() $\dim (E_j)=d_j$
for
$\dim (E_j)=d_j$
for
![]() $1\leq j\leq i$
, such that for any
$1\leq j\leq i$
, such that for any
![]() $y\in \Lambda $
, one has
$y\in \Lambda $
, one has
To prove this proposition, we require the following definitions. Let
![]() $\mathcal {G}(\mathfrak {X})$
denote the Grassmannian of closed subspaces of
$\mathcal {G}(\mathfrak {X})$
denote the Grassmannian of closed subspaces of
![]() $\mathfrak {X}$
, endowed with the Hausdorff metric
$\mathfrak {X}$
, endowed with the Hausdorff metric
![]() $d_H$
, defined by
$d_H$
, defined by
 $$ \begin{align*}d_H(E,F) = \max\bigg\{\sup\limits_{u\in S_E}\mathrm{dist}(u,S_F),\sup\limits_{v\in S_F}\mathrm{dist}(v,S_E) \bigg\}\quad\text{for all } E,F\in \mathcal{G}(\mathfrak{X}),\end{align*} $$
$$ \begin{align*}d_H(E,F) = \max\bigg\{\sup\limits_{u\in S_E}\mathrm{dist}(u,S_F),\sup\limits_{v\in S_F}\mathrm{dist}(v,S_E) \bigg\}\quad\text{for all } E,F\in \mathcal{G}(\mathfrak{X}),\end{align*} $$
where
![]() $S_F=\{v\in F:\|v\|=1 \}$
,
$S_F=\{v\in F:\|v\|=1 \}$
,
![]() $\mathrm{dist}(u,S_F)=\inf \{\|u-v\|:v\in S_F\}$
. Denote by
$\mathrm{dist}(u,S_F)=\inf \{\|u-v\|:v\in S_F\}$
. Denote by
![]() $\mathcal {G}_j(\mathfrak {X})$
,
$\mathcal {G}_j(\mathfrak {X})$
,
![]() $\mathcal {G}^j({\mathfrak {X}})$
the Grassmannian of j-dimensional and j-codimensional closed subspaces, respectively. Then by [Reference Kato15, Ch. IV, §2.1],
$\mathcal {G}^j({\mathfrak {X}})$
the Grassmannian of j-dimensional and j-codimensional closed subspaces, respectively. Then by [Reference Kato15, Ch. IV, §2.1],
![]() $(\mathcal {G}({\mathfrak {X}}),d_H)$
is a complete metric space, and
$(\mathcal {G}({\mathfrak {X}}),d_H)$
is a complete metric space, and
![]() $\mathcal {G}_j({\mathfrak {X}})$
,
$\mathcal {G}_j({\mathfrak {X}})$
,
![]() $\mathcal {G}^j(\mathfrak {X})$
are closed in
$\mathcal {G}^j(\mathfrak {X})$
are closed in
![]() $\mathcal {G}(\mathfrak {X})$
. To compute
$\mathcal {G}(\mathfrak {X})$
. To compute
![]() $d_H$
conveniently, we introduce the gap
$d_H$
conveniently, we introduce the gap
![]() $\hat {\delta }$
, defined by
$\hat {\delta }$
, defined by
 $$ \begin{align*} \hat{\delta}(E,F) = \max\bigg\{\sup\limits_{u\in S_E}\mathrm{dist}(u,F),\sup\limits_{v\in S_F}\mathrm{dist}(v,E) \bigg\}\quad\text{for all } E,F\in \mathcal{G}({\mathfrak{X}}).\end{align*} $$
$$ \begin{align*} \hat{\delta}(E,F) = \max\bigg\{\sup\limits_{u\in S_E}\mathrm{dist}(u,F),\sup\limits_{v\in S_F}\mathrm{dist}(v,E) \bigg\}\quad\text{for all } E,F\in \mathcal{G}({\mathfrak{X}}).\end{align*} $$
Note that the gap is not a metric on
![]() $\mathcal {G}(\mathfrak {X})$
, but
$\mathcal {G}(\mathfrak {X})$
, but
See [Reference Kato15, Ch. IV, §2.1] for a proof.
Before proving Proposition 4.1, we give the following lemma first.
Lemma 4.2. Let
![]() $A \in L(\mathfrak {X})$
. If there exists a splitting
$A \in L(\mathfrak {X})$
. If there exists a splitting
and
![]() $A|_{H}$
is a bijection, then
$A|_{H}$
is a bijection, then
Proof. Define
![]() $T:\mathfrak {X}\to \mathfrak {X}$
by
$T:\mathfrak {X}\to \mathfrak {X}$
by
![]() $T=(A|_{H} )^{-1}\circ \pi _1\circ A$
, where
$T=(A|_{H} )^{-1}\circ \pi _1\circ A$
, where
![]() $\pi _1$
is the projection associated with equation (4.5) onto
$\pi _1$
is the projection associated with equation (4.5) onto
![]() $A(H)$
parallel to F. Since
$A(H)$
parallel to F. Since
![]() $A|_{H}$
is a bijection, T is well defined. Then it follows from T having image H and kernel
$A|_{H}$
is a bijection, T is well defined. Then it follows from T having image H and kernel
![]() $ A^{-1}(F)$
that the conclusion holds.
$ A^{-1}(F)$
that the conclusion holds.
We now prove Proposition 4.1.
Proof of Proposition 4.1
Fix any
![]() $i\in \mathbb {N}_{k_0}$
,
$i\in \mathbb {N}_{k_0}$
,
![]() $0<\varepsilon <\varepsilon _i$
, and
$0<\varepsilon <\varepsilon _i$
, and
![]() $1\leq j\leq i$
. We first assume
$1\leq j\leq i$
. We first assume
![]() $y\in \Lambda ^*,$
and then by the definition of
$y\in \Lambda ^*,$
and then by the definition of
![]() $\Lambda ^*$
, there exist
$\Lambda ^*$
, there exist
![]() $\{x_n\}_{n\in \mathbb {Z}}\subset F_m$
, such that
$\{x_n\}_{n\in \mathbb {Z}}\subset F_m$
, such that
For any
![]() $n\in \mathbb {Z}$
, let
$n\in \mathbb {Z}$
, let
![]() $\mathfrak {X}=H_j(x_{n})\oplus F_j(x_{n})$
be the Oseledets decomposition at
$\mathfrak {X}=H_j(x_{n})\oplus F_j(x_{n})$
be the Oseledets decomposition at
![]() $x_n$
, where
$x_n$
, where
![]() $H_j(x_{n})=E_1(x_{n})\oplus \cdots \oplus E_j(x_{n})$
. We first prove
$H_j(x_{n})=E_1(x_{n})\oplus \cdots \oplus E_j(x_{n})$
. We first prove
![]() $\{\mathcal {A}_{f^{-mn}y}^{mn}H_j(x_{-n})\}_{n\geq 1}$
is a Cauchy sequence in
$\{\mathcal {A}_{f^{-mn}y}^{mn}H_j(x_{-n})\}_{n\geq 1}$
is a Cauchy sequence in
![]() $\mathcal {G}(\mathfrak {X})$
. Denote
$\mathcal {G}(\mathfrak {X})$
. Denote
![]() $\widetilde {H}_j(x_{-n})=\mathcal {A}_{f^{-m(n+1)}y}^{m}H_j(x_{-n-1}).$
Then,
$\widetilde {H}_j(x_{-n})=\mathcal {A}_{f^{-m(n+1)}y}^{m}H_j(x_{-n-1}).$
Then,
By Lemma 3.5,
![]() $\widetilde {H}_j(x_{-n})\subset U_j(x_{-n},\theta _0)$
,
$\widetilde {H}_j(x_{-n})\subset U_j(x_{-n},\theta _0)$
,
![]() $\mathcal {A}_{f^{-mn}y}^{mn}\widetilde {H}_j(x_{-n})\subset U_j(x_{0},\theta _0)$
, and
$\mathcal {A}_{f^{-mn}y}^{mn}\widetilde {H}_j(x_{-n})\subset U_j(x_{0},\theta _0)$
, and
![]() $\mathcal {A}_{f^{-mn}y}^{mn}$
is injective on
$\mathcal {A}_{f^{-mn}y}^{mn}$
is injective on
![]() $ U_j(x_{-n},\theta _0)$
. Thus, we have
$ U_j(x_{-n},\theta _0)$
. Thus, we have
Now, for any
![]() $u\in H_j(x_{-n})$
,
$u\in H_j(x_{-n})$
,
 $$ \begin{align} & \mathrm{dist}\bigg(\frac{\mathcal{A}_{f^{-mn}y}^{mn}(u)}{\|\mathcal{A}_{f^{-mn}y}^{mn}(u)\|},\mathcal{A}_{f^{-m(n+1)}y}^{m(n+1)}H_j(x_{-n-1})\bigg)\nonumber\\ &\quad= \inf_{v\in \widetilde{H}_j(x_{-n}) } \bigg\|\frac{\mathcal{A}_{f^{-mn}y}^{mn}(u)}{\|\mathcal{A}_{f^{-mn}y}^{mn}(u)\|}- \mathcal{A}_{f^{-mn}y}^{mn}(v) \bigg\|\nonumber\\ &\quad= \frac{\|u\|}{\|\mathcal{A}_{f^{-mn}y}^{mn}(u)\|}\cdot\inf_{v\in \widetilde{H}_j(x_{-n}) }\bigg\|\mathcal{A}_{f^{-mn}y}^{mn}\bigg(\frac{u}{\|u\|}- v\bigg) \bigg\|. \end{align} $$
$$ \begin{align} & \mathrm{dist}\bigg(\frac{\mathcal{A}_{f^{-mn}y}^{mn}(u)}{\|\mathcal{A}_{f^{-mn}y}^{mn}(u)\|},\mathcal{A}_{f^{-m(n+1)}y}^{m(n+1)}H_j(x_{-n-1})\bigg)\nonumber\\ &\quad= \inf_{v\in \widetilde{H}_j(x_{-n}) } \bigg\|\frac{\mathcal{A}_{f^{-mn}y}^{mn}(u)}{\|\mathcal{A}_{f^{-mn}y}^{mn}(u)\|}- \mathcal{A}_{f^{-mn}y}^{mn}(v) \bigg\|\nonumber\\ &\quad= \frac{\|u\|}{\|\mathcal{A}_{f^{-mn}y}^{mn}(u)\|}\cdot\inf_{v\in \widetilde{H}_j(x_{-n}) }\bigg\|\mathcal{A}_{f^{-mn}y}^{mn}\bigg(\frac{u}{\|u\|}- v\bigg) \bigg\|. \end{align} $$
By equation (4.6), for
![]() $\mathcal {A}_{f^{-mn}y}^{mn}({u}/{\|u\|})\in \mathfrak {X}$
, there exists
$\mathcal {A}_{f^{-mn}y}^{mn}({u}/{\|u\|})\in \mathfrak {X}$
, there exists
![]() $v_n\in \widetilde {H}_j(x_{-n})$
such that
$v_n\in \widetilde {H}_j(x_{-n})$
such that
 $$ \begin{align*} \mathcal{A}_{f^{-mn}y}^{mn}\bigg(\frac{u}{\|u\|}\bigg)-\mathcal{A}_{f^{-mn}y}^{mn}(v_n)\in F_j(x_0)\subset V_j(x_0,\theta_0). \end{align*} $$
$$ \begin{align*} \mathcal{A}_{f^{-mn}y}^{mn}\bigg(\frac{u}{\|u\|}\bigg)-\mathcal{A}_{f^{-mn}y}^{mn}(v_n)\in F_j(x_0)\subset V_j(x_0,\theta_0). \end{align*} $$
Then it follows from equation (4.7) and Lemma 3.5 that

Claim. There exists
![]() $c=c(\delta )>0$
, such that
$c=c(\delta )>0$
, such that
![]() $\|{u}/{\|u\|}- v_n\|\leq c.$
$\|{u}/{\|u\|}- v_n\|\leq c.$
Proof of the claim
Using equation (4.6) and Lemma 4.2, we obtain
Let
![]() $\pi _2$
be the projection operator associated with equation (4.8) onto
$\pi _2$
be the projection operator associated with equation (4.8) onto
![]() $\mathcal {A}_y^{-mn}F_j(x_0)$
parallel to
$\mathcal {A}_y^{-mn}F_j(x_0)$
parallel to
![]() $\widetilde {H}_j(x_{-n})$
. Then,
$\widetilde {H}_j(x_{-n})$
. Then,
 $$ \begin{align*}\frac{u}{\|u\|}- v_n=\pi_2\bigg(\frac{u}{\|u\|}\bigg)\in \mathcal{A}_y^{-mn}F_j(x_0).\end{align*} $$
$$ \begin{align*}\frac{u}{\|u\|}- v_n=\pi_2\bigg(\frac{u}{\|u\|}\bigg)\in \mathcal{A}_y^{-mn}F_j(x_0).\end{align*} $$
Since the splitting
![]() $\mathfrak {X}=H_j(x)\oplus F_j(x)$
is uniformly continuous on
$\mathfrak {X}=H_j(x)\oplus F_j(x)$
is uniformly continuous on
![]() $\mathcal {R}^{\mathcal {A}}_\delta $
, there exists
$\mathcal {R}^{\mathcal {A}}_\delta $
, there exists
![]() ${c=c(\delta )>0}$
such that for any
${c=c(\delta )>0}$
such that for any
![]() $x\in \mathcal {R}^{\mathcal {A}}_\delta $
and any
$x\in \mathcal {R}^{\mathcal {A}}_\delta $
and any
![]() $H\subset U_j(x,\theta _0), F\subset V_j(x,\theta _0)$
with
$H\subset U_j(x,\theta _0), F\subset V_j(x,\theta _0)$
with
![]() $\mathfrak {X}=H\oplus F$
, one has
$\mathfrak {X}=H\oplus F$
, one has
where
![]() $\pi ^H, \pi ^F$
are the projections associated with the splitting
$\pi ^H, \pi ^F$
are the projections associated with the splitting
![]() $\mathfrak {X}=H\oplus F$
. Therefore,
$\mathfrak {X}=H\oplus F$
. Therefore,
 $$ \begin{align*}\bigg\|\frac{u}{\|u\|}- v_n\bigg\|=\bigg\|\pi_2\bigg(\frac{u}{\|u\|}\bigg)\bigg\|\leq c. \end{align*} $$
$$ \begin{align*}\bigg\|\frac{u}{\|u\|}- v_n\bigg\|=\bigg\|\pi_2\bigg(\frac{u}{\|u\|}\bigg)\bigg\|\leq c. \end{align*} $$
This proves the claim.
The claim gives

Similarly, for any
![]() $v\in H_j(x_{-n-1})$
, we have
$v\in H_j(x_{-n-1})$
, we have

Thus,
which implies
![]() $\{\mathcal {A}_{f^{-mn}y}^{mn}H_j(x_{-n})\}_{n\geq 1}$
is a Cauchy sequence in
$\{\mathcal {A}_{f^{-mn}y}^{mn}H_j(x_{-n})\}_{n\geq 1}$
is a Cauchy sequence in
![]() $(\mathcal {G}(\mathfrak {X}),d_H)$
.
$(\mathcal {G}(\mathfrak {X}),d_H)$
.
Now we prove
![]() $\{\mathcal {A}_{f^{mn}y}^{-mn}F_j(x_{n})\}_{n\geq 1}$
is a Cauchy sequence in
$\{\mathcal {A}_{f^{mn}y}^{-mn}F_j(x_{n})\}_{n\geq 1}$
is a Cauchy sequence in
![]() $(\mathcal {G}(\mathfrak {X}),d_H)$
. By Lemma 3.5,
$(\mathcal {G}(\mathfrak {X}),d_H)$
. By Lemma 3.5,
![]() $\mathcal {A}_{y}^{mn}{H}_j(x_{0})\subset U_j(x_n,\theta _0)$
and
$\mathcal {A}_{y}^{mn}{H}_j(x_{0})\subset U_j(x_n,\theta _0)$
and
![]() $\mathcal {A}_{y}^{mn}$
is injective on
$\mathcal {A}_{y}^{mn}$
is injective on
![]() ${H}_j(x_{0})$
. Thus,
${H}_j(x_{0})$
. Thus,
![]() $\mathfrak {X}=\mathcal {A}_{y}^{mn}{H}_j(x_{0})\oplus F_j(x_n).$
Using Lemma 4.2, we obtain
$\mathfrak {X}=\mathcal {A}_{y}^{mn}{H}_j(x_{0})\oplus F_j(x_n).$
Using Lemma 4.2, we obtain
For any
![]() $u\in \mathcal {A}_{f^{m(n+1)}y}^{-m(n+1)}F_j(x_{n+1})$
with
$u\in \mathcal {A}_{f^{m(n+1)}y}^{-m(n+1)}F_j(x_{n+1})$
with
![]() $\|u\|=1$
, choose
$\|u\|=1$
, choose
![]() $v_n\in \mathcal {A}_{f^{mn}y}^{-mn}F_j(x_n)$
such that
$v_n\in \mathcal {A}_{f^{mn}y}^{-mn}F_j(x_n)$
such that
Then, by Lemma 3.5,

However, since
![]() $u\in \mathcal {A}_{f^{m(n+1)}y}^{-m(n+1)}F_j(x_{n+1})\subset \mathcal {A}_{f^{mn}y}^{-mn}V_j(x_n,\theta _0)$
and
$u\in \mathcal {A}_{f^{m(n+1)}y}^{-m(n+1)}F_j(x_{n+1})\subset \mathcal {A}_{f^{mn}y}^{-mn}V_j(x_n,\theta _0)$
and
![]() $v_n\in \mathcal {A}_{f^{mn}y}^{-mn}F_j(x_n)\subset \mathcal {A}_{f^{mn}y}^{-mn}V_j(x_n,\theta _0)$
, Lemma 3.5 gives
$v_n\in \mathcal {A}_{f^{mn}y}^{-mn}F_j(x_n)\subset \mathcal {A}_{f^{mn}y}^{-mn}V_j(x_n,\theta _0)$
, Lemma 3.5 gives

where
![]() $\pi ^F$
is the projection associated with equation (4.10) onto
$\pi ^F$
is the projection associated with equation (4.10) onto
![]() $\mathcal {A}_{f^{mn}y}^{-mn}F_j(x_n)$
parallel to
$\mathcal {A}_{f^{mn}y}^{-mn}F_j(x_n)$
parallel to
![]() $H_j(x_{0})$
and the constant c is given by equation (4.9). Therefore, equations (4.11) and (4.12) show that for any
$H_j(x_{0})$
and the constant c is given by equation (4.9). Therefore, equations (4.11) and (4.12) show that for any
![]() $u\in \mathcal {A}_{f^{m(n+1)}y}^{-m(n+1)}F_j(x_{n+1})$
with
$u\in \mathcal {A}_{f^{m(n+1)}y}^{-m(n+1)}F_j(x_{n+1})$
with
![]() $\|u\|=1$
,
$\|u\|=1$
,
Similarly, for any
![]() $v\in \mathcal {A}_{f^{mn}y}^{-mn}F_j(x_{n})$
with
$v\in \mathcal {A}_{f^{mn}y}^{-mn}F_j(x_{n})$
with
![]() $\|v\|=1$
, we have
$\|v\|=1$
, we have
Thus,
which implies
![]() $\{\mathcal {A}_{f^{mn}y}^{-mn}F_j(x_{n})\}_{n\geq 1}$
is a Cauchy sequence in
$\{\mathcal {A}_{f^{mn}y}^{-mn}F_j(x_{n})\}_{n\geq 1}$
is a Cauchy sequence in
![]() $(\mathcal {G}(\mathfrak {X}),d_H)$
.
$(\mathcal {G}(\mathfrak {X}),d_H)$
.
Let
Since
![]() $\mathfrak {X}= \mathcal {A}_y^{mn}H_j(x_{0})\oplus F_j(x_{n})$
, by Lemma 4.2,
$\mathfrak {X}= \mathcal {A}_y^{mn}H_j(x_{0})\oplus F_j(x_{n})$
, by Lemma 4.2,
![]() $\mathfrak {X}= H_j(x_{0})\oplus \mathcal {A}_{f^{mn}y}^{-mn} F_j(x_{n})$
. Thus,
$\mathfrak {X}= H_j(x_{0})\oplus \mathcal {A}_{f^{mn}y}^{-mn} F_j(x_{n})$
. Thus,
where
![]() $D_j=d_1+\cdots +d_j$
. It follows from
$D_j=d_1+\cdots +d_j$
. It follows from
![]() $\mathcal {G}_{D_j}(\mathfrak {X})$
and
$\mathcal {G}_{D_j}(\mathfrak {X})$
and
![]() $\mathcal {G}^{D_j}(\mathfrak {X})$
being closed subsets of
$\mathcal {G}^{D_j}(\mathfrak {X})$
being closed subsets of
![]() $\mathcal {G}(\mathfrak {X})$
that
$\mathcal {G}(\mathfrak {X})$
that
![]() $H_j(y)\in \mathcal {G}_{D_j}(\mathfrak {X}),F_j(y)\in \mathcal {G}^{D_j}(\mathfrak {X})$
. Notice that
$H_j(y)\in \mathcal {G}_{D_j}(\mathfrak {X}),F_j(y)\in \mathcal {G}^{D_j}(\mathfrak {X})$
. Notice that
![]() $H_j(y)\subset U_j(x_0,\theta _0)$
and
$H_j(y)\subset U_j(x_0,\theta _0)$
and
![]() $ F_j(y)\subset \mathcal {A}_{f^{m}y}^{-m}V_j(x_1,\theta _0)\subset V_j(x_0,\theta _0)$
. We conclude
$ F_j(y)\subset \mathcal {A}_{f^{m}y}^{-m}V_j(x_1,\theta _0)\subset V_j(x_0,\theta _0)$
. We conclude
Additionally, by Lemma 3.5, we have
In general, for any
![]() $z\in \Lambda ,$
there exists
$z\in \Lambda ,$
there exists
![]() $0\leq k\leq m-1,y\in \Lambda ^*$
such that
$0\leq k\leq m-1,y\in \Lambda ^*$
such that
![]() $z=f^ky.$
Similar to the proof above, we can also get
$z=f^ky.$
Similar to the proof above, we can also get
satisfying
![]() $\mathfrak {X}= H_j(z)\oplus F_j(z), H_j(z)\in \mathcal {G}_{D_j}(\mathfrak {X}),F_j(z)\in \mathcal {G}^{D_j}(\mathfrak {X})$
, and
$\mathfrak {X}= H_j(z)\oplus F_j(z), H_j(z)\in \mathcal {G}_{D_j}(\mathfrak {X}),F_j(z)\in \mathcal {G}^{D_j}(\mathfrak {X})$
, and
Claim. The splitting
![]() $ \mathfrak {X}= H_j(z)\oplus F_j(z)$
is
$ \mathfrak {X}= H_j(z)\oplus F_j(z)$
is
![]() $\mathcal {A}$
-invariant on
$\mathcal {A}$
-invariant on
![]() $\Lambda $
.
$\Lambda $
.
Proof of the claim
Before proving the invariance of the splitting, we show that for any
![]() ${y\in \Lambda ^*,0\leq k\leq m-1}$
and any
${y\in \Lambda ^*,0\leq k\leq m-1}$
and any
![]() $H_{n,k}\in \mathcal {G}_{D_j}(\mathfrak {X})$
satisfying
$H_{n,k}\in \mathcal {G}_{D_j}(\mathfrak {X})$
satisfying
![]() $H_{n,k} \subset U_j(f^kx_{-n},\theta _0)$
, one has
$H_{n,k} \subset U_j(f^kx_{-n},\theta _0)$
, one has
Indeed, recall that
![]() $\mathfrak {X}=\mathcal {A}_{f^{-mn}(f^ky)}^{mn}H_{n,k}\oplus F_j(x_0)$
. Thus for any
$\mathfrak {X}=\mathcal {A}_{f^{-mn}(f^ky)}^{mn}H_{n,k}\oplus F_j(x_0)$
. Thus for any
![]() $u\in H_j(f^kx_{-n})$
, similar to the estimation above, we have
$u\in H_j(f^kx_{-n})$
, similar to the estimation above, we have

which implies
![]() $d_H(\mathcal {A}_{f^{-mn}(f^ky)}^{mn}H_j(x_{-n}),\mathcal {A}_{f^{-mn}(f^ky)}^{mn}{H_{n,k}})\to 0.$
Hence,
$d_H(\mathcal {A}_{f^{-mn}(f^ky)}^{mn}H_j(x_{-n}),\mathcal {A}_{f^{-mn}(f^ky)}^{mn}{H_{n,k}})\to 0.$
Hence,
Now for any
![]() $z \in \Lambda ,$
we may assume
$z \in \Lambda ,$
we may assume
![]() $z=f^k(y)$
for some
$z=f^k(y)$
for some
![]() $y\in \Lambda ^*$
and
$y\in \Lambda ^*$
and
![]() $0\leq k\leq m-1$
. If
$0\leq k\leq m-1$
. If
![]() $0\leq k\leq m-2$
, then by equation (3.9),
$0\leq k\leq m-2$
, then by equation (3.9),
![]() $A(f^{-mn}z)H_j(f^kx_{-n})\subset U_j(f^{k+1}x_{-n},\theta _0)$
; if
$A(f^{-mn}z)H_j(f^kx_{-n})\subset U_j(f^{k+1}x_{-n},\theta _0)$
; if
![]() $k=m-1$
, then by equation (3.17),
$k=m-1$
, then by equation (3.17),
![]() $A(f^{-mn}z)H_j(f^{m-1}x_{-n})\subset U_j(x_{-n+1},\theta _0)$
. Thus, equation (4.15) gives
$A(f^{-mn}z)H_j(f^{m-1}x_{-n})\subset U_j(x_{-n+1},\theta _0)$
. Thus, equation (4.15) gives
Therefore, for any
![]() $u\in H_j(z),$
$u\in H_j(z),$
 $$ \begin{align*} &\mathrm{dist}(A(z)u,\mathcal{A}_{f^{-mn}(fz)}^{mn}A(f^{-mn}z)H_j(f^kx_{-n}) )\\ &\quad\leq \|A(z)\|\cdot \mathrm{dist}(u,\mathcal{A}_{f^{-mn}(z)}^{mn}H_j(f^kx_{-n}) )\\ &\quad\leq \|A(z)\|\cdot d_H(H_j(z),\mathcal{A}_{f^{-mn}(z)}^{mn}H_j(f^kx_{-n}) )\to 0, \end{align*} $$
$$ \begin{align*} &\mathrm{dist}(A(z)u,\mathcal{A}_{f^{-mn}(fz)}^{mn}A(f^{-mn}z)H_j(f^kx_{-n}) )\\ &\quad\leq \|A(z)\|\cdot \mathrm{dist}(u,\mathcal{A}_{f^{-mn}(z)}^{mn}H_j(f^kx_{-n}) )\\ &\quad\leq \|A(z)\|\cdot d_H(H_j(z),\mathcal{A}_{f^{-mn}(z)}^{mn}H_j(f^kx_{-n}) )\to 0, \end{align*} $$
which implies
![]() $A(z)u\in H_j(fz)$
. Thus,
$A(z)u\in H_j(fz)$
. Thus,
![]() $A(z)H_j(z)\subset H_j(fz)$
. It can be proved analogously that
$A(z)H_j(z)\subset H_j(fz)$
. It can be proved analogously that
![]() $A(z)F_j(z)\subset F_j(fz)$
. Since
$A(z)F_j(z)\subset F_j(fz)$
. Since
![]() $\dim (A(z)H_j(z))= \dim (H_j(fz))$
, we have
$\dim (A(z)H_j(z))= \dim (H_j(fz))$
, we have
![]() $A(z)H_j(z)=H_j(fz)$
. Then by the remark in §2.1, the splitting
$A(z)H_j(z)=H_j(fz)$
. Then by the remark in §2.1, the splitting
![]() $ \mathfrak {X}= H_j(z)\oplus F_j(z)$
is
$ \mathfrak {X}= H_j(z)\oplus F_j(z)$
is
![]() $\mathcal {A}$
-invariant on
$\mathcal {A}$
-invariant on
![]() $\Lambda $
.
$\Lambda $
.
Claim. The splitting
![]() $ \mathfrak {X}= H_j(z)\oplus F_j(z)$
is continuous on
$ \mathfrak {X}= H_j(z)\oplus F_j(z)$
is continuous on
![]() $\Lambda $
.
$\Lambda $
.
Proof of the claim
Let
![]() $\pi ^{H_j}_z$
,
$\pi ^{H_j}_z$
,
![]() $\pi ^{F_j}_z$
be the projection operators associated with
$\pi ^{F_j}_z$
be the projection operators associated with
![]() $ \mathfrak {X}= H_j(z)\oplus F_j(z)$
. Then for any
$ \mathfrak {X}= H_j(z)\oplus F_j(z)$
. Then for any
![]() $\tilde {z}\in \Lambda ,u\in H_j(\tilde {z})$
, let
$\tilde {z}\in \Lambda ,u\in H_j(\tilde {z})$
, let
![]() $w=\mathcal {A}_{\tilde {z}}^{-mn}(u)\in H_j(f^{-mn}\tilde {z})$
, by the invariance of the splitting and equations (4.9), (4.13), and (4.14), we may estimate
$w=\mathcal {A}_{\tilde {z}}^{-mn}(u)\in H_j(f^{-mn}\tilde {z})$
, by the invariance of the splitting and equations (4.9), (4.13), and (4.14), we may estimate

Thus,

which gives
Similarly, for
![]() $v\in F_j(\tilde {z})$
,
$v\in F_j(\tilde {z})$
,

Therefore,
Now for any
![]() $\tau>0,$
take n large enough such that
$\tau>0,$
take n large enough such that
![]() $c\cdot e^{(\unicode{x3bb} _{j+1}-\unicode{x3bb} _j+8\varepsilon )mn}<\tau ,$
and then take
$c\cdot e^{(\unicode{x3bb} _{j+1}-\unicode{x3bb} _j+8\varepsilon )mn}<\tau ,$
and then take
![]() $\delta>0$
small enough such that for any
$\delta>0$
small enough such that for any
![]() $\tilde {z}\in B(z,\delta ),$
$\tilde {z}\in B(z,\delta ),$
Then we have
![]() $\|\pi ^{H_j}_z|_{F_j(\tilde {z})}\|\leq 2 \tau ,\|\pi ^{F_j}_z|_{H_j(\tilde {z})}\leq 2\tau .$
Thus by [Reference Blumenthal and Morris4, Remark 10],
$\|\pi ^{H_j}_z|_{F_j(\tilde {z})}\|\leq 2 \tau ,\|\pi ^{F_j}_z|_{H_j(\tilde {z})}\leq 2\tau .$
Thus by [Reference Blumenthal and Morris4, Remark 10],
 $$ \begin{align*}d_H(F_j(z),F_j(\tilde{z}))&\leq 4D_j\|\pi^{H_j}_z|_{F_j(\tilde{z})}\|\leq 8D_j\tau,\\ d_H(H_j(z),H_j(\tilde{z}))&\leq 4D_j\|\pi^{F_j}_z|_{H_j(\tilde{z})}\|\leq 8D_j\tau,\end{align*} $$
$$ \begin{align*}d_H(F_j(z),F_j(\tilde{z}))&\leq 4D_j\|\pi^{H_j}_z|_{F_j(\tilde{z})}\|\leq 8D_j\tau,\\ d_H(H_j(z),H_j(\tilde{z}))&\leq 4D_j\|\pi^{F_j}_z|_{H_j(\tilde{z})}\|\leq 8D_j\tau,\end{align*} $$
which gives the continuity of
![]() $F_j(z)$
and
$F_j(z)$
and
![]() $H_j(z)$
.
$H_j(z)$
.
At last, for any
![]() $z\in \Lambda ,1\leq j\leq i$
, let
$z\in \Lambda ,1\leq j\leq i$
, let
![]() $E_j(z):=H_j(z)\cap F_{j-1}(z)$
, where
$E_j(z):=H_j(z)\cap F_{j-1}(z)$
, where
![]() $F_0(z):={\mathfrak {X}}$
. Then,
$F_0(z):={\mathfrak {X}}$
. Then,
![]() $\dim (E_j)=d_j$
. Since
$\dim (E_j)=d_j$
. Since
and
![]() $\dim (A(z)E_j(z))=d_j=\dim (E_j(fz))$
, we have
$\dim (A(z)E_j(z))=d_j=\dim (E_j(fz))$
, we have
![]() $A(z)E_j(z)=E_j(fz).$
Therefore, we obtain a continuous
$A(z)E_j(z)=E_j(fz).$
Therefore, we obtain a continuous
![]() $\mathcal {A}$
-invariant splitting on
$\mathcal {A}$
-invariant splitting on
![]() $\Lambda $
:
$\Lambda $
:
with
![]() $\dim (E_j)=d_j \text { for all } 1\leq j\leq i$
. Additionally, by equations (4.13) and (4.14), we conclude
$\dim (E_j)=d_j \text { for all } 1\leq j\leq i$
. Additionally, by equations (4.13) and (4.14), we conclude
This completes the proof.
5 Proof of Theorem 2.4
We begin by estimating the growth rate of the volume function
![]() $\sigma _{k}(\mathcal {A}_x^n)$
, where
$\sigma _{k}(\mathcal {A}_x^n)$
, where
![]() $\sigma _{k}(\mathcal {A}_x^n)$
is the singular value of index k of
$\sigma _{k}(\mathcal {A}_x^n)$
is the singular value of index k of
![]() $\mathcal {A}_x^n$
which is given in §2.3.
$\mathcal {A}_x^n$
which is given in §2.3.
Lemma 5.1. Under the assumption of Theorem 2.1, for any
![]() $k\geq 1$
and
$k\geq 1$
and
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x\in M$
, one has
$x\in M$
, one has
where
![]() $\chi _{k}(\mathcal {A},\mu )=\unicode{x3bb} _i$
if
$\chi _{k}(\mathcal {A},\mu )=\unicode{x3bb} _i$
if
![]() $\dim (E_1\oplus \cdots \oplus E_{i-1})<k\leq \dim (E_1\oplus \cdots \oplus E_{i})$
, that is,
$\dim (E_1\oplus \cdots \oplus E_{i-1})<k\leq \dim (E_1\oplus \cdots \oplus E_{i})$
, that is,
![]() $\chi _{1}(\mathcal {A},\mu )\ge \chi _{2}(\mathcal {A},\mu )\ge \cdots $
are the Lyapunov exponents of
$\chi _{1}(\mathcal {A},\mu )\ge \chi _{2}(\mathcal {A},\mu )\ge \cdots $
are the Lyapunov exponents of
![]() $\mathcal {A}$
with respect to
$\mathcal {A}$
with respect to
![]() $\mu $
counted with multiplicities.
$\mu $
counted with multiplicities.
Proof. Suppose that
![]() $\dim (E_1\oplus \cdots \oplus E_{i-1})<k\leq \dim (E_1\oplus \cdots \oplus E_{i})$
. Denote
$\dim (E_1\oplus \cdots \oplus E_{i-1})<k\leq \dim (E_1\oplus \cdots \oplus E_{i})$
. Denote
![]() $\widetilde {E}_i(x)=E_1(x)\oplus \cdots \oplus E_{i}(x)$
and let
$\widetilde {E}_i(x)=E_1(x)\oplus \cdots \oplus E_{i}(x)$
and let
![]() $\mathfrak {X}=\widetilde {E}_i(x)\oplus F_i(x)$
be the Oseledets splitting given by Theorem 2.1. Let
$\mathfrak {X}=\widetilde {E}_i(x)\oplus F_i(x)$
be the Oseledets splitting given by Theorem 2.1. Let
![]() $\pi _E(x)$
be the projection associated with
$\pi _E(x)$
be the projection associated with
![]() $\mathfrak {X}=\widetilde {E}_i(x)\oplus F_i(x)$
onto
$\mathfrak {X}=\widetilde {E}_i(x)\oplus F_i(x)$
onto
![]() $\widetilde {E}_i(x)$
parallel to
$\widetilde {E}_i(x)$
parallel to
![]() $F_i(x)$
. To prove
$F_i(x)$
. To prove
![]() $\lim _{n\to \infty }(1/n)\log \sigma _{k}(\mathcal {A}_x^n)\le \chi _{k}(\mathcal {A},\mu )$
, for any subspace
$\lim _{n\to \infty }(1/n)\log \sigma _{k}(\mathcal {A}_x^n)\le \chi _{k}(\mathcal {A},\mu )$
, for any subspace
![]() $V\subset \mathfrak {X}$
with
$V\subset \mathfrak {X}$
with
![]() $\dim (V)=k,$
we divide the proof into two cases:
$\dim (V)=k,$
we divide the proof into two cases:
![]() $\dim (\pi _E(x)(V))=k$
and
$\dim (\pi _E(x)(V))=k$
and
![]() $\dim (\pi _E(x)(V))<k.$
$\dim (\pi _E(x)(V))<k.$
Case I:
![]() $\dim (\pi _E(x)(V))=k.$
Since
$\dim (\pi _E(x)(V))=k.$
Since
![]() $k>\dim (E_1\oplus \cdots \oplus E_{i-1})$
, there exists
$k>\dim (E_1\oplus \cdots \oplus E_{i-1})$
, there exists
![]() $v_0\in V$
with
$v_0\in V$
with
![]() $\|v_0\|=1$
such that
$\|v_0\|=1$
such that
![]() $v_E:=\pi _E(x)(v_0)\in E_{i}(x)$
. Let
$v_E:=\pi _E(x)(v_0)\in E_{i}(x)$
. Let
![]() $v_0=v_E+v_F$
. Then
$v_0=v_E+v_F$
. Then
 $$ \begin{align*} \inf\limits_{v\in V\setminus\{0\}}\frac{\|\mathcal{A}_x^n(v)\|}{\|v\|}\leq \|\mathcal{A}_x^n(v_0)\| &\leq \|\mathcal{A}_x^n(v_E)\|+\|\mathcal{A}_x^n(v_F)\|\\ & \leq \|\mathcal{A}_x^n|_{E_i(x)}\|\cdot \|\pi_E(x)(v_0)\|+\|\mathcal{A}_x^n|_{F_i(x)}\|\cdot \|\pi_F(x)(v_0)\|\\ &\leq \|\mathcal{A}_x^n|_{E_i(x)}\|\cdot \|\pi_E(x)\|+\|\mathcal{A}_x^n|_{F_i(x)}\|\cdot \|\pi_F(x)\|. \end{align*} $$
$$ \begin{align*} \inf\limits_{v\in V\setminus\{0\}}\frac{\|\mathcal{A}_x^n(v)\|}{\|v\|}\leq \|\mathcal{A}_x^n(v_0)\| &\leq \|\mathcal{A}_x^n(v_E)\|+\|\mathcal{A}_x^n(v_F)\|\\ & \leq \|\mathcal{A}_x^n|_{E_i(x)}\|\cdot \|\pi_E(x)(v_0)\|+\|\mathcal{A}_x^n|_{F_i(x)}\|\cdot \|\pi_F(x)(v_0)\|\\ &\leq \|\mathcal{A}_x^n|_{E_i(x)}\|\cdot \|\pi_E(x)\|+\|\mathcal{A}_x^n|_{F_i(x)}\|\cdot \|\pi_F(x)\|. \end{align*} $$
By Theorem 2.1, for any
![]() $\varepsilon>0$
, there exist
$\varepsilon>0$
, there exist
![]() $N\geq 1$
such that for any
$N\geq 1$
such that for any
![]() $n\geq N$
,
$n\geq N$
,
 $$ \begin{align*} & \|\mathcal{A}_x^n|_{E_i(x)}\|\cdot \|\pi_E(x)\|+\|\mathcal{A}_x^n|_{F_i(x)}\|\cdot \|\pi_F(x)\|\\ &\quad\leq e^{(\unicode{x3bb} _i+\varepsilon)n} \cdot \|\pi_E(x)\|+e^{(\unicode{x3bb} _{i+1}+\varepsilon)n}\cdot \|\pi_F(x)\| \\ &\quad=e^{(\unicode{x3bb} _i+\varepsilon)n} (\|\pi_E(x)\|+e^{(\unicode{x3bb} _{i+1}-\unicode{x3bb} _i)n}\cdot \|\pi_F(x)\|)\\ &\quad\leq e^{(\unicode{x3bb} _i+2\varepsilon)n}. \end{align*} $$
$$ \begin{align*} & \|\mathcal{A}_x^n|_{E_i(x)}\|\cdot \|\pi_E(x)\|+\|\mathcal{A}_x^n|_{F_i(x)}\|\cdot \|\pi_F(x)\|\\ &\quad\leq e^{(\unicode{x3bb} _i+\varepsilon)n} \cdot \|\pi_E(x)\|+e^{(\unicode{x3bb} _{i+1}+\varepsilon)n}\cdot \|\pi_F(x)\| \\ &\quad=e^{(\unicode{x3bb} _i+\varepsilon)n} (\|\pi_E(x)\|+e^{(\unicode{x3bb} _{i+1}-\unicode{x3bb} _i)n}\cdot \|\pi_F(x)\|)\\ &\quad\leq e^{(\unicode{x3bb} _i+2\varepsilon)n}. \end{align*} $$
Hence,
Case II:
![]() $\dim (\pi _E(x)(V))<k.$
Then there exists
$\dim (\pi _E(x)(V))<k.$
Then there exists
![]() $0\neq v_1\in F_i(x)\cap V.$
Thus,
$0\neq v_1\in F_i(x)\cap V.$
Thus,
Therefore, we conclude that
 $$ \begin{align*}\limsup\limits_{n\to\infty}\frac1n\log \sigma_{k}(\mathcal{A}_x^n)=\limsup\limits_{n\to\infty}\frac1n\log\bigg(\sup\limits_{\dim(V)=k}\inf\limits_{v\in V\setminus\{0\}}\frac{\|\mathcal{A}_x^n(v)\|}{\|v\|}\bigg)\le \unicode{x3bb} _i+2\varepsilon.\end{align*} $$
$$ \begin{align*}\limsup\limits_{n\to\infty}\frac1n\log \sigma_{k}(\mathcal{A}_x^n)=\limsup\limits_{n\to\infty}\frac1n\log\bigg(\sup\limits_{\dim(V)=k}\inf\limits_{v\in V\setminus\{0\}}\frac{\|\mathcal{A}_x^n(v)\|}{\|v\|}\bigg)\le \unicode{x3bb} _i+2\varepsilon.\end{align*} $$
Since
![]() $\varepsilon>0$
is arbitrary,
$\varepsilon>0$
is arbitrary,
However, choose
![]() $V_0\subset \widetilde {E}_i(x)$
with
$V_0\subset \widetilde {E}_i(x)$
with
![]() $\dim (V_0)=k$
. Then,
$\dim (V_0)=k$
. Then,
 $$ \begin{align*} \sigma_{k}(\mathcal{A}_x^n)=\sup\limits_{\dim(V)=k}\inf\limits_{v\in V\setminus\{0\}}\frac{\|\mathcal{A}_x^n(v)\|}{\|v\|}&\geq \inf\limits_{v\in V_0\setminus\{0\}}\frac{\|\mathcal{A}_x^n(v)\|}{\|v\|}\\ &\geq \inf\limits_{v\in \widetilde{E}_i(x)\setminus\{0\}}\frac{\|\mathcal{A}_x^n(v)\|}{\|v\|}. \end{align*} $$
$$ \begin{align*} \sigma_{k}(\mathcal{A}_x^n)=\sup\limits_{\dim(V)=k}\inf\limits_{v\in V\setminus\{0\}}\frac{\|\mathcal{A}_x^n(v)\|}{\|v\|}&\geq \inf\limits_{v\in V_0\setminus\{0\}}\frac{\|\mathcal{A}_x^n(v)\|}{\|v\|}\\ &\geq \inf\limits_{v\in \widetilde{E}_i(x)\setminus\{0\}}\frac{\|\mathcal{A}_x^n(v)\|}{\|v\|}. \end{align*} $$
Similar to the proof of Thieullen’s paper [Reference Thieullen28, pp. 68–69], for any
![]() $\varepsilon>0$
, there exists a measurable function
$\varepsilon>0$
, there exists a measurable function
![]() $C_\varepsilon (x)$
such that
$C_\varepsilon (x)$
such that
It follows that

Since
![]() $\varepsilon>0$
is arbitrary, we conclude
$\varepsilon>0$
is arbitrary, we conclude
This completes the proof.
We now prove Theorem 2.4.
Proof of Theorem 2.4
By [Reference Ban, Cao and Hu2, Proposition 2.1] and [Reference Zhang32, Lemma 2],
 $$ \begin{align*}P(A,s) =\lim_{n\to\infty} P\bigg(f, \frac1n \phi^s(A(\cdot,n))\bigg)= \inf_{ n \ge 1} P\bigg(f, \frac1n \phi^s(A(\cdot,n))\bigg),\end{align*} $$
$$ \begin{align*}P(A,s) =\lim_{n\to\infty} P\bigg(f, \frac1n \phi^s(A(\cdot,n))\bigg)= \inf_{ n \ge 1} P\bigg(f, \frac1n \phi^s(A(\cdot,n))\bigg),\end{align*} $$
where
![]() $\phi ^s(A(\cdot ,n))=\phi ^s(\cdot ,n)$
is given by equation (2.3). For every
$\phi ^s(A(\cdot ,n))=\phi ^s(\cdot ,n)$
is given by equation (2.3). For every
![]() $n \in \mathbb {N}$
, since the map
$n \in \mathbb {N}$
, since the map
is continuous at A, it gives that
![]() $A\mapsto P(A,s)$
is upper semi-continuous at A.
$A\mapsto P(A,s)$
is upper semi-continuous at A.
Therefore, it suffices to prove the lower semi-continuity. Since the entropy map
![]() $\mu \mapsto h_\mu (f)$
is upper semi-continuous, by the variational principle of sub-additive topological pressure (Theorem 2.3), there exists an ergodic measure
$\mu \mapsto h_\mu (f)$
is upper semi-continuous, by the variational principle of sub-additive topological pressure (Theorem 2.3), there exists an ergodic measure
![]() $\mu \in \mathcal E(M,f)$
such that
$\mu \in \mathcal E(M,f)$
such that
where
![]() $ \mathcal {F}_*(\Phi ,\mu )=\lim \nolimits _{n\to \infty }(1/n)\int \phi ^s(A(x,n)) d\mu $
. By equations (2.2), (2.3), and Lemma 5.1, one has
$ \mathcal {F}_*(\Phi ,\mu )=\lim \nolimits _{n\to \infty }(1/n)\int \phi ^s(A(x,n)) d\mu $
. By equations (2.2), (2.3), and Lemma 5.1, one has
For any
![]() $\varepsilon> 0$
and
$\varepsilon> 0$
and
![]() $i>s$
, by Theorem 2.2, one can construct a horseshoe
$i>s$
, by Theorem 2.2, one can construct a horseshoe
![]() $\Lambda _{\varepsilon }$
such that
$\Lambda _{\varepsilon }$
such that
-
(1)
 $h_{\mathrm {top}}(f|_{\Lambda _{\varepsilon }})> h_{\mu }(f) - \varepsilon $
;
$h_{\mathrm {top}}(f|_{\Lambda _{\varepsilon }})> h_{\mu }(f) - \varepsilon $
; -
(2) there is an
 $\mathcal {A}$
-invariant splitting over
$\mathcal {A}$
-invariant splitting over
 $\Lambda _\varepsilon $
,
$\Lambda _\varepsilon $
,  $$ \begin{align*}\mathfrak{X}=E_1(x)\oplus\cdots\oplus E_i(x)\oplus F_i(x);\end{align*} $$
$$ \begin{align*}\mathfrak{X}=E_1(x)\oplus\cdots\oplus E_i(x)\oplus F_i(x);\end{align*} $$
-
(3) for any
 $x \in \Lambda _\varepsilon , $
we have
$x \in \Lambda _\varepsilon , $
we have 
where
![]() $\unicode{x3bb} _1\ge \unicode{x3bb} _2\ge \cdots $
are the Lyapunov exponents of
$\unicode{x3bb} _1\ge \unicode{x3bb} _2\ge \cdots $
are the Lyapunov exponents of
![]() $\mathcal {A}$
with respect to
$\mathcal {A}$
with respect to
![]() $\mu .$
$\mu .$
Therefore, if
![]() $B: M \to L(\mathfrak {X})$
is close to A, then:
$B: M \to L(\mathfrak {X})$
is close to A, then:
-
(i) there is an
 $\mathcal {B}$
-invariant splitting over
$\mathcal {B}$
-invariant splitting over
 $\Lambda _\varepsilon $
,
$\Lambda _\varepsilon $
,  $$ \begin{align*}\mathfrak{X}=E_1^\prime(x)\oplus\cdots\oplus E_i^\prime(x)\oplus F_i^\prime(x);\end{align*} $$
$$ \begin{align*}\mathfrak{X}=E_1^\prime(x)\oplus\cdots\oplus E_i^\prime(x)\oplus F_i^\prime(x);\end{align*} $$
-
(ii) for any
 $x \in \Lambda _\varepsilon , $
we have
$x \in \Lambda _\varepsilon , $
we have 
Take an f-invariant ergodic measure
![]() $\nu $
on
$\nu $
on
![]() $\Lambda _\varepsilon $
such that
$\Lambda _\varepsilon $
such that
![]() $h_{\nu }(f) = h_{\mathrm {top}}(f|_{\Lambda _{\varepsilon }})$
. Then by the proof of Lemma 5.1, for
$h_{\nu }(f) = h_{\mathrm {top}}(f|_{\Lambda _{\varepsilon }})$
. Then by the proof of Lemma 5.1, for
![]() $\nu $
-a.e.
$\nu $
-a.e.
![]() $x\in M,$
$x\in M,$
Thus, we conclude that
 $$ \begin{align*} P(B,s) &\geq P_{\Lambda_\varepsilon}(B,s)\\ &\ge h_{\nu}(f)+\lim_{n\to\infty}\frac1n\int\phi^s(\mathcal{B}(x,n))\,d\nu\\ &\geq h_\mu(f)-\varepsilon +[\chi_1(A,\mu)+\cdots+ \chi_{[s]}(A,\mu)+(s-[s]) \chi_{[s]+1}(A,\mu)]-2s\varepsilon \\ &\ge P(A,s) - (2s+1) \varepsilon, \end{align*} $$
$$ \begin{align*} P(B,s) &\geq P_{\Lambda_\varepsilon}(B,s)\\ &\ge h_{\nu}(f)+\lim_{n\to\infty}\frac1n\int\phi^s(\mathcal{B}(x,n))\,d\nu\\ &\geq h_\mu(f)-\varepsilon +[\chi_1(A,\mu)+\cdots+ \chi_{[s]}(A,\mu)+(s-[s]) \chi_{[s]+1}(A,\mu)]-2s\varepsilon \\ &\ge P(A,s) - (2s+1) \varepsilon, \end{align*} $$
where
![]() $P_{\Lambda _\varepsilon }(B,s)$
denotes the topological pressure of f restricted on
$P_{\Lambda _\varepsilon }(B,s)$
denotes the topological pressure of f restricted on
![]() $\Lambda _\varepsilon $
. This yields the lower semi-continuity of the topological pressure.
$\Lambda _\varepsilon $
. This yields the lower semi-continuity of the topological pressure.
Acknowledgments
The authors would like to thank the referee for their careful reading and valuable comments which helped improve the paper substantially. Moreover, observed by the referee, the injectivity of the cocycle is not needed in this paper. Yongluo Cao is the corresponding author. Yongluo Cao is partially supported by National Key R&D Program of China (2022YFA1005802), NSFC (11790274). Rui Zou is partially supported by National Key R&D Program of China (2022YFA1007800), NSFC (11901305,12271386).