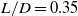Nomenclature
-
 $a$
$a$
-
number of nodes in the boundary layer normal to the wall
-
 $A$
$A$
-
Bernstein polynomial weighting coefficients
-
 ${A_{hi}}$
${A_{hi}}$
-
highlight area,
 ${{\rm{m}}^2}$
${{\rm{m}}^2}$
-
 $b$
$b$
-
average spacing on the fancowl surface in the axial direction
-
 $BP$
$BP$
-
Bernstein polynomial
-
 $c$
$c$
-
number of nodes in the circumferential direction
-
 ${\bf{c}}$
${\bf{c}}$
-
a column vector of the covariance of
 ${\bf{X}}$
${\bf{X}}$
-
 $C$
$C$
-
class function
-
 ${\bf{C}}$
${\bf{C}}$
-
covariance matrix
-
 $\widetilde{\boldsymbol{C}}$
$\widetilde{\boldsymbol{C}}$
-
covariance matrix of augmented dataset
-
 ${C_{D - {\rm{cruise}}}}$
${C_{D - {\rm{cruise}}}}$
-
ratio of the drag force at the fancowl to the force produced by the dynamic pressure multiplied by the area at highlight
-
 ${C_{fx}}$
${C_{fx}}$
-
skin-friction coefficient along the wing sections
-
 $d$
$d$
-
number of nodes in the radial direction
-
 ${\bf{d}}$
${\bf{d}}$
-
difference in trends between the low-fidelity and high-fidelity data
-
 $distance$
$distance$
-
distance criterion
-
 ${D_{{\rm{nac}}}}$
${D_{{\rm{nac}}}}$
-
drag force at the fancowl
-
 $e$
$e$
-
number of nodes from the nacelle to the farfield
-
 ${f_i}$
${f_i}$
-
location of the intake throat (fraction of intake length)
-
 ${f_{{\rm{max}}}}$
${f_{{\rm{max}}}}$
-
location of the maximum radius (fraction of nacelle length)
-
 $f_{sk}^i$
$f_{sk}^i$
-
normalised
 $k$
-th objective function at the
$k$
-th objective function at the
 $i$
-th sampling point
$i$
-th sampling point -
 ${G_i}$
${G_i}$
-
Pareto fitness at the
 $i$
-th sampling point
$i$
-th sampling point -
 $IP{R_{{\rm{takeoff}}}}$
$IP{R_{{\rm{takeoff}}}}$
-
ratio of the total pressure at the fanface to the total pressure of the freestream at takeoff condition
-
 $k$
$k$
-
number of design variables
-
 $K$
$K$
-
binomial coefficient
-
 ${l_{{\rm{nac}}}}$
${l_{{\rm{nac}}}}$
-
nacelle length, m
-
 ${M_\infty }$
${M_\infty }$
-
freestream Mach number
-
 $M{G_i}$
$M{G_i}$
-
modified Pareto fitness at the
 $i$
-th sampling point
$i$
-th sampling point -
 $MLE$
$MLE$
-
maximum likelihood estimation
-
 ${N_1},{N_2}$
${N_1},{N_2}$
-
class function leading-edge and trailing-edge parametres
-
 ${n_{{\rm{hi}}}}$
${n_{{\rm{hi}}}}$
-
number of high-fidelity samples
-
 ${n_{{\rm{lo}}}}$
${n_{{\rm{lo}}}}$
-
number of low-fidelity samples
-
 ${p_j}$
${p_j}$
-
correlation parametre
-
 ${P_{{\rm{st}}}}$
${P_{{\rm{st}}}}$
-
freestream static pressure, Pa
-
 ${P_{\rm{t}}}$
${P_{\rm{t}}}$
-
inlet total pressure, Pa
-
 ${P_0}$
${P_0}$
-
freestream total pressure, Pa
-
 ${\bar P_{0,{\textit{fanface}}}}$
${\bar P_{0,{\textit{fanface}}}}$
-
mean total pressure at the fanface, Pa
-
 $\rho $
$\rho $
-
scaling factor
-
 ${r_i}$
${r_i}$
-
intake throat radius, m
-
 ${r_{if}}$
${r_{if}}$
-
initial forebody radius of curvature, m
-
 ${r_{{\textit{fan}}}}$
${r_{{\textit{fan}}}}$
-
radius of fan, m
-
 ${r_{{\textit{hi}}}}$
${r_{{\textit{hi}}}}$
-
radius of highlight, m
-
 ${r_{{\textit{max}}}}$
${r_{{\textit{max}}}}$
-
maximum radius of the fancowl, m
-
 ${r_{{\textit{te}}}}$
${r_{{\textit{te}}}}$
-
radius of trailing-edge, m
-
 $S$
$S$
-
shape function
-
 ${T_{{\rm{st}}}}$
${T_{{\rm{st}}}}$
-
Freestream static temperature, K
-
 ${T_{\rm{t}}}$
${T_{\rm{t}}}$
-
inlet total temperature, K
-
 ${V_\infty }$
${V_\infty }$
-
freestream air speed, m/s
-
 $x_j^{\left( i \right)}$
$x_j^{\left( i \right)}$
-
 $j$
-th design variable of
$j$
-th design variable of
 $i$
-th sample
$i$
-th sample -
 ${\bf{x}}$
${\bf{x}}$
-
predicted sample location
-
 ${\bf{X}}$
${\bf{X}}$
-
samples locations
-
 ${{\bf{X}}_{{\rm{hi}}}}$
${{\bf{X}}_{{\rm{hi}}}}$
-
high-fidelity sample locations
-
 ${{\bf{X}}_{{\rm{lo}}}}$
${{\bf{X}}_{{\rm{lo}}}}$
-
low-fidelity sample locations
-
 $\widetilde{\boldsymbol{X}}$
$\widetilde{\boldsymbol{X}}$
-
argumented dataset by argumenting the observed data with the predicted data
-
 ${X_k}$
${X_k}$
-
sample set of the
 $k$
-th cluster
$k$
-th cluster -
 $\chi _{{\textit{infill}}}^{(\textit{k})}$
$\chi _{{\textit{infill}}}^{(\textit{k})}$
-
selected high-fidelity infill samples
-
 $y_1^ + $
$y_1^ + $
-
first cell y-plus
-
 $\hat{\textrm{y}}_{{\rm{hi}}}\!\left( {\bf{x}} \right)$
$\hat{\textrm{y}}_{{\rm{hi}}}\!\left( {\bf{x}} \right)$
-
maximum likelihood estimates for the predicted data
-
 $\tilde{\textbf{y}}$
$\tilde{\textbf{y}}$
-
values at
 $\widetilde{\textrm{X}}$
$\widetilde{\textrm{X}}$
-
 ${\bf{Y}}$
${\bf{Y}}$
-
values at sample locations
-
 ${{\bf{Y}}_{{\rm{lo}}}}\!\left( {{{\bf{X}}_{{\rm{lo}}}}} \right)$
${{\bf{Y}}_{{\rm{lo}}}}\!\left( {{{\bf{X}}_{{\rm{lo}}}}} \right)$
-
values at low-fidelity sample locations
-
 ${{\bf{Y}}_{{\rm{hi}}}}\!\left( {{{\bf{X}}_{{\rm{hi}}}}} \right)$
${{\bf{Y}}_{{\rm{hi}}}}\!\left( {{{\bf{X}}_{{\rm{hi}}}}} \right)$
-
values at high-fidelity sample locations
-
 ${{\rm{Z}}_{\rm{d}}}\!\left( . \right)$
${{\rm{Z}}_{\rm{d}}}\!\left( . \right)$
-
difference between
 ${{\rm{Z}}_{{\rm{lo}}}}\!\left( . \right)$
and
${{\rm{Z}}_{{\rm{lo}}}}\!\left( . \right)$
and
 ${{\rm{Z}}_{{\rm{hi}}}}\!\left( . \right)$
${{\rm{Z}}_{{\rm{hi}}}}\!\left( . \right)$
-
 ${{\rm{Z}}_{{\rm{hi}}}}\!\left( . \right)$
${{\rm{Z}}_{{\rm{hi}}}}\!\left( . \right)$
-
gaussian process of high-fiedlity simulations
-
 ${{\rm{Z}}_{{\rm{lo}}}}\!\left( . \right)$
${{\rm{Z}}_{{\rm{lo}}}}\!\left( . \right)$
-
gaussian process of low-fiedlity simulations
- CRM
-
common research model
- ACARE
-
Advisory Council for Aviation Research and Innovation in Europe
- NLF
-
natural laminar flow
- CFD
-
computational fluid dynamics
- LHS
-
Latin hypercube sampling
- CST
-
class/shape transformation
- iCST
-
intuitive class/shape transformation
- IGD
-
inverted generational distance
- HV
-
hypervolume
- IPR
-
intake pressure recovery
Greek Symbol
-
 ${\rho _\infty }$
${\rho _\infty }$
-
freestream air density,
 ${\rm{kg}}/{{\rm{m}}^3}$
${\rm{kg}}/{{\rm{m}}^3}$
-
 $\eta $
$\eta $
-
non-dimensional span station(0 = root, 1 = tip)
-
 $\zeta $
$\zeta $
-
non-dimensional aerofoil abscissa,
 $y/c$
$y/c$
-
 $\psi $
$\psi $
-
non-dimensional aerofoil ordinate,
 $x/c$
$x/c$
-
 ${\theta _j}$
${\theta _j}$
-
correlation coefficient of
 $j$
-th design variable
$j$
-th design variable -
 ${\theta _{{\rm{lo}}}}$
${\theta _{{\rm{lo}}}}$
-
correlation parametre
-
 ${\theta _{\rm{d}}}$
${\theta _{\rm{d}}}$
-
correlation parametre
-
 ${\hat {\boldsymbol\theta}_{\rm{d}}}$
${\hat {\boldsymbol\theta}_{\rm{d}}}$
-
maximum likelihood estimates for
 ${\theta _{\rm{d}}}$
${\theta _{\rm{d}}}$
-
 ${\sigma _{\rm{d}}}$
${\sigma _{\rm{d}}}$
-
standard deviation of
 ${{\rm{Z}}_{\rm{d}}}\!\left( . \right)$
${{\rm{Z}}_{\rm{d}}}\!\left( . \right)$
-
 ${\sigma _{{\rm{lo}}}}$
${\sigma _{{\rm{lo}}}}$
-
standard deviation of
 ${{\rm{Z}}_{{\rm{lo}}}}\!\left( . \right)$
${{\rm{Z}}_{{\rm{lo}}}}\!\left( . \right)$
-
 ${\hat \sigma _{\rm{d}}}$
${\hat \sigma _{\rm{d}}}$
-
maximum likelihood estimates for
 ${\sigma _{\rm{d}}}$
${\sigma _{\rm{d}}}$
-
 ${\hat \sigma _{{\rm{lo}}}}$
${\hat \sigma _{{\rm{lo}}}}$
-
maximum likelihood estimates for
 ${\sigma _{{\rm{lo}}}}$
${\sigma _{{\rm{lo}}}}$
-
 ${\psi _{\rm{d}}}$
${\psi _{\rm{d}}}$
-
correlation in
 ${{\rm{Z}}_{\rm{d}}}\!\left( . \right)$
${{\rm{Z}}_{\rm{d}}}\!\left( . \right)$
-
 ${\psi _{{\rm{lo}}}}$
${\psi _{{\rm{lo}}}}$
-
correlation in
 ${{\rm{Z}}_{{\rm{lo}}}}\!\left( . \right)$
${{\rm{Z}}_{{\rm{lo}}}}\!\left( . \right)$
-
 ${{\rm{\Psi }}_{\rm{d}}}$
${{\rm{\Psi }}_{\rm{d}}}$
-
matrix of correlations of the form
 ${\psi _{\rm{d}}}$
${\psi _{\rm{d}}}$
-
 ${{\rm{\Psi }}_{{\rm{lo}}}}$
${{\rm{\Psi }}_{{\rm{lo}}}}$
-
matrix of correlations of the form
 ${\psi _{{\rm{lo}}}}$
${\psi _{{\rm{lo}}}}$
-
 ${\rm{\Phi }}$
${\rm{\Phi }}$
-
circumferential angle
-
 ${\beta _{{\textit{nac}}}}$
${\beta _{{\textit{nac}}}}$
-
boat-tail angle
-
 $\hat \mu $
$\hat \mu $
-
maximum likelihood estimates for mean of
 ${\widetilde{\boldsymbol{y}}}$
${\widetilde{\boldsymbol{y}}}$
-
 ${\hat \mu _{\rm{d}}}$
${\hat \mu _{\rm{d}}}$
-
maximum likelihood estimates for the mean of
 ${\bf{d}}$
${\bf{d}}$
1.0 Introduction
Engine nacelle is a key component of an aircraft and typically consists of an inlet cowl, a fancowl, a thrust reverser, a core cowl and a primary exhaust nozzle. It plays an important role in the flight mission to provide smooth aerodynamic fairing for internal core components while ensuring a smooth airflow into the engine [Reference Raghunathan, Benard and Watterson1]. The aerodynamic shape optimisation of an engine nacelle is complicated. The configuration is non-axisymmetrically controlled using relatively large design variables. In addition, an entire flight mission includes different operating conditions, such as takeoff, crosswind and cruise. If all these conditions are to be addressed, multi-objective optimisation must be used, which inevitably increases the complexity of the optimisation process.
The design requirements for engine nacelles continue to change. The Advisory Council for Aviation Research and Innovation in Europe (ACARE) proposed the goal of flight path 2050 to reduce
![]() ${\rm{C}}{{\rm{O}}_2}$
and
${\rm{C}}{{\rm{O}}_2}$
and
![]() ${\rm{N}}{{\rm{O}}_{\rm{x}}}$
emissions by 75% and 90% per passenger kilometer, respectively, compared to a typical new aircraft in 2000 [Reference Krein and Williams2]. As for civil aero-engines, to achieve these goals, the bypass ratio is increasing [Reference Birch3] by lowering the fan-pressure ratio [Reference Guha4]. Consequently, the fan diameter must be increased to allow more mass flow through the fan to generate a similar level of thrust. As the nacelle size increases, so does the associated drag and weight [Reference Peters, Spakovszky, Lord and Rose5]. Therefore, advanced nacelle designs with shorter inlets and exhaust nozzles are required to ensure that the achieved performance benefits are not outweighed by the increased installation drag and propulsion-system weight [Reference Silva, Lundbladh, Petit and Xisto6–Reference Magrini, Buosi and Benini8].
${\rm{N}}{{\rm{O}}_{\rm{x}}}$
emissions by 75% and 90% per passenger kilometer, respectively, compared to a typical new aircraft in 2000 [Reference Krein and Williams2]. As for civil aero-engines, to achieve these goals, the bypass ratio is increasing [Reference Birch3] by lowering the fan-pressure ratio [Reference Guha4]. Consequently, the fan diameter must be increased to allow more mass flow through the fan to generate a similar level of thrust. As the nacelle size increases, so does the associated drag and weight [Reference Peters, Spakovszky, Lord and Rose5]. Therefore, advanced nacelle designs with shorter inlets and exhaust nozzles are required to ensure that the achieved performance benefits are not outweighed by the increased installation drag and propulsion-system weight [Reference Silva, Lundbladh, Petit and Xisto6–Reference Magrini, Buosi and Benini8].
Over the past 20 years, surrogate-based aerodynamic shape optimisation of engine nacelles has been conducted for various objectives. Song and Keane [Reference Song and Keane9] built a surrogate model using kriging to find better designs with higher pressure recovery and larger scarf angles for a three-dimensional (3D) subsonic civil engine nacelle. Fang et al. [Reference Fang, Zhang, Li and Chen10] developed a platform for optimising a 3D powered-on nacelle of a transonic civil aircraft to minimise drag and increase internal volume. Nacelle optimisation has been obtained through hybrid methods that combine the non-dominated sorting genetic algorithm-II (NSGA-II) and kriging models. Zhong and Li [Reference Zhong and Li11] developed a 3D shape design and optimisation method for natural laminar flow (NLF) nacelles to minimise frictional drag. The procedure starts with two-dimensional (2D) optimisation of the profile to narrow down the design space for 3D optimisation. This is followed by building a kriging surrogate model and adopting an adaptive simulated annealing algorithm to find the best design. Yao et al. [Reference Yao, Ma and Yang12] established an adaptive-surrogate-based robust optimisation strategy for NLF nacelles to increase the favourable pressure gradient region and volume ratio of the nacelle by increasing its lip radius and reducing its maximum diameter.
To better investigate the performance of the engine nacelle during the cruise condition, except for the cruise drag, typically the spillage drag (CD-spill) and the drag rise Mach number (MDR) are considered [Reference Robinson, MacManus, Heidebrecht and Grech13–Reference Tejero, Christie, MacManus and Sheaf18]. Robinson et al. [Reference Robinson, MacManus, Heidebrecht and Grech13] demonstrated a multi-objective optimisation method using an evolutionary genetic algorithm and applied it to aerodynamic shape optimisation in a 2D axisymmetric nacelle to study its performance under different conditions. Kriging was used as the RSM interpolation tool, and NSGA-II was adopted to explore the 3D Pareto surfaces. Tejero et al. [Reference Tejero, Christie, MacManus and Sheaf18] presented an adapted method whose main principle is that, as the genetic algorithm progresses through generations, the optimisation focuses on narrower parts of the design space where the optimal designs are likely to be located to improve the prediction accuracy. Surrogate models have been constructed using the kriging interpolation methods, and NSGA-II has been used to explore the Pareto surfaces. In addition to the three objectives mentioned above, Schreiner et al. [Reference Schreiner, Tejero, MacManus and Sheaf19] considered two off-design windmilling conditions to extend the approach to account for off-design conditions. These are the cruise engine-out conditions (CD-windmill) and diversion conditions (CD-diversion).
To date, few studies have focused on the optimisation of short nacelles. Cipriani [Reference Cipriani20] constructed an optimisation framework based on kriging as a surrogate model and investigated the effects of the geometrical parametres of the short-intake bottom line on the aerodynamic behaviour at the fanface under takeoff conditions. Sanchez Moreno et al. [Reference Sanchez Moreno, MacManus and Hueso Rebassa21] proposed a method for compact and aerodynamically robust nacelle optimisation using a single-fidelity surrogate modeling approach based on Euler computations, whereas kriging interpolation and artificial neural networks are used for low-order models.
As discussed above, surrogate models are built only on high-fidelity data. Recently, there has been a trend to blend low-fidelity data with high-fidelity data to further improve prediction accuracy [Reference Kampolis and Giannakoglou22]. Cokriging [Reference Kennedy and O’Hagan23] was proposed by Kennedy and O’Hagan by blending the information from high-fidelity data and low-fidelity data. This has been widely used in aerodynamic optimisation problems. Toal and Keane [Reference Toal and Keane24] showed that cokriging is as effective as that produced using a traditional multipoint process when optimising a transonic aerofoil but with a reduction in the total number of computational fluid dynamics (CFD) simulations. Priyanka et al. [Reference Priyanka, Sivapragasam and Narahari25] carried out aerodynamic shape optimisation of an aerofoil using cokriging and obtained 18.08% and 38.70% improvements for maximising
![]() ${C_l}$
and
${C_l}$
and
![]() $C_l^{3/2}/{C_d}$
, respectively, compared with the baseline NACA0012 aerofoil. Tejero et al. [Reference Tejero, MacManus and Hueso-Rebassa26] optimised an installed aero-engine short nacelle using cokriging and obtained a new configuration with an increment of 0.65% in the net vehicle force. However, there is no open literature on multi-objective optimisation of short nacelles based on a multi-fidelity surrogate model.
$C_l^{3/2}/{C_d}$
, respectively, compared with the baseline NACA0012 aerofoil. Tejero et al. [Reference Tejero, MacManus and Hueso-Rebassa26] optimised an installed aero-engine short nacelle using cokriging and obtained a new configuration with an increment of 0.65% in the net vehicle force. However, there is no open literature on multi-objective optimisation of short nacelles based on a multi-fidelity surrogate model.
In this study, a short nacelle with a length-to-diameter ratio
![]() $L/D = 0.35$
was selected as the design object. A cokriging model was adopted as the surrogate model. Takeoff and cruise conditions were considered in the optimisation process to determine the optimal design. The remainder of this paper is organised as follows. In Section 2.0, the individual modules within the optimisation framework are described in detail and the proposed optimisation framework is validated using two test functions. Section 3.0 presents the results and discussion of the aerodynamic shape optimisation of a non-axisymmetric nacelle. Finally, Section 4.0 presents the conclusions.
$L/D = 0.35$
was selected as the design object. A cokriging model was adopted as the surrogate model. Takeoff and cruise conditions were considered in the optimisation process to determine the optimal design. The remainder of this paper is organised as follows. In Section 2.0, the individual modules within the optimisation framework are described in detail and the proposed optimisation framework is validated using two test functions. Section 3.0 presents the results and discussion of the aerodynamic shape optimisation of a non-axisymmetric nacelle. Finally, Section 4.0 presents the conclusions.
2.0 Methodology
An integrated adaptive cokriging-based multi-objective optimisation framework was applied in this study, denoted as MO-ACK [Reference Shi, Long and Baoyin27]. A flowchart of the MO-ACK is shown in Fig. 1. The framework comprised several fundamental modules, including sampling methods, parametric geometry definition, automatic mesh generation, performance computation of nacelle designs, surrogate models, optimisation algorithms and infilling methods.

Figure 1. Flowchart of the MO-ACK optimisation framework.
The optimisation routine was initialised using nested Latin hypercube sampling (LHS) to create the initial samples. Such designs are useful for conducting multiple simulation experiments with varying levels of accuracy [Reference Qian28]. Subsequently, initial samples of different levels of accuracy were evaluated in parallel by means of CFD to obtain the data of interest, which was used as the input transferred to the surrogate model. Generally, there are more samples with low-level accuracy than those with high-level accuracy, because the calculation time of a single sample with low-level accuracy is shorter than that with high-level accuracy. Consequently, the computational time spent on high-level accuracy samples is at the same level. The cokriging model was then used as a surrogate model to predict objective values. It can effectively blend two sets of data to achieve a higher prediction accuracy. The NSGA-II [Reference Deb, Pratap, Agarwal and Meyarivan29] was driven by the trained surrogate model during the optimisation step to explore the Pareto front. After each optimisation step, the sample dataset was updated by infilling the new samples until the termination condition was achieved. The details of these modules are described below.
2.1 Geometry definition
Kulfan [Reference Kulfan and Bussoletti30, Reference Kulfan31] proposed a unique and powerful geometry representation method called class/shape transformation (CST). The analytical CST geometry representation methodology provides a unified and systematic approach to present a wide variety of 2D and 3D geometries, encompassing a significantly large design space with relatively few parametres. Zhu and Qin [Reference Zhu and Qin32] extended the CST method and proposed a new aerofoil parameterisation method called intuitive class/shape transformation (iCST), which combines the flexibility and accuracy of the CST method with the intuitiveness of the PARSEC method. Christie et al. [Reference Christie, Heidebrecht and MacManus33] developed a system that analytically calculates the transformation matrix for a set of geometric constraints based on the iCST method and successfully applied it to construct a 3D axisymmetric nacelle. The iCST method has been successfully applied to parameterise various aerodynamic shape optimisation problems [Reference Goulos, Stankowski and Otter34].
In this study, the iCST method was applied to parameterise the surface of the fan cowl and intake. This method consists of shape and class functions. The class function is used to define the general classes of geometry, whereas the shape function is used to define specific shapes within the geometry class. The general mathematical expression of CST is of the following form:
where
![]() $C_{{N_2}}^{{N_1}}$
is the class function,
$C_{{N_2}}^{{N_1}}$
is the class function,
![]() $S\!\left( \psi \right)$
is the shape function, and
$S\!\left( \psi \right)$
is the shape function, and
![]() $\psi {\rm{\Delta }}{\zeta _{TE}}$
controls the trailing-edge thickness. The mathematical expression of the class function is of the following form:
$\psi {\rm{\Delta }}{\zeta _{TE}}$
controls the trailing-edge thickness. The mathematical expression of the class function is of the following form:
where
![]() ${N_1}$
and
${N_1}$
and
![]() ${N_2}$
are tuned to obtain different shapes, as shown in Fig. 2. For a round-nose aerofoil, usually
${N_2}$
are tuned to obtain different shapes, as shown in Fig. 2. For a round-nose aerofoil, usually
![]() ${N_1} = 0.5$
and
${N_1} = 0.5$
and
![]() ${N_2} = 1.0$
.
${N_2} = 1.0$
.

Figure 2. Illustration of the effects of
![]() ${N_1}$
and
${N_1}$
and
![]() ${N_2}$
on the class function.
${N_2}$
on the class function.
The shape function was constructed using a Bernstein polynomial with different weight coefficients. The mathematical expression of the Bernstein polynomials is
In addition, the shape function used in this study can be expressed as
In this work, the open source common research model (CRM) was used and was modified based on the fan diameter to meet the short nacelle
![]() $L/D = 0.35$
requirement. The target geometry can be obtained using appropriate weight coefficients. For an axisymmetric nacelle geometry, the aero-lines of the fancowl and intake were first created using the iCST method and then revolved to construct the surface. The aero-lines of the fancowl and intake were defined by several variables, as shown in Fig. 3. To simplify the optimisation process and comply with the specific design requirements, six design variables (
$L/D = 0.35$
requirement. The target geometry can be obtained using appropriate weight coefficients. For an axisymmetric nacelle geometry, the aero-lines of the fancowl and intake were first created using the iCST method and then revolved to construct the surface. The aero-lines of the fancowl and intake were defined by several variables, as shown in Fig. 3. To simplify the optimisation process and comply with the specific design requirements, six design variables (
![]() ${r_{if}},{r_{{\rm{max}}}},{f_{{\rm{max}}}},{\beta _{{\rm{nac}}}},{r_i}$
, and
${r_{if}},{r_{{\rm{max}}}},{f_{{\rm{max}}}},{\beta _{{\rm{nac}}}},{r_i}$
, and
![]() ${f_i}$
) were chosen to parameterise a single aero-line, whereas the remaining parametres were set as constants during the optimisation process. As shown in Fig. 3,
${f_i}$
) were chosen to parameterise a single aero-line, whereas the remaining parametres were set as constants during the optimisation process. As shown in Fig. 3,
![]() ${r_{if}}$
denotes the initial forebody radius of curvature,
${r_{if}}$
denotes the initial forebody radius of curvature,
![]() ${r_{{\rm{max}}}}$
denotes the maximum radius of the fancowl,
${r_{{\rm{max}}}}$
denotes the maximum radius of the fancowl,
![]() ${f_{{\rm{max}}}}$
denotes the location of the maximum radius, expressed as a fraction,
${f_{{\rm{max}}}}$
denotes the location of the maximum radius, expressed as a fraction,
![]() ${\beta _{{\rm{nac}}}}$
represents the boat-tail angle,
${\beta _{{\rm{nac}}}}$
represents the boat-tail angle,
![]() ${r_i}$
denotes the intake throat radius, and
${r_i}$
denotes the intake throat radius, and
![]() ${f_i}$
denotes the location of the intake throat, which is expressed as a fraction. The size of the fan and the specific engine limit some of the parametres to being constant. Specifically, when designing an engine nacelle, the
${f_i}$
denotes the location of the intake throat, which is expressed as a fraction. The size of the fan and the specific engine limit some of the parametres to being constant. Specifically, when designing an engine nacelle, the
![]() ${r_{{\rm{fan}},}},{r_{{\rm{hi}}}},{r_{{\rm{te}},}}\;{l_{{\rm{nac}}}}$
and
${r_{{\rm{fan}},}},{r_{{\rm{hi}}}},{r_{{\rm{te}},}}\;{l_{{\rm{nac}}}}$
and
![]() ${l_{{\rm{int}}}}$
should match the size of the engine because the aerodynamic shape optimisation of the nacelle is usually performed after the design of the engine. The non-asymmetry of the nacelle was achieved based on three different aero-lines at
${l_{{\rm{int}}}}$
should match the size of the engine because the aerodynamic shape optimisation of the nacelle is usually performed after the design of the engine. The non-asymmetry of the nacelle was achieved based on three different aero-lines at
![]() ${\rm{\Phi }} = {0^ \circ },{\rm{\Phi }} = {90^ \circ }$
, and
${\rm{\Phi }} = {0^ \circ },{\rm{\Phi }} = {90^ \circ }$
, and
![]() ${\rm{\Phi }} = {180^ \circ }$
, as shown in Fig. 4, with
${\rm{\Phi }} = {180^ \circ }$
, as shown in Fig. 4, with
![]() ${\rm{\Phi }} = {0^ \circ }$
being the top aero-line of the nacelle. It is worth mentioning that the aero-lines at
${\rm{\Phi }} = {0^ \circ }$
being the top aero-line of the nacelle. It is worth mentioning that the aero-lines at
![]() ${\rm{\Phi }} = {90^ \circ }$
and
${\rm{\Phi }} = {90^ \circ }$
and
![]() ${\rm{\Phi }} = {270^ \circ }$
were the same, owing to the left-right symmetry.
${\rm{\Phi }} = {270^ \circ }$
were the same, owing to the left-right symmetry.

Figure 3. Design variables of aero-lines.

Figure 4. Schematic of the boundary conditions.
2.2 Computational method
In this study, the numerical simulations were performed using an in-house CFD solver. The finite-volume method was applied to discretise the governing equations. The implicit Gauss–Seidel method was employed for the time discretisation. Scalar dissipation coupled with the central difference was used to discretise the spatial derivative. The shear stress transport (SST) k-w turbulence model was adopted to close the Reynolds-averaged Navier–Stokes (RANS) equation. Ideal compressible air was assumed for all the simulations. The freestream condition was specified using a pressure farfield boundary condition by setting the static pressure
![]() ${P_{{\rm{st}}}}$
, static temperature
${P_{{\rm{st}}}}$
, static temperature
![]() ${T_{{\rm{st}}}}$
, and Mach number
${T_{{\rm{st}}}}$
, and Mach number
![]() ${M_\infty }$
. The takeoff and cruise flight conditions were considered in this study. The exit-pressure boundary condition was applied at the duct ends, extended by 1.8 fan radii downstream of the fan location. It’s understood that fan has a significant effect on the flow around with the inlet, especially under the high angle-of-attack. Usually, the presence of fan will improve the performance of nacelle inlet under the large angle. Hence, the current optimisation framework of short nacelle will provide a conservative design. In the future, a fan model will be implemented to improve the optimisation framework for short nacelle. The inlet conditions for the bypass ducts were determined by using
${M_\infty }$
. The takeoff and cruise flight conditions were considered in this study. The exit-pressure boundary condition was applied at the duct ends, extended by 1.8 fan radii downstream of the fan location. It’s understood that fan has a significant effect on the flow around with the inlet, especially under the high angle-of-attack. Usually, the presence of fan will improve the performance of nacelle inlet under the large angle. Hence, the current optimisation framework of short nacelle will provide a conservative design. In the future, a fan model will be implemented to improve the optimisation framework for short nacelle. The inlet conditions for the bypass ducts were determined by using
![]() ${P_{\rm{t}}}$
and
${P_{\rm{t}}}$
and
![]() ${T_{\rm{t}}}$
.
${T_{\rm{t}}}$
.
To verify the accuracy and validity of the in-house solver, two cases were used as test cases: one was the ONERA M6 wing [Reference Diskin, Anderson and Pandya35] and the other was the NACA-1-Series inlets [Reference Re and Abeyounis36]. A description of the ONERA-M6 case is presented in Table 1. The surface pressure coefficients calculated using the in-house solver are shown in Fig. 5 and were compared with the data calculated using the FUN3D solver [Reference Anderson and Bonhaus37–Reference Nielsen39] and the experimental data. Here,
![]() $\eta $
refers to the span station (0 = root; 1 = tip), and the x-location was non-dimensionalised by the local chord. The skin friction coefficient calculated using the in-house solver is shown in Fig. 6 for comparison with the data calculated using the FUN3D solver. Evidently, in both figures, the results calculated using the in-house solver show good agreement with the FUN3D results. Moreover, in Fig. 5, the in-house solver performs even better than the FUN3D solver when
$\eta $
refers to the span station (0 = root; 1 = tip), and the x-location was non-dimensionalised by the local chord. The skin friction coefficient calculated using the in-house solver is shown in Fig. 6 for comparison with the data calculated using the FUN3D solver. Evidently, in both figures, the results calculated using the in-house solver show good agreement with the FUN3D results. Moreover, in Fig. 5, the in-house solver performs even better than the FUN3D solver when
![]() $\eta = 0.44$
and
$\eta = 0.44$
and
![]() $\eta = 0.65$
, and the in-house pressure coefficient distribution is smoother when
$\eta = 0.65$
, and the in-house pressure coefficient distribution is smoother when
![]() $x/c = 0.56$
and
$x/c = 0.56$
and
![]() $x/c = 0.48$
than the FUN3D pressure coefficient distribution.
$x/c = 0.48$
than the FUN3D pressure coefficient distribution.
Table 1. ONERA M6 case description


Figure 5. Comparisons of surface-pressure coefficients along the wing sections.
An axisymmetric NACA 1-85-43.9, with a contraction ratio of 1.250, was adopted as the second test case. Examples of the computed wall-pressure coefficient
![]() ${C_p}$
distribution along the chord normalised abscissa
${C_p}$
distribution along the chord normalised abscissa
![]() $x/c$
are shown in Fig. 7 for four Mach numbers and mass flow capture ratios (MFCRs) [Reference Magrini and Benini40]. Evidently, in all four different boundary conditions, the results calculated using the in-house solver show good agreement with the experimental results. The above results show that the in-house solver is suitable for the subsequent optimisation procedures.
$x/c$
are shown in Fig. 7 for four Mach numbers and mass flow capture ratios (MFCRs) [Reference Magrini and Benini40]. Evidently, in all four different boundary conditions, the results calculated using the in-house solver show good agreement with the experimental results. The above results show that the in-house solver is suitable for the subsequent optimisation procedures.
To mesh the 3D non-axisymmetric nacelle, ANSYS ICEM was used to create a structured mesh for the computational domain. The first cell height was set to achieve
![]() $y_1^ + \approx 1$
with a stretching ratio of 1.2. The mesh details are shown in Fig. 8. As shown in Fig. 9, there are five main parametres for controlling grid variation. The first parametre
$y_1^ + \approx 1$
with a stretching ratio of 1.2. The mesh details are shown in Fig. 8. As shown in Fig. 9, there are five main parametres for controlling grid variation. The first parametre
![]() $a$
indicates the number of nodes in the boundary layer normal to the wall. The second parametre,
$a$
indicates the number of nodes in the boundary layer normal to the wall. The second parametre,
![]() $b$
, indicates the average spacing on the fancowl surface in the axial direction, which also influences the inner surface grid distribution owing to the structured block. The number of nodes in the circumferential and radial directions was determined using the third parametre
$b$
, indicates the average spacing on the fancowl surface in the axial direction, which also influences the inner surface grid distribution owing to the structured block. The number of nodes in the circumferential and radial directions was determined using the third parametre
![]() $c$
and fourth parametre
$c$
and fourth parametre
![]() $d$
, respectively. The number of nodes from the nacelle to the farfield was determined using the fifth parametre,
$d$
, respectively. The number of nodes from the nacelle to the farfield was determined using the fifth parametre,
![]() $e$
. The other parametres remained unchanged. Table 2 summarises these parametres. Tables 3 and 4 summarises the boundary conditions used in this study. A mesh-independence study was performed for three different mesh sizes (3.9 M, 8.67 M, and 15.8 M), as shown in Fig. 10. It can be observed that the drag coefficient at cruise condition and pressure recovery at takeoff condition reached the grid convergence at a mesh size of 8.67 M. Therefore, this mesh size was adopted for the following high-fidelity CFD simulation, whereas the mesh size of 3.9 M was adopted for the low-fidelity CFD simulation.
$e$
. The other parametres remained unchanged. Table 2 summarises these parametres. Tables 3 and 4 summarises the boundary conditions used in this study. A mesh-independence study was performed for three different mesh sizes (3.9 M, 8.67 M, and 15.8 M), as shown in Fig. 10. It can be observed that the drag coefficient at cruise condition and pressure recovery at takeoff condition reached the grid convergence at a mesh size of 8.67 M. Therefore, this mesh size was adopted for the following high-fidelity CFD simulation, whereas the mesh size of 3.9 M was adopted for the low-fidelity CFD simulation.

Figure 6. Comparisons of skin-friction coefficients along the wing sections with results from FUN3D.

Figure 7. Comparisons of wall-pressure coefficients on the inlet forebody exterior and lip over a range of mass-flow ratios.

Figure 8. Mesh details of the nacelle surface and symmetry plane.

Figure 9. Illustration of grid independence varying parametres.
2.3 Multi-fidelity analysis
In engineering optimisation problems, high-fidelity samples are often difficult to obtain, whereas low-fidelity samples are easier to obtain. With the help of low-fidelity samples, the prediction accuracy of the surrogate model was improved. To make good use of the low-fidelity samples, multi-fidelity analysis was performed, and a multi-fidelity surrogate model was constructed. In this study, cokriging was adopted as the metamodel in the optimisation process. The mathematical formula for cokriging is detailed below.
Table 2. Parametres in grid independence

Table 3. Cruise boundary conditions

Table 4. Takeoff boundary conditions


Figure 10. Grid-independence study results showing the cruse and takeoff condition.
The samples used in cokriging are expressed using Equation (5), which consists of low- and high-fidelity samples.
 \begin{align}{\bf{X}} = \left( {\begin{array}{l}{{{\bf{X}}_{{\rm{lo}}}}}\\[5pt] {{{\bf{X}}_{{\rm{hi}}}}}\end{array}} \right) = {\!\left( {{\bf{x}}_{{\rm{lo}}}^{\!\left( 1 \right)} \cdots {\bf{x}}_{{\rm{lo}}}^{\!\left( {{n_{{\rm{lo}}}}} \right)}{\bf{x}}_{{\rm{hi}}}^{\!\left( 1 \right)} \cdots {\bf{x}}_{{\rm{hi}}}^{\!\left( {{n_{{\rm{hi}}}}} \right)}} \right)^{\rm{T}}}\end{align}
\begin{align}{\bf{X}} = \left( {\begin{array}{l}{{{\bf{X}}_{{\rm{lo}}}}}\\[5pt] {{{\bf{X}}_{{\rm{hi}}}}}\end{array}} \right) = {\!\left( {{\bf{x}}_{{\rm{lo}}}^{\!\left( 1 \right)} \cdots {\bf{x}}_{{\rm{lo}}}^{\!\left( {{n_{{\rm{lo}}}}} \right)}{\bf{x}}_{{\rm{hi}}}^{\!\left( 1 \right)} \cdots {\bf{x}}_{{\rm{hi}}}^{\!\left( {{n_{{\rm{hi}}}}} \right)}} \right)^{\rm{T}}}\end{align}
where
![]() ${{\bf{X}}_{{\rm{lo}}}}$
denotes the low-fidelity sample locations,
${{\bf{X}}_{{\rm{lo}}}}$
denotes the low-fidelity sample locations,
![]() ${{\bf{X}}_{{\rm{hi}}}}$
denotes the high-fidelity sample locations, and the high-fidelity sample locations coincided with a subset of the low-fidelity sample locations
${{\bf{X}}_{{\rm{hi}}}}$
denotes the high-fidelity sample locations, and the high-fidelity sample locations coincided with a subset of the low-fidelity sample locations
![]() ${{\bf{X}}_{{\rm{hi}}}} \subset {{\bf{X}}_{{\rm{lo}}}}$
. In addition,
${{\bf{X}}_{{\rm{hi}}}} \subset {{\bf{X}}_{{\rm{lo}}}}$
. In addition,
![]() ${n_{{\rm{lo}}}}$
represents the number of low-fidelity samples and
${n_{{\rm{lo}}}}$
represents the number of low-fidelity samples and
![]() ${n_{{\rm{hi}}}}$
represents the number of high-fidelity samples. The value at
${n_{{\rm{hi}}}}$
represents the number of high-fidelity samples. The value at
![]() ${\bf{X}}$
was treated as if it were a realisation of a stochastic process.
${\bf{X}}$
was treated as if it were a realisation of a stochastic process.
 \begin{align}{\bf{Y}} = \left( {\begin{array}{l}{{{\bf{Y}}_{{\rm{lo}}}}\!\left( {{{\bf{X}}_{{\rm{lo}}}}} \right)}\\[5pt] {{{\bf{Y}}_{{\rm{hi}}}}\!\left( {{{\bf{X}}_{{\rm{hi}}}}} \right)}\end{array}} \right) = {\!\left( {{{\bf{Y}}_{{\rm{lo}}}}\!\left( {{\bf{X}}_{{\rm{lo}}}^{\!\left( 1 \right)}} \right) \cdots {{\bf{Y}}_{{\rm{lo}}}}\!\left( {{\bf{X}}_{{\rm{lo}}}^{\!\left( {{n_{{\rm{lo}}}}} \right)}} \right){{\bf{Y}}_{{\rm{hi}}}}\!\left( {{\bf{X}}_{{\rm{hi}}}^{\!\left( 1 \right)}} \right) \cdots {{\bf{Y}}_{{\rm{hi}}}}\!\left( {{\bf{X}}_{{\rm{hi}}}^{\!\left( {{n_{{\rm{hi}}}}} \right)}} \right)} \right)^{\rm{T}}}\end{align}
\begin{align}{\bf{Y}} = \left( {\begin{array}{l}{{{\bf{Y}}_{{\rm{lo}}}}\!\left( {{{\bf{X}}_{{\rm{lo}}}}} \right)}\\[5pt] {{{\bf{Y}}_{{\rm{hi}}}}\!\left( {{{\bf{X}}_{{\rm{hi}}}}} \right)}\end{array}} \right) = {\!\left( {{{\bf{Y}}_{{\rm{lo}}}}\!\left( {{\bf{X}}_{{\rm{lo}}}^{\!\left( 1 \right)}} \right) \cdots {{\bf{Y}}_{{\rm{lo}}}}\!\left( {{\bf{X}}_{{\rm{lo}}}^{\!\left( {{n_{{\rm{lo}}}}} \right)}} \right){{\bf{Y}}_{{\rm{hi}}}}\!\left( {{\bf{X}}_{{\rm{hi}}}^{\!\left( 1 \right)}} \right) \cdots {{\bf{Y}}_{{\rm{hi}}}}\!\left( {{\bf{X}}_{{\rm{hi}}}^{\!\left( {{n_{{\rm{hi}}}}} \right)}} \right)} \right)^{\rm{T}}}\end{align}
The local features of the low-fidelity and high-fidelity simulations were represented as the Gaussian process
![]() ${{\rm{Z}}_{{\rm{lo}}}}\!\left( . \right)$
. and
${{\rm{Z}}_{{\rm{lo}}}}\!\left( . \right)$
. and
![]() ${{\rm{Z}}_{{\rm{hi}}}}\!\left( . \right)$
. Based on the auto-regressive model, the high-fidelity simulation was approximated as a low-fidelity simulation multiplied by a scaling factor
${{\rm{Z}}_{{\rm{hi}}}}\!\left( . \right)$
. Based on the auto-regressive model, the high-fidelity simulation was approximated as a low-fidelity simulation multiplied by a scaling factor
![]() $\rho $
plus a Gaussian process
$\rho $
plus a Gaussian process
![]() ${{\rm{Z}}_{\rm{d}}}\!\left( . \right)$
, which represented the difference between
${{\rm{Z}}_{\rm{d}}}\!\left( . \right)$
, which represented the difference between
![]() $\rho {{\rm{Z}}_{{\rm{lo}}}}\!\left( . \right)$
and
$\rho {{\rm{Z}}_{{\rm{lo}}}}\!\left( . \right)$
and
![]() ${{\rm{Z}}_{{\rm{hi}}}}\!\left( . \right)$
. The approximation is expressed as
${{\rm{Z}}_{{\rm{hi}}}}\!\left( . \right)$
. The approximation is expressed as
The covariance matrix is constructed as
 \begin{align}{\bf{C}} = \left( {\begin{array}{c@{\quad}c}{\sigma _{{\rm{lo}}}^2{{\boldsymbol{\Psi }}_{{\rm{lo}}}}\!\left( {{{\bf{X}}_{{\rm{lo}}}},{{\bf{X}}_{{\rm{lo}}}}} \right)} & {\rho \sigma _{{\rm{lo}}}^2{{\boldsymbol{\Psi }}_{{\rm{lo}}}}\!\left( {{{\bf{X}}_{{\rm{lo}}}},{{\bf{X}}_{{\rm{hi}}}}} \right)}\\[5pt] {\rho \sigma _{{\rm{lo}}}^2{{\boldsymbol{\Psi }}_{{\rm{lo}}}}\!\left( {{{\bf{X}}_{\rm{h}}},{{\bf{X}}_{{\rm{lo}}}}} \right)} & {\rho \sigma _{{\rm{lo}}}^2{{\boldsymbol{\Psi }}_{{\rm{lo}}}}\!\left( {{{\bf{X}}_{{\rm{hi}}}},{{\bf{X}}_{{\rm{hi}}}}} \right) + \sigma _{\rm{d}}^2{{\boldsymbol{\Psi }}_{\rm{d}}}\!\left( {{{\bf{X}}_{{\rm{hi}}}},{{\bf{X}}_{{\rm{hi}}}}} \right)}\end{array}} \right)\end{align}
\begin{align}{\bf{C}} = \left( {\begin{array}{c@{\quad}c}{\sigma _{{\rm{lo}}}^2{{\boldsymbol{\Psi }}_{{\rm{lo}}}}\!\left( {{{\bf{X}}_{{\rm{lo}}}},{{\bf{X}}_{{\rm{lo}}}}} \right)} & {\rho \sigma _{{\rm{lo}}}^2{{\boldsymbol{\Psi }}_{{\rm{lo}}}}\!\left( {{{\bf{X}}_{{\rm{lo}}}},{{\bf{X}}_{{\rm{hi}}}}} \right)}\\[5pt] {\rho \sigma _{{\rm{lo}}}^2{{\boldsymbol{\Psi }}_{{\rm{lo}}}}\!\left( {{{\bf{X}}_{\rm{h}}},{{\bf{X}}_{{\rm{lo}}}}} \right)} & {\rho \sigma _{{\rm{lo}}}^2{{\boldsymbol{\Psi }}_{{\rm{lo}}}}\!\left( {{{\bf{X}}_{{\rm{hi}}}},{{\bf{X}}_{{\rm{hi}}}}} \right) + \sigma _{\rm{d}}^2{{\boldsymbol{\Psi }}_{\rm{d}}}\!\left( {{{\bf{X}}_{{\rm{hi}}}},{{\bf{X}}_{{\rm{hi}}}}} \right)}\end{array}} \right)\end{align}
where
![]() ${{\boldsymbol{\Psi }}_{{\rm{lo}}}}\!\left( {{{\bf{X}}_{{\rm{lo}}}},{{\bf{X}}_{{\rm{hi}}}}} \right)$
denotes a matrix of correlations of the form
${{\boldsymbol{\Psi }}_{{\rm{lo}}}}\!\left( {{{\bf{X}}_{{\rm{lo}}}},{{\bf{X}}_{{\rm{hi}}}}} \right)$
denotes a matrix of correlations of the form
![]() ${\psi _{{\rm{lo}}}}$
between data
${\psi _{{\rm{lo}}}}$
between data
![]() ${{\bf{X}}_{{\rm{lo}}}}$
and
${{\bf{X}}_{{\rm{lo}}}}$
and
![]() ${{\bf{X}}_{{\rm{hi}}}}$
. Similarly,
${{\bf{X}}_{{\rm{hi}}}}$
. Similarly,
![]() ${{\boldsymbol{\Psi }}_{{\rm{lo}}}}\!\left( {{{\bf{X}}_{{\rm{lo}}}},{{\bf{X}}_{{\rm{lo}}}}} \right)$
denotes a matrix of correlations of the form
${{\boldsymbol{\Psi }}_{{\rm{lo}}}}\!\left( {{{\bf{X}}_{{\rm{lo}}}},{{\bf{X}}_{{\rm{lo}}}}} \right)$
denotes a matrix of correlations of the form
![]() ${\psi _{{\rm{lo}}}}$
between data
${\psi _{{\rm{lo}}}}$
between data
![]() ${{\bf{X}}_{{\rm{lo}}}}$
and
${{\bf{X}}_{{\rm{lo}}}}$
and
![]() ${{\boldsymbol{\Psi }}_{{\rm{hi}}}}\!\left( {{{\bf{X}}_{{\rm{hi}}}},{{\bf{X}}_{{\rm{hi}}}}} \right)$
denotes a matrix of correlations of the form
${{\boldsymbol{\Psi }}_{{\rm{hi}}}}\!\left( {{{\bf{X}}_{{\rm{hi}}}},{{\bf{X}}_{{\rm{hi}}}}} \right)$
denotes a matrix of correlations of the form
![]() ${\psi _{{\rm{lo}}}}$
between data
${\psi _{{\rm{lo}}}}$
between data
![]() ${{\bf{X}}_{{\rm{hi}}}}$
. Furthermore,
${{\bf{X}}_{{\rm{hi}}}}$
. Furthermore,
![]() ${{\boldsymbol{\Psi }}_{\rm{d}}}\!\left( {{{\bf{X}}_{{\rm{hi}}}},{{\bf{X}}_{{\rm{hi}}}}} \right)$
denotes a matrix of correlations of the form
${{\boldsymbol{\Psi }}_{\rm{d}}}\!\left( {{{\bf{X}}_{{\rm{hi}}}},{{\bf{X}}_{{\rm{hi}}}}} \right)$
denotes a matrix of correlations of the form
![]() ${\psi _{\rm{d}}}$
between data
${\psi _{\rm{d}}}$
between data
![]() ${{\bf{X}}_{{\rm{hi}}}}$
. Here, the squared exponential kernel was selected to describe the correlation between random variables, where
${{\bf{X}}_{{\rm{hi}}}}$
. Here, the squared exponential kernel was selected to describe the correlation between random variables, where
![]() ${p_j}$
was fixed at
${p_j}$
was fixed at
![]() ${p_{\!\left( {1,2, \ldots ,k} \right)}} = 2$
. The specific expression is as follows:
${p_{\!\left( {1,2, \ldots ,k} \right)}} = 2$
. The specific expression is as follows:
 \begin{align}cor\!\left[ {Y\!\left( {{{\bf{x}}^{\!\left( i \right)}}} \right),Y\!\left( {{{\bf{x}}^{\!\left( l \right)}}} \right)} \right] = {\rm{exp}}\!\left( { - \mathop \sum \limits_{j = 1}^k {\theta _j}{{\left| {x_j^{\!\left( i \right)} - x_j^{\!\left( l \right)}} \right|}^{{p_j}}}} \right)\end{align}
\begin{align}cor\!\left[ {Y\!\left( {{{\bf{x}}^{\!\left( i \right)}}} \right),Y\!\left( {{{\bf{x}}^{\!\left( l \right)}}} \right)} \right] = {\rm{exp}}\!\left( { - \mathop \sum \limits_{j = 1}^k {\theta _j}{{\left| {x_j^{\!\left( i \right)} - x_j^{\!\left( l \right)}} \right|}^{{p_j}}}} \right)\end{align}
where
![]() $k$
is the number of design variables,
$k$
is the number of design variables,
![]() ${\theta _j}$
represents the correlation coefficient of
${\theta _j}$
represents the correlation coefficient of
![]() $j$
-th design variable, and
$j$
-th design variable, and
![]() $x_j^{\!\left( i \right)}$
is the
$x_j^{\!\left( i \right)}$
is the
![]() $j$
-th design variable of
$j$
-th design variable of
![]() $i$
-th sample.
$i$
-th sample.
The basis of cokriging is that our prediction of a new expensive sample is assumed to be consistent with the observed data and the maximum-likelihood-estimations for the model parametres. Therefore, we augmented the observed data with a predicted value and maximised the likelihood of this augmented data by varying our prediction while keeping the model parametres fixed. The augmented dataset is defined as follows:
 \begin{align}\tilde{\textbf{X}} = \left( {\begin{array}{c}{{{\bf{X}}_{{\rm{lo}}}}}\\[5pt] {{{\bf{X}}_{{\rm{hi}}}}}\\[5pt] {\bf{X}}\end{array}} \right) = {\!\left( {{\bf{x}}_{{\rm{lo}}}^{\!\left( 1 \right)} \cdots {\bf{x}}_{{\rm{lo}}}^{\!\left( {{n_{{\rm{lo}}}}} \right)}{\bf{x}}_{{\rm{hi}}}^{\!\left( 1 \right)} \cdots {\bf{x}}_{{\rm{hi}}}^{\!\left( {{n_{{\rm{hi}}}}} \right)}{\bf{x}}} \right)^{\rm{T}}}\end{align}
\begin{align}\tilde{\textbf{X}} = \left( {\begin{array}{c}{{{\bf{X}}_{{\rm{lo}}}}}\\[5pt] {{{\bf{X}}_{{\rm{hi}}}}}\\[5pt] {\bf{X}}\end{array}} \right) = {\!\left( {{\bf{x}}_{{\rm{lo}}}^{\!\left( 1 \right)} \cdots {\bf{x}}_{{\rm{lo}}}^{\!\left( {{n_{{\rm{lo}}}}} \right)}{\bf{x}}_{{\rm{hi}}}^{\!\left( 1 \right)} \cdots {\bf{x}}_{{\rm{hi}}}^{\!\left( {{n_{{\rm{hi}}}}} \right)}{\bf{x}}} \right)^{\rm{T}}}\end{align}
In addition, the values at locations with a predicted value are defined as
The new covariance matrix
![]() $\widetilde{\boldsymbol{C}}$
can be expressed as
$\widetilde{\boldsymbol{C}}$
can be expressed as
 \begin{align}\tilde{\boldsymbol{C}} = \left( {\begin{array}{c@{\quad}c@{\quad}c}{\hat \sigma _{{\rm{lo}}}^2{{\boldsymbol{\Psi }}_{{\rm{lo}}}}\!\left( {{{\bf{X}}_{{\rm{lo}}}},{{\bf{X}}_{{\rm{lo}}}}} \right)} & {\rho \hat \sigma _{{\rm{lo}}}^2{{\boldsymbol{\Psi }}_{{\rm{lo}}}}\!\left( {{{\bf{X}}_{{\rm{lo}}}},{{\bf{X}}_{{\rm{hi}}}}} \right)} & {\rho \hat \sigma _{{\rm{lo}}}^2{{\boldsymbol{\Psi }}_{{\rm{lo}}}}\!\left( {{{\bf{X}}_{{\rm{lo}}}},{\bf{x}}} \right)}\\[5pt] {\rho \hat \sigma _{{\rm{lo}}}^2{{\boldsymbol{\Psi }}_{{\rm{lo}}}}\!\left( {{{\bf{X}}_{{\rm{hh}}}},{{\bf{X}}_{{\rm{lo}}}}} \right)} & {\rho _{{\rm{lo}}}^2\hat \sigma _{{\rm{lo}}}^2{{\boldsymbol{\Psi }}_{{\rm{lo}}}}\!\left( {{{\bf{X}}_{{\rm{hi}}}},{{\bf{X}}_{{\rm{hi}}}}} \right) + \hat \sigma _{\rm{d}}^2{{\boldsymbol{\Psi }}_{\rm{d}}}\!\left( {{{\bf{X}}_{{\rm{hi}}}},{{\bf{X}}_{{\rm{hi}}}}} \right)} & {\!\left( {{\rho ^2}\hat \sigma _{{\rm{lo}}}^2 + \hat \sigma _{\rm{d}}^2} \right){{\boldsymbol{\Psi }}_{\rm{d}}}\!\left( {{{\bf{X}}_{{\rm{hi}}}},{\bf{x}}} \right)}\\[5pt] {\rho \hat \sigma _{{\rm{lo}}}^2{{\boldsymbol{\Psi }}_{{\rm{lo}}}}{{\left( {{{\bf{X}}_{{\rm{lo}}}},{\bf{x}}} \right)}^{\rm{T}}}} & {\!\left( {{\rho ^2}\hat \sigma _{{\rm{lo}}}^2 + \hat \sigma _{\rm{d}}^2} \right){{\boldsymbol{\Psi }}_{\rm{d}}}{{\left( {{{\bf{X}}_{{\rm{hi}}}},{\bf{x}}} \right)}^{\rm{T}}}} & {{\rho ^2}\hat \sigma _{{\rm{lo}}}^2 + \hat \sigma _{\rm{d}}^2}\end{array}} \right)\end{align}
\begin{align}\tilde{\boldsymbol{C}} = \left( {\begin{array}{c@{\quad}c@{\quad}c}{\hat \sigma _{{\rm{lo}}}^2{{\boldsymbol{\Psi }}_{{\rm{lo}}}}\!\left( {{{\bf{X}}_{{\rm{lo}}}},{{\bf{X}}_{{\rm{lo}}}}} \right)} & {\rho \hat \sigma _{{\rm{lo}}}^2{{\boldsymbol{\Psi }}_{{\rm{lo}}}}\!\left( {{{\bf{X}}_{{\rm{lo}}}},{{\bf{X}}_{{\rm{hi}}}}} \right)} & {\rho \hat \sigma _{{\rm{lo}}}^2{{\boldsymbol{\Psi }}_{{\rm{lo}}}}\!\left( {{{\bf{X}}_{{\rm{lo}}}},{\bf{x}}} \right)}\\[5pt] {\rho \hat \sigma _{{\rm{lo}}}^2{{\boldsymbol{\Psi }}_{{\rm{lo}}}}\!\left( {{{\bf{X}}_{{\rm{hh}}}},{{\bf{X}}_{{\rm{lo}}}}} \right)} & {\rho _{{\rm{lo}}}^2\hat \sigma _{{\rm{lo}}}^2{{\boldsymbol{\Psi }}_{{\rm{lo}}}}\!\left( {{{\bf{X}}_{{\rm{hi}}}},{{\bf{X}}_{{\rm{hi}}}}} \right) + \hat \sigma _{\rm{d}}^2{{\boldsymbol{\Psi }}_{\rm{d}}}\!\left( {{{\bf{X}}_{{\rm{hi}}}},{{\bf{X}}_{{\rm{hi}}}}} \right)} & {\!\left( {{\rho ^2}\hat \sigma _{{\rm{lo}}}^2 + \hat \sigma _{\rm{d}}^2} \right){{\boldsymbol{\Psi }}_{\rm{d}}}\!\left( {{{\bf{X}}_{{\rm{hi}}}},{\bf{x}}} \right)}\\[5pt] {\rho \hat \sigma _{{\rm{lo}}}^2{{\boldsymbol{\Psi }}_{{\rm{lo}}}}{{\left( {{{\bf{X}}_{{\rm{lo}}}},{\bf{x}}} \right)}^{\rm{T}}}} & {\!\left( {{\rho ^2}\hat \sigma _{{\rm{lo}}}^2 + \hat \sigma _{\rm{d}}^2} \right){{\boldsymbol{\Psi }}_{\rm{d}}}{{\left( {{{\bf{X}}_{{\rm{hi}}}},{\bf{x}}} \right)}^{\rm{T}}}} & {{\rho ^2}\hat \sigma _{{\rm{lo}}}^2 + \hat \sigma _{\rm{d}}^2}\end{array}} \right)\end{align}
Based on the Gaussian process theory, we obtain
where
 \begin{align}{\bf{c}} = \left( {\begin{array}{c}{\rho \hat \sigma _{{\rm{lo}}}^2{{\boldsymbol{\Psi }}_{{\rm{lo}}}}\!\left( {{{\bf{X}}_{{\rm{lo}}}},{\bf{x}}} \right)}\\[5pt] {\!\left( {{\rho ^2}\hat \sigma _{{\rm{lo}}}^2 + \hat \sigma _{\rm{d}}^2} \right){{\boldsymbol{\Psi }}_{\rm{d}}}\!\left( {{{\bf{X}}_{{\rm{hi}}}},{\bf{x}}} \right)}\end{array}} \right)\end{align}
\begin{align}{\bf{c}} = \left( {\begin{array}{c}{\rho \hat \sigma _{{\rm{lo}}}^2{{\boldsymbol{\Psi }}_{{\rm{lo}}}}\!\left( {{{\bf{X}}_{{\rm{lo}}}},{\bf{x}}} \right)}\\[5pt] {\!\left( {{\rho ^2}\hat \sigma _{{\rm{lo}}}^2 + \hat \sigma _{\rm{d}}^2} \right){{\boldsymbol{\Psi }}_{\rm{d}}}\!\left( {{{\bf{X}}_{{\rm{hi}}}},{\bf{x}}} \right)}\end{array}} \right)\end{align}
Here
![]() $\textbf{1}$
is an
$\textbf{1}$
is an
![]() $n \times 1$
column vectors of ones. To obtain
$n \times 1$
column vectors of ones. To obtain
![]() ${\mu _{{\rm{lo}}}}$
,
${\mu _{{\rm{lo}}}}$
,
![]() $\hat \sigma _{{\rm{lo}}}^2$
, and
$\hat \sigma _{{\rm{lo}}}^2$
, and
![]() ${\theta _{{\rm{lo}}}}$
for the low-fidelity Gaussian process
${\theta _{{\rm{lo}}}}$
for the low-fidelity Gaussian process
![]() ${{\rm{Z}}_{{\rm{lo}}}}\!\left( {\bf{x}} \right)$
, we can maximise the ln-likelihood as
${{\rm{Z}}_{{\rm{lo}}}}\!\left( {\bf{x}} \right)$
, we can maximise the ln-likelihood as
The MLEs of
and
![]() ${\widehat{\boldsymbol\theta}_{{\rm{lo}}}}$
could be obtained by maximising the following equation after substituting Equations (17) and (18) in Equation (16):
${\widehat{\boldsymbol\theta}_{{\rm{lo}}}}$
could be obtained by maximising the following equation after substituting Equations (17) and (18) in Equation (16):
To estimate
![]() ${\mu _{\rm{d}}},\sigma _{\rm{d}}^2,{\boldsymbol\theta _{\rm{d}}}$
, and
${\mu _{\rm{d}}},\sigma _{\rm{d}}^2,{\boldsymbol\theta _{\rm{d}}}$
, and
![]() $\rho $
, we defined the following:
$\rho $
, we defined the following:
Similarly,
![]() ${\mu _{\rm{d}}}$
and
${\mu _{\rm{d}}}$
and
![]() $\sigma _{\rm{d}}^2$
were obtained by maximising the ln-likelihood of the expensive sample as
$\sigma _{\rm{d}}^2$
were obtained by maximising the ln-likelihood of the expensive sample as
Equation (21) yields the MLEs of the following as:
Furthermore,
![]() ${\widehat{\boldsymbol\theta}_{\rm{d}}}$
could be obtained by maximising the following equation after substituting Equations (22) and (23) in Equation (21)
${\widehat{\boldsymbol\theta}_{\rm{d}}}$
could be obtained by maximising the following equation after substituting Equations (22) and (23) in Equation (21)
With the above derivation, it is possible to use cokriging to make effective predictions. For more details about derivation and implementation, resources could be found in Refs [Reference Sobester, Forrester and Keane41, Reference Bouhlel, Hwang and Bartoli42].
2.4 Infill strategy
To improve the prediction accuracy of the surrogate models, the low- and high-fidelity samples must be updated after each iteration until the termination condition is achieved. Infilling low- and high-fidelity samples were generated from the current Pareto front to refine the surrogate models. Specifically, to update the high-fidelity samples, the current
![]() ${X_{{\rm{Parete}}}}$
was first clustered using the K-means clustering method. The Pareto fitness function (MG) was then calculated for each point in
${X_{{\rm{Parete}}}}$
was first clustered using the K-means clustering method. The Pareto fitness function (MG) was then calculated for each point in
![]() ${X_{{\rm{Parete}}}}$
[Reference Shi, Long and Baoyin27, Reference Kitayama, Srirat, Arakawa and Yamazaki43]:
${X_{{\rm{Parete}}}}$
[Reference Shi, Long and Baoyin27, Reference Kitayama, Srirat, Arakawa and Yamazaki43]:
where
![]() ${G_i}$
denotes the Pareto fitness at the
${G_i}$
denotes the Pareto fitness at the
![]() $i$
-th sampling point, and
$i$
-th sampling point, and
![]() $f_{sk}^i$
is the normalised
$f_{sk}^i$
is the normalised
![]() $k$
-th objective function at the
$k$
-th objective function at the
![]() $i$
-th sampling point, given by
$i$
-th sampling point, given by
where
![]() ${f_{k,i}}$
is the
${f_{k,i}}$
is the
![]() $k$
-th objective function at the
$k$
-th objective function at the
![]() $i$
-th sampling point, and
$i$
-th sampling point, and
![]() ${f_{k,{\rm{max}}}}$
and
${f_{k,{\rm{max}}}}$
and
![]() ${f_{k,{\rm{min}}}}$
denote the maximum and minimum values of the
${f_{k,{\rm{min}}}}$
denote the maximum and minimum values of the
![]() $k$
-th objective function among all sampling points, respectively. When the Pareto fitness
$k$
-th objective function among all sampling points, respectively. When the Pareto fitness
![]() ${G_i}$
is greater than one, the sampling point is a Pareto-optimal solution. A modified Pareto fitness function was calculated to construct a function that generates local minima around a set of Pareto-optimal solutions.
${G_i}$
is greater than one, the sampling point is a Pareto-optimal solution. A modified Pareto fitness function was calculated to construct a function that generates local minima around a set of Pareto-optimal solutions.
 \begin{align}M{G_i} = \left\{ {\begin{array}{c@{\quad}c}{\!\left( {1 - {G_i}} \right) + 2 \times {G_{{\rm{max}}}}} & {{G_i} \lt 1}\\[5pt] {{G_i}} & {{G_i} \geq 1}\end{array}\;\;\; i = 1,2, \cdots ,m} \right.\end{align}
\begin{align}M{G_i} = \left\{ {\begin{array}{c@{\quad}c}{\!\left( {1 - {G_i}} \right) + 2 \times {G_{{\rm{max}}}}} & {{G_i} \lt 1}\\[5pt] {{G_i}} & {{G_i} \geq 1}\end{array}\;\;\; i = 1,2, \cdots ,m} \right.\end{align}
A lower MG value indicates that the sample is closer to the Pareto front, and the sample point with the minimum MG value in each cluster was selected as the high-fidelity infill sample point, as follows:
where
![]() ${X_k}$
is the sample set of the
${X_k}$
is the sample set of the
![]() $k$
-th cluster and
$k$
-th cluster and
![]() $\chi _{{\rm{infill}}}^{\!\left( k \right)}$
are the selected high-fidelity infill samples. Specifically, all Pareto fronts were selected to update the low-fidelity samples.
$\chi _{{\rm{infill}}}^{\!\left( k \right)}$
are the selected high-fidelity infill samples. Specifically, all Pareto fronts were selected to update the low-fidelity samples.
With the high-fidelity and low-fidelity infill strategies described above, both exploration and exploitation could be performed.
2.5 Genetic algorithm
The NSGA-II, originally proposed by Deb, was adopted in this study because of its proven capabilities for global optimisation in flow aerodynamic applications. NSGA-II generates offspring using specific types of crossover and mutation and then selects the next generation according to a non-dominated sorting and crowding distance comparison. The initial seed was set at 36, with 36 individuals in the following generation and a total of 5,000 generations. The mutation probability was set at 0.1 and the crossover rate was set at 0.9. The selection operator was set as a tournament, the mutation operator was set as a polynomial mutation, and the crossover operator was set as the simulated binary crossover.
2.6 Validation and verification
Two test functions were used to validate the effectiveness of the MO-ACK framework. To demonstrate the role of multi-fidelity, a multi-objective optimisation framework based on kriging (MO-AK) was also tested. Comprehensive evaluation indicators were introduced to evaluate the performance of the multi-objective optimisation process, such as the hypervolume (HV) indicator [Reference Zitzler and Thiele44] and inverted generational distance (IGD) indicator [Reference Czyz and Jaszkiewicz45]. In this study, the HV indicator was calculated through optimisation iterations to measure the convergence and diversity of the Pareto front solutions. A higher value of HV indicates better capability for exploring the Pareto front. As shown in Fig. 11, the two main factors in the HV indicator are the reference point and the non-dominated solution. When non-dominated solutions are obtained, a reference point must be validated. A schematic of a 2D HV indicator is shown in Fig. 11. The HV indicator used in higher dimensional problems follows this analogy.
2.6.1 FON test function optimisation
The definition of the FON two-objective test function, composed of high-fidelity and low-fidelity functions, is as follows [Reference Huband, Hingston, Barone and While46]:
 \begin{align}\eqalign{ {\rm{Minimise}}:\;\;{f_1}\!\left( {{x_1},{x_2}, \cdots ,{x_5}} \right) = 1 - {\rm{exp}}\!\left( { - \mathop \sum \limits_{i = 1}^5 {{\!\left( {{x_i} - {1 \over {\sqrt 5 }}} \right)}^2}} \right) \cr {\rm{Minimise}}:\;\;{f_2}\!\left( {{x_1},{x_2}, \cdots ,{x_5}} \right) = 1 - {\rm{exp}}\!\left( { - \mathop \sum \limits_{i = 1}^5 {{\!\left( {{x_i} + {1 \over {\sqrt 5 }}} \right)}^2}} \right) \cr {\rm{Minimise}}:\;\;{f_{11}}\!\left( {{x_1},{x_2}, \cdots ,{x_5}} \right) = 1 - {\rm{exp}}\!\left( { - \mathop \sum \limits_{i = 1}^5 {{\!\left( {0.5{x_i} - 0.1 - {1 \over {\sqrt 5 }}} \right)}^2}} \right) \cr {\rm{Minimise}}:\;\;{f_{12}}\!\left( {{x_1},{x_2}, \cdots ,{x_5}} \right) = 1 - {\rm{exp}}\!\left( { - \mathop \sum \limits_{i = 1}^5 {{\!\left( {0.6{x_i} + 0.1 + {1 \over {\sqrt 5 }}} \right)}^2}} \right) \cr} \end{align}
\begin{align}\eqalign{ {\rm{Minimise}}:\;\;{f_1}\!\left( {{x_1},{x_2}, \cdots ,{x_5}} \right) = 1 - {\rm{exp}}\!\left( { - \mathop \sum \limits_{i = 1}^5 {{\!\left( {{x_i} - {1 \over {\sqrt 5 }}} \right)}^2}} \right) \cr {\rm{Minimise}}:\;\;{f_2}\!\left( {{x_1},{x_2}, \cdots ,{x_5}} \right) = 1 - {\rm{exp}}\!\left( { - \mathop \sum \limits_{i = 1}^5 {{\!\left( {{x_i} + {1 \over {\sqrt 5 }}} \right)}^2}} \right) \cr {\rm{Minimise}}:\;\;{f_{11}}\!\left( {{x_1},{x_2}, \cdots ,{x_5}} \right) = 1 - {\rm{exp}}\!\left( { - \mathop \sum \limits_{i = 1}^5 {{\!\left( {0.5{x_i} - 0.1 - {1 \over {\sqrt 5 }}} \right)}^2}} \right) \cr {\rm{Minimise}}:\;\;{f_{12}}\!\left( {{x_1},{x_2}, \cdots ,{x_5}} \right) = 1 - {\rm{exp}}\!\left( { - \mathop \sum \limits_{i = 1}^5 {{\!\left( {0.6{x_i} + 0.1 + {1 \over {\sqrt 5 }}} \right)}^2}} \right) \cr} \end{align}
where
![]() ${f_1}$
and
${f_1}$
and
![]() ${f_2}$
denote the high-fidelity functions, and
${f_2}$
denote the high-fidelity functions, and
![]() ${f_{11}}$
and
${f_{11}}$
and
![]() ${f_{12}}$
denote the low-fidelity functions. The design space of the test function is
${f_{12}}$
denote the low-fidelity functions. The design space of the test function is
![]() ${x_1},{x_2}, \cdots ,{x_5} \in \!\left[ { - 4,4} \right]$
.
${x_1},{x_2}, \cdots ,{x_5} \in \!\left[ { - 4,4} \right]$
.

Figure 11. Schematic of a 2D HV indicator.
The optimisation routine was initialised with LHS to create 20 initial high-fidelity samples and 40 initial low-fidelity samples. During each iteration, the high-fidelity samples were updated by adding five samples using the high-fidelity infill strategy. Meanwhile, the low-fidelity samples were updated by adding 10 samples, including the samples added to the high-fidelity samples using the low-fidelity infill strategy. The optimisation routine ended when the prescribed 24 iterations were met. This was consecutively tested in eight trials. The results of the eight trials are shown in Fig. 12. Moreover, 500,000 samples were generated by LHS, and the HV was calculated as the reference, as shown in Fig. 12.
As observed from Fig. 12, the MO-ACK model outperformed the MO-AK model in terms of achieving higher diversity because its HV was larger after five iterations in all trials. Eight trials were initialised with random LHS; therefore, the initial HV values were different. Both MO-ACK and MO-AK performed better than the reference. It can also be observed from the boxplots of the HV values from the eight trials that the MO-ACK has a larger mean HV value than the MO-AK. The NSGA-II was also included for comparison. The population size was set to 28 and the maximum generation was set to 20. As shown in Fig. 13, the NSGA-II exhibited the worst performance.
In comparison to the MO-AK model, we can conclude that the MO-ACK model can effectively explore the Pareto front of a relatively low-dimension optimisation problem.
2.6.2 DTLZ2 test function optimisation
The definition of the DTLZ2 three-objective test functions, composed of high-fidelity and low-fidelity functions, is as follows [Reference Huband, Hingston, Barone and While46]:

Figure 12. HV results of the FON test function.

Figure 13. Boxplots of the HV values of the FON test function from the eight trials.
 \begin{align}\eqalign{ {\rm{Minimise}}:\;\;{f_1}\!\left( {{x_1},{x_2}, \cdots ,{x_{18}}} \right) = \left( {1 + g} \right){\rm{cos}}\!\left( {0.5{x_1}\pi } \right){\rm{cos}}\!\left( {0.5{x_2}\pi } \right) \cr {\rm{Minimise}}:\;\;{f_2}\!\left( {{x_1},{x_2}, \cdots ,{x_{18}}} \right) = \left( {1 + g} \right){\rm{cos}}\!\left( {0.5{x_1}\pi } \right){\rm{sin}}\!\left( {0.5{x_2}\pi } \right) \cr {\rm{Minimise}}:\;\;{f_3}\!\left( {{x_1},{x_2}, \cdots ,{x_{18}}} \right) = \left( {1 + g} \right){\rm{sin}}\!\left( {0.5{x_1}\pi } \right) \cr g = \mathop \sum \limits_{i = 3}^{18} {\!\left( {{x_i} - 0.5} \right)^2} \cr {f_{11}}\!\left( {{x_1},{x_2}, \cdots ,{x_{18}}} \right) = \left( {0.5 + 1.5g} \right){\rm{cos}}\!\left( {0.6{x_1}\pi } \right){\rm{cos}}\!\left( {0.4{x_2}\pi } \right), \cr {f_{12}}\!\left( {{x_1},{x_2}, \cdots ,{x_{18}}} \right) = \left( {0.3 + 1.2g} \right){\rm{cos}}\!\left( {0.4{x_1}\pi } \right){\rm{sin}}\!\left( {0.6{x_2}\pi } \right), \cr {f_{13}}\!\left( {{x_1},{x_2}, \cdots ,{x_{18}}} \right) = \left( {0.4 + 1.3g} \right){\rm{sin}}\!\left( {0.5{x_1}\pi } \right) \cr {g_c} = \mathop \sum \limits_{i = 3}^{18} {\!\left( {0.8{x_i} - 0.3} \right)^2} \cr} \end{align}
\begin{align}\eqalign{ {\rm{Minimise}}:\;\;{f_1}\!\left( {{x_1},{x_2}, \cdots ,{x_{18}}} \right) = \left( {1 + g} \right){\rm{cos}}\!\left( {0.5{x_1}\pi } \right){\rm{cos}}\!\left( {0.5{x_2}\pi } \right) \cr {\rm{Minimise}}:\;\;{f_2}\!\left( {{x_1},{x_2}, \cdots ,{x_{18}}} \right) = \left( {1 + g} \right){\rm{cos}}\!\left( {0.5{x_1}\pi } \right){\rm{sin}}\!\left( {0.5{x_2}\pi } \right) \cr {\rm{Minimise}}:\;\;{f_3}\!\left( {{x_1},{x_2}, \cdots ,{x_{18}}} \right) = \left( {1 + g} \right){\rm{sin}}\!\left( {0.5{x_1}\pi } \right) \cr g = \mathop \sum \limits_{i = 3}^{18} {\!\left( {{x_i} - 0.5} \right)^2} \cr {f_{11}}\!\left( {{x_1},{x_2}, \cdots ,{x_{18}}} \right) = \left( {0.5 + 1.5g} \right){\rm{cos}}\!\left( {0.6{x_1}\pi } \right){\rm{cos}}\!\left( {0.4{x_2}\pi } \right), \cr {f_{12}}\!\left( {{x_1},{x_2}, \cdots ,{x_{18}}} \right) = \left( {0.3 + 1.2g} \right){\rm{cos}}\!\left( {0.4{x_1}\pi } \right){\rm{sin}}\!\left( {0.6{x_2}\pi } \right), \cr {f_{13}}\!\left( {{x_1},{x_2}, \cdots ,{x_{18}}} \right) = \left( {0.4 + 1.3g} \right){\rm{sin}}\!\left( {0.5{x_1}\pi } \right) \cr {g_c} = \mathop \sum \limits_{i = 3}^{18} {\!\left( {0.8{x_i} - 0.3} \right)^2} \cr} \end{align}
where
![]() ${f_1}$
,
${f_1}$
,
![]() ${f_2}$
, and
${f_2}$
, and
![]() ${f_3}$
denote the high-fidelity functions, and
${f_3}$
denote the high-fidelity functions, and
![]() ${f_{11}}$
,
${f_{11}}$
,
![]() ${f_{12}}$
, and
${f_{12}}$
, and
![]() ${f_{13}}$
denote the low-fidelity functions. Furthermore, the design space of the test function is
${f_{13}}$
denote the low-fidelity functions. Furthermore, the design space of the test function is
![]() ${x_1},{x_2}, \cdots ,{x_{18}} \in \!\left[ {0,1} \right]$
.
${x_1},{x_2}, \cdots ,{x_{18}} \in \!\left[ {0,1} \right]$
.
The optimisation routine was initialised with LHS to create 120 initial high-fidelity samples and 240 initial low-fidelity samples. During each iteration, the high-fidelity samples were updated by adding 18 samples using the high-fidelity infill strategy. Meanwhile, the low-fidelity samples were updated by adding 36 samples, including the samples added to the high-fidelity samples using the low-fidelity infill strategy. The optimisation routine ended when the four prescribed iterations were met. This was consecutively tested in eight trials. The results of the eight trials are shown in Fig. 14. Moreover, 500,000 samples were generated by LHS, and the HV was calculated as the reference, as shown in Fig. 14.

Figure 14. HV results of the DTLZ2 test function.
As observed from Fig. 14, the MO-ACK model outperformed the MO-AK model in terms of achieving higher diversity because its HV was larger after five iterations in all trials. Eight trials were initialised with random LHS; therefore, the initial HV values were different. All eight trials of the MO-ACK obtained higher HV values than the reference, whereas all eight trials of the MO-AK obtained lower HV values. It can also be observed from the boxplots of the HV values from the eight trials that the MO-ACK has a larger mean HV value than the MO-AK. The NSGA-II was also included for comparison. The population size was set to 32, and the maximum generation was set to 6. As shown in Fig. 15, the NSGA-II exhibited the worst performance.

Figure 15. Boxplots of the HV values of the DTLZ2 test function from the eight trials.
We may infer that the MO-ACK model can more effectively explore the Pareto front of a high-dimensional optimisation problem than the MO-AK model.
3.0 Results and discussion
The proposed optimisation framework was adopted to investigate the aerodynamic shape optimisation of an aero-engine nacelle under different operating conditions. The optimisation routine was initialised with LHS to create 120 initial high-fidelity samples and 240 initial low-fidelity samples. Subsequently, the iCST method was applied to construct the nacelle geometry, which was input to ANSYS ICEM to automatically create a structured mesh using a custom script. Computations were carried out using an in-house solver to obtain the target values. The obtained data were then processed and passed to a surrogate model as input. The Pareto front was explored using the NSGA-II. During each iteration, the high-fidelity samples were updated by adding four samples using the high-fidelity infill strategy. Meanwhile, the low-fidelity samples were updated by adding eight samples, including the samples added to the high-fidelity samples, using the low-fidelity infill strategy. The optimisation routine ended when the prescribed maximum iterations were met. To compare the ability to explore the Pareto front of different optimisation strategies, the MO-AK-based optimisation was also applied. To eliminate the influence of the initial samples, same high-fidelity initial samples were used for both MO-ACK-based optimisation and MO-AK-based optimisation.
Three aero-lines were used to construct the geometry of the non-axisymmetric nacelle. Each aero-line was controlled using six design variables (
![]() ${r_{if}},{r_{{\rm{max}}}},{f_{{\rm{max}}}},{\beta _{{\rm{nac}}}},{r_i}$
, and
${r_{if}},{r_{{\rm{max}}}},{f_{{\rm{max}}}},{\beta _{{\rm{nac}}}},{r_i}$
, and
![]() ${f_i}$
). The lower and upper bounds of these six parametres were the same for each aero-line, as listed in Table 5.
${f_i}$
). The lower and upper bounds of these six parametres were the same for each aero-line, as listed in Table 5.
Two nacelle performance metrics were employed as the objective functions for the optimistion routine. The drag coefficient (
![]() ${C_{D - {\rm{cruise}}}}$
) was evaluated under cruise conditions, whereas the intake pressure recovery (IPR) was evaluated under takeoff conditions. To assess the fancowl drag, the method described by Christie et al. [Reference Christie, Ramirez and MacManus47] was used, which uses surface integrals, velocity, and pressure distribution on the AIP and the farfield state to compute the sum of the forces on the entry streamtube and fancowl, ignoring the forces on the post-exit streamtube at data flow conditions of the nozzle.
${C_{D - {\rm{cruise}}}}$
) was evaluated under cruise conditions, whereas the intake pressure recovery (IPR) was evaluated under takeoff conditions. To assess the fancowl drag, the method described by Christie et al. [Reference Christie, Ramirez and MacManus47] was used, which uses surface integrals, velocity, and pressure distribution on the AIP and the farfield state to compute the sum of the forces on the entry streamtube and fancowl, ignoring the forces on the post-exit streamtube at data flow conditions of the nozzle.
Here,
![]() ${C_{D - {\rm{cruise}}}}$
was defined as the ratio of the drag force at the fancowl to the force produced by the dynamic pressure multiplied by the area at highlight, as follows:
${C_{D - {\rm{cruise}}}}$
was defined as the ratio of the drag force at the fancowl to the force produced by the dynamic pressure multiplied by the area at highlight, as follows:
Furthermore,
![]() $IP{R_{{\rm{takeoff}}}}$
was defined as the ratio of the mean total pressure at the fanface to the total pressure of the freestream, as follows:
$IP{R_{{\rm{takeoff}}}}$
was defined as the ratio of the mean total pressure at the fanface to the total pressure of the freestream, as follows:
Table 5. Design variable bounds


Figure 16. Pareto fronts for MO-AK and MO-ACK.

Figure 17. Comparisons of HV between the results of MO-AK and MO-ACK.
After the optimisation routine, the Pareto front in terms of
![]() ${C_{D - {\rm{cruise}}}}$
) and
${C_{D - {\rm{cruise}}}}$
) and
![]() $IP{R_{{\rm{takeoff}}}}$
is graphically shown in Fig. 16. To exhibit the Pareto front in the lower left, the Y-axis data are represented using
$IP{R_{{\rm{takeoff}}}}$
is graphically shown in Fig. 16. To exhibit the Pareto front in the lower left, the Y-axis data are represented using
![]() $1 - IP{R_{{\rm{takeoff}}}}$
instead of
$1 - IP{R_{{\rm{takeoff}}}}$
instead of
![]() $IP{R_{{\rm{takeoff}}}}$
. This Pareto front consisted of all the samples evaluated during the optimisation routine, where the added and initial samples are marked with “o” and “+”, respectively. Specifically, the samples added by the MO-ACK-based method are colored orange, whereas the samples added by the MO-AK-based method are colored blue. The non-dominated solutions are highlighted with a larger marker “o”. As shown in Fig. 16, the added samples are mainly clustered in the lower left, where the solutions are much closer to the Pareto front than the initial samples. The Pareto front from the MO-ACK shows a significant improvement in the convergence and diversity of solutions over the Pareto front from the MO-AK. It is also quantitatively described using the HV metrics, as shown in Fig. 17. It can be seen that the first increase in HV from the MO-ACK-based optimisation framework is 0.0180, whereas it is only 0.0047 from the MO-AK-based optimisation framework. Moreover, the HV from the MO-ACK-based optimisation framework ends with a value of 0.9189 after the 4th iteration, whereas the MO-AK-based optimisation framework ends with a value of 0.9143. It is clear that the MO-ACK-based optimisation framework can achieve a higher HV value, which means finding better solutions in terms of convergence and diversity, compared to the MO-AK-based optimisation framework. It can be found that with the help of the low-fidelity samples, the MO-ACK-based optimisation framework can more efficiently explore the design space. These results are summarised in Table 6.
$IP{R_{{\rm{takeoff}}}}$
. This Pareto front consisted of all the samples evaluated during the optimisation routine, where the added and initial samples are marked with “o” and “+”, respectively. Specifically, the samples added by the MO-ACK-based method are colored orange, whereas the samples added by the MO-AK-based method are colored blue. The non-dominated solutions are highlighted with a larger marker “o”. As shown in Fig. 16, the added samples are mainly clustered in the lower left, where the solutions are much closer to the Pareto front than the initial samples. The Pareto front from the MO-ACK shows a significant improvement in the convergence and diversity of solutions over the Pareto front from the MO-AK. It is also quantitatively described using the HV metrics, as shown in Fig. 17. It can be seen that the first increase in HV from the MO-ACK-based optimisation framework is 0.0180, whereas it is only 0.0047 from the MO-AK-based optimisation framework. Moreover, the HV from the MO-ACK-based optimisation framework ends with a value of 0.9189 after the 4th iteration, whereas the MO-AK-based optimisation framework ends with a value of 0.9143. It is clear that the MO-ACK-based optimisation framework can achieve a higher HV value, which means finding better solutions in terms of convergence and diversity, compared to the MO-AK-based optimisation framework. It can be found that with the help of the low-fidelity samples, the MO-ACK-based optimisation framework can more efficiently explore the design space. These results are summarised in Table 6.
The results of the optimisation routine under different conditions are discussed below. Because the Pareto solutions are mutually non-dominated, they are all feasible and acceptable in engineering practices. To better illustrate the effectiveness of the optimisation framework, a more detailed investigation of the nacelle designs with the highest
![]() $IP{R_{{\rm{takeoff}}}}$
identified using the MO-ACK and MO-AK models, referred to as A1 and B1, respectively, was carried out. The base sample was axisymmetric; therefore, the scarf angle was zero.
$IP{R_{{\rm{takeoff}}}}$
identified using the MO-ACK and MO-AK models, referred to as A1 and B1, respectively, was carried out. The base sample was axisymmetric; therefore, the scarf angle was zero.
Table 6. Comparison of the optimisation results from the MO-ACK and MO-AK optimisation frameworks

The comparison of the baseline and the optimal nacelle geometry designs of A1 and B1 is shown in Fig. 18. In comparison to the azimuthal section
![]() $\psi = {0^ \circ }$
,
$\psi = {0^ \circ }$
,
![]() $\psi = {90^ \circ }$
and
$\psi = {90^ \circ }$
and
![]() $\psi = {180^ \circ }$
of the baseline, the three lines of both optimal nacelle geometry designs of A1 and B1 are thinner. For the azimuthal section
$\psi = {180^ \circ }$
of the baseline, the three lines of both optimal nacelle geometry designs of A1 and B1 are thinner. For the azimuthal section
![]() $\psi = {0^ \circ }$
, design B1 has highest rates of change in curvature, corresponding to the highest peaks in isentropic Mach number. For the azimuthal section
$\psi = {0^ \circ }$
, design B1 has highest rates of change in curvature, corresponding to the highest peaks in isentropic Mach number. For the azimuthal section
![]() $\psi = {90^ \circ }$
, design A1 has highest rates of change in curvature. For the azimuthal section
$\psi = {90^ \circ }$
, design A1 has highest rates of change in curvature. For the azimuthal section
![]() $\psi = {180^ \circ }$
, the rates of change in curvature of design B1 is slightly larger than that of design A1. In all azimuthal sections, design A1 and design B1 have smaller boat-tail angles than base sample. For the intake geometry, design A1 and design B1 are similar in all azimuthal sections and have a smaller thickness compared to the base sample. The following is a further flow field analysis.
$\psi = {180^ \circ }$
, the rates of change in curvature of design B1 is slightly larger than that of design A1. In all azimuthal sections, design A1 and design B1 have smaller boat-tail angles than base sample. For the intake geometry, design A1 and design B1 are similar in all azimuthal sections and have a smaller thickness compared to the base sample. The following is a further flow field analysis.

Figure 18. Comparisons of the nacelle geometry for the selected designs at different azimuthal sections.
3.1 Results under cruise condition
Designs A1 and B1 exhibited significant reductions in terms of
![]() ${C_{D - {\rm{cruise}}}}$
compared to the configuration of the base sample. While design A1 exhibited a reduction of 23.6% while design B1 exhibited a reduction of 22.2%. As shown in Fig. 19, the large variation in the nacelle drag characteristics was caused by a fundamental change in the associated nacelle transonic flow aerodynamics. The pressure distributions of all designs are shown in Fig. 20. As shown in Fig. 21, the isentropic Mach number distributions of the base sample configuration on all four aero-lines were almost the same because of their axisymmetric characteristics. The location of the peak isentropic Mach number at the top aero-line (
${C_{D - {\rm{cruise}}}}$
compared to the configuration of the base sample. While design A1 exhibited a reduction of 23.6% while design B1 exhibited a reduction of 22.2%. As shown in Fig. 19, the large variation in the nacelle drag characteristics was caused by a fundamental change in the associated nacelle transonic flow aerodynamics. The pressure distributions of all designs are shown in Fig. 20. As shown in Fig. 21, the isentropic Mach number distributions of the base sample configuration on all four aero-lines were almost the same because of their axisymmetric characteristics. The location of the peak isentropic Mach number at the top aero-line (
![]() $\psi = {0^ \circ }$
) was significantly different for the three selected designs and varied by 2.474. Design A1, which had the highest
$\psi = {0^ \circ }$
) was significantly different for the three selected designs and varied by 2.474. Design A1, which had the highest
![]() $IP{R_{{\rm{takeoff}}}}$
found throughout the optimisation process, had an initial acceleration to terminate with a strong shockwave at
$IP{R_{{\rm{takeoff}}}}$
found throughout the optimisation process, had an initial acceleration to terminate with a strong shockwave at
![]() $X = 0.14$
. Design A1 had a well-defined shockwave at
$X = 0.14$
. Design A1 had a well-defined shockwave at
![]() $X = 0.14$
, whereas the configuration of the base sample had a similar shockwave at
$X = 0.14$
, whereas the configuration of the base sample had a similar shockwave at
![]() $X = 1.697$
. Compared to the other two configurations, design B1 had a shockwave in the shortest position at
$X = 1.697$
. Compared to the other two configurations, design B1 had a shockwave in the shortest position at
![]() $X = - 0.777$
. Unlike the other two, which experienced accelerations at the start, design B1 experienced a stable process at the beginning. For the azimuthal section
$X = - 0.777$
. Unlike the other two, which experienced accelerations at the start, design B1 experienced a stable process at the beginning. For the azimuthal section
![]() $\psi = {45^ \circ }$
, design A1 had a similar benign transonic flow structure compared to design B1. For the azimuthal section
$\psi = {45^ \circ }$
, design A1 had a similar benign transonic flow structure compared to design B1. For the azimuthal section
![]() $\psi = {90^ \circ }$
, design A1 had a well-defined shock wave at
$\psi = {90^ \circ }$
, design A1 had a well-defined shock wave at
![]() $X = - 0.325$
. Design B1 and the configuration of the base sample had similar flow structures except for the intensity of the associated transonic flow aerodynamics. For instance, the configuration of the base sample had an isentropic Mach number of 1.207, whereas design B1 had a Mach number of 1.177. For the azimuthal section
$X = - 0.325$
. Design B1 and the configuration of the base sample had similar flow structures except for the intensity of the associated transonic flow aerodynamics. For instance, the configuration of the base sample had an isentropic Mach number of 1.207, whereas design B1 had a Mach number of 1.177. For the azimuthal section
![]() $\psi = {180^ \circ }$
, design B1 still had flow structures similar to those of the base sample. Design B1 had a double shockwave structure with the first shockwave located at
$\psi = {180^ \circ }$
, design B1 still had flow structures similar to those of the base sample. Design B1 had a double shockwave structure with the first shockwave located at
![]() $X = - 0.370$
and the second shockwave at
$X = - 0.370$
and the second shockwave at
![]() $X = 1.510$
. The base sample had a double shockwave structure with the first shockwave located at
$X = 1.510$
. The base sample had a double shockwave structure with the first shockwave located at
![]() $X = - 0.322$
and the second shockwave at
$X = - 0.322$
and the second shockwave at
![]() $X = 1.870$
. Design A1 had an initial acceleration and terminated with a shockwave at
$X = 1.870$
. Design A1 had an initial acceleration and terminated with a shockwave at
![]() $X = 0.245$
.
$X = 0.245$
.
The design with the largest radius of curvature at the azimuthal section
![]() $\psi = {0^ \circ }$
and
$\psi = {0^ \circ }$
and
![]() $\psi = {90^ \circ }$
has the highest peaks in isentropic Mach number, which is consistent in Figs 18 and 21. For the azimuthal section
$\psi = {90^ \circ }$
has the highest peaks in isentropic Mach number, which is consistent in Figs 18 and 21. For the azimuthal section
![]() $\psi = {180^ \circ }$
, design A1 and design B1 have similar geometric configurations, but there is a significant difference at isentropic Mach number distributions, which indicates the sensitivity of the flow field to geometry and the strong nonlinearity of the transonic flow aerodynamics.
$\psi = {180^ \circ }$
, design A1 and design B1 have similar geometric configurations, but there is a significant difference at isentropic Mach number distributions, which indicates the sensitivity of the flow field to geometry and the strong nonlinearity of the transonic flow aerodynamics.

Figure 19. Comparison of the isentropic Mach number contours for the selected designs.

Figure 20. Comparison of the pressure contours for the selected designs.

Figure 21. Comparisons of the isentropic Mach number for the selected designs at different azimuthal sections.
3.2 Results under takeoff condition
Designs A1 and B1 had significant improvements in terms of
![]() $IP{R_{{\rm{takeoff}}}}$
compared to the configuration of the base sample. While design A1 had a reduction of 1.63%, design B1 had 1.59%. In Fig. 22, the total pressure distribution on the fanface under the takeoff condition is clearly illustrated. For the base sample, there was a distinct low-pressure area at the lower part of the fanface. This may occur because of the flow separation induced by the shockwave or adverse pressure gradient. This is an undesirable situation during takeoff. If internal separation occurs, the resulting fan entrance distortion could be critical to causing excessively high fan-blade stresses and may even cause core-compressor stalls. Designs A1 and B1 had significant improvements in
$IP{R_{{\rm{takeoff}}}}$
compared to the configuration of the base sample. While design A1 had a reduction of 1.63%, design B1 had 1.59%. In Fig. 22, the total pressure distribution on the fanface under the takeoff condition is clearly illustrated. For the base sample, there was a distinct low-pressure area at the lower part of the fanface. This may occur because of the flow separation induced by the shockwave or adverse pressure gradient. This is an undesirable situation during takeoff. If internal separation occurs, the resulting fan entrance distortion could be critical to causing excessively high fan-blade stresses and may even cause core-compressor stalls. Designs A1 and B1 had significant improvements in
![]() $IP{R_{{\rm{takeoff}}}}$
compared to the base sample. As shown in Fig. 22, the low-pressure area at the lower part of the fanface of designs A1 and B1 became significantly smaller. This also indicates that the
$IP{R_{{\rm{takeoff}}}}$
compared to the base sample. As shown in Fig. 22, the low-pressure area at the lower part of the fanface of designs A1 and B1 became significantly smaller. This also indicates that the
![]() $IP{R_{{\rm{takeoff}}}}$
was higher. As shown in Fig. 18, design A1 and design B1 are similar in all azimuthal sections and have a smaller thickness compared to the base sample. Combined with the flow field analysis in Fig. 22, these designs allow for a lower total pressure loss when the airflow reaches the fan surface. Compared to design B1, the low-pressure area of design A1 was smaller and more concentrated in the lower part.
$IP{R_{{\rm{takeoff}}}}$
was higher. As shown in Fig. 18, design A1 and design B1 are similar in all azimuthal sections and have a smaller thickness compared to the base sample. Combined with the flow field analysis in Fig. 22, these designs allow for a lower total pressure loss when the airflow reaches the fan surface. Compared to design B1, the low-pressure area of design A1 was smaller and more concentrated in the lower part.

Figure 22. Contours of the total pressure at the fanface for the selected designs.

Figure 23. Parallel coordinates plot of optimised designs coloured by
![]() ${C_{D - {\rm{cruise}}}}$
.
${C_{D - {\rm{cruise}}}}$
.

Figure 24. Parallel coordinates plot of optimised designs coloured by
![]() $IP{R_{{\rm{takeoff}}}}$
.
$IP{R_{{\rm{takeoff}}}}$
.
3.3 Influence of the design variables on the nacelle performance
Parallel coordinate plots represent the regions of the design space where the non-dominated solutions are concentrated [Reference Tejero, Robinson, MacManus and Sheaf15]. Here the ten samples of MO-ACK closest to the origin are selected as in Fig. 1, and the distance criterion formula is defined as follows:
Parallel coordinates plot of optimised designs coloured by
![]() ${C_{D - {\rm{cruise}}}}$
is shown in Fig. 23. Parallel coordinates plot of optimised designs coloured by
${C_{D - {\rm{cruise}}}}$
is shown in Fig. 23. Parallel coordinates plot of optimised designs coloured by
![]() $IP{R_{{\rm{takeoff}}}}$
is shown in Fig. 24. The figures show that the range of variation of design variables
$IP{R_{{\rm{takeoff}}}}$
is shown in Fig. 24. The figures show that the range of variation of design variables
![]() ${r_{if}}$
and
${r_{if}}$
and
![]() ${r_i}$
is small in all azimuthal sections and converges to the design space boundary. This provides some guidelines for design space considerations for subsequent preliminary designs. The overall trend of the design parametres is consistent in the azimuthal section
${r_i}$
is small in all azimuthal sections and converges to the design space boundary. This provides some guidelines for design space considerations for subsequent preliminary designs. The overall trend of the design parametres is consistent in the azimuthal section
![]() $\psi = {0^ \circ }$
and azimuthal section
$\psi = {0^ \circ }$
and azimuthal section
![]() $\psi = {180^ \circ }$
, and differs significantly from azimuthal section
$\psi = {180^ \circ }$
, and differs significantly from azimuthal section
![]() $\psi = {90^ \circ }$
. In the azimuthal section
$\psi = {90^ \circ }$
. In the azimuthal section
![]() $\psi = {0^ \circ }$
, design variable
$\psi = {0^ \circ }$
, design variable
![]() ${f_{{\rm{max}}}}$
has the largest range of variation, which is consistent in the azimuthal section
${f_{{\rm{max}}}}$
has the largest range of variation, which is consistent in the azimuthal section
![]() $\psi = {180^ \circ }$
, but in the azimuthal section
$\psi = {180^ \circ }$
, but in the azimuthal section
![]() $\psi = {90^ \circ }$
, design variable
$\psi = {90^ \circ }$
, design variable
![]() ${r_{{\rm{max}}}}$
has the largest range of variation. Overall, the range of design variables changed the least in the azimuthal section
${r_{{\rm{max}}}}$
has the largest range of variation. Overall, the range of design variables changed the least in the azimuthal section
![]() $\psi = {90^ \circ }$
and the most in the azimuthal section
$\psi = {90^ \circ }$
and the most in the azimuthal section
![]() $\psi = {180^ \circ }$
. This is likely because throughout the multi-objective optimisation process, the takeoff condition was taken into account but the crosswind condition was not. This also demonstrates the complexity of multi-objective optimisation of non-axisymmetric nacelles.
$\psi = {180^ \circ }$
. This is likely because throughout the multi-objective optimisation process, the takeoff condition was taken into account but the crosswind condition was not. This also demonstrates the complexity of multi-objective optimisation of non-axisymmetric nacelles.
4.0 Conclusion
In this study, a novel multi-fidelity surrogate-based multi-objective optimisation framework was proposed. The framework was compared to a conventional single-fidelity surrogate-based multi-objective optimisation framework to verify the effect of multi-fidelity. The two-objective and three-objective test functions were adopted, and the results show that with the help of a low-fidelity dataset, the optimisation method can find the Pareto solutions with better convergence and higher diversity.
The proposed MO-ACK framework was also applied to the aerodynamic shape optimisation of a non-axisymmetric nacelle. It encompassed several fundamental modules, including LHS, geometry parameterisation based on iCST, automatic mesh generation using ANSYS ICEM, CFD numerical analysis using an in-house solver, cokriging-based model, NSGA-II, and an infilling method for both high-fidelity and low-fidelity data. The two-objective and three-objective test functions were used to validate the effectiveness of the proposed framework. The results show that the MO-ACK outperformed the MO-AK and NSGA-II in terms of Pareto-front exploration. The optimised nacelles on the Pareto front from both optimisation strategies showed better aerodynamic performance than the base sample, which means a higher pressure-recovery ratio in the fanface under takeoff conditions and lower drag under cruise conditions. Compared to the results of the MO-AK framework optimisation, the Pareto front obtained from the MO-ACK framework optimisation had a higher HV value, which increased by 4.1% and 3.5% compared to the initial HV value. The nacelle designs with the highest
![]() $IP{R_{{\rm{takeoff}}}}$
of the Pareto front identified with the configuration of the MO-ACK and MO-AK frameworks were selected as the optimised designs and referred to as A1 and B1, respectively. In terms of
$IP{R_{{\rm{takeoff}}}}$
of the Pareto front identified with the configuration of the MO-ACK and MO-AK frameworks were selected as the optimised designs and referred to as A1 and B1, respectively. In terms of
![]() ${C_{D - {\rm{cruise}}}}$
), designs A1 and B1 had significant reductions compared to the configuration of the base sample. While design A1 had a reduction of 23.6%, design B1 had a reduction of 22.2%. In terms of
${C_{D - {\rm{cruise}}}}$
), designs A1 and B1 had significant reductions compared to the configuration of the base sample. While design A1 had a reduction of 23.6%, design B1 had a reduction of 22.2%. In terms of
![]() $IP{R_{{\rm{takeoff}}}}$
, designs A1 and B1 had significant improvements compared to the configuration of the base sample. While design A1 had a reduction of 1.63%, design B1 had a reduction of 1.59%. Therefore, it can be concluded that the proposed optimisation framework can be applied to the aerodynamic shape optimisation of engine nacelles under cruise and takeoff conditions.
$IP{R_{{\rm{takeoff}}}}$
, designs A1 and B1 had significant improvements compared to the configuration of the base sample. While design A1 had a reduction of 1.63%, design B1 had a reduction of 1.59%. Therefore, it can be concluded that the proposed optimisation framework can be applied to the aerodynamic shape optimisation of engine nacelles under cruise and takeoff conditions.
Acknowledgements
This study is supported in part by the Zhejiang University/University of Illinois at Urbana-Champaign Institute and Natural Science Foundation of China (Grant No.52106060 and 92152202). It was led by supervisor Jiahuan Cui.