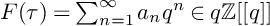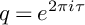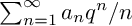1 Introduction
One of the arithmetic features of modular and quasi-modular forms is integrality of the coefficients in their Fourier expansions. This is trivially seen on the generators
 $$ \begin{align} E_2(\tau)=1-24\sum_{n=1}^{\infty}\frac{nq^n}{1-q^n}, \quad E_4(\tau)=1+240\sum_{n=1}^{\infty}\frac{n^3q^n}{1-q^n}, \quad E_6(\tau)=1-504\sum_{n=1}^{\infty}\frac{n^5q^n}{1-q^n} \end{align} $$
$$ \begin{align} E_2(\tau)=1-24\sum_{n=1}^{\infty}\frac{nq^n}{1-q^n}, \quad E_4(\tau)=1+240\sum_{n=1}^{\infty}\frac{n^3q^n}{1-q^n}, \quad E_6(\tau)=1-504\sum_{n=1}^{\infty}\frac{n^5q^n}{1-q^n} \end{align} $$
of the ring of quasi-modular forms, as well as on the discriminant cusp form
 $$ \begin{align*}\Delta(\tau)=q\prod_{m=1}^{\infty}(1-q^m)^{24}=\frac{E_4^3-E_6^2}{1728}, \end{align*} $$
$$ \begin{align*}\Delta(\tau)=q\prod_{m=1}^{\infty}(1-q^m)^{24}=\frac{E_4^3-E_6^2}{1728}, \end{align*} $$
where
![]() $q=q(\tau )=e^{2\pi i\tau }$
for
$q=q(\tau )=e^{2\pi i\tau }$
for
![]() $\tau $
from the upper half-plane
$\tau $
from the upper half-plane
![]() $\operatorname {Im}\tau>0$
. All q-expansions above converge for q inside the unit disk, and in fact have polynomial growth of the coefficients. A more surprising fact, brought to the mathematical community by Ramanujan [Reference Ramanujan, Hardy, Aiyar and Wilson21] more than 100 years ago, is that the three Eisenstein series in (1) satisfy the algebraic system of differential equations
$\operatorname {Im}\tau>0$
. All q-expansions above converge for q inside the unit disk, and in fact have polynomial growth of the coefficients. A more surprising fact, brought to the mathematical community by Ramanujan [Reference Ramanujan, Hardy, Aiyar and Wilson21] more than 100 years ago, is that the three Eisenstein series in (1) satisfy the algebraic system of differential equations
where
 $$ \begin{align*}\delta=\frac1{2\pi i}\frac{{\mathrm d}}{{\mathrm d}\tau}=q\frac{{\mathrm d}}{{\mathrm d} q}. \end{align*} $$
$$ \begin{align*}\delta=\frac1{2\pi i}\frac{{\mathrm d}}{{\mathrm d}\tau}=q\frac{{\mathrm d}}{{\mathrm d} q}. \end{align*} $$
Ramanujan’s notation for the Eisenstein series (1) was
![]() $P(q),Q(q),R(q)$
, respectively, as he mainly viewed them as functions of the q-nome. Since the functions
$P(q),Q(q),R(q)$
, respectively, as he mainly viewed them as functions of the q-nome. Since the functions
![]() $E_2,E_4,E_6$
are algebraically independent over
$E_2,E_4,E_6$
are algebraically independent over
![]() $\mathbb C$
, and even over
$\mathbb C$
, and even over
![]() $\mathbb C(q)$
and over
$\mathbb C(q)$
and over
![]() $\mathbb C(\tau ,q)$
[Reference Mahler19,Reference Resnikoff22], this fine structure gives rise to remarkable applications in transcendental number theory to the values of quasi-modular forms. One particular notable example in this direction is a famous theorem of Nesterenko [Reference Nesterenko20], which states that, given a complex number q with
$\mathbb C(\tau ,q)$
[Reference Mahler19,Reference Resnikoff22], this fine structure gives rise to remarkable applications in transcendental number theory to the values of quasi-modular forms. One particular notable example in this direction is a famous theorem of Nesterenko [Reference Nesterenko20], which states that, given a complex number q with
![]() ${0<|q|<1}$
, at least three of the four quantities
${0<|q|<1}$
, at least three of the four quantities
![]() $q,P(q),Q(q),R(q)$
are algebraically independent over
$q,P(q),Q(q),R(q)$
are algebraically independent over
![]() $\mathbb Q$
.
$\mathbb Q$
.
Establishing transformation properties of a double integral, which characterizes the output voltage of a Hall plate affected by the shape of the plates and sizes of the contacts and which is—for this reason—dubbed magnetic, in the work [Reference Borcherds7], Broadhurst and Zudilin came across a meromorphic modular form (on a congruence subgroup), whose anti-derivative had integral coefficients in its q-expansion and was not a modular object itself. This arithmetic observation was subsequently proved by Li and Neururer in [Reference Li and Neururer17] who also noticed that the formal anti-derivative
 $$ \begin{align*}\tilde F_{4a}=\delta^{-1}\biggl(\frac{\Delta}{E_4^2}\biggr)=\int_0^q\frac{\Delta}{E_4^2}\,\frac{{\mathrm d} q}q \end{align*} $$
$$ \begin{align*}\tilde F_{4a}=\delta^{-1}\biggl(\frac{\Delta}{E_4^2}\biggr)=\int_0^q\frac{\Delta}{E_4^2}\,\frac{{\mathrm d} q}q \end{align*} $$
of the meromorphic modular form
![]() $F_{4a}(\tau )=\Delta /E_4^2$
has integer coefficients in its q-expansion. (They proved a slightly weaker version about the integrality of the anti-derivative of
$F_{4a}(\tau )=\Delta /E_4^2$
has integer coefficients in its q-expansion. (They proved a slightly weaker version about the integrality of the anti-derivative of
![]() $64\Delta /E_4^2$
.) The function
$64\Delta /E_4^2$
.) The function
![]() $F_{4a}(\tau )$
has weight 4 and possesses the double pole at
$F_{4a}(\tau )$
has weight 4 and possesses the double pole at
![]() $\tau =\rho =e^{2\pi i/3}$
in the fundamental domain, and a simple analysis reveals that it is not the image under
$\tau =\rho =e^{2\pi i/3}$
in the fundamental domain, and a simple analysis reveals that it is not the image under
![]() $\delta $
of an element from the (differentially closed) field
$\delta $
of an element from the (differentially closed) field
![]() $\mathbb C(q,E_2,E_4,E_6)$
. This implies that the anti-derivative
$\mathbb C(q,E_2,E_4,E_6)$
. This implies that the anti-derivative
![]() $\tilde F_{4a}=\delta ^{-1}F_{4a}$
is transcendental over the field, and hence the addition of
$\tilde F_{4a}=\delta ^{-1}F_{4a}$
is transcendental over the field, and hence the addition of
![]() $\tilde F_{4a}$
to the latter increases the transcendence degree by 1. Following the background in [Reference Borcherds7], Li and Neururer coined the name magnetic modular form to a meromorphic modular form like
$\tilde F_{4a}$
to the latter increases the transcendence degree by 1. Following the background in [Reference Borcherds7], Li and Neururer coined the name magnetic modular form to a meromorphic modular form like
![]() $F_{4a}$
. A principal goal of this note is to investigate the magnetic modular phenomenon further and to give more examples of those.
$F_{4a}$
. A principal goal of this note is to investigate the magnetic modular phenomenon further and to give more examples of those.
Theorem 1. The meromorphic modular forms
![]() $F_{4a}(\tau )=\Delta /E_4^2$
and
$F_{4a}(\tau )=\Delta /E_4^2$
and
![]() $F_{4b}(\tau )=E_4\Delta /E_6^2$
of weight
$F_{4b}(\tau )=E_4\Delta /E_6^2$
of weight
![]() $4$
are magnetic. In other words, their anti-derivatives
$4$
are magnetic. In other words, their anti-derivatives
![]() $\delta ^{-1}F_{4a}$
and
$\delta ^{-1}F_{4a}$
and
![]() $\delta ^{-1}F_{4b}$
have integral q-expansions.
$\delta ^{-1}F_{4b}$
have integral q-expansions.
Theorem 2. The meromorphic modular form
![]() $F_6(\tau )=E_6\Delta /E_4^3$
of weight
$F_6(\tau )=E_6\Delta /E_4^3$
of weight
![]() $6$
is doubly magnetic: its first and second anti-derivatives
$6$
is doubly magnetic: its first and second anti-derivatives
![]() $\delta ^{-1}F_6$
and
$\delta ^{-1}F_6$
and
![]() $\delta ^{-2}F_6$
have integral q-expansions.
$\delta ^{-2}F_6$
have integral q-expansions.
There are other instances in the literature of related integrality phenomena; however, the existing methods of proofs seem to be quite different from what we use below. Investigating the solution space of the linear differential equation
in [Reference Honda and Kaneko13], Honda and Kaneko found that, when
![]() $k=4$
, it is spanned by
$k=4$
, it is spanned by
![]() $E_4$
and
$E_4$
and
 $$ \begin{align*}\tilde E_4=E_4\cdot\delta^{-1}\biggl(\frac{\Delta^{5/6}}{E_4^2}\biggr)\in q^{5/6}\mathbb Q[[q]]. \end{align*} $$
$$ \begin{align*}\tilde E_4=E_4\cdot\delta^{-1}\biggl(\frac{\Delta^{5/6}}{E_4^2}\biggr)\in q^{5/6}\mathbb Q[[q]]. \end{align*} $$
They numerically observed and proved some related results about the p-integrality of
![]() $\tilde E_4$
for primes
$\tilde E_4$
for primes
![]() $p\equiv 1\bmod 3$
. This theme was later analyzed and generalized in [Reference Ahlgren and Andersen2,Reference Guerzhoy11,Reference Guerzhoy12]. Bringing some parallel to that investigations, it is easy to check that the functions
$p\equiv 1\bmod 3$
. This theme was later analyzed and generalized in [Reference Ahlgren and Andersen2,Reference Guerzhoy11,Reference Guerzhoy12]. Bringing some parallel to that investigations, it is easy to check that the functions
![]() $E_4$
and
$E_4$
and
![]() $E_4\,\delta ^{-1}(\Delta /E_4^2)$
(both with integer coefficients in their q-expansions!) span the solution space of the differential equation
$E_4\,\delta ^{-1}(\Delta /E_4^2)$
(both with integer coefficients in their q-expansions!) span the solution space of the differential equation
![]() $Df=0$
, where
$Df=0$
, where
 $$ \begin{align*}D=\delta^2-E_2\delta+\frac1{36}\biggl(7E_2^2-5E_4-2\frac{E_2E_6}{E_4}\biggr) =D_5+\frac16\biggl(E_2\frac{\delta E_4}{E_4}-5\delta E_2\biggr). \end{align*} $$
$$ \begin{align*}D=\delta^2-E_2\delta+\frac1{36}\biggl(7E_2^2-5E_4-2\frac{E_2E_6}{E_4}\biggr) =D_5+\frac16\biggl(E_2\frac{\delta E_4}{E_4}-5\delta E_2\biggr). \end{align*} $$
At the same time, the only quasi-modular solutions of
![]() $D_5y=0$
are spanned by
$D_5y=0$
are spanned by
![]() $\delta E_4$
(see [Reference Kaneko and Koike15, Th. 2]).
$\delta E_4$
(see [Reference Kaneko and Koike15, Th. 2]).
A somewhat different account of strong divisibility of the coefficients of modular forms shows up in the context of arithmetic properties of traces of singular moduli initiated in Zagier’s work [Reference Zagier23]. As this topic remains quite popular, we only list a selection of contributions [Reference Ahlgren1,Reference Ahlgren and Ono3,Reference Duke and Jenkins8,Reference Edixhoven9,Reference Guerzhoy10,Reference Jenkins14]. The methods involved make use of the Shimura correspondence, which is also the main ingredient of our proof of Theorems 1 and 2.
2 Magnetic quasi-modular forms
In this part, we formalize the notion of magnetic forms and give results, which may be thought of as generalizations of Theorems 1 and 2, but use the theorems as principal steps.
Consider the family
of meromorphic quasi-modular forms. Their q-expansions all belong to
![]() $\mathbb Z[[q]]$
. For
$\mathbb Z[[q]]$
. For
![]() $k\in \mathbb Z$
even, denote by
$k\in \mathbb Z$
even, denote by
![]() $W_k$
the
$W_k$
the
![]() $\mathbb {Q}$
-vector space in
$\mathbb {Q}$
-vector space in
![]() $\mathbb Q\otimes _{\mathbb {Z}}\mathbb Z[[q]]$
(the q-series
$\mathbb Q\otimes _{\mathbb {Z}}\mathbb Z[[q]]$
(the q-series
![]() $f\in \mathbb Q[[q]]$
with
$f\in \mathbb Q[[q]]$
with
![]() $Nf\in \mathbb Z[[q]]$
for some
$Nf\in \mathbb Z[[q]]$
for some
![]() $N\in \mathbb Z_{>0}$
) spanned by the q-expansions of the forms
$N\in \mathbb Z_{>0}$
) spanned by the q-expansions of the forms
![]() $f_{a,b,c}$
of weight k, that is, with
$f_{a,b,c}$
of weight k, that is, with
![]() $2a+4b+6c=k$
. Because
$2a+4b+6c=k$
. Because
the differential operator
![]() $\delta $
defines a well-defined map
$\delta $
defines a well-defined map
![]() $W_k\to W_{k+2}$
. Clearly, the image
$W_k\to W_{k+2}$
. Clearly, the image
![]() $\delta W_k$
in
$\delta W_k$
in
![]() $W_{k+2}$
is a
$W_{k+2}$
is a
![]() $\mathbb Q$
-subspace in
$\mathbb Q$
-subspace in
![]() $\mathbb Q\otimes _{\mathbb {Z}}q\mathbb {Z}[[q]]$
; we call
$\mathbb Q\otimes _{\mathbb {Z}}q\mathbb {Z}[[q]]$
; we call
![]() $W_{k+2}^0$
the cuspidal subspace of
$W_{k+2}^0$
the cuspidal subspace of
![]() $W_{k+2}$
, that is, the set of all elements in
$W_{k+2}$
, that is, the set of all elements in
![]() $W_{k+2}$
with vanishing constant term in their q-expansion.
$W_{k+2}$
with vanishing constant term in their q-expansion.
We say that an element
![]() $v\in W_k^0$
is magnetic if its formal anti-derivative
$v\in W_k^0$
is magnetic if its formal anti-derivative
 $$ \begin{align*}\delta^{-1}v=\int_0^q v\,\frac{{\mathrm d} q}{q}\in \mathbb{Q}\otimes_{\mathbb{Z}} q\mathbb{Z}[[q]]. \end{align*} $$
$$ \begin{align*}\delta^{-1}v=\int_0^q v\,\frac{{\mathrm d} q}{q}\in \mathbb{Q}\otimes_{\mathbb{Z}} q\mathbb{Z}[[q]]. \end{align*} $$
We also call it strongly magnetic if
![]() $\delta ^{-1}v\in q\mathbb {Z}[[q]]$
. With the magnetic property, we can associate the equivalence relation
$\delta ^{-1}v\in q\mathbb {Z}[[q]]$
. With the magnetic property, we can associate the equivalence relation
![]() $\sim $
on
$\sim $
on
![]() $W_k$
writing
$W_k$
writing
![]() $v\sim w$
if and only if the difference
$v\sim w$
if and only if the difference
![]() $v-w$
is in
$v-w$
is in
![]() $W_k^0$
and is magnetic.
$W_k^0$
and is magnetic.
Let
![]() $V_k$
(respectively,
$V_k$
(respectively,
![]() $V_k^0$
) be the
$V_k^0$
) be the
![]() $\mathbb {Q}$
-vector subspace of
$\mathbb {Q}$
-vector subspace of
![]() $W_k$
(respectively, of
$W_k$
(respectively, of
![]() $W_k^0$
) generated by the forms
$W_k^0$
) generated by the forms
![]() $f_{a,b,c}$
with
$f_{a,b,c}$
with
![]() $a\in \{0,1,\dots ,k-2\}$
. According to relation (3), this range of a makes the subspace
$a\in \{0,1,\dots ,k-2\}$
. According to relation (3), this range of a makes the subspace
![]() $V_k$
stable under the
$V_k$
stable under the
![]() $\delta $
-differentiation. Notice that
$\delta $
-differentiation. Notice that
![]() $\delta V_2\subseteq V_{4}^0$
.
$\delta V_2\subseteq V_{4}^0$
.
Theorem 3. Any element of
![]() $V_4^0$
is magnetic.
$V_4^0$
is magnetic.
Remark 1. It seems that the elements of
![]() $W_4^0$
with
$W_4^0$
with
![]() $a>2$
(i.e., outside the range assumed in
$a>2$
(i.e., outside the range assumed in
![]() $V_4^0$
) with the magnetic property are those that come as linear combinations of
$V_4^0$
) with the magnetic property are those that come as linear combinations of
![]() $\delta $
-derivatives of elements from
$\delta $
-derivatives of elements from
![]() $W_2$
. In other words, we expect that the choice of
$W_2$
. In other words, we expect that the choice of
![]() $V_4^0$
in the theorem as a magnetic space of weight 4 to be sharp.
$V_4^0$
in the theorem as a magnetic space of weight 4 to be sharp.
Proof. Derivation of Theorem 3 from Theorem 1
It follows from Theorem 1 that the forms
are magnetic; in other words, we have the equivalences
![]() $f_{0,-2,2}\sim f_{0,1,0}$
and
$f_{0,-2,2}\sim f_{0,1,0}$
and
![]() $f_{1,2,-1}\sim f_{0,1,0}$
.
$f_{1,2,-1}\sim f_{0,1,0}$
.
Any element in
![]() $V_4$
can be written as
$V_4$
can be written as
![]() $E_2^aP(E_4,E_6)/(E_4^mE_6^n)$
, for some
$E_2^aP(E_4,E_6)/(E_4^mE_6^n)$
, for some
![]() $a,m,n$
non-negative integers,
$a,m,n$
non-negative integers,
![]() $a\le 2$
, and
$a\le 2$
, and
![]() $P(x,y)\in \mathbb Q[x,y]$
. Such an expression clearly splits into a linear combination of the form
$P(x,y)\in \mathbb Q[x,y]$
. Such an expression clearly splits into a linear combination of the form
![]() $f_{a,b,c}\in V_4$
with
$f_{a,b,c}\in V_4$
with
![]() $0\le a\le 2$
and either
$0\le a\le 2$
and either
![]() $b\ge 0$
or
$b\ge 0$
or
![]() $c\ge 0$
. If both
$c\ge 0$
. If both
![]() $b\ge 0$
and
$b\ge 0$
and
![]() $c\ge 0$
, then we get only two elements in
$c\ge 0$
, then we get only two elements in
![]() $V_4$
, namely,
$V_4$
, namely,
![]() $f_{0,1,0}$
and
$f_{0,1,0}$
and
![]() $f_{2,0,0} = f_{0,1,0} + 12\delta f_{1,0,0}$
, both equivalent to
$f_{2,0,0} = f_{0,1,0} + 12\delta f_{1,0,0}$
, both equivalent to
![]() $f_{0,1,0}$
. Therefore, we only need to prove the theorem in two situations:
$f_{0,1,0}$
. Therefore, we only need to prove the theorem in two situations:
![]() $b\ge 0$
and
$b\ge 0$
and
![]() $c<0$
, or
$c<0$
, or
![]() $b<0$
and
$b<0$
and
![]() $c\ge 0$
.
$c\ge 0$
.
If
![]() $b\ge 0$
and
$b\ge 0$
and
![]() $c<0$
, then there is only one form
$c<0$
, then there is only one form
![]() $f_{a,b,c}\in V_4$
with
$f_{a,b,c}\in V_4$
with
![]() $c=-1$
. Indeed, solving
$c=-1$
. Indeed, solving
![]() $4=2a+4b+6c=2a+4b-6$
, we get
$4=2a+4b+6c=2a+4b-6$
, we get
![]() $a=1$
and
$a=1$
and
![]() $b=2$
. By the hypothesis, this form
$b=2$
. By the hypothesis, this form
![]() $f_{1,2,-1}\sim f_{0,1,0}$
. For
$f_{1,2,-1}\sim f_{0,1,0}$
. For
![]() $c\le -2$
, we use equation (3) (with
$c\le -2$
, we use equation (3) (with
![]() $k=2$
) in the form
$k=2$
) in the form
and induction on
![]() $-c$
to conclude that
$-c$
to conclude that
![]() $f_{a,b,c}$
is equivalent to a linear combination of
$f_{a,b,c}$
is equivalent to a linear combination of
![]() $f_{1,2,-1}$
and
$f_{1,2,-1}$
and
![]() $f_{0,1,0}$
, and hence to
$f_{0,1,0}$
, and hence to
![]() $f_{0,1,0}$
alone. (Notice that prefactors
$f_{0,1,0}$
alone. (Notice that prefactors
![]() $a/12$
and
$a/12$
and
![]() $(a-2)/12$
leave the terms on the right-hand side in
$(a-2)/12$
leave the terms on the right-hand side in
![]() $V_4$
.)
$V_4$
.)
If
![]() $b<0$
(and
$b<0$
(and
![]() $c\ge 0$
), we use equation (3) in the form
$c\ge 0$
), we use equation (3) in the form
When
![]() $b=-1$
and
$b=-1$
and
![]() $b=-2$
, the only forms
$b=-2$
, the only forms
![]() $f_{a,b,c}\in V_4$
possible with
$f_{a,b,c}\in V_4$
possible with
![]() $c\ge 0$
are
$c\ge 0$
are
![]() $f_{1,-1,1}$
and
$f_{1,-1,1}$
and
![]() $f_{0,-2,2}$
, respectively. Substituting
$f_{0,-2,2}$
, respectively. Substituting
![]() $a=0$
,
$a=0$
,
![]() $b=-2$
, and
$b=-2$
, and
![]() $c=2$
in (4) leads to
$c=2$
in (4) leads to
implying
![]() $f_{1,-1,1}\sim f_{0,-2,2}\sim f_{0,1,0}$
from the hypothesis. For
$f_{1,-1,1}\sim f_{0,-2,2}\sim f_{0,1,0}$
from the hypothesis. For
![]() $b\le -3$
, we use (4) to conclude by induction on
$b\le -3$
, we use (4) to conclude by induction on
![]() $-b$
that any such
$-b$
that any such
![]() $f_{a,b,c}$
is equivalent to a linear combination of
$f_{a,b,c}$
is equivalent to a linear combination of
![]() $f_{0,-2,2}$
,
$f_{0,-2,2}$
,
![]() $f_{1,-1,1}$
, and
$f_{1,-1,1}$
, and
![]() $f_{0,1,0}$
, and hence to
$f_{0,1,0}$
, and hence to
![]() $f_{0,1,0}$
. This completes the proof of the theorem.
$f_{0,1,0}$
. This completes the proof of the theorem.
Remark 2. It follows from the proof that we can replace the generator
![]() $f_{0,-2,2}-f_{0,1,0}$
with
$f_{0,-2,2}-f_{0,1,0}$
with
![]() $f_{1,-1,1}-f_{0,1,0}$
. Furthermore, alternative choices for
$f_{1,-1,1}-f_{0,1,0}$
. Furthermore, alternative choices for
![]() $f_{0,-2,2}-f_{0,1,0}$
and
$f_{0,-2,2}-f_{0,1,0}$
and
![]() $f_{1,2,-1}-f_{0,1,0}$
are
$f_{1,2,-1}-f_{0,1,0}$
are
![]() $\tilde F_j=E_2\cdot (\delta E_j)/E_j$
or
$\tilde F_j=E_2\cdot (\delta E_j)/E_j$
or
![]() $\hat F_j=(\delta ^2E_j)/E_j$
, for
$\hat F_j=(\delta ^2E_j)/E_j$
, for
![]() $j=4,6$
.
$j=4,6$
.
For weight
![]() $6$
, the situation is slightly different. Only the following is true.
$6$
, the situation is slightly different. Only the following is true.
Theorem 4. Let
![]() $U_6$
be the subspace of
$U_6$
be the subspace of
![]() $V_6$
spanned over
$V_6$
spanned over
![]() $\mathbb Q$
by
$\mathbb Q$
by
![]() $f_{a,b,c}$
with the additional constraint
$f_{a,b,c}$
with the additional constraint
![]() $c\ge 0$
, and
$c\ge 0$
, and
![]() $U_6^0=U_6\cap V_6^0$
its cuspidal subspace. Then any element of
$U_6^0=U_6\cap V_6^0$
its cuspidal subspace. Then any element of
![]() $U_6^0$
is magnetic.
$U_6^0$
is magnetic.
Remark 3. In fact, it seems that the space
![]() $U_6^0$
possesses the strongly magnetic property: the anti-derivative of any difference of two
$U_6^0$
possesses the strongly magnetic property: the anti-derivative of any difference of two
![]() $f_{a,b,c}$
from
$f_{a,b,c}$
from
![]() $U_6$
has an integral q-expansion.
$U_6$
has an integral q-expansion.
Proof. For
![]() $c=0$
, we only have two elements
$c=0$
, we only have two elements
![]() $f_{3,0,0}$
and
$f_{3,0,0}$
and
![]() $f_{1,1,0}$
in
$f_{1,1,0}$
in
![]() $U_6$
, and
$U_6$
, and
![]() $f_{3,0,0}\sim f_{1,1,0}$
since
$f_{3,0,0}\sim f_{1,1,0}$
since
![]() $ f_{3,0,0}- f_{1,1,0}=6\delta f_{2,0,0}$
. Moreover, they are both strongly equivalent to
$ f_{3,0,0}- f_{1,1,0}=6\delta f_{2,0,0}$
. Moreover, they are both strongly equivalent to
![]() $f_{0,0,1}$
, because
$f_{0,0,1}$
, because
![]() $f_{1,1,0}-f_{0,0,1}=3\delta E_4$
.
$f_{1,1,0}-f_{0,0,1}=3\delta E_4$
.
For
![]() $c=1$
, we find out that
$c=1$
, we find out that
![]() $f_{0,0,1}$
,
$f_{0,0,1}$
,
![]() $f_{2,-1,1}$
, and
$f_{2,-1,1}$
, and
![]() $f_{4,-2,1}$
are in
$f_{4,-2,1}$
are in
![]() $U_6$
. Then
$U_6$
. Then
![]() $f_{4,-2,1}$
is strongly equivalent to any of
$f_{4,-2,1}$
is strongly equivalent to any of
![]() $f_{3,0,0}$
,
$f_{3,0,0}$
,
![]() $f_{1,1,0}$
, and
$f_{1,1,0}$
, and
![]() $f_{0,0,1}$
in accordance with
$f_{0,0,1}$
in accordance with
![]() $ f_{4,-2,1}-f_{3,0,0}=3\delta f_{4,-1,0}$
and the above. With the help of Theorem 2 and derivation
$ f_{4,-2,1}-f_{3,0,0}=3\delta f_{4,-1,0}$
and the above. With the help of Theorem 2 and derivation
we see that the same is true for
![]() $f_{2,-1,1}$
.
$f_{2,-1,1}$
.
We have just shown that any element in the subspace
![]() $U_6^0$
generated by
$U_6^0$
generated by
![]() $f_{a,b,c}$
with
$f_{a,b,c}$
with
![]() $c\in \{0,1\}$
does have the (strongly) magnetic property. For the rest of our theorem, we proceed by induction over c using the following consequence of equation (3) when
$c\in \{0,1\}$
does have the (strongly) magnetic property. For the rest of our theorem, we proceed by induction over c using the following consequence of equation (3) when
![]() $k=4$
:
$k=4$
:
3 A magnetic extension of the field of quasi-modular forms
The functions
![]() $\tau ,q,E_2,E_4,E_6$
are algebraically independent over
$\tau ,q,E_2,E_4,E_6$
are algebraically independent over
![]() $\mathbb C$
(see [Reference Mahler19,Reference Resnikoff22]). We can identify the differential field
$\mathbb C$
(see [Reference Mahler19,Reference Resnikoff22]). We can identify the differential field
![]() $\mathbb C\langle \tau ,q,E_2,E_4,E_6\rangle $
generated by them over
$\mathbb C\langle \tau ,q,E_2,E_4,E_6\rangle $
generated by them over
![]() $\mathbb C$
with the differential field
$\mathbb C$
with the differential field
![]() $\mathcal {K}=\mathbb C\langle \tau ,q,X,Y,Z\rangle $
equipped with the derivation
$\mathcal {K}=\mathbb C\langle \tau ,q,X,Y,Z\rangle $
equipped with the derivation
 $$ \begin{align*}D=\frac1{2\pi i}\,\frac\partial{\partial\tau}+q\frac\partial{\partial q} +\frac1{12}(X^2-Y)\frac\partial{\partial X}+\frac13(XY-Z)\frac\partial{\partial Y}+\frac12(XZ-Y^2)\frac\partial{\partial Z}. \end{align*} $$
$$ \begin{align*}D=\frac1{2\pi i}\,\frac\partial{\partial\tau}+q\frac\partial{\partial q} +\frac1{12}(X^2-Y)\frac\partial{\partial X}+\frac13(XY-Z)\frac\partial{\partial Y}+\frac12(XZ-Y^2)\frac\partial{\partial Z}. \end{align*} $$
Our goal is to demonstrate that the elements
 $$ \begin{align*}v_1=\frac{XZ}{Y}-Y \quad\text{and}\quad v_2=\frac{XY^2}{Z}-Z \end{align*} $$
$$ \begin{align*}v_1=\frac{XZ}{Y}-Y \quad\text{and}\quad v_2=\frac{XY^2}{Z}-Z \end{align*} $$
corresponding to
![]() $f_{1,-1,1}-f_{0,1,0}$
and
$f_{1,-1,1}-f_{0,1,0}$
and
![]() $f_{1,2,-1}-f_{0,1,0}$
do not have D-anti-derivatives in
$f_{1,2,-1}-f_{0,1,0}$
do not have D-anti-derivatives in
![]() $\mathcal {K}$
(not even in
$\mathcal {K}$
(not even in
![]() $\mathcal {K}\langle D^{-1}v_2\rangle $
and
$\mathcal {K}\langle D^{-1}v_2\rangle $
and
![]() $\mathcal {K}\langle D^{-1}v_1\rangle $
, respectively). This follows trivially from noticing that
$\mathcal {K}\langle D^{-1}v_1\rangle $
, respectively). This follows trivially from noticing that
![]() $\operatorname {ord}_Yv_1=-1$
and
$\operatorname {ord}_Yv_1=-1$
and
![]() $\operatorname {ord}_Zv_2=-1$
, so that if either
$\operatorname {ord}_Zv_2=-1$
, so that if either
![]() $D^{-1}v_1$
or
$D^{-1}v_1$
or
![]() $D^{-1}v_2$
existed, then
$D^{-1}v_2$
existed, then
![]() ${\operatorname {ord}_YD^{-1}v_1<0}$
and
${\operatorname {ord}_YD^{-1}v_1<0}$
and
![]() $\operatorname {ord}_ZD^{-1}v_2<0$
, hence
$\operatorname {ord}_ZD^{-1}v_2<0$
, hence
![]() $\operatorname {ord}_Yv_1=\operatorname {ord}_YD(D^{-1}v_1)\le -2$
and similarly
$\operatorname {ord}_Yv_1=\operatorname {ord}_YD(D^{-1}v_1)\le -2$
and similarly
![]() $\operatorname {ord}_Zv_2\le -2$
, contradiction.
$\operatorname {ord}_Zv_2\le -2$
, contradiction.
By [Reference Kaplansky16, Lem. 3.9] applied twice, the anti-derivatives
are algebraically independent over the field
![]() $\mathbb C\langle \tau ,q,E_2,E_4,E_6\rangle $
, and the extended differential field
$\mathbb C\langle \tau ,q,E_2,E_4,E_6\rangle $
, and the extended differential field
has transcendence degree 7 over
![]() $\mathbb C$
and is a Picard–Vessiot extension of the differential field
$\mathbb C$
and is a Picard–Vessiot extension of the differential field
![]() $\mathbb C\langle \tau ,q,E_2,E_4,E_6\rangle $
. Again, by identifying the former through the isomorphism
$\mathbb C\langle \tau ,q,E_2,E_4,E_6\rangle $
. Again, by identifying the former through the isomorphism
with the differential field
![]() $\hat {\mathcal {K}}=\mathbb C\langle \tau ,q,X,Y,Z,S,T\rangle $
equipped with the derivation
$\hat {\mathcal {K}}=\mathbb C\langle \tau ,q,X,Y,Z,S,T\rangle $
equipped with the derivation
 $$ \begin{align*} \hat D&=\frac1{2\pi i}\,\frac\partial{\partial\tau}+q\frac\partial{\partial q} +\frac1{12}(X^2-Y)\frac\partial{\partial X}+\frac13(XY-Z)\frac\partial{\partial Y}+\frac12(XZ-Y^2)\frac\partial{\partial Z} \\[6pt] &\qquad +\biggl(\frac{XZ}{Y}-Y\biggr)\frac\partial{\partial S} +\biggl(\frac{XY^2}{Z}-Z\biggr)\frac\partial{\partial T}, \end{align*} $$
$$ \begin{align*} \hat D&=\frac1{2\pi i}\,\frac\partial{\partial\tau}+q\frac\partial{\partial q} +\frac1{12}(X^2-Y)\frac\partial{\partial X}+\frac13(XY-Z)\frac\partial{\partial Y}+\frac12(XZ-Y^2)\frac\partial{\partial Z} \\[6pt] &\qquad +\biggl(\frac{XZ}{Y}-Y\biggr)\frac\partial{\partial S} +\biggl(\frac{XY^2}{Z}-Z\biggr)\frac\partial{\partial T}, \end{align*} $$
we want to demonstrate that the element
 $$ \begin{align*}v_3=\frac{X^2Z}{Y}-Z \end{align*} $$
$$ \begin{align*}v_3=\frac{X^2Z}{Y}-Z \end{align*} $$
corresponding to
![]() $f_{2,-1,1}-f_{0,0,1}$
does not have a
$f_{2,-1,1}-f_{0,0,1}$
does not have a
![]() $\hat D$
-anti-derivative in
$\hat D$
-anti-derivative in
![]() $\hat {\mathcal {K}}$
.
$\hat {\mathcal {K}}$
.
Assume on the contrary that there is an element
![]() $u_3\in \hat {\mathcal {K}}$
such that
$u_3\in \hat {\mathcal {K}}$
such that
![]() $\hat Du_3=v_3$
. Notice that the functions
$\hat Du_3=v_3$
. Notice that the functions
![]() $\tau $
,
$\tau $
,
![]() $q=e^{2\pi i\tau }$
,
$q=e^{2\pi i\tau }$
,
![]() $E_2(\tau )$
,
$E_2(\tau )$
,
![]() $E_4(\tau )$
, and
$E_4(\tau )$
, and
![]() $E_6(\tau )$
are all analytic at
$E_6(\tau )$
are all analytic at
![]() $\tau =\rho =e^{2\pi i/3}$
, the latter three having the values
$\tau =\rho =e^{2\pi i/3}$
, the latter three having the values
 $$ \begin{align*}E_2(\rho)=\frac{2\sqrt3}{\pi}, \quad E_4(\rho)=0, \quad E_6(\rho)=\biggl(\frac{3\Gamma(\frac13)^6}{8\pi^4}\biggr)^3. \end{align*} $$
$$ \begin{align*}E_2(\rho)=\frac{2\sqrt3}{\pi}, \quad E_4(\rho)=0, \quad E_6(\rho)=\biggl(\frac{3\Gamma(\frac13)^6}{8\pi^4}\biggr)^3. \end{align*} $$
With the help of Ramanujan’s system (2), we find out that
so that
 $$ \begin{align*}\begin{aligned} f_{1,-1,1}-f_{0,1,0} &=\frac{3iE_2(\rho)}{2\pi}\,\frac1{\tau-\rho}+O(1), \\[6pt] f_{2,-1,1}-f_{0,0,1} &=\frac{3iE_2(\rho)^2}{2\pi}\,\frac1{\tau-\rho}+O(1) \end{aligned} \quad\text{as}\; \tau\to\rho \end{align*} $$
$$ \begin{align*}\begin{aligned} f_{1,-1,1}-f_{0,1,0} &=\frac{3iE_2(\rho)}{2\pi}\,\frac1{\tau-\rho}+O(1), \\[6pt] f_{2,-1,1}-f_{0,0,1} &=\frac{3iE_2(\rho)^2}{2\pi}\,\frac1{\tau-\rho}+O(1) \end{aligned} \quad\text{as}\; \tau\to\rho \end{align*} $$
and
![]() $f_{1,2,-1}-f_{0,1,0}$
is analytic at
$f_{1,2,-1}-f_{0,1,0}$
is analytic at
![]() $\tau =\rho $
. In turn, this implies that
$\tau =\rho $
. In turn, this implies that
 $$ \begin{align*}\begin{aligned} \tilde E_{4a}&=-3E_2(\rho)\ln(\tau-\rho)+g_1(\tau), \\[6pt] \delta^{-1}(f_{2,-1,1}-f_{0,0,1}) &=-3E_2(\rho)^2\ln(\tau-\rho)+g_3(\tau) \end{aligned} \quad\text{as}\; \tau\to\rho \end{align*} $$
$$ \begin{align*}\begin{aligned} \tilde E_{4a}&=-3E_2(\rho)\ln(\tau-\rho)+g_1(\tau), \\[6pt] \delta^{-1}(f_{2,-1,1}-f_{0,0,1}) &=-3E_2(\rho)^2\ln(\tau-\rho)+g_3(\tau) \end{aligned} \quad\text{as}\; \tau\to\rho \end{align*} $$
for some functions
![]() $g_1(\tau )$
and
$g_1(\tau )$
and
![]() $g_3(\tau )$
analytic at
$g_3(\tau )$
analytic at
![]() $\tau =\rho $
, while
$\tau =\rho $
, while
![]() $\tilde E_{4b}(\tau )$
is analytic there. To summarize, the function
$\tilde E_{4b}(\tau )$
is analytic there. To summarize, the function
 $$ \begin{align*}\delta^{-1}(f_{2,-1,1}-f_{0,0,1}) -\frac{2\sqrt3}\pi\,\tilde E_{4a}(\tau) =\delta^{-1}(f_{2,-1,1}-f_{0,0,1}) -E_2(\rho)\tilde E_{4a}(\tau) \end{align*} $$
$$ \begin{align*}\delta^{-1}(f_{2,-1,1}-f_{0,0,1}) -\frac{2\sqrt3}\pi\,\tilde E_{4a}(\tau) =\delta^{-1}(f_{2,-1,1}-f_{0,0,1}) -E_2(\rho)\tilde E_{4a}(\tau) \end{align*} $$
is analytic at
![]() $\tau =\rho $
, and hence only representable as a rational function of
$\tau =\rho $
, and hence only representable as a rational function of
![]() $\tau ,q,E_2,E_4, E_6,\tilde E_{4b}$
. Using the isomorphism
$\tau ,q,E_2,E_4, E_6,\tilde E_{4b}$
. Using the isomorphism
![]() $\varphi $
, we conclude that
$\varphi $
, we conclude that
 $$ \begin{align*}u=u_3-\frac{2\sqrt3}\pi\,S\in\hat{\mathcal{K}} \end{align*} $$
$$ \begin{align*}u=u_3-\frac{2\sqrt3}\pi\,S\in\hat{\mathcal{K}} \end{align*} $$
is a polynomial in
![]() $\tau ,q,X,Y,Z,T$
. The latter is seen to be impossible after the operator
$\tau ,q,X,Y,Z,T$
. The latter is seen to be impossible after the operator
![]() $\hat D$
is applied to u and to
$\hat D$
is applied to u and to
 $u_3-\dfrac {2\sqrt 3}\pi \,S$
leading to a rational expression of S in terms of the other generators of
$u_3-\dfrac {2\sqrt 3}\pi \,S$
leading to a rational expression of S in terms of the other generators of
![]() $\hat {\mathcal {K}}$
. The contradiction we arrive at implies that the anti-derivative
$\hat {\mathcal {K}}$
. The contradiction we arrive at implies that the anti-derivative
is transcendental over the field
![]() $\mathbb C\langle \tau ,q,E_2,E_4,E_6,\tilde E_{4a},\tilde E_{4b}\rangle $
. On replacing the generators of the latter with the anti-derivatives of magnetic modular forms from Theorems 1 and 2, we obtain the following result.
$\mathbb C\langle \tau ,q,E_2,E_4,E_6,\tilde E_{4a},\tilde E_{4b}\rangle $
. On replacing the generators of the latter with the anti-derivatives of magnetic modular forms from Theorems 1 and 2, we obtain the following result.
Theorem 5. The differentially closed field
generated by
![]() $\tau $
,
$\tau $
,
![]() $q=e^{2\pi i\tau }$
, the Eisenstein series (1), and the anti-derivatives
$q=e^{2\pi i\tau }$
, the Eisenstein series (1), and the anti-derivatives
 $$ \begin{align*}\tilde F_{4a}=\delta^{-1}\biggl(\frac{\Delta}{E_4^2}\biggr), \quad \tilde F_{4b}=\delta^{-1}\biggl(\frac{E_4\Delta}{E_6^2}\biggr), \quad \tilde F_6=\delta^{-1}\biggl(\frac{E_6\Delta}{E_4^3}\biggr) \end{align*} $$
$$ \begin{align*}\tilde F_{4a}=\delta^{-1}\biggl(\frac{\Delta}{E_4^2}\biggr), \quad \tilde F_{4b}=\delta^{-1}\biggl(\frac{E_4\Delta}{E_6^2}\biggr), \quad \tilde F_6=\delta^{-1}\biggl(\frac{E_6\Delta}{E_4^3}\biggr) \end{align*} $$
with integral coefficients in their q-expansions, has transcendence degree
![]() $8$
over
$8$
over
![]() $\mathbb C$
.
$\mathbb C$
.
Remark 4. Another way to see that no
![]() $u_3$
exists in
$u_3$
exists in
![]() $\hat {\mathcal {K}}$
such that
$\hat {\mathcal {K}}$
such that
![]() $\hat Du_3=v_3$
is by casting
$\hat Du_3=v_3$
is by casting
![]() $u_3$
in the form
$u_3$
in the form
![]() $p/q$
with
$p/q$
with
![]() $p,q$
in the ring
$p,q$
in the ring
![]() $\mathcal R[S]$
, where
$\mathcal R[S]$
, where
![]() $\mathcal R=\mathbb C\langle \tau ,q,X,Y,Z,T\rangle $
, and
$\mathcal R=\mathbb C\langle \tau ,q,X,Y,Z,T\rangle $
, and
![]() $\gcd (p,q)=1$
. After clearing the denominators in
$\gcd (p,q)=1$
. After clearing the denominators in
![]() $\hat D(p/q)=v_3$
and comparing the degree in S on both sides, one concludes that
$\hat D(p/q)=v_3$
and comparing the degree in S on both sides, one concludes that
![]() $\hat Dq=uq$
for some
$\hat Dq=uq$
for some
![]() $u\in \mathcal R$
(i.e., independent of S). This leads to conclusion
$u\in \mathcal R$
(i.e., independent of S). This leads to conclusion
![]() $q\in \mathcal R$
, so that
$q\in \mathcal R$
, so that
![]() $u_3$
is a polynomial in S. Finally, the equation
$u_3$
is a polynomial in S. Finally, the equation
![]() $\hat Du_3=X^2Z/Y-Z$
is seen to be impossible by comparing the order in Y on both sides.
$\hat Du_3=X^2Z/Y-Z$
is seen to be impossible by comparing the order in Y on both sides.
Exercise 1. We leave to the reader the exercise to prove that the anti-derivative of
![]() $\tilde F_6$
(in turn, the second anti-derivative of
$\tilde F_6$
(in turn, the second anti-derivative of
![]() $F_6$
) is transcendental over the field in Theorem 5.
$F_6$
) is transcendental over the field in Theorem 5.
4 Half-integral weight weakly holomorphic modular forms
Following the ideas in [Reference Li and Neururer17], we cast magnetic modular forms of weight
![]() $2k$
as the images of weakly holomorphic eigenforms of weight
$2k$
as the images of weakly holomorphic eigenforms of weight
![]() $k+1/2$
under the Shimura–Borcherds (SB) lift. In our settings, an input for the lift is a form
$k+1/2$
under the Shimura–Borcherds (SB) lift. In our settings, an input for the lift is a form
![]() $f(\tau )=\sum _{n\gg -\infty }a(n)q^n$
from the Kohnen plus space
$f(\tau )=\sum _{n\gg -\infty }a(n)q^n$
from the Kohnen plus space
![]() $M_{k+1/2}^{!,+}$
(meaning that
$M_{k+1/2}^{!,+}$
(meaning that
![]() $a(n)$
vanishes when
$a(n)$
vanishes when
![]() $(-1)^kn\not \equiv 0,1\bmod 4$
); the output is the meromorphic modular form
$(-1)^kn\not \equiv 0,1\bmod 4$
); the output is the meromorphic modular form
![]() $\Psi (f)(\tau )=\sum _{n>0}A(n)q^n$
with
$\Psi (f)(\tau )=\sum _{n>0}A(n)q^n$
with
 $$ \begin{align} A(n)=\sum_{d\mid n}\bigg(\frac dD\bigg)d^{k-1}a(|D|\,n^2/d^2), \end{align} $$
$$ \begin{align} A(n)=\sum_{d\mid n}\bigg(\frac dD\bigg)d^{k-1}a(|D|\,n^2/d^2), \end{align} $$
where
![]() $D=D_k=1$
for k even (so that the Kronecker–Jacobi symbol
$D=D_k=1$
for k even (so that the Kronecker–Jacobi symbol
![]() $\big (\frac dD\big )$
is always 1) and
$\big (\frac dD\big )$
is always 1) and
![]() $D=D_k=-3$
for k odd. In other words,
$D=D_k=-3$
for k odd. In other words,
 $$ \begin{align} \Psi=\Psi_k\colon f=\sum_{n\gg-\infty}a(n)q^n \mapsto F=\sum_{n>0}q^n\sum_{d\mid n}\bigg(\frac d{D_k}\bigg)d^{k-1}a(|D_k|\,n^2/d^2), \end{align} $$
$$ \begin{align} \Psi=\Psi_k\colon f=\sum_{n\gg-\infty}a(n)q^n \mapsto F=\sum_{n>0}q^n\sum_{d\mid n}\bigg(\frac d{D_k}\bigg)d^{k-1}a(|D_k|\,n^2/d^2), \end{align} $$
and the latter expression is just
![]() $F=\sum _{n>0}q^n\sum _{d\mid n}d^{k-1}a(n^2/d^2)$
when k is even. We also distinguish the Kohnen plus cuspidal space
$F=\sum _{n>0}q^n\sum _{d\mid n}d^{k-1}a(n^2/d^2)$
when k is even. We also distinguish the Kohnen plus cuspidal space
![]() $S_{k+1/2}^{!,+}$
in
$S_{k+1/2}^{!,+}$
in
![]() $M_{k+1/2}^{!,+}$
by imposing the additional constraint
$M_{k+1/2}^{!,+}$
by imposing the additional constraint
![]() $a(0)=0$
.
$a(0)=0$
.
Our examples of forms from
![]() $M_{k+1/2}^{!,+}$
with
$M_{k+1/2}^{!,+}$
with
![]() $k=2$
involved in the proof of Theorem 1 are the following three:
$k=2$
involved in the proof of Theorem 1 are the following three:
 $$ \begin{align*} g_0(\tau)&=\theta(\tau)\,(\theta(\tau)^4-20 E_{2,4}(\tau)) \\[6pt] &=1 - 10q - 70q^4 - 48q^5 - 120q^8 - 250q^9 - \dotsb - 550q^{16} - \dotsb \\[6pt] &\quad - 1210q^{25} - \dotsb - 1750q^{36} - \dotsb - 3370q^{49} -\dotsb, \\[6pt] g_1(\tau)&=\frac{\theta(\tau)E_4(4\tau)^2E_6(4\tau)}{\Delta(4\tau)} \\[6pt] &=q^{-4} + 2q^{-3} + 2 - 196884q^4 - \dotsb - 85975040q^9 - \dotsb \\[6pt] &\quad - 86169224844q^{16} - \dotsb - 51186246451200q^{25} - \dotsb \\[6pt] &\quad - 35015148280961780q^{36} - \dotsb - 21434928162930081792q^{49} - \dotsb, \nonumber \\ g_2(\tau)&=\frac{g_0(\tau)E_4(4\tau)^3}{\Delta(4\tau)} \\[6pt] &=q^{-4} - 10q^{-3} + 674 - 7488q + 144684q^4 - \dotsb - 224,574,272q^9 - \dotsb \\[6pt] &\quad - 42882054732q^{16} - \dotsb - 63793268216640q^{25} - \dotsb \\[6pt] &\quad - 31501841125150388q^{36} - \dotsb - 22385069000981561664q^{49} - \dotsb, \end{align*} $$
$$ \begin{align*} g_0(\tau)&=\theta(\tau)\,(\theta(\tau)^4-20 E_{2,4}(\tau)) \\[6pt] &=1 - 10q - 70q^4 - 48q^5 - 120q^8 - 250q^9 - \dotsb - 550q^{16} - \dotsb \\[6pt] &\quad - 1210q^{25} - \dotsb - 1750q^{36} - \dotsb - 3370q^{49} -\dotsb, \\[6pt] g_1(\tau)&=\frac{\theta(\tau)E_4(4\tau)^2E_6(4\tau)}{\Delta(4\tau)} \\[6pt] &=q^{-4} + 2q^{-3} + 2 - 196884q^4 - \dotsb - 85975040q^9 - \dotsb \\[6pt] &\quad - 86169224844q^{16} - \dotsb - 51186246451200q^{25} - \dotsb \\[6pt] &\quad - 35015148280961780q^{36} - \dotsb - 21434928162930081792q^{49} - \dotsb, \nonumber \\ g_2(\tau)&=\frac{g_0(\tau)E_4(4\tau)^3}{\Delta(4\tau)} \\[6pt] &=q^{-4} - 10q^{-3} + 674 - 7488q + 144684q^4 - \dotsb - 224,574,272q^9 - \dotsb \\[6pt] &\quad - 42882054732q^{16} - \dotsb - 63793268216640q^{25} - \dotsb \\[6pt] &\quad - 31501841125150388q^{36} - \dotsb - 22385069000981561664q^{49} - \dotsb, \end{align*} $$
where
![]() $\theta (\tau )=\sum _{n\in \mathbb Z}q^{n^2}$
and
$\theta (\tau )=\sum _{n\in \mathbb Z}q^{n^2}$
and
 $$ \begin{align} E_{2,4}(\tau) =\frac{-E_2(\tau)+3E_2(2\tau)-2E_2(4\tau)}{24} =\sum_{\substack{n=1\\ n\;\text{odd}}}^{\infty} q^n\sum_{d\mid n}d. \end{align} $$
$$ \begin{align} E_{2,4}(\tau) =\frac{-E_2(\tau)+3E_2(2\tau)-2E_2(4\tau)}{24} =\sum_{\substack{n=1\\ n\;\text{odd}}}^{\infty} q^n\sum_{d\mid n}d. \end{align} $$
The modular form
![]() $g_0(\tau )$
is known by the name of normalized Cohen–Eisenstein series of weight
$g_0(\tau )$
is known by the name of normalized Cohen–Eisenstein series of weight
![]() $5/2$
.
$5/2$
.
Lemma 1.
-
(a) The weight
 $5/2$
weakly holomorphic modular form lies in the Kohnen plus cuspidal space
$5/2$
weakly holomorphic modular form lies in the Kohnen plus cuspidal space $$ \begin{align*}f_{4a}(\tau) = \frac{7}{8} g_0(\tau) + \frac{1}{768} g_1(\tau) - \frac{1}{768} g_2(\tau) = \frac{1}{64}q^{-3} + q - 506q^4 + \dotsb \end{align*} $$
$$ \begin{align*}f_{4a}(\tau) = \frac{7}{8} g_0(\tau) + \frac{1}{768} g_1(\tau) - \frac{1}{768} g_2(\tau) = \frac{1}{64}q^{-3} + q - 506q^4 + \dotsb \end{align*} $$
 $S^{!,+}_{5/2}$
, and its SB lift
$S^{!,+}_{5/2}$
, and its SB lift
 $\Psi (f_{4a})$
is
$\Psi (f_{4a})$
is
 $F_{4a}=\Delta /E_4^2$
.
$F_{4a}=\Delta /E_4^2$
.
-
(b) The weight
 $5/2$
weakly holomorphic modular form lies in the Kohnen plus cuspidal space
$5/2$
weakly holomorphic modular form lies in the Kohnen plus cuspidal space $$ \begin{align*}f_{4b}(\tau) = \frac{19}{18} g_0(\tau) -\frac{5}{648} g_1(\tau) - \frac{1}{648} g_2(\tau) = -\frac{1}{108}q^{-4} + q + 1222q^4 + \dotsb \end{align*} $$
$$ \begin{align*}f_{4b}(\tau) = \frac{19}{18} g_0(\tau) -\frac{5}{648} g_1(\tau) - \frac{1}{648} g_2(\tau) = -\frac{1}{108}q^{-4} + q + 1222q^4 + \dotsb \end{align*} $$
 $S^{!,+}_{5/2}$
, and its SB lift
$S^{!,+}_{5/2}$
, and its SB lift
 $\Psi (f_{4b})$
is
$\Psi (f_{4b})$
is
 $E_4\Delta /E_6^2$
.
$E_4\Delta /E_6^2$
.
Moreover,
![]() $f_{4a}\in \frac {1}{64} q^{-3}\mathbb {Z}[[q]]$
and
$f_{4a}\in \frac {1}{64} q^{-3}\mathbb {Z}[[q]]$
and
![]() $f_{4b}\in \frac {1}{108} q^{-4}\mathbb {Z}[[q]]$
.
$f_{4b}\in \frac {1}{108} q^{-4}\mathbb {Z}[[q]]$
.
The identification
![]() $\Psi (f_{4a})=F_{4a}$
is already in Borcherds’ [Reference Broadhurst and Zudilin5, Exam. 14.4].
$\Psi (f_{4a})=F_{4a}$
is already in Borcherds’ [Reference Broadhurst and Zudilin5, Exam. 14.4].
Proof. Indeed, we only need to check that
![]() $f_{4a},f_{4b}$
have vanishing constant term and that the first three coefficients in the q-expansions of
$f_{4a},f_{4b}$
have vanishing constant term and that the first three coefficients in the q-expansions of
![]() $\Psi (f_{4a})$
,
$\Psi (f_{4a})$
,
![]() $\Psi (f_{4b})$
agree with those of the predicted meromorphic modular forms; we choose to check the first seven coefficients.
$\Psi (f_{4b})$
agree with those of the predicted meromorphic modular forms; we choose to check the first seven coefficients.
For the integrality statement, we use the alternative expressions
 $$ \begin{align*}64f_{4a}(\tau)= \frac{f_{14+1/2}^*(\tau)}{\Delta(4\tau)} \end{align*} $$
$$ \begin{align*}64f_{4a}(\tau)= \frac{f_{14+1/2}^*(\tau)}{\Delta(4\tau)} \end{align*} $$
and
 $$ \begin{align*}-108f_{4b}(\tau)= \frac{ f_{14+1/2}(\tau)\,(j(4\tau)-674)+10 f_{14+1/2}^*(\tau)}{\Delta(4\tau)}, \end{align*} $$
$$ \begin{align*}-108f_{4b}(\tau)= \frac{ f_{14+1/2}(\tau)\,(j(4\tau)-674)+10 f_{14+1/2}^*(\tau)}{\Delta(4\tau)}, \end{align*} $$
where the forms
![]() $f_{b+1/2}(\tau ), f^*_{b+1/2}(\tau )$
are the holomorphic modular forms of weight
$f_{b+1/2}(\tau ), f^*_{b+1/2}(\tau )$
are the holomorphic modular forms of weight
![]() $b+1/2$
with integral q-expansions from the table in [Reference Duke and Jenkins8, Appendix] and
$b+1/2$
with integral q-expansions from the table in [Reference Duke and Jenkins8, Appendix] and
![]() $j(\tau )=E_4(\tau )^3/\Delta (\tau )$
is the elliptic modular invariant.
$j(\tau )=E_4(\tau )^3/\Delta (\tau )$
is the elliptic modular invariant.
As we see further, for certain forms
![]() $\sum _{n\gg -\infty }a(n)q^n\in S^{!,+}_{5/2}$
with integral q-expansions (in particular, for the forms
$\sum _{n\gg -\infty }a(n)q^n\in S^{!,+}_{5/2}$
with integral q-expansions (in particular, for the forms
![]() $64f_{4a}$
and
$64f_{4a}$
and
![]() $108f_{4b}$
), one can make use of Hecke operators to conclude with the divisibility
$108f_{4b}$
), one can make use of Hecke operators to conclude with the divisibility
![]() $n\mid a(n^2)$
for
$n\mid a(n^2)$
for
![]() $n>0$
. This readily implies that
$n>0$
. This readily implies that
![]() $64F_{4a}$
and
$64F_{4a}$
and
![]() $108F_{4b}$
in Theorem 1 are strongly magnetic modular forms, since the relation in (5) translates the divisibility into
$108F_{4b}$
in Theorem 1 are strongly magnetic modular forms, since the relation in (5) translates the divisibility into
 $$ \begin{align*}\frac{A(n)}n =\sum_{d\mid n}\frac{a(n^2/d^2)}{n/d} =\sum_{d\mid n}\frac{a(d^2)}{d}\in\mathbb Z. \end{align*} $$
$$ \begin{align*}\frac{A(n)}n =\sum_{d\mid n}\frac{a(n^2/d^2)}{n/d} =\sum_{d\mid n}\frac{a(d^2)}{d}\in\mathbb Z. \end{align*} $$
A detailed analysis below reveals that the factors
![]() $64$
and
$64$
and
![]() $108$
can be also removed.
$108$
can be also removed.
5 The square part and Hecke operators
We refer the reader to [Reference Borcherds6,Reference Duke and Jenkins8] for the definition of Hecke operators
![]() $\mathcal {T}_p$
and
$\mathcal {T}_p$
and
![]() $T_{p^2}$
on integral weight
$T_{p^2}$
on integral weight
![]() $2k$
and half-integral weight
$2k$
and half-integral weight
![]() $k+1/2$
modular forms (including weakly holomorphic or meromorphic), respectively. As in the case of the SB lift
$k+1/2$
modular forms (including weakly holomorphic or meromorphic), respectively. As in the case of the SB lift
![]() $\Psi =\Psi _k$
in (6), these definitions make perfect sense for any Laurent series
$\Psi =\Psi _k$
in (6), these definitions make perfect sense for any Laurent series
![]() $f=\sum _{n\gg -\infty }a(n)q^n$
, not necessarily of modular origin, but with the weight
$f=\sum _{n\gg -\infty }a(n)q^n$
, not necessarily of modular origin, but with the weight
![]() $2k$
or
$2k$
or
![]() $k+1/2$
additionally supplied. We refer to the finite sum
$k+1/2$
additionally supplied. We refer to the finite sum
![]() $\sum _{n<0}a(n)q^n$
as to the principal part of f. We take
$\sum _{n<0}a(n)q^n$
as to the principal part of f. We take
for a character
![]() $\chi \colon \mathbb {Z}\to \mathbb C$
, and define
$\chi \colon \mathbb {Z}\to \mathbb C$
, and define
and
where
![]() $\chi _p(n)=\chi _{p,k}(n)=\big (\frac {(-1)^kn}p\big )$
is the Kronecker–Jacobi symbol.
$\chi _p(n)=\chi _{p,k}(n)=\big (\frac {(-1)^kn}p\big )$
is the Kronecker–Jacobi symbol.
A simple calculation shows that
![]() $\Psi _k(f){\kern 1.5pt|\kern 1.5pt}(\mathcal {T}_p,2k)=\Psi _k\big (f{\kern 1.5pt|\kern 1.5pt}(T_{p^2},k+1/2)\big )$
, which we can reproduce in a simplified form
$\Psi _k(f){\kern 1.5pt|\kern 1.5pt}(\mathcal {T}_p,2k)=\Psi _k\big (f{\kern 1.5pt|\kern 1.5pt}(T_{p^2},k+1/2)\big )$
, which we can reproduce in a simplified form
when k is fixed.
Lemma 2. Given a positive integer k, assume that there are no cusp forms of weight
![]() $2k$
. For a prime p, let
$2k$
. For a prime p, let
![]() $f\in M^{!,+}_{k+1/2}$
have p-integral coefficients and satisfy
$f\in M^{!,+}_{k+1/2}$
have p-integral coefficients and satisfy
![]() $p^2>-\operatorname {ord}_q(f)$
. Then
$p^2>-\operatorname {ord}_q(f)$
. Then
Proof. Following the argument in [Reference Borcherds6, Proof of Lem. 3.1], we can write
 $$ \begin{align} T_{p^2}^n =\sum_{\substack{a,b,c,r\ge0\\ a+b+c=n\\ r\le\min\{a,c\}}} \alpha_{a,b,c,r}\cdot p^{(2k-1)c+(k-1)b}\cdot U_{p^2}^{a-r}\chi_p^bV_{p^2}^{c-r}, \end{align} $$
$$ \begin{align} T_{p^2}^n =\sum_{\substack{a,b,c,r\ge0\\ a+b+c=n\\ r\le\min\{a,c\}}} \alpha_{a,b,c,r}\cdot p^{(2k-1)c+(k-1)b}\cdot U_{p^2}^{a-r}\chi_p^bV_{p^2}^{c-r}, \end{align} $$
where
![]() $\alpha _{a,b,c,r}$
are some integers. This writing can be easily deduced from
$\alpha _{a,b,c,r}$
are some integers. This writing can be easily deduced from
![]() $V_{p^2}\chi _p =\chi _p U_{p^2}= 0$
and the fact that
$V_{p^2}\chi _p =\chi _p U_{p^2}= 0$
and the fact that
![]() $V_{p^2}U_{p^2}$
is the identity. We only need to analyze the principal part of
$V_{p^2}U_{p^2}$
is the identity. We only need to analyze the principal part of
![]() $f{\kern 1.5pt|\kern 1.5pt} T_{p^2}^n$
which, by the hypothesis
$f{\kern 1.5pt|\kern 1.5pt} T_{p^2}^n$
which, by the hypothesis
![]() $\dim S_{2k}=0$
, determines it uniquely.
$\dim S_{2k}=0$
, determines it uniquely.
If
![]() $r<a$
, then
$r<a$
, then
![]() $f{\kern 1.5pt|\kern 1.5pt} U_{p^2}^{a-r}\chi _p^b V_{p^2}^{c-r}$
has no principal part, because the latter is killed by a single action of
$f{\kern 1.5pt|\kern 1.5pt} U_{p^2}^{a-r}\chi _p^b V_{p^2}^{c-r}$
has no principal part, because the latter is killed by a single action of
![]() $U_{p^2}$
(since
$U_{p^2}$
(since
![]() $a_{-p^2m}=0$
for any
$a_{-p^2m}=0$
for any
![]() $m\ge 0$
). Therefore, we may assume that
$m\ge 0$
). Therefore, we may assume that
![]() $a=r\le c$
. This implies that
$a=r\le c$
. This implies that
![]() $(2k-1)c+(k-1)b\ge (k-1)(2c+b)\ge (k-1)n$
, and hence the principal of
$(2k-1)c+(k-1)b\ge (k-1)(2c+b)\ge (k-1)n$
, and hence the principal of
![]() $ f{\kern 1.5pt|\kern 1.5pt} T_{p^2}^n$
part is divisible by
$ f{\kern 1.5pt|\kern 1.5pt} T_{p^2}^n$
part is divisible by
![]() $p^{(k-1)n}$
. This, in turn, implies that
$p^{(k-1)n}$
. This, in turn, implies that
![]() $f{\kern 1.5pt|\kern 1.5pt} T_{p^2}^n=p^{(k-1)n}\cdot g$
for some
$f{\kern 1.5pt|\kern 1.5pt} T_{p^2}^n=p^{(k-1)n}\cdot g$
for some
![]() $g\in \mathcal {M}_{k+1/2}^{!,+}$
with p-integral coefficients, since there is a basis
$g\in \mathcal {M}_{k+1/2}^{!,+}$
with p-integral coefficients, since there is a basis
![]() $\{g_m=q^m+O(q):m\in \mathbb {Z},\;(-1)^km\equiv 0\}$
of
$\{g_m=q^m+O(q):m\in \mathbb {Z},\;(-1)^km\equiv 0\}$
of
![]() $M^{!,+}_{k+1/2}$
whose elements have all coefficients integral (see [Reference Duke and Jenkins8, Prop. 2]).
$M^{!,+}_{k+1/2}$
whose elements have all coefficients integral (see [Reference Duke and Jenkins8, Prop. 2]).
In parallel with (6), define
 $$ \begin{align*} \Phi=\Phi_k\colon g=\sum_{n\gg-\infty}b(n)q^n \mapsto \sum_{n>0}q^{|D_k|n^2}\sum_{d\mid n}\bigg(\frac d{D_k}\bigg)d^{k-1}\mu(d)b(n/d), \end{align*} $$
$$ \begin{align*} \Phi=\Phi_k\colon g=\sum_{n\gg-\infty}b(n)q^n \mapsto \sum_{n>0}q^{|D_k|n^2}\sum_{d\mid n}\bigg(\frac d{D_k}\bigg)d^{k-1}\mu(d)b(n/d), \end{align*} $$
where
![]() $\mu (\,\cdot \,)$
is the Möbius function and, as before,
$\mu (\,\cdot \,)$
is the Möbius function and, as before,
![]() $D_k=2\cdot (-1)^k-1\in \{1,-3\}$
. We further define the square part of a Laurent series
$D_k=2\cdot (-1)^k-1\in \{1,-3\}$
. We further define the square part of a Laurent series
![]() $f=\sum _{n\gg -\infty }a(n)q^n$
as
$f=\sum _{n\gg -\infty }a(n)q^n$
as
 $$ \begin{align*}f^{\square}=\sum_{n>0} a(|D_k|n^2) q^{|D_k| n^2}. \end{align*} $$
$$ \begin{align*}f^{\square}=\sum_{n>0} a(|D_k|n^2) q^{|D_k| n^2}. \end{align*} $$
The definitions immediately lead to the following conclusions.
Lemma 3. We have
![]() $\Phi (\Psi (f))=f^{\square }$
. In particular, if
$\Phi (\Psi (f))=f^{\square }$
. In particular, if
![]() $\Psi (f)\in q\mathbb {Z}[[q]]$
, then
$\Psi (f)\in q\mathbb {Z}[[q]]$
, then
![]() $f^{\square }\in q\mathbb {Z}[[q]]$
.
$f^{\square }\in q\mathbb {Z}[[q]]$
.
Notice that
![]() $f_{4a}^\square , f_{4b}^\square \in q\mathbb {Z}[[q]]$
by this lemma, because both
$f_{4a}^\square , f_{4b}^\square \in q\mathbb {Z}[[q]]$
by this lemma, because both
![]() $F_{4a}=\Psi (f_{4a})$
and
$F_{4a}=\Psi (f_{4a})$
and
![]() $F_{4b}=\Psi (f_{4b})$
are in
$F_{4b}=\Psi (f_{4b})$
are in
![]() $q\mathbb {Z}[[q]]$
.
$q\mathbb {Z}[[q]]$
.
In addition to this, we list some other easily verifiable properties about the interaction of Hecke operators and square parts.
Lemma 4. Given a Laurent series
![]() $f=\sum _{n\gg -\infty }a(n)q^n$
and positive integer k, the following statements are true.
$f=\sum _{n\gg -\infty }a(n)q^n$
and positive integer k, the following statements are true.
-
(a)
 $\Psi (f){\kern 1.5pt|\kern 1.5pt}\mathcal {T}_p^n=\Psi (f{\kern 1.5pt|\kern 1.5pt} T_{p^2}^n)$
for
$\Psi (f){\kern 1.5pt|\kern 1.5pt}\mathcal {T}_p^n=\Psi (f{\kern 1.5pt|\kern 1.5pt} T_{p^2}^n)$
for
 $n=1,2,\dots $
.
$n=1,2,\dots $
. -
(b)
 $\Psi (f)=\Psi (f^\square )$
.
$\Psi (f)=\Psi (f^\square )$
. -
(c)
 $(f{\kern 1.5pt|\kern 1.5pt} T_{p^2})^{\square }=f^{\square }{\kern 1.5pt|\kern 1.5pt} T_{p^2}$
termwise, that is,
$(f{\kern 1.5pt|\kern 1.5pt} T_{p^2})^{\square }=f^{\square }{\kern 1.5pt|\kern 1.5pt} T_{p^2}$
termwise, that is,
 $(f{\kern 1.5pt|\kern 1.5pt} U_{p^2})^{\square }=f^{\square }{\kern 1.5pt|\kern 1.5pt} U_{p^2}$
,
$(f{\kern 1.5pt|\kern 1.5pt} U_{p^2})^{\square }=f^{\square }{\kern 1.5pt|\kern 1.5pt} U_{p^2}$
,
 $(f{\kern 1.5pt|\kern 1.5pt} V_{p^2})^{\square }=f^{\square }{\kern 1.5pt|\kern 1.5pt} V_{p^2}$
, and
$(f{\kern 1.5pt|\kern 1.5pt} V_{p^2})^{\square }=f^{\square }{\kern 1.5pt|\kern 1.5pt} V_{p^2}$
, and
 $(f{\kern 1.5pt|\kern 1.5pt} \chi _p)^{\square }=f^{\square }{\kern 1.5pt|\kern 1.5pt} \chi _p$
.
$(f{\kern 1.5pt|\kern 1.5pt} \chi _p)^{\square }=f^{\square }{\kern 1.5pt|\kern 1.5pt} \chi _p$
. -
(d) If the coefficients of f are integral and
 $k\ge 2$
, then
$k\ge 2$
, then
 $f{\kern 1.5pt|\kern 1.5pt} T_{p^2}\equiv f{\kern 1.5pt|\kern 1.5pt} U_p^2\bmod p$
.
$f{\kern 1.5pt|\kern 1.5pt} T_{p^2}\equiv f{\kern 1.5pt|\kern 1.5pt} U_p^2\bmod p$
.
Proof of Theorem 1
Consider
![]() $f\in \{f_{4a},f_{4b}\}$
. For a prime
$f\in \{f_{4a},f_{4b}\}$
. For a prime
![]() $p\ge 5$
, the form f is p-integral and we have
$p\ge 5$
, the form f is p-integral and we have
![]() $\operatorname {ord}_q(f)\ge -4$
; therefore, Lemma 2 with
$\operatorname {ord}_q(f)\ge -4$
; therefore, Lemma 2 with
![]() $k=2$
applies to result in
$k=2$
applies to result in
Applying SB map (6), we deduce that, for
![]() $F=\Psi (f)\in \{F_{4a},F_{4b}\}$
, we have
$F=\Psi (f)\in \{F_{4a},F_{4b}\}$
, we have
![]() $F{\kern 1.5pt|\kern 1.5pt} \mathcal {T}_p^n\equiv 0 \bmod p^{n}$
for all
$F{\kern 1.5pt|\kern 1.5pt} \mathcal {T}_p^n\equiv 0 \bmod p^{n}$
for all
![]() $n\ge 1$
, and hence
$n\ge 1$
, and hence
![]() $F{\kern 1.5pt|\kern 1.5pt} U_{p}^n\equiv 0 \bmod p^{n}$
; in other words,
$F{\kern 1.5pt|\kern 1.5pt} U_{p}^n\equiv 0 \bmod p^{n}$
; in other words,
![]() $F=\sum _{m>0}A(m)q^m$
has the strong p-magnetic property:
$F=\sum _{m>0}A(m)q^m$
has the strong p-magnetic property:
for any prime
![]() $p\ge 5$
. This argument also works for
$p\ge 5$
. This argument also works for
![]() $f=f_{4a}$
in the case of
$f=f_{4a}$
in the case of
![]() $p=3$
, because
$p=3$
, because
![]() $f_{4a}$
is
$f_{4a}$
is
![]() $3$
-integral.
$3$
-integral.
Consider now
![]() $p=3$
and
$p=3$
and
![]() $f=f_{4b}$
, in which case we only know that
$f=f_{4b}$
, in which case we only know that
![]() $27f$
is
$27f$
is
![]() $3$
-integral. Take the (unique!) element
$3$
-integral. Take the (unique!) element
![]() $g_r\in M_{5/2}^{!, +}$
with q-expansion
$g_r\in M_{5/2}^{!, +}$
with q-expansion
![]() $g_r=q^{-4\cdot 9^r}+O(q)$
; by [Reference Duke and Jenkins8, Prop. 2], it has integral coefficients. We first show that
$g_r=q^{-4\cdot 9^r}+O(q)$
; by [Reference Duke and Jenkins8, Prop. 2], it has integral coefficients. We first show that
![]() $g_0^\square {\kern 1.5pt|\kern 1.5pt} T_9^n\equiv 0 \bmod 3^{n+3}$
. For
$g_0^\square {\kern 1.5pt|\kern 1.5pt} T_9^n\equiv 0 \bmod 3^{n+3}$
. For
![]() $n=0$
, this is true, because
$n=0$
, this is true, because
![]() $g_0=-108\cdot f_{4b}$
and
$g_0=-108\cdot f_{4b}$
and
![]() $f_{4b}^\square $
is in
$f_{4b}^\square $
is in
![]() $q\mathbb {Z}[[q]]$
. For
$q\mathbb {Z}[[q]]$
. For
![]() $n=1$
, we observe that
$n=1$
, we observe that
![]() $\Psi (-\frac {1}{108}g_0{\kern 1.5pt|\kern 1.5pt} T_9)=F_{4b}{\kern 1.5pt|\kern 1.5pt} \mathcal {T}_3$
and
$\Psi (-\frac {1}{108}g_0{\kern 1.5pt|\kern 1.5pt} T_9)=F_{4b}{\kern 1.5pt|\kern 1.5pt} \mathcal {T}_3$
and
![]() $F_{4b}\equiv \Delta \bmod 3$
(since both
$F_{4b}\equiv \Delta \bmod 3$
(since both
![]() $E_4,E_6\equiv 1\bmod 3$
). This implies that
$E_4,E_6\equiv 1\bmod 3$
). This implies that
![]() $F_{4b}{\kern 1.5pt|\kern 1.5pt} \mathcal {T}_3\equiv \Delta {\kern 1.5pt|\kern 1.5pt} \mathcal {T}_3\equiv 0 \bmod 3$
, and hence
$F_{4b}{\kern 1.5pt|\kern 1.5pt} \mathcal {T}_3\equiv \Delta {\kern 1.5pt|\kern 1.5pt} \mathcal {T}_3\equiv 0 \bmod 3$
, and hence
meaning that
![]() $g_0^\square {\kern 1.5pt|\kern 1.5pt} T_9^n\equiv 0 \bmod 3^{n+3}$
is true when
$g_0^\square {\kern 1.5pt|\kern 1.5pt} T_9^n\equiv 0 \bmod 3^{n+3}$
is true when
![]() $n=1$
. Since
$n=1$
. Since
![]() $g_0{\kern 1.5pt|\kern 1.5pt} T_9=27 g_1-3g_0$
, we also deduce from this that
$g_0{\kern 1.5pt|\kern 1.5pt} T_9=27 g_1-3g_0$
, we also deduce from this that
![]() $g_1^\square \equiv 0 \bmod 3$
.
$g_1^\square \equiv 0 \bmod 3$
.
For n general, we want to write
![]() $g_0{\kern 1.5pt|\kern 1.5pt} T_9^n$
as a
$g_0{\kern 1.5pt|\kern 1.5pt} T_9^n$
as a
![]() $\mathbb {Z}$
-linear combination of
$\mathbb {Z}$
-linear combination of
![]() $g_r$
with
$g_r$
with
![]() $r=0,1,\dots ,n$
. Looking at the principal part of
$r=0,1,\dots ,n$
. Looking at the principal part of
![]() $g_0{\kern 1.5pt|\kern 1.5pt} T_9^n$
, one finds out that only terms of the form
$g_0{\kern 1.5pt|\kern 1.5pt} T_9^n$
, one finds out that only terms of the form
![]() $q^{-4\cdot 3^{2m}}$
appear, so that subtracting the related linear combination of
$q^{-4\cdot 3^{2m}}$
appear, so that subtracting the related linear combination of
![]() $f_r$
leads to a holomorphic cusp form, which then must vanish. To examine this linear combination in more details, we proceed as in the proof of Lemma 2:
$f_r$
leads to a holomorphic cusp form, which then must vanish. To examine this linear combination in more details, we proceed as in the proof of Lemma 2:
 $$ \begin{align*}g_0{\kern1.5pt|\kern1.5pt} T_9^n =\sum_{a,b,c,r} \alpha_{a,b,c,r}\cdot 3^{3c+b}\cdot g_0{\kern1.5pt|\kern1.5pt} U_9^{a-r}\chi_3^bV_9^{c-3} \end{align*} $$
$$ \begin{align*}g_0{\kern1.5pt|\kern1.5pt} T_9^n =\sum_{a,b,c,r} \alpha_{a,b,c,r}\cdot 3^{3c+b}\cdot g_0{\kern1.5pt|\kern1.5pt} U_9^{a-r}\chi_3^bV_9^{c-3} \end{align*} $$
(see (8)). As already noticed in that proof, only the terms with
![]() $r=a\le c$
contribute to the principal part, and thus to the linear combination; the terms with
$r=a\le c$
contribute to the principal part, and thus to the linear combination; the terms with
![]() $r=a$
contribute by the subsum
$r=a$
contribute by the subsum
 $$ \begin{align*}\sum_{a,b,c} \alpha_{a,b,c,a}\cdot (-1)^b\cdot 3^{3c+b}\cdot g_{c-a}. \end{align*} $$
$$ \begin{align*}\sum_{a,b,c} \alpha_{a,b,c,a}\cdot (-1)^b\cdot 3^{3c+b}\cdot g_{c-a}. \end{align*} $$
Now, notice that if
![]() $2c\ge a+3$
, then the coefficient is divisible by
$2c\ge a+3$
, then the coefficient is divisible by
![]() $3^{n+3}$
. In the remaining situations, we have
$3^{n+3}$
. In the remaining situations, we have
![]() $2a\le 2c<a+3$
, in particular
$2a\le 2c<a+3$
, in particular
![]() $a\in \{0,1,2\}$
, and we use the following analysis:
$a\in \{0,1,2\}$
, and we use the following analysis:
-
(a) If
 $a=2$
, then the inequalities imply that
$a=2$
, then the inequalities imply that
 $c=2$
, and hence
$c=2$
, and hence
 $b=n-4$
; the corresponding term is then a multiple of
$b=n-4$
; the corresponding term is then a multiple of
 $3^{3\cdot 2+n-4}g_0$
.
$3^{3\cdot 2+n-4}g_0$
. -
(b) If
 $a=1$
, then
$a=1$
, then
 $c=1$
, and hence
$c=1$
, and hence
 $b=n-2$
; the corresponding term happens to be a multiple of
$b=n-2$
; the corresponding term happens to be a multiple of
 $3^{3\cdot 1+n-2}g_0$
.
$3^{3\cdot 1+n-2}g_0$
. -
(c) If
 $a=0$
, then
$a=0$
, then
 $c\in \{0,1\}$
. The term corresponding to
$c\in \{0,1\}$
. The term corresponding to
 $c=0$
is a multiple of
$c=0$
is a multiple of
 $3^ng_0$
, whereas the term corresponding to
$3^ng_0$
, whereas the term corresponding to
 $c=1$
is a multiple of
$c=1$
is a multiple of
 $3^{n+2}\cdot g_1$
.
$3^{n+2}\cdot g_1$
.
Gathering all the terms, we end up with an expression
where g is integral and both
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are integers. Taking the square parts on both sides and using the results for
$\beta $
are integers. Taking the square parts on both sides and using the results for
![]() $n=0,1$
, we deduce that
$n=0,1$
, we deduce that
![]() $g_0^\square {\kern 1.5pt|\kern 1.5pt} T_9^n\equiv 0 \bmod 3^{n+3}$
for any
$g_0^\square {\kern 1.5pt|\kern 1.5pt} T_9^n\equiv 0 \bmod 3^{n+3}$
for any
![]() $n=0,1,\dots $
. Finally, we apply the SB map to this congruence to deduce that
$n=0,1,\dots $
. Finally, we apply the SB map to this congruence to deduce that
![]() $F_{4b}{\kern 1.5pt|\kern 1.5pt} \mathcal {T}_3^n\equiv 0 \bmod 3^n$
for all
$F_{4b}{\kern 1.5pt|\kern 1.5pt} \mathcal {T}_3^n\equiv 0 \bmod 3^n$
for all
![]() $n\ge 0$
. In other words, this implies the congruences (9) for
$n\ge 0$
. In other words, this implies the congruences (9) for
![]() $p=3$
.
$p=3$
.
Turning now our attention to the prime
![]() $p=2$
, notice that the Hecke operator
$p=2$
, notice that the Hecke operator
![]() $T_4$
does not respect the Kohnen plus space. However, if we define the projection
$T_4$
does not respect the Kohnen plus space. However, if we define the projection
 $$ \begin{align*}K^+=K_k^+\colon \sum_{n\in\mathbb Z} a(n) q^n \mapsto \sum_{\substack{n\in\mathbb Z\\ (-1)^kn\equiv0,1\bmod4}} a(n) q^n, \end{align*} $$
$$ \begin{align*}K^+=K_k^+\colon \sum_{n\in\mathbb Z} a(n) q^n \mapsto \sum_{\substack{n\in\mathbb Z\\ (-1)^kn\equiv0,1\bmod4}} a(n) q^n, \end{align*} $$
then the operator
![]() $T_4'=K^+\circ T_4$
maps the space
$T_4'=K^+\circ T_4$
maps the space
![]() $M_{k+1/2}^{!,+}$
onto itself and inherits all the properties used above for
$M_{k+1/2}^{!,+}$
onto itself and inherits all the properties used above for
![]() $T_{p^2}$
when
$T_{p^2}$
when
![]() $p>2$
. We use this operator
$p>2$
. We use this operator
![]() $T_4'$
in place of
$T_4'$
in place of
![]() $T_4$
to complete the proof of our Theorem 1. Notice that in both cases
$T_4$
to complete the proof of our Theorem 1. Notice that in both cases
![]() $f=f_{4a}$
and
$f=f_{4a}$
and
![]() $f=f_{4b}$
has powers of
$f=f_{4b}$
has powers of
![]() $2$
in the denominator of its main term. For an ease of the argument, we treat the two cases separately, although the same strategy is used for both, along the line with the proof above of relation (9) for
$2$
in the denominator of its main term. For an ease of the argument, we treat the two cases separately, although the same strategy is used for both, along the line with the proof above of relation (9) for
![]() $p=3$
.
$p=3$
.
When
![]() $f=f_{4b}$
, we need to prove that
$f=f_{4b}$
, we need to prove that
![]() $F_{4b}{\kern 1.5pt|\kern 1.5pt} \mathcal {T}_{2}^n\equiv 0 \bmod 2^n$
, which is in turn implied by the congruence
$F_{4b}{\kern 1.5pt|\kern 1.5pt} \mathcal {T}_{2}^n\equiv 0 \bmod 2^n$
, which is in turn implied by the congruence
![]() $f_{4b}^\square {\kern 1.5pt|\kern 1.5pt} {T_4'}^n\equiv 0\bmod 2^n$
. Introduce
$f_{4b}^\square {\kern 1.5pt|\kern 1.5pt} {T_4'}^n\equiv 0\bmod 2^n$
. Introduce
![]() $g_r=q^{-4\cdot 4^r}+O(q)\in M_{5/2}^{!,+}$
with integral q-expansions for
$g_r=q^{-4\cdot 4^r}+O(q)\in M_{5/2}^{!,+}$
with integral q-expansions for
![]() $r=0,1,\dots $
and notice that
$r=0,1,\dots $
and notice that
![]() $f_{4b}=-\frac {1}{108}\cdot g_0$
. The induction on
$f_{4b}=-\frac {1}{108}\cdot g_0$
. The induction on
![]() $r\ge 0$
shows that the recursion
$r\ge 0$
shows that the recursion
![]() $g_r{\kern 1.5pt|\kern 1.5pt} T_4'=8g_{r+1}+g_{r-1}$
takes place, with the convention that
$g_r{\kern 1.5pt|\kern 1.5pt} T_4'=8g_{r+1}+g_{r-1}$
takes place, with the convention that
![]() $g_{-1}=0$
. This in turn leads to
$g_{-1}=0$
. This in turn leads to
for some integral
![]() $g\in M_{5/2}^{!,+}$
and
$g\in M_{5/2}^{!,+}$
and
![]() $\alpha ,\beta \in \mathbb {Z}$
. Taking the square parts on both sides and using that
$\alpha ,\beta \in \mathbb {Z}$
. Taking the square parts on both sides and using that
![]() $F_{4b}\equiv \Delta \bmod 8$
, and hence
$F_{4b}\equiv \Delta \bmod 8$
, and hence
![]() $\Phi (F_{4b}{\kern 1.5pt|\kern 1.5pt}\mathcal {T}_2)\equiv \Phi (\Delta {\kern 1.5pt|\kern 1.5pt}\mathcal {T}_2)\equiv 0\bmod 8$
, we conclude with
$\Phi (F_{4b}{\kern 1.5pt|\kern 1.5pt}\mathcal {T}_2)\equiv \Phi (\Delta {\kern 1.5pt|\kern 1.5pt}\mathcal {T}_2)\equiv 0\bmod 8$
, we conclude with
![]() $g_0^\square {\kern 1.5pt|\kern 1.5pt} {T_4'}^n\equiv 0\bmod 2^{n+2}$
, and hence with (9) for
$g_0^\square {\kern 1.5pt|\kern 1.5pt} {T_4'}^n\equiv 0\bmod 2^{n+2}$
, and hence with (9) for
![]() $p=2$
and
$p=2$
and
![]() $F=F_{4b}$
.
$F=F_{4b}$
.
For
![]() $f=f_{4a}$
, we introduce the family
$f=f_{4a}$
, we introduce the family
![]() $g_r=q^{-3\cdot 4^r}+O(q)\in M_{5/2}^{!,+}$
, where
$g_r=q^{-3\cdot 4^r}+O(q)\in M_{5/2}^{!,+}$
, where
![]() $r=0,1,\dots $
, which is invariant under the action of the operator
$r=0,1,\dots $
, which is invariant under the action of the operator
![]() $T_4'$
, and proceed similarly to get exactly the same recursion
$T_4'$
, and proceed similarly to get exactly the same recursion
![]() $g_r{\kern 1.5pt|\kern 1.5pt} T_4'=8g_{r+1}+g_{r-1}$
for
$g_r{\kern 1.5pt|\kern 1.5pt} T_4'=8g_{r+1}+g_{r-1}$
for
![]() $r\ge 0$
with
$r\ge 0$
with
![]() $g_{-1}=0$
. On using
$g_{-1}=0$
. On using
![]() $g_0=\frac 1{64}f_{4a}$
,
$g_0=\frac 1{64}f_{4a}$
,
for
![]() $n\ge 3$
, and
$n\ge 3$
, and
![]() $F_{4a}\equiv \Delta \bmod 8$
, we conclude with
$F_{4a}\equiv \Delta \bmod 8$
, we conclude with
![]() $g_0^\square {\kern 1.5pt|\kern 1.5pt} {T_4'}^n\equiv 0\bmod 2^{n+6}$
implying
$g_0^\square {\kern 1.5pt|\kern 1.5pt} {T_4'}^n\equiv 0\bmod 2^{n+6}$
implying
![]() $F_{4a}{\kern 1.5pt|\kern 1.5pt} \mathcal {T}_{2}^n\equiv 0 \bmod 2^n$
as required.
$F_{4a}{\kern 1.5pt|\kern 1.5pt} \mathcal {T}_{2}^n\equiv 0 \bmod 2^n$
as required.
Proof of Theorem 2
We now work with
![]() $k=3$
. Consider
$k=3$
. Consider
 $$ \begin{align*}f(\tau)=-\frac{1}{384}\,\frac{f_{15+1/2}^*(\tau)}{\Delta(4\tau)}\in \mathcal{M}_{k+1/2}^{!,+}, \end{align*} $$
$$ \begin{align*}f(\tau)=-\frac{1}{384}\,\frac{f_{15+1/2}^*(\tau)}{\Delta(4\tau)}\in \mathcal{M}_{k+1/2}^{!,+}, \end{align*} $$
where
![]() $f_{b+1/2}^*$
is the weight
$f_{b+1/2}^*$
is the weight
![]() $b+1/2$
modular form from the table in [Reference Duke and Jenkins8, Appendix]. One can easily check (through the first few coefficients) that
$b+1/2$
modular form from the table in [Reference Duke and Jenkins8, Appendix]. One can easily check (through the first few coefficients) that
![]() $\Psi (f)=F_6$
and from the expression above we also know that f has p-integral coefficients for any
$\Psi (f)=F_6$
and from the expression above we also know that f has p-integral coefficients for any
![]() $p\ge 5$
. It follows from Lemma 2 (applied this time with
$p\ge 5$
. It follows from Lemma 2 (applied this time with
![]() $k=3$
) that
$k=3$
) that
![]() $f{\kern 1.5pt|\kern 1.5pt} T_{p^2}^n\equiv 0 \bmod p^{2n}$
. Therefore,
$f{\kern 1.5pt|\kern 1.5pt} T_{p^2}^n\equiv 0 \bmod p^{2n}$
. Therefore,
![]() $F_6{\kern 1.5pt|\kern 1.5pt} \mathcal {T}_p^n\equiv 0\bmod p^{2n}$
for all
$F_6{\kern 1.5pt|\kern 1.5pt} \mathcal {T}_p^n\equiv 0\bmod p^{2n}$
for all
![]() $n\ge 0$
implying that
$n\ge 0$
implying that
![]() $F_6{\kern 1.5pt|\kern 1.5pt} U_p^n\equiv 0 \bmod p^{2n}$
and that, for
$F_6{\kern 1.5pt|\kern 1.5pt} U_p^n\equiv 0 \bmod p^{2n}$
and that, for
![]() $F_6=\sum _{m>0} A(m) q^m$
, we have
$F_6=\sum _{m>0} A(m) q^m$
, we have
for any prime
![]() $p\ge 5$
.
$p\ge 5$
.
Since
![]() $384=3\cdot 2^7$
, for
$384=3\cdot 2^7$
, for
![]() $p=3$
, we see that
$p=3$
, we see that
![]() $3f$
is
$3f$
is
![]() $3$
-integral. Repeating the argument from Lemma 2 and using the fact that f is a multiple of the unique element in
$3$
-integral. Repeating the argument from Lemma 2 and using the fact that f is a multiple of the unique element in
![]() $ \mathcal {M}_{7/2}^{!,+}$
with the integral q-expansion
$ \mathcal {M}_{7/2}^{!,+}$
with the integral q-expansion
![]() $q^{-1}+O(q)$
, we deduce that
$q^{-1}+O(q)$
, we deduce that
![]() $f{\kern 1.5pt|\kern 1.5pt} T_9^n=3^{2n}\cdot (g+ \alpha f)$
with
$f{\kern 1.5pt|\kern 1.5pt} T_9^n=3^{2n}\cdot (g+ \alpha f)$
with
![]() $\alpha $
an integer and g a
$\alpha $
an integer and g a
![]() $3$
-integral modular form. Indeed, the principal part of
$3$
-integral modular form. Indeed, the principal part of
![]() $f{\kern 1.5pt|\kern 1.5pt} T_9^n$
is a
$f{\kern 1.5pt|\kern 1.5pt} T_9^n$
is a
![]() $\mathbb {Z}$
-linear combination of the principal parts of
$\mathbb {Z}$
-linear combination of the principal parts of
If
![]() $c-a\ge 1$
, the principal part of
$c-a\ge 1$
, the principal part of
![]() $(3^{c-a} f){\kern 1.5pt|\kern 1.5pt} \chi _{3}^b V_9^{c-a}$
is
$(3^{c-a} f){\kern 1.5pt|\kern 1.5pt} \chi _{3}^b V_9^{c-a}$
is
![]() $3$
-integral; when
$3$
-integral; when
![]() $c=a$
, the principal part of
$c=a$
, the principal part of
![]() $ f{\kern 1.5pt|\kern 1.5pt} \chi _{3}^b$
is an integral multiple of the principal part of f. Thus,
$ f{\kern 1.5pt|\kern 1.5pt} \chi _{3}^b$
is an integral multiple of the principal part of f. Thus,
![]() $f{\kern 1.5pt|\kern 1.5pt} T_9^n=3^{2n}\cdot (g+ \alpha \cdot f)$
implies (applying the SB lift to both sides) that
$f{\kern 1.5pt|\kern 1.5pt} T_9^n=3^{2n}\cdot (g+ \alpha \cdot f)$
implies (applying the SB lift to both sides) that
![]() $F_6{\kern 1.5pt|\kern 1.5pt} \mathcal {T}_3^n\equiv 0 \bmod 3^{2n}$
, and hence we deduce that (10) is true also for
$F_6{\kern 1.5pt|\kern 1.5pt} \mathcal {T}_3^n\equiv 0 \bmod 3^{2n}$
, and hence we deduce that (10) is true also for
![]() $p=3$
.
$p=3$
.
To prove the relation (10) for
![]() $p=2$
, we proceed as in the proof of Theorem 1. We introduce the
$p=2$
, we proceed as in the proof of Theorem 1. We introduce the
![]() $T_4'$
-invariant family of weight
$T_4'$
-invariant family of weight
![]() $7/2$
weakly holomorphic modular forms
$7/2$
weakly holomorphic modular forms
![]() $g_r=q^{-4^r}+O(q)$
with integral q-expansions with the help of [Reference Duke and Jenkins8, Prop. 2]. Again, we write the expression of
$g_r=q^{-4^r}+O(q)$
with integral q-expansions with the help of [Reference Duke and Jenkins8, Prop. 2]. Again, we write the expression of
![]() $g_0{\kern 1.5pt|\kern 1.5pt} {T_4'}^n$
as
$g_0{\kern 1.5pt|\kern 1.5pt} {T_4'}^n$
as
![]() $\mathbb {Z}$
-linear combination of
$\mathbb {Z}$
-linear combination of
![]() $g_r$
with
$g_r$
with
![]() $r=0,1,\dots ,n$
and analyze the powers of
$r=0,1,\dots ,n$
and analyze the powers of
![]() $2$
appearing in the coefficients; similarly, we can prove that
$2$
appearing in the coefficients; similarly, we can prove that
![]() $g_0^\square {\kern 1.5pt|\kern 1.5pt} {T_4'}^n\equiv 0 \bmod 2^{2n+7}$
for any
$g_0^\square {\kern 1.5pt|\kern 1.5pt} {T_4'}^n\equiv 0 \bmod 2^{2n+7}$
for any
![]() $n\ge 0$
. For
$n\ge 0$
. For
![]() $n=0$
, this comes from the integrality of
$n=0$
, this comes from the integrality of
![]() $f^\square $
, whereas for
$f^\square $
, whereas for
![]() $n=1$
, we get it, again, by noticing that
$n=1$
, we get it, again, by noticing that
![]() $F_6\equiv E_6\Delta \bmod 2^{4}$
while
$F_6\equiv E_6\Delta \bmod 2^{4}$
while
![]() $E_6\Delta $
being an eigenform of weight 18 with slope
$E_6\Delta $
being an eigenform of weight 18 with slope
![]() $4$
at the prime
$4$
at the prime
![]() $2$
. The induction argument follows mutatis mutandis as in the proof of Theorem 1.
$2$
. The induction argument follows mutatis mutandis as in the proof of Theorem 1.
6 Miscellania on half-integral weight modular forms
In this part, not well related to the proofs of Theorems 1 and 2, we indicate a different strategy of constructing half-integral weight weakly holomorphic modular forms using a traditional rising operator.
Standard examples of weight
![]() $1/2$
modular forms (see [Reference Bringmann, Guerzhoy and Kane4, Sec. 14, Exam. 2]) include the theta function
$1/2$
modular forms (see [Reference Bringmann, Guerzhoy and Kane4, Sec. 14, Exam. 2]) include the theta function
![]() $\theta (\tau )=\sum _{n\in \mathbb Z}q^{n^2}$
and
$\theta (\tau )=\sum _{n\in \mathbb Z}q^{n^2}$
and
 $$ \begin{align*} h_0(\tau) &=\frac{ E_{2,4}(\tau) \theta(\tau) \,(\theta(\tau)^4-2E_{2,4}(\tau))\,(\theta(\tau)^4-16E_{2,4}(\tau))\,E_6(4\tau)}{\Delta(4\tau)}+56\theta(\tau) \\[6pt] &=q^{-3}-248q+26752q^4+\dotsb, \end{align*} $$
$$ \begin{align*} h_0(\tau) &=\frac{ E_{2,4}(\tau) \theta(\tau) \,(\theta(\tau)^4-2E_{2,4}(\tau))\,(\theta(\tau)^4-16E_{2,4}(\tau))\,E_6(4\tau)}{\Delta(4\tau)}+56\theta(\tau) \\[6pt] &=q^{-3}-248q+26752q^4+\dotsb, \end{align*} $$
where
![]() $E_{2,4}(\tau )$
is given in (7). The images of
$E_{2,4}(\tau )$
is given in (7). The images of
![]() $12\theta $
and
$12\theta $
and
![]() $4\theta +h_0$
under the multiplicative Borcherds lift
$4\theta +h_0$
under the multiplicative Borcherds lift
 $$ \begin{align*}\Psi^{\text{mult}}\colon\sum_{n\gg-\infty}c(n)q^n \mapsto q^{-h}\prod_{n>0}(1-q^n)^{c(n^2)} \end{align*} $$
$$ \begin{align*}\Psi^{\text{mult}}\colon\sum_{n\gg-\infty}c(n)q^n \mapsto q^{-h}\prod_{n>0}(1-q^n)^{c(n^2)} \end{align*} $$
are the modular forms
![]() $\Delta (\tau )$
and
$\Delta (\tau )$
and
![]() $E_4(\tau )$
, respectively (see [Reference Bringmann, Guerzhoy and Kane4, Th. 14.1] for the definition of h). Although it is not useful for our results in this note, we remark that the two weakly holomorphic modular forms can serve as constructors of some weight
$E_4(\tau )$
, respectively (see [Reference Bringmann, Guerzhoy and Kane4, Th. 14.1] for the definition of h). Although it is not useful for our results in this note, we remark that the two weakly holomorphic modular forms can serve as constructors of some weight
![]() $5/2$
modular forms from §4.
$5/2$
modular forms from §4.
Lemma 5. The raising operator
maps
![]() ${M}_{k+1/2}^{!, +}$
onto
${M}_{k+1/2}^{!, +}$
onto
![]() ${M}_{k+5/2}^{!, +}$
.
${M}_{k+5/2}^{!, +}$
.
Proof. Observe that
![]() $E_2(\tau )-4E_2(4\tau )$
is a modular form of weight 2 for
$E_2(\tau )-4E_2(4\tau )$
is a modular form of weight 2 for
![]() $\Gamma _0(4)$
, so that the difference between the usual raising operator and
$\Gamma _0(4)$
, so that the difference between the usual raising operator and
![]() $\mathcal {D}$
is the multiplication by a weight 2 modular form, thus indeed
$\mathcal {D}$
is the multiplication by a weight 2 modular form, thus indeed
![]() $\mathcal {D}\colon {M}_{k+1/2}^{!}\to {M}_{k+5/2}^{!}$
. On the other hand, both
$\mathcal {D}\colon {M}_{k+1/2}^{!}\to {M}_{k+5/2}^{!}$
. On the other hand, both
![]() $\delta $
and multiplication by any modular form
$\delta $
and multiplication by any modular form
![]() $f(4\tau )$
preserve the Kohnen plus space condition, and the lemma follows.
$f(4\tau )$
preserve the Kohnen plus space condition, and the lemma follows.
For the functions
![]() $g_0$
,
$g_0$
,
![]() $f_{4a}$
, and
$f_{4a}$
, and
![]() $f_{4b}$
in §4, we find out that
$f_{4b}$
in §4, we find out that
and
 $$ \begin{align*}108 f_{4b}=-\frac{6}{25}\mathcal{D}\biggl(2 h_0-1006\theta-\frac{\theta E_6(4\tau)^2}{\Delta(4\tau)}\biggr). \end{align*} $$
$$ \begin{align*}108 f_{4b}=-\frac{6}{25}\mathcal{D}\biggl(2 h_0-1006\theta-\frac{\theta E_6(4\tau)^2}{\Delta(4\tau)}\biggr). \end{align*} $$
Table 1 Strong magnetic modular forms of weight
![]() $4$
(where
$4$
(where
![]() $f_m=q^{-m}+O(q)$
denotes the unique weakly holomorphic cusp form in
$f_m=q^{-m}+O(q)$
denotes the unique weakly holomorphic cusp form in
![]() $M_{5/2}^{!,+}$
).
$M_{5/2}^{!,+}$
).

where
 \begin{array}{rl}P_{23}(j)&=141826 j^5-286458244\cdot 5^3 j^4+5214621227\cdot 5^6 j^3+3414887843776\cdot 5^9 j^2\\[6pt] &\qquad-47816219216827\cdot 5^{12} j+4378632\cdot 187^3\cdot 5^{15}.\end{array}
\begin{array}{rl}P_{23}(j)&=141826 j^5-286458244\cdot 5^3 j^4+5214621227\cdot 5^6 j^3+3414887843776\cdot 5^9 j^2\\[6pt] &\qquad-47816219216827\cdot 5^{12} j+4378632\cdot 187^3\cdot 5^{15}.\end{array}
7 Concluding remarks
Although we expect that our discussion above exhausts all elements with the magnetic property in
![]() $W_4^0$
, many such exist for
$W_4^0$
, many such exist for
![]() $W_{2k}^0$
with
$W_{2k}^0$
with
![]() $k>2$
, for example, the q-series
$k>2$
, for example, the q-series
![]() $E_2^m\cdot (\delta E_j)/E_j$
for
$E_2^m\cdot (\delta E_j)/E_j$
for
![]() $j=4,6$
and
$j=4,6$
and
![]() $m=1,2,3,4,6$
(but not for
$m=1,2,3,4,6$
(but not for
![]() $m=5$
). Constructing magnetic modular forms—meromorphic ones with poles at quadratic irrationalities from the upper half-plane—is a routine on the basis of SB lift (6); Table 1 lists a few instances of this production explicitly in terms of the j-invariant
$m=5$
). Constructing magnetic modular forms—meromorphic ones with poles at quadratic irrationalities from the upper half-plane—is a routine on the basis of SB lift (6); Table 1 lists a few instances of this production explicitly in terms of the j-invariant
![]() $j(\tau )=E_4^3/\Delta $
. Generating the forms with multiple magnetic property in higher weights is a tougher task; one such example
$j(\tau )=E_4^3/\Delta $
. Generating the forms with multiple magnetic property in higher weights is a tougher task; one such example
![]() $E_4^2(j -3\cdot 2^{10})/j^2$
can be found in the more recent work [Reference Löbrich and Schwagenscheidt18] of Löbrich and Schwagenscheidt; another example of a triply magnetic form of weight 8 is
$E_4^2(j -3\cdot 2^{10})/j^2$
can be found in the more recent work [Reference Löbrich and Schwagenscheidt18] of Löbrich and Schwagenscheidt; another example of a triply magnetic form of weight 8 is
 $$ \begin{align*}E_4^2\,\frac{13 j^3 - 443556 j^2 + 1610452125 j - 98280\cdot 15^6}{(j+15^3)^4}. \end{align*} $$
$$ \begin{align*}E_4^2\,\frac{13 j^3 - 443556 j^2 + 1610452125 j - 98280\cdot 15^6}{(j+15^3)^4}. \end{align*} $$
We have observed that in all such instances the related numerators, viewed as polynomials in j, have real zeros only. Furthermore, there are weaker divisibility conditions (resembling the Honda–Kaneko congruences [Reference Honda and Kaneko13]) for individual summands of magnetic forms; for example, the anti-derivatives of
 $$ \begin{align*}\frac{E_4j}{(j-2\cdot 30^3)^2} \quad\text{and}\quad \frac{E_4}{(j-2\cdot 30^3)^2} \end{align*} $$
$$ \begin{align*}\frac{E_4j}{(j-2\cdot 30^3)^2} \quad\text{and}\quad \frac{E_4}{(j-2\cdot 30^3)^2} \end{align*} $$
are already p-integral for primes
![]() $p\equiv 5\ \textrm{mod}\ 6$
. We have not tried to investigate this arithmetic subphenomenon.
$p\equiv 5\ \textrm{mod}\ 6$
. We have not tried to investigate this arithmetic subphenomenon.
There is a good reason to believe that all such magnetic forms originate from suitable Shimura--Borcherds lifts. However, maybe, there is more in this story—then time will show.
Acknowledgment
We thank the anonymous referee for their critical reading and valuable comments: those really helped to reduce errors and improve the exposition.