Article contents
Topological Quantum Field Theory and Strong Shift Equivalence
Published online by Cambridge University Press: 20 November 2018
Abstract
Given a 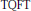 $\text{TQFT}$ in dimension
$\text{TQFT}$ in dimension 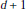 $d\,+\,1$, and an infinite cyclic covering of a closed (
$d\,+\,1$, and an infinite cyclic covering of a closed (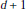 $d\,+\,1$)-dimensional manifold
$d\,+\,1$)-dimensional manifold 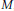 $M$, we define an invariant taking values in a strong shift equivalence class of matrices. The notion of strong shift equivalence originated in R. Williams’ work in symbolic dynamics. The Turaev-Viro module associated to a
$M$, we define an invariant taking values in a strong shift equivalence class of matrices. The notion of strong shift equivalence originated in R. Williams’ work in symbolic dynamics. The Turaev-Viro module associated to a 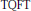 $\text{TQFT}$ and an infinite cyclic covering is then given by the Jordan form of this matrix away from zero. This invariant is also defined if the boundary of
$\text{TQFT}$ and an infinite cyclic covering is then given by the Jordan form of this matrix away from zero. This invariant is also defined if the boundary of 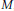 $M$ has an
$M$ has an
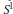 ${{S}^{1}}$ factor and the infinite cyclic cover of the boundary is standard. We define a variant of a
${{S}^{1}}$ factor and the infinite cyclic cover of the boundary is standard. We define a variant of a 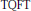 $\text{TQFT}$ associated to a finite group
$\text{TQFT}$ associated to a finite group 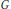 $G$ which has been studied by Quinn. In this way, we recover a link invariant due to D. Silver and S. Williams. We also obtain a variation on the Silver-Williams invariant, by using the
$G$ which has been studied by Quinn. In this way, we recover a link invariant due to D. Silver and S. Williams. We also obtain a variation on the Silver-Williams invariant, by using the 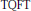 $\text{TQFT}$ associated to
$\text{TQFT}$ associated to 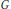 $G$ in its unmodified form.
$G$ in its unmodified form.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1999
References
- 4
- Cited by


