Introduction
Radio echo-sounding has become a routine method for measuring ice thickness, but, because high-frequency radio waves cannot penetrate sea-water, it is necessary to use seismic shooting for finding the depth of water under ice shelves. A pilot project to investigate George VI Sound was undertaken in January 1981. On a 40 km traverse of George VI Ice Shelf at about 72°S (Fig.1) seismic reflection soundings were taken at 23 stations. Because of the acknowledged difficulties of interpreting seismic records on ice shelves, due to the usually weak echo from the ice-sea boundary and multiple reflections within the water layer (Reference RöthlisbergerRöthlisberger 1972), the whole line was covered by continuous radio echo-sounding to give an independent measure of ice thickness. It was found, however, that for 22 of the 23 sites an ice-shelf bottom echo could be readily distinguished, allowing an accurate comparison to be made between seismic and radio echo; travel times. The principal parameter affecting seismic and radio wave velocities is ice density; therefore an estimate could be made of the mean ice density at each station.

Fig. 1 (a). Location map for George VI Ice Shelf.

Fig. 1 (b). Map of part of George VI Ice Shelf showing line sounded across the ice shelf and extent of surface melt pools seen in Landsat images taken in January 1973. Contour lines are of ice thickness (m).
Sounding Methods
Six geophones, sensitive to vertical motion, were used in a straight-line pattern with 10 m separation. The seismic traces were recorded by a Savage and Parsons 12-12 oscillograph onto ultraviolet sensitive paper. Time marks were generated every 2 ms, allowing echo times to be read to a precision of 1 ms. Calibration runs were carried out in a laboratory to check the accuracy of the timing over the temperature range encountered in the field (down to −10°C). Shot holes were drilled by a hand corer usually to a depth of between 2 or 3 m about 30 m from the nearest geophone. An uphole geophone was used to record the detonation time.
Although each shot hole was stemmed with snow and ice cores to increase the coupling of the blast with the ice, there was a wide, but systematic, variation in the results of the explosion. On the west side of the ice shelf, where hard ice lenses and wet snow made drilling difficult, there was much ejected material. Towards the centre of the line the surface would visibly heave and leave a crater about 2 m in diameter. At the eastern end of the traverse no shock could be felt Dr heard and there was no visible expression of the blast. Only by looking at the record could it be ascertained that there had been a successful explosion.
A standard 60 MHz ice sounding pulsed radar was used with a single aerial to give a continuous profile of ice thickness. Tests were carried out to determine propagation delays through the system.
Theory
The velocity in ice at both seismic and radio waves varies with density. For seismic P-waves, there are various relationships in the literature connecting velocity with density and temperature (Reference RobinRobin 1958, Reference KohnenKohnen 1972, Reference BennettBennett unpublished). The dependence of velocity upon temperature is small (around −2.3 m s−1 K−1) and for the temperature regime of George VI Ice Shelf would be contained within the spread of velocity values derived from different formulations. The discrepancies between the various formulations can be small at the higher densities (Reference KohnenKohnen 1972) so, in order to follow an analytic approach, we shall use a linear equation of the form
Vp(z) = aρ(z) + b
where Vp is the P-wave velocity at depth z, ρ the density and a and b are constants. The average velocity V p over the ice-shelf thickness H is given by
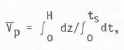
where ts is the (one-way) travel time and

Assuming a density-depth relationship of the form

where ρi is the density of ice, 0.917 Mg m−3, ρs the density of the snow or firn at the top surface z = 0, and k a constant, then

The integral is of a standard form, so that

Taking the thickness of the ice shelf to be much greater than the decay factor
al1ows the mean density ρ to be written as

so that

where Vp = aρi + b
and

For radio waves, the linear relationship between refractive index n and density, given by Reference Robin, Evans and BaileyRobin and others (1969)
can be used to relate radio wave velocity VR to density by

where c is the velocity of light in vacuo (300 m μs−1). Thus, the average velocity V R through the ice is given by

If the one-way travel time for radio waves is tR, then the ice thickness is given by
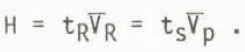
Using Equations (1) and (2) gives

and hence an expression for the average ice shelf density is given by

Timing Corrections
The two-way travel times measured for the seismic and radar echoes both need several corrections to eliminate significant systematic errors. For the seismic times, an allowance was made for the depth of the shot hole and its horizontal distance from the geophones, and the timing marks were calibrated. In the radio echo case, using a single aerial with a transmit/receive (T/R) switch, a correction was made for the length of cable from the T/R switch to the aerial. In addition, because the received echo was attenuated by about 90 dB compared with the direct transmitter pulse, a correction allowing for the rise time of the echo was applied. This correction was determined in the laboratory by accurately timing pulses of different amplitudes and was of the order 0.2 μs. After allowing for reading errors, the final accuracies were estimated as ±2 ms for the seismic data and ±0.05 μs for the radio echo data. A large part of the error in the seismic data arises from the correction for the shot-hole depth. Because the hole is in the lowest density firn where the seismic velocity is lowest, uncertainties in the actual density structure or in the depth of the hole have their greatest effect. The error figures are probably overestimated, but should be large enough to allow for any residual systematic error due to uncertainties in the values taken for the velocity-density relationships, which would include any temperature dependence.
Results
Equation (3) was used to calculate the average ice-shelf density ρ using values for Vp = 3860 m s−1 (Reference RobinRobin 1958) and A = 1.25 m3 Mg−1. Although strictly the value of A depends on the surface snow density ρs, the final value for ρ is insensitive to this parameter and any errors are contained within the uncertainties in the echo times. The variation of ρ along the line is shown in Figure 2. There appears to be a grouping of values about two means, with the 13 westernmost sites forming one population and the nine easternmost sites forming another distinct one. The variance-ratio F of the two groups shows that Student’s ‘t’ test is applicable with the result that the western group, with a mean density of 0.915 ± 0.010 Mg m−3, is significantly different to the eastern group, with a mean density of 0.884 ± 0.007 Mg m−3 at a probability level of less than 0.1%.

Fig. 2 Calculated mean density along line. The change in direction of the line occurred about 16 km from the western end (origin of distance coordinate).
Discussion
The broad grouping of the density values can be simply related to local surface conditions. In the summer, a large area of George VI Ice Shelf is covered with melt pools (Reference Bishop and WaltonBishop and Walton 1981). Landsat pictures taken in 1973 show extensive melt features in the area covered by the western part of the line. Thus the break in mean density values about half-way along the line could be explained by a change in surface melt conditions there. The change in near-surface densities is also associated with the variation in physical surface effects of the explosion described earlier.
The sounding line followed approximately a flow-line in the ice shelf, but some of the variation in mean densities within the two main groups may reflect a real lateral variation, as suggested for the Ross Ice Shelf to explain differences in shallow seismic short-refraction studies (Reference Kirchner, Bentley and RobertsonKirchner and others 1979).
A knowledge of how density varies with position is important when attempting to model the flow of ice shelves (Reference ThomasThomas 1973, Reference SandersonSanderson 1979, Reference Morland and ShoemakerMorland and Shoemaker 1982). Reference ThomasThomas (1973) showed how the double integral of density over depth could affect the calculated horizontal strain-rate by a factor of two compared with a constant density with depth approximation. Reference SandersonSanderson (1979) assumed for his models that the mean ice-shelf density was constant. However, Reference Morland and ShoemakerMorland and Shoemaker (1982) have pointed out the inconsistency of considering a variation of density with depth but ignoring a variation with horizontal position. The problem lies in the mass-balance equation (assuming now steady state for simplicity)
where ρ and u are the density and velocity (u,v,w) fields in a rectangular coordinate frame (x,y,z), z being vertical and x horizontal in the direction of motion. The usual assumption of incompressibility implies ∇ · u = 0, but the term (∇ρ) · u may not be negligible on ice shelves. Reference PatersonPaterson (1976) assumed that, near the centre of an ice cap, (w/ρ)∂ρ/∂z was the only significant term that needed to be considered to correct the vertical strain-rate for effects of compaction, but on an ice shelf the term (u/ρ)∂ρ/∂x might be in some circumstances of the same order as ∂u/∂x. Near the centre of the line sounded on George VI Ice Shelf, the term
(ρ = mean density) is about 0.2 x 10−2 a−2 compared with the measured (compressive) strain-rate of around 10 x 10−2 a−1 on a nearby stake scheme. In this case the assumption made by Reference Bishop and WaltonBishop and Walton (1981) that terms containing horizontal mean density gradients could be ignored seems justified. This however is a weaker condition than saying that horizontal density gradients at a point can be ignored. More data on the variation of density with position on an ice shelf are required to judge the importance of their spatial gradients.
John Anderson (later killed in a crevasse accident) and Richard Crabtree provided enthusiastic support and companionship during an intensive but short field programme.





