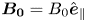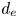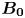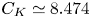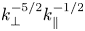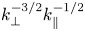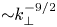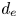1. Introduction
There are many ways to investigate the problem of energy transfer through the different scales in a turbulent plasma, but one of the most rigorous is the theory of wave turbulence. This theory is limited to systems composed of a sea of weakly interacting waves. Since the nonlinearities are weak, it is possible to describe how the dynamics of the system develops in a time asymptotically long compared with the period of the waves considered (Nazarenko Reference Nazarenko2011). The importance of the wave turbulence theory is, first, the fact that a natural closure can be achieved with a uniformity of the asymptotic development (Benney & Saffman Reference Benney and Saffman1966; Benney & Newell Reference Benney and Newell1969) and, second, the possibility of deriving exact solutions (Kolmogorov–Zakharov spectra) of the wave kinetic equations (Zakharov, L'Vov & Falkovich Reference Zakharov, L'Vov and Falkovich1992). The wave turbulence regime is a highly studied subject in physics, both theoretically and experimentally. Examples are provided e.g. in hydrodynamics with surface waves (Zakharov & Filonenko Reference Zakharov and Filonenko1967; Falcon & Mordant Reference Falcon and Mordant2022), internal gravity waves (Caillol & Zeitlin Reference Caillol and Zeitlin2000; Dematteis & Lvov Reference Dematteis and Lvov2021) and inertial waves (Galtier Reference Galtier2003; Yarom & Sharon Reference Yarom and Sharon2014; Monsalve et al. Reference Monsalve, Brunet, Gallet and Cortet2020); in plasma physics with magnetohydrodynamics (MHD) (Galtier et al. Reference Galtier, Nazarenko, Newell and Pouquet2000; Kuznetsov Reference Kuznetsov2001; Meyrand, Kiyani & Galtier Reference Meyrand, Kiyani and Galtier2015), Hall-MHD (Galtier Reference Galtier2006; Meyrand et al. Reference Meyrand, Kiyani, Gürcan and Galtier2018) and rotating MHD (Galtier Reference Galtier2014); in acoustic waves (Zakharov & Sagdeev Reference Zakharov and Sagdeev1970; Newell & Aucoin Reference Newell and Aucoin1971; L'vov et al. Reference L'vov, L'vov, Newell and Zakharov1997), optical waves (Dyachenko et al. Reference Dyachenko, Newell, Pushkarev and Zakharov1992), elastic waves (Düring, Josserand & Rica Reference Düring, Josserand and Rica2006; Hassaini et al. Reference Hassaini, Mordant, Miquel, Krstulovic and Düring2019), Kelvin waves (Laurie et al. Reference Laurie, L'vov, Nazarenko and Rudenko2010), in Bose–Einstein condensates (Nazarenko & Onorato Reference Nazarenko and Onorato2006) and even with gravitational waves (Galtier & Nazarenko Reference Galtier and Nazarenko2017, Reference Galtier and Nazarenko2021).
Here, we are interested in the plasma dynamics at scales where the electron inertia plays a non-negligible role. In our approach, the mass difference between ions and electrons is such that the ions will be considered static to form a neutralizing background. Therefore, at the time scale of interest, only the electron dynamics is relevant. This is the domain of electron magnetohydrodynamics (EMHD) and inertial electron magnetohydrodynamics (IEMHD) which describe, respectively, the scales $\ell \gg d_e$![]() and $d_e \gg \ell \gg r_e$
and $d_e \gg \ell \gg r_e$![]() , where $r_e$
, where $r_e$![]() is the electron Larmor radius. Our study will focus on the latter case. Although it is difficult for current spacecraft to measure the plasma dynamics corresponding to the electron inertia scales, it is interesting to see what the theoretical description can predict. The EMHD and IEMHD approximations are widely used models to study, for example, magnetic reconnection or space plasma turbulence (Bulanov, Pegoraro & Sakharov Reference Bulanov, Pegoraro and Sakharov1992; Biskamp, Schwarz & Drake Reference Biskamp, Schwarz and Drake1996; Biskamp et al. Reference Biskamp, Schwarz, Zeiler, Celani and Drake1999; Dastgeer, Das & Kaw Reference Dastgeer, Das and Kaw2000a; Dastgeer et al. Reference Dastgeer, Das, Kaw and Diamond2000b; Cho & Lazarian Reference Cho and Lazarian2004; Cho Reference Cho2011; Kim & Cho Reference Kim and Cho2015). More information is given in Milanese et al. (Reference Milanese, Loureiro, Daschner and Boldyrev2020), where an exhaustive list of plasmas driven by the IEMHD model is given with the parameter regimes. In this paper, we present the theory of wave turbulence for IEMHD in the presence of a relatively strong and uniform external magnetic field $\boldsymbol {B_0}$
is the electron Larmor radius. Our study will focus on the latter case. Although it is difficult for current spacecraft to measure the plasma dynamics corresponding to the electron inertia scales, it is interesting to see what the theoretical description can predict. The EMHD and IEMHD approximations are widely used models to study, for example, magnetic reconnection or space plasma turbulence (Bulanov, Pegoraro & Sakharov Reference Bulanov, Pegoraro and Sakharov1992; Biskamp, Schwarz & Drake Reference Biskamp, Schwarz and Drake1996; Biskamp et al. Reference Biskamp, Schwarz, Zeiler, Celani and Drake1999; Dastgeer, Das & Kaw Reference Dastgeer, Das and Kaw2000a; Dastgeer et al. Reference Dastgeer, Das, Kaw and Diamond2000b; Cho & Lazarian Reference Cho and Lazarian2004; Cho Reference Cho2011; Kim & Cho Reference Kim and Cho2015). More information is given in Milanese et al. (Reference Milanese, Loureiro, Daschner and Boldyrev2020), where an exhaustive list of plasmas driven by the IEMHD model is given with the parameter regimes. In this paper, we present the theory of wave turbulence for IEMHD in the presence of a relatively strong and uniform external magnetic field $\boldsymbol {B_0}$![]() . The equivalent theory for EMHD has already been published (Galtier & Bhattacharjee Reference Galtier and Bhattacharjee2003) but not yet for IEMHD. Strong IEMHD turbulence has recently received new attention with the study of the weakly compressible case (Chen & Boldyrev Reference Chen and Boldyrev2017; Roytershteyn et al. Reference Roytershteyn, Boldyrev, Delzanno, Chen, Grošelj and Loureiro2019). The objective was to study the nature of plasma turbulence in the Earth's magnetosheath. The main prediction, phenomenological in nature, is a magnetic spectrum in $k_\perp ^{-11/3}$
. The equivalent theory for EMHD has already been published (Galtier & Bhattacharjee Reference Galtier and Bhattacharjee2003) but not yet for IEMHD. Strong IEMHD turbulence has recently received new attention with the study of the weakly compressible case (Chen & Boldyrev Reference Chen and Boldyrev2017; Roytershteyn et al. Reference Roytershteyn, Boldyrev, Delzanno, Chen, Grošelj and Loureiro2019). The objective was to study the nature of plasma turbulence in the Earth's magnetosheath. The main prediction, phenomenological in nature, is a magnetic spectrum in $k_\perp ^{-11/3}$![]() (see also Meyrand & Galtier Reference Meyrand and Galtier2010) which is less steep than the prediction we will derive in this paper. In the meantime, a rigorous derivation (using systematic asymptotic expansions) based on a more general model including electron inertia and finite Larmor radius corrections has been proposed (Passot, Sulem & Tassi Reference Passot, Sulem and Tassi2017; Passot & Sulem Reference Passot and Sulem2019). This more general approach allows the study of several different limits, and recovery in particular of the model discussed previously (Chen & Boldyrev Reference Chen and Boldyrev2017). In fact, the weakly compressible IEMHD equations have the same mathematical structure as the incompressible case when the ion $\beta _i$
(see also Meyrand & Galtier Reference Meyrand and Galtier2010) which is less steep than the prediction we will derive in this paper. In the meantime, a rigorous derivation (using systematic asymptotic expansions) based on a more general model including electron inertia and finite Larmor radius corrections has been proposed (Passot, Sulem & Tassi Reference Passot, Sulem and Tassi2017; Passot & Sulem Reference Passot and Sulem2019). This more general approach allows the study of several different limits, and recovery in particular of the model discussed previously (Chen & Boldyrev Reference Chen and Boldyrev2017). In fact, the weakly compressible IEMHD equations have the same mathematical structure as the incompressible case when the ion $\beta _i$![]() (the ratio between ion thermal pressure and magnetic pressure) is moderately small. Therefore, the physics of wave turbulence that we will describe in this paper has a broader impact than strictly speaking the incompressible case and can be applied for both inertial whistler waves (IWW) and inertial kinetic Alfvén waves (IKAW). A similar situation exists for scales larger than $d_e$
(the ratio between ion thermal pressure and magnetic pressure) is moderately small. Therefore, the physics of wave turbulence that we will describe in this paper has a broader impact than strictly speaking the incompressible case and can be applied for both inertial whistler waves (IWW) and inertial kinetic Alfvén waves (IKAW). A similar situation exists for scales larger than $d_e$![]() : in the presence of a strong $\boldsymbol {B_0}$
: in the presence of a strong $\boldsymbol {B_0}$![]() , the equations describing the nonlinear dynamics of kinetic Alfvén waves and whistler waves have exactly the same mathematical form, which means that the physics of wave turbulence is similar for both problems (Galtier & Meyrand Reference Galtier and Meyrand2015). Although a fully kinetic approach is a priori required to describe plasma dynamics at electron inertial scales, all of these reduced fluid models can provide interesting insight when considering small fluctuations around a Maxwellian equilibrium state. In this paper, we follow this precept and apply the powerful tool of wave turbulence to extract new properties useful for a better understanding of space plasmas.
, the equations describing the nonlinear dynamics of kinetic Alfvén waves and whistler waves have exactly the same mathematical form, which means that the physics of wave turbulence is similar for both problems (Galtier & Meyrand Reference Galtier and Meyrand2015). Although a fully kinetic approach is a priori required to describe plasma dynamics at electron inertial scales, all of these reduced fluid models can provide interesting insight when considering small fluctuations around a Maxwellian equilibrium state. In this paper, we follow this precept and apply the powerful tool of wave turbulence to extract new properties useful for a better understanding of space plasmas.
The structure of the article is as follows. In § 2, we propose a quick (and therefore simplified) derivation of the system of equations that we will use for the theory of wave turbulence. In § 3, we introduce the canonical variables and derive the dynamical equation describing the wave amplitude variation. In § 4, a phenomenology of wave turbulence is developed to get a simple heuristic explanation for the solutions (Kolmogorov–Zakharov spectra) derived later. In § 5, we derive the wave kinetic equations from which we show the detailed conservation of invariants. In § 6, we obtain the exact stationary solutions in the anisotropic limit $k_\| \ll k_\perp$![]() and the locality of these solutions is proved. In § 7, we consider the limit of super-local interactions and derive the associated nonlinear diffusion equation for the energy. In § 8, we compute the sign of the energy flux which gives the direction of the cascade, and find the Kolmogorov constant. We conclude in § 9 with a discussion of possible applications of our results, and ways in which these results can be extended.
and the locality of these solutions is proved. In § 7, we consider the limit of super-local interactions and derive the associated nonlinear diffusion equation for the energy. In § 8, we compute the sign of the energy flux which gives the direction of the cascade, and find the Kolmogorov constant. We conclude in § 9 with a discussion of possible applications of our results, and ways in which these results can be extended.
2. Inertial electron magnetohydrodynamics
The goal of this section is to quickly derive in a simplified way the set of equations describing the dynamics of non-relativistic electrons at inertial scales in a fully ionized plasma. For this reason, the assumption of incompressibility will be used. A complete derivation is found in Chen & Boldyrev (Reference Chen and Boldyrev2017) and in Passot et al. (Reference Passot, Sulem and Tassi2017).
2.1. Governing equations
The basic fluid equations governing the electron dynamics in an incompressible (dissipationless) plasma are
where $\boldsymbol {u}_e(\boldsymbol {x},t)$![]() is the electron velocity, $\rho _e(\boldsymbol {x},t)= m_e n_0$
is the electron velocity, $\rho _e(\boldsymbol {x},t)= m_e n_0$![]() is the constant electron mass density, with $m_e$
is the constant electron mass density, with $m_e$![]() the electron mass and $n_0$
the electron mass and $n_0$![]() the density, $P_e(\boldsymbol {x},t)$
the density, $P_e(\boldsymbol {x},t)$![]() is the electron pressure, $q_e>0$
is the electron pressure, $q_e>0$![]() is the modulus of the electron charge, $\boldsymbol {B}(\boldsymbol {x},t)$
is the modulus of the electron charge, $\boldsymbol {B}(\boldsymbol {x},t)$![]() is the magnetic field, $\boldsymbol {E}(\boldsymbol {x},t)$
is the magnetic field, $\boldsymbol {E}(\boldsymbol {x},t)$![]() is the electric field, $\mu_0$
is the electric field, $\mu_0$![]() is the vacuum permeability, $\boldsymbol {J}(\boldsymbol {x},t) = n_0 q_e (\boldsymbol {u}_i - \boldsymbol {u}_e )$
is the vacuum permeability, $\boldsymbol {J}(\boldsymbol {x},t) = n_0 q_e (\boldsymbol {u}_i - \boldsymbol {u}_e )$![]() is the electric current and $\boldsymbol {u}_i(\boldsymbol {x},t)$
is the electric current and $\boldsymbol {u}_i(\boldsymbol {x},t)$![]() is the ion velocity (assumed to be zero). Normalizing the magnetic field to the (electron) Alfvén velocity and then taking the rotational of (2.1) combined with the Maxwell–Faraday law (2.2), one obtains
is the ion velocity (assumed to be zero). Normalizing the magnetic field to the (electron) Alfvén velocity and then taking the rotational of (2.1) combined with the Maxwell–Faraday law (2.2), one obtains
where $d_e = \sqrt {m_e/(n_0 q_e^{2} \mu _0)}$![]() is the electron inertial length. Now, we introduce a relatively strong and uniform (normalized) magnetic field $\boldsymbol {b}_0 = b_0 \hat {\boldsymbol {e}}_\|$
is the electron inertial length. Now, we introduce a relatively strong and uniform (normalized) magnetic field $\boldsymbol {b}_0 = b_0 \hat {\boldsymbol {e}}_\|$![]() that defines the parallel direction. In the limit of IEMHD, the spatial variations of $\boldsymbol {b}$
that defines the parallel direction. In the limit of IEMHD, the spatial variations of $\boldsymbol {b}$![]() are done on a characteristic length $L \ll d_e$
are done on a characteristic length $L \ll d_e$![]() and mainly in the plane perpendicular to $\hat {\boldsymbol {e}}_\|$
and mainly in the plane perpendicular to $\hat {\boldsymbol {e}}_\|$![]() . Thus, at the leading order, we have
. Thus, at the leading order, we have
and also $\boldsymbol {J} = - n_0 q_e \boldsymbol {u}_e$![]() , which can be written $d_e \boldsymbol {j} = - \boldsymbol {u}_e$
, which can be written $d_e \boldsymbol {j} = - \boldsymbol {u}_e$![]() with the normalized electric current $\boldsymbol {j} \equiv \boldsymbol {\nabla } \times \boldsymbol {b}$
with the normalized electric current $\boldsymbol {j} \equiv \boldsymbol {\nabla } \times \boldsymbol {b}$![]() . The magnetic field having a zero divergence, we define $\boldsymbol {b} \equiv \boldsymbol {b}_0 - \boldsymbol {\nabla } \times ( g \boldsymbol {e}_x + \psi \boldsymbol {e}_z )$
. The magnetic field having a zero divergence, we define $\boldsymbol {b} \equiv \boldsymbol {b}_0 - \boldsymbol {\nabla } \times ( g \boldsymbol {e}_x + \psi \boldsymbol {e}_z )$![]() , where $\hat {\boldsymbol {e}}_z$
, where $\hat {\boldsymbol {e}}_z$![]() is a unit vector (hereafter, we will assume $\hat {\boldsymbol {e}}_z = \hat {\boldsymbol {e}}_\|$
is a unit vector (hereafter, we will assume $\hat {\boldsymbol {e}}_z = \hat {\boldsymbol {e}}_\|$![]() which is valid at leading order for a relatively strong uniform magnetic field $\boldsymbol {b}_0$
which is valid at leading order for a relatively strong uniform magnetic field $\boldsymbol {b}_0$![]() ), $\psi (\boldsymbol {x},t)$
), $\psi (\boldsymbol {x},t)$![]() a streamfunction and $g(\boldsymbol {x},t)$
a streamfunction and $g(\boldsymbol {x},t)$![]() a function satisfying the relation $\partial _y g \equiv b_\|$
a function satisfying the relation $\partial _y g \equiv b_\|$![]() . We obtain the relation
. We obtain the relation
where, hereafter, the $z$![]() -derivative is assumed to be negligible compared with the perpendicular derivative. Replacing $\boldsymbol {b}$
-derivative is assumed to be negligible compared with the perpendicular derivative. Replacing $\boldsymbol {b}$![]() by its expression, the electron velocity can be expressed as a function of the magnetic field components
by its expression, the electron velocity can be expressed as a function of the magnetic field components
Projecting equation (2.7) in the perpendicular plane to $\hat {\boldsymbol {e}}_\|$![]() , we find
, we find

The non-trivial relation

allows us to simplify the previous equation and, by expressing $\boldsymbol {u}_e$![]() as a function of $\psi$
as a function of $\psi$![]() , we obtain, after some algebraic manipulations,
, we obtain, after some algebraic manipulations,
with $\varOmega _e \equiv b_0 / d_e$![]() the cyclotron frequency of electrons (note that, here, $\varOmega _e$
the cyclotron frequency of electrons (note that, here, $\varOmega _e$![]() is constant due to the assumption of incompressibility).
is constant due to the assumption of incompressibility).
Now, a projection of (2.7) in the $\hat {\boldsymbol {e}}_\|$![]() direction gives directly
direction gives directly
It is straightforward to show that the first term of the right-hand side is exactly zero. Then, by expressing $\boldsymbol {b}$![]() and $\boldsymbol {u}_e$
and $\boldsymbol {u}_e$![]() as functions of $\psi$
as functions of $\psi$![]() and $b_\|$
and $b_\|$![]() , we obtain
, we obtain
Equations (2.12) and (2.14) describe the dynamics of electrons at inertial scales. They have been derived in a more general framework and using kinetic arguments by Chen & Boldyrev (Reference Chen and Boldyrev2017) and Passot et al. (Reference Passot, Sulem and Tassi2017). Here, we have used the incompressibility condition to propose a (less accurate but more) fast derivation of a system that a priori describes only IWW. However, it is interesting to note that at inertial electron scales: (i) IKAW and IWW can have the same dispersion relation and the only difference is that the transition to the inertial regime occurs at $k_\perp ^{2} d_e^{2} \simeq 1$![]() for IWW rather than $k_\perp ^{2} d_e^{2} \simeq 1 + 2/ \beta _i$
for IWW rather than $k_\perp ^{2} d_e^{2} \simeq 1 + 2/ \beta _i$![]() for IKAW; (ii) the nonlinear equations governing the dynamics of IKAW and IWW are mathematically similar (up to a change of variable from $b_z$
for IKAW; (ii) the nonlinear equations governing the dynamics of IKAW and IWW are mathematically similar (up to a change of variable from $b_z$![]() to $\rho _e$
to $\rho _e$![]() Chen & Boldyrev Reference Chen and Boldyrev2017; Passot et al. Reference Passot, Sulem and Tassi2017), which means that the physics of wave turbulence developed in this paper applies to both waves. A similar situation is found at scales larger than $d_e$
Chen & Boldyrev Reference Chen and Boldyrev2017; Passot et al. Reference Passot, Sulem and Tassi2017), which means that the physics of wave turbulence developed in this paper applies to both waves. A similar situation is found at scales larger than $d_e$![]() : in the presence of a strong $\boldsymbol {B_0}$
: in the presence of a strong $\boldsymbol {B_0}$![]() , the equations describing the nonlinear dynamics of kinetic Alfvén waves and whistler waves have exactly the same mathematical form, which means that the physics of wave turbulence is similar for both problems (Galtier & Meyrand Reference Galtier and Meyrand2015).
, the equations describing the nonlinear dynamics of kinetic Alfvén waves and whistler waves have exactly the same mathematical form, which means that the physics of wave turbulence is similar for both problems (Galtier & Meyrand Reference Galtier and Meyrand2015).
2.2. Three-dimensional quadratic invariants
In the absence of forcing and dissipation, the system (2.12)–(2.14) has two quadratic invariants. The first invariant is the energy which is written at the leading order
where $\langle \rangle$![]() is a spatial average or, equivalently by ergodicity, an ensemble average. Here, $E$
is a spatial average or, equivalently by ergodicity, an ensemble average. Here, $E$![]() can also be interpreted as the kinetic energy of electrons. As shown in Appendix A, both $E_\perp$
can also be interpreted as the kinetic energy of electrons. As shown in Appendix A, both $E_\perp$![]() and $E_\|$
and $E_\|$![]() are separately conserved at the nonlinear level, however, energy is exchanged between the two at the linear level, thanks to the presence of waves. This definition of energy is valid for both IWW and for IKAW in the limit of small $\beta _i$
are separately conserved at the nonlinear level, however, energy is exchanged between the two at the linear level, thanks to the presence of waves. This definition of energy is valid for both IWW and for IKAW in the limit of small $\beta _i$![]() .
.
The second quadratic invariant is the momentum that can be written at the leading order
Here, $H$![]() can be interpreted as the kinetic helicity of electrons. Unlike energy, the momentum is not positive defined. As we will see later, the wave kinetic equations conserve these two invariants on the resonant manifold.
can be interpreted as the kinetic helicity of electrons. Unlike energy, the momentum is not positive defined. As we will see later, the wave kinetic equations conserve these two invariants on the resonant manifold.
2.3. Dispersion relation
In the linear regime, the Fourier transform of (2.12) and (2.14) gives
where the Fourier transform used is
Hereafter, we use the notation $b_k \equiv {b_\|}_k$![]() . If the wavevector $\boldsymbol {k}$
. If the wavevector $\boldsymbol {k}$![]() is decomposed as $\boldsymbol {k} = k_\perp \hat {\boldsymbol {e}}_\perp + k_\| \hat {\boldsymbol {e}}_\|$
is decomposed as $\boldsymbol {k} = k_\perp \hat {\boldsymbol {e}}_\perp + k_\| \hat {\boldsymbol {e}}_\|$![]() , then the linear dispersion relation reads
, then the linear dispersion relation reads
One can find the following solutions to the linear IEMHD equations in Fourier space:
with $f$![]() and $g$
and $g$![]() two arbitrary functions.
two arbitrary functions.
3. Wave amplitude equation
In Fourier space, IEMHD equations (2.12) and (2.14) become
with $\delta _{pq}^{k} \equiv \delta ( \boldsymbol {k} - \boldsymbol {p} - \boldsymbol {q})$![]() the Dirac distribution coming from the Fourier transform of the nonlinear terms. We introduce the canonical variables as follows:
the Dirac distribution coming from the Fourier transform of the nonlinear terms. We introduce the canonical variables as follows:
where $s_k =\pm$![]() is the directional polarization that defines the direction of the wave propagation with $s_k k_\| \ge 0$
is the directional polarization that defines the direction of the wave propagation with $s_k k_\| \ge 0$![]() . After a little calculation, we find
. After a little calculation, we find

By making the following change of variable $A_{\boldsymbol {k}}^{s_k} = \epsilon a_{\boldsymbol {k}}^{s_k} \, {\rm e}^{-{\rm i} s_k \omega _k t}$![]() , where $\epsilon \ll 1$
, where $\epsilon \ll 1$![]() is a small positive parameter, the linear part of this equation vanishes and we obtain the fundamental equation describing the slow temporal evolution – thanks to $\epsilon$
is a small positive parameter, the linear part of this equation vanishes and we obtain the fundamental equation describing the slow temporal evolution – thanks to $\epsilon$![]() – of the wave amplitude
– of the wave amplitude

with $\varOmega ^{k}_{pq} \equiv s_k \omega _k - s_p \omega _p - s_q \omega _q$![]() and $\mathcal {H}_{\boldsymbol {kpq}}^{s_k s_p s_q} \equiv \hat {\boldsymbol {e}}_\| \boldsymbol {\cdot } (\boldsymbol {p}_\perp \times \boldsymbol {q}_\perp ) ( q_\perp ^{2} + s_k s_q k_\perp q_\perp ) / (k_\perp p_\perp q_\perp )$
and $\mathcal {H}_{\boldsymbol {kpq}}^{s_k s_p s_q} \equiv \hat {\boldsymbol {e}}_\| \boldsymbol {\cdot } (\boldsymbol {p}_\perp \times \boldsymbol {q}_\perp ) ( q_\perp ^{2} + s_k s_q k_\perp q_\perp ) / (k_\perp p_\perp q_\perp )$![]() the nonlinear interaction coefficient which depends on the nonlinearities of the system. The presence of the complex exponential is fundamental for the asymptotic closure: as we are interested in the long-time behaviour with respect to the linear time scale ($1/\omega$
the nonlinear interaction coefficient which depends on the nonlinearities of the system. The presence of the complex exponential is fundamental for the asymptotic closure: as we are interested in the long-time behaviour with respect to the linear time scale ($1/\omega$![]() ), the contribution of the exponential is mostly zero. Only (secular) terms for which $\varOmega ^{k}_{pq}=0$
), the contribution of the exponential is mostly zero. Only (secular) terms for which $\varOmega ^{k}_{pq}=0$![]() will survive (Benney & Saffman Reference Benney and Saffman1966; Newell, Nazarenko & Biven Reference Newell, Nazarenko and Biven2001). Adding to this the relation imposed by the Dirac distribution, we can obtain the following resonance condition (symmetries in $\boldsymbol {p}$
will survive (Benney & Saffman Reference Benney and Saffman1966; Newell, Nazarenko & Biven Reference Newell, Nazarenko and Biven2001). Adding to this the relation imposed by the Dirac distribution, we can obtain the following resonance condition (symmetries in $\boldsymbol {p}$![]() and $\boldsymbol {q}$
and $\boldsymbol {q}$![]() are used):
are used):
After a few manipulations, we find the (anisotropic) relationships
which will be useful to prove the conservation of the quadratic invariants. This is also useful to highlight the anisotropic character of the system. Indeed, let us consider the particular case of super-local interactions which give, in general, a dominant contribution to the turbulent dynamics. In this case, we have $k_\perp \simeq p_\perp \simeq q_\perp$![]() and the resonance condition simplifies into
and the resonance condition simplifies into
If $k_\|$![]() is non-zero, the left-hand term will only give a non-negligible contribution when $s_p=-s_q$
is non-zero, the left-hand term will only give a non-negligible contribution when $s_p=-s_q$![]() . We do not consider the case $s_p=s_q$
. We do not consider the case $s_p=s_q$![]() which is not relevant to first order in the case of local interactions, as can be seen in expression (3.5), which then becomes negligible (it is easier to see that in (3.11)–(3.12) after using the symmetry in $\boldsymbol {p}$
which is not relevant to first order in the case of local interactions, as can be seen in expression (3.5), which then becomes negligible (it is easier to see that in (3.11)–(3.12) after using the symmetry in $\boldsymbol {p}$![]() and $\boldsymbol {q}$
and $\boldsymbol {q}$![]() ). The immediate consequence is that either the middle or the right term has its numerator cancelling (to first order), which implies that the associated denominator must also cancel (to first order) to satisfy the equality: for example, if $s_k=s_p$
). The immediate consequence is that either the middle or the right term has its numerator cancelling (to first order), which implies that the associated denominator must also cancel (to first order) to satisfy the equality: for example, if $s_k=s_p$![]() then $q_\| \simeq 0$
then $q_\| \simeq 0$![]() . This condition means that the transfer in the parallel direction is negligible because the integration in the parallel direction of (3.5) is then reduced to a few modes (since $p_\| \simeq k_\|$
. This condition means that the transfer in the parallel direction is negligible because the integration in the parallel direction of (3.5) is then reduced to a few modes (since $p_\| \simeq k_\|$![]() ) which strongly limits the transfer between the parallel modes. The cascade in the parallel direction is thus possible but relatively weak compared with the one in the perpendicular direction.
) which strongly limits the transfer between the parallel modes. The cascade in the parallel direction is thus possible but relatively weak compared with the one in the perpendicular direction.
Before applying the spectral formalism of wave turbulence, it is necessary to symmetrize the fundamental equation (3.5) under the exchange of $\boldsymbol {p}$![]() and $\boldsymbol {q}$
and $\boldsymbol {q}$![]() . To do this, we take advantage of the summation over the $s_p$
. To do this, we take advantage of the summation over the $s_p$![]() and $s_q$
and $s_q$![]() polarizations and introduce
polarizations and introduce
to finally obtain, after a little calculation,

where
This operator has, among others, the following symmetries
Equation (3.11) is our fundamental equation, the starting point to derive the wave kinetic equations. Note that the nonlinear coupling associated with the wavevectors $\boldsymbol {p}$![]() and $\boldsymbol {q}$
and $\boldsymbol {q}$![]() vanishes when they are collinear ($k=0$
vanishes when they are collinear ($k=0$![]() is a particular case). Additionally, the nonlinear coupling vanishes whenever the wavenumbers $p_\perp$
is a particular case). Additionally, the nonlinear coupling vanishes whenever the wavenumbers $p_\perp$![]() and $q_\perp$
and $q_\perp$![]() are equal if their associated polarities $s_p$
are equal if their associated polarities $s_p$![]() and $s_q$
and $s_q$![]() are also equal. This was also observed in EMHD (for scales larger than $d_e$
are also equal. This was also observed in EMHD (for scales larger than $d_e$![]() ) and seems to be a general property of helical waves (Kraichnan Reference Kraichnan1973; Waleffe Reference Waleffe1992; Turner Reference Turner2000; Galtier Reference Galtier2003; Galtier & Bhattacharjee Reference Galtier and Bhattacharjee2003).
) and seems to be a general property of helical waves (Kraichnan Reference Kraichnan1973; Waleffe Reference Waleffe1992; Turner Reference Turner2000; Galtier Reference Galtier2003; Galtier & Bhattacharjee Reference Galtier and Bhattacharjee2003).
4. Phenomenology of wave turbulence
Before going into the deep analysis of the wave turbulence regime, it is important to have a simple (phenomenological) picture in mind of the physical process that we are going to describe. According to the properties given in § 3, if we assume that the nonlinear transfer is mainly driven by super-local interactions $( k \sim p \sim q )$![]() , which is a classical assumption in the turbulence phenomenology, then we can consider only stochastic collisions between counter-propagating waves $(s_p = - s_q)$
, which is a classical assumption in the turbulence phenomenology, then we can consider only stochastic collisions between counter-propagating waves $(s_p = - s_q)$![]() to derive the form of the spectra. Note that non-local interactions (which include copropagating waves) also provide a contribution to the nonlinear dynamics but, as will be shown in § 6.4 with the convergence study, their contributions are not dominant for the formation of a stationary spectrum.
to derive the form of the spectra. Note that non-local interactions (which include copropagating waves) also provide a contribution to the nonlinear dynamics but, as will be shown in § 6.4 with the convergence study, their contributions are not dominant for the formation of a stationary spectrum.
To find the transfer time and then the energy spectrum, we first need to evaluate the modification of a wave produced by one collision. Starting from the momentum equation (for simplicity we write the wave amplitude as $a_\ell$![]() and assume anisotropy with $k \sim k_\perp$
and assume anisotropy with $k \sim k_\perp$![]() ), we have
), we have
where $\tau _1$![]() is the duration of one collision; in other words, after a collision, the distortion of a wave is $\varDelta _1 a_\ell \simeq a_\ell ^{2} / \ell _\perp$
is the duration of one collision; in other words, after a collision, the distortion of a wave is $\varDelta _1 a_\ell \simeq a_\ell ^{2} / \ell _\perp$![]() . This distortion is going to increase with time in such a way that, after $N$
. This distortion is going to increase with time in such a way that, after $N$![]() stochastic collisions, the cumulative effect may be evaluated like a random walk (Galtier Reference Galtier2016)
stochastic collisions, the cumulative effect may be evaluated like a random walk (Galtier Reference Galtier2016)

The transfer time, $\tau _\mathrm {tr}$![]() , that we are looking for is the time for which the cumulative distortion is of order one, i.e. of the order of the wave itself
, that we are looking for is the time for which the cumulative distortion is of order one, i.e. of the order of the wave itself
Then, we obtain
where $\tau _\mathrm {NL} \equiv \ell _\perp / a_\ell$![]() . This is basically the formula that we are going to use to evaluate the energy spectra. Let us consider IWW/IKAW for which $\tau _1 \sim 1/\omega _k \sim k_\perp / k_\parallel$
. This is basically the formula that we are going to use to evaluate the energy spectra. Let us consider IWW/IKAW for which $\tau _1 \sim 1/\omega _k \sim k_\perp / k_\parallel$![]() . A classical calculation with a constant energy flux $\varepsilon \sim E_\ell / \tau _\mathrm {tr}$
. A classical calculation with a constant energy flux $\varepsilon \sim E_\ell / \tau _\mathrm {tr}$![]() , leads finally to the bi-dimensional axisymmetric energy spectrum
, leads finally to the bi-dimensional axisymmetric energy spectrum
As we will see in § 6.3, this corresponds to the exact solution of the wave turbulence theory. The same calculation could be done for the momentum but, as we will see, it presents a more subtle behaviour that the phenomenology cannot describe.
5. Kinetic equations
5.1. Definition of the energy density tensor
We now move on to a statistical description. We use the ensemble average $\langle \rangle$![]() and define the following spectral correlators (cumulants) for homogeneous turbulence (we assume $\langle a_k^{s_k}\rangle =0$
and define the following spectral correlators (cumulants) for homogeneous turbulence (we assume $\langle a_k^{s_k}\rangle =0$![]() ):
):
with ${\rm e}^{s_k'}( \boldsymbol {k}') = e_{\boldsymbol {k}'}^{s_k'}$![]() . We observe the presence of the delta function $\delta ^{s_k}_{s_k'}$
. We observe the presence of the delta function $\delta ^{s_k}_{s_k'}$![]() meaning that two-point correlations of opposite polarities have no long-time influence in the wave turbulence regime. The other delta function is the consequence of the statistical homogeneity assumption. The objective of the wave turbulence theory is to derive a self-consistent equation for the time evolution of this spectral correlator; this is the kinetic equation. In this development, we have to face the classical closure problem: a hierarchy of statistical equations of increasingly higher order emerges. In contrast to strong turbulence, in the weak wave turbulence regime we can use the time scale separation to achieve a natural closure of the system (Benney & Saffman Reference Benney and Saffman1966; Newell et al. Reference Newell, Nazarenko and Biven2001). After a lengthy (but classical) algebra, we obtain the time evolution equation of the energy density tensor (we leave the details of the derivation to Appendix B)
meaning that two-point correlations of opposite polarities have no long-time influence in the wave turbulence regime. The other delta function is the consequence of the statistical homogeneity assumption. The objective of the wave turbulence theory is to derive a self-consistent equation for the time evolution of this spectral correlator; this is the kinetic equation. In this development, we have to face the classical closure problem: a hierarchy of statistical equations of increasingly higher order emerges. In contrast to strong turbulence, in the weak wave turbulence regime we can use the time scale separation to achieve a natural closure of the system (Benney & Saffman Reference Benney and Saffman1966; Newell et al. Reference Newell, Nazarenko and Biven2001). After a lengthy (but classical) algebra, we obtain the time evolution equation of the energy density tensor (we leave the details of the derivation to Appendix B)

where
and $\varOmega _{kpq} \equiv s_k \omega _k + s_p \omega _p + s_q \omega _q$![]() and $\delta _{kpq} = \delta (\boldsymbol {k} + \boldsymbol {p} + \boldsymbol {q})$
and $\delta _{kpq} = \delta (\boldsymbol {k} + \boldsymbol {p} + \boldsymbol {q})$![]() . This equation is the main result of the wave turbulence formalism. It describes the statistical properties of IWW or IKAW turbulence at the leading order, i.e. for three-wave interactions.
. This equation is the main result of the wave turbulence formalism. It describes the statistical properties of IWW or IKAW turbulence at the leading order, i.e. for three-wave interactions.
5.2. Detailed conservation of quadratic invariants
In § 2.2 we introduced the three-dimensional invariants of IEMHD. The first test that the wave turbulence equations must pass is the detailed conservation – i.e. for each triad ($\boldsymbol {k}, \boldsymbol {p}, \boldsymbol {q}$![]() ) – of these invariants. Starting from the definitions (2.15) and (2.16), we define the energy and momentum spectra
) – of these invariants. Starting from the definitions (2.15) and (2.16), we define the energy and momentum spectra
Before checking the energy conservation, it is interesting to note that, when one of the polarized energy density tensors $e_{\boldsymbol {k}}^{\pm }$![]() is zero, the other invariant is extremal and verifies the relation $H(\boldsymbol {k}) = \pm k_\perp E(\boldsymbol {k})$
is zero, the other invariant is extremal and verifies the relation $H(\boldsymbol {k}) = \pm k_\perp E(\boldsymbol {k})$![]() , which is in agreement with the realizability condition (Schwarz inequality) $\vert H(\boldsymbol {k}) \vert \le k_\perp E(\boldsymbol {k})$
, which is in agreement with the realizability condition (Schwarz inequality) $\vert H(\boldsymbol {k}) \vert \le k_\perp E(\boldsymbol {k})$![]() . From (5.2), we obtain the equation for the (total) energy
. From (5.2), we obtain the equation for the (total) energy

Without forcing and dissipation, energy must be conserved and this conservation is done at the level of triadic interactions (detailed energy conservation). The demonstration is straightforward. By applying a cyclic permutation of wavevectors and polarizations, we find

which proves the conservation of (kinetic) energy on the resonant manifold for each triadic interaction.
For the second invariant $H(t)$![]() , one has
, one has

The same manipulations as before lead immediately to

This proves the conservation of momentum (kinetic helicity) on the resonant manifold for each triadic interaction.
5.3. Helical turbulence
From the wave turbulence equation (5.2), we can deduce several general properties. First, we observe that there is no coupling between the waves associated with the $\boldsymbol {p}$![]() and $\boldsymbol {q}$
and $\boldsymbol {q}$![]() wavevectors when these wavevectors are collinear. Second, the nonlinear coupling disappears whenever the wavenumbers $p_\perp$
wavevectors when these wavevectors are collinear. Second, the nonlinear coupling disappears whenever the wavenumbers $p_\perp$![]() and $q_\perp$
and $q_\perp$![]() are equal if their associated polarities $s_p$
are equal if their associated polarities $s_p$![]() and $s_q$
and $s_q$![]() are also equal. These properties are also observed in EMHD (for scales larger than $d_e$
are also equal. These properties are also observed in EMHD (for scales larger than $d_e$![]() ) and more generally for other helical waves (Kraichnan Reference Kraichnan1973; Waleffe Reference Waleffe1992; Turner Reference Turner2000; Galtier Reference Galtier2003; Galtier & Bhattacharjee Reference Galtier and Bhattacharjee2003). Note that they can already be deduced directly from the fundamental equation (3.5). Third, the wave modes ($k_\| > 0$
) and more generally for other helical waves (Kraichnan Reference Kraichnan1973; Waleffe Reference Waleffe1992; Turner Reference Turner2000; Galtier Reference Galtier2003; Galtier & Bhattacharjee Reference Galtier and Bhattacharjee2003). Note that they can already be deduced directly from the fundamental equation (3.5). Third, the wave modes ($k_\| > 0$![]() ) are decoupled from the slow mode ($k_\|=0$
) are decoupled from the slow mode ($k_\|=0$![]() ) which is not described by these wave kinetic equations. This situation is thus different from wave turbulence in incompressible MHD where the slow mode has a profound influence on the nonlinear dynamics.
) which is not described by these wave kinetic equations. This situation is thus different from wave turbulence in incompressible MHD where the slow mode has a profound influence on the nonlinear dynamics.
6. Turbulent spectra as exact solutions
6.1. Wave kinetic equations for the invariants
The objective of this section is to derive, in the stationary case, the exact power law solutions of the kinetic equations for the two invariants, energy and momentum. To do so, it is necessary to simplify the equations, written for $E(\boldsymbol {k})$![]() and $H(\boldsymbol {k})$
and $H(\boldsymbol {k})$![]() , using the axisymmetric assumption. First of all, we have
, using the axisymmetric assumption. First of all, we have

We now develop the energy density tensors inside the integral in terms of energy and momentum spectra. We note that only terms containing the products of two $E(\boldsymbol {k})$![]() or two $H(\boldsymbol {k})$
or two $H(\boldsymbol {k})$![]() will survive for energy, whereas only the products of $E(\boldsymbol {k}) H(\boldsymbol {k})$
will survive for energy, whereas only the products of $E(\boldsymbol {k}) H(\boldsymbol {k})$![]() will survive for helicity. After some algebra, we find for the energy
will survive for helicity. After some algebra, we find for the energy

and for the momentum

If we exchange in the integrand the dummy variables, $\boldsymbol {p}$![]() and $\boldsymbol {q}$
and $\boldsymbol {q}$![]() , as well as $s_p$
, as well as $s_p$![]() and $s_q$
and $s_q$![]() , we can simplify further the previous expressions to obtain
, we can simplify further the previous expressions to obtain

with

6.2. The axisymmetric wave turbulence equations
To simplify the problem, we will consider an axial symmetry with respect to the external magnetic field and introduce the two-dimensional anisotropic spectra
which result from an integration over the angles in the plane perpendicular to the mean magnetic field (see figure 1). In polar coordinates $\mathrm {d}\boldsymbol {p} \, \mathrm {d}\boldsymbol {q} = p_\perp \, \mathrm {d} \alpha _q \, \mathrm {d} p_\perp \, \mathrm {d} p_\| \, \mathrm {d} q_\|$![]() and, thanks to the Al-Kashi formula: $q_\perp ^{2} = k_\perp ^{2} + p_\perp ^{2} - 2 k_\perp p_\perp \cos \alpha _q$
and, thanks to the Al-Kashi formula: $q_\perp ^{2} = k_\perp ^{2} + p_\perp ^{2} - 2 k_\perp p_\perp \cos \alpha _q$![]() , we find at fixed $k_\perp$
, we find at fixed $k_\perp$![]() and $p_\perp$
and $p_\perp$![]() , $q_\perp \, \mathrm {d} q_\perp = k_\perp p_\perp \sin \alpha _q \, \mathrm {d} \alpha _q$
, $q_\perp \, \mathrm {d} q_\perp = k_\perp p_\perp \sin \alpha _q \, \mathrm {d} \alpha _q$![]() . Using expression (5.3), we then obtain the kinetic equations
. Using expression (5.3), we then obtain the kinetic equations

where $\varDelta _\perp$![]() the integration domain verifies the resonance condition $\boldsymbol {k}_\perp + \boldsymbol {p}_\perp + \boldsymbol {q}_\perp = \boldsymbol {0}$
the integration domain verifies the resonance condition $\boldsymbol {k}_\perp + \boldsymbol {p}_\perp + \boldsymbol {q}_\perp = \boldsymbol {0}$![]() and
and

with $\alpha _q$![]() the angle between $\boldsymbol {k}_\perp$
the angle between $\boldsymbol {k}_\perp$![]() and $\boldsymbol {p}_\perp$
and $\boldsymbol {p}_\perp$![]() in the triangle defined by the triadic interaction $( \boldsymbol {k}_\perp, \boldsymbol {p}_\perp, \boldsymbol {q}_\perp )$
in the triangle defined by the triadic interaction $( \boldsymbol {k}_\perp, \boldsymbol {p}_\perp, \boldsymbol {q}_\perp )$![]() (see figure 1). Equation (6.8) will be used to derive exact solutions also called Kolmogorov–Zakharov spectra.
(see figure 1). Equation (6.8) will be used to derive exact solutions also called Kolmogorov–Zakharov spectra.

Figure 1. Triadic relation $\boldsymbol {k}_\perp + \boldsymbol {p}_\perp + \boldsymbol {q}_\perp = \boldsymbol {0}$![]() .
.
6.3. Kolmogorov–Zakharov spectra
Equation (6.8) has sufficient symmetry to apply the bi-homogeneous conformal Kuznetsov –Zakharov transformation (Zakharov et al. Reference Zakharov, L'Vov and Falkovich1992). This transformation has been applied to several problems involving anisotropy (Kuznetsov Reference Kuznetsov2001; Galtier Reference Galtier2003, Reference Galtier2006). It is a generalization of the Zakharov transformation applied for isotropic turbulence (in the context of strong two-dimensional hydrodynamic turbulence, see also Kraichnan Reference Kraichnan1967). With such an operation, we are able to find the exact stationary solutions of the kinetic equations in power law form. The bihomogeneity of the integrals in the wavenumbers $k_\perp$![]() and $k_\|$
and $k_\|$![]() allows us to use the transformations (see figure 2)
allows us to use the transformations (see figure 2)

Figure 2. Illustration of the Kuznetsov–Zakharov transformation. It consists of swapping regions I and III with regions II and IV, respectively. We specify that the grey band is defined up to infinity and corresponds to the domain $\varDelta _\perp$![]() . The same manipulation is done on the parallel wavenumbers.
. The same manipulation is done on the parallel wavenumbers.
We apply this transformation first on the energy equation (6.8) which means that we are looking for constant energy flux solutions. We seek stationary solutions in the power law form,
where $C_E$![]() and $C_H$
and $C_H$![]() are two constants with $C_E \ge 0$
are two constants with $C_E \ge 0$![]() . (We consider only positive parallel wavenumber since it is symmetric in $k_\|$
. (We consider only positive parallel wavenumber since it is symmetric in $k_\|$![]() .) The new form of the integral, resulting from the summation of the integrand in its primary form and after the Kuznetsov–Zakharov transformation, can be written as
.) The new form of the integral, resulting from the summation of the integrand in its primary form and after the Kuznetsov–Zakharov transformation, can be written as

with the pure energy contribution

and the pure helicity contribution

We can distinguish two different types of solutions. First, there are the thermodynamic equilibrium solutions, which correspond to the equipartition state for which the energy flux is zero. The power laws which verify this condition are
These results can be easily verified by a direct substitution in the original kinetic equations. In general, this stationary state cannot be reached in the presence of helicity because the value $s_k s_p = -1$![]() prevents the cancellation of the integral. There is, however, a particular case where the solutions exist: it is the state of maximal helicity for which either $e_{\boldsymbol {k}}^{+}=0$
prevents the cancellation of the integral. There is, however, a particular case where the solutions exist: it is the state of maximal helicity for which either $e_{\boldsymbol {k}}^{+}=0$![]() or $e_{\boldsymbol {k}}^{-}=0$
or $e_{\boldsymbol {k}}^{-}=0$![]() . Then, we have the relation $H_k=\pm k_\perp E_k$
. Then, we have the relation $H_k=\pm k_\perp E_k$![]() . But this state is not viable as we can see on (5.2): for example, if $e_{\boldsymbol {k}}^{-}=0$
. But this state is not viable as we can see on (5.2): for example, if $e_{\boldsymbol {k}}^{-}=0$![]() at time $t=0$
at time $t=0$![]() , it will not remain zero at time $t>0$
, it will not remain zero at time $t>0$![]() . This means that this solution is only possible if there is an external mechanism that forces the system to remain in the maximal helicity state.
. This means that this solution is only possible if there is an external mechanism that forces the system to remain in the maximal helicity state.
The most interesting solutions are those for which the energy flux is constant, non-zero and finite. These exact solutions are called Kolmogorov-Zakharov (KZ) spectra and correspond to the values which make the integral cancel in a non-trivial way and independently of the polarizations. These spectra are
There are not constrained by the polarization and can therefore be reached by the system even in the presence of helicity.
For the helicity equation, using the same manipulations as before, we obtain

The zero helicity flux solutions satisfy
which correspond to the thermodynamic spectra found for energy (this can be seen directly from (6.9)). For the KZ spectra, we have a family of solutions that meet the following criteria:
The situation is worse than for energy because none of the constant helicity flux solutions (thermodynamic or KZ) can be reached in general because of the presence of the product $s_ks_p$![]() which, let us recall, prevents the cancellation of the term in the right-hand side of expression (6.22). Only the maximal helicity state allows the existence of these stationary spectra but, as said above, it is not a naturally viable state. (Note that this property found in weak wave turbulence may not be true in strong turbulence.)
which, let us recall, prevents the cancellation of the term in the right-hand side of expression (6.22). Only the maximal helicity state allows the existence of these stationary spectra but, as said above, it is not a naturally viable state. (Note that this property found in weak wave turbulence may not be true in strong turbulence.)
In conclusion, the most relevant solutions are the KZ spectra at constant energy flux. In § 8 we will further investigate the corresponding exact solution for $H=0$![]() in order to find the direction of the energy cascade and the expression of the Kolmogorov constant. In space plasma physics, we often compare theoretical predictions with the magnetic spectrum $E_k^{B}$
in order to find the direction of the energy cascade and the expression of the Kolmogorov constant. In space plasma physics, we often compare theoretical predictions with the magnetic spectrum $E_k^{B}$![]() which is well measured by spacecraft (with the Taylor hypothesis, the frequency is used as a proxy for the wavenumber). In our case, a simple dimensional analysis based on the definition of energy (2.15), leads to the relation $E_k \sim k_\perp ^{2} E_k^{B}$
which is well measured by spacecraft (with the Taylor hypothesis, the frequency is used as a proxy for the wavenumber). In our case, a simple dimensional analysis based on the definition of energy (2.15), leads to the relation $E_k \sim k_\perp ^{2} E_k^{B}$![]() . Consequently, we obtain $E_k^{B} \sim k_\perp ^{-9/2}$
. Consequently, we obtain $E_k^{B} \sim k_\perp ^{-9/2}$![]() , which is steeper than the predictions made at scales larger than $d_e$
, which is steeper than the predictions made at scales larger than $d_e$![]() .
.
6.4. Locality condition
We have seen that the most interesting exact solutions of the kinetic equations are the KZ spectra at constant energy flux. However, these solutions are only fully relevant if they satisfy the locality condition. Mathematically, this condition means that the integral must be convergent. If it is not the case, it means physically that the inertial range is not independent of the largest or smallest scales, where forcing and dissipation are expected. The calculation of the locality condition is highly non-trivial in this anisotropic case. It requires a careful treatment that we leave to Appendix C. Note that the study of locality is still a subject of investigation (Dematteis, Polzin & Lvov Reference Dematteis, Polzin and Lvov2022). In the absence of helicity, we find the following conditions:
We obtain a classical result for wave turbulence in the sense that the power law indices of the KZ spectra fall exactly in the middle of the convergence domain (see figure 3).

Figure 3. Domain of convergence of the energy integral. The black dot at the centre of the domain corresponds to the KZ energy spectrum.
7. Super-local interactions
In this section, we shall study the limit of local triadic interactions (in the perpendicular direction) for which the wave kinetic equations simplify significantly. From to the results found in the previous section, we know that it is mainly relevant to study the energy only. In the strongly anisotropic limit $k_\| \ll k_\perp$![]() , (6.8) writes
, (6.8) writes

By definition (the small parameter $\epsilon$![]() is absorbed in the time variable)
is absorbed in the time variable)

is the nonlinear operator which describes the energy transfer between modes which verifies the following symmetry:
In the limit of super-local interactions, we can write
with $0 \ll \epsilon _p \ll 1$![]() and $0 \ll \epsilon _q \ll 1$
and $0 \ll \epsilon _q \ll 1$![]() . We can introduce an arbitrary function $f ( k_\perp, k_\| )$
. We can introduce an arbitrary function $f ( k_\perp, k_\| )$![]() and integrate the kinetic equation to find
and integrate the kinetic equation to find

Neglecting the parallel wavenumber contribution (this assumption is fully compatible with the weak cascade along the parallel direction – see arguments based on the resonance condition), for local interactions we have

At the main order, we can write

Using an integration by parts, we find the relation

The asymptotic form of $T_{\boldsymbol {k p q}}^{s_k s_p s_q}$![]() can be found by using the locality in the perpendicular direction. In particular, we find the relations
can be found by using the locality in the perpendicular direction. In particular, we find the relations

After simplification, we arrive at

With this form we see that the transfer will be significantly higher when $s_p =-s_q$![]() , therefore we will only consider this type of interaction. Then, the expression of the transfer reduces to
, therefore we will only consider this type of interaction. Then, the expression of the transfer reduces to
The resonance condition leads to two possible combinations for the parallel wavenumbers,
The solution corresponds either to $q_\| = 0$![]() or $p_\| = 0$
or $p_\| = 0$![]() , which means in particular that the strong locality assumption is not allowed for the parallel direction. The second solution cancels the transfer, therefore, we will only consider the first solution for which we have (with $p_\|=-k_\|$
, which means in particular that the strong locality assumption is not allowed for the parallel direction. The second solution cancels the transfer, therefore, we will only consider the first solution for which we have (with $p_\|=-k_\|$![]() )
)

We finally obtain the nonlinear diffusion equation

where $C = \tilde \epsilon ^{4} / ({2^{11}} \sqrt {3} \varOmega _e )$![]() . This equation has been derived analytically from the kinetic equations in the limit of super-local (perpendicular) interactions when $H=0$
. This equation has been derived analytically from the kinetic equations in the limit of super-local (perpendicular) interactions when $H=0$![]() . It gives a first interesting description of wave turbulence in IEMHD. In particular, the thermodynamic and KZ spectra are exact solutions. We can also prove that the corresponding energy flux is positive, and thus that the cascade is direct.
. It gives a first interesting description of wave turbulence in IEMHD. In particular, the thermodynamic and KZ spectra are exact solutions. We can also prove that the corresponding energy flux is positive, and thus that the cascade is direct.
It is interesting to note that a similar nonlinear diffusion equation has been obtained, in the same approximation of wave turbulence, for EMHD (David & Galtier Reference David and Galtier2019; Passot & Sulem Reference Passot and Sulem2019) and rotating hydrodynamics (Galtier & David Reference Galtier and David2020). The numerical simulations of this equation reveal the existence of a $k_\perp ^{-8/3}$![]() energy spectrum during the non-stationary phase that is steeper than the KZ spectrum. This solution has been understood as a self-similar solution of the second kind (which means it cannot be predicted analytically). It is also shown that, once the energy spectrum reaches the dissipative scales, a spectral bounce appears which affects the whole inertial range to finally form the expected KZ spectrum in $k_\perp ^{-5/2}$
energy spectrum during the non-stationary phase that is steeper than the KZ spectrum. This solution has been understood as a self-similar solution of the second kind (which means it cannot be predicted analytically). It is also shown that, once the energy spectrum reaches the dissipative scales, a spectral bounce appears which affects the whole inertial range to finally form the expected KZ spectrum in $k_\perp ^{-5/2}$![]() .
.
8. Direction of the energy cascade and Kolmogorov constant
8.1. Direct energy cascade
In this section, we will study the sign of the energy flux from the kinetic equations (6.15) and prove that the cascade in the perpendicular direction is direct. In cylindrical coordinates (see figure 4), we have (Zakharov et al. Reference Zakharov, L'Vov and Falkovich1992)
where $\boldsymbol {\varPi }$![]() is the energy flux vector, $\varPi _\perp$
is the energy flux vector, $\varPi _\perp$![]() and $\varPi _\|$
and $\varPi _\|$![]() its perpendicular and parallel components (axisymmetric turbulence is assumed), respectively. Introducing the axisymmetric spectra $E_k \equiv 2 {\rm \pi}k_\perp E(\boldsymbol {k})$
its perpendicular and parallel components (axisymmetric turbulence is assumed), respectively. Introducing the axisymmetric spectra $E_k \equiv 2 {\rm \pi}k_\perp E(\boldsymbol {k})$![]() , $\varPi _\perp \equiv 2 {\rm \pi}k_\perp \varPi _\perp (\boldsymbol {k})$
, $\varPi _\perp \equiv 2 {\rm \pi}k_\perp \varPi _\perp (\boldsymbol {k})$![]() and $\varPi _\| \equiv 2 {\rm \pi}k_\perp \varPi _\|(\boldsymbol {k})$
and $\varPi _\| \equiv 2 {\rm \pi}k_\perp \varPi _\|(\boldsymbol {k})$![]() , we obtain
, we obtain

Figure 4. Schematic representation of an axisymmetric flux in Fourier space. Each cylindrical shell corresponds to a specific value of $k_\perp$![]() . In theory, they form a continuum but here their discrete nature serves as an illustration.
. In theory, they form a continuum but here their discrete nature serves as an illustration.
We now introduce the adimensional variables $\tilde {p}_\perp \equiv p_\perp / k_\perp$![]() , $\tilde {q}_\perp \equiv q_\perp / k_\perp$
, $\tilde {q}_\perp \equiv q_\perp / k_\perp$![]() , $\tilde {p}_\| \equiv p_\|/ k_\|$
, $\tilde {p}_\| \equiv p_\|/ k_\|$![]() and $\tilde {q}_\| \equiv q_\| / k_\|$
and $\tilde {q}_\| \equiv q_\| / k_\|$![]() . We seek power law solutions of the form (6.14a,b) and then obtain
. We seek power law solutions of the form (6.14a,b) and then obtain
where

and

Taking the limits, corresponding to the KZ spectra, $( x, y, \tilde {x}, \tilde {y} ) \rightarrow ( 5/2, 1/2, 3/2, 1/2 )$![]() , thanks to l'H$\hat{{\rm o}}$
, thanks to l'H$\hat{{\rm o}}$![]() pital's rule, we can write
pital's rule, we can write
where

and

Therefore, the ratio of the two fluxes is

Since it is proportional to $k_\| / k_\perp$![]() , we expect $\varPi _\|^{\mathrm {KZ}} \ll \varPi _\perp ^{\mathrm{KZ}}$
, we expect $\varPi _\|^{\mathrm {KZ}} \ll \varPi _\perp ^{\mathrm{KZ}}$![]() , which is in agreement with the analysis based on the resonance condition to find the direction of the cascade. In the absence of helicity, the ratio (8.9) only depends on $k_\| / k_\perp \ll 1$
, which is in agreement with the analysis based on the resonance condition to find the direction of the cascade. In the absence of helicity, the ratio (8.9) only depends on $k_\| / k_\perp \ll 1$![]() and $I_\| / I_\perp$
and $I_\| / I_\perp$![]() ; we numerically find $I_\| / I_\perp \simeq 0.73$
; we numerically find $I_\| / I_\perp \simeq 0.73$![]() , then the previous expectation is fulfilled.
, then the previous expectation is fulfilled.
We can also find the sign of the energy flux and thus prove the direction of the cascade. Since the perpendicular flux is dominant, we will neglect the parallel flux and only look for the sign of $I_\perp$![]() . A numerical evaluation reveals a positive value, which means that $\varPi _\perp > 0$
. A numerical evaluation reveals a positive value, which means that $\varPi _\perp > 0$![]() and that the energy cascade is direct in the transverse direction.
and that the energy cascade is direct in the transverse direction.
In figure 5, we show the sign of the integrands of $I_\perp$![]() and $I_\|$
and $I_\|$![]() obtained from a numerical evaluation of expressions (8.7). We see that for $I_\perp$
obtained from a numerical evaluation of expressions (8.7). We see that for $I_\perp$![]() the integrand is always positive, while for $I_\|$
the integrand is always positive, while for $I_\|$![]() the integrand can be either positive or negative depending on the perpendicular wavenumbers (for large perpendicular wavenumbers it is always positive) but overall, after integration, the positive sign dominates in the sense that the integral $I_\| >0$
the integrand can be either positive or negative depending on the perpendicular wavenumbers (for large perpendicular wavenumbers it is always positive) but overall, after integration, the positive sign dominates in the sense that the integral $I_\| >0$![]() . Therefore, the parallel cascade is also direct but it is composed of different contributions, with (a minority of) triadic interactions contributing to an inverse transfer.
. Therefore, the parallel cascade is also direct but it is composed of different contributions, with (a minority of) triadic interactions contributing to an inverse transfer.

Figure 5. (a) Integrand of $I_\perp$![]() as a function of $\tilde {p}_\perp$
as a function of $\tilde {p}_\perp$![]() and $\tilde {q}_\perp$
and $\tilde {q}_\perp$![]() ; a positive value is always observed. (b) Integrand of $I_\|$
; a positive value is always observed. (b) Integrand of $I_\|$![]() which changes sign as a function of (small) $\tilde {p}_\perp$
which changes sign as a function of (small) $\tilde {p}_\perp$![]() and $\tilde {q}_\perp$
and $\tilde {q}_\perp$![]() .
.
8.2. Kolmogorov constant
If we neglect the parallel flux and helicity, we can also obtain the expression of the Kolmogorov constant $C_K$![]() for which we can numerically get an estimate. To do so, we take advantage of the Dirac distributions to integrate the parallel wavenumbers. Then, since $I_\perp$
for which we can numerically get an estimate. To do so, we take advantage of the Dirac distributions to integrate the parallel wavenumbers. Then, since $I_\perp$![]() is only defined on the region $\varDelta _\perp$
is only defined on the region $\varDelta _\perp$![]() , we introduce the change of variable $\tilde {q}_\perp \equiv \xi - \tilde {p}_\perp$
, we introduce the change of variable $\tilde {q}_\perp \equiv \xi - \tilde {p}_\perp$![]() where $\xi \in [1,+\infty [$
where $\xi \in [1,+\infty [$![]() and $\tilde {p}_\perp \in [({\xi -1})/{2},\ ({\xi +1})/{2} ]$
and $\tilde {p}_\perp \in [({\xi -1})/{2},\ ({\xi +1})/{2} ]$![]() that confines the integration to this domain. One finds at a given $k_\parallel$
that confines the integration to this domain. One finds at a given $k_\parallel$![]() ,
,
The numerical convergence of $C_K$![]() to this value in shown in figure 6.
to this value in shown in figure 6.

Figure 6. Convergence of $C_K$![]() as a function of $\xi$
as a function of $\xi$![]() .
.
9. Discussion and conclusion
In this paper, we have developed a wave turbulence theory for inertial electron MHD (i.e. for scales smaller than $d_e$![]() ) mediated by three-wave interactions between IWW or between inertial kinetic Alfvén waves. The asymptotic wave kinetic equations are derived for the two quadratic invariants of the system, namely energy and momentum. The theory is expected to be relevant mainly for ion–electron plasmas such as the Earth's magnetosheath, the solar corona or the solar wind (Milanese et al. Reference Milanese, Loureiro, Daschner and Boldyrev2020), but also for electron–positron plasmas (Loureiro & Boldyrev Reference Loureiro and Boldyrev2018). We show that this turbulence is mainly characterized by a direct energy cascade in the direction perpendicular to the strong applied magnetic field. The role of the second invariant, the momentum or kinetic helicity, is less important because in general there is no exact solution at constant helicity flux (except for the state of maximal helicity). By converting the exact solution (KZ spectrum) into units of magnetic field, which is easier to measure in space plasma, we find a magnetic energy spectrum $E^{B} \sim k_\perp ^{-9/2}$
) mediated by three-wave interactions between IWW or between inertial kinetic Alfvén waves. The asymptotic wave kinetic equations are derived for the two quadratic invariants of the system, namely energy and momentum. The theory is expected to be relevant mainly for ion–electron plasmas such as the Earth's magnetosheath, the solar corona or the solar wind (Milanese et al. Reference Milanese, Loureiro, Daschner and Boldyrev2020), but also for electron–positron plasmas (Loureiro & Boldyrev Reference Loureiro and Boldyrev2018). We show that this turbulence is mainly characterized by a direct energy cascade in the direction perpendicular to the strong applied magnetic field. The role of the second invariant, the momentum or kinetic helicity, is less important because in general there is no exact solution at constant helicity flux (except for the state of maximal helicity). By converting the exact solution (KZ spectrum) into units of magnetic field, which is easier to measure in space plasma, we find a magnetic energy spectrum $E^{B} \sim k_\perp ^{-9/2}$![]() . It is interesting to note that this power law is steeper than that observed in the solar wind at sub-MHD scales (satisfying $k d_e < 1$
. It is interesting to note that this power law is steeper than that observed in the solar wind at sub-MHD scales (satisfying $k d_e < 1$![]() ) with a power law index often close to $-8/3$
) with a power law index often close to $-8/3$![]() (Alexandrova et al. Reference Alexandrova, Lacombe, Mangeney, Grappin and Maksimovic2012; Podesta Reference Podesta2013; Sahraoui, Hadid & Huang Reference Sahraoui, Hadid and Huang2020) whereas at $kd_e > 1$
(Alexandrova et al. Reference Alexandrova, Lacombe, Mangeney, Grappin and Maksimovic2012; Podesta Reference Podesta2013; Sahraoui, Hadid & Huang Reference Sahraoui, Hadid and Huang2020) whereas at $kd_e > 1$![]() , power law indices close to $-11/3$
, power law indices close to $-11/3$![]() are observed (Sahraoui et al. Reference Sahraoui, Goldstein, Robert and Khotyaintsev2009, Reference Sahraoui, Hadid and Huang2020) as well as $-9/2$
are observed (Sahraoui et al. Reference Sahraoui, Goldstein, Robert and Khotyaintsev2009, Reference Sahraoui, Hadid and Huang2020) as well as $-9/2$![]() (Sahraoui et al. Reference Sahraoui, Huang, Belmont, Goldstein, Rétino, Robert and Patoul2013) but in a narrow frequency range. The former matches the strong turbulence prediction (Biskamp et al. Reference Biskamp, Schwarz, Zeiler, Celani and Drake1999; Meyrand & Galtier Reference Meyrand and Galtier2010) while the latter is in adequation with the wave turbulence one. In absence of helicity, we prove that the energy cascade is direct and numerically estimate the Kolmogorov constant using its analytical expression. We also prove that the KZ spectrum is in the domain of convergence, showing the relevance of the exact solution.
(Sahraoui et al. Reference Sahraoui, Huang, Belmont, Goldstein, Rétino, Robert and Patoul2013) but in a narrow frequency range. The former matches the strong turbulence prediction (Biskamp et al. Reference Biskamp, Schwarz, Zeiler, Celani and Drake1999; Meyrand & Galtier Reference Meyrand and Galtier2010) while the latter is in adequation with the wave turbulence one. In absence of helicity, we prove that the energy cascade is direct and numerically estimate the Kolmogorov constant using its analytical expression. We also prove that the KZ spectrum is in the domain of convergence, showing the relevance of the exact solution.
An interesting point concerns the dynamics of the two-dimensional state (i.e. the slow modes for which $k_\|=0$![]() ). We see from the kinetic equation (6.8) that the nonlinear transfer for energy and helicity decreases linearly with $k_\|$
). We see from the kinetic equation (6.8) that the nonlinear transfer for energy and helicity decreases linearly with $k_\|$![]() , and for the value $k_\|=0$
, and for the value $k_\|=0$![]() the transfer is exactly null. This means that the dynamics of the slow modes decouples from the three-dimensional state. Actually, the slow modes are not described by the wave turbulence theory which is based on the time scales separation $1/\omega \ll \tau _\mathrm {NL}$
the transfer is exactly null. This means that the dynamics of the slow modes decouples from the three-dimensional state. Actually, the slow modes are not described by the wave turbulence theory which is based on the time scales separation $1/\omega \ll \tau _\mathrm {NL}$![]() (when $k_\| \to 0$
(when $k_\| \to 0$![]() this inequality cannot be satisfied). The possibility that higher-order processes, such as four-wave interactions, could lead to a coupling between two-dimensional and three-dimensional modes has been discussed in the past by Smith & Waleffe (Reference Smith and Waleffe1999) in the context of inertial waves in rotating hydrodynamics. Since it is a similar problem, this scenario could also be relevant here.
this inequality cannot be satisfied). The possibility that higher-order processes, such as four-wave interactions, could lead to a coupling between two-dimensional and three-dimensional modes has been discussed in the past by Smith & Waleffe (Reference Smith and Waleffe1999) in the context of inertial waves in rotating hydrodynamics. Since it is a similar problem, this scenario could also be relevant here.
In the limit of super-local (perpendicular) interactions, we derive a nonlinear diffusion equation that is similar to that found in electron MHD at scales larger than $d_e$![]() . Interestingly, this equation is also similar to the case of inertial wave turbulence (fast rotating hydrodynamic turbulence). In fact, the link is deeper than that since the two problems share the same kinetic equations (within a factor) with the same dispersion relation (within a factor). This connection is due to a strong asymmetry imposed by a mean magnetic field on the one hand, and by the axis rotation on the other hand. It is also due to the helical nature of the waves. This reinforces the bridge between plasma physics and fluid mechanics (see also Galtier & David Reference Galtier and David2020) and suggests that laboratory experiments (Yarom & Sharon Reference Yarom and Sharon2014; Monsalve et al. Reference Monsalve, Brunet, Gallet and Cortet2020) can help to better understand space plasma physics at a scale still difficult to detect by current spacecraft.
. Interestingly, this equation is also similar to the case of inertial wave turbulence (fast rotating hydrodynamic turbulence). In fact, the link is deeper than that since the two problems share the same kinetic equations (within a factor) with the same dispersion relation (within a factor). This connection is due to a strong asymmetry imposed by a mean magnetic field on the one hand, and by the axis rotation on the other hand. It is also due to the helical nature of the waves. This reinforces the bridge between plasma physics and fluid mechanics (see also Galtier & David Reference Galtier and David2020) and suggests that laboratory experiments (Yarom & Sharon Reference Yarom and Sharon2014; Monsalve et al. Reference Monsalve, Brunet, Gallet and Cortet2020) can help to better understand space plasma physics at a scale still difficult to detect by current spacecraft.
Acknowledgements
Editor Francesco Califano thanks the referees for their advice in evaluating this article.
Declaration of interest
The authors report no conflict of interest.
Appendix A. Detailed conservation of energy
We recall the relations $u_\|= d_e \nabla ^{2}_\perp \psi$![]() and $\textbf {u}_\perp = d_e (- \partial _y b_\| \hat {\boldsymbol {e}}_x + \partial _x b_\| \hat {\boldsymbol {e}}_y)$
and $\textbf {u}_\perp = d_e (- \partial _y b_\| \hat {\boldsymbol {e}}_x + \partial _x b_\| \hat {\boldsymbol {e}}_y)$![]() which allow us, in Fourier space, to obtain the expressions of the energy density respectively in the directions parallel and perpendicular to the mean magnetic field: $\vert u_{\|,k}\vert ^{2}= d_e^{2} k_\perp ^{4} \vert \psi _k \vert ^{2}$
which allow us, in Fourier space, to obtain the expressions of the energy density respectively in the directions parallel and perpendicular to the mean magnetic field: $\vert u_{\|,k}\vert ^{2}= d_e^{2} k_\perp ^{4} \vert \psi _k \vert ^{2}$![]() and $\vert u_{\perp,k}\vert ^{2}= d_e^{2} k_\perp ^{2} \vert b_k\vert ^{2}$
and $\vert u_{\perp,k}\vert ^{2}= d_e^{2} k_\perp ^{2} \vert b_k\vert ^{2}$![]() (with $b_k \equiv {b_\|}_k$
(with $b_k \equiv {b_\|}_k$![]() ). From the equations describing the temporal evolution of $\psi$
). From the equations describing the temporal evolution of $\psi$![]() and $b_\|$
and $b_\|$![]() in Fourier space, we obtain the evolution of the energy density (we used the properties $\psi _{-k}^{*} = \psi _k$
in Fourier space, we obtain the evolution of the energy density (we used the properties $\psi _{-k}^{*} = \psi _k$![]() and $b_{-k}^{*} = b_k$
and $b_{-k}^{*} = b_k$![]() )
)


where we have used the relation $\hat {\boldsymbol {e}}_\| \boldsymbol {\cdot } (\hat {\boldsymbol {e}}_{p_\perp } \times \hat {\boldsymbol {e}}_{q_\perp } ) = \sin \alpha _k$![]() and $\textrm {c.c.}$
and $\textrm {c.c.}$![]() denotes the complex conjugate. Parallel $E_\|^{u}$
denotes the complex conjugate. Parallel $E_\|^{u}$![]() and perpendicular $E_\perp ^{u}$
and perpendicular $E_\perp ^{u}$![]() energies being the sum of these quantities over the all wavenumbers, we find
energies being the sum of these quantities over the all wavenumbers, we find
with $S_\|^{u} ( k_\perp, p_\perp, q_\perp )$![]() and $S_\perp ^{u} ( k_\perp, p_\perp, q_\perp )$
and $S_\perp ^{u} ( k_\perp, p_\perp, q_\perp )$![]() the nonlinear interaction coefficient defined as
the nonlinear interaction coefficient defined as
The remarkable property is that the nonlinear contributions are both conserved over time since $S_\|^{u} ( k_\perp, p_\perp, q_\perp )$![]() and $S_\perp ^{u} ( k_\perp, p_\perp, q_\perp )$
and $S_\perp ^{u} ( k_\perp, p_\perp, q_\perp )$![]() verify the following relations:
verify the following relations:
Then, the parallel and perpendicular components of the energy are conserved individually at the nonlinear level. The exchanges between the two are only done at the linear level.
Appendix B. Derivation of the wave kinetic equations
We start from (3.11) and write successively equations for the second- and third-order moments,

and

A natural closure arises for times asymptotically large compared with the linear wave time scale (see e.g. Newell et al. Reference Newell, Nazarenko and Biven2001; Nazarenko Reference Nazarenko2011; Newell & Rumpf Reference Newell and Rumpf2011). An important aspect is the uniformity of the development which was discussed first by Benney & Saffman (Reference Benney and Saffman1966). In this case, the fourth-order moment does not contribute at large time and, therefore, the nonlinear regeneration of third-order moments depends essentially on products of second-order moments
Thanks to the integration on the dummy variables $\boldsymbol {p}$![]() and $\boldsymbol {q}$
and $\boldsymbol {q}$![]() , to their symmetry and the symmetry between the polarizations $s_p$
, to their symmetry and the symmetry between the polarizations $s_p$![]() and $s_q$
and $s_q$![]() , we make the following simplification in advance:
, we make the following simplification in advance:
and also introduce the spectral energy density $e^{s_k'}( \boldsymbol {k}') = e_{\boldsymbol {k}'}^{s_k'}$![]() as
as
where $\delta _{kk'} = \delta (\boldsymbol {k} + \boldsymbol {k}')$![]() and $\delta ^{s_k}_{s_k'} = \delta (s_k - s_k')$
and $\delta ^{s_k}_{s_k'} = \delta (s_k - s_k')$![]() . The last delta condition ensures that the contribution is non-negligible over long times. We then write
. The last delta condition ensures that the contribution is non-negligible over long times. We then write
We note that, on the one hand, $\delta _{pq}$![]() imposes $\boldsymbol {p}=-\boldsymbol {q}$
imposes $\boldsymbol {p}=-\boldsymbol {q}$![]() and, on the other hand, $\delta _{pq}^{k}$
and, on the other hand, $\delta _{pq}^{k}$![]() imposes $\boldsymbol {k}=\boldsymbol {p}+\boldsymbol {q}$
imposes $\boldsymbol {k}=\boldsymbol {p}+\boldsymbol {q}$![]() . Thus, these two conditions lead to $\boldsymbol {k}=\boldsymbol {0}$
. Thus, these two conditions lead to $\boldsymbol {k}=\boldsymbol {0}$![]() . Since $L_{\boldsymbol {0pq}}^{s_k s_p s_q}= 0$
. Since $L_{\boldsymbol {0pq}}^{s_k s_p s_q}= 0$![]() , the first term on the right-hand side is zero and we get
, the first term on the right-hand side is zero and we get

After integration and summation over the polarizations, we obtain

where $\varOmega _{kk'k''} = s_k \omega _k + s_k' \omega _k' + s_k'' \omega _k''$![]() . Further simplifications can be made. Firstly, the energy density tensor describes a homogeneous turbulence so that $e_{\boldsymbol {-k}}^{s_k}=e_{\boldsymbol {k}}^{s_k}$
. Further simplifications can be made. Firstly, the energy density tensor describes a homogeneous turbulence so that $e_{\boldsymbol {-k}}^{s_k}=e_{\boldsymbol {k}}^{s_k}$![]() . Secondly, the interaction coefficient has the following symmetry $L_{\boldsymbol {-k-k'-k''}}^{s_k s_k' s_k''}=L_{\boldsymbol {kk'k''}}^{s_k s_k' s_k''}$
. Secondly, the interaction coefficient has the following symmetry $L_{\boldsymbol {-k-k'-k''}}^{s_k s_k' s_k''}=L_{\boldsymbol {kk'k''}}^{s_k s_k' s_k''}$![]() . Thirdly, we introduce $L_{\boldsymbol {kpq}}^{s_k s_p s_q} \equiv (s_q q_\perp - s_p p_\perp ) M_{\boldsymbol {kpq}}^{s_k s_p s_q}$
. Thirdly, we introduce $L_{\boldsymbol {kpq}}^{s_k s_p s_q} \equiv (s_q q_\perp - s_p p_\perp ) M_{\boldsymbol {kpq}}^{s_k s_p s_q}$![]() which is convenient for the calculations. We obtain
which is convenient for the calculations. We obtain

We observe that $M_{\boldsymbol {kk'k''}}^{s_k s_k' s_k''}=M_{\boldsymbol {k''kk'}}^{s_k'' s_k s_k'}=-M_{\boldsymbol {k'kk''}}^{s_k' s_k s_k''}$![]() thus the previous expression can be simplified
thus the previous expression can be simplified

We note that $s_k'' k'' - s_k' k' = s_k'' k'' - s_k k + s_k k - s_k' k'$![]() , and thus
, and thus

After integration over time, one has

with
Now, we can introduce expression (B14) for the third-order moment into (B1)

where $I_1$![]() and $I_2$
and $I_2$![]() are the two integrals involving the interaction coefficients $L_{\boldsymbol {-kpq}}^{s_k s_p s_q}$
are the two integrals involving the interaction coefficients $L_{\boldsymbol {-kpq}}^{s_k s_p s_q}$![]() and $L_{\boldsymbol {-k'pq}}^{s_k' s_p s_q}$
and $L_{\boldsymbol {-k'pq}}^{s_k' s_p s_q}$![]() , respectively. Expressing $L_{\boldsymbol {kpq}}^{s_k s_p s_q}$
, respectively. Expressing $L_{\boldsymbol {kpq}}^{s_k s_p s_q}$![]() as a function of $M_{\boldsymbol {kpq}}^{s_k s_p s_q}$
as a function of $M_{\boldsymbol {kpq}}^{s_k s_p s_q}$![]() , the first integral becomes
, the first integral becomes

We note that ${\rm \Delta} (\varOmega _{-kpq}) \, \mathrm {e}^{\textrm {i} \varOmega ^{k}_{pq} t} = {\rm \Delta} (\varOmega _{pq}^{k})$![]() . The long-time behaviour is given by the Riemann–Lebesgue lemma
. The long-time behaviour is given by the Riemann–Lebesgue lemma
After a last change of variable, we find $(\boldsymbol {p},\boldsymbol {q})\to (-\boldsymbol {p},-\boldsymbol {q})$![]()

The same manipulation with $I_2$![]() without performing the change of variable leads to
without performing the change of variable leads to

and the sum of these two integrals gives

Using the symmetries of the resonant conditions, we have

The parameter $\delta (\varOmega _{kpq} )$![]() allows us to finally rewrite the term in the second line as follows:
allows us to finally rewrite the term in the second line as follows:

These are the kinetic equations for IEMHD wave turbulence.
Appendix C. Locality criteria
The objective of this section is to find the locality domain of the power law solutions at constant energy flux and (for simplicity) in the absence of helicity. In other words, we want to check whether the contribution of non-local interactions is not dominant. There are three areas (regions A, B and C in figure 7) for which the interactions are non-local. To do this, it is convenient to introduce the adimensional wavenumbers $\tilde {p}_\perp \equiv p_\perp /k_\perp$![]() , $\tilde {p}_\| \equiv p_\|/k_\|$
, $\tilde {p}_\| \equiv p_\|/k_\|$![]() , $\tilde {q}_\perp \equiv q_\perp /k_\perp$
, $\tilde {q}_\perp \equiv q_\perp /k_\perp$![]() and $\tilde {q}_\| \equiv q_\|/k_\|$
and $\tilde {q}_\| \equiv q_\|/k_\|$![]() . We obtain ($H=0$
. We obtain ($H=0$![]() )
)

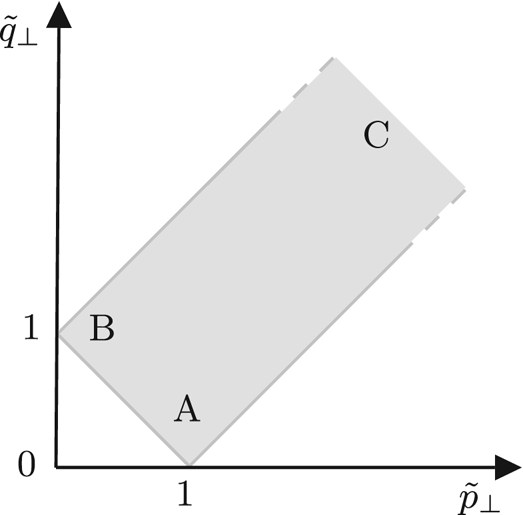
Figure 7. The kinetic equations are integrated on a domain verifying $\boldsymbol {k} + \boldsymbol {p} + \boldsymbol {q} = \boldsymbol {0}$![]() . The grey strip corresponds to this domain for the adimensional perpendicular wavevectors. A, B and C (at infinity) are the non-local regions where the convergence of the integrals must be checked.
. The grey strip corresponds to this domain for the adimensional perpendicular wavevectors. A, B and C (at infinity) are the non-local regions where the convergence of the integrals must be checked.
This expression can be integrated in the parallel directions. We recall the following property:
Then, we have
We obtain

where $\sin \alpha _q= \sqrt {1 - (1 + \tilde {p}_\perp ^{2} - \tilde {q}_\perp ^{2} )^{2} (2 \tilde {p}_\perp )^{-2}}$![]() .
.
C.1. Zone A
We define $\tilde {p}_\perp = 1 + r \cos \beta$![]() and $\tilde {q}_\perp = r \sin \beta$
and $\tilde {q}_\perp = r \sin \beta$![]() , with $r \ll 1$
, with $r \ll 1$![]() and $\beta \in [{\rm \pi} /4, 3 {\rm \pi}/4 ]$
and $\beta \in [{\rm \pi} /4, 3 {\rm \pi}/4 ]$![]() . Two cases must be distinguished: when $s_k = s_p$
. Two cases must be distinguished: when $s_k = s_p$![]() and when $s_k = -s_p$
and when $s_k = -s_p$![]() . An evaluation (to leading order) of the different terms of the integral (C5) is given in Table 1. Note that these evaluations take into account the possible cancellation of the integral due to $\beta$
. An evaluation (to leading order) of the different terms of the integral (C5) is given in Table 1. Note that these evaluations take into account the possible cancellation of the integral due to $\beta$![]() symmetry.
symmetry.

When $s_k=s_p$![]() , the criterion of convergence of the kinetic equation (C5) will be given by the following integral:
, the criterion of convergence of the kinetic equation (C5) will be given by the following integral:

Therefore, there is convergence if $x+2y < 4$![]() . When $s_k=-s_p$
. When $s_k=-s_p$![]() , we have
, we have

and the convergence is obtained if $x + y < 6$![]() .
.
C.2. Zone B
We define $\tilde {p}_\perp = r \cos \beta$![]() and $\tilde {q}_\perp = 1+ r \sin \beta$
and $\tilde {q}_\perp = 1+ r \sin \beta$![]() , with this time $\beta \in [-{\rm \pi} /4, {\rm \pi}/4 ]$
, with this time $\beta \in [-{\rm \pi} /4, {\rm \pi}/4 ]$![]() . We have two cases: $s_k=s_q$
. We have two cases: $s_k=s_q$![]() and $s_k=-s_q$
and $s_k=-s_q$![]() . An evaluation (to leading order) of the different terms of the integral (C5) is given in Table 2. Note that these evaluations take into account the possible cancellation of the integral due to $\beta$
. An evaluation (to leading order) of the different terms of the integral (C5) is given in Table 2. Note that these evaluations take into account the possible cancellation of the integral due to $\beta$![]() symmetry.
symmetry.

When $s_k=s_q$![]() , the criterion of convergence of the kinetic equation (C5) will be given by the following integral:
, the criterion of convergence of the kinetic equation (C5) will be given by the following integral:

Therefore, there is convergence if $x+2y < 4$![]() . When $s_k=-s_q$
. When $s_k=-s_q$![]() , we have
, we have

and the convergence is obtained if $x + y < 4$![]() .
.
C.3. Zone C
We define $\tilde {p}_\perp = (\tau _2-\tau _1)/2$![]() and $\tilde {q}_\perp = (\tau _1+\tau _2)/2$
and $\tilde {q}_\perp = (\tau _1+\tau _2)/2$![]() , with $-1 \le \tau _1 \le 1$
, with $-1 \le \tau _1 \le 1$![]() and $1 \ll \tau _2$
and $1 \ll \tau _2$![]() . We have two cases: $s_p=s_q$
. We have two cases: $s_p=s_q$![]() and $s_p=-s_q$
and $s_p=-s_q$![]() . An evaluation (to leading order) of the different terms of the integral (C5) is given in Table 3. Note that these evaluations take into account the possible cancellation of the integral due to $\tau _1$
. An evaluation (to leading order) of the different terms of the integral (C5) is given in Table 3. Note that these evaluations take into account the possible cancellation of the integral due to $\tau _1$![]() symmetry.
symmetry.

When $s_p=s_q$![]() , the criterion of convergence of the kinetic equation (C5) will be given by the following integral:
, the criterion of convergence of the kinetic equation (C5) will be given by the following integral:
Therefore, there is convergence if $3 < x + 2y$![]() . When $s_p=-s_q$
. When $s_p=-s_q$![]() , we have
, we have
and the convergence is obtained if $2 < x + y$![]() .
.
In conclusion, a solution is local if the following conditions are satisfied:
We notice that the KZ spectrum for the energy corresponds to $x+2y=3.5$![]() and $x+y=3$
and $x+y=3$![]() . These values are thus exactly in the middle of the convergence domain.
. These values are thus exactly in the middle of the convergence domain.