Using Eye-Tracking to Understand Decision-Making in Conjoint Experiments

Abstract

Conjoint experiments are popular, but there is a paucity of research on respondents’ underlying decision-making processes. We leverage eye-tracking methodology and a series of conjoint experiments, administered to university students and local community members, to examine how respondents process information in conjoint surveys. There are two main findings. First, attribute importance measures inferred from the stated choice data are correlated with attribute importance measures based on eye movement. This validation test supports the interpretation of common conjoint metrics, such as average marginal component effects (AMCEs), as measures of attribute importance. Second, when we experimentally increase the number of attributes and profiles in the conjoint table, respondents view a larger absolute number of cells but a smaller fraction of the total cells displayed. Moving from two to three profiles, respondents search more within-profile, rather than within-attribute, to build summary evaluations. However, respondents’ stated choices remain fairly stable regardless of the number of attributes and profiles in the conjoint table. Together, these patterns speak to the robustness of conjoint experiments and are consistent with a bounded rationality mechanism. Respondents adapt to complexity by selectively incorporating relevant new information to focus on important attributes, while ignoring less relevant information to reduce cognitive processing costs.

1 Introduction

Recent years have seen the frequent use of conjoint experiments in political science and other disciplines (Bansak et al. 2020). Conjoint experiments ask survey respondents to rank or rate profiles that are combinations of multiple attributes with randomly assigned values such as profiles of political candidates, policy packages, or consumer products. Conjoint experiments are popular because they allow researchers to understand how respondents weigh the various attributes and to test competing theories about which attributes are most important (Green and Rao 1971; Green and Srinivasan 1990; Hainmueller, Hopkins, and Yamamoto 2014).

Researchers have also begun to examine methodological issues in conjoint experimentation, both in terms of statistical methods (Hainmueller, Hopkins, and Yamamoto 2014; de la Cuesta et al. 2019; Egami and Imai 2019; Leeper, Hobolt, and Tilley 2020) as well as survey design (Hainmueller, Hangartner, and Yamamoto 2015; Bansak et al. 2018, 2019; Horiuchi, Markovich, and Yamamoto 2020). However, there are still many open methodological questions about the use and design of conjoint experiments. One important gap is the paucity of systematic knowledge about the underlying decision-making processes that respondents use when completing conjoint surveys. Research in conjoint experiments typically only collects data on the stated choices that respondents make and then use these data to infer the importance that respondents attach to the attributes, typically by estimating average marginal component effects (AMCEs) or related metrics such as attribute marginal $R^{2}$ values (Hainmueller, Hopkins, and Yamamoto 2014). This means that the mental processes behind these stated choices largely remain a black box.

In this study, we take a step toward better understanding the underlying information processing of respondents in conjoint experiments. We leverage eye-tracking data that provides us with detailed information on how respondents process information as they complete conjoint surveys. We focus on two distinct research questions. First, we ask to what extent measurements of the underlying information processing support the interpretation of commonly used metrics that are estimated from self-reported respondent choices (such as AMCEs and attribute marginal $R^{2}$ values) as valid measures of attribute importance. Neuroscience research has shown that visual attention is indicative of cognitive processes in the sense that humans tend to fixate their eyes more on information they deem to be of high utility in a choice task (Just and Carpenter 1976; Hoffman 1998; Findlay and Walker 1999; Kim, Seligman, and Kable 2012). ¹ Eye-tracking therefore provides us with a direct and fine-grained measure that captures the importance respondents attach to different pieces of information. If the choices respondents report after being exposed to different attribute values accurately reflect the importance they attach to each attribute, then we would expect conjoint choice metrics to be positively correlated with attribute importance as measured by eye movement.

The second research question we ask is if and how respondents adjust their underlying information processing in response to changes in the design of the conjoint experiment. In particular, we are interested in the effects of increasing the complexity of the choice task through adding more attributes and profiles to the conjoint table. Learning how respondents’ information-processing changes is important because it can inform decisions about the design of conjoint experiments. If respondents adjust to added complexity by paying less attention in general, their choices would not accurately reflect attribute importance as conjoint tables become too large. In contrast, if respondents are able to adjust to added complexity in ways that allow them to process relevant information more efficiently, then increasing the complexity of the conjoint task will not necessarily compromise the inferences that can be drawn from the observed choices.

To investigate these research questions, we designed a conjoint experiment asking subjects to choose between the profiles of candidates for president. The survey was administered in the Fuqua Behavioral Lab at Duke University on computers equipped with eye-trackers that take unobtrusive, high-frequency measures of eye movements throughout the survey. Subjects completed a series of six conjoint design blocks with twenty decision tasks in each block. Each block had a different conjoint design that featured five, eight, or eleven attributes and two or three candidate profiles to choose from in a given task. All subjects completed all six blocks in a randomly assigned order, providing us with both within- and between-subject variation across the experimental conditions.

There are three sets of findings from the study. The first pertains to the validation of respondent choices. We find that there is a clear correspondence between attribute importance measures inferred from the stated choice data and attribute importance measures based on eye movement. In particular, the estimated AMCEs of the attributes are positively correlated with the number of eye fixations associated with the attributes across the full sample. At the individual level, the relative rankings of the attributes as measured by their marginal $R^{2}$ are positively correlated with their relative rankings in terms of the frequency of eye fixations. This supports the interpretation of conjoint metrics estimated from self-reported choices as valid measures of attribute importance.

The second set of findings pertains to the stability of the AMCEs when increasing the complexity of the conjoint design. As we increase the complexity by adding attributes and moving from a comparison between two to three profiles, respondents visually process a smaller fraction of cells in the conjoint table. Yet, even though respondents process a smaller amount of the total information presented, the estimated AMCEs remain fairly stable such that the observed choices lead to relatively similar conclusions about attribute importance.

The third set of findings relates to explaining the seemingly paradoxical result that choices remain stable despite increased complexity. Consistent with a decision-making process of bounded rationality (Simon 1957) as an “adaptive toolbox” (Gigerenzer and Todd 1999), we find that subjects react to increased complexity by selectively incorporating relevant additional information. They focus on new information about attributes that matter to them, but ignore additional information they consider irrelevant to reduce the computational cost of processing more information. Consistent with this, we find that even though subjects on average view a smaller proportion of the total number of cells as the design gets more complex, they still view a considerably larger number of cells. In addition to adjusting the amount of information processed, respondents also adjust the search strategy that determines the order in which the information is processed. In particular, respondents tend to adjust their search patterns and shift toward searching more within-profile to build summary evaluations, rather than searching within-attribute, when faced with comparing three profiles instead of two profiles. There is little to no change in search patterns when merely the number of attributes increases.

Our findings help explain why conjoint designs can be robust to increasing complexity, at least within the context of our experiment. As respondents employ adjustment mechanisms to filter out information that is less relevant to them and more efficiently process the information that is more relevant to them, the stated choices that researchers observe remain fairly similar since they are primarily driven by the important attributes. In the concluding discussion, we elaborate on some of the implications of our findings for the interpretation and design of conjoint experiments.

2 Research Questions and Literature Review

2.1 Validation of AMCEs through Eye-tracking

One of the key features that differentiates conjoint experiments from traditional survey experiments is that conjoints require respondents to navigate the rather complex task of ranking or rating multiattribute profiles. Typically the profiles are presented in a so-called conjoint table, where the rows contain the attribute values and the columns contain the profiles. Figure 1 shows two example conjoint tables from our experiment, which asked respondents to choose between the profiles of candidates for president. In the first conjoint table, there are five attributes and two profiles for a total of ten cells with randomly assigned attribute values. The second table contains eleven attributes and three profiles resulting in 33 cells.

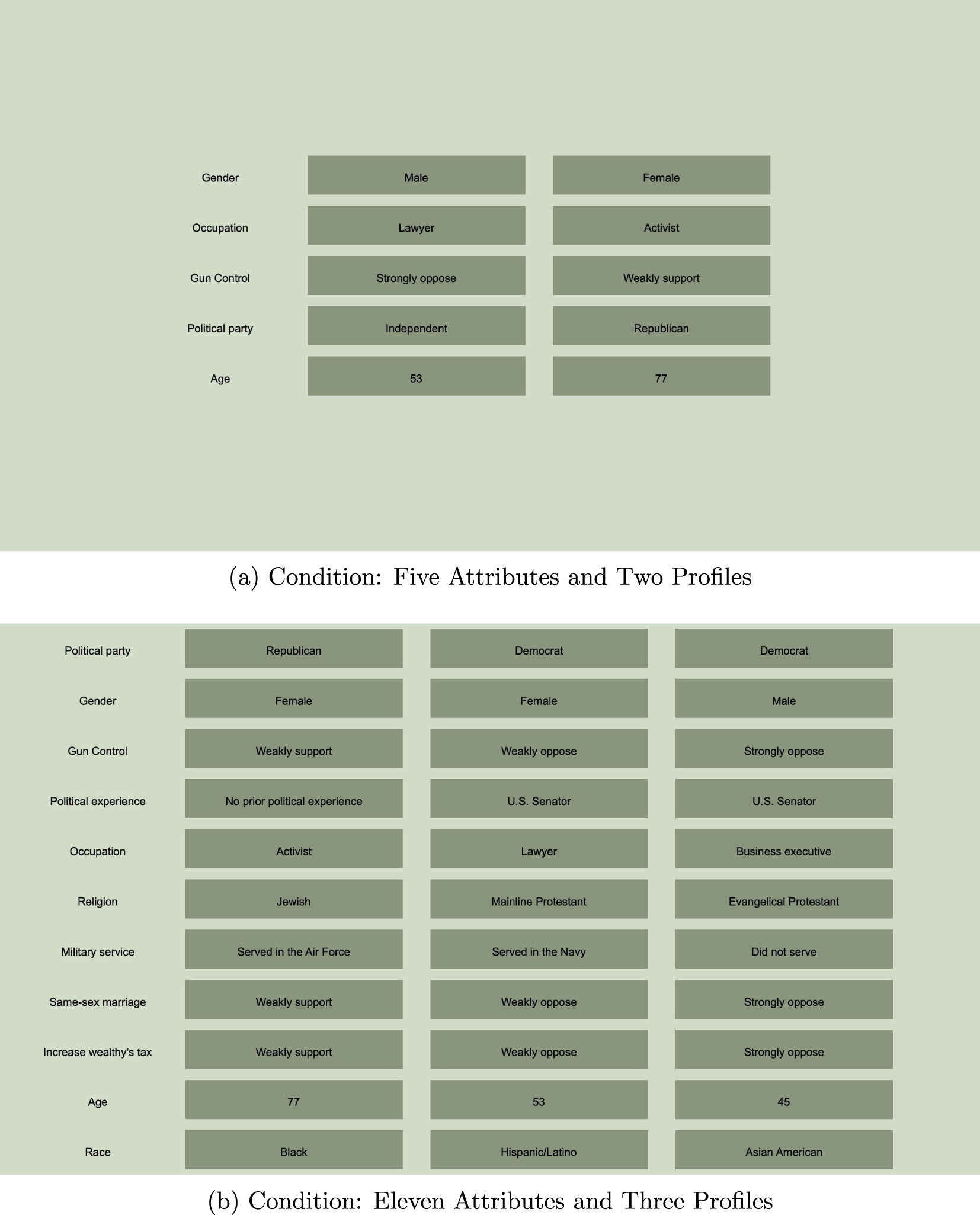
Figure 1. Example Screenshot from Conjoint Experiment.

How do respondents navigate this complexity? We have little systematic evidence on the underlying mental processes that respondents engage in when completing conjoint surveys. In a typical conjoint experiment, these processes are unobserved; researchers collect data on respondents’ choices and infer the importance respondents attach to each attribute. One common method to infer attribute importance is to estimate AMCEs. They capture the average effect of changing the value of an attribute on the probability that the profile is selected, averaging over the randomization distribution of the other attributes (Hainmueller, Hopkins, and Yamamoto 2014).

While AMCEs are frequently used, we do not know whether respondents’ underlying information processes actually support the interpretation of AMCEs (or functions of the AMCEs such as attribute marginal $R^{2}$ ) as measuring attribute importance. In this study, we leverage data from eye-tracking to provide a validation exercise for these metrics. In particular, we ask how well AMCEs and marginal $R^{2}$ values, which are based on the stated choices, correspond with more direct measures of attribute importance based on eye movement. Eye-tracking data are uniquely suited to this validation task because they provide a direct measure of attribute importance that is less affected by survey response biases.

Eye-tracking can be used to measure attribute salience, self-reported measures of which can suffer from survey response biases (Jenke and Munger 2019). Studies in the decision-making, marketing, and neuroscience literatures have found that the frequency of fixations correlates with the importance of an attribute in a task, with more fixations given to parts of the stimulus that are relevant to the task goal. This is termed the “utility effect” and has been established over many studies such that it has been termed “the most robust observation on eye movements in decision making” (Orquin and Loose 2013). When making a decision, participants more often look at the option they ultimately choose (Wedell and Senter 1997; Glaholt, Wu, and Reingold 2009; Kim, Seligman, and Kable 2012). This finding of increased fixation frequency correlating with high utility objects extends from the chosen alternative to attributes respondents consider more important in their decision (Van Raaij 1977; Jacob and Karn 2003; Glaholt, Wu, and Reingold 2009; Kim, Seligman, and Kable 2012). ²

In past research, other process-tracing methods such as information boards and verbal protocols have also been used to capture decision-making processes. However, such paradigms may prevent subjects from using automatic processing because information search and comparisons must be conducted in a slower, more encumbered fashion than is natural (Lohse and Johnson 1996). Eye-tracking is widely considered the preeminent process-tracing tool in terms of maximizing internal validity.

Therefore, if conjoint metrics estimated from the stated choice data accurately reflect the importance respondents attach to each attribute, we would expect those metrics to be positively correlated with attribute importance as measured by the number of eye fixations on each attribute. But if we find no such correlation or even a negative correlation, this would suggest that commonly used conjoint metrics are a poor indication of attribute importance and instead are highly affected by various types of potential survey response biases.

One piece of existing evidence we have on this question is from a related study in the marketing literature. Meißner and Decker (2010) and Meißner, Musalem, and Huber (2016) employ eye-tracking in a conjoint setting to examine respondents’ choices between coffee makers using pictorial information. Although they use somewhat different measures and methods than our study, their findings largely indicate support for the idea that respondents consistently fixate more on attributes of higher importance according to the stated choice data.

2.2 Design Effects in Conjoint Experiments

Our second research question examines whether and how respondents adjust their modes of information gathering and processing in response to changes in the conjoint design. Typical conjoint designs used in political science involve a pair of two profiles and around five to ten different attributes. Yet there has been little research on how the specific design of the conjoint affects responses. One exception is Bansak et al. (2019), who examined how increasing the number of attributes affects response behavior in conjoints. They find that there is only a modest decrease in AMCE magnitudes and marginal $R^{2}$ s when respondents are assigned to conjoint tasks with more attributes. ³

One of the novel contributions of our study over Bansak et al. (2019) is that we not only consider increased complexity in terms of the number of attributes, but also the number of candidate profiles. In particular, we consider how respondents adjust their behavior when we move from a paired contest between two profiles to a side-by-side comparison between three profiles. Examining the effects of adding a third profile is important because it constitutes a more structural modification of the choice task than simply adding attributes. In particular, adding a third profile means that it may be more challenging for respondents to compare profiles. For example, to rank three profiles on a single specific attribute, respondents now have to keep track of three (instead of one) pairwise comparisons to identify their preferred profile. In addition, the relative rankings of the three profiles likely vary across attributes, which means that respondents need to engage in complex trade-offs to identify their overall top choice among the three multiattribute profiles. ⁴

In addition to examining how changes in the conjoint design affect response behavior, another contribution of our study is that we move beyond measuring only the stated choices and shed light on respondents’ underlying information processes, which might help explain why the AMCEs remained fairly stable even when more attributes were added. In other words, while the early findings in Bansak et al. (2019) are encouraging for the potential robustness of conjoint experiments, they leave open the important question of why the AMCEs remain rather stable even when the complexity of the conjoint task increases. What decision-making mechanisms or cognitive strategies might explain this pattern? We move toward answering this question by examining how eye movement, a direct measure of visual attention, reacts to changes in the conjoint design. Getting at the underlying mechanisms is essential because it provides us with a more general understanding of how changing the design affects the quality of response data.

A first hypothesis is that increased complexity results in respondents paying less attention in general and as a result the quality of the responses will suffer. A second alternative hypothesis is that respondents are able to effectively process all of the information given to them regardless of complexity (within some reasonable limit), and hence added complexity affects neither response quality nor patterns of information processing. A third alternative hypothesis, drawing on the theory of bounded rationality (Simon 1957), is that respondents react to increased complexity by adjusting their processes to more efficiently focus on the information they determine is most relevant. In contrast to axiomatic theories of expected utility that postulate maximization of utility and consistency of choices as a sine qua non of rational behavior, theories of bounded rationality emphasize the costs of processing information and the benefits of applying fast and frugal heuristics to decide among multiattribute alternatives (Gigerenzer and Goldstein 1996). Based on this framework, we might expect our subjects to adapt to a more complex decision environment by using information-processing strategies and choice heuristics to efficiently filter out additional information they deem less relevant and to selectively incorporate additional information they deem more relevant (Payne et al. 1993; Bettman, Luce, and Payne 1998).

Such adjustment mechanisms may affect the amount of information that is processed. As the conjoint design becomes more complex, subjects may not automatically incorporate all of the additional information that is being presented into their decision-making. Instead, they may try to process the subset of additional information that is most relevant to their choices. With increasing complexity, the cognitive effort of processing all the information available, which is necessary to identify the utility-maximizing choice, increases as well (see, e.g., Kahneman 1973). To balance this trade-off between cognitive effort and decision accuracy, subjects may settle for a solution that is good enough rather than attempt to find the optimal solution, which would require processing the full information (Simon 1955). To examine this adjustment mechanism, we consider the number of cells in the conjoint table that are visually fixated upon by subjects and examine how both the fraction of cells as well as the total number of cells viewed change as we increase the size of the conjoint table by adding attributes and profiles.

In addition to adjusting the amount of information that is processed, bounded rationality suggests that subjects may also adapt to more complexity by changing the order in which subjects process the cells in the conjoint table. Past research on such adjustment heuristics has focused on a variety of choice tasks, ranging from the selection of a particular detergent to choosing political candidates and using a variety of process-tracing methodologies (which are predecisional measures that give insight into psychological mechanisms), including “think aloud” protocols, information boards, and mouse-tracking (for reviews, see, e.g., Ford et al. 1989; Payne et al. 1993; Bettman, Luce, and Payne 1998; Lau and Redlawsk 2006). This research shows that decision-makers will predominantly use one of two information-processing strategies when searching through a multiattribute table of alternatives. They will tend to either transition horizontally, by comparing adjacent cells in the same row, or transition vertically, by comparing adjacent cells in the same column (see, e.g., Jacoby, Speller, and Berning 1974; Herstein 1981; Lau and Redlawsk 2006; Amasino et al. 2019). The observed pattern of these transitions allows for inferences about the search process: The more a subject uses horizontal transitions (in our table orientation), the more the search process may be characterized as one of within-attribute comparisons where the subject goes back and forth between the profiles and compares them on each attribute. The more a subject uses vertical transitions (in our table orientation), the more the search process may be characterized as one of within-profile comparisons, where the subject builds a summary of a given profile by processing the attributes within that profile and then moves on to the next profile (Tversky 1969; Payne 1982; Payne et al. 1993; Bockenholt and Hynan 1994; Lau and Redlawsk 2006).

Eye-tracking is ideally suited to capture such changes in respondents’ search strategy. In particular, our design enables us to examine whether adding attributes or profiles to the conjoint table will result in respondents adjusting their search strategy by increasingly relying on within-attribute or within-profile search. Such changes may be particularly pronounced when increasing the number of profiles. When faced with comparing three profiles instead of two profiles, more subjects may adopt a strategy of searching within-profile to build summary evaluations that are used to compare the three profiles against each other, rather than searching within-attribute.

Before describing our experimental design, it is worth emphasizing that outside of the methodological research on conjoints, there is a significant body of work in political science that has used process-tracing methods to study how voters process information when choosing between candidates (for a review, see Lau and Redlawsk 2006). In particular, in their pioneering work on voter decision-making, Lau and Redlawsk have developed a dynamic processing-tracing methodology. In their experimental setup, boxes with information about candidates appear on a computer screen that gradually scrolls down to mimic the flow of information voters face in a campaign, and subjects can access information about the attributes of candidates by clicking on the boxes (Lau and Redlawsk 1997, 2001, 2006). Lau and Redlawsk use the data from their dynamic process tracing environment (DPTE) to explicitly study how subjects use cognitive heuristics to gather information and combine it into voting decisions. Although there are some significant differences between conjoints and the DPTE in the way in which candidate information is presented and how subjects can access attribute information, our leveraging of eye-tracking data in the context of conjoints in this study is in many ways complementary to the work of Lau and Redlawsk. We share a motivation to better understand the underlying decision-making processes that respondents utilize to search for information and make choices between multiattribute profiles.

3 Research Design

3.1 Experiment

Our design involved a conjoint experiment in which subjects were asked to decide between the profiles of candidates for president. ⁵ More specifically, subjects were shown sets of candidate profiles and asked to choose their preferred candidate from each set. We use the term “decision task” to denote each time a subject chose a candidate from a set of displayed profiles. In total, each subject completed 120 decision tasks, and the decision tasks varied according to the design described below. The stimulus presentation software used was MATLAB and Psychtoolbox.

In each decision task, subjects were shown multiple candidate profiles that were presented side by side in a standard conjoint table, where each candidate profile included multiple “attributes” (characteristics describing the candidate). We varied the number of candidates and attributes shown in each decision task across several experimental conditions in order to analyze the effects of the conjoint design on respondent behavior. Specifically, there were six experimental conditions, which consisted of conjoint blocks with a sequence of 20 decision tasks each. For each block, the number of attributes per profile in the conjoint table was set to either five, eight, or eleven attributes and the number of profiles to either two or three. We chose these values to capture the range of settings that are commonly found in applications of conjoints in political science. Figure 1 shows example screenshots of the experimental conditions with the lowest and highest number of attributes and profiles. As is evident, the level of complexity varies greatly as the conjoint table increases from a minimum of ten cells (two profiles with five attributes each) to maximum of 33 cells (three profiles with eleven attributes each).

Each subject completed all six blocks for a total of 120 decision tasks, with the six blocks presented in a randomly assigned order for each subject. To determine which attributes to include in the candidate profiles for each block, the appropriate number of attributes were randomly drawn from a full list of eleven attributes. For the sake of realism, the party and gender attributes were always included. The order in which the attributes were displayed in the table was also randomly assigned for each subject–block. This prevented the confounding of attention due to subjects’ interest with attention due to the placement of the object but still gave the task enough predictability to minimize eye movements due to searching for a piece of information. ⁶ For each subject within each block, the number of attributes, the order of the attributes, and the number of profiles remained fixed, but the values (levels) of the attributes displayed for each profile were randomly assigned across the decision tasks. The design therefore provides us with within- as well as between-subject variation in the conjoint design. The inter-stimulus interval between the decision tasks was one second, during which subjects viewed a fixation cross in one of five areas of the screen. To give subjects a break in the middle of the experiment, we showed them a seven-minute cut from Charlie Chaplin’s The Circus after three blocks were completed.

The full list of attributes and attribute values are listed in Table 1. For most attributes, the values were assigned with equal probability. However, for some attributes—including race, military service, and religion—weights were adjusted to give a higher probability to more common groups to increase the ecological validity of the survey experiment. Appendix Section A provides more details on the randomization weights for all attribute values.

Subjects were introduced to their decision tasks with the following instructions: “Your task is to decide which of the candidates you would vote for, for President, if you had to cast a vote. If you prefer candidate 1, the leftmost candidate, press the ‘1’ key above on the number line. For candidate 2, press the ‘2’ key, and for candidate 3 the ‘3’ key. The candidates are always numbered from left to right.” ⁷ Then, during the tasks, subjects simply pressed 1, 2, or 3 to choose between the candidates. ⁸ Using these stated choice data, we created an outcome variable that was coded as one if the subjects chose the candidate profile and zero if not. To avoid the effects of time pressure (Reutskaja et al. 2011) or idleness (Hsee, Yang, and Wang 2010), we gave subjects as much time as they needed to choose between the candidates on each decision task rather than impose a fixed exposure time. At the end of the full set of conjoint tasks, the subjects also answered some basic demographic questions.

Finally, while having the subjects complete 120 decision tasks may seem like a considerable burden that could potentially affect response quality for later tasks, we do not find this to be the case. Consistent with Bansak et al. (2018), who find little degradation in response quality over thirty decision tasks as measured by AMCEs and marginal $R^{2}$ values, we find similar response quality robustness over the course of the 120 decision tasks in the present study (details are provided in the Results section). We also note that similar numbers of tasks are common in decision experiments in behavioral economics (e.g., Semmann, Krambeck, and Milinski 2003), marketing (e.g., Reibstein, Bateson, and Boulding 1988), and neuroscience research (e.g., Figner et al. 2010).

Table 1. List of attributes and values for conjoint experiment.

3.2 Eye-Tracking Technology and Methods

The computers on which subjects completed the conjoint survey were equipped with a video-based, remote Tobii T60XL eye-tracker to track eye movement with a screen resolution of 1280 x 1024 pixels and a screen size of 17 inches TFT. The eye-tracker automatically adjusts to various physical and physiological conditions, including the subject’s eye color and sight correction (meaning that glasses can be worn), and does not require subjects to wear headsets or use head-rest/chin-rest devices. Luminance matching was not used, as every screen in every decision task was the same in terms of color and because no pupillometry was utilized in analyses. Eye properties were determined through a calibration process completed prior to the experiment, which consisted of fixation on five predetermined screen positions sequentially, allowing the system to solve for the location of the pupil. The eye-tracker locates a subject’s gaze by calculating the relationship of the reflection of an infrared light off of the cornea and the retina. The system’s accuracy is within $0.5^{\circ }$ (in visual angle) with less than $1^{\circ }$ of error resulting from head motion and less than $0.3^{\circ }$ drift over time. The sampling rate of the Tobii T60XL is 60 hertz, meaning that it records 60 gaze locations per second. This is within the conventional range, likely to produce a fixation error of $+/-10~\text{ms}$ or less (as compared to the typical fixation time of 200–300 ms). Subjects were seated approximately 700 mm from the screen. An exclusion criterion was applied such that subjects were excluded from the sample if more than 25% of their gaze points were unidentifiable during a decision task. This can be caused by excessive head movement, occlusion of the pupil by the eyelid or eyelashes, the subject looking away from the screen, or faulty calibration. Only one subject was excluded for this reason.

Fixation analysis was used to analyze eye movement patterns. A fixation is a period in which eyes remain relatively still. Our measure of importance using eye-tracking is fixation frequency, which is the number of fixations in an area of interest (AOI) per decision task. Fixation frequency is often used to indicate the amount of interest allocated to an area (Fitts, Jones, and Milton 1950; Jacob and Karn 2003; Orquin and Holmqvist 2018). ⁹ It is up to the researcher to define these areas, which typically include some space around the text or picture of focus to account for issues with accuracy and precision (Holmqvist et al. 2011). For our AOIs, the vertical space between the text of the attribute values ( $1.32^{\circ }$ ) was halved and then added on to the beginning, end, top, and bottom of each attribute value. Consequently, the AOIs touched vertically but did not overlap. Thus, a fixation that was slightly vertically offset from the text would have been counted as a fixation on the attribute it was closer to vertically. Each AOI had a height of $3.03^{\circ }$ . The width of each AOI differed by the texts’ lengths, such that the room for error was regularized across attributes and attribute values. The widths ranged from $2.19^{\circ }$ (for a candidate’s age) to $17.02^{\circ }$ (“no prior political experience”).

In calculating the location of the gaze, one can either average both eyes or use the position of the dominant eye. We used the average, which improves accuracy and precision (Cui and Hondzinski 2006), unless one of the eyes was not found by the eye-tracker, in which case the eye with data was used to indicate fixation location. We differentiated between saccades (rapid eye movements) and fixations by using an I-VT classification algorithm. Key in this algorithm is the setting of the velocity threshold parameter: if the eyes are moving at a velocity above the parameter, the sample is classified as a saccade, and if the velocity is below this parameter, the sample is classified as a fixation. We followed Olsen and Matos (2012) in setting the velocity threshold to be $30^{\circ }/\text{second}$ . Another important parameter is the minimum fixation duration, against which the duration of the fixation is checked and reclassified as an unknown eye movement if the minimum fixation duration exceeds it. We set our parameter at 60 ms, as short fixations are common when reading (Over et al. 2007). Appendix Section C provides more details on the eye-tracking methodology and algorithms used for preprocessing the eye-tracking data.

3.3 Sample

Our sample consists of 122 subjects, who completed the conjoint experiment in the period between July 5 and July 31, 2019. ¹⁰ The subjects were drawn from the Duke Behavioral Research subject pool and included undergraduate and graduate students from the university (39% of the sample) as well as members of the local community. 86% of the sample identified as Democrats or Democrat-leaning, 9% identified as Republican or Republican-leaning, and 5% identified as pure independents. 75% identified as slightly to extremely liberal, and 25% identified as slightly to extremely conservative. We also asked subjects to identify their ideology on economic and social issues separately. 57% were economically liberal and 85% were socially liberal (with none identifying as moderate in either case). The mean score on political knowledge questions was 1.8 out of 3.

The mean age of the sample was thirty-one years old. 37% of the sample were male. The subjects were 56% white, 15% African American, 18% Asian, 6% Hispanic, and 5% other. Subjects received a compensation of $15 for participating in the experiment. The median completion time for the experiment, not including the demographic survey, was 34.75 minutes with an interquartile range of 24.89 to 44.61 minutes. Appendix Section B provides more information on the subject pool and descriptive statistics of the sample. ¹¹

4 Results

4.1 Validating AMCEs with Eye-Tracking

Our first set of results relates to the validation exercise of comparing the AMCE and $R^{2}$ estimates based on the stated choice data and the visual attention measures from the eye-tracking data. ¹² Figure 2 presents the AMCE estimates with 95% confidence intervals for all eleven attributes that are computed from the full data pooling across all experimental conditions. ¹³ We find that the largest effects pertain to the candidates’ policy positions, with subjects being around 45 percentage points less likely on average to select profiles of candidates that strongly oppose gun control, taxes on the wealthy, and same-sex marriage as compared to candidates that strongly support these policies. The other attributes have smaller but still meaningful effects. In particular, subjects have a higher probability of selecting profiles of candidates who are Democrats or Independents rather than Republicans, who are younger, who served in the Marine Corps, who are not Protestant, and who are White or Black as compared to Hispanic, Asian, or Native American.

Figure 2. AMCEs in the Pooled Data.

How do the AMCEs correspond to the visual attention measures from the eye-tracking data? Figure 3 plots the mean proportion of fixations per attribute across decision tasks, thus providing summary measures of the relative amount of attention given to each attribute on average. We find that there is a clear correspondence between the AMCEs and the visual importance in the sense that the attributes with the largest AMCEs are also the ones that received the most visual attention. In particular, the three policy positions are by far the most fixated upon. Among the other attributes the ordering is less clear. The political party attribute has the fourth highest proportion of fixations while the other attributes receive similarly lower levels of attention. ¹⁴ However, an issue here may be that aggregating the results across all subjects can lead to smaller AMCEs for attributes on which subjects have more heterogeneous preferences.

Figure 3. Mean Proportion of Fixations per Attribute (Pooled Data).

Thus, to more directly test whether stated choices and visual attention on the attributes are correlated, we also performed a within-subject analysis. Specifically, we computed for all subjects within each block their personal rankings of the attributes in terms of their number of eye fixations and their individual-level marginal $R^{2}$ based on the stated choice data. The marginal $R^{2}$ values are a function of the AMCEs for individual attributes, and each marginal $R^{2}$ value provides a single summary measure of the overall influence of an attribute, making it better suited than the AMCEs for evaluating the relative importance of attributes (see Bansak et al. (2019) for details). For each subject–block, the individual-level marginal $R^{2}$ is obtained independently for each attribute via a regression of the outcome (whether a candidate was selected) on the dummy variables for each value of the attribute in question (excluding all other attributes). Because the attributes were randomized independently of one another, each of these marginal $R^{2}$ values thus in expectation isolates the individual-level influence of the attribute in question. ¹⁵

For each subject–block, we then compute the Spearman correlation between the two ranking vectors: the attribute ranking in terms of the individual-level number of eye fixations and the attribute ranking in terms of the individual-level marginal $R^{2}$ . The resulting distribution of Spearman correlation coefficients computed for all subjects and blocks is displayed in the left panel of Figure 4. Even though the $R^{2}$ -based estimates of the rankings are necessarily noisy—given the limited amount of data per subject–block and the fact that there are likely to be many near ties among the less important attributes—we find that there is overall a clear correspondence between the rankings of the attribute importance in terms of the $R^{2}$ values and rankings in terms of visual attention. The median correlation is 0.32, and about 81% of the correlations are positive. To formally test the significance of these results, we conduct a two-tailed randomization inference test of the sharp null hypothesis that there is a correlation of zero for all subjects (i.e., subjects randomly fixate and choose profiles) by randomly shuffling the ranking vectors and re-computing the Spearman correlation coefficients for each subject–block. We conduct 10,000 random shuffles and find both statistics (median correlation of 0.32, and proportion of positive correlations of 0.81) to be statistically significant with $p<0.0001$ . That is, in none of the random shuffles did we compute a median correlation greater in absolute value than 0.32 or a proportion of positive correlations greater than 0.81 (or less than 0.19).

As a visual comparison, the right panel shows the distribution of correlation coefficients from a placebo check, where we perform a single random re-shuffle of the ranking vectors to mimic random looking and clicking. We see that the placebo distribution looks markedly different. Moreover, in the appendix we have replicated this analysis for each experimental condition separately, and the results are similar across all six conditions.

Overall, these findings show that while the correlation between the conjoint metrics estimated from stated choice data and measures of visual attention is not perfect, it is mostly positive and sizable. This supports the interpretation of AMCEs and functions thereof (e.g., marginal $R^{2}$ ) as measures of attribute importance, given that eye movement more directly indicates subjects’ underlying decision-making processes. Our results on validation are also broadly consistent with Meißner, Musalem, and Huber (2016), who found a connection between attribute importance and fixations in a marketing conjoint context.

Figure 4. Correlation between Attribute Importance in Choice and Eye-Tracking Data (Pooled Data).

4.2 Design Effects on AMCEs and Visual Attention

We now turn to our findings on how changes in the conjoint design affect the AMCEs and the underlying decision-making processes as suggested by eye-tracking. Figure 5 shows the estimates of the AMCEs broken down by the six different experimental conditions, which range from less complex conjoint tables with five attributes and two profiles to fairly complex conjoint tables with eleven attributes and three profiles. We find that the AMCEs are fairly stable across the increasing levels of complexity. For example, the AMCEs of moving from a candidate who strongly opposes to strongly supports gun control is fifty-two percentage points (95% CI: 40-65) in the least complex condition (five attributes and two profiles) compared to forty-six percentage points (CI: 39-53) in the most complex condition (eleven attributes and three profiles). For taxes on the wealthy, the AMCEs are 41 percentage points (CI: 29-54) in the least and 46 percentage points (CI: 39-53) in the most complex condition. Similarly, the AMCEs of comparing a Republican versus a Democratic candidate range from 16 percentage points (CI: 12-20) in the least to ten percentage points (CI: 7-13) in the most complex condition. ¹⁶ The effects and ranking of attributes in terms of overall magnitudes of the AMCEs are also substantively stable for the other attributes, with only some modest variation.

Figure 5. AMCEs by Experimental Condition.

Given this stability in the AMCEs, one might then wonder whether and how respondents adjust their visual attention as the complexity of the design increases. Figure 6(a) shows the proportion of cells in the conjoint table that are viewed by the subjects averaged across the decision tasks in each of the six experimental conditions. We find that there is a marked decline in the proportion of cells that the subjects view as the complexity increases. While subjects on average view about 71% of cells in the condition with five attributes and two profiles, this metric decreases monotonically as complexity increases, until subjects view only 45% of cells in the condition with eleven attributes and three profiles. Holding the number of attributes constant, the average proportion of cells viewed drops by about ten percentage points when moving from two to three profiles. Conditional on any number of attributes (or conditional upon either number of profiles), the differences between the mean proportion of cells viewed across two- versus three-profile tables (or all pairwise differences between the mean proportion of cells viewed across five-, eight-, and eleven-attribute tables) are all statistically significant with $p<0.0001$ . These results show that subjects adjust to the increased complexity of the conjoint by processing a smaller fraction of the information presented to them.

Figure 6. Changes in Visual Attention Across Conjoint Designs.

Using locally estimated scatterplot smoothing (LOESS) regression fits, Figure 6(b) shows that there is also a decline, albeit a much smaller one, in the proportion of cells viewed across the sequence of choice tasks completed over time. For instance, in the condition with five attributes and two profiles, while subjects on average view about 75% of cells in their first decision task in this block, this average declines at a roughly linear rate to about 70% of cells at the twentieth choice task in the block. Moreover, this linear decline from earlier to later tasks in a given block is similar across experimental conditions. This result suggests that as subjects become more familiar with the conjoint tasks, they similarly fixate on a smaller fraction of the information presented. This result is consistent with previous work in marketing finding that the number of cells fixated decreases over the course of an experiment (Meißner, Musalem, and Huber 2016).

Figure 6(c) replicates the previous result but focuses only on the first block completed by each respondent. We find that the adjustment is particularly concentrated in this very first block, when subjects are just beginning to familiarize themselves with the conjoint task. In their very first decision task, subjects on average view a considerably higher fraction of cells than in subsequent decision tasks. This initial high fraction of viewed cells is consistent with the idea that subjects familiarize themselves with the full set of attributes. ¹⁷ As subjects complete their first task and move to the second, third, and eventually the last task in their first block, the fraction of viewed cells drops at a roughly linear rate until the last task. Again, this decline is similar across conditions.

Taken together, these results demonstrate that subjects adjust their information gathering processes and focus their visual attention on a smaller fraction of the overall information presented to them as the conjoint table grows in complexity and as they become more familiar with the decision tasks.

4.3 Mechanisms

The previous findings have shown that as the size of the conjoint table increases, respondents adjust by processing a smaller fraction of the presented information. And yet the AMCEs, which reflect the choices that respondents make, remain fairly similar across the different designs. What might explain this seemingly paradoxical result? How can respondents make similar choices even though they process a smaller fraction of the information? Our interpretation is that these results are consistent with a theory of bounded rationality (Simon 1957) as an “adaptive toolbox” (Gigerenzer and Todd 1999). The core idea here is that subjects can adapt to a more complex decision environment by employing information-processing strategies and choice heuristics that allow them to efficiently sift through the additional information, filter out its less relevant components, and selectively focus on the relevant pieces (Payne et al. 1993; Gigerenzer and Goldstein 1996; Bettman, Luce, and Payne 1998). In other words, rather than exert the cognitive effort of processing all the information available to find the optimal choice, respondents rely on shortcuts and only selectively process additional information to find a solution that is good enough (Simon 1955).

One implication of this boundedly rational decision-making is that as complexity increases, we would expect subjects to process a relatively smaller subset of the information environment. At the same time, we would also expect that subjects try to process more information in total. In other words, while the fraction of cells viewed is expected to decline with complexity, we would expect that the absolute number of cells viewed increases as subjects are looking to selectively incorporate the additional information that is most useful to them to make a better choice.

Figure 7 shows that these implications of the bounded rationality mechanism are consistent with the fixation pattern that we find in our data. In particular, we find that as the complexity of the design increases, subjects view a considerably larger number of cells and employ a larger number of total fixations. For example, in the simplest design with five attributes and two profiles, subjects have on average about 17 fixations per decision task. In contrast, in the most complex design with eleven attributes and three profiles, subjects have on average about 32 fixations per decision task. Conditional on any number of attributes (or conditional upon either number of profiles), the differences between the mean number of fixations across two- versus three-profile tables (or all pairwise differences between the mean number of fixations across five-, eight-, and eleven-attribute tables) are all statistically significant with $p<0.01$ . In terms of the mean number of cells viewed across conditions, these differences are all statistically significant with $p<0.0001$ . Substantively, the average number of cells viewed increases from about seven to 15 when comparing the simplest and most complex designs. This represents a considerable increase in the total amount of information that is being processed. At the same time, however, this relative increase in fixations and number of cells viewed does not match the relative increase in the number of cells presented in the conjoint table, which increases from ten to 33 between the simplest and most complex designs. It is for this reason that we find our earlier result, displayed in Figure 6(a), that the proportion of information processed decreases even as the absolute amount of information processed increases.

Figure 7. Changes in Visual Attention Across Conjoint Designs: Number of Cells Viewed, Number of Fixations, and Attribute-wise versus Profile-wise Search.

A second implication of the bounded rationality mechanism is that subjects will adapt to more complexity through various choice heuristics (for reviews, see, Ford et al. 1989; Payne et al. 1993; Bettman, Luce, and Payne 1998; Lau and Redlawsk 2006). One set of heuristics relates to the order in which subjects process the cells in the conjoint table. In particular, we may expect that when faced with comparing three profiles instead of two profiles, more subjects may adopt a strategy of searching within-profile to build summary evaluations that are used to compare the three profiles against each other, rather than searching within-attribute.

Figure 7(c) plots the fraction of decision tasks in which subjects exhibit a positive “search metric” for each experimental condition. The search metric (Bockenholt and Hynan 1994) measures a subject’s preference for within-profile versus within-attribute transitions by comparing the number of vertical to horizontal transitions. Importantly, the search metric was derived to take into account the number of attributes and profiles within a choice task in order to adjust for the differential probability of within-profile versus within-attribute transitions if subjects were to randomly transition around the table. Thus, it allows for a fair comparison of search strategy across conjoint tables of varying composition. A positive search metric means that the subject prefers within-profile searching whereby information is predominantly processed in our tables via vertical transitions between cells, while a negative search metric means the subject prefers within-attribute searching with horizontal transition-based processing.

There are two key results from this search metric analysis. First, conditional on the number of profiles, increasing the number of attributes has no systematic effect on the search metric. In other words, subjects’ search strategy is not systematically affected by the number of attributes presented (at least within the confines of the number of attributes we evaluated). This makes sense from the perspective of bounded rationality: since adding attributes (which may or may not be important to the subject) does not fundamentally change the choice task, we should not expect subjects to change their general search strategy even as they view a smaller proportion of the total information.

As our second result, however, we find that holding the number of attributes constant, there is a noticeable increase in the fraction of decision tasks in which subjects exhibit a positive search metric as we move from two to three profiles in the conjoint table. When faced with decision tasks that involve only two candidate profiles, the average proportion of tasks with a positive search metric is 32.6% (pooling across the five-, eight-, and eleven-attribute conditions). When the number of candidates increases from two to three, the proportion of decision tasks with a positive search metric increases by approximately ten, 13, and six percentage points, respectively (for the five-, eight-, and eleven-attribute conditions). Each of these estimates is statistically significant with $p<0.01$ . This shows that when faced with comparing three profiles instead of two profiles, more subjects adopt a strategy of searching within-profile to build summary evaluations that are used to compare the three profiles against each other, rather than searching within-attribute. In contrast to the addition of attributes, the addition of another profile to choose from is a more fundamental structural modification of the choice task, and thus it is sensible that this design change more substantially affects the subjects’ search strategy.

But what cognitive process could explain the specific result that a higher proportion of subjects prioritize a within-profile search over a within-attribute search as the number of profiles increases? We conjecture that within-attribute comparisons become computationally more costly relative to within-profile comparisons when the conjoint design moves from two to three profiles (while holding the number of attributes fixed). Specifically, subjects searching within-attribute would need to keep in their heads and continually update three values representing the utility of each of the candidates. We expect that doing so is cognitively costly and hence an increasing number of subjects will prefer to process each candidate individually, which necessitates only updating one utility value at a time.

Note that our study provides little direct evidence regarding whether subjects are using memory-based or online processing in their decision-making (Hastie and Park 1986; Lodge, McGraw, and Stroh 1989; Kim and Garrett 2012). Online processing asserts that individuals do not remember detailed past information about an object; instead, their evaluation is represented by a utility value, into which new information is integrated upon exposure in a “running tally.” This contrasts with a memory-based process, by which individuals retrieve information from their long-term memories and render their judgement by weighting the remembered evidence and computing a summary judgement. We do not have a memory measure, which is necessary in order to distinguish between a subject making a single summary judgement versus keeping a running tally of her impression of a candidate. Additionally, whether a subject looks within-profile or within-attribute does not disambiguate between the two theories. A subject may be using an online model and look within-attribute, remembering a utility value for each profile that is updated as she progresses through the issues. Or, she may be using the online model and look within-profile, keeping only a single value for that candidate in mind and updating that value while proceeding through the attributes.

In addition to supporting the idea that subjects exhibit stated choice and visual fixation patterns that are consistent with theories of bounded rationality, our data also indicate that subjects become more efficient in this approach as they become more familiar with the choice task. As subjects evaluate more profiles, their familiarity with the attributes and the attributes’ associated range of values increases. This in turn allows them to focus more quickly on the more important attributes and visually process fewer pieces of information, thereby reducing the computational costs for making choices and allowing them to use boundedly rational heuristics more efficiently over time. Figure 8 demonstrates this pattern. In the upper panel, we see that the AMCEs (pooled across blocks) are similar when we split the sample and compare the first ten and last ten decision tasks within each block. This pattern of stability across tasks is consistent with the results in Bansak et al. (2018) and indicates that subjects continue to make similar choices as they progress through more tasks. ¹⁸ Yet, as shown in the bottom panel of Figure 8, which displays LOESS regression fits, subjects markedly reduce their number of fixations as they complete more tasks. This suggests that subjects learn to become more efficient in making their choices. Meißner, Musalem, and Huber (2016) find a similar pattern in a marketing conjoint example.

Figure 8. Changes in Visual Attention Across Tasks within Block: AMCEs and #of Fixations.

Together, these findings are consistent with theories of bounded rationality that emphasize the role of choice heuristics for making decisions among multiattribute alternatives. They suggest that subjects adapt to information environments of increasing complexity by adopting strategies to selectively incorporate relevant additional information on attributes that matter most to them, and also by efficiently ignoring less relevant additional information to deal with the increased computational cost.

4.4 Response Robustness across Tasks

One possible concern with the design of our experiment relates to the large number of tasks completed by the subjects. As noted earlier, similar numbers of tasks are common in decision experiments in behavioral economics, marketing, and neuroscience research. Nonetheless, there is still a question as to whether the response quality or choice behavior of the subjects in our experiment degraded or changed as they progressed through their decision tasks. This could be the result of fatigue over time, changing levels of social desirability bias over repeat tasks, simple loss of interest in the exercise after many tasks, or other survey-taking phenomena that could affect the choices (preferences) that respondents make (express) over the course of a survey. Substantial changes in subjects’ choice patterns over decision tasks would then call into question the extent to which results from later tasks are informative or generalizable to survey designs that do not include as many decision tasks.

As already shown in Figure 8(a), we do not find evidence that our subjects’ choice patterns differ meaningfully across the first half and second half of their decision tasks within each block. However, Figure 8(a) pools the results across all six blocks, and it may be that a more abrupt change in choice patterns occurs during the subjects’ earlier tasks. Thus, we replicate this analysis using only data from the first block each subject completed. The results, shown in Figure A.8 in the appendix, similarly reveal little to no change in choice patterns.

Figure 9. Distribution of $p$ -Values for Interactions between the AMCEs and Decision Task Number.

In addition, to more formally evaluate whether the subjects’ choice patterns changed systematically across decision tasks, we estimate the interactions between each AMCE and the task number (i.e., a numeric variable indicating the task number, from 1 to 120) within the same regression framework used to estimate the AMCEs themselves. We then assess the distribution of the $p$ -values from these interaction estimates (36 $p$ -values for 36 interactions) for evidence of systematic trends over tasks. Specifically, we use quantile–quantile plots to compare the observed distribution of the $p$ -values to the theoretical null distribution under the assumption of no interactions between the task number and any of the AMCEs. We conduct two versions of this analysis—one pooling over all six blocks and one using only the first block each subject completed—with the results shown in Figure 9. For each point in the plots, the $y$ -axis corresponds to a particular quantile of the observed $p$ -values while the $x$ -axis corresponds to the theoretical value at the same quantile under the null distribution. The closeness with which the points track along the identity line in both plots indicates close correspondence between the observed and null distributions, indicating that the interactions between the task number and the AMCEs are indeed zero or close to zero. ¹⁹ This provides evidence that the AMCEs do not meaningfully vary as a function of the decision task number, which suggests little to no degradation of response quality or change in choice patterns as subjects completed more decision tasks.

5 Limitations

Underlying eye-tracking studies is the assumption that attention is focused at the point of visual fixation. The eye–mind hypothesis (Just and Carpenter 1976) states that the lag between fixations and cognitive processing in the brain is minimal, meaning that an object being fixated upon is also being processed cognitively. However, several limitations and exceptions to this hypothesis have been demonstrated. There is some temporal overlap in processing across fixations (Russo 1978). During the current fixation one may still be processing the previously fixated information. Such delays in attention typically last about 70–80 ms (Holmqvist et al. 2011) out of a typical fixation time of 200–300 ms. One also may shift their attention via peripheral vision to process information that is not yet fixated upon (Rayner and Duffy 1986). Additionally, task design can make a difference in the coupling of mental processing and eye movements, such as if subjects are uncertain about where information is located. We take the steps recommended by Just and Carpenter (1976) to minimize the effects of such interpretability issues on our results: making the task goal clear to subjects, keeping screens empty of any extraneous or distracting peripheral items, reducing scanning urgency, and making the location of objects well known through instructions. We additionally minimize the effect of saccadic suppression in our results given that we use fixation density rather than total fixation duration as our measure. Given this, visual attention can be inferred from fixation points (Hoffman 1998).

Another limitation of our study is that because the eye-tracking technology necessitated bringing the subjects into a lab, our evidence is based on a single sample of respondents from a subject pool at Duke University. The composition of our sample differs from those of typical conjoint survey samples in several respects. In particular, our sample is skewed toward Democrats, younger ages, and females. This raises the question of whether our results generalize to typical conjoint survey samples. While external validity is of course best addressed through replicating our experiment in other samples, there are several pieces of evidence that suggest that our findings may travel to other samples. First, research has shown that findings from student samples can provide a valuable guide for generalizability (Druckman and Kam 2011). Second, we have no strong theoretical reason to expect that the validation tests and design effects we observed are strongly moderated by characteristics that are unique to our sample. For example, it is not readily apparent why Democrats should react differently than Republicans in terms of adjusting their information-processing strategies to increases in the complexity of the conjoint design, and we are not aware of any studies documenting such differential behavior. In fact, similar boundedly rational behaviors have been observed across a wide variety of samples (Jones 2003). Third, our finding that AMCEs remain similar across conjoint tables with varying levels of complexity has also been observed in Bansak et al. (2019) for respondents from two different online panels that are often used for survey research. In the appendix, we replicate and extend the results from Bansak et al. (2019) and show that this stability in AMCEs despite increased complexity is similar for both Democratic and Republican respondents in their samples. Although we lack eye-tracking data from their respondents, the similarity of the patterns gives some credence to the conjecture that these respondents (both Democrats and Republicans) may have similarly adjusted their decision-making processes to deal with the increased complexity.

Another question in terms of generalizability involves whether our results from candidate conjoint experiments generalize to voter behavior in real-world elections. It is important to recognize that our study was not designed with this goal in mind. Instead, our focus was on internal validity to learn about behavior in conjoint surveys. While there exists some evidence that response behavior in conjoint surveys can replicate real-world voting in referendums in some settings (Hainmueller, Hangartner, and Yamamoto 2015), we would advise against generalizing our results too far in this direction. Other experimental designs, such as the DPTE by Lau and Redlawsk (2006), have been specifically designed to improve external validity. The comparability of different designs in terms of external validity is an interesting question for future research.

6 Discussion

The surge in the use of conjoint analysis in political science in recent years highlights the need for increased methodological research into the design and interpretation of conjoint experiments. In this study, we have leveraged eye-tracking methodology to examine how respondents process information when completing conjoint surveys. Bringing eye-tracking data to the analysis of conjoint survey behavior allows us to begin opening up the black box of decision-making and shed some new light on the underlying mechanisms that determine how respondents process information in conjoint experiments.

Our study has several findings. First, we find that there is a positive correlation between commonly used metrics used to infer attribute importance based on the stated choice data (i.e., AMCEs and marginal $R^{2}$ values) and direct measures of attribute importance based on visual fixations. Second, we find that when the complexity of the conjoint table increases through the addition of attributes and profiles, AMCEs remain fairly stable, but subjects process a lower fraction of the cells in the conjoint table and a larger total number of cells. In addition, holding the number of attributes constant, more subjects use a within-profile versus a within-attribute search as the number of profiles increases from two to three. In contrast, holding the number of profiles constant, there was little to no change in the search metric when increasing the number of attributes. In addition, AMCEs remain fairly stable as subjects become more familiar with the task, even though the number of fixations declines, suggesting that subjects learn to make similar choices more efficiently while processing less information. Overall, these findings are consistent with a theory of bounded rationality that highlights how respondents are able to adapt to increased complexity in the conjoint table by relying on simplifying choice heuristics that allow them to make similar choices while balancing the trade-offs between decision accuracy and increased cognitive effort.

Our study makes several contributions. First, we were able to provide a validation test comparing the behavioral importance of attributes based on eye-tracking data to metrics based on self-reported choices. AMCEs and functions thereof are commonly used measures of attribute importance in typical conjoint analyses, and our validation tests support their interpretation as measures of attribute salience.

Second, we provide evidence on the extent to which subjects adjust their choice behavior in response to changes in the complexity of the conjoint decision task. Our finding that AMCEs are robust to increasing the number of attributes is consistent with Bansak et al. (2019), who found a similar pattern in their online surveys. Here, we also find similar stability in AMCEs for a more structural modification of the conjoint design that moves from two to three profiles.

Third, our study provides an explanation for why the AMCEs remain stable despite the increased complexity. In particular, we show that, consistent with theories of bounded rationality that emphasize the trade-off between decision accuracy and cognitive effort, subjects adapt their visual processing to filter out less relevant information and focus on more relevant information. Our findings here are largely consistent with Meißner, Musalem, and Huber (2016), who concluded that conjoint choices are “relatively free of distorting effects from task layout or random exposures” because subjects “identify simple processes that enable conjoint respondents to perform a difficult task efficiently.”

Fourth, our study has direct implications for the design of conjoint experiments. Our findings speak to the robustness of conjoint experiments when increasing the complexity of the conjoint table with respect to the number of attributes and profiles. Our finding about the robustness property of conjoint experiments is important given that researchers who are interested in reducing “masking” (Bansak et al. 2019) may prefer to include a larger number of attributes.

Importantly, our validation results should not be read as confirming that AMCEs or eye-tracking data will always provide valid measures of attribute importance. Depending on the topic of the study or the nature of the respondents, response biases may still be an important concern in conjoint experiments. For example, a savvy respondent may try to conceal racist motivations by choosing profiles without considering the race attribute. Although there is some evidence that conjoint experiments may help to mitigate some problems with social desirability bias (Horiuchi, Markovich, and Yamamoto 2020), more research is needed on this issue.

Similarly, our results should not be read as confirming that AMCEs will always remain stable, regardless of the complexity with which the conjoint may be designed. Although we explored stability across a range of designs that varied the number of attributes and number of profiles, there is likely some level of complexity that we did not reach in our study where respondents would be overwhelmed and no longer provide useful responses. This breaking point appears to be beyond the scope of conventionally sized conjoint tables in political science research, though it is possible that respondents become overwhelmed more quickly with conjoint designs involving decision tasks that are more complex or less familiar than choosing between political candidates.

Our study also suggests some important next steps for future work. Using eye-tracking data opens the door for future research to study additional questions in conjoint analysis, as well as survey design more generally. In political science, the first step was taken by Galesic et al. (2008), who used eye-tracking in a survey design study. But there are ample opportunities to leverage eye-tracking to address questions of interest to political methodology. Follow-up questions include, inter alia, analysis of social desirability bias, decision-making strategies, and heterogeneity in information processing. We hope that our study design can serve as a blueprint for future studies.