INTRODUCTION
Significant progress in measles control has been made as a consequence of implementing the World Health Organization (WHO) and United Nations Children's Fund (UNICEF) strategy for measles mortality reduction [1]. Measles deaths in Africa decreased by an estimated 91% from 2000 to 2006, accounting for 70% of the global decline in measles mortality [2]. The global measles mortality reduction goal set forth in the WHO-UNICEF Global Immunization Vision and Strategy (GIVS) for 2006–2015 is to reduce measles deaths by 90% by 2010 compared to the estimated 757 000 deaths in 2000 [3].
Maintaining current gains and making further reductions in measles incidence and mortality will face several obstacles [Reference Orenstein4]. One challenge to continued progress in measles control is the need for repeated mass measles vaccination campaigns, designated supplementary immunization activities (SIAs). An initial SIA, the catch-up campaign, will typically target all children aged between 6 months and 14 years independent of vaccination status. Follow-up SIAs, typically targeting children aged 9 months to 4 years, are currently recommended when the estimated number of susceptible children reaches the size of one birth cohort, generally every 2–4 years after the catch-up [5]. However, the frequency with which these campaigns must be performed to prevent epidemics is uncertain. Because these programmes are resource intensive, the long-term sustainability of SIAs is unclear. These activities require resources and staff of the primary healthcare system, and public support in the face of decreasing disease burden. Countries and regions will increasingly need evidence-based methods to determine the optimal timing of repeat measles SIAs, maximizing the efficient use of scarce resources while minimizing the frequency and size of measles outbreaks.
The impact of recurring SIAs, sometimes termed pulsed vaccination, on measles transmission has been explored in modelling studies [Reference Agur6]. Several authors have estimated the frequency and coverage of SIAs that must be maintained to sustain low levels of transmission in theoretical models [Reference Shulgin, Stone and Agur7, Reference Nokes and Swinton8], but these models have used simplified representations of population structure and the performance of vaccine programmes. These studies do not provide guidance on the use of setting specific data to inform policy and depend on assumptions about measles transmission dynamics that may not apply to all settings. Here we provide a data-driven approach to estimating the population immunity achieved by different vaccination strategies in the absence of circulating measles, thereby providing a lower limit to the level of population immunity achieved by these strategies independent of assumptions about transmission dynamics.
Over the longer term SIAs are not considered an optimal or sustainable approach to measles control. In addition to increasing the number of children reached by the standard 9-month dose, the eventual addition of a second dose at 12, 15 or 24 months has been considered as one method of maintaining high levels of measles immunity in Africa [9]. Because the current vaccine is not efficacious at young ages, a substantial proportion of those at risk (especially in high birth-rate countries) cannot be protected, and utilization of measles vaccine targeted at 9-month-olds is lower than for neonatal vaccines such as diphtheria-tetanus-pertussis (DTP). Research into novel measles vaccines provides hopes for a future neonatal vaccine that can overcome the basic shortcomings of the current vaccine [Reference Pan10, Reference Griffin, Pan and Moss11].
The ultimate goal of measles control is elimination. The proportion of the population that must be immune to eliminate measles is dependent on the basic reproductive rate (R 0) of measles by the well known formula: 1−1/R 0 [Reference Hethcote12]. Estimates of R 0 for measles typically range from 12 to 20 [Reference Anderson and May13], although a recent study estimated R 0 values ranging from 4·7 to 15·7 in Niger [Reference Grais14]. Using the average age of hospitalized cases of measles [Reference Scott15], we estimate R 0 in Zambia to be 12·6. A population immunity of 95% is necessary to prevent outbreaks if R 0 is 20, 94% if R 0 is 15·7, and 92% if R 0 is 12.
In 2003, Zambia conducted a catch-up SIA targeting children aged 6 months to 14 years that achieved an estimated 97% coverage [16]. A follow-up SIA was conducted in 2007. We used data obtained from a survey conducted in Lusaka, Zambia in 2006 to develop models of measles vaccination coverage. We then performed numerical simulations to predict levels of measles population immunity under multiple alternative immunization strategies. We compared strategies supplementing routine measles vaccination with: (1) additional doses of measles vaccine administered through routine immunization services; (2) additional does administered through SIAs; and (3) a hypothetical measles vaccine administered in early infancy.
METHODS
Research on human subjects was approved by the University of Zambia Research Ethics Committee and the Johns Hopkins University Bloomberg School of Public Health Institutional Review Board.
Study population
In July 2006, 3 years after a national measles SIA, we conducted a cross-sectional survey in Lusaka, Zambia to assess measles vaccination coverage and population immunity to measles virus using oral fluid specimens [Reference Lowther17]. The sampling frame for the random selection of households was constructed from a publicly available Quickbird™ satellite image obtained from DigitalGlobe Services Inc. (USA). Children aged between 9 months and 5 years residing in a randomly selected household were eligible for enrolment. When an eligible child was identified, written informed consent was obtained from the caretaker or guardian. After obtaining informed consent, a questionnaire was administered to collect information on demographic characteristics and the health status of the child, including vaccination history. When possible, the dates of vaccination were recorded from the child's under-5 card. Oral fluid samples were obtained from children aged 9 months to 5 years using Oracol® oral-specimen collection devices (Malvern Medical Developments Ltd, UK) and tested for antibodies to measles virus by enzyme immunoassay (Microimmune Ltd, UK) validated for oral fluid. During 3 weeks in July and August 2006, 1242 potential residences were visited, 1194 residences were identified, and 1069 children from 691 residences were enrolled. Our analysis is based on 1015 children from 668 households who provided an adequate oral fluid specimen and for whom a caretaker completed the interview.
Age-specific probability of vaccination
To estimate the age-specific probability of measles vaccination, log-spline semi-parametric probability density functions (p.d.f.s) were fit to reported vaccination status using semi-parametric methods based on log-splines [Reference Venables and Ripley18]. If the date of vaccination was available from the child's under-5 vaccination card, we considered the time of vaccination to be known exactly. If the vaccination record was unavailable but the caretaker reported the child had been vaccinated, data were considered to be left-censored at the time of the interview. If the child had not been vaccinated at the time of the interview, data were considered to be right-censored at the time of the interview. We fit three models to determine the best method for modeling the effect of vaccination during the 2003 SIA. Model 1 was fit to all children with known measles vaccination status (n=969). Model 2 considered the same children (n=969), but children reported to have been vaccinated only in the 2003 SIA were classified as unvaccinated. Model 3 used survey data only from children aged <42 months, too young to have participated in the 2003 SIA (n=688). Models 2 and 3 were extended to give children alive during the 2003 SIA an independent probability of vaccination during the SIA of 96·9%, based on measles vaccine coverage levels reported by the WHO [16]. Models were compared based on the likelihood of producing the observed age distribution of measles vaccination. Similar methods were used to fit the p.d.f. of receiving one, two, or three doses of DTP vaccine to data from the same survey. These p.d.f.s were used to model the uptake of a hypothetical neonatal measles vaccine administered in early infancy.
Population immunity to measles
In addition to the age-specific probability of vaccination, population immunity to measles is a function of the rate of decline of passively acquired maternal antibodies and the age-specific probability of primary vaccine failure. We modelled protection from passively acquired maternal antibodies and primary vaccine failure independently. Based on data from Kenya, passively acquired maternal antibodies to measles virus were estimated to have a half-life of 46·1 days and to decay at a constant rate, corresponding to an exponential decay function of exp(−0·45t), where t is age in months [Reference Caceres, Strebel and Sutter19]. We assumed all children were protected by maternal antibodies at birth and protection decayed proportionally with levels of maternal antibody. A logistic model of vaccine failure was fit to data on seropositivity in the absence of passively acquired maternal antibodies in 6-, 9-, and 12-month-old children in the USA [Reference Gans20]. Using a conservative estimate of the immunological endpoint representing immunity, we estimated that the probability of successful vaccination follows the logistic function 1/[1+exp(−(−3·77+0·59t))]; we assumed that at no age does vaccine efficacy exceed 97%. The age-specific probabilities of protection by maternal antibodies and vaccination were combined to determine the age-specific probability of measles immunity in the absence of circulating measles virus.
The percentage of the population protected from measles can be determined by applying these probabilities to the age distribution of the population. Specifically, the probability of being immune at age t is Pr(V)+Pr(M) – Pr(V)×Pr(M), where V indicates immunity from vaccination and M indicates immunity from maternal antibodies. Using the model of vaccine efficacy and vaccine uptake described above, Pr(V) can be calculated by applying the distributions described above. We used population growth and mortality data from the 2001/2002 Zambia Demographic Health Survey to model the age structure of the population [21] and checked our model against projections by the US Census Bureau for the year 2000/2001 [22].
Using this model of measles population immunity, we performed numerical simulations projecting population immunity under different control programmes in the absence of circulating wild-type measles virus. Model estimates of the June 2006 immunological profile of the population were compared to the results of the 2006 antibody survey, adjusted for the manufacturer's reported sensitivity (93%) and specificity (98%) of the oral fluid assay. With the modelled immunological profile of the 2006 population as baseline, we predicted population immunity to measles at monthly intervals for 15 years. SIAs were considered to give each child in the appropriate age range an independent probability of being vaccinated on 15 June equivalent to the coverage of the hypothetical SIA. Different routine vaccination schedules were considered as time-shifted versions of the p.d.f. for routine vaccination estimated from the 2006 survey or as having the programme goals fulfilled (e.g. 97% of the population vaccinated during the 9th month of life). The probability of being included in each vaccination programme is assumed to be independent of participation in any other. To estimate the effect of a hypothetical neonatal measles vaccine administered in the first months of life, we assumed the age-specific probability of vaccination with the neonatal vaccine was the same as for the first dose of DTP vaccine (for a one-dose measles vaccine) or the second dose of DTP vaccine (for a two-dose measles vaccine). This hypothetical vaccine was assumed to confer the same level of protection as the currently used measles vaccine at age 9½ months (86·4%), and to have no efficacy after the first dose using a two-dose schedule (i.e. two doses were required to have any protective effect). To predict measles population immunity for all age groups, we assumed persons aged >5 years to have levels of immunity equivalent to 5-year-old children who received a second dose of measles vaccine during the 2003 SIA (99%). This assumption is justified by the fact that, prior to the 2003 SIA, wild-type measles virus circulated widely in Zambia with an average age of infection of 2·9 years, and the 2003 SIA targeted children to 14 years of age [Reference Scott15, 16]. Hence, the majority of persons aged >5 years in 2006 were likely to be immune to measles either through vaccination or natural infection.
Simulations and statistical analyses were performed using the R statistical package (version 2.8). All confidence intervals were calculated using bootstrapping [Reference Duda, Hart and Stork23]. Further details on numerical simulations are available in the online Supplementary material.
RESULTS
The model with the best fit to the observed age distribution of measles vaccination was model 3, which combined survey-reported vaccination status for children aged <42 months with WHO-reported coverage of the 2003 SIA. Using this model, the probability of measles vaccination was low before age 9 months, peaked between 9 and 10 months, and decreased thereafter but remained elevated into the second year of life (Fig. 1). In the absence of a SIA, 83% of children were estimated to have been vaccinated against measles by age 2 years. According to the best fit model, over 90% of children received at least one dose of DTP vaccine by age 5 months and at least two doses by age 9 months (Fig. 1).

Fig. 1. Age-specific probability of vaccination, using a model fit to data from survey respondents aged <42 months, compared to the actual percentage of children vaccinated by a given age reported in a 2006 survey conducted in Lusaka, Zambia. SIA, Supplementary immunization activity; DTP, diphtheria-tetanus-pertussis.
In children too young to have participated in the 2003 SIA, our model overestimated the proportion of children with detectable antibodies to measles virus but was within projected error limits (Fig. 2). In children old enough to have participated in the 2003 SIA, our predictions deviated from the observed percentage of children with detectable antibodies to measles virus and the impact of the 2003 SIA was not apparent in the observed data (Fig. 2). However, the percentage positive by the antibody test may be affected by the time since vaccination, potentially obscuring the effect of the 2003 SIA. It is also possible that vaccinations delivered during the 2003 SIA were less efficacious, although the fact that measles circulation in Zambia was interrupted by this campaign makes this unlikely [16].

Fig. 2. Predicted levels of population immunity compared to the actual proportion of children with detectable antibodies to measles virus using an oral fluid assay, adjusted for manufacturer's reported sensitivity and specificity. SIA, Supplementary immunization activity.
We compared 30 different vaccination schedules (Tables 1 and 2) and estimated the level of population immunity that would be expected in the absence of natural measles virus transmission in children aged <5 years and for all age groups. Selected results are presented in Figures 3 and 4, and detailed results are presented in the online Supplementary material (Fig. S1, Table S1). We projected that immunity to measles virus in children aged <5 years would stabilize at about 68% immune if current routine vaccine coverage remained unchanged and no supplemental activities were performed. Population immunity for all ages would decline consistently, dropping below 93% within 10 years. The addition of a routine second dose at age 12 months would greatly increase immunity in children aged <5 years, reaching 81% if coverage were equivalent to that at age 9 months, 78% if coverage were reduced by a quarter, and 74% if coverage were reduced by half. Programmes in which the second dose of measles vaccine is administered at ages 15 or 24 months result in lower levels of population immunity in children aged <5 years.

Fig. 3. Predicted levels of immunity achieved by differing measles vaccination schedules. The left panels show the percentage aged <5 years (thick blue line) and the entire population (thin grey line) predicted to be immune to measles in the absence of circulating virus for 10 years after instituting the given vaccination programme. The right panels show the percentage of children aged 0–60 months predicted to be immune to measles by age after the given programme has been in place for 10 years.

Fig. 4. Predicted levels of immunity achieved by augmenting current routine vaccination with supplementary immunization activities (SIAs). The left panels show the percentage aged <5 years (thick blue line) and the entire population (thin grey line) predicted to be immune to measles in the absence of circulating virus for 10 years after instituting the given programme. The right panels show the percentage of children aged 0–60 months predicted to be immune to measles immediately preceding (solid orange line) and following (dashed blue line) the last SIA shown.
Table 1. Hypothetical measles vaccination programmes not including supplementary immunization activities. ‘Current’ vaccination probability refers to the probability density function fit to the 2006 survey data. A vaccine with ‘normal’ efficacy is assumed to have the same age-specific vaccine failure rate as the current vaccine

Curr, Current; mo., months; DTP, diphtheria-tetanus-pertussis.
* For two-dose neonatal programmes, it is assumed that the first dose gives no protection and 86·4% are protected after two doses.
Table 2. Hypothetical measles vaccination programmes supplementing current routine vaccination coverage with SIAs. The probability of being included in a SIA is assumed to be independent of participation in previous SIAs and routine vaccination. SIAs are assumed to target children aged 6–48 months
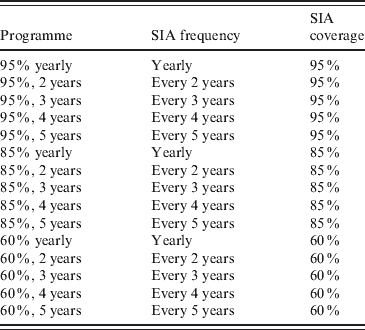
SIA, Supplementary immunization activity.
Supplementing routine vaccination with periodic SIAs in 6- to 48-month-old children can further raise levels of population immunity; however, the frequency of SIAs substantially affects the impact on population immunity (Fig. 5). SIAs at 5-year intervals will routinely miss a 1½-year-wide birth cohort, allowing immunity levels in children aged <5 years to fall to the same levels as with routine vaccination (68%) in the months before the SIA is repeated. High-coverage SIAs generally achieve higher peak levels of population immunity even if conducted less frequently than lower-coverage SIAs (e.g. 86% in <5-year-olds for 95% coverage every 5 years vs. 83% for 60% coverage every 2 years). However, the frequency of SIAs is more important than the coverage of individual SIAs in raising the mean and minimum levels of population immunity (Fig. 5). More frequent SIAs may be preferable even at the expense of substantial drops in the vaccine coverage of each SIA. As an example, the mean population immunity of 95%-coverage SIAs conducted every 5 years is 74% vs. a mean of 76% for 60% coverage every 2 years.

Fig. 5. Comparison of programmes including SIAs by projected population immunity in the absence of circulating measles virus 5–15 years after implementation: (a) minimum immunity in children aged <5 years; (b) mean immunity in children aged <5 years; (c) minimum immunity in total population; and (d) mean immunity in total population.
A hypothetical neonatal measles vaccine that is 86·4% efficacious in infants and achieves the same coverage as the current DTP vaccine would raise immunity in <5-year-olds to 84%. If combined with a second dose of the current vaccine at 12 months, immunity levels of 94% could be achieved. If two doses were required, and age-specific uptake matched that of the second dose of DTP vaccine, these immunity levels would fall to 80% and 91%, respectively.
DISCUSSION
The goal of this analysis was to determine programmes that could maintain population immunity at high levels in the absence of transmission. We used specific information on the performance of immunization campaigns in Zambia to create detailed estimates of population-level immunity in the absence of transmission. We expected that the qualitative results of our analysis will be applicable to much of sub-Saharan Africa. However, using our methods any country can create similar quantitative estimates of population-level immunity that apply to their situation.
The maximum level of population immunity attained by a programme indicates if levels of immunity adequate to interrupt measles virus transmission are achieved (estimated to be 92–95%). The mean level of population immunity indicates on average how near the programme is to this goal. However, the minimum immunity over a period may be most important for public health, as this determines if a population falls to immunity levels where a measles epidemic becomes possible. Our analysis indicates that frequent, low-coverage SIAs sustain higher mean and minimum levels of immunity than less frequent, high-coverage SIAs.
A second dose of measles vaccination delivered by the routine vaccination programme also maintains high levels of population immunity. We find that a second dose targeting children shortly after the probability of successful immunization plateaus with age (12 months) and results in the highest mean and minimum levels of population immunity among two-dose strategies with the existing vaccine. A vaccine that could be delivered in early infancy could increase coverage substantially in Africa, due to the high uptake of early vaccines (e.g. DTP) and the large population aged <9 months.
More frequent SIAs and programmes that provide a second dose of vaccine provide opportunities for vaccination both when children are young, reducing their time at risk, and when vaccine is most likely to be efficacious. In contrast, less frequent SIAs provide fewer opportunities for each birth cohort to be immunized; completely missing some cohorts if the size of the age range targeted is less than the time between SIAs.
Our analysis does not include information on the logistics of performing each campaign. Detailed information on the logistical requirements of conducting more frequent, lower-coverage SIAs compared to less frequent, high-coverage campaigns would provide further, important criteria on which to evaluate the programes proposed in this work.
Our analysis indicates that vaccination programmes vary in the length of time it takes population immunity levels to stabilize. If a country decides to implement a second routine dose of measles vaccine, policy-makers must decide when they should switch resources from conducting SIAs to administering the second dose. To reduce the time necessary to achieve projected immunity levels, new programmes should be started shortly after a SIA or natural epidemic. The spikes in population immunity provided by these activities or events will bring population immunity levels closer to (or even above) the immunity levels attainable by the new programme, thereby substantially reducing the time needed to realize those results.
Little is known about the proportion of children vaccinated during SIAs or receiving second routine doses who were not vaccinated through routine immunization services. An analysis of a SIA in Kenya found reductions in susceptibility consistent with equal probabilities of vaccination for both previously vaccinated and unvaccinated individuals [Reference Ohuma24]. Wood et al. found a ~25% increase in the proportion susceptible at age 4 years in the presence of significant correlation between vaccine programmes in a simulation designed to model a developed setting [Reference Wood25]. We were unable to perform a similar analysis due to the high coverage of the 2003 SIA and problems with recall 3 years post-campaign. Positive correlation of vaccination probability in routine and supplemental doses reduces programme effectiveness by increasing the number of children receiving multiple doses and the number receiving none at all. Negative correlation would have the opposite effect, spreading vaccine doses over a wider population. Increased information on the correlation of vaccine outcomes in multiple programmes would improve our results. If lower-coverage SIAs are performed, monitoring is essential to make sure that there is no subpopulation that is consistently missed by the programme and that the long-term immunization goals are being met.
We chose to simulate population immunity in the absence of transmission. Natural transmission will increase population immunity over our model predictions, but this extra protection should not be dependent upon when setting policy. Ultimately, countries that have eliminated transmission will face the prospect of maintaining herd immunity through vaccination alone. We are optimistic that each of the countries of Africa will reduce measles transmission to low levels in the coming years (WHO AFRO proposes a goal of >98% reduction by 2012) [26].
WHO guidelines suggest that Zambia should conduct follow-up SIAs every 5 years [5], but our analysis suggests that Zambia would benefit from more frequent SIAs. In 2006, measles virus began circulating widely in Zambia for the first time since the 2003 SIA [27]. We projected that about 71% of <5-year-olds and 94% of the general population were immune at that time. If the goal is to maintain measles immunity above these levels, SIAs should be performed every 2 years with at least 60% coverage or every 3 years with at least 85% coverage. Frequent SIAs of this type could contain measles transmission until the long-term goal of implementing an evidence-based, sustainable and effective routine programme can be achieved.
NOTE
Supplementary material accompanies this paper on the Journal's website (http://journals.cambridge.org/hyg).
ACKNOWLEDGEMENTS
The field work was supported by the Thrasher Research Fund (02828-9). S.A.L was supported by the National Eye Institute Training Grant (EY 07127), pre-doctoral Clinical Trials Training Program in Vision Research, National Institutes of Health, Department of Health and Human Services. The modelling and simulation work was supported by grants from the Bill and Melinda Gates Foundation (The Measles Vaccine Initiative, The Vaccine Modeling Initiative). Derek Cummings holds a Burroughs Wellcome Career Award at the Scientific Interface. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
S. A. Lowther is currently affiliated with Centers for Disease Control and Prevention, Atlanta, GA, USA.
DECLARATION OF INTEREST
None.








