Hyper-Fit: Fitting Linear Models to Multidimensional Data with Multivariate Gaussian Uncertainties

Abstract

Astronomical data is often uncertain with errors that are heteroscedastic (different for each data point) and covariant between different dimensions. Assuming that a set of D-dimensional data points can be described by a (D − 1)-dimensional plane with intrinsic scatter, we derive the general likelihood function to be maximised to recover the best fitting model. Alongside the mathematical description, we also release the hyper-fit package for the R statistical language (github.com/asgr/hyper.fit) and a user-friendly web interface for online fitting (hyperfit.icrar.org). The hyper-fit package offers access to a large number of fitting routines, includes visualisation tools, and is fully documented in an extensive user manual. Most of the hyper-fit functionality is accessible via the web interface. In this paper, we include applications to toy examples and to real astronomical data from the literature: the mass-size, Tully–Fisher, Fundamental Plane, and mass-spin-morphology relations. In most cases, the hyper-fit solutions are in good agreement with published values, but uncover more information regarding the fitted model.

1 INTRODUCTION

There is a common conception that the method used for fitting multidimensional data is a matter of subjective choice. However, if the problem is mathematically well-defined, the optimal fitting solution is, in many cases, unique. This paper presents the optimal maximum likelihood fitting solution (with the caveats that a maximum likelihood fitting approach entails) for the frequently encountered case schematised in Figure 1, where D-dimensional data (i) have multivariate Gaussian uncertainties (these may be different for each data point), and (ii) randomly sample a (D − 1)-dimensional plane (a line if D = 2, a plane if D = 3, a hyperplane if D ⩾ 4) with intrinsic Gaussian scatter. In particular, the data have no defined predictor/response variable. Hence, standard regression analysis does not apply, and in general, it would yield different geometric solutions depending on axis-ordering (though see von Toussaint 2015, which presents the necessary prior modifications to make traditional intrinsic-scatter-free regression analysis rotationally invariant).

Figure 1. Schematic representation of the linear model (blue) fitted to the data points (red). Both the model and the data are assumed to have Gaussian distributions, representing intrinsic model scatter and statistical measurement uncertainties, respectively. In both cases, 1σ-contours are shown as dashed lines.

Within the assumptions above, the (D − 1)-dimensional plane that best explains the observed data is unique and can be fit using a traditional likelihood method. In this paper, we present the general D-dimensional form of the likelihood function and release a package for the R statistical programming language (hyper-fit) that optimally fits data using this likelihood approach. We also release a user-friendly web interface to run hyper-fit online and apply our algorithm to common relations in galaxy population studies.

Other authors have investigated the problem of regression and correlation analysis (Kelly 2007; Hogg, Bovy, & Lang 2010; Kelly 2011; von Toussaint 2015) with the aim of improving on the ad-hoc use of standard linear or multi-variate regression, reduced χ² analysis, computationally expensive (and usually unnecessary) bootstrap resampling, and the ‘bisector method’ that is sometimes wrongly assumed to be invariant with respect to an arbitrary rotation of the data. Of recent work that is familiar in the astronomical community, Kelly (2007) presents a comprehensive approach for linear regression analysis with support for non-detections, and made available idl code that can analyse multi-dimensional data with a single predictor variable. More recently, Hogg et al. (2010) describes the approach to attack such joint regression problems in two dimensions. Taylor et al. (2015) describes an approach to extend the work of Hogg et al. (2010) to multiple Gaussian mixture models to model the red and blue populations in the Galaxy And Mass Assembly survey (Liske et al. 2015). Here, we extend Hogg et al. (2010) to arbitrary dimensions and include a suite of tools to aid scientists with such analysis.

In Section 2, we describe the likelihood method for an arbitrary number of dimensions and for different projection systems (to allow for maximum flexibility in its application). In Section 3, we describe and publicly release the hyper-fit package for R, a user friendly and fully-documented package that can be applied to such problems. We also introduce a simple web interface for the package. In Section 4, we show simple applications of hyper-fit to toy examples, including the dataset presented in Hogg et al. (2010). In Section 5, we show more advanced examples taken directly from published astronomy papers, where we can compare our fitting procedure against the relationships presented in the original work. In the appendix, we add a discussion regarding the subtle biases contained in an extraction of model intrinsic scatter, and provide a route to properly account for a non-uniformly sampled data. We also illustrate the implementation of the 2D-fitting problem in hierarchical Bayesian inference software, with an illustrative model using Just Another Gibbs Sampler ( jags¹).

2 MATHEMATICAL DERIVATION

This section develops the general theory for fitting data points in D dimensions by a (D − 1)-dimensional plane, such as fitting points in two dimensions by a line (Figure 1). As described in Section 1, we assume that the data represent a random sample of a population exactly described by a (D − 1)-dimensional plane with intrinsic Gaussian scatter, referred to as the ‘generative model’. The objective is to determine the most likely generative model, by fitting simultaneously for the (D − 1)-dimensional plane and the intrinsic Gaussian scatter, given data points with multivariate Gaussian uncertainties: the uncertainties are (1) different for each data point (heteroscedasticity), (2) independent between different data points, and (3) covariant between orthogonal directions, e.g. x-errors and y-errors can be correlated. We first present the general method in D dimensions in coordinate-free form (Section 2.1) and in Cartesian coordinates (Section 2.2). Explicit equations for the two-dimensional case are given in Section 2.3. Subtleties and generalisations are presented in the appendix.

2.1 Coordinate-free solution in D dimensions

Consider N data points i = 1, . . ., N in D dimensions. These points are specified by the measured positions $\mathbf {x}_i\in {\mathbb {R}^D}$ relative to a fixed origin $\mathcal {O}\in {\mathbb {R}^D}$, and Gaussian measurement uncertainties expressed by the symmetric covariance matrices C_i. We can then fully express our knowledge about a point i as the probability density function (PDF) ρ(x|x_i), describing the probability that point i is truly at the position x given the measured position x_i. In the case where the intrinsic distribution of points in any direction is uniform (the case of non-uniform point distributions is discussed in Appendix B), this PDF is symmetric, i.e. ρ(x|x_i) = ρ(x_i|x), and reads

(1) $$\begin{equation} \rho (\mathbf {x}_i|\mathbf {x}) = \frac{1}{\sqrt{(2\pi )^D|{\mathbf {C}}_i|}}\,e^{-\frac{1}{2}(\mathbf {x}-\mathbf {x}_i)^\top {\mathbf {C}}_i^{-1}(\mathbf {x}-\mathbf {x}_i)}. \end{equation}$$

In Figure 1, these PDFs are shown as red shading.

The data points are assumed to be randomly sampled from a PDF, called the generative model, defined by a (D − 1)-dimensional plane $\mathcal {H}\subset {\mathbb {R}^D}$ (a line if D = 2, a plane if D = 3, a hyperplane if D ⩾ 4) with Gaussian scatter σ_⊥ orthogonal to $\mathcal {H}$. Note that the scatter remains Gaussian along any other direction, not parallel to $\mathcal {H}$. The blue shading in Figure 1 represents this generative model, with the solid line indicating the central line $\mathcal {H}$ and the dashed lines being the parallel lines at a distance σ_⊥ from $\mathcal {H}$. The plane $\mathcal {H}$ is fully specified by the normal vector ${\mathbf {n}}\perp \mathcal {H}$ going from $\mathcal {O}$ to $\mathcal {H}$, and the distance of a point $\mathbf {x}\in {\mathbb {R}^D}$ from $\mathcal {H}$ equals $|\hat{{\mathbf {n}}}^\top \mathbf {x}-n|$, where n = |n| and $\hat{{\mathbf {n}}}={\mathbf {n}}/n$. Thus, $\mathcal {H}$ is the ensemble of points x that satisfy

(2) $$\begin{equation} \hat{{\mathbf {n}}}^\top \mathbf {x}-n = 0\,. \end{equation}$$

Given this parameterisation, the generative model is fully described by the PDF

(3) $$\begin{equation} \rho _m(\mathbf {x}) = \frac{1}{\sqrt{2\pi \sigma _\perp ^2}}\,e^{-\frac{(\hat{{\mathbf {n}}}^\top \mathbf {x}-n)^2}{2\sigma _\perp ^2}}, \end{equation}$$

expressing the probability of generating a point at position x. Note that we here assume that the generative model is infinitely uniform along any dimension in the plane. If the selection function was, e.g. a power law distribution, then ρ(x|x_i) ≠ ρ(x_i|x), and Equation (3) cannot be a simply stated. Such scenarios are discussed in Appendix B.

The likelihood of measuring data point i at position x_i then equals

(4) $$\begin{equation} \mathcal {L}_i = \int _{\mathbb {R}^D}\!\!d\mathbf {x}\,\rho (\mathbf {x}_i|\mathbf {x})\rho _m(\mathbf {x}) = \frac{1}{\sqrt{2\pi s_{\perp ,i}^2}}\,e^{-\frac{(\hat{{\mathbf {n}}}^\top \mathbf {x}_i-n)^2}{2s_{\perp ,i}^2}}, \end{equation}$$

where $s_{\perp ,i}^2\equiv \sigma _\perp ^2+\hat{{\mathbf {n}}}^\top {\mathbf {C}}_i\hat{{\mathbf {n}}}$. Following the Bayesian theorem and assuming uniform priors on $\hat{{\mathbf {n}}}$ and σ_⊥, the most likely model maximises the total likelihood $\mathcal {L}=\prod _{i=1}^{N}\mathcal {L}_i$ and hence its logarithm $\ln \mathcal {L}$. Up to an additive constant $\frac{N}{2}\ln (2\pi )$,

(5) $$\begin{equation} \ \ln \mathcal {L}= -\frac{1}{2}\sum _{i=1}^{N} \left[\ln (s_{\perp ,i}^2)+\frac{(\hat{{\mathbf {n}}}^\top \mathbf {x}_i-n)^2}{s_{\perp ,i}^2}\right]. \end{equation}$$

Note that Equation (5) is manifestly rotationally invariant in this coordinate-free notation, as expected when fitting data without a preferred choice of predictor/response variables. For the purpose of numerical optimisation, free parameters in the form of unit vectors are rather impractical, because of their requirement to have a fixed norm. It is therefore helpful to express Equation (5) entirely in terms of n, without using $\hat{{\mathbf {n}}}$ and n,

(6) $$\begin{equation} \ln \mathcal {L}= \!-\frac{1}{2}\sum _{i=1}^{N}\!\left[\ln \!\left(\!\sigma _\perp ^2\!\!+\!\frac{{\mathbf {n}}\!^\top \!{\mathbf {C}}_i{\mathbf {n}}}{{\mathbf {n}}\!^\top {\mathbf {n}}}\!\right)\!+\!\frac{({\mathbf {n}}^\top [\mathbf {x}_i-{\mathbf {n}}])^2}{\sigma _\perp ^2{\mathbf {n}}\!^\top \!{\mathbf {n}}\!+\!{\mathbf {n}}\!^\top \!{\mathbf {C}}_i{\mathbf {n}}}\right]\!.\!\! \end{equation}$$

In summary, assuming that the data samples a linear generative model described by Equation (3), the model-parameters that best describe the data are found by maximising the likelihood function given in Equation (5) or (6).

2.2 Notations in Cartesian coordinates

For plotting and further manipulation, it is often useful to work in a Cartesian coordinate system with D orthogonal coordinates j = 1, . . ., D. The typical expression of a linear model in such coordinates is

(7) $$\begin{equation} x_D = {\Sigma _{j=1}^{D-1}}\alpha _j x_j+\beta , \end{equation}$$

where x_j is the j-th coordinate of x = (x ₁, . . ., x_D)^⊤, α_j = ∂x_D/∂x_j is the slope along the coordinate j, and β is the zero-point along the coordinate D. Equation (7) can be rewritten as α^⊤x + β = 0, where α^⊤ ≡ (α₁, . . ., α_{N − 1}, −1) is a normal vector of the (D − 1)-dimensional plane. The Gaussian scatter about this plane is now parameterised with the scatter σ_D along the coordinate D. A vector calculation shows that the transformation between the coordinate-free model parameters {n, σ_⊥} and the coordinate-dependent parameters {α, β, σ_D} takes the form

(8) $$\begin{eqnarray} {\mathbf {n}}& =& -\beta \mathbf {\alpha }(\mathbf {\alpha }^\top \mathbf {\alpha })^{-1}\nonumber\\ \sigma _\perp & = & \sigma _D(\mathbf {\alpha }^\top \mathbf {\alpha })^{-1/2} \end{eqnarray}$$

or, inversely,

(9) $$\begin{eqnarray} \mathbf {\alpha }& =& -{\mathbf {n}}/n_D \nonumber\\ \beta & = & ({\mathbf {n}}^\top {\mathbf {n}})/n_D \\ \sigma _D & = & \sigma _\perp ({\mathbf {n}}^\top {\mathbf {n}})^{1/2}/|n_D|. \nonumber \end{eqnarray}$$

In practice, one can always fit for {n, σ_⊥} by maximising Equation (6) and then convert {n, σ_⊥} to {α, β, σ_D}, if desired. Alternatively, we can rewrite Equation (6) directly in terms of the parameters {α, β, σ_D} as

(10) $$\begin{equation} \ln \mathcal {L}= \frac{1}{2}\sum _{i=1}^{N} \left[\ln \frac{\mathbf {\alpha }^\top \mathbf {\alpha }}{\sigma _D^2+\mathbf {\alpha }^\top {\mathbf {C}}_i\mathbf {\alpha }}-\frac{(\mathbf {\alpha }^\top \mathbf {x}_i+\beta )^2}{\sigma _D^2+\mathbf {\alpha }^\top {\mathbf {C}}_i\mathbf {\alpha }}\right], \end{equation}$$

however, this formulation of the likelihood is prone to optimisation problems since the parameters diverge when $\mathcal {H}$ becomes parallel to the coordinate D.

2.3 Two-dimensional case

Let us now consider the special case of N points in D = 2 dimensions (Figure 1), adopting the standard ‘xy’ notation, where x replaces x ₁ and y replaces x ₂ = x_D. The data points are specified by the positions x_i = (x_i, y_i)^⊤ and heteroscedastic Gaussian errors σ_{x, i} and σ_{y, i} with correlation coefficients c_i; thus the covariance matrix elements are (C_i)_xx = σ²_{x, i}, (C_i)_yy = σ²_{y, i}, (C_i)_xy = σ_{xy, i} = c_iσ_{x, i}σ_{y, i}. These points are to be fitted by a line

(11) $$\begin{equation} y = \alpha x+\beta , \end{equation}$$

which we can also parameterise by the normal vector n = n(cos ϕ, sin ϕ)^⊤ going from the origin to the line. The parameters α, β, and σ_y (σ_y = σ_D being the intrinsic scatter along y) are then given by [following Equation (9)]

(12) $$\begin{equation} \alpha = \frac{-1}{\tan \phi },\beta =\frac{n}{\sin \phi },\sigma _y=\frac{\sigma _\perp }{|\sin \phi |}, \end{equation}$$

which manifestly diverge as the line becomes vertical ($\phi \in \pi \mathbb {Z}$). In these notations, Equations (5) and (10) simplify to

(13) $$\begin{eqnarray} \ln \mathcal {L}& =& -\frac{1}{2}\sum _{i=1}^{N} \left[\ln s^2_{\perp ,i}\!+\frac{(x_i\cos \phi \!+\!y_i\sin \phi \!-\!n)^2}{s^2_{\perp ,i}}\right]\nonumber\\ & = & \frac{1}{2}\sum _{i=1}^{N} \left[\ln \frac{\alpha ^2+1}{s^2_{y,i}}-\frac{(\alpha x_i-y_i+\beta )^2}{s^2_{y,i}}\right], \end{eqnarray}$$

where s ²_{⊥, i} ≡ σ²_⊥ + σ²_{x, i}cos ²ϕ + σ_{y, i}²sin ²ϕ + 2σ_{xy, i}cos ϕsin ϕ and s ²_{y, i} ≡ σ²_y + σ²_{x, i}α² + σ_{y, i}² − 2σ_{xy, i}α (reminder: σ_y is the intrinsic vertical scatter of the model, whereas σ_{y, i} is the vertical uncertainty of point i). The most likely fit to the data is obtained by maximising Equation (13), either through adjusting the parameters (ϕ, n, σ_⊥) or (α, β, σ_y). Following Appendix A, unbiased estimators for the population-model (as opposed to the sample-model) of the scatter σ_⊥ or σ_y and its variance σ²_⊥ or σ²_y can be obtained via Equations (A2) and (A1), respectively.

It is worth stressing that the exact Equation (13) never reduces to the frequently used, simple minimisation of χ² ≡ ∑_i(y_i − αx_i − β)², not even if the data has zero uncertainties and if the intrinsic scatter is fixed. This reflects the fact that the χ²-minimisation breaks the rotational invariance by assuming a uniform prior for the slope α (rather than the angle ϕ). The term ln (α² + 1) in Equation (13) is needed to recover the rotational invariance.

3 NUMERICAL IMPLEMENTATION

Having established the above mathematical framework for calculating the likelihood for a multi-dimensional fit, we developed a fully documented and tested R package called hyper-fit. This is available through a github repository² and can be installed from within R with the following commands:

• > install.packages(‘magicaxis’, dependencies=TRUE)

• > install.packages(‘MASS’, dependencies=TRUE)

• > install.packages(‘rgl’, dependencies=TRUE)

• > install.packages(‘devtools’)

• > library(devtools)

• > install_github(‘asgr/

• LaplacesDemon’)

• > install_github(‘asgr/hyper.fit’)

To load the package into your R session, run

• > library(hyper.fit)

The core function that utilises the maths presented in the previous Section is hyper.like, which calculates the likelihood (Equation 6) for a given set of hyperplane parameters and a given dataset. This dataset can be error-free, or include covariant and heteroscedastic errors. To fit a hyperplane, the hyper.like function is accessed by hyper.fit, a utility fitting function that attempts to optimally fit a generative model to the data. The package includes a number of user-friendly summary and plotting outputs in order to visualise the fitted model and investigate its quality. The full 35 pages manual detailing the hyper-fit package can be viewed at hyperfit.icrar.org, and is included within the help files of the package itself (e.g. see > ?hyper.fit within R once the package is loaded.).

3.1 Hyper.like

The basic likelihood function hyper.like requires the user to specify a vector of model parameters parm, an N × D dimensional position matrix X (where N is the number of data points and D the dimensionality of the dataset, i.e. 10 rows by 2 columns in the case of 10 data points with x and y positions) and a D × D × N array covarray containing the covariance error matrix for each point stacked along the last index. A simple example looks like

• > hyper.like(parm, X, covarray)

parm must be specified as the normal vector n that points from the origin to the hyperplane concatenated with the intrinsic scatter σ_⊥ orthogonal to the hyperplane. E.g. if the user wants to calculate the likelihood of a plane in 3D with equation z = 2x + 3y + 1 and intrinsic scatter along the z-axis of 4, this becomes a normal vector with elements [ − 0.143, −0.214, 0.071] with intrinsic scatter orthogonal to the hyperplane equal to 1.07. In this case, parm=c(-0.143, -0.214, 0.071, 1.07), i.e. as expected, a 3D plane with intrinsic scatter is fully described by 4 ( = D + 1) parameters. Because of the large number of coordinate systems that unambiguously define a hyperplane (and many of them might be useful in different circumstances), the hyper-fit package also includes the function hyper.convert that allows the user to convert between coordinate systems simply. In astronomy, the Euclidian z = α[1]x + α[2]y + β system is probably the most common (e.g. Fundamental Plane definition, Faber et al. 1987; Binney & Merrifield 1998), but this has limitations when it comes to efficient high dimensional hyperplane fitting, as we discuss later.

3.2 Hyper.fit

In practice, we expect most user interaction with the hyper-fit package will be via the higher level hyper.fit function (hence the name of the package). For example, to find an optimal fit for the data in the N × D dimensional matrix X (see Section 3.1) with no specified error, it suffices to run

• > fit=hyper.fit(X)

This function interacts with the hyper.like function and attempts to find the best generative hyperplane model via a number of schemes. The user has access to three main high-level fitting routines: the base Roptim function (available with all installations), the LaplaceApproximation function, and the LaplacesDemon function (both available in the laplacesdemon package).

3.2.1 Optim

optim is the base R parameter optimisation routine. It allows the user to generically find the maximum or minimum of a target function via a number of built-in schemes that are popular in the statistical optimisation community. The default option is to use a Nelder–Mead (Nelder & Mead 1965) optimiser that uses only function values. This is robust but relatively slow, with the advantage that it will work reasonably well for non-differentiable functions, i.e. it does not compute the local hessian at every step. Conjugate gradient (Hestenes & Stiefel 1952); quasi-Newtonian BFGS (Broyden, Fletcher, Goldfarb, and Shanno; Fletcher 1970); and simulated annealing (Belisle 1992) are some of the other popular methods available to the user. All of these schemes are fully documented within the optim manual pages that is included with any standard R implementation.

3.2.2 LaplaceApproximation

To offer the user more flexibility, we also allow access to the non-base open-source MIT-licensed laplacesdemon package that users can install from github.com/asgr/ LaplacesDemon (the direct R installation code is provided above). It is developed by Statisticat and currently contains 18 different optimisation schemes. Many of these are shared with optim (e.g. the default option of Nelder–Mead; conjugate gradient descent), but many are unique to the package (e.g. Levenberg–Marquardt, Marquardt 1963; particle swarm optimisation, Kennedy & Eberhart 1995).

The LaplaceApproximation function offers a host of high level user tools, and with these object oriented extensions, it tends to be slower to converge compared to the same method in optim. The large range of methods means the user should be able to find a robustly converged solution in most situations, without having to resort to much more computationally expensive Markov-Chain Monte-Carlo (MCMC) methods accessed through the LaplacesDemon function which is also available in the laplacesdemon package.

The LaplaceApproximation function and the wider laplacesdemon package is extensively documented, both in the bundled manual and at the www.bayesian-inference.com website³ maintained by the package developers.

3.2.3 LaplacesDemon

The final hyperplane fitting function that users of hyper-fit have access to is LaplacesDemon which is also included in the laplacesdemon package. The function includes a suite of 41 MCMC routines, and the number is still growing. For hyper-fit, the default routine is Griddy–Gibbs (Ritter & Tanner 1992), a component-wise algorithm that approximates the conditional distribution by evaluating the likelihood model at a set of points on a grid. This proved to have attractive qualities and well-behaved systematics for relatively few effective samples during testing on toy models. The user also has access to a large variety of routine families, including Gibbs; Metropolis–Hasting (Hastings 1970); slice sampling (Neal 2003); and Hamiltonian Monte Carlo (Duane et al. 1987).

In practice, the user should investigate the range of options available, and the optimal routine for a given problem might not simply be the default provided. To aid the user in choosing an appropriate scheme, the laplacesdemon package includes a comprehensive suite of analysis tools to analyse the post convergence Markov-Chains. The potential advantages to use an MCMC approach to analyse the generative likelihood model are manifold, allowing the user of hyper-fit to investigate complex high-dimensional multi-modal problems that might not be well suited to the traditional downhill gradient approaches included in optim and LaplaceApproximation. Again, the function is extensively described both in the laplacesdemon package and on the www.bayesian-inference.com website ⁴.

3.3 Plot

The hyper-fit package comes with a class sensitive plotting function where the user is able to execute a command such as

• > plot(hyper.fit(X))

where X is a 2 × N or 3 × N matrix. The plot displays the data with the best fit. If (uncorrelated or correlated) Gaussian errors are given, e.g. via plot(hyper.fit(X,covarray)), they are displayed as 2D ellipses or 3D ellipsoids, respectively. The built-in plotting only works in 2 or 3 dimensions (i.e. x,y or x,y,z data), which will likely be the two most common hyperplane fitting situations encountered in astronomical applications.

3.4 Summary

The hyper-fit package comes with a class sensitive summary function where the user is able to execute a command such as

• > summary(hyper.fit(X))

where X can be any (D × N)-array with D ⩾ 2 dimensions. Using summary for 2D data will produce an output similar to

• > summary(fitnoerror)

• Call used was:

• hyper.fit(X = cbind(xval, yval))

• Data supplied was 5rows × 2cols.

• Requested parameters:

• alpha1 beta.vert scat.vert

• 0.4680861 0.6272718 0.2656171

• Errors for parameters:

• err_alpha1 err_beta.vert err_scat.vert

• 0.12634307 0.11998805 0.08497509

• The full parameter covariance matrix:

• alpha1 beta.vert scat.vert

• alpha1 0.015962572 -0.0021390417 0.0016270601

• beta.vert -0.002139042 0.0143971319 -0.0002182796

• scat.vert 0.001627060 -0.0002182796 0.0072207660

• The sum of the log-likelihood for the best fit parameters:

• LL

• 4.623924

• Unbiased population estimator for the intrinsic scatter:

• scat.vert

• 0.3721954

• Standardised parameters vertically projected along dimension 2 (yval):

• alpha1 beta.vert scat.vert

• 0.4680861 0.6272718 0.2656171

• Standardised generative hyperplane equation with unbiased population estimator for the intrinsic scatter, vertically projected along dimension 2 (yval):

• yval ~ N(mu= 0.4681*xval + 0.6273, sigma= 0.3722)

3.5 Web interface

To aid the accessibility of the tools, we have developed in this paper, a high-level web interface to the hyper-fit package has been developed that runs on a permanent virtual server using RShiny ⁵. The hyper-fit computations are executed remotely, and the web interface itself is in standard JavaScript and accessible using any modern popular web browser. This website interface to hyper-fit can be accessed at hyperfit.icrar.org. The hyper-fit website also hosts the latest version of the manual, and the most recent version of the associated hyper-fit paper. The design philosophy for the page is heavily influenced by modern web design, where the emphasis is on clean aesthetics, simplicity, and intuitiveness. The front page view of the web interface is shown in Figure 2.

Figure 2. The front page view of the hyper-fit web tool available at hyperfit.icrar.org. The web tool allows users to interact with hyper-fit through a simple GUI interface, with nearly all hyper-fit functionality available to them. The code itself runs remotely on a machine located at ICRAR, and the user’s computer is only used to render the website graphics.

The hyper-fit web tool allows access to nearly all of the functionality of hyper-fit, with a few key restrictions:

• • Only 2D or 3D analysis available (Rhyper-fit allows for arbitrary ND analysis)

• • Uploaded files are limited to 2 000 or fewer row entries (Rhyper-fit allows for hard-disk limited size datasets)

• • When using the LaplaceApproximation or LaplacesDemon algorithms only 20 000 iterations are allowed (Rhyper-fit has no specific limit on the number of iterations)

• • A number of the more complex LaplacesDemon methods are unavailable to the user because the specification options are too complex to describe via a web interface (Rhyper-fit allows access to all LaplacesDemon methods)

In practice, for the vast majority of typical use cases, these restrictions will not limit the utility of the analysis offered by the web tool. For the extreme combination of 2 000 rows of data and 20 000 iterations of one of the LaplacesDemon MCMC samplers, users might need to wait a couple of minutes for results.

4 MOCK EXAMPLES

In this Section, we give some examples using two sets of idealised mock data.

4.1 Simple examples

To help novice users get familiar with R and the hyper-fit package, we start this Section by building the basic example shown in Figure 1. We first create the central x and y positions of the five data points, encoded in the five-element vectors x_val and y_val,

• > xval = c(-1.22, -0.78, 0.44, 1.01, 1.22)

• > yval = c(-0.15, 0.49, 1.17, 0.72, 1.22)

We can obtain the hyper-fit solution and plot the result (seen in Figure 3) with

• > fitnoerror=hyper.fit(cbind(xval, yval))

• > plot(fitnoerror) (Figure 3)

Since this example has no errors associated with the data positions, the generative model created has a large intrinsic scatter that broadly encompasses the data points (dashed lines in Figure 3). Extending the analysis, we can add x-errors x_err (standard deviations of the errors along the x-dimension) and y-errors y_err and recalculate the fit and plot (Figure 4) with

• > xerr = c(0.12, 0.14, 0.20, 0.07, 0.06)

• > yerr = c(0.13, 0.03, 0.07, 0.11, 0.08)

• > fitwitherror=hyper.fit(cbind(xval, yval), vars=cbind(xerr, yerr)^2)

• > plot(fitwitherror) (Figure 4)

Since we have added errors to the data, the intrinsic scatter required in the generative model is reduced. To extend this 2D example to the full complexity of Figure 1, we assume that we know xy_cor (the correlation between the errors for each individual data point) and recalculate the fit and plot (Figure 5) with

• > xycor = c(0.90, -0.40, -0.25, 0.00, -0.20)

• > fitwitherrorandcor=hyper.fit(cbind

• > (xval, yval), covarray=

• > makecovarray2d(xerr, yerr, xycor))

• > plot(fitwitherrorandcor) (Figure 5)

The effect of including the correlations can be quite subtle, but inspecting the intersections on the y-axis, it is clear that both the best-fitting line and the intrinsic scatter have slightly changed. To see how dramatic the effect of large errors can be on the estimated intrinsic scatter, we can simply inflate our errors by a large factor. We recalculate the fit and plot (Figure 6) with

• > fitwithbigerrorandcor=hyper.fit

• (cbind(xval, yval), covarray=makecovarray2d(xerr*1.9, yerr*1.9, xycor))

• > plot(fitwithbigerrorandcor) (Figure 6)

Per-data-point error covariance is often overlooked during regression analysis because of the lack of readily available tools to correctly make use of the information, but the impact of correctly using them can be non-negligible. As a final simple example, we take the input for Figure 6 and simply rotate the covariance matrix by 90°. We recalculate the fit and plot (Figure 7) with

• > fitwithbigerrorandrotcor=hyper.fit

• > (cbind(xval, yval), covarray=makecovarray2d(yerr*1.9, xerr*1.9, -xycor))

• > plot(fitwithbigerrorandrotcor) (Figure 7)

The impact of simply rotating the covariance matrix is to flatten the preferred slope and to slightly reduce the intrinsic scatter.

Figure 3. 2D fit with no errors. Figure shows the default plot output of the hyper.plot2d function (accessed via the class specific plot method) included as part of the R hyper-fit package, where the best generative model for the data is shown as a solid line with the intrinsic scatter indicated by dashed lines. The colouring of the points shows the ‘tension’ with respect to the best-fit linear model and the measurement errors (zero in this case), where redder colours indicate data that is less likely to be explainable.

Figure 4. 2D fit with uncorrelated (between x and y) errors. The errors are represented by 2D ellipses at the location of the xy-data. See Figure 3 for further details on this Figure. The reduction in the intrinsic scatter required to explain the data compared to Figure 3 is noticeable (see the dashed line intersects on the y-axis).

Figure 5. 2D fit with correlated (between x and y) errors. The errors are represented by 2D ellipses at the location of the xy-data. See Figure 3 for further details on this Figure. The keen reader might notice that this Figure uses data from the Figure 1 schematic.

Figure 6. 2D fit with correlated (between x and y) errors. The errors here are a factor 1.9 times larger than used in Figure 5. See Figure 3 for further details on this Figure.

Figure 7. 2D fit with correlated (between x and y) errors. The errors here are a factor 1.9 times larger than used in Figure 5 and the correlation matrix is rotated by 90°. See Figure 3 for further details on this Figure.

4.2 Hogg example

In the arXiv paper by Hogg et al. (2010), the general approach to the problem of generative fitting is explored, along with exercises for the user. The majority of the paper is concerned with 2D examples, and an idealised data set (Table 1 in the paper) is included to allow readers to recreate their fits and plots. This dataset comes bundled with the hyper-fit package, making it easy to recreate many of the examples of Hogg et al. (2010). Towards the end of their paper, they include an exercise on fitting 2D data with covariant errors. We can generate the hyper-fit solution to this exercise and create the relevant plots (Figure 8) with

• > data(hogg)

• > hoggcovarray= makecovarray2d(hogg[-3,‘x_err’], hogg[-3,‘y_err’], hogg[-3,‘corxy’])

• > plot(hyper.fit(hogg[-3,c(‘x’, ‘y’)], covarray=hoggcovarray)) (Figure 8)

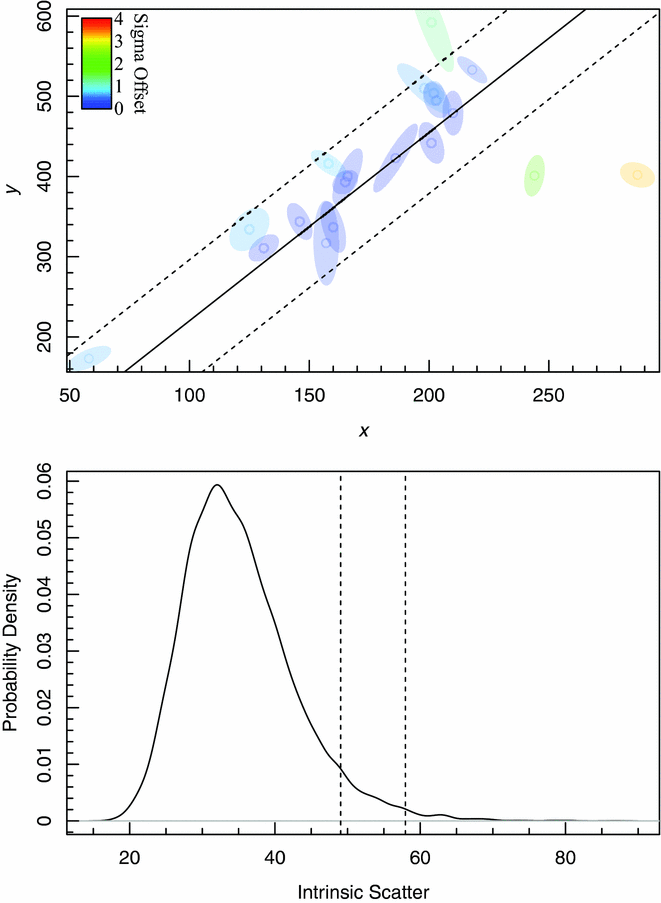
The fit we generate agrees very closely with the example in Hogg et al. (2010), which is not surprising since the likelihood function we maximise is identical, bar a normalising factor (i.e. an additive constant in $\ln \mathcal {L}$). The differences seen between Hogg’s Figure 14 and the bottom panel of our Figure 8, showing the projected posterior chain density distribution of the intrinsic scatter parameter, are likely to be due to our specific choice of MCMC solver. In our hyper-fit example, we use Componentwise Hit-And-Run Metropolis (CHARM, Turchin 1971), being a particularly simple MCMC for a novice user to specify, and one that performs well as long as the number of data points is greater than ~ 10.

Figure 8. 2D toy data with correlated (between x and y) errors taken from Hogg et al. (2010). The top panel shows the fit to the Hogg et al. (2010) data minus row 3, as per exercise 17 and Figure 13 of Hogg et al. (2010), the bottom panel shows the MCMC posterior chains for the intrinsic scatter, as per Figure 14 of Hogg et al. (2010). The vertical dashed lines specify the 95^th and 99^th percentile range of the posterior chains, as requested for the original exercise. See Figure 3 for further details on the top two panels of this Figure.

5 ASTROPHYSICAL EXAMPLES

In this Section, we have endeavoured to include a mixture of real examples from published astronomy papers. In some cases, aspects of the data are strictly proprietary (in the sense that the tables used to generate paper Figures have not been explicitly published), but the respective authors have allowed us to include the required data in our package.

5.1 2D Mass-size relation

The galaxy mass-size relation is a topic of great popularity in the current astronomical literature (Shen et al. 2003; Trujillo et al. 2004; Lange et al. 2015). The hyper-fit package includes data taken from the bottom-right panel of Figure 3 from Lange et al. (2015). To do our fit on these data and create Figure 9, we make use of the published data errors and the $1/V_{\text{max}}$ weights calculated for each galaxy by running

• > data(GAMAsmVsize)

• > plot(hyper.fit(GAMAsmVsize[,c (‘logmstar’, ‘logrekpc’)], vars=GAMAsmVsize[,c(‘logmstar_err’, ‘logrekpc_err’)]^2, weights=GAMAsmVsize[,‘weights’])) (Figure 9)

This analysis produces a mass-size relation of

$$\begin{eqnarray*} \log _{10}R_e &\sim & \mathcal {N}[\mu =(0.382\pm 0.006) \log _{10} \mathcal {M}_{*}-(3.53\pm 0.06),\nonumber\\ &&\sigma =0.145\pm 0.003], \end{eqnarray*}$$

where R_e is the effective radius of the galaxy in kpc, $\mathcal {N}$ is the normal distribution with parameters μ (mean) and σ (standard deviation), and $\mathcal {M}_{*}$ is the stellar mass in solar mass units. The relation published in Lange et al. (2015) is $\log _{10}R_e = 0.46\pm 0.02 (\log _{10} \mathcal {M}_{*})-4.38\pm 0.03$. The function in Lange et al. (2015) is noticeably steeper due to being fit to the running median with weighting determined by the spread in the data and the number of data points in the stellar mass bin, rather than directly to the data including the error.

Figure 9. GAMA mass-size relation data taken from Lange et al. (2015) See Figure 4 for further details on this Figure.

5.2 2D Tully–Fisher relation

One of the most common relationships in extragalactic astronomy is the so-called Tully–Fisher relation (TFR, Tully & Fisher 1977). This tight coupling between inclination corrected disc rotation velocity and the absolute magnitude (or, more fundamentally, stellar mass) of spiral galaxies is an important redshift-independent distance indicator, as well as a probe for galaxy evolution studies. Here, we use TFR data included in the hyper-fit package that has been taken from Figure 4 of Obreschkow & Meyer (2013), where we fit the data and create Figure 10 with

• > data(TFR)

• > plot(hyper.fit(TFR[,c(‘logv’, ‘M_K’)], vars=TFR[,c(‘logv_err’, ‘M_K_err’)]^2)) (Figure 10)

This yields a TFR of

$$\begin{eqnarray*} M_K &\sim &\mathcal {N}[\mu =(-9.3\pm 0.4) \log _{10} v_{\text{circ}}-(2.5\pm 0.9),\nonumber\\ \sigma &=&0.22\pm 0.04], \end{eqnarray*}$$

where M_K is the absolute K-band magnitude and $v_{\text{circ}}$ is the maximum rotational velocity of the disc in km s⁻¹. Obreschkow & Meyer (2013) find

$$\begin{eqnarray*} M_K &\sim & \mathcal {N}[\mu =(-9.3\pm 0.3) \log _{10} v_{\text{circ}}-(2.5\pm 0.7),\nonumber\\ \sigma &=&0.22\pm 0.06], \end{eqnarray*}$$

where all the fit parameters comfortably agree within quoted errors. The parameter errors in Obreschkow & Meyer (2013) were recovered via bootstrap resampling of the data points, whereas hyper-fit used the covariant matrix via the inverse of the parameter Hessian matrix. Using hyper-fit, we find marginally less constraint on the slope and intercept, but slightly more on the intrinsic scatter.

Figure 10. Tully–Fisher data taken from Obreschkow & Meyer (2013), with the best-fit hyper-fit generative model for the data shown as a solid line and the intrinsic scatter indicated with dashed lines. See Figure 3 for further details on this Figure.

5.3 3D fundamental plane

Moving to a 3D example, perhaps the most common application in the literature is the Fundamental Plane for elliptical galaxies (Faber 1987; Binney & Merrifield 1998). This also offers a route to a redshift-independent distance estimator, but from a 3D relation rather than a 2D relation (although an approximate 2D version also exists for elliptical galaxies via the Faber–Jackson relation; Faber & Jackson 1976). In hyper-fit, we include 6dFGS data released in Campbell et al. (2014), where we fit the data and generate Figure 11 with

• > data(FP6dFGS)

• > plot(hyper.fit(FP6dFGS[,c (‘logIe_J’, ‘logsigma’, ‘logRe_J’)], vars=FP6dFGS[,c (‘logIe_J_err’, ‘logsigma_err’, ‘logRe_J_err’)]^2, weights=FP6dFGS[,‘weights’])) (Figure 11)

This yields a Fundamental Plane relation of

$$\begin{eqnarray*} \log _{10} Re_J &\sim & \mathcal {N}[\mu = -(0.853 \pm 0.005) \log _{10} Ie_J \nonumber\\ && +\, (1.508 \pm 0.012) \log _{10}\sigma _{\text{vel}} - (0.42 \pm 0.03),\nonumber\\ \sigma &=&0.060\pm 0.001], \end{eqnarray*}$$

where Re_J (in kpc) is the effect radius in the J-band, Ie_J (in mag arcsec⁻²) is the average surface brightness intensity within Re_J and $\sigma _{\text{vel}}$ (in km s⁻¹) is the central velocity dispersion. Magoulas et al. (2012) find

$$\begin{eqnarray*} \log _{10} Re_J &\sim & \mathcal {N}[\mu = -(0.89 \pm 0.01) \log _{10} Ie_J \nonumber\\ &&+\, (1.52 \pm 0.03) \log _{10}\sigma _{\text{vel}} - (0.19 \pm 0.01),\nonumber\\ \sigma &=&0.12\pm 0.01]. \end{eqnarray*}$$

It is notable that our fit requires substantially less intrinsic scatter than Magoulas et al. (2012). It is difficult to assess the origin of this difference since the methods used to fit the plane differ between this work and Magoulas et al. (2012), where the latter fit a 3D generative Gaussian with 8° of parameter freedom, which is substantially more general than the 3D plane with only 4° of parameter freedom that hyper-fit used.

Figure 11. 6dFGS Fundamental Plane data and hyper-fit fit. The two panels are different orientations of the default plot output of the hyper.plot3d function (accessed via the class specific plot method) included as part of the R hyper-fit package, where the best-fit hyper-fit generative model for the data is shown as a translucent grey 3D plane. The package function is interactive, allowing the user the rotate the data and the overlaid 3D plane to any desired orientation. See Figure 3 for further details on this Figure.

5.4 3D mass-spin-morphology relation

The final example of hyper-fit uses astronomical data from Obreschkow & Glazebrook (2014). They measured the fundamental relationship between mass (here the baryon mass (stars+cold gass) of the disc), spin (here the specific baryon angular momentum of the disc), and morphology (as measured by the bulge-to-total mass ratio). Hereafter, this relation is referred to as the MJB relation. This dataset is interesting to analyse with hyper-fit because it includes error correlation between mass and spin, caused by their common dependence on distance. In hyper-fit, we included the MJB data presented in Obreschkow & Glazebrook (2014). We can fit these data and generate Figure 12 with

• > data(MJB)

• > plot(hyper.fit(X=MJB[,c(‘logM’, ‘logj’, ‘B.T’)], covarray=makecovarray3d(MJB$logM_err, MJB$logj_err, MJB$B.T_err, MJB$corMJ, 0, 0))) (Figure 12)

This leads to a MJB relation of

$$\begin{eqnarray*} B/T &-& (0.34 \pm 0.03) \log _{10} j - (0.04 \pm 0.01),\\ \sigma &=&0.002\pm 0.006], \end{eqnarray*}$$

where B/T is the galaxy bulge-to-total ratio, $\mathcal {M}$ is the disc baryon mass in 10¹⁰ solar masses, and j is the specific baryon angular momentum in 10⁻³ kpc km s⁻¹ (see Obreschkow & Glazebrook 2014, for details on measuring this quantity). Obreschkow & Glazebrook (2014) find

$$\begin{eqnarray*} B/T &\sim & \mathcal {N}[\mu = (0.34 \pm 0.03) \log _{10} \mathcal {M} \nonumber\\ &&-\, (0.35 \pm 0.04) \log _{10} j - (0.04 \pm 0.02),\nonumber\\ \sigma &=&0]. \end{eqnarray*}$$

The agreement between hyper-fit and Obreschkow & Glazebrook (2014) is excellent, with all parameters consistent within quoted 1σ errors. Our results are consistent with zero intrinsic scatter within parameter errors. In fact, running the analysis using MCMC and the CHARM algorithm, we used hyper-fit to directly sample the likelihood of the intrinsic scatter being exactly 0. This is possible because we use the wall condition that any intrinsic scatter sample below 0 (which is non-physical) is assigned to be exactly 0. We find that 90.4% of the posterior chain samples have intrinsic scatter of exactly 0 post application of the wall condition (which imposes a spike + slab posterior), which can be interpreted to mean that the data is consistent with P(σ = 0) = 0.904.

Figure 12. Mass-spin-morphology (MJB) data and hyper-fit fit. The two panels are different orientations of the default plot output. All error ellipsoids overlap with the best-fit 3D plane found using hyper-fit, implying that the generative model does not require any additional scatter. Indeed the observed data is unusually close to the plane, implying slightly overestimated errors. See Figures 3 and 11 for further details on this Figure.

This agrees with the assessment in Obreschkow & Glazebrook (2014), where they conclude that the 3D plane generated does not require any additional scatter to explain the observed data, probably indicating that the errors have been overestimated⁶.

6 CONCLUSION

In this paper, we have extended previous work (Kelly 2007; Hogg et al. 2010; Kelly 2011) to describe the general form of the D dimensional generative hyperplane model with intrinsic scatter. We have also provided the fully-documented hyper-fit package for the R statistical programming language, available immediately for installation via github⁷. A user friendly Shiny web interface has also been developed and can be accessed at hyperfit.icrar.org. The hyper-fit version released in conduction with this paper is v1.0.2, and regular updates and support are planned.

To make the package as user-friendly as possible, we have provided examples for simple 2D datasets, as well as complex 3D datasets utilising heteroscedastic covariant errors taken from Obreschkow & Glazebrook (2014). We compared the published fits to the new hyper-fit estimates, and in most cases find good agreement for the hyperplane parameters (not all original papers attempt to make an intrinsic scatter estimate). hyper-fit offers users access to higher level statistics (e.g. the parameter covariance matrix) and includes simple class sensitive summary and plot functions to assist in analysing the quality of the generative model.

The ambition is for hyper-fit to be regularly updated based on feedback and suggestions from the astronomy and statistics community. As such, in the long term, the documentation included as part of the package might supersede some details provided in this paper.

7 FUTURE WORK

The current R hyper-fit package does not have a mechanism for handling censored data, and we currently implicitly assume a uniform population distribution along the hyperplane. Both of these issues can arise with astronomy data, where typically some fraction of sources might be left censored (i.e. below a certain value but uncertain where, and usually represented by an upper limit) and sampled from an unknown power-law type distribution (hyper-fit allows for the description of known power-law selection functions, see Appendix B). A future extension for hyper-fit will allow for multi-parameter censoring, i.e. where a data point might exist some subset of parameters (e.g. stellar mass and redshift) but only has an upper limit for others (e.g. star-formation rate and HI mass). Kelly (2007) allows for censoring of the response variable, but not multiple observables simultaneously. It is possible to account for such censoring using a hierarchical Bayesian inference software program, such as bugs, jags, or stan. An example jags model of the hyper-fit scheme is provided in Appendix C. We also aim to allow generic distribution functions along and perpendicular to the hyperplane including power-laws and Gaussian mixture models. Again, using a hierarchical Bayesian inference, software program is one potential route to achieve this, but at the expense of generalisability and simplicity.