Published online by Cambridge University Press: 20 November 2018
0. Introduction. Functors 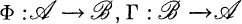 form an equivalence of categories (see [8,]) if Γ(Φ(A)) ≅ A and Φ (Γ(B)) ≅ B naturally for all objects A from
form an equivalence of categories (see [8,]) if Γ(Φ(A)) ≅ A and Φ (Γ(B)) ≅ B naturally for all objects A from 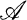 and B from
and B from 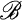 . Letting
. Letting 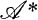 denote the opposite of
denote the opposite of 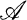 we say that
we say that 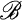 and
and 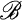 are dual if there is an equivalence between
are dual if there is an equivalence between 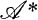 and
and 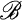 .
.
Let τ be a similarity type of finitary operation symbols. We let Lτ denote the first order language (with equality) using nonlogical symbols from τ, and consider the class  of all algebras of type τ as a category by declaring the morphisms to be all homomorphisms in the usual sense (i.e., those functions preserving the atomic sentences of Lτ). If
of all algebras of type τ as a category by declaring the morphisms to be all homomorphisms in the usual sense (i.e., those functions preserving the atomic sentences of Lτ). If 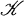 is a class in
is a class in  (i.e.,
(i.e., 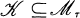 and
and 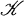 is closed under isomorphism), we view
is closed under isomorphism), we view 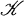 as a full subcategory of
as a full subcategory of  , and we define the order of
, and we define the order of 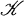 to be the number of symbols occurring in τ.
to be the number of symbols occurring in τ.