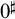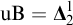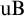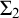THE CONSISTENCY STRENGTH OF THE PERFECT SET PROPERTY FOR UNIVERSALLY BAIRE SETS OF REALS

Abstract

We show that the statement “every universally Baire set of reals has the perfect set property” is equiconsistent modulo ZFC with the existence of a cardinal that we call virtually Shelah for supercompactness (VSS). These cardinals resemble Shelah cardinals and Shelah-for-supercompactness cardinals but are much weaker: if $0^\sharp $ exists then every Silver indiscernible is VSS in L. We also show that the statement $\operatorname {\mathrm {uB}} = {\boldsymbol {\Delta }}^1_2$ , where $\operatorname {\mathrm {uB}}$ is the pointclass of all universally Baire sets of reals, is equiconsistent modulo ZFC with the existence of a $\Sigma _2$ -reflecting VSS cardinal.

1 Introduction

A set of reals, meaning a subset of the Baire space $\omega ^\omega $ , is called universally Baire if its preimages under all continuous functions from all topological spaces have the Baire property (Feng et al. [2]). We denote the pointclass of all universally Baire sets of reals by uB. The universally Baire sets of reals include the ${\boldsymbol {\Sigma }}^1_1$ (analytic) and ${\boldsymbol {\Pi }}^1_1$ (coanalytic) sets of reals, but not necessarily the ${\Delta ^1_2}$ sets of reals. Every universally Baire set of reals is Lebesgue measurable and has the Baire property. If there is a Woodin cardinal then every universally Baire set of reals has the perfect set property, ¹ whereas if $\omega _1^L = \omega _1$ then there is a set of reals that is $\Pi ^1_1$ , hence universally Baire, but fails to have the perfect set property (Gödel; see Kanamori [8, Theorem 13.12]).

In this article we will describe the exact consistency strength of the theory ZFC+ “every universally Baire set of reals has the perfect set property” in terms of a large cardinal that we call virtually Shelah for supercompactness (VSS). ² It is likely that this theory was already known to be much weaker than a Woodin cardinal, since it is not difficult to force it over L if $0^\sharp $ exists, but we are not aware of reference for this.

First we briefly review the notion of a virtual large cardinal property. Many large cardinal properties are defined in terms of elementary embeddings $j : M \to N$ where M and N are structures. (If M and N are sets with no structure given, we consider them as structures with the $\in $ relation). Such a definition can be weakened to a “virtual” large cardinal property by only requiring j to exist in some generic extension of V. Examples of virtual large cardinal properties are remarkability, which is a virtual form of Magidor’s characterization of supercompactness (Schindler [12, Lemma 1.6]), and the generic Vopěnka principle, which is a virtual form of Vopěnka’s principle (Bagaria et al. [1]).

For a thorough introduction to virtual large cardinal properties, see Gitman and Schindler [5]. For an application of virtual large cardinals to descriptive set theory involving $\aleph _1$ -Suslin sets instead of universally Baire sets, see Wilson [18].

Note that for set-sized structures M and N in V, if some generic extension of V contains an elementary embedding of M into N, then by the absoluteness of elementary embeddability of countable structures (see Bagaria et al. [1, Lemma 2.6]) every generic extension of V by the poset $\operatorname {\mathrm {Col}}(\omega ,M)$ contains such an elementary embedding. The converse implication holds also, of course, and we may abbreviate these equivalent conditions by the phrase “there is a generic elementary embedding of M into N.”

Recall that a cardinal $\kappa $ is called Shelah if for every function $f : \kappa \to \kappa $ there is a transitive class M and an elementary embedding $j:V \to M$ with $\operatorname {\mathrm {crit}}(j) = \kappa $ and $V_{j(f)(\kappa )} \subset M$ . Note that for any ordinal $\lambda \ge \kappa +1$ , the restriction $j \restriction V_\lambda $ is sufficient to derive an extender E whose ultrapower embedding $j_E$ witnesses the Shelah property of $\kappa $ as well as j does. Making the convenient choice $\lambda = \max \{j(f)(\kappa ),\kappa +1\}$ , we obtain the following definition as a kind of virtualization. ³

Definition 1.1. A cardinal $\kappa $ is virtually Shelah for supercompactness (VSS) if for every function $f : \kappa \to \kappa $ there is an ordinal $\lambda> \kappa $ , a transitive set M with $V_\lambda \subset M$ , and a generic elementary embedding $j : V_\lambda \to M$ with $\operatorname {\mathrm {crit}}(j) = \kappa $ and $j(f)(\kappa ) \le \lambda $ .

The VSS property follows immediately from the Shelah property but is much weaker: Proposition 3.1 will show that if $0^\sharp $ exists then every Silver indiscernible is VSS in L, a result that is typical of virtual large cardinal properties.

Our main result is stated below. It relates models of ZFC with VSS cardinals to models of ZFC in which the universally Baire sets are few in number and have nice properties. It also includes a combinatorial statement about order types of countable sets of ordinals.

Theorem 1.2. The following statements are equiconsistent modulo ZFC.

1. 1. There is a VSS cardinal.

2. 2. $\left |\operatorname {\mathrm {uB}}\right | = \omega _1$ .

3. 3. Every set of reals in $L(\mathbb {R},\operatorname {\mathrm {uB}})$ is Lebesgue measurable.

4. 4. Every set of reals in $L(\mathbb {R},\operatorname {\mathrm {uB}})$ has the perfect set property.

5. 5. Every universally Baire set of reals has the perfect set property.

6. 6. For every function $f: \omega _1 \to \omega _1$ there is an ordinal $\lambda> \omega _1$ such that for a stationary set of $\sigma \in \mathcal {P}_{\omega _1}(\lambda )$ we have $\sigma \cap \omega _1 \in \omega _1$ and $\operatorname {\mathrm {o.\!t.}}(\sigma ) \ge f(\sigma \cap \omega _1)$ . ⁴

We will show that if statement 1 holds then statements 2–4 hold after forcing with the Levy collapse poset to make a VSS cardinal equal to $\omega _1$ . Clearly statement 4 implies statement 5, and we will show that statements 2 and 3 also imply statement 5. We will show that statement 5 implies statement 6. Finally, we will show that if statement 6 holds, then statement 1 holds in L as witnessed by $\omega _1^V$ .

We will also prove an equiconsistency result at a slightly higher level of consistency strength, namely that of a $\Sigma _2$ -reflecting VSS cardinal. A cardinal $\kappa $ is called $\Sigma _n$ -reflecting if it is inaccessible and $V_\kappa \prec _{\Sigma _n} V$ . This definition is particularly natural in the case $n = 2$ because the $\Sigma _2$ statements about a parameter a are the statements that can be expressed in the form “there is an ordinal $\lambda $ such that $V_\lambda \models \varphi [a]$ ” where $\varphi $ is a formula in the language of set theory. Because the existence of a VSS cardinal above any given cardinal $\alpha $ is a $\Sigma _2$ statement about $\alpha $ , if $\kappa $ is a $\Sigma _2$ -reflecting VSS cardinal then $V_\kappa $ satisfies ZFC+ “there is a proper class of VSS cardinals.”

The existence of a $\Sigma _2$ -reflecting cardinal is equiconsistent modulo ZFC with the statement ${\boldsymbol {\Delta }}^1_2 \subset \operatorname {\mathrm {uB}}$ by Feng et al. [2, Theorem 3.3], who showed that if $\kappa $ is $\Sigma _2$ -reflecting then ${\boldsymbol {\Delta }}^1_2 \subset \operatorname {\mathrm {uB}}$ holds after the Levy collapse forcing to make $\kappa $ equal to $\omega _1$ , and conversely that if ${\boldsymbol {\Delta }}^1_2 \subset \operatorname {\mathrm {uB}}$ then $\omega _1^V$ is $\Sigma _2$ -reflecting in L.

The reverse inclusion $\operatorname {\mathrm {uB}} \subset {\boldsymbol {\Delta }}^1_2$ is consistent relative to ZFC by Larson and Shelah [9], who showed that if $V = L[x]$ for some real x then there is a proper forcing extension in which every universally measurable set of reals—and hence every universally Baire set of reals—is ${\boldsymbol {\Delta }}^1_2$ . Of course this proper forcing is not the Levy collapse; as we will show, forcing both inclusions to hold simultaneously requires more large cardinals in the ground model.

Combining the argument of Feng et al. [2, Theorem 3.3] with parts of the proof of Theorem 1.2, we will show:

Theorem 1.3. The following statements are equiconsistent modulo ZFC.

1. 1. There is a $\Sigma _2$ -reflecting VSS cardinal.

2. 2. $\operatorname {\mathrm {uB}} = {\boldsymbol {\Delta }}^1_2$ .

The remaining sections of this paper are outlined as follows. In Section 2 we will prove some consequences of Definition 1.1 that will be needed for our main results, including a reformulation of the definition in which $\kappa $ is $j(\operatorname {\mathrm {crit}}(j))$ instead of $\operatorname {\mathrm {crit}}(j)$ , justifying the name “virtually Shelah for supercompactness” (Proposition 2.5). In Section 3 we will prove some relations between VSS cardinals and other large cardinals that will not be needed for our main results. In Section 4 we will review some properties of universally Baire sets and establish some equivalent conditions for a universally Baire set to be thin, meaning to contain no perfect subset. In Section 5 we will prove Theorem 1.2. In Section 6 we will prove Theorem 1.3.

2 Consequences of the VSS property

Recall that a cardinal $\kappa $ is called ineffable if for every sequence of sets $\langle A_\alpha : \alpha < \kappa \rangle $ such that $A_\alpha \subset \alpha $ for all $\alpha < \kappa $ , there is a set $A \subset \kappa $ such that $\{\alpha < \kappa : A \cap \alpha = A_\alpha \}$ is stationary. The following result is typical of virtual large cardinals (see Schindler [12, Lemma 1.4]).

Proposition 2.1. Every VSS cardinal is ineffable.

Proof Let $\kappa $ be a VSS cardinal. Then there is an ordinal $\lambda> \kappa $ , a transitive set M such that $V_\lambda \subset M$ , and a generic elementary embedding $j : V_\lambda \to M$ with $\operatorname {\mathrm {crit}}(j) = \kappa $ . (Here we will not need $j(f)(\kappa ) \le \lambda $ for any particular function f.)

Let $\vec {A}$ be a $\kappa $ -sequence of sets such that $\vec {A}(\alpha ) \subset \alpha $ for every ordinal $\alpha < \kappa $ . Then we may define a subset $A \subset \kappa $ by $A = j(\vec {A})(\kappa )$ . We will show that the set

$$ \begin{align*}S = \{\alpha < \kappa : A \cap \alpha = \vec{A}(\alpha)\}\end{align*} $$

is stationary. Letting C be a club set in $\kappa $ we have $\kappa \in j(C)$ , and because

$$ \begin{align*}j(A) \cap \kappa = A = j(\vec{A})(\kappa),\end{align*} $$

we have $\kappa \in j(S)$ also, so it follows that

$$ \begin{align*}\kappa \in j(C) \cap j(S) = j(C \cap S),\end{align*} $$

and by the elementarity of j we have $C \cap S \ne \emptyset $ .

A better lower bound for the consistency strength of VSS cardinals will be given in Section 3 along with an upper bound. For our main results we will only need the fact that every VSS cardinal is an inaccessible limit of inaccessible cardinals, which is a consequence of Proposition 2.1.

The following lemma shows (among other things) that the domain of a generic elementary embedding witnessing the VSS property may be taken to be an inaccessible rank initial segment of V, which implies that the domain and codomain both satisfy ZFC.

Lemma 2.2. Let $\kappa $ be a VSS cardinal and let $f : \kappa \to \kappa $ . Then there is an inaccessible cardinal $\lambda> \kappa $ , a transitive model M of ZFC with $V_\lambda \subset M$ , and a generic elementary embedding $j : V_\lambda \to M$ with $\operatorname {\mathrm {crit}}(j) = \kappa $ and $j(f)(\kappa ) < \lambda < j(\kappa )$ .

Proof Because $\kappa $ is a limit of inaccessible cardinals we may define a function $g : \kappa \to \kappa $ such that $g(\alpha )$ is the least inaccessible cardinal greater than $\max \{f(\alpha ), \alpha \}$ for all $\alpha < \kappa $ . Because $\kappa $ is VSS with respect to the function $g+1$ defined by $\alpha \mapsto g(\alpha )+1$ , there is an ordinal $\beta> \kappa $ , a transitive set N with $V_\beta \subset N$ , and a generic elementary embedding

$$ \begin{align*}j: V_\beta \to N \text{ with } \operatorname{\mathrm{crit}}(j) = \kappa \text{ and } j(g)(\kappa) < \beta.\end{align*} $$

By the definition of g from f and the elementarity of j it follows that $j(g)(\kappa )$ is the least inaccessible cardinal in N greater than $\max \{j(f)(\kappa ), \kappa \}$ . Because $j(g)$ is a function from $j(\kappa )$ to $j(\kappa )$ we have $j(g)(\kappa ) < j(\kappa )$ . Letting $\lambda = j(g)(\kappa )$ we therefore have $\lambda> \kappa $ and

$$ \begin{align*}j(f)(\kappa) < \lambda < j(\kappa).\end{align*} $$

Because $\lambda < \beta $ and $V_\beta \subset N$ , the inaccessibility of $\lambda $ is absolute from N to V. Define $j_1 = j \restriction V_\lambda $ and M = $j(V_\lambda ) = V_{j(\lambda )}^N$ . Then $j_1 : V_\lambda \to M$ is a generic elementary embedding with $\operatorname {\mathrm {crit}}(j_1) = \kappa $ and $j_1(f)(\kappa ) < \lambda < j_1(\kappa )$ as desired. Because $V_\lambda $ satisfies ZFC it follows by the elementarity of $j_1$ that M satisfies ZFC.

It follows from Lemma 2.2 that every VSS cardinal has an inaccessible cardinal above it. Because inaccessibility is preserved by small forcing, combining this fact with the proof of Theorem 1.2 (as outlined following the statement of the theorem) yields the following curious consequence.

Proposition 2.3. The following statements are equiconsistent modulo ZFC.

1. 1. Every universally Baire set of reals has the perfect set property.

2. 2. Every universally Baire set of reals has the perfect set property and there is an inaccessible cardinal.

Note that the natural attempt to show that statement 2 has strictly higher consistency strength than statement 1 fails because for an inaccessible cardinal $\lambda $ , the pointclass $\operatorname {\mathrm {uB}}^{V_\lambda }$ might not be equal to $\operatorname {\mathrm {uB}}$ . For example, if $V = L[U]$ where U is a normal measure on $\lambda $ , then it follows from Feng et al. [2, Theorem 3.4] that $\boldsymbol {\Sigma }^1_2 \subset \operatorname {\mathrm {uB}}^{V_\lambda }$ and $\boldsymbol {\Sigma }^1_2 \not \subset \operatorname {\mathrm {uB}}$ .

Like other known virtual large cardinal properties, the virtual Shelah-for-supercompactness property is downward absolute to L:

Proposition 2.4. Every VSS cardinal is VSS in L.

Proof Let $\kappa $ be a VSS cardinal and let $f : \kappa \to \kappa $ be a function in L. Then by Lemma 2.2 there is an inaccessible cardinal $\lambda> \kappa $ , a transitive model M of ZFC with $V_\lambda \subset M$ , and a generic elementary embedding $j : V_\lambda \to M$ with $\operatorname {\mathrm {crit}}(j) = \kappa $ and $j(f)(\kappa ) < \lambda < j(\kappa )$ . Note that $L^{V_\lambda } = L_\lambda $ and $L^M = L_\theta $ where $\theta = \mathrm {Ord}^M$ . Moreover, because $\lambda $ is inaccessible we have $L_\lambda = V_\lambda ^L$ . For the elementary embedding $j_1 = j \restriction V_\lambda ^L$ we have

$$ \begin{align*}j_1 : V_\lambda^L \to L_\theta \text{ and } \operatorname{\mathrm{crit}}(j_1) = \kappa \text{ and } j_1(f) = j(f).\end{align*} $$

Let $G \subset \operatorname {\mathrm {Col}}(\omega ,V_\lambda ^L)$ be a V-generic filter. Then by the absoluteness of elementary embeddability of countable structures there is an elementary embedding $j_2 \in L[G]$ such that

$$ \begin{align*}j_2 : V_\lambda^L \to L_\theta \text{ and } \operatorname{\mathrm{crit}}(j_2) = \kappa \text{ and } j_2(f) = j(f).\end{align*} $$

We have $V_\lambda ^L = L_\lambda \subset L_\theta $ and $j_2(f)(\kappa ) = j(f)(\kappa ) < \lambda $ , so $j_2$ witnesses the VSS property for $\kappa $ in L with respect to f.

In Proposition 2.5, we characterize VSS cardinals by a property in which $\kappa $ is the image of the critical point, as in the characterizations of supercompact and virtually supercompact (i.e., remarkable) cardinals by Magidor [10, Theorem 1] and Schindler [12, Lemma 1.6] respectively. Note that if statement 2 of Proposition 2.5 is unvirtualized by requiring j to exist in V, the result is equivalent to the property called “Shelah for supercompactness” by Perlmutter [11, Definition 2.7]. This justifies the name “virtually Shelah for supercompactness.”

Proposition 2.5. For every cardinal $\kappa $ the following statements are equivalent:

1. 1. $\kappa $ is VSS.

2. 2. For every function $f : \kappa \to \kappa $ there are ordinals $\bar {\lambda }$ and $\lambda $ and a generic elementary embedding $j :V_{\bar {\lambda }} \to V_\lambda $ with the properties $j(\operatorname {\mathrm {crit}}(j)) = \kappa $ and $f \in \operatorname {\mathrm {ran}}(j)$ and $f(\operatorname {\mathrm {crit}}(j)) \le \bar {\lambda }$ . ⁵

Proof (1) $\!\implies\! $ (2): Assume that $\kappa $ is VSS and let $f: \kappa \to \kappa $ . By Lemma 2.2 there is an inaccessible cardinal $\lambda> \kappa $ , a transitive model M of ZFC with $V_\lambda \subset M$ , and a generic elementary embedding

$$ \begin{align*}j : V_\lambda \to M \text{ with }\operatorname{\mathrm{crit}}(j) = \kappa \text{ and }j(f)(\kappa) < \lambda < j(\kappa).\end{align*} $$

Define $\beta = \max \{j(f)(\kappa ), \kappa +1\}$ , so $\kappa < \beta < \lambda $ and $V_\beta ^M = V_\beta $ . Let $j_1 = j \restriction V_\beta $ and note that

$$ \begin{align*}j_1 : V_\beta \to V_{j(\beta)}^M \text{ and } \operatorname{\mathrm{crit}}(j_1) = \kappa \text{ and } j_1(\kappa) = j(\kappa) \text{ and } j_1(f) = j(f).\end{align*} $$

Let $G \subset \operatorname {\mathrm {Col}}(\omega ,V_\beta )$ be a V-generic filter. Because $M[G]$ is wellfounded, by the absoluteness of elementary embeddability of countable structures there is an elementary embedding $j_2 \in M[G]$ such that

$$ \begin{align*}j_2 : V_\beta \to V_{j(\beta)}^M \text{ and } \operatorname{\mathrm{crit}}(j_2) = \kappa \text{ and } j_2(\kappa) = j(\kappa) \text{ and } j_2(f) = j(f).\end{align*} $$

Then we have

$$ \begin{align*}j_2(\operatorname{\mathrm{crit}}(j_2)) = j(\kappa) \text{ and } j(f) \in \operatorname{\mathrm{ran}}(j_2) \text{ and }j(f)(\operatorname{\mathrm{crit}}(j_2)) \le \beta,\end{align*} $$

because $j(f)(\kappa ) \le \beta $ . By the elementarity of j and the definability of forcing there is an ordinal $\bar {\beta } < \lambda $ such that, letting $g \subset \operatorname {\mathrm {Col}}(\omega ,V_{\bar {\beta }})$ be a V-generic filter, there is an elementary embedding $j_3 \in V_\lambda [g]$ with

$$ \begin{align*}j_3 : V_{\bar{\beta}} \to V_{\beta} \text{ and } j_3(\operatorname{\mathrm{crit}}(j_3)) = \kappa \text{ and } f \in \operatorname{\mathrm{ran}}(j_3) \text{ and } f(\operatorname{\mathrm{crit}}(j_3)) \le \bar{\beta}.\end{align*} $$

Therefore statement 2 holds for f.

(2) $\!\implies\! $ (1): Assume that statement 2 holds and let $f: \kappa \to \kappa $ . Note that statement 2 implies the ineffability of $\kappa $ by an argument similar to Proposition 2.1. It follows that $\kappa $ is a limit of inaccessible cardinals, so by increasing the values of f we may assume that for all $\alpha < \kappa $ , $f(\alpha )$ is an inaccessible cardinal greater than $\alpha $ and we may furthermore define $f^+(\alpha )$ to be the least inaccessible cardinal greater than $f(\alpha )$ . Applying statement 2 to the function $f^+: \kappa \to \kappa $ yields ordinals $\bar {\lambda }$ and $\lambda $ and a generic elementary embedding

$$ \begin{align*}j :V_{\bar{\lambda}} \to V_\lambda \text{ with } j(\bar{\kappa}) = \kappa \text{ and } f^+ \in \operatorname{\mathrm{ran}}(j) \text{ and } f^+(\bar{\kappa}) \le \bar{\lambda},\end{align*} $$

where $\bar {\kappa } = \operatorname {\mathrm {crit}}(j)$ . By restricting j if necessary we may assume that $\bar {\lambda }$ is equal to $f^+(\bar {\kappa })$ and is therefore an inaccessible cardinal less than $\kappa $ . Let $\bar {\beta } = f(\bar {\kappa })$ and $\beta = j(\bar {\beta })$ .

Note that $f^+ \in \operatorname {\mathrm {ran}}(j)$ implies $f \in \operatorname {\mathrm {ran}}(j)$ because for all $\alpha < \kappa $ , $f(\alpha )$ is definable in $V_\lambda $ as the largest inaccessible cardinal less than $f^+(\alpha )$ , so we may define $\bar {f} = j^{-1}(f)$ . Then we have $\bar {f} : \bar {\kappa } \to \bar {\kappa }$ and $\bar {\beta } = j(\bar {f})(\bar {\kappa })$ . Note that

$$ \begin{align*} \bar{\kappa} < \bar{\beta} < \bar{\lambda} < \kappa < \beta < \lambda.\end{align*} $$

For the elementary embedding $j_1 = j \restriction V_{\bar {\beta }}$ we have

$$ \begin{align*} j_1 : V_{\bar{\beta}} \to V_\beta \text{ and } \operatorname{\mathrm{crit}}(j_1) = \bar{\kappa} \text { and } j_1(\bar{\kappa}) = \kappa \text{ and } j_1(\bar{f}) = f.\end{align*} $$

Let $g \subset \operatorname {\mathrm {Col}}(\omega , V_{\bar {\beta }})$ be a V-generic filter. Then by the absoluteness of elementary embeddability of countable structures there is an elementary embedding $j_2 \in V[g]$ such that

$$ \begin{align*} j_2 : V_{\bar{\beta}} \to V_\beta \text{ and } \operatorname{\mathrm{crit}}(j_2) = \bar{\kappa} \text { and } j_2(\bar{\kappa}) = \kappa \text{ and } j_2(\bar{f}) = f.\end{align*} $$

Letting $M = V_\beta $ we therefore have

$$ \begin{align*} V_{\bar{\beta}} \subset M \text{ and } j_2 : V_{\bar{\beta}} \to M \text{ and } \operatorname{\mathrm{crit}}(j_2) = \bar{\kappa} \text { and } j_2(\bar{f})(\bar{\kappa}) = \bar{\beta}.\end{align*} $$

Because $\bar {\lambda }$ is inaccessible in V and remains so in $V[g]$ , a Skolem hull argument in $V[g]$ yields a transitive set $M' \in V_{\bar {\lambda }}[g]$ and an elementary embedding $j_3 \in V_{\bar {\lambda }}[g]$ such that

$$ \begin{align*} V_{\bar{\beta}} \subset M' \text{ and } j_3 : V_{\bar{\beta}} \to M' \text{ and } \operatorname{\mathrm{crit}}(j_3) = \bar{\kappa} \text { and } j_3(\bar{f})(\bar{\kappa}) = \bar{\beta}.\end{align*} $$

Let $G \subset \operatorname {\mathrm {Col}}(\omega , V_\beta )$ be a V-generic filter. By the elementarity of j and the definability of forcing, there is a transitive set $M'' \in V_{\lambda }[G]$ and an elementary embedding $j_4 \in V_{\lambda }[G]$ with

$$ \begin{align*}V_{\beta} \subset M'' \text{ and } j_4 : V_{\beta} \to M'' \text{ and } \operatorname{\mathrm{crit}}(j_4) = \kappa \text{ and } j_4(f)(\kappa) = \beta.\end{align*} $$

Therefore $\kappa $ is VSS with respect to f.

3 Relation to other large cardinal properties

It is clear from the definitions that every Shelah cardinal (and a fortiori every Shelah-for-supercompactness cardinal) is VSS. In fact the VSS property is much weaker than either of these traditional large cardinal properties by the following result, which is typical of virtual large cardinals:

Proposition 3.1. If $0^\sharp $ exists then every Silver indiscernible is a VSS cardinal in L.

Proof Assume that $0^\sharp $ exists and let $\kappa $ be a Silver indiscernible. Then there is an elementary embedding $j: L \to L$ with $\operatorname {\mathrm {crit}}(j) = \kappa $ . Let $f : \kappa \to \kappa $ be a function in L and define $\lambda = \max \{j(f)(\kappa ), \kappa +1\}$ . For the elementary embedding $j_1 = j \restriction V_\lambda ^L$ we have

$$ \begin{align*} j_1 : V_\lambda^L \to V_{j(\lambda)}^L \text{ and } \operatorname{\mathrm{crit}}(j_1) = \kappa \text{ and } j_1(\kappa) = j(\kappa) \text{ and } j_1(f) = j(f).\end{align*} $$

Let $G \subset \operatorname {\mathrm {Col}}(\omega ,V_\lambda ^L)$ be a V-generic filter. Then by the absoluteness of elementary embeddability of countable structures there is an elementary embedding $j_2 \in L[G]$ such that

$$ \begin{align*} j_2 : V_\lambda^L \to V_{j(\lambda)}^L \text{ and } \operatorname{\mathrm{crit}}(j_2) = \kappa \text{ and } j_2(\kappa) = j(\kappa) \text{ and } j_2(f) = j(f).\end{align*} $$

We have $j_2(f)(\kappa ) = j(f)(\kappa ) \le \lambda $ , so $j_2$ witnesses the VSS property for $\kappa $ in L with respect to the function f.

We can obtain a better upper bound for the consistency strength of VSS cardinals in terms of the hierarchy of $\alpha $ -iterable cardinals defined by Gitman [3]. If $0^\sharp $ exists then every Silver indiscernible is $\alpha $ -iterable in L for every ordinal $\alpha < \omega _1^L$ by Gitman and Welch [6, Theorem 3.11], and we will show that 2-iterable cardinals already exceed VSS cardinals in consistency strength. We will not need the definition of $\alpha $ -iterability below, only a certain established consequence of it in the case $\alpha = 2$ .

Proposition 3.2. If $\kappa $ is a $2$ -iterable cardinal then $\kappa $ is a stationary limit of cardinals that are VSS in $V_\kappa $ .

Proof Assume that $\kappa $ is 2-iterable. Then by Gitman and Welch [6, Theorem 4.7] there is a transitive model M of ZFC with $V_\kappa \in M$ and an elementary embedding $j : M \to N$ with critical point equal to $\kappa $ where N is a transitive model of ZFC and $M = V_{j(\kappa )}^N$ .

First, we show that $\kappa $ is VSS in N. Let $f : \kappa \to \kappa $ be in N and therefore also in M. Define $\lambda = \max \{j(f)(\kappa ), \kappa + 1\}$ . Because $j(f)$ is a function from $j(\kappa )$ to $j(\kappa )$ we have $\lambda < j(\kappa ) = \mathrm {Ord}^M$ , so $V_\lambda ^M = V_\lambda ^N$ and we have an elementary embedding $j_1 = j \restriction V_\lambda ^M$ with

$$ \begin{align*} j_1 : V_\lambda^N \to V_{j(\lambda)}^N \text{ and } \operatorname{\mathrm{crit}}(j_1) = \kappa \text{ and } j_1(\kappa) = j(\kappa)\text{ and } j_1(f) = j(f).\end{align*} $$

Let $G \subset \operatorname {\mathrm {Col}}(\omega ,V_\lambda ^N)$ be a V-generic filter. Then by the absoluteness of elementary embeddability of countable structures there is an elementary embedding $j_2 \in N[G]$ such that

$$ \begin{align*} j_2 : V_\lambda^N \to V_{j(\lambda)}^N \text{ and } \operatorname{\mathrm{crit}}(j_2) = \kappa \text{ and } j_2(\kappa) = j(\kappa)\text{ and } j_2(f) = j(f).\end{align*} $$

Because $j_2(f)(\kappa ) = j(f)(\kappa ) \le \lambda $ , this elementary embedding $j_2$ witnesses the VSS property for $\kappa $ in N with respect to f.

Now let C be club in $\kappa $ . Then $\kappa \in j(C)$ , so the model N satisfies the statement “there is a VSS cardinal in $j(C)$ ” and by the elementarity of j it follows that the model M satisfies the statement “there is a VSS cardinal in C.” Let $\bar {\kappa } \in C$ be VSS in M. Because we have $j(\bar {\kappa }) = \bar {\kappa }$ and

$$ \begin{align*}j(V_\kappa) = j(V_\kappa^M) = V_{j(\kappa)}^N = M,\end{align*} $$

it follows by the elementarity of j that $\bar {\kappa }$ is VSS in $V_\kappa $ .

Because the set of all ordinals $\alpha < \kappa $ such that $V_\alpha \prec _{\Sigma _2} V_\kappa $ is club in $\kappa $ , the conclusion of Proposition 3.2 implies that $\kappa $ is a stationary limit of cardinals that are both $\Sigma _2$ -reflecting and VSS in $V_\kappa $ . (Note that the VSS property is upward absolute from $V_\kappa $ to V but the $\Sigma _2$ -reflecting property might not be.) It follows that ZFC+ “there is a $\Sigma _2$ -reflecting VSS cardinal” has lower consistency strength than ZFC+ “there is a 2-iterable cardinal.”

Recall that every VSS cardinal is ineffable by Proposition 2.1. We can obtain a better lower bound for the consistency strength of VSS cardinals in terms of the virtually A-extendible cardinals defined by Gitman and Hamkins [4, Definition 6]: For a cardinal $\alpha $ and a class A (meaning either a definable class in ZFC or more generally an arbitrary class in GBC) we say that $\alpha $ is virtually A-extendible if for every ordinal $\beta> \alpha $ there is an ordinal $\theta $ and a generic elementary embedding

$$ \begin{align*}j : \langle V_\beta; \mathord{\in},A \cap V_\beta\rangle \to \langle V_\theta; \mathord{\in},A \cap V_\theta\rangle,\end{align*} $$

with $ \operatorname {\mathrm {crit}}(j) = \alpha $ and $j(\alpha )> \beta $ .

Proposition 3.3. If $\kappa $ is a VSS cardinal then the structure $\langle V_\kappa , V_{\kappa +1}; \mathord {\in }\rangle $ satisfies the statement “for every class A there is a virtually A-extendible cardinal.” ⁶

Proof Let $\kappa $ be a VSS cardinal, let $A \subset V_\kappa $ , and assume toward a contradiction that no cardinal less than $\kappa $ is virtually A-extendible in $\langle V_\kappa , V_{\kappa +1}; \mathord {\in }\rangle $ . Then we may define a function $f:\kappa \to \kappa $ such that for every ordinal $\alpha < \kappa $ , $f(\alpha )$ is the least ordinal greater than $\alpha $ such that for every ordinal $\theta < \kappa $ there is no generic elementary embedding from $\langle V_{f(\alpha )}; \mathord {\in },A \cap V_{f(\alpha )}\rangle $ to $\langle V_\theta; \mathord {\in },A \cap V_\theta \rangle $ that has critical point $\alpha $ and maps $\alpha $ above $f(\alpha )$ .

Because $\kappa $ is VSS, by Lemma 2.2 there is an inaccessible cardinal $\lambda> \kappa $ , a transitive model M of ZFC with $V_\lambda \subset M$ , and a generic elementary embedding

$$ \begin{align*}j : V_\lambda \to M \text{ with } \operatorname{\mathrm{crit}}(j) = \kappa \text { and }j(f)(\kappa) < \lambda < j(\kappa).\end{align*} $$

Defining $\beta = j(f)(\kappa )$ , we have

$$ \begin{align*}\kappa < \beta < \lambda < j(\kappa) < j(\beta) < \mathrm{Ord}^M\kern-1.2pt .\end{align*} $$

Let $j_1 = j \restriction V_\beta $ , considered as an elementary embedding whose domain is the structure $\langle V_\beta; \mathord {\in }, j(A) \cap V_\beta \rangle $ . Then we have

$$ \begin{align*}j_1 : \langle V_\beta; \mathord{\in}, j(A) \cap V_\beta\rangle \to \langle V_{j(\beta)}^M; \mathord{\in}, j(j(A) \cap V_\beta)\rangle \text{ and } \operatorname{\mathrm{crit}}(j_1) = \kappa \text{ and } j_1(\kappa) = j(\kappa).\end{align*} $$

Let $G \subset \operatorname {\mathrm {Col}}(\omega ,V_\beta )$ be a V-generic filter. Then by the absoluteness of elementary embeddability of countable structures there is an elementary embedding $j_2 \in M[G]$ such that

$$ \begin{align*}j_2 : \langle V_\beta; \mathord{\in}, j(A) \cap V_\beta\rangle \to \langle V_{j(\beta)}^M; \mathord{\in}, j(j(A) \cap V_\beta)\rangle \text{ and } \operatorname{\mathrm{crit}}(j_2) = \kappa \text{ and } j_2(\kappa) = j(\kappa).\end{align*} $$

Note that $j_2(\kappa ) = j(\kappa )> j(f)(\kappa ) = \beta $ . By the elementarity of j and the definability of forcing it follows that there is a cardinal $\alpha < \kappa $ such that, letting $g \subset \operatorname {\mathrm {Col}}(\omega ,V_{f(\alpha )})$ be a V-generic filter, there is an elementary embedding $j_3 \in V_\lambda [g]$ with

$$ \begin{align*}j_3 : \langle V_{f(\alpha)}; \mathord{\in}, A \cap V_{f(\alpha)}\rangle \to \langle V_{\beta}; \mathord{\in}, j(A) \cap V_\beta\rangle \text{ and } \operatorname{\mathrm{crit}}(j_3) = \alpha \text{ and } j_3(\alpha)> f(\alpha).\end{align*} $$

Because $V_\lambda \subset M$ we have $j_3 \in M[g]$ , and because $\beta < j(\kappa )$ it then follows by the elementarity of j that there is an ordinal $\theta < \kappa $ and an elementary embedding $j_4 \in V_\lambda [g]$ such that

$$ \begin{align*}j_4 : \langle V_{f(\alpha)}; \mathord{\in}, A \cap V_{f(\alpha)}\rangle \to \langle V_{\theta}; \mathord{\in}, A \cap V_\theta\rangle \text{ and } \operatorname{\mathrm{crit}}(j_4) = \alpha \text{ and } j_4(\alpha)> f(\alpha).\end{align*} $$

The existence of such a generic elementary embedding $j_4$ contradicts the definition of the function f.

We can state a further consequence of the VSS property in terms of the generic Vopěnka principle defined by Bagaria et al. [1], which says that for every proper class of structures of the same type there is a generic elementary embedding from one of the structures into another. The generic Vopěnka principle, formalized as a statement in GBC, follows from the existence of a virtually A-extendible cardinal for every class A by Gitman and Hamkins [4, Theorem 7]. ⁷ Combining this fact with Proposition 3.3 gives the following result.

Corollary 3.4. If $\kappa $ is a VSS cardinal then the structure $\langle V_\kappa , V_{\kappa +1}; \mathord {\in }\rangle $ satisfies the generic Vopěnka principle.

Remark 3.5. Gitman and Hamkins [4, Theorem 7] showed more specifically that the generic Vopěnka principle is equivalent to the existence of a proper class of weakly virtually A-extendible cardinals for every class A, where the definition of weak virtual A-extendibility is obtained from the definition of virtual A-extendibility by removing the requirement that the image of the critical point is greater than the rank of the domain structure. Solovay et al. [16, Theorem 6.9] proved an analogous result in the non-virtual setting, where Kunen’s inconsistency erases the distinction between weak extendibility and extendibility: Vopěnka’s principle is equivalent to the existence of an A-extendible cardinal for every class A.

4 Thin universally Baire sets of reals

In this section we will establish some equivalent conditions for a universally Baire set of reals to be thin, meaning to have no perfect subset. To do this we will need a characterization of universal Baireness in terms of trees and forcing due to Feng et al. [2].

For a class X, a tree on X is a subset of $X^{\mathord {<}\omega }$ that is closed under initial segments. For a tree T on X we let $[T]$ denote the set of all infinite branches of T. Note that $[T]$ is a closed subset of $X^\omega $ (where X has the discrete topology) and conversely every closed subset of $X^\omega $ is the set of branches of some tree on X.

We will typically consider trees on $\omega \times \mathrm {Ord}$ , whose elements we may think of either as finite sequences of pairs or as pairs of equal-length finite sequences. Because we require trees to be sets, a tree on $\omega \times \mathrm {Ord}$ is actually a tree on $\omega \times \gamma $ for some ordinal $\gamma $ , but there is usually no need to specify a particular ordinal.

The letter $\operatorname {\mathrm {p}}$ denotes projection:

$$ \begin{align*}\operatorname{\mathrm{p}}[T]= \{x \in \omega^\omega : \langle x,f\rangle \in [T] \text{ for some }f \in \mathrm{Ord}^\omega\}.\end{align*} $$

For a tree T on $\omega \times \mathrm {Ord}$ and a real $x \in \omega ^\omega $ we define the section $T_x$ of T as the set of all $s \in \mathrm {Ord}^{\mathord {<}\omega }$ such that $\langle x \restriction \left | s \right |, s\rangle \in T$ . Note that $T_x$ is a tree on $\mathrm {Ord}$ that is illfounded if and only if $x \in \operatorname {\mathrm {p}}[T]$ , so the statement $x \in \operatorname {\mathrm {p}}[T]$ is absolute to all transitive models of ZFC containing x and T by the absoluteness of wellfoundedness.

A pair of trees $\langle T,\tilde {T}\rangle $ on $\omega \times \mathrm {Ord}$ is complementing if

$$ \begin{align*}\operatorname{\mathrm{p}}[T] = \omega^\omega \setminus \operatorname{\mathrm{p}}[\tilde{T}]\end{align*} $$

and for a poset $\mathbb {P}$ it is $\mathbb {P}$ -absolutely complementing if it is complementing in every generic extension of V by $\mathbb {P}$ . The statement $\operatorname {\mathrm {p}}[T] \cap \operatorname {\mathrm {p}}[\tilde {T}] = \emptyset $ is generically absolute by the absoluteness of wellfoundedness of the tree of all triples $\langle r,s_1,s_2\rangle $ such that $\langle r, s_1\rangle \in T$ and $\langle r,s_2\rangle \in \tilde {T}$ , so a complementing pair of trees $\langle T,\tilde {T}\rangle $ is $\mathbb {P}$ -absolutely complementing if and only if $\operatorname {\mathrm {p}}[T] \cup \operatorname {\mathrm {p}}[\tilde {T}] = \omega ^\omega $ in every generic extension of V by $\mathbb {P}$ . A tree T is called $\mathbb {P}$ -absolutely complemented if there is a tree $\tilde {T}$ such that the pair $\langle T,\tilde {T}\rangle $ is $\mathbb {P}$ -absolutely complementing.

We say that a set of reals A is $\mathbb {P}$ -Baire if $A = \operatorname {\mathrm {p}}[T]$ for some $\mathbb {P}$ -absolutely complemented tree T on $\omega \times \mathrm {Ord}$ . By Feng et al. [2, Theorem 2.1] a set of reals is universally Baire if and only if it is $\mathbb {P}$ -Baire for every poset $\mathbb {P}$ . We will adopt this characterization of universal Baireness as our definition from now on.

For a cardinal $\kappa $ , we say that a set of reals is $\kappa $ -universally Baire if it is $\mathbb {P}$ -Baire for every poset $\mathbb {P}$ of cardinality less than $\kappa $ . We denote the pointclass of all $\kappa $ -universally Baire sets of reals by $\operatorname {\mathrm {uB}}_\kappa $ . Note that if $\kappa $ is inaccessible, then a set of reals is $\kappa $ -universally Baire if and only if it is $\operatorname {\mathrm {Col}}(\omega ,\mathord {<}\kappa )$ -Baire. ⁸

If a set of reals A is $\mathbb {P}$ -Baire and $G \subset \mathbb {P}$ is a V-generic filter, then the canonical extension of A to $V[G]$ is the set of reals $A^{V[G]}$ in $V[G]$ defined by

$$ \begin{align*}A^{V[G]} = \operatorname{\mathrm{p}}[T]^{V[G]},\end{align*} $$

where T is a $\mathbb {P}$ -absolutely complemented tree in V such that $A = \operatorname {\mathrm {p}}[T]^V$ . By a standard argument using the absoluteness of wellfoundedness, this definition of the canonical extension does not depend on the choice of T.

For every positive integer n, all of the above definitions and facts about universally Baire sets of reals can easily be generalized to universally Baire n-ary relations on the reals by replacing trees on $\omega \times \mathrm {Ord}$ with trees on $\omega ^n \times \mathrm {Ord}$ .

Now we can establish some equivalent conditions for thinness. The equivalence of statements 1 and 2 seems to be well known (and perhaps the others are also) but we are not aware of a reference.

Lemma 4.1. For every universally Baire set of reals A, the following statements are equivalent in ZFC.

1. 1. A is thin.

2. 2. $A^{V[G]} = A^V$ for every generic extension $V[G]$ of V.

3. 3. For every $n < \omega $ , every subset of $A^n$ is universally Baire.

4. 4. There is a universally Baire wellordering of A.

Proof (1) $\!\implies\! $ (2): Assume that statement 2 fails, so there is a generic extension $V[G]$ of V by a poset $\mathbb {P}$ and a real $x \in A^{V[G]} \setminus V$ . Letting $\langle T,\tilde {T}\rangle $ be a $\mathbb {P}$ -absolutely complementing pair of trees for A in V we have $x \in \operatorname {\mathrm {p}}[T]^{V[G]} \setminus L[T]$ , so by Mansfield’s theorem in $V[G]$ (see Jech [7, Lemma 25.24]) there is a perfect tree $U \in L[T]$ on $\omega $ such that $[U] \subset \operatorname {\mathrm {p}}[T]$ in $V[G]$ . This implies $[U] \subset A$ in V, so A is not thin.

(2) $\!\implies\! $ (3): Assume statement 2 and let $\mathbb {P}$ be a poset. Then there is a tree $T_{\neg A}$ on $\omega \times \mathrm {Ord}$ such that

$$ \begin{align*}{} \mathbin{\Vdash}_{\mathbb{P}} \operatorname{\mathrm{p}}[T_{\neg A}] = \omega^\omega \setminus A.\end{align*} $$

Let $n< \omega $ . From $T_{\neg A}$ , one can define a tree $T_{\neg A^n}$ on $\omega ^n \times \mathrm {Ord}$ such that

$$ \begin{align*}{} \mathbin{\Vdash}_{\mathbb{P}} \operatorname{\mathrm{p}}[T_{\neg A^n}] = (\omega^\omega)^n \setminus A^n\kern-1.2pt .\end{align*} $$

Now let $B \subset A^n$ . We will show that B is $\mathbb {P}$ -Baire. Take trees $T_B$ and $T_{A^n \setminus B}$ on $\omega ^n \times \left |B\right |$ and $\omega ^n \times \left |A^n \setminus B\right |$ respectively that project to B and $A^n \setminus B$ respectively in every generic extension. (Such trees can be trivially defined for every pointset.) From $T_{\neg A^n}$ and $T_{A^n \setminus B}$ , one can define a tree $T_{\neg B}$ on $\omega ^n \times \mathrm {Ord}$ such that every generic extension satisfies $\operatorname {\mathrm {p}}[T_{\neg B}] = \operatorname {\mathrm {p}}[T_{\neg A^n}] \cup \operatorname {\mathrm {p}}[T_{A^n \setminus B}]$ . Then we have

$$ \begin{align*}{} \mathbin{\Vdash}_{\mathbb{P}} \operatorname{\mathrm{p}}[T_{\neg B}] = (\omega^\omega)^n \setminus B,\end{align*} $$

so the pair of trees $\langle T_B, T_{\neg {B}}\rangle $ witnesses that B is $\mathbb {P}$ -Baire.

(3) $\!\implies\! $ (4): This follows directly from the existence of a wellordering of A given by the axiom of choice.

(4) $\!\implies\! $ (1): Suppose toward a contradiction that some universally Baire set of reals A has a universally Baire wellordering but is not thin. Because A has a perfect subset there is a continuous injection $f : 2^\omega \to \omega ^\omega $ whose range is contained in A. Taking the preimage of a universally Baire wellordering of A under the continuous function $f \times f$ we obtain a wellordering of $2^\omega $ with the Baire property, which leads to a contradiction using the Kuratowski–Ulam theorem (see Kanamori [8, Corollary 13.10]).

5 Proof of Theorem 1.2

The following “universally Baire reflection” lemma is the key to obtaining consequences of the VSS property by forcing. Our statement of the lemma will use the following definition. For a V-generic filter G on the Levy collapse poset $\operatorname {\mathrm {Col}}(\omega ,\mathord {<}\kappa )$ and an ordinal $\alpha < \kappa $ we define $G \restriction \alpha = G \cap \operatorname {\mathrm {Col}}(\omega ,\mathord {<}\alpha )$ , which is a V-generic filter on $\operatorname {\mathrm {Col}}(\omega ,\mathord {<}\alpha )$ .

Lemma 5.1. Let $\kappa $ be a VSS cardinal, let $G \subset \operatorname {\mathrm {Col}}(\omega ,\mathord {<}\kappa )$ be a V-generic filter, and let A be a universally Baire set of reals in $V[G]$ . Then there is an ordinal $\alpha < \kappa $ and a $\kappa $ -universally Baire set of reals $A_0$ in $V[G\restriction \alpha ]$ such that $A = A_0^{V[G]}$ .

Proof Suppose toward a contradiction that for every ordinal $\alpha < \kappa $ we have

$$ \begin{align*}\forall A_0 \in \operatorname{\mathrm{uB}}_\kappa^{V[G\restriction\alpha]}\, A_0^{V[G]} \ne A.\end{align*} $$

Then for every ordinal $\alpha < \kappa $ , because $\kappa $ is inaccessible in $V[G \restriction \alpha ]$ and we have

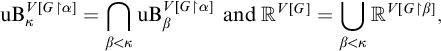$$ \begin{align*} \operatorname{\mathrm{uB}}_\kappa^{V[G \restriction \alpha]} = \bigcap_{\beta < \kappa} \operatorname{\mathrm{uB}}_\beta^{V[G \restriction \alpha]} \text{ and } \mathbb{R}^{V[G]} = \bigcup_{\beta < \kappa} \mathbb{R}^{V[G\restriction \beta]},\end{align*} $$

it follows that for all sufficiently large ordinals $\beta < \kappa $ we have $\beta> \alpha $ and

$$ \begin{align*}\forall A_0 \in \operatorname{\mathrm{uB}}^{V[G\restriction\alpha]}_{\beta}\, A_0^{V[G \restriction \beta]} \ne A \cap V[G \restriction \beta].\end{align*} $$

Then by the $\kappa $ -chain condition for $\operatorname {\mathrm {Col}}(\omega ,\mathord {<}\kappa )$ it follows that there is a function $f : \kappa \to \kappa $ in V such that for all $\alpha < \kappa $ we have $f(\alpha )> \alpha $ and

$$ \begin{align*}\forall A_0 \in \operatorname{\mathrm{uB}}^{V[G\restriction\alpha]}_{f(\alpha)}\, A_0^{V[G \restriction f(\alpha)]} \ne A \cap V[G \restriction f(\alpha)].\end{align*} $$

Because $\kappa $ is a limit of inaccessible cardinals in V we may additionally assume that $f(\alpha )$ is inaccessible in V for every ordinal $\alpha < \kappa $ .

Because $\kappa $ is VSS, by Lemma 2.2 there is an inaccessible cardinal $\lambda> \kappa $ , a transitive model M of ZFC in V with $V_\lambda \subset M$ , and a generic elementary embedding

$$ \begin{align*} j : V_{\lambda} \to M \text{ with } \operatorname{\mathrm{crit}}(j) = \kappa \text{ and } j(f)(\kappa) < \lambda < j(\kappa).\end{align*} $$

Defining $\beta = j(f)(\kappa )$ , we have

$$ \begin{align*}\kappa < \beta < \lambda < j(\kappa) < j(\beta) < \mathrm{Ord}^M\kern-1.2pt .\end{align*} $$

Note that $\beta $ is inaccessible in M by our assumption on f and the elementarity of j, and because $V_\lambda \subset M$ and $\beta < \lambda $ this implies that $\beta $ is also inaccessible in V.

We can extend j to a generic elementary embedding

$$ \begin{align*}{\hat \jmath} : V_{\lambda}[G] \to M[H],\end{align*} $$

where $H\subset \operatorname {\mathrm {Col}}(\omega ,\mathord {<}j(\kappa ))$ is an V-generic filter such that $H \restriction \kappa = G$ . By the fact that $\beta = j(f)(\kappa )$ and the elementarity of ${\hat \jmath }$ it follows that

$$ \begin{align*}\forall A_0 \in \operatorname{\mathrm{uB}}^{M[G]}_{\beta}\,A_0^{M[H \restriction \beta]} \ne {\hat \jmath}(A) \cap M[H \restriction \beta].\end{align*} $$

We will now obtain a contradiction by showing

$$ \begin{align*}A \in \operatorname{\mathrm{uB}}^{M[G]}_{\beta} \text{ and } A^{M[H \restriction \beta]} = {\hat \jmath}(A) \cap M[H \restriction \beta].\end{align*} $$

In $V[G]$ , because A is universally Baire we may take a $\operatorname {\mathrm {Col}}(\omega ,\mathord {<}\beta )$ -absolutely complementing pair of trees $\langle T,\tilde {T}\rangle $ on $\omega \times \mathrm {Ord}$ such that $\operatorname {\mathrm {p}}[T] = A$ . We may assume that $\langle T,\tilde {T}\rangle \in V_{\lambda }[G]$ : if necessary, replace T and $\tilde {T}$ by their images under the transitive collapse of an elementary substructure of a sufficiently large rank initial segment of $V[G]$ containing $V_\beta [G] \cup \{\beta ,T,\tilde {T}\}$ and having cardinality $\beta $ . Because $V_\lambda \subset M$ we have $V_\lambda [G] \subset M[G]$ and the pair $\langle T,\tilde {T}\rangle \in V_{\lambda }[G]$ witnesses $A \in \operatorname {\mathrm {uB}}^{M[G]}_{\beta }$ as desired.

We have $\langle {\hat \jmath }(T), {\hat \jmath }(\tilde {T})\rangle \in M[H]$ and it follows by the elementarity of ${\hat \jmath }$ that

$$ \begin{align*}\operatorname{\mathrm{p}}[{\hat \jmath}(T)]^{M[H]} = {\hat \jmath}(A).\end{align*} $$

Mapping branches pointwise by j gives the inclusions

$$ \begin{align*}\operatorname{\mathrm{p}}[T] \subset \operatorname{\mathrm{p}}[{\hat \jmath}(T)] \text{ and } \operatorname{\mathrm{p}}[\tilde{T}] \subset \operatorname{\mathrm{p}}[{\hat \jmath}(\tilde{T})],\end{align*} $$

which are absolute to transitive models containing these trees, so in particular they hold in $M[H]$ . Because the pair $\langle T,\tilde {T}\rangle $ is $\operatorname {\mathrm {Col}}(\omega ,\mathord {<}\beta )$ -absolutely complementing in $V[G]$ and the pair $\langle {\hat \jmath }(T), {\hat \jmath }(\tilde {T})\rangle $ is complementing in $M[H]$ , these inclusions become equalities when restricted to the reals of $M[H \restriction \beta ]$ , so

$$ \begin{align*}A^{M[H \restriction \beta]} = \operatorname{\mathrm{p}}[T]^{M[H \restriction \beta]} = \operatorname{\mathrm{p}}[ {\hat \jmath}(T)]^{M[H \restriction \beta]} = {\hat \jmath}(A) \cap M[H \restriction \beta],\end{align*} $$

completing the desired contradiction.

We can use Lemma 5.1 to show that the consistency of statement 1 of Theorem 1.2 (which says there is a VSS cardinal) implies the consistency of statements 2–4, and the corresponding statement for the Baire property:

Proposition 5.2. Let $\kappa $ be a VSS cardinal and let $G \subset \operatorname {\mathrm {Col}}(\omega ,\mathord {<}\kappa )$ be a V-generic filter. Then the following statements hold in $V[G]$ :

• • $\left |\operatorname {\mathrm {uB}}\right | = \omega _1$ .

• • Every set of reals in $L(\operatorname {\mathrm {uB}}, \mathbb {R})$ is Lebesgue measurable, has the Baire property, and has the perfect set property.

Proof By Lemma 5.1 every universally Baire set of reals in $V[G]$ is definable in a uniform way from V, G, and elements of $V_\kappa $ , namely an ordinal $\alpha < \kappa $ and a $\operatorname {\mathrm {Col}}(\omega ,\mathord {<}\alpha )$ -name for a $\kappa $ -universally Baire set of reals. (Recall that the canonical extension of a $\kappa $ -universally Baire set of reals does not depend on any choice of trees.) Because the rank initial segment $V_\kappa $ of the ground model has cardinality $\omega _1$ in $V[G]$ , it follows that $V[G]$ satisfies $\left |\operatorname {\mathrm {uB}}\right | = \omega _1$ .

Now let B be a set of reals in $L(\operatorname {\mathrm {uB}}, \mathbb {R})^{V[G]}$ . Then B is definable in $V[G]$ from a universally Baire set A, a real x, and an ordinal $\xi $ . By Lemma 5.1 there is an ordinal $\alpha < \kappa $ and a tree T on $\omega \times \mathrm {Ord}$ in $V[G \restriction \alpha ]$ such that $A = \operatorname {\mathrm {p}}[T]^{V[G]}$ . Letting $\dot {T} \in V$ be a $\operatorname {\mathrm {Col}}(\omega ,\mathord {<}\alpha )$ name for T and letting $y \in V[G]$ be a real coding x and the hereditarily countable set $G \restriction \alpha $ , the set B is definable in $V[G]$ from the parameter $\langle \xi , \dot {T}\rangle \in V$ and the real parameter y. Then B has the three claimed regularity properties by Lemmas III.1.4, III.1.6, and III.1.7 respectively of Solovay [14].

Proceeding with the proof of Theorem 1.2, note that statement 4 of the theorem, which says that every set of reals in $L(\operatorname {\mathrm {uB}}, \mathbb {R})$ has the perfect set property, obviously implies statement 5 of the theorem, which says that every universally Baire set of reals has the perfect set property.

We will show that statements 2 and 3 also imply statement 5.

Assume that statement 5 fails, so there is an uncountable thin universally Baire set A. Then by Lemma 4.1 every subset of A is also universally Baire, so $\left |\operatorname {\mathrm {uB}}\right | \ge 2^{\omega _1}$ and therefore statement 2 fails. To show that statement 3 fails, meaning that there is a non-measurable set of reals in $L(\operatorname {\mathrm {uB}}, \mathbb {R})$ , it suffices by Shelah [13, Theorem 5.1B] to show that $L(\operatorname {\mathrm {uB}}, \mathbb {R})$ satisfies DC and the statement “there is a set of reals of cardinality $\aleph _1$ .” Because every countable sequence of universally Baire sets (or reals) is coded by a single universally Baire set (or real), DC in V implies $\text {DC}_{\operatorname {\mathrm {uB}} \cup \mathbb {R}}$ in $L(\operatorname {\mathrm {uB}}, \mathbb {R})$ , which in turn implies DC in $L(\operatorname {\mathrm {uB}}, \mathbb {R})$ by the proof of Solovay [15, Lemma 1.4]. Because A is universally Baire and thin, it has a universally Baire wellordering by Lemma 4.1. Because A is uncountable, this wellordering has an initial segment of order type $\omega _1$ , giving a set of reals of cardinality $\aleph _1$ in $L(\operatorname {\mathrm {uB}}, \mathbb {R})$ as desired.

Next we show that statement 5 implies statement 6:

Lemma 5.3. Assume that every universally Baire set of reals has the perfect set property. Then for every function $f: \omega _1 \to \omega _1$ there is an ordinal $\lambda> \omega _1$ such that for a stationary set of $\sigma \in \mathcal {P}_{\omega _1}(\lambda )$ we have $\sigma \cap \omega _1 \in \omega _1$ and $\operatorname {\mathrm {o.\!t.}}(\sigma ) \ge f(\sigma \cap \omega _1)$ .

Proof Assume toward a contradiction that some function $f: \omega _1 \to \omega _1$ fails to have this property. For every ordinal $\lambda> \omega _1$ the set $\{\sigma \in \mathcal {P}_{\omega _1}(\lambda ) : \sigma \cap \omega _1 \in \omega _1\}$ is always club in $\mathcal {P}_{\omega _1}(\lambda )$ , so it follows from our assumption that the set of all $\sigma \in \mathcal {P}_{\omega _1}(\lambda )$ such that $\sigma \cap \omega _1 \in \omega _1$ and $\operatorname {\mathrm {o.\!t.}}(\sigma ) < f(\sigma \cap \omega _1)$ contains a club set in $\mathcal {P}_{\omega _1}(\lambda )$ . (This statement holds for $\lambda \le \omega _1$ as well, since it is weaker for smaller $\lambda $ .) Increasing the values of f if necessary, we may assume that f is a strictly increasing function.

We may consider every real x as coding a structure $\langle \omega; E_x \rangle $ where $E_x$ is a binary relation on $\omega $ . More precisely, for all $m,n \in \omega $ we let $\langle m,n\rangle \in E_x$ if and only if $x(2^m3^n) = 0$ . We may use AC to choose for every countable ordinal $\beta $ a real $x_\beta $ that codes $\beta $ in the sense that $\langle \omega; E_{x_\beta }\rangle \cong \langle \beta , \in \rangle $ . We claim that the set of reals

$$ \begin{align*} A = \{x_\beta : \beta \in \operatorname{\mathrm{ran}}(f)\}, \end{align*} $$

which is uncountable, is also universally Baire and thin. This will contradict our assumption that every universally Baire set of reals has the perfect set property.

Because $\left |A\right | = \omega _1$ we may trivially define a tree T on $\omega \times \omega _1$ from A such that $\operatorname {\mathrm {p}}[T] = A$ in every generic extension of V. To prove the claim, it will therefore suffice to show that for every poset $\mathbb {P}$ there is a tree $\tilde {T}$ on $\omega \times \mathrm {Ord}$ such that the pair $\langle T,\tilde {T}\rangle $ is $\mathbb {P}$ -absolutely complementing, which for this trivial tree T simply means

$$ \begin{align*} {} \mathbin{\Vdash}_{\mathbb{P}} \operatorname{\mathrm{p}}[\tilde{T}] = \omega^\omega \setminus A.\end{align*} $$

This will show that A is universally Baire by definition, and also that A is thin by condition 2 of Lemma 4.1. (Note that our assumption on f is only needed to prove universal Baireness of A. The thinness of A follows from the more general fact that the set $\{x_\beta : \beta <\omega _1\}$ is thin, which can be proved using the boundedness lemma; see Jech [7, Corollary 25.14].)

Fix a poset $\mathbb {P}$ and let $\eta = \max \{|\mathbb {P}|^+,\omega _1\}$ . Using our hypothesis on the existence of club sets, for every ordinal $\lambda $ in the interval $[\omega _1,\eta )$ we may choose a function

$$ \begin{align*}g_\lambda : \lambda^{\mathord{<}\omega} \to \lambda,\end{align*} $$

such that for every $g_\lambda $ -closed set $\sigma \in \mathcal {P}_{\omega _1}(\lambda )$ we have $\sigma \cap \omega _1 \in \omega _1$ and $\operatorname {\mathrm {o.\!t.}}(\sigma ) < f(\sigma \cap \omega _1)$ . (If $\mathbb {P}$ is countable then this interval is empty and there is nothing to do in this step.) Moreover, we can choose $g_\lambda $ to satisfy the additional property that for every $g_\lambda $ -closed set $\sigma \in \mathcal {P}_{\omega _1}(\lambda )$ the set $\sigma \cap \omega _1$ is f-closed. Then because f is strictly increasing, these properties imply that for every $g_\lambda $ -closed set $\sigma \in \mathcal {P}_{\omega _1}(\lambda )$ the order type of $\sigma $ is not in the range of f.

As a first step in defining the tree $\tilde {T}$ , note that there is a tree $\tilde {T}_1$ on $\omega \times \omega $ in V such that in every generic extension of V we have

$$ \begin{align*} \operatorname{\mathrm{p}}[\tilde{T}_1] = \{x \in \omega^\omega: \langle \omega;E_x\rangle \text{ is not a well-ordering}\},\end{align*} $$

because this set of reals is $\Sigma ^1_1$ .

As a second step in defining $\tilde {T}$ , note that for every ordinal $\beta < \omega _1^V$ there is a tree $\tilde {T}_{2,\beta }$ on $\omega \times \omega $ in V such that in every generic extension of V we have

$$ \begin{align*}\operatorname{\mathrm{p}}[\tilde{T}_{2,\beta}] = \{x \in \omega^\omega : \langle \omega;E_x\rangle \cong \langle \beta;\mathord{\in}\rangle \text{ and } x \notin A\},\end{align*} $$

because this set of reals is $\Sigma ^1_1(x_\beta )$ where $x_\beta $ is our chosen code of $\beta $ . (The condition $x \notin A$ in the definition of this set either subtracts the single point $x_\beta $ from the set or leaves it unchanged, according to whether or not $\beta $ is in the range of f.)

As a third step in defining $\tilde {T}$ , note that for every ordinal $\lambda \in [\omega _1^V, \eta )$ there is a tree $\tilde {T}_{3,\lambda }$ on $\omega \times \lambda $ in V such that in every generic extension of V we have

$$ \begin{align*}\operatorname{\mathrm{p}}[\tilde{T}_{3,\lambda}] = \{x \in \omega^\omega : \langle \omega;E_x\rangle \cong \langle \sigma;\mathord{\in}\rangle \text{ for some}\ g_\lambda\text{-closed set}\ \sigma \in \mathcal{P}_{\omega_1}(\lambda)\}.\end{align*} $$

To show this, it suffices to represent the set of all such reals x as the projection of a closed subset of $\omega ^\omega \times \lambda ^\omega $ onto its first coordinate. Using a definable pairing function $\lambda \times \omega \cong \lambda $ , it equivalently suffices to represent the set of all such reals x as the projection of a closed subset of $\omega ^\omega \times \lambda ^\omega \times \omega ^\omega $ onto its first coordinate. An example of such a closed set is the set of all triples $\langle x, h, y\rangle \in \omega ^\omega \times \lambda ^\omega \times \omega ^\omega $ such that h is an embedding $\langle \omega; E_x\rangle \to \langle \lambda ;\mathord {\in }\rangle $ and y is a function telling us how far we have to look ahead in order to verify that the range of h is $g_\lambda $ -closed. To be precise, we require that for all $n < \omega $ the pointwise image of the set $\{ h(i) : i < n \}^{\mathord {<}n}$ under $g_\lambda $ is contained in $\{ h(i) : i < y(n) \}$ .

Now we can define a tree $\tilde {T}$ on $\omega \times \eta $ in V as an amalgamation of these trees, so in every generic extension of V we have

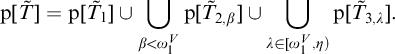$$ \begin{align*}\operatorname{\mathrm{p}}[\tilde{T}] = \operatorname{\mathrm{p}}[\tilde{T}_1] \cup \bigcup_{\beta < \omega_1^V} \operatorname{\mathrm{p}}[\tilde{T}_{2,\beta}] \cup \bigcup_{\lambda \in [\omega_1^V, \eta)} \operatorname{\mathrm{p}}[\tilde{T}_{3,\lambda}].\end{align*} $$

Let $G \subset \mathbb {P}$ be a V-generic filter and let x be a real in $V[G]$ . We want to show

$$ \begin{align*}x \in A \iff x \notin \operatorname{\mathrm{p}}[\tilde{T}].\end{align*} $$

Assume that $x \in A$ . Then clearly we have $x \notin \operatorname {\mathrm {p}}[\tilde {T}_1]$ and $x \notin \operatorname {\mathrm {p}}[\tilde {T}_{2,\beta }]$ for all $\beta < \omega _1^V$ . By the definition of A we have $x = x_\beta $ for some $\beta $ in the range of f. Now let $\lambda \in [\omega _1^V, \eta )$ . As previously noted, the order type of a $g_\lambda $ -closed set $\sigma \in \mathcal {P}_{\omega _1}(\lambda )^V$ cannot be in the range of f, so we have $x \notin \operatorname {\mathrm {p}}[\tilde {T}_{3,\lambda }]$ in V and equivalently in $V[G]$ . Therefore $x \notin \operatorname {\mathrm {p}}[\tilde {T}]$ .

Conversely, assume that $x \notin A$ . If $\langle \omega ;E_x\rangle $ is not a wellordering then we have $x \in \operatorname {\mathrm {p}}[\tilde {T}_1]$ . If $\langle \omega ;E_x\rangle $ is a wellordering of order type less than $\omega _1^V$ then let $\beta $ be its order type and note that $x \in \operatorname {\mathrm {p}}[\tilde {T}_{2,\beta }]$ . If $\langle \omega ;E_x\rangle $ is a wellordering of order type greater than or equal to $\omega _1^V$ then let $\lambda $ be its order type. Note that $\lambda < \eta $ because $\eta $ was chosen to be large enough that forcing with $\mathbb {P}$ does not collapse it to be countable. Therefore $\lambda \in [\omega _1^V,\eta )$ and we have $x \in \operatorname {\mathrm {p}}[\tilde {T}_{3,\lambda }]$ because $\langle \omega ;E_x\rangle \cong \langle \lambda ;\mathord {\in }\rangle $ and the set $\lambda \in \mathcal {P}_{\omega _1}(\lambda )^{V[G]}$ is trivially $g_\lambda $ -closed. In every case we have shown the desired conclusion that $x \in \operatorname {\mathrm {p}}[\tilde {T}]$ .

Finally, we show that if statement 6 holds then statement 1 holds in L:

Lemma 5.4. Assume that for every function $f: \omega _1 \to \omega _1$ there is an ordinal $\lambda> \omega _1$ such that for a stationary set of $\sigma \in \mathcal {P}_{\omega _1}(\lambda )$ we have $\sigma \cap \omega _1 \in \omega _1$ and $\operatorname {\mathrm {o.\!t.}}(\sigma ) \ge f(\sigma \cap \omega _1)$ . Then $\omega _1^V$ is VSS in L.

Proof Let $\kappa = \omega _1^V$ . First we will show that $\kappa $ is inaccessible in L. Because $\kappa $ is regular in V it is regular in L, so by GCH in L it remains to show that $\kappa $ is a limit cardinal in L. Suppose toward a contradiction that there is a cardinal $\eta < \kappa $ of L such that $(\eta ^+)^L = \kappa $ and define the function $f : \kappa \to \kappa $ in L such that for every ordinal $\alpha < \kappa $ , $f(\alpha )$ is the least ordinal $\beta> \max \{\alpha , \eta \}$ such that $L_\beta \models \left | \alpha \right | \le \eta $ . (Note that $\beta < \kappa $ by Gödel’s condensation lemma.)

By our assumption there is an ordinal $\lambda> \kappa $ such that for a stationary set of $\sigma \in \mathcal {P}_\kappa (\lambda )$ in V we have $\sigma \cap \kappa \in \kappa $ and $\operatorname {\mathrm {o.\!t.}}(\sigma ) \ge f(\sigma \cap \kappa )$ . Because the set of all $X \in \mathcal {P}_\kappa (L_\lambda )$ such that $X \prec L_\lambda $ , $X \cap \kappa \in \kappa $ , and $\eta \cup \{\eta \} \subset X$ is club in $\mathcal {P}_\kappa (L_\lambda )$ , there is such a set X with the additional property that $\bar {\lambda } \ge f(\bar {\kappa })$ where $\bar {\kappa } = X \cap \kappa $ and $\bar {\lambda } = \operatorname {\mathrm {o.\!t.}}(X \cap \lambda )$ . Note that

$$ \begin{align*} \eta < \bar{\kappa} < f(\bar{\kappa}) \le \bar{\lambda} < \kappa < \lambda.\end{align*} $$

By the condensation lemma, X is the range of an elementary embedding

$$ \begin{align*}j : L_{\bar{\lambda}} \to L_\lambda \text{ with } \operatorname{\mathrm{crit}}(j) = \bar{\kappa} \text{ and } j(\bar{\kappa}) = \kappa.\end{align*} $$

By the definition of f we have $L_{f(\bar {\kappa })} \models \left | \bar {\kappa } \right | \le \eta $ , and because $f(\bar {\kappa }) \le \bar {\lambda }$ it follows that $L_{\bar {\lambda }} \models \left | \bar {\kappa } \right | \le \eta $ . Then we have $L_\lambda \models \left | \kappa \right | \le \eta $ by the elementarity of j, contradicting the fact that $\kappa $ is a cardinal in V.

Now because $\kappa $ is inaccessible in L it follows that $L_\beta = V_\beta ^L$ for a cofinal set of ordinals $\beta < \kappa $ . We will use this fact to show that L satisfies statement 2 of Proposition 2.5, which is an equivalent condition for $\kappa $ to be VSS.

Let $f : \kappa \to \kappa $ be a function in L and define the function $g: \kappa \to \kappa $ in L where for every ordinal $\alpha < \kappa $ , $g(\alpha )$ is the least ordinal $\beta \ge \max \{f(\alpha ), \alpha +1\}$ such that $L_\beta = V_\beta ^L$ . Applying our assumption to the function $g + 1$ , we obtain an ordinal $\lambda> \kappa $ such that for a stationary set of $\sigma \in \mathcal {P}_\kappa (\lambda )$ in V we have $\sigma \cap \kappa \in \kappa $ and $\operatorname {\mathrm {o.\!t.}}(\sigma )> g(\sigma \cap \kappa )$ . By increasing $\lambda $ if necessary, we may assume that $L_\lambda = V_\lambda ^L$ .

Because the set of all $X \in \mathcal {P}_\kappa (L_\lambda )$ such that $X \prec L_\lambda $ , $X \cap \kappa \in \kappa $ , and $f \in X$ is club in $\mathcal {P}_\kappa (L_\lambda )$ , there is such a set X with the additional property that $\bar {\lambda }> g(\bar {\kappa })$ where $\bar {\kappa } = X \cap \kappa $ and $\bar {\lambda } = \operatorname {\mathrm {o.\!t.}}(X \cap \lambda )$ . By the condensation lemma, X is the range of an elementary embedding

$$ \begin{align*}j : L_{\bar{\lambda}} \to L_\lambda \text{ with } \operatorname{\mathrm{crit}}(j) = \bar{\kappa} \text{ and } j(\bar{\kappa}) = \kappa.\end{align*} $$

Define $\bar {\beta } = g(\bar {\kappa })$ and $\beta = j(\bar {\beta })$ and $\bar {f} = j^{-1}(f)$ . Note that

$$ \begin{align*} \bar{\kappa} < \bar{\beta} < \bar{\lambda} < \kappa < \beta < \lambda.\end{align*} $$

We have $L_{\bar {\beta }} = V_{\bar {\beta }}^L$ because $\bar {\beta }$ is in the range of the function g. Therefore $L_{\bar {\lambda }} \models L_{\bar {\beta }} = V_{\bar {\beta }}$ and it follows by the elementarity of j that $L_\lambda \models L_\beta = V_\beta $ . Because $L_\lambda = V_\lambda ^L$ , this implies $L_\beta = V_\beta ^L$ . For the elementary embedding $j_1 = j \restriction V_{\bar {\beta }}^L$ we have

$$ \begin{align*} j_1: V_{\bar{\beta}}^L \to V_\beta^L \text{ and } \operatorname{\mathrm{crit}}(j_1) = \bar{\kappa} \text{ and } j_1(\bar{\kappa}) = \kappa \text{ and } j_1(\bar{f}) = f.\end{align*} $$

Let $G \subset \operatorname {\mathrm {Col}}(\omega ,V_{\bar {\beta }}^L)$ be a V-generic filter. Then by the absoluteness of elementary embeddability of countable structures there is an elementary embedding $j_2 \in L[G]$ such that

$$ \begin{align*} j_2: V_{\bar{\beta}}^L \to V_\beta^L \text{ and } \operatorname{\mathrm{crit}}(j_2) = \bar{\kappa} \text{ and } j_2(\bar{\kappa}) = \kappa \text{ and } j_2(\bar{f}) = f.\end{align*} $$

Because $f(\bar {\kappa }) \le g(\bar {\kappa }) = \bar {\beta }$ , this elementary embedding $j_2$ witnesses statement 2 of Proposition 2.5 for $\kappa $ in L with respect to the function f.

This completes the proof of Theorem 1.2. The following question remains open.

Question 5.5. What is the consistency strength of the theory ZFC+ “every set of reals in $L(\mathbb {R},\operatorname {\mathrm {uB}})$ has the Baire property”?

An upper bound for the consistency strength is ZFC+ “there is a VSS cardinal” by Proposition 5.2. We do not know any nontrivial lower bound.

6 Proof of Theorem 1.3

When forcing with the Levy collapse over L, the VSS property can be used to limit the complexity of the universally Baire sets of reals in the generic extension:

Proposition 6.1. Let $\kappa $ be a VSS cardinal in L and let $G \subset \operatorname {\mathrm {Col}}(\omega ,\mathord {<}\kappa )$ be an L-generic filter. Then $L[G] \models \operatorname {\mathrm {uB}} \subset {\boldsymbol {\Delta }}^1_2$ .

Proof Let A be a universally Baire set of reals in $L[G]$ . Then by Lemma 5.1 there is an ordinal $\alpha < \kappa $ and a $\kappa $ -universally Baire set of reals $A_0$ in $L[G\restriction \alpha ]$ such that $A = A_0^{L[G]}$ . Increasing $\alpha $ if necessary, we may assume that it is a successor ordinal, so $G\restriction \alpha $ is countable in $L[G\restriction \alpha ]$ and therefore $L[G\restriction \alpha ] = L[z]$ for some real $z \in L[G]$ . Take a $\operatorname {\mathrm {Col}}(\omega ,\mathord {<}\kappa )$ -absolutely complementing pair of trees $\langle T, \tilde {T}\rangle $ in $L[z]$ such that $\operatorname {\mathrm {p}}[T]^{L[z]} = A_0$ and therefore $\operatorname {\mathrm {p}}[T]^{L[G]} = A$ . Define the sets of reals

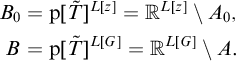$$ \begin{align*} B_0 &= \operatorname{\mathrm{p}}[\tilde{T}]^{L[z]} = \mathbb{R}^{L[z]} \setminus A_0,\\ B &= \operatorname{\mathrm{p}}[\tilde{T}]^{L[G]} = \mathbb{R}^{L[G]} \setminus A. \end{align*} $$

We claim that for every real $x \in L[G]$ we have $x \in A$ if and only if there is a tree $T' \in L[z]$ such that $x \in \operatorname {\mathrm {p}}[T']$ and $\operatorname {\mathrm {p}}[T'] \cap B_0 = \emptyset $ . To prove the forward direction of the claim, note that if $x \in A$ then we can simply let $T' = T$ .

To prove the reverse direction of the claim, let x be a real in $L[G]$ and assume that $x \in \operatorname {\mathrm {p}}[T']$ for some tree $T' \in L[z]$ such that $\operatorname {\mathrm {p}}[T'] \cap B_0 = \emptyset $ . Because $\operatorname {\mathrm {p}}[T'] \cap B_0 = \emptyset $ and $B_0 = \operatorname {\mathrm {p}}[\tilde {T}]^{L[z]}$ we have

$$ \begin{align*}L[z] \models \operatorname{\mathrm{p}}[T'] \cap \operatorname{\mathrm{p}}[\tilde{T}] = \emptyset.\end{align*} $$

The statement $\operatorname {\mathrm {p}}[T'] \cap \operatorname {\mathrm {p}}[\tilde {T}] = \emptyset $ is absolute between $L[z]$ and $L[G]$ by the absoluteness of wellfoundedness of the tree of all triples $\langle r, s_1, s_2\rangle $ such that $\langle r,s_1\rangle \in T'$ and $\langle r,s_2\rangle \in \tilde {T}$ , so because $x \in \operatorname {\mathrm {p}}[T']$ we have $x \notin \operatorname {\mathrm {p}}[\tilde {T}]$ and therefore $x \in \operatorname {\mathrm {p}}[T] = A$ .

We can use the claim to define A in $L[G]$ without reference to T. Because the class $L[z]$ is $\Sigma _1(z)$ and the statement $y \notin \operatorname {\mathrm {p}}[T']$ (where y is a real) is witnessed by the existence of a rank function for the section tree $T_y$ , it follows from the claim that A is $\Sigma _1(z,B_0)$ . Because $\text {HC} \prec _{\Sigma _1} V$ , this implies that A is $\Sigma _1^{\text {HC}}(z,B_0)$ and is therefore $\Sigma ^1_2(z,b)$ where b is a real coding $B_0$ . A symmetric argument shows that B is ${\boldsymbol {\Sigma }}^1_2$ in $L[G]$ , so A and B are both ${\boldsymbol {\Delta }}^1_2$ in $L[G]$ .

Proposition 6.1 is not useful as a relative consistency result because the theory ZFC+ “ $\operatorname {\mathrm {uB}} \subset {\boldsymbol {\Delta }}^1_2$ ” is equiconsistent with ZFC by the theorem of Larson and Shelah mentioned in the introduction. However, we can combine Proposition 6.1 with the theorem of Feng et al. mentioned in the introduction to obtain an equiconsistency result at the level of a $\Sigma _2$ -reflecting VSS cardinal:

Proof of Theorem 1.3 Assume that there is a $\Sigma _2$ -reflecting VSS cardinal $\kappa $ . Then $\kappa $ is clearly $\Sigma _2$ -reflecting in L and moreover it is VSS in L by Lemma 2.4. Let $G \subset \operatorname {\mathrm {Col}}(\omega ,\mathord {<}\kappa )$ be an L-generic filter. Because $\kappa $ is $\Sigma _2$ -reflecting in L we have ${\boldsymbol {\Delta }}^1_2 \subset \operatorname {\mathrm {uB}}$ in $L[G]$ by the proof of Feng et al. [2, Theorem 3.3]. On the other hand, because $\kappa $ is VSS in L we have $\operatorname {\mathrm {uB}} \subset {\boldsymbol {\Delta }}^1_2$ in $L[G]$ by Proposition 6.1.

Conversely, assume $\operatorname {\mathrm {uB}} = {\boldsymbol {\Delta }}^1_2$ . Because ${\boldsymbol {\Delta }}^1_2 \subset \operatorname {\mathrm {uB}}$ , the cardinal $\omega _1^V$ is $\Sigma _2$ -reflecting in L by the proof of Feng et al. [2, Theorem 3.3]. Also because ${\boldsymbol {\Delta }}^1_2 \subset \operatorname {\mathrm {uB}}$ , every ${\boldsymbol {\Sigma }}^1_2$ set of reals has the perfect set property by Feng et al. [2, Theorem 2.4]. Combining this with the assumption that $\operatorname {\mathrm {uB}} \subset {\boldsymbol {\Delta }}^1_2$ shows that every $\operatorname {\mathrm {uB}}$ set has the perfect set property, so $\omega _1^V$ is VSS in L by Lemmas 5.3 and 5.4.