Data assimilation in sea-ice monitoring

Abstract

The detection of small changes in concentration or thickness in the Arctic or Antarctic ice cover is an important topic in the current global-climate-change debate. Change detection using satellite data alone requires rigorous error analysis for their derived ice products, including inter-satellite validation for long time series. All models of physical processes are only approximations, and the best models of complicated physical processes have errors and uncertainties. A promising approach is data assimilation, combining model, in situ data and satellite remote-sensing data. Sea-ice monitoring from satellite, ice-model estimates, and the potential benefit of combining the two are discussed in some detail. In a case-study we demonstrate how the sea-ice backscatter for the Beaufort Sea region was derived using a backscattering model in combination with an ice model. We conclude that, for data assimilation, the first steps include the use of simple models, moving, with success at this level, to progressively more complex models. We also recommend reconfiguring the current remote-sensing data to include precise time tags with each pixel. For example, the current Special Sensor Microwave Imager data might be reissued in a time-tagged orbital (or gridded) format as opposed to the currently available daily averaged gridded data. Finally, error statistics and quality-control information also need to be readily available in a form useful for assimilation. The effectiveness of data-assimilation techniques is directly linked to the availability of data error statistics.

Introduction

Global climate models are unanimous in projecting enhanced climate warming in the polar regions. This warming is associated with projected changes in sea-ice cover. Detection of such changes in polar ice requires both an accurate assessment of the present state of the ice cover and reliable information on historical variability (in order to determine the significance of observed changes). These data are also useful in evaluating the sea-ice component of climate, forecast and process models.

A major challenge to the sea-ice research community is how to address the need for a uniform, consistent, gridded dataset describing the state of the polar sea ice and its variability in time and space. This is especially troublesome since most remotely sensed information provides only indirect measurements of the key elements of sea-ice dynamics, ice concentration, ice movement, ice thickness and turbulent energy fluxes through the ocean-ice-atmosphere interfaces. Remote sensing of ice motion is possible, but at space- and time-scales that are insufficient to capture the full range of important surface processes. Compounding this problem, in situ measurements of ice properties are from temporally and spatially limited case-studies.

All models of physical processes are only approximations to the ˚truth", and even the best models of complicated physical processes have built-in errors and uncertainties. There is need to bring the models closer to reality by means of information derived from observations of the actual physical processes. However, in situ data on sea-ice processes are rather scarce, and satellite data are probably the next best information available for remote polar regions.

Data-assimilation techniques, coupled with satellite remote-sensing and other observations, have a high potential to improve our understanding of the sea-ice state, including the variables needed for improved climate models. In the following, we will discuss the current status of data assimilation in sea-ice monitoring in view of present and future satellite sensors, with special focus on sea-ice parameters such as ice concentration, ice thickness, ice motion and deformation.

This paper does not provide a review of the latest data-assimilation techniques, but rather a road-map, outlining the important first steps toward integration of data-assimilation techniques with remote-satellite sensing data. We hope that this approach will take sea-ice monitoring beyond the empirical and physically simple algorithms in use today.

Sea-Ice Remote Sensing and Physical Models

For sea-ice monitoring, we currently have a variety of datasets of varying quality, spatial and temporal coverage. Great effort has been devoted to extracting sea-ice information from satellite data, principally the passive-microwave instruments such as the Scanning Multichannel Microwave Radiometer (SMMR) and the Special Sensor Microwave/ Imager (SSM/I), and several radars from European, Japanese and Canadian satellites. A 17 year time series of ice concentration and extent has been compiled from the SMMR and SSM/I instruments (Cavalieri and others, 1997). This time series is derived using statistical/empincal-based algorithms and provides estimates with 5–8% error envelope in winter and 15% or so in summer (Steffen and Schweiger, 1991). Radar data provide high-resolution snapshots of the ice state. Systems such as the RADARSAT geophysical processor system (RGPS) provide estimates of ice growth, ice type and ice movement during the winter months on approximately a 3 day time-step (Kwok and Baltzer, 1995). However, the RGPS does not currently function through the summer melt season.

A selection of one- and two-dimensional physically based sea-ice models is available. These models are used in stand-alone mode or as components in climate-system models. The trend in model development is toward more complexity and higher resolution, for example incorporating the ice-thickness distribution instead of a one- or two-level approximation (e.g. Flato and Hibler, 1995), finer grid spacing and time resolutions, anisotropic rheologies and more detailed thermodynamics. Alternative approaches such as the Kalman filter and model/data hybrids such as the RGPS and Lagrangian Parcel models are being pursued (Rothrock and Thomas, 1992). But we have yet to closely link the data and models to provide a comprehensive view of the sea ice. Some studies have been completed which link data and models (Kwok and others, 1995; Thomas and others, 1996). So far the community is only beginning direct data assimilation into dynamical models.

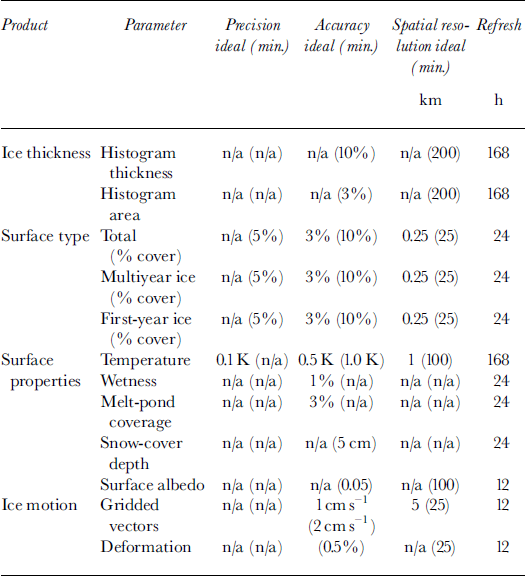
In Table 1 we have summarized the scientific observations requirements commonly used by the science community for sea-ice monitoring. Data assimilation will provide a framework, which we believe will improve the measurements of the following ice-related parameters: (1) ice concentration, mainly during the melt season, at higher temporal resolutions between observations, (2) ice thickness and mass estimates, and (3) ice motion/deformation. Note that the targeted parameters do not represent the complete list of needed observations inTable 1.

Table 1. Scientific observation requirements

The following is a case-study illustrating the combination of a physical sea-ice model with remote-sensing data. An ice model was combined with a model of radar-backscatter values to simulate G-band synthetic-aperture radar (SAR) data from the European Remote-sensing Satellite ERS-1. The simulation of the Arctic ice cover was achieved using a two-layer dynamic/thermodynamic ice model based on the formulations of Hibler (1979) and Hibler and Walsh (1982), as described by Maslanik and Silcox (1993). Model runs were carried out at 160 km spatial resolution with a 24 hour time-step over a 13 month period. Daily geostrophic wind fields were obtained from the U.S. National Center for Environmental Prediction (NGEP) model output; air pressures, climatological air temperatures and humidity values were obtained from Crutcher and Meserve (1970); and oceanic heat flux and geostrophic ocean currents were taken from ice-ocean simulations of Hibler and Bryan (1987). Periods for the occurrence of wet snow, melt ponds and young ice were derived using the NCEP temperature data. The physical model output, expressed as cover fractions of open water, first-year ice, multiyear ice, young ice, wet snow and melt ponds, is shown in Figure 1. Backscatter values for all of these surface types were simulated using empirically derived values for the ice types and an exponential relationship between ocean surface backscatter and wind speed (Wismann, 1993). Figure 2 shows the estimated backscatter produced by the forward simulation model compared with the actual ERS-1 SAR calibrated backscatter time series. The root-mean-square difference between the two time series is only 0.65 dB. The forward simulation was able to reproduce the summer melt and autumn freeze-up events seen in the SAR data. In a full data-assimilation model, the ice-type coverage might be adjusted iteratively to obtain the greatest correspondence with the actual SAR data. The model would thus serve as a robust and physically consistent ice-type classifier: one without the problems inherent in simpler classifiers based on thresholds or statistics (Steffen and Heinrichs, 1994).

Fig. 1. Time series of coverage by six different surface types used for the forward simulation model. Types included are open water (OW), first –year (FY) ice, multiyear (MY) ice, frost-flower-covered young ice (YI), wet snow (WS) and melt ponds (MP).

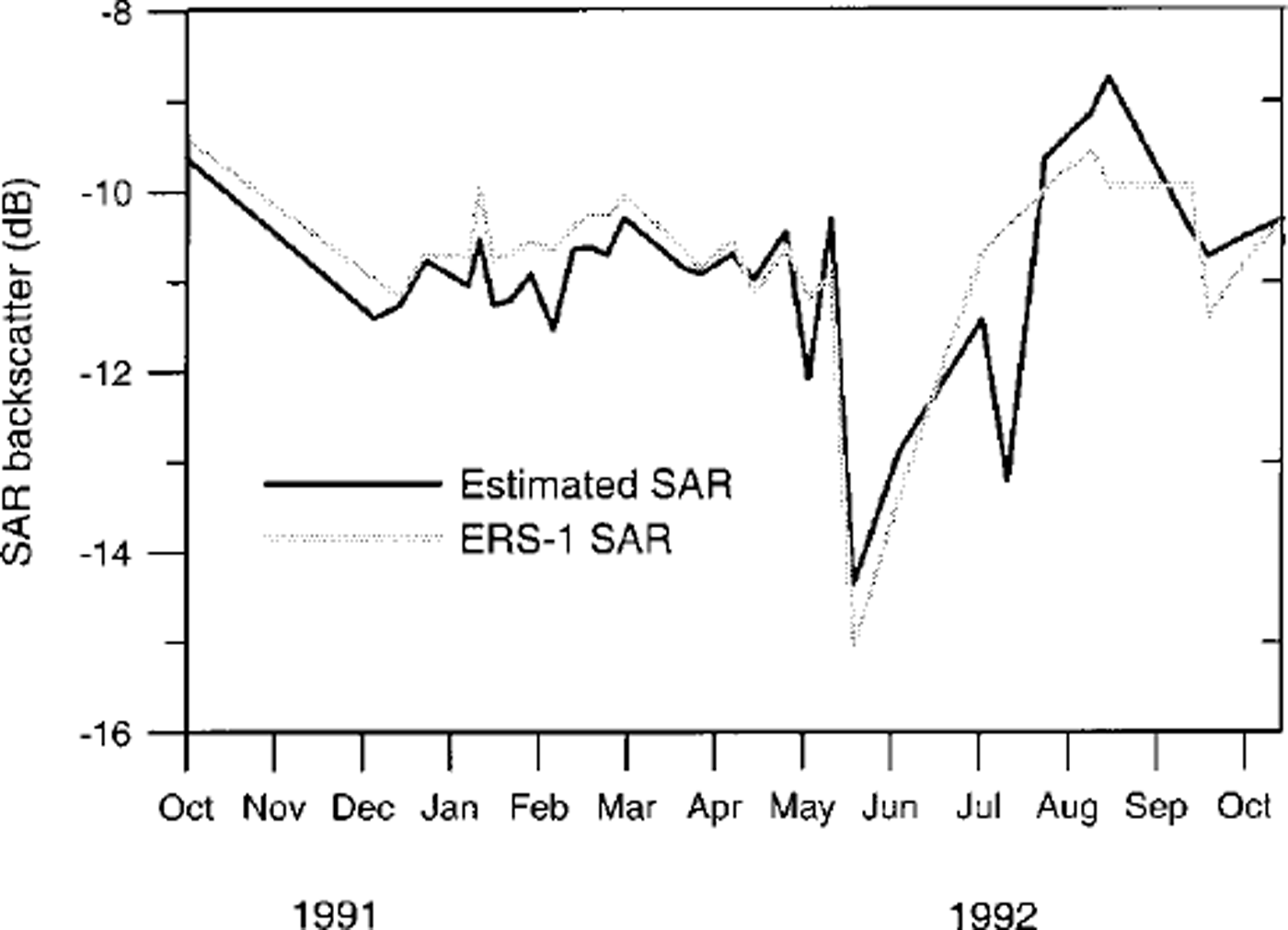
Fig. 2. Comparison between actual ERS-1 SAR backscatter time series and estimates from the forward simulation model.

Data Assimilation for Sea Ice

Data assimilation is a method to produce a four-dimensional representation of the state of a physical system. It is derived from: (1) a heterogeneous array of in situ and remote-sensing measurements which sample imperfectly and irregularly in space and time; (2) known physics of the system; and (3) prior information (including prior analyses). From a theoretical point of view, data assimilation can be viewed as the quantitative analysis of information using the principles of estimation theory.

The most general approach to data assimilation, called the Bayesian approach, is based on a definition of information in terms of probabilities. The conditional probability of a particular analysis field given the observational data is calculated, and the analysis field that yields the greatest probability is chosen. Because of the large number of probabilities that need to be calculated, the Bayesian approach is not computationally efficient.

A more practical technique, which is currently used to produce analysis fields for NGEP and other operational centers, is the variational approach. This method, like other data-assimilation approaches, begins with a model d = m(g), where g is the gridded data field, m is a model that estimates observational data (either remote-sensing or in situ) from the gridded field, and d is a vector of the modeled observational data without instrument error. The vector d can also be thought of as a forward simulation vector. The variational formulation defines a cost function as the fit of the assimilated field to observations plus a set of penalties to force the solution to be smooth. The data-assimilation problem then becomes finding the g that minimizes the cost function. This can be done by formalizing the data-assimilation problem as g ― g_p = K[m(g_ρ) ― d₀], where g_p is the previous gridded field, d₀ is the actual measured vector of observations, and K is a matrix that relates the observational errors to the model prediction errors. For the variational approach, K is obtained using the cost function.

Other approaches that have been used for data assimilation include function fitting and successive corrections, optimal interpolation, Kalman filters and smoothers, and ensemble techniques (Monte Carlo models). All of these approaches can be formalized similarly to the variational approach, the difference being how the matrix K is obtained. The variational approach, because it has been used for operational products, and because a software base exists in the form of the 3DVAR and 4DVAR programs, may be the lowest-risk approach for assimilation of sea-ice fields. However, if the models involved are highly non-linear, or if there is no sufficiently accurate model m, other techniques may be useful.

The requirements for any of the data-assimilation approaches include models (forward simulation models, interpolation operators and operators to extrapolate prior information) and error statistics for the observations (the nature of the distributions, independence, biases, variances, covariances, and the likelihood of extreme events). The importance of these error statistics to data assimilation cannot be overemphasized. Without accurate information from sensor engineers and operational data-processing sites, the accuracy of the assimilation process cannot be estimated a priori.

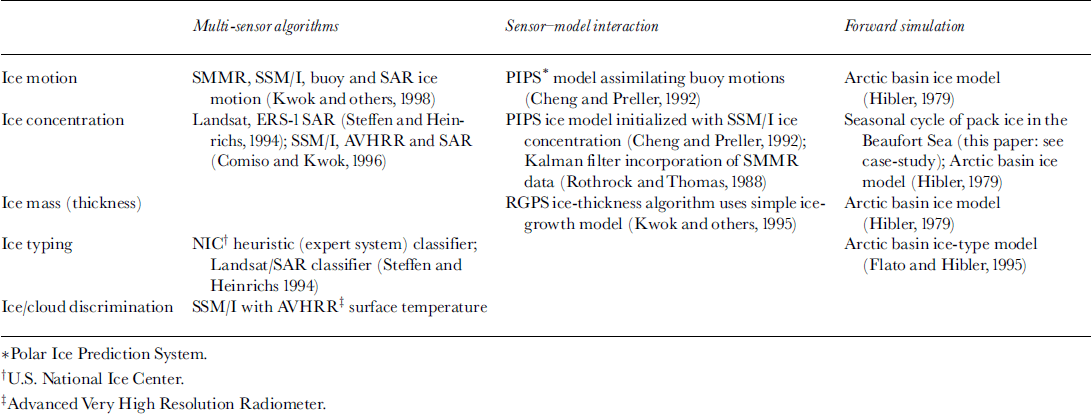
A significant amount of work has been done already on the techniques required for data assimilation within sea-ice models, although the individual pieces remain separated. Several promising studies have attempted to use data from multiple sensors to generate sea-ice products (Steffen and Heinrichs, 1994; Comiso and Kwok, 1996; Kwok and others, 1998). In general, the use of multiple data sources improved either the product accuracy or the robustness of the algorithms. A number of operational or potentially operational ice-prediction systems have incorporated remote-sensing data to constrain the model output (Rothrock and Thomas, 1988; Chang and Preller, 1992; Kwok and others, 1995). A product generation system has been designed to use a simple ice-growth model as a component. An under-studied area is the use of a forward simulation approach, which combines ice conditions predicted by a physical model with conversion of these conditions to spectral radiances, reflectance, backscatter or brightness temperature using radiative-transfer and/or microwave-scattering models. A case-study was presented in this paper using a backscattering model combined with an ice model to predict the seasonality of the sea-ice backscatter coefficient. Quite sophisticated radiative-transfer and microwave-scattering models exist, but these need to be intimately coupled to the ice models, and their error characteristics further assessed. Table 2 lists, by variable, a few studies identified that can fit into one of three categories, multi-sensor algorithms, sensor-model interaction and forward simulation. This list is not complete and should only serve as an example.

Table 2. Known efforts that are potentially useful as stepping-stones towards data assimilation of sea-ice parameters

Prospect of Data Assimilation in Sea-Ice Monitoring

The hypothetical sea-ice data-assimilation scheme (Fig. 3) shows the complexity for a full-scale assimilation effort. This approach uses atmospheric and ocean forcing to initiate a sea-ice model that conserves momentum, mass and heat, with satellite-derived geophysical data or satellite radiances as additional data input. The scheme proposes to assimilate buoy velocity, satellite-derived velocity, deformation, ice thickness, snow depth, lead orientation and floe size, in descending order of readiness.

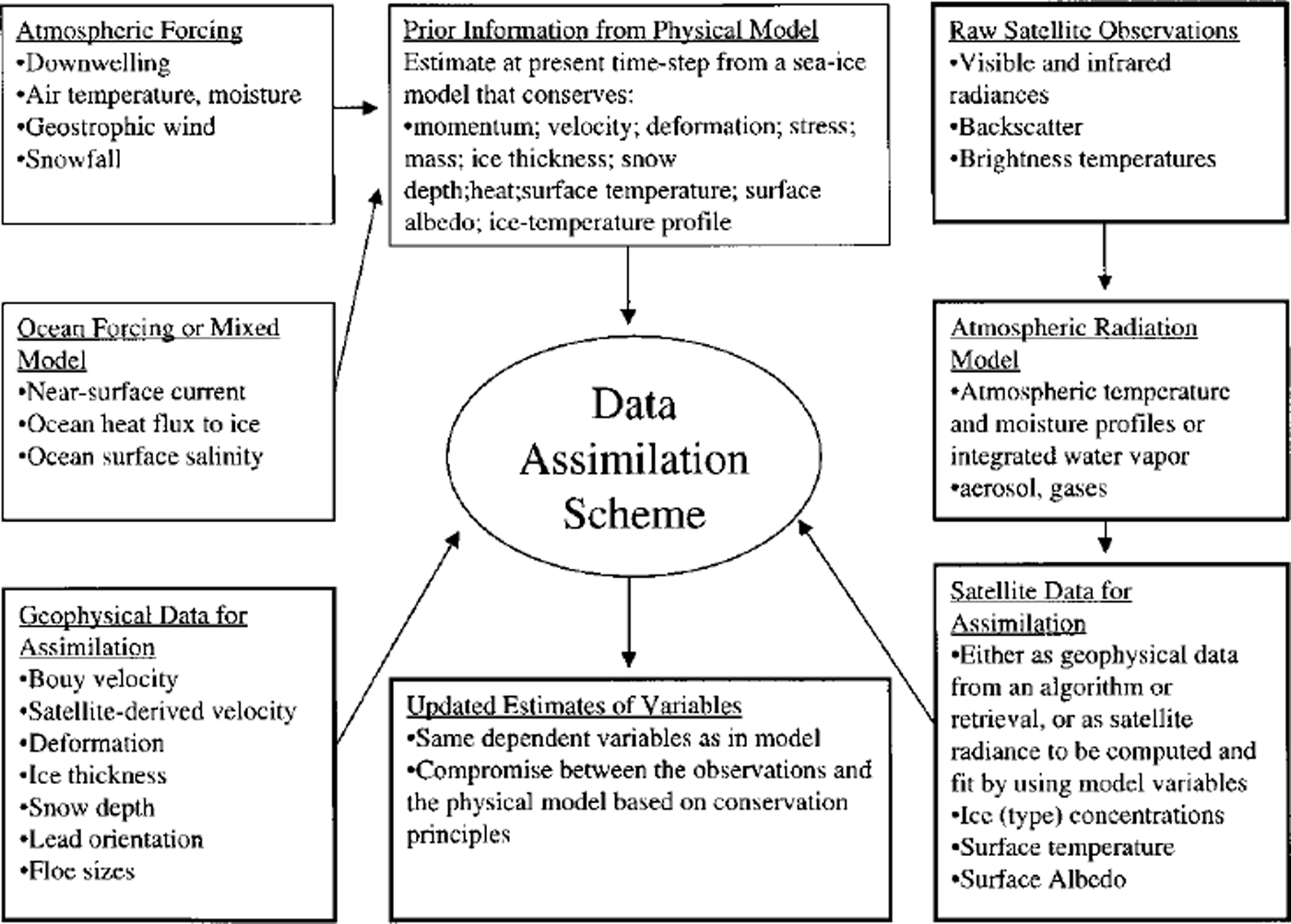
Fig. 3. Suggestion of eventual sea-ice data-assimilation scheme. The fainter boxes represent the traditional sea-ice model with forcing. The heavier boxes involve data assimilation. This diagram was originally drafted by D. Rothrock, APL, University of Washington, Seattle, for his presentation at the data-assimilation workshop in Boulder, CO, December 1997.

All methods of data assimilation attempt to estimate values that have a lower error than either the model or the data. A system that is appropriate for assimilation is shown in Figure 4a. Model and observational errors are somewhat comparable, so neither dominates the assimilation solution. In the system shown in Figure 4b, the assimilation does not accomplish the error reduction but may provide a suitable way to interpolate the observations to a grid. The opposite situation can occur when the model solutions are of little value, and thus the observations dominate (Fig. 4c).

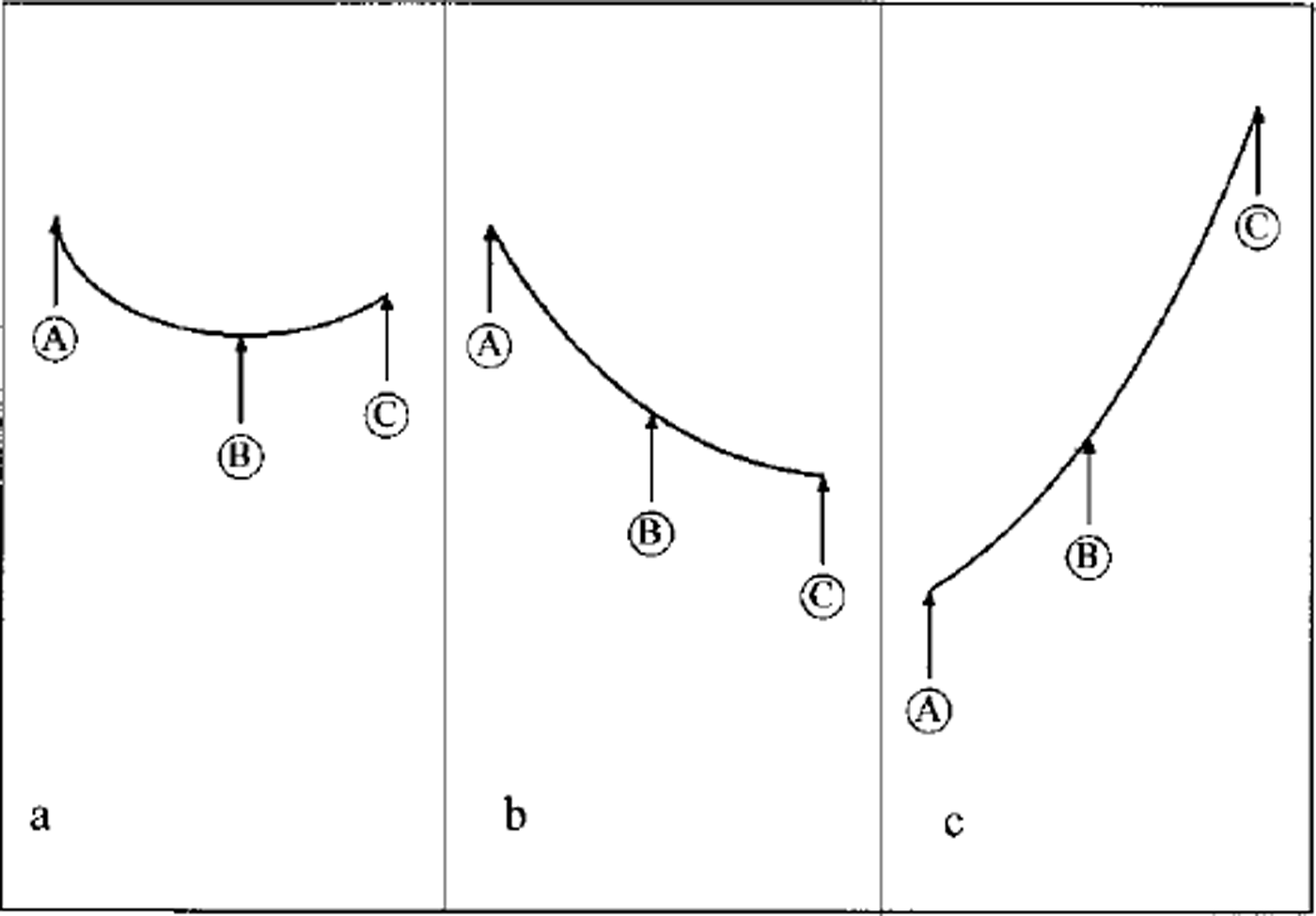
Fig. 4. Error variance for observations (A), assimilated variables ( B) and modeled variables (C) for three cases (see text).

The key question to be asked is how well do we know the error variance of observations (i.e. satellite data) and modeled data? Observation error statistics remain poorly defined, in terms of the requirements for assimilation applications.

Models used in a sea-ice data-assimilation scheme that are based on conservation equations for quantities like momentum, mass and heat provide a means to test the effectiveness of assimilation. Changes in conserved quantities brought about by assimilation of observed data can be evaluated, which in turn allows errors in the prescribed forcing and model parameters to be corrected. The aim is to have a data-assimilation scheme in which biases in both the observations and the model are removed to the extent possible, so that long-term average sources and sinks added to the model’s conservation equations by data assimilation are near zero.

Ice-motion observations are available from buoy and drift-station data and more recently from satellite sources. This kinematic information can be used in a data-assimilation scheme in several ways. Assimilating ice velocity is perhaps the most straightforward; and although this provides a constraint on the large-scale transport patterns, it may not be a sufficient constraint on focal deformation. Assimilation of strain-rate estimates could provide a more direct constraint on ice deformation (and hence focal thickness buildup). However, deformation estimates derived from high-resolution velocity fields are only possible from recent SAR data but with a relatively long time-span between samples (Kwok and others, 1998). Estimates from lower-resolution passive-microwave- and scatterometer-derived velocity fields may be useful, which would cover the period since 1987 using higher-resolution SSM/I data, and the period 1979–87 using lower-resolution SMMR imagery (Agnew and others, 1997). Buoy-derived velocity estimates are available from 1979 onwards (Thorndike and Colony, 1980; Rigor and Heiberg, 1997). These provide the most precise motion information available for specific locations and are thus useful within assimilation. However, they are deemed unsuitable for detailed strain-rate estimation given the relatively sparse spatial distribution of Arctic buoys.

Because sea-ice motion is so discontinuous and deformation is highly concentrated spatially, we recommend that modelers and data analysts guard against any smoothing of kinematic data. Data should be assimilated at no coarser spacing than a model’s resolution; any smoothing beyond that imposed by a model’s grid spacing would mask the natural concentration of deformation into features such as leads, flaws, ridges and shear-zone slip lines. Similarly, because ice kinematics show high-frequency spectral content, temporal information should not be lost by excessive smoothing but should be retained at the temporal resolution of models.

At present, many of the datasets that could be used for assimilation are available only at 1–3 day time-scales. Archived products should be expanded to include data at the full temporal as well as spatial resolution at which the data were acquired. This should also include the time of acquisition for each data value, and also perhaps ancillary parameters that may affect data quality, such as sensor scan angle, etc. In many cases this implies that orbital data should be made available to test data-assimilation schemes. Some assimilation strategies require radiance-level data that have been subjected to a minimum of processing using adjustments or product-generation algorithms. In general, this suggests that the standard approaches to product generation and archiving would need to be reconsidered in the context of assimilation requirements.

We acknowledge that data-assimilation constraints for the science community and for the operational forecast community are quite different, but not contradictory. The operational forecast community needs the product in a timely manner but at lower resolution, whereas the science community has no production time constraint and will probably use more complex models.

Recommendations

In conclusion, we provide some recommendations, in particular targeted for those just starting to make use of data assimilation in sea-ice monitoring.

1. (1) Use simple data-assimilation models in pilot studies to gain a better understanding of data and model error characteristics, and to determine which assimilation methods are best suited to particular applications and data types. The variational data-assimilation model appears promising.

2. (2) Take an incremental approach. We suggest the following three steps could provide adequate validation before more effort is invested in the next, more complex step.

3. (a) Use data assimilation in (possibly) low-resolution models to find to the first order whether data assimilation will improve sea-ice parameterization (e.g. ice concentration compared with dynamical model; then include ice thickness and deformation).

4. (b) Use data assimilation in higher-resolution models, which incorporate multiple variables, and high-frequency variations.

5. (c) Couple radiative models to ice models to explore assimilation methods that operate on raw data rather than geophysical products. Evaluate results by intercomparisons of error statistics and simulated low-level data.

6. (3) Investigate coupling of efforts between operational and research groups to make more efficient use of resources. Both communities can benefit from data assimilation, but have slightly different goals.

7. (4) Without accurate error statistics, data assimilation will be less successful, since the error uncertainty will remain in the assimilated variables. Thus data producers must place more emphasis on error assessment of both data fields and the models themselves. At a minimum, data distributors must take steps to secure data error statistics from data producers. In the case of satellite data, this means compiling sensor engineering data and pre-launch test data, as well as assessments of on-orbit sensor errors.

8. (5) Many of the assimilated data are available only at 1–3 day time-scales, whereas the available physical models are capable of assimilating variables more frequently. Therefore, datasets will need to be reconfigured and/or reissued if they are to provide much higher-temporal-resolution input data.

9. (6) Datasets (e.g. passive-microwave satellite data) must carry time tags for each pixel since the actual time of the observation is essential in data assimilation.

10. (7) We suggest that a passive-microwave test dataset (SSM/I) with error assessment and time tags for each orbit should be made available to the user community (e.g. U.S. National Snow and Ice Data Center Distributed Active Archive Center (NSIDC-DAAC)).