Article contents
Low-lying zeros of quadratic Dirichlet 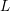 $L$-functions: lower order terms for extended support
$L$-functions: lower order terms for extended support
Published online by Cambridge University Press: 26 April 2017
Abstract
We study the 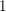 $1$-level density of low-lying zeros of Dirichlet
$1$-level density of low-lying zeros of Dirichlet 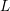 $L$-functions attached to real primitive characters of conductor at most
$L$-functions attached to real primitive characters of conductor at most 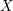 $X$. Under the generalized Riemann hypothesis, we give an asymptotic expansion of this quantity in descending powers of
$X$. Under the generalized Riemann hypothesis, we give an asymptotic expansion of this quantity in descending powers of 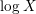 $\log X$, which is valid when the support of the Fourier transform of the corresponding even test function
$\log X$, which is valid when the support of the Fourier transform of the corresponding even test function 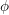 $\unicode[STIX]{x1D719}$ is contained in
$\unicode[STIX]{x1D719}$ is contained in 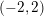 $(-2,2)$. We uncover a phase transition when the supremum
$(-2,2)$. We uncover a phase transition when the supremum  $\unicode[STIX]{x1D70E}$ of the support of
$\unicode[STIX]{x1D70E}$ of the support of 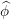 $\widehat{\unicode[STIX]{x1D719}}$ reaches
$\widehat{\unicode[STIX]{x1D719}}$ reaches 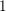 $1$, both in the main term and in the lower order terms. A new lower order term appearing at
$1$, both in the main term and in the lower order terms. A new lower order term appearing at 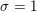 $\unicode[STIX]{x1D70E}=1$ involves the quantity
$\unicode[STIX]{x1D70E}=1$ involves the quantity 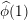 $\widehat{\unicode[STIX]{x1D719}}(1)$, and is analogous to a lower order term which was isolated by Rudnick in the function field case.
$\widehat{\unicode[STIX]{x1D719}}(1)$, and is analogous to a lower order term which was isolated by Rudnick in the function field case.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Authors 2017
References
- 7
- Cited by


