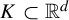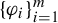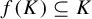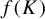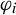On a self-embedding problem for self-similar sets

Abstract

Let $K\subset {\mathbb {R}}^d$ be a self-similar set generated by an iterated function system $\{\varphi _i\}_{i=1}^m$ satisfying the strong separation condition and let f be a contracting similitude with $f(K)\subseteq K$. We show that $f(K)$ is relatively open in K if all $\varphi _i$ share a common contraction ratio and orthogonal part. We also provide a counterexample when the orthogonal parts are allowed to vary. This partially answers a question of Elekes, Keleti and Máthé [Ergod. Th. & Dynam. Sys. 30 (2010), 399–440]. As a byproduct of our argument, when $d=1$ and K admits two homogeneous generating iterated function systems satisfying the strong separation condition but with contraction ratios of opposite signs, we show that K is symmetric. This partially answers a question of Feng and Wang [Adv. Math. 222 (2009), 1964–1981].

1 Introduction

For $1\leq i\leq m$ , let $\varphi _i(x)=r_iO_ix+a_i$ be a contracting similitude on ${\mathbb {R}}^d$ , where ${0<r_i<1}$ is the contraction ratio, $O_i$ is an orthogonal transformation on ${\mathbb {R}}^d$ and $a_i\in {\mathbb {R}}^d$ . Let K be the self-similar attractor generated by the iterated function system (or IFS in short) $\Phi :=\{\varphi _1,\ldots ,\varphi _m\}$ , that is, K is the unique non-empty compact set such that $K=\bigcup _{i=1}^m \varphi _i(K)$ . Sometimes $\Phi $ is also referred to as a generating IFS of K. For a detailed introduction to self-similar sets and IFSs, please refer to the classical textbook [9].

The IFS $\Phi $ is said to satisfy the open set condition (OSC) if there is a non-empty open set O such that $\bigcup _{i=1}^m \varphi _i(O)\subset O$ and $\varphi _1(O),\ldots ,\varphi _m(O)$ are pairwise disjoint; and to satisfy the strong separation condition (SSC) when $\varphi _1(K),\ldots ,\varphi _m(K)$ are pairwise disjoint. It is well known that SSC implies OSC. Under these separation conditions, the self-similar attractor K has been extensively studied in many aspects, especially the fractal dimensions and self-similar measures [8, 9, 14–17]. Despite this, a number of geometric structures of K remain mysterious even with the assumption of OSC or SSC. For example, if there is a contracting similitude f that embeds K into itself, what can we say about f? It is quite reasonable to guess that such a mapping cannot be too peculiar and there are existing results that describe this phenomenon.

In [12], Feng and Wang studied this problem (or more precisely, the generating IFS problem) on the real line. One of their results is the so-called logarithmic commensurability theorem: if $\varphi _i(x)=rx+a_i$ for a common $0<r<1$ , $\mathrm {dim}_{\mathrm {H}}\ K<1$ and the OSC is assumed, then $f(K)\subseteq K$ implies that $({\log r_f}/{\log r})\in {\mathbb {Q}}$ , where $r_f$ is the contraction ratio of f. In other words, $r_f$ should be a rational power of r.

Later, Elekes, Keleti and Máthé [7] generalized this result to the higher dimensional cases with OSC replaced by SSC. Please see Lemma 2.4 for the explicit statement. Their paper also contains many more interesting findings. For example, they proved that assuming the SSC, there are only finitely many similitudes f for which $f(K)\subseteq K$ and $f(K)$ intersects at least two level-1 cells (please see Definition 2.1), and for any self-similar measure $\mu $ , the collection of interior points of $f(K)$ with respect to K has the same $\mu $ -mass as $f(K)$ .

Another related work is that of Algom and Hochman [3] which studied the self-embedding problem for Bedford–McMullen carpets. They discovered that if a carpet is created by an $m\times n$ grid with $({\log m}/{\log n})\notin {\mathbb {Q}}$ and is not a product set, then any similitude mapping it into itself must be an isometry composed of reflections about lines parallel to the axes.

There is also research on variants of the above embedding problem including, among others, affine embeddings of self-similar sets [2] and embeddings between self-similar or self-affine sets [1, 4, 10, 13].

The paper is mainly devoted to a seemingly innocent question as follows.

Question 1.1. [7, Question 9.3]

If $\Phi $ satisfies the SSC and f is a contracting similitude mapping K into itself, must $f(K)$ be relatively open in K?

As was mentioned before, Elekes, Keleti and Máthé [7] showed that $f(K)$ contains many interior points. Unfortunately, this is still far from the openness of the whole set $f(K)$ . If $f(K)$ is simply a level-n cell (see Definition 2.1) for some $n\geq 1$ , then it is certainly open. Nevertheless, there are indeed many scenarios in which $f(K)$ crosses two or more cells (please refer to [7, Theorem 6.2] for an example). The way $f(K)$ embeds K can be very intricate and we rarely know anything about it.

Our first result is to establish the openness of $f(K)$ when all similitudes in $\Phi $ share a common contraction ratio and orthogonal transformation.

Theorem 1.2. Let $K\subset {\mathbb {R}}^d$ be the self-similar set generated by an IFS $\Phi =\{\varphi _i\}_{i=1}^m$ , where $\varphi _i(x)=r_iO_ix+a_i$ . Suppose $\Phi $ satisfies the SSC and f is a similitude with $f(K)\subseteq K$ . If $r_i=r$ and $O_i=O$ for all $1\leq i\leq m$ , where $0<r<1$ and O is a $d\times d$ orthogonal matrix, then $f(K)$ is relatively open in K.

Somewhat surprisingly, when the orthogonal parts are allowed to vary, we are able to construct a ‘counterexample’ (please see Example 2.6) to the above openness statement. In other words, we have the following result.

Theorem 1.3. Removing the assumption that $O_i\equiv O$ in Theorem 1.2, $f(K)$ need not to be relatively open in K.

We remark that in Theorem 1.2, one cannot hope to relax the SSC to the OSC. For example, $\{\tfrac 12x,\tfrac 12x+\tfrac 12\}$ is a generating IFS of the unit interval $[0,1]$ which satisfies the OSC, but $f([0,1])$ is clearly not an open subset of $[0,1]$ for any contracting similitude f.

There is also a forklore open question closely related to Question 1.1: are there two self-similar IFSs on ${\mathbb {R}}^d$ which generate the same attractor, such that one satisfies the OSC but not the SSC, and the other satisfies the SSC? Recently, Feng, Ruan and Xiong [11] gave a negative answer for homogeneous cases. More precisely, they proved that if a self-similar set admits a homogeneous generating IFS (that is, all the similitudes in that IFS share a common contraction ratio) with OSC but not SSC, then any generating self-similar IFS of it cannot satisfy the SSC. As pointed out in their paper, an affirmative answer to Question 1.1 would lead to a negative answer to the above question. Thus, if we not only require the IFS to be homogeneous but also to satisfy the ‘same orthogonal parts’ assumption, then we get a stronger conclusion (Theorem 1.2); but if the orthogonal parts can vary, then one cannot expect an affirmative answer of Question 1.1. For research on generating IFSs of self-similar sets, interested readers can refer to [5, 6, 12] and references therein.

Finally, by using the idea in the proof of Theorem 1.2, we can give a partial positive answer to another interesting question as follows.

Question 1.4. [12, Open Question 1]

Let $\{rx+a_i\}_{i=1}^m$ and $\{-rx+b_j\}_{j=1}^{m'}$ be two self-similar IFSs on ${\mathbb {R}}$ generating the same attractor S. If both of them satisfy the OSC, must S be symmetric?

This was answered in the affirmative in [12] under a strong assumption called the convex open set condition, that is, the open set in the definition of the OSC can be chosen as a non-degenerate open interval. We are able to prove the desired symmetry under the SSC.

Theorem 1.5. Let $S\subset {\mathbb {R}}$ be a self-similar set. Suppose there are two generating IFSs $\{rx+a_i\}_{i=1}^m$ and $\{-rx+b_j\}_{j=1}^{m'}$ of S and both of them satisfy the SSC. Then $-S=S+c$ for some $c\in {\mathbb {R}}$ .

To prove Theorems 1.2 and 1.5, we first select a large n, group together those level-n cells that are close enough to each other, and regard each of them as a chain. For Theorem 1.2, we use an observation in [7] to reduce it to the case when f shares a common linear part with $\varphi _i$ . By carefully examining the locations of these chains, one can see that the image of every chain under f is exactly the image of some chain under some maps in $\Phi $ , which proves the theorem. Using similar ideas, if a self-similar set S admits two generating IFSs as in Theorem 1.5, one can show that there is a one-to-one correspondence between level- $1$ cells (with respect to one IFS) and those cells (with respect to the other one), from which it is standard to establish the symmetry.

We will use $|A|$ to denote the diameter of a set $A\subset {\mathbb {R}}^d$ , and we denote by

$$ \begin{align*} \operatorname{\mathrm{dist}}(A,B) = \inf\{\|x-y\|: x\in A, y\in B\}, \quad A,B\subset{\mathbb{R}}^d \end{align*} $$

the distance between A and B.

The paper is organized as follows. In §2, we prove Theorem 1.2 and construct an example to establish Theorem 1.3. In §3, we prove Theorem 1.5.

2 The relative openness problem

Let $\varphi _i,K$ be as in the beginning and let f be a similitude with $f(K)\subseteq K$ . We may of course assume that $f(K)$ is a proper subset of K. Write $f(x)=r_fO_fx+a_f$ , where ${0<r_f<1}$ , $O_f$ is an orthogonal matrix and $a_f\in {\mathbb {R}}^d$ . Write $\Lambda =\{1,2,\ldots ,m\}$ to be the alphabet and to be the set of words of length n. Also, let $\Lambda ^*=\bigcup _{n=1}^\infty \Lambda ^n$ denote the collection of all finite words.

Definition 2.1. For $n\geq 1$ and , we will refer to as a level-n cell.

Let us start with a special case where the linear part of f coincides with the common one of similitudes in $\Phi $ . This is actually not far away from general cases.

Proposition 2.2. Assume that $r_i=r$ and $O_i=O$ for all $1\leq i\leq m$ , where $0<r<1$ and O is an orthogonal transformation on ${\mathbb {R}}^d$ . If we not only have $f(K)\subset K$ but also $r_f=r$ and $O_f=O$ , then $f(K)$ is relatively open in K.

Proof. For convenience, we may assume that $|K|=1$ and write

$$ \begin{align*} I = \{1\leq i\leq m: \varphi_i(K)\cap f(K)\neq\varnothing\}. \end{align*} $$

If $\#I=1$ , say $I=\{i_0\}$ , then $f(K)\subseteq \varphi _{i_0}(K)$ . We claim that $f(K)=\varphi _{i_0}(K)$ . Otherwise, since $f(K)$ is a closed subset of $\varphi _{i_0}(K)$ , there is some $\omega \in \Lambda ^*$ such that $\varphi _{i_0\omega }(K)\cap f(K) = \varnothing $ . Writing $\alpha =\mathrm {dim}_{\mathrm {H}} K$ , it is well known that $0<{\mathcal {H}}^\alpha (K)<\infty $ (see [9, Theorem 9.3]). Thus,

$$ \begin{align*} {\mathcal{H}}^\alpha(f(K)) \leq {\mathcal{H}}^\alpha(\varphi_{i_0}(K)\setminus\varphi_{i_0\omega}(K)) < {\mathcal{H}}^\alpha(\varphi_{i_0}(K)) = r^\alpha{\mathcal{H}}^\alpha(K) = {\mathcal{H}}^\alpha(f(K)), \end{align*} $$

which leads to a contradiction. In particular, $f(K)$ is open as a level- $1$ cell. So it remains to consider when $\#I\geq 2$ .

Let $n\geq 1$ be so large that $r^n<\delta :=\min _{i\neq j} \operatorname {\mathrm {dist}}(\varphi _i(K),\varphi _j(K))$ . As a result, recalling that $|K|=1$ , the diameter of every level-n cell is strictly less than $\delta $ . For $\mathcal {J}\subseteq \Lambda ^{n-1}$ , we call a chain if the following two conditions are met:

1. (1) for any pair of , we can always find a sequence such that , , and for all $1\leq k\leq p-1$ ;

2. (2) for any , .

Let $\mathcal {E}$ denote the collection of all chains. Under these conditions, it is not hard to see that for any $E\in \mathcal {E}$ , there is exactly one $i\in I$ and $E'\in \mathcal {E}$ such that $f(E)\subseteq \varphi _i(E')$ .

To prove the proposition, it suffices to show that for every $E\in \mathcal {E}$ , there is some $E'\in \mathcal {E}$ and some $i\in I$ such that $f(E)=\varphi _i(E')$ . Suppose in contrast that there exists $E_0\in \mathcal {E}$ not obeying this claim. Pick $i_1\in I$ and $E_1\in \mathcal {E}$ so that $f(E_0)\subset \varphi _{i_1}(E_1)$ . Inductively, for each $k\geq 1$ , we can find the unique $i_{k+1}\in I$ and $E_{k+1}\in \mathcal {E}$ such that $f(E_k)\subseteq \varphi _{i_{k+1}}(E_{k+1})$ . Since $f,\varphi _{i_{k+1}}$ have the same contraction ratio, $|E_k|\leq |E_{k+1}|$ and ${\mathcal {H}}^\alpha (E_k)\leq {\mathcal {H}}^\alpha (E_{k+1})$ for all k. Roughly speaking, the size of these chains is ‘increasing’. Also, if ${f(E_k)\subsetneq \varphi _{i_{k+1}}(E_{k+1})}$ , then ${\mathcal {H}}^\alpha (E_k)<{\mathcal {H}}^\alpha (E_{k+1})$ .

Since $E_0$ does not obey our claim, $f(E_0)\subsetneq \varphi _{i_1}(E_1)$ . So ${\mathcal {H}}^\alpha (E_0)<{\mathcal {H}}^\alpha (E_1)$ and hence $E_0\neq E_1$ . Since there are only finitely many chains in $\mathcal {E}$ , we can find $1\leq s<t$ such that $E_s=E_t$ . Of course, we may assume that $(s,t)$ is the earliest such pair. Note that

$$ \begin{align*} {\mathcal{H}}^\alpha(E_s) \leq {\mathcal{H}}^\alpha(E_{s+1})\leq\cdots\leq {\mathcal{H}}^\alpha(E_t)={\mathcal{H}}^\alpha(E_s). \end{align*} $$

Combining with the observation in the end of the last paragraph, $f(E_k)=\varphi _{i_{k+1}}(E_{k+1})$ for all $s\leq k\leq t-1$ . Equivalently,

(2.1) $$ \begin{align} rOE_k+a = rOE_{k+1}+a_{i_{k+1}}\quad \text{for all } s\leq k\leq t-1. \end{align} $$

Since $f(E_{s-1})\subseteq \varphi _{i_s}(E_s)$ and $E_s=E_t$ , we have

$$ \begin{align*} \varphi_{i_t}(E_{s-1}) = rOE_{s-1}+a_{i_t} &= (rOE_{s-1} + a) +(a_{i_t}-a) \\ &= f(E_{s-1}) + (a_{i_t}-a) \\ &\subseteq \varphi_{i_s}(E_s) + (a_{i_t}-a) \\ &= rOE_s+a_{i_s}+a_{i_t}-a \\ &= rOE_t+a_{i_t}+a_{i_s}-a \\ &= rOE_{t-1}+a+a_{i_s}-a = \varphi_{i_{s}}(E_{t-1}), \end{align*} $$

where the second last equality follows from equation (2.1). In particular, $\varphi _{i_t}(K)\cap \varphi _{i_s}(K)\neq \varnothing $ . Then $i_t=i_s$ because of the SSC assumption. As a result, $E_{s-1}\subseteq E_{t-1}$ . However, by the definition of chains, we must have $E_{s-1}=E_{t-1}$ . This contradicts the ‘earliest appearance’ assumption on $(s,t)$ .

Remark 2.3. It is noteworthy that the above proof actually reveals more than the relative openness of $f(K)$ . More precisely, it shows that $f(K)$ is a finite union of level-n cells of K, where n is the smallest integer such that $r^n<\min _{i\neq j} \operatorname {\mathrm {dist}}(\varphi _i(K),\varphi _j(K))$ . Furthermore, the assumption ‘ $O_i\equiv O$ ’ can be relaxed as ‘ $O_i=O$ for all $i\in I$ ’.

To prove Theorem 1.2, we need the following two observations.

Lemma 2.4. [7]

Let g be a similitude on ${\mathbb {R}}^d$ . If $g(K)\subset K$ , then there are some integer $k\geq 1$ and two words such that .

Lemma 2.5. If $f^q(K)$ is an open subset of K for some integer $q>1$ , then so is $f(K)$ .

Proof. Otherwise, there is some $x\in K$ and a sequence $\{y_n\}_{n=1}^\infty \subset K$ such that $y_n\to f(x)$ but $y_n\notin f(K)$ . So $f^{q-1}(y_n)\to f^{q-1}(f(x))=f^{q}(x)$ but $f^{q-1}(y_n)\notin f^{q-1}(f(K))=f^q(K)$ , which contradicts the openness of $f^q(K)$ .

Proof of Theorem 1.2

By Lemma 2.4, we have for some $k\geq 1$ and . Let $n,n'$ be the length of and , respectively. Comparing the linear parts, we have $r_f^{k}r^nO_f^kO^n=r^{n'}O^{n'}$ . So $r_f^k=r^{n'-n}$ and $O_f^k=O^{n'-n}$ . Now, applying Proposition 2.2 to $\{\varphi _\omega : \omega \in \Lambda ^{n'-n}\}$ and $f^k$ , we see that $f^k(K)$ is an open subset of K. Then the theorem follows immediately from Lemma 2.5.

Below we present a counterexample when the orthogonal parts vary.

Example 2.6. For $\theta \in [0,2\pi ]$ , let $R_\theta =(\! \begin {smallmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end {smallmatrix}\!)$ be the corresponding rotation matrix as usual. We consider the IFS $\{\varphi _1,\ldots ,\varphi _9\}$ , where

$$ \begin{align*} \begin{aligned} \varphi_1(x)&=\tfrac{1}{6}x+(-\tfrac{15}{8},\tfrac{15}{8}), \quad \varphi_2(x)=\tfrac{1}{6}x+(-\tfrac{5}{2},-\tfrac{5}{4}), \quad \varphi_3(x)=\tfrac{1}{6}R_{3\pi/2}x+(-\tfrac{5}{4},-\tfrac{5}{4}), \\[5pt] \varphi_4(x)&=\tfrac{1}{6}R_{\pi/2}x+(-\tfrac{5}{2},-\tfrac{5}{2}), \quad \varphi_5(x)=\tfrac{1}{6}R_{\pi}x+(-\tfrac{5}{4},-\tfrac{5}{2}),\quad \!\varphi_6(x)=\tfrac{1}{6}x+(\tfrac{5}{4},-\tfrac{5}{4}),\\[5pt] \varphi_7(x)&=\tfrac{1}{6}R_{3\pi/2}x+(\tfrac{5}{2},-\tfrac{5}{4}), \quad \!\!\varphi_8(x)=\tfrac{1}{6}R_{\pi/2}x+(\tfrac{5}{4},-\tfrac{5}{2}), \!\quad \!\varphi_9(x)=\tfrac{1}{6}R_{\pi}x+(\tfrac{5}{2},-\tfrac{5}{2}). \end{aligned} \end{align*} $$

Letting $I=[-3,3]^2$ , it is easy to see that $\bigcup _{i=1}^9 \varphi _i(I)\subset I$ and hence one can use I as the initial invariant set to get the attractor K by iteration. In particular, $K\subset I$ . Moreover, $\varphi _1(I),\ldots ,\varphi _9(I)$ are disjoint and hence so are $\varphi _1(K),\ldots ,\varphi _9(K)$ . That is to say, this IFS satisfies the SSC. Please see Figure 1 for an illustration.

Figure 1. An illustration of the IFS and the attractor.

Write $E_2=\bigcup _{i=2}^5 \varphi _i(K)$ , $E_3=\bigcup _{i=6}^9 \varphi _i(K)$ , $P=[-3,-\tfrac 34]^2$ and $Q=[\tfrac 34,3]\times [-3, -\tfrac 34]$ . Clearly, $E_2$ and $E_3$ only differ by a translation. A key ingredient here is the symmetry of $E_2$ (respectively $E_3$ ): rotating it counterclockwise by any angle in $\{{\pi }/{2},\pi ,{3\pi }/{2}\}$ at the centre of P (respectively Q) gives us exactly the same set. Also, note that $K=\varphi _1(K)\cup E_2\cup E_3$ .

Consider $f(x)=\tfrac 16x+(\tfrac{15}{8},-(\tfrac{15}{8}))$ , where $(\tfrac{15}{8},-(\tfrac{15}{8}))$ is nothing but the centre of Q. We first claim that $f(K)\subset K$ . A direct computation gives us the following properties:

1. (1) $f\varphi _1=\varphi _6f$ ;

2. (2) $f(E_2)=\varphi _8(E_3)$ and $f(E_3)=\varphi _9(E_3)$ (due to the symmetry of $E_2,E_3$ ).

By property (2), writing $A=\varphi _8(E_3)\cup \varphi _9(E_3)$ , we have

$$ \begin{align*} f(K) &= f(\varphi_1(K)\cup E_2 \cup E_3) \\ &= f\varphi_1(K) \cup f(E_2) \cup f(E_3) \\ &= f\varphi_1(K) \cup \varphi_8(E_3)\cup \varphi_9(E_3) \\ &= f\varphi_1(K) \cup A. \end{align*} $$

Combining with property (1),

$$ \begin{align*} f(K) = \varphi_6f(K)\cup A = \varphi_6(\varphi_6f(K)\cup A) \cup A = \varphi_6^2f(K) \cup \varphi_6(A)\cup A. \end{align*} $$

An induction argument immediately implies

(2.2) $$ \begin{align} f(K) = \varphi^n_6f(K) \cup \bigcup_{k=0}^{n-1}\varphi_6^k(A)\quad \text{for all } n\geq 1. \end{align} $$

Note that $\operatorname {\mathrm {dist}}(\varphi ^n_6f(K),\bigcup _{k=0}^{n-1}\varphi _6^k(A))\leq |\varphi _6^{n-1}(K)|$ , which tends to zero as $n\to \infty $ . Thus,

$$ \begin{align*} f(K) = \overline{\bigcup_{k=0}^\infty \varphi_6^k(A)} \subset \overline{K} = K. \end{align*} $$

To see that $f(K)$ is not an open subset of K, let $x_1\in K$ be the fixed point of $\varphi _1$ . By equation (2.2) and recalling the definition of A, we have for all $n\geq 1$ that

$$ \begin{align*} f(K) \cap \varphi_6^n\varphi_7(K) &= \bigg( \varphi_6^{n+1}(K)\cup \bigcup_{k=0}^n \varphi_6^k(A) \bigg) \cap \varphi_6^n\varphi_7(K) \\ &= ( \varphi_6^{n+1}(K) \cap \varphi_6^n\varphi_7(K) ) \cup \bigcup_{k=0}^n ( \varphi_6^k(A) \cap \varphi_6^n\varphi_7(K) ) \\ &= \varnothing. \end{align*} $$

However, since $f\varphi _1=\varphi _6f$ and $\varphi _1^n(x_1)=x_1$ ,

$$ \begin{align*} \operatorname{\mathrm{dist}}(f(x_1),\varphi_6^n\varphi_7(K)) &\leq \operatorname{\mathrm{dist}}(f\varphi_1^n(K),\varphi_6^n\varphi_7(K)) \\ &= \operatorname{\mathrm{dist}}(\varphi_6^nf(K),\varphi_6^n\varphi_7(K)) \\ &\leq |\varphi_6^n(K)|, \end{align*} $$

which tends to $0$ as $n\to \infty $ . Therefore, $f(x_1)$ is not an interior point of $f(K)$ .

3 The symmetry problem

Let S, $\{rx+a_i\}_{i=1}^m$ and $\{-rx+b_j\}_{j=1}^{m'}$ be as in Theorem 1.5. Note that the SSC implies that $m'r^s=1=mr^s$ , where s denotes the Hausdorff dimension of S. In particular, ${m'=m}$ . To prove Theorem 1.5, we need a simple observation.

Lemma 3.1. If there are $t_1<t_2<\cdots <t_m$ and $\alpha \in {\mathbb {R}}$ such that both of $\bigcup _{i=1}^m (S+t_i)$ , $\bigcup _{i=1}^m ((-S+\alpha )+t_i)$ are disjoint unions and they are identical, then $S=-S+\alpha $ .

Proof. For notational simplicity, write $S'=-S+\alpha $ . Suppose in contrast that $S\neq S'$ . Similarly as in the beginning of the proof of Proposition 2.2, any one of S, $S'$ cannot be a proper subset of the other. So both of $S\setminus S'$ and $S'\setminus S$ are non-empty. Since $\bigcup _{i=1}^m (S+t_i)=\bigcup _{i=1}^m (S'+t_i)$ , it is not hard to see that

(3.1) $$ \begin{align} \bigcup_{i=1}^m ((S\setminus S')+t_i) &= \bigcup_{i=1}^m (S\setminus(S\cap S')+t_i)\nonumber\\ &= \bigg( \bigcup_{i=1}^m (S+t_i) \bigg) \setminus \bigg( \bigcup_{i=1}^m ((S\cap S')+t_i) \bigg)\nonumber\\&= \bigg( \bigcup_{i=1}^m (S'+t_i) \bigg) \setminus\bigg( \bigcup_{i=1}^m ((S\cap S')+t_i) \bigg)\nonumber \\ &= \bigcup_{i=1}^m ((S'\setminus S)+t_i), \end{align} $$

where the second equality is due to the disjointness of $\{S+t_i\}_{i=1}^m$ .

Write $e=\inf (S\setminus S')$ and $e'=\inf (S'\setminus S)$ . Then by equation (3.1),

$$ \begin{align*} e+t_1=\inf \bigg( \bigcup_{i=1}^m ((S\setminus S')+t_i) \bigg) = \inf \bigg( \bigcup_{i=1}^m ((S'\setminus S)+t_i) \bigg) = e'+t_1. \end{align*} $$

So $e=e'$ . Choose $\{x_k\}_{k=1}^\infty \subset S\setminus S'$ with $\lim _{k\to \infty } x_k=e$ and let $0<\delta <t_2-t_1$ be any small real number. Such a sequence exists because both of S, $S'$ are perfect sets. Note that when k is sufficiently large, $x_k+t_1<e+t_1+\delta <e+t_2$ , implying that ${x_k+t_1\notin (S\setminus S')+t_j}$ for all $2\leq j\leq m$ . Since $e=e'$ , we also have for all large k that $x_k+t_1<e'+t_2$ and hence $x_k+t_1\notin (S'\setminus S)+t_j$ for all $2\leq j\leq m$ . By equation (3.1), $x_k+t_1\in (S'\setminus S)+t_1$ for all large k. However, this contradicts the fact that ${x_k\in S\setminus S'}$ .

Proof of Theorem 1.5

Without loss of generality, we may assume the convex hull of S to be $[0,1]$ and both of $\{a_i\}_{i=1}^m$ , $\{b_i\}_{i=1}^m$ are increasing sequences. In particular, ${a_1=0}$ and ${b_1=r}$ . For convenience, let $\varphi _i(x)=rx+a_i$ and $\psi _i(x)=-rx+b_i$ . Then $a_i$ , ${a^{\prime }_i :=b_i-r}$ are the left end points of $\varphi _i(S)$ , $\psi _i(S)$ , respectively. Using Lemma 3.1, it suffices to show that $a^{\prime }_i=a_i$ for all $1\leq i\leq m$ . We will prove this by induction.

Similarly as in the proof of Proposition 2.2, pick $n\geq 1$ so large that

$$ \begin{align*} r^n<\min_{i\neq j}\operatorname{\mathrm{dist}}(\varphi_i(S),\varphi_j(S)), \end{align*} $$

adopt the definition of chains there (using this integer n) and denote by $\mathcal {E}$ the collection of chains of S. By definition, the convex hulls of these chains are disjoint. This allows us to enumerate $\mathcal {E}=\{E_1,\ldots ,E_N\}$ so that $E_1,\ldots ,E_N$ are located from left to right. Since every $\psi _i$ can be regarded as a self-embedding similitude of $S=\bigcup _{i=1}^m \varphi _i(S)$ , similarly again as in the proof of Proposition 2.2, for each $1\leq i\leq m$ and $1\leq t\leq N$ , there are unique $i',t'$ such that $\psi _i(E_t)\subseteq \varphi _{i'}(E_{t'})$ .

Clearly, $a^{\prime }_1=b_1-r=0=a_1$ . Suppose $a^{\prime }_i=a_i$ for all $1\leq i\leq p$ . Recall that $a_i$ , $a^{\prime }_i$ are the left end point of $\varphi _i(S)$ and $\psi _i(S)$ , respectively. Since $\psi _i(E_N)$ lies on the left end of $\psi _i(K)$ , we have for all $1\leq i\leq p$ that $\psi _i(E_N)\cap \varphi _i(E_1)\neq \varnothing $ . Thus, $\psi _i(E_N)\subseteq \varphi _i(E_1)$ . Also, the inclusion in turn indicates that

(3.2) $$ \begin{align} \varphi_i(E_N) = rE_N+a_i &= -(-rE_N+b_i)+a_i+b_i \nonumber\\ &= -\psi_i(E_N)+a_i+b_i \nonumber\\ &\subseteq -\varphi_i(E_1)+a_i+b_i \nonumber\\ &= -rE_1+b_i \nonumber\\ &= \psi_i(E_1). \end{align} $$

In particular, $\psi _i(E_1)\cap \varphi _i(E_N)\neq \varnothing $ . It then follows from the ‘uniqueness’ statement in the end of the last paragraph that $\psi _i(E_1)\subseteq \varphi _i(E_N)$ . Together with equation (3.2), $\varphi _i(E_N)=\psi _i(E_1)$ for $1\leq i\leq p$ . As a result, ${\mathcal {H}}^s(E_1)={\mathcal {H}}^s(E_N)$ and hence $\varphi _i(E_1)=\psi _i(E_N)$ for $1\leq i\leq p$ (due to the inclusion relationship before equation (3.2)).

If $a^{\prime }_{p+1}<a_{p+1}$ , then $a^{\prime }_{p+1}\in \bigcup _{i=1}^p \varphi _i(S)$ . Thus, $\psi _{p+1}(E_N)\cap \bigcup _{i=1}^p \varphi _i(S)\neq \varnothing $ and hence $\psi _{p+1}(E_N)\subset \bigcup _{i=1}^p \varphi _i(S)$ . So there are $1\leq k\leq p$ , $1\leq s\leq N$ such that $\psi _{p+1}(E_N)\subseteq \varphi _k(E_s)$ . A similar argument as in equation (3.2) implies that $\psi _{p+1}(E_s)=\varphi _k(E_N)$ . However, we also have by the induction hypothesis that $\psi _k(E_1)=\varphi _k(E_N)$ . So

$$ \begin{align*} \psi_k(S)\cap\psi_{p+1}(S) &\supseteq \psi_k(E_1) \cap \psi_{p+1}(E_s) \\ &= \psi_k(E_1)\cap\varphi_k(E_N) = \psi_{k}(E_1) \neq\varnothing, \end{align*} $$

which contradicts the SSC. Similarly, $a_{p+1}<a^{\prime }_{p+1}$ is impossible. So $a^{\prime }_{p+1}=a_{p+1}$ . This completes the induction.