1. Introduction
Understanding the flow in ice divides is of singular importance owing to their being favoured locations for ice-core drilling. The non-linear rheology of ice means that over a zone a few ice-sheet thicknesses wide the flow in the vicinity of ice divides cannot be described by the shallow-ice approximation (Raymond, 1983). In particular, the vertical strain rate is markedly different, leading to different predicted age–depth relationships (Raymond, 1983; Reeh, 1988) in stationary divides than in the remaining part of the ice sheet. The different vertical velocities lead to a theoretical prediction that marker layers in the divide area will be higher than in the flanking areas, a phenomenon popularly known as “Raymond bumps”. The variation of steady divide position with asymmetric forcing of the ice sheet (e.g. by accumulation rate) has been considered by Weertman (1973) and, in the specific context of the influence of divide migration on flow modelling of the GRIP and GISP2 cores, by Anandakrishnan and others (1994).
Movement of the divide causes these flow patterns to migrate horizontally through the ice, which is itself flowing. There is clearly an important issue of the expected transient variation of ice-divide position; if this is only expected to be a few ice-sheet thicknesses, the complicating influence will be concentrated in a small area, while, if the expected variation of divide position is large, the complicating influence will only exist in a particular ice zone for a short time and it may be possible to neglect it. Larger variation in divide position will spread out the Raymond bumps. If, as seems likely, the Special flow fields in divides are liable to produce folding of the ice (Alley and others, 1995), then repeated reversals of divide-migration direction may potentially produce repealed folding events within the ice. One purpose of this paper is to investigate whether stochastic variability of climate can produce these reversals in divide-migration direction. This is potentially an explanation for folding seen in many sites distant from the divide; ice becomes heavily folded under a (stochastically) migrating divide, and then is transported, folded, to the distant sites. Even if pure shear is occurring in the rest of the ice sheet, the folding will be preserved, although the limbs will clearly be heavily attenuated.
The investigation in this paper concentrates on divide motion forced by anti-symmetric accumulation forcing. It is obvious that margin position can have a far greater influence on divide position than any other factor, but in ice sheets like on Greenland and around the Antarctic Peninsula, margin position is determined by the heavily red-shifted sea-level record, which may not produce the same short-term variability in divide position.
The technical procedure used in this paper is based on the recognition that while the flow within ice divides cannot be calculated using the shallow-ice approximation, their position (to the order of the ice-sheet thickness) can. If the movement of the divide over a period of interest is greater than the breadth of the region of anomalous flow, then the shallow-ice approximation can be used to determine how large a region the moving divide can be expected to cover. Nevertheless, we expect from the analysis presented by Weertman (1973) that the expected variation in divide position, normalized by the span, will be small, possibly smaller than typical finite-difference grids, with the implication that moving-grid techniques need to be used, and also implying that study of the linearized ice-sheet evolution equations can yield applicable equations. We thus perform the anti-symmetric perturbation around the Vialov–Nye fixed-span solution through a coordinate stretching, using the correct regularity condition for the moving divide and solve the consequent eigen problem, Ice divides are difficult areas to work with theoretically, and this is also true when considering application of the shallow-ice approximation (Hutter, 1983; Szidarovszky and others, 1989). The profile is singular (e.g. Fowler, 1992) and the nature of the singularity describing the anti-symmetric, migrating divide has only been established recently (Hindmarsh, unpublished). It is clearly important that analyses which have been correctly executed should be used to examine the stochastic variability of divides.
The analyses reported in this paper tell us that, for internal deformation of ice according to a Glen rheology, the time-scale for decay of the slowest anti-symmetric mode is 16 times less than the fundamental thickness/accumulation-rate time-scale for the ice sheet, implying relaxation times of 200 years for the Antarctic Peninsula divides and around 600 years for the central Greenland divide. Steady-state divide position is most sensitive to accumulation forcing near the divide, but large divide motions are forced most efficiently by an accumulation distribution which reaches ils maximum half-way between divide and margin. The corresponding relaxation constant for symmetric configurations is 9 times the fundamental time-scale (Hindmarsh, unpublished). Other configurations with O(1) variations in basal topography yield eigenvalues of between 6 and 15 times the fundamental rate, with an increase in relief of basal topography causing divides to decay more slowly from anti-symmetric perturbation.
We consider the evolution of the slowest mode being stochastically forced by the anti-symmetric accumulation-rate variation projected on to the eigenfunction associated with the slowest mode. This yields a Langevin equation whose asymptotic behaviour is, for forcing by white noise, an Ornstein–Uhlenbeck process which relates the expected variation of the divide position to the expected variation of the anti-symmetric accumulation rate.
2. The Stokes’ Equation and the Ice-Sheet Equation
In this paper we shall restrict consideration to plane flow. In two space dimensions the Stokes’ equations, which describe momentum balance, are

where τ ij represents the components of the deviator stress tensor and we represent the horizontal and vertical dimensions by x 1, x 2 or x, z as convenient. The acceleration due to gravity is represented by g i and the pressure by p. Specification of a viscous relationship and appropriate boundary conditions permits solution of the Stokes” equations, which are usually obtained numerically. Normally we consider a reduced model obtained from an affine scaling of the Stokes’ equations. This scaling is equivalent to the “stretched coordinates” used by Hutter (1981) which are completely different from the stretched coordinates we use later. The affine scaling yields simple functional forms for the vertical variation of the stress field and a considerable computational saving, further manipulation of the reduced model results in the ice-sheet equation

where H(x, t) is the thickness of the ice sheet, s(x, t) is the upper surface, a is the surface mass-balance exchange and t denotes time. Boundary conditions for this model are
These equations describe the evolution of ice-sheet thickness where the flow mechanism is either internal deformation according to some non-linearly viscous flow law or sliding according to some Weertman-type law. The analyses we shall carry out are not in principle limited to these situations but tractability, which we are seeking in the first instance, does appear to impose such limits.
The most important point to grasp is that in a small region of length a few ice-sheet thicknesses around the ice divide (where the surface slope is zero) the reduced model is known not to apply. However, while the flow in this region must therefore be computed using the Stokes equations, large-scale variations in its position are determined principally by flow in regions where the reduced model holds, and one can therefore compute divide translation on the large scale by solution of the evolution Equation (2). Because the flow in the region of the divide gives different age–depth relationships in cores (Raymond, 1983; Reeh, 1988) to those found in the rest of the ice sheet, migration of the divide will disturb age–depth relationships. The purpose of the analysis is to estimate the likely magnitude of this effect.
The quantity C is directly related to either a weighted vertical average rate factor Ā d defined below in Equation (17) of the rate factor A d used in the viscous relationship
where E is a second invariant of the deformation rate and τ is a second invariant of the deviator stress (Glen, 1955) or comes from a sliding relation of the form

(Weertman, 1957) where U b is the sliding velocity. We construct the following quantities for use in the general evolution equation



The derivation of the evolution Equation (2) using the shallow-ice approximation is standard (Hutter, 1983; Morland, 1984; Fowler, 1992). The following derivation is not essentially different from these and may also be found in Hindmarsh (unpublished). Let vertical distances be scaled by a thickness magnitude [H], horizontal distances by a magnitude [S], accumulation rates by [a], time by [t] = [H]/[a] and rate factor [C] by

The scale magnitude of the shear stress [τ xz ] is given by

Where
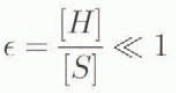
is the aspect ratio of the problem and [p] is the pressure magnitude. We also note that we have used density and gravitational acceleration magnitudes [ρ] and [g]. Henceforth, all quantities are assumed to be dimensionless.
The shallow-ice approximation (Hutter, 1983) expands the Stokes’ equations in terms of the aspect ratio, treating it as a global parameter representing deviation from static conditions. The quasi-static formula for the shear stress introduced into glaciology by Nye 1952)
is re-obtained as the asymptotic approximation

and the shallow-ice approximation also yields

while the viscous relationship may be approximated

Substitution of the approximate relationship (13) and two integrations with respect to z yields a formula for the ice flux q,

where

and where
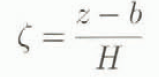
is a normalized vertical coordinate and b represents the base of the ice sheet. If instead we are dealing with sliding, then

and use of the continuity equation
results in the non-linear diffusion type Equation (2).
The Vialov–Nye (VN) (Vialov, 1958; Nye, 1959) solution is computed by setting ∂ t H = 0 and a = am0, C = C m0, both constants, in Equation (2) and integrating the resulting ordinary differential equation (ODE). It is convenient to work in terms of a normalized profile η(ξ), where

The VN solution is

and

where
We shall also use the construction

Following Weertman (1973), one may compute the effect of a step change in the parameters on the divide position. Consider an ice sheet where the distance from left and right margins to divide are S L, S R, respectively. Since the elevations of the two sections must be equal at the divide by definition, we see that

where additional subscripts R and L indicate the constant values of accumulation rate or rate factor on the left or right side of the divide. For example, a 2:1 ratio in accumulation rates yields
when we choose v = 3 ⇒ δ = 4. The normalized deviation of the divide from the centre position is given by

for the ease mentioned above.
We are also interested in more general eases, where the bed profile is varying smoothly but with O(1) variations in elevation. This does not violate reduced model assumptions (Morland and Johnson, 1980) but does now mean that the zeroth-order solution is no longer analytical. With VN boundary conditions, one may integrate from the margin where the discharge and elevation are known and obtain the divide elevation without any need for shooting. The equation for the steady profile is

which has first integral

and s(x) is obtained by numerical solution of this ODE. This is singular at the margin x = L, where it is known (e.g. Hindmarsh, 1995) that the local expansion is of form

and we can solve for k by noting that at this order at and near the margin q = aL and substituting for s and ∂ x s in the flux relations (16) and (19) to obtain

whence we solve for k,

Starting the integration at the margin, a forward Euler starting step over a discretization interval ∆ x is given by

The profile is then integrated back to the divide using Taylor expansions. At the final step we use the divide local expansion (Fowler, 1992)

where k d is a constant. We may compute

and thus s(0), and we define
3. Anti-Symmetric Linearizations around the Vn Solution
Linearizations around the VN solution have been considered in detail by Hindmarsh (unpublished). There, symmetric and anti-symmetric perturbations are considered in detail, and the resulting numerical eigenvalue problem is solved in a number of ways in order to ensure accuracy, using (i) finite discretization methods and (ii) Prüfer–Pruess shooting methods (see Pryce, 1993). We refer the interested reader to Hindmarsh (unpublished) for further details of the techniques used. We shall use the more accurate Prüfer–Pruess method. In this section we extend the analysis of Hindmarsh (unpublished) by considering beds which have general symmetric topography in the zeroth-order solution.
3.1. Regularity conditions for a moving divide
In the general asymmetric case the divide will move. Since the divide curvature is in general singular (Weertman, 1961; Fowler, 1992), we need to examine the nature of the expansion around the moving divide to assure ourselves that we are respecting regularity conditions. We summarize the construction of Hindmarsh (unpublished).
There are three requirements for a moving divide expansion, which we suppose occurs at a point x = x d; (i) the slope is zero; under reduced model assumptions, this implies that the flux is zero; (ii) there is a finite lowering rate. i.e. ∂q/∂x is finite; (iii) there is a finite migration rate. Under shallow-ice approximations, the divide slope is zero. Since the divide is the point ∂ x s(x = x d ) ≡ 0, we may write

where M d is the migration velocity of the divide. The differentiated form of the mass conservation condition is

(surface mass-exchange gradient does not enter into the analysis at this order) and assuming that the profile s is sufficiently well behaved at the divide that ∂ x ∂ t s = ∂ t ∂ x s (which tan be confirmed a posteriori) we can substitute the differentiated conservation condition into Equation (33) to eliminate ∂ x ∂ t s to obtain
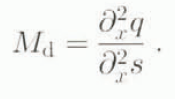
We consider a more general case where the divide is at x = x
d and define a local coordinate ![]() = x − x
d
, and -set k = sgn(x − x
d). The expansion consistent with these requirements is
= x − x
d
, and -set k = sgn(x − x
d). The expansion consistent with these requirements is

where the first two terms are the usual divide expansion (Fowler, 1992) and the third term enables the divide to move. The constants e 1 and e 2 emerge from solutions to the parabolic equation describing the evolution of ice-sheet profile (Equation (2)). The constant e 1 tells us about the curvature of the divide, (if e 1 = 0, the divide is flat), while the constant e 2 tells us about the asymmetry of the divide.
3.2. The stretched coordinate system
If a divide moves, there will clearly be a position where the perturbed slope is non-zero but the zeroth-order solution has zero slope. For flux relations where the slope enters non-linearly (here, as a result of Glen’s power-law deformation relationship), this will cause any assumption about the perturbed quantities being much smaller than the zeroth-order solution quantities to be violated. The standard resolution to this technical problem is to use stretched coordinates (e.g. Halfar, 1981; Fowler, 1992) illustrated in Figure 1. Rather than let the profile perturb, we let the independent space coordinate stretch in such a way that the transformed ice-sheet evolution equation satisfies the assumptions of a perturbation being small. We then construct an evolution equation for the profile perturbation. Because this is an anti-symmetric perturbation, by construction the average elevation and in particular the elevation at the perturbed divide will not change.

Fig. 1. The stretched coordinate system. Vertical axis ξ, horizontal axis ξ*. Solid line is the symmetric VN solution ξ = η(ξ), ξ = ξ*, while dashed line is a non-symmetric solution η(ξ(ξ*)), ξ = 1 + ξ* − ξ* 2. The dolled tine is a graph of ξ − ξ* = 1 − ξ* 2, which represents the deviation of the stretched coordinate system from the configuration yielding a symmetric ice-sheet profile, In this paper, non-symmetric ice-sheet configurations are described by similar coordinate stretchings.
The procedure used has been given in detail by Hindmarsh (unpublished) and the important features are described here. To construct the stretched coordinate system we write

and solve for ξ with ξ *, t * as the independent variables. Here ξ * = 0 defines the divide position which is given directly by ξ = X(0, t *). The key point is that ξ is the physical coordinate but ξ * is the independent variable.
We may construct an evolution equation for η from Equations (2), (21) and (22):

Then, by substituting into the above equation the dynamic stretching transformation (Equation (36)) and eliminating η(ξ, t) in favour of η 0(ξ *) a non-linear evolution equation for Χ(ξ * ,t), given in Hindmarsh (1996), is obtained. We shall treat the small perturbation ease and consider a linearized problem which can therefore be superposed on to solutions from the symmetric perturbation, Halfar (1981), who carried out an anti-symmetric ice-sheet perturbation using a stretched coordinate system, found infinite tangents at the divide, but no such problems are found here, presumably because we ensure that we respect the regularity condition for an asymmetric divide (Equation (35)). Thus, we perturb the Stretched coordinate system, again using a small parameter μ, writing
We must have Χ 1(−1, t) = X 1(−1, t) = 0, in order to ensure that the position of the margin is fixed (a condition of the VN solution), while the value of X 1(0, t) determines the position of the divide in ξ space and in x space. (Physically, t * is identical to t.) We allow perturbations in the accumulation
where the perturbed forcing function is an anti-symmetric function of the spatial coordinate.
Hindmarsh (unpublished) showed that to zeroth order the ice-sheet evolution equation is simply

which is true by construction, and to first order

where
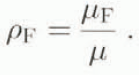
it we wine
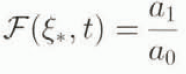
and multiply Equation (41) by a Sturm–Liouville multiplier S(ξ *),we find that we can write the evolution equation for X 1 in a self-adjoint form

Where

and where we have taken (v − 1)/2 = O(1). This equation is to be solved over the domain ξ * ∈ [0, 1] and X 1 will be an even function about zero.
The small parameter μ is now interpreted an acceptable relative modelling error ℰ in the perturbed divide position, which will thus depend upon how the solution is being used. Under steady conditions, the lefthand side of Equation (44) is zero, and to balance the righthand side we need

i.e. the acceptable (anti-symmetric) forcing magnitude is v limes the acceptable relative error in the perturbed position. Provided this is accepted as an operational rule, it is now computationally convenient to take μ F = μ = ρ F = 1, and this convention will be followed in the rest of this paper.
Let its consider for the moment the homogeneous problem, setting ![]() a
= 0, we write X
1(ξ
*,t
*) in a separated form
a
= 0, we write X
1(ξ
*,t
*) in a separated form
substitute this into Equation (44) to obtain


where λ is the eigenvalue of the problem. The time equation has solution
where T *0 represents an initial condition, and the second order equation in space can be written in Sturm-Liouville from as

4. Computation Of The Eigenvalues
Solutions to the linearized eigenvalue problem and computation of Green’s functions have been considered for the perturbation about the VN solution and have been described in detail by Hindmarsh (unpublished), who compared the results from finite-difference discretizations and shooting methods. The perturbation problem is as above, and we note that the Prüfer–Pruess solver we use (SLEDGE; Pruess and Fulton, 1993) has automatic end-point analysers, which deal with the singular nature of the boundary-value ordinary differential equation for the perturbation.
We consider results for five diffèrent cases, all of which have a bed-function defined by

and with {b 0} = 2 v /(γ+1) × [0, 0.25, 0.5, 0.75, 1, 1.25], and v = 3, δ = 4, γ = 7 and ξ ℓ = 1/2. These are values suitable for internal deformation of the ice according to Glen’s flow relation. The results of the computation of the zeroth’Order solution are shown in Figure 2 and indicate features like the maximum ice elevation, which does not increase at the same rate as the maximum bed elevation.

Fig. 2. Zereth-order profiles z = s(x) (solid line) for five bed profiles z = b(x) (dotted line) including a fat bed. Highest ice-sheet profiles correspond to highest bed profiles, etc. Horizontal axis x, vertical axis z.
Computations by SLEDGE yielded the eigenvalues shown in Table 1 for the slower modes. These eigenvalues can be regarded as relaxation-rate constants in inverse time units set by the scale [a]/[H]. Relaxation time-scales for a typical Antarctic Peninsula ice cap, the Greenland ice sheet and East Antarctica are indicated in this table. The computed eigenvalues show that divide relaxation limes for the Antarctic Peninsula are between 200 and 500 years, for Greenland are 500–1000 years and for East Antarctica are 5000–10 000 years. Forcing at frequencies higher than these values will be filtered by the ice sheet. This is likely to be true of forcings not considered explicitly in VN-type models, for example of margin position by sea-level rise and fall. Sturm–Liouville theory shows that
This relationship is accurate enough for our purposes for i ≥ 1 and the constant of proportionality can be deduced with sufficient accuracy from Table 1 as being the same as the eigenvalue for the first mode.
Table 1. Eigenvalues and relaxation time-scales for linearized divide motion. The meaning of the parameters describing cases 1–9 are explained in the text, and the first eigenvalue λ1 and the value of the corresponding eigenvalue at the divide ℇ1(0) are indicated. The corresponding divide-motion relaxation times for Greenland (G, [H] = 3000 m, [a] = 0.3 m year−1, [t] = 100 00 years), Antarctic Peninsula (AP, [H] = 1000 m, [a] = 0.3 m year−1, [t] = 3000 years), East Antarctica (EA, [H] = 3000 m, [a] = 0.03 m year−1, [t] = 10 000 years) are shown. Case 10 refers to the predictions of the relaxation time by the 0D scale model, where the eigenvalue is 1/(2n +2): this corresponds to a symmetric perturbation (see Hindmarsh, unpublished)

5. Divide Migration
5.1. Steady divide position
It is shown in the Appendix that we may solve the non-homogeneous equation through the equation


where y is a dummy variable, ℇ i (ξ *) is an eigenfunction for mode i, the kernel K is a non-symmetric influence function (see Equation (66) in the Appendix) and G is a symmetric Green’s function.
This has been computed for the case v = 3, m = 5 δ = 4, γ =7. We are only really interested in K(0, y). This is the sensitivity of divide position to anti-symmetric forcing at position y and is illustrated in Figure 3. The key point is that steady-state divide position is most sensitively affected by accumulation close to the divide, which is perhaps obvious, but, as we shall shortly see, the sensitivity in the area around the divide belongs to the modes with the fastest response times, with the implication that stochastic excitation of these modes will not produce great variations in divide position.

Fig. 3. Divide position sensitivity functions K(0, y) for accumulation for the case v = 3, δ 5 = 4, γ = 7. Horizontal axis y.
5.2. Time-dependent behaviour
The different modes of the solution can be forced or excited by accumulation-rate variations. Each mode samples the anti-symmetric distribution differently in space, Let us consider a set of forcing functions ![]() so that
so that

where R i (t) is a function of time only. (Here. a si , is redundant, but in the stochastic counterpart to this ODE, a si , will be seen to be equivalent to the standard deviation of the forcing.)
Sturm–Liouville theory shows that the eigenfunction solutions to Equation (51) form a complete set, and are orthogonal with respect to the weighting function ![]() (ξ
*) given by Equation (45). The former fact means that we can write arbitrary
(ξ
*) given by Equation (45). The former fact means that we can write arbitrary ![]() as
as

The completeness of the eigenfunctions means drat we may write

and by using the definition of ![]() , orthogonality and the original partial differential equation (PDE) in Equation (44) we obtain
, orthogonality and the original partial differential equation (PDE) in Equation (44) we obtain
i.e. an ODE for the mode magnitude. This standard derivation is sketched in the Appendix.
The ξ
* dependence of the functions ![]() i
represents the sampling of the accumulation rate by the different modes. This dependence is plotted in Figure 4, which clearly shows that the slower modes sample preferentially approximately halfway between divide and margin, while the faster modes sample closer and closer to the divide. Even though for any one mode there is strong sampling at the margin, the sign oscillates with mode number magnitude and will cancel for smooth accumulation distributions. It must also be remembered that this is an anti-symmetric perturbation, with an increase in accumulation on one side of the ice sheet implying an equivalent decrease on the other side.
i
represents the sampling of the accumulation rate by the different modes. This dependence is plotted in Figure 4, which clearly shows that the slower modes sample preferentially approximately halfway between divide and margin, while the faster modes sample closer and closer to the divide. Even though for any one mode there is strong sampling at the margin, the sign oscillates with mode number magnitude and will cancel for smooth accumulation distributions. It must also be remembered that this is an anti-symmetric perturbation, with an increase in accumulation on one side of the ice sheet implying an equivalent decrease on the other side.

Fig. 4. Sampling of accumulation distribution by the solution modes, divided by their eigenvalue so as to indicate then relative importance in time-dependent behaviour. Horizontal position coordinate is ξ, ξ = 0 indicates divide. Even though the modes sample heavily near the margin, the sign changes with each mode and, in general, the effect will sum to zero. At the divide, sampling is all positive. Values for non-integral mode numbers have no mathematical inclining and are only drawn to improve the display.
We are less interested in the actual eigenfunctions X
1
, but we shall need the result that for v = 3, δ = 4, γ = 7 (internal deformation according to a Glen rheology) ℇ(0) ![]() 2 for all the cases considered here (table 1).
2 for all the cases considered here (table 1).
6. Stochastic Forcing of divide Position
We now present the main application of the paper, which is consideration of the stochastic forcing of divide position by and-symmetric accumulation forcing. The scientific issue is whether random variations in climate are likely to have produced large enough variations in divide position to affect seriously dating. This question cannot be answered fully without detailed modelling of the transition zone (see Schott and others (1992) for an example of modelling a stationary divide).
Let us write down the stochastic counterpart to the deterministic ODE in Equation (58) derived in the Appendix.
a Langevin equation for mode i,. where T *i is now a stochastic process ana Ξ it denotes a white-noise forcing with unit variance, i.e. where the spectral power density is independent of the wave number. At the moment we are more interested in the evolution and Steady-State value of 〈T i 2〉, the variance of mode i. This particular Langevin equation in the stochastic process T *i , with the restoring force linear in the deviation, and with the white-noise term entering additively, yields as its solution an Ornstein–Uhlenbeck process. We are interested in its asymptotic behaviour as t → ∞. It can be shown (e.g. Grimmet and Stirzaker, 1992, p.519) that the resulting probability distribution for T *i is Gaussian with the following relationship between the standard deviations

When one is considering a system of Langevin equations, the solution is more complicated, because one must specify the correlation between the white-noise processes driving the different ODEs. Since, in our case, the different modes are sampling the accumulation rate in space according to Figure 4, the cross-correlation between the noise processes driving each of the modes depends upon the spatial autocorrelation of the accumulation. Such considerations are somewhat beyond the coverage of available data. We thus suppose that the accumulation rate, although a white-noise process in time, is perfectly autocorrelated in space. Under these assumptions, the effects of random forcing of each mode are additive and we shall for simplicity consider the effects of forcing the slowest mode as this will be a valid order-of-magnitude estimate.
We are particularly interested in whether fluctuations in divide position are less or greater than the ice-sheet thickness, as this is the breadth of the region of anomalous flow (Raymond, 1983; Reeh, 1988). The divide position is given by X(0, t) = ℇ(0)T
1. As a basis for comparison, let us consider the case when the horizontal fluctuations in divide position have the same standard deviation as hall the ice-sheet depth (we lake half the ice-sheet depth because the divide position is fluctuating about both sides of the mean position). This occurs when the standard deviation of divide position is σ
εX = ![]() =
= ![]() = ε/2. The critical standard deviation σ
εa of the antisymmetric component of the accumulation rate required to produce this magnitude of divide-position fluctuation may be computed from this relationship and the Ornstein–Uhlenbeck solution in Equation (60), and is found to be
= ε/2. The critical standard deviation σ
εa of the antisymmetric component of the accumulation rate required to produce this magnitude of divide-position fluctuation may be computed from this relationship and the Ornstein–Uhlenbeck solution in Equation (60), and is found to be
Taking ε = (0.001 → 0.01) for typical ice sheets, the first eigenvalue of the anti-symmetric perturbation to be (6 → 16) and ℇ(0) = 2 (see Table 1), gives us a range of possible answers for the standard deviation of the critical standard deviation of the anti-symmetric accumulation-rate distribution σ εa , which are given in Table 2. The smaller this required standard deviation of anti-symmetric accumulation-rate distribution, the more likely it will be that the age–depth relations will have been influenced by stochastic forcing. To make this conclusion more precise, we need to look at some observed standard deviations.
Table 2. Standard deviation of anti-symmetric accumulation rate required to produce a normal probability distribution of divide position with standard deviation half the ice-sheet thickness

Problems in estimating standard deviations of accumulation rates have been discussed by Fisher and others (1985). They estimate normalized standard deviations of accumulation rates as being between 0.12 and 0.14 for Greenland (computed from column 3, table II, Fisher and others (1985)). The aspect ratio in Greenland is around 0.003. Fisher and others also suggested that the stochastic process is “blue”, that is it contains proportionally more power in the high-frequency part of the spectrum than in the low.
D. A. Peel (personal communication) stated that in the Antarctic Peninsula region the typical normalized standard deviation of inter-annual accumulation-rate values determined directly from stratigraphic measurements on ice cores is 0.3. Deposition noise (local spatial variations) and definition noise (error in assigning a calendar date to a stratigraphic horizon) are estimated to contribute an effective standard deviation of 0.13–0.17 (for accumulation rates of 0.9–0.4 m water year−1, respectively) to this estimate. The standard deviation of the true accumulation rate is then estimated at 0.22–0.26. The aspect ratio in the Antarctic Peninsula is around 0.004.
Unsmoothed periodograms of accumulation data from the Antarctic Peninsula (personal communication from R. Mulvaney) have been computed (see Fig. 5). Period-ograms are simply Fast Fourier transformations (FFT) of the data, and are very noisy, but do represent the data in its frequency domain in its least processed form. All that has been done here is to detrend the data, which removes the very lowest frequency components. The spectra, although noisy, are flat, showing that to a first approximation, these accumulation distributions can be viewed as a white-noise process rather than typical geophysical red-noise processes. This is consistent with the view of Fisher and others that accumulation-rate processes are white or blue rather than red. Normalized standard deviations are between 0.2 and 0.3. Elimination of deposition noise and definition noise still leave significant high-frequency variation which can be related to regional climate fluctuations such as the El Niño oscillation (personal communication from D. A. Peel).

Fig. 5. Unsmoothed periodograms of accumulation rates obtained from four Antarctic Peninsula sites (personal communication from R. Mulvaney). Horizontal axes are log10 of the frequency in a−1, while vertical axes are the log10 of the spectral power density. The periodograms show a flat response indicative of while noise.
It is not known to what extent these accumulation-rate processes are symmetric or anti-symmetric about the divides. If they are anti-symmetric (unlikely), the Antarctic Peninsula values would cause divide fluctuations to be 10–20 times greater than the breadth of the anomalous zone, which actually helps core dating, as the disruption is spread over a wider area. If the anti-symmetric component were a one-tenth of the measured standard deviation, fluctuations would be concentrated in the breadth of the anomalous zone, and increase the number of refolding events as each area would experience a larger number of flow-direction reversals.
In Greenland, if all the noise were anti-symmetric, this would cause the divide position to fluctuate over a zone 5–13 times the breadth of the anomalous zone. If one-tenth of the noise were anti-symmetric, this would cause divide fluctuations to be one-half of the zone of anomalous mechanics (the case λ = 6 corresponds to high elevation immediately beneath the divide and may not be realistic). This is likely to be enough to haw-significant observable effects.
When the estimated standard deviation of the divide is less than the breadth of the anomalous zone, the answer is not robust, as the flow within the anomalous zone can be expected to affect the standard deviation. It is nut known whether it will clamp or amplify the standard deviation.
7. Conclusions and Suggestions for Further Work
We have considered the problem of forcing of divide position through a linearization about the VN solution which includes the correct regularity condition for divide motion. A time constant for divide relaxation has been computed, and found to be 16 times smaller than the H/a time-scale for ice sheets, with plausible ranges of between 6 and 20 times the fundamental time-scale. High basal relief reduces the rate of relaxation. Divide-position relaxation time-scales are estimated to be about 200 years for the Antarctic Peninsula and 600 years for Greenland.
Depending on the geometry of the ice sheet and the bed topography, standard deviations of anti-symmetric accumulation distributions of between 0.003 and 0.08 are required to cause the divide to fluctuate in position with standard deviation half the breadth of the anomalous zone of ice flow. Larger deviations will spread the disruption over a larger area, diluting its effect, while smaller deviations will concentrate it, making flow modelling easier. Given that observed standard deviations (whose symmetry properties are not known) can be as high as 0.25, it seems very likely that divide position exhibits significant stochastic variation driven by accumulation-gradient variability.
Asymmetric migration of margin position has the dominating secular effect on divide position, but in much of Greenland and most of Antarctica this secular change will be forced by sea-level change, and not produce the higher-frequency forcing that seems to be present in the climate record and thus in accumulation forcing. Repeated reversals in divide-migration direction will produce conditions favourable for multiple-folding events, and thus forcing of divide position by accumulation-rate variations may have a more disruptive effect on ice cores than the larger changes induced by margin migration.
There is clearly a need for knowledge of the statistical characteristics of accumulation in time and in space. Radar-echo transects from divide to both margins might be able to pick up sufficient shallow layering to determine whether the random anti-symmetric component of accumulation variation is sufficiently strong to disrupt flow in divide areas.
It is likely that there is a sufficiently large anti-symmetric noise component to cause Raymond bumps to be spread out both in the Antarctic Peninsula and in Greenland.
Acknowledgements
I have had instructive conversations with A. Fowler, K. Hutter, R. Mulvaney, D. A. Peel, J. Pryce, E. Waddington and E. Wolff I should like to thank R. Greve for a careful and constructive review and K. Hutter for an excellent editing job. I used the SLEDGE driver written by M. Marietta.
Appendix
Kernel functions and mode-evolution equations
Consider tin inhomogeneous partial differential equation in self-adjoint form

Here, ![]() is a forcing flint lion with some physical meaning — for example, the first-order accumulation a
1 If we consider the corresponding homogeneous equation,
is a forcing flint lion with some physical meaning — for example, the first-order accumulation a
1 If we consider the corresponding homogeneous equation,

a standard separation of variable technique (i.e. setting X 1(ξ *,.t) = Χ *(ξ *)T(t)) can be used to yield two ordinary differential equations, the spatial one being in Sturm–Liouville form i.e.
Such an equation has eigenfunction solutions ℇ i (ξ *), i ∈ N which are orthogonal with respect to the weighting function, i.e.

where δ ij is the Kronecker delta and we have normalized the eigenfunctious appropriately. The eigenfunctions form a complete set and we may thus write

Substitution of this relation into the PDE in Equation (16). yields

which if one uses Equation (63) can be written

If we then multiply the whole equation by the eigen functions ℇ i (x), j ∈ N and integrate over the domain of the differential equation using y as a dummy variable we obtain

which, upon using the orthogonality relationships and Equations (55) and (56), becomes diagonabzed, yielding the system of equations

We are particularly interested in steady state, when

and using

we obtain the steady distribution in the form

By defining a Green’s function

we may solve the non-homogeneous equation through the equation

One may equally rewrite this as

and one has an equation with a non-symmetric kernel K we shall call the influence function.









