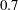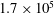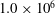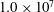1. Introduction
Thermally driven turbulence plays a major role in several natural phenomena, from oceanic and atmospheric circulations to convection in stars and planets. Equally apparent is the importance of turbulent thermal convection in industrial processes, which range from passive cooling of nuclear reactors to the controlled growth of crystals from the melt (Ahlers, Grossmann & Lohse Reference Ahlers, Grossmann and Lohse2009). A canonical flow for approaching all the cases above is Rayleigh–Bénard convection (RBC), which consists of a fluid layer heated from below and cooled from above in a vertically bounded domain (Siggia Reference Siggia1994).
At the present time, there are four major directions in the study of turbulent RBC (Xia Reference Xia2013). The first one concerns the scaling properties of heat transport, that is, how the Nusselt (
![]() $\mathit{Nu}$
) number depends on the Rayleigh (
$\mathit{Nu}$
) number depends on the Rayleigh (
![]() $\mathit{Ra}$
) and Prandtl (
$\mathit{Ra}$
) and Prandtl (
![]() $\mathit{Pr}$
) numbers. In this context, Grossmann & Lohse (Reference Grossmann and Lohse2000) proposed a theoretical model that has been found to fit experimental data over a wide range of parameters (Chillà & Schumacher Reference Chillà and Schumacher2012). Nevertheless, it is not clear if the unifying theory holds at very large
$\mathit{Pr}$
) numbers. In this context, Grossmann & Lohse (Reference Grossmann and Lohse2000) proposed a theoretical model that has been found to fit experimental data over a wide range of parameters (Chillà & Schumacher Reference Chillà and Schumacher2012). Nevertheless, it is not clear if the unifying theory holds at very large
![]() $\mathit{Ra}$
in the so-called ultimate regime; indeed, the existence of this state has not yet been confirmed (Xia Reference Xia2013). The effect of buoyancy on statistical properties of turbulence represents another major challenge nowadays. Despite many attempts, a clear identification of the Bolgiano–Obukhov scaling and the recovery of the Kolmogorov one at small scales is still missing (Lohse & Xia Reference Lohse and Xia2010). The last two topics of interest are boundary layer dynamics and coherent structures. These aspects play a paramount role in the transport mechanisms of heat and momentum, and hence a great effort has been made to study these two topics in order to refine the theoretical models (Grossmann & Lohse Reference Grossmann and Lohse2004; Stevens, Verzicco & Lohse Reference Stevens, Verzicco and Lohse2010).
$\mathit{Ra}$
in the so-called ultimate regime; indeed, the existence of this state has not yet been confirmed (Xia Reference Xia2013). The effect of buoyancy on statistical properties of turbulence represents another major challenge nowadays. Despite many attempts, a clear identification of the Bolgiano–Obukhov scaling and the recovery of the Kolmogorov one at small scales is still missing (Lohse & Xia Reference Lohse and Xia2010). The last two topics of interest are boundary layer dynamics and coherent structures. These aspects play a paramount role in the transport mechanisms of heat and momentum, and hence a great effort has been made to study these two topics in order to refine the theoretical models (Grossmann & Lohse Reference Grossmann and Lohse2004; Stevens, Verzicco & Lohse Reference Stevens, Verzicco and Lohse2010).
A topic that eludes precise classification concerns the description of turbulent RBC both in the physical space and in the space of turbulent scales. A focus on this subject seems to be well justified by the inherent multi-scale feature of convective turbulence. Indeed, the production, transport and dissipation of kinetic energy and temperature variance depend both on the scale considered and on the position in the physical space. In this scenario, a compound description in the physical/scale space is required for the correct understanding and modelling of the physics. The current literature shows many useful analyses of turbulent RBC in terms of the budgets of turbulent kinetic and temperature variance (Deardorff & Willis Reference Deardorff and Willis1967; Wörner & Grötzbach Reference Wörner and Grötzbach1998) and, more recently, of mechanical energy budgets (Gayen, Hughes & Griffiths Reference Gayen, Hughes and Griffiths2013). Nevertheless, these approaches are limited to a description in physical space alone. On the other hand, some works are devoted to an analysis only in the space of scales; see Domaradzki et al. (Reference Domaradzki, Liu, Härtel and Kleiser1994) for a numerical study of the inter-scale energy transfer in RBC. The present work completes the above-mentioned approaches by analysing, for the first time, turbulent RBC in the compound physical/scale space domain. To this end, generalized forms of both the Kolmogorov (Hill Reference Hill2002) and Yaglom equations are employed. These sophisticated tools are evolution equations for the second-order moment of the velocity (Kolmogorov equation) and temperature (Yaglom equation) increments between two points. As shown for the first time in Marati, Casciola & Piva (Reference Marati, Casciola and Piva2004) for a channel flow, the generalized Kolmogorov equation unveils an intricate and highly scale-dependent dynamics of turbulence. In the same context, a multi-dimensional description is found to be crucial for the understanding of the formation and sustainment of turbulent fluctuations (Cimarelli, De Angelis & Casciola Reference Cimarelli, De Angelis and Casciola2013).
The present work displays a similar approach for multi-scale analysis of turbulent RBC. Our goal here is to shed light on the self-regenerating cycle of turbulence in RBC by linking the scale-by-scale budgets obtained from the generalized Kolmogorov/Yaglom equation with the classic single-point energy budgets and the flow topology. Three direct numerical simulations (DNS) of turbulent RBC in a laterally unbounded domain between two parallel and horizontal walls have been performed at Prandtl number
![]() $\mathit{Pr}=0.7$
and at Rayleigh numbers
$\mathit{Pr}=0.7$
and at Rayleigh numbers
![]() $1.7\times 10^{5}$
,
$1.7\times 10^{5}$
,
![]() $1.0\times 10^{6}$
and
$1.0\times 10^{6}$
and
![]() $1.0\times 10^{7}$
. It is well known that an increase in the Rayleigh number affects the flow topology in such a way that the turbulent structures, the so-called thermal plumes, become less coherent due to the increasing intensity of the turbulent background. However, a clear footprint of the presence of thermal plumes can be observed also at large Rayleigh numbers, highlighting how these structures play a crucial role in the statistical behaviour of convective turbulence. In the text, data from the simulation at larger
$1.0\times 10^{7}$
. It is well known that an increase in the Rayleigh number affects the flow topology in such a way that the turbulent structures, the so-called thermal plumes, become less coherent due to the increasing intensity of the turbulent background. However, a clear footprint of the presence of thermal plumes can be observed also at large Rayleigh numbers, highlighting how these structures play a crucial role in the statistical behaviour of convective turbulence. In the text, data from the simulation at larger
![]() $\mathit{Ra}$
will be mainly discussed and, when specifically stated, compared with the two simulations at lower
$\mathit{Ra}$
will be mainly discussed and, when specifically stated, compared with the two simulations at lower
![]() $\mathit{Ra}$
. In fact, in the latter a more coherent pattern of thermal plumes is expected to lead to a clearer and better-defined statistical footprint.
$\mathit{Ra}$
. In fact, in the latter a more coherent pattern of thermal plumes is expected to lead to a clearer and better-defined statistical footprint.
The paper is organized as follows. In § 2 the governing equations of RBC together with the numerical method employed for the DNS are presented. Section 3 discusses the instantaneous topology highlighting the features of the self-sustained life cycle of turbulent coherent structures. The first half of the paper ends with the analysis of turbulent kinetic energy and temperature variance budgets in § 4. These equations allow us to provide a first statistical characterization of turbulent RBC by identifying some distinct regions inside the flow, which will be useful for the reading of the next part of the paper. In § 5, starting from a generalized form of the classical Kolmogorov and Yaglom equations, the budgets for the second-order moments of the velocity and temperature increments are obtained for the RBC case. Then, the detailed scale-by-scale balances are presented for different regions and linked with the flow phenomenology. Finally, in the last section a summary of the main findings and some concluding remarks are made.
2. Equations and numerical method
The governing equations for the RBC are the momentum, continuity and temperature equations in the Boussinesq approximation,
Table 1. Parameters of the simulations.
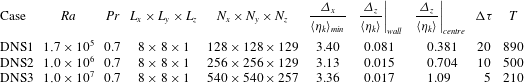
The Boussinesq equations (2.1a–c
) are solved using a pseudospectral method that discretizes space with Chebyshev polynomials in the
![]() $z$
direction and with Fourier modes in the
$z$
direction and with Fourier modes in the
![]() $x$
and
$x$
and
![]() $y$
directions. Time integration is performed with a fourth-order Runge–Kutta scheme for the nonlinear terms and a second-order-accurate Crank–Nicolson scheme for the linear ones. Further details of the numerical scheme can be found in Lundbladh, Henningson & Johansson (Reference Lundbladh, Henningson and Johansson1992). Table 1 reports the main parameters of the simulations. Three DNS are performed for a fixed
$y$
directions. Time integration is performed with a fourth-order Runge–Kutta scheme for the nonlinear terms and a second-order-accurate Crank–Nicolson scheme for the linear ones. Further details of the numerical scheme can be found in Lundbladh, Henningson & Johansson (Reference Lundbladh, Henningson and Johansson1992). Table 1 reports the main parameters of the simulations. Three DNS are performed for a fixed
![]() $\mathit{Pr}=0.7$
at
$\mathit{Pr}=0.7$
at
![]() $\mathit{Ra}=1.7\times 10^{5}$
,
$\mathit{Ra}=1.7\times 10^{5}$
,
![]() $1.0\times 10^{6}$
and
$1.0\times 10^{6}$
and
![]() $1.0\times 10^{7}$
in a rectangular box of sizes
$1.0\times 10^{7}$
in a rectangular box of sizes
![]() $L_{x}=8$
,
$L_{x}=8$
,
![]() $L_{y}=8$
and
$L_{y}=8$
and
![]() $L_{z}=1$
along
$L_{z}=1$
along
![]() $x$
,
$x$
,
![]() $y$
and
$y$
and
![]() $z$
, respectively, where the Cartesian coordinate system is cell-centred, with the
$z$
, respectively, where the Cartesian coordinate system is cell-centred, with the
![]() $xy$
plane parallel to the horizontal plates and the
$xy$
plane parallel to the horizontal plates and the
![]() $z$
axis pointing in the direction opposite to that of gravitational acceleration. Periodic boundary conditions are imposed at the lateral sidewalls, whereas isothermal and no-slip boundary conditions are used on the top and bottom plates. The number of horizontal (
$z$
axis pointing in the direction opposite to that of gravitational acceleration. Periodic boundary conditions are imposed at the lateral sidewalls, whereas isothermal and no-slip boundary conditions are used on the top and bottom plates. The number of horizontal (
![]() $N_{x},~N_{y}$
) and vertical (
$N_{x},~N_{y}$
) and vertical (
![]() $N_{z}$
) fully dealiased modes and polynomials must be sufficiently high to solve the smallest length scale of the problem, which is the Kolmogorov length scale
$N_{z}$
) fully dealiased modes and polynomials must be sufficiently high to solve the smallest length scale of the problem, which is the Kolmogorov length scale
![]() ${\it\eta}_{k}$
, since
${\it\eta}_{k}$
, since
![]() $\mathit{Pr}<1$
. Hence the corresponding grid spacings in physical space (
$\mathit{Pr}<1$
. Hence the corresponding grid spacings in physical space (
![]() ${\it\Delta}_{x}$
,
${\it\Delta}_{x}$
,
![]() ${\it\Delta}_{y}$
,
${\it\Delta}_{y}$
,
![]() ${\it\Delta}_{z}$
) should be smaller than or at least of the same order as
${\it\Delta}_{z}$
) should be smaller than or at least of the same order as
![]() ${\it\eta}_{k}$
.
${\it\eta}_{k}$
.
The average Kolmogorov length scale
![]() $\langle {\it\eta}_{k}\rangle (z)$
is computed a posteriori from the datasets. Hereafter, the angular brackets operator
$\langle {\it\eta}_{k}\rangle (z)$
is computed a posteriori from the datasets. Hereafter, the angular brackets operator
![]() $\langle \,\cdot \,\rangle$
denotes the spatial average along the homogeneous directions
$\langle \,\cdot \,\rangle$
denotes the spatial average along the homogeneous directions
![]() $x$
and
$x$
and
![]() $y$
and the ensemble average over the different configurations. As shown in table 1, for all the DNS, the minimum value of the average Kolmogorov length scale
$y$
and the ensemble average over the different configurations. As shown in table 1, for all the DNS, the minimum value of the average Kolmogorov length scale
![]() $\langle {\it\eta}_{k}\rangle _{min}=\langle {\it\eta}_{k}\rangle |_{wall}$
is shown to be of the same order as the horizontal mesh size
$\langle {\it\eta}_{k}\rangle _{min}=\langle {\it\eta}_{k}\rangle |_{wall}$
is shown to be of the same order as the horizontal mesh size
![]() ${\it\Delta}_{x}={\it\Delta}_{y}$
. Owing to the Chebyshev expansion, the vertical resolution varies with the wall distance,
${\it\Delta}_{x}={\it\Delta}_{y}$
. Owing to the Chebyshev expansion, the vertical resolution varies with the wall distance,
![]() ${\it\Delta}_{z}={\it\Delta}_{z}(z)$
, thus allowing us to solve the Kolmogorov length scale both at the wall and at the cell centre as shown in table 1. Let us note that the resolution employed in the vertical direction for DNS1 amply exceeds the requirement. A way to further assess the employed resolution is by checking the consistency relation
${\it\Delta}_{z}={\it\Delta}_{z}(z)$
, thus allowing us to solve the Kolmogorov length scale both at the wall and at the cell centre as shown in table 1. Let us note that the resolution employed in the vertical direction for DNS1 amply exceeds the requirement. A way to further assess the employed resolution is by checking the consistency relation
![]() $\langle \mathit{Nu}\rangle _{V}=1+\sqrt{\mathit{Ra }\mathit{ Pr}}\,\langle w{\it\theta}\rangle _{V}=1+\sqrt{\mathit{Ra }\mathit{ Pr}}\,\langle \tilde{{\it\epsilon}}\rangle _{V}=\sqrt{\mathit{Ra }\mathit{ Pr}}\,\langle \tilde{{\it\chi}}\rangle _{V}$
, as proposed in Verzicco & Camussi (Reference Verzicco and Camussi2003). Here,
$\langle \mathit{Nu}\rangle _{V}=1+\sqrt{\mathit{Ra }\mathit{ Pr}}\,\langle w{\it\theta}\rangle _{V}=1+\sqrt{\mathit{Ra }\mathit{ Pr}}\,\langle \tilde{{\it\epsilon}}\rangle _{V}=\sqrt{\mathit{Ra }\mathit{ Pr}}\,\langle \tilde{{\it\chi}}\rangle _{V}$
, as proposed in Verzicco & Camussi (Reference Verzicco and Camussi2003). Here,
![]() $\langle \,\cdot \,\rangle _{V}$
denotes the spatial average over the whole fluid domain and over different configurations,
$\langle \,\cdot \,\rangle _{V}$
denotes the spatial average over the whole fluid domain and over different configurations,
![]() $\mathit{Nu}$
is the Nusselt number,
$\mathit{Nu}$
is the Nusselt number,
![]() $\tilde{{\it\epsilon}}=\sqrt{\mathit{Pr }/\mathit{Ra}}\,(\partial u_{i}/\partial x_{j})(\partial u_{i}/\partial x_{j})$
is the pseudo-dissipation of kinetic energy and
$\tilde{{\it\epsilon}}=\sqrt{\mathit{Pr }/\mathit{Ra}}\,(\partial u_{i}/\partial x_{j})(\partial u_{i}/\partial x_{j})$
is the pseudo-dissipation of kinetic energy and
![]() $\tilde{{\it\chi}}=(\mathit{Pr}\mathit{Ra})^{-1/2}(\partial {\it\theta}/\partial x_{i})(\partial {\it\theta}/\partial x_{i})$
is the dissipation of the temperature squared. All DNS appear to be adequately resolved, as they satisfy the criterion with a good approximation, as shown in table 2.
$\tilde{{\it\chi}}=(\mathit{Pr}\mathit{Ra})^{-1/2}(\partial {\it\theta}/\partial x_{i})(\partial {\it\theta}/\partial x_{i})$
is the dissipation of the temperature squared. All DNS appear to be adequately resolved, as they satisfy the criterion with a good approximation, as shown in table 2.
Table 2. Comparison of the different terms of the consistency relation.
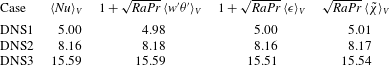
Velocity and temperature fields, after the initial transient is washed out, are collected with a time interval
![]() ${\rm\Delta}{\it\tau}$
and for a period
${\rm\Delta}{\it\tau}$
and for a period
![]() $T$
. The time interval is significantly longer than the large eddy turnover time
$T$
. The time interval is significantly longer than the large eddy turnover time
![]() $2H/U_{f}=2$
in order to collect fields that are likely to be uncorrelated; see table 1. An estimate of the statistical convergence of the data is displayed by the accuracy with which the Kolmogorov and Yaglom equations are satisfied; see circles in figures 10, 11, 13 and 14. As shown by these observables, the overall statistical convergence is achieved with a good accuracy. The fact that both the Kolmogorov and Yaglom equations are satisfied is also evidence of the fact that the terms associated with the possible presence of a mean flow are negligible. Indeed, it should be pointed out that a mean velocity field would exist locally in time and space due to the presence of large-scale circulations which erratically reverse their directions on time scales exceeding the large eddy turnover time as reported in Van Reeuwijk, Jonker & Hanjalić (Reference Van Reeuwijk, Jonker and Hanjalić2005), Brown & Ahlers (Reference Brown and Ahlers2006) and Xi, Zhou & Xia (Reference Xi, Zhou and Xia2006).
$2H/U_{f}=2$
in order to collect fields that are likely to be uncorrelated; see table 1. An estimate of the statistical convergence of the data is displayed by the accuracy with which the Kolmogorov and Yaglom equations are satisfied; see circles in figures 10, 11, 13 and 14. As shown by these observables, the overall statistical convergence is achieved with a good accuracy. The fact that both the Kolmogorov and Yaglom equations are satisfied is also evidence of the fact that the terms associated with the possible presence of a mean flow are negligible. Indeed, it should be pointed out that a mean velocity field would exist locally in time and space due to the presence of large-scale circulations which erratically reverse their directions on time scales exceeding the large eddy turnover time as reported in Van Reeuwijk, Jonker & Hanjalić (Reference Van Reeuwijk, Jonker and Hanjalić2005), Brown & Ahlers (Reference Brown and Ahlers2006) and Xi, Zhou & Xia (Reference Xi, Zhou and Xia2006).
It is well known that by increasing the Rayleigh number the characteristic length scales of the problem decrease. For that reason, in what follows, many statistical quantities are expressed as a function of spatial variables that are normalized by the characteristic length
![]() $H/\mathit{Nu}$
and denoted with the superscript
$H/\mathit{Nu}$
and denoted with the superscript
![]() $\ast$
. This length scale, which is twice the commonly defined thermal boundary layer thickness, will allow for a more appropriate comparison of the scales and regions analysed at different Rayleigh numbers.
$\ast$
. This length scale, which is twice the commonly defined thermal boundary layer thickness, will allow for a more appropriate comparison of the scales and regions analysed at different Rayleigh numbers.
3. Flow topology
As Kadanoff (Reference Kadanoff2001) describes, turbulent RBC is a nonlinear system with a natural tendency towards self-organization. Coherent thermal and velocity structures emerge from the chaotic regime, combine themselves and create a sort of persistent machinery. It is generally assumed that the most prominent structure in turbulent convection is the so-called thermal plume, which can be defined as a localized portion of fluid having a temperature contrast with the background (Chillà & Schumacher Reference Chillà and Schumacher2012). Plumes are responsible for the transport of a large amount of heat across the convection cell (Shang et al.
Reference Shang, Qiu, Tong and Xia2003, Reference Shang, Qiu, Tong and Xia2004), and there are a lot of studies devoted to this subject (Ching et al.
Reference Ching, Guo, Shang, Tong and Xia2004; Zhou, Sun & Xia Reference Zhou, Sun and Xia2007; Shishkina & Wagner Reference Shishkina and Wagner2008). The flow topology observed for the DNS at
![]() $\mathit{Ra}=1.7\times 10^{5}$
is characterized by large and smooth plumes which emerge distinctly from the turbulent background. As the turbulence intensity increases, for
$\mathit{Ra}=1.7\times 10^{5}$
is characterized by large and smooth plumes which emerge distinctly from the turbulent background. As the turbulence intensity increases, for
![]() $\mathit{Ra}=1.0\times 10^{6}$
and
$\mathit{Ra}=1.0\times 10^{6}$
and
![]() $\mathit{Ra}=1.0\times 10^{7}$
, the flow structure become smaller and less coherent.
$\mathit{Ra}=1.0\times 10^{7}$
, the flow structure become smaller and less coherent.
Figure 1(a) shows two isosurfaces of temperature coloured with the vertical velocity component for
![]() $\mathit{Ra}=1.0\times 10^{7}$
. As can be seen, hot and cold plumes detach respectively from the lower and the upper plate, accelerate through the bulk of the flow under the action of buoyancy forces and, finally, impinge on the opposite wall. In the core, thermal plumes have a mushroom-like shape, whereas close to the walls they have a sheet-like one. Generally speaking, the sheet-like plumes create a fine network across the plates and the mushroom-like plumes are emitted from the intersection spots. This behaviour seems particularly evident in figure 1(b), which represents the top view of the hot isosurface displayed in figure 1(a). The isosurface shows ejections of hot fluid in the regions where different sheet-like plumes collide and merge.
$\mathit{Ra}=1.0\times 10^{7}$
. As can be seen, hot and cold plumes detach respectively from the lower and the upper plate, accelerate through the bulk of the flow under the action of buoyancy forces and, finally, impinge on the opposite wall. In the core, thermal plumes have a mushroom-like shape, whereas close to the walls they have a sheet-like one. Generally speaking, the sheet-like plumes create a fine network across the plates and the mushroom-like plumes are emitted from the intersection spots. This behaviour seems particularly evident in figure 1(b), which represents the top view of the hot isosurface displayed in figure 1(a). The isosurface shows ejections of hot fluid in the regions where different sheet-like plumes collide and merge.
In figure 2(a,b), the hot isosurface coloured with the horizontal divergence of the velocity field,
![]() $\text{div}_{{\rm\pi}}=\partial u/\partial x+\partial v/\partial y$
, is shown. The use of
$\text{div}_{{\rm\pi}}=\partial u/\partial x+\partial v/\partial y$
, is shown. The use of
![]() $\text{div}_{{\rm\pi}}$
allows us to clearly identify the plume impingement and to see that the emersion of sheet-like structures is mainly due to the latter phenomenon. Indeed, it is shown that the heads of the plumes which impinge on the plate induce a strong positive divergence,
$\text{div}_{{\rm\pi}}$
allows us to clearly identify the plume impingement and to see that the emersion of sheet-like structures is mainly due to the latter phenomenon. Indeed, it is shown that the heads of the plumes which impinge on the plate induce a strong positive divergence,
![]() $\text{div}_{{\rm\pi}}>0$
. Hence, it appears clearly that the presence of concurrent regions of strong positive divergence leads to interface filaments, the sheet-like plumes, where there is a strong convergence,
$\text{div}_{{\rm\pi}}>0$
. Hence, it appears clearly that the presence of concurrent regions of strong positive divergence leads to interface filaments, the sheet-like plumes, where there is a strong convergence,
![]() $\text{div}_{{\rm\pi}}<0$
, of the velocity field. In this view, the intersection of different filaments leads to a large concentration of momentum, which is in turn responsible, together with the buoyancy forces, for the ejection of mushroom-like plumes, closing the self-sustained life cycle of these structures. In order to separate the contributions of impingement from those of ejection, the conditional statistics
$\text{div}_{{\rm\pi}}<0$
, of the velocity field. In this view, the intersection of different filaments leads to a large concentration of momentum, which is in turn responsible, together with the buoyancy forces, for the ejection of mushroom-like plumes, closing the self-sustained life cycle of these structures. In order to separate the contributions of impingement from those of ejection, the conditional statistics
![]() $\langle \text{div}_{{\rm\pi}}\rangle _{+}$
and
$\langle \text{div}_{{\rm\pi}}\rangle _{+}$
and
![]() $-\langle \text{div}_{{\rm\pi}}\rangle _{-}$
, where
$-\langle \text{div}_{{\rm\pi}}\rangle _{-}$
, where
![]() $\langle \text{div}_{{\rm\pi}}\rangle _{+}=\langle \text{div}_{{\rm\pi}}\rangle$
for
$\langle \text{div}_{{\rm\pi}}\rangle _{+}=\langle \text{div}_{{\rm\pi}}\rangle$
for
![]() $\text{div}_{{\rm\pi}}>0$
and
$\text{div}_{{\rm\pi}}>0$
and
![]() $\langle \text{div}_{{\rm\pi}}\rangle _{-}=\langle \text{div}_{{\rm\pi}}\rangle$
for
$\langle \text{div}_{{\rm\pi}}\rangle _{-}=\langle \text{div}_{{\rm\pi}}\rangle$
for
![]() $\text{div}_{{\rm\pi}}<0$
, are analysed. These quantities allow us to display the magnitude of both the impingement (
$\text{div}_{{\rm\pi}}<0$
, are analysed. These quantities allow us to display the magnitude of both the impingement (
![]() $\langle \text{div}_{{\rm\pi}}\rangle _{+}$
) and the ejection (
$\langle \text{div}_{{\rm\pi}}\rangle _{+}$
) and the ejection (
![]() $\langle \text{div}_{{\rm\pi}}\rangle _{-}$
) as a function of the distance from the wall. Independently from the Rayleigh number considered, the impingement reaches its maximum at a distance from the wall
$\langle \text{div}_{{\rm\pi}}\rangle _{-}$
) as a function of the distance from the wall. Independently from the Rayleigh number considered, the impingement reaches its maximum at a distance from the wall
![]() $z^{\ast }=(0.5-|z|)^{\ast }=0.3$
, while the ejection is peaked slightly further away from the wall at
$z^{\ast }=(0.5-|z|)^{\ast }=0.3$
, while the ejection is peaked slightly further away from the wall at
![]() $z^{\ast }=0.5$
; see figure 3(a) for
$z^{\ast }=0.5$
; see figure 3(a) for
![]() $\mathit{Ra}=1.0\times 10^{7}$
.
$\mathit{Ra}=1.0\times 10^{7}$
.

Figure 1. (a) Isosurfaces of temperature (
![]() ${\it\theta}=0.2$
down and
${\it\theta}=0.2$
down and
![]() ${\it\theta}=-0.2$
up) coloured by the vertical velocity component
${\it\theta}=-0.2$
up) coloured by the vertical velocity component
![]() $w$
and (b) top view of the isosurface at
$w$
and (b) top view of the isosurface at
![]() ${\it\theta}=0.2$
for
${\it\theta}=0.2$
for
![]() $\mathit{Ra}=1.0\times 10^{7}$
.
$\mathit{Ra}=1.0\times 10^{7}$
.

Figure 2. (a) Isosurface of temperature (
![]() ${\it\theta}=0.2$
) coloured by the horizontal divergence of the velocity field,
${\it\theta}=0.2$
) coloured by the horizontal divergence of the velocity field,
![]() $\text{div}_{{\rm\pi}}$
, for
$\text{div}_{{\rm\pi}}$
, for
![]() $\mathit{Ra}=1.0\times 10^{7}$
. (b) Close-up of part of (a) with superimposed velocity vectors.
$\mathit{Ra}=1.0\times 10^{7}$
. (b) Close-up of part of (a) with superimposed velocity vectors.
To gain information about the scales of impingement, let us now consider the autocorrelation function of the divergence
![]() $R=\langle \text{div}_{{\rm\pi}}({\bf\pi},z)\,\text{div}_{{\rm\pi}}({\bf\pi}+\boldsymbol{r},z)\rangle /\langle \text{div}_{{\rm\pi}}^{2}({\bf\pi},z)\rangle$
, where
$R=\langle \text{div}_{{\rm\pi}}({\bf\pi},z)\,\text{div}_{{\rm\pi}}({\bf\pi}+\boldsymbol{r},z)\rangle /\langle \text{div}_{{\rm\pi}}^{2}({\bf\pi},z)\rangle$
, where
![]() ${\bf\pi}=(x,y)$
and
${\bf\pi}=(x,y)$
and
![]() $\boldsymbol{r}=(r_{x},r_{y})$
are respectively the position and the separation vectors in the
$\boldsymbol{r}=(r_{x},r_{y})$
are respectively the position and the separation vectors in the
![]() $xy$
plane at height
$xy$
plane at height
![]() $z$
. Taking into account the planar homogeneity and isotropy, the dependence of
$z$
. Taking into account the planar homogeneity and isotropy, the dependence of
![]() $R$
on both the position vector
$R$
on both the position vector
![]() ${\bf\pi}$
and the direction of
${\bf\pi}$
and the direction of
![]() $\boldsymbol{r}$
vanishes, hence
$\boldsymbol{r}$
vanishes, hence
![]() $R=R(r,z)$
, where
$R=R(r,z)$
, where
![]() $r=|\boldsymbol{r}|$
. At the distance from the wall
$r=|\boldsymbol{r}|$
. At the distance from the wall
![]() $z^{\ast }=0.3$
, the uncorrelation is found to occur at
$z^{\ast }=0.3$
, the uncorrelation is found to occur at
![]() $r^{\ast }=3$
for all the
$r^{\ast }=3$
for all the
![]() $\mathit{Ra}$
considered; see figure 3(b) for
$\mathit{Ra}$
considered; see figure 3(b) for
![]() $\mathit{Ra}=1.0\times 10^{7}$
. This separation can be reasonably considered as the characteristic width of the impinging plumes. Indeed, the strength of the impingement reaches its maximum and dominates over the ejection at
$\mathit{Ra}=1.0\times 10^{7}$
. This separation can be reasonably considered as the characteristic width of the impinging plumes. Indeed, the strength of the impingement reaches its maximum and dominates over the ejection at
![]() $z^{\ast }=0.3$
, as can be seen in figure 3(a). Furthermore, as the uncorrelation separation does not change with the Rayleigh number, it can be inferred that the characteristic length of the impinging plume scales with the thermal boundary layer thickness.
$z^{\ast }=0.3$
, as can be seen in figure 3(a). Furthermore, as the uncorrelation separation does not change with the Rayleigh number, it can be inferred that the characteristic length of the impinging plume scales with the thermal boundary layer thickness.

Figure 3. (a) Behaviour of
![]() $\langle \text{div}_{{\rm\pi}}\rangle _{+}$
(solid line) and
$\langle \text{div}_{{\rm\pi}}\rangle _{+}$
(solid line) and
![]() $-\langle \text{div}_{{\rm\pi}}\rangle _{-}$
(dashed line) as functions of
$-\langle \text{div}_{{\rm\pi}}\rangle _{-}$
(dashed line) as functions of
![]() $z^{\ast }$
. (b) Behaviour of the autocorrelation function
$z^{\ast }$
. (b) Behaviour of the autocorrelation function
![]() $R$
as a function of
$R$
as a function of
![]() $r^{\ast }$
and for
$r^{\ast }$
and for
![]() $z^{\ast }=0.3$
. Results are shown for
$z^{\ast }=0.3$
. Results are shown for
![]() $\mathit{Ra}=1.0\times 10^{7}$
.
$\mathit{Ra}=1.0\times 10^{7}$
.
Let us now investigate in more detail the impingement and the ejection of thermal plumes. Figure 4(a,b) shows respectively the skewness
![]() $S$
and the kurtosis
$S$
and the kurtosis
![]() $K$
of the velocity components, pressure and temperature for
$K$
of the velocity components, pressure and temperature for
![]() $\mathit{Ra}=1.0\times 10^{7}$
as functions of the distance from the wall
$\mathit{Ra}=1.0\times 10^{7}$
as functions of the distance from the wall
![]() $z^{\ast }$
. The high-order moments of
$z^{\ast }$
. The high-order moments of
![]() $u$
and
$u$
and
![]() $v$
are shown to be equal for statistical isotropy in the horizontal directions, hence only the statistics of
$v$
are shown to be equal for statistical isotropy in the horizontal directions, hence only the statistics of
![]() $u$
are discussed. At the centreline
$u$
are discussed. At the centreline
![]() $z^{\ast }=7.8$
, every variable except the pressure
$z^{\ast }=7.8$
, every variable except the pressure
![]() $p$
is almost normally distributed, as both the skewness and the kurtosis are not far from the Gaussian values
$p$
is almost normally distributed, as both the skewness and the kurtosis are not far from the Gaussian values
![]() $S_{N}=0$
and
$S_{N}=0$
and
![]() $K_{N}=3$
. The horizontal velocity component
$K_{N}=3$
. The horizontal velocity component
![]() $u$
remains normally distributed throughout the flow whereas the probability density functions (p.d.f.s) of both the wall-normal velocity component
$u$
remains normally distributed throughout the flow whereas the probability density functions (p.d.f.s) of both the wall-normal velocity component
![]() $w$
and the temperature
$w$
and the temperature
![]() ${\it\theta}$
dramatically diverge from Gaussianity as the wall is approached. Close to the wall, the p.d.f. of
${\it\theta}$
dramatically diverge from Gaussianity as the wall is approached. Close to the wall, the p.d.f. of
![]() $w$
is considerably skewed towards negative fluctuations and the kurtosis is peaked. This means that, as the wall approaches,
$w$
is considerably skewed towards negative fluctuations and the kurtosis is peaked. This means that, as the wall approaches,
![]() $w$
is more likely to assume large negative values by intermittent extreme events. Regarding the temperature,
$w$
is more likely to assume large negative values by intermittent extreme events. Regarding the temperature,
![]() $S_{{\it\theta}}$
changes sign close to the wall and
$S_{{\it\theta}}$
changes sign close to the wall and
![]() $K_{{\it\theta}}$
reaches a minimum roughly at the same location, allowing for the identification of two distinct regions, one in the centre of the channel (
$K_{{\it\theta}}$
reaches a minimum roughly at the same location, allowing for the identification of two distinct regions, one in the centre of the channel (
![]() $z^{\ast }>0.5$
) and the other closer to the wall (
$z^{\ast }>0.5$
) and the other closer to the wall (
![]() $z^{\ast }<0.5$
). Inside the latter region, the product
$z^{\ast }<0.5$
). Inside the latter region, the product
![]() $S_{w}S_{{\it\theta}}$
is always non-negative, which reasonably means that plume impingement is the intermittent event that dominates this layer. Just outside the near-wall region, we can observe that
$S_{w}S_{{\it\theta}}$
is always non-negative, which reasonably means that plume impingement is the intermittent event that dominates this layer. Just outside the near-wall region, we can observe that
![]() $S_{w}S_{{\it\theta}}$
becomes negative and
$S_{w}S_{{\it\theta}}$
becomes negative and
![]() $S_{w}$
decreases its slope. This behaviour may be related to the protrusion of sheet-like plumes and the emission of mushroom-like ones, which should become statistically relevant sufficiently away from the wall. At the centreline, all p.d.f.s, except for the pressure one, become even less skewed as the intermittent events related to the ascending plumes balance the events related to the descending ones.
$S_{w}$
decreases its slope. This behaviour may be related to the protrusion of sheet-like plumes and the emission of mushroom-like ones, which should become statistically relevant sufficiently away from the wall. At the centreline, all p.d.f.s, except for the pressure one, become even less skewed as the intermittent events related to the ascending plumes balance the events related to the descending ones.
Let us now focus on the p.d.f. of
![]() $p$
. Inside the core of the flow,
$p$
. Inside the core of the flow,
![]() $S_{p}$
is negative and
$S_{p}$
is negative and
![]() $K_{p}$
is maximum; hence negative and intense pressure fluctuations are the most common intermittent events in this region. Indeed, inside the core of the flow, both hot and cold plumes are subjected to an acceleration, and hence negative pressure fluctuations are fairly reasonable. On the contrary, close to the walls,
$K_{p}$
is maximum; hence negative and intense pressure fluctuations are the most common intermittent events in this region. Indeed, inside the core of the flow, both hot and cold plumes are subjected to an acceleration, and hence negative pressure fluctuations are fairly reasonable. On the contrary, close to the walls,
![]() $S_{p}$
is positive and
$S_{p}$
is positive and
![]() $K_{p}$
is minimum, which means that positive and less intense intermittent fluctuations are more probable. As Wörner & Grötzbach (Reference Wörner and Grötzbach1998) pointed out in their work, the rising/falling plumes are decelerated as they approach the upper/lower plate and hence positive pressure fluctuations are enhanced by the impingement.
$K_{p}$
is minimum, which means that positive and less intense intermittent fluctuations are more probable. As Wörner & Grötzbach (Reference Wörner and Grötzbach1998) pointed out in their work, the rising/falling plumes are decelerated as they approach the upper/lower plate and hence positive pressure fluctuations are enhanced by the impingement.

Figure 4. (a) Skewness and (b) kurtosis of
![]() $u$
(solid line),
$u$
(solid line),
![]() $w$
(dashed line),
$w$
(dashed line),
![]() $p$
(dot-dashed line) and
$p$
(dot-dashed line) and
![]() ${\it\theta}$
(dotted line) as functions of
${\it\theta}$
(dotted line) as functions of
![]() $z^{\ast }$
for
$z^{\ast }$
for
![]() $\mathit{Ra}=1.0\times 10^{7}$
.
$\mathit{Ra}=1.0\times 10^{7}$
.
4. Spatial redistribution of turbulent kinetic energy and temperature variance
In order to provide a more quantitative description of the self-sustained turbulent cycles, we proceed by analysing the balance equations for the turbulent kinetic energy and the temperature variance. Based on these budgets, distinct regions where the second-order moments are produced, transported and dissipated are both identified and phenomenologically explained.
We start with the analysis of the turbulent kinetic energy budget,
where the prime indicates the fluctuating component,
![]() $k=(u_{i}^{\prime }u_{i}^{\prime })/2$
is the instantaneous turbulent kinetic energy density and
$k=(u_{i}^{\prime }u_{i}^{\prime })/2$
is the instantaneous turbulent kinetic energy density and
![]() $\langle {\it\epsilon}\rangle$
is the average pseudo-dissipation of turbulent kinetic energy, defined as
$\langle {\it\epsilon}\rangle$
is the average pseudo-dissipation of turbulent kinetic energy, defined as
The first three terms of the turbulent kinetic energy equation are the inertial, the pressure and the viscous contributions to the transport of
![]() $\langle k\rangle$
across the horizontal planes of the domain. The last two terms, hereafter called production and dissipation, are a source due to buoyancy and a sink due to viscosity.
$\langle k\rangle$
across the horizontal planes of the domain. The last two terms, hereafter called production and dissipation, are a source due to buoyancy and a sink due to viscosity.

Figure 5. (a) Turbulent kinetic energy budget as a function of
![]() $z^{\ast }$
for
$z^{\ast }$
for
![]() $\mathit{Ra}=1.0\times 10^{7}$
: inertial transport (dashed line), pressure transport (dotted line), viscous transport (long dashed line), production (dot-dot-dashed line) and dissipation (solid line). The details of the central region are shown in the inset. (b) Profiles of
$\mathit{Ra}=1.0\times 10^{7}$
: inertial transport (dashed line), pressure transport (dotted line), viscous transport (long dashed line), production (dot-dot-dashed line) and dissipation (solid line). The details of the central region are shown in the inset. (b) Profiles of
![]() $\langle k\rangle$
(solid line),
$\langle k\rangle$
(solid line),
![]() $\langle u^{2}\rangle$
(dashed line) and
$\langle u^{2}\rangle$
(dashed line) and
![]() $\langle w^{2}\rangle$
(dot-dashed line) as functions of
$\langle w^{2}\rangle$
(dot-dashed line) as functions of
![]() $z^{\ast }$
.
$z^{\ast }$
.
In figure 5(a), the terms of (4.1) are plotted as functions of the distance from the wall
![]() $z^{\ast }$
for
$z^{\ast }$
for
![]() $\mathit{Ra}=1.0\times 10^{7}$
. Three distinct regions are recognizable: a bulk region in the core of the flow, a transitional layer, and a viscous boundary layer closer to the wall. The bulk is defined as the region where the velocity fluctuations are sustained by buoyant production rather than transport processes, and ranges from the centreline at
$\mathit{Ra}=1.0\times 10^{7}$
. Three distinct regions are recognizable: a bulk region in the core of the flow, a transitional layer, and a viscous boundary layer closer to the wall. The bulk is defined as the region where the velocity fluctuations are sustained by buoyant production rather than transport processes, and ranges from the centreline at
![]() $z^{\ast }=7.8$
to
$z^{\ast }=7.8$
to
![]() $z^{\ast }=0.78$
, where the production term equals the pressure transport term, i.e.
$z^{\ast }=0.78$
, where the production term equals the pressure transport term, i.e.
![]() $-\text{d}\langle w^{\prime }p^{\prime }\rangle /\text{d}z=\langle w^{\prime }{\it\theta}^{\prime }\rangle$
. The bulk region is a nearly homogeneous layer, in which all terms are almost constant. Moreover, the production is found to be dominant and to exceed the dissipation. This energy excess,
$-\text{d}\langle w^{\prime }p^{\prime }\rangle /\text{d}z=\langle w^{\prime }{\it\theta}^{\prime }\rangle$
. The bulk region is a nearly homogeneous layer, in which all terms are almost constant. Moreover, the production is found to be dominant and to exceed the dissipation. This energy excess,
![]() $\langle w^{\prime }{\it\theta}^{\prime }\rangle -\langle {\it\epsilon}\rangle$
, is transported towards the wall regions, where the dissipation dominates over the production. In the bulk, the transport is mainly due to pressure and inertial mechanisms since the viscous diffusion is essentially negligible. The region of the flow where most of the energy is provided by inviscid transport mechanisms rather than production processes is called the transitional layer and ranges from
$\langle w^{\prime }{\it\theta}^{\prime }\rangle -\langle {\it\epsilon}\rangle$
, is transported towards the wall regions, where the dissipation dominates over the production. In the bulk, the transport is mainly due to pressure and inertial mechanisms since the viscous diffusion is essentially negligible. The region of the flow where most of the energy is provided by inviscid transport mechanisms rather than production processes is called the transitional layer and ranges from
![]() $z^{\ast }=0.78$
to
$z^{\ast }=0.78$
to
![]() $z^{\ast }=0.13$
, where the viscous transport term equals the pressure term, i.e.
$z^{\ast }=0.13$
, where the viscous transport term equals the pressure term, i.e.
![]() $\sqrt{\mathit{Pr }/\mathit{Ra}}\,\text{d}^{2}\langle k\rangle /\text{d}z^{2}=-\text{d}\langle w^{\prime }p^{\prime }\rangle /\text{d}z$
. In this layer, the production is smaller than the dissipation, and the resulting energy defect is mainly compensated by a positive pressure transport, meaning that the energy excess coming from the bulk is partially released to this layer. On the contrary, the viscous transport is negative, meaning that the transitional layer, in turn, releases kinetic energy towards the wall through diffusion processes. Lastly, inside the viscous boundary layer defined for
$\sqrt{\mathit{Pr }/\mathit{Ra}}\,\text{d}^{2}\langle k\rangle /\text{d}z^{2}=-\text{d}\langle w^{\prime }p^{\prime }\rangle /\text{d}z$
. In this layer, the production is smaller than the dissipation, and the resulting energy defect is mainly compensated by a positive pressure transport, meaning that the energy excess coming from the bulk is partially released to this layer. On the contrary, the viscous transport is negative, meaning that the transitional layer, in turn, releases kinetic energy towards the wall through diffusion processes. Lastly, inside the viscous boundary layer defined for
![]() $z^{\ast }<0.13$
, the turbulent kinetic energy diffuses through viscous mechanisms and it is massively dissipated.
$z^{\ast }<0.13$
, the turbulent kinetic energy diffuses through viscous mechanisms and it is massively dissipated.
In order to understand how the different velocity components contribute to the turbulent kinetic energy, it is useful to split the balance equation (4.1) into a set of equations, one for each component of
![]() $\langle k\rangle$
:
$\langle k\rangle$
:

Figure 6. (a) Budget of
![]() $\langle w^{\prime 2}\rangle$
and (b) budget of
$\langle w^{\prime 2}\rangle$
and (b) budget of
![]() $\langle u^{\prime 2}\rangle$
as a function of
$\langle u^{\prime 2}\rangle$
as a function of
![]() $z^{\ast }$
: inertial transport (dashed line), pressure–strain rate term (dot-dashed line), pressure transport (dotted line), viscous transport (long dashed line), production (dot-dot-dashed line) and dissipation (solid line). The details of the central region are shown in the insets.
$z^{\ast }$
: inertial transport (dashed line), pressure–strain rate term (dot-dashed line), pressure transport (dotted line), viscous transport (long dashed line), production (dot-dot-dashed line) and dissipation (solid line). The details of the central region are shown in the insets.
The three components of the average pseudo-dissipation,
![]() $\langle {\it\epsilon}_{x}\rangle$
,
$\langle {\it\epsilon}_{x}\rangle$
,
![]() $\langle {\it\epsilon}_{y}\rangle$
and
$\langle {\it\epsilon}_{y}\rangle$
and
![]() $\langle {\it\epsilon}_{z}\rangle$
, are defined as
$\langle {\it\epsilon}_{z}\rangle$
, are defined as
It can be observed that the sum of (4.3a–c
) is equal to (4.1), where the sum of the pressure–strain rate terms
![]() $\langle p^{\prime }\partial u_{i}^{\prime }/\partial x_{i}\rangle$
is equal to zero for incompressibility. The production term is present only in the equation for
$\langle p^{\prime }\partial u_{i}^{\prime }/\partial x_{i}\rangle$
is equal to zero for incompressibility. The production term is present only in the equation for
![]() $\langle w^{\prime 2}\rangle$
, since the vertical velocity component is the only one which directly receives energy from the buoyancy force. Analysing the balance for
$\langle w^{\prime 2}\rangle$
, since the vertical velocity component is the only one which directly receives energy from the buoyancy force. Analysing the balance for
![]() $\langle w^{\prime 2}\rangle$
plotted in figure 6(a), it emerges that the vertical dissipation is negligible compared to production almost everywhere. In the bulk region, the energy excess
$\langle w^{\prime 2}\rangle$
plotted in figure 6(a), it emerges that the vertical dissipation is negligible compared to production almost everywhere. In the bulk region, the energy excess
![]() $\langle w^{\prime }{\it\theta}^{\prime }\rangle -\langle {\it\epsilon}_{z}\rangle +\langle p^{\prime }\partial w^{\prime }/\partial z\rangle$
is transported towards the wall mainly by pressure mechanisms, since the viscous and inertial terms are substantially negligible. In the transitional layer, the production due to buoyancy decreases and the wall-normal fluctuations are sustained by the energy provided through the pressure transport. In this layer, the pressure–strain rate term is negative and reaches its maximum intensity. This term is actually the main sink term for
$\langle w^{\prime }{\it\theta}^{\prime }\rangle -\langle {\it\epsilon}_{z}\rangle +\langle p^{\prime }\partial w^{\prime }/\partial z\rangle$
is transported towards the wall mainly by pressure mechanisms, since the viscous and inertial terms are substantially negligible. In the transitional layer, the production due to buoyancy decreases and the wall-normal fluctuations are sustained by the energy provided through the pressure transport. In this layer, the pressure–strain rate term is negative and reaches its maximum intensity. This term is actually the main sink term for
![]() $\langle w^{\prime 2}\rangle$
since the vertical dissipation is negligible also close to the wall.
$\langle w^{\prime 2}\rangle$
since the vertical dissipation is negligible also close to the wall.
On the contrary, by considering the budget of
![]() $\langle u^{\prime 2}\rangle$
plotted in figure 6(b), which is equal to the budget of
$\langle u^{\prime 2}\rangle$
plotted in figure 6(b), which is equal to the budget of
![]() $\langle v^{\prime 2}\rangle$
for isotropy, it is clear that the pressure–strain rate acts as a source. In particular, in the transitional layer, this term is positive and reaches its maximum, highlighting an inter-component exchange of energy from the wall-normal to the wall-parallel directions. For the wall-parallel components of energy, the quantity
$\langle v^{\prime 2}\rangle$
for isotropy, it is clear that the pressure–strain rate acts as a source. In particular, in the transitional layer, this term is positive and reaches its maximum, highlighting an inter-component exchange of energy from the wall-normal to the wall-parallel directions. For the wall-parallel components of energy, the quantity
![]() $\langle p^{\prime }\partial u^{\prime }/\partial x\rangle -\langle {\it\epsilon}_{x}\rangle$
provides an energy excess inside the transitional layer, which is then transported towards the viscous boundary layer and towards the bulk region by viscous diffusion and inertial transport, respectively, where it is finally dissipated.
$\langle p^{\prime }\partial u^{\prime }/\partial x\rangle -\langle {\it\epsilon}_{x}\rangle$
provides an energy excess inside the transitional layer, which is then transported towards the viscous boundary layer and towards the bulk region by viscous diffusion and inertial transport, respectively, where it is finally dissipated.
Summarizing, buoyancy is effective only for the wall-normal component of turbulent kinetic energy and limited to the bulk region. Indeed, as shown in figure 5(b), the maximum of
![]() $\langle w^{\prime 2}\rangle$
is located at the centreline. The resulting energy excess is transported by pressure mechanisms to the transitional layer, where it is released to the wall-parallel components of velocity through the pressure–strain rate terms, which have a maximum where the peak of
$\langle w^{\prime 2}\rangle$
is located at the centreline. The resulting energy excess is transported by pressure mechanisms to the transitional layer, where it is released to the wall-parallel components of velocity through the pressure–strain rate terms, which have a maximum where the peak of
![]() $\langle u^{\prime 2}\rangle$
occurs. Finally, the wall-parallel components redistribute this energy across the bulk and the viscous boundary layer, where it is dissipated. It should be noted that the energy associated with
$\langle u^{\prime 2}\rangle$
occurs. Finally, the wall-parallel components redistribute this energy across the bulk and the viscous boundary layer, where it is dissipated. It should be noted that the energy associated with
![]() $\langle w^{\prime 2}\rangle$
is almost totally released to the wall-parallel components inside the transitional layer. Indeed, as shown in figure 5(b), the viscous layer appears as a two-dimensional layer since
$\langle w^{\prime 2}\rangle$
is almost totally released to the wall-parallel components inside the transitional layer. Indeed, as shown in figure 5(b), the viscous layer appears as a two-dimensional layer since
![]() $\langle w^{\prime 2}\rangle$
is very small.
$\langle w^{\prime 2}\rangle$
is very small.
The temperature field plays an active role in RBC. Therefore the analysis of the turbulent kinetic energy balance alone is insufficient to understand how the self-sustained motion works. The evolution equation for the temperature variance
![]() $\langle {\it\theta}^{\prime 2}\rangle$
is
$\langle {\it\theta}^{\prime 2}\rangle$
is
where
![]() ${\it\Theta}$
is the mean temperature and
${\it\Theta}$
is the mean temperature and
![]() $\langle {\it\chi}\rangle$
is the average rate of thermal dissipation, defined as
$\langle {\it\chi}\rangle$
is the average rate of thermal dissipation, defined as
The first two terms of (4.5) are the inertial and the viscous transports, whereas the last two terms are the production and the dissipation. The different terms of the balance are reported in figure 7(a) for
![]() $\mathit{Ra}=1.0\times 10^{7}$
. Similarly to the budget for
$\mathit{Ra}=1.0\times 10^{7}$
. Similarly to the budget for
![]() $\langle k\rangle$
, three well-separated regions are observable: a thermal boundary layer, a thermal transitional layer, and a thermal bulk region. The thermal transitional layer is defined as the region where production dominates, and it extends from
$\langle k\rangle$
, three well-separated regions are observable: a thermal boundary layer, a thermal transitional layer, and a thermal bulk region. The thermal transitional layer is defined as the region where production dominates, and it extends from
![]() $z^{\ast }=0.16$
, where production equals viscous diffusion, i.e.
$z^{\ast }=0.16$
, where production equals viscous diffusion, i.e.
![]() $-2\langle w^{\prime }{\it\theta}^{\prime }\rangle (\text{d}{\it\Theta}/\text{d}z)=(1/\sqrt{\mathit{Pr }\mathit{ Ra}})\,\text{d}^{2}\langle {\it\theta}^{\prime 2}\rangle /\text{d}z^{2}$
, to
$-2\langle w^{\prime }{\it\theta}^{\prime }\rangle (\text{d}{\it\Theta}/\text{d}z)=(1/\sqrt{\mathit{Pr }\mathit{ Ra}})\,\text{d}^{2}\langle {\it\theta}^{\prime 2}\rangle /\text{d}z^{2}$
, to
![]() $z^{\ast }=2.4$
, where production equals inertial transport, i.e.
$z^{\ast }=2.4$
, where production equals inertial transport, i.e.
![]() $-2\langle w^{\prime }{\it\theta}^{\prime }\rangle (\text{d}{\it\Theta}/\text{d}z)=-\text{d}\langle {\it\theta}^{\prime 2}w^{\prime }\rangle /\text{d}z$
. In this layer, production exceeds dissipation and the net temperature variance excess,
$-2\langle w^{\prime }{\it\theta}^{\prime }\rangle (\text{d}{\it\Theta}/\text{d}z)=-\text{d}\langle {\it\theta}^{\prime 2}w^{\prime }\rangle /\text{d}z$
. In this layer, production exceeds dissipation and the net temperature variance excess,
![]() $-2\langle w^{\prime }{\it\theta}^{\prime }\rangle \,\text{d}{\it\Theta}/\text{d}z-2\langle {\it\chi}\rangle$
, is carried away by the transport terms and sent towards the wall and towards the core, which are sink regions, i.e.
$-2\langle w^{\prime }{\it\theta}^{\prime }\rangle \,\text{d}{\it\Theta}/\text{d}z-2\langle {\it\chi}\rangle$
, is carried away by the transport terms and sent towards the wall and towards the core, which are sink regions, i.e.
![]() $-2\langle w^{\prime }{\it\theta}^{\prime }\rangle \,\text{d}{\it\Theta}/\text{d}z-2\langle {\it\chi}\rangle <0$
. The viscosity transports the temperature variance mainly towards the wall, while inertia carries out transport mainly towards the core. Indeed, inside the thermal bulk region (
$-2\langle w^{\prime }{\it\theta}^{\prime }\rangle \,\text{d}{\it\Theta}/\text{d}z-2\langle {\it\chi}\rangle <0$
. The viscosity transports the temperature variance mainly towards the wall, while inertia carries out transport mainly towards the core. Indeed, inside the thermal bulk region (
![]() $z^{\ast }>2.4$
) the production is negligible and the temperature fluctuations are sustained by the inertial transport and dissipated by viscosity. On the contrary, inside the thermal boundary layer (
$z^{\ast }>2.4$
) the production is negligible and the temperature fluctuations are sustained by the inertial transport and dissipated by viscosity. On the contrary, inside the thermal boundary layer (
![]() $z^{\ast }<0.16$
) the temperature variance is fed by the viscous transport and, once again, dissipated by viscosity.
$z^{\ast }<0.16$
) the temperature variance is fed by the viscous transport and, once again, dissipated by viscosity.

Figure 7. (a) Budget of the temperature variance as a function of
![]() $z^{\ast }$
for
$z^{\ast }$
for
![]() $\mathit{Ra}=1.0\times 10^{7}$
: inertial transport (dashed line), viscous transport (long dashed line), production (dot-dashed line) and dissipation (solid line). The details of the central region are shown in the inset. (b) Profiles of
$\mathit{Ra}=1.0\times 10^{7}$
: inertial transport (dashed line), viscous transport (long dashed line), production (dot-dashed line) and dissipation (solid line). The details of the central region are shown in the inset. (b) Profiles of
![]() $\langle {\it\theta}^{\prime 2}\rangle$
and of
$\langle {\it\theta}^{\prime 2}\rangle$
and of
![]() ${\it\Theta}$
(inset) as a function of
${\it\Theta}$
(inset) as a function of
![]() $z^{\ast }$
.
$z^{\ast }$
.

Figure 8. (a) Behaviour of production, the sum of pressure and inertial transport and the viscous transport of turbulent kinetic energy
![]() $\langle k\rangle$
as functions of
$\langle k\rangle$
as functions of
![]() $z^{\ast }$
for the different Rayleigh numbers:
$z^{\ast }$
for the different Rayleigh numbers:
![]() $\mathit{Ra}=1.7\times 10^{5}$
(solid line),
$\mathit{Ra}=1.7\times 10^{5}$
(solid line),
![]() $\mathit{Ra}=1.0\times 10^{6}$
(dotted line) and
$\mathit{Ra}=1.0\times 10^{6}$
(dotted line) and
![]() $\mathit{Ra}=1.0\times 10^{7}$
(dashed line). (b) Behaviour of production, inertial and viscous transport of temperature variance
$\mathit{Ra}=1.0\times 10^{7}$
(dashed line). (b) Behaviour of production, inertial and viscous transport of temperature variance
![]() $\langle {\it\theta}^{\prime 2}\rangle$
as functions of
$\langle {\it\theta}^{\prime 2}\rangle$
as functions of
![]() $z^{\ast }$
for the same three Rayleigh numbers.
$z^{\ast }$
for the same three Rayleigh numbers.
The production and transport terms of the turbulent kinetic energy and temperature variance budgets are reported in figure 8(a,b) for the different Rayleigh numbers. It is possible to identify viscous/thermal bulk regions, transitional and boundary layers also at lower
![]() $\mathit{Ra}$
, thus suggesting that the physical understanding of the energetics of the flow made so far is substantially unaltered by the Rayleigh number, at least for the range of values considered in the present work. From a quantitative point of view, the intensities of the single processes of transport and production are modulated. While the magnitudes of the terms of the temperature variance budget increase with
$\mathit{Ra}$
, thus suggesting that the physical understanding of the energetics of the flow made so far is substantially unaltered by the Rayleigh number, at least for the range of values considered in the present work. From a quantitative point of view, the intensities of the single processes of transport and production are modulated. While the magnitudes of the terms of the temperature variance budget increase with
![]() $\mathit{Ra}$
, the magnitudes of those of the turbulent kinetic energy budget decrease. In contrast to the fact that by increasing the Rayleigh number the turbulence level of the system increases, this behaviour is related to the adoption of the free-fall velocity
$\mathit{Ra}$
, the magnitudes of those of the turbulent kinetic energy budget decrease. In contrast to the fact that by increasing the Rayleigh number the turbulence level of the system increases, this behaviour is related to the adoption of the free-fall velocity
![]() $U_{f}$
as the characteristic velocity. By means of other velocity scales such as
$U_{f}$
as the characteristic velocity. By means of other velocity scales such as
![]() ${\it\kappa}/H$
, this behaviour would be reversed, with the terms of the equation for
${\it\kappa}/H$
, this behaviour would be reversed, with the terms of the equation for
![]() $\langle k\rangle$
increasing their intensity with
$\langle k\rangle$
increasing their intensity with
![]() $\mathit{Ra}$
. It is worth noting that, despite intensity, the behaviour of the terms of both the equations for
$\mathit{Ra}$
. It is worth noting that, despite intensity, the behaviour of the terms of both the equations for
![]() $\langle k\rangle$
and for
$\langle k\rangle$
and for
![]() $\langle {\it\theta}^{\prime 2}\rangle$
as a function of the wall distance normalized with
$\langle {\it\theta}^{\prime 2}\rangle$
as a function of the wall distance normalized with
![]() $H/\mathit{Nu}$
is nearly independent of the Rayleigh number, i.e. the location of the peaks is roughly the same for the different
$H/\mathit{Nu}$
is nearly independent of the Rayleigh number, i.e. the location of the peaks is roughly the same for the different
![]() $\mathit{Ra}$
.
$\mathit{Ra}$
.
Let us now discuss the self-sustaining mechanism of turbulence in RBC in terms of energetics of the flow. From the flow topology shown in the previous section, it emerges that mushroom-like plumes are accelerated throughout the bulk region by buoyancy. Close to the wall, the impingement redistributes the momentum of the plumes towards the wall-parallel directions (
![]() $\text{div}_{{\rm\pi}}>0$
) and creates sheet-like plumes (
$\text{div}_{{\rm\pi}}>0$
) and creates sheet-like plumes (
![]() $\text{div}_{{\rm\pi}}<0$
) which, in turn, trigger the emission of new plumes. In addition to that, the single-point analysis of the flow allows us to depict a more detailed picture. Generally speaking, the kinetic energy of the mushroom-like plumes is produced by buoyancy in the bulk region, where
$\text{div}_{{\rm\pi}}<0$
) which, in turn, trigger the emission of new plumes. In addition to that, the single-point analysis of the flow allows us to depict a more detailed picture. Generally speaking, the kinetic energy of the mushroom-like plumes is produced by buoyancy in the bulk region, where
![]() $\langle w^{\prime }{\it\theta}^{\prime }\rangle -\langle {\it\epsilon}\rangle >0$
, and it is transported towards the transitional layer by pressure mechanisms; see figure 5(a). Here, the kinetic energy begins to flow from the normal towards the horizontal components by pressure–strain rate correlation phenomena; see figure 6(a,b). This energy exchange between the different components of
$\langle w^{\prime }{\it\theta}^{\prime }\rangle -\langle {\it\epsilon}\rangle >0$
, and it is transported towards the transitional layer by pressure mechanisms; see figure 5(a). Here, the kinetic energy begins to flow from the normal towards the horizontal components by pressure–strain rate correlation phenomena; see figure 6(a,b). This energy exchange between the different components of
![]() $\langle k\rangle$
can be intuitively related to the impingement of mushroom-like plumes. Indeed, the impinging head of the plume induces a positive divergence of the horizontal velocity field, and hence the momentum of the wall-normal velocity component is redirected to the wall-parallel ones.
$\langle k\rangle$
can be intuitively related to the impingement of mushroom-like plumes. Indeed, the impinging head of the plume induces a positive divergence of the horizontal velocity field, and hence the momentum of the wall-normal velocity component is redirected to the wall-parallel ones.
In agreement with this picture, the peak of
![]() $\langle \text{div}_{{\rm\pi}}\rangle _{+}$
occurs almost at the same distance from the wall as the peak of the pressure–strain rate terms; compare figure 3(a) with figure 6(a,b). Hence, the impingement is clearly responsible for the inter-component exchange of kinetic energy. The wall-parallel components
$\langle \text{div}_{{\rm\pi}}\rangle _{+}$
occurs almost at the same distance from the wall as the peak of the pressure–strain rate terms; compare figure 3(a) with figure 6(a,b). Hence, the impingement is clearly responsible for the inter-component exchange of kinetic energy. The wall-parallel components
![]() $\langle u^{\prime 2}\rangle$
and
$\langle u^{\prime 2}\rangle$
and
![]() $\langle v^{\prime 2}\rangle$
are then partially transported by viscosity towards the viscous boundary layer, where they are dissipated; see figure 6(b). The residual energy flows from the horizontal components towards the normal one, creating a network of thin filaments, the sheet-like plumes. From the point of view of the temperature field, the interaction between the mechanically extracted sheet-like plumes and the strong mean temperature gradient of the transitional layer induces temperature fluctuations strong enough to be enriched by buoyancy. As can be seen by comparing figure 3(a) with figure 7(a), the production of temperature fluctuations reaches its maximum exactly where the peak of
$\langle v^{\prime 2}\rangle$
are then partially transported by viscosity towards the viscous boundary layer, where they are dissipated; see figure 6(b). The residual energy flows from the horizontal components towards the normal one, creating a network of thin filaments, the sheet-like plumes. From the point of view of the temperature field, the interaction between the mechanically extracted sheet-like plumes and the strong mean temperature gradient of the transitional layer induces temperature fluctuations strong enough to be enriched by buoyancy. As can be seen by comparing figure 3(a) with figure 7(a), the production of temperature fluctuations reaches its maximum exactly where the peak of
![]() $\langle \text{div}_{{\rm\pi}}\rangle _{-}$
occurs. Hence, the ejection of plumes is responsible for the sustainment of thermal fluctuations (see figure 7
b), which force the lift-up of new plumes, closing the self-sustained cycle.
$\langle \text{div}_{{\rm\pi}}\rangle _{-}$
occurs. Hence, the ejection of plumes is responsible for the sustainment of thermal fluctuations (see figure 7
b), which force the lift-up of new plumes, closing the self-sustained cycle.
5. Scale-by-scale budget of scale energy and scale variance
The self-sustained mechanisms of turbulence, described so far in terms of coherent structures and single-point turbulent kinetic energy and temperature variance budgets, are here studied in a multi-scale framework. Indeed, the mechanisms of production, transport and dissipation of turbulent velocity and temperature structures, previously shown, are actually multi-scale phenomena that depend not only on the position within the flow but also on the scale considered. In this scenario, a compound description in the physical/scale space is required for the correct understanding and modelling of the physics behind the turbulent regenerating cycle in RBC. Appropriate candidates to consider for a simultaneous description of turbulent dynamics in physical and scale space are the two-point statistical observables, such as the second-order structure function for the velocity
![]() $\langle {\it\delta}u^{2}\rangle =\langle {\it\delta}u_{i}{\it\delta}u_{i}\rangle$
and for the temperature
$\langle {\it\delta}u^{2}\rangle =\langle {\it\delta}u_{i}{\it\delta}u_{i}\rangle$
and for the temperature
![]() $\langle {\it\delta}{\it\theta}^{2}\rangle =\langle {\it\delta}{\it\theta}{\it\delta}{\it\theta}\rangle$
, where
$\langle {\it\delta}{\it\theta}^{2}\rangle =\langle {\it\delta}{\it\theta}{\it\delta}{\it\theta}\rangle$
, where
![]() ${\it\delta}{\it\beta}={\it\beta}^{\prime }(x_{i}+r_{i})-{\it\beta}^{\prime }(x_{i})$
denotes the fluctuating increment of the generic quantity
${\it\delta}{\it\beta}={\it\beta}^{\prime }(x_{i}+r_{i})-{\it\beta}^{\prime }(x_{i})$
denotes the fluctuating increment of the generic quantity
![]() ${\it\beta}$
between points
${\it\beta}$
between points
![]() $x_{i}$
and
$x_{i}$
and
![]() $x_{i}+r_{i}$
. The second-order structure function depends both on the separation vector
$x_{i}+r_{i}$
. The second-order structure function depends both on the separation vector
![]() $r_{i}$
and on the spatial location of the mid-point
$r_{i}$
and on the spatial location of the mid-point
![]() $X_{ci}=x_{i}+r_{i}/2$
. The present flow is statistically homogeneous and isotropic in the horizontal planes, hence the physical space dependence reduces simply to the position in the wall-normal direction, i.e.
$X_{ci}=x_{i}+r_{i}/2$
. The present flow is statistically homogeneous and isotropic in the horizontal planes, hence the physical space dependence reduces simply to the position in the wall-normal direction, i.e.
![]() $Z_{c}=z+r_{z}/2$
, where
$Z_{c}=z+r_{z}/2$
, where
![]() $r_{z}=r_{3}$
. In order to reduce the degrees of freedom of the analysis, we set
$r_{z}=r_{3}$
. In order to reduce the degrees of freedom of the analysis, we set
![]() $r_{z}=0$
, since the space of wall-normal scales implies averages over the statistically inhomogeneous direction
$r_{z}=0$
, since the space of wall-normal scales implies averages over the statistically inhomogeneous direction
![]() $z$
. Furthermore, the two-dimensional space of wall-parallel scales
$z$
. Furthermore, the two-dimensional space of wall-parallel scales
![]() $(r_{x},r_{y})$
, where
$(r_{x},r_{y})$
, where
![]() $r_{x}=r_{1}$
and
$r_{x}=r_{1}$
and
![]() $r_{y}=r_{2}$
, can be contracted into a single scalar quantity
$r_{y}=r_{2}$
, can be contracted into a single scalar quantity
![]() $r$
by considering the average over a circle
$r$
by considering the average over a circle
![]() $C$
of radius
$C$
of radius
![]() $r$
belonging to wall-parallel planes; see Marati et al. (Reference Marati, Casciola and Piva2004) for a similar approach. This operator is defined for the generic quantity
$r$
belonging to wall-parallel planes; see Marati et al. (Reference Marati, Casciola and Piva2004) for a similar approach. This operator is defined for the generic quantity
![]() ${\it\beta}$
as
${\it\beta}$
as

Figure 9. (a) Isolines of the
![]() $r$
average of
$r$
average of
![]() $\langle {\it\delta}u^{2}\rangle$
and (b) isolines of the
$\langle {\it\delta}u^{2}\rangle$
and (b) isolines of the
![]() $r$
average of
$r$
average of
![]() $\langle {\it\delta}{\it\theta}^{2}\rangle$
in the
$\langle {\it\delta}{\it\theta}^{2}\rangle$
in the
![]() $(r^{\ast },Z_{c}^{\ast })$
space.
$(r^{\ast },Z_{c}^{\ast })$
space.
The
![]() $r$
average of
$r$
average of
![]() $\langle {\it\delta}u^{2}\rangle$
and
$\langle {\it\delta}u^{2}\rangle$
and
![]() $\langle {\it\delta}{\it\theta}^{2}\rangle$
can be considered as a rough measure of the kinetic energy and temperature variance at scale
$\langle {\it\delta}{\it\theta}^{2}\rangle$
can be considered as a rough measure of the kinetic energy and temperature variance at scale
![]() $r$
and position
$r$
and position
![]() $Z_{c}$
and will be hereafter called scale energy and scale variance. Figure 9(a,b) shows the isolines of scale energy and scale variance at
$Z_{c}$
and will be hereafter called scale energy and scale variance. Figure 9(a,b) shows the isolines of scale energy and scale variance at
![]() $\mathit{Ra}=1.0\times 10^{7}$
in the
$\mathit{Ra}=1.0\times 10^{7}$
in the
![]() $(r^{\ast },Z_{c}^{\ast })$
space, where
$(r^{\ast },Z_{c}^{\ast })$
space, where
![]() $Z_{c}^{\ast }=(0.5-|Z_{c}|)^{\ast }$
corresponds with the distance from the wall
$Z_{c}^{\ast }=(0.5-|Z_{c}|)^{\ast }$
corresponds with the distance from the wall
![]() $z^{\ast }$
as we consider
$z^{\ast }$
as we consider
![]() $r_{z}^{\ast }=0$
. According to the profiles of turbulent kinetic energy and temperature variance shown in figures 5(b) and 7(b), both scale energy and scale variance reach their maxima close to the wall. Extending this picture, the space of scales
$r_{z}^{\ast }=0$
. According to the profiles of turbulent kinetic energy and temperature variance shown in figures 5(b) and 7(b), both scale energy and scale variance reach their maxima close to the wall. Extending this picture, the space of scales
![]() $r$
reveals that both scale energy and scale variance reach their maxima at large scales and decrease moving to small dissipative scales. Starting from a generalized form of the Kolmogorov (see § 5.1) and Yaglom (see § 5.2) equations, the scale-by-scale budgets for
$r$
reveals that both scale energy and scale variance reach their maxima at large scales and decrease moving to small dissipative scales. Starting from a generalized form of the Kolmogorov (see § 5.1) and Yaglom (see § 5.2) equations, the scale-by-scale budgets for
![]() $\langle {\it\delta}u^{2}\rangle$
and
$\langle {\it\delta}u^{2}\rangle$
and
![]() $\langle {\it\delta}{\it\theta}^{2}\rangle$
are evaluated at specific locations
$\langle {\it\delta}{\it\theta}^{2}\rangle$
are evaluated at specific locations
![]() $Z_{c}^{\ast }$
and, after a detailed study, the results are interpreted in terms of the flow topology.
$Z_{c}^{\ast }$
and, after a detailed study, the results are interpreted in terms of the flow topology.
5.1. The generalized Kolmogorov equation
Using the momentum (2.1a
) and the continuity (2.1b
) equations, a balance for
![]() $\langle {\it\delta}u^{2}\rangle$
(Marati et al.
Reference Marati, Casciola and Piva2004) can be derived following the procedure described by Hill (Reference Hill2002) as
$\langle {\it\delta}u^{2}\rangle$
(Marati et al.
Reference Marati, Casciola and Piva2004) can be derived following the procedure described by Hill (Reference Hill2002) as
 $$\begin{eqnarray}\displaystyle & & \displaystyle -\frac{\partial \langle w^{\ast }{\it\delta}u^{2}\rangle }{\partial Z_{c}}-2\frac{\partial \langle {\it\delta}p{\it\delta}w\rangle }{\partial Z_{c}}+\frac{1}{2}\sqrt{\frac{\mathit{ Pr }}{\mathit{Ra}}}\frac{\partial ^{2}\langle {\it\delta}u^{2}\rangle }{\partial Z_{c}^{2}}-\frac{\partial \langle {\it\delta}u^{2}{\it\delta}u_{i}\rangle }{\partial r_{i}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,2\sqrt{\frac{\mathit{ Pr }}{\mathit{Ra }}}\frac{\partial ^{2}\langle {\it\delta}u^{2}\rangle }{\partial r_{j}\partial r_{j}}+2\langle {\it\delta}{\it\theta}{\it\delta}w\rangle -4\langle {\it\epsilon}^{\ast }\rangle =0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle -\frac{\partial \langle w^{\ast }{\it\delta}u^{2}\rangle }{\partial Z_{c}}-2\frac{\partial \langle {\it\delta}p{\it\delta}w\rangle }{\partial Z_{c}}+\frac{1}{2}\sqrt{\frac{\mathit{ Pr }}{\mathit{Ra}}}\frac{\partial ^{2}\langle {\it\delta}u^{2}\rangle }{\partial Z_{c}^{2}}-\frac{\partial \langle {\it\delta}u^{2}{\it\delta}u_{i}\rangle }{\partial r_{i}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,2\sqrt{\frac{\mathit{ Pr }}{\mathit{Ra }}}\frac{\partial ^{2}\langle {\it\delta}u^{2}\rangle }{\partial r_{j}\partial r_{j}}+2\langle {\it\delta}{\it\theta}{\it\delta}w\rangle -4\langle {\it\epsilon}^{\ast }\rangle =0,\end{eqnarray}$$
where the asterisk denotes the mid-point average,
![]() ${\it\beta}^{\ast }=({\it\beta}^{\prime }(x_{i})+{\it\beta}^{\prime }(x_{i}+r_{i}))/2$
. Equation (5.2) is referred to as the generalized Kolmogorov equation. Indeed, it represents an extension to an inhomogeneous flow of the balance proposed by Kolmogorov (Reference Kolmogorov1941) for homogeneous and isotropic turbulence. The terms with the
${\it\beta}^{\ast }=({\it\beta}^{\prime }(x_{i})+{\it\beta}^{\prime }(x_{i}+r_{i}))/2$
. Equation (5.2) is referred to as the generalized Kolmogorov equation. Indeed, it represents an extension to an inhomogeneous flow of the balance proposed by Kolmogorov (Reference Kolmogorov1941) for homogeneous and isotropic turbulence. The terms with the
![]() $r$
derivative are associated with a transfer of scale energy through scales, while those with the
$r$
derivative are associated with a transfer of scale energy through scales, while those with the
![]() $Z_{c}$
derivative correspond to a transport of scale energy across different layers due to vertical inhomogeneity. Hereafter, ‘transfer’ and ‘transport’ are used to specify implicitly an exchange of energy in the scale space and in the physical space, respectively. The first, second and third terms of (5.2) are respectively the inertial, pressure and viscous contributions to the transport, whereas the fourth and fifth terms are respectively the inertial and viscous contributions to the transfer. The last two terms are the production and dissipation of scale energy due to buoyancy and viscosity. Equation (5.2) manifests a well-defined asymptotic behaviour as larger and larger scales are approached. For
$Z_{c}$
derivative correspond to a transport of scale energy across different layers due to vertical inhomogeneity. Hereafter, ‘transfer’ and ‘transport’ are used to specify implicitly an exchange of energy in the scale space and in the physical space, respectively. The first, second and third terms of (5.2) are respectively the inertial, pressure and viscous contributions to the transport, whereas the fourth and fifth terms are respectively the inertial and viscous contributions to the transfer. The last two terms are the production and dissipation of scale energy due to buoyancy and viscosity. Equation (5.2) manifests a well-defined asymptotic behaviour as larger and larger scales are approached. For
![]() $r\gg l$
, where
$r\gg l$
, where
![]() $l$
is the relevant correlation length, quantities evaluated at
$l$
is the relevant correlation length, quantities evaluated at
![]() $x_{i}$
and
$x_{i}$
and
![]() $x_{i}^{\prime }$
are uncorrelated and (5.2) reduces, within a factor of four, to the mid-point average of the turbulent kinetic energy budget (4.1).
$x_{i}^{\prime }$
are uncorrelated and (5.2) reduces, within a factor of four, to the mid-point average of the turbulent kinetic energy budget (4.1).
Equation (5.2) is written in the four-dimensional space
![]() $(r_{x},r_{y},r_{z},Z_{c})$
. By considering
$(r_{x},r_{y},r_{z},Z_{c})$
. By considering
![]() $r_{z}=0$
and by applying the
$r_{z}=0$
and by applying the
![]() $r$
-averaging operator defined in (5.1)–(5.2), we obtain the so-called
$r$
-averaging operator defined in (5.1)–(5.2), we obtain the so-called
![]() $r$
-averaged form of the generalized Kolmogorov equation,
$r$
-averaged form of the generalized Kolmogorov equation,
where each term corresponds to the appropriate term in (5.2). To streamline the notation, the overall transport term
![]() $T_{c}$
and the overall transfer term
$T_{c}$
and the overall transfer term
![]() $T_{r}$
of scale energy are introduced:
$T_{r}$
of scale energy are introduced:
thus we can rewrite (5.3) as
Equation (5.5) allows us to appreciate the amount of scale energy provided at a certain scale
![]() $r$
and geometric location
$r$
and geometric location
![]() $Z_{c}$
by the buoyancy forces through
$Z_{c}$
by the buoyancy forces through
![]() ${\it\Pi}$
and how much energy is dissipated by viscous forces through
${\it\Pi}$
and how much energy is dissipated by viscous forces through
![]() $E$
. The net amount of scale energy is transferred towards other scales and positions of the flow as described by the terms
$E$
. The net amount of scale energy is transferred towards other scales and positions of the flow as described by the terms
![]() $T_{r}$
and
$T_{r}$
and
![]() $T_{c}$
, respectively. When the transport term is negative,
$T_{c}$
, respectively. When the transport term is negative,
![]() $T_{c}<0$
, scale energy is drained to feed regions closer to the wall, whereas, when it is positive,
$T_{c}<0$
, scale energy is drained to feed regions closer to the wall, whereas, when it is positive,
![]() $T_{c}>0$
, scale energy is received from regions located further away from the wall. Analogously, when the transfer term is negative,
$T_{c}>0$
, scale energy is received from regions located further away from the wall. Analogously, when the transfer term is negative,
![]() $T_{r}<0$
, scale energy is drained to feed larger scales forming a reverse cascade, whereas, when it is positive,
$T_{r}<0$
, scale energy is drained to feed larger scales forming a reverse cascade, whereas, when it is positive,
![]() $T_{r}>0$
, scale energy is received from larger scales forming a more classical forward cascade. In what follows, the scale-by-scale energy budgets at different distances from the wall, in the bulk region, transitional layer and viscous boundary layer, are shown for
$T_{r}>0$
, scale energy is received from larger scales forming a more classical forward cascade. In what follows, the scale-by-scale energy budgets at different distances from the wall, in the bulk region, transitional layer and viscous boundary layer, are shown for
![]() $\mathit{Ra}=1.0\times 10^{7}$
. The main plot in each figure displays the terms
$\mathit{Ra}=1.0\times 10^{7}$
. The main plot in each figure displays the terms
![]() $T_{c}$
,
$T_{c}$
,
![]() $T_{r}$
,
$T_{r}$
,
![]() ${\it\Pi}$
,
${\it\Pi}$
,
![]() $E$
and their sum
$E$
and their sum
![]() $T_{c}+T_{r}+{\it\Pi}+E$
. The accuracy with which this sum satisfies (5.5) is interpreted as a measure of the statistical convergence of the data. Finally, the insets show the different contributions of
$T_{c}+T_{r}+{\it\Pi}+E$
. The accuracy with which this sum satisfies (5.5) is interpreted as a measure of the statistical convergence of the data. Finally, the insets show the different contributions of
![]() $T_{c}$
and
$T_{c}$
and
![]() $T_{r}$
.
$T_{r}$
.

Figure 10. Terms of the generalized Kolmogorov equation as a function of
![]() $r^{\ast }$
in (a) the bulk region at
$r^{\ast }$
in (a) the bulk region at
![]() $Z_{c}^{\ast }=2.5$
and (b) the high transitional layer at
$Z_{c}^{\ast }=2.5$
and (b) the high transitional layer at
![]() $Z_{c}^{\ast }=0.6$
. Main panel:
$Z_{c}^{\ast }=0.6$
. Main panel:
![]() ${\it\Pi}$
(solid line),
${\it\Pi}$
(solid line),
![]() $T_{c}$
(dashed line),
$T_{c}$
(dashed line),
![]() $T_{r}$
(dot-dashed line),
$T_{r}$
(dot-dashed line),
![]() $E$
(long dashed line) and
$E$
(long dashed line) and
![]() $T_{c}+T_{r}+{\it\Pi}+E$
(circles). Left inset:
$T_{c}+T_{r}+{\it\Pi}+E$
(circles). Left inset:
![]() $I_{c}$
(solid line),
$I_{c}$
(solid line),
![]() $P$
(dashed line) and
$P$
(dashed line) and
![]() $D_{c}$
(dot-dashed line). Right inset:
$D_{c}$
(dot-dashed line). Right inset:
![]() $I_{r}$
(solid line) and
$I_{r}$
(solid line) and
![]() $D_{r}$
(dashed line).
$D_{r}$
(dashed line).
We start by analysing the bulk region. According to the turbulent kinetic energy budget shown in § 4, this is the region where the velocity fluctuations are produced and transported towards the wall. As shown in figure 10(a), at
![]() $Z_{c}^{\ast }=2.5$
, the production of scale energy is concentrated at large scales, where it exceeds the dissipation. Here, the scale-energy excess is drained by the transport term
$Z_{c}^{\ast }=2.5$
, the production of scale energy is concentrated at large scales, where it exceeds the dissipation. Here, the scale-energy excess is drained by the transport term
![]() $T_{c}<0$
and the transfer term
$T_{c}<0$
and the transfer term
![]() $T_{r}<0$
to be redistributed in the
$T_{r}<0$
to be redistributed in the
![]() $(r^{\ast },Z_{c}^{\ast })$
space. The transport
$(r^{\ast },Z_{c}^{\ast })$
space. The transport
![]() $T_{c}$
subtracts scale energy to feed the near-wall region of the flow. In particular, as shown in the left inset of figure 10(a), the transport at large separations is mainly performed by the pressure term
$T_{c}$
subtracts scale energy to feed the near-wall region of the flow. In particular, as shown in the left inset of figure 10(a), the transport at large separations is mainly performed by the pressure term
![]() $P$
and the inertial term
$P$
and the inertial term
![]() $I_{c}$
, while the viscous contribution
$I_{c}$
, while the viscous contribution
![]() $D_{c}$
is negligible. Unexpectedly, the transfer term gives rise to a reverse cascade from small to larger scales,
$D_{c}$
is negligible. Unexpectedly, the transfer term gives rise to a reverse cascade from small to larger scales,
![]() $T_{r}<0$
. In particular, as shown in the right inset of figure 10(a), this large-scale reverse transfer is performed by
$T_{r}<0$
. In particular, as shown in the right inset of figure 10(a), this large-scale reverse transfer is performed by
![]() $I_{r}$
and hence by inertial mechanisms. While considering smaller scales, we observe that the transport term
$I_{r}$
and hence by inertial mechanisms. While considering smaller scales, we observe that the transport term
![]() $T_{c}$
is still negative and reaches its minimum, thus highlighting that the scales that contribute most to the transport of scale energy towards the wall are not the largest but the intermediate ones. As shown in the left inset of figure 10(a), this transport is mainly carried out by the pressure term
$T_{c}$
is still negative and reaches its minimum, thus highlighting that the scales that contribute most to the transport of scale energy towards the wall are not the largest but the intermediate ones. As shown in the left inset of figure 10(a), this transport is mainly carried out by the pressure term
![]() $P$
. At these intermediate small scales, the overall transfer
$P$
. At these intermediate small scales, the overall transfer
![]() $T_{r}$
becomes positive, recovering a more classical forward cascade towards smaller scales. This forward cascade is sustained by the inertial term
$T_{r}$
becomes positive, recovering a more classical forward cascade towards smaller scales. This forward cascade is sustained by the inertial term
![]() $I_{r}$
at intermediate scales, while at the smallest scales by viscous diffusion
$I_{r}$
at intermediate scales, while at the smallest scales by viscous diffusion
![]() $D_{r}$
, as shown in the right inset of figure 10(a).
$D_{r}$
, as shown in the right inset of figure 10(a).
We focus now on the scale-by-scale budgets within the transitional layer. As highlighted by the single-point budget shown in § 4, the turbulent kinetic energy of this layer is sustained by a pressure-driven transport coming from the bulk. On the contrary, the viscous transport is negative, which means that this layer, in turn, feeds the viscous boundary layer through a diffusive process. The scale-by-scale budget at
![]() $Z_{c}^{\ast }=0.6$
is shown in figure 10(b). As can be seen, the production due to buoyancy is still significant and concentrated at large scales but, contrary to the bulk region, an energy excess is not observed, i.e.
$Z_{c}^{\ast }=0.6$
is shown in figure 10(b). As can be seen, the production due to buoyancy is still significant and concentrated at large scales but, contrary to the bulk region, an energy excess is not observed, i.e.
![]() ${\it\Pi}+E<0$
at every scale. In this physical location, the scale energy is sustained at large and intermediate scales by a positive overall transport term
${\it\Pi}+E<0$
at every scale. In this physical location, the scale energy is sustained at large and intermediate scales by a positive overall transport term
![]() $T_{c}$
and, in particular, by the pressure contribution
$T_{c}$
and, in particular, by the pressure contribution
![]() $P$
, as shown in the left inset of figure 10(b). The viscous transport term
$P$
, as shown in the left inset of figure 10(b). The viscous transport term
![]() $D_{c}$
is also significant at large scales but it is negative, actually draining scale energy to feed the viscous boundary layer. The overall transfer term
$D_{c}$
is also significant at large scales but it is negative, actually draining scale energy to feed the viscous boundary layer. The overall transfer term
![]() $T_{r}$
still highlights a double feature of forward transfer at small scales and reverse transfer at large ones. With respect to the budget at
$T_{r}$
still highlights a double feature of forward transfer at small scales and reverse transfer at large ones. With respect to the budget at
![]() $Z_{c}^{\ast }=2.5$
in the bulk region, two main differences appear. The first one is that the reverse transfer is stronger and the range of scales involved is increased. The second one is relative to the nature of the reverse transfer mechanisms. Indeed, in this case the transfer from small to large scales is driven by the viscous term
$Z_{c}^{\ast }=2.5$
in the bulk region, two main differences appear. The first one is that the reverse transfer is stronger and the range of scales involved is increased. The second one is relative to the nature of the reverse transfer mechanisms. Indeed, in this case the transfer from small to large scales is driven by the viscous term
![]() $D_{r}$
rather than by the inertial term
$D_{r}$
rather than by the inertial term
![]() $I_{r}$
; see the right inset of figure 10(b). It is worth pointing out that the overall transport term
$I_{r}$
; see the right inset of figure 10(b). It is worth pointing out that the overall transport term
![]() $T_{c}$
is not always positive, but negative values are observed for small scales, meaning that these separations are still pumping scale energy almost through inviscid mechanisms (
$T_{c}$
is not always positive, but negative values are observed for small scales, meaning that these separations are still pumping scale energy almost through inviscid mechanisms (
![]() $T_{c}\approx I_{c}+P<0$
) towards the wall region while the larger ones are receiving scale energy from the bulk (
$T_{c}\approx I_{c}+P<0$
) towards the wall region while the larger ones are receiving scale energy from the bulk (
![]() $T_{c}>0$
). This is an interesting feature that could be explained as a compound effect of both transport in physical space and transfer in the space of scales, as follows. From the bulk region, scale energy flows towards the wall by means of pressure transport processes since
$T_{c}>0$
). This is an interesting feature that could be explained as a compound effect of both transport in physical space and transfer in the space of scales, as follows. From the bulk region, scale energy flows towards the wall by means of pressure transport processes since
![]() $P<0$
at intermediate/large scales. At the same time, scale energy is transferred towards larger scales, since
$P<0$
at intermediate/large scales. At the same time, scale energy is transferred towards larger scales, since
![]() $T_{r}<0$
. As a consequence, moving towards the wall, the first scales that gain scale energy from the inviscid transport are the larger ones, while the small scales are still feeding the transport towards the wall.
$T_{r}<0$
. As a consequence, moving towards the wall, the first scales that gain scale energy from the inviscid transport are the larger ones, while the small scales are still feeding the transport towards the wall.

Figure 11. As figure 10 but in (a) the low transitional layer at
![]() $Z_{c}^{\ast }=0.2$
and (b) the viscous boundary layer at
$Z_{c}^{\ast }=0.2$
and (b) the viscous boundary layer at
![]() $Z_{c}^{\ast }=0.1$
.
$Z_{c}^{\ast }=0.1$
.
The scale-by-scale budget at
![]() $Z_{c}^{\ast }=0.2$
, corresponding to the part of the transitional layer closer to the wall, is shown in figure 11(a). In this location, production is negligible at all separations and scale energy is entirely provided by transport. As for
$Z_{c}^{\ast }=0.2$
, corresponding to the part of the transitional layer closer to the wall, is shown in figure 11(a). In this location, production is negligible at all separations and scale energy is entirely provided by transport. As for
![]() $Z_{c}^{\ast }=0.6$
, the pressure transport term is positive while the viscous one is negative. A gain of energy from the overall transport term throughout the entire range of scales and a lack of a reverse cascade are the main differences with the scale-by-scale budget at
$Z_{c}^{\ast }=0.6$
, the pressure transport term is positive while the viscous one is negative. A gain of energy from the overall transport term throughout the entire range of scales and a lack of a reverse cascade are the main differences with the scale-by-scale budget at
![]() $Z_{c}^{\ast }=0.6$
. Indeed, as shown by the isolines of
$Z_{c}^{\ast }=0.6$
. Indeed, as shown by the isolines of
![]() $T_{r}$
in the
$T_{r}$
in the
![]() $(r^{\ast },Z_{c}^{\ast })$
space plotted in figure 12(a), the reverse transfer reaches its maximum intensity and extension at
$(r^{\ast },Z_{c}^{\ast })$
space plotted in figure 12(a), the reverse transfer reaches its maximum intensity and extension at
![]() $Z_{c}^{\ast }=0.45$
, which is just a little away from the wall compared to
$Z_{c}^{\ast }=0.45$
, which is just a little away from the wall compared to
![]() $Z_{c}^{\ast }=0.2$
but well within the transitional layer. It can be seen by recalling figure 3(a) that the peak of
$Z_{c}^{\ast }=0.2$
but well within the transitional layer. It can be seen by recalling figure 3(a) that the peak of
![]() $\langle \text{div}_{{\rm\pi}}\rangle _{+}$
, which occurs at
$\langle \text{div}_{{\rm\pi}}\rangle _{+}$
, which occurs at
![]() $z^{\ast }=0.3$
, is located close to the maximum reverse cascade. Furthermore, the dashed line plotted in figure 12(a) crosses the isoline
$z^{\ast }=0.3$
, is located close to the maximum reverse cascade. Furthermore, the dashed line plotted in figure 12(a) crosses the isoline
![]() $T_{r}=0$
at
$T_{r}=0$
at
![]() $r^{\ast }=7$
, which is not very different from the characteristic length of the impinging plumes,
$r^{\ast }=7$
, which is not very different from the characteristic length of the impinging plumes,
![]() $r^{\ast }=3$
, observed at
$r^{\ast }=3$
, observed at
![]() $z^{\ast }=0.3$
; see figure 3(b). According to these observations, the reverse energy transfer seems to be strongly related to the enlargement of the plumes during impingement. How the results from the scale-by-scale budgets are related with the turbulent structures will be further analysed in the last paragraph of this section.
$z^{\ast }=0.3$
; see figure 3(b). According to these observations, the reverse energy transfer seems to be strongly related to the enlargement of the plumes during impingement. How the results from the scale-by-scale budgets are related with the turbulent structures will be further analysed in the last paragraph of this section.
Let us consider the scale-by-scale budget within the viscous boundary layer at
![]() $Z_{c}^{\ast }=0.1$
. As already shown by means of the turbulent kinetic energy budget, this layer is characterized by a strong energy dissipation, which is fed by a viscous transport. According to this picture, the scale-by-scale budget shown in figure 11(b) highlights that the production term is negligible at all scales and that the overall transport term
$Z_{c}^{\ast }=0.1$
. As already shown by means of the turbulent kinetic energy budget, this layer is characterized by a strong energy dissipation, which is fed by a viscous transport. According to this picture, the scale-by-scale budget shown in figure 11(b) highlights that the production term is negligible at all scales and that the overall transport term
![]() $T_{c}$
is deputed for the sustaining of turbulent fluctuations. In particular, scale energy is found to be provided essentially by the viscous transport term
$T_{c}$
is deputed for the sustaining of turbulent fluctuations. In particular, scale energy is found to be provided essentially by the viscous transport term
![]() $D_{c}$
and the pressure term
$D_{c}$
and the pressure term
![]() $P$
, as shown in the left inset of figure 11(b). In turn, this scale energy available at large scales is transferred towards small scales by the overall transfer term
$P$
, as shown in the left inset of figure 11(b). In turn, this scale energy available at large scales is transferred towards small scales by the overall transfer term
![]() $T_{r}$
, where it is finally dissipated. As shown in the right inset of figure 11(b), this forward transfer is mainly due to the viscous diffusion term
$T_{r}$
, where it is finally dissipated. As shown in the right inset of figure 11(b), this forward transfer is mainly due to the viscous diffusion term
![]() $D_{r}$
also at large scales.
$D_{r}$
also at large scales.

Figure 12. (a) Isolines of
![]() $T_{r}$
in the
$T_{r}$
in the
![]() $(r^{\ast },Z_{c}^{\ast })$
space for (a)
$(r^{\ast },Z_{c}^{\ast })$
space for (a)
![]() $\mathit{Ra}=1.0\times 10^{7}$
and (b)
$\mathit{Ra}=1.0\times 10^{7}$
and (b)
![]() $\mathit{Ra}=1.7\times 10^{5}$
. Dashed lines denotes the value of
$\mathit{Ra}=1.7\times 10^{5}$
. Dashed lines denotes the value of
![]() $Z_{c}^{\ast }$
at which the range of scales characterized by
$Z_{c}^{\ast }$
at which the range of scales characterized by
![]() $T_{r}<0$
is maximum. The values of the isolines are percentage of the maximum of
$T_{r}<0$
is maximum. The values of the isolines are percentage of the maximum of
![]() $T_{r}$
.
$T_{r}$
.
As for the single-point budgets, the Rayleigh number does not affect the physical understanding of the multi-scale features of RBC, at least for the range of values considered here. From a quantitative point of view, the intensity of the terms of the generalized Kolmogorov equation significantly change with
![]() $\mathit{Ra}$
, but the behaviour in the
$\mathit{Ra}$
, but the behaviour in the
![]() $(r^{\ast },Z_{c}^{\ast })$
space remains almost unaltered. As an example, by comparing the isolines of
$(r^{\ast },Z_{c}^{\ast })$
space remains almost unaltered. As an example, by comparing the isolines of
![]() $T_{r}$
for
$T_{r}$
for
![]() $\mathit{Ra}=1.0\times 10^{7}$
and
$\mathit{Ra}=1.0\times 10^{7}$
and
![]() $\mathit{Ra}=1.7\times 10^{5}$
(see figure 12
a,b, respectively), it can be noted that from a physical point of view the double feature of forward and reverse transfer is almost unaltered by
$\mathit{Ra}=1.7\times 10^{5}$
(see figure 12
a,b, respectively), it can be noted that from a physical point of view the double feature of forward and reverse transfer is almost unaltered by
![]() $\mathit{Ra}$
. Indeed, the reverse cascade phenomena are present at both
$\mathit{Ra}$
. Indeed, the reverse cascade phenomena are present at both
![]() $\mathit{Ra}$
, taking place at the larger scales of the bulk region and reaching their maximum closer to the wall in the transitional layer, while the forward cascade phenomena characterize the intermediate/small scales of the bulk and transitional region and the entire space of scales of the boundary layer for both
$\mathit{Ra}$
, taking place at the larger scales of the bulk region and reaching their maximum closer to the wall in the transitional layer, while the forward cascade phenomena characterize the intermediate/small scales of the bulk and transitional region and the entire space of scales of the boundary layer for both
![]() $\mathit{Ra}$
.
$\mathit{Ra}$
.
Let us now investigate how the multi-scale description of turbulent RBC given by the generalized Kolmogorov equation extends our understanding of the flow topology. From the profile of
![]() $\langle k\rangle$
plotted in figure 5(b) we have seen that most of the turbulent kinetic energy belongs to the bulk region. This energy can be associated with the plumes, and it is shown that these structures are sustained by buoyancy and transferred towards the wall mainly by pressure mechanisms. In the transitional layer, the plumes feel the impermeability condition of the wall and redistribute the energy associated with their wall-normal component to the wall-parallel ones through pressure–strain rate correlation mechanisms. Finally, the two-dimensional wall-parallel components of the turbulent kinetic energy are diffused towards the wall and dissipated by viscous mechanisms in the viscous boundary layer. In this context, a negative (positive) overall transfer term
$\langle k\rangle$
plotted in figure 5(b) we have seen that most of the turbulent kinetic energy belongs to the bulk region. This energy can be associated with the plumes, and it is shown that these structures are sustained by buoyancy and transferred towards the wall mainly by pressure mechanisms. In the transitional layer, the plumes feel the impermeability condition of the wall and redistribute the energy associated with their wall-normal component to the wall-parallel ones through pressure–strain rate correlation mechanisms. Finally, the two-dimensional wall-parallel components of the turbulent kinetic energy are diffused towards the wall and dissipated by viscous mechanisms in the viscous boundary layer. In this context, a negative (positive) overall transfer term
![]() $T_{r}$
can be reasonably associated with an enlargement (contraction) of plumes in the horizontal planes. In the bulk region, the compound effect of a reverse transfer and an overall transport towards the wall can be interpreted as the enlargement of the wall-parallel section of the plume while moving towards the wall. This phenomenon is mainly driven by the inertial term
$T_{r}$
can be reasonably associated with an enlargement (contraction) of plumes in the horizontal planes. In the bulk region, the compound effect of a reverse transfer and an overall transport towards the wall can be interpreted as the enlargement of the wall-parallel section of the plume while moving towards the wall. This phenomenon is mainly driven by the inertial term
![]() $I_{r}$
in the space of scales and by the pressure term
$I_{r}$
in the space of scales and by the pressure term
![]() $P$
in the physical space. In the transitional layer, the impingement of the plumes occurs. The enlargement of the head of the plumes is characterized by a strong reverse energy transfer driven by viscous diffusive mechanisms. As a result of the coupling of the reverse transfer with the spatial transport, the large scales are the first to be fed by the flux emerging from the bulk region, while small scales are still transporting scale energy towards the wall. Hence, the core of the plumes, while pushing to the wall, feels the presence of the wall after their exterior, which experiences a diffusive enlargement.
$P$
in the physical space. In the transitional layer, the impingement of the plumes occurs. The enlargement of the head of the plumes is characterized by a strong reverse energy transfer driven by viscous diffusive mechanisms. As a result of the coupling of the reverse transfer with the spatial transport, the large scales are the first to be fed by the flux emerging from the bulk region, while small scales are still transporting scale energy towards the wall. Hence, the core of the plumes, while pushing to the wall, feels the presence of the wall after their exterior, which experiences a diffusive enlargement.
5.2. The generalized Yaglom equation
Let us now focus on the multi-scale analysis of the temperature field. In the same way as we derived the generalized Kolmogorov equation, a balance for
![]() $\langle {\it\delta}{\it\theta}^{2}\rangle$
can be obtained from the temperature equation (2.1c
),
$\langle {\it\delta}{\it\theta}^{2}\rangle$
can be obtained from the temperature equation (2.1c
),
 $$\begin{eqnarray}\displaystyle & & \displaystyle -\frac{\partial \langle w^{\ast }{\it\delta}{\it\theta}^{2}\rangle }{\partial Z_{c}}+\frac{1}{2\sqrt{\mathit{Pr }\mathit{ Ra}}}\frac{\partial ^{2}\langle {\it\delta}{\it\theta}^{2}\rangle }{\partial Z_{c}^{2}}-\frac{\partial \langle {\it\delta}{\it\theta}^{2}{\it\delta}u_{i}\rangle }{\partial r_{i}}+\frac{2}{\sqrt{\mathit{Pr }\mathit{ Ra}}}\frac{\partial ^{2}\langle {\it\delta}{\it\theta}^{2}\rangle }{\partial r_{j}\partial r_{j}}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,2\langle w^{\ast }{\it\delta}{\it\theta}\rangle \frac{\partial {\it\delta}{\it\Theta}}{\partial Z_{c}}-2\langle {\it\delta}w{\it\delta}{\it\theta}\rangle \left(\frac{\text{d}{\it\Theta}}{\text{d}Z_{c}}\right)^{\!\ast }-4\langle {\it\chi}^{\ast }\rangle =0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle -\frac{\partial \langle w^{\ast }{\it\delta}{\it\theta}^{2}\rangle }{\partial Z_{c}}+\frac{1}{2\sqrt{\mathit{Pr }\mathit{ Ra}}}\frac{\partial ^{2}\langle {\it\delta}{\it\theta}^{2}\rangle }{\partial Z_{c}^{2}}-\frac{\partial \langle {\it\delta}{\it\theta}^{2}{\it\delta}u_{i}\rangle }{\partial r_{i}}+\frac{2}{\sqrt{\mathit{Pr }\mathit{ Ra}}}\frac{\partial ^{2}\langle {\it\delta}{\it\theta}^{2}\rangle }{\partial r_{j}\partial r_{j}}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,2\langle w^{\ast }{\it\delta}{\it\theta}\rangle \frac{\partial {\it\delta}{\it\Theta}}{\partial Z_{c}}-2\langle {\it\delta}w{\it\delta}{\it\theta}\rangle \left(\frac{\text{d}{\it\Theta}}{\text{d}Z_{c}}\right)^{\!\ast }-4\langle {\it\chi}^{\ast }\rangle =0,\end{eqnarray}$$
which is called hereafter the generalized Yaglom equation. Indeed, it represents an extension to an inhomogeneous flow of the balance proposed by Yaglom (Reference Yaglom1949) for homogeneous and isotropic turbulence; see Gauding et al. (Reference Gauding, Wick, Pitsch and Peters2014) for an intermediate generalization to homogeneous but anisotropic scalar turbulence. The first and second terms of (5.6) are the inertial and viscous contributions to the transport in physical space, respectively, whereas the third and fourth terms are the inertial and viscous contributions to the transfer in the space of scales. The last three terms are, in order, the two contributions to production and the dissipation of scale variance.
Analogously to the generalized Kolmogorov budget, (5.6) tends, within a factor of two, to the mid-point average of the equation for the temperature variance (4.5) as larger and larger scales are approached. By considering
![]() $r_{z}=0$
and by applying the
$r_{z}=0$
and by applying the
![]() $r$
-averaging operator defined in (5.1), we obtain the
$r$
-averaging operator defined in (5.1), we obtain the
![]() $r$
-averaged form of the generalized Yaglom equation,
$r$
-averaged form of the generalized Yaglom equation,
where the contribution from the fifth term of (5.6) vanishes since
![]() ${\it\delta}{\it\Theta}=0$
for
${\it\delta}{\it\Theta}=0$
for
![]() $r_{z}=0$
. Each term of (5.7) corresponds to the appropriate term in (5.6). Again, to streamline the notation, the overall transport and transfer terms,
$r_{z}=0$
. Each term of (5.7) corresponds to the appropriate term in (5.6). Again, to streamline the notation, the overall transport and transfer terms,
![]() $T_{c}^{{\it\theta}}$
and
$T_{c}^{{\it\theta}}$
and
![]() $T_{r}^{{\it\theta}}$
respectively, are introduced:
$T_{r}^{{\it\theta}}$
respectively, are introduced:
Thus we can rewrite (5.7) as
In what follows, the scale-by-scale budgets inside the thermal bulk region, the thermal transitional layer and the thermal boundary layer are shown for
![]() $\mathit{Ra}=1.0\times 10^{7}$
. The main plot in each figure shows the terms
$\mathit{Ra}=1.0\times 10^{7}$
. The main plot in each figure shows the terms
![]() $T_{c}^{{\it\theta}}$
,
$T_{c}^{{\it\theta}}$
,
![]() $T_{r}^{{\it\theta}}$
,
$T_{r}^{{\it\theta}}$
,
![]() ${\it\Pi}^{{\it\theta}}$
,
${\it\Pi}^{{\it\theta}}$
,
![]() $E^{{\it\theta}}$
and their sum
$E^{{\it\theta}}$
and their sum
![]() $T_{c}^{{\it\theta}}+T_{r}^{{\it\theta}}+{\it\Pi}^{{\it\theta}}+E^{{\it\theta}}$
. As for the scale-energy budget, the accuracy with which this sum satisfies (5.9) is a measure of the statistical convergence of the data. Finally, the insets display the different contributions of
$T_{c}^{{\it\theta}}+T_{r}^{{\it\theta}}+{\it\Pi}^{{\it\theta}}+E^{{\it\theta}}$
. As for the scale-energy budget, the accuracy with which this sum satisfies (5.9) is a measure of the statistical convergence of the data. Finally, the insets display the different contributions of
![]() $T_{c}^{{\it\theta}}$
and
$T_{c}^{{\it\theta}}$
and
![]() $T_{r}^{{\it\theta}}$
.
$T_{r}^{{\it\theta}}$
.

Figure 13. Terms of the generalized Yaglom equation as a function of
![]() $r^{\ast }$
in the thermal transitional layer at (a)
$r^{\ast }$
in the thermal transitional layer at (a)
![]() $Z_{c}^{\ast }=0.75$
and (b)
$Z_{c}^{\ast }=0.75$
and (b)
![]() $Z_{c}^{\ast }=0.4$
. Main panel:
$Z_{c}^{\ast }=0.4$
. Main panel:
![]() ${\it\Pi}^{{\it\theta}}$
(solid line),
${\it\Pi}^{{\it\theta}}$
(solid line),
![]() $T_{c}^{{\it\theta}}$
(dashed line),
$T_{c}^{{\it\theta}}$
(dashed line),
![]() $T_{r}^{{\it\theta}}$
(dot-dashed line),
$T_{r}^{{\it\theta}}$
(dot-dashed line),
![]() $E^{{\it\theta}}$
(long dashed line) and
$E^{{\it\theta}}$
(long dashed line) and
![]() $T_{c}^{{\it\theta}}+T_{r}^{{\it\theta}}+{\it\Pi}^{{\it\theta}}+E^{{\it\theta}}$
(circles). Left inset:
$T_{c}^{{\it\theta}}+T_{r}^{{\it\theta}}+{\it\Pi}^{{\it\theta}}+E^{{\it\theta}}$
(circles). Left inset:
![]() $I_{c}^{{\it\theta}}$
(solid line) and
$I_{c}^{{\it\theta}}$
(solid line) and
![]() $D_{c}^{{\it\theta}}$
(dashed line). Right inset:
$D_{c}^{{\it\theta}}$
(dashed line). Right inset:
![]() $I_{r}^{{\it\theta}}$
(solid line) and
$I_{r}^{{\it\theta}}$
(solid line) and
![]() $D_{r}^{{\it\theta}}$
(dashed line).
$D_{r}^{{\it\theta}}$
(dashed line).
Let us analyse the scale-by-scale budget at
![]() $Z_{c}^{\ast }=0.75$
, displayed in figure 13(a), which corresponds to the central part of the thermal transitional layer. As shown by the temperature variance equation in § 4, this layer is the source region for the temperature fluctuations. Production dominates dissipation and the temperature variance excess is transported away to feed temperature fluctuations inside both the thermal bulk and the thermal boundary layer. The scale-by-scale budget confirms this picture, showing a strong production, which exceeds dissipation for a large range of scales. This scale-variance excess is partially drained by the overall transport term
$Z_{c}^{\ast }=0.75$
, displayed in figure 13(a), which corresponds to the central part of the thermal transitional layer. As shown by the temperature variance equation in § 4, this layer is the source region for the temperature fluctuations. Production dominates dissipation and the temperature variance excess is transported away to feed temperature fluctuations inside both the thermal bulk and the thermal boundary layer. The scale-by-scale budget confirms this picture, showing a strong production, which exceeds dissipation for a large range of scales. This scale-variance excess is partially drained by the overall transport term
![]() $T_{c}^{{\it\theta}}$
, which is significantly negative and, as shown in the left inset of figure 13(a), is driven by the inertial term
$T_{c}^{{\it\theta}}$
, which is significantly negative and, as shown in the left inset of figure 13(a), is driven by the inertial term
![]() $I_{c}^{{\it\theta}}$
. The scale variance drained by
$I_{c}^{{\it\theta}}$
. The scale variance drained by
![]() $T_{c}^{{\it\theta}}$
is then directed towards the wall and the centreline. Considering the space of scales, an interesting behaviour is observed for the overall transfer term
$T_{c}^{{\it\theta}}$
is then directed towards the wall and the centreline. Considering the space of scales, an interesting behaviour is observed for the overall transfer term
![]() $T_{r}^{{\it\theta}}$
. At small scales,
$T_{r}^{{\it\theta}}$
. At small scales,
![]() $T_{r}^{{\it\theta}}$
is positive, highlighting the presence of a forward transfer of scale variance, while, at larger scales, it becomes negative, implying a reverse transfer from small to large scales. As shown in the right inset of figure 13(a), the reverse transfer is driven by the inertial term
$T_{r}^{{\it\theta}}$
is positive, highlighting the presence of a forward transfer of scale variance, while, at larger scales, it becomes negative, implying a reverse transfer from small to large scales. As shown in the right inset of figure 13(a), the reverse transfer is driven by the inertial term
![]() $I_{r}^{{\it\theta}}$
, while the forward transfer is driven by the viscous term
$I_{r}^{{\it\theta}}$
, while the forward transfer is driven by the viscous term
![]() $D_{r}^{{\it\theta}}$
. By considering the scale-by-scale budget at
$D_{r}^{{\it\theta}}$
. By considering the scale-by-scale budget at
![]() $Z_{c}^{\ast }=0.4$
, shown in figure 13(b), we observe that the production and the resulting scale-variance excess are even stronger compared with the scale-by-scale budget at
$Z_{c}^{\ast }=0.4$
, shown in figure 13(b), we observe that the production and the resulting scale-variance excess are even stronger compared with the scale-by-scale budget at
![]() $Z_{c}^{\ast }=0.75$
. Indeed, at
$Z_{c}^{\ast }=0.75$
. Indeed, at
![]() $z^{\ast }=0.4$
, the single-point production of temperature variance reaches its maximum, as shown in figure 7(a). As a consequence, also the overall transport term
$z^{\ast }=0.4$
, the single-point production of temperature variance reaches its maximum, as shown in figure 7(a). As a consequence, also the overall transport term
![]() $T_{c}^{{\it\theta}}$
is stronger and drains a large amount of scale variance, redirecting it towards other regions of the flow. As shown in the left inset of figure 13(b), the viscous transport term
$T_{c}^{{\it\theta}}$
is stronger and drains a large amount of scale variance, redirecting it towards other regions of the flow. As shown in the left inset of figure 13(b), the viscous transport term
![]() $D_{c}^{{\it\theta}}$
is no longer negligible and contributes significantly, together with the inertial term
$D_{c}^{{\it\theta}}$
is no longer negligible and contributes significantly, together with the inertial term
![]() $I_{c}^{{\it\theta}}$
, to drain the scale-variance excess.
$I_{c}^{{\it\theta}}$
, to drain the scale-variance excess.
Concerning the transfer in the space of scales, we observe a stronger reverse transfer, which involves a larger range of separations. The main difference between the budget at
![]() $Z_{c}^{\ast }=0.75$
and the budget at
$Z_{c}^{\ast }=0.75$
and the budget at
![]() $Z_{c}^{\ast }=0.4$
is that, in the latter, the action of viscous diffusion on the transfer in the space of scales is never negligible even at large separations, where it contributes significantly to
$Z_{c}^{\ast }=0.4$
is that, in the latter, the action of viscous diffusion on the transfer in the space of scales is never negligible even at large separations, where it contributes significantly to
![]() $T_{r}^{{\it\theta}}$
. The observed reverse transfer for the scale variance appears to be related to the reverse transfer observed in § 5.1 for the scale energy. Indeed, both the reverse transfers take place almost at the same scales and positions. Hence, it is arguable that the two observed reverse transfers are both a footprint of the same phenomenon, in particular, of the enlargement of thermal and velocity structure due to the impingement. Accordingly, the peak of
$T_{r}^{{\it\theta}}$
. The observed reverse transfer for the scale variance appears to be related to the reverse transfer observed in § 5.1 for the scale energy. Indeed, both the reverse transfers take place almost at the same scales and positions. Hence, it is arguable that the two observed reverse transfers are both a footprint of the same phenomenon, in particular, of the enlargement of thermal and velocity structure due to the impingement. Accordingly, the peak of
![]() $\langle \text{div}_{{\rm\pi}}\rangle _{+}$
is found to occur at
$\langle \text{div}_{{\rm\pi}}\rangle _{+}$
is found to occur at
![]() $z^{\ast }=0.3$
(see figure 3
a), which is close to the wall distance of maximum reverse cascade shown in figure 15(a) with a dashed line. Furthermore, at this distance from the wall, the cross-over between forward and reverse transfer (
$z^{\ast }=0.3$
(see figure 3
a), which is close to the wall distance of maximum reverse cascade shown in figure 15(a) with a dashed line. Furthermore, at this distance from the wall, the cross-over between forward and reverse transfer (
![]() $T_{r}^{{\it\theta}}=0$
) occurs at
$T_{r}^{{\it\theta}}=0$
) occurs at
![]() $r^{\ast }=3$
, which is exactly the characteristic length of the impinging plumes,
$r^{\ast }=3$
, which is exactly the characteristic length of the impinging plumes,
![]() $r^{\ast }=3$
, observed at
$r^{\ast }=3$
, observed at
![]() $z^{\ast }=0.3$
; see figure 3(b). It should be noted that the same exact correspondence between the characteristic scales of the inertial transfer and the planar divergence is not found for the velocity field; compare figure 12(a) with figure 3(b). This is probably related to the fact that the plumes are thermal structures rather than being structures of momentum. Clearly, these thermal structures leave a footprint also on the velocity field, but a direct correspondence between the scale of impingement and the cross-over scale between reverse and direct cascades is expected more for the scale variance than for the scale energy.
$z^{\ast }=0.3$
; see figure 3(b). It should be noted that the same exact correspondence between the characteristic scales of the inertial transfer and the planar divergence is not found for the velocity field; compare figure 12(a) with figure 3(b). This is probably related to the fact that the plumes are thermal structures rather than being structures of momentum. Clearly, these thermal structures leave a footprint also on the velocity field, but a direct correspondence between the scale of impingement and the cross-over scale between reverse and direct cascades is expected more for the scale variance than for the scale energy.

Figure 14. As figure 13 but in (a) the thermal bulk region at
![]() $Z_{c}^{\ast }=5$
and (b) the thermal boundary layer at
$Z_{c}^{\ast }=5$
and (b) the thermal boundary layer at
![]() $Z_{c}^{\ast }=0.1$
.
$Z_{c}^{\ast }=0.1$
.
We proceed by analysing in detail the scale-by-scale budget in the thermal bulk region at
![]() $Z_{c}^{\ast }=5$
, shown in figure 14(a). As anticipated by the single-point temperature variance budget, the production term is almost negligible and the temperature fluctuations are sustained by the inertial transport. The scale-by-scale budget confirms this picture. Indeed, even if we are considering the inner part of the thermal bulk region, the production term is small and the scale variance is sustained by the overall transport term
$Z_{c}^{\ast }=5$
, shown in figure 14(a). As anticipated by the single-point temperature variance budget, the production term is almost negligible and the temperature fluctuations are sustained by the inertial transport. The scale-by-scale budget confirms this picture. Indeed, even if we are considering the inner part of the thermal bulk region, the production term is small and the scale variance is sustained by the overall transport term
![]() $T_{c}^{{\it\theta}}$
, which in turn is driven by the inertial term
$T_{c}^{{\it\theta}}$
, which in turn is driven by the inertial term
![]() $I_{c}^{{\it\theta}}$
, as shown in the left inset of figure 14(a). The scale variance supplied at large scales by the transport term is then transferred by
$I_{c}^{{\it\theta}}$
, as shown in the left inset of figure 14(a). The scale variance supplied at large scales by the transport term is then transferred by
![]() $T_{r}^{{\it\theta}}$
towards small scales and dissipated. Indeed,
$T_{r}^{{\it\theta}}$
towards small scales and dissipated. Indeed,
![]() $T_{r}^{{\it\theta}}$
is always positive and, as shown in the right inset of figure 14(a), is dominated by the inertial term
$T_{r}^{{\it\theta}}$
is always positive and, as shown in the right inset of figure 14(a), is dominated by the inertial term
![]() $I_{r}^{{\it\theta}}$
at large scales and by the viscous term
$I_{r}^{{\it\theta}}$
at large scales and by the viscous term
![]() $D_{r}^{{\it\theta}}$
at smaller scales.
$D_{r}^{{\it\theta}}$
at smaller scales.
Let us now analyse the scale-by-scale budget within the thermal boundary layer at
![]() $Z_{c}^{\ast }=0.1$
, shown in figure 14(b). By comparing this picture with the one referring to the thermal bulk region at
$Z_{c}^{\ast }=0.1$
, shown in figure 14(b). By comparing this picture with the one referring to the thermal bulk region at
![]() $Z_{c}^{\ast }=5$
, shown in figure 14(a), a reasonable similarity can be observed. Indeed, both regions lack in production and receive scale variance from the thermal transitional layer. The overall transport term
$Z_{c}^{\ast }=5$
, shown in figure 14(a), a reasonable similarity can be observed. Indeed, both regions lack in production and receive scale variance from the thermal transitional layer. The overall transport term
![]() $T_{c}^{{\it\theta}}$
sustains temperature fluctuations at large scales and an overall transfer term
$T_{c}^{{\it\theta}}$
sustains temperature fluctuations at large scales and an overall transfer term
![]() $T_{r}^{{\it\theta}}$
redistributes this scale variance towards small scales, where it is dissipated. The only difference with the thermal bulk comes from the nature of the transport and transfer processes. Indeed, in the thermal boundary layer, viscosity dominates the whole space of scales. As shown in both the insets of figure 14(b), the scale-variance injection at large scales by the overall transport is significantly provided by the viscous term
$T_{r}^{{\it\theta}}$
redistributes this scale variance towards small scales, where it is dissipated. The only difference with the thermal bulk comes from the nature of the transport and transfer processes. Indeed, in the thermal boundary layer, viscosity dominates the whole space of scales. As shown in both the insets of figure 14(b), the scale-variance injection at large scales by the overall transport is significantly provided by the viscous term
![]() $D_{c}^{{\it\theta}}$
, while the redistribution towards small scales by
$D_{c}^{{\it\theta}}$
, while the redistribution towards small scales by
![]() $T_{r}^{{\it\theta}}$
is mainly driven by the viscous diffusion term
$T_{r}^{{\it\theta}}$
is mainly driven by the viscous diffusion term
![]() $D_{r}^{{\it\theta}}$
also at large scales.
$D_{r}^{{\it\theta}}$
also at large scales.
In closing this section, we address the multi-dimensional behaviour of scale variance at the different Rayleigh numbers. As for the generalized Kolmogorov equation, the considerations we made by analysing the generalized Yaglom equation for
![]() $\mathit{Ra}=1.0\times 10^{7}$
are not affected by
$\mathit{Ra}=1.0\times 10^{7}$
are not affected by
![]() $\mathit{Ra}$
from a physical point of view. Despite the fact that the intensity of the terms of the generalized Yaglom equation change with
$\mathit{Ra}$
from a physical point of view. Despite the fact that the intensity of the terms of the generalized Yaglom equation change with
![]() $\mathit{Ra}$
, the behaviour in the
$\mathit{Ra}$
, the behaviour in the
![]() $(r^{\ast },Z_{c}^{\ast })$
space remains almost unaltered. As shown in figure 15(a,b), where the isolines of
$(r^{\ast },Z_{c}^{\ast })$
space remains almost unaltered. As shown in figure 15(a,b), where the isolines of
![]() $T_{r}^{{\it\theta}}$
for
$T_{r}^{{\it\theta}}$
for
![]() $\mathit{Ra}=1.0\times 10^{7}$
and
$\mathit{Ra}=1.0\times 10^{7}$
and
![]() $\mathit{Ra}=1.7\times 10^{5}$
are reported, the double feature of forward and reverse transfer is almost the same for the two
$\mathit{Ra}=1.7\times 10^{5}$
are reported, the double feature of forward and reverse transfer is almost the same for the two
![]() $\mathit{Ra}$
reported. This scaling also characterizes the other terms of the budget. These results suggest that the same dynamics of the plumes affect the flows at the different
$\mathit{Ra}$
reported. This scaling also characterizes the other terms of the budget. These results suggest that the same dynamics of the plumes affect the flows at the different
![]() $\mathit{Ra}$
considered, even if the coherence of the flow structures changes dramatically from
$\mathit{Ra}$
considered, even if the coherence of the flow structures changes dramatically from
![]() $\mathit{Ra}=1.7\times 10^{5}$
to
$\mathit{Ra}=1.7\times 10^{5}$
to
![]() $\mathit{Ra}=1.0\times 10^{7}$
.
$\mathit{Ra}=1.0\times 10^{7}$
.

Figure 15. (a) Isolines of
![]() $T_{r}^{{\it\theta}}$
in the
$T_{r}^{{\it\theta}}$
in the
![]() $(r^{\ast },Z_{c}^{\ast })$
space for (a)
$(r^{\ast },Z_{c}^{\ast })$
space for (a)
![]() $\mathit{Ra}=1.0\times 10^{7}$
and (b)
$\mathit{Ra}=1.0\times 10^{7}$
and (b)
![]() $\mathit{Ra}=1.7\times 10^{5}$
. Dashed lines denotes the value of
$\mathit{Ra}=1.7\times 10^{5}$
. Dashed lines denotes the value of
![]() $Z_{c}^{\ast }$
at which the range of scales characterized by
$Z_{c}^{\ast }$
at which the range of scales characterized by
![]() $T_{r}^{{\it\theta}}<0$
is maximum. The values of the isolines are percentage of the maximum of
$T_{r}^{{\it\theta}}<0$
is maximum. The values of the isolines are percentage of the maximum of
![]() $T_{r}^{{\it\theta}}$
.
$T_{r}^{{\it\theta}}$
.
6. Conclusions
Convective turbulence is one of the most interesting fluid phenomena, where production of turbulent fluctuations is embedded in the system rather than being provided by an external agent. The inhomogeneous and anisotropic features of the self-sustained processes in such a flow makes the problem very difficult to understand and model. Indeed, the presence of the walls induces a spatial modulation of the scale-by-scale interactions of turbulence. In this scenario, a compound description in the physical and scale space of the turbulent dynamics is required. In the present paper, starting from a properly defined form of the Kolmogorov and Yaglom equations, a scale-by-scale balance for the turbulent velocity and temperature fluctuations is presented. This approach allows us to analyse for the first time how kinetic energy and temperature variance are produced, transported and dissipated simultaneously in physical and scale space. DNS data of turbulent RBC for Prandtl number
![]() $0.7$
and Rayleigh numbers
$0.7$
and Rayleigh numbers
![]() $10^{5}$
,
$10^{5}$
,
![]() $10^{6}$
and
$10^{6}$
and
![]() $10^{7}$
are used for the analysis. To provide a mechanistic description of the phenomenon by which turbulent velocity and temperature fluctuations are generated and sustained at different scales and locations, a detailed description of the scale-by-scale budgets is linked to the classical single-point energy budgets and to the commonly accepted model of the life cycle of the turbulent structures.
$10^{7}$
are used for the analysis. To provide a mechanistic description of the phenomenon by which turbulent velocity and temperature fluctuations are generated and sustained at different scales and locations, a detailed description of the scale-by-scale budgets is linked to the classical single-point energy budgets and to the commonly accepted model of the life cycle of the turbulent structures.
Concerning the velocity field, three distinct regions are identified as relevant in our flow: a bulk region, a transitional layer, and a viscous boundary layer. In the bulk region, the mushroom-like plumes are locally sustained at relatively large scales by production due to buoyancy, which exceeds the local rate of energy dissipation. This scale energy excess is transported towards the wall by pressure mechanisms and transferred towards larger scales by inertial mechanisms, meaning that the mushroom-like plumes enlarge through inviscid mechanisms while moving towards the wall. Turbulent velocity fluctuations inside the transitional layer are sustained by the pressure transport rather than by the buoyant production. The large scales are those fed by the spatial flux coming from the bulk, while small scales are still transporting scale energy towards the viscous boundary layer, as a consequence of the coupling between the reverse transfer towards large scales and the transport towards the wall. Within the transitional layer, the reverse transfer is found to be strong and driven by viscous diffusion. This behaviour characterizes the plume impingement on the wall, identified here by means of the divergence of the horizontal velocity field, as mainly a viscous process. During the impingement, the plumes feel the presence of the wall through the pressure field and they enlarge by viscous diffusion, transferring their turbulent kinetic energy from the wall-normal to the wall-parallel components. These are large-scale phenomena, since, at small scales, plumes are characterized by a viscous forward cascade and a viscous transport towards the wall, where scale energy is finally dissipated.
Concerning the temperature field, a thermal bulk region, a thermal transitional layer and a thermal boundary layer are identified analogously to the velocity field. The thermal transitional layer is actually the source region, where the production of scale variance is strong and exceeds dissipation at large scales. This statistical observable can be related with the lift-up of thermal plumes from the sheet-like ones, closing the life cycle of the plume. The scale variance excess, at large scales, is transported towards the thermal boundary layer and towards the thermal bulk by viscous and pressure mechanisms, respectively, and transferred towards larger scales by viscous mechanisms. This reverse transfer occurs almost in the same locations as the reverse transfer of scale energy, suggesting that both observations are related to the same phenomenon of plume impingement. Inside the thermal bulk and thermal boundary layer, temperature fluctuations are sustained at large scales by the transport and a forward transfer occurs draining at large scales and feeding the dissipative ones.
The observed complex scale-by-scale dynamics could have strong repercussions on the theoretical approaches to convective turbulence. In the classical picture, the spectrum of scales is divided into three ranges: a large-scale one, an intermediate one and a small-scale one. In the large-scale range, turbulent fluctuations are produced through buoyancy mechanisms and a Bolgiano–Obukhov subrange is expected to take place as suggested by Ching et al. (Reference Ching, Tsang, Fok, He and Tong2013). In an intermediate range of scales, the energy content of the large scales flows down towards smaller ones through an inviscid cascade process reproducing the classical Kolmogorov inertial subrange as reported by experiments (Kunnen et al. Reference Kunnen, Clercx, Geurts, Van Bokhoven, Akkermans and Verzicco2008; Ching et al. Reference Ching, Tsang, Fok, He and Tong2013) and numerical simulations (Calzavarini, Toschi & Tripiccione Reference Calzavarini, Toschi and Tripiccione2002; Kunnen et al. Reference Kunnen, Clercx, Geurts, Van Bokhoven, Akkermans and Verzicco2008; Kaczorowski & Xia Reference Kaczorowski and Xia2013). Finally, in the viscosity-dominated range at small scales, turbulent energy is dissipated. This picture does not take into account the observed presence of spatially evolving forward and reverse cascades. The flow of scale energy from the large production scales to the small dissipative ones is never at the same wall distance as the Bolgiano–Obukhov and Kolmogorov subranges assume, and involves in between larger scales. More explicitly, production at intermediate/large scales in the bulk region feed larger scales in the transitional layer (reverse cascade towards the wall), which in turn feed smaller scales in the boundary layer (forward cascade towards the wall) where dissipation occurs. These fundamental processes characterize the self-sustaining cycle of turbulence and should be taken into account in the modelling approaches of convective turbulence.