1 Motivation
Functional and logic programming are the most prominent declarative programming paradigms. Functional programming provides a compact notation, due to nested expressions, and demand-driven (optimal) evaluation strategies, whereas logic programming provides flexibility due to free variables, unification, and built-in search. Thus, both paradigms have their advantages for application programming so that it is reasonable to offer their features in a single language. One option to achieve this is to extend a logic language with functional syntax (equations, nested functional expressions) and transform evaluable functions into predicates and flatten nested expressions (Barbuti et al. Reference Barbuti, Bellia, Levi and Martelli1984; Casas et al. Reference Casas, Cabeza and Hermenegildo2006; Naish Reference Naish1991). Hence, logic programming can be considered as the more general paradigm. On the other hand, functional programming supports efficient, in particular, optimal evaluation strategies, by exploiting functional dependencies during evaluation so that it provides more modularity and new programming concepts, like programming with infinite data structures (Hughes Reference Hughes1990). In Prolog systems which support coroutining, that is, delaying the evaluation of literals when arguments are not sufficiently instantiated, one can exploit coroutining to implement the basic idea of lazy evaluation (Casas et al. Reference Casas, Cabeza and Hermenegildo2006; Naish Reference Naish1991). However, the use of coroutines might add new problems. For instance, computations with coroutining introduce the risk of incompleteness by floundering (Lloyd Reference Lloyd1987). Furthermore, coroutining might yield infinite search spaces due to delaying literals generated by recursively defined predicates (Hanus Reference Hanus1995). Although the operational behavior of particular programs can be improved with coroutines, there are no general results characterizing classes of programs where this always leads to an improved operational behavior.
Amalgamated functional logic languages (Antoy and Hanus Reference Antoy and Hanus2010) are an approach to support flexible as well as efficient evaluation strategies. For instance, the language Curry (Hanus Reference Hanus2016) is based on an optimal and logically sound and complete strategy (Antoy et al. Reference Antoy, Echahed and Hanus2000; Antoy Reference Antoy1997). The motivation of this paper is to show that functional logic languages are actually superior to pure logic languages. Instead of transforming functions into predicates, we present a sequence of transformations which map logic programs into functional logic programs. Using a sophisticated mapping based on inferring functional dependencies, we obtain a fully automatic transformation tool which can reduce the computational efforts. In particular, infinite search spaces w.r.t. logic programs can be reduced to finite ones w.r.t. the transformed functional logic programs.
This paper is structured as follows. The next section reviews basic notions of logic and functional logic programming. Section 3 presents a simple embedding of logic into functional logic programs, which is extended in Sections 4 and 5 by considering functional dependencies. Section 6 discusses the inference of such dependencies and Section 7 adds some extensions. This final transformation is implemented in a tool sketched in Section 8. We evaluate our transformation in Section 9 before we conclude. Due to lack of space, some details and proofs are omitted. They are available in a longer version of this paper. Footnote 1
2 Logic and functional logic programming
In this section, we fix our notation for logic programs and briefly review some relevant features of functional logic programming. More details are in the textbook of Lloyd (Reference Lloyd1987) and in surveys on functional logic programming (Antoy and Hanus Reference Antoy and Hanus2010; Hanus Reference Hanus2013).
In logic programming (we use Prolog syntax for concrete examples), terms are constructed from variables (
![]() $X,Y\ldots$
), numbers, atom constants (
$X,Y\ldots$
), numbers, atom constants (
![]() $c,d,\ldots$
), and functors or term constructors (
$c,d,\ldots$
), and functors or term constructors (
![]() $f,g,\ldots$
) applied to a sequence of terms, like
$f,g,\ldots$
) applied to a sequence of terms, like
![]() $f(t_1,\ldots,t_n)$
. A literal
$f(t_1,\ldots,t_n)$
. A literal
![]() $p(t_1,\ldots,t_n)$
is a predicate p applied to a sequence of terms, and a goal
$p(t_1,\ldots,t_n)$
is a predicate p applied to a sequence of terms, and a goal
![]() $L_1,\ldots,L_k$
is a sequence of literals, where □ denotes the empty goal (
$L_1,\ldots,L_k$
is a sequence of literals, where □ denotes the empty goal (
![]() $k = 0$
). Predicates are defined by clauses L :- B, where the head L is a literal and the body B is a goal (a fact is a clause with an empty body □, otherwise it is a rule). A logic program is a sequence of clauses.
$k = 0$
). Predicates are defined by clauses L :- B, where the head L is a literal and the body B is a goal (a fact is a clause with an empty body □, otherwise it is a rule). A logic program is a sequence of clauses.
Logic programs are evaluated by SLD-resolution steps, where we consider the leftmost selection rule here. Thus, if
![]() $G = L_1,\ldots,L_k$
is a goal and L :- B is a variant of a program clause (with fresh variables) such that there exists a most general unifier
Footnote 2
(mgu)
$G = L_1,\ldots,L_k$
is a goal and L :- B is a variant of a program clause (with fresh variables) such that there exists a most general unifier
Footnote 2
(mgu)
![]() $\sigma$
of
$\sigma$
of
![]() $L_1$
and L, then
$L_1$
and L, then
![]() $G \vdash_\sigma \sigma(B, L_2,\ldots,L_k)$
is a resolution step. We denote by
$G \vdash_\sigma \sigma(B, L_2,\ldots,L_k)$
is a resolution step. We denote by
![]() $G_1 \vdash^{*}_\sigma G_m$
a sequence
$G_1 \vdash^{*}_\sigma G_m$
a sequence
![]() $G_1 \vdash_{\sigma_1} G_2 \vdash_{\sigma_2} \ldots \vdash_{\sigma_{m-1}} G_m$
of resolution steps with
$G_1 \vdash_{\sigma_1} G_2 \vdash_{\sigma_2} \ldots \vdash_{\sigma_{m-1}} G_m$
of resolution steps with
![]() $\sigma = \sigma_{m-1} \circ \dots \circ \sigma_1$
. A computed answer for a goal G is a substitution
$\sigma = \sigma_{m-1} \circ \dots \circ \sigma_1$
. A computed answer for a goal G is a substitution
![]() $\sigma$
(usually restricted to the variables occurring in G) with
$\sigma$
(usually restricted to the variables occurring in G) with
![]() $G \vdash^{*}_\sigma$
□.
$G \vdash^{*}_\sigma$
□.
Example 1 The following logic program defines the well-known predicate app for list concatenation, a predicate app3 to concatenate three lists, and a predicate dup which is satisfied if the second argument occurs at least two times in the list provided as the first argument:
The computed answers for the goal dup([1,2,2,1],Z) are
![]() $\{\mathtt{Z} \mapsto \mathtt{1}\}$
and
$\{\mathtt{Z} \mapsto \mathtt{1}\}$
and
![]() $\{\mathtt{Z} \mapsto \mathtt{2}\}$
. They can be computed by a Prolog system, but after showing these answers, Prolog does not terminate due to an infinite search space. Actually, Prolog does not terminate for the goal dup([],Z) since it enumerates arbitrary long lists for the first argument of app3.
$\{\mathtt{Z} \mapsto \mathtt{2}\}$
. They can be computed by a Prolog system, but after showing these answers, Prolog does not terminate due to an infinite search space. Actually, Prolog does not terminate for the goal dup([],Z) since it enumerates arbitrary long lists for the first argument of app3.
Functional logic programming (Antoy and Hanus Reference Antoy and Hanus2010; Hanus Reference Hanus2013) integrates the most important features of functional and logic languages in order to provide a variety of programming concepts. Functional logic languages support higher order functions and lazy (demand-driven) evaluation from functional programming as well as nondeterministic search and computing with partial information from logic programming. The declarative multiparadigm language Curry (Hanus Reference Hanus2016), which we use in this paper, is a functional logic language with advanced programming concepts. Its syntax is close to Haskell (Peyton Jones Reference Peyton Jones2003), that is, variables and names of defined operations start with lowercase letters and the names of data constructors start with an uppercase letter. The application of an operation f to e is denoted by juxtaposition (“
![]() $f~e$
”).
$f~e$
”).
In addition to Haskell, Curry allows free (logic) variables in program rules (equations) and initial expressions. Function calls with free variables are evaluated by a possibly nondeterministic instantiation of arguments.
Example 2 The following Curry program Footnote 3 defines the operations of Example 1 in a functional manner, where logic features (free variables z and _) are exploited to define dup:
“|” introduces a condition, and “=:=” denotes semantic unification, that is, the expressions on both sides are evaluated before unifying them.
Since app can be called with free variables in arguments, the condition in the definition of dup is solved by instantiating z and the anonymous free variables “_” to appropriate values (i.e., expressions without defined functions) before reducing the function calls. This corresponds to narrowing (Reddy Reference Reddy1985; Slagle Reference Slagle1974).
![]() $t \rightsquigarrow_\sigma t'$
is a narrowing step if there is some nonvariable position p in t, an equation (program rule)
$t \rightsquigarrow_\sigma t'$
is a narrowing step if there is some nonvariable position p in t, an equation (program rule)
![]() $l \;\mathtt{=}\; r$
, and an mgu
$l \;\mathtt{=}\; r$
, and an mgu
![]() $\sigma$
of
$\sigma$
of
![]() $t|_p$
and l such that
$t|_p$
and l such that
![]() $t' = \sigma(t[r]_p)$
,
Footnote 4
that is, t’ is obtained from t by replacing the subterm
$t' = \sigma(t[r]_p)$
,
Footnote 4
that is, t’ is obtained from t by replacing the subterm
![]() $t|_p$
by the equation’s right-hand side and applying the unifier. This definition also applies to conditional equations
$t|_p$
by the equation’s right-hand side and applying the unifier. This definition also applies to conditional equations
![]() $l \;\mathtt{|}\; c \;\mathtt{=}\; r$
which are considered as syntactic sugar for the unconditional equation
$l \;\mathtt{|}\; c \;\mathtt{=}\; r$
which are considered as syntactic sugar for the unconditional equation
![]() $l \;\mathtt{=}\; c \;\mathtt{\&>}\; r$
, where the operation “&>” is defined by True &> x = x.
$l \;\mathtt{=}\; c \;\mathtt{\&>}\; r$
, where the operation “&>” is defined by True &> x = x.
Curry is based on the needed narrowing strategy (Antoy et al. Reference Antoy, Echahed and Hanus2000) which also uses non-most-general unifiers in narrowing steps to ensure the optimality of computations. Needed narrowing is a demand-driven evaluation strategy, that is, it supports computations with infinite data structures (Hughes Reference Hughes1990) and can avoid superfluous computations. The latter property is our motivation to transform logic programs into Curry programs, since this can reduce infinite search spaces to finite ones. For instance, the evaluation of the expression dup [] has a finite computation space: the generation of longer lists for the first argument of app3 is avoided since there is no demand for such lists.
dup is a nondeterministic operation since it might deliver more than one result for a given argument, for example, the evaluation of dup[1,2,2,1] yields the values 1 and 2. Nondeterministic operations, which can formally be interpreted as mappings from values into sets of values (González-Moreno et al. Reference González-Moreno, Hortalá-González, López-Fraguas and Rodrguez-Artalejo1999), are an important feature of contemporary functional logic languages. For the transformation described in this paper, this feature has the advantage that it is not important to transform predicates into purely mathematical functions (having at most one result for a given combination of arguments).
Curry has many more features that are useful for application programming, like set functions (Antoy and Hanus Reference Antoy and Hanus2009) to encapsulate search, and standard features from functional programming, like modules or monadic I/O (Wadler Reference Wadler1997). However, the kernel of Curry described so far should be sufficient to understand the transformation described in the following sections.
3 Conservative transformation
Functional logic programming is an extension of pure logic programming. Hence, there is a straightforward way to map logic programs into functional logic programs: map each predicate into a Boolean function and transform each clause into a (conditional) equation. We call this mapping the conservative transformation since it keeps the basic structure of derivations. Since narrowing-based functional logic languages support free variables as well as overlapping rules, this mapping does not change the set of computed solutions (in contrast to a purely functional target language where always the first matching rule is selected).
As a first step to describe this transformation, we have to map terms from logic into functional logic notation. Since terms in logic programming (here: Prolog syntax) have a direct correspondence to data terms (as used in Curry), the mapping of terms is just a change of syntax (e.g., uppercase variables are mapped into lowercase, and lowercase constants and constructors are mapped into their uppercase equivalents). We denote this term transformation by
![]() $[\![\cdot]\!]_{\mathcal{T}}$
, that is,
$[\![\cdot]\!]_{\mathcal{T}}$
, that is,
![]() $[\![\cdot]\!]_{\mathcal{T}}$
is a syntactic transformation which maps a (Prolog) term, written inside the brackets, into a (Curry) data term. It is defined by a case distinction as follows:
$[\![\cdot]\!]_{\mathcal{T}}$
is a syntactic transformation which maps a (Prolog) term, written inside the brackets, into a (Curry) data term. It is defined by a case distinction as follows:

Based on this term transformation, we define a mapping
![]() $[\![\cdot]\!]_{\mathcal{C}}$
from logic into functional logic programs where facts and rules are transformed into unconditional and conditional equations, respectively (the symbol “&&” is an infix operator in Curry denoting the Boolean conjunction):
$[\![\cdot]\!]_{\mathcal{C}}$
from logic into functional logic programs where facts and rules are transformed into unconditional and conditional equations, respectively (the symbol “&&” is an infix operator in Curry denoting the Boolean conjunction):
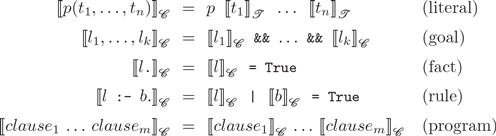
Example 3 Consider the following program to add two natural numbers in Peano representation, where o represents zero and s represents the successor of a natural (Sterling and Shapiro Reference Sterling and Shapiro1994):
The conservative transformation produces the following Curry program:
Note that the first rule would not be allowed in functional languages, like Haskell, since the left-hand side is not linear due to the two occurrences of the pattern variable y. For compatibility with logic programming, such multiple occurrences of variables in patterns are allowed in Curry, where they are considered as syntactic sugar for explicit unification constraints. Thus, the first rule is equivalent to
Apart from small steps to handle conditions and conjunctions, there is a strong correspondence between the derivations steps in the logic programs and the functional logic programs obtained by the conservative transformation. Therefore, the following result can be proved by induction on the length of the resolution and narrowing derivations, respectively.
Theorem 1 (Correctness of the conservative transformation) Let P be a logic program and G a goal. There is a resolution derivation
![]() $G \vdash^{*}_\sigma$
□ w.r.t. P if and only if there is a narrowing derivation
$G \vdash^{*}_\sigma$
□ w.r.t. P if and only if there is a narrowing derivation
![]() $[\![G]\!]_{\mathcal{C}} \buildrel {*} \over \rightsquigarrow_{\sigma}$
True w.r.t.
$[\![G]\!]_{\mathcal{C}} \buildrel {*} \over \rightsquigarrow_{\sigma}$
True w.r.t.
![]() $[\![P]\!]_{\mathcal{C}}$
.
$[\![P]\!]_{\mathcal{C}}$
.
4 Functional transformation
The conservative transformation simply maps n-ary predicates into n-ary Boolean functions. In order to exploit features from functional logic programming, one should mark at least one argument as a result argument with the intended meaning that the operation maps values for the remaining arguments into values for the result arguments. For instance, consider the predicate plus defined in Example 3. Here, the third argument could be considered as a result argument since plus maps values for the first two arguments into a value for the third argument. Hence, the definition of plus can also be transformed into the following functional logic program:
We call this the functional transformation and denote it by
![]() $[\![\cdot]\!]_{\mathcal{F}}$
. At this point we do not replace the occurrence of z in the right-hand side by plus x y since this might lead to a different semantics, as we will see later.
$[\![\cdot]\!]_{\mathcal{F}}$
. At this point we do not replace the occurrence of z in the right-hand side by plus x y since this might lead to a different semantics, as we will see later.
It is interesting to note that, without such a replacement, it is not really relevant which arguments are considered as results. For instance, if the first two arguments of plus are marked as result arguments, we obtain the following program by the functional transformation:
This specifies a nondeterministic operation which returns, for a given natural number n, all splittings into two numbers such that their sum is equal to n:
Later we will show how to prefer the transformation into deterministic operations, since they will lead to a better operational behavior. For the moment we should keep in mind that the selection of result arguments could be arbitrary. In order to fix it, we assume that, for each n-ary predicate p, there is an assignment
![]() ${\mathcal{R}}(p/n) \subseteq \{1,\ldots,n\}$
which defines the result argument positions, for example,
${\mathcal{R}}(p/n) \subseteq \{1,\ldots,n\}$
which defines the result argument positions, for example,
![]() ${\mathcal{R}}(\mathtt{plus}/3) = \{3\}$
or
${\mathcal{R}}(\mathtt{plus}/3) = \{3\}$
or
![]() ${\mathcal{R}}(\mathtt{plus}/3) = \{1,2\}$
. In practice, one can specify the result argument positions for a predicate by a specific directive, for example,
${\mathcal{R}}(\mathtt{plus}/3) = \{1,2\}$
. In practice, one can specify the result argument positions for a predicate by a specific directive, for example,
or
If the set of result argument positions for an n-ary predicate is
![]() $\{n\}$
, it can also be omitted in the directive, as in
$\{n\}$
, it can also be omitted in the directive, as in
Our tool, described below, respects such directives or tries to infer them automatically.
With these prerequisites in mind, we denote the functional transformation w.r.t. a result argument position mapping
![]() ${\mathcal{R}}$
by
${\mathcal{R}}$
by
![]() $[\![\cdot]\!]^{\mathcal{R}}_{\mathcal{F}}$
. To define this transformation, we use the following notation to split the arguments of a predicate call
$[\![\cdot]\!]^{\mathcal{R}}_{\mathcal{F}}$
. To define this transformation, we use the following notation to split the arguments of a predicate call
![]() $p(t_1,\ldots,t_n)$
into the result and the remaining arguments. If
$p(t_1,\ldots,t_n)$
into the result and the remaining arguments. If
![]() ${\mathcal{R}}(p/n) = \{\pi_1,\ldots,\pi_u\}$
and
${\mathcal{R}}(p/n) = \{\pi_1,\ldots,\pi_u\}$
and
![]() $\{\pi'_1,\ldots,\pi'_v\} = \{1,\ldots,n\} \setminus {\mathcal{R}}(p/n)$
(where
$\{\pi'_1,\ldots,\pi'_v\} = \{1,\ldots,n\} \setminus {\mathcal{R}}(p/n)$
(where
![]() $\pi_i < \pi_{i+1}$
and
$\pi_i < \pi_{i+1}$
and
![]() $\pi'_j < \pi'_{j+1}$
), then the result arguments are
$\pi'_j < \pi'_{j+1}$
), then the result arguments are
![]() $r_i = t_{\pi_i}$
, for
$r_i = t_{\pi_i}$
, for
![]() $i \in \{1,\ldots,u\}$
, and the remaining arguments are
$i \in \{1,\ldots,u\}$
, and the remaining arguments are
![]() $a_j = t_{\pi'_j}$
, for
$a_j = t_{\pi'_j}$
, for
![]() $j \in \{1,\ldots,v\}$
. Then
$j \in \{1,\ldots,v\}$
. Then
![]() $[\![\cdot]\!]^{\mathcal{R}}_{\mathcal{F}}$
is defined as follows:
$[\![\cdot]\!]^{\mathcal{R}}_{\mathcal{F}}$
is defined as follows:
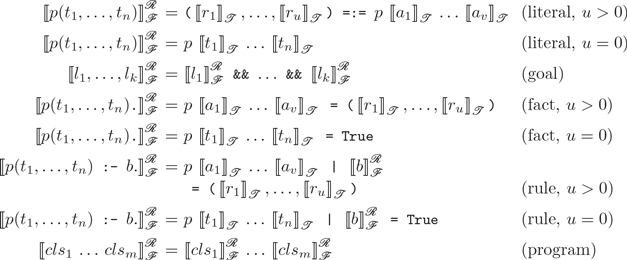
As already mentioned, the actual selection of result positions is not relevant so that we have the following result, which can be proved similarly to Theorem 1:
Theorem 2 (Correctness of the functional transformation) Let P be a logic program,
![]() ${\mathcal{R}}$
a result argument position mapping for all predicates in P, and G a goal. There is a resolution derivation
${\mathcal{R}}$
a result argument position mapping for all predicates in P, and G a goal. There is a resolution derivation
![]() $G \vdash^{*}_\sigma$
□ w.r.t. P if and only if there is a narrowing derivation
$G \vdash^{*}_\sigma$
□ w.r.t. P if and only if there is a narrowing derivation
![]() $[\![G]\!]^{\mathcal{R}}_{\mathcal{F}} \buildrel {*} \over \rightsquigarrow_{\sigma}$
True w.r.t.
$[\![G]\!]^{\mathcal{R}}_{\mathcal{F}} \buildrel {*} \over \rightsquigarrow_{\sigma}$
True w.r.t.
![]() $[\![P]\!]^{\mathcal{R}}_{\mathcal{F}}$
.
$[\![P]\!]^{\mathcal{R}}_{\mathcal{F}}$
.
5 Demand functional transformation
Consider the result of the functional transformation of plus w.r.t. the result argument position mapping
![]() ${\mathcal{R}}(\mathtt{plus}/3) = \{3\}$
:
${\mathcal{R}}(\mathtt{plus}/3) = \{3\}$
:
Since the value of z is determined by the expression plus
![]() $\;\textit{x}\;$
y, we could be tempted to replace the unification in the condition by a local binding for z:
$\;\textit{x}\;$
y, we could be tempted to replace the unification in the condition by a local binding for z:
Since z is used only once, we could inline the definition of z and obtain the purely functional definition
Although this transformation looks quite natural, there is a potential problem with this transformation. In a strict language, where arguments are evaluated before jumping into the function’s body (“call by value”), there is no difference between these versions of plus. However, there is also no operational advantage of this transformation. An advantage could come from the nonstrict or demand-driven evaluation of functions, as used in Haskell or Curry and discussed by Hughes (Reference Hughes1990) and Huet and Lévy (Reference Huet and Lévy1991). For instance, consider the predicate isPos which returns True if the argument is nonzero
and the expression
![]() $\mathtt{isPos}(\mathtt{plus}\,n_1 n_2)$
, where
$\mathtt{isPos}(\mathtt{plus}\,n_1 n_2)$
, where
![]() $n_1$
is a big natural number. A strict language requires
$n_1$
is a big natural number. A strict language requires
![]() $n_1 + 1$
rewrite steps to evaluate this expression, whereas a nonstrict language needs only two steps w.r.t. the purely functional definition of plus.
$n_1 + 1$
rewrite steps to evaluate this expression, whereas a nonstrict language needs only two steps w.r.t. the purely functional definition of plus.
The potential problem of this transformation comes from the fact that it does not require the evaluation of subexpressions which do not contribute to the overall result. For instance, consider the functions
and the expression
![]() $e =\;\mathtt{const\,0(dec\,0)}$
. Following the mathematical principle of “replacing equals by equals”, e is equivalent to O, but a strict language does not compute this value.
$e =\;\mathtt{const\,0(dec\,0)}$
. Following the mathematical principle of “replacing equals by equals”, e is equivalent to O, but a strict language does not compute this value.
Hence, it is a matter of taste whether we want to stick to purely equational reasoning, that is, ignore the evaluation of subexpressions that do not contribute to the result, or strictly evaluate all subexpressions independent of their demand.
Footnote 5
Since nonstrict evaluation yields reduced search spaces (as discussed below), we accept this slight change in the semantics and define the demand functional transformation
![]() $[\![\cdot]\!]^{\mathcal{R}}_{\mathcal{D}}$
as follows. Its definition is identical to
$[\![\cdot]\!]^{\mathcal{R}}_{\mathcal{D}}$
as follows. Its definition is identical to
![]() $[\![\cdot]\!]^{\mathcal{R}}_{\mathcal{F}}$
except for the translation of a literal in a goal. Instead of a unification,
$[\![\cdot]\!]^{\mathcal{R}}_{\mathcal{F}}$
except for the translation of a literal in a goal. Instead of a unification,
![]() $[\![\cdot]\!]^{\mathcal{R}}_{\mathcal{D}}$
generates a local binding
$[\![\cdot]\!]^{\mathcal{R}}_{\mathcal{D}}$
generates a local binding ![]() if the result arguments
if the result arguments
![]() $r_1,\ldots,r_u$
are variables which do not occur in the rule’s left-hand side or in result arguments of other goal literals. The latter restriction avoids inconsistent bindings for a variable. Since such bindings are evaluated on demand in nonstrict languages, this change has the effect that the transformed programs might require fewer steps to compute a result.
$r_1,\ldots,r_u$
are variables which do not occur in the rule’s left-hand side or in result arguments of other goal literals. The latter restriction avoids inconsistent bindings for a variable. Since such bindings are evaluated on demand in nonstrict languages, this change has the effect that the transformed programs might require fewer steps to compute a result.
In order to produce more compact and readable program, local bindings of single variables, that is, x = e, are inlined if possible, that is, if there is only a single occurrence of x in the rule, this occurrence is replaced by e and the binding is deleted. This kind of inlining is the inverse of the normalization of functional programs presented by Launchbury (Reference Launchbury1993) to specify a natural semantics for lazy evaluation.
Example 4 Consider the usual definition of naive reverse:
The demand functional transformation translates this program into the Curry program
Thanks to the functional logic features of Curry, one can use the transformed program similarly to the logic program. For instance, the equation app xs ys =:= [1,2,3] computes all splittings of the list [1,2,3], and rev ps =:= ps computes palindromes ps.
An advantage of this transformation becomes apparent for nested applications of recursive predicates. For instance, consider the concatenation of three lists, as shown in Example 1:
The demand functional transformation maps it into
The Prolog goal app3(Xs,Ys,Zs,[]) has an infinite search space, that is, it does not terminate after producing the solution Xs=[], Ys=[], Zs=[].. In contrast, Curry has a finite search space since the demand-driven evaluation avoids the superfluous generation of longer lists. This shows the advantage of transforming logic programs into functional logic programs: the operational behavior is improved, that is, the size of the search space could be reduced due to the demand-driven exploration of the search space, whereas the positive features, like backward computations, are kept.
A slight disadvantage of the demand functional transformation is the fact that it requires the specification of the result argument position mapping
![]() ${\mathcal{R}}$
, for example, by explicit function directives. In the next section, we show how it can be automatically inferred.
${\mathcal{R}}$
, for example, by explicit function directives. In the next section, we show how it can be automatically inferred.
6 Inferring result argument positions
As already discussed above, the selection of result arguments is not relevant for the applicability of our transformation. For instance, the predicate
could be transformed into the function
as well as into the nondeterministic operation
or just kept as a predicate:
In general, it is difficult to say what is the best representation of a predicate as a function. One could argue that deterministic operations are preferable, but there are also examples where nondeterministic operations lead to reduced search spaces. For instance, the complexity of the classical permutation sort can be improved by defining the computation of permutations as a nondeterministic operation (González-Moreno et al. Reference González-Moreno, Hortalá-González, López-Fraguas and Rodrguez-Artalejo1999; Hanus Reference Hanus2013).
A possible criterion can be derived from the theory of term rewriting (Huet and Lévy Reference Huet and Lévy1991) and functional logic programming (Antoy et al. Reference Antoy, Echahed and Hanus2000). If the function definitions are inductively sequential (Antoy Reference Antoy1992), that is, the left-hand sides of the rules of each function contain arguments with a unique case distinction, the demand-driven evaluation (needed narrowing) is optimal in the number of computed solutions and the length of successful derivations (Antoy et al. Reference Antoy, Echahed and Hanus2000). In the following, we present a definition of this criterion adapted to logic programs.
In many logic programs, there is a single argument which allows a unique case distinction between all clauses, for example, the first argument in the predicates app, rev, or plus shown above. However, there are also predicates requiring more than one argument for a unique selection of a matching rule. For instance, consider Ackermann’s function as a logic program, as presented by Sterling and Shapiro (Reference Sterling and Shapiro1994):
The first argument distinguishes between the cases of an atom o and a structure s(M), but, for the latter case, two rules might be applicable. Hence, the second argument is necessary to distinguish between these rules. Therefore, we call
![]() $\{1,2\}$
a set of inductively sequential argument positions for this predicate.
$\{1,2\}$
a set of inductively sequential argument positions for this predicate.
A precise definition of inductively sequential argument positions is based on the notion of definitional trees (Antoy Reference Antoy1992). The following definition is adapted to our needs.
Definition 1 (Inductively sequential arguments) A partial definitional tree
![]() ${\mathcal{T}}$
with a literal l is either a clause node of the form
${\mathcal{T}}$
with a literal l is either a clause node of the form
![]() $clause(l ~\mathtt{:-}~ b)$
with some goal b or a branch node of the form
$clause(l ~\mathtt{:-}~ b)$
with some goal b or a branch node of the form
![]() $branch(l,p,{\mathcal{T}}_1,\ldots,{\mathcal{T}}_k)$
, where p is a position of a variable x in l,
$branch(l,p,{\mathcal{T}}_1,\ldots,{\mathcal{T}}_k)$
, where p is a position of a variable x in l,
![]() $f_1,\ldots,f_k$
are pairwise different functors,
$f_1,\ldots,f_k$
are pairwise different functors,
![]() $\sigma_i = \{ x \mapsto f_i(x_1,\ldots,x_{a_i}) \}$
where
$\sigma_i = \{ x \mapsto f_i(x_1,\ldots,x_{a_i}) \}$
where
![]() $x_1,\ldots,x_{a_i}$
are new pairwise distinct variables, and, for all i in
$x_1,\ldots,x_{a_i}$
are new pairwise distinct variables, and, for all i in
![]() $\{1,\ldots,k\}$
, the child
$\{1,\ldots,k\}$
, the child
![]() ${\mathcal{T}}_i$
is a partial definitional tree with literal
${\mathcal{T}}_i$
is a partial definitional tree with literal
![]() $\sigma_i(l)$
.
$\sigma_i(l)$
.
A definitional tree of an n-ary predicate p defined by a set of clauses cs is a partial definitional tree
![]() ${\mathcal{T}}$
with literal
${\mathcal{T}}$
with literal
![]() $p(x_1,\ldots,x_n)$
, where
$p(x_1,\ldots,x_n)$
, where
![]() $x_1,\ldots,x_n$
are pairwise distinct variables, such that a variant of each clause of cs is represented in exactly one clause node of
$x_1,\ldots,x_n$
are pairwise distinct variables, such that a variant of each clause of cs is represented in exactly one clause node of
![]() ${\mathcal{T}}$
. In this case,
${\mathcal{T}}$
. In this case,
![]() $p/n$
is called inductively sequential.
$p/n$
is called inductively sequential.
A set
![]() $D \subseteq \{1,\ldots,n\}$
of argument positions of
$D \subseteq \{1,\ldots,n\}$
of argument positions of
![]() $p/n$
is called inductively sequential if there is a definitional tree
$p/n$
is called inductively sequential if there is a definitional tree
![]() ${\mathcal{T}}$
of
${\mathcal{T}}$
of
![]() $p/n$
such that all positions occurring in branch nodes of
$p/n$
such that all positions occurring in branch nodes of
![]() ${\mathcal{T}}$
with more than one child are equal or below a position in D.
${\mathcal{T}}$
with more than one child are equal or below a position in D.
The predicate ackermann shown above has the inductively sequential argument sets
![]() $\{1,2,3\}$
and
$\{1,2,3\}$
and
![]() $\{1,2\}$
. For the predicates app and rev (see Example 4),
$\{1,2\}$
. For the predicates app and rev (see Example 4),
![]() $\{1\}$
is the minimal set of inductively sequential argument positions.
$\{1\}$
is the minimal set of inductively sequential argument positions.
Our inference of result argument positions for a n-ary predicate p is based on the following heuristic:
-
1. Find a minimal set D of inductively sequential argument positions of
 $p/n$
.
$p/n$
. -
2. If D exists and the set
 $R = \{1,\ldots,n\} \setminus D$
is not empty, select the maximum value m of R as the result argument, that is,
$R = \{1,\ldots,n\} \setminus D$
is not empty, select the maximum value m of R as the result argument, that is,
 ${\mathcal{R}}(p/n) = \{m\}$
, otherwise
${\mathcal{R}}(p/n) = \{m\}$
, otherwise
 ${\mathcal{R}}(p/n) = \varnothing$
.
${\mathcal{R}}(p/n) = \varnothing$
.
Thus, a predicate is transformed into a function only if there are some inductively sequential arguments and some other arguments. In this case, we select the maximum argument position, since this is usually the intended one in practical programs. Moreover, a single result argument allows a better nesting of function calls which leads to a better demand-driven evaluation.
Minimal sets of inductively sequential argument positions can be computed by analyzing the heads of all clauses. There might be different inductively sequential argument sets for a given set of clauses. For instance, the predicate q defined by the clauses
has two minimal sets of inductively sequential arguments:
![]() $\{1\}$
and
$\{1\}$
and
![]() $\{2\}$
. The actual choice of arguments is somehow arbitrary. If predicates are inductively sequential, the results of Antoy et al. (Reference Antoy, Echahed and Hanus2000) ensure that the programs obtained by our transformation with the heuristic described above can be evaluated in an optimal manner.
$\{2\}$
. The actual choice of arguments is somehow arbitrary. If predicates are inductively sequential, the results of Antoy et al. (Reference Antoy, Echahed and Hanus2000) ensure that the programs obtained by our transformation with the heuristic described above can be evaluated in an optimal manner.
A special case of our heuristic to infer result argument positions are predicates defined by a single rule. Since such a definition is clearly nonoverlapping and inductively sequential, all such predicates might be considered as functions. However, this might lead to unintended function definitions, for example, if a predicate is defined by a single clause containing a conjunction of literals. Therefore, we use the following heuristic. A predicate defined by a single rule is transformed into a function only if the last argument of the head is not a variable or a variable which occurs in a result argument position in the rule’s body. The first case is reasonable to transform predicates which define constants, as
into constant definitions, as
An example for the second case is the automatic transformation of app3 into a function, as shown in Section 5.
Although these heuristics yield the expected transformations in most practical cases (they have been developed during the experimentation with our tool, see below), one can always override them using an explicit function directive in the logic program.
7 Extensions
Our general objective is the transformation of pure logic programs into functional logic ones. Prolog programs often use many impure features which cannot be directly translated into a language like Curry. This is intended, because functional logic languages are an approach to demonstrate how to avoid impure features and side effects by concepts from functional programming. For instance, I/O operations, offered in Prolog as predicates with side effects, can be represented in functional (logic) languages by monadic operations which structure effectful computations (Wadler Reference Wadler1997). Encapsulated search (findall) or cuts in Prolog, whose behavior depends on the search strategy and ordering of rules, can be represented in functional logic programming in a strategy-independent manner as set functions (Antoy and Hanus Reference Antoy and Hanus2009) or default rules (Antoy and Hanus Reference Antoy and Hanus2017). Thus, a complete transformation of Prolog programs into Curry programs might have to distinguish between “green” and “red” cuts, which is not computable. Nevertheless, it is possible to transform some Prolog features which we discuss in the following.
A useful feature of Prolog is the built-in arithmetic which avoids to compute with numbers in Peano arithmetic. For instance, consider the definition of the predicate length to relate a list with its number of elements:
Since the first argument position is inductively sequential, it is reasonable to transform length into a function with
![]() ${\mathcal{R}}(\mathtt{length}/2) = \{2\}$
. Furthermore, the predicate “is” evaluates its second argument to a number and returns this result by unifying it with its first argument. Thus,
${\mathcal{R}}(\mathtt{length}/2) = \{2\}$
. Furthermore, the predicate “is” evaluates its second argument to a number and returns this result by unifying it with its first argument. Thus,
![]() ${\mathcal{R}}(\mathtt{is}/2) = \{1\}$
. Using this result argument position mapping, the demand functional transformation yields the program
${\mathcal{R}}(\mathtt{is}/2) = \{1\}$
. Using this result argument position mapping, the demand functional transformation yields the program
where the occurrence of is is omitted since it behaves as the identity function.
Arbitrary Prolog cuts cannot be translated (or only into awkward code). However, Prolog cuts can be avoided by using Prolog’s if-then-else construct. If the condition is a simple predicate, like a deterministic test or an arithmetic comparison, it can be translated into a functional if-then-else construct. For instance, consider the following definition of the factorial function as a Prolog predicate:
Translating this into a function (note that variable F is used in a result argument position in the body) with the arithmetic operations transformed as discussed above, we obtain the functional definition
With these extensions, many other arithmetic functions are automatically transformed into their typical functional definition.
8 Implementation
In order to evaluate our approach, we have implemented the transformation described in this paper as a tool pl2curry in Curry so that it can easily be installed by Curry’s package manager. Footnote 6 pl2curry has various options to influence the transformation strategy (e.g., conservative, without let bindings, without result position inference, etc). In the default mode, the demand functional transformation is used where result arguments are inferred if they are not explicitly specified by function directives. The tool assumes that the logic program is written in standard Prolog syntax. It reads the Prolog file and transforms it into an abstract representation, Footnote 7 from which a Curry program is generated that can be directly loaded into a Curry system.
A delicate practical issue of the transformation is the typing of the transformed programs. Curry is a strongly typed language with parametric types and type classes (Wadler and Blott Reference Wadler and Blott1989). Since logic programs and standard Prolog do not contain type information, our tool defines a single type Term containing all atoms and functors occurring in the logic program. Although this works fine for smaller programs, it could be improved by using type information. For instance, CIAO-Prolog (Hermenegildo et al. Reference Hermenegildo, Bueno, Carro, López-Garca, Mera, Morales and Puebla2012) supports the definition of regular and Hindley-Milner types, which could be translated into algebraic data types, or Barbosa et al. (Reference Barbosa, Florido and Santos Costa2021) describe a tool to infer similar types from logic programs. Although there is some interest toward adding types to Prolog programs (Schrijvers et al. Reference Schrijvers, Santos Costa, Wielemaker and Demoen2008), there is no general agreement about its syntax and structure. Therefore, the translation of more refined types is omitted from the current implementation but it could be added in the future.
9 Evaluation
The main motivation for this work is to show that functional logic programs have concrete operational advantages compared to pure logic programs. This has been demonstrated by defining transformations for logic programs into functional logic programs. The simplest transformations (conservative and functional) keeps the structure of computations, whereas the demand functional transformation has the potential advantage to reduce the computation space by evaluating fewer subexpressions.
The practical comparison of original and transformed programs is not straightforward since it depends on the underlying implementation to execute these programs. Compilers for functional languages might contain good optimizations since they must not be prepared for nondeterministic computations (although Prolog systems based on Warren’s Abstract Machine (A t-Kaci 1991; Warren Reference Warren1983) implement specific indexing techniques to support deterministic branching when it is possible). This can be demonstrated by some typical examples: the naive reverse of list structures (see Example 4), the highly recursive tak function used in various benchmarks (Partain Reference Partain1993) for logic and functional languages, and the Ackermann function (see Section 6). Since these logic programs are automatically transformed into purely functional programs using our demand functional transformation, we can execute the original logic programs with Prolog systems and the transformed programs with Haskell (GHC) and Curry (KiCS2 Braß el et al. 2011) systems (since the functional kernel of Curry use the same syntax as Haskell). KiCS2 compiles Curry programs to Haskell programs by representing nondeterministic computations as search trees, that is, the generated Haskell functions return a tree of all result values. Table 1 contains the average execution times in seconds Footnote 8 of reversing a list with 4096 elements, the function tak applied to arguments (27,16,8), implemented with built-in integers (takInt) and Peano numbers (takPeano), and the Ackermann function applied to the Peano representation of the numbers (3,9).
Table 1. Execution times of Prolog, Haskell, and Curry programs
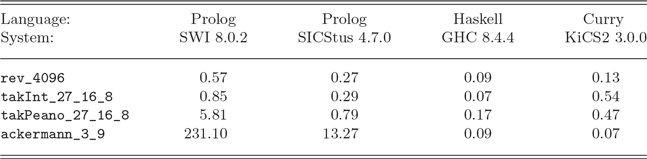
Note that the demand strategy has no real advantage in these examples. The values of all subexpressions are required so that the same resolution/rewrite steps, possibly in a different order, are performed in Prolog and Haskell/Curry. Therefore, the results show the dependency on the actual language implementations. Although the table indicates the superiority of the functional programs (in particular, GHC seems to implement recursion quite efficiently), one might also obtain better results for a logic programming system by sophisticated implementation techniques, for example, by specific compilation techniques based on mode information, as done in Mercury (Somogyi et al. Reference Somogyi, Henderson and Conway1996), or by statically analyzing programs to optimize the generated code (Van Roy and Despain Reference Van Roy and Despain1990). For instance, the large execution times of the Prolog version of the Ackermann function are probably due to the fact that the function is defined by pattern matching on two arguments whereas typical Prolog systems implement indexing on one argument only. Nevertheless, the results for the Curry system KiCS2 show a clear improvement without loosing the flexibility of logic programming, since the same Curry program can compute result values as well as search for required argument values. Note that all systems of these benchmarks use unbounded integers, whereas KiCS2 has a more complex representation of integers in order to support searching demanded values for free integer variables (Braß el et al. 2008).
Because it is difficult to draw definite conclusions from the absolute execution times, we want to emphasize the qualitative improvement of our transformation. The demand functional transformation might reduce the number of evaluation steps and leads to a demand-driven exploration of the search space. In the best case, it can reduce infinite search spaces to finite ones. We already discussed such examples before. For instance, our transformation automatically maps the logic program of Example 1 into the functional logic program of Example 2 so that the infinite search space of the predicate dup applied to an empty list is cut down to a small finite search space for the function dup. As a similar example, the goal plus(X,Y,R), plus(R,Z,o) (w.r.t. Example 3) has an infinite search space, whereas the transformed expression plus (plus
![]() $\;\textit{x}\;$
y) z =:= O has a finite search space w.r.t. the demand functional transformation.
$\;\textit{x}\;$
y) z =:= O has a finite search space w.r.t. the demand functional transformation.
These examples show that our transformation has a considerable advantage when goals containing several recursive predicates are used to search for solutions. Such goals naturally occur when complex data structures, like XML structures, are explored. The good behavior of functional logic programs on such applications is exploited by Hanus (Reference Hanus2011) to implement a domain-specific language for XML processing as a library in Curry. Without the demand-driven evaluation strategy, many of the library functions would not terminate. Actually, the library has similar features as the logic-based language Xcerpt (Bry and Schaffert Reference Bry and Schaffert2002) which uses a specialized unification procedure to ensure finite matching and unification w.r.t XML terms.
10 Conclusions
We presented methods to transform logic programs into functional logic programs. By specifying one or more arguments as results to transform predicates into functions and evaluating them with a demand-driven strategy, we showed with various examples that this transformation is able to reduce the computation space. Although this effect depends on the concrete examples, our transformation never introduces new or superfluous steps in successful computations. We also discussed a heuristic to infer result arguments for predicates. It is based on detecting inductively sequential argument positions so that the programs transformed by our method benefit from strong completeness and optimality results of functional logic programming (Antoy et al. Reference Antoy, Echahed and Hanus2000; Antoy Reference Antoy1997).
In principle, it is not necessary to switch to another programming language since demand-driven functional computations can be implemented in Prolog systems supporting coroutining. However, one has to be careful about the precise evaluation strategy implemented in this way. For instance, Naish (Reference Naish1991) implements lazy evaluation in Prolog by representing closures as terms and use when declarations to delay insufficiently instantiated function calls. This might lead to floundering so that completeness is lost when predicates are transformed into functions. Moreover, delaying recursively defined predicates could result in infinite search spaces which can be avoided by complete strategies (Hanus Reference Hanus1995). Casas et al. (Reference Casas, Cabeza and Hermenegildo2006) use coroutining to implement lazy evaluation and offer a notation for functions which are mapped into Prolog predicates. Although this syntactic transformation might yield the same values and search space as functional logic languages, there are no formal results justifying this transformation. On the other hand, there are various approaches to implement lazy narrowing strategies in Prolog (Antoy and Hanus Reference Antoy and Hanus2000; Jiménez-Martin et al. Reference Jiménez-Martin, Marino-Carballo and Moreno-Navarro1992; LoogenLopezFraguasRodriguezArtalejo93PLILP; López-Fraguas and Sánchez-Hernández Reference López-Fraguas and Sánchez-Hernández1999). In this sense, our results provide a systematic method to improve computations in logic programs by mapping predicates into functions and applying sound and complete evaluation strategies to the transformed programs. In particular, if predicates are defined with inductively sequential arguments (as all examples in this paper), the needed narrowing strategy is optimal, that is, the set of computed solutions is minimal and successful derivations have the shortest possible length (Antoy et al. Reference Antoy, Echahed and Hanus2000). This does not restrict the flexibility of logic programming but might reduce the computation space. Although our implemented tool maps logic programs into Curry programs, one could also map them back into Prolog programs by compiling the demand-driven evaluation strategy into appropriate features of Prolog (e.g., coroutining).
There is a long history to improve the execution of logic programs by modified control rules (Bruynooghe et al. Reference Bruynooghe, De Schreye and Krekels1989; Narain Reference Narain1986). However, these proposals usually consider the operational level so that a declarative justification (soundness and completeness) is missing. In this sense, our work provides a justification for specific control rules used in logic programming, since it is based on soundness and completeness results for functional logic programs.
For future work it is interesting to use a refined representation of types (as discussed in Section 8) or to consider other methods to infer result positions, for example, by a program analysis taking into account the data flow between arguments of literals in goals.




