1. Introduction
The subglacial setting in which temperate ice rests on a soft bed is most important for modulating fast glacier flow and mobilizing basal sediment (Reference ClarkeClarke, 2005). Interactions among water, ice and sediment in this environment can result in abrupt temporal and spatial variations in glacier velocity. On large scales these variations may be manifested as surging (e.g. Reference Clarke, Collins and ThompsonClarke and others, 1984), spatiotemporal switching of ice-stream flow (e.g. Reference Kamb, Alley and BindschadlerKamb, 2001) and lurching behavior of parts of ice sheets that has been measured directly (Reference Bindschadler, King, Alley, Anandakrishnan and PadmanBindschadler and others, 2003) and inferred from seismicity (Reference Ekström, Nettles and AbersEkstro¨m and others, 2003, Reference Ekström, Nettles and Tsai2006). Also, very high rates of basal sediment transport have been postulated for glaciers that are soft-bedded and warm-based (Reference Hooke and ElverhøiHooke and Elverhøi, 1996; Reference Dowdeswell and SiegertDowdeswell and Siegert, 1999). Moreover, under these conditions some of the most poorly understood of glacial landforms, such as drumlins (e.g. Reference Boulton, Menzies, Rose, Rotterdam and BalkemaBoulton, 1987) and megascale lineations (e.g. Reference Ottesen and DowdeswellOttesen and Dowdeswell, 2006), are thought to have developed.
The most detailed observations of soft-bed processes beneath glaciers have been made with instruments inserted through boreholes drilled to the bed, from either ice tunnels (e.g. Reference Boulton and HindmarshBoulton and Hindmarsh, 1987) or glacier surfaces (e.g. Reference Blake, Clarke and Ge´rinBlake and others, 1992; Reference Kamb, Alley and BindschadlerKamb, 2001). These observations, although illuminating, have been limited by the restricted range of instruments that can be inserted through boreholes. Moreover, interpretations are complicated by ambiguities regarding instrument position, bed geometry and bed disturbance by hot-water drilling.
Our goal was to avoid these difficulties by building and studying a 1.3m3 prism of simulated till beneath Engabreen, Norway, (Reference IversonIverson and others, 2003) where tunnels through the subglacial rock provide access to the bed. Our results provide a field demonstration of regelation infiltration of ice into a till bed (e.g. Reference Iverson and SemmensIverson and Semmens, 1995; Reference ClarkeClarke, 2005; Reference Christoffersen, Tulaczyk, Carsey and BeharChristoffersen and others, 2006), help illustrate the relationship between basal water pressure and the coupling between ice and till (e.g. Reference Fischer and ClarkeFischer and Clarke, 2001) and provide new insights into controls on the vertical distribution of bed deformation (e.g. Reference Boulton, Dobbie and ZatsepinBoulton and others, 2001). Associated analysis indicates that regelation infiltration occurred at rates in agreement with theory, and a new model of ploughing clarifies how changes in the thickness of a water layer at the bed surface control the basal flow mechanism.
2. Background
2.1. Regelation infiltration
In a process that Reference ClarkeClarke (2005) calls regelation infiltration, temperate ice may move downward into the pores of subglacial sediment by melting and refreezing. Evidence for this process comes from laboratory experiments (Reference IversonIverson, 1993; Reference Iverson and SemmensIverson and Semmens, 1995). Its rate is controlled by the bed-normal pressure gradient across the sediment layer that has been entrained, which depends on the effective pressure at the bed and the thickness of the layer.
Although the isotopic composition (Reference Iverson and SouchezIverson and Souchez, 1996) and structure (Reference Truffer, Motyka, Harrison, Echelmeyer, Fisk and TulaczykTruffer and others, 1999; Reference Christoffersen, Tulaczyk, Carsey and BeharChristoffersen and others, 2006) of some basal ice facies are consistent with sediment entrainment by regelation infiltration, it may be prevented or inhibited beneath glaciers. In fine-grained sediments interfacial-curvature and pre-melting effects (Reference O’Neill and MillerO’Neill and Miller, 1985; Reference Rempel, Wettlaufer and Grae WorsterRempel and others, 2004) can hold water sufficiently tightly in the pore space to inhibit refreezing there. Reference Alley, Cuffey, Evenson, Strasser, Lawson and LarsonAlley and others (1997) estimated that regelation should be impeded for sediment grains smaller than fine to medium silt. In addition, regelation infiltration may be inhibited by sliding of ice across the bed, with frictional heat impeding refreezing (Reference Alley, Cuffey, Evenson, Strasser, Lawson and LarsonAlley and others, 1997).
Field measurements have not yet demonstrated that regelation infiltration occurs. Studying this process subglacially is important because it may provide a general mechanism of sediment entrainment for wet-based glaciers (e.g. Reference IversonIverson, 2000; Reference Christoffersen, Tulaczyk, Carsey and BeharChristoffersen and others, 2006). Moreover, if regelation infiltration is common then, as noted by Boulton and others (2001), ice-infiltrated sediment, rather than clean ice, overlies the wet sediment of the bed. Slip at such an interface has not been studied.
2.2. Basal slip of ice over a soft bed
Resistance to basal movement of soft-bedded portions of glaciers is commonly assumed to be equal to the deformation resistance of the bed (e.g. Reference PatersonPaterson, 1994; Reference Tulaczyk, Kamb and EngelhardtTulaczyk and others, 2000b; Reference Bindschadler, King, Alley, Anandakrishnan and PadmanBindschadler and others, 2003), such that the bed deforms in shear at its yield strength. There is considerable evidence from modern glaciers, however, that under some conditions ice slips across the surface of the bed, without shearing it significantly at depth (Reference Blake, Fischer and ClarkeBlake and others, 1994; Reference Iverson, Hanson, Hooke and JanssonIverson and others, 1995; Reference Hooke, Hanson, Iverson, Jansson and FischerHooke and others, 1997; Reference Boulton, Dobbie and ZatsepinBoulton and others, 2001; Reference Kamb, Alley and BindschadlerKamb, 2001; Reference Truffer and HarrisonTruffer and Harrison, 2006). In particular, some borehole experiments indicate that when basal water pressure is rising and high the bed relaxes elastically in shear up-glacier as slip occurs at the bed surface (Reference Fischer and ClarkeFischer and Clarke, 1997; Reference Iverson, Baker, Hooke, Hanson and JanssonIverson and others, 1999). Some field evidence indicates that such slip can be responsible for major glacier speed-up events (Reference Truffer and HarrisonTruffer and Harrison, 2006). Also, extreme sensitivity of ice-sheet velocity to seemingly insignificant changes in stress (Reference Bindschadler, King, Alley, Anandakrishnan and PadmanBindschadler and others, 2003) indicates that even a small decrease in flow resistance caused by slip over a soft bed could affect flow dynamics over wide areas.
The question of where most basal motion occurs and how it depends on water pressure still lacks a definitive answer, in part due to ambiguity in interpreting existing borehole data. For example, Reference Tulaczyk, Kamb and EngelhardtTulaczyk and others (2000a) argued that up-glacier rotation of tiltmeters in basal till reflected expansion of till as pore-water pressure rose, rather than elastic relaxation in shear and associated slip of ice across the bed surface. Also, the processes operating at the bed surface are unclear. Movement there is assumed to occur by a combination of ice sliding past bed clasts that protrude upward into the glacier and ploughing of such clasts across the bed surface (Reference Brown, Hallet and BoothBrown and others, 1987; Reference AlleyAlley, 1989; Reference IversonIverson, 1999). These models, however, have considered basal ice to be clean. If ice generally intrudes into sediment pores, so ice-infiltrated sediment slides over the bed surface, the physical relevance of these models is dubious.
2.3. Profile of bed deformation
Some data indicate that when the bed shears, rates of shear strain generally increase upward toward the bed surface (Reference Boulton and HindmarshBoulton and Hindmarsh, 1987; Reference Boulton and DobbieBoulton and Dobbie, 1998; Reference Boulton, Dobbie and ZatsepinBoulton and others, 2001), so the velocity profile is concave-down. Early discussion attributed this strain pattern to an ad hoc rheological rule for till in which the rate of shear deformation was assumed to be directly proportional to the shear stress and inversely proportional to the effective pressure (Reference Boulton and HindmarshBoulton and Hindmarsh, 1987). Since effective pressure, and hence shearing resistance, increases more rapidly with depth than shear stress – at least in the absence of upwardly flowing pore water – shear-strain rates, according to this rule, should decrease downward (Reference AlleyAlley, 1989). However, diverse laboratory studies do not support this rheological rule (Reference KambKamb, 1991; Reference Iverson, Hooyer and BakerIverson and others, 1998; Reference Tulaczyk, Kamb and EngelhardtTulaczyk and others, 2000a). These studies, in agreement with most geotechnical literature, indicate that the most appropriate first-order model for till is that of a Coulomb material in which shear-strain rate is independent of shear stress.
This finding has prompted other explanations for the deformation profile. Reference Iverson, Hooyer and BakerIverson and others (1998) suggested that shear zones in Coulomb till will migrate due to increases in shear-zone strength caused by shear-induced dilation and an associated reduction in pore pressure, thereby distributing strain as observed. Others have suggested that repeated water-pressure variations at the bed surface and associated downward diffusion of pore pressure would cause vertical migration of the locus of shear that could lead to the observed profile (Reference Tulaczyk, Mickelson and AttigTulaczyk, 1999; Reference Tulaczyk, Kamb and EngelhardtTulaczyk and others, 2000a). A third hypothesis invokes movement of particles in till resulting from very brief, local departures from quasi-static stress equilibrium caused by the failure of stress-bearing grain networks (Reference Iverson and IversonIverson and Iverson, 2001). The frictional strength of the bed increases more rapidly with depth than the applied shear stress, so the small force imbalances that drive grain movement tend to be smaller at depth than near the bed surface. Thus, relative movements between grains and resultant shear-strain rates tend to decrease with depth in the bed. This explanation for the concave-down profile is similar to that of Reference AlleyAlley (1989) but relies on experimental studies of grain-bridge failure and grain displacements calculated from Newton’s second law rather than on the Reference Boulton and HindmarshBoulton and Hindmarsh (1987) rheological rule.
3. Research Questions
We address three questions in our field experiments: (1) Can a temperate glacier entrain till by regelation infiltration and, if so, are rates of infiltration comparable to those predicted by theory? (2) How does partitioning of basal movement between slip at the bed surface and bed deformation depend on basal water pressure and what processes at the bed surface are responsible for this partitioning? (3) Can the concave-down velocity profiles measured by Boulton and colleagues be reproduced and, if so, does this strain pattern necessarily require a specific till rheology (Reference Boulton and HindmarshBoulton and Hindmarsh, 1987), dilatant strengthening (Reference Iverson, Hooyer and BakerIverson and others, 1998) or basal water-pressure fluctuations (Tulaczyk and others, 2000a)?
4. Methodology
Engabreen is a temperate outlet glacier of the Svartisen ice cap in northern Norway. Its bed consists of gneiss and schist bedrock with meter- to decameter-scale undulations and no overlying till layer, except in rare circumstances (e.g. Reference Hooke and IversonHooke and Iverson, 1995). Tunnels in the rock beneath the glacier have been excavated as part of a hydropower installation. One of these tunnels extends to the ice–bed interface (Fig. 1), where the glacier is 213 m thick and slopes at ~10°. A removable door across the mouth of the tunnel prevents ice from squeezing into it. This tunnel is sufficiently dry during fall, winter and early spring to provide safe access for subglacial experiments. The Svartisen Subglacial Laboratory is housed beneath the glacier in a larger tunnel nearby and has provided infrastructure for studies of various basal processes (Reference Jansson, Kohler and PohjolaJansson and others, 1996; Reference Cohen, Hooke, Iverson and KohlerCohen and others, 2000, Reference Cohen, Iverson, Hooyer, Fischer, Jackson and Moore2005, Reference Cohen, Hooyer, Iverson, Thomason and Jackson2006; Reference IversonIverson and others, 2003; Reference Lappegard, Kohler, Jackson and HagenLappegard and others, 2006). An essential part of this infrastructure is a warm-water drill that allows tunnels (usually ~5 m2 in crosssection) to be melted through ice along the bed.

Fig. 1. Site of the till prism, access points to the bed of Engabreen and the bed morphology. The ice tunnel melted to the site of the till prism was started from the tunnel access to the bed. The vertical shaft was the site of the sliding velocity measurement. Contour interval 1 m.
4.1. Till prism and instruments
To study soft-bed processes, a till prism was constructed in a bedrock trough beneath the glacier. A tunnel was melted through the basal ice to a relatively flat section of the bed, ~10m from the mouth of the bed-access tunnel (Fig. 1). A trough was blasted in the bed there that was ~1.8 m long, 1.6 m wide and 0.45 m deep. The trough was oriented roughly parallel to bedrock striae and was deepest on its up-glacier side (Fig. 2). Lateral walls of the bedrock trough were irregular and sloped more gently than the headwall. Three 32 mm boreholes were drilled through the rock bed from the down-glacier end of the trough to the underlying rock tunnel (Fig. 1), spanning a distance of ~4m. Two of these boreholes were for instrument cables. A pipe that extended downward into the rock tunnel was cemented in the third borehole to use as a conduit for pumping water upward from the tunnel to the bed surface.

Fig. 2. Till prism in a flow-parallel cross-section with instruments..
No source of till was available in the tunnel system, so a synthetic till was used. Supraglacial till was available in the end moraines of Engabreen, but these moraines lie 700 m below and ~5 km away from the site of the experiment, making transport of a sufficient volume of this till to the bed-access point prohibitively laborious and time-consuming. We thus manufactured several cubic meters of synthetic till by digging sediment from the floor of the rock-tunnel system. This sediment was the product of blasting, which produces a power-law relationship between the number and sizes of grains similar to that of some basal tills (Reference Hooke and IversonHooke and Iverson, 1995). The synthetic till was, by mass, 10% gravel, 70% sand and 20% silt and clay, and the relationship between the number and sizes of grains was indeed well fitted by a power law (Fig. 3). The relatively small silt-and-clay fraction, characteristic of many basal tills (e.g. Reference HaldorsenHaldorsen, 1981; Reference Hooke and IversonHooke and Iverson, 1995; Reference Truffer, Motyka, Harrison, Echelmeyer, Fisk and TulaczykTruffer and others, 1999), caused the till’s permeability to be high and thereby reduced the likelihood that its dilation or contraction during shear would produce non-hydrostatic pore pressures (e.g. Reference Moore and IversonMoore and Iverson, 2002). Avoiding this complication helped clarify interpretations.

Fig. 3. Particle-size distribution of the simulated till used in the experiments. Mass fractions were obtained by mechanical sieving, and the number and mean diameter of each particle-size class were determined using the method described by Reference Hooke and IversonHooke and Iverson (1995). The exponent of the power-law fit is –3.37. The coefficient of determination (r 2) of the fit is 0.99.
Approximately 3 tons of simulated till were added to the trough in layers, 50–100mm thick, and various instruments were added to the till as the trough was filled (Fig. 2). To measure shear deformation, vertical columns of four tiltmeters were placed in the till prism spanning its thickness at two locations, and vertical columns of beads, 16 or 18 mm in diameter, were positioned within 0.1 m of the tiltmeter columns for excavation after the experiment. The tiltmeters consisted of biaxial, electrolytic cells (Fredericks Company, model 0717-2201) mounted in plastic cylinders, 16 mm in diameter and 50 mm long. Three pore-pressure sensors were installed in the till prism, up-glacier from the mouth of the water-entry pipe. Two of these were placed 1.3 m up-glacier from the pipe at different heights above the bed;the third was placed 0.5–0.6 m up-glacier from the pipe (Fig. 2). A disk-shaped earth-pressure (EP) cell, oriented horizontally in the till, recorded total normal stress exerted over a circular sensing face 102 mm in diameter. A strain-meter, 0.33 m long, was placed vertically in the till. This piston-like instrument, which had anchors at its ends that gripped the till, recorded till expansion or contraction along a direction parallel to its long axis. Both the earth-pressure cell and the strainmeter were free to rotate in the till during shear, although it was hoped, based on laboratory observations of clast rotation in shearing till (Reference Hooyer and IversonHooyer and Iverson, 2000), that the disk-shaped pressure cell would not rotate out of the plane of shear. The pore-pressure sensors, earth-pressure cells and strainmeters were vibrating-wire sensors (Geokon models 4500S-500, 4800X-1-500 and 4430-X, respectively). When the prism was completed, gravel-sized clasts, painted gold, were embedded partway in the till to mark the bed surface.
Cables from the instruments were fed down two of the boreholes to the underlying tunnel. All instruments had separate cables, reducing the chance of mechanical inter-action of instruments. Hollow rubber stoppers, which had been threaded onto each bundle of cables, were hammered into the mouths of the boreholes to inhibit water leakage from the bed. All instruments in the prism were excited and logged with a Campbell CR10x data logger and multiplexer.
Also, ~11 m directly down-glacier from the till prism, sliding velocity was measured at the mouth of a vertical shaft used in other experiments (Fig. 1) (Reference Cohen, Hooke, Iverson and KohlerCohen and others, 2000, Reference Cohen, Iverson, Hooyer, Fischer, Jackson and Moore2005). This was done by measuring the displacement of an anchor entrained in the ice. The anchor was connected to a thin cable that extended into the rock tunnel below, where an extensometer (Unimeasure, model HX-PA-60) recorded the withdrawal of the cable during sliding.
4.2. Procedure
In March 2001 and April 2002, experiments were conducted that lasted 7–12 days. In each experiment, after the till prism was constructed, the ice tunnel was evacuated, and the door across the mouth of the bed-access tunnel was closed. After a period of several days, the ice tunnel shrunk until tiltmeters, the earth-pressure cell and the strainmeter indicated that ice had begun closing on the surface of the prism. Once reasonably steady conditions in the till prism had been achieved, a series of pump tests were conducted. In each of these tests, water at ~2°C was pumped for a few hours to the glacier sole. In 2001 a high-discharge pump, operated in the rock tunnel, was used to pump a steady discharge of 8Ls–1. In 2002 a lower-discharge (0.13 Ls–1) pump was used. During these pump tests, water pressure varied from nearly atmospheric to above the ice-overburden pressure.
Following the 2001 experiment, a tunnel was melted through the ice back to the till prism. Although every effort was made to expose the prism without eroding it with water from the drill, some disturbance of the prism was unavoidable. Nevertheless, bead-displacement profiles were measured, undisturbed portions of the till prism were closely examined, some instruments were recovered and undisturbed samples were collected to compute the final till porosity. Unfortunately, logistical problems prevented excavation of the prism after the 2002 experiment.
Ancillary laboratory data were collected to characterize some of the mechanical properties of the simulated till. A series of drained direct-shear experiments (Reference Lambe and WhitmanLambe and Whitman, 1969) were performed on remolded specimens at various normal stresses (10–500 kPa) to determine the friction angle and cohesion of the till. In addition, the till was compressed incrementally in a fixed-ring consolidometer (Lambe and Whitman, 1969) to provide baseline data on till compressibility, hydraulic diffusivity and permeability. The till specimen was then unloaded and reloaded to provide data for the case of overconsolidated till.
5. Results
Figures 4 and 5 show records from tiltmeters, earth-pressure cells, strainmeters and the mean record from pore-pressure sensors during the 2001 and 2002 experiments. As in most borehole studies of soft-bed processes, some instruments did not return meaningful signals throughout the experiments. In 2001 all of the tiltmeters in one of the two columns (not shown in Fig. 4) stopped working 2 days into the experiment. During both years, other tiltmeters near the ice–till interface failed late in the experiments. Also, a multiplexer malfunction in 2002 resulted in the loss of 5 days of tiltmeter data (Fig. 5a and b).

Fig. 4. Time series from the 2001 experiment. Signals from the four tiltmeters of column 2 are labeled according to the original heights of their upper ends above the base of the till prism. All sensors of column 1 stopped working 2 days into the experiment and are not shown. Pump tests correspond to the two periods of elevated porewater pressure.

Fig. 5. Time series from the 2002 experiment. Signals from the tiltmeters, which were placed originally in vertical columns, are labeled according to the original heights of their upper ends above the base of the till prism. Beginnings of pump tests correspond to abrupt increases in pore-water pressure.
The experiments began with closure of the ice tunnel, causing progressively increasing contact of ice with the prism (Figs 4 and 5). During closure, tiltmeters recorded irregular deformation that began hours before the downward stress on the prism, recorded by the earth-pressure cell, began to increase. In 2001 this stress ramped up to a value commensurate with the ice thickness (~2000 kPa) in 1.6 days and then became steady (Fig. 4b). In 2002 the stress on the earth-pressure cell increased similarly but after 1 day abruptly peaked at ~1500 kPa and then fell to ~900kPa before becoming steady (Fig. 5c). In both years extension of the strainmeter began to occur prior to the increase in stress on the earth-pressure cell. This extension reached a peak during closure, then declined slightly before becoming steady at approximately the time when the stress on the earth-pressure cell became steady (Figs 4b and 5c).
For 2–3 days after closure was over, stress on the earth-pressure cells remained steady (Figs 4 and 5). Pore pressure remained very near atmospheric during this period in 2001 and crept up slightly, to ~300 kPa, in 2002. In 2001, tiltmeters recorded little deformation during this period (Fig. 4a). In 2002 a preliminary pump test was conducted on 18 April (Fig. 5c) that was quickly aborted when tiltmeters delivered physically untenable signals that led to the diagnosis of the multiplexer problem. Once this problem was corrected, the tiltmeters indicated that some deformation of the prism had occurred during the previous 5 days (Fig. 5a and b), perhaps during the later stages of closure or the preliminary pump test.
Sliding velocity was relatively steady at 44 ± 7 ma–1 in 2001. In 2002, no velocity measurement succeeded. However, sliding velocity measured in 2003 (Reference Cohen, Iverson, Hooyer, Fischer, Jackson and MooreCohen and others, 2005) fell within the same narrow range as in 2001, so the velocity was probably similar in 2002.
5.1. Pump-test hydrology
During the last stage of these experiments, repeated pump tests were conducted, which differed in 2001 and 2002. In 2001 a discharge of 8Ls–1 was pumped to the prism until a hydraulic connection along the ice–rock interface adjacent to the prism was established with the mouth of the access tunnel (Fig. 1). This connection was indicated by turbid water flowing into the access tunnel. Pumping was then stopped, both to minimize erosion of the till prism by water and because pore pressure could not be sustained. Pressure decreased to near atmospheric within minutes of turning off the pump. Two pump tests of several hours were completed in 2001 (Fig. 4b), with a maximum pore-water pressure of ~1600 kPa.
In 2002 during pump tests at the smaller discharge (0.13 Ls–1), hydraulic connection with the mouth of the access tunnel was never established. Rather, during the four 3–5 hour pump tests starting 19 April (Fig. 5c), water flowed from the till prism along an unknown drainage path. During the first of these pump tests, pore pressure cycled about the ice-overburden pressure because the pump had to be switched on and off every 5–20 min to avoid sustained pore pressure in excess of the ice-overburden pressure. In the subsequent three pump tests, pore pressure was sustained at a relatively steady value of ~1800 kPa with the pump on continuously. After the pump was shut off, water pressure decayed at a rate two orders of magnitude slower than in 2001. Thus the drainage path away from the till prism was far less conductive in 2002 than in 2001.
During pump tests each year, pore pressure at the up-glacier and down-glacier locations of pore-pressure sensors (Fig. 2) varied nearly synchronously and equivalently, but the direction and magnitude of the hydraulic gradient within the prism differed (Fig. 6). In 2001 prior to the pump tests, the pore-pressure gradient (measured parallel to the length of the prism over a longitudinal distance of 0.8 m) was near zero. The pump tests caused water flow up-glacier across the prism, as indicated by a negative pore-pressure gradient (<–200 kPam–1). The value of this gradient gradually became less negative during the pump tests (Fig. 6a). During 2002 before the pump tests, there was a small negative pore-pressure gradient, indicating minor water flow up-glacier across the prism. During and after pump tests, however, the gradient reversed (became positive) (Fig. 6b). This indicates that water introduced to the down-glacier edge of the prism (Fig. 2) drained largely down-glacier away from the prism, rather than, as in 2001, up-glacier across the prism. Also, in 2002 the pore-pressure gradient across the prism was a maximum of ~15 kPa m–1, less than 10% of the negative gradient during pumping in 2001.

Fig. 6. Up-glacier and down-glacier pore-water pressure and porepressure gradient during and after pump tests of (a) 2001 and (b) 2002. A positive gradient implies down-glacier water flow across the till prism. Duration of pump tests shown with dotted lines.
Another aspect of the pump-test hydrology is that the total stress recorded by the earth-pressure cells was perturbed by pumping water to the glacier sole. Increases in pore pressure resulted in increases in total stress on the earth-pressure cells that were sometimes >50% of the pore-pressure increase (Figs 4b and 5c).
5.2. Tiltmeter records
During the early stages of pump tests, tiltmeters accelerated their rotation down-glacier but then generally either stopped rotating or began rotating up-glacier until some time after the pump test was over. If, as in past studies (e.g. Reference Blake, Clarke and Ge´rinBlake and others, 1992), tiltmeters are assumed to rotate passively during shear, till shear strain, γ, can be computed from the down-glacier tilt angle, θ d, as γ = 1/2 tan θ d. In Figure 7a shear strain is plotted for the four tiltmeters of the column that functioned during the period spanned by the pump tests. To allow direct comparison of shear-strain records during this period, shear-strain values were set to zero early on 25 March. Shear-strain rates, as indicated by the slope of the plots, increased initially during pump tests but eventually became negative (up-glacier rotation), as high pore-water pressure was sustained. This reversal in shear direction occurred in both pump tests but was pronounced in the second, longer test. At the end of the pump tests, when pore pressure fell rapidly, there was renewed down-glacier shear, although this shear occurred after, rather than during, the pore-pressure decrease and associated increase in effective pressure (Fig. 7b). Overall, shear-strain variations during pump tests were affected by, but did not mirror, changes in effective pressure on the bed.

Fig. 7. (a) Strain records calculated from rotation of tiltmeters (column 2) in 2001. Distances are heights of the tops of tiltmeters above the base of the prism. The highest tiltmeter in the column stopped working at ~1930 h, 26 March. Pore-water pressure is the mean value from the three sensors. (b) The last 8 hours of the tiltmeter record shown in (a), spanning the end of the second pump test, together with mean effective pressure on the bed and the signal from the strainmeter. Mean effective pressure is the difference between the total normal stress on the bed measured with the earthpressure cell and the mean pore-water pressure. The strainmeter was not normal to the bed at this stage of the experiment but was sufficiently upright that abrupt contraction at the end of the pump test reflects contraction of the prism.
Tiltmeters from pump tests of the 2002 experiment behaved similarly. Figure 8 shows shear strains, set to zero prior to the pump tests, indicated by the two uppermost tiltmeters of each column that delivered reliable signals. There was a clear tendency for tiltmeters to rotate up-glacier or stop rotating down-glacier either at the beginning of or during pump tests. However, the highest tiltmeter in column 2 (placed with its upper surface 0.42 m above the base of the rock trough and 0.04 m below the bed surface) behaved differently during the third pump test (Fig. 8, bottom panel);shortly after this test began, this tiltmeter increased its rate of rotation to a relatively steady value more than an order of magnitude larger than that exhibited by any other tiltmeter during either year. This tiltmeter stopped working about 4 hours later.

Fig. 8. Strain records calculated from rotation of tiltmeters in 2002. Uppermost two tiltmeters in each column that worked for most of the pump tests are shown (the two uppermost tiltmeters in column 1 are not shown because they had both stopped working by the end of the first pump test). Distances are heights of the tops of the tiltmeters above the base of the prism. Note the high shear strains indicated by the tiltmeter record in the lowest panel. The top of this tiltmeter (uppermost tiltmeter of column 2) is inferred to have been deflected by sliding ice at ~1700h, 20 April.
Tiltmeter rotation and associated strain and time-averaged strain rates generally increased upward toward the bed surface (Figs 4a, 5b and 7a). Tiltmeter rotation was interpolated linearly over depth intervals in the bed centered on the tiltmeters to estimate vertical profiles of horizontal till displacement (Fig. 9). The compaction of the till prism due to the pressure of the ice, described in section 5.3, was accounted for in generating these profiles. Profiles were generally concave-down over both the period spanned by the pump tests and the longer period between the start of the experiment and when one tiltmeter in the columns failed (Fig. 9). The primary exception was column 1 in 2002, in which shear strains were greater at depth, due to irregular deformation early in the experiment during ice closure on the till (Fig. 5a).

Fig. 9. Deformation profiles computed from tiltmeter rotation during (a) 2001 and (b) 2002. Profiles labeled ‘Pump tests’ were computed based on tiltmeter rotation during only the periods spanning the pump tests. Profiles labeled ‘Long-term’ were computed over the full period when all tiltmeters functioned properly (20–26 March in 2001; 11–21 April in 2002). Thus, the long-term profiles include the effects of irregular deformation during ice closure on the till.
5.3. Post-experimental observations
Excavation of the till prism in 2001 revealed that its initial upper surface was not the bed surface at the end of the experiment. Painted clasts placed at the initial bed surface had basal ice above them identical to dirty basal ice usually observed at the bed of Engabreen (2–11% debris by volume (Reference Cohen, Iverson, Hooyer, Fischer, Jackson and MooreCohen and others, (2005)). However, below the painted clasts there was a layer of ice-cemented till (Fig. 10). In the undisturbed part of the prism that could be excavated, this ice-cemented layer was 50–80mm thick. The contact between the basal ice and ice-cemented till was sharp, and there was flow-parallel asymmetry of this contact around some clasts (Fig. 10), consistent with ice sliding past them. The contact between the ice-cemented till and the underlying till (the final bed surface) was also sharp, with clear separation between the two materials.

Fig. 10. Basal ice after excavating part of the till prism from the experiment of 2001. The painted clast was initially halfway buried in the surface of the till prism when ice closed on it. After the experiment, ice-cemented till extended 50–80mm below the clast. Overlying the clast was basal ice with sparse debris like that usually observed at the bed of Engabreen (Reference Cohen, Iverson, Hooyer, Fischer, Jackson and MooreCohen and others, 2005). Sliding direction was from left to right.
Samples collected for bulk density measurements in 2001 indicated a final mean bulk density for the till prism of 2190± 30kg m–3, corresponding to a porosity of 19.6 ± 1.2%. Samples collected before the experiment had a mean dry bulk density of 1830 ± 50kgm–3, or a porosity of 33.4 ± 1.8%. The measured reduction in porosity corresponded to mean thinning of the till layer of about 18% in 2001. This amount of thinning was assumed also in 2002, when the till prism could not be excavated, to construct the velocity profiles of Figure 9b.
Bead columns placed near each of the two tiltmeter columns in 2001 were successfully exposed and measured (Fig. 11). Several beads at the top of both columns were found displaced down-glacier but at a high angle to the glacier flow direction. We inferred that these beads were scraped by ice from the bed surface during ice-tunnel closure, so data from these beads are not plotted in Figure 11. Down-glacier bead displacements near tiltmeter column 1, which stopped working during the first 2 days of the experiment, indicate major shear strain focused near the bed. Bead displacements near tiltmeter column 2 indicate a weakly concave-down velocity profile, similar in shape to that constructed from the signals of the tiltmeters from this column (Fig. 11). However, the bead profile indicates shear displacements a factor of three larger than those indicated by the tiltmeter signals. This difference apparently reflects till deformation during the 3 days of the experiment after the uppermost tiltmeter in column 2 stopped working;the displacement record computed from column 2 (Fig. 11) does not include that period.

Fig. 11. Bead profiles from 2001. Tiltmeter column 1 stopped working about 2 days into the experiment, so a profile calculated from only tiltmeter column 2 (see also Fig. 9a, ‘Longterm’) is shown.
5.4. Ancillary laboratory data
Results of direct-shear tests, conducted until steady shear stresses were attained, yielded a friction angle of 32.3° with zero cohesion, consistent with the high sand content of the till (Fig. 12a). Till compressibility, α, (Reference Freeze, Cherry and Englewood CliffsFreeze and Cherry, 1979; Reference ClarkeClarke, 1987) decreased with increasing normal stress, as is expected due to the resultant reduction in porosity, and was about an order of magnitude smaller during reloading of the till once it had been overconsolidated (Fig. 12b). Hydraulic diffusivity, D, (Reference Freeze, Cherry and Englewood CliffsFreeze and Cherry, 1979) was estimated using the rate of change of consolidation after loading increments (e.g. Reference BowlesBowles, 1992); D = 1.0–3.2 × 10–5 m2 s–1 (Fig. 12b). Owing to the negligibly small compressibility of water, hydraulic conductivity, K, is well approximated by K = ρwgDα, where ρw is water density and g is gravitational acceleration. Values of K calculated from D and α decreased from 5 × 10–7 to 5 × 10–9ms–1 with increasing normal stress.

Fig. 12. (a) Results of direct-shear tests with the simulated till. As indicated by the regression, the friction angle is 32.3° with a standard error of 2°. The cohesion is 1 kPa with a standard error of 10 kPa. (b) Compressibility and hydraulic diffusivity of the till as a function of total normal stress, determined from tests with a fixedring consolidometer. Diffusivity remained relatively constant with increasing normal stress because reductions in permeability were compensated by reductions in compressibility.
6. Analysis and Discussion
6.1. Closure
The irregular deformation recorded by the tiltmeters during closure is interpreted to reflect partial bulldozing of the till prism by ice closing on its sides, prior to loading of the prism by ice from above it (Figs 4a and 5a and b). This interpretation is supported by deformation that began before stress on the earth-pressure cells had begun increasing (Figs 4b and 5c). Bulldozing is also indicated by one of the bead profiles from 2001, which indicated a steep velocity gradient near the base of the prism (Fig. 11). Deformation of the till prism during ice closure is also illustrated by the strainmeters, which extended substantially, either due to shear that stretched the instruments or vertical extension associated with bulldozing (Figs 4b and 5c). The subsequent contraction of these instruments that occurred as stresses on the earth-pressure cells were increasing is interpreted as reflecting consolidation of the till as ice closed on it from above, although this underestimates the true consolidation, due to rotation of the strainmeters from their initially vertical orientation during deformation. Given the irregular deformation during closure, our discussion focuses primarily on bed deformation during the pump tests.
6.2. Total normal stresses
Although conditions in the prism became relatively steady once closure was complete, in 2002 the steady-state pressure on the earth-pressure cell was about 50% (900–1000 kPa) of that expected from the ice thickness (Fig. 5c). This is interpreted as reflecting rotation of the instrument, so that its sensing face deviated substantially from horizontal; when granular materials are loaded vertically in confined compression, horizontal stresses can be less than half the applied stress (Reference Lambe and WhitmanLambe and Whitman, 1969, p. 127). Thus, this instrument probably did not record the total downward stress on the prism. In 2001 there was little rotation of the earth-pressure cell, as indicated by its near-horizontal orientation upon excavation of the prism and by its steady-state signal, which was commensurate with the ice-overburden pressure (Fig. 4b).
The increase in total stress on the earth-pressure cells during pump tests when pore-water pressure was increased (Figs 4b and 5c) was probably a product of the limited footprint of the pressure pulse. The dilation of till and upward movement of ice that would result from a spatially uniform increase in basal pressure was impeded by ice outside the margins of the till prism that was outside the pressure-pulse footprint. Thus, no upward movement of ice was permitted, other than elastic flexure, so some of the increase in water pressure resulted in an increase in downward total stress on the prism. This result is a reminder that spatial gradients in basal water pressure can locally affect the total stress that ice exerts on the bed (e.g. Reference Murray and ClarkeMurray and Clarke, 1995; Reference Lappegard, Kohler, Jackson and HagenLappegard and others, 2006). In 2001 this effect of water pressure on total normal stress was successfully measured and factored into calculations presented hereinafter; this was not possible for the experiment of 2002, in which the earth-pressure cell rotated.
6.3. Regelation infiltration
Observations after the 2001 experiment indicate that the position of the bed surface (interface between dirty ice and ice-free till) moved into the prism 50–80 mm over the part of it that could be successfully excavated, with resultant entrainment of till (Fig. 10). Although the till prism could not be excavated in 2002, the abrupt, sustained increase in rotation rate of the uppermost tiltmeter of column 2 (Fig. 8, bottom panel) provides evidence that downward migration of the bed surface also occurred during that year’s experiment. On the afternoon of 20 April (~1700h), the rate of rotation of this tiltmeter increased abruptly by more than an order of magnitude. This higher rotation rate was commensurate with a change in horizontal velocity across the tiltmeter equal to 60% of the sliding speed. We infer that the upper end of the tiltmeter was deflected by sliding ice, thereby dramatically increasing its rotation rate. The failure of this tiltmeter 4 hours later is consistent with this explanation. The top of this tiltmeter was originally 40± 15 mm below the bed surface. Accounting for the tiltmeter’s rotation, which would have reduced the elevation of its upper end, the top of this tiltmeter would have been 55 ± 15 mm below the initial bed surface when its top was deflected by ice. Unfortunately, the uppermost tiltmeter from the other column (Fig. 5a) never delivered a meaningful signal, so yielded no information about the position of the bed surface with time.
Possible mechanisms for downward migration of the bed surface include freeze-on by regelation in the lee of a bed obstacle, net freeze-on of water by conductive cooling, net freeze-on by supercooling and regelation infiltration (Reference Alley, Cuffey, Evenson, Strasser, Lawson and LarsonAlley and others, 1997). Refreezing in the lee of a bed obstacle can be ruled out because, although the trough that contained the till prism was blasted on the down-glacier side of a subdued bump, this bump had a wavelength of several meters, far larger than expected for significant regelation (e.g. Reference PatersonPaterson, 1994). Also, net freeze-on by conductive cooling can be precluded because Engabreen is a fully temperate glacier with basal ice containing more than 2% water (Reference Cohen, Hooke, Iverson and KohlerCohen, 2000). The bed sloped down-glacier at the site of prism, both locally and regionally, so freeze-on by supercooling is not a viable hypothesis.
We conclude that the most likely mechanism for the downward migration of the bed surface was regelation infiltration. To test this hypothesis, theory grounded on the regelation model of Reference PhilipPhilip (1980) can be used to calculate the depth of infiltration as a function of time for comparison with our observations. Following Reference Iverson and SemmensIverson and Semmens (1995) and Reference IversonIverson (2000), temperate ice will regelate into a granular layer at a speed, v r, given by
where Ks is a constant fully derivable from first principles (Reference PhilipPhilip, 1980), H is the thickness of the ice-infiltrated sediment layer, P i is the normal stress acting on the upper boundary of that layer and P w is the pore-water pressure in the bed. K s is proportional to the apparent conductivity of sediment to ice, such that K s ρg, with ρ the ice density, is analogous to the conductivity of Darcian flow. The rate of change in the thickness of the ice-infiltrated layer, dH/dt, is
where ṁ is the basal melt rate. Neglecting heat advected by basal water and dissipated by water flow, the basal melt rate depends on the flux of heat from the bed, q b, and on the heat flux produced by basal motion at a velocity U and under a shear stress τ:
where n is the porosity of the ice-infiltrated till layer and L is the volumetric latent heat of fusion. Combining Equations (1) and (2) and integrating yields
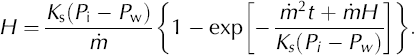
Equation (4), together with Equation (3), was used to calculate the thickness of the ice-infiltrated till layer as a function of time (Fig. 13) for comparison with both the direct observation at the end of the 2001 experiment (Fig. 10) and the thickness inferred in 2002 from the abrupt increase in tiltmeter rotation rate (Fig. 8, bottom panel). Table 1 lists the ranges of parameter values used to calculate the upper and lower bounds of the model prediction. Basal melt rates were higher than normal (0.54–1.06 m a–1). They were calculated using the measured value of U, ranges of local τ measured by Reference Cohen, Iverson, Hooyer, Fischer, Jackson and MooreCohen and others (2005) at Engabreen, ranges of n defined by the initial and final porosity of the prism, and ranges of q b indicated by the temperature gradient in the rock bed. This gradient was controlled by the air temperature of the rock tunnel ~4 m below the till prism (2°C); one-dimensional heat flow was assumed to calculate q b, using a thermal conductivity appropriate for granitic rock (3.3 W m–1 °C–1). Values of K s in Table 1 reflect the melting-point depression for air-saturated ice and the range of till porosity considered (Reference Iverson and SemmensIverson and Semmens, 1995). In the experiments, P i – P w varied with time, so the time-averaged value was used (Table 1). This value provides a good estimate of the total infiltration depth over the duration of the experiments but smooths irregularities in the rate of infiltration-depth increase caused by unsteady P i – P w.

Fig. 13. Regelation infiltration depth during the experiments of 2001 and 2002, calculated using regelation theory grounded on the model of Reference PhilipPhilip (1980) and adapted by Reference IversonIverson (2000). Ranges of parameter values used in the calculation to arrive at upper and lower bounds are listed in Table 1. Error bars for the 2001 data point reflect the range of intrusion depths observed upon excavating the till prism. Error bars for the 2002 data point reflect the uncertainty of the position of the top of the tiltmeter that is inferred to have been deflected by the glacier sole (see text and Fig. 8, bottom panel).
Table 1. Parameter values used to calculate infiltration depth

Although the thickness of the ice-infiltrated layer was observed only once during each year, Figure 13 indicates that the model, with no adjustment of parameters, is in good agreement with these observations. This agreement supports the hypothesis that regelation infiltration entrained till at the top of the prism, despite the higher-than-normal basal melt rate. Moreover, the good agreement indicates interfacial-curvature and pre-melting effects that can hold water tightly in the till pores did not impede regelation discernibly, although these effects might have become evident had the time-averaged value of P i – P w during the experiments been smaller. Our results also indicate that the component of ice motion parallel to the bed surface did not grossly impede regelation. Our pump tests, however, probably did impede regelation by increasing pore-water pressure in the prism and causing transient separation between ice-infiltrated till and the prism, as discussed in section 6.4. The latter of these effects could not be incorporated in the calculation of infiltration depth (Fig. 13) but, owing to the limited duration of the pump tests, did not have a perceptible effect on the results.
6.4. Water-layer thickness and glacier–bed coupling
Periods of up-glacier tiltmeter rotation during pump tests (Figs 7 and 8) are interpreted as periods of relaxation of the prism in shear when slip occurred at the bed surface. During these events, the shear traction supported by the bed surface became less than the bulk yield strength of the till, halting permanent deformation of the till down-glacier and causing its elastic relaxation up-glacier (Reference IversonIverson and others, 2003). An alternative interpretation is that up-glacier rotation simply reflected periods of till dilation associated with increasing pore-water pressure, which would cause a tiltmeter tilting down-glacier to rotate up-glacier (Reference Tulaczyk, Kamb and EngelhardtTulaczyk and others, 2000a). This hypothesis is not tenable in this case because substantial up-glacier rotation occurred commonly when water pressure was either steady or decreasing (Figs 7a and 8). Moreover, there were sometimes lags between pore-pressure changes and tiltmeter response (Fig. 7b).
A past interpretation of similar tiltmeter records attributed slip of ice over the bed to thickening of a water layer between clean ice and the bed surface (Reference IversonIverson, 1999). This thickening was thought to submerge some particles at the bed surface, thereby concentrating shear stresses on larger particles sufficiently to activate ploughing and associated slip of the glacier across the bed. In the case of the ice-infiltrated till layer overlying the bed surface in these experiments, this water layer can be considered to be a thin zone of very high porosity (Fig. 14), probably caused by a combination of elastic uplift of the glacier sole and winnowing of particles at the bed surface by water flow through this porous zone.

Fig. 14. Ice-infiltrated till sliding over a water-saturated till bed. A water layer separates much of the ice-infiltrated till from the bed. Only particles of sufficient size protrude through the layer and plough during slip of the glacier across the bed surface.
Unlike past studies, in this case the water-layer thickness can be independently estimated as a function of time and compared with the record of till deformation. Although the water layer could not be observed directly, near-synchronous variations in water pressure at the up-glacier and down-glacier positions in the prism suggest that flow across the prism occurred primarily at the bed surface rather than through the till pores (Fig. 6). Time lags between the two pressure signals were discernible but <5 min in duration. Had water flowed up- or down-glacier primarily through the till, the minimum diffusive time lag would have been on the order of ![]() D, where x
d is the lateral distance between sensors (0.8–0.9 m) and D is the maximum hydraulic diffusivity of the till (3 × 10–5 m2 s–1). For these experiments,
D, where x
d is the lateral distance between sensors (0.8–0.9 m) and D is the maximum hydraulic diffusivity of the till (3 × 10–5 m2 s–1). For these experiments, ![]() D was greater than ~5.5 hours, far longer than the lags observed. However, if sensors were a few centimeters away from the water layer at the glacier sole, as a result of regelation infiltration of the bed, with essentially instant-aneous transmission of pressure through the water layer, then the timescale for vertical diffusion through the till to the water layer would have been on the order of a few minutes, as observed, rather than hours. Most water, therefore, must have flowed across the prism through a water layer at the bed surface, and the pressure gradient recorded by the sensors was comparable to that driving flow through this layer (Fig. 6).
D was greater than ~5.5 hours, far longer than the lags observed. However, if sensors were a few centimeters away from the water layer at the glacier sole, as a result of regelation infiltration of the bed, with essentially instant-aneous transmission of pressure through the water layer, then the timescale for vertical diffusion through the till to the water layer would have been on the order of a few minutes, as observed, rather than hours. Most water, therefore, must have flowed across the prism through a water layer at the bed surface, and the pressure gradient recorded by the sensors was comparable to that driving flow through this layer (Fig. 6).
Thus, if, in addition to the pressure gradient, the water discharge through the layer is known, the water-layer thickness, d w, can be estimated, for the case of laminar flow (e.g. Reference WeertmanWeertman, 1972; Reference Engelhardt and KambEngelhardt and Kamb, 1997):
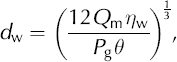
where Q
m is the mean water discharge per unit width across the prism, η
w is the dynamic viscosity of water near 0°C, P
g is the pressure gradient between the water-pressure sensors, ignoring the negligible difference in sensor elevation, and θ is the fraction of the layer’s cross-sectional area that is not blocked by particles that span the layer. This equation applies strictly to steady-state flow. However, the characteristic period required for steady flow to develop after a change in P
g is ![]() /ν, where ν is the kinematic viscosity of water (e.g. Reference BatchelorBatchelor, 1967). This period is on the order of 1 s for a 1 mm thick layer, so Equation (5) is appropriate for P
g fluctuating over the much longer periods of interest herein.
/ν, where ν is the kinematic viscosity of water (e.g. Reference BatchelorBatchelor, 1967). This period is on the order of 1 s for a 1 mm thick layer, so Equation (5) is appropriate for P
g fluctuating over the much longer periods of interest herein.
In 2001 P g was negative (Fig. 6a), indicating that water pumped to the down-glacier end of the prism flowed up-glacier across the prism. Assuming uniform radial flow in all directions from the mouth of the borehole across the prism, the spatially averaged discharge per unit width across the prism and between the two pressure sensors was Q m = 1.2 × 10–3 m2 s–1. This value yields a Reynolds number less than 1000 (670), so the laminar-flow assumption of Equation (5) is correct (Reference Vennard and StreetVennard and Street, 1982). Using this value of Q m and the pressure gradient of Figure 6a in Equation (5) to calculate d w during the two pump tests of 2001 yields noisy values of 0.4–1.0mm (Fig. 15a). This estimate assumes that θ = 1.0 is a good approximation due to the limited area of real contact between particles in ice and the bed – an assumption justified in section 6.5. Up-glacier rotation of tiltmeters, interpreted to reflect slip of ice across the bed surface, occurred at d w ~ 0.7 mm in the second pump test when the transition from bed deformation at depth to sustained slip occurred most clearly (Fig. 15a). In 2002 the same calculation is not possible because during pumping the pressure gradient was positive (Fig. 6b), indicating that water introduced to the down-glacier end of the prism did not flow up-glacier across the prism but rather escaped down-glacier. Thus, the discharge across the prism during pump tests from that year is unknown. However, the water-layer thickness can be estimated in 2002 during the periods following pump tests. After pumping was stopped, water pressure decreased slowly in the prism, as did the down-glacier gradient in water pressure (Fig. 6b). The dominant source of water flowing in the water layer during these periods would have been pore-water that was squeezed from the till prism as effective pressure on the prism increased. If all water produced by this till consolidation flowed down-glacier through the water layer toward the side of the prism where water had escaped during pumping, then the mean discharge per unit width across the prism between the pressure sensors was

Fig. 15. (a) Water-layer thickness during pump tests of 2001, calculated from the constant water discharge during pumping and the measured pressure gradient. Shear-strain record is from the uppermost tiltmeter in column 2 (see Fig. 7a). Dashed line shows when the uppermost tiltmeter began sustained up-glacier rotation, indicating slip at the bed surface, and points to the associated water-layer thickness. (b) Water-layer thickness after pump tests of 2002, calculated using the water discharge squeezed from the consolidating till prism. Upper and lower bounds of water-layer thickness are shown, corresponding to virgin and reloaded till, respectively. Shear-strain record is from the uppermost tiltmeter in column 1 that worked during all of the pump tests. Dashed lines indicate when sustained up-glacier rotation of this tiltmeter began after pump tests.
where α is the till compressibility (Fig. 12b), V t is the volume of the till prism upstream of the down-glacier pressure sensor and w is the width of the prism (Table 2). Equation (6) ignores the compressibility of water, which is small relative to that of till (Reference Freeze, Cherry and Englewood CliffsFreeze and Cherry, 1979), and the flux of water from basal melt, which was a negligibly small fraction of the discharge of water squeezed from the till during consolidation. Note that till compressibility probably decreased with time after pumping, as effective stress increased and the porosity of the till decreased during consolidation, as indicated by the consolidometer tests (Fig. 12b). Substituting Equation (6) into (5) yields the water-layer thickness during till consolidation after the pump tests of 2002:

Table 2. Constants used to calculate water-layer thickness, submergence ratio and the slip parameter

Numerical values of d w were obtained during the periods after pump tests by fitting a power function to P w with time and differentiating it, using the regressions of α as a function of effective pressure (Fig. 12b), and applying measured values of P g (Fig. 6b). Upper and lower bounds of water-layer thickness are shown in Figure 15b, using compressibility values measured for virgin and reloaded till, respectively.
For the three pump tests in 2002 for which this calculation was possible, down-glacier deformation of till was reactivated at water-layer thicknesses of ~0.05–0.25 mm (Fig. 15b), somewhat thinner than when slip was initiated in 2001 (~0.7 mm). This difference may reflect system hysteresis, such that the water-layer thickness necessary for slip was different during rising (2001) and falling (2002) water pressure. Alternatively, it may reflect an overestimate of the water discharge across the prism in 2001, when considerable discharge was observed entering the mouth of the horizontal access tunnel, down-glacier from the prism (Fig. 1). If more water escaped down-glacier from the water entry point than flowed up-glacier across the prism, then the 2001 water-layer thickness would have been overestimated by an amount proportional to the flow asymmetry. This and other uncertainties, such as the poorly known true azimuth of water flow at the bed surface, highlight that these are crude estimates of water-layer thickness.
Despite these uncertainties, however, these data indicate that water-layer thickness is a major factor modulating the tendency for glacier slip over the bed surface. This has been assumed but not demonstrated in previous studies (Reference Brown, Hallet and BoothBrown and others, 1987; Reference AlleyAlley, 1989; Reference IversonIverson, 1999).
6.5. Model of basal slip by ploughing
These results indicate that when basal water pressure and discharge are sufficiently large at a till bed, ice slips across the bed rather than deforming it at depth. This observation is consistent with those from several other glaciers (Reference Blake, Fischer and ClarkeBlake and others, 1994; Reference Engelhardt and KambEngelhardt and Kamb, 1998; Reference Iverson, Baker, Hooke, Hanson and JanssonIverson and others, 1999; Reference Truffer and HarrisonTruffer and Harrison, 2006). Also, our results confirm the expectation that when water pressure is sufficiently low, the bed does not deform at depth owing to its high shear strength (e.g. Fig. 4).
Our goal now is to develop a slip model that reproduces this behavior, incorporating the effect of the water-layer thickness. The model must describe friction between the glacier sole and the bed, bearing in mind that regelation infiltration caused ice-infiltrated till, rather than mildly dirty ice, to be in contact with the till surface. Friction at this contact will depend on resistance to ploughing of particles that are sufficiently large to span the water layer, so these particles are both held in the ice-infiltrated till of the glacier sole and protrude into the bed, as shown in Figure 14. In contrast to the case of clean ice resting on a soft bed, in which sliding of ice by the classical mechanisms (e.g. Reference LliboutryLliboutry, 1979) may limit the shear traction on some particles rather than ploughing (e.g. Reference Brown, Hallet and BoothBrown and others, 1987; Reference IversonIverson, 1999), intergranular friction within the ice-infiltrated till of the glacier sole will inhibit the classical sliding mechanisms. Thus, we consider the shear traction on the soft bed to result exclusively from resistance to ploughing of individual particles through the bed surface, so that resistance to ploughing of particles through the wet bed is always less than resistance to movement of particles through the ice-infiltrated till. Particles effectively act as asperities at the base of the ice-infiltrated till layer that drag across the bed, which yields locally around them. The smallest of these particle asperities are drowned in the water layer and do not contribute to the shear traction on the bed surface (Fig. 14).
The bed-parallel component of force exerted on ploughing particles, Fx, depends on the ploughing resistance of the bed, s (bed-parallel stress exerted by the bed on particles in the ice). Thus, Fx = s(A – A s), where A is the total area of the bed and A s is area of the bed submerged in the water layer. The quantity, A – A s, is the area of the bed in direct contact with particles protruding from the glacier sole. The bed-normal weight of the glacier, Fz, is partitioned between ploughing particles and water under a pressure P w (e.g. Reference ClarkeClarke, 2005). Thus, Fz = p(A – As ) + P w A s, where static stress equilibrium requires that p is the resistance to penetration of particles downward into the soft bed. The ratio between Fx and Fz , after dividing both expressions by the total area of the bed, yields a friction coefficient, μ 1, for the glacier–bed interface:
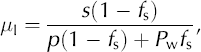
where f s is the fractional area of the bed submerged in the water layer. Thus, the shear traction on the bed due to ploughing is μ I P 0, where P 0 is the total normal stress on the bed.
A geotechnical theory of the movement of cones and piles through sediment (Reference Senneset, Janbu, Chaney and DemarsSenneset and Janbu, 1985), applied previously to subglacial ploughing (Reference IversonIverson, 1999, Reference Iverson2004; Reference Fischer, Porter, Schuler, Evans and GudmundssonFischer and others, 2001) and tested in experiments (Reference Senneset, Janbu, Chaney and DemarsSenneset and Janbu, 1985; Reference Iverson, Jansson and HookeIverson and others, 1994), provides clear guidance for estimating the penetration resistance, p, and ploughing resistance, s:
where P e is the effective pressure (P 0 – P w). NF is a dimensionless bearing-capacity factor that depends on the friction angle, φ, of the sediment and the orientation of conjugate slip surfaces in till near the ploughing element, described by the angle β (Reference Iverson, Jansson and HookeIverson and others, 1994):

Use of Equations (9) and (10) acknowledges that till is a Coulomb material, in which resistance to deformation is independent of deformation rate and linearly dependent on P e. Laboratory experiments with till support this idealization (Kamb, 1991; Reference Iverson, Hooyer and BakerIverson and others, 1998; Tulazcyk and others, 2000a), with the exception of the study of Reference Ho, Vela, Jenson, Clark, Sheahan and KaliakinHo and others (1996) in which steady-state deformation rates were not achieved. Cohesion is assumed to be zero, which was true, within error limits, for the till of the sediment prism (Fig. 12a);even in clay-rich tills with non-zero cohesion, cohesion is usually subordinate to the frictional component of till strength except at very low effective pressures. The coefficient 0.5 in Equation (10) is the ratio of the transverse to plan-view cross-sectional areas of ploughing clasts in contact with till. This value of the ratio is appropriate for spherical clasts buried halfway in the bed – a reasonable mean position for ploughing particles (Reference Brown, Hallet and BoothBrown and others, 1987; Reference IversonIverson, 1999), although values of this coefficient for individual particles probably vary through nearly the full possible range (0–1.0). Moreover, Equation (10) applies only if excess pore pressures did not develop in the zone of compression in till down-glacier from ploughing particles (e.g. Reference IversonIverson, 1999). Scaling arguments, tested in laboratory ploughing experiments (Reference ThomasonThomason 2006), indicate that the high hydraulic diffusivity of the till used in the prism (10–5 m2 s–1) prevented excess pore pressures (Appendix A). Finally, Equations (9) and (10) are strictly valid only for deformation fields near ploughing particles that do not interact, an assumption justified hereinafter.
To rewrite Equation (8) in a more convenient form, we define the ratio of the submerged to unsubmerged fractions of the bed as the submergence ratio, S
R = f
s/(1–f
s). Substituting Equations (9) and (10) into Equation (8) and defining the normalized effective pressure as ![]() = P
e/P
0 yields the friction coefficient at the bed surface in terms of only dimensionless variables:
= P
e/P
0 yields the friction coefficient at the bed surface in terms of only dimensionless variables:

An analogous friction coefficient, μ T, characterizes the overall resistance of the till bed to shear. Again neglecting till cohesion, the shear strength of till, τ s, is given by the Coulomb–Terzaghi criterion: τ s = P etan φ. Dividing both sides of this equation by the total normal stress, P 0, yields the friction coefficient for till shear:
For values of ![]() that satisfy μ
I > μ
T, the glacier will slip across the bed by ploughing, rather than shearing it at depth. Thus, dividing Equation (13) by Equation (12) yields a slip parameter, χs, which predicts whether slip will occur as a function of
that satisfy μ
I > μ
T, the glacier will slip across the bed by ploughing, rather than shearing it at depth. Thus, dividing Equation (13) by Equation (12) yields a slip parameter, χs, which predicts whether slip will occur as a function of ![]() :
:

For χ s > 1, there will be slip by ploughing; for χ s ≤ 1, the glacier sole will grip the bed sufficiently to deform it at a shear stress equal to the bed shear strength.
The constants N
F and φ in Equation (14) are well known, but computing χ
s from ![]() also requires estimating S
R, the submergence ratio. S
R depends on
also requires estimating S
R, the submergence ratio. S
R depends on ![]() through its effect on the water-layer thickness and also depends on the size distribution of ploughing particle asperities on the glacier sole. To establish S
R as a function of
through its effect on the water-layer thickness and also depends on the size distribution of ploughing particle asperities on the glacier sole. To establish S
R as a function of ![]() , we first assume that the size distribution of ploughing particle asperities reflects the till grain-size distribution. The number of grains, N, of radius R is given by the relation N = kR
−m
, where k and m are fitted constants (Fig. 3). As shown in Appendix B, the submergence ratio, as a function of water-layer thickness, d
w, is then
, we first assume that the size distribution of ploughing particle asperities reflects the till grain-size distribution. The number of grains, N, of radius R is given by the relation N = kR
−m
, where k and m are fitted constants (Fig. 3). As shown in Appendix B, the submergence ratio, as a function of water-layer thickness, d
w, is then
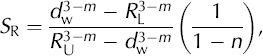
where R
L and R
U are the upper and lower size limits of the grain-size distribution. The empirical relationships between d
w and ![]() during the pump tests of 2001 (Fig. 15a) and during the till consolidation that followed the pump tests of 2002 (Fig. 15b) are shown in Figure 16. During these periods there were exponential decreases in d
w with increasing
during the pump tests of 2001 (Fig. 15a) and during the till consolidation that followed the pump tests of 2002 (Fig. 15b) are shown in Figure 16. During these periods there were exponential decreases in d
w with increasing ![]() . Using these relationships to specify d
w in Equation (15), submergence ratios from 6 to 38 are indicated over the measured ranges of
. Using these relationships to specify d
w in Equation (15), submergence ratios from 6 to 38 are indicated over the measured ranges of ![]() , such that 86–98% of the bed area was submerged (Fig. 16). This result supports our assumptions that θ was close to 1.0 in Equations (5) and (7) (Table 2) and that ploughing particles were isolated sufficiently to have non-interacting deformation fields. More importantly, these calculations indicate the general form of the function S
R(
, such that 86–98% of the bed area was submerged (Fig. 16). This result supports our assumptions that θ was close to 1.0 in Equations (5) and (7) (Table 2) and that ploughing particles were isolated sufficiently to have non-interacting deformation fields. More importantly, these calculations indicate the general form of the function S
R(![]() ); submergence ratios, like d
w, decreased exponentially with increasing
); submergence ratios, like d
w, decreased exponentially with increasing ![]() .
.

Fig. 16. Calculated water-layer thicknesses and submergence ratios during the two pump tests of 2001 and during the periods of till consolidation following the three final pump tests of 2002. The 2002 values are minima because the compressibility of the till upon reloading was used to compute water-layer thickness; owing to till shear between pump tests and associated dilation, the till compressibility may have been higher, approaching the value for virgin till (see Fig. 15).
Various functions that describe an exponential reduction in submergence ratio, S
R, with increasing ![]() (Fig. 17a) were considered in Equation (14) to explore how the slip parameter χ
s varies with
(Fig. 17a) were considered in Equation (14) to explore how the slip parameter χ
s varies with ![]() . For values of S
R comparable to those indicated by the data at low effective pressures (trial cases i–iii in Fig. 17a), slip over the bed (χ
s > 1) is predicted for sufficiently small and sufficiently large values of
. For values of S
R comparable to those indicated by the data at low effective pressures (trial cases i–iii in Fig. 17a), slip over the bed (χ
s > 1) is predicted for sufficiently small and sufficiently large values of ![]() , with bed deformation only at intermediate values. These predictions are in broad agreement with our tiltmeter observations (e.g. Figs 7 and 8) and observations elsewhere (e.g. Reference Blake, Fischer and ClarkeBlake and others, 1994; Reference Iverson, Baker, Hooke, Hanson and JanssonIverson and others, 1999). Only for values of S
R smaller than those indicated by our data (case iv in Fig. 17a) is slip not predicted at low effective pressures. For linear reductions in S
R with increasing
, with bed deformation only at intermediate values. These predictions are in broad agreement with our tiltmeter observations (e.g. Figs 7 and 8) and observations elsewhere (e.g. Reference Blake, Fischer and ClarkeBlake and others, 1994; Reference Iverson, Baker, Hooke, Hanson and JanssonIverson and others, 1999). Only for values of S
R smaller than those indicated by our data (case iv in Fig. 17a) is slip not predicted at low effective pressures. For linear reductions in S
R with increasing ![]() , values of the slip parameter indicate that the observed switching from bed deformation to slip of ice by ploughing under effective pressures approaching zero is far less likely (Fig. 17b). Thus, the tendency for the water-layer thickness and the submerged area of the bed to change most rapidly at low effective pressures appears to help instigate switching between basal flow mechanisms.
, values of the slip parameter indicate that the observed switching from bed deformation to slip of ice by ploughing under effective pressures approaching zero is far less likely (Fig. 17b). Thus, the tendency for the water-layer thickness and the submerged area of the bed to change most rapidly at low effective pressures appears to help instigate switching between basal flow mechanisms.

Fig. 17. Slip parameter as a function of normalized effective pressure for various submergence ratios that (a) decrease exponentially with increasing effective pressure, as was observed in the experiments, and (b) decrease linearly with increasing effective pressure. Slip parameters indicate that the observed switching between slip and bed deformation is more likely for the exponential case.
The result that slip by ploughing prevails at sufficiently high effective pressures (Fig. 17a and b) stems from the factor of 0.5 in the expression for ploughing resistance (Equation (10)). This factor (the ratio of transverse to plan-view cross-sectional areas of ploughing particles in contact with till) results from only partial penetration of particles in the bed and causes ploughing resistance that is less than resistance to bed shear as ![]() approaches 1.0 in Equation (14).
approaches 1.0 in Equation (14).
6.6. Distribution of bed deformation
The observation from tiltmeter rotations that shear-strain rates generally increased upward toward the bed surface (Figs 7 and 9) agrees with observations of Boulton and colleagues within natural subglacial till layers (Reference Boulton and HindmarshBouton and Hindmarsh, 1987; Reference Boulton and DobbieBoulton and Dobbie, 1998; Reference Boulton, Dobbie and ZatsepinBoulton and others, 2001). The bead data are less illuminating because they include the irregular deformation (e.g. bulldozing) that accompanied closure of ice on the prism. The bead data also include the period of melting when the till prism was exposed. Removal of the weight of ice from the top of the prism’s down-glacier end by melting could have resulted in slump-related deformation. This may explain why so much of the till deformation recorded by the beads occurred during the last 3 days of the experiment, after the failure of the uppermost tiltmeter in column 1 (Fig. 11). Unfortunately, no tiltmeter data were successfully logged during the exposure of the prism by melting, so this hypothesis cannot be checked.
The concave-down velocity profiles that developed in these experiments allow us to conclude that several processes are not necessary for distributed deformation of till. Any explanation that requires viscous deformation resistance can be precluded, since experimental data on a number of tills provide no evidence for it (Reference ClarkeClarke, 2005), and there is no reason to assert that this till should have anomalous mechanical properties. Dilatant strengthening (Reference Iverson, Hanson, Hooke and JanssonIverson and others, 1998), which can lead to pseudoviscous effects (Reference Moore and IversonMoore and Iverson, 2002), can be precluded owing to the high diffusivity of the till (Appendix C). Multiple water-pressure fluctuations at the bed surface, with diffusion of pore pressure to various depths in the till (Reference Tulaczyk, Kamb and EngelhardtTulaczyk and others, 2000a), can also be dismissed;water pressure varied nearly simultaneously and uniformly in the prism (Fig. 6) due to its high diffusivity. Moreover, during a single pump test, most of the thickness of the prism sheared (Fig. 7a).
We favor the hypothesis that strain that increases in magnitude toward the bed surface results simply from decreasing friction with decreasing depth in the bed (Reference IversonIverson and Iverson, 2001). This friction is briefly and locally overcome when grain bridges fail at various depths in the bed. Movement in the bed depends on the magnitude of the resultant stress imbalances, which will tend to be largest near the bed surface where frictional resistance is smallest. With stress imbalances largest near the bed surface, relative displacements among grains are largest there also, resulting in shear strain that increases upward.
6.7. Effects of prism size
An important consideration is whether the small size of the prism affected these results, particularly the tendency for ice to slip across the bed surface during periods of sufficiently sustained high pore pressure. Although the down-glacier end of the trough that contained the till was tapered (Fig. 2), longitudinal stress gradients in the prism may have impeded its shear deformation. Nevertheless, the prism did deform in shear between pump tests when pore pressure was lower (Fig. 8). Thus, the conclusion that the bed surface was preferentially weakened by pumping relative to the till at depth is sound.
The small footprint of the prism also prevented the expected feedback between basal water pressure and the rate of basal ice movement;any change in the resistance to basal motion over the area of the prism would not have caused a significant change in basal ice velocity, owing to lateral and longitudinal stress gradients in the ice. However, the lack of this velocity feedback would not have affected the partitioning between slip and shear deformation of the bed. As noted, the intrinsic strength of till, as a Coulomb material, is independent of its deformation rate. Thus, neither the shear strength of the bed nor the drag on particle asperities ploughing through the bed surface would have been affected by changes in the rate of basal motion. Also, possible ratestrengthening associated with dilation and associated pore-pressure reduction (e.g. Reference Moore and IversonMoore and Iverson, 2002) was prevented by the high hydraulic diffusivity of the till (Appendix C).
During pump tests shear stresses must have shifted between the till prism and adjacent bedrock as water pressure and discharge fluctuated. Similar stress reorganization has been observed beneath soft-bedded glaciers previously (e.g. Reference Fischer and ClarkeFischer and Clarke, 1997; Reference Iverson, Baker, Hooke, Hanson and JanssonIverson and others, 1999; Reference Kavanaugh and ClarkeKavanaugh and Clarke, 2001, Reference Kavanaugh and Clarke2006; Reference Truffer, Echelmeyer and HarrisonTruffer and others, 2001). Thus, we view the stress redistribution of these tests not as an experimental artifact but as a small-scale example of stress redistribution prompted by spatially non-uniform changes in basal hydrology.
7. Conclusions
Our measurements provide the first field demonstration that glacier ice can infiltrate a soft bed with a till-like grain-size distribution and at rates consistent with regelation theory. Unlike other proposed mechanisms of sediment entrainment, regelation does not require an adverse bed slope (e.g. Reference Alley, Lawson, Larson, Evenson and BakerAlley and others, 2003) or departures from fully temperate conditions (e.g. Reference Christoffersen and TulaczykChristoffersen and Tulaczyk, 2003). As a result, ice-infiltrated till, rather than relatively clean ice, may commonly be in contact with the surfaces of soft beds, contrary to existing treatments of slip at the bed surface (Reference Brown, Hallet and BoothBrown and others, 1987; Reference AlleyAlley, 1989; Reference IversonIverson, 1999; Reference Kavanaugh and ClarkeKavanaugh and Clarke, 2006).
Consistent with expectation, the glacier slipped across the bed surface at near zero pore-water pressure; deformation of the prism was activated by pumping water to it, which increased pore pressure and weakened the till. However, deformation commonly ceased if pore-water pressure within a few hundred kilopascals of the ice-overburden pressure was sustained. During these periods, ice slipped across the bed surface. This switching between bed deformation and slip at low effective pressure occurred at sub-millimeter water-layer thicknesses, which controlled the area of the bed subject to ploughing by particle asperities at the base of the ice-infiltrated till. Model calculations account for the observed slip at low and high effective pressures and for bed deformation at intermediate effective pressures. Non-linear water-layer thickening with decreasing effective pressure reduced friction at the bed surface more than in the till bed, causing slip at low effective pressures rather than bed deformation.
When the prism deformed, it sheared pervasively over most of its thickness. Shear strain generally decreased with depth, yielding the concave-down velocity profile observed in some previous studies. Viscous deformation resistance, dilatant strengthening and pore-pressure diffusion from the ice–till interface played no role in distributing this deformation.
These observations demonstrate that small changes in water-layer thickness can prompt slip of glaciers over soft beds. Such slip may result in abrupt increases in glacier velocity, consistent with recent interpretations of observations at Black Rapids Glacier, Alaska, USA (Reference Truffer and HarrisonTruffer and Harrison, 2006). This mechanism of glacier motion over a soft bed needs to be considered in evaluating abrupt velocity increases elsewhere (e.g. on the ice plain of Whillans Ice Stream, West Antarctica (Reference Bindschadler, King, Alley, Anandakrishnan and PadmanBindschadler and others, 2003)). Resistance to basal movement may be overestimated by equating it with the bed shearing resistance, as commonly done in models of soft-bedded glaciers (Reference AlleyAlley, 1989; Reference Clark, Licciardi, MacAyeal and JensonClark and others, 1996; Reference Licciardi, Clark, Jenson and MacAyealLicciardi and others, 1998; Reference Tulaczyk, Kamb and EngelhardtTulaczyk and others, 2000b; Reference Fowler, Murray and NgFowler and others, 2001; Reference Bindschadler, King, Alley, Anandakrishnan and PadmanBindschadler and others, 2003). In addition, estimates of basal sediment transport by bed deformation that neglect such slip (e.g. Reference Jenson, Clark, MacAyeal, Ho and VelaJenson and others, 1995; Reference Dowdeswell and SiegertDowdeswell and Siegert, 1999; Reference Siegert and DowdeswellSiegert and Dowdeswell, 2002) may grossly overestimate sediment fluxes.
Regelation infiltration and slip by ploughing at low effective pressures cannot occur simultaneously, owing to the ice–bed separation required for slip. Periods of regelation and slip are expected to alternate as basal water discharge and effective pressure change seasonally and diurnally.
The observation that regelation infiltration can leave ice-infiltrated sediment in contact with a soft bed indicates that slip resistance at the bed surface can be dominantly frictional rather than viscous, contrary to most model assumptions (e.g. Reference AlleyAlley, 1989; Reference Kavanaugh and ClarkeKavanaugh and Clarke, 2006). Thus, increases in the rate of basal motion will not be accompanied by increases in slip resistance. Unlike the case of clean ice on a soft bed, the rate strengthening provided by ice sliding past clasts partway lodged in the glacier sole (e.g. Reference Brown, Hallet and BoothBrown and others, 1987) will be inhibited or prevented in ice-infiltrated till. Moreover, the till bed, if it deforms at depth, will not rate-strengthen, except transiently under the specific range of parameter space that promotes dilatant strengthening (Reference Moore and IversonMoore and Iverson, 2002).
With only frictional sources of slip resistance, the ice–bed interface can be mechanically more akin to a crustal fault than what has traditionally been assumed (e.g. Reference PatersonPaterson, 1994). We view the abrupt lurching behavior of parts of ice sheets, like that observed in West Antarctica (Reference Bindschadler, King, Alley, Anandakrishnan and PadmanBindschadler and others, 2003) and inferred beneath the Greenland ice sheet from far-field seismicity data (Reference Ekström, Nettles and AbersEkström and others, 2003, Reference Ekström, Nettles and Tsai2006), as possible indications that glacier beds can be dominated over large areas by resistance to basal movement that is frictional rather than viscous (see also Reference TulaczykTulaczyk, 2006). Future research should explore whether this friction can decrease with increasing slip rate – an essential requirement for stick–slip motion on crustal faults (e.g. Reference ScholzScholz, 2002).
Acknowledgements
We thank M. Rousselot and A. Flint for help in the field, and W. Harrison, J. Kavanaugh and J. Walder for comments on the manuscript. We also thank A. Rempel who corrected an important error. This work was supported by a grant from the US National Science Foundation, OPP-9911559.
Appendix A
Experiments in which hemispheres were pushed through various basal tills indicate that pore-water pressure in excess of hydrostatic can develop, thereby weakening till and reducing ploughing resistance (Thomason, 2006). These experiments indicate, in agreement with Iverson (1999), that significant excess pore pressures do not develop if the timescale for compaction of till down-glacier from ploughing particles is larger than the timescale for pore-pressure diffusion out of the compacted zone. The timescale for compaction, t c, is δ/Up, where δ is the characteristic length scale for compaction and Up is the velocity of the ploughing particle. The value of δ is approximately equal to the diameter of the ploughing particle (Thomason, 2006). The timescale for pore-pressure diffusion, t d is δ2/D where δ is commensurate with the length of the diffusion path and D is the hydraulic diffusivity. Owing to the dependence of t d on δ2, excess pore pressures will be most probable near the largest ploughing particles. If we choose the largest particles of our field experiments, then δ ~ 0.02 m. We assume the velocity of ploughing particles to be equal to the measured slip velocity of the basal ice, ~44m a–1, a reasonable assumption for particles in the ice-infiltrated till of the glacier sole. The measured hydraulic diffusivity was ~10–5 m2 s–1. Using these values, t c = 14 300 s and t d = 40 s. Thus, owing to the high diffusivity of the simulated till, pore-pressure diffusion would have occurred far too rapidly to result in excess pore pressures sufficient to invalidate Equations (9) and (10).
Appendix B
The area of the bed submerged by the water layer can be estimated from the water-layer thickness and the till grain-size distribution. The submergence ratio, S R, is by definition
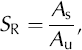
where A u is the unsubmerged area of the bed in direct contact with particle asperities on the glacier sole. To determine As, note that the number of particles, N, of radius R is given by N = kR –m , as indicated by Figure 3, where k and m are fitted constants. Assuming that, on average, particles are halfway embedded in the glacier sole, the area of particles, A R, occupied by clasts of size R and their associated porosity, n, is NπR 2/ (1 – n). Thus,
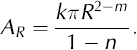
Integrating this equation from the radius of the smallest particle in the till bed, R L, to the water-layer thickness, d w, yields an estimate of the area of particles submerged in the layer:

Particles with radii larger than d w will tend not to be submerged in the water layer. Integrating Equation (B2) from d w to the radius of the largest particle in the till bed, R U, with n = 0, yields the area of the bed covered by particles sufficiently large to span the water layer and hence plough:
Substituting Equations (B3) and (B4) into Equation (B1) yields the submergence ratio as given by Equation (15).
Appendix C
A scaling argument similar to that of Appendix A and supported by stress-controlled ring-shear experiments with various tills (Moore and Iverson, 2002) indicates that dilatant strengthening did not occur during shear of the till. Dilatant strengthening can be precluded if the timescale for pore dilation during shear is long relative to the timescale for pore-pressure diffusion into the dilating pores of the shear zone. For a shear zone of thickness h, the timescale for pore dilation, t p, is h/v sφ, where v s is the shearing velocity and φ is the dilatancy, the ratio of shear-zone dilation (thickening) to shear displacement. The timescale for pore-pressure diffusion into the shear zone, t ds, is h 2/D. In laboratory experiments with two different basal tills φ varied, depending upon porosity, between 0.01 and 0.25 (Moore and Iverson, 2002). Choosing φ = 0.25 to minimize tp, considering the full till thickness (h ~ 0.5 m) to maximize t ds, choosing the measured sliding speed for the shearing velocity (v s = 44ma–1) and using the measured hydraulic diffusivity (D ~ 10–5m2 s–1) yields t p = 1.4 × 106s and t ds = 2.5 × 104s. Thus, owing to the high diffusivity of the till, pore-pressure diffusion would have outpaced pore opening by more than a factor of 50. Dilatant strengthening was therefore unlikely.




















