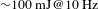1. Introduction
1.1. High-power coherent beam combination laser
Pulsed lasers with high power and a high repetition rate are greatly needed in many application fields, such as laser machining/annealing, neutron/proton generation, particle acceleration, laser fusion energy development, etc.[Reference Bachmann1–Reference Miller, Moses and Wuest4].
Beam combination can contribute to the development of these high-power, high-repetition-rate lasers. There are two main lines of research in beam combination, namely beam combination of fiber lasers and beam combination of bulk lasers. There are many research groups in the field of fiber beam combination lasers, including the ICAN Program[Reference Wang, Zhou, Ma, Leng, Xu and Liu5–Reference Mourou, Brocklesby, Tajima and Limpert8]. Since the output power of an optical fiber laser is limited, a large number of fiber lasers need to be combined to get high enough power[Reference Farrow, Kline, Hadley and Smith9]. On the other hand, bulk lasers have higher output power and a relatively small number of lasers are needed to achieve high power and a high repetition rate, compared with fiber-based lasers. To build a coherent beam combination (CBC) laser, the wavefronts of the combining beams should be flat, and their piston errors, the relative phases between the laser beams, should be zero[Reference Fan10]. The ![]() $\text{M}^{2}$ factor of a single-mode fiber laser is very good, so it is greatly advantageous to combine fiber lasers because only the piston errors need to be considered. Meanwhile, high-power bulk lasers tend to have lower beam quality than fiber lasers and it is very difficult to combine the beams. The main sources of a bulk laser’s low beam quality are the thermal lensing effect, pumping inhomogeneity and filamentation due to self-focusing.
$\text{M}^{2}$ factor of a single-mode fiber laser is very good, so it is greatly advantageous to combine fiber lasers because only the piston errors need to be considered. Meanwhile, high-power bulk lasers tend to have lower beam quality than fiber lasers and it is very difficult to combine the beams. The main sources of a bulk laser’s low beam quality are the thermal lensing effect, pumping inhomogeneity and filamentation due to self-focusing.
To coherently combine bulk lasers, one should flatten the wavefront of the combining beams via active control or passive control. Active control utilizes an adaptive mirror[Reference Goodno, Komine, McNaught, Weiss, Redmond, Long, Simpson, Cheung, Howland, Epp, Weber, McClellan, Sollee and Injeyan11], but it is difficult to make a perfect wavefront in this way. There are passive control methods using a phase conjugate mirror (PCM), and they can compensate for the distorted wavefront during amplification to give a lower ![]() $\text{M}^{2}$ factor[Reference Fisher12]. Stimulated Brillouin scattering (SBS)[Reference Zel’dovich, Popovichev, Ragulsky and Faizullov13] and degenerate four-wave mixing (DFWM)[Reference Andreev, Khazanov, Kuznetsov, Pasmanik, Shklovsky and Sidorin14] are typical phase conjugation methods commonly used for bulk lasers. The SBS-PCM needs only one convex focusing lens, so it is optically very simple, but the phase of the reflected beam is inherently random because it originates from thermal noise[Reference Damzen, Vlad, Babin and Mocofanescu15]. The DFWM method maintains the phase of the reflected beam, but when it is applied to beam combination, the optical system becomes very complicated. Many studies have focused on phase locking of the reflected beam from an SBS-PCM[Reference Loree, Watkins, Johnson, Kurnit and Fisher16–Reference Andreev, Palashov, Pasmanik and Khazanov19]. They are mostly classified as the back-seeding method[Reference Loree, Watkins, Johnson, Kurnit and Fisher16] and the focal point overlapping method[Reference Rockwell and Giuliano17, Reference Valley, Lombardi and Aprahamian18]. In the back-seeding method, the phase of an SBS wave follows the phase of a back-seeding beam so that the phase conjugation property disappears. On the other hand, in the overlapping method, the energy focused into a common focal point increases as the number of beams grows. Therefore, the number of combining beams is limited due to the energy limit at the focal spot, and the focal spot of each beam can move due to thermal effects, self-focusing effects, etc.
$\text{M}^{2}$ factor[Reference Fisher12]. Stimulated Brillouin scattering (SBS)[Reference Zel’dovich, Popovichev, Ragulsky and Faizullov13] and degenerate four-wave mixing (DFWM)[Reference Andreev, Khazanov, Kuznetsov, Pasmanik, Shklovsky and Sidorin14] are typical phase conjugation methods commonly used for bulk lasers. The SBS-PCM needs only one convex focusing lens, so it is optically very simple, but the phase of the reflected beam is inherently random because it originates from thermal noise[Reference Damzen, Vlad, Babin and Mocofanescu15]. The DFWM method maintains the phase of the reflected beam, but when it is applied to beam combination, the optical system becomes very complicated. Many studies have focused on phase locking of the reflected beam from an SBS-PCM[Reference Loree, Watkins, Johnson, Kurnit and Fisher16–Reference Andreev, Palashov, Pasmanik and Khazanov19]. They are mostly classified as the back-seeding method[Reference Loree, Watkins, Johnson, Kurnit and Fisher16] and the focal point overlapping method[Reference Rockwell and Giuliano17, Reference Valley, Lombardi and Aprahamian18]. In the back-seeding method, the phase of an SBS wave follows the phase of a back-seeding beam so that the phase conjugation property disappears. On the other hand, in the overlapping method, the energy focused into a common focal point increases as the number of beams grows. Therefore, the number of combining beams is limited due to the energy limit at the focal spot, and the focal spot of each beam can move due to thermal effects, self-focusing effects, etc.
Thus, we need to develop a scalable beam combination technique using an SBS-PCM that produces a phase-controllable SBS wave.
1.2. Beam combination laser using an SBS-PCM
H. J. Kong, the main author of this paper, proposed the simplest technique for controlling the phase of an SBS-PCM[Reference Kong, Lee and Lee20]. A beam combination laser using this ‘self-phase controlled’ SBS-PCM (SC-SBS-PCM) is indefinitely scalable because the combining beams are not optically interconnected. The only requirements are a linewidth, a pulse width and the minimum energy of the beams for efficient SBS to occur[Reference Kong, Lee and Lee21]. The linewidth of the beams should be smaller than the Brillouin bandwidth, and the pulse width of the beams should be several times the acoustic lifetime, typically several nanoseconds. Moreover, the energy of the beams should be larger than several mJ because the reflectivity of an SBS-PCM is highly nonlinear to its input energy. These are general prerequisites for an SBS-PCM and not special conditions for the SC-SBS-PCM. The SBS medium, where the SBS process occurs, could be any phase of matter, solid, liquid, gas or plasma. A solid SBS material must be replaced when damage occurs, while a fluid SBS material like liquid, gas or plasma dissipates the damaged part and heals itself. In our research, fluorocarbonate liquids are utilized as the SBS material because they have good SBS properties[Reference Hasi, Lu, Gong, Liu, Li and He22].
The feasibility of a beam combination laser using fluorocarbonate SBS-PCMs has been proved experimentally in the low power range of several W[Reference Kong, Lee, Lee and Guo23–Reference Kong, Shin and Park31]. Currently we are working on experimental verification of this beam combination laser with an average output power in the kW range. As mentioned above, the output power of a beam combination laser using an SC-SBS-PCM can be freely scaled. It should be noted that in this beam combination laser, the output power of each sub-beam is limited by the power limit of the SC-SBS-PCM. Moreover, the output power of the laser can be increased without additional problems by enlarging the size of the combined beam. Therefore, if this research is performed successfully, it will be an important step towards realization of the Dream laser, a hypothetical laser having unlimited power and a high repetition rate. We named the beam combination laser system employed in this research the ‘Kumgang laser’.
1.3. Kumgang laser
A project for a 4 kW beam combination laser system using SC-SBS-PCMs began in 2012 and the laser is called ‘Kumgang’, meaning diamond (or very important) in Korean. Four sub-beams, each with an energy of ![]() $0.1~\text{J}/10~\text{ns}$ pulse width and a repetition rate of 10 kHz, are coherently combined to produce an output beam with an energy of 0.4 J. It is a master oscillator power amplifier (MOPA) system and all of its pre- and main amplifiers are diode-pumped Nd:YAG amplifiers. The project will be completed by the end of 2015 and its first industrial application will be patterned 2D laser cutting of a printed circuit board (PCB) substrate.
$0.1~\text{J}/10~\text{ns}$ pulse width and a repetition rate of 10 kHz, are coherently combined to produce an output beam with an energy of 0.4 J. It is a master oscillator power amplifier (MOPA) system and all of its pre- and main amplifiers are diode-pumped Nd:YAG amplifiers. The project will be completed by the end of 2015 and its first industrial application will be patterned 2D laser cutting of a printed circuit board (PCB) substrate.

Figure 1. The schematic diagram of the Kumgang laser system.
Table 1. Beam combination methods.

Table 2. CBC methods.

Figure 1 shows the schematic diagram of the Kumgang laser. The front end consists of a CW laser-diode master oscillator, an acousto-optic modulator (AOM) for 10 kHz pulse generation, fiber-based amplifier(s), and a regenerative amplifier for boosting the power. The average output power of the front end is 5 W [0.5 mJ/10 ns/10 kHz]. Diode-pumped Nd:YAG amplifiers in the pre-amplifier stage amplify the beam in a double-pass configuration. The output beam of the pre-amplifier stage has a power of 200 W [20 mJ/10 ns/10 kHz]. The coherent beam divider/combiner divides the beam from the pre-amplifier stage and combines the beams after amplification through the main amplifier stage. The volume Bragg grating (VBG) coherent beam divider/combiner is currently being researched[Reference Case32, Reference Lu, Flores, Bochove, Roach, Smirnov and Glebov33]. A polarizing beam splitter (PBS) will be used for the beam combiner before the VBG is developed. The main amplifier stage is composed of a diode-pumped Nd:YAG amplifier chain and an SC-SBS-PCM. When completed, each divided sub-beam from the coherent beam divider/combiner will be amplified to 1 kW with a double-pass configuration. After the coherent combination, the final output beam will have an energy of 400 mJ per pulse with a pulse width of 10 ns and a repetition rate of 10 kHz, making the average output power 4 kW.
In Section 2, the general methods of beam combination are presented and two notable CBC methods are explained in detail. In Section 3, a beam combination laser system using SC-SBS-PCMs is described in detail. In Section 4, each subsystem of the Kumgang laser is shown with its prime application, the two-dimensional cutting of a PCB substrate. Finally, in Section 5, possible future projects for generating high-power fs/ps lasers are discussed.
2. CBC laser
2.1. Methods of beam combination
There are several methods of constructing beam combination lasers[Reference Fan10]. In general, they are divided into two categories, incoherent beam combination (IBC) and CBC. In IBC, the relative phases between the combining beams are ignored and only the directions of propagation are aligned, while in CBC, the relative phases are measured and controlled to be zero.
Table 1 summarizes the beam combination methods. There are three types of IBC. The frequency combining method combines beams with different wavelengths. The radiance of a frequency combined beam increases with the number of combining beams, but the spectral radiance is always the same. When building high-power beam combination lasers, frequency beam combination is less favorable, mainly due to the limited frequency range of high-power laser sources and additional difficulties in generating and handling beams with several frequencies.
The other two methods are monochromatic. The side-by-side beam combination method combines the beams blindly, only aligning them side by side, and does not consider their relative phases. The radiance does not scale with the number of combining beams and the focused beam pattern is irregular and random. This type of beam combination is only applicable when only the power of the beam is important. It is of no use for most applications where the focused beam intensity is critical.
The last type of IBC is the polarization combining method. Two beams with the same frequency and opposite polarization can be combined using a PBS or other polarization optics. Since the relative phase between the two beams is random, the output polarization is random and undetermined. Therefore, one cannot combine more than two beams using this method.
There are two types of CBC as shown in Table 2. The first one is wavefront combination/tiled-aperture combination. Like the side-by-side beam combination, it combines the beams in parallel, but by controlling the piston phases to be zero, the radiance scales as the number of beams combined. The advantage is that the output power of the wavefront combined beam is always the sum of the combining beams. Meanwhile, the beam quality can be degraded greatly compared with the individual combining beams. The arrangement of the combining beams causes the focused intensity pattern to scatter because the pattern is the product of the focused intensity pattern of one beam and the diffraction pattern of a two-dimensional multislit. If the piston phases are not exactly zero, the beam quality decreases and the focused intensity pattern becomes distorted. The wavefront beam combination can be performed using mirrors or wedges. The beams are directed to neighboring but non-overlapping positions and their propagation directions are aligned by tilting the optical devices. When many diverging beams are combined, e.g., when combining an array of laser diodes (LDs) or fiber lasers coupled to free space, a lens array can be used.
The other method of CBC is amplitude combination. It combines the beams to have the same position and the same direction. In this case, control of the relative phases is very important and it directly affects the output power by interference. The most beneficial property of amplitude beam combination is that the beam quality remains unchanged compared with the combining beams. This is because the shape of the combining beams is the same as that of the combined beam. On the other hand, the output power of the amplitude combined beam fluctuates as the piston phases deviate from zero. When all the piston phases are zero, the output power is maximal and is the same as the sum of the combining beams. Otherwise, the output power is lower than the sum. A beam splitter can combine two beams with the same polarization and power. The output power of the beam splitter is dependent on the phase difference between the two beams, and when the difference is zero, the output power is twice the power of the combining beams. One can combine ![]() $2^{N}$ beams by cascading the process
$2^{N}$ beams by cascading the process ![]() $N$ times. Amplitude beam combination using a PBS is a special case of beam splitting. Using two beams with opposite polarizations, the output power of the PBS is the sum of the two beams, but the polarization of the output is random and typically elliptical. By controlling the relative phase between the two beams, the output polarization is fixed to a known state and the combined output beam can be combined with another beam by the same method. A grating can also coherently combine the beams. This is done either by combining several high-order beams into a zeroth-order beam, or by combining several first-order beams of co-existing gratings into a common zeroth-order beam. In any case, the output power can be reduced without controlling the relative phases.
$N$ times. Amplitude beam combination using a PBS is a special case of beam splitting. Using two beams with opposite polarizations, the output power of the PBS is the sum of the two beams, but the polarization of the output is random and typically elliptical. By controlling the relative phase between the two beams, the output polarization is fixed to a known state and the combined output beam can be combined with another beam by the same method. A grating can also coherently combine the beams. This is done either by combining several high-order beams into a zeroth-order beam, or by combining several first-order beams of co-existing gratings into a common zeroth-order beam. In any case, the output power can be reduced without controlling the relative phases.
In beam combination using MOPA systems, the laser beam from the master oscillator is divided into several beams. After the amplification from the power amplifier, they are combined to make the output beam. Typically, the beam dividing optics and the beam combining optics are the same. When using the wavefront dividing method, division of the beam into sub-beams with sharp edges induces severe diffraction with very dangerous intensity spikes. To eliminate them, sophisticated methods like serrated apertures are needed and, therefore, the power of the divided beam is typically lower than that of the amplitude dividing method. Considering this limitation and other factors, the amplitude dividing/combining method will be employed for the Kumgang laser. Two possible methods of amplitude combination are presented below.
2.2. Amplitude beam combination using a PBS
Figure 2 shows a schematic diagram of a four-beam MOPA beam combination laser with the amplitude dividing method using a PBS. It employs a double-pass amplification scheme. PBS1 and quarter-wave plate (QWP1) serve as a beam diverter. When the laser passes through QWP1 and back, the polarization of the beam is rotated by ![]() $90^{\circ }$ and the output beam is reflected on PBS1. PBS2 divides the input beam into two beams. With a proper angle of half-wave plate (HWP1), PBS2 can divide the beam into two beams with the same power. Likewise, HWP2, PBS3, HWP3 and PBS4 divide the two beams into four beams. Four power amplifier chains amplify each beam in a double-pass configuration. To measure the relative phases between the beams, at each combining stage, a small portion of the combined beam is directed towards a measurement stage. Each measurement stage consists of one QWP, one PBS and two energy meters. By measuring the energy on the two energy meters, the relative phase between two combining beams can be calculated[Reference Kong, Shin, Yoon and Beak28]. If there are remaining phase errors between beams while the phase is being controlled, part of the beam leaks at PBS1 and PBS2, and the output power decreases.
$90^{\circ }$ and the output beam is reflected on PBS1. PBS2 divides the input beam into two beams. With a proper angle of half-wave plate (HWP1), PBS2 can divide the beam into two beams with the same power. Likewise, HWP2, PBS3, HWP3 and PBS4 divide the two beams into four beams. Four power amplifier chains amplify each beam in a double-pass configuration. To measure the relative phases between the beams, at each combining stage, a small portion of the combined beam is directed towards a measurement stage. Each measurement stage consists of one QWP, one PBS and two energy meters. By measuring the energy on the two energy meters, the relative phase between two combining beams can be calculated[Reference Kong, Shin, Yoon and Beak28]. If there are remaining phase errors between beams while the phase is being controlled, part of the beam leaks at PBS1 and PBS2, and the output power decreases.

Figure 2. The MOPA beam combination laser with the amplitude combining method using PBSs: EM1–EM6, energy meters.
2.3. Amplitude beam combination using a VBG

Figure 3. MOPA beam combination laser with the amplitude combining method using a VBG.
Figure 3 shows a schematic diagram of a four-beam MOPA beam combination laser with the amplitude dividing method using a VBG. It employs a double-pass amplification scheme. The PBS and QWP serve as a beam diverter as before. The VBG is a grating in which variation in the refractive index is engraved within a material. When a beam passes the VBG, the input beam (zeroth-order beam) is gradually converted into a refracted beam (first-order beam) throughout the thickness of the VBG. Only slight modulation of the refractive index is needed to achieve 100% efficiency. By etching multiple gratings, a beam divider/combiner for many beams can be made. This multiplexed VBG divides the input beam (common zeroth-order beam) into multiple output beams (first-order beams from each grating). The recent development of photorefractive glass makes high power and high damage threshold application of the VBG possible. To measure the relative phases between the combining beams, an additional phase measurement device is needed. If there is a remaining phase error between the beams while the phase is being controlled, part of the beam leaks at the VBG, and the output power decreases.
3. CBC laser using an SBS-PCM
3.1. SBS-PCM
The SBS-PCM is one type of PCM. The SBS phenomenon can be explained as follows[Reference Shen34–Reference Menzel and Eichler37]. When a beam is focused into the SBS material, a small portion of the beam is spontaneously scattered by random thermal phonons, and the scattered beams interfere with the incoming beam and create weak optical gratings. These optical gratings generate acoustic gratings by an electrostriction effect. The acoustic gratings are generally weak and dissipate quickly. However, if a scattered beam happens to have the opposite direction to the incoming beam, the acoustic grating generated by it has the same direction and phase as the original thermal phonon that created that scattered beam, and the amplified phonon scatters the incoming beam even further. If the incoming beam has high peak power, the feedback loop is powerful enough that a significant portion of the incoming beam is scattered to make a ‘reflected’ beam. The reflectivity can be higher than 90%[Reference Kong, Lee and Lee21]. Since only a beam with a precisely opposite direction of the incoming beam is generated by the SBS process, the reflected beam is a phase conjugation of the incoming beam.
The main amplifiers in an MOPA beam combination laser are not exactly the same. Therefore, the wavefronts of the divided beams are distorted in different ways. Unless these distortions are compensated for, CBC cannot be achieved. By using a double-pass amplification scheme and utilizing the SBS-PCM as a back reflector of the main amplifier, the wavefronts are restored after the second pass due to the phase conjugation property of the SBS. In this case, CBC is possible if the piston phases are controlled. Unfortunately, since the reflected beam from the SBS-PCM originates from random thermal noise, the phases of the reflections are random, and the piston phases cannot be controlled.
3.2. Self-phase control of an SBS-PCM

Figure 4. Types of SBS-PCM: (a) conventional SBS-PCM and (b) self-phase-locking SBS-PCM with PZT.
Figure 4(a) shows a conventional SBS-PCM. Convex lenses focus incoming beams into the SBS cells. As mentioned above, the relative phase between the reflected beams from SBS cell #1 and SBS cell #2 is random. Figure 4(b) shows one type of SC-SBS-PCM, in which concave mirrors focus the incoming beams. Unlike Figure 4(a), a standing wave from the incoming beam and the focused beam generates a grating and the grating initiates the SBS process. Since the grating is generated at a definite position and time, the relative phase between the incoming beam and the reflected beam is fixed, and the relative phase between the reflected beams from the two SBS cells is also fixed. By attaching a piezoelectric transducer (PZT) to one of the concave mirrors, the path length difference between the two beams can be controlled up to a wavelength. In practice, the path lengths of the beams fluctuate slowly due to air convection and other thermal effects. By measuring the piston phase, the path length fluctuation can be compensated for.

Figure 5. Experimental setup of the self-phase-locked SBS-PCM: BS, beam splitter; W1 and W2, wedges; CM1 and CM2, concave mirrors.

Figure 6. Experimental result of the self-phase-locked SBS-PCM. (a) A mosaic intensity pattern. It is generated by lining up one line of the intensity profile pattern recorded at each CCD image. (b) The measured relative phase. The standard deviation of the measured phase fluctuation is ![]() ${\it\lambda}/35.7$.
${\it\lambda}/35.7$.

Figure 7. Experimental setup of beam combination using an SBS-PCM and a feedback loop: M, mirror; W, wedged window; CM, concave mirror.
3.3. Experimental results for the beam combination laser using a SC-SBS-PCM
The principles of the SC-SBS-PCM were experimentally verified in 2005[Reference Kong, Lee and Lee20]. Since then, the results have improved and the method has been applied to four-beam coherent combination lasers with both the wavefront dividing method and the amplitude dividing method[Reference Kong, Lee, Lee and Guo23–Reference Kong, Shin and Park31].
Figure 5 shows the experimental setup for verifying the principles of the SC-SBS-PCM[Reference Lee, Kong and Nakatsuka24]. A 1064 nm laser beam with a pulse width of 8 ns and a repetition rate of 10 Hz is divided into two beams. The input energy of each SBS-PCM is 10 mJ. After reflection from the self-phase-locked SBS-PCM, small parts of each beam are reflected by wedges. A CCD camera records the interference pattern between the beams. From the interference pattern, the relative phase between the beams is measured.
Figure 6(a) shows a mosaic intensity pattern. It is generated by lining up one line of the intensity profile pattern recorded at each CCD image. Figure 6(b) shows the measured relative phase. The standard deviation of the measured phase fluctuation is ![]() ${\it\lambda}/35.7$.
${\it\lambda}/35.7$.

Figure 8. Experimental result of beam combination using an SBS-PCM and a feedback loop: (a) without operating the feedback loop and (b) with operation of the feedback loop.

Figure 9. Experimental setup of the four-beam combination using an SBS-PCM with the amplitude dividing method: ![]() $\text{D}_{\text{1P}}$,
$\text{D}_{\text{1P}}$, ![]() $\text{D}_{\text{1S}}$,
$\text{D}_{\text{1S}}$, ![]() $\text{D}_{\text{2P}}$,
$\text{D}_{\text{2P}}$, ![]() $\text{D}_{\text{2S}}$,
$\text{D}_{\text{2S}}$, ![]() $\text{D}_{\text{3P}}$,
$\text{D}_{\text{3P}}$, ![]() $\text{D}_{\text{3S}}$ and
$\text{D}_{\text{3S}}$ and ![]() $\text{D}_{\text{out}}$, energy detectors; CM, concave mirror.
$\text{D}_{\text{out}}$, energy detectors; CM, concave mirror.
Figure 7 shows the experimental setup for controlling the phase of the SC-SBS-PCM[Reference Kong, Shin, Yoon and Beak29]. In this case, a two-beam aperture with a beam diameter of 8 mm is used. After passing through the PBS, the prism divides the beam. A Faraday rotator (FR) rotates the polarization of the beam by ![]() $45^{\circ }$. After reflection from the SC-SBS-PCM and the second pass of the FR, the polarization of the beam is now perpendicular to the input beam and the combined beam is reflected at the PBS. The method for measuring the relative phase is the same as in Figure 5. Using the measured relative phase, the PZT is operated to compensate for the path length fluctuation.
$45^{\circ }$. After reflection from the SC-SBS-PCM and the second pass of the FR, the polarization of the beam is now perpendicular to the input beam and the combined beam is reflected at the PBS. The method for measuring the relative phase is the same as in Figure 5. Using the measured relative phase, the PZT is operated to compensate for the path length fluctuation.
Figure 8(a) shows the relative phase between the two beams during 100 s when the PZT is not moving. Path length fluctuation causes the relative phase to drift. Figure 8(b) shows the same result when the feedback is on and the PZT is moving to compensate for the phase difference between the beams. The standard deviation of the measured phase fluctuation is ![]() ${\it\lambda}/28.8$.
${\it\lambda}/28.8$.
Figure 9 shows the experimental setup of the four-beam combination laser with the amplitude dividing method[Reference Kong, Shin, Yoon and Beak28] using a PBS. A detailed explanation of the measurement of the relative phases can be found in Ref. [Reference Kong, Shin, Yoon and Beak28]. Using the measured phase between beam 1 and beam 2 ![]() $({\rm\Delta}{\rm\Phi}_{12})$, PZT1 is operated to compensate for the phase difference. Likewise, using the measured phase between beam 3 and beam 4
$({\rm\Delta}{\rm\Phi}_{12})$, PZT1 is operated to compensate for the phase difference. Likewise, using the measured phase between beam 3 and beam 4 ![]() $({\rm\Delta}{\rm\Phi}_{34})$, PZT2 is operated. From the measured phase between the combined beam of 1&2 and the combined beam of 3&4
$({\rm\Delta}{\rm\Phi}_{34})$, PZT2 is operated. From the measured phase between the combined beam of 1&2 and the combined beam of 3&4 ![]() $({\rm\Delta}{\rm\Phi}_{13})$ both PZT2 and PZT3 are operated to compensate for the path length difference.
$({\rm\Delta}{\rm\Phi}_{13})$ both PZT2 and PZT3 are operated to compensate for the path length difference.

Figure 10. Measured phase fluctuation of four-beam combination using an SBS-PCM with the amplitude dividing method.
Figure 10 shows the relative phases between beams during 200 s (2000 shots). ![]() ${\rm\Delta}{\rm\Phi}_{12}$,
${\rm\Delta}{\rm\Phi}_{12}$, ![]() ${\rm\Delta}{\rm\Phi}_{34}$ and
${\rm\Delta}{\rm\Phi}_{34}$ and ![]() ${\rm\Delta}{\rm\Phi}_{13}$ are all stabilized and have standard deviations of
${\rm\Delta}{\rm\Phi}_{13}$ are all stabilized and have standard deviations of ![]() ${\it\lambda}/34.3$,
${\it\lambda}/34.3$, ![]() ${\it\lambda}/44.1$ and
${\it\lambda}/44.1$ and ![]() ${\it\lambda}/37.6$, respectively. The output energy is also stabilized to 6.16% of the average in standard deviation.
${\it\lambda}/37.6$, respectively. The output energy is also stabilized to 6.16% of the average in standard deviation.
Figure 11 shows the experimental setup of the four-beam combination amplifier with the wavefront dividing method[Reference Shin, Park, Kong and Yoon30]. The laser beam from the oscillator is expanded four times by the beam expander consisting of a concave lens and a convex lens. The four-beam aperture shapes the input beam into four 6 mm beams. After separation, each divided beam passes through the amplifier twice in a double-pass configuration. The FR rotates the polarization of the beam by ![]() $90^{\circ }$ and minimizes the thermal depolarization of the amplifier. At the end of each beam line, SC-SBS-PCMs reflect the beam. Inside one of the beam lines (beam 1), a wedge is installed to make a reference beam (beam 0). The reference beam is expanded and makes an interference pattern with the output beam. From the interference pattern, the relative phases between the reference beam and the four beams can be calculated (
$90^{\circ }$ and minimizes the thermal depolarization of the amplifier. At the end of each beam line, SC-SBS-PCMs reflect the beam. Inside one of the beam lines (beam 1), a wedge is installed to make a reference beam (beam 0). The reference beam is expanded and makes an interference pattern with the output beam. From the interference pattern, the relative phases between the reference beam and the four beams can be calculated (![]() ${\rm\Delta}{\rm\Phi}_{01}$,
${\rm\Delta}{\rm\Phi}_{01}$, ![]() ${\rm\Delta}{\rm\Phi}_{02}$,
${\rm\Delta}{\rm\Phi}_{02}$, ![]() ${\rm\Delta}{\rm\Phi}_{03}$ and
${\rm\Delta}{\rm\Phi}_{03}$ and ![]() ${\rm\Delta}{\rm\Phi}_{04}$).
${\rm\Delta}{\rm\Phi}_{04}$).
Figure 12 shows the relative phase between beams during 250 s (2500 shots). ![]() ${\rm\Delta}{\rm\Phi}_{01}$ is the interference between beam 1 and the reference beam. Both beams are from the same SBS-PCM and
${\rm\Delta}{\rm\Phi}_{01}$ is the interference between beam 1 and the reference beam. Both beams are from the same SBS-PCM and ![]() ${\rm\Delta}{\rm\Phi}_{01}$ is stabilized to
${\rm\Delta}{\rm\Phi}_{01}$ is stabilized to ![]() ${\it\lambda}/68.8$.
${\it\lambda}/68.8$. ![]() ${\rm\Delta}{\rm\Phi}_{02}$,
${\rm\Delta}{\rm\Phi}_{02}$, ![]() ${\rm\Delta}{\rm\Phi}_{03}$ and
${\rm\Delta}{\rm\Phi}_{03}$ and ![]() ${\rm\Delta}{\rm\Phi}_{04}$ are the interferences between different beam lines, and they are all stabilized and have standard deviations of
${\rm\Delta}{\rm\Phi}_{04}$ are the interferences between different beam lines, and they are all stabilized and have standard deviations of ![]() ${\it\lambda}/26.5$,
${\it\lambda}/26.5$, ![]() ${\it\lambda}/28.0$ and
${\it\lambda}/28.0$ and ![]() ${\it\lambda}/26.1$, respectively. The input energy of the beam after the beam aperture is
${\it\lambda}/26.1$, respectively. The input energy of the beam after the beam aperture is ![]() $32.2\pm 0.3~\text{mJ}$ and the output energy of the amplified combined beam is
$32.2\pm 0.3~\text{mJ}$ and the output energy of the amplified combined beam is ![]() $169\pm 6~\text{mJ}$.
$169\pm 6~\text{mJ}$.
4. Kumgang laser
The Kumgang laser, which is now under construction, will be a high-power, high-repetition-rate beam combination laser that uses SC-SBS-PCMs. Four sub-beams, each with a power of 1 kW, are combined to make a 10 kHz/10 ns laser beam with a pulse energy of 400 mJ. Therefore, the total output power is 4 kW. The research on the Kumgang laser and its application started in 2012 and will be completed by the end of 2015.
4.1. Front-end subsystem

Figure 11. Experimental setup of the four-beam combination amplifier using an SBS-PCM with the wavefront dividing method: HWP1 and HWP2, half-wave plates; BS, beam splitter; P1–P3, Prisms; M1–M3, mirrors; AMP1–AMP4, amplifiers; C1–C4, concave mirrors; W, wedge.

Figure 12. Measured phase fluctuation of the four-beam combination amplifier using an SBS-PCM with the wavefront dividing method.

Figure 13. Schematic diagram of the front end: FC/APC, fiber connector/angled physical contact; WDM, wavelength division multiplexor; BPF, bandpass filter; FC, fiber collimator; HR1 and HR2; high-reflectivity mirrors; A1 and A2, apertures.
Figure 13 shows the schematic diagram of the Kumgang laser’s front-end subsystem. It consists of two parts, a 10 kHz master oscillator and a Nd:YAG regenerative amplifier. Recent technological developments of the LD enable stable and temperature tunable LDs with a narrow linewidth. By controlling the temperature of the LD, its frequency can be adjusted to match the frequency that the Nd:YAG amplifies most. The light from the laser diode passes through the AOM. The AOM is operated by a function generator to make a 10 kHz/10 ns pulse train. The pulse train has very stable timing and is almost free of jitter. Laser pulses now pass through an Yb fiber amplifier, which is pumped by another LD operating at 976 nm. To clear out unwanted frequency components generated by the fiber, the laser beam passes through a bandpass filter before it is coupled out of the fiber.
The Nd:YAG regenerative amplifier amplifies the beam further. The beam passes through FR1, HWP1 and PBS. The PBS acts as an output coupler. Next, the FR2 rotates the polarization of the beam by ![]() $45^{\circ }$ and HWP2 reverses the effect of FR2. When the beam is injected into the regenerative amplifier through the thin-film polarizer (TFP1), the Pockels cell (PC) is in the ‘open’ state and does not change the polarization of the injected beam. The QWP rotates the polarization and the beam is reflected at TFP1. While the beam is being amplified at the gain module (GM) for the first time, the PC changes to a ‘closed’ state and reverses the effect of the QWP. Now the beam is trapped in the regenerative amplifier and passes between the high-reflectivity mirrors HR1 and HR2 many times. After sufficient amplification, the PC changes back to the ‘open’ state and the beam leaves the regenerative amplifier. The net effect on the polarization of the returning beam by FR2 and HWP2 is a
$45^{\circ }$ and HWP2 reverses the effect of FR2. When the beam is injected into the regenerative amplifier through the thin-film polarizer (TFP1), the Pockels cell (PC) is in the ‘open’ state and does not change the polarization of the injected beam. The QWP rotates the polarization and the beam is reflected at TFP1. While the beam is being amplified at the gain module (GM) for the first time, the PC changes to a ‘closed’ state and reverses the effect of the QWP. Now the beam is trapped in the regenerative amplifier and passes between the high-reflectivity mirrors HR1 and HR2 many times. After sufficient amplification, the PC changes back to the ‘open’ state and the beam leaves the regenerative amplifier. The net effect on the polarization of the returning beam by FR2 and HWP2 is a ![]() $90^{\circ }$ rotation and the beam is reflected at the PBS. The average output power of the front-end subsystem is 5 W (0.5 mJ/10 ns/10 kHz).
$90^{\circ }$ rotation and the beam is reflected at the PBS. The average output power of the front-end subsystem is 5 W (0.5 mJ/10 ns/10 kHz).
4.2. Pre-amplifier subsystem

Figure 14. Schematic diagram of the pre-amplifier: RL1–RL5, relay lens pairs; PR1 and PR2, polarization rotators; HR, high-reflectivity mirror.
The pre-amplifier subsystem is depicted in Figure 14. The beam from the front-end subsystem first enters an isolator (ISO). The ISO blocks the backward scattered beam and the spontaneously emitted CW background from going back to the front end. After passing through the HWP, the beam enters pre-amplifier stage I. There are two GMs in pre-amplifier stage I. The amplifying medium of the pre-amplifier GM is a Nd:YAG rod with a diameter of 4.5 mm and a length of 96 mm. The water-cooled GM is pumped by five 200 W LDs operated at 807 nm. To minimize the thermal depolarization effect, the polarization rotator rotates the polarization of the beam by ![]() $90^{\circ }$ between two GMs. After passing through the FR twice, the beam is amplified again in the second pass. Relay lens pairs relay the image of the beam from the input position of the pre-amplifier to GM1, to GM2 and to the high-reflectivity mirror and back.
$90^{\circ }$ between two GMs. After passing through the FR twice, the beam is amplified again in the second pass. Relay lens pairs relay the image of the beam from the input position of the pre-amplifier to GM1, to GM2 and to the high-reflectivity mirror and back.
Pre-amplifier stage II has another two GMs with the same specifications as stage I. In this case, the beam passes through the amplifiers only once. An image of the beam at the output position of pre-amplifier stage I is relayed to GM3 and to GM4. The average output power of the pre-amplifier subsystem is 200 W (20 mJ/10 ns/10 kHz).
4.3. Main amplifier subsystem

Figure 15. Schematic diagram of the main amplifier: RL1–RL20, relay lens pairs; CM1–CM4, concave mirrors.
Figure 15 shows the main amplifier subsystem. The beam from the pre-amplifier subsystem is directed to the beam divider/combiner. The VBG coherent beam divider/combiner is currently under research. A PBS will be used for the beam combiner until the VBG is developed. Details of the proposed beam divider/combiner are explained in Section 2. After the division, the four sub-beams have a power of 50 W each. Four main amplifier modules amplify the sub-beams in the double-pass configuration. Each amplifier module has four main amplifier GMs, which are larger than the pre-amplifier GMs. The amplifying medium of the main amplifier GM is a Nd:YAG rod with a diameter of 6.35 mm and a length of 144 mm. The water cooled GM is pumped by five 400 W LDs operated at 807 nm. The quartz rotators rotate the polarization of the beam by ![]() $90^{\circ }$ after the first and the third GM to minimize thermal depolarization. Image relaying lenses relay the beam image from the output position of the pre-amplifier to the GMs one by one, and to the SBS-PCM and back.
$90^{\circ }$ after the first and the third GM to minimize thermal depolarization. Image relaying lenses relay the beam image from the output position of the pre-amplifier to the GMs one by one, and to the SBS-PCM and back.
After passing through the FR, the beam is reflected from the SC-SBS-PCM. The SC-SBS-PCM generates a phase conjugated wave, so any wavefront distortion in the first pass is compensated for automatically in the second pass. After amplification, each sub-beam has a power of 1 kW (100 mJ/10 ns/10 kHz), and four sub-beams are combined at the beam divider/combiner. A phase measurement device measures the relative phases between the four sub-beams. The exact nature of the phase measurement device needs to be studied and is dependent on the beam divider/combiner. Three of the four concave mirrors in the SC-SBS-PCMs are attached to the PZT. The relative phases are compensated for by the movement of these PZTs. The output beam of the Kumgang laser will be a 4 kW, 10 kHz pulse train. Each pulse will have a pulse width of 10 ns and an energy of 400 mJ.
4.4. Applications of the Kumgang laser
There are two distinct pulse width ranges among short-pulse lasers. For applications requiring high power and high peak power, ns pulsed lasers are suitable. The Kumgang laser falls in this category. On the other hand, for applications requiring high power and extremely high peak power, ps and/or fs pulsed lasers are suitable. This category will be discussed in Section 5.
There are many applications for high-power ns pulsed lasers like the Kumgang laser. For defense, high-power lasers with powers of over 100 kW can be effective weapons for intercepting missiles, rockets and mortar shells with soft-kill/hard-kill methods. Further, using a neutron beam or x-ray generated by a laser, explosives and nuclear materials can be detected early. For medical applications, proton beams generated by lasers can be directed to cancer cells deep within the body and kill them while minimizing collateral damage. Neutron and proton beams can also generate radioactive isotopes that can be used in various fields including medical imaging. For manufacturing, laser peening technology can harden the surface of a material more than conventional peening. On the other hand, extreme UV (EUV) light can be generated with high brightness by high-power ns lasers. Using this EUV light, the linewidth of the lithography used in the semiconductor industry can be reduced severalfold. The laser fusion driver of inertial confinement fusion is also of great interest. To cost-effectively generate electricity, the laser fusion driver should operate with a repetition rate of at least 0.1 Hz and an energy of at least several kJ, and the whole fusion power plant will require one to two hundred such laser drivers.

Figure 16. Schematic diagram of 2D laser processing using the Kumgang laser.

Figure 17. Schematic diagram of the generation of a fs/ps laser using the Kumgang laser as a pump source: OPA1–OPA3, optical parametric amplifiers.
The Kumgang laser aims for 2D cutting of a PCB substrate using holography. Figure 16 shows a schematic diagram of this application. The output beam of the Kumgang laser, with a power of 4 kW and a repetition rate of 10 kHz, passes through a glass hologram. The glass hologram deforms the wavefront of the laser beam and the desired cutting pattern is generated at the surface of the PCB. The conventional laser cutting industry uses CW or quasi-CW lasers. These have low peak power and need to scan a surface to operate. Since the output peak power of the Kumgang laser will be much higher than these CW lasers, the peak intensity at the PCB surface can be higher than the material processing threshold throughout the entire 2D pattern. With no moving parts, the processing time can be reduced significantly.
5. High-power fs/ps lasers generated by the Kumgang laser
5.1. Optical parametric chirped-pulse amplification
Since the peak power of fs/ps lasers is very high compared with ns lasers, chirped-pulse amplification (CPA) is usually employed to amplify fs/ps lasers to high power. It stretches the pulse width to a nanosecond range by dispersive optics. After amplification of the stretched and low-peak-power pulses, a compressor reverses the effect of the stretcher, creating a fs/ps pulse with higher energy. Due to many problems regarding the amplifying medium like thermal effects, amplified spontaneous emission and parasitic lasing, CPA has its limitations.
Optical parametric CPA (OPCPA) is a novel technology for building high-power fs/ps lasers. Instead of using a laser medium with a large amplification linewidth like CPA, a nonlinear crystal amplifies the chirped beam by an optical parametric amplification (OPA) process. Since absorption and emission do not occur in the crystal, the thermal load is very low and the problems originating from spontaneous emission disappear. For efficient OPA to occur, the pump beam of the OPA should have a comparable pulse width to the amplifying beam. The Kumgang laser, a high-power, high-repetition-rate ns pulsed laser, will be a good pump beam for OPCPA of fs/ps lasers with a pulse energy of several tens of mJ and a repetition rate of 10 kHz.
Figure 17 shows the schematic diagram of a high-power, high-repetition-rate fs/ps laser using OPCPA. The Kumgang laser has a repetition rate of 10 kHz and a pulse energy of 400 mJ. Using a nonlinear crystal, the wavelength of the Kumgang laser is converted from 1064 to 532 nm. Meanwhile, a short-pulse oscillator generates a signal beam with a pulse width in the fs/ps range and a repetition rate of 10 kHz, which is in synchronization with the Kumgang laser optically or electronically. After passing through a stretcher, the signal beam is chirped and has a pulse width in the ns range. OPA crystals amplify the stretched pulse using the pump beam from the Kumgang laser. There are several OPA stages, and through the stages, the signal beam is amplified. After the final OPA stage, a compressor reduces the pulse width to the fs/ps range by inducing inverse chirp. A dazzler is inserted between the stretcher and the OPA stages to compensate for the residual chirping error. The final output beam is a 10 kHz pulse train with a pulse width in the fs/ps range.
5.2. Applications for a high-power, high-repetition-rate fs/ps laser
High-power, high-repetition-rate fs/ps lasers have many applications. The extremely high peak power and intensity enable various new fields. First of all, a high-brightness x-ray can be generated from the high-power fs/ps laser by various methods, including high-harmonic generation. High-brightness x-rays can probe very small and very fast processes in chemistry, materials science and medical science. On the other hand, a high-power fs/ps laser can generate a gamma-ray by Compton scattering. The properties of the laser-based gamma-ray can be adjusted easily and it is very useful in nuclear science. Furthermore, laser wakefield acceleration of protons and other ions has applications in cancer therapy and in the field of materials science. In addition, these accelerated ions can generate high-energy and high-density neutron beams by nuclear reaction. Since the neutron has no charge, it can penetrate matter at a long distance. Moreover, depending on the energy of the neutron beam, it can examine suspicious baggage non-destructively or treat cancer. Finally, the high electric field itself can probe linear and nonlinear relativistic effects in matter and in the vacuum.
6. Summary
Beam combination of lasers can contribute to the development of high-power, high-repetition-rate lasers. The SC-SBS-PCM used in a double-pass amplifier can compensate for the distorted wavefront from the amplifiers. Since the SC-SBS-PCM has a very simple and independently configured optical scheme, scalable beam combination of bulk pulsed lasers is possible.
An SC-SBS-PCM was demonstrated several times at the academic low power level of several watts. Using PZTs, the path length fluctuation between the beam lines is controlled. Four beam combination lasers using both the wavefront dividing method and the amplitude dividing method were proved experimentally.
The Kumgang laser, a beam combination laser combining four 1 kW beams to make 4 kW output (400 mJ/10 ns/10 kHz), is now under development to test whether this scheme is appropriate for high-power lasers. The Kumgang laser has four subsystems. The front-end subsystem generates the seed beam using a LD oscillator and an AOM. It amplifies the seed beam to 5 W (0.5 mJ/10 ns/10 kHz) using a fiber amplifier and a regenerative amplifier. The pre-amplifier subsystem amplifies the beam further to 200 W (20 mJ/10 ns/10 kHz) using Nd:YAG amplifiers. After dividing it into four sub-beams, the main amplifier amplifies each beam to 1 kW (100 mJ/10 ns/10 kHz) in a double-pass configuration. The wavefront combining method using a VHG or a PBS will be employed for the Kumgang laser.
There are many applications for high-power, high-repetition-rate lasers. One of the possibilities is to use a ns pulsed laser like the Kumgang as a pump source for ps/fs pulse generation by OPCPA. If the Kumgang laser functions successfully, it will be the most important step towards a Dream laser with ns, ps or fs pulse width, which is, a hypothetical laser with unlimited power and a high repetition rate.
Acknowledgements
This work was supported by the ‘Dual Use Technology Program’ at the Agency for Defense Development (ADD) of the Republic of Korea (UM12012RD1).