Introduction
The shortwave radiation balance is the largest energy source of most glaciers (Reference Male and GrangerMale and Granger, 1981; Reference Gardner and SharpGardner and Sharp, 2010) and is determined by the magnitude of the incoming radiation and the albedo (the fraction of reflected to incoming shortwave radiation). Snow and ice albedo is known to change with time, from very high values immediately after a snowfall event (up to 0.98) to values as low as 0.46 for clean old snow and to 0.06 for dirty ice (Reference Cuffey and PatersonCuffey and Paterson, 2010). The reasons for this include snow metamorphosis and the concurrent increase in grain size, a change in water content and the exposure of dust particles at the surface. As soon as ice is exposed, the albedo remains constant on the scale of days to weeks (Reference Oerlemans and KnapOerlemans and Knap, 1998). However, it has been shown that long-term trends of decreasing ice albedo may occur as a result of a sequence of negative mass-balance years and the subsequent accumulation of dust on glacier surfaces (Reference Oerlemans, Giesen and Van den BroekeOerle-mans and others, 2009).
Other daily or sub-daily albedo variations can occur as a result of precipitation or cloud cover. Fresh snow, even if it is just a thin layer, increases albedo significantly (Reference Oerlemans and KnapOerlemans and Knap, 1998; Reference Brock, Willis and SharpBrock and others, 2000). Clouds have been shown to increase albedo for several reasons, including that they lead to an alteration in the effective zenith angle of the incident radiation due to an increase of its diffuse fraction (e.g. Reference Cutler, Demuth, Munro and YoungCutler, 2006). Furthermore, clouds are more absorbent in the near-infrared spectrum, leaving radiation that is relatively richer in the shortwave part of the spectrum, where albedo is generally higher (Reference Gardner and SharpGardner and Sharp, 2010; Kuipers Reference Kuipers Munneke, Reijmer and Van den BroekeMunneke and others, 2011). The first effect (effective zenith angle) can lead to either an increase or a decrease of the albedo, depending on the incident angle of incoming solar radiation (e.g. Reference Cutler, Demuth, Munro and YoungCutler, 2006). Generally, the limit of 508 is accepted as the boundary below which an increase of albedo is expected (as a result of an increased effective zenith angle), whereas above 50° a decrease of albedo occurs. The second effect (enrichment of the shortwave part of the spectrum) leads to an increase of surface albedo (e.g. Reference PirazziniPirazzini, 2004; Reference Gardner and SharpGardner and Sharp, 2010). Jonsell and others (2003) found that the increase of albedo due to clouds is stronger for snow than for ice surfaces. They attributed this finding mainly to the lower albedo of ice causing the multiple reflections between the surface and the cloud to be less efficient at increasing albedo.
Albedo measurements have to be interpreted carefully by taking into account the slope and aspect of the surface. Unattended automated weather stations (AWSs) generally have the radiation sensors levelled parallel to the horizon, whereas the actual surface may be slightly inclined. Incident radiation measured horizontally has to be corrected to obtain the true incident radiation at the surface. Assuming isotropic reflection and a plane surface, the measured or apparent albedo can be corrected to obtain the true albedo (Reference MannsteinMannstein, 1985; Reference Grenfell, Warren and MullenGrenfell and others, 1994; Reference Sicart, Ribstein, Wagnon and BrunsteinSicart and others, 2001). The surface microtopography plays another role, a topic that is rarely considered in the literature from a quantitative perspective because of the difficulties in measuring albedo at representative locations within the micro-topography. For example, Kotlyakov and Lebedeva (1974) reported a decreased albedo in the troughs of penitentes, which they attribute to increased humidity there. Pirazzini (2004) reviewed the literature on the effect of morphological features on albedo, focusing mainly on sastrugi in Antarctica. They concluded that generally two effects take place. Firstly, the effective zenith angle changes because direct radiation hits walls directed towards, or away from, the direct radiation. Secondly, ‘light trapping’ occurs due to multiple reflections between the features. Both effects lead to a reduction in albedo (Reference KuhnKuhn, 1974; Reference Warren, Brandt and HintonWarren and others, 1998). Also, Corripio and Purves (2005) found through simulations that penitentes decrease albedo by 8% compared with flat snow surfaces (see table 5 in Reference Corripio, Purves, De Jong, Collins and RanziCorripio and Purves, 2005).
Table 1. Site characteristics for the two AWSs. X, Y and Z are Universal Transverse Mercator (UTM) coordinates

In the semi-arid Andes the topic of snow and ice albedo is even more important for glaciological studies than in other regions for several reasons. The incoming shortwave radiation is very high because of small zenith angles and a very dry and clean atmosphere compared with higher latitudes. The study location is very high (>5200 m a.s.l.) and the atmosphere is thin, another reason for high values of incoming shortwave radiation. Furthermore, as we will show, the albedo is generally low, which increases the relative importance of the net shortwave radiation as an energy-balance component. The generally small diffuse fraction of the incoming radiation means that the light spectrum and the reflective properties of the surface are likely to change more strongly when clouds occur.
The aims of this study are (1) to present albedo measurements on adjacent sites with different characteristics, (2) to quantify their long- and short-term fluctuations as well as their drivers, (3) to present a reliable cloud quantification scheme to (4) investigate the effects of cloud cover on albedo variations, and (5) to investigate whether including the daily albedo cycle or the albedo change through clouds in surface energy-balance calculations is important in the semi-arid Andes.
Location
Radiation data from two AWSs at nearby sites are presented. The study area is in the upper Huasco valley, in the semi-arid Andes of Chile’s Norte Chico region (27–33º S), in a very dry region on the fringes of the Atacama Desert, with relatively low temperatures at high elevations (e.g. Reference Gascoin, Kinnard, Ponce, Lhermitte, MacDonell and RabatelRabatel and others, 2011; Reference MacDonell, Kinnard, Mölg, Nicholson and AbermannMacDonell and others, 2013a). Extremely high incident solar radiation occurs, such that maximum hourly average values are up to 99% of the solar constant (Table 1), and very limited cloud cover occurs.
Above 4000 m, 11% or 17 km2 of land area in the Huasco basin is glacier-covered (Reference Nicholson, Marín, Lopez, Rabatel, Bown and RiveraNicholson and others, 2009; Reference Gascoin, Kinnard, Ponce, Lhermitte, MacDonell and RabatelGascoin and others, 2011). The Guanaco AWS is on the upper part of Guanaco glacier, which is relatively large for the region (1.8 km2), whereas the Toro 1 AWS is on a 0.06 km2 ‘glacieret’ (a small ice body on which no sign of surface motion is present; Reference CogleyCogley and others, 2011). For simplicity, for the remainder of the text we refer to both sites as glaciers. Basic site characteristics, including the data period used, are summarized in Table 1, and an overview map is provided in Figure 1. Despite their proximity, the sites differ significantly in terms of accumulation processes, surface properties and precipitation amounts. Very little snow accumulates at Guanaco AWS due to its proximity to a crest, and the strong wind and surface scouring related to that. In contrast, Toro 1 is more wind-protected and receives more precipitation (Reference MacDonell, Nicholson and KinnardMacDonell and others, 2013b). At both sites, all precipitation falls in solid form. Surface properties also vary significantly. At Guanaco there is either clean and smooth ice or snow, whereas Toro 1 has a very dirty ice surface in summer (debris cover present) and the area around the AWS is covered with tall penitentes (up to 2 m high), which typically start to form in December and become covered by snow in late April. In winter the penitentes are snowed in entirely and the surface is smooth.
Data And Methods
Shortwave radiation was measured at two AWSs with upward- and downward-looking Kipp & Zonen CM3 pyranometers sampling every 10 s, with hourly averages stored. Coordinates, time periods available and site characteristics are listed in Table 1. Slope and aspect are derived from a 2005 digital elevation model (DEM) with 4 m spatial resolution constructed from a stereo pair of Ikonos satellite images. The DEM was resampled to 20 m cell size to obtain a representative slope and aspect value, which smooths microscale surface roughness. Field measurements of these parameters are difficult to obtain and limited to a point not necessarily representative of the area. Nonetheless, manual slope measurements were carried out at three stakes around each AWS at least once a year by placing a 1 m long inclinometer on the glacier surface. These measurements gave values within 2° of the DEM values.
Broadband albedo values derived from measured outgoing shortwave radiation with values <60 W m−2 and zenith angles >65° (hourly means) are discarded as instruments give unreliable responses for very low incoming shortwave radiation values and high zenith angles (Reference Jonsell, Hock and HolmgrenJonsell and others, 2003; Reference BrockBrock, 2004). High zenith angles occur only at the very edges of the day and thus very likely lead to misinterpretation (i.e. a fraction of the averaged hour may receive only incoming or outgoing radiation).
Correction of albedo
The hourly albedo values have been corrected according to Grenfell and others (1994), modifying the ‘apparently’ measured albedo α app to obtain α true, the albedo for the inclined surface, which we consequently call or the ‘broadband albedo’,

where θ sun is the solar zenith angle, θ surf is the slope of the surface (rad) and φ is the solar azimuth defined as zero when the sun is in the uphill direction from the slope. It was essential to apply this correction in order to remove strong asymmetries in the daily clear-sky albedo cycle due to the fact that the pyranometers are levelled horizontally over a slightly sloping surface (Table 1; Reference Sicart, Ribstein, Wagnon and BrunsteinSicart and others, 2001). A good estimate of slope and aspect of the site where albedo is measured is a crucial input for Eqn (1). Sicart and others (2001) performed a thorough error analysis on that topic and showed that the results vary insignificantly if pixel averages instead of individual point measurements are taken to determine slope and aspect. Assuming an error of 208 for aspect and ±3.4º for slope, they found the error in individual hourly albedo values to be up to ±8%, but mostly between ±5%.

Fig. 1. Ikonos image (2005) of the upper Huasco river catchment showing the location of the AWSs (circles) on Guanaco and Toro 1 glaciers. Figure adapted from MacDonell and others (2013b).
As in Jonsell and others (2003), hourly albedo values of >0.9 have been set to 0.9, a typical value for fresh snow (Reference Cuffey and PatersonCuffey and Paterson, 2010). Daily albedo values were calculated by dividing the total daily outgoing shortwave radiation by the total daily incoming radiation.
Discerning cloudy from cloud-free days
In order to quantify the effective influence of clouds on albedo it is first necessary to reliably discern cloudy from cloud-free days. Several studies use theoretically calculated ‘potential clear-sky’ radiation fluxes based on the solar constant, the atmospheric turbidity and the solar incident angle (e.g. Reference BrockBrock, 2004), and subsequent scaling with the measured incoming shortwave radiation. This means that incoming shortwave radiation is expressed as the fraction of the potential incoming shortwave radiation (effective cloud cover, n eff). The disadvantage of theoretically calculated potential incoming radiation to derive n eff is that turbidity values have to be either measured or assumed. Furthermore, handling data from unattended on-glacier AWSs over several years implies slight tilts in the radiation sensor or minor time offsets when the logger is reconfigured. Especially in an environment such as our study area, where incoming shortwave radiation values change very rapidly at the edges of the day, these small deviations can lead to artifacts when comparing with theoretical values. Taking advantage of the fact that the climate at the site is characterized by many entirely clear-sky days, we developed a simple alternative method to discern cloud-free from cloudy days and obtain a time series of potential incoming shortwave radiation. This series is later scaled to the incoming radiation measured on cloudy days to derive the diurnal cycle of the effective cloud cover n eff.
Daily total incident radiation sums are taken as the start, including both cloudy and cloud-free days. Running means (window length 3 days because cloudy conditions are episodic and generally of short duration) are calculated iteratively, such that after each iteration the values lower than the running mean are replaced with the running mean. The procedure is repeated until changes between iterations converge and become insignificant (stopping criterion0.03% change in the total value between successive iterations after 43 iterations). The resulting time series is interpreted as the total (potential) clear-sky daily incoming shortwave radiation. Days with total incoming radiation sums >90% of this potential daily sum (corresponding to the instrument error; Table 2) are considered to be cloud-free (cl = 0), and the remaining days to be cloudy (cl = 1).
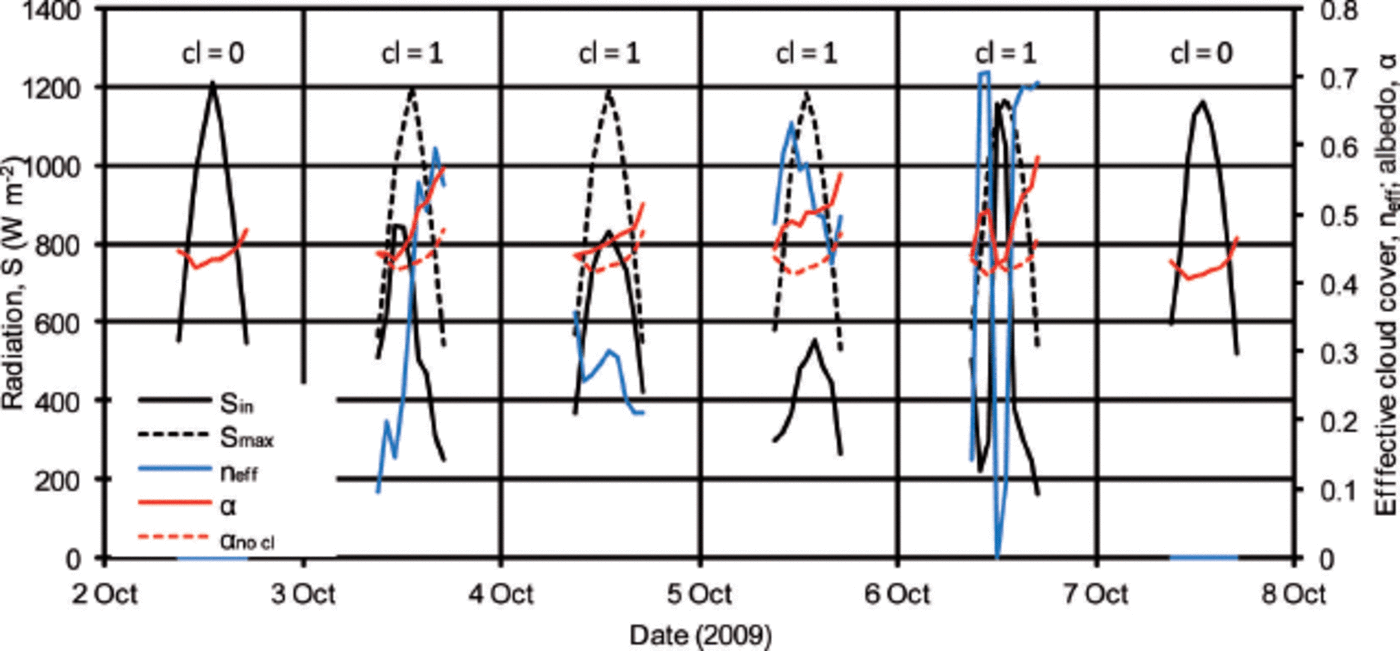
Fig. 2. An example of how n eff and α no cl are derived showing data for 2–7 October 2009. S in is the measured incoming shortwave radiation (black, solid), S max is the maximal possible incoming shortwave radiation (black, dashed), n eff is the effective cloud cover (blue, solid) derived from S in and S max, α is the measured and slope-corrected albedo (red, solid) and α no cl is the albedo without the cloud-induced increase (red, dashed). Note that 2 and 7 October are entirely cloud-free days (cl = 0), whereas 3–6 October showed almost continuous cloud cover.
Quantification of cloud cover
Figure 2 shows an example of how n eff is derived on an hourly scale and later how the effect of clouds on increase in albedo is quantified, once cloudy days have been discerned from cloud-free days. The steps outlined above showed that, in this example, 2 and 7 October were cloud-free days (cl = 0), whereas 3–6 October show cloud cover (cl = 1). The potential incoming clear-sky radiation (S max) on cloudy days (3–6 October) is then linearly interpolated from the incoming radiation (S in) measured on the two closest cloud-free days (in this case, 2 and 7 October). The slightly decreasing maximum value of S max over this example of a few days illustrates the interpolation between the cycle of the cloud-free days. However, the difference between 2 and 7 October is small and within the measurement uncertainty, and can therefore not be interpreted further. From these data the transmissivity is derived by simply dividing hourly S in by S max. The effective cloud cover n eff (blue line in Fig. 2) is then calculated as 1 minus the transmissivity, and has values between 0 and 1. The method to derive n eff is different from previous studies in the area. MacDonell and others (2013b) compared incoming shortwave radiation with the theoretical maximum at the site, but their results showed artificial asymmetries at the start and end of each day (i.e. the theoretically calculated potential incoming radiation curve does not fit perfectly over the measured incoming shortwave radiation). For energy-balance totals this is not significant and also the cloud climatology of this study (see below) does not deviate strongly from Figure 4 of MacDonell and others (2013b). However, as we are interested here in investigating individual hourly albedo changes to hourly cloud conditions, the method of MacDonell and others (2013b) was not suitable and therefore the presented method has been applied. Other studies also use longwave radiation data to quantify cloud cover (e.g. Reference Dürr and PhiliponaDürr and Philippona, 2004; Kuipers Reference Kuipers Munneke, Reijmer and Van den BroekeMunneke and others, 2011). Owing to data gaps in the longwave radiation data of our records, and the focus on shortwave radiation in this study, we did not include these approaches.
Quantification of the effect of clouds on albedo
Albedo time series for cases where n eff > 0 are investigated to understand the relation between clouds, albedo rise and zenith angle. Data from an ultrasonic ranger (see Table 2 for specifications), which measured the variations in surface elevation and hence the occurrence of snowfall events, were used in order to distinguish cloudy days with snowfall from cloudy days without snowfall. For the subsequent analysis we focus on days without snowfall to examine the albedo rise from clouds alone (i.e. independent of the effect of snowfall). Additionally, daily time-lapse photographs (between 12:00 and 14:00) were used to qualitatively detect precipitation events on the two glaciers. A comparison with the ultrasonic ranger shows that there were several cases when no precipitation was recorded by the sensor but traces of snow were visible on the photographs. The reason for this is that very thin snowfalls frequently occur in this area and are below the measurement accuracy of the instrument, especially given the roughness of the surface at the study sites (Table 2). The aim was therefore to employ a number of measures that enable a conservative interpretation of albedo rise due to cloud, as it is preferable to miss some cases when cloud but not precipitation occurred, as opposed to misattributing an albedo rise to cloud when it is actually a consequence of snowfall. Therefore, we do not analyze cloud-induced albedo rise at any station, in the event that at one of the stations precipitation was recorded. Furthermore, to be conservative, any day following a day of measured precipitation at any station is not considered. Finally, we ran a manual check for every remaining day on which cloud but not precipitation occurred. The previous day’s albedo cycle was superimposed on the actual day’s cycle. If a significant difference was visible (>0.05), we checked the database of time-lapse photographs (Table 2), and in many cases a thin layer of snow was visible. In such cases we removed the day from the sample for both sites, as it is likely that a misinterpretation occurred. The remaining albedo cycles were treated as follows (using Fig. 2 as an example): all days shown in Figure 2 did not have snowfall; the solid red curves are the measured and corrected hourly albedo values (α) as described above. Now the daily cycles α of for the nearest cloud-free days (2 and 7 October) are used, and their hourly values linearly interpolated for the intervening period when clouds occurred (3–6 October). This is how the cloud-free albedo (α no cl, dashed red curves) is derived. The difference between α and α no cl can now be interpreted as the albedo rise that is due to cloud (Δα clouds). This approach is similar to that of other studies using daily values (e.g. Reference Cutler, Demuth, Munro and YoungCutler, 2006), and differs slightly from Brock (2004) who used the daily minimum of albedo and scaled these minimal values with the hourly means (fig. 4 of Reference BrockBrock, 2004).
Table 2. Sensor specifications and accuracies. The same types of sensor were deployed on both AWSs


Fig. 3. (a) Mean daily albedo and (b) mean daily snow height for Guanaco (blue) and Toro 1 (red) glaciers.
Results
Figure 3 shows the mean daily albedo for Guanaco and Toro 1 (Fig. 3a) and the respective snow height (Fig. 3b). Generally, although the sites are relatively close to each other, their results are very different. Toro 1 shows the strongest seasonal cycle, which generally follows the snow-pack evolution. As soon as the snow disappears and the ice is exposed (e.g. January 2009, February 2010, March 2011), very low albedo values are recorded (as low as 0.2). With a continuous thick snowpack, values of ~0.65 are reached (e.g. September 2010), with spikes up to 0.9, which are attributable to fresh snowfall events (Fig. 3b) or clouds. Guanaco lacks distinct seasonal snowpack and albedo cycles. Generally, its minimum albedo values are higher (~0.4) than those of Toro 1. The high-frequency variations (spikes due to snow or cloud) of both glaciers are qualitatively similar. Individual seasons differ strongly and no long-term trend is detectable at either station.
Monthly means of daily albedo cycles under cloud-free conditions are presented in Figure 4. All days having n eff = 0 during the whole day are defined as cloud-free days (for Guanaco 69% and for Toro 1 59% of all days). From the results of Figure 3 it is to be expected that albedo values and their evolution throughout the year will vary for the individual glaciers, meaning that we would expect a different sequence of mean monthly daily cycles in Figure 4 for each glacier. This is evident, with Guanaco showing comparably little month-to-month variation and generally higher values in the later summer months (January–March) than in spring (e.g. September, October).

Fig. 4. Daily cycles of cloud-free albedo (corrected for aspect and slope) on (a) Guanaco and (b) Toro 1. Each curve represents the monthly mean of all albedo cycles under entirely cloud-free conditions. Note that there may be months when the curves include both snow and ice albedo (Fig. 2).
In contrast, Toro 1 shows a typical and very pronounced albedo evolution, with generally lower values in austral summer (e.g. December–February) when the surface is ice and/or debris is exposed. The highest values are experienced in late winter (August, September) when the snowpack is thickest, all penitentes are covered and a smooth surface is present.
There is a pronounced daily cycle present on both glaciers. Generally, albedo is higher in the morning and evening than at noon, and the daily cycle is stronger in summer months than in winter months. In late austral winter and early spring a decrease in albedo during the day is visible on Toro 1. Generally speaking, daily cycles are present at both sites, and albedo can vary on a cloud-free day by up to 0.15.
Figure 5 shows how cloud cover is distributed throughout the year. The fewest cloudy days occur in austral autumn (March–April) and throughout late spring and early summer (September–November), and the highest number occur in June. Looking at the mean n eff of the hours with clouds in a month (grey curve in Fig. 5a), the spring and summer months clearly show thicker cloud cover than the winter months, although clouds occur less frequently (bars). Figure 5b shows the mean daily cycle of n eff for each month individually. The austral summer months show a distinct rise in the early afternoon, indicating optically thicker clouds, whereas the other months have a more uniform daily cycle.

Fig. 5. (a) Annual cycle of cloud distribution as a fraction of days (bars) and the mean n eff of the cloudy hours only (thick grey curve) along with one standard deviation (thin grey curves) and (b) diurnal average evolution of n eff for the individual months. Data from Toro 1 AWS are shown as an example; however, the key features are the same for Guanaco.
Figure 6 shows the quantification of the cloud-induced albedo rise and its relation to n eff. A large scatter is visible for values of n eff > 0.2. A nonlinear relationship is suspected. The red curve shows the cumulative relative frequency of Δαclouds(ξ) and can be interpreted as the fraction of the total sample that is at or below a given value of Δαclouds. As such, the median albedo rise due to clouds is 0.04, in 75% of the total it is <0.1, and in 95% it is <0.2. Only ~1% of all hourly values show an albedo rise of >0.3.
Discussion
Generally, the significant diurnal cycle on both sites is related to the solar incident angle and a higher probability that photons can leave the snowpack if they hit the surface at grazing angles (Reference Gardner and SharpGardner and Sharp, 2010). We found that on Toro 1 the diurnal cycle is more pronounced than on Guanaco. This may be due to the growth of penitentes in summer on Toro 1. When the radiation hits the surface with penitentes around noon, the troughs are reached directly and their moist and dusty surface reduces the overall albedo, whereas at high zenith angles (mornings and afternoons) the walls of the penitentes increase the effective albedo in relation to the noon albedo. The reduction of Toro 1 albedo in the afternoon of austral spring months coincides with the timing of snow metamorphosis, and could be related to a change in snow grain size or water content, in line with other studies (e.g. Reference PirazziniPirazzini, 2004). The more pronounced daily cycle in summer than in winter is likely due to larger diurnal ranges of variation in the solar incident angle in summer.
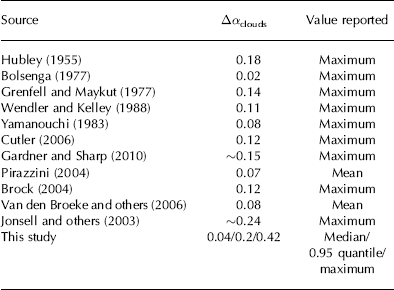
Table 3. Albedo rise as a result of cloud cover (maximum or mean values) according to various studies
We attribute the unusual annual evolution of the daily albedo cycle (Fig. 4) for Guanaco (higher values of albedo in summer than in winter) to the accumulation particularities of this site. Little snow accumulates throughout the year and it is the wind that determines whether the snow that falls in episodic events can remain. Gascoin and others (2013) and MacDonell and others (2013a) show a clear seasonal cycle of wind speed at the Guanaco site, with lower wind speed in summer, which is the likely cause for comparably more snow being accumulated there during these months, and the higher albedo values between January and March than in winter (fig. 2 of Reference MacDonell, Kinnard, Mölg, Nicholson and AbermannMacDonell and others, 2013a).
The inverse relationship between cloud frequency and effective cloud cover as shown in Figure 5 is explained by different cloud types that occur in the study area in different seasons. Winter cloud cover is mainly of a frontal, advective type, which is generally thinner and can last on the scale of days, whereas in summer convective clouds dominate, which generally develop in the afternoon and reach substantially thickened dimensions in the evening but dissolve overnight.
For the albedo rise caused by clouds, Table 3 summarizes a comparison with values from previous studies. Proposed values vary strongly and lie between 0.02 and 0.24 as a maximum value for cloud-induced albedo change.
The values we present are generally within the suggested mean values found in other studies; however, individual maximum values exceed them. There are several possible explanations for this. Many of the studies mentioned above were conducted in the polar regions, but none of them in low latitudes as in our study. High-latitude regions receive large zenith angles through which the zenith angle effect on cloud-induced albedo rise partly balances the spectral shift (e.g. Reference Gardner and SharpGardner and Sharp, 2010). Therefore the total albedo rise is expected to be reduced. In contrast, at small zenith angles, both the zenith angle effect and the spectral shift are positive and lead to an increase in albedo, making the higher numbers of our study plausible. Another peculiarity of our site is that under cloud-free conditions the diffuse part of the shortwave radiation is very low, as only a very small part of the incoming radiation is scattered or absorbed. This is evident in the high values of incoming radiation (e.g. Reference MacDonell, Nicholson and KinnardMacDonell and others, 2013b; Table 1). A low fraction of diffuse radiation also suggests a spectrum at the surface that is similar to the solar spectrum at the top of the atmosphere, which is relatively rich in the longer wavelengths of the shortwave spectrum (compared with incident radiation that is composed of a higher fraction of diffuse radiation; e.g. Reference PirazziniPirazzini, 2004). This is again where the spectral albedo is lower, and helps to explain both the generally low albedo values encountered at our site (Fig. 3) and the fact that clouds cause a stronger spectral shift in incoming radiation, thereby leading to a stronger albedo rise under such circumstances.

Fig. 6. Hourly values of the cloud-induced albedo rise (Δαclouds) vs n eff for both stations (points). The red curve is not a regression; it shows the cumulative relative occurrenceξ.
Our results make it possible to assess the significance of including both the diurnal cycle of albedo and the albedo rise due to clouds in surface energy-balance calculations. For this purpose we present a full year of data (1 October 2010 to 30 September 2011) and calculate the corrected shortwave radiation balance with measured hourly albedo values (S net, I) and compare them with S net, II, which is calculated with the noon albedo value used for the entire day (e.g. Reference BrockBrock, 2004), i.e. not considering the daily cycle (Table 4). The overestimation of the shortwave balance (OE S net, II) is 14% for Guanaco and 13% for Toro 1. Considering the daily mean albedo instead of the noon albedo (i.e. dividing total outgoing by total incoming shortwave radiation) to calculate the net shortwave radiation (S net, III), the overestimation is reduced but still significant (OE S net, III 13% for Guanaco, 9% for Toro 1). This result means that the diurnal albedo cycle should be included in surface energy-balance calculations. Arendt (1999) showed for a glacier in the Canadian Arctic that the diurnal albedo cycle is significant for the surface energy balance there, leading to a decrease of the net shortwave radiation of up to 16%.
Table 4. Overview of results for October 2010–September 2011. S in, hor is the total incoming radiation flux on the horizontal plane, S net, I is the total net shortwave radiation calculated with hourly albedo values, S net, II is calculated with the noon albedo value applied throughout the day, S net, III is calculated with the daily total albedo value (total S out/total S in) applied throughout the day, and S net, IV is calculated by subtracting the albedo rise due to clouds from the measured hourly albedo cycle. OE S net, II, OE S net, III and OE S net, IV are the percentage overestimations in the net shortwave balance for Snet, II, Snet, III and Snet, IV each referring to Snet, I.

Subtracting the albedo rise due to clouds from the measured hourly slope-corrected albedo and then calculating the net shortwave balance (S net, IV) leads to an overestimation (OE S net, IV) of 0.4% compared with S net, I for both glaciers. Hence our study shows that at high-altitude arid sites such as ours the cloud-induced albedo rise can be neglected for energy-balance studies. This is surprising given the significant Δαclouds values that have been shown above (Fig. 6). However, cloudy days are infrequent (Fig. 5) and, furthermore, the lower incident radiation on cloudy days makes them less significant for the annual shortwave radiation balance. This conclusion is therefore valid for similar dry climates and should be re-evaluated for climatic conditions where cloudy days occur more frequently.
Conclusions
This study shows the complicated temporal evolution of snow and ice albedo at two adjacent sites in the semi-arid Andes of Chile. The site-specific complexity has to be taken into account when it comes to calibrating spatial energy-balance models with point AWS albedo measurements. The representativeness of individual sites should be carefully evaluated for entire glaciers or catchments. There is a significant diurnal cycle of albedo that generally follows the zenith angle. This has to be taken into account in surface energy-balance calculations, whereas the effect of clouds on albedo rise is insignificant in this respect. This is explained by the infrequent occurrence of clouds in the very dry climate of the semi-arid Andes and the low incoming radiation on cloudy days. Future work should focus on acquiring spatially distributed albedo maps as an input to distributed energy-balance models. Furthermore, remote-sensing approaches to derive albedo must take into account the small-scale variations in a heterogeneous study area such as the semi-arid Andes.
Acknowledgements
This study was financed by Compañia Minera Nevada (CMN). CMN did not interfere in the data interpretation and conclusions reached in this study. We thank the CMN for logistical support, and the glaciology group at CEAZA for help in the field. S. MacDonell was supported by FONDECYT postdoctoral grant No. 3110053. We acknowledge the financial support of FONDECYT grant No. 1130598. We also thank M. Kuhn and M. Petlicki for their comments.












