Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ni, Wei-Jay
and
Capart, Hervé
2015.
Cross-sectional imaging of refractive-index-matched liquid-granular flows.
Experiments in Fluids,
Vol. 56,
Issue. 8,
Revil-Baudard, Thibaud
Chauchat, Julien
Hurther, David
and
Barraud, Pierre-Alain
2015.
Investigation of sheet-flow processes based on novel acoustic high-resolution velocity and concentration measurements – ERRATUM.
Journal of Fluid Mechanics,
Vol. 769,
Issue. ,
p.
723.
Berzi, Diego
and
Fraccarollo, Luigi
2015.
Turbulence Locality and Granularlike Fluid Shear Viscosity in Collisional Suspensions.
Physical Review Letters,
Vol. 115,
Issue. 19,
Jenkins, James T.
Meiburg, Eckart
and
Valance, Alexandre
2015.
Report on the Program “Fluid-mediated particle transport in geophysical flows” at the Kavli Institute for Theoretical Physics, UC Santa Barbara, September 23 to December 12, 2013.
Physics of Fluids,
Vol. 27,
Issue. 9,
Maurin, Raphael
Chauchat, Julien
and
Frey, Philippe
2016.
Dense granular flow rheology in turbulent bedload transport.
Journal of Fluid Mechanics,
Vol. 804,
Issue. ,
p.
490.
Berzi, Diego
and
Fraccarollo, Luigi
2016.
Intense sediment transport: Collisional to turbulent suspension.
Physics of Fluids,
Vol. 28,
Issue. 2,
Finn, Justin R.
Li, Ming
and
Apte, Sourabh V.
2016.
Particle based modelling and simulation of natural sand dynamics in the wave bottom boundary layer.
Journal of Fluid Mechanics,
Vol. 796,
Issue. ,
p.
340.
Liu, Detian
Liu, Xiaofeng
Fu, Xudong
and
Wang, Guangqian
2016.
Quantification of the bed load effects on turbulent open‐channel flows.
Journal of Geophysical Research: Earth Surface,
Vol. 121,
Issue. 4,
p.
767.
Bareš, Vojtěch
Zrostlík, Štěpán
Picek, Tomáš
Krupička, Jan
and
Matoušek, Václav
2016.
On local velocity measurement in gravity-driven flows with intense bedload of coarse lightweight particles.
Flow Measurement and Instrumentation,
Vol. 51,
Issue. ,
p.
68.
Houssais, M.
Ortiz, C. P.
Durian, D. J.
and
Jerolmack, D. J.
2016.
Rheology of sediment transported by a laminar flow.
Physical Review E,
Vol. 94,
Issue. 6,
Zrostlík, Štěpán
Bareš, Vojtěch
Krupička, Jan
Picek, Tomáš
Matoušek, Václav
Dančová, P.
and
Veselý, M.
2016.
Distribution of velocity and turbulent characteristics in coarse-sediment laden flows above erodible plane bed in open channel.
EPJ Web of Conferences,
Vol. 114,
Issue. ,
p.
02144.
Revil-Baudard, T.
Chauchat, J.
Hurther, D.
and
Eiff, O.
2016.
Turbulence modifications induced by the bed mobility in intense sediment-laden flows.
Journal of Fluid Mechanics,
Vol. 808,
Issue. ,
p.
469.
van der Zanden, J.
van der A, D. A.
Hurther, D.
Cáceres, I.
O'Donoghue, T.
and
Ribberink, J. S.
2016.
Near‐bed hydrodynamics and turbulence below a large‐scale plunging breaking wave over a mobile barred bed profile.
Journal of Geophysical Research: Oceans,
Vol. 121,
Issue. 8,
p.
6482.
van der Zanden, J.
van der A, D.A.
Hurther, D.
Cáceres, I.
O’Donoghue, T.
and
Ribberink, J.S.
2017.
Suspended sediment transport around a large-scale laboratory breaker bar.
Coastal Engineering,
Vol. 125,
Issue. ,
p.
51.
Zhou, Zheyu
Hsu, Tian‐Jian
Cox, Daniel
and
Liu, Xiaofeng
2017.
Large‐eddy simulation of wave‐breaking induced turbulent coherent structures and suspended sediment transport on a barred beach.
Journal of Geophysical Research: Oceans,
Vol. 122,
Issue. 1,
p.
207.
Cheng, Zhen
Hsu, Tian-Jian
and
Calantoni, Joseph
2017.
SedFoam: A multi-dimensional Eulerian two-phase model for sediment transport and its application to momentary bed failure.
Coastal Engineering,
Vol. 119,
Issue. ,
p.
32.
Houssais, Morgane
and
Jerolmack, Douglas J.
2017.
Toward a unifying constitutive relation for sediment transport across environments.
Geomorphology,
Vol. 277,
Issue. ,
p.
251.
Chauchat, Julien
Cheng, Zhen
Nagel, Tim
Bonamy, Cyrille
and
Hsu, Tian-Jian
2017.
SedFoam-2.0: a 3-D two-phase flow numerical model for sediment transport.
Geoscientific Model Development,
Vol. 10,
Issue. 12,
p.
4367.
Cheng, Zhen
Chauchat, Julien
Hsu, Tian-Jian
and
Calantoni, Joseph
2018.
Eddy interaction model for turbulent suspension in Reynolds-averaged Euler–Lagrange simulations of steady sheet flow.
Advances in Water Resources,
Vol. 111,
Issue. ,
p.
435.
Krupička, Jan
Matoušek, Václav
Picek, Tomáš
Zrostlík, Štěpán
and
Dančová, P.
2018.
Validation of laser-penetration- and electrical-conductivity-based methods of concentration measurement in flow with intense transport of coarse sediment.
EPJ Web of Conferences,
Vol. 180,
Issue. ,
p.
02048.
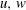 $u,w$) and sediment concentration and to measure the time evolution of the bed interface position. Ensemble averaging over 11 similar experiment realisations is done to evaluate the mean profiles of streamwise velocity, concentration, sediment flux and Reynolds shear stress. The repeatability, stationarity and uniformity of the flow are carefully checked for a Shields number
$u,w$) and sediment concentration and to measure the time evolution of the bed interface position. Ensemble averaging over 11 similar experiment realisations is done to evaluate the mean profiles of streamwise velocity, concentration, sediment flux and Reynolds shear stress. The repeatability, stationarity and uniformity of the flow are carefully checked for a Shields number 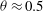 ${\it\theta}\approx 0.5$ and a suspension number of
${\it\theta}\approx 0.5$ and a suspension number of 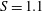 $S=1.1$. The mean profile analysis allows to separate the flow into two distinct layers: a suspension layer dominated by turbulence and a bed layer dominated by granular interactions. The bed layer can be further subdivided into a frictional layer capped by a collisional layer. In the suspension layer, the mixing length profile is linear with a strongly reduced von Karman parameter equal to 0.225. The Schmidt number is found to be constant in this region with a mean value of
$S=1.1$. The mean profile analysis allows to separate the flow into two distinct layers: a suspension layer dominated by turbulence and a bed layer dominated by granular interactions. The bed layer can be further subdivided into a frictional layer capped by a collisional layer. In the suspension layer, the mixing length profile is linear with a strongly reduced von Karman parameter equal to 0.225. The Schmidt number is found to be constant in this region with a mean value of 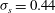 ${\it\sigma}_{s}=0.44$. The present results are then interpreted in terms of existing modelling approaches and the underlying assumptions are discussed. In particular, the well-known Rouse profile is shown to predict the concentration profile adequately in the suspension layer provided that all the required parameters can be evaluated separately. However, the strong intermittency of the flow observed in the bed layer under the impact of turbulent large-scale coherent flow structures suggests the limitations of averaged steady two-phase flow models.
${\it\sigma}_{s}=0.44$. The present results are then interpreted in terms of existing modelling approaches and the underlying assumptions are discussed. In particular, the well-known Rouse profile is shown to predict the concentration profile adequately in the suspension layer provided that all the required parameters can be evaluated separately. However, the strong intermittency of the flow observed in the bed layer under the impact of turbulent large-scale coherent flow structures suggests the limitations of averaged steady two-phase flow models.


