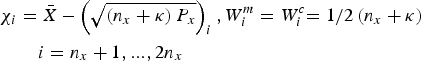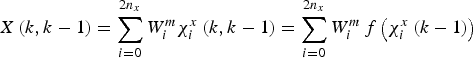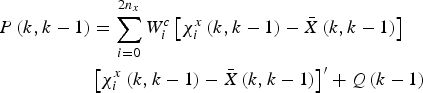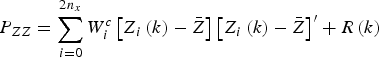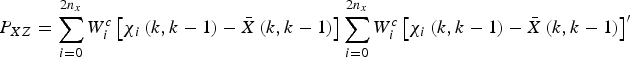1. INTRODUCTION
With the rapid development of transportation, more and more road tunnels have been constructed. Tunnels often play a role in reducing traffic jams, shortening driving distances and allowing faster journeys. However, tunnels bring challenges in vehicle navigation and positioning.
For vehicle positioning, the Global Positioning System (GPS) is currently the most widely used technology (Skog and Handel, Reference Skog and Handel2009). However, GPS suffers from performance degradation in GPS-denied environments such as tunnels due to the signal blockage. To overcome this problem, the common solution is that GPS is integrated with an Inertial Navigation System (INS) or Dead Reckoning (DR) system (Toledo-Moreo et al., Reference Toledo-Moreo, Zamora-Izquierdo and Ubeda-Miarro2007; Zhang and Xu, Reference Zhang and Xu2012; Tzoreff and Bobrovsky, Reference Tzoreff and Bobrovsky2012). Both INS and DR contain inertial sensors. For automotive applications, only low-cost inertial sensors based on Micro Electromechanical Systems (MEMS) technology are affordable. Due to the presence of noise in the MEMS-based sensors measurements and the integration process, the INS and DR solutions drift over time. This drift can cause rapid positioning performance degradation during GPS outages (Bhatt et al., Reference Bhatt, Aggarwal, Devabhaktuni and Bhattacharya2014), especially in GPS-denied environments such as long tunnels. Other sensors, such as vehicle motion sensors, cameras and radar are used to compensate for errors (Schleicher et al., Reference Schleicher, Bergasa, Ocan and Barea2010; Li and Zhang, Reference Li and Zhang2010; Jo et al., Reference Jo, Chu and Sunwoo2012). These sensors can partially correct the accumulated errors, but the compensation effect is poor when GPS is in a long-time failure. The main reason is the lack of the position observation to correct the error.
As an alternative, there has been rapid development of wireless location technologies (Liu et al., Reference Liu, Darabi and Banerjee2007; Zhou and Shi, Reference Zhou and Shi2009; Curran et al., Reference Curran, Furey and Lunney2011; Kaemarungsi and Krishnamurthy, Reference Kaemarungsi and Krishnamurthy2012) in recent years, such as Wireless Local Area Networks (WLAN), Bluetooth, Ultra Wide Band (UWB) and Radio Frequency Identification (RFID). Among them, RFID has attracted wide attention due to its advantages of non-touch, low-cost and high accuracy (Zhou and Shi, Reference Zhou and Shi2009; Ting et al., Reference Ting, Kwok, Tsang and Ho2011; Park and Lee, Reference Park and Lee2013), especially in the field of indoor positioning. RFID-based indoor positioning technology typically employs the Received Signal Strength (RSS), Time Of Arrival (TOA), Time Difference Of Arrival (TDOA) or Angle Of Arrival (AOA) to compute the object's location. The RSS-based location algorithms are the most widely used for indoor positioning because the algorithms are simple and need no additional hardware.
RFID-based technology has also been studied for outdoor applications (Boccadoro et al., Reference Boccadoro, Martinelli and Pagnottelli2010). Chon et al. (Reference Chon, Jun and Jung2004) applied RFID technology to the vehicle positioning field for the first time, and the feasibility of RFID-based vehicle positioning at high speed was preliminarily verified. Zhang et al. (Reference Zhang, Jiang and Kuang2011) used Active RFID Positioning (ARP) technology to achieve vehicle positioning. Cheng et al. (Reference Cheng, Cheng and Song2012) employed passive RFID tags for vehicle navigation. Lee et al. (Reference Lee, Oh and Gerla2012) used RFID to improve GPS accuracy in GPS-denied environments. In these methods, only the RFID information is used. Therefore, the positioning accuracy and the output frequency are not high enough to meet the performance requirements for many applications. In addition, these methods can only provide position information and cannot provide speed or attitude information that is also important to location-related services. Because of the similarity between tunnel and indoor environments, RFID technology can be considered as a possible solution to achieve vehicle positioning in tunnels. However, the disadvantages of an RFID-based positioning algorithm as discussed above, i.e., low accuracy, low output frequency and the lack of speed or attitude information, still exist in tunnel positioning.
For vehicle positioning, DR is a widely used technology in GPS-denied environments that uses driving direction and speed to reckon the position of the vehicle. The commonly used sensors include electronic compass, wheel speed sensor, and other in-vehicle sensors. DR has the advantage that it is totally self-contained. However, for numerical integration processing, this method suffers from serious accumulative integration errors, and these large errors are strongly time correlated and can cause rapid performance degradation due to the lack of position observations.
To combine the advantages of RFID and DR methods to achieve accurate and reliable positioning performance in tunnels, the multi-sensor fusion method provides a viable solution. Due to the complementary natures of these two types of sensors, the RFID can be fused with several in-vehicle DR sensors to realise positioning in completely GPS-denied areas. In other words, RFID can provide the position observation to correct the accumulative integration errors of DR, and DR can provide speed and attitude information of the vehicle to improve the positioning accuracy and output frequency of RFID. However, to the author's knowledge, there has been little recent and relevant research on the topic of fusion positioning specialised for vehicles in tunnels by using RFID and in-vehicle sensors.
Several information fusion algorithms have been proposed in the field of vehicle navigation by using GPS and DR, such as Extended Kalman Filter (EKF) (Toledo-Moreo et al., Reference Toledo-Moreo, Zamora-Izquierdo and Ubeda-Miarro2007; Skog and Handel, Reference Skog and Handel2009), Unscented Kalman Kilter (UKF) (Jung et al., Reference Jung, Kim, Kim, Jung and Kim2014) and Particle Filter (PF)(Georgy et al., Reference Georgy, Noureldin, Korenberg and Bayoumi2010), which can provide a way to propose a suitable algorithm for RFID/DR fusion. Among the existing algorithms, Federated Unscented Kalman Filter (FUKF) is a novel and effective algorithm to achieve GPS/DR fusion positioning (Xu et al., Reference Xu, Zhang, Quan and Lin2009; Zhang et al., Reference Zhang, Liu and Du2007). Due to the ability to deal with nonlinear problems and a fault tolerance ability, the FUKF is employed to achieve RFID/DR fusion in this paper.
This paper proposes a vehicle positioning strategy based on the fusion of RFID and in-vehicle sensors in completely GPS-denied environments such as tunnels. This strategy employs a two-step approach, namely, the calculation of the distances between the RFID tags and the reader based on RSS, and then the global fusion estimation of vehicle position. The algorithms for both distance estimation and global fusion are developed to obtain higher performance. The main contributions of this paper can be summarised as follows:
(1) A Least Square Support Vector Machine (LSSVM)-based algorithm is developed to estimate the distances based on RSS. Compared to other estimation methods such as propagation models, the proposed algorithm has many advantages, such as high precision, high generalisation ability and strong adaptability for different environments, which can significantly improve the performance of subsequent global fusion.
(2) Since the fusion of the RFID and in-vehicle sensors has seldom been discussed in related literature, this paper presents an in-depth study to derive our fusion algorithm. First, a RFID-based positioning method utilising EKF is developed (RFID-EKF), which only uses the RFID and aims to validate the feasibility of a RFID-based positioning algorithm for vehicles in tunnels. Then low cost in-vehicle sensors are introduced to fuse with RFID to achieve fusion positioning (abbreviated as Fusion-EKF), and the improved vehicle motion model is developed and adopted to establish an EKF state model. Finally, our global fusion algorithm is proposed on the basis of Fusion-EKF to lower its costs.
(3) A novel Federated Unscented Kalman Filter (FUKF) is designed to realise the global fusion. To overcome the disadvantage of RFID-based positioning algorithms, low cost in-vehicle sensors, such as electronic compass and wheel speed sensors, are introduced to fuse with RFID. In this algorithm, the obvious advantage is that due to the application of a decentralized federated filter, the layout of tags can be optimised to significantly reduce the number of tags and thus lower the costs. In the actual implementation of local filtering of the federated filter, the UKF algorithm is developed to replace the EKF since it has better ability to deal with a nonlinear problem than EKF.
The remainder of the paper is organised as follows. Section 2 gives an overview of the structure of the proposed strategy. The distance estimation algorithm is given in Section 3. The RFID-EKF and Fusion-EKF algorithm are discussed in Section 4. Section 5 presents the FUKF algorithm for global fusion. Experimental results are provided in Sections 6. The paper is concluded in Section 7.
2. PROPOSED STRATEGY FOR VEHICLE POSITIONING
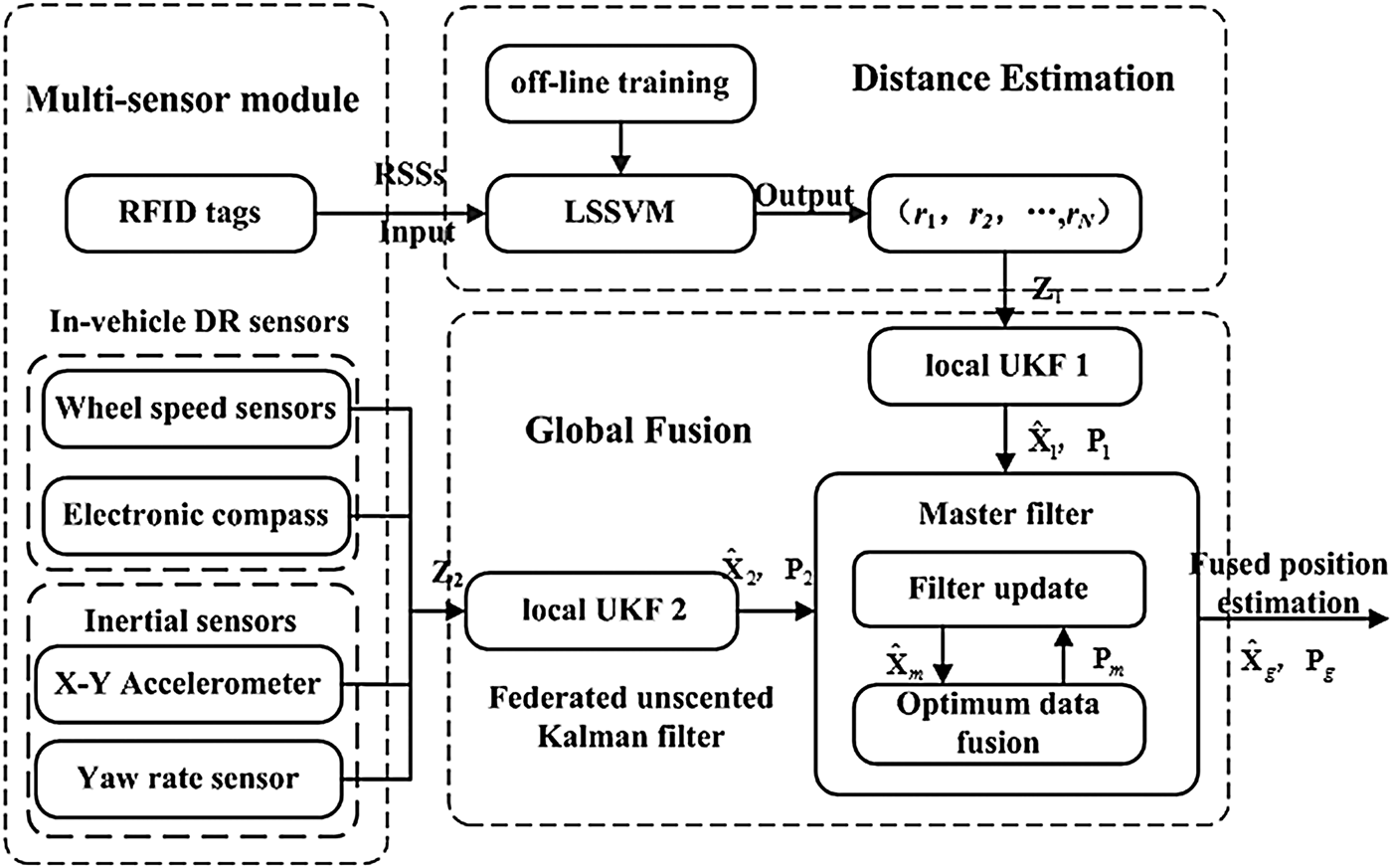
The proposed strategy is shown in Figure 1. Figure 1 is mainly composed of three parts, i.e., multi-sensor module, LSSVM-based distance estimation algorithm, and FUKF for global fusion.

Figure 1. Proposed fusion strategy.
The multi-sensor module includes such sensors as MEMS-based inertial sensors, wheel speed sensors, electronic compass and the low-cost active RFID hardware devices (a reader and a number of tags). The low-cost active RFID hardware devices are characterised by low price and low output frequency. The MEMS-based inertial sensors used here only include two orthogonal accelerometers and a yaw gyro, rather than a full INS which would be expensive.
The LSSVM algorithm is developed to estimate the distance information between RFID reader and tags, i.e., r 1, r 2 …r N, based on RSS. The LSSVM has been verified to be effective and robust for modelling the systems with nonlinearity, parametric and modelling uncertainties. Rather than the propagation model method that is the main approach for distance estimation in indoor positioning based on RSS, the LSSVM can achieve better performance in real world applications since the accuracy of the propagation model may be influenced by the environment.
The FUKF is proposed to realise global fusion. The improved vehicle motion model is adopted to establish the state equation. With an optimised layout of tags, the number of tags is reduced for lower costs. The federated filter is designed to ensure the accuracy and reliability of positioning in the condition that fewer tags are needed. In the actual implementation of local filtering of the federated filter, EKF is the most commonly used algorithm for nonlinear systems. However, EKF is mainly suitable for mild nonlinear systems. The first-order local linearization procedure of EKF introduces approximation errors and even causes divergence of the filter. To overcome these problems a UKF is developed to replace EKF in the design of the local filter. The main advantage of UKF is that it does not use any linearization for calculating the state prediction covariance. Consequently, it has more accurate covariance and Kalman gain estimates, and this leads to more exact fusion results. Since the actual vehicle motions are arbitrary nonlinear processes, UKF is more suitable than EKF that has better ability to deal with nonlinear problems. In the FUKF module of Figure 1, Z1 and Z2 are the observation vectors from RFID and in-vehicle sensors, respectively; ![]() ${\hat X}_g $ and
${\hat X}_g $ and ![]() ${P}_g $ represent the fused state and its variance;
${P}_g $ represent the fused state and its variance; ![]() ${\hat X}_j $ and
${\hat X}_j $ and ![]() ${P}_j $ (j = 1,2) represent the state estimation and variance of the j-th local filter;
${P}_j $ (j = 1,2) represent the state estimation and variance of the j-th local filter; ![]() ${\hat X}_m $ and
${\hat X}_m $ and ![]() ${P}_m $ represent the state estimation and variance of the master filter.
${P}_m $ represent the state estimation and variance of the master filter.
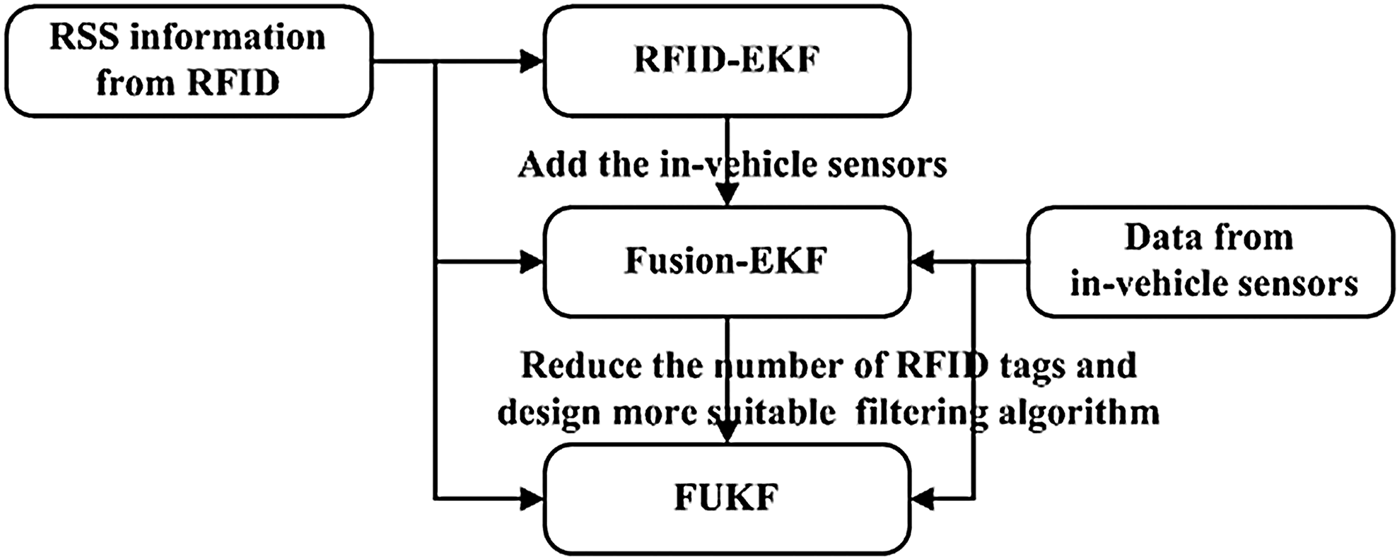
To demonstrate the derivation process of our global fusion algorithm, Figure 2 shows the relationships of RFID-EKF, Fusion-EKF and FUKF algorithms.

Figure 2. The relationships of RFID-EKF, Fusion-EKF and FUKF.
It can be seen in Figure 2 that RFID-EKF only uses RFID to estimate the vehicle position. The data from low-cost in-vehicle sensors is added to aid the RFID in Fusion-EKF. Therefore, the positioning results of Fusion-EKF have higher accuracy and output frequency due to the in-vehicle sensors.
On the basis of RFID-EKF, the FUKF is developed to reduce the number of tags. FUKF also combines the data from RFID and in-vehicle sensors. However, due to the optimised layout of tags and the application of the federated filter, FUKF needs fewer RFID tags than Fusion-EKF to reduce the costs for practical application. The federated filter is designed to tolerate and isolate the faulty RSS information or even non-existence of RFID information.
The specific implementation of these algorithms and the comparison of each will be discussed in a later section.
3. LSSVM FOR DISTANCE ESTIMATION
It seems that the first challenge for the positioning strategy is how to mathematically model the relationship between RSS and distance. Theoretically, in unobstructed free space, Friis transmission equation (Zhou and Shi, Reference Zhou and Shi2009) can be applied. However, in real world applications, this model becomes less useful. For example, RFID signals in tunnels usually exhibit multipath propagation due to the effect from obstructing structures such as walls. For this reason, this paper proposes a LSSVM-based algorithm to model the relationship between RSS and distance.
LSSVM is a powerful tool to model nonlinear functions and can be trained offline utilising the experiment data collected in a specific environment (Dong and Luo, Reference Dong and Luo2013). Compared to other modelling methods such as Artificial Neural Networks (ANN), LSSVM has a higher generalisation ability to accommodate the requirement of different application environments.
It has been found that there is a nonlinear correlation between RSS and distance. Although modelling this correlation is difficult, it is possible to build correlation with the designed LSSVM after adequate training. In this paper, the input of LSSVM is RSS, and the output is the distance between the RFID reader and tag. The training data is collected through experiments in different situations. The training process is completely offline, and the trained LSSVM model is used to estimate the distance online. To ensure the effectiveness of LSSVM, the same group of tags and reader is selected in the training stage and online estimation stage. Meanwhile, a large mount of data in different situations is collected to guarantee the training is rich.
Take a training set ![]() $\left\{ {x_k, y_k} \right\}_{k = 1}^N $, where x k is input RSS vector, y k is output distance vector.
$\left\{ {x_k, y_k} \right\}_{k = 1}^N $, where x k is input RSS vector, y k is output distance vector. ![]() $x_k, y_k \in {R}^1 $,
$x_k, y_k \in {R}^1 $, ![]() ${R}^1 $ is the one-dimensional vector space. In feature space, the LSSVM model takes the form:
${R}^1 $ is the one-dimensional vector space. In feature space, the LSSVM model takes the form:
where ![]() ${\omega} \in {R}^{n_h} $ is an adjustable weight vector; the nonlinear mapping
${\omega} \in {R}^{n_h} $ is an adjustable weight vector; the nonlinear mapping ![]() $\varphi (.):{R}^1 \to {R}^{n_h} $ maps the input data into a higher dimensional feature space; b is the scalar threshold.
$\varphi (.):{R}^1 \to {R}^{n_h} $ maps the input data into a higher dimensional feature space; b is the scalar threshold.
The optimisation problem is
 $$\min J({ \omega}, b,e) = \displaystyle{1 \over 2}{ \omega} ^T { \omega} + \displaystyle{1 \over 2}\gamma \sum\limits_{k = 1}^N {e_k^2} $$
$$\min J({ \omega}, b,e) = \displaystyle{1 \over 2}{ \omega} ^T { \omega} + \displaystyle{1 \over 2}\gamma \sum\limits_{k = 1}^N {e_k^2} $$Due to the equality constraints:
where e k is the error variable and γ ≥ 0 is a regularisation constant. To solve the optimisation problem, the Lagrangian function is introduced:
 $$L_{LS - SVM} = \displaystyle{1 \over 2}{ \omega} ^T { \omega} + \displaystyle{1 \over 2}\gamma \sum\limits_{k = 1}^N {e_k^2} - \sum\limits_{k = 1}^N {\alpha _k \left\{ {{ \omega} ^T \varphi ({X}_k ) + b + e_k - y_k} \right\}} $$
$$L_{LS - SVM} = \displaystyle{1 \over 2}{ \omega} ^T { \omega} + \displaystyle{1 \over 2}\gamma \sum\limits_{k = 1}^N {e_k^2} - \sum\limits_{k = 1}^N {\alpha _k \left\{ {{ \omega} ^T \varphi ({X}_k ) + b + e_k - y_k} \right\}} $$Where α k are the Lagrange multipliers, according to Karush Kuhn Tucker (KKT) optimization conditions that are illustrated in Equation (5):
 $$\left\{ \matrix{\displaystyle{{\partial L_{LS - SVM}} \over {\partial { \omega}}} = 0 \to { \omega} = \sum\limits_{k = 1}^N {\alpha _k \varphi (x_k )} \hfill \cr \displaystyle{{\partial L_{LS - SVM}} \over {\partial b}} = 0 \to \sum\limits_{k = 1}^N {\alpha _k} = 0 \hfill \cr \displaystyle{{\partial L_{LS - SVM}} \over {\partial e_k}} = 0 \to \alpha _k = \gamma e_k, k = 1, \cdots, N \hfill \cr \displaystyle{{\partial L_{LS - SVM}} \over {\partial \alpha _k}} = 0 \to { \omega} ^T \varphi (x_k ) + b + e_k - y_k = 0,k = 1, \cdots, N \hfill} \right.$$
$$\left\{ \matrix{\displaystyle{{\partial L_{LS - SVM}} \over {\partial { \omega}}} = 0 \to { \omega} = \sum\limits_{k = 1}^N {\alpha _k \varphi (x_k )} \hfill \cr \displaystyle{{\partial L_{LS - SVM}} \over {\partial b}} = 0 \to \sum\limits_{k = 1}^N {\alpha _k} = 0 \hfill \cr \displaystyle{{\partial L_{LS - SVM}} \over {\partial e_k}} = 0 \to \alpha _k = \gamma e_k, k = 1, \cdots, N \hfill \cr \displaystyle{{\partial L_{LS - SVM}} \over {\partial \alpha _k}} = 0 \to { \omega} ^T \varphi (x_k ) + b + e_k - y_k = 0,k = 1, \cdots, N \hfill} \right.$$ Eliminating ![]() ${ \omega} $ and e k will yield a linear system instead of a quadratic programming problem:
${ \omega} $ and e k will yield a linear system instead of a quadratic programming problem:
where ![]() ${Y} = \left[ {y_1, \cdots, y_N} \right]^T, {\it 1}_N = \left[ {{\rm 1}, \cdots, {\rm 1}} \right]^T $ and
${Y} = \left[ {y_1, \cdots, y_N} \right]^T, {\it 1}_N = \left[ {{\rm 1}, \cdots, {\rm 1}} \right]^T $ and ![]() ${\alpha} = \left[ {\alpha _1, \cdots, \alpha _N} \right]^T $.
${\alpha} = \left[ {\alpha _1, \cdots, \alpha _N} \right]^T $. ![]() ${\bf \rm I}_N $ is a N × N identity matrix.
${\bf \rm I}_N $ is a N × N identity matrix. ![]() $\it \Omega$ is the kernel matrix defined by
$\it \Omega$ is the kernel matrix defined by
The Radial Basis Function (RBF) has been used here as the kernel function K(·,·), which is given by
 $$K(x,x_k ) = \exp \left\{ { - \displaystyle{{\left\Vert {x - x_k} \right\Vert _2^2} \over {2\sigma ^2}}} \right\},k = 1, \cdots, N$$
$$K(x,x_k ) = \exp \left\{ { - \displaystyle{{\left\Vert {x - x_k} \right\Vert _2^2} \over {2\sigma ^2}}} \right\},k = 1, \cdots, N$$
where ![]() $\left\Vert {x - x_k} \right\Vert_2^2 $ is the squared Euclidean distance between the two feature vectors; σ is the width of RBF.
$\left\Vert {x - x_k} \right\Vert_2^2 $ is the squared Euclidean distance between the two feature vectors; σ is the width of RBF.
Further, the result of the LS-SVM model for function estimation becomes
 $$f\,(x) = \sum\limits_{k = 1}^N {\alpha _k K(x,x_k )} + b$$
$$f\,(x) = \sum\limits_{k = 1}^N {\alpha _k K(x,x_k )} + b$$where α k and b are the solutions to Equation (6). The design values of γ and σ can be determined during the training of LS-SVM.
After offline training, Equation (9) can be used to estimate the distance between tag and reader based on measured RSS online.
4. RFID-EKF AND Fusion-EKF
The second step of the proposed strategy is to estimate the vehicle position based on the distances. In this paper, the global fusion algorithm for positioning is derived by RFID-EKF and Fusion-EKF. To illustrate the advantages of our global fusion algorithm, RFID-EKF and Fusion-EKF algorithm are designed in this section, and will be compared with FUKF in Section 6.
4.1. System Setup
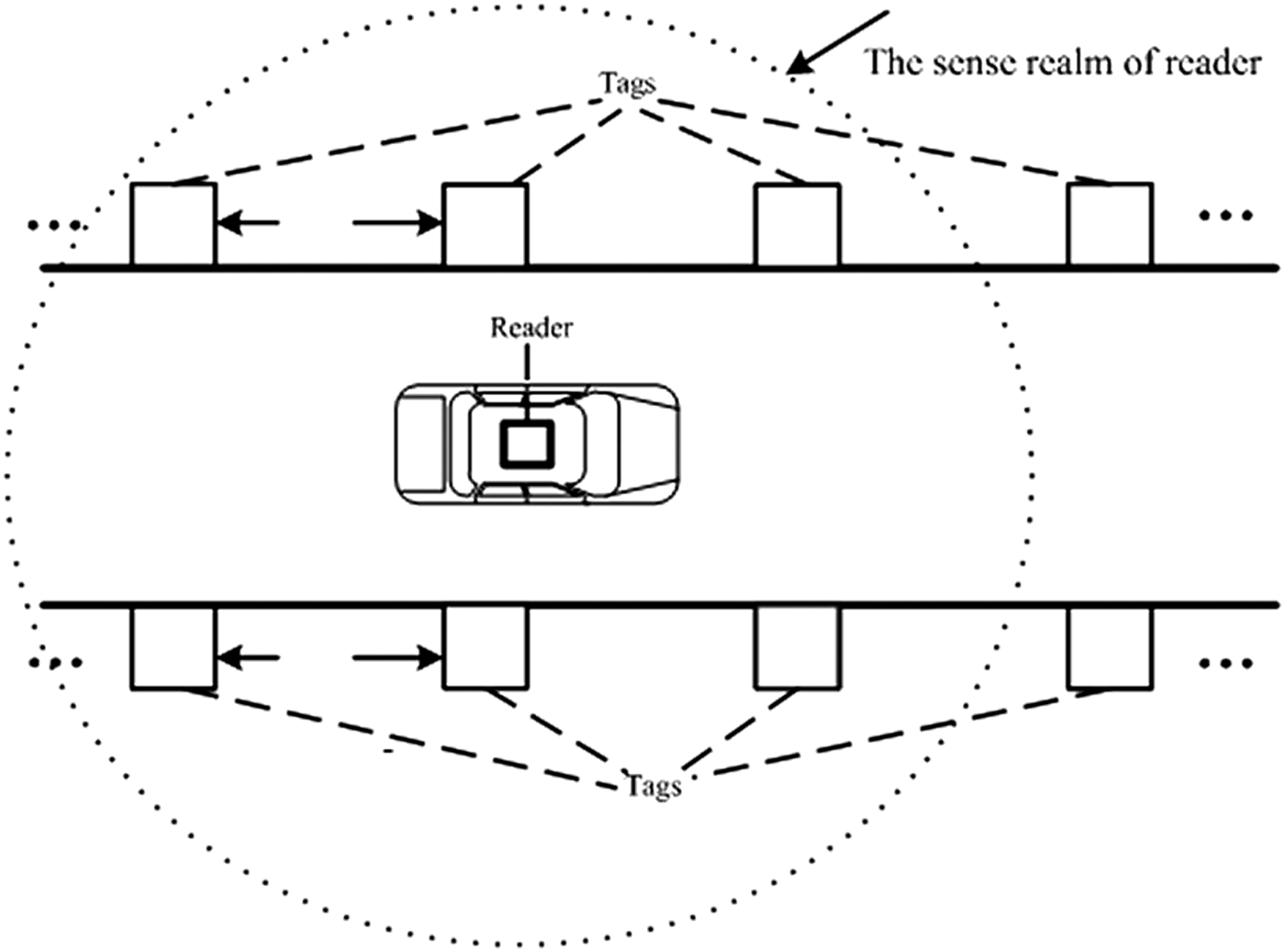
The RFID-EKF and Fusion-EKF algorithm have the same layout style of RFID tags and reader. The active RFID reader is installed on the top of the vehicle, and the active RFID tags are placed on both sidewalls of the tunnel, as shown in Figure 3. On each side, the tags are placed at regular intervals that are set according to the characteristics of the reader and tags to ensure at least four tags can be detected by reader at any moment, i.e., the interval is 6 m in this paper. The exact position of each tag can be determined beforehand, and the position of the reader can be considered as the position of the vehicle.

Figure 3. The layout style of RFID tags for RFID-EKF and Fusion-EKF.
4.2. RFID-EKF
The RFID-EKF algorithm only uses RFID to estimate the vehicle position. For indoor location, the most widely used method is the so-called multi-lateration method. However, the values of calculation distance usually have a large error due to phenomena such as fading, absorption and multipath of propagation and even the failure of tags, which may cause a large positioning error. To solve the problem discussed above, a RFID-EKF algorithm is designed.
Assuming that RSSs of N tags can be measured by the reader at the time k, the distances between reader and tags, r 1(k), r 2(k)…r N(k), can be calculated by Equation (9).
The discretised state equation and measurement equation can be written as
where k refers to the discrete-time step; ![]() ${X}_{{\rm RFID}} \left( k \right){\rm =} \left[ {\matrix{ {p_e \left( k \right)} & {p_n \left( k \right)} \cr}} \right]^{\prime} $ is the state vector; the state transition matrix
${X}_{{\rm RFID}} \left( k \right){\rm =} \left[ {\matrix{ {p_e \left( k \right)} & {p_n \left( k \right)} \cr}} \right]^{\prime} $ is the state vector; the state transition matrix ![]() ${A}_{{\rm RFID}} {\rm =} \left[ {\matrix{ 1 & 0 \cr 0 & 1 \cr}} \right]$; W RFID and V RFID are the system and measurement noise vectors, and their covariance matrices are Q RFID and R RFID, respectively;
${A}_{{\rm RFID}} {\rm =} \left[ {\matrix{ 1 & 0 \cr 0 & 1 \cr}} \right]$; W RFID and V RFID are the system and measurement noise vectors, and their covariance matrices are Q RFID and R RFID, respectively; ![]() ${Z}_{{\rm RFID}} = \left[ {\matrix{ {r_1 \left( k \right)} & {r_2 \left( k \right)} & {...} & {r_N \left( k \right)} \cr}} \right]^{\prime} $ is the observation vector and h RFID is the corresponding observation function and can be described by:
${Z}_{{\rm RFID}} = \left[ {\matrix{ {r_1 \left( k \right)} & {r_2 \left( k \right)} & {...} & {r_N \left( k \right)} \cr}} \right]^{\prime} $ is the observation vector and h RFID is the corresponding observation function and can be described by:
 $$\eqalign{{{h}_{{\rm RFID}}}\left( k \right) & = \left[ {\matrix{ {{h_{11}}\left( k \right)} \cr {...} \cr {{h_{1N}}\left( k \right)} \cr } } \right],\,{h_{1i}}\left( k \right) \cr & = \sqrt {{{\left( {{\,p_e}\left( k \right) - {x_i}\left( k \right)} \right)}^2} + {{\left( {{\,p_n}\left( k \right) - {y_i}\left( k \right)} \right)}^2}} {\rm + }{n_{{r_i}}}\quad \left( {i = 1,2...,N} \right)}$$
$$\eqalign{{{h}_{{\rm RFID}}}\left( k \right) & = \left[ {\matrix{ {{h_{11}}\left( k \right)} \cr {...} \cr {{h_{1N}}\left( k \right)} \cr } } \right],\,{h_{1i}}\left( k \right) \cr & = \sqrt {{{\left( {{\,p_e}\left( k \right) - {x_i}\left( k \right)} \right)}^2} + {{\left( {{\,p_n}\left( k \right) - {y_i}\left( k \right)} \right)}^2}} {\rm + }{n_{{r_i}}}\quad \left( {i = 1,2...,N} \right)}$$ p e(k) and p n(k) represent the east and north coordinates of the vehicle CoG (Centre of gravity) in the global positioning frame, respectively. (x i, yi) are the known coordinates of the i-th tag. ![]() $n_{r_i} $ denotes the corresponding observation noise vector.
$n_{r_i} $ denotes the corresponding observation noise vector.
The EKF process consists of the following two phases:
Time update:
Measurement update:
 $$\eqalign{{K}_{{\rm RFID}} (k) & = {P}_{{\rm RFID}} (k,k - 1) \cdot {H^{\prime}}_1 (k) \cr & \quad \cdot \left[ {{H}_{{\rm RFID}} (k){P}_{{\rm RFID}} (k,k - 1){H^{\prime}}_{{\rm RFID}} (k) + {R}_{{\rm RFID}} (k)} \right]^{ - 1}}$$
$$\eqalign{{K}_{{\rm RFID}} (k) & = {P}_{{\rm RFID}} (k,k - 1) \cdot {H^{\prime}}_1 (k) \cr & \quad \cdot \left[ {{H}_{{\rm RFID}} (k){P}_{{\rm RFID}} (k,k - 1){H^{\prime}}_{{\rm RFID}} (k) + {R}_{{\rm RFID}} (k)} \right]^{ - 1}}$$ $$\eqalign{{\hat X}_{{\rm RFID}} (k) & = {\hat X}_{{\rm RFID}} (k,k - 1) + {K}_{{\rm RFID}} (k) \cr & \quad \times \left[ {{Z}_{{\rm RFID}} (k) - {h}_{{\rm RFID}} \left( {{\hat X}_{{\rm RFID}} (k,k - 1)} \right)} \right]}$$
$$\eqalign{{\hat X}_{{\rm RFID}} (k) & = {\hat X}_{{\rm RFID}} (k,k - 1) + {K}_{{\rm RFID}} (k) \cr & \quad \times \left[ {{Z}_{{\rm RFID}} (k) - {h}_{{\rm RFID}} \left( {{\hat X}_{{\rm RFID}} (k,k - 1)} \right)} \right]}$$
where I is an identity matrix, H RFID are the Jacobian matrices of the measurement function ![]() ${h}_{{\rm RFID}} \left( \cdot \right)$ with respect to X RFID:
${h}_{{\rm RFID}} \left( \cdot \right)$ with respect to X RFID:
 $${H}_{{\rm RFID}} \left( k \right) = \left[ {\matrix{ {{{\left( {\,p_e \left( {k,k - 1} \right) - x_1 \left( k \right)} \right)} / {D_1 \left( k \right)}}} & {{{\left( {\,p_n \left( {k,k - 1} \right) - y_1 \left( k \right)} \right)} / {D_1 \left( k \right)}}} \cr {...} & {...} \cr {{{\left( {\,p_e \left( {k,k - 1} \right) - x_N \left( k \right)} \right)} / {D_N \left( k \right)}}} & {{{\left( {\,p_e \left( {k,k - 1} \right) - y_N \left( k \right)} \right)} / {D_N \left( k \right)}}} \cr}} \right]\semicolon$$
$${H}_{{\rm RFID}} \left( k \right) = \left[ {\matrix{ {{{\left( {\,p_e \left( {k,k - 1} \right) - x_1 \left( k \right)} \right)} / {D_1 \left( k \right)}}} & {{{\left( {\,p_n \left( {k,k - 1} \right) - y_1 \left( k \right)} \right)} / {D_1 \left( k \right)}}} \cr {...} & {...} \cr {{{\left( {\,p_e \left( {k,k - 1} \right) - x_N \left( k \right)} \right)} / {D_N \left( k \right)}}} & {{{\left( {\,p_e \left( {k,k - 1} \right) - y_N \left( k \right)} \right)} / {D_N \left( k \right)}}} \cr}} \right]\semicolon$$Since only the RFID is employed to achieve vehicle positioning, this algorithm can only provide the position information, and the positioning accuracy and the output frequency are not high enough, i.e., the output frequency is always less than 1 Hz.
4.3. Fusion-EKF
To overcome the disadvantages of RFID-EKF, the Fusion-EKF algorithm is developed to correct the positioning errors and improve the output frequency. The difference between Fusion-EKF and RFID-EKF is that some in-vehicle sensors are introduced to fuse with the RFID information in Fusion-EKF. To describe the vehicle motion in a tunnel, the improved vehicle motion model is established. The state vector is
where v e(k) and v n(k) are the east and north velocity. ψ(k) is the yaw angle. To represent two typical vehicle movements, i.e., the straight line and curvilinear motions, the longitudinal acceleration a x, the lateral accelerations a y and the yaw rate ω z are introduced as system input vectors in the vehicle motion model. The improved vehicle motion model equation is shown as follows:
 $$\eqalign{{X}_{{\rm Fusion}} \left( {k,k - 1} \right) & = {\,f}_{{\rm Fusion}} \left( {{X}_2 \left( {k - 1} \right),{U}_{{\rm Fusion}} \left( k \right)} \right) \cr & = \left[ {\matrix{ {\,p_e \left( {k - 1} \right) + v_e \left( {k - 1} \right)T + \displaystyle{1 \over 2}\left[ {a_x \cos \psi \left( {k - 1} \right) - a_y \sin \psi \left( {k - 1} \right)} \right]T^2} \cr {v_e \left( {k - 1} \right) + \left[ {a_x \cos \psi \left( {k - 1} \right) - a_y \sin \psi \left( {k - 1} \right)} \right]T} \cr {\,p_n \left( {k - 1} \right) + v_n \left( {k - 1} \right)T + \displaystyle{1 \over 2}\left[ {a_x \sin \psi \left( {k - 1} \right) + a_y \cos \psi \left( {k - 1} \right)} \right]T^2} \cr {v_n \left( {k - 1} \right) + \left[ {a_x \sin \psi \left( {k - 1} \right) + a_y \cos \psi \left( {k - 1} \right)} \right]T} \cr {\psi \left( {k - 1} \right) + \omega _z} \cr}} \right]}$$
$$\eqalign{{X}_{{\rm Fusion}} \left( {k,k - 1} \right) & = {\,f}_{{\rm Fusion}} \left( {{X}_2 \left( {k - 1} \right),{U}_{{\rm Fusion}} \left( k \right)} \right) \cr & = \left[ {\matrix{ {\,p_e \left( {k - 1} \right) + v_e \left( {k - 1} \right)T + \displaystyle{1 \over 2}\left[ {a_x \cos \psi \left( {k - 1} \right) - a_y \sin \psi \left( {k - 1} \right)} \right]T^2} \cr {v_e \left( {k - 1} \right) + \left[ {a_x \cos \psi \left( {k - 1} \right) - a_y \sin \psi \left( {k - 1} \right)} \right]T} \cr {\,p_n \left( {k - 1} \right) + v_n \left( {k - 1} \right)T + \displaystyle{1 \over 2}\left[ {a_x \sin \psi \left( {k - 1} \right) + a_y \cos \psi \left( {k - 1} \right)} \right]T^2} \cr {v_n \left( {k - 1} \right) + \left[ {a_x \sin \psi \left( {k - 1} \right) + a_y \cos \psi \left( {k - 1} \right)} \right]T} \cr {\psi \left( {k - 1} \right) + \omega _z} \cr}} \right]}$$
where ![]() ${f}_{{\rm Fusion}} \left( \cdot \right)$ denotes the process function of the improved vehicle motion model. T is the sampling interval.
${f}_{{\rm Fusion}} \left( \cdot \right)$ denotes the process function of the improved vehicle motion model. T is the sampling interval. ![]() ${U}_{{\rm Fusion}} = \left[ {\matrix{ {a_x} & {a_y \quad \omega _z} \cr}} \right]^{\prime} $ is the input vector.
${U}_{{\rm Fusion}} = \left[ {\matrix{ {a_x} & {a_y \quad \omega _z} \cr}} \right]^{\prime} $ is the input vector.
The observation equation can be established as:
 $$\eqalign{{Z}_{{\rm Fusion}} & = {h}_{{\rm Fusion}} \left[ {{X}_{{\rm Fusion}} \left( k \right)} \right] \cr & = \left[ {\matrix{ {\sqrt {\left( {\,p_e \left( k \right) - x_1 \left( k \right)} \right)^2 + \left( {\,p_n \left( k \right) - y_1 \left( k \right)} \right)^2} {\rm +} n_{r_1}} \cr {...} \cr {\sqrt {\left( {\,p_e \left( k \right) - x_N \left( k \right)} \right)^2 + \left( {\,p_n \left( k \right) - y_N \left( k \right)} \right)^2} {\rm +} n_{r_N}} \cr {v_e \left( k \right)\cos \psi \left( k \right) + v_n \left( k \right)\sin \psi \left( k \right) + n_v} \cr {\psi \left( k \right) + n_\psi} \cr}} \right]}$$
$$\eqalign{{Z}_{{\rm Fusion}} & = {h}_{{\rm Fusion}} \left[ {{X}_{{\rm Fusion}} \left( k \right)} \right] \cr & = \left[ {\matrix{ {\sqrt {\left( {\,p_e \left( k \right) - x_1 \left( k \right)} \right)^2 + \left( {\,p_n \left( k \right) - y_1 \left( k \right)} \right)^2} {\rm +} n_{r_1}} \cr {...} \cr {\sqrt {\left( {\,p_e \left( k \right) - x_N \left( k \right)} \right)^2 + \left( {\,p_n \left( k \right) - y_N \left( k \right)} \right)^2} {\rm +} n_{r_N}} \cr {v_e \left( k \right)\cos \psi \left( k \right) + v_n \left( k \right)\sin \psi \left( k \right) + n_v} \cr {\psi \left( k \right) + n_\psi} \cr}} \right]}$$
where ![]() ${Z}_{{\rm Fusion}} = \left[ {\matrix{ {r_1} & {...} & {r_N} & {v_{wheel}} & {\psi _{compass}} \cr}} \right]^{\prime} $ is the observation vector and h Fusion is the corresponding observation function. v wheel is the longitudinal linear velocity in the vehicle body frame which measured by the wheel speed sensors; ψ compass is the observed yaw angle. n v and n ψ denote the corresponding observation noise vector.
${Z}_{{\rm Fusion}} = \left[ {\matrix{ {r_1} & {...} & {r_N} & {v_{wheel}} & {\psi _{compass}} \cr}} \right]^{\prime} $ is the observation vector and h Fusion is the corresponding observation function. v wheel is the longitudinal linear velocity in the vehicle body frame which measured by the wheel speed sensors; ψ compass is the observed yaw angle. n v and n ψ denote the corresponding observation noise vector.
Then the execution of EKF can be divided into time update stage and measurement update stage as Equations (11)-(15). Compared to RFID-EKF, the output frequency of the Fusion-EKF algorithm is increased to 10 Hz from the value 1 Hz of RFID-EKF. Meanwhile, the fusion algorithm can provide the speed and attitude information which RFID was unable to provide.
5. GLOBAL FUSION ALGORITHM BASED ON FUKF
Although the Fusion-EKF algorithm can achieve better positioning performance than RFID-EKF, the costs of Fusion-EKF are high due to the high density layout of tags. To reduce the costs of Fusion-EKF with very little sacrifice of accuracy is the major goal of our fusion algorithm. On the basis of Fusion-EKF, the FUKF is proposed to reduce the number of tags. Compared to Fusion-EKF, a significant advantage of FUKF is that the tags can be placed at long distance intervals rather than covering the whole tunnel, due to the optimised layout of tags.
In practice, there are two aspects that should be considered: (1) different sensors have different sampling rates. The sampling rate of the RFID is always lower than that of in-vehicle sensors. (2) RFID fails to provide reliable positioning information if there is no RSS signal. Considering these two aspects, it is more suitable to adopt a decentralized filtering algorithm, therefore, the decentralized federated filter is designed to realise global fusion. The UKF algorithm is developed to design the local filter. For the vehicle, UKF has the following advantages over the commonly-used EKF: (1) UKF eliminates the calculation of Jacobian matrices in EKF and makes the estimation procedure easier; (2) it increases the estimation accuracy by considering at least the second order Taylor expansion to satisfy the nonlinear characteristics in the process of vehicle operation; (3) Strong robustness on the changes of the actual vehicle system parameters, and lower sensitivity to system noise, measurement noise and the initial statistical properties.
5.1. The optimised layout of tags
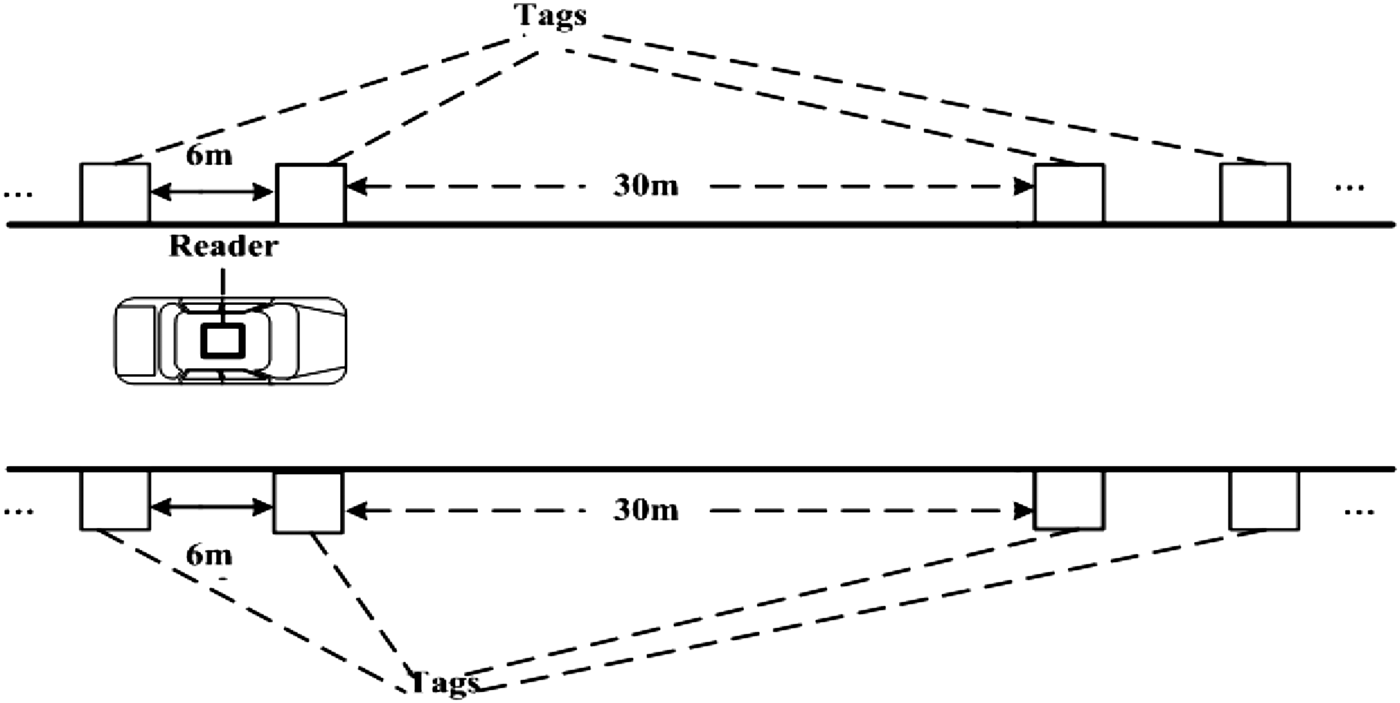
For Fusion-EKF, four tags are placed in a region. Each side has two tags and the interval between the two tags is 6 m. Then another four tags in accordance with this layout are placed at every 30 m interval, as shown in Figure 4.

Figure 4. The optimised layout style of RFID tags for FUKF.
From Figure 4, the DR method is used to estimate the vehicle's position, and the RFID data is used to compensate for the accumulated errors when the vehicle is close to the tags and can receive the RSS signal.
5.2. System Model
To avoid the shortages in the central data fusion, a distributed data fusion model based on federated UKF is adopted to achieve global fusion for vehicle positioning. The system model can be seen in Figure 1. The federated filter is composed of one master filter and two local filters. In Figure 1, the state estimation of one local filter is independent of the other. ![]() ${\hat X}_g $ and
${\hat X}_g $ and ![]() ${P}_g $ represent the fused state and its variance.
${P}_g $ represent the fused state and its variance. ![]() ${\hat X}_j $ and
${\hat X}_j $ and ![]() ${P}_j $ (j = 1,2) represent the state estimation and its variance of the j-th local filter.
${P}_j $ (j = 1,2) represent the state estimation and its variance of the j-th local filter. ![]() ${\hat X}_m $ and
${\hat X}_m $ and ![]() ${P}_m $ represent the state estimation and its variance of the master filter.
${P}_m $ represent the state estimation and its variance of the master filter.
In Figure 1, RFID and DR in-vehicle sensors estimate the position of the vehicle with its own UKF local filter. The position of the vehicle is fused in the master filter according to the state estimation results of every UKF local filter. The model of Figure 1 has much lower computation complexity and better system fault tolerance. When no RSS signal exists, the positioning results of the RFID-based local filter are always inaccurate or even faulty. However, the faults can hardly influence the final precision of the fused position due to the distributed fusion model. Therefore, the distributed data fusion model shown in Figure 1 is more suitable to be used in the proposed positioning strategy which needs fewer tags.
5.3. UKF local filter
The UKF filter chooses a set of sigma sample points to compute the mean and covariance of the state distribution. Assuming that the state estimation vector of the UKF local filter is ![]() ${X}\left( k \right){\rm =} \left[ {\matrix{ {p_e \left( k \right)} & {p_n \left( k \right)} & {v_e \left( k \right)} & {v_n \left( k \right)} & {\psi \left( k \right)} \cr}} \right]^{\prime} $, the discretized state equation and measurement equation can be written as:
${X}\left( k \right){\rm =} \left[ {\matrix{ {p_e \left( k \right)} & {p_n \left( k \right)} & {v_e \left( k \right)} & {v_n \left( k \right)} & {\psi \left( k \right)} \cr}} \right]^{\prime} $, the discretized state equation and measurement equation can be written as:
where W is the system noise vector. V j is the measurement noise vectors of j-th local filters. Q and R are the covariance matrices of W and V. ![]() ${U} = \left[ {\matrix{ {a_x} & {a_y \quad \omega _z} \cr}} \right]^{\prime} $ is the input vector.
${U} = \left[ {\matrix{ {a_x} & {a_y \quad \omega _z} \cr}} \right]^{\prime} $ is the input vector. ![]() ${f}\left( \cdot \right)$ denotes the nonlinear system functions and can be described by improved vehicle motion model as Equation (16). Zj is the observation vectors of j-th local filter and h j is the corresponding observation function.
${f}\left( \cdot \right)$ denotes the nonlinear system functions and can be described by improved vehicle motion model as Equation (16). Zj is the observation vectors of j-th local filter and h j is the corresponding observation function.
 $${{h}_1}\left[ {{X}\left( k \right)} \right] = \left[ {\matrix{ {\sqrt {{{\left( {{\,p_e}\left( k \right) - {x_1}\left( k \right)} \right)}^2} + {{\left( {{\,p_n}\left( k \right) - {y_1}\left( k \right)} \right)}^2}} {\rm + }{n_{{r_1}}}} \cr {...} \cr {\sqrt {{{\left( {{\,p_e}\left( k \right) - {x_N}\left( k \right)} \right)}^2} + {{\left( {{\,p_n}\left( k \right) - {y_N}\left( k \right)} \right)}^2}} {\rm + }{n_{{r_N}}}} \cr } } \right]$$
$${{h}_1}\left[ {{X}\left( k \right)} \right] = \left[ {\matrix{ {\sqrt {{{\left( {{\,p_e}\left( k \right) - {x_1}\left( k \right)} \right)}^2} + {{\left( {{\,p_n}\left( k \right) - {y_1}\left( k \right)} \right)}^2}} {\rm + }{n_{{r_1}}}} \cr {...} \cr {\sqrt {{{\left( {{\,p_e}\left( k \right) - {x_N}\left( k \right)} \right)}^2} + {{\left( {{\,p_n}\left( k \right) - {y_N}\left( k \right)} \right)}^2}} {\rm + }{n_{{r_N}}}} \cr } } \right]$$For the j-th local filter, the UKF consists of the following steps:
(1) Set the initial values for state mean
 ${\hat X}_0 $ and error covariance
${\hat X}_0 $ and error covariance  ${P}_0 $.
${P}_0 $.(2) Compute the 2n x + 1 sigma sampling points χ i and their weighted coefficient W i.
(21) $$\chi _0 = {\bar X},W_0^m = {\kappa / {\left( {n_x + \kappa} \right)}},W_0^c = {\kappa / {\left( {n_x + \kappa} \right)}} + \left( {1 - \alpha ^2 + \beta} \right)\quad \quad i = 0$$(22)
$$\chi _0 = {\bar X},W_0^m = {\kappa / {\left( {n_x + \kappa} \right)}},W_0^c = {\kappa / {\left( {n_x + \kappa} \right)}} + \left( {1 - \alpha ^2 + \beta} \right)\quad \quad i = 0$$(22) $$\chi _i = {\bar X} + \left( {\sqrt {\left( {n_x + \kappa} \right){P}_x}} \right)_i, W_i^m = W_i^c {{ = 1} / {2\left( {n_x + \kappa} \right)}}\quad \quad i = 1,...,n_x $$(23)where
$$\chi _i = {\bar X} + \left( {\sqrt {\left( {n_x + \kappa} \right){P}_x}} \right)_i, W_i^m = W_i^c {{ = 1} / {2\left( {n_x + \kappa} \right)}}\quad \quad i = 1,...,n_x $$(23)where $$\eqalign{& \chi _i = {\bar X} - \left( {\sqrt {\left( {n_x + \kappa} \right){P}_x}} \right)_i, W_i^m = W_i^c {{ = 1} / {2\left( {n_x + \kappa} \right)}} \cr & \quad \quad i = n_x + 1,...,2n_x}$$
$$\eqalign{& \chi _i = {\bar X} - \left( {\sqrt {\left( {n_x + \kappa} \right){P}_x}} \right)_i, W_i^m = W_i^c {{ = 1} / {2\left( {n_x + \kappa} \right)}} \cr & \quad \quad i = n_x + 1,...,2n_x}$$ ${\bar X}$ and
${\bar X}$ and  ${P}_x $ are the mean vector and the covariance matrix of the n x-dimensional distribution. κ is a scaling parameter, and
${P}_x $ are the mean vector and the covariance matrix of the n x-dimensional distribution. κ is a scaling parameter, and  $\left( {\sqrt {\left( {n_x + \kappa} \right){P}_x}} \right)_i $ represents the i-th row of the matrix square root. α determines the spread of the sigma points around
$\left( {\sqrt {\left( {n_x + \kappa} \right){P}_x}} \right)_i $ represents the i-th row of the matrix square root. α determines the spread of the sigma points around  ${\bar X}$. β is used to incorporate prior knowledge of the distribution of
${\bar X}$. β is used to incorporate prior knowledge of the distribution of  ${\bar X}$.
${\bar X}$.(3) Compute the predicted state mean and the predicted covariance as:
(24) $$\chi _i^x \left( {k,k - 1} \right) = {\,f}\left( {\chi _i \left( k \right),{U}\left( k \right)} \right)\quad $$(25)
$$\chi _i^x \left( {k,k - 1} \right) = {\,f}\left( {\chi _i \left( k \right),{U}\left( k \right)} \right)\quad $$(25) $${X}\left( {k,k - 1} \right) = \sum\limits_{i = 0}^{2n_x} {W_i^m \chi _i^x \left( {k,k - 1} \right)} = \sum\limits_{i = 0}^{2n_x} {W_i^m {\,f}\left( {\chi _i^x \left( {k - 1} \right)} \right)} $$(26)
$${X}\left( {k,k - 1} \right) = \sum\limits_{i = 0}^{2n_x} {W_i^m \chi _i^x \left( {k,k - 1} \right)} = \sum\limits_{i = 0}^{2n_x} {W_i^m {\,f}\left( {\chi _i^x \left( {k - 1} \right)} \right)} $$(26) $$\eqalign{{P}\left( {k,k - 1} \right) & = \sum\limits_{i = 0}^{2n_x} {W_i^c} \left[ {\chi _i^x \left( {k,k - 1} \right) - {\bar X}\left( {k,k - 1} \right)} \right] \cr & \left[ {\chi _i^x \left( {k,k - 1} \right) - {\bar X}\left( {k,k - 1} \right)} \right]^{\prime} + {Q}\left( {k - 1} \right)}$$(27)
$$\eqalign{{P}\left( {k,k - 1} \right) & = \sum\limits_{i = 0}^{2n_x} {W_i^c} \left[ {\chi _i^x \left( {k,k - 1} \right) - {\bar X}\left( {k,k - 1} \right)} \right] \cr & \left[ {\chi _i^x \left( {k,k - 1} \right) - {\bar X}\left( {k,k - 1} \right)} \right]^{\prime} + {Q}\left( {k - 1} \right)}$$(27) $${Z}_i \left( k \right) = {h}\left( {\chi _i} \right)\quad i = 0,...,2n_x $$(28)
$${Z}_i \left( k \right) = {h}\left( {\chi _i} \right)\quad i = 0,...,2n_x $$(28) $${\bar Z} = \sum\limits_{i = 0}^{2n_x} {W_i^m {Z}_i \left( k \right)} $$
$${\bar Z} = \sum\limits_{i = 0}^{2n_x} {W_i^m {Z}_i \left( k \right)} $$(4) Update the state mean and covariance as
(29) $${P}_{ZZ} = \sum\limits_{i = 0}^{2n_x} {W_i^c \left[ {{Z}_i \left( k \right) - {\bar Z}} \right]} \left[ {{Z}_i \left( k \right) - {\bar Z}} \right]^{\prime} + {R}\left( k \right)$$(30)
$${P}_{ZZ} = \sum\limits_{i = 0}^{2n_x} {W_i^c \left[ {{Z}_i \left( k \right) - {\bar Z}} \right]} \left[ {{Z}_i \left( k \right) - {\bar Z}} \right]^{\prime} + {R}\left( k \right)$$(30) $${P}_{XZ} = \sum\limits_{i = 0}^{2n_x} {W_i^c \left[ {\chi _i \left( {k,k - 1} \right) - {\bar X}\left( {k,k - 1} \right)} \right]} \sum\limits_{i = 0}^{2n_x} {W_i^c \left[ {\chi _i \left( {k,k - 1} \right) - {\bar X}\left( {k,k - 1} \right)} \right]} ^{\prime} $$(31)
$${P}_{XZ} = \sum\limits_{i = 0}^{2n_x} {W_i^c \left[ {\chi _i \left( {k,k - 1} \right) - {\bar X}\left( {k,k - 1} \right)} \right]} \sum\limits_{i = 0}^{2n_x} {W_i^c \left[ {\chi _i \left( {k,k - 1} \right) - {\bar X}\left( {k,k - 1} \right)} \right]} ^{\prime} $$(31) $${K}\left( k \right) = {P}_{XZ} {P}_{ZZ} ^{ - 1} $$(32)
$${K}\left( k \right) = {P}_{XZ} {P}_{ZZ} ^{ - 1} $$(32) $${X}\left( k \right) = {X}\left( {k,k - 1} \right) + {K}\left( k \right)\left[ {{Z}\left( k \right) - {\bar Z}} \right]$$(33)
$${X}\left( k \right) = {X}\left( {k,k - 1} \right) + {K}\left( k \right)\left[ {{Z}\left( k \right) - {\bar Z}} \right]$$(33) $${P}\left( k \right) = {P}\left( {k,k - 1} \right) + {K}\left( k \right){P}_{ZZ} \left( k \right){K^{\prime}}\left( k \right)$$
$${P}\left( k \right) = {P}\left( {k,k - 1} \right) + {K}\left( k \right){P}_{ZZ} \left( k \right){K^{\prime}}\left( k \right)$$
5.4. Data Fusion in the Master Filter
In the federated UKF filter, the process information Q−1(k) and P−1(k) are distributed between the local filters and the master filter as follows:
 $$\matrix{ {{{Q}_j}\left( k \right) = {\beta _j}^{ - 1} {Q}\left( k \right)} & {} \cr {} & {\,j = {\rm 1},{\rm 2}, m} \cr {{{P}_j}\left( k \right) = {\beta _j}^{ - 1} {P}\left( k \right)} & {} \cr } $$
$$\matrix{ {{{Q}_j}\left( k \right) = {\beta _j}^{ - 1} {Q}\left( k \right)} & {} \cr {} & {\,j = {\rm 1},{\rm 2}, m} \cr {{{P}_j}\left( k \right) = {\beta _j}^{ - 1} {P}\left( k \right)} & {} \cr } $$where m represents the master filter, β j is the information distribution coefficient and satisfies
 $$\sum\limits_{\,j = 1}^2 {\beta _j}+ \beta _m = 1$$
$$\sum\limits_{\,j = 1}^2 {\beta _j}+ \beta _m = 1$$In this paper, β m = 0. For β 1 and β 2, a simple determining rule is that when the number of measured tags is less than 4, β 1 = 0·05, β 2 = 0·95, else β 1 = 0·8, β 2 = 0·2.
Finally, all of the vehicle position estimations in every UKF local filter are fused in the master filter. The fused state estimation and the covariance matrix can be expressed as:
 $${P}_g \left( k \right) = \left[ {\sum\limits_{\,j = 1}^{2,m} {{P}_j^{ - 1} \left( k \right)}} \right]^{ - 1} $$
$${P}_g \left( k \right) = \left[ {\sum\limits_{\,j = 1}^{2,m} {{P}_j^{ - 1} \left( k \right)}} \right]^{ - 1} $$ $${\hat X}_g \left( k \right) = {P}_g \left( k \right)\sum\limits_{\,j = 1}^{2,m} {{P}_j^{ - 1} {\hat X}_j} $$
$${\hat X}_g \left( k \right) = {P}_g \left( k \right)\sum\limits_{\,j = 1}^{2,m} {{P}_j^{ - 1} {\hat X}_j} $$6. EXPERIMENTAL RESULTS
To validate and evaluate the performance of the proposed positioning algorithm, experiments were conducted on a Buick Sail SRV vehicle. It was equipped with RFID hardware devices sampled at 1 Hz, Crossbow MEMS-based IMU-440 inertial sensors sampled at 100 Hz as well as wheel speed sensors sampled at 100 Hz and an electronic compass sampled at 10 Hz. The sensor accuracies (1σ) are 0·1 m/s2 for the accelerometers and 0·20/s for the yaw rate sensor. Moreover, an accurate Differential GPS (DGPS) NovAtel L1L2/RT2 was used as a reference for performance evaluation.
6.1. Modelling of the relationship between RSS and distance
In the experiment, the RFID hardware devices, as shown in Figure 5, included one NWR-01 RFID reader with an antenna, and a number of NWI-01 active RFID tags (the operating frequency band is 417·05~435·9 MHz). The output frequency of RFID hardware devices is 1 Hz. The RSS range of a tag is normalised to 0–255, and the maximum measured distance of tag is 9 m. However, many experiments show that the RSS signal will deteriorate when the RFID tags are placed beyond 6 m from the reader, ergo the effective transmission distance of the RSS signal is 6 m. Therefore to ensure the reliability of the RSS signal the interval between tags is 6 m in this paper.

Figure 5. RFID hardware devices.
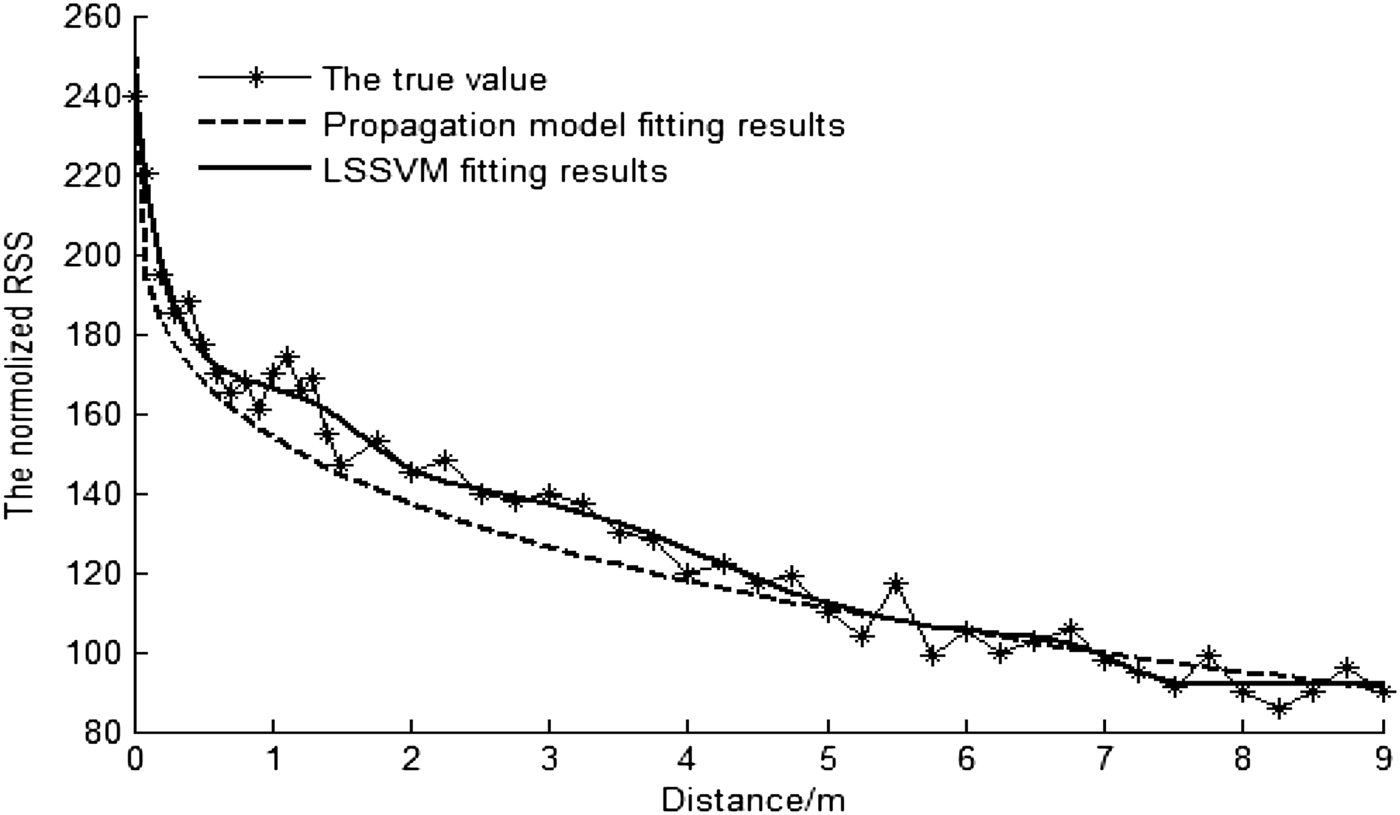
In different situations such as in the laboratory, the outdoor test site and a tunnel, we fit the curve that shows the relationship of RSS with distance between the reader and the active tag using LSSVM. The RSSs are collected at different distances between the tag and the reader. In the 0–1·5 m range, the collecting gap is 0·1 m, and in 1·5–9 m range, the collecting gap is 0·25 m. There are four tags at each collecting location, and the collecting time is five minutes. The average value of RSS is considered as the true RSS value of this location. For comparison, the propagation model-based algorithm utilising Friis transmission equation is also investigated. The fitting results of the relationship between RSS and distance in the outdoor test site is shown in Figure 6. The distance estimation errors in the tunnel are shown in Figure 7. In Figure 7, the distance estimation errors are compared in different values of RSS. The mean and Standard Deviation (STD) of the RSS fitting errors in different situations are shown in Table 1.

Figure 6. The fitting results of the relationship in outdoor test site.

Figure 7. The distance estimation errors in tunnel.
Table 1. The Mean and Standard deviation of the RSS fitting errors.

It can be seen in Figures 6 and 7 and Table 1 that the LSSVM achieves better performance than the propagation model, which can provide the more accurate distance information and improve the performance of the subsequent positioning algorithm. Especially in the tunnel, due to environmental effects such as multipath propagation, the estimation performance of the propagation model degrades significantly. The LSSVM achieves clearly better performance since the LSSVM is capable of learning in specific environments and has strong adaptability for different environments.
6.2. Experimental design
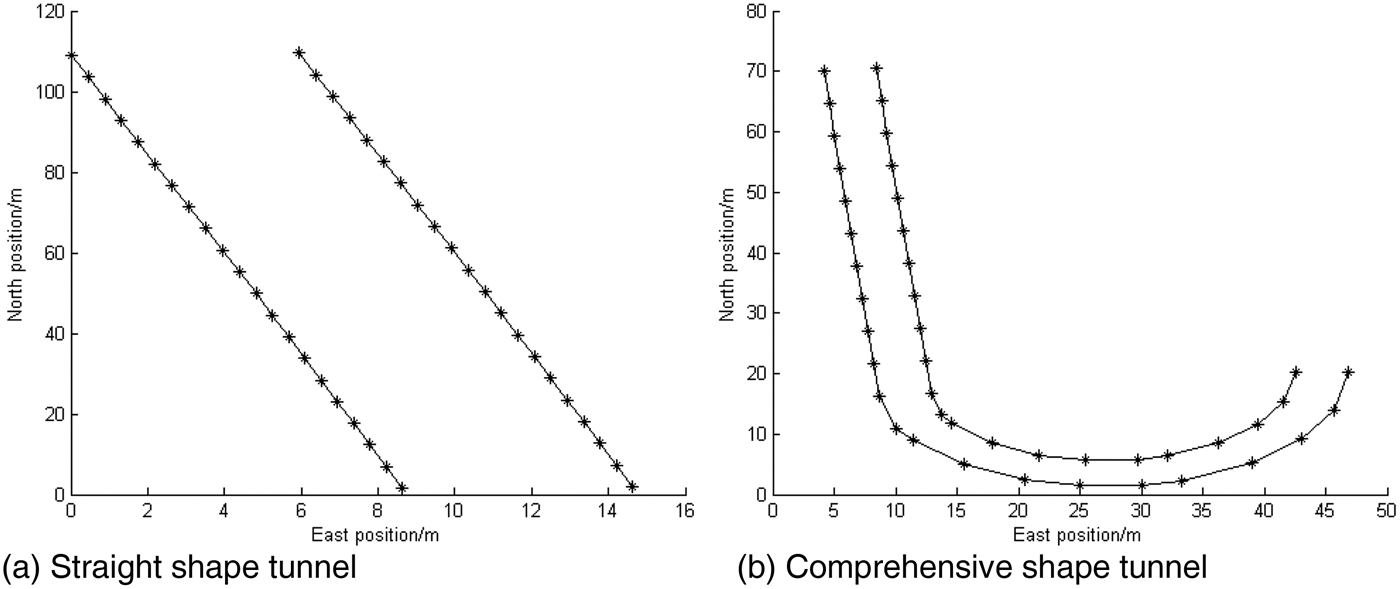
Because of experimental condition limitations, the simulated tunnels were set in outdoor open space so that the reference trajectory could be obtained by DGPS. The width of the tunnels is set to 6 m. To cover the different shapes of actual tunnels, the shapes of the tunnels are respectively set to straight shape and comprehensive shape (contains straight line and curvilinear part), as shown in Figure 8. In order to be easier to understand, the actual coordinates of start points are adjusted to the coordinate (0, 0) by adding some offsets, i.e., for the straight shape tunnel the coordinate (0, 0) indicate the actual coordinate (East: 2822, North: −18060), and all the coordinates in the figure convert to the actual coordinates needed to add the offset (2822, −18060). For the comprehensive shape tunnel, the offset is (2830, −18020). This also applies to the following diagram of trajectories.

Figure 8. The setting shape of the tunnels.
In Figure 8, the symbol “*” represents the active RFID tags, and tags are placed on both sides of the tunnel edge. For RFID-EKF and Fusion-EKF, the gap along the direction of the tunnel between adjacent tags is 6 m. For FUKF, the number of tags is obviously reduced, as shown in Figure 9.

Figure 9. The tag layout for FUKF.
During the experiments, all sensor data were collected, and the positioning algorithm was evaluated using the logged data.
6.3. Validation of Positioning Performance
6.3.1. Performance of RFID-EKF
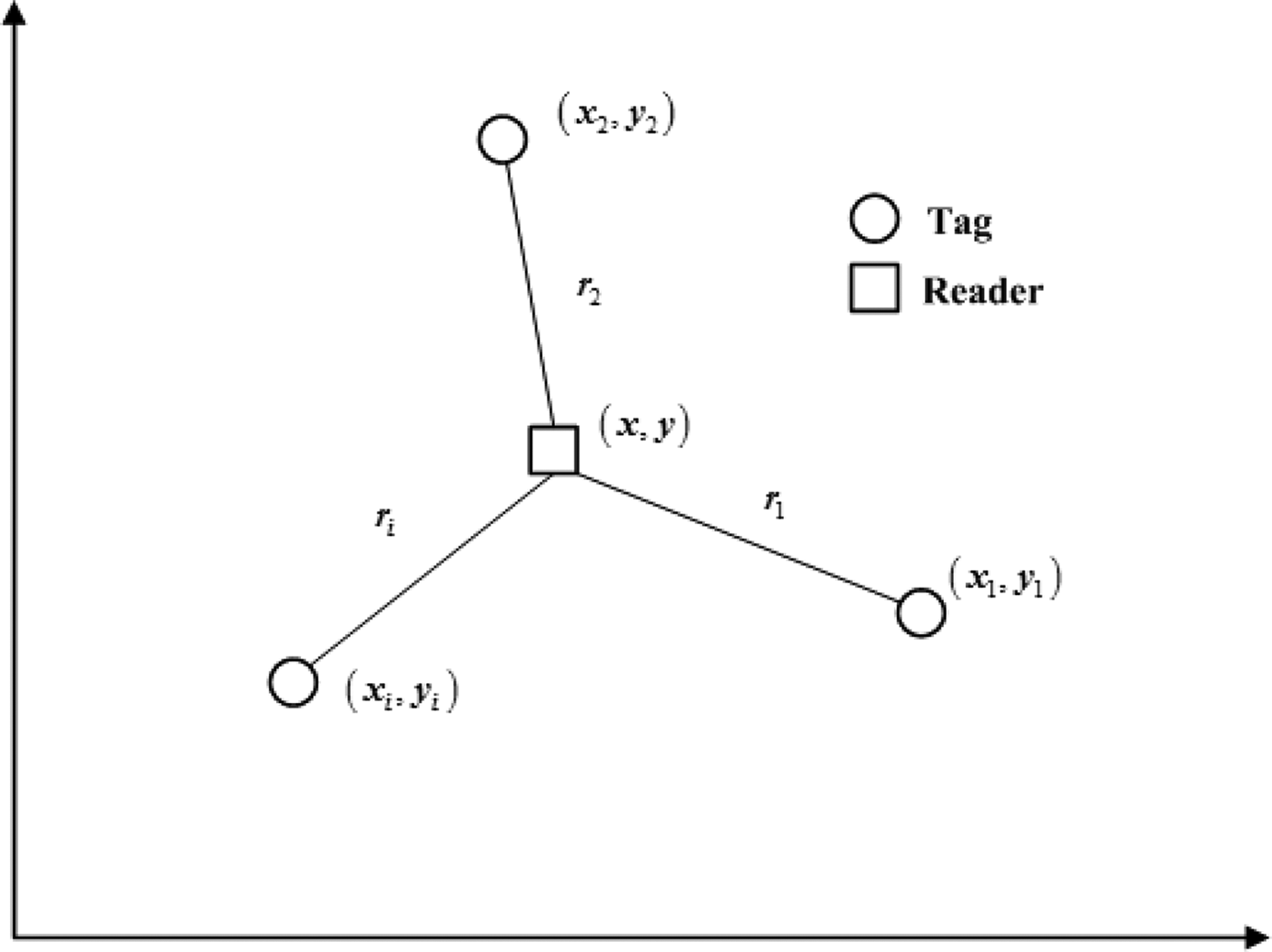
To verify and validate the feasibility of RFID used for vehicle positioning in a tunnel, the RFID-EKF algorithm discussed above is first evaluated through experiments. Moreover, to evaluate the effect of RFID-EKF, the multi-lateration method is also investigated for comparison. The multi-lateration method is the most widely used method for indoor location. Figure 10 shows the schematic of 2-D localisation using multi-lateration.

Figure 10. Schematic of multi-lateration method.
From Figure 10, if there are i tags (i> = 3) with known coordinates (x i, yi), and the distances between the reader with unknown coordinates (x, y) and tags are estimated to be r i, we can obtain:
 $$\left\{ \matrix{r_1^2 = \left( {x - x_1^2} \right)^2 + \left( {y - y_1^2} \right)^2 \hfill \cr r_2^2 = \left( {x - x_2^2} \right)^2 + \left( {y - y_2^2} \right)^2 \hfill \cr \quad \quad \quad \quad \quad... \hfill \cr r_i^2 = \left( {x - x_i^2} \right)^2 + \left( {y - y_i^2} \right)^2 \hfill} \right.$$
$$\left\{ \matrix{r_1^2 = \left( {x - x_1^2} \right)^2 + \left( {y - y_1^2} \right)^2 \hfill \cr r_2^2 = \left( {x - x_2^2} \right)^2 + \left( {y - y_2^2} \right)^2 \hfill \cr \quad \quad \quad \quad \quad... \hfill \cr r_i^2 = \left( {x - x_i^2} \right)^2 + \left( {y - y_i^2} \right)^2 \hfill} \right.$$By solving this equation group, the coordinates of the reader can be calculated.
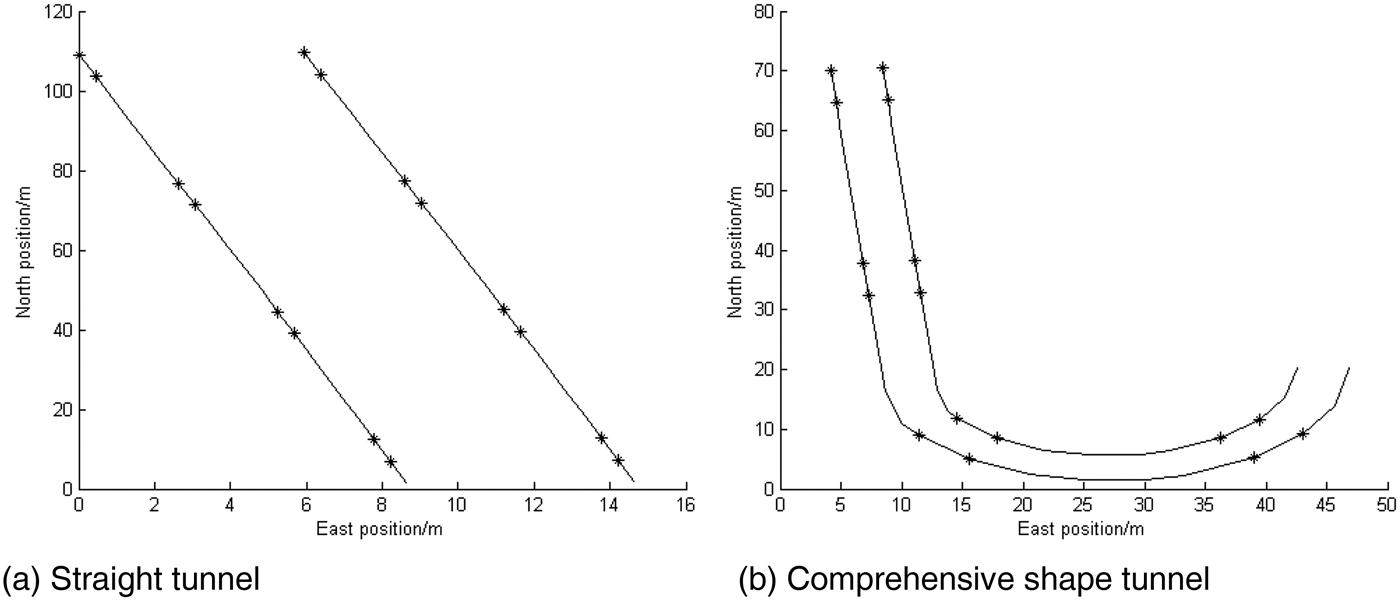
The reference and estimated vehicle trajectories in a comprehensive shape tunnel test are shown in Figure 11, the Euclidean distance errors are shown in Figure12.

Figure 11. The vehicle trajectories.

Figure 12. The Euclidean distance errors.
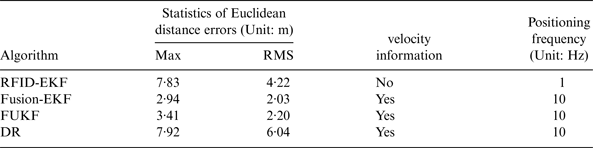
From Figures 11 and 12 it can be seen that the performance of RFID-EKF is clearly improved compared with that of multi-lateration. However, from Figure 12, we can see that the positioning errors are large when the vehicle is outside the tunnel (0–6 s and 69–76 s). This is because the reader cannot detect enough tags in these areas, i.e., the number of tags is less than three. Table 2 shows statistics of Euclidean distance errors when the vehicle is driving in the tunnel (7–68 s).
Table 2. Statistics of Euclidean distance errors (Unit: m).

From Table 2, we can see that when the vehicle is driving in the tunnel, the Root Mean Square (RMS) value of the Euclidean distance error of RFID-EKF algorithm is decreased to 5·07 m, i.e., about 48% accuracy improvement over the multi-lateration method, and the max value of the Euclidean distance error of RFID-EKF algorithm is obviously reduced to 9·27 m from the value 20·18 m of multi-lateration. This performance can meet the positioning requirement of actual driving situations since the GPS is available outside the tunnel. The further statistics and analysis of RFID-EKF will be described in the next section.
However, there are some wild values in Figure 12 that can be attributed to the RSS measurements being severely contaminated with large temporal variations. The smoothing and filtering ability of EKF can partly compensate the adverse influence on the positioning performance. Due to the poor correction effect of EKF, a further improvement may be to rely on the fusion with the in-vehicle sensors and the more advanced algorithm.
6.3.2. Straight line driving test
For preliminary validation and evaluation of the performance of the proposed algorithm, a total of nine straight line driving tests were carried out. The straight line driving test situations include acceleration, deceleration and uniform motion under different vehicle speeds. For brevity, only one test is shown here as an example because similar conclusions can be obtained by other tests. A DR-based algorithm which only uses the in-vehicle sensors to reckon the vehicle's position is also investigated for comparison. The reference and estimated vehicle trajectories in the experiment are shown in Figure 13. Figure 14 illustrates the Euclidean distance errors of four algorithms. For four positioning algorithms, i.e., RFID-EKF, Fusion-EKF, FUKF and DR, Table 3 gives their performances.

Figure 13. Vehicle trajectories.

Figure 14. The Euclidean distance errors.
Table 3. The positioning performance of different algorithms.

From Table 3, it is clear that DR has the worst positioning performance, i.e., both the maximum and RMS values of its Euclidean distance error are the largest. The reason is that the DR algorithm will accumulate large errors over time due to factors such as measurement errors and the characteristics of the integration process.
RFID-EKF can achieve better performance than DR. However, the maximum value of its Euclidean distance error is large. The reason is that the estimation results of the distances between tags and reader contain a lot of noise, and sometimes the tags can fail.
Among the four algorithms, the Fusion-EKF achieves the optimal accuracy and reliability. For example, the RMS value of Euclidean distance error of Fusion-EKF is reduced to 2·03 m from the value 4·22 m for RFID-EKF. It can be attributed to the fact that the in-vehicle sensors provide more accurate and richer vehicle state information for fusion positioning, which can remarkably improve the system observability and enhance the positioning reliability. Meanwhile, its positioning frequency is increased to 10 Hz from the 1 Hz value of RFID, and velocity information can be provided. Compared to DR, the RMS value of the Euclidean distance error of Fusion-EKF has about 66% accuracy improvement; this is because the position observation by RFID is compensated for the accumulated errors.
For the FUKF, its positioning accuracy is clearly improved compared with that of RFID-EKF and DR. For instance, the RMS value of Euclidean distance error of FUKF is decreased to 2·20 m, i.e., about 48% accuracy improvement over RFID-EKF and 64% accuracy improvement over DR. The positioning performance of FUKF is approximately the same as that of Fusion-EKF. However, the number of tags is reduced to 16 from 42 for Fusion-EKF, and thus the cost is remarkably reduced with very little sacrifice of accuracy.
The experiment's results show that the Fusion-EKF and FUKF can achieve better performance than the RFID-EKF and DR. Due to the in-vehicle sensors, the velocity and heading angle information can be provided by the algorithms, and the positioning frequencies of Fusion-EKF and FUKF are increased to 10 Hz from the 1 Hz value of RFID-EKF.
To achieve balance between positioning accuracy and costs, FUKF is considered to be the most appropriate algorithm in actual application.
6.3.3. Comprehensive test
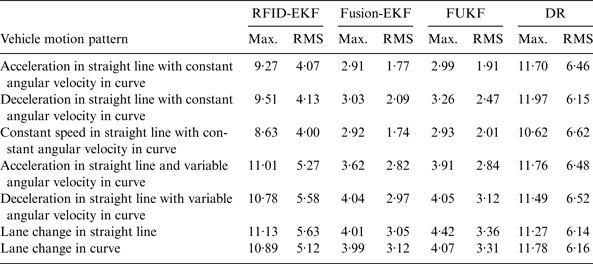
For further validaton and evaluation of the performance of the proposed algorithm, the comprehensive test scenario contains the straight line situation and the curvilinear situation. In order to cover the different typical motion patterns of vehicles in a tunnel, i.e., straight line (acceleration or deceleration), curve, and lane change etc, a total of 21 comprehensive tests have been carried out. The statistics of the Euclidean distance errors are summarised in Table 4.
Table 4. Statistics of Euclidean Distance Errors in comprehensive test (Unit:m).

From Table 4, it is clear that Fusion-EKF achieves the optimal performance, and the positioning accuracy of FUKF is approximately the same as that of Fusion-EKF with fewer costs. As an example, the vehicle trajectories in a test are shown in Figure 15.

Figure 15. The reference and estimated vehicle trajectories in a comprehensive test.
From Table 4 and Figure 15, similar conclusions can be obtained as the straight line test. Due to the improved vehicle motion model, Fusion-EKF and FUKF can adapt to the comprehensive shape tunnel containing both a straight line part and curvilinear part. The experiments results show that the FUKF algorithm can achieve better positioning performance than the RFID-EKF and DR. Although the positioning accuracy of FUKF is slightly lower than Fusion-EKF, the cost of FUKF is remarkably reduced over Fusion-EKF.
The low-cost GPS is the most widely used vehicle positioning sensor with accuracies of (1σ) of about 3 m for position. From Table 4, we can see that the positioning accuracy of FUKF is approximately the same as that of low-cost GPS with higher frequency. Therefore, the positioning performance of FUKF can meet the requirement of vehicle positioning in a tunnel when low-cost GPS is unavailable.
To further evaluate the performance of vehicle speed estimation, Figure 16 shows that the comparison of vehicle speed errors between the raw sensor data measured by the wheel speed sensors and the estimation results from the proposed algorithm. The speed measured by DGPS was used as the true value. It can be seen in Figure 16, through the filtering process of UKF, that the speed accuracy can be significantly improved over the measured results of wheel sensors.

Figure 16. The speed errors of raw sensor data and estimated results.
In summary, taking into consideration the positioning performance and costs, FUKF is the most feasible method for practical application due to its low cost and high accuracy.
7. CONCLUSIONS
To realise accurate positioning for vehicles in a tunnel, this paper has presented a RFID/ in-vehicle sensors-integrated vehicle positioning strategy. The strategy employs a two-step approach, namely, the calculation of the distances between the RFID tags and the reader based on RSS, and then the global fusion estimation of vehicle position.
In the proposed strategy, both a distance estimation algorithm and a global fusion algorithm have been developed. First, the LSSVM algorithm is developed to obtain distance between RFID tag and reader based on RSS, which can provide accurate observation data for the subsequent global fusion. Further, the federated UKF algorithm has been proposed to realise the global fusion. To derive the global fusion algorithm, RFID-EKF and Fusion-EKF algorithm are designed. In the federated UKF algorithm, both positioning performance and costs are taken into consideration. The decentralised federated filter is adopted to reduce the number of tags, and UKF is employed to design the local filter due to its better ability to deal with nonlinear problems than EKF. For the proposed strategy, the effectiveness of both its distance estimation and global fusion algorithms has been comprehensively verified. During GPS outages in a tunnel, the proposed strategy has shown more obvious advantages and achieved more accurate and reliable performance compared with other methods.
The proposed vehicle positioning algorithms for use in a tunnel can equally be adapted to other GPS-denied environments such as urban areas. It should be noted that the experiments were only conducted in an outdoor environment rather than real enclosed environments due to the limitation of our experimental conditions. In enclosed environments, the multipath phenomenon may seriously affect the reliability of RFID, for example, the RSS measurements are severely contaminated with large temporal variation. Meanwhile, the low output frequency of RFID and the dynamic characteristic may affect sensor fusion severely. Future work will focus on these problems, including how to deal with out-dated information and how to meet the requirements of the wide driving-manoeuvre range of vehicle operation in the actual tunnel environments, and how to fuse other information to further enhance performance.
ACKNOWLEDGMENTS
This work is supported by the National Natural Science Foundation of China (Grant No. 61273236), the Jiangsu Planned Projects for Postdoctoral Research Funds (Grant No. 1401012C), the Fundamental Research Funds for the Central Universities (Grant No. 2242015R20017) and the Project Funded by China Postdoctoral Science Foundation (Grant No. 2015M571631).