Lagrangian approach to nonlinear waves in non-dispersive and dispersive rotating shallow water magnetohydrodynamics

Abstract

A Lagrangian approach to both hydrostatic non-dispersive in the short-wave range and non-hydrostatic dispersive rotating shallow-water magnetohydrodynamics is developed, and used to analyse weakly and fully nonlinear waves described by the model. Hyperbolic structure in the non-dispersive case is displayed and Riemann invariants are constructed. Characteristic equations are used to establish criteria of breaking and formation of shocks by magneto-gravity waves, and conditions of the appearance of contact discontinuities in Alfvén waves. As in the case of non-magnetic rotating shallow water, rotation cannot prevent breaking. The Lagrangian equations of the model are reduced to a single partial differential ‘master’ equation, which is used to analyse the propagation of weakly nonlinear waves of both families, with or without weak rotation, and with or without weak short-wave dispersion. Corresponding modulation equations are constructed and their main properties sketched. The same master equation is used to obtain fully nonlinear finite-amplitude wave solutions in particular cases of no short-wave dispersion or no rotation.

1. Introduction

A rotating shallow water magnetohydrodynamics, or magnetic rotating shallow water (MRSW), model was proposed by Gilman (2000) for a simplified description of non-dissipative dynamics of the solar tachocline and is being used to model various astrophysical phenomena, e.g. see the recent works of Magill et al. (2019) and Petrosyan et al. (2020). As the ‘pure’ shallow water model, rotating (RSW) or not (SW), MRSW can be obtained by vertical averaging of the full ‘parent’ equations, which are in this case the equations of magnetohydrodynamics (MHD) in the rotating frame. The averaging is performed between a pair of material surfaces, which should be at the same time magnetic surfaces, using (magneto-)hydrostatic and columnar motion approximations (Dellar 2002; Zeitlin 2013). The hydrostatic approximation, which is the basis for the standard RSW and MRSW models can be relaxed, and non-hydrostatic corrections can be taken into account perturbatively, assuming that non-dimensional thickness is sufficiently small, i.e. the layer is sufficiently shallow. If applied to the non-magnetic shallow-water model, this gives the well-known Serre–Green–Naghdi (SGN) equations (Serre 1953; Green & Naghdi 1976). A fundamental difference between SW and SGN equations is that linear non-dispersive gravity waves of the former acquire short-wave dispersion in the latter. As a consequence, if nonlinear, the gravity waves do not break forming shocks, as in SW, but rather form sharp fronts followed by rapidly oscillating wave-tails, see e.g. LeMetayer, Gavriliuk & Hank (2010), which become soliton tails in the limit of weak nonlinearity when the SGN system leads to the famous Korteweg–de Vries (KdV) equation in the case of unidirectional waves. If rotation is introduced in SW, it produces a long-wave dispersion which does not prohibit breaking of inertia-gravity waves (Zeitlin, Medvedev & Plougonven 2003). In the limit of weak nonlinearity and weak dispersion due to rotation, the RSW equations give the reduced Ostrovsky equation, also called Ostrovsky–Hunter or Vakhnenko equation, see Grimshaw, Helfrich & Johnson (2012) and references therein, which is integrable in a range of parameters, but also exhibits wave breaking in another range. In the limit of weak nonlinearity and weak dispersion due to rotation, the rotating SGN equations (rSGN) give the full Ostrovsky equation (Ostrovsky 1978), which is also called rotation-modified KdV, and does not allow for soliton solutions, see e.g. Galkin & Stepanyants (1991).

However, while fully nonlinear waves inevitably break in non-dispersive SW, the long-wave dispersion due to rotation is known to be sufficient to grant steady-propagating wave solutions in the non-magnetic RSW model, see Shrira (1981, 1986). These waves are nonlinear counterparts of harmonic linear inertia-gravity waves, to which they tend in the limit of vanishing nonlinearity. Soliton and cnoidal wave solutions are known in non-rotating SGN model, giving in the limit of small nonlinearity corresponding solutions of the KdV equation, and there exists extensive literature on this subject, see e.g. Choi & Camassa (1999), Deng, Guo & Wang (2013), Dutykh & Ionescu-Kruse (2016) and Zhang, Shi & Han (2020).

A natural question arises as to whether all these facts can be transposed from the RSW to MRSW model. The relaxation of hydrostatic approximation was first applied to MRSW by Dellar (2003), who thus derived a dispersive (rotating) shallow water magnetohydrodynamics (DMRSW) model and analysed its basic properties, including the linear wave spectrum. Nonlinear wave solutions of the model in the non-rotating limit were also sketched. An alternative derivation of DMRSW based on the Hamiltonian formulation of the MHD equations and its reduction to columnar motion was also given. As for the finite-amplitude waves, it was shown by Shecter, Boyd & Gilman (2001), see also Zeitlin, Lusso & Bouchut (2015), that the above-mentioned solutions of the RSW equations can be generalized to the MRSW model, with appearance of a second family of such waves in the presence of a mean magnetic field.

A linear wave spectrum of the non-rotating hydrostatic MSW model consists of non-dispersive magneto-gravity waves and transverse Alfvén waves. In the presence of rotation, they become low- and high-frequency branches of magneto-inertia-gravity waves, see e.g. Zeitlin et al. (2015), which are weakly dispersive in the long-wave range and non-dispersive in the opposite short-wave range. Non-hydrostatic corrections in DMRSW lead to dispersion in the short-wave sector (Dellar 2003), same as in the rSGN system.

The purpose of the present paper is to investigate the interplay between the effects of nonlinearity, rotation and deviations from hydrostatics upon the two species of waves in MSW: magneto-gravity and Alfvén waves. On the one hand, we will analyse the situation when all of these effects are weak and derive the corresponding modulation equations for the quasi-linear waves. On the other hand, we will track the influence of the dispersion and magnetic field on the fully nonlinear wave solutions known in RSW, as well as the influence of the magnetic field on the essentially nonlinear phenomenon of wave-breaking and shock formation.

Usually, the first approach to such kinds of studies is to work in the simplest one-dimensional configuration. However, inclusion of the transverse component of velocity is unavoidable because of rotation, so we will use the so-called 1.5D MRSW model with no dependence on one of the spatial coordinates, but with velocity along this coordinate maintained (Zeitlin et al. 2015), along the lines of Zeitlin et al. (2003), where the RSW model was analysed in this way. It happens that the Lagrangian approach, which was fully exploited by Zeitlin et al. (2003) and was briefly sketched by Zeitlin et al. (2015) for the 1.5D MRSW model, provides a universal and handy framework for studying the model and, by allowing the reduction of the whole DMRSW system to a single nonlinear partial differential equation (PDE), the ‘master equation’, which leads to considerable conceptual and technical simplifications with respect to the standard Eulerian approach. Thus, by applying the Lax (1973) method to fully nonlinear Lagrangian equations of the model, we will be able to show that rotation and mean magnetic field combined cannot prevent breaking of magneto-gravity waves and formation of shocks, and that Alfvén waves do not break, but can form tangential discontinuities in the wake of shocks. By applying the method of multiple time scale asymptotic expansions to the master equation, we will be able to show that weakly nonlinear non-hydrostatic magneto-gravity waves in the presence of rotation and mean magnetic field obey the same Ostrovsky equation as their non-magnetic counterparts, while Alfvén waves in the same regime remain linear, but acquire rotation-induced dispersion. We will also show how the known finite-amplitude stationary-wave solutions of the system can be easily obtained from the master equation.

The paper is organized as follows. In § 2, we recall the MRSW and DMRSW models, proceed by their 1.5D reduction and develop Lagrangian formulation of the resulting systems. We then reduce the DMRSW system, without any approximation, to a single equation for displacements of Lagrangian parcels. In § 3, we show that the non-dispersive MRSW is a hyperbolic system and obtain conditions for wave-breaking and shock formation. In § 4, applying an appropriate scaling, we develop a perturbation theory in the amplitude of the Lagrangian displacements, considering the rotation and/or non-hydrostatic effects to be weak or just absent. We thus obtain, in the leading order, the modulation equations for the amplitudes of propagating waves of the both above-mentioned families in the following dynamical regimes: (1) hydrostatic non-rotating; (2) hydrostatic weakly rotating; (3) weakly non-hydrostatic non-rotating; and (4) weakly non-hydrostatic weakly rotating, and briefly sketch their properties. In § 5, we find exact fully nonlinear wave solutions of the system in various limiting cases and discuss their characteristics. Section 6 contains a summary of the obtained results and a discussion.

2. The DMRSW model, the 1.5D reduction and the Lagrangian formulation

2.1. The model and its 1.5D reduction

The equations of the DMRSW model in the rotating $(x,\,y)$ plane read (Dellar 2003):

(2.1)$$\begin{gather} D_{t} \boldsymbol{v} + f \hat{\boldsymbol{z}} \wedge \boldsymbol{v}+ g \boldsymbol{\nabla} h = \frac{1}{h} \boldsymbol{\nabla} ( h \boldsymbol{b} \otimes \boldsymbol{b} ) + \frac{1}{3h} \boldsymbol{\nabla} [-h^{2} D^{2}_{t}h + h^{3} (\boldsymbol{\nabla} \boldsymbol{\cdot} \boldsymbol{b})^{2} - h^{3} \boldsymbol{b}\boldsymbol{\cdot} \boldsymbol{\nabla} (\boldsymbol{\nabla} \boldsymbol{\cdot} \boldsymbol{b})], \end{gather}$$

(2.2)$$\begin{gather}D_{t}h + h {\boldsymbol{\nabla}} \boldsymbol{\cdot} \boldsymbol{v} = 0, \end{gather}$$

(2.3)$$\begin{gather}\boldsymbol{\nabla} \boldsymbol{\cdot} ( h \boldsymbol{b} ) = 0, \end{gather}$$

(2.4)$$\begin{gather}D_{t} \boldsymbol{b} = \frac{1}{h} \boldsymbol{\nabla} ( h \boldsymbol{v} \otimes \boldsymbol{b} ) , \end{gather}$$

where $D_{t} =\partial _{t}\boldsymbol {v} + \boldsymbol {v}\boldsymbol{\cdot}\boldsymbol {\nabla }$ is the material (Lagrangian) derivative, $f$ is the Coriolis parameter and $g$ is the gravity acceleration. (We used (2.2) to replace $h {\boldsymbol {\nabla }} \boldsymbol{\cdot} \boldsymbol {v}$ by $-D_{t}h$ in (2.1).) The dynamical variables of the model are the thickness of the layer $h$, the velocity $\boldsymbol {v} = u\hat {\boldsymbol {x}} + v \hat {\boldsymbol {y}}$ and the magnetic field $\boldsymbol {b}= a\hat {\boldsymbol {x}} + b \hat {\boldsymbol {y}}$ in the plane, where $(\hat {\boldsymbol {x}}, \hat {\boldsymbol {y}}, \hat {\boldsymbol {z}})$ are unit vectors along the respective axes, $\boldsymbol {\nabla } = \hat {\boldsymbol {x}} \partial _{x}+ \hat {\boldsymbol {y}} \partial _{y}$. The notation $\boldsymbol {\nabla } ( \boldsymbol{\mathsf{A}} \otimes \boldsymbol{\mathsf{B}} )$ is a shorthand for tensor notation: the $i$th component of such an expression is given by $\partial _{j} A_i B_j$, with summation over repeated indices from 1 to 3. We will work in the $f$-plane approximation, where Coriolis parameter $f$ is constant. According to the standard in geophysics conventions, $x$ and $y$ coordinates will be called zonal and meridional, respectively, and the components of the vector fields will be called correspondingly. The difference between DMRSW and (magneto)hydrostatic MRSW models resides in the last term on the right-hand side of (2.1), which is absent in the latter model.

The 1.5D reduction of this system consists in eliminating all dependence on one of the spatial coordinates, which we choose to be the zonal one, in a way that $\partial _{x}(\ldots ) \equiv 0$ for any quantity. It is easy to see that, as follows from (2.3) and (2.4), under this hypothesis, the meridional component of the magnetic field ceases to be independent:

(2.5)\begin{equation} hb = B H = \text{const.}\ \Rightarrow\ b = \frac{B H}{h}, \end{equation}

where $H$ is the mean thickness of the layer and $B$ is a mean meridional magnetic field. In fact, as magnetic fields in the DMRSW system, as it is written in (2.1)–(2.4), have dimensions of velocity, $B$ is at the same time the Alfvén wave speed $c_{a}$. Using (2.5) , the 1.5D DMRSW is written, in components, as

(2.6)\begin{align} \left.\begin{array}{c@{}} D_{t} u - f v =\displaystyle \dfrac{B}{h} a_{y},\\ D_{t}v + f u + g h_{y}= \displaystyle \dfrac{B}{h} \left(\displaystyle \dfrac{B}{h} \right)_{y} + \displaystyle \dfrac{1}{3 h} \left[ - h^{2}D^{2}_{t} h + h \left( \left[\left(\displaystyle \dfrac{B}{h} \right)_{y}\right]^{2} - \displaystyle \dfrac{B}{h} \left(\displaystyle \dfrac{B}{h} \right)_{yy} \right)\right]_{y},\\ D_{t} a = \displaystyle\dfrac{B}{h} u_{y},\\ D_{t}h + (v h)_{y} = 0, \end{array} \right\} \end{align}

where we used the shorthand notation $\partial _{y}(\ldots ) \equiv (\ldots )_{y}$, and from now on, $D_{t}= \partial _{t} + v \partial _{y}$. An analogous system, with the only difference that variables were not depending on $y$ instead of $x$, was used by Dellar (2003) for a study of the linear wave spectrum. We should stress that in the $f$-plane approximation we are using, the orientation of the coordinate axes is arbitrary, so $y$ could also be considered as a zonal coordinate. In this case, $v$ becomes the zonal velocity, $-u$ becomes meridional velocity, and $b$ and $-a$ are zonal and meridional components of the magnetic field. Then, in the absence of a magnetic field, the resulting system becomes the one considered by Zeitlin et al. (2003). Let us also mention that the $f$-plane approximation in (2.6) can be relaxed and the Coriolis parameter considered as a linear function of $y$: $f = f_{0} + \beta y$. The beta-plane approximation is appropriate for large-scale motions, which are sensible to the planet/star curvature. Non-hydrostatic effects are unimportant in such a case, so maintaining them in the equations of motion is not justified. As our goal is to study the simultaneous influence of non-hydrostatic and rotation effects, and in addition rotation will be considered weak in § 4, we will stick to the $f$-plane in what follows.

2.2. Lagrangian formulation of the 1.5D DMRSW model and scaling

Let us recall that in the Lagrangian description of the 1.5D RSW model (Zeitlin et al. 2003), the motion of the fluid layer is described in terms of the trajectories of Lagrangian parcels – fluid columns of variable depth $h$ with current positions $Y(y_{0},\tau )$ depending on the initial position $y_{0}$, the Lagrangian label, and on time $\tau$. The fluid motion, thus, is a time-dependent mapping of the domain of the flow, the whole $y$-axis in the present case, onto itself. According to the principle of Euler–Lagrange duality in hydrodynamics, the Lagrangian velocity of the fluid parcels $\partial _{\tau }Y \equiv \dot {Y}$ is the Eulerian velocity $v$ measured at the point $y = Y$. From now on, we will be using the dot and the prime notation respectively for the derivatives of Lagrangian variables with respect to time and with respect to space labels. The mass conservation in Lagrangian terms is just the conservation of the volume of the parcel, i.e. its area in the 1.5D case:

(2.7)\begin{equation} h(Y)\,{\rm d}Y = h_{0} \,{\rm d}y_{0}, \end{equation}

where $h_{0}$ is an initial thickness distribution. In what follows, we identify the above-used Eulerian coordinate with $Y$ and reserve the notation $y$ for the so-called mass-weighted coordinate (label) which is obtained from $y_{0}$ by a change of variables ‘straightening’ the initial thickness: $h_{0} \rightarrow H = \textrm {const.}$, see Zeitlin et al. (2003). Thus,

(2.8)\begin{equation} h(Y)\,{\rm d}Y = H\,{\rm d}\kern0.05em y,\quad \rightarrow\quad h(Y) = \frac{H}{J},\quad J := \frac{\partial Y}{\partial y} \equiv Y', \end{equation}

where we introduced the Jacobian $J$ of the Lagrangian mapping. Notice that, as follows from the definition (2.8),

(2.9)\begin{equation} \dot{Y} = v(y,\tau). \end{equation}

We are now ready to rewrite (2.6) in Lagrangian form. We should emphasize that a Lagrangian description of the full (non-dissipative) three-dimensional MHD is known, and had been used in the seminal paper of Newcomb (1962) to construct an action principle for MHD. We should also mention in passing that the DMRSW equations could be directly obtained from this action by using mass-weighted coordinates, restricting vertical integration to a layer of finite depth and imposing the hypothesis of columnar motion, similar to the procedure leading to rSGN equations from the action principle for non-dissipative hydrodynamics, cf. e.g. Dellar & Salmon (2005). We, however, do not need such full machinery in the present 1.5D situation. There is no Lagrangian motion in the transverse direction, so it is sufficient to make a change of variables $Y \rightarrow y$ in the zonal fields $u$ and $a$, similar to what was done in ‘pure’ 1.5D RSW (Zeitlin et al. 2003), while the Lagrangian expression of the meridional magnetic field is already given by (2.5) and (2.8). The Lagrangian equations of the DMRSW model thus read:

(2.10)\begin{equation} \left.\begin{array}{c@{}} \ddot{Y} + f u + \displaystyle\dfrac{g H}{Y'} \left( \dfrac{1}{Y'}\right)' - c^{2}_{a}Y'' = \dfrac{H^{2}}{3} \left[ - \dfrac{1}{Y'^{2}}\ddot{\left( \dfrac{1}{Y'}\right)} + \dfrac{c^{2}_{a}}{Y'^{2}} \left( \dfrac{1}{Y'}\right)''\right]',\\ \dot{u} - f \dot{Y} - c_{a} a'=0,\\ \dot{a} - c_{a} u' = 0. \end{array} \right\} \end{equation}

The Lagrangian equations of the MRSW model are the same, modulo the term on the right-hand side of the first equation which should be set to zero in this case.

Notice that if the $f$-plane approximation is relaxed as explained earlier, the substitution $f \rightarrow f_{0} + \beta Y$ should be made in (2.10), with $f_{0} \equiv 0$ on the equatorial beta plane.

It is useful for what follows to rewrite this system in terms of variables $u,\ v,\ J, a$:

(2.11)\begin{equation} \left.\begin{array}{c@{}} \dot{v} + f u - \displaystyle \dfrac{g H}{J^{3}} J' - c^{2}_{a}J' = \dfrac{H^{2}}{3} \left[ - \dfrac{1}{J^{2}}\ddot{\left( \dfrac{1}{J}\right)} + \dfrac{c^{2}_{a}}{J^{2}} \left( \dfrac{1}{J}\right)''\right]',\\ \dot{J} - v' = 0,\\ \dot{u} - f v - c_{a} a'=0,\\ \dot{a} - c_{a} u' = 0. \end{array} \right\} \end{equation}

Notice that if $c_{a}\equiv 0$ and non-hydrostatic effects (the right-hand side of the first equation of each system) are neglected, (2.10) and (2.11) become the Lagrangian equations for 1.5D RSW obtained by Zeitlin et al. (2003) (only there, they were equations for zonal and not meridional motion). At the same time, setting $c_{a}\equiv 0$ and keeping the non-hydrostatic terms gives Lagrangian formulation of the rSGN model. A crucial difference of (2.10) with (2.11) is the non-conservation of the geostrophic momentum $M = u - f\kern0.07em Y$ which, in turn, means non-conservation of potential vorticity, a known fact for MRSW and DMRSW (Dellar 2003) which becomes obvious in Lagrangian description. The conservation of the geostrophic momentum allowed Zeitlin et al. (2003) to express the transverse velocity in terms of the Lagrangian position and thus obtain, without any approximations, a closed nonlinear second-order in time equation for the latter, which contained the entire evolution of the system. In the present case, the extra variables can be also eliminated in favour of $Y$, but due to the non-conservation of the geostrophic momentum, the resulting equation is of the fourth order in time. Indeed, cross-differentiating the second and the third equations in (2.10) gives

(2.12)\begin{equation} \ddot{u} - c^{2}_{a}u'' = f \ddot{Y}, \end{equation}

and, therefore, $u$ can be eliminated from the equation for $Y$ by additional differentiations.

Let us proceed with the scaling of the resulting equations. For our purposes, we use the ‘wave’ scaling based on the horizontal scale $L$, vertical scale $H$ and the velocity scale based on the maximal velocity of gravity waves:

(2.13a–c)\begin{equation} y \sim L,\quad u \sim \sqrt{g H}, \quad t \sim L/\sqrt{g H}. \end{equation}

Two characteristic non-dimensional parameters can be built from these scales and the Coriolis parameter $f$:

(2.14a,b)\begin{equation} \gamma = Bu^{-1/2} = \frac{f\kern0.06em L}{\sqrt{g H}}, \quad \delta= \frac{H}{3 L}, \end{equation}

the first being the non-dimensional Coriolis parameter, and at the same time the inverse square root of the Burger number, and the second being the effective shallowness of the layer. They control respectively the rotation and non-hydrostatic effects. It is also helpful, cf. Zeitlin et al. (2003), to introduce the deviations $\phi (\tau, y)$ of the Lagrangian parcels from their initial positions: $Y = y + \phi$. The system of non-dimensional equations for $\phi$ and $u$ reads:

(2.15)$$\begin{gather} \ddot{\phi} + \gamma u - \frac{\phi''}{(1+ \phi')^{3}} - c^{2}_{a}\phi'' =-\delta^{2} \left\{\frac{1}{(1+ \phi')^{2}}\left[ \ddot{\left( \frac{1}{1+ \phi'}\right)} - c^{2}_{a} \left(\frac{1}{1+ \phi'}\right)''\right]\right\}', \end{gather}$$

(2.16)$$\begin{gather}\ddot{u} - c^{2}_{a}u'' = \gamma \ddot{\phi}, \end{gather}$$

and the passage between DMRSW and MRSW models is achieved by switching on/off the parameter $\delta$. The last step consists in eliminating $u$ by applying the wave operator $\partial ^{2}_{\tau \tau } - c^{2}_{a} \partial ^{2}_{y y}$ to (2.15), which gives the following closed equation for $\phi$:

(2.17)\begin{align} &(\partial^{2}_{\tau \tau} - c^{2}_{a} \partial^{2}_{y y}) \left( \ddot{\phi} - \frac{\phi''}{(1+ \phi')^{3}} - c^{2}_{a}\phi'' + \delta^{2} \left[ \frac{1}{(1+ \phi')^{2}} ( \partial^{2}_{\tau \tau} - c^{2}_{a} \partial^{2}_{y y} ) \left(\frac{1}{1+ \phi'}\right)\right]' \right)\nonumber\\ &\quad + \gamma^{2} \ddot{\phi} = 0, \end{align}

and we recall that $\dot {(\ldots )} \equiv \partial _{\tau } (\ldots ),\, (\ldots )' \equiv \partial _{y}$.

We should stress that no approximation was made in obtaining the ‘master’ equation (2.17), which is equivalent, up to zero modes of the wave operator, to the original system of equations and contains the full information on the evolution of the system starting from an arbitrary set of initial conditions for $Y$, and equivalently, for $\phi$. Let us mention that the initial value of $Y$ is $y$, by construction, the inverse of the initial value of $Y'$ gives initial $h$, and therefore initial $b$, initial value of $\dot {Y}$ gives initial $v$, and combinations of initial second derivatives of $Y$ allow to determine initial $u$ and $a$. For example, magneto-geostrophic adjustment of arbitrary initial perturbations, which was studied numerically in the framework of the standard MRSW by Zeitlin et al. (2015), that is, in the limit $\delta \rightarrow 0$ of the system (2.1)–(2.4), can be studied solely with (2.17), although such analysis is out of the scope of the present paper. We will use (2.17) both for development of the perturbation theory in wave amplitudes and for finding exact nonlinear wave solutions in § 5, but will start in the next section with finding conditions of shock formation in the non-dispersive limit.

3. Hyperbolic structure and shock formation in non-dispersive 1.5D MRSW

Equation (2.11) with non-hydrostatic terms set to zero can be written in the form

(3.1) \begin{equation} \left( \begin{array}{@{}c@{}} \dot{v} \\ \dot{J}\\ \dot{u}\\ \dot{a} \end{array} \right) +\left( \begin{array}{@{}cccc@{}} 0 & - \dfrac{g H}{J^{3}} - c^{2}_{a} & 0 & 0 \\ -1 & 0 & 0 & 0\\ 0 & 0 & 0 & - c_{a}\\ 0 & 0 & - c_{a} & 0 \end{array} \right)\partial_{y} \left(\begin{array}{@{}c@{}} v \\ J\\ u\\ a \end{array} \right) = \left( \begin{array}{@{}cccc@{}} 0 & 0 & - f & 0 \\ 0 & 0 & 0 & 0\\ f & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{array} \right)\left(\begin{array}{@{}c@{}} v \\ J\\ u\\ a \end{array} \right)\!. \end{equation}

It is, thus, a quasi-linear system, which is hyperbolic if the left eigenvalues of the characteristic matrix

(3.2) \begin{equation} M = \left( \begin{array}{@{}cccc@{}} 0 & - \dfrac{g H}{J^{3}} - c^{2}_{a} & 0 & 0 \\ -1 & 0 & 0 & 0\\ 0 & 0 & 0 & - c_{a}\\ 0 & 0 & - c_{a} & 0 \end{array} \right) \end{equation}

are non-zero and different. The matrix $M$ is block-diagonal, with the blocks

(3.3a,b) \begin{equation} M^{(1)} = \left( \begin{array}{@{}cc@{}} 0 & - \dfrac{g H}{J^{3}} - c^{2}_{a} \\ -1 & 0 \end{array} \right)\!, \quad M^{(2)} = \left( \begin{array}{@{}cc@{}} 0 & - c_{a}\\ - c_{a} & 0 \end{array} \right). \end{equation}

The left eigenvalues $\mu$ – the characteristic velocities of magneto-gravity and Alfvén wave signals – can be straightforwardly found for respective blocks:

(3.4a,b)\begin{equation} \mu^{(1)}_{{\pm}} ={\pm}\left( \frac{g H}{J^{3}} + c^{2}_{a} \right)^{{1}/{2}}, \quad \mu^{(2)}_{{\pm}} ={\pm} c_{a}. \end{equation}

The corresponding left eigenvectors are

(3.5a,b)\begin{equation} l^{(1)}_{{\pm}} = \left( 1, \, \pm\left( \frac{g H}{J^{3}} + c^{2}_{a} \right)^{{1}/{2}} \right)\!, \quad l^{(2)}_{{\pm}} = (1,\, \pm 1). \end{equation}

Notice that the block $M^{(1)}$ and, as a consequence, its eigenvalues and eigenvectors coincide, up to the change

(3.6)\begin{equation} \frac{g H}{J^{3}} \rightarrow \frac{g H}{J^{3}} + c^{2}_{a}, \end{equation}

with the characteristic matrix of the 1.5D RSW, cf. Zeitlin et al. (2003). The Riemann invariants $w^{(i)}_{\pm }$, which obey the equations

(3.7)\begin{equation} \frac{{\rm d} w^{(i)}_{{\pm}}}{{\rm d} t_{{\pm}}} \equiv \dot{w}^{(i)}_{{\pm}} + \mu^{(i)}_{{\pm}} w'^{(i)}_{{\pm}} = f ( (i - 1) v + (i - 2) u ) ,\quad i = 1,2, \end{equation}

can be always found for each $2 \times 2$ block, according to Pfaff's theorem. (We introduced here the time derivatives ${\textrm {d}}/{\textrm {d} t^{(i)}_{\pm }}$ along the characteristics of both types $i = 1,2$, as in Zeitlin et al. (2003), and deliberately keep the same notation for the sake of comparisons.) However, the seemingly innocuous difference (3.6) renders impossible expression of the corresponding Riemann invariants in terms of elementary functions. Their expressions are

(3.8)\begin{equation} w^{(1)}_{{\pm}} = v \mp-\frac{2J \sqrt{c^2 + \dfrac{gH}{J^3}} \,{}_{2}F_{1}\left(-\dfrac{1}{2}, -\dfrac{1}{6}, \dfrac{5}{6}, -\dfrac{c^2 J^3}{gH}\right)}{\sqrt{1 + \dfrac{c^2 J^3}{gH}}}, \end{equation}

where $_{2}F_{1}$ is the hypergeometric function. The Riemann invariants of the block $M^{(2)}$ are simply

(3.9)\begin{equation} w^{(2)}_{{\pm}} = u \pm a. \end{equation}

Let us recall that a simple and efficient method (Lax 1973) for looking for shock formation consists in analysing whether the derivatives of the Riemann invariants become infinite in finite time. The equations for the Riemann invariants of the block $(1)$ having the same form as in Lagrangian 1.5D RSW (Zeitlin et al. 2003), with the only difference in the expressions of the eigenvalues (3.6), the equations for their derivatives $r^{(1)}_{\pm }$ have the same form as well and may be treated in the same way. By the change of variables $R^{(1)}_{\pm } = \textrm {e}^{\lambda } r^{(1)}_{\pm }$ with $\lambda = \frac {3}{2}|w_+ - w_-|$, the following generalized Riccatti equation is obtained:

(3.10)\begin{equation} \frac{{\rm d} R^{(1)}_{{\pm}}}{{\rm d} t^{(1)}_{{\pm}}} =-{\rm e}^{-\lambda} \frac{\partial \mu^{(1)}_{{\pm}}}{\partial w^{(1)}_{{\pm}}} (R^{(1)})^{2}_{{\pm}} - f u'. \end{equation}

It is the same as in Zeitlin et al. (2003), with the only difference residing in the factor ${\partial \mu ^{(1)}_{\pm }}/{\partial w^{(1)}_{\pm }}$ due to the different form of Riemann invariants. This factor is a rather cumbersome expression, as compared to its simple analogue in 1.5D RSW. It can be obtained by changing the variable from $J$ to $\mu ^{(1)}$ in (3.8), differentiating with respect to $\mu ^{(1)}$ and taking the inverse. It can be shown by direct computation that the result is positive for any relation between $\sqrt {g H}$ and $c_{a}$, like the corresponding expression of Zeitlin et al. (2003). Hence, the same conclusions as in Zeitlin et al. (2003) hold, with the replacement $v \rightarrow - u$, namely if the initial $-u'$ is sufficiently negative, breaking always takes place, but it also takes place for sufficiently negative initial values of Riemann invariants. Thus, magnetic field and rotation do not prevent breaking of magneto-gravity waves and shock formation.

As for the second family of Alfvén waves, the corresponding eigenvalues of the block $M^{(2)}$ are constant, so the equations for the derivatives of the corresponding Riemann invariants are, simply

(3.11)\begin{equation} \frac{{\rm d} r^{(2)}_{{\pm}}}{{\rm d} t^{(2)}_{{\pm}}} = f v'. \end{equation}

As the corresponding characteristics are straight lines, they cannot intersect, so there is no shock formation by Alfvén waves in this sense. However, the solutions of (3.11) can become singular in finite time, provided the right-hand side goes to infinity in finite time. This is the case if there is a shock formation in magneto-gravity waves which, thus engenders a singularity in $u$ and/or $a$. This singularity is, in fact, a manifestation of the known MHD tangential discontinuity, e.g. Landau & Lifshitz (1984) in the present 1.5D context, and can be, therefore, generated in the model in the wake of a shock.

4. Perturbative analysis of wave propagation

4.1. Linear waves

We now proceed with analysis of small-amplitude wave motions in MRSW and DMRSW. For this, we introduce the parameter $\epsilon$ measuring the wave amplitude, by rescaling $\phi \rightarrow \epsilon \phi$ in (2.17). We are interested in the regimes of weak rotation, that is, $\gamma \rightarrow 0$, and weak non-hydrostaticity, that is, $\delta \rightarrow 0$, so we will consider that the parameters $\gamma ^{2}$ and $\delta ^{2}$ entering (2.17) are of the order of $\epsilon$ or smaller. Solutions of (2.17) are sought in the form

(4.1)\begin{equation} \phi = \epsilon \phi_{0} + \epsilon^{2} \phi_{1}. \end{equation}

Linear waves arise in the leading order in $\epsilon$ of (2.17):

(4.2)\begin{equation} \left( \frac{\partial^{2}}{\partial \tau^{2}} - c^{2}_{a} \frac{\partial^{2}}{\partial y^{2}}\right) \left( \frac{\partial^{2}\phi}{\partial \tau^{2}} - (1+ c^{2}_{a})\frac{\partial^{2}\phi}{\partial y^{2}} \right) = 0. \end{equation}

Although there are only two independent variables $\tau$ and $y$ in the system, it is convenient to introduce four of their linear combinations, the characteristic variables with corresponding characteristic velocities $c_{a}$ and $c = \sqrt {1 + c^{2}_{a}}$ for each kind of waves, as follows:

(4.3a,b)\begin{equation} \xi_{{\pm}} = y \pm c_{a} \tau, \quad \chi_{{\pm}} = y \pm c \tau. \end{equation}

Notice that the characteristic velocity $c$ is obtained from the eigenvalue $\mu ^{(1)}$ of the characteristic matrix of the previous section by linearization.

Equation (4.2) and its general solution, modulo a constant which can be excluded by imposing decay boundary conditions on the $y$-axis, which we suppose hereafter, are

(4.4)\begin{equation} \frac{\partial^{4} \phi_{0}}{\partial \xi_+ \partial \xi_- \partial \chi_+ \partial \chi_-} = 0\ \Rightarrow\ \phi_{0} = f_+(\chi_+) + f_-(\chi_-) + g_+(\xi_+) + g_-(\xi_-), \end{equation}

where $f_{\pm }$ and $g_{\pm }$ are arbitrary (localized) functions of their arguments. The physical meaning of the thus obtained solution is obvious: it represents wave packets of non-dispersive Alfvén and magneto-gravity waves moving leftward or rightward along the $y$-axis with phase velocities $c_{a}$ and $c$, and with envelope functions $g_{\pm }$ and $f_{\pm }$, respectively.

4.2. Weakly nonlinear waves with dispersive corrections

Nonlinear and dispersive corrections to these linear wave solutions, as usual, lead to a modulation of their amplitudes. To take this effect into account and following the standard recipes, we introduce a slow-time dependence of the amplitude: $\phi _{0} = \phi _{0}(\tau, T, y)$, with $T = O(\epsilon ^{-1}\tau )$, and thus make a replacement

(4.5)\begin{equation} \partial_{\tau} \rightarrow \partial_{\tau} + \epsilon \partial_{T} \end{equation}

in (4.2). We recall that we supposed that $\gamma ^{2}, \delta ^{2} = O(\epsilon )$. For easy tracking of the terms due to rotation and non-hydrostaticity, respectively we put

(4.6a,b)\begin{equation} \gamma^{2} = \epsilon \bar{\gamma},\quad \delta^{2} = \epsilon \bar{\delta}, \end{equation}

with $\bar {\gamma }, \bar {\delta }$ being either one or zero. We rewrite (2.17) with these changes:

(4.7) \begin{align} &( ( \partial_{\tau} + \epsilon \partial_{T} ) ^{2} - c^{2}_{a} \partial^{2}_{y y} ) \left[ ( \partial_{\tau} + \epsilon \partial_{T} ) ^{2}(\epsilon\phi_{0} + \epsilon^{2} \phi_{1}) - \left( \frac{1}{(1+ (\epsilon\phi_{0} + \epsilon^{2} \phi_{1})')^{3}} + c^{2}_{a}\right) \right.\nonumber\\ &\quad \,\times (\epsilon\phi_{0} + \epsilon^{2} \phi_{1})''+\epsilon \bar{\delta} \left[ \frac{1}{(1+ (\epsilon\phi_{0} + \epsilon^{2} \phi_{1})')^{2}}\left( ( \partial_{\tau} + \epsilon \partial_{T} ) {\left( \frac{( \partial_{\tau} + \epsilon \partial_{T} ) (\epsilon\phi_{0} + \epsilon^{2} \phi_{1})'}{(1+ (\epsilon\phi_{0} + \epsilon^{2} \phi_{1})')^{2}}\right)}\right. \right.\nonumber\\ &\quad \!\left. \left.\left. -\,c^{2}_{a} \left(\frac{( (\epsilon\phi_{0} + \epsilon^{2} \phi_{1} ) '}{(1+ (\epsilon\phi_{0} + \epsilon^{2} \phi_{1})')^{2}}\right)'\right)\right]' \right]' +\epsilon \bar{\gamma} ( \partial_{\tau} + \epsilon \partial_{T} ) ^{2 }(\epsilon\phi_{0} + \epsilon^{2} \phi_{1}) = 0, \end{align}

where we kept, for compactness, the prime notation for differentiation with respect to $y$ where it does not lead to confusion.

The terms of the first order in $\epsilon$ in (4.7) give linear wave equation (4.2) for $\phi _{0}$, with solutions (4.4). Collecting the terms of the second order in $\epsilon$ gives

(4.8) \begin{align} &\big( \partial^{2}_{ \tau^{2}} - c^{2}_{a} \partial^{2}_{y^{2}} \big) \big( \partial^{2}_{\tau^{2}} - \big(1+ c^{2}_{a}\big)\partial^{2}_{y^{2}} \big)\phi_{1} \nonumber\\ &\quad =- 2 \big[\big( \partial^{2}_{\tau^{2}} - c^{2}_{a}\partial^{2}_{y^{2}} \big) +\big( \partial^{2}_{\tau^{2}} - (1+ c^{2}_{a})\partial^{2}_{y^{2}} \big)\big]\partial^{2}_{\tau T}\phi_{0} - \big( \partial^{2}_{ \tau^{2}} - c^{2}_{a} \partial^{2}_{y^{2}} \big) 3 \phi'_{0}\phi''_{0}\nonumber\\ &\qquad -\bar{\delta} \big( \big( \partial^{2}_{\tau^{2}} - c^{2}_{a} \partial^{2}_{y^{2}} \big) \phi''_{0} \big) '' - \bar{\gamma} \partial^{2}_{\tau^{2}} \phi_{0}. \end{align}

We will now rewrite this equation using the characteristic variables introduced in (4.3) and the linear wave solution (4.4) for $\phi _{0}$, where the functions $f_{\pm }$ and $g_{\pm }$ are now supposed to depend on the slow time $T$, in addition to their characteristic arguments. We first replace the wave operators $( \partial ^{2}_{ \tau ^{2}} - c^{2}_{a} \partial ^{2}_{y^{2}} )$ and $( \partial ^{2}_{\tau ^{2}} - (1+ c^{2}_{a})\partial ^{2}_{y^{2}} )$ by their expressions in terms of $\chi _{\pm }$ and $\xi _{\pm }$ and get, not forgetting that these variables are not mutually independent,

(4.9) \begin{align} \frac{\partial^{4} \phi_{1}}{\partial \xi_+ \partial \xi_- \partial \chi_+ \partial \chi_-} &=-(\mathcal{R}_{1} + \mathcal{R}_{2} +\mathcal{R}_{3} + \mathcal{R}_{4})\nonumber\\ &\equiv- 2\partial^{2}_{\xi_+ \xi_-} \partial^{2}_{\tau T}[ \,f_+(\chi_+) + f_-(\chi_-)] - 2\partial^{2}_{\chi_+ \chi_-} \partial^{2}_{\tau T}[ g_+(\xi_+) + g_-(\xi_-)]\nonumber\\ &\quad -3 \partial^{2}_{\xi_+ \xi_-} [ \partial_{y}( \,f_+(\chi_+) + f_-(\chi_-) + g_+(\xi_+) + g_-(\xi_-) ) \partial^2_{y^{2}}( \,f_+(\chi_+)\notag\\ &\quad + f_-(\chi_-) + g_+(\xi_+) + g_-(\xi_-) ) ]\nonumber\\ &\quad - \bar{\delta}\, \partial^{2}_{y^{2}}[ \partial^{2}_{\xi_+ \xi_-} \partial^{2}_{y^{2}}( \,f_+(\chi_+) + f_-(\chi_-) + g_+(\xi_+) + g_-(\xi_-) ) ]\nonumber\\ &\quad -\bar{\gamma} \, \partial^{2}_{\tau^{2}}( \,f_+(\chi_+) + f_-(\chi_-) + g_+(\xi_+) + g_-(\xi_-) ) . \end{align}

Using the changes of variables

(4.10)\begin{equation} \left.\begin{array}{c@{}} \displaystyle y = \dfrac{1}{2} ( \chi_+ + \chi_- ) ,\quad \tau = \dfrac{1}{2 c} ( \chi_+ - \chi_- ) ,\\ \displaystyle y = \dfrac{1}{2} ( \xi_+ + \xi_- ) ,\quad \tau = \dfrac{1}{2 c_{a}} ( \xi_+ - \xi_- ) , \end{array}\right\} \end{equation}

we get

(4.11a,b)\begin{equation} \chi_{{\pm}} = \alpha_{{\pm}} \xi_+ + \alpha_{{\mp}} \xi_-, \quad \xi_{{\pm}} = \beta_{{\pm}} \chi_+ + \beta_{{\mp}} \chi_-, \end{equation}

where we introduced the notation

(4.12a,b)\begin{equation} \alpha_{{\pm}} = \frac{1 \pm \dfrac{c}{c_{a}}}{2}, \quad \beta_{{\pm}} = \frac{1 \pm \dfrac{c_{a}}{c}}{2}. \end{equation}

Notice that, as follows from the definition, $c = \sqrt {1 + c^{2}_{a}} > c_{a}$; therefore,

(4.13a–c)\begin{equation} \beta_{{\pm}} > 0, \quad \alpha_+ >0, \quad \alpha_-<0. \end{equation}

With the help of these formulae, all derivatives in (4.9) could be transformed into derivatives of the functions $f_{\pm },\ g_{\pm }$ with respect to their characteristic arguments. In this way, we get the following expressions for the terms $\mathcal {R}_{i},\ i = 1, 2,3,4$ on the right-hand side of (4.9):

(4.14) \begin{gather} \mathcal{R}_{1} = 2\partial_{T} [ c \alpha_+\alpha_- (\, f'''_+(\chi_+) - f'''_- (\chi_-) ) + c_{a} \beta_+\beta_- ( g'''_+(\xi_+) - g'''_- (\xi_-) ) ], \end{gather}

(4.15) \begin{align} \mathcal{R}_{2} &= 3\{\alpha_+\alpha_- (\, f'''_+(\chi_+) + f'''_- (\chi_-) ) ( g''_+(\xi_+) + g''_- (\xi_-) + f''_+(\chi_+) + f''_- (\chi_-) ) \nonumber\\ &\quad +\, ( g''_- (\xi_-) + \alpha_- f''_+(\chi_+) + \alpha_+ f''_- (\chi_-) ) ( g'''_+(\xi_+) + \alpha_+ f'''_+(\chi_+) + \alpha_- f'''_- (\chi_-) ) \nonumber\\ &\quad +\, ( g''_+ (\xi_+) + \alpha_{+ } f''_+(\chi_+) + \alpha_- f''_- (\chi_-) ) ( g'''_-(\xi_-) + \alpha_- f''_+(\chi_+) + \alpha_+ f'''_- (\chi_-) ) \nonumber\\ &\quad +\,\alpha_+\alpha_- ( g'_+(\xi_+) + g'_-(\xi_-) + f'_+(\chi_+) + f'_-(\chi_-) ) (\, f''''_+(\chi_+) + f''''_- (\chi_-) ) \}, \end{align}

(4.16) \begin{gather} \mathcal{R}_{3} = \bar{\delta}\, \alpha_+\alpha_- (\, f''''''_+(\xi_+) + f''''''_-(\xi_-) ) , \end{gather}

(4.17) \begin{gather}\mathcal{R}_{4} = \bar{\gamma} [ c^{2} (\, f''_+(\chi_+) + f''_- (\chi_-) ) + c^{2}_{a} ( g''_+(\xi_+) + g''_- (\xi_-) ) ], \end{gather}

where from now on, the prime denotes the derivative of the functions $f_{\pm }$ and $g_{\pm }$ with respect to their characteristic arguments.

Equation (4.9) allows to determine the first correction to the linear Alfvén and magneto-gravity waves, unless its right-hand side contains resonant terms which produce a secular growth of the solution and thus a breakdown of the perturbation theory. This terms are, indeed present, but the above-introduced slow-time dependence allows to ‘kill’ them, according to the well-known procedure, and thus obtain the modulation equations for the amplitudes of the linear waves. In view of (4.11), (4.9) can be regarded either as a second-order partial differential equation with respect to the pair of independent variables $\chi _{\pm }$ or with respect to the pair $\xi _{\pm }$. It is easy to realize that in both cases, the only resonant terms are those depending only on one variable in the chosen pair of independent variables, as integration of both sides of the equation over the other variable produces a linear growth in the latter, in this case. Hence, a combination of such terms occurring in the right-hand side of (4.9), taking into account the expressions (4.14)–(4.17), should be equal to zero. Inspection of the expression (4.15) immediately shows an essential difference between the resonances in $\xi _{\pm }$ and in $\chi _{\pm }$, as there are neither nonlinear nor short-wave dispersive resonant terms in the former case. We should stress that the absence of the former is fully consistent with the results of § 3.

Elimination of the resonances in $\chi _{\pm }$ results in the following modulation equation for left- and right-moving magneto-gravity waves:

(4.18)\begin{equation} \pm\! 2 c \alpha_+\alpha_-\partial_{T} f'''_{{\pm}} + 3\alpha_-\alpha_+( 3 f''_{\pm}\, f'''_{{\pm}} + f'_{\pm}\, f''''_{{\pm}} ) + \bar{\gamma} c^{2} f''_{{\pm}} + \bar{\delta}\, \alpha_+\alpha_- f''''''_{{\pm}} = 0. \end{equation}

Similarly, elimination of the resonances in $\xi _{\pm }$ results in the modulation equation for left- and right-moving Alfvén waves:

(4.19)\begin{equation} \pm\! 2 c_{a} \beta_+\beta_-\partial_{T} g'''_{{\pm}} + \bar{\gamma} c^{2}_{a} g''_{{\pm}} = 0. \end{equation}

4.2.1. Magneto-gravity waves

Let us first recall that for small displacements of Lagrangian parcels, the non-dimensional thickness is

(4.20)\begin{equation} h = (1 + \epsilon \phi')^{-1} \approx 1 - \epsilon \phi', \end{equation}

where prime denotes the $y$-derivative, cf. (2.8). Therefore, up to a sign, $\phi '$, and hence each of $g'$ and $f'$ is a non-dimensional deviation $\eta (y, \tau )$ of the free surface from the state of rest.

Let us rewrite (4.18) in terms of $\eta _{\pm }$, the deviations of the surface produced by respectively left- and right-moving waves, dividing all terms by $\alpha _+\alpha _- <0$ (cf. (4.13)):

(4.21)\begin{equation} \mp\! 2 c \partial_{T} \eta''_{{\pm}} + 3( 3 \eta'_{{\pm}} \eta''_{{\pm}} + \eta_{{\pm}} \eta'''_{{\pm}} ) - \bar{\gamma} \frac{c^{2}}{\alpha_+\alpha_-} \eta'_{{\pm}} - \bar{\delta} \eta'''''_{{\pm}} = 0. \end{equation}

It can be easily checked that this equation can be rewritten as

(4.22)\begin{equation} ( ({\mp} c \partial_{T} \eta_{{\pm}} + 3 \eta_{{\pm}} \eta'_{{\pm}} - \bar{\delta}\, \eta'''_{{\pm}} ) ' + \varGamma \eta_{{\pm}} ) ' = 0, \end{equation}

where we rescaled the slow time $T\rightarrow T/2$ and introduced $\varGamma = \bar {\gamma } ({c^{2}}/{|\alpha _+\alpha _-|})>0$, which can be integrated once, giving for rapid decay boundary conditions:

(4.23)\begin{equation} ({\mp} c \partial_{T} \eta_{{\pm}} + 3 \eta_{{\pm}} \eta'_{{\pm}} - \bar{\delta}\, \eta'''_{{\pm}} ) ' + \varGamma \eta_{{\pm}} = 0. \end{equation}

This is the Ostrovsky equation (Ostrovsky 1978), which is also called rotation-modified KdV equation. There exist an abundant literature on this equation, but dwelling into it is out of the scope of the present paper. We would only like to emphasize that, as already mentioned in § 1, unlike the famous KdV equation, this equation does not have soliton solutions, unless the coefficients $\bar {\delta }$ and $\varGamma$ have opposite signs (Galkin & Stepanyants 1991), which is not the case here. The equation does not produce shock formation either.

Vanishing rotation, vanishing short-wave dispersion or both give, under rapid decay boundary conditions, the following equations describing different dynamical regimes:

• (i) no rotation, no dispersion $\varGamma = 0,\,\bar {\delta } = 0$

  Hopf or inviscid Burgers equation:

  (4.24)\begin{equation} \pm\! c \partial_{T} \eta_{{\pm}} + 3 \eta_{{\pm}} \eta'_{{\pm}} = 0 \end{equation}
  describing wave-breaking and shock formation in finite time;

• (ii) no rotation, dispersion $\varGamma = 0,\ \bar {\delta } \neq 0$

  Fully integrable Korteweg–de Vries equation with solitary wave solutions:

  (4.25)\begin{equation} \mp\! c \partial_{T} \eta_{{\pm}} + 3 \eta_{{\pm}} \eta'_{{\pm}}- \bar{\delta} \eta'''_{{\pm}} = 0; \end{equation}

• (iii) rotation, no dispersion $\varGamma \neq 0,\ \bar {\delta } = 0$

  Reduced Ostrovsky (Ostrovsky–Hunter, Vakhnenko) equation:

  (4.26)\begin{equation} \pm\! c \partial_{T} \eta_{{\pm}} + 3 \eta_{{\pm}} \eta'_{{\pm}} + \varGamma \eta_{{\pm}} = 0, \end{equation}
  which is integrable in a range of parameters, and produces wave-breaking and shock formation in another range (Grimshaw et al. 2012).

Thus, weakly nonlinear magneto-gravity waves undergo the modulation described by the Ostrovsky equation. In the limits of negligible rotation and/or dispersion, the modulation produces coherent structures, respectively solitons or shocks.

4.2.2. Alfvén waves

The analysis of the modulation equation for Alfvén waves is much simpler. Equation (4.19) under rapid decay boundary conditions can be integrated twice, giving the following second-order linear PDE:

(4.27)\begin{equation} \pm\! \partial_{T} g'_{{\pm}}(\xi_{{\pm}}) + \bar{\varGamma}\, g_{{\pm}}(\xi_{{\pm}}) = 0, \end{equation}

where we defined $\bar {\varGamma } = {\bar {\gamma } c_{a}}/{2 \beta _+\beta _-} >0$. By introducing ‘bi-characteristic’ variables $\rho _{\pm }=\xi \pm T$ for each $\xi _{\pm }$, this equation is transformed into the well-known and exhaustively studied Klein–Gordon equation:

(4.28)\begin{equation} \frac{\partial^{2} g_{{\pm}}}{\partial \rho^{2}_+} - \frac{\partial^{2} g_{{\pm}}}{\partial \rho^{2}_-} \pm \bar{\varGamma} g_{{\pm}} = 0, \end{equation}

and may be analysed as such. Thus, the modulation of weakly nonlinear Alfvén waves, unlike magneto-gravity waves, does not produce coherent structures, having a purely dispersive character which is due exclusively to rotation.

5. Fully nonlinear steady-propagating waves

In this section, we are looking for steady propagating solutions of (2.17), that is, solutions depending only on the combination $y - V \tau$ of the independent variables, where $V = \textrm {const.}$ is the propagation velocity. Denoting now by prime the derivative with respect to $y - V \tau$, we get from (2.17), by using the variable $J = 1 + \phi '$ instead of $\phi$,

(5.1)\begin{equation} ( V^{2} - c^{2}_{a} ) \left[ \left[ ( V^{2} - c^{2}_{a} ) J + \displaystyle \frac{1}{2 J^{2}} \right]' + \delta \left[ \frac{V^{2} - c^{2}_{a}}{J^{2}} \left( \frac{1}{J}\right)'' \right]' \right]'' + \gamma^{2} V^{2} J' = 0. \end{equation}

This equation can be immediately integrated once, giving

(5.2)\begin{align} ( V^{2} - c^{2}_{a} ) \left[ \left[ ( V^{2} - c^{2}_{a} ) J + \displaystyle \frac{1}{2 J^{2}} \right]' + \delta \left[ \frac{V^{2} - c^{2}_{a}}{J^{2}} \left( \frac{1}{J}\right)'' \right]' \right]' + \gamma^{2} V^{2} J = A = \text{const}. \end{align}

It is hard to analyse this equation in its full complexity and we were unable, at present, to prove or disprove the existence of its periodic finite-amplitude wave solutions. We only show below, for illustrative purposes, how the known in limiting cases solutions are obtained in the Lagrangian framework.

5.1. Non-dispersive rotating case $\delta = 0,\ \gamma \neq 0$

Equation (5.2) in this case becomes

(5.3)\begin{equation} ( V^{2} - c^{2}_{a} ) \left[ ( V^{2} - c^{2}_{a} ) J + \frac{1}{2 J^{2}} \right]'' + \gamma^{2} V^{2} J = A. \end{equation}

The method of treating it is the same as in Zeitlin et al. (2003), where fully nonlinear wave solutions were obtained in Lagrangian RSW. First, the constant $A$ can be determined if solutions are sought in a form of periodic waves. By integrating (5.3) over one period of the wave, we get

(5.4)\begin{equation} A = \gamma^{2} V^{2}. \end{equation}

After substituting this result in (5.3) and multiplying by $[ ( V^{2} - c^{2}_{a} ) J + ({1}/{2 J^{2}}) ]'$, we can integrate the equation once more, and get

(5.5)\begin{align} &\frac{1}{2}( V^{2} - c^{2}_{a} ) \left(\left[ ( V^{2} - c^{2}_{a} ) J + \frac{1}{2 J^{2}} \right]'\right)^{2}\nonumber\\ &\quad + \gamma^{2} V^{2} \left[ ( V^{2} - c^{2}_{a} ) \left(\frac{J^{2}}{2} - J\right)+ \frac{1}{J} - \frac{1}{2 J^{2}} \right]= B = \text{const.} \end{align}

The first term of this equation can be rewritten as $( V^{2} - c^{2}_{a} ) [ ( V^{2} - c^{2}_{a} ) - {1}/{J^{3}} ]^{2} ({J'^{2}}/{2})$, and we thus arrive at the following ordinary differential equation for $J$:

(5.6)\begin{equation} \frac{J'^{2}}{2} + \frac{ \gamma^{2} V^{2} \left[ ( V^{2} - c^{2}_{a} ) \left( \dfrac{J^{2}}{2} -J\right)+ \dfrac{1}{J} - \dfrac{1}{2 J^{2}} \right] - B}{( V^{2} - c^{2}_{a} ) \left[ ( V^{2} - c^{2}_{a} ) - \dfrac{1}{J^{3}} \right]^{2} } = 0, \end{equation}

which is equivalent to a mechanical particle-in-a-well problem with a ‘particle’ with unit mass at position $J$, evolving at zero energy level in a ‘potential’ $\mathcal {V}(J)$ depending on parameters $B, C \equiv \gamma V, \varDelta \equiv V^{2} - c^{2}_{a}$:

(5.7)\begin{equation} \mathcal{V}(B,C, \varDelta; J) = \frac{C^{2} \left[ \varDelta \left( \dfrac{J^{2}}{2} -J\right)+ \dfrac{1}{J} - \dfrac{1}{2 J^{2}} \right] - B}{\varDelta \left[ \varDelta - \displaystyle \dfrac{1}{J^{3}} \right]^{2} } . \end{equation}

The constant $C$ may be absorbed in the independent variable: $y - V\tau \rightarrow C(\kern0.06em y - V\tau )$ and the constant $B$: $B \rightarrow \bar {B} = B/C^{2}$, which results in the potential depending effectively only on two parameters $\varDelta$ and $\bar {B}$. We will not present the analysis of the resulting particle-in-a-well problem, which follows that presented by Shecter et al. (2001) and Zeitlin et al. (2015), although it was performed in these papers in the Eulerian framework. We should only recall that two types of solutions are possible when respectively $\varDelta >1$ and $\varDelta <0$: finite-amplitude magneto-gravity and Alfvén waves. We present the form of the potential well in (5.6) in these two cases in figure 1, demonstrating the existence of respective solutions.

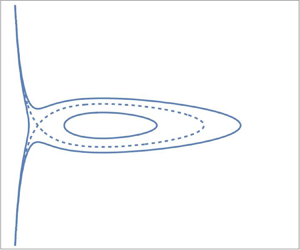
Figure 1. Graphs of potential (5.7) as a function of $J$ at: (a) $\bar {B} = -0.97$, $\varDelta = 3$; (b) $\bar {B} = -0.97$, $\varDelta = -5$; and (c) a zoom of panel (b) showing that the left zero of the potential there is positive. Periodic finite-amplitude wave solutions with bounded $h \propto 1/J$ correspond to the intervals between successive positive zeros of the potential.

5.2. Dispersive non-rotating case $\delta \neq 0,\ \gamma = 0$

The double derivative in (5.1) should be lifted or, equivalently, (5.1) is integrated twice with integration constants equal to zero, as there is no need to differentiate twice (2.15) in this case because the original equations for $u$ and $v$ are uncoupled in the absence of rotation. Hence,

(5.8)\begin{equation} ( V^{2} - c^{2}_{a} ) \left[ ( V^{2} - c^{2}_{a} ) J + \frac{1}{2 J^{2}} \right]' + \delta \left[ \frac{V^{2} - c^{2}_{a}}{J^{2}} \left( \frac{1}{J}\right)'' \right]' = 0. \end{equation}

This equation can be integrated again, with an integration constant $A$. We thus have

(5.9)\begin{equation} ( V^{2} - c^{2}_{a} ) J + \frac{1}{2 J^{2}} + \delta \frac{V^{2} - c^{2}_{a}}{J^{2}} \left( \frac{1}{J}\right)'' = A. \end{equation}

Unlike the previous case, integration over the period of a supposed periodic wave solution does not allow to determine the constant $A$ because of the second term in (5.9), so we leave the equation as it is. It is natural to come back to the non-dimensional thickness variable $h = J^{-1}$ in (5.9) which gives, after the introduction of the above-defined $\varDelta$ and rescaling of $A$: $A \rightarrow \bar {A}= A/\varDelta$,

(5.10)\begin{equation} \delta h'' + \frac{1}{2 \varDelta} + \frac{1}{h^{3}} - \frac{\bar{A}}{h^{2}}=0. \end{equation}

This is, once more, a particle-in-a-well mechanical problem, where $\delta$ plays the role of particle mass and $h$ its position, and can be treated by standard techniques. (In fact, the equation can be directly integrated in terms of elliptic functions, but we will limit ourselves here by a qualitative analysis of solutions.) By multiplying the left-hand side by $h'$ and integrating once with an integration constant $E$, we get

(5.11)\begin{equation} \delta \frac{h'^{2}}{2} + \frac{h}{2 \varDelta} - \frac{1}{2~h^{2}} + \frac{\bar{A}}{h} = E. \end{equation}

Here, the first term is the ‘particle's kinetic energy and the rest of the left-hand side is a potential:

(5.12)\begin{equation} \mathcal{V}( \bar{A},\varDelta; h) = \frac{h}{2 \varDelta} - \frac{1}{2h^{2}} + \frac{\bar{A}}{h}. \end{equation}

As said, (5.11) can be explicitly integrated by the method of separation of variables, but existence of periodic and/or decaying solutions can be analysed qualitatively in a very simple way by looking for the existence of potential well(s) in $\mathcal {V}(h)$ at positive $h$. It easy to see that such a well can exist only at $\varDelta >0$, that is, if the velocity of the solution exceeds the Alfvén velocity. In figure 2, we give an example of such a well. As follows from the figure, the potential has a maximum at $h=h_{max}\approx 0.54$ and a minimum at $h = h_{min} \approx 1.68 > h_{max}$, growing monotonically at $h > h_{min}$. Following the standard mechanical interpretation, for $\mathcal {V}(h_{min}) < E < \mathcal {V}(h_{max})$, the ‘particle’ oscillates between two zeros of $E - \mathcal {V}(h)$ (closed contour in figure 2b), which corresponds to periodic wave solutions for $h(y - V \tau )$ in our MSW problem, and for $E = \mathcal {V}(h_{max})$, the ‘particle’ follows the separatrix trajectory (dashed contour), reaching the ‘top of the hill’ in infinite ‘time’, which corresponds to a solitary wave solution for $h$ which rises monotonically from its asymptotic value $h = h_{max}$ at $y - V \tau \rightarrow -\infty$ to the maximum value given by the non-trivial solution $h > h_{max}$ of the equation $E = \mathcal {V}(h_{max}) = \mathcal {V}(h)$, and then monotonically descending to the asymptotic value $h = h_{max}$ at $y - V \tau \rightarrow +\infty$.

Figure 2. (a) Graph of the potential (5.12) as a function of $h$ at $\bar {A} = 2$, $\varDelta = 1$, and (b) the corresponding phase portrait of the system (5.10) in the ($h,\ h'$) plane. Dashed, separatrix trajectory.

The existence of such solutions of both types for SGN equations is known, e.g. Dutykh & Ionescu-Kruse (2016). We are not aware, to the best of our knowledge, of their derivation in the Lagrangian framework. The specificity of these solutions, which were already sketched by Dellar (2003) in the present magnetized system, is that their speed of translation is limited from below by the Alfvén velocity.

6. Summary and discussion

We have, thus, developed a Lagrangian description for non-dispersive and dispersive non-rotating and rotating shallow-water magnetohydrodynamics, and showed that it provides a universal and convenient framework for understanding the properties of nonlinear magneto-gravity and Alfvén waves in these models. With the help of this approach, in the non-dispersive case, we were able to fully analyse the hyperbolic structure of the system, construct Riemann invariants, prove that magneto-gravity waves can break and form shocks in spite of rotation, find necessary conditions for this process, and also establish its relation to the appearance of tangential discontinuities of the magnetic field.

We also showed that Lagrangian approach allows to reduce the equations of the full system to a single PDE, a ‘master’ equation, both in hydrostatic and non-hydrostatic cases, which greatly simplifies the analysis of both weakly and fully nonlinear wave solutions. Using the master equation, we established modulation equations for weakly nonlinear waves, and showed that while the modulation of magneto-gravity waves is described, in general, by the Ostrovsky equation, which in the absence of rotation and non-hydrostatic effects degenerates and becomes respectively the Korteweg–de Vries and Ostrovsky–Hunter equation, the modulation of Alfvén waves is due solely to rotation and is described by the Klein–Gordon equation. Again, by analysing the master equation, we demonstrated in a simple way the existence of solutions of the model in the form of finite-amplitude periodic waves if either dispersion or rotation are absent, and the existence of solitary waves in the latter case, thus generalizing the known for the SGN system results to the magnetic case. Existence of finite-amplitude solutions with both rotation and dispersion being present is a much more difficult problem, but we believe that the progress here would be easier to make using the single master equation. This problem is postponed to a future work.

We should emphasize that the coherent structures produced by nonlinear waves and studied above, shocks and tangential discontinuities in the case of strong nonlinearity and negligible short-wave dispersion, and eventual solitary and cnoidal waves in the case of weak nonlinearity and non-negligible dispersion, are important dynamical actors in M(R)SW turbulence and especially in so-called weak- or wave- turbulence regimes, as is the case in RSW for the former, e.g. Lahaye & Zeitlin (2012). The shocks are locations of enhanced dissipation, while solitons possess non-trivial transport properties. That is why properties and conditions of the existence of these coherent structures are of primary importance. However, these structures should be well resolved in dedicated numerical schemes and their correct reproduction provides crucial tests for reliability of these latter.

Let us finally mention that the approach developed in the present paper could be pursued, following the lines of Zeitlin et al. (2003), for axisymmetric motions in the DMRSW model, using the corresponding expressions for non-hydrostatic terms in the momentum equations obtained by LeMetayer et al. (2010).