The penetration of light into natural snow cover is of interest both to Geologists and those concerned with the thermodynamics of snow ablation and metamorphosis. An estimate of the optical extinction coefficient at a particular wavelength in terms of physical properties frequently measured in the field—such as density and grain size—would often be of considerable utility. This note suggests a model for such an estimate.
The basic radiation transfer model applied to snow by Reference Dunkle and BevansDunkle and Bevans (1956) is attributed to Schuster, and in its modified form to Schwartzchild. The same formal relations may be deduced from a variety of physical assumptions. A recent derivation by Reference Dunkle and BevansKottler (1964) is briefly outlined below.
A slab of dispersed material is considered, of depth dx where dx is less than the average distance between adjacent reflecting surfaces in the medium. The parameters in the radiation balance will refer to average physical properties of the medium in the horizontal planes.
The slab is assumed to be thin enough so that only primary and secondary scattering need be considered. The latter is assumed to be “isotropic” in the sense that, if a pencil of light is scattered from a point P on a surface in the slab in the direction θ relative to the x-axis, the contributions to that pencil between P and the surface of the slab from secondary scattering from other pencils originating at P with various angles θ' is independent of θ'
If a forward flux Y is defined as the integral over all values of θ, taken in the forward sense on the x-axis, and a backward flux Z is similarly defined for a negative sense, it may be shown that
where k is the average volume absorptivity of the medium for diffuse radiation and r, in the nomenclature of Dunkle and Bevans, is the “distributed reflectivity” of the medium.
If the differential balance equations above are integrated over a semi-infinite physically uniform slab, with diffuse illumination at x = 0,
where
If the variations in the radiation field in that plane may be neglected or are uncorrelated with the variations of grain size in the local medium structure, the absorptivity k refers to the average absorptivity of the medium along a collection of straight-line segments drawn for a uniform random distribution of angles to the vertical axis.
For a statistically homogeneous porous material, the average fraction of such segments which will lie in the solid phase will be (1 − η) where η is the absolute porosity (Reference Fara and ScheideggerFara and Scheidegger, 1961). Thus, for the case of light with wavelength λ in snow
where kλ is the absorption coefficient for radiation of wavelength λ of ice at the local snow temperature.
The reflectivity in a real snow cover must depend mainly on the area of ice-to-air interface S per unit volume of the snow. Considered as an equivalent set of ice laminae, the ice-to-air surfaces would face in one of three directions relative to the incident ray; the effective reflecting surface would be S/3, and if r 0, is the reflectivity of an ice-air interface at normal incidence,
The specific surface of a porous material has no self-evident relation to either grain size or density (Reference ScheideggerScheidegger, 1954). In the case of soils and industrial powders, it is usually determined by the capillary rise method or by its close correlation with the Darcy permeability or flow resistance of the material. By the Carmen modification of the Kozney equation (Reference ScheideggerScheidegger, 1954);
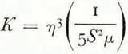
where μ is the dynamic viscosity of the fluid, K is the Darcy coefficient defined in terms of the flow-measurements by
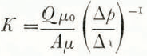
where Q the volume of flow of fluid through a sample length Δx and area A in response to a pressure drop of Δp. μ 0 is the viscosity at some reference pressure and temperature, generally 0°C in the case of air-flow through snow. The air permeability of natural snow has been studied extensively by Reference BenderBender (1957) among others.
No simultaneous measurements of optical transmissivity and air permeability are available in the literature. The most detailed physical descriptions of the snow samples used for observations on light transmission supply only the density and average grain size estimated by sieve analysis or inspection. Fortunately, the relation between the air permeability and these two parameters has been well established on an empirical basis for natural snow. For snow deposited with little or no wind loading the value of K in cm2 s−1 bar−1
where d is the mean sieve grain size in mm of snow. Substitution of Equations (4) and (6), and the value of μ 0 = 170.8 μ, into (1) yields the predictive relationship for β in cm−1
Reference Dunkle and BevansDunkle and Bevans (1956) use a value of 0.018 for r 0 at all wavelengths, which is based on the index of refraction for ice given by available literature. Direct measurements of the reflectivity of glacier ice for a range of wavelengths in the visible spectrum were made by Sauber in 1938, and are presented in Reference MantisMantis (1951) These indicate much higher values of from 0.43 to 0.50 over the visual spectrum. These values are probably more relevant to the reflection within a snow cover.
The question of the temperature dependence of τ 0 is unresolved. In succeeding calculations, the value 0.45 is assumed for the wavelengths and temperatures to be considered,
The only data available in the literature on the transmission of monochromatic radiation in uniform natural snow cover for which both grain size and density are explicitly stated are those for a spring snow cover studied by Reference MellorMellor (1966) and those given by Reference LiljequistLiljequist (1956) for a fine-grained Antarctic snow layer. Both were rather dense with densities of 0.41 Mg m−3 and 0.43 Mg m−3, respectively. The estimated grain size for the first, however, is 2.0 mm compared with 0.3 mm for the Antarctic snow.
Liljequist measured the attenuation of the downward flux of radiation with a selenium cell covered by one of four photographic filters; the values for λ at maximum transparency are given in Table I. The spectral response of the cell-filter combination as given in the paper is relatively concentrated, 0.63 to 0.73 for the red filter, but considerably more disperse for the shorter wavelengths.
Table I. Comparison of observed and predicted extinction coefficients tkom measurements by Reference LiljequistLiljequist (1956)

This problem is not particularly acute for the blue filter, since the value of Kλ is relatively insensitive to λ in this region, but for the remaining two filters, one would expect erroneous results due to the selective attenuation of the various sunlight components and the non-uniformity of the incident solar spectrum. The observed values of β and those predicted from Equation (7) are shown in Table I. The values for the red and the blue filter measurements are within 20%. The greatest deviation, 33%, is for the orange filter (λ = 0.595 μm). The spectral response for this combination extends from 0.51 μm to 0.72 μm, which encompasses the bulk of the solar spectrum and includes a tenfold increase in kλ
Comparison with the data for the one natural snow sample included in Mellor's measurements is disappointing. Equation (7) would predict values of β almost an order of magnitude less than those observed, as well as a steady increase in β with increasing wavelength, which is not observed in the data. Since the sample was refrozen wet spring snow, it is possible that the structure was so disturbed that the empirical relation given by Equation (6) would no longer apply.
The derivation of Equation (7) seems direct and physically plausible as well as being consistent with the known decrease of attenuation with grain size for a given density. It is obvious that more attenuation measurements are needed for any valid test. These must be with sensors with a narrow and well defined spectral response, and must include measurements of density and either air permeability or grain size.



