1 Introduction
Delimited control is a powerful programming language mechanism for control flow manipulation that was developed in the late ’80s in the context of functional programming (Felleisen (Reference Felleisen1988); Danvy and Filinski (Reference Danvy and Filinski1990)). Schrijvers et al. (Reference Schrijvers, Demoen, Desouter and Wielemaker2013) have recently ported this mechanism to Prolog.
Compared to both low-level abstract machine extensions and high-level global program transformations, delimited control is much more light-weight and robust for implementing new control flow and dataflow features. Indeed, the Prolog port has enabled powerful applications in Prolog, such as high-level implementations of both tabling (Reference Desouter, van Dooren and SchrijversDesouter et al. (2015)) and algebraic effects and handlers (Saleh and Schrijvers (Reference Saleh and Schrijvers2016)). Yet, at the same time, there is much untapped potential, as the port fails to recognise the unique nature of Prolog when compared with functional and imperative languages that have previously adopted delimited control.
Indeed, computations in other languages have only one continuation, i.e., one way to proceed from the current point to a result. In contrast, at any point in a Prolog continuation, there may be multiple ways to proceed and obtain a result. More specifically, we can distinguish 1) the success or conjunctive continuation which proceeds with the current state of the continuation; and 2) the failure or disjunctive continuation which bundles the alternative ways to proceed, e.g., if the conjunctive continuation fails.
The original delimited control only accounts for one continuation, which Schrijvers et al. have unified with Prolog’s conjunctive continuation. More specifically, for a given subcomputation, they allow to wrest the current conjunctive continuation from its track, and to resume it at leisure, however many times as desired. Yet, this entirely ignores the disjunctive continuation, which remains as and where it is.
In this work, we adapt delimited control to embrace the whole of Prolog and capture both the conjunctive and the disjunctive continuations. This makes it possible to manipulate Prolog’s built-in search for custom search strategies and enables clean implementations of, e.g., findall/3 and branch-and-bound. This new version of delimited control has an executable specification in the form of a meta-interpreter (Section 3), that can run both the above examples, amongst others. Appendices to this paper are available in the extended version (Vandenbroucke and Schrijvers (Reference Vandenbroucke and Schrijvers2021)) and the paper’s code is available in the online repository at https://github.com/alexandervandenbroucke/tplp-disjunctive-delimited-continuations.
2 Overview and Motivation
We briefly review conjunctive delimited control, explain its obliviousness to Prolog disjunctions, and introduce disjunctive delimited control by example.
2.1 Background: Conjunctive Delimited Control
In earlier work, Schrijvers et al. (Reference Schrijvers, Demoen, Desouter and Wielemaker2013) have introduced a Prolog-compatible interface for delimited control that consists of two predicates: reset/3 and shift/1.
Motivation While library developers and advanced users typically do not build in new language features in Prolog, they have traditionally been able to add various language extensions by means of Prologs rich meta-programming and program transformation facilities. Examples are definite clause grammars (DCGs), extended DCGs (Van Roy (Reference Van Roy1989)), Ciao Prologs structured state threading (Reference Ivanovic, Morales Caballero, Carro and HermenegildoIvanovic et al. (2009)) and logical loops (Schimpf (Reference Schimpf2002)). However, there are several important disadvantages to non-local program transformations for defining new language features: A transformation that combines features can be quite complex and is fragile under language evolution. Moreover, existing code bases typically need pervasive changes to, e.g., include DCGs.
Delimited continuations enable new language features at the program level rather than as program transformations. This makes features based on delimited continuations more light-weight and more robust with respect to changes, and it does not require pervasive changes to existing code.
Behavior The predicate reset(Goal,ShiftTerm,Cont) executes Goal, and, (a) if Goal fails, reset/3 also fails; (b) if Goal succeeds, then reset/3 also succeeds and unifies Cont and ShiftTerm with 0; (c) if Goal calls shift(Term), then the execution of Goal is suspended and reset/3 succeeds immediately, unifying ShiftTerm with Term and Cont with the remainder of Goal. The shift/reset pair resembles the more familiar catch/throw predicates, with the following differences: shift/1 does not copy its argument (i.e., it does not refresh the variables), it does not delete choice points, and also communicates the remainder of Goal to reset/3.
Example Consider DCGs, a language extension to sequentially access the elements of an implicit list. It is conventionally defined by a program transformation that requires special syntax to mark DCG clauses H –> B and to mark non-DCG goals {G}. The delimited control approach requires neither. It introduces two new predicates: c(E) consumes the next element E in the implicit list, and phrase(G,Lin,Lout) runs goal G with implicit list Lin and returns unconsumed remainder Lout. For instance, the following predicate implements the grammar
![]() $(ab)^n$
and returns n.
$(ab)^n$
and returns n.
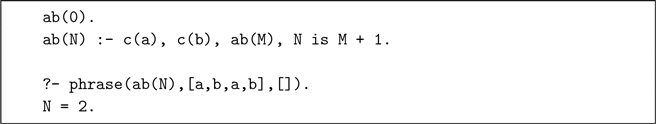
The two DCG primitives are implemented as follows in terms of shift/1 and reset/3.

In words, phrase/3 executes the given goal within a reset/3 and analyzes the possible outcomes. If Cont == 0, this means the goal succeeds without consuming any input. Then the remainder Lout is equal to the input list Lin. Alternatively, the execution of the goal has been suspended midway by the invocation of a shift/1 because it wants to consume an element from the implicit list with c/1. In that case, Term has been instantiated with a request c(E) for an element E. This request is satisfied by instantiating E with the first element of Lin. Finally, the remainder of the suspended goal, Cont (the continuation), is resumed with the remainder of the list Lmid.
Other examples of language features implemented in terms of delimited control are co-routines, algebraic effects (Saleh and Schrijvers (Reference Saleh and Schrijvers2016)) and tabling (Reference Desouter, van Dooren and SchrijversDesouter et al. (2015)).
Obliviousness to Disjunctions This form of delimited control only captures the conjunctive continuation. For instance reset((shift(a),G1),Term,Cont) captures in Cont goal G1 that appears in conjunction to shift(a). In a low-level operational sense, this corresponds to delimited control in other (imperative and functional) languages where the only possible continuation to capture is the computation that comes sequentially after the shift. Thus, this approach is very useful for enabling conventional applications of delimited control in Prolog.
In functional and imperative languages, delimited control can also be characterised at a more conceptual level as capturing the entire remainder of a computation. Indeed, in those languages the sequential continuation coincides with the entire remainder of a computation. Yet, the existing Prolog approach fails to capture the entire remainder of a goal, as it only captures the conjunctive continuation and ignores any disjunctions. This can be illustrated by the reset((shift(a),G1;G2),Term,Cont) which only captures the conjunctive continuation G1 in Cont and not the disjunctive continuation G2. In other words, only the conjunctive part of the goal’s remainder is captured.
This is a pity because disjunctions are a key feature of Prolog and many advanced manipulations of Prolog’s control flow involve manipulating those disjunctions in one way or another.
2.2 Delimited Continuations with Disjunction
This paper presents an approach to delimited control for Prolog that is in line with the conceptual view that the whole remainder of a goal should be captured, including in particular the disjunctive continuation.
For this purpose we modify the reset/3 interface, where depending on Goal, reset(Pattern,Goal,Result) has three possible outcomes:
-
1. If Goal fails, then the reset succeeds and unifies Result with failure. For instance,

-
2. If Goal succeeds, then Result is unified with success(PatternCopy, DisjCont) and the reset succeeds. Here DisjCont is a goal that represents the disjunctive remainder of Goal. For instance,

Observe that, similar to findall/3, the logical variables in DisjCont have been renamed apart to avoid interference between the branches of the computation. To be able to identify any variables of interest after renaming, we provide PatternCopy as a likewise renamed-apart copy of Pattern.
If there is no disjunctive remainder, DisjCont will simply be fail.
-
3. If Goal calls shift(Term), then the reset succeeds and Result is unified with shift(Term,ConjCont,PatternCopy,DisjCont). This contains in addition to the disjunctive continuation also the conjunctive continuation. The latter is not renamed apart and can share variables with Pattern and Term. For instance,

Note that reset(P,G,R) always succeeds if R is unbound and never leaves choicepoints.
Encoding not/1 As a small warm-up exercise, we show how to encode not/1.

This encoding calls Goal through reset/3 and checks that the result is failure; in this case the pattern argument of reset/3 is irrelevant. If the outcome is anything else, not(Goal) clearly fails as required.
Encoding findall/3 Section 4 presents larger applications of disjunctive delimited control, but our encoding of findall/3 with already gives an idea of the expressive power:

This encoding is structured around a reset/3 call of the given Goal followed by a case analysis of the result. Here we assume that shift/1 is not called in Goal, which is a reasonable assumption for plain findall/3.
Encoding !/0 Our encoding of the !/0 operator illustrates the use of shift/1:

The encoding provides cut/0 as a substitute for !/0. Where the scope of regular cut is determined lexically, we use scope/1 here to define it dynamically. For instance, we encode

The logic of cut is captured in the definition of scope/1; all the cut/0 predicate does is request the execution of a cut with shift/1.
In scope/1, the Goal is copied to avoid instantiation by any of the branches. The copied goal is executed inside a reset/3 with the copied goal itself as the pattern. The scope_result/3 predicate handles the result:
-
failure propagates with fail;
-
success creates a disjunction to either unify the initial goal with the now instantiated copy to propagate bindings, or to invoke the disjunctive continuation;
-
shift(cut) discards the disjunctive continuation and proceeds with the conjunctive continuation only.
Encoding Non-Backtrackable State Disjunctive delimited control can also be used to express custom dataflows, such as non-backtrackable state. For the sake of simplicity, we encode here a single nameless global state. This can be easily extended to support SICStus Prolog’s blackboard primitives or SWI-Prolog’s non-backtrackable variables.
The state is read and written with respectively get/1 and put/1. For instance, predicate q/1 writes 1 to the global state in the first clause, fails and backtracks to the next clause to read and use the value of the global state.

The run_state(Goal,Initstate,FinalState) is the analog of DCG’s phrase/3 for running a goal with a given initial value for the global state and resulting final value.

As this query illustrates, the value 1 written in the first branch survives the backtracking and is still available in the second branch.
Figure 1 shows the implementation of this non-backtrackable state interface. Both get/1 and put/1 are defined in terms of shift/1. The run_state/3 predicate calls the goal inside reset/3 and subsequently handles the result with state_handler/5. The latter auxiliary predicate essentially acts as a meta-interpreter for the non-deterministic structure of the goal without resorting to Prolog’s underlying backtracking. This way it avoids backtracking over the global state.

Fig 1. Encoding of non-backtrackable state.
3 Meta-Interpreter Semantics
We provide an accessible definition of disjunctive delimited control in the form of a meta-interpreter. Broadly speaking, it consists of two parts: the core interpreter, and a top level predicate to initialise the core and interpret the results.
3.1 Core Interpreter
Figure 2 defines the interpreter’s core predicate, eval(Conj, PatIn, Disj, PatOut, Result). It captures the behaviour of reset(Pattern,Goal,Result) where the goal is given in the form of a list of goals, Conj, together with the alternative branches, Disj. The latter is renamed apart from Conj to avoid conflicting instantiations.

Fig 2. Meta-Interpreter Core.
The pattern that identifies the variables of interest (similar to findall/3) is present in three forms. Firstly, PatIn is an input argument that shares the variables of interest with Conj (but not with Disj). Secondly, PatOut outputs the instantiated pattern when the goal succeeds or suspends on a shift/1. Thirdly, the alternative branches Disj are of the form alt(BranchPatIn,BranchGoal) with their own copy of the pattern.
When the conjunction is empty (1–4), the output pattern is unified with the input pattern, and success/2 is populated with the information from the alternative branches.
When the first conjunct is true/0 (5–6), it is dropped and the meta-interpreter proceeds with the remainder of the conjunction. When it is a composite conjunction (G1,G2) (7–8), the individual components are added separately to the list of conjunctions.
When the first conjunct is fail/0 (9–10), the meta-interpreter backtracks explicitly by means of auxiliary predicate backtrack/3 (see Fig. 3). If there is no alternative branch, it sets the Result to failure.

Fig 3. Auxiliary Predicates for Meta-Interpreter Core.
Otherwise, it resumes with the alternative branch. Note that by managing its own backtracking, eval/5 is entirely deterministic with respect to the meta-level Prolog system.
When the first conjunct is a disjunction (G1;G2) (11–14), the meta-interpreter adds (a renamed apart copy of) (G2,Conj) to the alternative branches with disjoin/3 (see Fig. 3) and proceeds with [G1|Conj].
Note that we have introduced a custom built-in conj(Conj) that turns a list of goals into an actual conjunction. It is handled (15–17) by prepending the goals to the current list of conjuncts, and never actually builds the explicit conjunction.
When the first goal is shift(Term) (18–21), this is handled similarly to an empty conjunction, except that the result is a shift/4 term which contains Term and the remainder of the conjunction in addition the branch information.
When the first goal is a reset(RPattern,RGoal,RResult) (22–27), the meta-interpreter sets up an isolated call to eval/5 for this goal. When the call returns, the meta-interpreter passes on the results and resumes the current conjunction Conj. Notice that we are careful that this does not result in meta-level failure by meta-interpreting the unification.
Finally, when the first goal is a call to a user-defined predicate (28–33), the meta-interpreter collects the bodies of the predicate’s clauses whose head unifies with the call. If there are none, it backtracks explicitly. Otherwise, it builds an explicit disjunction with disjoin_clauses (see Fig. 3), which it pushes on the conjunction stack.
An example execution trace of the interpreter can be found in (Vandenbroucke and Schrijvers Reference Vandenbroucke and Schrijvers2021, Appendix C).
3.2 Toplevel
The toplevel(Goal)-predicate (see Fig. 4) initialises the core interpreter with a conjunction containing only the given goal, the pattern and pattern copy set to (distinct) copies of the goal, and an empty disjunction. It interprets the result by non-deterministically producing all the answers to Goal and signalling an error for any unhandled shift/1.

Fig 4. Meta-Interpreter Toplevel.
3.3 Performance Discussion
Our meta-interpreter is an executable specification that allows prototyping new language features on top of disjunctive control. Yet, it clearly has scalability issues. Notably, the interpreter makes use of copy_term/2 at every disjunction. This can easily lead to a quadratic runtime on its own. Moreover, several applications (like our encoding of cut) add further uses of copy_term/2 on top of that.
These scalability issues can be partly mitigated by providing native (e.g., WAM-level) support for disjunctive control. We expect that more significant (algorithmic) gains can be obtained by providing native support for new language features implemented with delimited control, effectively moving them from the prototyping stage to the production stage. This way unnecessary overhead, that stems from the generic nature of disjunctive control, can be removed in favour of exploiting feature-specific properties. An example of a language feature that has undergone a similar evolution is SWI-Prolog’s tabling (Desouter et al. Reference Desouter, van Dooren and Schrijvers2015), which was originally implemented with conjunctive delimited control and pure Prolog datastructures, and later several of its components were re-implemented in C for greater performance.
4 Case Studies
To illustrate the usefulness and practicality of our approach, we present two case studies that use the new reset/3 and shift/1: branch-and-bound search and probalistic programming in both the PRISM and ProbLog flavors.
4.1 Branch-and-Bound: Nearest Neighbour Search
Branch-and-bound is a well-known general optimisation strategy, where the solutions in certain areas or branches of the search space are known to be bounded. Such branches can be pruned, when their bound does not improve upon a previously found solution, eliminating large swaths of the search space in a single stroke.
We provide an implementation Footnote 1 of branch-and-bound (see Figure 5) that is generic, i.e., it is not specialised for any application. In particular it is not specific to nearest neighbour search, the problem on which we demonstrate the branch-and-bound approach here.

Fig 5. Branch-and-Bound Effect Handler.
The framework requires minimal instrumentation: it suffices to begin every prunable branch with bound(V), where V is a lower bound on the values in the branch. Footnote 2
-
1. If the Goal succeeds normally (i.e., Result is success), then Data contains a new solution, which is only accepted if it is an improvement over the existing Value. The handler then tries the next Branch.
-
2. If the Goal calls bound(V), V is compared to the current best Value:
-
if it is less than the current value, then Cont could produce a solution that improves upon the current value, and thus must be explored. The alternative Branch is disjoined to Cont, and DataCopy is restored to Data (ensuring that a future reset/3 copies the right variables);
-
if it is larger than or equal to the current value, then Cont can be safely discarded.
-
-
3. Finally, if the goal fails entirely, Min is the current minimum Value.
Nearest Neighbour Search The code in Figure 6 shows how the branch and bound framework efficiently solves the problem of finding the point (in a given set) that is nearest to a given target point on the Euclidean plane.

Fig 6. 2D Nearest Neighbour Search with Branch-and-Bound.
The run_nn/3 predicate takes a point (X,Y), a Binary Space Partitioning (BSP)-tree Footnote 3 that represents the set of points, and returns the point, nearest to (X,Y). The algorithm implemented by nn/3 recursively descends the BSP-tree. At each node, it first tries the partition to which the target point belongs, then the point in the node, and finally the other partition. For this final step we can give an easy lower bound: any point in the other partition must be at least as far away as the (perpendicular) distance from the given point to the partition boundary.
As an example, we search for the point nearest to
![]() $(1,0.1)$
in the set
$(1,0.1)$
in the set
![]() $\{(0.5,0.5),$
(0,0),
$\{(0.5,0.5),$
(0,0),
![]() $(-0.5,0),$
$(-0.5,0),$
![]() $(-0.75,-0.5)\}$
. Figure 7 shows a BSP-tree containing these points, the solid lines demarcate the partitions. The algorithm visits the points
$(-0.75,-0.5)\}$
. Figure 7 shows a BSP-tree containing these points, the solid lines demarcate the partitions. The algorithm visits the points
![]() $(0.5,0.5)$
and (0,0), in that order. The shaded area is never visited, since the distance from (1,0.1) to the vertical boundary through (0,0) is greater than the distance to
$(0.5,0.5)$
and (0,0), in that order. The shaded area is never visited, since the distance from (1,0.1) to the vertical boundary through (0,0) is greater than the distance to
![]() $(0.5,0.5)$
(1 and about 0.64). The corresponding call to run_nn/3 is:
$(0.5,0.5)$
(1 and about 0.64). The corresponding call to run_nn/3 is:


Fig 7. Nearest-Neighbour Search using a BSP-tree.
4.2 Probabilistic Programming
Probabilistic programming languages (PPLs) are programming languages designed for probabilistic modelling. In a probabilistic model, components behave in a variety of ways—just like in a non-deterministic model—but do so with a certain probability.
Instead of a single deterministic value, the execution of a probabilistic program results in a probability distribution of a set of values. This result is produced by probabilistic inference (Reference Wood, van de Meent and MansinghkaWood et al. (2014)), for which there are many strategies and algorithms, the discussion of which is out of scope here. Instead, we focus on two concrete probabilistic logic programming languages: PRISM (Sato (Reference Sato2009)) and PRISM (Reference Fierens, den Broeck, Renkens, Shterionov, Gutmann, Thon, Janssens and RaedtFierens et al. (2015)).
PRISM-Style Probabilistic Logic Programming A PRISM program looks just like a regular Prolog program extended with two special predicates:
-
values_x(Switch,Values,Probabilities) This predicate defines a probabilistic switch Switch, that can assume a value from Values with the probability that is given at the corresponding position in Probabilities (the contents of Probabilitie should sum to one).
-
msw(Switch,Value) This predicate samples a value Value from a switch Switch. For instance, if the program contains a switch declared as values_x(coin, [h,t], [0.4,0.6]), then msw(coin,V) assigns h (for heads) to V with probability 0.4, and t (for tails) with probability 0.6. Remark that each distinct call to msw leads to a different sample from that switch. For instance, in the query msw(coin,X),msw(coin,Y), the outcome could be either (X = h, Y = h),(X = t, Y = t), (X = h, Y = t) or (X = t,Y = h).
Consider the following PRISM program, the running example for this section:

This example defines two predicates: twoheads which is true if both coins are heads, and onehead which is true if either coin is heads. However, note the special structure of onehead: PRISM requires the exclusiveness condition, that is, branches of a disjunction cannot be both satisfied at the same time. The simpler goal msw(coin1,heads) ; msw(coin2, heads) violates this assumption.
The code in Figure 8 interprets this program. Line 1 defines msw/2 as a simple shift. Next, lines 3–5 define the prism/1 wrapper predicate that computes and prints a goal’s probability. Lines 7–10 install a reset/3 call over the goal, and analyse the result. The result is analysed in the remaining lines: A failure never succeeds, and thus has success probability 0.0 (line 12). Conversely, a successful computation has a success probability of 1.0 (line 13). Finally, the probability of a switch (lines 14–18) is the sum of the probability of the remainder of the program given each possible value of the switch multiplied with the probability of that value, and summed with the probability of the alternative branch.

Fig 8. An implementation of PRISM-style probabilistic logic programming.
The predicate msw_prob finds the joint probability of all choices. It iterates over the list of values, and sums the probability of their continuations.

Now, we can compute the probabilities of the two predicates above:

ProbLog-Style Probabilistic Logic Programming We now encode the loop-free, definite fragment of ProbLog on top of the above encoding of PRISM. Our encoding uses a different syntax for probabilistic facts than ProbLog: Footnote 4

For the declaration of probabilistic facts we use the PRISM notation (because that is what we are leveraging underneath). For the invocation of these facts, we use a special fact/1 predicate.
Semantically, ProbLog distinguishes itself on several accounts from PRISM. Consider the following variant of twoheads/0.
PRISM assigns the probability 0.25 to twoheads1 because it treats the two occurrences of heads1 as independent samples. In contrast, ProbLog treats them as referring to the same sample and thus assigns probability 0.5 to twoheads1.
ProbLog also does not require the branches of disjunctions to be mutually exclusive. Consider the following variant of onehead/0.
In PRISM, onehead1 is not well-defined because the two branches are not exclusive. ProbLog in contrast considers onehead1 to be true when heads1 is true, which has probability 50%. The second branch does not affect the probability; it is redundant.
We implement this ProbLog semantics in the problog/1 predicate as a “pre-processor” for the prism/1 encoding of PRISM. Hence, a toplevel ProbLog goals G is meant to be called as prism(problog(G)).
The main work of problog/1 is done by problog/2 which keeps track of a list Pc of F-V pairs of already sampled probabilistic facts F and their sampled value V; initially this list is empty. The problog/2 predicate calls the current goal with reset/3 and analyzes the result. In case of success or failure, it propagates that success or failure, which means it will be handled by prism/1.
In case the goal calls a probabilistic fact with fact/1, this results in a shift/1 which is intercepted by reset/3 and handled in one of two ways. If the fact was already sampled before and its value is thus available in the Pc list, the computation proceeds with that value. Otherwise, the msw/2 predicate is used to sample the fact’s value, which is stored in the Pc list for future uses, and the computation proceeds accordingly. The treatment of msw/2 and working out the probabilities is delegated to prism/1.
The interplay between problog/1 and prism/1 is somewhat subtle. So let us consider what happens in the case of the two example queries above.
-
fact(heads1), fact(heads1) The first occurrence of heads1 appeals to msw(heasd1,V), but the second only observes the already sampled value. Hence, prism only sees one sampling and assigns probability 0.5.

-
fact(heads1); fact(heads1) The first occurrence of heads1 appeals to msw(heasd1,V) and essentially rearranges the goal to

When the sampling yields value t, the V = t unification in the left branch succeeds and the alternative branch is discarded. When the sampling yields value f, the unification fails and the right branch is executed: The second and remaining occurrence of fact(heads1) now consults the recorded f value—rather than sampling again—and also fails because it is not t. Hence, overall there is one success and this success involved one sampling with probability 0.5.

5 Properties of the Meta-Interpreter
In this section, we establish two important correctness properties of our meta-interpreter with respect to standard SLD resolution. Together these establish that disjunctive delimited control is a conservative extension. This means that programs that do not use the feature behave the same as before.
The proofs of these properties are in (Vandenbroucke and Schrijvers Reference Vandenbroucke and Schrijvers2021, Appendix A). The first theorem establishes the soundness of the meta-interpreter, i.e., if a program (not containing shift/1 or reset/3) evaluates to success, then an SLD-derivation of the same answer must exist.
Theorem 1
(Soundness) For all lists of goals
![]() $[A_1,\ldots,A_n]$
, terms
$[A_1,\ldots,A_n]$
, terms
![]() $\alpha,\beta,\gamma,\nu$
, variables P,R conjunctions
$\alpha,\beta,\gamma,\nu$
, variables P,R conjunctions
![]() $B_1,\ldots,B_m$
;
$B_1,\ldots,B_m$
;
![]() $C_1,\ldots,C_k$
and substitutions
$C_1,\ldots,C_k$
and substitutions
![]() $\theta$
, if
$\theta$
, if
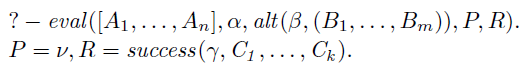 \[ \begin{array}{l} ?- \mathit{eval}([A_1,\ldots,A_n],\alpha,\mathit{alt}(\beta,(B_1,\ldots,B_m)),P,R).\\ P = \nu, R = \mathit{success(\gamma,C_1,\ldots,C_k)}. \end{array} \]
\[ \begin{array}{l} ?- \mathit{eval}([A_1,\ldots,A_n],\alpha,\mathit{alt}(\beta,(B_1,\ldots,B_m)),P,R).\\ P = \nu, R = \mathit{success(\gamma,C_1,\ldots,C_k)}. \end{array} \]
and the program contains neither shift/1 nor reset/3, then SLD-resolution Footnote 5 finds the following derivation:
 \[ \begin{array}{c} \leftarrow (A_1,\ldots,A_n,\mathit{true}) ; (\alpha = \beta,B_1,\ldots,B_m)\\ \vdots\\ \square\\ \text{(with solution $\theta$ s.t. $\alpha\theta = \nu$)} \end{array} \]
\[ \begin{array}{c} \leftarrow (A_1,\ldots,A_n,\mathit{true}) ; (\alpha = \beta,B_1,\ldots,B_m)\\ \vdots\\ \square\\ \text{(with solution $\theta$ s.t. $\alpha\theta = \nu$)} \end{array} \]
Conversely, we want to argue that the meta-interpreter is complete, i.e., if SLD-derivation finds a refutation, then meta-interpretation—provided that it terminates—must find the same answer eventually. The theorem is complicated somewhat by the fact that the first answer that the meta-interpreter arrives at might not be the desired one due to the order of the clauses in the program. To deal with this problem, we use the operator ![]() , which is like
, which is like ![]() , but allows a different permutation of the program in every step.
, but allows a different permutation of the program in every step.
Theorem 2
(Completeness) For any goal
![]() $\leftarrow A_1,\ldots,A_n$
, if it has solution
$\leftarrow A_1,\ldots,A_n$
, if it has solution
![]() $\theta$
, then
$\theta$
, then
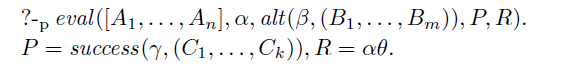
Together, these two theorems show that our meta-interpreter is a conservative extension of the conventional Prolog semantics.
6 Related Work
We briefly discuss the main areas of related work.
Continuations in
![]() $\lambda$
-Prolog Perhaps most closely related to our work is that of Brisset and Ridoux (1993), who present a continuation-passing style semantics for
$\lambda$
-Prolog Perhaps most closely related to our work is that of Brisset and Ridoux (1993), who present a continuation-passing style semantics for
![]() $\lambda$
-Prolog. Their semantics distinguishes three different continuations: the classic success and failure continuations, and a third “cut failure” continuation which cut uses to overwrite the failure continuation with. They also expose the first two continuations, through the well-known call-with-current-continuation operator from functional programming for the success continuation and an analog operator for the failure continuation. They illustrate how the latter can be used to make cut work appropriately for meta-calls.
$\lambda$
-Prolog. Their semantics distinguishes three different continuations: the classic success and failure continuations, and a third “cut failure” continuation which cut uses to overwrite the failure continuation with. They also expose the first two continuations, through the well-known call-with-current-continuation operator from functional programming for the success continuation and an analog operator for the failure continuation. They illustrate how the latter can be used to make cut work appropriately for meta-calls.
A syntactic difference with our work is that they provide two seperate operators to capture the success and failure continuation rather than a single one. More importantly, their operators capture the full continuation while ours capture delimited continuations. Filinski (Reference Filinski1996) has shown that the latter are more expressive than the former.
Conjunctive Delimited Control Disjunctive delimited control is the culmination of a line of research on mechanisms to modify Prolog’s control flow and search, which started with the hook-based approach of Tor (Reference Schrijvers, Demoen, Triska and DesouterSchrijvers et al. (2014a)) and was followed by the development of conjunctive delimited control for Prolog (Schrijvers et al. (2013; Reference Schrijvers, Wu, Desouter and Demoen2014b)).
The listing of Figure 10 shows that disjunctive delimited control entirely subsumes conjunctive delimited control. It encodes the conjunctive reset conj_reset/3 in terms of our disjunctive reset/3, while using the same shift/1. The conjunctive behaviour is recovered by disjoining the captured disjunctive branch. We believe that Tor is similarly superseded.

Fig 9. An implementation of PRISM-style probabilistic logic programming.

Fig 10. Encoding of conjunctive delimited control.
Abdallah (Reference Abdallah2017) presents a higher-level interface for (conjunctive) delimited control on top of that of Schrijvers et al. (Reference Schrijvers, Demoen, Desouter and Wielemaker2013).In particular, it features prompts, first conceived in a Haskell implementation by Dyvbig et al. (Reference Dyvbig, Jones and Sabry2005), which allow shifts to dynamically specify up to what reset to capture the continuation. We believe that it is not difficult to add a similar prompt mechanism on top of our disjunctive version of delimited control.
Interoperable Engines Tarau and Majumdar (Reference Tarau and Majumdar2009)’s Interoperable Engines propose engines as a means for co-operative coroutines in Prolog. An engine is an independent instance of a Prolog interpreter that provides answers to the main interpreter on request.
The predicate new_engine(Pattern,Goal,Interactor) creates a new engine with answer pattern Pattern that will execute Goal and is identified by Interactor. The predicate get(Interactor,Answer) has an engine execute its goal until it produces an answer (either by proving the Goal, or explicitly with return/1). After this predicate returns, more answers can be requested, by calling get/2 again with the same engine identifier. The full interface also allows bi-directional communication between engines, but that is out of scope here.
Figure 11 shows that we can implement the get/2 engine interface in terms of delimited control (the full code is available in the online repository).The opposite, implementing disjunctive delimited control with engines, seems impossible as engines do not provide explicit control over the disjunctive continuation. Indeed, get/2 can only follow Prolog’s natural left-to-right control flow and thus we cannot, e.g., run the disjunctive continuation before the conjunctive continuation, which is trivial with disjunctive delimited control.

Fig 11. Interoperable Engines in terms of delimited control.
Functional Programming Models of Nondeterminism and Backtracking Prolog-style nondeterminism, and in particular its backtracking approach, have been widely studied from a Functional Programming perspective and various abstraction mechanisms have been proposed to capture it.
Carlsson (Reference Carlsson1984) has shown how to implement Prolog-style backtracking with a single “success” continuation. A decade later, Gudeman (Reference Gudeman1992) uses a second “failure” continuation in the denotational semantics of the goal-oriented Icon language to conveniently express control flow manipulations.
Wadler (Reference Wadler1985) has shown how to encode backtracking with lazy lists, Spivey (Reference Spivey1990) noticed that this fit the category theoretical structure of monads which was further expanded upon by Wadler (Reference Wadler1990). Later, Hinze (Reference Hinze2012) has shown that the lazy list monad and the two-continuation approach, which also has monadic structure, are two equivalent representations obtained from the same adjunction.
Another related development is that of algebraic effects & handlers, pioneered by Plotkin and Pretnar (Reference Plotkin and Pretnar2013), a high-level mechanism for modelling side effects such as nondeterminism. Kammar et al. (2013) have shown that this mechanism can be implemented both in terms of delimited control and of the so-called free monad. The latter reifies the computation as a tree-like data structure. We can find precursors of this approach in Curry’s encapsulated search tree (Braßel et al. (2004)) and the monadic constraint programming framework (Reference Schrijvers, Stuckey and WadlerSchrijvers et al. (2009)), which both expose an explicit search tree that can be manipulated to obtain various search strategies.
Tabling without non-bactrackable variables Tabling (Swift and Warren (Reference Swift and Warren2012); Reference Santos Costa, Rocha and DamasSantos Costa et al. (2012)) is a well-known technique that eliminates the sensitivity of SLD-resolution to clause and goal ordering, allowing a larger class of programs to terminate. As a bonus, it may improve the run-time performance (at the expense of increased memory consumption).
One way to implement tabling—with minimal engineering impact to the Prolog engine—is the tabling-as-a-library approach proposed by Desouter et al. (Reference Desouter, van Dooren and Schrijvers2015). This approach requires (global) mutable variables that are not erased by backtracking to store their data structures in a persistent manner. With the new reset/3 predicate, this is no longer needed, as (non-backtracking) state can be implemented in directly with disjunctive delimited control.
Probabilistic Logic Programming The implementation techniques used by existing probabilistic logic programming systems use more elaborate and sophisticated approaches than the lightweight technique we have presented. PRISM is implemented on top of B-Prolog (Sato and Kameya (Reference Sato and Kameya2001)) and uses its tabling mechanism to execute programs that are transformed to collect rather than execute msw/2 calls. Based on the answer tables, support graphs are constructed from which the probabilities are computed.
The first version of ProbLog (Reference Kimmig, Demoen, Raedt, Costa and RochaKimmig et al. (2011)) used a similar tabling-based approach to collect all the proofs of a goal and post-process these. The present version of ProbLog (Reference Fierens, den Broeck, Renkens, Shterionov, Gutmann, Thon, Janssens and RaedtFierens et al. (2015)) converts a program to a weighted boolean formula, then converts this to a circuit in deterministic, decomposable negation normal form (Darwiche (Reference Darwiche2004)) which can be directly evaluated with structural recursion.
7 Conclusion and Future Work
We have presented disjunctive delimited control, an extension to delimited control that takes Prolog’s non-deterministic nature into account. This is a conservative extension that enables implementing disjunction-related language features and extensions as a library.
In future work, we plan to explore a WAM-level implementation of disjunctive delimited control, inspired by the stack freezing functionality of tabling engines, to gain access to the disjunctive continuations efficiently. Similarly, the use of copy_term/2 necessitated by the current API has a detrimental impact on performance, which might be overcome by a sharing or shallow copying scheme.
Inspired by the impact of conjunctive delimited control, which has brought tabling to SWI-Prolog, we believe that further development of disjunctive delimited control is worthwhile. Indeed, it has the potential of bringing powerful disjunctive control abstractions like branch-and-bound search to a wider range of Prolog systems.
Acknowledgments
We are grateful to Paul Tarau and the anonymous LOPSTR 2021 reviewers for their helpful feedback. Part of this work was funded by FWO grant G0D1419N and by KU Leuven grant C14/20/079.




















