Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-29T04:11:51.041Z Has data issue: false hasContentIssue false
  • English
  • Français

Particle radial distribution function and relative velocity measurement in turbulence at small particle-pair separations

Published online by Cambridge University Press:  30 June 2021

Adam Hammond  and
Hui Meng
Adam Hammond
Affiliation:
Department of Mechanical and Aerospace Engineering, University at Buffalo, Buffalo, NY 14260, USA
Hui Meng*
Affiliation:
Department of Mechanical and Aerospace Engineering, University at Buffalo, Buffalo, NY 14260, USA
*
†Email address for correspondence: huimeng@buffalo.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

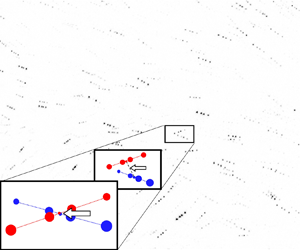
Particle collisions in turbulent flow are critical to particle agglomeration and droplet coalescence. The collision kernel can be evaluated by radial distribution function (RDF) and radial relative velocity (RV) between particles at small separations $r$. Previously, the smallest $r$ was limited to roughly the Kolmogorov length $\eta$ due to particle position uncertainty and image overlap. We report a new approach to measuring RDF and RV near contact ($r/a \approx 2.07$, where $a$ is particle radius). Three-dimensional particle tracking velocimetry using the four-pulse shake-the-box algorithm recorded short tracks with the interpolated midpoints registered as particle positions, avoiding image overlap and track mismatch. We measured RDF and RV of inertial particles in a one metre diameter isotropic air turbulence chamber with Taylor Reynolds number $Re_\lambda =324$, $a=12 - 16\ \mathrm {\mu }\textrm {m}$ $({\approx }0.12\eta )$ and Stokes number ${\approx }0.7$. At large $r$ the measured RV agrees with the literature, but when $r<20\eta$ the first moment of negative RV starts to increase, reaching 10 times higher values than direct numerical simulations of non-interacting particles. Likewise, RDF scales as $r^{-0.39}$ when $r>\eta$, reflecting the well-known scaling for polydisperse particles, but when $r\lessapprox \eta$, RDF scales as $r^{-6}$, yielding 1000 times higher near-contact RDF than simulations. Such RV enhancement and extreme clustering at small $r$ can be attributed to particle–particle interactions including hydrodynamic interactions, which are not well-understood. Uncertainty analysis substantiates the observed trends. This first-ever simultaneous RDF and RV measurement at small separations provides a clear glimpse into the clustering and relative velocities of particles in turbulence near-contact.

JFM classification

Multiphase and Particle-laden Flows: Particle/fluid flow Turbulent Flows: Isotropic turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 921 , 25 August 2021 , A16
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ayala, O., Rosa, B., Wang, L.-P. & Grabowski, W.W. 2008 Effects of turbulence on the geometric collision rate of sedimenting droplets. Part 1. Results from direct numerical simulation. New J. Phys. 10 (7), 075015.CrossRefGoogle Scholar
Ayala, O., Parishani, H., Chen, L., Rosa, B. & Wang, L.-P. 2014 DNS of hydrodynamically interacting droplets in turbulent clouds: parallel implementation and scalability analysis using 2D domain decomposition. Comput. Phys. Commun. 185 (12), 3269–3290.CrossRefGoogle Scholar
Batchelor, G. & Green, J.-T. 1972 The hydrodynamic interaction of two small freely-moving spheres in a linear flow field. J. Fluid Mech. 56 (2), 375–400.CrossRefGoogle Scholar
Bewley, G.P., Saw, E.-W. & Bodenschatz, E. 2013 Observation of the sling effect. New J. Phys. 15 (8), 083051.CrossRefGoogle Scholar
Bordás, R., Roloff, C., Thévenin, D. & Shaw, R. 2013 Experimental determination of droplet collision rates in turbulence. New J. Phys. 15 (4), 045010.CrossRefGoogle Scholar
Bragg, A.D. & Collins, L.R. 2014 New insights from comparing statistical theories for inertial particles in turbulence: II. Relative velocities. New J. Phys. 16, 055014.CrossRefGoogle Scholar
Brunk, B.K., Koch, D.L. & Lion, L.W. 1997 Hydrodynamic pair diffusion in isotropic random velocity fields with application to turbulent coagulation. Phys. Fluids 9 (9), 2670–2691.CrossRefGoogle Scholar
Brunk, B.K., Koch, D.L. & Lion, L.W. 1998 Turbulent coagulation of colloidal particles. J. Fluid Mech. 364, 81–113.CrossRefGoogle Scholar
Cao, L., Pan, G., de Jong, J., Woodward, S. & Meng, H. 2008 Hybrid digital holographic imaging system for three-dimensional dense particle field measurement. Appl. Opt. 47 (25), 4501–4508.CrossRefGoogle ScholarPubMed
Dhariwal, R. & Bragg, A.D. 2018 Small-scale dynamics of settling, bidisperse particles in turbulence. J. Fluid Mech. 839, 594–620.CrossRefGoogle Scholar
Dou, Z., Bragg, A.D., Hammond, A.L., Liang, Z., Collins, L.R. & Meng, H. 2018 a Effects of Reynolds number and Stokes number on particle-pair relative velocity in isotropic turbulence: a systematic experimental study. J. Fluid Mech. 839, 271–292.CrossRefGoogle Scholar
Dou, Z., Ireland, P.J., Bragg, A.D., Liang, Z., Collins, L.R. & Meng, H. 2018 b Particle-pair relative velocity measurement in high-Reynolds-number homogeneous and isotropic turbulence using 4-frame particle tracking velocimetry. Exp. Fluids 59 (2), 30.CrossRefGoogle Scholar
Dou, Z.W., Pecenak, Z.K., Cao, L.J., Woodward, S.H., Liang, Z. & Meng, H. 2016 PIV measurement of high-Reynolds-number homogeneous and isotropic turbulence in an enclosed flow apparatus with fan agitation. Meas. Sci. Technol. 27 (3), 035305.CrossRefGoogle Scholar
Falkovich, G. & Pumir, A. 2007 Sling effect in collisions of water droplets in turbulent clouds. J. Atmos. Sci. 64 (12), 4497–4505.CrossRefGoogle Scholar
Falkovich, G., Fouxon, A. & Stepanov, M. 2002 Acceleration of rain initiation by cloud turbulence. Nature 419 (6903), 151–154.CrossRefGoogle ScholarPubMed
Ireland, P.J., Bragg, A.D. & Collins, L.R. 2016 The effect of Reynolds number on inertial particle dynamics in isotropic turbulence. Part 1. Simulations without gravitational effects. J. Fluid Mech. 796, 617–658.CrossRefGoogle Scholar
de Jong, J., Salazar, J.P.L.C., Woodward, S.H., Collins, L.R. & Meng, H. 2010 Measurement of inertial particle clustering and relative velocity statistics in isotropic turbulence using holographic imaging. Intl J. Multiphase Flow 36 (4), 324–332.CrossRefGoogle Scholar
Kearney, R.V. & Bewley, G.P. 2020 Lagrangian tracking of colliding droplets. Exp. Fluids 61 (7), 155.CrossRefGoogle Scholar
Larsen, M.L. & Shaw, R. 2018 A method for computing the three-dimensional radial distribution function of cloud particles from holographic images. Atmos. Meas. Tech. 11 (7), 4261.CrossRefGoogle Scholar
Lu, J. & Shaw, R.A. 2015 Charged particle dynamics in turbulence: theory and direct numerical simulations. Phys. Fluids 27 (6), 065111.CrossRefGoogle Scholar
Meng, H., Gang, P., Ye, P. & Woodward, S.H. 2004 Holographic particle image velocimetry: from film to digital recording. Meas. Sci. Technol. 15 (4), 673.CrossRefGoogle Scholar
Moffat, R.J. 1988 Describing the uncertainties in experimental results. Exp. Therm. Fluid Sci. 1 (1), 3–17.CrossRefGoogle Scholar
Novara, M., Schanz, D., Geisler, R., Gesemann, S., Voss, C. & Schröder, A. 2019 Multi-exposed recordings for 3D Lagrangian particle tracking with multi-pulse shake-the-box. Exp. Fluids 60 (3), 44.CrossRefGoogle Scholar
Reade, W.C. & Collins, L.R. 2000 Effect of preferential concentration on turbulent collision rates. Phys. Fluids 12 (10), 2530–2540.CrossRefGoogle Scholar
Rosa, B., Parishani, H., Ayala, O., Grabowski, W.W. & Wang, L.-P. 2013 Kinematic and dynamic collision statistics of cloud droplets from high-resolution simulations. New J. Phys. 15 (4), 045032.CrossRefGoogle Scholar
Salazar, J.P.L.C., De Jong, J., Cao, L.J., Woodward, S.H., Meng, H. & Collins, L.R. 2008 Experimental and numerical investigation of inertial particle clustering in isotropic turbulence. J. Fluid Mech. 600, 245–256.CrossRefGoogle Scholar
Saw, E.-W., Salazar, J.P., Collins, L.R. & Shaw, R.A. 2012 a Spatial clustering of polydisperse inertial particles in turbulence: I. Comparing simulation with theory. New J. Phys. 14 (10), 105030.CrossRefGoogle Scholar
Saw, E.-W., Shaw, R.A., Salazar, J.P. & Collins, L.R. 2012 b Spatial clustering of polydisperse inertial particles in turbulence: II. Comparing simulation with experiment. New J. Phys. 14 (10), 105031.CrossRefGoogle Scholar
Saw, E.-W., Bewley, G.P., Bodenschatz, E., Ray, S.S. & Bec, J. 2014 Extreme fluctuations of the relative velocities between droplets in turbulent airflow. Phys. Fluids (1994-present) 26 (11), 111702.CrossRefGoogle Scholar
Schanz, D., Gesemann, S., Schröder, A., Wieneke, B. & Novara, M. 2012 Non-uniform optical transfer functions in particle imaging: calibration and application to tomographic reconstruction. Meas. Sci. Technol. 24 (2), 024009.CrossRefGoogle Scholar
Schanz, D., Gesemann, S. & Schröder, A. 2016 Shake-the-box: Lagrangian particle tracking at high particle image densities. Exp. Fluids 57 (5), 70.CrossRefGoogle Scholar
Sellappan, P., Alvi, F.S. & Cattafesta, L.N. 2020 Lagrangian and Eulerian measurements in high-speed jets using multi-pulse shake-the-box and fine scale reconstruction (vic#). Exp. Fluids 61 (7), 1–17.CrossRefGoogle Scholar
Shaw, R.A. 2003 Particle-turbulence interations in atmospheric clouds. Annu. Rev. Fluid Mech. 35 (1), 183–227.CrossRefGoogle Scholar
Squires, K.D. & Eaton, J.K. 1991 Preferential concentration of particles by turbulence. Phys. Fluids A 3 (5), 1169–1178.CrossRefGoogle Scholar
Sundaram, S. & Collins, L.R. 1997 Collision statistics in an isotropic particle-laden turbulent suspension. 1. Direct numerical simulations. J. Fluid Mech. 335, 75–109.CrossRefGoogle Scholar
Tavoularis, S., Bennett, J. & Corrsin, S. 1978 Velocity-derivative skewness in small Reynolds number, nearly isotropic turbulence. J. Fluid Mech. 88 (1), 63–69.CrossRefGoogle Scholar
Wang, L.-P., Wexler, A.S. & Zhou, Y. 2000 Statistical mechanical description and modelling of turbulent collision of inertial particles. J. Fluid Mech. 415, 117–153.CrossRefGoogle Scholar
Wang, L.-P., Ayala, O., Kasprzak, S.E. & Grabowski, W.W. 2005 Theoretical formulation of collision rate and collision efficiency of hydrodynamically interacting cloud droplets in turbulent atmosphere. J. Atmos. Sci. 62 (7), 2433–2450.CrossRefGoogle Scholar
Wang, L.-P., Ayala, O., Rosa, B. & Grabowski, W.W. 2008 Turbulent collision efficiency of heavy particles relevant to cloud droplets. New J. Phys. 10 (7), 075013.CrossRefGoogle Scholar
Wieneke, B. 2008 Volume self-calibration for 3D particle image velocimetry. Exp. Fluids 45 (4), 549–556.CrossRefGoogle Scholar
Yavuz, M.A., Kunnen, R.P.J., van Heijst, G.J.F. & Clercx, H.J.H. 2018 Extreme small-scale clustering of droplets in turbulence driven by hydrodynamic interactions. Phys. Rev. Lett. 120 (24), 244504.CrossRefGoogle ScholarPubMed
Zhou, Y., Wexler, A.S. & Wang, L.-P. 2001 Modelling turbulent collision of bidisperse inertial particles. J. Fluid Mech. 433, 77.CrossRefGoogle Scholar