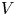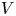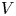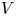1. Introduction
In this work, we obtain large $n$![]() asymptotics of the Toeplitz determinant
asymptotics of the Toeplitz determinant
where $f$![]() is supported on the unit circle $\mathbb {T}=\{z\in \mathbb {C}:|z|=1\}$
is supported on the unit circle $\mathbb {T}=\{z\in \mathbb {C}:|z|=1\}$![]() and is of the form
and is of the form
We assume that $V$![]() and $W$
and $W$![]() are analytic in a neighbourhood of $\mathbb {T}$
are analytic in a neighbourhood of $\mathbb {T}$![]() and that the potential $V$
and that the potential $V$![]() is real-valued on $\mathbb {T}$
is real-valued on $\mathbb {T}$![]() . The function $\omega (z)=\omega (z;\vec \alpha,\vec \beta )$
. The function $\omega (z)=\omega (z;\vec \alpha,\vec \beta )$![]() in (1.2) contains Fisher–Hartwig singularities and is defined in (1.8) below. Since the functions $V$
in (1.2) contains Fisher–Hartwig singularities and is defined in (1.8) below. Since the functions $V$![]() and $W$
and $W$![]() are analytic on $\mathbb {T}$
are analytic on $\mathbb {T}$![]() , there exists an open annulus $U$
, there exists an open annulus $U$![]() containing $\mathbb {T}$
containing $\mathbb {T}$![]() on which they admit Laurent series representations of the form
on which they admit Laurent series representations of the form


where $V_{k}, W_{k}\in \mathbb {C}$![]() are the Fourier coefficients of $V$
are the Fourier coefficients of $V$![]() and $W$
and $W$![]() , i.e. $V_{k} = {1}/{2\pi }\int _0^{2\pi }V(e^{i\theta })e^{-ik\theta }{\rm d}\theta$
, i.e. $V_{k} = {1}/{2\pi }\int _0^{2\pi }V(e^{i\theta })e^{-ik\theta }{\rm d}\theta$![]() and similarly for $W_{k}$
and similarly for $W_{k}$![]() . Associated to $V$
. Associated to $V$![]() there is an equilibrium measure $\mu _{V}$
there is an equilibrium measure $\mu _{V}$![]() , which is the unique minimizer of the functional
, which is the unique minimizer of the functional
among all Borel probability measures $\mu$![]() on $\mathbb {T}$
on $\mathbb {T}$![]() . In this paper, we make the assumption that $\mu$
. In this paper, we make the assumption that $\mu$![]() is supported on the whole unit circle. We further assume that $V$
is supported on the whole unit circle. We further assume that $V$![]() is regular, i.e. that the function $\psi$
is regular, i.e. that the function $\psi$![]() given by
given by

is strictly positive on $\mathbb {T}$![]() . Under these assumptions, we show in appendix A that
. Under these assumptions, we show in appendix A that
The function $\omega$![]() appearing in (1.2) is defined by
appearing in (1.2) is defined by

where $\omega _{\alpha _{k}}(z)$![]() and $\omega _{\beta _{k}}(z)$
and $\omega _{\beta _{k}}(z)$![]() are defined for $z=e^{i\theta }$
are defined for $z=e^{i\theta }$![]() by
by
and
At $t_k=e^{i\theta _{k}}$![]() , the functions $\omega _{\alpha _{k}}$
, the functions $\omega _{\alpha _{k}}$![]() and $\omega _{\beta _{k}}$
and $\omega _{\beta _{k}}$![]() have root- and jump-type singularities, respectively. Note that $\omega _{\beta _{k}}$
have root- and jump-type singularities, respectively. Note that $\omega _{\beta _{k}}$![]() is continuous at $z=1$
is continuous at $z=1$![]() if $k \neq 0$
if $k \neq 0$![]() . We allow the parameters $\theta _{1},\ldots,\theta _{m}$
. We allow the parameters $\theta _{1},\ldots,\theta _{m}$![]() to vary with $n$
to vary with $n$![]() , but we require them to lie in a compact subset of $(0,2\pi )_{\mathrm {ord}}^{m}:=\{(\theta _{1},\ldots,\theta _{m}): 0 < \theta _{1} < \cdots < \theta _{m} < 2\pi \}$
, but we require them to lie in a compact subset of $(0,2\pi )_{\mathrm {ord}}^{m}:=\{(\theta _{1},\ldots,\theta _{m}): 0 < \theta _{1} < \cdots < \theta _{m} < 2\pi \}$![]() .
.
To summarize, the $n \times n$![]() Toeplitz determinant (1.1) depends on $n$
Toeplitz determinant (1.1) depends on $n$![]() , $m$
, $m$![]() , $V$
, $V$![]() , $W$
, $W$![]() , $\vec {t} = (t_{1},\ldots,t_{m})$
, $\vec {t} = (t_{1},\ldots,t_{m})$![]() , $\vec {\alpha }=(\alpha _1,\ldots,\alpha _m)$
, $\vec {\alpha }=(\alpha _1,\ldots,\alpha _m)$![]() and $\vec {\beta } = (\beta _{1},\ldots,\beta _{m})$
and $\vec {\beta } = (\beta _{1},\ldots,\beta _{m})$![]() , but for convenience the dependence on $m$
, but for convenience the dependence on $m$![]() and $\vec {t}$
and $\vec {t}$![]() is omitted in the notation $D_n(\vec \alpha,\vec \beta,V,W)$
is omitted in the notation $D_n(\vec \alpha,\vec \beta,V,W)$![]() . We now state our main result.
. We now state our main result.
Theorem 1.1 Large $n$ asymptotics of $D_{n}(\vec {\alpha },\vec {\beta },V,W)$
asymptotics of $D_{n}(\vec {\alpha },\vec {\beta },V,W)$
Let $m \in \mathbb {N} :=\{0,1,\ldots \}$![]() , and let $t_{k}=e^{i\theta _{k}}$
, and let $t_{k}=e^{i\theta _{k}}$![]() , $\alpha _{k}\in \mathbb {C}$
, $\alpha _{k}\in \mathbb {C}$![]() and $\beta _{k} \in \mathbb {C}$
and $\beta _{k} \in \mathbb {C}$![]() be such that
be such that

Let $V: \mathbb {T}\to \mathbb {R}$![]() and $W: \mathbb {T}\to \mathbb {C}$
and $W: \mathbb {T}\to \mathbb {C}$![]() , and suppose $V$
, and suppose $V$![]() and $W$
and $W$![]() can be extended to analytic functions in a neighbourhood of $\mathbb {T}$
can be extended to analytic functions in a neighbourhood of $\mathbb {T}$![]() . Suppose that the equilibrium measure ${\rm d}\mu _V(e^{i\theta })=\psi (e^{i\theta }){\rm d}\theta$
. Suppose that the equilibrium measure ${\rm d}\mu _V(e^{i\theta })=\psi (e^{i\theta }){\rm d}\theta$![]() associated to $V$
associated to $V$![]() is supported on $\mathbb {T}$
is supported on $\mathbb {T}$![]() and that $\psi > 0$
and that $\psi > 0$![]() on $\mathbb {T}$
on $\mathbb {T}$![]() . Then, as $n \to \infty$
. Then, as $n \to \infty$![]() ,
,
with $\beta _{\max } = \max \{ |{\rm Re\,} \beta _{1}|,\ldots,|{\rm Re\,} \beta _{m}| \}$![]() and
and

where $G$![]() is Barnes’ $G$
is Barnes’ $G$![]() -function. Furthermore, the above asymptotics are uniform for all $\alpha _{k}$
-function. Furthermore, the above asymptotics are uniform for all $\alpha _{k}$![]() in compact subsets of $\{z \in \mathbb {C}: {\rm Re\,} z >-1\}$
in compact subsets of $\{z \in \mathbb {C}: {\rm Re\,} z >-1\}$![]() , for all $\beta _{k}$
, for all $\beta _{k}$![]() in compact subsets of $\{z \in \mathbb {C}: {\rm Re\,} z \in (-\frac {1}{2},\frac {1}{2})\}$
in compact subsets of $\{z \in \mathbb {C}: {\rm Re\,} z \in (-\frac {1}{2},\frac {1}{2})\}$![]() and for all $(\theta _{1},\ldots,\theta _{m})$
and for all $(\theta _{1},\ldots,\theta _{m})$![]() in compact subsets of $(0,2\pi )_{\mathrm {ord}}^{m}$
in compact subsets of $(0,2\pi )_{\mathrm {ord}}^{m}$![]() . The above asymptotics can also be differentiated with respect to $\alpha _{0},\ldots,\alpha _{m},\beta _{0},\ldots,\beta _{m}$
. The above asymptotics can also be differentiated with respect to $\alpha _{0},\ldots,\alpha _{m},\beta _{0},\ldots,\beta _{m}$![]() as follows: if $k_{0},\ldots,k_{2m+1}\in \mathbb {N}$
as follows: if $k_{0},\ldots,k_{2m+1}\in \mathbb {N}$![]() , $k_{0}+\ldots +k_{2m+1}\geq 1$
, $k_{0}+\ldots +k_{2m+1}\geq 1$![]() and $\partial ^{\vec {k}}:=\partial _{\alpha _{0}}^{k_{0}}\ldots \partial _{\alpha _{m}}^{k_{m}}\partial _{\beta _{0}}^{k_{m+1}}\ldots \partial _{\beta _{m}}^{k_{2m+1}}$
and $\partial ^{\vec {k}}:=\partial _{\alpha _{0}}^{k_{0}}\ldots \partial _{\alpha _{m}}^{k_{m}}\partial _{\beta _{0}}^{k_{m+1}}\ldots \partial _{\beta _{m}}^{k_{2m+1}}$![]() , then
, then
where $\widehat {D}_{n}$![]() denotes the right-hand side of (1.11) without the error term.
denotes the right-hand side of (1.11) without the error term.
1.1 History and related work
In the case when the potential $V(z)$![]() in (1.2) vanishes identically, the asymptotic evaluation of Toeplitz determinants of the form (1.1) has a long and distinguished history. The first important result was obtained by Szegő in 1915 who determined the leading behaviour of $D_{n}(\vec {\alpha },\vec {\beta },V,W)$
in (1.2) vanishes identically, the asymptotic evaluation of Toeplitz determinants of the form (1.1) has a long and distinguished history. The first important result was obtained by Szegő in 1915 who determined the leading behaviour of $D_{n}(\vec {\alpha },\vec {\beta },V,W)$![]() in the case when $\vec {\alpha } = \vec {\beta } = \vec {0}$
in the case when $\vec {\alpha } = \vec {\beta } = \vec {0}$![]() and $V = 0$
and $V = 0$![]() , that is, when the symbol $f(z)$
, that is, when the symbol $f(z)$![]() is given by $f(z) = e^{W(z)}$
is given by $f(z) = e^{W(z)}$![]() . In our notation, this result, known as the first Szegő limit theorem [Reference Szegő45], can be expressed as
. In our notation, this result, known as the first Szegő limit theorem [Reference Szegő45], can be expressed as
Later, in the 1940s, it became clear from the pioneering work of Kaufmann and Onsager that a more detailed understanding of the error term in (1.13) could be used to compute two-point correlation functions in the two-dimensional Ising model in the thermodynamic limit [Reference Kaufman and Onsager39]. This inspired Szegő to seek for a stronger version of (1.13). The outcome was the so-called strong Szegő limit theorem [Reference Szegő46], which in our notation states that

We observe that if $V = 0$![]() , then ${\rm d}\mu _V(e^{i\theta }) = \frac {{\rm d}\theta }{2\pi }$
, then ${\rm d}\mu _V(e^{i\theta }) = \frac {{\rm d}\theta }{2\pi }$![]() ; thus, Szegő's theorems are consistent with our main result, theorem 1.11, in the special case when $\vec {\alpha } = \vec {\beta } = \vec {0}$
; thus, Szegő's theorems are consistent with our main result, theorem 1.11, in the special case when $\vec {\alpha } = \vec {\beta } = \vec {0}$![]() and $V = 0$
and $V = 0$![]() . (The strong Szegő theorem actually holds under much weaker assumptions on $W$
. (The strong Szegő theorem actually holds under much weaker assumptions on $W$![]() than what is assumed in this paper, see e.g. the survey [Reference Basor7].)
than what is assumed in this paper, see e.g. the survey [Reference Basor7].)
In a groundbreaking paper from 1968, Fisher and Hartwig introduced a class of singular symbols $f(z)$![]() for which they convincingly conjectured a detailed asymptotic formula for the associated Toeplitz determinant [Reference Fisher and Hartwig32]. The Fisher–Hartwig class consists of symbols $f(z)$
for which they convincingly conjectured a detailed asymptotic formula for the associated Toeplitz determinant [Reference Fisher and Hartwig32]. The Fisher–Hartwig class consists of symbols $f(z)$![]() of form (1.2) with $V = 0$
of form (1.2) with $V = 0$![]() . In our notation, the Fisher–Hartwig conjecture can be formulated as
. In our notation, the Fisher–Hartwig conjecture can be formulated as

where $C_4$![]() is a constant to be determined, and the Fisher–Hartwig singularities are encoded in the vectors $\vec {\alpha }$
is a constant to be determined, and the Fisher–Hartwig singularities are encoded in the vectors $\vec {\alpha }$![]() and $\vec {\beta }$
and $\vec {\beta }$![]() . Symbols with Fisher–Hartwig singularities arise in many applications. For example, in the 1960s, Lenard proved [Reference Lenard41] that no Bose–Einstein condensation exists in the ground state for a one-dimensional system of impenetrable bosons by considering Toeplitz determinants with symbols of the form $f(z) = |z-e^{i\theta _1}| |z - e^{-i\theta _1}|$
. Symbols with Fisher–Hartwig singularities arise in many applications. For example, in the 1960s, Lenard proved [Reference Lenard41] that no Bose–Einstein condensation exists in the ground state for a one-dimensional system of impenetrable bosons by considering Toeplitz determinants with symbols of the form $f(z) = |z-e^{i\theta _1}| |z - e^{-i\theta _1}|$![]() with $\theta _1 \in {\mathbb {R}}$
with $\theta _1 \in {\mathbb {R}}$![]() . Lenard's proof hinges on an inequality whose proof was provided by Szegő, see [Reference Lenard41, Theorem 2]. We observe that (1.15) is consistent with theorem 1.11 in the special case when $V = 0$
. Lenard's proof hinges on an inequality whose proof was provided by Szegő, see [Reference Lenard41, Theorem 2]. We observe that (1.15) is consistent with theorem 1.11 in the special case when $V = 0$![]() .
.
There are too many works devoted to proofs and generalizations of the Fisher–Hartwig conjecture (1.15) for us to cite them all, but we refer to [Reference Basor4, Reference Böttcher and Silbermann11, Reference Widom47] for some early works, and to [Reference Basor and Morrison5, Reference Basor and Tracy6, Reference Böttcher10, Reference Deift, Its and Krasovsky25] for four reviews. The current state-of-the-art for non-merging singularities and for $\vec {\alpha }$![]() , $\vec {\beta }$
, $\vec {\beta }$![]() in compact subsets was set by Ehrhardt in his 1997 Ph.D. thesis (see [Reference Ehrhardt29]) and by Deift, Its and Krasovsky in [Reference Deift, Its and Krasovsky24, Reference Deift, Its and Krasovsky26]. Since our proof builds on the results for the case of $V = 0$
in compact subsets was set by Ehrhardt in his 1997 Ph.D. thesis (see [Reference Ehrhardt29]) and by Deift, Its and Krasovsky in [Reference Deift, Its and Krasovsky24, Reference Deift, Its and Krasovsky26]. Since our proof builds on the results for the case of $V = 0$![]() , we have included a version of the asymptotic formulas of [Reference Deift, Its and Krasovsky24, Reference Deift, Its and Krasovsky26, Reference Ehrhardt29] in theorem 4.1. We also refer to [Reference Claeys and Krasovsky21, Reference Fahs31] for studies of merging Fisher–Hartwig singularities with $V=0$
, we have included a version of the asymptotic formulas of [Reference Deift, Its and Krasovsky24, Reference Deift, Its and Krasovsky26, Reference Ehrhardt29] in theorem 4.1. We also refer to [Reference Claeys and Krasovsky21, Reference Fahs31] for studies of merging Fisher–Hartwig singularities with $V=0$![]() , and to [Reference Charlier and Claeys17] for the case of large discontinuities with $V=0$
, and to [Reference Charlier and Claeys17] for the case of large discontinuities with $V=0$![]() .
.
Note that if $V=V_{0}$![]() is a constant, then $D_{n}(\vec {\alpha },\vec {\beta },V_{0},W)=e^{-n^{2}V_{0}}D_{n}(\vec {\alpha },\vec {\beta },0,W)$
is a constant, then $D_{n}(\vec {\alpha },\vec {\beta },V_{0},W)=e^{-n^{2}V_{0}}D_{n}(\vec {\alpha },\vec {\beta },0,W)$![]() .
.
The novelty of the present work is that we consider symbols that include a non-constant potential $V$![]() ; we are not aware of any previous works on the unit circle including such potentials. Our main result is formulated under the assumption that ${\rm Re\,} \beta _{k} \in (-\frac {1}{2},\frac {1}{2})$
; we are not aware of any previous works on the unit circle including such potentials. Our main result is formulated under the assumption that ${\rm Re\,} \beta _{k} \in (-\frac {1}{2},\frac {1}{2})$![]() for all $k$
for all $k$![]() . The general case where ${\rm Re\,} \beta _{k} \in \mathbb {R}$
. The general case where ${\rm Re\,} \beta _{k} \in \mathbb {R}$![]() was treated in the case of $V=0$
was treated in the case of $V=0$![]() in [Reference Deift, Its and Krasovsky24]. Asymptotic formulas for Hankel determinants with a one-cut regular potential $V$
in [Reference Deift, Its and Krasovsky24]. Asymptotic formulas for Hankel determinants with a one-cut regular potential $V$![]() and Fisher–Hartwig singularities were obtained in [Reference Berestycki, Webb and Wong8, Reference Charlier14, Reference Charlier and Gharakhloo19], and the corresponding multi-cut case was considered in [Reference Charlier, Fahs, Webb and Wong18]. Our proofs draw on some of the techniques developed in these papers.
and Fisher–Hartwig singularities were obtained in [Reference Berestycki, Webb and Wong8, Reference Charlier14, Reference Charlier and Gharakhloo19], and the corresponding multi-cut case was considered in [Reference Charlier, Fahs, Webb and Wong18]. Our proofs draw on some of the techniques developed in these papers.
1.2 Application: a determinantal point process on the unit circle
The Toeplitz determinant (1.1) admits the Heine representation

This suggests that the results of theorem 1.11 can be applied to obtain information about the point process on $\mathbb {T}$![]() defined by the probability measure
defined by the probability measure

where $Z_{n} = D_{n}(\vec {0},\vec {0},V,0)$![]() is the normalization constant (also called the partition function). In what follows, we use theorem 1.11 to obtain smooth statistics, log statistics, counting statistics and rigidity bounds for the point process (1.17). In the case of constant $V$
is the normalization constant (also called the partition function). In what follows, we use theorem 1.11 to obtain smooth statistics, log statistics, counting statistics and rigidity bounds for the point process (1.17). In the case of constant $V$![]() , the point process (1.17) describes the distribution of eigenvalues of matrices drawn from the circular unitary ensemble and has already been widely studied. We are not aware of any earlier work where the process (1.17) is considered explicitly for non-constant $V$
, the point process (1.17) describes the distribution of eigenvalues of matrices drawn from the circular unitary ensemble and has already been widely studied. We are not aware of any earlier work where the process (1.17) is considered explicitly for non-constant $V$![]() . However, the point process (1.17), but with $nV(e^{i\phi })$
. However, the point process (1.17), but with $nV(e^{i\phi })$![]() replaced by the highly oscillatory potential $V(e^{in\phi })$
replaced by the highly oscillatory potential $V(e^{in\phi })$![]() , is studied in [Reference Baik2, Reference Forrester34]. We also refer to [Reference Bourgade and Falconet12, Reference Byun and Seo13] for other determinantal generalizations of the circular unitary ensemble.
, is studied in [Reference Baik2, Reference Forrester34]. We also refer to [Reference Bourgade and Falconet12, Reference Byun and Seo13] for other determinantal generalizations of the circular unitary ensemble.
Let $\mathsf {p}_{n}(z):=\prod _{j=1}^{n}(e^{i\phi _{j}}-z)$![]() be the characteristic polynomial associated to (1.17), and define $\log \mathsf {p}_{n}(z)$
be the characteristic polynomial associated to (1.17), and define $\log \mathsf {p}_{n}(z)$![]() for $z \in \mathbb {T}\setminus \{e^{i\phi _{1}},\ldots,e^{i\phi _{n}}\}$
for $z \in \mathbb {T}\setminus \{e^{i\phi _{1}},\ldots,e^{i\phi _{n}}\}$![]() by
by

where $\arg _{0} z \in [0,2\pi )$![]() . In particular, if $\theta _{k}\notin \{\phi _{1},\ldots,\phi _{n}\}$
. In particular, if $\theta _{k}\notin \{\phi _{1},\ldots,\phi _{n}\}$![]() ,
,

where $N_{n}(\theta ):=\#\{\phi _{j} \in [0,\theta ]\} \in \{0,1,\ldots,n\}$![]() . Using the first identity in (1.18) and the fact that $\{\theta _{0},\ldots,\theta _{m}\} \cap \{\phi _{1},\ldots,\phi _{n}\} = \emptyset$
. Using the first identity in (1.18) and the fact that $\{\theta _{0},\ldots,\theta _{m}\} \cap \{\phi _{1},\ldots,\phi _{n}\} = \emptyset$![]() with probability one, it is straightforward to see that
with probability one, it is straightforward to see that

Furthermore, if $\beta _{0}=-\beta _{1}-\ldots -\beta _{m}$![]() , then the second identity in (1.18) together with (1.19) implies
, then the second identity in (1.18) together with (1.19) implies

Lemma 1.2 For any $z \in \mathbb {T}$![]() , we have
, we have
Proof. The equilibrium measure $\mu _{V}$![]() is uniquely characterized by the Euler–Lagrange variational equality
is uniquely characterized by the Euler–Lagrange variational equality
where $\ell \in \mathbb {R}$![]() is a constant, see e.g. [Reference Saff and Totik42]. In particular, the identity (1.21) is equivalent to the statement that $\ell =V_{0}$
is a constant, see e.g. [Reference Saff and Totik42]. In particular, the identity (1.21) is equivalent to the statement that $\ell =V_{0}$![]() . The equality $\ell =V_{0}$
. The equality $\ell =V_{0}$![]() can be established by integrating (1.23) over $z=e^{i\phi } \in \mathbb {T}$
can be established by integrating (1.23) over $z=e^{i\phi } \in \mathbb {T}$![]() and dividing by $2\pi$
and dividing by $2\pi$![]() :
:
where we have used the well-known (see e.g. [Reference Saff and Totik42, Example 0.5.7]) identity $\int _{0}^{2\pi } \log |e^{i\phi }-e^{i\theta }| \frac {{\rm d}\phi }{2\pi } =0$![]() for $\theta \in [0,2\pi )$
for $\theta \in [0,2\pi )$![]() . This proves (1.21). Identity (1.22) follows from (1.6) and (1.3).
. This proves (1.21). Identity (1.22) follows from (1.6) and (1.3).
Combining (1.20), theorem 1.1 and lemma 1.2, we get the following.
Theorem 1.3 Let $m \in \mathbb {N},$![]() and let $t_{k}=e^{i\theta _{k}},$
and let $t_{k}=e^{i\theta _{k}},$![]() $\alpha _{0},\ldots,\alpha _{m}\in \mathbb {C}$
$\alpha _{0},\ldots,\alpha _{m}\in \mathbb {C}$![]() and $u_{1},\ldots,u_{m} \in \mathbb {C}$
and $u_{1},\ldots,u_{m} \in \mathbb {C}$![]() be such that
be such that
Let $V: \mathbb {T}\to \mathbb {R},$![]() $W: \mathbb {T}\to \mathbb {C}$
$W: \mathbb {T}\to \mathbb {C}$![]() and suppose $V,$
and suppose $V,$![]() $W$
$W$![]() can be extended to analytic functions in a neighbourhood of $\mathbb {T}$
can be extended to analytic functions in a neighbourhood of $\mathbb {T}$![]() . Suppose that the equilibrium measure ${\rm d}\mu _V(e^{i\theta })=\psi (e^{i\theta }){\rm d}\theta$
. Suppose that the equilibrium measure ${\rm d}\mu _V(e^{i\theta })=\psi (e^{i\theta }){\rm d}\theta$![]() associated to $V$
associated to $V$![]() is supported on $\mathbb {T}$
is supported on $\mathbb {T}$![]() and that $\psi > 0$
and that $\psi > 0$![]() on $\mathbb {T}$
on $\mathbb {T}$![]() . Then, as $n \to \infty,$
. Then, as $n \to \infty,$![]() we have
we have

with $u_{\max } = \max \{ |{\rm Im\,} u_{1}|,\ldots,|{\rm Im\,} u_{m}| \}$![]() and
and





where $G$![]() is Barnes’ $G$
is Barnes’ $G$![]() -function and $u_{0}:=-u_{1}-\ldots -u_{m}$
-function and $u_{0}:=-u_{1}-\ldots -u_{m}$![]() . Furthermore, the above asymptotics are uniform for all $\alpha _{k}$
. Furthermore, the above asymptotics are uniform for all $\alpha _{k}$![]() in compact subsets of $\{z \in \mathbb {C}: {\rm Re\,} z >-1\}$
in compact subsets of $\{z \in \mathbb {C}: {\rm Re\,} z >-1\}$![]() , for all $u_{k}$
, for all $u_{k}$![]() in compact subsets of $\{z \in \mathbb {C}: {\rm Im\,} z \in (-\pi,\pi )\}$
in compact subsets of $\{z \in \mathbb {C}: {\rm Im\,} z \in (-\pi,\pi )\}$![]() and for all $(\theta _{1},\ldots,\theta _{m})$
and for all $(\theta _{1},\ldots,\theta _{m})$![]() in compact subsets of $(0,2\pi )_{\mathrm {ord}}^{m}$
in compact subsets of $(0,2\pi )_{\mathrm {ord}}^{m}$![]() . The above asymptotics can also be differentiated with respect to $\alpha _{0},\ldots,\alpha _{m},u_{1},\ldots,u_{m}$
. The above asymptotics can also be differentiated with respect to $\alpha _{0},\ldots,\alpha _{m},u_{1},\ldots,u_{m}$![]() as follows: if $k_{0},\ldots,k_{2m}\in \mathbb {N}$
as follows: if $k_{0},\ldots,k_{2m}\in \mathbb {N}$![]() , $k_{0}+\ldots +k_{2m}\geq 1$
, $k_{0}+\ldots +k_{2m}\geq 1$![]() and $\partial ^{\vec {k}}:=\partial _{\alpha _{0}}^{k_{0}}\ldots \partial _{\alpha _{m}}^{k_{m}}\partial _{u_{1}}^{k_{m+1}}\ldots \partial _{u_{m}}^{k_{2m}}$
and $\partial ^{\vec {k}}:=\partial _{\alpha _{0}}^{k_{0}}\ldots \partial _{\alpha _{m}}^{k_{m}}\partial _{u_{1}}^{k_{m+1}}\ldots \partial _{u_{m}}^{k_{2m}}$![]() , then as $n \to + \infty$
, then as $n \to + \infty$![]()

where $\widehat {E}_{n}$![]() denotes the right-hand side of (1.24) without the error term.
denotes the right-hand side of (1.24) without the error term.
Our first corollary is concerned with the smooth linear statistics of (1.17). For $V=0$![]() , the central limit theorem stated in corollary 1.4 was already obtained in [Reference Johansson38].
, the central limit theorem stated in corollary 1.4 was already obtained in [Reference Johansson38].
Corollary 1.4 Smooth statistics
Let $V$![]() and $W$
and $W$![]() be as in theorem 1.3, and assume furthermore that $W:\mathbb {T}\to \mathbb {R}$
be as in theorem 1.3, and assume furthermore that $W:\mathbb {T}\to \mathbb {R}$![]() . Let $\{\kappa _{j}\}_{j=1}^{+\infty }$
. Let $\{\kappa _{j}\}_{j=1}^{+\infty }$![]() be the cumulants of $\sum _{j=1}^{n}W(e^{i\phi _{j}})$
be the cumulants of $\sum _{j=1}^{n}W(e^{i\phi _{j}})$![]() , i.e.
, i.e.
As $n \to + \infty$![]() , we have
, we have

Moreover, if $W$![]() is non-constant, then
is non-constant, then

converges in distribution to a standard normal random variable.
Our second corollary considers linear statistics for a test function with a $\log$![]() -singularity at $t$
-singularity at $t$![]() . We let $\gamma _{\mathrm {E}}\approx 0.5772$
. We let $\gamma _{\mathrm {E}}\approx 0.5772$![]() denote Euler's constant.
denote Euler's constant.
Corollary 1.5 $\log |\cdot |$ -statistics
-statistics
Let $t=e^{i\theta } \in \mathbb {T}$![]() with $\theta \in [0,2\pi ),$
with $\theta \in [0,2\pi ),$![]() and let $\{\kappa _{j}\}_{j=1}^{+\infty }$
and let $\{\kappa _{j}\}_{j=1}^{+\infty }$![]() be the cumulants of $\log |\mathsf {p}_{n}(t)|,$
be the cumulants of $\log |\mathsf {p}_{n}(t)|,$![]() i.e.
i.e.
As $n \to + \infty$![]() , we have
, we have

and

converges in distribution to a standard normal random variable.
Counting statistics of determinantal point processes have been widely studied over the years [Reference Costin and Lebowitz22, Reference Soshnikov44] and is still a subject of active research, see e.g. the recent works [Reference Charlier16, Reference Dai, Xu and Zhang23, Reference Smith, Le Doussal, Majumdar and Schehr43]. Our third corollary established various results on the counting statistics of (1.17).
Corollary 1.6 Counting statistics
Let $t=e^{i\theta } \in \mathbb {T}$![]() be bounded away from $t_{0}:=1$
be bounded away from $t_{0}:=1$![]() , with $\theta \in (0,2\pi )$
, with $\theta \in (0,2\pi )$![]() , and let $\{\kappa _{j}\}_{j=1}^{+\infty }$
, and let $\{\kappa _{j}\}_{j=1}^{+\infty }$![]() be the cumulants of $N_{n}(\theta )$
be the cumulants of $N_{n}(\theta )$![]() , i.e.
, i.e.
As $n \to + \infty$![]() , we have
, we have

and $\frac {N_{n}(\theta )-n\int _{0}^{\theta } {\rm d}\mu _V(e^{i\phi })}{\sqrt {\log n}/\pi }$![]() converges in distribution to a standard normal random variable.
converges in distribution to a standard normal random variable.
Remark 1.7 There are several differences between smooth, $\log$![]() - and counting statistics that are worth pointing out:
- and counting statistics that are worth pointing out:
• The variance of the smooth statistics is of order $1$
 , while the variances of the $\log$
, while the variances of the $\log$ - and counting statistics are of order $\log n$
- and counting statistics are of order $\log n$ .
.• The third and higher order cumulants of the smooth statistics are all ${\mathcal {O}}(n^{-1})$
 , while for the $\log$
, while for the $\log$ -statistics the corresponding cumulants are all of order $1$
-statistics the corresponding cumulants are all of order $1$ . On the other hand, the third and higher order cumulants of the counting statistics are as follows: the odd cumulants are $o(1)$
. On the other hand, the third and higher order cumulants of the counting statistics are as follows: the odd cumulants are $o(1)$ , while the even cumulants are of order $1$
, while the even cumulants are of order $1$ . This phenomenon for the counting statistics was already noticed in [Reference Smith, Le Doussal, Majumdar and Schehr43, eq (29)] for a class of determinantal point processes.
. This phenomenon for the counting statistics was already noticed in [Reference Smith, Le Doussal, Majumdar and Schehr43, eq (29)] for a class of determinantal point processes.
Another consequence of theorem 1.3 is the following result about the individual fluctuations of the ordered angles. Corollary 1.8 is an analogue for (1.17) of Gustavsson's well-known result [Reference Gustavsson36, Theorem 1.2] for the Gaussian unitary ensemble.
Corollary 1.8 Ordered statistics
Let $\xi _{1}\leq \xi _{2} \leq \ldots \leq \xi _{n}$![]() denote the ordered angles,
denote the ordered angles,
and let $\eta _{k}$![]() be the classical location of the $k$
be the classical location of the $k$![]() -th smallest angle $\xi _{k}$
-th smallest angle $\xi _{k}$![]() ,
,
Let $t=e^{i\theta } \in \mathbb {T}$![]() with $\theta \in (0,2\pi )$
with $\theta \in (0,2\pi )$![]() . Let $k_{\theta }=[n \int _{0}^{\theta }{\rm d}\mu _V(e^{i\phi })],$
. Let $k_{\theta }=[n \int _{0}^{\theta }{\rm d}\mu _V(e^{i\phi })],$![]() where $[x]:= \lfloor x + \frac {1}{2}\rfloor$
where $[x]:= \lfloor x + \frac {1}{2}\rfloor$![]() is the closest integer to $x$
is the closest integer to $x$![]() . As $n \to + \infty,$
. As $n \to + \infty,$![]() $\frac {n\psi (e^{i\eta _{k_{\theta }}})}{\sqrt {\log n}/\pi }(\xi _{k_{\theta }}-\eta _{k_{\theta }})$
$\frac {n\psi (e^{i\eta _{k_{\theta }}})}{\sqrt {\log n}/\pi }(\xi _{k_{\theta }}-\eta _{k_{\theta }})$![]() converges in distribution to a standard normal random variable.
converges in distribution to a standard normal random variable.
There has been a lot of progress in recent years towards understanding the global rigidity of various point processes, see e.g. [Reference Arguin, Belius and Bourgade1, Reference Claeys, Fahs, Lambert and Webb20, Reference Erdős, Yau and Yin30]. Our next corollary is a contribution in this direction: it establishes global rigidity upper bounds for (i) the counting statistics of (1.17) and (ii) the ordered statistics of (1.17).
Corollary 1.9 Rigidity
For each $\epsilon >0$![]() sufficiently small, there exist $c>0$
sufficiently small, there exist $c>0$![]() and $n_{0}>0$
and $n_{0}>0$![]() such that
such that

for all $n \geq n_{0}$![]() .
.
Remark 1.10 It follows from (1.36) that $\lim _{n\to \infty }\mathbb {P}( \max _{1 \leq k \leq n} \psi (e^{i\eta _{k}})|\xi _{k}-\eta _{k}| \leq (1+\epsilon )\frac {1}{\pi }\frac {\log n}{n} ) = 1$![]() . We believe that the upper bound $(1+\epsilon )\frac {1}{\pi }$
. We believe that the upper bound $(1+\epsilon )\frac {1}{\pi }$![]() is sharp, in the sense that we expect the following to hold true:
is sharp, in the sense that we expect the following to hold true:
Our belief is supported by the fact that (1.37) was proved in [Reference Arguin, Belius and Bourgade1, Theorem 1.5] for $V=0$![]() , $\psi (e^{i\theta })=\frac {1}{2\pi }$
, $\psi (e^{i\theta })=\frac {1}{2\pi }$![]() .
.
2. Differential identity for $D_n$
Our general strategy to prove theorem 1.1 is inspired by the earlier works [Reference Berestycki, Webb and Wong8, Reference Charlier14, Reference Deift, Its and Krasovsky24, Reference Krasovsky40]. The first step consists of establishing a differential identity which expresses derivatives of $\log D_n(\vec \alpha,\vec \beta,V,W)$![]() in terms of the solution $Y$
in terms of the solution $Y$![]() to a Riemann–Hilbert (RH) problem (see proposition 2.2). Throughout the paper, $\mathbb {T}$
to a Riemann–Hilbert (RH) problem (see proposition 2.2). Throughout the paper, $\mathbb {T}$![]() is oriented in the counterclockwise direction. We first state the RH problem for $Y$
is oriented in the counterclockwise direction. We first state the RH problem for $Y$![]() .
.
RH problem for $Y(\cdot ) = Y_n(\cdot ;\vec \alpha,\vec \beta,V,W)$
(a) $Y : {\mathbb {C}} \setminus \mathbb {T} \to \mathbb {C}^{2 \times 2}$
 is analytic.
is analytic.(b) For each $z \in \mathbb {T}\setminus \{t_{0},\ldots,t_{m}\}$
 , the boundary values $\lim _{z' \to z}Y(z')$
, the boundary values $\lim _{z' \to z}Y(z')$ from the interior and exterior of $\mathbb {T}$
from the interior and exterior of $\mathbb {T}$ exist, and are denoted by $Y_+(z)$
exist, and are denoted by $Y_+(z)$ and $Y_{-}(z)$
and $Y_{-}(z)$ respectively. Furthermore, $Y_+$
respectively. Furthermore, $Y_+$ and $Y_{-}$
and $Y_{-}$ are continuous on $\mathbb {T}\setminus \{t_{0},\ldots,t_{m}\}$
are continuous on $\mathbb {T}\setminus \{t_{0},\ldots,t_{m}\}$ , and are related by the jump condition
(2.1)\begin{equation} Y_+(z) = Y_-(z)\begin{pmatrix}1 & z^{{-}n}f(z) \\ 0 & 1\end{pmatrix}, \qquad z \in \mathbb{T}\setminus \{t_{0},\ldots,t_{m}\}, \end{equation}where $f$
, and are related by the jump condition
(2.1)\begin{equation} Y_+(z) = Y_-(z)\begin{pmatrix}1 & z^{{-}n}f(z) \\ 0 & 1\end{pmatrix}, \qquad z \in \mathbb{T}\setminus \{t_{0},\ldots,t_{m}\}, \end{equation}where $f$
 is given by (1.2).
is given by (1.2).(c) $Y$
 has the following asymptotic behaviour at infinity:
\[ Y(z) = (1+{\mathcal{O}}(z^{{-}1}))z^{n \sigma_{3}}, \qquad \mbox{as } z \to \infty, \]where $\sigma _{3} = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}$
has the following asymptotic behaviour at infinity:
\[ Y(z) = (1+{\mathcal{O}}(z^{{-}1}))z^{n \sigma_{3}}, \qquad \mbox{as } z \to \infty, \]where $\sigma _{3} = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}$
 .
.(d) As $z \rightarrow t_k$
 , $k=0, \ldots, m$
, $k=0, \ldots, m$ , $z \in {\mathbb {C}} \setminus \mathbb {T}$
, $z \in {\mathbb {C}} \setminus \mathbb {T}$ ,
\[ Y(z) = \begin{cases} \begin{pmatrix} {\mathcal{O}}(1) & {\mathcal{O}}(1) + {\mathcal{O}}({|z-t_k|}^{\alpha_{k}}) \\ {\mathcal{O}}(1) & {\mathcal{O}}(1) + {\mathcal{O}}({|z-t_k|}^{\alpha_{k}}) \end{pmatrix}, & \mbox{if } {\rm Re\,} \alpha_k \ne 0, \\ \begin{pmatrix} {\mathcal{O}}(1) & {\mathcal{O}}(\log{|z-t_k|}) \\ {\mathcal{O}}(1) & {\mathcal{O}}(\log{|z-t_k|}) \end{pmatrix}, & \mbox{if } {\rm Re\,} \alpha_k = 0. \end{cases} \]
,
\[ Y(z) = \begin{cases} \begin{pmatrix} {\mathcal{O}}(1) & {\mathcal{O}}(1) + {\mathcal{O}}({|z-t_k|}^{\alpha_{k}}) \\ {\mathcal{O}}(1) & {\mathcal{O}}(1) + {\mathcal{O}}({|z-t_k|}^{\alpha_{k}}) \end{pmatrix}, & \mbox{if } {\rm Re\,} \alpha_k \ne 0, \\ \begin{pmatrix} {\mathcal{O}}(1) & {\mathcal{O}}(\log{|z-t_k|}) \\ {\mathcal{O}}(1) & {\mathcal{O}}(\log{|z-t_k|}) \end{pmatrix}, & \mbox{if } {\rm Re\,} \alpha_k = 0. \end{cases} \]
Suppose $\{p_k(z) = \kappa _{k} z^{k}+\ldots \}_{k\geq 0}$![]() and $\{\hat {p}_k(z)=\kappa _{k} z^{k}+\ldots \}_{k\geq 0}$
and $\{\hat {p}_k(z)=\kappa _{k} z^{k}+\ldots \}_{k\geq 0}$![]() are two families of polynomials satisfying the orthogonality conditions
are two families of polynomials satisfying the orthogonality conditions

Then the function $Y(z)$![]() defined by
defined by

solves the RH problem for $Y$![]() . It was first noticed by Fokas, Its and Kitaev [Reference Fokas, Its and Kitaev33] that orthogonal polynomials can be characterized by RH problems (for a contour on the real line). The above RH problem for $Y$
. It was first noticed by Fokas, Its and Kitaev [Reference Fokas, Its and Kitaev33] that orthogonal polynomials can be characterized by RH problems (for a contour on the real line). The above RH problem for $Y$![]() , whose jumps lie on the unit circle, was already considered in e.g. [Reference Baik, Deift and Johansson3, eq. (1.26)] and [Reference Deift, Its and Krasovsky24, eq. (3.1)] for more specific $f$
, whose jumps lie on the unit circle, was already considered in e.g. [Reference Baik, Deift and Johansson3, eq. (1.26)] and [Reference Deift, Its and Krasovsky24, eq. (3.1)] for more specific $f$![]() .
.
The monic orthogonal polynomials $\kappa _{n}^{-1}p_{n}, \kappa _{n}^{-1}\hat {p}_{n}$![]() , and also $Y$
, and also $Y$![]() , are unique (if they exist). The orthogonal polynomials exist if $f$
, are unique (if they exist). The orthogonal polynomials exist if $f$![]() is strictly positive almost everywhere on $\mathbb {T}$
is strictly positive almost everywhere on $\mathbb {T}$![]() (this is the case if $W$
(this is the case if $W$![]() is real-valued, $\alpha _{k}>-1$
is real-valued, $\alpha _{k}>-1$![]() and $i\beta _{k} \in (-\frac {1}{2},\frac {1}{2})$
and $i\beta _{k} \in (-\frac {1}{2},\frac {1}{2})$![]() ). More generally, a sufficient condition to ensure existence of $p_{n}, \hat {p}_{n}$
). More generally, a sufficient condition to ensure existence of $p_{n}, \hat {p}_{n}$![]() (and therefore of $Y$
(and therefore of $Y$![]() ) is that $D_{n}^{(n)} \neq 0 \neq D_{n+1}^{(n)}$
) is that $D_{n}^{(n)} \neq 0 \neq D_{n+1}^{(n)}$![]() , where $D_{l}^{(n)} =: \det (f_{j-k})_{j,k=0,\ldots,l-1}$
, where $D_{l}^{(n)} =: \det (f_{j-k})_{j,k=0,\ldots,l-1}$![]() , $l\geq 1$
, $l\geq 1$![]() (note that $D_{n}^{(n)}=D_{n}(\vec {\alpha },\vec {\beta },V,W)$
(note that $D_{n}^{(n)}=D_{n}(\vec {\alpha },\vec {\beta },V,W)$![]() ), see e.g. [Reference Claeys and Krasovsky21, Section 2.1]. In fact,
), see e.g. [Reference Claeys and Krasovsky21, Section 2.1]. In fact,

and $\kappa _k= (D_{k}^{(n)})^{1/2}/(D_{k+1}^{(n)})^{1/2}$![]() . (Note that $p_{k}$
. (Note that $p_{k}$![]() , $\hat {p}_{k}$
, $\hat {p}_{k}$![]() and $\kappa _{k}$
and $\kappa _{k}$![]() are unique only up to multiplicative factors of $-1$
are unique only up to multiplicative factors of $-1$![]() . This can be fixed with a choice of the branch for the above roots. However, since $Y$
. This can be fixed with a choice of the branch for the above roots. However, since $Y$![]() only involves $\kappa _{n}^{-1}p_{n}$
only involves $\kappa _{n}^{-1}p_{n}$![]() and $\kappa _{n-1}\hat {p}_{n-1}$
and $\kappa _{n-1}\hat {p}_{n-1}$![]() , which are unique, this choice for the branch is unimportant for us.) If $D_{k}^{(n)}\neq 0$
, which are unique, this choice for the branch is unimportant for us.) If $D_{k}^{(n)}\neq 0$![]() for $k=0,1,\ldots,n+1$
for $k=0,1,\ldots,n+1$![]() , it follows that
, it follows that

Lemma 2.1 Let $n \in \mathbb {N}$![]() be fixed, and assume that $D_k^{(n)}(f)\neq 0$
be fixed, and assume that $D_k^{(n)}(f)\neq 0$![]() , $k = 0,1,\ldots,n+1$
, $k = 0,1,\ldots,n+1$![]() . For any $z\ne 0$
. For any $z\ne 0$![]() , we have
, we have

where $Y(\cdot ) = Y_n(\cdot ;\vec \alpha,\vec \beta,V,W)$![]() .
.
Proof. The assumptions imply that $\kappa _k= (D_k^{(n)})^{1/2}/(D_{k+1}^{(n)})^{1/2}$![]() is finite and nonzero and that $p_k, \hat {p}_k$
is finite and nonzero and that $p_k, \hat {p}_k$![]() exist for all $k \in \{0,\ldots,n\}$
exist for all $k \in \{0,\ldots,n\}$![]() . Note that (a) $\det Y: {\mathbb {C}} \setminus {\mathbb {T}} \to {\mathbb {C}}$
. Note that (a) $\det Y: {\mathbb {C}} \setminus {\mathbb {T}} \to {\mathbb {C}}$![]() is analytic, (b) $(\det Y)_+(z) = (\det Y)_{-}(z)$
is analytic, (b) $(\det Y)_+(z) = (\det Y)_{-}(z)$![]() for $z \in {\mathbb {T}}\setminus \{t_{0},\ldots,t_{m}\}$
for $z \in {\mathbb {T}}\setminus \{t_{0},\ldots,t_{m}\}$![]() , (c) $\det Y(z) = o(|z-t_{k}|^{-1})$
, (c) $\det Y(z) = o(|z-t_{k}|^{-1})$![]() as $z \to t_{k}$
as $z \to t_{k}$![]() and (d) $\det Y(z) = 1+o(1)$
and (d) $\det Y(z) = 1+o(1)$![]() as $z\to \infty$
as $z\to \infty$![]() . Hence, using successively Morera's theorem, Riemann's removable singularities theorem and Liouville's theorem, we conclude that $\det Y \equiv 1$
. Hence, using successively Morera's theorem, Riemann's removable singularities theorem and Liouville's theorem, we conclude that $\det Y \equiv 1$![]() . Using (2.3) and the fact that $\det Y \equiv 1$
. Using (2.3) and the fact that $\det Y \equiv 1$![]() , we obtain
, we obtain

Using the recurrence relation (see [Reference Deift, Its and Krasovsky24, Lemma 2.2])
we then find

The claim now directly follows from the Christoffel–Darboux formula [Reference Deift, Its and Krasovsky24, Lemma 2.3].
Proposition 2.2 Let $n \in \mathbb {N}_{\geq 1}:=\{1,2,\ldots \}$![]() be fixed and suppose that $f$
be fixed and suppose that $f$![]() depends smoothly on a parameter $\gamma$
depends smoothly on a parameter $\gamma$![]() . If $D_k^{(n)}(f)\neq 0$
. If $D_k^{(n)}(f)\neq 0$![]() for $k = n-1,n,n+1$
for $k = n-1,n,n+1$![]() , then the following differential identity holds
, then the following differential identity holds
Remark 2.3 Identity (2.7) will be used (with a particular choice of $\gamma$![]() ) in the proof of proposition 4.4 to deform the potential, see (4.8).
) in the proof of proposition 4.4 to deform the potential, see (4.8).
Proof. We first prove the claim under the stronger assumption that $D_k^{(n)}(f)\neq 0$![]() for $k = 0,1,\ldots,n+1$
for $k = 0,1,\ldots,n+1$![]() . In this case, $\kappa _k= (D_k^{(n)})^{1/2}/(D_{k+1}^{(n)})^{1/2}$
. In this case, $\kappa _k= (D_k^{(n)})^{1/2}/(D_{k+1}^{(n)})^{1/2}$![]() is finite and nonzero and $p_k, \hat {p}_k$
is finite and nonzero and $p_k, \hat {p}_k$![]() exist for all $k = 0,1,\ldots,n$
exist for all $k = 0,1,\ldots,n$![]() . Replacing $z^{-j}$
. Replacing $z^{-j}$![]() with $\hat {p}_{j}(z^{-1})\kappa _j^{-1}$
with $\hat {p}_{j}(z^{-1})\kappa _j^{-1}$![]() in the first orthogonality condition in (2.2) (with $k=j$
in the first orthogonality condition in (2.2) (with $k=j$![]() ), and differentiating with respect to $\gamma$
), and differentiating with respect to $\gamma$![]() , we obtain, for $j = 0, \ldots, n-1$
, we obtain, for $j = 0, \ldots, n-1$![]() ,
,

The second term on the right-hand side can be simplified as follows:

where the first and second equalities use the first and second relations in (2.2), respectively. Combining (2.8) and (2.9), we find
Taking the log of both sides of (2.5) and differentiating with respect to $\gamma$![]() , we get
, we get

An application of lemma 2.1 completes the proof under the assumption that $D_k^{(n)}(f)\neq 0$![]() , $k = 0,1,\ldots,n+1$
, $k = 0,1,\ldots,n+1$![]() . Since the existence of $Y$
. Since the existence of $Y$![]() only relies on the weaker assumption $D_k^{(n)}(f)\neq 0$
only relies on the weaker assumption $D_k^{(n)}(f)\neq 0$![]() , $k = n-1,n,n+1$
, $k = n-1,n,n+1$![]() , the claim follows from a simple continuity argument.
, the claim follows from a simple continuity argument.
3. Steepest descent analysis
In this section, we use the Deift-Zhou [Reference Deift and Zhou28] steepest descent method to obtain large $n$![]() asymptotics for $Y$
asymptotics for $Y$![]() .
.
3.1 Equilibrium measure and $g$ -function
-function
The first step of the method is to normalize the RH problem at $\infty$![]() by means of a so-called $g$
by means of a so-called $g$![]() -function built in terms of the equilibrium measure (1.7). Recall from (1.3), (1.4) and (1.6) that $U$
-function built in terms of the equilibrium measure (1.7). Recall from (1.3), (1.4) and (1.6) that $U$![]() is an open annulus containing $\mathbb {T}$
is an open annulus containing $\mathbb {T}$![]() in which $V$
in which $V$![]() , $W$
, $W$![]() and $\psi$
and $\psi$![]() are analytic.
are analytic.
Define the function $g:\mathbb {C}\setminus ((-\infty,-1]\cup \mathbb {T} )\to \mathbb {C}$![]() by
by
where for $s = e^{i \theta } \in \mathbb {T}$![]() and $\theta \in [-\pi,\pi )$
and $\theta \in [-\pi,\pi )$![]() , the function $z \mapsto \log _{s} (z-s)$
, the function $z \mapsto \log _{s} (z-s)$![]() is analytic in $\mathbb {C}\setminus ((-\infty,-1]\cup \{e^{i \theta '}: -\pi \leq \theta ' \leq \theta \})$
is analytic in $\mathbb {C}\setminus ((-\infty,-1]\cup \{e^{i \theta '}: -\pi \leq \theta ' \leq \theta \})$![]() and such that $\log _{s} (2)=\log |2|$
and such that $\log _{s} (2)=\log |2|$![]() .
.
Lemma 3.1 The function $g$![]() defined in (3.1) is analytic in $\mathbb {C}\setminus ((-\infty,-1]\cup \mathbb {T} )$
defined in (3.1) is analytic in $\mathbb {C}\setminus ((-\infty,-1]\cup \mathbb {T} )$![]() , satisfies $g(z) = \log z + {\mathcal {O}}(z^{-1})$
, satisfies $g(z) = \log z + {\mathcal {O}}(z^{-1})$![]() as $z \to \infty$
as $z \to \infty$![]() and possesses the following properties:
and possesses the following properties:
where $\hat {c}=\int _{-\pi }^{\pi } \theta \psi (e^{i\theta }) {\rm d}\theta$![]() and $\arg z \in (-\pi,\pi )$
and $\arg z \in (-\pi,\pi )$![]() .
.
Proof. In the case where the equilibrium measure satisfies the symmetry $\psi (e^{i\theta })=\psi (e^{-i\theta })$![]() , we have $\hat {c}=0$
, we have $\hat {c}=0$![]() and in this case (3.2)–(3.4) follow from [Reference Baik, Deift and Johansson3, Lemma 4.2]. In the more general setting of a non-symmetric equilibrium measure, (3.2)–(3.4) can be proved along the same lines as [Reference Baik, Deift and Johansson3, proof of Lemma 4.2] (the main difference is that $F(\pi )=\pi$
and in this case (3.2)–(3.4) follow from [Reference Baik, Deift and Johansson3, Lemma 4.2]. In the more general setting of a non-symmetric equilibrium measure, (3.2)–(3.4) can be proved along the same lines as [Reference Baik, Deift and Johansson3, proof of Lemma 4.2] (the main difference is that $F(\pi )=\pi$![]() in [Reference Baik, Deift and Johansson3, proof of Lemma 4.2] should here be replaced by $F(\pi )=\pi +\hat {c}$
in [Reference Baik, Deift and Johansson3, proof of Lemma 4.2] should here be replaced by $F(\pi )=\pi +\hat {c}$![]() ).
).
It follows from (3.3) that
Substituting (3.2) into the Euler–Lagrange equality (1.23) and recalling that ${\rm d}\mu _V(s) = \psi (s) \frac {{\rm d}s}{is}$![]() , we get
, we get
where the principal branch is taken for the logarithm. Consider the function

where the contour of integration (except for the starting point $-1$![]() ) lies in $U \setminus ((-\infty,0]\cup \mathbb {T})$
) lies in $U \setminus ((-\infty,0]\cup \mathbb {T})$![]() and the first part of the contour lies in $\{z : {\rm Im\,} z \geq 0\}$
and the first part of the contour lies in $\{z : {\rm Im\,} z \geq 0\}$![]() . Since $\psi$
. Since $\psi$![]() is real-valued on $\mathbb {T}$
is real-valued on $\mathbb {T}$![]() , we have ${\rm Re\,} \xi (z)=0$
, we have ${\rm Re\,} \xi (z)=0$![]() for $z \in \mathbb {T}$
for $z \in \mathbb {T}$![]() . Using the Cauchy–Riemann equations in polar coordinates and the compactness of the unit circle, we verify that there exists an open annulus $U' \subseteq U$
. Using the Cauchy–Riemann equations in polar coordinates and the compactness of the unit circle, we verify that there exists an open annulus $U' \subseteq U$![]() containing $\mathbb {T}$
containing $\mathbb {T}$![]() such that ${\rm Re\,} \xi (z) > 0$
such that ${\rm Re\,} \xi (z) > 0$![]() for $z \in U'\setminus \mathbb {T}$
for $z \in U'\setminus \mathbb {T}$![]() . Redefining $U$
. Redefining $U$![]() if necessary, we can (and do) assume that $U'=U$
if necessary, we can (and do) assume that $U'=U$![]() . Furthermore, for $z = e^{i\theta } \in \mathbb {T}$
. Furthermore, for $z = e^{i\theta } \in \mathbb {T}$![]() , $\theta \in (-\pi,\pi )$
, $\theta \in (-\pi,\pi )$![]() , we have
, we have
Analytically continuing $\xi (z)-g(z)$![]() in (3.9), we obtain
in (3.9), we obtain
Note also that
where $\xi _{\pm }(x) := \lim _{\epsilon \to 0^+}\xi (z\pm i\epsilon )$![]() for $x \in U\cap ((-\infty,-1)\cup (-1,0))$
for $x \in U\cap ((-\infty,-1)\cup (-1,0))$![]() .
.
3.2 Transformations $Y\rightarrow T\rightarrow S$
The first transformation $Y\rightarrow T$![]() is defined by
is defined by
For $z \in \mathbb {T} \setminus \{t_{0},\ldots,t_{m}\}$![]() , the function $T$
, the function $T$![]() satisfies the jump relation $T_+=T{\_}J_T$
satisfies the jump relation $T_+=T{\_}J_T$![]() where the jump matrix $J_T$
where the jump matrix $J_T$![]() is given by
is given by
Combining the above with (3.4), (3.6) and (3.8), we conclude that $T$![]() satisfies the following RH problem.
satisfies the following RH problem.
RH problem for $T$
(a) $T: {\mathbb {C}} \setminus \mathbb {T} \rightarrow {\mathbb {C}}^{2\times 2}$
 is analytic.
is analytic.(b) The boundary values $T_+$
 and $T_{-}$
and $T_{-}$ are continuous on $\mathbb {T}\setminus \{t_{0},\ldots,t_{m}\}$
are continuous on $\mathbb {T}\setminus \{t_{0},\ldots,t_{m}\}$ and are related by
\[ T_+(z) = T_-(z)\begin{pmatrix} e^{{-}2n\xi_+(z)} & e^{W(z)} \omega(z) \\ 0 & e^{{-}2n\xi_{-}(z)} \end{pmatrix}, \qquad z \in \mathbb{T} \setminus \{t_{0},\ldots,t_{m}\}. \]
and are related by
\[ T_+(z) = T_-(z)\begin{pmatrix} e^{{-}2n\xi_+(z)} & e^{W(z)} \omega(z) \\ 0 & e^{{-}2n\xi_{-}(z)} \end{pmatrix}, \qquad z \in \mathbb{T} \setminus \{t_{0},\ldots,t_{m}\}. \]
(c) As $z \to \infty$
 , $T(z) = I + {\mathcal {O}}(z^{-1})$
, $T(z) = I + {\mathcal {O}}(z^{-1})$ .
.(d) As $z \rightarrow t_k$
 , $k = 0, \ldots, m$
, $k = 0, \ldots, m$ , $z \in {\mathbb {C}} \setminus \mathbb {T}$
, $z \in {\mathbb {C}} \setminus \mathbb {T}$ ,
\[ T(z) = \begin{cases} \begin{pmatrix} {\mathcal{O}}(1) & {\mathcal{O}}(1) + {\mathcal{O}}({|z-t_k|}^{\alpha_{k}}) \\ {\mathcal{O}}(1) & {\mathcal{O}}(1) + {\mathcal{O}}({|z-t_k|}^{\alpha_{k}}) \end{pmatrix}, & \mbox{if } {\rm Re\,} \alpha_k \ne 0, \\ \begin{pmatrix} {\mathcal{O}}(1) & {\mathcal{O}}(\log{|z-t_k|}) \\ {\mathcal{O}}(1) & {\mathcal{O}}(\log{|z-t_k|}) \end{pmatrix}, & \mbox{if } {\rm Re\,} \alpha_k = 0. \end{cases} \]
,
\[ T(z) = \begin{cases} \begin{pmatrix} {\mathcal{O}}(1) & {\mathcal{O}}(1) + {\mathcal{O}}({|z-t_k|}^{\alpha_{k}}) \\ {\mathcal{O}}(1) & {\mathcal{O}}(1) + {\mathcal{O}}({|z-t_k|}^{\alpha_{k}}) \end{pmatrix}, & \mbox{if } {\rm Re\,} \alpha_k \ne 0, \\ \begin{pmatrix} {\mathcal{O}}(1) & {\mathcal{O}}(\log{|z-t_k|}) \\ {\mathcal{O}}(1) & {\mathcal{O}}(\log{|z-t_k|}) \end{pmatrix}, & \mbox{if } {\rm Re\,} \alpha_k = 0. \end{cases} \]
The jumps of $T$![]() for $z \in \mathbb {T}\setminus \{t_{0},\ldots,t_{m}\}$
for $z \in \mathbb {T}\setminus \{t_{0},\ldots,t_{m}\}$![]() can be factorized as
can be factorized as

Before proceeding to the second transformation, we first describe the analytic continuations of the functions appearing in the above factorization. The functions $\omega _{\beta _{k}}$![]() , $k =0,\ldots,m$
, $k =0,\ldots,m$![]() , have a straightforward analytic continuation from $\mathbb {T} \setminus \{t_{k}\}$
, have a straightforward analytic continuation from $\mathbb {T} \setminus \{t_{k}\}$![]() to $\mathbb {C}\setminus \{\lambda t_{k}: \lambda \geq 0\}$
to $\mathbb {C}\setminus \{\lambda t_{k}: \lambda \geq 0\}$![]() , which is given by
, which is given by

where $\arg _{0} z \in [0,2\pi )$![]() , $t_{k}^{-\beta _{k}} := e^{-i\beta _{k} \theta _{k}}$
, $t_{k}^{-\beta _{k}} := e^{-i\beta _{k} \theta _{k}}$![]() and $z^{\beta _{k}} := |z|^{\beta _{k}}e^{i\beta _{k} \arg _{0} z}$
and $z^{\beta _{k}} := |z|^{\beta _{k}}e^{i\beta _{k} \arg _{0} z}$![]() . For the root-type singularities, we follow [Reference Deift, Its and Krasovsky24] and analytically continue $\omega _{\alpha _{k}}$
. For the root-type singularities, we follow [Reference Deift, Its and Krasovsky24] and analytically continue $\omega _{\alpha _{k}}$![]() from $\mathbb {T}\setminus \{t_{k}\}$
from $\mathbb {T}\setminus \{t_{k}\}$![]() to $\mathbb {C}\setminus \{\lambda t_{k}: \lambda \geq 0\}$
to $\mathbb {C}\setminus \{\lambda t_{k}: \lambda \geq 0\}$![]() as follows
as follows

where $\hat {\arg }_{k} z \in (\theta _{k},\theta _{k}+2\pi )$![]() , and
, and

Now, we open lenses around $\mathbb {T}\setminus \{t_{0},\ldots,t_{m}\}$![]() as shown in figure 1. The part of the lens-shaped contour lying in $\{|z|<1\}$
as shown in figure 1. The part of the lens-shaped contour lying in $\{|z|<1\}$![]() is denoted $\gamma _+$
is denoted $\gamma _+$![]() , and the part lying in $\{|z|>1\}$
, and the part lying in $\{|z|>1\}$![]() is denoted $\gamma _{-}$
is denoted $\gamma _{-}$![]() . We require that $\gamma _+,\gamma _{-} \subset U$
. We require that $\gamma _+,\gamma _{-} \subset U$![]() . The transformation $T \mapsto S$
. The transformation $T \mapsto S$![]() is defined by
is defined by

Note from (3.11)–(3.12) that $e^{-2n\xi (z)}$![]() is analytic in $U \cap ((-\infty,-1)\cup (-1,0))$
is analytic in $U \cap ((-\infty,-1)\cup (-1,0))$![]() . It can be verified using the RH problem for $T$
. It can be verified using the RH problem for $T$![]() and (3.15) that $S$
and (3.15) that $S$![]() satisfies the following RH problem.
satisfies the following RH problem.

Figure 1. The jump contour for $S$![]() with $m=2$
with $m=2$![]() .
.
RH problem for $S$
(a) $S : {\mathbb {C}} \setminus (\gamma _+ \cup \gamma _{-} \cup \mathbb {T}) \to \mathbb {C}^{2 \times 2}$
 is analytic, where $\gamma _+, \gamma _-$
is analytic, where $\gamma _+, \gamma _-$ are the contours in figure 1 lying inside and outside $\mathbb {T}$
are the contours in figure 1 lying inside and outside $\mathbb {T}$ , respectively.
, respectively.(b) The jumps for $S$
 are as follows.
\begin{align*} & S_+(z) = S_-(z)\begin{pmatrix} 0 & e^{W(z)}\omega(z) - e^{{-}W(z)}\omega(z)^{{-}1} & 0 \end{pmatrix}, & & z \in \mathbb{T}\setminus \{t_{0},\ldots,t_{m}\}, \\ & S_+(z) = S_-(z)\begin{pmatrix} 1 & 0 \\ e^{{-}W(z)}\omega(z)^{{-}1}e^{{-}2n\xi(z)} & 1 \end{pmatrix}, & & z \in \gamma_+{\cup} \gamma_{-}. \end{align*}
are as follows.
\begin{align*} & S_+(z) = S_-(z)\begin{pmatrix} 0 & e^{W(z)}\omega(z) - e^{{-}W(z)}\omega(z)^{{-}1} & 0 \end{pmatrix}, & & z \in \mathbb{T}\setminus \{t_{0},\ldots,t_{m}\}, \\ & S_+(z) = S_-(z)\begin{pmatrix} 1 & 0 \\ e^{{-}W(z)}\omega(z)^{{-}1}e^{{-}2n\xi(z)} & 1 \end{pmatrix}, & & z \in \gamma_+{\cup} \gamma_{-}. \end{align*}
(c) As $z \rightarrow \infty$
 , $S(z) = I + {\mathcal {O}}(z^{-1})$
, $S(z) = I + {\mathcal {O}}(z^{-1})$ .
.(d) As $z \to t_{k}$
 , $k = 0,\ldots,m$
, $k = 0,\ldots,m$ , we have
\begin{align*} & \displaystyle S(z) = \left\{\begin{array}{@{}ll} \begin{pmatrix} {\mathcal{O}}(1) & {\mathcal{O}}(\log (z-t_{k})) \\ {\mathcal{O}}(1) & {\mathcal{O}}(\log (z-t_{k})) \end{pmatrix}, & \mbox{if } z \mbox{ is outside the lenses}, \\ \begin{pmatrix} {\mathcal{O}}(\log (z-t_{k})) & {\mathcal{O}}(\log (z-t_{k})) \\ {\mathcal{O}}(\log (z-t_{k})) & {\mathcal{O}}(\log (z-t_{k})) \end{pmatrix}, & \mbox{if } z \mbox{ is inside the lenses}, \end{array}\right.\\ & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \displaystyle \mbox{ if } {\rm Re\,} \alpha_{k} = 0, \\ & \displaystyle S(z) = \left\{\begin{array}{@{}ll} \begin{pmatrix} {\mathcal{O}}(1) & {\mathcal{O}}(1) \\ {\mathcal{O}}(1) & {\mathcal{O}}(1) \end{pmatrix}, & \mbox{if } z \mbox{ is outside the lenses}, \\ \begin{pmatrix} {\mathcal{O}}((z-t_{k})^{-\alpha_{k}}) & {\mathcal{O}}(1) \\ {\mathcal{O}}((z-t_{k})^{-\alpha_{k}}) & {\mathcal{O}}(1) \end{pmatrix}, & \mbox{if } z \mbox{ is inside the lenses}, \end{array} \right.\\ & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \displaystyle \mbox{ if } {\rm Re\,} \alpha_{k} > 0, \\ & \displaystyle S(z) = \begin{pmatrix} {\mathcal{O}}(1) & {\mathcal{O}}((z-t_{k})^{\alpha_{k}}) \\ {\mathcal{O}}(1) & {\mathcal{O}}((z-t_{k})^{\alpha_{k}}) \end{pmatrix},\\ & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \displaystyle \mbox{ if } {\rm Re\,} \alpha_{k} < 0. \end{align*}
, we have
\begin{align*} & \displaystyle S(z) = \left\{\begin{array}{@{}ll} \begin{pmatrix} {\mathcal{O}}(1) & {\mathcal{O}}(\log (z-t_{k})) \\ {\mathcal{O}}(1) & {\mathcal{O}}(\log (z-t_{k})) \end{pmatrix}, & \mbox{if } z \mbox{ is outside the lenses}, \\ \begin{pmatrix} {\mathcal{O}}(\log (z-t_{k})) & {\mathcal{O}}(\log (z-t_{k})) \\ {\mathcal{O}}(\log (z-t_{k})) & {\mathcal{O}}(\log (z-t_{k})) \end{pmatrix}, & \mbox{if } z \mbox{ is inside the lenses}, \end{array}\right.\\ & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \displaystyle \mbox{ if } {\rm Re\,} \alpha_{k} = 0, \\ & \displaystyle S(z) = \left\{\begin{array}{@{}ll} \begin{pmatrix} {\mathcal{O}}(1) & {\mathcal{O}}(1) \\ {\mathcal{O}}(1) & {\mathcal{O}}(1) \end{pmatrix}, & \mbox{if } z \mbox{ is outside the lenses}, \\ \begin{pmatrix} {\mathcal{O}}((z-t_{k})^{-\alpha_{k}}) & {\mathcal{O}}(1) \\ {\mathcal{O}}((z-t_{k})^{-\alpha_{k}}) & {\mathcal{O}}(1) \end{pmatrix}, & \mbox{if } z \mbox{ is inside the lenses}, \end{array} \right.\\ & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \displaystyle \mbox{ if } {\rm Re\,} \alpha_{k} > 0, \\ & \displaystyle S(z) = \begin{pmatrix} {\mathcal{O}}(1) & {\mathcal{O}}((z-t_{k})^{\alpha_{k}}) \\ {\mathcal{O}}(1) & {\mathcal{O}}((z-t_{k})^{\alpha_{k}}) \end{pmatrix},\\ & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \displaystyle \mbox{ if } {\rm Re\,} \alpha_{k} < 0. \end{align*}
Since $\gamma _+,\gamma _{-} \subset U$![]() and ${\rm Re\,} \xi (z) > 0$
and ${\rm Re\,} \xi (z) > 0$![]() for $z \in U\setminus \mathbb {T}$
for $z \in U\setminus \mathbb {T}$![]() (recall the discussion below (3.7)), the jump matrices $S_{-}(z)^{-1}S_+(z)$
(recall the discussion below (3.7)), the jump matrices $S_{-}(z)^{-1}S_+(z)$![]() on $\gamma _+\cup \gamma _{-}$
on $\gamma _+\cup \gamma _{-}$![]() are exponentially close to $I$
are exponentially close to $I$![]() as $n \to + \infty$
as $n \to + \infty$![]() , and this convergence is uniform outside fixed neighbourhoods of $t_{0},\ldots,t_{m}$
, and this convergence is uniform outside fixed neighbourhoods of $t_{0},\ldots,t_{m}$![]() .
.
Our next task is to find suitable approximations (called ‘parametrices’) for $S$![]() in different regions of the complex plane.
in different regions of the complex plane.
3.3 Global parametrix $P^{(\infty )}$
In this subsection, we will construct a global parametrix $P^{(\infty )}$![]() that is defined as the solution to the following RH problem. We will show in subsection 3.5 below that $P^{(\infty )}$
that is defined as the solution to the following RH problem. We will show in subsection 3.5 below that $P^{(\infty )}$![]() is a good approximation of $S$
is a good approximation of $S$![]() outside fixed neighbourhoods of $t_{0},\ldots,t_{m}$
outside fixed neighbourhoods of $t_{0},\ldots,t_{m}$![]() .
.
RH problem for $P^{(\infty )}$
(a) $P^{(\infty )}:\mathbb {C}\setminus \mathbb {T} \to \mathbb {C}^{2\times 2}$
 is analytic.
is analytic.(b) The jumps are given by
(3.16)\begin{align} P^{(\infty)}_+(z) = P^{(\infty)}_-(z) \begin{pmatrix} 0 & e^{W(z)}\omega(z) - e^{{-}W(z)}\omega(z)^{{-}1} & 0 \end{pmatrix},\nonumber\\ z \in \mathbb{T}\setminus \{t_{0},\ldots,t_{m}\}. \end{align}
(c) As $z \to \infty$
 , we have $P^{(\infty )}(z) = I + {\mathcal {O}}(z^{-1})$
, we have $P^{(\infty )}(z) = I + {\mathcal {O}}(z^{-1})$ .
.(d) As $z \to t_{k}$
 from $|z| \lessgtr 1$
from $|z| \lessgtr 1$ , $k\in \{0,\ldots,m\}$
, $k\in \{0,\ldots,m\}$ , we have $P^{(\infty )}(z) = {\mathcal {O}}(1)(z-t_{k})^{-(\frac {\alpha _{k}}{2}\pm \beta _{k})\sigma _{3}}$
, we have $P^{(\infty )}(z) = {\mathcal {O}}(1)(z-t_{k})^{-(\frac {\alpha _{k}}{2}\pm \beta _{k})\sigma _{3}}$ .
.
The unique solution to the above RH problem is given by

where $D(z)$![]() is the Szegő function defined by
is the Szegő function defined by

The branches of the logarithms in (3.19) can be arbitrarily chosen as long as $\log \omega _{\alpha _k}(s)$![]() and $\log \omega _{\beta _k}(s)$
and $\log \omega _{\beta _k}(s)$![]() are continuous on $\mathbb {T} \setminus t_k$
are continuous on $\mathbb {T} \setminus t_k$![]() . The function $D$
. The function $D$![]() is analytic on $\mathbb {C}\setminus \mathbb {T}$
is analytic on $\mathbb {C}\setminus \mathbb {T}$![]() and satisfies the jump condition $D_+(z) = D_-(z)e^{W(z)}\omega (z)$
and satisfies the jump condition $D_+(z) = D_-(z)e^{W(z)}\omega (z)$![]() on $\mathbb {T} \setminus \{t_0, \ldots, t_m\}$
on $\mathbb {T} \setminus \{t_0, \ldots, t_m\}$![]() . The expressions for $D_{\alpha _{k}}$
. The expressions for $D_{\alpha _{k}}$![]() and $D_{\beta _{k}}$
and $D_{\beta _{k}}$![]() can be simplified as in [Reference Deift, Its and Krasovsky24, eqs. (4.9)–(4.10)]; we have
can be simplified as in [Reference Deift, Its and Krasovsky24, eqs. (4.9)–(4.10)]; we have

where $\hat {\arg }_{k}$![]() was defined below (3.14). Using (1.4), we can also simplify $D_{W}$
was defined below (3.14). Using (1.4), we can also simplify $D_{W}$![]() as
as

3.4 Local parametrices $P^{(t_k)}$
In this subsection, we build parametrices $P^{(t_k)}(z)$![]() in small open disks $\mathcal {D}_{t_k}$
in small open disks $\mathcal {D}_{t_k}$![]() of $t_k$
of $t_k$![]() , $k=0,\ldots,m$
, $k=0,\ldots,m$![]() . The disks $\mathcal {D}_{t_k}$
. The disks $\mathcal {D}_{t_k}$![]() are taken sufficiently small such that $\mathcal {D}_{t_k} \subset U$
are taken sufficiently small such that $\mathcal {D}_{t_k} \subset U$![]() and $\mathcal {D}_{t_k} \cap \mathcal {D}_{t_j} = \emptyset$
and $\mathcal {D}_{t_k} \cap \mathcal {D}_{t_j} = \emptyset$![]() for $j \neq k$
for $j \neq k$![]() . Since we assume that the $t_{k}$
. Since we assume that the $t_{k}$![]() 's remain bounded away from each other, we can (and do) choose the radii of the disks to be fixed. The parametrices $P^{(t_k)}(z)$
's remain bounded away from each other, we can (and do) choose the radii of the disks to be fixed. The parametrices $P^{(t_k)}(z)$![]() are defined as the solution to the following RH problem. We will show in subsection 3.5 below that $P^{(t_k)}$
are defined as the solution to the following RH problem. We will show in subsection 3.5 below that $P^{(t_k)}$![]() is a good approximation for $S$
is a good approximation for $S$![]() in $\mathcal {D}_{t_k}$
in $\mathcal {D}_{t_k}$![]() .
.
RH problem for $P^{(t_{k})}$
(a) $P^{(t_k)}: \mathcal {D}_{t_{k}}\setminus (\mathbb {T} \cup \gamma _+ \cup \gamma _{-}) \to \mathbb {C}^{2\times 2}$
 is analytic.
is analytic.(b) For $z\in (\mathbb {T} \cup \gamma _+ \cup \gamma _{-})\cap \mathcal {D}_{t_{k}}$
 , $P_{-}^{(t_k)}(z)^{-1}P_+^{(t_k)}(z)=S_{-}(z)^{-1}S_+(z)$
, $P_{-}^{(t_k)}(z)^{-1}P_+^{(t_k)}(z)=S_{-}(z)^{-1}S_+(z)$ .
.(c) As $n\to +\infty$
 , $P^{(t_k)}(z)=(I+{\mathcal {O}}(n^{-1+2|{\rm Re\,} \beta _{k}|}))P^{(\infty )}(z)$
, $P^{(t_k)}(z)=(I+{\mathcal {O}}(n^{-1+2|{\rm Re\,} \beta _{k}|}))P^{(\infty )}(z)$ uniformly for $z\in \partial \mathcal {D}_{t_k}$
uniformly for $z\in \partial \mathcal {D}_{t_k}$ .
.(d) As $z\to t_k$
 , $S(z)P^{(t_k)}(z)^{-1}={\mathcal {O}}(1)$
, $S(z)P^{(t_k)}(z)^{-1}={\mathcal {O}}(1)$ .
.
A solution to the above RH problem can be constructed using hypergeometric functions as in [Reference Deift, Its and Krasovsky24, Reference Foulquié Moreno, Martinez-Finkelshtein and Sousa35]. Consider the function
where the path is a straight line segment from $t_{k}$![]() to $z$
to $z$![]() . This is a conformal map from $\mathcal {D}_{t_k}$
. This is a conformal map from $\mathcal {D}_{t_k}$![]() to a neighbourhood of $0$
to a neighbourhood of $0$![]() , which satisfies
, which satisfies
If $\mathcal {D}_{t_{k}} \cap (-\infty,0] = \emptyset$![]() , $f_{t_{k}}$
, $f_{t_{k}}$![]() can also be expressed as
can also be expressed as

If $\mathcal {D}_{t_{k}} \cap (-\infty,0] \neq \emptyset$![]() , then instead we have
, then instead we have

If $t_{k}=-1$![]() , (3.23) also holds with $\xi _{\pm }(t_k) := \lim _{\epsilon \to 0^+}\xi _{\pm }(e^{(\pi - \epsilon )i})=0$
, (3.23) also holds with $\xi _{\pm }(t_k) := \lim _{\epsilon \to 0^+}\xi _{\pm }(e^{(\pi - \epsilon )i})=0$![]() . We define $\omega _{k}$
. We define $\omega _{k}$![]() and $\widetilde {W}_{k}$
and $\widetilde {W}_{k}$![]() by
by

where $\hat {\theta }(z;k)=1$![]() if ${\rm Im\,} z <0$
if ${\rm Im\,} z <0$![]() and $k=0$
and $k=0$![]() and $\hat {\theta }(z;k)=0$
and $\hat {\theta }(z;k)=0$![]() otherwise, $z^{\beta _{k}} := |z|^{\beta _{k}}e^{i\beta _{k} \arg _{0} z}$
otherwise, $z^{\beta _{k}} := |z|^{\beta _{k}}e^{i\beta _{k} \arg _{0} z}$![]() ,
,
and (see figure 2)


Figure 2. The four quadrants $Q_{\pm,k}^{R}$![]() , $Q_{\pm,k}^{L}$
, $Q_{\pm,k}^{L}$![]() near $t_k$
near $t_k$![]() and their images under the map $f_{t_k}$
and their images under the map $f_{t_k}$![]() .
.
The argument $\check {\arg }_{k}(z-t_{k})$![]() in (3.24) is defined to have a discontinuity for $z \in (\overline {Q_{-,k}^{L}} \cap \overline {Q_{-,k}^{R}}) \cup [z_{\star,k},t_{k}\infty )$
in (3.24) is defined to have a discontinuity for $z \in (\overline {Q_{-,k}^{L}} \cap \overline {Q_{-,k}^{R}}) \cup [z_{\star,k},t_{k}\infty )$![]() , $z_{\star,k}:=\overline {Q_{-,k}^{L}} \cap \overline {Q_{-,k}^{R}}\cap \partial \mathcal {D}_{t_{k}}$
, $z_{\star,k}:=\overline {Q_{-,k}^{L}} \cap \overline {Q_{-,k}^{R}}\cap \partial \mathcal {D}_{t_{k}}$![]() , and such that $\check {\arg }_{k}((1-0_+)t_{k}-t_{k})=\theta _{k}+\pi$
, and such that $\check {\arg }_{k}((1-0_+)t_{k}-t_{k})=\theta _{k}+\pi$![]() . Note that $\check {\arg }_{k}(z-t_{k})$
. Note that $\check {\arg }_{k}(z-t_{k})$![]() is merely a small deformation of the argument $\hat {\arg }_{k}(z-t_{k})$
is merely a small deformation of the argument $\hat {\arg }_{k}(z-t_{k})$![]() defined below (3.14). This small deformation is needed to ensure that $E_{t_{k}}$
defined below (3.14). This small deformation is needed to ensure that $E_{t_{k}}$![]() in (3.26) below is analytic in $\mathcal {D}_{t_{k}}$
in (3.26) below is analytic in $\mathcal {D}_{t_{k}}$![]() .
.
Note that $\omega _{k}$![]() is analytic in $\mathcal {D}_{t_{k}}$
is analytic in $\mathcal {D}_{t_{k}}$![]() . We now use the confluent hypergeometric model RH problem, whose solution is denoted $\Phi _{\mathrm {HG}}(z;\alpha _{k},\beta _{k})$
. We now use the confluent hypergeometric model RH problem, whose solution is denoted $\Phi _{\mathrm {HG}}(z;\alpha _{k},\beta _{k})$![]() (see appendix B for the definition and properties of $\Phi _{\mathrm {HG}}$
(see appendix B for the definition and properties of $\Phi _{\mathrm {HG}}$![]() ). If $k \neq 0$
). If $k \neq 0$![]() and $\mathcal {D}_{t_{k}} \cap (-\infty,0] = \emptyset$
and $\mathcal {D}_{t_{k}} \cap (-\infty,0] = \emptyset$![]() , we define
, we define
where $E_{t_{k}}$![]() is given by
is given by

Here the branch of $f_{t_k}(z)^{\beta _k}$![]() is such that $f_{t_k}(z)^{\beta _k} = |f_{t_{k}}(z)|^{\beta _k} e^{\beta _k i\arg f_{t_{k}}(z)}$
is such that $f_{t_k}(z)^{\beta _k} = |f_{t_{k}}(z)|^{\beta _k} e^{\beta _k i\arg f_{t_{k}}(z)}$![]() with $\arg f_{t_k}(z) \in (-\frac {\pi }{2}, \frac {3\pi }{2})$
with $\arg f_{t_k}(z) \in (-\frac {\pi }{2}, \frac {3\pi }{2})$![]() , and the branch for the square root of $\omega _{k}(z)$
, and the branch for the square root of $\omega _{k}(z)$![]() can be chosen arbitrarily as long as $\omega _{k}(z)^{1/2}$
can be chosen arbitrarily as long as $\omega _{k}(z)^{1/2}$![]() is analytic in $\mathcal {D}_{t_{k}}$
is analytic in $\mathcal {D}_{t_{k}}$![]() (note that $P^{(t_{k})}(z)$
(note that $P^{(t_{k})}(z)$![]() is invariant under a sign change of $\omega _{k}(z)^{1/2}$
is invariant under a sign change of $\omega _{k}(z)^{1/2}$![]() ). If $k \neq 0$
). If $k \neq 0$![]() , $\mathcal {D}_{t_{k}} \cap (-\infty,0] \neq \emptyset$
, $\mathcal {D}_{t_{k}} \cap (-\infty,0] \neq \emptyset$![]() and ${\rm Im\,} t_{k} \geq 0$
and ${\rm Im\,} t_{k} \geq 0$![]() (resp. ${\rm Im\,} t_{k} < 0$
(resp. ${\rm Im\,} t_{k} < 0$![]() ), then we define $P^{(t_{k})}(z)$
), then we define $P^{(t_{k})}(z)$![]() as in (3.25) but with $\xi (z)$
as in (3.25) but with $\xi (z)$![]() replaced by $\xi (z)+\pi i \theta _{-}(z)$
replaced by $\xi (z)+\pi i \theta _{-}(z)$![]() (resp. $\xi (z)+\pi i \theta _+(z)$
(resp. $\xi (z)+\pi i \theta _+(z)$![]() ), where
), where

Using the definition of $\widetilde {W}_{k}$![]() and the jumps (3.16) of $P^{(\infty )}$
and the jumps (3.16) of $P^{(\infty )}$![]() , we verify that $E_{t_{k}}$
, we verify that $E_{t_{k}}$![]() has no jumps in $\mathcal {D}_{t_{k}}$
has no jumps in $\mathcal {D}_{t_{k}}$![]() . Moreover, since $P^{(\infty )}(z) = {\mathcal {O}}(1)(z-t_{k})^{-(\frac {\alpha _{k}}{2}\pm \beta _{k})\sigma _{3}}$
. Moreover, since $P^{(\infty )}(z) = {\mathcal {O}}(1)(z-t_{k})^{-(\frac {\alpha _{k}}{2}\pm \beta _{k})\sigma _{3}}$![]() as $z\to t_{k}$
as $z\to t_{k}$![]() , $\pm (1-|z|) > 0$
, $\pm (1-|z|) > 0$![]() , we infer from (3.26) that $E_{t_{k}}(z) = {\mathcal {O}}(1)$
, we infer from (3.26) that $E_{t_{k}}(z) = {\mathcal {O}}(1)$![]() as $z \to t_{k}$
as $z \to t_{k}$![]() , and therefore $E_{t_{k}}$
, and therefore $E_{t_{k}}$![]() is analytic in $\mathcal {D}_{t_{k}}$
is analytic in $\mathcal {D}_{t_{k}}$![]() . Using (3.26), we see that $E_{t_{k}}(z) = {\mathcal {O}}(1)n^{\beta _{k}\sigma _{3}}$
. Using (3.26), we see that $E_{t_{k}}(z) = {\mathcal {O}}(1)n^{\beta _{k}\sigma _{3}}$![]() as $n \to \infty$
as $n \to \infty$![]() , uniformly for $z \in \mathcal {D}_{t_{k}}$
, uniformly for $z \in \mathcal {D}_{t_{k}}$![]() . Since $P^{(t_{k})}$
. Since $P^{(t_{k})}$![]() and $S$
and $S$![]() have the same jumps on $(\mathbb {T}\cup \gamma _+\cup \gamma _{-})\cap \mathcal {D}_{t_{k}}$
have the same jumps on $(\mathbb {T}\cup \gamma _+\cup \gamma _{-})\cap \mathcal {D}_{t_{k}}$![]() , $S(z)P^{(t_{k})}(z)^{-1}$
, $S(z)P^{(t_{k})}(z)^{-1}$![]() is analytic in $\mathcal {D}_{t_{k}} \setminus \{t_{k}\}$
is analytic in $\mathcal {D}_{t_{k}} \setminus \{t_{k}\}$![]() . Furthermore, by (B.5) and condition (d) in the RH problem for $S$
. Furthermore, by (B.5) and condition (d) in the RH problem for $S$![]() , as $z \to t_{k}$
, as $z \to t_{k}$![]() from outside the lenses we have that $S(z)P^{(t_{k})}(z)^{-1}$
from outside the lenses we have that $S(z)P^{(t_{k})}(z)^{-1}$![]() is ${\mathcal {O}}(\log (z-t_{k}))$
is ${\mathcal {O}}(\log (z-t_{k}))$![]() if ${\rm Re\,} \alpha _{k} = 0$
if ${\rm Re\,} \alpha _{k} = 0$![]() , is ${\mathcal {O}}(1)$
, is ${\mathcal {O}}(1)$![]() if ${\rm Re\,} \alpha _{k} > 0$
if ${\rm Re\,} \alpha _{k} > 0$![]() , and is ${\mathcal {O}}((z-t_{k})^{\alpha _{k}})$
, and is ${\mathcal {O}}((z-t_{k})^{\alpha _{k}})$![]() if ${\rm Re\,} \alpha _{k} < 0$
if ${\rm Re\,} \alpha _{k} < 0$![]() . In all cases, the singularity of $S(z)P^{(t_{k})}(z)^{-1}$
. In all cases, the singularity of $S(z)P^{(t_{k})}(z)^{-1}$![]() at $z = t_{k}$
at $z = t_{k}$![]() is removable and therefore $P^{(t_{k})}$
is removable and therefore $P^{(t_{k})}$![]() in (3.25) satisfies condition (d) of the RH problem for $P^{(t_{k})}$
in (3.25) satisfies condition (d) of the RH problem for $P^{(t_{k})}$![]() .
.
The value of $E_{t_{k}}(t_{k})$![]() can be obtained by taking the limit $z \to t_{k}$
can be obtained by taking the limit $z \to t_{k}$![]() in (3.26) (e.g. from the quadrant $Q_{+,k}^{R}$
in (3.26) (e.g. from the quadrant $Q_{+,k}^{R}$![]() ). Using (3.17), (3.18), (3.20), (3.22) and (3.26), we obtain
). Using (3.17), (3.18), (3.20), (3.22) and (3.26), we obtain
where

In (3.28), the branch of $\omega _{\alpha _{j}}^{\frac {1}{2}}(t_{k})$![]() is as in (3.24) and $\omega _{\beta _{j}}^{\frac {1}{2}}(t_{k})$
is as in (3.24) and $\omega _{\beta _{j}}^{\frac {1}{2}}(t_{k})$![]() is defined by
is defined by

The expression for $\Lambda _k$![]() can be further simplified as follows. A simple computation shows that
can be further simplified as follows. A simple computation shows that

for $z \in \mathbb {T}$![]() . Therefore, the product in brackets in (3.28) can be rewritten as
. Therefore, the product in brackets in (3.28) can be rewritten as

and thus
where

Using (3.25) and (B.2), we obtain

as $n \to \infty$![]() uniformly for $z \in \partial \mathcal {D}_{t_{k}}$
uniformly for $z \in \partial \mathcal {D}_{t_{k}}$![]() , where $\tau (\alpha _{k},\beta _{k})$
, where $\tau (\alpha _{k},\beta _{k})$![]() is defined in (B.3).
is defined in (B.3).
3.5 Small norm RH problem
We consider the function $R$![]() defined by
defined by

We have shown in the previous section that $P^{(t_{k})}$![]() and $S$
and $S$![]() have the same jumps on $\mathbb {T} \cup \gamma _+ \cup \gamma _{-}$
have the same jumps on $\mathbb {T} \cup \gamma _+ \cup \gamma _{-}$![]() and that $S(z)P^{(t_{k})}(z)^{-1}={\mathcal {O}}(1)$
and that $S(z)P^{(t_{k})}(z)^{-1}={\mathcal {O}}(1)$![]() as $z\to t_{k}$
as $z\to t_{k}$![]() . Hence, $R$
. Hence, $R$![]() is analytic in $\cup _{k=0}^m\mathcal {D}_{t_k}$
is analytic in $\cup _{k=0}^m\mathcal {D}_{t_k}$![]() . Using also the RH problems for $S$
. Using also the RH problems for $S$![]() , $P^{(\infty )}$
, $P^{(\infty )}$![]() and $P^{(t_{k})}$
and $P^{(t_{k})}$![]() , we conclude that $R$
, we conclude that $R$![]() satisfies the following RH problem.
satisfies the following RH problem.
RH problem for $R$
(a) $R : {\mathbb {C}} \setminus \Gamma _{R} \to \mathbb {C}^{2 \times 2}$
 is analytic, where $\Gamma _{R} = \cup _{k=0}^{m} \partial \mathcal {D}_{t_{k}} \cup ((\gamma _+ \cup \gamma _{-}) \setminus \cup _{k=0}^{m} \mathcal {D}_{t_{k}})$
is analytic, where $\Gamma _{R} = \cup _{k=0}^{m} \partial \mathcal {D}_{t_{k}} \cup ((\gamma _+ \cup \gamma _{-}) \setminus \cup _{k=0}^{m} \mathcal {D}_{t_{k}})$ and the circles $\partial \mathcal {D}_{t_{k}}$
and the circles $\partial \mathcal {D}_{t_{k}}$ are oriented in the clockwise direction.
are oriented in the clockwise direction.(b) The jumps are given by
\begin{align*} & R_+(z) = R_{-}(z) P^{(\infty)}(z)& \\ & \quad \times\!\begin{pmatrix} 1 & 0 \\ e^{{-}W(z)}\omega(z)^{{-}1}e^{{-}2n\xi(z)} & 1 \end{pmatrix} P^{(\infty)}(z)^{{-}1}, & \!\!\!z \in (\gamma_+{\cup} \gamma_{-}) {\setminus} \cup_{k=0}^{m} \overline{\mathcal{D}_{t_{k}}},\\ & R_+(z) = R_{-}(z) P^{(t_{k})}(z)P^{(\infty)}(z)^{{-}1}, & z \in \partial \mathcal{D}_{t_{k}}, \, k=0,\ldots,m. \end{align*}
(c) As $z \to \infty$
 , $R(z) = I + {\mathcal {O}}(z^{-1})$
, $R(z) = I + {\mathcal {O}}(z^{-1})$ .
.(d) As $z \to z^{*}\in \Gamma _{R}^{*}$
 , where $\Gamma _{R}^{*}$
, where $\Gamma _{R}^{*}$ is the set of self-intersecting points of $\Gamma _{R}$
is the set of self-intersecting points of $\Gamma _{R}$ , we have $R(z) = {\mathcal {O}}(1)$
, we have $R(z) = {\mathcal {O}}(1)$ .
.
Recall that ${\rm Re\,} \xi (z) \geq c > 0$![]() for $z \in (\gamma _+ \cup \gamma _{-}) \setminus \cup _{k=0}^{m} \mathcal {D}_{t_{k}}$
for $z \in (\gamma _+ \cup \gamma _{-}) \setminus \cup _{k=0}^{m} \mathcal {D}_{t_{k}}$![]() . Moreover, we see from (3.17) that $P^{(\infty )}(z)$
. Moreover, we see from (3.17) that $P^{(\infty )}(z)$![]() is bounded for $z$
is bounded for $z$![]() away from the points $t_{0},\ldots,t_{m}$
away from the points $t_{0},\ldots,t_{m}$![]() . Using also (3.30), we conclude that as $n \to + \infty$
. Using also (3.30), we conclude that as $n \to + \infty$![]()
where $J_{R}(z):=R_{-}^{-1}(z)R_+(z)$![]() and
and

Furthermore, it is easy to see that the ${\mathcal {O}}$![]() -terms in (3.32)–(3.33) are uniform for $(\theta _{1},\ldots,\theta _{m})$
-terms in (3.32)–(3.33) are uniform for $(\theta _{1},\ldots,\theta _{m})$![]() in any given compact subset $\Theta \subset (0,2\pi )_{\mathrm {ord}}^{m}$
in any given compact subset $\Theta \subset (0,2\pi )_{\mathrm {ord}}^{m}$![]() , for $\alpha _{0},\ldots,\alpha _{m}$
, for $\alpha _{0},\ldots,\alpha _{m}$![]() in any given compact subset $\mathfrak {A}\subset \{z \in \mathbb {C}: {\rm Re\,} z >-1\}$
in any given compact subset $\mathfrak {A}\subset \{z \in \mathbb {C}: {\rm Re\,} z >-1\}$![]() , and for $\beta _{0},\ldots,\beta _{m}$
, and for $\beta _{0},\ldots,\beta _{m}$![]() in any given compact subset $\mathfrak {B}\subset \{z \in \mathbb {C}: {\rm Re\,} z \in (-\frac {1}{2},\frac {1}{2})\}$
in any given compact subset $\mathfrak {B}\subset \{z \in \mathbb {C}: {\rm Re\,} z \in (-\frac {1}{2},\frac {1}{2})\}$![]() . Therefore, $R$
. Therefore, $R$![]() satisfies a small norm RH problem, and the existence of $R$
satisfies a small norm RH problem, and the existence of $R$![]() for all sufficiently large $n$
for all sufficiently large $n$![]() can be proved using standard theory [Reference Deift, Kriecherbauer, McLaughlin, Venakides and Zhou27, Reference Deift and Zhou28] as follows. Define the operator $\mathcal {C}:L^{2}(\Gamma _{R})\to L^{2}(\Gamma _{R})$
can be proved using standard theory [Reference Deift, Kriecherbauer, McLaughlin, Venakides and Zhou27, Reference Deift and Zhou28] as follows. Define the operator $\mathcal {C}:L^{2}(\Gamma _{R})\to L^{2}(\Gamma _{R})$![]() by $\mathcal {C}f(z) = \frac {1}{2\pi i}\int _{\Gamma _{R}}\frac {f(s)}{s-z}dz$
by $\mathcal {C}f(z) = \frac {1}{2\pi i}\int _{\Gamma _{R}}\frac {f(s)}{s-z}dz$![]() , and denote $\mathcal {C}_+f$
, and denote $\mathcal {C}_+f$![]() and $\mathcal {C}_{-}f$
and $\mathcal {C}_{-}f$![]() for the left and right non-tangential limits of $\mathcal {C}f$
for the left and right non-tangential limits of $\mathcal {C}f$![]() . Since $\Gamma _{R}$
. Since $\Gamma _{R}$![]() is a compact set, by (3.32)–(3.33) we have $J_{R}-I \in L^{2}(\Gamma _{R})\cap L^{\infty }(\Gamma _{R})$
is a compact set, by (3.32)–(3.33) we have $J_{R}-I \in L^{2}(\Gamma _{R})\cap L^{\infty }(\Gamma _{R})$![]() , and we can define
, and we can define

Using $\| \mathcal {C}_{J_{R}} \|_{L^{2}(\Gamma _{R}) \to L^{2}(\Gamma _{R})} \leq C \|J_{R}-I\|_{L^{\infty }(\Gamma _{R})}$![]() and (3.32)–(3.33), we infer that there exists $n_{0}=n_{0}(\Theta,\mathfrak {A},\mathfrak {B})$
and (3.32)–(3.33), we infer that there exists $n_{0}=n_{0}(\Theta,\mathfrak {A},\mathfrak {B})$![]() such that $\| \mathcal {C}_{J_{R}} \|_{L^{2}(\Gamma _{R}) \to L^{2}(\Gamma _{R})} <1$
such that $\| \mathcal {C}_{J_{R}} \|_{L^{2}(\Gamma _{R}) \to L^{2}(\Gamma _{R})} <1$![]() for all $n \geq n_{0}$
for all $n \geq n_{0}$![]() , all $(\theta _{1},\ldots,\theta _{m})\in \Theta$
, all $(\theta _{1},\ldots,\theta _{m})\in \Theta$![]() , all $\alpha _{0},\ldots,\alpha _{m} \in \mathfrak {A}$
, all $\alpha _{0},\ldots,\alpha _{m} \in \mathfrak {A}$![]() and all $\beta _{0},\ldots,\beta _{m}\in \mathfrak {B}$
and all $\beta _{0},\ldots,\beta _{m}\in \mathfrak {B}$![]() . Hence, for $n \geq n_{0}$
. Hence, for $n \geq n_{0}$![]() , $I-\mathcal {C}_{J_{R}}:L^{2}(\Gamma _{R}) \to L^{2}(\Gamma _{R})$
, $I-\mathcal {C}_{J_{R}}:L^{2}(\Gamma _{R}) \to L^{2}(\Gamma _{R})$![]() can be inverted as a Neumann series and thus $R$
can be inverted as a Neumann series and thus $R$![]() exists and is given by
exists and is given by
Using (3.34), (3.32) and (3.33), we obtain
uniformly for $(\theta _{1},\ldots,\theta _{m})\in \Theta$![]() , $\alpha _{0},\ldots,\alpha _{m} \in \mathfrak {A}$
, $\alpha _{0},\ldots,\alpha _{m} \in \mathfrak {A}$![]() and $\beta _{0},\ldots,\beta _{m}\in \mathfrak {B}$
and $\beta _{0},\ldots,\beta _{m}\in \mathfrak {B}$![]() , where $R^{(1)}$
, where $R^{(1)}$![]() is given by
is given by

Since the jumps $J_{R}$![]() are analytic in a neighbourhood of $\Gamma _{R}$
are analytic in a neighbourhood of $\Gamma _{R}$![]() , expansion (3.35) holds uniformly for $z \in \mathbb {C}\setminus \Gamma _{R}$
, expansion (3.35) holds uniformly for $z \in \mathbb {C}\setminus \Gamma _{R}$![]() . It also follows from (3.34) that (3.35) can be differentiated with respect to $z$
. It also follows from (3.34) that (3.35) can be differentiated with respect to $z$![]() without increasing the error term. For $z \in \mathbb {C}\setminus \cup _{k=0}^{m} \mathcal {D}_{t_{k}}$
without increasing the error term. For $z \in \mathbb {C}\setminus \cup _{k=0}^{m} \mathcal {D}_{t_{k}}$![]() , a residue calculation using (3.22), (3.27) and (3.30) shows that (recall that $\partial \mathcal {D}_{t_{k}}$
, a residue calculation using (3.22), (3.27) and (3.30) shows that (recall that $\partial \mathcal {D}_{t_{k}}$![]() is oriented in the clockwise direction)
is oriented in the clockwise direction)

Remark 3.2 Above, we have discussed the uniformity of (3.32)–(3.33) and (3.35) in the parameters $\theta _{k},\alpha _{k},\beta _{k}$![]() . In § 4, we will also need the following fact, which can be proved via a direct analysis (we omit the details here, see e.g. [Reference Berestycki, Webb and Wong8, Lemma 4.35] for a similar situation): If $V$
. In § 4, we will also need the following fact, which can be proved via a direct analysis (we omit the details here, see e.g. [Reference Berestycki, Webb and Wong8, Lemma 4.35] for a similar situation): If $V$![]() is replaced by $sV$
is replaced by $sV$![]() , then (3.32)–(3.33) and (3.35) also hold uniformly for $s \in [0,1]$
, then (3.32)–(3.33) and (3.35) also hold uniformly for $s \in [0,1]$![]() .
.
Remark 3.3 If $k_{0},\ldots,k_{2m+1}\in \mathbb {N}$![]() , $k_{0}+\ldots +k_{2m+1}\geq 1$
, $k_{0}+\ldots +k_{2m+1}\geq 1$![]() and $\partial ^{\vec {k}}:=\partial _{\alpha _{0}}^{k_{0}}\ldots \partial _{\alpha _{m}}^{k_{m}}\partial _{\beta _{0}}^{k_{m+1}}\ldots \partial _{\beta _{m}}^{k_{2m+1}}$
and $\partial ^{\vec {k}}:=\partial _{\alpha _{0}}^{k_{0}}\ldots \partial _{\alpha _{m}}^{k_{m}}\partial _{\beta _{0}}^{k_{m+1}}\ldots \partial _{\beta _{m}}^{k_{2m+1}}$![]() , then by (3.17) we have
, then by (3.17) we have
and by the same type of arguments that led to (3.30) we have

It follows that
If $W$![]() is replaced by $tW$
is replaced by $tW$![]() , $t \in [0,1]$
, $t \in [0,1]$![]() , then the asymptotics (3.32), (3.33) and (3.35) are uniform with respect to $t$
, then the asymptotics (3.32), (3.33) and (3.35) are uniform with respect to $t$![]() and can also be differentiated any number of times with respect to $t$
and can also be differentiated any number of times with respect to $t$![]() without worsening the error term.
without worsening the error term.
4. Integration in $V$
Our strategy is inspired by [Reference Berestycki, Webb and Wong8] and considers a linear deformation in the potential (in [Reference Berestycki, Webb and Wong8] the authors study Hankel determinants related to point processes on the real line, see also [Reference Charlier14, Reference Charlier, Fahs, Webb and Wong18, Reference Charlier and Gharakhloo19] for subsequent works using similar deformation techniques). Consider the potential $\hat {V}_{s}:=sV$![]() , where $s \in [0,1]$
, where $s \in [0,1]$![]() . It is immediate to verify that
. It is immediate to verify that
with ${\rm d}\mu _{\hat {V}_{0}}(e^{i\theta }):=\frac {1}{2\pi }{\rm d}\theta$![]() and $\ell _{0}=0$
and $\ell _{0}=0$![]() . Using a linear combination of (4.1) and (1.23) (writing $\hat {V}_{s}=(1-s)\hat {V}_{0}+sV$
. Using a linear combination of (4.1) and (1.23) (writing $\hat {V}_{s}=(1-s)\hat {V}_{0}+sV$![]() ), we infer that
), we infer that
holds for each $s \in [0,1]$![]() with $\ell _{s}:=s \ell$
with $\ell _{s}:=s \ell$![]() and ${\rm d}\mu _{\hat {V}_{s}}(e^{i\theta })=\psi _{s}(e^{i\theta }){\rm d}\theta$
and ${\rm d}\mu _{\hat {V}_{s}}(e^{i\theta })=\psi _{s}(e^{i\theta }){\rm d}\theta$![]() , $\psi _{s}(e^{i\theta }):=\frac {1-s}{2\pi }+s\psi (e^{i\theta })$
, $\psi _{s}(e^{i\theta }):=\frac {1-s}{2\pi }+s\psi (e^{i\theta })$![]() . In particular, this shows that $\psi _{s}(e^{i\theta })>0$
. In particular, this shows that $\psi _{s}(e^{i\theta })>0$![]() for all $s \in [0,1]$
for all $s \in [0,1]$![]() and all $\theta \in [0,2\pi )$
and all $\theta \in [0,2\pi )$![]() . Hence, we can (and will) use the analysis of § 3 with $V$
. Hence, we can (and will) use the analysis of § 3 with $V$![]() replaced by $\hat {V}_{s}$
replaced by $\hat {V}_{s}$![]() .
.
We first recall the following result, which will be used for our proof.
Theorem 4.1 Taken from [Reference Deift, Its and Krasovsky24, Reference Ehrhardt29]
Let $m \in \mathbb {N}$![]() , and let $t_{k}=e^{i\theta _{k}}$
, and let $t_{k}=e^{i\theta _{k}}$![]() , $\alpha _{k}$
, $\alpha _{k}$![]() and $\beta _{k}$
and $\beta _{k}$![]() be such that
be such that
Let $W: \mathbb {T}\to \mathbb {R}$![]() be analytic, and define $W_+$
be analytic, and define $W_+$![]() and $W_{-}$
and $W_{-}$![]() as in (1.4). As $n \to +\infty$
as in (1.4). As $n \to +\infty$![]() , we have
, we have
where

where $G$![]() is Barnes’ $G$
is Barnes’ $G$![]() -function. Furthermore, the above asymptotics are uniform for all $\alpha _{k}$
-function. Furthermore, the above asymptotics are uniform for all $\alpha _{k}$![]() in compact subsets of $\{z \in \mathbb {C}: {\rm Re\,} z >-1\}$
in compact subsets of $\{z \in \mathbb {C}: {\rm Re\,} z >-1\}$![]() , for all $\beta _{k}$
, for all $\beta _{k}$![]() in compact subsets of $\{z \in \mathbb {C}: {\rm Re\,} z \in (-\frac {1}{2},\frac {1}{2})\}$
in compact subsets of $\{z \in \mathbb {C}: {\rm Re\,} z \in (-\frac {1}{2},\frac {1}{2})\}$![]() and for all $(\theta _{1},\ldots,\theta _{m})$
and for all $(\theta _{1},\ldots,\theta _{m})$![]() in compact subsets of $(0,2\pi )_{\mathrm {ord}}^{m}$
in compact subsets of $(0,2\pi )_{\mathrm {ord}}^{m}$![]() .
.
Remark 4.2 The above theorem, but with the ${\mathcal {O}}$![]() -term replaced by $o(1)$
-term replaced by $o(1)$![]() , was proved by Ehrhardt in [Reference Ehrhardt29]. The stronger estimate ${\mathcal {O}}( n^{-1+ 2\beta _{\max }} )$
, was proved by Ehrhardt in [Reference Ehrhardt29]. The stronger estimate ${\mathcal {O}}( n^{-1+ 2\beta _{\max }} )$![]() was obtained in [Reference Deift, Its and Krasovsky26, Remark 1.4]. (In fact the results [Reference Deift, Its and Krasovsky26, Reference Ehrhardt29] are valid for more general values of the $\beta _{k}$
was obtained in [Reference Deift, Its and Krasovsky26, Remark 1.4]. (In fact the results [Reference Deift, Its and Krasovsky26, Reference Ehrhardt29] are valid for more general values of the $\beta _{k}$![]() 's, but this will not be needed for us.)
's, but this will not be needed for us.)
Lemma 4.3 For $z\in \mathbb {T}$![]() , we have
, we have
where ${\int\hskip -1,05em -\,}$![]() stands for principal value integral.
stands for principal value integral.
Proof. The first identity (4.4) can be proved by a direct residue calculation using (1.3) and (1.6). We give here another proof, more in the spirit of [Reference Berestycki, Webb and Wong8, Lemma 5.8] and [Reference Charlier and Gharakhloo19, Lemma 8.1]. Let $H,\varphi :\mathbb {C}\setminus \mathbb {T}\to \mathbb {C}$![]() be functions given by
be functions given by

Clearly, $H(\infty )=0$![]() , and for $z\in \mathbb {T}$
, and for $z\in \mathbb {T}$![]() we have
we have
where for the last equality we have used (3.6). So $H(z)\equiv 0$![]() by Liouville's theorem. Identity (4.4) now follows from relations (3.5) and
by Liouville's theorem. Identity (4.4) now follows from relations (3.5) and
The second identity (4.5) follows from a direct residue computation, using (1.3).
Proposition 4.4 As $n\to +\infty$![]() ,
,

where

Proof. We will use (2.7) with $V=\hat {V}_{s}$![]() and $\gamma =s$
and $\gamma =s$![]() , i.e.
, i.e.
where $f(z)=e^{-n\hat {V}_{s}(z)}\omega (z)$![]() and $Y(\cdot ) = Y_{n}(\cdot ;\vec {\alpha },\vec {\beta },\hat {V}_{s},W)$
and $Y(\cdot ) = Y_{n}(\cdot ;\vec {\alpha },\vec {\beta },\hat {V}_{s},W)$![]() . Recall from proposition 2.2 that (4.8) is valid only when $D_{k}^{(n)}(f) \neq 0$
. Recall from proposition 2.2 that (4.8) is valid only when $D_{k}^{(n)}(f) \neq 0$![]() , $k=n-1,n,n+1$
, $k=n-1,n,n+1$![]() . However, it follows from the analysis of subsection 3.5 (see also remark 3.2) that the right-hand side of (4.8) exists for all $n$
. However, it follows from the analysis of subsection 3.5 (see also remark 3.2) that the right-hand side of (4.8) exists for all $n$![]() sufficiently large, for all $(\theta _{1},\ldots,\theta _{m})\in \Theta$
sufficiently large, for all $(\theta _{1},\ldots,\theta _{m})\in \Theta$![]() , all $\alpha _{0},\ldots,\alpha _{m}\in \mathfrak {A}$
, all $\alpha _{0},\ldots,\alpha _{m}\in \mathfrak {A}$![]() , all $\beta _{0},\ldots,\beta _{m}\in \mathfrak {B}$
, all $\beta _{0},\ldots,\beta _{m}\in \mathfrak {B}$![]() and all $s \in [0,1]$
and all $s \in [0,1]$![]() . Hence, we can extend (4.8) by continuity (see also [Reference Charlier14, Reference Charlier and Gharakhloo19, Reference Deift, Its and Krasovsky26, Reference Its and Krasovsky37, Reference Krasovsky40] for similar situations with more details provided). By (2.1), for $z\in \mathbb {T}\setminus \{t_{0},\ldots,t_{m}\}$
. Hence, we can extend (4.8) by continuity (see also [Reference Charlier14, Reference Charlier and Gharakhloo19, Reference Deift, Its and Krasovsky26, Reference Its and Krasovsky37, Reference Krasovsky40] for similar situations with more details provided). By (2.1), for $z\in \mathbb {T}\setminus \{t_{0},\ldots,t_{m}\}$![]() we have
we have
and thus, using that $\partial _s\log f(z) = -nV(z)$![]() is analytic in a neighbourhood of $\mathbb {T}$
is analytic in a neighbourhood of $\mathbb {T}$![]() ,
,
where $\mathcal {C}_i \subset \{z:|z|<1\}\cap U$![]() is a closed curve oriented counterclockwise and surrounding $0$
is a closed curve oriented counterclockwise and surrounding $0$![]() , and $\mathcal {C}_e \subset \{z:|z|>1\} \cap U$
, and $\mathcal {C}_e \subset \{z:|z|>1\} \cap U$![]() is a closed curve oriented clockwise and surrounding $0$
is a closed curve oriented clockwise and surrounding $0$![]() . We choose $\mathcal {C}_i$
. We choose $\mathcal {C}_i$![]() and $\mathcal {C}_e$
and $\mathcal {C}_e$![]() such that they do not intersect $\mathbb {T}\cup \gamma _+\cup \gamma _{-}\cup \mathcal {D}_{t_0}\cup \cdots \cup \mathcal {D}_{t_m}$
such that they do not intersect $\mathbb {T}\cup \gamma _+\cup \gamma _{-}\cup \mathcal {D}_{t_0}\cup \cdots \cup \mathcal {D}_{t_m}$![]() .
.
Inverting the transformations $Y \mapsto T \mapsto S \mapsto R$![]() of § 3 using (3.13), (3.15) and (3.31), for $z \in \mathcal {C}_e\cup \mathcal {C}_i$
of § 3 using (3.13), (3.15) and (3.31), for $z \in \mathcal {C}_e\cup \mathcal {C}_i$![]() we find
we find

Substituting the above in (4.11), we find the following exact identity:
where
Using $\partial _s\log f(z) = -nV(z)$![]() and (3.5) (with $\psi$
and (3.5) (with $\psi$![]() replaced by $\psi _{s}$
replaced by $\psi _{s}$![]() ), we find
), we find
and since $\psi _{s}=\frac {1-s}{2\pi }+s\psi$![]() ,
,

Now we turn to the analysis of $I_{2,s}$![]() . Using (3.17), we obtain
. Using (3.17), we obtain
where $\varphi$![]() is defined in (4.6). Also, by (3.18), (3.20) and (3.21), we have
is defined in (4.6). Also, by (3.18), (3.20) and (3.21), we have

where $W_\pm$![]() are defined in (1.4), and by (1.6), we have
are defined in (1.4), and by (1.6), we have

Substituting (4.16) and (4.17) in (4.13), and doing a residue computation, we obtain

where for the last equality we have used (4.5) and (4.18). Clearly, $I_{2,s}$![]() is independent of $s$
is independent of $s$![]() , and therefore $\int _{0}^{1}I_{2,s}{\rm d}s = c_{2}n$
, and therefore $\int _{0}^{1}I_{2,s}{\rm d}s = c_{2}n$![]() . We now analyse $I_{3,s}$
. We now analyse $I_{3,s}$![]() as $n \to + \infty$
as $n \to + \infty$![]() . From (3.35), we have
. From (3.35), we have
and, using first (3.17) and then (3.36),

Therefore, as $n \to + \infty$![]()

Partial integration yields
and thus, by (4.4), we have

Since the above asymptotics are uniform for $s \in [0,1]$![]() (see remark 3.2), the claim follows.
(see remark 3.2), the claim follows.
Theorem 1.1 now directly follows by combining proposition 4.4 with theorem 4.1. (The estimate (1.12) follows from remark 3.3.)
5. Proofs of corollaries 1.4, 1.5, 1.6, 1.8, 1.9
Let $e^{\phi _{1}},\ldots,e^{i\phi _{n}}$![]() be distributed according to (1.17) with $\phi _{1},\ldots,\phi _{n}\in [0,2\pi )$
be distributed according to (1.17) with $\phi _{1},\ldots,\phi _{n}\in [0,2\pi )$![]() . Recall that $N_{n}(\theta ) = \#\{\phi _{j}\in [0,\theta )\}$
. Recall that $N_{n}(\theta ) = \#\{\phi _{j}\in [0,\theta )\}$![]() and that the angles $\phi _{1},\ldots,\phi _{n}$
and that the angles $\phi _{1},\ldots,\phi _{n}$![]() arranged in increasing order are denoted by $0 \leq \xi _{1} \leq \xi _{2} \leq \ldots \leq \xi _{n} < 2\pi$
arranged in increasing order are denoted by $0 \leq \xi _{1} \leq \xi _{2} \leq \ldots \leq \xi _{n} < 2\pi$![]() .
.
Proof of corollary 1.4.
The asymptotics for the cumulants $\{\kappa _{j}\}_{j=1}^{+\infty }$![]() follow directly from (1.30), theorem 1.3 (with $m=0$
follow directly from (1.30), theorem 1.3 (with $m=0$![]() , $\alpha _{0}=0$
, $\alpha _{0}=0$![]() and with $W$
and with $W$![]() replaced by $tW$
replaced by $tW$![]() ) and the fact that (1.24) can be differentiated any number of time with respect to $t$
) and the fact that (1.24) can be differentiated any number of time with respect to $t$![]() without worsening the error term (see remark 3.3). Furthermore, if $W$
without worsening the error term (see remark 3.3). Furthermore, if $W$![]() is non-constant, then $\sum _{k = 1}^{+\infty } kW_{k}W_{-k} = \sum _{k = 1}^{+\infty } k|W_{k}|^{2} > 0$
is non-constant, then $\sum _{k = 1}^{+\infty } kW_{k}W_{-k} = \sum _{k = 1}^{+\infty } k|W_{k}|^{2} > 0$![]() (because $W$
(because $W$![]() is assumed to be real-valued) and from theorem 1.3 (with $m=0$
is assumed to be real-valued) and from theorem 1.3 (with $m=0$![]() , $\alpha _{0}=0$
, $\alpha _{0}=0$![]() and with $W$
and with $W$![]() replaced by $\frac {tW}{(2\sum _{k = 1}^{+\infty } kW_{k}W_{-k})^{1/2}}$
replaced by $\frac {tW}{(2\sum _{k = 1}^{+\infty } kW_{k}W_{-k})^{1/2}}$![]() , $t \in \mathbb {R}$
, $t \in \mathbb {R}$![]() ) we also have
) we also have

as $n \to + \infty$![]() with $t\in \mathbb {R}$
with $t\in \mathbb {R}$![]() arbitrary but fixed. The convergence in distribution stated in corollary 1.4 now follows from standard theorems (see e.g. [Reference Billingsley9, top of page 415]).
arbitrary but fixed. The convergence in distribution stated in corollary 1.4 now follows from standard theorems (see e.g. [Reference Billingsley9, top of page 415]).
Proof of corollary 1.5.
The proof is similar to the proof of corollary 1.4. The main difference is that (i) for the asymptotics of the cumulants, one needs to use theorem 1.3 with $W=0$![]() , $m=0$
, $m=0$![]() if $t = 1$
if $t = 1$![]() , and with $W=0$
, and with $W=0$![]() , $m=1$
, $m=1$![]() , $\alpha _0 = 0$
, $\alpha _0 = 0$![]() , $u_{1}=0$
, $u_{1}=0$![]() if $t \in \mathbb {T} \setminus \{1\}$
if $t \in \mathbb {T} \setminus \{1\}$![]() , and (ii) for the convergence in distribution, one needs to use theorem 1.3 with $W=0$
, and (ii) for the convergence in distribution, one needs to use theorem 1.3 with $W=0$![]() , $m=0$
, $m=0$![]() and $\alpha _{0}$
and $\alpha _{0}$![]() replaced by $\alpha \sqrt {2}/\sqrt {\log n}$
replaced by $\alpha \sqrt {2}/\sqrt {\log n}$![]() , $\alpha \in \mathbb {R}$
, $\alpha \in \mathbb {R}$![]() fixed, if $t = 1$
fixed, if $t = 1$![]() , and with $W=0$
, and with $W=0$![]() , $m=1$
, $m=1$![]() , $\alpha _0 = 0$
, $\alpha _0 = 0$![]() , $u_{1}=0$
, $u_{1}=0$![]() and $\alpha _1$
and $\alpha _1$![]() replaced by $\alpha \sqrt {2}/\sqrt {\log n}$
replaced by $\alpha \sqrt {2}/\sqrt {\log n}$![]() , $\alpha \in \mathbb {R}$
, $\alpha \in \mathbb {R}$![]() fixed, if $t \in \mathbb {T}\setminus \{1\}$
fixed, if $t \in \mathbb {T}\setminus \{1\}$![]() .
.
Proof of corollary 1.6.
This proof is also similar to the proof of corollary 1.4. For the asymptotics of the cumulants, one needs to use theorem 1.3 with $W=0$![]() , $m=1$
, $m=1$![]() , $\alpha _{0}=\alpha _{1}=0$
, $\alpha _{0}=\alpha _{1}=0$![]() and for the convergence in distribution, one needs to use theorem 1.3 with $W=0$
and for the convergence in distribution, one needs to use theorem 1.3 with $W=0$![]() , $m=1$
, $m=1$![]() , $\alpha _{0}=\alpha _{1}=0$
, $\alpha _{0}=\alpha _{1}=0$![]() , and with $u_{1}$
, and with $u_{1}$![]() replaced by $\pi u/\sqrt {\log n}$
replaced by $\pi u/\sqrt {\log n}$![]() , $u\in \mathbb {R}$
, $u\in \mathbb {R}$![]() fixed.
fixed.
Proof of corollary 1.8.
The proof is inspired by Gustavsson [Reference Gustavsson36, Theorem 1.2]. Let $\theta \in (0,2\pi )$![]() and $k_{\theta }=[n \int _{0}^{\theta }{\rm d}\mu _{V}(e^{i \phi })]$
and $k_{\theta }=[n \int _{0}^{\theta }{\rm d}\mu _{V}(e^{i \phi })]$![]() , where $[x]:= \lfloor x + \frac {1}{2}\rfloor$
, where $[x]:= \lfloor x + \frac {1}{2}\rfloor$![]() , and consider the random variable
, and consider the random variable

where $\mu _{n}(\xi ) := n\int _{0}^{\xi }{\rm d}\mu _{V}(e^{i \phi })$![]() and $\sigma _{n} := \frac {1}{\pi }\sqrt {\log n}$
and $\sigma _{n} := \frac {1}{\pi }\sqrt {\log n}$![]() . For $y \in \mathbb {R}$
. For $y \in \mathbb {R}$![]() , we have
, we have
Letting $\tilde {\theta } := \mu _{n}^{-1}(k_{\theta } + y \sigma _{n} )$![]() , we can rewrite (5.2) as
, we can rewrite (5.2) as

As $n \to +\infty$![]() , we have
, we have
Since theorem 1.3 also holds in the case where $\theta$![]() depends on $n$
depends on $n$![]() but remains bounded away from $0$
but remains bounded away from $0$![]() , the same is true for the convergence in distribution in corollary 1.6. By (5.4), $\tilde {\theta }$
, the same is true for the convergence in distribution in corollary 1.6. By (5.4), $\tilde {\theta }$![]() remains bounded away from $0$
remains bounded away from $0$![]() , and therefore corollary 1.6 together with (5.3) implies that $Y_{n}$
, and therefore corollary 1.6 together with (5.3) implies that $Y_{n}$![]() converges in distribution to a standard normal random variable. Since
converges in distribution to a standard normal random variable. Since

as $n\to + \infty$![]() , this implies the convergence in distribution in the statement of corollary 1.8.
, this implies the convergence in distribution in the statement of corollary 1.8.
Proof of corollary 1.9.
Let $\mu _{n}(\xi ) := n\int _{0}^{\xi }{\rm d}\mu _{V}(e^{i \phi })$![]() , $\sigma _{n} := \frac {1}{\pi }\sqrt {\log n}$
, $\sigma _{n} := \frac {1}{\pi }\sqrt {\log n}$![]() , and for $\theta \in [0,2\pi )$
, and for $\theta \in [0,2\pi )$![]() , let $\overline {N}_{n}(\theta ) := N_{n}(\theta )-\mu _{n}(\theta )$
, let $\overline {N}_{n}(\theta ) := N_{n}(\theta )-\mu _{n}(\theta )$![]() . Using theorem 1.3 with $W=0$
. Using theorem 1.3 with $W=0$![]() , $m \in {\mathbb {N}}_{>0}$
, $m \in {\mathbb {N}}_{>0}$![]() , $\alpha _{0}=\ldots =\alpha _{m}=0$
, $\alpha _{0}=\ldots =\alpha _{m}=0$![]() and $u_{1},\ldots,u_{m} \in \mathbb {R}$
and $u_{1},\ldots,u_{m} \in \mathbb {R}$![]() , we infer that for any $\delta \in (0,\pi )$
, we infer that for any $\delta \in (0,\pi )$![]() and $M>0$
and $M>0$![]() , there exists $n_{0}'=n_{0}'(\delta,M)\in \mathbb {N}$
, there exists $n_{0}'=n_{0}'(\delta,M)\in \mathbb {N}$![]() and $\mathrm {C}=\mathrm {C}(\delta,M)>0$
and $\mathrm {C}=\mathrm {C}(\delta,M)>0$![]() such that
such that
for all $n\geq n_{0}'$![]() , $(\theta _{1},\ldots, \theta _{m})$
, $(\theta _{1},\ldots, \theta _{m})$![]() in compact subsets of $(0,2\pi )_{\mathrm {ord}}^{m}\cap (\delta,2\pi -\delta )^{m}$
in compact subsets of $(0,2\pi )_{\mathrm {ord}}^{m}\cap (\delta,2\pi -\delta )^{m}$![]() and $u_{1},\ldots,u_{m} \in [-M,M]$
and $u_{1},\ldots,u_{m} \in [-M,M]$![]() , and where $u_{0}=-u_{1}-\ldots -u_{m}$
, and where $u_{0}=-u_{1}-\ldots -u_{m}$![]() .
.
Lemma 5.1 For any $\delta \in (0,\pi )$![]() , there exists $c>0$
, there exists $c>0$![]() such that for all large enough $n$
such that for all large enough $n$![]() and small enough $\epsilon >0$
and small enough $\epsilon >0$![]() ,
,

Proof. A naive adaptation of [Reference Charlier15, Lemma 8.1] (an important difference between [Reference Charlier15] and our situation is that $\sigma _{n} = \frac {\sqrt {\log n}}{\sqrt {2}\pi }$![]() in [Reference Charlier15] while here we have $\smash {\sigma _{n} = \frac {\sqrt {\log n}}{\pi }}$
in [Reference Charlier15] while here we have $\smash {\sigma _{n} = \frac {\sqrt {\log n}}{\pi }}$![]() ) yields
) yields

Inequality (5.5) can in fact be used to obtain the stronger statement (5.6).Footnote 1 Recall that $\eta _{k}= \mu _{n}^{-1}(k)$![]() is the classical location of the $k$
is the classical location of the $k$![]() -th smallest point $\xi _{k}$
-th smallest point $\xi _{k}$![]() and is defined in (1.34). Since $\mu _{n}$
and is defined in (1.34). Since $\mu _{n}$![]() and $N_{n}$
and $N_{n}$![]() are increasing functions, for $x\in [\eta _{k-1},\eta _k]$
are increasing functions, for $x\in [\eta _{k-1},\eta _k]$![]() with $k \in \{1,\ldots,n\}$
with $k \in \{1,\ldots,n\}$![]() , we have
, we have
which implies
where $\mathcal {K}_{n} = \{k: \eta _{k}>\delta \mbox { and } \eta _{k-1}<2\pi -\delta \}$![]() . Hence, for any $v>0$
. Hence, for any $v>0$![]() ,
,
Let $\epsilon _{0}>0$![]() be small and fixed, and let $\mathcal {I}$
be small and fixed, and let $\mathcal {I}$![]() be an arbitrary but fixed subset of $(0,\epsilon _{0}]$
be an arbitrary but fixed subset of $(0,\epsilon _{0}]$![]() . Claim (5.6) will follow if we can prove for any $\epsilon \in \mathcal {I}$
. Claim (5.6) will follow if we can prove for any $\epsilon \in \mathcal {I}$![]() that
that
for some $c_{1}=c_{1}(\mathcal {I})>0$![]() . Let $m \in {\mathbb {N}}$
. Let $m \in {\mathbb {N}}$![]() be fixed and $S_{m}$
be fixed and $S_{m}$![]() and $S_{m}'$
and $S_{m}'$![]() be the following two collections of points of size $m$
be the following two collections of points of size $m$![]()

Let $X_{n}(\theta ):= (N_{n}(\theta )-\mu _{n}(\theta ))/\sigma _{n}$![]() . For any $\theta \in [\delta,2\pi -\delta ]$
. For any $\theta \in [\delta,2\pi -\delta ]$![]() , we have by corollary 1.6 that $\mathbb {E}[X_{n}(\theta )] = {\mathcal {O}}(\frac {\sqrt {\log n}}{n})$
, we have by corollary 1.6 that $\mathbb {E}[X_{n}(\theta )] = {\mathcal {O}}(\frac {\sqrt {\log n}}{n})$![]() and $\mbox {Var}[X_{n}(\theta )] \leq 2$
and $\mbox {Var}[X_{n}(\theta )] \leq 2$![]() for all large enough $n$
for all large enough $n$![]() . Hence, by Chebyshev's inequality, for any fixed $\ell > 0$
. Hence, by Chebyshev's inequality, for any fixed $\ell > 0$![]() , $\mathbb {P}(\frac {|X_{n}|}{\sigma _{n}} \geq \ell ) \leq \frac {3}{\ell ^{2}\sigma _{n}^{2}}$
, $\mathbb {P}(\frac {|X_{n}|}{\sigma _{n}} \geq \ell ) \leq \frac {3}{\ell ^{2}\sigma _{n}^{2}}$![]() for all large enough $n$
for all large enough $n$![]() . Using this inequality with $\ell =\frac {\pi \epsilon }{2}$
. Using this inequality with $\ell =\frac {\pi \epsilon }{2}$![]() together with a union bound, we get
together with a union bound, we get

and then

The reason for introducing two subsets $S_{m},S_{m}'$![]() is the following: for any $k \in \mathcal {K}_{n}$
is the following: for any $k \in \mathcal {K}_{n}$![]() , one must have that $\eta _{k}$
, one must have that $\eta _{k}$![]() remains bounded away from at least one of $S_{m},S_{m}'$
remains bounded away from at least one of $S_{m},S_{m}'$![]() (so that (5.5) can be applied). Indeed, suppose for example that $\theta$
(so that (5.5) can be applied). Indeed, suppose for example that $\theta$![]() is bounded away from $S_{m}$
is bounded away from $S_{m}$![]() , then by (5.5) (with $m$
, then by (5.5) (with $m$![]() replaced by $m+1$
replaced by $m+1$![]() and with $u_{1}=u$
and with $u_{1}=u$![]() and $u_{2}=\ldots =u_{m+1}=-\frac {u}{m}$
and $u_{2}=\ldots =u_{m+1}=-\frac {u}{m}$![]() ) we have
) we have

and similarly,

Hence, if $\eta _{k}$![]() remains bounded away from $S_{m}$
remains bounded away from $S_{m}$![]() , we have (with $\gamma :=\pi (1+\epsilon /2)$
, we have (with $\gamma :=\pi (1+\epsilon /2)$![]() and $\alpha := \frac {1}{2}(1+\frac {1}{m})$
and $\alpha := \frac {1}{2}(1+\frac {1}{m})$![]() )
)


We obtain the same bound (5.11) if $\eta _{k}$![]() in (5.10) is instead bounded away from $S_{m}'$
in (5.10) is instead bounded away from $S_{m}'$![]() . The above exponent is less than $-1$
. The above exponent is less than $-1$![]() provided that $m$
provided that $m$![]() is sufficiently large relative to $\epsilon$
is sufficiently large relative to $\epsilon$![]() . Since the number of points in $\mathcal {K}_{n}$
. Since the number of points in $\mathcal {K}_{n}$![]() is proportional to $n$
is proportional to $n$![]() , claim (5.6) now directly follows from (5.9) (recall also (5.8)).
, claim (5.6) now directly follows from (5.9) (recall also (5.8)).
Lemma 5.2 Let $\delta \in (0,\frac {\pi }{2})$![]() and $\epsilon > 0$
and $\epsilon > 0$![]() . For all sufficiently large $n$
. For all sufficiently large $n$![]() , if the event
, if the event
holds true, then we have

Proof. The proof is almost identical to the proof of [Reference Charlier15, Lemma 8.2] so we omit it.
By combining lemmas 5.1 and 5.2, we arrive at the following result (the proof is very similar to [Reference Charlier15, Proof of (1.38)], so we omit it).
Lemma 5.3 For any $\delta \in (0,\pi )$![]() , there exists $c>0$
, there exists $c>0$![]() such that for all large enough $n$
such that for all large enough $n$![]() and small enough $\epsilon >0$
and small enough $\epsilon >0$![]() ,
,
Extending lemmas 5.1 and 5.3 to $\delta =0$ .
.
In this paper, the support of $\mu _{V}$![]() is $\mathbb {T}$
is $\mathbb {T}$![]() . Therefore, the point $1 \in \mathbb {T}$
. Therefore, the point $1 \in \mathbb {T}$![]() should play no special role in the study of the global rigidity of the points, which suggests that (5.6) and (5.14) should still hold with $\delta =0$
should play no special role in the study of the global rigidity of the points, which suggests that (5.6) and (5.14) should still hold with $\delta =0$![]() . The next lemma shows that this is indeed the case.
. The next lemma shows that this is indeed the case.
Lemma 5.4 Proof of (1.35)
For each small enough $\epsilon >0$![]() , there exists $c>0$
, there exists $c>0$![]() such that
such that

for all large enough $n$![]() .
.
Proof. For $-\pi \leq \theta < 0$![]() , let $\tilde {N}_{n}(\theta ):=\#\{\phi _{j}-2\pi \in (-\pi,\theta ]\}$
, let $\tilde {N}_{n}(\theta ):=\#\{\phi _{j}-2\pi \in (-\pi,\theta ]\}$![]() , and for $0 \leq \theta < \pi$
, and for $0 \leq \theta < \pi$![]() , let $\tilde {N}_{n}(\theta ):=\#(\{\phi _{j}-2\pi \in (-\pi,0]\}\cup \{\phi _{j} \in [0,\theta ]\})$
, let $\tilde {N}_{n}(\theta ):=\#(\{\phi _{j}-2\pi \in (-\pi,0]\}\cup \{\phi _{j} \in [0,\theta ]\})$![]() . For $-\pi \leq \theta < \pi$
. For $-\pi \leq \theta < \pi$![]() , define also $\tilde {\mu }_{n}(\theta ):=n\int _{-\pi }^{\theta }{\rm d}\mu _{V}(e^{i\phi })$
, define also $\tilde {\mu }_{n}(\theta ):=n\int _{-\pi }^{\theta }{\rm d}\mu _{V}(e^{i\phi })$![]() . In the same way as for lemma 5.1, the following holds: for any $\delta \in (0,\pi )$
. In the same way as for lemma 5.1, the following holds: for any $\delta \in (0,\pi )$![]() , there exists $c_{1}>0$
, there exists $c_{1}>0$![]() such that for all large enough $n$
such that for all large enough $n$![]() and small enough $\epsilon >0$
and small enough $\epsilon >0$![]() ,
,

Clearly,

and therefore

Thus, for all large enough $n$![]() ,
,

Combining the above with (5.6) (with $c$![]() replaced by $c_{2}$
replaced by $c_{2}$![]() ), we obtain
), we obtain

Let $X_{n}:= (N_{n}(\pi )-\mu _{n}(\pi ))/\sigma _{n}$![]() . By corollary 1.6, $\mathbb {E}[X_{n}] = {\mathcal {O}}(\frac {\sqrt {\log n}}{n})$
. By corollary 1.6, $\mathbb {E}[X_{n}] = {\mathcal {O}}(\frac {\sqrt {\log n}}{n})$![]() and $\mbox {Var}[X_{n}] \leq 2$
and $\mbox {Var}[X_{n}] \leq 2$![]() for all large enough $n$
for all large enough $n$![]() . Hence, by Chebyshev's inequality, for any fixed $\ell > 0$
. Hence, by Chebyshev's inequality, for any fixed $\ell > 0$![]() , $\mathbb {P}(\frac {|X_{n}|}{\sigma _{n}} \geq \ell ) \leq \frac {3}{\ell ^{2}\sigma _{n}^{2}}$
, $\mathbb {P}(\frac {|X_{n}|}{\sigma _{n}} \geq \ell ) \leq \frac {3}{\ell ^{2}\sigma _{n}^{2}}$![]() for all large enough $n$
for all large enough $n$![]() . Applying this inequality with $\ell = \pi (1+(1+\epsilon )\epsilon ) - \pi (1+\epsilon ) = \pi \epsilon ^{2}$
. Applying this inequality with $\ell = \pi (1+(1+\epsilon )\epsilon ) - \pi (1+\epsilon ) = \pi \epsilon ^{2}$![]() we see that if $\mathbb {P}(A)$
we see that if $\mathbb {P}(A)$![]() denotes the left-hand side of (5.15), then
denotes the left-hand side of (5.15), then

Together with (5.15), this gives

for some $c_{3}=c_{3}(\epsilon )>0$![]() , which proves the claim.
, which proves the claim.
The upper bound (1.36) can be proved using the same idea as in the proof of lemma 5.4.
Acknowledgements
The work of all three authors was supported by the European Research Council, Grant Agreement No. 682537. C. C. also acknowledges support from the Swedish Research Council, Grant No. 2021-04626. J. L. also acknowledges support from the Swedish Research Council, Grant No. 2021-03877, and the Ruth and Nils-Erik Stenbäck Foundation. We are very grateful to the referees for valuable suggestions, and in particular for providing us with a proof of (5.6).
Appendix A. Equilibrium measure
Assume that $\mu _{V}$![]() is supported on $\mathbb {T}$
is supported on $\mathbb {T}$![]() . We make the ansatz that $\mu _{V}$
. We make the ansatz that $\mu _{V}$![]() is of form (1.7) for some $\psi$
is of form (1.7) for some $\psi$![]() . Let $g$
. Let $g$![]() be as in (3.1). Substituting (3.2) in (1.23) and differentiating, we obtain
be as in (3.1). Substituting (3.2) in (1.23) and differentiating, we obtain
Since $g'(z) = \frac {1}{z}+{\mathcal {O}}(z^{-2})$![]() as $z \to \infty$
as $z \to \infty$![]() , we deduce that
, we deduce that
where $\varphi (z) := +1$![]() if $|z|>1$
if $|z|>1$![]() and $\varphi (z) := -1$
and $\varphi (z) := -1$![]() if $|z|<1$
if $|z|<1$![]() . Using (A.1) in (3.5), it follows that
. Using (A.1) in (3.5), it follows that
Recall from (1.3) that $V$![]() is analytic in the open annulus $U$
is analytic in the open annulus $U$![]() and real-valued on $\mathbb {T}$
and real-valued on $\mathbb {T}$![]() , and therefore
, and therefore
(It is straightforward to check that the series $\sum _{k \geq 1} k V_{k}z^{k-1}$![]() and $\sum _{k \geq 1} k\overline {V_{k}}z^{-k-1}$
and $\sum _{k \geq 1} k\overline {V_{k}}z^{-k-1}$![]() are convergent in $U$
are convergent in $U$![]() .) Direct computation gives
.) Direct computation gives

which, by (A.2), proves that $\psi$![]() is given by (1.6). Since the right-hand side of (1.6) is positive on $\mathbb {T}$
is given by (1.6). Since the right-hand side of (1.6) is positive on $\mathbb {T}$![]() (by our assumption that $V$
(by our assumption that $V$![]() is regular), we conclude that $\psi (e^{i\theta }){\rm d}\theta$
is regular), we conclude that $\psi (e^{i\theta }){\rm d}\theta$![]() is a probability measure satisfying the Euler–Lagrange condition (1.23). Therefore, $\psi (e^{i\theta }){\rm d}\theta$
is a probability measure satisfying the Euler–Lagrange condition (1.23). Therefore, $\psi (e^{i\theta }){\rm d}\theta$![]() minimizes (1.5), i.e. $\psi (e^{i\theta }){\rm d}\theta$
minimizes (1.5), i.e. $\psi (e^{i\theta }){\rm d}\theta$![]() is the equilibrium measure associated to $V$
is the equilibrium measure associated to $V$![]() . Since the equilibrium measure is unique [Reference Saff and Totik42], this proves (1.7).
. Since the equilibrium measure is unique [Reference Saff and Totik42], this proves (1.7).
Appendix B. Confluent hypergeometric model RH problem
(a) $\Phi _{\mathrm {HG}} : \mathbb {C} \setminus \Sigma _{\mathrm {HG}} \rightarrow \mathbb {C}^{2 \times 2}$
 is analytic, where $\Sigma _{\mathrm {HG}}$
is analytic, where $\Sigma _{\mathrm {HG}}$ is shown in figure 3.
is shown in figure 3.(b) For $z \in \Gamma _{k}$
 (see figure 3), $k = 1,\ldots,8$
(see figure 3), $k = 1,\ldots,8$ , $\Phi _{\mathrm {HG}}$
, $\Phi _{\mathrm {HG}}$ obeys the jump relations
(B.1)\begin{equation} \Phi_{\mathrm{HG},+}(z) = \Phi_{\mathrm{HG},-}(z)J_{k}, \end{equation}where
obeys the jump relations
(B.1)\begin{equation} \Phi_{\mathrm{HG},+}(z) = \Phi_{\mathrm{HG},-}(z)J_{k}, \end{equation}where \begin{align*} & J_{1} = \begin{pmatrix} 0 & e^{{-}i\pi \beta} - e^{i\pi\beta} & 0 \end{pmatrix}, \quad J_{5} = \begin{pmatrix} 0 & e^{i\pi\beta} - e^{{-}i\pi\beta} & 0 \end{pmatrix},\\ & J_{3} = J_{7} = \begin{pmatrix} e^{\frac{i\pi\alpha}{2}} & 0 \\ 0 & e^{-\frac{i\pi\alpha}{2}} \end{pmatrix}, \\ & J_{2} = \begin{pmatrix} 1 & 0 \\ e^{{-}i\pi\alpha}e^{i\pi\beta} & 1 \end{pmatrix}\hspace{-0.1cm}, \hspace{-0.3cm} \quad J_{4} = \begin{pmatrix} 1 & 0 \\ e^{i\pi\alpha}e^{{-}i\pi\beta} & 1 \end{pmatrix}\hspace{-0.1cm}, \hspace{-0.3cm} \quad J_{6} = \begin{pmatrix} 1 & 0 \\ e^{{-}i\pi\alpha}e^{{-}i\pi\beta} & 1 \end{pmatrix}\hspace{-0.1cm}, \\ & J_{8} = \begin{pmatrix} 1 & 0 \\ e^{i\pi\alpha}e^{i\pi\beta} & 1 \end{pmatrix}. \end{align*}
\begin{align*} & J_{1} = \begin{pmatrix} 0 & e^{{-}i\pi \beta} - e^{i\pi\beta} & 0 \end{pmatrix}, \quad J_{5} = \begin{pmatrix} 0 & e^{i\pi\beta} - e^{{-}i\pi\beta} & 0 \end{pmatrix},\\ & J_{3} = J_{7} = \begin{pmatrix} e^{\frac{i\pi\alpha}{2}} & 0 \\ 0 & e^{-\frac{i\pi\alpha}{2}} \end{pmatrix}, \\ & J_{2} = \begin{pmatrix} 1 & 0 \\ e^{{-}i\pi\alpha}e^{i\pi\beta} & 1 \end{pmatrix}\hspace{-0.1cm}, \hspace{-0.3cm} \quad J_{4} = \begin{pmatrix} 1 & 0 \\ e^{i\pi\alpha}e^{{-}i\pi\beta} & 1 \end{pmatrix}\hspace{-0.1cm}, \hspace{-0.3cm} \quad J_{6} = \begin{pmatrix} 1 & 0 \\ e^{{-}i\pi\alpha}e^{{-}i\pi\beta} & 1 \end{pmatrix}\hspace{-0.1cm}, \\ & J_{8} = \begin{pmatrix} 1 & 0 \\ e^{i\pi\alpha}e^{i\pi\beta} & 1 \end{pmatrix}. \end{align*}
(c) As $z \to \infty$
 , $z \notin \Sigma _{\mathrm {HG}}$
, $z \notin \Sigma _{\mathrm {HG}}$ , we have
(B.2)\begin{equation} \Phi_{\mathrm{HG}}(z) = \left( I + \sum_{k=1}^{\infty} \frac{\Phi_{\mathrm{HG},k}}{z^{k}} \right) z^{-\beta\sigma_{3}}e^{-\frac{z}{2}\sigma_{3}}M^{{-}1}(z), \end{equation}where
, we have
(B.2)\begin{equation} \Phi_{\mathrm{HG}}(z) = \left( I + \sum_{k=1}^{\infty} \frac{\Phi_{\mathrm{HG},k}}{z^{k}} \right) z^{-\beta\sigma_{3}}e^{-\frac{z}{2}\sigma_{3}}M^{{-}1}(z), \end{equation}where (B.3)\begin{align} \Phi_{\mathrm{HG},1} & = \left(\beta^{2}-\frac{\alpha^{2}}{4}\right) \begin{pmatrix} -1 & \tau(\alpha,\beta) - \tau(\alpha,-\beta) & 1 \end{pmatrix}, \nonumber\\ \tau(\alpha,\beta) & ={-}\frac{\Gamma\left( \frac{\alpha}{2}-\beta \right)}{\Gamma\left( \frac{\alpha}{2}+\beta + 1 \right)}, \end{align}and
(B.3)\begin{align} \Phi_{\mathrm{HG},1} & = \left(\beta^{2}-\frac{\alpha^{2}}{4}\right) \begin{pmatrix} -1 & \tau(\alpha,\beta) - \tau(\alpha,-\beta) & 1 \end{pmatrix}, \nonumber\\ \tau(\alpha,\beta) & ={-}\frac{\Gamma\left( \frac{\alpha}{2}-\beta \right)}{\Gamma\left( \frac{\alpha}{2}+\beta + 1 \right)}, \end{align}and (B.4)\begin{equation} M(z) = \left\{ \begin{array}{l l} \displaystyle e^{\dfrac{i\pi\alpha}{4} \sigma_{3}}e^{- i\pi\beta \sigma_{3}}, & \displaystyle \dfrac{\pi}{2} < \arg z < \pi, \\ \displaystyle e^{-\dfrac{i\pi\alpha}{4} \sigma_{3}}e^{{-}i\pi\beta \sigma_{3}}, & \displaystyle \pi < \arg z < \dfrac{3\pi}{2}, \\ e^{\dfrac{i\pi\alpha}{4}\sigma_{3}} \begin{pmatrix} 0 & 1 - 1 & 0 \end{pmatrix}, & -\dfrac{\pi}{2} < \arg z < 0, \\ e^{-\dfrac{i\pi\alpha}{4}\sigma_{3}} \begin{pmatrix} 0 & 1 - 1 & 0 \end{pmatrix}, & 0 < \arg z < \dfrac{\pi}{2}. \end{array} \right. \end{equation}In (B.2), $z^{-\beta }$
(B.4)\begin{equation} M(z) = \left\{ \begin{array}{l l} \displaystyle e^{\dfrac{i\pi\alpha}{4} \sigma_{3}}e^{- i\pi\beta \sigma_{3}}, & \displaystyle \dfrac{\pi}{2} < \arg z < \pi, \\ \displaystyle e^{-\dfrac{i\pi\alpha}{4} \sigma_{3}}e^{{-}i\pi\beta \sigma_{3}}, & \displaystyle \pi < \arg z < \dfrac{3\pi}{2}, \\ e^{\dfrac{i\pi\alpha}{4}\sigma_{3}} \begin{pmatrix} 0 & 1 - 1 & 0 \end{pmatrix}, & -\dfrac{\pi}{2} < \arg z < 0, \\ e^{-\dfrac{i\pi\alpha}{4}\sigma_{3}} \begin{pmatrix} 0 & 1 - 1 & 0 \end{pmatrix}, & 0 < \arg z < \dfrac{\pi}{2}. \end{array} \right. \end{equation}In (B.2), $z^{-\beta }$
 has a cut along $i\mathbb {R}^{-}$
has a cut along $i\mathbb {R}^{-}$ so that $z^{-\beta } = |z|^{-\beta }e^{-\beta i \arg (z)}$
so that $z^{-\beta } = |z|^{-\beta }e^{-\beta i \arg (z)}$ with $-\frac {\pi }{2} < \arg z < \frac {3\pi }{2}$
with $-\frac {\pi }{2} < \arg z < \frac {3\pi }{2}$ . As $z \to 0$
. As $z \to 0$ , we have
(B.5)\begin{align} \begin{aligned} \displaystyle \Phi_{\mathrm{HG}}(z) & = \left\{\begin{array}{@{}ll} \begin{pmatrix} {\mathcal{O}}(1) & {\mathcal{O}}(\log z) \\ {\mathcal{O}}(1) & {\mathcal{O}}(\log z) \end{pmatrix}, & \mbox{if } z \in II \cup III \cup VI \cup VII, \\ \begin{pmatrix} {\mathcal{O}}(\log z) & {\mathcal{O}}(\log z) \\ {\mathcal{O}}(\log z) & {\mathcal{O}}(\log z) \end{pmatrix}, & \mbox{if } z \in I\cup IV \cup V \cup VIII, \end{array} \right.,\nonumber\\ & \displaystyle \mbox{ if } {\rm Re\,} \alpha = 0, \\\displaystyle \Phi_{\mathrm{HG}}(z) & = \left\{ \begin{array}{@{}ll} \begin{pmatrix} {\mathcal{O}}(z^{\frac{\alpha}{2}}) & {\mathcal{O}}(z^{-\frac{\alpha}{2}}) \\ {\mathcal{O}}(z^{\frac{\alpha}{2}}) & {\mathcal{O}}(z^{-\frac{\alpha}{2}}) \end{pmatrix}, & \mbox{if } z \in II \cup III \cup VI \cup VII, \\ \begin{pmatrix} {\mathcal{O}}(z^{-\frac{\alpha}{2}}) & {\mathcal{O}}(z^{-\frac{\alpha}{2}}) \\ {\mathcal{O}}(z^{-\frac{\alpha}{2}}) & {\mathcal{O}}(z^{-\frac{\alpha}{2}}) \end{pmatrix}, & \mbox{if } z \in I\cup IV \cup V \cup VIII, \end{array} \right. ,\nonumber\\ & \displaystyle \mbox{ if } {\rm Re\,} \alpha > 0, \\\displaystyle \Phi_{\mathrm{HG}}(z) & = \begin{pmatrix} {\mathcal{O}}(z^{\frac{\alpha}{2}}) & {\mathcal{O}}(z^{\frac{\alpha}{2}}) \\ {\mathcal{O}}(z^{\frac{\alpha}{2}}) & {\mathcal{O}}(z^{\frac{\alpha}{2}}) \end{pmatrix}, \quad \displaystyle \mbox{ if } {\rm Re\,} \alpha < 0. \end{aligned} \end{align}
, we have
(B.5)\begin{align} \begin{aligned} \displaystyle \Phi_{\mathrm{HG}}(z) & = \left\{\begin{array}{@{}ll} \begin{pmatrix} {\mathcal{O}}(1) & {\mathcal{O}}(\log z) \\ {\mathcal{O}}(1) & {\mathcal{O}}(\log z) \end{pmatrix}, & \mbox{if } z \in II \cup III \cup VI \cup VII, \\ \begin{pmatrix} {\mathcal{O}}(\log z) & {\mathcal{O}}(\log z) \\ {\mathcal{O}}(\log z) & {\mathcal{O}}(\log z) \end{pmatrix}, & \mbox{if } z \in I\cup IV \cup V \cup VIII, \end{array} \right.,\nonumber\\ & \displaystyle \mbox{ if } {\rm Re\,} \alpha = 0, \\\displaystyle \Phi_{\mathrm{HG}}(z) & = \left\{ \begin{array}{@{}ll} \begin{pmatrix} {\mathcal{O}}(z^{\frac{\alpha}{2}}) & {\mathcal{O}}(z^{-\frac{\alpha}{2}}) \\ {\mathcal{O}}(z^{\frac{\alpha}{2}}) & {\mathcal{O}}(z^{-\frac{\alpha}{2}}) \end{pmatrix}, & \mbox{if } z \in II \cup III \cup VI \cup VII, \\ \begin{pmatrix} {\mathcal{O}}(z^{-\frac{\alpha}{2}}) & {\mathcal{O}}(z^{-\frac{\alpha}{2}}) \\ {\mathcal{O}}(z^{-\frac{\alpha}{2}}) & {\mathcal{O}}(z^{-\frac{\alpha}{2}}) \end{pmatrix}, & \mbox{if } z \in I\cup IV \cup V \cup VIII, \end{array} \right. ,\nonumber\\ & \displaystyle \mbox{ if } {\rm Re\,} \alpha > 0, \\\displaystyle \Phi_{\mathrm{HG}}(z) & = \begin{pmatrix} {\mathcal{O}}(z^{\frac{\alpha}{2}}) & {\mathcal{O}}(z^{\frac{\alpha}{2}}) \\ {\mathcal{O}}(z^{\frac{\alpha}{2}}) & {\mathcal{O}}(z^{\frac{\alpha}{2}}) \end{pmatrix}, \quad \displaystyle \mbox{ if } {\rm Re\,} \alpha < 0. \end{aligned} \end{align}

Figure 3. The jump contour $\Sigma _{\mathrm {HG}}$![]() for $\Phi _{\mathrm {HG}}(z)$
for $\Phi _{\mathrm {HG}}(z)$![]() . The ray $\Gamma _{k}$
. The ray $\Gamma _{k}$![]() is oriented from $0$
is oriented from $0$![]() to $\infty$
to $\infty$![]() , and forms an angle with $\mathbb {R}^+$
, and forms an angle with $\mathbb {R}^+$![]() which is a multiple of $\frac {\pi }{4}$
which is a multiple of $\frac {\pi }{4}$![]() .
.
This model RH problem was first introduced and solved explicitly in [Reference Its and Krasovsky37] for the case $\alpha = 0$![]() , and then in [Reference Deift, Its and Krasovsky24, Reference Foulquié Moreno, Martinez-Finkelshtein and Sousa35] for the general case. The constant matrices $\Phi _{\mathrm {HG},k}$
, and then in [Reference Deift, Its and Krasovsky24, Reference Foulquié Moreno, Martinez-Finkelshtein and Sousa35] for the general case. The constant matrices $\Phi _{\mathrm {HG},k}$![]() depend analytically on $\alpha$
depend analytically on $\alpha$![]() and $\beta$
and $\beta$![]() (they can be found explicitly, see e.g. [Reference Foulquié Moreno, Martinez-Finkelshtein and Sousa35, eq. (56)]). Consider the matrix
(they can be found explicitly, see e.g. [Reference Foulquié Moreno, Martinez-Finkelshtein and Sousa35, eq. (56)]). Consider the matrix

where $G$![]() and $H$
and $H$![]() are related to the Whittaker functions:
are related to the Whittaker functions:
The solution $\Phi _{\mathrm {HG}}$![]() is given by
is given by