1. Introduction
In the European Alps, glacier mass balance results mainly from accumulation (mass input) of snow in winter and ablation (mass loss) due to the melting of snow and ice in summer. Fluctuations of mass-balance seasonal components are therefore strongly related to climate fluctuations. More generally, glacier mass balances are well-known useful indicators of climate change over the last few centuries (Reference Oerlemans and FortuinOerlemans and Fortuin, 1992; Reference HaeberliHaeberli, 1995; Reference VincentVincent, 2002; Reference Vincent, Kappenberger, Valla, Bauder, Funk and Le MeurVincent and others, 2004; Reference Kaser, Cogley, Dyurgerov, Meier and OhmuraKaser and others, 2006; Reference SolomonSolomon and others, 2007).
However, inferring the climatic signal from a glacier mass-balance series is not an easy task. For example, the glacier-wide balance obtained from spatial averaging of point mass balances (measured at individual locations) is a function of glacier geometry (Reference Ohmura, Bauder, Müller and KappenbergerOhmura and others, 2007). To overcome this problem, Reference Elsberg, Harrison, Echelmeyer and KrimmelElsberg and others (2001) have proposed a method that corrects surface and elevation changes in the integrated glacier-wide balance. An alternative is to directly use surface point mass balances (Reference RasmussenRasmussen, 2004; Reference Vincent, Kappenberger, Valla, Bauder, Funk and Le MeurVincent and others, 2004; Reference Huss and BauderHuss and Bauder, 2009; Reference Thibert and VincentThibert and Vincent, 2009), but this implies separating the overall annual effect from the spatial variability at the glacier surface. This can be done using variance decompositions (analysis of variance: ANOVA).
The suitability of annual point mass-balance time series for linear variance decomposition was first proposed by Reference Meier and TangbornMeier and Tangborn (1965) and Reference HoinkesHoinkes (1970). Reference LliboutryLliboutry (1974) generalized the approach by proposing what is formally an incomplete two-way ANOVA model:
where N
1 denotes the normal distribution and ![]() the annual (superscript a) point mass balance observed at spatial coordinates (xi
, yi
) during the glaciological year, t ∊ [t
0, t
0 + T −1 ], where t
0 is the first year considered and T is the total number of years with observations.
the annual (superscript a) point mass balance observed at spatial coordinates (xi
, yi
) during the glaciological year, t ∊ [t
0, t
0 + T −1 ], where t
0 is the first year considered and T is the total number of years with observations. ![]() is the spatial term. The notation indicates that the measurements are made using stakes i ∊ [1, N], for which the number and positions are chosen to provide a good vision of the spatial variability at the glacier surface. The constraint
is the spatial term. The notation indicates that the measurements are made using stakes i ∊ [1, N], for which the number and positions are chosen to provide a good vision of the spatial variability at the glacier surface. The constraint ![]() is used to ensure model identifiability, so that
is used to ensure model identifiability, so that ![]() is the annual deviation. The residuals of standard deviation,
is the annual deviation. The residuals of standard deviation, ![]() , are assumed to be independent and Gaussian. The model is referred to as incomplete because the interaction terms between space and time are not distinguished from the residuals.
, are assumed to be independent and Gaussian. The model is referred to as incomplete because the interaction terms between space and time are not distinguished from the residuals.
Evaluating the glacier-wide balance involves integration over the glacier surface. Under an assumption of equally weighted measurement points, the glacier-wide mean balance over the studied period is ![]() . Note that the way spatial averaging is performed has little influence on the annual deviations, and that implementation of other choices (e.g. area–altitude distribution weighting coefficients) than the direct arithmetic mean used here is straightforward. Furthermore, the annual glacier-wide balance is then simply
. Note that the way spatial averaging is performed has little influence on the annual deviations, and that implementation of other choices (e.g. area–altitude distribution weighting coefficients) than the direct arithmetic mean used here is straightforward. Furthermore, the annual glacier-wide balance is then simply ![]() , uppercase letters denoting glacier-wide variables. This highlights that the mean annual deviation of the balance
, uppercase letters denoting glacier-wide variables. This highlights that the mean annual deviation of the balance ![]() at all measurement sites equals the glacier-wide annual deviation. Therefore, the
at all measurement sites equals the glacier-wide annual deviation. Therefore, the ![]() time series extracted by the model from point balances also apply to the wide balance, and can be used to characterize the response of the glacier to climate fluctuations.
time series extracted by the model from point balances also apply to the wide balance, and can be used to characterize the response of the glacier to climate fluctuations.
Because of its simplicity and ability to fit various point mass-balance series, this model has met with great success in the glaciological community (Reference Vallon and LeivaVallon and Leiva, 1981; Reference KuhnKuhn, 1984; Reference RasmussenRasmussen, 2004; Reference Thibert, Blanc, Vincent and EckertThibert and others, 2008; Reference Thibert and VincentThibert and Vincent, 2009). However, some studies have reported discrepancies between model results and real datasets, caused by unsteady spatial terms or temporal terms decreasing at high elevations (Reference Oerlemans and HoogendoornOerlemans and Hoogendoorn, 1989; Reference Funk, Morelli and StahelFunk and others 1997; Reference Vallon, Vincent and ReynaudVallon and others, 1998; Reference Dyurgerov and DwyerDyurgerov and Dwyer, 2001; Reference SorucoSoruco and others, 2009).
From a more methodological point of view, a first limitation of the model proposed by Reference LliboutryLliboutry (1974) is that it does not explicitly consider the two specific contributions of summer and winter balance components to the annual balance. Reference Rasmussen and AndreassenRasmussen and Andreassen (2005) therefore applied their variance analysis separately to both winter and summer components of the balance, with good agreement between model results and data for studies concerning Norway. Although it represents a big step forward from a physical point of view, such an approach remains questionable. Indeed, by modelling the different components of the balance separately, it neglects the fact that they are correlated. Their correlations must therefore be estimated empirically from the obtained annual terms. In statistics, empirical estimation denotes a procedure that does not explicitly rely on a model fitted on data using a procedure such as mean square error minimization. This leads to different estimates, with generally higher estimation errors. Furthermore, among winter, summer and annual balance, only two contributions are usually measured (the third being calculated from), so that neglecting the correlation between the two measured variables may imply underestimating the uncertainty around the third unobserved variable.
A second limitation of Lliboutry’s model is that it implicitly considers stationary conditions over the period of record, with random annual fluctuations around a mean balance, which is inappropriate in the context of a marked climate change. Standard time series can be used to extract structured patterns (e.g. memory effects, systematic trends, break points) from the βt
series, with the ultimate goal of relating them to similar behaviours in more direct climatic data series. However, this poses an even greater statistical problem. Indeed the ![]() are unobserved, so that the uncertainty related to their estimation must be taken into account when estimating the investigated temporal patterns. Not doing so may lead to an overestimation of the significance levels of the temporal patterns because the studied series are only a few decades long.
are unobserved, so that the uncertainty related to their estimation must be taken into account when estimating the investigated temporal patterns. Not doing so may lead to an overestimation of the significance levels of the temporal patterns because the studied series are only a few decades long.
The objective of this paper is therefore to reconsider the problem of extracting a climatic trend from a glacier mass balance recorded by a sampling site network using a variance decomposition. To do so, we first propose an expansion of Lliboutry’s model adapted to correlated pairs. Second, we show how hierarchy (Reference WikleWikle, 2003; Reference Clark and GelfandClark and Gelfand, 2006) can be used to isolate the annual terms and explicitly model their temporal structure within the same statistical framework (Reference Carlin, Gelfand and SmithCarlin and others, 1992; Reference Banerjee, Carlin and GelfandBanerjee and others, 2004), so as to relax in a consistent manner the underlying assumption of stationary conditions. Inspired by work in other fields (Reference ClarkClark, 2005; Reference Eckert, Parent, Bélanger and GarciaEckert and others, 2007, Reference Eckert, Parent, Kies and Baya2010c), implementation is performed using Bayesian schemes thanks to the availability of simulation-based methods for parameter estimation (Reference TannerTanner, 1992; Reference Gaucherel, Campillo, Misson, Guiot and BoreuxGaucherel and others, 2008). The proposed approach and for instance the effectiveness of the different model components are illustrated using the six-decade Sarennes mass-balance series.
2. Data and Site
The mass-balance series of Glacier de Sarennes (45°07′ N, 6°07′ E), Massif des Grandes Rousses, France, has been measured since t
0 = 1949 (Reference VallaValla, 1989; Reference Thibert, Blanc, Vincent and EckertThibert and others, 2008). Sarennes is a small south-facing glacier whose surface decreased from 0.85 km2 in 1952 to 0.41 km2 in 2003. Over the period of record, the elevation ranges from 2800 to 3100 m a.s.l. (Fig. 1). On this glacier, the winter balance, ![]() , is measured from cores drilled at the end of the winter. The annual balance,
, is measured from cores drilled at the end of the winter. The annual balance,![]() , is measured in late summer from emergence variations of stakes inserted in the ice of the ablation zone and cores drilled in the accumulation zone. The summer balance term at each location,
, is measured in late summer from emergence variations of stakes inserted in the ice of the ablation zone and cores drilled in the accumulation zone. The summer balance term at each location, ![]() , is then estimated from
, is then estimated from ![]() . Point balances
. Point balances ![]() are measured at five sites for which the mean elevation over the period of record is respectively 2860, 2920, 2945, 2995 and 3020 m a.s.l. Mean altitude change over the period of record is −36 m, ranging from −61 m in the lower part, to −15 m in high-elevation areas. From 1949 to 1957, only two to four sites were sampled, and only four since 2003 because of the retreat of the tongue. The 1949–2008 experimental table is therefore a partially complete dataset for the three terms of the balance (27 missing values). These annual data are expressed in m w.e.a−1 and are published on http://wwwlgge.ujf-grenoble.fr/ServiceObs/.
are measured at five sites for which the mean elevation over the period of record is respectively 2860, 2920, 2945, 2995 and 3020 m a.s.l. Mean altitude change over the period of record is −36 m, ranging from −61 m in the lower part, to −15 m in high-elevation areas. From 1949 to 1957, only two to four sites were sampled, and only four since 2003 because of the retreat of the tongue. The 1949–2008 experimental table is therefore a partially complete dataset for the three terms of the balance (27 missing values). These annual data are expressed in m w.e.a−1 and are published on http://wwwlgge.ujf-grenoble.fr/ServiceObs/.
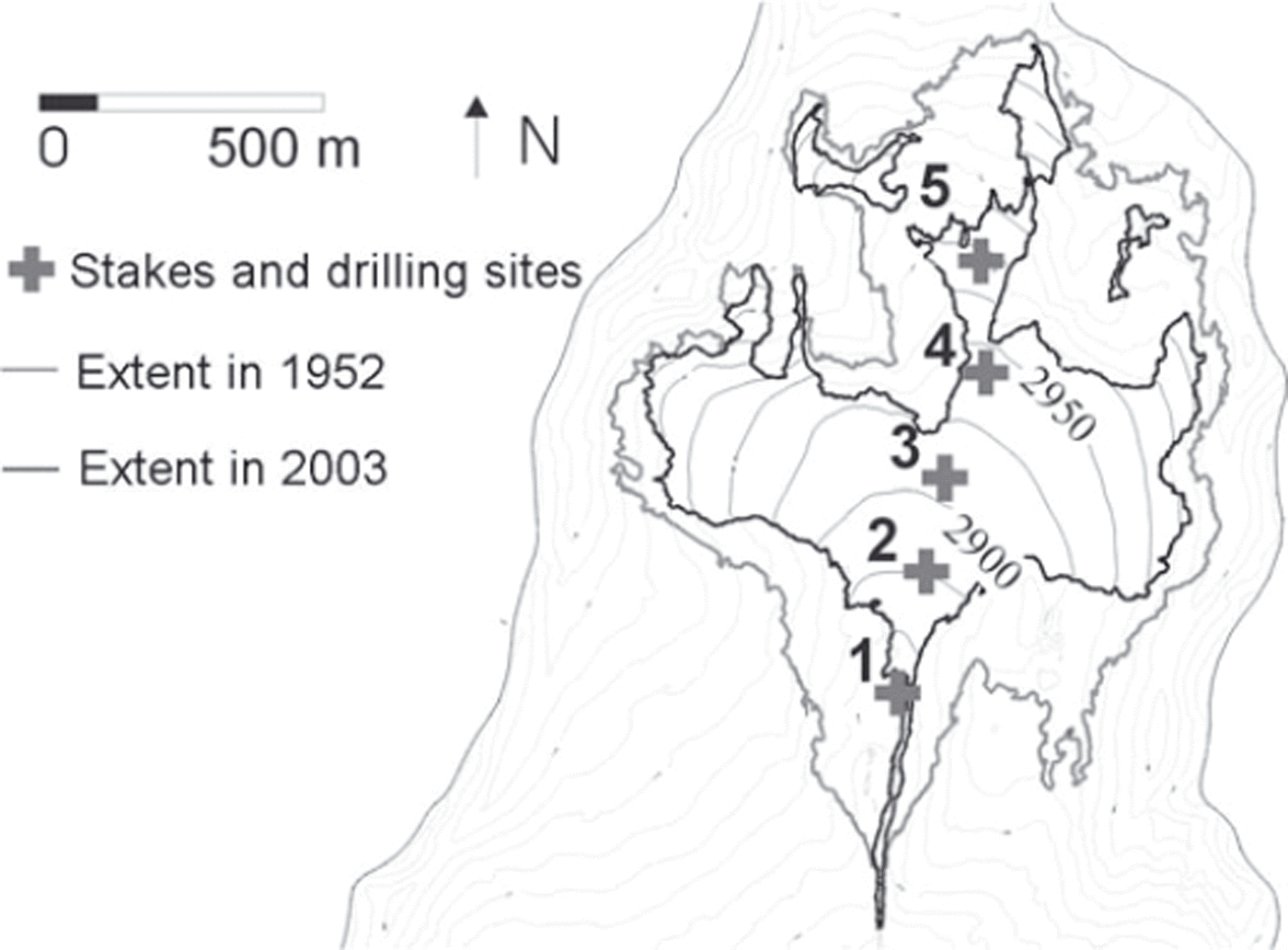
Fig. 1. Location of stakes where balances are measured on Glacier de Sarennes. Contours on the glacier are at 25 m intervals.
Measurements are not performed at fixed dates: the investigated annual mass changes refer to the so-called floating date system. Durations of mass-balance year are therefore variable, and account for both the effects of changes in accumulation and ablation rates, and of their duration. Note that, as field visits do not coincide in general with the glacier minimum or maximum mass, data differ somewhat from the theoretical stratigraphic system in which annual balance is defined between one year’s minimum and the next year’s, and winter balance between one year’s maximum and the previous year’s. However, we assume that these differences are small, and do not apply a correction.
A routinely calculated glacier-wide balance (published in World Glacier Monitoring Service (WGMS) glacier mass-balance bulletins) uses an integration relationship based on area–altitude distribution weighting coefficients (Reference VallaValla, 1989; Reference Thibert, Blanc, Vincent and EckertThibert and others, 2008). Over the 1949–2007 period, this calculation gives a mean annual glacier-wide balance of −0.92 m w.e. a−1,while mean annual glacier-wide winter and summer balances are 1.68 and −2.60 m w.e. a−1, respectively. Additional annual mass-balance data estimated by photogrammetry (geodetic balance) are available in 1981 (Reference Valla and PiedalluValla and Piedallu, 1997), 1952 and 2003 (Reference Thibert, Blanc, Vincent and EckertThibert and others, 2008) for comparison and control.
3. Methods
3.1. Bivariate formulation of Lliboutry’s model
To generalize Lliboutry’s model to the actually observed pair ![]() , we introduce spatial terms
, we introduce spatial terms ![]() and temporal terms
and temporal terms ![]() for winter balance under the additional constraint
for winter balance under the additional constraint ![]() :
:
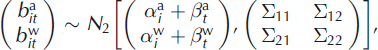
where superscript w denotes the winter period. The overall mean ![]() is the mean glacier-wide winter balance over the studied period, whereas the
is the mean glacier-wide winter balance over the studied period, whereas the ![]() series represents the annual deviations to the mean. N
2 denotes the two-dimensional (2-D) Gaussian vector of variance–covariance matrix ∑ which includes the marginal variances
series represents the annual deviations to the mean. N
2 denotes the two-dimensional (2-D) Gaussian vector of variance–covariance matrix ∑ which includes the marginal variances ![]() and
and ![]() . The residual pair
. The residual pair ![]() reflects the discrepancy between the observations and the linear model which is expected to be low if the model fits the data properly. It is simply given by:
reflects the discrepancy between the observations and the linear model which is expected to be low if the model fits the data properly. It is simply given by:
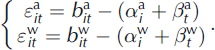
The main advantage of the joint formulation is that the covariance ![]() is also available, providing easy access to the correlation coefficient
is also available, providing easy access to the correlation coefficient ![]() between the residual pair
between the residual pair ![]() :
:
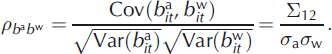
This makes recourse to an empirical estimation procedure such as that used by Reference Rasmussen and AndreassenRasmussen and Andreassen (2005) unnecessary.
The pair of annual deviations ![]() is assumed to be sampled from a 2-D Gaussian vector of variance–covariance matrix ∑
β
. Its mean is set to zero for consistency with the imposed constraints:
is assumed to be sampled from a 2-D Gaussian vector of variance–covariance matrix ∑
β
. Its mean is set to zero for consistency with the imposed constraints:
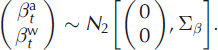
The hidden quantities ![]() have a hybrid status, i.e. they behave as observations with regard to the overall parameters, but they are parameters with regard to the observations. Such a multilayer construction characterizes a hierarchical structure. Its advantage over a non-hierarchical approach is to explicitly model the similarity of the different annual terms through the different terms of the ∑
β
covariance matrix. The marginal variances
have a hybrid status, i.e. they behave as observations with regard to the overall parameters, but they are parameters with regard to the observations. Such a multilayer construction characterizes a hierarchical structure. Its advantage over a non-hierarchical approach is to explicitly model the similarity of the different annual terms through the different terms of the ∑
β
covariance matrix. The marginal variances ![]() and
and ![]() quantify the magnitude of interannual fluctuations of respectively annual and winter deviations. As for the residuals, the covariance between annual and winter balance is given by
quantify the magnitude of interannual fluctuations of respectively annual and winter deviations. As for the residuals, the covariance between annual and winter balance is given by ![]() , which provides easy access to their correlation coefficient
, which provides easy access to their correlation coefficient ![]() . It is definitely non-negligible, since mass balance physically depends on winter balance:
. It is definitely non-negligible, since mass balance physically depends on winter balance:
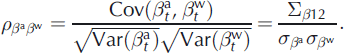
The summer balance is obtained by subtracting winter balance from mass balance:
where superscript s denotes summer balance terms. Because of the properties of Gaussian linear models, it is also normally distributed:
and its variance decomposition into a spatial term ![]() , an annual term
, an annual term ![]() verifying
verifying ![]() and a residual
and a residual ![]() is readily available:
is readily available:
Keeping an arithmetic averaging over the glacier surface, the mean summer balance over the studied period is then simply ![]() . Moreover, marginal N variances for the summer balance residual
. Moreover, marginal N variances for the summer balance residual ![]() and for the annual deviation to the mean summer balance
and for the annual deviation to the mean summer balance ![]() can be computed from the covariance matrixes ∑ and ∑
β
, respectively. This implies that the error made while estimating the summer balance using Equation (9) is higher than if mass balance and winter balance were independent, but remains smaller than σ
a+σ
w for σ
s, and smaller than
can be computed from the covariance matrixes ∑ and ∑
β
, respectively. This implies that the error made while estimating the summer balance using Equation (9) is higher than if mass balance and winter balance were independent, but remains smaller than σ
a+σ
w for σ
s, and smaller than ![]() for
for ![]() :
:
Finally, the correlation coefficients between summer balance and the two other terms are not explicitly available in the model and must therefore be estimated empirically. Since all residuals and annual deviations are, by definition, centred random numbers, the correlation coefficients ![]() and
and ![]() between the residuals pairs
between the residuals pairs ![]() and
and ![]() are given by:
are given by:
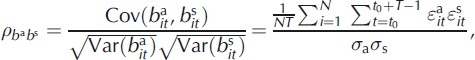
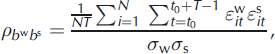
whereas the correlation coefficients ![]() and
and ![]() between the annual deviations are given by:
between the annual deviations are given by:
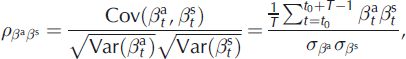
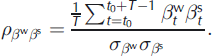
Equation (2) separates different independent effects using variance decomposition. We introduce the ratios λ a, λ w and λ s (Equations (18–20)) to quantify the specific contribution (% of variance) to the total variability of the annual terms for annual, winter and summer balances respectively. Note that the denominator is an approximation of the total variability neglecting the spatial variability of the αi terms. This is reasonable for a small glacier such as Sarennes (Reference Thibert and VincentThibert and Vincent, 2009), but would not be appropriate for a wider glacier covering a large elevation range:
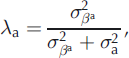
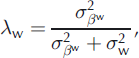
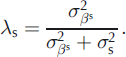
Figure 2a summarizes this first model, noted M1, using a direct acyclic graph (Reference LauritzenLauritzen, 1996). On the one hand, the parameters ![]() , i ∈ [1, N] and hidden variables
, i ∈ [1, N] and hidden variables ![]() have to be estimated using the data. On the other hand, all the other unknown quantities such as the summer terms, correlation coefficients and ratios are explicit combinations of
have to be estimated using the data. On the other hand, all the other unknown quantities such as the summer terms, correlation coefficients and ratios are explicit combinations of ![]() and
and ![]() , which somewhat restricts the dimension of the estimation problem. With regard to Reference Rasmussen and AndreassenRasmussen and Andreassen’s (2005) approach, our model offers a fair quantification of the uncertainty levels thanks to the explicit modelling of the covariances ∑ and ∑
β
. With respect to Lliboutry’s model, it is also characterized by its fully bivariate nature. Figure 2b indicates how point variables are related to glacier-wide variables.
, which somewhat restricts the dimension of the estimation problem. With regard to Reference Rasmussen and AndreassenRasmussen and Andreassen’s (2005) approach, our model offers a fair quantification of the uncertainty levels thanks to the explicit modelling of the covariances ∑ and ∑
β
. With respect to Lliboutry’s model, it is also characterized by its fully bivariate nature. Figure 2b indicates how point variables are related to glacier-wide variables.
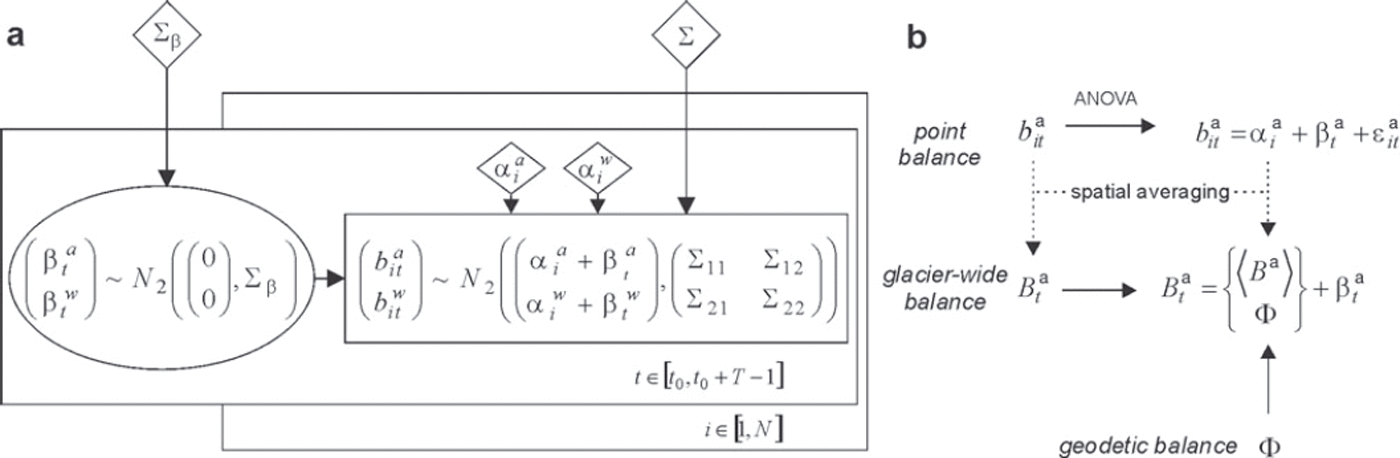
Fig. 2. (a) Direct acyclic graph of model M1. Arrows express conditional dependence, circled nodes represent stochastic hidden variables, diamonds represent the overall parameters and rectangles indicate observed values. (b) Links between point and glacier-wide variables illustrated for the annual term. The alternative to estimate the mean annual glacier-wide balance from a geodetic balance (photogrammetry), Φ, instead of the ![]() spatial mean 〈B
a〉 is also indicated.
spatial mean 〈B
a〉 is also indicated.
3.2. Extracting structured temporal trends
With model M1, the annual terms ![]() are modelled as if they were exchangeable, which means that they are assumed to be sampled from the same distribution whatever the considered year. This makes it possible to quantify the interannual variability, for instance thanks to the temporal ratios of Equations (18–20). On the other hand, a possible structured time trend that affects the whole glacier in a similar way and may therefore be related to climate change cannot be inferred. To overcome this limitation, we relax in this subsection the assumption of exchangeability of the
are modelled as if they were exchangeable, which means that they are assumed to be sampled from the same distribution whatever the considered year. This makes it possible to quantify the interannual variability, for instance thanks to the temporal ratios of Equations (18–20). On the other hand, a possible structured time trend that affects the whole glacier in a similar way and may therefore be related to climate change cannot be inferred. To overcome this limitation, we relax in this subsection the assumption of exchangeability of the ![]() . Moreover, for better consistency with the physical processes involved, we prefer working with the seasonal pair
. Moreover, for better consistency with the physical processes involved, we prefer working with the seasonal pair ![]() rather than with the pair
rather than with the pair ![]() .
.
A time-series analysis of the ![]() can theoretically be achieved using various time-series models developed in other fields, such as econometrics (Reference Booth and SmithBooth and Smith, 1982), hydrology (Reference Rao and TirtotjondroRao and Titrojondro, 1996), meteorology (Reference BloomfieldBloomfield, 1992) or climatology (Reference Von Storch and Zwiersvon Storch and Zwiers, 2002). The choice of the time-series model must be made with regard to the investigated temporal pattern, for example, memory effects, monotonic trends or change points for the mean (Reference Mearns, Rosenzweig and GoldbergMearns and others, 1997), variance (Reference DiazDiaz, 1982) or extreme values (Reference Nogaj, Parey and Dacunha-CastelleNogaj and others, 2007).
can theoretically be achieved using various time-series models developed in other fields, such as econometrics (Reference Booth and SmithBooth and Smith, 1982), hydrology (Reference Rao and TirtotjondroRao and Titrojondro, 1996), meteorology (Reference BloomfieldBloomfield, 1992) or climatology (Reference Von Storch and Zwiersvon Storch and Zwiers, 2002). The choice of the time-series model must be made with regard to the investigated temporal pattern, for example, memory effects, monotonic trends or change points for the mean (Reference Mearns, Rosenzweig and GoldbergMearns and others, 1997), variance (Reference DiazDiaz, 1982) or extreme values (Reference Nogaj, Parey and Dacunha-CastelleNogaj and others, 2007).
However, the balance between the available information and the number of model unknowns must also be considered to make it possible to extract the temporal structure from the hidden variables without producing an uncertainty level that is too high for any practical conclusions. We therefore restrict our purpose to a relatively simple change-point model with limited parameters. This model is relevant to Glacier de Sarennes data (see section 4) and has already been applied to similar problems in hydrology (Reference Perreault, Bernier, Bobée and ParentPerreault and others, 2000a,Reference Perreault, Bernier, Bobée and Parentb).
We designate (τ
w, τ
s) as the years of possible change points separating two periods of different conditions for winter and summer balances respectively. Before and after the change points, both the ![]() (Equations (21) and (22)) and the
(Equations (21) and (22)) and the ![]() (Equations (23) and (24)) are broken down into random noises and structured linear trends. The random noises, with respective variances
(Equations (23) and (24)) are broken down into random noises and structured linear trends. The random noises, with respective variances ![]() : and
: and ![]() , model the unstructured interannual fluctuations. The notation
, model the unstructured interannual fluctuations. The notation ![]() , for example, indicates that the parameter
, for example, indicates that the parameter ![]() can take different values before and after the change point, so as to allow τ
s and/or τ
w to also reflect a change point in variance. The linear trends, expressed as w
*(t) = a
w:+b
w:
t and s
*(t) = a
s: + b
s:t, are designed to capture gradual changes affecting summer and/or winter mass-balance terms. Seasonal components of the balance being expressed in m w.e. a−1, the trend slopes (b
w., b
s.) are expressed in m w.e.a−2. Depending on the continuity of w
*(t) and s
*(t) around τ
w and τ
s, the change points can be brutal, with a clear separation of two budget regimes, or just a distinction between two different trends (b
w1, b
w2) and/or (b
s1, b
s2). This model, noted M2, is therefore flexible enough to capture monotonic trends and various types of changes in mean and variance for both summer and winter balances:
can take different values before and after the change point, so as to allow τ
s and/or τ
w to also reflect a change point in variance. The linear trends, expressed as w
*(t) = a
w:+b
w:
t and s
*(t) = a
s: + b
s:t, are designed to capture gradual changes affecting summer and/or winter mass-balance terms. Seasonal components of the balance being expressed in m w.e. a−1, the trend slopes (b
w., b
s.) are expressed in m w.e.a−2. Depending on the continuity of w
*(t) and s
*(t) around τ
w and τ
s, the change points can be brutal, with a clear separation of two budget regimes, or just a distinction between two different trends (b
w1, b
w2) and/or (b
s1, b
s2). This model, noted M2, is therefore flexible enough to capture monotonic trends and various types of changes in mean and variance for both summer and winter balances:
The trend for annual mass balance, a *(t), is easily accessible due to the linearity of the model:
If τ s = τ w, there are two linear trends b a: = b w: + b s: and intercepts a a: = a w: + a s: in mass balance. However, as soon as τ s ≠ τ w, three possibly different linear trends and intercepts are obtained for respectively t ≤ min (τ s, τ w), t ∊ [min (τ s, τ w) + 1, max (τ s, τ w)] and t ≥ max (τ s, τ w) + 1. This makes it possible to model different combinations of changes in winter and summer budgets, leading to three possible regimes of change in mass balance.
A major difference between models M1 and M2 is that, with model M2, the variance of the annual deviations is no longer constant, depending on the existence of change points in the data. Nevertheless, it is possible to use Equations (26–28), where E denotes the mathematical expectation, to globally evaluate the dispersion of the annual terms in a way similar to that used in model M1:
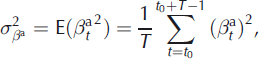
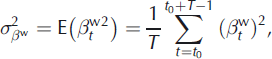
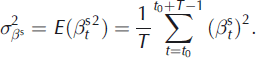
These global variances can be used to compute global temporal ratios quantifying the specific contribution to the total variability of the annual terms all over the studied period using Equations (18–20). Similarly, the global coefficient correlations ![]() and
and ![]() can be evaluated using Equations (16) and (17) respectively. For
can be evaluated using Equations (16) and (17) respectively. For ![]() , however, Equation (6) is no longer valid, and empirical estimation must be used. This shows that, with regard to model M1, the bivariate formulation at the annual level is lost with model M2:
, however, Equation (6) is no longer valid, and empirical estimation must be used. This shows that, with regard to model M1, the bivariate formulation at the annual level is lost with model M2:
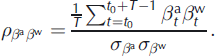
Finally, to compare the respective contributions to the annual variability of the temporal structure and the random fluctuations, we define the global ratios μ a, μ w and μ s (Equations (30–32)). They are able to indicate whether the hypothesized structured linear trends with change points explain a large part of the annual variability of annual, winter and summer balances respectively, in a way similar to that of the classical determination coefficient R 2 in a non-hierarchical linear regression:
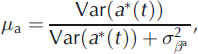
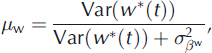
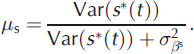
Obviously, the different proposed ratios as well as the correlation coefficients between the ![]() can also be computed separately before and after the change points τ
w and τ
s instead of globally over the entire observation period. This is, for instance, straightforward for λ
s, since it only implies computing the ratio with the two values
can also be computed separately before and after the change points τ
w and τ
s instead of globally over the entire observation period. This is, for instance, straightforward for λ
s, since it only implies computing the ratio with the two values ![]() and
and ![]() However, for mass balance, the three possible periods must be considered, which multiplies the number of indicators to be interpreted without necessarily adding much information to the analysis. This is the main reason why we mainly consider the global quantities over the T years of study.
However, for mass balance, the three possible periods must be considered, which multiplies the number of indicators to be interpreted without necessarily adding much information to the analysis. This is the main reason why we mainly consider the global quantities over the T years of study.
Summing up, by comparison with the first model, model M2 involves the additional parameters ![]() and hidden variables w
*(t), s
*(t) that have to be estimated from the data. All of them are related to the quantification of the temporal structure, which is assumed to be well modelled by two linear trends possibly separated by change points. The rest of the model is not modified, except for the correlation structure at the annual level, which is no longer constrained by ∑
β
12.
and hidden variables w
*(t), s
*(t) that have to be estimated from the data. All of them are related to the quantification of the temporal structure, which is assumed to be well modelled by two linear trends possibly separated by change points. The rest of the model is not modified, except for the correlation structure at the annual level, which is no longer constrained by ∑
β
12.
3.3. Bayesian inference and associated MCMC sampling
The different models proposed in this paper have been inferred within a Bayesian framework (Reference BergerBerger, 1985; Reference Parent and BernierParent and Bernier, 2007). The principle is to compute the joint posterior probability distribution function (PDF) of all parameters, hidden variables and missing values. Poorly informative marginal priors were used to ‘let the data speak for themselves’. For instance, pseudo-uniform priors were chosen for the spatial terms, poorly informative inverse gamma and inverse Wishart priors for the variances and variance–covariance matrixes, and poorly informative normal priors for the trend parameters.
Markov chain Monte Carlo (MCMC) schemes have been used to sample the joint posterior PDF. These powerful simulation methods are detailed, for example, by Reference Gilks, Richardson and SpiegelhalterGilks and others (1996) and Reference BrooksBrooks (1998). Examples of applications in a related field are given by Reference Eckert, Parent, Naaim and RichardEckert and others (2008, Reference Eckert, Naaim and Parent2010b). In our case, the efficient Gibbs sampler (Reference Geman and GemanGeman and Geman, 1984) could be run easily because of the Gaussian nature of a variance analysis that makes the full conditional distributions of the different parameters and hidden variables accessible.
Convergence of the MCMC sequence was checked by graphical comparison and various tests on the distributions obtained with different chains starting at different points of the parameter space (Reference Brooks and GelmanBrooks and Gelman, 1998). When the ergodic state was clearly reached, a sample of the joint posterior distribution was stored. For each quantity of interest, a point estimate and the related uncertainty was obtained by considering the marginal posterior mean and the related 95% credibility interval (i.e. the Bayesian counterpart of the classical confidence interval). Figure 3 shows an example of the marginal posterior distributions obtained for six quantities of interest. All are nicely shaped and unimodal, which indicates that information contained in the prior has been updated with the data and that the point estimates are meaningful. Among the distributions presented, those corresponding to σ
a and ![]() are direct results of the MCMC procedure. The others were obtained by computing their values at each step of the sampling procedure.
are direct results of the MCMC procedure. The others were obtained by computing their values at each step of the sampling procedure.
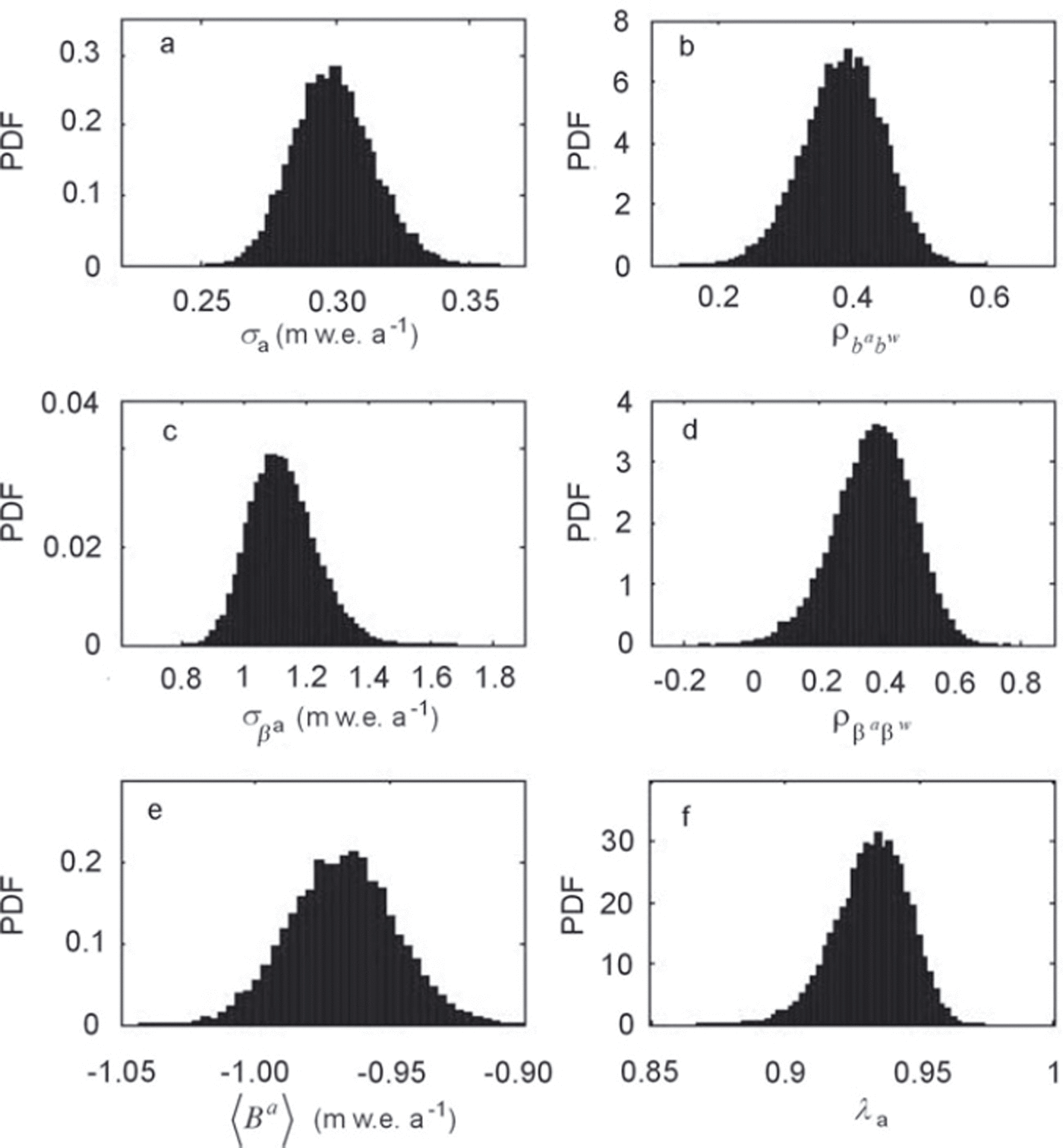
Fig. 3. Marginal PDFs for a few parameters, model M1. (a) Standard deviation for the annual balance residuals. (b) Correlation coefficient between annual and winter balance residuals. (c) Standard deviations for annual balance deviations. (d) Correlation coefficient between annual and winter balance deviations. (e) Glacier-wide mean balance over the period of record. (f) Ratio between variance of annual deviations and total annual variance.
4. Results
4.1. Lliboutry’s bivariate model
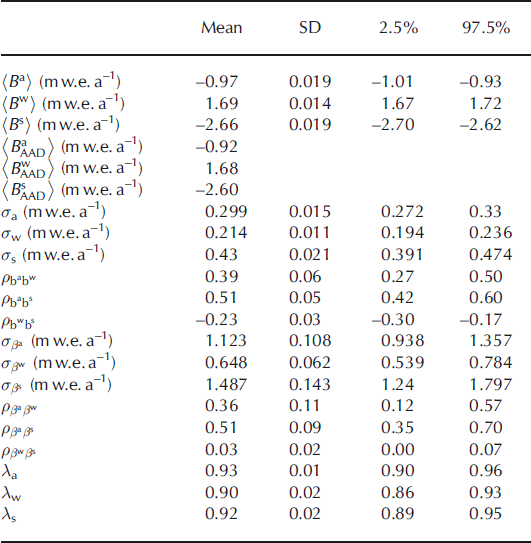
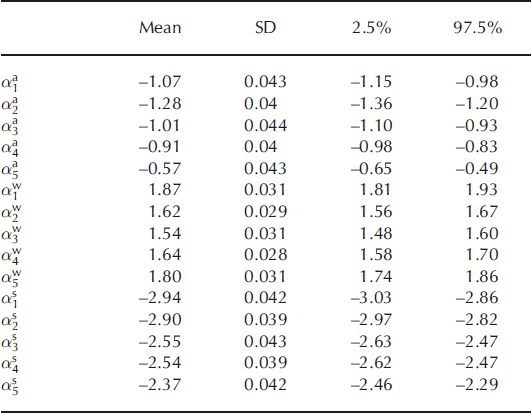
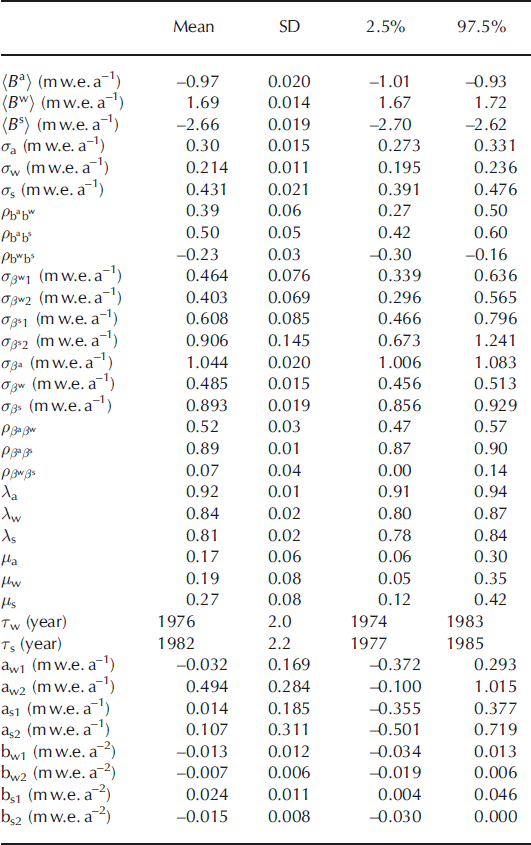
Table 1 summarizes the estimates obtained by applying model M1 to the Sarennes series. It appears that 〈B
a〉, the glacier-wide mean annual balance computed over the whole period under the assumption of equally weighted sites, is strongly negative. The glacier has lost ∼1 m w.e. a−1 because, in mean, summer balance has been much larger in absolute value (−2.66 m w.e. a−1) than winter balance (1.69 m w.e. a−1). These results do not differ significantly from those obtained with the altitude–area integration relationship ![]() ; Table 1). They are also clearly consistent with previous studies of the same glacier (Reference VallaValla, 1989; Reference Vincent and VallonVincent and Vallon, 1997; Reference Thibert, Blanc, Vincent and EckertThibert and others, 2008; Reference Thibert and VincentThibert and Vincent, 2009) and other glaciers in the French and Swiss Alps (Reference Müller and KappenbergerMüller and Kappenberger, 1991; Reference VincentVincent, 2002; Reference Vincent, Kappenberger, Valla, Bauder, Funk and Le MeurVincent and others, 2004; Reference Huss and BauderHuss and Bauder, 2009).
; Table 1). They are also clearly consistent with previous studies of the same glacier (Reference VallaValla, 1989; Reference Vincent and VallonVincent and Vallon, 1997; Reference Thibert, Blanc, Vincent and EckertThibert and others, 2008; Reference Thibert and VincentThibert and Vincent, 2009) and other glaciers in the French and Swiss Alps (Reference Müller and KappenbergerMüller and Kappenberger, 1991; Reference VincentVincent, 2002; Reference Vincent, Kappenberger, Valla, Bauder, Funk and Le MeurVincent and others, 2004; Reference Huss and BauderHuss and Bauder, 2009).
Table 1. Posterior characteristics of model M1 applied on Glacier de Sarennes point mass-balance series for the 1949–2007 period. SD denotes standard deviation, 2.5% and 97.5% denote the lower and upper bound of the 95% credible interval. For comparison, mean annual glacier-wide balances obtained with the glaciological method using the area–altitude distribution averaging (AAD subscripts) are also indicated for the annual, winter and summer terms
Marginal variances (σ
a, σ
w, σ
s) of the residuals are equal to 0.3, 0.21 and 0.43 m w.e. a−1 for annual, winter and summer balance respectively, which is consistent with the inequalities of Equation (12). Marginal variances of the annual terms ![]() ,
, ![]() ,
, ![]() are more than three times higher. Moreover, spatial variability is relatively small (the values obtained on the five stakes are not very different from each other for all three variables; Table 2), which is consistent with the small size of the glacier. Note also that estimation error is small for the three αi
series, i.e. not more than 0.044 m w.e.a−1. All this indicates that the interannual variability between the
are more than three times higher. Moreover, spatial variability is relatively small (the values obtained on the five stakes are not very different from each other for all three variables; Table 2), which is consistent with the small size of the glacier. Note also that estimation error is small for the three αi
series, i.e. not more than 0.044 m w.e.a−1. All this indicates that the interannual variability between the ![]() is the major source of variability at the glacier scale, constraining the three ratios λ
a, λ
w and λ
s to be above 90%. It also a posteriori justifies neglecting the spatial variability while computing the ratios of Equations (18–20).
is the major source of variability at the glacier scale, constraining the three ratios λ
a, λ
w and λ
s to be above 90%. It also a posteriori justifies neglecting the spatial variability while computing the ratios of Equations (18–20).
Table 2. Spatial α i terms, model M1 applied on Glacier de Sarennes point mass-balance series for the 1949–2007 period. Indices 1–5 correspond to the five stakes located in Figure 1. Units are m w.e. a−1
Residuals account for nonlinear effects that are not systematic in space and/or time and cannot therefore be captured in the α and β terms. Their correlations are all significantly nonzero at the 95% credibility level, which indicates that when the linear model performs poorly for one of the three terms of the balance, it is also biased for the two others. The positive values for ![]() and
and ![]() are easily understandable since when a local excess of winter mass input or summer mass loss occurs at a given stake in a given year, it influences accordingly the annual mass balance at this location. A nonzero value for
are easily understandable since when a local excess of winter mass input or summer mass loss occurs at a given stake in a given year, it influences accordingly the annual mass balance at this location. A nonzero value for ![]() is less intuitive. A physical explanation for a nonzero correlation between winter and summer balance residuals could be local excesses due to avalanches or local excesses/deficits due to snowdrift. In case of an excess, the corresponding albedo feedback in the summer balance would then result in a positive correlation. Indeed, an expanded snow ablation period would decrease ablation due to higher albedo at the glacier surface and reduced shortwave radiation absorption. Therefore, an enhanced (less negative) summer balance would be expected. In our case,
is less intuitive. A physical explanation for a nonzero correlation between winter and summer balance residuals could be local excesses due to avalanches or local excesses/deficits due to snowdrift. In case of an excess, the corresponding albedo feedback in the summer balance would then result in a positive correlation. Indeed, an expanded snow ablation period would decrease ablation due to higher albedo at the glacier surface and reduced shortwave radiation absorption. Therefore, an enhanced (less negative) summer balance would be expected. In our case, ![]() is negative, and harder to interpret, but anyway the correlation remains low (−0.23).
is negative, and harder to interpret, but anyway the correlation remains low (−0.23).
At the level of annual terms, things are simpler: a very strong positive correlation ![]() exists between annual and summer balance. Identically, annual and winter balances are well correlated (
exists between annual and summer balance. Identically, annual and winter balances are well correlated (![]() being significantly positive). Finally, winter and summer balances are uncorrelated with
being significantly positive). Finally, winter and summer balances are uncorrelated with ![]() . This suggests that the albedo feedback mentioned above is not effective at the overall glacier scale.
. This suggests that the albedo feedback mentioned above is not effective at the overall glacier scale.
In the Bayesian framework, the joint posterior distribution of the annual deviations ![]() is obtained. It is summarized in Figure 4 using box plots. The glacier-wide annual terms are obtained by adding the interannual mean, i.e. 〈B
a〉,〈B
w〉 and 〈B
s〉 respectively, to each value (Fig. 2b). For all three series, the interannual fluctuations are very strong, so that the different annual terms are largely significantly different from each other at the 95% credibility level. This reflects the variability under unsteady climatic forcing conditions of the accumulation and ablation processes governing the two seasonal components of the balance. Even if apparently random fluctuations are strong, glacier-wide balance (i.e.
is obtained. It is summarized in Figure 4 using box plots. The glacier-wide annual terms are obtained by adding the interannual mean, i.e. 〈B
a〉,〈B
w〉 and 〈B
s〉 respectively, to each value (Fig. 2b). For all three series, the interannual fluctuations are very strong, so that the different annual terms are largely significantly different from each other at the 95% credibility level. This reflects the variability under unsteady climatic forcing conditions of the accumulation and ablation processes governing the two seasonal components of the balance. Even if apparently random fluctuations are strong, glacier-wide balance (i.e. ![]() ), although remaining almost always negative, seems to increase during slightly more than the first half of the studied period, and then to decrease again, reaching strongly negative values at the end of the study period. On the other hand, the winter mass input decreases over the entire study period, but with a strong shift in the middle. Glacier-wide summer balance is nothing more than the difference between the two other terms, with values much lower after 1985 than before.
), although remaining almost always negative, seems to increase during slightly more than the first half of the studied period, and then to decrease again, reaching strongly negative values at the end of the study period. On the other hand, the winter mass input decreases over the entire study period, but with a strong shift in the middle. Glacier-wide summer balance is nothing more than the difference between the two other terms, with values much lower after 1985 than before.
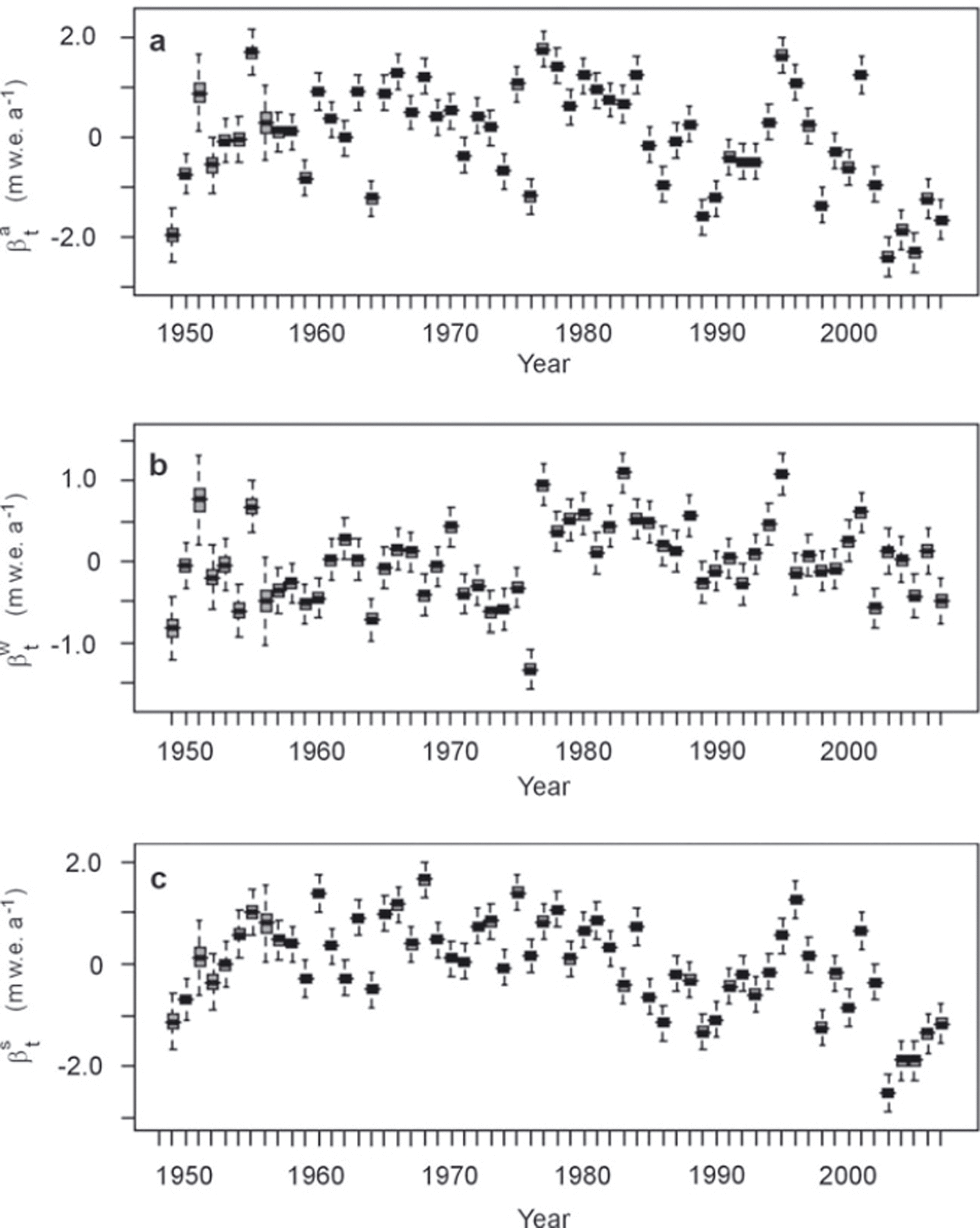
Fig. 4. Box plots of βt terms (annual deviations), model M1. (a) Annual balance, (b) winter balance, (c) summer balance. The posterior mean is shown in black, the interquartile range in grey and the 95% credibility interval by dashed lines. Extremely similar plots are obtained with models M1–M5. As shown in Figure 2b, the glacier-wide terms can be obtained by adding to each βt term the interannual mean given in Table 1, i.e. 〈B a〉,〈B w〉 and 〈B s〉 , respectively.
Even if the behaviour of the different annual terms is not identical, there is evidence in the three time series that changes separating different structured trends have occurred around the middle of the study period. This confirms the results of Reference Vincent and VallonVincent and Vallon (1997), reporting a strong positive accumulation change (+17%) on Sarennes since 1977 and a large increase in summer ablation and ablation rates (50%) since 1981. The latter has been thoroughly analysed by Reference Vincent, Kappenberger, Valla, Bauder, Funk and Le MeurVincent and others (2004). However, in these approaches, a single stake was used, and the significance of these changes was not assessed using specific statistical tests. Furthermore, annual terms were considered as observed, without taking into account the uncertainty related to their estimation. This justifies testing the hierarchical and non-exchangeable model M2 on the same dataset in section 4.2 to identify temporal break points in means/trends/variances of the three annual terms.
For the three βt series, estimation error measured as the width of the 95% credible interval for each estimate remains nearly constant over the whole period. The only exceptions correspond to the years for which one or several measurements are missing (e.g. 1951, three missing values out of five, or 1956, four missing values out of five), and for which estimation error is then logically higher. This ability to fairly reflect the level of available information is for us an important advantage of our modelling approach with regard to empirical estimation procedures. Furthermore, the uncertainty around the annual estimates remains tenable even with two or three missing measurements out of five. This is another clear benefit of a bivariate hierarchical model. Indeed, correlations between the different variables (Equation (2)) and from one year to another (Equation (5)) are explicitly modelled, so that information is transferred from one variable/year to another, thus reducing all credible intervals, and especially those corresponding to years with one or several missing values.
Similarly, missing data are estimated with credibility levels depending on the number of measurements for the considered stake/year. Figure 5a thus presents the annual balance at stake 3. Measurements exist between 1958 and 2007. Between 1949 and 1957, missing values are estimated on the basis of correlations between variables, sites and years. Variance of the estimated missing value is lower for 1957 than for 1956, since one more measurement is available (Fig. 5b and c).
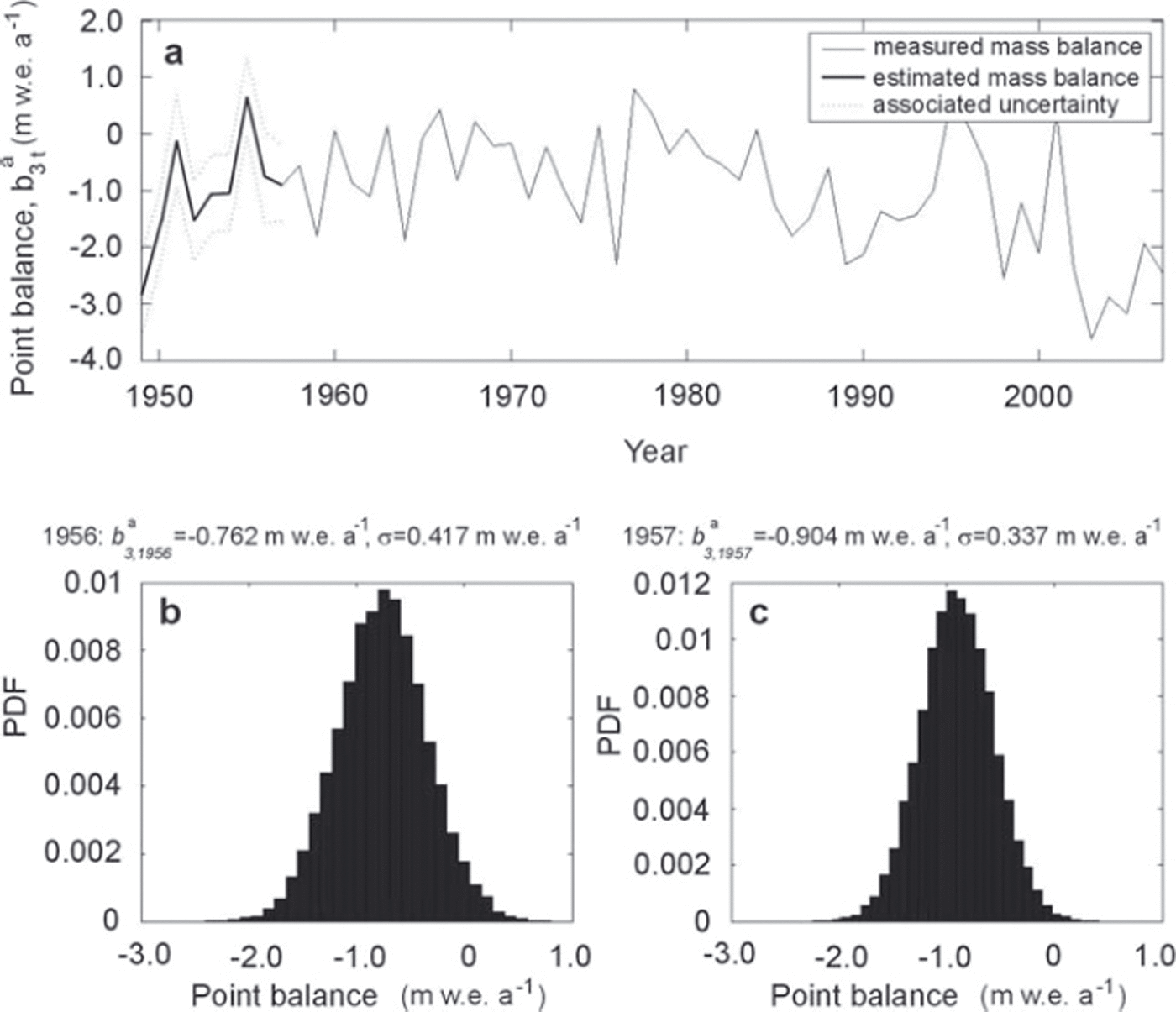
Fig. 5. Estimation of missing data in the annual mass-balance series at stake 3 (missing values from 1949 to 1957). (a) Completion of the record at stake 3, ![]() , and associated uncertainty for the missing values. (b, c) Posterior distribution of mass balance at stake 3 estimated in (b) 1956 and (c) 1957.
, and associated uncertainty for the missing values. (b, c) Posterior distribution of mass balance at stake 3 estimated in (b) 1956 and (c) 1957.
Finally, model adequacy with respect to data can be checked by comparing the residuals ![]() with the centred linear model with variance covariance E. Figure 6 shows that, for the point mass-balance series, model fit is relatively good, with no bias and a nearly Gaussian distribution of the residuals, which is not surprising since the two-way ANOVA model has been known since Lliboutry’s work to be well suited to mass-balance series. Model fit is also not that bad for the winter point balances, which has been less often reported. However, with a statistical test such as the Kolmogorov–Smirnov test, the null hypothesis that both residuals are sampled from centred normal distributions of respective marginal variances
with the centred linear model with variance covariance E. Figure 6 shows that, for the point mass-balance series, model fit is relatively good, with no bias and a nearly Gaussian distribution of the residuals, which is not surprising since the two-way ANOVA model has been known since Lliboutry’s work to be well suited to mass-balance series. Model fit is also not that bad for the winter point balances, which has been less often reported. However, with a statistical test such as the Kolmogorov–Smirnov test, the null hypothesis that both residuals are sampled from centred normal distributions of respective marginal variances ![]() and
and ![]() is questionable: it is accepted at the 95% significance level for annual balance, but only with a p value of 0.2, and rejected at the same significance level for winter balance with a p value of 0.02, just below the rejection threshold.
is questionable: it is accepted at the 95% significance level for annual balance, but only with a p value of 0.2, and rejected at the same significance level for winter balance with a p value of 0.02, just below the rejection threshold.
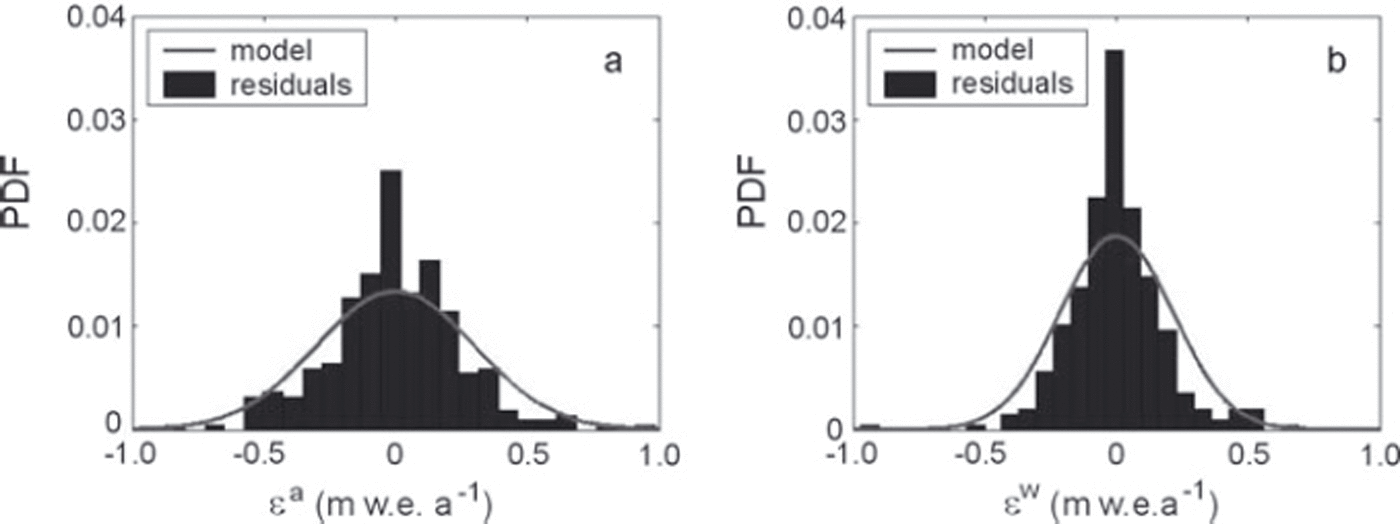
Fig. 6. PDF of residuals for linear model M1 in annual (a) and winter (b) point mass-balance series.
These results indicate a small but significant discrepancy between the model and reality, especially for winter balance. In the latter case, it is probably related to the lower stability from year to year of the spatial structure of winter balance because of processes such as avalanches or snowdrifts whose influence has already been mentioned while discussing ![]() . The development of a ski resort on a part of the glacier and snow grooming may also have affected nonlinearly the spatial distribution of winter snow deposition. Another reason for the relatively low p values obtained is related to the normality test which is somewhat severe here as the quantity of available data is relatively large. This is not the case in other glaciological studies applying Lliboutry’s model which generally rely on much shorter measurement series. Note in any case that we are primarily interested in the annual terms that capture the main part of data variability rather than in the residuals, making the obtained low p values sufficient with regard to the scope of the study.
. The development of a ski resort on a part of the glacier and snow grooming may also have affected nonlinearly the spatial distribution of winter snow deposition. Another reason for the relatively low p values obtained is related to the normality test which is somewhat severe here as the quantity of available data is relatively large. This is not the case in other glaciological studies applying Lliboutry’s model which generally rely on much shorter measurement series. Note in any case that we are primarily interested in the annual terms that capture the main part of data variability rather than in the residuals, making the obtained low p values sufficient with regard to the scope of the study.
4.2. Change-point model
Model M2 shares many common features with model M1, so that some of the results are identical when both models are applied to the Sarennes dataset. For instance, this is the case for most of the quantities related to the observation layer: overall means, residual variances and correlation coefficients, as well as spatial terms. Their values (Table 3) therefore do not need to be discussed again.
Table 3. Posterior characteristics, model M2 applied on Glacier de Sarennes point mass-balance series for the 1949–2007 period.
However, as soon as the temporal aspect is considered, differences appear between models M1 and M2. The introduction in model M2 of a non-exchangeable structure and the related absence of an explicit specification of the correlation structure between the triplets ![]() explains why the overall variances
explains why the overall variances ![]() and correlation coefficients
and correlation coefficients ![]() differ slightly with model M2 (Table 3) from their previous values (Table 1).
differ slightly with model M2 (Table 3) from their previous values (Table 1).
More precisely, all marginal variances ![]() are reduced, and
are reduced, and ![]() no longer satisfies Equation (11). This is logical, since the means of the
no longer satisfies Equation (11). This is logical, since the means of the ![]() are, with model M2, functions of time rather than set to zero, allowing better fitting to the data. As a consequence, the temporal ratios λ
w and λ
s are lowered by ∼10% compared to their values with model M1, but the interannual variability remains largely predominant, still representing >80% of the total variability. For the correlation coefficients, the main features are slightly enhanced with regard to model M1:
are, with model M2, functions of time rather than set to zero, allowing better fitting to the data. As a consequence, the temporal ratios λ
w and λ
s are lowered by ∼10% compared to their values with model M1, but the interannual variability remains largely predominant, still representing >80% of the total variability. For the correlation coefficients, the main features are slightly enhanced with regard to model M1: ![]() and
and ![]() are more strongly positive, whereas there is still no correlation between winter and summer balance components. All these differences are, however, insufficient to make the
are more strongly positive, whereas there is still no correlation between winter and summer balance components. All these differences are, however, insufficient to make the ![]() time series from model M2 graphically distinguishable from those of model M1 displayed in Figure 4.
time series from model M2 graphically distinguishable from those of model M1 displayed in Figure 4.
The values obtained for μ a, μ w and μ s show that the assumed linear time trends represent ∼20% of the inter-annual variability of annual and winter balances, and 27% of the interannual variability of summer balance (Table 3). The years of change found for winter and summer balances are significantly different. The posterior distribution of τ w shows a well-marked main mode in 1976, indicating strong evidence that a change actually occurred around that year for winter balance. For summer mass balance, the main mode is less marked in 1982, and other plausible years range between 1981 and 1984 (Fig. 7). This suggests that, for Glacier de Sarennes, the winter mass-balance regime changed ∼6 years before the summer balance regime.
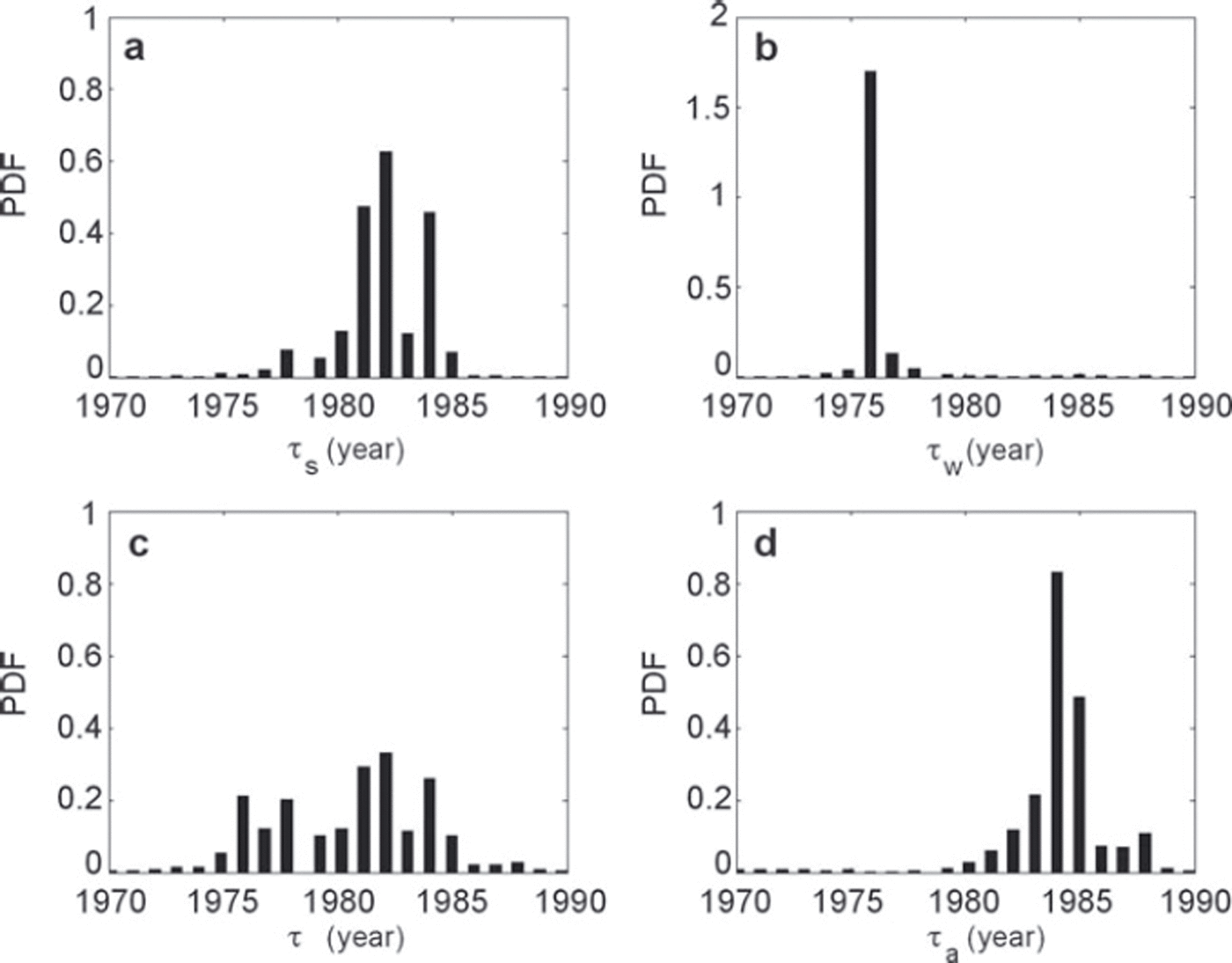
Fig. 7. (a, b) Posterior distributions of the year of change for model M2 for summer (a) and winter (b) balances. (c, d) Posterior distributions for change points in additional models M3 (c) and M4 (d).
![]() is only slightly lower than
is only slightly lower than ![]() , so τ
w cannot be considered as a change point in variance for the winter balance. On the other hand, for summer balance, variance around the interannual trend
, so τ
w cannot be considered as a change point in variance for the winter balance. On the other hand, for summer balance, variance around the interannual trend ![]() is much higher than
is much higher than ![]() . τ
s is therefore also a change point in variance separating two periods with interannual variabilities differing from the overall variance
. τ
s is therefore also a change point in variance separating two periods with interannual variabilities differing from the overall variance ![]() of Equation (28).
of Equation (28).
The mean trends and the related uncertainties are shown in Figure 8. The box plots may look quite wide, but this is because the linear fits are made on hidden variables, thus taking into account the uncertainty related to the ![]() for the estimation of the time trends. This may prevent firm conclusions, but once again properly reflects the amount of information present in the data. Logically, the uncertainty level is higher at the beginning and at the end of the study period where information density is lower, as well as around the change points. This is especially true for a
*(t) which is influenced by both change points (τ
w, τ
s).
for the estimation of the time trends. This may prevent firm conclusions, but once again properly reflects the amount of information present in the data. Logically, the uncertainty level is higher at the beginning and at the end of the study period where information density is lower, as well as around the change points. This is especially true for a
*(t) which is influenced by both change points (τ
w, τ
s).
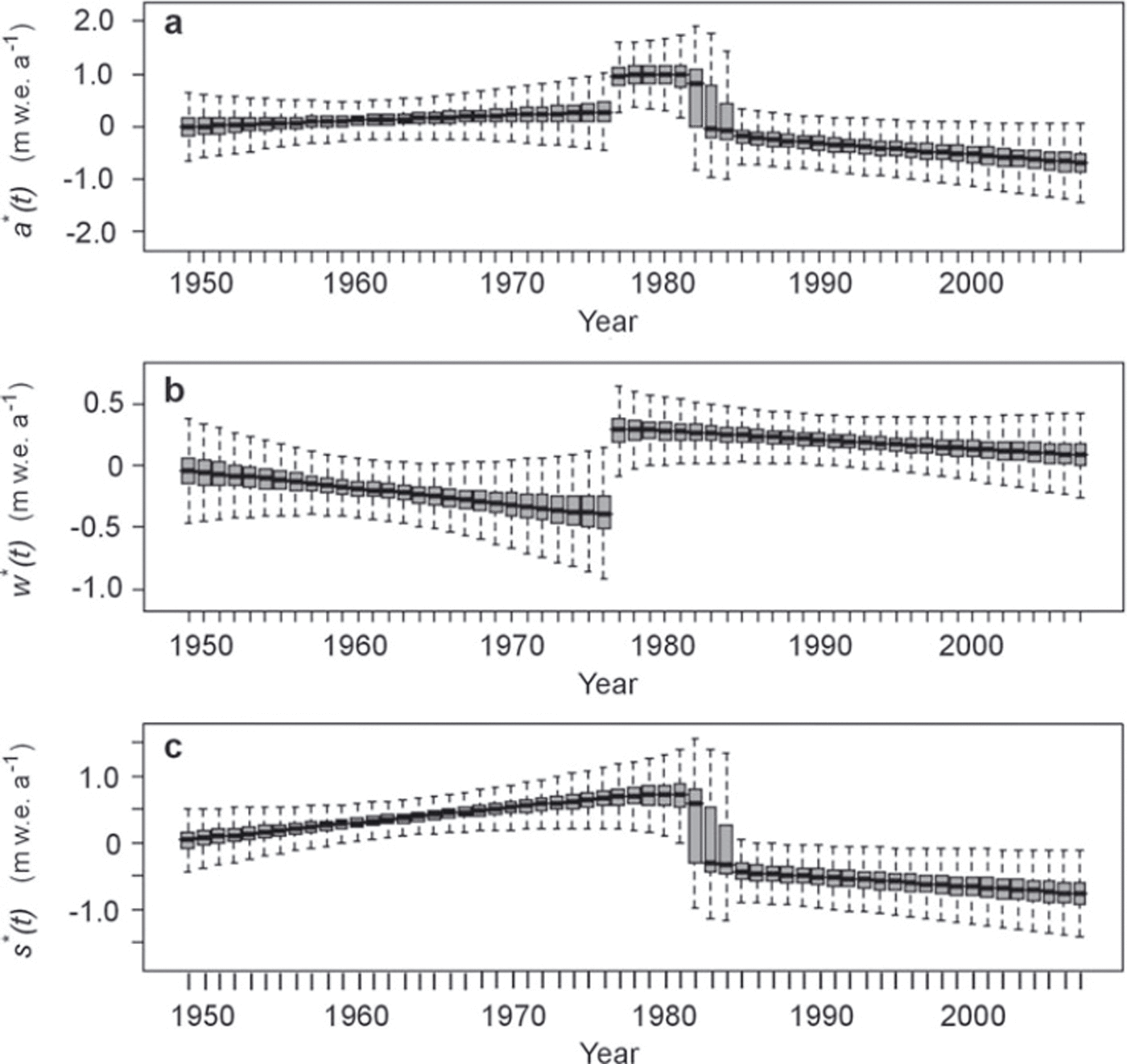
Fig. 8. Box plots of the structured trends, model M2: (a) annual balance, (b) winter balance and (c) summer balance. The posterior mean is shown in black, the interquartile range in grey and the 95% credibility interval by dashed lines.
Looking closer, the two trend parameters (b
s1, b
s2) are significantly nonzero at the 95% credibility level, positive before the change point and negative after. On the other hand, the two b
w. trend parameters and the four intercepts are not significantly nonzero at the 95% credibility level (Table 3). However, even if checking that zero belongs to a credible interval is in some ways the Bayesian counterpart of a classical significance test, it is not a test in the strict sense of the term, and the shape of the posterior distribution must be taken into account to properly interpret the results. For instance, the marginal posterior distributions of the (b
w1, b
w2) trend parameters are far from centred around zero, indicating that there is a high probability that they may be nonzero. The decreasing trend before and after the strong shift τ
w must therefore be noted, even if it is definitely less marked than the two trends in the summer mass-balance series. Hence, the high uncertainty around the most probable values must be linked to the difficulty of extracting information from hidden layers rather than to the absence in the ![]() series of any temporal structure.
series of any temporal structure.
For winter balance, the structured trend is strongly discontinuous around τ
w = 1976, indicating that the change is sudden. Between 1949 and 1976, the mean glacier-wide winter budget ![]() , but is not uniformly distributed since there is a decrease of −0.37 m w.e. a−1 over this period (b
w1 = −0.013 m w.e. a−2). In 1977, winter mass input increases strongly and its mean
, but is not uniformly distributed since there is a decrease of −0.37 m w.e. a−1 over this period (b
w1 = −0.013 m w.e. a−2). In 1977, winter mass input increases strongly and its mean ![]() between 1977 and 2007 is 1.88 m w.e. a−1.Note though that, as observed before 1976, winter mass balance slowly decreases in this second period by 0.20 m w.e. a−1until 2007 (b
w2 = −0.007 m w.e. a−2). Mean glacier-wide winter balance was therefore lower than the long-term mean 〈B
w〉 = 1.69 m w.e. a−1 before the change point, and higher than the long-term mean after the change point, with the years of lowest values being just before the change point in 1976, and the years with the highest values just after.
between 1977 and 2007 is 1.88 m w.e. a−1.Note though that, as observed before 1976, winter mass balance slowly decreases in this second period by 0.20 m w.e. a−1until 2007 (b
w2 = −0.007 m w.e. a−2). Mean glacier-wide winter balance was therefore lower than the long-term mean 〈B
w〉 = 1.69 m w.e. a−1 before the change point, and higher than the long-term mean after the change point, with the years of lowest values being just before the change point in 1976, and the years with the highest values just after.
Regarding summer balance, the transition lasts ∼4–5 years around τ
s = 1982. During these 4–5 years, it is shifted down by about 1.11 m w.e. a−1. Before 1982, mean glacier-wide summer balance is ![]() , that is 0.4 m w.e. a−1 more than the long-term mean 〈B
s〉. Furthermore, during this first period, summer glacier-wide balance increases by 0.62 m w.e. a−1 (b
s1 = +0.024 m w.e. a −2). After 1982, summer balances are significantly lower,
, that is 0.4 m w.e. a−1 more than the long-term mean 〈B
s〉. Furthermore, during this first period, summer glacier-wide balance increases by 0.62 m w.e. a−1 (b
s1 = +0.024 m w.e. a −2). After 1982, summer balances are significantly lower, ![]() , i.e. nearly 0.6 m w.e.a−1 below the long-term mean. During this second period, there is also a decreasing trend from year to year (b
s2 = −0.015 m w.e. a−2), with summer glacier-wide balance more in deficit by 0.30 m w.e. a−1 between τ
s and 2007.
, i.e. nearly 0.6 m w.e.a−1 below the long-term mean. During this second period, there is also a decreasing trend from year to year (b
s2 = −0.015 m w.e. a−2), with summer glacier-wide balance more in deficit by 0.30 m w.e. a−1 between τ
s and 2007.
For glacier-wide annual balance, three regimes are separated by the two change points, τw and τs:
-
1. Before τw = 1976, Glacier de Sarennes loses mass with a mean annual wide balance of −0.80 m w.e. a−1, but the trend goes from strongly negative balances to less negative balances from year to year (b a = +0.011 m w.e. a−2), mainly due to less negative summer balances.
-
2. Between 1976 and 1982, glacier-wide winter balances increase strongly while the summer regime has not yet changed. As a result, the mean mass balance is slightly above 0 m w.e. a−1 and the glacier, very close to equilibrium, maintains its mass. The trend is to higher mass gain from year to year in this short period with b a = +0.017 m w.e. a−2, because the increase in the winter balance comes over the summer budget.
-
3. After the summer balance shift down in τ s = 1982, the glacier loses mass, with a mean balance of −1.36 m w.e. a−1. Furthermore, due to the concordance of unfavourable trends in winter and summer balances, there is a well-marked trend towards higher mass loss from year to year, with b a = −0.022 m w.e. a−2.
These results are in good agreement with the available mean annual geodetic balances mentioned in section 2. Indeed, these independent data indicate that the mean annual balances over the periods 1952–81 and 1981–2003 are −0.36 and −0.99 m a−1, respectively, thus confirming the large increase in mass loss between the two periods.
5. Discussion
5.1. Model efficiency and usefulness of its different components
The change-point model M2 previously discussed introduces two different ruptures for winter and summer balances, which have been shown to be acceptable for the Sarennes series. We have tested a simpler model, M3, with a single change point, τ, in the two series. The main mode in the distribution of τ is then in 1982 (Fig. 7c), i.e. the year obtained for τ s with model M2 (Fig. 7a). This year is identified since it is the most significant of the (τ w, τ s) pair. The change-point selection is, however, less clear than with model M2 because τ = 1982 does not correspond at all to the winter balance series. As a result, the winter trend, w *(t), is then very close to zero whatever t (not shown). A single change point must therefore be rejected on the basis of Sarennes data.
We have also analysed the effect of setting a change point τ a in the annual balance instead of the change point τ s in the summer balance. This results in a well-marked main mode in 1984 in τ a’s posterior PDF, thus slightly later than τ s (Fig. 7d). However, the main difference between this model M4 and model M2 is in the trends s *(t) and a *(t) around the change points (not shown). The mass-balance trend is positive (b a1 = +0.027 m w.e.a−2) until 1984, then becomes slightly negative (b a2 = −0.013 m w.e. a−2). On the other hand, for summer balance, since τ w ≠ τ a, three subperiods appear. Having two change points in summer balance and only one in annual balance is highly unlikely and justifies preferring model M2.
Finally, nonlinear effects have been neglected until here. Removing this assumption requires adding, with suitable constraints to ensure model identifiability, interaction terms ![]() , for the annual balance and
, for the annual balance and ![]() for the winter balance in model M2, leading to the full bivariate ANOVA model M5:
for the winter balance in model M2, leading to the full bivariate ANOVA model M5:
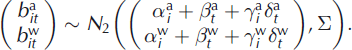
Among all ![]() , only
, only ![]() is significantly nonzero at the 95% credibility level for Sarennes. This indicates that only stake 1 behaves differently from the glacier’s mean in some specific years, and only for winter balance. This can be explained by enhanced winter accumulation due to snowdrifts/ avalanches in the area of stake 1. As discussed in section 4, these effects were part of the residuals with models M1–M4 and are, with this model, captured in the interaction term.
is significantly nonzero at the 95% credibility level for Sarennes. This indicates that only stake 1 behaves differently from the glacier’s mean in some specific years, and only for winter balance. This can be explained by enhanced winter accumulation due to snowdrifts/ avalanches in the area of stake 1. As discussed in section 4, these effects were part of the residuals with models M1–M4 and are, with this model, captured in the interaction term.
Second-order temporal terms (δt ’s) are all very small, indicating no year with excess or deficits in mass balance and/or winter balance that are not captured by the βt ’s (Fig. 9). This confirms that most of the temporal structure is actually captured by the linear temporal terms. Note that the δt ’s are somewhat more significant for winter than for annual balance, which makes sense since it has been established with model M1 that the decomposition between space and time is more adapted to the data for annual balance than for winter balance.
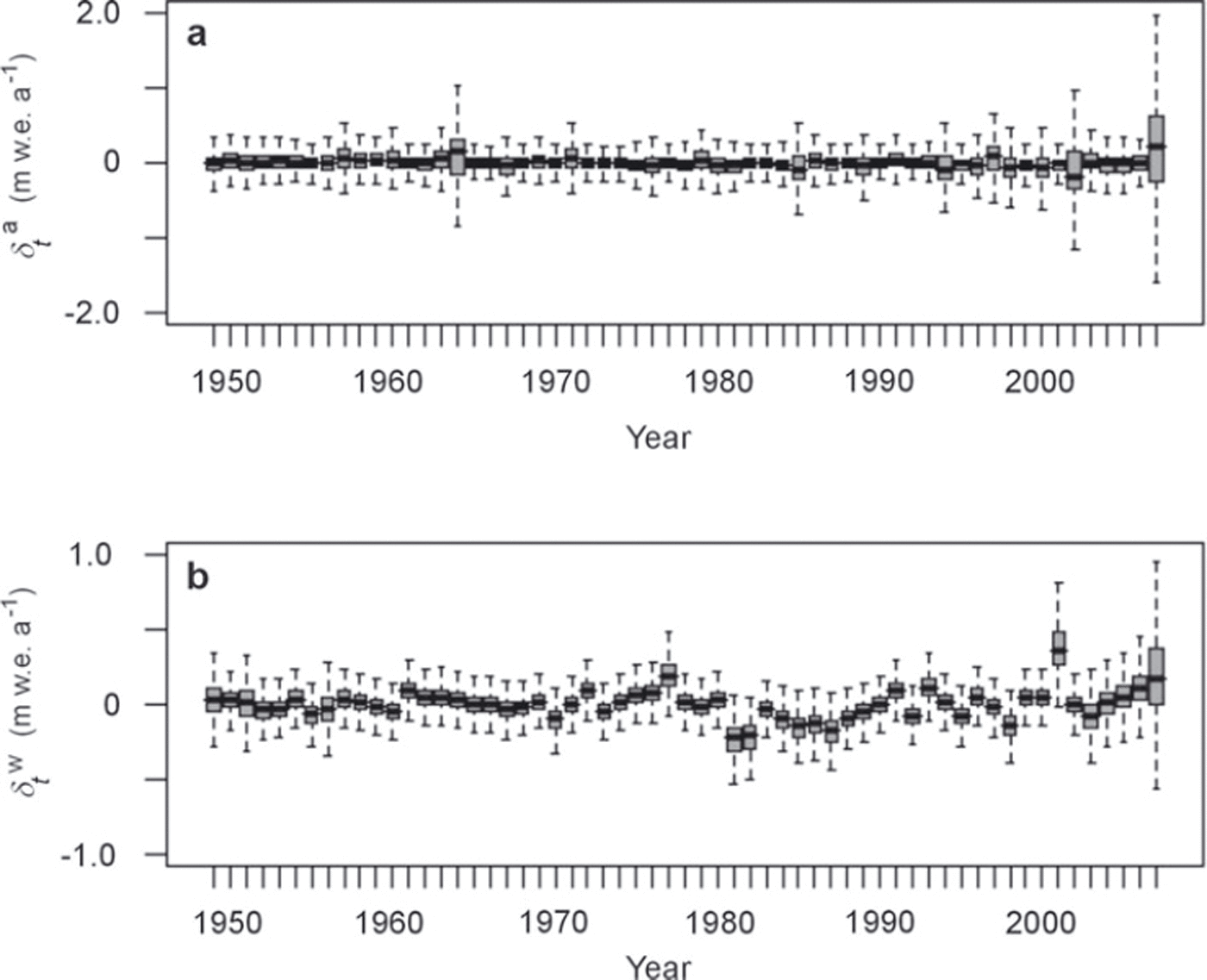
Fig. 9. Box plots of the additional nonlinear temporal terms in the annual (a) and winter (b) balances, model M5. The posterior mean is shown in black, the interquartile range in grey and the 95% credibility interval by dashed lines. Temporal cross terms ![]() and
and ![]() are displayed in physical units, whereas spatial terms, γ, are arbitrarily normalized to unity.
are displayed in physical units, whereas spatial terms, γ, are arbitrarily normalized to unity.
Adequacy between model and data measured in terms of variance of residuals or using a model selection tool such as the deviance information criterion (DIC; Reference Spiegelhalter, Best, Carlin and van der LindeSpiegelhalter and others, 2002) is better with model M5 than with model M2 (and than with any other model) because model M5 is much more flexible due to the new parameters introduced. However, standard deviations for the three interaction terms (estimated, e.g., as ![]() for annual balance) range from 0.122 to 0.185 m w.e. a−1only for the three components of the balance. This is not negligible, but not high enough to represent a large part of data variability, so that the normality of the residuals is still rejected with model M5 for winter balance (Kolmogorov–Smirnov test). Furthermore, as a consequence of model structure, the three obtained βt
series and underlying trends are fully identical with model M5 to those provided by model M2. Model M5 cannot therefore be considered as really superior to model M2, being much more complex in terms of specification and inference without providing much valuable additional information.
for annual balance) range from 0.122 to 0.185 m w.e. a−1only for the three components of the balance. This is not negligible, but not high enough to represent a large part of data variability, so that the normality of the residuals is still rejected with model M5 for winter balance (Kolmogorov–Smirnov test). Furthermore, as a consequence of model structure, the three obtained βt
series and underlying trends are fully identical with model M5 to those provided by model M2. Model M5 cannot therefore be considered as really superior to model M2, being much more complex in terms of specification and inference without providing much valuable additional information.
5.2. Interpretation of temporal patterns
In this work, fluctuations of different seasonal components in mass balance have been related to time taken as an explicit covariate rather than to seasonal climatic descriptors such as cumulated winter snow depth or summer mean temperature. The main justification of such a time-explicit framework is its flexibility: it does not impose a forced link with climate, and therefore allows the extraction of refined temporal patterns as close as those present in the data. On the other hand, their climatic relevance is then not granted, and one must be extremely cautious when considering trends, change points, and their interpretation in term of climatic drivers.
For instance, Sarennes has a cumulative wide balance of −48 m w.e. over the period of record, and there is an average elevation decrease of 53 m over the entire glacier surface. We would therefore expect an enhanced surface energy exchange due to the elevation gradient of mass balance. Assuming a value of −0.66 m w.e. a−1(100 m)−1 for the mass-balance gradient, a mean annual elevation decrease of −0.89 m a−1 over six decades results in a negative trend in mass balance of −0.0059 m w.e. a−2 due to the lowering of the glacier surface. This represents nearly 27% of the trend detected by model M2 in the annual balance time series, which is not a direct consequence of changes in climatic forcing but rather a feedback from the glacier. Another potential source of glacier topography retroaction is the decrease in area at low elevations which removes negative contributions to the glacier-total balance (Reference Elsberg, Harrison, Echelmeyer and KrimmelElsberg and others, 2001). However, this effect has no impact here because the ![]() terms are not spatial integrated balances, but uniform annual deviations from the mean surface balance at all individual measurement locations.
terms are not spatial integrated balances, but uniform annual deviations from the mean surface balance at all individual measurement locations.
Nevertheless, other observations support the assumption that the major explanation of our results is recent climate change. For example, the same trends in summer balances have been reported for other French and Swiss glaciers with analogous temporal break points (Reference VincentVincent, 2002; Reference Huss, Bauder, Funk and HockHuss and others, 2008). The rise in winter precipitation since 1977 that has been found has a more regional signification. Indeed, no specific trend is reported in glacier winter balances in the eastern Swiss Alps, for instance on Silvretta and Clariden glaciers (Reference Müller and KappenbergerMüller and Kappenberger, 1991; Reference Huss and BauderHuss and Bauder, 2009). Nevertheless, closer to Sarennes, Aletschgletscher, Valais, Switzerland, displays a synchronous change point in winter balance around 1974–76, though less significant in magnitude than for Sarennes (Reference Huss and BauderHuss and Bauder, 2009). Furthermore, this change point is present in various snow and weather series in the French Alps (Reference Durand, Laternser, Giraud, Etchevers, Lesaffre and MérindolDurand and others, 2009a,Reference Durand, Giraud, Laternser, Etchevers, Mérindol and Lesaffreb) and avalanche runout elevation series (Reference Eckert, Parent, Kies and BayaEckert and others, 2010c), which supports its climatic relevance, at least at the scale of the French Alps and their close surroundings.
These preliminary interpretations have now to be expanded by analysing in detail the correlations between the different mass-balance series obtained, their underlying trends, and seasonal climatic data. This was not done in this study because its scope was mainly methodological. The different models’ components have therefore been used much more to discuss the advantages of our approach compared to previous ones than to evaluate the contribution of Glacier de Sarennes as a proxy indicator of climate change around the French Alps. Hence, this will be the scope of further work which will involve cross-comparison of the refined indicators provided by our analysis of Sarennes’ exceptionally long and complete series with systematic variations of the constraining climatic factors at large and local scales.
5.3. Implication for the overall and cumulative balances
In a previous paper (Reference Thibert and VincentThibert and Vincent, 2009), a combination of the variance decomposition of the annual mass-balance series using Lliboutry’s classical linear model with aerial photogrammetry was proposed. By minimizing systematic errors, this gives the best possible estimate of the glacier-wide balance. The same goal can be achieved with model M2 instead of Lliboutry’s model over the periods 1952–81 and 1981–2003 on which, as mentioned in section 2, the mean geodetic balances are available. Note that even if the period of record is only divided into two periods, before and after 1981, instead of the three periods identified by model M2 (before τ w = 1976, between τ w and τ s = 1982, and after τ f), 1981 is approximately the middle of the 6–7year long 1977–84 period of high mass-balance regime.
As indicated by Reference Thibert and VincentThibert and Vincent (2009), because of the linearity of the variance decomposition, the glacier-wide balance, ![]() , can be evaluated from the annual deviation,
, can be evaluated from the annual deviation, ![]() , and the mean annual balance,Φ 4), obtained from photogrammetry according to Figure 2b:
, and the mean annual balance,Φ 4), obtained from photogrammetry according to Figure 2b:
The upper-case letters ![]() designate spatially integrated values as opposed to point measurements such as in Equation (2), for example. In our case, Φ takes two different values, before and after 1981. Furthermore, since no photogrammetry measurement is available for the initial and final years of record, the glacier total balance is calculated from the
designate spatially integrated values as opposed to point measurements such as in Equation (2), for example. In our case, Φ takes two different values, before and after 1981. Furthermore, since no photogrammetry measurement is available for the initial and final years of record, the glacier total balance is calculated from the ![]() terms. The cumulative balance,
terms. The cumulative balance, ![]() , for glaciological year t is then given by:
, for glaciological year t is then given by:
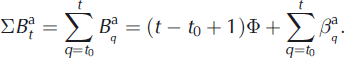
Under model M2, ![]() is centred on a linear time trend with slope b
a. which is homogeneous to a rate. The sum of the
is centred on a linear time trend with slope b
a. which is homogeneous to a rate. The sum of the ![]() terms then has a second- order time dependence such as:
terms then has a second- order time dependence such as:
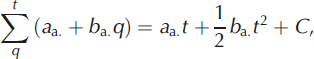
where C is a constant which can be determined for each of the two considered periods using the control mass balances from photogrammetry and by imposing continuity around the change points. Over each period, the cumulative glacier-wide balance is therefore a parabolic function of time, with curvature given by the sum in winter and summer balance trends:
Considering the two periods given by photogrammetry instead of the three given by the variance analysis is thus equivalent to neglecting the slight increase in the mass-balance trend between 1977 and 1982 (from +0.011 to +0.017 m w.e. a−2).
The obtained cumulative glacier-wide balance perfectly matches the parabolic trend in 1952, 1981 and 2003 as a result of the fitting of the mean annual balance to photogrammetry measurements performed on these dates (Fig. 10). For all other years, the obtained parabolic curve also fits the data well, which is remarkable since it results from integrating the mean trend provided by model M2 rather than from direct fitting to cumulated data at each stake. This provides another argument in favour of the assumption of robust underlying linear trends for the changes in mean winter and summer balances.
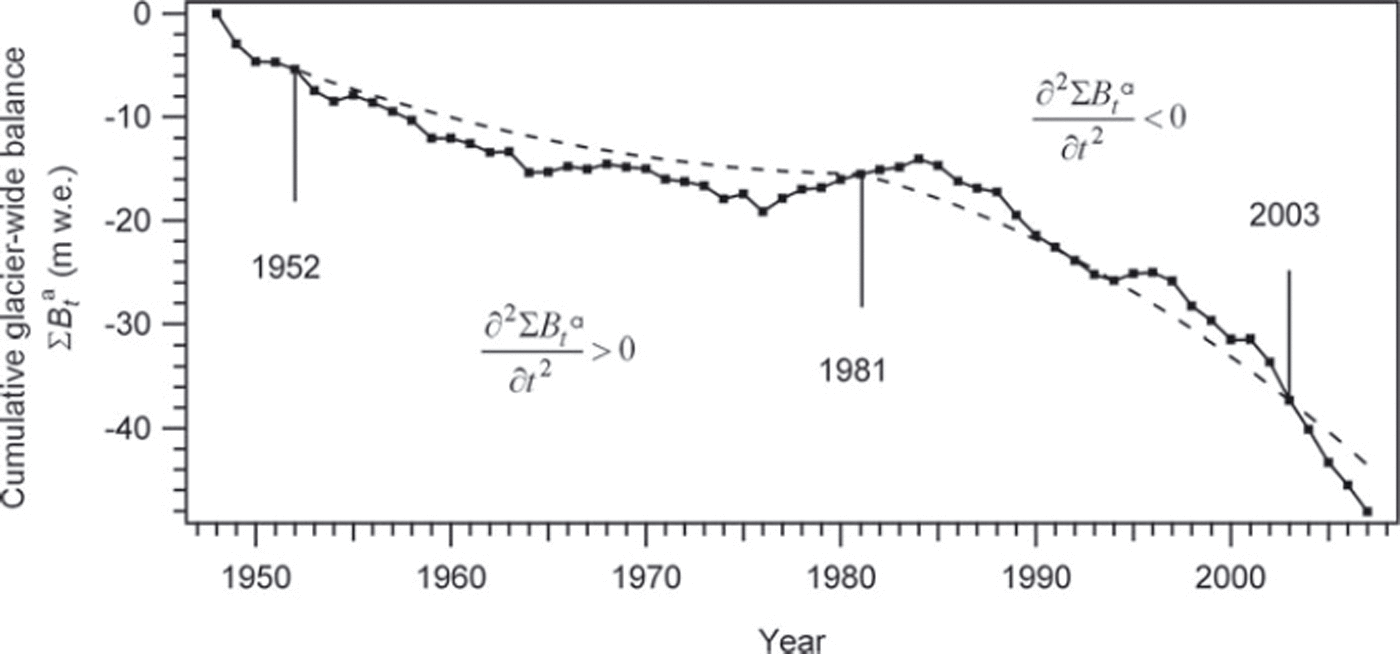
Fig. 10. Cumulative glacier-wide balance, ![]() , obtained by combining photogrammetry performed in 1952, 1981 and 2003, and annual
, obtained by combining photogrammetry performed in 1952, 1981 and 2003, and annual ![]() terms centred on a linear time trend given by model M2. As a result of the two linear trends in annual balances, trends in cumulative balance,
terms centred on a linear time trend given by model M2. As a result of the two linear trends in annual balances, trends in cumulative balance, ![]() , are parabolic over the 1949–81 and 1981–2007 periods.
, are parabolic over the 1949–81 and 1981–2007 periods.
For instance, the curvature of the cumulative balance is positive before 1981 (+0.011 m w.e. a−2) and negative since (−0.022 m w.e. a−2). In mean, i.e. when the predominant temporal pattern is separated from interannual variability modelled as random, mass loss decelerated before 1981 while Sarennes was approaching an equilibrium state, which was reached in the early 1980s. On the other hand, in the last 25 years, the predominant pattern is an accelerated glacier mass loss clearly indicated by the negative curvature of the cumulative balance. This shows that Sarennes is rapidly moving away from the last equilibrium state of the 1980s. Even considering that a part of this acceleration in mass loss (27%) is retroactive due to glacier topography, this confirms that the glacier is now still far from its equilibrium state under the current climate and/ or that climate change is still in progress.
6. Conclusion and Outlooks
In this paper, a hierarchical modelling framework has been developed to study the spatio-temporal variability of the three components of a glacier mass-balance series, so as to take into account the different seasonal processes. Bayesian estimation was used because of its convenience for hierarchical modelling, but without recourse to informative priors, so as to extract an unperturbed temporal signal from the data. With regard to previous more empirical modelling procedures, this constitutes an important step forward in the study of mass-balance series since it allows an appropriate extraction of refined temporal patterns.
Another important feature of our approach is that it uses a complete bivariate dataset of measured surface balances as input, so as to capture the mean effect at the glacier scale. The extracted temporal signal is therefore free of any effect related to the geometry (surface) and the dynamics of the glacier that affect surface integrated balances, except the retroaction due to elevation changes discussed in section 5.2. It therefore offers an advantageous alternative to the arbitrary selection of a single site, which may discard a part of the climatic information present in the overall data and also lead to misleading conclusions because of local effects.
In detail, a fully multivariate extension was first proposed for Lliboutry’s well-known linear ANOVA model. Even if the assumption of Gaussian residuals remains questionable for winter balance, application to the exceptional Sarennes data series has shown that a linear variance decomposition satisfactorily represents the different components of a glacier mass balance. Furthermore, the explicit quantification of all variability sources and correlations was found useful to properly represent the uncertainty around each estimate, and to quantify missing values based on information transferred between sites/years/variables.
Next, different non-exchangeable structures capable of capturing change points and various types of systematic trends were considered. Hierarchy was shown to take into account the uncertainty related to the for their estimation. Different change points in 1976 (highly discontinuous) and 1982 ![]() (much more transitional) separating different mean trends for respectively winter balance and summer balance as well as different variances for summer balance were highlighted. They explain the complex patterns existing in the corresponding annual mass-balance series.
(much more transitional) separating different mean trends for respectively winter balance and summer balance as well as different variances for summer balance were highlighted. They explain the complex patterns existing in the corresponding annual mass-balance series.
This hierarchical model is able to identify predominant structured patterns, in our case linear trends with break points, among other interannual fluctuations modelled as Gaussian white noises. Thus, ∼20% of the interannual variability of Sarennes winter balance series is related to two linear time trends separated by the change point in 1976, while the rest of the temporal variability is captured by a constant white noise before and after the change point. A relatively analogous feature is identified for summer balance, with 27% of variance related to two linear trends separated by the 1982 change point, but with a white noise which is significantly higher over more recent years. The fraction of the signal captured by the linear trends is not that high, but neither is it negligible. It is presumably of the correct order of magnitude for a marked linear drift due to climate change (including the retroaction due to elevation change) with regard to the truly random interannual fluctuations and to other systematic effects such as periodic fluctuations, long memory effects, multiple change points, etc., which cannot be captured with our model. Furthermore, it is sufficient to well represent the predominant quasi-parabolic pattern in the cumulative balance, for instance the accelerated mass loss over the last 25 years.
As a final illustration of the value of our hierarchical model for decomposing the data in two steps, Figure 11 compares, for the glacier-wide balance, the annual empirical estimates ![]() , to the two components provided by model M2: the annual estimates
, to the two components provided by model M2: the annual estimates ![]() , and the mean trend, a*(t) + 〈Ba
〉, as well as their 95% credibility intervals. The interannual variability of empirical estimates is clearly very well captured by the annual estimates provided by the model, with a low smoothing effect due to the capacity of the hierarchical model to transfer information from one year to another. The extraction of the mean trend can be considered as a second smoothing that distinguishes the predominant pattern from the interannual variability, i.e. the distinct behaviours before τ
w and after τ
s separated by ∼6 years of high mass-balance regime.
, and the mean trend, a*(t) + 〈Ba
〉, as well as their 95% credibility intervals. The interannual variability of empirical estimates is clearly very well captured by the annual estimates provided by the model, with a low smoothing effect due to the capacity of the hierarchical model to transfer information from one year to another. The extraction of the mean trend can be considered as a second smoothing that distinguishes the predominant pattern from the interannual variability, i.e. the distinct behaviours before τ
w and after τ
s separated by ∼6 years of high mass-balance regime.
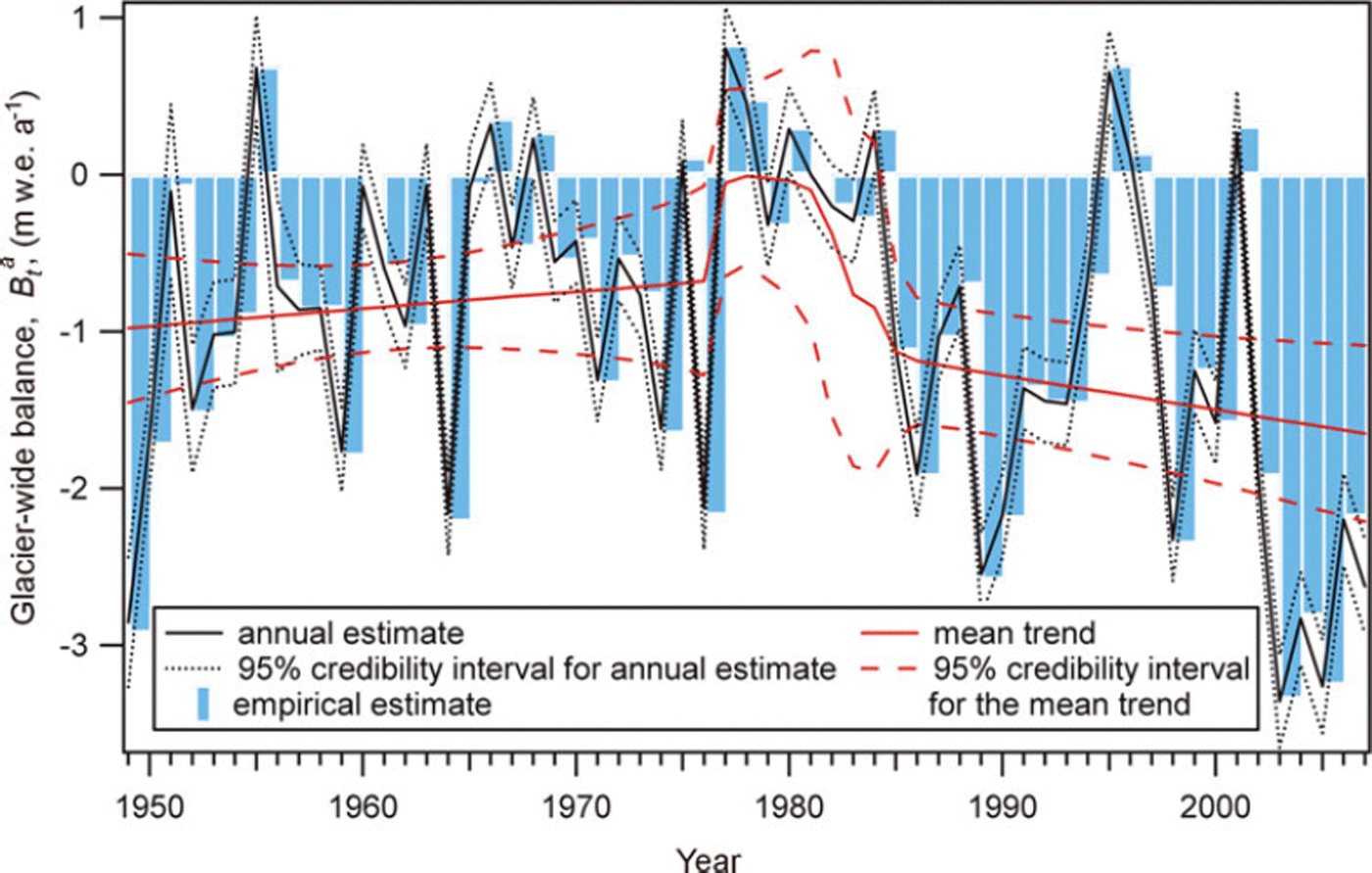
Fig. 11. Summary of glacier-wide annual balance ![]() decomposition using hierarchy. Empirical estimates are plotted against annual estimates and mean trend from model M2, and respective 95% credibility intervals.
decomposition using hierarchy. Empirical estimates are plotted against annual estimates and mean trend from model M2, and respective 95% credibility intervals.
Although primarily methodological, our model construction approach was guided by the structure of the studied data. For instance, two change points in the seasonal components of the balance were found to be much better than only one in fitting the data variability, and parameterization in terms of winter and summer balance for the time trends gave much more realistic results than a direct analysis of the actually observed couple, winter and annual balances. Finally, even if the interaction terms were able to capture a small part of the data variability, they were shown to be relatively unnecessary, especially for the study of the βt series which is the primary purpose of this paper. Nevertheless, things could be different for other case studies for which the different proposed model structures M1–M5 could be compared and tested.
Further work could test different modelling extensions. For the temporal trend, more advanced time-series models including nonlinear trends and/or multiple change points instead of only one could be employed, so as to be able to distinguish other types of systematic changes from the ‘true’ random fluctuations. However, it must be kept in mind that a compromise between model complexity and robustness must be found. Indeed, application to the Sarennes data has shown that, even with our relatively simple model, we are close to the significance limit for several parameters because of the difficulty of extracting information from hidden variables. It would therefore appear to be difficult to expand the model much without losing confidence in the obtained patterns, thus making their climatic relevance questionable.
Other modelling improvements could involve explicit modelling of the spatial structure between the αi ’s using geostatistical methods and/or specific elevation effects. An additional hierarchical level could also be considered in the variance decomposition, so as to simultaneously process data from several glaciers instead of only one as previously investigated by Reference Letréguilly and ReynaudLetréguilly and Reynaud (1990) with Lliboutry’s model. These latter points could lead to a more accurate distinction between true spatial gradients and orographic effects, as well as between inter- and intraglacier spatial variabilities.
However, starting from the proposed basis, the priority is now to bridge the gap with the analysis of direct climatic data as mentioned in section 5.2 in order to reinforce the interpretation of our results in terms of links with climate change. Indeed, since our approach is purely statistical and time-explicit, it has, when used alone, nearly no predictive power. Evaluating the chances of persistence of the highlighted trends beyond 2007 so as to extrapolate the evolution of the different seasonal components of the balance beyond the last studied data therefore involves introducing additional information and/or physical constraints into the analysis. This could be done by using seasonal climatic covariates in the proposed statistical model and/or using its results to constrain and calibrate a physical model of glacier evolution.
Acknowledgements
We are grateful to the many people who have contributed to the constitution of the exceptional data series for Glacier de Sarennes, especially L. de Crécy and F. Valla. Thank to their efforts, data collection has been, despite limited funds, nearly exhaustive for 60 years. The last years of the record were funded by GLACIOCLIM (http://www-lgge.ujfgrenoble.fr/ServiceObs/) through Observatoire des Sciences de l’Univers de Grenoble (OSUG) and Institut des Sciences de l’Univers (INSU). The authors also thank R. Hock and two anonymous reviewers whose comments led to an improved paper.
















