Introduction
Changes in the cryosphere associated with a warming climate have been documented worldwide through modelling studies (e.g. Reference Radić and HockRadić and Hock, 2006; Reference Huss, Bauder, Funk and HockHuss and others, 2008; Reference Immerzeel, Pellicciotti and BierkensImmerzeel and others, 2013), ground measurements (e.g. Reference Huss and BauderHuss and Bauder, 2009; Reference Zemp, Hoelzle and HaeberliZemp and others, 2009; Reference Fujita and NuimuraFujita and Nuimura, 2011; Reference YaoYao and others, 2012) and spaceborne remote-sensing observations (e.g. Reference Rignot, Rivera and CasassaRignot and others, 2003; Reference Paul, Kääb, Maisch, Kellenberger and HaeberliPaul and others, 2004; Reference Bolch, Menounos and WheateBolch and others, 2010, Reference Bolch, Pieczonka and Benn2011; Reference Kääb, Berthier, Nuth, Gardelle and ArnaudKääb and others, 2012). Remote-sensing studies are increasingly used, as they allow derivation of glacier changes for remote regions where ground data are scarce. They also enable reconstruction of changes in glacier area and volume over large regions and, despite limitations in the upper accumulation areas (Reference Nuimura, Fujita, Yamaguchi and SharmaNuimura and others, 2012), provide evidence of areal and mass changes at the glacier scale, in contrast to the point scale of most ground measurements (e.g. direct mass-balance records). Remotely sensed data have also been increasingly used to calibrate and validate distributed glaciohydrological models (Reference Immerzeel, Petersen, Ragettli and PellicciottiImmerzeel and others, 2014). Their main disadvantage is that they usually provide only integrated or average values of changes over several years (the interval between images) and do not offer any insight into the relationship between climate and the observed changes (Reference CogleyCogley, 2012). Despite this limitation, they have provided key evidence of changes in glaciers and ice caps worldwide (e.g. Reference GardnerGardner and others, 2013), and suggested future avenues of research (e.g. Reference Gardelle, Berthier and ArnaudGardelle and others, 2012a; Reference Kääb, Berthier, Nuth, Gardelle and ArnaudKääb and others, 2012).
In the Hindu Kush–Karakoram–Himalaya (HKH) region such studies represent a key source of information on the current and past status of the cryosphere, given the lack of ground observations due to remoteness and difficult access (Reference CogleyCogley, 2011; Reference BolchBolch and others, 2012; Reference VincentVincent and others, 2013), as well as the scarcity of modelling studies (Reference BolchBolch and others, 2012; Reference Ragettli, Pellicciotti, Bordoy and ImmerzeelRagettli and others, 2013; Reference Immerzeel, Petersen, Ragettli and PellicciottiImmerzeel and others, 2014). The current debate about the fate of Himalayan glaciers is mostly based on remote-sensing studies, and while numerous authors have called for better and more numerous ground observations (Reference CogleyCogley, 2011), satellite-based observations still remain our main source of information about ongoing glacier changes. Remote-sensing data in the HKH region have been used to reconstruct frontal variations (Reference Haritashya, Bishop, Shroder, Bush and BulleyHaritashya and others, 2009; Reference Sarikaya, Bishop, Shroder and AliSarikaya and others, 2013), areal changes (Reference LiuLiu and others, 2010; Reference BolchBolch and others, 2012; Reference KriegelKriegel and others, 2013) and volume and mass changes through differencing of digital elevation models (DEMs) (e.g. Reference Berthier, Arnaud, Kumar, Ahmad, Wagnon and ChevallierBerthier and others, 2007; Reference Bolch, Pieczonka and BennBolch and others, 2011; Reference Gardelle, Berthier and ArnaudGardelle and others, 2012a, Reference Gardelle, Berthier, Arnaud and Kääb2013; Reference Kääb, Berthier, Nuth, Gardelle and ArnaudKääb and others, 2012; Reference Nuimura, Fujita, Yamaguchi and SharmaNuimura and others, 2012; Reference VincentVincent and others, 2013). Most of these studies systematically identify a negative mass balance of the glaciers in the HKH region. The average values do not significantly deviate from the global mean, but the spatial variability is very large (Reference BolchBolch and others, 2012; Reference Kääb, Berthier, Nuth, Gardelle and ArnaudKääb and others, 2012; Reference Gardelle, Berthier, Arnaud and KääbGardelle and others, 2013) and comparison between studies is difficult because they use different remote-sensing products, spatial resolution and delineation methods and refer to different periods (Reference Unger-ShayestehUnger-Shayesteh and others, 2013). The majority of the studies in the region focus on a very recent period, from about 2000 to the end of the decade (2008–11).
Many glaciers in the HKH region are debris-covered (Reference Scherler, Bookhagen and StreckerScherler and others, 2011; Reference Nuimura, Fujita, Yamaguchi and SharmaNuimura and others, 2012). While the effect of debris over glacier ice is well understood at the point scale, it is much less so at the scale of the entire glacier (Reference Kääb, Berthier, Nuth, Gardelle and ArnaudKääb and others, 2012). Both numerical studies (Reference Nicholson and BennNicholson and Benn, 2006; Reference Reid and BrockReid and Brock, 2010; Reference Reid, Carenzo, Pellicciotti and BrockReid and others, 2012) and measurements in the field (Reference Mihalcea, Mayer, Diolaiuti, Lambrecht, Smiraglia and TartariMihalcea and others, 2006) have shown that a thin layer of debris (less than a few centimetres) enhances melt compared with debris-free conditions, through increased absorption of solar radiation and a shorter vertical distance for heat conduction. Above that critical thickness, melt is inhibited through reduced absorption of solar radiation and the debris insulating effect. At the glacier-wide scale, however, recent studies based on remote sensing have suggested that debris-covered glaciers might be losing as much mass as nondebris-covered glaciers (Reference Gardelle, Berthier and ArnaudGardelle and others, 2012a; Reference Kääb, Berthier, Nuth, Gardelle and ArnaudKääb and others, 2012). Possible reasons are the decreasing mass transport from the accumulation region (Reference Quincey, Luckman and BennQuincey and others, 2009) and the supraglacial ponds and ice cliffs that form on the tongues of many debris-covered glaciers (Reference Sakai, Takeuchi, Fujita and NakawoSakai and others, 2000, Reference Sakai, Nakawo and Fujita2002; Reference Han, Wang, Wei and LiuHan and others, 2010). It has been suggested these absorb large amounts of energy and thus contribute substantially to the wastage of glaciers (Reference Kääb, Berthier, Nuth, Gardelle and ArnaudKääb and others, 2012; Reference Nuimura, Fujita, Yamaguchi and SharmaNuimura and others, 2012; Reference Zhang, Hirabayashi and LiuZhang and others, 2012). While this has been demonstrated for single supraglacial ponds or ice cliffs (Reference Sakai, Takeuchi, Fujita and NakawoSakai and others, 2000, Reference Sakai, Nakawo and Fujita2002), their role has never been quantified at the scale of the entire glacier and with respect to the total mass balance.
It has also been suggested that the presence of thick, widespread supraglacial debris leads to nearly uniform downwasting of glacier ice, as opposed to the terminus retreat typical of non-debris-covered glaciers (Reference Bolch, Buchroithner, Pieczonka and KunertBolch and others, 2008; Reference BennBenn and others, 2012), thus altering the linear dependence of mass balance on elevation typical of clean-ice glaciers (Reference BennBenn and others, 2012; Reference Dobhal, Mehta and SrivastavaDobhal and others, 2013). Debris cover has often been observed to thicken approaching the terminus, potentially reversing the ablation gradient and promoting a reduction in slope of the glacier tongue (Reference Hambrey, Quincey, Glasser, Reynolds, Richardson and ClemmensHambrey and others, 2008; Reference BennBenn and others, 2012). Thus, the glaciers often exhibit a very low longitudinal elevation gradient (<10%), which, in turn, limits the control of vertical temperature lapse rates on longitudinal variations in ablation, as an increase in local temperature increases ice melt over an extensive portion of the glacier tongue, rather than over a localized area proximal to the terminus (as for more steeply sloping glaciers). As a result, the local mass balance of debris-covered glaciers is distinctively nonlinear and non-monotonic (Reference Dobhal, Mehta and SrivastavaDobhal and others, 2013). To thoroughly understand the response of glaciers to climate, it is therefore necessary to monitor mass (volume) directly, rather than length. For these reasons, temporal changes in glacier length and area do not provide a good indication of glacier health. It is more effective to measure changes in glacier volume (and thus mass) if effective means can be found (Reference Scherler, Bookhagen and StreckerScherler and others, 2011; Reference Nuimura, Fujita, Yamaguchi and SharmaNuimura and others, 2012). Our study demonstrates one such method.
In this paper, we reconstruct geodetic mass balances for the four main debris-covered glaciers in the upper Langtang River basin, central Nepalese Himalaya, between 1974 and 1999. We use Hexagon imagery from 1974 and the Shuttle Radar Topography Mission (SRTM) DEM from February 2000. Geodetic mass balances have not previously been derived for this part of the Himalaya. We analyse differences in thinning patterns among the four glaciers and the spatial variability over each glacier, and use surface velocities and a map of supraglacial lakes derived from Landsat images to interpret the observed patterns. We show that the strongest thinning occurs in areas with low slopes and low velocities, and suggest that supraglacial ponds and ice cliffs that are likely to form on these areas might be responsible for the high mass losses suggested by the DEM differencing.
Background: Geodetic Mass-Balance Studies in the HKH Region
Geodetic mass-balance studies in the HKH region are either site-specific or, more recently, have looked at the entire HKH region (Reference Kääb, Berthier, Nuth, Gardelle and ArnaudKääb and others, 2012) or at selected locations along the east-to-west HKH transect (Reference Gardelle, Berthier, Arnaud and KääbGardelle and others, 2013). In Nepal, Reference Bolch, Pieczonka and BennBolch and others (2011) reconstructed mass losses for ten glaciers in the Sagarmatha (Everest) area, eastern Nepal Himalaya, for the period 1962–2007, using stereo Corona imagery (1962 and 1970), Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) DEMs from 2002 and Cartosat-1 images from 2007. They showed that glaciers had lost mass since 1970, with a specific mass loss for the period 1970–2007 of 0.32 ± 0.08 m w.e. a−1 averaged over all ten glaciers. Reference Nuimura, Fujita, Yamaguchi and SharmaNuimura and others (2012) computed glacier elevation changes in the same Khumbu region (total area 183.3 km2) for the period 1992–2008 using a 1992 map obtained from aerial photos, the SRTM DEM 2000 and ASTER-derived DEMs from 2000–08. They obtained a regional average mass balance of −0.40 ± 0.25 m w.e. a−1 for the period 1992–2008, and partly confirmed the evidence of gradual acceleration in glacier thinning in the more recent period suggested by Reference Bolch, Pieczonka and BennBolch and others (2011). They also commented that uncertainties in these estimates are very large. In the Indian western Himalaya, Reference Berthier, Arnaud, Kumar, Ahmad, Wagnon and ChevallierBerthier and others (2007) used the SRTM DEM 2000 and a 2004 DEM derived from two SPOT-5 satellite optical images to derive elevation and mass changes for all glaciers in the Spiti/Lahaul region in Himachal Pradesh. They measured thinning on most glaciers, including debris-covered glaciers, and obtained an overall specific mass balance of −0.7 to −0.85 m w.e. a−1 (depending on the density used in the accumulation area). Larger glaciers lost mass at higher rates than smaller glaciers (Reference Berthier, Arnaud, Kumar, Ahmad, Wagnon and ChevallierBerthier and others, 2007). Reference VincentVincent and others (2013) revisited those estimates and extended the record with an additional SPOT-5 optical stereo image-set acquired in 2011. Reference Berthier, Arnaud, Kumar, Ahmad, Wagnon and ChevallierBerthier and others (2007) applied no correction for the penetration of the radar signal into snow and ice to the SRTM DEM. This was corrected using the first-order estimate of Reference Gardelle, Berthier and ArnaudGardelle and others (2012a) and error estimates were provided. The new regional mass balance for the Lahaul and Spiti region (868 km2 of glaciers) was −0.65 ± 0.17 m w.e. a−1, slightly less negative than in the previous study. On the Tibetan Plateau, Reference Zhang, Fujita, Liu, Liu and WangZhang and others (2010) calculated elevation changes of −1.1 ± 0.4 m a−1 for the ablation area of Hailuogou Glacier for the period 1966–2009, from DEMs obtained from 2009 ASTER images, differential GPS data from 2008 and aerial photographs acquired in 1966 and 1989. They also found that since 1989 thinning had accelerated significantly. In the central Karakoram, Reference Gardelle, Berthier and ArnaudGardelle and others (2012a) calculated the regional mass balance of glaciers between 1999 and 2008 from differences between the 2000 SRTM DEM and a DEM generated from SPOT-5 optical stereo imagery acquired in December 2008. They obtained a highly heterogeneous spatial pattern of glacier elevation changes and high thinning rates for debris-covered glaciers. The mass balance for the entire region (5615 km2) was +0.10 ± 0.22 m w.e. a−1, and confirmed evidence of a Karakoram anomaly characterized by a mass gain or a neutral mass balance. Reference Gardelle, Berthier, Arnaud and KääbGardelle and others (2013) extended the analysis of Reference Gardelle, Berthier and ArnaudGardelle and others (2012a) to nine sites in the Pamir– Karakoram–Himalaya (PKH) region, for approximately the same period (2000 to 2008–11), again using the 2000 SRTM DEM and recent (2008–11) DEMs obtained from SPOT-5 stereo imagery. They obtained a contrasting response for the glaciers in the PKH region, with moderate ice losses in the eastern and central Himalaya (−0.22 ± 0.12 to –0.33 ± 0.14 m w.e. a−1), larger losses in the western Himalaya (−0.45 ± 0.13 m w.e. a−1) and a slight positive mass balance at the regional scale for the central Karakoram (confirming the previous findings) and the western Pamir (+0.14 ± 0.13 m w.e. a−1). Reference Kääb, Berthier, Nuth, Gardelle and ArnaudKääb and others (2012) used satellite laser altimetry (from the Ice, Cloud and land Elevation Satellite (ICESat)) over 2003–09 and the SRTM DEM to derive glacier elevation and mass-balance changes for the entire HKH region. They derived widespread glacier wastage in the eastern, central and southwestern parts of the HKH, while in the Karakoram there was little glacier thinning. The 2003–08 specific mass balance for the entire HKH region was −0.21 ± 0.05 m w.e. a−1, less negative than the estimated global average for glaciers and ice caps.
Hence, the majority of studies in the HKH region focus on a very recent period, from ∼2000 to the end of the decade (2008–11) and few studies have looked at changes over longer periods (Reference Zhang, Fujita, Liu, Liu and WangZhang and others, 2010; Reference Bolch, Pieczonka and BennBolch and others, 2011; Reference Nuimura, Fujita, Yamaguchi and SharmaNuimura and others, 2012). Evidence of a remarkably differentiated response along the very large eastto-west Himalaya transect is slowly emerging (Reference Kääb, Berthier, Nuth, Gardelle and ArnaudKääb and others, 2012; Reference Gardelle, Berthier, Arnaud and KääbGardelle and others, 2013), but studies that have looked in detail at small-scale, intra-basin variability are lacking, as are insights about the causes of such differentiated responses at the catchment scale and the main controlling mechanisms.
Study Site
The Langtang River basin is located in the monsoon-dominated central part of the Himalaya, north of Kathmandu, Nepal. Its drainage area is 585 km2, of which 155 km2 is glacierized. The elevation ranges from 1406 m in Syafru Besi to the summit of Langtang Lirung at 7234 m. The Langtang River flows through the main valley, which is typically U-shaped. The climate is dominated by monsoon circulation, with predominant easterly winds in the summer and westerly winds from October to May. In this work, we focus on the upper Langtang River basin (Fig. 1), with an outlet below the village of Kyanjing, as this is the section of the basin where most of the glaciers are concentrated. Its area is 350 km2, with a total glacier area of ∼31%, a debris-covered glacier area of ∼24% and an elevation range ∼3650–∼7160 m. The major glaciers in the basin are debris-covered on their tongues, with most of the debris found at <5200 m. Debris thickness is spatially variable, but field observations (unpublished) have shown a very thick cover (>60 cm) over most of Lirung Glacier, with thin debris localized on sloped surfaces. The composition of the debris layer on both Lirung and Langtang Glaciers is highly heterogeneous, from very fine silt to large boulders exceeding several metres in height (field observations, unpublished).

Fig. 1. (a) True colour image of the Landsat ETM+ covering the domain of the upper Langtang valley (Landsat ETM+ image is from September 2001). (b) Map of the upper Langtang valley in the Nepalese Himalaya, showing the four main glaciers investigated in this study: Lirung, Shalbachum, Langshisha and Langtang glaciers. The extents for both 1974 and 1999 are shown. Also shown is the debris extent in 1999 and the upper basin watershed (in pale blue).
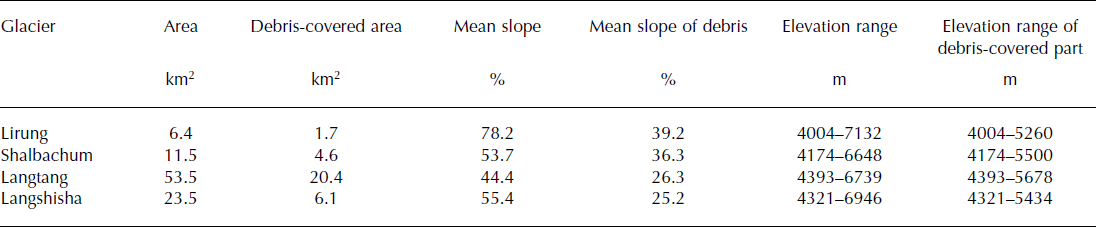
We analyse the four main glaciers in the upper valley (Lirung, Shalbachum, Langtang and Langshisha glaciers; Fig. 1; Table 1). Lirung Glacier, with the greatest elevation range (∼4004–7132 m a.s.l; Table 1), has been the site of glaciological investigations in the past (e.g. Reference Sakai, Takeuchi, Fujita and NakawoSakai and others, 2000, Reference Sakai, Nakawo and Fujita2002), and has recently been monitored again, in the 2012 and 2013 ablation seasons by an expedition from ETH Zürich (e.g. Reference Immerzeel, Petersen, Ragettli and PellicciottiImmerzeel and others, 2014; Reference RagettliRagetti and others, 2015). The largest glacier is Langtang Glacier, the most remote of the four (Table 1). It has also been the site of field investigations from May to October 2014. No previous measurements on this glacier exist. Numerous supraglacial lakes and ponds were observed on the tongues of both Lirung and Langtang Glaciers in May and October 2013. Shalbachum and Langshisha Glaciers have never been monitored. Characteristics of the four glaciers are reported in Table 1.
Table 1. Characteristics of the studied glaciers in the upper Langtang River basin. Area based on Hexagon DEM and outlines of 1974
Data
Digital elevation models (DEMs)
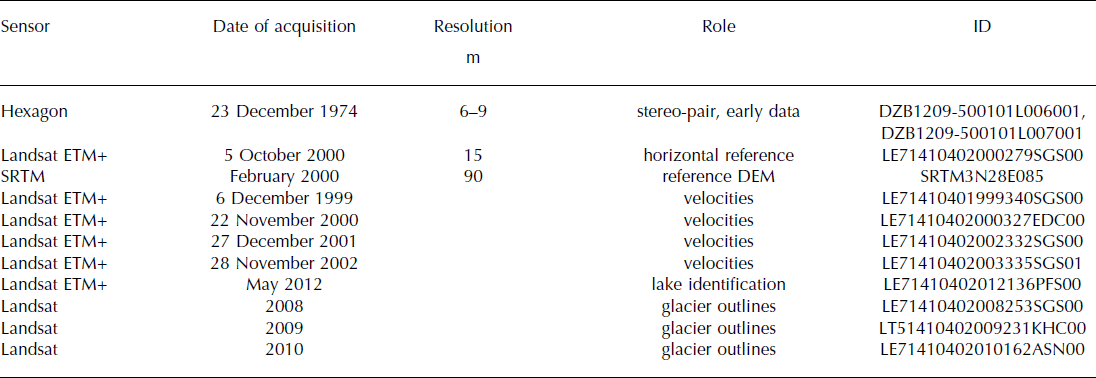
We use two main types of remote-sensing data for geodetic estimation of glacier volume changes: (1) Hexagon satellite data and (2) the SRTM DEM V3.0. We also use Landsat Enhanced Thematic Mapper Plus (ETM+) data for image coregistration and to assist with interpretation of the results. Selection of scenes was based on minimum snow cover and minimum cloudiness and we favoured scenes at the end of the ablation season.
Satellite images of the KeyHole camera system KH-9 (Hexagon) were declassified by the US Government in 2002 and are now publicly available. Hexagon operated from March 1973 to October 1980. Two datasets covering the study region are available from the US Geological Survey. Clouds and annual timing prevented one from being used, so we accessed and have used a pair of stereo images from November 1974, mission No. 1209-5, acquired on 23 November 1974 (Table 3). Knowledge of the technical details of Hexagon is still limited, as the mission-related documentation has not been declassified (Reference Surazakov and AizenSurazakov and Aizen, 2010). Horizontal accuracies of <6 m for flat terrain and ∼10 m for mountainous terrain were obtained, while the analysis of the vertical accuracy revealed a root-mean-square error (rmse) of 6.2 m over flat terrain and ∼19 m over mountainous terrain in comparison with precise ICESat laser altimetry data (Reference Surazakov and AizenSurazakov and Aizen, 2010; Reference Pieczonka, Bolch, Wei and LiuPieczonka and others, 2013).
The data of the SRTM were acquired during a 10 day mission in February 2000 on board the space shuttle Endeavour. It had an altitude of 233 km and captured elevation data from 80% of the Earth’s land surfaces between 60°N and 56°S. Data are available at a spacing of 3 arcsec (∼90 m) in the study region (Table 3). Reference BamlerBamler (1999) indicated that the SRTM DEM should meet an absolute vertical accuracy of 16 m, a relative vertical height accuracy of 10 m and an absolute horizontal accuracy of 20 m, each value expressed as linear error at 90% confidence. Reference Fujita, Suzuki, Nuimura and SakaiFujita and others (2008) evaluated DEM accuracies in the Bhutanese Himalaya. Reference Berthier, Arnaud, Vincent and RémyBerthier and others (2006) found that at high elevations the SRTM DEM tends to underestimate elevations (by up to 10 m), while it tends to overestimate the elevations in valleys. The SRTM DEM has been increasingly used for analysis of mass changes in the HKH region (Reference Gardelle, Berthier and ArnaudGardelle and others, 2012a, Reference Gardelle, Berthier, Arnaud and Kääb2013; Reference Kääb, Berthier, Nuth, Gardelle and ArnaudKääb and others, 2012; Reference Nuimura, Fujita, Yamaguchi and SharmaNuimura and others, 2012), while Hexagon data so far have only have been considered in the Tien Shan (Reference Pieczonka, Bolch, Wei and LiuPieczonka and others, 2013).
Surface velocities
To assist with interpretation of the derived volumetric changes, we have utilized ETM+ imagery to determine glacier velocities and supraglacial lake distributions. These datasets and their processing are described here. Cloud-free minimum-snow-cover annual Landsat scenes were chosen for analysis of surface velocities for the period 1999–2003 (acquisition dates 6 December 1999, 22 November 2000, 27 December 2001, 28 November 2002, 1 December 2003). The VisiCorr framework was used to apply the IMCORR cross-correlation feature-tracking algorithm (Reference Scambos, Dutkiewicz, Wilson and BindschadlerScambos and others, 1992; Reference DowdeswellDowdeswell, 2003) to the 15 m resolution panchromatic bands (0.52–0.90 μm), with a minimum correlation score of 6. Shadow-, cloud- and snowline-affected results were eliminated manually, and the resulting points were used to assess the co-registration of non-glacial terrain. No systematic biases were observed, so the assessed match displacements were converted to mean annual velocities for each of the periods. A coverage of the resulting glacier velocities appears in Figure 2 for the period November 2000–December 2001.

Fig. 2. Left: Glacier velocities for the four main glaciers of the upper Langtang River basin between 22 November 2000 and 27 December 2001, revealing extensive areas of ice nearing stagnation. Velocities are derived by a feature-tracking algorithm applied to Landsat ETM+ panchromatic imagery. Right: Distribution of supraglacial pond features, showing common occurrence on debris-covered tongues, with the largest features coinciding with the greatest surface lowering. Supraglacial ponds are presented for May 2012 using methods adapted from Reference Gardelle, Arnaud and BerthierGardelle and others (2011) with Landsat ETM+ imagery. Lakes are outlined for visibility at this scale. Also indicated are the 1999 glacier extent and debris cover.
The feature-tracking algorithm produced the clearest results for the debris-covered portions of the basin’s glaciers, which exhibit readily identifiable features at the 15 m scale. As seen in Figure 2, all four glaciers show a strong decrease in flow velocity through the debris-covered tongue approaching the glacier terminus. While velocities at the head of the debris-covered area are commonly 20–40 m a−1, extensive portions of all four glaciers have deformed ∼10 m a−1 through successive years. Using this value as a threshold, the lower 8.5 km of Langtang Glacier is nearly stagnant, while for Langshisha, Shalbachum and Lirung glaciers the nearly stagnant portions are the lower 3.3, 1.8 and 1.2 km, respectively. Shalbachum Glacier surface velocities remain sustained up to this point (1.8 km), while the other three glaciers exhibit a patchy pattern, including local flow increases, probably related to topographic constraint and sustained snow and ice avalanching.
Supraglacial lakes
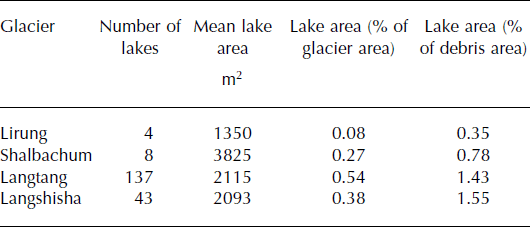
Landsat multispectral data were also used to evaluate the spatial pattern of supraglacial ponding. Landsat Thematic Mapper (TM) and ETM+ data for the period 2000–13 were atmospherically corrected using the LandCor MATLAB® routines to apply the 6S atmospheric transfer code (Reference Kotchenova and VermoteKotchenova and Vermote, 2007; Reference Zelazowski, Sayer, Thomas and GraingerZelazowski and others, 2011) to produce modelled surface reflectances for bands 1–5 and 7. A lake-mapping procedure was adapted from the work of Reference Gardelle, Arnaud and BerthierGardelle and others (2011), also including cloud-and shadow-masking routines to exclude locations not suitable for lake delineation. A typical pre-monsoon lake coverage (May 2012) appears in Figure 2. About 0.5–1.5% of debris area is covered by ponded water during May 2012. One should notice that analysis is limited to observations of grid resolution 30 m, while field observations have documented many smaller lakes (Table 2). Only the largest (wider) glaciers can form very large lakes, which may be why Lirung and Shalbachum Glaciers show less supraglacial ponding (Table 2). Also taking this into account, lakes seem to appear in highest density immediately downstream of clean ice in May.
Table 2. Number and area of lakes identified on the four main glaciers of the upper Langtang valley
Methods
Glacier elevation changes for the period 1974–2000 are obtained by differencing the SRTM and the Hexagon DEM. Below we describe the steps for generation of the Hexagon DEM and for uncertainty assessment. The volumetric changes were calculated by subtracting the two DEMs within the outline of the larger extent and multiplying by the cell size of the raster grid (e.g. Reference KobletKoblet and others, 2010). Planimetric glacier changes can be quantified directly from the orthorectified images, and areal changes were directly assessed from the differences in glacier outlines. The length changes were estimated by comparing the central flowlines.
DEM generation, co-registration and glacier outlines
The first step for the generation of a DEM from Hexagon data is to define ground-control points (GCPs). The horizontal coordinates of 233 GCPs were defined based on the Landsat ETM+ scene from the year 2000, while the vertical coordinates were taken from the SRTM DEM. The images were processed with the Leica Photogrammetry Suite of ERDAS Imagine 9.2. The sampling distance (grid size) of the final DEMs was set to 30 m.
Co-registration was applied to the DEMs in order to minimize errors associated with shifts and systematic errors, as well as tectonic uplift (e.g. Reference Nuth and KääbNuth and Kääb, 2011). Reference Berthier, Arnaud, Kumar, Ahmad, Wagnon and ChevallierBerthier and others (2007) determined the mean horizontal shift by minimizing the standard deviation (σ) of the elevation difference between two DEMs. Reference Nuth and KääbNuth and Kääb (2011) proposed using a polynomial of first or second order to correct an elevation dependency, which is usually expressed by an overestimation of the elevation in valley bottoms, while slopes and mountain ridges tend to be underestimated. Both methods were applied to an excerpt of glacier-free terrain, where no elevation change is expected, resulting in a considerable improvement in the accuracy of the Hexagon DEM (Table 4). The initial rmse of the elevation differences (rmse-z) was 16.2 m, but decreased to 11.7 m after both corrections.
The glacier outlines were manually delineated (Reference Nuimura, Fujita, Yamaguchi and SharmaNuimura and others, 2012). For the accumulation areas we used three Landsat scenes from 2008, 2009 and 2010 (Table 3), which were the best images available over the entire period. We assume that the accumulation areas did not change significantly over time. The tongues were re-delineated for the two time slices (1974 and 2000), using the orthorectified satellite images and DEMs (slope maps and hillshades) of the corresponding years. To quantify the uncertainty associated with the manual delineation, we repeated the delineation three times, following a variant of the round-robin approach suggested by Reference PaulPaul and others (2013). We compared the expert manual delineation with the Global Land Ice Measurements from Space (GLIMS) database. Debris extent was also manually digitized (as by Reference Gardelle, Berthier, Arnaud and KääbGardelle and others, 2013).
Table 3. Overview of data used in this study for DEM generation and calculations of areal and volumetric changes, as well as for derivation of surface velocities and supraglacial lakes
Uncertainty of elevation change estimates
To assess the uncertainty of glacier elevation changes and mass balance, we use a statistical estimator over stable terrain. The normalized median absolute deviation (NMAD) is a robust estimator for the standard deviation if many outliers are present (Reference Höhle and HöhleHöhle and Höhle, 2009). It is defined as
where Δhj describe the individual errors, j = 1, …, n and m Δh is the median of the errors. It is equivalent to the standard deviation in case of normality (Reference Höhle and HöhleHöhle and Höhle, 2009). In accordance with Reference Pieczonka, Bolch, Wei and LiuPieczonka and others (2013), the 68.3% quantile of the absolute elevation differences over stable terrain was computed to test the assumption of normality. Although the NMAD (13.2 m) is quite close to the standard deviation (15.5 m) over stable terrain (Table 4), it differs noticeably from the 68.3% quantile (5.0 m) (Table 5). Thus, non-normality of the elevation differences was assumed and the 68.3% quantile was used as uncertainty of the elevation differences both on glacier-free and glacier-covered terrain.
Table 4. Influence of post-processing steps on elevation changes, dh (calculated as the arithmetic mean), for the period 1974–99 for glacierized (subscript gl) and glacier-free, stable (subscript st) terrain. med: median; std: standard deviation; rmse-z: root-meansquare error of elevation differences
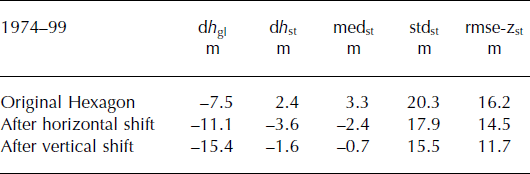
Table 5. Statistics of the elevation differences (m) between the 2000 SRTM and the 1974 Hexagon DEM. σ is the standard deviation, NMAD is the normalized median absolute deviation and Q68.3 is the 68.3% quantile of the absolute elevation differences

Definition of outliers
Before averaging elevation changes, unexpected elevation changes that are likely to be outliers were excluded. There is no best method to identify outliers, and various approaches have been used. Reference Gardelle, Berthier, Arnaud and KääbGardelle and others (2013) used a threshold of ±80 m for non-surging glaciers, identified from visual analysis of the elevation differences maps, while Reference Nuimura, Fujita, Yamaguchi and SharmaNuimura and others (2012) excluded outliers with accuracy worse than 5 m a−1, which for our study period corresponds to 125 m. In this work, pixels are defined as outliers when the absolute elevation differences differ by >2σ in the observed elevation differences within a glacier. Since no established method exists to identify and remove outliers, but results might be sensitive to their definition, we test thresholds of 1σ, 2σ and 3σ to investigate the dependency of our results on the assumption made. We also test the approach of Reference Nuimura, Fujita, Yamaguchi and SharmaNuimura and others (2012). By using the standard deviations we avoid an arbitrary or subjective threshold. Analysis of the elevation difference maps shows that these high values are found at high elevations, where the accuracy of the DEMs might be questionable. We therefore analysed the elevation changes for 100 m elevation intervals. In each band, we averaged all the pixels after excluding the outliers, following the assumption that elevation changes in the same elevation band should be similar. Pixels with no data and outliers were assigned the value of the mean elevation change of the 100 m elevation band (e.g. Reference Gardelle, Berthier, Arnaud and KääbGardelle and others, 2013).
Glacier density
An estimate of snow and ice density is required to convert the volume change into mass balance. Many recent studies do not differentiate between accumulation and ablation area (Reference ZempZemp and others, 2010) and use a value of ice density of 900 kg m−3 for both (Reference Gardelle, Berthier and ArnaudGardelle and others, 2012a; Reference VincentVincent and others, 2013), invoking Sorge’s law to justify this assumption (Reference Gardelle, Berthier and ArnaudGardelle and others, 2012a). This is a potential source of error (Reference ZempZemp and others, 2010).
In the ablation zone we use the commonly assumed value of 900 kg m−3 (density of ice) (Reference PatersonPaterson, 1994), while the density is less constrained in the accumulation zone due to the coexistence of snow and ice. Reference Hagg, Braun, Uvarov and MakarevichHagg and others (2004) assumed a mean density of 650 kg m−3 and Reference Berthier, Arnaud, Kumar, Ahmad, Wagnon and ChevallierBerthier and others (2007) of 600 kg m−3 in the accumulation area. Due to this uncertainty, two scenarios are considered in this study. In the first, the entire glacier is assumed to have a density of 900 kg m−3 (e.g. Reference Gardelle, Berthier and ArnaudGardelle and others, 2012a), while in the second, densities of 900 and 600 kg m−3 are used in the ablation and accumulation areas, respectively. The latter requires an estimation of the equilibrium-line altitude (ELA). Due to lack of measurements, this is approximated using the AAR (accumulation–area ratio) method with a threshold value of 0.66 (Reference Gross, Kerschner and PatzeltGross and others, 1977). To take into account the uncertainty introduced by applying this method to debris-covered glaciers, the ELA is varied by ±200 m and the effect on the mass balance is evaluated.
Correction for penetration of the SRTM radar beam
A further uncertainty results from the penetration depth of the radar beam into snow and ice for the SRTM DEM, which was acquired in the C-band. At this wavelength (5.6 cm), the penetration of the radar signal into snow or ice can reach several metres (Reference Gardelle, Berthier, Arnaud and KääbGardelle and others, 2013). The SRTM DEM might therefore underestimate glacier elevations. Several authors have therefore referred to the 2000 SRTM DEM as representative of the elevation of the glacier at the end of the 1999 melt season (Reference Berthier, Arnaud, Kumar, Ahmad, Wagnon and ChevallierBerthier and others, 2007). Reference Gardelle, Berthier, Arnaud and KääbGardelle and others (2013) estimated the penetration depth by differencing the SRTM C-band and X-band. Since X-band penetration is low compared with C-band penetration, they regarded the difference in elevation between the two DEMs as a first estimate of C-band penetration over glaciers (Reference Gardelle, Berthier and ArnaudGardelle and others, 2012b). This estimate was not available for the west Nepal location, but they calculated a value of 1.4 m for the Everest region. Reference Kääb, Berthier, Nuth, Gardelle and ArnaudKääb and others (2012) calculated penetration estimates of 2.5 ± 0.5 m for east Nepal and 1.5 ± 04 m for west Nepal. We therefore used the value of 1.5 m for west Nepal (very close to the value for the Everest region of Reference Gardelle, Berthier, Arnaud and KääbGardelle and others, 2013). We also tested the sensitivity of our estimates to the 2.5 m value (for east Nepal) of Reference Kääb, Berthier, Nuth, Gardelle and ArnaudKääb and others (2012).
Results
Areal changes
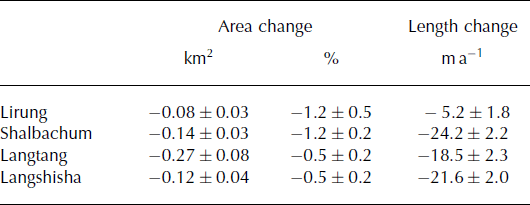
Areal changes are reported in Table 6 for the four glaciers separately. A decrease in glacier area is evident for all four glaciers. The strongest relative loss has been experienced by Lirung (−1.2 ± 0.5%) and Shalbachum (−1.2 ± 0.2%) Glaciers, while the highest retreat rate was found for Shalbachum Glacier (−24.2 ± 2.2 m a−1 for the period 1974–99). Changes in area are mostly localized on the glaciers’ terminal fronts (Fig. 1).
Table 6. Glacier area and length changes over the period 1974–99
Compared with shrinkage rates reported by other authors for glaciers in high Asia, our values are relatively small. Reference KriegelKriegel and others (2013) obtained an area loss of 23% for the glaciers in the Naryin catchment, Tien Shan, in Kyrgyzstan. The glaciers investigated in our study are all heavily debris-covered on their tongues, so that losses of mass occur typically by downwasting rather than tongue retreat (Reference Bolch, Buchroithner, Pieczonka and KunertBolch and others, 2008; Reference Nuimura, Fujita, Yamaguchi and SharmaNuimura and others, 2012). Changes in areas and frontal positions are therefore not indicative of the actual changes in glacier volumes and mass and should be regarded with caution (Reference Nuimura, Fujita, Yamaguchi and SharmaNuimura and others, 2012). While relative changes in area are minimal, frontal variations are non-negligible, especially for Shalbachum, Langshisha and Langtang (Table 6), in contrast to results reported by Reference Scherler, Bookhagen and StreckerScherler and others (2011) at the very large scale. Our results, however, agree with those of Reference Zhang, Fujita, Liu, Liu and WangZhang and others (2010, Reference Zhang, Fujita, Liu, Liu and Nuimura2011), who showed that the terminus of debris-covered Hailuogou Glacier, Tibetan Plateau, retreated at a high rate. They attributed this to the large ablation occurring on the termini of debris-covered glaciers because of the coexistence of inhomogeneous surfaces, ponds and cliffs that are very dynamic in time and lead to collapse of tongue terminal zones and glacier fronts.
Volumetric and mass changes
Elevation changes are shown in Figure 3, and the corresponding mass balances listed in Table 7 for different assumptions of glacier density. Important differences are evident among the glaciers, as seen in Figure 3, with the largest thinning observed for Langshisha Glacier (see also Table 7). The debris-covered section of Langshisha Glacier has the shallowest slope of all four glaciers (and is located at relatively high elevations; Table 1), which might explain the strongest thinning observed (see Discussion).
Table 7. Mass balances (m w.e. a−1) for the four glaciers of the upper Langtang valley. Values are obtained with the assumption of 1.5 and 2.5 m for penetration depth and outliers defined as above twice the standard deviation (2σ). We test both calculations with a density of 900 kg m−3 for the entire glacier (option 1) and of 900 kg m−3 for the ablation area and 600 kg m−3 for the accumulation area (option 2), using the AAR approach to determine the ELA. We also show results obtained by varying the ELA ±200 m (with penetration depth of 1.5 m (option 2+)), to test the influence of the ELA derivation on the calculated mass balance
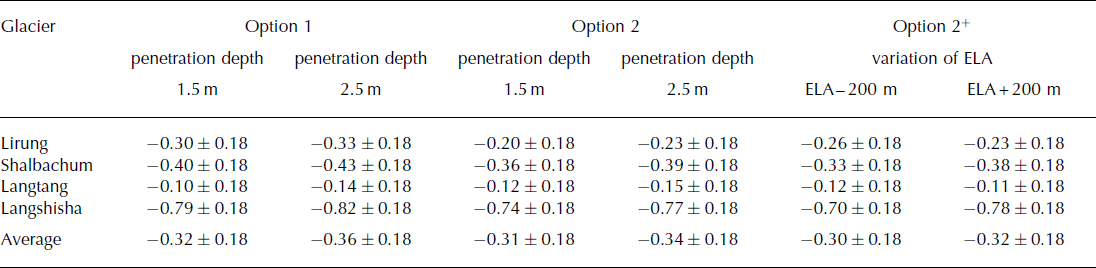

Fig. 3. Glacier elevation differences for the four glaciers of the upper Langtang River basin between 1974 and 2000 for the entire upper catchment. Also indicated are the glacier outlines and debris extent (in 1999). The background image shows a shaded relief representation of the Hexagon DEM (from 1974).
Important spatial variations in thinning rates can also be observed on the individual glaciers, and for Langtang Glacier in particular, where thinning is strongest away from the terminus, between ∼4600 and 5300 m. This confirms previous evidence that debris-covered glaciers do not exhibit the linear dependence of mass balance on elevation typical of debris-free glaciers (Reference BennBenn and others, 2012; Reference Nuimura, Fujita, Yamaguchi and SharmaNuimura and others, 2012; Reference Dobhal, Mehta and SrivastavaDobhal and others, 2013). Figure 4 shows the altitudinal distribution of elevation changes, together with the altitudinal distribution of glacier area. It is evident that no linear mass-balance gradient exists for the glaciers in the valley. Instead, all four glaciers present a change of slope in the relationship: losses increase (i.e. are more negative) or remain roughly constant with increasing elevation up to a certain elevation, which varies between glaciers; it is 4800–5000 m for Shalbachum, Lirung and Langtang glaciers (Fig. 4a–c) and 5000–5200 m for Langshisha Glacier (Fig. 4d). Above this elevation, the relationship changes and the losses decrease (i.e. elevation differences become increasingly less negative) with elevation. Both segments of the relationship are approximately linear (Fig. 4). These elevations correspond approximately to the maximum extent of the debris cover (Table 1). Our results thus indicate that on the investigated debris-covered glaciers the pattern of mass loss is different to that of debris-free glaciers (Reference Zhang, Fujita, Liu, Liu and NuimuraZhang and others, 2011). The highest mass losses are not concentrated on the lower tongues, but somewhere close to the ELA. For the smaller glaciers, in particular (Lirung and Shalbachum), volume losses are higher in the upper non-debris-covered areas than in the lower tongues. Similar results were obtained by Reference Nuimura, Fujita, Yamaguchi and SharmaNuimura and others (2012) (compare our Fig. 4 with Nuimura and others’ fig. 7) and Reference Dobhal, Mehta and SrivastavaDobhal and others (2013). In the case of Lirung Glacier, more melt occurs over the south-facing debris-free steep areas at high elevation than over the debris-covered tongue. Elevation changes are positive only over ∼4600–5000 m (Fig. 4a) and could be due to increased serac fall rates as the headwall glacier destabilizes.
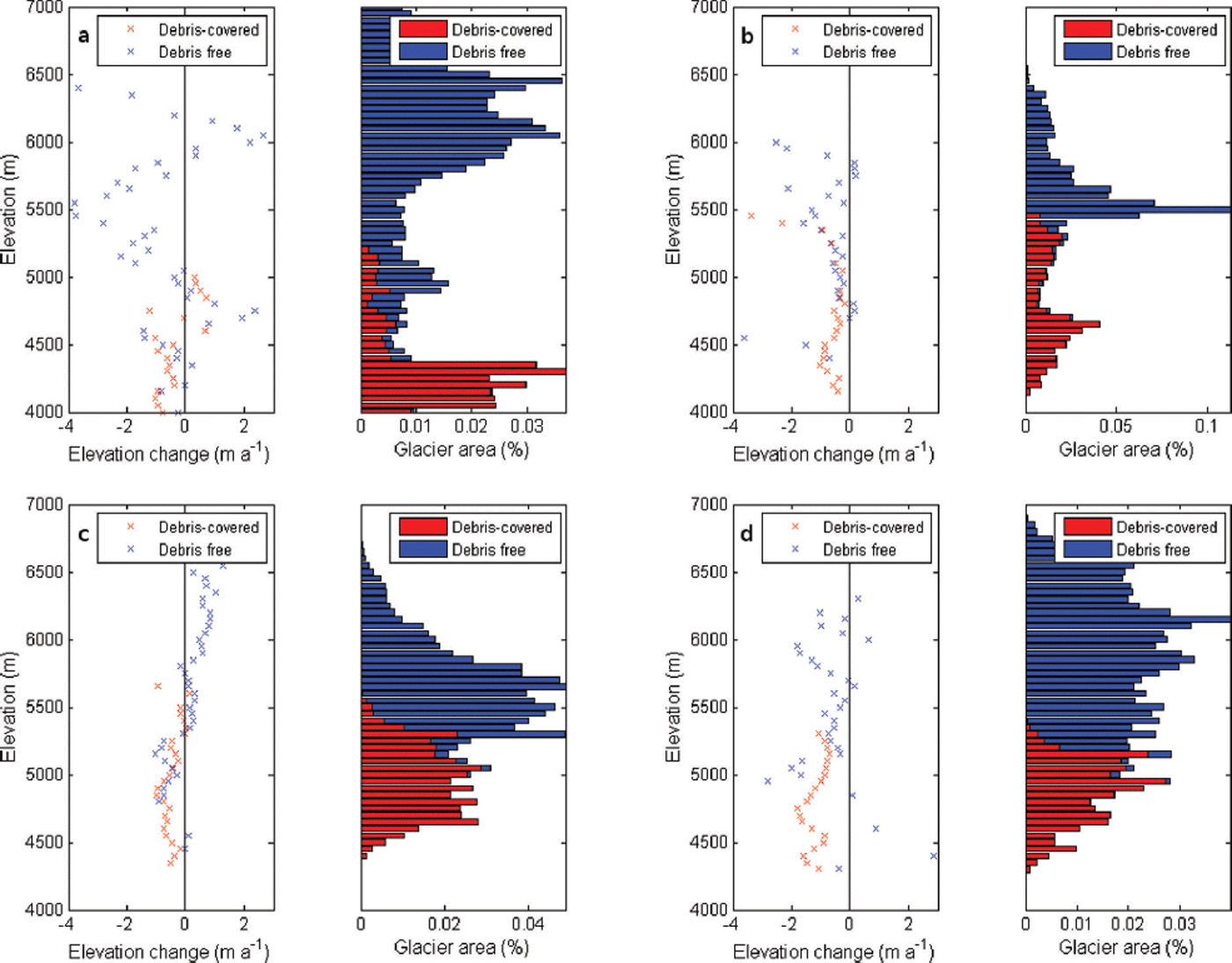
Fig. 4. Altitudinal distribution of the mean annual elevation change (left) and glacier area (right) over 50 m elevation bands for the four glaciers: (a) Lirung; (b) Shalbachum; (c) Langtang; and (d) Langshisha. Elevation differences are calculated with outliers defined as pixels with values >2σ and a correction for penetration error of 1.5 m.
Elevation changes calculated for the debris-covered portions of each glacier are listed in Table 8. Values are rather similar, with the exception of Langshisha Glacier, for which elevation differences are much more negative (Table 8). The definition of outliers does not have a strong impact on the estimates (Table 8), as most of the outliers are in the higher sections of the glaciers. Elevation changes over the non-debris-covered portions of the four glaciers are also reported. They are smaller than those over the debris-covered portions, but comparison is complicated by the fact that they lie in different altitudinal bands, where the climatic forcing is likely to be very different.
Table 8. Elevation changes (m a−1) on the debris-covered and non-debris-covered sections of the glaciers, separately for each glacier. Values are obtained with the assumption of 1.5 m for penetration depth and outliers defined as both 1σ and 2σ

Discussion
Spatial heterogeneity of surface elevation changes
Our results suggest a heterogeneous pattern of mass-balance and ice volume changes in the upper Langtang valley. Glacier losses have been demonstrated to be heterogeneous at large basin scales (e.g. Reference KriegelKriegel and others, 2013). We have shown that heterogeneity is also large within a relatively small catchment, such as the upper Langtang River basin, and this cautions against extrapolation of mass-balance values from single glaciers to larger scales. It also calls for caution in the extrapolation of point or local observations to the glacier (and catchment-wide) scale, given the heterogeneity on any individual glacier. Reasons that have been used in the past to explain heterogeneity at large scales are aspect, hypsometry and glacier size distribution (Reference KriegelKriegel and others, 2013). However, none of these factors alone can explain the observed losses.
For debris-covered glaciers, mass-loss patterns are complicated by complex surface conditions with supraglacial lakes, ice cliffs and heterogeneity of debris cover, especially towards their termini, which may lead to spatially inhomogeneous surface ablation (Reference Zhang, Fujita, Liu, Liu and NuimuraZhang and others, 2011). While it is not entirely clear what factors explain differences in thinning rates between the four glaciers, the spatial heterogeneity on the individual glaciers seems to be associated with areas of low velocity. This is evident for all four glaciers (Figs 2 and 3). Areas of low velocity are associated with formation of supraglacial lakes and ponds, development of ice cliffs, highly irregular topography and the breakdown of englacial and subglacial conduits (Reference Zhang, Fujita, Liu, Liu and NuimuraZhang and others, 2011, Reference Zhang, Hirabayashi and Liu2012; Reference BennBenn and others, 2012). It has been suggested that supraglacial ponds and ice cliffs considerably enhance glacier ablation (Reference Sakai, Takeuchi, Fujita and NakawoSakai and others, 2000) and this might therefore explain the observed association between thinning and velocity decay.
Reference Nuimura, Fujita, Yamaguchi and SharmaNuimura and others (2012) used slope to interpret thinning patterns. They analysed elevation changes in relation to the slope of the debris-covered areas for glaciers in the Khumbu region and found a higher lowering (−0.87 m a−1) for large glaciers with <5° slopes in debris-covered areas and relatively low rates of surface lowering (0.35 m a−1) for debris-covered areas of small glaciers with a mean slope >5°. They suggested that gently sloping glaciers have complex, heterogeneous topography, characterized by many ponds and ice cliffs. These features can absorb large amounts of energy (Reference Sakai, Takeuchi, Fujita and NakawoSakai and others, 2000, Reference Sakai, Nakawo and Fujita2002) and, when widely distributed across debris-covered areas, can result in higher total melt rates from the entire glacier than previously thought. They therefore concluded that glaciers with gentle slopes (conducive to the formation of lakes and ice cliffs) experience greater thinning than those with steep slopes in their debris-covered sections. Our observations on the tongues of both Lirung and Langtang Glaciers confirmed the very rough topography and presence of numerous supraglacial lakes and ice cliffs.
Figure 5 shows the elevation differences along the glacier centre line for the four glaciers, together with the mean corresponding slope. The average is the mean of five parallel length profiles, to avoid a random or erroneous selection of the flowline. It is evident that on all glaciers thinning is stronger for the gentler slopes, especially in the lower sections of the tongues, confirming the hypothesis of Reference Nuimura, Fujita, Yamaguchi and SharmaNuimura and others (2012). While this effect is very clear, especially for Lirung and Langshisha Glaciers (Fig. 5a and d), local effects, as well as dynamics, might also play a role, as suggested by the fact that the four profiles of thinning rates are highly inhomogeneous. On Langtang Glacier, the strongest thinning is observed at 50–60% of the total distance from the glacier front, where velocities are lower. Slope can therefore be used as a proxy for stagnant, debris-covered glacier sections where ice cliffs and lakes are prone to form, favouring increases in ice losses. Gentle slopes in combination with thick debris are able to counteract the temperature control on mass balance typical of clean-ice glaciers, by which mass balance decreases with elevation because of lower temperatures at higher elevations. Thick debris (as observed on the tongues of the upper Langtang valley glaciers) reduces ablation on the glacier lower sections, while stagnant portions higher up over the debris-covered sections favour the formation of ponds and cliffs and therefore increase overall mass loss (Fig. 4).
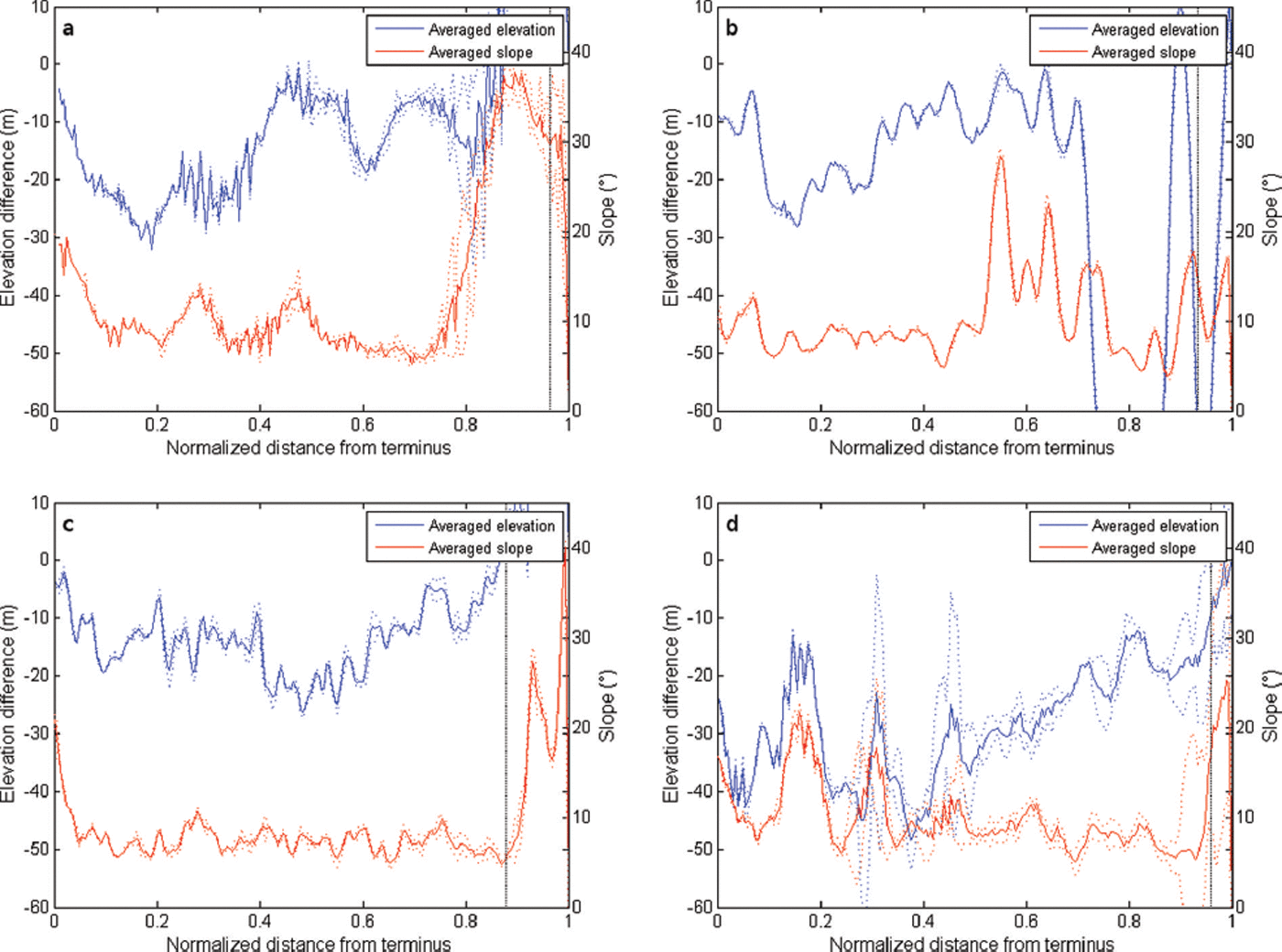
Fig. 5. Normalized length profiles with average elevation difference in 1974–99 (blue) and average slope in 1999 (orange), where the average results are from five parallel length profiles for each of the four glaciers: (a) Lirung; (b) Shalbachum; (c) Langtang; and (d) Langshisha. Uncertainty range is the standard deviation (dotted); debris limit (vertical dotted line). Curves of both elevation changes and slope were smoothed with a ten-window moving average.
This specific behaviour of glaciers mantled in a thick cover of debris also results in a specific response to a warming climate: for these glaciers, an increase in local temperature increases ice melt over an extensive portion of the glacier tongue, rather than a localized area proximal to the terminus (as for steeper-sloping glaciers). Consequently, debris-covered glaciers are thought to respond to climate warming initially by (1) downwasting and supraglacial ponding, followed by (2) proglacial lake formation if a terminal moraine presents suitable conditions and, finally, (3) retreat by calving or terminal cliff backwasting (Reference Sakai, Nishimura, Kadota and TakeuchiSakai and others, 2009; Reference Sakai and FujitaSakai and Fujita, 2010; Reference BennBenn and others, 2012). A significant retreat of the front of flat (low-gradient) debris-covered glaciers is therefore only expected at an advanced stage of climate response.
This complex interplay of controlling factors for debris-covered glaciers defies the application of standard glaciological concepts (such as that of an elevation mass-balance gradient). Glacier size has been used to interpret patterns of glacier changes. Several authors have suggested that smaller glaciers are shrinking/thinning at higher rates than larger ones (e.g. Reference Unger-ShayestehUnger-Shayesteh and others, 2013). Evidence for debris-covered glaciers is not conclusive, as other studies have found that the larger glaciers lose mass more than smaller ones (e.g. Reference Berthier, Arnaud, Kumar, Ahmad, Wagnon and ChevallierBerthier and others, 2007; Reference Nuimura, Fujita, Yamaguchi and SharmaNuimura and others, 2012). Our results show that the large Langtang Glacier has the least-negative mass balance of all four glaciers studied here (Table 8) (independently of assumptions about ice density and definition of outliers, and corrections for penetration depth). This seems to be due to a combination of factors, and size alone seems a poor predictor of glacier changes for debris-covered glaciers. Indeed, it seems clear from the analysis above, and from other studies, that thinning patterns at the catchment scale are extremely heterogeneous and can be explained only by a complex interplay of many factors (dynamics, surface features (e.g. supraglacial ponds and ice cliffs), conduit collapse, as well as climatic patterns), for which remote-sensing studies cannot provide adequate insight.
Comparison with other studies
Patterns of mass loss in the HKH region are highly variable (Reference Kääb, Berthier, Nuth, Gardelle and ArnaudKääb and others, 2012; Reference Gardelle, Berthier, Arnaud and KääbGardelle and others, 2013), with evidence of mass-balance gains in the Pamir and Karakoram regions, moderate ice losses occurring in the eastern and central Himalaya (−0.22 ± 0.12 to −0.33 ± 0.14 m w.e. a−1) and larger losses in the western Himalaya (−0.45 ± 0.13 m w.e. a−1)(Reference Gardelle, Berthier, Arnaud and KääbGardelle and others, 2013). These differences are explained by climatic regimes as well as glacier features, so a comparison between different geographic regions is not straightforward. A comparison between our results and other studies is also difficult, because they use different remote-sensing products, spatial resolution and delineation methods, and mostly refer, with the exception of the Khumbu Himalaya (eastern Nepal Himalaya), to more recent periods of analysis.
A meaningful comparison is only possible for studies in the same climatic region. Even given differences in methods, there seems to be a general agreement with mass-balance values derived in other studies of the Nepalese Himalaya. The mass loss of the glaciers in the upper Langtang valley that we obtained, equal to 0.33 ± 0.18 m w.e. a−1 for the period 1974–99, is similar to the value of 0.32 ± 0.08 m w.e. a−1 obtained for ten glaciers (nine of which are also heavily debris-covered; area 47 km2) by Reference Bolch, Pieczonka and BennBolch and others (2011) in the Khumbu valley. The heavily debris-covered Khumbu Glacier, which has shown no significant area change but has a large stagnant part, lost 0.28 ± 0.22 m w.e. a−1 in the period 1970–2002 (Reference Bolch, Buchroithner, Pieczonka and KunertBolch and others, 2008, Reference Bolch, Pieczonka and Benn2011), a value closer to the one we obtained for Lirung Glacier. Reference Nuimura, Fujita, Yamaguchi and SharmaNuimura and others (2012) obtained a regional average mass balance in the same Khumbu region (total area ∼180 km2), of −0.40 ± 0.25 m w.e. a−1 for the period 1992–2008, which seems to support the evidence of gradual acceleration in glacier thinning in the more recent period (also suggested by Reference Bolch, Pieczonka and BennBolch and others, 2011). Reference Gardelle, Berthier, Arnaud and KääbGardelle and others (2013), however, found a mass loss in the Khumbu area for the period 2000–11 of the same order as Reference Bolch, Pieczonka and BennBolch and others (2011) for 1970–2007. Hence, a possible increase in mass loss during the past decade requires further investigation, and an extension of the analysis to a more recent time, as well as resolution of shorter time intervals. Further work should also be devoted to shedding light on the apparent finding that there are no significant differences in specific mass balance between debris-covered and debris-free glaciers (Reference Kääb, Berthier, Nuth, Gardelle and ArnaudKääb and others, 2012), as a truly comparative assessment is hindered by the different elevational distributions of debris-covered and debris-free ice on the same glacier or in the same basin (Table 1; Fig. 4). At our study site, no such comparison was possible for this reason, as is indeed the case for most of the studies conducted in the HKH region (Reference Zhang, Fujita, Liu, Liu and WangZhang and others, 2010; Reference Nuimura, Fujita, Yamaguchi and SharmaNuimura and others, 2012).
Uncertainty and assumptions
The assumption of an AAR of 0.66 used to identify the position of the ELA might be a source of error in our mass-balance estimates. Most studies in the region do not differentiate between accumulation and ablation areas, and assume that the mass lost in the interval between DEMs is all glacier ice, and thus use a constant value of ice density (usually assumed to be 900 kg m−3) for the entire glacier area (Reference Gardelle, Berthier and ArnaudGardelle and others, 2012a, Reference Gardelle, Berthier, Arnaud and Kääb2013; Reference Nuimura, Fujita, Yamaguchi and SharmaNuimura and others, 2012; Reference VincentVincent and others, 2013). Despite being commonly applied, this assumption is disputable, but our sensitivity analysis has shown that estimates are not substantially different if we assign a different density to the accumulation area (Table 7). A similar result was obtained by Reference Gardelle, Berthier and ArnaudGardelle and others (2012a), who tested their results when assuming that, in the accumulation area, only firn (density 600 kg m−3) is lost or gained. The regional mass balance changed from +0.11 ± 0.22 to +0.05 ± 0.16 m a−1, but for the two extreme scenarios always remained close to zero, not affecting the main results. Since changes are small for the two scenarios, this also suggests that errors associated with the exact definition of the accumulation and ablation areas should not be major.
Other authors have made different assumptions to estimate the ELA. Reference Gardelle, Berthier, Arnaud and KääbGardelle and others (2013) assumed that the ELA was equal to the elevation of the transient snowline at the end of the ablation season (after the end of the monsoon) and derived the ELA from just one image (Landsat 2000), using it for the entire period. As the authors recognized, the ELA (assuming that it can be taken as the elevation of the transient snowline, which might not be the case) should have been derived for every year of the study period. This is a time-consuming task that the authors did not carry out. In our case, the task was impossible, as our study period is much longer that of Reference Gardelle, Berthier, Arnaud and KääbGardelle and others (2013). They looked at 8–11 years (depending on the site), for the period 1974–2000, when very few images were available to reconstruct the elevation of the transient snowline.
The definition of outliers based on 1σ, 2σ or 3σ does not seem to introduce significant errors, as estimates remained close and their differences well within the uncertainty of the method. The average basin mass balance was −0.33, −0.32 and −0.30 ± 0.18 m w.e. a−1, for the three assumptions of 1σ, 2σ and 3σ, respectively (for a penetration depth of 1.5 m and an overall density of 900 kg m−3). The average mass balance obtained with the outliers definition of Reference Nuimura, Fujita, Yamaguchi and SharmaNuimura and others (2012) was −0.28 ± 0.18 m w.e. a−1, again not remarkably different.
Conclusions
We have examined elevation changes for the four main glaciers of the upper Langtang valley, central Himalaya, Nepal. All four glaciers are heavily debris-covered on their tongues. We derived thinning rates by differencing a Hexagon DEM (1974) and a SRTM DEM for 2000. Our study adds to the increasing amount of work based on remote-sensing methods that attempts to reconstruct glacier changes in an inaccessible part of the world that contains the largest glacierized area outside the polar regions. Our study is one of the few that extend as far back as the 1970s, owing to the use of the Hexagon satellite data. Only Reference Bolch, Pieczonka and BennBolch and others (2011) and Reference Nuimura, Fujita, Yamaguchi and SharmaNuimura and others (2012) have analysed a period of multiple decades. All other works, making use of recently available datasets (SRTM, SPOT-5, ICESat) focus only on the most recent decade. Our main conclusions are as follows:
-
1. The mean mass balance for the debris-covered glaciers of the upper Langtang River basin (−0.32 ± 0.18 m w.e. a−1) is similar to values in central and western Nepal. In particular, it is similar to the values of Reference Nuimura, Fujita, Yamaguchi and SharmaNuimura and others (2012) for the Khumbu region, but slightly less negative. Estimates are affected by a number of assumptions made when deriving mass balance, and in particular (i) the density used to convert glacier volume changes into mass balance, (ii) the correction for penetration depth of the radar beam for the SRTM DEM and (iii) the way outliers are defined. Each of these factors introduces some variability in the results. The relative importance of these assumptions depends on glacier characteristics (Table 7), and we suggest that attention should be paid to each of them. Even considering the variability associated with these assumptions, the mean catchment values are within similar ranges to values from other studies in the Nepalese Himalaya.
-
2. However, the value obtained for the catchment is a result of averaging very distinct mass balances for the individual glaciers. We obtain large differences among the four main glaciers, all debris-covered on their tongues, with high mass losses over Langshisha Glacier (0.79 ± 0.18 m w.e. a−1) and low losses for the largest, Langtang Glacier (0.10 ± 0.18 m w.e. a−1). These heterogeneous values result from complex processes that are only beginning to be understood (Reference BennBenn and others, 2012). However, we could also clearly identify a causal relationship between glacier slope, surface velocity and thinning rate, with high thinning occurring at locations of gentle slope and decaying velocity. These results call for a more detailed, physically based investigation into processes occurring on the highly heterogeneous surface and subsurface systems of debris-covered glaciers. They also clearly indicate that no extrapolation of point or glacier values of mass balance to the catchment scale can be safely made.
-
3. Our results confirm recent evidence that mass balance of debris-covered glaciers is characteristically nonlinear with elevation. Over each glacier analysed, surface elevation losses were spatially highly variable, with a maximum in the ablation area at varying distances from the glacier terminus, but less variable for the lower portion of the tongues. On these, mass losses remain fairly constant (or even increase with elevation) for a consistent portion of the tongue (Fig. 4), because the thick debris neutralizes or limits the air-temperature control on mass balance. Analysis of surface velocities shows that there is a clear decay in velocities, with the upper sections moving at ∼20–60 m a−1 and decaying down-glacier to <10–15 m a−1, thus confirming evidence of stagnating tongues. The tongues have not retreated significantly since 1974 (at least in comparison with debris-free glaciers), but are instead downwasting, all at a similar pace. The exception is Langshisha Glacier, for which losses over the debris-covered tongue are higher than for the other glaciers. These upper sections, characterized by gentle slopes, favour the formation of supraglacial ponds and ice cliffs, which contribute significantly to the total downwasting of the glacier, by absorbing large amounts of energy. It thus seems important that integrated studies include an accurate description of climatically driven ablation in glacier-scale models that are also able to account for the effect of supraglacial ponds and ice cliffs on glacier ablation and mass balance.
-
4. Because of the strong predominance of debris-covered glaciers in the upper Langtang Valley, no sound comparison is possible, and little can be inferred about the so-called debris-cover anomaly, by which debris-mantled glaciers seem to be losing as much mass as debris-free glaciers. The average values obtained for the glaciers seem to be close to those of other regions in Nepal, but most of these companion studies also focused on catchments with a predominance of debris-covered glaciers (e.g. Reference Bolch, Pieczonka and BennBolch and others, 2011). Comparison with recent studies is also difficult because most looked at only a recent period (from about 2000 to 2008 or 2011; e.g. Reference Gardelle, Berthier, Arnaud and KääbGardelle and others, 2013) and indeed future work could look into shorter time intervals to resolve temporal variability. This could be accomplished by processing more numerous images and DEMs when available. However, it seems imperative that modelling studies incorporating the physics of the processes occurring in the debris mantles and subglacial systems of debris-covered glaciers be used. If we intend to understand the actual rates of mass loss and volume changes and their drivers, these modelling studies are needed in combination with high-resolution observations to reproduce the response of such complex systems.
Acknowledgements
The first two authors contributed equally to this work. We thank Paolo Burlando who supported C. Stephan’s work at ETH. T. Bolch acknowledges funding through Deutsche Forschungsgemeinschaft (DFG; BO 3199/2-1) and the European Space Agency (ESA) project Glaciers_cci (4000101778101-AM). We are grateful for the cooperation with the International Centre for Integrated Mountain Development, Kathmandu. The reviews of Koji Fujita and an anonymous reviewer helped to improve the paper, as did the comments of Scientific Editor Ted Scambos, who is warmly acknowledged.














