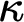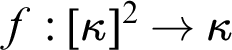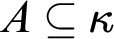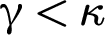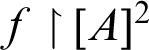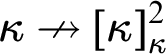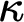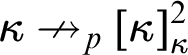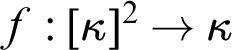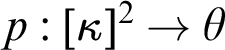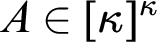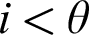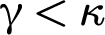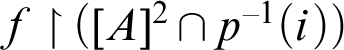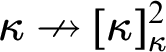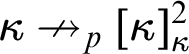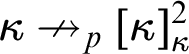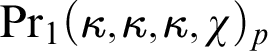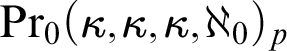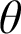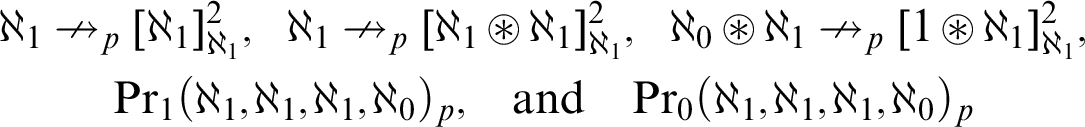1. Introduction
The theory of strong colorings branched off Ramsey theory in 1933 when Sierpinski constructed a coloring on
 $[\mathbb R]^2$
that contradicted the uncountable generalization of Ramsey’s theorem. For many years, pair-colorings which keep their range even after they are restricted to all unordered pairs from an arbitrary, sufficiently large set were called “bad”; now they are called “strong.”
$[\mathbb R]^2$
that contradicted the uncountable generalization of Ramsey’s theorem. For many years, pair-colorings which keep their range even after they are restricted to all unordered pairs from an arbitrary, sufficiently large set were called “bad”; now they are called “strong.”
Definition 1. Let
![]() $\lambda \le \kappa $
be cardinals. A strong
$\lambda \le \kappa $
be cardinals. A strong
![]() $\lambda $
-coloring on
$\lambda $
-coloring on
![]() $\kappa $
is a function
$\kappa $
is a function
 $f:[\kappa ]^2\to \lambda $
such that
$f:[\kappa ]^2\to \lambda $
such that
 $\lambda ={\operatorname {ran}}(f\restriction [A]^2)$
for every
$\lambda ={\operatorname {ran}}(f\restriction [A]^2)$
for every
![]() $A\in [\kappa ]^{\kappa }$
.
$A\in [\kappa ]^{\kappa }$
.
By Ramsey’s theorem there are no strong
![]() $\lambda $
-colorings on
$\lambda $
-colorings on
![]() $\omega $
for
$\omega $
for
![]() $\lambda>1$
. Sierpinski constructed a strong two-coloring on the continuum and on
$\lambda>1$
. Sierpinski constructed a strong two-coloring on the continuum and on
![]() $\aleph _1$
.
$\aleph _1$
.
Assertions of existence of strong colorings with various cardinal parameters are conveniently phrased with partition-calculus symbols. The (negative) square-brackets symbol
 $$ \begin{align*} \kappa\nrightarrow[\kappa]^2_{\lambda}, \end{align*} $$
$$ \begin{align*} \kappa\nrightarrow[\kappa]^2_{\lambda}, \end{align*} $$
asserts the existence of a strong
![]() $\lambda $
-coloring on
$\lambda $
-coloring on
![]() $\kappa $
. Recall that the symbol for Ramsey’s theorem for pairs,
$\kappa $
. Recall that the symbol for Ramsey’s theorem for pairs,
 $$ \begin{align} \omega\to(\omega)^2_n \end{align} $$
$$ \begin{align} \omega\to(\omega)^2_n \end{align} $$
reads “for every
 $f:[\omega ]^2\to n$
there is an infinite subset
$f:[\omega ]^2\to n$
there is an infinite subset
![]() $A\subseteq \omega $
such that
$A\subseteq \omega $
such that
 $f\restriction [A]^2$
is constant (omits all colors but one).” The square brackets in place of the rounded ones stand for “omits at least one color”; with the negation on the arrow, the symbol
$f\restriction [A]^2$
is constant (omits all colors but one).” The square brackets in place of the rounded ones stand for “omits at least one color”; with the negation on the arrow, the symbol
 $\kappa \nrightarrow [\kappa ]^2_{\lambda }$
means, then, “not for all colorings
$\kappa \nrightarrow [\kappa ]^2_{\lambda }$
means, then, “not for all colorings
 $f:[\kappa ]^2\to \lambda $
at least one color can be omitted on
$f:[\kappa ]^2\to \lambda $
at least one color can be omitted on
 $[A]^2$
for some
$[A]^2$
for some
![]() $A\subseteq \kappa $
of cardinality
$A\subseteq \kappa $
of cardinality
![]() $|A|=\kappa $
.” That is, there exists a strong
$|A|=\kappa $
.” That is, there exists a strong
![]() $\lambda $
-coloring on
$\lambda $
-coloring on
![]() $\kappa $
.
$\kappa $
.
When
![]() $2$
is replaced with some
$2$
is replaced with some
![]() $d>0$
the symbol states the existence of an analogous coloring of unordered d-tuples. As Ramsey’s theorem holds for all finite
$d>0$
the symbol states the existence of an analogous coloring of unordered d-tuples. As Ramsey’s theorem holds for all finite
![]() $d>0$
, strong d-dimensional colorings can also exist only on uncountable cardinals. In what follows we shall address almost exclusively the case
$d>0$
, strong d-dimensional colorings can also exist only on uncountable cardinals. In what follows we shall address almost exclusively the case
![]() $d=2$
.
$d=2$
.
Definition 2. Given a coloring
 $f:[\kappa ]^2\to \lambda $
, a set
$f:[\kappa ]^2\to \lambda $
, a set
 $X\subseteq [\kappa ]^2$
is f -strong if
$X\subseteq [\kappa ]^2$
is f -strong if
![]() ${\operatorname {ran}} (f\restriction X)={\operatorname {ran}} (f)$
.
${\operatorname {ran}} (f\restriction X)={\operatorname {ran}} (f)$
.
The collection of f-strong subsets of
 $[\kappa ]^2$
is clearly upwards closed and not necessarily closed under intersections.
$[\kappa ]^2$
is clearly upwards closed and not necessarily closed under intersections.
Different square-bracket symbols require that different families of sets are f-strong with respect to the coloring f whose existence each symbol asserts. The symbol above asserts the existence of f such that every
![]() $\kappa $
-square, that is, every
$\kappa $
-square, that is, every
 $[A]^2$
for some
$[A]^2$
for some
![]() $A\in [\kappa ]^{\kappa }$
, is f-strong. A
$A\in [\kappa ]^{\kappa }$
, is f-strong. A
![]() $(\lambda ,\kappa )$
-rectangle in
$(\lambda ,\kappa )$
-rectangle in
 $[\kappa ]^2$
is a set of the form
$[\kappa ]^2$
is a set of the form
![]() $A\circledast B= \{\{\alpha ,\beta \}: \alpha <\beta <\kappa , \; \alpha \in A \text { and } \beta \in B\}$
. Every
$A\circledast B= \{\{\alpha ,\beta \}: \alpha <\beta <\kappa , \; \alpha \in A \text { and } \beta \in B\}$
. Every
![]() $\kappa $
-square contains a
$\kappa $
-square contains a
![]() $(\mu _1,\mu _2)$
-rectangle if
$(\mu _1,\mu _2)$
-rectangle if
![]() $\mu _1\le \mu _2\le \kappa $
; the symbol
$\mu _1\le \mu _2\le \kappa $
; the symbol
 $$ \begin{align*} \kappa\nrightarrow [\mu_1\circledast\mu_2]^2_{\lambda},\end{align*} $$
$$ \begin{align*} \kappa\nrightarrow [\mu_1\circledast\mu_2]^2_{\lambda},\end{align*} $$
which asserts the existence of
 $f:[\kappa ]^2\to \lambda $
such that every
$f:[\kappa ]^2\to \lambda $
such that every
![]() $(\mu _1,\mu _2)$
-rectangle
$(\mu _1,\mu _2)$
-rectangle
 $A\circledast B\subseteq [\kappa ]^2$
is f-strong, is, then, stronger than
$A\circledast B\subseteq [\kappa ]^2$
is f-strong, is, then, stronger than
 $\kappa \nrightarrow [\kappa ]^2_{\lambda }$
.
$\kappa \nrightarrow [\kappa ]^2_{\lambda }$
.
The next two strong-coloring symbols go beyond specifying which sets ought to be f-strong. They require the existence of certain patterns in the preimage of each color.
-
(1) A coloring
 $f:[\kappa ]^2\to \lambda $
witnesses the symbol if for every
$f:[\kappa ]^2\to \lambda $
witnesses the symbol if for every $$ \begin{align*} \operatorname{Pr}_1(\kappa,\mu,\lambda,\chi) \end{align*} $$
$$ \begin{align*} \operatorname{Pr}_1(\kappa,\mu,\lambda,\chi) \end{align*} $$
 $\xi <\chi $
and a pairwise disjoint family
$\xi <\chi $
and a pairwise disjoint family
 $\mathcal A\subseteq [\kappa ]^{<\xi }$
of cardinality
$\mathcal A\subseteq [\kappa ]^{<\xi }$
of cardinality
 $|\mathcal A|=\mu $
and color
$|\mathcal A|=\mu $
and color
 $\unicode{x3b3} <\lambda $
there are
$\unicode{x3b3} <\lambda $
there are
 $a,b\in \mathcal A$
with
$a,b\in \mathcal A$
with
 $\max a< \min b$
such that
$\max a< \min b$
such that
 $f(\alpha ,\beta )=\unicode{x3b3} $
for all
$f(\alpha ,\beta )=\unicode{x3b3} $
for all
 $\alpha \in a$
and
$\alpha \in a$
and
 $\beta \in b$
. The quantified
$\beta \in b$
. The quantified
 $\xi $
above is needed only in the case that
$\xi $
above is needed only in the case that
 $\chi \ge {\operatorname {cf}}(\kappa )$
, which received attention very recently. When
$\chi \ge {\operatorname {cf}}(\kappa )$
, which received attention very recently. When
 $\chi <{\operatorname {cf}}(\kappa )$
we omit
$\chi <{\operatorname {cf}}(\kappa )$
we omit
 $\xi $
from the definition and require only that
$\xi $
from the definition and require only that
 $A\subseteq [\kappa ]^{<\chi }$
instead.
$A\subseteq [\kappa ]^{<\chi }$
instead.
-
(2) A coloring
 $f:[\kappa ]^2\to \lambda $
witnesses the symbol if for every
$f:[\kappa ]^2\to \lambda $
witnesses the symbol if for every $$ \begin{align*} \operatorname{Pr}_0(\kappa,\mu,\lambda,\chi) \end{align*} $$
$$ \begin{align*} \operatorname{Pr}_0(\kappa,\mu,\lambda,\chi) \end{align*} $$
 $\xi <\chi $
, a pairwise disjoint family
$\xi <\chi $
, a pairwise disjoint family
 $\mathcal A\subseteq [\kappa ]^{\xi }$
of cardinality
$\mathcal A\subseteq [\kappa ]^{\xi }$
of cardinality
 $|\mathcal A|=\mu $
and a matrix
$|\mathcal A|=\mu $
and a matrix
 $\{\unicode{x3b3} _{i,j}:i,j<\xi \}\subseteq \lambda $
there are
$\{\unicode{x3b3} _{i,j}:i,j<\xi \}\subseteq \lambda $
there are
 $a,b\in \mathcal A$
with
$a,b\in \mathcal A$
with
 $\max a< \min b$
such that
$\max a< \min b$
such that
 $f(\alpha (i),\beta (j))=\unicode{x3b3} _{i,j}$
for all
$f(\alpha (i),\beta (j))=\unicode{x3b3} _{i,j}$
for all
 $i,j<\xi $
, where
$i,j<\xi $
, where
 $a(i),b(j)$
are the
$a(i),b(j)$
are the
 $i^{\text {th}}$
and
$i^{\text {th}}$
and
 $j^{\text {th}}$
elements of a and of b, respectively, in increasing order.
$j^{\text {th}}$
elements of a and of b, respectively, in increasing order.
For
![]() $\chi>2$
and
$\chi>2$
and
![]() $\mu \ge \aleph _0$
,
$\mu \ge \aleph _0$
,
![]() $\operatorname {Pr}_1(\kappa ,\mu ,\lambda ,\chi )$
implies
$\operatorname {Pr}_1(\kappa ,\mu ,\lambda ,\chi )$
implies
 $\kappa \nrightarrow [\mu ]^2_{\lambda }$
(see 8 below). If
$\kappa \nrightarrow [\mu ]^2_{\lambda }$
(see 8 below). If
![]() $\chi < {\operatorname {cf}}(\mu )$
then
$\chi < {\operatorname {cf}}(\mu )$
then
![]() $\operatorname {Pr}_0(\kappa ,\mu ,\lambda ,\chi )$
implies
$\operatorname {Pr}_0(\kappa ,\mu ,\lambda ,\chi )$
implies
![]() $\operatorname {Pr}_1(\kappa ,\mu ,\lambda ,\chi )$
.
$\operatorname {Pr}_1(\kappa ,\mu ,\lambda ,\chi )$
.
Let us conclude the introduction with the remark that some authors use the term “strong coloring” only for colorings which witness
![]() $\operatorname {Pr}_1$
or a stronger symbol.
$\operatorname {Pr}_1$
or a stronger symbol.
2 A brief history of strong colorings
Strong
![]() $\kappa $
-colorings on various cardinals
$\kappa $
-colorings on various cardinals
![]() $\kappa $
were constructed by Erdős, Hajnál, Milner and Rado in the 1950s and 1960s from instances of the GCH. For every cardinal
$\kappa $
were constructed by Erdős, Hajnál, Milner and Rado in the 1950s and 1960s from instances of the GCH. For every cardinal
![]() $\kappa $
they were able to construct from
$\kappa $
they were able to construct from
![]() $2^{\kappa }=\kappa ^+$
colorings
$2^{\kappa }=\kappa ^+$
colorings
 $f:[\kappa ^+]^2\to \kappa ^+$
which witnessed
$f:[\kappa ^+]^2\to \kappa ^+$
which witnessed
 $$ \begin{align*} \kappa^+\nrightarrow [\kappa\circledast \kappa^+]^2_{\kappa^+},\end{align*} $$
$$ \begin{align*} \kappa^+\nrightarrow [\kappa\circledast \kappa^+]^2_{\kappa^+},\end{align*} $$
and even colorings which witnesses the stronger

whose meaning is that inside every
![]() $(\kappa ,\kappa ^+)$
-rectangle
$(\kappa ,\kappa ^+)$
-rectangle
![]() $A\circledast B\subseteq \kappa ^+$
there is a
$A\circledast B\subseteq \kappa ^+$
there is a
![]() $(1,\kappa ^+)$
-rectangle
$(1,\kappa ^+)$
-rectangle
![]() $\{\alpha \}\circledast B\subseteq A\circledast B$
such that
$\{\alpha \}\circledast B\subseteq A\circledast B$
such that
![]() ${\operatorname {ran}} (f\restriction (\{\alpha \}\circledast B))=\kappa ^+$
(see Section 49 in [Reference Erdős, Hajnal, Máté and Rado5]). A coloring
${\operatorname {ran}} (f\restriction (\{\alpha \}\circledast B))=\kappa ^+$
(see Section 49 in [Reference Erdős, Hajnal, Máté and Rado5]). A coloring
 $f[\kappa ^+]^2\to \kappa ^+$
witnesses this symbol if and only if for every
$f[\kappa ^+]^2\to \kappa ^+$
witnesses this symbol if and only if for every
 $B\in [\kappa ^+]^{\kappa ^+}$
, for all but fewer than
$B\in [\kappa ^+]^{\kappa ^+}$
, for all but fewer than
![]() $\kappa $
ordinals
$\kappa $
ordinals
![]() $\alpha <\kappa ^+$
the full range
$\alpha <\kappa ^+$
the full range
![]() $\kappa ^+$
is attained by f on the set
$\kappa ^+$
is attained by f on the set
![]() $\{\alpha \}\circledast B=\{\{\alpha ,\beta \}:\alpha <\beta \in B\}$
.
$\{\alpha \}\circledast B=\{\{\alpha ,\beta \}:\alpha <\beta \in B\}$
.
Galvin [Reference Galvin15], who was motivated by the problem of productivity of chain conditions and by earlier work of Laver, used
![]() $2^{\kappa }=\kappa ^+$
to obtain a new class of two-colorings, which in modern notation witness
$2^{\kappa }=\kappa ^+$
to obtain a new class of two-colorings, which in modern notation witness
![]() $\operatorname {Pr}_1(\kappa ^+,\kappa ^+,2,\aleph _0)$
, and used these colorings for constructing counter examples to the productivity of the
$\operatorname {Pr}_1(\kappa ^+,\kappa ^+,2,\aleph _0)$
, and used these colorings for constructing counter examples to the productivity of the
![]() $\kappa ^+$
-chain condition. A straightforward modification of Galvin’s proof actually gives
$\kappa ^+$
-chain condition. A straightforward modification of Galvin’s proof actually gives
![]() $\operatorname {Pr}_1(\kappa ^+,\kappa ^+,\kappa ^+,\aleph _0)$
on all successor cardinals from
$\operatorname {Pr}_1(\kappa ^+,\kappa ^+,\kappa ^+,\aleph _0)$
on all successor cardinals from
![]() $2^{\kappa }=\kappa ^+$
.
$2^{\kappa }=\kappa ^+$
.
A remarkable breakthrough in the theory of strong colorings was the invention of the method of ordinal-walks by Todorčević [Reference Todorčević41] (or, as it was originally called, minimal walks). Todorčević applied his method to construct strong colorings on all successors of regulars in ZFC with no additional axioms. With the same method Todorčević [Reference Todorčević43] got in ZFC the square bracket symbol for triples
 $\omega _2\nrightarrow [\omega _1]^3_{\omega }$
and proved that
$\omega _2\nrightarrow [\omega _1]^3_{\omega }$
and proved that
 $\omega _2\nrightarrow [\omega _1]^2_{\omega _1}$
is equivalent to the negation of the
$\omega _2\nrightarrow [\omega _1]^2_{\omega _1}$
is equivalent to the negation of the
![]() $(\aleph _2,\aleph _1)$
Chang conjecture. The rectangular symbol
$(\aleph _2,\aleph _1)$
Chang conjecture. The rectangular symbol
 $\kappa ^+\nrightarrow [\kappa ^+\circledast \kappa ^+]^2_{\kappa ^+}$
has been obtained since in ZFC on all succesors of uncountable regular cardinals
$\kappa ^+\nrightarrow [\kappa ^+\circledast \kappa ^+]^2_{\kappa ^+}$
has been obtained since in ZFC on all succesors of uncountable regular cardinals
![]() $\kappa $
by Shelah via further developments of ordinal-walks. Moore [Reference Moore20] developed ordinal-walks further and provided the missing
$\kappa $
by Shelah via further developments of ordinal-walks. Moore [Reference Moore20] developed ordinal-walks further and provided the missing
![]() $\kappa ^+=\aleph _1$
case. Rinot and Todorčević [Reference Rinot and Todorčević28] present a unified proof of the rectangle version for all successors of regulars with a completely arithmetic oscillation function.
$\kappa ^+=\aleph _1$
case. Rinot and Todorčević [Reference Rinot and Todorčević28] present a unified proof of the rectangle version for all successors of regulars with a completely arithmetic oscillation function.
Shelah, following Galvin [Reference Galvin15], phrased the strong coloring relations
![]() $\operatorname {Pr}_1(\kappa ,\mu ,\lambda ,\chi )$
and
$\operatorname {Pr}_1(\kappa ,\mu ,\lambda ,\chi )$
and
![]() $\operatorname {Pr}_0(\kappa ,\mu ,\lambda ,\chi )$
(and a few more!) and proved
$\operatorname {Pr}_0(\kappa ,\mu ,\lambda ,\chi )$
(and a few more!) and proved
![]() $\operatorname {Pr}_1(\kappa ^{++},\kappa ^{++},\kappa ^{++},\kappa )$
for every regular
$\operatorname {Pr}_1(\kappa ^{++},\kappa ^{++},\kappa ^{++},\kappa )$
for every regular
![]() $\kappa $
in ZFC [Reference Shelah34]. Shelah also proved a criterion for stepping up from
$\kappa $
in ZFC [Reference Shelah34]. Shelah also proved a criterion for stepping up from
![]() $\operatorname {Pr}_1$
to
$\operatorname {Pr}_1$
to
![]() $\operatorname {Pr}_0$
: if
$\operatorname {Pr}_0$
: if
![]() $\operatorname {Pr}_1(\kappa ,\kappa ,\lambda ,\chi )$
holds,
$\operatorname {Pr}_1(\kappa ,\kappa ,\lambda ,\chi )$
holds,
![]() $\lambda =\lambda ^{<\chi }$
and there is some “interpolant” cardinal
$\lambda =\lambda ^{<\chi }$
and there is some “interpolant” cardinal
![]() $\rho $
such that
$\rho $
such that
![]() $\rho ^{<\chi }\le \lambda $
,
$\rho ^{<\chi }\le \lambda $
,
![]() $2^{\rho }\ge \kappa $
and
$2^{\rho }\ge \kappa $
and
![]() ${\operatorname {cf}}(\kappa )>\rho ^{<\chi }$
, then
${\operatorname {cf}}(\kappa )>\rho ^{<\chi }$
, then
![]() $\operatorname {Pr}_0(\kappa ,\kappa ,\lambda ,\chi )$
holds (Lemma 4.5(3), p. 170 of [Reference Shelah38]). In particular, chosing
$\operatorname {Pr}_0(\kappa ,\kappa ,\lambda ,\chi )$
holds (Lemma 4.5(3), p. 170 of [Reference Shelah38]). In particular, chosing
![]() $\rho =\lambda $
as the interpolant,
$\rho =\lambda $
as the interpolant,
![]() $\operatorname {Pr}_1(\lambda ^+,\lambda ^+,\lambda ^+,\aleph _0)\Rightarrow \operatorname {Pr}_0(\lambda ^+,\lambda ^+,\lambda ^+,\aleph _0)$
for every cardinal
$\operatorname {Pr}_1(\lambda ^+,\lambda ^+,\lambda ^+,\aleph _0)\Rightarrow \operatorname {Pr}_0(\lambda ^+,\lambda ^+,\lambda ^+,\aleph _0)$
for every cardinal
![]() $\lambda $
; so for all regular cardinals
$\lambda $
; so for all regular cardinals
![]() $\kappa $
,
$\kappa $
,
![]() $\operatorname {Pr}_0(\kappa ^{++},\kappa ^{++},\kappa ^{++},\aleph _0)$
holds in ZFC (
$\operatorname {Pr}_0(\kappa ^{++},\kappa ^{++},\kappa ^{++},\aleph _0)$
holds in ZFC (
![]() $\operatorname {Pr}_1(\aleph _1,\aleph _1,3,\aleph _0)$
cannot hold in ZFC because under MA the product of two ccc spaces is ccc). See the survey in [Reference Rinot25] for more background on strong colorings and non-productivity of chain conditions.
$\operatorname {Pr}_1(\aleph _1,\aleph _1,3,\aleph _0)$
cannot hold in ZFC because under MA the product of two ccc spaces is ccc). See the survey in [Reference Rinot25] for more background on strong colorings and non-productivity of chain conditions.
On successors of singulars, Todorčević [Reference Todorčević41] proved that the pcf assumption
![]() $\operatorname {pp}(\mu )=\mu ^+$
for a singular
$\operatorname {pp}(\mu )=\mu ^+$
for a singular
![]() $\mu $
implies
$\mu $
implies
 $\mu ^+\nrightarrow [\mu ^+]^2_{\mu ^+}$
. Shelah proved
$\mu ^+\nrightarrow [\mu ^+]^2_{\mu ^+}$
. Shelah proved
![]() $\operatorname {Pr}_1(\mu ^+,\mu ^+,{\operatorname {cf}}(\mu ),{\operatorname {cf}}(\mu ))$
for every singular
$\operatorname {Pr}_1(\mu ^+,\mu ^+,{\operatorname {cf}}(\mu ),{\operatorname {cf}}(\mu ))$
for every singular
![]() $\mu $
(4.1 p. 67 of [Reference Shelah38]). Eisworth [Reference Eisworth9] proved
$\mu $
(4.1 p. 67 of [Reference Shelah38]). Eisworth [Reference Eisworth9] proved
![]() $\operatorname {Pr}_1(\mu ^+\mu ^+,\mu ^+,{\operatorname {cf}}(\mu ))$
from
$\operatorname {Pr}_1(\mu ^+\mu ^+,\mu ^+,{\operatorname {cf}}(\mu ))$
from
![]() $\operatorname {pp}(\mu )=\mu ^+$
. Then Rinot, building on Eisworth’s [Reference Eisworth9, Reference Eisworth10], proved that for every singular
$\operatorname {pp}(\mu )=\mu ^+$
. Then Rinot, building on Eisworth’s [Reference Eisworth9, Reference Eisworth10], proved that for every singular
![]() $\mu $
,
$\mu $
,
![]() $\operatorname {Pr}_1(\mu ^+,\mu ^+,\mu ^+,{\operatorname {cf}}(\mu ))$
holds iff
$\operatorname {Pr}_1(\mu ^+,\mu ^+,\mu ^+,{\operatorname {cf}}(\mu ))$
holds iff
 $\mu ^+\nrightarrow [\mu ^+]^2_{\mu ^+}$
holds. In particular, via Shelah’s criterion,
$\mu ^+\nrightarrow [\mu ^+]^2_{\mu ^+}$
holds. In particular, via Shelah’s criterion,
 $\operatorname {Pr}_0(\mu ^+,\mu ^+,\mu ^+,\aleph _0)\iff \mu ^+\nrightarrow [\mu ^+]^2_{\mu ^+}$
for all singular
$\operatorname {Pr}_0(\mu ^+,\mu ^+,\mu ^+,\aleph _0)\iff \mu ^+\nrightarrow [\mu ^+]^2_{\mu ^+}$
for all singular
![]() $\mu $
[Reference Rinot23]. Quite recently, Peng and Wu proved in [Reference Peng and Wu21] that
$\mu $
[Reference Rinot23]. Quite recently, Peng and Wu proved in [Reference Peng and Wu21] that
![]() $\operatorname {Pr}_0(\aleph _1,\aleph _1,\aleph _1,n)$
holds for all
$\operatorname {Pr}_0(\aleph _1,\aleph _1,\aleph _1,n)$
holds for all
![]() $n<\omega $
outright in ZFC.
$n<\omega $
outright in ZFC.
The most recent progress on strong colorings is made in a series of papers by Rinot and his collaborators. The result in [Reference Rinot24], shown to be optimal in Theorem 3.4 in [Reference Lambie-Hanson and Rinot19], establishes the property
![]() $\operatorname {Pr}_1(\lambda ,\lambda ,\lambda ,\chi )$
for regular
$\operatorname {Pr}_1(\lambda ,\lambda ,\lambda ,\chi )$
for regular
![]() $\lambda>\chi ^+$
from a non-reflecting stationary subset of
$\lambda>\chi ^+$
from a non-reflecting stationary subset of
![]() $\lambda $
composed of ordinals of cofinality
$\lambda $
composed of ordinals of cofinality
![]() $\ge \chi $
(using a new oscillation function called
$\ge \chi $
(using a new oscillation function called
![]() $\operatorname {P\ell }_6$
). In [Reference Rinot25], Rinot gets the same result from
$\operatorname {P\ell }_6$
). In [Reference Rinot25], Rinot gets the same result from
![]() $\square (\lambda )$
, thus establishing that if
$\square (\lambda )$
, thus establishing that if
![]() $\lambda ={\operatorname {cf}}(\lambda )>\aleph _1$
and the
$\lambda ={\operatorname {cf}}(\lambda )>\aleph _1$
and the
![]() $\lambda $
-chain condition is productive, then
$\lambda $
-chain condition is productive, then
![]() $\lambda $
is weakly compact in L. Then Rinot and Zhang prove in [Reference Rinot and Zhang29] that for every regular cardinal
$\lambda $
is weakly compact in L. Then Rinot and Zhang prove in [Reference Rinot and Zhang29] that for every regular cardinal
![]() $\kappa $
,
$\kappa $
,
![]() $2^{\kappa }=\kappa ^+$
implies
$2^{\kappa }=\kappa ^+$
implies
![]() $\operatorname {Pr}_1(\kappa ^+,\kappa ^+,\kappa ^+,\kappa )$
and for every inaccessible
$\operatorname {Pr}_1(\kappa ^+,\kappa ^+,\kappa ^+,\kappa )$
and for every inaccessible
![]() $\lambda $
such that
$\lambda $
such that
![]() $\square (\lambda )$
and
$\square (\lambda )$
and
![]() $\diamondsuit ^*(\lambda )$
both hold,
$\diamondsuit ^*(\lambda )$
both hold,
![]() $\operatorname {Pr}_1(\lambda ,\lambda ,\lambda ,\lambda )$
holds as well (this is the case in which our remark about
$\operatorname {Pr}_1(\lambda ,\lambda ,\lambda ,\lambda )$
holds as well (this is the case in which our remark about
![]() $\xi $
at the end of (1) of Definition 3 is relevant). In the other direction it is proved in [Reference Rinot and Zhang29] that
$\xi $
at the end of (1) of Definition 3 is relevant). In the other direction it is proved in [Reference Rinot and Zhang29] that
![]() $\operatorname {Pr}_1(\kappa ^+,\kappa ^+,2,\kappa )$
fails for every singular cardinal
$\operatorname {Pr}_1(\kappa ^+,\kappa ^+,2,\kappa )$
fails for every singular cardinal
![]() $\kappa $
and that
$\kappa $
and that
![]() $\operatorname {Pr}_1(\kappa ^+,\kappa ^+,2,{\operatorname {cf}}(\kappa )^+)$
fails for a singular limit
$\operatorname {Pr}_1(\kappa ^+,\kappa ^+,2,{\operatorname {cf}}(\kappa )^+)$
fails for a singular limit
![]() $\kappa $
of strongly compact cardinals.
$\kappa $
of strongly compact cardinals.
Ramsey’s theorem prohibits the existence of strong colorings with more than one color on countable sets for which all infinite subsets are strong, but in topological partition theory, strong colorings may exist also on countable spaces. Baumgartner [Reference Baumgartner3], following some unpublished work by Galvin, constructed a coloring
 $c:[\mathbb Q]^2\to \omega $
which attains all colors on every homeomorphic copy of
$c:[\mathbb Q]^2\to \omega $
which attains all colors on every homeomorphic copy of
![]() $\mathbb Q$
. Todorčević [Reference Todorčević44] obtained the rectangular version of Baumgartner’s result and very recently, Raghavan and Todorčević [Reference Raghavan and Todorčević22] proved that if a Woodin cardinal exists then for every natural number
$\mathbb Q$
. Todorčević [Reference Todorčević44] obtained the rectangular version of Baumgartner’s result and very recently, Raghavan and Todorčević [Reference Raghavan and Todorčević22] proved that if a Woodin cardinal exists then for every natural number
![]() $k>2$
, for every coloring
$k>2$
, for every coloring
 $c:[\mathbb R]^2\to k$
there is homeomorphic copy of
$c:[\mathbb R]^2\to k$
there is homeomorphic copy of
![]() $\mathbb Q$
in
$\mathbb Q$
in
![]() $\mathbb R$
on which at most two colors occur, confirming thus a conjecture of Galvin from the 1970s. They also proved that any regular topological space of cardinality
$\mathbb R$
on which at most two colors occur, confirming thus a conjecture of Galvin from the 1970s. They also proved that any regular topological space of cardinality
![]() $\aleph _n$
admits a coloring of
$\aleph _n$
admits a coloring of
![]() $(n+2)$
-tuples which attains all
$(n+2)$
-tuples which attains all
![]() $\omega $
colors on every subspace which is homeomorphic to
$\omega $
colors on every subspace which is homeomorphic to
![]() $\mathbb Q$
.
$\mathbb Q$
.
3 Strong-coloring symbols over partitions
We introduce now the main new notion of symbols with an additional parameter p, where p is a partition of unordered pairs. Suppose
 $p:[\kappa ]^2\to \theta $
is a partition of unordered pairs from
$p:[\kappa ]^2\to \theta $
is a partition of unordered pairs from
![]() $\kappa $
. A preliminary definition of the square brackets symbol
$\kappa $
. A preliminary definition of the square brackets symbol
 $\kappa \nrightarrow _p[\kappa ]^2_{\kappa }$
with parameter p has been mentioned in the abstract: there exists a coloring
$\kappa \nrightarrow _p[\kappa ]^2_{\kappa }$
with parameter p has been mentioned in the abstract: there exists a coloring
 $f:[\kappa ]^2\to \kappa $
such that for every
$f:[\kappa ]^2\to \kappa $
such that for every
![]() $A\in [\kappa ]^{\kappa }$
there is some p-cell
$A\in [\kappa ]^{\kappa }$
there is some p-cell
![]() $i<\theta $
such that for all
$i<\theta $
such that for all
![]() $\unicode{x3b3} <\kappa $
there is
$\unicode{x3b3} <\kappa $
there is
 $\{\alpha ,\beta \}\in [A]^2$
such that
$\{\alpha ,\beta \}\in [A]^2$
such that
![]() $p(\alpha ,\beta )=i$
and
$p(\alpha ,\beta )=i$
and
![]() $f(\alpha ,\beta )=\unicode{x3b3} $
.
$f(\alpha ,\beta )=\unicode{x3b3} $
.
However, for
![]() $\operatorname {Pr}_1$
or for
$\operatorname {Pr}_1$
or for
![]() $\operatorname {Pr}_0$
it is not possible to require a prescribed pattern on
$\operatorname {Pr}_0$
it is not possible to require a prescribed pattern on
![]() $a\circledast b$
in both f and p when
$a\circledast b$
in both f and p when
![]() $a,b$
belong to an arbitrary
$a,b$
belong to an arbitrary
![]() $\mathcal A$
, as all such
$\mathcal A$
, as all such
![]() $a\circledast b$
might meet more than one p-cell. What we do, then, is replace this definition by a different one. The new definition is equivalent to the initial definition in all square-bracket symbols by Fact 5 below, and works for
$a\circledast b$
might meet more than one p-cell. What we do, then, is replace this definition by a different one. The new definition is equivalent to the initial definition in all square-bracket symbols by Fact 5 below, and works for
![]() $\operatorname {Pr}_1$
and
$\operatorname {Pr}_1$
and
![]() $\operatorname {Pr}_0$
.
$\operatorname {Pr}_0$
.
Definition 4. Suppose
 $f:[\kappa ]^d\to \lambda $
is a coloring and
$f:[\kappa ]^d\to \lambda $
is a coloring and
 $p:[\kappa ]^d\to \theta $
is a partition for a cardinal
$p:[\kappa ]^d\to \theta $
is a partition for a cardinal
![]() $\kappa $
and natural
$\kappa $
and natural
![]() $d>0$
. Then:
$d>0$
. Then:
-
(1) For a function
 $\zeta :\theta \to \lambda $
and
$\zeta :\theta \to \lambda $
and
 $\overline \alpha \in [\kappa ]^d$
we say that
$\overline \alpha \in [\kappa ]^d$
we say that
 $f \text { hits } \zeta \text { over } p \text { at } \overline \alpha $
, if
$f \text { hits } \zeta \text { over } p \text { at } \overline \alpha $
, if
 $f(\overline \alpha )=\zeta (p(\overline \alpha ))$
.
$f(\overline \alpha )=\zeta (p(\overline \alpha ))$
. -
(2) A set
 $X\subseteq [\kappa ]^d$
is
$X\subseteq [\kappa ]^d$
is
 $(f,p)$
-strong if for every
$(f,p)$
-strong if for every
 $\zeta \in \lambda ^{\theta }$
there is
$\zeta \in \lambda ^{\theta }$
there is
 $\overline \alpha \in X$
such that f hits
$\overline \alpha \in X$
such that f hits
 $\zeta $
over p at
$\zeta $
over p at
 $\overline \alpha $
.
$\overline \alpha $
.
Thus, the initial definition of an
![]() $(f,p)$
-strong
$(f,p)$
-strong
 $X\subseteq [\kappa ]^d$
— that
$X\subseteq [\kappa ]^d$
— that
 $(X\cap p^{-1}(i))$
is f-strong for some fixed p-cell i—is replaced in (2) above with the requirement that every assignment of colors to p-cells
$(X\cap p^{-1}(i))$
is f-strong for some fixed p-cell i—is replaced in (2) above with the requirement that every assignment of colors to p-cells
![]() $\zeta :\theta \to \lambda $
is hit by some
$\zeta :\theta \to \lambda $
is hit by some
![]() $\overline d\in X$
. The advantage of the new definition is that an assignment
$\overline d\in X$
. The advantage of the new definition is that an assignment
![]() $\zeta $
can be hit in any p-cell, so defining
$\zeta $
can be hit in any p-cell, so defining
![]() $\operatorname {Pr}_1$
and
$\operatorname {Pr}_1$
and
![]() $\operatorname {Pr}_0$
over a partition will now make sense.
$\operatorname {Pr}_0$
over a partition will now make sense.
Topologically, a set
 $X\subseteq [\kappa ]^d$
is
$X\subseteq [\kappa ]^d$
is
![]() $(f,p)$
-strong iff the collection
$(f,p)$
-strong iff the collection
 $\{u_{\langle p(\overline \alpha ),f(\overline \alpha )\rangle }:\overline \alpha \in X\}$
is an open cover of the space
$\{u_{\langle p(\overline \alpha ),f(\overline \alpha )\rangle }:\overline \alpha \in X\}$
is an open cover of the space
![]() $\lambda ^{\theta }$
of all
$\lambda ^{\theta }$
of all
![]() $\theta $
-sequences over
$\theta $
-sequences over
![]() $\lambda $
with the product topology, where
$\lambda $
with the product topology, where
![]() $u_{\langle i,\unicode{x3b3} \rangle }$
is the basic open set
$u_{\langle i,\unicode{x3b3} \rangle }$
is the basic open set
 $\{\zeta \in \lambda ^{\theta }: \zeta (i)=\unicode{x3b3} \}$
.
$\{\zeta \in \lambda ^{\theta }: \zeta (i)=\unicode{x3b3} \}$
.
The definitions of the main symbols over partitions which we shall work with are in Definition 7 below; an impatient reader can proceed there directly. We precede this definition with two useful facts about
![]() $(f,p)$
-strong sets.
$(f,p)$
-strong sets.
If
 $X\subseteq [\kappa ]^d$
is
$X\subseteq [\kappa ]^d$
is
![]() $(f,p)$
-strong then for every
$(f,p)$
-strong then for every
![]() $\unicode{x3b3} <\lambda $
there is
$\unicode{x3b3} <\lambda $
there is
![]() $\overline \alpha \in X$
such that
$\overline \alpha \in X$
such that
![]() $f(\overline \alpha )=\unicode{x3b3} $
since if
$f(\overline \alpha )=\unicode{x3b3} $
since if
![]() $\zeta $
is the constant sequence with value
$\zeta $
is the constant sequence with value
![]() $\unicode{x3b3} $
and
$\unicode{x3b3} $
and
![]() $\overline \alpha \in X$
is such that
$\overline \alpha \in X$
is such that
![]() $f(\overline \alpha )=\zeta (p(\overline \alpha ))$
then
$f(\overline \alpha )=\zeta (p(\overline \alpha ))$
then
![]() $f(\overline \alpha )=\unicode{x3b3} $
. This also follows from the next fact:
$f(\overline \alpha )=\unicode{x3b3} $
. This also follows from the next fact:
Fact 5. A set
 $X\subseteq [\kappa ]^d$
is
$X\subseteq [\kappa ]^d$
is
![]() $(f,p)$
-strong if and only if there is some
$(f,p)$
-strong if and only if there is some
![]() $i<\theta $
such that
$i<\theta $
such that
 $\lambda ={\operatorname {ran}} (f\restriction (X\cap p^{-1}(i)))$
.
$\lambda ={\operatorname {ran}} (f\restriction (X\cap p^{-1}(i)))$
.
Proof Suppose first that that
![]() $i<\theta $
is fixed so that
$i<\theta $
is fixed so that
 $\lambda ={\operatorname {ran}} (f\restriction (X\cap p^{-1}(i)))$
. Let
$\lambda ={\operatorname {ran}} (f\restriction (X\cap p^{-1}(i)))$
. Let
![]() $\zeta \in \lambda ^{\theta }$
be arbitrary and let
$\zeta \in \lambda ^{\theta }$
be arbitrary and let
![]() $\unicode{x3b3} =\zeta (i)$
. Fix some
$\unicode{x3b3} =\zeta (i)$
. Fix some
![]() $\overline \alpha \in X$
such that
$\overline \alpha \in X$
such that
![]() $f(\overline \alpha )=\unicode{x3b3} $
and
$f(\overline \alpha )=\unicode{x3b3} $
and
![]() $p(\overline \alpha )=i$
. Now
$p(\overline \alpha )=i$
. Now
![]() $f(\overline \alpha )=\zeta (p(\overline \alpha ))$
as required.
$f(\overline \alpha )=\zeta (p(\overline \alpha ))$
as required.
For the other direction suppose to the contrary that for every
![]() $i<\lambda $
there is some
$i<\lambda $
there is some
![]() $\zeta (i)\in (\lambda \setminus {\operatorname {ran}}(f\restriction X))$
. Since X is
$\zeta (i)\in (\lambda \setminus {\operatorname {ran}}(f\restriction X))$
. Since X is
![]() $(f,p)$
-strong, find
$(f,p)$
-strong, find
![]() $\overline \alpha \in X$
such that f hits
$\overline \alpha \in X$
such that f hits
![]() $\zeta $
over p at
$\zeta $
over p at
![]() $\overline \alpha $
. Let
$\overline \alpha $
. Let
![]() $i=p(\overline \alpha )$
. Now
$i=p(\overline \alpha )$
. Now
![]() $f(\overline \alpha )=\zeta (i)\notin {\operatorname {ran}} (f\restriction X)$
—a contradiction. ⊣
$f(\overline \alpha )=\zeta (i)\notin {\operatorname {ran}} (f\restriction X)$
—a contradiction. ⊣
Suppose that
 $h:[\kappa ]^d\to \lambda ^{<\mu }$
is some function into sequences of length
$h:[\kappa ]^d\to \lambda ^{<\mu }$
is some function into sequences of length
![]() $<\mu $
. For every partition
$<\mu $
. For every partition
 $p:[\kappa ]^d\to \theta $
for some
$p:[\kappa ]^d\to \theta $
for some
![]() $\theta <\mu $
, let
$\theta <\mu $
, let
 $h_p:[\kappa ]^d\to \lambda \cup \{*\}$
be defined by
$h_p:[\kappa ]^d\to \lambda \cup \{*\}$
be defined by
 $$ \begin{align*} h_p(\overline \alpha)= \begin{cases} h(\overline\alpha)(p(\overline\alpha)) & \text{ if } p(\overline\alpha)\in {\operatorname {dom}\,}(h(\overline\alpha)),\\ * & \text{ otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} h_p(\overline \alpha)= \begin{cases} h(\overline\alpha)(p(\overline\alpha)) & \text{ if } p(\overline\alpha)\in {\operatorname {dom}\,}(h(\overline\alpha)),\\ * & \text{ otherwise.} \end{cases} \end{align*} $$
Then for every
 $\overline \alpha \in [\kappa ]^d$
, if
$\overline \alpha \in [\kappa ]^d$
, if
 $h_p(\overline \alpha )\neq *$
then
$h_p(\overline \alpha )\neq *$
then
![]() $h_p$
hits
$h_p$
hits
![]() $h(\overline \alpha )$
over p at
$h(\overline \alpha )$
over p at
![]() $\overline \alpha $
. In particular, every
$\overline \alpha $
. In particular, every
 $X\subseteq [\kappa ]^d$
which is h-strong is also
$X\subseteq [\kappa ]^d$
which is h-strong is also
 $(h_p,p)$
-strong for every partition p of
$(h_p,p)$
-strong for every partition p of
 $[\kappa ]^d$
to
$[\kappa ]^d$
to
![]() $\theta <\mu $
cells. A simple book-keeping argument can waive the dependence of
$\theta <\mu $
cells. A simple book-keeping argument can waive the dependence of
![]() $h_p$
on p for a set of
$h_p$
on p for a set of
![]() $\le \lambda ^{<\mu }$
partitions:
$\le \lambda ^{<\mu }$
partitions:
Lemma 6. Suppose
 $h:[\kappa ]^d\to \lambda ^{<\mu }$
is given and
$h:[\kappa ]^d\to \lambda ^{<\mu }$
is given and
![]() $\overline p=\langle p_{\delta }:\delta <\lambda ^{<\mu }\rangle $
is a sequence such that
$\overline p=\langle p_{\delta }:\delta <\lambda ^{<\mu }\rangle $
is a sequence such that
 $p_{\delta }:[\kappa ]^d\to \theta _{\delta }$
and
$p_{\delta }:[\kappa ]^d\to \theta _{\delta }$
and
![]() $\theta _{\delta }<\mu $
for all
$\theta _{\delta }<\mu $
for all
![]() $\delta <\lambda ^{<\mu }$
. Then there is a single coloring
$\delta <\lambda ^{<\mu }$
. Then there is a single coloring
 $f:[\kappa ]^d\to \lambda $
such that for all
$f:[\kappa ]^d\to \lambda $
such that for all
 $X\subseteq [\kappa ]^d$
, if X is h-strong then X is
$X\subseteq [\kappa ]^d$
, if X is h-strong then X is
![]() $(f,p_{\delta })$
-strong for all
$(f,p_{\delta })$
-strong for all
![]() $\delta <\lambda ^{<\mu }$
.
$\delta <\lambda ^{<\mu }$
.
Proof Suppose
 $h:[\kappa ]^d\to \lambda ^{<\mu }$
and
$h:[\kappa ]^d\to \lambda ^{<\mu }$
and
![]() $\overline p=\langle p_{\delta }:\delta <\lambda ^{<\mu }\rangle $
are given, where
$\overline p=\langle p_{\delta }:\delta <\lambda ^{<\mu }\rangle $
are given, where
 $p_{\delta }:[\kappa ]^d\to \theta _{\delta }$
and
$p_{\delta }:[\kappa ]^d\to \theta _{\delta }$
and
![]() $\theta _{\delta }<\mu $
for every
$\theta _{\delta }<\mu $
for every
![]() $\delta <\lambda ^{<\mu }$
.
$\delta <\lambda ^{<\mu }$
.
Let
 $R=\bigcup \{\{\delta \}\times \lambda ^{\theta _{\delta }}:\delta <\lambda ^{<\mu }\}$
. As
$R=\bigcup \{\{\delta \}\times \lambda ^{\theta _{\delta }}:\delta <\lambda ^{<\mu }\}$
. As
![]() $|R|=\lambda ^{<\mu }$
, we may fix a bijection
$|R|=\lambda ^{<\mu }$
, we may fix a bijection
![]() $t:\lambda ^{<\mu }\to R$
and let
$t:\lambda ^{<\mu }\to R$
and let
![]() $g=t\circ h$
. So
$g=t\circ h$
. So
 $g:[\kappa ]^d\to R$
and every
$g:[\kappa ]^d\to R$
and every
 $X\subseteq [\kappa ]^d$
is g-strong iff it is h-strong.
$X\subseteq [\kappa ]^d$
is g-strong iff it is h-strong.
Define
 $f:[\kappa ]^d\to \lambda $
by
$f:[\kappa ]^d\to \lambda $
by
Let
 $X\subseteq [\kappa ]^d$
be given and assume that X is h-strong. Let
$X\subseteq [\kappa ]^d$
be given and assume that X is h-strong. Let
![]() $\delta <\lambda ^{<\mu }$
and some desirable
$\delta <\lambda ^{<\mu }$
and some desirable
![]() $\zeta \in \lambda ^{\theta _{\delta }}$
be given. As X is h-strong, it is also g-strong, so fix
$\zeta \in \lambda ^{\theta _{\delta }}$
be given. As X is h-strong, it is also g-strong, so fix
![]() ${\overline \alpha }\in X$
such that
${\overline \alpha }\in X$
such that
![]() $g(\overline \alpha )=\langle \delta ,\zeta \rangle $
. Now it holds by the definition of f that
$g(\overline \alpha )=\langle \delta ,\zeta \rangle $
. Now it holds by the definition of f that
![]() $f(\overline \alpha )=\zeta (p_{\delta }(\overline \alpha ))$
, that is f hits
$f(\overline \alpha )=\zeta (p_{\delta }(\overline \alpha ))$
, that is f hits
![]() $\zeta $
over
$\zeta $
over
![]() $p_{\delta }$
at
$p_{\delta }$
at
![]() $\overline \alpha \in X$
.⊣
$\overline \alpha \in X$
.⊣
We define now the main symbols over a partition. We state only the case for pairs. The definitions of the square-bracket symbols for
![]() $d\neq 2$
are similar.
$d\neq 2$
are similar.
Definition 7. Suppose
 $p:[\kappa ]^2\to \theta $
is a partition of all unordered pairs from a cardinal
$p:[\kappa ]^2\to \theta $
is a partition of all unordered pairs from a cardinal
![]() $\kappa $
.
$\kappa $
.
-
(1) The symbol
asserts the existence of a coloring $$ \begin{align*} \kappa\nrightarrow_p[\mu]^2_{\lambda} \end{align*} $$
$$ \begin{align*} \kappa\nrightarrow_p[\mu]^2_{\lambda} \end{align*} $$
 $f:[\kappa ]^2\to \lambda $
such that for all
$f:[\kappa ]^2\to \lambda $
such that for all
 $A\in [\kappa ]^{\mu }$
, for every
$A\in [\kappa ]^{\mu }$
, for every
 $\zeta \in \lambda ^{\theta }$
there is
$\zeta \in \lambda ^{\theta }$
there is
 $\{ \alpha ,\beta \}\in [A]^2$
such that
$\{ \alpha ,\beta \}\in [A]^2$
such that
 $f(\alpha , \beta )=\zeta (p(\alpha ,\beta ))$
.
$f(\alpha , \beta )=\zeta (p(\alpha ,\beta ))$
.
-
(2) The symbol
asserts the existence of a coloring $$ \begin{align*} \kappa\nrightarrow_p[\mu_1\circledast\mu_2]^2_{\lambda} \end{align*} $$
$$ \begin{align*} \kappa\nrightarrow_p[\mu_1\circledast\mu_2]^2_{\lambda} \end{align*} $$
 $f:[\kappa ]^2\to \lambda $
such that for all
$f:[\kappa ]^2\to \lambda $
such that for all
 $A\in [\kappa ]^{\mu _1}$
and
$A\in [\kappa ]^{\mu _1}$
and
 $B\in [\kappa ]^{\mu _2}$
, for every
$B\in [\kappa ]^{\mu _2}$
, for every
 $\zeta \in \lambda ^{\theta }$
there is
$\zeta \in \lambda ^{\theta }$
there is
 $\{\alpha ,\beta \}\in A\circledast B$
such that
$\{\alpha ,\beta \}\in A\circledast B$
such that
 $f( \alpha ,\beta )=\zeta (p(\alpha ,\beta ))$
.
$f( \alpha ,\beta )=\zeta (p(\alpha ,\beta ))$
.
-
(3) The symbol
asserts the existence of a coloring $$ \begin{align*}\operatorname{Pr}_1(\kappa,\mu,\lambda,\chi)_p\end{align*} $$
$$ \begin{align*}\operatorname{Pr}_1(\kappa,\mu,\lambda,\chi)_p\end{align*} $$
 $f:[\kappa ]^2\to \lambda $
such that for every
$f:[\kappa ]^2\to \lambda $
such that for every
 $\xi <\chi $
and a family
$\xi <\chi $
and a family
 $\mathcal A\subseteq [\kappa ]^{<\xi }$
of pairwise disjoint nonempty subsets of
$\mathcal A\subseteq [\kappa ]^{<\xi }$
of pairwise disjoint nonempty subsets of
 $\kappa $
such that
$\kappa $
such that
 $|\mathcal A|=\mu $
, for every
$|\mathcal A|=\mu $
, for every
 $\zeta \in \lambda ^{\theta }$
there are
$\zeta \in \lambda ^{\theta }$
there are
 $a,b\in \mathcal A$
such that
$a,b\in \mathcal A$
such that
 $\max a<\min b$
and
$\max a<\min b$
and
 $f(\alpha ,\beta )=\zeta (p(\alpha ,\beta ))$
for all
$f(\alpha ,\beta )=\zeta (p(\alpha ,\beta ))$
for all
 $\{\alpha ,\beta \}\in a\circledast b$
.
$\{\alpha ,\beta \}\in a\circledast b$
.
-
(4) The symbol
asserts the existence of a coloring $$ \begin{align*} \operatorname{Pr}_0(\kappa,\mu,\lambda,\chi)_p\end{align*} $$
$$ \begin{align*} \operatorname{Pr}_0(\kappa,\mu,\lambda,\chi)_p\end{align*} $$
 $f:[\kappa ]^2\to \lambda $
such that for every
$f:[\kappa ]^2\to \lambda $
such that for every
 $\xi <\chi $
, a pairwise disjoint family
$\xi <\chi $
, a pairwise disjoint family
 $\mathcal A\subseteq [\kappa ]^{\xi }$
of cardinality
$\mathcal A\subseteq [\kappa ]^{\xi }$
of cardinality
 $|\mathcal A|=\mu $
and a matrix
$|\mathcal A|=\mu $
and a matrix
 $\{\zeta _{i,j}:i,j<\xi \}\subseteq \lambda ^{\theta }$
there are
$\{\zeta _{i,j}:i,j<\xi \}\subseteq \lambda ^{\theta }$
there are
 $a,b\in \mathcal A$
with
$a,b\in \mathcal A$
with
 $\max a< \min b$
such that
$\max a< \min b$
such that
 $f(a(i),b(j))=\zeta _{i,j}(p(a(i),b(j))$
for all
$f(a(i),b(j))=\zeta _{i,j}(p(a(i),b(j))$
for all
 $i,j<\xi $
, where
$i,j<\xi $
, where
 $a(i),b(j)$
are the
$a(i),b(j)$
are the
 $i^{\text {th}}$
and
$i^{\text {th}}$
and
 $j^{\text {th}}$
elements of a and of b, respectively, in increasing order. If
$j^{\text {th}}$
elements of a and of b, respectively, in increasing order. If
 $\chi < {\operatorname {cf}}(\mu )$
then
$\chi < {\operatorname {cf}}(\mu )$
then
 $\operatorname {Pr}_0(\kappa ,\mu ,\lambda ,\chi )_p$
implies
$\operatorname {Pr}_0(\kappa ,\mu ,\lambda ,\chi )_p$
implies
 $\operatorname {Pr}_1(\kappa ,\mu ,\lambda ,\chi )_p$
.
$\operatorname {Pr}_1(\kappa ,\mu ,\lambda ,\chi )_p$
.
-
(5) Suppose
 $\overline p=\langle p_{\delta }:\delta <\delta (*)\rangle $
is a sequence of partitions
$\overline p=\langle p_{\delta }:\delta <\delta (*)\rangle $
is a sequence of partitions
 $p_{\delta }:[\kappa ]^2\to \theta _{\delta }$
. In each of the four symbols above, writing
$p_{\delta }:[\kappa ]^2\to \theta _{\delta }$
. In each of the four symbols above, writing
 $\overline p$
instead of p means there exists a single coloring which witnesses simultaneously the relation with
$\overline p$
instead of p means there exists a single coloring which witnesses simultaneously the relation with
 $p_{\delta }$
in place of p for each
$p_{\delta }$
in place of p for each
 $\delta <\delta (*)$
.
$\delta <\delta (*)$
.
By Fact 5, the first two symbols are equivalently defined by requiring that for every
 $X\subseteq [\kappa ]^2$
which is a
$X\subseteq [\kappa ]^2$
which is a
![]() $\mu $
-square or is a
$\mu $
-square or is a
![]() $(\mu _1,\mu _2)$
-rectangle there is a single cell
$(\mu _1,\mu _2)$
-rectangle there is a single cell
![]() $i<\theta $
(which depends on X) such that
$i<\theta $
(which depends on X) such that
 $X\cap p^{-1}(i)$
is f-strong.
$X\cap p^{-1}(i)$
is f-strong.
Fact 8. Suppose
![]() $\kappa \ge \mu \ge \lambda $
are cardinals. Then every coloring f which witnesses
$\kappa \ge \mu \ge \lambda $
are cardinals. Then every coloring f which witnesses
 $\operatorname {Pr}_1(\kappa ,\mu ,\lambda ,3)_p$
witnesses also
$\operatorname {Pr}_1(\kappa ,\mu ,\lambda ,3)_p$
witnesses also
 $\kappa \nrightarrow _p[\mu \circledast \mu ]^2_{\lambda }$
. In particular,
$\kappa \nrightarrow _p[\mu \circledast \mu ]^2_{\lambda }$
. In particular,
 $$ \begin{align*} \operatorname{Pr}_1(\kappa,\mu,\lambda,3)_p \,\,\, \Rightarrow \,\,\, \kappa\nrightarrow_p[\mu\circledast \mu]^2_{\lambda}\end{align*} $$
$$ \begin{align*} \operatorname{Pr}_1(\kappa,\mu,\lambda,3)_p \,\,\, \Rightarrow \,\,\, \kappa\nrightarrow_p[\mu\circledast \mu]^2_{\lambda}\end{align*} $$
for every partition
 $p:[\kappa ]^2\to \theta $
.
$p:[\kappa ]^2\to \theta $
.
Proof Fix
 $f:[\kappa ]^2\to \lambda $
which witnesses
$f:[\kappa ]^2\to \lambda $
which witnesses
 $\operatorname {Pr}_1(\kappa ,\mu ,\lambda ,3)_p$
. Let
$\operatorname {Pr}_1(\kappa ,\mu ,\lambda ,3)_p$
. Let
 $A\circledast B\subseteq [\kappa ]^2$
be an arbitrary
$A\circledast B\subseteq [\kappa ]^2$
be an arbitrary
![]() $(\mu ,\mu )$
-rectangle. Find inductively a pair-wise disjoint
$(\mu ,\mu )$
-rectangle. Find inductively a pair-wise disjoint
![]() $\mathcal A=\{a_i:i<\mu \}\subseteq A\circledast B$
. Given some
$\mathcal A=\{a_i:i<\mu \}\subseteq A\circledast B$
. Given some
![]() $\zeta \in \lambda ^{\theta }$
, fix
$\zeta \in \lambda ^{\theta }$
, fix
![]() $a=\{\alpha, \beta \}$
and
$a=\{\alpha, \beta \}$
and
![]() $b=\{\unicode{x3b3},\, \delta \}$
from
$b=\{\unicode{x3b3},\, \delta \}$
from
![]() $\mathcal A$
such that
$\mathcal A$
such that
![]() $\alpha <\beta <\unicode{x3b3} <\delta $
and such that f hits
$\alpha <\beta <\unicode{x3b3} <\delta $
and such that f hits
![]() $\zeta $
over p at all (four) elements
$\zeta $
over p at all (four) elements
![]() $\{x,y\}\in a\circledast b$
. In particular, f hits
$\{x,y\}\in a\circledast b$
. In particular, f hits
![]() $\zeta $
over p at
$\zeta $
over p at
![]() $\{\alpha,\,\delta \}$
which belongs to
$\{\alpha,\,\delta \}$
which belongs to
![]() $A\circledast B$
. ⊣
$A\circledast B$
. ⊣
The next lemma is the main tool for adding a partition parameter to a strong-coloring symbol.
Lemma 9. Suppose
![]() $\kappa \ge \mu \ge \lambda \ge \rho $
are cardinals. Then for every sequence of partitions
$\kappa \ge \mu \ge \lambda \ge \rho $
are cardinals. Then for every sequence of partitions
![]() $\overline p=\langle p_{\delta }:\delta <\lambda ^{<\rho }\rangle $
in which
$\overline p=\langle p_{\delta }:\delta <\lambda ^{<\rho }\rangle $
in which
 $p_{\delta }:[\kappa ]^2\to \theta _{\delta }$
and
$p_{\delta }:[\kappa ]^2\to \theta _{\delta }$
and
![]() $\theta _{\delta }<\rho $
for
$\theta _{\delta }<\rho $
for
![]() $\delta <\lambda ^{<\rho }$
:
$\delta <\lambda ^{<\rho }$
:
-
(1)
 $$ \begin{align*} \\[-40pt] \kappa\nrightarrow [\mu]^2_{\lambda^{<\rho}} \;\;\;\Rightarrow\;\;\; \kappa\nrightarrow_{\overline p}[\mu]^2_{\lambda}.\end{align*} $$
$$ \begin{align*} \\[-40pt] \kappa\nrightarrow [\mu]^2_{\lambda^{<\rho}} \;\;\;\Rightarrow\;\;\; \kappa\nrightarrow_{\overline p}[\mu]^2_{\lambda}.\end{align*} $$
-
(2) For all
 $\mu '\le \mu $
,
$\mu '\le \mu $
,  $$ \begin{align*}\kappa\nrightarrow [\mu'\circledast \mu]^2_{\lambda^{<\rho}}\;\;\;\Rightarrow\;\;\; \kappa\nrightarrow_{\overline p} [\mu'\circledast \mu]^2_{\lambda}.\end{align*} $$
$$ \begin{align*}\kappa\nrightarrow [\mu'\circledast \mu]^2_{\lambda^{<\rho}}\;\;\;\Rightarrow\;\;\; \kappa\nrightarrow_{\overline p} [\mu'\circledast \mu]^2_{\lambda}.\end{align*} $$
-
(3)

-
(4) For all
 $\chi>0$
,
$\chi>0$
,  $$ \begin{align*}\operatorname{Pr}_0(\kappa,\mu,\lambda^{<\rho},\chi)\;\;\;\Rightarrow\;\;\; \operatorname{Pr}_0(\kappa,\mu,\lambda,\chi)_{\overline p}.\end{align*} $$
$$ \begin{align*}\operatorname{Pr}_0(\kappa,\mu,\lambda^{<\rho},\chi)\;\;\;\Rightarrow\;\;\; \operatorname{Pr}_0(\kappa,\mu,\lambda,\chi)_{\overline p}.\end{align*} $$
-
(5) For all
 $\chi>0$
,
$\chi>0$
,  $$ \begin{align*}\operatorname{Pr}_1(\kappa,\mu,\lambda^{<\rho},\chi)\;\;\;\Rightarrow\;\;\; \operatorname{Pr}_1(\kappa,\mu,\lambda,\chi)_{\overline p}.\end{align*} $$
$$ \begin{align*}\operatorname{Pr}_1(\kappa,\mu,\lambda^{<\rho},\chi)\;\;\;\Rightarrow\;\;\; \operatorname{Pr}_1(\kappa,\mu,\lambda,\chi)_{\overline p}.\end{align*} $$
Proof Given any of the first three symbols in the hypotheses above, fix a coloring
 $h:[\kappa ]^2\to \lambda ^{<\rho }$
which witnesses it. Suppose
$h:[\kappa ]^2\to \lambda ^{<\rho }$
which witnesses it. Suppose
![]() $\overline p=\langle p_{\delta }:\delta <\lambda ^{<\rho }\rangle $
is given, where
$\overline p=\langle p_{\delta }:\delta <\lambda ^{<\rho }\rangle $
is given, where
 $p_{\delta }:[\kappa ]^2\to \theta _{\delta }$
and
$p_{\delta }:[\kappa ]^2\to \theta _{\delta }$
and
![]() $\theta _{\delta }<\rho $
for every
$\theta _{\delta }<\rho $
for every
![]() $\delta <\lambda ^{<\rho }$
.
$\delta <\lambda ^{<\rho }$
.
By Lemma 6 fix
 $f:[\kappa ]^2\to \lambda $
such that every
$f:[\kappa ]^2\to \lambda $
such that every
 $X\subseteq [\kappa ]^2$
which is h-strong is also
$X\subseteq [\kappa ]^2$
which is h-strong is also
![]() $(f,p_{\delta })$
-strong for all
$(f,p_{\delta })$
-strong for all
![]() $\delta <\lambda ^{<\rho }$
. Let
$\delta <\lambda ^{<\rho }$
. Let
![]() $\delta <\lambda ^{<\rho }$
be arbitrary. Suppose that
$\delta <\lambda ^{<\rho }$
be arbitrary. Suppose that
 $X\subseteq [\kappa ]^2$
is some
$X\subseteq [\kappa ]^2$
is some
![]() $\mu $
-square
$\mu $
-square
 $[A]^2$
or X is some
$[A]^2$
or X is some
![]() $(\mu ',\mu )$
-rectangle
$(\mu ',\mu )$
-rectangle
![]() $A\circledast B$
. Then X is
$A\circledast B$
. Then X is
![]() $(f,p_{\delta })$
-strong. This proves the first two implications. For the third, let
$(f,p_{\delta })$
-strong. This proves the first two implications. For the third, let
![]() $A\circledast B$
be some
$A\circledast B$
be some
![]() $(\kappa ,\kappa ^+)$
-rectangle. By the hypothesis, there is some
$(\kappa ,\kappa ^+)$
-rectangle. By the hypothesis, there is some
![]() $\alpha \in A$
such that
$\alpha \in A$
such that
![]() $\{\alpha \}\circledast B$
is h-strong, hence it is also
$\{\alpha \}\circledast B$
is h-strong, hence it is also
![]() $(f,p_{\delta })$
-strong.
$(f,p_{\delta })$
-strong.
To prove the fourth implication, let, as in the proof of Lemma 6,
 $R=\bigcup \bigl \{\{\delta \}\times \lambda ^{\theta _{\delta }}:\delta <\lambda ^{<\rho }\bigr \}$
, let
$R=\bigcup \bigl \{\{\delta \}\times \lambda ^{\theta _{\delta }}:\delta <\lambda ^{<\rho }\bigr \}$
, let
 $g:[\kappa ]^2\to R$
witness
$g:[\kappa ]^2\to R$
witness
![]() $\operatorname {Pr}_0(\kappa ,\mu ,\lambda ^{<\rho },\chi )$
and let
$\operatorname {Pr}_0(\kappa ,\mu ,\lambda ^{<\rho },\chi )$
and let
![]() $f(\alpha ,\beta )=\zeta (p_{\delta }(\alpha ,\beta ))$
when
$f(\alpha ,\beta )=\zeta (p_{\delta }(\alpha ,\beta ))$
when
![]() $g(\alpha ,\beta )=\langle \delta ,\zeta \rangle $
. Suppose
$g(\alpha ,\beta )=\langle \delta ,\zeta \rangle $
. Suppose
![]() $\xi <\chi $
and
$\xi <\chi $
and
 $\mathcal A\subseteq [\kappa ]^{\xi }$
is pair-wise disjoint and
$\mathcal A\subseteq [\kappa ]^{\xi }$
is pair-wise disjoint and
![]() $|\mathcal A|=\mu $
. Given any
$|\mathcal A|=\mu $
. Given any
![]() $\delta <\lambda ^{<\rho }$
and
$\delta <\lambda ^{<\rho }$
and
 $\{\zeta _{i,j}:i,j<\xi \}\subseteq \lambda ^{\theta _{\delta }}$
, use the fact g witnesses
$\{\zeta _{i,j}:i,j<\xi \}\subseteq \lambda ^{\theta _{\delta }}$
, use the fact g witnesses
![]() $\operatorname {Pr}_0(\kappa ,\mu ,\lambda ^{<\rho },\chi )$
to fix
$\operatorname {Pr}_0(\kappa ,\mu ,\lambda ^{<\rho },\chi )$
to fix
![]() $a,b\in \mathcal A$
such that
$a,b\in \mathcal A$
such that
![]() $\max a<\min b$
and
$\max a<\min b$
and
 $f(\alpha (i),\beta (j))=\langle \delta ,\zeta _{i,j}\rangle $
for all
$f(\alpha (i),\beta (j))=\langle \delta ,\zeta _{i,j}\rangle $
for all
![]() $i,j<\xi $
, where
$i,j<\xi $
, where
![]() $a(i)$
and
$a(i)$
and
![]() $b(j)$
are the
$b(j)$
are the
![]() $i^{\text {th}}$
and
$i^{\text {th}}$
and
 $j^{\text {th}}$
members of a and of b respectively. Now
$j^{\text {th}}$
members of a and of b respectively. Now
 $f(a(i),b(j))=\zeta _{i,j}(p_{\delta }(a(i),b(j))$
as required.
$f(a(i),b(j))=\zeta _{i,j}(p_{\delta }(a(i),b(j))$
as required.
The proof of the last implication is gotten from the fourth by using constant
![]() $\zeta _{i,j}=\zeta $
. ⊣
$\zeta _{i,j}=\zeta $
. ⊣
4 Valid symbols over partitions in ZFC and in ZFC with additional axioms
Question 10. Suppose
![]() $\kappa \ge \rho $
are cardinals. Which strong-coloring symbols in
$\kappa \ge \rho $
are cardinals. Which strong-coloring symbols in
![]() $\kappa $
hold over all
$\kappa $
hold over all
![]() $<\rho $
partitions?
$<\rho $
partitions?
Clearly, every coloring which witnesses a strong-coloring symbol
![]() $\Phi $
over some partition p, witnesses the symbol gotten by deleting p from
$\Phi $
over some partition p, witnesses the symbol gotten by deleting p from
![]() $\Phi $
. The question of existence of strong colorings over partition therefore refines the question of existence of strong colorings in the classical sense.
$\Phi $
. The question of existence of strong colorings over partition therefore refines the question of existence of strong colorings in the classical sense.
Let us mention two obvious constraints on obtaining strong-coloring symbols over partitions. Given any coloring
 $f:[\kappa ]^2\to \lambda $
with
$f:[\kappa ]^2\to \lambda $
with
![]() $\lambda \ge 2$
, let us define, for
$\lambda \ge 2$
, let us define, for
![]() $\alpha <\beta <\kappa $
,
$\alpha <\beta <\kappa $
,
![]() $p(\alpha ,\beta )=0\iff f(\alpha ,\beta )=0$
and
$p(\alpha ,\beta )=0\iff f(\alpha ,\beta )=0$
and
![]() $p(\alpha ,\beta )=1$
otherwise. Then f does not witness
$p(\alpha ,\beta )=1$
otherwise. Then f does not witness
 $\kappa \nrightarrow _p [\kappa ]^2_{\lambda }$
. Hence:
$\kappa \nrightarrow _p [\kappa ]^2_{\lambda }$
. Hence:
Fact 11. No single coloring witnesses
 $\kappa \nrightarrow _p [\kappa ]^2_{\lambda }$
for all two-partitions p if
$\kappa \nrightarrow _p [\kappa ]^2_{\lambda }$
for all two-partitions p if
![]() $\lambda>1$
.
$\lambda>1$
.
If
![]() $\theta \ge {\operatorname {cf}}(\kappa )$
then there is a partition
$\theta \ge {\operatorname {cf}}(\kappa )$
then there is a partition
 $p:[\kappa ]^2\to \theta $
with
$p:[\kappa ]^2\to \theta $
with
 $|p^{-1}(i)|<\kappa $
for every
$|p^{-1}(i)|<\kappa $
for every
![]() $i<\theta $
, so
$i<\theta $
, so
 $\kappa \nrightarrow _p[\kappa ]^2_{\kappa }$
cannot hold. This narrows down the discussion of
$\kappa \nrightarrow _p[\kappa ]^2_{\kappa }$
cannot hold. This narrows down the discussion of
 $\kappa \nrightarrow _p[\kappa ]^2_{\kappa }$
to partitions
$\kappa \nrightarrow _p[\kappa ]^2_{\kappa }$
to partitions
 $p:[\kappa ^2]\to \theta $
with
$p:[\kappa ^2]\to \theta $
with
![]() $\theta <{\operatorname {cf}}(\kappa )$
.
$\theta <{\operatorname {cf}}(\kappa )$
.
4.1 Symbols which are valid in ZFC
Every infinite cardinal
![]() $\lambda $
satisfies
$\lambda $
satisfies
![]() $\lambda ^{<\aleph _0}=\lambda $
. Therefore, by Lemma 9, every symbol with
$\lambda ^{<\aleph _0}=\lambda $
. Therefore, by Lemma 9, every symbol with
![]() $\lambda \ge \aleph _0$
colors which holds in ZFC continues to hold in ZFC over any sequence of length
$\lambda \ge \aleph _0$
colors which holds in ZFC continues to hold in ZFC over any sequence of length
![]() $\lambda $
of finite partitions.
$\lambda $
of finite partitions.
Let us state ZFC symbols over partitions whose classical counterparts were mentioned in §2 above:
Theorem 12. For every regular cardinal
![]() $\kappa $
and a sequence of length
$\kappa $
and a sequence of length
![]() $\kappa ^+$
of finite partitions of
$\kappa ^+$
of finite partitions of
 $[\kappa ^+]^2$
,
$[\kappa ^+]^2$
,
 $$ \begin{align*} \kappa^+\nrightarrow_{\overline p}[\kappa^+\circledast \kappa^+]^2_{\kappa^+}. \end{align*} $$
$$ \begin{align*} \kappa^+\nrightarrow_{\overline p}[\kappa^+\circledast \kappa^+]^2_{\kappa^+}. \end{align*} $$
Proof The symbol without
![]() $\overline p$
holds by the results of Todorčević, Moore and Shelah. Now apply Lemma 9(1). ⊣
$\overline p$
holds by the results of Todorčević, Moore and Shelah. Now apply Lemma 9(1). ⊣
In particular,
Corollary 13. For every finite partition
 $p:[\omega _1]^2\to n$
,
$p:[\omega _1]^2\to n$
,
 $$ \begin{align*} \omega_1\nrightarrow_p [\omega_1\circledast \omega_1]^2_{\omega_1} \;\;\; \text{ and } \;\;\; \omega_1\nrightarrow_p[\omega_1]^2_{\omega_1}. \end{align*} $$
$$ \begin{align*} \omega_1\nrightarrow_p [\omega_1\circledast \omega_1]^2_{\omega_1} \;\;\; \text{ and } \;\;\; \omega_1\nrightarrow_p[\omega_1]^2_{\omega_1}. \end{align*} $$
Theorem 14. For every sequence of length
![]() $\omega _2$
of finite partitions of
$\omega _2$
of finite partitions of
 $[\omega _2]^3$
,
$[\omega _2]^3$
,
 $$ \begin{align*} \omega_2\nrightarrow_{\overline p}[\omega_1]^3_{\omega}, \end{align*} $$
$$ \begin{align*} \omega_2\nrightarrow_{\overline p}[\omega_1]^3_{\omega}, \end{align*} $$
and
 $\omega _2\nrightarrow _{\overline p}[\omega _1]^3_{\omega _1}$
is equivalent to the negation of the
$\omega _2\nrightarrow _{\overline p}[\omega _1]^3_{\omega _1}$
is equivalent to the negation of the
![]() $(\aleph _2,\aleph _1)$
Chang conjecture.
$(\aleph _2,\aleph _1)$
Chang conjecture.
Proof The symbol
 $\omega _2\nrightarrow [\omega _1]^3_{\omega }$
holds by Todorevic’s [Reference Todorčević43], and now apply Lemma 6 as in the proof of Lemma 9. ⊣
$\omega _2\nrightarrow [\omega _1]^3_{\omega }$
holds by Todorevic’s [Reference Todorčević43], and now apply Lemma 6 as in the proof of Lemma 9. ⊣
Theorem 15. For every cardinal
![]() $\kappa $
and a list
$\kappa $
and a list
![]() $\overline p$
of length
$\overline p$
of length
![]() $\kappa ^{++}$
of finite partitions of
$\kappa ^{++}$
of finite partitions of
 $[\kappa ^{++}]^2$
,
$[\kappa ^{++}]^2$
,
 $$ \begin{align*} \operatorname{Pr}_1(\kappa^{++},\kappa^{++},\kappa^{++},\kappa)_{\overline p}. \end{align*} $$
$$ \begin{align*} \operatorname{Pr}_1(\kappa^{++},\kappa^{++},\kappa^{++},\kappa)_{\overline p}. \end{align*} $$
Proof By Shelah’s [Reference Shelah34] and Lemma 9(4). ⊣
Theorem 16. For every cardinal
![]() $\kappa $
and a list
$\kappa $
and a list
![]() $\overline p$
of length
$\overline p$
of length
![]() $\kappa ^{++}$
of finite partitions of
$\kappa ^{++}$
of finite partitions of
 $[\kappa ^{++}]^2$
,
$[\kappa ^{++}]^2$
,
 $$ \begin{align*} \operatorname{Pr}_0(\kappa^{++},\kappa^{++},\kappa^{++},\aleph_0)_{\overline p}. \end{align*} $$
$$ \begin{align*} \operatorname{Pr}_0(\kappa^{++},\kappa^{++},\kappa^{++},\aleph_0)_{\overline p}. \end{align*} $$
Proof By Shelah’s [Reference Shelah34], 4.5(3) p. 170 in [Reference Shelah38] and Lemma 9(5). ⊣
Theorem 17. For every singular cardinal
![]() $\mu $
and a sequence of length
$\mu $
and a sequence of length
![]() ${\operatorname {cf}}(\mu )$
of finite partitions of
${\operatorname {cf}}(\mu )$
of finite partitions of
 $[\mu ^+]^2$
,
$[\mu ^+]^2$
,
 $$ \begin{align*} \operatorname{Pr}_1(\mu^+,\mu^+,{\operatorname {cf}}(\mu),{\operatorname {cf}}(\mu))_{\overline p}.\end{align*} $$
$$ \begin{align*} \operatorname{Pr}_1(\mu^+,\mu^+,{\operatorname {cf}}(\mu),{\operatorname {cf}}(\mu))_{\overline p}.\end{align*} $$
Proof By Shelah’s 4.1 p. 67 of [Reference Shelah38] and Lemma 9(4). ⊣
Theorem 18. For every singular
![]() $\mu $
and a sequence
$\mu $
and a sequence
![]() $\overline p$
of length
$\overline p$
of length
![]() $\mu ^+$
of finite partitions of
$\mu ^+$
of finite partitions of
 $[\mu ^+]^2$
,
$[\mu ^+]^2$
,
 $$ \begin{align*} \mu^+\nrightarrow[\mu^+]^2_{\mu^+}\Rightarrow \operatorname{Pr}_1(\mu^+,\mu^+,\mu^+,{\operatorname {cf}}(\mu))_{\overline p} \wedge \operatorname{Pr}_0(\mu^+,\mu^+,\mu^+,\aleph_0)_{\overline p}. \end{align*} $$
$$ \begin{align*} \mu^+\nrightarrow[\mu^+]^2_{\mu^+}\Rightarrow \operatorname{Pr}_1(\mu^+,\mu^+,\mu^+,{\operatorname {cf}}(\mu))_{\overline p} \wedge \operatorname{Pr}_0(\mu^+,\mu^+,\mu^+,\aleph_0)_{\overline p}. \end{align*} $$
Proof Suppose
 $\mu ^+\nrightarrow [\mu ^+]^2_{\mu ^+}$
. By Rinot’s [Reference Rinot23], also
$\mu ^+\nrightarrow [\mu ^+]^2_{\mu ^+}$
. By Rinot’s [Reference Rinot23], also
![]() $\operatorname {Pr}_1(\mu ^+,\mu ^+,\mu ^+,{\operatorname {cf}}(\mu ))$
holds. The first conjuct now follows by Lemma 9(4). To get the second conjunct observes that by the first conjunct we have in particular
$\operatorname {Pr}_1(\mu ^+,\mu ^+,\mu ^+,{\operatorname {cf}}(\mu ))$
holds. The first conjuct now follows by Lemma 9(4). To get the second conjunct observes that by the first conjunct we have in particular
![]() $\operatorname {Pr}_1(\mu ^+,\mu ^+,\mu ^+,\aleph _0)$
. The second conjunct follows now by 4.5(3) in [Reference Shelah38] and Lemma 9(5). ⊣
$\operatorname {Pr}_1(\mu ^+,\mu ^+,\mu ^+,\aleph _0)$
. The second conjunct follows now by 4.5(3) in [Reference Shelah38] and Lemma 9(5). ⊣
4.2 Symbols from instances of the GCH or of the SCH
If the GCH holds then every regular cardinal
![]() $\lambda $
satisfies
$\lambda $
satisfies
![]() $\lambda ^{<\lambda }=\lambda $
. Thus,
$\lambda ^{<\lambda }=\lambda $
. Thus,
Theorem 19 GCH
In Theorems (12)-(18) above, “finite partitions” may be replaced by
![]() $<\lambda $
-partitions.
$<\lambda $
-partitions.
The GCH also makes Shelah’s implication 4.5(3) from [Reference Shelah38] valid in additional cases. For example,
Theorem 20 GCH
For every regular cardinal
![]() $\kappa $
and a sequence
$\kappa $
and a sequence
![]() $\overline p$
of length
$\overline p$
of length
![]() $\kappa ^{++}$
of
$\kappa ^{++}$
of
![]() $\kappa ^+$
-partitions,
$\kappa ^+$
-partitions,
 $$ \begin{align*} \operatorname{Pr}_0(\kappa^{++},\kappa^{++},\kappa^{++},\kappa)_{\overline p}. \end{align*} $$
$$ \begin{align*} \operatorname{Pr}_0(\kappa^{++},\kappa^{++},\kappa^{++},\kappa)_{\overline p}. \end{align*} $$
Proof By Shelah’s [Reference Shelah34] we have
![]() $\operatorname {Pr}_1(\kappa ^{++},\kappa ^{++},\kappa ^{++},\kappa )$
in ZFC. Let
$\operatorname {Pr}_1(\kappa ^{++},\kappa ^{++},\kappa ^{++},\kappa )$
in ZFC. Let
![]() $\rho =\kappa ^+$
. By the GCH,
$\rho =\kappa ^+$
. By the GCH,
![]() $\rho ^{<\kappa }=\rho $
and
$\rho ^{<\kappa }=\rho $
and
![]() $(\kappa ^{++})^{<\kappa }=\kappa ^{++}$
, so
$(\kappa ^{++})^{<\kappa }=\kappa ^{++}$
, so
![]() $\rho $
qualifies as an interpolant in 4.5(3) p. 170 in [Reference Shelah38] and
$\rho $
qualifies as an interpolant in 4.5(3) p. 170 in [Reference Shelah38] and
![]() $\operatorname {Pr}_0(\kappa ^{++},\kappa ^{++},\kappa ^{++},\kappa )$
follows. Now use GCH again with Lemma 9(5). ⊣
$\operatorname {Pr}_0(\kappa ^{++},\kappa ^{++},\kappa ^{++},\kappa )$
follows. Now use GCH again with Lemma 9(5). ⊣
Theorem 21. For every cardinal
![]() $\kappa $
, if
$\kappa $
, if
![]() $2^{\kappa }=\kappa ^+$
then for every sequence p of length
$2^{\kappa }=\kappa ^+$
then for every sequence p of length
![]() $\kappa ^+$
of
$\kappa ^+$
of
![]() $\kappa $
-partitions of
$\kappa $
-partitions of
 $[\kappa ]^2$
,
$[\kappa ]^2$
,

Proof The symbol
 follows from
follows from
![]() $2^{\kappa }=\kappa ^+$
by the and Erdoős–Hajnal–Milner theorem (see Section 49 in [Reference Erdős, Hajnal, Máté and Rado5]). Use now Lemma 9(2). ⊣
$2^{\kappa }=\kappa ^+$
by the and Erdoős–Hajnal–Milner theorem (see Section 49 in [Reference Erdős, Hajnal, Máté and Rado5]). Use now Lemma 9(2). ⊣
Theorem 22. For every singular cardinal
![]() $\mu $
, if
$\mu $
, if
![]() $\operatorname {pp}(\mu )=\mu ^+$
then for every sequence
$\operatorname {pp}(\mu )=\mu ^+$
then for every sequence
![]() $\overline p$
of length
$\overline p$
of length
![]() $\mu ^+$
of finite partitions of
$\mu ^+$
of finite partitions of
 $[\mu ^+]^2$
,
$[\mu ^+]^2$
,
 $$ \begin{align*} \operatorname{Pr}_1(\mu^+,\mu^+,\mu^+,{\operatorname {cf}}(\mu))_{\overline p}. \end{align*} $$
$$ \begin{align*} \operatorname{Pr}_1(\mu^+,\mu^+,\mu^+,{\operatorname {cf}}(\mu))_{\overline p}. \end{align*} $$
Proof By
![]() $\operatorname {pp}(\mu )=\mu ^+$
and Eisworth’s theorem [Reference Eisworth10],
$\operatorname {pp}(\mu )=\mu ^+$
and Eisworth’s theorem [Reference Eisworth10],
![]() $\operatorname {Pr}_1(\mu ^+,\mu ^+,\mu ^+,{\operatorname {cf}}(\mu ))$
holds. Now use Lemma 9(4). ⊣
$\operatorname {Pr}_1(\mu ^+,\mu ^+,\mu ^+,{\operatorname {cf}}(\mu ))$
holds. Now use Lemma 9(4). ⊣
Theorem 23 GCH
For every singular cardinal
![]() $\mu $
and a sequence
$\mu $
and a sequence
![]() $\overline p$
of length
$\overline p$
of length
![]() $\mu ^+$
of
$\mu ^+$
of
![]() $\mu $
-partitions of
$\mu $
-partitions of
 $[\mu ^+]^2$
,
$[\mu ^+]^2$
,
 $$ \begin{align*} \operatorname{Pr}_0(\mu^+,\mu^+,\mu^+,{\operatorname {cf}}(\mu))_{\overline p}. \end{align*} $$
$$ \begin{align*} \operatorname{Pr}_0(\mu^+,\mu^+,\mu^+,{\operatorname {cf}}(\mu))_{\overline p}. \end{align*} $$
Proof By Eisworth’s theorem it holds that
![]() $\operatorname {Pr}_1(\mu ^+,\mu ^+,\mu ^+,{\operatorname {cf}}(\mu ))$
. By the GCH and Shelah’s 4.5(3) in [Reference Shelah38], also
$\operatorname {Pr}_1(\mu ^+,\mu ^+,\mu ^+,{\operatorname {cf}}(\mu ))$
. By the GCH and Shelah’s 4.5(3) in [Reference Shelah38], also
![]() $\operatorname {Pr}_0(\mu ^+,\mu ^+,\mu ^+,{\operatorname {cf}}(\mu ))$
holds. Finally, as
$\operatorname {Pr}_0(\mu ^+,\mu ^+,\mu ^+,{\operatorname {cf}}(\mu ))$
holds. Finally, as
![]() $(\mu ^+)^{\mu }=\mu ^+$
, by Lemma 9(5), for every sequence
$(\mu ^+)^{\mu }=\mu ^+$
, by Lemma 9(5), for every sequence
![]() $\overline p$
of length
$\overline p$
of length
![]() $\mu ^+$
of
$\mu ^+$
of
![]() $\mu $
-partitions of
$\mu $
-partitions of
![]() $[\mu ]^+$
it holds that
$[\mu ]^+$
it holds that
 $\operatorname {Pr}_0(\mu ^+,\mu ^+,\mu ^+,{\operatorname {cf}}(\mu ))_{\overline p}$
. ⊣
$\operatorname {Pr}_0(\mu ^+,\mu ^+,\mu ^+,{\operatorname {cf}}(\mu ))_{\overline p}$
. ⊣
In the next theorem a different cardinal arithmetic assumption appears:
Theorem 24. If
![]() $\mu $
is a singular cardinal and
$\mu $
is a singular cardinal and
 $2^{{\operatorname {cf}}(\mu )}>\mu $
then for every sequence
$2^{{\operatorname {cf}}(\mu )}>\mu $
then for every sequence
![]() $\overline p$
of length
$\overline p$
of length
![]() $\mu ^+$
of finite partitions of
$\mu ^+$
of finite partitions of
 $[\mu ^+]^2$
,
$[\mu ^+]^2$
,
 $$ \begin{align*} \operatorname{Pr}_0(\mu^+,\mu^+,{\operatorname {cf}}(\mu),\aleph_0)_{\overline p}. \end{align*} $$
$$ \begin{align*} \operatorname{Pr}_0(\mu^+,\mu^+,{\operatorname {cf}}(\mu),\aleph_0)_{\overline p}. \end{align*} $$
Proof By Shelah’s 4.1 p. 67 the symbol
![]() $\operatorname {Pr}_1(\mu ^+,\mu ^+,{\operatorname {cf}}(\mu ),{\operatorname {cf}}(\mu ))$
holds in ZFC. Choose
$\operatorname {Pr}_1(\mu ^+,\mu ^+,{\operatorname {cf}}(\mu ),{\operatorname {cf}}(\mu ))$
holds in ZFC. Choose
![]() $\rho ={\operatorname {cf}}(\mu )$
. So
$\rho ={\operatorname {cf}}(\mu )$
. So
![]() $2^{\rho }\ge \mu ^+$
,
$2^{\rho }\ge \mu ^+$
,
 $\rho ^{<\aleph _0}=\rho $
and
$\rho ^{<\aleph _0}=\rho $
and
 ${\operatorname {cf}}(\mu ^+)>\rho ^{<\aleph _0}$
, so
${\operatorname {cf}}(\mu ^+)>\rho ^{<\aleph _0}$
, so
![]() $\rho $
qualifies as an interpolant cardinal in 4.5(3) p. 170 in [Reference Shelah38] and
$\rho $
qualifies as an interpolant cardinal in 4.5(3) p. 170 in [Reference Shelah38] and
![]() $\operatorname {Pr}_0(\mu ^+,\mu ^+,{\operatorname {cf}}(\mu ),\aleph _0)$
follows. Now use Lemma 9(5). ⊣
$\operatorname {Pr}_0(\mu ^+,\mu ^+,{\operatorname {cf}}(\mu ),\aleph _0)$
follows. Now use Lemma 9(5). ⊣
Lastly in this section, we show that
 , an axiom (stated in the proof below), which does not imply
, an axiom (stated in the proof below), which does not imply
![]() $2^{\kappa }=\kappa ^+$
, implies the following rectangular square-brackets symbol.
$2^{\kappa }=\kappa ^+$
, implies the following rectangular square-brackets symbol.
Theorem 25. If
![]() $\kappa $
is a cardinal and
$\kappa $
is a cardinal and

holds then for every sequence of partitions
![]() $\overline p=\langle p_{\unicode{x3b3} }:\unicode{x3b3} <\kappa ^+\rangle $
, where
$\overline p=\langle p_{\unicode{x3b3} }:\unicode{x3b3} <\kappa ^+\rangle $
, where
 $p_{\unicode{x3b3} }:[\kappa ^+]^2\to \lambda _{\unicode{x3b3} }$
and
$p_{\unicode{x3b3} }:[\kappa ^+]^2\to \lambda _{\unicode{x3b3} }$
and
 $\lambda _{\unicode{x3b3} }<{\operatorname {cf}}(\kappa )$
for each
$\lambda _{\unicode{x3b3} }<{\operatorname {cf}}(\kappa )$
for each
![]() $\unicode{x3b3} <\kappa ^+$
, it holds that
$\unicode{x3b3} <\kappa ^+$
, it holds that

That is, there exists a coloring
 $f:[\kappa ^+]^2\to \kappa ^+$
such that for every
$f:[\kappa ^+]^2\to \kappa ^+$
such that for every
![]() $(\kappa ^+,\kappa ^+)$
-rectangle
$(\kappa ^+,\kappa ^+)$
-rectangle
![]() $A\circledast B$
and
$A\circledast B$
and
![]() $\unicode{x3b3} <\omega _1$
there is
$\unicode{x3b3} <\omega _1$
there is
![]() $j<\lambda _{\unicode{x3b3} }$
and
$j<\lambda _{\unicode{x3b3} }$
and
![]() $X\in [A]^{\kappa }$
such that
$X\in [A]^{\kappa }$
such that
 $$ \begin{align*} \kappa^+={\operatorname {ran}} \bigl( f\restriction [(X\circledast B)\cap p_{\unicode{x3b3}}^{-1}(j)] \bigr). \end{align*} $$
$$ \begin{align*} \kappa^+={\operatorname {ran}} \bigl( f\restriction [(X\circledast B)\cap p_{\unicode{x3b3}}^{-1}(j)] \bigr). \end{align*} $$
Proof Suppose a sequence of partitions
![]() $\overline p =\langle p_{\unicode{x3b3} }:\unicode{x3b3} <\kappa ^+\rangle $
is given as above and we shall define the required f assuming
$\overline p =\langle p_{\unicode{x3b3} }:\unicode{x3b3} <\kappa ^+\rangle $
is given as above and we shall define the required f assuming
 . Fix a sequence
. Fix a sequence
![]() $\langle X_i:i<\kappa ^+\rangle $
which witnesses
$\langle X_i:i<\kappa ^+\rangle $
which witnesses
 , that is:
, that is:
![]() $X_i\subseteq \kappa ^+$
,
$X_i\subseteq \kappa ^+$
,
![]() ${\operatorname {otp}} (X_i)=\kappa $
for each
${\operatorname {otp}} (X_i)=\kappa $
for each
![]() $i<\kappa ^+$
and for every
$i<\kappa ^+$
and for every
 $A\in [\kappa ^+]^{\kappa ^+}$
there exists some
$A\in [\kappa ^+]^{\kappa ^+}$
there exists some
![]() $i<\kappa ^+$
such that
$i<\kappa ^+$
such that
![]() $X_i\subseteq A$
.
$X_i\subseteq A$
.
Let
![]() $\beta <\kappa ^+$
be arbitrary. Towards defining
$\beta <\kappa ^+$
be arbitrary. Towards defining
![]() $f(\alpha ,\beta )$
for
$f(\alpha ,\beta )$
for
![]() $\alpha <\beta $
, let us define, for every triple
$\alpha <\beta $
, let us define, for every triple
![]() $\langle \unicode{x3b3} ,i,j\rangle $
such that
$\langle \unicode{x3b3} ,i,j\rangle $
such that
![]() $\unicode{x3b3} ,i<\beta $
and
$\unicode{x3b3} ,i<\beta $
and
![]() $j<\lambda _{\unicode{x3b3} }$
,
$j<\lambda _{\unicode{x3b3} }$
,
 $$ \begin{align} A^{\beta}_{\langle \unicode{x3b3},i,j\rangle} = \{\alpha<\beta: \alpha\in X_i \wedge p_{\unicode{x3b3}}(\alpha,\beta)=j\}. \end{align} $$
$$ \begin{align} A^{\beta}_{\langle \unicode{x3b3},i,j\rangle} = \{\alpha<\beta: \alpha\in X_i \wedge p_{\unicode{x3b3}}(\alpha,\beta)=j\}. \end{align} $$
Let
 $$ \begin{align} \mathcal A_{\beta}= \left\{A^{\beta}_{\langle \unicode{x3b3},i,j\rangle}: \unicode{x3b3},i<\beta\wedge j<\lambda_{\unicode{x3b3}} \wedge |A^{\beta}_{\langle \unicode{x3b3},i,j\rangle}|=\kappa\right\}. \end{align} $$
$$ \begin{align} \mathcal A_{\beta}= \left\{A^{\beta}_{\langle \unicode{x3b3},i,j\rangle}: \unicode{x3b3},i<\beta\wedge j<\lambda_{\unicode{x3b3}} \wedge |A^{\beta}_{\langle \unicode{x3b3},i,j\rangle}|=\kappa\right\}. \end{align} $$
As
![]() $\mathcal A_{\beta }$
is a family of at most
$\mathcal A_{\beta }$
is a family of at most
![]() $\kappa $
subsets of
$\kappa $
subsets of
![]() $\beta $
, each of cardinality
$\beta $
, each of cardinality
![]() $\kappa $
, we may fix a disjoint refinement
$\kappa $
, we may fix a disjoint refinement
 $\mathcal D_{\beta }=\{D^{\beta }_{\langle \unicode{x3b3} ,i,j\rangle }: A^{\beta }_{\langle \unicode{x3b3} ,i,j\rangle }\in \mathcal A_{\beta }\}$
, that is, each
$\mathcal D_{\beta }=\{D^{\beta }_{\langle \unicode{x3b3} ,i,j\rangle }: A^{\beta }_{\langle \unicode{x3b3} ,i,j\rangle }\in \mathcal A_{\beta }\}$
, that is, each
 $D^{\beta }_{\langle \unicode{x3b3} ,i,j\rangle }\subseteq A^{\beta }_{\langle \unicode{x3b3} ,i,j\rangle }$
has cardinality
$D^{\beta }_{\langle \unicode{x3b3} ,i,j\rangle }\subseteq A^{\beta }_{\langle \unicode{x3b3} ,i,j\rangle }$
has cardinality
![]() $\kappa $
and
$\kappa $
and
 $\langle \unicode{x3b3} ,i,j\rangle \neq\langle \unicode{x3b3} ',i',j'\rangle \Rightarrow D^{\beta }_{\langle \unicode{x3b3} ,i,j \rangle }\cap D^{\beta }_{\langle \unicode{x3b3} ',i',j'\rangle }=\emptyset $
for any
$\langle \unicode{x3b3} ,i,j\rangle \neq\langle \unicode{x3b3} ',i',j'\rangle \Rightarrow D^{\beta }_{\langle \unicode{x3b3} ,i,j \rangle }\cap D^{\beta }_{\langle \unicode{x3b3} ',i',j'\rangle }=\emptyset $
for any
 $A^{\beta }_{\langle \unicode{x3b3} ,i,j\rangle }, A^{\beta }_{\langle \unicode{x3b3} ',i',j'\rangle }\in \mathcal A_{\beta }$
.
$A^{\beta }_{\langle \unicode{x3b3} ,i,j\rangle }, A^{\beta }_{\langle \unicode{x3b3} ',i',j'\rangle }\in \mathcal A_{\beta }$
.
Let us define now
![]() $f(\alpha ,\beta )$
for all
$f(\alpha ,\beta )$
for all
![]() $\alpha $
below our fixed
$\alpha $
below our fixed
![]() $\beta $
by cases. For each
$\beta $
by cases. For each
 $D^{\beta }_{\langle \unicode{x3b3} ,i,j\rangle }\in \mathcal D_{\beta }$
define
$D^{\beta }_{\langle \unicode{x3b3} ,i,j\rangle }\in \mathcal D_{\beta }$
define
 $f\restriction (D^{\beta }_{\langle \unicode{x3b3} ,i,j\rangle }\circledast \{\beta \})$
to be some function onto
$f\restriction (D^{\beta }_{\langle \unicode{x3b3} ,i,j\rangle }\circledast \{\beta \})$
to be some function onto
![]() $\beta $
. This is possible since
$\beta $
. This is possible since
 $| D^{\beta }_{\langle \unicode{x3b3} ,i,j\rangle }|=\kappa $
and
$| D^{\beta }_{\langle \unicode{x3b3} ,i,j\rangle }|=\kappa $
and
![]() $\beta <\kappa ^+$
(so
$\beta <\kappa ^+$
(so
 $| D^{\beta }_{\langle \unicode{x3b3} ,i,j\rangle }|=|\beta |$
) and because the
$| D^{\beta }_{\langle \unicode{x3b3} ,i,j\rangle }|=|\beta |$
) and because the
 $D^{\beta }_{\langle \unicode{x3b3} ,i,j\rangle }$
are pairwise disjoint, hence
$D^{\beta }_{\langle \unicode{x3b3} ,i,j\rangle }$
are pairwise disjoint, hence
 $(D^{\beta }_{\langle \unicode{x3b3} ,i,j\rangle } \circledast \{\beta \})\cap (D^{\beta }_{\langle \unicode{x3b3} ',i',j'\rangle }\circledast \{\beta \}) =\emptyset $
when
$(D^{\beta }_{\langle \unicode{x3b3} ,i,j\rangle } \circledast \{\beta \})\cap (D^{\beta }_{\langle \unicode{x3b3} ',i',j'\rangle }\circledast \{\beta \}) =\emptyset $
when
![]() $\langle \unicode{x3b3} ,i,j\rangle \neq\langle \unicode{x3b3} ',i',j'\rangle $
.
$\langle \unicode{x3b3} ,i,j\rangle \neq\langle \unicode{x3b3} ',i',j'\rangle $
.
For
![]() $\alpha \in \beta \setminus \bigcup \mathcal D_{\beta }$
define
$\alpha \in \beta \setminus \bigcup \mathcal D_{\beta }$
define
![]() $f(\alpha ,\beta )$
arbitrarily (say, as
$f(\alpha ,\beta )$
arbitrarily (say, as
![]() $0$
). As
$0$
). As
![]() $\beta $
was arbitrary, we have defined
$\beta $
was arbitrary, we have defined
![]() $f(\alpha ,\beta )$
for all
$f(\alpha ,\beta )$
for all
![]() $\alpha <\beta <\kappa ^+$
. By this definition, for all
$\alpha <\beta <\kappa ^+$
. By this definition, for all
![]() $\beta <\kappa ^+ $
and
$\beta <\kappa ^+ $
and
 $D^{\beta }_{\langle \unicode{x3b3} ,i,j\rangle }\in \mathcal D_{\beta }$
,
$D^{\beta }_{\langle \unicode{x3b3} ,i,j\rangle }\in \mathcal D_{\beta }$
,
 $$ \begin{align} \beta={\operatorname {ran}} (f\restriction (D^{\beta}_{\langle \unicode{x3b3},i,j\rangle}\circledast \{\beta\}). \end{align} $$
$$ \begin{align} \beta={\operatorname {ran}} (f\restriction (D^{\beta}_{\langle \unicode{x3b3},i,j\rangle}\circledast \{\beta\}). \end{align} $$
To see that f satisfies what Theorem 25 states, let
![]() $A,B\subseteq \kappa ^+$
be arbitrary with
$A,B\subseteq \kappa ^+$
be arbitrary with
![]() $|A|=|B|=\kappa ^+$
and let
$|A|=|B|=\kappa ^+$
and let
![]() $\unicode{x3b3} <\kappa ^+$
be given. Using the properties of the
$\unicode{x3b3} <\kappa ^+$
be given. Using the properties of the
 -sequence, fix some
-sequence, fix some
![]() $i<\kappa ^+$
such that
$i<\kappa ^+$
such that
As
![]() $X_i\subseteq \kappa ^+$
and
$X_i\subseteq \kappa ^+$
and
![]() ${\operatorname {otp}}(X_i)=\kappa $
,
${\operatorname {otp}}(X_i)=\kappa $
,
![]() $\mathrm{sup} (X_i)<\kappa ^+$
, hence
$\mathrm{sup} (X_i)<\kappa ^+$
, hence
![]() $\beta _0:=\max \{\unicode{x3b3} ,i,\mathrm{sup} X_i\}<\kappa ^+$
.
$\beta _0:=\max \{\unicode{x3b3} ,i,\mathrm{sup} X_i\}<\kappa ^+$
.
If
![]() $\beta \in B$
is any ordinal such that
$\beta \in B$
is any ordinal such that
![]() $\beta>\beta _0$
then
$\beta>\beta _0$
then
![]() $X_i\subseteq \beta $
and as
$X_i\subseteq \beta $
and as
![]() $|X_i|=\kappa $
while
$|X_i|=\kappa $
while
![]() $\lambda _{\unicode{x3b3} }<{\operatorname {cf}}\kappa $
, there exists some
$\lambda _{\unicode{x3b3} }<{\operatorname {cf}}\kappa $
, there exists some
 $j(\beta )<\lambda _{\unicode{x3b3} }$
such that
$j(\beta )<\lambda _{\unicode{x3b3} }$
such that
 $$ \begin{align*} |\{\alpha\in X_i: p_{\unicode{x3b3}}(\alpha,\beta)=j \}|=\kappa,\end{align*} $$
$$ \begin{align*} |\{\alpha\in X_i: p_{\unicode{x3b3}}(\alpha,\beta)=j \}|=\kappa,\end{align*} $$
 $$ \begin{align*} A^{\beta}_{\langle \unicode{x3b3},i,j(\beta)\rangle}\in \mathcal A_{\beta}. \end{align*} $$
$$ \begin{align*} A^{\beta}_{\langle \unicode{x3b3},i,j(\beta)\rangle}\in \mathcal A_{\beta}. \end{align*} $$
By the regularity of
![]() $\kappa ^+$
and the assumption that
$\kappa ^+$
and the assumption that
![]() $\lambda _{\unicode{x3b3} }<{\operatorname {cf}}\kappa <\kappa ^+$
, we can fix some
$\lambda _{\unicode{x3b3} }<{\operatorname {cf}}\kappa <\kappa ^+$
, we can fix some
![]() $B'\subseteq B\setminus (\beta _0+1)$
and
$B'\subseteq B\setminus (\beta _0+1)$
and
 $j(*)<\lambda _{\unicode{x3b3} }$
such that
$j(*)<\lambda _{\unicode{x3b3} }$
such that
![]() $j(\beta )=j(*)$
for all
$j(\beta )=j(*)$
for all
![]() $\beta \in B$
.
$\beta \in B$
.
For each
![]() $\beta \in B'$
it holds, then, that
$\beta \in B'$
it holds, then, that
 $A^{\beta }_{\langle \unicode{x3b3} ,i,j(*)\rangle }$
belongs to
$A^{\beta }_{\langle \unicode{x3b3} ,i,j(*)\rangle }$
belongs to
![]() $\mathcal A_{\beta }$
, and therefore also
$\mathcal A_{\beta }$
, and therefore also
 $$ \begin{align} D^{\beta}_{\langle \unicode{x3b3},i,j(*)\rangle}\in \mathcal D_{\beta}. \end{align} $$
$$ \begin{align} D^{\beta}_{\langle \unicode{x3b3},i,j(*)\rangle}\in \mathcal D_{\beta}. \end{align} $$
Now, for each
![]() $\beta \in B'$
we have by (6) and (4) that
$\beta \in B'$
we have by (6) and (4) that
 $$ \begin{align*} \beta={\operatorname {ran}}(c\restriction D^{\beta}_{\langle \unicode{x3b3},i,j(*)\rangle}\circledast \{\beta\}),\end{align*} $$
$$ \begin{align*} \beta={\operatorname {ran}}(c\restriction D^{\beta}_{\langle \unicode{x3b3},i,j(*)\rangle}\circledast \{\beta\}),\end{align*} $$
and as
 $D^{\beta }_{\langle \unicode{x3b3} ,i,j(*)\rangle }\subseteq X_i\cap p_{\unicode{x3b3} }^{-1}(j(*))$
by (2),
$D^{\beta }_{\langle \unicode{x3b3} ,i,j(*)\rangle }\subseteq X_i\cap p_{\unicode{x3b3} }^{-1}(j(*))$
by (2),
 $$ \begin{align*} \beta={\operatorname{ran}}(f\restriction [(X_i\circledast \{\beta\})\cap p_{\unicode{x3b3}}^{-1}(j(*))]). \end{align*} $$
$$ \begin{align*} \beta={\operatorname{ran}}(f\restriction [(X_i\circledast \{\beta\})\cap p_{\unicode{x3b3}}^{-1}(j(*))]). \end{align*} $$
As
![]() $B'\subseteq B$
is unbounded in
$B'\subseteq B$
is unbounded in
![]() $\kappa ^+$
it follows, after setting
$\kappa ^+$
it follows, after setting
![]() $X=X_i$
and
$X=X_i$
and
![]() $j=j(*)$
, that
$j=j(*)$
, that
 $$ \begin{align*} \kappa^+= f\restriction [(X\circledast B)\cap p_{\unicode{x3b3}}^{-1}(j)]. \end{align*} $$
$$ \begin{align*} \kappa^+= f\restriction [(X\circledast B)\cap p_{\unicode{x3b3}}^{-1}(j)]. \end{align*} $$
⊣
5 Independence results on
 $\aleph _1$
$\aleph _1$
In this section we shall show that the existence of strong colorings over countable partitions of
 $[\omega _1]^2$
is independent over ZFC and over ZFC +
$[\omega _1]^2$
is independent over ZFC and over ZFC +
![]() $2^{\aleph _0}>\aleph _1$
.
$2^{\aleph _0}>\aleph _1$
.
Theorem 26. If the CH holds, then the following five symbols are valid for every sequence of partitions
![]() $\overline p=\langle p_{\delta }:\delta <\omega _1\rangle $
where
$\overline p=\langle p_{\delta }:\delta <\omega _1\rangle $
where
 $p_{\delta }:[\omega _1]^2\to \omega $
:
$p_{\delta }:[\omega _1]^2\to \omega $
:
-
•
 $\displaystyle \aleph _1\nrightarrow _{\overline p}[\aleph _1]^2_{\aleph _1},$
$\displaystyle \aleph _1\nrightarrow _{\overline p}[\aleph _1]^2_{\aleph _1},$
-
•
 $\displaystyle \aleph _1\nrightarrow _{\overline p}[\aleph _1\circledast \aleph _1]^2_{\aleph _1},$
$\displaystyle \aleph _1\nrightarrow _{\overline p}[\aleph _1\circledast \aleph _1]^2_{\aleph _1},$
-
•

-
•
 $\displaystyle \operatorname {Pr}_1(\aleph _1,\aleph _1,\aleph _1,\aleph _0)_{\overline p},$
$\displaystyle \operatorname {Pr}_1(\aleph _1,\aleph _1,\aleph _1,\aleph _0)_{\overline p},$
-
•
 $\displaystyle \operatorname {Pr}_0(\aleph _1,\aleph _1,\aleph _1,\aleph _0)_{\overline p}.$
$\displaystyle \operatorname {Pr}_0(\aleph _1,\aleph _1,\aleph _1,\aleph _0)_{\overline p}.$
Proof Assume CH, that is,
![]() $2^{\aleph _0}=\aleph _1$
. Then
$2^{\aleph _0}=\aleph _1$
. Then
![]() $\operatorname {Pr}_1(\aleph _1,\aleph _1,\aleph _1,\aleph _0)$
holds by (a slight strengthening of) Galvin’s theorem. By Shelah’s 4.5(3) from [Reference Shelah38], also
$\operatorname {Pr}_1(\aleph _1,\aleph _1,\aleph _1,\aleph _0)$
holds by (a slight strengthening of) Galvin’s theorem. By Shelah’s 4.5(3) from [Reference Shelah38], also
![]() $\operatorname {Pr}_0(\aleph _1,\aleph _1,\aleph _1,\aleph _0)$
holds. The CH also implies that
$\operatorname {Pr}_0(\aleph _1,\aleph _1,\aleph _1,\aleph _0)$
holds. The CH also implies that
 $(\aleph _1)^{\aleph _0}=(2^{\aleph _0})^{\aleph _0}=2^{\aleph _0}=\aleph _1$
. By Lemma 9(5), then, for every
$(\aleph _1)^{\aleph _0}=(2^{\aleph _0})^{\aleph _0}=2^{\aleph _0}=\aleph _1$
. By Lemma 9(5), then, for every
![]() $\omega _1$
-sequence
$\omega _1$
-sequence
![]() $\overline p$
of countable partitions of
$\overline p$
of countable partitions of
 $[\omega _1]^2$
it holds that
$[\omega _1]^2$
it holds that
 $$ \begin{align*} \operatorname{Pr}_0(\aleph_1,\aleph_1,\aleph_1,\aleph_0)_{\overline p} \end{align*} $$
$$ \begin{align*} \operatorname{Pr}_0(\aleph_1,\aleph_1,\aleph_1,\aleph_0)_{\overline p} \end{align*} $$
and therefore by Lemma 8 also
 $$ \begin{align*} \operatorname{Pr}_1(\aleph_1,\aleph_1,\aleph_1,\aleph_0)_{\overline p}, \;\;\;\omega_1\nrightarrow_{\overline p}[\omega_1]^2_{\omega_1} \;\;\; \text{ and } \;\;\; \omega_1\nrightarrow_{\overline p}[\omega_1\circledast\omega_1]^2_{\omega_1}.\end{align*} $$
$$ \begin{align*} \operatorname{Pr}_1(\aleph_1,\aleph_1,\aleph_1,\aleph_0)_{\overline p}, \;\;\;\omega_1\nrightarrow_{\overline p}[\omega_1]^2_{\omega_1} \;\;\; \text{ and } \;\;\; \omega_1\nrightarrow_{\overline p}[\omega_1\circledast\omega_1]^2_{\omega_1}.\end{align*} $$
Similarly, by the CH and Theorem 21 in the previous section,

⊣
We prove next that these five symbols are valid in all models of ZFC obtained by adding
![]() $\aleph _2$
Cohen reals over an arbitrary model V of ZFC, and, more generally, by forcing with a finite-support
$\aleph _2$
Cohen reals over an arbitrary model V of ZFC, and, more generally, by forcing with a finite-support
![]() $\omega _2$
-iteration of
$\omega _2$
-iteration of
![]() $\sigma $
-linked posets over an arbitrary model V of ZFC.
$\sigma $
-linked posets over an arbitrary model V of ZFC.
Before proving yet another combinatorial property in a Cohen extension let us recall Roitman’s [Reference Roitman30] proof that the addition of a single Cohen real introduces an S-space, Todorčević’s presentation in [Reference Todorčević42], p. 26 and Rinot’s blog-post [Reference Rinot26] in which it is shown that a single Cohen real introduces
![]() $\operatorname {Pr}_0(\aleph _1,\aleph _1,\aleph _0,\aleph _0)$
. For a short proof of Shelah’s theorem that a single Cohen real introduces a Suslin line see [Reference Steprāns40]. Fleissner [Reference Fleissner14] proved that adding
$\operatorname {Pr}_0(\aleph _1,\aleph _1,\aleph _0,\aleph _0)$
. For a short proof of Shelah’s theorem that a single Cohen real introduces a Suslin line see [Reference Steprāns40]. Fleissner [Reference Fleissner14] proved that adding
![]() $\lambda $
Cohen reals introduces two ccc spaces whose product is not
$\lambda $
Cohen reals introduces two ccc spaces whose product is not
![]() $\lambda $
-cc. Hajnal and Komjath [Reference Hajnal and Komjath17] proved that adding one Cohen subset to a cardinal
$\lambda $
-cc. Hajnal and Komjath [Reference Hajnal and Komjath17] proved that adding one Cohen subset to a cardinal
![]() $\kappa =\kappa ^{<\kappa }$
forces the statement
$\kappa =\kappa ^{<\kappa }$
forces the statement
![]() $Q(\kappa ^+)$
they defined, following [Reference Erdős, Galvin and Hajnal4]: for every graph
$Q(\kappa ^+)$
they defined, following [Reference Erdős, Galvin and Hajnal4]: for every graph
![]() $G=\langle \kappa ^+,E\rangle $
with
$G=\langle \kappa ^+,E\rangle $
with
![]() $\chi (G)=\kappa ^+$
there is a coloring
$\chi (G)=\kappa ^+$
there is a coloring
![]() $f:E\to \kappa ^+$
such that for every partition of
$f:E\to \kappa ^+$
such that for every partition of
![]() $\kappa ^+$
to
$\kappa ^+$
to
![]() $\kappa $
parts, all colors are gotten by f on edges from a single part. It is still open if
$\kappa $
parts, all colors are gotten by f on edges from a single part. It is still open if
![]() $Q(\aleph _1)$
holds in ZFC.
$Q(\aleph _1)$
holds in ZFC.
Theorem 27. If
![]() $\mathbb C_{\aleph _2}$
is the partial order for adding
$\mathbb C_{\aleph _2}$
is the partial order for adding
![]() $\aleph _2$
Cohen reals then for every sequence
$\aleph _2$
Cohen reals then for every sequence
![]() $\overline p =\langle p_{\delta }:\delta <\omega _1\rangle $
of partitions
$\overline p =\langle p_{\delta }:\delta <\omega _1\rangle $
of partitions
 $p_{\delta }:[\omega _1]^2\to \omega $
in the forcing extension by
$p_{\delta }:[\omega _1]^2\to \omega $
in the forcing extension by
![]() $\mathbb C_{\aleph _2}$
,
$\mathbb C_{\aleph _2}$
,

Proof Let
![]() $\mathbb {C}_{\alpha }$
be the partial order of finite partial functions from
$\mathbb {C}_{\alpha }$
be the partial order of finite partial functions from
 $[\alpha ]^2$
to
$[\alpha ]^2$
to
![]() $\omega $
. Let V be a model of set theory and let
$\omega $
. Let V be a model of set theory and let
![]() $G\subseteq \mathbb C_{\omega _2}$
be generic over V. Then
$G\subseteq \mathbb C_{\omega _2}$
be generic over V. Then
 $\bigcup G:[\omega _2]^2\to \omega $
.
$\bigcup G:[\omega _2]^2\to \omega $
.
Now suppose that
![]() $\overline p=\langle p_{\delta }:\delta <\omega _1\rangle $
is an arbitrary sequence of partitions
$\overline p=\langle p_{\delta }:\delta <\omega _1\rangle $
is an arbitrary sequence of partitions
 $p_{\delta }:[\omega _1]^2\to \omega $
in
$p_{\delta }:[\omega _1]^2\to \omega $
in
![]() $V[G]$
. As there is some
$V[G]$
. As there is some
![]() $\alpha \in \omega _2$
such that
$\alpha \in \omega _2$
such that
![]() $\overline p\in V[G\cap \mathbb C_{\alpha }]$
, it may be assumed that
$\overline p\in V[G\cap \mathbb C_{\alpha }]$
, it may be assumed that
![]() $\overline p\in V$
. Let
$\overline p\in V$
. Let
 $c= \bigcup G\restriction [\omega _1]^2$
. So
$c= \bigcup G\restriction [\omega _1]^2$
. So
 $c:[\omega _1]^2\to \omega $
. In V, fix a sequence
$c:[\omega _1]^2\to \omega $
. In V, fix a sequence
![]() $\langle e_{\alpha }:\omega \le \alpha <\omega _1\rangle $
, where
$\langle e_{\alpha }:\omega \le \alpha <\omega _1\rangle $
, where
![]() $e_{\alpha }: \omega \to \alpha $
is a bijection. In the generic extension, define a coloring
$e_{\alpha }: \omega \to \alpha $
is a bijection. In the generic extension, define a coloring
 $f:[\omega _1]^2\to \omega _1$
by
$f:[\omega _1]^2\to \omega _1$
by
 $$ \begin{align*} f(\alpha,\beta)=e_{\beta}(c(\alpha,\beta)),\end{align*} $$
$$ \begin{align*} f(\alpha,\beta)=e_{\beta}(c(\alpha,\beta)),\end{align*} $$
for
![]() $\beta \ge \omega $
and as
$\beta \ge \omega $
and as
![]() $0$
otherwise.
$0$
otherwise.
To see that f witnesses
 $\displaystyle \aleph _1\nrightarrow _{\overline p}[\aleph _1]^2_{\aleph _1}$
suppose that there is some
$\displaystyle \aleph _1\nrightarrow _{\overline p}[\aleph _1]^2_{\aleph _1}$
suppose that there is some
![]() $\delta<\omega_1$
for which f fails to witness
$\delta<\omega_1$
for which f fails to witness
 $\displaystyle \aleph _1\nrightarrow _{\overline p}[\aleph _1]^2_{\aleph _1}$
. This means that in
$\displaystyle \aleph _1\nrightarrow _{\overline p}[\aleph _1]^2_{\aleph _1}$
. This means that in
![]() $V^G$
there are
$V^G$
there are
![]() $A\in [\omega _1]^{\omega }$
and
$A\in [\omega _1]^{\omega }$
and
![]() $B\in [\omega _1]^{\omega _1}$
such that for all
$B\in [\omega _1]^{\omega _1}$
such that for all
![]() $\alpha \in A$
there is some
$\alpha \in A$
there is some
 $W(\alpha )\in \omega _1^{\omega }$
such that for all
$W(\alpha )\in \omega _1^{\omega }$
such that for all
![]() $\beta \in B\setminus (\alpha +1)$
it holds that
$\beta \in B\setminus (\alpha +1)$
it holds that
![]() $f(\alpha ,\beta )\neq W(\alpha )(p_{\delta }(\alpha ,\beta ))$
. Let
$f(\alpha ,\beta )\neq W(\alpha )(p_{\delta }(\alpha ,\beta ))$
. Let
![]() $\dot A$
and
$\dot A$
and
![]() $\dot W$
be countable names for A and W and let
$\dot W$
be countable names for A and W and let
![]() $\dot B$
be a name for B. Let
$\dot B$
be a name for B. Let
![]() $r\in G$
decide
$r\in G$
decide
![]() $\delta $
and force
$\delta $
and force
 $$ \begin{align*} r\Vdash_{} ``(\forall \alpha\in \dot A)(\forall \beta\in \dot B\setminus (\alpha+1))\,(f(\alpha,\beta))\neq \dot W(\alpha)(p_{\delta}(\alpha,\beta)).\text{''} \end{align*} $$
$$ \begin{align*} r\Vdash_{} ``(\forall \alpha\in \dot A)(\forall \beta\in \dot B\setminus (\alpha+1))\,(f(\alpha,\beta))\neq \dot W(\alpha)(p_{\delta}(\alpha,\beta)).\text{''} \end{align*} $$
Let
![]() $\mathfrak M$
be a countable elementary submodel of
$\mathfrak M$
be a countable elementary submodel of
 $H(\omega _2,\dot A, \dot B, \dot {W}, r) $
.
$H(\omega _2,\dot A, \dot B, \dot {W}, r) $
.
Fix an extension
![]() $r'\in G$
of r and an ordinal
$r'\in G$
of r and an ordinal
![]() $\beta \in \omega _1\setminus \mathrm{sup} (\mathfrak M\cap \omega _1)$
such that
$\beta \in \omega _1\setminus \mathrm{sup} (\mathfrak M\cap \omega _1)$
such that
 $r'\Vdash \beta \in \dot B$
. Let
$r'\Vdash \beta \in \dot B$
. Let
![]() $r_0=r'\cap \mathfrak M$
. Inside
$r_0=r'\cap \mathfrak M$
. Inside
![]() $\mathfrak M$
extend
$\mathfrak M$
extend
![]() $r_0$
to
$r_0$
to
![]() $r_1$
such that
$r_1$
such that
![]() $r_1\Vdash _{} ``\alpha \in \dot A\text{''}$
for an ordinal
$r_1\Vdash _{} ``\alpha \in \dot A\text{''}$
for an ordinal
![]() $\alpha $
which is not in
$\alpha $
which is not in
![]() $\bigcup {\operatorname {dom}\,}(r')$
and
$\bigcup {\operatorname {dom}\,}(r')$
and
![]() $r_1$
decides
$r_1$
decides
![]() $W(\alpha )(p_{\delta }(\alpha ,\beta ))$
. Thus,
$W(\alpha )(p_{\delta }(\alpha ,\beta ))$
. Thus,
![]() $\{\alpha ,\beta \}\notin {\operatorname {dom}\,}(r'\cup r_1)$
. Let
$\{\alpha ,\beta \}\notin {\operatorname {dom}\,}(r'\cup r_1)$
. Let
 $$ \begin{align*}r^*=r'\cup r_1\cup \bigl\{\langle \{\alpha,\beta\},e^{-1}_{\beta}(W(\alpha)(p_{\delta}(\alpha,\beta))\rangle\bigr\}. \end{align*} $$
$$ \begin{align*}r^*=r'\cup r_1\cup \bigl\{\langle \{\alpha,\beta\},e^{-1}_{\beta}(W(\alpha)(p_{\delta}(\alpha,\beta))\rangle\bigr\}. \end{align*} $$
Since
![]() $r^*$
extends r and
$r^*$
extends r and
 $f(\alpha ,\beta )=e_{\beta }(c(\alpha ,\beta ))=W(\alpha )(p_{\delta }(\alpha ,\beta ))$
, this is a contradiction to the choice of r.⊣
$f(\alpha ,\beta )=e_{\beta }(c(\alpha ,\beta ))=W(\alpha )(p_{\delta }(\alpha ,\beta ))$
, this is a contradiction to the choice of r.⊣
The forcing for adding a single Cohen real is obviously
![]() $\sigma $
-linked. Thus, the next theorem applies to a broader class of posets than Cohen forcing. The previous theorem holds also in this generality.
$\sigma $
-linked. Thus, the next theorem applies to a broader class of posets than Cohen forcing. The previous theorem holds also in this generality.
Theorem 28. If
![]() $\mathbb P$
is an
$\mathbb P$
is an
![]() $\omega _2$
-length finite support iteration of
$\omega _2$
-length finite support iteration of
![]() $\sigma $
-linked partial orders then
$\sigma $
-linked partial orders then
 $$ \begin{align*} 1\Vdash_{\mathbb P}``\operatorname{Pr}_{0}(\aleph_{1},\aleph_{1},\aleph_{1},\aleph_0)_{\bar{p}}\mathrm{''} \end{align*} $$
$$ \begin{align*} 1\Vdash_{\mathbb P}``\operatorname{Pr}_{0}(\aleph_{1},\aleph_{1},\aleph_{1},\aleph_0)_{\bar{p}}\mathrm{''} \end{align*} $$
for any
![]() $\omega _1$
sequence of partitions
$\omega _1$
sequence of partitions
![]() $\bar {p} = \langle p_{\delta }:\delta <\omega _1\rangle $
such that
$\bar {p} = \langle p_{\delta }:\delta <\omega _1\rangle $
such that
 $p_{\delta }:[\omega _1]^2\to \omega $
for all
$p_{\delta }:[\omega _1]^2\to \omega $
for all
![]() $\delta <\omega _1$
.
$\delta <\omega _1$
.
Proof Let
![]() $\mathbb {P}_{\alpha }$
be the finite support iteration of the first
$\mathbb {P}_{\alpha }$
be the finite support iteration of the first
![]() $\alpha $
partial orders and suppose that
$\alpha $
partial orders and suppose that
 $$ \begin{align} 1\Vdash_{{\mathbb P}_{\alpha}} ``\mathbb Q_{\alpha} = \bigcup_{n\in\omega} \mathbb Q_{\alpha,n} \text{ and each } \mathbb Q_{\alpha,n} \text{ is linked,''} \end{align} $$
$$ \begin{align} 1\Vdash_{{\mathbb P}_{\alpha}} ``\mathbb Q_{\alpha} = \bigcup_{n\in\omega} \mathbb Q_{\alpha,n} \text{ and each } \mathbb Q_{\alpha,n} \text{ is linked,''} \end{align} $$
Let
 $B: [\omega _2]^2\to \omega _2$
be a bijection and let
$B: [\omega _2]^2\to \omega _2$
be a bijection and let
![]() $e_{\xi }:\omega \to \xi $
be a bijection for each infinite
$e_{\xi }:\omega \to \xi $
be a bijection for each infinite
![]() $\xi \in \omega _1$
. Let V be a model of set theory, let
$\xi \in \omega _1$
. Let V be a model of set theory, let
![]() $G\subseteq \mathbb P$
be generic over V and let
$G\subseteq \mathbb P$
be generic over V and let
![]() $G_{\alpha }$
be the generic filter induced on
$G_{\alpha }$
be the generic filter induced on
![]() $\mathbb Q_{\alpha }$
by G.
$\mathbb Q_{\alpha }$
by G.
Now suppose that a sequence of partitions
![]() $\bar {p} = \langle p_{\delta }:\delta <\omega _1\rangle $
such that
$\bar {p} = \langle p_{\delta }:\delta <\omega _1\rangle $
such that
 $p_{\delta }:[\omega _1]^2\to \omega $
belongs to
$p_{\delta }:[\omega _1]^2\to \omega $
belongs to
![]() $V[G]$
. As there is some
$V[G]$
. As there is some
![]() $\alpha \in \omega _2$
such that
$\alpha \in \omega _2$
such that
![]() $\bar {p}\in V[G\cap \mathbb P_{\alpha }]$
, it may be assumed that
$\bar {p}\in V[G\cap \mathbb P_{\alpha }]$
, it may be assumed that
![]() $\bar {p}\in V$
. There is no harm in assuming that B maps
$\bar {p}\in V$
. There is no harm in assuming that B maps
 $ [\omega _1]^2$
to
$ [\omega _1]^2$
to
![]() $\omega _1$
so let
$\omega _1$
so let
 $c: [\omega _1]^2\to \omega _1$
be defined by
$c: [\omega _1]^2\to \omega _1$
be defined by
![]() $c(\alpha ,\beta ) = \xi $
if and only if
$c(\alpha ,\beta ) = \xi $
if and only if
![]() $q_{B(\alpha ,\beta ),k}\in G_{B(\alpha ,\beta )}$
and
$q_{B(\alpha ,\beta ),k}\in G_{B(\alpha ,\beta )}$
and
 $\xi = e_{B(\alpha ,\beta )}(k)$
.
$\xi = e_{B(\alpha ,\beta )}(k)$
.
To see that c witnesses
 $\operatorname {Pr}_0(\aleph _1,\aleph _1,\aleph _1,\aleph _0)_{\bar {p}}$
suppose that:
$\operatorname {Pr}_0(\aleph _1,\aleph _1,\aleph _1,\aleph _0)_{\bar {p}}$
suppose that:
-
•
 $\delta \in \omega _1.$
$\delta \in \omega _1.$
-
•
 $k>0.$
$k>0.$
-
•
 $\dot \alpha _{\xi ,i}<\omega _1$
are
$\dot \alpha _{\xi ,i}<\omega _1$
are
 $\mathbb P$
-names for
$\mathbb P$
-names for
 $\xi <\omega _1$
and
$\xi <\omega _1$
and
 $1\le i\le k$
of distinct ordinals such that for every
$1\le i\le k$
of distinct ordinals such that for every
 $\xi <\omega _1$
the sequence
$\xi <\omega _1$
the sequence
 $\langle \dot \alpha _{\xi ,i}:1\le i\le \kappa \rangle $
is increasing with i.
$\langle \dot \alpha _{\xi ,i}:1\le i\le \kappa \rangle $
is increasing with i. -
•
 $\left (\dot {N}_{i,j}\right )$
is a
$\left (\dot {N}_{i,j}\right )$
is a
 $\mathbb P$
-name for a
$\mathbb P$
-name for a
 $k\times k$
matrix with entries in
$k\times k$
matrix with entries in
 ${\omega _1}^{\omega }$
.
${\omega _1}^{\omega }$
.
We may fix
![]() $q_{\xi }\in G$
such that:
$q_{\xi }\in G$
such that:
-
(1)
 $q_{\xi }\Vdash _{\mathbb P} ``\dot {\alpha }_{\xi ,i} = \alpha _{\xi ,i}\;\text{''}$
for all
$q_{\xi }\Vdash _{\mathbb P} ``\dot {\alpha }_{\xi ,i} = \alpha _{\xi ,i}\;\text{''}$
for all
 $1\le i\le k,$
$1\le i\le k,$
-
(2)
 $\{\alpha _{\xi ,1},\alpha _{\xi , 2}, \ldots , \alpha _{\xi , k}\}\subseteq d_{\xi } = \bigcup B^{-1}({\operatorname {dom}\,}(q_{\xi })),$
$\{\alpha _{\xi ,1},\alpha _{\xi , 2}, \ldots , \alpha _{\xi , k}\}\subseteq d_{\xi } = \bigcup B^{-1}({\operatorname {dom}\,}(q_{\xi })),$
-
(3) for all
 $\mu \in {\operatorname {dom}\,}(q_{\xi })$
there is
$\mu \in {\operatorname {dom}\,}(q_{\xi })$
there is
 $n_{\mu ,\xi }$
such that
$n_{\mu ,\xi }$
such that
 $q_{\xi }\restriction \mu \Vdash _{{\mathbb P}_{\mu }} ``q_{\xi }(\mu )\in \mathbb Q_{\mu , n_{\mu ,\xi }}.\text{''}$
$q_{\xi }\restriction \mu \Vdash _{{\mathbb P}_{\mu }} ``q_{\xi }(\mu )\in \mathbb Q_{\mu , n_{\mu ,\xi }}.\text{''}$
Let
![]() $\{\mathfrak M_{\eta }\}_{\eta \in \omega +1}$
be countable elementary submodels of
$\{\mathfrak M_{\eta }\}_{\eta \in \omega +1}$
be countable elementary submodels of
 $$ \begin{align*}H(\omega_2,\{q_{\xi}, \{\alpha_{\xi,1},\alpha_{\xi, 2}, \ldots , \alpha_{\xi, k}\}\}_{\xi\in\omega_1},B, \dot{N}, G)\end{align*} $$
$$ \begin{align*}H(\omega_2,\{q_{\xi}, \{\alpha_{\xi,1},\alpha_{\xi, 2}, \ldots , \alpha_{\xi, k}\}\}_{\xi\in\omega_1},B, \dot{N}, G)\end{align*} $$
such that
![]() $\mathfrak M_j\prec \mathfrak M_{j+1}\prec \mathfrak M_{\omega }$
and
$\mathfrak M_j\prec \mathfrak M_{j+1}\prec \mathfrak M_{\omega }$
and
![]() $\omega _1\cap \mathfrak M_j \in \mathfrak M_{j+1}$
for each
$\omega _1\cap \mathfrak M_j \in \mathfrak M_{j+1}$
for each
![]() $j\in \omega $
. Let
$j\in \omega $
. Let
![]() $\xi _{\omega } \in \omega _1\setminus \mathfrak M_{\omega }$
. By elementarity there are
$\xi _{\omega } \in \omega _1\setminus \mathfrak M_{\omega }$
. By elementarity there are
![]() $\xi _j\in \omega _1\cap \mathfrak M_j$
such that:
$\xi _j\in \omega _1\cap \mathfrak M_j$
such that:
-
(1)
 ${\operatorname {dom}\,}(q_{\xi _{\omega }})\cap \mathfrak M_j\subseteq {\operatorname {dom}\,}(q_{\xi _j}).$
${\operatorname {dom}\,}(q_{\xi _{\omega }})\cap \mathfrak M_j\subseteq {\operatorname {dom}\,}(q_{\xi _j}).$
-
(2)
 $ n_{\mu ,\xi _j} = n_{\mu ,\xi _{\omega }}$
for each
$ n_{\mu ,\xi _j} = n_{\mu ,\xi _{\omega }}$
for each
 $\mu \in {\operatorname {dom}\,}(q_{\xi _{\omega }})\cap \mathfrak M_j$
.
$\mu \in {\operatorname {dom}\,}(q_{\xi _{\omega }})\cap \mathfrak M_j$
.
Note that
![]() $\{\alpha _{\xi _{\omega },1},\alpha _{\xi _{\omega }, 2}, \ldots , \alpha _{\xi _{\omega }, k}\}\cap \mathfrak M_{\omega }=\varnothing $
and hence
$\{\alpha _{\xi _{\omega },1},\alpha _{\xi _{\omega }, 2}, \ldots , \alpha _{\xi _{\omega }, k}\}\cap \mathfrak M_{\omega }=\varnothing $
and hence
 $$ \begin{align} (\forall j\in \omega)(\forall u\in k)(\forall v\in k) \ B(\alpha_{\xi_j,u},\alpha_{\xi_{\omega},v})\notin \mathfrak M_{\omega} . \end{align} $$
$$ \begin{align} (\forall j\in \omega)(\forall u\in k)(\forall v\in k) \ B(\alpha_{\xi_j,u},\alpha_{\xi_{\omega},v})\notin \mathfrak M_{\omega} . \end{align} $$
Furthermore, note that
 $\bigcup B^{-1}({\operatorname {dom}\,}(q_{\xi _{\omega }}))$
is finite and so there is J such that
$\bigcup B^{-1}({\operatorname {dom}\,}(q_{\xi _{\omega }}))$
is finite and so there is J such that
 $$ \begin{align*}\bigcup B^{-1}({\operatorname {dom}\,}(q_{\xi_{\omega}}))\cap \mathfrak M_{\omega}\subseteq \mathfrak M_J .\end{align*} $$
$$ \begin{align*}\bigcup B^{-1}({\operatorname {dom}\,}(q_{\xi_{\omega}}))\cap \mathfrak M_{\omega}\subseteq \mathfrak M_J .\end{align*} $$
From (9) it follows that
 $$ \begin{align}B(\alpha_{\xi_J,u},\alpha_{\xi_{\omega},v})\notin {\operatorname {dom}\,}(q_{\xi_J})\cup {\operatorname {dom}\,}(q_{\xi_{\omega}}) .\end{align} $$
$$ \begin{align}B(\alpha_{\xi_J,u},\alpha_{\xi_{\omega},v})\notin {\operatorname {dom}\,}(q_{\xi_J})\cup {\operatorname {dom}\,}(q_{\xi_{\omega}}) .\end{align} $$
From condition (19) in the choice of
![]() $q_{\xi }$
and condition (1) in the choice of
$q_{\xi }$
and condition (1) in the choice of
![]() $\xi _j$
, it follows that there is
$\xi _j$
, it follows that there is
![]() $q^*$
such that
$q^*$
such that
![]() $q^*\leq q_{\xi _J}$
and
$q^*\leq q_{\xi _J}$
and
![]() $q^*\leq q_{\xi _{\omega }}$
and
$q^*\leq q_{\xi _{\omega }}$
and
 ${\operatorname {dom}\,}(q^*)= {\operatorname {dom}\,}(q_{\xi _J}) \cup {\operatorname {dom}\,}(q_{\xi _{\omega }})$
.
${\operatorname {dom}\,}(q^*)= {\operatorname {dom}\,}(q_{\xi _J}) \cup {\operatorname {dom}\,}(q_{\xi _{\omega }})$
.
Let
![]() $\mathcal {A}\in \mathfrak {M_{\omega }}$
be a maximal antichain such that for every conditions
$\mathcal {A}\in \mathfrak {M_{\omega }}$
be a maximal antichain such that for every conditions
![]() $r\in \mathcal A$
,
$r\in \mathcal A$
,
 $$ \begin{align*}r\Vdash_{\mathbb P} ``M_{u,v} = \dot{N}_{u,v}(p_{\delta}(a_{\xi_J,u}, a_{\xi_{\omega},v}))\text{''}\end{align*} $$
$$ \begin{align*}r\Vdash_{\mathbb P} ``M_{u,v} = \dot{N}_{u,v}(p_{\delta}(a_{\xi_J,u}, a_{\xi_{\omega},v}))\text{''}\end{align*} $$
for some
![]() $k\times k$
matrix
$k\times k$
matrix
![]() $\left (M_{i,j}\right )$
with entries in
$\left (M_{i,j}\right )$
with entries in
![]() $\omega _1$
.
$\omega _1$
.
By the countable chain condition,
![]() $\mathcal {A}$
is countable and hence
$\mathcal {A}$
is countable and hence
![]() $\mathcal {A}\subseteq \mathfrak {M_{\omega }}$
. Let
$\mathcal {A}\subseteq \mathfrak {M_{\omega }}$
. Let
![]() $r\in \mathcal {A}$
be such that r is compatible with
$r\in \mathcal {A}$
be such that r is compatible with
![]() $q^*$
and let
$q^*$
and let
![]() $\left (M_{i,j}\right )$
be the
$\left (M_{i,j}\right )$
be the
![]() $k\times k$
matrix which witnesses that
$k\times k$
matrix which witnesses that
![]() $r\in \mathcal {A}$
. Let
$r\in \mathcal {A}$
. Let
![]() $q^{**}\le q^*, r$
.
$q^{**}\le q^*, r$
.
Note that
 $B(\alpha _{\xi _J,u},\alpha _{\xi _{\omega },v})\notin {\operatorname {dom}\,}(q^{**})$
because
$B(\alpha _{\xi _J,u},\alpha _{\xi _{\omega },v})\notin {\operatorname {dom}\,}(q^{**})$
because
 ${\operatorname {dom}\,}(q^{**})\setminus ({\operatorname {dom}\,}(q_{\xi _J})\cup {\operatorname {dom}\,}(q_{\xi _{\omega }}))\subseteq \mathfrak M_{\omega }$
and (9) and (10) hold. Let
${\operatorname {dom}\,}(q^{**})\setminus ({\operatorname {dom}\,}(q_{\xi _J})\cup {\operatorname {dom}\,}(q_{\xi _{\omega }}))\subseteq \mathfrak M_{\omega }$
and (9) and (10) hold. Let
 $$ \begin{align*}\hat{q}(\theta)= \begin{cases} q^{**}(\theta) & \text{ if } \theta \notin \{B(a_{\xi_J,u}, a_{\xi_{\omega},v})\}_{u,v\in k},\\ q_{\theta , e^{-1}_{B(a_{\xi_J,u}, a_{\xi_{\omega},v})}(M_{u,v})} & \text{ if } \theta = B(a_{\xi_J,u}, a_{\xi_{\omega},v}). \end{cases}\end{align*} $$
$$ \begin{align*}\hat{q}(\theta)= \begin{cases} q^{**}(\theta) & \text{ if } \theta \notin \{B(a_{\xi_J,u}, a_{\xi_{\omega},v})\}_{u,v\in k},\\ q_{\theta , e^{-1}_{B(a_{\xi_J,u}, a_{\xi_{\omega},v})}(M_{u,v})} & \text{ if } \theta = B(a_{\xi_J,u}, a_{\xi_{\omega},v}). \end{cases}\end{align*} $$
Then by the definition of c
 $$ \begin{align*}\hat{q}\Vdash_{\mathbb P} ``c(\alpha_{\xi_J, u}, \alpha_{\xi_{\omega}, v}) = M_{u,v} = \dot{N}_{u,v}((p_{\delta}(a_{\xi_J,u}, a_{\xi_{\omega},v}))\text{''}\end{align*} $$
$$ \begin{align*}\hat{q}\Vdash_{\mathbb P} ``c(\alpha_{\xi_J, u}, \alpha_{\xi_{\omega}, v}) = M_{u,v} = \dot{N}_{u,v}((p_{\delta}(a_{\xi_J,u}, a_{\xi_{\omega},v}))\text{''}\end{align*} $$
for each u and v as required. ⊣
Corollary 29. It is consistent with
![]() ${MA}_{\aleph _1}(\sigma \text {-linked})$
that
${MA}_{\aleph _1}(\sigma \text {-linked})$
that
 $\operatorname {Pr}_{0}(\aleph _1,\aleph _1,\aleph _1,\aleph _0)_{\bar p}$
holds for any
$\operatorname {Pr}_{0}(\aleph _1,\aleph _1,\aleph _1,\aleph _0)_{\bar p}$
holds for any
![]() $\omega _1$
sequence of partitions
$\omega _1$
sequence of partitions
![]() $\bar {p} = \{p_{\xi }\}_{\xi \in \omega _1}$
such that
$\bar {p} = \{p_{\xi }\}_{\xi \in \omega _1}$
such that
 $p_{\xi }:[\omega _1]^2\to \omega $
.
$p_{\xi }:[\omega _1]^2\to \omega $
.
Now we prove that the symbol
 $$ \begin{align*} \omega_1\nrightarrow_p [\omega_1]^2_{\omega_1} \end{align*} $$
$$ \begin{align*} \omega_1\nrightarrow_p [\omega_1]^2_{\omega_1} \end{align*} $$
can consistently fail for some
 $p:[\omega _1]^2\to \omega $
.
$p:[\omega _1]^2\to \omega $
.
We actually prove more. The failure of the symbol above over a partition
 $p:[\omega _1]^2\to \omega $
, symbolically written as
$p:[\omega _1]^2\to \omega $
, symbolically written as
 $$ \begin{align*} \omega_1\rightarrow_p[\omega_1]^2_{\omega_1}, \end{align*} $$
$$ \begin{align*} \omega_1\rightarrow_p[\omega_1]^2_{\omega_1}, \end{align*} $$
means that for every coloring
 $f:[\omega _1]^2\to \omega _1$
there is a set
$f:[\omega _1]^2\to \omega _1$
there is a set
 $A\in [\omega _1]^{\aleph _1}$
such that
$A\in [\omega _1]^{\aleph _1}$
such that
 $f\restriction ([A]^2\cap p^{-1}(i))$
omits at least one color for every
$f\restriction ([A]^2\cap p^{-1}(i))$
omits at least one color for every
![]() $i<\omega $
. Let us introduce the following symbol:
$i<\omega $
. Let us introduce the following symbol:
 $$ \begin{align*} \omega_1\rightarrow_p[\omega_1]^2_{\omega_1\setminus \omega_1}, \end{align*} $$
$$ \begin{align*} \omega_1\rightarrow_p[\omega_1]^2_{\omega_1\setminus \omega_1}, \end{align*} $$
to say that for every coloring
 $f:[\omega _1]^2\to \omega _1$
there is a set
$f:[\omega _1]^2\to \omega _1$
there is a set
 $A\in [\omega _1]^{\aleph _1}$
such that for every
$A\in [\omega _1]^{\aleph _1}$
such that for every
![]() $i<\omega $
a set of size
$i<\omega $
a set of size
![]() $\aleph _1$
of colors is omitted by
$\aleph _1$
of colors is omitted by
 $f\restriction ([A]^2\cap p^{-1}(i))$
. An even stronger failure (via breaking
$f\restriction ([A]^2\cap p^{-1}(i))$
. An even stronger failure (via breaking
![]() $\omega _1$
to two disjoint equinumerous sets and identifying all colors in each part) is
$\omega _1$
to two disjoint equinumerous sets and identifying all colors in each part) is
 $$ \begin{align*} \omega_1\rightarrow_p[\omega_1]^2_2.\end{align*} $$
$$ \begin{align*} \omega_1\rightarrow_p[\omega_1]^2_2.\end{align*} $$
It is the consistency of the latter symbol which we prove. Note that with the rounded-brackets symbol in (1) from the introduction we may write this failure as:
 $$ \begin{align*} \omega_1\rightarrow_p(\omega_1)^2_2,\end{align*} $$
$$ \begin{align*} \omega_1\rightarrow_p(\omega_1)^2_2,\end{align*} $$
whose meaning is that for every coloring
 $f:[\omega _1]^2\to 2$
there is
$f:[\omega _1]^2\to 2$
there is
 $A\in [\omega _1]^{\aleph _1}$
such that for every
$A\in [\omega _1]^{\aleph _1}$
such that for every
![]() $i<\omega $
the set
$i<\omega $
the set
 $[A]^2\cap p^{-1}(i)$
is f-monochromatic. Thus, while
$[A]^2\cap p^{-1}(i)$
is f-monochromatic. Thus, while
 $\omega _1\nrightarrow [\omega _1]^2_{\omega _1}$
holds in ZFC, it is consistent that for a suitable countable partition p the symbol
$\omega _1\nrightarrow [\omega _1]^2_{\omega _1}$
holds in ZFC, it is consistent that for a suitable countable partition p the symbol
 $\omega _1\nrightarrow _p[\omega _1]^2_{\omega _1}$
fails pretty badly.
$\omega _1\nrightarrow _p[\omega _1]^2_{\omega _1}$
fails pretty badly.
Theorem 30. It is consistent that
![]() $2^{\aleph _0}=\aleph _2$
and there is a partition
$2^{\aleph _0}=\aleph _2$
and there is a partition
 $p:[\omega _1]^2 \to \omega $
such that
$p:[\omega _1]^2 \to \omega $
such that
 $$ \begin{align*} \omega_1\rightarrow_p [\omega_1]^2_2. \end{align*} $$
$$ \begin{align*} \omega_1\rightarrow_p [\omega_1]^2_2. \end{align*} $$
Corollary 31. It is consistent that
![]() $2^{\aleph _0}=\aleph _2$
and there is some
$2^{\aleph _0}=\aleph _2$
and there is some
 $p:[\omega _1]^2\to \omega $
such that
$p:[\omega _1]^2\to \omega $
such that
 $$ \begin{align*} \omega_1\rightarrow_p[\omega_1]^2_{\omega_1\setminus \omega_1} \;\;\;\text{ and hence }\;\;\; \omega_1\rightarrow_p[\omega_1]^2_{\omega_1}. \end{align*} $$
$$ \begin{align*} \omega_1\rightarrow_p[\omega_1]^2_{\omega_1\setminus \omega_1} \;\;\;\text{ and hence }\;\;\; \omega_1\rightarrow_p[\omega_1]^2_{\omega_1}. \end{align*} $$
Proof of the Theorem
Let
![]() $\mathbb P$
be the partial order of finite partial functions from
$\mathbb P$
be the partial order of finite partial functions from
 $[\omega _1]^2 \to \omega $
ordered by inclusion. More precisely, each condition
$[\omega _1]^2 \to \omega $
ordered by inclusion. More precisely, each condition
![]() $q\in \mathbb P$
has associated to it a finite subset of
$q\in \mathbb P$
has associated to it a finite subset of
![]() $\omega _1$
which, abusing notation, will be called
$\omega _1$
which, abusing notation, will be called
![]() ${\operatorname {dom}\,}(q)$
. Then q is a function
${\operatorname {dom}\,}(q)$
. Then q is a function
 $[{\operatorname {dom}\,}(q)]^2\rightarrow \omega $
.
$[{\operatorname {dom}\,}(q)]^2\rightarrow \omega $
.
Given any partition
 $p:[\omega _1]^2 \to \omega $
and a colouring
$p:[\omega _1]^2 \to \omega $
and a colouring
 $c:[\omega _1]^2 \to 2$
define the partial order
$c:[\omega _1]^2 \to 2$
define the partial order
![]() $\mathbb Q(p,c)$
to be the set of all pairs
$\mathbb Q(p,c)$
to be the set of all pairs
![]() $(h,w)$
such that
$(h,w)$
such that
-
•
 $w\in [\omega _1]^{<\aleph _0},$
$w\in [\omega _1]^{<\aleph _0},$
-
•
 $h:m\to 2$
for some
$h:m\to 2$
for some
 $m\in \omega $
so that
$m\in \omega $
so that
 $m\supseteq p([w]^2),$
$m\supseteq p([w]^2),$
-
•
 $c(\{\alpha ,\beta \}) \neq h(p(\{\alpha ,\beta \}))$
for each
$c(\{\alpha ,\beta \}) \neq h(p(\{\alpha ,\beta \}))$
for each
 $\{\alpha ,\beta \}\in [w]^2$
$\{\alpha ,\beta \}\in [w]^2$
and order
![]() $\mathbb Q(p,c)$
by coordinatewise extension. Let V be a model of set theory in which
$\mathbb Q(p,c)$
by coordinatewise extension. Let V be a model of set theory in which
![]() $2^{\aleph _1} = \aleph _2$
and let
$2^{\aleph _1} = \aleph _2$
and let
![]() $\{c_{\xi }\}_{\xi \in \omega _2}$
enumerate cofinally often the subsets of hereditary cardinality less than
$\{c_{\xi }\}_{\xi \in \omega _2}$
enumerate cofinally often the subsets of hereditary cardinality less than
![]() $\aleph _2$
. If
$\aleph _2$
. If
![]() $G\subseteq \mathbb P$
is generic over V, in
$G\subseteq \mathbb P$
is generic over V, in
![]() $V[G]$
define
$V[G]$
define
![]() $p_G=\bigcup G$
. Then define a finite support iteration
$p_G=\bigcup G$
. Then define a finite support iteration
![]() $\{\mathbb Q_{\zeta }\}_{\zeta \in \omega _2}$
such that
$\{\mathbb Q_{\zeta }\}_{\zeta \in \omega _2}$
such that
![]() $\mathbb Q_1=\mathbb P$
and if
$\mathbb Q_1=\mathbb P$
and if
![]() $c_{\zeta }$
is a
$c_{\zeta }$
is a
![]() $\mathbb Q_{\zeta }$
-name such that
$\mathbb Q_{\zeta }$
-name such that
 $1\Vdash _{{\mathbb Q}_{\zeta }} ``c_{\zeta }:[\omega _1]^2 \to 2\text{''}$
then
$1\Vdash _{{\mathbb Q}_{\zeta }} ``c_{\zeta }:[\omega _1]^2 \to 2\text{''}$
then
 $\mathbb Q_{\zeta +1} = \mathbb Q_{\zeta }\ast \mathbb Q(p_G,c_{\zeta })$
.
$\mathbb Q_{\zeta +1} = \mathbb Q_{\zeta }\ast \mathbb Q(p_G,c_{\zeta })$
.
It suffices to establish the following two claims.
Claim 32. For each
![]() $\zeta \in \omega _2$
greater than
$\zeta \in \omega _2$
greater than
![]() $1$
and
$1$
and
![]() $\eta \in \omega _1$
the set of
$\eta \in \omega _1$
the set of
![]() $q\in \mathbb Q_{\zeta +1}$
such that
$q\in \mathbb Q_{\zeta +1}$
such that
 $$ \begin{align*}q\restriction \zeta\Vdash_{{\mathbb Q}_{\zeta}} ``q(\zeta ) = (h,w)\text{ and } w\setminus \eta\neq \varnothing\mathrm{''}\end{align*} $$
$$ \begin{align*}q\restriction \zeta\Vdash_{{\mathbb Q}_{\zeta}} ``q(\zeta ) = (h,w)\text{ and } w\setminus \eta\neq \varnothing\mathrm{''}\end{align*} $$
is dense in
![]() $\mathbb Q_{\zeta +1}$
.
$\mathbb Q_{\zeta +1}$
.
Proof Given q it may be assumed that there are h and w such that
 $$ \begin{align*}q\restriction \zeta\Vdash_{{\mathbb Q}_{\zeta}} ``q(\zeta ) = (\check{h},\check{w}).\text{''}\end{align*} $$
$$ \begin{align*}q\restriction \zeta\Vdash_{{\mathbb Q}_{\zeta}} ``q(\zeta ) = (\check{h},\check{w}).\text{''}\end{align*} $$
Let
![]() $\theta \in \omega _1$
be so large that
$\theta \in \omega _1$
be so large that
![]() $\theta>\max ({\operatorname {dom}\,}(q(0))),\max (w),\eta $
. Let
$\theta>\max ({\operatorname {dom}\,}(q(0))),\max (w),\eta $
. Let
![]() $f:w\to \omega $
be any one-to-one function so that
$f:w\to \omega $
be any one-to-one function so that
![]() ${\operatorname {ran}}(f)\cap {\operatorname {dom}\,}(h)=\emptyset $
and let
${\operatorname {ran}}(f)\cap {\operatorname {dom}\,}(h)=\emptyset $
and let
![]() $f_{\theta }:\{\{\theta ,\rho \}\}_{\rho \in w}\to \omega $
be defined by
$f_{\theta }:\{\{\theta ,\rho \}\}_{\rho \in w}\to \omega $
be defined by
![]() $f_{\theta }(\{\theta ,\rho \}) = f(\rho )$
. Note that since
$f_{\theta }(\{\theta ,\rho \}) = f(\rho )$
. Note that since
![]() $q(0)\cup f_{\theta }\in \mathbb P$
it is possible to find
$q(0)\cup f_{\theta }\in \mathbb P$
it is possible to find
![]() $\bar {q}\leq q\restriction \zeta $
such that:
$\bar {q}\leq q\restriction \zeta $
such that:
-
•
 $f_{\theta }\subseteq \bar {q}(0)$
and
$f_{\theta }\subseteq \bar {q}(0)$
and -
•
 $\bar {q}\Vdash _{{\mathbb Q}_{\zeta }} ``c_{\zeta }(\{\theta ,\rho \}) = \check {k}_{\rho }\text{''}$
for some family of integers
$\bar {q}\Vdash _{{\mathbb Q}_{\zeta }} ``c_{\zeta }(\{\theta ,\rho \}) = \check {k}_{\rho }\text{''}$
for some family of integers
 $\{k_{\rho }\}_{\rho \in w}$
equal to
$\{k_{\rho }\}_{\rho \in w}$
equal to
 $0$
or
$0$
or
 $1$
.
$1$
.
Then let
 $\bar {h}\supseteq h$
be any finite function such that
$\bar {h}\supseteq h$
be any finite function such that
 $\bar {h}(f(\rho ))=1- k_{\rho }$
and let
$\bar {h}(f(\rho ))=1- k_{\rho }$
and let
![]() $\bar {w} = w\cup \{\theta \}$
. Then
$\bar {w} = w\cup \{\theta \}$
. Then
 $\bar {q}\ast (\bar {h},\bar {w})$
is the desired condition. ⊣
$\bar {q}\ast (\bar {h},\bar {w})$
is the desired condition. ⊣
Claim 33. The partial order
![]() $\mathbb Q_{\omega _2}$
satisfies the ccc.
$\mathbb Q_{\omega _2}$
satisfies the ccc.
Proof By a standard argument, there is a dense subset of
![]() $\mathbb Q_{\omega _2}$
of conditions q such that for each
$\mathbb Q_{\omega _2}$
of conditions q such that for each
![]() $\zeta \in {\operatorname {dom}\,}(q)$
with
$\zeta \in {\operatorname {dom}\,}(q)$
with
![]() $\zeta>0$
, there are h and w so that
$\zeta>0$
, there are h and w so that
 $q\restriction \zeta \Vdash _{{\mathbb Q}_{\omega _2}} ``q(\zeta ) = (\check {h},\check {w}).\text{''}$
We will assume that all conditions that we work with are members of this dense subset.
$q\restriction \zeta \Vdash _{{\mathbb Q}_{\omega _2}} ``q(\zeta ) = (\check {h},\check {w}).\text{''}$
We will assume that all conditions that we work with are members of this dense subset.
Let
![]() $\{ q_{\xi }:\xi <\omega _1\}$
be conditions in
$\{ q_{\xi }:\xi <\omega _1\}$
be conditions in
![]() $\mathbb Q_{\omega _2}$
. By thinning out, we can assume that their domains form a
$\mathbb Q_{\omega _2}$
. By thinning out, we can assume that their domains form a
![]() $\Delta $
-system with root
$\Delta $
-system with root
![]() $\{0,\zeta _0,\zeta _1,\ldots ,\zeta _k\}$
. We can further assume that:
$\{0,\zeta _0,\zeta _1,\ldots ,\zeta _k\}$
. We can further assume that:
-
• each of the sets
 $\{{\operatorname {dom}\,}(q_{\xi }(0)):\xi <\omega _1\}$
, and
$\{{\operatorname {dom}\,}(q_{\xi }(0)):\xi <\omega _1\}$
, and
 $\{w_{\xi ,\zeta _i}:\xi <\omega _1\}$
for each
$\{w_{\xi ,\zeta _i}:\xi <\omega _1\}$
for each
 $i\le k$
form a
$i\le k$
form a
 $\Delta $
-system,
$\Delta $
-system, -
• the functions
 $q_{\xi }(0)$
agree on the root of the
$q_{\xi }(0)$
agree on the root of the
 $\Delta $
-system of their domains, and
$\Delta $
-system of their domains, and -
• there are
 $h_i$
,
$h_i$
,
 $i\le k$
, so that for all
$i\le k$
, so that for all
 $\xi <\omega $
we have
$\xi <\omega $
we have
 $h_i=h_{\xi ,\zeta _i}$
,
$h_i=h_{\xi ,\zeta _i}$
,
where
 $q_{\xi }\restriction \zeta \Vdash _{{\mathbb Q}_{\omega _2}} ``q_{\xi }(\zeta ) = (\check {h}_{\xi ,\zeta },\check {w}_{\xi ,\zeta }).\text{''}$
$q_{\xi }\restriction \zeta \Vdash _{{\mathbb Q}_{\omega _2}} ``q_{\xi }(\zeta ) = (\check {h}_{\xi ,\zeta },\check {w}_{\xi ,\zeta }).\text{''}$
Let
 $\delta =\max \{{\operatorname {dom}\,}(q_0(0)),w_{0,\zeta _i}:i\le k\}$
. Pick
$\delta =\max \{{\operatorname {dom}\,}(q_0(0)),w_{0,\zeta _i}:i\le k\}$
. Pick
![]() $\unicode{x3b3} <\omega _1$
so that each of the values
$\unicode{x3b3} <\omega _1$
so that each of the values
 $$ \begin{align*}\min({\operatorname {dom}\,}(q_{\unicode{x3b3}}(0))\setminus {\operatorname {dom}\,}(q_0(0))),\min(w_{\unicode{x3b3},\zeta_i}\setminus w_{0,\zeta_i}) \text{ for } i\le k,\end{align*} $$
$$ \begin{align*}\min({\operatorname {dom}\,}(q_{\unicode{x3b3}}(0))\setminus {\operatorname {dom}\,}(q_0(0))),\min(w_{\unicode{x3b3},\zeta_i}\setminus w_{0,\zeta_i}) \text{ for } i\le k,\end{align*} $$
are above
![]() $\delta $
(if defined).
$\delta $
(if defined).
Arguing as in Claim 32, we see that
![]() $q_0$
and
$q_0$
and
![]() $q_{\unicode{x3b3} }$
are compatible conditions. ⊣
$q_{\unicode{x3b3} }$
are compatible conditions. ⊣
This completes the proof of the theorem.⊣
Definition 34. The symbol
 $$ \begin{align*}\kappa\to_p [\kappa]^2_{\lambda,<\mu} \end{align*} $$
$$ \begin{align*}\kappa\to_p [\kappa]^2_{\lambda,<\mu} \end{align*} $$
for a partition
 $p:[\kappa ]^2\to \theta $
means that for every coloring
$p:[\kappa ]^2\to \theta $
means that for every coloring
 $f:[\kappa ]^2\to \lambda $
there is a set
$f:[\kappa ]^2\to \lambda $
there is a set
![]() $A\in [\kappa ]^{\kappa }$
such that
$A\in [\kappa ]^{\kappa }$
such that
 $|{\operatorname {ran}} (f\restriction ( [A]^2\cap p^{-1}(i)))|<\mu $
for all
$|{\operatorname {ran}} (f\restriction ( [A]^2\cap p^{-1}(i)))|<\mu $
for all
![]() $i<\theta $
.
$i<\theta $
.
Note that for
![]() $\mu \le \lambda $
this symbol is stronger than
$\mu \le \lambda $
this symbol is stronger than
 $\kappa \to _p [\kappa ]^2_{\lambda \setminus \lambda }$
. Thus the next theorem, which uses ideas from [Reference Shelah and Steprāns39], gives a stronger consistency than the previous one.
$\kappa \to _p [\kappa ]^2_{\lambda \setminus \lambda }$
. Thus the next theorem, which uses ideas from [Reference Shelah and Steprāns39], gives a stronger consistency than the previous one.
Theorem 35. Given any regular
![]() $\kappa>\aleph _1$
it is consistent that:
$\kappa>\aleph _1$
it is consistent that:
-
•
 $ \operatorname {\mathrm {\textbf {non}}}(\mathcal L)= \aleph _1$
,
$ \operatorname {\mathrm {\textbf {non}}}(\mathcal L)= \aleph _1$
, -
•
 $\mathfrak b = \aleph _2 = 2^{\aleph _0}$
,
$\mathfrak b = \aleph _2 = 2^{\aleph _0}$
, -
•
 $2^{\aleph _1} = \kappa $
, and
$2^{\aleph _1} = \kappa $
, and -
• there is a
 $p:[\omega _1]^2\to \omega $
such that
$p:[\omega _1]^2\to \omega $
such that
 $\omega _1\rightarrow _p [\omega _1]^2_{\omega ,<\omega }$
.
$\omega _1\rightarrow _p [\omega _1]^2_{\omega ,<\omega }$
.
Theorem 36. Given any regular
![]() $\kappa>\aleph _1$
it is consistent that:
$\kappa>\aleph _1$
it is consistent that:
-
•
 $ \operatorname {\mathrm {\textbf {non}}}(\mathcal M)= \aleph _1$
,
$ \operatorname {\mathrm {\textbf {non}}}(\mathcal M)= \aleph _1$
, -
•
 $\mathfrak b = \aleph _1 $
,
$\mathfrak b = \aleph _1 $
, -
•
 $\mathfrak d = \aleph _2 = 2^{\aleph _0}$
,
$\mathfrak d = \aleph _2 = 2^{\aleph _0}$
, -
•
 $2^{\aleph _1} = \kappa $
, and
$2^{\aleph _1} = \kappa $
, and -
• there is a
 $p:[\omega _1]^2\to \omega $
such that
$p:[\omega _1]^2\to \omega $
such that
 $\omega _1\rightarrow _p [\omega _1]^2_{\omega ,<\omega }$
.
$\omega _1\rightarrow _p [\omega _1]^2_{\omega ,<\omega }$
.
The proofs of both theorems are similar, using ideas from [Reference Shelah and Steprāns39]; only the proof of Theorem 35 will be given in detail. Both rely on the following definition:
Definition 37. Let
![]() $\mu $
be some probability measure on
$\mu $
be some probability measure on
![]() $\omega $
under which each singleton has positive measure, for example
$\omega $
under which each singleton has positive measure, for example
![]() $\mu (\{n\}) = 2^{-n}$
. A sequence of functions
$\mu (\{n\}) = 2^{-n}$
. A sequence of functions
![]() $\mathcal P = \{p_{\eta }\}_{\eta \in \omega _1}$
will be said to have full outer measure if:
$\mathcal P = \{p_{\eta }\}_{\eta \in \omega _1}$
will be said to have full outer measure if:
-
•
 $p_{\eta }:\eta \to \omega $
and
$p_{\eta }:\eta \to \omega $
and -
• for each
 $\eta \in \omega _1$
the set
$\eta \in \omega _1$
the set
 $\{p_{\beta }\restriction \eta \}_{\beta> \eta }$
has measure one in the measure space
$\{p_{\beta }\restriction \eta \}_{\beta> \eta }$
has measure one in the measure space
 $(\omega ^{\eta },\mu ^{\eta })$
.
$(\omega ^{\eta },\mu ^{\eta })$
.
The sequence
![]() $\mathcal P$
is defined to be nowhere meagre similarly, by requiring that for each
$\mathcal P$
is defined to be nowhere meagre similarly, by requiring that for each
![]() $\eta \in \omega _1$
the set
$\eta \in \omega _1$
the set
![]() $\{p_{\beta }\restriction \eta \}_{\beta> \eta }$
is nowhere meagre in
$\{p_{\beta }\restriction \eta \}_{\beta> \eta }$
is nowhere meagre in
![]() $(\omega ^{\eta },\mu ^{\eta })$
with the usual product topology. In both cases define
$(\omega ^{\eta },\mu ^{\eta })$
with the usual product topology. In both cases define
![]() $p = p(\mathcal P)$
by
$p = p(\mathcal P)$
by
 $p(\alpha , \beta ) = p_{\beta }(\alpha )$
if
$p(\alpha , \beta ) = p_{\beta }(\alpha )$
if
![]() $\alpha < \beta $
.
$\alpha < \beta $
.
By enumerating all functions from a countable ordinal into
![]() $\omega $
, we have:
$\omega $
, we have:
Proposition 38. Assuming the Continuum Hypothesis there is a sequence
![]() $\mathcal P = \{p_{\eta }\}_{\eta \in \omega _1}$
such that
$\mathcal P = \{p_{\eta }\}_{\eta \in \omega _1}$
such that
![]() $\{p_{\beta }\restriction \eta \}_{\beta> \eta } = \omega ^{\eta }$
for each
$\{p_{\beta }\restriction \eta \}_{\beta> \eta } = \omega ^{\eta }$
for each
![]() $\eta \in \omega _1$
. Hence
$\eta \in \omega _1$
. Hence
![]() $\mathcal P$
has full outer measure as in Definition 37
.
$\mathcal P$
has full outer measure as in Definition 37
.
While it is, of course, impossible to preserve the property that
![]() $\{p_{\beta }\restriction \eta \}_{\beta> \eta } = \omega ^{\eta }$
when adding reals, the goal of the following arguments is to show that the properties of Definition 37 can be preserved in certain circumstances. The following definition is from [Reference Shelah and Steprāns39] and will play a key role in this context.
$\{p_{\beta }\restriction \eta \}_{\beta> \eta } = \omega ^{\eta }$
when adding reals, the goal of the following arguments is to show that the properties of Definition 37 can be preserved in certain circumstances. The following definition is from [Reference Shelah and Steprāns39] and will play a key role in this context.
Definition 39. A function
 $\psi : {\omega }^{<\omega } \to [\omega _1]^{<\aleph _0}$
satisfying that
$\psi : {\omega }^{<\omega } \to [\omega _1]^{<\aleph _0}$
satisfying that
![]() $\psi (s)\cap \psi (t)=\varnothing $
unless
$\psi (s)\cap \psi (t)=\varnothing $
unless
![]() $s=t$
will be said to have disjoint range. If for each
$s=t$
will be said to have disjoint range. If for each
![]() $t\in {\omega }^{<\omega }$
there is k such that
$t\in {\omega }^{<\omega }$
there is k such that
![]() $|\psi (t^{\frown } j)|<k$
for all
$|\psi (t^{\frown } j)|<k$
for all
![]() $j\in \omega $
then
$j\in \omega $
then
![]() $\psi $
will be called bounded with disjoint range. If G is a filter of subtrees of
$\psi $
will be called bounded with disjoint range. If G is a filter of subtrees of
![]() $ {\omega }^{<\omega }$
and
$ {\omega }^{<\omega }$
and
![]() $\psi $
has disjoint range define
$\psi $
has disjoint range define
 $$ \begin{align*}S(G,\psi) = \bigcup_{t\in\bigcap G} \psi(t) .\end{align*} $$
$$ \begin{align*}S(G,\psi) = \bigcup_{t\in\bigcap G} \psi(t) .\end{align*} $$
If G is a generic filter of trees over a model V define
It is shown in [Reference Shelah and Steprāns39] that Lemmas 40 and 42 hold.
Lemma 40. If
![]() $G\subseteq \mathbb L$
is generic over V then
$G\subseteq \mathbb L$
is generic over V then
![]() $\mathcal S_b(G)$
is a P-ideal in
$\mathcal S_b(G)$
is a P-ideal in
![]() $V[G]$
.
$V[G]$
.
Lemma 41 is the content of Section 3 of [Reference Abraham and Todorčević1]. Recall that if
![]() $\mathcal I$
is an ideal then X is said to be orthogonal to
$\mathcal I$
is an ideal then X is said to be orthogonal to
![]() $\mathcal I$
if
$\mathcal I$
if
![]() $X\cap A$
is finite for each
$X\cap A$
is finite for each
![]() $A\in \mathcal I$
.
$A\in \mathcal I$
.
Lemma 41 Abraham and Todorčević
Let
![]() $\mathcal I$
be a P-ideal on
$\mathcal I$
be a P-ideal on
![]() $\omega _1$
that is generated by a family of
$\omega _1$
that is generated by a family of
![]() $\aleph _1$
countable sets and such that
$\aleph _1$
countable sets and such that
![]() $\omega _1$
is not the union of countably many sets orthogonal to
$\omega _1$
is not the union of countably many sets orthogonal to
![]() $\mathcal I$
. Then there is a proper partial order
$\mathcal I$
. Then there is a proper partial order
![]() ${\mathbb P}_{\mathcal I}$
, that adds no reals, even when iterated with countable support, such that there is a
${\mathbb P}_{\mathcal I}$
, that adds no reals, even when iterated with countable support, such that there is a
![]() ${\mathbb P}_{\mathcal I}$
-name
${\mathbb P}_{\mathcal I}$
-name
![]() $\dot {Z}$
for an uncountable subset of
$\dot {Z}$
for an uncountable subset of
![]() $\omega _1$
such that
$\omega _1$
such that
 $ 1\Vdash _{{\mathbb P}_{\mathcal I}} ``(\forall \eta \in \omega _1) \ \dot {Z}\cap \eta \in \mathcal I.\mathrm{''} $
$ 1\Vdash _{{\mathbb P}_{\mathcal I}} ``(\forall \eta \in \omega _1) \ \dot {Z}\cap \eta \in \mathcal I.\mathrm{''} $
Lemma 42. If
![]() $G\subseteq \mathbb L$
is generic over V and
$G\subseteq \mathbb L$
is generic over V and
![]() ${\mathbb P}_{{\mathcal S}_b(G)}$
is the partial order of Lemma 41
using Lemma 40
and
${\mathbb P}_{{\mathcal S}_b(G)}$
is the partial order of Lemma 41
using Lemma 40
and
![]() $H\subseteq {\mathbb P}_{{\mathcal S}_b(G)}$
is generic over
$H\subseteq {\mathbb P}_{{\mathcal S}_b(G)}$
is generic over
![]() $V[G]$
then in
$V[G]$
then in
![]() $V[G][H]$
there is an uncountable
$V[G][H]$
there is an uncountable
![]() $R\subseteq \omega _1$
such that
$R\subseteq \omega _1$
such that
![]() $R\cap Y\neq \varnothing $
for each uncountable
$R\cap Y\neq \varnothing $
for each uncountable
![]() $Y\in V[G]$
and such that
$Y\in V[G]$
and such that
 $[R]^{\aleph _0}\subseteq {\mathcal S}_b(G)$
.
$[R]^{\aleph _0}\subseteq {\mathcal S}_b(G)$
.
Lemma 43. Let
![]() $\mathcal P$
be a sequence with full outer measure and suppose that
$\mathcal P$
be a sequence with full outer measure and suppose that
![]() $p = p(\mathcal P)$
. Suppose further that
$p = p(\mathcal P)$
. Suppose further that
-
•
 $c:[\omega _1]^2 \to \omega $
,
$c:[\omega _1]^2 \to \omega $
, -
•
 $G\subseteq \mathbb L$
is generic over V, and
$G\subseteq \mathbb L$
is generic over V, and -
•
 $H\subseteq \mathbb P_{{\mathcal S}_b(\dot {G})}$
is generic over
$H\subseteq \mathbb P_{{\mathcal S}_b(\dot {G})}$
is generic over
 $V[G]$
.
$V[G]$
.
Then there is an uncountable
![]() $X\subseteq \omega _1$
in
$X\subseteq \omega _1$
in
![]() $V[G][H]$
and
$V[G][H]$
and
![]() $L:\omega \to \omega $
such that
$L:\omega \to \omega $
such that
![]() $L(p(\alpha ,\beta ))>c(\alpha ,\beta )$
for all
$L(p(\alpha ,\beta ))>c(\alpha ,\beta )$
for all
 $\{\alpha ,\beta \}\in [X]^2$
.
$\{\alpha ,\beta \}\in [X]^2$
.
Proof In
![]() $V[G]$
let
$V[G]$
let
![]() $L = \bigcap {G}$
be the Laver real. In
$L = \bigcap {G}$
be the Laver real. In
![]() $V[G][H]$
let R be the uncountable set given by Lemma 42. Construct by induction distinct
$V[G][H]$
let R be the uncountable set given by Lemma 42. Construct by induction distinct
![]() $\rho _{\xi }\in R$
such that if
$\rho _{\xi }\in R$
such that if
![]() $\eta \in \xi $
then
$\eta \in \xi $
then
 $L(p(\rho _{\xi },\rho _{\eta }))>c(\rho _{\xi },\rho _{\eta }) $
. To carry out the induction assume that
$L(p(\rho _{\xi },\rho _{\eta }))>c(\rho _{\xi },\rho _{\eta }) $
. To carry out the induction assume that
![]() $R_{\eta }= \{\rho _{\xi }\}_{\xi \in \eta }$
have been chosen and satisfy the inductive hypothesis.
$R_{\eta }= \{\rho _{\xi }\}_{\xi \in \eta }$
have been chosen and satisfy the inductive hypothesis.
By the choice of R it follows that
 $R_{\eta }\in {\mathcal S}_b(G)$
. Since
$R_{\eta }\in {\mathcal S}_b(G)$
. Since
 $\mathbb P_{{\mathcal S}_b(\dot {G})}$
adds no new reals it follows that
$\mathbb P_{{\mathcal S}_b(\dot {G})}$
adds no new reals it follows that
![]() $R_{\eta } \in V[G]$
and so there is
$R_{\eta } \in V[G]$
and so there is
![]() $T\in G$
and
$T\in G$
and
![]() $\psi \in V$
with bounded, disjoint range such that
$\psi \in V$
with bounded, disjoint range such that
 $T\Vdash _{\mathbb L} ``\dot {R}_{\eta } = S(\dot {G},\psi ).\text{''}$
Let
$T\Vdash _{\mathbb L} ``\dot {R}_{\eta } = S(\dot {G},\psi ).\text{''}$
Let
![]() $\mu $
be so large that
$\mu $
be so large that
 $T\Vdash _{\mathbb L} ``\dot {R}_{\eta } \subseteq \mu \text{''}$
and let r be the root of T. For
$T\Vdash _{\mathbb L} ``\dot {R}_{\eta } \subseteq \mu \text{''}$
and let r be the root of T. For
![]() $t\in T$
define
$t\in T$
define
 $\mathcal W_t=\left \{x\in 2^{\mu } \ \left | \ x\restriction \psi (t)\text { has constant value } |t| \right .\right \} $
and then define
$\mathcal W_t=\left \{x\in 2^{\mu } \ \left | \ x\restriction \psi (t)\text { has constant value } |t| \right .\right \} $
and then define
 $$ \begin{align*}\mathcal W_t^+ = \left\{x\in 2^{\mu} \ \left| \ (\exists^{\infty} s\in \textstyle{\textbf{succ}_T(t)}) \ x\in {\mathcal W}_s \right.\right\} .\end{align*} $$
$$ \begin{align*}\mathcal W_t^+ = \left\{x\in 2^{\mu} \ \left| \ (\exists^{\infty} s\in \textstyle{\textbf{succ}_T(t)}) \ x\in {\mathcal W}_s \right.\right\} .\end{align*} $$
Note that
![]() ${\mathcal W}_t^+$
has measure one in
${\mathcal W}_t^+$
has measure one in
![]() $2^{\mu }$
for each
$2^{\mu }$
for each
![]() $t\supseteq r$
. To see this note that for a random
$t\supseteq r$
. To see this note that for a random
![]() $h\in 2^{\mu }$
the probability that
$h\in 2^{\mu }$
the probability that
![]() $h(\zeta ) = |t| + 1$
is
$h(\zeta ) = |t| + 1$
is
![]() $2^{-(|t|+1)}$
. Also, note that since
$2^{-(|t|+1)}$
. Also, note that since
![]() $\psi $
is bounded—see Definition 39—there is some k such that
$\psi $
is bounded—see Definition 39—there is some k such that
![]() $|\psi (s)|\leq k$
for each
$|\psi (s)|\leq k$
for each
![]() $s\in \textbf {succ}_T(t)$
. Hence, the probability of h belonging to
$s\in \textbf {succ}_T(t)$
. Hence, the probability of h belonging to
![]() ${\mathcal W}_{s}$
is bounded below by
${\mathcal W}_{s}$
is bounded below by
![]() $2^{-(|t|+1)k}$
for all
$2^{-(|t|+1)k}$
for all
![]() $s\in \textbf {succ}_T(t)$
and these events are independent because the
$s\in \textbf {succ}_T(t)$
and these events are independent because the
![]() $\psi (s)$
are pairwise disjoint for
$\psi (s)$
are pairwise disjoint for
![]() $s\in \textbf {succ}_T(t)$
.
$s\in \textbf {succ}_T(t)$
.
Define f on
 $\bigcup _{j\leq |r|}\psi (r\restriction j)$
to have constant value
$\bigcup _{j\leq |r|}\psi (r\restriction j)$
to have constant value
![]() $|r|$
and note that the domain of f is disjoint from each
$|r|$
and note that the domain of f is disjoint from each
![]() $\psi (s)$
where
$\psi (s)$
where
![]() $s\supsetneq r$
. Hence the probability that
$s\supsetneq r$
. Hence the probability that
![]() $f\subseteq h$
is non-zero and independent from belonging to each
$f\subseteq h$
is non-zero and independent from belonging to each
![]() ${\mathcal W}^+$
. Since p has full outer measure it follows that
${\mathcal W}^+$
. Since p has full outer measure it follows that
 $$ \begin{align*}\Bigg\{\beta\in \omega_1 \ \Bigg| \ f\subseteq p_{\beta}\restriction \mu\in\bigcap_{r\subseteq t\in T}{\mathcal W}_{t}^+ \Bigg\}\end{align*} $$
$$ \begin{align*}\Bigg\{\beta\in \omega_1 \ \Bigg| \ f\subseteq p_{\beta}\restriction \mu\in\bigcap_{r\subseteq t\in T}{\mathcal W}_{t}^+ \Bigg\}\end{align*} $$
is uncountable and belongs to
![]() $V[G]$
. Therefore by Lemma 42 there is some
$V[G]$
. Therefore by Lemma 42 there is some
![]() $\beta \in R\setminus R_{\eta }$
such that
$\beta \in R\setminus R_{\eta }$
such that
![]() $f\subseteq p_{\beta }\restriction \mu $
and such that for all
$f\subseteq p_{\beta }\restriction \mu $
and such that for all
![]() $t\in T$
containing r there are infinitely many
$t\in T$
containing r there are infinitely many
![]() $s\in \textstyle {\textbf {succ}_T(t)}$
such that
$s\in \textstyle {\textbf {succ}_T(t)}$
such that
![]() $p(\alpha ,\beta ) = |s|$
for all
$p(\alpha ,\beta ) = |s|$
for all
![]() $\alpha \in \psi (s)$
.
$\alpha \in \psi (s)$
.
Using this and the definition of f, it is possible to start with r and successively thin out the successors of each
![]() $t\in T$
to find a tree
$t\in T$
to find a tree
![]() $T^*\subseteq T$
with root r such that
$T^*\subseteq T$
with root r such that
![]() $p(\alpha ,\beta ) = |t| $
for all
$p(\alpha ,\beta ) = |t| $
for all
![]() $t\in T^*$
and for all
$t\in T^*$
and for all
![]() $\alpha \in \psi (t)$
. Once again starting with r and removing only finitely many elements of
$\alpha \in \psi (t)$
. Once again starting with r and removing only finitely many elements of
![]() $\textbf {succ}_{T^*}(t)$
for each
$\textbf {succ}_{T^*}(t)$
for each
![]() $t\in T^*$
it is possible to find
$t\in T^*$
it is possible to find
![]() $T^{**}\subseteq T^*$
with root r such that
$T^{**}\subseteq T^*$
with root r such that
and this implies that
 $$ \begin{align*} T^{**}\, {\Vdash}_{\mathbb L} ``(\forall \alpha\in {\dot{R}}_{\eta}) \ \dot{L}(p(\alpha,\beta))>c(\alpha,\beta).\text{''} \end{align*} $$
$$ \begin{align*} T^{**}\, {\Vdash}_{\mathbb L} ``(\forall \alpha\in {\dot{R}}_{\eta}) \ \dot{L}(p(\alpha,\beta))>c(\alpha,\beta).\text{''} \end{align*} $$
Since this holds for any T, genericity yields that in
![]() $V[G][H]$
there is some
$V[G][H]$
there is some
![]() $\beta \in R\setminus R_{\eta }$
such that
$\beta \in R\setminus R_{\eta }$
such that
 $L(p(\rho _{\xi },\beta ))>c(\rho _{\xi },\beta )$
for each
$L(p(\rho _{\xi },\beta ))>c(\rho _{\xi },\beta )$
for each
![]() $\xi \in \eta $
. Define
$\xi \in \eta $
. Define
![]() $\rho _{\eta } = \beta $
to continue the induction. Since limit stages are immediate, this completes the proof. ⊣
$\rho _{\eta } = \beta $
to continue the induction. Since limit stages are immediate, this completes the proof. ⊣
Proof of Theorem 35
The required model is the one obtained by starting with a model of the Continuum Hypothesis in which
![]() $2^{\aleph _1}=\kappa $
. Then iterate with countable support the partial order
$2^{\aleph _1}=\kappa $
. Then iterate with countable support the partial order
 ${\mathbb L}\ast {\mathbb P}_{{\mathcal S}_b\dot {G})}$
. In the initial model there is, by Proposition 38, a sequence with full outer measure. To see this, begin by observing that it is shown in Theorem 7.3.39 of [Reference Bartoszyński and Judah2] that
${\mathbb L}\ast {\mathbb P}_{{\mathcal S}_b\dot {G})}$
. In the initial model there is, by Proposition 38, a sequence with full outer measure. To see this, begin by observing that it is shown in Theorem 7.3.39 of [Reference Bartoszyński and Judah2] that
![]() $\mathbb L$
preserves
$\mathbb L$
preserves
![]() $\sqsubseteq ^{\textbf {Random}}$
. Since
$\sqsubseteq ^{\textbf {Random}}$
. Since
 ${\mathbb P}_{{\mathcal S}(\dot {G})}$
is proper and adds no new reals it is immediate that it also preserves
${\mathbb P}_{{\mathcal S}(\dot {G})}$
is proper and adds no new reals it is immediate that it also preserves
![]() $ \sqsubseteq ^{\textbf {Random}}$
. It follows by Theorem 6.1.13 of [Reference Bartoszyński and Judah2] that the entire countable support iteration preserves outer measure sets and, hence, any sequence with full outer measure in the initial model maintains this property throughout the iteration.
$ \sqsubseteq ^{\textbf {Random}}$
. It follows by Theorem 6.1.13 of [Reference Bartoszyński and Judah2] that the entire countable support iteration preserves outer measure sets and, hence, any sequence with full outer measure in the initial model maintains this property throughout the iteration.
To see that for every function
 $c:[\omega _1]^2\to \omega $
there is an uncountable set witnessing
$c:[\omega _1]^2\to \omega $
there is an uncountable set witnessing
![]() $\aleph _1{\rightarrow }_p[\aleph _{1}]_{\aleph _0,<\aleph _0}$
use Lemma 3.4 and Lemma 3.6 of [Reference Abraham and Todorčević1] to conclude that each partial order in the
$\aleph _1{\rightarrow }_p[\aleph _{1}]_{\aleph _0,<\aleph _0}$
use Lemma 3.4 and Lemma 3.6 of [Reference Abraham and Todorčević1] to conclude that each partial order in the
![]() $\omega _2$
length iteration is proper and has the
$\omega _2$
length iteration is proper and has the
![]() $\aleph _2$
-pic of Definition 2.1 on page 409 of [Reference Shelah35]. By Lemma 2.4 on page 410 of [Reference Shelah35] it follows that the iteration has the
$\aleph _2$
-pic of Definition 2.1 on page 409 of [Reference Shelah35]. By Lemma 2.4 on page 410 of [Reference Shelah35] it follows that the iteration has the
![]() $\aleph _2$
chain condition and, hence, that c appears at some stage. It is then routine to apply Lemma 43.
$\aleph _2$
chain condition and, hence, that c appears at some stage. It is then routine to apply Lemma 43.
That
![]() $\mathfrak b=\aleph _2$
is a standard argument using that Laver forcing adds a dominating real. ⊣
$\mathfrak b=\aleph _2$
is a standard argument using that Laver forcing adds a dominating real. ⊣
Remark 44. The proof of Theorem 36 is similar but uses Miller reals instead of Laver reals. This requires that nowhere meagreness play the role of full outer measure.
Remark 45. Note that there is no partition p such that
 $$ \begin{align*} \omega_1{\rightarrow}_p [\omega_1]^2_{\omega_1,<\omega_1} \end{align*} $$
$$ \begin{align*} \omega_1{\rightarrow}_p [\omega_1]^2_{\omega_1,<\omega_1} \end{align*} $$
because a colouring
 $c:[\omega _1]^2\to \omega _1$
that is a bijection will provide a counterexample.
$c:[\omega _1]^2\to \omega _1$
that is a bijection will provide a counterexample.
6 Concluding Remarks and Open Questions
It turns out, via Lemma 9, that getting strong coloring symbols over finite partitions is not harder than getting them without partitions; so one immediately gets many strong coloring symbols over partitions outright in ZFC. If the number of colors
![]() $\lambda $
raised to the number of cells in a partition is not too large, Lemma 9 applies again, and consequently all GCH symbols gotten by Erdoős, Hajnal and Milner on
$\lambda $
raised to the number of cells in a partition is not too large, Lemma 9 applies again, and consequently all GCH symbols gotten by Erdoős, Hajnal and Milner on
![]() $\kappa ^+$
hold under the GCH over arbitrary
$\kappa ^+$
hold under the GCH over arbitrary
![]() $\kappa $
-partitions. Even without instances of the GCH, strong colorings symbols over countable partitions are valid in Cohen-type forcing extenstions, by Theorems 27 and 28.
$\kappa $
-partitions. Even without instances of the GCH, strong colorings symbols over countable partitions are valid in Cohen-type forcing extenstions, by Theorems 27 and 28.
Yet, it is not the case that every time a strong-coloring symbol holds at a successor of a regular, it also holds over countable partitions: by Theorems 30 and 35 the ZFC symbol
 $\aleph _1\nrightarrow [\aleph _1]^2_{\aleph _1}$
, and hence all stronger ones, consistently fail quite badly over sufficiently generic countable partitions. Thus, strong coloring symbols over partitions are a subject of their own, in which the independence phenomenon is manifested prominently.
$\aleph _1\nrightarrow [\aleph _1]^2_{\aleph _1}$
, and hence all stronger ones, consistently fail quite badly over sufficiently generic countable partitions. Thus, strong coloring symbols over partitions are a subject of their own, in which the independence phenomenon is manifested prominently.
Many natural questions about the combinatorial and set-theoretic connections between coloring and partition arise. We hope that this subject will get attention in the near future both in the infinite combinatorics and in the forcing communities. For example, by Fact 11, there is always a set of
![]() $2$
-partitions of
$2$
-partitions of
 $[\kappa ^+]^2$
such that no coloring is strong over all of them. What is the least cardinality of such a set? In the case of
$[\kappa ^+]^2$
such that no coloring is strong over all of them. What is the least cardinality of such a set? In the case of
![]() $\theta =\kappa =\aleph _0$
, the results in Section 5 show that this cardinal may be as small as 1 or at least as large as
$\theta =\kappa =\aleph _0$
, the results in Section 5 show that this cardinal may be as small as 1 or at least as large as
![]() $\aleph _2=\kappa ^{++}$
. Can this number ever be
$\aleph _2=\kappa ^{++}$
. Can this number ever be
![]() $\kappa $
or, say,
$\kappa $
or, say,
![]() $\kappa ^+<2^{\kappa }$
?
$\kappa ^+<2^{\kappa }$
?
We conclude with a short selection of open questions.
Question 46. If
 $\operatorname {Pr}_1(\aleph _1,\aleph _1,\aleph _1,\aleph _0)_p$
holds for all countable p, does also
$\operatorname {Pr}_1(\aleph _1,\aleph _1,\aleph _1,\aleph _0)_p$
holds for all countable p, does also
 $\operatorname {Pr}_0(\aleph _1,\aleph _1,\aleph _1,\aleph _0)_p$
hold for all countable p?
$\operatorname {Pr}_0(\aleph _1,\aleph _1,\aleph _1,\aleph _0)_p$
hold for all countable p?
Question 47. Suppose
 $\operatorname {Pr}_0(\aleph _1,\aleph _1,\aleph _0,\aleph _0)_p$
holds for some countable partition p. Does
$\operatorname {Pr}_0(\aleph _1,\aleph _1,\aleph _0,\aleph _0)_p$
holds for some countable partition p. Does
 $\operatorname {Pr}_0(\aleph _1,\aleph _1,\aleph _1,\aleph _0)_p$
hold as well?
$\operatorname {Pr}_0(\aleph _1,\aleph _1,\aleph _1,\aleph _0)_p$
hold as well?
Without partitions, both implications above hold.
Question 48. Does
![]() $MA_{\sigma \text {-linked}}$
or
$MA_{\sigma \text {-linked}}$
or
![]() $\mathfrak p = \mathfrak c$
or even full
$\mathfrak p = \mathfrak c$
or even full
![]() $MA_{\aleph _1}$
imply that
$MA_{\aleph _1}$
imply that
 $\operatorname {Pr}_{0}(\aleph _1,\aleph _1,\aleph _1,\aleph _0)_{\bar p}$
holds for every
$\operatorname {Pr}_{0}(\aleph _1,\aleph _1,\aleph _1,\aleph _0)_{\bar p}$
holds for every
![]() $\omega _1$
sequence of partitions
$\omega _1$
sequence of partitions
![]() $\bar {p} = \langle p_{\delta }:\delta <\omega _1\rangle $
such that
$\bar {p} = \langle p_{\delta }:\delta <\omega _1\rangle $
such that
 $p_{\delta }:[\omega _1]^2\to \omega $
?
$p_{\delta }:[\omega _1]^2\to \omega $
?
Question 49. Is it consistent that there is a partition p such that
 $$ \begin{align*}\aleph_1\rightarrow_p [\aleph_1]^2_{\aleph_0,<k}\end{align*} $$
$$ \begin{align*}\aleph_1\rightarrow_p [\aleph_1]^2_{\aleph_0,<k}\end{align*} $$
for some integer k?
Question 50. Is

consistent for all
![]() $\aleph _0$
- or
$\aleph _0$
- or
![]() $\aleph _1$
-partitions p? That is, can there be a coloring
$\aleph _1$
-partitions p? That is, can there be a coloring
 $f:[\omega _2]^2\to \omega _2$
such that for every (one, or sequence of
$f:[\omega _2]^2\to \omega _2$
such that for every (one, or sequence of
![]() $\omega _2$
many)
$\omega _2$
many)
![]() $\omega _1$
-partition(s) of
$\omega _1$
-partition(s) of
 $[\omega _2]^2$
, for every
$[\omega _2]^2$
, for every
![]() $B\in [\omega _2]^{\omega _2}$
, for all but finitely many
$B\in [\omega _2]^{\omega _2}$
, for all but finitely many
![]() $\alpha <\omega _2$
there is
$\alpha <\omega _2$
there is
![]() $i<\omega _1$
such that for every color
$i<\omega _1$
such that for every color
![]() $\zeta <\omega _2$
there is
$\zeta <\omega _2$
there is
![]() $\beta \in B$
such that
$\beta \in B$
such that
![]() $p(\alpha ,\beta )=i$
and
$p(\alpha ,\beta )=i$
and
![]() $f(\alpha ,\beta )=\zeta $
.
$f(\alpha ,\beta )=\zeta $
.
The consistency of this symbol is open even without the p. A negative answer may be easier to get with p.
Added in proof: Problems 46–49 above are solved in [Reference Kojman, Rinot and Steprans18].
Acknowledgments
The first author’s research for this paper was partially supported by an Israeli Science Foundation grant number 665/20. The third author’s research for this paper was partially supported by NSERC of Canada.