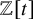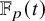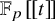1 Introduction
Les grassmanniennes affines
![]() $\operatorname {Gr}_G$
de k-groupes réductifs G sont des k-ind-schémas qui ont été introduits dans les années 90 en théorie géométrique des représentations pour étudier le champ des G-fibrés sur une courbe à l’aide de l’uniformisation de Beauville–Laszlo [Reference Beauville and LaszloBL94]. Cependant, leur importance n’a été mise en relief que dans les décennies suivantes, dans fondamentalement deux programmes : d’un côté, l’équivalence de Satake géométrique, et de l’autre, la théorie des modèles entiers de variétés de Shimura ou plutôt de ce qu’on appelle leurs modèles locaux. Pour cette dernière application, il faut comprendre vraiment la structure géométrique de certains sous-schémas fermés de
$\operatorname {Gr}_G$
de k-groupes réductifs G sont des k-ind-schémas qui ont été introduits dans les années 90 en théorie géométrique des représentations pour étudier le champ des G-fibrés sur une courbe à l’aide de l’uniformisation de Beauville–Laszlo [Reference Beauville and LaszloBL94]. Cependant, leur importance n’a été mise en relief que dans les décennies suivantes, dans fondamentalement deux programmes : d’un côté, l’équivalence de Satake géométrique, et de l’autre, la théorie des modèles entiers de variétés de Shimura ou plutôt de ce qu’on appelle leurs modèles locaux. Pour cette dernière application, il faut comprendre vraiment la structure géométrique de certains sous-schémas fermés de
![]() $\operatorname {Gr}_G$
. En fait, la stratégie adoptée à la suite de Faltings [Reference FaltingsFa03] pour parvenir aux résultats désirés consiste à tirer profit du fait que l’on ait une réalisation entière de la grassmannienne affine. Lorsqu’on veut traiter les groupes non constants et tordus, la situation devient plus compliquée et les divers travaux monumentaux [Reference Pappas and RapoportPR08], [Reference ZhuZh14], [Reference Pappas and ZhuPZ13] de Pappas–Rapoport–Zhu consacrés à ce problème ne réussirent pas à éviter des hypothèses de ramification modérée - à savoir la grassmannienne affine tordue n’est réalisée qu’au-dessus de
$\operatorname {Gr}_G$
. En fait, la stratégie adoptée à la suite de Faltings [Reference FaltingsFa03] pour parvenir aux résultats désirés consiste à tirer profit du fait que l’on ait une réalisation entière de la grassmannienne affine. Lorsqu’on veut traiter les groupes non constants et tordus, la situation devient plus compliquée et les divers travaux monumentaux [Reference Pappas and RapoportPR08], [Reference ZhuZh14], [Reference Pappas and ZhuPZ13] de Pappas–Rapoport–Zhu consacrés à ce problème ne réussirent pas à éviter des hypothèses de ramification modérée - à savoir la grassmannienne affine tordue n’est réalisée qu’au-dessus de
![]() $\mathbb {Z}[1/e]$
, où l’on note e l’indice de ramification.
$\mathbb {Z}[1/e]$
, où l’on note e l’indice de ramification.
Dans l’article présent, on se propose d’étendre la théorie existante pour les groupes quasi-déployés aux cas de ramification sauvage et d’obtenir ainsi des réalisations entières des grassmanniennes affines tordues, voir le théorème 1.4. L’étape-clé est la construction d’un certain
![]() $\mathbb {Z}[t]$
-groupe
$\mathbb {Z}[t]$
-groupe
![]() $\underline {\mathscr {G}_{\mathbf {f}}}$
affine, lisse et connexe, qu’on regarde comme une famille entière de groupes parahoriques au-dessus de chaque corps premier et dont la grassmannienne affine est celle qu’on cherche, sous des hypothèses légères sur le
$\underline {\mathscr {G}_{\mathbf {f}}}$
affine, lisse et connexe, qu’on regarde comme une famille entière de groupes parahoriques au-dessus de chaque corps premier et dont la grassmannienne affine est celle qu’on cherche, sous des hypothèses légères sur le
![]() $\mathbb {Q}(t)$
-groupe G fibre générique de
$\mathbb {Q}(t)$
-groupe G fibre générique de
![]() $\underline {\mathscr {G}_{\mathbf {f}}}$
, voir le théorème 1.3. Notre approche diffère de celle de [Reference Pappas and ZhuPZ13] en ce que les auteurs de ce dernier article choisissent relever leurs groupes en caractéristique mixte aux anneaux des polynômes, tandis que nous adoptons le point de vue de la réduction de la caractéristique nulle à la positive. Toutefois, on s’attend à ce que notre article fournisse les outils nécessaires, voir le théorème 1.5, pour faire des avances dans la théorie des modèles locaux p-adiques en des cas de ramification sauvage, telle qu’elle fut exposée dans les travaux de Scholze–Weinstein [Reference Scholze and WeinsteinSW20] et de He–Pappas–Rapoport [Reference He, Pappas and RapoportHPR18], voir notre dissertation [Reference Pereira LourençoPL20] et le dernier paragraphe de cette introduction.
$\underline {\mathscr {G}_{\mathbf {f}}}$
, voir le théorème 1.3. Notre approche diffère de celle de [Reference Pappas and ZhuPZ13] en ce que les auteurs de ce dernier article choisissent relever leurs groupes en caractéristique mixte aux anneaux des polynômes, tandis que nous adoptons le point de vue de la réduction de la caractéristique nulle à la positive. Toutefois, on s’attend à ce que notre article fournisse les outils nécessaires, voir le théorème 1.5, pour faire des avances dans la théorie des modèles locaux p-adiques en des cas de ramification sauvage, telle qu’elle fut exposée dans les travaux de Scholze–Weinstein [Reference Scholze and WeinsteinSW20] et de He–Pappas–Rapoport [Reference He, Pappas and RapoportHPR18], voir notre dissertation [Reference Pereira LourençoPL20] et le dernier paragraphe de cette introduction.
Signalons que, afin d’étudier l’arithmétique de nos groupes en les caractéristiques sauvages, il faut utiliser la théorie générale et classification des groupes pseudo-réductifs sur les corps développée par Conrad–Gabber–Prasad [Reference Conrad, Gabber and PrasadCGP15], ainsi que leur théorie schématique de Bruhat–Tits sur les corps discrètement valués, complets et à corps résiduels parfaits, qui fut développée en [Reference LourençoLou21]. Cet outil-là a été développé pour qu’on puisse démontrer certaines propriétés générales concernant les groupes algébriques linéaires sur les corps de fonctions, comme en [Reference ConradCo12] ou [Reference RosengartenRo18]. Néanmoins, le présent article est le seul à mettre au centre de l’attention les groupes pseudo-réductifs non standards, depuis les travaux de Tits consacrés aux groupes de Kac–Moody, [Reference TitsTi84] et [Reference TitsTi89], où les
![]() $\mathbb {Z}[t^{\pm 1}]$
-groupes
$\mathbb {Z}[t^{\pm 1}]$
-groupes
![]() $\underline {G}$
furent construits, voir la question 1.1. Cependant, ce fut originalement à travers l’article [Reference LevinLev16] de Levin, consacré aux modèles locaux p-adiques pour les restrictions des scalaires de groupes modérés, que nous sommes conduit au cadre pseudo-réductif, car celui-là faisait implicitement usage des extensions purement inséparables.
$\underline {G}$
furent construits, voir la question 1.1. Cependant, ce fut originalement à travers l’article [Reference LevinLev16] de Levin, consacré aux modèles locaux p-adiques pour les restrictions des scalaires de groupes modérés, que nous sommes conduit au cadre pseudo-réductif, car celui-là faisait implicitement usage des extensions purement inséparables.
Pour conclure en ce qui touche aux références historiques, nous aimerions rappeler au lecteur que, dans le cadre de Kac–Moody, la communauté mathématique avait déjà étudié à fond les variétés de drapeaux sur
![]() $\mathbb {C}$
typiquement de dimension infinie associées aux algèbres de Kac–Moody
$\mathbb {C}$
typiquement de dimension infinie associées aux algèbres de Kac–Moody
![]() $\mathfrak {g}$
, qui admettent un prolongement naturel en des
$\mathfrak {g}$
, qui admettent un prolongement naturel en des
![]() $\mathbb {Z}$
-ind-schémas d’après Mathieu [Reference MathieuMat88]. Comme produit dérivé des résultats qu’on va présenter, se dégage un dictionnaire arithmétique complet entre les grassmanniennes affines tordues et les variétés de drapeaux de Kac–Moody affines, voir le §6, ce qui était attendu en les caractéristiques petites depuis longtemps. Le théorème 1.4 sur la normalité des variétés de Schubert retient néanmoins son importance, parce que leurs définitions ne se ressemblent guère et qu’on y recourt pour établir la comparaison. Il ne doit être alors aucune surprise que Tits soit arrivé au milieu de sa recherche sur les groupes de Kac–Moody aux constructions sur lesquelles on s’appuie, et que cette théorie soit progressivement devenue une grosse source d’inspiration de cet article.
$\mathbb {Z}$
-ind-schémas d’après Mathieu [Reference MathieuMat88]. Comme produit dérivé des résultats qu’on va présenter, se dégage un dictionnaire arithmétique complet entre les grassmanniennes affines tordues et les variétés de drapeaux de Kac–Moody affines, voir le §6, ce qui était attendu en les caractéristiques petites depuis longtemps. Le théorème 1.4 sur la normalité des variétés de Schubert retient néanmoins son importance, parce que leurs définitions ne se ressemblent guère et qu’on y recourt pour établir la comparaison. Il ne doit être alors aucune surprise que Tits soit arrivé au milieu de sa recherche sur les groupes de Kac–Moody aux constructions sur lesquelles on s’appuie, et que cette théorie soit progressivement devenue une grosse source d’inspiration de cet article.
1.1 Groupes tordus sur
 $\mathbb {Z}[t]$
.
$\mathbb {Z}[t]$
.
Soient k un corps algébriquement clos,
![]() $K=k (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) $
le corps de séries de Laurent à coefficients dans k et G un K-groupe réductif, connexe, quasi-déployé, simplement connexe et absolument presque simple. Fixons un épinglage
$K=k (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) $
le corps de séries de Laurent à coefficients dans k et G un K-groupe réductif, connexe, quasi-déployé, simplement connexe et absolument presque simple. Fixons un épinglage
![]() $(H, T_H, B_H, X_H)$
au-dessus de
$(H, T_H, B_H, X_H)$
au-dessus de
![]() $\mathbb {Z}$
de la
$\mathbb {Z}$
de la
![]() $\mathbb {Z}$
-forme déployée H de G et un isomorphisme
$\mathbb {Z}$
-forme déployée H de G et un isomorphisme
![]() $G \otimes _K K^{\mathrm {s\acute {e}p}} \simeq H \otimes _K K^{\mathrm {s\acute {e}p}}$
de telle sorte que le groupe de Galois
$G \otimes _K K^{\mathrm {s\acute {e}p}} \simeq H \otimes _K K^{\mathrm {s\acute {e}p}}$
de telle sorte que le groupe de Galois
![]() $\operatorname {Gal}(K^{\mathrm {s\acute {e}p}}/K)$
opère sur le membre de droite par automorphismes qui préservent l’épinglage donné. Comme le groupe
$\operatorname {Gal}(K^{\mathrm {s\acute {e}p}}/K)$
opère sur le membre de droite par automorphismes qui préservent l’épinglage donné. Comme le groupe
![]() $\operatorname {Aut}(H, T_H, B_H, X_H)$
est isomorphe au groupe d’automorphismes du diagramme de Dynkin de H, il s’identifie au groupe symétrique
$\operatorname {Aut}(H, T_H, B_H, X_H)$
est isomorphe au groupe d’automorphismes du diagramme de Dynkin de H, il s’identifie au groupe symétrique
![]() $\mathfrak {S}_e$
d’indice
$\mathfrak {S}_e$
d’indice
![]() $e=1$
,
$e=1$
,
![]() $2$
ou
$2$
ou
![]() $3$
. Si e est différent de la caractéristique p de k, alors la plus petite extension de K déployant G est
$3$
. Si e est différent de la caractéristique p de k, alors la plus petite extension de K déployant G est
![]() $L=k (\hspace {-0,7mm}( {t^{1/e}} )\hspace {-0,7mm}) $
et l’on a un isomorphisme
$L=k (\hspace {-0,7mm}( {t^{1/e}} )\hspace {-0,7mm}) $
et l’on a un isomorphisme
![]() $G =(\operatorname {R}_{L/K} H)^{\Gamma }$
, où
$G =(\operatorname {R}_{L/K} H)^{\Gamma }$
, où
![]() $\operatorname {R}_{L/K} H$
désigne la restriction des scalaires à la Weil de H sur laquelle
$\operatorname {R}_{L/K} H$
désigne la restriction des scalaires à la Weil de H sur laquelle
![]() $\Gamma :=\operatorname {Gal}(L/K)$
opère de façon galoisienne sur les coefficients et diagrammatique sur H, cf. constr. 2.2.2. Cependant, si
$\Gamma :=\operatorname {Gal}(L/K)$
opère de façon galoisienne sur les coefficients et diagrammatique sur H, cf. constr. 2.2.2. Cependant, si
![]() $e=p$
, alors le même type d’énoncé reste valide, mais il faut remplacer l’extension
$e=p$
, alors le même type d’énoncé reste valide, mais il faut remplacer l’extension
![]() $k (\hspace {-0,7mm}( {t^{1/e}} )\hspace {-0,7mm}) $
de
$k (\hspace {-0,7mm}( {t^{1/e}} )\hspace {-0,7mm}) $
de
![]() $k (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) $
par des classes d’isomorphisme en nombre infini de clôtures galoisiennes d’extensions séparables de degré e.
$k (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) $
par des classes d’isomorphisme en nombre infini de clôtures galoisiennes d’extensions séparables de degré e.
Cette différence arithmétique se manifeste aussi dans la mesure où les groupes G à ramification modérée et indice de Tits fixé, voir la classification de [Reference TitsTi66], qu’on vient de décrire peuvent être rassemblés dans un
![]() $\mathbb {Z}[1/e][t^{\pm 1}]$
-groupe lisse, affine et connexe
$\mathbb {Z}[1/e][t^{\pm 1}]$
-groupe lisse, affine et connexe
![]() $\underline {G}$
, en prenant la même définition comme invariants de la restriction des scalaires du groupe de Chevalley H. La question qui a déclenché ce travail fut la suivante :
$\underline {G}$
, en prenant la même définition comme invariants de la restriction des scalaires du groupe de Chevalley H. La question qui a déclenché ce travail fut la suivante :
Question 1.1. Y a-t-il un prolongement “canonique” de G en un schéma en groupes
![]() $\underline {G}$
au-dessus de
$\underline {G}$
au-dessus de
![]() $\mathbb {Z}[t^{\pm 1}]$
? Si oui, quel groupe obtient-on en caractéristique e ?
$\mathbb {Z}[t^{\pm 1}]$
? Si oui, quel groupe obtient-on en caractéristique e ?
La réponse est heureusement toujours affirmative et ce schéma en groupes fut originalement construit par Tits [Reference TitsTi84], en faisant usage des techniques de recollement de Bruhat–Tits [Reference Bruhat and TitsBT84a], voir le th. 3.2.5, pour se ramener à construire une “donnée radicielle schématique”
![]() $(\underline {T}, \underline {U_a})_{a \in \Phi ^{\operatorname {nd}}}$
constituée de certains
$(\underline {T}, \underline {U_a})_{a \in \Phi ^{\operatorname {nd}}}$
constituée de certains
![]() $\mathbb {Z}[t^{\pm 1}]$
-modèles naturels induits par le choix d’un système cohérent d’épinglages, voir la déf. 3.3.3. Il est toujours loisible d’identifier le
$\mathbb {Z}[t^{\pm 1}]$
-modèles naturels induits par le choix d’un système cohérent d’épinglages, voir la déf. 3.3.3. Il est toujours loisible d’identifier le
![]() $\mathbb {Z}[t^{\pm 1}]$
-groupe
$\mathbb {Z}[t^{\pm 1}]$
-groupe
![]() $\underline {G}$
à un sous-schéma en groupes fermé de la restriction des scalaires de H le long de
$\underline {G}$
à un sous-schéma en groupes fermé de la restriction des scalaires de H le long de
![]() $\mathbb {Z}[\zeta _e,t^{1/e}]/\mathbb {Z}[t]$
, voir la prop. 3.3.9, mais on doit s’attendre au besoin de modifier à la Tits par quelques facteurs de
$\mathbb {Z}[\zeta _e,t^{1/e}]/\mathbb {Z}[t]$
, voir la prop. 3.3.9, mais on doit s’attendre au besoin de modifier à la Tits par quelques facteurs de
![]() $2$
le choix canonique de quasi-épinglages dû à Steinberg [Reference SteinbergSt59] et [Reference SteinbergSt68], cf. défs. 2.2.6 et 2.3.4. Il s’ensuit que
$2$
le choix canonique de quasi-épinglages dû à Steinberg [Reference SteinbergSt59] et [Reference SteinbergSt68], cf. défs. 2.2.6 et 2.3.4. Il s’ensuit que
![]() $\underline {G}$
est lisse, affine et à fibres connexes.
$\underline {G}$
est lisse, affine et à fibres connexes.
Quant au groupe algébrique que l’on obtient en caractéristique e, le lecteur aura peut-être soupçonné qu’il ne s’agit pas non plus d’un groupe réductif, à cause de la présence d’une extension de corps purement inséparable
![]() $\mathbb {F}_e(t^{1/e})/\mathbb {F}_e(t)$
, et en fait
$\mathbb {F}_e(t^{1/e})/\mathbb {F}_e(t)$
, et en fait
![]() $\underline {G}\otimes \mathbb {F}_e(t)$
est un groupe pseudo-réductif non standard et pseudo-déployé au sens de [Reference Conrad, Gabber and PrasadCGP15], comme mentionné plus haut, cf. prop. 3.3.7. Ces groupes pseudo-réductifs non standards forment une classe assez exceptionnelle qui a été découverte par Tits et qui n’existe qu’en caractéristiques petites
$\underline {G}\otimes \mathbb {F}_e(t)$
est un groupe pseudo-réductif non standard et pseudo-déployé au sens de [Reference Conrad, Gabber and PrasadCGP15], comme mentionné plus haut, cf. prop. 3.3.7. Ces groupes pseudo-réductifs non standards forment une classe assez exceptionnelle qui a été découverte par Tits et qui n’existe qu’en caractéristiques petites
![]() $p\leq 3$
. La raison d’être de tels groupes, selon les auteurs de [Reference Conrad, Gabber and PrasadCGP15], est qu’il y ait des phénomènes de p-divisibilité dans le système de racines
$p\leq 3$
. La raison d’être de tels groupes, selon les auteurs de [Reference Conrad, Gabber and PrasadCGP15], est qu’il y ait des phénomènes de p-divisibilité dans le système de racines
![]() $\Phi _G$
. Nous préférons les regarder comme le fruit de la volonté de prendre avec insistance des
$\Phi _G$
. Nous préférons les regarder comme le fruit de la volonté de prendre avec insistance des
![]() $\Gamma $
-invariants galoisiens-diagrammatiques d’un groupe déployé, lorsque cela cesse d’être naïvement possible.
$\Gamma $
-invariants galoisiens-diagrammatiques d’un groupe déployé, lorsque cela cesse d’être naïvement possible.
Venons-en à présent aux constructions de type parahorique. Soit S le plus grand tore déployé de G contenu dans le Cartan T. Admettons pour l’instant l’existence d’identifications canoniques entre les appartements
![]() $\mathscr {A}(\underline {G},\underline {S},\mathbb {F}_p (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
en caractéristiques différentes, voir la prop. 3.4.1, qu’on note plutôt
$\mathscr {A}(\underline {G},\underline {S},\mathbb {F}_p (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
en caractéristiques différentes, voir la prop. 3.4.1, qu’on note plutôt
![]() $\mathscr {A}(\underline {G}, \underline {S}, \mathbb {Z} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
pour signaler que la combinatoire est indépendante de l’arithmétique. Ceci soulève le même type de questions que plus haut, comparer avec la question 1.1 :
$\mathscr {A}(\underline {G}, \underline {S}, \mathbb {Z} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
pour signaler que la combinatoire est indépendante de l’arithmétique. Ceci soulève le même type de questions que plus haut, comparer avec la question 1.1 :
Question 1.2. Si on se donne une partie bornée et non vide
![]() $\Omega \subset \mathscr {A}(\underline {G}, \underline {S}, \mathbb {Z} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
, existe-t-il un
$\Omega \subset \mathscr {A}(\underline {G}, \underline {S}, \mathbb {Z} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
, existe-t-il un
![]() $\mathbb {Z}[t]$
-groupe lisse, affine et connexe de type “immobilier”
$\mathbb {Z}[t]$
-groupe lisse, affine et connexe de type “immobilier”
![]() $\underline {\mathscr {G}_{\Omega }}$
modelant
$\underline {\mathscr {G}_{\Omega }}$
modelant
![]() $\underline {G}$
?
$\underline {G}$
?
Le mot “immobilier” dans l’énoncé veut dire tout simplement que, au-dessus de
![]() $\mathbb {F}_p [\hspace {-0,5mm}[ {t} ]\hspace {-0,5mm}] $
pour tout
$\mathbb {F}_p [\hspace {-0,5mm}[ {t} ]\hspace {-0,5mm}] $
pour tout
![]() $p \in \mathbb {P} \cup \{0\}$
, on obtient des modèles en groupes canoniquement associés à
$p \in \mathbb {P} \cup \{0\}$
, on obtient des modèles en groupes canoniquement associés à
![]() $\Omega $
au sens de la théorie de Bruhat–Tits généralisée de [Reference LourençoLou21]. Il faut noter que, en dehors de
$\Omega $
au sens de la théorie de Bruhat–Tits généralisée de [Reference LourençoLou21]. Il faut noter que, en dehors de
![]() $\{e=0\}$
, soit dans [Reference Pappas and RapoportPR08], soit dans [Reference Pappas and ZhuPZ13], on peut essentiellement trouver une construction de ce schéma en groupes à l’aide des techniques des
$\{e=0\}$
, soit dans [Reference Pappas and RapoportPR08], soit dans [Reference Pappas and ZhuPZ13], on peut essentiellement trouver une construction de ce schéma en groupes à l’aide des techniques des
![]() $\Gamma $
-invariants, mais lorsqu’on insiste pour travailler à coefficients entiers, il n’existe pas à notre connaissance une référence dans la littérature où ce schéma en groupes soit construit. Pour construire cet objet, on se propose de trouver une donnée radicielle valuée et puis d’appliquer le théorème sur l’existence de solutions aux lois birationnelles.
$\Gamma $
-invariants, mais lorsqu’on insiste pour travailler à coefficients entiers, il n’existe pas à notre connaissance une référence dans la littérature où ce schéma en groupes soit construit. Pour construire cet objet, on se propose de trouver une donnée radicielle valuée et puis d’appliquer le théorème sur l’existence de solutions aux lois birationnelles.
Ceci étant, précisons le cadre un petit peu plus général dans lequel on va travailler. On se donne un
![]() $\mathbb {Q}(t)$
-groupe réductif connexe G quasi-déployé,
$\mathbb {Q}(t)$
-groupe réductif connexe G quasi-déployé,
![]() $\mathbb {Q}(\zeta _e,t^{1/e})$
-déployé,
$\mathbb {Q}(\zeta _e,t^{1/e})$
-déployé,
![]() $\mathbb {Q} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) $
-résiduellement déployé, dont le tore maximal T est induit, ainsi qu’un système cohérent d’épinglages à la Tits des sous-groupes radiciels
$\mathbb {Q} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) $
-résiduellement déployé, dont le tore maximal T est induit, ainsi qu’un système cohérent d’épinglages à la Tits des sous-groupes radiciels
![]() $U_a$
. Le groupe de Tits
$U_a$
. Le groupe de Tits
![]() $\underline {G}$
, ainsi que ses modèles immobiliers
$\underline {G}$
, ainsi que ses modèles immobiliers
![]() $\underline {\mathscr {G}_\Omega }$
associés à une partie bornée et non vide
$\underline {\mathscr {G}_\Omega }$
associés à une partie bornée et non vide
![]() $\Omega \subseteq \mathscr {A}(\underline {G}, \underline {S}, \mathbb {Z} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
, se construisent de manière analogue, cf. défs. 3.3.5 et 3.4.6. Les conclusions de la première partie de l’article peuvent être résumées comme suit :
$\Omega \subseteq \mathscr {A}(\underline {G}, \underline {S}, \mathbb {Z} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
, se construisent de manière analogue, cf. défs. 3.3.5 et 3.4.6. Les conclusions de la première partie de l’article peuvent être résumées comme suit :
Théorème 1.3 (prop. 3.4.5, th. 3.4.10).
Sous les hypothèses précédentes, il existe un et un seul
![]() $\mathbb {Z}[t]$
-modèle en groupes lisse, affine, connexe et immobilier
$\mathbb {Z}[t]$
-modèle en groupes lisse, affine, connexe et immobilier
![]() $\underline {\mathscr {G}_\Omega }$
de
$\underline {\mathscr {G}_\Omega }$
de
![]() $\underline {G}$
associé à
$\underline {G}$
associé à
![]() $\Omega $
.
$\Omega $
.
On dit un mot sur la preuve de l’affinité. Malheureusement, on ne peut pas suivre l’argument de [Reference Pappas and ZhuPZ13] verbatim, car celui utilise la cohomologie de groupes et l’interprétation en tant que
![]() $\Gamma $
-invariants. Néanmoins, on réussit encore à démontrer l’affinité de la manière suivante. On observe que l’enveloppe affine, lequel est lisse d’après Raynaud [Reference RaynaudRay70], ne peut pas posséder des composantes connexes supplémentaires dans les fibres, en appliquant le fait que les groupes d’Iwahori–Weyl de
$\Gamma $
-invariants. Néanmoins, on réussit encore à démontrer l’affinité de la manière suivante. On observe que l’enveloppe affine, lequel est lisse d’après Raynaud [Reference RaynaudRay70], ne peut pas posséder des composantes connexes supplémentaires dans les fibres, en appliquant le fait que les groupes d’Iwahori–Weyl de
![]() $\underline {G}\otimes \mathbb {F}_p (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) $
ne dépendent pas de la caractéristique.
$\underline {G}\otimes \mathbb {F}_p (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) $
ne dépendent pas de la caractéristique.
1.2 La géométrie des grassmanniennes affines tordues
Soient A un anneau et
![]() $\mathrm {G}$
un
$\mathrm {G}$
un
![]() $A [\hspace {-0,5mm}[ {t} ]\hspace {-0,5mm}] $
-groupe affine et lisse. La grassmannienne affine
$A [\hspace {-0,5mm}[ {t} ]\hspace {-0,5mm}] $
-groupe affine et lisse. La grassmannienne affine
![]() $\operatorname {Gr}_{\mathrm {G}}$
de
$\operatorname {Gr}_{\mathrm {G}}$
de
![]() $\mathrm {G}$
est le pré-faisceau sur la catégorie des A-algèbres B qui classifie les
$\mathrm {G}$
est le pré-faisceau sur la catégorie des A-algèbres B qui classifie les
![]() $\mathrm {G}$
-torseurs sur le disque
$\mathrm {G}$
-torseurs sur le disque
![]() $B [\hspace {-0,5mm}[ {t} ]\hspace {-0,5mm}] $
munis d’une trivialisation sur le disque épointé
$B [\hspace {-0,5mm}[ {t} ]\hspace {-0,5mm}] $
munis d’une trivialisation sur le disque épointé
![]() $B (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) $
, cf. déf. 4.1.1. On dispose aussi des groupes d’arcs
$B (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) $
, cf. déf. 4.1.1. On dispose aussi des groupes d’arcs
![]() $L^+\mathrm {G}$
et de lacets
$L^+\mathrm {G}$
et de lacets
![]() $L\mathrm {G}$
donnés par
$L\mathrm {G}$
donnés par
![]() $R \mapsto \mathrm {G}(R [\hspace {-0,5mm}[ {t} ]\hspace {-0,5mm}] )$
et
$R \mapsto \mathrm {G}(R [\hspace {-0,5mm}[ {t} ]\hspace {-0,5mm}] )$
et
![]() $R\mapsto \mathrm {G}(R (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
, tels que le faisceau quotient
$R\mapsto \mathrm {G}(R (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
, tels que le faisceau quotient
![]() $L\mathrm {G}/L^+\mathrm {G}$
pour la topologie étale soit isomorphe à
$L\mathrm {G}/L^+\mathrm {G}$
pour la topologie étale soit isomorphe à
![]() $\operatorname {Gr}_{\mathrm {G}}$
. Sa représentabilité par un A-ind-schéma en est assurée dès que A soit un anneau de Dedekind et
$\operatorname {Gr}_{\mathrm {G}}$
. Sa représentabilité par un A-ind-schéma en est assurée dès que A soit un anneau de Dedekind et
![]() $\mathrm {G}$
soit lisse, affine et connexe, cf. prop. 4.1.2.
$\mathrm {G}$
soit lisse, affine et connexe, cf. prop. 4.1.2.
On s’intéresse surtout au cas où
![]() $A=\mathbb {Z}$
et
$A=\mathbb {Z}$
et
![]() $\mathrm {G}=\underline {\mathscr {G}_{\mathbf {f}}}$
est parahorique associé à une facette
$\mathrm {G}=\underline {\mathscr {G}_{\mathbf {f}}}$
est parahorique associé à une facette
![]() $\mathbf {f} \subset \mathscr {A}(\underline {G},\underline {S},\mathbb {Z} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
, en reprenant les notations de la partie précédente concernant les groupes tordus, cf. question 1.2 et théorème 1.3. La parahoricité est condition nécessaire et suffisante pour que la grassmannienne affine soit un ind-schéma projectif, cf. 4.1.3, grâce à un théorème de Richarz [Reference RicharzRi16] que nous avons étendu au cas pseudo-réductif dans [Reference LourençoLou21].
$\mathbf {f} \subset \mathscr {A}(\underline {G},\underline {S},\mathbb {Z} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
, en reprenant les notations de la partie précédente concernant les groupes tordus, cf. question 1.2 et théorème 1.3. La parahoricité est condition nécessaire et suffisante pour que la grassmannienne affine soit un ind-schéma projectif, cf. 4.1.3, grâce à un théorème de Richarz [Reference RicharzRi16] que nous avons étendu au cas pseudo-réductif dans [Reference LourençoLou21].
Pour une alcôve fixe
![]() $\mathbf {a}$
adhérente à
$\mathbf {a}$
adhérente à
![]() $\mathbf {f}$
et chaque classe
$\mathbf {f}$
et chaque classe
![]() $w \in \widetilde {W}/W_{\textbf {f}}$
du groupe d’Iwahori–Weyl, on dispose du schéma de Schubert
$w \in \widetilde {W}/W_{\textbf {f}}$
du groupe d’Iwahori–Weyl, on dispose du schéma de Schubert
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq w}$
, défini comme l’orbite fermée sous
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq w}$
, défini comme l’orbite fermée sous
![]() $L^+\underline {\mathscr {G}_{\mathbf {a}}}$
d’un représentant convenable
$L^+\underline {\mathscr {G}_{\mathbf {a}}}$
d’un représentant convenable
![]() $n_w \in L\underline {N}(\mathbb {Z})$
de w, cf. déf. 4.1.4. Pour étudier leur géométrie, on se sert des schémas de Demazure
$n_w \in L\underline {N}(\mathbb {Z})$
de w, cf. déf. 4.1.4. Pour étudier leur géométrie, on se sert des schémas de Demazure
![]() $\operatorname {Dem}_{\mathfrak {w}}$
lisses et projectifs sur
$\operatorname {Dem}_{\mathfrak {w}}$
lisses et projectifs sur
![]() $\mathbb {Z}$
, produit tordu de droites de Schubert, tel que le morphisme vers la grassmannienne se factorise en une application birationnelle et surjective
$\mathbb {Z}$
, produit tordu de droites de Schubert, tel que le morphisme vers la grassmannienne se factorise en une application birationnelle et surjective
![]() $\operatorname {Dem}_{\mathfrak {w}} \rightarrow \operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq w}$
. Voici le résultat central :
$\operatorname {Dem}_{\mathfrak {w}} \rightarrow \operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq w}$
. Voici le résultat central :
Théorème 1.4 (th. 4.1.5).
Supposons que
![]() $G^{\mathrm {d\acute {e}r}}=G^{\operatorname {sc}}$
. Alors les schémas de Schubert
$G^{\mathrm {d\acute {e}r}}=G^{\operatorname {sc}}$
. Alors les schémas de Schubert
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq w}$
sont géométriquement normaux sur
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq w}$
sont géométriquement normaux sur
![]() $\mathbb {Z}$
, de Cohen–Macaulay et leurs fibres modulo
$\mathbb {Z}$
, de Cohen–Macaulay et leurs fibres modulo
![]() $p>0$
sont scindées.
$p>0$
sont scindées.
La démonstration du théorème ci-dessus ressemble à celles de Faltings [Reference FaltingsFa03] lorsque G est déployé ou de Pappas–Rapoport [Reference Pappas and RapoportPR08] au-dessus de
![]() $\mathbb {Z}[1/e]$
, mais il y a des différences importantes que nous allons expliquer dans la suite. Avant de commencer, nous voudrions aussi signaler que l’hypothèse
$\mathbb {Z}[1/e]$
, mais il y a des différences importantes que nous allons expliquer dans la suite. Avant de commencer, nous voudrions aussi signaler que l’hypothèse
![]() $G^{\mathrm {d\acute {e}r}}=G^{\operatorname {sc}}$
est impérative, si l’on veut éviter des complications dont la découverte fut le sujet de notre collaboration récente avec Haines–Richarz [Reference Haines, Lourenço and RicharzHLR20] : en effet, dans ce cas les schémas de Schubert possèdent des fibres spéciales non réduites à réduits non normaux, cf. cors. 4.3.8 et 4.3.7.
$G^{\mathrm {d\acute {e}r}}=G^{\operatorname {sc}}$
est impérative, si l’on veut éviter des complications dont la découverte fut le sujet de notre collaboration récente avec Haines–Richarz [Reference Haines, Lourenço and RicharzHLR20] : en effet, dans ce cas les schémas de Schubert possèdent des fibres spéciales non réduites à réduits non normaux, cf. cors. 4.3.8 et 4.3.7.
La première étape est composée d’un traitement exhaustif de la structure du groupe d’arcs
![]() $L^+\underline {\mathscr {G}_{\mathbf {f}}}$
, voir les props. 4.2.4 et 4.2.6, telle que de son opposé le groupe de cordes
$L^+\underline {\mathscr {G}_{\mathbf {f}}}$
, voir les props. 4.2.4 et 4.2.6, telle que de son opposé le groupe de cordes
![]() $L^-\underline {\mathscr {G}_{\mathbf {f}}}$
. Notre approche de celui-ci est en fonction d’une extension convenable du
$L^-\underline {\mathscr {G}_{\mathbf {f}}}$
. Notre approche de celui-ci est en fonction d’une extension convenable du
![]() $\mathbb {A}_{\mathbb {Z}}^1$
-groupe
$\mathbb {A}_{\mathbb {Z}}^1$
-groupe
![]() $\underline {\mathscr {G}_{\mathbf {f}}}$
à
$\underline {\mathscr {G}_{\mathbf {f}}}$
à
![]() $\mathbb {P}_{\mathbb {Z}}^1$
, qui nous permet de poser
$\mathbb {P}_{\mathbb {Z}}^1$
, qui nous permet de poser
![]() $L^-\underline {\mathscr {G}_{\mathbf {f}}}(R)=\underline {\mathscr {G}_{\mathbf {f}}}(R[t^{-1}])$
, cf. déf. 4.2.8. La méthode de preuve ici adoptée pour la plupart des propriétés fondamentales concernant le groupe de cordes se distingue ainsi complètement de celle de de Cataldo–Haines–Li dans [Reference de Cataldo, Haines and LidHL18] pour les groupes déployés (reprise dans [Reference Haines, Lourenço and RicharzHLR20] pour les groupes tordus modérément ramifiés), en substituant aux calculs interminables une analyse raffinée n’impliquant que l’action de rotation, voir le th. 4.2.9.
$L^-\underline {\mathscr {G}_{\mathbf {f}}}(R)=\underline {\mathscr {G}_{\mathbf {f}}}(R[t^{-1}])$
, cf. déf. 4.2.8. La méthode de preuve ici adoptée pour la plupart des propriétés fondamentales concernant le groupe de cordes se distingue ainsi complètement de celle de de Cataldo–Haines–Li dans [Reference de Cataldo, Haines and LidHL18] pour les groupes déployés (reprise dans [Reference Haines, Lourenço and RicharzHLR20] pour les groupes tordus modérément ramifiés), en substituant aux calculs interminables une analyse raffinée n’impliquant que l’action de rotation, voir le th. 4.2.9.
Puis on construit les
![]() $L^-\underline {\mathscr {G}_{\mathbf {a}}}$
-orbites fermées
$L^-\underline {\mathscr {G}_{\mathbf {a}}}$
-orbites fermées
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}^{\geq w}$
dans la grassmannienne affine à la suite de [Reference FaltingsFa03], cf. th. 4.2.16, dont des quotients locaux pour certains sous-groupes de congruence sont de type fini de codimension
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}^{\geq w}$
dans la grassmannienne affine à la suite de [Reference FaltingsFa03], cf. th. 4.2.16, dont des quotients locaux pour certains sous-groupes de congruence sont de type fini de codimension
![]() $l(w)$
, et même géométriquement normaux et de Cohen–Macaulay, d’après Kashiwara–Shimozono [Reference Kashiwara and ShimozonoKS09]. Ces résultats et constructions devraient être mis en relief, car ils sont incontournables pour qu’on parvienne à obtenir tous les faisceaux inversibles amples de la grassmannienne affine
$l(w)$
, et même géométriquement normaux et de Cohen–Macaulay, d’après Kashiwara–Shimozono [Reference Kashiwara and ShimozonoKS09]. Ces résultats et constructions devraient être mis en relief, car ils sont incontournables pour qu’on parvienne à obtenir tous les faisceaux inversibles amples de la grassmannienne affine
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
, cf. cor. 4.3.10, s’agissant d’une lacune très sérieuse dans la preuve du théorème de normalité dans [Reference Pappas and RapoportPR08] en caractéristique
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
, cf. cor. 4.3.10, s’agissant d’une lacune très sérieuse dans la preuve du théorème de normalité dans [Reference Pappas and RapoportPR08] en caractéristique
![]() $p=2$
.
$p=2$
.
Pour la deuxième étape, on fait usage des fibrés en droites amples pour montrer que les variétés de Schubert normalisées en caractéristique p sont scindées, cf. prop. 4.3.1, donc les schémas de Schubert normalisés satisfont aux propriétés du théorème 1.4, formant en outre un ind-schéma
![]() $\widetilde {\operatorname {Gr}}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
opéré par les groupes de lacets
$\widetilde {\operatorname {Gr}}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
opéré par les groupes de lacets
![]() $L\underline {U_\pm }$
associés aux sous-groupes radiciels, cf. cor. 4.3.2. Alors que la normalité en caractéristique
$L\underline {U_\pm }$
associés aux sous-groupes radiciels, cf. cor. 4.3.2. Alors que la normalité en caractéristique
![]() $0$
est due à Kumar [Reference KumarKum87], il ne reste qu’à montrer que l’application d’espaces tangents induite par la normalisation est surjective, dès que
$0$
est due à Kumar [Reference KumarKum87], il ne reste qu’à montrer que l’application d’espaces tangents induite par la normalisation est surjective, dès que
![]() $G=G^{\operatorname {sc}}$
. Malheureusement, l’algèbre de Lie de
$G=G^{\operatorname {sc}}$
. Malheureusement, l’algèbre de Lie de
![]() $L\underline {G}$
sur
$L\underline {G}$
sur
![]() $\mathbb {Z}$
n’est topologiquement pas engendrée par celles associées aux sous-groupes radicielles, dès que
$\mathbb {Z}$
n’est topologiquement pas engendrée par celles associées aux sous-groupes radicielles, dès que
![]() $\Phi _G$
soit non réduit, cf. lem. 4.3.5, en vertu de quelques facteurs quadratiques méchants, ce qui n’était jamais le cas sous les hypothèses de [Reference FaltingsFa03] ou de [Reference Pappas and RapoportPR08]. Pour remédier à ce problème, nous devons considérer les espaces de distributions, c’est-à-dire opérateurs différentiels supérieurs, cf. lem. 4.3.6.
$\Phi _G$
soit non réduit, cf. lem. 4.3.5, en vertu de quelques facteurs quadratiques méchants, ce qui n’était jamais le cas sous les hypothèses de [Reference FaltingsFa03] ou de [Reference Pappas and RapoportPR08]. Pour remédier à ce problème, nous devons considérer les espaces de distributions, c’est-à-dire opérateurs différentiels supérieurs, cf. lem. 4.3.6.
Ceci fournit en outre le lien entre nos schémas de Schubert et ceux de Mathieu [Reference MathieuMat88] encadrés dans la théorie de Kac–Moody, cf. §6.1, dont les groupes d’arcs parahoriques sont définis par dualité en fonction de tels opérateurs différentiels supérieurs, cf. lem. 6.2.1. Puis la comparaison des schémas de Schubert s’ensuit en appliquant les théorèmes de normalité, voir le th. 6.2.4. Bien sûr, le lecteur cynique pourrait objecter à ce stade, nonobstant l’énorme travail géométrique que l’on a eu besoin de faire en avance, que les grassmanniennes affines ici construites ne sont alors que des objets bien connus depuis trente ans.
En réponse à cela, nous objecterions que la déformation de Beilinson–Drinfeld [Reference Beilinson and DrinfeldBD96], nous ne l’avions pas ! Par là, on entend le pré-faisceau
![]() $\operatorname {GR}_{\mathrm {G}}$
associé à une courbe lisse affine relative
$\operatorname {GR}_{\mathrm {G}}$
associé à une courbe lisse affine relative
![]() $A \rightarrow B$
sur un anneau A et à un B-groupe affine
$A \rightarrow B$
sur un anneau A et à un B-groupe affine
![]() $\mathrm {G}$
, qui fait correspondre à toute B-algèbre C les classes d’isomorphisme de
$\mathrm {G}$
, qui fait correspondre à toute B-algèbre C les classes d’isomorphisme de
![]() $\mathrm {G}$
-torseurs sur
$\mathrm {G}$
-torseurs sur
![]() $B\otimes _A C$
munis d’une trivialisation en dehors du graphe
$B\otimes _A C$
munis d’une trivialisation en dehors du graphe
![]() $B \otimes _A C \rightarrow C $
, cf. déf. 5.1.1. On a aussi des groupes de lacets
$B \otimes _A C \rightarrow C $
, cf. déf. 5.1.1. On a aussi des groupes de lacets
![]() $L \mathrm {G}$
et d’arcs
$L \mathrm {G}$
et d’arcs
![]() $L^+ \mathrm {G}$
opérant sur
$L^+ \mathrm {G}$
opérant sur
![]() $\operatorname {GR}_{\mathrm {G}}$
et dont le quotient pour la topologie étale
$\operatorname {GR}_{\mathrm {G}}$
et dont le quotient pour la topologie étale
![]() $L \mathrm {G}/L^+\mathrm {G}=\operatorname {GR}_{\mathrm {G}}$
s’identifie à la grassmannienne affine.
$L \mathrm {G}/L^+\mathrm {G}=\operatorname {GR}_{\mathrm {G}}$
s’identifie à la grassmannienne affine.
Soient alors
![]() $A=\mathbb {Z}$
,
$A=\mathbb {Z}$
,
![]() $B=\mathbb {Z}[t]$
et
$B=\mathbb {Z}[t]$
et
![]() $\mathrm {G}=\underline {\mathscr {G}_{\mathbf {f}}}$
comme ci-dessus. La grassmannienne affine globale
$\mathrm {G}=\underline {\mathscr {G}_{\mathbf {f}}}$
comme ci-dessus. La grassmannienne affine globale
![]() $\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
est représentable par un ind-schéma projectif, voir la prop. 5.1.2 et le th. 5.1.3. Cet ind-schéma admet certains sous-schémas fermés invariants par le groupe d’arcs pour chaque copoids géométrique dominant
$\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
est représentable par un ind-schéma projectif, voir la prop. 5.1.2 et le th. 5.1.3. Cet ind-schéma admet certains sous-schémas fermés invariants par le groupe d’arcs pour chaque copoids géométrique dominant
![]() $\mu $
de G, voir la déf. 5.1.6, appelés les schémas globaux de Schubert
$\mu $
de G, voir la déf. 5.1.6, appelés les schémas globaux de Schubert
![]() $\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq \mu }$
et définis sur
$\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq \mu }$
et définis sur
![]() $\mathbb {Z}[\zeta _\infty , t^{1/\infty }]$
. Encore mieux, l’on a une description géométrique de ces variétés de Schubert globales.
$\mathbb {Z}[\zeta _\infty , t^{1/\infty }]$
. Encore mieux, l’on a une description géométrique de ces variétés de Schubert globales.
Théorème 1.5 (th. 5.2.1, th. 5.2.2).
Supposons que
![]() $G^{\mathrm {d\acute {e}r}}=G^{\operatorname {sc}}$
. Alors les schémas de Schubert globaux
$G^{\mathrm {d\acute {e}r}}=G^{\operatorname {sc}}$
. Alors les schémas de Schubert globaux
![]() $\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq \mu }$
sont normaux, plats, géométriquement réduits et leurs fibres sont égales au lieu admissible de
$\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq \mu }$
sont normaux, plats, géométriquement réduits et leurs fibres sont égales au lieu admissible de
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}\otimes k [\hspace {-0,5mm}[ {z_x} ]\hspace {-0,5mm}] }$
.
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}\otimes k [\hspace {-0,5mm}[ {z_x} ]\hspace {-0,5mm}] }$
.
Le lieu admissible est classiquement défini en termes de l’application de Kottwitz, mais ici, on se sert de la finitude au sens inductif de
![]() $\operatorname {GR}_{\underline {\mathscr {T}}}$
, cf. lem. 5.1.5. Faisons aussi quelques commentaires relativement à la démonstration du théorème, dont l’affirmation reste nouvelle en ce degré de généralité même pour les groupes déployés ou tordus modérément ramifiés. L’empêchement le plus sérieux est qu’on ne sait plus sur une base bidimensionnelle si
$\operatorname {GR}_{\underline {\mathscr {T}}}$
, cf. lem. 5.1.5. Faisons aussi quelques commentaires relativement à la démonstration du théorème, dont l’affirmation reste nouvelle en ce degré de généralité même pour les groupes déployés ou tordus modérément ramifiés. L’empêchement le plus sérieux est qu’on ne sait plus sur une base bidimensionnelle si
![]() $\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq \mu }$
est plat, contrairement à ce qui se passe sur les anneaux de dimension
$\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq \mu }$
est plat, contrairement à ce qui se passe sur les anneaux de dimension
![]() $1$
, auquel cas l’assertion résulterait du théorème de cohérence de Zhu [Reference ZhuZh14], cf. th. 5.2.1. Toutefois, cette assertion plus faible sur un anneau de dimension
$1$
, auquel cas l’assertion résulterait du théorème de cohérence de Zhu [Reference ZhuZh14], cf. th. 5.2.1. Toutefois, cette assertion plus faible sur un anneau de dimension
![]() $1$
permet d’entendre assez bien le normalisé de
$1$
permet d’entendre assez bien le normalisé de
![]() $\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq \mu }$
et de montrer que l’application de normalisation est un isomorphisme, cf. th. 5.2.2.
$\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq \mu }$
et de montrer que l’application de normalisation est un isomorphisme, cf. th. 5.2.2.
Enfin, venons-en bref aux applications à la théorie des modèles locaux. Ceux-ci sont étroitement liés à l’arithmétique des variétés de Shimura et plus récemment Scholze–Weinstein [Reference Scholze and WeinsteinSW20] ont conjecturé qu’un certain v-faisceau de Schubert minuscule dans leur grassmannienne affine p-adique soit représentable par un schéma projectif, plat et géométriquement réduit. Dans une première version de cet article, nous avons généralisé les arguments de [Reference Scholze and WeinsteinSW20] et de He–Pappas–Rapoport [Reference He, Pappas and RapoportHPR18], afin de prouver la conjecture en presque tous les cas de type abélien. Vu que l’article présent est devenu trop grand et que l’encadrement perfectoïde p-adique ne ressemble guère aux méthodes employées, on s’est décidé de revenir sur la conjecture générale dans un futur travail. Les gens intéressés trouveront des informations supplémentaires dans [Reference Pereira LourençoPL20, IV].
1.3 Leitfaden
L’article est organisé à peu près comme l’introduction. Le §2 est un rappel de divers concepts fondamentaux autour des épinglages de sous-groupes radiciels et de leurs systèmes cohérents. Au §3 il s’agit de construire les
![]() $\mathbb {Z}[t]$
-groupes immobiliers tordus
$\mathbb {Z}[t]$
-groupes immobiliers tordus
![]() $\underline {\mathscr {G}_\Omega }$
qui sont la base de tout ce travail. Le §4 concerne la géométrie des grassmanniennes affines tordues entières associées aux groupes parahoriques
$\underline {\mathscr {G}_\Omega }$
qui sont la base de tout ce travail. Le §4 concerne la géométrie des grassmanniennes affines tordues entières associées aux groupes parahoriques
![]() $\underline {\mathscr {G}_{\mathbf {f}}}$
, tandis que l’on étudie au §5 la déformation de Beilinson–Drinfeld et démontre notre variante du théorème de la cohérence. Enfin, on décrit dans §6 le lien entre notre théorie et celle de Kac–Moody au sens de Mathieu. Maintenant, on va détailler le contenu de chaque sous-section.
$\underline {\mathscr {G}_{\mathbf {f}}}$
, tandis que l’on étudie au §5 la déformation de Beilinson–Drinfeld et démontre notre variante du théorème de la cohérence. Enfin, on décrit dans §6 le lien entre notre théorie et celle de Kac–Moody au sens de Mathieu. Maintenant, on va détailler le contenu de chaque sous-section.
Le §2.1 explique quelques notions préparatoires concernant les automorphismes de groupes épinglés et les systèmes de Chevalley–Steinberg. Le §2.2 concerne la construction de formes tordues quasi-déployées associées à ces données. Au §2.3, nous éclaircissons l’aspect technique qu’on appelle la modification de Tits, et dans §2.4 on aborde une procédure d’élargissement central. Le §3.1 s’agit d’une rétrospective de la théorie de Bruhat–Tits visant le cas pseudo-réductif. Au §3.2, nous donnons une nouvelle approche des données radicielles schématiques de Bruhat–Tits, particulièrement utile sur les bases de dimension supérieure. Dans §3.3 les
![]() $\mathbb {Z}[t^{\pm 1}]$
-groupes de Tits
$\mathbb {Z}[t^{\pm 1}]$
-groupes de Tits
![]() $\underline {G}$
sont construits et puis dans §3.4 il en est de même de leurs
$\underline {G}$
sont construits et puis dans §3.4 il en est de même de leurs
![]() $\mathbb {Z}[t]$
-modèles immobiliers
$\mathbb {Z}[t]$
-modèles immobiliers
![]() $\underline {\mathscr {G}_{\Omega }}$
. Nous démontrons notamment qu’ils sont lisses, affines et connexes.
$\underline {\mathscr {G}_{\Omega }}$
. Nous démontrons notamment qu’ils sont lisses, affines et connexes.
Au §4.1, on commence par présenter les définitions et propriétés basiques des grassmanniennes affines. Le §4.2 établit certains résultats structuraux sur les groupes d’arcs
![]() $L^+\underline {\mathscr {G}_{\mathbf {f}}}$
parahoriques, ainsi que leurs opposés, les groupes de cordes
$L^+\underline {\mathscr {G}_{\mathbf {f}}}$
parahoriques, ainsi que leurs opposés, les groupes de cordes
![]() $L^-\underline {\mathscr {G}_{\mathbf {f}}}$
, qui sont exploités pour introduire les cycles de Schubert. Dans §4.3 nous démontrons le théorème de normalité sur les schémas de Schubert. À partir du §5.1 on se penche sur la déformation globale de Beilinson–Drinfeld
$L^-\underline {\mathscr {G}_{\mathbf {f}}}$
, qui sont exploités pour introduire les cycles de Schubert. Dans §4.3 nous démontrons le théorème de normalité sur les schémas de Schubert. À partir du §5.1 on se penche sur la déformation globale de Beilinson–Drinfeld
![]() $\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
et l’on montre le théorème de la cohérence sur les schémas de Schubert globaux au §5.2. Le §6.1 sert de briève introduction aux notions de la théorie de Kac–Moody, tandis qu’au §6.2 le lien entre les deux théories des groupes est établi.
$\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
et l’on montre le théorème de la cohérence sur les schémas de Schubert globaux au §5.2. Le §6.1 sert de briève introduction aux notions de la théorie de Kac–Moody, tandis qu’au §6.2 le lien entre les deux théories des groupes est établi.
1.4 Remerciements
Premièrement, il faut évidemment que je remercie mon directeur de thèse Prof. Dr. P. Scholze, qui m’a suggéré d’étudier les modèles locaux des variétés de Shimura et m’a aidé constamment avec des conseils précieux. Ensuite, je tiens à remercier vivement T. Haines et T. Richarz, qui ont toujours montré un grand intérêt pour mon travail, qui ont partagé très généreusement leurs idées mathématiques avec moi et qui m’ont appris beaucoup, notamment pendant l’écriture de [Reference Haines, Lourenço and RicharzHLR20]. Je veux remercier aussi le Prof. Dr. G. Faltings en tant que deuxième rapporteur de ma dissertation [Reference Pereira LourençoPL20]. B. Conrad mérite aussi une mention distinguée pour sa façon d’échanger de courriels très énergique et à la vitesse de l’éclair. C’est avec grand plaisir que je remercie J. Anschütz, G. Pappas, M. Santos et X. Zhu pour des discussions fructueuses autour de ce sujet et/ou des commentaires pertinents sur le texte. De plus, je tiens à remercier A.-C. le Bras, qui a corrigé plusieurs fautes de français. Enfin, un remerciement spécial est adressé au rapporteur, qui n’a pas seulement fait des suggestions très pertinentes et attentives, mais qui m’a aussi forcé à renoncer à mes aspirations littéraires et ainsi à faire l’écriture de cet article correctement. Du point de vue historique, je suis immensément redevable à J. Tits, pour la façon parfois inattendue dont son travail a imprégné tout ce que j’ai fait, et sans lequel je n’aurais jamais pu résoudre le cas non réduit.
1.5 Notations et conventions
Tous les anneaux considérés seront unitaires et commutatifs. Le foncteur de restriction des scalaires le long d’une extension plate et finie
![]() $A \rightarrow B$
d’anneaux sera noté
$A \rightarrow B$
d’anneaux sera noté
![]() $\operatorname {R}_{B/A}$
. On dit qu’un A-groupe G est connexe si toutes ses fibres sont connexes. Dans le présent article, on ne s’occupera que des formes tordues quasi-déployées. Sauf mention contraire, les immeubles ici considérés sont les réduits et pas les élargis. Tous les ind-schémas sont stricts.
$\operatorname {R}_{B/A}$
. On dit qu’un A-groupe G est connexe si toutes ses fibres sont connexes. Dans le présent article, on ne s’occupera que des formes tordues quasi-déployées. Sauf mention contraire, les immeubles ici considérés sont les réduits et pas les élargis. Tous les ind-schémas sont stricts.
2 Automorphismes de Dynkin et leurs formes tordues
2.1 Systèmes de Chevalley–Steinberg
Donnons-nous un schéma en groupes de Chevalley H sur
![]() $\mathbb {Z}$
muni d’un épinglage, c’est-à-dire de la donnée d’un couple de Killing
$\mathbb {Z}$
muni d’un épinglage, c’est-à-dire de la donnée d’un couple de Killing
![]() $T_H \subseteq B_H \subseteq H$
constitué par un tore maximal et un Borel, la base correspondante
$T_H \subseteq B_H \subseteq H$
constitué par un tore maximal et un Borel, la base correspondante
![]() $\Delta _H$
du système de racines
$\Delta _H$
du système de racines
![]() $\Phi _H$
de H suivant
$\Phi _H$
de H suivant
![]() $T_H$
et des isomorphismes
$T_H$
et des isomorphismes
![]() $y_\alpha :\mathbb {G}_a \rightarrow U_\alpha $
pour toute racine simple
$y_\alpha :\mathbb {G}_a \rightarrow U_\alpha $
pour toute racine simple
![]() $\alpha \in \Delta _H$
. La définition suivante d’une base de Chevalley est tirée directement de [Reference Bruhat and TitsBT84a, 3.2.1, 3.2.2].
$\alpha \in \Delta _H$
. La définition suivante d’une base de Chevalley est tirée directement de [Reference Bruhat and TitsBT84a, 3.2.1, 3.2.2].
Définition 2.1.1. On dit qu’une famille d’isomorphismes
![]() $y_\alpha :\mathbb {G}_a \rightarrow U_\alpha $
pour toute racine
$y_\alpha :\mathbb {G}_a \rightarrow U_\alpha $
pour toute racine
![]() $\alpha \in \Phi _H$
forme un système de Chevalley du groupe épinglé H, si
$\alpha \in \Phi _H$
forme un système de Chevalley du groupe épinglé H, si
-
1. les
 $y_\alpha $
pour les racines positives simples
$y_\alpha $
pour les racines positives simples
 $\alpha \in \Delta _H$
sont les épinglages donnés,
$\alpha \in \Delta _H$
sont les épinglages donnés, -
2. l’élément
 $n_\alpha =y_\alpha (1)y_{-\alpha }(1)y_\alpha (1)$
normalise
$n_\alpha =y_\alpha (1)y_{-\alpha }(1)y_\alpha (1)$
normalise
 $T_H$
pour toute racine
$T_H$
pour toute racine
 $\alpha \in \Phi _H$
,
$\alpha \in \Phi _H$
, -
3. et l’on a
 $n_\alpha y_\beta (r)n_\alpha ^{-1}=y_{s_\alpha (b)}(\epsilon _{\alpha ,\beta } r)$
, pour un certain signe
$n_\alpha y_\beta (r)n_\alpha ^{-1}=y_{s_\alpha (b)}(\epsilon _{\alpha ,\beta } r)$
, pour un certain signe
 $\epsilon _{\alpha ,\beta } \in \{\pm 1\}$
, où
$\epsilon _{\alpha ,\beta } \in \{\pm 1\}$
, où
 $\alpha , \beta \in \Phi _H$
et
$\alpha , \beta \in \Phi _H$
et
 $s_\alpha $
désigne la réflexion dans le groupe de Weyl
$s_\alpha $
désigne la réflexion dans le groupe de Weyl
 $W_H$
par rapport à
$W_H$
par rapport à
 $\alpha $
.
$\alpha $
.
Il faut noter qu’il n’est pas possible en général de se débarrasser de ces signes méchants
![]() $\epsilon _{\alpha ,\beta }$
. Par conséquent, le choix du prolongement d’épinglage dans un système de Chevalley n’est pas unique, parce qu’on se permet toujours de remplacer
$\epsilon _{\alpha ,\beta }$
. Par conséquent, le choix du prolongement d’épinglage dans un système de Chevalley n’est pas unique, parce qu’on se permet toujours de remplacer
![]() $y_\alpha $
et
$y_\alpha $
et
![]() $y_{-\alpha }$
par leurs inverses, pour
$y_{-\alpha }$
par leurs inverses, pour
![]() $\alpha \in \Phi _H \setminus \pm \Delta _H$
. Notre convention pour le signe de la racine opposée
$\alpha \in \Phi _H \setminus \pm \Delta _H$
. Notre convention pour le signe de la racine opposée
![]() $-\alpha $
diffère de celle de [SGA3, exp. XXIII, 1.2] comme le lecteur le verra dans l’exemple ci-dessous :
$-\alpha $
diffère de celle de [SGA3, exp. XXIII, 1.2] comme le lecteur le verra dans l’exemple ci-dessous :
Exemple 2.1.2. Soit H le groupe de rang un
![]() $\operatorname {SL}_2$
épinglé de la manière habituelle :
$\operatorname {SL}_2$
épinglé de la manière habituelle :
![]() $T_H$
est le tore diagonal,
$T_H$
est le tore diagonal,
![]() $B_H$
le groupe des matrices triangulaires supérieures et
$B_H$
le groupe des matrices triangulaires supérieures et
![]() $y_\alpha : \mathbb {G}_a \rightarrow U_\alpha $
est donné par:
$y_\alpha : \mathbb {G}_a \rightarrow U_\alpha $
est donné par:
 $$ \begin{align} r \mapsto \begin{pmatrix} 1 & r\\ 0 & 1 \end{pmatrix}.\end{align} $$
$$ \begin{align} r \mapsto \begin{pmatrix} 1 & r\\ 0 & 1 \end{pmatrix}.\end{align} $$
Alors, le seul système de Chevalley de ce groupe épinglé satisfait à la formule
 $$ \begin{align} y_{-\alpha}(r)= \begin{pmatrix} 1 & 0\\ -r & 1 \end{pmatrix},\end{align} $$
$$ \begin{align} y_{-\alpha}(r)= \begin{pmatrix} 1 & 0\\ -r & 1 \end{pmatrix},\end{align} $$
puisque des calculs fournissent
 $n_\alpha = n_{-\alpha }= \begin {pmatrix} 0 & 1\\ -1 & 0 \end {pmatrix}$
.
$n_\alpha = n_{-\alpha }= \begin {pmatrix} 0 & 1\\ -1 & 0 \end {pmatrix}$
.
Alors, [SGA3, exp. XXIII, prop. 6.2] affirme qu’il existe toujours un système de Chevalley pour un tel groupe épinglé H :
Proposition 2.1.3 (Chevalley).
Il y a un et un seul système de Chevalley au signe près de H prolongeant l’épinglage donné.
Démonstration. Écrivons une racine arbitraire
![]() $\alpha \in \Phi _H$
comme la transformée
$\alpha \in \Phi _H$
comme la transformée
![]() $w(\beta )$
d’une racine positive simple
$w(\beta )$
d’une racine positive simple
![]() $\beta \in \Delta _H$
. L’élément w admet une écriture
$\beta \in \Delta _H$
. L’élément w admet une écriture
![]() $s_1\dots s_k$
comme produit de réflexions
$s_1\dots s_k$
comme produit de réflexions
![]() $s_i$
associées aux racines simples. On a ainsi
$s_i$
associées aux racines simples. On a ainsi
ce qui nous permet aussi de définir une famille d’isomorphismes
![]() $y_\alpha $
en prenant un signe quelconque. On n’a qu’à vérifier que telle construction, malgré ses choix arbitraires, préserve l’épinglage donné lorsque appliquée à une racine simple. Ceci est le contenu du [SGA3, exp. XXIII, lem. 6.3], lequel repose sur des calculs en rang
$y_\alpha $
en prenant un signe quelconque. On n’a qu’à vérifier que telle construction, malgré ses choix arbitraires, préserve l’épinglage donné lorsque appliquée à une racine simple. Ceci est le contenu du [SGA3, exp. XXIII, lem. 6.3], lequel repose sur des calculs en rang
![]() $2$
.
$2$
.
Considérons maintenant le groupe
![]() $\Xi _H$
d’automorphismes de la donnée radicielle épinglée correspondante à
$\Xi _H$
d’automorphismes de la donnée radicielle épinglée correspondante à
![]() $\Delta _H \subseteq \Phi _H \subseteq X^*(T_H)$
et identifions-le au groupe des automorphismes de H fixant l’épinglage donné, d’après le [SGA3, exp. XXIV, th. 1.3]. On peut associer à ces données un nouveau système de racines
$\Delta _H \subseteq \Phi _H \subseteq X^*(T_H)$
et identifions-le au groupe des automorphismes de H fixant l’épinglage donné, d’après le [SGA3, exp. XXIV, th. 1.3]. On peut associer à ces données un nouveau système de racines
![]() $\Phi _G $
dans
$\Phi _G $
dans
![]() $X^*(T_H)^{\Xi _H}$
formé par les moyennes
$X^*(T_H)^{\Xi _H}$
formé par les moyennes
des orbites finies de
![]() $\Phi _H$
pour l’action de
$\Phi _H$
pour l’action de
![]() $\Xi _H$
(ceci conserve son sens même si
$\Xi _H$
(ceci conserve son sens même si
![]() $\Xi _H$
est infini), cf. [Reference HainesHai15, lem. 4.2]. Ce système de racines vient muni d’une application évidente de restriction
$\Xi _H$
est infini), cf. [Reference HainesHai15, lem. 4.2]. Ce système de racines vient muni d’une application évidente de restriction
![]() $\Phi _H \rightarrow \Phi _G$
. On remarque que la définition suivante d’un système de Chevalley–Steinberg coïncide avec celle de [Reference Bruhat and TitsBT84a, 4.1.3] et de [Reference LandvogtLan96, déf. 4.2], sauf que les auteurs y travaillent avec les formes tordues quasi-déployées qu’on étudiera au §2.2.
$\Phi _H \rightarrow \Phi _G$
. On remarque que la définition suivante d’un système de Chevalley–Steinberg coïncide avec celle de [Reference Bruhat and TitsBT84a, 4.1.3] et de [Reference LandvogtLan96, déf. 4.2], sauf que les auteurs y travaillent avec les formes tordues quasi-déployées qu’on étudiera au §2.2.
Définition 2.1.4. Un système de Chevalley s’appelle de Chevalley–Steinberg si, pour tout automorphisme
![]() $\sigma \in \Xi _H$
, l’on a
$\sigma \in \Xi _H$
, l’on a
![]() $\sigma (y_\alpha (r))= y_{\sigma (\alpha )}(\epsilon _{\alpha ,\sigma } r)$
où
$\sigma (y_\alpha (r))= y_{\sigma (\alpha )}(\epsilon _{\alpha ,\sigma } r)$
où
![]() $\epsilon _{\alpha ,\sigma } \in \{\pm 1\}$
et est même égal à
$\epsilon _{\alpha ,\sigma } \in \{\pm 1\}$
et est même égal à
![]() $1$
si la moyenne
$1$
si la moyenne
![]() $a \in \Phi _{G}^{\operatorname {nd}}$
n’est pas divisible.
$a \in \Phi _{G}^{\operatorname {nd}}$
n’est pas divisible.
En particulier, une condition suffisante pour que le signe
![]() $\epsilon _{\alpha ,\sigma }$
soit toujours égal à
$\epsilon _{\alpha ,\sigma }$
soit toujours égal à
![]() $1$
est que
$1$
est que
![]() $\Phi _G$
soit réduit, c’est-à-dire que
$\Phi _G$
soit réduit, c’est-à-dire que
![]() $H^{\operatorname {sc}}$
ne contienne aucun facteur isomorphe à
$H^{\operatorname {sc}}$
ne contienne aucun facteur isomorphe à
![]() $\operatorname {SL}_{2n+1}$
. L’exemple suivant montre que cette condition est aussi nécessaire :
$\operatorname {SL}_{2n+1}$
. L’exemple suivant montre que cette condition est aussi nécessaire :
Exemple 2.1.5. Soit H le groupe
![]() $\operatorname {SL}_3$
épinglé de la façon canonique, c’est-à-dire
$\operatorname {SL}_3$
épinglé de la façon canonique, c’est-à-dire
![]() $T_H$
est le tore diagonal,
$T_H$
est le tore diagonal,
![]() $B_H$
le sous-groupes des matrices triangulaires unipotentes et les sous-groupes radiciels associés aux racines positives simples
$B_H$
le sous-groupes des matrices triangulaires unipotentes et les sous-groupes radiciels associés aux racines positives simples
![]() $\alpha $
et
$\alpha $
et
![]() $\beta $
sont donnés par
$\beta $
sont donnés par
 $$ \begin{align}y_\alpha: r\mapsto \begin{pmatrix} 1& r & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{pmatrix}, y_\beta: r\mapsto \begin{pmatrix} 1& 0 & 0\\ 0 & 1 & r\\ 0 & 0 & 1 \end{pmatrix}.\end{align} $$
$$ \begin{align}y_\alpha: r\mapsto \begin{pmatrix} 1& r & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{pmatrix}, y_\beta: r\mapsto \begin{pmatrix} 1& 0 & 0\\ 0 & 1 & r\\ 0 & 0 & 1 \end{pmatrix}.\end{align} $$
D’après [Reference ConradCo14, ex. 7.1.5], on sait que le seul automorphisme
![]() $\sigma $
du groupe épinglé H est :
$\sigma $
du groupe épinglé H est :
 $$ \begin{align} \begin{pmatrix} a& b & c\\ d & e & f\\ g & h & i \end{pmatrix}\mapsto \begin{pmatrix} ei-fh & af-cd & bf-ce\\ ah-bg & ai-cg & bi-ch\\ dh-eg & di-fg & ae-bd \end{pmatrix},\end{align} $$
$$ \begin{align} \begin{pmatrix} a& b & c\\ d & e & f\\ g & h & i \end{pmatrix}\mapsto \begin{pmatrix} ei-fh & af-cd & bf-ce\\ ah-bg & ai-cg & bi-ch\\ dh-eg & di-fg & ae-bd \end{pmatrix},\end{align} $$
ce qui entraîne
![]() $\epsilon _{\alpha +\beta ,\sigma }=-1$
comme voulu. Par alternative, nous pourrions avoir calculé directement l’effet de
$\epsilon _{\alpha +\beta ,\sigma }=-1$
comme voulu. Par alternative, nous pourrions avoir calculé directement l’effet de
![]() $\sigma $
sur
$\sigma $
sur
![]() $\operatorname {Lie}H$
, utilisant le crochet.
$\operatorname {Lie}H$
, utilisant le crochet.
Ce sont justement ces signes méchants, qui nous forceront à traiter de façon spéciale les groupes unitaires de dimension impaire, voir l’ex. 2.2.4 et surtout le §2.3. Finissons-en par énoncer l’existence des systèmes de Chevalley–Steinberg, dont la démonstration remonte essentiellement à l’œuvre [Reference SteinbergSt59] de Steinberg.
Proposition 2.1.6 (Steinberg).
Il existe toujours un système de Chevalley–Steinberg.
Démonstration. Vu que
![]() $\sigma $
est un automorphisme et que les
$\sigma $
est un automorphisme et que les
![]() $\mathbb {Z}$
-automorphismes de
$\mathbb {Z}$
-automorphismes de
![]() $\mathbb {G}_a$
sont déterminés par les signes
$\mathbb {G}_a$
sont déterminés par les signes
![]() $\{\pm 1\}$
, on déduit que
$\{\pm 1\}$
, on déduit que
![]() $\sigma (y_\alpha (r))= y_{\sigma (\alpha )}(\epsilon _{\alpha ,\sigma } r)$
avec
$\sigma (y_\alpha (r))= y_{\sigma (\alpha )}(\epsilon _{\alpha ,\sigma } r)$
avec
![]() $\epsilon _{\alpha ,\sigma } \in \{\pm 1\}$
. Fixé un système de Chevalley quelconque du groupe épinglé H, on doit montrer que, quitte à faire des changements de signes, on arrive à la condition
$\epsilon _{\alpha ,\sigma } \in \{\pm 1\}$
. Fixé un système de Chevalley quelconque du groupe épinglé H, on doit montrer que, quitte à faire des changements de signes, on arrive à la condition
![]() $\epsilon _{\alpha ,\sigma }=1$
pour toutes les racines
$\epsilon _{\alpha ,\sigma }=1$
pour toutes les racines
![]() $\alpha \in \Phi _H$
telles que leurs moyennes
$\alpha \in \Phi _H$
telles que leurs moyennes
![]() $a\in \Phi _G^{\operatorname {nd}}$
soient non divisibles.
$a\in \Phi _G^{\operatorname {nd}}$
soient non divisibles.
On se ramène aisément au cas où H est adjoint simple. Le cas des involutions fut traité dans [Reference SteinbergSt59, lem. 3.2] et le cas du groupe symétrique
![]() $\mathfrak {S}_3$
en trois éléments fut vérifié dans la preuve de [Reference LandvogtLan96, prop. 4.4].
$\mathfrak {S}_3$
en trois éléments fut vérifié dans la preuve de [Reference LandvogtLan96, prop. 4.4].
2.2 Formes tordues et quasi-systèmes de Chevalley
Soient k un corps et G un k-groupe réductif et connexe. Rappelons que G s’appelle quasi-déployé si le centralisateur de tout sous-k-tore déployé maximal S est un tore maximal T. En particulier, on peut toujours choisir un sous-groupe de Borel
![]() $B\supset T\supset S$
correspondant à une base
$B\supset T\supset S$
correspondant à une base
![]() $\Delta _G$
du système de racines
$\Delta _G$
du système de racines
![]() $\Phi _G$
de G relativement à S. Soit
$\Phi _G$
de G relativement à S. Soit
![]() $l/k$
une extension galoisienne à groupe
$l/k$
une extension galoisienne à groupe
![]() $\Gamma $
déployant G. Le lemme suivant est du folklore :
$\Gamma $
déployant G. Le lemme suivant est du folklore :
Lemme 2.2.1. Soit H la k-forme déployée de G munie d’un épinglage. Alors, quitte à conjuguer par
![]() $H^{\mathrm {ad}}(l)$
, il y a un et un seul prolongement de l’isomorphisme donné
$H^{\mathrm {ad}}(l)$
, il y a un et un seul prolongement de l’isomorphisme donné
![]() $G_l\simeq H_l$
à un isomorphisme de triples
$G_l\simeq H_l$
à un isomorphisme de triples
![]() $(G,B,T)\otimes _k l \simeq (H,B_H,T_H)\otimes _k l$
tel que l’action de
$(G,B,T)\otimes _k l \simeq (H,B_H,T_H)\otimes _k l$
tel que l’action de
![]() $\Gamma $
transportée au membre de droite préserve l’épinglage.
$\Gamma $
transportée au membre de droite préserve l’épinglage.
Il en résulte un certain homomorphisme
![]() $\tau : \Gamma \rightarrow \Xi _H$
vers le groupe d’automorphismes épinglés, tel que l’opération de
$\tau : \Gamma \rightarrow \Xi _H$
vers le groupe d’automorphismes épinglés, tel que l’opération de
![]() $\Gamma $
sur
$\Gamma $
sur
![]() $G_l$
transportée à
$G_l$
transportée à
![]() $H_l$
devienne égale à
$H_l$
devienne égale à
![]() $\gamma \mapsto \tau (\gamma )\otimes \gamma $
.
$\gamma \mapsto \tau (\gamma )\otimes \gamma $
.
Démonstration. L’unicité est évidente en vertu du [SGA3, exp. XXIV, th. 1.3]. Grâce aux théorèmes de conjugaison pour les tores maximaux et les paraboliques minimaux qui les contiennent, cf. par exemple [Reference Conrad, Gabber and PrasadCGP15, th. C.2.3, th. C.2.5], on peut choisir
![]() $h \in H(l)$
, tel que
$h \in H(l)$
, tel que
![]() $\varphi : G_l \simeq H_l$
envoie
$\varphi : G_l \simeq H_l$
envoie
![]() $(B,T)$
sur
$(B,T)$
sur
![]() $(B_H,T_H)$
. Pour préserver l’épinglage, il suffit de conjuguer par un élément de
$(B_H,T_H)$
. Pour préserver l’épinglage, il suffit de conjuguer par un élément de
![]() $T^{\operatorname {ad}}(l)$
.
$T^{\operatorname {ad}}(l)$
.
Par conséquent, tous les k-formes G quasi-déployées et l-déployées du k-groupe épinglé H s’obtiennent par une procédure très explicite de tordument comme suit :
Construction 2.2.2. Soient
![]() $\Gamma $
le groupe de Galois de
$\Gamma $
le groupe de Galois de
![]() $l/k$
et
$l/k$
et
![]() $\tau : \Gamma \rightarrow \Xi _H$
un homomorphisme de groupes continu. Comme
$\tau : \Gamma \rightarrow \Xi _H$
un homomorphisme de groupes continu. Comme
![]() $\Gamma $
commute aux k-automorphismes de H, l’homomorphisme
$\Gamma $
commute aux k-automorphismes de H, l’homomorphisme
![]() $\tau :\Gamma \rightarrow \Xi _H$
induit une classe
$\tau :\Gamma \rightarrow \Xi _H$
induit une classe
![]() $c_\tau \in H^1(k,\operatorname {Aut}_{l}(H))$
et l’on note G le k-groupe réductif, connexe et quasi-déployé obtenu en tordant H par
$c_\tau \in H^1(k,\operatorname {Aut}_{l}(H))$
et l’on note G le k-groupe réductif, connexe et quasi-déployé obtenu en tordant H par
![]() $c_\tau $
, comp. avec [Reference ConradCo14, lem. 7.1.1, prop. 7.1.6]. Plus explicitement, si
$c_\tau $
, comp. avec [Reference ConradCo14, lem. 7.1.1, prop. 7.1.6]. Plus explicitement, si
![]() $\Gamma $
est fini, considérons la restriction des scalaires
$\Gamma $
est fini, considérons la restriction des scalaires
![]() $\operatorname {R}_{l/k} H$
munie de l’opération de
$\operatorname {R}_{l/k} H$
munie de l’opération de
![]() $\Gamma $
qui fait correspondre à
$\Gamma $
qui fait correspondre à
![]() $\gamma $
l’automorphisme
$\gamma $
l’automorphisme
![]() $\tau (\gamma ) \otimes \gamma $
. Si l’on pose alors
$\tau (\gamma ) \otimes \gamma $
. Si l’on pose alors
![]() $G=(\operatorname {R}_{l/k} H)^{\Gamma }$
, on obtient la k-forme quasi-déployée cherchée de H.
$G=(\operatorname {R}_{l/k} H)^{\Gamma }$
, on obtient la k-forme quasi-déployée cherchée de H.
La définition classique d’un quasi-épinglage d’un groupe quasi-déployé G consiste de la donnée d’un couple de Killing
![]() $B\supset T$
et d’un élément
$B\supset T$
et d’un élément
![]() $X \in \operatorname {Lie} B$
, tel que son image dans
$X \in \operatorname {Lie} B$
, tel que son image dans
![]() $\operatorname {Lie}B_H$
coïncide avec la somme des vecteurs générateurs
$\operatorname {Lie}B_H$
coïncide avec la somme des vecteurs générateurs
![]() $Y_\alpha =y_\alpha (1) \in \operatorname {Lie}U_\alpha $
pour chaque racine simple
$Y_\alpha =y_\alpha (1) \in \operatorname {Lie}U_\alpha $
pour chaque racine simple
![]() $\alpha \in \Delta _H$
, cf. [SGA3, exp. XXIV, 3.9]. Bien que cela est raisonnable, nous aurons besoin de recourir plutôt à d’isomorphismes décrivant les sous-groupes radiciels
$\alpha \in \Delta _H$
, cf. [SGA3, exp. XXIV, 3.9]. Bien que cela est raisonnable, nous aurons besoin de recourir plutôt à d’isomorphismes décrivant les sous-groupes radiciels
![]() $U_a$
pour les racines relatives
$U_a$
pour les racines relatives
![]() $a \in \Phi _G$
, où ce symbole-ci désigne le système de racines relatifFootnote 1 de G par rapport à S.
$a \in \Phi _G$
, où ce symbole-ci désigne le système de racines relatifFootnote 1 de G par rapport à S.
Ensuite, on étudie la structure des sous-groupes radiciels
![]() $U_a$
lorsque
$U_a$
lorsque
![]() $a \in \Phi _G^{\operatorname {nd}}$
n’est pas divisible.
$a \in \Phi _G^{\operatorname {nd}}$
n’est pas divisible.
Exemple 2.2.3 (non-multipliable).
Supposons que
![]() $H=\prod _{I} \operatorname {SL}_2$
, épinglé comme d’habitude et où I est un ensemble fini sur lequel
$H=\prod _{I} \operatorname {SL}_2$
, épinglé comme d’habitude et où I est un ensemble fini sur lequel
![]() $\Gamma $
agit de façon transitive. Alors, le groupe
$\Gamma $
agit de façon transitive. Alors, le groupe
![]() $\Gamma $
y opère canoniquement par d’automorphismes de Dynkin qui échangent les différents facteurs simples de rang
$\Gamma $
y opère canoniquement par d’automorphismes de Dynkin qui échangent les différents facteurs simples de rang
![]() $1$
, selon l’action naturelle de
$1$
, selon l’action naturelle de
![]() $\Gamma $
sur l’espace homogène I. On veut calculer le groupe
$\Gamma $
sur l’espace homogène I. On veut calculer le groupe
![]() $G=(\operatorname {R}_{l/k} H)^\Gamma $
. Mais si
$G=(\operatorname {R}_{l/k} H)^\Gamma $
. Mais si
![]() $(h_{\gamma })\in \operatorname {SL}_2(R\otimes _kl)^{I}$
est invariant par
$(h_{\gamma })\in \operatorname {SL}_2(R\otimes _kl)^{I}$
est invariant par
![]() $\Gamma $
, alors
$\Gamma $
, alors
![]() $\sigma (h_{i})=h_{\sigma i}$
. Par conséquent, on arrive à la conclusion que
$\sigma (h_{i})=h_{\sigma i}$
. Par conséquent, on arrive à la conclusion que
![]() $G \simeq \operatorname {R}_{m_0/k} \operatorname {SL}_2$
, où
$G \simeq \operatorname {R}_{m_0/k} \operatorname {SL}_2$
, où
![]() $m_0$
désigne le corps fixe du stabilisateurs
$m_0$
désigne le corps fixe du stabilisateurs
![]() $ \Gamma _0 \subset \Gamma $
de
$ \Gamma _0 \subset \Gamma $
de
![]() $i_0 \in I$
, et que l’inclusion dans
$i_0 \in I$
, et que l’inclusion dans
![]() $\operatorname {R}_{l/k} H$
est donnée par la diagonale tordue
$\operatorname {R}_{l/k} H$
est donnée par la diagonale tordue
![]() $(\gamma )_{\gamma \in \Gamma /\Gamma _0}$
.
$(\gamma )_{\gamma \in \Gamma /\Gamma _0}$
.
Revenons alors au cas général d’une racine relative ni divisible ni multipliable
![]() $a \in \Phi _G^{\operatorname {nd,nm}}$
obtenue en moyennant
$a \in \Phi _G^{\operatorname {nd,nm}}$
obtenue en moyennant
![]() $\alpha \in \Phi _H$
. En termes d’un système de Chevalley–Steinberg de notre groupe épinglé H, on obtient un isomorphisme
$\alpha \in \Phi _H$
. En termes d’un système de Chevalley–Steinberg de notre groupe épinglé H, on obtient un isomorphisme
où l’on note
![]() $l_a$
le corps fixe du stabilisateur de
$l_a$
le corps fixe du stabilisateur de
![]() $\alpha $
pour l’action de
$\alpha $
pour l’action de
![]() $\Gamma $
, car
$\Gamma $
, car
![]() $\epsilon _{\alpha ,\gamma }=1$
pour tout
$\epsilon _{\alpha ,\gamma }=1$
pour tout
![]() $\gamma \in \Gamma $
, comp. aussi avec [Reference Bruhat and TitsBT84a, 4.1.5]. Si l’on avait choisi soit un autre système de Chevalley, soit une racine conjuguée de
$\gamma \in \Gamma $
, comp. aussi avec [Reference Bruhat and TitsBT84a, 4.1.5]. Si l’on avait choisi soit un autre système de Chevalley, soit une racine conjuguée de
![]() $\alpha $
, on n’aurait changé
$\alpha $
, on n’aurait changé
![]() $x_a$
qu’au signe et à la conjugaison près, cf. aussi [Reference Bruhat and TitsBT84a, 4.1.7]. On va dire que deux tels isomorphismes sont similaires et donc que
$x_a$
qu’au signe et à la conjugaison près, cf. aussi [Reference Bruhat and TitsBT84a, 4.1.7]. On va dire que deux tels isomorphismes sont similaires et donc que
![]() $x_a$
ne dépend que de a à similitude près.
$x_a$
ne dépend que de a à similitude près.
Exemple 2.2.4 (multipliable).
Considérons maintenant
![]() $H=\operatorname {SL}_3$
muni de l’épinglage usuel et supposons que
$H=\operatorname {SL}_3$
muni de l’épinglage usuel et supposons que
![]() $l/k$
soit une extension quadratique séparable. Dans l’exemple 2.1.5, nous avons déterminé l’involution de Dynkin
$l/k$
soit une extension quadratique séparable. Dans l’exemple 2.1.5, nous avons déterminé l’involution de Dynkin
![]() $\sigma $
de
$\sigma $
de
![]() $\operatorname {SL}_3$
. Le groupe échéant
$\operatorname {SL}_3$
. Le groupe échéant
![]() $G=(\operatorname {R}_{l/k}H)^\Gamma $
sera toujours noté
$G=(\operatorname {R}_{l/k}H)^\Gamma $
sera toujours noté
![]() $\operatorname {SU}_{3,l/k}$
et regardé en tant que fermé de
$\operatorname {SU}_{3,l/k}$
et regardé en tant que fermé de
![]() $\operatorname {R}_{l/k}\operatorname {SL}_3$
; il s’agit même du groupe unitaire attaché à la forme quadratique
$\operatorname {R}_{l/k}\operatorname {SL}_3$
; il s’agit même du groupe unitaire attaché à la forme quadratique
![]() $xy+yx-z^2$
. Son système de racines est
$xy+yx-z^2$
. Son système de racines est
![]() $\Phi _G=\{\pm a, \pm 2a\}$
et on souhaiterait d’avoir une description explicite du groupe
$\Phi _G=\{\pm a, \pm 2a\}$
et on souhaiterait d’avoir une description explicite du groupe
![]() $U_a$
. Grâce à l’exemple sus-mentionné, on tire
$U_a$
. Grâce à l’exemple sus-mentionné, on tire
 $$ \begin{align} U_a =\Bigg\{ \begin{pmatrix} 1& r & s\\ 0 & 1 & \sigma(r)\\ 0 & 0 & 1 \end{pmatrix} : s+\sigma(s)=r\sigma(r) \Bigg\}. \end{align} $$
$$ \begin{align} U_a =\Bigg\{ \begin{pmatrix} 1& r & s\\ 0 & 1 & \sigma(r)\\ 0 & 0 & 1 \end{pmatrix} : s+\sigma(s)=r\sigma(r) \Bigg\}. \end{align} $$
Notant
![]() $x_a(r,s)$
la matrice ci-dessus, on peut regarder
$x_a(r,s)$
la matrice ci-dessus, on peut regarder
![]() $x_a$
comme un isomorphisme entre un certain groupe matriciel et le groupe algébrique abstrait
$x_a$
comme un isomorphisme entre un certain groupe matriciel et le groupe algébrique abstrait
![]() $U_a$
. En termes du système de Chevalley–Steinberg de
$U_a$
. En termes du système de Chevalley–Steinberg de
![]() $\operatorname {SL}_3$
, il s’écrit de la façon suivante :
$\operatorname {SL}_3$
, il s’écrit de la façon suivante :
Cet exemple nous amène à introduire de la notation pour ce groupe matriciel unipotent, cf. aussi [Reference Bruhat and TitsBT84a, 4.1.9].
Définition 2.2.5. Soit
![]() $l/k$
une extension quadratique séparable. Le groupe unipotent pluriel
$l/k$
une extension quadratique séparable. Le groupe unipotent pluriel
![]() $\mathbb {G}_{p,l/k}$
est le sous-groupe des matrices triangulaires supérieures unipotentes de
$\mathbb {G}_{p,l/k}$
est le sous-groupe des matrices triangulaires supérieures unipotentes de
![]() $\operatorname {R}_{l/k}\operatorname {SL}_3$
de la forme de (2.2.3).
$\operatorname {R}_{l/k}\operatorname {SL}_3$
de la forme de (2.2.3).
Soient
![]() $a \in \Phi _G^{\operatorname {m}}$
une racine relative multipliable et
$a \in \Phi _G^{\operatorname {m}}$
une racine relative multipliable et
![]() $\alpha ,\beta \in \Phi _H$
deux racines conjuguées dont la somme est une racine et dont les moyennes sont égales à a. En termes d’un système de Chevalley–Steinberg commode de notre groupe épinglé H, on obtient un isomorphisme
$\alpha ,\beta \in \Phi _H$
deux racines conjuguées dont la somme est une racine et dont les moyennes sont égales à a. En termes d’un système de Chevalley–Steinberg commode de notre groupe épinglé H, on obtient un isomorphisme
 $$ \begin{align} (r,s)\mapsto \prod_{\{\gamma\alpha,\gamma\beta\}} y_{\gamma\beta}(\gamma\sigma(r))y_{\gamma(\alpha+\beta)}(\gamma(s))y_{\gamma\alpha}(\gamma(r)), \end{align} $$
$$ \begin{align} (r,s)\mapsto \prod_{\{\gamma\alpha,\gamma\beta\}} y_{\gamma\beta}(\gamma\sigma(r))y_{\gamma(\alpha+\beta)}(\gamma(s))y_{\gamma\alpha}(\gamma(r)), \end{align} $$
où l’on note
![]() $l_a$
le corps fixe du stabilisateur de
$l_a$
le corps fixe du stabilisateur de
![]() $\alpha $
pour l’action de
$\alpha $
pour l’action de
![]() $\Gamma $
et
$\Gamma $
et
![]() $l_{2a}$
celui de
$l_{2a}$
celui de
![]() $\alpha +\beta $
, et
$\alpha +\beta $
, et
![]() $\sigma $
l’involution de
$\sigma $
l’involution de
![]() $l_a/l_{2a}$
, voir [Reference Bruhat and TitsBT84a, 4.1.9]. Notons que les ensembles
$l_a/l_{2a}$
, voir [Reference Bruhat and TitsBT84a, 4.1.9]. Notons que les ensembles
![]() $\{\gamma \alpha ,\gamma \beta \}$
doivent être regardés comme étant ordonnés et
$\{\gamma \alpha ,\gamma \beta \}$
doivent être regardés comme étant ordonnés et
![]() $\gamma $
doit préserver cet ordre, pour que cette écriture ait du sens, donc on dira que
$\gamma $
doit préserver cet ordre, pour que cette écriture ait du sens, donc on dira que
![]() $\gamma \alpha $
resp.
$\gamma \alpha $
resp.
![]() $\gamma \beta $
est un relèvement de premier type resp. second type de a. Finalement, l’isomorphisme
$\gamma \beta $
est un relèvement de premier type resp. second type de a. Finalement, l’isomorphisme
![]() $x_a$
ne dépend que de a à similitude près, cf. [Reference Bruhat and TitsBT84a, 4.1.13] et voir [Reference Bruhat and TitsBT84a, A.4] pour les opérations permises dans ce cas.
$x_a$
ne dépend que de a à similitude près, cf. [Reference Bruhat and TitsBT84a, 4.1.13] et voir [Reference Bruhat and TitsBT84a, A.4] pour les opérations permises dans ce cas.
L’ensemble des isomorphismes
![]() $x_a$
pour
$x_a$
pour
![]() $a \in \Delta _G$
resp.
$a \in \Delta _G$
resp.
![]() $a \in \Phi _G$
ainsi obtenus est exactement ce que nous aurions envie d’appeler un quasi-épinglage resp. quasi-système de Chevalley. La seule nuisance est qu’une telle notion nous semble à l’instant extrinsèque et dépendante de la réalisation de G comme
$a \in \Phi _G$
ainsi obtenus est exactement ce que nous aurions envie d’appeler un quasi-épinglage resp. quasi-système de Chevalley. La seule nuisance est qu’une telle notion nous semble à l’instant extrinsèque et dépendante de la réalisation de G comme
![]() $\Gamma $
-invariants d’une restriction des scalaires de H. L’approche idéale pour s’y référer intrinsèquement est celle de [Reference LourençoLou21, 2.4], dont le truc principal est de considérer plutôt les homomorphismes naturels
$\Gamma $
-invariants d’une restriction des scalaires de H. L’approche idéale pour s’y référer intrinsèquement est celle de [Reference LourençoLou21, 2.4], dont le truc principal est de considérer plutôt les homomorphismes naturels
prolongeant les isomorphismes
![]() $x_a$
, selon a appartienne à
$x_a$
, selon a appartienne à
![]() $\Phi _G^{\operatorname {nd,nm}}$
ou à
$\Phi _G^{\operatorname {nd,nm}}$
ou à
![]() $\Phi _G^{\operatorname {m}}$
. En effet, leur existence découle de la description des groupes quasi-déployés de rang
$\Phi _G^{\operatorname {m}}$
. En effet, leur existence découle de la description des groupes quasi-déployés de rang
![]() $1$
conformément aux ex. 2.2.3 et 2.2.4. Voici la [Reference LourençoLou21, déf. 2.4] :
$1$
conformément aux ex. 2.2.3 et 2.2.4. Voici la [Reference LourençoLou21, déf. 2.4] :
Définition 2.2.6. Soit
![]() $G \supset B \supset T \supset S$
un groupe quasi-déployé. Un quasi-épinglage de G est une collection d’homomorphismes
$G \supset B \supset T \supset S$
un groupe quasi-déployé. Un quasi-épinglage de G est une collection d’homomorphismes
![]() $\zeta _a$
de
$\zeta _a$
de
![]() $\operatorname {R}_{l_a/k} \operatorname {SL}_2$
vers G si
$\operatorname {R}_{l_a/k} \operatorname {SL}_2$
vers G si
![]() $a \in \Delta _G^{\operatorname {nd,nm}}$
(resp. de
$a \in \Delta _G^{\operatorname {nd,nm}}$
(resp. de
![]() $\operatorname {R}_{l_{2a}/k} \operatorname {SU}_{3,l_a/l_{2a}}$
si
$\operatorname {R}_{l_{2a}/k} \operatorname {SU}_{3,l_a/l_{2a}}$
si
![]() $a \in \Delta _G^{\operatorname {m}}$
) tels que leurs restrictions aux tores diagonaux déployés soient égales à
$a \in \Delta _G^{\operatorname {m}}$
) tels que leurs restrictions aux tores diagonaux déployés soient égales à
![]() $a^{\vee }:\mathbb {G}_m \rightarrow G$
et que les matrices triangulaires supérieures unipotentes s’envoient sur
$a^{\vee }:\mathbb {G}_m \rightarrow G$
et que les matrices triangulaires supérieures unipotentes s’envoient sur
![]() $U_a$
. Un quasi-système de Chevalley de G quasi-épinglé est une extension de la collection
$U_a$
. Un quasi-système de Chevalley de G quasi-épinglé est une extension de la collection
![]() $\zeta _a$
aux racines non divisibles
$\zeta _a$
aux racines non divisibles
![]() $a \in \Phi _G^{\operatorname {nd}}$
de telle sorte que
$a \in \Phi _G^{\operatorname {nd}}$
de telle sorte que
![]() $\operatorname {int}(m_a) \circ \zeta _b$
soit semblable à
$\operatorname {int}(m_a) \circ \zeta _b$
soit semblable à
![]() $\zeta _{s_a(b)}$
.
$\zeta _{s_a(b)}$
.
Les
![]() $m_a$
s’écrivent comme
$m_a$
s’écrivent comme
![]() $\prod _{\gamma \alpha } n_{\gamma \alpha }$
dans le cas non multipliable (resp.
$\prod _{\gamma \alpha } n_{\gamma \alpha }$
dans le cas non multipliable (resp.
![]() $\prod _{\gamma (\alpha +\beta )} n_{\gamma (\alpha +\beta )}$
dans le cas multipliable), voir la déf. 2.1.1 pour le cas déployé. Ceux-ci se généralisentFootnote 2 en des éléments
$\prod _{\gamma (\alpha +\beta )} n_{\gamma (\alpha +\beta )}$
dans le cas multipliable), voir la déf. 2.1.1 pour le cas déployé. Ceux-ci se généralisentFootnote 2 en des éléments
pour toute racine
![]() $a\in \Phi _G^{\operatorname {nd},\operatorname {nm}}$
ni divisible ni multipliable, et
$a\in \Phi _G^{\operatorname {nd},\operatorname {nm}}$
ni divisible ni multipliable, et
pour toute racine multipliable
![]() $a \in \Phi _G^{\operatorname {m}}$
, voir [Reference Bruhat and TitsBT84a, 4.1.5, 4.1.11].
$a \in \Phi _G^{\operatorname {m}}$
, voir [Reference Bruhat and TitsBT84a, 4.1.5, 4.1.11].
Proposition 2.2.7. Les classes de similitude des quasi-systèmes de Chevalley de G forment un torseur trivial sous
![]() $T^{\operatorname {ad}}(k)/T^{\operatorname {ad}}[2](k)$
.
$T^{\operatorname {ad}}(k)/T^{\operatorname {ad}}[2](k)$
.
Démonstration. On renvoie à [Reference LourençoLou21, prop. 2.5] pour plus de détails. Ce que deux classes de similitude de quasi-systèmes de Chevalley ne diffèrent qu’en conjuguant par
![]() $T^{\operatorname {ad}}(k)/T^{\operatorname {ad}}[2](k)$
est presque évidente. La méthode de preuve dans le cas déployé permet d’étendre un quasi-épinglage donné à une famille d’homomorphismes
$T^{\operatorname {ad}}(k)/T^{\operatorname {ad}}[2](k)$
est presque évidente. La méthode de preuve dans le cas déployé permet d’étendre un quasi-épinglage donné à une famille d’homomorphismes
![]() $\zeta _a$
. Pour vérifier qu’ils satisfont à la contrainte de similitude, on utilise les formules explicites pour les
$\zeta _a$
. Pour vérifier qu’ils satisfont à la contrainte de similitude, on utilise les formules explicites pour les
![]() $x_a$
,
$x_a$
,
![]() $m_a$
, etc. en termes des
$m_a$
, etc. en termes des
![]() $y_\alpha $
,
$y_\alpha $
,
![]() $n_\alpha $
, etc. pour se ramener au cas déployé.
$n_\alpha $
, etc. pour se ramener au cas déployé.
Remarque 2.2.8. Outre les résultats de conjugaison, qui ne marchent qu’au-dessus des corps, le genre de constructions entreprises dans ce numéro, voir par exemple la constr. 2.2.2, s’étendent facilement aux bases générales. On en laisse le soin au lecteur.
2.3 La modification de Tits
Malheureusement, le prolongement naturel du groupe
![]() $\mathbb {G}_{p,l/k}$
, voir la déf. 2.2.5, au cas où les coefficients sont entiers (ceci doit être pris au sens du §3) n’est plus lisse en caractéristique résiduelle égale à
$\mathbb {G}_{p,l/k}$
, voir la déf. 2.2.5, au cas où les coefficients sont entiers (ceci doit être pris au sens du §3) n’est plus lisse en caractéristique résiduelle égale à
![]() $2$
. Par conséquent, on va introduire un certain k-groupe unipotent
$2$
. Par conséquent, on va introduire un certain k-groupe unipotent
![]() $\mathbb {G}^{\operatorname {T}}_{p,l/k}$
explicite à la suite de [Reference TitsTi84, annexe 2], qui s’identifie encore, lorsque
$\mathbb {G}^{\operatorname {T}}_{p,l/k}$
explicite à la suite de [Reference TitsTi84, annexe 2], qui s’identifie encore, lorsque
![]() $2$
est inversible dans k, au groupe unipotent pluriel de la déf. 2.2.5 noté
$2$
est inversible dans k, au groupe unipotent pluriel de la déf. 2.2.5 noté
![]() $\mathbb {G}^{\operatorname {CS}}_{p,l/k}$
pendant tout ce numéro. L’avantage de la variante
$\mathbb {G}^{\operatorname {CS}}_{p,l/k}$
pendant tout ce numéro. L’avantage de la variante
![]() $\mathbb {G}^{\operatorname {T}}_{p,l/k}$
de Tits est qu’elle admet une description plus commode en termes du sous-espace vectoriel
$\mathbb {G}^{\operatorname {T}}_{p,l/k}$
de Tits est qu’elle admet une description plus commode en termes du sous-espace vectoriel
![]() $l^0 \subset l$
des éléments de trace nulle, qui s’étendra sans peine de manière lisse au cas où les coefficients sont entiers, voir la déf. 3.3.3.
$l^0 \subset l$
des éléments de trace nulle, qui s’étendra sans peine de manière lisse au cas où les coefficients sont entiers, voir la déf. 3.3.3.
Définition 2.3.1. Soit k un corps de caractéristique différente de
![]() $2$
et
$2$
et
![]() $l/k$
une extension quadratique. Alors,
$l/k$
une extension quadratique. Alors,
![]() $\mathbb {G}^{\operatorname {T}}_{p,l/k}$
est la variété
$\mathbb {G}^{\operatorname {T}}_{p,l/k}$
est la variété
![]() $\operatorname {R}_{l/k}\mathbb {A}^1_l \times \mathbb {A}^1_{l_0}$
munie de la loi de groupe
$\operatorname {R}_{l/k}\mathbb {A}^1_l \times \mathbb {A}^1_{l_0}$
munie de la loi de groupe
Ici, l’on regarde
![]() $\mathbb {A}^1_{l_0}$
comme la droite affine sur k au moyen d’un isomorphisme quelconque de k-espaces vectoriels
$\mathbb {A}^1_{l_0}$
comme la droite affine sur k au moyen d’un isomorphisme quelconque de k-espaces vectoriels
![]() $k \simeq l_0$
.
$k \simeq l_0$
.
Notons que cette définition se ressemble à celle de [Reference Bruhat and TitsBT84a, 4.1.15], sauf en ce qui concerne le choix d’un élément
![]() $\lambda $
de trace
$\lambda $
de trace
![]() $1$
, bien que nous avons choisi
$1$
, bien que nous avons choisi
![]() $\lambda =1$
. Nous en tirons l’isomorphisme
$\lambda =1$
. Nous en tirons l’isomorphisme
lequel profite du fait que
![]() $2$
est inversible dans k. Avant de continuer, étudions la situation limite en caractéristique
$2$
est inversible dans k. Avant de continuer, étudions la situation limite en caractéristique
![]() $2$
, qui est implicitement liée avec toutes les modification que nous sommes en train d’introduire :
$2$
, qui est implicitement liée avec toutes les modification que nous sommes en train d’introduire :
Remarque 2.3.2. Supposons pour l’instant que
![]() $l/k$
est une extension quadratique inséparable de caractéristique
$l/k$
est une extension quadratique inséparable de caractéristique
![]() $2$
, c’est-à-dire
$2$
, c’est-à-dire
![]() $\sigma $
est trivial. Alors la déf. 2.2.5 préserve son sens et l’on obtient un isomorphisme
$\sigma $
est trivial. Alors la déf. 2.2.5 préserve son sens et l’on obtient un isomorphisme
![]() $\mathbb {G}^{\operatorname {CS}}_{p,l/k}=\operatorname {R}_{l/k}\alpha _2 \times \operatorname {R}_{l/k}\mathbb {G}_a $
, donc le groupe commutatif dont il s’agit n’est pas lisse. Par contre, si l’on remplace
$\mathbb {G}^{\operatorname {CS}}_{p,l/k}=\operatorname {R}_{l/k}\alpha _2 \times \operatorname {R}_{l/k}\mathbb {G}_a $
, donc le groupe commutatif dont il s’agit n’est pas lisse. Par contre, si l’on remplace
![]() $l^0$
dans la déf. 2.3.1 par un choix arbitraire de complément linéaire de k dans l, alors on obtient que
$l^0$
dans la déf. 2.3.1 par un choix arbitraire de complément linéaire de k dans l, alors on obtient que
![]() $\mathbb {G}^{\operatorname {T}}_{p,l/k}$
s’identifie au groupe commutatif lisse
$\mathbb {G}^{\operatorname {T}}_{p,l/k}$
s’identifie au groupe commutatif lisse
![]() $\operatorname {R}_{l/k}\mathbb {G}_a \times \mathbb {G}_a$
.
$\operatorname {R}_{l/k}\mathbb {G}_a \times \mathbb {G}_a$
.
Moyennant l’isomorphisme donné
![]() $\mathbb {G}^{\operatorname {T}}_{p,l/k} \simeq \mathbb {G}^{\operatorname {CS}}_{p,l/k}$
, on peut donc considérer les isomorphismes du quasi-système de Chevalley de G introduit précédemment, voir la déf. 2.2.6, comme partant du membre de gauche. On obtient alors l’écriture
$\mathbb {G}^{\operatorname {T}}_{p,l/k} \simeq \mathbb {G}^{\operatorname {CS}}_{p,l/k}$
, on peut donc considérer les isomorphismes du quasi-système de Chevalley de G introduit précédemment, voir la déf. 2.2.6, comme partant du membre de gauche. On obtient alors l’écriture
dans le cas où
![]() $\Phi _H$
est irréductible (en général, il faut considérer un produit à plusieurs termes). Cet état de choses est indésirable en vertu du §3, puisque le morphisme vers H, pour qu’il soit prolongeable aux coefficients entiers, cf. prop. 3.3.9, ne devrait pas impliquer des divisions par
$\Phi _H$
est irréductible (en général, il faut considérer un produit à plusieurs termes). Cet état de choses est indésirable en vertu du §3, puisque le morphisme vers H, pour qu’il soit prolongeable aux coefficients entiers, cf. prop. 3.3.9, ne devrait pas impliquer des divisions par
![]() $2$
. On souhaiterait donc modifier les isomorphismes du système de Chevalley–Steinberg de H, de manière que
$2$
. On souhaiterait donc modifier les isomorphismes du système de Chevalley–Steinberg de H, de manière que
![]() $x_a$
s’exprime en fonction de u, v et de leurs conjugués à coefficients entiers. Ceci sera achevé au lem. 2.3.5.
$x_a$
s’exprime en fonction de u, v et de leurs conjugués à coefficients entiers. Ceci sera achevé au lem. 2.3.5.
Exemple 2.3.3. Reprenons les exemples 2.1.5 et 2.2.4, alors
![]() $H=\operatorname {SL}_3$
et
$H=\operatorname {SL}_3$
et
![]() $G=\operatorname {SU}_{3,l/k}$
. D’après la prop. 2.2.7, on se permet de conjuguer le système de Chevalley de H par un élément de
$G=\operatorname {SU}_{3,l/k}$
. D’après la prop. 2.2.7, on se permet de conjuguer le système de Chevalley de H par un élément de
![]() $T_H^{\operatorname {ad}}(k)$
. Choisissons d’abord
$T_H^{\operatorname {ad}}(k)$
. Choisissons d’abord
![]() $\varpi _{\alpha }^\vee (2)$
. En notant le quasi-système de Chevalley et le système de Chevalley–Steinberg par
$\varpi _{\alpha }^\vee (2)$
. En notant le quasi-système de Chevalley et le système de Chevalley–Steinberg par
![]() $x_{\bullet }^{\operatorname {CS}}$
et
$x_{\bullet }^{\operatorname {CS}}$
et
![]() $y_{\bullet }^{\operatorname {CS}}$
, posons alors
$y_{\bullet }^{\operatorname {CS}}$
, posons alors
![]() $y_{\bullet }^{\operatorname {T}}=\operatorname {int}(\varpi _{\alpha }^\vee (2)) \circ y_{\bullet }^{\operatorname {CS}}$
. On en tire les relations suivantes :
$y_{\bullet }^{\operatorname {T}}=\operatorname {int}(\varpi _{\alpha }^\vee (2)) \circ y_{\bullet }^{\operatorname {CS}}$
. On en tire les relations suivantes :
En particulier, il suffit de prendre
![]() $x_a^{\operatorname {T}}(u,v)=x_a^{\operatorname {CS}}(2u,4v)$
et
$x_a^{\operatorname {T}}(u,v)=x_a^{\operatorname {CS}}(2u,4v)$
et
![]() $x_{-a}^{\operatorname {T}}(u,v)=x_{-a}^{\operatorname {CS}}(u,v)$
, pour que la contrainte d’intégralité soit satisfaite.
$x_{-a}^{\operatorname {T}}(u,v)=x_{-a}^{\operatorname {CS}}(u,v)$
, pour que la contrainte d’intégralité soit satisfaite.
Cependant, il faut typiquement modifier aussi les isomorphismes associés aux racines ni divisibles ni multipliables. La définition suivante généralise de façon naturelle la modification de Tits dans le cas où H est simplement connexe et simple, voir [Reference TitsTi84, pp. 216-217] :
Définition 2.3.4 (Tits).
Soient c la somme des racines simples multipliables de G et
![]() $\gamma $
la somme de leurs relèvements de premier type. Alors, on pose
$\gamma $
la somme de leurs relèvements de premier type. Alors, on pose
et l’on dit que les quasi-systèmes correspondants sont de Tits. Ici,
![]() $\chi _{+}$
désigne la fonction caractéristique de
$\chi _{+}$
désigne la fonction caractéristique de
![]() $\Phi _G^+$
dans
$\Phi _G^+$
dans
![]() $\Phi _G$
.
$\Phi _G$
.
Nous sommes amené à définir les
pour toute racine
![]() $a\in \Phi _G^{\operatorname {nd},\operatorname {nm}}$
ni divisible ni multipliable, et
$a\in \Phi _G^{\operatorname {nd},\operatorname {nm}}$
ni divisible ni multipliable, et
pour toute racine multipliable
![]() $a \in \Phi _G^{\operatorname {m}}$
, où l’on pose
$a \in \Phi _G^{\operatorname {m}}$
, où l’on pose
![]() $s(u,v)=v+u\sigma (u)$
. Nous posons aussi
$s(u,v)=v+u\sigma (u)$
. Nous posons aussi
![]() $m_a^{\operatorname {T}}=m_a^{\operatorname {T}}(1)$
si a n’est ni divisible ni multipliable, et
$m_a^{\operatorname {T}}=m_a^{\operatorname {T}}(1)$
si a n’est ni divisible ni multipliable, et
![]() $m_a^{\operatorname {T}}=m_a^{\operatorname {T}}(1,0)$
si a est multipliable.
$m_a^{\operatorname {T}}=m_a^{\operatorname {T}}(1,0)$
si a est multipliable.
Considérons l’action de
![]() $\Gamma $
par automorphismes de Dynkin sur le groupe épinglé
$\Gamma $
par automorphismes de Dynkin sur le groupe épinglé
![]() $(H,y_\alpha ^{\operatorname {CS}})$
selon le système de Chevalley-Steinberg originel et transportons-la au groupe épinglé
$(H,y_\alpha ^{\operatorname {CS}})$
selon le système de Chevalley-Steinberg originel et transportons-la au groupe épinglé
![]() $(H,y_\alpha ^{\operatorname {T}})$
. Il est important de remarquer que ces automorphismes ne préservent pas le système de Tits non plus, car ils introduisent des facteurs de
$(H,y_\alpha ^{\operatorname {T}})$
. Il est important de remarquer que ces automorphismes ne préservent pas le système de Tits non plus, car ils introduisent des facteurs de
![]() $2$
supplémentaires. Plus tard, il faudra en faire usage et ces automorphismes seront dénommés désormais de Dynkin–Tits.
$2$
supplémentaires. Plus tard, il faudra en faire usage et ces automorphismes seront dénommés désormais de Dynkin–Tits.
Enregistrons la propriété la plus significative de cette modification.
Lemme 2.3.5. Les coordonnées des
![]() $x_a^{\operatorname {T}}$
par rapport aux
$x_a^{\operatorname {T}}$
par rapport aux
![]() $y_\alpha ^{\operatorname {T}}$
sont des polynômes entiers dans les variables
$y_\alpha ^{\operatorname {T}}$
sont des polynômes entiers dans les variables
![]() $\gamma (u)$
,
$\gamma (u)$
,
![]() $\gamma (v)$
et les
$\gamma (v)$
et les
![]() $m_b^{\operatorname {T}}$
permutent les
$m_b^{\operatorname {T}}$
permutent les
![]() $x_a^{\operatorname {T}}$
à similitude près.
$x_a^{\operatorname {T}}$
à similitude près.
Démonstration. On laisse le soin au lecteur de vérifier que les facteurs de
![]() $2$
concernés s’annulent, puisqu’il serait fastidieux de reproduire tous les calculs, comp. aussi avec l’ex. 2.3.3.
$2$
concernés s’annulent, puisqu’il serait fastidieux de reproduire tous les calculs, comp. aussi avec l’ex. 2.3.3.
Sauf mention contraire, on travaillera toujours dans la suite avec de quasi-systèmes de Tits et pas de Chevalley–Steinberg, donc on se permettra d’omettre l’exposant
![]() $\operatorname {T}$
, lorsqu’aucune confusion n’est à craindre, cf. §3.3 en particulier.
$\operatorname {T}$
, lorsqu’aucune confusion n’est à craindre, cf. §3.3 en particulier.
2.4 Des extensions centrales
Dans cet article, on travaillera souvent en même temps avec une classe de groupes tordus à groupe adjoint donné et l’une des tâches les plus courantes consistera à ramener le cas général au simplement connexe dès que possible, voir les preuves de la prop. 3.3.7 et du th. 4.1.5. Pour cette raison, nous décrivons maintenant une manière très sympathique, à la suite de [Reference Conrad, Gabber and PrasadCGP15, §1.4], de modifier un
![]() $\mathbb {Z}$
-groupe déployé et épinglé H en son tore maximal
$\mathbb {Z}$
-groupe déployé et épinglé H en son tore maximal
![]() $T_H$
.
$T_H$
.
Soit
![]() $\widetilde {T}_H$
un
$\widetilde {T}_H$
un
![]() $\mathbb {Z}$
-tore déployé muni des morphismes
$\mathbb {Z}$
-tore déployé muni des morphismes
![]() $T_H \rightarrow \widetilde {T}_H \rightarrow T_H^{\operatorname {ad}}$
, dont le composé est l’application naturelle. Comme
$T_H \rightarrow \widetilde {T}_H \rightarrow T_H^{\operatorname {ad}}$
, dont le composé est l’application naturelle. Comme
![]() $T_H^{\operatorname {ad}}$
s’identifie canoniquement au groupe des automorphismes de H laissant
$T_H^{\operatorname {ad}}$
s’identifie canoniquement au groupe des automorphismes de H laissant
![]() $T_H$
stable point par point, voir par exemple [Reference Conrad, Gabber and PrasadCGP15, th. 1.3.9, th. A.4.6], ceci équivaut à se donner une opération de
$T_H$
stable point par point, voir par exemple [Reference Conrad, Gabber and PrasadCGP15, th. 1.3.9, th. A.4.6], ceci équivaut à se donner une opération de
![]() $\widetilde {T}_H$
sur H ainsi qu’un morphisme équivariant
$\widetilde {T}_H$
sur H ainsi qu’un morphisme équivariant
![]() $T_H \rightarrow \widetilde {T}_H$
. En particulier, l’application anti-diagonale
$T_H \rightarrow \widetilde {T}_H$
. En particulier, l’application anti-diagonale
donnée par
![]() $t \mapsto (t^{-1}, t)$
, identifie
$t \mapsto (t^{-1}, t)$
, identifie
![]() $T_H$
à un sous-groupe fermé central de
$T_H$
à un sous-groupe fermé central de
![]() $H \rtimes \widetilde {T}_H$
.
$H \rtimes \widetilde {T}_H$
.
Proposition 2.4.1. Le faisceau en groupes quotient
![]() $(H \rtimes \widetilde {T}_H)/T_H$
de l’application (2.4.1) est représentable par un
$(H \rtimes \widetilde {T}_H)/T_H$
de l’application (2.4.1) est représentable par un
![]() $\mathbb {Z}$
-groupe déployé
$\mathbb {Z}$
-groupe déployé
![]() $\widetilde {H}$
à tore maximal
$\widetilde {H}$
à tore maximal
![]() $\widetilde {T}_H$
et à groupe adjoint
$\widetilde {T}_H$
et à groupe adjoint
![]() $H^{\mathrm {ad}}$
.
$H^{\mathrm {ad}}$
.
Démonstration. La représentabilité d’un quotient plat sur une base régulière de dimension
![]() $1$
est un résultat d’Anantharaman, cf. [Reference AnantharamanAna73, §4]. Les propriétés restantes se vérifient au-dessus de chaque corps algébriquement clos, voir [Reference Conrad, Gabber and PrasadCGP15, prop. 1.4.3].
$1$
est un résultat d’Anantharaman, cf. [Reference AnantharamanAna73, §4]. Les propriétés restantes se vérifient au-dessus de chaque corps algébriquement clos, voir [Reference Conrad, Gabber and PrasadCGP15, prop. 1.4.3].
En particulier, on en tire une suite exacte courte
car le tore maximal
![]() $T_H$
opère sur H en préservant le groupe dérivé, d’où le relèvement de l’opération au revêtement simplement connexe
$T_H$
opère sur H en préservant le groupe dérivé, d’où le relèvement de l’opération au revêtement simplement connexe
![]() $H^{\operatorname {sc}}$
. Vu que
$H^{\operatorname {sc}}$
. Vu que
![]() $T_H^{\operatorname {sc}}$
est induit et que le groupe dérivé de
$T_H^{\operatorname {sc}}$
est induit et que le groupe dérivé de
![]() $H^{\operatorname {sc}}\rtimes T_H$
est simplement connexe, cette extension centrale de H est habituellement appelée une z-extension, cf. [Reference Milne and ShihMS82, prop. 3.1]. Puisque sa formation ne dépend que du choix du tore maximal
$H^{\operatorname {sc}}\rtimes T_H$
est simplement connexe, cette extension centrale de H est habituellement appelée une z-extension, cf. [Reference Milne and ShihMS82, prop. 3.1]. Puisque sa formation ne dépend que du choix du tore maximal
![]() $T_H$
, nous parlerons souvent de la z-extension canonique du groupe épinglé H.
$T_H$
, nous parlerons souvent de la z-extension canonique du groupe épinglé H.
Traitons enfin le cas des formes tordues quasi-déployées comme dans §2.2. Soient alors
![]() $l/k$
une extension galoisienne à groupe de Galois
$l/k$
une extension galoisienne à groupe de Galois
![]() $\Gamma $
, H un k-groupe épinglé muni d’une action de
$\Gamma $
, H un k-groupe épinglé muni d’une action de
![]() $\Gamma $
par automorphismes de Dynkin (ou bien de Dynkin–Tits en dehors de la caractéristique
$\Gamma $
par automorphismes de Dynkin (ou bien de Dynkin–Tits en dehors de la caractéristique
![]() $2$
, cf. §2.3) et G le groupe obtenu par torsion comme dans la constr. 2.2.2. En se donnant de nouveau un k-tore déployé
$2$
, cf. §2.3) et G le groupe obtenu par torsion comme dans la constr. 2.2.2. En se donnant de nouveau un k-tore déployé
![]() $\widetilde {T}_H$
opéré par
$\widetilde {T}_H$
opéré par
![]() $\Gamma $
et des k-morphismes
$\Gamma $
et des k-morphismes
![]() $T_H \rightarrow \widetilde {T}_H\rightarrow T_H^{\operatorname {ad}}$
invariants par
$T_H \rightarrow \widetilde {T}_H\rightarrow T_H^{\operatorname {ad}}$
invariants par
![]() $\Gamma $
, on arrive aux applications de tores tordus
$\Gamma $
, on arrive aux applications de tores tordus
![]() $T \rightarrow \widetilde {T} \rightarrow T^{\operatorname {ad}}$
, ce qu’on utilise pour définir le modifié central
$T \rightarrow \widetilde {T} \rightarrow T^{\operatorname {ad}}$
, ce qu’on utilise pour définir le modifié central
de G, lequel est réductif connexe à tore maximal égal à T, cf. prop. 2.4.1. D’autre part, l’action de
![]() $\Gamma $
sur H se prolonge naturellement en une action sur la modification centrale
$\Gamma $
sur H se prolonge naturellement en une action sur la modification centrale
![]() $\widetilde {H}$
.
$\widetilde {H}$
.
Lemme 2.4.2. Le groupe
![]() $\widetilde {G}$
s’identifie canoniquement à la forme tordue quasi-déployée associée à
$\widetilde {G}$
s’identifie canoniquement à la forme tordue quasi-déployée associée à
![]() $\widetilde {H}$
muni de l’action naturelle de
$\widetilde {H}$
muni de l’action naturelle de
![]() $\Gamma $
.
$\Gamma $
.
Il résulte de même la z-extension canonique, comp. avec (2.4.2) :
dont l’avantage principal n’est pas seulement sa naturalité, mais aussi que plusieurs propriétés convenables de G soient préservées, comme nous verrons plus tard, cf. par exemple l’hyp. 3.3.1.
3 Familles entières de groupes parahoriques
Dans cette partie, on construit au §3.4 les
![]() $\mathbb {A}^1_{\mathbb {Z}}$
-modèles en groupes “immobiliers”
$\mathbb {A}^1_{\mathbb {Z}}$
-modèles en groupes “immobiliers”
![]() $\underline {\mathscr {G}_{\Omega }}$
des groupes de Tits
$\underline {\mathscr {G}_{\Omega }}$
des groupes de Tits
![]() $\underline {G}$
sur
$\underline {G}$
sur
![]() $\mathbb {G}_{m,\mathbb {Z}}$
introduits au §3.3 et l’on étudie leurs propriétés, démontrant notamment leur affinité, cf. th. 3.4.10.
$\mathbb {G}_{m,\mathbb {Z}}$
introduits au §3.3 et l’on étudie leurs propriétés, démontrant notamment leur affinité, cf. th. 3.4.10.
3.1 Théorie de Bruhat–Tits pour les groupes pseudo-réductifs
Comme il a été expliqué dans l’introduction, le but principal de cet article nous amène à travailler avec des groupes pseudo-réductifs en tant que spécialisations en caractéristiques petites et/ou mauvaises de certains groupes réductifs, voir la prop. 3.3.7.
Commençons par rappeler cette notion pour ceux qui ne la connaissent pas bien :
Définition 3.1.1. Soient k un corps et G un k-groupe lisse, affine et connexe. On dit que G est pseudo-réductif s’il ne contient aucun sous-k-groupe invariant, unipotent, lisse et connexe (autrement dit, si son k-radical unipotent
![]() $R_{u,k}G$
s’annule).
$R_{u,k}G$
s’annule).
Cette classe des groupes pseudo-réductifs contient nettement celle des groupes réductifs connexes et est stable par extensions des scalaires séparables, voir [Reference Conrad, Gabber and PrasadCGP15, prop. 1.1.9]. Voici l’exemple prototypique, cf. [Reference Conrad, Gabber and PrasadCGP15, prop. 1.1.10], d’un groupe pseudo-réductif qui n’est pas réductif :
Exemple 3.1.2. Soient
![]() $l/k$
une extension finie non-triviale et purement inséparable de corps et H un l-groupe réductif. Alors,
$l/k$
une extension finie non-triviale et purement inséparable de corps et H un l-groupe réductif. Alors,
![]() $G=\operatorname {R}_{l/k}H$
est pseudo-réductif, vu que, si l’on note U le k-radical unipotent de G, alors l’image de
$G=\operatorname {R}_{l/k}H$
est pseudo-réductif, vu que, si l’on note U le k-radical unipotent de G, alors l’image de
![]() $U_l \subset G_l$
dans H est lisse, connexe, distinguée et unipotente, donc
$U_l \subset G_l$
dans H est lisse, connexe, distinguée et unipotente, donc
![]() $U=1$
se réduit à l’unité lui-même. D’autre part, G n’est pas réductif, car la p-torsion du centre de
$U=1$
se réduit à l’unité lui-même. D’autre part, G n’est pas réductif, car la p-torsion du centre de
![]() $G(k^{\operatorname {alg}})=H(l\otimes _k k^{\operatorname {alg}})$
est un groupe infini, comp. avec [Reference Conrad, Gabber and PrasadCGP15, lem. 1.2.1], d’après un calcul élémentaire appliquant que
$G(k^{\operatorname {alg}})=H(l\otimes _k k^{\operatorname {alg}})$
est un groupe infini, comp. avec [Reference Conrad, Gabber and PrasadCGP15, lem. 1.2.1], d’après un calcul élémentaire appliquant que
![]() $l\otimes _k k^{\operatorname {alg}}$
est une
$l\otimes _k k^{\operatorname {alg}}$
est une
![]() $k^{\operatorname {alg}}$
-algèbre non réduite.
$k^{\operatorname {alg}}$
-algèbre non réduite.
Malgré cet exemple, on pourrait craindre qu’il ne soit typiquement pas possible d’apprivoiser ces groupes pseudo-réductifs et qu’ils n’admettent aucun théorème raisonnable, soit de structure, soit de classification. Au contraire, Borel–Tits avaient déjà découvert dans [Reference Borel and TitsBoT78] que leur structure générale ressemble beaucoup à celle des groupes réductifs et connexes :
Théorème 3.1.3 (Borel–Tits).
Tous les tores déployés maximaux de G sont conjugués par
![]() $G(k)$
. Étant donné un tore déployé maximal S de G, alors l’ensemble des poids
$G(k)$
. Étant donné un tore déployé maximal S de G, alors l’ensemble des poids
![]() $\Phi _G$
de l’action de S sur l’algèbre de Lie
$\Phi _G$
de l’action de S sur l’algèbre de Lie
![]() $\mathfrak {g}$
de G se prolonge naturellement en une donnée radicielle
$\mathfrak {g}$
de G se prolonge naturellement en une donnée radicielle
![]() $(X_*(S),X^*(S),\Phi _G^\vee ,\Phi _G)$
. Les espaces de poids
$(X_*(S),X^*(S),\Phi _G^\vee ,\Phi _G)$
. Les espaces de poids
![]() $\mathfrak {g}_a\oplus \mathfrak {g}_{2a}$
sont sous-jacents à l’un et un seul sous-k-groupe lisse, unipotent et connexe
$\mathfrak {g}_a\oplus \mathfrak {g}_{2a}$
sont sous-jacents à l’un et un seul sous-k-groupe lisse, unipotent et connexe
![]() $U_a$
de G, tel que l’application produit
$U_a$
de G, tel que l’application produit
 $$ \begin{align}\prod_{a \in \Phi_G^-} U_{-a} \times Z_G(S) \times \prod_{a \in \Phi_G^+} U_a \rightarrow G,\end{align} $$
$$ \begin{align}\prod_{a \in \Phi_G^-} U_{-a} \times Z_G(S) \times \prod_{a \in \Phi_G^+} U_a \rightarrow G,\end{align} $$
soit une immersion ouverte, quel que soit le choix de racines positives et quel que soit l’ordre en lequel le produit est mis. Ces données ne dépendent de S qu’à
![]() $G(k)$
-conjugaison près.
$G(k)$
-conjugaison près.
Démonstration. Toutes les affirmations avaient été annoncées en [Reference Borel and TitsBoT78], dont les preuves n’étaient qu’esquissées. Puis Conrad–Gabber–Prasad ont fourni dans leur œuvre [Reference Conrad, Gabber and PrasadCGP15] des arguments complets, voir [Reference Conrad, Gabber and PrasadCGP15, prop. 2.1.8, th. C.2.3, th. C.2.15, prop. C.2.26].
L’autre question qu’on s’est naturellement posée était de savoir s’il est loisible de classifier tous les groupes pseudo-réductifs. Tits avait déjà remarqué dans l’importance de l’application canonique
où
![]() $k'$
est le corps de définition du radical unipotent géométrique
$k'$
est le corps de définition du radical unipotent géométrique
![]() $R_u G_{k^{\operatorname {alg}}}$
et
$R_u G_{k^{\operatorname {alg}}}$
et
![]() $G'$
le
$G'$
le
![]() $k^{\operatorname {alg}}$
-quotient réductif de
$k^{\operatorname {alg}}$
-quotient réductif de
![]() $G_{k^{\operatorname {alg}}}$
. On ne peut pas s’attendre typiquement à ce que
$G_{k^{\operatorname {alg}}}$
. On ne peut pas s’attendre typiquement à ce que
![]() $i_G$
soit injectif, soit surjectif, parce que G peut être modifié centralement par la procédure de modification centrale de (2.4.3), et vu que les groupes pseudo-réductifs commutatifs sont habituellement n’importe quoi, cf. [Reference Conrad, Gabber and PrasadCGP15, ex. 1.6.3, ex. 1.6.4, §11.3]. À ces phénomènes de Cartan près, une classification exhaustive a été trouvée par Conrad–Gabber–Prasad, cf. [Reference Conrad, Gabber and PrasadCGP15, th. 5.1.1, th. 10.2.1].
$i_G$
soit injectif, soit surjectif, parce que G peut être modifié centralement par la procédure de modification centrale de (2.4.3), et vu que les groupes pseudo-réductifs commutatifs sont habituellement n’importe quoi, cf. [Reference Conrad, Gabber and PrasadCGP15, ex. 1.6.3, ex. 1.6.4, §11.3]. À ces phénomènes de Cartan près, une classification exhaustive a été trouvée par Conrad–Gabber–Prasad, cf. [Reference Conrad, Gabber and PrasadCGP15, th. 5.1.1, th. 10.2.1].
Théorème 3.1.4 (Conrad–Gabber–Prasad).
Soit k un corps de caractéristique p satisfaisant à
![]() $[k:k^p]\leq p$
dès que p est positif. Alors tous les groupes pseudo-réductifs s’obtiennent naturellement à partir des groupes simplement connexes, des exotiques et des barcelonais en combinant les opérations produit, restriction des scalaires et modification centrale.
$[k:k^p]\leq p$
dès que p est positif. Alors tous les groupes pseudo-réductifs s’obtiennent naturellement à partir des groupes simplement connexes, des exotiques et des barcelonais en combinant les opérations produit, restriction des scalaires et modification centrale.
Les groupes exotiques, voir [Reference Conrad, Gabber and PrasadCGP15, déf. 7.2.6], et les barcelonais, cf. [Reference Conrad, Gabber and PrasadCGP15, déf. 10.1.2], n’existent qu’en caractéristiques petites
![]() $p=2$
ou
$p=2$
ou
![]() $3$
et sont reliés à certains phénomènes de p-divisibilité du système de racines
$3$
et sont reliés à certains phénomènes de p-divisibilité du système de racines
![]() $\Phi _G$
. Dans la suite, nous allons éclaircir leur aspect dans le cas quasi-déployé.
$\Phi _G$
. Dans la suite, nous allons éclaircir leur aspect dans le cas quasi-déployé.
Remarque 3.1.5. Le th. 3.1.4 vaut plus généralement lorsque
![]() $p \neq 2$
ou
$p \neq 2$
ou
![]() $p=2$
et
$p=2$
et
![]() $[k:k^2]\leq 2$
. Le cas restant où
$[k:k^2]\leq 2$
. Le cas restant où
![]() $p=2$
et
$p=2$
et
![]() $[k:k^2]>2$
fut traité par Conrad–Prasad dans [Reference Conrad and PrasadCP16], en supposant que G est localement de type minimal, voir [Reference Conrad and PrasadCP16, §1.6, th. de str.].
$[k:k^2]>2$
fut traité par Conrad–Prasad dans [Reference Conrad and PrasadCP16], en supposant que G est localement de type minimal, voir [Reference Conrad and PrasadCP16, §1.6, th. de str.].
Penchons-nous d’abord sur le cas exotique :
Exemple 3.1.6 (exotique).
Soient k un corps imparfait de caractéristique p satisfaisant à
![]() $[k:k^p]= p$
et G un groupe exotique basique et quasi-déployé, voir [Reference Conrad, Gabber and PrasadCGP15, déf. 7.2.6]. Alors, on a
$[k:k^p]= p$
et G un groupe exotique basique et quasi-déployé, voir [Reference Conrad, Gabber and PrasadCGP15, déf. 7.2.6]. Alors, on a
![]() $p=2,3$
,
$p=2,3$
,
![]() $\Phi _G$
est irréductible et possède une p-arête, donc on peut appliquer [Reference Conrad and PrasadCP16, lem. C.2.2] pour déduire que G est pseudo-déployé. D’après [Reference Conrad, Gabber and PrasadCGP15, th. 7.2.3], le
$\Phi _G$
est irréductible et possède une p-arête, donc on peut appliquer [Reference Conrad and PrasadCP16, lem. C.2.2] pour déduire que G est pseudo-déployé. D’après [Reference Conrad, Gabber and PrasadCGP15, th. 7.2.3], le
![]() $k^{1/p}$
-quotient réductif
$k^{1/p}$
-quotient réductif
![]() $G'$
de G est déployé et simplement connexe à système de racines
$G'$
de G est déployé et simplement connexe à système de racines
![]() $\Phi _G$
, tandis que l’application canonique
$\Phi _G$
, tandis que l’application canonique
![]() $ i_G :G \rightarrow \operatorname {R}_{k^{1/p}/k} G'$
de (3.1.2) est une immersion fermée. Soit
$ i_G :G \rightarrow \operatorname {R}_{k^{1/p}/k} G'$
de (3.1.2) est une immersion fermée. Soit
l’isogénie très spéciale, voir [Reference Conrad, Gabber and PrasadCGP15, déf. 7.1.3], définie sur
![]() $k^{1/p}$
, où
$k^{1/p}$
, où
![]() $\overline {G}'$
est un groupe déployé et simplement connexe de type dual. Alors, l’image de G par la restriction des scalaires
$\overline {G}'$
est un groupe déployé et simplement connexe de type dual. Alors, l’image de G par la restriction des scalaires
de l’isogénie très spéciale
![]() $\pi '$
est un k-Levi
$\pi '$
est un k-Levi
![]() $\overline {G} $
du membre de droite, c’est-à-dire un k-descendu de
$\overline {G} $
du membre de droite, c’est-à-dire un k-descendu de
![]() $\overline {G}'$
, et G s’identifie à l’image réciproque par
$\overline {G}'$
, et G s’identifie à l’image réciproque par
![]() $\pi $
de ce Levi
$\pi $
de ce Levi
![]() $\overline {G}$
dans
$\overline {G}$
dans
![]() $\operatorname {R}_{k^{1/p}/k} G'$
, voir [Reference Conrad, Gabber and PrasadCGP15, déf. 7.2.6].
$\operatorname {R}_{k^{1/p}/k} G'$
, voir [Reference Conrad, Gabber and PrasadCGP15, déf. 7.2.6].
On peut trouver un
![]() $k^{1/p}$
-système de Chevalley, cf. déf. 2.1.1, de
$k^{1/p}$
-système de Chevalley, cf. déf. 2.1.1, de
![]() $G'$
(resp. k-système de Chevalley de
$G'$
(resp. k-système de Chevalley de
![]() $\overline {G}$
) tels que l’isogénie très spéciale s’identifie à
$\overline {G}$
) tels que l’isogénie très spéciale s’identifie à
 $$ \begin{align}\pi: x^{\prime}_a(r) \mapsto \begin{cases} \overline{x}_{\overline{a}}(r^p), a \in \Phi_{G}^<\\ \overline{x}_{\overline{a}}(r), a \in \Phi_G^> \end{cases}\end{align} $$
$$ \begin{align}\pi: x^{\prime}_a(r) \mapsto \begin{cases} \overline{x}_{\overline{a}}(r^p), a \in \Phi_{G}^<\\ \overline{x}_{\overline{a}}(r), a \in \Phi_G^> \end{cases}\end{align} $$
restreinte aux groupes radiciels relativement à
![]() $S'$
(resp.
$S'$
(resp.
![]() $\overline {S}$
) et à
$\overline {S}$
) et à
 $$ \begin{align}\pi:a^\vee(r) \mapsto \begin{cases} \overline{a}^\vee(r^p), a \in \Phi_G^<\\ \overline{a}^\vee(r), a \in \Phi_G^> \end{cases}\end{align} $$
$$ \begin{align}\pi:a^\vee(r) \mapsto \begin{cases} \overline{a}^\vee(r^p), a \in \Phi_G^<\\ \overline{a}^\vee(r), a \in \Phi_G^> \end{cases}\end{align} $$
restreinte aux facteurs multiplicatifs associés aux coracines, comp. avec [Reference Conrad, Gabber and PrasadCGP15, prop. 7.1.5], où les exposantes
![]() $<,>$
notent les racines courtes, resp. longues de
$<,>$
notent les racines courtes, resp. longues de
![]() $\Phi _G$
.
$\Phi _G$
.
Ainsi, on obtient des isomorphismes
où
![]() $k_a=k^{1/p}$
si
$k_a=k^{1/p}$
si
![]() $a \in \Phi _G^<$
,
$a \in \Phi _G^<$
,
![]() $k_a=k$
si
$k_a=k$
si
![]() $a \in \Phi _G^>$
et
$a \in \Phi _G^>$
et
![]() $Z^a$
désigne l’intersection
$Z^a$
désigne l’intersection
![]() $Z \cap \langle U_a, U_{-a}\rangle $
, cf. [Reference Conrad, Gabber and PrasadCGP15, rem. 7.2.8].
$Z \cap \langle U_a, U_{-a}\rangle $
, cf. [Reference Conrad, Gabber and PrasadCGP15, rem. 7.2.8].
Le groupe pseudo-réductif suivant est aussi pseudo-déployé, mais son système de racines absolu n’est pas réduit, c’est-à-dire de type
![]() $BC_n$
.Footnote 3
$BC_n$
.Footnote 3
Exemple 3.1.7 (barcelonais).
Soient k un corps imparfait de caractéristique
![]() $2$
tel que
$2$
tel que
![]() $[k:k^2]= 2$
et G un groupe pseudo-réductif barcelonais basique, cf. [Reference Conrad, Gabber and PrasadCGP15, déf. 10.1.2]. Alors, on sait déjà que G est pseudo-déployé et que son
$[k:k^2]= 2$
et G un groupe pseudo-réductif barcelonais basique, cf. [Reference Conrad, Gabber and PrasadCGP15, déf. 10.1.2]. Alors, on sait déjà que G est pseudo-déployé et que son
![]() $k^{1/2}$
-quotient réductif
$k^{1/2}$
-quotient réductif
![]() $G'$
est déployé et simplement connexe à système de racines
$G'$
est déployé et simplement connexe à système de racines
![]() $\Phi _G^{\operatorname {nm}}$
, cf. [Reference Conrad, Gabber and PrasadCGP15, th. 2.3.10]. L’application correspondante
$\Phi _G^{\operatorname {nm}}$
, cf. [Reference Conrad, Gabber and PrasadCGP15, th. 2.3.10]. L’application correspondante
![]() $i_G: G \rightarrow \operatorname {R}_{k^{1/2}/k}G'$
, voir (3.1.2), induit des isomorphismes
$i_G: G \rightarrow \operatorname {R}_{k^{1/2}/k}G'$
, voir (3.1.2), induit des isomorphismes
entre les Cartans et les sous-groupes radiciels associés aux racines ni divisibles ni multipliables, voir [Reference Conrad, Gabber and PrasadCGP15, th. 9.4.7]. Cependant, d’après [Reference Conrad, Gabber and PrasadCGP15, prop. 9.5.2, prop. 9.6.8] le morphisme
![]() $U_a \rightarrow \operatorname {R}_{k^{1/2}/k} U^{\prime }_{2a}$
pour
$U_a \rightarrow \operatorname {R}_{k^{1/2}/k} U^{\prime }_{2a}$
pour
![]() $a \in \Phi _G^m$
peut être identifié avec
$a \in \Phi _G^m$
peut être identifié avec
donné par
![]() $(u,v)\mapsto u^2+v$
, où l’on note
$(u,v)\mapsto u^2+v$
, où l’on note
![]() $\mathbb {G}_{p,k^{1/2}/k}$
le groupe unipotent pluriel modifié selon la définition limite de la rem. 2.3.2 (ceci ne dépend pas à isomorphisme près du choix d’un complément k-linéaire
$\mathbb {G}_{p,k^{1/2}/k}$
le groupe unipotent pluriel modifié selon la définition limite de la rem. 2.3.2 (ceci ne dépend pas à isomorphisme près du choix d’un complément k-linéaire
![]() $k_0= k\subset k^{1/2}$
pour
$k_0= k\subset k^{1/2}$
pour
![]() $\alpha \in k^{1/2}\setminus k$
). On signale que la construction de [Reference Conrad, Gabber and PrasadCGP15, §§9.6-9.7] utilise les lois birationnelles strictes par réduction au cas de
$\alpha \in k^{1/2}\setminus k$
). On signale que la construction de [Reference Conrad, Gabber and PrasadCGP15, §§9.6-9.7] utilise les lois birationnelles strictes par réduction au cas de
![]() $\operatorname {R}_{k^{1/2}/k}G'$
, tandis que Tits a réalisé G explicitement comme une sorte de groupe unitaire de dimension impaire dégénéré en caractéristique
$\operatorname {R}_{k^{1/2}/k}G'$
, tandis que Tits a réalisé G explicitement comme une sorte de groupe unitaire de dimension impaire dégénéré en caractéristique
![]() $2$
, voir [Reference TitsTi84, pp. 218-219]. Par alternative, voir les props. 3.3.7 et 3.3.9.
$2$
, voir [Reference TitsTi84, pp. 218-219]. Par alternative, voir les props. 3.3.7 et 3.3.9.
Motivés par l’étude des groupes algébriques sur les corps valués, Bruhat–Tits ont crée leur théorie des immeubles et des modèles en groupes immobiliers, cf. [Reference Bruhat and TitsBT72] et [Reference Bruhat and TitsBT84a]. Les exemples précédents montrent que les points rationnels des groupes pseudo-réductifs ne s’éloignent beaucoup de ceux des groupes réductifs. Solleveld s’y est appuyé dans [Reference SolleveldSol18] pour parvenir à construire des immeubles et, dans [Reference LourençoLou21, déf. 3.5, th. 4.9], nous avons construit les schémas en groupes.
Théorème 3.1.8 (Solleveld, L.).
La théorie de Bruhat–Tits s’étend aux groupes pseudo-réductifs sur les corps complets et résiduellement parfaits.
Remarque 3.1.9. Cet énoncé devrait être valable sur les corps discrètement valués et henséliens k et pour les k-groupes
![]() $\widehat {k}$
-pseudo-réductifs et
$\widehat {k}$
-pseudo-réductifs et
![]() $k^{\operatorname {nr}}$
-quasi-déployés. Dans [Reference LourençoLou21], on suppose encore que
$k^{\operatorname {nr}}$
-quasi-déployés. Dans [Reference LourençoLou21], on suppose encore que
![]() $\widehat {k}/k$
est séparable et que le corps résiduel est parfait. Ce dernier a été éliminé dans [Reference Pereira LourençoPL20, IV, §§3.1-3.2] et Conrad m’a convaincu que le premier devrait être superflue.
$\widehat {k}/k$
est séparable et que le corps résiduel est parfait. Ce dernier a été éliminé dans [Reference Pereira LourençoPL20, IV, §§3.1-3.2] et Conrad m’a convaincu que le premier devrait être superflue.
Notre construction des immeubles de Bruhat–Tits dans [Reference LourençoLou21] est pareille à celle de [Reference Bruhat and TitsBT84a]. Supposons encore que G soit quasi-déployé. À chaque sous-tore déployé maximal S de G, on associe un appartement
![]() $\mathscr {A}(G,S,k)$
, en vérifiant les axiomes de [Reference Bruhat and TitsBT72, déf. 6.1.1, déf. 6.2.1] pour appliquer le [Reference Bruhat and TitsBT72, th. 6.5], cf. aussi [Reference Bruhat and TitsBT72, déf. 7.4.2]. Le seul point compliqué est donc de trouver une valuation
$\mathscr {A}(G,S,k)$
, en vérifiant les axiomes de [Reference Bruhat and TitsBT72, déf. 6.1.1, déf. 6.2.1] pour appliquer le [Reference Bruhat and TitsBT72, th. 6.5], cf. aussi [Reference Bruhat and TitsBT72, déf. 7.4.2]. Le seul point compliqué est donc de trouver une valuation
![]() $\varphi $
de la donnée radicielle abstraite
$\varphi $
de la donnée radicielle abstraite
![]() $(Z(k),U_a(k))$
, pour lequel nous recourons à un quasi-système de Chevalley de G, cf. déf. 2.2.6 et [Reference LourençoLou21, prop. 2.5] pour le cas pseudo-réductif. Alors, on pose
$(Z(k),U_a(k))$
, pour lequel nous recourons à un quasi-système de Chevalley de G, cf. déf. 2.2.6 et [Reference LourençoLou21, prop. 2.5] pour le cas pseudo-réductif. Alors, on pose
selon que
![]() $a\in \Phi _G^{\operatorname {nd,nm}}$
est une racine ni divisible ni multipliable, ou que
$a\in \Phi _G^{\operatorname {nd,nm}}$
est une racine ni divisible ni multipliable, ou que
![]() $a \in \Phi _G^{\operatorname {m}}$
est multipliable et
$a \in \Phi _G^{\operatorname {m}}$
est multipliable et
![]() $G^a$
réductif, ou que
$G^a$
réductif, ou que
![]() $a \in \Phi _G^{\operatorname {m}}$
est multipliable et
$a \in \Phi _G^{\operatorname {m}}$
est multipliable et
![]() $G^a$
non standard. Ici, l’on note
$G^a$
non standard. Ici, l’on note
![]() $\omega $
la valuation additive de k étendue à sa clôture algébrique et satisfaisant à
$\omega $
la valuation additive de k étendue à sa clôture algébrique et satisfaisant à
![]() $\omega (k^\times )=\mathbb {Z}$
.
$\omega (k^\times )=\mathbb {Z}$
.
Disons un mot sur les modèles entiers de G associés aux parties non vides et bornées
![]() $\Omega $
de l’appartement
$\Omega $
de l’appartement
![]() $\mathscr {A}(G,S,k)\subset \mathscr {I}(G,k)$
, où G est encore supposé quasi-déployé. D’un côté, il faut construire le modèle de Néron connexe
$\mathscr {A}(G,S,k)\subset \mathscr {I}(G,k)$
, où G est encore supposé quasi-déployé. D’un côté, il faut construire le modèle de Néron connexe
![]() $\mathscr {Z}$
d’un groupe pseudo-réductif commutatif Z, ce qui fut achevé par Bosch–Lütkebohmert–Raynaud dans [Reference Bosch, Lütkebohmert and RaynaudBLR90, th. 10.2.2]. De l’autre côté, on a besoin de trouver les modèles entiers
$\mathscr {Z}$
d’un groupe pseudo-réductif commutatif Z, ce qui fut achevé par Bosch–Lütkebohmert–Raynaud dans [Reference Bosch, Lütkebohmert and RaynaudBLR90, th. 10.2.2]. De l’autre côté, on a besoin de trouver les modèles entiers
![]() $\mathscr {U}_{a,\Omega }$
stabilisant
$\mathscr {U}_{a,\Omega }$
stabilisant
![]() $\Omega $
pour toute racine non divisible
$\Omega $
pour toute racine non divisible
![]() $a \in \Phi _G^{\operatorname {nd}}$
, ne s’agissant que des calculs simples, voir [Reference Bruhat and TitsBT84a, §4.3] et [Reference LourençoLou21, lem. 4.4]. Enfin, on recolle ces données en appliquant la théorie des lois birationnelles, voir [Reference LourençoLou21, §4.1, th. 4.2], ce qu’on reprendra d’ailleurs toute de suite au §3.2, cf. ths. 3.2.4 et 3.2.5.
$a \in \Phi _G^{\operatorname {nd}}$
, ne s’agissant que des calculs simples, voir [Reference Bruhat and TitsBT84a, §4.3] et [Reference LourençoLou21, lem. 4.4]. Enfin, on recolle ces données en appliquant la théorie des lois birationnelles, voir [Reference LourençoLou21, §4.1, th. 4.2], ce qu’on reprendra d’ailleurs toute de suite au §3.2, cf. ths. 3.2.4 et 3.2.5.
Remarque 3.1.10. Presque tous les résultats que nous avons mentionnés s’étendent aux groupes quasi-réductifs, dont le k-radical unipotent n’est peu-être pas non plus trivial, mais bien ployé, c’est-à-dire sans sous-groupe unipotent additif, voir [Reference Bruhat and TitsBT84a, 1.1.12] et [Reference Conrad, Gabber and PrasadCGP15, déf. B.2.1]. Ceci a été caché dans cette section afin de ne pas effrayer le lecteur sans raison.
3.2 Données radicielles schématiques
Dans ce paragraphe, on discute le concept des données radicielles schématiques dû à Bruhat–Tits, cf. [Reference Bruhat and TitsBT84a, déf. 3.1.1]. Leur but, comme le lecteur bientôt comprendra, est de construire des A-modèles en groupes
![]() $\mathscr {G}$
de G avec de bonnes propriétés par “recollement fermé” de A-modèles en groupes correspondants pour chaque terme individuel Z et
$\mathscr {G}$
de G avec de bonnes propriétés par “recollement fermé” de A-modèles en groupes correspondants pour chaque terme individuel Z et
![]() $U_a$
de la grosse cellule, où
$U_a$
de la grosse cellule, où
![]() $a \in \Phi _G^{\operatorname {nd}}$
décrit l’ensemble des racines non divisibles.
$a \in \Phi _G^{\operatorname {nd}}$
décrit l’ensemble des racines non divisibles.
Définition 3.2.1 (Bruhat–Tits, à peu près).
Soient A un anneau noethérien et intègre, K son corps de fractions, G un K-groupe pseudo-réductif et S un sous-tore déployé maximal. Une donnée radicielle dans G par rapport à S au-dessus de A est la donnée de A-modèles en groupes lisses, affines et connexes
![]() $\mathscr {Z}$
de
$\mathscr {Z}$
de
![]() $Z=Z_G(S)$
(resp.
$Z=Z_G(S)$
(resp.
![]() $\mathscr {U}_a$
du sous-groupe radiciel
$\mathscr {U}_a$
du sous-groupe radiciel
![]() $U_a$
attaché à la racine non divisible
$U_a$
attaché à la racine non divisible
![]() $a \in \Phi _G^{\operatorname {nd}}$
) tels que :
$a \in \Phi _G^{\operatorname {nd}}$
) tels que :
-
(DRS 0) l’injection de S dans Z se prolonge en un morphisme
 $\mathscr {S} \rightarrow \mathscr {Z}$
, où
$\mathscr {S} \rightarrow \mathscr {Z}$
, où
 $\mathscr {S}$
désigne le seul groupe diagonalisable à isomorphisme unique près modelant S.
$\mathscr {S}$
désigne le seul groupe diagonalisable à isomorphisme unique près modelant S. -
(DRS 1) l’application conjugaison
 $Z \times U_a \rightarrow U_a$
se prolonge en une application
$Z \times U_a \rightarrow U_a$
se prolonge en une application
 $\mathscr {Z} \times \mathscr {U}_a \rightarrow \mathscr {U}_a$
.
$\mathscr {Z} \times \mathscr {U}_a \rightarrow \mathscr {U}_a$
. -
(DRS 2) si
 $b \neq -a$
, l’application commutateur
$b \neq -a$
, l’application commutateur
 $U_a \times U_b \rightarrow \prod _{c\in ] a, b[} U_c$
se prolonge en un morphisme
$U_a \times U_b \rightarrow \prod _{c\in ] a, b[} U_c$
se prolonge en un morphisme
 $\mathscr {U}_a \times \mathscr {U}_b \rightarrow \prod _{c\in ] a, b[} \mathscr {U}_c$
, où l’on note
$\mathscr {U}_a \times \mathscr {U}_b \rightarrow \prod _{c\in ] a, b[} \mathscr {U}_c$
, où l’on note
 $] a, b[$
la partie de
$] a, b[$
la partie de
 $\Phi _{G}^{\operatorname {nd}}$
contenue dans
$\Phi _{G}^{\operatorname {nd}}$
contenue dans
 $\mathbb {Q}_{> 0}a+\mathbb {Q}_{ >0}b$
.
$\mathbb {Q}_{> 0}a+\mathbb {Q}_{ >0}b$
. -
(DRS 3) si on note
 $W_a$
l’image réciproque par l’immersion fermée
$W_a$
l’image réciproque par l’immersion fermée
 $U_a \times U_{-a} \hookrightarrow G$
du fermé local
$U_a \times U_{-a} \hookrightarrow G$
du fermé local
 $ C_a:=U_{-a} \times Z \times U_a\subset G$
, cf. (3.1.1), alors il existe un ouvert
$ C_a:=U_{-a} \times Z \times U_a\subset G$
, cf. (3.1.1), alors il existe un ouvert
 $\mathscr {U}_{\pm a} \subset \mathscr {W}_a\subset \mathscr {U}_a \times \mathscr {U}_{-a}$
modelant
$\mathscr {U}_{\pm a} \subset \mathscr {W}_a\subset \mathscr {U}_a \times \mathscr {U}_{-a}$
modelant
 $W_a$
tel que l’inclusion
$W_a$
tel que l’inclusion
 $W_a \subset C_a$
se prolonge en une application
$W_a \subset C_a$
se prolonge en une application
 $\mathscr {W}_a \rightarrow \mathscr {C}_a:=\mathscr {U}_{-a} \times \mathscr {Z} \times \mathscr {U}_a$
.
$\mathscr {W}_a \rightarrow \mathscr {C}_a:=\mathscr {U}_{-a} \times \mathscr {Z} \times \mathscr {U}_a$
.
Remarque 3.2.2. Il y a deux différences entre notre définition et celle de Bruhat–Tits, comp. avec [Reference Bruhat and TitsBT84a, déf. 3.1.1]: on ne demande pas que l’application
![]() $\mathscr {S} \rightarrow \mathscr {Z}$
soit une immersion fermée, puisque cela est superflue, voir [SGA3, exp. IX, cor. 2.5, th. 6.8]; notre voisinage ouvert
$\mathscr {S} \rightarrow \mathscr {Z}$
soit une immersion fermée, puisque cela est superflue, voir [SGA3, exp. IX, cor. 2.5, th. 6.8]; notre voisinage ouvert
![]() $\mathscr {W}_a$
contient les fermés
$\mathscr {W}_a$
contient les fermés
![]() $\mathscr {U}_{\pm a}$
et pas seulement la section unité, pour que la loi birationnelle sur
$\mathscr {U}_{\pm a}$
et pas seulement la section unité, pour que la loi birationnelle sur
![]() $\mathscr {C}:=\mathscr {U}_-\times \mathscr {Z} \times \mathscr {U}_+$
soit automatiquement stricte, cf. déf. 3.2.3 et th. 3.2.5.
$\mathscr {C}:=\mathscr {U}_-\times \mathscr {Z} \times \mathscr {U}_+$
soit automatiquement stricte, cf. déf. 3.2.3 et th. 3.2.5.
Notre démonstration du théorème concernant l’existence du recollé
![]() $\mathscr {G}$
fera usage des lois birationnelles de groupes.
$\mathscr {G}$
fera usage des lois birationnelles de groupes.
Définition 3.2.3. Soient A un anneau noethérien et X un A-schéma séparé de type fini. Alors, une loi birationnelle de groupe sur X est la donnée d’un morphisme A-rationnel
![]() $m: X \times X \rightarrow X$
tel qu’il soit associatif et que les applications de translation universelles à la gauche
$m: X \times X \rightarrow X$
tel qu’il soit associatif et que les applications de translation universelles à la gauche
![]() $(\operatorname {id},m)$
resp. à la droite
$(\operatorname {id},m)$
resp. à la droite
![]() $(m, \operatorname {id})$
soient A-birationnelles. On dit que la loi birationnelle est stricte si les applications de translation universelles sont X-birationnelles relativement aux deux projections
$(m, \operatorname {id})$
soient A-birationnelles. On dit que la loi birationnelle est stricte si les applications de translation universelles sont X-birationnelles relativement aux deux projections
![]() $X\times X \rightarrow X$
.
$X\times X \rightarrow X$
.
On suit la terminologie de [Reference Bosch, Lütkebohmert and RaynaudBLR90] en dénommant un morphisme de présentation finie A-rationnel si son lieu ouvert de définition est à A-fibres denses. Étant donnée une loi birationnelle de groupe sur X, la question qui se pose est de la prolonger birationnellement à un schéma en groupes
![]() $\overline {X}$
.
$\overline {X}$
.
Théorème 3.2.4 (Existence de solutions).
Gardons les notations de la déf. 3.2.3. Alors, il existe un et un seul A-groupe séparé de type fini
![]() $\overline {X}$
muni d’un morphisme A-birationnel
$\overline {X}$
muni d’un morphisme A-birationnel
![]() $X \dashrightarrow \overline {X}$
préservant les lois birationnelles de groupe. Si la loi birationnelle de X est stricte ou si A est normal et X lisse, alors l’application rationnelle
$X \dashrightarrow \overline {X}$
préservant les lois birationnelles de groupe. Si la loi birationnelle de X est stricte ou si A est normal et X lisse, alors l’application rationnelle
![]() $X \dashrightarrow \overline {X}$
se prolonge en une immersion ouverte définie partout.
$X \dashrightarrow \overline {X}$
se prolonge en une immersion ouverte définie partout.
Démonstration. On ne fera que résumer la chronologie du degré de généralité dont le théorème d’existence de solutions de lois birationnelles en groupes a été démontré. Alors, au-dessus des corps ce résultat remonte à Weil. Puis il fut amélioré par Artin, voir [SGA3, exp. XVIII, th. 3.7], sur des bases assez générales, mais la solution n’était donnée qu’en espaces algébriques. Finalement, Bosch–Lütkebohmert–Raynaud, voir [Reference Bosch, Lütkebohmert and RaynaudBLR90, th. 6.6.1], montrèrent que la solution
![]() $\overline {X}$
est un schéma. Observons qu’on s’est toujours ramené au cas où la loi birationnelle est stricte, d’après [Reference Bosch, Lütkebohmert and RaynaudBLR90, prop. 5.2.2]. Enfin, si la base est normale et X lisse, alors on n’a pas besoin de remplacer la grosse cellule par un ouvert A-schématiquement dense grâce au [Reference Bosch, Lütkebohmert and RaynaudBLR90, th. 5.1.5].
$\overline {X}$
est un schéma. Observons qu’on s’est toujours ramené au cas où la loi birationnelle est stricte, d’après [Reference Bosch, Lütkebohmert and RaynaudBLR90, prop. 5.2.2]. Enfin, si la base est normale et X lisse, alors on n’a pas besoin de remplacer la grosse cellule par un ouvert A-schématiquement dense grâce au [Reference Bosch, Lütkebohmert and RaynaudBLR90, th. 5.1.5].
Théorème 3.2.5 (Bruhat–Tits, à peu près).
Reprenons les notations de la déf. 3.2.1. Alors, il existe un et un seul A-groupe séparé, lisse et connexe
![]() $\mathscr {G}$
modelant G tel que :
$\mathscr {G}$
modelant G tel que :
-
1. les inclusions
 $Z \rightarrow G$
et
$Z \rightarrow G$
et
 $U_a \rightarrow G$
pour tout
$U_a \rightarrow G$
pour tout
 $a \in \Phi _G^{\operatorname {nd}}$
se prolongent en des isomorphismes de
$a \in \Phi _G^{\operatorname {nd}}$
se prolongent en des isomorphismes de
 $\mathscr {Z}$
et
$\mathscr {Z}$
et
 $\mathscr {U}_a$
sur des sous-A-groupes fermés de
$\mathscr {U}_a$
sur des sous-A-groupes fermés de
 $\mathscr {G}$
.
$\mathscr {G}$
. -
2. pour tout système de racines positives
 $\Phi _G^+$
et tout ordre mis sur
$\Phi _G^+$
et tout ordre mis sur
 $\Phi _G^+$
, le morphisme
$\Phi _G^+$
, le morphisme
 $\prod _{a \in \Phi _G^{\operatorname {nd},+}} \mathscr {U}_a \rightarrow \mathscr {G}$
soit un isomorphisme sur un sous-A-groupe fermé
$\prod _{a \in \Phi _G^{\operatorname {nd},+}} \mathscr {U}_a \rightarrow \mathscr {G}$
soit un isomorphisme sur un sous-A-groupe fermé
 $\mathscr {U}_+$
de
$\mathscr {U}_+$
de
 $\mathscr {G}$
.
$\mathscr {G}$
. -
3. l’application produit
 $\mathscr {U}_-\times \mathscr {Z} \times \mathscr {U}_+ \rightarrow \mathscr {G}$
définisse un ouvert du membre de droite.
$\mathscr {U}_-\times \mathscr {Z} \times \mathscr {U}_+ \rightarrow \mathscr {G}$
définisse un ouvert du membre de droite.
Avant de initier la preuve en tant que telle, résumons son histoire complexe.
Remarque 3.2.6. Dans [Reference Bruhat and TitsBT84a, 3.1.3], Bruhat–Tits évoquent leur envie d’appliquer les lois birationnelles pour répondre à la question, mais [SGA3, exp. XVIII, th. 3.7] ne fournissait que des solutions en espaces algébriques et non pas en schémas – le livre [Reference Bosch, Lütkebohmert and RaynaudBLR90] n’avait pas encore été écrit, cf. th. 3.2.4. Par conséquent, ils consacrent 30 pages à son argument alternatif avec la théorie des représentations, cf. [Reference Bruhat and TitsBT84a, §3.8, 3.9.4]. Sur un anneau de valuation discrète, Landvogt donnera une démonstration appliquant les lois birationnelles, voir [Reference LandvogtLan96, §§5–6], tout en empruntant des idées superflues de [Reference Bruhat and TitsBT84a, §3].
Démonstration. Lorsqu’on se donne un ordre grignotant sur
![]() $\Phi ^+$
, cf. [Reference Bruhat and TitsBT84a, 3.1.2], alors [Reference Bruhat and TitsBT84a, §3.3] fournit une loi de groupe dans le produit
$\Phi ^+$
, cf. [Reference Bruhat and TitsBT84a, 3.1.2], alors [Reference Bruhat and TitsBT84a, §3.3] fournit une loi de groupe dans le produit
![]() $\mathscr {U}_+=\prod _{a \in \Phi ^{+,\operatorname {nd}}}\mathscr {U}_{a}$
, en argumentant par récurrence sur la longueur des parties positivement closes
$\mathscr {U}_+=\prod _{a \in \Phi ^{+,\operatorname {nd}}}\mathscr {U}_{a}$
, en argumentant par récurrence sur la longueur des parties positivement closes
![]() $\Psi $
de
$\Psi $
de
![]() $\Phi ^{+,\operatorname {nd}}$
et en appliquant la règle (DRS 2). Comme les groupes trouvés sont toujours lisses et connexes, le fait que
$\Phi ^{+,\operatorname {nd}}$
et en appliquant la règle (DRS 2). Comme les groupes trouvés sont toujours lisses et connexes, le fait que
![]() $\mathscr {U}_+$
s’écrit comme produit de ses sous-groupes fermés
$\mathscr {U}_+$
s’écrit comme produit de ses sous-groupes fermés
![]() $\mathscr {U}_{a}$
rangés dans un ordre quelconque résulte du théorème principal de Zariski et de la même indépendance de l’ordre au-dessus des corps, ce qui est déjà classique, voir par exemple [Reference Conrad, Gabber and PrasadCGP15, prop. C.2.26]. Notons également que
$\mathscr {U}_{a}$
rangés dans un ordre quelconque résulte du théorème principal de Zariski et de la même indépendance de l’ordre au-dessus des corps, ce qui est déjà classique, voir par exemple [Reference Conrad, Gabber and PrasadCGP15, prop. C.2.26]. Notons également que
![]() $\mathscr {Z}$
opère sur
$\mathscr {Z}$
opère sur
![]() $\mathscr {U}_+$
canoniquement d’après la règle (DRS 1), donnant lieu à un A-groupe noté parfois
$\mathscr {U}_+$
canoniquement d’après la règle (DRS 1), donnant lieu à un A-groupe noté parfois
![]() $\mathscr {Z}\mathscr {U}_+:=\mathscr {Z} \ltimes \mathscr {U}_+$
.
$\mathscr {Z}\mathscr {U}_+:=\mathscr {Z} \ltimes \mathscr {U}_+$
.
Pour construire
![]() $\mathscr {G}$
satisfaisant à la troisième propriété, il suffit de construire une loi birationnelle stricte sur
$\mathscr {G}$
satisfaisant à la troisième propriété, il suffit de construire une loi birationnelle stricte sur
![]() $\mathscr {C}_{+}:=\mathscr {U}_-\times \mathscr {Z} \times \mathscr {U}_+$
pour un choix quelconque
$\mathscr {C}_{+}:=\mathscr {U}_-\times \mathscr {Z} \times \mathscr {U}_+$
pour un choix quelconque
![]() $\Phi ^+$
de racines positives, d’après le th. 3.2.5. Il reste à définir une application birationnelle
$\Phi ^+$
de racines positives, d’après le th. 3.2.5. Il reste à définir une application birationnelle
![]() $\mathscr {C}_{+} \dashrightarrow \mathscr {C}_{-}$
prolongeant l’identité de G dans la fibre générique et contenant la section unité, car cela permettrait de définir des applications rationnelles de produit et d’inversion dans
$\mathscr {C}_{+} \dashrightarrow \mathscr {C}_{-}$
prolongeant l’identité de G dans la fibre générique et contenant la section unité, car cela permettrait de définir des applications rationnelles de produit et d’inversion dans
![]() $\mathscr {C}_{+}$
, en commutant tous les facteurs et en multipliant ou inversant lorsqu’il le faut.
$\mathscr {C}_{+}$
, en commutant tous les facteurs et en multipliant ou inversant lorsqu’il le faut.
Montrons plus généralement la même assertion pour chaque paire de systèmes de racines positives
![]() $\Phi ^+$
et
$\Phi ^+$
et
![]() $\Psi ^+$
par récurrence sur le cardinal des rayons de
$\Psi ^+$
par récurrence sur le cardinal des rayons de
![]() $ \Phi ^+ \cap \Psi ^- $
. Si cette intersection ne contient que le rayon radiciel
$ \Phi ^+ \cap \Psi ^- $
. Si cette intersection ne contient que le rayon radiciel
![]() $\mathbb {Q}_{>0}a \cap \Phi $
engendré par la racine non divisible
$\mathbb {Q}_{>0}a \cap \Phi $
engendré par la racine non divisible
![]() $a \in \Phi $
, alors l’axiome (DRS 3) en fournit un morphisme rationnel
$a \in \Phi $
, alors l’axiome (DRS 3) en fournit un morphisme rationnel
défini dans un voisinage ouvert de la section unité, où
![]() $\mathscr {V}^{\pm }:= \mathscr {U}_{\Phi ^{\pm ,\operatorname {nd}}\setminus \{\pm a\}}$
. La construction montre aussi que la loi birationnelle est indépendante du système de racines positives
$\mathscr {V}^{\pm }:= \mathscr {U}_{\Phi ^{\pm ,\operatorname {nd}}\setminus \{\pm a\}}$
. La construction montre aussi que la loi birationnelle est indépendante du système de racines positives
![]() $\Phi ^+$
choisi, donc il en sera de même du groupe
$\Phi ^+$
choisi, donc il en sera de même du groupe
![]() $\mathscr {G}$
obtenu à la fin.
$\mathscr {G}$
obtenu à la fin.
Pour que la loi birationnelle esquissée ci-dessus soit stricte, il faut et il suffit que le morphisme multiplication
![]() $\mathscr {C}_+ \times \mathscr {C}_+ \dashrightarrow \mathscr {C}_+$
soit un épimorphisme, vu que la grosse cellule
$\mathscr {C}_+ \times \mathscr {C}_+ \dashrightarrow \mathscr {C}_+$
soit un épimorphisme, vu que la grosse cellule
![]() $\mathscr {C}_+$
est géométriquement connexe, cf. [Reference Conrad, Gabber and PrasadCGP15, rem. 9.6.3]. Or, considérant le fermé
$\mathscr {C}_+$
est géométriquement connexe, cf. [Reference Conrad, Gabber and PrasadCGP15, rem. 9.6.3]. Or, considérant le fermé
![]() $\mathscr {U}_- \times \mathcal {Z}\mathscr {U}_+ \subset \mathscr {C}_+ \times \mathscr {C}_{+}$
dont les points sont de la forme
$\mathscr {U}_- \times \mathcal {Z}\mathscr {U}_+ \subset \mathscr {C}_+ \times \mathscr {C}_{+}$
dont les points sont de la forme
![]() $(a,1,1,b)$
, on déduit aisément que ceux-ci appartiennent au lieu de définition du morphisme multiplication, compte tenu de ce que les morphismes d’échange (3.2.1) soient définis autour de
$(a,1,1,b)$
, on déduit aisément que ceux-ci appartiennent au lieu de définition du morphisme multiplication, compte tenu de ce que les morphismes d’échange (3.2.1) soient définis autour de
![]() $\mathscr {Z} \mathscr {U}_{\pm }$
.
$\mathscr {Z} \mathscr {U}_{\pm }$
.
Maintenant, on dispose d’un A-groupe lisse, séparé et connexe
![]() $\mathscr {G}$
qui modèle G et qui contient les différents
$\mathscr {G}$
qui modèle G et qui contient les différents
![]() $\mathscr {C}_{\Phi ^+}$
en tant qu’ouverts, et il faut encore voir que les sous-groupes localement fermés
$\mathscr {C}_{\Phi ^+}$
en tant qu’ouverts, et il faut encore voir que les sous-groupes localement fermés
![]() $\mathscr {Z}$
et
$\mathscr {Z}$
et
![]() $\mathscr {U}_+$
sont effectivement fermés. Or l’image réciproque de
$\mathscr {U}_+$
sont effectivement fermés. Or l’image réciproque de
![]() $\mathscr {Z}\mathscr {U}_+$
par le revêtement fidèlement plat
$\mathscr {Z}\mathscr {U}_+$
par le revêtement fidèlement plat
![]() $\mathscr {C}_{\Phi ^-} \times \mathscr {C}_{\Phi ^+} \rightarrow \mathscr {G}$
est déterminée par la condition fermée
$\mathscr {C}_{\Phi ^-} \times \mathscr {C}_{\Phi ^+} \rightarrow \mathscr {G}$
est déterminée par la condition fermée
![]() $b_1b_2=1$
, où
$b_1b_2=1$
, où
![]() $(a_1,b_1, b_2, a_2) \in \mathscr {Z}\mathscr {U}_+ \times (\mathscr {U}_-)^2 \times \mathscr {Z} \mathscr {U}_+$
, ce qui achève la vérification de l’affirmation par descente fidèlement plate.
$(a_1,b_1, b_2, a_2) \in \mathscr {Z}\mathscr {U}_+ \times (\mathscr {U}_-)^2 \times \mathscr {Z} \mathscr {U}_+$
, ce qui achève la vérification de l’affirmation par descente fidèlement plate.
En principe, on voudrait que le groupe
![]() $\mathscr {G}$
soit affine, mais cela ne découle ni de la construction avec des lois birationnelles ni de celle de [Reference Bruhat and TitsBT84a, §3.8, 3.9.4] : en effet, [Reference RaynaudRay70, §VII.3] fournit un exemple d’un groupe quasi-affine, lisse et connexe qui n’est pas affine; remarquons néanmoins que, par contre, celui de [Reference Bruhat and TitsBT84a, 3.2.15] s’avère affine. Toutefois, l’on a :
$\mathscr {G}$
soit affine, mais cela ne découle ni de la construction avec des lois birationnelles ni de celle de [Reference Bruhat and TitsBT84a, §3.8, 3.9.4] : en effet, [Reference RaynaudRay70, §VII.3] fournit un exemple d’un groupe quasi-affine, lisse et connexe qui n’est pas affine; remarquons néanmoins que, par contre, celui de [Reference Bruhat and TitsBT84a, 3.2.15] s’avère affine. Toutefois, l’on a :
Proposition 3.2.7 (Raynaud, à peu près).
Soient A un anneau noethérien et régulier de dimension inférieure ou égale à
![]() $2$
et
$2$
et
![]() $\mathscr {G}$
un A-modèle en groupes lisse, connexe et séparé de G. Alors, la A-algèbre
$\mathscr {G}$
un A-modèle en groupes lisse, connexe et séparé de G. Alors, la A-algèbre
![]() $\Gamma (\mathscr {G}, \mathcal {O}_{\mathscr {G}})$
est munie d’une structure canonique de A-algèbre de Hopf plate de type fini. De plus, le A-groupe résultant
$\Gamma (\mathscr {G}, \mathcal {O}_{\mathscr {G}})$
est munie d’une structure canonique de A-algèbre de Hopf plate de type fini. De plus, le A-groupe résultant
![]() $\mathscr {G}^{\mathrm {af}}:=\operatorname {Spec} \Gamma (\mathscr {G}, \mathcal {O}_{\mathscr {G}})$
est lisse, affine et sa composante neutre s’identifie à
$\mathscr {G}^{\mathrm {af}}:=\operatorname {Spec} \Gamma (\mathscr {G}, \mathcal {O}_{\mathscr {G}})$
est lisse, affine et sa composante neutre s’identifie à
![]() $\mathscr {G}$
par l’application naturelle.
$\mathscr {G}$
par l’application naturelle.
Démonstration. Le groupe
![]() $\mathscr {G}$
est tout d’abord quasi-affine grâce au [Reference RaynaudRay70, cor. VII.2.2], ce qu’on peut appliquer car A est normal et
$\mathscr {G}$
est tout d’abord quasi-affine grâce au [Reference RaynaudRay70, cor. VII.2.2], ce qu’on peut appliquer car A est normal et
![]() $\mathscr {G}$
est lisse, séparé et géométriquement connexe. Raynaud avait montré en [Reference RaynaudRay70, prop. VII.3.1], que, lorsqu’on se trouve dans les circonstances énoncées,
$\mathscr {G}$
est lisse, séparé et géométriquement connexe. Raynaud avait montré en [Reference RaynaudRay70, prop. VII.3.1], que, lorsqu’on se trouve dans les circonstances énoncées,
![]() $\Gamma (\mathscr {G}, \mathcal {O}_{\mathscr {G}})$
était fidèlement plate sur A et, par suite, que
$\Gamma (\mathscr {G}, \mathcal {O}_{\mathscr {G}})$
était fidèlement plate sur A et, par suite, que
![]() $\mathscr {G}^{\operatorname {af}}$
était un A-groupe plat admettant
$\mathscr {G}^{\operatorname {af}}$
était un A-groupe plat admettant
![]() $\mathscr {G}$
comme sous-groupe ouvert par le morphisme canonique
$\mathscr {G}$
comme sous-groupe ouvert par le morphisme canonique
![]() $\mathscr {G} \rightarrow \mathscr {G}^{\operatorname {af}}$
. Pour aider le lecteur, nous allons expliquer brièvement la démonstration de la platitude, comp. avec [Reference RaynaudRay70, lem. VII.3.2].
$\mathscr {G} \rightarrow \mathscr {G}^{\operatorname {af}}$
. Pour aider le lecteur, nous allons expliquer brièvement la démonstration de la platitude, comp. avec [Reference RaynaudRay70, lem. VII.3.2].
Soit B un A-module fini contenu dans
![]() $\Gamma (\mathscr {G},\mathcal {O}_{\mathscr {G}})$
. Alors, B induit un fibré vectoriel au-dessus d’un ouvert cofini U de
$\Gamma (\mathscr {G},\mathcal {O}_{\mathscr {G}})$
. Alors, B induit un fibré vectoriel au-dessus d’un ouvert cofini U de
![]() $S=\operatorname {Spec} A$
, qui s’étend donc en un A-module libre et fini
$S=\operatorname {Spec} A$
, qui s’étend donc en un A-module libre et fini
![]() $\tilde {B} = \Gamma (U,B\otimes \mathcal {O}_S)$
, d’après [Reference Dieudonné and GrothendieckEGAIV, th. 5.10.5, prop. 5.11.1]. Mais par changement de base plat, on déduit l’égalité
$\tilde {B} = \Gamma (U,B\otimes \mathcal {O}_S)$
, d’après [Reference Dieudonné and GrothendieckEGAIV, th. 5.10.5, prop. 5.11.1]. Mais par changement de base plat, on déduit l’égalité
![]() $\Gamma (U,\pi _*\mathcal {O}_{\mathscr {G}})=\Gamma (S,\pi _*\mathcal {O}_{\mathscr {G}})$
du deuxième lemme d’extension de Riemann
$\Gamma (U,\pi _*\mathcal {O}_{\mathscr {G}})=\Gamma (S,\pi _*\mathcal {O}_{\mathscr {G}})$
du deuxième lemme d’extension de Riemann
![]() $\Gamma (U,\mathcal {O}_S)=A$
. Alors, ceci entrâine que
$\Gamma (U,\mathcal {O}_S)=A$
. Alors, ceci entrâine que
![]() $\tilde {B} \subseteq \Gamma (\mathscr {G},\mathcal {O}_{\mathscr {G}})$
, d’où une écriture de cette dernière A-algèbre comme la colimite filtrée de ses sous-A-modules plats. Ce que
$\tilde {B} \subseteq \Gamma (\mathscr {G},\mathcal {O}_{\mathscr {G}})$
, d’où une écriture de cette dernière A-algèbre comme la colimite filtrée de ses sous-A-modules plats. Ce que
![]() $\mathscr {G}^{\operatorname {af}}$
soit maintenant un A-groupe affine et (fidèlement) plat est trivial, cf. [SGA3, exp. VIB, lem. 11.1].
$\mathscr {G}^{\operatorname {af}}$
soit maintenant un A-groupe affine et (fidèlement) plat est trivial, cf. [SGA3, exp. VIB, lem. 11.1].
Malheureusement, il n’est pas clair que
![]() $\Gamma (\mathscr {G}, \mathcal {O}_{\mathscr {G}})$
soit une A-algèbre de type fini. Néanmoins, d’après [Reference AnantharamanAna73, prop. 2.3.1] ou [SGA3, exp. VIB, prop. 12.9], on peut trouver un ouvert cofini U de
$\Gamma (\mathscr {G}, \mathcal {O}_{\mathscr {G}})$
soit une A-algèbre de type fini. Néanmoins, d’après [Reference AnantharamanAna73, prop. 2.3.1] ou [SGA3, exp. VIB, prop. 12.9], on peut trouver un ouvert cofini U de
![]() $\operatorname {Spec} A$
tel que
$\operatorname {Spec} A$
tel que
![]() $\mathscr {G}_U$
soit affine sur U, d’où en particulier la présentation finie de
$\mathscr {G}_U$
soit affine sur U, d’où en particulier la présentation finie de
![]() $\mathscr {G}^{\operatorname {af}}$
au-dessus de U. Par descente fidèlement plate et quasi-compacte, on se ramène au cas où A est un anneau local d’idéal maximal
$\mathscr {G}^{\operatorname {af}}$
au-dessus de U. Par descente fidèlement plate et quasi-compacte, on se ramène au cas où A est un anneau local d’idéal maximal
![]() $\mathfrak {m}$
,
$\mathfrak {m}$
,
![]() $\mathfrak {m}$
-adiquement séparé et complet, et à corps résiduel k algébriquement clos.
$\mathfrak {m}$
-adiquement séparé et complet, et à corps résiduel k algébriquement clos.
Nous affirmons d’abord que
![]() $\mathscr {G}^{\operatorname {af}}$
est de type fini au-dessus de
$\mathscr {G}^{\operatorname {af}}$
est de type fini au-dessus de
![]() $A/\mathfrak {m}^n$
pour tout entier positif n, ce qui résulte immédiatement du cas
$A/\mathfrak {m}^n$
pour tout entier positif n, ce qui résulte immédiatement du cas
![]() $n=1$
grâce au lemme de Nakayama nilpotent. Alors, le monomorphisme
$n=1$
grâce au lemme de Nakayama nilpotent. Alors, le monomorphisme
![]() $\mathscr {G}_k \rightarrow \mathscr {G}^{\operatorname {af}}_k$
est ouvert par hypothèse et fermé d’après le [SGA3, exp. VIB, lem. 11.18.1], identifiant donc le membre de gauche à la composante neutre de
$\mathscr {G}_k \rightarrow \mathscr {G}^{\operatorname {af}}_k$
est ouvert par hypothèse et fermé d’après le [SGA3, exp. VIB, lem. 11.18.1], identifiant donc le membre de gauche à la composante neutre de
![]() $\mathscr {G}^{\operatorname {af}}_k$
. Vu que le faisceau quotient
$\mathscr {G}^{\operatorname {af}}_k$
. Vu que le faisceau quotient
![]() $\pi _0(\mathscr {G}_k^{\operatorname {af}}):=\mathscr {G}^{\operatorname {af}}_k/\mathscr {G}_k$
est représentable par un groupe proétale, cf. [Reference Demazure and GabrielDG70, III, §3, 7.7], dont la section unité est ouverte, on en tire que
$\pi _0(\mathscr {G}_k^{\operatorname {af}}):=\mathscr {G}^{\operatorname {af}}_k/\mathscr {G}_k$
est représentable par un groupe proétale, cf. [Reference Demazure and GabrielDG70, III, §3, 7.7], dont la section unité est ouverte, on en tire que
![]() $\pi _0(\mathscr {G}_k^{\operatorname {af}})$
est un groupe étale fini et que le k-groupe
$\pi _0(\mathscr {G}_k^{\operatorname {af}})$
est un groupe étale fini et que le k-groupe
![]() $\mathscr {G}_k^{\operatorname {af}}$
est forcément de type fini.
$\mathscr {G}_k^{\operatorname {af}}$
est forcément de type fini.
En sachant que le schéma affine
![]() $\mathscr {G}^{\operatorname {af}}$
est lisse au-dessus de chaque quotient artinien de A, on peut relever par récurrence tout point de
$\mathscr {G}^{\operatorname {af}}$
est lisse au-dessus de chaque quotient artinien de A, on peut relever par récurrence tout point de
![]() $\mathscr {G}^{\operatorname {af}}$
à valeurs dans k en un A-point correspondant (de façon non unique évidemment) et par translation de
$\mathscr {G}^{\operatorname {af}}$
à valeurs dans k en un A-point correspondant (de façon non unique évidemment) et par translation de
![]() $\mathscr {G}$
dans
$\mathscr {G}$
dans
![]() $\mathscr {G}^{\operatorname {af}}$
par ces points, on dérive la lissité de ce dernier.
$\mathscr {G}^{\operatorname {af}}$
par ces points, on dérive la lissité de ce dernier.
3.3 Les groupes de Tits sur
 $\mathbb {G}_{m,\mathbb {Z}}$
$\mathbb {G}_{m,\mathbb {Z}}$
Dans le présent paragraphe, nous allons construire les
![]() $\mathbb {G}_{m,\mathbb {Z}}$
-groupes de Tits à la suite de [Reference TitsTi84, annexe 2], mission pour laquelle les notations du §2 seront reprises. Néanmoins, il faudra que des hypothèses additionnelles soient faites :
$\mathbb {G}_{m,\mathbb {Z}}$
-groupes de Tits à la suite de [Reference TitsTi84, annexe 2], mission pour laquelle les notations du §2 seront reprises. Néanmoins, il faudra que des hypothèses additionnelles soient faites :
Hypothèse 3.3.1. Sauf mention contraire, G sera un
![]() $\mathbb {Q}(t)$
-groupe réductif connexe, quasi-déployé,
$\mathbb {Q}(t)$
-groupe réductif connexe, quasi-déployé,
![]() $\mathbb {Q}(\zeta _e,t^{1/e})$
-déployé pour un certain entier positif e. Étant donné un tore déployé maximal
$\mathbb {Q}(\zeta _e,t^{1/e})$
-déployé pour un certain entier positif e. Étant donné un tore déployé maximal
![]() $S \subset G$
, on fixe un couple de Killing
$S \subset G$
, on fixe un couple de Killing
![]() $Z_G(S)=T \subset B$
et un quasi-système de Tits
$Z_G(S)=T \subset B$
et un quasi-système de Tits
![]() $(x_a)_{a \in \Phi _G}$
, voir la déf. 2.3.4. On suppose de plus que T est induit et que
$(x_a)_{a \in \Phi _G}$
, voir la déf. 2.3.4. On suppose de plus que T est induit et que
![]() $G_{\mathbb {Q} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) }$
est résiduellement déployé.
$G_{\mathbb {Q} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) }$
est résiduellement déployé.
Les notions correspondantes pour la forme déployée H de G seront notées
![]() $T_H$
,
$T_H$
,
![]() $B_H$
,
$B_H$
,
![]() $(y_\alpha )_{\alpha \in \Phi _H}$
et
$(y_\alpha )_{\alpha \in \Phi _H}$
et
![]() $\Gamma $
désignera le groupe de Galois de
$\Gamma $
désignera le groupe de Galois de
![]() $\mathbb {Q}(\zeta _e,t^{1/e})/\mathbb {Q}(t)$
opérant sur H par automorphismes de Dynkin–Tits, cf. §§2.2-2.3.
$\mathbb {Q}(\zeta _e,t^{1/e})/\mathbb {Q}(t)$
opérant sur H par automorphismes de Dynkin–Tits, cf. §§2.2-2.3.
Tout d’abord signalons que le déploiement résiduel de
![]() $G_{\mathbb {Q} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) }$
dans l’hyp. 3.3.1 sert à que les extensions de
$G_{\mathbb {Q} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) }$
dans l’hyp. 3.3.1 sert à que les extensions de
![]() $\mathbb {Q}(t)$
associées aux racines
$\mathbb {Q}(t)$
associées aux racines
![]() $a \in \Phi _G$
soient conjuguées de
$a \in \Phi _G$
soient conjuguées de
![]() $\mathbb {Q}(t_a)$
, où
$\mathbb {Q}(t_a)$
, où
![]() $t_a=t^{1/e_a}$
et le nombre naturel
$t_a=t^{1/e_a}$
et le nombre naturel
![]() $e_a$
divise e, c’est-à-dire que l’on ait des quasi-épinglages
$e_a$
divise e, c’est-à-dire que l’on ait des quasi-épinglages
si
![]() $a \in \Phi ^{\operatorname {nd,nm}}_G$
n’est ni divisible ni multipliable ou
$a \in \Phi ^{\operatorname {nd,nm}}_G$
n’est ni divisible ni multipliable ou
si
![]() $a \in \Phi _G^{\operatorname {m}}$
est multipliable. D’autre part, le fait que T soit induit entraîne que le tore maximal s’exprime comme produit de facteurs de la forme
$a \in \Phi _G^{\operatorname {m}}$
est multipliable. D’autre part, le fait que T soit induit entraîne que le tore maximal s’exprime comme produit de facteurs de la forme
 $$ \begin{align} T\simeq\prod_{j\in J}\operatorname{R}_{\mathbb{Q}(t^{1/d_j})/\mathbb{Q}(t)} \mathbb{G}_m \end{align} $$
$$ \begin{align} T\simeq\prod_{j\in J}\operatorname{R}_{\mathbb{Q}(t^{1/d_j})/\mathbb{Q}(t)} \mathbb{G}_m \end{align} $$
avec
![]() $d_j$
des diviseurs naturels de e.
$d_j$
des diviseurs naturels de e.
Pour conclure, notons que, si G remplit l’hyp. 3.3.1, alors il en est de même de son revêtement simplement connexe
![]() $G^{\operatorname {sc}}$
, de son groupe adjoint
$G^{\operatorname {sc}}$
, de son groupe adjoint
![]() $G^{\operatorname {ad}}$
, voir [Reference Bruhat and TitsBT84a, prop. 4.4.16], et de la z-extension canonique associée
$G^{\operatorname {ad}}$
, voir [Reference Bruhat and TitsBT84a, prop. 4.4.16], et de la z-extension canonique associée
![]() $\widetilde {G}$
au sens de (2.4.3), d’où la richesse véritable de la classe d’exemples ici considérés.
$\widetilde {G}$
au sens de (2.4.3), d’où la richesse véritable de la classe d’exemples ici considérés.
Remarque 3.3.2. Notons que, dans [Reference TitsTi84, p. 215], le groupe G est supposé simplement connexe et sa forme déployée H simple, ce qui s’approche plus de l’hypothèse régnante de la version précédente de cet article : d’un côté, cela nous permet de supposer
![]() $e \leq 3$
et nous ramène à travailler avec un nombre fini de familles de diagrammes de Dynkin irréductibles; de l’autre côté, presque tous les affirmations valables sous l’hyp. 3.3.1 seront typiquement déduites de celles-ci.
$e \leq 3$
et nous ramène à travailler avec un nombre fini de familles de diagrammes de Dynkin irréductibles; de l’autre côté, presque tous les affirmations valables sous l’hyp. 3.3.1 seront typiquement déduites de celles-ci.
Ensuite, on se penche sur la construction d’un certain schéma en groupes
![]() $\underline {G}$
sur
$\underline {G}$
sur
![]() $\mathbb {G}_{m, \mathbb {Z}}=\operatorname {Spec} \mathbb {Z}[t^{\pm 1}]$
prolongeant G à la suite de Tits, cf. [Reference TitsTi84, p. 217]. Son observation cruciale consiste à remarquer que le tore maximal T et les sous-groupes radiciels
$\mathbb {G}_{m, \mathbb {Z}}=\operatorname {Spec} \mathbb {Z}[t^{\pm 1}]$
prolongeant G à la suite de Tits, cf. [Reference TitsTi84, p. 217]. Son observation cruciale consiste à remarquer que le tore maximal T et les sous-groupes radiciels
![]() $U_a$
pour
$U_a$
pour
![]() $a \in \Phi _G^{\operatorname {nd}}$
admettent des
$a \in \Phi _G^{\operatorname {nd}}$
admettent des
![]() $\mathbb {Z}[t^{\pm 1}]$
-modèles naturels.
$\mathbb {Z}[t^{\pm 1}]$
-modèles naturels.
Définition 3.3.3 (Tits).
Soit
 $$ \begin{align} \underline{T}:=\prod_{j \in J}\operatorname{R}_{\mathbb{Z}[t^{\pm 1/d_j}]/\mathbb{Z}[t^{\pm 1}]}\mathbb{G}_{m,\mathbb{Z}[t^{\pm 1/d_j}]} \end{align} $$
$$ \begin{align} \underline{T}:=\prod_{j \in J}\operatorname{R}_{\mathbb{Z}[t^{\pm 1/d_j}]/\mathbb{Z}[t^{\pm 1}]}\mathbb{G}_{m,\mathbb{Z}[t^{\pm 1/d_j}]} \end{align} $$
le
![]() $\mathbb {Z}[t^{\pm 1}]$
-modèle en groupes de T défini par transport de structure le long de l’isomorphisme (3.3.3). Pour les racines
$\mathbb {Z}[t^{\pm 1}]$
-modèle en groupes de T défini par transport de structure le long de l’isomorphisme (3.3.3). Pour les racines
![]() $a \in \Phi ^{\operatorname {nd,nm}}$
aux rayons singuliers, soient
$a \in \Phi ^{\operatorname {nd,nm}}$
aux rayons singuliers, soient
les
![]() $\mathbb {Z}[t^{\pm 1}]$
-modèles en groupes de
$\mathbb {Z}[t^{\pm 1}]$
-modèles en groupes de
![]() $U_a$
définis par transport de structure le long de
$U_a$
définis par transport de structure le long de
![]() $x_a$
, voir (3.3.1). Pour chaque racine multipliable
$x_a$
, voir (3.3.1). Pour chaque racine multipliable
![]() $a \in \Phi _G^{\operatorname {m}}$
, soit
$a \in \Phi _G^{\operatorname {m}}$
, soit
le
![]() $\mathbb {Z}[t^{\pm 1}]$
-modèle en groupes de
$\mathbb {Z}[t^{\pm 1}]$
-modèle en groupes de
![]() $U_a$
définis par transport de structure le long de
$U_a$
définis par transport de structure le long de
![]() $x_a$
, voir (3.3.2), où l’on note
$x_a$
, voir (3.3.2), où l’on note
![]() $\mathbb {G}_{p,\mathbb {Z}[t_a^{\pm 1}]/\mathbb {Z}[t_{2a}^{\pm 1}]}$
le
$\mathbb {G}_{p,\mathbb {Z}[t_a^{\pm 1}]/\mathbb {Z}[t_{2a}^{\pm 1}]}$
le
![]() $\mathbb {Z}[t_{2a}^{\pm 1}]$
-schéma
$\mathbb {Z}[t_{2a}^{\pm 1}]$
-schéma
![]() $\operatorname {R}_{\mathbb {Z}[t_a^{\pm 1}]/\mathbb {Z}[t_{2a}^{\pm 1}]}\mathbb {A}^1_{\mathbb {Z}[t_a^{\pm 1}]} \times t_a\mathbb {A}^1_{\mathbb {Z}[t_{2a}^{\pm 1}]}$
muni de la loi de groupe induite par (2.3.1), où l’on note
$\operatorname {R}_{\mathbb {Z}[t_a^{\pm 1}]/\mathbb {Z}[t_{2a}^{\pm 1}]}\mathbb {A}^1_{\mathbb {Z}[t_a^{\pm 1}]} \times t_a\mathbb {A}^1_{\mathbb {Z}[t_{2a}^{\pm 1}]}$
muni de la loi de groupe induite par (2.3.1), où l’on note
![]() $t_a\mathbb {A}^1_{\mathbb {Z}[t_{2a}^{\pm 1}]} \subset \operatorname {R}_{\mathbb {Z}[t_a^{\pm 1}]/\mathbb {Z}[t_{2a}^{\pm 1}]}\mathbb {A}^1_{\mathbb {Z}[t_a^{\pm 1}]}$
le sous-schéma où la trace s’annule.
$t_a\mathbb {A}^1_{\mathbb {Z}[t_{2a}^{\pm 1}]} \subset \operatorname {R}_{\mathbb {Z}[t_a^{\pm 1}]/\mathbb {Z}[t_{2a}^{\pm 1}]}\mathbb {A}^1_{\mathbb {Z}[t_a^{\pm 1}]}$
le sous-schéma où la trace s’annule.
Observons que
![]() $\underline {T}$
ne dépend pas du choix de l’isomorphisme de (3.3.3), en vertu de son identification au modèle de Néron connexe de T sur
$\underline {T}$
ne dépend pas du choix de l’isomorphisme de (3.3.3), en vertu de son identification au modèle de Néron connexe de T sur
![]() $\mathbb {Z}[t^{\pm 1}]$
, cf. [Reference Bruhat and TitsBT84a, 4.4.8], [Reference Bosch, Lütkebohmert and RaynaudBLR90, prop. 10.1.4] et [Reference Pereira LourençoPL20, prop. 3.8]. Nous montrons ci-dessous que la donnée
$\mathbb {Z}[t^{\pm 1}]$
, cf. [Reference Bruhat and TitsBT84a, 4.4.8], [Reference Bosch, Lütkebohmert and RaynaudBLR90, prop. 10.1.4] et [Reference Pereira LourençoPL20, prop. 3.8]. Nous montrons ci-dessous que la donnée
![]() $(\underline {T},\underline {U_a})_{a \in \Phi _G^{\operatorname {nd}}}$
est radicielle schématique, cf. [Reference TitsTi84, p. 217].
$(\underline {T},\underline {U_a})_{a \in \Phi _G^{\operatorname {nd}}}$
est radicielle schématique, cf. [Reference TitsTi84, p. 217].
Proposition 3.3.4 (Tits).
La donnée
![]() $(\underline {T},\underline {U_a})_{a \in \Phi _G^{\operatorname {nd}}}$
satisfait aux axiomes (DRS0-3) de la déf. 3.2.1.
$(\underline {T},\underline {U_a})_{a \in \Phi _G^{\operatorname {nd}}}$
satisfait aux axiomes (DRS0-3) de la déf. 3.2.1.
Démonstration. Ceci découle essentiellement du fait que l’application conjugaison
l’application commutateur
et l’application rationnelle d’échange
préservent leur sens avec
![]() $\mathbb {Z}[t^{\pm 1}]$
-coefficients, c’est-à-dire que se prolongent nettement en des morphismes rationnels entre les produits des modèles
$\mathbb {Z}[t^{\pm 1}]$
-coefficients, c’est-à-dire que se prolongent nettement en des morphismes rationnels entre les produits des modèles
![]() $\underline {T}$
et
$\underline {T}$
et
![]() $\underline {U_a}$
pour toute racine
$\underline {U_a}$
pour toute racine
![]() $a \in \Phi _G^{\operatorname {nd}}$
non divisible. L’effet de la similitude n’est pas à craindre, restant visible dans la fibre générique.
$a \in \Phi _G^{\operatorname {nd}}$
non divisible. L’effet de la similitude n’est pas à craindre, restant visible dans la fibre générique.
En effet, pour l’action de
![]() $\underline {T}$
sur
$\underline {T}$
sur
![]() $\underline {U_a}$
, on peut se ramener, par naturalité des modèles de Néron connexes, au cas où G est adjoint de rang relatif
$\underline {U_a}$
, on peut se ramener, par naturalité des modèles de Néron connexes, au cas où G est adjoint de rang relatif
![]() $1$
. Alors, on voit par construction que
$1$
. Alors, on voit par construction que
![]() $\underline {T}$
s’identifie à
$\underline {T}$
s’identifie à
![]() $\operatorname {R}_{\mathbb {Z}[t_a^{\pm 1}]/\mathbb {Z}[t^{\pm 1}]}\mathbb {G}_m$
par un certain morphisme a, choisi de telle sorte que les formules
$\operatorname {R}_{\mathbb {Z}[t_a^{\pm 1}]/\mathbb {Z}[t^{\pm 1}]}\mathbb {G}_m$
par un certain morphisme a, choisi de telle sorte que les formules
décrivent l’opération de
![]() $\underline {T}$
sur
$\underline {T}$
sur
![]() $\underline {U_a}$
à similitude près, voir aussi [Reference Bruhat and TitsBT84a, prop. 4.4.19].
$\underline {U_a}$
à similitude près, voir aussi [Reference Bruhat and TitsBT84a, prop. 4.4.19].
La règle (DRS 2) concerne les applications commutateur
pour des racines non divisibles
![]() $a,b$
engendrant des
$a,b$
engendrant des
![]() $\mathbb {Q}$
-droites différentes. Leurs fibres génériques s’écrivent à similitude près comme dans [Reference Bruhat and TitsBT84a, A.6] et on voit aisément que les applications y décrites se prolongent aux coefficients entiers. Pour être exhaustif, nous allons écrire les applications commutateur lorsque l’une des racines a, b ou c est multipliable, vu qu’elles ont été affectées par la modification de Tits, voir la déf. 2.3.4 :
$\mathbb {Q}$
-droites différentes. Leurs fibres génériques s’écrivent à similitude près comme dans [Reference Bruhat and TitsBT84a, A.6] et on voit aisément que les applications y décrites se prolongent aux coefficients entiers. Pour être exhaustif, nous allons écrire les applications commutateur lorsque l’une des racines a, b ou c est multipliable, vu qu’elles ont été affectées par la modification de Tits, voir la déf. 2.3.4 :
où
![]() $s(u,v)$
désigne la somme quadratique
$s(u,v)$
désigne la somme quadratique
![]() $N(u)+v$
. En particulier, les sous-groupes radiciels multipliables commutent les uns avec les autres en caractéristique
$N(u)+v$
. En particulier, les sous-groupes radiciels multipliables commutent les uns avec les autres en caractéristique
![]() $2$
, ce qui pourrait surprendre le lecteur, mais qui répondre à nos attentes, compte tenu de la classification des groupes pseudo-réductifs, voir l’ex. 3.1.7 et le th. 3.3.7.
$2$
, ce qui pourrait surprendre le lecteur, mais qui répondre à nos attentes, compte tenu de la classification des groupes pseudo-réductifs, voir l’ex. 3.1.7 et le th. 3.3.7.
Enfin, pour que l’axiome (DRS 3) soit rempli, il faut se donner une certaine section globale
Posant
![]() $\underline {W_a}$
l’ouvert distingué de
$\underline {W_a}$
l’ouvert distingué de
![]() $\underline {U_a}\times \underline {U_{-a}}$
où
$\underline {U_a}\times \underline {U_{-a}}$
où
![]() $d_a$
ne s’annule pas, qui doit contenir les fermés
$d_a$
ne s’annule pas, qui doit contenir les fermés
![]() $\underline {U_{\pm a}}$
, on a besoin encore d’une application
$\underline {U_{\pm a}}$
, on a besoin encore d’une application
Dans la fibre générique, on trouve l’écriture de ces applications à similitude près dans [Reference Bruhat and TitsBT84a, 4.1.6, 4.1.12].
Enregistrons toutefois leurs prolongements entiers pour référence future. Si
![]() $a \in \Phi _G^{\operatorname {nd,nm}}$
n’est ni divisible ni multipliable, alors
$a \in \Phi _G^{\operatorname {nd,nm}}$
n’est ni divisible ni multipliable, alors
et, en posant
![]() $t(r,r')=1-rr'$
et
$t(r,r')=1-rr'$
et
![]() $\underline {W_a}$
l’ouvert spécial déterminé par
$\underline {W_a}$
l’ouvert spécial déterminé par
![]() $d_a$
, on en tire
$d_a$
, on en tire
où
![]() $a^{\vee }$
désigne l’application composée d’un certain isomorphisme
$a^{\vee }$
désigne l’application composée d’un certain isomorphisme
![]() $\operatorname {R}_{\mathbb {Z}[t_a^{\pm 1}]/\mathbb {Z}[t^{\pm 1}]}\mathbb {G}_m \simeq \underline {T}^{\operatorname {sc},a} $
unique à conjugaison près avec le morphisme naturel
$\operatorname {R}_{\mathbb {Z}[t_a^{\pm 1}]/\mathbb {Z}[t^{\pm 1}]}\mathbb {G}_m \simeq \underline {T}^{\operatorname {sc},a} $
unique à conjugaison près avec le morphisme naturel
![]() $\underline {T}^{\operatorname {sc},a} \rightarrow \underline {T}$
. Si
$\underline {T}^{\operatorname {sc},a} \rightarrow \underline {T}$
. Si
![]() $a \in \Phi _G^{\operatorname {m}}$
est multipliable, il s’avère par des calculs impliquant la modification de Tits que l’on a
$a \in \Phi _G^{\operatorname {m}}$
est multipliable, il s’avère par des calculs impliquant la modification de Tits que l’on a
où l’on note
![]() $t(u,v,u',v'):=1-2\sigma (u)u'+s(u,v)s(u',v')$
, et on en déduit aussi que la première coordonnée de
$t(u,v,u',v'):=1-2\sigma (u)u'+s(u,v)s(u',v')$
, et on en déduit aussi que la première coordonnée de
![]() $\beta _a(x_a(u,v),x_{-a}(u',v'))$
s’écrit comme le monstre suivant
$\beta _a(x_a(u,v),x_{-a}(u',v'))$
s’écrit comme le monstre suivant
mais sans aucun facteur de
![]() $2$
non souhaitable. On voit de même que sa dernière coordonnée est pareille à la première, quitte à échanger quelques primes et à conjuguer, et que la deuxième est égale à
$2$
non souhaitable. On voit de même que sa dernière coordonnée est pareille à la première, quitte à échanger quelques primes et à conjuguer, et que la deuxième est égale à
![]() $(2a)^{\vee }(t(u,v,u',v'))$
, où l’on note
$(2a)^{\vee }(t(u,v,u',v'))$
, où l’on note
![]() $(2a)^\vee $
l’applicationFootnote 4 composée
$(2a)^\vee $
l’applicationFootnote 4 composée
![]() $\operatorname {R}_{\mathbb {Z}[t_a^{\pm 1}]/\mathbb {Z}[t^{\pm 1}]}\mathbb {G}_m \simeq \underline {T}^{\operatorname {sc},a}\rightarrow \underline {T}$
.
$\operatorname {R}_{\mathbb {Z}[t_a^{\pm 1}]/\mathbb {Z}[t^{\pm 1}]}\mathbb {G}_m \simeq \underline {T}^{\operatorname {sc},a}\rightarrow \underline {T}$
.
Grâce à cette proposition, nous pouvons appliquer le th. 3.2.5 pour obtenir un
![]() $\mathbb {Z}[t^{\pm 1}]$
-groupe lisse, connexe et séparé
$\mathbb {Z}[t^{\pm 1}]$
-groupe lisse, connexe et séparé
![]() $\underline {G}$
.
$\underline {G}$
.
Définition 3.3.5 (Tits).
Le groupe de Tits
![]() $\underline {G}$
est le
$\underline {G}$
est le
![]() $\mathbb {Z}[t^{\pm 1}]$
-modèle en groupes séparé, lisse et connexe de G qui découle du th. 3.2.5 appliqué à la donnée radicielle schématique
$\mathbb {Z}[t^{\pm 1}]$
-modèle en groupes séparé, lisse et connexe de G qui découle du th. 3.2.5 appliqué à la donnée radicielle schématique
![]() $(\underline {T},\underline {U_a})_{a\in \Phi _G^{\operatorname {nd}}}$
.
$(\underline {T},\underline {U_a})_{a\in \Phi _G^{\operatorname {nd}}}$
.
Remarquons tout d’abord quelques propriétés importantes :
Remarque 3.3.6. Tous les faits qui suivent sans démonstration ultérieure résultent d’une comparaison des grosses cellules correspondantes, vu l’unicité des solutions aux lois birationnelles :
-
1. Si G est la restriction des scalaires d’un groupe déployé
 $H'$
le long de
$H'$
le long de
 $\mathbb {Q}(t^{1/d})/\mathbb {Q}(t)$
, alors
$\mathbb {Q}(t^{1/d})/\mathbb {Q}(t)$
, alors
 $\underline {G}$
en est de même la restriction des scalaires
$\underline {G}$
en est de même la restriction des scalaires
 $\operatorname {R}_{\mathbb {Z}[t^{\pm 1/d}]/\mathbb {Z}[t^{\pm 1}]}H'$
.
$\operatorname {R}_{\mathbb {Z}[t^{\pm 1/d}]/\mathbb {Z}[t^{\pm 1}]}H'$
. -
2. Si l’on inverse le degré de ramification e, on obtient un
 $\mathbb {Z}[1/e, t^{\pm 1}]$
-groupe réductif
$\mathbb {Z}[1/e, t^{\pm 1}]$
-groupe réductif
 $\underline {G}[1/e]$
donné par les
$\underline {G}[1/e]$
donné par les
 $\Gamma $
-invariants de
$\Gamma $
-invariants de
 $\operatorname {R}_{\mathbb {Z}[1/e, t^{\pm 1/d}]/\mathbb {Z}[1/e, t^{\pm 1}]}\underline {H}$
, voir [Reference Pappas and ZhuPZ13, 3.c.1].
$\operatorname {R}_{\mathbb {Z}[1/e, t^{\pm 1/d}]/\mathbb {Z}[1/e, t^{\pm 1}]}\underline {H}$
, voir [Reference Pappas and ZhuPZ13, 3.c.1]. -
3. On verra ci-dessous, cf. prop. 3.3.7, que la fibre générique
 $G_{\eta _p}:=\underline {G}\otimes \mathbb {F}_p(t)$
de la réduction modulo p est toujours pseudo-réductive et quasi-déployée à système de racines
$G_{\eta _p}:=\underline {G}\otimes \mathbb {F}_p(t)$
de la réduction modulo p est toujours pseudo-réductive et quasi-déployée à système de racines
 $\Phi _G$
. Si
$\Phi _G$
. Si
 $\Phi _H$
est irréductible et
$\Phi _H$
est irréductible et
 $\Gamma $
n’y opère pas trivialement (donc on peut choisir
$\Gamma $
n’y opère pas trivialement (donc on peut choisir
 $e=2,3$
), alors le th. 3.1.4 entraîne que
$e=2,3$
), alors le th. 3.1.4 entraîne que
 $G_{\eta _e}^{\operatorname {sc}}$
est soit exotique basique, soit barcelonais basique.
$G_{\eta _e}^{\operatorname {sc}}$
est soit exotique basique, soit barcelonais basique. -
4. Nous verrons plus tard que
 $\underline {G}$
est même affine et non pas seulement quasi-affine, voir la prop. 3.2.7 et la prop. 3.3.9.
$\underline {G}$
est même affine et non pas seulement quasi-affine, voir la prop. 3.2.7 et la prop. 3.3.9.
Notons
![]() $G_{\eta _p}$
la fibre générique
$G_{\eta _p}$
la fibre générique
![]() $\underline {G}\otimes \mathbb {F}_p(t)$
de la réduction
$\underline {G}\otimes \mathbb {F}_p(t)$
de la réduction
![]() $G_p:=\underline {G}\otimes \mathbb {F}_p[t^{\pm 1}]$
modulo p de
$G_p:=\underline {G}\otimes \mathbb {F}_p[t^{\pm 1}]$
modulo p de
![]() $\underline {G}$
.
$\underline {G}$
.
Proposition 3.3.7. Le
![]() $\mathbb {F}_p(t)$
-groupe lisse, affine et connexe
$\mathbb {F}_p(t)$
-groupe lisse, affine et connexe
![]() $G_{\eta _p}$
est pseudo-réductif, quasi-déployé et son système de racines relatif s’identifie à
$G_{\eta _p}$
est pseudo-réductif, quasi-déployé et son système de racines relatif s’identifie à
![]() $\Phi _G$
. De plus, les
$\Phi _G$
. De plus, les
![]() $\eta _p$
-fibres des isomorphismes
$\eta _p$
-fibres des isomorphismes
![]() $x_a$
définissent un quasi-système de Tits.
$x_a$
définissent un quasi-système de Tits.
La notion de quasi-système de Tits n’a été pas définie pour les groupes pseudo-réductifs exotiques ou barcelonais, la raison étant que pour ces groupes il n’a aucun sens a priori de distinguer entre quasi-systèmes de Tits et de Chevalley, voir [Reference LourençoLou21, déf. 2.4]. On pourrait alors prendre l’énoncé en petites caractéristiques comme définition même.
Démonstration. Par construction avec les lois birationnelles, l’on a une suite de sous-groupes fermés
![]() $\underline {S} \subset \underline {T} \subset \underline {B} \subset \underline {G}$
lisses et connexes. On voit que les fibrés vectoriels
$\underline {S} \subset \underline {T} \subset \underline {B} \subset \underline {G}$
lisses et connexes. On voit que les fibrés vectoriels
![]() $\operatorname {Lie}\underline {T}$
resp.
$\operatorname {Lie}\underline {T}$
resp.
![]() $\operatorname {Lie}\underline {U_a}$
ne sont que les espaces propres à poids nul resp. non nul pour l’action de
$\operatorname {Lie}\underline {U_a}$
ne sont que les espaces propres à poids nul resp. non nul pour l’action de
![]() $\underline {S}$
sur
$\underline {S}$
sur
![]() $\operatorname {Lie}\,\underline {G}$
. En particulier, cela caractérise uniquement leurs fibres
$\operatorname {Lie}\,\underline {G}$
. En particulier, cela caractérise uniquement leurs fibres
![]() $S_{\eta _p} \subset T_{\eta _p} \subset B_{\eta _p} \subset G_{\eta _p}$
comme sous-groupes fermés de
$S_{\eta _p} \subset T_{\eta _p} \subset B_{\eta _p} \subset G_{\eta _p}$
comme sous-groupes fermés de
![]() $G_{\eta _p}$
par le th. 3.1.3 - l’assertion cruciale reste valable plus généralement pour les groupes lisses, affines et connexes.
$G_{\eta _p}$
par le th. 3.1.3 - l’assertion cruciale reste valable plus généralement pour les groupes lisses, affines et connexes.
Il suffit donc de montrer, en vertu de [Reference Bruhat and TitsBT84a, 1.1.11] et de [Reference Conrad, Gabber and PrasadCGP15, th. C.2.29], que
![]() $T_{\eta _p}$
est pseudo-réductif (ce qui est manifestement le cas) et que les sous-groupes
$T_{\eta _p}$
est pseudo-réductif (ce qui est manifestement le cas) et que les sous-groupes
![]() $G_{a,\eta _p}$
engendrés par
$G_{a,\eta _p}$
engendrés par
![]() $C_{a,\eta _p}$
sont pseudo-réductifs. Autrement dit, on peut supposer G de rang relatif
$C_{a,\eta _p}$
sont pseudo-réductifs. Autrement dit, on peut supposer G de rang relatif
![]() $1$
, et même simplement connexe, en faisant usage des z-extensions. En effet, comme G résulte de
$1$
, et même simplement connexe, en faisant usage des z-extensions. En effet, comme G résulte de
![]() $G^{\operatorname {sc}}$
par modification centrale, cf. (2.4.4), alors les lois birationnelles fournissent un isomorphisme de
$G^{\operatorname {sc}}$
par modification centrale, cf. (2.4.4), alors les lois birationnelles fournissent un isomorphisme de
![]() $\mathbb {Z}[t^{\pm 1}]$
-groupes :
$\mathbb {Z}[t^{\pm 1}]$
-groupes :
d’où le fait que
![]() $G_{\eta _p}$
soit un modifié central de
$G_{\eta _p}$
soit un modifié central de
![]() $G^{\operatorname {sc}}_{\eta _p}$
par le groupe commutatif pseudo-réductif
$G^{\operatorname {sc}}_{\eta _p}$
par le groupe commutatif pseudo-réductif
![]() $T_{\eta _p}$
, ramenant l’assertion au cas où G est simplement connexe.
$T_{\eta _p}$
, ramenant l’assertion au cas où G est simplement connexe.
Supposons que
![]() $G=\operatorname {R}_{\mathbb {Q}(t_a)/\mathbb {Q}(t)}\operatorname {SL}_2$
ou que
$G=\operatorname {R}_{\mathbb {Q}(t_a)/\mathbb {Q}(t)}\operatorname {SL}_2$
ou que
![]() $p \neq 2$
et
$p \neq 2$
et
![]() $G=\operatorname {R}_{\mathbb {Q}(t_{2a})/\mathbb {Q}(t)}\operatorname {SU}_{3,\mathbb {Q}(t_a)/\mathbb {Q}(t_{2a})}$
. Alors, on sait déjà que
$G=\operatorname {R}_{\mathbb {Q}(t_{2a})/\mathbb {Q}(t)}\operatorname {SU}_{3,\mathbb {Q}(t_a)/\mathbb {Q}(t_{2a})}$
. Alors, on sait déjà que
![]() $G_{\eta _p}=\operatorname {R}_{\mathbb {F}_p(t_a)/\mathbb {F}_p(t)}\operatorname {SL}_2$
ou que
$G_{\eta _p}=\operatorname {R}_{\mathbb {F}_p(t_a)/\mathbb {F}_p(t)}\operatorname {SL}_2$
ou que
![]() $G_{\eta _p}=\operatorname {R}_{\mathbb {F}_p(t_{2a})/\mathbb {F}_p(t)}\operatorname {SU}_{3,\mathbb {F}_p(t_{2a})/\mathbb {F}_p(t_a)}$
sont pseudo-réductifs, voir la rem. 3.3.6. Si
$G_{\eta _p}=\operatorname {R}_{\mathbb {F}_p(t_{2a})/\mathbb {F}_p(t)}\operatorname {SU}_{3,\mathbb {F}_p(t_{2a})/\mathbb {F}_p(t_a)}$
sont pseudo-réductifs, voir la rem. 3.3.6. Si
![]() $p=2$
et
$p=2$
et
![]() $G=\operatorname {R}_{\mathbb {Q}(t_{2a})/\mathbb {Q}(t)}\operatorname {SU}_{3,\mathbb {Q}(t_a)/\mathbb {Q}(t_{2a})}$
, alors (3.3.20) et (3.3.21) se simplifient en caractéristique
$G=\operatorname {R}_{\mathbb {Q}(t_{2a})/\mathbb {Q}(t)}\operatorname {SU}_{3,\mathbb {Q}(t_a)/\mathbb {Q}(t_{2a})}$
, alors (3.3.20) et (3.3.21) se simplifient en caractéristique
![]() $2$
comme suit :
$2$
comme suit :
et
ce qui coïncide avec (3.3.18) et (3.3.19) pour le couple
![]() $(s(u,v),s(u',v'))$
. Par suite, notre loi birationnelle dans la grosse cellule
$(s(u,v),s(u',v'))$
. Par suite, notre loi birationnelle dans la grosse cellule
![]() $C_{\eta _2} \subset G_{\eta _2}$
coïncide avec celle du groupe barcelonais de rang relatif
$C_{\eta _2} \subset G_{\eta _2}$
coïncide avec celle du groupe barcelonais de rang relatif
![]() $1$
et de dimension
$1$
et de dimension
![]() $\dim G$
, voir ex. 3.1.7.
$\dim G$
, voir ex. 3.1.7.
Enfin, pour que les isomorphismes donnés
![]() $x_a$
constituent un quasi-système de Tits, il faut essentiellement remarquer que les
$x_a$
constituent un quasi-système de Tits, il faut essentiellement remarquer que les
![]() $m_b$
permutent les classes de similitude des
$m_b$
permutent les classes de similitude des
![]() $x_a$
pour toutes racines non divisibles
$x_a$
pour toutes racines non divisibles
![]() $a,b \in \Phi _G^{\operatorname {nd}}$
. Cela résulte par densité de l’assertion correspondante dans la fibre générique, c’est-à-dire pour G, donc remplie grâce au lem. 2.3.5.
$a,b \in \Phi _G^{\operatorname {nd}}$
. Cela résulte par densité de l’assertion correspondante dans la fibre générique, c’est-à-dire pour G, donc remplie grâce au lem. 2.3.5.
Remarque 3.3.8. Être pseudo-réductif n’est pas une condition géométrique et donc n’admet aucune formulation relative en familles qui soit pratique. En particulier, on peut montrer facilement que, si e est un choix minimal d’entier tel que l’extension
![]() $\mathbb {Q}(\zeta _e,t^{1/e})/\mathbb {Q}(t)$
déploie G, alors
$\mathbb {Q}(\zeta _e,t^{1/e})/\mathbb {Q}(t)$
déploie G, alors
![]() $G_{\eta _p}$
n’est pas réductif pour tout p divisant e, et tous les autres fibres du
$G_{\eta _p}$
n’est pas réductif pour tout p divisant e, et tous les autres fibres du
![]() $\mathbb {F}_p[t^{\pm 1}]$
-groupe
$\mathbb {F}_p[t^{\pm 1}]$
-groupe
![]() $G_p$
ont un radical unipotent non trivial sur
$G_p$
ont un radical unipotent non trivial sur
![]() $\mathbb {F}_p$
. Cependant, nous verrons dans la suite, cf. prop. 5.1.4, que
$\mathbb {F}_p$
. Cependant, nous verrons dans la suite, cf. prop. 5.1.4, que
![]() $G_p$
possède une structure arithmétique assez remarquable, étant un modèle parahorique spécial de sa fibre générique.
$G_p$
possède une structure arithmétique assez remarquable, étant un modèle parahorique spécial de sa fibre générique.
Parfois il sera plus commode d’avoir une description plus concise et explicite du groupe de Tits
![]() $\underline {G}$
en fonction de
$\underline {G}$
en fonction de
![]() $\operatorname {R}_{\mathbb {Z}[\zeta _e,t^{\pm 1/e}]/\mathbb {Z}[t^{\pm 1}]} H$
, où H est vu comme
$\operatorname {R}_{\mathbb {Z}[\zeta _e,t^{\pm 1/e}]/\mathbb {Z}[t^{\pm 1}]} H$
, où H est vu comme
![]() $\mathbb {Z}$
-groupe épinglé au moyen des épinglages
$\mathbb {Z}$
-groupe épinglé au moyen des épinglages
![]() $y_\alpha $
du système de Tits associé.
$y_\alpha $
du système de Tits associé.
Proposition 3.3.9. On a une immersion fermée naturelle
![]() $\underline {G}\rightarrow \operatorname {R}_{\mathbb {Z}[\zeta _e,t^{\pm 1/e}]/\mathbb {Z}[t^{\pm 1}]} H$
prolongeant l’application générique. En particulier,
$\underline {G}\rightarrow \operatorname {R}_{\mathbb {Z}[\zeta _e,t^{\pm 1/e}]/\mathbb {Z}[t^{\pm 1}]} H$
prolongeant l’application générique. En particulier,
![]() $\underline {G}$
est affine sur
$\underline {G}$
est affine sur
![]() $\mathbb {G}_{m,\mathbb {Z}}$
.
$\mathbb {G}_{m,\mathbb {Z}}$
.
Commentons également un truc qui s’avère très utile dans certaines situations. Si on se contente de construire le schéma en groupes
![]() $\underline {G}$
au-dessus de
$\underline {G}$
au-dessus de
![]() $\mathbb {Z}[\zeta _e,t^{\pm 1}]$
, alors l’extension de déploiement (générique)
$\mathbb {Z}[\zeta _e,t^{\pm 1}]$
, alors l’extension de déploiement (générique)
![]() $\mathbb {Z}[\zeta _e,t^{\pm 1}] \rightarrow \mathbb {Z}[\zeta _e,t^{\pm 1/e}]$
devient cyclique, et on peut substituer le groupe cyclique
$\mathbb {Z}[\zeta _e,t^{\pm 1}] \rightarrow \mathbb {Z}[\zeta _e,t^{\pm 1/e}]$
devient cyclique, et on peut substituer le groupe cyclique
![]() $\Gamma _0$
à son sur-groupe
$\Gamma _0$
à son sur-groupe
![]() $\Gamma $
. Par la même argumentation ci-dessous, on arrive à réaliser
$\Gamma $
. Par la même argumentation ci-dessous, on arrive à réaliser
![]() $\underline {G}\otimes \mathbb {Z}[\zeta _e]$
comme sous-groupe fermé de
$\underline {G}\otimes \mathbb {Z}[\zeta _e]$
comme sous-groupe fermé de
![]() $\operatorname {R}_{\mathbb {Z}[\zeta _e, t^{\pm 1/e}]/\mathbb {Z}[\zeta _e,t^{\pm 1}]} H$
contenu dans les
$\operatorname {R}_{\mathbb {Z}[\zeta _e, t^{\pm 1/e}]/\mathbb {Z}[\zeta _e,t^{\pm 1}]} H$
contenu dans les
![]() $\Gamma _0$
-invariants.
$\Gamma _0$
-invariants.
Démonstration. Montrons tout d’abord que les applications restreintes aux tores
resp. aux sous-groupes radiciels
si
![]() $a\in \Phi _G$
n’est ni divisible ni multipliable, et
$a\in \Phi _G$
n’est ni divisible ni multipliable, et
 $$ \begin{align}\underline{U_a} \rightarrow \prod_{\{\gamma\alpha,\gamma\beta\}} \operatorname{R}_{\mathbb{Z}[\zeta_e,t^{\pm 1/e}]/\mathbb{Z}[t^{\pm 1}]}U_{H,\gamma\alpha} U_{H,\gamma(\alpha+\beta)}U_{H,\gamma\beta}\end{align} $$
$$ \begin{align}\underline{U_a} \rightarrow \prod_{\{\gamma\alpha,\gamma\beta\}} \operatorname{R}_{\mathbb{Z}[\zeta_e,t^{\pm 1/e}]/\mathbb{Z}[t^{\pm 1}]}U_{H,\gamma\alpha} U_{H,\gamma(\alpha+\beta)}U_{H,\gamma\beta}\end{align} $$
si
![]() $a \in \Phi _G^{\operatorname {m}}$
est multipliable, sont des immersions fermées. Le cas du centralisateur résulte de ce que les modèles de Néron connexes des tores induits sont leurs modèles canoniques, cf. [Reference Bruhat and TitsBT84a, 4.4.6, 4.4.8]. À son tour, le cas des sous-groupes radiciels est une conséquence des calculs supprimés du lem. 2.3.5.
$a \in \Phi _G^{\operatorname {m}}$
est multipliable, sont des immersions fermées. Le cas du centralisateur résulte de ce que les modèles de Néron connexes des tores induits sont leurs modèles canoniques, cf. [Reference Bruhat and TitsBT84a, 4.4.6, 4.4.8]. À son tour, le cas des sous-groupes radiciels est une conséquence des calculs supprimés du lem. 2.3.5.
Par suite, la [Reference Bruhat and TitsBT84a, prop. 2.2.10] entraîne que l’application naturelle
est une immersion localement fermée. Soit
![]() $\widehat {\mathbb {Z}[t]}_{(p)}$
le séparé complété du localisé de
$\widehat {\mathbb {Z}[t]}_{(p)}$
le séparé complété du localisé de
![]() $\mathbb {Z}[t]$
dans l’idéal premier
$\mathbb {Z}[t]$
dans l’idéal premier
![]() $(p)$
: il s’agit d’un anneau de valuation discrète à uniformisante p et à corps résiduel
$(p)$
: il s’agit d’un anneau de valuation discrète à uniformisante p et à corps résiduel
![]() $\mathbb {F}_p(t)$
. L’image schématique du groupe parahorique spécial
$\mathbb {F}_p(t)$
. L’image schématique du groupe parahorique spécial
![]() $\underline {G} \otimes \widehat {\mathbb {Z}[t]}_{(p)}$
dans la restriction des scalaires correspondante de
$\underline {G} \otimes \widehat {\mathbb {Z}[t]}_{(p)}$
dans la restriction des scalaires correspondante de
![]() $ H$
est un sous-groupe fermé, affine et lisse, dont la composante neutre reste égale, d’où l’égalité par [Reference Bruhat and TitsBT84a, prop. 4.6.21].
$ H$
est un sous-groupe fermé, affine et lisse, dont la composante neutre reste égale, d’où l’égalité par [Reference Bruhat and TitsBT84a, prop. 4.6.21].
En particulier, la propriété d’être une immersion fermée se propage à un ouvert cofini U de
![]() $\operatorname {Spec} \mathbb {Z}[t^{\pm 1}]$
. Pour conclure, il ne reste qu’à appliquer le lemme ci-dessous concernant l’existence d’une opération tordue fonctorielle de
$\operatorname {Spec} \mathbb {Z}[t^{\pm 1}]$
. Pour conclure, il ne reste qu’à appliquer le lemme ci-dessous concernant l’existence d’une opération tordue fonctorielle de
![]() $\mathbb {G}_{m,\mathbb {Z}[t^{\pm 1}]}$
sur
$\mathbb {G}_{m,\mathbb {Z}[t^{\pm 1}]}$
sur
![]() $\underline {G}$
et sur
$\underline {G}$
et sur
![]() $\operatorname {R}_{\mathbb {Z}[\zeta _et^{1/e}]/\mathbb {Z}[t]} H$
. En effet, cette action relève celle de la e-ième puissance sur
$\operatorname {R}_{\mathbb {Z}[\zeta _et^{1/e}]/\mathbb {Z}[t]} H$
. En effet, cette action relève celle de la e-ième puissance sur
![]() $\operatorname {Spec} \mathbb {Z}[t^{\pm 1}]$
, dont les translatés de U recouvrent tout le spectre.
$\operatorname {Spec} \mathbb {Z}[t^{\pm 1}]$
, dont les translatés de U recouvrent tout le spectre.
Ce lemme a joué un rôle important dans la fin de la démonstration précédente.
Lemme 3.3.10. L’action e-ième puissance de
![]() $\mathbb {G}_{m,\mathbb {Z}}$
sur soi-même se relève en une action tordue sur le
$\mathbb {G}_{m,\mathbb {Z}}$
sur soi-même se relève en une action tordue sur le
![]() $\mathbb {G}_{m,\mathbb {Z}}$
-groupe
$\mathbb {G}_{m,\mathbb {Z}}$
-groupe
![]() $\underline {G}$
.
$\underline {G}$
.
Démonstration. Voyons que la e-puissance définit une opération
![]() $\mathbb {G}_{m,\mathbb {Z}} \times \mathbb {G}_{m,\mathbb {Z}} \rightarrow \mathbb {G}_{m,\mathbb {Z}}$
donnée par
$\mathbb {G}_{m,\mathbb {Z}} \times \mathbb {G}_{m,\mathbb {Z}} \rightarrow \mathbb {G}_{m,\mathbb {Z}}$
donnée par
![]() $(r,t)\mapsto r^et$
. Considérons maintenant le
$(r,t)\mapsto r^et$
. Considérons maintenant le
![]() $\mathbb {G}_{m,\mathbb {Z}}$
-groupe
$\mathbb {G}_{m,\mathbb {Z}}$
-groupe
![]() $\operatorname {R}_{\mathbb {Z}[t^{\pm 1/d}]/\mathbb {Z}[t^{\pm 1}]}\mathbb {G}_{a}$
classifiant des éléments
$\operatorname {R}_{\mathbb {Z}[t^{\pm 1/d}]/\mathbb {Z}[t^{\pm 1}]}\mathbb {G}_{a}$
classifiant des éléments
![]() $a \in R[t^{1/d}]$
. Alors, la correspondance
$a \in R[t^{1/d}]$
. Alors, la correspondance
![]() $(r,t,a) \mapsto (r^et,a)$
en détermine un relèvement de l’opération puissance. La même écriture marche aussi pour les restrictions des scalaires du groupe multiplicatif
$(r,t,a) \mapsto (r^et,a)$
en détermine un relèvement de l’opération puissance. La même écriture marche aussi pour les restrictions des scalaires du groupe multiplicatif
![]() $\mathbb {G}_m$
et du groupe unipotent pluriel
$\mathbb {G}_m$
et du groupe unipotent pluriel
![]() $\mathbb {G}_p$
. Finalement, nous laissons au lecteur le soin de vérifier que cette action préserve les morphismes des axiomes des données radicielles schématiques – voir la déf. 3.2.1 et les formules de la preuve de la prop. 3.3.4 – d’où son prolongement à
$\mathbb {G}_p$
. Finalement, nous laissons au lecteur le soin de vérifier que cette action préserve les morphismes des axiomes des données radicielles schématiques – voir la déf. 3.2.1 et les formules de la preuve de la prop. 3.3.4 – d’où son prolongement à
![]() $\underline {G}$
par fonctorialité du th. 3.2.4.
$\underline {G}$
par fonctorialité du th. 3.2.4.
Dans la version précédente de l’article, nous avons démontré par un calcul presque direct que, au cas où G est absolument simple et simplement connexe à système de racines
![]() $\Phi _G$
réduit, la fibre générique
$\Phi _G$
réduit, la fibre générique
![]() $G_{\eta _e}$
était pseudo-réductive exotique basique. Voici le raisonnement :
$G_{\eta _e}$
était pseudo-réductive exotique basique. Voici le raisonnement :
Exemple 3.3.11. Supposons que G est absolument simple, simplement connexe et non déployé à système de racines
![]() $\Phi _G$
réduit et que
$\Phi _G$
réduit et que
![]() $e\leq 3$
. Grâce à la prop. 3.3.9, on a une immersion fermée
$e\leq 3$
. Grâce à la prop. 3.3.9, on a une immersion fermée
Vu que la partie galoisienne de l’opération de
![]() $\Gamma _0$
sur cette restriction des scalaires s’évapore tout simplement en caractéristique e, le membre de droite s’écrit comme
$\Gamma _0$
sur cette restriction des scalaires s’évapore tout simplement en caractéristique e, le membre de droite s’écrit comme
![]() $\operatorname {R}_{\mathbb {F}_e(t^{1/e})/\mathbb {F}_e(t)} H^{\Gamma _0}$
, où
$\operatorname {R}_{\mathbb {F}_e(t^{1/e})/\mathbb {F}_e(t)} H^{\Gamma _0}$
, où
![]() $\Gamma _0$
opère par
$\Gamma _0$
opère par
![]() $\mathbb {F}_e$
-automorphismes de Dynkin sur le
$\mathbb {F}_e$
-automorphismes de Dynkin sur le
![]() $\mathbb {F}_e$
-groupe épinglé H.
$\mathbb {F}_e$
-groupe épinglé H.
D’après Steinberg, cf. [Reference SteinbergSt68, th. 8.2] et [Reference HainesHai18, prop. 5.1], le groupe algébrique
![]() $H^{\Gamma _0}$
est lisse, connexe, semi-simple, absolument presque simple et simplement connexe déployé à système de racines
$H^{\Gamma _0}$
est lisse, connexe, semi-simple, absolument presque simple et simplement connexe déployé à système de racines
![]() $\Phi _G$
ayant
$\Phi _G$
ayant
![]() $T^{\Gamma _0}$
comme
$T^{\Gamma _0}$
comme
![]() $\mathbb {F}_e$
-tore maximal. Ce tore se décompose en produit de groupes multiplicatifs
$\mathbb {F}_e$
-tore maximal. Ce tore se décompose en produit de groupes multiplicatifs
![]() $\mathbb {G}_m$
numérotés par les racines simples
$\mathbb {G}_m$
numérotés par les racines simples
![]() $a \in \Delta _G$
et donnés par les formules
$a \in \Delta _G$
et donnés par les formules
Ses groupes radiciels numérotés par
![]() $a \in \Phi _G$
sont égaux à
$a \in \Phi _G$
sont égaux à
![]() $(\prod _{\gamma \alpha } U_{\gamma \alpha })^{\Gamma _0}$
et donnés par les épinglages
$(\prod _{\gamma \alpha } U_{\gamma \alpha })^{\Gamma _0}$
et donnés par les épinglages
qui forment un
![]() $\mathbb {F}_e$
-système de Chevalley, comme on vérifie aisément. Alors, il suffit de remarquer que ces applications sont naturellement compatibles avec celles du quasi-système de Tits de G, donc le
$\mathbb {F}_e$
-système de Chevalley, comme on vérifie aisément. Alors, il suffit de remarquer que ces applications sont naturellement compatibles avec celles du quasi-système de Tits de G, donc le
![]() $\mathbb {F}_e(t)$
-groupe
$\mathbb {F}_e(t)$
-groupe
![]() $G_{\eta _e}$
s’identifie au seul
$G_{\eta _e}$
s’identifie au seul
![]() $\mathbb {F}_e(t)$
-groupe pseudo-réductif exotique basique à système de racines
$\mathbb {F}_e(t)$
-groupe pseudo-réductif exotique basique à système de racines
![]() $\Phi _G$
de l’ex. 3.1.6, compte tenu de l’unicité des solutions aux lois birationnelles, cf. th. 3.2.4.
$\Phi _G$
de l’ex. 3.1.6, compte tenu de l’unicité des solutions aux lois birationnelles, cf. th. 3.2.4.
3.4 Modèles en groupes immobiliers sur
 $\mathbb {A}_{\mathbb {Z}}^1$
$\mathbb {A}_{\mathbb {Z}}^1$
Dans ce numéro, nous allons introduire les
![]() $\mathbb {A}_{\mathbb {Z}}^1$
-modèles en groupes immobiliers
$\mathbb {A}_{\mathbb {Z}}^1$
-modèles en groupes immobiliers
![]() $\underline {\mathscr {G}_{ \Omega }}$
, voir la déf. 3.4.6, des groupes de Tits
$\underline {\mathscr {G}_{ \Omega }}$
, voir la déf. 3.4.6, des groupes de Tits
![]() $\underline {G}$
, voir la déf. 3.3.5. Au-dessus de
$\underline {G}$
, voir la déf. 3.3.5. Au-dessus de
![]() $\mathbb {Z}[1/e]$
, ces groupes avaient été découverts par Pappas–Rapoport dans le cas simplement connexe, voir [Reference Pappas and RapoportPR08, 7.a, (7.2)], puis définis plus généralement par Pappas–Zhu, voir [Reference Pappas and ZhuPZ13, th. 4.1]. Notre gros résultat est celui de l’affinité du modèle immobilier
$\mathbb {Z}[1/e]$
, ces groupes avaient été découverts par Pappas–Rapoport dans le cas simplement connexe, voir [Reference Pappas and RapoportPR08, 7.a, (7.2)], puis définis plus généralement par Pappas–Zhu, voir [Reference Pappas and ZhuPZ13, th. 4.1]. Notre gros résultat est celui de l’affinité du modèle immobilier
![]() $\underline {\mathscr {G}_{ \Omega }}$
, voir le th. 3.4.10, lequel résulte d’une approche radicalement différente de celle de Pappas–Rapoport–Zhu, en faisant justement usage des propriétés combinatoires élémentaires, cf. prop. 3.4.1, et de la lissité de l’enveloppe affine, cf. prop. 3.2.7.
$\underline {\mathscr {G}_{ \Omega }}$
, voir le th. 3.4.10, lequel résulte d’une approche radicalement différente de celle de Pappas–Rapoport–Zhu, en faisant justement usage des propriétés combinatoires élémentaires, cf. prop. 3.4.1, et de la lissité de l’enveloppe affine, cf. prop. 3.2.7.
Avant de définir les données radicielles schématiques, on a besoin du lemme suivant sur la combinatoire des
![]() $\mathbb {F}_p (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) $
-groupes déduits de
$\mathbb {F}_p (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) $
-groupes déduits de
![]() $\underline {G}$
par changement de base, en variant la caractéristique p.
$\underline {G}$
par changement de base, en variant la caractéristique p.
Proposition 3.4.1. Il existent des bijections canoniques entre les différents appartements
![]() $\mathscr {A}(G_{\eta _p},S_{\eta _p},\mathbb {F}_p (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
, pour toute caractéristique
$\mathscr {A}(G_{\eta _p},S_{\eta _p},\mathbb {F}_p (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
, pour toute caractéristique
![]() $p \in \mathbb {P} \cup \{0\}$
, invariantes par l’action des groupes d’Iwahori–Weyl.
$p \in \mathbb {P} \cup \{0\}$
, invariantes par l’action des groupes d’Iwahori–Weyl.
Démonstration. Identifions d’abord les groupes d’Iwahori–Weyl
![]() $\widetilde {W}_p$
de
$\widetilde {W}_p$
de
![]() $G_{\eta _p}$
par rapport à
$G_{\eta _p}$
par rapport à
![]() $S_{\eta _p}$
en caractéristiques différentes. Soit
$S_{\eta _p}$
en caractéristiques différentes. Soit
![]() $\underline {N}$
le normalisateur de
$\underline {N}$
le normalisateur de
![]() $\underline {S}$
dans
$\underline {S}$
dans
![]() $\underline {G}$
, qui en est un
$\underline {G}$
, qui en est un
![]() $\mathbb {Z}[t^{\pm 1}]$
-sous-groupe fermé affine et lisse, comme l’affirme [SGA3, exp. XI, cor. 5.3 bis]. Posons
$\mathbb {Z}[t^{\pm 1}]$
-sous-groupe fermé affine et lisse, comme l’affirme [SGA3, exp. XI, cor. 5.3 bis]. Posons
 $$ \begin{align}\underline{\mathscr{T}}:=\prod_{j\in J}\operatorname{R}_{\mathbb{Z}[t^{1/d_j}]/\mathbb{Z}[t]}\mathbb{G}_{m} \end{align} $$
$$ \begin{align}\underline{\mathscr{T}}:=\prod_{j\in J}\operatorname{R}_{\mathbb{Z}[t^{1/d_j}]/\mathbb{Z}[t]}\mathbb{G}_{m} \end{align} $$
le modèle de Néron connexe de T sur
![]() $\mathbb {Z}[t]$
. On montre que l’homomorphisme de groupes naturel
$\mathbb {Z}[t]$
. On montre que l’homomorphisme de groupes naturel
est toujours bijectif, ce qui fournira par zig-zag l’isomorphisme cherché. Le lemme de la serpente nous permet de traiter distinctement les sous-groupes des translations
et les quotients des transformations vectorielles
On voit que le cas des translations est trivial, en calculant explicitement avec la décomposition (3.4.1), ce qui revient au même de dire que la valuation t-adique est indépendante des coefficients.
Maintenant, on se penche sur la partie des transformations vectorielles. Vu que
![]() $\underline {T} \rightarrow \underline {N}$
est une immersion fermée, l’application (3.4.4) est injective en caractéristique nulle
$\underline {T} \rightarrow \underline {N}$
est une immersion fermée, l’application (3.4.4) est injective en caractéristique nulle
![]() $p=0$
. D’autre part, les éléments
$p=0$
. D’autre part, les éléments
![]() $m_a$
du normalisateur qu’on avait évoqués à (2.3.11) et (2.3.12) sont définis sur
$m_a$
du normalisateur qu’on avait évoqués à (2.3.11) et (2.3.12) sont définis sur
![]() $\mathbb {Z}[t^{\pm 1}]$
, voir la preuve de la prop. 3.3.4, et y induisent les réflexions
$\mathbb {Z}[t^{\pm 1}]$
, voir la preuve de la prop. 3.3.4, et y induisent les réflexions
![]() $s_a$
du groupe de Weyl de
$s_a$
du groupe de Weyl de
![]() $\Phi _G$
. Par suite, les applications de (3.4.4) sont même bijectives pour tout premier p, comme il suit d’une comparaison d’ordres.
$\Phi _G$
. Par suite, les applications de (3.4.4) sont même bijectives pour tout premier p, comme il suit d’une comparaison d’ordres.
Maintenant, on peut définir une valuation
![]() $\varphi _p \in \mathscr {A}(G_{\eta _p}, S_{\eta _p}, \mathbb {F}_p (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
, pour chaque caractéristique
$\varphi _p \in \mathscr {A}(G_{\eta _p}, S_{\eta _p}, \mathbb {F}_p (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
, pour chaque caractéristique
![]() $p \in \mathbb {P} \cup \{0\}$
, en termes du quasi-système de Tits naturel de
$p \in \mathbb {P} \cup \{0\}$
, en termes du quasi-système de Tits naturel de
![]() $G_{\eta _p}$
, cf. prop. 3.3.7, de la manière suivante :
$G_{\eta _p}$
, cf. prop. 3.3.7, de la manière suivante :
où la valuation additive t-adique
![]() $\omega _p: \mathbb {F}_p (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) ^{\operatorname {alg}}\rightarrow \mathbb {R}$
est déterminée uniquement par la contrainte
$\omega _p: \mathbb {F}_p (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) ^{\operatorname {alg}}\rightarrow \mathbb {R}$
est déterminée uniquement par la contrainte
![]() $\omega _p(t)=1$
, comp. avec la valuation de [Reference LourençoLou21, déf. 3.1] donnée par (3.1.12), (3.1.13) et (3.1.14).
$\omega _p(t)=1$
, comp. avec la valuation de [Reference LourençoLou21, déf. 3.1] donnée par (3.1.12), (3.1.13) et (3.1.14).
La prochaine étape consiste à identifier les appartements
![]() $\mathscr {A}(G_{\eta _p},S_{\eta _p},\mathbb {F}_p (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
de façon équivariante. En choisissant
$\mathscr {A}(G_{\eta _p},S_{\eta _p},\mathbb {F}_p (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
de façon équivariante. En choisissant
![]() $\varphi _p$
pour origine de cet appartement, il ne devient autre que le sous-
$\varphi _p$
pour origine de cet appartement, il ne devient autre que le sous-
![]() $\mathbb {R}$
-espace vectoriel de
$\mathbb {R}$
-espace vectoriel de
![]() $X_*(S_{\eta _p}) \otimes _{\mathbb {Z}}{\mathbb {R}}$
engendré par les coracines
$X_*(S_{\eta _p}) \otimes _{\mathbb {Z}}{\mathbb {R}}$
engendré par les coracines
![]() $\Phi _G^\vee $
, d’où en particulier des isomorphismes
$\Phi _G^\vee $
, d’où en particulier des isomorphismes
pour toute paire de caractéristiques
![]() $p,q \in \mathbb {P} \cup \{0\}$
. Il est aisé de voir que cette identification fait correspondre les racines affines de chaque appartement ainsi que leurs échelonnages, voir [Reference LourençoLou21, déf. 3.3].
$p,q \in \mathbb {P} \cup \{0\}$
. Il est aisé de voir que cette identification fait correspondre les racines affines de chaque appartement ainsi que leurs échelonnages, voir [Reference LourençoLou21, déf. 3.3].
Démontrons enfin l’équivariance de l’isomorphisme donné par (3.4.7), qu’il suffit de la vérifier pour une partie génératrice. Pour les translations l’assertion devient évidente, vu que
![]() $z \in T_{\eta _p}(\mathbb {F}_p (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
opère par la translation par le vecteur
$z \in T_{\eta _p}(\mathbb {F}_p (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
opère par la translation par le vecteur
![]() $\nu (z)$
tel que
$\nu (z)$
tel que
![]() $a(\nu (z))=-\omega _p(a(z)) $
, voir [Reference Bruhat and TitsBT84a, 4.2.7], et que la valuation t-adique est indépendante de la caractéristique, voir (3.4.3). Les classes des
$a(\nu (z))=-\omega _p(a(z)) $
, voir [Reference Bruhat and TitsBT84a, 4.2.7], et que la valuation t-adique est indépendante de la caractéristique, voir (3.4.3). Les classes des
![]() $m_a \in \underline {N}(\mathbb {Z}[t^{\pm 1}])$
à leur tour opèrent par des réflexions correspondantes
$m_a \in \underline {N}(\mathbb {Z}[t^{\pm 1}])$
à leur tour opèrent par des réflexions correspondantes
![]() $s_a$
du groupe de Weyl fixant l’origine.
$s_a$
du groupe de Weyl fixant l’origine.
Remarque 3.4.2. Il y a d’autres changements de base intéressants qu’on avait étudiés plus soigneusement dans la version précédente de cet article.
-
1. Soient
 $e=2,3$
,
$e=2,3$
,
 $G=G^{\operatorname {sc}}$
absolument simple et simplement connexe à système de racines
$G=G^{\operatorname {sc}}$
absolument simple et simplement connexe à système de racines
 $\Phi _G$
réduit. Pour tout
$\Phi _G$
réduit. Pour tout
 $a \in \overline {\mathbb {F}}_e^{\times }$
, on obtient d’isomorphismes naturels (3.4.8)d’appartements, bien que d’autres structures combinatoires comme les groupes d’Iwahori–Weyl. Cela découle du fait que
$a \in \overline {\mathbb {F}}_e^{\times }$
, on obtient d’isomorphismes naturels (3.4.8)d’appartements, bien que d’autres structures combinatoires comme les groupes d’Iwahori–Weyl. Cela découle du fait que $$ \begin{align}\mathscr{A}(G_{\eta_e}, S_{\eta_e}, \overline{\mathbb{F}}_e (\hspace{-0,7mm}( {t-a} )\hspace{-0,7mm}) ) \simeq \mathscr{A}(G_{\eta_e}, S_{\eta_e}, \mathbb{F}_e (\hspace{-0,7mm}( {t} )\hspace{-0,7mm}) )\end{align} $$
$$ \begin{align}\mathscr{A}(G_{\eta_e}, S_{\eta_e}, \overline{\mathbb{F}}_e (\hspace{-0,7mm}( {t-a} )\hspace{-0,7mm}) ) \simeq \mathscr{A}(G_{\eta_e}, S_{\eta_e}, \mathbb{F}_e (\hspace{-0,7mm}( {t} )\hspace{-0,7mm}) )\end{align} $$
 $G_{\eta _e}$
vienne muni d’un quasi-système de Tits global et que la ramification de
$G_{\eta _e}$
vienne muni d’un quasi-système de Tits global et que la ramification de
 $\mathbb {A}^{1/e}_{\mathbb {F}_e}\rightarrow \mathbb {A}^1_{\mathbb {F}_e}$
soit constante. Toutefois, si l’on essayait de faire le même jeu avec les groupes barcelonais, on se serait heurt à ce que la valuation de
$\mathbb {A}^{1/e}_{\mathbb {F}_e}\rightarrow \mathbb {A}^1_{\mathbb {F}_e}$
soit constante. Toutefois, si l’on essayait de faire le même jeu avec les groupes barcelonais, on se serait heurt à ce que la valuation de
 $t^{1/2}$
ne soit pas constante parmi les diverses places de
$t^{1/2}$
ne soit pas constante parmi les diverses places de
 $\mathbb {A}^1_{\mathbb {F}_e}$
, d’où le besoin de remplacer l’origine de
$\mathbb {A}^1_{\mathbb {F}_e}$
, d’où le besoin de remplacer l’origine de
 $\mathscr {A}(G_{\eta _e}, S_{\eta _e}, \mathbb {F}_e (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
à système de racines résiduel
$\mathscr {A}(G_{\eta _e}, S_{\eta _e}, \mathbb {F}_e (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
à système de racines résiduel
 $\Phi _G^{\operatorname {nd}}$
par un point spécial avec
$\Phi _G^{\operatorname {nd}}$
par un point spécial avec
 $\Phi _G^{\operatorname {nm}}$
pour système de racines résiduel.
$\Phi _G^{\operatorname {nm}}$
pour système de racines résiduel.
-
2. Soient
 $\mathcal {O}$
un anneau de valuation discrète de caractéristique mixte
$\mathcal {O}$
un anneau de valuation discrète de caractéristique mixte
 $(0,p)$
,
$(0,p)$
,
 $\varpi $
une uniformisante de
$\varpi $
une uniformisante de
 $\mathcal {O}$
et K son corps de fraction. Alors, l’on tire aussi un isomorphisme équivariant (3.4.9)d’appartements, où
$\mathcal {O}$
et K son corps de fraction. Alors, l’on tire aussi un isomorphisme équivariant (3.4.9)d’appartements, où $$ \begin{align}\mathscr{A}(\underline{G}\otimes_{\mathbb{Z}[t]} K, \underline{S}\otimes_{\mathbb{Z}[t]} K,K) \simeq \mathscr{A}(G_{\eta_p}, S_{\eta_p}, \mathbb{F}_p (\hspace{-0,7mm}( {t} )\hspace{-0,7mm}) )\end{align} $$
$$ \begin{align}\mathscr{A}(\underline{G}\otimes_{\mathbb{Z}[t]} K, \underline{S}\otimes_{\mathbb{Z}[t]} K,K) \simeq \mathscr{A}(G_{\eta_p}, S_{\eta_p}, \mathbb{F}_p (\hspace{-0,7mm}( {t} )\hspace{-0,7mm}) )\end{align} $$
 $\mathbb {Z}[t]\rightarrow \mathcal {O}$
est le seul homomorphisme qui applique t sur
$\mathbb {Z}[t]\rightarrow \mathcal {O}$
est le seul homomorphisme qui applique t sur
 $\varpi $
; en particulier, l’hypothèse de ramification modérée dans [Reference Pappas and ZhuPZ13, 4.a.2] est inutile. Ce changement de base de type diagonal prend un rôle proéminent dans la théorie des modèles locaux des variétés de Shimura, voir [Reference Pappas and ZhuPZ13, §§8-9] et [Reference Pereira LourençoPL20, IV, §4.1].
$\varpi $
; en particulier, l’hypothèse de ramification modérée dans [Reference Pappas and ZhuPZ13, 4.a.2] est inutile. Ce changement de base de type diagonal prend un rôle proéminent dans la théorie des modèles locaux des variétés de Shimura, voir [Reference Pappas and ZhuPZ13, §§8-9] et [Reference Pereira LourençoPL20, IV, §4.1].
Dorénavant, on fera plusieurs fois l’abus de langage d’écrire
![]() $\mathscr {A}(\underline {G},\underline {S},\mathbb {Z} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
lorsqu’on parle de tous les appartements
$\mathscr {A}(\underline {G},\underline {S},\mathbb {Z} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
lorsqu’on parle de tous les appartements
![]() $\mathscr {A}(G_{\eta _p},S_{\eta _p},\mathbb {F}_p (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
pour
$\mathscr {A}(G_{\eta _p},S_{\eta _p},\mathbb {F}_p (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
pour
![]() $p \in \mathbb {P}\cup \{0\}$
en même temps, identifiés selon (3.4.7). L’information combinatoire qu’on vient de rassembler dans la prop. 3.4.1 nous permettra ainsi d’introduire les
$p \in \mathbb {P}\cup \{0\}$
en même temps, identifiés selon (3.4.7). L’information combinatoire qu’on vient de rassembler dans la prop. 3.4.1 nous permettra ainsi d’introduire les
![]() $\mathbb {A}^1_{\mathbb {Z}}$
-modèles immobiliers
$\mathbb {A}^1_{\mathbb {Z}}$
-modèles immobiliers
![]() $\underline {\mathscr {G}_{ \Omega }}$
, voir la déf. 3.4.6, des
$\underline {\mathscr {G}_{ \Omega }}$
, voir la déf. 3.4.6, des
![]() $\mathbb {G}_{m,\mathbb {Z}}$
-groupes de Tits
$\mathbb {G}_{m,\mathbb {Z}}$
-groupes de Tits
![]() $\underline {G}$
, où
$\underline {G}$
, où
![]() $\Omega $
désigne une partie bornée et non vide de
$\Omega $
désigne une partie bornée et non vide de
![]() $\mathscr {A}(\underline {G},\underline {S},\mathbb {Z} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
.
$\mathscr {A}(\underline {G},\underline {S},\mathbb {Z} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
.
On commence par rappeler la structure de certains modèles entiers lisses et connexes du groupe additif, à la suite de [Reference Bruhat and TitsBT84a, 1.4.1].
Exemple 3.4.3. Soit A un anneau noethérien intègre à corps de fraction K. À chaque idéal fraccionaire
![]() $\mathfrak {a} \subset K$
, on lui associe le modèle en groupes
$\mathfrak {a} \subset K$
, on lui associe le modèle en groupes
![]() $\mathfrak {a} \otimes \mathbb {G}_a$
dont les points à valeurs dans R sont donnés par
$\mathfrak {a} \otimes \mathbb {G}_a$
dont les points à valeurs dans R sont donnés par
![]() $\mathfrak {a} \otimes _A R$
. Autrement dit, quitte à localiser pour que
$\mathfrak {a} \otimes _A R$
. Autrement dit, quitte à localiser pour que
![]() $\mathfrak {a}=(a)$
soit principal, ceci n’est autre que le A-groupe
$\mathfrak {a}=(a)$
soit principal, ceci n’est autre que le A-groupe
![]() $\mathbb {G}_a$
regardé en tant que modèle de
$\mathbb {G}_a$
regardé en tant que modèle de
![]() $\mathbb {G}_{a,K}$
au moyen de
$\mathbb {G}_{a,K}$
au moyen de
![]() $\mathbb {G}_{a,K}\xrightarrow {\cdot a}\mathbb {G}_{a,K}$
.
$\mathbb {G}_{a,K}\xrightarrow {\cdot a}\mathbb {G}_{a,K}$
.
L’étape suivante consiste à définir les données radicielles schématiques, pour lequel il faut introduire un outil combinatoire additionnel. Soient
![]() $\Omega \subset \mathscr {A}(\underline {G},\underline {S},\mathbb {Z} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
une partie non vide et bornée et
$\Omega \subset \mathscr {A}(\underline {G},\underline {S},\mathbb {Z} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
une partie non vide et bornée et
la fonction quasi-concave et optimale attachée à
![]() $\Omega $
, voir [Reference Bruhat and TitsBT84a, 4.6.26]. Notons que
$\Omega $
, voir [Reference Bruhat and TitsBT84a, 4.6.26]. Notons que
![]() $f_\Omega $
dépend aussi du choix de l’origine
$f_\Omega $
dépend aussi du choix de l’origine
![]() $\varphi $
de l’appartement
$\varphi $
de l’appartement
![]() $\mathscr {A}(\underline {G},\underline {S},\mathbb {Z} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
que nous avons introduite à la prop. 3.4.1, cf. (3.4.7).
$\mathscr {A}(\underline {G},\underline {S},\mathbb {Z} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
que nous avons introduite à la prop. 3.4.1, cf. (3.4.7).
Définition 3.4.4. Soient G un
![]() $\mathbb {Q}(t)$
-groupe remplissant l’hyp. 3.3.1,
$\mathbb {Q}(t)$
-groupe remplissant l’hyp. 3.3.1,
![]() $\Omega $
une partie non vide et bornée de l’appartement
$\Omega $
une partie non vide et bornée de l’appartement
![]() $\mathscr {A}(\underline {G},\underline {S},\mathbb {Z} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
et
$\mathscr {A}(\underline {G},\underline {S},\mathbb {Z} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
et
![]() $f_\Omega $
la fonction (3.4.10) définie par (3.4.11). Définissons le modèle
$f_\Omega $
la fonction (3.4.10) définie par (3.4.11). Définissons le modèle
![]() $\underline {\mathscr {T}}$
de
$\underline {\mathscr {T}}$
de
![]() $\underline {T}$
par (3.4.1). Quant aux sous-groupes radiciels, définissons-le par transport de structure le long des quasi-épinglage comme suit :
$\underline {T}$
par (3.4.1). Quant aux sous-groupes radiciels, définissons-le par transport de structure le long des quasi-épinglage comme suit :
lorsque
![]() $a\in \Phi _G^{\operatorname {nd,nm}}$
n’est ni divisible ni multipliable, ou
$a\in \Phi _G^{\operatorname {nd,nm}}$
n’est ni divisible ni multipliable, ou
où
![]() $t^{f_{\Omega }(a),f_{\Omega }(2a)} \mathbb {G}_{p,\mathbb {Z}[t_a]/\mathbb {Z}[t_{2a}]}$
signifie le produit
$t^{f_{\Omega }(a),f_{\Omega }(2a)} \mathbb {G}_{p,\mathbb {Z}[t_a]/\mathbb {Z}[t_{2a}]}$
signifie le produit
![]() $t^{f_\Omega (a)} \mathbb {G}_{a,\mathbb {Z}[t_{a}]} \times t^{f_\Omega (2a)}\mathbb {G}_{a,\mathbb {Z}[t_{2a}]}$
.
$t^{f_\Omega (a)} \mathbb {G}_{a,\mathbb {Z}[t_{a}]} \times t^{f_\Omega (2a)}\mathbb {G}_{a,\mathbb {Z}[t_{2a}]}$
.
Signalons que le
![]() $\mathbb {Z}[t]$
-modèle en groupes
$\mathbb {Z}[t]$
-modèle en groupes
![]() $\underline {\mathscr {U}_{a, \Omega }}$
est bien défini, car
$\underline {\mathscr {U}_{a, \Omega }}$
est bien défini, car
![]() $t^{f_\Omega (a)}$
est une puissance entière de
$t^{f_\Omega (a)}$
est une puissance entière de
![]() $t_a$
. On a fait un abus de langage pareil dans l’écriture de
$t_a$
. On a fait un abus de langage pareil dans l’écriture de
![]() $\underline {\mathscr {U}_{a, \Omega }}$
, lorsque
$\underline {\mathscr {U}_{a, \Omega }}$
, lorsque
![]() $a\in \Phi _G^{\operatorname {m}}$
est multipliable, vu que
$a\in \Phi _G^{\operatorname {m}}$
est multipliable, vu que
![]() $t^{f_\Omega (2a)}$
n’appartient jamais à
$t^{f_\Omega (2a)}$
n’appartient jamais à
![]() $\mathbb {Z}[t_{2a}]$
, mais bien à son complément
$\mathbb {Z}[t_{2a}]$
, mais bien à son complément
![]() $t_a\mathbb {Z}[t_{2a}]$
dans
$t_a\mathbb {Z}[t_{2a}]$
dans
![]() $\mathbb {Z}[t_a]$
. Il faudrait d’ailleurs montrer que la loi de groupe de
$\mathbb {Z}[t_a]$
. Il faudrait d’ailleurs montrer que la loi de groupe de
![]() $\mathbb {G}_{p,\mathbb {Q}(t_{a})/\mathbb {Q}(t_{2a})}$
se prolonge à son modèle entier, ce qui sera vérifié implicitement pendant la preuve de la proposition suivante.
$\mathbb {G}_{p,\mathbb {Q}(t_{a})/\mathbb {Q}(t_{2a})}$
se prolonge à son modèle entier, ce qui sera vérifié implicitement pendant la preuve de la proposition suivante.
Proposition 3.4.5. Les schémas en groupes
![]() $(\underline {\mathscr {T}}, \underline {\mathscr {U}_{a, \Omega }})_{a \in \Phi _G^{\operatorname {nd}}}$
forment une donnée radicielle schématique au-dessus de
$(\underline {\mathscr {T}}, \underline {\mathscr {U}_{a, \Omega }})_{a \in \Phi _G^{\operatorname {nd}}}$
forment une donnée radicielle schématique au-dessus de
![]() $\mathbb {Z}[t]$
prolongeant celle de la prop. 3.3.4.
$\mathbb {Z}[t]$
prolongeant celle de la prop. 3.3.4.
Démonstration. On peut certes démontrer que nos modèles entiers satisfont aux règles de la déf. 3.2.1 par la même procédure de la prop. 3.3.4. Toutefois, il est plus vite d’observer le truc suivant à la Beauville–Laszlo [Reference Beauville and LaszloBL95, th.] : on a l’égalité
pour toute
![]() $\mathbb {Z}[t]$
-algèbre plate A. Cela implique qu’on peut toujours construire des homomorphismes entre de tels anneaux par recollement au-dessus de
$\mathbb {Z}[t]$
-algèbre plate A. Cela implique qu’on peut toujours construire des homomorphismes entre de tels anneaux par recollement au-dessus de
![]() $\mathbb {Z}[t^{\pm 1}]$
et puis
$\mathbb {Z}[t^{\pm 1}]$
et puis
![]() $\mathbb {Q} [\hspace {-0,5mm}[ {t} ]\hspace {-0,5mm}] $
. Par conséquent, on s’est ramené, d’un côté, au cas où t est inversible, ce qui a été déjà réalisé dans la prop. 3.3.4, et d’autre côté, au cas des modèles immobiliers du
$\mathbb {Q} [\hspace {-0,5mm}[ {t} ]\hspace {-0,5mm}] $
. Par conséquent, on s’est ramené, d’un côté, au cas où t est inversible, ce qui a été déjà réalisé dans la prop. 3.3.4, et d’autre côté, au cas des modèles immobiliers du
![]() $\mathbb {Q} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) $
-groupe réductif et connexe
$\mathbb {Q} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) $
-groupe réductif et connexe
![]() $G_{\mathbb {Q} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) }$
, grâce au cor. 3.4.7. Mais ce dernier cas est dû à Bruhat–Tits, cf. [Reference Bruhat and TitsBT84a, th. 4.5.4].
$G_{\mathbb {Q} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) }$
, grâce au cor. 3.4.7. Mais ce dernier cas est dû à Bruhat–Tits, cf. [Reference Bruhat and TitsBT84a, th. 4.5.4].
On peut finalement définir les
![]() $\mathbb {Z}[t]$
-modèles immobiliers
$\mathbb {Z}[t]$
-modèles immobiliers
![]() $\underline {\mathscr {G}_{ \Omega }}$
du groupe de Tits
$\underline {\mathscr {G}_{ \Omega }}$
du groupe de Tits
![]() $\underline {G}$
.
$\underline {G}$
.
Définition 3.4.6. Soit
![]() $\underline {G}$
un
$\underline {G}$
un
![]() $\mathbb {G}_{m,\mathbb {Z}}$
-groupe de Tits, voir la déf. 3.3.5, et
$\mathbb {G}_{m,\mathbb {Z}}$
-groupe de Tits, voir la déf. 3.3.5, et
![]() $\Omega \subset \mathscr {A}( \underline {G},\underline {S},\mathbb {Z} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
une partie non vide et bornée. On leur associe son
$\Omega \subset \mathscr {A}( \underline {G},\underline {S},\mathbb {Z} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
une partie non vide et bornée. On leur associe son
![]() $\mathbb {A}^1_{\mathbb {Z}}$
-modèle immobilier
$\mathbb {A}^1_{\mathbb {Z}}$
-modèle immobilier
![]() $\underline {\mathscr {G}_\Omega }$
déduit du th. 3.2.5 appliqué à la donnée radicielle schématique de la prop. 3.4.5.
$\underline {\mathscr {G}_\Omega }$
déduit du th. 3.2.5 appliqué à la donnée radicielle schématique de la prop. 3.4.5.
Particularisant les schémas en groupes ci-dessus, on obtient à l’évidence ceux de la théorie de Bruhat–Tits pseudo-réductive qu’on avait mentionnée au th. 3.1.8.
Corollaire 3.4.7. Le
![]() $\mathbb {F}_p [\hspace {-0,5mm}[ {t} ]\hspace {-0,5mm}] $
-modèle de
$\mathbb {F}_p [\hspace {-0,5mm}[ {t} ]\hspace {-0,5mm}] $
-modèle de
![]() $G_{\eta _p}$
déduit du
$G_{\eta _p}$
déduit du
![]() $\mathbb {A}_{\mathbb {Z}}^1$
-modèle immobilier
$\mathbb {A}_{\mathbb {Z}}^1$
-modèle immobilier
![]() $\underline {\mathscr {G}_{ \Omega }}$
de la déf. 3.4.6 par le changement de base
$\underline {\mathscr {G}_{ \Omega }}$
de la déf. 3.4.6 par le changement de base
![]() $\mathbb {Z}[t]\rightarrow \mathbb {F}_p [\hspace {-0,5mm}[ {t} ]\hspace {-0,5mm}] $
s’identifie au
$\mathbb {Z}[t]\rightarrow \mathbb {F}_p [\hspace {-0,5mm}[ {t} ]\hspace {-0,5mm}] $
s’identifie au
![]() $\mathbb {F}_p [\hspace {-0,5mm}[ {t} ]\hspace {-0,5mm}] $
-modèle immobilier
$\mathbb {F}_p [\hspace {-0,5mm}[ {t} ]\hspace {-0,5mm}] $
-modèle immobilier
![]() $\mathscr {G}_{\Omega ,p}$
de
$\mathscr {G}_{\Omega ,p}$
de
![]() $G_{\eta _p}$
associé à
$G_{\eta _p}$
associé à
![]() $\Omega \subset \mathscr {A}(G_{\eta _p},S_{\eta _p},\mathbb {F}_p (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
.
$\Omega \subset \mathscr {A}(G_{\eta _p},S_{\eta _p},\mathbb {F}_p (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
.
Démonstration. Il ne suffit que de considérer les termes de la donnée radicielle schématique, cf. déf.3.4.4. Mais si l’on tue p dans les coefficients entiers et complète pour la topologie t-adique, alors on obtient encore le modèle de Néron connexe du centralisateur, voir [Reference Pereira LourençoPL20, prop. 3.3.8], et les stabilisateurs radiciels de
![]() $\Omega $
, voir [Reference Bruhat and TitsBT84a, 4.3.2, 4.3.4] et [Reference LourençoLou21, lem. 4.4], en identifiant celui à une partie convenable de
$\Omega $
, voir [Reference Bruhat and TitsBT84a, 4.3.2, 4.3.4] et [Reference LourençoLou21, lem. 4.4], en identifiant celui à une partie convenable de
![]() $\mathscr {A}(G_{\eta _p},S_{\eta _p},\mathbb {F}_p (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
selon la prop. 3.4.1.
$\mathscr {A}(G_{\eta _p},S_{\eta _p},\mathbb {F}_p (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
selon la prop. 3.4.1.
Enfin, on va relier les
![]() $\mathbb {A}^1_{\mathbb {Z}}$
-modèles immobiliers
$\mathbb {A}^1_{\mathbb {Z}}$
-modèles immobiliers
![]() $\underline {\mathscr {G}_{ \Omega }}$
de G avec ceux de H, tel que l’on avait fait pour leurs groupes de Tits, cf. prop. 3.3.9. On remarque que l’isomorphisme
$\underline {\mathscr {G}_{ \Omega }}$
de G avec ceux de H, tel que l’on avait fait pour leurs groupes de Tits, cf. prop. 3.3.9. On remarque que l’isomorphisme
![]() $G_{\mathbb {Q}(\zeta _e,t^{1/e})} \simeq H$
induit un plongement
$G_{\mathbb {Q}(\zeta _e,t^{1/e})} \simeq H$
induit un plongement
d’appartements, donc
![]() $\Omega $
peut être regardé comme partie du membre de droite. Le résultat ci-dessous ne sera jamais appliqué dans le reste de l’article.
$\Omega $
peut être regardé comme partie du membre de droite. Le résultat ci-dessous ne sera jamais appliqué dans le reste de l’article.
Proposition 3.4.8. Le morphisme naturel
![]() $\underline {\mathscr {G}_{ \Omega }} \rightarrow \operatorname {R}_{\mathbb {Z}[\zeta _e,t^{1/e}]/\mathbb {Z}[t]} \underline {\mathscr {H}_{\Omega }}$
induit par l’inclusion (3.4.15) est un plongement localement fermé.
$\underline {\mathscr {G}_{ \Omega }} \rightarrow \operatorname {R}_{\mathbb {Z}[\zeta _e,t^{1/e}]/\mathbb {Z}[t]} \underline {\mathscr {H}_{\Omega }}$
induit par l’inclusion (3.4.15) est un plongement localement fermé.
Démonstration. On reprendre la preuve de la prop. 3.3.9 pour voir que l’adhérence schématique de T et des
![]() $U_a$
dans le membre de droite s’identifie aux modèles immobiliers souhaités de la déf. 3.4.4. D’après [Reference Bruhat and TitsBT84a, prop. 2.2.10], ceci termine la preuve de la propriété énoncée. On s’attend à ce que l’image fermée du membre de gauche soit un sous-
$U_a$
dans le membre de droite s’identifie aux modèles immobiliers souhaités de la déf. 3.4.4. D’après [Reference Bruhat and TitsBT84a, prop. 2.2.10], ceci termine la preuve de la propriété énoncée. On s’attend à ce que l’image fermée du membre de gauche soit un sous-
![]() $\mathbb {Z}[t]$
-groupe plat et fermé du membre de droite (dont la composante neutre s’identifierait à
$\mathbb {Z}[t]$
-groupe plat et fermé du membre de droite (dont la composante neutre s’identifierait à
![]() $\underline {\mathscr {G}_{ \Omega }}$
), mais cela pourrait éventuellement n’être pas le cas, cf. [Reference Bruhat and TitsBT84a, 3.2.15], et il semble que nos méthodes soient insuffisantes pour y parvenir.
$\underline {\mathscr {G}_{ \Omega }}$
), mais cela pourrait éventuellement n’être pas le cas, cf. [Reference Bruhat and TitsBT84a, 3.2.15], et il semble que nos méthodes soient insuffisantes pour y parvenir.
Remarque 3.4.9. Dans une autre direction, lorsque G est un groupe classique, il serait aussi très intéressant d’interpréter les groupes parahoriques comme classifiant les automorphismes de certains chaînes périodiques de réseaux munis de formes quadratiques comme en [Reference Pappas and ZhuPZ13, §5], ou [Reference TitsTi84, pp. 218-219], ce qui peut être regardé comme une généralisation aux bases bidimensionnelles de [Reference Rapoport and ZinkRZ96, §3, annexe]. Voir aussi [Reference Bruhat and TitsBT84b], [Reference Bruhat and TitsBT87] et [Reference KirchKir17] pour des cas classiques non modérément ramifiés sur un anneau de valuation discrète.
Enfin, on mettre un terme à nos enquêtes sur la théorie des groupes, en démontrant que les
![]() $\mathbb {Z}[t]$
-groupes lisses, séparés et connexes
$\mathbb {Z}[t]$
-groupes lisses, séparés et connexes
![]() $\underline {\mathscr {G}_\Omega }$
sont même affines, duquel on profitera plus tard pour faire la géométrie des grassmanniennes affines, voir les §§4-5 et en particulier les props. 4.1.2 et 5.1.2.
$\underline {\mathscr {G}_\Omega }$
sont même affines, duquel on profitera plus tard pour faire la géométrie des grassmanniennes affines, voir les §§4-5 et en particulier les props. 4.1.2 et 5.1.2.
Théorème 3.4.10. Le schéma en groupes
![]() $\underline {\mathscr {G}_{\Omega }}$
est affine sur
$\underline {\mathscr {G}_{\Omega }}$
est affine sur
![]() $\mathbb {A}^1_{\mathbb {Z}}$
.
$\mathbb {A}^1_{\mathbb {Z}}$
.
On va démontrer ce résultat fondamental de manière complètement différente à celle de [Reference Pappas and ZhuPZ13, th. 4.1] dans le cas modérément ramifié. En effet, ce dernier article procède par deux étapes : dans le cas déployé, des techniques de dilatation sont appliquées, voir [Reference Waterhouse and WeisfeilerWW80, §1] et [Reference Bosch, Lütkebohmert and RaynaudBLR90, §3.2] pour le cas de la dimension
![]() $1$
et [Reference MayeuxMRR20, §3] en dimension supérieure; dans le cas tordu, un calcul cohomologique en termes de
$1$
et [Reference MayeuxMRR20, §3] en dimension supérieure; dans le cas tordu, un calcul cohomologique en termes de
![]() $\Gamma $
-invariants est évoqué.
$\Gamma $
-invariants est évoqué.
Dans notre cadre généralisé, même si l’on sait déjà que
![]() $\underline {G}$
est affine sur
$\underline {G}$
est affine sur
![]() $\mathbb {Z}[t^{\pm 1}]$
d’après la prop. 3.3.9, nous ne disposons pas d’une interprétation galoisienne pure, pour qu’on puisse calculer des groupes de cohomologie. Nos arguments sont donc beaucoup plus abstraits, mais aussi élémentaires en ce qui concerne les outils techniques.
$\mathbb {Z}[t^{\pm 1}]$
d’après la prop. 3.3.9, nous ne disposons pas d’une interprétation galoisienne pure, pour qu’on puisse calculer des groupes de cohomologie. Nos arguments sont donc beaucoup plus abstraits, mais aussi élémentaires en ce qui concerne les outils techniques.
Démonstration. On doit prouver que l’enveloppe affine
![]() $\underline {\mathscr {G}_{\Omega }^{\operatorname {af}}}$
est connexe, voir la prop. 3.2.7, et on s’est ramené à traiter les fibres géométriques en les idéaux maximaux
$\underline {\mathscr {G}_{\Omega }^{\operatorname {af}}}$
est connexe, voir la prop. 3.2.7, et on s’est ramené à traiter les fibres géométriques en les idéaux maximaux
![]() $(p,t)$
de
$(p,t)$
de
![]() $\mathbb {Z}[t]$
, pour
$\mathbb {Z}[t]$
, pour
![]() $p>0$
un nombre premier. Soient
$p>0$
un nombre premier. Soient
![]() $\underline {\mathscr {N}_{\Omega }}$
(resp.
$\underline {\mathscr {N}_{\Omega }}$
(resp.
![]() $\underline {\mathscr {N}_{\Omega }^{\operatorname {af}}}$
) le normalisateur de
$\underline {\mathscr {N}_{\Omega }^{\operatorname {af}}}$
) le normalisateur de
![]() $\underline {\mathscr {S}}$
dans
$\underline {\mathscr {S}}$
dans
![]() $\underline {\mathscr {G}_{\Omega }}$
(resp. dans l’enveloppe affine
$\underline {\mathscr {G}_{\Omega }}$
(resp. dans l’enveloppe affine
![]() $\underline {\mathscr {G}_{\Omega }^{\operatorname {af}}}$
), qui sont sous-
$\underline {\mathscr {G}_{\Omega }^{\operatorname {af}}}$
), qui sont sous-
![]() $\mathbb {Z}[t]$
-groupes fermés et lisses, cf. [SGA3, exp. XI, cor. 2.4 bis, cor. 6.11]. Chaque composante connexe de cette fibre géométrique peut être représentée par un point de
$\mathbb {Z}[t]$
-groupes fermés et lisses, cf. [SGA3, exp. XI, cor. 2.4 bis, cor. 6.11]. Chaque composante connexe de cette fibre géométrique peut être représentée par un point de
![]() $\underline {\mathscr {N}_{\Omega }^{\operatorname {af}}}$
à valeurs dans
$\underline {\mathscr {N}_{\Omega }^{\operatorname {af}}}$
à valeurs dans
![]() $\breve {\mathbb {Z}}_p [\hspace {-0,5mm}[ {t} ]\hspace {-0,5mm}] $
, grâce au lemme d’Hensel joint au cor. 3.4.7 et au fait correspondant en théorie de Bruhat–Tits, voir [Reference LourençoLou21, prop. 2.12] et [Reference Bruhat and TitsBT84a, cor. 4.6.21]. Alors, la non connexité de
$\breve {\mathbb {Z}}_p [\hspace {-0,5mm}[ {t} ]\hspace {-0,5mm}] $
, grâce au lemme d’Hensel joint au cor. 3.4.7 et au fait correspondant en théorie de Bruhat–Tits, voir [Reference LourençoLou21, prop. 2.12] et [Reference Bruhat and TitsBT84a, cor. 4.6.21]. Alors, la non connexité de
![]() $\underline {\mathscr {G}_{\Omega }^{\operatorname {af}}}$
au-dessus de
$\underline {\mathscr {G}_{\Omega }^{\operatorname {af}}}$
au-dessus de
![]() $\breve {\mathbb {Z}}_p [\hspace {-0,5mm}[ {t} ]\hspace {-0,5mm}] $
contredit à l’évidence l’affirmation selon laquelle les flèches
$\breve {\mathbb {Z}}_p [\hspace {-0,5mm}[ {t} ]\hspace {-0,5mm}] $
contredit à l’évidence l’affirmation selon laquelle les flèches
sont bijectives, puisque la descente de Beauville–Laszlo, voir [Reference Beauville and LaszloBL95, th.], en fournit l’égalité
comme sous-groupes de
![]() $\underline {N}(\breve {\mathbb {Q}}_p (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
.
$\underline {N}(\breve {\mathbb {Q}}_p (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
.
Maintenant, nous montrons cette assertion, c’est-à-dire que les applications (3.4.16) et (3.4.17) sont bijectives. En effet, nous avons déjà vu pendant la preuve de la prop. 3.4.1 que les diverses variantes des groupes d’Iwahori-Weyl sont toutes canoniquement isomorphes, quels que soient les coefficients utilisés, cf. (3.4.2). Par suite, il reste à avérer que les applications d’ensembles finis
sont bijectives. D’une part, le cardinal du membre de droite de ces applications ne dépend pas de la caractéristique des coefficients, puisqu’il s’identifie en tout cas au groupe de Weyl résiduel
![]() $W(\Phi _{\Omega })$
du sous-système de racines
$W(\Phi _{\Omega })$
du sous-système de racines
![]() $\Omega $
-résiduel
$\Omega $
-résiduel
voir [Reference Bruhat and TitsBT84a, cor. 4.6.12] et [Reference LourençoLou21, lem. 4.6] pour une preuve de cette affirmation. D’autre part, la première flèche (3.4.19) est surjective par le lemme d’Hensel et la deuxième (3.4.20) est injective, parce que
![]() $\underline {\mathscr {T}}$
est fermé dans
$\underline {\mathscr {T}}$
est fermé dans
![]() $\underline {\mathscr {N}_{\Omega }}$
.
$\underline {\mathscr {N}_{\Omega }}$
.
Remarque 3.4.11. Rappelons succinctement la stratégie de preuve de la version précédente du texte dans le cas parahorique : la première étape consistait à exploiter que les stabilisateurs soient automatiquement connexes si
![]() $G=G^{\operatorname {sc}}$
pour montrer la connexité de l’enveloppe affine; la deuxième étape ramenait le problème par modification centrale aux modèles de Néron des tores pas forcément induits, dès que
$G=G^{\operatorname {sc}}$
pour montrer la connexité de l’enveloppe affine; la deuxième étape ramenait le problème par modification centrale aux modèles de Néron des tores pas forcément induits, dès que
![]() $G^{\mathrm {d\acute {e}r}}=G^{\operatorname {sc}}$
; la troisième étape explicitait ceux-ci grâce à la classification des tores cycliques lorsque
$G^{\mathrm {d\acute {e}r}}=G^{\operatorname {sc}}$
; la troisième étape explicitait ceux-ci grâce à la classification des tores cycliques lorsque
![]() $e \leq 3$
. À la fin, cette preuve était encore plus longue que l’actuelle et ne fonctionnait que dans un cadre limitant.
$e \leq 3$
. À la fin, cette preuve était encore plus longue que l’actuelle et ne fonctionnait que dans un cadre limitant.
4 La géométrie des grassmanniennes affines tordues entières
Cette partie est consacrée à l’étude géométrique des grassmanniennes affines
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
attachées aux
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
attachées aux
![]() $\mathbb {A}_{\mathbb {Z}}^1$
-modèles parahoriques
$\mathbb {A}_{\mathbb {Z}}^1$
-modèles parahoriques
![]() $\underline {\mathscr {G}_{\mathbf {f}}}$
des groupes de Tits
$\underline {\mathscr {G}_{\mathbf {f}}}$
des groupes de Tits
![]() $\underline {G}$
déjà introduits à la déf. 3.4.6. On démontre notamment que les schémas de Schubert
$\underline {G}$
déjà introduits à la déf. 3.4.6. On démontre notamment que les schémas de Schubert
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq w}$
, cf. déf. 4.1.4, sont géométriquement normaux et scindés en caractéristique
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq w}$
, cf. déf. 4.1.4, sont géométriquement normaux et scindés en caractéristique
![]() $p>0$
, cf. th. 4.1.5.
$p>0$
, cf. th. 4.1.5.
4.1 Rappels et préparatifs
Nous allons rappeler au lecteur les notions et résultats principales concernant les grassmanniennes affines, lesquelles seront les objets géométriques centraux de nos investigations. Voici la définition :
Définition 4.1.1. Soient A un anneau et
![]() $\mathrm {G}$
un schéma en groupes lisse sur
$\mathrm {G}$
un schéma en groupes lisse sur
![]() $A [\hspace {-0,5mm}[ {t} ]\hspace {-0,5mm}] $
. La grassmannienne affine
$A [\hspace {-0,5mm}[ {t} ]\hspace {-0,5mm}] $
. La grassmannienne affine
![]() $\operatorname {Gr}_{\mathrm {G}}$
est le pré-faisceau en ensembles de la catégorie des A-algèbres, tel que
$\operatorname {Gr}_{\mathrm {G}}$
est le pré-faisceau en ensembles de la catégorie des A-algèbres, tel que
![]() $\operatorname {Gr}_{\mathrm {G}}(R)$
soit l’ensemble des classes d’isomorphisme de
$\operatorname {Gr}_{\mathrm {G}}(R)$
soit l’ensemble des classes d’isomorphisme de
![]() $\mathrm {G}$
-fibrés
$\mathrm {G}$
-fibrés
![]() $\mathcal {E}$
sur
$\mathcal {E}$
sur
![]() $R [\hspace {-0,5mm}[ {t} ]\hspace {-0,5mm}] $
munis d’une trivialisation au-dessus de
$R [\hspace {-0,5mm}[ {t} ]\hspace {-0,5mm}] $
munis d’une trivialisation au-dessus de
![]() $R (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) $
.
$R (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) $
.
Il s’agit d’un faisceau en ensembles pour la topologie plate. Le groupe de lacets
![]() $L\mathrm {G}:R \mapsto \mathrm {G}(R (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
de G, qui est représentable par un ind-schéma affine de type fini, cf. [Reference Pappas and RapoportPR08, 1.a], y opère par changement de trivialisation. Notant
$L\mathrm {G}:R \mapsto \mathrm {G}(R (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
de G, qui est représentable par un ind-schéma affine de type fini, cf. [Reference Pappas and RapoportPR08, 1.a], y opère par changement de trivialisation. Notant
![]() $L^+\mathrm {G}:R \mapsto \mathrm {G}(R [\hspace {-0,5mm}[ {t} ]\hspace {-0,5mm}] )$
le groupe d’arcs de
$L^+\mathrm {G}:R \mapsto \mathrm {G}(R [\hspace {-0,5mm}[ {t} ]\hspace {-0,5mm}] )$
le groupe d’arcs de
![]() $\mathrm {G}$
, qui est naturellement contenu dans
$\mathrm {G}$
, qui est naturellement contenu dans
![]() $L\mathrm {G}$
et représentable par un schéma pro-lisse, cf. [Reference ZhuZh17, prop. 1.3.2], on peut réaliser la grassmannienne affine comme le faisceau quotient
$L\mathrm {G}$
et représentable par un schéma pro-lisse, cf. [Reference ZhuZh17, prop. 1.3.2], on peut réaliser la grassmannienne affine comme le faisceau quotient
![]() $L\mathrm {G}/L^+\mathrm {G}$
pour la topologie étale, cf. [Reference ZhuZh17, prop. 1.3.6], de manière compatible à l’action à la gauche de
$L\mathrm {G}/L^+\mathrm {G}$
pour la topologie étale, cf. [Reference ZhuZh17, prop. 1.3.6], de manière compatible à l’action à la gauche de
![]() $L\mathrm {G}$
.
$L\mathrm {G}$
.
La question de savoir quand la grassmannienne affine d’un groupe est représentable est encore subtile, mais nous avons le résultat suivant :
Proposition 4.1.2 (Pappas–Zhu).
Soient A un anneau de Dedekind et
![]() $\mathrm {G}$
un
$\mathrm {G}$
un
![]() $A [\hspace {-0,5mm}[ {t} ]\hspace {-0,5mm}] $
-groupe lisse, affine et connexe. Alors,
$A [\hspace {-0,5mm}[ {t} ]\hspace {-0,5mm}] $
-groupe lisse, affine et connexe. Alors,
![]() $\operatorname {Gr}_{\mathrm {G}}$
est représentable par un ind-schéma quasi-projectif de type fini.
$\operatorname {Gr}_{\mathrm {G}}$
est représentable par un ind-schéma quasi-projectif de type fini.
Esquisse de la preuve. Lorsque
![]() $\mathrm {G}=\operatorname {GL}_n$
, la grassmannienne affine admet une interprétation comme espace classifiant de
$\mathrm {G}=\operatorname {GL}_n$
, la grassmannienne affine admet une interprétation comme espace classifiant de
![]() $R [\hspace {-0,5mm}[ {t} ]\hspace {-0,5mm}] $
-réseaux dans
$R [\hspace {-0,5mm}[ {t} ]\hspace {-0,5mm}] $
-réseaux dans
![]() $R (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) $
, d’où son écriture comme colimite de fermés de grassmanniennes finies, cf. [Reference ZhuZh17, th. 1.1.3]. Sous les contraintes énoncées, alors [Reference Pappas and ZhuPZ13, cor. 11.8] affirme l’existence d’une immersion fermée
$R (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) $
, d’où son écriture comme colimite de fermés de grassmanniennes finies, cf. [Reference ZhuZh17, th. 1.1.3]. Sous les contraintes énoncées, alors [Reference Pappas and ZhuPZ13, cor. 11.8] affirme l’existence d’une immersion fermée
![]() $\mathrm {G} \rightarrow \operatorname {GL}_n$
à quotient représentable et quasi-affine pour la topologie plate - cela repose essentiellement sur les travaux de Thomason, voir [Reference ThomasonTho87]. Mais dans ce cas, on parvient à prouver que le morphisme induit
$\mathrm {G} \rightarrow \operatorname {GL}_n$
à quotient représentable et quasi-affine pour la topologie plate - cela repose essentiellement sur les travaux de Thomason, voir [Reference ThomasonTho87]. Mais dans ce cas, on parvient à prouver que le morphisme induit
![]() $\operatorname {Gr}_{\mathrm {G}} \rightarrow \operatorname {Gr}_{\operatorname {GL}_n}$
est représentable par une immersion quasi-compacte, cf. [Reference ZhuZh17, prop. 1.2.6].
$\operatorname {Gr}_{\mathrm {G}} \rightarrow \operatorname {Gr}_{\operatorname {GL}_n}$
est représentable par une immersion quasi-compacte, cf. [Reference ZhuZh17, prop. 1.2.6].
L’autre question qui se pose concerne la projectivité de
![]() $\operatorname {Gr}_{\mathrm {G}}$
. Pour obtenir une classification complète, on se borne au cas où A est un corps parfait.
$\operatorname {Gr}_{\mathrm {G}}$
. Pour obtenir une classification complète, on se borne au cas où A est un corps parfait.
Proposition 4.1.3 (Pappas–Rapoport, Richarz, L.).
Soient k un corps parfait,
![]() $\mathrm {G}$
un
$\mathrm {G}$
un
![]() $k [\hspace {-0,5mm}[ {t} ]\hspace {-0,5mm}] $
-schéma en groupes lisse, affine et connexe. Pour que
$k [\hspace {-0,5mm}[ {t} ]\hspace {-0,5mm}] $
-schéma en groupes lisse, affine et connexe. Pour que
![]() $\operatorname {Gr}_{\mathrm {G}}$
soit un ind-schéma projectif, il faut et il suffit que
$\operatorname {Gr}_{\mathrm {G}}$
soit un ind-schéma projectif, il faut et il suffit que
![]() $\mathrm {G}$
soit parahorique au sens de [Reference LourençoLou21].
$\mathrm {G}$
soit parahorique au sens de [Reference LourençoLou21].
Esquisse de la preuve. On reprend les arguments de [Reference LourençoLou21, th. 5.2]. Pour la suffisance, on peut supposer sans perte de généralité que
![]() $\mathrm {G}=\mathrm {I}$
est d’Iwahori et que
$\mathrm {G}=\mathrm {I}$
est d’Iwahori et que
![]() $\operatorname {Gr}_{\mathrm {I}}$
est connexe. En particulier, les
$\operatorname {Gr}_{\mathrm {I}}$
est connexe. En particulier, les
![]() $\mathrm {I}$
-orbites fermées de
$\mathrm {I}$
-orbites fermées de
![]() $\operatorname {Gr}_{\mathrm {I}}$
sont numérotées par
$\operatorname {Gr}_{\mathrm {I}}$
sont numérotées par
![]() $w \in W^{\operatorname {af}}$
, où ce dernier symbole désigne le groupe de Weyl affine, d’après la décomposition de Bruhat de [Reference LourençoLou21, prop. 3.7]. Cela veut dire que w peut s’exprimer dans la forme d’un produit de réflexions fondamentales; soit
$w \in W^{\operatorname {af}}$
, où ce dernier symbole désigne le groupe de Weyl affine, d’après la décomposition de Bruhat de [Reference LourençoLou21, prop. 3.7]. Cela veut dire que w peut s’exprimer dans la forme d’un produit de réflexions fondamentales; soit
![]() $\mathfrak {w}=[s_1: \dots :s_n]$
le mot réduit correspondant. Considérons la variété de Demazure
$\mathfrak {w}=[s_1: \dots :s_n]$
le mot réduit correspondant. Considérons la variété de Demazure
où l’on note
![]() $\mathrm {P}_s$
le groupe parahorique minimal associé à s. On peut montrer que ceci est une fibration en droites projectives localement triviale pour la topologie ouverte, donc représentable par une variété projective lisse, voir [Reference Pappas and RapoportPR08, prop. 8.7, prop. 8.8] et aussi cor. 4.2.5. Son image dans
$\mathrm {P}_s$
le groupe parahorique minimal associé à s. On peut montrer que ceci est une fibration en droites projectives localement triviale pour la topologie ouverte, donc représentable par une variété projective lisse, voir [Reference Pappas and RapoportPR08, prop. 8.7, prop. 8.8] et aussi cor. 4.2.5. Son image dans
![]() $\operatorname {Gr}_{\mathrm {I}}$
par le morphisme multiplication est la variété de Schubert
$\operatorname {Gr}_{\mathrm {I}}$
par le morphisme multiplication est la variété de Schubert
![]() $\operatorname {Gr}_{\mathrm {I},\leq w}$
, qui est donc projective.
$\operatorname {Gr}_{\mathrm {I},\leq w}$
, qui est donc projective.
Quant à la nécessité, on voit facilement que la fibre générique de
![]() $\mathrm {G}$
est sans
$\mathrm {G}$
est sans
![]() $\mathbb {G}_a$
central, en appliquant ce que
$\mathbb {G}_a$
central, en appliquant ce que
![]() $\operatorname {Gr}_{\mathbb {G}_a}$
est l’ind-droite affine
$\operatorname {Gr}_{\mathbb {G}_a}$
est l’ind-droite affine
![]() $\mathbb {A}_k^\infty $
infinie, cf. [Reference LourençoLou21, th. 5.2]. Enfin, le fait que
$\mathbb {A}_k^\infty $
infinie, cf. [Reference LourençoLou21, th. 5.2]. Enfin, le fait que
![]() $\mathrm {G}$
soit parahorique résulte d’après la preuve de [Reference RicharzRi16, th. 1.19] d’un théorème sur les sous-groupes bornés maximaux de
$\mathrm {G}$
soit parahorique résulte d’après la preuve de [Reference RicharzRi16, th. 1.19] d’un théorème sur les sous-groupes bornés maximaux de
![]() $\mathrm {G}(k (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
, cf. [Reference Bruhat and TitsBT72, th. 3.3.1], et du lien avec les sous-groupes paraboliques de la fibre spéciale, cf. [Reference Bruhat and TitsBT84a, th. 4.6.33] et [Reference LourençoLou21, th. 4.7], couplés au fait que les sous-groupes de congruence de
$\mathrm {G}(k (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
, cf. [Reference Bruhat and TitsBT72, th. 3.3.1], et du lien avec les sous-groupes paraboliques de la fibre spéciale, cf. [Reference Bruhat and TitsBT84a, th. 4.6.33] et [Reference LourençoLou21, th. 4.7], couplés au fait que les sous-groupes de congruence de
![]() $L^+\mathrm {G}$
sont toujours pro-unipotents, voir le début de §4.2, particulièrement (4.2.1).
$L^+\mathrm {G}$
sont toujours pro-unipotents, voir le début de §4.2, particulièrement (4.2.1).
Reprenons maintenant les notations des §§3.3-3.4, c’est-à-dire : G est un
![]() $\mathbb {Q}(t)$
-groupe quasi-déployé,
$\mathbb {Q}(t)$
-groupe quasi-déployé,
![]() $\mathbb {Q}(\zeta _e,t^{1/e})$
-déployé,
$\mathbb {Q}(\zeta _e,t^{1/e})$
-déployé,
![]() $\mathbb {Q} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) $
-résiduellement déployé et à tore maximal induit, muni d’un couple de Killing relatif
$\mathbb {Q} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) $
-résiduellement déployé et à tore maximal induit, muni d’un couple de Killing relatif
![]() $S \subset T \subset B \subset G$
et d’un quasi-système de Tits, voir l’hyp. 3.3.1;
$S \subset T \subset B \subset G$
et d’un quasi-système de Tits, voir l’hyp. 3.3.1;
![]() $\underline {G}$
est le
$\underline {G}$
est le
![]() $\mathbb {G}_{m,\mathbb {Z}}$
-groupe de Tits sur
$\mathbb {G}_{m,\mathbb {Z}}$
-groupe de Tits sur
![]() $\mathbb {Z}[t^{\pm 1}]$
qui lui est associé par la déf. 3.3.5; et les
$\mathbb {Z}[t^{\pm 1}]$
qui lui est associé par la déf. 3.3.5; et les
![]() $\underline {\mathscr {G}_{\mathbf {f}}}$
, où
$\underline {\mathscr {G}_{\mathbf {f}}}$
, où
![]() $\mathbf {f}\subset \mathscr {A}(\underline {G},\underline {S},\mathbb {Z} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
est une facette, sont les
$\mathbf {f}\subset \mathscr {A}(\underline {G},\underline {S},\mathbb {Z} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
est une facette, sont les
![]() $\mathbb {A}^1_{\mathbb {Z}}$
-modèles parahoriques que nous avons construits à la déf. 3.4.6 et qui sont lisses, affines et connexes sur
$\mathbb {A}^1_{\mathbb {Z}}$
-modèles parahoriques que nous avons construits à la déf. 3.4.6 et qui sont lisses, affines et connexes sur
![]() $\mathbb {Z}[t]$
, grâce au th. 3.4.10.
$\mathbb {Z}[t]$
, grâce au th. 3.4.10.
Alors, la grassmannienne affine
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
sur
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
sur
![]() $\operatorname {Spec} \mathbb {Z}$
est, en quelque sorteFootnote 5 , une variété de drapeaux affine entière du groupe tordu
$\operatorname {Spec} \mathbb {Z}$
est, en quelque sorteFootnote 5 , une variété de drapeaux affine entière du groupe tordu
![]() $\underline {G}$
. On s’intéresse aux sous-schémas intègres et invariants par
$\underline {G}$
. On s’intéresse aux sous-schémas intègres et invariants par
![]() $L^+\underline {\mathscr {G}_{\mathbf {a}}}$
de
$L^+\underline {\mathscr {G}_{\mathbf {a}}}$
de
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
, où
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
, où
![]() $\mathbf {a}$
est une alcôve dont l’adhérence contient
$\mathbf {a}$
est une alcôve dont l’adhérence contient
![]() $\mathbf {a}$
, qu’on appelle les schémas de Schubert :
$\mathbf {a}$
, qu’on appelle les schémas de Schubert :
Définition 4.1.4. Soient
![]() $w \in \widetilde {W}/W_{\mathbf {f}}$
et
$w \in \widetilde {W}/W_{\mathbf {f}}$
et
![]() $n_w \in \underline {N}(\mathbb {Z}[t^{\pm 1}])$
un représentant de w. Alors, le schéma de Schubert
$n_w \in \underline {N}(\mathbb {Z}[t^{\pm 1}])$
un représentant de w. Alors, le schéma de Schubert
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq w}$
est l’image schématique de l’application orbite
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq w}$
est l’image schématique de l’application orbite
![]() $L^+\underline {\mathscr {G}_{\mathbf {a}}} \rightarrow \operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
donnée par
$L^+\underline {\mathscr {G}_{\mathbf {a}}} \rightarrow \operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
donnée par
![]() $g \mapsto g\cdot n_w$
.
$g \mapsto g\cdot n_w$
.
Ces schémas sont automatiquement intègres, plats et projectifs et indépendantes du choix d’un représentant
![]() $n_w$
de w. Les relations d’inclusion entre eux sont induites par l’ordre de Bruhat dans le double quotient
$n_w$
de w. Les relations d’inclusion entre eux sont induites par l’ordre de Bruhat dans le double quotient
![]() $\widetilde {W}/W_{\mathbf {f}}$
, voir [Reference RicharzRi13, prop. 2.8]. Notre théorème principal concerne leur géométrie :
$\widetilde {W}/W_{\mathbf {f}}$
, voir [Reference RicharzRi13, prop. 2.8]. Notre théorème principal concerne leur géométrie :
Théorème 4.1.5 (Faltings, Pappas–Rapoport, L.).
Supposons que
![]() $G^{\mathrm {d\acute {e}r}}=G^{\operatorname {sc}}$
. Alors, les schémas de Schubert
$G^{\mathrm {d\acute {e}r}}=G^{\operatorname {sc}}$
. Alors, les schémas de Schubert
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq w}$
sont géométriquement normaux sur
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq w}$
sont géométriquement normaux sur
![]() $\mathbb {Z}$
, de Cohen–Macaulay et leurs fibres modulo
$\mathbb {Z}$
, de Cohen–Macaulay et leurs fibres modulo
![]() $p>0$
sont scindées.
$p>0$
sont scindées.
Faisons quelques remarques sur l’énoncé :
Remarque 4.1.6.
-
1. Au-dessus de
 $\mathbb {Z}[1/e]$
, le théorème est dû à Pappas–Rapoport, voir [Reference Pappas and RapoportPR08, th. 8.4, 9.g], dont la preuve remonte à Faltings, voir [Reference FaltingsFa03, th. 8], pour les groupes déployés.
$\mathbb {Z}[1/e]$
, le théorème est dû à Pappas–Rapoport, voir [Reference Pappas and RapoportPR08, th. 8.4, 9.g], dont la preuve remonte à Faltings, voir [Reference FaltingsFa03, th. 8], pour les groupes déployés. -
2. L’hypothèse que le groupe dérivé soit simplement connexe ne peut être pas soulevée, comme nous l’avons démontré très récemment avec Haines–Richarz, voir [Reference Haines, Lourenço and RicharzHLR20, th. 1.1] et cor. 4.3.7. En effet, les schémas
 $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq w}$
ne seront typiquement pas à fibres réduites sans cette hypothèse, cf. [Reference Haines, Lourenço and RicharzHLR20, th. 1.5, prop. 3.4].
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq w}$
ne seront typiquement pas à fibres réduites sans cette hypothèse, cf. [Reference Haines, Lourenço and RicharzHLR20, th. 1.5, prop. 3.4].
La démonstration du th. 4.1.5 sera faite en diverses étapes pendant tous les numéros restants du §4. Outre le traitement complet de la théorie de la grosse cellule et des diviseurs/cycles de Schubert au §4.2, notre preuve au §4.3 contient une petite sophistication technique (ou devrait-on dire complication ?), en ce que le lem. 4.3.5 de Faltings–Pappas–Rapoport est faux en caractéristique résiduelle
![]() $2$
si
$2$
si
![]() $\Phi _G$
n’est pas réduit et doit être remplacé par son analogue différentiel supérieur, cf. lem. 4.3.6.
$\Phi _G$
n’est pas réduit et doit être remplacé par son analogue différentiel supérieur, cf. lem. 4.3.6.
4.2 Groupes de cordes et cycles de Schubert
Ce numéro est consacré à mieux comprendre la structure du groupe de lacets
![]() $L\underline {\mathscr {G}_{\mathbf {f}}}$
, de son sous-groupe d’arcs
$L\underline {\mathscr {G}_{\mathbf {f}}}$
, de son sous-groupe d’arcs
![]() $L^+\underline {\mathscr {G}_{\mathbf {f}}}$
et de ce qu’on appellera son sous-groupe de cordes
$L^+\underline {\mathscr {G}_{\mathbf {f}}}$
et de ce qu’on appellera son sous-groupe de cordes
![]() $L^-\underline {\mathscr {G}_{\mathbf {f}}}$
, voir la déf. 4.2.8. On s’en sert pour définir quelques cycles de codimension finie dans la grassmannienne affine
$L^-\underline {\mathscr {G}_{\mathbf {f}}}$
, voir la déf. 4.2.8. On s’en sert pour définir quelques cycles de codimension finie dans la grassmannienne affine
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
, voir le th. 4.2.16, dont les diviseurs parmi eux engendrent le groupe de Picard, cf. cor. 4.3.10, et jouent un rôle essentiel dans la preuve du th. 4.1.5, voir en particulier la prop. 4.3.1 et le lem. 4.3.4.
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
, voir le th. 4.2.16, dont les diviseurs parmi eux engendrent le groupe de Picard, cf. cor. 4.3.10, et jouent un rôle essentiel dans la preuve du th. 4.1.5, voir en particulier la prop. 4.3.1 et le lem. 4.3.4.
Le groupe d’arcs
![]() $L^+\underline {\mathscr {G}_{\mathbf {f}}}$
possède une filtration canonique exhaustive et séparée
$L^+\underline {\mathscr {G}_{\mathbf {f}}}$
possède une filtration canonique exhaustive et séparée
donnée par les n-ièmes sous-groupes de congruence, c’est-à-dire les noyaux des applications
![]() $L^+\underline {\mathscr {G}_{\mathbf {f}}} \rightarrow L^n\underline {\mathscr {G}_{\mathbf {f}}}:=\operatorname {R}_{\mathbb {Z}[t]/(t^n)/\mathbb {Z}}\underline {\mathscr {G}_{\mathbf {f}}}$
de réduction modulo
$L^+\underline {\mathscr {G}_{\mathbf {f}}} \rightarrow L^n\underline {\mathscr {G}_{\mathbf {f}}}:=\operatorname {R}_{\mathbb {Z}[t]/(t^n)/\mathbb {Z}}\underline {\mathscr {G}_{\mathbf {f}}}$
de réduction modulo
![]() $t^n$
. Notons que les sous-quotients successifs
$t^n$
. Notons que les sous-quotients successifs
![]() $L^{(n)}\underline {\mathscr {G}_{\mathbf {f}}}/ L^{(n+1)}\underline {\mathscr {G}_{\mathbf {f}}}$
de la filtration de congruence sont isomorphes à la fibre spéciale
$L^{(n)}\underline {\mathscr {G}_{\mathbf {f}}}/ L^{(n+1)}\underline {\mathscr {G}_{\mathbf {f}}}$
de la filtration de congruence sont isomorphes à la fibre spéciale
![]() $\underline {\mathscr {G}_{\mathbf {f},s}}:=\underline {\mathscr {G}_{\mathbf {f}}}\otimes _{\mathbb {Z}[t], t\mapsto 0} \mathbb {Z}$
si
$\underline {\mathscr {G}_{\mathbf {f},s}}:=\underline {\mathscr {G}_{\mathbf {f}}}\otimes _{\mathbb {Z}[t], t\mapsto 0} \mathbb {Z}$
si
![]() $n=0$
, et au fibré vectoriel de Lie de
$n=0$
, et au fibré vectoriel de Lie de
![]() $\underline {\mathscr {G}_{\mathbf {f},s}}$
comme groupe additif sinon, voir soit [Reference Demazure and GabrielDG70, tome I, ch. II, §4, nº3, prop. 3.2], soit [Reference Richarz and ScholbachRS20, prop. A.9]. Par suite,
$\underline {\mathscr {G}_{\mathbf {f},s}}$
comme groupe additif sinon, voir soit [Reference Demazure and GabrielDG70, tome I, ch. II, §4, nº3, prop. 3.2], soit [Reference Richarz and ScholbachRS20, prop. A.9]. Par suite,
![]() $L^{(1)} \underline {\mathscr {G}_{\textbf {f}}}$
est un schéma en groupes pro-lisse, pro-unipotent et connexe. Il ne reste qu’à entendre la fibre spéciale entière
$L^{(1)} \underline {\mathscr {G}_{\textbf {f}}}$
est un schéma en groupes pro-lisse, pro-unipotent et connexe. Il ne reste qu’à entendre la fibre spéciale entière
![]() $\underline {\mathscr {G}_{\mathbf {f},s}}$
comme extension d’un certain quotient réductif (qui n’existe pas forcément sur les entiers a priori) et d’un radical unipotent; on s’en occupera dans la suite, voir la prop. 4.2.4.
$\underline {\mathscr {G}_{\mathbf {f},s}}$
comme extension d’un certain quotient réductif (qui n’existe pas forcément sur les entiers a priori) et d’un radical unipotent; on s’en occupera dans la suite, voir la prop. 4.2.4.
Avant de se concentrer sur cette décomposition de Levi, il faut discuter le rôle de l’action de rotation de
![]() $\mathbb {G}_m$
sur le groupe de lacets
$\mathbb {G}_m$
sur le groupe de lacets
![]() $L\underline {G}$
déduite de l’action tordue du lem. 3.3.10. Cela fournit par linéarisation une opération
$L\underline {G}$
déduite de l’action tordue du lem. 3.3.10. Cela fournit par linéarisation une opération
![]() $\mathbb {Z}$
-linéaire de
$\mathbb {Z}$
-linéaire de
![]() $\mathbb {G}_m$
sur
$\mathbb {G}_m$
sur
![]() $L\underline {G}$
et on vérifie facilement que l’opération induite sur son algèbre de Lie est donnée par
$L\underline {G}$
et on vérifie facilement que l’opération induite sur son algèbre de Lie est donnée par
![]() $t^{1/e} \mapsto at^{1/e}$
. Il est facile de voir que les groupes d’arcs parahoriques
$t^{1/e} \mapsto at^{1/e}$
. Il est facile de voir que les groupes d’arcs parahoriques
![]() $L^+\underline {\mathscr {G}_{\mathbf {f}}}$
sont stables par cette opération, soit en généralisant la preuve du lem. 3.3.10 à l’anneau de polynômes
$L^+\underline {\mathscr {G}_{\mathbf {f}}}$
sont stables par cette opération, soit en généralisant la preuve du lem. 3.3.10 à l’anneau de polynômes
![]() $\mathbb {Z}[t]$
, soit en utilisant l’espace d’arcs de la grosse cellule. Tout cela nos permet d’introduire la terminologie suivante :
$\mathbb {Z}[t]$
, soit en utilisant l’espace d’arcs de la grosse cellule. Tout cela nos permet d’introduire la terminologie suivante :
Définition 4.2.1. Les racines affines de
![]() $\underline {G}$
sont l’ensemble
$\underline {G}$
sont l’ensemble
![]() $\Phi ^{\operatorname {af}}_G$
des poids non nuls de
$\Phi ^{\operatorname {af}}_G$
des poids non nuls de
![]() $\underline {S}\times \mathbb {G}_{m,\mathbb {Z}}$
dans
$\underline {S}\times \mathbb {G}_{m,\mathbb {Z}}$
dans
![]() $L\underline {G}$
, où le facteur multiplicatif y opère par rotation.
$L\underline {G}$
, où le facteur multiplicatif y opère par rotation.
Bien qu’il y ait un lien entre cette notion de racines affines et celle utilisée dans [Reference Bruhat and TitsBT72, 1.3.3, 6.2.6], on avertit le lecteur qu’il y a des nouvelles racines “imaginaires”, ainsi appelées dans la théorie des algèbres de Kac–Moody, cf. [Reference KacKac90, §5.2], provenant de l’algèbre de Lie de
![]() $L\underline {T}$
et qui restent invisibles pour le groupe d’Iwahori–Weyl
$L\underline {T}$
et qui restent invisibles pour le groupe d’Iwahori–Weyl
![]() $\widetilde {W}$
.
$\widetilde {W}$
.
Lemme 4.2.2. Le système des racines affines
![]() $\Phi ^{\operatorname {af}}_G$
se décompose en une
$\Phi ^{\operatorname {af}}_G$
se décompose en une
![]() $W^{\operatorname {af}}$
-orbite simplement transitive
$W^{\operatorname {af}}$
-orbite simplement transitive
![]() $\Phi ^{\mathrm{r}\acute{\rm e}}_G$
formées des
$\Phi ^{\mathrm{r}\acute{\rm e}}_G$
formées des
![]() $a +n$
pour
$a +n$
pour
![]() $a \in \Phi _G$
et
$a \in \Phi _G$
et
![]() $n \in \Gamma _a'$
et une partie dénombrable
$n \in \Gamma _a'$
et une partie dénombrable
![]() $\Phi ^{\operatorname {im}}_G$
de
$\Phi ^{\operatorname {im}}_G$
de
![]() $\widetilde {W}$
-points fixes
$\widetilde {W}$
-points fixes
![]() $n \in \mathbb {Z}_{\neq 0}$
. Pour chaque racine réelle
$n \in \mathbb {Z}_{\neq 0}$
. Pour chaque racine réelle
![]() $\alpha \in \Phi ^{\mathrm{r}\acute{\rm e}}_G$
, il y a un et un seul sous-groupe fermé additif
$\alpha \in \Phi ^{\mathrm{r}\acute{\rm e}}_G$
, il y a un et un seul sous-groupe fermé additif
![]() $\underline {V_\alpha }$
de
$\underline {V_\alpha }$
de
![]() $L\underline {G}$
tel que son sous-algèbre de Lie soit l’espace de poids de dimension associé à
$L\underline {G}$
tel que son sous-algèbre de Lie soit l’espace de poids de dimension associé à
![]() $\alpha $
.
$\alpha $
.
On ne tentera pas de parler d’une donnée radicielle infinie et on renvoie aux sources de la théorie de Kac–Moody pour ce genre de notions, voir [Reference KacKac90] pour plus de références. Puisque les racines imaginaires forment deux rayons radiciels de cardinal infini, on a du mal à entendre leurs sous-groupes radiciels.
Démonstration. La détermination du système de racines affines est élémentaire, en appliquant ce que
![]() $L\underline {C}\rightarrow L\underline {G}$
est formellement étale, où
$L\underline {C}\rightarrow L\underline {G}$
est formellement étale, où
![]() $\underline {C}=\underline {U_-}\times \underline {T}\times \underline {U_+}$
désigne la grosse cellule, voir [Reference Haines, Lourenço and RicharzHLR20, lem. 7.5] pour un énoncé du même genre, donc les poids non nuls peuvent être calculés au moyen des quasi-épinglages des sous-groupes radiciels et du tore maximal.
$\underline {C}=\underline {U_-}\times \underline {T}\times \underline {U_+}$
désigne la grosse cellule, voir [Reference Haines, Lourenço and RicharzHLR20, lem. 7.5] pour un énoncé du même genre, donc les poids non nuls peuvent être calculés au moyen des quasi-épinglages des sous-groupes radiciels et du tore maximal.
Quant à l’existence des sous-groupes radiciels réels, il suffit de poser
![]() $x_a(t^n\mathbb {G}_{a,\mathbb {Z}}) \subset L\underline {G}$
pour voir que cela remplit les contraintes énoncées. Notons que quand a engendre un rayon radiciel pluriel, on entend par cela
$x_a(t^n\mathbb {G}_{a,\mathbb {Z}}) \subset L\underline {G}$
pour voir que cela remplit les contraintes énoncées. Notons que quand a engendre un rayon radiciel pluriel, on entend par cela
![]() $x_a(t^n\mathbb {G}_{a,\mathbb {Z}},0)$
, si
$x_a(t^n\mathbb {G}_{a,\mathbb {Z}},0)$
, si
![]() $a \in \Phi _G^{\operatorname {m}}$
est multipliable, et
$a \in \Phi _G^{\operatorname {m}}$
est multipliable, et
![]() $x_{a/2}(0,t^n\mathbb {G}_{a,\mathbb {Z}})$
si
$x_{a/2}(0,t^n\mathbb {G}_{a,\mathbb {Z}})$
si
![]() $a\in \Phi _G^{\operatorname {d}}$
est divisible. Pour l’unicité, on prend l’intersection affine et unipotente de deux choix possibles. Vu que l’algèbre de Lie de cette intersection est non triviale, la fibre générique n’est autre que
$a\in \Phi _G^{\operatorname {d}}$
est divisible. Pour l’unicité, on prend l’intersection affine et unipotente de deux choix possibles. Vu que l’algèbre de Lie de cette intersection est non triviale, la fibre générique n’est autre que
![]() $V_{\alpha ,0}$
, voir [Reference Demazure and GabrielDG70, IV, §2, cor. 4.5], d’où l’égalité par considération de l’adhérence.
$V_{\alpha ,0}$
, voir [Reference Demazure and GabrielDG70, IV, §2, cor. 4.5], d’où l’égalité par considération de l’adhérence.
On dit enfin un mot sur l’opération du groupe d’Iwahori–Weyl
![]() $\widetilde {W}$
sur
$\widetilde {W}$
sur
![]() $\Phi ^{\operatorname {af}}_G$
. Vu que
$\Phi ^{\operatorname {af}}_G$
. Vu que
![]() $L\underline {N}$
opère sur
$L\underline {N}$
opère sur
![]() $L\underline {G}$
par conjugaison en préservant
$L\underline {G}$
par conjugaison en préservant
![]() $\underline {S} \subset L\underline {S}$
de façon compatible à l’action de rotation, ces automorphismes préservent les espaces propres de
$\underline {S} \subset L\underline {S}$
de façon compatible à l’action de rotation, ces automorphismes préservent les espaces propres de
![]() $\underline {S}\times \mathbb {G}_{m,\mathbb {Z}}$
. Elle est évidemment triviale dès que
$\underline {S}\times \mathbb {G}_{m,\mathbb {Z}}$
. Elle est évidemment triviale dès que
![]() $\alpha \in \Phi _{G}^{\operatorname {im}}$
est imaginaire, et coïncide avec l’action habituelle de
$\alpha \in \Phi _{G}^{\operatorname {im}}$
est imaginaire, et coïncide avec l’action habituelle de
![]() $\widetilde {W}$
sur les racines réelles au-sens de Bruhat–Tits, en les identifiant aux racines affines de
$\widetilde {W}$
sur les racines réelles au-sens de Bruhat–Tits, en les identifiant aux racines affines de
![]() $\mathscr {A}(\underline {G},\underline {S}, \mathbb {Z} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
.
$\mathscr {A}(\underline {G},\underline {S}, \mathbb {Z} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
.
Les parties parahoriques de
![]() $\Phi _G^{\operatorname {af}}$
au sens de [Reference Bruhat and TitsBT72, 1.5.1] sont aussi bien entendues :
$\Phi _G^{\operatorname {af}}$
au sens de [Reference Bruhat and TitsBT72, 1.5.1] sont aussi bien entendues :
Proposition 4.2.3. Les parties parahoriques de
![]() $\Phi _G^{\operatorname {af}}$
sont mis en bijection au signe près avec les facettes
$\Phi _G^{\operatorname {af}}$
sont mis en bijection au signe près avec les facettes
![]() $\mathbf {f} \subset \mathscr {A}(\underline {G},\underline {S},\mathbb {Z} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
, au moyen de l’application qui fait correspondre à
$\mathbf {f} \subset \mathscr {A}(\underline {G},\underline {S},\mathbb {Z} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
, au moyen de l’application qui fait correspondre à
![]() $\mathbf {f}$
l’ensemble
$\mathbf {f}$
l’ensemble
![]() $\Phi ^{\operatorname {af}}_{\mathbf {f},\geq 0}$
des poids non nuls de
$\Phi ^{\operatorname {af}}_{\mathbf {f},\geq 0}$
des poids non nuls de
![]() $\underline {S}\times \mathbb {G}_{m,\mathbb {Z}}$
dans
$\underline {S}\times \mathbb {G}_{m,\mathbb {Z}}$
dans
![]() $L^+\underline {\mathscr {G}_{\mathbf {f}}}$
.
$L^+\underline {\mathscr {G}_{\mathbf {f}}}$
.
La partie parahorique opposée de
![]() $\Phi ^{\operatorname {af}}_{\mathbf {f},\geq 0}$
sera notée
$\Phi ^{\operatorname {af}}_{\mathbf {f},\geq 0}$
sera notée
![]() $\Phi ^{\operatorname {af}}_{\mathbf {f},\leq 0}$
et l’on voit que leur intersection
$\Phi ^{\operatorname {af}}_{\mathbf {f},\leq 0}$
et l’on voit que leur intersection
![]() $\Phi ^{\operatorname {af}}_{\mathbf {f},0}$
s’identifie naturellement, par restriction au sous-tore
$\Phi ^{\operatorname {af}}_{\mathbf {f},0}$
s’identifie naturellement, par restriction au sous-tore
![]() $\underline {S}$
, au sous-système de racines résiduel
$\underline {S}$
, au sous-système de racines résiduel
![]() $\Phi _{\mathbf {f}} \subset \Phi _G$
associé à
$\Phi _{\mathbf {f}} \subset \Phi _G$
associé à
![]() $\mathbf {f}$
par (3.4.21).
$\mathbf {f}$
par (3.4.21).
Démonstration. On peut considérer la partition symétrique de
![]() $\Phi _G^{\operatorname {af}}$
dont les racines positives sont celles de la forme
$\Phi _G^{\operatorname {af}}$
dont les racines positives sont celles de la forme
![]() $n \in \mathbb {Z}_{>0}$
, ou bien
$n \in \mathbb {Z}_{>0}$
, ou bien
![]() $a+n$
avec
$a+n$
avec
![]() $a \in \Phi _G^+$
et
$a \in \Phi _G^+$
et
![]() $n \in \Gamma ^{\prime }_{a}\cap \mathbb {R}_{\geq 0}$
ou
$n \in \Gamma ^{\prime }_{a}\cap \mathbb {R}_{\geq 0}$
ou
![]() $a \in \Phi _G^-$
et
$a \in \Phi _G^-$
et
![]() $n \in \Gamma ^{\prime }_{a}\cap \mathbb {R}_{>0}$
, voir (3.4.11). Mais cela n’est autre que l’ensemble des poids non nuls de
$n \in \Gamma ^{\prime }_{a}\cap \mathbb {R}_{>0}$
, voir (3.4.11). Mais cela n’est autre que l’ensemble des poids non nuls de
![]() $L^+\underline {\mathscr {G}_{\mathbf {a}}}$
, où
$L^+\underline {\mathscr {G}_{\mathbf {a}}}$
, où
![]() $\mathbf {a}$
désigne l’alcôve dominante adhérente à l’origine. Ceci étant, on s’en sert aussi pour récupérer les racines négatives simples de
$\mathbf {a}$
désigne l’alcôve dominante adhérente à l’origine. Ceci étant, on s’en sert aussi pour récupérer les racines négatives simples de
![]() $\Phi _G^{\mathrm{r}\acute{\rm e}}$
: pour chaque cloison
$\Phi _G^{\mathrm{r}\acute{\rm e}}$
: pour chaque cloison
![]() $\mathbf {f}_i$
dans l’adhérence de
$\mathbf {f}_i$
dans l’adhérence de
![]() $\mathbf {a}$
, on considère la racine réelle qui est poids de
$\mathbf {a}$
, on considère la racine réelle qui est poids de
![]() $L^+\underline {\mathscr {G}_{\mathbf {f}_i}}$
mais pas de
$L^+\underline {\mathscr {G}_{\mathbf {f}_i}}$
mais pas de
![]() $L^+\underline {\mathscr {G}_{\mathbf {a}}}$
, ce qui montre l’assertion dans le cas parahorique minimal. En général, les sous-groupes ainsi que les parties parahoriques sont engendrées à un sens convenable par les minimaux qui y sont contenus et la proposition est achevée.
$L^+\underline {\mathscr {G}_{\mathbf {a}}}$
, ce qui montre l’assertion dans le cas parahorique minimal. En général, les sous-groupes ainsi que les parties parahoriques sont engendrées à un sens convenable par les minimaux qui y sont contenus et la proposition est achevée.
Nos sous-groupes radiciels affines nous permettent de choisir canoniquement les facteurs de Levi promis au début de ce numéro.
Proposition 4.2.4. Le groupe d’arcs
![]() $L^+\underline {\mathscr {G}_{\mathbf {f}}}$
admet un et un seul sous-
$L^+\underline {\mathscr {G}_{\mathbf {f}}}$
admet un et un seul sous-
![]() $\mathbb {Z}$
-groupe fermé et distingué, pro-unipotent, pro-lisse et connexe maximal
$\mathbb {Z}$
-groupe fermé et distingué, pro-unipotent, pro-lisse et connexe maximal
![]() $L^{++}\underline {\mathscr {G}_{\mathbf {f}}}$
, ainsi qu’un unique sous-
$L^{++}\underline {\mathscr {G}_{\mathbf {f}}}$
, ainsi qu’un unique sous-
![]() $\mathbb {Z}$
-groupe réductif
$\mathbb {Z}$
-groupe réductif
![]() $\underline {M_{\mathbf {f}}}$
contenant
$\underline {M_{\mathbf {f}}}$
contenant
![]() $\underline {S}$
et invariant par l’action de rotation tel que
$\underline {S}$
et invariant par l’action de rotation tel que
![]() $\underline {M_{\mathbf {f}}} \ltimes L^{++}\underline {\mathscr {G}_{\mathbf {f}}} \rightarrow L^{+}\underline {\mathscr {G}_{\mathbf {f}}}$
soit un isomorphisme.
$\underline {M_{\mathbf {f}}} \ltimes L^{++}\underline {\mathscr {G}_{\mathbf {f}}} \rightarrow L^{+}\underline {\mathscr {G}_{\mathbf {f}}}$
soit un isomorphisme.
Par suite, nous dénommons
![]() $L^{++}\underline {\mathscr {G}_{\mathbf {f}}}$
le radical pro-unipotent,
$L^{++}\underline {\mathscr {G}_{\mathbf {f}}}$
le radical pro-unipotent,
![]() $\underline {M_{\mathbf {f}}}$
le facteur de Levi et l’écriture suivant
$\underline {M_{\mathbf {f}}}$
le facteur de Levi et l’écriture suivant
la décomposition de Levi de
![]() $L^{+}\underline {\mathscr {G}_{\mathbf {f}}}$
.
$L^{+}\underline {\mathscr {G}_{\mathbf {f}}}$
.
Démonstration. Si l’on géométrise [Reference Bruhat and TitsBT84a, prop. 4.6.10] et/ou [Reference LourençoLou21, lem. 4.6], on arrive à la conclusion qu’il y a une partie non vide et bornée
![]() $\Omega :=\operatorname {tour}(\mathbf {f})$
, appelée l’entourage de
$\Omega :=\operatorname {tour}(\mathbf {f})$
, appelée l’entourage de
![]() $\mathbf {f}$
, voir aussi [Reference Pereira LourençoPL20, IV, lem. 3.5], telle que le sous-groupe
$\mathbf {f}$
, voir aussi [Reference Pereira LourençoPL20, IV, lem. 3.5], telle que le sous-groupe
![]() $L^+\underline {\mathscr {G}_{\Omega }} \subset L^+\underline {\mathscr {G}_{\mathbf {f}}}$
est pro-soluble et dont les sous-groupes radiciels sont ceux de ce qui s’avérera le radical pro-unipotent
$L^+\underline {\mathscr {G}_{\Omega }} \subset L^+\underline {\mathscr {G}_{\mathbf {f}}}$
est pro-soluble et dont les sous-groupes radiciels sont ceux de ce qui s’avérera le radical pro-unipotent
![]() $L^{++}\underline {\mathscr {G}_{\mathbf {f}}}$
; autrement dit, la seule différence entre
$L^{++}\underline {\mathscr {G}_{\mathbf {f}}}$
; autrement dit, la seule différence entre
![]() $L^+\underline {\mathscr {G}_{\Omega }}$
et le groupe
$L^+\underline {\mathscr {G}_{\Omega }}$
et le groupe
![]() $L^{++}\underline {\mathscr {G}_{\mathbf {f}}}$
est le sous-tore déployé maximal du premier. Notons que la pro-solubilité de ce groupe entraîne qu’on ait un isomorphisme de schémas
$L^{++}\underline {\mathscr {G}_{\mathbf {f}}}$
est le sous-tore déployé maximal du premier. Notons que la pro-solubilité de ce groupe entraîne qu’on ait un isomorphisme de schémas
![]() $L^+\underline {\mathscr {C}_{\Omega }}\simeq L^+\underline {\mathscr {G}_{\Omega }}$
, où
$L^+\underline {\mathscr {C}_{\Omega }}\simeq L^+\underline {\mathscr {G}_{\Omega }}$
, où
![]() $\underline {\mathscr {C}_{\Omega }}$
désigne le produit
$\underline {\mathscr {C}_{\Omega }}$
désigne le produit
![]() $\underline {\mathscr {U}_{-,\Omega }}\times \underline {\mathscr {T}} \times \underline {\mathscr {U}_{+,\Omega }}$
.
$\underline {\mathscr {U}_{-,\Omega }}\times \underline {\mathscr {T}} \times \underline {\mathscr {U}_{+,\Omega }}$
.
En particulier, on s’est presque ramené a construire le radical pro-unipotent
![]() $L^{++}\underline {\mathscr {T}}$
au cas où
$L^{++}\underline {\mathscr {T}}$
au cas où
![]() $G=T$
est un tore. Dans cet endroit, on utilise la décomposition (3.4.1) comme produit de restrictions des scalaires de groupes multiplicatifs et l’on observe que
$G=T$
est un tore. Dans cet endroit, on utilise la décomposition (3.4.1) comme produit de restrictions des scalaires de groupes multiplicatifs et l’on observe que
il s’ensuit que le premier groupe de congruence par rapport à la variable
![]() $t^{1/d}$
en fournit le radical pro-unipotent cherché.
$t^{1/d}$
en fournit le radical pro-unipotent cherché.
En général, on pose
et l’on vérifie que ce sous-schéma fermé de
![]() $L^+\underline {\mathscr {G}_{ \mathbf {f}}}$
possède une structure naturelle de groupe en vérifiant que les applications conjugaison, commutateur et échange des axiomes de la déf. 3.2.1 y sont bien définies. Son unicité est claire, vu que les spécialisés
$L^+\underline {\mathscr {G}_{ \mathbf {f}}}$
possède une structure naturelle de groupe en vérifiant que les applications conjugaison, commutateur et échange des axiomes de la déf. 3.2.1 y sont bien définies. Son unicité est claire, vu que les spécialisés
![]() $L^{++}\mathscr {G}_{\mathbf {f},p}$
en caractéristique
$L^{++}\mathscr {G}_{\mathbf {f},p}$
en caractéristique
![]() $p \in \mathbb {P} \cup \{0\}$
de ce sous-schéma en groupes redonnent le radical pro-unipotent habituel selon [Reference Bruhat and TitsBT84a, prop. 4.6.10] et [Reference LourençoLou21, lem. 4.6].
$p \in \mathbb {P} \cup \{0\}$
de ce sous-schéma en groupes redonnent le radical pro-unipotent habituel selon [Reference Bruhat and TitsBT84a, prop. 4.6.10] et [Reference LourençoLou21, lem. 4.6].
Enfin, on veut construire le facteur de Levi
![]() $\underline {M_{\mathbf {f}}}$
. Son unicité découle de ce que son algèbre de Lie est le seul complément
$\underline {M_{\mathbf {f}}}$
. Son unicité découle de ce que son algèbre de Lie est le seul complément
![]() $\mathbb {Z}$
-linéaire invariant par
$\mathbb {Z}$
-linéaire invariant par
![]() $\operatorname {Lie}(\underline {S}\times \mathbb {G}_{m,\mathbb {Z}})$
du radical pro-nilpotent de
$\operatorname {Lie}(\underline {S}\times \mathbb {G}_{m,\mathbb {Z}})$
du radical pro-nilpotent de
![]() $\operatorname {Lie}L^+\underline {\mathscr {G}_{\mathbf {f}}}$
, donc ses sous-groupes radiciels
$\operatorname {Lie}L^+\underline {\mathscr {G}_{\mathbf {f}}}$
, donc ses sous-groupes radiciels
![]() $\underline {V_\alpha }$
relativement à S sont forcément de la forme
$\underline {V_\alpha }$
relativement à S sont forcément de la forme
![]() $x_a(t^{f_{\mathbf {f}}(a)}\mathbb {G}_a)$
pour toute racine résiduelle
$x_a(t^{f_{\mathbf {f}}(a)}\mathbb {G}_a)$
pour toute racine résiduelle
![]() $a \in \Phi _{\mathbf {f}}$
, cf. (3.4.21) et prop. 4.2.3. Montrons d’abord que la grosse cellule du sous-groupe
$a \in \Phi _{\mathbf {f}}$
, cf. (3.4.21) et prop. 4.2.3. Montrons d’abord que la grosse cellule du sous-groupe
![]() $\underline {M_{\mathbf {f}}} \subset L^+\underline {\mathscr {G}_{\mathbf {f}}}$
que nous voulons construire, constituée par le produit des sous-groupes radiciels
$\underline {M_{\mathbf {f}}} \subset L^+\underline {\mathscr {G}_{\mathbf {f}}}$
que nous voulons construire, constituée par le produit des sous-groupes radiciels
![]() $\underline {V_\alpha }$
et de
$\underline {V_\alpha }$
et de
![]() $\underline {S}$
, en hérite une loi birationnelle. En effet, il s’avérera par les calculs explicites des applications des axiomes (DRS 1-3) que cette loi birationelle coïncide avec celle du groupe épinglé à tore maximal
$\underline {S}$
, en hérite une loi birationnelle. En effet, il s’avérera par les calculs explicites des applications des axiomes (DRS 1-3) que cette loi birationelle coïncide avec celle du groupe épinglé à tore maximal
![]() $\underline {S}$
et système de racines
$\underline {S}$
et système de racines
![]() $\Phi _{\mathbf {f}}$
au moyen d’un système de Chevalley convenable.
$\Phi _{\mathbf {f}}$
au moyen d’un système de Chevalley convenable.
Étudions d’abord les morphismes d’échange des facteurs. On peut voir d’après (3.3.18) et (3.3.20) que le lieu ouvert distingué de définition de l’application échange est donné par
![]() $1-rs$
. Puis (3.3.19) et (3.3.21) entraînent que
$1-rs$
. Puis (3.3.19) et (3.3.21) entraînent que
![]() $\beta _a$
s’écrive comme
$\beta _a$
s’écrive comme
ce qui coïncide avec l’application voulue. Cela est légèrement plus compliqué lorsque
![]() $a \in \Phi _{\mathbf {f}}$
est une racine multipliable ou divisible dans
$a \in \Phi _{\mathbf {f}}$
est une racine multipliable ou divisible dans
![]() $\Phi _G$
, mais les écritures se simplifient nettement et il faut juste observer que
$\Phi _G$
, mais les écritures se simplifient nettement et il faut juste observer que
![]() $(2a)^\vee =a^\vee /2$
.
$(2a)^\vee =a^\vee /2$
.
Finalement, nous traitons l’application commutateur, voir la règle (DR2) de la déf. 3.2.1. Pour cela on peut supposer
![]() $G^{\operatorname {ad}}$
absolument simple et non déployé, les morphismes les plus intéressants parmi ceux écrits dans [Reference Bruhat and TitsBT84a, A.6] étant ceux dont la longueur des racines impliquées n’est pas constante. On suppose premièrement que le système de racines
$G^{\operatorname {ad}}$
absolument simple et non déployé, les morphismes les plus intéressants parmi ceux écrits dans [Reference Bruhat and TitsBT84a, A.6] étant ceux dont la longueur des racines impliquées n’est pas constante. On suppose premièrement que le système de racines
![]() $\Phi _G$
est réduit et qu’il possède une arête double. L’éventualité la plus intéressante est lorsque
$\Phi _G$
est réduit et qu’il possède une arête double. L’éventualité la plus intéressante est lorsque
![]() $a,b \in \Phi _{\mathbf {f}}\cap \Phi _G^<$
sont racines courtes dont la somme est longue, cf. [Reference Bruhat and TitsBT84a, A.6 b)]. Alors, on obtient
$a,b \in \Phi _{\mathbf {f}}\cap \Phi _G^<$
sont racines courtes dont la somme est longue, cf. [Reference Bruhat and TitsBT84a, A.6 b)]. Alors, on obtient
 $$ \begin{align}[x_a(t^{f_{\mathbf{f}}(a)}r),x_b(t^{f_{\mathbf{f}}(b)}s)]\sim\begin{cases} x_{a+b}(2t^{f_{\mathbf{f}}(a+b)}rs) \text{, si } a+b\in\Phi_{\mathbf{f}}\\ 0 \text{, sinon,}\end{cases} \end{align} $$
$$ \begin{align}[x_a(t^{f_{\mathbf{f}}(a)}r),x_b(t^{f_{\mathbf{f}}(b)}s)]\sim\begin{cases} x_{a+b}(2t^{f_{\mathbf{f}}(a+b)}rs) \text{, si } a+b\in\Phi_{\mathbf{f}}\\ 0 \text{, sinon,}\end{cases} \end{align} $$
car l’ensemble des valeurs de la valuation
![]() $\varphi _{a+b}$
est égal à
$\varphi _{a+b}$
est égal à
![]() $\mathbb {Z}$
et la trace de
$\mathbb {Z}$
et la trace de
![]() $t^{1/2}\mathbb {Z}[t]$
s’annule. Alors, l’application commutateur est vraiment la cherchée (au signe près), d’après la règle de Chevalley, voir [SGA3, exp. XXIII, cor. 6.5]. Si nous supposons ensuite que
$t^{1/2}\mathbb {Z}[t]$
s’annule. Alors, l’application commutateur est vraiment la cherchée (au signe près), d’après la règle de Chevalley, voir [SGA3, exp. XXIII, cor. 6.5]. Si nous supposons ensuite que
![]() $\Phi _G$
est réduit et qu’il possède une arête triple, alors nous nous concentrons sur le cas où
$\Phi _G$
est réduit et qu’il possède une arête triple, alors nous nous concentrons sur le cas où
![]() $a,b \in \Phi _{\mathbf {f}}\cap \Phi _G^<$
sont courtes,
$a,b \in \Phi _{\mathbf {f}}\cap \Phi _G^<$
sont courtes,
![]() $a+b \in \Phi _G^<$
est courte (automatiquement dans
$a+b \in \Phi _G^<$
est courte (automatiquement dans
![]() $\Phi _{\mathbf {f}}$
) et
$\Phi _{\mathbf {f}}$
) et
![]() $2a+b, a+2b \in \Phi _G^>$
sont longues, cf. [Reference Bruhat and TitsBT84a, A.6 d) et e)]. On en déduit les formules :
$2a+b, a+2b \in \Phi _G^>$
sont longues, cf. [Reference Bruhat and TitsBT84a, A.6 d) et e)]. On en déduit les formules :
 $$ \begin{align}[x_a(t^{f_{\mathbf{f}}(a)}r),x_b(t^{f_{\mathbf{f}}(b)}s)]\sim\begin{cases} \prod_{p,q} x_{c}( (p+q)t^{f_{\mathbf{f}}(c)}rs)\text{, si } 2a+b\in\Phi_{\mathbf{f}}\\x_{a+b}( t^{f_{\mathbf{f}}(a+b)}rs) \text{, sinon,}\end{cases} \end{align} $$
$$ \begin{align}[x_a(t^{f_{\mathbf{f}}(a)}r),x_b(t^{f_{\mathbf{f}}(b)}s)]\sim\begin{cases} \prod_{p,q} x_{c}( (p+q)t^{f_{\mathbf{f}}(c)}rs)\text{, si } 2a+b\in\Phi_{\mathbf{f}}\\x_{a+b}( t^{f_{\mathbf{f}}(a+b)}rs) \text{, sinon,}\end{cases} \end{align} $$
où
![]() $c=pa+qb$
décrit l’ensemble
$c=pa+qb$
décrit l’ensemble
![]() $]a,b[$
. Le premier cas correspond à l’un sous-système de racines résiduel
$]a,b[$
. Le premier cas correspond à l’un sous-système de racines résiduel
![]() $\Phi _{\mathbf {f}}$
de type
$\Phi _{\mathbf {f}}$
de type
![]() $G_2$
et le deuxième à l’un de type
$G_2$
et le deuxième à l’un de type
![]() $A_2$
.
$A_2$
.
Finalement, si
![]() $\Phi _G$
est non réduit, on peut procéder de la même manière. Par exemple, si
$\Phi _G$
est non réduit, on peut procéder de la même manière. Par exemple, si
![]() $a,b\in \Phi _{\mathbf {f}} \cap \Phi _G^{\operatorname {nd,nm}}$
et
$a,b\in \Phi _{\mathbf {f}} \cap \Phi _G^{\operatorname {nd,nm}}$
et
![]() $a+b \in \Phi _G^{\operatorname {d}}$
est divisible, alors le commutateur s’écrit, cf. (3.3.13), comme l’anti-trace de
$a+b \in \Phi _G^{\operatorname {d}}$
est divisible, alors le commutateur s’écrit, cf. (3.3.13), comme l’anti-trace de
![]() $rs$
, ce qui s’annule si et seulement si
$rs$
, ce qui s’annule si et seulement si
![]() $a+b \notin \Phi _{\mathbf {f}}$
, et sinon a constante de Chevalley égale à
$a+b \notin \Phi _{\mathbf {f}}$
, et sinon a constante de Chevalley égale à
![]() $2$
, comme prédit par la règle de Chevalley, cf. [SGA3, exp. XXIII, cor. 6.5]; si
$2$
, comme prédit par la règle de Chevalley, cf. [SGA3, exp. XXIII, cor. 6.5]; si
![]() $a,b\in \Phi _{\mathbf {f}} \cap \Phi _G^{\operatorname {m}}$
et
$a,b\in \Phi _{\mathbf {f}} \cap \Phi _G^{\operatorname {m}}$
et
![]() $a+b \in \Phi _G^{\operatorname {nd,nm}}$
, alors la constante
$a+b \in \Phi _G^{\operatorname {nd,nm}}$
, alors la constante
![]() $2$
qui est parue dans l’écriture due à Tits, cf. (3.3.14), est aussi correcte, grâce à la règle de Chevalley. En ce qui concerne le cas où
$2$
qui est parue dans l’écriture due à Tits, cf. (3.3.14), est aussi correcte, grâce à la règle de Chevalley. En ce qui concerne le cas où
![]() $a \in \Phi _{\mathbf {f}}\cap \Phi _G^{\operatorname {m}}$
,
$a \in \Phi _{\mathbf {f}}\cap \Phi _G^{\operatorname {m}}$
,
![]() $b \in \Phi _{\mathbf {f}} \cap \Phi _G^{\operatorname {nd,nm}} $
et
$b \in \Phi _{\mathbf {f}} \cap \Phi _G^{\operatorname {nd,nm}} $
et
![]() $a+b,2a+2b, 2a+b \in \Phi _G$
, cf. (3.3.15), on en laisse le soin au lecteur, vu que les écritures sont assez simples.
$a+b,2a+2b, 2a+b \in \Phi _G$
, cf. (3.3.15), on en laisse le soin au lecteur, vu que les écritures sont assez simples.
Les paragraphes ci-dessus fournissent par fonctorialité des lois birationnelles une application
![]() $\underline {M_{\mathbf {f}}} \rightarrow L^{+}\underline {\mathscr {G}_{\mathbf {f}}}$
et ils montrent aussi que le faisceau quotient
$\underline {M_{\mathbf {f}}} \rightarrow L^{+}\underline {\mathscr {G}_{\mathbf {f}}}$
et ils montrent aussi que le faisceau quotient
![]() $L^+\underline {\mathscr {G}_{\mathbf {f}}}/L^{++}\underline {\mathscr {G}_{\mathbf {f}}}$
pour la topologie plate, lequel est représentable par un
$L^+\underline {\mathscr {G}_{\mathbf {f}}}/L^{++}\underline {\mathscr {G}_{\mathbf {f}}}$
pour la topologie plate, lequel est représentable par un
![]() $\mathbb {Z}$
-groupe lisse, affine et connexe d’après un théorème d’Anantharaman, cf. [Reference AnantharamanAna73, th. 4.A], s’identifie à
$\mathbb {Z}$
-groupe lisse, affine et connexe d’après un théorème d’Anantharaman, cf. [Reference AnantharamanAna73, th. 4.A], s’identifie à
![]() $\underline {M_{\mathbf {f}}}$
au moyen du morphisme composé. Ceci n’est plus que la décomposition de Levi (4.2.2) qu’on avait cherchée.
$\underline {M_{\mathbf {f}}}$
au moyen du morphisme composé. Ceci n’est plus que la décomposition de Levi (4.2.2) qu’on avait cherchée.
Voici une conséquence pertinente de la prop. précédente :
Corollaire 4.2.5. Soit
![]() $\mathbf {a}$
une alcôve adhérente à
$\mathbf {a}$
une alcôve adhérente à
![]() $\mathbf {f}$
. Alors,
$\mathbf {f}$
. Alors,
![]() $L^+\underline {\mathscr {G}_{\mathbf {f}}}/L^+\underline {\mathscr {G}_{\mathbf {a}}}$
est représentable par un schéma projectif lisse et la projection
$L^+\underline {\mathscr {G}_{\mathbf {f}}}/L^+\underline {\mathscr {G}_{\mathbf {a}}}$
est représentable par un schéma projectif lisse et la projection
![]() $L^+\underline {\mathscr {G}_{\mathbf {f}}}\rightarrow L^+\underline {\mathscr {G}_{\mathbf {f}}}/L^+\underline {\mathscr {G}_{\mathbf {a}}}$
est un
$L^+\underline {\mathscr {G}_{\mathbf {f}}}\rightarrow L^+\underline {\mathscr {G}_{\mathbf {f}}}/L^+\underline {\mathscr {G}_{\mathbf {a}}}$
est un
![]() $L^+\underline {\mathscr {G}_{\mathbf {a}}}$
-torseur localement trivial pour la topologie ouverte.
$L^+\underline {\mathscr {G}_{\mathbf {a}}}$
-torseur localement trivial pour la topologie ouverte.
Démonstration. La première assertion résulte de [Reference Bruhat and TitsBT84a, th. 4.6.33] et [Reference LourençoLou21, th. 4.7], lequel fournit un sous-groupe borélien
![]() $\underline {B_{\mathbf {a},\mathbf {f}}}$
de
$\underline {B_{\mathbf {a},\mathbf {f}}}$
de
![]() $\underline {M_{\mathbf {f}}}$
contenant le tore maximal fixé
$\underline {M_{\mathbf {f}}}$
contenant le tore maximal fixé
![]() $\underline {S}$
tel que l’image réciproque de
$\underline {S}$
tel que l’image réciproque de
![]() $\underline {B_{\mathbf {a},\mathbf {f}}}$
dans
$\underline {B_{\mathbf {a},\mathbf {f}}}$
dans
![]() $L^+\underline {\mathscr {G}_{\mathbf {f}}}$
coïncide avec
$L^+\underline {\mathscr {G}_{\mathbf {f}}}$
coïncide avec
![]() $L^+\underline {\mathscr {G}_{\mathbf {a}}}$
. En particulier, le faisceau quotient
$L^+\underline {\mathscr {G}_{\mathbf {a}}}$
. En particulier, le faisceau quotient
![]() $L^+\underline {\mathscr {G}_{\mathbf {f}}}/L^+\underline {\mathscr {G}_{\mathbf {a}}}$
pour la topologie étale est représentable par le
$L^+\underline {\mathscr {G}_{\mathbf {f}}}/L^+\underline {\mathscr {G}_{\mathbf {a}}}$
pour la topologie étale est représentable par le
![]() $\mathbb {Z}$
-schéma projectif et lisse
$\mathbb {Z}$
-schéma projectif et lisse
![]() $\underline {M_{\mathbf {f}}}/\underline {B_{\mathbf {a},\mathbf {f}}}$
(égal à
$\underline {M_{\mathbf {f}}}/\underline {B_{\mathbf {a},\mathbf {f}}}$
(égal à
![]() $\mathbb {P}^1_{\mathbb {Z}}$
si
$\mathbb {P}^1_{\mathbb {Z}}$
si
![]() $\mathbf {f}$
est un cloison) et le morphisme quotient
$\mathbf {f}$
est un cloison) et le morphisme quotient
![]() $L^+\underline {\mathscr {G}_{\mathbf {f}}} \rightarrow L^+\underline {\mathscr {G}_{\mathbf {f}}}/L^+\underline {\mathscr {G}_{\mathbf {a}}}$
possède des sections localement pour la topologie ouverte, car il en est de même de la projection vers
$L^+\underline {\mathscr {G}_{\mathbf {f}}} \rightarrow L^+\underline {\mathscr {G}_{\mathbf {f}}}/L^+\underline {\mathscr {G}_{\mathbf {a}}}$
possède des sections localement pour la topologie ouverte, car il en est de même de la projection vers
![]() $\underline {M_{\mathbf {f}}}$
et de l’application
$\underline {M_{\mathbf {f}}}$
et de l’application
![]() $\underline {M_{\mathbf {f}}}\rightarrow \underline {M_{\mathbf {f}}}/\underline {B_{\mathbf {a},\mathbf {f}}}$
, cf. [SGA3, exp. XXVI, cor. 5.9].
$\underline {M_{\mathbf {f}}}\rightarrow \underline {M_{\mathbf {f}}}/\underline {B_{\mathbf {a},\mathbf {f}}}$
, cf. [SGA3, exp. XXVI, cor. 5.9].
Dans la prop. 4.2.4, on a montré l’existence du radical pro-unipotent
![]() $ L^{++}\underline {\mathscr {G}_{\mathbf {f}}}$
et maintenant on va voir qu’il s’identifie au produit direct de ses sous-groupes radiciels
$ L^{++}\underline {\mathscr {G}_{\mathbf {f}}}$
et maintenant on va voir qu’il s’identifie au produit direct de ses sous-groupes radiciels
![]() $\underline {V_{\alpha }}$
, cf. lem. 4.2.2, pris correctement dans la catégorie des pro-groupes.
$\underline {V_{\alpha }}$
, cf. lem. 4.2.2, pris correctement dans la catégorie des pro-groupes.
Proposition 4.2.6. Soit I une partie finie de racines réelles dans
![]() $\Phi _{\mathbf {f},>0}^{\operatorname {af}}$
à complément saturé au sens de [Reference Conrad, Gabber and PrasadCGP15, déf. C.2.25]. Alors, le radical pro-unipotent
$\Phi _{\mathbf {f},>0}^{\operatorname {af}}$
à complément saturé au sens de [Reference Conrad, Gabber and PrasadCGP15, déf. C.2.25]. Alors, le radical pro-unipotent
![]() $L^{++}\underline {\mathscr {G}_{\mathbf {f}}}$
admet un unique sous-groupe fermé et pro-lisse
$L^{++}\underline {\mathscr {G}_{\mathbf {f}}}$
admet un unique sous-groupe fermé et pro-lisse
![]() $L^{++}_I\underline {\mathscr {G}_{\mathbf {f}}}$
stable sous
$L^{++}_I\underline {\mathscr {G}_{\mathbf {f}}}$
stable sous
![]() $\underline {S}\times \mathbb {G}_{m,\mathbb {Z}}$
tel que les applications produit
$\underline {S}\times \mathbb {G}_{m,\mathbb {Z}}$
tel que les applications produit
soient des isomorphismes, quel que soit l’ordre mis sur I. En particulier, si l’on pose
![]() $I_w=\Phi _{\mathbf {a},>0}^{\mathrm{r}\acute{\rm e}} \cap w\Phi _{\mathbf {f},\leq 0}^{\mathrm{r}\acute{\rm e}}$
et
$I_w=\Phi _{\mathbf {a},>0}^{\mathrm{r}\acute{\rm e}} \cap w\Phi _{\mathbf {f},\leq 0}^{\mathrm{r}\acute{\rm e}}$
et
![]() $L^{++}_w=L^{++}_{I_w}$
pour alléger la notation, alors
$L^{++}_w=L^{++}_{I_w}$
pour alléger la notation, alors
![]() $L^{++}_{w}\underline {\mathscr {G}_{\mathbf {f}}} =L^{++}\underline {\mathscr {G}_{\mathbf {a}}} \cap n_wL^{++}\underline {\mathscr {G}_{\mathbf {f}}}n_w^{-1}$
pour tout représentant
$L^{++}_{w}\underline {\mathscr {G}_{\mathbf {f}}} =L^{++}\underline {\mathscr {G}_{\mathbf {a}}} \cap n_wL^{++}\underline {\mathscr {G}_{\mathbf {f}}}n_w^{-1}$
pour tout représentant
![]() $n_w\in LN(\mathbb {Z})$
de w.
$n_w\in LN(\mathbb {Z})$
de w.
Démonstration. Montrons d’abord que le morphisme suivant
 $$ \begin{align} \left[\prod_{\alpha\in J}\underline{V_\alpha} \right] \times L^{++}\underline{\mathscr{T}}/L^{(n)}\underline{\mathscr{T}} \rightarrow L^{++}\underline{\mathscr{G}_{\mathbf{f}}}/L^{(n)}\underline{\mathscr{G}_{\mathbf{f}}} \end{align} $$
$$ \begin{align} \left[\prod_{\alpha\in J}\underline{V_\alpha} \right] \times L^{++}\underline{\mathscr{T}}/L^{(n)}\underline{\mathscr{T}} \rightarrow L^{++}\underline{\mathscr{G}_{\mathbf{f}}}/L^{(n)}\underline{\mathscr{G}_{\mathbf{f}}} \end{align} $$
est un isomorphisme, où
![]() $\alpha $
décrit l’ensemble J des racines du membre de droite par rapport à
$\alpha $
décrit l’ensemble J des racines du membre de droite par rapport à
![]() $\underline {S}\times \mathbb {G}_{m, \mathbb {Z}}$
et les sous-groupes radiciels
$\underline {S}\times \mathbb {G}_{m, \mathbb {Z}}$
et les sous-groupes radiciels
![]() $\underline {V_\alpha }$
sont mis dans un ordre quelconque. Après les changements de base
$\underline {V_\alpha }$
sont mis dans un ordre quelconque. Après les changements de base
![]() $\mathbb {Z} \rightarrow \mathbb {F}_p$
à tout corps premier, ceci n’est plus que la décomposition habituelle d’un groupe unipotent lisse opéré par un tore de [Reference Bruhat and TitsBT84a, 1.1.7] et/ou [Reference Conrad, Gabber and PrasadCGP15, prop. C.2.26]. En particulier, le
$\mathbb {Z} \rightarrow \mathbb {F}_p$
à tout corps premier, ceci n’est plus que la décomposition habituelle d’un groupe unipotent lisse opéré par un tore de [Reference Bruhat and TitsBT84a, 1.1.7] et/ou [Reference Conrad, Gabber and PrasadCGP15, prop. C.2.26]. En particulier, le
![]() $\mathbb {Z}$
-morphisme donné par (4.2.9) de
$\mathbb {Z}$
-morphisme donné par (4.2.9) de
![]() $\mathbb {Z}$
-schémas lisses est bijectif et birationnel, donc un isomorphisme d’après le théorème principal de Zariski.
$\mathbb {Z}$
-schémas lisses est bijectif et birationnel, donc un isomorphisme d’après le théorème principal de Zariski.
Choisissons n assez grand tel que
![]() $\underline {V_\alpha } \cap L^{(n)}\underline {\mathscr {G}_{\mathbf {f}}}=1$
pour toute racine réelle
$\underline {V_\alpha } \cap L^{(n)}\underline {\mathscr {G}_{\mathbf {f}}}=1$
pour toute racine réelle
![]() $\alpha \in I$
. Si l’on note
$\alpha \in I$
. Si l’on note
![]() $L^{++}_I \underline {\mathscr {G}_{\mathbf {f}}}$
l’image réciproque dans
$L^{++}_I \underline {\mathscr {G}_{\mathbf {f}}}$
l’image réciproque dans
![]() $L^{++}\underline {\mathscr {G}_{\mathbf {f}}}$
du sous-groupe de
$L^{++}\underline {\mathscr {G}_{\mathbf {f}}}$
du sous-groupe de
![]() $L^{++}\underline {\mathscr {G}_{\mathbf {f}}}/L^{(n)}\underline {\mathscr {G}_{\mathbf {f}}}$
complémentaire de
$L^{++}\underline {\mathscr {G}_{\mathbf {f}}}/L^{(n)}\underline {\mathscr {G}_{\mathbf {f}}}$
complémentaire de
![]() $\prod _{\alpha \in I}\underline {V_\alpha }$
, cf. (4.2.9), on obtient ce qu’on avait souhaité. L’unicité est une conséquence de la détermination de l’algèbre de Lie et l’équivalence du foncteur Lie pour les groupes pro-unipotents en caractéristique nulle, voir [Reference KumarKum02, th. 4.4.19], ce qui caractérise le modèle entier en prenant l’adhérence.
$\prod _{\alpha \in I}\underline {V_\alpha }$
, cf. (4.2.9), on obtient ce qu’on avait souhaité. L’unicité est une conséquence de la détermination de l’algèbre de Lie et l’équivalence du foncteur Lie pour les groupes pro-unipotents en caractéristique nulle, voir [Reference KumarKum02, th. 4.4.19], ce qui caractérise le modèle entier en prenant l’adhérence.
Tournons-nous vers le cas qui s’avérera fondamental dans la suite, celui de la partie
![]() $I_w= \Phi _{\mathbf {a},>0}^{\mathrm{r}\acute{\rm e}}\cap w\Phi _{\mathbf {f},\leq 0}^{\mathrm{r}\acute{\rm e}}$
de cardinal
$I_w= \Phi _{\mathbf {a},>0}^{\mathrm{r}\acute{\rm e}}\cap w\Phi _{\mathbf {f},\leq 0}^{\mathrm{r}\acute{\rm e}}$
de cardinal
![]() $l(w)$
et de la décomposition (4.2.8) pour
$l(w)$
et de la décomposition (4.2.8) pour
![]() $I=I_w$
. L’inclusion
$I=I_w$
. L’inclusion
![]() $L^{++}_w\underline {\mathscr {G}_{\mathbf {f}}} \subset L^{++}\underline {\mathscr {G}_{\mathbf {a}}} \cap n_wL^{++}\underline {\mathscr {G}_{\mathbf {f}}}n_w^{-1}$
est presque évidente et se démontre aisément, dont le soin est laissé au lecteur. Il reste à observer que l’intersection de
$L^{++}_w\underline {\mathscr {G}_{\mathbf {f}}} \subset L^{++}\underline {\mathscr {G}_{\mathbf {a}}} \cap n_wL^{++}\underline {\mathscr {G}_{\mathbf {f}}}n_w^{-1}$
est presque évidente et se démontre aisément, dont le soin est laissé au lecteur. Il reste à observer que l’intersection de
![]() $\prod _{\beta \in w^{-1}I_w} \underline {V_{\beta }}$
avec
$\prod _{\beta \in w^{-1}I_w} \underline {V_{\beta }}$
avec
![]() $L^{++}\underline {\mathscr {G}_{\mathbf {f}}}$
est triviale, où l’on peut ordonner les racines réelles à goût. En effet, les racines peuvent être supposées avoir été ordonnées de telle façon que le produit soit contenu dans l’espace de lacets
$L^{++}\underline {\mathscr {G}_{\mathbf {f}}}$
est triviale, où l’on peut ordonner les racines réelles à goût. En effet, les racines peuvent être supposées avoir été ordonnées de telle façon que le produit soit contenu dans l’espace de lacets
![]() $L\underline {C}$
de la grosse cellule de
$L\underline {C}$
de la grosse cellule de
![]() $\underline {G}$
, ainsi que le radical pro-unipotent
$\underline {G}$
, ainsi que le radical pro-unipotent
![]() $L^{++}\underline {\mathscr {G}_{\mathbf {f}}}$
, voir la prop. 4.2.4. L’affirmation cherchée en résulte par des calculs élémentaires et grâce à ce que
$L^{++}\underline {\mathscr {G}_{\mathbf {f}}}$
, voir la prop. 4.2.4. L’affirmation cherchée en résulte par des calculs élémentaires et grâce à ce que
![]() $\beta =w^{-1}\alpha \in \Phi _{\mathbf {f},\leq 0}^{\mathrm{r}\acute{\rm e}}$
pour tout
$\beta =w^{-1}\alpha \in \Phi _{\mathbf {f},\leq 0}^{\mathrm{r}\acute{\rm e}}$
pour tout
![]() $\alpha \in I_w$
.
$\alpha \in I_w$
.
Ensuite, on va mettre en valeur le fait qu’il y ait une certaine symétrie entre les parties parahoriques
![]() $\Phi _{\mathbf {f},\geq 0}^{\operatorname {af}}$
et leurs opposées
$\Phi _{\mathbf {f},\geq 0}^{\operatorname {af}}$
et leurs opposées
![]() $\Phi _{\mathbf {f},\leq 0}^{\operatorname {af}}$
.
$\Phi _{\mathbf {f},\leq 0}^{\operatorname {af}}$
.
Lemme 4.2.7. Il existe un et un seul isomorphisme de complexes simpliciaux
qui fait correspondre à une facette
![]() $\mathbf {f} $
du membre de gauche la seule facette
$\mathbf {f} $
du membre de gauche la seule facette
![]() $\operatorname {op}(\mathbf {f})$
du membre de droite telle que
$\operatorname {op}(\mathbf {f})$
du membre de droite telle que
![]() $\Phi _{\operatorname {op}(\mathbf {f}),\geq 0}^{\operatorname {af}}=\Phi _{\mathbf {f},\leq 0}^{\operatorname {af}}$
comme parties du groupe de caractères de
$\Phi _{\operatorname {op}(\mathbf {f}),\geq 0}^{\operatorname {af}}=\Phi _{\mathbf {f},\leq 0}^{\operatorname {af}}$
comme parties du groupe de caractères de
![]() $\underline {S}\times \mathbb {G}_{m,\mathbb {Z}}$
. En particulier,
$\underline {S}\times \mathbb {G}_{m,\mathbb {Z}}$
. En particulier,
![]() $\operatorname {op}$
est équivariant sous l’action de
$\operatorname {op}$
est équivariant sous l’action de
![]() $\widetilde {W}=\underline {N}(\mathbb {Z}[t^{\pm 1}])/\underline {S}(\mathbb {Z})$
.
$\widetilde {W}=\underline {N}(\mathbb {Z}[t^{\pm 1}])/\underline {S}(\mathbb {Z})$
.
Démonstration. On remarque que cela est raisonnable, puisque la
![]() $\mathbb {G}_m$
-opération fut définie en termes de la variable t, d’où l’inversion de signe lorsqu’on veut la remplacer par
$\mathbb {G}_m$
-opération fut définie en termes de la variable t, d’où l’inversion de signe lorsqu’on veut la remplacer par
![]() $t^{-1}$
. L’existence et unicité d’une application
$t^{-1}$
. L’existence et unicité d’une application
![]() $\operatorname {op}$
telle que dans (4.2.10) avec les propriétés énoncées est un exercice élémentaire en ensembles simpliciaux et leurs réalisations géométriques, d’après la prop. 4.2.3, ce qui donne aussi l’équivariance par le groupe d’Iwahori–Weyl. Signalons toutefois que (4.2.10) ne coïncide pas avec l’application d’oubli des uniformisantes, car les alcôves dominantes du membre de gauche sont appliquées sur les alcôves anti-dominantes du membre de droite.
$\operatorname {op}$
telle que dans (4.2.10) avec les propriétés énoncées est un exercice élémentaire en ensembles simpliciaux et leurs réalisations géométriques, d’après la prop. 4.2.3, ce qui donne aussi l’équivariance par le groupe d’Iwahori–Weyl. Signalons toutefois que (4.2.10) ne coïncide pas avec l’application d’oubli des uniformisantes, car les alcôves dominantes du membre de gauche sont appliquées sur les alcôves anti-dominantes du membre de droite.
La méthode du numéro §3.4 peut donc être appliquée pour construire le
![]() $\mathbb {Z}[t^{-1}]$
-modèle parahorique
$\mathbb {Z}[t^{-1}]$
-modèle parahorique
![]() $\underline {\mathscr {G}_{\operatorname {op}(\mathbf {f})}}$
associé à la facette
$\underline {\mathscr {G}_{\operatorname {op}(\mathbf {f})}}$
associé à la facette
![]() $\operatorname {op}(\mathbf {f})$
, cf. déf. 3.4.6. Ceci donne par recollement au-dessus de
$\operatorname {op}(\mathbf {f})$
, cf. déf. 3.4.6. Ceci donne par recollement au-dessus de
![]() $\mathbb {Z}[t^{\pm 1}]$
le long du groupe de Tits
$\mathbb {Z}[t^{\pm 1}]$
le long du groupe de Tits
![]() $\underline {G}$
un
$\underline {G}$
un
![]() $\mathbb {P}_{\mathbb {Z}}^1$
-schéma en groupes affine, lisse et connexe
$\mathbb {P}_{\mathbb {Z}}^1$
-schéma en groupes affine, lisse et connexe
![]() $\underline {\mathscr {G}_{\mathbf {f}, \operatorname {op}(\mathbf {f})}}$
, voir th. 3.4.10. Désormais, on note ce schéma en groupes
$\underline {\mathscr {G}_{\mathbf {f}, \operatorname {op}(\mathbf {f})}}$
, voir th. 3.4.10. Désormais, on note ce schéma en groupes
![]() $\underline {\mathscr {G}_{\mathbf {f}}}$
tout simplement.
$\underline {\mathscr {G}_{\mathbf {f}}}$
tout simplement.
Définition 4.2.8. Le groupe de cordesFootnote 6 de
![]() $\underline {\mathscr {G}_{\mathbf {f}}}$
est le faisceau en ensembles
$\underline {\mathscr {G}_{\mathbf {f}}}$
est le faisceau en ensembles
![]() $L^-\underline {\mathscr {G}_{\mathbf {f}}}$
sur les
$L^-\underline {\mathscr {G}_{\mathbf {f}}}$
sur les
![]() $\mathbb {Z}$
-algèbres donné par la correspondance
$\mathbb {Z}$
-algèbres donné par la correspondance
Le faisceau en ensembles
![]() $L^{\operatorname {gr}}\underline {G}$
qui fait correspondre
$L^{\operatorname {gr}}\underline {G}$
qui fait correspondre
est ce qu’on appelle le groupe d’élastiques de
![]() $\underline {G}$
.
$\underline {G}$
.
Par le lemme de descente de Beauville–Laszlo, voir [Reference Beauville and LaszloBL95, th.], on a une égalité de faisceaux
![]() $L^-\underline {\mathscr {G}_{\mathbf {f}}}=L_{t^{-1}}^+\underline {\mathscr {G}_{\mathbf {f}}} \cap L^{\operatorname {gr}}\underline {G}$
, où l’intersection est prise dedans
$L^-\underline {\mathscr {G}_{\mathbf {f}}}=L_{t^{-1}}^+\underline {\mathscr {G}_{\mathbf {f}}} \cap L^{\operatorname {gr}}\underline {G}$
, où l’intersection est prise dedans
![]() $L_{t^{-1}}\underline {G}$
. On pose aussi
$L_{t^{-1}}\underline {G}$
. On pose aussi
qu’on regarde comme le radical ind-unipotent du groupe de cordes, dénomination laquelle n’a aucun sens précis pour l’instant, mais voir cependant (4.2.15). On note aussi
![]() $L^{--}_I\underline {\mathscr {G}_{\mathbf {f}}}$
et
$L^{--}_I\underline {\mathscr {G}_{\mathbf {f}}}$
et
![]() $L^{--}_w\underline {\mathscr {G}_{\mathbf {f}}}$
les sous-groupes évidentes de
$L^{--}_w\underline {\mathscr {G}_{\mathbf {f}}}$
les sous-groupes évidentes de
![]() $L^{--}\underline {\mathscr {G}_{\mathbf {f}}}$
, voir la prop. 4.2.6, déduits du recollement à la Beauville–Laszlo. Cela nous permet ainsi de déduire sans peine plusieurs propriétés concernant
$L^{--}\underline {\mathscr {G}_{\mathbf {f}}}$
, voir la prop. 4.2.6, déduits du recollement à la Beauville–Laszlo. Cela nous permet ainsi de déduire sans peine plusieurs propriétés concernant
![]() $L^-\underline {\mathscr {G}_{\mathbf {f}}}$
:
$L^-\underline {\mathscr {G}_{\mathbf {f}}}$
:
Théorème 4.2.9. On a une égalité de sous-faisceaux
du groupe de lacets
![]() $L\underline {G}$
, ainsi qu’une décomposition de Levi opposée
$L\underline {G}$
, ainsi qu’une décomposition de Levi opposée
et une décomposition radicielle pour toute partie finie
![]() $I\subset \Phi ^{\operatorname {af}}_{\mathbf {f},< 0}$
à complément saturé
$I\subset \Phi ^{\operatorname {af}}_{\mathbf {f},< 0}$
à complément saturé
En particulier, il en résulte, pour tout
![]() $w \in \widetilde {W}/W_{\mathbf {f}}$
et tout représentant
$w \in \widetilde {W}/W_{\mathbf {f}}$
et tout représentant
![]() $n_w \in L^{\operatorname {gr}}N(\mathbb {Z})$
, la décomposition suivante :
$n_w \in L^{\operatorname {gr}}N(\mathbb {Z})$
, la décomposition suivante :
Démonstration. Évidemment l’application
![]() $\underline {M_{\mathbf {f}}} \rightarrow L\underline {G}$
se factorise à travers du fermé
$\underline {M_{\mathbf {f}}} \rightarrow L\underline {G}$
se factorise à travers du fermé
![]() $L^-\underline {\mathscr {G}_{\mathbf {f}}}$
du but, puisque cela est valable au-dessus d’un ouvert schématiquement dense de la source. La décomposition de Levi (4.2.15), telle que la radicielle (4.2.16), découlent alors facilement de ce qu’on avait prouvé pour les groupes d’arcs (par rapport à la variable
$L^-\underline {\mathscr {G}_{\mathbf {f}}}$
du but, puisque cela est valable au-dessus d’un ouvert schématiquement dense de la source. La décomposition de Levi (4.2.15), telle que la radicielle (4.2.16), découlent alors facilement de ce qu’on avait prouvé pour les groupes d’arcs (par rapport à la variable
![]() $t^{-1}$
), cf. (4.2.2). On en tire au moins l’inclusion
$t^{-1}$
), cf. (4.2.2). On en tire au moins l’inclusion
la plus facile de l’égalité (4.2.14).
D’autre part, l’intersection contemplée dans le membre de droite de (4.2.14) coïncide avec le foncteur
lequel est représentable par un
![]() $\mathbb {Z}$
-schéma en groupes affine et lisse. En effet, l’affinité et la présentation finie se ramènent au cas du même foncteur associé aux espaces affines. D’ailleurs, pour montrer que le critère de lissité formelle soit remplit, il faut vérifier l’annulation de certaines classes d’obstruction
$\mathbb {Z}$
-schéma en groupes affine et lisse. En effet, l’affinité et la présentation finie se ramènent au cas du même foncteur associé aux espaces affines. D’ailleurs, pour montrer que le critère de lissité formelle soit remplit, il faut vérifier l’annulation de certaines classes d’obstruction
dans le premier groupe de cohomologie de l’algèbre de Lie de
![]() $\underline {\mathscr {G}_{\mathbf {f}}}$
, cf. [SGA1, exp. III, cor. 5.4]. Mais celle-ci admet une écriture en tant que somme d’images directes de
$\underline {\mathscr {G}_{\mathbf {f}}}$
, cf. [SGA1, exp. III, cor. 5.4]. Mais celle-ci admet une écriture en tant que somme d’images directes de
![]() $\mathcal {O}_{\mathbb {P}_{\mathbb {Z}}^1}$
ou
$\mathcal {O}_{\mathbb {P}_{\mathbb {Z}}^1}$
ou
![]() $\mathcal {O}_{\mathbb {P}_{\mathbb {Z}}^1}(-1)$
le long de morphismes finis
$\mathcal {O}_{\mathbb {P}_{\mathbb {Z}}^1}(-1)$
le long de morphismes finis
![]() $\mathbb {P}_{\mathbb {Z}}^1\rightarrow \mathbb {P}_{\mathbb {Z}}^1$
.
$\mathbb {P}_{\mathbb {Z}}^1\rightarrow \mathbb {P}_{\mathbb {Z}}^1$
.
Il suffit de montrer que le
![]() $\mathbb {Z}$
-groupe affine et lisse
$\mathbb {Z}$
-groupe affine et lisse
![]() $L^{++}\underline {\mathscr {G}_{\mathbf {f}}}\cap L^-\underline {\mathscr {G}_{\mathbf {f}}}$
est trivial. Mais il est aussi unipotent, puisque contenu dans le radical pro-unipotent, et étale, grâce à l’annulation de son fibré vectoriel de Lie. En caractéristique
$L^{++}\underline {\mathscr {G}_{\mathbf {f}}}\cap L^-\underline {\mathscr {G}_{\mathbf {f}}}$
est trivial. Mais il est aussi unipotent, puisque contenu dans le radical pro-unipotent, et étale, grâce à l’annulation de son fibré vectoriel de Lie. En caractéristique
![]() $0$
, les groupes unipotents et étales ne sont autres que les triviaux, cf. [Reference Demazure and GabrielDG70, IV, §2, cor. 4.5], donc par adhérence plate
$0$
, les groupes unipotents et étales ne sont autres que les triviaux, cf. [Reference Demazure and GabrielDG70, IV, §2, cor. 4.5], donc par adhérence plate
![]() $L^{++}\underline {\mathscr {G}_{\mathbf {f}}}\cap L^-\underline {\mathscr {G}_{\mathbf {f}}}$
est trivial aussi.
$L^{++}\underline {\mathscr {G}_{\mathbf {f}}}\cap L^-\underline {\mathscr {G}_{\mathbf {f}}}$
est trivial aussi.
Quant à la dernière assertion, cf. (4.2.17), nous l’avons déjà vu à (4.2.8), quitte à faire la descente de Beauville–Laszlo et à constater que
![]() $L^{--}\underline {\mathscr {G}_{\mathbf {a}}} \cap n_wL^+\underline {\mathscr {G}_{\mathbf {f}}}n_w^{-1}$
est égal au produit des sous-groupes radiciels qu’il contienne. Néanmoins, si ce n’était pas le cas, alors son intersection avec le sous-groupe
$L^{--}\underline {\mathscr {G}_{\mathbf {a}}} \cap n_wL^+\underline {\mathscr {G}_{\mathbf {f}}}n_w^{-1}$
est égal au produit des sous-groupes radiciels qu’il contienne. Néanmoins, si ce n’était pas le cas, alors son intersection avec le sous-groupe
![]() $L^{--}_w\underline {\mathscr {G}_{\mathbf {f}}}$
ne serait pas triviale, ce qui est un absurde.
$L^{--}_w\underline {\mathscr {G}_{\mathbf {f}}}$
ne serait pas triviale, ce qui est un absurde.
Remarque 4.2.10. La définition du groupe de cordes n’est jamais parue dans la littérature que dans des cas particuliers. de Cataldo–Haines–Li ont introduit en [Reference de Cataldo, Haines and LidHL18, §3] le radical ind-unipotent pour les groupes déployés, en prenant l’intersection de ceux associés aux alcôves entourantes. Par là, on ne retrouve autre que nos groupes, en vertu de [Reference de Cataldo, Haines and LidHL18, prop. 3.6.4]. En [Reference Haines, Lourenço and RicharzHLR20], nous avons étendu avec Haines–Richarz ce même radical ind-unipotent au cas tordu et modérément ramifié en prenant des
![]() $\Gamma $
-invariants, voir [Reference Haines, Lourenço and RicharzHLR20, éq. (3.12)], ce qui est évidemment encore compatible avec la définition actuelle.
$\Gamma $
-invariants, voir [Reference Haines, Lourenço and RicharzHLR20, éq. (3.12)], ce qui est évidemment encore compatible avec la définition actuelle.
Corollaire 4.2.11. L’application multiplication
est une immersion ouverte et affine.
Démonstration. On prouve ce corollaire à la suite de [Reference Haines, Lourenço and RicharzHLR20, lem. 3.6], observant que le morphisme (4.2.21) satisfait aux propriétés énoncées si et seulement s’il en est de même du morphisme quotient
d’après la descente plate. La première application, cf. (4.2.21), est représentable en schémas affines, parce que
![]() $L^{--}\underline {\mathscr {G}_{\mathbf {f}}}\rightarrow L\underline {G}$
est une immersion fermée et que
$L^{--}\underline {\mathscr {G}_{\mathbf {f}}}\rightarrow L\underline {G}$
est une immersion fermée et que
![]() $L^+\underline {\mathscr {G}_{\mathbf {f}}}$
est représentable par un schéma affine. La deuxième, cf. (4.2.22), est aussi de présentation finie, car ses deux membres admettent des présentations inductives par de
$L^+\underline {\mathscr {G}_{\mathbf {f}}}$
est représentable par un schéma affine. La deuxième, cf. (4.2.22), est aussi de présentation finie, car ses deux membres admettent des présentations inductives par de
![]() $\mathbb {Z}$
-schémas de type fini.
$\mathbb {Z}$
-schémas de type fini.
Mais on a déjà vu au th. 4.2.9 que (4.2.21) détermine un monomorphisme, cf. (4.2.14) et (4.2.15), donc on n’a besoin que de vérifier le critère de lissité formelle. Comme tous les foncteurs en groupes sont formellement lisses, cela se ramène à un calcul de fibrés vectoriels de Lie, lequel donne un isomorphisme.
Le lemme de descente de Beauville–Laszlo, cf. [Reference Beauville and LaszloBL95, th.], fournit un morphisme de
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
vers le champ algébrique
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
vers le champ algébrique
![]() $\operatorname {Fib}_{\underline {\mathscr {G}_{\mathbf {f}}}, \mathbb {P}_{\mathbb {Z}}^1}$
lisse et localement de type fini qui paramètre les
$\operatorname {Fib}_{\underline {\mathscr {G}_{\mathbf {f}}}, \mathbb {P}_{\mathbb {Z}}^1}$
lisse et localement de type fini qui paramètre les
![]() $\underline {\mathscr {G}_{\mathbf {f}}}$
-fibrés sur la droite projective.
$\underline {\mathscr {G}_{\mathbf {f}}}$
-fibrés sur la droite projective.
Corollaire 4.2.12. La cellule ouverte
![]() $L^{--}\underline {\mathscr {G}_{\mathbf {f}}}$
de
$L^{--}\underline {\mathscr {G}_{\mathbf {f}}}$
de
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
coïncide avec l’image réciproque du sous-champ ouvert de
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
coïncide avec l’image réciproque du sous-champ ouvert de
![]() $\operatorname {Fib}_{\underline {\mathscr {G}_{\mathbf {f}}}, \mathbb {P}_{\mathbb {Z}}^1}$
formé des fibrés triviaux.
$\operatorname {Fib}_{\underline {\mathscr {G}_{\mathbf {f}}}, \mathbb {P}_{\mathbb {Z}}^1}$
formé des fibrés triviaux.
Démonstration. L’affirmation se démontre à la suite de [Reference Haines and RicharzHR21, lem. 3.1], dont le point plus délicat était de constater la
![]() $H^1$
-trivialité de
$H^1$
-trivialité de
![]() $\operatorname {Lie}\underline {\mathscr {G}_{\mathbf {f}}}$
, voir (4.2.20), ce qu’on a fait pendant la démonstration du th. 4.2.9.
$\operatorname {Lie}\underline {\mathscr {G}_{\mathbf {f}}}$
, voir (4.2.20), ce qu’on a fait pendant la démonstration du th. 4.2.9.
Voici une description dynamique des groupes d’arcs
![]() $L^+\underline {\mathscr {G}_{\mathbf {f}}}$
et de cordes
$L^+\underline {\mathscr {G}_{\mathbf {f}}}$
et de cordes
![]() $L^-\underline {\mathscr {G}_{\mathbf {f}}}$
à composantes connexes près.
$L^-\underline {\mathscr {G}_{\mathbf {f}}}$
à composantes connexes près.
Proposition 4.2.13. Soit
![]() $\mu : \mathbb {G}_{m,\mathbb {Z}} \rightarrow \underline {S} \times \mathbb {G}_{m,\mathbb {Z}}$
un copoids tel que l’ensemble des racines affines
$\mu : \mathbb {G}_{m,\mathbb {Z}} \rightarrow \underline {S} \times \mathbb {G}_{m,\mathbb {Z}}$
un copoids tel que l’ensemble des racines affines
![]() $\alpha \in \Phi _{G}^{\operatorname {af}}$
appliquées sur la demi droite non négative soit égal à
$\alpha \in \Phi _{G}^{\operatorname {af}}$
appliquées sur la demi droite non négative soit égal à
![]() $\Phi _{\mathbf {f},\geq 0}$
. Alors, le groupe d’arcs
$\Phi _{\mathbf {f},\geq 0}$
. Alors, le groupe d’arcs
![]() $L^+\underline {\mathscr {G}_{\mathbf {f}}}$
resp. le groupe de cordes
$L^+\underline {\mathscr {G}_{\mathbf {f}}}$
resp. le groupe de cordes
![]() $L^-\underline {\mathscr {G}_{\mathbf {f}}}$
s’identifie à la composante neutre de l’attracteur resp. du répulseur de
$L^-\underline {\mathscr {G}_{\mathbf {f}}}$
s’identifie à la composante neutre de l’attracteur resp. du répulseur de
![]() $L\underline {G}$
pour l’action de
$L\underline {G}$
pour l’action de
![]() $\mathbb {G}_{m,\mathbb {Z}}$
induite par
$\mathbb {G}_{m,\mathbb {Z}}$
induite par
![]() $\mu $
.
$\mu $
.
Démonstration. On remarque qu’un tel copoids
![]() $\mu $
avec les propriétés désirées existe toujours, grâce à la prop. 4.2.3. Pour plus de détails sur les
$\mu $
avec les propriétés désirées existe toujours, grâce à la prop. 4.2.3. Pour plus de détails sur les
![]() $\mathbb {G}_m$
-opérations et leurs généralités, le lecteur est renvoyé à [Reference Conrad, Gabber and PrasadCGP15, §2.1] et [Reference RicharzRi19a, §1]. Ce dernier montre au [Reference RicharzRi19a, th. 1.8] que les actions qui stabilisent un recouvrement ouvert (ou plus généralement étale) par des affines admettent des attracteurs et des répulseurs représentables et ceci s’étend facilement au cadre des ind-schémas.
$\mathbb {G}_m$
-opérations et leurs généralités, le lecteur est renvoyé à [Reference Conrad, Gabber and PrasadCGP15, §2.1] et [Reference RicharzRi19a, §1]. Ce dernier montre au [Reference RicharzRi19a, th. 1.8] que les actions qui stabilisent un recouvrement ouvert (ou plus généralement étale) par des affines admettent des attracteurs et des répulseurs représentables et ceci s’étend facilement au cadre des ind-schémas.
On montre tout d’abord que l’attracteur de l’espace de lacets de la grosse cellule
![]() $L\underline {C}$
est le bon. Supposons que a est une racine ni multipliable ni divisible. Alors, l’action de
$L\underline {C}$
est le bon. Supposons que a est une racine ni multipliable ni divisible. Alors, l’action de
![]() $\mathbb {G}_m$
sur
$\mathbb {G}_m$
sur
![]() $L\underline {U_a}$
induite par
$L\underline {U_a}$
induite par
![]() $\mu $
est donnée par
$\mu $
est donnée par
en termes du quasi-système de Tits choisi. Alors, les points à valeurs dans R de l’attracteur s’écrivent comme le sous-groupe additif des séries formelles dans
![]() $R (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) $
tronquées par
$R (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) $
tronquées par
![]() $i=-n/m$
. On voit ainsi que cela coïncide avec
$i=-n/m$
. On voit ainsi que cela coïncide avec
![]() $L^+\underline {\mathscr {U}_a}$
, comme on le voulait. Quant au cas des racines multipliables et du tore, on en laisse le soin au lecteur.
$L^+\underline {\mathscr {U}_a}$
, comme on le voulait. Quant au cas des racines multipliables et du tore, on en laisse le soin au lecteur.
Maintenant, on démontre que le groupe de cordes
![]() $L^-\underline {\mathscr {G}_{\mathbf {f}}}$
, qui est stable par
$L^-\underline {\mathscr {G}_{\mathbf {f}}}$
, qui est stable par
![]() $\mu $
et ind-affine, est son propre répulseur. En fait, le répulseur est représentable par un sous-
$\mu $
et ind-affine, est son propre répulseur. En fait, le répulseur est représentable par un sous-
![]() $\mathbb {Z}$
-ind-groupe fermé, et l’on sait qu’il contient l’espace de cordes de la grosse cellule
$\mathbb {Z}$
-ind-groupe fermé, et l’on sait qu’il contient l’espace de cordes de la grosse cellule
![]() $L^-\underline {\mathscr {C}_{\mathbf {f}}}$
. Par suite, l’immersion fermée du répulseur vers
$L^-\underline {\mathscr {C}_{\mathbf {f}}}$
. Par suite, l’immersion fermée du répulseur vers
![]() $L^-\underline {\mathscr {G}_{\mathbf {f}}}$
est formellement étale et de présentation finie, donc un isomorphisme sur un ouvert. Néanmoins, le groupe de cordes est connexe, grâce au cor. 4.2.11 et au lem. 4.2.14, donc l’inclusion voulue est achevée.
$L^-\underline {\mathscr {G}_{\mathbf {f}}}$
est formellement étale et de présentation finie, donc un isomorphisme sur un ouvert. Néanmoins, le groupe de cordes est connexe, grâce au cor. 4.2.11 et au lem. 4.2.14, donc l’inclusion voulue est achevée.
Considérons maintenant l’attracteur de l’ouvert translaté, voir le cor. 4.2.11,
pour chaque
![]() $w\in \widetilde {W}/W_{\mathbf {f}}$
, où cette égalité suit d’appliquer la décomposition (4.2.17). Son attracteur peut être calculé sans grande peine, s’avérant égal à la cellule de Schubert
$w\in \widetilde {W}/W_{\mathbf {f}}$
, où cette égalité suit d’appliquer la décomposition (4.2.17). Son attracteur peut être calculé sans grande peine, s’avérant égal à la cellule de Schubert
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}},w}$
. En particulier, l’attracteur de
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}},w}$
. En particulier, l’attracteur de
![]() $L\underline {G}$
est un sous-groupe fermé réunion disjointe de certaines cellules de Schubert
$L\underline {G}$
est un sous-groupe fermé réunion disjointe de certaines cellules de Schubert
![]() $L^+\mathscr {G}_{\mathbf {a}} \cdot n_w \cdot L^+\mathscr {G}_{\mathbf {f}}$
fermées pour une partie
$L^+\mathscr {G}_{\mathbf {a}} \cdot n_w \cdot L^+\mathscr {G}_{\mathbf {f}}$
fermées pour une partie
![]() $W_\mu \subset \widetilde {W}/ W_{\mathbf {f}}$
constitué de quelques éléments de longueur
$W_\mu \subset \widetilde {W}/ W_{\mathbf {f}}$
constitué de quelques éléments de longueur
![]() $0$
, ce qui termine la démonstration.
$0$
, ce qui termine la démonstration.
Le cas du groupes de cordes est traité de façon similaire, mais on a besoin de substituer la grassmannienne épaisse
![]() $L\underline {G}/L^-\underline {\mathscr {G}_{\mathbf {f}}}$
à la grassmannienne affine, laquelle est représentable par un schéma de type infini. Comme la détermination précise du répulseur ne sera jamais utilisée dans la suite, mais juste le fait que nos groupes d’arcs/de cordes soient attractifs/répulsifs, voir la démonstration du th. 4.2.16, on omettre les détails qui seront laissés au lecteur.
$L\underline {G}/L^-\underline {\mathscr {G}_{\mathbf {f}}}$
à la grassmannienne affine, laquelle est représentable par un schéma de type infini. Comme la détermination précise du répulseur ne sera jamais utilisée dans la suite, mais juste le fait que nos groupes d’arcs/de cordes soient attractifs/répulsifs, voir la démonstration du th. 4.2.16, on omettre les détails qui seront laissés au lecteur.
Avant de initier l’étude géométrique des
![]() $L^-\underline {\mathscr {G}_{\mathbf {f}}}$
-orbites fermées de
$L^-\underline {\mathscr {G}_{\mathbf {f}}}$
-orbites fermées de
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
, voir le th. 4.2.16, il va falloir déterminer quelques doubles quotients pour les numéroter.
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
, voir le th. 4.2.16, il va falloir déterminer quelques doubles quotients pour les numéroter.
Lemme 4.2.14. On a une bijection naturelle de type Birkhoff
pour un corps quelconque k.
Démonstration. L’orbite
est un fermé local bien défini de
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
et isomorphe à
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
et isomorphe à
![]() $L_w^{--}\underline {\mathscr {G}_{\mathbf {f}}}$
en tant que ind-schéma, d’après (4.2.17) et (4.2.24). L’assertion (4.2.25) revient alors au même que dire que ces orbites soient disjointes et recouvrent l’espace topologique sous-jacent à
$L_w^{--}\underline {\mathscr {G}_{\mathbf {f}}}$
en tant que ind-schéma, d’après (4.2.17) et (4.2.24). L’assertion (4.2.25) revient alors au même que dire que ces orbites soient disjointes et recouvrent l’espace topologique sous-jacent à
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
.
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
.
Par suite, le corps k peut être supposé algébriquement clos, sans perte de généralité. Afin d’établer la bijection (4.2.25) dans ce cas, on peut procéder verbatim comme dans la preuve de la [Reference Heinloth, Ngô and YunHNY13, prop. 1.1], ce qui nous ramène au cas où G est simplement connexe et absolument presque simple. Évidemment on ne doit pas oublier les bizarres groupes exotiques et barcelonais, auquel cas on applique les [Reference Conrad, Gabber and PrasadCGP15, prop. 7.3.3, prop. 9.9.2] et [Reference LourençoLou21, prop. 3.6] pour ramener la question dont il s’agit à la décomposition de Birkhoff d’un groupe déployé.
Remarque 4.2.15. Cette décomposition de Birkhoff est très bien connue aussi en théorie des groupes de Kac–Moody, voir les articles et exposés suivants [Reference TitsTi87], [Reference TitsTi89] et [Reference TitsTi92] de Tits, ainsi que le survol [Reference MarquisMar18] de Marquis. Dans son interprétation, les points à valeurs dans k de nos groupes d’arcs et de cordes sont devenus des sous-groupes paraboliques opposés d’un groupe de Kac–Moody, voir §6, et forment partie d’une BN-paire raffinée, cf. [Reference RousseauRou16, prop. 3.16].
Comme nous avons mentionné au lemme précédent, cf. (4.2.26), l’orbite
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}^w$
associée à
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}^w$
associée à
![]() $w \in \widetilde {W}/W_{\mathbf {f}}$
admet une immersion affine dans
$w \in \widetilde {W}/W_{\mathbf {f}}$
admet une immersion affine dans
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
. Ci-dessous, on parvient à saisir leurs adhérences schématiques
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
. Ci-dessous, on parvient à saisir leurs adhérences schématiques
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}^{\geq w}$
qu’on appelle les cycles de Schubert. Ce sont les plus grands sous-ind-schémas ind-fermés de
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}^{\geq w}$
qu’on appelle les cycles de Schubert. Ce sont les plus grands sous-ind-schémas ind-fermés de
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
qui contiennent
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
qui contiennent
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}^w$
et ils se définissent en termes d’une présentation de
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}^w$
et ils se définissent en termes d’une présentation de
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
par schémas.
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
par schémas.
Théorème 4.2.16 (Faltings, Kashiwara–Shimozono, L.).
Le cycle de Schubert
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}^{\geq w}$
est un fermé plat de codimension
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}^{\geq w}$
est un fermé plat de codimension
![]() $l(w)$
, stratifié dans la réunion des
$l(w)$
, stratifié dans la réunion des
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}^{v}$
, pour
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}^{v}$
, pour
![]() $v\geq w$
, et à quotients locaux
$v\geq w$
, et à quotients locaux
![]() $L^{--}\underline {\mathscr {G}_{\mathbf {a}}}(n)\backslash \operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}^{v\geq w}$
géométriquement normaux de Cohen–Macaulay, pour n assez grand et qui dépend de v.
$L^{--}\underline {\mathscr {G}_{\mathbf {a}}}(n)\backslash \operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}^{v\geq w}$
géométriquement normaux de Cohen–Macaulay, pour n assez grand et qui dépend de v.
Démonstration. Le jeu à la fois combinatoire et géométrique de Faltings, cf. [Reference FaltingsFa03, p. 48], permet de déduire que
est fermé et que la réunion
 $$ \begin{align}\operatorname{Gr}_{\underline{\mathscr{G}_{\mathbf{f}}}}^{u\geq}:=\bigcup_{u \geq w \in \widetilde{W}/W_{\mathbf{f}}} n_wL^{--}\underline{\mathscr{G}_{\mathbf{f}}}\end{align} $$
$$ \begin{align}\operatorname{Gr}_{\underline{\mathscr{G}_{\mathbf{f}}}}^{u\geq}:=\bigcup_{u \geq w \in \widetilde{W}/W_{\mathbf{f}}} n_wL^{--}\underline{\mathscr{G}_{\mathbf{f}}}\end{align} $$
est un ouvert stable par
![]() $L^{-}\underline {\mathscr {G}_{\mathbf {a}}}$
. Décrivons ces raisonnements en passant pour aider le lecteur. Considérant le schéma de Richardson
$L^{-}\underline {\mathscr {G}_{\mathbf {a}}}$
. Décrivons ces raisonnements en passant pour aider le lecteur. Considérant le schéma de Richardson
donné par l’intersection d’un cycle avec un schéma de Schubert, et dont la géométrie sera étudiée plus tard au cor. 4.3.9, on affirme que ceci est non vide si et seulement si
![]() $w \leq v$
; ce critère implique d’immédiat les affirmations précédentes, voir (4.2.27) et (4.2.24).
$w \leq v$
; ce critère implique d’immédiat les affirmations précédentes, voir (4.2.27) et (4.2.24).
La suffisance de ce critère n’est plus qu’une simple application de la résolution de Demazure, qui permet de produire une droite projective dont la droite affine est contenue dans
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}^{w}$
et dont la section infinie est égale à
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}^{w}$
et dont la section infinie est égale à
![]() $n_u \cdot e$
, où
$n_u \cdot e$
, où
![]() $w < u \leq v$
, d’où la conclusion par récurrence. Pour la nécessité, on peut remplacer le schéma de Richardson par une demi-cellule
$w < u \leq v$
, d’où la conclusion par récurrence. Pour la nécessité, on peut remplacer le schéma de Richardson par une demi-cellule
non vide sans perte de généralité. Mais nous avons vu, cf. (4.2.24), que la cellule de Schubert
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}, v}$
se plonge dans l’ouvert
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}, v}$
se plonge dans l’ouvert
![]() $n_vL^{--}\underline {\mathscr {G}_{\mathbf {f}}}$
. Par conséquent, celui-ci doit couper l’orbite schématiquement dense
$n_vL^{--}\underline {\mathscr {G}_{\mathbf {f}}}$
. Par conséquent, celui-ci doit couper l’orbite schématiquement dense
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}^{w}$
. Multipliant par un élément convenable de
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}^{w}$
. Multipliant par un élément convenable de
![]() $L^{--}\underline {\mathscr {G}_{\mathbf {a}}}$
à la gauche, on revient à ce que la cellule de Richardson
$L^{--}\underline {\mathscr {G}_{\mathbf {a}}}$
à la gauche, on revient à ce que la cellule de Richardson
est non vide, voir (4.2.24). Mais on a toujours une
![]() $\mathbb {G}_m$
-opération pour un certain choix convenable d’un copoids dans
$\mathbb {G}_m$
-opération pour un certain choix convenable d’un copoids dans
![]() $\underline {S} \times \mathbb {G}_{m,\mathbb {Z}}$
qui fait contracter les
$\underline {S} \times \mathbb {G}_{m,\mathbb {Z}}$
qui fait contracter les
![]() $L^-\underline {\mathscr {G}_{\mathbf {a}}}$
-orbites en
$L^-\underline {\mathscr {G}_{\mathbf {a}}}$
-orbites en
![]() $n_w \cdot e$
, voir prop. 4.2.13, et qui préserve les schémas de Schubert, d’où l’inégalité cherchée.
$n_w \cdot e$
, voir prop. 4.2.13, et qui préserve les schémas de Schubert, d’où l’inégalité cherchée.
Soit
![]() $L^{-}\underline {\mathscr {G}_{\mathbf {a}}}(n)$
le sous-groupe fermé de
$L^{-}\underline {\mathscr {G}_{\mathbf {a}}}(n)$
le sous-groupe fermé de
![]() $L^-\underline {\mathscr {G}_{\mathbf {a}}}$
engendré par le n-ième sous-groupe de congruence (par rapport à
$L^-\underline {\mathscr {G}_{\mathbf {a}}}$
engendré par le n-ième sous-groupe de congruence (par rapport à
![]() $t^{-1}$
) et par
$t^{-1}$
) et par
![]() $L^{--}\underline {\mathscr {T}}$
. Si l’on choisit l’entier n assez grand, alors on peut supposer que
$L^{--}\underline {\mathscr {T}}$
. Si l’on choisit l’entier n assez grand, alors on peut supposer que
![]() $L^{--}\underline {\mathscr {G}_{\mathbf {a}}}(n)$
soit contenu dans
$L^{--}\underline {\mathscr {G}_{\mathbf {a}}}(n)$
soit contenu dans
![]() $L^{--}_w\underline {\mathscr {G}_{\mathbf {f}}}$
pour tout
$L^{--}_w\underline {\mathscr {G}_{\mathbf {f}}}$
pour tout
![]() $w \leq v$
. Ceci entraîne que le faisceau quotient
$w \leq v$
. Ceci entraîne que le faisceau quotient
![]() $L^{--}\underline {\mathscr {G}_{\mathbf {a}}}(n)\backslash \operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}^{v\geq }$
pour la topologie plate est représentable par un schéma lisse, appliquant la décomposition radicielle (4.2.16) joint à (4.2.24) comme d’habitude, comp. aussi avec [Reference FaltingsFa03, lem. 6], et que la projection
$L^{--}\underline {\mathscr {G}_{\mathbf {a}}}(n)\backslash \operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}^{v\geq }$
pour la topologie plate est représentable par un schéma lisse, appliquant la décomposition radicielle (4.2.16) joint à (4.2.24) comme d’habitude, comp. aussi avec [Reference FaltingsFa03, lem. 6], et que la projection
a des sections localement pour la topologie ouverte. Puis, vu que le cycle de Schubert restreint
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}^{v\geq w}$
est
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}^{v\geq w}$
est
![]() $L^-\underline {\mathscr {G}_{\mathbf {a}}}$
-invariant, il se descend en un fermé représentable
$L^-\underline {\mathscr {G}_{\mathbf {a}}}$
-invariant, il se descend en un fermé représentable
compte tenu de la platitude de
![]() $L^-\underline {\mathscr {G}_{\mathbf {a}}}(n)$
, cf. lem. 4.3.3, cor. 4.2.11 et (4.2.16). En grandissant v arbitrairement pour recouvrir la grassmannienne toute entière, on obtient une immersion fermée
$L^-\underline {\mathscr {G}_{\mathbf {a}}}(n)$
, cf. lem. 4.3.3, cor. 4.2.11 et (4.2.16). En grandissant v arbitrairement pour recouvrir la grassmannienne toute entière, on obtient une immersion fermée
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}^{\geq w}\hookrightarrow \operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
, comp. avec [Reference FaltingsFa03, th. 7].
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}^{\geq w}\hookrightarrow \operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
, comp. avec [Reference FaltingsFa03, th. 7].
Ceci nous permet d’introduire des propriétés géométriques locales pour la topologie lisse pour ces quotients
![]() $L^{--}\underline {\mathscr {G}_{\mathbf {a}}}(n)\backslash \operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}^{v\geq w}$
des cycles de Schubert. On démontre leur normalité par récurrence sur la longueur de w à la suite de Kashiwara–Shimozono, cf. [Reference Kashiwara and ShimozonoKS09, prop. 3.2]. Pour cela, on peut supposer
$L^{--}\underline {\mathscr {G}_{\mathbf {a}}}(n)\backslash \operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}^{v\geq w}$
des cycles de Schubert. On démontre leur normalité par récurrence sur la longueur de w à la suite de Kashiwara–Shimozono, cf. [Reference Kashiwara and ShimozonoKS09, prop. 3.2]. Pour cela, on peut supposer
![]() $\mathbf {f}=\mathbf {a}$
et
$\mathbf {f}=\mathbf {a}$
et
![]() $w \in W^{\operatorname {af}}$
. On va faire l’abus de langage de travailler avec les cycles de Schubert en lieu de leurs quotients locaux
$w \in W^{\operatorname {af}}$
. On va faire l’abus de langage de travailler avec les cycles de Schubert en lieu de leurs quotients locaux
![]() $L^{--}\underline {\mathscr {G}_{\mathbf {a}}}(n)\backslash \operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}^{v\geq w}$
.
$L^{--}\underline {\mathscr {G}_{\mathbf {a}}}(n)\backslash \operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}^{v\geq w}$
.
On commence par leurs fibres réduites sur les corps premiers
![]() $\mathbb {F}_p$
,
$\mathbb {F}_p$
,
![]() $p \in \mathbb {P}\cup \{0\}$
. On note que le cas fondamental
$p \in \mathbb {P}\cup \{0\}$
. On note que le cas fondamental
![]() $w=1$
découle de ce que
$w=1$
découle de ce que
![]() $\operatorname {Gr}_{\mathscr {G}_{\mathbf {a},p}}$
est lisse. Par équivariance sous
$\operatorname {Gr}_{\mathscr {G}_{\mathbf {a},p}}$
est lisse. Par équivariance sous
![]() $L^-\mathscr {G}_{\mathbf {a},p}$
, on voit que le lieu normal de
$L^-\mathscr {G}_{\mathbf {a},p}$
, on voit que le lieu normal de
![]() $\operatorname {Gr}_{\mathscr {G}_{\mathbf {a},p}}^{\geq w}$
, c’est-à-dire le support du faisceau
$\operatorname {Gr}_{\mathscr {G}_{\mathbf {a},p}}^{\geq w}$
, c’est-à-dire le support du faisceau
![]() $\widetilde {\mathcal {O}}/\mathcal {O}$
, est une réunion ouverte et non vide d’orbites et on choisit
$\widetilde {\mathcal {O}}/\mathcal {O}$
, est une réunion ouverte et non vide d’orbites et on choisit
![]() $v> w$
minimal tel que la restriction de
$v> w$
minimal tel que la restriction de
![]() $\operatorname {Gr}_{\mathscr {G}_{\mathbf {a},p}}^{v}$
n’y appartienne. Soit aussi
$\operatorname {Gr}_{\mathscr {G}_{\mathbf {a},p}}^{v}$
n’y appartienne. Soit aussi
![]() $s \in W^{\operatorname {af}}$
une réflexion simple telle que
$s \in W^{\operatorname {af}}$
une réflexion simple telle que
![]() $vs<v$
et considérons la
$vs<v$
et considérons la
![]() $\mathbb {P}^1_{\mathbb {Z}}$
-fibration
$\mathbb {P}^1_{\mathbb {Z}}$
-fibration
où
![]() $\mathbf {f}$
désigne le cloison de
$\mathbf {f}$
désigne le cloison de
![]() $\mathbf {a}$
associé à s. Le cas
$\mathbf {a}$
associé à s. Le cas
![]() $ws>w$
s’exclut aisément grâce à la minimalité de v, donc on tire
$ws>w$
s’exclut aisément grâce à la minimalité de v, donc on tire
![]() $ws<w$
et l’on sait que
$ws<w$
et l’on sait que
![]() $\operatorname {Gr}_{\mathscr {G}_{\mathbf {a},p}}^{\geq ws} $
et
$\operatorname {Gr}_{\mathscr {G}_{\mathbf {a},p}}^{\geq ws} $
et
![]() $\operatorname {Gr}_{\mathscr {G}_{\mathbf {f},p}}^{\geq w} $
sont normaux par récurrence. Tirant en arrière la normalisation du faisceau structural le long de
$\operatorname {Gr}_{\mathscr {G}_{\mathbf {f},p}}^{\geq w} $
sont normaux par récurrence. Tirant en arrière la normalisation du faisceau structural le long de
![]() $\pi $
, on en déduit que
$\pi $
, on en déduit que
![]() $\pi _*\mathcal {O}=\pi _*\widetilde {\mathcal {O}}$
, donc leur conoyau est trivial sur
$\pi _*\mathcal {O}=\pi _*\widetilde {\mathcal {O}}$
, donc leur conoyau est trivial sur
![]() $\operatorname {Gr}_{\mathscr {G}_{\mathbf {a},p}}^{v} $
, compte tenu de l’annulation de
$\operatorname {Gr}_{\mathscr {G}_{\mathbf {a},p}}^{v} $
, compte tenu de l’annulation de
![]() $R^1\pi _*\mathcal {O}$
, voir [Reference Kashiwara and ShimozonoKS09, lem. 3.1], et de ce que
$R^1\pi _*\mathcal {O}$
, voir [Reference Kashiwara and ShimozonoKS09, lem. 3.1], et de ce que
![]() $\pi $
restreinte à l’orbite
$\pi $
restreinte à l’orbite
![]() $\operatorname {Gr}_{\mathscr {G}_{\mathbf {a},p}}^{v}$
devient un isomorphisme.
$\operatorname {Gr}_{\mathscr {G}_{\mathbf {a},p}}^{v}$
devient un isomorphisme.
Pour finir la preuve, il faut noter que le normalisé de
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {a}}}}^{\geq w}$
sur
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {a}}}}^{\geq w}$
sur
![]() $\mathbb {Z}$
admet un ouvert lisse et à fibres denses, donc leurs fibres sont géométriquement réduites par le critère de Serre. Par suite, une application du lemme de Nakayama fournit l’affirmation cherchée. Pour montrer que ces cycles sont de Cohen–Macaulay, on renvoie le lecteur à [Reference Kashiwara and ShimozonoKS09, prop. 3.4].
$\mathbb {Z}$
admet un ouvert lisse et à fibres denses, donc leurs fibres sont géométriquement réduites par le critère de Serre. Par suite, une application du lemme de Nakayama fournit l’affirmation cherchée. Pour montrer que ces cycles sont de Cohen–Macaulay, on renvoie le lecteur à [Reference Kashiwara and ShimozonoKS09, prop. 3.4].
Remarque 4.2.17. La clé de cette preuve de normalité quotiente est l’étude de l’ouverte induit par le groupe de cordes et des décompositions du th. 4.2.9. Ces trucs ne fonctionnent pas pour les schémas de Schubert, parce qu’on ne dispose d’aucun élément maximal, pour qu’on puisse raisonner par récurrence descendante sur la longueur. En effet, d’après les découvertes que nous avons faites avec Haines–Richarz dans [Reference Haines, Lourenço and RicharzHLR20], sans l’hypothèse “le groupe dérivé est simplement connexe”, alors les variétés de Schubert en caractéristique mauvaises ne sont typiquement pas normales, voir [Reference Haines, Lourenço and RicharzHLR20, th. 2.5] et le cor. 4.3.7, et la grassmannienne affine
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
n’est en général pas géométriquement réduite, voir [Reference Haines, Lourenço and RicharzHLR20, prop. 7.10] et le cor. 4.3.8.
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
n’est en général pas géométriquement réduite, voir [Reference Haines, Lourenço and RicharzHLR20, prop. 7.10] et le cor. 4.3.8.
En guise d’application, on obtient le théorème d’uniformisation des
![]() $\underline {\mathscr {G}_{\mathbf {f}}}$
-fibrés sur la droite projective, dû à Beuaville–Laszlo pour
$\underline {\mathscr {G}_{\mathbf {f}}}$
-fibrés sur la droite projective, dû à Beuaville–Laszlo pour
![]() $\operatorname {SL}_n$
, cf. [Reference Beauville and LaszloBL94, prop. 3.4], à Drinfeld–Simpson pour les groupes déployés, cf. [Reference Drinfeld and SimpsonDS95, th. 3], et à Heinloth pour les groupes tordus modérément ramifiés, voir [Reference HeinlothHei10, th. 4, th. 5].
$\operatorname {SL}_n$
, cf. [Reference Beauville and LaszloBL94, prop. 3.4], à Drinfeld–Simpson pour les groupes déployés, cf. [Reference Drinfeld and SimpsonDS95, th. 3], et à Heinloth pour les groupes tordus modérément ramifiés, voir [Reference HeinlothHei10, th. 4, th. 5].
Corollaire 4.2.18. Le champ classifiant
![]() $\operatorname {Fib}_{\underline {\mathscr {G}_{\mathbf {f}}}, \mathbb {P}^1}$
des
$\operatorname {Fib}_{\underline {\mathscr {G}_{\mathbf {f}}}, \mathbb {P}^1}$
des
![]() $\mathscr {G}_{\mathbf {f}}$
-fibrés sur la droite projective s’identifie au champ quotient
$\mathscr {G}_{\mathbf {f}}$
-fibrés sur la droite projective s’identifie au champ quotient
![]() $[L^-\underline {\mathscr {G}_{\mathbf {f}}}\backslash \operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}]$
pour la topologie ouverte.
$[L^-\underline {\mathscr {G}_{\mathbf {f}}}\backslash \operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}]$
pour la topologie ouverte.
Démonstration. La détermination dans la preuve du th. 4.2.16 des quotients de type fini des ouverts
![]() $\operatorname {Gr}_{\underline {\mathscr {G}}}^{v\geq }$
, cf. (4.2.32) et (4.2.33), montre que le champ quotient
$\operatorname {Gr}_{\underline {\mathscr {G}}}^{v\geq }$
, cf. (4.2.32) et (4.2.33), montre que le champ quotient
![]() $[L^-\underline {\mathscr {G}_{\mathbf {f}}}\backslash \operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}]$
possède des sections localement pour la topologie ouverte et qu’il est un champ d’Artin lisse. Vu que
$[L^-\underline {\mathscr {G}_{\mathbf {f}}}\backslash \operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}]$
possède des sections localement pour la topologie ouverte et qu’il est un champ d’Artin lisse. Vu que
![]() $\operatorname {Fib}_{\underline {\mathscr {G}_{\mathbf {f}}}, \mathbb {P}_{\mathbb {Z}}^1}$
est aussi un champ d’Artin lisse d’après [Reference HeinlothHei10, prop. 1] et que l’uniformisation
$\operatorname {Fib}_{\underline {\mathscr {G}_{\mathbf {f}}}, \mathbb {P}_{\mathbb {Z}}^1}$
est aussi un champ d’Artin lisse d’après [Reference HeinlothHei10, prop. 1] et que l’uniformisation
est un monomorphisme formellement lisse, il suffit de montrer sa surjectivité essentielle. Mais cela résulte d’une application soigneuse du théorème de Steinberg, voir [Reference HeinlothHei10, th. 4], qui reste valable pour les groupes pseudo-réductifs, cf. [Reference Conrad, Gabber and PrasadCGP15, prop. 7.3.3., prop. 9.9.2] et [Reference LourençoLou21, prop. 2.2, cor. 2.3].
Remarque 4.2.19. Signalons que nous avons eu besoin d’éviter le calcul d’espaces tangents à la manière de [Reference HeinlothHei10, lem. 6, lem. 7], parce que le lem. 4.3.5 est insuffisant lorsque
![]() $\Phi _G$
est non réduit et la caractéristique résiduelle égale à
$\Phi _G$
est non réduit et la caractéristique résiduelle égale à
![]() $2$
. Cependant, nous ne savons pas démontrer le théorème de réduction au Borel, cf. [Reference Drinfeld and SimpsonDS95, th. 2] et [Reference HeinlothHei10, prop. 25], car le quotient
$2$
. Cependant, nous ne savons pas démontrer le théorème de réduction au Borel, cf. [Reference Drinfeld and SimpsonDS95, th. 2] et [Reference HeinlothHei10, prop. 25], car le quotient
![]() $\underline {\mathscr {G}_{\mathbf {f}}}/\underline {\mathscr {B}_{\mathbf {f}}}$
cesse d’être projectif même sur
$\underline {\mathscr {G}_{\mathbf {f}}}/\underline {\mathscr {B}_{\mathbf {f}}}$
cesse d’être projectif même sur
![]() $\mathbb {G}_{m,\mathbb {Z}}$
.
$\mathbb {G}_{m,\mathbb {Z}}$
.
4.3 Normalité des schémas de Schubert
Le but de ce numéro est de finalement démontrer le théorème de normalité concernant les schémas de Schubert
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
, cf. th. 4.1.5. Signalons que le résultat dual de normalité pour les quotients locaux des cycles de Schubert du th. 4.2.16 ne nous aidera pas, vu que les schémas de Schubert ne sont pas invariants sous
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
, cf. th. 4.1.5. Signalons que le résultat dual de normalité pour les quotients locaux des cycles de Schubert du th. 4.2.16 ne nous aidera pas, vu que les schémas de Schubert ne sont pas invariants sous
![]() $L^-\underline {\mathscr {G}_{\mathbf {f}}}$
. En lieu de cette notion, il va falloir travailler avec la colimite filtrée des normalisations, dont la première étape consiste à montrer que cela est raisonnable, voir prop. 4.3.1 et cor. 4.3.2. Puis on aura besoin de relever au sens formel la cellule ouverte
$L^-\underline {\mathscr {G}_{\mathbf {f}}}$
. En lieu de cette notion, il va falloir travailler avec la colimite filtrée des normalisations, dont la première étape consiste à montrer que cela est raisonnable, voir prop. 4.3.1 et cor. 4.3.2. Puis on aura besoin de relever au sens formel la cellule ouverte
![]() $L^{--}\underline {\mathscr {G}_{\mathbf {f}}}$
de la grassmannienne affine à sa normalisée, voir lem. 4.3.6 et (4.3.23). Désormais, on fixe une alcôve
$L^{--}\underline {\mathscr {G}_{\mathbf {f}}}$
de la grassmannienne affine à sa normalisée, voir lem. 4.3.6 et (4.3.23). Désormais, on fixe une alcôve
![]() $\mathbf {a}$
contenant
$\mathbf {a}$
contenant
![]() $\mathbf {f}$
dans son adhérence.
$\mathbf {f}$
dans son adhérence.
Proposition 4.3.1. Les morphismes de normalisation
sont des homéomorphismes universels, les applications de transition
entre les normalisées sont des immersions fermées et la désingularisation de Demazure se factorise à travers les normalisées
de sorte que la première flèche soit une désingularisation rationnelle.
En caractéristique positive
![]() $p>0$
, les normalisées
$p>0$
, les normalisées
![]() $\widetilde {\operatorname {Gr}}_{\mathscr {G}_{\mathbf {f},p},\leq w}$
sont compatiblement scindées les unes avec les autres.
$\widetilde {\operatorname {Gr}}_{\mathscr {G}_{\mathbf {f},p},\leq w}$
sont compatiblement scindées les unes avec les autres.
Rappelons qu’un schéma X de caractéristique positive
![]() $p>0$
est scindé si l’homomorphisme de
$p>0$
est scindé si l’homomorphisme de
![]() $\mathcal {O}_X$
-modules
$\mathcal {O}_X$
-modules
![]() $\mathcal {O}_X \rightarrow F_*\mathcal {O}_X$
correspondant au frobenius absolu possède une section. On renvoie à [Reference Brion and KumarBK05, §1] pour toutes les propriétés basiques de cette notion fondamental pendant la démonstration ci-dessous.
$\mathcal {O}_X \rightarrow F_*\mathcal {O}_X$
correspondant au frobenius absolu possède une section. On renvoie à [Reference Brion and KumarBK05, §1] pour toutes les propriétés basiques de cette notion fondamental pendant la démonstration ci-dessous.
Démonstration. On peut suivre exactement les démonstrations de [Reference FaltingsFa03, lem. 9] et/ou de [Reference Pappas and RapoportPR08, prop. 9.7]. La résolution de Demazure
pour
![]() $w\in W^{\operatorname {af}}/W_{\mathbf {f}} $
et
$w\in W^{\operatorname {af}}/W_{\mathbf {f}} $
et
![]() $\mathfrak {w}$
une décomposition en réflexions simples
$\mathfrak {w}$
une décomposition en réflexions simples
![]() $s_i$
d’un relèvement de w à
$s_i$
d’un relèvement de w à
![]() $W^{\operatorname {af}}$
de la même longueur, étant birationnelle et projective, les fibres géométriques réduites s’écrivent comme fibrations itérées en droites projectives, d’où leur connexité. Autrement dit, la variété de Schubert normalisée
$W^{\operatorname {af}}$
de la même longueur, étant birationnelle et projective, les fibres géométriques réduites s’écrivent comme fibrations itérées en droites projectives, d’où leur connexité. Autrement dit, la variété de Schubert normalisée
![]() $\widetilde {\operatorname {Gr}}_{\mathscr {G}_{\mathbf {f},p},\leq w}$
est le membre du milieu de la factorisation de Stein de la résolution de Demazure, cf. (4.3.3), et les applications de normalisation (4.3.1) sont des homéomorphismes universels. Il s’ensuit du même raisonnement que les images directes supérieures du faisceau structural de
$\widetilde {\operatorname {Gr}}_{\mathscr {G}_{\mathbf {f},p},\leq w}$
est le membre du milieu de la factorisation de Stein de la résolution de Demazure, cf. (4.3.3), et les applications de normalisation (4.3.1) sont des homéomorphismes universels. Il s’ensuit du même raisonnement que les images directes supérieures du faisceau structural de
![]() $\operatorname {Dem}_{\mathfrak {w}}$
sont triviales.
$\operatorname {Dem}_{\mathfrak {w}}$
sont triviales.
Ensuite, un scindage du frobenius
![]() $\mathcal {O} \rightarrow F_*\mathcal {O}$
de
$\mathcal {O} \rightarrow F_*\mathcal {O}$
de
![]() $\operatorname {Dem}_{\mathfrak {w}}$
est construit, en appliquant le critère de Mehta–Ramanathan, voir [Reference Brion and KumarBK05, prop. 1.3.11]. Sous-jacent à tout cela, se trouve le point le plus délicat, à savoir, l’existence d’un faisceau inversible ample
$\operatorname {Dem}_{\mathfrak {w}}$
est construit, en appliquant le critère de Mehta–Ramanathan, voir [Reference Brion and KumarBK05, prop. 1.3.11]. Sous-jacent à tout cela, se trouve le point le plus délicat, à savoir, l’existence d’un faisceau inversible ample
![]() $\mathcal {L}$
sur la grassmannienne affine
$\mathcal {L}$
sur la grassmannienne affine
![]() $\operatorname {Gr}_{\mathscr {G}_{\mathbf {f},p}}$
à degré
$\operatorname {Gr}_{\mathscr {G}_{\mathbf {f},p}}$
à degré
![]() $1$
sur tous les droites de Schubert, comp. avec [Reference GörtzGo01, prop. 3.3.11] et [Reference Brion and KumarBK05, prop. 2.2.2], pour qu’on puisse calculer le fibré canonique de
$1$
sur tous les droites de Schubert, comp. avec [Reference GörtzGo01, prop. 3.3.11] et [Reference Brion and KumarBK05, prop. 2.2.2], pour qu’on puisse calculer le fibré canonique de
![]() $\operatorname {Dem}_{\mathfrak {w}}$
. Mais cela découle manifestement de notre construction des cycles de Schubert, voir th. 4.2.16 ainsi que le cor. 4.3.10. Ceci comble une lacune de [Reference Pappas and RapoportPR08, prop. 9.6], dont les auteurs ont négligé que les arguments de Görtz avec des réseaux, voir [Reference GörtzGo01, §3.3.6] sont insuffisantes au cas général. Voir aussi l’erreur de [Reference Pappas and RapoportPR08, 10.a.1] signalée par [Reference ZhuZh14, rem. 2.1].
$\operatorname {Dem}_{\mathfrak {w}}$
. Mais cela découle manifestement de notre construction des cycles de Schubert, voir th. 4.2.16 ainsi que le cor. 4.3.10. Ceci comble une lacune de [Reference Pappas and RapoportPR08, prop. 9.6], dont les auteurs ont négligé que les arguments de Görtz avec des réseaux, voir [Reference GörtzGo01, §3.3.6] sont insuffisantes au cas général. Voir aussi l’erreur de [Reference Pappas and RapoportPR08, 10.a.1] signalée par [Reference ZhuZh14, rem. 2.1].
Ce scindage est par construction évidemment compatible aux sous-variétés de Demazure
et se descend donc en un scindage des variétés de Schubert normalisées. Par suite, les applications de transition (4.3.2) déduites des factorisations de Stein (4.3.3) sont des immersion fermées, compte tenu de ce que les schémas scindés sont toujours faiblement normaux, cf. [Reference Brion and KumarBK05, prop. 1.2.5]. Le cas de la caractéristique nulle découle de la semi-continuité supérieure, cf. [Reference Brion and KumarBK05, §1.6].
Revenons aux coefficients entiers et considérons les schémas de Schubert
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}, \leq w}$
définis sur
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}, \leq w}$
définis sur
![]() $\mathbb {Z}$
. Le premier obstacle qu’on rencontre consiste à que les fibres
$\mathbb {Z}$
. Le premier obstacle qu’on rencontre consiste à que les fibres
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}, \leq w}\otimes \mathbb {F}_p$
ne soient pas réduites en caractéristique positive, ce qui sera typiquement le cas quand p divise le cardinal de
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}, \leq w}\otimes \mathbb {F}_p$
ne soient pas réduites en caractéristique positive, ce qui sera typiquement le cas quand p divise le cardinal de
![]() $\pi _1(G^{\mathrm {d\acute {e}r}})$
, voir [Reference Haines, Lourenço and RicharzHLR20, th. 2.5, prop. 3.4] et le cor. 4.3.7. Cependant, pour les normalisés on n’a rien à craindre :
$\pi _1(G^{\mathrm {d\acute {e}r}})$
, voir [Reference Haines, Lourenço and RicharzHLR20, th. 2.5, prop. 3.4] et le cor. 4.3.7. Cependant, pour les normalisés on n’a rien à craindre :
Corollaire 4.3.2. Considérons la factorisation de Stein sur les entiers
des schémas de Schubert. Alors la deuxième flèche est le morphisme de normalisation, le membre du milieu est géométriquement normal et les morphismes de transition
sont des immersions fermées. En particulier, leur colimite
forme un ind-schéma plat opéré par
![]() $L^+\underline {\mathscr {G}_{\mathbf {f}}}$
.
$L^+\underline {\mathscr {G}_{\mathbf {f}}}$
.
Démonstration. On doit observer que l’image directe des sections globales le long de la résolution de Demazure commute aux changements de base quelconques, ce que l’on déduit de l’annulation des images directes supérieures en caractéristique positive, voir la prop. 4.3.1, [Reference FaltingsFa03, p. 52] et [Reference GörtzGo03, prop. 3.13]. Les morphismes de transition
entre les schémas de Schubert normalisés sont des immersions fermées, car on le sait déjà pour les fibres spéciales. Le mot plat est appliqué pour les ind-schémas au sens de [Reference Haines, Lourenço and RicharzHLR20, déf. 8.1].
Enfin, pour voir que l’opération du groupe d’arcs se relève en la colimite
![]() $\widetilde {\operatorname {Gr}}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
, il suffit de remarquer que
$\widetilde {\operatorname {Gr}}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
, il suffit de remarquer que
![]() $L^+\underline {\mathscr {G}_{\mathbf {f}}}$
est pro-lisse et que la normalisation faible absolue est fonctorielle, cf. [StaProj, 0EUS], et commute aux produits géométriquement réduits, cf. [Reference ManaresiMan80, th. III.1, th. V.2].
$L^+\underline {\mathscr {G}_{\mathbf {f}}}$
est pro-lisse et que la normalisation faible absolue est fonctorielle, cf. [StaProj, 0EUS], et commute aux produits géométriquement réduits, cf. [Reference ManaresiMan80, th. III.1, th. V.2].
Le lemme suivant est aussi fondamental et provient de notre collaboration [Reference Haines, Lourenço and RicharzHLR20] avec Haines–Richarz :
Lemme 4.3.3 (Haines–L.–Richarz).
La grassmannienne affine
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
est plate sur
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
est plate sur
![]() $\mathbb {Z}$
.
$\mathbb {Z}$
.
Démonstration. La preuve du lemme à la suite de [Reference Haines, Lourenço and RicharzHLR20, prop. 8.8] se fait en deux étapes. On voit d’abord que le voisinage formel
![]() $\operatorname {Spf} \mathcal {O}$
de la section identité est plate, ce qui peut être ramené à un calcul n’impliquant que la grosse cellule
$\operatorname {Spf} \mathcal {O}$
de la section identité est plate, ce qui peut être ramené à un calcul n’impliquant que la grosse cellule
![]() $\underline {\mathscr {C}_{\mathbf {f}}}$
, cf. [Reference Haines, Lourenço and RicharzHLR20, lem. 8.4].
$\underline {\mathscr {C}_{\mathbf {f}}}$
, cf. [Reference Haines, Lourenço and RicharzHLR20, lem. 8.4].
À ce stade, on pourrait imaginer que tout serait fini, cf. la preuve du cor. 4.2.11. Néanmoins, l’adhérence plate n’est pas forcément représentable, donc il faut évoquer une technique légèrement plus sophistiquée due à Faltings, cf. [Reference FaltingsFa03, preuve du cor. 11] et [Reference Haines, Lourenço and RicharzHLR20, lem. 8.6]. Celle-ci affirme que, pour que notre plongement ind-fermé soit un isomorphisme, il suffit d’étudier les points à valeurs dans les anneaux artiniens locaux. Comme ceux-ci peuvent être translatés vers le voisinage formel de l’unité, grâce à la décomposition de Bruhat sur les corps, voir [Reference Bruhat and TitsBT72, th. 6.5.1] et [Reference LourençoLou21, prop. 3.7], on en obtient la platitude de la grassmannienne affine.
Il sera essentiel pour nous de savoir en avance que les variétés de Schubert sont normales en caractéristique nulle, voir la démonstration ci-dessous du th. 4.1.5. L’argument suivant est dû à Kumar, voir [Reference KumarKum87, th. 2.16], dans le cadre de Kac–Moody et a été adapté par Faltings, voir [Reference FaltingsFa03, p. 52], aux grassmanniennes affines de groupes déployés et puis répété dans le cas tordu par Pappas–Rapoport, voir [Reference Pappas and RapoportPR08, 9.f].
Lemme 4.3.4 (Kumar, Faltings, Pappas–Rapoport).
Les variétés de Schubert
![]() $\operatorname {Gr}_{\mathscr {G}_{\mathbf {f},0},\leq w}$
sont normales en caractéristique nulle.
$\operatorname {Gr}_{\mathscr {G}_{\mathbf {f},0},\leq w}$
sont normales en caractéristique nulle.
Démonstration. Soit G simplement connexe sans perte de généralité, d’où le fait que la grassmannienne affine soit réduite, voir [Reference Pappas and RapoportPR08, prop. 9.9] ainsi que le cor. 4.3.8. Soit
![]() $\mathcal {L}$
un faisceau inversible effectif sur
$\mathcal {L}$
un faisceau inversible effectif sur
![]() $\operatorname {Gr}_{\mathscr {G}_{\mathbf {f},0}}$
induit par le th. 4.2.16, cf. aussi cor. 4.3.10. Alors,
$\operatorname {Gr}_{\mathscr {G}_{\mathbf {f},0}}$
induit par le th. 4.2.16, cf. aussi cor. 4.3.10. Alors,
![]() $\mathcal {L}$
est par construction sans points de base en un ouvert non vide et même partout par translation, cf. [Reference FaltingsFa03, th. 7]. En passant à la normalisée
$\mathcal {L}$
est par construction sans points de base en un ouvert non vide et même partout par translation, cf. [Reference FaltingsFa03, th. 7]. En passant à la normalisée
![]() $\widetilde {\operatorname {Gr}}_{\mathscr {G}_{\mathbf {f},0}}$
, alors le groupe de Picard devient engendré par ces faisceaux effectifs, voir le cor. 4.3.10, ce qui permet de déduire l’ampleur de ces derniers sur la grassmannienne
$\widetilde {\operatorname {Gr}}_{\mathscr {G}_{\mathbf {f},0}}$
, alors le groupe de Picard devient engendré par ces faisceaux effectifs, voir le cor. 4.3.10, ce qui permet de déduire l’ampleur de ces derniers sur la grassmannienne
![]() $\operatorname {Gr}_{\mathscr {G}_{\mathbf {f},0}}$
elle-même. Finalement, on remarque que l’opération naturelle de
$\operatorname {Gr}_{\mathscr {G}_{\mathbf {f},0}}$
elle-même. Finalement, on remarque que l’opération naturelle de
![]() $L^-\underline {\mathscr {G}_{\mathbf {a}}}$
sur
$L^-\underline {\mathscr {G}_{\mathbf {a}}}$
sur
![]() $\mathcal {L}$
se prolonge et se relève en une action de l’extension centrale universelle
$\mathcal {L}$
se prolonge et se relève en une action de l’extension centrale universelle
par des raisonnements généraux, voir aussi le cor. 4.3.11.
Considérons maintenant l’application
de
![]() $\mathbb {Q}$
-espaces vectoriels non nuls déduite de la colimite des mêmes morphismes pour les variétés de Schubert. On en déduit une action de l’algèbre de Lie de l’extension centrale
$\mathbb {Q}$
-espaces vectoriels non nuls déduite de la colimite des mêmes morphismes pour les variétés de Schubert. On en déduit une action de l’algèbre de Lie de l’extension centrale
![]() $\widehat {LG}$
de (4.3.10) sur les
$\widehat {LG}$
de (4.3.10) sur les
![]() $\mathbb {Q}$
-espaces vectoriels non nuls de (4.3.11). On peut même montrer que les deux
$\mathbb {Q}$
-espaces vectoriels non nuls de (4.3.11). On peut même montrer que les deux
![]() $\operatorname {Lie}\widehat {LG}$
-modules sont irréductibles au même plus grand poids au sens de la théorie de Kac–Moody, donc isomorphes, cf. [Reference Pappas and RapoportPR08, 9.f]. Comme
$\operatorname {Lie}\widehat {LG}$
-modules sont irréductibles au même plus grand poids au sens de la théorie de Kac–Moody, donc isomorphes, cf. [Reference Pappas and RapoportPR08, 9.f]. Comme
![]() $\mathcal {L}$
était arbitraire, on achève facilement la conclusion voulue que les variétés de Schubert sont normales, cf. [Reference FaltingsFa03, p. 52]. Pour une preuve plus élémentaire mais moins éclairante, voir aussi [Reference KumarKum97, annexe].
$\mathcal {L}$
était arbitraire, on achève facilement la conclusion voulue que les variétés de Schubert sont normales, cf. [Reference FaltingsFa03, p. 52]. Pour une preuve plus élémentaire mais moins éclairante, voir aussi [Reference KumarKum97, annexe].
Récapitulons les faits qui ont été établis ci-dessus : on a un morphisme
![]() $L^+\underline {\mathscr {G}_{\mathbf {f}}}$
-équivariant de normalisation
$L^+\underline {\mathscr {G}_{\mathbf {f}}}$
-équivariant de normalisation
entre ind-schémas plats, voir le cor. 4.3.2 et le lem. 4.3.3, qui est un isomorphisme sur le réduit du membre de droite en caractéristique nulle, voir le lem. 4.3.4. Typiquement, la grassmannienne n’est pas réduite, voir [Reference Pappas and RapoportPR08, th. 6.1, prop. 6.5] ainsi que le cor. 4.3.8, si G n’est pas semi-simple, et il y a aussi des problèmes de non normalité en caractéristiques mauvaises selon notre collaboration avec Haines–Richarz, voir [Reference Haines, Lourenço and RicharzHLR20, th. 2.5] et le cor. 4.3.7. Ainsi, on suppose dorénavant que
est simplement connexe, ce qui est évidemment suffisant afin de montrer le th. 4.1.5.
Comme nous avons dit auparavant, notre but est de construire l’application réciproque du morphisme naturel
entre les voisinages formels de l’originel, voir la démonstration ci-dessous du th. 4.1.5. Tous les deux membres sont des schéma en groupes formels affines de type infini, voir le cor. 4.2.11 et appliquer le foncteur de normalisation faible absolue, cf. [Reference ManaresiMan80, th. III.1, th. V.2]. Ce raisonnement entraîne, de plus, que le morphisme (4.3.14) soit aussi opéré par tout groupe d’arcs parahorique
![]() $L^+\underline {\mathscr {G}_{\mathbf {g}}}$
associé aux facettes
$L^+\underline {\mathscr {G}_{\mathbf {g}}}$
associé aux facettes
![]() $\mathbf {g} \subset \mathscr {A}(\underline {G},\underline {S},\mathbb {Z} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
, et en particulier, par les groupes de lacets radiciels
$\mathbf {g} \subset \mathscr {A}(\underline {G},\underline {S},\mathbb {Z} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
, et en particulier, par les groupes de lacets radiciels
![]() $L\underline {U_a}$
. Ce fait sera exploité décisivement pour déduire que les algèbres de Lie à coefficients dans
$L\underline {U_a}$
. Ce fait sera exploité décisivement pour déduire que les algèbres de Lie à coefficients dans
![]() $\mathbb {Z}$
de ces deux groupes infinis sont isomorphes, voir les lems. 4.3.5, 4.3.6 et (4.3.23).
$\mathbb {Z}$
de ces deux groupes infinis sont isomorphes, voir les lems. 4.3.5, 4.3.6 et (4.3.23).
Afin de motiver la discussion à venir, voici une adaptation du lemme-clef de Pappas–Rapoport, voir [Reference Pappas and RapoportPR08, prop. 9.3], que nous avons déjà mentionné ailleurs.
Lemme 4.3.5. Supposons que
![]() $G=G^{\operatorname {sc}}$
est simplement connexe et soit R n’importe quel anneau. Alors, la R-algèbre de Lie de
$G=G^{\operatorname {sc}}$
est simplement connexe et soit R n’importe quel anneau. Alors, la R-algèbre de Lie de
![]() $L^{\operatorname {gr}}\underline {G}$
est engendrée par celles de
$L^{\operatorname {gr}}\underline {G}$
est engendrée par celles de
![]() $L^{\operatorname {gr}}\underline {U_\pm }$
, si et seulement si
$L^{\operatorname {gr}}\underline {U_\pm }$
, si et seulement si
![]() $\Phi _G$
est réduit ou si
$\Phi _G$
est réduit ou si
![]() $2 \in R^\times $
est inversible.
$2 \in R^\times $
est inversible.
Démonstration. On s’est ramené au cas où G est de rang relatif
![]() $1$
et absolument simple, c’est-à-dire soit
$1$
et absolument simple, c’est-à-dire soit
![]() $\operatorname {SL}_2$
, soit
$\operatorname {SL}_2$
, soit
![]() $\operatorname {SU}_{3}$
. Dans le cas non pluriel, on a
$\operatorname {SU}_{3}$
. Dans le cas non pluriel, on a
![]() $[t^ne_a,t^me_{-a}]=\pm t^{n+m}h_a$
, où les
$[t^ne_a,t^me_{-a}]=\pm t^{n+m}h_a$
, où les
![]() $e_a$
engendrent l’algèbre de Lie de
$e_a$
engendrent l’algèbre de Lie de
![]() $\underline {U_a}$
et les
$\underline {U_a}$
et les
![]() $h_a$
de
$h_a$
de
![]() $\underline {T}$
, comme d’habitude. Dans le cas pluriel, on peut choisir les générateurs
$\underline {T}$
, comme d’habitude. Dans le cas pluriel, on peut choisir les générateurs
![]() $e_{\pm a}$
et
$e_{\pm a}$
et
![]() $e_{\pm 2a}$
des espaces de poids de
$e_{\pm 2a}$
des espaces de poids de
![]() $\operatorname {Lie}\underline {G}$
, de telle manière que
$\operatorname {Lie}\underline {G}$
, de telle manière que
![]() $[t^ne_a,t^me_{-a}]=\pm 2t^{n+m}h_a$
et
$[t^ne_a,t^me_{-a}]=\pm 2t^{n+m}h_a$
et
![]() $[t^ne_{2a},t^me_{-2a}]=\pm t^{n+m}h_a$
, cf. (3.3.20) et (3.3.21). En particulier, si
$[t^ne_{2a},t^me_{-2a}]=\pm t^{n+m}h_a$
, cf. (3.3.20) et (3.3.21). En particulier, si
![]() $2 \notin R^\times $
, on voit que la sous-algèbre de Lie engendré par les espaces de poids non nuls ne contient pas les éléments de la forme
$2 \notin R^\times $
, on voit que la sous-algèbre de Lie engendré par les espaces de poids non nuls ne contient pas les éléments de la forme
![]() $t^{n}h_a$
, où
$t^{n}h_a$
, où
![]() $n\in \frac {1}{2}\mathbb {Z} \setminus \mathbb {Z}$
décrit l’ensemble des demi entiers non entiers.
$n\in \frac {1}{2}\mathbb {Z} \setminus \mathbb {Z}$
décrit l’ensemble des demi entiers non entiers.
En conclusion, le crochet de Lie ne suffit pas pour qu’on retrouve l’algèbre de Lie de
![]() $\operatorname {Spf} \mathcal {O}$
toute entière, en n’opérant qu’avec les sous-groupes radiciels, ne soit qu’on exclut les systèmes de racines non réduits (c’était le choix de la version préliminaire de cet article) ou que la caractéristique paire soit à éviter (moins souhaitable pour nous). La solution consiste à substituer des opérateurs différentiels supérieurs aux linéaires.
$\operatorname {Spf} \mathcal {O}$
toute entière, en n’opérant qu’avec les sous-groupes radiciels, ne soit qu’on exclut les systèmes de racines non réduits (c’était le choix de la version préliminaire de cet article) ou que la caractéristique paire soit à éviter (moins souhaitable pour nous). La solution consiste à substituer des opérateurs différentiels supérieurs aux linéaires.
Autrement dit, on fera usage de l’algèbre des distributions
![]() $\operatorname {Dist}\mathcal {O}$
constituée des opérateurs linéaires continus
$\operatorname {Dist}\mathcal {O}$
constituée des opérateurs linéaires continus
![]() $\delta :\mathcal {O} \rightarrow \mathbb {Z}$
qui s’annulent sur une puissance de l’idéal
$\delta :\mathcal {O} \rightarrow \mathbb {Z}$
qui s’annulent sur une puissance de l’idéal
![]() $\mathcal {I}$
définissant la section origine. Pour la notion habituelle en géométrie algébrique et ses propriétés, on renvoie le lecteur à [Reference Bruhat and TitsBT84a, §1.3] et à [Reference JantzenJa07, I, §7]; pour les ind-schémas au-dessus des corps, la discussion du concept au début de [Reference Haines, Lourenço and RicharzHLR20, §7.1] est aussi recommandée.
$\mathcal {I}$
définissant la section origine. Pour la notion habituelle en géométrie algébrique et ses propriétés, on renvoie le lecteur à [Reference Bruhat and TitsBT84a, §1.3] et à [Reference JantzenJa07, I, §7]; pour les ind-schémas au-dessus des corps, la discussion du concept au début de [Reference Haines, Lourenço and RicharzHLR20, §7.1] est aussi recommandée.
Lemme 4.3.6. Gardons les notations du lem. 4.3.5. Alors, la R-algèbre de distributions de
![]() $L^{\operatorname {gr}}\underline {G}$
est engendrée par celles de
$L^{\operatorname {gr}}\underline {G}$
est engendrée par celles de
![]() $L^{\operatorname {gr}}\underline {U_\pm }$
.
$L^{\operatorname {gr}}\underline {U_\pm }$
.
Démonstration. Alors, l’algèbre de distributions
![]() $\operatorname {Dist}L^{\operatorname {gr}}\underline {G}$
ne dépend que de l’espace d’élastiques
$\operatorname {Dist}L^{\operatorname {gr}}\underline {G}$
ne dépend que de l’espace d’élastiques
![]() $L^{\operatorname {gr}}\underline {C}$
de la grosse cellule
$L^{\operatorname {gr}}\underline {C}$
de la grosse cellule
![]() $\underline {C} \subset \underline {G}$
. Comme les distributions transforment les produits directs en tensoriels, dès que les voisinages infinitésimaux de l’origine soient des R-modules projectifs, voir [Reference Bruhat and TitsBT84a, 1.3.5], on en tire que l’algèbre
$\underline {C} \subset \underline {G}$
. Comme les distributions transforment les produits directs en tensoriels, dès que les voisinages infinitésimaux de l’origine soient des R-modules projectifs, voir [Reference Bruhat and TitsBT84a, 1.3.5], on en tire que l’algèbre
![]() $\operatorname {Dist}L^{\operatorname {gr}}\underline {G}$
est engendrée par celles de
$\operatorname {Dist}L^{\operatorname {gr}}\underline {G}$
est engendrée par celles de
![]() $L^{\operatorname {gr}}\underline {T}$
et de
$L^{\operatorname {gr}}\underline {T}$
et de
![]() $L^{\operatorname {gr}}\underline {U_a}$
, où a décrit la partie
$L^{\operatorname {gr}}\underline {U_a}$
, où a décrit la partie
![]() $\Phi _G^{\operatorname {nd}}$
des racines non divisibles.
$\Phi _G^{\operatorname {nd}}$
des racines non divisibles.
Comme d’habitude, l’affirmation se réduit aux cas absolument simples de rang relatif
![]() $1$
et on commence par déduire du morphisme échange de l’axiome (DRS 3), voir les formules explicites 3.3.19 et 3.3.21, l’existence d’un morphisme rationnel :
$1$
et on commence par déduire du morphisme échange de l’axiome (DRS 3), voir les formules explicites 3.3.19 et 3.3.21, l’existence d’un morphisme rationnel :
où la deuxième flèche est la multiplication et la composée se factorise à travers
![]() $\underline {T}$
. Ensuite, nous prenons
$\underline {T}$
. Ensuite, nous prenons
![]() $L^{\operatorname {gr}}$
et complétons autour de la section unité pour obtenir une application définie partout au sens formel; nous allons montrer que le morphisme induit des distributions est surjectif.
$L^{\operatorname {gr}}$
et complétons autour de la section unité pour obtenir une application définie partout au sens formel; nous allons montrer que le morphisme induit des distributions est surjectif.
Les équations qui décrivent l’échange pour le groupe
![]() $\operatorname {SL}_2$
son si simples que le soin des calculs pertinents sera laissé au lecteur. Dans le cas de
$\operatorname {SL}_2$
son si simples que le soin des calculs pertinents sera laissé au lecteur. Dans le cas de
![]() $\operatorname {SU}_3$
, on pose soit
$\operatorname {SU}_3$
, on pose soit
soit
Si l’on identifie le sous-groupe des éléments
![]() $1-rt^n$
dans le complété de
$1-rt^n$
dans le complété de
![]() $L^{\operatorname {gr}}\underline {T}$
à la droite affine formelle, alors on obtient un morphisme plat
$L^{\operatorname {gr}}\underline {T}$
à la droite affine formelle, alors on obtient un morphisme plat
donné lorsqu’on se trouve dans le cas (4.3.16) par
soit par
lorsqu’on se trouve dans le cas (4.3.17). Les applications des modules de distributions qui en résultent sont en tout cas surjectives.
Ce lemme combiné avec l’équivariance de la normalisation entraîne que
est même surjectif. D’autre part, les algèbres de distributions sont toujours sans torsion et on sait déjà que le
![]() $\mathbb {Q}$
-localisé de l’homomorphisme (4.3.21) est bijectif, cf. lem. 4.3.4, lem. 4.3.3 et cor. 4.3.8, d’où la bijectivité à coefficients entiers de (4.3.21).
$\mathbb {Q}$
-localisé de l’homomorphisme (4.3.21) est bijectif, cf. lem. 4.3.4, lem. 4.3.3 et cor. 4.3.8, d’où la bijectivité à coefficients entiers de (4.3.21).
Puis on observe sans peine que l’algèbre de Lie
est un sous-module saturé de l’algèbre de distributions, c’est-à-dire le conoyau est sans torsion : en effet, si
![]() $n\delta $
s’annule sur
$n\delta $
s’annule sur
![]() $\mathcal {I}^2$
, alors la distribution
$\mathcal {I}^2$
, alors la distribution
![]() $\delta $
s’annule aussi sur
$\delta $
s’annule aussi sur
![]() $\mathcal {I}^2$
. Par suite, l’homomorphisme
$\mathcal {I}^2$
. Par suite, l’homomorphisme
est bijectif. Maintenant, on est prêt à prouver le théorème de normalité des schémas de Schubert, cf. th. 4.1.5.
Démonstration du th. 4.1.5. On affirme qu’il suffit de construire une section de l’homomorphisme de normalisation
entre les anneaux locaux séparés complétés du schéma de Schubert associé à w et de son normalisé le long de leurs sections origines. En effet, le support du conoyau des faisceaux structuraux serait ainsi trivial, car stable par
![]() $L^+\underline {\mathscr {G}_{\mathbf {a}}}$
et fermé.
$L^+\underline {\mathscr {G}_{\mathbf {a}}}$
et fermé.
On procède par un argument inductif de déformation, comp. avec [Reference FaltingsFa03, p. 53] et [Reference Pappas and RapoportPR08, 9.g]. Grâce à la résolution de Demazure, l’anneau
![]() $\mathcal {O}_w$
peut être filtré par une suite d’idéaux décroissante et exhaustive
$\mathcal {O}_w$
peut être filtré par une suite d’idéaux décroissante et exhaustive
telle que leurs conoyaux
![]() $A_n$
soient plats sur
$A_n$
soient plats sur
![]() $\mathbb {Z}$
ayant
$\mathbb {Z}$
ayant
![]() $I_{n-1}$
pour idéal de carré nul. Alors, le point canonique
$I_{n-1}$
pour idéal de carré nul. Alors, le point canonique
![]() $s_n$
de
$s_n$
de
![]() $\operatorname {Spf} \mathcal {O}_w$
à valeurs dans
$\operatorname {Spf} \mathcal {O}_w$
à valeurs dans
![]() $A_n$
peut être relevé uniquement en un point
$A_n$
peut être relevé uniquement en un point
![]() $\widetilde {s}_n$
de
$\widetilde {s}_n$
de
![]() $\operatorname {Spf} \widetilde {\mathcal {O}}_w$
.
$\operatorname {Spf} \widetilde {\mathcal {O}}_w$
.
En effet, comme les espaces tangents commutent aux changements de base plats, on peut appliquer le critère de lissité formelle, ainsi que l’isomorphisme (4.3.23), pour relever uniquement
![]() $s_{n+1}$
à
$s_{n+1}$
à
![]() $\operatorname {Spf} \widetilde {\mathcal {O}}$
. Vu que ce relèvement n’est autre que l’identité en caractéristique nulle, voir le lem. 4.3.4, la section
$\operatorname {Spf} \widetilde {\mathcal {O}}$
. Vu que ce relèvement n’est autre que l’identité en caractéristique nulle, voir le lem. 4.3.4, la section
![]() $\widetilde {s}_n \in \operatorname {Spf} \widetilde {\mathcal {O}}(A_n)$
doit se factoriser à travers
$\widetilde {s}_n \in \operatorname {Spf} \widetilde {\mathcal {O}}(A_n)$
doit se factoriser à travers
![]() $\operatorname {Spf} \widetilde {\mathcal {O}}_w$
. En particulier, les
$\operatorname {Spf} \widetilde {\mathcal {O}}_w$
. En particulier, les
![]() $\widetilde {s}_n$
s’assemblent les unes avec les autres pour donner un morphisme
$\widetilde {s}_n$
s’assemblent les unes avec les autres pour donner un morphisme
![]() $\operatorname {Spec} \mathcal {O}_w \rightarrow \operatorname {Spec} \widetilde {\mathcal {O}}_w$
, par le lemme de Chevalley.
$\operatorname {Spec} \mathcal {O}_w \rightarrow \operatorname {Spec} \widetilde {\mathcal {O}}_w$
, par le lemme de Chevalley.
En collaboration avec Haines–Richarz, voir [Reference Haines, Lourenço and RicharzHLR20], nous avons déterminé tous les groupes G dont les variétés de Schubert en caractéristique positive sont toutes normales, sous des hypothèses de ramification modérée, cf. [Reference Haines, Lourenço and RicharzHLR20, prop. 2.1, th. 2.5]. Ceci s’étend aussi au présent cadre.
Corollaire 4.3.7 (Haines–L.–Richarz).
Pour que les variétés de Schubert
![]() $\operatorname {Gr}_{\mathscr {G}_{\mathbf {f},p},\leq w}$
soient toutes normales, il faut et il suffit que p ne divise pas l’ordre du groupe fondamental
$\operatorname {Gr}_{\mathscr {G}_{\mathbf {f},p},\leq w}$
soient toutes normales, il faut et il suffit que p ne divise pas l’ordre du groupe fondamental
![]() $\pi _1(G^{\mathrm {d\acute {e}r}})$
du groupe dérivé.
$\pi _1(G^{\mathrm {d\acute {e}r}})$
du groupe dérivé.
Démonstration. L’affirmation cruciale qu’on va prouver est que le noyau de
est étale si et seulement si p ne divise pas l’ordre n du groupe fondamental du dérivé de G. En effet, on voit par réduction au cas déployé, cf. prop. 3.3.9, que le noyau générique modulo p est contenu dans
![]() $T^{\operatorname {sc}}_{\eta _p}[n]$
. Si
$T^{\operatorname {sc}}_{\eta _p}[n]$
. Si
![]() $(p,n)=1$
, ce sous-groupe de n-torsion est fini étale. Sinon, on peut déduire grâce à [Reference HeinlothHei10, ass. 12] que le noyau contient toutefois un sous-groupe fini et multiplicatif d’ordre n, donc non étale. Armés de telle information, on peut appliquer l’argument principal de [Reference Haines, Lourenço and RicharzHLR20, prop. 2.1] pour déduire l’existence d’une obstruction dans les cas souhaités.
$(p,n)=1$
, ce sous-groupe de n-torsion est fini étale. Sinon, on peut déduire grâce à [Reference HeinlothHei10, ass. 12] que le noyau contient toutefois un sous-groupe fini et multiplicatif d’ordre n, donc non étale. Armés de telle information, on peut appliquer l’argument principal de [Reference Haines, Lourenço and RicharzHLR20, prop. 2.1] pour déduire l’existence d’une obstruction dans les cas souhaités.
Le corollaire suivant est dû à plusieurs mathématiciens qui l’ont démontré à des degrés divers de généralité.
Corollaire 4.3.8 (Faltings, Pappas–Rapoport, Haines–L.–Richarz).
La grassmannienne affine
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
est réduite si et seulement si G est semi-simple. Pour que ses fibres soient aussi réduites, il faut et il suffit que G soit simplement connexe.
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
est réduite si et seulement si G est semi-simple. Pour que ses fibres soient aussi réduites, il faut et il suffit que G soit simplement connexe.
Démonstration. On prend l’opportunité pour reprouver que la grassmannienne affine est géométriquement réduite au cas où G est simplement connexe, sans recourir ni à [Reference FaltingsFa03, cor. 11] en caractéristique nulle ni au lem. 4.3.3. Le voisinage formel
![]() $\operatorname {Spf} \mathcal {O}_p$
de la grassmannienne affine
$\operatorname {Spf} \mathcal {O}_p$
de la grassmannienne affine
![]() $\operatorname {Gr}_{\mathscr {G}_{\mathbf {f},p}}$
modulo p est contenu dans la colimite des schémas de Schubert, parce que tous les deux sont opérés par les groupes de lacets radiciels, donc les algèbres de distributions coïncident, voir le lem. 4.3.6. Les points à valeurs dans les anneaux artiniens locaux se translatent sans peine vers ce voisinage formel, d’où notre affirmation.
$\operatorname {Gr}_{\mathscr {G}_{\mathbf {f},p}}$
modulo p est contenu dans la colimite des schémas de Schubert, parce que tous les deux sont opérés par les groupes de lacets radiciels, donc les algèbres de distributions coïncident, voir le lem. 4.3.6. Les points à valeurs dans les anneaux artiniens locaux se translatent sans peine vers ce voisinage formel, d’où notre affirmation.
En caractéristique nulle, on peut montrer aisément que
![]() $\operatorname {Gr}_{\mathscr {G}_{\mathbf {f},0}}$
est réduite si et seulement si G est semi-simple, voir [Reference Pappas and RapoportPR08, th. 6.1, prop. 6.5], d’où l’assertion à coefficients entiers grâce au lem. 4.3.3. Lorsque G est semi-simple à groupe fondamental
$\operatorname {Gr}_{\mathscr {G}_{\mathbf {f},0}}$
est réduite si et seulement si G est semi-simple, voir [Reference Pappas and RapoportPR08, th. 6.1, prop. 6.5], d’où l’assertion à coefficients entiers grâce au lem. 4.3.3. Lorsque G est semi-simple à groupe fondamental
![]() $\pi _1(G)$
non trivial, un nombre premier p divisant le cardinal en est choisi et nous observons que le noyau de
$\pi _1(G)$
non trivial, un nombre premier p divisant le cardinal en est choisi et nous observons que le noyau de
![]() $G^{\operatorname {sc}}_{\eta _p}\rightarrow G_{\eta _p}$
n’est pas étale, à cause de [Reference HeinlothHei10, ass. 12]. Par conséquent, il s’avère par une application soigneuse des arguments de [Reference Haines, Lourenço and RicharzHLR20, §7] que
$G^{\operatorname {sc}}_{\eta _p}\rightarrow G_{\eta _p}$
n’est pas étale, à cause de [Reference HeinlothHei10, ass. 12]. Par conséquent, il s’avère par une application soigneuse des arguments de [Reference Haines, Lourenço and RicharzHLR20, §7] que
![]() $\operatorname {Gr}_{\mathscr {G}_{\mathbf {f},p}}$
n’est pas réduite. Il semble que ceci pourrait aussi découler de l’étude du morphisme d’algèbre de distributions entières, mais nous n’avons pas pu montrer que le conoyau est sans torsion divisible, comme par exemple
$\operatorname {Gr}_{\mathscr {G}_{\mathbf {f},p}}$
n’est pas réduite. Il semble que ceci pourrait aussi découler de l’étude du morphisme d’algèbre de distributions entières, mais nous n’avons pas pu montrer que le conoyau est sans torsion divisible, comme par exemple
![]() $\mathbb {Q}/\mathbb {Z}$
.
$\mathbb {Q}/\mathbb {Z}$
.
Cette section se conclut par donner une application à la géométrie des schémas de Richardson
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}, \leq v}^{\geq w}$
sur les entiers, cf. (4.2.29), qui n’est parue dans la littérature des groupes de Kac–Moody affines, tant que nous le savons, cf. aussi [Reference Kumar and SchwedeKS14, rem. 5.10], mais qui est probablement connue parmi les experts, voir [Reference Brion and LakshmibaiBL01, lem. 1] pour les variétés de drapeaux finies et [Reference Kumar and SchwedeKS14, th. 3.1] en caractéristique nulle.
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}, \leq v}^{\geq w}$
sur les entiers, cf. (4.2.29), qui n’est parue dans la littérature des groupes de Kac–Moody affines, tant que nous le savons, cf. aussi [Reference Kumar and SchwedeKS14, rem. 5.10], mais qui est probablement connue parmi les experts, voir [Reference Brion and LakshmibaiBL01, lem. 1] pour les variétés de drapeaux finies et [Reference Kumar and SchwedeKS14, th. 3.1] en caractéristique nulle.
Corollaire 4.3.9 (Brion–Lakshimibai, Mathieu–Kumar–Schwede, L.).
Sous l’hypothèse
![]() $G^{\mathrm {d\acute {e}r}}=G^{\operatorname {sc}}$
, alors les schémas de Richardson sont plats, intègres de dimension relative
$G^{\mathrm {d\acute {e}r}}=G^{\operatorname {sc}}$
, alors les schémas de Richardson sont plats, intègres de dimension relative
![]() $l(v)-l(w)$
, de Cohen–Macaulay et géométriquement normaux à fibres compatiblement scindées en caractéristique positive.
$l(v)-l(w)$
, de Cohen–Macaulay et géométriquement normaux à fibres compatiblement scindées en caractéristique positive.
Démonstration. La preuve qui va suivre est reprise de [Reference Brion and LakshmibaiBL01, lem. 1]. On considère la fibration
localement triviale pour la topologie ouverte, voir cor. 4.2.11, dont les fibres sont isomorphes à certaines variétés de Schubert. Puis on prend l’ind-schéma Z déduit par changement de base le long de
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}^{\geq w} $
et qui est opéré par
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}^{\geq w} $
et qui est opéré par
![]() $L^-\underline {\mathscr {G}_{\mathbf {a}}}$
par multiplication à la gauche, vu que le même vaut pour
$L^-\underline {\mathscr {G}_{\mathbf {a}}}$
par multiplication à la gauche, vu que le même vaut pour
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}^{\geq w} $
. D’autre part, l’on a une application projection canonique de Z vers
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}^{\geq w} $
. D’autre part, l’on a une application projection canonique de Z vers
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {a}}}}$
, dont le produit fibré avec la section origine s’identifie sans peine au schéma de Richardson
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {a}}}}$
, dont le produit fibré avec la section origine s’identifie sans peine au schéma de Richardson
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}, \leq v}^{\geq w}$
. Évoquant la
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}, \leq v}^{\geq w}$
. Évoquant la
![]() $L^-\underline {\mathscr {G}_{\mathbf {a}}}$
-équivariance de ce morphisme, nous arrivons à ce que l’image réciproque dans Z de la cellule ouverte
$L^-\underline {\mathscr {G}_{\mathbf {a}}}$
-équivariance de ce morphisme, nous arrivons à ce que l’image réciproque dans Z de la cellule ouverte
![]() $L^{--}\underline {\mathscr {G}_{\mathbf {a}}}$
de
$L^{--}\underline {\mathscr {G}_{\mathbf {a}}}$
de
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {a}}}}$
est isomorphe à son produit avec
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {a}}}}$
est isomorphe à son produit avec
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}, \leq v}^{\geq w}$
. En particulier, les propriétés géométriques qui ont été énoncées sauf le scindage découlent très vite de leurs analogues pour les schémas de Schubert, cf. th. 4.1.5, ainsi que pour les quotients locaux des cycles de Schubert, cf. th. 4.2.16.
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}, \leq v}^{\geq w}$
. En particulier, les propriétés géométriques qui ont été énoncées sauf le scindage découlent très vite de leurs analogues pour les schémas de Schubert, cf. th. 4.1.5, ainsi que pour les quotients locaux des cycles de Schubert, cf. th. 4.2.16.
Le part sur le scindage est un théorème non publié de Mathieu, qui fut rédigé par Kumar–Schwede en [Reference Kumar and SchwedeKS14, prop. 5.3]. L’outil principal est une notion de scindage
![]() $L^+\underline {\mathscr {G}_{\mathbf {a}}}$
-canonique au sens de [Reference Brion and KumarBK05, déf. 4.1.1], en termes du sous-tore maximal
$L^+\underline {\mathscr {G}_{\mathbf {a}}}$
-canonique au sens de [Reference Brion and KumarBK05, déf. 4.1.1], en termes du sous-tore maximal
![]() $\underline {S}$
et des sous-groupes radiciels
$\underline {S}$
et des sous-groupes radiciels
![]() $\underline {V_\alpha }$
associés aux racines réelles simples positives
$\underline {V_\alpha }$
associés aux racines réelles simples positives
![]() $\alpha \in \Delta _G^{\mathrm{r}\acute{\rm e}}$
. On s’en sert pour montrer que les cycles de Schubert en caractéristique p sont compatiblement scindés, en appliquant l’opération du Borel opposé
$\alpha \in \Delta _G^{\mathrm{r}\acute{\rm e}}$
. On s’en sert pour montrer que les cycles de Schubert en caractéristique p sont compatiblement scindés, en appliquant l’opération du Borel opposé
![]() $L^-\underline {\mathscr {G}_{\mathbf {a}}}$
, donc il en est de même des schémas de Richardson.
$L^-\underline {\mathscr {G}_{\mathbf {a}}}$
, donc il en est de même des schémas de Richardson.
On obtient la description ci-dessous du groupe de Picard des schémas de Schubert
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq w}$
.
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq w}$
.
Corollaire 4.3.10. Si
![]() $G^{\mathrm {d\acute {e}r}}=G^{\operatorname {sc}}$
, alors le foncteur de Picard rigidifié
$G^{\mathrm {d\acute {e}r}}=G^{\operatorname {sc}}$
, alors le foncteur de Picard rigidifié
est localement libre en les faisceaux inversibles induits par les diviseurs de Richardson
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}, \leq w}^{\geq s}$
, où la longueur de
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}, \leq w}^{\geq s}$
, où la longueur de
![]() $s \leq w$
est égale à
$s \leq w$
est égale à
![]() $1$
.
$1$
.
Démonstration. Remarquant que les quotients locaux de (4.2.33) avec n assez grand définissent des
![]() $1$
-cycles intègres dans des schémas lisses, on arrive aux fibrés en droites
$1$
-cycles intègres dans des schémas lisses, on arrive aux fibrés en droites
![]() $\mathcal {L}_s$
sur
$\mathcal {L}_s$
sur
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
munis d’une section globale invariante par
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
munis d’une section globale invariante par
![]() $L^-\underline {\mathscr {G}_{\mathbf {a}}}$
. D’après le cor. 4.3.9, nous savons que le degré de
$L^-\underline {\mathscr {G}_{\mathbf {a}}}$
. D’après le cor. 4.3.9, nous savons que le degré de
![]() $\mathcal {L}_s$
restreint à la droite projective
$\mathcal {L}_s$
restreint à la droite projective
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}, \leq t}$
est égal à
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}, \leq t}$
est égal à
![]() $1$
ou
$1$
ou
![]() $0$
selon que s et t sont égaux ou différents.
$0$
selon que s et t sont égaux ou différents.
Il reste à vérifier que les degrés d’un fibré
![]() $\mathcal {L}$
sur les droites projectives stables sous
$\mathcal {L}$
sur les droites projectives stables sous
![]() $L^+\underline {\mathscr {G}_{\mathbf {a}}}$
le caractérisent à isomorphisme près. Ceci n’est qu’un exercice en utilisant les résolutions de Demazure, en vertu du th. 4.1.5, cf. [Reference FaltingsFa03, cor. 12] et [Reference MathieuMat88, XII, prop. 6].
$L^+\underline {\mathscr {G}_{\mathbf {a}}}$
le caractérisent à isomorphisme près. Ceci n’est qu’un exercice en utilisant les résolutions de Demazure, en vertu du th. 4.1.5, cf. [Reference FaltingsFa03, cor. 12] et [Reference MathieuMat88, XII, prop. 6].
Typiquement l’opération de
![]() $L^{--}\underline {\mathscr {G}_{\mathbf {a}}}$
sur les fibrés en droites ne s’étend pas au groupe de lacets
$L^{--}\underline {\mathscr {G}_{\mathbf {a}}}$
sur les fibrés en droites ne s’étend pas au groupe de lacets
![]() $L\underline {G}$
, voir le cor. 4.3.11 ci-dessous, mais juste à une extension centrale de ceci par le groupe multiplicatif. En effet, à chaque faisceau inversible
$L\underline {G}$
, voir le cor. 4.3.11 ci-dessous, mais juste à une extension centrale de ceci par le groupe multiplicatif. En effet, à chaque faisceau inversible
![]() $\mathcal {L}$
sur la grassmannienne affine
$\mathcal {L}$
sur la grassmannienne affine
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
, on lui associe le foncteur
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
, on lui associe le foncteur
qui paramétrise les éléments
![]() $g \in L\underline {G}(R)$
joints aux isomorphismes
$g \in L\underline {G}(R)$
joints aux isomorphismes
![]() $g^*\mathcal {L}\xrightarrow {\alpha }\mathcal {L}$
. Il s’ensuit aisément du th. 4.1.5 que, si
$g^*\mathcal {L}\xrightarrow {\alpha }\mathcal {L}$
. Il s’ensuit aisément du th. 4.1.5 que, si
![]() $G=G^{\operatorname {sc}}$
est simplement connexe, alors le foncteur
$G=G^{\operatorname {sc}}$
est simplement connexe, alors le foncteur
![]() $\widehat {L\underline {G}}\{\mathcal {L}\}$
est un
$\widehat {L\underline {G}}\{\mathcal {L}\}$
est un
![]() $\mathbb {Z}$
-ind-groupe extension centrale de
$\mathbb {Z}$
-ind-groupe extension centrale de
![]() $L\underline {G}$
par
$L\underline {G}$
par
![]() $\mathbb {G}_{m,\mathbb {Z}}$
.
$\mathbb {G}_{m,\mathbb {Z}}$
.
Corollaire 4.3.11. Si
![]() $G=G^{\operatorname {sc}}$
est presque simple, alors la correspondance
$G=G^{\operatorname {sc}}$
est presque simple, alors la correspondance
induite par (4.3.29) définit un homomorphisme
dont l’image est libre de rang
![]() $1$
.
$1$
.
Démonstration. Que l’extension centrale (4.3.29) soit scindée revient au même que dire que le faisceau inversible
![]() $\mathcal {L}$
admette une structure
$\mathcal {L}$
admette une structure
![]() $L\underline {G}$
-équivariante. Compte tenu de ce que le groupe des caractères de
$L\underline {G}$
-équivariante. Compte tenu de ce que le groupe des caractères de
![]() $L\underline {G}$
est trivial, puisque ce dernier est schématiquement engendré par
$L\underline {G}$
est trivial, puisque ce dernier est schématiquement engendré par
![]() $L\underline {U_\pm }$
, comp. avec la preuve de prop. 4.2.13, on voit que la structure équivariante est uniquement déterminée, lorsqu’elle existe, c’est-à-dire l’application
$L\underline {U_\pm }$
, comp. avec la preuve de prop. 4.2.13, on voit que la structure équivariante est uniquement déterminée, lorsqu’elle existe, c’est-à-dire l’application
est injective dont l’image s’identifie au noyau de l’homomorphisme (4.3.31). Le raisonnement ci-dessus montre aussi que
![]() $c_{\mathbf {f}}$
commute aux changements de facettes.
$c_{\mathbf {f}}$
commute aux changements de facettes.
Comme l’origine est stable par
![]() $L^+\underline {\mathscr {G}_{\mathbf {f}}}$
, une telle structure équivariante donne un caractère entier
$L^+\underline {\mathscr {G}_{\mathbf {f}}}$
, une telle structure équivariante donne un caractère entier
du groupe d’arcs par restriction à la fibre de
![]() $\mathcal {L}$
. Réciproquement, un
$\mathcal {L}$
. Réciproquement, un
![]() $\mathbb {Z}$
-caractère
$\mathbb {Z}$
-caractère
![]() $\chi $
de
$\chi $
de
![]() $\underline {M_{\mathbf {f}}}$
fournit par inflation à
$\underline {M_{\mathbf {f}}}$
fournit par inflation à
![]() $L^+\underline {\mathscr {G}_{\mathbf {f}}}$
et puis par induction à
$L^+\underline {\mathscr {G}_{\mathbf {f}}}$
et puis par induction à
![]() $L\underline {G}$
un faisceau inversible
$L\underline {G}$
un faisceau inversible
sur la grassmannienne affine muni d’une opération compatible par le groupe de lacets
![]() $L\underline {G}$
, cf. [Reference IversenIv76, prop. 1.5]. En particulier, il en résulte que le groupe de Picard équivariant
$L\underline {G}$
, cf. [Reference IversenIv76, prop. 1.5]. En particulier, il en résulte que le groupe de Picard équivariant
s’identifie au groupe de caractères du groupe épinglé
![]() $\underline {M_{\mathbf {f}}}$
, dont le rang coïncide avec la dimension de
$\underline {M_{\mathbf {f}}}$
, dont le rang coïncide avec la dimension de
![]() $\mathbf {f}$
, tandis que le rang de
$\mathbf {f}$
, tandis que le rang de
![]() $\operatorname {Pic}(\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}})$
est strictement supérieur par une unité, cf. cor. 4.3.10.
$\operatorname {Pic}(\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}})$
est strictement supérieur par une unité, cf. cor. 4.3.10.
Pour voir que l’image de
![]() $c_{\mathbf {f}}$
est libre, on peut supposer que
$c_{\mathbf {f}}$
est libre, on peut supposer que
![]() $\mathbf {f}=\mathbf {a}$
est une alcôve. Appliquant encore la même identification (4.3.35) pour calculer le groupe de Picard des droites de Schubert, on remarque alors sans peine que (4.3.32) s’écrit au signe près comme
$\mathbf {f}=\mathbf {a}$
est une alcôve. Appliquant encore la même identification (4.3.35) pour calculer le groupe de Picard des droites de Schubert, on remarque alors sans peine que (4.3.32) s’écrit au signe près comme
où
![]() $a_s \in \Phi _{\mathbf {f}_s}$
en est la seule racine positive. On laisse le soin au lecteur de montrer que le membre de gauche se projette isomorphiquement sur le quotient du membre de droite obtenu en oubliant le faisceau inversible
$a_s \in \Phi _{\mathbf {f}_s}$
en est la seule racine positive. On laisse le soin au lecteur de montrer que le membre de gauche se projette isomorphiquement sur le quotient du membre de droite obtenu en oubliant le faisceau inversible
![]() $\mathcal {L}_s$
correspondant à la réflexion simple s ne fixant pas un point spécial x adhérente à
$\mathcal {L}_s$
correspondant à la réflexion simple s ne fixant pas un point spécial x adhérente à
![]() $\mathbf {a}$
, dont le système de racines résiduel
$\mathbf {a}$
, dont le système de racines résiduel
![]() $\Phi _x=\Phi _G^{\operatorname {nm}}$
ne contienne que les racines non multipliables.
$\Phi _x=\Phi _G^{\operatorname {nm}}$
ne contienne que les racines non multipliables.
Désormais, pour abréger, on note c le seul épimorphisme
pour l’alcôve donnée
![]() $\mathbf {a}$
, dont le noyau coïncide avec le sous-groupe des faisceaux inversibles qui admettent une structure
$\mathbf {a}$
, dont le noyau coïncide avec le sous-groupe des faisceaux inversibles qui admettent une structure
![]() $L\underline {G}$
-équivariante, cf. (4.3.32) et tel que les faisceaux en droites semi-amples soient appliqués sur
$L\underline {G}$
-équivariante, cf. (4.3.32) et tel que les faisceaux en droites semi-amples soient appliqués sur
![]() $\mathbb {Z}_{\geq 0}$
. L’entier
$\mathbb {Z}_{\geq 0}$
. L’entier
![]() $c(\mathcal {L})$
s’appelle la charge centrale de
$c(\mathcal {L})$
s’appelle la charge centrale de
![]() $\mathcal {L}$
et l’extension centrale
$\mathcal {L}$
et l’extension centrale
![]() $\widehat {L\underline {G}}$
de 4.3.29 obtenu en prenant
$\widehat {L\underline {G}}$
de 4.3.29 obtenu en prenant
![]() $\mathcal {L}$
tel que
$\mathcal {L}$
tel que
![]() $c(\mathcal {L})=1$
s’appelle l’extension centrale universelle de
$c(\mathcal {L})=1$
s’appelle l’extension centrale universelle de
![]() $L\underline {G}$
.
$L\underline {G}$
.
5 Déformation globale sur la droite affine cyclotomique
La partie présente est consacrée à l’étude des déformations à la Beilinson–Drinfeld des grassmanniennes affines associées aux groupes parahoriques
![]() $\underline {\mathscr {G}_{\mathbf {f}}}$
sur la droite affine à coefficients cyclotomiques entiers, cf. prop. 3.4.5. On démontre notamment leur projectivité et aussi un théorème de cohérence à la Zhu, cf. [Reference ZhuZh14, ths. 2, 3] à coefficients cyclotomiques entiers. Ceci sera appliqué dans un travail futur pour répondre à la conjecture de Scholze–Weinstein sur les modèles locaux, cf. [Reference Scholze and WeinsteinSW20, conj. 21.4.1], dans des cas non modérément ramifiés, voir aussi [Reference Pereira LourençoPL20, IV, §4.2].
$\underline {\mathscr {G}_{\mathbf {f}}}$
sur la droite affine à coefficients cyclotomiques entiers, cf. prop. 3.4.5. On démontre notamment leur projectivité et aussi un théorème de cohérence à la Zhu, cf. [Reference ZhuZh14, ths. 2, 3] à coefficients cyclotomiques entiers. Ceci sera appliqué dans un travail futur pour répondre à la conjecture de Scholze–Weinstein sur les modèles locaux, cf. [Reference Scholze and WeinsteinSW20, conj. 21.4.1], dans des cas non modérément ramifiés, voir aussi [Reference Pereira LourençoPL20, IV, §4.2].
5.1 Projectivité et le lieu admissible
La grassmannienne affine qui fut étudiée au §4 était de nature locale, en ce qui concerne sa dépendance de la donnée d’une uniformisante, cf. déf. 4.1.1. Si nous voulons la déformer en un équivalent global, il faut faire varier l’uniformisante, et l’on arrive à la définition suivante due à Beilinson–Drinfeld, cf. [Reference Beilinson and DrinfeldBD96, 4.3.14] :
Définition 5.1.1. Soient A un anneau, X une courbe lisse au-dessus de A et
![]() $\mathrm {G}$
un schéma en groupes sur X. La grassmannienne affine globale
$\mathrm {G}$
un schéma en groupes sur X. La grassmannienne affine globale
![]() $\operatorname {GR}_{\mathrm {G}}$
associée à cette donnée est le pré-faisceau sur X qui, à chaque application
$\operatorname {GR}_{\mathrm {G}}$
associée à cette donnée est le pré-faisceau sur X qui, à chaque application
![]() $Y\rightarrow X$
quasi-compacte de A-schémas, lui associe les classes d’isomorphisme de
$Y\rightarrow X$
quasi-compacte de A-schémas, lui associe les classes d’isomorphisme de
![]() $\mathrm {G}$
-torseurs au-dessus de
$\mathrm {G}$
-torseurs au-dessus de
![]() $X\otimes _A Y$
munis d’une trivialisation en dehors du graphe
$X\otimes _A Y$
munis d’une trivialisation en dehors du graphe
![]() $\Gamma _{Y/X}$
de
$\Gamma _{Y/X}$
de
![]() $Y\rightarrow X$
.
$Y\rightarrow X$
.
On dispose aussi pour ces objets globaux des groupes d’arcs et de lacets
où
![]() $D_{R/X}$
désigne le séparé complété de la R-courbe
$D_{R/X}$
désigne le séparé complété de la R-courbe
![]() $R\otimes _A X$
le long du graphe
$R\otimes _A X$
le long du graphe
![]() $\Gamma _{R/X}$
, dont le quotient pour la topologie étale s’identifie à
$\Gamma _{R/X}$
, dont le quotient pour la topologie étale s’identifie à
![]() $\operatorname {GR}_{\mathrm {G}}$
, cf. [Reference RicharzRi16, lem. 1.12]. Le produit fibré de
$\operatorname {GR}_{\mathrm {G}}$
, cf. [Reference RicharzRi16, lem. 1.12]. Le produit fibré de
![]() $\operatorname {GR}_{\mathrm {G}}$
avec une section
$\operatorname {GR}_{\mathrm {G}}$
avec une section
![]() $x:\operatorname {Spec} A \rightarrow X$
devient ainsi isomorphe, d’après la descente de Beauville–Laszlo, à la grassmannienne affine locale
$x:\operatorname {Spec} A \rightarrow X$
devient ainsi isomorphe, d’après la descente de Beauville–Laszlo, à la grassmannienne affine locale
![]() $\operatorname {Gr}_{\mathrm {G}_{X,x}}$
associée au
$\operatorname {Gr}_{\mathrm {G}_{X,x}}$
associée au
![]() $A [\hspace {-0,5mm}[ {z_x} ]\hspace {-0,5mm}] $
-groupe
$A [\hspace {-0,5mm}[ {z_x} ]\hspace {-0,5mm}] $
-groupe
![]() $\mathrm {G}_{X,x}$
déduit de
$\mathrm {G}_{X,x}$
déduit de
![]() $\mathrm {G}$
par changement de base, où
$\mathrm {G}$
par changement de base, où
![]() $A [\hspace {-0,5mm}[ {z_x} ]\hspace {-0,5mm}] $
est le voisinage formel de X en la section x. Nous avertissons le lecteur que, si l’on applique cette identification pour étudier les fibres géométriques de
$A [\hspace {-0,5mm}[ {z_x} ]\hspace {-0,5mm}] $
est le voisinage formel de X en la section x. Nous avertissons le lecteur que, si l’on applique cette identification pour étudier les fibres géométriques de
![]() $\operatorname {GR}_{\mathrm {G}}$
sur les points génériques d’une fibre
$\operatorname {GR}_{\mathrm {G}}$
sur les points génériques d’une fibre
![]() $X_k$
de
$X_k$
de
![]() $X\rightarrow \operatorname {Spec} A$
, alors il pourrait être compliqué de saisir correctement le séparé complété l’uniformisante
$X\rightarrow \operatorname {Spec} A$
, alors il pourrait être compliqué de saisir correctement le séparé complété l’uniformisante
![]() $z_x$
résultante et que ceci a déjà provoqué d’ailleurs quelques maladresses dans la littérature, cf. [Reference RicharzRi19b].
$z_x$
résultante et que ceci a déjà provoqué d’ailleurs quelques maladresses dans la littérature, cf. [Reference RicharzRi19b].
Proposition 5.1.2 (Pappas–Zhu).
Soient A un anneau de Dedekind, X une A-courbe lisse et géométriquement connexe et
![]() $\operatorname {G}$
un X-groupe lisse, affine et connexe. Alors, la grassmannienne affine globale
$\operatorname {G}$
un X-groupe lisse, affine et connexe. Alors, la grassmannienne affine globale
![]() $\operatorname {GR}_{\operatorname {G}}$
est représentable par un ind-schéma séparé de type fini.
$\operatorname {GR}_{\operatorname {G}}$
est représentable par un ind-schéma séparé de type fini.
Démonstration. L’assertion se démontre par la même procédure de la prop. 4.1.2.
On veut analyser les grassmanniennes affine globales de nos modèles parahoriques
![]() $\underline {\mathscr {G}_{\mathbf {f}}}$
des groupes de Tits
$\underline {\mathscr {G}_{\mathbf {f}}}$
des groupes de Tits
![]() $\underline {G}$
sur la droite affine
$\underline {G}$
sur la droite affine
![]() $\mathbb {A}^1_{\mathbb {Z}}$
.
$\mathbb {A}^1_{\mathbb {Z}}$
.
Théorème 5.1.3 (Pappas–Zhu, L.).
La grassmannienne affine globale
![]() $\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
est projective.
$\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
est projective.
Vérifions tout d’abord que les fibres se comportent comme envisagéFootnote 7.
Lemme 5.1.4. Les fibres géométriques de
![]() $\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
sont projectives.
$\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
sont projectives.
Démonstration. On n’a besoin que de comprendre les fibres géométriques sur les points fermés du schéma de Jacobson
![]() $\mathbb {A}^1_{\mathbb {Z}}$
, parce que la partie des fibres propres est constructible. Mais alors le lemme résulte de ce que
$\mathbb {A}^1_{\mathbb {Z}}$
, parce que la partie des fibres propres est constructible. Mais alors le lemme résulte de ce que
![]() $\underline {\mathscr {G}_{\mathbf {f}}}\otimes \mathbb {F}^{\operatorname {alg}}_p [\hspace {-0,5mm}[ {u} ]\hspace {-0,5mm}] $
soit parahorique, où
$\underline {\mathscr {G}_{\mathbf {f}}}\otimes \mathbb {F}^{\operatorname {alg}}_p [\hspace {-0,5mm}[ {u} ]\hspace {-0,5mm}] $
soit parahorique, où
![]() $u=t-a$
et
$u=t-a$
et
![]() $a \in \mathbb {F}^{\operatorname {alg}}_p$
, cf. prop. 3.4.5 et rem. 3.4.2. Voir aussi [Reference Pappas and ZhuPZ13, prop. 6.4].
$a \in \mathbb {F}^{\operatorname {alg}}_p$
, cf. prop. 3.4.5 et rem. 3.4.2. Voir aussi [Reference Pappas and ZhuPZ13, prop. 6.4].
L’étape suivante tourne autour des tores induits.
Lemme 5.1.5.
![]() $\operatorname {GR}_{\underline {\mathscr {T}}}$
est une réunion disjointe dénombrable de schémas finis.
$\operatorname {GR}_{\underline {\mathscr {T}}}$
est une réunion disjointe dénombrable de schémas finis.
Démonstration. Cela résulte presque directement de [Reference Haines and RicharzHR20, lem. 3.8, §4.4.2]. Dans une première version de l’article, nous avons suivi plutôt les démonstrations de [Reference ZhuZh14, prop. 3.4] et [Reference LevinLev16, prop. 4.2.8], en construisant des sections explicites.
La fibre géométrique générique de
![]() $\operatorname {GR}_{\underline {\mathscr {T}}}$
en caractéristique nulle est isomorphe à la grassmannienne affine locale constante
$\operatorname {GR}_{\underline {\mathscr {T}}}$
en caractéristique nulle est isomorphe à la grassmannienne affine locale constante
![]() $\operatorname {Gr}_{T_H}$
, donc numérotée par le groupe des cocaractères géométriques
$\operatorname {Gr}_{T_H}$
, donc numérotée par le groupe des cocaractères géométriques
![]() $X_*(T_H)$
du tore T, comp. avec [Reference Pappas and ZhuPZ13, prop. 6.5]. Le point associé au copoids
$X_*(T_H)$
du tore T, comp. avec [Reference Pappas and ZhuPZ13, prop. 6.5]. Le point associé au copoids
![]() $\mu \in X_*(T_H)$
s’étend uniquement par le lemme précédent en un point
$\mu \in X_*(T_H)$
s’étend uniquement par le lemme précédent en un point
de la grassmannienne affine globale à valeurs dans le spectre de
![]() $\mathbb {Z}[\zeta _\infty ,t^{1/\infty }]$
. Les spécialisés de
$\mathbb {Z}[\zeta _\infty ,t^{1/\infty }]$
. Les spécialisés de
![]() $z^\mu $
aux corps k le long de
$z^\mu $
aux corps k le long de
![]() $x: \operatorname {Spec} k \rightarrow \mathbb {A}^{1/\infty }$
sont des translations dans le groupe d’Iwahori–Weyl de
$x: \operatorname {Spec} k \rightarrow \mathbb {A}^{1/\infty }$
sont des translations dans le groupe d’Iwahori–Weyl de
![]() $\underline {\mathscr {T}}\otimes k (\hspace {-0,7mm}( {z_{x}} )\hspace {-0,7mm}) $
, où
$\underline {\mathscr {T}}\otimes k (\hspace {-0,7mm}( {z_{x}} )\hspace {-0,7mm}) $
, où
![]() $z_{x}$
désigne une uniformisante associée à ce point géométrique. Habituellement, ceux-ci sont interprétés en termes de l’application de Kottwitz, mais celle-ci n’est malheureusement pas disponible dans notre cadre.
$z_{x}$
désigne une uniformisante associée à ce point géométrique. Habituellement, ceux-ci sont interprétés en termes de l’application de Kottwitz, mais celle-ci n’est malheureusement pas disponible dans notre cadre.
Définition 5.1.6. Soit
![]() $\mu \in X_*(T_H)_+$
un cocaractère géométrique dominant de T. Le schéma de Schubert global, noté
$\mu \in X_*(T_H)_+$
un cocaractère géométrique dominant de T. Le schéma de Schubert global, noté
![]() $\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}}, \leq \mu }$
, est l’image schématique du morphisme orbite
$\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}}, \leq \mu }$
, est l’image schématique du morphisme orbite
défini au-dessus de
![]() $\mathbb {A}^{1/\infty }$
.
$\mathbb {A}^{1/\infty }$
.
Disons un mot sur quelques fait élémentaires concernant ce schéma de Schubert global. Il est sans torsion, stable sous
![]() $L^+\underline {\mathscr {G}_{\mathbf {f}}}$
et projectif, grâce à la preuve de [Reference Pappas and ZhuPZ13, prop. 6.5]. Néanmoins, on ne sait pas pour l’instant s’il est plat, voir cependant le th. 5.2.2.
$L^+\underline {\mathscr {G}_{\mathbf {f}}}$
et projectif, grâce à la preuve de [Reference Pappas and ZhuPZ13, prop. 6.5]. Néanmoins, on ne sait pas pour l’instant s’il est plat, voir cependant le th. 5.2.2.
Quoiqu’il en soit, les réduits des fibres géométriques de
![]() $\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}}, \leq \{\mu \}}$
sont isomorphes à la réunion de certaines variétés de Schubert de la grassmannienne affine locale
$\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}}, \leq \{\mu \}}$
sont isomorphes à la réunion de certaines variétés de Schubert de la grassmannienne affine locale
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}\otimes k [\hspace {-0,5mm}[ {z_x} ]\hspace {-0,5mm}] }$
correspondante. Ceci nous amène à la définition du lieu admissible :
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}\otimes k [\hspace {-0,5mm}[ {z_x} ]\hspace {-0,5mm}] }$
correspondante. Ceci nous amène à la définition du lieu admissible :
 $$ \begin{align}\operatorname{Adm}_{\underline{\mathscr{G}_{\mathbf{f}}}\otimes k [\hspace{-0,5mm}[ {z_x} ]\hspace{-0,5mm}] ,\leq \mu}:= \bigcup_{\lambda\in W_G\cdot \mu} \operatorname{Gr}_{\underline{\mathscr{G}_{\mathbf{f}}}\otimes k [\hspace{-0,5mm}[ {z_x} ]\hspace{-0,5mm}] , \leq z^{\lambda}},\end{align} $$
$$ \begin{align}\operatorname{Adm}_{\underline{\mathscr{G}_{\mathbf{f}}}\otimes k [\hspace{-0,5mm}[ {z_x} ]\hspace{-0,5mm}] ,\leq \mu}:= \bigcup_{\lambda\in W_G\cdot \mu} \operatorname{Gr}_{\underline{\mathscr{G}_{\mathbf{f}}}\otimes k [\hspace{-0,5mm}[ {z_x} ]\hspace{-0,5mm}] , \leq z^{\lambda}},\end{align} $$
où l’on note
![]() $W_G$
le groupe de Weyl du système de racines relatif
$W_G$
le groupe de Weyl du système de racines relatif
![]() $\Phi _G$
, lequel est évidemment contenu dans la fibre
$\Phi _G$
, lequel est évidemment contenu dans la fibre
On verra ci-dessous que ces deux sous-schémas fermés coïncident dès que le dérivé de G est simplement connexe.
Démonstration du th. 5.1.3. La représentabilité par un ind-schéma quasi-projectif fut déjà remarquée dans la prop. 5.1.2 et il suffit de montrer l’ind-propreté de
![]() $\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
. Leurs fibres géométriques sont projectives d’après le lem. 5.1.4. Nous avons déjà remarqué que les schémas de Schubert globales sont projectifs, en répétant la preuve de [Reference Pappas and ZhuPZ13, prop. 6.5].
$\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
. Leurs fibres géométriques sont projectives d’après le lem. 5.1.4. Nous avons déjà remarqué que les schémas de Schubert globales sont projectifs, en répétant la preuve de [Reference Pappas and ZhuPZ13, prop. 6.5].
Par suite, il reste à prouver que tout point de
![]() $\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
en est contenu dans la colimite de ses sous-schémas de Schubert. Mais la fibre géométrique de celle-ci sur
$\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
en est contenu dans la colimite de ses sous-schémas de Schubert. Mais la fibre géométrique de celle-ci sur
![]() $\overline {x}$
contienne dedans toutes les variétés de Schubert de
$\overline {x}$
contienne dedans toutes les variétés de Schubert de
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}\otimes k [\hspace {-0,5mm}[ {z_{\overline {x}}} ]\hspace {-0,5mm}] }$
associées aux translations du groupe d’Iwahori–Weyl, recouvrant totalement l’espace topologique de cette grassmannienne affine locale.
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}\otimes k [\hspace {-0,5mm}[ {z_{\overline {x}}} ]\hspace {-0,5mm}] }$
associées aux translations du groupe d’Iwahori–Weyl, recouvrant totalement l’espace topologique de cette grassmannienne affine locale.
5.2 Le théorème de la cohérence
Enfin, on étudie la géométrie du schéma de Schubert global
![]() $\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq \mu }$
dans le cas où le dérivé
$\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq \mu }$
dans le cas où le dérivé
![]() $G^{\mathrm {d\acute {e}r}}=G^{\operatorname {sc}}$
est simplement connexe. Pour formuler le th. 5.2.2 ci-dessous, on a besoin de montrer d’abord sa variante cohomologique due à Pappas–Rapoport, cf. [Reference Pappas and RapoportPR08, conj. 10.5], et améliorée par Zhu, cf. [Reference ZhuZh14, th. 2].
$G^{\mathrm {d\acute {e}r}}=G^{\operatorname {sc}}$
est simplement connexe. Pour formuler le th. 5.2.2 ci-dessous, on a besoin de montrer d’abord sa variante cohomologique due à Pappas–Rapoport, cf. [Reference Pappas and RapoportPR08, conj. 10.5], et améliorée par Zhu, cf. [Reference ZhuZh14, th. 2].
Théorème 5.2.1 (Zhu).
Soit
![]() $\mathcal {L}$
un faisceau inversible ample sur
$\mathcal {L}$
un faisceau inversible ample sur
![]() $\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}}}^{\mathrm {r\acute {e}d}}$
et supposons que
$\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}}}^{\mathrm {r\acute {e}d}}$
et supposons que
![]() $G^{\mathrm {d\acute {e}r}}=G^{\operatorname {sc}}$
. Étant donné
$G^{\mathrm {d\acute {e}r}}=G^{\operatorname {sc}}$
. Étant donné
![]() $\mu \in X_*(T_H)$
, alors l’entier positif
$\mu \in X_*(T_H)$
, alors l’entier positif
ne dépend pas du choix de x.
Démonstration. Le premier truc que nous devons établir est que, pour un faisceau ample inversible sur la grassmannienne globale
![]() $\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq \mu }$
, alors la charge centrale de la restriction de
$\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq \mu }$
, alors la charge centrale de la restriction de
![]() $\mathcal {L}$
à
$\mathcal {L}$
à
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}\otimes k [\hspace {-0,5mm}[ {z_x} ]\hspace {-0,5mm}] }$
définie à (4.3.37) est un invariant de
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}\otimes k [\hspace {-0,5mm}[ {z_x} ]\hspace {-0,5mm}] }$
définie à (4.3.37) est un invariant de
![]() $\mathcal {L}$
qui ne dépend pas du point x. On remarque que, lorsque le groupe d’Iwahori-Weyl
$\mathcal {L}$
qui ne dépend pas du point x. On remarque que, lorsque le groupe d’Iwahori-Weyl
![]() $\widetilde {W}$
de
$\widetilde {W}$
de
![]() $\underline {\mathscr {G}_{\mathbf {f}}}\otimes k (\hspace {-0,7mm}( {z_x} )\hspace {-0,7mm}) $
n’est pas irréductible, la charge centrale doit plutôt s’entendre comme un n-uplet d’entiers, chacun d’eux associé à une composante irréductible du groupe d’Iwahori-Weyl; que la charge centrale soit constante doit être entendu au sens des morphismes de spécialisation de la grassmannienne affine globale.
$\underline {\mathscr {G}_{\mathbf {f}}}\otimes k (\hspace {-0,7mm}( {z_x} )\hspace {-0,7mm}) $
n’est pas irréductible, la charge centrale doit plutôt s’entendre comme un n-uplet d’entiers, chacun d’eux associé à une composante irréductible du groupe d’Iwahori-Weyl; que la charge centrale soit constante doit être entendu au sens des morphismes de spécialisation de la grassmannienne affine globale.
Ceci se trouve dans [Reference ZhuZh14, prop. 4.1] à coefficients dans k pour les groupes modérément ramifiés, mais nous allons donner une preuve explicite dans le cas où la grassmannienne affine est associée à un groupe pseudo-réductif exotique et barcelonais. Autrement dit, nous supposons que
![]() $\Phi _G$
est irréductible et que
$\Phi _G$
est irréductible et que
![]() $p=e=2,3$
. Or, selon les ex. 3.1.6 et 3.1.7, nous disposons d’une application canonique
$p=e=2,3$
. Or, selon les ex. 3.1.6 et 3.1.7, nous disposons d’une application canonique
où
![]() $\overline {G}$
est la restriction des scalaires purement inséparable d’un
$\overline {G}$
est la restriction des scalaires purement inséparable d’un
![]() $\mathbb {F}_e$
-groupe déployé simplement connexe, tel que l’on ait des bijections d’immeubles
$\mathbb {F}_e$
-groupe déployé simplement connexe, tel que l’on ait des bijections d’immeubles
de points entiers et rationnels
induisant un homéomorphisme universel
cf. [Reference LourençoLou21, prop. 3.6]. Les morphismes induits
![]() $\mathbb {P}^1_s \rightarrow \mathbb {P}^1_s$
entre les droites de Schubert ont degrés soit
$\mathbb {P}^1_s \rightarrow \mathbb {P}^1_s$
entre les droites de Schubert ont degrés soit
![]() $1$
, soit e, bien déterminés par la combinatoire. Pour que la charge centrale soit constante, il faut alors balancer cet effet de sorte que les raisons
$1$
, soit e, bien déterminés par la combinatoire. Pour que la charge centrale soit constante, il faut alors balancer cet effet de sorte que les raisons
![]() $a_s^{\vee }/\overline {a}^\vee _s$
des coefficients de Kac–Moody, c’est-à-dire la valeur
$a_s^{\vee }/\overline {a}^\vee _s$
des coefficients de Kac–Moody, c’est-à-dire la valeur
![]() $c(\mathcal {L}_s)$
de la charge centrale c dans
$c(\mathcal {L}_s)$
de la charge centrale c dans
![]() $\mathcal {L}_s$
, cf. cor. 4.3.11, associés à l’un et l’autre groupe soient égaux à e ou à
$\mathcal {L}_s$
, cf. cor. 4.3.11, associés à l’un et l’autre groupe soient égaux à e ou à
![]() $1$
, selon les degrés ci-dessus soient égaux à
$1$
, selon les degrés ci-dessus soient égaux à
![]() $1$
ou e. La relation prévue entre les coefficients peut être facilement vérifiée aux tableaux de [Reference CarterCa05, annexe]. Ici on utilise alors la comparaison du §6, cf. (6.2.6).
$1$
ou e. La relation prévue entre les coefficients peut être facilement vérifiée aux tableaux de [Reference CarterCa05, annexe]. Ici on utilise alors la comparaison du §6, cf. (6.2.6).
Finalement, nous voulons montrer des égalités
 $$ \begin{align}\dim_{\mathbb{F}_p}H^0\left(\bigcup_{i=1}^{n}\operatorname{Gr}_{\mathscr{G}_{\mathbf{f},p},\leq w_i},\mathcal{L}\right)=\dim_{\mathbb{F}_l}H^0\left(\bigcup_{i=1}^{n}\operatorname{Gr}_{\mathscr{G}_{\mathbf{f},l},\leq w_i},\mathcal{L}\right),\end{align} $$
$$ \begin{align}\dim_{\mathbb{F}_p}H^0\left(\bigcup_{i=1}^{n}\operatorname{Gr}_{\mathscr{G}_{\mathbf{f},p},\leq w_i},\mathcal{L}\right)=\dim_{\mathbb{F}_l}H^0\left(\bigcup_{i=1}^{n}\operatorname{Gr}_{\mathscr{G}_{\mathbf{f},l},\leq w_i},\mathcal{L}\right),\end{align} $$
où
![]() $w_i \in \widetilde {W}/W_{\mathbf {f}}$
sont des éléments quelconques,
$w_i \in \widetilde {W}/W_{\mathbf {f}}$
sont des éléments quelconques,
![]() $p,l \in \mathbb {P} \cup \{0\}$
sont des caractéristiques des corps premiers et
$p,l \in \mathbb {P} \cup \{0\}$
sont des caractéristiques des corps premiers et
![]() $\mathcal {L}$
est un faisceau inversible très ample sur
$\mathcal {L}$
est un faisceau inversible très ample sur
![]() $\operatorname {Gr}_{\mathscr {G}_{\mathbf {f}}}$
, cf. [Reference ZhuZh14, cor. 4.4]. Cela revient au même que savoir que la formation des réunions des schémas de Schubert commute aux changements de base quelconques. Nous observons d’abord que, grâce à un argument avec une suite exacte du type Mayer–Vietoris, on a une formule
$\operatorname {Gr}_{\mathscr {G}_{\mathbf {f}}}$
, cf. [Reference ZhuZh14, cor. 4.4]. Cela revient au même que savoir que la formation des réunions des schémas de Schubert commute aux changements de base quelconques. Nous observons d’abord que, grâce à un argument avec une suite exacte du type Mayer–Vietoris, on a une formule
 $$ \begin{align}\dim_{\mathbb{F}_p}H^0\left(\bigcup_{i=1}^{n}\operatorname{Gr}_{\mathscr{G}_{\mathbf{f},p},\leq w_i},\mathcal{L}\right)= \sum_{J \subseteq I} (-1)^{j-1} \dim_{\mathbb{F}_p} H^0\left(\bigcap_{j\in J}\operatorname{Gr}_{\mathscr{G}_{\mathbf{f},p},\leq w_j},\mathcal{L}\right)\end{align} $$
$$ \begin{align}\dim_{\mathbb{F}_p}H^0\left(\bigcup_{i=1}^{n}\operatorname{Gr}_{\mathscr{G}_{\mathbf{f},p},\leq w_i},\mathcal{L}\right)= \sum_{J \subseteq I} (-1)^{j-1} \dim_{\mathbb{F}_p} H^0\left(\bigcap_{j\in J}\operatorname{Gr}_{\mathscr{G}_{\mathbf{f},p},\leq w_j},\mathcal{L}\right)\end{align} $$
de type inclusion-exclusion, puisque les groupes de cohomologie supérieurs s’annulent. Comme les intersections des variétés de Schubert sont réduites sont réduites, puisque scindées dès que
![]() $p>0$
, cf. prop. 4.3.1, elles coïncident avec la réunion
$p>0$
, cf. prop. 4.3.1, elles coïncident avec la réunion
 $$ \begin{align} \bigcap_{j\in J}\operatorname{Gr}_{\mathscr{G}_{\mathbf{f}},p,\leq w_j}= \bigcup_{k \in K} \operatorname{Gr}_{\mathscr{G}_{\mathbf{f}},p,\leq v_k}\end{align} $$
$$ \begin{align} \bigcap_{j\in J}\operatorname{Gr}_{\mathscr{G}_{\mathbf{f}},p,\leq w_j}= \bigcup_{k \in K} \operatorname{Gr}_{\mathscr{G}_{\mathbf{f}},p,\leq v_k}\end{align} $$
des variétés de Schubert contenues là, où l’ensemble des
![]() $v_k$
ne dépend pas de la caractéristique p, voir [Reference RicharzRi13, prop. 2.8]. En particulier, on se ramène par récurrence décroissante au cas où
$v_k$
ne dépend pas de la caractéristique p, voir [Reference RicharzRi13, prop. 2.8]. En particulier, on se ramène par récurrence décroissante au cas où
![]() $\lvert I \rvert =1$
, lequel résulte de notre résultat sur les schémas de Schubert, voir th. 4.1.5.
$\lvert I \rvert =1$
, lequel résulte de notre résultat sur les schémas de Schubert, voir th. 4.1.5.
Sur une base unidimensionnelle, le théorème précédent suffit pour démontrer que les schémas de Schubert globaux ont de fibres géométriques réduites, données par les lieux admissibles, cf. [Reference ZhuZh14, th. 3, §4.2] ainsi que [Reference Pappas and ZhuPZ13, th. 9.1]. Dans la présente situation, il va falloir être plus soigneux avec l’argumentation géométrique.
Théorème 5.2.2 (L.).
Si le groupe dérivé
![]() $G^{\mathrm {d\acute {e}r}}=G^{\operatorname {sc}}$
est simplement connexe, alors le schéma de Schubert global
$G^{\mathrm {d\acute {e}r}}=G^{\operatorname {sc}}$
est simplement connexe, alors le schéma de Schubert global
![]() $\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq \mu }$
est normal, plat, géométriquement réduit et connexe, à fibres égales à
$\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq \mu }$
est normal, plat, géométriquement réduit et connexe, à fibres égales à
![]() $\operatorname {Adm}_{\underline {\mathscr {G}_{\mathbf {f}}}\otimes k [\hspace {-0,5mm}[ {z_x} ]\hspace {-0,5mm}] ,\leq \mu }$
.
$\operatorname {Adm}_{\underline {\mathscr {G}_{\mathbf {f}}}\otimes k [\hspace {-0,5mm}[ {z_x} ]\hspace {-0,5mm}] ,\leq \mu }$
.
Démonstration. Nous avons déjà vu à (5.1.6) et (5.1.7) que le lieu admissible
se trouve dedans la fibre spéciale du schéma de Schubert en tant que sous-schémas fermés de grassmannienne affine locale
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}\otimes k [\hspace {-0,5mm}[ {z_x} ]\hspace {-0,5mm}] }$
. Afin d’obtenir l’égalité désirée, il faudra calculer les sections globales de fibrés en droites très amples, dont l’outil principal est le th. 5.2.1.
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}\otimes k [\hspace {-0,5mm}[ {z_x} ]\hspace {-0,5mm}] }$
. Afin d’obtenir l’égalité désirée, il faudra calculer les sections globales de fibrés en droites très amples, dont l’outil principal est le th. 5.2.1.
Cependant, cette utilisation aura lieu seulement quand le schéma en question est plat sur la base, pour que la caractéristique d’Euler des fibres soit localement constante. Par suite, le th. 5.2.1 entraîne que l’affirmation du présent énoncé est vraie au-dessus d’un ouvert
![]() $U \subset \mathbb {A}^{1/\infty }$
à complément pro-fini. De plus, en prenant des changements de base aux anneaux de valuation V de rang
$U \subset \mathbb {A}^{1/\infty }$
à complément pro-fini. De plus, en prenant des changements de base aux anneaux de valuation V de rang
![]() $1$
sur le schéma de Schubert global dont le point fermé s’envoie sur un point générique de la fibre sur x, on en déduit que l’espace topologique de
$1$
sur le schéma de Schubert global dont le point fermé s’envoie sur un point générique de la fibre sur x, on en déduit que l’espace topologique de
![]() $\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq \mu }$
est le bon, c’est-à-dire notre assertion sur ses fibres est valable à structures non réduites près. En particulier, le schéma de Schubert global est régulier en codimension
$\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq \mu }$
est le bon, c’est-à-dire notre assertion sur ses fibres est valable à structures non réduites près. En particulier, le schéma de Schubert global est régulier en codimension
![]() $1$
par comparaison de cardinaux.
$1$
par comparaison de cardinaux.
Considérons ainsi le schéma de Schubert global normalisé
![]() $\widetilde {\operatorname {GR}}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq \mu }$
dans son corps des fractions. Celui-ci est plat sur la base grâce au [Reference RaynaudRay70, lem. VII.3.2], voir aussi la prop. 3.2.7, vu que la codimension du lieu plat du schéma de Schubert global est au moins
$\widetilde {\operatorname {GR}}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq \mu }$
dans son corps des fractions. Celui-ci est plat sur la base grâce au [Reference RaynaudRay70, lem. VII.3.2], voir aussi la prop. 3.2.7, vu que la codimension du lieu plat du schéma de Schubert global est au moins
![]() $2$
et que celui-ci est régulier en codimension
$2$
et que celui-ci est régulier en codimension
![]() $1$
. Puis, on affirme que l’application
$1$
. Puis, on affirme que l’application
est une immersion fermée pour tout point x à valeurs dans k. En effet, le
![]() $\mathbb {A}^{1/\infty }_k$
-schéma plat
$\mathbb {A}^{1/\infty }_k$
-schéma plat
déduit par changement de base s’applique isomorphiquement d’après le théorème principal de Zariski sur l’adhérence plate de
car cette dernière est normale, géométriquement réduite et à fibres données par les lieux admissibles, cf. th. 5.2.1. Enfin, le fait que l’application de normalisation
soit un isomorphisme devient une conséquence du lemme de Nakayama, comp. avec la fin de la preuve de [Reference Pappas and ZhuPZ13, prop. 8.1].
Remarque 5.2.3. Pour finir cette section, étendrons-nous un peu sur les schémas déduits du schéma de Schubert global
![]() $\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq \mu }$
par quelques changements de base particuliers. En caractéristiques égales, les objets échéants généralisent à un certain sens les modèles locaux en caractéristiques égales au sens de Zhu, voir [Reference ZhuZh14, déf. 3.1, th. 3], et au sens de Richarz, voir [Reference RicharzRi16, déf. 2.5]. En caractéristique mixte, alors on obtient en même temps les modèles locaux au sens de Pappas–Zhu, voir [Reference Pappas and ZhuPZ13, déf. 7.1, th. 9.1] et de Levin, voir [Reference LevinLev16, déf. 4.2.1, th. 4.3.2], mais aussi quelques-uns nouveaux en des cas sauvagement ramifiés. En guise d’application, nous avons étendu [Reference He, Pappas and RapoportHPR18, th. 2.14, cor. 2.16] concernant la conjecture de Scholze–Weinstein sur les modèles locaux à presque tous les cas de type abélien dans [Reference Pereira LourençoPL20, IV, prop. 4.22, cor. 4.24]. Récemment, on a fait des avances non négligeables sur le cas général de la conjecture, dont on rapportera dans un article futur.
$\operatorname {GR}_{\underline {\mathscr {G}_{\mathbf {f}}},\leq \mu }$
par quelques changements de base particuliers. En caractéristiques égales, les objets échéants généralisent à un certain sens les modèles locaux en caractéristiques égales au sens de Zhu, voir [Reference ZhuZh14, déf. 3.1, th. 3], et au sens de Richarz, voir [Reference RicharzRi16, déf. 2.5]. En caractéristique mixte, alors on obtient en même temps les modèles locaux au sens de Pappas–Zhu, voir [Reference Pappas and ZhuPZ13, déf. 7.1, th. 9.1] et de Levin, voir [Reference LevinLev16, déf. 4.2.1, th. 4.3.2], mais aussi quelques-uns nouveaux en des cas sauvagement ramifiés. En guise d’application, nous avons étendu [Reference He, Pappas and RapoportHPR18, th. 2.14, cor. 2.16] concernant la conjecture de Scholze–Weinstein sur les modèles locaux à presque tous les cas de type abélien dans [Reference Pereira LourençoPL20, IV, prop. 4.22, cor. 4.24]. Récemment, on a fait des avances non négligeables sur le cas général de la conjecture, dont on rapportera dans un article futur.
6 Le lien avec le cadre de Kac–Moody
Nous arrivons maintenant au paragraphe concernant le lien entre les
![]() $\mathbb {Z}[t^{\pm 1}]$
-groupes de Tits
$\mathbb {Z}[t^{\pm 1}]$
-groupes de Tits
![]() $\underline {G}$
de la déf. 3.3.5, ainsi que leurs
$\underline {G}$
de la déf. 3.3.5, ainsi que leurs
![]() $\mathbb {Z}[t]$
-modèles parahoriques
$\mathbb {Z}[t]$
-modèles parahoriques
![]() $\underline {\mathscr {G}_{\mathbf {f}}}$
associés aux facettes
$\underline {\mathscr {G}_{\mathbf {f}}}$
associés aux facettes
![]() $\mathbf {f} \subset \mathscr {A}(\underline {G},\underline {S},\mathbb {Z} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
par la déf. 3.4.6, et les
$\mathbf {f} \subset \mathscr {A}(\underline {G},\underline {S},\mathbb {Z} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
par la déf. 3.4.6, et les
![]() $\mathbb {Z}$
-groupes
$\mathbb {Z}$
-groupes
![]() $\mathcal {G}_{\mathbb {Z}}$
de (6.1.24), ainsi que leurs sous-groupes paraboliques
$\mathcal {G}_{\mathbb {Z}}$
de (6.1.24), ainsi que leurs sous-groupes paraboliques
![]() $\mathcal {P}^{\pm }_{\mathbb {Z}}$
à (6.1.17) et (6.1.26), construits par Mathieu dans le cadre de Kac–Moody affine, voir les cors. 6.2.3 et 6.2.5. Cela résulte également d’un théorème de comparaison entre nos grassmanniennes affines
$\mathcal {P}^{\pm }_{\mathbb {Z}}$
à (6.1.17) et (6.1.26), construits par Mathieu dans le cadre de Kac–Moody affine, voir les cors. 6.2.3 et 6.2.5. Cela résulte également d’un théorème de comparaison entre nos grassmanniennes affines
![]() $\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
et les variétés de drapeaux affines
$\operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
et les variétés de drapeaux affines
![]() $\mathcal {F}_{\mathfrak {g}/\mathfrak {p},\mathbb {Z}}$
de Kac-Moody, cf. th. 6.2.4. À la fin, on pourra regarder les
$\mathcal {F}_{\mathfrak {g}/\mathfrak {p},\mathbb {Z}}$
de Kac-Moody, cf. th. 6.2.4. À la fin, on pourra regarder les
![]() $\underline {\mathscr {G}_{\mathbf {f}}}$
comme des sortes de “délacés” des groupes de Kac–Moody affines à coefficients entiers.
$\underline {\mathscr {G}_{\mathbf {f}}}$
comme des sortes de “délacés” des groupes de Kac–Moody affines à coefficients entiers.
6.1 Les
 $\mathbb {Z}$
-groupes de Kac–Moody et leurs variétés de drapeaux
$\mathbb {Z}$
-groupes de Kac–Moody et leurs variétés de drapeaux
Rappelons les notions basiques sur les algèbres de Kac–Moody et les groupes qui leur sont associés.
On dit qu’une matrice
![]() $A \in M_n(\mathbb {Z})$
carrée d’ordre n à entrées entières est de Cartan généralisée, cf. [Reference MarquisMar18, déf. 3.7], si les conditions suivantes sont remplies :
$A \in M_n(\mathbb {Z})$
carrée d’ordre n à entrées entières est de Cartan généralisée, cf. [Reference MarquisMar18, déf. 3.7], si les conditions suivantes sont remplies :
![]() $a_{ii}=2$
,
$a_{ii}=2$
,
![]() $a_{ij} \in \mathbb {Z}_{\leq 0}$
et
$a_{ij} \in \mathbb {Z}_{\leq 0}$
et
![]() $a_{ij} \neq 0$
si et seulement si
$a_{ij} \neq 0$
si et seulement si
![]() $a_{ji} \neq 0$
. On fixe désormais une matrice de Cartan généralisée A de rang r, supposée d’ailleurs symétrisable.
$a_{ji} \neq 0$
. On fixe désormais une matrice de Cartan généralisée A de rang r, supposée d’ailleurs symétrisable.
La définition suivante est une synthèse de [Reference MarquisMar18, déf. 3.10, déf. 7.9] :
Définition 6.1.1. Une réalisation entière de A est la donnée d’un
![]() $5$
-tuplet
$5$
-tuplet
qui se compose d’un
![]() $\mathbb {Q}$
-espace vectoriel
$\mathbb {Q}$
-espace vectoriel
![]() $\mathfrak {t}$
de dimension
$\mathfrak {t}$
de dimension
![]() $2n-r$
, des
$2n-r$
, des
![]() $\mathbb {Z}$
-réseaux duaux
$\mathbb {Z}$
-réseaux duaux
et des parties libres
à matrice d’accouplement A, c’est-à-dire
![]() $\langle \alpha _i^{\vee }, \alpha _j\rangle =a_{ij}$
, de sorte que, lorsqu’on pose
$\langle \alpha _i^{\vee }, \alpha _j\rangle =a_{ij}$
, de sorte que, lorsqu’on pose
 $$ \begin{align}Q=\bigoplus_{i=1}^n\mathbb{Z} \alpha_i \text{ et }Q^{\vee}=\bigoplus_{i=1}^n \mathbb{Z} \alpha_i^\vee,\end{align} $$
$$ \begin{align}Q=\bigoplus_{i=1}^n\mathbb{Z} \alpha_i \text{ et }Q^{\vee}=\bigoplus_{i=1}^n \mathbb{Z} \alpha_i^\vee,\end{align} $$
alors
![]() $Q \subset P$
,
$Q \subset P$
,
![]() $Q^{\vee } \subset P^\vee $
et
$Q^{\vee } \subset P^\vee $
et
![]() $P^{\vee }/Q^{\vee }$
est sans torsion.
$P^{\vee }/Q^{\vee }$
est sans torsion.
Ces données sont uniquement déterminées par la matrice A à isomorphisme unique près, cf. [Reference MarquisMar18, ex. 3.11, ex. 7.10]. Les algèbres de Kac-Moody sont définies en termes des présentations comme suit, comp. avec [Reference MathieuMat88, ch. I, (I)-(VII)] et [Reference MarquisMar18, déf. 3.17].
Définition 6.1.2. L’algèbre de Kac–Moody
![]() $\mathfrak {g}$
attachée à A est la
$\mathfrak {g}$
attachée à A est la
![]() $\mathbb {Q}$
-algèbre de Lie engendrée par
$\mathbb {Q}$
-algèbre de Lie engendrée par
![]() $\mathfrak {t}$
et par des
$\mathfrak {t}$
et par des
![]() $\mathfrak {t}$
-vecteurs propres
$\mathfrak {t}$
-vecteurs propres
![]() $e_i$
et
$e_i$
et
![]() $f_i$
à valeurs propres
$f_i$
à valeurs propres
![]() $\pm \alpha _i$
, où
$\pm \alpha _i$
, où
![]() $i=1, \dots , n$
, tels que
$i=1, \dots , n$
, tels que
et soumis aux relations de Serre
pour tout
![]() $1\leq i \neq j \leq n$
.
$1\leq i \neq j \leq n$
.
Ainsi que pour les algèbres de Lie semi-simples, il faut regarder
![]() $\mathfrak {t}$
comme sous-algèbre de Cartan de
$\mathfrak {t}$
comme sous-algèbre de Cartan de
![]() $\mathfrak {g}$
et les
$\mathfrak {g}$
et les
![]() $e_i$
et
$e_i$
et
![]() $f_i$
comme vecteurs radiciels associés aux racines simples
$f_i$
comme vecteurs radiciels associés aux racines simples
![]() $\pm \alpha _i$
du système de racines
$\pm \alpha _i$
du système de racines
![]() $\Phi $
de
$\Phi $
de
![]() $\mathfrak {g}$
suivant
$\mathfrak {g}$
suivant
![]() $\mathfrak {t}$
.
$\mathfrak {t}$
.
Expliquons la construction des
![]() $\mathbb {Q}$
-sous-groupes paraboliques de Kac–Moody à la suite de Kumar, voir [Reference KumarKum02, ch. VI]. Étant donnée une sous-algébre parabolique positive
$\mathbb {Q}$
-sous-groupes paraboliques de Kac–Moody à la suite de Kumar, voir [Reference KumarKum02, ch. VI]. Étant donnée une sous-algébre parabolique positive
invariante sous
![]() $\mathfrak {t}$
, alors on a un choix unique de décomposition
$\mathfrak {t}$
, alors on a un choix unique de décomposition
![]() $\mathfrak {t}$
-équivariante de Levi
$\mathfrak {t}$
-équivariante de Levi
Ceci nous amène à considérer, d’un côté, le seul
![]() $\mathbb {Z}$
-groupe épinglé
$\mathbb {Z}$
-groupe épinglé
![]() $\mathcal {M}_{\mathbb {Z}}$
associé à la donnée radicielle de
$\mathcal {M}_{\mathbb {Z}}$
associé à la donnée radicielle de
![]() $\mathfrak {m}$
induite par la réalisation entière (6.1.1) ci-dessus, et de l’autre côté, le seul
$\mathfrak {m}$
induite par la réalisation entière (6.1.1) ci-dessus, et de l’autre côté, le seul
![]() $\mathbb {Q}$
-groupe pro-unipotent
$\mathbb {Q}$
-groupe pro-unipotent
associé au séparé complété de
![]() $\mathfrak {n}^+$
pour sa topologie naturelle, d’après [Reference KumarKum02, th. 4.4.19]. Puis, on voit que l’exponentielle relève l’action de l’algèbre de Lie en une opération
$\mathfrak {n}^+$
pour sa topologie naturelle, d’après [Reference KumarKum02, th. 4.4.19]. Puis, on voit que l’exponentielle relève l’action de l’algèbre de Lie en une opération
de sorte qu’on puisse prendre le produit semi-direct
En ce qui concerne les modèles entiers des groupes de Kac–Moody, la stratégie adoptée remonte à Kostant [Reference KostantKos66]. L’idée est que leur géométrie devrait être codifiée dans la famille de leurs opérateurs différentiels supérieurs, cf. preuve du th. 4.1.5 en §4.3. Par suite, on a besoin de trouver un
![]() $\mathbb {Z}$
-réseau convenable
$\mathbb {Z}$
-réseau convenable
dedans l’algèbre enveloppante de l’algèbre de Kac–Moody
![]() $\mathfrak {g}$
. Ceci fut mené dans le présent cadre par Tits, voir [Reference TitsTi13], [Reference TitsTi87, §4] et [Reference MarquisMar18, déf. 7.3].
$\mathfrak {g}$
. Ceci fut mené dans le présent cadre par Tits, voir [Reference TitsTi13], [Reference TitsTi87, §4] et [Reference MarquisMar18, déf. 7.3].
Définition 6.1.3. La
![]() $\mathbb {Z}$
-forme de Kostant–Tits notée
$\mathbb {Z}$
-forme de Kostant–Tits notée
![]() $U_{\mathbb {Z}}(\mathfrak {g})$
de l’algèbre enveloppante de
$U_{\mathbb {Z}}(\mathfrak {g})$
de l’algèbre enveloppante de
![]() $\mathfrak {g}$
est la sous-
$\mathfrak {g}$
est la sous-
![]() $\mathbb {Z}$
-algèbre associative
$\mathbb {Z}$
-algèbre associative
 $$ \begin{align} U_{\mathbb{Z}}(\mathfrak{g}):=\mathbb{Z}\left[\frac{e_i^n}{n!},\frac{f_i^n}{n!},\binom{h}{n} \right] \end{align} $$
$$ \begin{align} U_{\mathbb{Z}}(\mathfrak{g}):=\mathbb{Z}\left[\frac{e_i^n}{n!},\frac{f_i^n}{n!},\binom{h}{n} \right] \end{align} $$
engendrée par des puissances divisées tordues, où
![]() $h \in P^\vee $
.
$h \in P^\vee $
.
Alors, on peut prolonger le
![]() $\mathbb {Q}$
-groupe pro-algébrique
$\mathbb {Q}$
-groupe pro-algébrique
![]() $\mathcal {U}^+_{\mathbb {Q}}$
en un
$\mathcal {U}^+_{\mathbb {Q}}$
en un
![]() $\mathbb {Z}$
-schéma en groupes affine et plat
$\mathbb {Z}$
-schéma en groupes affine et plat
en prenant pour sections globales le dual gradué de
![]() $U_{\mathbb {Z}}(\mathfrak {n}^+)$
, cf. [Reference MarquisMar18, déf. 8.41]; celui-ci coïncide avec la partie de
$U_{\mathbb {Z}}(\mathfrak {n}^+)$
, cf. [Reference MarquisMar18, déf. 8.41]; celui-ci coïncide avec la partie de
![]() $\Gamma (\mathcal {U}^+_{\mathbb {Q}}, \mathcal {O})$
duale au réseau de (6.1.13) par rapport à l’accouplement
$\Gamma (\mathcal {U}^+_{\mathbb {Q}}, \mathcal {O})$
duale au réseau de (6.1.13) par rapport à l’accouplement
provenant du lien entre les distributions et l’algèbre enveloppante de Lie, cf. [Reference MathieuMat88, lem. 8] et [Reference TitsTi89, 6.2]. On remarque que le
![]() $\mathbb {Z}$
-groupe épinglé
$\mathbb {Z}$
-groupe épinglé
![]() $\mathcal {M}_{\mathbb {Z}}$
opère encore sur
$\mathcal {M}_{\mathbb {Z}}$
opère encore sur
![]() $\mathcal {U}_{\mathbb {Z}}^+$
d’où le modèle entier
$\mathcal {U}_{\mathbb {Z}}^+$
d’où le modèle entier
voir [Reference RousseauRou16, cor. 3.10].
Il y a une théorie des
![]() $\mathfrak {g}$
-modules irréductibles intégrables
$\mathfrak {g}$
-modules irréductibles intégrables
![]() $V(\lambda )$
de plus grand poids
$V(\lambda )$
de plus grand poids
![]() $\lambda $
, où ce dernier est un caractère régulier dominant de
$\lambda $
, où ce dernier est un caractère régulier dominant de
![]() $\mathcal {M}_{\mathbb {Z}}$
, cf. [Reference KacKac90, §9] et [Reference MarquisMar18, §4.1], déterminés en tant que quotients du module de Verma
$\mathcal {M}_{\mathbb {Z}}$
, cf. [Reference KacKac90, §9] et [Reference MarquisMar18, §4.1], déterminés en tant que quotients du module de Verma
La
![]() $\mathbb {Z}$
-forme
$\mathbb {Z}$
-forme
![]() $U_{\mathbb {Z}}(\mathfrak {g})$
nous permet d’introduire le réseau
$U_{\mathbb {Z}}(\mathfrak {g})$
nous permet d’introduire le réseau
donné par l’image de
![]() $U_{\mathbb {Z}}(\mathfrak {g})\otimes _{U_{\mathbb {Z}}(\mathfrak {p}^+)} \mathbb {Z}_\lambda $
suivant (6.1.18), voir [Reference MarquisMar18, ex. 7.23]. Ceci étant, on se tourne vers les schémas de Schubert sur les entiers, cf. [Reference MathieuMat89, p. 37].
$U_{\mathbb {Z}}(\mathfrak {g})\otimes _{U_{\mathbb {Z}}(\mathfrak {p}^+)} \mathbb {Z}_\lambda $
suivant (6.1.18), voir [Reference MarquisMar18, ex. 7.23]. Ceci étant, on se tourne vers les schémas de Schubert sur les entiers, cf. [Reference MathieuMat89, p. 37].
Définition 6.1.4. Soit
![]() $\lambda $
un poids régulier dominant de
$\lambda $
un poids régulier dominant de
![]() $\mathcal {M}_{\mathbb {Z}}$
. Alors, à chaque
$\mathcal {M}_{\mathbb {Z}}$
. Alors, à chaque
![]() $w \in W/W_{\mathfrak {p}}$
, on lui associe le schéma de Schubert
$w \in W/W_{\mathfrak {p}}$
, on lui associe le schéma de Schubert
donné par l’orbite fermée d’un générateur
![]() $v_{w\lambda }$
de l’espace de poids
$v_{w\lambda }$
de l’espace de poids
![]() $w\lambda $
de
$w\lambda $
de
![]() $V_{\mathbb {Z}}(\lambda )$
dedans l’ind-espace projectif qui lui est associé.
$V_{\mathbb {Z}}(\lambda )$
dedans l’ind-espace projectif qui lui est associé.
Heureusement, les schémas de Schubert normalisés ne dépendent que du niveau parabolique
![]() $\mathfrak {p}$
et pas du choix de poids
$\mathfrak {p}$
et pas du choix de poids
![]() $\lambda $
, grâce à un argument topologique, cf. [Reference MathieuMat88, lem. 55], avec les schémas de Demazure
$\lambda $
, grâce à un argument topologique, cf. [Reference MathieuMat88, lem. 55], avec les schémas de Demazure
Puis on dispose de même du théorème de normalité dans le cadre de Kac–Moody :
Théorème 6.1.5 (Mathieu, Littelmann).
Les schémas de Schubert
![]() $\mathcal {S}_{w,\mathbb {Z}}$
associés à
$\mathcal {S}_{w,\mathbb {Z}}$
associés à
![]() $w \in W/W_{\mathfrak {p}}$
sont géométriquement normaux.
$w \in W/W_{\mathfrak {p}}$
sont géométriquement normaux.
Esquisse de la preuve. Ceci repose sur la formule de caractère de Demazure pour les
![]() $U_{\mathbb {Z}}(\mathfrak {g})$
-modules irréductibles
$U_{\mathbb {Z}}(\mathfrak {g})$
-modules irréductibles
![]() $V_{\mathbb {Z}}(\lambda )$
de plus grand poids. Mathieu recourt dans [Reference MathieuMat89, cor. 1] aux techniques de scindage pour les variétés de Schubert normalisées en caractéristique
$V_{\mathbb {Z}}(\lambda )$
de plus grand poids. Mathieu recourt dans [Reference MathieuMat89, cor. 1] aux techniques de scindage pour les variétés de Schubert normalisées en caractéristique
![]() $p>0$
, tandis que Littelmann applique sa méthodes des chemins pour y parvenir, cf. [Reference LittelmannLit98, §8].
$p>0$
, tandis que Littelmann applique sa méthodes des chemins pour y parvenir, cf. [Reference LittelmannLit98, §8].
La variété de drapeaux de Kac–Moody à niveau parabolique
![]() $\mathfrak {p}$
introduite par Mathieu est donc la limite inductive filtrée
$\mathfrak {p}$
introduite par Mathieu est donc la limite inductive filtrée
des schémas de Schubert. Il ne reste qu’à ériger le groupe complet
![]() $\mathcal {G}_{\mathbb {Z}}$
de Kac–Moody.
$\mathcal {G}_{\mathbb {Z}}$
de Kac–Moody.
Supposons pour l’instant que
![]() $\mathfrak {p}^+=\mathfrak {b}^+$
est une sous-algèbre borélienne. On remarque d’abord que le schéma de Demazure
$\mathfrak {p}^+=\mathfrak {b}^+$
est une sous-algèbre borélienne. On remarque d’abord que le schéma de Demazure
![]() $D_{\mathfrak {w},\mathbb {Z}}$
de (6.1.21) possède un
$D_{\mathfrak {w},\mathbb {Z}}$
de (6.1.21) possède un
![]() $\mathcal {B}_{\mathbb {Z}}^+$
-torseur naturel
$\mathcal {B}_{\mathbb {Z}}^+$
-torseur naturel
Il en résulte alors un
![]() $\mathcal {B}_{\mathbb {Z}}^+$
-torseur canonique sur
$\mathcal {B}_{\mathbb {Z}}^+$
-torseur canonique sur
![]() $\mathcal {S}_{w,\mathbb {Z}}$
noté
$\mathcal {S}_{w,\mathbb {Z}}$
noté
![]() $\mathcal {G}_{w,\mathbb {Z}}$
et déterminé en tant que l’enveloppe affine de
$\mathcal {G}_{w,\mathbb {Z}}$
et déterminé en tant que l’enveloppe affine de
![]() $\mathcal {E}_{\mathfrak {w},\mathbb {Z}}$
, voir [Reference MathieuMat88, prop. 26]. Ainsi, l’on note
$\mathcal {E}_{\mathfrak {w},\mathbb {Z}}$
, voir [Reference MathieuMat88, prop. 26]. Ainsi, l’on note
l’ind-schéma en groupes affine sur
![]() $\mathbb {Z}$
qui est la limite directe des torseurs précédents, comp. avec [Reference MathieuMat89, p. 45] et [Reference RousseauRou16, §3.6].
$\mathbb {Z}$
qui est la limite directe des torseurs précédents, comp. avec [Reference MathieuMat89, p. 45] et [Reference RousseauRou16, §3.6].
Plus généralement, les sous-groupes paraboliques positifs
![]() $\mathcal {P}_{\mathbb {Z}}^+$
se plongent dans
$\mathcal {P}_{\mathbb {Z}}^+$
se plongent dans
![]() $\mathcal {G}_{\mathbb {Z}}$
en tant que sous-
$\mathcal {G}_{\mathbb {Z}}$
en tant que sous-
![]() $\mathbb {Z}$
-groupes fermés, tels que le quotient pour la topologie plate
$\mathbb {Z}$
-groupes fermés, tels que le quotient pour la topologie plate
s’identifie canoniquement à la variété de drapeaux partielle.
En outre, le groupe de Kac–Moody possède également des sous-groupes paraboliques négatifs ou opposés
définis comme répulseurs dans
![]() $\mathcal {G}_{\mathbb {Z}}$
d’un copoids dominant régulier de
$\mathcal {G}_{\mathbb {Z}}$
d’un copoids dominant régulier de
![]() $\mathcal {M}_{\mathbb {Z}}$
, tels que l’on ait une décomposition de Levi
$\mathcal {M}_{\mathbb {Z}}$
, tels que l’on ait une décomposition de Levi
où l’on note
![]() $\mathcal {U}_{\mathbb {Z}}^-$
le répulseur strict, et que l’application
$\mathcal {U}_{\mathbb {Z}}^-$
le répulseur strict, et que l’application
définisse une immersion ouverte et affine, voir [Reference Haines, Lourenço and RicharzHLR20, lem. 4.1] pour toutes ces affirmations et comparer avec la prop. 4.2.13.
6.2 La comparaison avec les grassmanniennes affines
Maintenant, on va considérer toutes les constructions du paragraphe précédent dans le cas particulier où
![]() $\mathfrak {g}$
est de type affine, c’est-à-dire
$\mathfrak {g}$
est de type affine, c’est-à-dire
![]() $r=n-1$
.
$r=n-1$
.
Or, la classification des algèbres de Kac–Moody est faite en termes de diagrammes de Dynkin affines, cf. [Reference KacKac90, §4.8] et [Reference MarquisMar18, p. 77] : on a la partie des diagrammes non tordus
celle des diagrammes tordus réduits
et enfin le seul diagramme tordu non réduit
Quoiqu’il en soit, nous disposons em même temps d’un et d’un seul
![]() $\mathbb {Q}(t)$
-groupe G simplement connexe et absolument presque simple à isomorphisme près, satisfaisant à l’hyp. 3.3.1, et dont le diagramme de Dynkin affine est celui donné, qu’on fixera désormais. L’objet du présent paragraphe est de comparer les données géométriques de Kac–Moody affines décrites ci-dessus à celles du §4.
$\mathbb {Q}(t)$
-groupe G simplement connexe et absolument presque simple à isomorphisme près, satisfaisant à l’hyp. 3.3.1, et dont le diagramme de Dynkin affine est celui donné, qu’on fixera désormais. L’objet du présent paragraphe est de comparer les données géométriques de Kac–Moody affines décrites ci-dessus à celles du §4.
Traitons d’abord les opérateurs différentiels. On note ci-dessous
![]() $\widetilde {L\underline {G}}$
le produit semi-direct
$\widetilde {L\underline {G}}$
le produit semi-direct
de l’extension centrale universelle
![]() $ \widehat {L\underline {G}}$
de (4.3.37) par l’action de rotation du groupe multiplicatif
$ \widehat {L\underline {G}}$
de (4.3.37) par l’action de rotation du groupe multiplicatif
![]() $\mathbb {G}_{m,\mathbb {Z}}$
, voir le lem. 3.3.10. Ces définitions s’appliquent également aux groupes d’élastiques
$\mathbb {G}_{m,\mathbb {Z}}$
, voir le lem. 3.3.10. Ces définitions s’appliquent également aux groupes d’élastiques
![]() $L^{\operatorname {gr}}\underline {G}$
, donc on fera usage des mêmes notations.
$L^{\operatorname {gr}}\underline {G}$
, donc on fera usage des mêmes notations.
Lemme 6.2.1. Il y a un isomorphisme
![]() $W^{\operatorname {af}}$
-équivariant
$W^{\operatorname {af}}$
-équivariant
de
![]() $\mathbb {Z}$
-algèbres associatives.
$\mathbb {Z}$
-algèbres associatives.
Démonstration. La première étape consiste à construire l’isomorphisme rationnel, ce qui ramène le problème à trouver un isomorphisme
compte tenu de ce que le membre de droite de (6.2.5) n’est autre que l’algèbre enveloppante de celui de (6.2.6). Cette dernière identification est toutefois une conséquence des descriptions explicites des algèbres de Kac–Moody affines
![]() $\mathfrak {g}$
dans [Reference KacKac90, ths. 7.4, 8.3], jointes à la détermination de la charge centrale dans (4.3.36).
$\mathfrak {g}$
dans [Reference KacKac90, ths. 7.4, 8.3], jointes à la détermination de la charge centrale dans (4.3.36).
Penchons-nous sur l’égalité
de réseaux entiers des algèbres de Lie. Il s’avère que la base évidente du membre de droite induite par le quasi-système de Tits est une base de Chevalley du membre de gauche au sens de [Reference MitzmanMit85, §§2-3]; on attire l’attention particulière du lecteur à la modification de [Reference MitzmanMit85, (3.5.33)] pour le cas non réduit, qui correspond exactement à celle de la déf. 2.3.4.
Or, comme
 $$ \begin{align}\operatorname{Dist}(\mathbb{G}_{a,\mathbb{Z}})=\mathbb{Z}\Big[\frac{X^n}{n!}\Big] \text{ et } \operatorname{Dist}(\mathbb{G}_{m,\mathbb{Z}})=\mathbb{Z}\Big[\binom{X}{n}\Big],\end{align} $$
$$ \begin{align}\operatorname{Dist}(\mathbb{G}_{a,\mathbb{Z}})=\mathbb{Z}\Big[\frac{X^n}{n!}\Big] \text{ et } \operatorname{Dist}(\mathbb{G}_{m,\mathbb{Z}})=\mathbb{Z}\Big[\binom{X}{n}\Big],\end{align} $$
cf. [Reference JantzenJa07, I, ex. 7.8], on en tire l’inclusion
![]() $U_{\mathbb {Z}}(\mathfrak {g})\subset \operatorname {Dist}(\widetilde {L^{\operatorname {gr}}\underline {G}})$
énoncée par (6.2.5). D’autre part, le lem. 4.3.6 entraîne que cette dernière algèbre est engendrée par
$U_{\mathbb {Z}}(\mathfrak {g})\subset \operatorname {Dist}(\widetilde {L^{\operatorname {gr}}\underline {G}})$
énoncée par (6.2.5). D’autre part, le lem. 4.3.6 entraîne que cette dernière algèbre est engendrée par
![]() $\operatorname {Dist}(L^{\operatorname {gr}}\underline {U}^{\pm })$
et
$\operatorname {Dist}(L^{\operatorname {gr}}\underline {U}^{\pm })$
et
![]() $\operatorname {Dist}(\widetilde {S})$
. Par conséquent, on achève le lemme voulu.
$\operatorname {Dist}(\widetilde {S})$
. Par conséquent, on achève le lemme voulu.
Remarque 6.2.2. L’algèbre de distributions de
![]() $L^{\operatorname {gr}}\mathbb {G}_{m,\mathbb {Z}}$
peut être calculée explicitement. Celle-ci est donnée en fonction de certains polynômes en un nombre dénombrable de variables qui correspondent à une base de
$L^{\operatorname {gr}}\mathbb {G}_{m,\mathbb {Z}}$
peut être calculée explicitement. Celle-ci est donnée en fonction de certains polynômes en un nombre dénombrable de variables qui correspondent à une base de
![]() $\operatorname {Lie}(L^{\operatorname {gr}}\mathbb {G}_{m,\mathbb {Z}})$
, la difficulté résidant en les déterminer. Raisonnant par récurrence, on récupère les polynômes de Garland–Mitzman, voir [Reference GarlandGa78, (5.7), th. 5.8], [Reference MitzmanMit85, §4.1] et [Reference MarquisMar18, ex. 8.60].
$\operatorname {Lie}(L^{\operatorname {gr}}\mathbb {G}_{m,\mathbb {Z}})$
, la difficulté résidant en les déterminer. Raisonnant par récurrence, on récupère les polynômes de Garland–Mitzman, voir [Reference GarlandGa78, (5.7), th. 5.8], [Reference MitzmanMit85, §4.1] et [Reference MarquisMar18, ex. 8.60].
Grâce à la prop. 4.2.3, on dispose d’une correspondance bijective entre les facettes
![]() $\mathbf {f} \subset \mathscr {A}(\underline {G},\underline {S},\mathbb {Z} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
et les sous-algèbres paraboliques positives
$\mathbf {f} \subset \mathscr {A}(\underline {G},\underline {S},\mathbb {Z} (\hspace {-0,7mm}( {t} )\hspace {-0,7mm}) )$
et les sous-algèbres paraboliques positives
![]() $\mathfrak {p}^+ \subset \mathfrak {g}$
. Ceci se géométrise comme suit :
$\mathfrak {p}^+ \subset \mathfrak {g}$
. Ceci se géométrise comme suit :
Corollaire 6.2.3. Il y a un et un seul isomorphisme
relevant celui des algèbres de distributions graduées.
Démonstration. L’identification (6.2.6) concernant les algèbres de Lie fournit déjà un isomorphisme
entre les radicaux pro-unipotents sur les rationnels, d’après [Reference KumarKum02, th. 4.4.19]. D’autre part, les données entières définissant les facteurs de Levi de (6.1.17) et (4.2.2) coïncident aux extensions près, d’où une identification
Ceci entraîne qu’on puisse identifier
les schémas en groupes sur les rationnels comme envisagé.
Maintenant, nous voulons améliorer ce résultat en étendant les isomorphismes aux modèles entiers. On s’est ramené à construire un isomorphisme entre les radicaux unipotents. En vertu de [Reference Bruhat and TitsBT84a, rem. 3.5.1(1)], démontré dans [Reference JantzenJa07, I, prop. 10.12], on peut retrouver les
![]() $\mathbb {Z}$
-groupes lisses unipotents et connexes en connaissant leur algèbres de distributions. En particulier, l’affirmation en résulte du lem. 6.2.1, passant à la limite projective.
$\mathbb {Z}$
-groupes lisses unipotents et connexes en connaissant leur algèbres de distributions. En particulier, l’affirmation en résulte du lem. 6.2.1, passant à la limite projective.
Théorème 6.2.4 (Faltings, Pappas–Rapoport, L.).
Il y a des isomorphismes équivariants naturels
entre les schémas de Schubert associés à
![]() $w \in W^{\operatorname {af}}/W_{\mathbf {f}}$
en chacun des cadres, induisant un isomorphisme global
$w \in W^{\operatorname {af}}/W_{\mathbf {f}}$
en chacun des cadres, induisant un isomorphisme global
![]() $\mathcal {F}_{\mathfrak {g}/\mathfrak {p},\mathbb {Z}} \simeq \operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
.
$\mathcal {F}_{\mathfrak {g}/\mathfrak {p},\mathbb {Z}} \simeq \operatorname {Gr}_{\underline {\mathscr {G}_{\mathbf {f}}}}$
.
Démonstration. On reprend les arguments de [Reference Pappas and RapoportPR08, 8.d, 9.h]. Le cor. 6.2.3 fournit un isomorphisme équivariant des résolutions de Demazure, d’où l’identification des schémas de Schubert d’après [Reference MathieuMat88, lem. 33], appliquant simultanément les théorèmes de normalité en chacun des cadres étudies, cf. th. 4.1.5 et th. 6.1.5.
À son tour, la démonstration implicite de [Reference FaltingsFa03, p. 54] tire profit de ce que les sections globales duales des faisceaux amples s’identifient
aux modules irréductibles intégrables de l’algèbre de distributions. Identifiant les mêmes objets dans le cadre des grassmanniennes affines, on voit que tous les deux schémas de Schubert se plongent dans les mêmes espaces projectifs.
Le théorème ci-dessus permet ainsi de comparer également les groupes complets, complétant le dictionnaire entre la théorie de Kac–Moody affine et les grassmanniennes affines.
Corollaire 6.2.5 (Haines–L.–Richarz).
Il y a un isomorphisme canonique
induisant des identifications
entre les sous-groupes paraboliques et les sous-groupes d’arcs et/ou de cordes.
Démonstration. On renvoie à [Reference Haines, Lourenço and RicharzHLR20, prop. 4.3] pour plus de détails. Notons que l’identification des sous-groupes paraboliques opposés aux sous-groupes de cordes résultent plus aisément de la prop. 4.2.13 et de [Reference Haines, Lourenço and RicharzHLR20, lem. 4.1].
Conflict of Interest
The authors have no conflict of interest to declare.
Funding statement
The first version of this work was written during my doctoral studies at the Universität Bonn and was funded by the SFB/TR 45 of the DFG and the Leibniz prize of Prof. Dr. P. Scholze. The final version of this work was written while at Imperial College London and supported by the ERC Starting Grant 804176 of Prof. A. Caraiani within the Horizon 2020 program of the EU.