FISHING FOR COMPLEMENTS

Abstract

Given a presilting object in a triangulated category, we find necessary and sufficient conditions for the existence of a complement. This is done both for classic (pre)silting objects and for large (pre)silting objects. The key technique is the study of associated co-t-structures. As a consequence of our techniques we recover some known cases of the existence of complements, including for derived categories of some hereditary abelian categories and for silting-discrete algebras. Moreover, we also show that a finite-dimensional algebra is silting discrete if and only if every bounded large silting complex is equivalent to a compact one.

1 Introduction

The question about the existence of complements is a problem that goes back to the early days of tilting theory. Bongartz showed in 1981 that a partial tilting module over a finite-dimensional algebra $\Lambda $ always admits a finite-dimensional complement [14]. Here a partial tilting module is a finite-dimensional module without self-extensions that has projective dimension one. Already for projective dimension two, however, there are counterexamples to the corresponding generalized statement [42]. On the other hand, it was shown in [6] that complements do exist for partial tilting modules of any projective dimension if we relax the requirement that they ought to be finite dimensional, working with large tilting modules, that is, possibly infinite-dimensional tilting modules, instead. This result relies on the theory of cotorsion pairs developed in [22], which is a source of left and right approximations in the category $\mathsf {Mod}(\Lambda )$ of all $\Lambda $ -modules, with good homological behavior.

The analogous problem in silting theory asks whether a presilting object can be completed to a silting object. One has to distinguish between two parallel setups: the classic notion of (pre)silting object from [3], [32] which is mostly used in triangulated categories satisfying some finiteness conditions, and the more recent definition from [38], [41] designed for “large” triangulated categories with arbitrary coproducts. While in the references indicated, these subcategories are simply called (pre)silting, in this paper we will use the adjectives classic and large to distinguish them.

Bongartz completion extends to silting theory, see [21, §5], [45, Proposition 6.1], [17, Proposition 3.14]. The silting version is “basis-free”: the assumption that a partial 1-tilting module has a two-term projective resolution is replaced by the condition that the presilting object X is “two-term” with respect to a suitable classic silting object M. Moreover, in the classic setup, complements are known to exist in certain ambient triangulated categories, such as the bounded derived category of a hereditary abelian category, or the category $\mathsf {per}(\Lambda )$ of perfect complexes when $\Lambda $ is a piecewise hereditary algebra or a silting-discrete algebra [4], [17], [19]. On the other hand, recent work in [28], [29], [35] provides examples of finite-dimensional algebras for which $\mathsf {per}(\Lambda )$ contains classic presilting objects that cannot be completed to a classic silting object.

In analogy to [6], we show in the present paper that every classic presilting object in $\mathsf {per}(\Lambda )$ can be completed to a bounded complex of (possibly large) projectives which is a large silting object in the unbounded derived category $\mathsf {D}(\mathsf {Mod}(\Lambda ))$ . This relies on a development of the theory of cotorsion pairs in [43] providing a powerful existence result for co-t-structures which we state in Lemma 4.5.

In fact, we present general criteria for the existence of complements, both in the context of large and classic silting theory (Theorems 4.6 and 4.11). Under mild assumptions on the ambient triangulated category $\mathsf {T}$ , we prove that a presilting object X admits a complement if and only if there exists a silting object M satisfying the following conditions, where we denote by $\mathsf {X}$ and $\mathsf {M}$ the additive closures of X and M in $\mathsf {T}$ , respectively:

1. (i) X is intermediate with respect to M, that is, $\mathsf {M}\geqslant \mathsf {X}\geqslant \mathsf {M}[n]$ for some $n>0$ ;

2. (ii) $\mathsf {M}\geqslant \mathsf {X}$ and given the co-t-structures $(\mathsf {U}_X,\mathsf {V}_X:=(X[<0])^\perp )$ and $(\mathsf {U}_M,\mathsf {V}_M:=(M[<0])^\perp )$ associated to X and M, respectively, the intersection $\mathsf {V}_X \cap \mathsf {V}_M $ is again the coaisle of a co-t-structure in $\mathsf {T}$ .

Condition (i) is natural in the classic case, because the existence of a classic silting object entails that homomorphisms between two objects vanish after shifting one object far enough (Lemma 3.4). Condition (ii) is the co-t-structure analog of averaging of t-structures studied in [16], and it is always satisfied in the large setup thanks to Lemma 4.5. In the classic setup, the choice of the silting object M above matters. Indeed, the averaging condition (ii) may hold for certain objects M and fail for others, see Example 5.7. We summarize our main theorem as follows.

Theorem 1. Let $\mathsf {T}$ be a triangulated category. The following hold.

1. 1. (Theorem 4.6) If $\mathsf {T}$ is algebraic and compactly generated and if X is a large presilting object in $\mathsf {T}$ , then X admits a complement to a large silting object if and only if condition (i) above holds with respect to a large silting object M.

2. 2. (Theorem 4.11) If $\mathsf {add}(T)$ is precovering in $\mathsf {T}$ for every T in $\mathsf {T}$ (for example, if $\mathsf {T}$ is ${\mathbf {k}}$ -linear, Krull-Schmidt and Hom-finite over a field ${\mathbf {k}}$ ) and X is a classic presilting object in $\mathsf {T}$ , then X admits a complement to a classic silting object if and only if condition (ii) above holds with respect to a classic silting object M.

In the last part of the paper, we will show how to recover Bongartz completion and the existence of complements for classic presilting objects over hereditary abelian categories or silting-discrete algebras. The latter result also requires a characterisation of silting-discrete algebras that may be of independent interest.

Theorem 2 (Theorem 6.5).

A finite-dimensional algebra $\Lambda $ is silting discrete if and only if every bounded complex of projective modules which is a large silting object in $\mathsf {D}(\mathsf {Mod}(\Lambda ))$ is (additively) equivalent to a classic silting object in $\mathsf {per}(\Lambda )$ .

This can be regarded as a triangulated version of a result from [8] stating that $\Lambda $ is $\tau $ -tilting finite if and only if every silting module in $\mathsf {Mod}(\Lambda )$ is equivalent to a support $\tau $ -tilting module in $\mathsf {mod}(\Lambda )$ .

The article is organized as follows. In Sections 2 and 3, we collect some preliminaries and review the notions of silting or presilting objects and subcategories, together with their relationship with co-t-structures. Section 4 contains the general existence results for complements, while Section 5 recovers some known cases as applications of our criteria. Section 6 is devoted to silting-discrete algebras.

2 Preliminaries

In this section, we fix some notation and terminology. Unless stated otherwise, $\mathsf {T}$ will denote an abstract triangulated category with shift functor $[1]$ , and all subcategories will be strict and full. Furthermore, when considering abelian categories, we shall consider only those whose derived category exists, that is, we require that morphisms between any two given objects form a set rather than a proper class.

2.1 Subcategory constructions

For subcategories $\mathsf {U}$ , $\mathsf {V}$ and $\mathsf {X}$ of $\mathsf {T}$ , we consider the following subcategories of $\mathsf {T}$ :

We will use the following abbreviations:

$$\begin{align*}\mathsf{V}_{\mathsf{X}}= \mathsf{X}[<0]^\perp, \quad \mathsf{W}_{\mathsf{X}}= \mathsf{X}[\geqslant 0]^\perp, \quad \mathsf{U}_{\mathsf{X}}={}^\perp(\mathsf{V}_{\mathsf{X}}). \end{align*}$$

In the notation of [7–9], [41], we have $\mathsf {V}_{\mathsf {X}}=\mathsf {X}^{\perp _{>0}}$ , $\mathsf {W}_{\mathsf {X}}= \mathsf {X}^{\perp _{\leqslant 0}}$ , $\mathsf {U}_{\mathsf {X}}={}^{\perp _0}(\mathsf {V}_{\mathsf {X}})$ . Note that $\mathsf {V}_{\mathsf {X}}$ is a suspended subcategory, while $\mathsf {W}_{\mathsf {X}}$ and $\mathsf {U}_{\mathsf {X}}$ are cosuspended subcategories. When $\mathsf {X}$ consists of a single object X, we just write $\mathsf {thick}_{}(X),\mathsf {Add}(X), \mathsf {V}_X,\mathsf {W}_X$ etc.

We say that a subcategory $\mathsf {X}$ of $\mathsf {T}$ weakly generates $\mathsf {T}$ if $(\mathsf {X}[\mathbb {Z}])^\perp =0$ . The adverb “weakly” here refers to the fact that if $\mathsf {thick}_{}(\mathsf {X}) = \mathsf {T}$ then $\mathsf {X}$ weakly generates $\mathsf {T}$ , while the converse does not hold in general.

2.2 Precovering and pre-enveloping subcategories

Let $\mathsf {U}$ be a subcategory of $\mathsf {T}$ and T be an object of $\mathsf {T}$ . A morphism $f \colon U_T \to T$ is called a $\mathsf {U}$ -precover (or a right $\mathsf {U}$ -approximation) of T if the induced homomorphism

$$\begin{align*}\operatorname{\mathrm{\mathsf{Hom}}}_{\mathsf{T}}(U,f) \colon \operatorname{\mathrm{\mathsf{Hom}}}_{\mathsf{T}}(U,U_T) \to \operatorname{\mathrm{\mathsf{Hom}}}_{\mathsf{T}}(U,T) \end{align*}$$

is surjective for each object U of $\mathsf {U}$ . If each object T of $\mathsf {T}$ admits a $\mathsf {U}$ -precover then $\mathsf {U}$ is said to be precovering in $\mathsf {T}$ . There are dual notions of $\mathsf {U}$ -pre-envelope and pre-enveloping subcategory.

2.3 t-structures and co-t-structures

Two kinds of torsion pairs in triangulated categories play an important role in silting theory.

Definition 2.1 [27, Definition 2.2].

A pair $(\mathsf {U},\mathsf {V})$ of idempotent-complete additive subcategories of a triangulated category $\mathsf {T}$ is said to be a torsion pair in $\mathsf {T}$ if

1. (1) $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {T}}(U,V)=0$ , for each U in $\mathsf {U}$ and V in $\mathsf {V}$ ;

2. (2) $\mathsf {T} = \mathsf {U} * \mathsf {V}$ .

For each object T of $\mathsf {T}$ , the triangle associated with the decomposition $\mathsf {T} = \mathsf {U} * \mathsf {V}$ is called the truncation triangle for T. The subcategories $\mathsf {U}$ and $\mathsf {V}$ are the aisle and coaisle, respectively, of the torsion pair. A torsion pair $(\mathsf {U},\mathsf {V})$ is said to be:

• • a t-structure if $\mathsf {U}[1] \subseteq \mathsf {U}$ (see [11]);

• • a co-t-structure if $\mathsf {U}[-1]\subseteq \mathsf {U}$ (see [39], or [13] under the name weight structure);

• • bounded if $\mathsf {T} = \bigcup _{n \in \mathbb {Z}} \mathsf {U}[n] = \bigcup _{n \in \mathbb {Z}}\mathsf {V}[n]$ ;

• • left nondegenerate if $\bigcap _{n\in \mathbb {Z}}\mathsf {U}[n]=0$ ;

• • right nondegenerate if $\bigcap _{n\in \mathbb {Z}}\mathsf {V}[n]=0$ ;

• • nondegenerate if it is both left and right nondegenerate;

• • generated by a set if there is a set of objects $\mathsf {X}$ in $\mathsf {T}$ such that $\mathsf {V}=\mathsf {X}^\perp $ .

After [13], given torsion pairs $(\mathsf {U},\mathsf {V})$ and $(\mathsf {V},\mathsf {W})$ , we say that the former is left adjacent to the latter or that the latter is right adjacent to the former.

In the case that $(\mathsf {U},\mathsf {V})$ is a t-structure, the subcategory $\mathsf {A} = \mathsf {U} \cap \mathsf {V}[1]$ called the heart. In the case that $(\mathsf {U},\mathsf {V})$ is a co-t-structure, the subcategory $\mathsf {C} = \mathsf {U}[1] \cap \mathsf {V}$ is called the coheart of the co-t-structure. A t-structure $(\mathsf {U},\mathsf {V})$ is called split if each truncation triangle given in condition $(2)$ above is a split triangle, that is, $\mathsf {T} = \mathsf {Add}(\mathsf {U},\mathsf {V})$ .

We recall a few useful results about t-structures and co-t-structures:

1. 1. The aisle of a torsion pair is always a precovering subcategory and the coaisle is always a pre-enveloping subcategory.

2. 2. The heart of a t-structure is an abelian category [11]. The coheart of a co-t-structure is an additive subcategory, but rarely abelian.

3. 3. The truncation triangles for a t-structure are functorially determined.

4. 4. A t-structure with heart $\mathsf {A}$ is bounded if and only if

   $$\begin{align*}\mathsf{T} = \bigcup_{i \geqslant j} \mathsf{A}[i] * \mathsf{A}[i-1] * \cdots * \mathsf{A}[j]. \end{align*}$$

We end this section with a couple of straightforward but useful observations about co-t-structures. For the first one, see also [13, Proposition 1.5.6].

Lemma 2.2. Let $(\mathsf {U}, \mathsf {V})$ be a co-t-structure in $\mathsf {T}$ . Then any object of $\mathsf {T}$ sits in a (possibly infinite) Postnikov tower, that is, a diagram of the form

where

$$\begin{align*}T_1\to T\to V_T\to T_1[1] \quad \text{and} \quad T_{i+1}\to T_{i}\to C_i[-i]\to T_{i+1}[1] \end{align*}$$

are triangles for all $i\geqslant 1$ , and such that $V_T$ lies in $\mathsf {V}$ , $T_i$ lies in $\mathsf {U}[1-i]$ and $C_i$ in the coheart $\mathsf {C} = \mathsf {U} [1] \cap \mathsf {V}$ for all $i\geqslant 1$ . Moreover, if T lies in $\mathsf {V}[-n]$ for some $n>0$ , then the Postnikov tower is finite, that is, $T_n$ lies in $\mathsf {C}[-n]$ .

As truncations with respect to co-t-structures are not unique, the Postnikov tower occurring in Lemma 2.2 is not necessarily unique.

Proof. The existence of the Postnikov tower follows by iteratively taking triangles, starting with $T_0 = T$ , and choosing the co-t-structure $(\mathsf {U}[-i],\mathsf {V}[-i])$ for each $T_i$ , $i\geqslant 0$ . It is then easy to observe that the third term in each truncation triangle sits in the subcategories claimed.

Suppose now that T lies in $\mathsf {V}[-n]$ for some $n>0$ . One can show by induction that $T_i \in \mathsf {V}[-n]$ for each $0 \leqslant i \leqslant n$ . Indeed, suppose that, for $i\geqslant 1$ , $T_{i-1}$ lies in $\mathsf {V}[-n]$ . One then reads off that $T_i \in \mathsf {V}[-n]$ from the truncation triangle

$$\begin{align*}C_{i-1}[-i] \to T_i \to T_{i-1} \to C_{i-1}[-i+1] \end{align*}$$

and the fact that $C_{i-1} [-i] \in \mathsf {C}[-i] \subseteq \mathsf {V}[-i] \subseteq \mathsf {V}[-n]$ . Hence, by construction of the tower, $T_n$ lies in $\mathsf {V}[-n]\cap \mathsf {U}[-n+1]=\mathsf {C}[-n]$ .

Corollary 2.3. Let $(\mathsf {U}, \mathsf {V})$ and $(\mathsf {U}', \mathsf {V}')$ be two co-t-structures in $\mathsf {T}$ with cohearts $\mathsf {C}$ and $\mathsf {C}'$ , respectively. Assume there is an integer $n>0$ such that $\mathsf {V}'[n]\subseteq \mathsf {V}\subseteq \mathsf {V}'$ . Then

$$\begin{align*}\mathsf{C}'\subseteq \mathsf{C}[-n] * \cdots * \mathsf{C}[-1] * \mathsf{C} \quad \text{and} \quad \mathsf{C} \subseteq \mathsf{C}' * \cdots * \mathsf{C}'[n-1] * \mathsf{C}'[n]. \end{align*}$$

In particular, it follows that $\mathsf {thick}_{}(\mathsf {C}')=\mathsf {thick}_{}(\mathsf {C}).$

Proof. First of all, notice that the assumption also yields $\mathsf {U}'[n] \supseteq \mathsf {U} \supseteq \mathsf {U}'$ . Take now M in $\mathsf {C}'=\mathsf {U}'[1]\cap \mathsf {V}'$ and consider a triangle

$$\begin{align*}U\to M\to V\to U[1] \end{align*}$$

with U in $\mathsf {U}$ and V in $\mathsf {V}$ . Since M lies in $\mathsf {V}'\subseteq \mathsf {V}[-n]$ , by Lemma 2.2 there is a finite Postnikov tower showing that the object U in the triangle lies in $\mathsf {C}[-n] * \cdots * \mathsf {C}[-1]$ . Observe further that M lies in $\mathsf {U}'[1]\subseteq \mathsf {U}[1]$ , hence V lies in $\mathsf {C}$ . We conclude that M lies in $\mathsf {C}[-n] * \cdots * \mathsf {C}[-1] * \mathsf {C}$ , as desired.

For the second inclusion, pick T in $\mathsf {C} = \mathsf {U}[1] \cap \mathsf {V} \subseteq \mathsf {U}'[n+1]\cap \mathsf {V}'$ and apply Lemma 2.2 on the object $T[-(n+1)]$ .

2.4 Derived categories

Our main examples come from various categories associated with a coherent ring R. Later in Section 6 we will restrict to the case of a finite-dimensional algebra over a field ${\mathbf {k}}$ ; for emphasis in this case we will denote the algebra by $\Lambda $ .

3 (Pre)silting and co-t-structures

There are two kinds of (pre)silting subcategories/objects in common use, depending on the context in which one is working. There is the classic definition of (pre)silting subcategory/object, used in “small” triangulated categories [3], [32], and the more recent definition of a silting object, better adapted to “large” triangulated categories [9], [38], [41]. We review these notions below.

3.1 Classic silting subcategories

Definition 3.1. Let $\mathsf {M}=\mathsf {add}(\mathsf {M})$ be a subcategory of a triangulated category $\mathsf {T}$ . We say that $\mathsf {M}$ is

• • classic presilting if $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {T}}(M, M^\prime [>0]) = 0$ for any objects M and $M^\prime $ of $\mathsf {M}$ ;

• • classic silting if it is classic presilting and $\mathsf {T} = \mathsf {thick}_{}(\mathsf {M})$ .

An object M in $\mathsf {T}$ is a classic (pre)silting object if $\mathsf {add}(M)$ is a classic (pre)silting subcategory of $\mathsf {T}$ .

A first fundamental fact about classic silting subcategories is their close relationship to co-t-structures.

Theorem 3.2 [36, Corollary 5.8].

Let $\mathsf {T}$ be a triangulated category. The assignment

$$\begin{align*}\mathsf{M}\mapsto(\mathsf{U}_{\mathsf{M}},\mathsf{V}_{\mathsf{M}}) \end{align*}$$

is a bijection between classic silting subcategories of $\mathsf {T}$ and bounded co-t-structures in $\mathsf {T}$ . Moreover, if $\mathsf {M}$ is a classic silting subcategory of $\mathsf {T}$ , the associated bounded co-t-structure has coheart $\mathsf {M}$ and satisfies $\mathsf {V}_{\mathsf {M}}= \operatorname {\mathrm {\mathsf {susp}}}(\mathsf {M})$ and $\mathsf {U}_{\mathsf {M}}= \operatorname {\mathrm {\mathsf {cosusp}}}(\mathsf {M}[-1])={}^\perp (\mathsf {M}[\geqslant 0])$ .

Note that there is a priori no condition imposed on a triangulated category where a classic silting subcategory lives. Nevertheless, the fact that $\mathsf {T} = \mathsf {thick}_{}(\mathsf {M})$ imposes that if $\mathsf {M}$ is skeletally small (e.g., when $\mathsf {M}=\mathsf {add}(M)$ for a silting object M), then so is $\mathsf {T}$ .

Example 3.3. Let R be a coherent ring. Then R is a classic silting object in $\mathsf {K}^b(\mathsf {proj}(R))$ and $\mathsf {Proj}(R)$ is a classic silting subcategory of $\mathsf {K}^b(\mathsf {Proj}(R))$ .

The existence of a silting subcategory does impose a condition on the behaviour of morphisms in the triangulated category.

Lemma 3.4 [3, Proposition 2.4].

Suppose $\mathsf {T}$ is a triangulated category containing a classic silting subcategory. Then, for any two objects X and Y in $\mathsf {T}$ , there is $n>0$ such that $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {T}}(X,Y[>n])=0$

3.2 Large silting objects

The existence of precovers and pre-envelopes, see Section 2.2, is central in silting theory. In the classic setting, the relevant precovers and pre-envelopes exist under suitable finiteness conditions on the category. In large silting theory, the existence of precovers and pre-envelopes is guaranteed provided we work with at most a set (rather than a proper class) of objects. As such, in the large setting we restrict our attention to large silting objects rather than subcategories.

In this subsection, $\mathsf {T}$ will be a triangulated category that admits all set-indexed coproducts.

Definition 3.5. An object M of $\mathsf {T}$ is called

• • large presilting if $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {T}}(M, M[>0]) = 0$ , and $\mathsf {V}_M$ is coproduct closed;

• • large silting if $(\mathsf {V}_M, \mathsf {W}_M)$ is a t-structure in $\mathsf {T}$ .

Two (pre)silting objects M and $M^\prime $ are said to be equivalent if $\mathsf {Add}(M)=\mathsf {Add}(M^\prime ).$

Remark 3.6. We make the following observations regarding large (pre)silting objects.

1. 1. It follows from the very definition of a t-structure that any large silting object is also a large presilting object.

2. 2. Any large (pre)silting object X gives rise to a classic silting subcategory $\mathsf {Add}(X)$ in $\mathsf {thick}_{}(\mathsf {Add}(X))$ because $\mathsf {V}_X$ is closed under coproducts.

The definition of large silting is borrowed from [41], while the notion of large presilting is closely related to the notion of partial silting introduced in [9], and in a wide range of categories they coincide, see Remark 3.8 below. The definition of partial silting from [9] has the additional requirement of the existence of a t-structure.

Similar to the classic silting case, for suitable triangulated categories, silting and presilting objects of $\mathsf {T}$ are related to co-t-structures in $\mathsf {T}$ . One context in which this relationship is well understood is that of a compactly generated triangulated category.

Definition 3.7. An object X in a triangulated category $\mathsf {T}$ with set-indexed coproducts is compact if the functor $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {T}}(X,-)$ commutes with set-indexed coproducts. We say that $\mathsf {T}$ is compactly generated if the subcategory of compact objects $\mathsf {T}^c$ is skeletally small and weakly generates $\mathsf {T}$ .

Remark 3.8. Compactly generated triangulated categories are examples of a larger class of triangulated categories called well generated. It follows from recent results of Neeman in [37] that our large presilting objects coincide with the partial silting objects of [9] in the wider context of well-generated triangulated categories. Moreover, Neeman’s result in [37] on the generation of t-structures has the further consequence that in a well-generated triangulated category, an object is large silting if and only if it is a large presilting object which weakly generates the category. This is observed in [9] after loc. cit. Lemma 3.3, as a consequence of [38, Theorem 1(2)]. Recently, the same relation between silting and presilting objects was extended to arbitrary triangulated categories with coproducts in [15].

Example 3.9. The condition that $\mathsf {V}_M$ is closed under coproducts in Definition 3.5 doesn’t require the object M to be compact. For an example, consider the large silting object M given by the projective resolution of an infinite dimensional tilting module T over a finite-dimensional algebra $\Lambda $ and observe that the associated aisle $\mathsf {V}_M$ is closed under coproducts, because it consists of the complexes Y in the aisle of the standard t-structure of $\Lambda $ whose zero cohomology $H^0(Y)$ is isomorphic to a quotient of a direct sum of copies of T (see, e.g., [10, Remark 3.6]).

Theorem 3.10 [9, Proposition 3.8, Theorem 3.9 and Corollary 3.10], [38, Theorem 2].

Let $\mathsf {T}$ be a compactly generated triangulated category. The assignment

$$\begin{align*}M \mapsto (\mathsf{U}_M, \mathsf{V}_M) \end{align*}$$

gives a bijection between equivalence classes of large (pre)silting objects in $\mathsf {T}$ and co-t-structures $(\mathsf {U},\mathsf {V})$ that are generated by a set and admit a right adjacent t-structure which is (right) nondegenerate. If M is a large silting object of $\mathsf {T}$ , the associated co-t-structure has coheart $\mathsf {Add}(M)$ , and $\mathsf {V}_{\mathsf {M}}= \operatorname {\mathrm {\mathsf {Susp}}}(M)$ is the smallest aisle of $\mathsf {T}$ containing M.

Remark 3.11. Let $\mathsf {T}$ be a compactly generated triangulated category. An object $M\in \mathsf {T}^c$ is classic (pre)silting in $\mathsf {T}^c$ if and only if it is large (pre)silting in $\mathsf {T}$ . Indeed, every object $M\in \mathsf {T}^c$ generates a t-structure $(\operatorname {\mathrm {\mathsf {Susp}}}(M), \mathsf {W}_M)$ in $\mathsf {T}$ (see, e.g., [5, Theorem A.1]), and if M is classic presilting we have $\operatorname {\mathrm {\mathsf {Susp}}}(M)\subseteq \mathsf {V}_M$ . If M is furthermore classic silting in $\mathsf {T}^c$ (and, hence, a weak generator in $\mathsf {T}$ ), a $\mathsf {W}_M$ -pre-envelope of an object X of $\mathsf {V}_M$ must lie in $M[\mathbb {Z}]^\perp $ , thus showing that X must lie in $\operatorname {\mathrm {\mathsf {Susp}}}(M)$ and that $\operatorname {\mathrm {\mathsf {Susp}}}(M)=\mathsf {V}_M$ . Conversely, every large silting object M is a weak generator in $\mathsf {T}$ , and from, for example, [34, Proposition 3.4.15], it follows that $\mathsf {thick}_{\mathsf {T}^c}(M) = \mathsf {thick}_{\mathsf {T}}(M) = \mathsf {T}^c$ .

4 Complements

Our main problem in this paper is that of finding necessary and sufficient conditions for a given (classic/large) presilting object to be a summand of a silting object. We will approach this problem by looking at associated co-t-structures.

Definition 4.1. A classic (respectively, large) presilting object X in a triangulated category $\mathsf {T}$ is said to admit a complement if there is an object V in $\mathsf {T}$ such that $X\oplus V$ is a classic (respectively, large) silting object.

4.1 Intermediate (pre)silting objects

We recall from [3] the following relation on classic presilting subcategories. When the subcategories are classic silting, this relation defines a partial order [3, Theorem 2.11].

Definition 4.2. For two classic presilting subcategories $\mathsf {X}$ and $\mathsf {Y}$ in a triangulated category $\mathsf {T}$ , we set

$$\begin{align*}\mathsf{X} \geqslant \mathsf{Y} \iff \operatorname{\mathrm{\mathsf{Hom}}}_{\mathsf{T}} (X, Y[>0])=0 \text{ for all } X \in \mathsf{X} \text{ and } Y \in \mathsf{Y}. \end{align*}$$

In our notation, we have that $\mathsf {X} \geqslant \mathsf {Y} \iff \mathsf {Y} \subseteq \mathsf {V}_{\mathsf {X}}$ .

It follows that if $\mathsf {X}$ is a classic presilting subcategory in $\mathsf {T}$ , then $\mathsf {X}[-1] \geqslant \mathsf {X} \geqslant \mathsf {X}[1]$ . We need the following minor generalization of [2, Lemma 3.6].

Lemma 4.3. Let $\mathsf {T}$ be a triangulated category. Given a classic presilting subcategory $\mathsf {X}$ and a classic silting subcategory $\mathsf {Y}$ of $\mathsf {T}$ , we have that

1. (a) $\mathsf {X} \geqslant \mathsf {Y}$ if and only if $\mathsf {V}_{\mathsf {Y}} \subseteq \mathsf {V}_{\mathsf {X}};$

2. (b) for any $n>0$ , $\mathsf {Y}\ge \mathsf {X}\ge \mathsf {Y}[n]$ if and only if $\mathsf {X}\subseteq \mathsf {Y}*\mathsf {Y}[1]*\cdots *\mathsf {Y}[n]$ .

The same statements hold when $\mathsf {T}$ is a compactly generated triangulated category, $\mathsf {X}=\mathsf {Add}(X)$ for a large presilting object X, and $\mathsf {Y}=\mathsf {Add}(Y)$ for a large silting object Y in $\mathsf {T}$ with X lying in $\mathsf {thick}_{}(\mathsf {Y})$ .

If condition (b) holds for $\mathsf {X}$ and $\mathsf {Y}$ as in the lemma then we say that $\mathsf {X}$ is intermediate with respect to $\mathsf {Y}$ .

Proof. (a) $\mathsf {V}_{\mathsf {X}}$ is closed under suspensions, extensions and direct summands, thus $\mathsf {Y} \subseteq \mathsf {V}_{\mathsf {X}}$ implies $\operatorname {\mathrm {\mathsf {susp}}}(\mathsf {Y}) \subseteq \mathsf {V}_{\mathsf {X}}$ , and the claim follows because $\mathsf {V}_{\mathsf {Y}} =\operatorname {\mathrm {\mathsf {susp}}}(\mathsf {Y})$ ; see Theorem 3.2.

(b) The if part is clear. For the converse, observe that

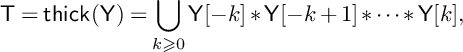$$\begin{align*}\mathsf{T}=\mathsf{thick}_{}(\mathsf{Y}) = \bigcup_{k\geqslant 0} \mathsf{Y}[-k] * \mathsf{Y}[-k+1] * \cdots * \mathsf{Y}[k], \end{align*}$$

where the last equality holds due to [3, Theorem 2.11] (see also [2, Lemma 3.5(c)]). Thus, there is $k\geqslant 0$ for which X lies in $\mathsf {Y}[-k]*\mathsf {Y}[-k+1]*\cdots *\mathsf {Y}[k]$ . Assuming that there is $n>0$ such that $\mathsf {Y}\ge \mathsf {X}\ge \mathsf {Y}[n]$ , we obtain the statement using [2, Lemma 3.5(b)].

Finally, in the context of the last assertion, we can use the same arguments to prove (a), taking into account that $\mathsf {V}_X$ is closed under coproducts, and that $\mathsf {V}_{\mathsf {Y}}=\operatorname {\mathrm {\mathsf {Susp}}}{Y}$ by Theorem 3.10. For (b), we observe that $\mathsf {X}=\mathsf {Add}(X)$ is a classic presilting subcategory in $\mathsf {thick}_{}(\mathsf {Y})$ and $\mathsf {Y}=\mathsf {Add}(Y)$ is a classic silting subcategory in $\mathsf {thick}_{}(\mathsf {Y})$ by Remark 3.6.

Given a silting object M, a useful recent result of Breaz allows us to identify large silting objects N which are intermediate with respect to M in a slightly less cumbersome manner. We will use this result in the Section 5.

Theorem 4.4 [15, Theorem 3.4].

Let $\mathsf {T}$ be a triangulated category with coproducts and M a large silting object in $\mathsf {T}$ . The following are equivalent for an object N in $\mathsf {T}$ .

1. 1. The object N is a large silting object such that $\mathsf {Add}(M) \geqslant \mathsf {Add}(N) \geqslant \mathsf {Add}(M[n])$ ;

2. 2. The object N satisfies:

   1. (i) N lies in $\mathsf {V}_M$ and there is $n>0$ such that $\mathsf {V}_M[n]\subseteq \mathsf {V}_N$ ;

   2. (ii) N is a weak generator; and,

   3. (iii) $\mathsf {Add}(N)$ lies in $\mathsf {V}_N$ .

4.2 Complements for large presilting

We are now ready to state the first result concerning the existence of complements in the context of algebraic, compactly generated triangulated categories. Recall from [30] that a triangulated category is algebraic if it is equivalent to the stable category of a Frobenius exact category. We first need the following observation from [43].

Lemma 4.5. Let $\mathsf {T}$ be an algebraic, compactly generated triangulated category. Suppose $\mathcal {S}$ is a set of objects such that $\mathcal {S}[-1] \subset \mathcal {S}$ (resp. $\mathcal {S}[1] \subset \mathcal {S}$ ). Then, $({}^\perp (\mathcal {S}^\perp ), \mathcal {S}^\perp )$ is a co-t-structure (resp. t-structure) in $\mathsf {T}$ .

Proof. By [30, §4.3, Theorem], $\mathsf {T}$ is equivalent to the derived category of a small differential graded category. From [44, Remark 2.15] it follows that there $\mathsf {T}$ can be seen as the stable category of an efficient Frobenius exact category in the sense of [43, Definition 2.6]. Finally, by [43, Proposition 3.3 and Corollary 3.5], any set $\mathcal {S}$ of objects such that $\mathcal {S}[-1] \subset \mathcal {S}$ (resp. $\mathcal {S}[1] \subset \mathcal {S}$ ) gives rise to a co-t-structure (resp. t-structure) $({}^\perp (\mathcal {S}^\perp ),\mathcal {S}^\perp )$ .

Theorem 4.6. Let $\mathsf {T}$ be an algebraic compactly generated triangulated category, and suppose that X is a large presilting object in $\mathsf {T}$ . The following statements are equivalent.

1. 1. X admits a complement V such that $X\oplus V$ is a large silting object in $\mathsf {T}$ .

2. 2. There is a large silting object M in $\mathsf {T}$ such that X lies in $\mathsf {thick}_{}(\mathsf {Add}(M))$ .

3. 3. There are a large silting object M in $\mathsf {T}$ and an integer $n>0$ such that

   $$\begin{align*}\mathsf{Add}(M)\geqslant \mathsf{Add}(X)\geqslant \mathsf{Add}(M[n]). \end{align*}$$

Moreover, for any M satisfying the equivalent conditions (2) and (3) above, there exists a complement V such that $\mathsf {thick}_{}(\mathsf {Add}(M))=\mathsf {thick}_{}(\mathsf {Add}(X\oplus V)).$

Proof. (1) $\Rightarrow $ (2): If X admits a complement, V say, then $M=X\oplus V$ is a large silting object satisfying (2).

(2) $\Rightarrow $ (3): If X lies in $\mathsf {thick}_{}(\mathsf {Add}(M))$ , it follows from [2, Lemma 3.5(c)] and Remark 3.6 that X lies in $\mathsf {Add}(M)[-k]*\mathsf {Add}(M)[-k+1]*\cdots *\mathsf {Add}(M)[k]$ for some $k>0$ . Choose $M':=M[-k]$ and it then follows from Lemma 4.3(b) that $\mathsf {Add}(M') \geqslant \mathsf {Add}(X) \geqslant \mathsf {Add}(M'[2k])$ .

(3) $\Rightarrow $ (1): First note that, as $\mathsf {T}$ is compactly generated, by Theorem 3.10 there are co-t-structures $(\mathsf {U}_X,\mathsf {V}_X)$ and $(\mathsf {U}_M,\mathsf {V}_M)$ with cohearts $\mathsf {Add}(X)$ and $\mathsf {Add}(M)$ , respectively. Aplying Lemma 4.5 on the set $\mathcal {S} = \{ M[k],X[k] \mid k<0\}$ , we obtain a co-t-structure

$$\begin{align*}(\mathsf{U}, \mathsf{V} := \mathsf{V}_M \cap \mathsf{V}_X). \end{align*}$$

We write $\mathsf {C} := \mathsf {U}[1] \cap \mathsf {V}$ for its coheart.

Consider now a decomposition of M with respect to this co-t-structure

(4.1)

with U in $\mathsf {U}$ and V in $\mathsf {V}$ . We claim that V is a complement for X. We proceed in a sequence of steps.

Step 1: We have $\mathsf {C} = \mathsf {Add}(X\oplus V)$ .

We first show that $\mathsf {Add}(X\oplus V) \subseteq \mathsf {C}$ . The object X lies in both $\mathsf {V}_X$ and $\mathsf {V}_M$ since it is large presilting and since $\mathsf {Add}(M)\geqslant \mathsf {Add}(X)$ by assumption, respectively. Moreover, since $\mathsf {V} \subseteq \mathsf {V}_X$ , it follows that $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {T}}(X,\mathsf {V}[1])=0$ , whence X lies in $\mathsf {U}[1] = {}^\perp \mathsf {V}[1]$ and we have that X lies in $\mathsf {C}$ . Similarly, as M belongs to $\mathsf {U}[1] = {}^\perp \mathsf {V}[1]$ , we observe from the triangle (4.1) that V lies in $\mathsf {U}[1]$ and, thus, in $\mathsf {C}$ . As $\mathsf {C}$ is closed under coproducts and direct summands, we see that $\mathsf {Add}(X\oplus V) \subseteq \mathsf {C}$ .

For the reverse inclusion, consider an object C of $\mathsf {C}$ together with an $\mathsf {Add}(X\oplus V)$ -precover $\varphi \colon K\to C$ , which exists since $\mathsf {T}$ has set-indexed coproducts. We have a triangle

and we claim that L lies in $\mathsf {V}[1]$ . It is clear that L lies in $\mathsf {V}$ since $\mathsf {V}$ is a suspended subcategory of $\mathsf {T}$ . Therefore, it remains only to show that $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {T}}(X,L)=0=\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {T}}(M,L)$ . For any map $f \colon X\longrightarrow L$ , we have that $\theta f = 0$ since K lies in $\mathsf {V}$ . Therefore, there is a map $\overline {f}\colon X\longrightarrow C$ such that $f=\psi \overline {f}$ . But $\varphi $ is an $\mathsf {Add}(X\oplus V)$ -precover and therefore $\overline {f}$ must factor through $\varphi $ , thus showing that $f=0$ and, hence, $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {T}}(X,L)=0$ . On the other hand, for any map $g\colon M\longrightarrow L$ , we also have that $\theta g=0$ . Thus, there is a map $\overline {g} \colon M\longrightarrow C$ such that $g=\psi \overline {g}$ . Since C lies in $\mathsf {V}$ , the map $\overline {g}$ must factor through the $\mathsf {V}$ -pre-envelope $\Psi $ from (4.1), that is, there is $\hat {g} \colon V \longrightarrow C$ such that $g = \psi \hat {g} \Psi $ . Again, because $\varphi $ is an $\mathsf {Add}(X\oplus V)$ -precover, $\hat {g}$ must factor through $\varphi $ , showing that $g=0$ . Hence L lies in $\mathsf {V}[1]$ as claimed, and thus $\psi =0$ and $\varphi $ is a split epimorphism. This proves that C lies in $\mathsf {Add}(X \oplus V)$ .

Step 2: The object $X \oplus V$ is a large presilting.

As $X\oplus V$ lies in the coheart of a co-t-structure, it satisfies $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {T}}(X\oplus V,X\oplus V[>0])=0$ . Since $\mathsf {V}$ is closed under coproducts, it suffices to show $\mathsf {V}_{X\oplus V} =\mathsf {V}$ . As $X\oplus V$ lies in $\mathsf {C} \subseteq \mathsf {U}[1]$ , we have that $\mathsf {V} \subseteq \mathsf {V}_{X\oplus V}$ . To see the reverse inclusion, we recall that by assumption and Lemma 4.3(a) there is $n>0$ such that $\mathsf {V}_{M[n]}\subseteq \mathsf {V}_X$ , and since $\mathsf {V}_M[n]=\mathsf {V}_{M[n]}$ and $\mathsf {V}=\mathsf {V}_X\cap \mathsf {V}_M$ , we find that

$$\begin{align*}\mathsf{V}_M[n] \subseteq \mathsf{V} \subseteq \mathsf{V}_M. \end{align*}$$

By Corollary 2.3, we have that M lies in $\mathsf {C}[-n] * \cdots * \mathsf {C}[-1] * \mathsf {C}$ . We conclude then that $\mathsf {V}_{\mathsf {C}} \subseteq \mathsf {V}_M$ , and since $\mathsf {C} = \mathsf {Add}(X\oplus V)$ by Step 1, we get the desired inclusion.

Step 3: The object $X\oplus V$ is a weak generator.

In order to conclude that $X\oplus V$ is a large silting object, by Remark 3.8 it suffices to show that $X\oplus V$ is a weak generator of $\mathsf {T}$ . We have seen in Step 2 that M lies in $\mathsf {thick}_{}(\mathsf {Add}(X\oplus V))$ . Hence, if Y lies in $(X\oplus V)[\mathbb {Z}]^\perp $ , it also lies in $M[\mathbb {Z}]^\perp $ . As M is a weak generator for $\mathsf {T}$ , it follows that $Y=0$ , as required.

We conclude that $X \oplus V$ is a large silting object and that V is a complement for X. This completes the proof of the equivalence of conditions (1), (2), and (3).

Finally, as shown above, for any large silting M satisfying the equivalent conditions (2) and (3), we can find a complement V of X such that $\mathsf {V}_M[n] \subseteq \mathsf {V}_{X\oplus V} \subseteq \mathsf {V}_M,$ and it follows from Corollary 2.3 and Theorem 3.10 that $\mathsf {thick}_{}(\mathsf {Add}(M))= \mathsf {thick}_{}(\mathsf {Add}(X\oplus V))$ .

Corollary 4.7. Let R be a coherent ring and let X be a large presilting object in $\mathsf {D}(R)$ . If X is a bounded complex of projective R-modules, then it admits a complement which is also a bounded complex of projective R-modules.

Proof. This follows directly from Theorem 4.6 since R is a large silting object in $\mathsf {D}(R)$ and X is a bounded complex of projective R-modules if and only if X lies in $\mathsf {thick}_{}(\mathsf {Add}(R))$ .

Remark 4.8. As a consequence of Corollary 4.7, every classic presilting object in $\mathsf {per}(R)$ admits a complement if we extend the ambient category to $\mathsf {D}(R)$ . In other words, classic presilting objects in $\mathsf {per}(R)$ admit complements if we regard them as large presilting objects in $\mathsf {D}(R)$ , cf. Remark 3.11. Moreover, these complements can always be found in $\mathsf {K}^b(\mathsf {Proj}(R))$ .

4.3 Complements to classic presilting

To establish a criterion for the existence of complements in the classic setting, we will imitate the strategy of Theorem 4.6. For this purpose, we need to associate co-t-structures to classic presilting objects. Fortunately, this happens frequently, as shown in the following proposition, which is essentially a reformulation of [26, Proposition 3.2].

Proposition 4.9. Let $\mathsf {T}$ be a triangulated category containing a classic silting subcategory. Let X be an object of $\mathsf {T}$ . The following statements hold.

1. 1. If $\mathsf {X}=\mathsf {add}(X)$ is precovering in $\mathsf {T}$ , then $\mathsf {X}$ is a classic presilting subcategory if and only if $(\mathsf {U}_{\mathsf {X}},\mathsf {V}_{\mathsf {X}})$ is a co-t-structure in $\mathsf {T}$ with coheart $\mathsf {X}$ .

2. 2. If $\mathsf {T}$ admits set-indexed self-coproducts, then $\mathsf {X}=\mathsf {Add}(X)$ is a classic presilting subcategory if and only if $(\mathsf {U}_{\mathsf {X}},\mathsf {V}_{\mathsf {X}})$ is a co-t-structure in $\mathsf {T}$ with coheart $\mathsf {X}$ .

Proof. Let $\mathsf {X}$ be a classic presilting subcategory in $\mathsf {T}$ . Observe first that assumption (P2) from [26, p. 7870] holds by Lemma 3.4 since we assume that $\mathsf {X}$ is additively generated by a single object. Moreover, by the proof of [26, Proposition 3.2], the following conditions are equivalent:

• • the subcategory $\mathsf {X}$ is precovering in $\mathsf {V}_{\mathsf {X}}$ , and assumption (P2) holds,

• • $(\mathsf {U}_{\mathsf {X}},\mathsf {V}_{\mathsf {X}}) $ is a co-t-structure in $\mathsf {T}$ with $\mathsf {U}_{\mathsf {X}}=\operatorname {\mathrm {\mathsf {cosusp}}}{\mathsf {X}[-1]}$ ,

and under these conditions $(\mathsf {U}_{\mathsf {X}},\mathsf {V}_{\mathsf {X}})$ has coheart $\mathsf {X}$ . This yields statement (1).

The proof of statement (2) is analogous once one observes that the existence of self-coproducts in $\mathsf {T}$ guarantees the existence of $\mathsf {Add}(X)$ -precovers. Indeed, for any object T of $\mathsf {T}$ an $\mathsf {Add}(X)$ -precover is given by taking the universal map $\varphi \colon X^{(\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {T}}(X,T))} \longrightarrow T$ .

Before stating our criterion for the existence of complements for classic presilting objects we need the following straightforward lemma.

Lemma 4.10. Suppose M is a classic silting object and X is a classic presilting object of $\mathsf {T}$ . Then X lies in $\mathsf {add}(M)$ if and only if $\mathsf {add}(M) \geqslant \mathsf {add}(X)$ and $\mathsf {add}(X) \geqslant \mathsf {add}(M)$ .

Proof. If X is an object of $\mathsf {add}(M)$ then the relations $\mathsf {add}(M) \geqslant \mathsf {add}(X)$ and $\mathsf {add}(X) \geqslant \mathsf {add}(M)$ are clear. Conversely, suppose $\mathsf {add}(M) \geqslant \mathsf {add}(X)$ and $\mathsf {add}(X) \geqslant \mathsf {add}(M)$ . Since $\mathsf {add}(M) \geqslant \mathsf {add}(X)$ , we have that X lies in $\mathsf {V}_M $ , and so we can decompose X as

$$\begin{align*}M_1 \to X \to V_1[1] \to M_1[1]\end{align*}$$

with $M_1$ in $\mathsf {add}(M)$ and $V_1$ in $\mathsf {V}_M$ . As $\mathsf {add}(X) \geqslant \mathsf {add}(M)$ , the morphism $X \to V_1[1]$ must be zero. Hence, the triangle splits and X is a direct summand of $M_1$ and thus an object of $\mathsf {add}(M)$ .

Theorem 4.11. Let $\mathsf {T}$ be a triangulated category such that $\mathsf {add}(T)$ is precovering for any object T in $\mathsf {T}$ . A classic presilting object X in $\mathsf {T}$ admits a complement if and only if there is a classic silting object M of $\mathsf {T}$ such that $\mathsf {add}(M) \geqslant \mathsf {add}(X)$ and for which the pair

$$\begin{align*}(\mathsf{U} := {}^\perp\mathsf{V}, \mathsf{V} := \mathsf{V}_X\cap\mathsf{V}_M), \end{align*}$$

is a co-t-structure. In this case we have that $\mathsf {add}(X)\geqslant \mathsf {add}(M[n])$ for some $n \geqslant 0$ .

Note that the condition that $\mathsf {add}(T)$ is precovering for any object T is automatically satisfied whenever $\mathsf {T}$ is a ${\mathbf {k}}$ -linear, Hom-finite triangulated category over a field ${\mathbf {k}}$ .

Proof. If X admits a complement, V say, then it is clear that $M = X \oplus V$ is a classic silting object satisfying the required conditions.

For the converse implication, suppose that M is a classic silting object M for which $\mathsf {add}(M) \geqslant \mathsf {add}(X)$ and such that $(\mathsf {U},\mathsf {V} := \mathsf {V}_X\cap \mathsf {V}_M)$ is a co-t-structure. If $\mathsf {add}(X) \geqslant \mathsf {add}(M)$ then $X \in \mathsf {add}(M)$ by Lemma 4.10 and M is, itself, a complement. Therefore, we assume that $\mathsf {add}(X) \ngeq \mathsf {add}(M)$ , in which case M does not lie in $\mathsf {V}$ . As in the proof of Theorem 4.6, we find a complement by truncating M with respect to $(\mathsf {U},\mathsf {V})$

(4.2)

Arguing as in Step 1 of the proof of Theorem 4.6, thanks to the assumption that the subcategory $\mathsf {add}(X\oplus V)$ is precovering, we conclude that $\mathsf {add}(X\oplus V)$ is the coheart of $(\mathsf {U},\mathsf {V})$ . In particular, $X\oplus V$ is a classic presilting object.

To see that $X \oplus V$ is a classic silting object, it is enough to check that $\mathsf {thick}_{}(M)=\mathsf {thick}_{}(X\oplus V)$ . By Lemma 3.4 there is $n>0$ such that $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {T}}(X,M[{>n}])=0$ , and we obtain $\mathsf {add}(M)\geqslant \mathsf {add}(X)\geqslant \mathsf {add}(M[n])$ . We can now proceed as in Step 2 of the proof of Theorem 4.6 to conclude that $\mathsf {V}_M[n] \subseteq \mathsf {V} \subseteq \mathsf {V}_M,$ and Corollary 2.3 yields $\mathsf {thick}_{}(M)=\mathsf {thick}_{}(X\oplus V)$ , as desired.

The following corollary applies to categories such as $\mathsf {K}^b(\mathsf {Proj}(R))$ or $\mathsf {D}^b(\mathsf {Mod}(R))$ which have the property that every object in them admits any set-indexed self-coproduct.

Corollary 4.12. Let $\mathsf {T}$ be a triangulated category admitting set-indexed self-coproducts. If X is an object such that $\mathsf {Add}(X)$ is a classic presilting subcategory, then there is a classic silting subcategory $\mathsf {N}$ containing $\mathsf {Add}(X)$ if and only if there is a classic silting subcategory $\mathsf {M}$ of $\mathsf {T}$ such that $\mathsf {M} \geqslant \mathsf {Add}(X)$ and there is a co-t-structure of the form $ (\mathsf {U},\mathsf {V} := \mathsf {V}_X \cap \mathsf {V}_{\mathsf {M}}). $

Proof. The existence of arbitrary self-coproducts in $\mathsf {T}$ implies that $\mathsf {Add}(Z)$ is precovering for any object Z in $\mathsf {T}$ . One can now apply the argument of the proof of Theorem 4.11 noting that as $\mathsf {M}$ is a classic silting subcategory, the classic silting subcategory $\mathsf {N}$ is constructed as $\mathsf {Add}(X \oplus V_M \mid M \in \mathsf {M})$ , where $V_M$ is constructed via the truncation triangles (4.2) as a $\mathsf {V}$ -pre-envelope of $M\in \mathsf {M}$ . Furthermore, the co-t-structure associated with $\mathsf {M}$ by Theorem 3.2 is bounded, so that there exists $n>0$ with $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {T}}(X,\mathsf {M}[>n])=0$ despite $\mathsf {M}$ being a silting subcategory rather than a silting object.

In light of the (proofs of) Theorems 4.6 and 4.11, we make the following definition.

Definition 4.13. Suppose X is a large (resp. classic) presilting object and M is a large (resp. classic) silting object. We call the large (resp. classic) silting object $V \oplus X$ constructed in the proof of Theorem 4.6 (resp. Theorem 4.11) the completion of X with respect to M.

5 Applications

In this section, we provide two immediate applications of our results in Section 4, namely, new proofs of the existence of complements for classic presilting objects in hereditary categories and of the classic Bongartz completion lemma for “two-term” presilting subcategories.

We recall the following well-known characterisation of split t-structures in terms of their hearts, cf. [18, Lemma 2.1 and Theorem 2.3] and [31, Proposition 1]. We include the argument for the convenience of the reader.

Proposition 5.1. Let $\mathsf {T}$ be a triangulated category and let $(\mathsf {V},\mathsf {W})$ be a bounded t-structure in $\mathsf {T}$ with heart $\mathsf {A}$ and associated cohomological functor $H \colon \mathsf {T} \to \mathsf {A}$ . Write ${H^i(X)=H(X[i])}$ for any X in $\mathsf {T}$ . The following conditions are equivalent.

1. (1) For all objects $A_1$ and $A_2$ of $\mathsf {A}$ , we have $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {T}}(A_1,A_2[2]) = 0$ .

2. (2) For each object T of $\mathsf {T}$ , we have $T \cong \bigoplus _{i \in \mathbb {Z}} H^{i}(T)[-i]$ .

3. (3) The t-structure $(\mathsf {V},\mathsf {W})$ is split.

Proof. $(1) \implies (2)$ . Observe that $\mathsf {A}[1] * \mathsf {A} = \mathsf {add}(\mathsf {A}[1],\mathsf {A})$ . The inclusion $\mathsf {A}[1] * \mathsf {A} \supseteq \mathsf {add}(\mathsf {A}[1],\mathsf {A})$ is clear, while the inclusion $\mathsf {A}[1] * \mathsf {A} \subseteq \mathsf {add}(\mathsf {A}[1],\mathsf {A})$ follows immediately from the condition $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {T}}(\mathsf {A},\mathsf {A}[2]) = 0$ . Finally, the characterisation of the boundedness of $(\mathsf {V},\mathsf {W})$ via

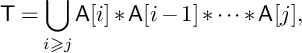$$\begin{align*}\mathsf{T} = \bigcup_{i \geqslant j} \mathsf{A}[i] * \mathsf{A}[i-1] * \cdots * \mathsf{A}[j], \end{align*}$$

and induction shows that

$$\begin{align*}\mathsf{T} = \bigcup_{i \geqslant j} \mathsf{add}(\mathsf{A}[i], \mathsf{A}[i-1], \ldots, \mathsf{A}[j]), \end{align*}$$

from which we see that each object of $\mathsf {T}$ decomposes into a direct sum of its cohomology with respect to $(\mathsf {V},\mathsf {W})$ .

$(2) \implies (3)$ . Write $T \cong \bigoplus _{i \in \mathbb {Z}} H^{i}(T)[-i]$ , the split triangle $\bigoplus _{i < 0} H^i(T)[-i] \to T \to \bigoplus _{i \geqslant 0} H^i(T)[-i] \to \big (\bigoplus _{i \le 0} H^i(T)[-i] \big )$ gives the truncation triangle for T.

$(3) \implies (1)$ . Take objects $A_1$ , $A_2$ of $\mathsf {A}$ and extend a morphism $A_1 \to A_2[2]$ to the triangle $A_2[1] \to C \to A_1 \to A_2[2]$ . As $A_2[1] \in \mathsf {A}[1] \subset \mathsf {V}$ and $A_1 \in \mathsf {A} \subset \mathsf {W}$ , this triangle is the truncation triangle of C with respect to the split t-structure $(\mathsf {V},\mathsf {W})$ , in which case the third map is zero.

We will be considering abelian categories $\mathsf {A}$ containing a projective object P such that every object of $\mathsf {A}$ is a quotient of an object in $\mathsf {add}(P)$ . In such categories, it is well known that if $\mathsf {A}$ has finite global dimension, then the bounded derived category $\mathsf {D}^b(\mathsf {A})$ is equivalent to the bounded homotopy category $\mathsf {K}^b(\mathsf {proj}(\mathsf {A}))$ of the additive category $\mathsf {proj}(\mathsf {A})=\mathsf {add}(P)$ of projective objects in $\mathsf {A}$ . This means, in particular, that P is a classic silting object in $\mathsf {D}^b(\mathsf {A}) = \mathsf {K}^b(\mathsf {proj}(\mathsf {A}))$ .

The following result intersects non-trivially [19, Theorem 1.2], which was proved using other methods. Recall that $\mathsf {A}$ is hereditary if $\operatorname {\mathrm {\mathsf {Ext}}}^2_{\mathsf {A}}(-,-) = 0$ .

Proposition 5.2 (Hereditary silting completion).

Suppose $\mathsf {A}$ is a hereditary abelian category with a projective object P such that every object in $\mathsf {A}$ is a quotient of an object in $\mathsf {add}(P)$ . Suppose further that $\mathsf {add}(T)$ is precovering for every object T in $\mathsf {D}^b(\mathsf {A})$ . If X is a classic presilting object in $\mathsf {D}^b(\mathsf {A})$ , then X admits a complement to a classic silting object in $\mathsf {D}^b(\mathsf {A})$ .

Proof. Under the hypotheses of the proposition, it is clear that P is a classic silting object in $\mathsf {D}^b(\mathsf {A})$ , and it is well known that the associated torsion pairs $(\mathsf {V}_P,\mathsf {W}_P)$ and $(\mathsf {U}_P,\mathsf {V}_P)$ in $\mathsf {D}^b(\mathsf {A})=\mathsf {thick}_{}(P)=\mathsf {K}^b(\mathsf {add}(P))$ are, respectively, the standard t-structure and its left adjacent co-t-structure. Note that the corresponding truncation triangles are given by the so-called smart and stupid truncations. Consider now the co-t-structure $(\mathsf {U}_X,\mathsf {V}_X)$ associated with the classic presilting object X (see Proposition 4.9(1)). We will show that $(\mathsf {add}(\mathsf {U}_P * \mathsf {U}_X),\mathsf {V}_P \cap \mathsf {V}_X)$ is a co-t-structure in $\mathsf {D}^b(\mathsf {A})$ . Closure under shifts and Hom-orthogonality are clear. Closure under summands is given by definition for $\mathsf {add}(\mathsf {U}_P * \mathsf {U}_X)$ and is clear for $\mathsf {V}_P \cap \mathsf {V}_X$ because it is defined by an orthogonality condition. It remains to obtain the decomposition triangle. Let D be an object of $\mathsf {D}^b(\mathsf {A})$ , consider the truncation triangle with respect to $(\mathsf {U}_P, \mathsf {V}_P)$ ,

$$\begin{align*}U_P \longrightarrow D \stackrel{f}{\longrightarrow} V_P \longrightarrow U_P[1]. \end{align*}$$

Now we truncate $V_P$ with respect to $(\mathsf {U}_X,\mathsf {V}_X)$ :

$$\begin{align*}U_X \longrightarrow V_P \stackrel{g}{\longrightarrow} V_X \longrightarrow U_X[1]. \end{align*}$$

Finally, we truncate $V_X$ with respect to the standard t-structure $(\mathsf {V}_P,\mathsf {W}_P)$ :

$$\begin{align*}\widetilde{V}_P \stackrel{h}{\longrightarrow} V_X \longrightarrow W_P \stackrel{0}{\longrightarrow} \widetilde{V}_P[1], \end{align*}$$

where $\widetilde {V}_P$ lies in $\mathsf {V}_P$ , $W_P$ lies in $\mathsf {W}_P$ and the third morphism is $0$ by Proposition 5.1 since $\mathsf {A}$ is hereditary and $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {D}^b(\mathsf {A})}(A_1, A_2[2]) = \operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {A}}(A_1,A_2[2])$ for objects $A_1$ and $A_2$ of $\mathsf {A}$ . In particular, $\widetilde {V}_P$ is a direct summand of $V_X$ and therefore lies in $\mathsf {V}_X$ and hence lies in $\mathsf {V}_P \cap \mathsf {V}_X$ . As $(\mathsf {V}_P, \mathsf {W}_P)$ is a t-structure, $h \colon \widetilde {V}_P \to V_X$ is a $\mathsf {V}_P$ -precover. Thus, there exists $\tilde {g} \colon V_P \to \widetilde {V}_P$ such that $g = h\tilde {g}$ . Applying the octahedral axiom to the composition $g = h\tilde {g}$ gives the following commutative diagram.

The split triangle forming the third column shows that C is a direct summand of $U_X$ and thus lies in $\mathsf {U}_X$ . Now applying the octahedral axiom to the composition $\tilde {g}f$ gives the following commutative diagram.

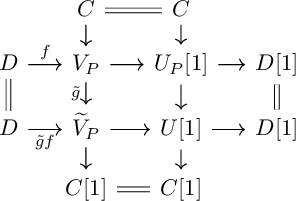
Observe that $U \in \mathsf {U}_P * \mathsf {U}_X$ , and hence

$$\begin{align*}U \longrightarrow D \stackrel{\tilde{g}f}{\longrightarrow} \widetilde{V}_P \longrightarrow U[1] \end{align*}$$

is a truncation triangle showing that $(\mathsf {add}(\mathsf {U}_P * \mathsf {U}_X),\mathsf {V}_P \cap \mathsf {V}_X)$ is a co-t-structure in $\mathsf {D}^b(\mathsf {A})$ and the result follows by Theorem 4.11.

Remark 5.3. Note that if $\mathsf {A}$ is a cocomplete hereditary abelian category with a projective generator P, then P is a silting object in $\mathsf {D}(\mathsf {A})$ and $\mathsf {D}^b(\mathsf {A})\cong \mathsf {K}^b(\mathsf {Proj}(\mathsf {A}))$ (see, e.g., [41, §4]). Thus, if $\mathsf {D}(\mathsf {A})$ is a compactly generated triangulated category, then a large presilting complex X in $\mathsf {D}^b(\mathsf {A})$ admits a complement to a large silting object in $\mathsf {D}(\mathsf {A})$ following Theorem 4.6 (just as argued in Corollary 4.7). Note, furthermore, that the complement found using Theorem 4.6 is an object in $\mathsf {D}^b(\mathsf {A})$ .

Next, we recover the classic Bongartz completion lemma for two-term classic presilting objects, see [21, §5], [45, Proposition 6.1], [17, Proposition 3.14].

Proposition 5.4 (Bongartz completion).

Let $\mathsf {T}$ be a triangulated category such that $\mathsf {add}(T)$ is precovering for any object T in $\mathsf {T}$ (e.g., a ${\mathbf {k}}$ -linear, Hom-finite triangulated category over a field ${\mathbf {k}}$ ). Let M be a classic silting object and X a classic presilting object in $\mathsf {T}$ which is two-term with respect to M, that is,

$$\begin{align*}\mathsf{add}(M)\ge\mathsf{add}(X)\ge\mathsf{add}(M[1]). \end{align*}$$

Then $\mathsf {V}_M \cap \mathsf {V}_X$ is the coaisle of a co-t-structure. In particular, there is V in $\mathsf {T}$ such that $X\oplus V$ is a classic silting object with $\mathsf {V}_{X\oplus V} = \mathsf {V}_M \cap \mathsf {V}_X$ .

Proof. We show that $(\mathsf {add}(\mathsf {U}_M * \mathsf {U}_X), \mathsf {V}_M \cap \mathsf {V}_X)$ is a co-t-structure in $\mathsf {T}$ . Closure under shifts, closure under summands and Hom-orthogonality are clear. It remains to obtain a decomposition triangle for each object T in $\mathsf {T}$ . We truncate first with respect to $(\mathsf {U}_M, \mathsf {V}_M)$ and then with respect to $(\mathsf {U}_X, \mathsf {V}_X)$ , which is a co-t-structure with coheart $\mathsf {add}(X)$ by Proposition 4.9. We obtain triangles

$$\begin{align*}U_M \longrightarrow T \stackrel{f}{\longrightarrow} V_M \longrightarrow U_M[1] \quad \text{and} \quad U_X \longrightarrow V_M \stackrel{g}{\longrightarrow} V_X \longrightarrow U_X[1], \end{align*}$$

with $U_M$ in $\mathsf {U}_M$ , $V_M$ in $\mathsf {V}_M$ , $U_X$ in $\mathsf {U}_X$ , and $V_X$ in $\mathsf {V}_X$ . By assumption and Lemma 4.3(a), we see that $V_M[1]$ lies in $\mathsf {V}_X$ , and so does $U_X[1]$ . Thus $U_X[1]$ lies in $\mathsf {C}_X = \mathsf {add}(X) \subseteq \mathsf {V}_M$ . Hence, $V_X$ lies in $\mathsf {V}_M \cap \mathsf {V}_X$ . Using the octahedral axiom, we get a triangle

$$\begin{align*}U \longrightarrow T \stackrel{gf}{\longrightarrow} V_X \longrightarrow U[1], \end{align*}$$

with U lying in $\mathsf {U}_M * \mathsf {U}_X$ , and we conclude that $(\mathsf {add}(\mathsf {U}_M * \mathsf {U}_X), \mathsf {V}_M \cap \mathsf {V}_X)$ is a co-t-structure. The existence of a complement now follows from Theorem 4.11.

Remark 5.5. In each of Propositions 5.2 and 5.4, we obtain a truncation triangle for the co-t-structure $(\mathsf {add}(\mathsf {U}_M * \mathsf {U}_X), \mathsf {V}_M \cap \mathsf {V}_X)$ by first truncating an object of $\mathsf {T}$ with respect to $(\mathsf {U}_M, \mathsf {V}_M)$ and then truncating the resulting object of $\mathsf {V}_M$ with respect to $(\mathsf {U}_X, \mathsf {V}_X)$ . One then observes, using two different arguments, that the object of $\mathsf {V}_X$ resulting from the second truncation is also an object of $\mathsf {V}_M$ . This is an example in which the naive truncation algorithm of [16, §2] terminates after two steps; see also [12]. It would be interesting to find conditions under which the naive or refined truncation algorithm [16, §3] terminates after finitely many steps (e.g., [16, Theorem 6.1]).

The (complete) silting object with respect to which the complement is taken matters. Attempting to complete a given presilting object with respect to different (complete) silting objects may yield different completions, or even a completion in one case and no completion in the other. The examples below exhibit both of these kinds of behavior.

Example 5.6. Let Q be the $A_3$ quiver below and let ${\mathbf {k}} Q$ be its path algebra.

Let $X = S_1$ , which is a classic presilting object in $\mathsf {D}^b({\mathbf {k}} Q)$ . We consider completions of X with respect to two different classic silting objects in $\mathsf {D}^b({\mathbf {k}} Q)$ . Consider the classic silting object $M = P_1 \oplus P_2 \oplus P_3$ . Then applying Theorem 4.11, we obtain the completion $V \oplus X = P_1 \oplus P_3 \oplus S_1$ from the decomposition triangle

$$\begin{align*}S_1[-1] \to P_3 \oplus P_2 \oplus P_3 \to P_3 \oplus P_1 \oplus P_1 \to S_1. \end{align*}$$

Now consider the classic silting object $N = P_2 \oplus P_1 \oplus S_2$ . In this case, applying Theorem 4.11 gives us the completion $V' \oplus X = P_1 \oplus I_2 \oplus S_1$ from the decomposition triangle

$$\begin{align*}S_1[-1] \oplus S_1[-1] \to P_2 \oplus P_1 \oplus S_2 \to P_1 \oplus P_1 \oplus I_2 \to S_1 \oplus S_1. \end{align*}$$

Note that the complement need not be basic; in each case, we have given the basic version.

The following example is based on the method in [16].

Example 5.7. Let Q be the $\widetilde {A}_2$ quiver below and let ${\mathbf {k}} Q$ be its path algebra.

The object $P_1 \oplus P_3 \oplus \tau S_2$ is a tilting object in $\mathsf {D}^b({\mathbf {k}} Q)$ , from which we deduce that is a classic silting object in $\mathsf {D}^b({\mathbf {k}} Q)$ . Let . Since $S_2$ is rigid, X is a classic presilting object in $\mathsf {D}^b({\mathbf {k}} Q)$ which lies in $\operatorname {\mathrm {\mathsf {susp}}} M = \mathsf {V}_M$ and $M[2] \in \mathsf {V}_X$ . By Proposition 4.9, $(\operatorname {\mathrm {\mathsf {cosusp}}} X[-1], \mathsf {V}_X)$ is a co-t-structure in $\mathsf {D}^b({\mathbf {k}} Q)$ . Consider

The suspended subcategory $\mathsf {V}$ is not pre-enveloping in $\mathsf {D}^b({\mathbf {k}} Q)$ and therefore it is not the co-aisle of a co-t-structure, see Figure 1 on page 18 for an illustration. Hence, X cannot be completed with respect to M. However, X can be completed with respect to because X is two-term with respect to N (see Proposition 5.4).

Figure 1 Each figure shows a region of the Auslander–Reiten quiver of $\mathsf {D}^b({\mathbf {k}} Q)$ . Top: the coaisle $\mathsf {V}_M$ associated with the silting object M is marked in red, with the silting object M marked in deeper red. Middle: the (unbounded) coaisle $\mathsf {V}_X$ associated with the presilting object $X = S_2[2] \in \mathsf {V}_M$ is marked in blue. Bottom: the intersection . One can see that no object in the transjective component containing the shifted projective objects admits a left $\mathsf {V}$ -approximation. $\mathsf {V}$ is not the coaisle of a co-t-structure.

6 Silting-discrete finite-dimensional algebras

In this section, $\Lambda $ will be a finite-dimensional algebra over a field ${\mathbf {k}}$ .

6.1 Classic silting objects versus large silting objects

We have seen in Remark 3.11 that an object M in $\mathsf {per}(\Lambda )$ is a classic silting object in $\mathsf {per}(\Lambda )$ if and only if it is a large silting object in $\mathsf {D}(\Lambda )$ . Consider the following pairs

where the orthogonals are taken inside $\mathsf {D}(\Lambda )$ .

Proposition 6.1 [24, Theorem 1.3], [38, Corollary 2], [41, Proposition 4.3], [33, Proposition 5.4].

Let $M \in \mathsf {per}(\Lambda )$ be a classic silting object.

1. 1. The pair of subcategories $(\mathsf {V}_M, \mathsf {W}_M)$ is a t-structure in $\mathsf {D}(\Lambda )$ .

2. 2. The cohomological functor $H^0_M \colon \mathsf {D}(\Lambda )\to \mathsf {H}_M$ associated with the t-structure $(\mathsf {V}_M,\mathsf {W}_M)$ induces an equivalence

   $$\begin{align*}H^0_M|_{\mathsf{Add}(M)} \colon \mathsf{Add}(M) \to \mathsf{Proj}(\mathsf{H}_M). \end{align*}$$
   In particular, $H^0(M)$ is a small projective generator of $\mathsf {H}_M$ , and the heart $\mathsf {H}_M$ is equivalent to $\mathsf {Mod}(\operatorname {\mathrm {\mathsf {End}}}(H^0(M)))$ .

3. 3. The pair $(\mathsf {v}_M,\mathsf {w}_M)$ is a t-structure in $\mathsf {D}^b(\Lambda )$ whose heart $\mathsf {h}_M$ is equivalent to $\mathsf {mod}(\operatorname {\mathrm {\mathsf {End}}}(M))$ .

We denote the class of large silting objects in $\mathsf {D}(\Lambda )$ , up to equivalence, by $\mathsf {Silt}(\Lambda )$ . Similarly, the class of classic silting objects in $\mathsf {per}(\Lambda )$ , up to equivalence, is denoted by $\mathsf {silt}(\Lambda )$ . As discussed in Remark 3.11, there is an embedding of $\mathsf {silt}(\Lambda )$ into $\mathsf {Silt}(\Lambda )$ and, by abuse of notation, we shall write $\mathsf {silt}(\Lambda ) \subseteq \mathsf {Silt}(\Lambda )$ . For a classic silting object M in $\mathsf {per}(\Lambda )$ and $n \ge 1$ , the partial order in Definition 4.2 defines the following subclasses of $\mathsf {Silt}(\Lambda )$ :

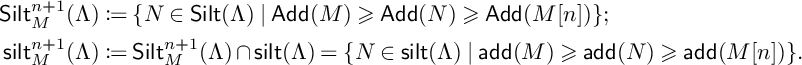
6.2 Silting modules, $\tau $ -tilting finiteness and silting discreteness

Silting modules were introduced in [7] as infinite-dimensional analogs of support $\tau $ -tilting modules. For the original definition of support $\tau $ -tilting module we refer to [1].

Definition 6.2 [7, Definition 3.7].

A $\Lambda $ -module M is a silting module if there is an exact sequence

with P and Q projective $\Lambda $ -modules such that the class

coincides with the class $\mathsf {Gen}(M)$ of modules which are epimorphic images of coproducts of M. Two silting modules M and N are said to be equivalent if $\mathsf {Add}(M)=\mathsf {Add}(N)$ .

Over a finite-dimensional algebra, a module is support $\tau $ -tilting if and only if it a finite-dimensional silting module [7, Proposition 3.15]. A finite-dimensional algebra is $\tau $ -tilting-finite if it has only finitely many support $\tau $ -tilting modules up to equivalence [20]. It turns out that these are precisely the algebras whose silting modules coincide, up to equivalence, with the support $\tau $ -tilting modules.

Theorem 6.3 [8, Theorem 4.8].

The following are equivalent for a finite-dimensional ${\mathbf {k}}$ -algebra $\Lambda $ .

1. 1. $\Lambda $ is $\tau $ -tilting-finite.

2. 2. Every silting $\Lambda $ -module is finite dimensional up to equivalence.

3. 3. Every torsion pair in $\mathsf {Mod}(\Lambda )$ is of the form $\mathsf {Gen}(T)$ for a finite-dimensional silting module T.

The triangulated category analog of $\tau $ -tilting finiteness is silting discreteness [4]. We recall the following characterization of a silting-discrete finite-dimensional algebra.

Theorem 6.4. The following statements are equivalent for $\Lambda $ .

1. 1. For any M in $\mathsf {silt}(\Lambda )$ and any $n>1$ , the set $\mathsf {silt}^{n}_{M}(\Lambda )$ is finite.

2. 2. For any M in $\mathsf {silt}(\Lambda )$ , the set $\mathsf {silt}^{2}_{M}(\Lambda )$ is finite.

3. 3. For any M in $\mathsf {silt}(\Lambda )$ , the finite-dimensional algebra $\operatorname {\mathrm {\mathsf {End}}}(M)$ is $\tau $ -tilting finite.

If these equivalent conditions hold then $\Lambda $ is called silting discrete.

Proof. The assertion $(1)\Leftrightarrow (2)$ is [4, Theorem 2.4], and the assertion $(2)\Leftrightarrow (3)$ is [25, Theorem 4.6].

6.3 Another characterisation of silting discreteness

In this section, we add a further characterization to the list in Theorem 6.4 by proving that silting-discrete finite-dimensional algebras are those whose large, bounded silting theory in $\mathsf {D}(\Lambda )$ coincides with the classic silting theory in $\mathsf {per}(\Lambda )$ . This can be regarded as a triangulated version of Theorem 6.3.

Theorem 6.5. A finite-dimensional algebra $\Lambda $ is silting discrete if and only if every large silting object in $\mathsf {D}(\Lambda )$ which lies in $\mathsf {K}^b(\mathsf {Proj}(\Lambda ))$ is perfect up to equivalence. In other words, $\Lambda $ is silting discrete if and only if $\mathsf {Silt}^{n}_{\Lambda }(\Lambda ) = \mathsf {silt}^{n}_{\Lambda }(\Lambda )$ for each $n>1$ .

We recover the following result of Aihara and Mizuno immediately from Theorem 6.5.

Corollary 6.6 [4, Theorem 2.15].

Let $\Lambda $ be a silting-discrete finite-dimensional algebra. Then every classic presilting object X in $\mathsf {per}(\Lambda )$ admits a complement in $\mathsf {per}(\Lambda )$ .

Proof. It follows from Remark 4.8 that X admits a complement to a large silting object in $\mathsf {D}(\Lambda )$ , that is, there is V such that $X\oplus V$ is large silting in $\mathsf {D}(\Lambda )$ , and moreover, V can be chosen in $\mathsf {K}^b(\mathsf {Proj}(\Lambda ))$ . Therefore $X\oplus V$ is a large silting object that is a bounded complex of projective $\Lambda $ -modules, and by Theorem 6.5, it is equivalent to a classic silting object in $\mathsf {per}(\Lambda )$ .

The rest of this section is devoted to the proof of Theorem 6.5. For the reverse implication, we will need the following generalization of [1, Theorem 3.2] and [7, Theorem 4.9] which follows the spirit of [25] in making a ‘basis-free’ statement.

Proposition 6.7. Let M a classic silting object in $\mathsf {per}(\Lambda )$ . Write $\Gamma =\operatorname {\mathrm {\mathsf {End}}}(M)$ and let $H^0:=H^0_M \colon \mathsf {D}(\Lambda ) \to \mathsf {Mod}(\Gamma )$ be the cohomological functor associated with the t-structure $(\mathsf {V}_M,\mathsf {W}_M)$ according to Proposition 6.1. There is a bijection

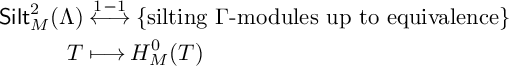$$ \begin{align*} \mathsf{Silt}^{2}_{M}(\Lambda) & \stackrel{1-1}{\longleftrightarrow} \{\text{silting}\ \Gamma\text{-modules up to equivalence}\} \\ T & \longmapsto H^0_M(T) \end{align*} $$

which restricts to a bijection

$$\begin{align*}\mathsf{silt}^{2}_{M}(\Lambda) \stackrel{1-1}{\longleftrightarrow} \{\text{support}\ \tau\text{-tilting}\ \Gamma\text{-modules up to equivalence}\}. \end{align*}$$

Proof. We fix the notation $\mathsf {U}_T:={}^\perp \mathsf {V}_T$ and $\mathsf {U}_M:={}^\perp \mathsf {V}_M$ for the left orthogonal subcategories of $\mathsf {V}_T$ and $\mathsf {V}_M$ in $\mathsf {D}(\Lambda )$ , as in previous sections.

We begin by showing the assignment is well defined. Suppose T is an object in $\mathsf {D}(\Lambda )$ that lies in $\mathsf {Silt}^{2}_{M}(\Lambda )$ . By Lemma 4.3(2) there is a triangle of the form

with $M_0$ and $M_1$ in $\mathsf {Add}(M)$ . By Proposition 6.1(2), applying the cohomological functor $H^0$ to this triangle we obtain a projective presentation of $H^0(T)$ :

We claim that $H^0(T)$ is a silting $\Gamma $ -module with respect to the projective presentation $\sigma $ .

Step 1: A $\Gamma $ -module X, regarded as an object of $\mathsf {H}_M$ , lies in $\mathcal {D}_\sigma $ if and only if it lies in $\mathsf {V}_T$ , or equivalently, $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {D}(\Lambda )}(T,X[1])=0$ .

The canonical maps $h_1 \colon M_1 \to H^0(M_1)$ and $h_2 \colon M_0 \to H^0(M_0)$ induce the following commutative diagram.

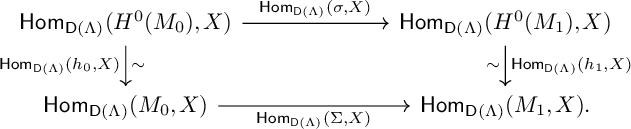
From this, we conclude that X lies in $\mathcal {D}_\sigma $ if and only if $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {D}(\Lambda )}(\Sigma ,X)$ is surjective. This occurs if and only if $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {D}(\Lambda )}(T,X[1])=0$ as $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {D}(\Lambda )}(M_0,X[1])=0$ . Moreover, this happens if and only if X lies in $\mathsf {V}_T$ . Indeed, X already lies in $V_T[-1]$ as $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {D}(\Lambda )}(T,X[i])=0$ for all $i>1$ because T lies in $\mathsf {U}_T[1]\subseteq \mathsf {U}_M[2]$ . This latter claim follows from the assumption $\mathsf {V}_M[1]\subseteq \mathsf {V}_T$ , which gives $\mathsf {U}_T\subseteq \mathsf {U}_M[1]$ .

Step 2: We have $\mathsf {Gen}(H^0(T)) \subseteq \mathcal {D}_\sigma $ .

It suffices to show that ${H^0(T)^{(I)}} $ lies in $ \mathcal {D}_\sigma $ for any set I, because $\mathcal {D}_\sigma $ is closed under quotients. Note that $H^0(T)^{(I)}\cong H^0(T^{(I)})$ because M is compact. As T and $T^{(I)}$ lie in $\mathsf {V}_M$ , truncating with respect to $(\mathsf {V}_M[1],\mathsf {W}_M[1])$ gives a triangle

As $\mathsf {V}_M[1]\subseteq \mathsf {V}_T$ and $T^{(I)} \in \mathsf {V}_T$ because T is large presilting, it follows that $H^0(T^{(I)})$ lies in $\mathsf {V}_T$ , and thus in $ \mathcal {D}_\sigma $ by Step 1.

Step 3: We have $\mathcal {D}_\sigma \subseteq \mathsf {Gen}(H^0(T))$ .

Let X be an object in $\mathcal {D}_\sigma $ and take the universal map $u\colon H^0(T)^{(I)} \to X$ , where I is a basis for the ${\mathbf {k}}$ -vector space $\operatorname {\mathrm {\mathsf {Hom}}}_\Gamma (H^0(T),X)$ . In order to prove that u is an epimorphism in $\mathsf {H}_M$ , we use the fact that $H^0(T)^{(I)}\cong H^0(T^{(I)})$ again and consider the triangle

We show that $H^0(K)=0$ . Since $H^0(M)$ is a projective generator of $\mathsf {H}_M$ by Proposition 6.1(2), this amounts to showing that $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {D}(\Lambda )}(M,K)=0$ . Now, by assumption $\mathsf {Add}(T)[-1]\ge \mathsf {Add}(M)\ge \mathsf {Add}(T)$ , so we know from Lemma 4.3(2) that M lies in $\mathsf {Add}(T[-1]) \ast \mathsf {Add}(T)$ . Thus, it suffices to check that

$$\begin{align*}\operatorname{\mathrm{\mathsf{Hom}}}_{\mathsf{D}(\Lambda)}(T,K)=0=\operatorname{\mathrm{\mathsf{Hom}}}_{\mathsf{D}(\Lambda)}(T,K[1]).\end{align*}$$

Since X is an object of $\mathsf {H}_M$ , any morphism $T \to X$ factors through the canonical map $T \to H^0(T)$ . This shows that $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {T}}(T,u)$ is an epimorphism. It follows that $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {D}(\Lambda )}(T,K)=0$ since $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {D}(\Lambda )}(T,H^0(T)^{(I)}[1])=0$ from Step 2. Moreover, as X lies in $\mathcal {D}_\sigma $ , we have from Step 1 that $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {D}(\Lambda )}(T,X[1])=0$ , and we conclude that $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {D}(\Lambda )}(T,K[1])=0$ . Hence we have that X lies in $\mathsf {Gen}(H^0(T))$ as claimed.

We have thus shown that the assignment $T \mapsto H^0(T)$ is well defined. In order to prove the bijectivity of this map, we observe the following.

Step 4: We have $\mathsf {V}_T=\mathsf {V}_M[1] * \mathsf {Gen}(H^0(T))$ .

Indeed, we have that $\mathsf {V}_M[1] * \mathsf {Gen}(H^0(T)) \subseteq \mathsf {V}_T$ by assumption and Step 1. For the reverse inclusion, truncate an object X in $\mathsf {V}_T$ with respect to the t-structure $(\mathsf {V}_M[1], \mathsf {W}_M[1])$

where, again, $W[1]=H^0(X)$ lies in $\mathsf {H}_M$ because $\mathsf {V}_T$ is contained in $\mathsf {V}_M$ . Now, $H^0(X)$ lies in $\mathsf {V}_T$ since $\mathsf {V}_M[1] \subseteq \mathsf {V}_T$ , whence $H^0(X)$ lies in $\mathcal {D}_\sigma = \mathsf {Gen}(H^0(T))$ by Step 1.

Step 5: The assignment $T \mapsto H^0(T)$ is injective.

Suppose $T_1$ and $T_2$ are objects of $\mathsf {Silt}^{2}_{M}(\Lambda )$ such that $\mathsf {Add}(H^0(T_1)) = \mathsf {Add}(H^0(T_2))$ . Then $\mathsf {Gen}(H^0(T_1)) = \mathsf {Gen}(H^0(T_2))$ , and by Step 4 we have $\mathsf {V}_{T_1} = \mathsf {V}_{T_2}$ . Now we use Theorem 3.10 asserting that a silting object is determined by the co-t-structure up to equivalence.

Step 6: The assignment $T \mapsto H^0(T)$ is surjective.

Suppose Y is a silting $\Gamma $ -module with respect to a map $\sigma \colon H^0(M_1)\to H^0(M_0)$ . By Proposition 6.1(2), $H^0|_{\mathsf {Add}(M)} \colon \mathsf {Add}(M) \to \mathsf {Proj}(\mathsf {H}_M) = \mathsf {Add}(H^0(M))$ is an equivalence, and so, there is a unique map $\Sigma \colon M_1 \to M_0$ such that $H^0(\Sigma )=\sigma $ . Thus, we set T to be the cone of $\Sigma $ , that is, we consider the triangle

from which we observe that $H^0(T)=Y$ and that T lies in $\mathsf {Add}(M)\ast \mathsf {Add}(M[1])$ . We check that T is a large silting object using Theorem 4.4. By the construction of T it is clear that T lies in $\mathsf {V}_M$ and that $\mathsf {V}_M[1]\subseteq \mathsf {V}_T$ . It remains to see that $\mathsf {Add}(T)$ is contained in $\mathsf {V}_T$ and that T is a weak generator.

We first show that $\mathsf {Add}(T)$ is contained in $\mathsf {V}_T$ . For a $\Gamma $ -module X, applying $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {D}(\Lambda )}(-,X)$ to the triangle above tells us that $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {D}(\Lambda )}(T,X[1])=0$ if and only if $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {D}(\Lambda )}(\Sigma , X)$ is surjective. Consider the commutative diagram:

(*)

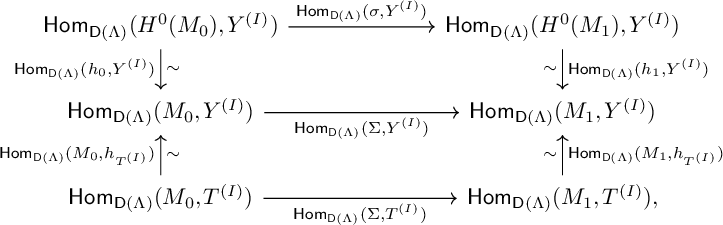
where $h_{T^{(I)}}\colon T^{(I)}\to H^0(T^{(I)})\cong H^0(T)^{(I)}=Y^{(I)}$ , $h_1\colon M_1\to H^0(M_1)$ and $h_0\colon M_0\to H^0(M_0)$ are the canonical maps coming from the fact that $M_1$ , $M_0$ , and $T^{(I)}$ lie in $\mathsf {V}_M$ . The top vertical maps are isomorphisms as in Step 1, and the bottom vertical maps are isomorphisms because M is silting and T lies in $\mathsf {V}_M$ . Since, by assumption, Y is a silting module with respect to $\sigma $ it follows that $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {D}(\Lambda )}(\Sigma ,T^{(I)})$ is surjective, as required.

Next, we argue that T is a weak generator exactly as in the proof of (4) $\Rightarrow $ (1) in [7, Theorem 4.9]; we transcribe the proof to our setting and notation for the convenience of the reader. Let Z be an object in $\mathsf {T}$ for which $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {D}(\Lambda )}(T,Z[j])=0$ for all j in $\mathbb {Z}$ . For i in $\mathbb {Z}$ , let $v_i$ denote the right adjoint of the inclusion of $\mathsf {V}_M[i]$ into $\mathsf {T}$ (i.e., $v_i$ is the truncation with respect to $\mathsf {V}_M[i]$ ). Since T lies in $\mathsf {V}_M$ , it follows that $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {D}(\Lambda )}(T,-)\cong \operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {D}(\Lambda )}(T,v_0(-))$ and, as $\mathsf {V}_M[1] \subseteq \mathsf {V}_T$ , there is a natural epimorphism

Hence, $H^j(Z)$ lies in the torsionfree class $Y^\perp $ in $\mathsf {H}_M$ for all j in $\mathbb {Z}$ . From the triangle

$$\begin{align*}H^0(Z[j+1])[-1] \longrightarrow v_1(Z[j+1]) \longrightarrow v_0(Z[j+1]) \longrightarrow H^0(Z[j+1]) \end{align*}$$

we deduce that $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {D}(\Lambda )}(T,v_1(Z[j+1]))=0$ . Notice that $v_1(Z[j+1])\cong v_0(Z[j])[1]$ , and thus $v_0(Z[j])$ lies in $\mathsf {V}_T$ for all j in $\mathbb {Z}$ . This implies that $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {D}(\Lambda )}(\Sigma ,v_0(Z[j]))$ is surjective and, using a diagram as in (*) above, that $\operatorname {\mathrm {\mathsf {Hom}}}_{\mathsf {D}(\Lambda )}(\sigma ,H^0(Z[j]))$ is surjective. This shows that $H^j(Z)$ lies in $\mathcal {D}_\sigma $ for all j in $\mathbb {Z}$ . Since $(\mathcal {D}_\sigma ,Y^\perp )$ is a torsion pair in $\mathsf {H}_M$ , we conclude that $H^j(Z)=0$ for all j and, since $(\mathsf {V}_M,\mathsf {W}_M)$ is nondegenerate, we conclude that $Z=0$ . This concludes the proof that T is indeed a large silting object in $\mathsf {D}(\Lambda )$ .

Thus, $T \mapsto H^0(T)$ is a bijection between silting $\Gamma $ -modules and $\mathsf {Silt}^{2}_{M}(\Lambda )$ .

Step 7: The assignment $T \mapsto H^0(T)$ restricts to bijection $\mathsf {silt}^{2}_{M}(\Lambda )$ and support $\tau $ -tilting $\Gamma $ -modules.

This bijection is well known, see [25, Theorem 4.6]. However, for completeness, we explain how the statement can be recovered as a restriction of the assignment in the cocomplete case above.

If T is compact, then T is an object in $\mathsf {add}(M) * \mathsf {add}(M[1])$ and, therefore, $H^0(T)$ is a finite-dimensional $\Gamma $ -module. Conversely, suppose $H^0(T)$ is a finite-dimensional silting $\Gamma $ -module witnessed by a projective presentation $\sigma $ in $\mathsf {proj}(\mathsf {H}_M) = \mathsf {add}(H^0(M))$ . As in Step 6, we can lift $\sigma $ to a map $\Sigma $ in $\mathsf {add}(M)$ . We then observe that the cone of $\Sigma $ is a compact silting object lying in $\mathsf {silt}^{2}_{M}(\Lambda )$ and whose zeroth cohomology is $H^0(T)$ .

We now turn to the forward implication in Theorem 6.5, which is implicitly contained in [40, Lemma 3.5]. We provide details for the convenience of the reader.

Lemma 6.8. Let $\Lambda $ be a silting-discrete, finite-dimensional ${\mathbf {k}}$ -algebra. Suppose M and S are large silting objects such that S lies in $\mathsf {per}(\Lambda )$ and M lies in $\mathsf {Silt}^{n}_{S}(\Lambda )$ for some natural number $n \geqslant 1$ . Then there exists a large silting object T in $\mathsf {per}(\Lambda )$ such that M lies in $\mathsf {Silt}^{2}_{T}(\Lambda )$ . In particular, $\mathsf {Silt}^{n}_{\Lambda }(\Lambda ) = \mathsf {silt}^{n}_{\Lambda }(\Lambda )$ for all $n> 0$ .

Proof. As M lies in $\mathsf {Silt}^{n}_{S}(\Lambda )$ , we have $\mathsf {V}_S[n] \subseteq \mathsf {V}_M \subseteq \mathsf {V}_S$ , or equivalently, $\mathsf {W}_S[n] \supseteq \mathsf {W}_M \supseteq \mathsf {W}_S$ . By Proposition 6.1(3), the pair $(\mathsf {v}_S,\mathsf {w}_S) = (\mathsf {V}_S \cap \mathsf {D}^b(\Lambda ), \mathsf {W}_S \cap \mathsf {D}^b(\Lambda ))$ is a t-structure in $\mathsf {D}^b(\Lambda )$ with heart $\mathsf {h}_S \simeq \mathsf {mod}(\Gamma )$ , where $\Gamma := \operatorname {\mathrm {\mathsf {End}}}_{\mathsf {D}(\Lambda )}(S)$ . Applying Lemma 4.5 on the set $\{S[k+1], M[k]\mid k\ge 0\}$ , we obtain a t-structure

$$\begin{align*}(\mathsf{V}, \mathsf{W}:= \mathsf{W}_S[1] \cap \mathsf{W}_M\big) \text{ in } \mathsf{D}(\Lambda). \end{align*}$$

One can check that

(6.1) $$ \begin{align}\mathsf{W}[n-1] \supseteq \mathsf{W}_M \supseteq \mathsf{W},\end{align} $$

(6.2) $$ \begin{align}\mathsf{W}_S[1] \supseteq \mathsf{W} \supseteq \mathsf{W}_S.\end{align} $$

It suffices to find a large silting object $N \in \mathsf {per}(\Lambda )$ such that $(\mathsf {V}, \mathsf {W}) = (\mathsf {V}_N, \mathsf {W}_N).$ Indeed, M then lies in $\mathsf {Silt}^{n-1}_{N}(\Lambda )$ by (6.1), and the result follows by induction.

The inclusions (6.2) show that the t-structure $(\mathsf {V} , \mathsf {W})$ is a Happel–Reiten–Smalø tilt of $(\mathsf {V}_S, \mathsf {W}_S)$ (see [23, Proposition 2.1]), that is, there is a torsion pair $(\mathcal {T},\mathcal {F})$ in $\mathsf {H}_S$ such that $(\mathsf {V} , \mathsf {W}) = (\mathsf {V}_S[1] * \mathcal {T}, \mathcal {F} * \mathsf {W}_S)$ , see for example [46, Proposition 2.1]. Since $\Lambda $ is silting discrete, it follows from Theorem 6.4 that $\Gamma $ is $\tau $ -tilting finite and, therefore, by Theorem 6.3, we have that $\mathcal {T}=\mathsf {Gen}(Y)$ , for a finite-dimensional silting $\Gamma $ -module. By Proposition 6.7, $Y=H^0(N)$ for some silting object N in $\mathsf {silt}^2_S(\Lambda )$ and, by Step 4 of proof of Proposition 6.7, it follows that $\mathsf {V}_N=\mathsf {V}_S[1] * \mathcal {T}=\mathsf {V}$ , as wanted.

For the last statement, pick an object T in $\mathsf {Silt}^{n}_{\Lambda }(\Lambda )$ . It lies in $\mathsf {Silt}^{2}_{M}(\Lambda )$ for some classic silting object in $\mathsf {per}(\Lambda )$ and corresponds to some silting $\operatorname {\mathrm {\mathsf {End}}}(M)$ -module under the bijection in Proposition 6.7. By assumption $\operatorname {\mathrm {\mathsf {End}}}(M)$ is $\tau $ -tilting finite, and by Theorem 6.3 we obtain that T lies in $\mathsf {silt}^{2}_{M}(\Lambda )$ . So T is a perfect complex and lies in $\mathsf {silt}^{n}_{\Lambda }(\Lambda )$ .

Proof of Theorem 6.5

One implication has just been proven in Lemma 6.8. For the other implication, suppose $\mathsf {Silt}^{n}_{\Lambda }(\Lambda ) = \mathsf {silt}^{n}_{\Lambda }(\Lambda )$ for all $n> 1$ . Given a classic silting object M in $\mathsf {per}(\Lambda )$ , it follows that $\mathsf {Silt}^{2}_{M}(\Lambda ) = \mathsf {silt}^{2}_{M}(\Lambda )$ . Indeed, as $M \in \mathsf {per}(\Lambda )$ there exists $n> 1$ such that $M \in \mathsf {Silt}^{n}_{\Lambda }(\Lambda )$ . Hence, for $N \in \mathsf {Silt}^{2}_{M}(\Lambda )$ , we have $N \in \mathsf {Silt}^{n+1}_{\Lambda }(\Lambda ) = \mathsf {silt}^{n+1}_{\Lambda }(\Lambda )$ and it follows that $N \in \mathsf {silt}^{2}_{M}(\Lambda )$ . By Proposition 6.7, this can be rephrased as a property of the algebra $\Gamma =\operatorname {\mathrm {\mathsf {End}}}(M)$ , namely, all silting $\Gamma $ -modules are finite dimensional up to equivalence. But this means that $\Gamma $ is $\tau $ -tilting finite by Theorem 6.3. By Theorem 6.4 we conclude that $\Lambda $ is silting discrete.