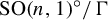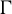1 Introduction
The group
![]() $G = \operatorname {SO}(n,1)^{\circ }$
with
$G = \operatorname {SO}(n,1)^{\circ }$
with
![]() $n\ge 2$
can be considered as the group of orientation preserving isometries of the hyperbolic space
$n\ge 2$
can be considered as the group of orientation preserving isometries of the hyperbolic space
![]() ${\mathbb H}^n$
. Let
${\mathbb H}^n$
. Let
![]() $\Gamma \subseteq G$
be a geometrically finite and Zariski dense subgroup of G with infinite covolume. In this paper, we establish an effective rate of equidistribution of orbits under the action of a horospherical subgroup
$\Gamma \subseteq G$
be a geometrically finite and Zariski dense subgroup of G with infinite covolume. In this paper, we establish an effective rate of equidistribution of orbits under the action of a horospherical subgroup
![]() $U \subseteq G$
under a certain exponential mixing assumption (Assumption 1.1).
$U \subseteq G$
under a certain exponential mixing assumption (Assumption 1.1).
An early result on the equidistribution of horocyclic flows in
![]() $G/\Gamma $
for
$G/\Gamma $
for
![]() $G= \operatorname {SL}_2(\mathbb R)$
and
$G= \operatorname {SL}_2(\mathbb R)$
and
![]() $\Gamma $
a lattice was obtained by Dani and Smillie in [Reference Dani and Smillie4]. They proved that if
$\Gamma $
a lattice was obtained by Dani and Smillie in [Reference Dani and Smillie4]. They proved that if
![]() $U=\{(\begin {smallmatrix}1 & t\\ 0 & 1 \end {smallmatrix}): t\in \mathbb R\}$
and if x does not have a closed U-orbit in
$U=\{(\begin {smallmatrix}1 & t\\ 0 & 1 \end {smallmatrix}): t\in \mathbb R\}$
and if x does not have a closed U-orbit in
![]() $G/\Gamma $
, then for every
$G/\Gamma $
, then for every
![]() $f \in C_c(X)$
,
$f \in C_c(X)$
,
 $$ \begin{align} \lim\limits_{T \to \infty} \frac{1}{T} \int_0^T f(u_t x)\,dt = m(f), \end{align} $$
$$ \begin{align} \lim\limits_{T \to \infty} \frac{1}{T} \int_0^T f(u_t x)\,dt = m(f), \end{align} $$
where m denotes the normalized Haar probability measure on X. The lattice case is well understood in general, thanks to Ratner’s celebrated theorems on unipotent flows [Reference Ratner28].
Results such as these are not considered to be effective, because they do not address the rate of convergence, and this is important in many applications. Burger proved effective equidistribution of horocyclic flows for
![]() $\operatorname {SL}_2(\mathbb R)/\Gamma $
when
$\operatorname {SL}_2(\mathbb R)/\Gamma $
when
![]() $\Gamma $
is a uniform lattice or convex cocompact with critical exponent at least
$\Gamma $
is a uniform lattice or convex cocompact with critical exponent at least
![]() $1/2$
in [Reference Burger3]. Sarnak proved effective equidistribution of translates of closed horocycles when
$1/2$
in [Reference Burger3]. Sarnak proved effective equidistribution of translates of closed horocycles when
![]() $\Gamma $
is a non-uniform lattice in [Reference Sarnak31]. More general results were obtained for non-uniform lattices using representation theoretic methods by Flaminio and Forni in [Reference Flaminio and Forni9], and also by Strömbergsson in [Reference Strömbergsson36]. The case where
$\Gamma $
is a non-uniform lattice in [Reference Sarnak31]. More general results were obtained for non-uniform lattices using representation theoretic methods by Flaminio and Forni in [Reference Flaminio and Forni9], and also by Strömbergsson in [Reference Strömbergsson36]. The case where
![]() $\Gamma =\operatorname {SL}_2(\mathbb Z)$
was also obtained independently by Sarnak and Ubis in [Reference Sarnak and Ubis32]. The higher dimensional setting has recently been considered by Katz [Reference Katz15] and McAdam [Reference McAdam21]. McAdam proved equidistribution of abelian horospherical flows in
$\Gamma =\operatorname {SL}_2(\mathbb Z)$
was also obtained independently by Sarnak and Ubis in [Reference Sarnak and Ubis32]. The higher dimensional setting has recently been considered by Katz [Reference Katz15] and McAdam [Reference McAdam21]. McAdam proved equidistribution of abelian horospherical flows in
![]() $\operatorname {SL}_n(\mathbb R)/\Gamma $
for
$\operatorname {SL}_n(\mathbb R)/\Gamma $
for
![]() $n \ge 3$
when
$n \ge 3$
when
![]() $\Gamma $
is a cocompact lattice or
$\Gamma $
is a cocompact lattice or
![]() $\operatorname {SL}_n(\mathbb Z)$
, and Katz proved equidistribution in greater generality when
$\operatorname {SL}_n(\mathbb Z)$
, and Katz proved equidistribution in greater generality when
![]() $\Gamma $
is a lattice in a semi-simple linear group without compact factors.
$\Gamma $
is a lattice in a semi-simple linear group without compact factors.
In infinite volume, we cannot hope for a result such as (1) for the Haar measure: by the Hopf ratio ergodic theorem, for almost every point,
 $$ \begin{align*} \lim\limits_{T \to \infty} \frac{1}{T}\int_0^T f(u_t x)\,dt = 0. \end{align*} $$
$$ \begin{align*} \lim\limits_{T \to \infty} \frac{1}{T}\int_0^T f(u_t x)\,dt = 0. \end{align*} $$
This tells us that this is not the correct measure to consider. A key characteristic of the Haar probability measure in the lattice case is that it is the unique U-invariant ergodic Radon measure that is not supported on a closed U orbit, [Reference Dani and Smillie4, Reference Furstenberg10]. By [Reference Burger3, Reference Roblin29, Reference Winter40], the measure with this property in the infinite volume setting is the Burger–Roblin (BR) measure, which is defined fully in §3. The correct normalization will be given by the Patterson–Sullivan (PS) measure, which is a geometrically defined measure on U orbits. This is also defined in §3.
Maucourant and Schapira proved equidistribution of horocycle flows on geometrically finite quotients of
![]() $\operatorname {SL}_2(\mathbb R)$
in [Reference Maucourant and Schapira20], and in [Reference Mohammadi and Oh24], Mohammadi and Oh generalize these results to geometrically finite quotients of
$\operatorname {SL}_2(\mathbb R)$
in [Reference Maucourant and Schapira20], and in [Reference Mohammadi and Oh24], Mohammadi and Oh generalize these results to geometrically finite quotients of
![]() $\operatorname {SO}(n,1)^{\circ }$
for
$\operatorname {SO}(n,1)^{\circ }$
for
![]() $n\ge 2$
, but these results are not effective. Oh and Shah also proved equidistribution on the unit tangent bundle of geometrically finite hyperbolic manifolds in [Reference Oh and Shah26]. In [Reference Edwards8], Edwards proves effective results for geometrically finite quotients of
$n\ge 2$
, but these results are not effective. Oh and Shah also proved equidistribution on the unit tangent bundle of geometrically finite hyperbolic manifolds in [Reference Oh and Shah26]. In [Reference Edwards8], Edwards proves effective results for geometrically finite quotients of
![]() $\operatorname {SL}_2(\mathbb R)$
.
$\operatorname {SL}_2(\mathbb R)$
.
In this paper, we extend these results to geometrically finite quotients of
![]() $\operatorname {SO}(n,1)^{\circ }$
, under the assumption of exponential mixing of the frame flow for the Bowen–Margulis– Sullivan (BMS) measure, which is defined in §3. More explicitly, in §§6–8 (but not §4 or §5), we will assume the following holds, where
$\operatorname {SO}(n,1)^{\circ }$
, under the assumption of exponential mixing of the frame flow for the Bowen–Margulis– Sullivan (BMS) measure, which is defined in §3. More explicitly, in §§6–8 (but not §4 or §5), we will assume the following holds, where
![]() $\{a_s : s \in \mathbb R\}$
denotes the frame flow on
$\{a_s : s \in \mathbb R\}$
denotes the frame flow on
![]() $G/\Gamma $
.
$G/\Gamma $
.
Assumption 1.1. (Exponential mixing)
There exist
![]() $c,\kappa>0$
and
$c,\kappa>0$
and
![]() $\ell \in \mathbb N$
which depend only on
$\ell \in \mathbb N$
which depend only on
![]() $\Gamma $
, such that for
$\Gamma $
, such that for
![]() $\psi ,\varphi \in C_c^{\infty }(G/\Gamma )$
and
$\psi ,\varphi \in C_c^{\infty }(G/\Gamma )$
and
![]() $s>0$
,
$s>0$
,
 $$ \begin{align*} \bigg|\int_{X}\psi(a_{s}x)\varphi(x)\,dm^{\operatorname{BMS}}(x)-m^{\operatorname{BMS}}(\psi)m^{\operatorname{BMS}}(\varphi)\bigg|<cS_{\ell}(\psi)S_{\ell}(\varphi)e^{-\kappa s}. \end{align*} $$
$$ \begin{align*} \bigg|\int_{X}\psi(a_{s}x)\varphi(x)\,dm^{\operatorname{BMS}}(x)-m^{\operatorname{BMS}}(\psi)m^{\operatorname{BMS}}(\varphi)\bigg|<cS_{\ell}(\psi)S_{\ell}(\varphi)e^{-\kappa s}. \end{align*} $$
Assumption 1.1 is known to hold when
![]() $\Gamma $
is convex cocompact by [Reference Sarkar and Winter30]. In [Reference Mohammadi and Oh23], Mohammadi and Oh prove such a result for geometrically finite
$\Gamma $
is convex cocompact by [Reference Sarkar and Winter30]. In [Reference Mohammadi and Oh23], Mohammadi and Oh prove such a result for geometrically finite
![]() $\Gamma $
under a spectral gap assumption (see Definition 2.1), using decay of matrix coefficients. Edwards and Oh recently proved effective mixing for the geodesic flow on the unit tangent bundle of a geometrically finite hyperbolic manifold when the critical exponent is larger than
$\Gamma $
under a spectral gap assumption (see Definition 2.1), using decay of matrix coefficients. Edwards and Oh recently proved effective mixing for the geodesic flow on the unit tangent bundle of a geometrically finite hyperbolic manifold when the critical exponent is larger than
![]() $(n-1)/2$
in [Reference Edwards and Oh7]. Further details about this assumption are discussed in §2.
$(n-1)/2$
in [Reference Edwards and Oh7]. Further details about this assumption are discussed in §2.
We will need to restrict consideration to points satisfying the following geometric property, which means that the point does not travel into a cusp ‘too fast’. Here, d is a left-invariant Riemannian metric on
![]() $G/\Gamma $
that projects to the hyperbolic distance on
$G/\Gamma $
that projects to the hyperbolic distance on
![]() ${\mathbb H}^n$
.
${\mathbb H}^n$
.
Definition 1.2. For
![]() $0<\varepsilon <1$
and
$0<\varepsilon <1$
and
![]() $s_0\ge 1$
, we say that
$s_0\ge 1$
, we say that
![]() $x\in G/\Gamma $
with
$x\in G/\Gamma $
with
![]() $x^- \in \Lambda (\Gamma )$
is
$x^- \in \Lambda (\Gamma )$
is
![]() $(\varepsilon ,s_0)$
-Diophantine if for all
$(\varepsilon ,s_0)$
-Diophantine if for all
![]() $s\ge s_0$
,
$s\ge s_0$
,
where
![]() $\mathcal {C}_0$
is a compact set arising from the thick-thin decomposition, and is fully defined in §3.2. We say that
$\mathcal {C}_0$
is a compact set arising from the thick-thin decomposition, and is fully defined in §3.2. We say that
![]() $x\in G/\Gamma $
with
$x\in G/\Gamma $
with
![]() $x^- \in \Lambda (\Gamma )$
is Diophantine if x is
$x^- \in \Lambda (\Gamma )$
is Diophantine if x is
![]() $(\varepsilon ,s_0)$
-Diophantine for some
$(\varepsilon ,s_0)$
-Diophantine for some
![]() $\varepsilon $
and
$\varepsilon $
and
![]() $s_0$
.
$s_0$
.
Here,
![]() $\Lambda (\Gamma )$
denotes the set of limit points of
$\Lambda (\Gamma )$
denotes the set of limit points of
![]() $\Gamma $
, and is defined fully in §3, as is the notation
$\Gamma $
, and is defined fully in §3, as is the notation
![]() $x^{\pm }$
. In the case that
$x^{\pm }$
. In the case that
![]() $\Gamma $
is a lattice, the condition
$\Gamma $
is a lattice, the condition
![]() $x^- \in \Lambda (\Gamma )$
is always satisfied. Also, if
$x^- \in \Lambda (\Gamma )$
is always satisfied. Also, if
![]() $\Gamma $
is convex cocompact, every point
$\Gamma $
is convex cocompact, every point
![]() $x \in G/\Gamma $
with
$x \in G/\Gamma $
with
![]() $x^-\in \Lambda (\Gamma )$
will be Diophantine, because all limit points are radial in this case (see §3).
$x^-\in \Lambda (\Gamma )$
will be Diophantine, because all limit points are radial in this case (see §3).
Note that x is
![]() $(\varepsilon ,s_0)$
-Diophantine if
$(\varepsilon ,s_0)$
-Diophantine if
![]() $(1-\varepsilon )s$
is a bound on the asymptotic excursion rate of the geodesic
$(1-\varepsilon )s$
is a bound on the asymptotic excursion rate of the geodesic
![]() $\{a_{-s}x\}$
, that is,
$\{a_{-s}x\}$
, that is,
Sullivan’s logarithm law for geodesics when
![]() $\Gamma $
is geometrically finite with
$\Gamma $
is geometrically finite with
![]() $\delta _{\Gamma }>(n-1)/2$
was shown in [Reference Kelmer and Oh16, Reference Stratmann and Velani35] (and is a strengthening of Sullivan’s logarithm law for non-compact lattices [Reference Sullivan38, §9]), and implies that for almost all
$\delta _{\Gamma }>(n-1)/2$
was shown in [Reference Kelmer and Oh16, Reference Stratmann and Velani35] (and is a strengthening of Sullivan’s logarithm law for non-compact lattices [Reference Sullivan38, §9]), and implies that for almost all
![]() $x \in G/\Gamma $
,
$x \in G/\Gamma $
,
where k is the maximal cusp rank. In [Reference Kelmer and Oh16], Kelmer and Oh showed a strengthening of the above, considering excursion to individual cusps and obtaining a limit for the shrinking target problem of the geodesic flow. Note also that the result stated in [Reference Kelmer and Oh16] is for
![]() $x\in {\operatorname {T}^1}(G/\Gamma $
), but since the distance function there is assumed to be K-invariant, where
$x\in {\operatorname {T}^1}(G/\Gamma $
), but since the distance function there is assumed to be K-invariant, where
![]() ${\mathbb H}^n=K\backslash G$
, and the set
${\mathbb H}^n=K\backslash G$
, and the set
![]() $\mathcal {C}_0$
is K-invariant as well (see §3.2), we can deduce the form above.
$\mathcal {C}_0$
is K-invariant as well (see §3.2), we can deduce the form above.
It follows from (3) that the limit on the left-hand side of (2) is zero for almost every point
![]() $x\in G/\Gamma $
(with respect to the invariant volume measure) in this case. Moreover, for any
$x\in G/\Gamma $
(with respect to the invariant volume measure) in this case. Moreover, for any
![]() $\varepsilon $
, the Hausdorff dimension of the set of directions in
$\varepsilon $
, the Hausdorff dimension of the set of directions in
![]() ${\operatorname {T}^1}({\mathbb H}^n/\Gamma )$
around a fixed point in
${\operatorname {T}^1}({\mathbb H}^n/\Gamma )$
around a fixed point in
![]() ${\mathbb H}^n/\Gamma $
that do not satisfy (2) is computed in [Reference Melián and Pestana22, Theorem 1]. For geometrically finite
${\mathbb H}^n/\Gamma $
that do not satisfy (2) is computed in [Reference Melián and Pestana22, Theorem 1]. For geometrically finite
![]() $\Gamma $
, the Hausdorff dimension of the set of directions around a fixed point that do not satisfy (2) can be found in [Reference Hill and Velani11, Reference Stratmann and Velani35].
$\Gamma $
, the Hausdorff dimension of the set of directions around a fixed point that do not satisfy (2) can be found in [Reference Hill and Velani11, Reference Stratmann and Velani35].
The main goal of this paper is to establish the following two theorems. Here,
![]() $m^{\operatorname {BR}}$
denotes the BR measure,
$m^{\operatorname {BR}}$
denotes the BR measure,
![]() $m^{\operatorname {BMS}}$
denotes the BMS measure, and
$m^{\operatorname {BMS}}$
denotes the BMS measure, and
![]() $\mu ^{\operatorname {PS}}$
denotes the PS measure. These measures are defined in §3. Throughout the paper, the notation
$\mu ^{\operatorname {PS}}$
denotes the PS measure. These measures are defined in §3. Throughout the paper, the notation
means there exists a constant c such that
If a subscript is denoted, e.g.
![]() $\ll _{\Gamma }$
, this explicitly indicates that this constant depends on
$\ll _{\Gamma }$
, this explicitly indicates that this constant depends on
![]() $\Gamma $
.
$\Gamma $
.
Let
![]() $U = \{u_{\textbf {t}} : \textbf {t} \in \mathbb R^{n-1}\}$
denote the expanding horospherical flow. Let
$U = \{u_{\textbf {t}} : \textbf {t} \in \mathbb R^{n-1}\}$
denote the expanding horospherical flow. Let
![]() $B_U(r)$
denote the ball in U of radius r with the max norm on
$B_U(r)$
denote the ball in U of radius r with the max norm on
![]() $\mathbb R^{n-1}$
. See §3 for more details on notation.
$\mathbb R^{n-1}$
. See §3 for more details on notation.
Theorem 1.3. Assume that
![]() $\Gamma $
satisfies Assumption 1.1. For any
$\Gamma $
satisfies Assumption 1.1. For any
![]() $0<\varepsilon <1$
and
$0<\varepsilon <1$
and
![]() $s_0\ge 1$
, there exist constants
$s_0\ge 1$
, there exist constants
![]() $\ell = \ell (\Gamma ) \in \mathbb N$
and
$\ell = \ell (\Gamma ) \in \mathbb N$
and
![]() $\kappa = \kappa (\Gamma , \varepsilon )>0$
satisfying for every
$\kappa = \kappa (\Gamma , \varepsilon )>0$
satisfying for every
![]() $\psi \in C_c^{\infty }(G/\Gamma )$
, there exists
$\psi \in C_c^{\infty }(G/\Gamma )$
, there exists
![]() $c = c(\Gamma ,\operatorname {supp}\psi )$
such that for every
$c = c(\Gamma ,\operatorname {supp}\psi )$
such that for every
![]() $x\in G/\Gamma $
that is
$x\in G/\Gamma $
that is
![]() $(\varepsilon ,s_0)$
-Diophantine, and for every
$(\varepsilon ,s_0)$
-Diophantine, and for every
![]() $r \gg _{\Gamma ,\varepsilon } s_0$
,
$r \gg _{\Gamma ,\varepsilon } s_0$
,
 $$ \begin{align*} \bigg|\frac{1}{\mu^{\operatorname{PS}}_x(B_U(r))} \int_{B_U(r)}\psi(u_{\textbf{t}} x)\,d\mu^{\operatorname{PS}}_x(\textbf{t}) - m^{\operatorname{BMS}}(\psi)\bigg| \le c S_{\ell}(\psi) r^{-\kappa}, \end{align*} $$
$$ \begin{align*} \bigg|\frac{1}{\mu^{\operatorname{PS}}_x(B_U(r))} \int_{B_U(r)}\psi(u_{\textbf{t}} x)\,d\mu^{\operatorname{PS}}_x(\textbf{t}) - m^{\operatorname{BMS}}(\psi)\bigg| \le c S_{\ell}(\psi) r^{-\kappa}, \end{align*} $$
where
![]() $S_{\ell }(\psi )$
is the
$S_{\ell }(\psi )$
is the
![]() $\ell $
-Sobolev norm.
$\ell $
-Sobolev norm.
For the Haar measure, we will prove the following equidistribution result.
Theorem 1.4. Assume that
![]() $\Gamma $
satisfies Assumption 1.1. For any
$\Gamma $
satisfies Assumption 1.1. For any
![]() $0<\varepsilon <1$
and
$0<\varepsilon <1$
and
![]() $s_0\ge 1$
, there exist
$s_0\ge 1$
, there exist
![]() $\ell =\ell (\Gamma )\in \mathbb N$
and
$\ell =\ell (\Gamma )\in \mathbb N$
and
![]() $\kappa =\kappa (\Gamma ,\varepsilon )>0$
satisfying for every
$\kappa =\kappa (\Gamma ,\varepsilon )>0$
satisfying for every
![]() $\psi \in C_c^{\infty }(G/\Gamma )$
, there exists
$\psi \in C_c^{\infty }(G/\Gamma )$
, there exists
![]() $c = c(\Gamma ,\operatorname {supp}\psi )$
such that for every
$c = c(\Gamma ,\operatorname {supp}\psi )$
such that for every
![]() $x\in G/\Gamma $
that is
$x\in G/\Gamma $
that is
![]() $(\varepsilon ,s_0)$
-Diophantine, and for all
$(\varepsilon ,s_0)$
-Diophantine, and for all
![]() $r \gg _{\Gamma ,\operatorname {supp}\psi ,\varepsilon } s_0$
,
$r \gg _{\Gamma ,\operatorname {supp}\psi ,\varepsilon } s_0$
,
 $$ \begin{align*} \bigg|\frac{1}{\mu^{\operatorname{PS}}_x(B_U(r))} \int_{B_U(r)}\psi(u_{\textbf{t}} x)\,d\textbf{t} - m^{\operatorname{BR}}(\psi)\bigg| \le c S_{\ell}(\psi)r^{-\kappa}, \end{align*} $$
$$ \begin{align*} \bigg|\frac{1}{\mu^{\operatorname{PS}}_x(B_U(r))} \int_{B_U(r)}\psi(u_{\textbf{t}} x)\,d\textbf{t} - m^{\operatorname{BR}}(\psi)\bigg| \le c S_{\ell}(\psi)r^{-\kappa}, \end{align*} $$
where
![]() $S_{\ell }(\psi )$
is the
$S_{\ell }(\psi )$
is the
![]() $\ell $
-Sobolev norm.
$\ell $
-Sobolev norm.
Note that the assumption that x is Diophantine is required to obtain quantitative non-divergence results in §4, which is key in proving the above theorems. The dependence on a Diophantine condition is necessary, and is analogous to known effective equidistribution results for when
![]() $\Gamma $
is a non-cocompact lattice (see [Reference McAdam21, Reference Strömbergsson36]).
$\Gamma $
is a non-cocompact lattice (see [Reference McAdam21, Reference Strömbergsson36]).
In [Reference Tamam and Warren39], we apply the above result to obtain a quantitative ratio theorem for the distribution of orbits for
![]() $\Gamma $
acting on
$\Gamma $
acting on
![]() $U \backslash G$
. This improves upon the work of Maucourant and Schapira in [Reference Maucourant and Schapira20].
$U \backslash G$
. This improves upon the work of Maucourant and Schapira in [Reference Maucourant and Schapira20].
A key step toward proving Theorem 1.3 is the following, which is proved in §6.
Theorem 1.5. Assume that
![]() $\Gamma $
satisfies Assumption 1.1. There exist
$\Gamma $
satisfies Assumption 1.1. There exist
![]() $\kappa = \kappa (\Gamma )$
and
$\kappa = \kappa (\Gamma )$
and
![]() $\ell = \ell (\Gamma )$
which satisfy the following: for any
$\ell = \ell (\Gamma )$
which satisfy the following: for any
![]() $\psi \in C_c^{\infty }(X)$
, there exists
$\psi \in C_c^{\infty }(X)$
, there exists
![]() $c = c(\Gamma , \operatorname {supp}\psi )>0$
such that for any
$c = c(\Gamma , \operatorname {supp}\psi )>0$
such that for any
![]() $f \in C_c^{\infty }(B_U(r))$
,
$f \in C_c^{\infty }(B_U(r))$
,
![]() $0<r<1$
,
$0<r<1$
,
![]() $x \in \operatorname {supp}m^{\operatorname {BMS}}$
, and
$x \in \operatorname {supp}m^{\operatorname {BMS}}$
, and
![]() $s\gg _{\Gamma } d(\mathcal {C}_0,x)$
, we have
$s\gg _{\Gamma } d(\mathcal {C}_0,x)$
, we have
 $$ \begin{align*} \bigg|\int_U \psi(a_s u_{\textbf{t}} x)f(\textbf{t})\,d\mu^{\operatorname{PS}}_x(\textbf{t}) - \mu^{\operatorname{PS}}_x(f)m^{\operatorname{BMS}}(\psi)\bigg| < cS_{\ell}(\psi)S_{\ell}(f)e^{-\kappa s}. \end{align*} $$
$$ \begin{align*} \bigg|\int_U \psi(a_s u_{\textbf{t}} x)f(\textbf{t})\,d\mu^{\operatorname{PS}}_x(\textbf{t}) - \mu^{\operatorname{PS}}_x(f)m^{\operatorname{BMS}}(\psi)\bigg| < cS_{\ell}(\psi)S_{\ell}(f)e^{-\kappa s}. \end{align*} $$
In §6, we also prove an analogous statement for the Haar measure. Such a result is proven in [Reference Mohammadi and Oh23] under a spectral gap assumption on
![]() $\Gamma $
, but we show in this paper how to prove it whenever the frame flow is exponentially mixing.
$\Gamma $
, but we show in this paper how to prove it whenever the frame flow is exponentially mixing.
The proof will use similar techniques as in [Reference Mohammadi and Oh24, Reference Oh and Shah26]; in particular, we will rely on Margulis’ ‘thickening trick’ from his thesis [Reference Margulis19].
In the proofs of our main theorems (Theorems 1.3 and 1.4), we use partition of unity arguments. In particular, the bounds we get are on slightly bigger sets. As a result, we need an effective bound on the PS measure of a small neighborhood of a boundary of a ball relative to the PS measure of that ball. The following theorem achieves this. It is shown using [Reference Das, Fishman, Simmons and Urbański5, Lemma 3.8] and [Reference Stratmann and Velani35, Theorem 2].
Theorem 1.6. There exists a constant
![]() $\alpha = \alpha (\Gamma )>0,$
such that for every
$\alpha = \alpha (\Gamma )>0,$
such that for every
![]() $x \in G/\Gamma $
that is
$x \in G/\Gamma $
that is
![]() $(\varepsilon ,s_0)$
-Diophantine, for every
$(\varepsilon ,s_0)$
-Diophantine, for every
![]() $0<s\le T^{{\varepsilon }/({1-\varepsilon })}$
, every
$0<s\le T^{{\varepsilon }/({1-\varepsilon })}$
, every
![]() $0<\xi \ll _{\Gamma } 1,$
and every
$0<\xi \ll _{\Gamma } 1,$
and every
![]() $T\gg _{\Gamma ,\varepsilon } s_0$
,
$T\gg _{\Gamma ,\varepsilon } s_0$
,
 $$ \begin{align*} \frac{\mu^{\operatorname{PS}}_{a_{-s}x}(B_U(\xi+T) )}{\mu^{\operatorname{PS}}_{a_{-s}x}(B_U(T))}-1\ll_{\Gamma} \xi^{\alpha}.\end{align*} $$
$$ \begin{align*} \frac{\mu^{\operatorname{PS}}_{a_{-s}x}(B_U(\xi+T) )}{\mu^{\operatorname{PS}}_{a_{-s}x}(B_U(T))}-1\ll_{\Gamma} \xi^{\alpha}.\end{align*} $$
In the appendix, a stronger version is obtained under the assumption that all cusps of
![]() $G/\Gamma $
have maximal rank.
$G/\Gamma $
have maximal rank.
This paper is organized as follows. In §2, we discuss under what conditions Assumption 1.1 is known to hold. In §3, we set out notation used in the article, and define the measures we will be using, along with proving some important facts about them. In §4, we prove quantitative non-divergence of horospherical orbits of Diophantine points, which is needed in the following sections. In §5, we control the PS measure of the boundary of a set by proving Theorem 1.6. In §6, we use Margulis’ ‘thickening trick’ to prove Theorem 1.5 and an analogous result for the Haar measure, which are key in the proofs of Theorems 1.3 and 1.4. In §7, we use quantitative non-divergence and Theorem 1.5 to prove Theorem 1.3. In §8, we use Theorem 1.6 and the Haar measure analogue of Theorem 1.5 to prove Theorem 1.4. Several technical details of the proof of Theorem 1.6 are in the appendix, §A, and in §A.3, we prove stronger statements hold in the setting that all cusps have maximal rank, because the PS measure is absolutely friendly (see [Reference Das, Fishman, Simmons and Urbański5, Theorem 1.9]).
2 Known exponential mixing results
Throughout the paper, we assume the existence of an exponential mixing result (see Assumption 1.1). In this section, we elaborate on the conditions under which such a result is known. Here we assume that
![]() $\Gamma $
is a Zariski dense discrete subgroup of G.
$\Gamma $
is a Zariski dense discrete subgroup of G.
There is a natural action of G on
![]() ${\mathbb H}^n$
and
${\mathbb H}^n$
and
![]() $\partial {\mathbb H}^n$
, the hyperbolic n-space and its boundary, respectively. Let
$\partial {\mathbb H}^n$
, the hyperbolic n-space and its boundary, respectively. Let
![]() $\Lambda (\Gamma )\subseteq \partial ({\mathbb H}^n)$
denote the limit set of X, that is, the set of all accumulation points of
$\Lambda (\Gamma )\subseteq \partial ({\mathbb H}^n)$
denote the limit set of X, that is, the set of all accumulation points of
![]() $\Gamma z$
for some
$\Gamma z$
for some
![]() $z\in {\mathbb H}^n\cup \partial ({\mathbb H}^n)$
. The convex core of X is the image in X of the minimal convex subset of
$z\in {\mathbb H}^n\cup \partial ({\mathbb H}^n)$
. The convex core of X is the image in X of the minimal convex subset of
![]() ${\mathbb H}^n$
which contains all geodesics connecting any two points in
${\mathbb H}^n$
which contains all geodesics connecting any two points in
![]() $\Lambda (\Gamma )$
. We say that
$\Lambda (\Gamma )$
. We say that
![]() $\Gamma $
is convex cocompact if the convex core of
$\Gamma $
is convex cocompact if the convex core of
![]() ${\mathbb H}^n /\Gamma $
is compact, and geometrically finite if a unit neighborhood of the convex core of
${\mathbb H}^n /\Gamma $
is compact, and geometrically finite if a unit neighborhood of the convex core of
![]() $\Gamma $
has finite volume.
$\Gamma $
has finite volume.
For
![]() $\Gamma $
convex cocompact, Assumption 1.1 was proved by Sarkar and Winter in [Reference Sarkar and Winter30, Theorem 1.1].
$\Gamma $
convex cocompact, Assumption 1.1 was proved by Sarkar and Winter in [Reference Sarkar and Winter30, Theorem 1.1].
Fix a point
![]() $w_o \in {\operatorname {T}^1}({\mathbb H}^n)$
and denote
$w_o \in {\operatorname {T}^1}({\mathbb H}^n)$
and denote
![]() $M = \operatorname {Stab}_G(w_o)$
. Denote by
$M = \operatorname {Stab}_G(w_o)$
. Denote by
![]() $\hat {G}$
and
$\hat {G}$
and
![]() $\hat {M}$
the unitary dual of G and M respectively. A representation
$\hat {M}$
the unitary dual of G and M respectively. A representation
![]() $(\pi ,\mathcal {H})\in \hat {G}$
is called tempered if for any K-finite
$(\pi ,\mathcal {H})\in \hat {G}$
is called tempered if for any K-finite
![]() $v\in \mathcal {H}$
, the associated matrix coefficient function
$v\in \mathcal {H}$
, the associated matrix coefficient function
![]() $g\mapsto \langle \pi (g)v,v\rangle $
belongs to
$g\mapsto \langle \pi (g)v,v\rangle $
belongs to
![]() $L^{2+\varepsilon }(G)$
for any
$L^{2+\varepsilon }(G)$
for any
![]() $\varepsilon>0$
, and non-tempered otherwise. The non-tempered part of
$\varepsilon>0$
, and non-tempered otherwise. The non-tempered part of
![]() $\hat {G}$
consists of the trivial representation, and complementary series representations
$\hat {G}$
consists of the trivial representation, and complementary series representations
![]() $\mathcal {U}(v,s-n+1)$
parameterized by
$\mathcal {U}(v,s-n+1)$
parameterized by
![]() $v\in \hat {M}$
and
$v\in \hat {M}$
and
![]() $s\in I_v$
, where
$s\in I_v$
, where
![]() $I_v\subseteq (({n-1})/{2},n-1)$
is an interval depending on v (see [Reference Hirai12]).
$I_v\subseteq (({n-1})/{2},n-1)$
is an interval depending on v (see [Reference Hirai12]).
Definition 2.1. The space
![]() $L^2(X)$
has a spectral gap if there exist
$L^2(X)$
has a spectral gap if there exist
![]() $({n-1})/{2}<s_0=s_0(\Gamma )<\delta $
and
$({n-1})/{2}<s_0=s_0(\Gamma )<\delta $
and
![]() $n_0=n_0(\Gamma )\in \mathbb {N}$
such that:
$n_0=n_0(\Gamma )\in \mathbb {N}$
such that:
-
(1) the multiplicity of
 $\mathcal {U}(v,\delta _{\Gamma }-n+1)$
contained in
$\mathcal {U}(v,\delta _{\Gamma }-n+1)$
contained in
 $L^2(X)$
is at most
$L^2(X)$
is at most
 $dim(v)^{n_0}$
for any
$dim(v)^{n_0}$
for any
 $v\in \hat {M}$
;
$v\in \hat {M}$
; -
(2)
 $L^2(X)$
does not weakly contain any
$L^2(X)$
does not weakly contain any
 $\mathcal {U}(v,s-n+1)$
with
$\mathcal {U}(v,s-n+1)$
with
 $s\in (s_0,\delta )$
and
$s\in (s_0,\delta )$
and
 $v\in \hat {M}$
.
$v\in \hat {M}$
.
According to [Reference Mohammadi and Oh23, Theorem 3.27], if
![]() $\delta _{\Gamma }>({n-1})/{2}$
for
$\delta _{\Gamma }>({n-1})/{2}$
for
![]() $n=2,3$
, or if
$n=2,3$
, or if
![]() $\delta _{\Gamma }>n-2$
for
$\delta _{\Gamma }>n-2$
for
![]() $n\ge 4$
, then
$n\ge 4$
, then
![]() $L^2(X)$
has a spectral gap. If
$L^2(X)$
has a spectral gap. If
![]() $\delta _{\Gamma }\leq ({n-1})/{2}$
, then there is no spectral gap, but it was conjectured that whenever
$\delta _{\Gamma }\leq ({n-1})/{2}$
, then there is no spectral gap, but it was conjectured that whenever
![]() $\delta _{\Gamma }>({n-1})/{2}$
,
$\delta _{\Gamma }>({n-1})/{2}$
,
![]() $L^2(X)$
has a spectral gap (see [Reference Mohammadi and Oh23]). Note that if there are cusps of maximal rank
$L^2(X)$
has a spectral gap (see [Reference Mohammadi and Oh23]). Note that if there are cusps of maximal rank
![]() $n-1$
, it follows that
$n-1$
, it follows that
![]() $\delta _{\Gamma }>({n-1})/{2}$
.
$\delta _{\Gamma }>({n-1})/{2}$
.
For
![]() $\Gamma $
geometrically finite such that
$\Gamma $
geometrically finite such that
![]() $L^2(X)$
has a spectral gap and
$L^2(X)$
has a spectral gap and
![]() $\delta _{\Gamma }> ({n-1})/{2}$
, Mohammadi and Oh stated in [Reference Mohammadi and Oh23, Theorem 1.6] an exponential mixing result similar to Assumption 1.1. In their statement, the constant c depends on
$\delta _{\Gamma }> ({n-1})/{2}$
, Mohammadi and Oh stated in [Reference Mohammadi and Oh23, Theorem 1.6] an exponential mixing result similar to Assumption 1.1. In their statement, the constant c depends on
![]() $\Gamma $
and the support of the functions. The dependence on the support of the functions arises in the last part of the proof (see [Reference Mohammadi and Oh23, §6.3]) and can be omitted by using the following lemma (the BR-measure is defined in §3.3), hence obtaining a result of the form needed in Assumption 1.1.
$\Gamma $
and the support of the functions. The dependence on the support of the functions arises in the last part of the proof (see [Reference Mohammadi and Oh23, §6.3]) and can be omitted by using the following lemma (the BR-measure is defined in §3.3), hence obtaining a result of the form needed in Assumption 1.1.
Lemma 2.2. If
![]() $\delta>(n-1)/2$
, then there exists
$\delta>(n-1)/2$
, then there exists
![]() $c=c(\Gamma )>0$
such that any
$c=c(\Gamma )>0$
such that any
![]() $B\subset X$
of diameter smaller than
$B\subset X$
of diameter smaller than
![]() $1$
satisfies
$1$
satisfies
Proof. For any
![]() $g\in G$
denote
$g\in G$
denote
where o is the projection of
![]() $w_o$
onto
$w_o$
onto
![]() ${\mathbb H}^n$
and for any
${\mathbb H}^n$
and for any
![]() $x\in {\mathbb H}^n$
,
$x\in {\mathbb H}^n$
,
![]() $\nu _x$
is the Patterson–Sullivan density defined in §3.1. Since
$\nu _x$
is the Patterson–Sullivan density defined in §3.1. Since
![]() $\Phi _0$
is
$\Phi _0$
is
![]() $\Gamma $
-invariant, it can be considered as a smooth function on X. Moreover, by assuming B contains
$\Gamma $
-invariant, it can be considered as a smooth function on X. Moreover, by assuming B contains
![]() $K=\operatorname {Stab}_G(o)$
and using the Cauchy–Schwartz inequality, we get
$K=\operatorname {Stab}_G(o)$
and using the Cauchy–Schwartz inequality, we get
 $$ \begin{align*} m^{\operatorname{BR}}(B)&=\int_{B}\Phi_0(g)\,dm^{\operatorname{Haar}}(g)\\ &\leq\sqrt{dm^{\operatorname{Haar}}(B)}\Vert \Phi_0\Vert _2\\ &\ll\Vert \Phi_0\Vert _2. \end{align*} $$
$$ \begin{align*} m^{\operatorname{BR}}(B)&=\int_{B}\Phi_0(g)\,dm^{\operatorname{Haar}}(g)\\ &\leq\sqrt{dm^{\operatorname{Haar}}(B)}\Vert \Phi_0\Vert _2\\ &\ll\Vert \Phi_0\Vert _2. \end{align*} $$
According to [Reference Sullivan37, §7] and by the assumption
![]() $\delta>(n-1)/2$
, we have that
$\delta>(n-1)/2$
, we have that
![]() $\phi _0\in L^2(X)$
.
$\phi _0\in L^2(X)$
.
3 Notation and preliminaries
Recall from §1 that
![]() $G = \operatorname {SO}(n,1)^{\circ }$
and
$G = \operatorname {SO}(n,1)^{\circ }$
and
![]() $\Gamma \subseteq G$
is a geometrically finite Kleinian subgroup of G. Denote
$\Gamma \subseteq G$
is a geometrically finite Kleinian subgroup of G. Denote
Here, G acts transitively on
![]() ${\mathbb H}^n$
, the hyperbolic n-space. Fix a reference point
${\mathbb H}^n$
, the hyperbolic n-space. Fix a reference point
![]() $o\in {\mathbb H}^n$
and let
$o\in {\mathbb H}^n$
and let
![]() $K=\text {Stab}_G(o)$
, then
$K=\text {Stab}_G(o)$
, then
![]() $K\backslash G=\mathbb {H}^n$
. Let
$K\backslash G=\mathbb {H}^n$
. Let
![]() $\pi :G\rightarrow {\mathbb H}^n$
be the projection
$\pi :G\rightarrow {\mathbb H}^n$
be the projection
We will abuse notation and also write
![]() $\pi $
for the induced map from
$\pi $
for the induced map from
![]() $G/\Gamma $
to
$G/\Gamma $
to
![]() ${\mathbb H}^n/\Gamma $
. For convenience, we will assume throughout the paper that we have chosen o so that
${\mathbb H}^n/\Gamma $
. For convenience, we will assume throughout the paper that we have chosen o so that
![]() $o\Gamma \in \pi (\mathcal {C}_0)$
, where
$o\Gamma \in \pi (\mathcal {C}_0)$
, where
![]() $\mathcal {C}_0$
is defined in §3.2. This says that
$\mathcal {C}_0$
is defined in §3.2. This says that
![]() $o\Gamma $
is in the convex core of
$o\Gamma $
is in the convex core of
![]() ${\mathbb H}^n/\Gamma $
.
${\mathbb H}^n/\Gamma $
.
Let d denote the left G-invariant metric on G which induces the hyperbolic metric on
![]() $K\backslash G=\mathbb {H}^n$
.
$K\backslash G=\mathbb {H}^n$
.
Recall from §2 that
![]() $\Lambda (\Gamma )\subseteq \partial ({\mathbb H}^n)$
denotes the limit set of X. We denote the Hausdorff dimension of
$\Lambda (\Gamma )\subseteq \partial ({\mathbb H}^n)$
denotes the limit set of X. We denote the Hausdorff dimension of
![]() $\Lambda (\Gamma )$
by
$\Lambda (\Gamma )$
by
![]() $\delta _{\Gamma }$
. It is equal to the critical exponent of
$\delta _{\Gamma }$
. It is equal to the critical exponent of
![]() $\Gamma $
(see [Reference Patterson27]).
$\Gamma $
(see [Reference Patterson27]).
We say that a limit point
![]() $\xi \in \Lambda (\Gamma )$
is radial if there exists a compact subset of X so that some (and hence every) geodesic ray toward
$\xi \in \Lambda (\Gamma )$
is radial if there exists a compact subset of X so that some (and hence every) geodesic ray toward
![]() $\xi $
has accumulation points in that set. An element
$\xi $
has accumulation points in that set. An element
![]() $g\in G$
is called parabolic if the set of fixed points of g in
$g\in G$
is called parabolic if the set of fixed points of g in
![]() $\partial (\mathbb {H}^n)$
is a singleton. We say that a limit point is parabolic if it is fixed by a parabolic element of
$\partial (\mathbb {H}^n)$
is a singleton. We say that a limit point is parabolic if it is fixed by a parabolic element of
![]() $\Gamma $
. A parabolic limit point
$\Gamma $
. A parabolic limit point
![]() $\xi \in \Lambda (\Gamma )$
is called bounded if the stabilizer
$\xi \in \Lambda (\Gamma )$
is called bounded if the stabilizer
![]() $\Gamma _{\xi }$
acts cocompactly on
$\Gamma _{\xi }$
acts cocompactly on
![]() $\Lambda (\Gamma )-\{\xi \}$
.
$\Lambda (\Gamma )-\{\xi \}$
.
We denote by
![]() $\Lambda _r (\Gamma )$
and
$\Lambda _r (\Gamma )$
and
![]() $\Lambda _{bp} (\Gamma )$
the set of all radial limit points and the set of all bounded parabolic limit points respectively. Since
$\Lambda _{bp} (\Gamma )$
the set of all radial limit points and the set of all bounded parabolic limit points respectively. Since
![]() $\Gamma $
is geometrically finite (see [Reference Bowditch2]),
$\Gamma $
is geometrically finite (see [Reference Bowditch2]),
Fix
![]() $w_o \in {\operatorname {T}^1}({\mathbb H}^n)$
and let
$w_o \in {\operatorname {T}^1}({\mathbb H}^n)$
and let
![]() $M = \operatorname {Stab}_G(w_o)$
so that
$M = \operatorname {Stab}_G(w_o)$
so that
![]() ${\operatorname {T}^1}({\mathbb H}^n)$
may be identified with
${\operatorname {T}^1}({\mathbb H}^n)$
may be identified with
![]() $M\backslash G$
. For
$M\backslash G$
. For
![]() $w \in {\operatorname {T}^1}({\mathbb H}^n)$
,
$w \in {\operatorname {T}^1}({\mathbb H}^n)$
,
denotes the forward and backward endpoints of the geodesic w determined. For
![]() $g \in G$
, we define
$g \in G$
, we define
Without loss of generality, we may assume that
![]() $w_o^{\pm }\in \Lambda (\Gamma )$
, and hence every
$w_o^{\pm }\in \Lambda (\Gamma )$
, and hence every
![]() $\gamma \in \Gamma $
will satisfy
$\gamma \in \Gamma $
will satisfy
![]() $\gamma ^{\pm }\in \Lambda (\Gamma ).$
$\gamma ^{\pm }\in \Lambda (\Gamma ).$
Let
![]() $A=\{a_s : s\in \mathbb R\}$
be a one parameter diagonalizable subgroup such that M and A commute, and such that the right action on
$A=\{a_s : s\in \mathbb R\}$
be a one parameter diagonalizable subgroup such that M and A commute, and such that the right action on
![]() $M\backslash G={\operatorname {T}^1}({\mathbb H}^n)$
corresponds to unit speed geodesic flow. We parameterize A by
$M\backslash G={\operatorname {T}^1}({\mathbb H}^n)$
corresponds to unit speed geodesic flow. We parameterize A by
![]() $A=\{a_s : s\in \mathbb R\}$
, where
$A=\{a_s : s\in \mathbb R\}$
, where
 $$ \begin{align} a_s = \begin{pmatrix} e^{s} & & \\ & I & \\ & & e^{-s} \end{pmatrix} \end{align} $$
$$ \begin{align} a_s = \begin{pmatrix} e^{s} & & \\ & I & \\ & & e^{-s} \end{pmatrix} \end{align} $$
and I denotes the
![]() $(n-1)\times (n-1)$
identity matrix.
$(n-1)\times (n-1)$
identity matrix.
Let U denote the expanding horospherical subgroup
let
![]() $\tilde U$
be the contracting horospherical subgroup
$\tilde U$
be the contracting horospherical subgroup
and let
![]() $P=MA\tilde U$
be the parabolic subgroup.
$P=MA\tilde U$
be the parabolic subgroup.
The group U is a connected abelian group, isomorphic to
![]() $\mathbb R^{n-1}$
. We may use the parameterization
$\mathbb R^{n-1}$
. We may use the parameterization
![]() $\textbf {t}\mapsto u_{\textbf {t}}$
so that for any
$\textbf {t}\mapsto u_{\textbf {t}}$
so that for any
![]() $s\in \mathbb R$
,
$s\in \mathbb R$
,
Similarly, we parameterize
![]() $\tilde U$
by
$\tilde U$
by
![]() $\textbf {t} \mapsto v_{\textbf {t}} \in \tilde {U}$
so that for
$\textbf {t} \mapsto v_{\textbf {t}} \in \tilde {U}$
so that for
![]() $s \in \mathbb R$
,
$s \in \mathbb R$
,
More explicitly, if
![]() $\textbf {t} \in \mathbb R^{n-1}$
is viewed as a row vector,
$\textbf {t} \in \mathbb R^{n-1}$
is viewed as a row vector,
 $$ \begin{align} u_{\textbf{t}} = \begin{pmatrix} 1 & \textbf{t} & \frac{1}{2}\Vert \textbf{t}\Vert ^2 \\ & I & \textbf{t}^T \\ & & 1 \end{pmatrix} \end{align} $$
$$ \begin{align} u_{\textbf{t}} = \begin{pmatrix} 1 & \textbf{t} & \frac{1}{2}\Vert \textbf{t}\Vert ^2 \\ & I & \textbf{t}^T \\ & & 1 \end{pmatrix} \end{align} $$
and
 $$ \begin{align*}v_{\textbf{t}} = \begin{pmatrix} 1 & & \\ \textbf{t}^T & I & \\ \frac{1}{2}\|\textbf{t}\|^2 & \textbf{t} & 1 \end{pmatrix}.\end{align*} $$
$$ \begin{align*}v_{\textbf{t}} = \begin{pmatrix} 1 & & \\ \textbf{t}^T & I & \\ \frac{1}{2}\|\textbf{t}\|^2 & \textbf{t} & 1 \end{pmatrix}.\end{align*} $$
For a subset H of G and
![]() $\eta>0$
,
$\eta>0$
,
![]() $H_{\eta }$
denotes the closed
$H_{\eta }$
denotes the closed
![]() $\eta $
-neighborhood of e in H, that is,
$\eta $
-neighborhood of e in H, that is,
For any
![]() $r>0$
, let
$r>0$
, let
where
![]() $\Vert \textbf {t}\Vert $
is the sup-norm of
$\Vert \textbf {t}\Vert $
is the sup-norm of
![]() $\textbf {t}\in \mathbb R^{n-1}$
.
$\textbf {t}\in \mathbb R^{n-1}$
.
Lemma 3.1. For
![]() $0<\eta <1/4$
and
$0<\eta <1/4$
and
![]() $p \in P_{\eta }$
, there exists
$p \in P_{\eta }$
, there exists
![]() $\rho _p : B_U(1) \to B_U(1+O(\eta ))$
that is a diffeomorphism onto its image and a constant
$\rho _p : B_U(1) \to B_U(1+O(\eta ))$
that is a diffeomorphism onto its image and a constant
![]() $D=D(\eta )<3\eta $
such that
$D=D(\eta )<3\eta $
such that
Explicitly, if
![]() $p = a_s v_{\textbf {r}}$
, then
$p = a_s v_{\textbf {r}}$
, then
![]() $\rho _p(\textbf {t}) = ({\textbf {t} - \tfrac 12\|\textbf {t}\|^2\textbf {r}})/{e^s(1-(\textbf {t}\cdot \textbf {r})+\tfrac 14\|\textbf {r}\|^2\|\textbf {t}\|^2)}$
.
$\rho _p(\textbf {t}) = ({\textbf {t} - \tfrac 12\|\textbf {t}\|^2\textbf {r}})/{e^s(1-(\textbf {t}\cdot \textbf {r})+\tfrac 14\|\textbf {r}\|^2\|\textbf {t}\|^2)}$
.
Proof. For
![]() $s \in \mathbb R$
and
$s \in \mathbb R$
and
![]() $\textbf {r} \in \mathbb R^{n-1}$
, let
$\textbf {r} \in \mathbb R^{n-1}$
, let
![]() $p = a_sv_{\textbf {r}}$
. Then
$p = a_sv_{\textbf {r}}$
. Then
 $$\begin{align*}p^{-1} = \begin{pmatrix} e^{-s} & & \\[3pt] -e^{-s} \textbf{r}^T & I & \\[3pt] \tfrac12e^{-s}\|\textbf{r}\|^2 & -\textbf{r} & e^{s} \end{pmatrix},\end{align*}$$
$$\begin{align*}p^{-1} = \begin{pmatrix} e^{-s} & & \\[3pt] -e^{-s} \textbf{r}^T & I & \\[3pt] \tfrac12e^{-s}\|\textbf{r}\|^2 & -\textbf{r} & e^{s} \end{pmatrix},\end{align*}$$
so
 $$ \begin{align*}u_{\textbf{t}} p^{-1} = \begin{pmatrix} e^{-s}(1-(\textbf{t}\cdot \textbf{r})+\frac{1}{4}\|\textbf{r}\|^2\|\textbf{t}\|^2) & \textbf{t} - \frac{1}{2} \|\textbf{t}\|^2 \textbf{r} & \frac{1}{2}e^{s}\|\textbf{t}\|^2 \\[3pt] -e^{-s}\textbf{r}^T + \frac{1}{2}e^{-s}\|\textbf{r}\|^2\textbf{t}^T & I - \textbf{t}^T \textbf{r} & e^{s}\textbf{t}^T \\[3pt] \frac{1}{2}e^{-s}\|\textbf{r}\|^2 & -\textbf{r} & e^{s}\end{pmatrix}.\end{align*} $$
$$ \begin{align*}u_{\textbf{t}} p^{-1} = \begin{pmatrix} e^{-s}(1-(\textbf{t}\cdot \textbf{r})+\frac{1}{4}\|\textbf{r}\|^2\|\textbf{t}\|^2) & \textbf{t} - \frac{1}{2} \|\textbf{t}\|^2 \textbf{r} & \frac{1}{2}e^{s}\|\textbf{t}\|^2 \\[3pt] -e^{-s}\textbf{r}^T + \frac{1}{2}e^{-s}\|\textbf{r}\|^2\textbf{t}^T & I - \textbf{t}^T \textbf{r} & e^{s}\textbf{t}^T \\[3pt] \frac{1}{2}e^{-s}\|\textbf{r}\|^2 & -\textbf{r} & e^{s}\end{pmatrix}.\end{align*} $$
Now, if
![]() $p' = a_{s'}v_{\textbf {r}'},$
we obtain that
$p' = a_{s'}v_{\textbf {r}'},$
we obtain that
 $$ \begin{align*}p'u_{\textbf{t}'} = \begin{pmatrix} e^{s'} & e^{s'}\textbf{t}' & \frac{1}{2}e^{s'}\|\textbf{t}'\|^2 \\[3pt] \textbf{r}^{\prime T} & \textbf{r}^{\prime T}\textbf{t}' + I & \frac{1}{2}\|\textbf{t}'\|^2\textbf{r}^{\prime T} + \textbf{t}^{\prime T} \\[3pt] \frac{1}{2}e^{-s'}\|\textbf{r}'\|^2 & \frac{1}{2}e^{-s'}\|\textbf{r}'\|^2\textbf{t}' + e^{-s'}\textbf{r}' & e^{-s'}(\frac{1}{4}\|\textbf{r}'\|^2\|\textbf{t}'\|^2 +(\textbf{r}'\cdot \textbf{t}')+1)\end{pmatrix}.\end{align*} $$
$$ \begin{align*}p'u_{\textbf{t}'} = \begin{pmatrix} e^{s'} & e^{s'}\textbf{t}' & \frac{1}{2}e^{s'}\|\textbf{t}'\|^2 \\[3pt] \textbf{r}^{\prime T} & \textbf{r}^{\prime T}\textbf{t}' + I & \frac{1}{2}\|\textbf{t}'\|^2\textbf{r}^{\prime T} + \textbf{t}^{\prime T} \\[3pt] \frac{1}{2}e^{-s'}\|\textbf{r}'\|^2 & \frac{1}{2}e^{-s'}\|\textbf{r}'\|^2\textbf{t}' + e^{-s'}\textbf{r}' & e^{-s'}(\frac{1}{4}\|\textbf{r}'\|^2\|\textbf{t}'\|^2 +(\textbf{r}'\cdot \textbf{t}')+1)\end{pmatrix}.\end{align*} $$
We wish to solve for
![]() $\textbf {t}'$
.
$\textbf {t}'$
.
Setting entries equal yields
and
Combining these implies that
 $$ \begin{align*}\textbf{t}' = \frac{\textbf{t} - {1}/{2}\|\textbf{t}\|^2\textbf{r}}{e^s(1-(\textbf{t}\cdot\textbf{r})+{1}/{4}\|\textbf{r}\|^2\Vert \textbf{t}\Vert ^2)}.\end{align*} $$
$$ \begin{align*}\textbf{t}' = \frac{\textbf{t} - {1}/{2}\|\textbf{t}\|^2\textbf{r}}{e^s(1-(\textbf{t}\cdot\textbf{r})+{1}/{4}\|\textbf{r}\|^2\Vert \textbf{t}\Vert ^2)}.\end{align*} $$
We define
![]() $\rho _p(\textbf {t})$
to be this quantity. One can directly check that it satisfies the claim.
$\rho _p(\textbf {t})$
to be this quantity. One can directly check that it satisfies the claim.
3.1 Patterson–Sullivan and Lebesgue measures
For
![]() $x, y \in {\mathbb H}^n$
and
$x, y \in {\mathbb H}^n$
and
![]() $\xi \in \partial ({\mathbb H}^n)$
, the Busemann function is given by
$\xi \in \partial ({\mathbb H}^n)$
, the Busemann function is given by
where
![]() $\xi _t$
is a geodesic ray towards
$\xi _t$
is a geodesic ray towards
![]() $\xi $
.
$\xi $
.
A family of finite measures
![]() $\{\mu _x : x\in {\mathbb H}^n\}$
on
$\{\mu _x : x\in {\mathbb H}^n\}$
on
![]() $\partial ({\mathbb H}^n)$
is called a
$\partial ({\mathbb H}^n)$
is called a
![]() $\Gamma $
-invariant conformal density of dimension
$\Gamma $
-invariant conformal density of dimension
![]() $\delta _{\mu }>0$
if for every
$\delta _{\mu }>0$
if for every
![]() $x,y\in {\mathbb H}^n$
,
$x,y\in {\mathbb H}^n$
,
![]() $\xi \in \partial ({\mathbb H}^n)$
, and
$\xi \in \partial ({\mathbb H}^n)$
, and
![]() $\gamma \in \Gamma $
,
$\gamma \in \Gamma $
,
where
![]() $\gamma _*\mu _x(F)=\mu _x(F\gamma )$
for any Borel subset F of
$\gamma _*\mu _x(F)=\mu _x(F\gamma )$
for any Borel subset F of
![]() $\partial ({\mathbb H}^n)$
.
$\partial ({\mathbb H}^n)$
.
We let
![]() $\{\nu _x\}_{x \in {\mathbb H}^n}$
denote the Patterson–Sullivan density on
$\{\nu _x\}_{x \in {\mathbb H}^n}$
denote the Patterson–Sullivan density on
![]() $\partial {\mathbb H}^n$
, that is, the unique (up to scalar multiplication) conformal density of dimension
$\partial {\mathbb H}^n$
, that is, the unique (up to scalar multiplication) conformal density of dimension
![]() $\delta _{\Gamma }$
.
$\delta _{\Gamma }$
.
For each
![]() $x\in {\mathbb H}^n$
, we denote by
$x\in {\mathbb H}^n$
, we denote by
![]() $m_x$
the unique probability measure on
$m_x$
the unique probability measure on
![]() $\partial ({\mathbb H}^n)$
which is invariant under the compact subgroup
$\partial ({\mathbb H}^n)$
which is invariant under the compact subgroup
![]() $\text {Stab}_G (x)$
. Then
$\text {Stab}_G (x)$
. Then
![]() $\{m_x : x\in {\mathbb H}^n\}$
forms a G-invariant conformal density of dimension
$\{m_x : x\in {\mathbb H}^n\}$
forms a G-invariant conformal density of dimension
![]() $n-1$
, called the Lebesgue density. Fix
$n-1$
, called the Lebesgue density. Fix
![]() $o \in {\mathbb H}^n$
.
$o \in {\mathbb H}^n$
.
For
![]() $g\in G$
, we can define measures on
$g\in G$
, we can define measures on
![]() $Ug$
using the conformal densities defined previously. The Patterson–Sullivan measure (abbreviated as the PS measure)
$Ug$
using the conformal densities defined previously. The Patterson–Sullivan measure (abbreviated as the PS measure)
and the Lebesgue measure
We similarly define the opposite PS measure on
![]() $\tilde Ug$
:
$\tilde Ug$
:
The conformal properties of
![]() $m_x$
and
$m_x$
and
![]() $\nu _x$
imply that these definitions are independent of the choice of
$\nu _x$
imply that these definitions are independent of the choice of
![]() $o\in {\mathbb H}^n$
.
$o\in {\mathbb H}^n$
.
We often view
![]() $\mu ^{\operatorname {PS}}_{Ug}$
as a measure on U via
$\mu ^{\operatorname {PS}}_{Ug}$
as a measure on U via
and similarly for
![]() $\mu ^{\operatorname {PS}-}_{\tilde U g}$
on
$\mu ^{\operatorname {PS}-}_{\tilde U g}$
on
![]() $\tilde U$
. For
$\tilde U$
. For
![]() $g \in G, s \in \mathbb R$
and
$g \in G, s \in \mathbb R$
and
![]() $E\subseteq U$
a Borel subset (or
$E\subseteq U$
a Borel subset (or
![]() $E \subseteq \tilde U$
for
$E \subseteq \tilde U$
for
![]() $\mu ^{\operatorname {PS}-}$
), these measures satisfy
$\mu ^{\operatorname {PS}-}$
), these measures satisfy
In particular,
The measure
is independent of the orbit
![]() $Ug$
and is simply the Lebesgue measure on
$Ug$
and is simply the Lebesgue measure on
![]() $U\equiv \mathbb R^{n-1}$
up to a scalar multiple.
$U\equiv \mathbb R^{n-1}$
up to a scalar multiple.
We will need the following fundamental results, which are stated for
![]() $\mu ^{\operatorname {PS}}$
and U, but also hold if we replace them with
$\mu ^{\operatorname {PS}}$
and U, but also hold if we replace them with
![]() $\mu ^{\operatorname {PS}-}$
and
$\mu ^{\operatorname {PS}-}$
and
![]() $\tilde U$
.
$\tilde U$
.
Lemma 3.2. The map
![]() $g \mapsto \mu ^{\operatorname {PS}}_g$
is continuous, where the topology on the space of regular Borel measures on U is given by
$g \mapsto \mu ^{\operatorname {PS}}_g$
is continuous, where the topology on the space of regular Borel measures on U is given by
![]() $\mu _n \to \mu \iff \mu _n(f)\to \mu (f)$
for all
$\mu _n \to \mu \iff \mu _n(f)\to \mu (f)$
for all
![]() $f\in C_c(U)$
.
$f\in C_c(U)$
.
Proof. This is clear from the definition of the PS measure, since it is defined using the Busemann function and stereographic projection.
Corollary 3.3. For any compact set
![]() $\Omega \subseteq G$
and any
$\Omega \subseteq G$
and any
![]() $r>0$
,
$r>0$
,
To define the PS measure on
![]() $Ux$
for
$Ux$
for
![]() $x \in X,$
note that
$x \in X,$
note that
and we can define the PS measure on
![]() $Ux \subseteq X$
, denoted
$Ux \subseteq X$
, denoted
![]() $\mu ^{\operatorname {PS}}_x$
, simply by pushforward of
$\mu ^{\operatorname {PS}}_x$
, simply by pushforward of
![]() $\mu ^{\operatorname {PS}}_g$
, where
$\mu ^{\operatorname {PS}}_g$
, where
![]() $x = g\Gamma $
. In general, defining
$x = g\Gamma $
. In general, defining
![]() $\mu ^{\operatorname {PS}}_x$
requires more care, see e.g. [Reference Mohammadi and Oh24, §2.3] for more details. As before, we can view
$\mu ^{\operatorname {PS}}_x$
requires more care, see e.g. [Reference Mohammadi and Oh24, §2.3] for more details. As before, we can view
![]() $\mu ^{\operatorname {PS}}_x$
as a measure on U via
$\mu ^{\operatorname {PS}}_x$
as a measure on U via
3.2 Thick–thin decomposition and the height function
There exists a finite set of
![]() $\Gamma $
-representatives
$\Gamma $
-representatives
![]() $\xi _1,\ldots ,\xi _q\in \Lambda _{bp}(\Gamma )$
. For
$\xi _1,\ldots ,\xi _q\in \Lambda _{bp}(\Gamma )$
. For
![]() $i=1,\ldots ,q$
, fix
$i=1,\ldots ,q$
, fix
![]() $g_i\in G$
such that
$g_i\in G$
such that
![]() $g_i^- =\xi _i$
, and for any
$g_i^- =\xi _i$
, and for any
![]() $R>0$
, set
$R>0$
, set
(recall,
![]() $K=\text {Stab}_G (o)$
). Each
$K=\text {Stab}_G (o)$
). Each
![]() $\mathcal {H}_i(R)$
is a horoball of depth R.
$\mathcal {H}_i(R)$
is a horoball of depth R.
The rank of
![]() $\mathcal {H}_i(R)$
is the rank of the finitely generated abelian subgroup
$\mathcal {H}_i(R)$
is the rank of the finitely generated abelian subgroup
![]() $\Gamma _{\xi _i}=\operatorname {Stab}_{\Gamma }(\xi _i)$
. We say that the cusp has maximal rank if
$\Gamma _{\xi _i}=\operatorname {Stab}_{\Gamma }(\xi _i)$
. We say that the cusp has maximal rank if
![]() $\operatorname {rank}\Gamma _{\xi }=n-1$
. It is known that each rank is strictly smaller than
$\operatorname {rank}\Gamma _{\xi }=n-1$
. It is known that each rank is strictly smaller than
![]() $2\delta _{\Gamma }$
.
$2\delta _{\Gamma }$
.
We denote
(For now, this is simply notation. The measure
![]() $m^{\operatorname {BMS}}$
will be defined in the next section, and this set is its support. It projects onto the convex core of
$m^{\operatorname {BMS}}$
will be defined in the next section, and this set is its support. It projects onto the convex core of
![]() ${\mathbb H}^n/\Gamma .$
) Note that the condition
${\mathbb H}^n/\Gamma .$
) Note that the condition
![]() $g^{\pm } \in \Lambda (\Gamma )$
is independent of the choice of representative of
$g^{\pm } \in \Lambda (\Gamma )$
is independent of the choice of representative of
![]() $x=g\Gamma $
in the above definition, because
$x=g\Gamma $
in the above definition, because
![]() $\Lambda (\Gamma )$
is
$\Lambda (\Gamma )$
is
![]() $\Gamma $
-invariant. Thus, the notation
$\Gamma $
-invariant. Thus, the notation
![]() $x^{\pm } \in \Lambda (\Gamma )$
is well defined, even though
$x^{\pm } \in \Lambda (\Gamma )$
is well defined, even though
![]() $x^{\pm }$
itself is not.
$x^{\pm }$
itself is not.
According to [Reference Bowditch2], there exists
![]() $R_0\geq 1$
such that
$R_0\geq 1$
such that
![]() $\mathcal {X}_1(R_0),\ldots ,\mathcal {X}_q(R_0)$
are disjoint, and for some compact set
$\mathcal {X}_1(R_0),\ldots ,\mathcal {X}_q(R_0)$
are disjoint, and for some compact set
![]() $\mathcal {C}_0\subset G/\Gamma $
,
$\mathcal {C}_0\subset G/\Gamma $
,
For
![]() $1\le i\le q$
and
$1\le i\le q$
and
![]() $R\ge R_0$
, denote
$R\ge R_0$
, denote
We will need a version of Sullivan’s shadow lemma, obtained by Schapira–Maucourant (see Proposition 5.1 and Remark 5.2 in [Reference Maucourant and Schapira20]).
Proposition 3.4. There exists a constant
![]() $\unicode{x3bb} =\unicode{x3bb} (\Gamma )\ge 1$
such that for all
$\unicode{x3bb} =\unicode{x3bb} (\Gamma )\ge 1$
such that for all
![]() $x \in \operatorname {supp}m^{\operatorname {BMS}}$
and all
$x \in \operatorname {supp}m^{\operatorname {BMS}}$
and all
![]() $T>0$
, we have
$T>0$
, we have
and
 $$ \begin{align} \unicode{x3bb}^{-1} T^{\delta_{\Gamma}}e^{(k_2(x,T)-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\pi(a_{\log T}x))} &\le \mu^{\operatorname{PS}-}_x(B_{\tilde U}(T)) \nonumber\\ &\le \unicode{x3bb} T^{\delta_{\Gamma}}e^{(k_2(x,T)-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\pi(a_{\log T}x))}, \end{align} $$
$$ \begin{align} \unicode{x3bb}^{-1} T^{\delta_{\Gamma}}e^{(k_2(x,T)-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\pi(a_{\log T}x))} &\le \mu^{\operatorname{PS}-}_x(B_{\tilde U}(T)) \nonumber\\ &\le \unicode{x3bb} T^{\delta_{\Gamma}}e^{(k_2(x,T)-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\pi(a_{\log T}x))}, \end{align} $$
where
![]() $k_1(x,T)$
is the rank of
$k_1(x,T)$
is the rank of
![]() $\mathcal {X}_i(R_0)$
if
$\mathcal {X}_i(R_0)$
if
![]() $a_{-\log T}x\in \mathcal {X}_i(R_0)$
for some
$a_{-\log T}x\in \mathcal {X}_i(R_0)$
for some
![]() $1\le i\le \ell $
and equals 0 if
$1\le i\le \ell $
and equals 0 if
![]() $a_{-\log T}x\in \mathcal {C}_0$
, and
$a_{-\log T}x\in \mathcal {C}_0$
, and
![]() $k_2(x,T)$
is defined analogously for
$k_2(x,T)$
is defined analogously for
![]() $a_{\log T}x$
. Recall the definition of
$a_{\log T}x$
. Recall the definition of
![]() $\pi $
from (4) as the projection from G to
$\pi $
from (4) as the projection from G to
![]() ${\mathbb H}^n$
.
${\mathbb H}^n$
.
Definition 3.5. For
![]() $x \in G/\Gamma $
, we define the height of x by
$x \in G/\Gamma $
, we define the height of x by
where
![]() $\pi :G/\Gamma \to {\mathbb H}^n/\Gamma $
is the projection map as in (4), recalling that
$\pi :G/\Gamma \to {\mathbb H}^n/\Gamma $
is the projection map as in (4), recalling that
![]() ${\mathbb H}^n/\Gamma \cong K\backslash G/\Gamma $
.
${\mathbb H}^n/\Gamma \cong K\backslash G/\Gamma $
.
Lemma 3.6. For any
![]() $x\in \operatorname {supp}m^{\operatorname {BMS}}$
and
$x\in \operatorname {supp}m^{\operatorname {BMS}}$
and
![]() $R\ge R_0$
, we have that
$R\ge R_0$
, we have that
Proof. The claim follows from the disjointness of
![]() $\mathcal {X}_i(R_0)$
,
$\mathcal {X}_i(R_0)$
,
![]() $1\le i\le q$
from
$1\le i\le q$
from
![]() $\mathcal {C}_0$
, and the fact that
$\mathcal {C}_0$
, and the fact that
![]() $\mathcal {X}_i(R)\subseteq \mathcal {X}_i(R_0)$
.
$\mathcal {X}_i(R)\subseteq \mathcal {X}_i(R_0)$
.
If
![]() $x\in \mathcal {C}(R)$
, then either
$x\in \mathcal {C}(R)$
, then either
![]() $x\in \mathcal {C}_0$
, in which case
$x\in \mathcal {C}_0$
, in which case
![]() $\operatorname {height}(x)=0$
and we are done, or
$\operatorname {height}(x)=0$
and we are done, or
![]() $x\in \mathcal {X}_i(R_0)$
. Assume the latter, then the Busemann function between x and the boundary of
$x\in \mathcal {X}_i(R_0)$
. Assume the latter, then the Busemann function between x and the boundary of
![]() $\mathcal {X}_i(R_0)$
(which intersects
$\mathcal {X}_i(R_0)$
(which intersects
![]() $\mathcal {C}_0)$
is at most
$\mathcal {C}_0)$
is at most
![]() $R-R_0$
. Thus, we may deduce the claim in this case.
$R-R_0$
. Thus, we may deduce the claim in this case.
Next, assume
![]() $x\in \mathcal {X}_i(R)$
for some i. The Busemann function between two points in different horoballs is at least
$x\in \mathcal {X}_i(R)$
for some i. The Busemann function between two points in different horoballs is at least
![]() $R-R_0$
. Since a point from
$R-R_0$
. Since a point from
![]() $\mathcal {X}_i(R)$
cannot go into
$\mathcal {X}_i(R)$
cannot go into
![]() $\mathcal {C}_0$
without passing through
$\mathcal {C}_0$
without passing through
![]() $\mathcal {X}_i(R_0),$
this is a lower bound for the distance between the base points, that is, the height.
$\mathcal {X}_i(R_0),$
this is a lower bound for the distance between the base points, that is, the height.
Corollary 3.7. Let
![]() $x \in G/\Gamma $
be
$x \in G/\Gamma $
be
![]() $(\varepsilon ,s_0)$
-Diophantine. Then
$(\varepsilon ,s_0)$
-Diophantine. Then
Proof. By Definition 1.2,
Hence, we have that
 $$ \begin{align*} \operatorname{height}(x)&\le d(\mathcal{C}_0,x)\\ &< d(\mathcal{C}_0, a_{-s_0}x)+d(a_{-s_0}x,x) \\ &< (1-\varepsilon)s_0+s_0.\\[-2.8pc] \end{align*} $$
$$ \begin{align*} \operatorname{height}(x)&\le d(\mathcal{C}_0,x)\\ &< d(\mathcal{C}_0, a_{-s_0}x)+d(a_{-s_0}x,x) \\ &< (1-\varepsilon)s_0+s_0.\\[-2.8pc] \end{align*} $$
The injectivity radius at
![]() $x \in X$
is defined to be the supremum over all
$x \in X$
is defined to be the supremum over all
![]() $\varepsilon>0$
such that the map
$\varepsilon>0$
such that the map
We denote the injectivity radius at x by
The injectivity radius of a set
![]() $\Omega $
is defined to be
$\Omega $
is defined to be
By the proof of [Reference Mohammadi and Oh25, Proposition 6.7], there exists a constant
![]() $\sigma = \sigma (\Gamma )> 0$
such that for all
$\sigma = \sigma (\Gamma )> 0$
such that for all
![]() $x \in \operatorname {supp}m^{\operatorname {BMS}}$
,
$x \in \operatorname {supp}m^{\operatorname {BMS}}$
,
The following fact is well known, but we include a proof for completion.
Lemma 3.8. There exists
![]() $T_0=T_0(\Gamma )>0$
which satisfies the following. Let
$T_0=T_0(\Gamma )>0$
which satisfies the following. Let
![]() $x \in G/\Gamma $
with
$x \in G/\Gamma $
with
![]() $x^- \in \Lambda (\Gamma )$
, and let
$x^- \in \Lambda (\Gamma )$
, and let
![]() $R>0$
be such that
$R>0$
be such that
![]() $d(\mathcal {C}_0,x)<R.$
Then there exists
$d(\mathcal {C}_0,x)<R.$
Then there exists
![]() $\textbf {t} \in B_U(2(R+T))$
such that
$\textbf {t} \in B_U(2(R+T))$
such that
In particular, for every
![]() $0<\varepsilon <1$
,
$0<\varepsilon <1$
,
![]() $s_0\ge 1$
, and
$s_0\ge 1$
, and
![]() $(\varepsilon ,s_0)$
-Diophantine point x, there exists
$(\varepsilon ,s_0)$
-Diophantine point x, there exists
![]() $|\textbf {t}|\ll _{\Gamma } s_0$
such that
$|\textbf {t}|\ll _{\Gamma } s_0$
such that
Proof. Let
![]() $g,h' \in G$
be such that
$g,h' \in G$
be such that
![]() $x=g\Gamma $
,
$x=g\Gamma $
,
![]() $h^{\prime -} =g^-$
,
$h^{\prime -} =g^-$
,
![]() $h'\Gamma \in K\mathcal {C}_0$
, and
$h'\Gamma \in K\mathcal {C}_0$
, and
Since
![]() $K\mathcal {C}_0$
is a compact set, by [Reference Mohammadi and Oh24, Lemma 3.3], there exists a constant
$K\mathcal {C}_0$
is a compact set, by [Reference Mohammadi and Oh24, Lemma 3.3], there exists a constant
![]() $T_0$
, which only depends on
$T_0$
, which only depends on
![]() $\mathcal {C}_0$
(that is, on
$\mathcal {C}_0$
(that is, on
![]() $\Gamma $
) such that for some
$\Gamma $
) such that for some
![]() $\textbf {t}\in B_U(T_0)$
,
$\textbf {t}\in B_U(T_0)$
,
Fix
![]() $h:=u_{\textbf {t}} h'$
and observe that
$h:=u_{\textbf {t}} h'$
and observe that
We must flow
![]() $h\Gamma $
with an element of A so that it lies on
$h\Gamma $
with an element of A so that it lies on
![]() $Ux.$
$Ux.$
Because
![]() $h^- = g^-,$
if
$h^- = g^-,$
if
![]() $s = \beta _{g^-}(h,g)$
, then
$s = \beta _{g^-}(h,g)$
, then
Since
![]() $\beta _{g^-}(h,g) \le d(h,g)$
, we arrive at
$\beta _{g^-}(h,g) \le d(h,g)$
, we arrive at
 $$ \begin{align*} d(g,a_s h)&\le d(g,h)+d(h,a_s h)\\ &\le 2d(g,h)\\ &\le 2(R+T). \end{align*} $$
$$ \begin{align*} d(g,a_s h)&\le d(g,h)+d(h,a_s h)\\ &\le 2d(g,h)\\ &\le 2(R+T). \end{align*} $$
For
![]() $(\varepsilon ,s_0)$
-Diophantine x, observe that
$(\varepsilon ,s_0)$
-Diophantine x, observe that
 $$ \begin{align*} d(\mathcal{C}_0,x)&\le d(\mathcal{C}_0,a_{-s_0}x) + d(a_{-s_0},x) \\ &< (1-\varepsilon)s_0+s_0 \\ &< 2s_0, \end{align*} $$
$$ \begin{align*} d(\mathcal{C}_0,x)&\le d(\mathcal{C}_0,a_{-s_0}x) + d(a_{-s_0},x) \\ &< (1-\varepsilon)s_0+s_0 \\ &< 2s_0, \end{align*} $$
so we see that
![]() $R=2s_0$
works for all such points.
$R=2s_0$
works for all such points.
3.3 Bowen–Margulis–Sullivan and Burger–Roblin measures
Recall
![]() $\pi : G \to {\mathbb H}^n$
from (4). In this section, we will abuse notation and write
$\pi : G \to {\mathbb H}^n$
from (4). In this section, we will abuse notation and write
![]() $\pi $
for the restriction of
$\pi $
for the restriction of
![]() $\pi $
to
$\pi $
to
![]() ${\operatorname {T}^1}({\mathbb H}^n)\cong M\backslash G.$
Recalling the fixed reference point
${\operatorname {T}^1}({\mathbb H}^n)\cong M\backslash G.$
Recalling the fixed reference point
![]() $o \in {\mathbb H}^n$
as before, the map
$o \in {\mathbb H}^n$
as before, the map
is a homeomorphism between
![]() ${\operatorname {T}^1}({\mathbb H}^n)$
and
${\operatorname {T}^1}({\mathbb H}^n)$
and
This homeomorphism allows us to define the Bowen–Margulis–Sullivan (BMS) and Burger–Roblin (BR) measures on
![]() ${\operatorname {T}^1}({\mathbb H}^n)$
, denoted by
${\operatorname {T}^1}({\mathbb H}^n)$
, denoted by
![]() $\tilde {m}^{\operatorname {BMS}}$
and
$\tilde {m}^{\operatorname {BMS}}$
and
![]() $\tilde {m}^{\operatorname {BR}}$
respectively:
$\tilde {m}^{\operatorname {BR}}$
respectively:
The conformal properties of
![]() $\{\nu _x\}$
and
$\{\nu _x\}$
and
![]() $\{m_x\}$
imply that these definitions are independent of the choice of
$\{m_x\}$
imply that these definitions are independent of the choice of
![]() $o\in {\mathbb H}^n$
. Using the identification of
$o\in {\mathbb H}^n$
. Using the identification of
![]() ${\operatorname {T}^1}({\mathbb H}^n)$
with
${\operatorname {T}^1}({\mathbb H}^n)$
with
![]() $M\backslash G$
, we lift the above measures to G so that they are all invariant under M from the left. By abuse of notation, we use the same notation (
$M\backslash G$
, we lift the above measures to G so that they are all invariant under M from the left. By abuse of notation, we use the same notation (
![]() $\tilde {m}^{\operatorname {BMS}}$
and
$\tilde {m}^{\operatorname {BMS}}$
and
![]() $\tilde {m}^{\operatorname {BR}}$
). These measures are right
$\tilde {m}^{\operatorname {BR}}$
). These measures are right
![]() $\Gamma $
-invariant, and hence induce locally finite Borel measures on X, which are the Bowen–Margulis–Sullivan measure
$\Gamma $
-invariant, and hence induce locally finite Borel measures on X, which are the Bowen–Margulis–Sullivan measure
![]() $m^{\operatorname {BMS}}$
and the Burger–Roblin measure
$m^{\operatorname {BMS}}$
and the Burger–Roblin measure
![]() $m^{\operatorname {BR}}$
respectively.
$m^{\operatorname {BR}}$
respectively.
Note that
and
Recall
![]() $P = MA\tilde {U}$
, which is exactly the stabilizer of
$P = MA\tilde {U}$
, which is exactly the stabilizer of
![]() $w_o^+$
in G. We can define another measure
$w_o^+$
in G. We can define another measure
![]() $\nu $
on
$\nu $
on
![]() $Pg$
for
$Pg$
for
![]() $g \in G$
, which will give us a product structure for
$g \in G$
, which will give us a product structure for
![]() $\tilde {m}^{\operatorname {BMS}}$
and
$\tilde {m}^{\operatorname {BMS}}$
and
![]() $\tilde {m}^{\operatorname {BR}}$
that will be useful in our approach. For any
$\tilde {m}^{\operatorname {BR}}$
that will be useful in our approach. For any
![]() $g\in G$
, define
$g\in G$
, define
on
![]() $Pg$
, where
$Pg$
, where
![]() $s = \beta _{(pg)^-}(o,pg(o))$
,
$s = \beta _{(pg)^-}(o,pg(o))$
,
![]() $p = mav \in MA\tilde {U}$
, and
$p = mav \in MA\tilde {U}$
, and
![]() $dm$
is the probability Haar measure on M.
$dm$
is the probability Haar measure on M.
Then for any
![]() $\psi \in C_c(G)$
and
$\psi \in C_c(G)$
and
![]() $g\in G$
, we have
$g\in G$
, we have
 $$ \begin{align} \tilde{m}^{\operatorname{BMS}}(\psi)=\int_{Pg}\int_U \psi(u_{\textbf{t}} pg)\,d\mu^{\operatorname{PS}}_{pg}(\textbf{t})\,d\nu(pg) \end{align} $$
$$ \begin{align} \tilde{m}^{\operatorname{BMS}}(\psi)=\int_{Pg}\int_U \psi(u_{\textbf{t}} pg)\,d\mu^{\operatorname{PS}}_{pg}(\textbf{t})\,d\nu(pg) \end{align} $$
and
 $$ \begin{align} \tilde{m}^{\operatorname{BR}}(\psi)=\int_{Pg}\int_U \psi(u_{\textbf{t}} pg)\,d\textbf{t} \,d\nu(pg). \end{align} $$
$$ \begin{align} \tilde{m}^{\operatorname{BR}}(\psi)=\int_{Pg}\int_U \psi(u_{\textbf{t}} pg)\,d\textbf{t} \,d\nu(pg). \end{align} $$
Lemma 3.9. There exists a constant
![]() $\unicode{x3bb} =\unicode{x3bb} (\Gamma )> 1$
such that for all
$\unicode{x3bb} =\unicode{x3bb} (\Gamma )> 1$
such that for all
![]() $g \in \operatorname {supp}\tilde {m}^{\operatorname {BMS}}$
and all
$g \in \operatorname {supp}\tilde {m}^{\operatorname {BMS}}$
and all
![]() $0<\varepsilon <\operatorname {inj}(g)$
, we have
$0<\varepsilon <\operatorname {inj}(g)$
, we have
 $$ \begin{align*}&\unicode{x3bb}^{-1} \varepsilon^{\delta_{\Gamma} +{1}/{2}(n-1)(n-2)+1}e^{(k_2(x,\varepsilon)-\delta_{\Gamma})d(\pi(\mathcal{C}_0), \pi(a_{\log \varepsilon}x))} \\[3pt] &\le \nu(P_{\varepsilon} g) \\[3pt] &\le \unicode{x3bb} \varepsilon^{\delta_{\Gamma} +{1}/{2}(n-1)(n-2)+1}e^{(k_2(x,\varepsilon)-\delta_{\Gamma})d(\pi(\mathcal{C}_0), \pi(a_{\log \varepsilon}x))},\end{align*} $$
$$ \begin{align*}&\unicode{x3bb}^{-1} \varepsilon^{\delta_{\Gamma} +{1}/{2}(n-1)(n-2)+1}e^{(k_2(x,\varepsilon)-\delta_{\Gamma})d(\pi(\mathcal{C}_0), \pi(a_{\log \varepsilon}x))} \\[3pt] &\le \nu(P_{\varepsilon} g) \\[3pt] &\le \unicode{x3bb} \varepsilon^{\delta_{\Gamma} +{1}/{2}(n-1)(n-2)+1}e^{(k_2(x,\varepsilon)-\delta_{\Gamma})d(\pi(\mathcal{C}_0), \pi(a_{\log \varepsilon}x))},\end{align*} $$
where
![]() $x = g\Gamma $
and
$x = g\Gamma $
and
![]() $k_2(x,\varepsilon )$
is as defined in Proposition 3.4.
$k_2(x,\varepsilon )$
is as defined in Proposition 3.4.
Proof. Let
![]() $x = g\Gamma $
. By Proposition 3.4, there exists
$x = g\Gamma $
. By Proposition 3.4, there exists
![]() $\tilde {\unicode{x3bb} }> 1$
such that for all such
$\tilde {\unicode{x3bb} }> 1$
such that for all such
![]() $\varepsilon $
,
$\varepsilon $
,
 $$ \begin{align} \tilde{\unicode{x3bb}}^{-1} \varepsilon^{\delta_{\Gamma}}e^{(k_2(x,\varepsilon)-\delta_{\Gamma})d(\pi(\mathcal{C}_0), \pi(a_{\log \varepsilon}x))} &\le \mu^{\operatorname{PS}-}_g(B_{\tilde U}(\varepsilon))\nonumber\\[4pt] &\le \tilde{\unicode{x3bb}} \varepsilon^{\delta_{\Gamma}}e^{(k_2(x,\varepsilon)-\delta_{\Gamma})d(\pi(\mathcal{C}_0), \pi(a_{\log \varepsilon}x))}. \end{align} $$
$$ \begin{align} \tilde{\unicode{x3bb}}^{-1} \varepsilon^{\delta_{\Gamma}}e^{(k_2(x,\varepsilon)-\delta_{\Gamma})d(\pi(\mathcal{C}_0), \pi(a_{\log \varepsilon}x))} &\le \mu^{\operatorname{PS}-}_g(B_{\tilde U}(\varepsilon))\nonumber\\[4pt] &\le \tilde{\unicode{x3bb}} \varepsilon^{\delta_{\Gamma}}e^{(k_2(x,\varepsilon)-\delta_{\Gamma})d(\pi(\mathcal{C}_0), \pi(a_{\log \varepsilon}x))}. \end{align} $$
From (24), if m denotes the probability Haar measure on M, we then have
 $$ \begin{align*} \nu(P_{\varepsilon} g) &\le \int_{A_{\varepsilon}}\int_{M_{\varepsilon}} \mu^{\operatorname{PS}-}_g(B_{\tilde U}(\varepsilon))\,dm\,ds\\[3pt] &\le C \tilde{\unicode{x3bb}} \varepsilon^{\delta_{\Gamma}+{1}/{2}(n-1)(n-2)+1}e^{(k_2(x,\varepsilon)-\delta_{\Gamma})d(\pi(\mathcal{C}_0), \pi(a_{\log \varepsilon}x))},\end{align*} $$
$$ \begin{align*} \nu(P_{\varepsilon} g) &\le \int_{A_{\varepsilon}}\int_{M_{\varepsilon}} \mu^{\operatorname{PS}-}_g(B_{\tilde U}(\varepsilon))\,dm\,ds\\[3pt] &\le C \tilde{\unicode{x3bb}} \varepsilon^{\delta_{\Gamma}+{1}/{2}(n-1)(n-2)+1}e^{(k_2(x,\varepsilon)-\delta_{\Gamma})d(\pi(\mathcal{C}_0), \pi(a_{\log \varepsilon}x))},\end{align*} $$
where C is determined by the scaling of the probability Haar measures on A and M. The lower bound follows similarly. Then,
![]() $\unicode{x3bb} =\max \{C \tilde {\unicode{x3bb} },\tilde {\unicode{x3bb} }\}$
satisfies the conclusion of the lemma.
$\unicode{x3bb} =\max \{C \tilde {\unicode{x3bb} },\tilde {\unicode{x3bb} }\}$
satisfies the conclusion of the lemma.
3.4 Admissible boxes and smooth partitions of unity
Recall that for
![]() $\eta>0$
, we denoted by
$\eta>0$
, we denoted by
![]() $G_{\eta }$
the closed
$G_{\eta }$
the closed
![]() $\eta $
-neighborhood of e in G.
$\eta $
-neighborhood of e in G.
Take
![]() $\varepsilon>0$
such that the map
$\varepsilon>0$
such that the map
For
![]() $x\in X$
and
$x\in X$
and
![]() $\eta _1>0$
,
$\eta _1>0$
,
![]() $\eta _2\geq 0$
less than
$\eta _2\geq 0$
less than
![]() $\operatorname {inj}(x)$
, we call
$\operatorname {inj}(x)$
, we call
an admissible box (with respect to the PS measure) if B is the injective image of
![]() $B_U(\eta _1)P_{\eta _2}$
in X under the map
$B_U(\eta _1)P_{\eta _2}$
in X under the map
![]() $h\mapsto h x$
and
$h\mapsto h x$
and
for all
![]() $p\in P_{\eta _2}$
. For
$p\in P_{\eta _2}$
. For
![]() $g\in G$
, we say that
$g\in G$
, we say that
![]() $B = B_U(\eta _1)P_{\eta _2}g$
is an admissible box if
$B = B_U(\eta _1)P_{\eta _2}g$
is an admissible box if
![]() $B = B_U(\eta _1)P_{\eta _2}x$
is one.
$B = B_U(\eta _1)P_{\eta _2}x$
is one.
Note that if
![]() $B_U(\eta _1)P_{\eta _2}g$
is an admissible box, then there exists
$B_U(\eta _1)P_{\eta _2}g$
is an admissible box, then there exists
![]() $\varepsilon>0$
such that
$\varepsilon>0$
such that
![]() $B_U (\eta _1+\varepsilon )P_{\eta _2 + \varepsilon }g$
is also an admissible box. Moreover, every point has an admissible box around it by [Reference Oh and Shah26, Lemma 2.17].
$B_U (\eta _1+\varepsilon )P_{\eta _2 + \varepsilon }g$
is also an admissible box. Moreover, every point has an admissible box around it by [Reference Oh and Shah26, Lemma 2.17].
The error terms in our main theorems are in terms of Sobolev norms, which we define here. For
![]() $\ell \in \mathbb N$
,
$\ell \in \mathbb N$
,
![]() $1\leq p\leq \infty $
, and
$1\leq p\leq \infty $
, and
![]() $\psi \in C^{\infty }(X)\cap L^p(X)$
, we consider the following Sobolev norm:
$\psi \in C^{\infty }(X)\cap L^p(X)$
, we consider the following Sobolev norm:
where the sum is taken over all monomials U in a fixed basis of
![]() $\mathfrak {g}=\mbox {Lie}(G)$
of order at most
$\mathfrak {g}=\mbox {Lie}(G)$
of order at most
![]() $\ell $
, and
$\ell $
, and
![]() $\Vert \cdot \Vert _p$
denotes the
$\Vert \cdot \Vert _p$
denotes the
![]() $L^p(X)$
-norm. Since we will be using
$L^p(X)$
-norm. Since we will be using
![]() $S_{2,\ell }$
most often, we set
$S_{2,\ell }$
most often, we set
Our proofs will require constructing smooth indicator functions and partitions of unity with controlled Sobolev norms. We prove such lemmas below.
Lemma 3.10. Let H be a horospherical subgroup of G (that is, U or
![]() $\tilde {U}$
). For every
$\tilde {U}$
). For every
![]() $\xi _1,\xi _2>0$
and
$\xi _1,\xi _2>0$
and
![]() $g \in G$
, there exists a non-negative smooth function
$g \in G$
, there exists a non-negative smooth function
![]() $\chi _{\xi _1,\xi _2}$
defined on
$\chi _{\xi _1,\xi _2}$
defined on
![]() $H_{\xi _1+\xi _2}g$
such that
$H_{\xi _1+\xi _2}g$
such that
![]() $0 \le \chi _{\xi _1,\xi _2}\le 1 $
,
$0 \le \chi _{\xi _1,\xi _2}\le 1 $
,
![]() $S_{\ell }(\chi _{\xi _1,\xi _2}) \ll _{n,\Gamma } \xi _1^{n-1}\xi _2^{-\ell -(n-1)/2},$
and
$S_{\ell }(\chi _{\xi _1,\xi _2}) \ll _{n,\Gamma } \xi _1^{n-1}\xi _2^{-\ell -(n-1)/2},$
and
 $$ \begin{align*}\chi_{\xi_1,\xi_2}(h) = \begin{cases} 0 & \text{ if } h \not\in H_{\xi_1+\xi_2 }g, \\ 1 &\text{ if } h \in H_{\xi_1-\xi_2}g.\end{cases}\end{align*} $$
$$ \begin{align*}\chi_{\xi_1,\xi_2}(h) = \begin{cases} 0 & \text{ if } h \not\in H_{\xi_1+\xi_2 }g, \\ 1 &\text{ if } h \in H_{\xi_1-\xi_2}g.\end{cases}\end{align*} $$
Proof. According to [Reference Kleinbock and Margulis17, Lemma 2.4.7(b)], there exists
![]() $c_1=c_1(n)>0$
such that for every
$c_1=c_1(n)>0$
such that for every
![]() $\xi>0$
, there exists a non-negative smooth function
$\xi>0$
, there exists a non-negative smooth function
![]() $\sigma _{\xi }$
defined on
$\sigma _{\xi }$
defined on
![]() $H_{\xi }$
such that
$H_{\xi }$
such that
For
![]() $g\in \Omega $
, let
$g\in \Omega $
, let
![]() $\chi _{\xi _1,\xi _2}={\mathbf {1}}_{H_{\xi _1} g}*\sigma _{\xi _2}$
. Then for any
$\chi _{\xi _1,\xi _2}={\mathbf {1}}_{H_{\xi _1} g}*\sigma _{\xi _2}$
. Then for any
![]() $h\in H$
, we have
$h\in H$
, we have
![]() $0\leq \chi _{\xi _1,\xi _2}(h)\leq 1$
and
$0\leq \chi _{\xi _1,\xi _2}(h)\leq 1$
and
 $$ \begin{align*} \chi_{\xi_1,\xi_2}(h)=\begin{cases} 0 & \text{if }h\notin H_{\xi_1+\xi_2}g,\\ 1& \text{if }h\in H_{\xi_1-\xi_2}g. \end{cases} \end{align*} $$
$$ \begin{align*} \chi_{\xi_1,\xi_2}(h)=\begin{cases} 0 & \text{if }h\notin H_{\xi_1+\xi_2}g,\\ 1& \text{if }h\in H_{\xi_1-\xi_2}g. \end{cases} \end{align*} $$
Since for some
![]() $c_2=c_2(\Gamma )>0$
,
$c_2=c_2(\Gamma )>0$
,
by the properties of the Sobolev norm and (28), we arrive at
Lemma 3.11. Let H be a horospherical subgroup of G,
![]() $r>0$
,
$r>0$
,
![]() $\ell \in \mathbb N$
, and let
$\ell \in \mathbb N$
, and let
![]() $E\subset H$
be bounded. Then, there exists a partition of unity
$E\subset H$
be bounded. Then, there exists a partition of unity
![]() $\sigma _1,\ldots ,\sigma _k$
of E in
$\sigma _1,\ldots ,\sigma _k$
of E in
![]() $H_r E$
, that is,
$H_r E$
, that is,
 $$ \begin{align*} \sum_{i=1}^k \sigma_i(x)=\begin{cases} 0 & \text{if }x\notin H_r E,\\ 1 & \text{if }x\in E, \end{cases}\end{align*} $$
$$ \begin{align*} \sum_{i=1}^k \sigma_i(x)=\begin{cases} 0 & \text{if }x\notin H_r E,\\ 1 & \text{if }x\in E, \end{cases}\end{align*} $$
such that for some
![]() $u_1,\ldots ,u_k\in E$
and all
$u_1,\ldots ,u_k\in E$
and all
![]() $1\leq i\leq k$
,
$1\leq i\leq k$
,
Moreover, if there exists
![]() $R>r$
such that
$R>r$
such that
![]() $E=H_R$
, then
$E=H_R$
, then
![]() $k\ll _n ({R}/{r})^{n-1}$
.
$k\ll _n ({R}/{r})^{n-1}$
.
Proof. Let
![]() $\{u_1,\ldots ,u_k\}$
be a maximal
$\{u_1,\ldots ,u_k\}$
be a maximal
![]() ${r}/{4}$
-separated set in E. Then
${r}/{4}$
-separated set in E. Then
 $$ \begin{align} E\subseteq\bigcup_{i=1}^k H_{r/2}u_i. \end{align} $$
$$ \begin{align} E\subseteq\bigcup_{i=1}^k H_{r/2}u_i. \end{align} $$
Let
![]() $1\leq i\leq k$
. According to [Reference Hörmander13, Theorem 1.4.2], there exists
$1\leq i\leq k$
. According to [Reference Hörmander13, Theorem 1.4.2], there exists
![]() $\chi _i\in C_c^{\infty }(H_{r} u_i)$
such that
$\chi _i\in C_c^{\infty }(H_{r} u_i)$
such that
![]() $0\leq \chi _i\leq 1$
,
$0\leq \chi _i\leq 1$
,
![]() $\chi _i(u)=1$
for any
$\chi _i(u)=1$
for any
![]() $u\in H_{r/2}u_i$
, and for
$u\in H_{r/2}u_i$
, and for
![]() $1\leq m\leq \ell $
,
$1\leq m\leq \ell $
,
(where the implied constant depends only on n). Let
![]() $\sigma _i$
be defined by
$\sigma _i$
be defined by
Then, each
![]() $\sigma _i\in C_c^{\infty }(H_{r} u_i)$
and
$\sigma _i\in C_c^{\infty }(H_{r} u_i)$
and
 $$ \begin{align*} 1-\sum_{i=1}^k\sigma_i=\prod_{i=1}^k(1-\chi_i)=0 \quad\mbox{on }\bigcup_{i=1}^k H_{r}u_i\end{align*} $$
$$ \begin{align*} 1-\sum_{i=1}^k\sigma_i=\prod_{i=1}^k(1-\chi_i)=0 \quad\mbox{on }\bigcup_{i=1}^k H_{r}u_i\end{align*} $$
implies that
![]() $\sum _{i=1}^k\sigma _i=1$
on
$\sum _{i=1}^k\sigma _i=1$
on
![]() $\bigcup _{i=1}^k H_{r/2}u_i$
.
$\bigcup _{i=1}^k H_{r/2}u_i$
.
By the rules for differentiating a product and (30) for
![]() $1\leq m\leq \ell $
, we have
$1\leq m\leq \ell $
, we have
where C is the multiplicity of the cover in (29). By Besicovitch covering theorem, C is bounded by a constant which depends only on n. Using the definition of the Sobolev norm, we arrive at
Now, assume there exists
![]() $R>r$
such that
$R>r$
such that
![]() $E=H_R$
. Since the geometry of H is of an Euclidean space of dimension
$E=H_R$
. Since the geometry of H is of an Euclidean space of dimension
![]() $\dim H$
, we then have
$\dim H$
, we then have
 $$ \begin{align*} k\ll_n\bigg(\frac{R}{r}\bigg)^{n-1}.\\[-3.6pc] \end{align*} $$
$$ \begin{align*} k\ll_n\bigg(\frac{R}{r}\bigg)^{n-1}.\\[-3.6pc] \end{align*} $$
Lemma 3.12. Let H be either U or G. There exists
![]() $\ell '=\ell '(H)>0$
such that for any integer
$\ell '=\ell '(H)>0$
such that for any integer
![]() $\ell>\ell '$
,
$\ell>\ell '$
,
![]() $\eta>0$
,
$\eta>0$
,
![]() $H\in \{U,G\}$
, and
$H\in \{U,G\}$
, and
![]() $f\in C_c^{\infty }(H)$
, there exist functions
$f\in C_c^{\infty }(H)$
, there exist functions
![]() $f_{\eta ,\pm }\in C_c^{\infty }(H)$
which are supported on an
$f_{\eta ,\pm }\in C_c^{\infty }(H)$
which are supported on an
![]() $2\eta $
neighborhood of
$2\eta $
neighborhood of
![]() $\operatorname {supp} f$
, and for any
$\operatorname {supp} f$
, and for any
![]() $h\in H$
, satisfy:
$h\in H$
, satisfy:
-
(1)
 $f_{\eta ,-}(h)\le \min _{w\in H_{\eta }}f(wh) \le \max _{w\in H_{\eta }}f(wh) \le f_{\eta ,+}(h)$
;
$f_{\eta ,-}(h)\le \min _{w\in H_{\eta }}f(wh) \le \max _{w\in H_{\eta }}f(wh) \le f_{\eta ,+}(h)$
; -
(2)
 $|f_{\eta ,\pm }(h)-f(h)|\ll _{\operatorname {supp} f} \eta S_{\ell }(f)$
;
$|f_{\eta ,\pm }(h)-f(h)|\ll _{\operatorname {supp} f} \eta S_{\ell }(f)$
; -
(3)
 $S_{\ell }(f_{\eta ,\pm })\ll _{H,\operatorname {supp} f}\eta ^{-2\ell } S_{\ell }(f).$
$S_{\ell }(f_{\eta ,\pm })\ll _{H,\operatorname {supp} f}\eta ^{-2\ell } S_{\ell }(f).$
Proof. First, according to [Reference Aubin1], there exists
![]() $\ell '\in \mathbb N$
such that any
$\ell '\in \mathbb N$
such that any
![]() $\ell>\ell '$
satisfies
$\ell>\ell '$
satisfies
![]() $S_{\infty ,1}(\psi )\ll _{\operatorname {supp} \psi } S_{\ell }(\psi )$
for any
$S_{\infty ,1}(\psi )\ll _{\operatorname {supp} \psi } S_{\ell }(\psi )$
for any
![]() $\psi \in C_c^{\infty }(H)$
.
$\psi \in C_c^{\infty }(H)$
.
Let
![]() $f^{\prime }_{\eta ,\pm }$
be defined by
$f^{\prime }_{\eta ,\pm }$
be defined by
for any
![]() $h\in H$
.
$h\in H$
.
As before, we use [Reference Kleinbock and Margulis17, Lemma 2.4.7(b)] to deduce that there exist
![]() $c_1=c_1(H)>0$
,
$c_1=c_1(H)>0$
,
![]() $n_1=n_1(H)$
, and a non-negative smooth function
$n_1=n_1(H)$
, and a non-negative smooth function
![]() $\sigma _{\eta }$
supported on
$\sigma _{\eta }$
supported on
![]() $H_{\eta }$
such that
$H_{\eta }$
such that
Define
![]() $f_{\eta ,\pm }$
by
$f_{\eta ,\pm }$
by
Then,
![]() $f_{\eta ,\pm }$
are smooth functions which are supported on a
$f_{\eta ,\pm }$
are smooth functions which are supported on a
![]() $2\eta $
neighborhood of
$2\eta $
neighborhood of
![]() $\operatorname {supp} f$
. Moreover, for any
$\operatorname {supp} f$
. Moreover, for any
![]() $h\in H$
,
$h\in H$
,
 $$ \begin{align} f^{\prime}_{\eta,+}(h) & = \int_{H_{\eta}}f^{\prime}_{\eta,+}(h)\sigma_{\eta}(u^{-1})\,dm^{\operatorname{Haar}}(u)\nonumber\\ & \le \int_{H_{\eta}}f^{\prime}_{2\eta,+}(uh)\sigma_{\eta}(u^{-1})\,dm^{\operatorname{Haar}}(u) \quad\text{by definition of } f^{\prime}_{2\eta,+}\\ & = f_{\eta,+}(h)\nonumber\\ & \le \int_{H_{\eta}}f^{\prime}_{3\eta,+}(h)\sigma_{\eta}(u^{-1})\,dm^{\operatorname{Haar}}(u) \quad\text{by (31) and definition of }f^{\prime}_{3\eta,+}\nonumber\\ & = f^{\prime}_{3\eta,+}(h).\nonumber \end{align} $$
$$ \begin{align} f^{\prime}_{\eta,+}(h) & = \int_{H_{\eta}}f^{\prime}_{\eta,+}(h)\sigma_{\eta}(u^{-1})\,dm^{\operatorname{Haar}}(u)\nonumber\\ & \le \int_{H_{\eta}}f^{\prime}_{2\eta,+}(uh)\sigma_{\eta}(u^{-1})\,dm^{\operatorname{Haar}}(u) \quad\text{by definition of } f^{\prime}_{2\eta,+}\\ & = f_{\eta,+}(h)\nonumber\\ & \le \int_{H_{\eta}}f^{\prime}_{3\eta,+}(h)\sigma_{\eta}(u^{-1})\,dm^{\operatorname{Haar}}(u) \quad\text{by (31) and definition of }f^{\prime}_{3\eta,+}\nonumber\\ & = f^{\prime}_{3\eta,+}(h).\nonumber \end{align} $$
In a similar way, one can show
proving the first inequality.
By the mean value theorem, for any
![]() $h\in H$
,
$h\in H$
,
![]() $w\in H_{3\eta }$
,
$w\in H_{3\eta }$
,
Since
![]() $f^{\prime }_{3\eta ,-}\le f_{\eta ,-} \le f_{\eta ,+} \le f^{\prime }_{3\eta ,+},$
there exist some
$f^{\prime }_{3\eta ,-}\le f_{\eta ,-} \le f_{\eta ,+} \le f^{\prime }_{3\eta ,+},$
there exist some
![]() $w_{+},w_{-}\in H_{3\eta }$
such that
$w_{+},w_{-}\in H_{3\eta }$
such that
and we have the second inequality.
Now, we have
By choosing
![]() $\ell '>n_1$
, we may deduce the last inequality.
$\ell '>n_1$
, we may deduce the last inequality.
4 Quantitative non-divergence
In this section, we prove a quantitative non-divergence result that is crucial in the following sections. We use the notation established in §3.2. The results in this section hold for any
![]() $\Gamma $
that is geometrically finite, without need for Assumption 1.1.
$\Gamma $
that is geometrically finite, without need for Assumption 1.1.
Recall from §1 that for
![]() $0<\varepsilon <1$
and
$0<\varepsilon <1$
and
![]() $s_0\ge 1$
, we say that
$s_0\ge 1$
, we say that
![]() $x\in X$
is
$x\in X$
is
![]() $(\varepsilon ,s_0)$
-Diophantine if for all
$(\varepsilon ,s_0)$
-Diophantine if for all
![]() $\tau>s_0$
,
$\tau>s_0$
,
where
![]() $\mathcal {C}_0$
is the compact set defined in §3.2. Let
$\mathcal {C}_0$
is the compact set defined in §3.2. Let
![]() $R_0$
and q also be as defined in §3.2.
$R_0$
and q also be as defined in §3.2.
This section is dedicated to the proof of the following theorem, which says (in a quantitative way) that most of the U orbit of a Diophantine point is not in the cusp.
Theorem 4.1. There exists
![]() $\beta>0$
satisfying the following: for every
$\beta>0$
satisfying the following: for every
![]() $0<\varepsilon <1$
and
$0<\varepsilon <1$
and
![]() $s_0\ge 1$
, and for every
$s_0\ge 1$
, and for every
![]() $(\varepsilon ,s_0)$
-Diophantine element
$(\varepsilon ,s_0)$
-Diophantine element
![]() $x\in X$
, every
$x\in X$
, every
![]() $R\ge R_0$
, every
$R\ge R_0$
, every
![]() $T\gg _{\Gamma ,\varepsilon }s_0$
, and every
$T\gg _{\Gamma ,\varepsilon }s_0$
, and every
![]() $0<s\le T^{\varepsilon }$
, we have
$0<s\le T^{\varepsilon }$
, we have
We now follow the notation of Mohammadi and Oh in [Reference Mohammadi and Oh25, §6]. Equip
![]() $\mathbb {R}^{n+1}$
with the Euclidean norm. Recall from §3.2 that for
$\mathbb {R}^{n+1}$
with the Euclidean norm. Recall from §3.2 that for
![]() $1\le i\le q$
,
$1\le i\le q$
,
![]() $g_i^-=\xi _i$
. Without loss of generality, we may further assume that
$g_i^-=\xi _i$
. Without loss of generality, we may further assume that
![]() $g_i$
satisfies
$g_i$
satisfies
![]() $\Vert g_i^{-1}e_1\Vert =~1.$
Let
$\Vert g_i^{-1}e_1\Vert =~1.$
Let
Lemma 4.2. For any
![]() $i=1,\ldots ,q$
,
$i=1,\ldots ,q$
,
![]() $\Gamma v_i$
is a discrete subset of
$\Gamma v_i$
is a discrete subset of
![]() $\mathbb {R}^{n+1}$
.
$\mathbb {R}^{n+1}$
.
Proof. Since
![]() $\xi _i$
is assumed to be a bounded parabolic limit point, by definition,
$\xi _i$
is assumed to be a bounded parabolic limit point, by definition,
![]() $(\Lambda (\Gamma )\setminus \{\xi _i\})/ \Gamma _{\xi _i}=(\Lambda (\Gamma )\setminus \{\xi _i\})/ \Gamma _{v_i}$
is compact, where
$(\Lambda (\Gamma )\setminus \{\xi _i\})/ \Gamma _{\xi _i}=(\Lambda (\Gamma )\setminus \{\xi _i\})/ \Gamma _{v_i}$
is compact, where
If
![]() $\gamma \in \Gamma _{v_i}$
, then
$\gamma \in \Gamma _{v_i}$
, then
![]() $\mathcal {H}_i(R_0)\gamma =\mathcal {H}_i(R_0)$
. Therefore, the visual map induces a homeomorphism between
$\mathcal {H}_i(R_0)\gamma =\mathcal {H}_i(R_0)$
. Therefore, the visual map induces a homeomorphism between
![]() $\mathcal {H}_i(R_0)/\Gamma _{v_i}$
and
$\mathcal {H}_i(R_0)/\Gamma _{v_i}$
and
![]() $(\partial {\mathbb H}^n\setminus \{\xi _i\})/\Gamma _{v_i}$
. It follows that the quotient of
$(\partial {\mathbb H}^n\setminus \{\xi _i\})/\Gamma _{v_i}$
. It follows that the quotient of
![]() $\{g^+\in \Lambda : g\in \mathcal {H}_i(R_0)\}$
by the action of
$\{g^+\in \Lambda : g\in \mathcal {H}_i(R_0)\}$
by the action of
![]() $\Gamma _{v_i}$
is compact. Using Iwasawa decomposition, it follows that there exists a compact set
$\Gamma _{v_i}$
is compact. Using Iwasawa decomposition, it follows that there exists a compact set
![]() $U_0\subset U$
such that for any
$U_0\subset U$
such that for any
![]() $g=kaug_i\in \mathcal {H}_i(R_0)$
such that
$g=kaug_i\in \mathcal {H}_i(R_0)$
such that
![]() $g^+\in \Lambda (\Gamma )$
,
$g^+\in \Lambda (\Gamma )$
,
![]() $k\in K$
,
$k\in K$
,
![]() $a\in A$
, and
$a\in A$
, and
![]() $u\in U$
, there exist
$u\in U$
, there exist
![]() $\gamma \in \Gamma _{v_i}$
,
$\gamma \in \Gamma _{v_i}$
,
![]() $k'\in K$
,
$k'\in K$
,
![]() $u'\in U_0$
so that
$u'\in U_0$
so that
![]() $g\gamma =k'au'g_i$
.
$g\gamma =k'au'g_i$
.
Since
![]() $\xi _i$
is assumed to be a parabolic limit point, there exists a parabolic element
$\xi _i$
is assumed to be a parabolic limit point, there exists a parabolic element
![]() $\gamma _0\in \Gamma _{\xi _i}$
, that is,
$\gamma _0\in \Gamma _{\xi _i}$
, that is,
![]() $\gamma _0=g_i^{-1}mug_i$
.
$\gamma _0=g_i^{-1}mug_i$
.
Assume for contradiction that there exists an infinite sequence
![]() $\{\gamma _j\}\in \Gamma $
such that
$\{\gamma _j\}\in \Gamma $
such that
![]() $\{\gamma _j v_i\}$
converges. Note that translating by an element of
$\{\gamma _j v_i\}$
converges. Note that translating by an element of
![]() $\gamma $
allows us to assume, without loss of generality, that the limit of this sequence is
$\gamma $
allows us to assume, without loss of generality, that the limit of this sequence is
![]() $0$
. Using the Iwasawa decomposition, we get that for all j, there exist
$0$
. Using the Iwasawa decomposition, we get that for all j, there exist
![]() $a_{t_j}\in A$
,
$a_{t_j}\in A$
,
![]() $k_j\in K$
, and uniformly bounded
$k_j\in K$
, and uniformly bounded
![]() $u_j\in U$
such that
$u_j\in U$
such that
![]() $\gamma _j=k_ja_{t_j}u_jg_i$
. Since
$\gamma _j=k_ja_{t_j}u_jg_i$
. Since
we may deduce that
![]() $t_j\rightarrow -\infty $
. In particular,
$t_j\rightarrow -\infty $
. In particular,
![]() $\gamma _j\in H_i(R_0)$
for all large enough j.
$\gamma _j\in H_i(R_0)$
for all large enough j.
We have
 $$ \begin{align*} \gamma_j\gamma_0\gamma_j^{-1} &=(k_ja_{t_j}u_jg_i)(g_i^{-1}mug_i)(g_i^{-1} u_j^{-1} a_{t_j}^{-1} k_{j}^{-1})\\ &=k_ja_{t_j}u_jm uu_j^{-1} a_{t_j}^{-1} k_j^{-1}. \end{align*} $$
$$ \begin{align*} \gamma_j\gamma_0\gamma_j^{-1} &=(k_ja_{t_j}u_jg_i)(g_i^{-1}mug_i)(g_i^{-1} u_j^{-1} a_{t_j}^{-1} k_{j}^{-1})\\ &=k_ja_{t_j}u_jm uu_j^{-1} a_{t_j}^{-1} k_j^{-1}. \end{align*} $$
Since
![]() $u_jmu_j^{-1}=m_ju^{\prime }_j\in MU$
, with
$u_jmu_j^{-1}=m_ju^{\prime }_j\in MU$
, with
![]() $u^{\prime }_j$
uniformly bounded, and since M centralizes A, we have
$u^{\prime }_j$
uniformly bounded, and since M centralizes A, we have
Since
![]() $u^{\prime }_j u$
is in a bounded subset of U, we get that
$u^{\prime }_j u$
is in a bounded subset of U, we get that
![]() $a_{t_j} u^{\prime }_j u a_{t_j}^{-1}\rightarrow e$
as
$a_{t_j} u^{\prime }_j u a_{t_j}^{-1}\rightarrow e$
as
![]() $t_j\rightarrow -\infty $
. Since K and M are compact, it then follows that the sequence
$t_j\rightarrow -\infty $
. Since K and M are compact, it then follows that the sequence
![]() $\gamma _j\gamma _0\gamma _j^{-1}$
has a convergent subsequence. This contradicts the discreteness of
$\gamma _j\gamma _0\gamma _j^{-1}$
has a convergent subsequence. This contradicts the discreteness of
![]() $\Gamma $
, since the
$\Gamma $
, since the
![]() $\gamma _j$
terms were assumed to be distinct.
$\gamma _j$
terms were assumed to be distinct.
For any
![]() $g\in G$
, we have that
$g\in G$
, we have that
![]() $g\Gamma \in \mathcal {X}_i(R)$
if and only if there exists
$g\Gamma \in \mathcal {X}_i(R)$
if and only if there exists
![]() $\gamma \in \Gamma $
such that
$\gamma \in \Gamma $
such that
Indeed, by the Iwasawa decomposition and (17), if
![]() $g\Gamma \in \mathcal {X}_i(R)$
, then there exist
$g\Gamma \in \mathcal {X}_i(R)$
, then there exist
![]() $\gamma \in \Gamma $
,
$\gamma \in \Gamma $
,
![]() $k\in K$
,
$k\in K$
,
![]() $s>R$
, and
$s>R$
, and
![]() $u\in U$
, such that
$u\in U$
, such that
Moreover, it follows from [Reference Mohammadi and Oh25, Lemmas 6.4 and 6.5] that the
![]() $\gamma $
in (33) is unique. Note that both lemmas are proved under the additional assumption that
$\gamma $
in (33) is unique. Note that both lemmas are proved under the additional assumption that
![]() $n=3$
, but the proofs also hold without it.
$n=3$
, but the proofs also hold without it.
However, by [Reference Mohammadi and Oh25, Lemma 6.5] and Lemma 4.2, there exists a constant
![]() $\eta _0 = \eta _0(\Gamma )>0$
such that if
$\eta _0 = \eta _0(\Gamma )>0$
such that if
![]() $g\Gamma \notin \mathcal {X}_i(R_0)$
, then for any
$g\Gamma \notin \mathcal {X}_i(R_0)$
, then for any
![]() $\gamma \in \Gamma $
,
$\gamma \in \Gamma $
,
Lemma 4.3. There exists
![]() $c=c(\Gamma )>0$
which satisfies the following. Let
$c=c(\Gamma )>0$
which satisfies the following. Let
![]() $\varepsilon , s_0>0$
and let
$\varepsilon , s_0>0$
and let
![]() $g \in G$
. If
$g \in G$
. If
![]() $x = g\Gamma $
is
$x = g\Gamma $
is
![]() $(\varepsilon ,s_0)$
-Diophantine, then for any
$(\varepsilon ,s_0)$
-Diophantine, then for any
![]() $T\gg _{\Gamma ,\varepsilon } s_0$
,
$T\gg _{\Gamma ,\varepsilon } s_0$
,
Proof. Fix
![]() $T>T_0=\max \{s_0,\eta _0^{{1}/({\varepsilon -1})}\}$
. We will first show that
$T>T_0=\max \{s_0,\eta _0^{{1}/({\varepsilon -1})}\}$
. We will first show that
for some constant
![]() $1>c=c(\Gamma )>0$
.
$1>c=c(\Gamma )>0$
.
There are two cases to consider. If
![]() $a_{-\log T}x\notin \mathcal {X}_i(R_0)$
, then (36) follows from (34) and the choice of T.
$a_{-\log T}x\notin \mathcal {X}_i(R_0)$
, then (36) follows from (34) and the choice of T.
Otherwise,
![]() $a_{-\log T}x\in \mathcal {X}_i(R)$
for some maximal
$a_{-\log T}x\in \mathcal {X}_i(R)$
for some maximal
![]() $R>R_0$
. According to Lemma 3.6, we have
$R>R_0$
. According to Lemma 3.6, we have
Then, because x is
![]() $(\varepsilon ,s_0)$
Diophantine and
$(\varepsilon ,s_0)$
Diophantine and
![]() $T> s_0,$
by (32), we may deduce that
$T> s_0,$
by (32), we may deduce that
Hence,
![]() $a_{-\log T}x \not \in \mathcal {X}_i((1-\varepsilon )\log T+R_0),$
so (33) implies (36).
$a_{-\log T}x \not \in \mathcal {X}_i((1-\varepsilon )\log T+R_0),$
so (33) implies (36).
Now, fix
![]() $\gamma \in \Gamma $
and
$\gamma \in \Gamma $
and
![]() $1\le i \le q$
, and let
$1\le i \le q$
, and let
 $$ \begin{align*} \begin{pmatrix} x_1\\ \vdots\\ x_{n+1} \end{pmatrix}=a_{-\log T}g\gamma v_i.\end{align*} $$
$$ \begin{align*} \begin{pmatrix} x_1\\ \vdots\\ x_{n+1} \end{pmatrix}=a_{-\log T}g\gamma v_i.\end{align*} $$
According to (36), there exists
![]() $1\leq k\leq n$
such that
$1\leq k\leq n$
such that
![]() $|x_k|>cT^{\varepsilon -1}$
. If
$|x_k|>cT^{\varepsilon -1}$
. If
![]() $|x_1|>cT^{\varepsilon -1}$
, then it follows from the action of
$|x_1|>cT^{\varepsilon -1}$
, then it follows from the action of
![]() $a_{-\log T}$
on
$a_{-\log T}$
on
![]() $\mathbb {R}^{n+1}$
that
$\mathbb {R}^{n+1}$
that
Otherwise, there exists
![]() $2\leq k\leq n$
such that
$2\leq k\leq n$
such that
![]() $|x_k|>cT^{\varepsilon -1}$
. Then, for any
$|x_k|>cT^{\varepsilon -1}$
. Then, for any
![]() $\textbf {t}\in \mathbb {R}^{n-1}$
, the first coordinate of
$\textbf {t}\in \mathbb {R}^{n-1}$
, the first coordinate of
![]() $u_{\textbf {t}}a_{-\log T}g\gamma v_i$
is
$u_{\textbf {t}}a_{-\log T}g\gamma v_i$
is
 $$ \begin{align*} x_1+\textbf{t}\cdot \mathbf{x}'+\frac{1}{2}\Vert \textbf{t}\Vert ^2 x_{n+1}\quad\mbox{where } \mathbf{x}'=\begin{pmatrix} x_2\\ \vdots\\ x_n \end{pmatrix}.\end{align*} $$
$$ \begin{align*} x_1+\textbf{t}\cdot \mathbf{x}'+\frac{1}{2}\Vert \textbf{t}\Vert ^2 x_{n+1}\quad\mbox{where } \mathbf{x}'=\begin{pmatrix} x_2\\ \vdots\\ x_n \end{pmatrix}.\end{align*} $$
In particular, by taking
![]() $t_k=\pm T$
(the kth entry in
$t_k=\pm T$
(the kth entry in
![]() $\textbf {t}$
) one can ensure that
$\textbf {t}$
) one can ensure that
![]() $\|a_{\log T}u_{\textbf {t}}a_{-\log T} g\gamma v_i\|>cT^{\varepsilon }$
.
$\|a_{\log T}u_{\textbf {t}}a_{-\log T} g\gamma v_i\|>cT^{\varepsilon }$
.
A measure
![]() $\mu $
is called D-Federer if for all
$\mu $
is called D-Federer if for all
![]() $v\in \operatorname {supp}(\mu )$
and
$v\in \operatorname {supp}(\mu )$
and
![]() $0 <\eta \leq 1$
,
$0 <\eta \leq 1$
,
It is proved in §A (specifically Corollary A.9) that there exists
![]() $D=D(\Gamma )>0$
such that
$D=D(\Gamma )>0$
such that
Indeed, Corollary A.9 actually establishes that there exists a constant
![]() $\sigma = \sigma (\Gamma )>0$
such that for all
$\sigma = \sigma (\Gamma )>0$
such that for all
![]() $x \in \operatorname {supp}m^{\operatorname {BMS}}, c>1,$
and
$x \in \operatorname {supp}m^{\operatorname {BMS}}, c>1,$
and
![]() $T>0$
,
$T>0$
,
For
![]() $f:\mathbb {R}^d\rightarrow \mathbb {R}$
and
$f:\mathbb {R}^d\rightarrow \mathbb {R}$
and
![]() $B\subset \mathbb {R}^d$
, let
$B\subset \mathbb {R}^d$
, let
Recall that
![]() $U \cong \mathbb R^{n-1}$
.
$U \cong \mathbb R^{n-1}$
.
Lemma 4.4. Let
![]() $\sigma = \sigma (\Gamma )>0$
be as in (38). Let
$\sigma = \sigma (\Gamma )>0$
be as in (38). Let
![]() $y \in \operatorname {supp}m^{\operatorname {BMS}}$
and let
$y \in \operatorname {supp}m^{\operatorname {BMS}}$
and let
![]() $f: B_U(\eta )\to \mathbb R^{n-1}$
be such that there exists
$f: B_U(\eta )\to \mathbb R^{n-1}$
be such that there exists
![]() $b\ne 0$
so that for every coordinate function
$b\ne 0$
so that for every coordinate function
![]() $f_i: B_U(\eta ) \to \mathbb R$
, there exist
$f_i: B_U(\eta ) \to \mathbb R$
, there exist
![]() $a_i\in \mathbb R$
, such that
$a_i\in \mathbb R$
, such that
Then for
![]() $0<\eta \le 1$
and
$0<\eta \le 1$
and
![]() $0<\varepsilon <1,$
we have
$0<\varepsilon <1,$
we have
 $$ \begin{align} \mu^{\operatorname{PS}}_y(\{\textbf{t}\in B_U(\eta):\|f(\textbf{t})\|<\varepsilon\})\ll_{\Gamma}\bigg(\frac{\varepsilon}{\Vert f\Vert _{B_U(\eta)}}\bigg)^{\sigma}\mu^{\operatorname{PS}}_y(B_U(\eta)), \end{align} $$
$$ \begin{align} \mu^{\operatorname{PS}}_y(\{\textbf{t}\in B_U(\eta):\|f(\textbf{t})\|<\varepsilon\})\ll_{\Gamma}\bigg(\frac{\varepsilon}{\Vert f\Vert _{B_U(\eta)}}\bigg)^{\sigma}\mu^{\operatorname{PS}}_y(B_U(\eta)), \end{align} $$
where
![]() $\|f(x)\|$
denotes the max norm.
$\|f(x)\|$
denotes the max norm.
Proof. First, note that if
![]() $\|f\|_{B_U(\eta )} < 2\varepsilon $
, then the result holds by assuming that the implied coefficient in (39) is bigger than
$\|f\|_{B_U(\eta )} < 2\varepsilon $
, then the result holds by assuming that the implied coefficient in (39) is bigger than
![]() $2^{\sigma }$
: in this case, the right-hand side is greater or equal to
$2^{\sigma }$
: in this case, the right-hand side is greater or equal to
 $$ \begin{align*}2^{\sigma}\bigg(\frac{\varepsilon}{\Vert f\Vert _{B_U(\eta)}}\bigg)^{\sigma}\mu^{\operatorname{PS}}_y(B_U(\eta)) &\ge2^{\sigma}\bigg(\frac{\varepsilon}{2\varepsilon}\bigg)^{\sigma}\mu^{\operatorname{PS}}_y(B_U(\eta))\\ & \ge\mu^{\operatorname{PS}}_y(\{\textbf{t}\in B_U(\eta):\|f(\textbf{t})\|<\varepsilon\}), \end{align*} $$
$$ \begin{align*}2^{\sigma}\bigg(\frac{\varepsilon}{\Vert f\Vert _{B_U(\eta)}}\bigg)^{\sigma}\mu^{\operatorname{PS}}_y(B_U(\eta)) &\ge2^{\sigma}\bigg(\frac{\varepsilon}{2\varepsilon}\bigg)^{\sigma}\mu^{\operatorname{PS}}_y(B_U(\eta))\\ & \ge\mu^{\operatorname{PS}}_y(\{\textbf{t}\in B_U(\eta):\|f(\textbf{t})\|<\varepsilon\}), \end{align*} $$
as desired. Thus, we now assume that
If
![]() $\|f(\textbf {t})\|\ge \varepsilon $
for all
$\|f(\textbf {t})\|\ge \varepsilon $
for all
![]() $\textbf {t} \in B_U(\eta )$
such that
$\textbf {t} \in B_U(\eta )$
such that
![]() $(u_{\textbf {t}} y)^+\notin \Lambda (\Gamma )$
, then there is nothing to prove. So assume that
$(u_{\textbf {t}} y)^+\notin \Lambda (\Gamma )$
, then there is nothing to prove. So assume that
![]() $\|f(\textbf {t})\|<\varepsilon $
and
$\|f(\textbf {t})\|<\varepsilon $
and
![]() $(u_{\textbf {t}} y)^+\in \Lambda (\Gamma )$
. Since each
$(u_{\textbf {t}} y)^+\in \Lambda (\Gamma )$
. Since each
![]() $f_i$
is linear, for all
$f_i$
is linear, for all
![]() $\textbf {t}'\in B_U(\eta )$
with
$\textbf {t}'\in B_U(\eta )$
with
![]() $\|f(\textbf {t}')\|<\varepsilon $
, we get that for all
$\|f(\textbf {t}')\|<\varepsilon $
, we get that for all
![]() $1\le i\le n-1$
,
$1\le i\le n-1$
,
Therefore,
Thus, by (38), we have that there exists
![]() $\sigma = \sigma (\Gamma )>0$
so that
$\sigma = \sigma (\Gamma )>0$
so that
 $$ \begin{align*} \mu^{\operatorname{PS}}_y(\{x \in B_U(\eta)y : \|f(x)\|<\varepsilon\})&\le\mu^{\operatorname{PS}}_z( B_U(2\varepsilon/b))\\ & \ll_{\Gamma}\bigg(\frac{2\varepsilon}{b\eta}\bigg)^{\sigma}\mu^{\operatorname{PS}}_z( B_U(\eta))\\ & \ll_{\Gamma}\bigg(\frac{2\varepsilon}{b\eta}\bigg)^{\sigma}\mu^{\operatorname{PS}}_y( B_U(3\eta))\\ & \ll_{\Gamma}\bigg(\frac{6\varepsilon}{b\eta}\bigg)^{\sigma}\mu^{\operatorname{PS}}_y( B_U(\eta)). \end{align*} $$
$$ \begin{align*} \mu^{\operatorname{PS}}_y(\{x \in B_U(\eta)y : \|f(x)\|<\varepsilon\})&\le\mu^{\operatorname{PS}}_z( B_U(2\varepsilon/b))\\ & \ll_{\Gamma}\bigg(\frac{2\varepsilon}{b\eta}\bigg)^{\sigma}\mu^{\operatorname{PS}}_z( B_U(\eta))\\ & \ll_{\Gamma}\bigg(\frac{2\varepsilon}{b\eta}\bigg)^{\sigma}\mu^{\operatorname{PS}}_y( B_U(3\eta))\\ & \ll_{\Gamma}\bigg(\frac{6\varepsilon}{b\eta}\bigg)^{\sigma}\mu^{\operatorname{PS}}_y( B_U(\eta)). \end{align*} $$
Assuming
![]() $\|f(\textbf {t})\|<\varepsilon $
for some
$\|f(\textbf {t})\|<\varepsilon $
for some
![]() $\textbf {t}\in B_U(\eta )$
(otherwise, as before, there is nothing to prove), for any
$\textbf {t}\in B_U(\eta )$
(otherwise, as before, there is nothing to prove), for any
![]() $\textbf {t}"\in B_U(\eta )$
and
$\textbf {t}"\in B_U(\eta )$
and
![]() $1\le i\le n-1$
, we have
$1\le i\le n-1$
, we have
Thus,
![]() $\Vert f\Vert _{B_U(\eta )y}-\varepsilon \le 2b\eta $
, so by (40),
$\Vert f\Vert _{B_U(\eta )y}-\varepsilon \le 2b\eta $
, so by (40),
which completes the proof.
A function f which satisfies (39) with the implied constant C for any
![]() $\varepsilon>0$
and any ball
$\varepsilon>0$
and any ball
![]() $B\subset U\subset \mathbb {R}^m$
is called
$B\subset U\subset \mathbb {R}^m$
is called
![]() $(C, \sigma )$
-good on U with respect to
$(C, \sigma )$
-good on U with respect to
![]() $\mu $
. Observe that
$\mu $
. Observe that
In the proof of the following theorem, we use similar ideas to those which appear in the proof of [Reference Kleinbock, Lindenstrauss and Weiss18, Lemma 5.2]. Note that the proof in this case is simplified by the third assumption, reflecting our rank-one setting.
Proposition 4.5. Given positive constants
![]() $C,\beta , D$
, and
$C,\beta , D$
, and
![]() $0<\eta <1$
, there exists
$0<\eta <1$
, there exists
![]() $C'=C'(C,\beta , D)>0$
with the following property. Suppose
$C'=C'(C,\beta , D)>0$
with the following property. Suppose
![]() $\mu $
is a D-Federer measure on
$\mu $
is a D-Federer measure on
![]() $\mathbb R^m$
,
$\mathbb R^m$
,
![]() $f:\mathbb R^m\rightarrow \operatorname {SL}_k(\mathbb R)$
is a continuous map,
$f:\mathbb R^m\rightarrow \operatorname {SL}_k(\mathbb R)$
is a continuous map,
![]() $0\le \varrho \le \eta $
,
$0\le \varrho \le \eta $
,
![]() $z\in \operatorname {supp}\mu $
,
$z\in \operatorname {supp}\mu $
,
![]() $\Lambda \subset \mathbb R^k$
,
$\Lambda \subset \mathbb R^k$
,
![]() $B=B(z,r_0)\subset \mathbb R^m$
, and
$B=B(z,r_0)\subset \mathbb R^m$
, and
![]() $\tilde B=B(z,3 r_0)$
satisfy the following.
$\tilde B=B(z,3 r_0)$
satisfy the following.
-
(1) For any
 $v\in \Lambda $
, the function
$v\in \Lambda $
, the function
 $\textbf {t}\mapsto \Vert f(\textbf {t})v\Vert $
is
$\textbf {t}\mapsto \Vert f(\textbf {t})v\Vert $
is
 $(C,\beta )$
-good on
$(C,\beta )$
-good on
 $\tilde B$
with respect to
$\tilde B$
with respect to
 $\mu $
.
$\mu $
. -
(2) For any
 $v\in \Lambda $
, there exists
$v\in \Lambda $
, there exists
 $\textbf {t}\in B$
such that
$\textbf {t}\in B$
such that
 $\Vert f(\textbf {t})v\Vert \geq \varrho $
.
$\Vert f(\textbf {t})v\Vert \geq \varrho $
. -
(3) For any
 $\textbf {t}\in B$
, there is at most one
$\textbf {t}\in B$
, there is at most one
 $v\in \Lambda $
which satisfies
$v\in \Lambda $
which satisfies
 $\Vert f(\textbf {t})v\Vert <\eta $
.
$\Vert f(\textbf {t})v\Vert <\eta $
.
Then, for any
![]() $0<\varepsilon <\varrho $
,
$0<\varepsilon <\varrho $
,
 $$ \begin{align*} \mu(\{\textbf{t}\in B : \text{there exists } v\in\Lambda\text{ such that }\Vert f(\textbf{t})v\Vert <\varepsilon\})\le C'\bigg(\frac{\varepsilon}{\varrho}\bigg)^{\beta}\mu(B). \end{align*} $$
$$ \begin{align*} \mu(\{\textbf{t}\in B : \text{there exists } v\in\Lambda\text{ such that }\Vert f(\textbf{t})v\Vert <\varepsilon\})\le C'\bigg(\frac{\varepsilon}{\varrho}\bigg)^{\beta}\mu(B). \end{align*} $$
Proof. For any
![]() $\textbf {t}\in B$
, denote
$\textbf {t}\in B$
, denote
Let
and for each
![]() $v \in \Lambda $
, define
$v \in \Lambda $
, define
Observe that by assumption (3), the
![]() $E_v$
terms are a disjoint cover of E. For each
$E_v$
terms are a disjoint cover of E. For each
![]() $\textbf {t} \in E_v$
, define
$\textbf {t} \in E_v$
, define
By assumption (2), we know that for every
![]() $\textbf {t}\in E$
, the set
$\textbf {t}\in E$
, the set
![]() $B(\textbf {t},r_{\textbf {t},v})$
does not contain B. Thus, since
$B(\textbf {t},r_{\textbf {t},v})$
does not contain B. Thus, since
![]() $\textbf {t}\in B$
, we deduce that
$\textbf {t}\in B$
, we deduce that
![]() $r_{\textbf {t},v}<2r_0$
. For any fixed
$r_{\textbf {t},v}<2r_0$
. For any fixed
![]() $r_{\textbf {t},v}<r^{\prime }_{\textbf {t},v}<2r_0$
, we have that
$r_{\textbf {t},v}<r^{\prime }_{\textbf {t},v}<2r_0$
, we have that
and by the definition of
![]() $r_{\textbf {t},v}$
, there exists
$r_{\textbf {t},v}$
, there exists
![]() $\textbf {s} \in B(\textbf {t},r^{\prime }_{\textbf {t},v})$
such that
$\textbf {s} \in B(\textbf {t},r^{\prime }_{\textbf {t},v})$
such that
Note that
![]() $\{B(\textbf {t},r_{\textbf {t},v}) : \textbf {t}\in E, v\in \Lambda \}$
is a cover of E. According to the Besicovitch covering theorem, there exists a countable subset
$\{B(\textbf {t},r_{\textbf {t},v}) : \textbf {t}\in E, v\in \Lambda \}$
is a cover of E. According to the Besicovitch covering theorem, there exists a countable subset
![]() $I\subset E\times \Lambda $
such that
$I\subset E\times \Lambda $
such that
![]() $\{B(\textbf {t},r_{\textbf {t},v}) : (\textbf {t},v)\in ~I\}$
is a cover of E with a covering number bounded by a constant which only depends on m. Thus,
$\{B(\textbf {t},r_{\textbf {t},v}) : (\textbf {t},v)\in ~I\}$
is a cover of E with a covering number bounded by a constant which only depends on m. Thus,
 $$ \begin{align} \sum_{(\textbf{t},v)\in I}\mu(B(\textbf{t},r_{\textbf{t},v})) \ll_{m} \mu\bigg(\bigcup_{(\textbf{t},v)\in I}B(\textbf{t},r_{\textbf{t},v})\bigg). \end{align} $$
$$ \begin{align} \sum_{(\textbf{t},v)\in I}\mu(B(\textbf{t},r_{\textbf{t},v})) \ll_{m} \mu\bigg(\bigcup_{(\textbf{t},v)\in I}B(\textbf{t},r_{\textbf{t},v})\bigg). \end{align} $$
By assumption (3) and the continuity of f, for any
![]() $(\textbf {t},v)\in I$
and
$(\textbf {t},v)\in I$
and
![]() $\mathbf{s}\in E\cap B(\textbf {t},r_{\textbf {t},v})$
,
$\mathbf{s}\in E\cap B(\textbf {t},r_{\textbf {t},v})$
,
Thus,
 $$ \begin{align*} \mu(\{\mathbf{s}\in B(\textbf{t},r_{\textbf{t},v}) : {f_{\Lambda}(\mathbf{s})}<\varepsilon\})&=\mu(\{\mathbf{s}\in B(\textbf{t},r_{\textbf{t},v}) : \Vert f(\mathbf{s})v\Vert <\varepsilon\})\\[3pt] &\le\mu(\{\mathbf{s}\in B(\textbf{t},r^{\prime}_{\textbf{t},v}) : \Vert f(\mathbf{s})v\Vert <\varepsilon\}).\end{align*} $$
$$ \begin{align*} \mu(\{\mathbf{s}\in B(\textbf{t},r_{\textbf{t},v}) : {f_{\Lambda}(\mathbf{s})}<\varepsilon\})&=\mu(\{\mathbf{s}\in B(\textbf{t},r_{\textbf{t},v}) : \Vert f(\mathbf{s})v\Vert <\varepsilon\})\\[3pt] &\le\mu(\{\mathbf{s}\in B(\textbf{t},r^{\prime}_{\textbf{t},v}) : \Vert f(\mathbf{s})v\Vert <\varepsilon\}).\end{align*} $$
Thus, assumption (1) and the assumption that
![]() $\mu $
is D-Federer together imply that
$\mu $
is D-Federer together imply that
 $$ \begin{align} \mu(\{\mathbf{s}\in B(\textbf{t},r_{\textbf{t},v}) : {f_{\Lambda}(\mathbf{s})}<\varepsilon\})&\le\mu(\{\mathbf{s}\in B(\textbf{t},r^{\prime}_{\textbf{t},v}) : \Vert f(\mathbf{s})v\Vert <\varepsilon\})\nonumber\\[3pt] & \le C\bigg(\frac{\varepsilon}{\varrho}\bigg)^{\beta}\mu(B(\textbf{t},r^{\prime}_{\textbf{t},v}))\nonumber\\[3pt] & \le CD \bigg(\frac{\varepsilon}{\varrho}\bigg)^{\beta}\mu(B(\textbf{t},r_{\textbf{t},v})). \end{align} $$
$$ \begin{align} \mu(\{\mathbf{s}\in B(\textbf{t},r_{\textbf{t},v}) : {f_{\Lambda}(\mathbf{s})}<\varepsilon\})&\le\mu(\{\mathbf{s}\in B(\textbf{t},r^{\prime}_{\textbf{t},v}) : \Vert f(\mathbf{s})v\Vert <\varepsilon\})\nonumber\\[3pt] & \le C\bigg(\frac{\varepsilon}{\varrho}\bigg)^{\beta}\mu(B(\textbf{t},r^{\prime}_{\textbf{t},v}))\nonumber\\[3pt] & \le CD \bigg(\frac{\varepsilon}{\varrho}\bigg)^{\beta}\mu(B(\textbf{t},r_{\textbf{t},v})). \end{align} $$
Since E covers the set of points for which
![]() $f_{\Lambda }$
is less than
$f_{\Lambda }$
is less than
![]() $\varepsilon $
, we may now conclude
$\varepsilon $
, we may now conclude
 $$ \begin{align*} &\mu(\{\textbf{t}\in B : f_{\Lambda}(\textbf{t})<\varepsilon\})\\ &\quad\le \sum_{(\textbf{t},v)\in I}\mu(\{\mathbf{s}\in B(\textbf{t},r_{\textbf{t},v}) : f_{\Lambda}(\textbf{t})<\varepsilon\}) \\ & \quad\le CD \sum_{(\textbf{t},v)\in I}\bigg(\frac{\varepsilon}{\varrho}\bigg)^{\beta}\mu(B(\textbf{t},r_{\textbf{t},v})) \quad \text{by (44)}\\ & \quad\ll_{m} CD \bigg(\frac{\varepsilon}{\varrho}\bigg)^{\beta}\mu\bigg(\bigcup_{(\textbf{t},v)\in I}B(\textbf{t},r_{\textbf{t},v})\bigg)\quad \text{by (43)}\\ & \quad\ll_{m} CD \bigg(\frac{\varepsilon}{\varrho}\bigg)^{\beta}\mu(\tilde B ) \quad \text{by (42)} \\ & \quad\ll_{m} CD^2 \bigg(\frac{\varepsilon}{\varrho}\bigg)^{\beta}\mu(B ) \quad\mu\text{ is }D\text{-Federer.}\\[-3.6pc] \end{align*} $$
$$ \begin{align*} &\mu(\{\textbf{t}\in B : f_{\Lambda}(\textbf{t})<\varepsilon\})\\ &\quad\le \sum_{(\textbf{t},v)\in I}\mu(\{\mathbf{s}\in B(\textbf{t},r_{\textbf{t},v}) : f_{\Lambda}(\textbf{t})<\varepsilon\}) \\ & \quad\le CD \sum_{(\textbf{t},v)\in I}\bigg(\frac{\varepsilon}{\varrho}\bigg)^{\beta}\mu(B(\textbf{t},r_{\textbf{t},v})) \quad \text{by (44)}\\ & \quad\ll_{m} CD \bigg(\frac{\varepsilon}{\varrho}\bigg)^{\beta}\mu\bigg(\bigcup_{(\textbf{t},v)\in I}B(\textbf{t},r_{\textbf{t},v})\bigg)\quad \text{by (43)}\\ & \quad\ll_{m} CD \bigg(\frac{\varepsilon}{\varrho}\bigg)^{\beta}\mu(\tilde B ) \quad \text{by (42)} \\ & \quad\ll_{m} CD^2 \bigg(\frac{\varepsilon}{\varrho}\bigg)^{\beta}\mu(B ) \quad\mu\text{ is }D\text{-Federer.}\\[-3.6pc] \end{align*} $$
Remark 4.6. Fix
![]() $x\in X$
such that
$x\in X$
such that
![]() $x^-\in \Lambda (\Gamma )$
. Since the PS measure
$x^-\in \Lambda (\Gamma )$
. Since the PS measure
![]() $\mu ^{\operatorname {PS}}_x$
is supported on
$\mu ^{\operatorname {PS}}_x$
is supported on
![]() $Ux\cap \operatorname {supp}m^{\operatorname {BMS}}$
, it follows from Lemma 4.4 and (37) that Proposition 4.5 holds for
$Ux\cap \operatorname {supp}m^{\operatorname {BMS}}$
, it follows from Lemma 4.4 and (37) that Proposition 4.5 holds for
![]() $\mu ^{\operatorname {PS}}_x$
and function f, which satisfies the assumption of Lemma 4.4.
$\mu ^{\operatorname {PS}}_x$
and function f, which satisfies the assumption of Lemma 4.4.
We are now ready to prove Theorem 4.1.
Proof of Theorem 4.1
Let
![]() $x_0=a_{-\log s}x$
and fix
$x_0=a_{-\log s}x$
and fix
![]() $g\in G$
such that
$g\in G$
such that
![]() $x=g\Gamma $
. By Lemma 4.3, for all
$x=g\Gamma $
. By Lemma 4.3, for all
![]() $T \gg _{\Gamma ,\varepsilon } s_0,$
we have (35), that is, that
$T \gg _{\Gamma ,\varepsilon } s_0,$
we have (35), that is, that
Let
![]() $f:\mathbb R^{n-1}\rightarrow \operatorname {SL}_{n+1}(\mathbb R)$
be defined by
$f:\mathbb R^{n-1}\rightarrow \operatorname {SL}_{n+1}(\mathbb R)$
be defined by
We first show that parts (1), (2), and (3) of Proposition 4.5 for
![]() $\mu =\mu ^{\operatorname {PS}}_{x_0}$
, f,
$\mu =\mu ^{\operatorname {PS}}_{x_0}$
, f,
![]() $\varrho =1$
,
$\varrho =1$
,
![]() $z=x_0$
,
$z=x_0$
,
![]() $r=T/s$
,
$r=T/s$
,
![]() $\eta =e^{-R_0}$
, and
$\eta =e^{-R_0}$
, and
Note that
![]() $0\notin \Lambda $
.
$0\notin \Lambda $
.
It follows from the action of
![]() $u_{\textbf {t}}$
on
$u_{\textbf {t}}$
on
![]() $\mathbb {R}^{n+1}$
that for any
$\mathbb {R}^{n+1}$
that for any
![]() $v\in \mathbb R^{n+1}$
, there exists
$v\in \mathbb R^{n+1}$
, there exists
![]() $v'=(v^{\prime }_1,\ldots ,v^{\prime }_{n+1})^T\in \mathbb R^{n+1}$
such that
$v'=(v^{\prime }_1,\ldots ,v^{\prime }_{n+1})^T\in \mathbb R^{n+1}$
such that
where
![]() $v"=(v^{\prime }_2,\ldots ,v^{\prime }_{n})^T$
. Thus, if
$v"=(v^{\prime }_2,\ldots ,v^{\prime }_{n})^T$
. Thus, if
![]() $v^{\prime }_{n+1}\ne 0$
, then
$v^{\prime }_{n+1}\ne 0$
, then
![]() $\textbf {t} \mapsto f(\textbf {t})v$
is bounded from below by a function which satisfies the assumption of Lemma 4.4. Therefore, by (41), for any
$\textbf {t} \mapsto f(\textbf {t})v$
is bounded from below by a function which satisfies the assumption of Lemma 4.4. Therefore, by (41), for any
![]() $v\in \Lambda $
, the function
$v\in \Lambda $
, the function
![]() $\textbf {t}\mapsto \Vert f(\textbf {t})v\Vert $
is
$\textbf {t}\mapsto \Vert f(\textbf {t})v\Vert $
is
![]() $(C,\beta )$
-good on
$(C,\beta )$
-good on
![]() $\tilde B$
with respect to
$\tilde B$
with respect to
![]() $\mu ^{\operatorname {PS}}_{x_0}$
for some
$\mu ^{\operatorname {PS}}_{x_0}$
for some
![]() $C=C(\Gamma )\ge 1$
,
$C=C(\Gamma )\ge 1$
,
![]() $\beta =\beta (\Gamma )>0$
, which proves (1) of Proposition 4.5. Note that these constants are uniform across all v so that
$\beta =\beta (\Gamma )>0$
, which proves (1) of Proposition 4.5. Note that these constants are uniform across all v so that
![]() $v_{n+1}'\ne 0.$
$v_{n+1}'\ne 0.$
However, if
![]() $v\neq 0$
and
$v\neq 0$
and
then
![]() $\textbf {t} \mapsto f(\textbf {t})v$
is bounded below by some positive constant, and since positive constant functions are
$\textbf {t} \mapsto f(\textbf {t})v$
is bounded below by some positive constant, and since positive constant functions are
![]() $(C,\beta )$
-good for any
$(C,\beta )$
-good for any
![]() $C\ge 1,\beta>0,$
we conclude that so is this function by (41).
$C\ge 1,\beta>0,$
we conclude that so is this function by (41).
By (6), we have
Since multiplication by
![]() $a_{-\log s}$
only changes the matrix entries by scaling, using (35), for
$a_{-\log s}$
only changes the matrix entries by scaling, using (35), for
![]() $i=1,\ldots ,q$
, we get
$i=1,\ldots ,q$
, we get
Thus, for any
![]() $s\le T^{\varepsilon }$
,
$s\le T^{\varepsilon }$
,
![]() $\|\textbf {t}\|<T/s$
, and
$\|\textbf {t}\|<T/s$
, and
![]() $v\in \Lambda $
,
$v\in \Lambda $
,
which establishes (2) of Proposition 4.5.
Since
![]() $\eta =e^{-R_0}$
and
$\eta =e^{-R_0}$
and
![]() $\mathcal {H}_i(R_0)$
terms are pairwise disjoint, part (3) of Proposition 4.5 follows from the uniqueness of
$\mathcal {H}_i(R_0)$
terms are pairwise disjoint, part (3) of Proposition 4.5 follows from the uniqueness of
![]() $\gamma $
in (33) and (34).
$\gamma $
in (33) and (34).
According to 37, the measure
![]() $\mu ^{\operatorname {PS}}_{x_0}$
is D-Federer for any
$\mu ^{\operatorname {PS}}_{x_0}$
is D-Federer for any
![]() $D>0$
. Thus, we may now use (33) and Proposition 4.5 to deduce
$D>0$
. Thus, we may now use (33) and Proposition 4.5 to deduce
 $$ \begin{align*} &\mu^{\operatorname{PS}}_{x_0}(B_U(T/s)\cap\mathcal{H}_i(R))\\[3pt] &\quad=\mu^{\operatorname{PS}}_{x_0}(\{\textbf{t}\in B_U(T/s) : \text{ there exists } \gamma\in\Gamma,1\le i\le q\text{ such that }\Vert f(\textbf{t})\gamma v_i\Vert <e^{-R}\})\\[3pt] &\quad\ll e^{-R \beta} \mu^{\operatorname{PS}}_{x_0}(B_U(T/s)x_0), \end{align*} $$
$$ \begin{align*} &\mu^{\operatorname{PS}}_{x_0}(B_U(T/s)\cap\mathcal{H}_i(R))\\[3pt] &\quad=\mu^{\operatorname{PS}}_{x_0}(\{\textbf{t}\in B_U(T/s) : \text{ there exists } \gamma\in\Gamma,1\le i\le q\text{ such that }\Vert f(\textbf{t})\gamma v_i\Vert <e^{-R}\})\\[3pt] &\quad\ll e^{-R \beta} \mu^{\operatorname{PS}}_{x_0}(B_U(T/s)x_0), \end{align*} $$
where the implied constant depends on n and
![]() $\Gamma $
.
$\Gamma $
.
5 Friendliness properties of the PS measure
In this section, we prove several key properties of the PS measure, including that slightly enlarging a ball does not increase the measure too much and that scaling the size of the ball has a bounded multiplicative increase on the measure. Note that the results in this section hold for any
![]() $\Gamma $
that is geometrically finite; we do not require Assumption 1.1. In the setting that all cusps have maximal rank, stronger statements hold. See the appendix, specifically §A.3, for more details.
$\Gamma $
that is geometrically finite; we do not require Assumption 1.1. In the setting that all cusps have maximal rank, stronger statements hold. See the appendix, specifically §A.3, for more details.
The main results in this section are the following, which both establish control over the measure of a slightly enlarged ball. Many technical details of the proofs are hidden in Proposition 5.4, which is proved in §A.
Theorem 5.1. There exists a constant
![]() $\alpha ' = \alpha '(\Gamma )>0$
such that for every
$\alpha ' = \alpha '(\Gamma )>0$
such that for every
![]() $x \in G/\Gamma $
that is
$x \in G/\Gamma $
that is
![]() $(\varepsilon ,s_0)$
-Diophantine, for every
$(\varepsilon ,s_0)$
-Diophantine, for every
![]() $0<s\le T^{{\varepsilon }/({1-\varepsilon })}$
, every
$0<s\le T^{{\varepsilon }/({1-\varepsilon })}$
, every
![]() $0<\xi \ll _{\Gamma } 1,$
and every
$0<\xi \ll _{\Gamma } 1,$
and every
![]() $T\gg _{\Gamma ,\varepsilon } s_0$
,
$T\gg _{\Gamma ,\varepsilon } s_0$
,
 $$ \begin{align*} \frac{\mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U(\xi+T) )}{\mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U(T))}-1\ll_{\Gamma} \xi^{\alpha'}.\end{align*} $$
$$ \begin{align*} \frac{\mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U(\xi+T) )}{\mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U(T))}-1\ll_{\Gamma} \xi^{\alpha'}.\end{align*} $$
Theorem 5.2. There exist
![]() $\alpha '=\alpha '(\Gamma )>0$
,
$\alpha '=\alpha '(\Gamma )>0$
,
![]() $\theta '=\theta '(\Gamma )\ge \alpha '$
,
$\theta '=\theta '(\Gamma )\ge \alpha '$
,
![]() $\omega '=\omega '(\Gamma )\ge 2\delta _{\Gamma }$
, such that for any
$\omega '=\omega '(\Gamma )\ge 2\delta _{\Gamma }$
, such that for any
![]() $g \in G$
with
$g \in G$
with
![]() $g^- \in \Lambda (\Gamma )$
and
$g^- \in \Lambda (\Gamma )$
and
![]() $0<\xi <\eta \ll _{\Gamma } e^{-\operatorname {height}(g\Gamma )},$
we have that
$0<\xi <\eta \ll _{\Gamma } e^{-\operatorname {height}(g\Gamma )},$
we have that
 $$ \begin{align*}\frac{\nu(P_{\xi+\eta}g)}{\nu(P_{\eta} g)}-1\ll_{\Gamma} e^{\omega'\operatorname{height}(g\Gamma)}\frac{\xi^{\alpha'}}{\eta^{\theta'}}.\end{align*} $$
$$ \begin{align*}\frac{\nu(P_{\xi+\eta}g)}{\nu(P_{\eta} g)}-1\ll_{\Gamma} e^{\omega'\operatorname{height}(g\Gamma)}\frac{\xi^{\alpha'}}{\eta^{\theta'}}.\end{align*} $$
Theorem 5.2 will be obtained as a corollary of the following.
Proposition 5.3. There exist constants
![]() $\alpha = \alpha (\Gamma )>0$
,
$\alpha = \alpha (\Gamma )>0$
,
![]() $\theta =\theta (\Gamma )\ge \alpha $
, and
$\theta =\theta (\Gamma )\ge \alpha $
, and
![]() $\omega =\omega (\Gamma )\ge 2\delta _{\Gamma }$
such that for
$\omega =\omega (\Gamma )\ge 2\delta _{\Gamma }$
such that for
![]() $x \in G/\Gamma $
, which satisfies
$x \in G/\Gamma $
, which satisfies
![]() $x^+\in \Lambda (\Gamma )$
, and
$x^+\in \Lambda (\Gamma )$
, and
![]() $0<\xi < \eta \ll _{\Gamma } e^{-\operatorname {height}(x)}$
, we have
$0<\xi < \eta \ll _{\Gamma } e^{-\operatorname {height}(x)}$
, we have
 $$ \begin{align*}\frac{\mu^{\operatorname{PS}}_x(B_U(\xi+\eta))}{\mu^{\operatorname{PS}}_x(B_U(\eta))}-1 \ll_{\Gamma} e^{\omega\operatorname{height}(x)}\frac{\xi^{\alpha}}{\eta^{\theta}}.\end{align*} $$
$$ \begin{align*}\frac{\mu^{\operatorname{PS}}_x(B_U(\xi+\eta))}{\mu^{\operatorname{PS}}_x(B_U(\eta))}-1 \ll_{\Gamma} e^{\omega\operatorname{height}(x)}\frac{\xi^{\alpha}}{\eta^{\theta}}.\end{align*} $$
We first show how to obtain Theorem 5.2 from Proposition 5.3.
Proof of Theorem 5.2 assuming Proposition 5.3
Using the product structure of
![]() $\nu $
, we can write
$\nu $
, we can write
 $$ \begin{align*}\nu(P_{\eta} g) = \int_{A_{\eta}}\int_{M_{\eta}} \mu^{\operatorname{PS}-}_g(B_{\tilde{U}} (\eta))\,dm\,ds.\end{align*} $$
$$ \begin{align*}\nu(P_{\eta} g) = \int_{A_{\eta}}\int_{M_{\eta}} \mu^{\operatorname{PS}-}_g(B_{\tilde{U}} (\eta))\,dm\,ds.\end{align*} $$
Then, by an analogous statement to Proposition 5.3 for
![]() $\mu ^{\operatorname {PS}-}$
, there exists a constant
$\mu ^{\operatorname {PS}-}$
, there exists a constant
![]() $c_0 = c_0(\Gamma )>0$
such that
$c_0 = c_0(\Gamma )>0$
such that
 $$ \begin{align*} \nu(P_{\eta+\xi}g) &= \int_{A_{\xi+\eta}}\int_{M_{\xi+\eta}}\mu^{\operatorname{PS}-}_g(B_{\tilde U}(\xi + \eta))\,dm\,ds \\[3pt] &\le\int_{A_{\xi+\eta}}\int_{M_{\xi+\eta}}\mu^{\operatorname{PS}-}_g(B_{\tilde U}(\eta))\bigg[1+c_0\frac{\xi^{\alpha}}{\eta^{\theta}} e^{\omega\operatorname{height}(g\Gamma)}\bigg]\, dm\, ds\\ &=\bigg[1+c_0\frac{\xi^{\alpha}}{\eta^{\theta}} e^{\omega\operatorname{height}(g\Gamma)}\bigg]\bigg[ \frac{(\xi+\eta)^{{1}/{2}(n-1)(n-2)+1}}{\eta^{{1}/{2}(n-1)(n-2)+1}}\nu(P_{\eta} g)\bigg]\\[4pt] &\le\bigg[1+c_0\frac{\xi^{\alpha}}{\eta^{\theta}} e^{\omega\operatorname{height}(g\Gamma)}\bigg]\bigg[1+c_1\frac{\xi}{\eta}\bigg]\nu(P_{\eta} g), \end{align*} $$
$$ \begin{align*} \nu(P_{\eta+\xi}g) &= \int_{A_{\xi+\eta}}\int_{M_{\xi+\eta}}\mu^{\operatorname{PS}-}_g(B_{\tilde U}(\xi + \eta))\,dm\,ds \\[3pt] &\le\int_{A_{\xi+\eta}}\int_{M_{\xi+\eta}}\mu^{\operatorname{PS}-}_g(B_{\tilde U}(\eta))\bigg[1+c_0\frac{\xi^{\alpha}}{\eta^{\theta}} e^{\omega\operatorname{height}(g\Gamma)}\bigg]\, dm\, ds\\ &=\bigg[1+c_0\frac{\xi^{\alpha}}{\eta^{\theta}} e^{\omega\operatorname{height}(g\Gamma)}\bigg]\bigg[ \frac{(\xi+\eta)^{{1}/{2}(n-1)(n-2)+1}}{\eta^{{1}/{2}(n-1)(n-2)+1}}\nu(P_{\eta} g)\bigg]\\[4pt] &\le\bigg[1+c_0\frac{\xi^{\alpha}}{\eta^{\theta}} e^{\omega\operatorname{height}(g\Gamma)}\bigg]\bigg[1+c_1\frac{\xi}{\eta}\bigg]\nu(P_{\eta} g), \end{align*} $$
where
![]() $c_1>0$
is an absolute constant (which depends only on n) arising from the binomial theorem. Therefore,
$c_1>0$
is an absolute constant (which depends only on n) arising from the binomial theorem. Therefore,
 $$ \begin{align} \frac{\nu(P_{\xi+\eta}g)}{\nu(P_{\eta} g)}-1\ll_{\Gamma} e^{\omega\operatorname{height}(g\Gamma)}\frac{\xi^{\alpha}}{\eta^{\theta}}\cdot\frac{\xi}{\eta}+\frac{\xi}{\eta}+e^{\omega\operatorname{height}(g\Gamma)}\frac{\xi^{\alpha}}{\eta^{\theta}}. \end{align} $$
$$ \begin{align} \frac{\nu(P_{\xi+\eta}g)}{\nu(P_{\eta} g)}-1\ll_{\Gamma} e^{\omega\operatorname{height}(g\Gamma)}\frac{\xi^{\alpha}}{\eta^{\theta}}\cdot\frac{\xi}{\eta}+\frac{\xi}{\eta}+e^{\omega\operatorname{height}(g\Gamma)}\frac{\xi^{\alpha}}{\eta^{\theta}}. \end{align} $$
Since
![]() $\xi <\eta $
, the first term on the left-hand side of (46) is dominated by the last term, and so
$\xi <\eta $
, the first term on the left-hand side of (46) is dominated by the last term, and so
 $$ \begin{align*}\frac{\nu(P_{\xi+\eta}g)}{\nu(P_{\eta} g)}-1\ll_{\Gamma}\frac{\xi}{\eta}+e^{\omega\operatorname{height}(g\Gamma)}\frac{\xi^{\alpha}}{\eta^{\theta}}.\end{align*} $$
$$ \begin{align*}\frac{\nu(P_{\xi+\eta}g)}{\nu(P_{\eta} g)}-1\ll_{\Gamma}\frac{\xi}{\eta}+e^{\omega\operatorname{height}(g\Gamma)}\frac{\xi^{\alpha}}{\eta^{\theta}}.\end{align*} $$
Since
![]() $e^{\omega \operatorname {height}(g\Gamma )}\ge 1$
, if we define
$e^{\omega \operatorname {height}(g\Gamma )}\ge 1$
, if we define
then both terms are dominated by
 $$ \begin{align*}e^{\omega\operatorname{height}(g\Gamma)}\frac{\xi^{\alpha'}}{\eta^{\theta'}},\end{align*} $$
$$ \begin{align*}e^{\omega\operatorname{height}(g\Gamma)}\frac{\xi^{\alpha'}}{\eta^{\theta'}},\end{align*} $$
which completes the proof.
The following result, showing that the PS measure is not concentrated near hyperplanes, is proved in the appendix to improve the readability of this section. See Proposition A.11 for the proof. This result builds upon the work of Das et al. in [Reference Das, Fishman, Simmons and Urbański5], where it is shown that the PS density
![]() $\nu _o$
is friendly when
$\nu _o$
is friendly when
![]() $\Gamma $
is geometrically finite.
$\Gamma $
is geometrically finite.
For a hyperplane
![]() $L \subset U \cong \mathbb R^{n-1}$
and
$L \subset U \cong \mathbb R^{n-1}$
and
![]() $\xi>0$
, define
$\xi>0$
, define
Proposition 5.4. Let
![]() $\Gamma $
be geometrically finite and Zariski dense. There exist constants
$\Gamma $
be geometrically finite and Zariski dense. There exist constants
![]() $\alpha = \alpha (\Gamma )>0, \omega =\omega (\Gamma ) \ge 0, $
and
$\alpha = \alpha (\Gamma )>0, \omega =\omega (\Gamma ) \ge 0, $
and
![]() $\theta = \theta (\Gamma )>\alpha $
satisfying the following: for any
$\theta = \theta (\Gamma )>\alpha $
satisfying the following: for any
![]() $x \in G/\Gamma $
with
$x \in G/\Gamma $
with
![]() $x^+\in \Lambda (\Gamma )$
, and for every
$x^+\in \Lambda (\Gamma )$
, and for every
![]() $\xi>0$
and
$\xi>0$
and
![]() $0<\eta \ll _{\Gamma } e^{-\operatorname {height}(x)}$
, we have that for every hyperplane L,
$0<\eta \ll _{\Gamma } e^{-\operatorname {height}(x)}$
, we have that for every hyperplane L,
We are now ready to prove Proposition 5.3.
Proof of Proposition 5.3
It follows from the geometry of
![]() $B_U(\xi +\eta )x-B_U(\eta )x$
that there exist hyperplanes
$B_U(\xi +\eta )x-B_U(\eta )x$
that there exist hyperplanes
![]() $L_1,\ldots ,L_m$
, where m only depends on n, such that
$L_1,\ldots ,L_m$
, where m only depends on n, such that
 $$ \begin{align*} B_U(\xi+\eta)x-B_U(\eta)x\subseteq\bigcup_{i=1}^{m} \mathcal{N}_U(L_i,2\xi).\end{align*} $$
$$ \begin{align*} B_U(\xi+\eta)x-B_U(\eta)x\subseteq\bigcup_{i=1}^{m} \mathcal{N}_U(L_i,2\xi).\end{align*} $$
For any
![]() $0<\xi <\eta \ll _{\Gamma } e^{-\operatorname {height}(x)},$
we have that
$0<\xi <\eta \ll _{\Gamma } e^{-\operatorname {height}(x)},$
we have that

By (37),
![]() $\mu ^{\operatorname {PS}}_x$
is D-Federer (see Corollary A.8 for more detail), in particular,
$\mu ^{\operatorname {PS}}_x$
is D-Federer (see Corollary A.8 for more detail), in particular,
Thus, we obtain
 $$ \begin{align*} \frac{\mu^{\operatorname{PS}}_x(B_U(\xi+\eta))}{\mu^{\operatorname{PS}}_x(B_U(\eta))} -1 \ll_{\Gamma}e^{{\omega}\operatorname{height}(x)}\frac{ \xi^{\alpha}}{\eta^{\theta}},\end{align*} $$
$$ \begin{align*} \frac{\mu^{\operatorname{PS}}_x(B_U(\xi+\eta))}{\mu^{\operatorname{PS}}_x(B_U(\eta))} -1 \ll_{\Gamma}e^{{\omega}\operatorname{height}(x)}\frac{ \xi^{\alpha}}{\eta^{\theta}},\end{align*} $$
and relabeling the constants completes the proof.
In (37), we saw that
![]() $\mu ^{\operatorname {PS}}_x$
is Federer when
$\mu ^{\operatorname {PS}}_x$
is Federer when
![]() $x \in \operatorname {supp}m^{\operatorname {BMS}}.$
Below, we show that
$x \in \operatorname {supp}m^{\operatorname {BMS}}.$
Below, we show that
![]() $\mu ^{\operatorname {PS}}_x$
satisfies a similar condition for sufficiently large balls when x is Diophantine, but not necessarily a BMS point.
$\mu ^{\operatorname {PS}}_x$
satisfies a similar condition for sufficiently large balls when x is Diophantine, but not necessarily a BMS point.
Corollary 5.5. There exists a constant
![]() $\sigma =\sigma (\Gamma )\ge \delta _{\Gamma }$
such that for every
$\sigma =\sigma (\Gamma )\ge \delta _{\Gamma }$
such that for every
![]() $c \ge 1$
and every
$c \ge 1$
and every
![]() $x \in G/\Gamma $
that is
$x \in G/\Gamma $
that is
![]() $(\varepsilon ,s_0)$
-Diophantine, if
$(\varepsilon ,s_0)$
-Diophantine, if
![]() $T \gg _{\Gamma ,\varepsilon } s_0 $
, then
$T \gg _{\Gamma ,\varepsilon } s_0 $
, then
Proof. By Lemma 3.8, for some
![]() $T_0\gg _{\Gamma ,\varepsilon } s_0$
, there exists
$T_0\gg _{\Gamma ,\varepsilon } s_0$
, there exists
Then for
![]() $T \ge T_0$
, we have
$T \ge T_0$
, we have
Since
![]() $c \ge 1,$
we therefore have that for
$c \ge 1,$
we therefore have that for
![]() $T \ge 2T_0,$
$T \ge 2T_0,$

Remark 5.6. Observe that if x is
![]() $(\varepsilon ,s_0)$
-Diophantine and
$(\varepsilon ,s_0)$
-Diophantine and
![]() $T \gg _{\Gamma ,\varepsilon } s_0$
, then T is sufficiently large to use Corollary 5.5 on
$T \gg _{\Gamma ,\varepsilon } s_0$
, then T is sufficiently large to use Corollary 5.5 on
![]() $a_{-s}x$
for
$a_{-s}x$
for
![]() $s>0.$
To see this, observe that in the notation of the proof of Corollary 5.5,
$s>0.$
To see this, observe that in the notation of the proof of Corollary 5.5,
![]() $T_0$
is such that for any
$T_0$
is such that for any
![]() $(\varepsilon ,s_0)$
-Diophantine point x, there exists
$(\varepsilon ,s_0)$
-Diophantine point x, there exists
![]() $y \in \operatorname {supp}m^{\operatorname {BMS}}$
and
$y \in \operatorname {supp}m^{\operatorname {BMS}}$
and
![]() $\textbf {t}\le T_0$
so that
$\textbf {t}\le T_0$
so that
![]() $x=u_{\textbf {t}} y$
. Then
$x=u_{\textbf {t}} y$
. Then
Thus, the distance to the nearest BMS point in the U orbit shrinks, and so T is still sufficiently large.
Proposition 5.7. Let
![]() $H_R = \{y \in G/\Gamma : \operatorname {height}(y)\le R\}$
. There exist constants
$H_R = \{y \in G/\Gamma : \operatorname {height}(y)\le R\}$
. There exist constants
![]() $\alpha = \alpha (\Gamma )>0,$
and
$\alpha = \alpha (\Gamma )>0,$
and
![]() $\omega =\omega (\Gamma )\ge 0$
such that for every
$\omega =\omega (\Gamma )\ge 0$
such that for every
![]() $x \in G/\Gamma $
that is
$x \in G/\Gamma $
that is
![]() $(\varepsilon ,s_0)$
-Diophantine and for every
$(\varepsilon ,s_0)$
-Diophantine and for every
![]() $0<\xi <1/2,$
and
$0<\xi <1/2,$
and
![]() $T\gg _{\Gamma ,\varepsilon } s_0$
,
$T\gg _{\Gamma ,\varepsilon } s_0$
,
 $$ \begin{align*} \frac{\mu^{\operatorname{PS}}_x((B_U(\xi+T) \cap H_R)-(B_U(T)\cap H_R) )}{\mu^{\operatorname{PS}}_x(B_U(T))}\ll_{\Gamma} e^{\omega R}{\xi^{\alpha}}.\end{align*} $$
$$ \begin{align*} \frac{\mu^{\operatorname{PS}}_x((B_U(\xi+T) \cap H_R)-(B_U(T)\cap H_R) )}{\mu^{\operatorname{PS}}_x(B_U(T))}\ll_{\Gamma} e^{\omega R}{\xi^{\alpha}}.\end{align*} $$
Proof. Let
![]() $T_0\gg _{\Gamma ,\varepsilon } s_0$
satisfy the conclusion of Lemma 3.8. For
$T_0\gg _{\Gamma ,\varepsilon } s_0$
satisfy the conclusion of Lemma 3.8. For
![]() $T \ge T_0$
, let
$T \ge T_0$
, let
and observe that
![]() $\mu ^{\operatorname {PS}}_x(E_T)=\mu ^{\operatorname {PS}}_x(\mathcal {N}(L,\xi )\cap B_U(T)\cap H_R).$
$\mu ^{\operatorname {PS}}_x(E_T)=\mu ^{\operatorname {PS}}_x(\mathcal {N}(L,\xi )\cap B_U(T)\cap H_R).$
Let
![]() $c_1=c_1(\Gamma )>0$
be the implied constant in Proposition 5.4. Fix
$c_1=c_1(\Gamma )>0$
be the implied constant in Proposition 5.4. Fix
![]() $r=c_1e^{-R}$
and let
$r=c_1e^{-R}$
and let
![]() $\{u_1,\ldots ,u_k\}$
be a maximal
$\{u_1,\ldots ,u_k\}$
be a maximal
![]() ${r}/{2}$
-separated set in
${r}/{2}$
-separated set in
![]() $E_{T-{r}/{4}}$
. Then,
$E_{T-{r}/{4}}$
. Then,
 $$ \begin{align*}E_T\subseteq\bigcup_{i=1}^k B_U(r)u_i.\end{align*} $$
$$ \begin{align*}E_T\subseteq\bigcup_{i=1}^k B_U(r)u_i.\end{align*} $$
Note also that by (37), we have that there exists a constant
![]() $c_2=c_2(\Gamma )>0$
such that for all
$c_2=c_2(\Gamma )>0$
such that for all
![]() $u_i$
,
$u_i$
,
Therefore,

By Corollary 5.5, there exists
![]() $\sigma =\sigma (\Gamma ) \ge \delta _{\Gamma }$
so that
$\sigma =\sigma (\Gamma ) \ge \delta _{\Gamma }$
so that
Let
It follows from the geometry of
![]() $B_U(\xi +T)x-B_U(T)x$
that there exist
$B_U(\xi +T)x-B_U(T)x$
that there exist
![]() $L_1,\ldots ,L_m$
, where m only depends on n, such that
$L_1,\ldots ,L_m$
, where m only depends on n, such that
 $$ \begin{align*} B_U(\xi+T)x-B_U(T)x\subseteq\bigcup_{i=1}^{m} \mathcal{N}_U(L_i,2\xi).\end{align*} $$
$$ \begin{align*} B_U(\xi+T)x-B_U(T)x\subseteq\bigcup_{i=1}^{m} \mathcal{N}_U(L_i,2\xi).\end{align*} $$
Thus, we also have
 $$ \begin{align*}(B_U(\xi + T)x - B_U(T)x) \cap H_R\subseteq\bigcup_{i=1}^{m} \mathcal{N}_U(L_i,2\xi).\end{align*} $$
$$ \begin{align*}(B_U(\xi + T)x - B_U(T)x) \cap H_R\subseteq\bigcup_{i=1}^{m} \mathcal{N}_U(L_i,2\xi).\end{align*} $$
We arrive at
 $$ \begin{align*} \frac{\mu^{\operatorname{PS}}_x((B_U(\xi+T) \cap H_R)-(B_U(T)\cap H_R) )}{\mu^{\operatorname{PS}}_x(B_U(T))} & \le \sum_{i=1}^m\frac{\mu^{\operatorname{PS}}_x(\mathcal{N}(L_i,2\xi)\cap B_U(\xi+T))}{\mu^{\operatorname{PS}}_x(B_U(T))}\\[4pt] & \ll_{\Gamma}m e^{\omega'R}{\xi^{\alpha}} \frac{\mu^{\operatorname{PS}}_x( B_U(\xi+T))}{\mu^{\operatorname{PS}}_x(B_U(T))}. \end{align*} $$
$$ \begin{align*} \frac{\mu^{\operatorname{PS}}_x((B_U(\xi+T) \cap H_R)-(B_U(T)\cap H_R) )}{\mu^{\operatorname{PS}}_x(B_U(T))} & \le \sum_{i=1}^m\frac{\mu^{\operatorname{PS}}_x(\mathcal{N}(L_i,2\xi)\cap B_U(\xi+T))}{\mu^{\operatorname{PS}}_x(B_U(T))}\\[4pt] & \ll_{\Gamma}m e^{\omega'R}{\xi^{\alpha}} \frac{\mu^{\operatorname{PS}}_x( B_U(\xi+T))}{\mu^{\operatorname{PS}}_x(B_U(T))}. \end{align*} $$
By Corollary 5.5 again, we conclude that
 $$ \begin{align*} \frac{\mu^{\operatorname{PS}}_x((B_U(\xi+T) \cap H_R)-(B_U(T)\cap H_R) )}{\mu^{\operatorname{PS}}_x(B_U(T))} \ll_{\Gamma}e^{\omega'R}\xi^{\alpha},\end{align*} $$
$$ \begin{align*} \frac{\mu^{\operatorname{PS}}_x((B_U(\xi+T) \cap H_R)-(B_U(T)\cap H_R) )}{\mu^{\operatorname{PS}}_x(B_U(T))} \ll_{\Gamma}e^{\omega'R}\xi^{\alpha},\end{align*} $$
which completes the proof.
We are now ready to prove Theorem 5.1.
Proof of Theorem 5.1
Observe that by Lemma 3.6, for any
![]() $R>R_0$
,
$R>R_0$
,
 $$ \begin{align} \mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U(T))&=\mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U(T)\cap H_{R-R_0}) + \mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U(T)\cap \mathcal{X}(R)),\nonumber\\[4pt] \mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U(T+\xi))&=\mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U(T+\xi)\cap H_{R-R_0}) + \mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U(T+\xi)\cap \mathcal{X}(R)). \end{align} $$
$$ \begin{align} \mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U(T))&=\mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U(T)\cap H_{R-R_0}) + \mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U(T)\cap \mathcal{X}(R)),\nonumber\\[4pt] \mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U(T+\xi))&=\mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U(T+\xi)\cap H_{R-R_0}) + \mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U(T+\xi)\cap \mathcal{X}(R)). \end{align} $$
By Theorem 4.1, for
![]() $T \gg _{\Gamma ,\varepsilon } s_0$
,
$T \gg _{\Gamma ,\varepsilon } s_0$
,
![]() $0<s\le T^{{\varepsilon }/({1-\varepsilon })}$
, and any
$0<s\le T^{{\varepsilon }/({1-\varepsilon })}$
, and any
![]() $R \ge R_0,$
$R \ge R_0,$
 $$ \begin{align*} \mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U(T+\xi)\cap \mathcal{X}(R))&= \mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U((s(T+\xi)/s) \cap \mathcal{X}(R)) \\[4pt] &\ll_{\Gamma} \mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U(T+\xi))e^{-\beta R}\\[4pt] &\ll_{\Gamma} \mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U(T))e^{-\beta R} \quad\text{by Corollary 5.5}. \end{align*} $$
$$ \begin{align*} \mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U(T+\xi)\cap \mathcal{X}(R))&= \mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U((s(T+\xi)/s) \cap \mathcal{X}(R)) \\[4pt] &\ll_{\Gamma} \mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U(T+\xi))e^{-\beta R}\\[4pt] &\ll_{\Gamma} \mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U(T))e^{-\beta R} \quad\text{by Corollary 5.5}. \end{align*} $$
Observe that use of Corollary 5.5 is justified if
![]() $T \gg _{\Gamma ,\varepsilon } s_0$
by Remark 5.6. Similarly, by Proposition 5.7 and the same reasoning as in Remark 5.6, for
$T \gg _{\Gamma ,\varepsilon } s_0$
by Remark 5.6. Similarly, by Proposition 5.7 and the same reasoning as in Remark 5.6, for
![]() $T \gg _{\Gamma ,\varepsilon } s_0$
, we have
$T \gg _{\Gamma ,\varepsilon } s_0$
, we have
Putting this together with (48), we conclude
 $$ \begin{align*} &\mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U(T+\xi))-\mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U(T))\\[4pt] &\quad\ll_{\Gamma} e^{\omega R}\xi^{\alpha} \mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U(T)) + 2e^{-\beta R}\mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U(T))\\[4pt] &\quad\ll_{\Gamma} (e^{\omega R}\xi^{\alpha} +2e^{-\beta R})\mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U(T)). \end{align*} $$
$$ \begin{align*} &\mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U(T+\xi))-\mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U(T))\\[4pt] &\quad\ll_{\Gamma} e^{\omega R}\xi^{\alpha} \mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U(T)) + 2e^{-\beta R}\mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U(T))\\[4pt] &\quad\ll_{\Gamma} (e^{\omega R}\xi^{\alpha} +2e^{-\beta R})\mu^{\operatorname{PS}}_{a_{-\log s}x}(B_U(T)). \end{align*} $$
Taking
![]() $R=-{\alpha }/({\omega +\beta })\log \xi $
implies the result, provided that
$R=-{\alpha }/({\omega +\beta })\log \xi $
implies the result, provided that
![]() $\xi $
is sufficiently small so that this is larger than
$\xi $
is sufficiently small so that this is larger than
![]() $R_0.$
Note that since
$R_0.$
Note that since
![]() $\alpha ,\omega ,\beta , R_0$
are all constants depending only on
$\alpha ,\omega ,\beta , R_0$
are all constants depending only on
![]() $\Gamma $
, this is equivalent to requiring
$\Gamma $
, this is equivalent to requiring
![]() $\xi \ll _{\Gamma } 1.$
$\xi \ll _{\Gamma } 1.$
6 Proof of Theorem 1.5
In this section, we keep the notation of §3.2. In particular, d denotes the hyperbolic distance,
![]() $\operatorname {height}$
is the height of a point in the convex core into the cusps, and
$\operatorname {height}$
is the height of a point in the convex core into the cusps, and
![]() $\mathcal {C}_0$
is the fixed compact set in
$\mathcal {C}_0$
is the fixed compact set in
![]() $G/\Gamma $
which is defined in §3.2.
$G/\Gamma $
which is defined in §3.2.
We will first prove the following proposition, which is a form of Theorem 1.5 for G. Theorem 1.5 will follow by a partition of unity argument.
Proposition 6.1. There exist
![]() $\kappa =\kappa (\Gamma )$
and
$\kappa =\kappa (\Gamma )$
and
![]() $\ell =\ell (\Gamma )$
which satisfy the following: let
$\ell =\ell (\Gamma )$
which satisfy the following: let
![]() $0<r<1$
,
$0<r<1$
,
![]() $\psi \in C_c^{\infty }(G)$
supported on an admissible box, and
$\psi \in C_c^{\infty }(G)$
supported on an admissible box, and
![]() $f\in C_c^{\infty }(B_U (r))$
. Then, there exists
$f\in C_c^{\infty }(B_U (r))$
. Then, there exists
![]() $c=c(\Gamma ,\operatorname {supp}\psi )>0$
such that for any
$c=c(\Gamma ,\operatorname {supp}\psi )>0$
such that for any
![]() $g\in \operatorname {supp}\tilde {m}^{\operatorname {BMS}}$
, and
$g\in \operatorname {supp}\tilde {m}^{\operatorname {BMS}}$
, and
![]() $s\gg _{\Gamma } \operatorname {height}(g\Gamma ),$
we have
$s\gg _{\Gamma } \operatorname {height}(g\Gamma ),$
we have
 $$ \begin{align*} &\bigg|\sum\limits_{\gamma \in \Gamma}\int_{U}\psi(a_su_{\textbf{t}} g\gamma)f(\textbf{t})\,d\mu^{\operatorname{PS}}_g(\textbf{t})- \mu^{\operatorname{PS}}_g(f)\tilde{m}^{\operatorname{BMS}}(\psi)\bigg|\\[3pt] &\quad<cS_{\ell}(\psi)S_{\ell}(f)e^{-\kappa s}\mu^{\operatorname{PS}}_g(B_U(1)). \end{align*} $$
$$ \begin{align*} &\bigg|\sum\limits_{\gamma \in \Gamma}\int_{U}\psi(a_su_{\textbf{t}} g\gamma)f(\textbf{t})\,d\mu^{\operatorname{PS}}_g(\textbf{t})- \mu^{\operatorname{PS}}_g(f)\tilde{m}^{\operatorname{BMS}}(\psi)\bigg|\\[3pt] &\quad<cS_{\ell}(\psi)S_{\ell}(f)e^{-\kappa s}\mu^{\operatorname{PS}}_g(B_U(1)). \end{align*} $$
Proof. Without loss of generality, assume that f and
![]() $\psi $
are non-negative functions. Step 1: Setup and approximations.
$\psi $
are non-negative functions. Step 1: Setup and approximations.
Let
![]() $\kappa ',\ell '$
satisfy the conclusion of Assumption 1.1, and let
$\kappa ',\ell '$
satisfy the conclusion of Assumption 1.1, and let
![]() $\ell>\ell '$
satisfy the conclusion of Lemma 3.12. Observe that
$\ell>\ell '$
satisfy the conclusion of Lemma 3.12. Observe that
![]() $\ell $
can be increased if necessary while maintaining this property.
$\ell $
can be increased if necessary while maintaining this property.
Because
![]() $\psi $
is supported on an admissible box, there exists
$\psi $
is supported on an admissible box, there exists
![]() $0<\eta _0<1/2$
(depending on
$0<\eta _0<1/2$
(depending on
![]() $\operatorname {supp}\psi $
) such that
$\operatorname {supp}\psi $
) such that
![]() $G_{3\eta _0}\operatorname {supp}\psi $
is still an admissible box. For
$G_{3\eta _0}\operatorname {supp}\psi $
is still an admissible box. For
![]() $0<\eta <\eta _0$
, let
$0<\eta <\eta _0$
, let
![]() $\psi _{\eta ,\pm }$
satisfy the conclusion of Lemma 3.12 for
$\psi _{\eta ,\pm }$
satisfy the conclusion of Lemma 3.12 for
![]() $G,3\eta $
, and
$G,3\eta $
, and
![]() $\psi $
. In particular, for all small
$\psi $
. In particular, for all small
![]() $\eta>0$
,
$\eta>0$
,
Since
![]() $\psi $
is uniformly continuous and the BMS measure is finite, we may deduce from Lemma 3.12(2) that
$\psi $
is uniformly continuous and the BMS measure is finite, we may deduce from Lemma 3.12(2) that
According to Lemma 3.1, for any
![]() $p \in P_{\eta }$
, there exists
$p \in P_{\eta }$
, there exists
![]() $\rho _p : B_U(1) \to B_U(1+O(\eta ))$
that is a diffeomorphism onto its image and a constant
$\rho _p : B_U(1) \to B_U(1+O(\eta ))$
that is a diffeomorphism onto its image and a constant
![]() $D=D(\eta )<3\eta $
such that
$D=D(\eta )<3\eta $
such that
Step 2: Assuming that f is supported on a small ball.
We start by proving that there exists
![]() $\kappa> 0$
such that if
$\kappa> 0$
such that if
![]() $f\in C_c^{\infty }(B_U(r_1))$
, where
$f\in C_c^{\infty }(B_U(r_1))$
, where
![]() $r_1\le \operatorname {inj}(g)$
, then for
$r_1\le \operatorname {inj}(g)$
, then for
![]() $s>0$
,
$s>0$
,
 $$ \begin{align} & \sum_{\gamma\in\Gamma}\int_U\psi(a_s u_{\textbf{t}} g\gamma)f(\textbf{t})\,d\mu^{\operatorname{PS}}_g (\textbf{t})-\tilde{m}^{\operatorname{BMS}}(\psi)\mu^{\operatorname{PS}}_g(f)\nonumber\\[3pt] &\quad\ll_{\Gamma,\operatorname{supp}\psi}S_{\ell}(\psi)S_{\ell}(f)e^{-2\kappa s}\mu^{\operatorname{PS}}_g(B_U(1)). \end{align} $$
$$ \begin{align} & \sum_{\gamma\in\Gamma}\int_U\psi(a_s u_{\textbf{t}} g\gamma)f(\textbf{t})\,d\mu^{\operatorname{PS}}_g (\textbf{t})-\tilde{m}^{\operatorname{BMS}}(\psi)\mu^{\operatorname{PS}}_g(f)\nonumber\\[3pt] &\quad\ll_{\Gamma,\operatorname{supp}\psi}S_{\ell}(\psi)S_{\ell}(f)e^{-2\kappa s}\mu^{\operatorname{PS}}_g(B_U(1)). \end{align} $$
For any
![]() $s>0$
and
$s>0$
and
![]() $\gamma \in \Gamma $
, from (51), we have that
$\gamma \in \Gamma $
, from (51), we have that
 $$ \begin{align*} &\int_{B_U(r_1)} \psi(a_s u_{\textbf{t}} g\gamma)f(\textbf{t})\,d\mu^{\operatorname{PS}}_g(\textbf{t}) \\[3pt] &\quad= \frac{1}{\nu(P_{\eta} g)}\int_{P_{\eta} g}\int_{B_U(r_1)}\psi(a_{s}u_{\textbf{t}} p^{-1} pg\gamma)f(\textbf{t})\,d\mu^{\operatorname{PS}}_{g}(\textbf{t})\,d\nu(pg)\\[3pt] &\quad\le \frac{1}{\nu(P_{\eta} g)} \int_{P_{\eta} g}\int_{B_U(r_1)} \psi_{\eta,+}(a_{s}u_{\rho_p(\textbf{t})}pg\gamma)f(\textbf{t})\,d\mu^{\operatorname{PS}}_{g}(\textbf{t})\,d\nu(pg), \end{align*} $$
$$ \begin{align*} &\int_{B_U(r_1)} \psi(a_s u_{\textbf{t}} g\gamma)f(\textbf{t})\,d\mu^{\operatorname{PS}}_g(\textbf{t}) \\[3pt] &\quad= \frac{1}{\nu(P_{\eta} g)}\int_{P_{\eta} g}\int_{B_U(r_1)}\psi(a_{s}u_{\textbf{t}} p^{-1} pg\gamma)f(\textbf{t})\,d\mu^{\operatorname{PS}}_{g}(\textbf{t})\,d\nu(pg)\\[3pt] &\quad\le \frac{1}{\nu(P_{\eta} g)} \int_{P_{\eta} g}\int_{B_U(r_1)} \psi_{\eta,+}(a_{s}u_{\rho_p(\textbf{t})}pg\gamma)f(\textbf{t})\,d\mu^{\operatorname{PS}}_{g}(\textbf{t})\,d\nu(pg), \end{align*} $$
where the last inequality follows since
![]() $a_s P_{3\eta }a_{-s}\subset P_{3\eta }$
for any positive s.
$a_s P_{3\eta }a_{-s}\subset P_{3\eta }$
for any positive s.
Step 2.1: Use the product structure of the BMS measure. For any
![]() $p\in P_{\eta }$
,
$p\in P_{\eta }$
,
![]() $(u_{\textbf {t}} g)^+= (u_{\rho _p (\textbf {t})}pg)^+$
, the measures
$(u_{\textbf {t}} g)^+= (u_{\rho _p (\textbf {t})}pg)^+$
, the measures
![]() $d\mu ^{\operatorname {PS}}_{g}(\textbf {t})$
and
$d\mu ^{\operatorname {PS}}_{g}(\textbf {t})$
and
![]() $d({\rho _p}_{\ast }\mu ^{\operatorname {PS}}_{pg}(\textbf {t}))=d\mu ^{\operatorname {PS}}_{pg}(\rho _p (\textbf {t}))$
are absolutely continuous with each other, and the Radon–Nikodym derivative at
$d({\rho _p}_{\ast }\mu ^{\operatorname {PS}}_{pg}(\textbf {t}))=d\mu ^{\operatorname {PS}}_{pg}(\rho _p (\textbf {t}))$
are absolutely continuous with each other, and the Radon–Nikodym derivative at
![]() $\textbf {t}$
is given by
$\textbf {t}$
is given by
 $$ \begin{align} \frac{d\mu^{\operatorname{PS}}_{g}(\textbf{t})}{d\mu^{\operatorname{PS}}_{pg}(\rho_p (\textbf{t}))}=e^{\delta_{\Gamma}\beta_{(u_{\textbf{t}} g)^+}(u_{\textbf{t}} g(o),u_{\rho_p(\textbf{t})}pg(o))}. \end{align} $$
$$ \begin{align} \frac{d\mu^{\operatorname{PS}}_{g}(\textbf{t})}{d\mu^{\operatorname{PS}}_{pg}(\rho_p (\textbf{t}))}=e^{\delta_{\Gamma}\beta_{(u_{\textbf{t}} g)^+}(u_{\textbf{t}} g(o),u_{\rho_p(\textbf{t})}pg(o))}. \end{align} $$
Let
![]() $0<\xi <\eta $
. Let
$0<\xi <\eta $
. Let
![]() $\chi _{\eta ,\xi }$
satisfy the conclusion of Lemma 3.10 for
$\chi _{\eta ,\xi }$
satisfy the conclusion of Lemma 3.10 for
![]() $H=P$
,
$H=P$
,
![]() $\xi _1=\eta -\xi $
,
$\xi _1=\eta -\xi $
,
![]() $\xi _2=\xi $
, and g. Let
$\xi _2=\xi $
, and g. Let
![]() $\varphi _{\eta ,g}$
be the function defined on
$\varphi _{\eta ,g}$
be the function defined on
![]() $B_U (1) P_{\eta }g$
given by
$B_U (1) P_{\eta }g$
given by
 $$ \begin{align*} \varphi_{\eta,g}(u_{\rho_p(\textbf{t})}pg):=\frac{f(\textbf{t})\chi_{\eta,\xi}(pg)}{\nu(P_{\eta} g)e^{\delta_{\Gamma}\beta_{(u_{\textbf{t}} g)^+}(u_{\textbf{t}} g(o),u_{\rho_p(\textbf{t})}pg(o))}}.\end{align*} $$
$$ \begin{align*} \varphi_{\eta,g}(u_{\rho_p(\textbf{t})}pg):=\frac{f(\textbf{t})\chi_{\eta,\xi}(pg)}{\nu(P_{\eta} g)e^{\delta_{\Gamma}\beta_{(u_{\textbf{t}} g)^+}(u_{\textbf{t}} g(o),u_{\rho_p(\textbf{t})}pg(o))}}.\end{align*} $$
We will need a bound on
![]() $S_{\ell }(\varphi _{\eta ,g}).$
To that end, note that
$S_{\ell }(\varphi _{\eta ,g}).$
To that end, note that
 $$ \begin{align*} |\beta_{(u_{\textbf{t}} g)^+}(u_{\textbf{t}} g(o), u_{\rho_p(\textbf{t})} pg(o))| &\le d(u_{\textbf{t}} g(o), u_{\rho_p(\textbf{t})}pg(o))\\[3pt] &= d(g(o), u_{-\textbf{t}} u_{\rho_p(\textbf{t})}pg(o)). \end{align*} $$
$$ \begin{align*} |\beta_{(u_{\textbf{t}} g)^+}(u_{\textbf{t}} g(o), u_{\rho_p(\textbf{t})} pg(o))| &\le d(u_{\textbf{t}} g(o), u_{\rho_p(\textbf{t})}pg(o))\\[3pt] &= d(g(o), u_{-\textbf{t}} u_{\rho_p(\textbf{t})}pg(o)). \end{align*} $$
Since
![]() $u_{-\textbf {t}} u_{\rho _p(\textbf {t})}p\in G_{5\eta }$
, the above is bounded by some absolute constant (depending only on
$u_{-\textbf {t}} u_{\rho _p(\textbf {t})}p\in G_{5\eta }$
, the above is bounded by some absolute constant (depending only on
![]() $\Gamma $
) for all
$\Gamma $
) for all
![]() $\eta <\tfrac 12$
. Observe that this bound holds on the support of
$\eta <\tfrac 12$
. Observe that this bound holds on the support of
![]() $f(\textbf {t})\chi _{\eta ,\xi }(pg).$
Moreover, because the Busemann function is Lipschitz, all of its derivatives are bounded.
$f(\textbf {t})\chi _{\eta ,\xi }(pg).$
Moreover, because the Busemann function is Lipschitz, all of its derivatives are bounded.
It then follows immediately from the product rule and the definition of the Sobolev norm that
By [Reference Kleinbock and Margulis17, Lemma 2.4.7(a)], Lemma 3.10, (54), and Lemma 3.9, we have
 $$ \begin{align} S_{\ell}(\varphi_{\eta,g})&\ll_{\Gamma,\ell} \nu(P_{\eta} g)^{-1} S_{\ell}(f)S_{\ell}(\chi_{\eta,\xi})\nonumber\\[3pt] &\ll_{\Gamma,\ell} \eta^{-(\delta_{\Gamma} + {1}/{2}(n-1)(n-2)+1)}e^{(\delta_{\Gamma} - k_2(x,\eta))d(\pi(\mathcal{C}_0),\pi(a_{\log \eta}g))}S_{\ell}(\chi_{\eta,\xi})S_{\ell}(f)\nonumber \\[3pt] &\ll_{\Gamma,\ell} e^{\delta_{\Gamma}(|\log \eta|+\operatorname{height}(g\Gamma))} \eta^{-(\delta_{\Gamma} + {1}/{2}(n-1)(n-2)+1)}\eta^{n-1} {\xi}^{-\ell-(n-1)/2} S_{\ell}(f)\nonumber\\[3pt] &\ll_{\Gamma,\ell} e^{\delta_{\Gamma} \operatorname{height}(g\Gamma)}\eta^{-(2\delta_{\Gamma} + {1}/{2}(n-1)(n-2)+1)}\eta^{n-1} {\xi}^{-\ell-(n-1)/2} S_{\ell}(f)\nonumber\\[3pt] &\ll_{\Gamma,\ell} e^{\delta_{\Gamma} \operatorname{height}(g\Gamma)} \eta^{4n-({1}/{2})n^2-3-2\delta_{\Gamma}}\xi^{-\ell-(n-1)/2}S_{\ell}(f). \end{align} $$
$$ \begin{align} S_{\ell}(\varphi_{\eta,g})&\ll_{\Gamma,\ell} \nu(P_{\eta} g)^{-1} S_{\ell}(f)S_{\ell}(\chi_{\eta,\xi})\nonumber\\[3pt] &\ll_{\Gamma,\ell} \eta^{-(\delta_{\Gamma} + {1}/{2}(n-1)(n-2)+1)}e^{(\delta_{\Gamma} - k_2(x,\eta))d(\pi(\mathcal{C}_0),\pi(a_{\log \eta}g))}S_{\ell}(\chi_{\eta,\xi})S_{\ell}(f)\nonumber \\[3pt] &\ll_{\Gamma,\ell} e^{\delta_{\Gamma}(|\log \eta|+\operatorname{height}(g\Gamma))} \eta^{-(\delta_{\Gamma} + {1}/{2}(n-1)(n-2)+1)}\eta^{n-1} {\xi}^{-\ell-(n-1)/2} S_{\ell}(f)\nonumber\\[3pt] &\ll_{\Gamma,\ell} e^{\delta_{\Gamma} \operatorname{height}(g\Gamma)}\eta^{-(2\delta_{\Gamma} + {1}/{2}(n-1)(n-2)+1)}\eta^{n-1} {\xi}^{-\ell-(n-1)/2} S_{\ell}(f)\nonumber\\[3pt] &\ll_{\Gamma,\ell} e^{\delta_{\Gamma} \operatorname{height}(g\Gamma)} \eta^{4n-({1}/{2})n^2-3-2\delta_{\Gamma}}\xi^{-\ell-(n-1)/2}S_{\ell}(f). \end{align} $$
Note that the dependence on
![]() $\ell $
arises from the exponential of the Busemann function in the denominator.
$\ell $
arises from the exponential of the Busemann function in the denominator.
Also, using the product structure of
![]() $\tilde {m}^{\operatorname {BMS}}$
in (25), we get
$\tilde {m}^{\operatorname {BMS}}$
in (25), we get
 $$ \begin{align*} & \frac{1}{\nu(P_{\eta}g)} \int_{P_{\eta} g}\int_{B_U(r_1)} \psi_{\eta,+}(a_{s}u_{\rho_p(\textbf{t})}pg\gamma)f(\textbf{t})\,d\mu^{\operatorname{PS}}_{g}(\textbf{t})\,d\nu(pg)\\[3pt] &\quad= \frac{1}{\nu(P_{\eta}g)}\int_{P_{\eta} g}\int_{B_U(r_1)} \psi_{\eta,+}(a_{s}u_{\rho_p(\textbf{t})}pg\gamma)f(\textbf{t})\frac{d\mu^{\operatorname{PS}}_{g}(\textbf{t})}{d\mu^{\operatorname{PS}}_{pg}(\rho_p (\textbf{t}))}\,d\mu^{\operatorname{PS}}_{pg}(\rho_p (\textbf{t}))\,d\nu(pg)\\[3pt] &\quad\leq\int_G \psi_{\eta,+}(a_{s}h\gamma)\varphi_{\eta,g}(h)\,d\tilde{m}^{\operatorname{BMS}}(h). \end{align*} $$
$$ \begin{align*} & \frac{1}{\nu(P_{\eta}g)} \int_{P_{\eta} g}\int_{B_U(r_1)} \psi_{\eta,+}(a_{s}u_{\rho_p(\textbf{t})}pg\gamma)f(\textbf{t})\,d\mu^{\operatorname{PS}}_{g}(\textbf{t})\,d\nu(pg)\\[3pt] &\quad= \frac{1}{\nu(P_{\eta}g)}\int_{P_{\eta} g}\int_{B_U(r_1)} \psi_{\eta,+}(a_{s}u_{\rho_p(\textbf{t})}pg\gamma)f(\textbf{t})\frac{d\mu^{\operatorname{PS}}_{g}(\textbf{t})}{d\mu^{\operatorname{PS}}_{pg}(\rho_p (\textbf{t}))}\,d\mu^{\operatorname{PS}}_{pg}(\rho_p (\textbf{t}))\,d\nu(pg)\\[3pt] &\quad\leq\int_G \psi_{\eta,+}(a_{s}h\gamma)\varphi_{\eta,g}(h)\,d\tilde{m}^{\operatorname{BMS}}(h). \end{align*} $$
Step 2.2: Use the exponential mixing assumption.
By defining
![]() $\Psi _{\eta ,+}(h\Gamma ) = \sum \nolimits _{\gamma \in \Gamma } \psi _{\eta ,+}(h\gamma )$
and
$\Psi _{\eta ,+}(h\Gamma ) = \sum \nolimits _{\gamma \in \Gamma } \psi _{\eta ,+}(h\gamma )$
and
![]() $\Phi _{\eta ,g}(h\Gamma ):=\sum \nolimits _{\gamma \in \Gamma }\varphi _{\eta ,g}(h\gamma ),$
we obtain
$\Phi _{\eta ,g}(h\Gamma ):=\sum \nolimits _{\gamma \in \Gamma }\varphi _{\eta ,g}(h\gamma ),$
we obtain
 $$ \begin{align*} \sum_{\gamma\in\Gamma}\int_G\psi_{\eta,+}(a_sh\gamma)\varphi_{\eta,g}(h)\,d\tilde{m}^{\operatorname{BMS}}(h)\leq\int_{X} \Psi_{\eta,+}(a_s x)\Phi_{\eta,g}(x)\,dm^{\operatorname{BMS}}(x)\end{align*} $$
$$ \begin{align*} \sum_{\gamma\in\Gamma}\int_G\psi_{\eta,+}(a_sh\gamma)\varphi_{\eta,g}(h)\,d\tilde{m}^{\operatorname{BMS}}(h)\leq\int_{X} \Psi_{\eta,+}(a_s x)\Phi_{\eta,g}(x)\,dm^{\operatorname{BMS}}(x)\end{align*} $$
for any positive s. Note that
In particular, (49) and (55) imply
 $$ \begin{align} &S_{\ell'}(\Psi_{\eta,+})\ll_{\operatorname{supp}\psi}\eta^{-2\ell}S_{\ell}(\psi)\quad\text{and}\nonumber\\[3pt] &S_{\ell'}(\Phi_{\eta,g}) \ll_{\Gamma} e^{\delta_{\Gamma} \operatorname{height}(g\Gamma)} \eta^{4n-({1}/{2})n^2-3-2\delta_{\Gamma}}\xi^{-\ell-(n-1)/2}S_{\ell}(f). \end{align} $$
$$ \begin{align} &S_{\ell'}(\Psi_{\eta,+})\ll_{\operatorname{supp}\psi}\eta^{-2\ell}S_{\ell}(\psi)\quad\text{and}\nonumber\\[3pt] &S_{\ell'}(\Phi_{\eta,g}) \ll_{\Gamma} e^{\delta_{\Gamma} \operatorname{height}(g\Gamma)} \eta^{4n-({1}/{2})n^2-3-2\delta_{\Gamma}}\xi^{-\ell-(n-1)/2}S_{\ell}(f). \end{align} $$
By Assumption 1.1,
 $$ \begin{align*} &\int\Psi_{\eta,+}(a_{s}x)\Phi_{\eta,g}(x)\,dm^{\operatorname{BMS}}(x)-m^{\operatorname{BMS}}(\Psi_{\eta,+})m^{\operatorname{BMS}}(\Phi_{\eta,g})\\ &\quad\ll_{\Gamma} S_{\ell'}(\Psi_{\eta,+})S_{\ell'}(\Phi_{\eta,g})e^{-\kappa' s}. \end{align*} $$
$$ \begin{align*} &\int\Psi_{\eta,+}(a_{s}x)\Phi_{\eta,g}(x)\,dm^{\operatorname{BMS}}(x)-m^{\operatorname{BMS}}(\Psi_{\eta,+})m^{\operatorname{BMS}}(\Phi_{\eta,g})\\ &\quad\ll_{\Gamma} S_{\ell'}(\Psi_{\eta,+})S_{\ell'}(\Phi_{\eta,g})e^{-\kappa' s}. \end{align*} $$
Then, by (57), there exists
![]() $c_1=c_1(\Gamma ,\operatorname {supp}\psi )$
such that
$c_1=c_1(\Gamma ,\operatorname {supp}\psi )$
such that
 $$ \begin{align*} &\sum_{\gamma\in\Gamma}\int_{B_U(r_1)} \psi(a_su_{\textbf{t}} g\gamma)f(\textbf{t})\,d\mu^{\operatorname{PS}}_g(\textbf{t})\\[3pt] &\quad<m^{\operatorname{BMS}}(\Psi_{\eta,+})m^{\operatorname{BMS}}(\Phi_{\eta,g})\\[3pt] &\qquad+c_1e^{\delta_{\Gamma} \operatorname{height}(g\Gamma)} \eta^{4n-({1}/{2})n^2-3-2\delta_{\Gamma}}\xi^{-\ell-(n-1)/2}S_{\ell}(\psi)S_{\ell}(f)e^{-\kappa' s}. \end{align*} $$
$$ \begin{align*} &\sum_{\gamma\in\Gamma}\int_{B_U(r_1)} \psi(a_su_{\textbf{t}} g\gamma)f(\textbf{t})\,d\mu^{\operatorname{PS}}_g(\textbf{t})\\[3pt] &\quad<m^{\operatorname{BMS}}(\Psi_{\eta,+})m^{\operatorname{BMS}}(\Phi_{\eta,g})\\[3pt] &\qquad+c_1e^{\delta_{\Gamma} \operatorname{height}(g\Gamma)} \eta^{4n-({1}/{2})n^2-3-2\delta_{\Gamma}}\xi^{-\ell-(n-1)/2}S_{\ell}(\psi)S_{\ell}(f)e^{-\kappa' s}. \end{align*} $$
Step 2.3: Rewrite in terms of
![]() $\psi $
and f.
$\psi $
and f.
Using Lemma 3.10 and (53), one can calculate
 $$ \begin{align*} m^{\operatorname{BMS}}(\Phi_{\eta,g})&=\int_{G}\varphi_{\eta,g}(h)\,d\tilde{m}^{\operatorname{BMS}}(h)\\[3pt] &=\frac{1}{\nu(P_{\eta} g)}\int_{Pg}\int_U\frac{f(\textbf{t})\chi_{\eta,\xi}(p)}{e^{\delta_{\Gamma}\beta_{(u_{\textbf{t}} g)^+}(u_{\textbf{t}} g(o),u_{\rho_p(\textbf{t})}pg(o))}}\,d\mu^{\operatorname{PS}}_{pg}(\rho_p (\textbf{t}))\,d\nu(pg)\\[3pt] &=\frac{1}{\nu(P_{\eta} g)}\int_{Pg}\int_U f(\textbf{t})\chi_{\eta,\xi}(p)\,d\mu^{\operatorname{PS}}_{g}(\textbf{t})\,d\nu(pg)\\[3pt] &\leq\frac{\nu(P_{\eta+\xi} g)}{\nu(P_{\eta} g)}\int_{B_U(r_1)}f(\textbf{t})\,d\mu^{\operatorname{PS}}_{g}(\textbf{t}). \end{align*} $$
$$ \begin{align*} m^{\operatorname{BMS}}(\Phi_{\eta,g})&=\int_{G}\varphi_{\eta,g}(h)\,d\tilde{m}^{\operatorname{BMS}}(h)\\[3pt] &=\frac{1}{\nu(P_{\eta} g)}\int_{Pg}\int_U\frac{f(\textbf{t})\chi_{\eta,\xi}(p)}{e^{\delta_{\Gamma}\beta_{(u_{\textbf{t}} g)^+}(u_{\textbf{t}} g(o),u_{\rho_p(\textbf{t})}pg(o))}}\,d\mu^{\operatorname{PS}}_{pg}(\rho_p (\textbf{t}))\,d\nu(pg)\\[3pt] &=\frac{1}{\nu(P_{\eta} g)}\int_{Pg}\int_U f(\textbf{t})\chi_{\eta,\xi}(p)\,d\mu^{\operatorname{PS}}_{g}(\textbf{t})\,d\nu(pg)\\[3pt] &\leq\frac{\nu(P_{\eta+\xi} g)}{\nu(P_{\eta} g)}\int_{B_U(r_1)}f(\textbf{t})\,d\mu^{\operatorname{PS}}_{g}(\textbf{t}). \end{align*} $$
Thus, by Theorem 5.2, there exist
![]() $\alpha ,\theta ,\omega ,c_0>0$
depending only on
$\alpha ,\theta ,\omega ,c_0>0$
depending only on
![]() $\Gamma $
such that for any
$\Gamma $
such that for any
![]() $0<\xi <\eta \ll _{\Gamma } e^{-\operatorname {height}(g\Gamma )}$
,
$0<\xi <\eta \ll _{\Gamma } e^{-\operatorname {height}(g\Gamma )}$
,
 $$ \begin{align*} m^{\operatorname{BMS}}(\Phi_{\eta,g})&\leq \bigg(1+c_2e^{\omega\operatorname{height}(g\Gamma)} \frac{\xi^{\alpha}}{\eta^{\theta}}\bigg)\int_{B_U(r_1)}f(\textbf{t})\,d\mu^{\operatorname{PS}}_{g}(\textbf{t})\\[3pt] &=\bigg(1+c_2e^{\omega\operatorname{height}(g\Gamma)} \frac{\xi^{\alpha}}{\eta^{\theta}}\bigg)\int_{B_U(r_1)}f(\textbf{t})\,d\mu^{\operatorname{PS}}_{g}(\textbf{t})\\[3pt] &=\bigg(1+c_2e^{\omega\operatorname{height}(g\Gamma)} \frac{\xi^{\alpha}}{\eta^{\theta}}\bigg)\mu^{\operatorname{PS}}_g(f). \end{align*} $$
$$ \begin{align*} m^{\operatorname{BMS}}(\Phi_{\eta,g})&\leq \bigg(1+c_2e^{\omega\operatorname{height}(g\Gamma)} \frac{\xi^{\alpha}}{\eta^{\theta}}\bigg)\int_{B_U(r_1)}f(\textbf{t})\,d\mu^{\operatorname{PS}}_{g}(\textbf{t})\\[3pt] &=\bigg(1+c_2e^{\omega\operatorname{height}(g\Gamma)} \frac{\xi^{\alpha}}{\eta^{\theta}}\bigg)\int_{B_U(r_1)}f(\textbf{t})\,d\mu^{\operatorname{PS}}_{g}(\textbf{t})\\[3pt] &=\bigg(1+c_2e^{\omega\operatorname{height}(g\Gamma)} \frac{\xi^{\alpha}}{\eta^{\theta}}\bigg)\mu^{\operatorname{PS}}_g(f). \end{align*} $$
Using (50), we get that there exists
![]() $c_3=c_3(\Gamma ,\operatorname {supp}\psi )$
such that
$c_3=c_3(\Gamma ,\operatorname {supp}\psi )$
such that
 $$ \begin{align*} m^{\operatorname{BMS}}(\Psi_{\eta,+})&\leq\int_G\psi_{\eta,+}(g)\,d\tilde{m}^{\operatorname{BMS}}(g)\\[4pt] &<\tilde{m}^{\operatorname{BMS}}(\psi)+c_3\eta S_{\ell}(\psi). \end{align*} $$
$$ \begin{align*} m^{\operatorname{BMS}}(\Psi_{\eta,+})&\leq\int_G\psi_{\eta,+}(g)\,d\tilde{m}^{\operatorname{BMS}}(g)\\[4pt] &<\tilde{m}^{\operatorname{BMS}}(\psi)+c_3\eta S_{\ell}(\psi). \end{align*} $$
To summarize, we have
 $$ \begin{align*} &\sum_{\gamma\in\Gamma}\int_{B_U(r_1)}\psi(a_s u_{\textbf{t}} g\gamma)f(\textbf{t})\,d\mu^{\operatorname{PS}}_g(\textbf{t})\\[3pt] &\quad\le \frac{1}{\nu(P_{\eta} g)}\sum_{\gamma\in\Gamma}\int_{P_{\eta} g}\int_{B_U(r_1)} \psi_{\eta,+}(a_{s}u_{\rho_p(\textbf{t})}pg\gamma)f(\textbf{t})\,d\mu^{\operatorname{PS}}_{g}(\textbf{t})\,d\nu(pg)\\[3pt] &\quad\leq\sum_{\gamma\in\Gamma}\int_G \psi_{\eta,+}(a_{s}h\gamma)\varphi_{\eta,g}(h)\,d\tilde{m}^{\operatorname{BMS}}(h)\\ &\quad\leq\int_{X} \Psi_{\eta,+}(a_s x)\Phi_{\eta,g}(x)\,dm^{\operatorname{BMS}}(x)\\[3pt] &\quad<m^{\operatorname{BMS}}(\Psi_{\eta,+})m^{\operatorname{BMS}}(\Phi_{\eta,g})+c_1{\eta}^{4n-({1}/{2})n^2-3-\delta_{\Gamma}-2\ell}{\xi}^{-\ell -(n-1)/2}S_{\ell}(\psi)S_{\ell}(f)e^{-\kappa' s}\\[3pt] &\quad<(\tilde{m}^{\operatorname{BMS}}(\psi)+c_3\eta S_{\ell}(\psi))\bigg(\bigg(1+c_2e^{\omega\operatorname{height}(g\Gamma)} \frac{\xi^{\alpha}}{\eta^{\theta}}\bigg)\mu^{\operatorname{PS}}_g(f)\bigg)\\[3pt] & \qquad+c_1e^{\delta_{\Gamma} \operatorname{height}(g\Gamma)} \eta^{4n-({1}/{2})n^2-3-2\delta_{\Gamma}}\xi^{-\ell-(n-1)/2}S_{\ell}(\psi)S_{\ell}(f)e^{-\kappa' s}. \end{align*} $$
$$ \begin{align*} &\sum_{\gamma\in\Gamma}\int_{B_U(r_1)}\psi(a_s u_{\textbf{t}} g\gamma)f(\textbf{t})\,d\mu^{\operatorname{PS}}_g(\textbf{t})\\[3pt] &\quad\le \frac{1}{\nu(P_{\eta} g)}\sum_{\gamma\in\Gamma}\int_{P_{\eta} g}\int_{B_U(r_1)} \psi_{\eta,+}(a_{s}u_{\rho_p(\textbf{t})}pg\gamma)f(\textbf{t})\,d\mu^{\operatorname{PS}}_{g}(\textbf{t})\,d\nu(pg)\\[3pt] &\quad\leq\sum_{\gamma\in\Gamma}\int_G \psi_{\eta,+}(a_{s}h\gamma)\varphi_{\eta,g}(h)\,d\tilde{m}^{\operatorname{BMS}}(h)\\ &\quad\leq\int_{X} \Psi_{\eta,+}(a_s x)\Phi_{\eta,g}(x)\,dm^{\operatorname{BMS}}(x)\\[3pt] &\quad<m^{\operatorname{BMS}}(\Psi_{\eta,+})m^{\operatorname{BMS}}(\Phi_{\eta,g})+c_1{\eta}^{4n-({1}/{2})n^2-3-\delta_{\Gamma}-2\ell}{\xi}^{-\ell -(n-1)/2}S_{\ell}(\psi)S_{\ell}(f)e^{-\kappa' s}\\[3pt] &\quad<(\tilde{m}^{\operatorname{BMS}}(\psi)+c_3\eta S_{\ell}(\psi))\bigg(\bigg(1+c_2e^{\omega\operatorname{height}(g\Gamma)} \frac{\xi^{\alpha}}{\eta^{\theta}}\bigg)\mu^{\operatorname{PS}}_g(f)\bigg)\\[3pt] & \qquad+c_1e^{\delta_{\Gamma} \operatorname{height}(g\Gamma)} \eta^{4n-({1}/{2})n^2-3-2\delta_{\Gamma}}\xi^{-\ell-(n-1)/2}S_{\ell}(\psi)S_{\ell}(f)e^{-\kappa' s}. \end{align*} $$
It follows from the proof of Lemma 3.12 that
![]() $\tilde {m}^{\operatorname {BMS}}(\psi )\ll _{\operatorname {supp}\psi }S_{\ell }(\psi )$
and
$\tilde {m}^{\operatorname {BMS}}(\psi )\ll _{\operatorname {supp}\psi }S_{\ell }(\psi )$
and
![]() $\mu ^{\operatorname {PS}}_g(f)\ll S_{\ell }(f)\mu ^{\operatorname {PS}}_g(B_U(1))$
. Then, using Proposition 3.4, we arrive at
$\mu ^{\operatorname {PS}}_g(f)\ll S_{\ell }(f)\mu ^{\operatorname {PS}}_g(B_U(1))$
. Then, using Proposition 3.4, we arrive at
 $$ \begin{align*} &\sum_{\gamma\in\Gamma}\int_{B_U(r_1)}\psi(a_s u_{\textbf{t}} g\gamma)f(\textbf{t})\,d\mu^{\operatorname{PS}}_g(\textbf{t})- \mu^{\operatorname{PS}}_g(f)\tilde{m}^{\operatorname{BMS}}(\psi)\\ &\quad\ll_{\Gamma}\bigg(e^{\omega\operatorname{height}(g\Gamma)} \frac{\xi^{\alpha}}{\eta^{\theta}} +e^{\delta_{\Gamma} \operatorname{height}(g\Gamma)} \eta^{4n-({1}/{2})n^2-3-2\delta_{\Gamma}}\xi^{-\ell-(n-1)/2}e^{-\kappa' s}\bigg)\\ &\qquad\cdot S_{\ell}(\psi)S_{\ell}(f)\mu^{\operatorname{PS}}_g(B_U(1)). \end{align*} $$
$$ \begin{align*} &\sum_{\gamma\in\Gamma}\int_{B_U(r_1)}\psi(a_s u_{\textbf{t}} g\gamma)f(\textbf{t})\,d\mu^{\operatorname{PS}}_g(\textbf{t})- \mu^{\operatorname{PS}}_g(f)\tilde{m}^{\operatorname{BMS}}(\psi)\\ &\quad\ll_{\Gamma}\bigg(e^{\omega\operatorname{height}(g\Gamma)} \frac{\xi^{\alpha}}{\eta^{\theta}} +e^{\delta_{\Gamma} \operatorname{height}(g\Gamma)} \eta^{4n-({1}/{2})n^2-3-2\delta_{\Gamma}}\xi^{-\ell-(n-1)/2}e^{-\kappa' s}\bigg)\\ &\qquad\cdot S_{\ell}(\psi)S_{\ell}(f)\mu^{\operatorname{PS}}_g(B_U(1)). \end{align*} $$
Define
 $$ \begin{align*}\kappa = \frac{3\alpha\theta\kappa'}{2\theta(2\ell+n-1)+9\alpha(2\delta_{\Gamma}+3+n^2/2-4n)},\end{align*} $$
$$ \begin{align*}\kappa = \frac{3\alpha\theta\kappa'}{2\theta(2\ell+n-1)+9\alpha(2\delta_{\Gamma}+3+n^2/2-4n)},\end{align*} $$
and note that by making
![]() $\ell $
larger if necessary, we guarantee
$\ell $
larger if necessary, we guarantee
![]() $\kappa>0$
.
$\kappa>0$
.
Recall from (22) that
For
![]() $s \ge \max \{\theta ,\omega \}\operatorname {height}(g\Gamma ) /\kappa $
, choose
$s \ge \max \{\theta ,\omega \}\operatorname {height}(g\Gamma ) /\kappa $
, choose
Note that
![]() $\eta < \operatorname {inj}(g\Gamma )$
by choice of s,
$\eta < \operatorname {inj}(g\Gamma )$
by choice of s,
![]() $\omega \operatorname {height}(g\Gamma )\le \kappa s$
, and
$\omega \operatorname {height}(g\Gamma )\le \kappa s$
, and
![]() $\xi <\eta $
since by Proposition 5.2,
$\xi <\eta $
since by Proposition 5.2,
![]() $\alpha <\theta $
. By Proposition 5.2, we have
$\alpha <\theta $
. By Proposition 5.2, we have
![]() $\omega>\delta _{\Gamma }$
; therefore,
$\omega>\delta _{\Gamma }$
; therefore,
![]() $\delta _{\Gamma } \operatorname {height}(g\Gamma )\le \kappa s$
. Note also that
$\delta _{\Gamma } \operatorname {height}(g\Gamma )\le \kappa s$
. Note also that
![]() $\max \{\theta ,\omega \}\operatorname {height}(g\Gamma ) /\kappa \ll _{\Gamma } \operatorname {height}(g\Gamma )$
.
$\max \{\theta ,\omega \}\operatorname {height}(g\Gamma ) /\kappa \ll _{\Gamma } \operatorname {height}(g\Gamma )$
.
With these choices, we obtain
 $$ \begin{align}e^{\omega\operatorname{height}(g\Gamma)}\bigg(\frac{\xi}{\eta^{\theta'}}\bigg)^{\alpha'} +e^{\delta_{\Gamma} \operatorname{height}(g\Gamma)} \eta^{4n-({1}/{2})n^2-3-2\delta_{\Gamma}}\xi^{-\ell-(n-1)/2}e^{-\kappa' s} \le 2e^{-2\kappa s}. \end{align} $$
$$ \begin{align}e^{\omega\operatorname{height}(g\Gamma)}\bigg(\frac{\xi}{\eta^{\theta'}}\bigg)^{\alpha'} +e^{\delta_{\Gamma} \operatorname{height}(g\Gamma)} \eta^{4n-({1}/{2})n^2-3-2\delta_{\Gamma}}\xi^{-\ell-(n-1)/2}e^{-\kappa' s} \le 2e^{-2\kappa s}. \end{align} $$
In a similar way, using
![]() $\psi _{\eta ,-}$
, one can show a lower bound, proving (52).
$\psi _{\eta ,-}$
, one can show a lower bound, proving (52).
Step 3: Covering argument for general f.
We now deduce the claim by decomposing f into a sum of functions, each defined on a ball of radius
![]() $r_1$
in U.
$r_1$
in U.
Let
![]() $u_1,\ldots ,u_k$
and
$u_1,\ldots ,u_k$
and
![]() $\sigma _1,\ldots ,\sigma _k\in C_c^{\infty }(B_U(r))$
satisfy the conclusion of Lemma 3.11 for
$\sigma _1,\ldots ,\sigma _k\in C_c^{\infty }(B_U(r))$
satisfy the conclusion of Lemma 3.11 for
![]() $E=B_U(r)$
and
$E=B_U(r)$
and
![]() $r_1$
. For
$r_1$
. For
![]() $1\leq i\leq k$
, let
$1\leq i\leq k$
, let
Then,
![]() $f\le \sum _{i-1}^k f_i$
, and by Lemma 3.11 and [Reference Kleinbock and Margulis17, Lemma 2.4.7(a)],
$f\le \sum _{i-1}^k f_i$
, and by Lemma 3.11 and [Reference Kleinbock and Margulis17, Lemma 2.4.7(a)],
Since each
![]() $f_i$
is supported on
$f_i$
is supported on
![]() $B_U(r_1)u_i$
for some
$B_U(r_1)u_i$
for some
![]() $u_i\in B_U(1)$
, by (52), we have
$u_i\in B_U(1)$
, by (52), we have
 $$ \begin{align*} & \sum_{\gamma\in\Gamma}\int_{B_U(r_1)}\psi(a_s u_{\textbf{t}} g\gamma)f_i(\textbf{t})\,d\mu^{\operatorname{PS}}_g(\textbf{t})-\tilde{m}^{\operatorname{BMS}}(\psi)\mu^{\operatorname{PS}}_g(f_i)\\ &\quad \ll_{\Gamma,\operatorname{supp}\psi}\mu^{\operatorname{PS}}_g(B_U(1)) S_{\ell}(\psi)S_{\ell}(f_i)e^{-2\kappa s}. \end{align*} $$
$$ \begin{align*} & \sum_{\gamma\in\Gamma}\int_{B_U(r_1)}\psi(a_s u_{\textbf{t}} g\gamma)f_i(\textbf{t})\,d\mu^{\operatorname{PS}}_g(\textbf{t})-\tilde{m}^{\operatorname{BMS}}(\psi)\mu^{\operatorname{PS}}_g(f_i)\\ &\quad \ll_{\Gamma,\operatorname{supp}\psi}\mu^{\operatorname{PS}}_g(B_U(1)) S_{\ell}(\psi)S_{\ell}(f_i)e^{-2\kappa s}. \end{align*} $$
Summing the above expressions for
![]() $i=1,\ldots ,k$
, we get
$i=1,\ldots ,k$
, we get
 $$ \begin{align*} &\sum_{\gamma\in\Gamma}\int_{B_U(r)}\psi(a_s u_{\textbf{t}} g\gamma)f(\textbf{t})\,d\mu^{\operatorname{PS}}_g(\textbf{t})-\tilde{m}^{\operatorname{BMS}}(\psi)\mu^{\operatorname{PS}}_g(f)\\[3pt] &\quad \ll k r_1^{-\ell+n-1}S_{\ell}(\psi)S_{\ell}(f)e^{-2\kappa s}\mu^{\operatorname{PS}}_g(B_U(1))\\[3pt] &\quad \ll\bigg(\frac{r}{r_1}\bigg)^{n-1} r_1^{-\ell+n-1}S_{\ell}(\psi)S_{\ell}(f)e^{-2\kappa s}\mu^{\operatorname{PS}}_g(B_U(1))\\[3pt] &\quad \ll r_1^{-\ell}S_{\ell}(\psi)S_{\ell}(f)e^{-2\kappa s}\mu^{\operatorname{PS}}_g(B_U(1))\\[3pt] &\quad \ll S_{\ell}(\psi)S_{\ell}(f)e^{-\kappa s}\mu^{\operatorname{PS}}_g(B_U(1)), \end{align*} $$
$$ \begin{align*} &\sum_{\gamma\in\Gamma}\int_{B_U(r)}\psi(a_s u_{\textbf{t}} g\gamma)f(\textbf{t})\,d\mu^{\operatorname{PS}}_g(\textbf{t})-\tilde{m}^{\operatorname{BMS}}(\psi)\mu^{\operatorname{PS}}_g(f)\\[3pt] &\quad \ll k r_1^{-\ell+n-1}S_{\ell}(\psi)S_{\ell}(f)e^{-2\kappa s}\mu^{\operatorname{PS}}_g(B_U(1))\\[3pt] &\quad \ll\bigg(\frac{r}{r_1}\bigg)^{n-1} r_1^{-\ell+n-1}S_{\ell}(\psi)S_{\ell}(f)e^{-2\kappa s}\mu^{\operatorname{PS}}_g(B_U(1))\\[3pt] &\quad \ll r_1^{-\ell}S_{\ell}(\psi)S_{\ell}(f)e^{-2\kappa s}\mu^{\operatorname{PS}}_g(B_U(1))\\[3pt] &\quad \ll S_{\ell}(\psi)S_{\ell}(f)e^{-\kappa s}\mu^{\operatorname{PS}}_g(B_U(1)), \end{align*} $$
where the first inequality is by Lemma 3.11, the second inequality follows from
![]() $r_1=\operatorname {inj}(g)>e^{-\kappa s/\ell }$
, the third is by (58) and because
$r_1=\operatorname {inj}(g)>e^{-\kappa s/\ell }$
, the third is by (58) and because
![]() $r<1$
, and the implied constants depend on
$r<1$
, and the implied constants depend on
![]() $\Gamma $
and
$\Gamma $
and
![]() $\operatorname {supp}\psi $
.
$\operatorname {supp}\psi $
.
As before, using similar arguments, one can show a lower bound, proving the claim.
We will now use a partition of unity argument to prove Theorem 1.5. For the reader’s convenience, we restate it in the following.
Theorem 6.2. There exist
![]() $\kappa = \kappa (\Gamma )$
and
$\kappa = \kappa (\Gamma )$
and
![]() $\ell = \ell (\Gamma )$
which satisfy the following: for any
$\ell = \ell (\Gamma )$
which satisfy the following: for any
![]() $\psi \in C_c^{\infty }(X)$
, there exists
$\psi \in C_c^{\infty }(X)$
, there exists
![]() $c = c(\Gamma , \operatorname {supp}\psi )>0$
such that for any
$c = c(\Gamma , \operatorname {supp}\psi )>0$
such that for any
![]() $f \in C_c^{\infty }(B_U(r))$
,
$f \in C_c^{\infty }(B_U(r))$
,
![]() $0<r<1$
,
$0<r<1$
,
![]() $x \in \operatorname {supp}m^{\operatorname {BMS}}$
, and
$x \in \operatorname {supp}m^{\operatorname {BMS}}$
, and
![]() $s\gg _{\Gamma } \operatorname {height}(x)$
, we have
$s\gg _{\Gamma } \operatorname {height}(x)$
, we have
 $$ \begin{align*} \bigg|\int_U \psi(a_s u_{\textbf{t}} x)f(\textbf{t})\,d\mu^{\operatorname{PS}}_x(\textbf{t}) - \mu^{\operatorname{PS}}_x(f)m^{\operatorname{BMS}}(\psi)\bigg| < cS_{\ell}(\psi)S_{\ell}(f)e^{-\kappa s}. \end{align*} $$
$$ \begin{align*} \bigg|\int_U \psi(a_s u_{\textbf{t}} x)f(\textbf{t})\,d\mu^{\operatorname{PS}}_x(\textbf{t}) - \mu^{\operatorname{PS}}_x(f)m^{\operatorname{BMS}}(\psi)\bigg| < cS_{\ell}(\psi)S_{\ell}(f)e^{-\kappa s}. \end{align*} $$
Proof. According to [Reference Oh and Shah26, Lemma 2.17], there exists an admissible box
![]() $B_y$
around y for any
$B_y$
around y for any
![]() $y\in X$
. Then,
$y\in X$
. Then,
![]() $\{B_y : y\in \operatorname {supp}\psi \}$
is an open cover of the compact set
$\{B_y : y\in \operatorname {supp}\psi \}$
is an open cover of the compact set
![]() $\operatorname {supp}\psi $
. Hence, there exists a minimal sub-cover
$\operatorname {supp}\psi $
. Hence, there exists a minimal sub-cover
![]() $B_{y_1},\ldots ,B_{y_k}$
. Using a similar construction to that in Lemma 3.11, there exist
$B_{y_1},\ldots ,B_{y_k}$
. Using a similar construction to that in Lemma 3.11, there exist
![]() $\sigma _1,\ldots , \sigma _k$
, a partition of unity for
$\sigma _1,\ldots , \sigma _k$
, a partition of unity for
![]() $\operatorname {supp}\psi $
, such that for
$\operatorname {supp}\psi $
, such that for
![]() $i=1,\ldots ,k$
, we have
$i=1,\ldots ,k$
, we have
![]() $\sigma _i \in C_c^{\infty }(B_{y_i})$
and for
$\sigma _i \in C_c^{\infty }(B_{y_i})$
and for
![]() $i=1,\ldots ,k$
and
$i=1,\ldots ,k$
and
![]() $m=1,\ldots ,\ell $
,
$m=1,\ldots ,\ell $
,
(the implied constant depends on the chosen sub-cover).
Define
![]() $\psi _i=\psi \sigma _i$
. Then
$\psi _i=\psi \sigma _i$
. Then
 $$ \begin{align} \psi=\sum_{i=1}^k\psi_i, \end{align} $$
$$ \begin{align} \psi=\sum_{i=1}^k\psi_i, \end{align} $$
and by (61) and the product rule, we have
According to Proposition 6.1 and Proposition 3.4, there exist
![]() $c=c(\Gamma ,\operatorname {supp}\psi )>0$
,
$c=c(\Gamma ,\operatorname {supp}\psi )>0$
,
![]() $\unicode{x3bb} =\unicode{x3bb} (\Gamma )>1$
such that for
$\unicode{x3bb} =\unicode{x3bb} (\Gamma )>1$
such that for
![]() $s\gg _{\Gamma } \operatorname {height}(x)$
,
$s\gg _{\Gamma } \operatorname {height}(x)$
,
 $$ \begin{align*} &\int_{B_U(r)} \psi(a_s u_{\textbf{t}} x)f(\textbf{t})d\textbf{t}\\ &\quad= \sum\limits_{i=1}^k \int_{B_U(r)} \psi_i(a_s u_{\textbf{t}} x)f(\textbf{t})\,d\textbf{t} \\ &\quad \le \sum\limits_{i=1}^k m^{\operatorname{BMS}}(\psi_i) \mu^{\operatorname{PS}}_x(f) + c S_{\ell}(\psi_i)S_{\ell}(f)e^{-\kappa s}\mu^{\operatorname{PS}}_x(B_U(1))\\ &\quad \le \sum\limits_{i=1}^k m^{\operatorname{BMS}}(\psi_i) \mu^{\operatorname{PS}}_x(f) + c \unicode{x3bb} S_{\ell}(\psi_i)S_{\ell}(f)e^{-\kappa s+(n-1-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\pi(x))}\\ &\quad\ll_{\Gamma,\operatorname{supp}\psi} m^{\operatorname{BMS}}(\psi) \mu^{\operatorname{PS}}_x(f) + c \unicode{x3bb} S_{\ell}(\psi)S_{\ell}(f)e^{-\kappa s+(n-1-\delta_{\Gamma})\operatorname{height}(x)}, \end{align*} $$
$$ \begin{align*} &\int_{B_U(r)} \psi(a_s u_{\textbf{t}} x)f(\textbf{t})d\textbf{t}\\ &\quad= \sum\limits_{i=1}^k \int_{B_U(r)} \psi_i(a_s u_{\textbf{t}} x)f(\textbf{t})\,d\textbf{t} \\ &\quad \le \sum\limits_{i=1}^k m^{\operatorname{BMS}}(\psi_i) \mu^{\operatorname{PS}}_x(f) + c S_{\ell}(\psi_i)S_{\ell}(f)e^{-\kappa s}\mu^{\operatorname{PS}}_x(B_U(1))\\ &\quad \le \sum\limits_{i=1}^k m^{\operatorname{BMS}}(\psi_i) \mu^{\operatorname{PS}}_x(f) + c \unicode{x3bb} S_{\ell}(\psi_i)S_{\ell}(f)e^{-\kappa s+(n-1-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\pi(x))}\\ &\quad\ll_{\Gamma,\operatorname{supp}\psi} m^{\operatorname{BMS}}(\psi) \mu^{\operatorname{PS}}_x(f) + c \unicode{x3bb} S_{\ell}(\psi)S_{\ell}(f)e^{-\kappa s+(n-1-\delta_{\Gamma})\operatorname{height}(x)}, \end{align*} $$
where the last line follows by the definition of
![]() $\operatorname {height}(x)$
, and (62) and (63). Moreover, we may assume that
$\operatorname {height}(x)$
, and (62) and (63). Moreover, we may assume that
![]() $s \ge {2(n-1-\delta _{\Gamma })}/{\kappa }\operatorname {height}(x)$
without changing the assumption
$s \ge {2(n-1-\delta _{\Gamma })}/{\kappa }\operatorname {height}(x)$
without changing the assumption
![]() $s\gg _{\Gamma } \operatorname {height}(x)$
. Then,
$s\gg _{\Gamma } \operatorname {height}(x)$
. Then,
as desired.
We will now use Theorem 1.5 to prove a similar result for the Haar measure. This will be necessary for the proof of Theorem 1.4. Note that such a result is proven in [Reference Mohammadi and Oh23] under a spectral gap assumption on
![]() $\Gamma $
, but we show here how to prove it whenever the frame flow is exponentially mixing.
$\Gamma $
, but we show here how to prove it whenever the frame flow is exponentially mixing.
Theorem 6.3. There exists
![]() $\kappa = \kappa (\Gamma )<1$
and
$\kappa = \kappa (\Gamma )<1$
and
![]() $\ell = \ell (\Gamma )$
that satisfy the following: let
$\ell = \ell (\Gamma )$
that satisfy the following: let
![]() $0<r<1$
, let
$0<r<1$
, let
![]() $f \in C_c^{\infty }(B_U(r))$
, and let
$f \in C_c^{\infty }(B_U(r))$
, and let
![]() $\psi \in C_c^{\infty }(X)$
be supported on an admissible box. Then there exists
$\psi \in C_c^{\infty }(X)$
be supported on an admissible box. Then there exists
![]() $c = c(\Gamma ,\operatorname {supp}\psi )>0$
such that for every
$c = c(\Gamma ,\operatorname {supp}\psi )>0$
such that for every
![]() $x \in \operatorname {supp}m^{\operatorname {BMS}}$
and
$x \in \operatorname {supp}m^{\operatorname {BMS}}$
and
![]() $s\gg _{\Gamma ,\operatorname {supp}\psi } \operatorname {height}(x)$
,
$s\gg _{\Gamma ,\operatorname {supp}\psi } \operatorname {height}(x)$
,
 $$ \begin{align*} \bigg| e^{(n-1-\delta_{\Gamma})s} \int_{B_U(r)}\psi(a_su_{\textbf{t}} x)f(\textbf{t})\,d\textbf{t} - \mu^{\operatorname{PS}}_x(f)m^{\operatorname{BR}}(\psi)\bigg|< cS_{\ell}(\psi)S_{\ell}(f)e^{-\kappa s}. \end{align*} $$
$$ \begin{align*} \bigg| e^{(n-1-\delta_{\Gamma})s} \int_{B_U(r)}\psi(a_su_{\textbf{t}} x)f(\textbf{t})\,d\textbf{t} - \mu^{\operatorname{PS}}_x(f)m^{\operatorname{BR}}(\psi)\bigg|< cS_{\ell}(\psi)S_{\ell}(f)e^{-\kappa s}. \end{align*} $$
Proof.
Step 1: Setup and approximations. Assume
![]() $s \gg _{\Gamma } \operatorname {height}(x)$
, and let
$s \gg _{\Gamma } \operatorname {height}(x)$
, and let
![]() $\kappa ,\ell '$
satisfy the conclusion of Theorem 1.5 and
$\kappa ,\ell '$
satisfy the conclusion of Theorem 1.5 and
![]() $\ell>\ell '$
satisfy the conclusion of Lemma 3.12.
$\ell>\ell '$
satisfy the conclusion of Lemma 3.12.
Since
![]() $\psi $
is assumed to be supported on an admissible box, there exist
$\psi $
is assumed to be supported on an admissible box, there exist
![]() $r_0,\eta ,\varepsilon _0,\varepsilon _1>0$
(depending only on
$r_0,\eta ,\varepsilon _0,\varepsilon _1>0$
(depending only on
![]() $\operatorname {supp} \psi $
) and
$\operatorname {supp} \psi $
) and
![]() $z\in X$
such that
$z\in X$
such that
and
where
![]() $B_U(r+\varepsilon _1) P_{\eta +\varepsilon _1}z$
is also an admissible box. Denote
$B_U(r+\varepsilon _1) P_{\eta +\varepsilon _1}z$
is also an admissible box. Denote
![]() $\eta '=\eta +\varepsilon _1$
and
$\eta '=\eta +\varepsilon _1$
and
![]() $r^{\prime }_0=r_0+\varepsilon _1$
.
$r^{\prime }_0=r_0+\varepsilon _1$
.
Without loss of generality, assume that f is a non-negative function. Continuously extend
![]() $\psi $
to
$\psi $
to
![]() $P_{\eta '}$
by defining
$P_{\eta '}$
by defining
![]() $\psi =0$
on
$\psi =0$
on
![]() $P_{\eta '}\setminus P_{\eta }$
.
$P_{\eta '}\setminus P_{\eta }$
.
For
![]() $0<\varepsilon <\varepsilon _0$
, let
$0<\varepsilon <\varepsilon _0$
, let
![]() $\psi _{\varepsilon ,\pm }$
and
$\psi _{\varepsilon ,\pm }$
and
![]() $f_{\varepsilon ,\pm }$
for Lemma 3.12 for
$f_{\varepsilon ,\pm }$
for Lemma 3.12 for
![]() $G,\varepsilon ,\psi $
and
$G,\varepsilon ,\psi $
and
![]() $U,\varepsilon ,f$
respectively. By Lemma 3.12,
$U,\varepsilon ,f$
respectively. By Lemma 3.12,
Moreover, by Lemma 3.12(2),
For
![]() $p \in P_{\eta '}$
, define
$p \in P_{\eta '}$
, define
Step 1.1: Construct a smooth approximation to
![]() $1/\varphi $
. Since the Busemann function is smooth and
$1/\varphi $
. Since the Busemann function is smooth and
![]() $\varphi $
is bounded below by a positive quantity on
$\varphi $
is bounded below by a positive quantity on
![]() $P_{\eta '}$
by Corollary 3.3, the mean value theorem implies that for any
$P_{\eta '}$
by Corollary 3.3, the mean value theorem implies that for any
![]() $0<\varepsilon <\varepsilon _0$
and all
$0<\varepsilon <\varepsilon _0$
and all
![]() $p, p' \in P_{\varepsilon },$
there exists a constant
$p, p' \in P_{\varepsilon },$
there exists a constant
![]() $d = d(\Gamma ,\operatorname {supp}\psi )$
such that
$d = d(\Gamma ,\operatorname {supp}\psi )$
such that
 $$ \begin{align} \bigg|\frac{1}{\varphi(p)} - \frac{1}{\varphi(p')}\bigg| \le \frac{d\varepsilon}{\varphi(p)}.\end{align} $$
$$ \begin{align} \bigg|\frac{1}{\varphi(p)} - \frac{1}{\varphi(p')}\bigg| \le \frac{d\varepsilon}{\varphi(p)}.\end{align} $$
By Lemma 3.10, for any
![]() $\xi>0$
, there exists a non-negative smooth function
$\xi>0$
, there exists a non-negative smooth function
![]() $\chi _{\xi }$
with
$\chi _{\xi }$
with
and
![]() $S_{\ell '}(\chi _{\xi }) \ll _{\Gamma ,n} (\varepsilon -\xi /2)^{n-1}(\xi /2)^{-\ell '-(n-1)/2}.$
Define
$S_{\ell '}(\chi _{\xi }) \ll _{\Gamma ,n} (\varepsilon -\xi /2)^{n-1}(\xi /2)^{-\ell '-(n-1)/2}.$
Define
 $$ \begin{align}\sigma(p):= \frac{1}{\varphi}\ast \frac{\chi_{\xi}}{m(P_{\varepsilon-\xi})},\end{align} $$
$$ \begin{align}\sigma(p):= \frac{1}{\varphi}\ast \frac{\chi_{\xi}}{m(P_{\varepsilon-\xi})},\end{align} $$
where m denotes the probability Haar measure on P. Then, assuming
![]() $\varepsilon _0<1/2$
and
$\varepsilon _0<1/2$
and
![]() $\xi \le \varepsilon ^2$
, by (67), (68), and (69), we have that
$\xi \le \varepsilon ^2$
, by (67), (68), and (69), we have that
 $$ \begin{align} \frac{1-d\varepsilon}{\varphi(p)} & \le\frac{1}{m(P_{\varepsilon-\xi})}\int_{pP_{\varepsilon - \xi}}\frac{1}{\varphi(p')}\,dp' \end{align} $$
$$ \begin{align} \frac{1-d\varepsilon}{\varphi(p)} & \le\frac{1}{m(P_{\varepsilon-\xi})}\int_{pP_{\varepsilon - \xi}}\frac{1}{\varphi(p')}\,dp' \end{align} $$
 $$ \begin{align} & \kern30pt \le \sigma(p) \nonumber\\ & \kern30pt \le \frac{1}{m(P_{\varepsilon-\xi})}\int_{pP_{\varepsilon}}\frac{1+d\varepsilon}{\varphi(p')}\,dp' \nonumber \\ & \le \bigg(\frac{\varepsilon}{\varepsilon-\xi}\bigg)^n\frac{1+d\varepsilon}{\varphi(p)}\nonumber\\[3pt] & \le\frac{1+d'\varepsilon}{\varphi(p)}, \end{align} $$
$$ \begin{align} & \kern30pt \le \sigma(p) \nonumber\\ & \kern30pt \le \frac{1}{m(P_{\varepsilon-\xi})}\int_{pP_{\varepsilon}}\frac{1+d\varepsilon}{\varphi(p')}\,dp' \nonumber \\ & \le \bigg(\frac{\varepsilon}{\varepsilon-\xi}\bigg)^n\frac{1+d\varepsilon}{\varphi(p)}\nonumber\\[3pt] & \le\frac{1+d'\varepsilon}{\varphi(p)}, \end{align} $$
for some absolute constant
![]() $d'>0$
.
$d'>0$
.
For
![]() $upz \in B_U(r^{\prime }_0) P_{\eta '} z$
and
$upz \in B_U(r^{\prime }_0) P_{\eta '} z$
and
![]() $0<\varepsilon <\varepsilon _0$
, let
$0<\varepsilon <\varepsilon _0$
, let
 $$ \begin{align*} \Psi_{\varepsilon,\pm}(upz)=\sigma(p)\int_{Upz}\psi_{c_1\varepsilon,\pm}(u_{\textbf{t}}pz)\,d\textbf{t}.\end{align*} $$
$$ \begin{align*} \Psi_{\varepsilon,\pm}(upz)=\sigma(p)\int_{Upz}\psi_{c_1\varepsilon,\pm}(u_{\textbf{t}}pz)\,d\textbf{t}.\end{align*} $$
Then, by (67),
 $$ \begin{align} \sup_{w\in G_{\varepsilon}}\Psi_{\varepsilon,\pm}(wupz) &=\sup_{w\in P_{\varepsilon}}\sigma(wp)\int_{Uwpz}\psi_{c_1\varepsilon,+}(u_{\textbf{t}}wpz)\,d\textbf{t}\nonumber\\[3pt] &\le(1+d'\varepsilon)\Psi_{2\varepsilon,\pm}. \end{align} $$
$$ \begin{align} \sup_{w\in G_{\varepsilon}}\Psi_{\varepsilon,\pm}(wupz) &=\sup_{w\in P_{\varepsilon}}\sigma(wp)\int_{Uwpz}\psi_{c_1\varepsilon,+}(u_{\textbf{t}}wpz)\,d\textbf{t}\nonumber\\[3pt] &\le(1+d'\varepsilon)\Psi_{2\varepsilon,\pm}. \end{align} $$
Step 2: Bounding with PS measure.
Let
By [Reference Mohammadi and Oh23, Lemma 6.2], there exists an absolute constant
![]() $c_1>0$
such that
$c_1>0$
such that
 $$ \begin{align} &e^{(n-1)s}\int_{B_U(r)}\psi(a_s u_{\textbf{t}} x)f(\textbf{t})\,d\textbf{t}\\[3pt] &\quad\le(1+c_1\varepsilon)\sum_{p\in P(f,\psi,x;s)}f_{c_1e^{-s}\eta}(a_{-s}pz)\int_{Upz}\psi_{c_1\varepsilon,+}(u_{\textbf{t}}pz)\,d\textbf{t}.\nonumber \end{align} $$
$$ \begin{align} &e^{(n-1)s}\int_{B_U(r)}\psi(a_s u_{\textbf{t}} x)f(\textbf{t})\,d\textbf{t}\\[3pt] &\quad\le(1+c_1\varepsilon)\sum_{p\in P(f,\psi,x;s)}f_{c_1e^{-s}\eta}(a_{-s}pz)\int_{Upz}\psi_{c_1\varepsilon,+}(u_{\textbf{t}}pz)\,d\textbf{t}.\nonumber \end{align} $$
It now follows from [Reference Mohammadi and Oh23, Lemma 6.5], (70), and (72) that there exists an absolute constant
![]() $c_2>0$
such that
$c_2>0$
such that
 $$ \begin{align*} &e^{-\delta_{\Gamma} s}\sum_{p\in P(f,\psi,x;s)}f_{c_1e^{-s}\eta}(a_{-s}pz)\int_{Upz}\psi_{c_1\varepsilon,+}(u_{\textbf{t}}pz)\,d\textbf{t}\\[3pt] &\quad\le\frac{(1+c_2\varepsilon)(1+d'\varepsilon)}{1-d\varepsilon}\int_U\Psi_{2c_2\varepsilon,+}(a_{s}u_{\textbf{t}}x)f_{(c_1+c_2)e^{-s}\varepsilon_0,+}(\textbf{t})\,d\mu^{\operatorname{PS}}_{x}(\textbf{t}). \end{align*} $$
$$ \begin{align*} &e^{-\delta_{\Gamma} s}\sum_{p\in P(f,\psi,x;s)}f_{c_1e^{-s}\eta}(a_{-s}pz)\int_{Upz}\psi_{c_1\varepsilon,+}(u_{\textbf{t}}pz)\,d\textbf{t}\\[3pt] &\quad\le\frac{(1+c_2\varepsilon)(1+d'\varepsilon)}{1-d\varepsilon}\int_U\Psi_{2c_2\varepsilon,+}(a_{s}u_{\textbf{t}}x)f_{(c_1+c_2)e^{-s}\varepsilon_0,+}(\textbf{t})\,d\mu^{\operatorname{PS}}_{x}(\textbf{t}). \end{align*} $$
Note that (70) is needed because our definition of
![]() $\Psi _{\varepsilon , +}$
is not identical to
$\Psi _{\varepsilon , +}$
is not identical to
![]() $\Psi $
as defined in [Reference Mohammadi and Oh23, Lemma 6.5]. The latter is bounded above by
$\Psi $
as defined in [Reference Mohammadi and Oh23, Lemma 6.5]. The latter is bounded above by
![]() ${1}/({1-d\varepsilon }) \Psi _{\varepsilon ,+}$
by (70).
${1}/({1-d\varepsilon }) \Psi _{\varepsilon ,+}$
by (70).
Combining the above with (73), we get that there exist constants
![]() $c_3,c_4=c_4(\Gamma ,\operatorname {supp}\psi )>0$
such that
$c_3,c_4=c_4(\Gamma ,\operatorname {supp}\psi )>0$
such that
 $$ \begin{align*} &e^{(n-1-\delta_{\Gamma})s}\int_{B_U(r)}\psi(a_s u_{\textbf{t}} x)f(\textbf{t})\,d\textbf{t}\\[3pt] &\quad\leq(1+c_4\varepsilon)\int_U\Psi_{c_3\varepsilon,+}(a_{s}u_{\textbf{t}}x)f_{c_3e^{-s}\varepsilon_0,+}(\textbf{t})\,d\mu^{\operatorname{PS}}_{x}(\textbf{t}). \end{align*} $$
$$ \begin{align*} &e^{(n-1-\delta_{\Gamma})s}\int_{B_U(r)}\psi(a_s u_{\textbf{t}} x)f(\textbf{t})\,d\textbf{t}\\[3pt] &\quad\leq(1+c_4\varepsilon)\int_U\Psi_{c_3\varepsilon,+}(a_{s}u_{\textbf{t}}x)f_{c_3e^{-s}\varepsilon_0,+}(\textbf{t})\,d\mu^{\operatorname{PS}}_{x}(\textbf{t}). \end{align*} $$
It follows from Theorem 1.5 that for some constant
![]() $c_5=c_5(\Gamma ,\operatorname {supp}\psi )>0$
,
$c_5=c_5(\Gamma ,\operatorname {supp}\psi )>0$
,
 $$ \begin{align} &e^{(n-1-\delta_{\Gamma})s}\int_{B_U(r)}\psi(a_s u_{\textbf{t}} x)f(\textbf{t})\,d\textbf{t}\nonumber\\[3pt] &\quad\leq(1+c_4\varepsilon)(\mu^{\operatorname{PS}}_x(f_{c_3e^{-s}\varepsilon_0,+})m^{\operatorname{BMS}}(\Psi_{c_3\varepsilon,+})+c_5S_{\ell'}(\Psi_{c_3\varepsilon,+})S_{\ell'}(f_{c_3e^{-s}\varepsilon_0,+})e^{-\kappa s}). \end{align} $$
$$ \begin{align} &e^{(n-1-\delta_{\Gamma})s}\int_{B_U(r)}\psi(a_s u_{\textbf{t}} x)f(\textbf{t})\,d\textbf{t}\nonumber\\[3pt] &\quad\leq(1+c_4\varepsilon)(\mu^{\operatorname{PS}}_x(f_{c_3e^{-s}\varepsilon_0,+})m^{\operatorname{BMS}}(\Psi_{c_3\varepsilon,+})+c_5S_{\ell'}(\Psi_{c_3\varepsilon,+})S_{\ell'}(f_{c_3e^{-s}\varepsilon_0,+})e^{-\kappa s}). \end{align} $$
Step 3: Bounding the error terms. We now show how to bound the various error terms to obtain the desired conclusion.
To compute
![]() $m^{\operatorname {BMS}}(\Psi )$
, we use (25), (65), and (71) to deduce that for some
$m^{\operatorname {BMS}}(\Psi )$
, we use (25), (65), and (71) to deduce that for some
![]() $c_6=c_6(\Gamma ,\operatorname {supp}\psi )$
, if
$c_6=c_6(\Gamma ,\operatorname {supp}\psi )$
, if
![]() $\xi = \varepsilon ^2$
,
$\xi = \varepsilon ^2$
,
 $$ \begin{align} &m^{\operatorname{BMS}}(\Psi_{c_3\varepsilon,+})\nonumber\\[3pt] &\quad\le (1+d'\varepsilon)\!\int_{P_{\eta'} z} \int_{B_U(r^{\prime}_0)} \frac{1}{\mu^{\operatorname{PS}}_{pz}(B_U(r^{\prime}_0)pz)} \int_{B_U(r^{\prime}_0)pz}\psi_{c_1\varepsilon,\pm}(u_{\textbf{t}}pz)\,d\textbf{t} \,d\mu^{\operatorname{PS}}_{pz}(\textbf{t})\,d\nu(pz)\nonumber\\[3pt] &\quad\le (1+d'\varepsilon)\int_{P_{\eta'} z} \int_{B_U(r^{\prime}_0)pz}\psi_{c_1\varepsilon,\pm}(u_{\textbf{t}}pz)\,d\textbf{t} \,d\nu(pz)\nonumber\\[3pt] &\quad\le (1+d'\varepsilon)(m^{\operatorname{BR}}(\psi)+c_6\varepsilon S_{\ell}(\psi)). \end{align} $$
$$ \begin{align} &m^{\operatorname{BMS}}(\Psi_{c_3\varepsilon,+})\nonumber\\[3pt] &\quad\le (1+d'\varepsilon)\!\int_{P_{\eta'} z} \int_{B_U(r^{\prime}_0)} \frac{1}{\mu^{\operatorname{PS}}_{pz}(B_U(r^{\prime}_0)pz)} \int_{B_U(r^{\prime}_0)pz}\psi_{c_1\varepsilon,\pm}(u_{\textbf{t}}pz)\,d\textbf{t} \,d\mu^{\operatorname{PS}}_{pz}(\textbf{t})\,d\nu(pz)\nonumber\\[3pt] &\quad\le (1+d'\varepsilon)\int_{P_{\eta'} z} \int_{B_U(r^{\prime}_0)pz}\psi_{c_1\varepsilon,\pm}(u_{\textbf{t}}pz)\,d\textbf{t} \,d\nu(pz)\nonumber\\[3pt] &\quad\le (1+d'\varepsilon)(m^{\operatorname{BR}}(\psi)+c_6\varepsilon S_{\ell}(\psi)). \end{align} $$
By Proposition 3.4, if s is sufficiently large so that
![]() $r+c_3e^{-s}\varepsilon _0\le 1$
(note that this requirement on s depends only on
$r+c_3e^{-s}\varepsilon _0\le 1$
(note that this requirement on s depends only on
![]() $\Gamma $
and
$\Gamma $
and
![]() $\operatorname {supp}\psi $
), we have that
$\operatorname {supp}\psi $
), we have that
Hence, by (65) and (76), we have
 $$ \begin{align} \mu^{\operatorname{PS}}_x(f_{c_3e^{-s}\varepsilon_0,+})-\mu^{\operatorname{PS}}_x(f)&\ll_{\Gamma}e^{- s}\varepsilon_0 S_{\ell}(f)\mu^{\operatorname{PS}}_x(B_U(r+c_3e^{-s}\varepsilon_0)) \nonumber \\[3pt] &\ll_{\Gamma} e^{-s}\varepsilon_0 S_{\ell}(f) e^{(n-1-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\pi(x))}. \end{align} $$
$$ \begin{align} \mu^{\operatorname{PS}}_x(f_{c_3e^{-s}\varepsilon_0,+})-\mu^{\operatorname{PS}}_x(f)&\ll_{\Gamma}e^{- s}\varepsilon_0 S_{\ell}(f)\mu^{\operatorname{PS}}_x(B_U(r+c_3e^{-s}\varepsilon_0)) \nonumber \\[3pt] &\ll_{\Gamma} e^{-s}\varepsilon_0 S_{\ell}(f) e^{(n-1-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\pi(x))}. \end{align} $$
According to [Reference Kleinbock and Margulis17, Lemma 2.4.7(a)] and (64), if
![]() $\xi = \varepsilon ^2$
and
$\xi = \varepsilon ^2$
and
then
 $$ \begin{align} S_{\ell'}(\Psi_{c_3\varepsilon,+}) &\ll_{\Gamma} S_{\ell'}(\psi_{c_3\varepsilon,+})S_{\ell'}(\sigma)\nonumber\\[3pt] &\ll_{\Gamma} (m(P_{\varepsilon-\xi}))^{-1} (\varepsilon-\xi/2)^{n-1}\xi^{-{\ell'}-(n-1)/2}\varepsilon^{-2\ell}S_{\ell}(\psi)\nonumber\\[3pt] &\ll \varepsilon^{-1-2\ell}\xi^{-{\ell'}-(n-1)/2}S_{\ell}(\psi) \nonumber\\[3pt] &\le e^{\kappa s/2} S_{\ell}(\psi). \end{align} $$
$$ \begin{align} S_{\ell'}(\Psi_{c_3\varepsilon,+}) &\ll_{\Gamma} S_{\ell'}(\psi_{c_3\varepsilon,+})S_{\ell'}(\sigma)\nonumber\\[3pt] &\ll_{\Gamma} (m(P_{\varepsilon-\xi}))^{-1} (\varepsilon-\xi/2)^{n-1}\xi^{-{\ell'}-(n-1)/2}\varepsilon^{-2\ell}S_{\ell}(\psi)\nonumber\\[3pt] &\ll \varepsilon^{-1-2\ell}\xi^{-{\ell'}-(n-1)/2}S_{\ell}(\psi) \nonumber\\[3pt] &\le e^{\kappa s/2} S_{\ell}(\psi). \end{align} $$
Using (74), (75), (77), and (79), we obtain
 $$ \begin{align} &e^{(n-1-\delta_{\Gamma})s}\int_{B_U(r)}\psi(a_su_{\textbf{t}} x)f(\textbf{t})\,d\textbf{t} - \mu^{\operatorname{PS}}_x(f)m^{\operatorname{BR}}(\psi)\nonumber\\[3pt] &\quad\le (1+c_4\varepsilon) [d'\varepsilon \mu^{\operatorname{PS}}_x(f)m^{\operatorname{BR}}(\psi) + (1+d'\varepsilon)\{ c_6 \varepsilon\mu^{\operatorname{PS}}_x(f)S_{\ell}(\psi)\nonumber\\[3pt] &\qquad+(e^{- s}\varepsilon_0 m^{\operatorname{BR}}(\psi)S_{\ell}(f) + c_6 e^{- s}\varepsilon_0 \varepsilon S_{\ell}(f) S_{\ell}(\psi))e^{(n-1-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\pi(x))}\}\nonumber\\[3pt] &\qquad+ c_8 S_{\ell}(\psi)S_{\ell}(f)e^{-\kappa s/2} ]. \end{align} $$
$$ \begin{align} &e^{(n-1-\delta_{\Gamma})s}\int_{B_U(r)}\psi(a_su_{\textbf{t}} x)f(\textbf{t})\,d\textbf{t} - \mu^{\operatorname{PS}}_x(f)m^{\operatorname{BR}}(\psi)\nonumber\\[3pt] &\quad\le (1+c_4\varepsilon) [d'\varepsilon \mu^{\operatorname{PS}}_x(f)m^{\operatorname{BR}}(\psi) + (1+d'\varepsilon)\{ c_6 \varepsilon\mu^{\operatorname{PS}}_x(f)S_{\ell}(\psi)\nonumber\\[3pt] &\qquad+(e^{- s}\varepsilon_0 m^{\operatorname{BR}}(\psi)S_{\ell}(f) + c_6 e^{- s}\varepsilon_0 \varepsilon S_{\ell}(f) S_{\ell}(\psi))e^{(n-1-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\pi(x))}\}\nonumber\\[3pt] &\qquad+ c_8 S_{\ell}(\psi)S_{\ell}(f)e^{-\kappa s/2} ]. \end{align} $$
These remaining error terms can be controlled as follows. Using (76), we can deduce
We also have that
Combining (80), (81), and (82) implies
 $$ \begin{align} &e^{(n-1-\delta_{\Gamma})s}\int_{B_U(r)}\psi(a_su_{\textbf{t}} x)f(\textbf{t})\,d\textbf{t} - \mu^{\operatorname{PS}}_x(f)m^{\operatorname{BR}}(\psi)\nonumber\\[3pt] &\quad\ll_{\Gamma, \operatorname{supp} \psi} S_{\ell}(\psi)S_{\ell}(f) \cdot [ d'\varepsilon + c_8e^{-\kappa s/2}+ \nonumber\\[3pt] &\qquad (1+d'\varepsilon)(c_6\varepsilon(1+e^{-s}\varepsilon_0) + e^{- s}\varepsilon_0)e^{(n-1-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\pi(x))} ]. \end{align} $$
$$ \begin{align} &e^{(n-1-\delta_{\Gamma})s}\int_{B_U(r)}\psi(a_su_{\textbf{t}} x)f(\textbf{t})\,d\textbf{t} - \mu^{\operatorname{PS}}_x(f)m^{\operatorname{BR}}(\psi)\nonumber\\[3pt] &\quad\ll_{\Gamma, \operatorname{supp} \psi} S_{\ell}(\psi)S_{\ell}(f) \cdot [ d'\varepsilon + c_8e^{-\kappa s/2}+ \nonumber\\[3pt] &\qquad (1+d'\varepsilon)(c_6\varepsilon(1+e^{-s}\varepsilon_0) + e^{- s}\varepsilon_0)e^{(n-1-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\pi(x))} ]. \end{align} $$
Finally, by the choice of
![]() $\varepsilon $
in (78) and because we may assume without loss of generality that
$\varepsilon $
in (78) and because we may assume without loss of generality that
![]() $\kappa <1$
, we obtain from (83) that there exists
$\kappa <1$
, we obtain from (83) that there exists
![]() $\kappa '<1$
such that
$\kappa '<1$
such that
 $$ \begin{align*} &e^{(n-1-\delta_{\Gamma})s}\int_{B_U(r)}\psi(a_su_{\textbf{t}} x)f(\textbf{t})\,d\textbf{t} - \mu^{\operatorname{PS}}_x(f)m^{\operatorname{BR}}(\psi)\\[3pt] &\quad\ll_{\Gamma,\operatorname{supp}\psi} S_{\ell}(\psi)S_{\ell}(f)e^{-\kappa' s + (n-1-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\pi(x))}. \end{align*} $$
$$ \begin{align*} &e^{(n-1-\delta_{\Gamma})s}\int_{B_U(r)}\psi(a_su_{\textbf{t}} x)f(\textbf{t})\,d\textbf{t} - \mu^{\operatorname{PS}}_x(f)m^{\operatorname{BR}}(\psi)\\[3pt] &\quad\ll_{\Gamma,\operatorname{supp}\psi} S_{\ell}(\psi)S_{\ell}(f)e^{-\kappa' s + (n-1-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\pi(x))}. \end{align*} $$
Recall that
![]() $d(\pi (\mathcal {C}_0),\pi (x))=\operatorname {height}(x)$
. Thus, if we assume that
$d(\pi (\mathcal {C}_0),\pi (x))=\operatorname {height}(x)$
. Thus, if we assume that
![]() $s \ge {2(n-1-\delta _{\Gamma })}/{\kappa '} \operatorname {height}(x)$
(which means
$s \ge {2(n-1-\delta _{\Gamma })}/{\kappa '} \operatorname {height}(x)$
(which means
![]() $s\gg _{\Gamma } \operatorname {height}(x)$
), then
$s\gg _{\Gamma } \operatorname {height}(x)$
), then
which completes the proof.
7 Proof of Theorem 1.3
In this section, we prove Theorem 1.3, which is restated in the following for the reader’s convenience. The proof relies on the quantitative non-divergence result in Theorems 4.1 and 1.5.
Theorem 7.1. For any
![]() $0<\varepsilon <1$
and
$0<\varepsilon <1$
and
![]() $s_0\ge 1$
, there exist constants
$s_0\ge 1$
, there exist constants
![]() $\ell = \ell (\Gamma ) \in \mathbb N$
and
$\ell = \ell (\Gamma ) \in \mathbb N$
and
![]() $\kappa = \kappa (\Gamma , \varepsilon )>0$
satisfying: for every
$\kappa = \kappa (\Gamma , \varepsilon )>0$
satisfying: for every
![]() $\psi \in C_c^{\infty }(G/\Gamma )$
, there exists
$\psi \in C_c^{\infty }(G/\Gamma )$
, there exists
![]() $c = c(\Gamma ,\operatorname {supp}\psi )$
such that every
$c = c(\Gamma ,\operatorname {supp}\psi )$
such that every
![]() $x\in G/\Gamma $
that is
$x\in G/\Gamma $
that is
![]() $(\varepsilon ,s_0)$
-Diophantine, and for every T with
$(\varepsilon ,s_0)$
-Diophantine, and for every T with
![]() $T^{1-\varepsilon /2} \gg _{\Gamma } s_0$
,
$T^{1-\varepsilon /2} \gg _{\Gamma } s_0$
,
 $$ \begin{align*}&\bigg|\frac{1}{\mu^{\operatorname{PS}}_x(B_U(T))} \int_{B_U(T)}\psi(u_{\textbf{t}} x)\,d\mu^{\operatorname{PS}}_x(\textbf{t}) - m^{\operatorname{BMS}}(\psi)\bigg| \le c S_{\ell}(\psi) T^{-\kappa},\end{align*} $$
$$ \begin{align*}&\bigg|\frac{1}{\mu^{\operatorname{PS}}_x(B_U(T))} \int_{B_U(T)}\psi(u_{\textbf{t}} x)\,d\mu^{\operatorname{PS}}_x(\textbf{t}) - m^{\operatorname{BMS}}(\psi)\bigg| \le c S_{\ell}(\psi) T^{-\kappa},\end{align*} $$
where
![]() $S_{\ell }(\psi )$
is the
$S_{\ell }(\psi )$
is the
![]() $\ell $
-Sobolev norm.
$\ell $
-Sobolev norm.
Proof. Let
![]() $\beta>0$
satisfy the conclusion of Theorem 4.1 for
$\beta>0$
satisfy the conclusion of Theorem 4.1 for
![]() $\varepsilon $
and
$\varepsilon $
and
![]() $s_0$
. Let
$s_0$
. Let
![]() $\kappa '>0$
,
$\kappa '>0$
,
![]() $\ell \in \mathbb {N}$
satisfy the conclusion of Theorem 1.5.
$\ell \in \mathbb {N}$
satisfy the conclusion of Theorem 1.5.
Since x is
![]() $(\varepsilon ,s_0)$
-Diophantine, by Theorem 4.1, for
$(\varepsilon ,s_0)$
-Diophantine, by Theorem 4.1, for
![]() $T_0\gg _{\Gamma } s_0$
and
$T_0\gg _{\Gamma } s_0$
and
![]() $R \ge R_0$
,
$R \ge R_0$
,
where
 $$ \begin{align*} \frac{1}{\mu^{\operatorname{PS}}_x(B_U(T))} \int_{B_U(T)} \psi(u_{\textbf{t}} x)\,d\mu^{\operatorname{PS}}_x(\textbf{t}) = \frac{1}{\mu^{\operatorname{PS}}_{x_0}(B_U(T_0))}\int_{B_U(T_0)}\psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)\,d\mu^{\operatorname{PS}}_{x_0}(\textbf{t}).\end{align*} $$
$$ \begin{align*} \frac{1}{\mu^{\operatorname{PS}}_x(B_U(T))} \int_{B_U(T)} \psi(u_{\textbf{t}} x)\,d\mu^{\operatorname{PS}}_x(\textbf{t}) = \frac{1}{\mu^{\operatorname{PS}}_{x_0}(B_U(T_0))}\int_{B_U(T_0)}\psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)\,d\mu^{\operatorname{PS}}_{x_0}(\textbf{t}).\end{align*} $$
Fix
![]() $R>R_0$
and define
$R>R_0$
and define
By the definition of
![]() ${\mathcal C}(R)$
,
${\mathcal C}(R)$
,
Let
![]() $\rho>0$
be smaller than half of the injectivity radius of
$\rho>0$
be smaller than half of the injectivity radius of
![]() $Q_0$
.
$Q_0$
.
First, by Lemma 3.11, there exist
![]() $\{y : y \in I_0\}\subseteq Q_0$
and
$\{y : y \in I_0\}\subseteq Q_0$
and
![]() $f_y \in C_c^{\infty }(B_U(2\rho )y)$
satisfying
$f_y \in C_c^{\infty }(B_U(2\rho )y)$
satisfying
and
 $$ \begin{align*}\sum\limits_{y} f_y = 1 \text{ on }E_1:= \bigcup_{y\in I_0} B_U(\rho)y\supseteq Q_0, \end{align*} $$
$$ \begin{align*}\sum\limits_{y} f_y = 1 \text{ on }E_1:= \bigcup_{y\in I_0} B_U(\rho)y\supseteq Q_0, \end{align*} $$
which are
![]() $0$
outside of
$0$
outside of
 $$ \begin{align*}E_2=\bigcup_{y\in I_0} B_U(2\rho)y.\end{align*} $$
$$ \begin{align*}E_2=\bigcup_{y\in I_0} B_U(2\rho)y.\end{align*} $$
Observe that
Thus,
 $$ \begin{align*}\int_{u_{\textbf{t}} x_0 \in E_1} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)\,d\mu^{\operatorname{PS}}_{x_0}(\textbf{t})\le \sum\limits_{y\in I_0} \int_{u_{\textbf{t}} x_0 \in B_U(2\rho)y} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)f_y(u_{\textbf{t}} x_0) \,d\mu^{\operatorname{PS}}_{x_0}(\textbf{t}). \end{align*} $$
$$ \begin{align*}\int_{u_{\textbf{t}} x_0 \in E_1} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)\,d\mu^{\operatorname{PS}}_{x_0}(\textbf{t})\le \sum\limits_{y\in I_0} \int_{u_{\textbf{t}} x_0 \in B_U(2\rho)y} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)f_y(u_{\textbf{t}} x_0) \,d\mu^{\operatorname{PS}}_{x_0}(\textbf{t}). \end{align*} $$
Because
![]() $Q_0 \subseteq \operatorname {supp}m^{\operatorname {BMS}}$
, we may use Proposition 3.4 to deduce that there exists
$Q_0 \subseteq \operatorname {supp}m^{\operatorname {BMS}}$
, we may use Proposition 3.4 to deduce that there exists
![]() $\unicode{x3bb} =\unicode{x3bb} (\Gamma )\ge 1$
such that for any
$\unicode{x3bb} =\unicode{x3bb} (\Gamma )\ge 1$
such that for any
![]() $y\in I_{0}$
, we have
$y\in I_{0}$
, we have
 $$ \begin{align*} \mu^{\operatorname{PS}}_y(B_U(\rho))&\ge\unicode{x3bb}^{-1}\rho^{\delta_{\Gamma}}e^{(k(y,\rho)-\delta_{\Gamma})d(\pi(\mathcal{C}_0), \pi(a_{-\log \rho}y))}\\[3pt] &\ge \unicode{x3bb}^{-1} \rho^{\delta_{\Gamma}}e^{-\delta_{\Gamma} d(\pi(\mathcal{C}_0), \pi(a_{-\log \rho}y))} \\[3pt] &\ge \unicode{x3bb}^{-1} \rho^{\delta_{\Gamma}}e^{-\delta_{\Gamma} (-\log\rho)}e^{-\delta_{\Gamma} \operatorname{height}(y)} \quad\text{since } \rho<1\\[3pt] &\gg_{\Gamma} \unicode{x3bb}^{-1} \rho^{2\delta_{\Gamma}}e^{-\delta_{\Gamma} \operatorname{height}(y)}\\[3pt] &\ge \unicode{x3bb}^{-1} \rho^{2\delta_{\Gamma}}e^{-\delta_{\Gamma} R}, \end{align*} $$
$$ \begin{align*} \mu^{\operatorname{PS}}_y(B_U(\rho))&\ge\unicode{x3bb}^{-1}\rho^{\delta_{\Gamma}}e^{(k(y,\rho)-\delta_{\Gamma})d(\pi(\mathcal{C}_0), \pi(a_{-\log \rho}y))}\\[3pt] &\ge \unicode{x3bb}^{-1} \rho^{\delta_{\Gamma}}e^{-\delta_{\Gamma} d(\pi(\mathcal{C}_0), \pi(a_{-\log \rho}y))} \\[3pt] &\ge \unicode{x3bb}^{-1} \rho^{\delta_{\Gamma}}e^{-\delta_{\Gamma} (-\log\rho)}e^{-\delta_{\Gamma} \operatorname{height}(y)} \quad\text{since } \rho<1\\[3pt] &\gg_{\Gamma} \unicode{x3bb}^{-1} \rho^{2\delta_{\Gamma}}e^{-\delta_{\Gamma} \operatorname{height}(y)}\\[3pt] &\ge \unicode{x3bb}^{-1} \rho^{2\delta_{\Gamma}}e^{-\delta_{\Gamma} R}, \end{align*} $$
where the last line follows by Lemma 3.6.
Since
![]() $e^{s_{\varepsilon }} = T^{\varepsilon /2}$
, it follows from (86) and the above, that if we choose
$e^{s_{\varepsilon }} = T^{\varepsilon /2}$
, it follows from (86) and the above, that if we choose
![]() $\rho $
and R such that
$\rho $
and R such that
then, by the choice of
![]() $f_y$
, we have
$f_y$
, we have
where the implied constant is absolute.
If we further assume that
(with the implied constant coming from Theorem 1.5), then
![]() $s_{\varepsilon } \gg _{\Gamma } R$
, and by (89), Theorem 1.5, and Lemma 3.6, there exist
$s_{\varepsilon } \gg _{\Gamma } R$
, and by (89), Theorem 1.5, and Lemma 3.6, there exist
![]() $c_1,c_2>0$
which depend only on
$c_1,c_2>0$
which depend only on
![]() $\Gamma $
and
$\Gamma $
and
![]() $\operatorname {supp}\psi $
such that
$\operatorname {supp}\psi $
such that
 $$ \begin{align*} &\sum_{y\in I_0} \int_{u_{\textbf{t}} x_0 \in B_U(2\rho)y} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)f_y(u_{\textbf{t}} x_0) \,d\mu^{\operatorname{PS}}_{x_0}(\textbf{t})\\[3pt] &\quad\le \sum_{y\in I_0} (m^{\operatorname{BMS}}(\psi)\mu^{\operatorname{PS}}_y(f_y)+c_1 S_{\ell}(\psi)S_{\ell}(f_y)e^{-\kappa' s_{\varepsilon}})\\[3pt] &\quad\le \sum_{y\in I_0} \mu^{\operatorname{PS}}_y(f_y)(m^{\operatorname{BMS}}(\psi)+c_2 S_{\ell}(\psi)e^{-\kappa' s_{\varepsilon}/2}). \end{align*} $$
$$ \begin{align*} &\sum_{y\in I_0} \int_{u_{\textbf{t}} x_0 \in B_U(2\rho)y} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)f_y(u_{\textbf{t}} x_0) \,d\mu^{\operatorname{PS}}_{x_0}(\textbf{t})\\[3pt] &\quad\le \sum_{y\in I_0} (m^{\operatorname{BMS}}(\psi)\mu^{\operatorname{PS}}_y(f_y)+c_1 S_{\ell}(\psi)S_{\ell}(f_y)e^{-\kappa' s_{\varepsilon}})\\[3pt] &\quad\le \sum_{y\in I_0} \mu^{\operatorname{PS}}_y(f_y)(m^{\operatorname{BMS}}(\psi)+c_2 S_{\ell}(\psi)e^{-\kappa' s_{\varepsilon}/2}). \end{align*} $$
By Theorem 5.1, there exists
![]() $c_3=c_3(\Gamma )>0$
such that if
$c_3=c_3(\Gamma )>0$
such that if
![]() $T_0\gg s_0$
, then there exist
$T_0\gg s_0$
, then there exist
![]() $\alpha =\alpha (\Gamma )>0$
,
$\alpha =\alpha (\Gamma )>0$
,
![]() $c_3=c_3(\Gamma )>0$
such that
$c_3=c_3(\Gamma )>0$
such that
 $$ \begin{align*} \sum\limits_{y\in I_0} \mu^{\operatorname{PS}}_y(f_y) &\le \mu^{\operatorname{PS}}_{x_0}(B_U(T_0+2\rho))\\ &\ll_{\Gamma} (1+c_3(2\rho)^{\alpha}) \mu^{\operatorname{PS}}_{x_0}(B_U(T_0)). \end{align*} $$
$$ \begin{align*} \sum\limits_{y\in I_0} \mu^{\operatorname{PS}}_y(f_y) &\le \mu^{\operatorname{PS}}_{x_0}(B_U(T_0+2\rho))\\ &\ll_{\Gamma} (1+c_3(2\rho)^{\alpha}) \mu^{\operatorname{PS}}_{x_0}(B_U(T_0)). \end{align*} $$
If
![]() $m^{\operatorname {BMS}}(\psi )+c_2 S_{\ell }(\psi )e^{-\kappa ' s_{\varepsilon }/2}\ge 0$
, we arrive at
$m^{\operatorname {BMS}}(\psi )+c_2 S_{\ell }(\psi )e^{-\kappa ' s_{\varepsilon }/2}\ge 0$
, we arrive at
 $$ \begin{align}&\sum_{y\in I_0} \int_{u_{\textbf{t}} x_0 \in B_U(2\rho)y} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)f_y(u_{\textbf{t}} x_0) \,d\mu^{\operatorname{PS}}_{x_0}(\textbf{t})\nonumber\\[3pt] &\quad\le\mu^{\operatorname{PS}}_{x_0}(B_U(T_0))(1+c_3(2\rho)^{\alpha})(m^{\operatorname{BMS}}(\psi) + c_2 S_{\ell}(\psi)e^{-\kappa' s_{\varepsilon}/2}). \end{align} $$
$$ \begin{align}&\sum_{y\in I_0} \int_{u_{\textbf{t}} x_0 \in B_U(2\rho)y} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)f_y(u_{\textbf{t}} x_0) \,d\mu^{\operatorname{PS}}_{x_0}(\textbf{t})\nonumber\\[3pt] &\quad\le\mu^{\operatorname{PS}}_{x_0}(B_U(T_0))(1+c_3(2\rho)^{\alpha})(m^{\operatorname{BMS}}(\psi) + c_2 S_{\ell}(\psi)e^{-\kappa' s_{\varepsilon}/2}). \end{align} $$
However, if
![]() $m^{\operatorname {BMS}}(\psi )+c_2 S_{\ell }(\psi )e^{-\kappa ' s_{\varepsilon }/2}<0$
, by (84), there exists
$m^{\operatorname {BMS}}(\psi )+c_2 S_{\ell }(\psi )e^{-\kappa ' s_{\varepsilon }/2}<0$
, by (84), there exists
![]() $c_6 = c_6(\Gamma )>0$
so that
$c_6 = c_6(\Gamma )>0$
so that
 $$ \begin{align} &\sum_{y\in I_0} \int_{u_{\textbf{t}} x_0 \in B_U(2\rho)y} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)f_y(u_{\textbf{t}} x_0) \,d\mu^{\operatorname{PS}}_{x_0}(\textbf{t}) \nonumber\\ &\quad\le \mu^{\operatorname{PS}}_{x_0}(Q_0)(m^{\operatorname{BMS}}(\psi)+c_2 S_{\ell}(\psi)e^{-\kappa' s_{\varepsilon}/2})\nonumber\\[3pt] &\quad\le \mu^{\operatorname{PS}}_{x_0}(B_U(T_0))(1-c_6e^{-\beta R})(m^{\operatorname{BMS}}(\psi)+c_2 S_{\ell}(\psi)e^{-\kappa' s_{\varepsilon}/2}). \end{align} $$
$$ \begin{align} &\sum_{y\in I_0} \int_{u_{\textbf{t}} x_0 \in B_U(2\rho)y} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)f_y(u_{\textbf{t}} x_0) \,d\mu^{\operatorname{PS}}_{x_0}(\textbf{t}) \nonumber\\ &\quad\le \mu^{\operatorname{PS}}_{x_0}(Q_0)(m^{\operatorname{BMS}}(\psi)+c_2 S_{\ell}(\psi)e^{-\kappa' s_{\varepsilon}/2})\nonumber\\[3pt] &\quad\le \mu^{\operatorname{PS}}_{x_0}(B_U(T_0))(1-c_6e^{-\beta R})(m^{\operatorname{BMS}}(\psi)+c_2 S_{\ell}(\psi)e^{-\kappa' s_{\varepsilon}/2}). \end{align} $$
Fix
such that
![]() $\rho $
also satisfies the assumption of Theorem 5.1, and R which satisfies (88) and (90). Thus, (91) and (93) imply in either case that
$\rho $
also satisfies the assumption of Theorem 5.1, and R which satisfies (88) and (90). Thus, (91) and (93) imply in either case that
 $$ \begin{align} &\frac{1}{\mu^{\operatorname{PS}}_{x_0}(B_U(T_0))} \int_{u_{\textbf{t}} x_0 \in E_1}\psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)\,d\mu^{\operatorname{PS}}_{x_0}(\textbf{t}) - m^{\operatorname{BMS}}(\psi) \nonumber\\[3pt] &\quad\ll_{\Gamma,\operatorname{supp}\psi} S_{\ell}(\psi)T^{-\kappa}, \end{align} $$
$$ \begin{align} &\frac{1}{\mu^{\operatorname{PS}}_{x_0}(B_U(T_0))} \int_{u_{\textbf{t}} x_0 \in E_1}\psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)\,d\mu^{\operatorname{PS}}_{x_0}(\textbf{t}) - m^{\operatorname{BMS}}(\psi) \nonumber\\[3pt] &\quad\ll_{\Gamma,\operatorname{supp}\psi} S_{\ell}(\psi)T^{-\kappa}, \end{align} $$
where we have used that by [Reference Aubin1],
![]() $\|\psi \|_{\infty } \ll _{\operatorname {supp} \psi } S_{\ell }(\psi )$
, so
$\|\psi \|_{\infty } \ll _{\operatorname {supp} \psi } S_{\ell }(\psi )$
, so
![]() $m^{\operatorname {BMS}}(\psi )\ll _{\operatorname {supp}\psi } S_{\ell }(\psi ).$
$m^{\operatorname {BMS}}(\psi )\ll _{\operatorname {supp}\psi } S_{\ell }(\psi ).$
By (84),
 $$ \begin{align*}\int_{B_U(T_0)x_0\setminus E_1} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)\,d\mu^{\operatorname{PS}}_{x_0}(\textbf{t}) &\le \|\psi\|_{\infty} \mu^{\operatorname{PS}}_{x_0}(B_U(T_0)\setminus E_1)\\[3pt] &\ll_{\operatorname{supp}\psi} S_{\ell}(\psi)\mu^{\operatorname{PS}}_{x_0}(B_U(T_0)x_0) e^{-\beta R}\\[3pt] &\ll_{\operatorname{supp}\psi} S_{\ell}(\psi)\mu^{\operatorname{PS}}_{x_0}(B_U(T_0)x_0) T^{-\kappa},\end{align*} $$
$$ \begin{align*}\int_{B_U(T_0)x_0\setminus E_1} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)\,d\mu^{\operatorname{PS}}_{x_0}(\textbf{t}) &\le \|\psi\|_{\infty} \mu^{\operatorname{PS}}_{x_0}(B_U(T_0)\setminus E_1)\\[3pt] &\ll_{\operatorname{supp}\psi} S_{\ell}(\psi)\mu^{\operatorname{PS}}_{x_0}(B_U(T_0)x_0) e^{-\beta R}\\[3pt] &\ll_{\operatorname{supp}\psi} S_{\ell}(\psi)\mu^{\operatorname{PS}}_{x_0}(B_U(T_0)x_0) T^{-\kappa},\end{align*} $$
where we have again used that by [Reference Aubin1],
![]() $\|\psi \|_{\infty } \ll _{\operatorname {supp} \psi } S_{\ell }(\psi )$
. Combining the above with (94) implies that
$\|\psi \|_{\infty } \ll _{\operatorname {supp} \psi } S_{\ell }(\psi )$
. Combining the above with (94) implies that
 $$ \begin{align*}&\frac{1}{\mu^{\operatorname{PS}}_{x_0}(B_U(T_0))} \int_{B_U(T_0)} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)\,d\mu^{\operatorname{PS}}_{x_0}(\textbf{t}) - m^{\operatorname{BMS}}(\psi) \\[3pt] &\quad\ll_{\Gamma,\operatorname{supp}\psi} S_{\ell}(\psi)T^{-\kappa}. \end{align*} $$
$$ \begin{align*}&\frac{1}{\mu^{\operatorname{PS}}_{x_0}(B_U(T_0))} \int_{B_U(T_0)} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)\,d\mu^{\operatorname{PS}}_{x_0}(\textbf{t}) - m^{\operatorname{BMS}}(\psi) \\[3pt] &\quad\ll_{\Gamma,\operatorname{supp}\psi} S_{\ell}(\psi)T^{-\kappa}. \end{align*} $$
For the lower bound, define
As before, according to Lemma 3.11, there exist
![]() $\{y : y \in I_1\}\subseteq Q_1$
and
$\{y : y \in I_1\}\subseteq Q_1$
and
![]() $f_y \in C_c^{\infty }(B_U(2\rho )y)$
satisfying
$f_y \in C_c^{\infty }(B_U(2\rho )y)$
satisfying
and
 $$ \begin{align*}\sum_{y\in I_1} f_y = 1 \text{ on }E_4:= \bigcup_{y\in I_1} B_U(\rho)y \supseteq Q_1,\end{align*} $$
$$ \begin{align*}\sum_{y\in I_1} f_y = 1 \text{ on }E_4:= \bigcup_{y\in I_1} B_U(\rho)y \supseteq Q_1,\end{align*} $$
and which are
![]() $0$
outside of
$0$
outside of
 $$ \begin{align} \bigcup_{y\in I_1} B_U(2\rho)y\subseteq B_U(T_0)x_0. \end{align} $$
$$ \begin{align} \bigcup_{y\in I_1} B_U(2\rho)y\subseteq B_U(T_0)x_0. \end{align} $$
Hence,
 $$ \begin{align*}\int_{u_{\textbf{t}} x_0 \in B_U(T_0)x_0} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)\,d\textbf{t}\ge \sum_{y\in I_1} \int_{u_{\textbf{t}} x_0 \in B_U(2\rho)y} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)f_y(u_{\textbf{t}} x_0)\,d\textbf{t}. \end{align*} $$
$$ \begin{align*}\int_{u_{\textbf{t}} x_0 \in B_U(T_0)x_0} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)\,d\textbf{t}\ge \sum_{y\in I_1} \int_{u_{\textbf{t}} x_0 \in B_U(2\rho)y} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)f_y(u_{\textbf{t}} x_0)\,d\textbf{t}. \end{align*} $$
Moreover, by the same argument as in (89), we deduce that
By Theorem 1.5 and (96), we have that
 $$ \begin{align*}&\sum_{y\in I_1} \int_{u_{\textbf{t}} x_0 \in B_U(2\rho)y} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)f_y(u_{\textbf{t}} x_0) \,d\textbf{t} \\ &\quad\ge \sum\limits_{y \in I_1} (\mu^{\operatorname{PS}}_{x_0}(f_y) m^{\operatorname{BMS}}(\psi) - c_4 S_{\ell}(\psi) S_{\ell}(f_y) e^{-\kappa' s_{\varepsilon}})\\ &\quad\ge \sum\limits_{y \in I_1} \mu^{\operatorname{PS}}_{x_0}(f_y)(m^{\operatorname{BMS}}(\psi) - c_5S_{\ell}(\psi)e^{-\kappa's_{\varepsilon}/2}),\end{align*} $$
$$ \begin{align*}&\sum_{y\in I_1} \int_{u_{\textbf{t}} x_0 \in B_U(2\rho)y} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)f_y(u_{\textbf{t}} x_0) \,d\textbf{t} \\ &\quad\ge \sum\limits_{y \in I_1} (\mu^{\operatorname{PS}}_{x_0}(f_y) m^{\operatorname{BMS}}(\psi) - c_4 S_{\ell}(\psi) S_{\ell}(f_y) e^{-\kappa' s_{\varepsilon}})\\ &\quad\ge \sum\limits_{y \in I_1} \mu^{\operatorname{PS}}_{x_0}(f_y)(m^{\operatorname{BMS}}(\psi) - c_5S_{\ell}(\psi)e^{-\kappa's_{\varepsilon}/2}),\end{align*} $$
where
![]() $c_5$
arises from
$c_5$
arises from
![]() $c_4$
and the implied constant in (96).
$c_4$
and the implied constant in (96).
Note that by replacing
![]() $\psi $
with
$\psi $
with
![]() $-\psi $
if necessary, we may assume that
$-\psi $
if necessary, we may assume that
![]() $m^{\operatorname {BMS}}(\psi ) - c_5S_{\ell }(\psi )e^{-\kappa 's_{\varepsilon }/2}<0$
. Thus, by observing that
$m^{\operatorname {BMS}}(\psi ) - c_5S_{\ell }(\psi )e^{-\kappa 's_{\varepsilon }/2}<0$
. Thus, by observing that
 $$ \begin{align*}\sum\limits_{y \in I_1} \mu^{\operatorname{PS}}_y(f_y) \le \mu^{\operatorname{PS}}_{x_0}(B_U(T_0)),\end{align*} $$
$$ \begin{align*}\sum\limits_{y \in I_1} \mu^{\operatorname{PS}}_y(f_y) \le \mu^{\operatorname{PS}}_{x_0}(B_U(T_0)),\end{align*} $$
we immediately conclude that
 $$ \begin{align*} &\frac{1}{\mu^{\operatorname{PS}}_{x_0}(B_U(T_0))} \int_{u_{\textbf{t}} x_0 \in E_1} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)\,d\mu^{\operatorname{PS}}_{x_0}(\textbf{t}) -m^{\operatorname{BMS}}(\psi)\\ &\quad\gg_{\Gamma,\operatorname{supp}\psi} S_{\ell}(\psi)e^{-\kappa's_{\varepsilon}/2}. \end{align*} $$
$$ \begin{align*} &\frac{1}{\mu^{\operatorname{PS}}_{x_0}(B_U(T_0))} \int_{u_{\textbf{t}} x_0 \in E_1} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)\,d\mu^{\operatorname{PS}}_{x_0}(\textbf{t}) -m^{\operatorname{BMS}}(\psi)\\ &\quad\gg_{\Gamma,\operatorname{supp}\psi} S_{\ell}(\psi)e^{-\kappa's_{\varepsilon}/2}. \end{align*} $$
Hence, (85) and (93) imply that
 $$ \begin{align*} \frac{1}{\mu^{\operatorname{PS}}_{x_0}(B_U(T_0))} \int_{u_{\textbf{t}} x_0 \in E_1} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)\,d\mu^{\operatorname{PS}}_{x_0}(\textbf{t}) -m^{\operatorname{BMS}}(\psi)\gg_{\Gamma,\operatorname{supp}\psi}- S_{\ell}(\psi)T^{-\kappa}. \end{align*} $$
$$ \begin{align*} \frac{1}{\mu^{\operatorname{PS}}_{x_0}(B_U(T_0))} \int_{u_{\textbf{t}} x_0 \in E_1} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)\,d\mu^{\operatorname{PS}}_{x_0}(\textbf{t}) -m^{\operatorname{BMS}}(\psi)\gg_{\Gamma,\operatorname{supp}\psi}- S_{\ell}(\psi)T^{-\kappa}. \end{align*} $$
8 Proof of Theorem 1.4
In this section, we will prove Theorem 1.4 using Theorem 6.3. We will use a partition of unity argument for a cover of the intersection of
![]() $B_U(r)x$
with a fixed compact set by small balls centered at PS points.
$B_U(r)x$
with a fixed compact set by small balls centered at PS points.
We will need the following lemma.
Lemma 8.1. There exists an absolute constant
![]() $c>0$
satisfying the following: for
$c>0$
satisfying the following: for
![]() $x\in X$
,
$x\in X$
,
![]() $y\in Ux$
,
$y\in Ux$
,
![]() $\psi \in C_c^{\infty }(X)$
supported on an admissible box of diameter smaller than
$\psi \in C_c^{\infty }(X)$
supported on an admissible box of diameter smaller than
![]() $1$
,
$1$
,
![]() $0<\rho <\operatorname {inj}(y)$
,
$0<\rho <\operatorname {inj}(y)$
,
![]() $f\in C_c^{\infty }(B_U(\rho )y)$
such that for
$f\in C_c^{\infty }(B_U(\rho )y)$
such that for
![]() $0\le f\le 1$
and
$0\le f\le 1$
and
![]() $s>c$
, we have
$s>c$
, we have
where
![]() $\ell \in \mathbb N$
satisfies the conclusion of Lemma 3.12.
$\ell \in \mathbb N$
satisfies the conclusion of Lemma 3.12.
Proof. Assume that for
![]() $0<\varepsilon _0,\varepsilon _1<1$
,
$0<\varepsilon _0,\varepsilon _1<1$
,
![]() $\psi $
is supported on the admissible box
$\psi $
is supported on the admissible box
![]() $B_U(\varepsilon _0)P_{\varepsilon _1}z$
for
$B_U(\varepsilon _0)P_{\varepsilon _1}z$
for
![]() $z\in X$
. Without loss of generality, we may assume that
$z\in X$
. Without loss of generality, we may assume that
![]() $\psi $
is non-negative. Fix
$\psi $
is non-negative. Fix
![]() $y\in Ux$
.
$y\in Ux$
.
For small
![]() $\eta>0$
,
$\eta>0$
,
![]() $h\in G_{\eta }\operatorname {supp}(\psi )$
, and
$h\in G_{\eta }\operatorname {supp}(\psi )$
, and
![]() $p\in P$
, let
$p\in P$
, let
 $$ \begin{align*} \psi_{\eta,+}(h):=\sup_{w\in G_{\eta}}\psi(wh),\quad\Psi_{\eta,+}(ph):=\int_{Uph}\psi_{\eta,+}(u_{\textbf{t}} ph)\,d\textbf{t}, \end{align*} $$
$$ \begin{align*} \psi_{\eta,+}(h):=\sup_{w\in G_{\eta}}\psi(wh),\quad\Psi_{\eta,+}(ph):=\int_{Uph}\psi_{\eta,+}(u_{\textbf{t}} ph)\,d\textbf{t}, \end{align*} $$
and for
![]() $upz\in B_U(\varepsilon _0)P_{\varepsilon _1}z$
, let
$upz\in B_U(\varepsilon _0)P_{\varepsilon _1}z$
, let
 $$ \begin{align*}\tilde{\Psi}_{\eta,+}(upz):=\frac{1}{\mu^{\operatorname{PS}}_{pz}(B_U(\varepsilon_0)pz)}\Psi_{\eta,+}(pz). \end{align*} $$
$$ \begin{align*}\tilde{\Psi}_{\eta,+}(upz):=\frac{1}{\mu^{\operatorname{PS}}_{pz}(B_U(\varepsilon_0)pz)}\Psi_{\eta,+}(pz). \end{align*} $$
By the choice of
![]() $\ell $
, for any
$\ell $
, for any
![]() $\eta>0$
and
$\eta>0$
and
![]() $h\in G_{\eta }\operatorname {supp}(\psi )$
,
$h\in G_{\eta }\operatorname {supp}(\psi )$
,
and
where the implied constants depend on
![]() $\operatorname {supp}\psi $
. Since the diameter of
$\operatorname {supp}\psi $
. Since the diameter of
![]() $\operatorname {supp}\psi $
is smaller than
$\operatorname {supp}\psi $
is smaller than
![]() $1$
, we may assume that the implied constants in the above are absolute. Then, for any
$1$
, we may assume that the implied constants in the above are absolute. Then, for any
![]() $u\in U$
such that
$u\in U$
such that
![]() $a_s uy=u'pz\in B_U(\varepsilon _0)P_{\varepsilon _1}z$
and
$a_s uy=u'pz\in B_U(\varepsilon _0)P_{\varepsilon _1}z$
and
![]() $0<\eta <1$
, we have
$0<\eta <1$
, we have
 $$ \begin{align} |\tilde\Psi_{\eta,+}(a_s u y)| &=\bigg|\frac{1}{\mu^{\operatorname{PS}}_{pz}(B_U(\varepsilon_0)pz)}\int_{U pz}\psi_{\eta,+}(u_{\textbf{t}} pz)\,d\textbf{t}\bigg|\nonumber\\[4pt] &=\frac{\mu^{\operatorname{Leb}}_{pz}(B_U(\varepsilon_0)pz)}{\mu^{\operatorname{PS}}_{pz}(B_U(\varepsilon_0)pz)} S_{\ell}(\psi)\nonumber\\[4pt] & \ll S_{\ell}(\psi), \end{align} $$
$$ \begin{align} |\tilde\Psi_{\eta,+}(a_s u y)| &=\bigg|\frac{1}{\mu^{\operatorname{PS}}_{pz}(B_U(\varepsilon_0)pz)}\int_{U pz}\psi_{\eta,+}(u_{\textbf{t}} pz)\,d\textbf{t}\bigg|\nonumber\\[4pt] &=\frac{\mu^{\operatorname{Leb}}_{pz}(B_U(\varepsilon_0)pz)}{\mu^{\operatorname{PS}}_{pz}(B_U(\varepsilon_0)pz)} S_{\ell}(\psi)\nonumber\\[4pt] & \ll S_{\ell}(\psi), \end{align} $$
where the implied constant depends only on
![]() $\operatorname {supp}\psi $
.
$\operatorname {supp}\psi $
.
For small
![]() $\eta>0$
and
$\eta>0$
and
![]() $uy\in B_U(\eta +\varepsilon _0) y$
, let
$uy\in B_U(\eta +\varepsilon _0) y$
, let
Using Lemmas 6.2 and 6.5 in [Reference Mohammadi and Oh23], we get that for some absolute constant
![]() $c'>0$
,
$c'>0$
,
 $$ \begin{align*} e^{(n-1-\delta_{\Gamma})s}\int_{B_U(\rho)y }\psi(a_{s}u_{\textbf{t}} y)f(u_{\textbf{t}} y)\,d\textbf{t} &\ll\int_{U}\tilde{\Psi}_{c'\rho,+}(a_su_{\textbf{t}} y)f_{c'e^{-s}\rho,+}(u_{\textbf{t}} y)\,d\mu^{\operatorname{PS}}_y(\textbf{t})\\[3pt] & \le\int_{B_U(\rho+c'e^{-s}\rho)y}\tilde{\Psi}_{c'\rho,+}(a_su_{\textbf{t}} y)\,d\mu^{\operatorname{PS}}_y(\textbf{t}), \end{align*} $$
$$ \begin{align*} e^{(n-1-\delta_{\Gamma})s}\int_{B_U(\rho)y }\psi(a_{s}u_{\textbf{t}} y)f(u_{\textbf{t}} y)\,d\textbf{t} &\ll\int_{U}\tilde{\Psi}_{c'\rho,+}(a_su_{\textbf{t}} y)f_{c'e^{-s}\rho,+}(u_{\textbf{t}} y)\,d\mu^{\operatorname{PS}}_y(\textbf{t})\\[3pt] & \le\int_{B_U(\rho+c'e^{-s}\rho)y}\tilde{\Psi}_{c'\rho,+}(a_su_{\textbf{t}} y)\,d\mu^{\operatorname{PS}}_y(\textbf{t}), \end{align*} $$
where the implied constant is absolute. Then, by (97), we get
 $$ \begin{align*} e^{(n-1-\delta_{\Gamma})s}\int_{B_U(\rho)y }\psi(a_{s}u_{\textbf{t}} y)f(u_{\textbf{t}} y)\,d\textbf{t} &\ll_{\operatorname{supp}\psi} \mu^{\operatorname{PS}}_y(B_U(\rho+c'e^{-s}\rho)) S_{\ell}(\psi)\\ &\le \mu^{\operatorname{PS}}_y(B_U(2\rho))S_{\ell}(\psi). \end{align*} $$
$$ \begin{align*} e^{(n-1-\delta_{\Gamma})s}\int_{B_U(\rho)y }\psi(a_{s}u_{\textbf{t}} y)f(u_{\textbf{t}} y)\,d\textbf{t} &\ll_{\operatorname{supp}\psi} \mu^{\operatorname{PS}}_y(B_U(\rho+c'e^{-s}\rho)) S_{\ell}(\psi)\\ &\le \mu^{\operatorname{PS}}_y(B_U(2\rho))S_{\ell}(\psi). \end{align*} $$
Choosing
![]() $c:=\log c'$
, we may conclude the claim.
$c:=\log c'$
, we may conclude the claim.
We are now ready to prove Theorem 1.4. For the reader’s convenience, we restate that theorem in the following.
Theorem 8.2. For any
![]() $0<\varepsilon <1$
and
$0<\varepsilon <1$
and
![]() $s_0\ge 1$
, there exist
$s_0\ge 1$
, there exist
![]() $\ell =\ell (\Gamma )\in \mathbb N$
and
$\ell =\ell (\Gamma )\in \mathbb N$
and
![]() $\kappa =\kappa (\Gamma ,\varepsilon )>0$
satisfying: for every
$\kappa =\kappa (\Gamma ,\varepsilon )>0$
satisfying: for every
![]() $\psi \in C_c^{\infty }(G/\Gamma )$
, there exists
$\psi \in C_c^{\infty }(G/\Gamma )$
, there exists
![]() $c = c(\Gamma ,\operatorname {supp}\psi )$
such that for every
$c = c(\Gamma ,\operatorname {supp}\psi )$
such that for every
![]() $x\in G/\Gamma $
that is
$x\in G/\Gamma $
that is
![]() $(\varepsilon ,s_0)$
-Diophantine, and for all T such that
$(\varepsilon ,s_0)$
-Diophantine, and for all T such that
![]() $T^{1-\varepsilon /2} \gg _{\Gamma ,\operatorname {supp}\psi } s_0$
,
$T^{1-\varepsilon /2} \gg _{\Gamma ,\operatorname {supp}\psi } s_0$
,
 $$ \begin{align*}\bigg|\frac{1}{\mu^{\operatorname{PS}}_x(B_U(T))} \int_{B_U(T)}\psi(u_{\textbf{t}} x)\,d\textbf{t} - m^{\operatorname{BR}}(\psi)\bigg| \le c S_{\ell}(\psi)T^{-\kappa},\end{align*} $$
$$ \begin{align*}\bigg|\frac{1}{\mu^{\operatorname{PS}}_x(B_U(T))} \int_{B_U(T)}\psi(u_{\textbf{t}} x)\,d\textbf{t} - m^{\operatorname{BR}}(\psi)\bigg| \le c S_{\ell}(\psi)T^{-\kappa},\end{align*} $$
where
![]() $S_{\ell }(\psi )$
is the
$S_{\ell }(\psi )$
is the
![]() $\ell $
-Sobolev norm.
$\ell $
-Sobolev norm.
Proof. We keep the notation of §4. By an argument similar to the proof of Theorem 1.5, we may assume that
![]() $\psi $
is supported on an admissible box. Because
$\psi $
is supported on an admissible box. Because
![]() $\psi $
is compactly supported, we may also assume
$\psi $
is compactly supported, we may also assume
![]() $\psi \ge 0$
by using a translation.
$\psi \ge 0$
by using a translation.
Let
![]() $\beta>0$
satisfy the conclusion of Theorem 4.1 for
$\beta>0$
satisfy the conclusion of Theorem 4.1 for
![]() $\varepsilon $
and
$\varepsilon $
and
![]() $s_0$
. Let
$s_0$
. Let
![]() $\kappa '>0$
,
$\kappa '>0$
,
![]() $\ell \in \mathbb {N}$
satisfy the conclusion of Theorem 6.3.
$\ell \in \mathbb {N}$
satisfy the conclusion of Theorem 6.3.
Since x is
![]() $(\varepsilon ,s_0)$
-Diophantine, by Theorem 4.1, for
$(\varepsilon ,s_0)$
-Diophantine, by Theorem 4.1, for
![]() $T_0\gg _{\Gamma } s_0$
and
$T_0\gg _{\Gamma } s_0$
and
![]() $R\ge R_0$
, we have
$R\ge R_0$
, we have
where
Observe that by (6), (13), and (14),
 $$ \begin{align*}\frac{1}{\mu^{\operatorname{PS}}_x(B_U(T))} \int_{B_U(T)}\psi(u_{\textbf{t}} x)\,d\textbf{t}=\frac{e^{(n-1-\delta)s_{\varepsilon}}}{\mu^{\operatorname{PS}}_{x_0}(B_U(T_0))} \int_{B_U(T_0)}\psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)\,d\textbf{t}.\end{align*} $$
$$ \begin{align*}\frac{1}{\mu^{\operatorname{PS}}_x(B_U(T))} \int_{B_U(T)}\psi(u_{\textbf{t}} x)\,d\textbf{t}=\frac{e^{(n-1-\delta)s_{\varepsilon}}}{\mu^{\operatorname{PS}}_{x_0}(B_U(T_0))} \int_{B_U(T_0)}\psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)\,d\textbf{t}.\end{align*} $$
Fix
![]() $R>R_0$
and define
$R>R_0$
and define
Since for any
![]() $R\geq R_0$
, the set
$R\geq R_0$
, the set
![]() ${\mathcal {C}}(R)$
is in the convex core of
${\mathcal {C}}(R)$
is in the convex core of
![]() ${\mathbb H}^n /\Gamma $
,
${\mathbb H}^n /\Gamma $
,
Let
![]() $\rho>0$
be smaller than half of the injectivity radius of
$\rho>0$
be smaller than half of the injectivity radius of
![]() $Q_0$
.
$Q_0$
.
First, by Lemma 3.11, there exist
![]() $\{y : y \in I_0\}\subseteq Q_0$
and
$\{y : y \in I_0\}\subseteq Q_0$
and
![]() $f_y \in C_c^{\infty }(B_U(2\rho )y)$
satisfying
$f_y \in C_c^{\infty }(B_U(2\rho )y)$
satisfying
and
 $$ \begin{align*}\sum\limits_{y} f_y = 1 \text{ on }E_1:= \bigcup_{y\in I_0} B_U(\rho)y\supseteq Q_0,\end{align*} $$
$$ \begin{align*}\sum\limits_{y} f_y = 1 \text{ on }E_1:= \bigcup_{y\in I_0} B_U(\rho)y\supseteq Q_0,\end{align*} $$
which are
![]() $0$
outside of
$0$
outside of
 $$ \begin{align*}E_2=\bigcup_{y\in I_0} B_U(2\rho)y.\end{align*} $$
$$ \begin{align*}E_2=\bigcup_{y\in I_0} B_U(2\rho)y.\end{align*} $$
By replacing references to Theorem 1.5 with references to Theorem 6.3, the exact same argument as in the proof of Theorem 1.3 will establish that for
![]() $T \gg _{\Gamma } e^{2R/\varepsilon }$
and
$T \gg _{\Gamma } e^{2R/\varepsilon }$
and
We get that if we assume without loss of generality that
![]() $\kappa '<2\beta $
and also that
$\kappa '<2\beta $
and also that
![]() $T\gg _{\Gamma } 1$
,
$T\gg _{\Gamma } 1$
,
 $$ \begin{align} &\frac{e^{(n-1-\delta_{\Gamma}) s_{\varepsilon}}}{\mu^{\operatorname{PS}}_{x_0}(B_U(T_0)x_0)} \int_{u_{\textbf{t}} x_0 \in E_1} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)\,d\textbf{t}-m^{\operatorname{BR}}(\psi) \ll_{\Gamma,\operatorname{supp}\psi} S_{\ell}(\psi)T^{-\kappa}. \end{align} $$
$$ \begin{align} &\frac{e^{(n-1-\delta_{\Gamma}) s_{\varepsilon}}}{\mu^{\operatorname{PS}}_{x_0}(B_U(T_0)x_0)} \int_{u_{\textbf{t}} x_0 \in E_1} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)\,d\textbf{t}-m^{\operatorname{BR}}(\psi) \ll_{\Gamma,\operatorname{supp}\psi} S_{\ell}(\psi)T^{-\kappa}. \end{align} $$
We now want to bound the integral over
![]() $B_U(T_0)x_0\setminus E_1$
. Using Lemma 3.11 again, we may deduce that there exist
$B_U(T_0)x_0\setminus E_1$
. Using Lemma 3.11 again, we may deduce that there exist
![]() $\{y : y \in I_1\}\subseteq B_U(T_0)x_0\setminus E_1$
and
$\{y : y \in I_1\}\subseteq B_U(T_0)x_0\setminus E_1$
and
![]() $f_y \in C_c^{\infty }(B_U(\rho /4)y)$
satisfying
$f_y \in C_c^{\infty }(B_U(\rho /4)y)$
satisfying
![]() $\sum \nolimits _{y\in I_1} f_y = 1$
on
$\sum \nolimits _{y\in I_1} f_y = 1$
on
![]() $ \bigcup \nolimits _{y\in I_1} B_U(\rho /8)y$
and
$ \bigcup \nolimits _{y\in I_1} B_U(\rho /8)y$
and
![]() $0$
outside of
$0$
outside of
 $$ \begin{align*}\bigcup\limits_{y\in I_1} B_U(\rho/4)y.\end{align*} $$
$$ \begin{align*}\bigcup\limits_{y\in I_1} B_U(\rho/4)y.\end{align*} $$
In particular, by the definition of
![]() $E_1$
, we have
$E_1$
, we have
 $$ \begin{align*} E_3:=\bigcup\limits_{y\in I_1} B_U(\rho/2)y\subseteq (B_U(T_0)x_0\setminus Q_0)\cup (B_U(T_0+\rho/2)x_0\setminus B_U(T_0))x_0. \end{align*} $$
$$ \begin{align*} E_3:=\bigcup\limits_{y\in I_1} B_U(\rho/2)y\subseteq (B_U(T_0)x_0\setminus Q_0)\cup (B_U(T_0+\rho/2)x_0\setminus B_U(T_0))x_0. \end{align*} $$
Using Lemma 8.1, we arrive at
 $$ \begin{align*} &e^{(n-1-\delta_{\Gamma})s_{\varepsilon}}\int_{B_U(T_0) \setminus E_1} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)\,d\textbf{t}\\ &\quad\le e^{(n-1-\delta_{\Gamma})s_{\varepsilon}}\sum_{y\in I_1} \int_{B_U(\rho/2)y} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} y)f_y(u_{\textbf{t}} y)\,d\textbf{t}\\ &\quad\ll\sum_{y\in I_1} S_{\ell}(\psi)\mu^{\operatorname{PS}}_y(B_U(\rho/2)y)\\ &\quad\le S_{\ell}(\psi)(\mu^{\operatorname{PS}}_{x_0}(B_U(T_0)x_0\setminus Q_0)+\mu^{\operatorname{PS}}_{x_0} ((B_U(T_0+\rho/2)\setminus B_U(T_0))x_0)). \end{align*} $$
$$ \begin{align*} &e^{(n-1-\delta_{\Gamma})s_{\varepsilon}}\int_{B_U(T_0) \setminus E_1} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)\,d\textbf{t}\\ &\quad\le e^{(n-1-\delta_{\Gamma})s_{\varepsilon}}\sum_{y\in I_1} \int_{B_U(\rho/2)y} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} y)f_y(u_{\textbf{t}} y)\,d\textbf{t}\\ &\quad\ll\sum_{y\in I_1} S_{\ell}(\psi)\mu^{\operatorname{PS}}_y(B_U(\rho/2)y)\\ &\quad\le S_{\ell}(\psi)(\mu^{\operatorname{PS}}_{x_0}(B_U(T_0)x_0\setminus Q_0)+\mu^{\operatorname{PS}}_{x_0} ((B_U(T_0+\rho/2)\setminus B_U(T_0))x_0)). \end{align*} $$
Thus, by Theorem 5.1, there exists
![]() $\alpha =\alpha (\Gamma )>0$
such that using (98) and (102), we arrive at
$\alpha =\alpha (\Gamma )>0$
such that using (98) and (102), we arrive at
 $$ \begin{align*} &e^{(n-1-\delta_{\Gamma})s_{\varepsilon}}\int_{B_U(T_0) \setminus E_1} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)\,d\textbf{t} \\ &\quad\ll_{\Gamma,\operatorname{supp}\psi} S_{\ell}(\psi)\mu^{\operatorname{PS}}_{x_0}(B_U(T_0)x_0)(e^{-\beta R}+\rho^{\alpha} )\\ &\quad\ll_{\Gamma,\operatorname{supp}\psi} S_{\ell}(\psi)\mu^{\operatorname{PS}}_{x_0}(B_U(T_0)x_0)T^{-\kappa}. \end{align*} $$
$$ \begin{align*} &e^{(n-1-\delta_{\Gamma})s_{\varepsilon}}\int_{B_U(T_0) \setminus E_1} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)\,d\textbf{t} \\ &\quad\ll_{\Gamma,\operatorname{supp}\psi} S_{\ell}(\psi)\mu^{\operatorname{PS}}_{x_0}(B_U(T_0)x_0)(e^{-\beta R}+\rho^{\alpha} )\\ &\quad\ll_{\Gamma,\operatorname{supp}\psi} S_{\ell}(\psi)\mu^{\operatorname{PS}}_{x_0}(B_U(T_0)x_0)T^{-\kappa}. \end{align*} $$
Using (103), we may now deduce
 $$ \begin{align*} \frac{e^{(n-1-\delta_{\Gamma})s_{\varepsilon}}}{\mu^{\operatorname{PS}}_{x_0}(B_U(T_0)x_0)}\int_{B_U(T_0)} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)\,d\textbf{t}-m^{\operatorname{BR}}(\psi)\ll_{\Gamma,\operatorname{supp}\psi} S_{\ell}(\psi)T^{-\kappa}.\end{align*} $$
$$ \begin{align*} \frac{e^{(n-1-\delta_{\Gamma})s_{\varepsilon}}}{\mu^{\operatorname{PS}}_{x_0}(B_U(T_0)x_0)}\int_{B_U(T_0)} \psi(a_{s_{\varepsilon}}u_{\textbf{t}} x_0)\,d\textbf{t}-m^{\operatorname{BR}}(\psi)\ll_{\Gamma,\operatorname{supp}\psi} S_{\ell}(\psi)T^{-\kappa}.\end{align*} $$
The lower bound follows similarly, as in the proof of Theorem 1.3.
Remark 8.3. The dependence of T on
![]() $\operatorname {supp}\psi $
in the previous proof arises from Theorem 6.3, through the quantity
$\operatorname {supp}\psi $
in the previous proof arises from Theorem 6.3, through the quantity
![]() $s_{\varepsilon }$
. Upon closer inspection, one can verify that this means T depends on
$s_{\varepsilon }$
. Upon closer inspection, one can verify that this means T depends on
![]() $\operatorname {supp}\psi $
through the maximum height of elements in
$\operatorname {supp}\psi $
through the maximum height of elements in
![]() $\operatorname {supp}\psi $
. In particular, we may choose a larger compact set containing
$\operatorname {supp}\psi $
. In particular, we may choose a larger compact set containing
![]() $\operatorname {supp}\psi $
and have T depend on that compact set, rather than
$\operatorname {supp}\psi $
and have T depend on that compact set, rather than
![]() $\operatorname {supp}\psi $
specifically.
$\operatorname {supp}\psi $
specifically.
Acknowledgments
We would like to thank Amir Mohammadi for suggesting this problem, as well as for his support and guidance. We would also like to thank Wenyu Pan for bringing [Reference Das, Fishman, Simmons and Urbański5] to our attention. We are also grateful to the anonymous referee for their insightful comments on an earlier version of this manuscript, which significantly improved the paper. The first author was partially supported by the Eric and Wendy Schmidt Fund for Strategic Innovation. The second author was supported in part by the National Science and Engineering Research Council of Canada (NSERC) PGSD3-502346-2017 and in part by the Zuckerman STEM Leadership Program.
A Appendix. Friendliness of the PS measure
For simplicity, in this section, we work in the Poincaré ball models of hyperbolic geometry
![]() $\mathbb D^n$
, instead of
$\mathbb D^n$
, instead of
![]() ${\mathbb H}^n$
. Recall that
${\mathbb H}^n$
. Recall that
![]() $\mathbb D^n$
and
$\mathbb D^n$
and
![]() ${\mathbb H}^n$
are isometric via the Cayley transform.
${\mathbb H}^n$
are isometric via the Cayley transform.
Denote by
![]() $d_E$
the Euclidean metric on
$d_E$
the Euclidean metric on
![]() $\mathbb R^m$
. For a subset
$\mathbb R^m$
. For a subset
![]() $S\subseteq \mathbb R^m$
and
$S\subseteq \mathbb R^m$
and
![]() $\xi>0$
, let
$\xi>0$
, let
For
![]() $v\in \mathbb R^m$
and
$v\in \mathbb R^m$
and
![]() $r>0$
, let
$r>0$
, let
be the Euclidean ball of radius r around v.
Definition A.1. Let
![]() $\mu $
be a measure defined on
$\mu $
be a measure defined on
![]() $\mathbb R^m$
.
$\mathbb R^m$
.
-
(1)
 $\mu $
is called Federer (respectively doubling) if for any
$\mu $
is called Federer (respectively doubling) if for any
 $c>1$
, there exists
$c>1$
, there exists
 $k_1>0$
such that for all
$k_1>0$
such that for all
 $v\in \operatorname {supp}(\mu )$
and
$v\in \operatorname {supp}(\mu )$
and
 $0 <\eta \leq 1$
(respectively
$0 <\eta \leq 1$
(respectively
 $\eta>0$
),
$\eta>0$
),  $$ \begin{align*} \mu(B(v,{c\eta}))\le k_1\mu(B(v,\eta)). \end{align*} $$
$$ \begin{align*} \mu(B(v,{c\eta}))\le k_1\mu(B(v,\eta)). \end{align*} $$
-
(2)
 $\mu $
is called decaying and non-planar if there exist
$\mu $
is called decaying and non-planar if there exist
 $\alpha ,c_2>0$
such that for all
$\alpha ,c_2>0$
such that for all
 $v\in \operatorname {supp}\mu $
,
$v\in \operatorname {supp}\mu $
,
 $\xi>0$
,
$\xi>0$
,
 $0<\eta \le 1$
, and every affine hyperplane
$0<\eta \le 1$
, and every affine hyperplane
 $L \subseteq \mathbb R^{n}$
, where
$L \subseteq \mathbb R^{n}$
, where $$ \begin{align*} \mu(\mathcal{N}(L,\xi\Vert d_L\Vert _{\mu,B(v,\eta)})\cap B(v,\eta)) \le c_2{\xi}^{\alpha} \mu (B(v,\eta)), \end{align*} $$
$$ \begin{align*} \mu(\mathcal{N}(L,\xi\Vert d_L\Vert _{\mu,B(v,\eta)})\cap B(v,\eta)) \le c_2{\xi}^{\alpha} \mu (B(v,\eta)), \end{align*} $$
 $$ \begin{align*} \Vert d_L\Vert _{\mu,B(v,\eta)}:=\sup\{d(\textbf{y},L) : \textbf{y}\in B(v,\eta)\cap\operatorname{supp}\mu\}. \end{align*} $$
$$ \begin{align*} \Vert d_L\Vert _{\mu,B(v,\eta)}:=\sup\{d(\textbf{y},L) : \textbf{y}\in B(v,\eta)\cap\operatorname{supp}\mu\}. \end{align*} $$
-
(3)
 $\mu $
is called friendly if it is Federer, decaying, and non-planar.
$\mu $
is called friendly if it is Federer, decaying, and non-planar.
In the case that all cusps have maximal rank (which vacuously includes the case of convex cocompact
![]() $\Gamma $
), a stronger statement holds, see §A.3.
$\Gamma $
), a stronger statement holds, see §A.3.
Theorem A.2. [Reference Das, Fishman, Simmons and Urbański5, Theorem 1.9]
Assume
![]() $\Gamma $
is geometrically finite and Zariski dense. Then the PS densities
$\Gamma $
is geometrically finite and Zariski dense. Then the PS densities
![]() $\{\nu _x\}_{x\in \mathbb D^n}$
are friendly. Moreover, in this case, the constants in Definition A.1 only depend on
$\{\nu _x\}_{x\in \mathbb D^n}$
are friendly. Moreover, in this case, the constants in Definition A.1 only depend on
![]() $\Gamma $
.
$\Gamma $
.
Note that, as in [Reference Das, Fishman, Simmons and Urbański5, Definition 1.1(1.3)], using closed thickenings, one obtains Definition A.1(2) by combining the separate definitions of decaying and of non-planar from [Reference Das, Fishman, Simmons and Urbański5]. The above result for the case
![]() $\Gamma $
is convex cocompact was proved in [Reference Stratmann and Urbański34, Theorem 2].
$\Gamma $
is convex cocompact was proved in [Reference Stratmann and Urbański34, Theorem 2].
In this section, we will prove the results in §5. In particular, because of the shadow lemma, Proposition 3.4, we will see that the leafwise PS measures
![]() $\{\mu ^{\operatorname {PS}}_x\}$
satisfy a stronger condition than that of friendliness. In general, we will begin by proving a statement for
$\{\mu ^{\operatorname {PS}}_x\}$
satisfy a stronger condition than that of friendliness. In general, we will begin by proving a statement for
![]() $\nu _o$
, then for
$\nu _o$
, then for
![]() $\mu ^{\operatorname {PS}}_x$
when
$\mu ^{\operatorname {PS}}_x$
when
![]() $x^+\in \Lambda (\Gamma ),$
and then finally a nicer statement for
$x^+\in \Lambda (\Gamma ),$
and then finally a nicer statement for
![]() $x \in \operatorname {supp}m^{\operatorname {BMS}}.$
$x \in \operatorname {supp}m^{\operatorname {BMS}}.$
The next lemma and subsequent corollaries are necessary to move between these measures.
As in §3.1, we fix
![]() $o\in \mathbb D^n$
. For any
$o\in \mathbb D^n$
. For any
![]() $x\in \mathbb D^n$
, define the Gromov distance at x of
$x\in \mathbb D^n$
, define the Gromov distance at x of
![]() $\xi ,\eta \in \partial \mathbb D^n$
by
$\xi ,\eta \in \partial \mathbb D^n$
by
where y is on the ray joining
![]() $\xi $
and
$\xi $
and
![]() $\eta $
. For any
$\eta $
. For any
![]() $x\in \mathbb D^n$
,
$x\in \mathbb D^n$
,
![]() $\xi \in \partial \mathbb D^n$
, and
$\xi \in \partial \mathbb D^n$
, and
![]() $r>0$
, let
$r>0$
, let
For
![]() $v\in {\operatorname {T}^1}(\mathbb {D}^n)$
, denote by
$v\in {\operatorname {T}^1}(\mathbb {D}^n)$
, denote by
![]() $\operatorname {Pr}_{v^-}:Uv\rightarrow \partial \mathbb D^n\setminus \{v^-\}$
the projection
$\operatorname {Pr}_{v^-}:Uv\rightarrow \partial \mathbb D^n\setminus \{v^-\}$
the projection
![]() $w\mapsto w^+$
.
$w\mapsto w^+$
.
The next lemma follows from §1.6 in [Reference Kaimanovich14], and [Reference Schapira33, Lemma 2.5 and Theorem 3.4].
Lemma A.3. There exist constants
![]() $\alpha _0>0$
,
$\alpha _0>0$
,
![]() $c>1$
such that for all
$c>1$
such that for all
![]() $g\in G$
and
$g\in G$
and
![]() $0<\eta \le \alpha _0$
, we have
$0<\eta \le \alpha _0$
, we have
According to [Reference Das, Simmons and Urbański6, Lemma 3.5.1] for any
![]() $\xi ,\eta \in \partial \mathbb D^n$
,
$\xi ,\eta \in \partial \mathbb D^n$
,
Using the triangle inequality on the hyperbolic distance and the definition of the Busemann function, one can show that for any
![]() $x\in \mathbb D^n$
and
$x\in \mathbb D^n$
and
![]() $\xi ,\eta \in \partial \mathbb D^n$
,
$\xi ,\eta \in \partial \mathbb D^n$
,
The following is a direct corollary of (A.1), (A.2), and Lemma A.3.
Corollary A.4. There exist constants
![]() $\alpha _0>0$
,
$\alpha _0>0$
,
![]() $c>1$
such that for all
$c>1$
such that for all
![]() $g\in G$
and
$g\in G$
and
![]() $0<\eta \le \alpha _0$
, we have
$0<\eta \le \alpha _0$
, we have
The next corollary will be necessary to obtain a non-planarity result for
![]() $\mu ^{\operatorname {PS}}_x.$
It follows from Corollary A.4 by covering the hyperplane with small balls using the fact that
$\mu ^{\operatorname {PS}}_x.$
It follows from Corollary A.4 by covering the hyperplane with small balls using the fact that
![]() $\eta \le 1$
to uniformly bound the
$\eta \le 1$
to uniformly bound the
![]() $d(o,\pi (g'))$
terms with
$d(o,\pi (g'))$
terms with
![]() $d(o,\pi (g))$
, where
$d(o,\pi (g))$
, where
![]() $g'$
is the center of one of the balls in this cover.
$g'$
is the center of one of the balls in this cover.
Corollary A.5. Let
![]() $\alpha _0$
be as in Corollary A.4. There exists a constant
$\alpha _0$
be as in Corollary A.4. There exists a constant
![]() $c>1$
so that for every
$c>1$
so that for every
![]() $g \in G$
, every
$g \in G$
, every
![]() $0<\xi <\eta \le \alpha _0,$
and every hyperplane L in
$0<\xi <\eta \le \alpha _0,$
and every hyperplane L in
![]() $\mathbb R^{n-1}$
, there exists a hyperplane
$\mathbb R^{n-1}$
, there exists a hyperplane
![]() $L'$
in
$L'$
in
![]() $\partial ({\mathbb H}^n)$
so that
$\partial ({\mathbb H}^n)$
so that
 $$ \begin{align*}&\mathcal{N}(L', c^{-1} e^{-d(o,\pi(g))}\xi)\cap B(g^+, c^{-1} e^{-d(o,\pi(g))}\eta)\\[3pt] &\quad\subseteq\operatorname{Pr}_{g^-}(\mathcal{N}(L,\xi)\cap B_U(\eta)g) \\[3pt] &\quad\subseteq\mathcal{N}(L', ce^{d(o,\pi(g))}\xi)\cap B(g^+, c e^{d(o,\pi(g))}\eta). \end{align*} $$
$$ \begin{align*}&\mathcal{N}(L', c^{-1} e^{-d(o,\pi(g))}\xi)\cap B(g^+, c^{-1} e^{-d(o,\pi(g))}\eta)\\[3pt] &\quad\subseteq\operatorname{Pr}_{g^-}(\mathcal{N}(L,\xi)\cap B_U(\eta)g) \\[3pt] &\quad\subseteq\mathcal{N}(L', ce^{d(o,\pi(g))}\xi)\cap B(g^+, c e^{d(o,\pi(g))}\eta). \end{align*} $$
Proof. Let
![]() $\{g_i\}_{i \in I}$
be chosen so that
$\{g_i\}_{i \in I}$
be chosen so that
By Corollary A.4,
Let
Observe that for
![]() $i \in I_2$
,
$i \in I_2$
,
![]() $g_i \in B_U(2)g.$
Then,
$g_i \in B_U(2)g.$
Then,
and
![]() $g_i = u_{\textbf {t}} g$
for
$g_i = u_{\textbf {t}} g$
for
![]() $|\textbf {t}|\le 2$
. Thus,
$|\textbf {t}|\le 2$
. Thus,
 $$ \begin{align*} d(\pi(g),\pi(g_i)) &= d(\pi(g),\pi(u_{\textbf{t}} g)) \\ &=d(g(o), u_{\textbf{t}} g(o)). \end{align*} $$
$$ \begin{align*} d(\pi(g),\pi(g_i)) &= d(\pi(g),\pi(u_{\textbf{t}} g)) \\ &=d(g(o), u_{\textbf{t}} g(o)). \end{align*} $$
This implies that there exists a constant
![]() $\hat {c}>1$
that is uniform for all
$\hat {c}>1$
that is uniform for all
![]() $g \in G$
so that for all
$g \in G$
so that for all
![]() $i \in I_2$
,
$i \in I_2$
,
Thus, for all
![]() $i \in I_2$
, we have
$i \in I_2$
, we have
Hence, for every
![]() $i \in I_2,$
$i \in I_2,$
 $$ \begin{align*} &B(g^+,\hat{c}^{-1} c^{-1}e^{-d(o,\pi(g))} \xi) \cap B(g^+,\hat{c}^{-1} c^{-1} e^{-d(o,\pi(g))}\eta)\\[3pt] &\quad\subseteq \operatorname{Pr}_{g^-}(B_U(\xi)g_i\cap B_U(\eta)g) \\[3pt] &\quad\subseteq B(g^+,\hat{c} ce^{d(o,\pi(g))} \xi) \cap B(g^+,\hat{c}c e^{d(o,\pi(g))}\eta). \end{align*} $$
$$ \begin{align*} &B(g^+,\hat{c}^{-1} c^{-1}e^{-d(o,\pi(g))} \xi) \cap B(g^+,\hat{c}^{-1} c^{-1} e^{-d(o,\pi(g))}\eta)\\[3pt] &\quad\subseteq \operatorname{Pr}_{g^-}(B_U(\xi)g_i\cap B_U(\eta)g) \\[3pt] &\quad\subseteq B(g^+,\hat{c} ce^{d(o,\pi(g))} \xi) \cap B(g^+,\hat{c}c e^{d(o,\pi(g))}\eta). \end{align*} $$
The result then follows by taking the union over all
![]() $i \in I_2$
.
$i \in I_2$
.
A.1 The PS measure is Federer
In this section, we prove more specific Federer statements for
![]() $\nu _o$
and
$\nu _o$
and
![]() $\mu ^{\operatorname {PS}}_x$
.
$\mu ^{\operatorname {PS}}_x$
.
Lemma A.6. There exists a constant
![]() $\sigma \ge \delta _{\Gamma }$
depending only on
$\sigma \ge \delta _{\Gamma }$
depending only on
![]() $\Gamma $
such that for any
$\Gamma $
such that for any
![]() $\unicode{x3bb} \in \Lambda (\Gamma ), \eta>0$
and
$\unicode{x3bb} \in \Lambda (\Gamma ), \eta>0$
and
![]() $c \ge 1,$
we have that
$c \ge 1,$
we have that
Proof. We will prove this for the balls
![]() $B_o(\unicode{x3bb} ,c\eta ),$
and
$B_o(\unicode{x3bb} ,c\eta ),$
and
![]() $B_o(\unicode{x3bb} ,\eta )$
using the Gromov distance. It then immediately follows for the Euclidean balls
$B_o(\unicode{x3bb} ,\eta )$
using the Gromov distance. It then immediately follows for the Euclidean balls
![]() $B(\unicode{x3bb} ,c\eta )$
and
$B(\unicode{x3bb} ,c\eta )$
and
![]() $B(\unicode{x3bb} ,\eta )$
by the Federer condition and (A.1).
$B(\unicode{x3bb} ,\eta )$
by the Federer condition and (A.1).
Let
![]() $\{\unicode{x3bb} _t\}_{t\ge 0}$
be a geodesic ray joining o to
$\{\unicode{x3bb} _t\}_{t\ge 0}$
be a geodesic ray joining o to
![]() $\unicode{x3bb} $
. By the shadow lemma for
$\unicode{x3bb} $
. By the shadow lemma for
![]() $\nu _o$
[Reference Stratmann and Velani35, Theorem 2] (see also [Reference Schapira33, Theorem 3.2]), we have that for any
$\nu _o$
[Reference Stratmann and Velani35, Theorem 2] (see also [Reference Schapira33, Theorem 3.2]), we have that for any
![]() $\eta>0,$
$\eta>0,$
 $$ \begin{align} \eta^{\delta_{\Gamma}}e^{(k(\unicode{x3bb}_{-\log \eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log \eta})}&\ll_{\Gamma}\nu_o(B_o(\unicode{x3bb},\eta ))\nonumber\\[3pt] &\ll_{\Gamma}\eta^{\delta_{\Gamma}}e^{(k(\unicode{x3bb}_{-\log \eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log \eta})}. \end{align} $$
$$ \begin{align} \eta^{\delta_{\Gamma}}e^{(k(\unicode{x3bb}_{-\log \eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log \eta})}&\ll_{\Gamma}\nu_o(B_o(\unicode{x3bb},\eta ))\nonumber\\[3pt] &\ll_{\Gamma}\eta^{\delta_{\Gamma}}e^{(k(\unicode{x3bb}_{-\log \eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log \eta})}. \end{align} $$
Here,
![]() $k(\unicode{x3bb} _{-\log \eta })$
denotes the rank of the cusp that
$k(\unicode{x3bb} _{-\log \eta })$
denotes the rank of the cusp that
![]() $\unicode{x3bb} _{-\log \eta }$
lies in; if it is in
$\unicode{x3bb} _{-\log \eta }$
lies in; if it is in
![]() $\pi (\mathcal {C}_0)$
, it is defined to be zero. (Recall the definition of
$\pi (\mathcal {C}_0)$
, it is defined to be zero. (Recall the definition of
![]() $\mathcal {C}_0$
from §3.2.) Note also that we have absorbed a constant depending on
$\mathcal {C}_0$
from §3.2.) Note also that we have absorbed a constant depending on
![]() $\operatorname {diam} \pi (\mathcal {C}_0)$
(hence only on
$\operatorname {diam} \pi (\mathcal {C}_0)$
(hence only on
![]() $\Gamma $
) to write the distance from
$\Gamma $
) to write the distance from
![]() $\pi (\mathcal {C}_0)$
rather than from the fixed reference point o.
$\pi (\mathcal {C}_0)$
rather than from the fixed reference point o.
It follows from (A.3) that it is enough to show that for some
![]() $\sigma \ge \delta _{\Gamma }$
,
$\sigma \ge \delta _{\Gamma }$
,
 $$ \begin{align*} \nu_o(B_o(\unicode{x3bb},c\eta ))&\ll_{\Gamma}(c\eta)^{\delta_{\Gamma}}e^{(k(\unicode{x3bb}_{-\log c\eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log c\eta})}\\[3pt] &\ll_{\Gamma}c^{\sigma}\eta^{\delta_{\Gamma}}e^{(k(\unicode{x3bb}_{-\log \eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log\eta})}\\[3pt] &\ll_{\Gamma}c^{\sigma}\nu_o(B_o(\unicode{x3bb},\eta )). \end{align*} $$
$$ \begin{align*} \nu_o(B_o(\unicode{x3bb},c\eta ))&\ll_{\Gamma}(c\eta)^{\delta_{\Gamma}}e^{(k(\unicode{x3bb}_{-\log c\eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log c\eta})}\\[3pt] &\ll_{\Gamma}c^{\sigma}\eta^{\delta_{\Gamma}}e^{(k(\unicode{x3bb}_{-\log \eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log\eta})}\\[3pt] &\ll_{\Gamma}c^{\sigma}\nu_o(B_o(\unicode{x3bb},\eta )). \end{align*} $$
Equivalently, it is enough to show that
 $$ \begin{align} & (k(\unicode{x3bb}_{-\log c\eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log c\eta})-(k(\unicode{x3bb}_{-\log \eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log\eta})\nonumber\\[3pt] &\quad\ll_{\Gamma}(\sigma-\delta_{\Gamma})\log c. \end{align} $$
$$ \begin{align} & (k(\unicode{x3bb}_{-\log c\eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log c\eta})-(k(\unicode{x3bb}_{-\log \eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log\eta})\nonumber\\[3pt] &\quad\ll_{\Gamma}(\sigma-\delta_{\Gamma})\log c. \end{align} $$
Case 1: Assume
![]() $k(\unicode{x3bb} _{-\log c\eta })\le k(\unicode{x3bb} _{-\log \eta })$
.
$k(\unicode{x3bb} _{-\log c\eta })\le k(\unicode{x3bb} _{-\log \eta })$
.
Then
 $$ \begin{align*} & (k(\unicode{x3bb}_{-\log c\eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log c\eta})-(k(\unicode{x3bb}_{-\log \eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log\eta})\\[3pt] &\quad\le (k(\unicode{x3bb}_{-\log\eta})-\delta_{\Gamma})(d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log c\eta}) - d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log\eta})) \\[3pt] &\quad\le (k(\unicode{x3bb}_{-\log\eta})-\delta_{\Gamma})\log c\\[3pt] &\quad\le (n-1-\delta_{\Gamma})\log c. \end{align*} $$
$$ \begin{align*} & (k(\unicode{x3bb}_{-\log c\eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log c\eta})-(k(\unicode{x3bb}_{-\log \eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log\eta})\\[3pt] &\quad\le (k(\unicode{x3bb}_{-\log\eta})-\delta_{\Gamma})(d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log c\eta}) - d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log\eta})) \\[3pt] &\quad\le (k(\unicode{x3bb}_{-\log\eta})-\delta_{\Gamma})\log c\\[3pt] &\quad\le (n-1-\delta_{\Gamma})\log c. \end{align*} $$
Case 2:
![]() $k(\unicode{x3bb} _{-\log c\eta })> k(\unicode{x3bb} _{-\log \eta })$
and
$k(\unicode{x3bb} _{-\log c\eta })> k(\unicode{x3bb} _{-\log \eta })$
and
![]() $k(\unicode{x3bb} _{-\log \eta })=0$
.
$k(\unicode{x3bb} _{-\log \eta })=0$
.
Then,
![]() $d(\pi (\mathcal {C}_0),\unicode{x3bb} _{-\log \eta })=0$
and
$d(\pi (\mathcal {C}_0),\unicode{x3bb} _{-\log \eta })=0$
and
Therefore,
 $$ \begin{align*} &(k(\unicode{x3bb}_{-\log c\eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log c\eta})-(k(\unicode{x3bb}_{-\log \eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log\eta})\\[3pt] &\quad\le(k(\unicode{x3bb}_{-\log c\eta})-\delta_{\Gamma})d((\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log c\eta})\\[3pt] &\quad\le(k(\unicode{x3bb}_{-\log c\eta})-\delta_{\Gamma})\log c\\[3pt] &\quad\le (n-1-\delta_{\Gamma})\log c. \end{align*} $$
$$ \begin{align*} &(k(\unicode{x3bb}_{-\log c\eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log c\eta})-(k(\unicode{x3bb}_{-\log \eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log\eta})\\[3pt] &\quad\le(k(\unicode{x3bb}_{-\log c\eta})-\delta_{\Gamma})d((\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log c\eta})\\[3pt] &\quad\le(k(\unicode{x3bb}_{-\log c\eta})-\delta_{\Gamma})\log c\\[3pt] &\quad\le (n-1-\delta_{\Gamma})\log c. \end{align*} $$
Case 3: Assume
![]() $k(\unicode{x3bb} _{-\log c\eta })> k(\unicode{x3bb} _{-\log \eta })$
and
$k(\unicode{x3bb} _{-\log c\eta })> k(\unicode{x3bb} _{-\log \eta })$
and
![]() $k(\unicode{x3bb} _{-\log \eta })>0$
. In particular,
$k(\unicode{x3bb} _{-\log \eta })>0$
. In particular,
![]() $\unicode{x3bb} _{-\log \eta }$
and
$\unicode{x3bb} _{-\log \eta }$
and
![]() $\unicode{x3bb} _{-\log c\eta }$
are in two different cusps, and hence there exists
$\unicode{x3bb} _{-\log c\eta }$
are in two different cusps, and hence there exists
![]() $1<r<c$
such that
$1<r<c$
such that
![]() $\unicode{x3bb} _{-\log r\eta }\in \pi (\mathcal {C}_0)$
. Then,
$\unicode{x3bb} _{-\log r\eta }\in \pi (\mathcal {C}_0)$
. Then,
 $$ \begin{align*} &d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log\eta})\le d(\unicode{x3bb}_{-\log r\eta},\unicode{x3bb}_{-\log\eta})\le \log r\le\log c\\[3pt] &d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log c\eta})\le d(\unicode{x3bb}_{-\log r\eta},\unicode{x3bb}_{-\log c\eta})\le \log (c/r)\le\log c. \end{align*} $$
$$ \begin{align*} &d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log\eta})\le d(\unicode{x3bb}_{-\log r\eta},\unicode{x3bb}_{-\log\eta})\le \log r\le\log c\\[3pt] &d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log c\eta})\le d(\unicode{x3bb}_{-\log r\eta},\unicode{x3bb}_{-\log c\eta})\le \log (c/r)\le\log c. \end{align*} $$
Note that since
![]() $k(\unicode{x3bb} _{-\log c\eta })\ge 2$
, we have
$k(\unicode{x3bb} _{-\log c\eta })\ge 2$
, we have
![]() $\delta _{\Gamma }>1$
, because
$\delta _{\Gamma }>1$
, because
![]() $\delta _{\Gamma }> k/2$
, where k is the maximal cusp rank. We arrive at
$\delta _{\Gamma }> k/2$
, where k is the maximal cusp rank. We arrive at
 $$ \begin{align*} (k(\unicode{x3bb}_{-\log{\eta}})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log\eta}) &\ge (1-\delta_{\Gamma}) d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log\eta})\\[3pt] &\ge (1-\delta_{\Gamma})\log c\\[3pt] (k(\unicode{x3bb}_{-\log{ c\eta}})-\delta_{\Gamma})d(\pi(\mathcal{C}_0,\unicode{x3bb}_{-\log c\eta}) &\le (n-1-\delta_{\Gamma}) d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log c\eta})\\[3pt] &\le (n-1-\delta_{\Gamma})\log c. \end{align*} $$
$$ \begin{align*} (k(\unicode{x3bb}_{-\log{\eta}})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log\eta}) &\ge (1-\delta_{\Gamma}) d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log\eta})\\[3pt] &\ge (1-\delta_{\Gamma})\log c\\[3pt] (k(\unicode{x3bb}_{-\log{ c\eta}})-\delta_{\Gamma})d(\pi(\mathcal{C}_0,\unicode{x3bb}_{-\log c\eta}) &\le (n-1-\delta_{\Gamma}) d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log c\eta})\\[3pt] &\le (n-1-\delta_{\Gamma})\log c. \end{align*} $$
It follows that
 $$ \begin{align*} &(k(\unicode{x3bb}_{-\log c\eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log c\eta})-(k(\unicode{x3bb}_{-\log \eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log\eta})\\[3pt] &\quad\le(n-1-\delta_{\Gamma})\log c-(1-\delta_{\Gamma})\log c\\[3pt] &\quad\le(n-2)\log c. \end{align*} $$
$$ \begin{align*} &(k(\unicode{x3bb}_{-\log c\eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log c\eta})-(k(\unicode{x3bb}_{-\log \eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log\eta})\\[3pt] &\quad\le(n-1-\delta_{\Gamma})\log c-(1-\delta_{\Gamma})\log c\\[3pt] &\quad\le(n-2)\log c. \end{align*} $$
Thus, choosing
completes the proof.
When
![]() $c<1$
, we obtain a similar result, with a slightly more involved argument.
$c<1$
, we obtain a similar result, with a slightly more involved argument.
Lemma A.7. There exists a constant
![]() $\sigma>0$
depending only on
$\sigma>0$
depending only on
![]() $\Gamma $
such that for any
$\Gamma $
such that for any
![]() $\unicode{x3bb} \in \Lambda (\Gamma ), \eta>0$
and
$\unicode{x3bb} \in \Lambda (\Gamma ), \eta>0$
and
![]() $0<c< 1,$
we have that
$0<c< 1,$
we have that
Proof. The proof is extremely similar to that of Lemma A.6.
By the shadow lemma, as in the proof of Lemma A.6, it is enough to show that for some
![]() $\sigma>0$
,
$\sigma>0$
,
 $$ \begin{align} & (k(\unicode{x3bb}_{-\log c\eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log c\eta})-(k(\unicode{x3bb}_{-\log \eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log\eta})\nonumber\\[3pt] &\quad\ll_{\Gamma}(\delta_{\Gamma}-\sigma) |\log c|. \end{align} $$
$$ \begin{align} & (k(\unicode{x3bb}_{-\log c\eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log c\eta})-(k(\unicode{x3bb}_{-\log \eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log\eta})\nonumber\\[3pt] &\quad\ll_{\Gamma}(\delta_{\Gamma}-\sigma) |\log c|. \end{align} $$
Case 1: Assume
![]() $k(\unicode{x3bb} _{-\log c\eta })\le k(\unicode{x3bb} _{-\log \eta })$
.
$k(\unicode{x3bb} _{-\log c\eta })\le k(\unicode{x3bb} _{-\log \eta })$
.
Then
 $$ \begin{align*} & (k(\unicode{x3bb}_{-\log c\eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log c\eta})-(k(\unicode{x3bb}_{-\log \eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log \eta})\\[3pt] &\quad\le (k(\unicode{x3bb}_{-\log c\eta})-\delta_{\Gamma})(d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log \eta}) - d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log c\eta})) \\[3pt] &\quad\le |k(\unicode{x3bb}_{-\log\eta})-\delta_{\Gamma}||\log c|. \end{align*} $$
$$ \begin{align*} & (k(\unicode{x3bb}_{-\log c\eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log c\eta})-(k(\unicode{x3bb}_{-\log \eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log \eta})\\[3pt] &\quad\le (k(\unicode{x3bb}_{-\log c\eta})-\delta_{\Gamma})(d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log \eta}) - d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log c\eta})) \\[3pt] &\quad\le |k(\unicode{x3bb}_{-\log\eta})-\delta_{\Gamma}||\log c|. \end{align*} $$
Let k be the maximal cusp rank. Since
![]() $ |k-\delta _{\Gamma }|<\delta _{\Gamma }$
, we get that
$ |k-\delta _{\Gamma }|<\delta _{\Gamma }$
, we get that
satisfies the claim. Case 2:
![]() $k(\unicode{x3bb} _{-\log c\eta })> k(\unicode{x3bb} _{-\log \eta })$
and
$k(\unicode{x3bb} _{-\log c\eta })> k(\unicode{x3bb} _{-\log \eta })$
and
![]() $k(\unicode{x3bb} _{-\log \eta })=0$
.
$k(\unicode{x3bb} _{-\log \eta })=0$
.
Then,
![]() $d(\pi (\mathcal {C}_0),\unicode{x3bb} _{-\log \eta })=0$
and
$d(\pi (\mathcal {C}_0),\unicode{x3bb} _{-\log \eta })=0$
and
Therefore,
 $$ \begin{align*} &(k(\unicode{x3bb}_{-\log c\eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log c\eta})-(k(\unicode{x3bb}_{-\log \eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log\eta})\\[3pt] &\quad\le(k(\unicode{x3bb}_{-\log c\eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log c\eta})\\[3pt] &\quad\le|k(\unicode{x3bb}_{-\log c\eta})-\delta_{\Gamma}||\log c|, \end{align*} $$
$$ \begin{align*} &(k(\unicode{x3bb}_{-\log c\eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log c\eta})-(k(\unicode{x3bb}_{-\log \eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log\eta})\\[3pt] &\quad\le(k(\unicode{x3bb}_{-\log c\eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log c\eta})\\[3pt] &\quad\le|k(\unicode{x3bb}_{-\log c\eta})-\delta_{\Gamma}||\log c|, \end{align*} $$
and the claim follows as in Case 1.
Case 3: Assume
![]() $k(\unicode{x3bb} _{-\log c\eta })> k(\unicode{x3bb} _{-\log \eta })$
and
$k(\unicode{x3bb} _{-\log c\eta })> k(\unicode{x3bb} _{-\log \eta })$
and
![]() $k(\unicode{x3bb} _{-\log \eta })>0$
. In particular,
$k(\unicode{x3bb} _{-\log \eta })>0$
. In particular,
![]() $\unicode{x3bb} _{-\log \eta }$
and
$\unicode{x3bb} _{-\log \eta }$
and
![]() $\unicode{x3bb} _{-\log c\eta }$
are in two different cusps, and hence there exists
$\unicode{x3bb} _{-\log c\eta }$
are in two different cusps, and hence there exists
![]() $c<r<1$
such that
$c<r<1$
such that
![]() $\unicode{x3bb} _{-\log r\eta }\in \pi (\mathcal {C}_0)$
. Then since
$\unicode{x3bb} _{-\log r\eta }\in \pi (\mathcal {C}_0)$
. Then since
![]() $r<1$
,
$r<1$
,
Note that since
![]() $k(\unicode{x3bb} _{-\log c\eta })\ge 2$
, we have
$k(\unicode{x3bb} _{-\log c\eta })\ge 2$
, we have
![]() $\delta _{\Gamma }>1$
. By (A.6) and (A.7), we arrive at
$\delta _{\Gamma }>1$
. By (A.6) and (A.7), we arrive at
We now have two cases. First, assume that
![]() $\log (r/c)(k(\unicode{x3bb} _{-\log c\eta })-\delta _{\Gamma })\le 0$
. Then
$\log (r/c)(k(\unicode{x3bb} _{-\log c\eta })-\delta _{\Gamma })\le 0$
. Then
![]() $k(\unicode{x3bb} _{-\log c\eta })-\delta _{\Gamma } \le 0,$
so by (A.8), we have that
$k(\unicode{x3bb} _{-\log c\eta })-\delta _{\Gamma } \le 0,$
so by (A.8), we have that
 $$ \begin{align*} &(k(\unicode{x3bb}_{-\log c\eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log c\eta})-(k(\unicode{x3bb}_{-\log \eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log\eta})\\[3pt] &\quad\le - (\delta_{\Gamma} -1 )\log c\\[3pt] &\quad= (\delta_{\Gamma} - 1 )|\log c|. \end{align*} $$
$$ \begin{align*} &(k(\unicode{x3bb}_{-\log c\eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log c\eta})-(k(\unicode{x3bb}_{-\log \eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log\eta})\\[3pt] &\quad\le - (\delta_{\Gamma} -1 )\log c\\[3pt] &\quad= (\delta_{\Gamma} - 1 )|\log c|. \end{align*} $$
Now, assume that
![]() $\log (r/c) (k(\unicode{x3bb} _{-\log c\eta })-\delta _{\Gamma })>0$
, that is, that
$\log (r/c) (k(\unicode{x3bb} _{-\log c\eta })-\delta _{\Gamma })>0$
, that is, that
![]() $k(\unicode{x3bb} _{-\log c\eta })-\delta _{\Gamma }>0$
. Then it follows from (A.7) that
$k(\unicode{x3bb} _{-\log c\eta })-\delta _{\Gamma }>0$
. Then it follows from (A.7) that
 $$ \begin{align} &(k(\unicode{x3bb}_{-\log c\eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log c\eta})-(k(\unicode{x3bb}_{-\log \eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log\eta})\nonumber\\[3pt] &\quad\le (k(\unicode{x3bb}_{-\log c\eta})-\delta_{\Gamma})\log(r/c)-(\delta_{\Gamma}-1)\log r. \end{align} $$
$$ \begin{align} &(k(\unicode{x3bb}_{-\log c\eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log c\eta})-(k(\unicode{x3bb}_{-\log \eta})-\delta_{\Gamma})d(\pi(\mathcal{C}_0),\unicode{x3bb}_{-\log\eta})\nonumber\\[3pt] &\quad\le (k(\unicode{x3bb}_{-\log c\eta})-\delta_{\Gamma})\log(r/c)-(\delta_{\Gamma}-1)\log r. \end{align} $$
Now, consider two further cases:
![]() $k(\unicode{x3bb} _{-\log c\eta })-\delta _{\Gamma }> \delta _{\Gamma } - 1$
or
$k(\unicode{x3bb} _{-\log c\eta })-\delta _{\Gamma }> \delta _{\Gamma } - 1$
or
![]() $k(\unicode{x3bb} _{-\log c\eta })-\delta _{\Gamma } \le \delta _{\Gamma } -1.$
In the first case, (A.11) is bounded above by
$k(\unicode{x3bb} _{-\log c\eta })-\delta _{\Gamma } \le \delta _{\Gamma } -1.$
In the first case, (A.11) is bounded above by
In the second case, note that (A.11) is equal to
and our assumption implies that the first term is negative. Thus, an upper bound is
where k is the maximal cusp rank, as before. Note that
![]() $k-\delta _{\Gamma } < \delta _{\Gamma }$
because
$k-\delta _{\Gamma } < \delta _{\Gamma }$
because
![]() $\delta _{\Gamma }>2k$
always holds.
$\delta _{\Gamma }>2k$
always holds.
Thus, choosing
completes the proof.
Using Lemma A.3, we obtain the following quantitative Federer-like statement for
![]() $\{\mu ^{\operatorname {PS}}_x\}_{x^+\in \Lambda (\Gamma )}$
.
$\{\mu ^{\operatorname {PS}}_x\}_{x^+\in \Lambda (\Gamma )}$
.
Corollary A.8. There exists constants
![]() $\sigma _1 = \sigma _1(\Gamma )\ge \delta _{\Gamma }$
,
$\sigma _1 = \sigma _1(\Gamma )\ge \delta _{\Gamma }$
,
![]() $\sigma _2 = \sigma _2(\Gamma )>0$
which satisfy the following: let
$\sigma _2 = \sigma _2(\Gamma )>0$
which satisfy the following: let
![]() $x \in G$
be such that
$x \in G$
be such that
![]() $x^+\in \Lambda (\Gamma )$
. Then for
$x^+\in \Lambda (\Gamma )$
. Then for
![]() $c>0$
and
$c>0$
and
![]() $\eta \ll _{\Gamma } c^{-1} e^{-\operatorname {height}(x)}$
, we have that
$\eta \ll _{\Gamma } c^{-1} e^{-\operatorname {height}(x)}$
, we have that
Proof. Fix
![]() $g\in G$
which satisfies
$g\in G$
which satisfies
![]() $x=g\Gamma $
and
$x=g\Gamma $
and
![]() $\operatorname {height}(x)=d(\pi (\mathcal {C}_0),\pi (g))$
. By (22),
$\operatorname {height}(x)=d(\pi (\mathcal {C}_0),\pi (g))$
. By (22),
![]() $\operatorname {inj}(x)$
and
$\operatorname {inj}(x)$
and
![]() $\operatorname {height}(x)$
are related, so that for
$\operatorname {height}(x)$
are related, so that for
![]() $\eta \ll _{\Gamma } c^{-1}\operatorname {height}(x),$
$\eta \ll _{\Gamma } c^{-1}\operatorname {height}(x),$
For any
![]() $0<\eta \le 1$
and
$0<\eta \le 1$
and
![]() $u_{\textbf {t}} \in B_U(\eta )$
, we have that
$u_{\textbf {t}} \in B_U(\eta )$
, we have that
 $$ \begin{align*} |\beta_{(u_{\textbf{t}} g)^+}(o,u_{\textbf{t}} g(o))| &\le d(u_{\textbf{t}}^{-1} (o),g(o)) \\[3pt] &\le d(u_{\textbf{t}}^{-1}(o),o)+d(o,g(o)) \\[3pt] &\le 2\operatorname{diam}(B_U(1)\pi(\mathcal{C}_0)) +\operatorname{height}(x). \end{align*} $$
$$ \begin{align*} |\beta_{(u_{\textbf{t}} g)^+}(o,u_{\textbf{t}} g(o))| &\le d(u_{\textbf{t}}^{-1} (o),g(o)) \\[3pt] &\le d(u_{\textbf{t}}^{-1}(o),o)+d(o,g(o)) \\[3pt] &\le 2\operatorname{diam}(B_U(1)\pi(\mathcal{C}_0)) +\operatorname{height}(x). \end{align*} $$
The above gives a bound on the Busemann function for the following when
![]() $\eta \le 1$
:
$\eta \le 1$
:
 $$ \begin{align} &e^{-\delta_{\Gamma} \operatorname{height}(x)}\nu_o(\operatorname{Pr}_{g^-}(B_U(\eta))) \nonumber\\[3pt] &\quad\ll_{\Gamma} \mu^{\operatorname{PS}}_g(B_U(\eta)) = \int_{\textbf{t} \in B_U(\eta)} e^{\delta_{\Gamma}\beta_{(u_{\textbf{t}} g)^+}(o,u_{\textbf{t}} g(o))} \,d\nu_o((u_{\textbf{t}} g)^+) \end{align} $$
$$ \begin{align} &e^{-\delta_{\Gamma} \operatorname{height}(x)}\nu_o(\operatorname{Pr}_{g^-}(B_U(\eta))) \nonumber\\[3pt] &\quad\ll_{\Gamma} \mu^{\operatorname{PS}}_g(B_U(\eta)) = \int_{\textbf{t} \in B_U(\eta)} e^{\delta_{\Gamma}\beta_{(u_{\textbf{t}} g)^+}(o,u_{\textbf{t}} g(o))} \,d\nu_o((u_{\textbf{t}} g)^+) \end{align} $$
Assume
![]() $c\ge 1$
. By Lemmas A.3 and A.6, we have that
$c\ge 1$
. By Lemmas A.3 and A.6, we have that
 $$ \begin{align} \nu_o(B(g^+,\eta))&= \nu_o(B(g^+,(\tilde{c}e^{\operatorname{height}(x)}\tilde{c}^{-1} e^{-\operatorname{height}(x)}\eta)) \nonumber \\[3pt] &\ll_{\Gamma} (\tilde{c}e^{\operatorname{height}(x)})^{\sigma_1} \nu_o(B(g^+,\tilde{c}e^{-\operatorname{height}(x)}\eta)). \end{align} $$
$$ \begin{align} \nu_o(B(g^+,\eta))&= \nu_o(B(g^+,(\tilde{c}e^{\operatorname{height}(x)}\tilde{c}^{-1} e^{-\operatorname{height}(x)}\eta)) \nonumber \\[3pt] &\ll_{\Gamma} (\tilde{c}e^{\operatorname{height}(x)})^{\sigma_1} \nu_o(B(g^+,\tilde{c}e^{-\operatorname{height}(x)}\eta)). \end{align} $$
Let
![]() $\tilde {c}>1$
be as in Corollary A.4. Then as long as
$\tilde {c}>1$
be as in Corollary A.4. Then as long as
we have the following:
 $$ \begin{align*} \mu^{\operatorname{PS}}_g(B_U(c\eta)) &\ll_{\Gamma} e^{\delta_{\Gamma} \operatorname{height}(x)} \nu_o(\operatorname{Pr}_{g^-}(B_U(c\eta)) \quad\text{by (116)}\\[3pt] &\ll_{\Gamma} e^{\delta_{\Gamma} \operatorname{height}(x)}\nu_o(B(g^+,\tilde{c}e^{\operatorname{height}(x)}c\eta)) \quad\text{by Corollary 9.4}\\[3pt] &\ll_{\Gamma} c^{\sigma} e^{(\delta_{\Gamma}+{\sigma_1})\operatorname{height}(x)}\nu_o(B(g^+,\eta)) \quad\text{by Lemma 9.6} \\[3pt] &\ll_{\Gamma} c^{\sigma_1} e^{(\delta_{\Gamma}+2{\sigma_1})\operatorname{height}(x)}\nu_o(B(g^+,\tilde{c}^{-1} e^{-\operatorname{height}(x)}\eta) \quad\text{by (117)}\\[3pt] &\ll_{\Gamma} c^{\sigma_1} e^{(\delta_{\Gamma}+2{\sigma_1})\operatorname{height}(x)}\nu_o(\operatorname{Pr}_{g^-}(B_U(\eta)))\quad\text{by Corollary 9.4}\\[3pt] &\ll_{\Gamma} c^{\sigma_1} e^{2(\delta_{\Gamma}+{\sigma_1})\operatorname{height}(x)}\mu^{\operatorname{PS}}_g(B_U(\eta)) \quad\text{by (115)}, \end{align*} $$
$$ \begin{align*} \mu^{\operatorname{PS}}_g(B_U(c\eta)) &\ll_{\Gamma} e^{\delta_{\Gamma} \operatorname{height}(x)} \nu_o(\operatorname{Pr}_{g^-}(B_U(c\eta)) \quad\text{by (116)}\\[3pt] &\ll_{\Gamma} e^{\delta_{\Gamma} \operatorname{height}(x)}\nu_o(B(g^+,\tilde{c}e^{\operatorname{height}(x)}c\eta)) \quad\text{by Corollary 9.4}\\[3pt] &\ll_{\Gamma} c^{\sigma} e^{(\delta_{\Gamma}+{\sigma_1})\operatorname{height}(x)}\nu_o(B(g^+,\eta)) \quad\text{by Lemma 9.6} \\[3pt] &\ll_{\Gamma} c^{\sigma_1} e^{(\delta_{\Gamma}+2{\sigma_1})\operatorname{height}(x)}\nu_o(B(g^+,\tilde{c}^{-1} e^{-\operatorname{height}(x)}\eta) \quad\text{by (117)}\\[3pt] &\ll_{\Gamma} c^{\sigma_1} e^{(\delta_{\Gamma}+2{\sigma_1})\operatorname{height}(x)}\nu_o(\operatorname{Pr}_{g^-}(B_U(\eta)))\quad\text{by Corollary 9.4}\\[3pt] &\ll_{\Gamma} c^{\sigma_1} e^{2(\delta_{\Gamma}+{\sigma_1})\operatorname{height}(x)}\mu^{\operatorname{PS}}_g(B_U(\eta)) \quad\text{by (115)}, \end{align*} $$
which completes the proof in this case.
The case
![]() $0<c<1$
can be shown in a similar way using Lemma A.7.
$0<c<1$
can be shown in a similar way using Lemma A.7.
When
![]() $x \in \operatorname {supp}m^{\operatorname {BMS}},$
a flowing argument with
$x \in \operatorname {supp}m^{\operatorname {BMS}},$
a flowing argument with
![]() $\{a_{-s}:s\ge 0\}$
allows us to remove the restriction that
$\{a_{-s}:s\ge 0\}$
allows us to remove the restriction that
![]() $\eta $
must be small in a way that depends on
$\eta $
must be small in a way that depends on
![]() $\operatorname {height}(x).$
More precisely, we obtain the corollary.
$\operatorname {height}(x).$
More precisely, we obtain the corollary.
Corollary A.9. If
![]() $\Gamma $
is geometrically finite and Zariski dense, then for any
$\Gamma $
is geometrically finite and Zariski dense, then for any
![]() $x\in \operatorname {supp}m^{\operatorname {BMS}}$
, the measure
$x\in \operatorname {supp}m^{\operatorname {BMS}}$
, the measure
![]() $\mu ^{\operatorname {PS}}_x$
is doubling, and the constants only depend on
$\mu ^{\operatorname {PS}}_x$
is doubling, and the constants only depend on
![]() $\Gamma $
. More precisely, there exist constants
$\Gamma $
. More precisely, there exist constants
![]() $\sigma _1 = \sigma _1(\Gamma )\ge \delta _{\Gamma }$
,
$\sigma _1 = \sigma _1(\Gamma )\ge \delta _{\Gamma }$
,
![]() $\sigma _2 = \sigma _2(\Gamma )>0$
such that for every
$\sigma _2 = \sigma _2(\Gamma )>0$
such that for every
![]() $c>0$
, every
$c>0$
, every
![]() $x \in \operatorname {supp}m^{\operatorname {BMS}}$
, and every
$x \in \operatorname {supp}m^{\operatorname {BMS}}$
, and every
![]() $T>0$
,
$T>0$
,
Proof. On a geometrically finite quotient, there exists a compact set
![]() $\Omega _0\subset X$
such that for every
$\Omega _0\subset X$
such that for every
![]() $x \in X$
with
$x \in X$
with
![]() $x^-\in \Lambda _r(\Gamma )$
, there exists a sequence
$x^-\in \Lambda _r(\Gamma )$
, there exists a sequence
![]() $s_n \to \infty $
such that
$s_n \to \infty $
such that
![]() $a_{-s_n}x \in \Omega _0$
.
$a_{-s_n}x \in \Omega _0$
.
Because
![]() $\Omega _0$
depends only on
$\Omega _0$
depends only on
![]() $\Gamma $
, the height of any point in
$\Gamma $
, the height of any point in
![]() $\Omega _0$
is bounded by a constant depending only on
$\Omega _0$
is bounded by a constant depending only on
![]() $\Gamma $
. Thus, by Corollary A.8, for all
$\Gamma $
. Thus, by Corollary A.8, for all
![]() $x \in \Omega _0 \cap \operatorname {supp}m^{\operatorname {BMS}}$
with
$x \in \Omega _0 \cap \operatorname {supp}m^{\operatorname {BMS}}$
with
![]() $x^-\in \Lambda _r(\Gamma )$
and for all
$x^-\in \Lambda _r(\Gamma )$
and for all
![]() $\eta \ll _{\Gamma } c^{-1},$
we have that
$\eta \ll _{\Gamma } c^{-1},$
we have that
Now, fix
![]() $x \in \operatorname {supp}m^{\operatorname {BMS}}$
with
$x \in \operatorname {supp}m^{\operatorname {BMS}}$
with
![]() $x^-\in \Lambda _r(\Gamma )$
. Let
$x^-\in \Lambda _r(\Gamma )$
. Let
![]() $T \ge 0$
and let
$T \ge 0$
and let
![]() $s>0$
be sufficiently large so that
$s>0$
be sufficiently large so that
![]() $e^{-s}T \ll _{\Gamma } c^{-1}$
and
$e^{-s}T \ll _{\Gamma } c^{-1}$
and
![]() $a_{-s}x \in \Omega _0.$
Then,
$a_{-s}x \in \Omega _0.$
Then,
 $$ \begin{align*} \mu^{\operatorname{PS}}_x(B_U(cT)) &= e^{\delta_{\Gamma} s}\mu^{\operatorname{PS}}_{a_{-s}x}(B_U(ce^{-s}T))\\[3pt] &\ll_{\Gamma} \max\{c^{\sigma_1}, c^{\sigma_2}\} e^{\delta_{\Gamma} s}\mu^{\operatorname{PS}}_{a_{-s}x}(B_U(e^{-s} T)) \quad\text{by (118)}\\[3pt] &\ll_{\Gamma} \max\{c^{\sigma_1}, c^{\sigma_2}\} \mu^{\operatorname{PS}}_{a_{-s}x}(B_U(T)), \end{align*} $$
$$ \begin{align*} \mu^{\operatorname{PS}}_x(B_U(cT)) &= e^{\delta_{\Gamma} s}\mu^{\operatorname{PS}}_{a_{-s}x}(B_U(ce^{-s}T))\\[3pt] &\ll_{\Gamma} \max\{c^{\sigma_1}, c^{\sigma_2}\} e^{\delta_{\Gamma} s}\mu^{\operatorname{PS}}_{a_{-s}x}(B_U(e^{-s} T)) \quad\text{by (118)}\\[3pt] &\ll_{\Gamma} \max\{c^{\sigma_1}, c^{\sigma_2}\} \mu^{\operatorname{PS}}_{a_{-s}x}(B_U(T)), \end{align*} $$
so the result holds for
![]() $x^- \in \Lambda _r(\Gamma ).$
$x^- \in \Lambda _r(\Gamma ).$
Since
![]() $x\mapsto \mu ^{\operatorname {PS}}_x$
is continuous (see Lemma 3.2) and the set of x with
$x\mapsto \mu ^{\operatorname {PS}}_x$
is continuous (see Lemma 3.2) and the set of x with
![]() $x^-\in \Lambda _r(\Gamma )$
is dense in the set of points
$x^-\in \Lambda _r(\Gamma )$
is dense in the set of points
![]() $y\in X$
which satisfy
$y\in X$
which satisfy
![]() $y^-\in \Lambda (\Gamma )$
, the result then follows for all
$y^-\in \Lambda (\Gamma )$
, the result then follows for all
![]() $x\in \operatorname {supp}m^{\operatorname {BMS}}.$
$x\in \operatorname {supp}m^{\operatorname {BMS}}.$
A.2 Non-planarity of the PS measure
For a subset
![]() $S\subseteq \mathbb R^{n-1}$
and
$S\subseteq \mathbb R^{n-1}$
and
![]() $\xi>0$
, let
$\xi>0$
, let
In the following, we use the shadow lemma for
![]() $\nu _o$
to obtain a stronger version of non-planarity than that in Definition A.1. From this, we will see that the PS measures when
$\nu _o$
to obtain a stronger version of non-planarity than that in Definition A.1. From this, we will see that the PS measures when
![]() $\Gamma $
is geometrically finite satisfies a non-planarity-like property. More specifically, the bound we get is independent of the hyperplane, but the size of
$\Gamma $
is geometrically finite satisfies a non-planarity-like property. More specifically, the bound we get is independent of the hyperplane, but the size of
![]() $\eta $
must be restricted in a way that depends on
$\eta $
must be restricted in a way that depends on
![]() $\operatorname {height}(x)$
, and a factor of
$\operatorname {height}(x)$
, and a factor of
![]() $\operatorname {height}(x)$
will appear.
$\operatorname {height}(x)$
will appear.
Theorem A.10. There exist
![]() $\theta =\theta (\Gamma )\ge 1$
,
$\theta =\theta (\Gamma )\ge 1$
,
![]() $\alpha =\alpha (\Gamma )>0$
which satisfy the following. For any
$\alpha =\alpha (\Gamma )>0$
which satisfy the following. For any
![]() $w \in {\mathbb H}^n$
,
$w \in {\mathbb H}^n$
,
![]() $\unicode{x3bb} \in \Lambda (\Gamma )$
,
$\unicode{x3bb} \in \Lambda (\Gamma )$
,
![]() $0<\eta \le 1$
, and
$0<\eta \le 1$
, and
![]() $\xi>0$
, we have
$\xi>0$
, we have
Proof. First, we show the result for o.
According to [Reference Das, Fishman, Simmons and Urbański5, Lemma 3.8], there exists
![]() $\beta>0$
such that for any
$\beta>0$
such that for any
![]() $\eta>0$
and any affine hyperplane
$\eta>0$
and any affine hyperplane
![]() $L\subset \mathbb R^n$
, we have
$L\subset \mathbb R^n$
, we have
For
![]() $\unicode{x3bb} \in \Lambda (\Gamma )$
and for
$\unicode{x3bb} \in \Lambda (\Gamma )$
and for
![]() $t\in \mathbb R$
, let
$t\in \mathbb R$
, let
![]() $\unicode{x3bb} _t$
be the unit speed geodesic ray from
$\unicode{x3bb} _t$
be the unit speed geodesic ray from
![]() ${o}$
to
${o}$
to
![]() $\unicode{x3bb} $
. It follows from the shadow lemma for
$\unicode{x3bb} $
. It follows from the shadow lemma for
![]() $\nu _o$
(see [Reference Stratmann and Velani35, Theorem 2], also [Reference Schapira33, Theorem 3.2]) that for any
$\nu _o$
(see [Reference Stratmann and Velani35, Theorem 2], also [Reference Schapira33, Theorem 3.2]) that for any
![]() $\eta>0$
, we have
$\eta>0$
, we have
where
![]() $k(\unicode{x3bb} _{-\log \eta })$
is the rank of the cusp containing
$k(\unicode{x3bb} _{-\log \eta })$
is the rank of the cusp containing
![]() $\unicode{x3bb} _{-\log \eta }$
(see §3.2). It follows from the fact that
$\unicode{x3bb} _{-\log \eta }$
(see §3.2). It follows from the fact that
![]() $k(\unicode{x3bb} _{-\log \eta })\ge 0$
and
$k(\unicode{x3bb} _{-\log \eta })\ge 0$
and
![]() $d({o},\unicode{x3bb} _{-\log \eta })\le -\log \eta $
, that
$d({o},\unicode{x3bb} _{-\log \eta })\le -\log \eta $
, that
Since
![]() $\nu _o$
is Federer (by Theorem A.2), using (A.1), we arrive at the same bound for Euclidean balls (with the implied constant changing):
$\nu _o$
is Federer (by Theorem A.2), using (A.1), we arrive at the same bound for Euclidean balls (with the implied constant changing):
Note that by the definition of
![]() $\Vert d_L\Vert _{\nu _o,B(\unicode{x3bb} ,\eta )}$
,
$\Vert d_L\Vert _{\nu _o,B(\unicode{x3bb} ,\eta )}$
,
It then follows from (A.16) and (A.17) that
Hence,
According to Theorem A.2, the PS density is friendly. In particular, it is decaying and non-planar, so there exists
![]() $\alpha> 0$
such that for all
$\alpha> 0$
such that for all
![]() $\unicode{x3bb} \in \Lambda (\Gamma )$
,
$\unicode{x3bb} \in \Lambda (\Gamma )$
,
![]() $0<\eta \le 1$
,
$0<\eta \le 1$
,
![]() $\xi>0$
, an affine hyperplane
$\xi>0$
, an affine hyperplane
![]() $L\subset \mathbb R^n$
, and
$L\subset \mathbb R^n$
, and
![]() $B=B(\unicode{x3bb} ,\eta )$
, we have
$B=B(\unicode{x3bb} ,\eta )$
, we have
The claim now follows for o from (A.18) and (A.19) by taking
![]() $\theta =2\delta _{\Gamma }/\beta $
.
$\theta =2\delta _{\Gamma }/\beta $
.
Second, we show the result for a general
![]() $w\in {\mathbb H}^n$
. Note that
$w\in {\mathbb H}^n$
. Note that
Thus, using this and the fact that
![]() $\{\nu _w\}_{w\in {\mathbb H}^n}$
is a conformal density satisfying (10), we arrive at
$\{\nu _w\}_{w\in {\mathbb H}^n}$
is a conformal density satisfying (10), we arrive at
 $$ \begin{align*} \nu_w(\mathcal{N}(L,\xi\eta^{\theta})\cap B(\unicode{x3bb},\eta))&\ll_{\Gamma} e^{\delta_{\Gamma} d(o,w)}\nu_o(\mathcal{N}(L,\xi\eta^{\theta})\cap B(\unicode{x3bb},\eta))\\[3pt] &\ll_{\Gamma}e^{\delta_{\Gamma} d(o,w)}\xi^{\alpha}\nu_o(B(\unicode{x3bb},\eta))\\[3pt] &\ll_{\Gamma} e^{2\delta_{\Gamma} d(o,w)}\xi^{\alpha}\nu_w(B(\unicode{x3bb},\eta)). \end{align*} $$
$$ \begin{align*} \nu_w(\mathcal{N}(L,\xi\eta^{\theta})\cap B(\unicode{x3bb},\eta))&\ll_{\Gamma} e^{\delta_{\Gamma} d(o,w)}\nu_o(\mathcal{N}(L,\xi\eta^{\theta})\cap B(\unicode{x3bb},\eta))\\[3pt] &\ll_{\Gamma}e^{\delta_{\Gamma} d(o,w)}\xi^{\alpha}\nu_o(B(\unicode{x3bb},\eta))\\[3pt] &\ll_{\Gamma} e^{2\delta_{\Gamma} d(o,w)}\xi^{\alpha}\nu_w(B(\unicode{x3bb},\eta)). \end{align*} $$
Last, note that by taking
![]() $\xi =\eta ^{1-\theta }$
, we conclude that
$\xi =\eta ^{1-\theta }$
, we conclude that
![]() $\theta \ge 1$
.
$\theta \ge 1$
.
Proposition A.11. Let
![]() $\Gamma $
be geometrically finite and Zariski dense. There exist constants
$\Gamma $
be geometrically finite and Zariski dense. There exist constants
![]() $\alpha = \alpha (\Gamma )>0, \omega =\omega (\Gamma ) \ge 0, $
and
$\alpha = \alpha (\Gamma )>0, \omega =\omega (\Gamma ) \ge 0, $
and
![]() $\theta = \theta (\Gamma )>\alpha $
satisfying the following: for any
$\theta = \theta (\Gamma )>\alpha $
satisfying the following: for any
![]() $x \in G/\Gamma $
with
$x \in G/\Gamma $
with
![]() $x^+\in \Lambda (\Gamma )$
, and for every
$x^+\in \Lambda (\Gamma )$
, and for every
![]() $\xi>0$
and
$\xi>0$
and
![]() $0<\eta \ll _{\Gamma } e^{-\operatorname {height}(x)}$
, we have that for every hyperplane L,
$0<\eta \ll _{\Gamma } e^{-\operatorname {height}(x)}$
, we have that for every hyperplane L,
Proof. Let
![]() $\alpha =\alpha (\Gamma ),\theta =\theta (\Gamma )>0$
satisfy the conclusion of Theorem A.10, and
$\alpha =\alpha (\Gamma ),\theta =\theta (\Gamma )>0$
satisfy the conclusion of Theorem A.10, and
![]() $c'>1$
satisfy the conclusion of Corollary A.4. Fix
$c'>1$
satisfy the conclusion of Corollary A.4. Fix
![]() $g\in G$
which satisfies
$g\in G$
which satisfies
![]() $x=g\Gamma $
and
$x=g\Gamma $
and
![]() $\operatorname {height}(x)=d(\pi (\mathcal {C}_0),\pi (g)).$
$\operatorname {height}(x)=d(\pi (\mathcal {C}_0),\pi (g)).$
By the same argument as in the proof of Corollary A.8 to bound the Busemann function when
![]() $\eta \le 1$
, we obtain
$\eta \le 1$
, we obtain
 $$ \begin{align*} &e^{-\delta_{\Gamma} \operatorname{height}(x)}\nu_o(\operatorname{Pr}_{g^-}(\mathcal{N}(L,\xi)x\cap B_U(\eta)x)) \\[3pt] &\quad\ll_{\Gamma} \mu^{\operatorname{PS}}_g(\mathcal{N}(L,\xi)\cap B_U(\eta)) = \int_{\textbf{t} \in \mathcal{N}(L,\xi)\cap B_U(\eta)} e^{\delta_{\Gamma}\beta_{(u_{\textbf{t}} g)^+}(o,u_{\textbf{t}} g(o))} \,d\nu_o((u_{\textbf{t}} g)^+) \\[3pt] &\quad\ll_{\Gamma} e^{\delta_{\Gamma} \operatorname{height}(x)} \nu_o(\operatorname{Pr}_{g^-}(\mathcal{N}(L,\xi)x\cap B_U(\eta)x)). \end{align*} $$
$$ \begin{align*} &e^{-\delta_{\Gamma} \operatorname{height}(x)}\nu_o(\operatorname{Pr}_{g^-}(\mathcal{N}(L,\xi)x\cap B_U(\eta)x)) \\[3pt] &\quad\ll_{\Gamma} \mu^{\operatorname{PS}}_g(\mathcal{N}(L,\xi)\cap B_U(\eta)) = \int_{\textbf{t} \in \mathcal{N}(L,\xi)\cap B_U(\eta)} e^{\delta_{\Gamma}\beta_{(u_{\textbf{t}} g)^+}(o,u_{\textbf{t}} g(o))} \,d\nu_o((u_{\textbf{t}} g)^+) \\[3pt] &\quad\ll_{\Gamma} e^{\delta_{\Gamma} \operatorname{height}(x)} \nu_o(\operatorname{Pr}_{g^-}(\mathcal{N}(L,\xi)x\cap B_U(\eta)x)). \end{align*} $$
Thus, for
![]() $\eta \ll _{\Gamma } e^{-\operatorname {height}(x)}$
(so that
$\eta \ll _{\Gamma } e^{-\operatorname {height}(x)}$
(so that
![]() $ce^{d(o,\pi (x))}\eta \le 1$
in the following, and we stay within the injectivity radius at x, using (22)), we have that
$ce^{d(o,\pi (x))}\eta \le 1$
in the following, and we stay within the injectivity radius at x, using (22)), we have that
 $$ \begin{align*} &\mu^{\operatorname{PS}}_x(\mathcal{N}_U(L,\xi)\cap B_U(\eta))\\[3pt] & \quad\ll_{\Gamma}e^{\delta_{\Gamma} \operatorname{height}(x)}\nu_o(\operatorname{Pr}_{g^-}(\mathcal{N}(L,\xi)\cap B_U(\eta)))\\[3pt] &\quad\ll_{\Gamma}e^{\delta_{\Gamma} \operatorname{height}(x)}\nu_o(\mathcal{N}(L', ce^{d(o,\pi(x))}\xi)\cap B(g^+, c e^{d(o,\pi(x))}\eta)) \quad\text{by Corollary 9.5}\\ & \quad\ll_{\Gamma}e^{\delta_{\Gamma} \operatorname{height}(x)} \bigg(\frac{\xi({c}e^{d(o,\pi(x))})^{1-\theta}}{\eta^{\theta}}\bigg)^{\alpha}\nu_o( B(g^+, ce^{d(o,\pi(x))}\eta)) \quad \text{by Theorem 9.10}\\[3pt] &\quad\ll_{\Gamma} e^{\delta_{\Gamma} \operatorname{height}(x)}\bigg(\frac{\xi(e^{d(o,\pi(x))})^{1-\theta}}{\eta^{\theta}}\bigg)^{\alpha} e^{d(o,\pi(x))\sigma}\nu_o(B(g^+,\eta)) \quad\text{by Lemma 9.6}\\[3pt] &\quad\ll_{\Gamma} e^{\delta_{\Gamma} \operatorname{height}(x)}\bigg(\frac{\xi(e^{d(o,\pi(x))})^{1-\theta}}{\eta^{\theta}}\bigg)^{\alpha}\\[3pt] &\qquad e^{2d(o,\pi(x))\sigma}\nu_o(B(g^+,c^{-1} e^{-d(o,\pi(x)}\eta)) \quad\text{by Corollary 9.4} \\[3pt] &\quad\ll_{\Gamma} e^{2\delta_{\Gamma} \operatorname{height}(x)+(\sigma+(1-\theta)\alpha) d(o,\pi(x))}\bigg(\frac{\xi}{\eta^{\theta}}\bigg)^{\alpha} \mu^{\operatorname{PS}}_x(B_U(\eta))\\[3pt] &\quad\ll_{\Gamma} e^{(2\delta_{\Gamma} + \sigma+(1-\theta)\alpha)\operatorname{height}(x)} \bigg(\frac{\xi}{\eta^{\theta}}\bigg)^{\alpha} \mu^{\operatorname{PS}}_x(B_U(\eta))\\[3pt] &\quad\ll_{\Gamma} e^{\omega\operatorname{height}(x)}\frac{\xi^{\alpha}}{\eta^{\theta'}} \mu^{\operatorname{PS}}_x(B_U(\eta)), \end{align*} $$
$$ \begin{align*} &\mu^{\operatorname{PS}}_x(\mathcal{N}_U(L,\xi)\cap B_U(\eta))\\[3pt] & \quad\ll_{\Gamma}e^{\delta_{\Gamma} \operatorname{height}(x)}\nu_o(\operatorname{Pr}_{g^-}(\mathcal{N}(L,\xi)\cap B_U(\eta)))\\[3pt] &\quad\ll_{\Gamma}e^{\delta_{\Gamma} \operatorname{height}(x)}\nu_o(\mathcal{N}(L', ce^{d(o,\pi(x))}\xi)\cap B(g^+, c e^{d(o,\pi(x))}\eta)) \quad\text{by Corollary 9.5}\\ & \quad\ll_{\Gamma}e^{\delta_{\Gamma} \operatorname{height}(x)} \bigg(\frac{\xi({c}e^{d(o,\pi(x))})^{1-\theta}}{\eta^{\theta}}\bigg)^{\alpha}\nu_o( B(g^+, ce^{d(o,\pi(x))}\eta)) \quad \text{by Theorem 9.10}\\[3pt] &\quad\ll_{\Gamma} e^{\delta_{\Gamma} \operatorname{height}(x)}\bigg(\frac{\xi(e^{d(o,\pi(x))})^{1-\theta}}{\eta^{\theta}}\bigg)^{\alpha} e^{d(o,\pi(x))\sigma}\nu_o(B(g^+,\eta)) \quad\text{by Lemma 9.6}\\[3pt] &\quad\ll_{\Gamma} e^{\delta_{\Gamma} \operatorname{height}(x)}\bigg(\frac{\xi(e^{d(o,\pi(x))})^{1-\theta}}{\eta^{\theta}}\bigg)^{\alpha}\\[3pt] &\qquad e^{2d(o,\pi(x))\sigma}\nu_o(B(g^+,c^{-1} e^{-d(o,\pi(x)}\eta)) \quad\text{by Corollary 9.4} \\[3pt] &\quad\ll_{\Gamma} e^{2\delta_{\Gamma} \operatorname{height}(x)+(\sigma+(1-\theta)\alpha) d(o,\pi(x))}\bigg(\frac{\xi}{\eta^{\theta}}\bigg)^{\alpha} \mu^{\operatorname{PS}}_x(B_U(\eta))\\[3pt] &\quad\ll_{\Gamma} e^{(2\delta_{\Gamma} + \sigma+(1-\theta)\alpha)\operatorname{height}(x)} \bigg(\frac{\xi}{\eta^{\theta}}\bigg)^{\alpha} \mu^{\operatorname{PS}}_x(B_U(\eta))\\[3pt] &\quad\ll_{\Gamma} e^{\omega\operatorname{height}(x)}\frac{\xi^{\alpha}}{\eta^{\theta'}} \mu^{\operatorname{PS}}_x(B_U(\eta)), \end{align*} $$
where
A.3 Absolute friendliness of the PS measure
When all cusps are of maximal rank, the PS measure is absolutely friendly, and stronger results hold. Note that if
![]() $\Gamma $
is convex cocompact, then there are no cusps, so this additional assumption is vacuously true.
$\Gamma $
is convex cocompact, then there are no cusps, so this additional assumption is vacuously true.
Definition A.12. Let
![]() $\mu $
be a measure defined on
$\mu $
be a measure defined on
![]() $\mathbb R^m$
.
$\mathbb R^m$
.
-
(1)
 $\mu $
is called absolutely decaying (respectively globally absolutely decaying) if there exist
$\mu $
is called absolutely decaying (respectively globally absolutely decaying) if there exist
 $\alpha ,c_2>0$
such that for all
$\alpha ,c_2>0$
such that for all
 $v \in \operatorname {supp}\mu $
, all
$v \in \operatorname {supp}\mu $
, all
 $0<\xi <\eta \le 1$
(respectively
$0<\xi <\eta \le 1$
(respectively
 $0<\xi <\eta $
), and every affine hyperplane
$0<\xi <\eta $
), and every affine hyperplane
 $L \subseteq \mathbb R^{n}$
,
$L \subseteq \mathbb R^{n}$
,  $$ \begin{align*} \mu(\mathcal{N}(L,\xi)\cap B(v,\eta)) \le c_2\bigg(\frac{\xi}{\eta}\bigg)^{\alpha} \mu (B(v,\eta)). \end{align*} $$
$$ \begin{align*} \mu(\mathcal{N}(L,\xi)\cap B(v,\eta)) \le c_2\bigg(\frac{\xi}{\eta}\bigg)^{\alpha} \mu (B(v,\eta)). \end{align*} $$
-
(2)
 $\mu $
is called absolutely friendly (respectively globally friendly) if it is Federer (respectively doubling) and absolutely decaying (respectively globally absolutely decaying).
$\mu $
is called absolutely friendly (respectively globally friendly) if it is Federer (respectively doubling) and absolutely decaying (respectively globally absolutely decaying).
It is easy to see that if a measure
![]() $\mu $
is globally friendly, then it is also absolutely friendly.
$\mu $
is globally friendly, then it is also absolutely friendly.
According to [Reference Stratmann and Urbański34, Theorem 2], if
![]() $\Gamma $
is convex cocompact or [Reference Das, Fishman, Simmons and Urbański5, Theorem 1.12], if
$\Gamma $
is convex cocompact or [Reference Das, Fishman, Simmons and Urbański5, Theorem 1.12], if
![]() $\Gamma $
is geometrically finite,
$\Gamma $
is geometrically finite,
![]() $\nu _o$
is absolutely friendly if and only if all cusps have maximal rank.
$\nu _o$
is absolutely friendly if and only if all cusps have maximal rank.
Theorem A.13. Assume that
![]() $\Gamma $
is Zariski dense and either convex cocompact or geometrically finite with all cusps having maximal rank. Then the PS measures
$\Gamma $
is Zariski dense and either convex cocompact or geometrically finite with all cusps having maximal rank. Then the PS measures
![]() $\{\mu ^{\operatorname {PS}}_x\}_{x^-\in \Lambda (\Gamma )}$
are globally friendly, and the constants in Definition A.12 only depend on
$\{\mu ^{\operatorname {PS}}_x\}_{x^-\in \Lambda (\Gamma )}$
are globally friendly, and the constants in Definition A.12 only depend on
![]() $\Gamma $
(in particular, they do not depend on x).
$\Gamma $
(in particular, they do not depend on x).
This follows by a flowing argument, similar to the doubling results for
![]() $x \in \operatorname {supp}m^{\operatorname {BMS}}$
proven before. The key difference is observed by contrasting Definition A.12(1) with Theorem A.10: when the powers of
$x \in \operatorname {supp}m^{\operatorname {BMS}}$
proven before. The key difference is observed by contrasting Definition A.12(1) with Theorem A.10: when the powers of
![]() $\xi , \eta $
match, a flowing argument may be used for BMS points. When they do not match, one introduces a power corresponding to how far one flows with
$\xi , \eta $
match, a flowing argument may be used for BMS points. When they do not match, one introduces a power corresponding to how far one flows with
![]() $a_{-s}$
.
$a_{-s}$
.
Corollary A.14. Assume that
![]() $\Gamma $
is Zariski dense and either convex cocompact or geometrically finite with all cusps having maximal rank. There exists
$\Gamma $
is Zariski dense and either convex cocompact or geometrically finite with all cusps having maximal rank. There exists
![]() $0<\alpha =\alpha (\Gamma )<1$
such that for any
$0<\alpha =\alpha (\Gamma )<1$
such that for any
![]() $x\in \operatorname {supp}m^{\operatorname {BMS}}$
,
$x\in \operatorname {supp}m^{\operatorname {BMS}}$
,
![]() $T>0$
, and
$T>0$
, and
![]() $0<\xi \le T$
, we have
$0<\xi \le T$
, we have
 $$ \begin{align*} \frac{\mu^{\operatorname{PS}}_x(B_U(T+\xi))}{\mu^{\operatorname{PS}}_x(B_U(T))} -1 \ll_{\Gamma}\bigg(\frac{\xi}{T}\bigg)^{\alpha}. \end{align*} $$
$$ \begin{align*} \frac{\mu^{\operatorname{PS}}_x(B_U(T+\xi))}{\mu^{\operatorname{PS}}_x(B_U(T))} -1 \ll_{\Gamma}\bigg(\frac{\xi}{T}\bigg)^{\alpha}. \end{align*} $$
Proof. Let
![]() $c_1=c_1(\Gamma ),c_2=c_2(\Gamma )>0$
and
$c_1=c_1(\Gamma ),c_2=c_2(\Gamma )>0$
and
![]() $\alpha =\alpha (\Gamma )>0$
satisfy the conclusion of Definition A.12 for
$\alpha =\alpha (\Gamma )>0$
satisfy the conclusion of Definition A.12 for
![]() $\mu ^{\operatorname {PS}}_x$
and
$\mu ^{\operatorname {PS}}_x$
and
![]() $k=2$
.
$k=2$
.
It follows from the geometry of
![]() $B_U(\xi +\eta )x-B_U(\eta )x$
that there exist
$B_U(\xi +\eta )x-B_U(\eta )x$
that there exist
![]() $L_1,\ldots ,L_m$
, where m only depends on n, such that
$L_1,\ldots ,L_m$
, where m only depends on n, such that
 $$ \begin{align*} B_U(\xi+T)x-B_U(T)x\subseteq\bigcup_{i=1}^{m} \mathcal{N}_U(L_i,2\xi).\end{align*} $$
$$ \begin{align*} B_U(\xi+T)x-B_U(T)x\subseteq\bigcup_{i=1}^{m} \mathcal{N}_U(L_i,2\xi).\end{align*} $$
Then, by Definition A.12, we have
 $$ \begin{align*} \frac{\mu^{\operatorname{PS}}_x(B_U(\xi+T))}{\mu^{\operatorname{PS}}_x(B_U(T))} -1 & =\frac{\mu^{\operatorname{PS}}_x(B_U(\xi+T)-B_U(T))}{\mu^{\operatorname{PS}}_x(B_U(T))}\\[3pt] &\le m c_2\bigg(\frac{\xi}{T}\bigg)^{\alpha}\frac{\mu^{\operatorname{PS}}_x(B_U(\xi+T))}{\mu^{\operatorname{PS}}_x(B_U(T))}\\[3pt] &\le m c_1 c_2\bigg(\frac{\xi}{T}\bigg)^{\alpha}.\\[-3.3pc] \end{align*} $$
$$ \begin{align*} \frac{\mu^{\operatorname{PS}}_x(B_U(\xi+T))}{\mu^{\operatorname{PS}}_x(B_U(T))} -1 & =\frac{\mu^{\operatorname{PS}}_x(B_U(\xi+T)-B_U(T))}{\mu^{\operatorname{PS}}_x(B_U(T))}\\[3pt] &\le m c_2\bigg(\frac{\xi}{T}\bigg)^{\alpha}\frac{\mu^{\operatorname{PS}}_x(B_U(\xi+T))}{\mu^{\operatorname{PS}}_x(B_U(T))}\\[3pt] &\le m c_1 c_2\bigg(\frac{\xi}{T}\bigg)^{\alpha}.\\[-3.3pc] \end{align*} $$