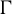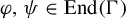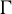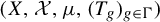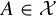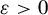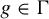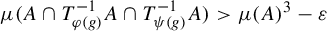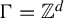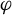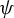1 Introduction
This paper is a continuation of work of the author together with Bergelson and Best [Reference Ackelsberg, Bergelson and Best1] and Bergelson and Shalom [Reference Ackelsberg, Bergelson and Shalom2] investigating the phenomenon of multiple recurrence with large intersections for actions of countable abelian groups (see also [Reference Shalom31]).
1.1 Background and motivation
The impetus for studying large intersections for multiple recurrence comes from the following two classical results.
Theorem 1.1. [Reference Khintchine24]
For any invertible measure-preserving system
![]() $(X, {\mathcal {X}}, \mu , T )$
, any
$(X, {\mathcal {X}}, \mu , T )$
, any
![]() $A \in {\mathcal {X}}$
, and any
$A \in {\mathcal {X}}$
, and any
![]() ${\varepsilon }> 0$
, the set
${\varepsilon }> 0$
, the set
has bounded gaps.
Theorem 1.2. [Reference Furstenberg12]
For any invertible measure-preserving system
![]() $(X, {\mathcal {X}}, \mu , T)$
, any
$(X, {\mathcal {X}}, \mu , T)$
, any
![]() $A \in {\mathcal {X}}$
with
$A \in {\mathcal {X}}$
with
![]() $\mu (A)> 0$
, and any positive integer
$\mu (A)> 0$
, and any positive integer
![]() $k \in {\mathbb {N}}$
,
$k \in {\mathbb {N}}$
,
 $$ \begin{align*} \liminf_{N-M \to \infty}{\frac{1}{N-M} \sum_{n=M}^{N-1}{\mu( A \cap T^{-n}A \cap \cdots \cap T^{-kn}A )}}> 0. \end{align*} $$
$$ \begin{align*} \liminf_{N-M \to \infty}{\frac{1}{N-M} \sum_{n=M}^{N-1}{\mu( A \cap T^{-n}A \cap \cdots \cap T^{-kn}A )}}> 0. \end{align*} $$
In particular, there exists
![]() $c> 0$
such that the set
$c> 0$
such that the set
has bounded gaps.
A subset of
![]() ${\mathbb {Z}}$
with bounded gaps is called syndetic. More generally, in a countable discrete abelian group
${\mathbb {Z}}$
with bounded gaps is called syndetic. More generally, in a countable discrete abelian group
![]() $(\Gamma , +)$
, a subset
$(\Gamma , +)$
, a subset
![]() $S \subseteq \Gamma $
is syndetic if finitely many translates of S cover
$S \subseteq \Gamma $
is syndetic if finitely many translates of S cover
![]() $\Gamma $
.
$\Gamma $
.
With the aim of finding a common refinement of Theorems 1.1 and 1.2, Bergelson, Host, and Kra [Reference Bergelson, Host and Kra6] asked whether, for a measure-preserving system
![]() $(X, {\mathcal {X}}, \mu , T)$
, a set
$(X, {\mathcal {X}}, \mu , T)$
, a set
![]() $A \in {\mathcal {X}}$
with
$A \in {\mathcal {X}}$
with
![]() $\mu (A)> 0$
, and
$\mu (A)> 0$
, and
![]() ${\varepsilon }> 0$
, the set
${\varepsilon }> 0$
, the set
is syndetic. They found that the answer depends on the length
![]() $(k+1)$
of the arithmetic progression.
$(k+1)$
of the arithmetic progression.
Theorem 1.3. [Reference Bergelson, Host and Kra6, Theorems 1.2 and 1.3]
-
(1) For any ergodic measure-preserving system
 $(X, {\mathcal {X}}, \mu , T )$
, any
$(X, {\mathcal {X}}, \mu , T )$
, any
 $A \in {\mathcal {X}}$
, and any
$A \in {\mathcal {X}}$
, and any
 ${\varepsilon }> 0$
, the sets and
${\varepsilon }> 0$
, the sets and $$ \begin{align*} \{ n \in {\mathbb{Z}} : \mu ( A \cap T^{-n}A \cap T^{-2n}A )> \mu(A)^3 - {\varepsilon} \} \end{align*} $$
are syndetic.
$$ \begin{align*} \{ n \in {\mathbb{Z}} : \mu ( A \cap T^{-n}A \cap T^{-2n}A )> \mu(A)^3 - {\varepsilon} \} \end{align*} $$
are syndetic. $$ \begin{align*} \{ n \in {\mathbb{Z}} : \mu ( A \cap T^{-n}A \cap T^{-2n}A \cap T^{-3n}A )> \mu(A)^4 - {\varepsilon} \} \end{align*} $$
$$ \begin{align*} \{ n \in {\mathbb{Z}} : \mu ( A \cap T^{-n}A \cap T^{-2n}A \cap T^{-3n}A )> \mu(A)^4 - {\varepsilon} \} \end{align*} $$
-
(2) There exists an ergodic measure-preserving system
 $(X, {\mathcal {X}}, \mu , T)$
with the following property. For any
$(X, {\mathcal {X}}, \mu , T)$
with the following property. For any
 $l \in {\mathbb {N}}$
, there exists
$l \in {\mathbb {N}}$
, there exists
 $A = A(l) \in {\mathcal {X}}$
with
$A = A(l) \in {\mathcal {X}}$
with
 $\mu (A)> 0$
such that for every
$\mu (A)> 0$
such that for every $$ \begin{align*} \mu ( A \cap T^{-n}A \cap T^{-2n}A \cap T^{-3n}A \cap T^{-4n}A ) \le \mu(A)^l \end{align*} $$
$$ \begin{align*} \mu ( A \cap T^{-n}A \cap T^{-2n}A \cap T^{-3n}A \cap T^{-4n}A ) \le \mu(A)^l \end{align*} $$
 $n \ne 0$
.
$n \ne 0$
.
Remark 1.4. The ergodicity assumption in item (1) cannot be dropped. An adaptation of Behrend’s construction of sets avoiding 3-term arithmetic progressions [Reference Behrend4] can be used to produce a counterexample for the non-ergodic transformation
![]() $T(x,y) = (x, y+x)$
on the 2-torus
$T(x,y) = (x, y+x)$
on the 2-torus
![]() ${\mathbb {T}}^2$
; see [Reference Bergelson, Host and Kra6, Theorem 2.1].
${\mathbb {T}}^2$
; see [Reference Bergelson, Host and Kra6, Theorem 2.1].
The combinatorial content of Theorem 1.3(1) is expressed by the following closely related result.
Theorem 1.5. [Reference Green17, Theorem 1.10], [Reference Green and Tao19, Theorem 1.12]
Let
![]() $\alpha , {\varepsilon }> 0$
.
$\alpha , {\varepsilon }> 0$
.
-
(1) There exists
 $N_3 = N_3(\alpha , {\varepsilon }) \in {\mathbb {N}}$
such that if
$N_3 = N_3(\alpha , {\varepsilon }) \in {\mathbb {N}}$
such that if
 $N \ge N_3$
and
$N \ge N_3$
and
 $A \subseteq \{1, \ldots , N\}$
has cardinality
$A \subseteq \{1, \ldots , N\}$
has cardinality
 $|A| \ge \alpha N$
, then there exists
$|A| \ge \alpha N$
, then there exists
 $d \in {\mathbb {N}}$
such that
$d \in {\mathbb {N}}$
such that  $$ \begin{align*} | \{ a \in {\mathbb{N}} : \{a, a+d, a+2d\} \subseteq A \} |> (\alpha^3 - {\varepsilon}) N. \end{align*} $$
$$ \begin{align*} | \{ a \in {\mathbb{N}} : \{a, a+d, a+2d\} \subseteq A \} |> (\alpha^3 - {\varepsilon}) N. \end{align*} $$
-
(2) There exists
 $N_4 = N_4(\alpha , {\varepsilon }) \in {\mathbb {N}}$
such that if
$N_4 = N_4(\alpha , {\varepsilon }) \in {\mathbb {N}}$
such that if
 $N \ge N_4$
and
$N \ge N_4$
and
 $A \subseteq \{1, \ldots , N\}$
has cardinality
$A \subseteq \{1, \ldots , N\}$
has cardinality
 $|A| \ge \alpha N$
, then there exists
$|A| \ge \alpha N$
, then there exists
 $d \in {\mathbb {N}}$
such that
$d \in {\mathbb {N}}$
such that  $$ \begin{align*} | \{ a \in {\mathbb{N}} : \{a, a+d, a+2d, a+3d\} \subseteq A \} |> (\alpha^4 - {\varepsilon}) N. \end{align*} $$
$$ \begin{align*} | \{ a \in {\mathbb{N}} : \{a, a+d, a+2d, a+3d\} \subseteq A \} |> (\alpha^4 - {\varepsilon}) N. \end{align*} $$
Remark 1.6
-
(1) The positive integers
 $d \in {\mathbb {N}}$
appearing in Theorem 1.5 are sometimes referred to as popular differences, since they are common differences for many arithmetic progressions contained in A.
$d \in {\mathbb {N}}$
appearing in Theorem 1.5 are sometimes referred to as popular differences, since they are common differences for many arithmetic progressions contained in A. -
(2) Theorem 1.3 can be converted directly into a combinatorial statement involving sets of positive upper Banach density by a version of the Furstenberg correspondence principle that produces ergodic measure-preserving systems; see [Reference Bergelson, Host and Kra6, §1.2]. However, no simple argument is known to deduce Theorem 1.5 from Theorem 1.3 or vice versa.
In other contexts in which a multiple recurrence result is known, one may again ask whether it is possible to find a corresponding Khintchine-type enhancement. Pursuing this line of inquiry, Bergelson, Tao, and Ziegler [Reference Bergelson, Tao and Ziegler9] established a Khintchine-type recurrence result for actions of the group
![]() ${\mathbb {F}}_p^{\infty }$
.
${\mathbb {F}}_p^{\infty }$
.
Theorem 1.7. [Reference Bergelson, Tao and Ziegler9, Theorems 1.12 and 1.13]
Fix a prime p and
![]() $a, b \in {\mathbb {F}}_p$
. For any ergodic measure-preserving
$a, b \in {\mathbb {F}}_p$
. For any ergodic measure-preserving
![]() ${\mathbb {F}}_p^{\infty }$
-system
${\mathbb {F}}_p^{\infty }$
-system
![]() $( X, {\mathcal {X}}, \mu , (T_g)_{g \in {\mathbb {F}}_p^{\infty }} )$
, any
$( X, {\mathcal {X}}, \mu , (T_g)_{g \in {\mathbb {F}}_p^{\infty }} )$
, any
![]() $A \in {\mathcal {X}}$
, and any
$A \in {\mathcal {X}}$
, and any
![]() ${\varepsilon }> 0$
, the sets
${\varepsilon }> 0$
, the sets
and
are syndetic.
A finitary combinatorial analog of Theorem 1.7 along the lines of Theorem 1.5 can be deduced using the methods established in [Reference Green17, Reference Green and Tao19], which in fact apply to general finite abelian groups. See also [Reference Green18, Lecture 4].
The most general multiple recurrence result with which we will concern ourselves is the following theorem, which can be seen as a consequence of [Reference Furstenberg and Katznelson13] or [Reference Austin3, Theorem B].
Theorem 1.8. Let
![]() $\Gamma $
be a countable discrete abelian group. Let
$\Gamma $
be a countable discrete abelian group. Let
![]() $k \in {\mathbb {N}}$
and let
$k \in {\mathbb {N}}$
and let
![]() $\varphi _1, \ldots , \varphi _k \in \mathrm{End}(\Gamma )$
. For any measure-preserving
$\varphi _1, \ldots , \varphi _k \in \mathrm{End}(\Gamma )$
. For any measure-preserving
![]() $\Gamma $
-system
$\Gamma $
-system
![]() $( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
and any set
$( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
and any set
![]() $A \in {\mathcal {X}}$
, the set
$A \in {\mathcal {X}}$
, the set
is syndetic.
Remark 1.9. When dealing with topological groups, one may wish to impose various continuity assumptions (for instance, on the endomorphisms
![]() $\varphi _1, \ldots , \varphi _k$
or on the action of
$\varphi _1, \ldots , \varphi _k$
or on the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $(X, {\mathcal {X}}, \mu )$
). Moreover, notions of largeness for subsets of
$(X, {\mathcal {X}}, \mu )$
). Moreover, notions of largeness for subsets of
![]() $\Gamma $
such as syndeticity and upper Banach density (discussed in §1.3) depend on the topology on
$\Gamma $
such as syndeticity and upper Banach density (discussed in §1.3) depend on the topology on
![]() $\Gamma $
. We assume that
$\Gamma $
. We assume that
![]() $\Gamma $
is discrete to avoid such topological issues.
$\Gamma $
is discrete to avoid such topological issues.
The foregoing discussion motivates the following general definition.
Definition 1.10. Let
![]() $\Gamma $
be a countable discrete abelian group. A family of endomorphisms
$\Gamma $
be a countable discrete abelian group. A family of endomorphisms
![]() $\varphi _1, \ldots , \varphi _k \in \mathrm {End}(\Gamma )$
has the large intersections property if the following holds: for any ergodic measure-preserving
$\varphi _1, \ldots , \varphi _k \in \mathrm {End}(\Gamma )$
has the large intersections property if the following holds: for any ergodic measure-preserving
![]() $\Gamma $
-system
$\Gamma $
-system
![]() $( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
, any
$( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
, any
![]() $A \in {\mathcal {X}}$
, and any
$A \in {\mathcal {X}}$
, and any
![]() ${\varepsilon }> 0$
, the set
${\varepsilon }> 0$
, the set
is syndetic.
We now give a brief summary of the previously known results about the large intersections property in general countable discrete abelian groups.
In [Reference Ackelsberg, Bergelson and Best1], a far-reaching generalization of Theorems 1.3 and 1.7 for configurations of length 3 and 4 was obtained (in a slight abuse of notation, we abbreviate a family of endomorphisms of the form
![]() $\{g \mapsto a_1 g, \ldots , g \mapsto a_k g\}$
by
$\{g \mapsto a_1 g, \ldots , g \mapsto a_k g\}$
by
![]() $\{a_1, \ldots , a_k\}$
).
$\{a_1, \ldots , a_k\}$
).
Theorem 1.11. [Reference Ackelsberg, Bergelson and Best1, Theorems 1.10 and 1.11]
Let
![]() $\Gamma $
be a countable discrete abelian group.
$\Gamma $
be a countable discrete abelian group.
-
(1) If
 $\varphi , \psi \in \mathrm {End}(\Gamma )$
are such that all three subgroups
$\varphi , \psi \in \mathrm {End}(\Gamma )$
are such that all three subgroups
 $\varphi (\Gamma )$
,
$\varphi (\Gamma )$
,
 $\psi (\Gamma )$
, and
$\psi (\Gamma )$
, and
 $(\psi - \varphi )(\Gamma )$
have finite index in
$(\psi - \varphi )(\Gamma )$
have finite index in
 $\Gamma $
, then
$\Gamma $
, then
 $\{\varphi , \psi \}$
has the large intersections property.
$\{\varphi , \psi \}$
has the large intersections property. -
(2) If
 $a, b \in {\mathbb {Z}}$
and all four subgroups
$a, b \in {\mathbb {Z}}$
and all four subgroups
 $a\Gamma $
,
$a\Gamma $
,
 $b\Gamma $
,
$b\Gamma $
,
 $(a+b)\Gamma $
, and
$(a+b)\Gamma $
, and
 $(b-a)\Gamma $
have finite index in
$(b-a)\Gamma $
have finite index in
 $\Gamma $
, then
$\Gamma $
, then
 $\{a, b, a+b\}$
has the large intersections property.
$\{a, b, a+b\}$
has the large intersections property.
Remark 1.12. Endomorphisms of groups with finite index conditions of the kind appearing in item (1) of Theorem 1.11 have led to fruitful developments in a number of areas of ergodic theory and combinatorics; see, e.g., [Reference Griesmer20, Reference Griesmer, Le and Lê21, Reference Le and Lê26, Reference Pilatte28, Reference Prendiville29].
Item (2) in Theorem 1.11 was also obtained independently by Shalom; see [Reference Shalom31, Theorem 1.3]. In joint work with Bergelson and Shalom, item (1) of Theorem 1.11 was strengthened as follows.
Theorem 1.13. [Reference Ackelsberg, Bergelson and Shalom2, Theorems 1.11 and 1.13]
Let
![]() $\Gamma $
be a countable discrete abelian group.
$\Gamma $
be a countable discrete abelian group.
-
(1) Suppose
 $\varphi , \psi \in \mathrm {End}(\Gamma )$
and two of the three subgroups
$\varphi , \psi \in \mathrm {End}(\Gamma )$
and two of the three subgroups
 $\varphi (\Gamma )$
,
$\varphi (\Gamma )$
,
 $\psi (\Gamma )$
, and
$\psi (\Gamma )$
, and
 $(\psi - \varphi )(\Gamma )$
have finite index in
$(\psi - \varphi )(\Gamma )$
have finite index in
 $\Gamma $
. Then
$\Gamma $
. Then
 $\{\varphi , \psi \}$
has the large intersections property.
$\{\varphi , \psi \}$
has the large intersections property. -
(2) Suppose
 $a, b \in {\mathbb {Z}}$
are distinct, non-zero integers such that
$a, b \in {\mathbb {Z}}$
are distinct, non-zero integers such that
 $(b-a)\Gamma $
has finite index in
$(b-a)\Gamma $
has finite index in
 $\Gamma $
. Then
$\Gamma $
. Then
 $\{a, b\}$
has the large intersections property.
$\{a, b\}$
has the large intersections property.
This result leaves the following as a natural open question.
Question 1.14. [Reference Ackelsberg, Bergelson and Shalom2, Question 1.12]
Let
![]() $\Gamma $
be a countable discrete abelian group. Suppose
$\Gamma $
be a countable discrete abelian group. Suppose
![]() $\varphi , \psi \in \mathrm {End}(\Gamma )$
such that
$\varphi , \psi \in \mathrm {End}(\Gamma )$
such that
![]() $(\psi - \varphi )(\Gamma )$
has finite index in
$(\psi - \varphi )(\Gamma )$
has finite index in
![]() $\Gamma $
. Does
$\Gamma $
. Does
![]() $\{\varphi , \psi \}$
have the large intersections property?
$\{\varphi , \psi \}$
have the large intersections property?
Remark 1.15. There are a variety of examples of pairs
![]() $\{\varphi , \psi \}$
without the large intersections property (see [Reference Ackelsberg, Bergelson and Best1, Example 10.2] and [Reference Ackelsberg, Bergelson and Shalom2, Theorem 1.14]), so it is necessary to impose some condition on
$\{\varphi , \psi \}$
without the large intersections property (see [Reference Ackelsberg, Bergelson and Best1, Example 10.2] and [Reference Ackelsberg, Bergelson and Shalom2, Theorem 1.14]), so it is necessary to impose some condition on
![]() $\varphi , \psi \in \mathrm {End}(\Gamma )$
(such as the finite index assumption in Question 1.14) to hope for the large intersections property.
$\varphi , \psi \in \mathrm {End}(\Gamma )$
(such as the finite index assumption in Question 1.14) to hope for the large intersections property.
The goal of this paper is to extend the techniques in [Reference Ackelsberg, Bergelson and Shalom2] to answer Question 1.14 affirmatively under a mild additional technical assumption. As we will see, this condition is always satisfied when the endomorphisms are obtained as multiplication by integers or when the group
![]() $\Gamma $
is equal to
$\Gamma $
is equal to
![]() ${\mathbb {Z}}^d$
for some
${\mathbb {Z}}^d$
for some
![]() $d \in {\mathbb {N}}$
. Hence, we are able to reproduce Theorem 1.13(2) and fully resolve Question 1.14 for
$d \in {\mathbb {N}}$
. Hence, we are able to reproduce Theorem 1.13(2) and fully resolve Question 1.14 for
![]() $\Gamma = {\mathbb {Z}}^d$
.
$\Gamma = {\mathbb {Z}}^d$
.
1.2 Main results
Our main result is the following theorem.
Theorem 1.16. Let
![]() $\Gamma $
be a countable discrete abelian group. Let
$\Gamma $
be a countable discrete abelian group. Let
![]() $\varphi , \psi \in \mathrm {End}(\Gamma )$
. Suppose there exist endomorphisms
$\varphi , \psi \in \mathrm {End}(\Gamma )$
. Suppose there exist endomorphisms
![]() $\eta , \varphi ', \psi ', \theta _1, \theta _2 \in \mathrm {End}(\Gamma )$
such that:
$\eta , \varphi ', \psi ', \theta _1, \theta _2 \in \mathrm {End}(\Gamma )$
such that:
-
(i)
 $\eta (\Gamma )$
is a finite index subgroup of
$\eta (\Gamma )$
is a finite index subgroup of
 $\Gamma $
;
$\Gamma $
; -
(ii)
 $\varphi = \varphi ' \circ \eta $
and
$\varphi = \varphi ' \circ \eta $
and
 $\psi = \psi ' \circ \eta $
;
$\psi = \psi ' \circ \eta $
; -
(iii)
 $\theta _1 \circ \varphi ' + \theta _2 \circ \psi '$
is injective; and
$\theta _1 \circ \varphi ' + \theta _2 \circ \psi '$
is injective; and -
(iv)
 $(\psi ' - \varphi ')(\Gamma )$
is a finite index subgroup of
$(\psi ' - \varphi ')(\Gamma )$
is a finite index subgroup of
 $\Gamma $
.
$\Gamma $
.
Then for any ergodic measure-preserving
![]() $\Gamma $
-system
$\Gamma $
-system
![]() $( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
, any
$( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
, any
![]() $A \in {\mathcal {X}}$
, and any
$A \in {\mathcal {X}}$
, and any
![]() ${\varepsilon }> 0$
, the set
${\varepsilon }> 0$
, the set
is syndetic.
Remark 1.17. The conditions (i)–(iv) in Theorem 1.16 may be forbidding at first glance. We give a brief explanation here and also refer the reader to the special cases outlined below for developing stronger intuition about each condition.
Conditions (i) and (ii) can be interpreted as follows. Define a new
![]() $\Gamma $
-action on
$\Gamma $
-action on
![]() $(X, {\mathcal {X}}, \mu )$
by
$(X, {\mathcal {X}}, \mu )$
by
![]() $S_g = T_{\eta (g)}$
. Then
$S_g = T_{\eta (g)}$
. Then
so it suffices to prove a statement about the system
![]() $( X, {\mathcal {X}}, \mu , (S_g)_{g \in \Gamma } )$
and the endomorphisms
$( X, {\mathcal {X}}, \mu , (S_g)_{g \in \Gamma } )$
and the endomorphisms
![]() $\varphi ', \psi ' \in \mathrm {End}(\Gamma )$
. The key consequence of condition (i) is that the new system
$\varphi ', \psi ' \in \mathrm {End}(\Gamma )$
. The key consequence of condition (i) is that the new system
![]() $( X, {\mathcal {X}}, \mu , (S_g)_{g \in \Gamma } )$
has only finitely many ergodic components, and our dynamical tools are flexible enough to handle this situation.
$( X, {\mathcal {X}}, \mu , (S_g)_{g \in \Gamma } )$
has only finitely many ergodic components, and our dynamical tools are flexible enough to handle this situation.
Condition (iii) imposes a level of non-triviality to the pair
![]() $\{\varphi ', \psi '\}$
by ensuring that the map
$\{\varphi ', \psi '\}$
by ensuring that the map
![]() $g \mapsto (\varphi '(g), \psi '(g))$
is injective. This condition also turns out to be crucial to describing the limiting behavior of double ergodic averages associated with
$g \mapsto (\varphi '(g), \psi '(g))$
is injective. This condition also turns out to be crucial to describing the limiting behavior of double ergodic averages associated with
![]() $\{\varphi ', \psi '\}$
.
$\{\varphi ', \psi '\}$
.
Finally, condition (iv) is the key assumption to get started with analyzing the relevant double ergodic average by invoking [Reference Ackelsberg, Bergelson and Shalom2, Theorem 4.10], which is proved using the van der Corput differencing trick (see Lemma 2.1). It is absolutely essential to the method used in this paper, though it is less clear whether condition (iv) is needed to obtain the desired conclusion. A concrete example where we do not know whether or not the large intersections property holds (and for which condition (iv) does not hold) is the following. Let
![]() $\Gamma = ({\mathbb {Q}}_{>0}, \cdot )$
be the group of positive rational numbers under multiplication (considered as a discrete group). Let
$\Gamma = ({\mathbb {Q}}_{>0}, \cdot )$
be the group of positive rational numbers under multiplication (considered as a discrete group). Let
![]() $a, b \in {\mathbb {N}}$
be coprime. It was asked in [Reference Ackelsberg, Bergelson and Shalom2, Question 1.18] whether the pair
$a, b \in {\mathbb {N}}$
be coprime. It was asked in [Reference Ackelsberg, Bergelson and Shalom2, Question 1.18] whether the pair
![]() $\{q \mapsto q^a, q \mapsto q^b\}$
has the large intersections property, and we are presently unable to make any substantial progress on this question. For this example, although condition (iv) does not hold, it is nevertheless the case that the group generated by
$\{q \mapsto q^a, q \mapsto q^b\}$
has the large intersections property, and we are presently unable to make any substantial progress on this question. For this example, although condition (iv) does not hold, it is nevertheless the case that the group generated by
![]() $\{q^a : q \in {\mathbb {Q}}_{>0}\}$
and
$\{q^a : q \in {\mathbb {Q}}_{>0}\}$
and
![]() $\{q^b : q \in {\mathbb {Q}}_{>0}\}$
has finite index in
$\{q^b : q \in {\mathbb {Q}}_{>0}\}$
has finite index in
![]() ${\mathbb {Q}}_{>0}$
(in fact, it is equal to
${\mathbb {Q}}_{>0}$
(in fact, it is equal to
![]() ${\mathbb {Q}}_{>0}$
), which eliminates many of the possible approaches to producing a counterexample. Additional discussion of the difficulties involved in this problem can be found in [Reference Ackelsberg, Bergelson and Shalom2, §2.7].
${\mathbb {Q}}_{>0}$
), which eliminates many of the possible approaches to producing a counterexample. Additional discussion of the difficulties involved in this problem can be found in [Reference Ackelsberg, Bergelson and Shalom2, §2.7].
We now turn to several consequences of Theorem 1.16.
Theorem 1.16 includes Theorem 1.13(2) as a special case. Given
![]() $a, b \in {\mathbb {Z}}$
such that
$a, b \in {\mathbb {Z}}$
such that
![]() $(b-a)\Gamma $
has finite index in
$(b-a)\Gamma $
has finite index in
![]() $\Gamma $
, let
$\Gamma $
, let
![]() $d = \gcd (a,b)$
,
$d = \gcd (a,b)$
,
![]() $a' = ({a}/{d})$
, and
$a' = ({a}/{d})$
, and
![]() $b' = ({b}/{d})$
. Since
$b' = ({b}/{d})$
. Since
![]() $d \mid b-a$
, we have
$d \mid b-a$
, we have
![]() $d\Gamma \supseteq (b-a)\Gamma $
, so
$d\Gamma \supseteq (b-a)\Gamma $
, so
![]() $d \Gamma $
has finite index in
$d \Gamma $
has finite index in
![]() $\Gamma $
. The integers
$\Gamma $
. The integers
![]() $a'$
and
$a'$
and
![]() $b'$
are coprime, so there exist
$b'$
are coprime, so there exist
![]() $c_1, c_2 \in {\mathbb {Z}}$
such that
$c_1, c_2 \in {\mathbb {Z}}$
such that
![]() $c_1a' + c_2b' = 1$
. Finally,
$c_1a' + c_2b' = 1$
. Finally,
![]() $(b' - a') \mid (b-a)$
, so
$(b' - a') \mid (b-a)$
, so
![]() $(b' - a')\Gamma \supseteq (b-a)\Gamma $
has finite index in
$(b' - a')\Gamma \supseteq (b-a)\Gamma $
has finite index in
![]() $\Gamma $
. Taking
$\Gamma $
. Taking
![]() $\varphi (g) = ag$
,
$\varphi (g) = ag$
,
![]() $\psi (g) = bg$
,
$\psi (g) = bg$
,
![]() $\eta (g) = dg$
,
$\eta (g) = dg$
,
![]() $\varphi '(g) = a'g$
,
$\varphi '(g) = a'g$
,
![]() $\psi '(g) = b'g$
,
$\psi '(g) = b'g$
,
![]() $\theta _1(g) = c_1g$
, and
$\theta _1(g) = c_1g$
, and
![]() $\theta _2(g) = c_2g$
and applying Theorem 1.16 reproduces the conclusion of Theorem 1.13(2).
$\theta _2(g) = c_2g$
and applying Theorem 1.16 reproduces the conclusion of Theorem 1.13(2).
Another illustrative special case of Theorem 1.16 is the following corollary.
Corollary 1.18. Let
![]() $\Gamma $
be a countable discrete abelian group. Let
$\Gamma $
be a countable discrete abelian group. Let
![]() $\varphi , \psi \in \mathrm {End}(\Gamma )$
such that
$\varphi , \psi \in \mathrm {End}(\Gamma )$
such that
![]() $\psi - \varphi $
is injective with finite index image. Then for any ergodic measure-preserving
$\psi - \varphi $
is injective with finite index image. Then for any ergodic measure-preserving
![]() $\Gamma $
-system
$\Gamma $
-system
![]() $( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
, any
$( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
, any
![]() $A \in {\mathcal {X}}$
, and any
$A \in {\mathcal {X}}$
, and any
![]() ${\varepsilon }> 0$
, the set
${\varepsilon }> 0$
, the set
is syndetic.
For the group
![]() $\Gamma = {\mathbb {Z}}^d$
, Corollary 1.18 takes the following shape.
$\Gamma = {\mathbb {Z}}^d$
, Corollary 1.18 takes the following shape.
Corollary 1.19. Let
![]() ${\mathbf {X}} = ( X, {\mathcal {X}}, \mu , (T_{\vec {n}})_{\vec {n} \in {\mathbb {Z}}^d} )$
be an ergodic
${\mathbf {X}} = ( X, {\mathcal {X}}, \mu , (T_{\vec {n}})_{\vec {n} \in {\mathbb {Z}}^d} )$
be an ergodic
![]() ${\mathbb {Z}}^d$
-system. Then for any integer matrices
${\mathbb {Z}}^d$
-system. Then for any integer matrices
![]() $M_1, M_2 \in M_{d \times d}({\mathbb {Z}})$
such that
$M_1, M_2 \in M_{d \times d}({\mathbb {Z}})$
such that
![]() $M_2 - M_1$
is non-singular, any
$M_2 - M_1$
is non-singular, any
![]() $A \in {\mathcal {X}}$
, and any
$A \in {\mathcal {X}}$
, and any
![]() ${\varepsilon }> 0$
, the set
${\varepsilon }> 0$
, the set
is syndetic.
In the case
![]() $d = 2$
, Corollary 1.19 was established in [Reference Ackelsberg, Bergelson and Shalom2] using a combination of different methods. If
$d = 2$
, Corollary 1.19 was established in [Reference Ackelsberg, Bergelson and Shalom2] using a combination of different methods. If
![]() $M_1$
is also non-singular, then the conclusion follows from [Reference Ackelsberg, Bergelson and Shalom2, Theorem 1.11], which is proved using methods similar to the current paper involving characteristic factors for multiple ergodic averages. In the case that both
$M_1$
is also non-singular, then the conclusion follows from [Reference Ackelsberg, Bergelson and Shalom2, Theorem 1.11], which is proved using methods similar to the current paper involving characteristic factors for multiple ergodic averages. In the case that both
![]() $M_1$
and
$M_1$
and
![]() $M_2$
are rank-one matrices, basic linear algebra combined with the Fubini property for uniform Cesàro limits (see [Reference Bergelson and Leibman7, Lemma 1.1]) allows one to prove a stronger result that implies, in particular, that the set
$M_2$
are rank-one matrices, basic linear algebra combined with the Fubini property for uniform Cesàro limits (see [Reference Bergelson and Leibman7, Lemma 1.1]) allows one to prove a stronger result that implies, in particular, that the set
is syndetic for any (not necessarily ergodic) measure-preserving system
![]() $( X, {\mathcal {X}}, \mu , (T_{\vec {n}})_{\vec {n} \in {\mathbb {Z}}^2} )$
, any
$( X, {\mathcal {X}}, \mu , (T_{\vec {n}})_{\vec {n} \in {\mathbb {Z}}^2} )$
, any
![]() $A \in {\mathcal {X}}$
, and any
$A \in {\mathcal {X}}$
, and any
![]() ${\varepsilon }> 0$
; see [Reference Ackelsberg, Bergelson and Shalom2, Theorem 7.1].
${\varepsilon }> 0$
; see [Reference Ackelsberg, Bergelson and Shalom2, Theorem 7.1].
The method for handling the case where both
![]() $M_1$
and
$M_1$
and
![]() $M_2$
are singular matrices does not easily generalize for
$M_2$
are singular matrices does not easily generalize for
![]() $d \ge 3$
. Instead, we produce a new proof avoiding any use of matrix manipulations that unifies the two different cases to apply to general
$d \ge 3$
. Instead, we produce a new proof avoiding any use of matrix manipulations that unifies the two different cases to apply to general
![]() $d \in {\mathbb {N}}$
and in fact to general countable discrete abelian groups.
$d \in {\mathbb {N}}$
and in fact to general countable discrete abelian groups.
1.3 Combinatorial consequences and questions
Recurrence results in ergodic theory translate into combinatorial statements about sets of positive density. Let us first make precise what we mean by the density of a subset of an abelian group. A Følner sequence in a countable discrete abelian group
![]() $\Gamma $
is a sequence
$\Gamma $
is a sequence
![]() $(\Phi _N)_{N \in {\mathbb {N}}}$
of finite subsets of
$(\Phi _N)_{N \in {\mathbb {N}}}$
of finite subsets of
![]() $\Gamma $
such that for any
$\Gamma $
such that for any
![]() $x \in \Gamma $
,
$x \in \Gamma $
,
The upper density of a set
![]() $E \subseteq \Gamma $
along a Følner sequence
$E \subseteq \Gamma $
along a Følner sequence
![]() $\Phi = (\Phi _N)_{N \in {\mathbb {N}}}$
is the quantity
$\Phi = (\Phi _N)_{N \in {\mathbb {N}}}$
is the quantity
The upper Banach density of
![]() $E \subseteq \Gamma $
is
$E \subseteq \Gamma $
is
![]() $d^*(E) = \sup _{\Phi } \overline {d}_{\Phi }(E)$
, where the supremum is over all Følner sequences in
$d^*(E) = \sup _{\Phi } \overline {d}_{\Phi }(E)$
, where the supremum is over all Følner sequences in
![]() $\Gamma $
. An immediate consequence of Theorem 1.16 together with a version of the Furstenberg correspondence principle for ergodic systems (see [Reference Bergelson and Ferré Moragues5, Theorem 2.8]) is the following theorem.
$\Gamma $
. An immediate consequence of Theorem 1.16 together with a version of the Furstenberg correspondence principle for ergodic systems (see [Reference Bergelson and Ferré Moragues5, Theorem 2.8]) is the following theorem.
Theorem 1.20. Let
![]() $\Gamma $
be a countable discrete abelian group. Let
$\Gamma $
be a countable discrete abelian group. Let
![]() $\varphi , \psi \in \mathrm {End}(\Gamma )$
be as in Theorem 1.16. Then for any
$\varphi , \psi \in \mathrm {End}(\Gamma )$
be as in Theorem 1.16. Then for any
![]() $E \subseteq \Gamma $
and any
$E \subseteq \Gamma $
and any
![]() ${\varepsilon }> 0$
, the set
${\varepsilon }> 0$
, the set
is syndetic.
This strongly suggests that various finitary combinatorial results hold. Namely, we conjecture that the following finitary version of Corollary 1.18 is true.
Conjecture 1.21. For
![]() $\alpha , {\varepsilon }> 0$
, there exists
$\alpha , {\varepsilon }> 0$
, there exists
![]() $N_0 = N_0(\alpha , {\varepsilon })$
with the property: for any finite abelian group G of order
$N_0 = N_0(\alpha , {\varepsilon })$
with the property: for any finite abelian group G of order
![]() $N \ge N_0$
, any
$N \ge N_0$
, any
![]() $\varphi , \psi \in \mathrm {End}(G)$
such that
$\varphi , \psi \in \mathrm {End}(G)$
such that
![]() $\psi - \varphi $
is an automorphism, and any set
$\psi - \varphi $
is an automorphism, and any set
![]() $A \subseteq G$
with
$A \subseteq G$
with
![]() $|A| \ge \alpha N$
, there exists
$|A| \ge \alpha N$
, there exists
![]() $y \in G \setminus \{0\}$
such that
$y \in G \setminus \{0\}$
such that
A natural conjecture in the setting of
![]() ${\mathbb {Z}}^d$
, building on Corollary 1.19, is the following conjecture.
${\mathbb {Z}}^d$
, building on Corollary 1.19, is the following conjecture.
Conjecture 1.22. Let
![]() $M_1, M_2 \in M_{d \times d}({\mathbb {Z}})$
such that
$M_1, M_2 \in M_{d \times d}({\mathbb {Z}})$
such that
![]() $M_2 - M_1$
is non-singular. For any
$M_2 - M_1$
is non-singular. For any
![]() $\alpha , {\varepsilon }> 0$
, there exists
$\alpha , {\varepsilon }> 0$
, there exists
![]() $N_0 = N_0(\alpha , {\varepsilon }, M_1, M_2) \in {\mathbb {N}}$
with the property: for any
$N_0 = N_0(\alpha , {\varepsilon }, M_1, M_2) \in {\mathbb {N}}$
with the property: for any
![]() $N \ge N_0$
and any set
$N \ge N_0$
and any set
![]() $A \subseteq \{1, \ldots , N\}^d$
with
$A \subseteq \{1, \ldots , N\}^d$
with
![]() $|A| \ge \alpha N^d$
, there exists
$|A| \ge \alpha N^d$
, there exists
![]() $\vec {y} \in {\mathbb {Z}}^d \setminus \{0\}$
such that
$\vec {y} \in {\mathbb {Z}}^d \setminus \{0\}$
such that
If one imposes the additional condition in Conjecture 1.21 that
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
are automorphisms, then the conjecture is known to be true by [Reference Berger, Sah, Sawhney and Tidor10, Theorem 7.3]. Similarly, if the matrices
$\psi $
are automorphisms, then the conjecture is known to be true by [Reference Berger, Sah, Sawhney and Tidor10, Theorem 7.3]. Similarly, if the matrices
![]() $M_1$
,
$M_1$
,
![]() $M_2$
, and
$M_2$
, and
![]() $M_2 - M_1$
in Conjecture 1.22 are all non-singular, then the conclusion holds by [Reference Berger, Sah, Sawhney and Tidor10, Theorem 1.1]. (For the particular matrices
$M_2 - M_1$
in Conjecture 1.22 are all non-singular, then the conclusion holds by [Reference Berger, Sah, Sawhney and Tidor10, Theorem 1.1]. (For the particular matrices
 $$ \begin{align*} M_1 = \left( \begin{array}{@{}cc@{}} 1 & 0 \\ 0 & 1 \end{array} \right) \quad \text{and} \quad M_2 = \left( \begin{array}{@{}cc@{}} 0 & -1 \\ 1 & 0 \end{array} \right)\!, \end{align*} $$
$$ \begin{align*} M_1 = \left( \begin{array}{@{}cc@{}} 1 & 0 \\ 0 & 1 \end{array} \right) \quad \text{and} \quad M_2 = \left( \begin{array}{@{}cc@{}} 0 & -1 \\ 1 & 0 \end{array} \right)\!, \end{align*} $$
this was also shown by [Reference Kovač25, Theorem 1].)
The ergodic theoretic methods used in this paper are not immediately applicable in the finitary setting. To resolve Conjectures 1.21 and 1.22, one should replace the dynamical tools with suitable analogs from higher order Fourier analysis.
1.4 Outline of the paper
The structure of the paper is as follows. Section 2 is preparatory, collecting the relevant background material that will be used in the proof of Theorem 1.16. The main technical results appear in §§3 and 4, where we prove the existence of extensions in which the Kronecker and quasi-affine factors interact nicely with a fixed pair of endomorphisms
![]() $\{\varphi , \psi \}$
. We then prove a formula for the limit of double ergodic averages associated with
$\{\varphi , \psi \}$
. We then prove a formula for the limit of double ergodic averages associated with
![]() $\{\varphi , \psi \}$
in §5. Finally, we complete the proof of Theorem 1.16 in §6.
$\{\varphi , \psi \}$
in §5. Finally, we complete the proof of Theorem 1.16 in §6.
2 Preliminaries
2.1 Uniform Cesàro limits and the van der Corput differencing lemma
Just as Furstenberg’s multiple recurrence theorem (Theorem 1.2) establishes a recurrence result by working with a multiple ergodic average, we will prove Theorem 1.16 by studying an associated double ergodic average. A sequence
![]() $(v_g)_{g \in \Gamma }$
in a (real or complex) topological vector space V has uniform Cesàro limit equal to
$(v_g)_{g \in \Gamma }$
in a (real or complex) topological vector space V has uniform Cesàro limit equal to
![]() $v \in V$
, denoted
$v \in V$
, denoted
![]() $\text {UC-}\lim \nolimits _{g \in \Gamma }{v_g} = v$
, if for any Følner sequence
$\text {UC-}\lim \nolimits _{g \in \Gamma }{v_g} = v$
, if for any Følner sequence
![]() $(\Phi _N)_{N \in {\mathbb {N}}}$
in
$(\Phi _N)_{N \in {\mathbb {N}}}$
in
![]() $\Gamma $
, one has
$\Gamma $
, one has
 $$ \begin{align*} \frac{1}{|\Phi_N|} \sum_{g \in \Phi_N}{v_g} {\xrightarrow[{N \to \infty}]{}} v. \end{align*} $$
$$ \begin{align*} \frac{1}{|\Phi_N|} \sum_{g \in \Phi_N}{v_g} {\xrightarrow[{N \to \infty}]{}} v. \end{align*} $$
In the group
![]() $\Gamma = {\mathbb {Z}}$
, the uniform Cesàro limit corresponds to the limit of averages appearing in Theorem 1.2, that is,
$\Gamma = {\mathbb {Z}}$
, the uniform Cesàro limit corresponds to the limit of averages appearing in Theorem 1.2, that is,
 $$ \begin{align*} \text{UC-}\lim_{n \in {\mathbb{Z}}}{v_n} = \lim_{N - M \to \infty}{\frac{1}{N-M} \sum_{n=M}^{N-1}{v_n}}. \end{align*} $$
$$ \begin{align*} \text{UC-}\lim_{n \in {\mathbb{Z}}}{v_n} = \lim_{N - M \to \infty}{\frac{1}{N-M} \sum_{n=M}^{N-1}{v_n}}. \end{align*} $$
One of the main tools for handling uniform Cesàro limits is the following version of the van der Corput differencing lemma.
Lemma 2.1. [Reference Ackelsberg, Bergelson and Best1, Lemma 2.2]
Let
![]() $\Gamma $
be a countable discrete abelian group and let
$\Gamma $
be a countable discrete abelian group and let
![]() $(u_g)_{g \in \Gamma }$
be a bounded sequence in a Hilbert space
$(u_g)_{g \in \Gamma }$
be a bounded sequence in a Hilbert space
![]() ${\mathcal {H}}$
. If
${\mathcal {H}}$
. If
exists for every
![]() $h \in \Gamma $
and
$h \in \Gamma $
and
![]() $\mathrm {UC}\text{-}\lim \nolimits _{h \in \Gamma }{\xi _h} = 0$
, then
$\mathrm {UC}\text{-}\lim \nolimits _{h \in \Gamma }{\xi _h} = 0$
, then
![]() $\mathrm {UC}\text{-}\lim \nolimits _{g \in \Gamma }{u_g} = 0$
.
$\mathrm {UC}\text{-}\lim \nolimits _{g \in \Gamma }{u_g} = 0$
.
2.2 Host–Kra factors
Let
![]() $\Gamma $
be a countable discrete abelian group and let
$\Gamma $
be a countable discrete abelian group and let
![]() ${\mathbf {X}} = ( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
be a measure-preserving
${\mathbf {X}} = ( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
be a measure-preserving
![]() $\Gamma $
-system. A factor of
$\Gamma $
-system. A factor of
![]() ${\mathbf {X}}$
is a
${\mathbf {X}}$
is a
![]() $(T_g)_{g \in \Gamma }$
-invariant sub-
$(T_g)_{g \in \Gamma }$
-invariant sub-
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() ${\mathcal {Y}} \subseteq {\mathcal {X}}$
. We may also refer to the system
${\mathcal {Y}} \subseteq {\mathcal {X}}$
. We may also refer to the system
![]() ${\mathbf {Y}} = ( X, {\mathcal {Y}}, \mu |_{{\mathcal {Y}}}, (T_g)_{g \in \Gamma } )$
, or any system isomorphic to
${\mathbf {Y}} = ( X, {\mathcal {Y}}, \mu |_{{\mathcal {Y}}}, (T_g)_{g \in \Gamma } )$
, or any system isomorphic to
![]() ${\mathbf {Y}}$
, as a factor of
${\mathbf {Y}}$
, as a factor of
![]() ${\mathbf {X}}$
.
${\mathbf {X}}$
.
The most important family of factors for our consideration is the family of Host–Kra factors. These factors are defined in terms of a family of seminorms, known as the Host–Kra seminorms [Reference Host and Kra23], which are an ergodic-theoretic counterpart to the Gowers uniformity norms [Reference Gowers16] in additive combinatorics.
Let
![]() ${\mathbf {X}} = ( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
be a measure-preserving
${\mathbf {X}} = ( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
be a measure-preserving
![]() $\Gamma $
-system. For
$\Gamma $
-system. For
![]() $g \in \Gamma $
and
$g \in \Gamma $
and
![]() $f : X \to {\mathbb {C}}$
, define
$f : X \to {\mathbb {C}}$
, define
![]() $\Delta _gf := \overline {f} \cdot T_g f$
. Then for
$\Delta _gf := \overline {f} \cdot T_g f$
. Then for
![]() $k \in {\mathbb {N}}$
and
$k \in {\mathbb {N}}$
and
![]() $g_1, \ldots , g_k \in \Gamma $
, we define
$g_1, \ldots , g_k \in \Gamma $
, we define
![]() $\Delta _{g_1, \ldots , g_k}$
inductively by
$\Delta _{g_1, \ldots , g_k}$
inductively by
![]() $\Delta _{g_1, \ldots , g_k}f := \Delta _{g_k} ( \Delta _{g_1, \ldots , g_{k-1}}f )$
. For
$\Delta _{g_1, \ldots , g_k}f := \Delta _{g_k} ( \Delta _{g_1, \ldots , g_{k-1}}f )$
. For
![]() $f \in L^{\infty }(\mu )$
and
$f \in L^{\infty }(\mu )$
and
![]() $k \in {\mathbb {N}}$
, we define the Host–Kra seminorm of order by
$k \in {\mathbb {N}}$
, we define the Host–Kra seminorm of order by
It is shown that
![]() ${{\vert \kern -0.25ex\vert \kern -0.25ex\vert {\cdot } \vert \kern -0.25ex\vert \kern -0.25ex\vert }_{{U^k}}}$
is indeed a seminorm for each
${{\vert \kern -0.25ex\vert \kern -0.25ex\vert {\cdot } \vert \kern -0.25ex\vert \kern -0.25ex\vert }_{{U^k}}}$
is indeed a seminorm for each
![]() $k \in {\mathbb {N}}$
in [Reference Bergelson, Tao and Ziegler8, Appendix A]. The corresponding Host–Kra factors are guaranteed by the following proposition.
$k \in {\mathbb {N}}$
in [Reference Bergelson, Tao and Ziegler8, Appendix A]. The corresponding Host–Kra factors are guaranteed by the following proposition.
Proposition 2.2. [Reference Bergelson, Tao and Ziegler8, Proposition 1.10]
Let
![]() $\Gamma $
be a countable discrete abelian group, let
$\Gamma $
be a countable discrete abelian group, let
![]() ${\mathbf {X}} = ( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
be a measure-preserving
${\mathbf {X}} = ( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
be a measure-preserving
![]() $\Gamma $
-system, and let
$\Gamma $
-system, and let
![]() $k \ge 0$
. There exists a factor
$k \ge 0$
. There exists a factor
![]() ${\mathcal {Z}}^k$
with the property that for every
${\mathcal {Z}}^k$
with the property that for every
![]() $f\in L^\infty (\mu )$
, one has
$f\in L^\infty (\mu )$
, one has
If
![]() ${\mathbf {X}} = ( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
is an ergodic system, then the first several Host–Kra factors are as follows.
${\mathbf {X}} = ( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
is an ergodic system, then the first several Host–Kra factors are as follows.
-
•
 ${\mathcal {Z}}^0$
is the trivial factor consisting of null and co-null subsets of X. (If
${\mathcal {Z}}^0$
is the trivial factor consisting of null and co-null subsets of X. (If
 ${\mathbf {X}}$
is not ergodic, then
${\mathbf {X}}$
is not ergodic, then
 ${\mathcal {Z}}^0 = {\mathcal {I}}$
, the
${\mathcal {Z}}^0 = {\mathcal {I}}$
, the
 $\sigma $
-algebra of all
$\sigma $
-algebra of all
 $(T_g)_{g \in \Gamma }$
-invariant sets.)
$(T_g)_{g \in \Gamma }$
-invariant sets.) -
•
 ${\mathcal {Z}}^1$
is the Kronecker factor. This is the smallest
${\mathcal {Z}}^1$
is the Kronecker factor. This is the smallest
 $\sigma $
-algebra with respect to which all eigenfunctions are measurable. As a measure-preserving system,
$\sigma $
-algebra with respect to which all eigenfunctions are measurable. As a measure-preserving system,
 ${\mathbf {Z}}^1$
is isomorphic to a rotational system. That is, there exists a compact abelian group Z and a homomorphism
${\mathbf {Z}}^1$
is isomorphic to a rotational system. That is, there exists a compact abelian group Z and a homomorphism
 $\alpha : \Gamma \to Z$
with dense image such that
$\alpha : \Gamma \to Z$
with dense image such that
 ${\mathbf {Z}}^1$
is isomorphic to the system
${\mathbf {Z}}^1$
is isomorphic to the system
 ${\mathbf {Z}} = (Z, \alpha )$
, where Z is equipped with the Haar measure and
${\mathbf {Z}} = (Z, \alpha )$
, where Z is equipped with the Haar measure and
 $g \in \Gamma $
acts by the rotation
$g \in \Gamma $
acts by the rotation
 $z \mapsto z + \alpha _g$
. Because of its relationship to the Kronecker factor, we refer to any ergodic rotational system
$z \mapsto z + \alpha _g$
. Because of its relationship to the Kronecker factor, we refer to any ergodic rotational system
 ${\mathbf {Z}} = (Z, \alpha )$
as an ergodic Kronecker system. Such systems are uniquely determined (up to isomorphism) by their discrete spectrum (that is, the group of eigenvalues), which is given by Moreover, the topological system underlying any ergodic Kronecker system is uniquely ergodic. See [Reference Ackelsberg, Bergelson and Best1, §2.4] for a more in-depth discussion of Kronecker systems in the context of actions of countable discrete abelian groups.
${\mathbf {Z}} = (Z, \alpha )$
as an ergodic Kronecker system. Such systems are uniquely determined (up to isomorphism) by their discrete spectrum (that is, the group of eigenvalues), which is given by Moreover, the topological system underlying any ergodic Kronecker system is uniquely ergodic. See [Reference Ackelsberg, Bergelson and Best1, §2.4] for a more in-depth discussion of Kronecker systems in the context of actions of countable discrete abelian groups. $$ \begin{align*} \Lambda = \{ \unicode{x3bb} \circ \alpha : \unicode{x3bb} \in \widehat{Z} \}. \end{align*} $$
$$ \begin{align*} \Lambda = \{ \unicode{x3bb} \circ \alpha : \unicode{x3bb} \in \widehat{Z} \}. \end{align*} $$
-
•
 ${\mathcal {Z}}^2$
is the quasi-affine (or Conze–Lesigne) factor. As a measure-preserving system,
${\mathcal {Z}}^2$
is the quasi-affine (or Conze–Lesigne) factor. As a measure-preserving system,
 ${\mathbf {Z}}^2$
is isomorphic to a group extension of the Kronecker factor,
${\mathbf {Z}}^2$
is isomorphic to a group extension of the Kronecker factor,
 ${\mathbf {Z}}^2 \cong {\mathbf {Z}}^1 \times _{\sigma } H$
, where the cocycle
${\mathbf {Z}}^2 \cong {\mathbf {Z}}^1 \times _{\sigma } H$
, where the cocycle
 $\sigma $
satisfies a certain functional equation known as the Conze–Lesigne equation; see Definition 2.11.
$\sigma $
satisfies a certain functional equation known as the Conze–Lesigne equation; see Definition 2.11.
Definition 2.3. Let
![]() $\Gamma $
be a countable discrete abelian group and let
$\Gamma $
be a countable discrete abelian group and let
![]() $k \ge 0$
. An ergodic measure-preserving
$k \ge 0$
. An ergodic measure-preserving
![]() $\Gamma $
-system
$\Gamma $
-system
![]() ${\mathbf {X}} = ( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
is a system of order k if
${\mathbf {X}} = ( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
is a system of order k if
![]() ${\mathcal {Z}}^k = {\mathcal {X}}$
.
${\mathcal {Z}}^k = {\mathcal {X}}$
.
Systems of order k have the following properties.
Proposition 2.4. [Reference Host and Kra23, §4.6]
Let
![]() $\Gamma $
be a countable discrete abelian group,
$\Gamma $
be a countable discrete abelian group,
![]() $k \ge 0$
, and
$k \ge 0$
, and
![]() ${\mathbf {X}} = ( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
an ergodic measure-preserving
${\mathbf {X}} = ( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
an ergodic measure-preserving
![]() $\Gamma $
-system.
$\Gamma $
-system.
-
(1) The Host–Kra factor
 ${\mathbf {Z}}^k$
is an order k system.
${\mathbf {Z}}^k$
is an order k system. -
(2) If
 ${\mathbf {X}}$
is an order k system and
${\mathbf {X}}$
is an order k system and
 ${\mathbf {Y}}$
is a factor of
${\mathbf {Y}}$
is a factor of
 ${\mathbf {X}}$
, then
${\mathbf {X}}$
, then
 ${\mathbf {Y}}$
is again a system of order k.
${\mathbf {Y}}$
is again a system of order k. -
(3) If
 ${\mathbf {Y}}$
is a system of order k and a factor of
${\mathbf {Y}}$
is a system of order k and a factor of
 ${\mathbf {X}}$
, then
${\mathbf {X}}$
, then
 ${\mathbf {Y}}$
is a factor of the Host–Kra factor
${\mathbf {Y}}$
is a factor of the Host–Kra factor
 ${\mathbf {Z}}^k$
.
${\mathbf {Z}}^k$
.
2.3 Relatively independent joinings
The proof of Theorem 1.16 requires that the Host–Kra factors have certain convenient properties that they may not have in general systems. To produce these desirable properties, we will work with an extension of the original system. The key construction to that end is the relatively independent joining of systems with respect to a common factor. Let
![]() ${\mathbf {X}}_1 = ( X_1, {\mathcal {X}}_1, \mu _1, ( T_{1,g} )_{g \in \Gamma } )$
and
${\mathbf {X}}_1 = ( X_1, {\mathcal {X}}_1, \mu _1, ( T_{1,g} )_{g \in \Gamma } )$
and
![]() ${\mathbf {X}}_2 = ( X_2, {\mathcal {X}}_2, \mu _2, ( T_{2,g} )_{g \in \Gamma } )$
be measure-preserving
${\mathbf {X}}_2 = ( X_2, {\mathcal {X}}_2, \mu _2, ( T_{2,g} )_{g \in \Gamma } )$
be measure-preserving
![]() $\Gamma $
-systems. Suppose
$\Gamma $
-systems. Suppose
![]() ${\mathbf {Y}} = ( Y, {\mathcal {Y}}, \nu , (S_g)_{g \in \Gamma } )$
is another measure-preserving
${\mathbf {Y}} = ( Y, {\mathcal {Y}}, \nu , (S_g)_{g \in \Gamma } )$
is another measure-preserving
![]() $\Gamma $
-system that arises as a factor of both of the systems
$\Gamma $
-system that arises as a factor of both of the systems
![]() ${\mathbf {X}}_1$
and
${\mathbf {X}}_1$
and
![]() ${\mathbf {X}}_2$
, say with factor maps
${\mathbf {X}}_2$
, say with factor maps
![]() $\pi _1 : X_1 \to Y$
and
$\pi _1 : X_1 \to Y$
and
![]() $\pi _2 : X_2 \to Y$
. The relatively independent joining (or fiber product) of
$\pi _2 : X_2 \to Y$
. The relatively independent joining (or fiber product) of
![]() ${\mathbf {X}}_1$
and
${\mathbf {X}}_1$
and
![]() ${\mathbf {X}}_2$
with respect to
${\mathbf {X}}_2$
with respect to
![]() ${\mathbf {Y}}$
is the system
${\mathbf {Y}}$
is the system
where the measure
![]() $\mu _1 \times _{{\mathbf {Y}}} \mu _2$
is defined by the equation
$\mu _1 \times _{{\mathbf {Y}}} \mu _2$
is defined by the equation
 $$ \begin{align*} \int_{X_1 \times X_2}{(f_1 \otimes f_2)\,d(\mu_1 \times_{{\mathbf{Y}}} \mu_2)} = \int_Y{{\mathbb{E} [ {f_1} \mid {{\mathcal{Y}}} ]} \cdot {\mathbb{E} [ {f_2} \mid {{\mathcal{Y}}} ]}\,d\nu}. \end{align*} $$
$$ \begin{align*} \int_{X_1 \times X_2}{(f_1 \otimes f_2)\,d(\mu_1 \times_{{\mathbf{Y}}} \mu_2)} = \int_Y{{\mathbb{E} [ {f_1} \mid {{\mathcal{Y}}} ]} \cdot {\mathbb{E} [ {f_2} \mid {{\mathcal{Y}}} ]}\,d\nu}. \end{align*} $$
Note that the measure
![]() $\mu _1 \times _{{\mathbf {Y}}} \mu _2$
is supported on the set
$\mu _1 \times _{{\mathbf {Y}}} \mu _2$
is supported on the set
The relatively independent joining construction allows us to take an extension of a Host–Kra factor of a given system and turn it into an extension of the full system.
Theorem 2.5. Let
![]() ${\mathbf {X}} = ( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
be an ergodic
${\mathbf {X}} = ( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
be an ergodic
![]() $\Gamma $
-system. Let
$\Gamma $
-system. Let
![]() $k \in {\mathbb {N}}$
. Suppose
$k \in {\mathbb {N}}$
. Suppose
![]() ${\mathbf {Z}}^k$
is the Host–Kra factor of
${\mathbf {Z}}^k$
is the Host–Kra factor of
![]() ${\mathbf {X}}$
of order k. Given any ergodic order k extension
${\mathbf {X}}$
of order k. Given any ergodic order k extension
![]() $\widetilde {{\mathbf {Z}}}^k$
of
$\widetilde {{\mathbf {Z}}}^k$
of
![]() ${\mathbf {Z}}^k$
, there exists an ergodic extension
${\mathbf {Z}}^k$
, there exists an ergodic extension
![]() $\widetilde {{\mathbf {X}}}$
of
$\widetilde {{\mathbf {X}}}$
of
![]() ${\mathbf {X}}$
such that
${\mathbf {X}}$
such that
![]() $\widetilde {{\mathbf {Z}}}^k$
is the Host–Kra factor of
$\widetilde {{\mathbf {Z}}}^k$
is the Host–Kra factor of
![]() $\widetilde {{\mathbf {X}}}$
of order k.
$\widetilde {{\mathbf {X}}}$
of order k.
Proof. Define
![]() $\widetilde {{\mathbf {X}}}$
as the relatively independent joining
$\widetilde {{\mathbf {X}}}$
as the relatively independent joining
![]() $\widetilde {{\mathbf {X}}} = {\mathbf {X}} \times _{{\mathbf {Z}}^k} \widetilde {{\mathbf {Z}}}^k$
. First,
$\widetilde {{\mathbf {X}}} = {\mathbf {X}} \times _{{\mathbf {Z}}^k} \widetilde {{\mathbf {Z}}}^k$
. First,
![]() $\widetilde {{\mathbf {Z}}}^k$
is an order k factor of
$\widetilde {{\mathbf {Z}}}^k$
is an order k factor of
![]() $\widetilde {{\mathbf {X}}}$
, so it is a factor of the Host–Kra factor of order k by Proposition 2.4(3).
$\widetilde {{\mathbf {X}}}$
, so it is a factor of the Host–Kra factor of order k by Proposition 2.4(3).
Conversely, we want to show that the Host–Kra factor of
![]() $\widetilde {{\mathbf {X}}}$
of order k is a factor of
$\widetilde {{\mathbf {X}}}$
of order k is a factor of
![]() $\widetilde {{\mathbf {Z}}}^k$
. Let
$\widetilde {{\mathbf {Z}}}^k$
. Let
![]() $(u_i)_{i \in {\mathbb {N}}}$
be an orthonormal basis in
$(u_i)_{i \in {\mathbb {N}}}$
be an orthonormal basis in
![]() $L^2(\widetilde {Z}^k)$
. Suppose
$L^2(\widetilde {Z}^k)$
. Suppose
![]() $f \in L^2(\widetilde {X})$
is measurable with respect to the Host–Kra factor of order k. Expand f in the basis
$f \in L^2(\widetilde {X})$
is measurable with respect to the Host–Kra factor of order k. Expand f in the basis
![]() $(u_i)_{i \in {\mathbb {N}}}$
:
$(u_i)_{i \in {\mathbb {N}}}$
:
Fix
![]() $i \in {\mathbb {N}}$
. Since
$i \in {\mathbb {N}}$
. Since ![]() is
is
![]() $\widetilde {{\mathcal {Z}}}^k$
-measurable and hence measurable with respect to the Host–Kra factor of order k, the product
$\widetilde {{\mathcal {Z}}}^k$
-measurable and hence measurable with respect to the Host–Kra factor of order k, the product ![]() remains measurable with respect to the Host–Kra factor of order k. Therefore,
remains measurable with respect to the Host–Kra factor of order k. Therefore, ![]() is measurable with respect to
is measurable with respect to
![]() ${\mathcal {Z}}^k$
by items (2) and (3) in Proposition 2.4. By direct computation, since
${\mathcal {Z}}^k$
by items (2) and (3) in Proposition 2.4. By direct computation, since
![]() $(u_j)_{j \in {\mathbb {N}}}$
is an orthonormal basis in
$(u_j)_{j \in {\mathbb {N}}}$
is an orthonormal basis in
![]() $L^2(\widetilde {Z}^k)$
, we have
$L^2(\widetilde {Z}^k)$
, we have

Thus,
![]() $a_i$
is
$a_i$
is
![]() ${\mathcal {Z}}^k$
-measurable for each
${\mathcal {Z}}^k$
-measurable for each
![]() $i \in {\mathbb {N}}$
. That is,
$i \in {\mathbb {N}}$
. That is,
![]() $a_i(x) = b_i(\pi _1(x))$
for some function
$a_i(x) = b_i(\pi _1(x))$
for some function
![]() $b_i : Z^k \to {\mathbb {C}}$
, where
$b_i : Z^k \to {\mathbb {C}}$
, where
![]() $\pi _1 : X \to Z^k$
is the factor map. However, letting
$\pi _1 : X \to Z^k$
is the factor map. However, letting
![]() $\pi _2 : \widetilde {Z}^k \to Z^k$
be the other factor map, one has
$\pi _2 : \widetilde {Z}^k \to Z^k$
be the other factor map, one has
![]() $\pi _1(x) = \pi _2(y)$
for almost every (a.e.)
$\pi _1(x) = \pi _2(y)$
for almost every (a.e.)
![]() $(x,y) \in \widetilde {X}$
. Hence,
$(x,y) \in \widetilde {X}$
. Hence,
is
![]() $\widetilde {{\mathcal {Z}}}^k$
-measurable.
$\widetilde {{\mathcal {Z}}}^k$
-measurable.
2.4 Hilbert space-valued functions and unique ergodicity
Let
![]() ${\mathcal {H}}$
be a Hilbert space. Given a compact metric space X, a probability measure
${\mathcal {H}}$
be a Hilbert space. Given a compact metric space X, a probability measure
![]() $\mu $
on X, and a continuous function
$\mu $
on X, and a continuous function
![]() $F : X \to {\mathcal {H}}$
, one can define the integral
$F : X \to {\mathcal {H}}$
, one can define the integral
![]() $\int _X{F\,d\mu }$
to be the element of
$\int _X{F\,d\mu }$
to be the element of
![]() ${\mathcal {H}}$
satisfying
${\mathcal {H}}$
satisfying
 $$ \begin{align*} {\bigg\langle {\int_X{F\,d\mu}}, {v} \bigg\rangle} = \int_X{{\langle {F(x)}, {v} \rangle}\,d\mu(x)} \end{align*} $$
$$ \begin{align*} {\bigg\langle {\int_X{F\,d\mu}}, {v} \bigg\rangle} = \int_X{{\langle {F(x)}, {v} \rangle}\,d\mu(x)} \end{align*} $$
for every
![]() $v \in {\mathcal {H}}$
.
$v \in {\mathcal {H}}$
.
A characterizing property of uniquely ergodic systems is the following: a topological system
![]() $( X, (T_g)_{g \in \Gamma } )$
is uniquely ergodic (with unique invariant measure
$( X, (T_g)_{g \in \Gamma } )$
is uniquely ergodic (with unique invariant measure
![]() $\mu $
) if and only if for any continuous function
$\mu $
) if and only if for any continuous function
![]() $F : X \to {\mathbb {C}}$
and any
$F : X \to {\mathbb {C}}$
and any
![]() $x_0 \in X$
,
$x_0 \in X$
,
The following lemma shows that the same result holds for Hilbert space-valued functions.
Lemma 2.6. Let
![]() $( X, (T_g)_{g \in \Gamma } )$
be a topological
$( X, (T_g)_{g \in \Gamma } )$
be a topological
![]() $\Gamma $
-system. Let
$\Gamma $
-system. Let
![]() ${\mathcal {H}}$
be a non-trivial Hilbert space. Then
${\mathcal {H}}$
be a non-trivial Hilbert space. Then
![]() $( X, (T_g)_{g \in \Gamma } )$
is uniquely ergodic (with unique invariant measure
$( X, (T_g)_{g \in \Gamma } )$
is uniquely ergodic (with unique invariant measure
![]() $\mu $
) if and only if for any continuous function
$\mu $
) if and only if for any continuous function
![]() $F : X \to {\mathcal {H}}$
and any
$F : X \to {\mathcal {H}}$
and any
![]() $x_0 \in X$
,
$x_0 \in X$
,
in
![]() ${\mathcal {H}}$
.
${\mathcal {H}}$
.
Proof. For the group
![]() $\Gamma = {\mathbb {Z}}$
, a proof of this fact appears in [Reference Host and Kra22, Lemma 4.3]. We follow the same strategy for a general countable discrete abelian group
$\Gamma = {\mathbb {Z}}$
, a proof of this fact appears in [Reference Host and Kra22, Lemma 4.3]. We follow the same strategy for a general countable discrete abelian group
![]() $\Gamma $
.
$\Gamma $
.
Suppose that for any continuous function
![]() $F : X \to {\mathcal {H}}$
and any
$F : X \to {\mathcal {H}}$
and any
![]() $x_0 \in X$
,
$x_0 \in X$
,
in
![]() ${\mathcal {H}}$
. Since
${\mathcal {H}}$
. Since
![]() ${\mathcal {H}}$
is non-trivial, it contains a copy of
${\mathcal {H}}$
is non-trivial, it contains a copy of
![]() ${\mathbb {C}}$
, so this implies if
${\mathbb {C}}$
, so this implies if
![]() $F : X \to {\mathbb {C}}$
is continuous and
$F : X \to {\mathbb {C}}$
is continuous and
![]() $x_0 \in X$
, then
$x_0 \in X$
, then
in
![]() ${\mathbb {C}}$
. Therefore,
${\mathbb {C}}$
. Therefore,
![]() $(X, (T_g)_{g \in \Gamma })$
is uniquely ergodic.
$(X, (T_g)_{g \in \Gamma })$
is uniquely ergodic.
Now suppose
![]() $( X, (T_g)_{g \in \Gamma } )$
is uniquely ergodic with unique invariant measure
$( X, (T_g)_{g \in \Gamma } )$
is uniquely ergodic with unique invariant measure
![]() $\mu $
. Replacing F by
$\mu $
. Replacing F by
![]() $F\hspace{-1pt} -\hspace{-1pt} \int _X{F\,d\mu }$
, we may assume without loss of generality that
$F\hspace{-1pt} -\hspace{-1pt} \int _X{F\,d\mu }$
, we may assume without loss of generality that
![]() $\int _X{F\,d\mu } = 0$
in
$\int _X{F\,d\mu } = 0$
in
![]() ${\mathcal {H}}$
. Put
${\mathcal {H}}$
. Put
![]() $u_g = F(T_gx_0) \in {\mathcal {H}}$
. For any
$u_g = F(T_gx_0) \in {\mathcal {H}}$
. For any
![]() $h \in \Gamma $
, the function
$h \in \Gamma $
, the function
![]() $\varphi _h : X \to {\mathbb {C}}$
defined by
$\varphi _h : X \to {\mathbb {C}}$
defined by
![]() $\varphi _h(x) = {\langle {F(T_hx)}, {F(x)} \rangle }$
is continuous. Hence, by unique ergodicity of
$\varphi _h(x) = {\langle {F(T_hx)}, {F(x)} \rangle }$
is continuous. Hence, by unique ergodicity of
![]() $(T_g)_{g \in \Gamma }$
,
$(T_g)_{g \in \Gamma }$
,
For
![]() $x \in X$
, consider the function
$x \in X$
, consider the function
![]() $\psi _x(y) = {\langle {F(y)}, {F(x)} \rangle }$
. This is a continuous function from X to
$\psi _x(y) = {\langle {F(y)}, {F(x)} \rangle }$
. This is a continuous function from X to
![]() ${\mathbb {C}}$
, so by unique ergodicity of
${\mathbb {C}}$
, so by unique ergodicity of
![]() $(T_h)_{h \in \Gamma }$
, we have
$(T_h)_{h \in \Gamma }$
, we have
 $$ \begin{align*} \text{UC-}\lim_{h \in \Gamma}{\psi_x(T_hy)} = \int_X{\psi_x\,d\mu} = {\bigg\langle {\int_X{F\,d\mu}}, {F(x)} \bigg\rangle} = 0 \end{align*} $$
$$ \begin{align*} \text{UC-}\lim_{h \in \Gamma}{\psi_x(T_hy)} = \int_X{\psi_x\,d\mu} = {\bigg\langle {\int_X{F\,d\mu}}, {F(x)} \bigg\rangle} = 0 \end{align*} $$
for every
![]() $y \in X$
. In particular, we may take
$y \in X$
. In particular, we may take
![]() $y = x$
, in which case
$y = x$
, in which case
Integrating over
![]() $x \in X$
and applying the dominated convergence theorem, it follows that
$x \in X$
and applying the dominated convergence theorem, it follows that
Thus, by Lemma 2.1,
![]() $\text {UC-}\lim \nolimits _{g \in \Gamma }{F(T_gx_0)} = 0$
in
$\text {UC-}\lim \nolimits _{g \in \Gamma }{F(T_gx_0)} = 0$
in
![]() ${\mathcal {H}}$
.
${\mathcal {H}}$
.
2.5 Cocycles and coboundaries
An important construction in ergodic theory is that of group extensions. For our purposes, we will need only to consider extensions by abelian groups, which creates various simplifications. Suppose
![]() ${\mathbf {X}} = ( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
is an ergodic
${\mathbf {X}} = ( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
is an ergodic
![]() $\Gamma $
-system. Given a compact abelian group
$\Gamma $
-system. Given a compact abelian group
![]() $(H,+)$
and a measurable function
$(H,+)$
and a measurable function
![]() $\sigma : \Gamma \times X \to H$
, we can define the group extension of
$\sigma : \Gamma \times X \to H$
, we can define the group extension of
![]() ${\mathbf {X}}$
by H over
${\mathbf {X}}$
by H over
![]() $\sigma $
as the system
$\sigma $
as the system
where
![]() $T^{\sigma }_g(x,y) := (T_gx, y + \sigma _g(x))$
. To obtain a
$T^{\sigma }_g(x,y) := (T_gx, y + \sigma _g(x))$
. To obtain a
![]() $\Gamma $
-action in this manner, the function
$\Gamma $
-action in this manner, the function
![]() $\sigma $
must satisfy the cocycle equation
$\sigma $
must satisfy the cocycle equation
for every
![]() $g, h \in \Gamma $
and
$g, h \in \Gamma $
and
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x \in X$
.
$x \in X$
.
Given any measurable function
![]() $F : X \to H$
, one may construct a cocycle
$F : X \to H$
, one may construct a cocycle
Such a cocycle is called a coboundary.
Two cocycles
![]() $\sigma $
and
$\sigma $
and
![]() $\tau $
are cohomologous, denoted
$\tau $
are cohomologous, denoted
![]() $\sigma \sim \tau $
, if their difference
$\sigma \sim \tau $
, if their difference
![]() $\tau - \sigma $
is a coboundary. The following result is an easy exercise.
$\tau - \sigma $
is a coboundary. The following result is an easy exercise.
Proposition 2.7. [Reference Glasner15, Lemma 3.20]
Let
![]() ${\mathbf {X}} = ( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
be a
${\mathbf {X}} = ( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
be a
![]() $\Gamma $
-system. Suppose H is a compact abelian group and
$\Gamma $
-system. Suppose H is a compact abelian group and
![]() $\sigma , \tau : \Gamma \times X \to H$
are cocycles such that
$\sigma , \tau : \Gamma \times X \to H$
are cocycles such that
![]() $\sigma \sim \tau $
. Then
$\sigma \sim \tau $
. Then
![]() ${\mathbf {X}} \times _{\sigma } H \cong {\mathbf {X}} \times _{\tau } H$
.
${\mathbf {X}} \times _{\sigma } H \cong {\mathbf {X}} \times _{\tau } H$
.
When analyzing a cocycle
![]() $\sigma : \Gamma \times X \to H$
taking values in a compact abelian group H, it is often useful to consider the family of cocycles
$\sigma : \Gamma \times X \to H$
taking values in a compact abelian group H, it is often useful to consider the family of cocycles
![]() $\chi \circ \sigma : \Gamma \times X \to S^1$
given by composition with characters
$\chi \circ \sigma : \Gamma \times X \to S^1$
given by composition with characters
![]() $\chi \in \widehat {H}$
.
$\chi \in \widehat {H}$
.
The following lemma gives a criterion for checking that a cocycle taking values in
![]() $S^1$
is a coboundary, when the base system is an action by rotations on a compact abelian group.
$S^1$
is a coboundary, when the base system is an action by rotations on a compact abelian group.
Lemma 2.8. [Reference Ackelsberg, Bergelson and Best1, Proposition 7.12]
Let
![]() ${\mathbf {Z}} = (Z,\alpha )$
be a Kronecker system and
${\mathbf {Z}} = (Z,\alpha )$
be a Kronecker system and
![]() $\sigma : \Gamma \times Z \to S^1$
a cocycle. The following are equivalent:
$\sigma : \Gamma \times Z \to S^1$
a cocycle. The following are equivalent:
-
(i)
 $\sigma $
is a coboundary;
$\sigma $
is a coboundary; -
(ii) for any sequence
 $(g_n)_{n \in {\mathbb {N}}}$
in
$(g_n)_{n \in {\mathbb {N}}}$
in
 $\Gamma $
such that
$\Gamma $
such that
 $\alpha _{g_n} \to 0$
in Z, one has
$\alpha _{g_n} \to 0$
in Z, one has
 $\sigma _{g_n} \to 1$
in
$\sigma _{g_n} \to 1$
in
 $L^2(Z)$
.
$L^2(Z)$
.
Remark 2.9. We do not assume that the Kronecker system
![]() $(Z, \alpha )$
appearing in Lemma 2.8 is ergodic. This will be important for some later applications, e.g., Theorem 4.1.
$(Z, \alpha )$
appearing in Lemma 2.8 is ergodic. This will be important for some later applications, e.g., Theorem 4.1.
Corollary 2.10. Let
![]() ${\mathbf {Z}} = (Z,\alpha )$
be a Kronecker system and suppose
${\mathbf {Z}} = (Z,\alpha )$
be a Kronecker system and suppose
![]() $\sigma : \Gamma \times Z \to S^1$
is a coboundary. Then there is a function
$\sigma : \Gamma \times Z \to S^1$
is a coboundary. Then there is a function
![]() $\omega : Z \times Z \to S^1$
such that
$\omega : Z \times Z \to S^1$
such that
![]() $t \mapsto \omega (t, \cdot )$
is a continuous map from Z to
$t \mapsto \omega (t, \cdot )$
is a continuous map from Z to
![]() $L^2(Z)$
and
$L^2(Z)$
and
If
![]() ${\mathbf {Z}}$
is ergodic, then
${\mathbf {Z}}$
is ergodic, then
![]() $\omega $
is defined uniquely almost everywhere.
$\omega $
is defined uniquely almost everywhere.
Proof. This follows from the proof of [Reference Ackelsberg, Bergelson and Best1, Proposition 7.12]. We give a different proof here. Since
![]() $\sigma $
is a coboundary, we may write
$\sigma $
is a coboundary, we may write
![]() $\sigma = \Delta F$
for some
$\sigma = \Delta F$
for some
![]() $F : Z \to S^1$
. That is,
$F : Z \to S^1$
. That is,
We may then take
![]() $\omega (t,z) = {F(z+t)}/{F(z)}$
.
$\omega (t,z) = {F(z+t)}/{F(z)}$
.
Two additional families of cocycles will play an important role in this paper.
Definition 2.11. Let
![]() $\Gamma $
be a countable discrete abelian group and let
$\Gamma $
be a countable discrete abelian group and let
![]() ${\mathbf {Z}} = (Z, \alpha )$
be an ergodic Kronecker system. A cocycle
${\mathbf {Z}} = (Z, \alpha )$
be an ergodic Kronecker system. A cocycle
![]() $\sigma : \Gamma \times Z \to S^1$
is:
$\sigma : \Gamma \times Z \to S^1$
is:
-
(1) cohomologous to a character if there exists
 $\gamma \in \widehat {\Gamma }$
such that
$\gamma \in \widehat {\Gamma }$
such that
 $\sigma _g(z) \sim \gamma (g)$
. That is, there exists a measurable function
$\sigma _g(z) \sim \gamma (g)$
. That is, there exists a measurable function
 $F : Z \to S^1$
such that for every
$F : Z \to S^1$
such that for every $$ \begin{align*} \sigma_g(z) = \gamma(g) \frac{F(z + \alpha_g)}{F(z)} \end{align*} $$
$$ \begin{align*} \sigma_g(z) = \gamma(g) \frac{F(z + \alpha_g)}{F(z)} \end{align*} $$
 $g \in \Gamma $
and a.e.
$g \in \Gamma $
and a.e.
 $z \in Z$
;
$z \in Z$
;
-
(2) quasi-affine (or a Conze–Lesigne cocycle) if for every
 $t \in Z$
, the cocycle is cohomologous to a character.
$t \in Z$
, the cocycle is cohomologous to a character. $$ \begin{align*} \frac{\sigma_g(z+t)}{\sigma_g(z)} \end{align*} $$
$$ \begin{align*} \frac{\sigma_g(z+t)}{\sigma_g(z)} \end{align*} $$
Remark 2.12. According to the definition above, a cocycle
![]() $\sigma : \Gamma \times Z \to S^1$
is quasi-affine if and only if for each
$\sigma : \Gamma \times Z \to S^1$
is quasi-affine if and only if for each
![]() $t \in Z$
, there exists a measurable function
$t \in Z$
, there exists a measurable function
![]() $F_t : Z \to S^1$
and a character
$F_t : Z \to S^1$
and a character
![]() $\gamma _t \in \widehat {\Gamma }$
such that
$\gamma _t \in \widehat {\Gamma }$
such that
 $$ \begin{align*} \frac{\sigma_g(z+t)}{\sigma_g(z)} = \gamma_t(g) \frac{F_t(z + \alpha_g)}{F_t(z)} \end{align*} $$
$$ \begin{align*} \frac{\sigma_g(z+t)}{\sigma_g(z)} = \gamma_t(g) \frac{F_t(z + \alpha_g)}{F_t(z)} \end{align*} $$
for every
![]() $g \in \Gamma $
and a.e.
$g \in \Gamma $
and a.e.
![]() $z \in Z$
. One may additionally ensure that the maps
$z \in Z$
. One may additionally ensure that the maps
![]() $(t, z) \mapsto F_t(z)$
from
$(t, z) \mapsto F_t(z)$
from
![]() $Z \times Z$
to
$Z \times Z$
to
![]() $S^1$
and
$S^1$
and
![]() $t \mapsto \gamma _t$
from Z to
$t \mapsto \gamma _t$
from Z to
![]() $\widehat {\Gamma }$
are Borel measurable by [Reference Lesigne27, Proposition 2] and [Reference Furstenberg and Weiss14, Proposition 10.5].
$\widehat {\Gamma }$
are Borel measurable by [Reference Lesigne27, Proposition 2] and [Reference Furstenberg and Weiss14, Proposition 10.5].
Suppose
![]() ${\mathbf {Z}} = (Z, \alpha )$
is an ergodic Kronecker system, H is a compact abelian group, and
${\mathbf {Z}} = (Z, \alpha )$
is an ergodic Kronecker system, H is a compact abelian group, and
![]() $\sigma : \Gamma \times Z \to H$
is a cocycle. If
$\sigma : \Gamma \times Z \to H$
is a cocycle. If
![]() $\chi \circ \sigma $
is quasi-affine for every
$\chi \circ \sigma $
is quasi-affine for every
![]() $\chi \in \widehat {H}$
, then the group extension
$\chi \in \widehat {H}$
, then the group extension
![]() ${\mathbf {X}} \times _{\sigma } H$
is called a quasi-affine or Conze–Lesigne system.
${\mathbf {X}} \times _{\sigma } H$
is called a quasi-affine or Conze–Lesigne system.
We now give characterizations of cocycles that are cohomologous to a character or quasi-affine in the same vein as Lemma 2.8.
Lemma 2.13. [Reference Ackelsberg, Bergelson and Best1, Proposition 7.13]
Let
![]() ${\mathbf {Z}} = (Z, \alpha )$
be an ergodic Kronecker system and
${\mathbf {Z}} = (Z, \alpha )$
be an ergodic Kronecker system and
![]() $\sigma : \Gamma \times Z \to S^1$
a cocycle. The following are equivalent:
$\sigma : \Gamma \times Z \to S^1$
a cocycle. The following are equivalent:
-
(i)
 $\sigma $
is cohomologous to a character;
$\sigma $
is cohomologous to a character; -
(ii) for every
 $t \in Z$
, is a coboundary;
$t \in Z$
, is a coboundary; $$ \begin{align*} \frac{\sigma_g(z+t)}{\sigma_g(z)} \end{align*} $$
$$ \begin{align*} \frac{\sigma_g(z+t)}{\sigma_g(z)} \end{align*} $$
-
(iii) there is a Borel set
 $A \subseteq Z$
with
$A \subseteq Z$
with
 $m_Z(A)> 0$
such that is a coboundary for every
$m_Z(A)> 0$
such that is a coboundary for every $$ \begin{align*} \frac{\sigma_g(z+t)}{\sigma_g(z)} \end{align*} $$
$$ \begin{align*} \frac{\sigma_g(z+t)}{\sigma_g(z)} \end{align*} $$
 $t \in A$
;
$t \in A$
;
-
(iv) for any sequence
 $(g_n)_{n \in {\mathbb {N}}}$
in
$(g_n)_{n \in {\mathbb {N}}}$
in
 $\Gamma $
with
$\Gamma $
with
 $\alpha _{g_n} \to 0$
in Z, there is a sequence
$\alpha _{g_n} \to 0$
in Z, there is a sequence
 $(c_n)_{n \in {\mathbb {N}}}$
in
$(c_n)_{n \in {\mathbb {N}}}$
in
 $S^1$
such that
$S^1$
such that
 $c_n \sigma _{g_n}(z) \to 1$
in
$c_n \sigma _{g_n}(z) \to 1$
in
 $L^2(Z)$
.
$L^2(Z)$
.
Lemma 2.14. [Reference Ackelsberg, Bergelson and Best1, Proposition 7.15]
Let
![]() ${\mathbf {Z}} = (Z, \alpha )$
be an ergodic Kronecker system and
${\mathbf {Z}} = (Z, \alpha )$
be an ergodic Kronecker system and
![]() $\sigma : \Gamma \times Z \to S^1$
a cocycle. The following are equivalent:
$\sigma : \Gamma \times Z \to S^1$
a cocycle. The following are equivalent:
-
(i)
 $\sigma $
is quasi-affine;
$\sigma $
is quasi-affine; -
(ii) there is a Borel set
 $A \subseteq Z$
with
$A \subseteq Z$
with
 $m_Z(A)> 0$
such that is cohomologous to a character for every
$m_Z(A)> 0$
such that is cohomologous to a character for every $$ \begin{align*} \frac{\sigma_g(z+t)}{\sigma_g(z)} \end{align*} $$
$$ \begin{align*} \frac{\sigma_g(z+t)}{\sigma_g(z)} \end{align*} $$
 $t \in A$
;
$t \in A$
;
-
(iii) for any sequence
 $(g_n)_{n \in {\mathbb {N}}}$
in
$(g_n)_{n \in {\mathbb {N}}}$
in
 $\Gamma $
with
$\Gamma $
with
 $\alpha _{g_n} \to 0$
in Z, there are sequences
$\alpha _{g_n} \to 0$
in Z, there are sequences
 $(c_n)_{n \in {\mathbb {N}}}$
in
$(c_n)_{n \in {\mathbb {N}}}$
in
 $S^1$
and
$S^1$
and
 $(\unicode{x3bb} _n)_{n \in {\mathbb {N}}}$
in
$(\unicode{x3bb} _n)_{n \in {\mathbb {N}}}$
in
 $\widehat {Z}$
such that
$\widehat {Z}$
such that
 $c_n \unicode{x3bb} _n(z) \sigma _{g_n}(z) \to 1$
in
$c_n \unicode{x3bb} _n(z) \sigma _{g_n}(z) \to 1$
in
 $L^2(Z)$
.
$L^2(Z)$
.
2.6 Mackey groups
Mackey groups play an essential role in this paper. We review the definition and the basic properties of the Mackey group in this section.
Let
![]() ${\mathbf {X}} = ( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
be an ergodic
${\mathbf {X}} = ( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
be an ergodic
![]() $\Gamma $
-system, H a compact abelian group, and
$\Gamma $
-system, H a compact abelian group, and
![]() $\sigma : \Gamma \times X \to H$
a cocycle. The range of
$\sigma : \Gamma \times X \to H$
a cocycle. The range of
![]() $\sigma $
is the closed subgroup
$\sigma $
is the closed subgroup
![]() $G_{\sigma }$
generated by
$G_{\sigma }$
generated by
![]() $\{\sigma _g(x) : g \in \Gamma , x \in X\}$
. The cocycle
$\{\sigma _g(x) : g \in \Gamma , x \in X\}$
. The cocycle
![]() $\sigma $
is minimal if there is no cohomologous cocycle
$\sigma $
is minimal if there is no cohomologous cocycle
![]() $\tau $
with
$\tau $
with
![]() $G_{\tau } \subsetneq ~G_{\sigma }$
.
$G_{\tau } \subsetneq ~G_{\sigma }$
.
Proposition 2.15. [Reference Glasner15, Theorem 3.25]
Any cocycle
![]() $\sigma : \Gamma \times X \to H$
is cohomologous to a minimal cocycle. Moreover, if two minimal cocycles are cohomologous, then they have the same range.
$\sigma : \Gamma \times X \to H$
is cohomologous to a minimal cocycle. Moreover, if two minimal cocycles are cohomologous, then they have the same range.
The Mackey group associated to
![]() $\sigma $
is defined to be the range of a minimal cocycle cohomologous to
$\sigma $
is defined to be the range of a minimal cocycle cohomologous to
![]() $\sigma $
. Several important properties of Mackey groups are collected in the following proposition.
$\sigma $
. Several important properties of Mackey groups are collected in the following proposition.
Proposition 2.16
-
(1) If M is the Mackey group associated to
 $\sigma $
, then the annihilator of M is
$\sigma $
, then the annihilator of M is  $$ \begin{align*} M^{\perp} = \{ \chi \in \widehat{H} : \chi \circ \sigma \text{ is a coboundary} \}. \end{align*} $$
$$ \begin{align*} M^{\perp} = \{ \chi \in \widehat{H} : \chi \circ \sigma \text{ is a coboundary} \}. \end{align*} $$
-
(2) If
 $\sigma $
and
$\sigma $
and
 $\tau $
are cohomologous, then their Mackey groups are equal.
$\tau $
are cohomologous, then their Mackey groups are equal. -
(3) The system
 ${\mathbf {X}} \times _{\sigma } H$
is ergodic if and only if
${\mathbf {X}} \times _{\sigma } H$
is ergodic if and only if
 $\sigma $
is minimal with range
$\sigma $
is minimal with range
 $G_{\sigma } = H$
.
$G_{\sigma } = H$
. -
(4) If
 $f : X \times H \to {\mathbb {C}}$
is
$f : X \times H \to {\mathbb {C}}$
is
 $(T^{\sigma }_g)_{g \in \Gamma }$
-invariant, then
$(T^{\sigma }_g)_{g \in \Gamma }$
-invariant, then
 $f(x, y+m) = f(x, y)$
for every
$f(x, y+m) = f(x, y)$
for every
 $m \in M$
and
$m \in M$
and
 $(\mu \times m_H)$
-a.e.
$(\mu \times m_H)$
-a.e.
 $(x,y) \in X \times H$
.
$(x,y) \in X \times H$
.
Proof. For property (1), see [Reference Host and Kra22, Proposition 2.5]. Properties (2) and (3) are proved in [Reference Glasner15, Theorem 3.25].
In the case
![]() $\Gamma = {\mathbb {Z}}$
, property (4) appears in [Reference Host and Kra22, Proposition 2.4] (see also [Reference Furstenberg and Weiss14, Proposition 7.1]). We give a quick proof for general
$\Gamma = {\mathbb {Z}}$
, property (4) appears in [Reference Host and Kra22, Proposition 2.4] (see also [Reference Furstenberg and Weiss14, Proposition 7.1]). We give a quick proof for general
![]() $\Gamma $
. Suppose
$\Gamma $
. Suppose
![]() $f : X \times H \to {\mathbb {C}}$
is
$f : X \times H \to {\mathbb {C}}$
is
![]() $( T^{\sigma }_g )_{g \in \Gamma }$
-invariant. We may expand f as a Fourier series:
$( T^{\sigma }_g )_{g \in \Gamma }$
-invariant. We may expand f as a Fourier series:
 $$ \begin{align*} f(x,y) = \sum_{\chi \in \widehat{H}}{c_{\chi}(x) \chi(y)}. \end{align*} $$
$$ \begin{align*} f(x,y) = \sum_{\chi \in \widehat{H}}{c_{\chi}(x) \chi(y)}. \end{align*} $$
Then
 $$ \begin{align*} ( T^{\sigma}_g f) (x,y) = \sum_{\chi \in \widehat{H}}{c_{\chi}(T_gx) \chi(y + \sigma_g(x))} = \sum_{\chi \in \widehat{H}}{c_{\chi}(T_gx) \chi(\sigma_g(x)) \chi(y)}. \end{align*} $$
$$ \begin{align*} ( T^{\sigma}_g f) (x,y) = \sum_{\chi \in \widehat{H}}{c_{\chi}(T_gx) \chi(y + \sigma_g(x))} = \sum_{\chi \in \widehat{H}}{c_{\chi}(T_gx) \chi(\sigma_g(x)) \chi(y)}. \end{align*} $$
The assumption that
![]() $T^{\sigma }_gf = f$
then implies
$T^{\sigma }_gf = f$
then implies
for every
![]() $\chi \in \widehat {H}$
. Hence, if
$\chi \in \widehat {H}$
. Hence, if
![]() $c_{\chi } \ne 0$
, then equation (2.1) expresses
$c_{\chi } \ne 0$
, then equation (2.1) expresses
![]() $\chi \circ \sigma $
as a coboundary. Thus,
$\chi \circ \sigma $
as a coboundary. Thus,
![]() $c_{\chi } = 0$
for
$c_{\chi } = 0$
for
![]() $\chi \notin M^{\perp }$
. For any
$\chi \notin M^{\perp }$
. For any
![]() $m \in M$
, we therefore have
$m \in M$
, we therefore have
 $$ \begin{align*} f(x,y+m) = \sum_{\chi \in M^{\perp}}{c_{\chi}(x) \chi(y + m)} = \sum_{\chi \in M^{\perp}}{c_{\chi}(x) \chi(y)} = f(x,y) \end{align*} $$
$$ \begin{align*} f(x,y+m) = \sum_{\chi \in M^{\perp}}{c_{\chi}(x) \chi(y + m)} = \sum_{\chi \in M^{\perp}}{c_{\chi}(x) \chi(y)} = f(x,y) \end{align*} $$
as claimed.
For a compact abelian group K, let
![]() ${\mathcal {M}}(Z, K)$
be the space of measurable functions
${\mathcal {M}}(Z, K)$
be the space of measurable functions
![]() $Z \to K$
with the topology of convergence in measure. One can show that a sequence
$Z \to K$
with the topology of convergence in measure. One can show that a sequence
![]() $(f_n)_{n \in {\mathbb {N}}}$
in
$(f_n)_{n \in {\mathbb {N}}}$
in
![]() ${\mathcal {M}}(Z,K)$
converges if and only if
${\mathcal {M}}(Z,K)$
converges if and only if
![]() $( \chi \circ f_n )_{n \in {\mathbb {N}}}$
converges in
$( \chi \circ f_n )_{n \in {\mathbb {N}}}$
converges in
![]() $L^2(Z)$
for every
$L^2(Z)$
for every
![]() $\chi \in \widehat {K}$
; see, e.g., [Reference Ackelsberg, Bergelson and Best1, Lemma 7.28]. The following is an easy consequence of Corollary 2.10 combined with the description of the Mackey group in item (1) of Proposition 2.16.
$\chi \in \widehat {K}$
; see, e.g., [Reference Ackelsberg, Bergelson and Best1, Lemma 7.28]. The following is an easy consequence of Corollary 2.10 combined with the description of the Mackey group in item (1) of Proposition 2.16.
Proposition 2.17. Let
![]() ${\mathbf {Z}} = (Z, \alpha )$
be an ergodic Kronecker system, H a compact abelian group, and
${\mathbf {Z}} = (Z, \alpha )$
be an ergodic Kronecker system, H a compact abelian group, and
![]() $\sigma : \Gamma \times Z \to H$
a cocycle with Mackey group
$\sigma : \Gamma \times Z \to H$
a cocycle with Mackey group
![]() $M \subseteq H$
. Then there is a function
$M \subseteq H$
. Then there is a function
![]() $\omega : Z \times Z \to H/M$
such that
$\omega : Z \times Z \to H/M$
such that
![]() $t \mapsto \omega (t, \cdot )$
is a continuous map from Z to
$t \mapsto \omega (t, \cdot )$
is a continuous map from Z to
![]() ${\mathcal {M}}(Z, H/M)$
and
${\mathcal {M}}(Z, H/M)$
and
Remark 2.18. If the cocycle
![]() $\sigma $
is minimal, then it takes values in the Mackey group M, in which case
$\sigma $
is minimal, then it takes values in the Mackey group M, in which case
![]() $\omega = 0$
.
$\omega = 0$
.
The Mackey group plays an important role in the analysis of ergodic averages, as demonstrated by the following result.
Proposition 2.19. Let
![]() ${\mathbf {X}} = ( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
be an ergodic
${\mathbf {X}} = ( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
be an ergodic
![]() $\Gamma $
-system, H a compact abelian group, and
$\Gamma $
-system, H a compact abelian group, and
![]() $\sigma : \Gamma \times X \to H$
a cocycle. Let M be the Mackey group associated to
$\sigma : \Gamma \times X \to H$
a cocycle. Let M be the Mackey group associated to
![]() $\sigma $
. Let
$\sigma $
. Let
![]() $f \in L^2(\mu \times m_H)$
. If for every
$f \in L^2(\mu \times m_H)$
. If for every
![]() $\chi \in M^{\perp }$
and
$\chi \in M^{\perp }$
and
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x \in X$
, one has
$x \in X$
, one has
then
in
![]() $L^2(\mu \times m_H)$
.
$L^2(\mu \times m_H)$
.
Proof. By the mean ergodic theorem, let
![]() $\widetilde {f} = \text {UC-}\lim \nolimits _{g \in \Gamma }{T^{\sigma }_gf}$
. We want to show
$\widetilde {f} = \text {UC-}\lim \nolimits _{g \in \Gamma }{T^{\sigma }_gf}$
. We want to show
![]() $\widetilde {f} = 0$
. Since
$\widetilde {f} = 0$
. Since
![]() $L^2(H, m_H)$
is spanned by characters, it suffices to show
$L^2(H, m_H)$
is spanned by characters, it suffices to show
for every
![]() $\chi \in \widehat {H}$
and
$\chi \in \widehat {H}$
and
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x \in X$
. We will prove this identity in cases, depending on whether or not
$x \in X$
. We will prove this identity in cases, depending on whether or not
![]() $\chi $
annihilates the Mackey group M.
$\chi $
annihilates the Mackey group M.
Case 1:
![]() $\chi \notin M^{\perp }$
. By item (4) of Proposition 2.16, for any
$\chi \notin M^{\perp }$
. By item (4) of Proposition 2.16, for any
![]() $m \in M$
and
$m \in M$
and
![]() $(\mu \times m_H)$
-a.e.
$(\mu \times m_H)$
-a.e.
![]() $(x,y) \in X \times H$
, we have
$(x,y) \in X \times H$
, we have
![]() $\widetilde {f}(x,y+m) = \widetilde {f}(x,y)$
. Therefore, for
$\widetilde {f}(x,y+m) = \widetilde {f}(x,y)$
. Therefore, for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x \in X$
,
$x \in X$
,
Taking
![]() $m \in M$
such that
$m \in M$
such that
![]() $\chi (m) \ne 1$
, this implies
$\chi (m) \ne 1$
, this implies
![]() $\int _H{\widetilde {f}(x,y) \chi (y)\,dy} = 0$
as claimed.
$\int _H{\widetilde {f}(x,y) \chi (y)\,dy} = 0$
as claimed.
Case 2:
![]() $\chi \in M^{\perp }$
. Note that
$\chi \in M^{\perp }$
. Note that
By item (1) of Proposition 2.16, there is a measurable function
![]() $F : X \to S^1$
such that
$F : X \to S^1$
such that
for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x \in X$
. We then compute directly:
$x \in X$
. We then compute directly:

In the last step, we have used the hypothesis ![]() .
.
Corollary 2.20. Let
![]() ${\mathbf {Z}} = (Z, \alpha )$
be an ergodic Kronecker system, H a compact abelian group, and
${\mathbf {Z}} = (Z, \alpha )$
be an ergodic Kronecker system, H a compact abelian group, and
![]() $\sigma : \Gamma \times Z \to H$
a cocycle. Let M be the Mackey group associated to
$\sigma : \Gamma \times Z \to H$
a cocycle. Let M be the Mackey group associated to
![]() $\sigma $
, and let
$\sigma $
, and let
![]() $\omega : Z \times Z \to H$
be a measurable map such that
$\omega : Z \times Z \to H$
be a measurable map such that
![]() $t \mapsto \omega (t, \cdot ) + M$
is a continuous map
$t \mapsto \omega (t, \cdot ) + M$
is a continuous map
![]() $Z \to {\mathcal {M}}(Z, H/M)$
and
$Z \to {\mathcal {M}}(Z, H/M)$
and
![]() $\omega (\alpha _g, z) \equiv \sigma _g(z) \,\pmod {M}$
. Then for any
$\omega (\alpha _g, z) \equiv \sigma _g(z) \,\pmod {M}$
. Then for any
![]() $f \in L^2(Z \times H)$
,
$f \in L^2(Z \times H)$
,
in
![]() $L^2(Z \times H)$
.
$L^2(Z \times H)$
.
Remark 2.21. Proposition 2.17 provides a function
![]() $\widetilde {\omega } : Z \times Z \to H/M$
corresponding to the cocycle
$\widetilde {\omega } : Z \times Z \to H/M$
corresponding to the cocycle
![]() $\sigma : \Gamma \times Z \to H$
. This can be lifted to a measurable function
$\sigma : \Gamma \times Z \to H$
. This can be lifted to a measurable function
![]() $\omega : Z \times Z \to H$
satisfying the conditions in the statement of Corollary 2.20 by the Kuratowski and Ryll-Nardewski measurable selection theorem (see [Reference Srivastava32, §5.2]).
$\omega : Z \times Z \to H$
satisfying the conditions in the statement of Corollary 2.20 by the Kuratowski and Ryll-Nardewski measurable selection theorem (see [Reference Srivastava32, §5.2]).
Proof of Corollary 2.20
By linearity, we may assume f is of the form
![]() $f = h \otimes \chi $
with
$f = h \otimes \chi $
with
![]() $\chi \in \widehat {H}$
. Then the right-hand side of equation (2.2) is equal to
$\chi \in \widehat {H}$
. Then the right-hand side of equation (2.2) is equal to
 $$ \begin{align} \chi(x) \bigg( \int_Z{h(z + t) \chi(\omega(t,z))\,dt} \bigg) \bigg( \int_M{\chi(m)\,dm} \bigg). \end{align} $$
$$ \begin{align} \chi(x) \bigg( \int_Z{h(z + t) \chi(\omega(t,z))\,dt} \bigg) \bigg( \int_M{\chi(m)\,dm} \bigg). \end{align} $$
If
![]() $\chi \notin M^{\perp }$
, then
$\chi \notin M^{\perp }$
, then
![]() $\text {UC-}\lim \nolimits _{g \in \Gamma }{T^{\sigma }_gf} = 0$
by Proposition 2.19. Moreover, equation (2.3) is clearly equal to zero.
$\text {UC-}\lim \nolimits _{g \in \Gamma }{T^{\sigma }_gf} = 0$
by Proposition 2.19. Moreover, equation (2.3) is clearly equal to zero.
Suppose
![]() $\chi \in M^{\perp }$
. Then equation (2.3) reduces to
$\chi \in M^{\perp }$
. Then equation (2.3) reduces to
 $$ \begin{align*} \chi(x) \bigg( \int_Z{h(z+t) \chi(\omega(t,z))\,dt} \bigg). \end{align*} $$
$$ \begin{align*} \chi(x) \bigg( \int_Z{h(z+t) \chi(\omega(t,z))\,dt} \bigg). \end{align*} $$
The left-hand side of equation (2.2) is equal to
Define
![]() $F : Z \times Z \to S^1$
by
$F : Z \times Z \to S^1$
by
![]() $F(t, z) := h(z + t) \chi (\omega (t,z))$
. Then, by Proposition 2.17,
$F(t, z) := h(z + t) \chi (\omega (t,z))$
. Then, by Proposition 2.17,
![]() $t \mapsto F(t, \cdot )$
is a continuous map from Z to
$t \mapsto F(t, \cdot )$
is a continuous map from Z to
![]() $L^2(Z)$
and
$L^2(Z)$
and
![]() $F(\alpha _g, z) = h(z + \alpha _g) \chi (\sigma _g(z))$
. Since
$F(\alpha _g, z) = h(z + \alpha _g) \chi (\sigma _g(z))$
. Since
![]() $(Z, \alpha )$
is uniquely ergodic, it follows by Lemma 2.6 that
$(Z, \alpha )$
is uniquely ergodic, it follows by Lemma 2.6 that
in
![]() $L^2(Z)$
. This completes the proof.
$L^2(Z)$
. This completes the proof.
3 Extensions
Definition 3.1. Let
![]() $\Phi $
be a family of endomorphisms of
$\Phi $
be a family of endomorphisms of
![]() $\Gamma $
. A group of characters
$\Gamma $
. A group of characters
![]() $\Lambda \subseteq \widehat {\Gamma }$
is:
$\Lambda \subseteq \widehat {\Gamma }$
is:
-
•
 $\Phi $
-complete if
$\Phi $
-complete if
 $\unicode{x3bb} \circ \varphi \in \Lambda $
for every
$\unicode{x3bb} \circ \varphi \in \Lambda $
for every
 $\unicode{x3bb} \in \Lambda $
and every
$\unicode{x3bb} \in \Lambda $
and every
 $\varphi \in \Phi $
;
$\varphi \in \Phi $
; -
•
 $\Phi $
-divisible if for every
$\Phi $
-divisible if for every
 $\unicode{x3bb} \in \Lambda $
and every
$\unicode{x3bb} \in \Lambda $
and every
 $\varphi \in \Phi $
, there exists
$\varphi \in \Phi $
, there exists
 $\unicode{x3bb} ' \in \Lambda $
such that
$\unicode{x3bb} ' \in \Lambda $
such that
 $\unicode{x3bb} ' \circ \varphi =\unicode{x3bb} $
.
$\unicode{x3bb} ' \circ \varphi =\unicode{x3bb} $
.
The main result of this section is the following extension theorem.
Theorem 3.2. Let
![]() $\Phi $
be any countable family of endomorphisms of
$\Phi $
be any countable family of endomorphisms of
![]() $\Gamma $
, and let
$\Gamma $
, and let
![]() $\Psi $
be a countable family of injective endomorphisms of
$\Psi $
be a countable family of injective endomorphisms of
![]() $\Gamma $
. Then for any ergodic
$\Gamma $
. Then for any ergodic
![]() $\Gamma $
-system
$\Gamma $
-system
![]() ${\mathbf {X}} = ( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
, there exists an ergodic extension
${\mathbf {X}} = ( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
, there exists an ergodic extension
![]() $\widetilde {{\mathbf {X}}}$
of
$\widetilde {{\mathbf {X}}}$
of
![]() ${\mathbf {X}}$
such that the discrete spectrum of
${\mathbf {X}}$
such that the discrete spectrum of
![]() $\widetilde {{\mathbf {X}}}$
is
$\widetilde {{\mathbf {X}}}$
is
![]() $\Phi $
-complete and
$\Phi $
-complete and
![]() $\Psi $
-divisible.
$\Psi $
-divisible.
We will derive Theorem 3.2 as a consequence of the following general result.
Theorem 3.3. Let
![]() ${\mathbf {X}} = ( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
be an ergodic
${\mathbf {X}} = ( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
be an ergodic
![]() $\Gamma $
-system, and let
$\Gamma $
-system, and let
![]() $\Lambda $
be the discrete spectrum of
$\Lambda $
be the discrete spectrum of
![]() ${\mathbf {X}}$
. For any countable set
${\mathbf {X}}$
. For any countable set
![]() $C \subseteq \widehat {\Gamma }$
, there is an ergodic extension
$C \subseteq \widehat {\Gamma }$
, there is an ergodic extension
![]() $\widetilde {{\mathbf {X}}}$
of
$\widetilde {{\mathbf {X}}}$
of
![]() ${\mathbf {X}}$
such that the discrete spectrum
${\mathbf {X}}$
such that the discrete spectrum
![]() $\widetilde {\Lambda }$
of
$\widetilde {\Lambda }$
of
![]() $\widetilde {{\mathbf {X}}}$
is equal to the group generated by
$\widetilde {{\mathbf {X}}}$
is equal to the group generated by
![]() $\Lambda $
and C.
$\Lambda $
and C.
Proof. This is a special case
![]() $(k=1)$
of Theorem 2.5. Indeed, if
$(k=1)$
of Theorem 2.5. Indeed, if
![]() $\widetilde {{\mathbf {Z}}}$
is an ergodic Kronecker system with discrete spectrum
$\widetilde {{\mathbf {Z}}}$
is an ergodic Kronecker system with discrete spectrum
![]() $\widetilde {\Lambda } = \langle \Lambda , C \rangle $
, then
$\widetilde {\Lambda } = \langle \Lambda , C \rangle $
, then
![]() $\widetilde {{\mathbf {Z}}}$
is an order 1 extension of
$\widetilde {{\mathbf {Z}}}$
is an order 1 extension of
![]() ${\mathbf {Z}}$
, and so there exists by Theorem 2.5 an ergodic extension
${\mathbf {Z}}$
, and so there exists by Theorem 2.5 an ergodic extension
![]() $\widetilde {{\mathbf {X}}}$
of
$\widetilde {{\mathbf {X}}}$
of
![]() ${\mathbf {X}}$
whose Kronecker factor is isomorphic to
${\mathbf {X}}$
whose Kronecker factor is isomorphic to
![]() $\widetilde {{\mathbf {Z}}}$
.
$\widetilde {{\mathbf {Z}}}$
.
Remark 3.4.
-
(1) A similar statement to Theorem 3.3 is proved in [Reference Ackelsberg, Bergelson and Shalom2, Theorem 4.3]. However, in [Reference Ackelsberg, Bergelson and Shalom2, Theorem 4.3], only one inclusion is established (namely, that
 $\widetilde {\Lambda }$
contains
$\widetilde {\Lambda }$
contains
 $\Lambda $
and C). It is nevertheless true that the construction in the proof of [Reference Ackelsberg, Bergelson and Shalom2, Theorem 4.3] produces a system with the correct discrete spectrum, as can be seen with some additional work. (In fact, though differently phrased, the construction is equivalent to taking the relatively independent joining of
$\Lambda $
and C). It is nevertheless true that the construction in the proof of [Reference Ackelsberg, Bergelson and Shalom2, Theorem 4.3] produces a system with the correct discrete spectrum, as can be seen with some additional work. (In fact, though differently phrased, the construction is equivalent to taking the relatively independent joining of
 ${\mathbf {X}}$
with the appropriate ergodic Kronecker system
${\mathbf {X}}$
with the appropriate ergodic Kronecker system
 $\widetilde {{\mathbf {Z}}}$
).
$\widetilde {{\mathbf {Z}}}$
). -
(2) The extension
 $\widetilde {{\mathbf {X}}}$
produced via Theorem 3.3 is not unique. For instance, any weakly mixing extension of
$\widetilde {{\mathbf {X}}}$
produced via Theorem 3.3 is not unique. For instance, any weakly mixing extension of
 $\widetilde {{\mathbf {X}}}$
will again satisfy the conclusion of the theorem. The minimal such extension (that is, the one appearing as a factor of any such extension) is precisely the relatively independent joining
$\widetilde {{\mathbf {X}}}$
will again satisfy the conclusion of the theorem. The minimal such extension (that is, the one appearing as a factor of any such extension) is precisely the relatively independent joining
 ${\mathbf {X}} \times _{{\mathbf {Z}}} \widetilde {{\mathbf {Z}}}$
.
${\mathbf {X}} \times _{{\mathbf {Z}}} \widetilde {{\mathbf {Z}}}$
.
Now we can prove Theorem 3.2.
Proof of Theorem 3.2
Let
![]() $\Lambda $
be the discrete spectrum of
$\Lambda $
be the discrete spectrum of
![]() ${\mathbf {X}}$
. We extend
${\mathbf {X}}$
. We extend
![]() $\Lambda $
in stages, alternating between
$\Lambda $
in stages, alternating between
![]() $\Phi $
-completeness and
$\Phi $
-completeness and
![]() $\Psi $
-divisibility.
$\Psi $
-divisibility.
First, we make a couple of convenient reductions to make the notation less cumbersome. Replacing
![]() $\Phi $
by
$\Phi $
by
![]() $\Phi \cup \Psi $
, we may assume that
$\Phi \cup \Psi $
, we may assume that
![]() $\Psi \subseteq \Phi $
. Let
$\Psi \subseteq \Phi $
. Let
![]() $\widetilde {\Phi }$
be the semigroup
$\widetilde {\Phi }$
be the semigroup
and let
![]() $\widetilde {\Psi }$
be the semigroup
$\widetilde {\Psi }$
be the semigroup
Since
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
are countable,
$\Psi $
are countable,
![]() $\widetilde {\Phi }$
and
$\widetilde {\Phi }$
and
![]() $\widetilde {\Psi }$
are also countable. Moreover, for
$\widetilde {\Psi }$
are also countable. Moreover, for
![]() $\widetilde {\psi } = \psi _1 \circ \cdots \circ \psi _k \in \widetilde {\Psi }$
, we have that
$\widetilde {\psi } = \psi _1 \circ \cdots \circ \psi _k \in \widetilde {\Psi }$
, we have that
![]() $\widetilde {\psi }$
is injective, since it is a composition of injective maps. Thus, replacing
$\widetilde {\psi }$
is injective, since it is a composition of injective maps. Thus, replacing
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
with
$\Psi $
with
![]() $\widetilde {\Phi }$
and
$\widetilde {\Phi }$
and
![]() $\widetilde {\Psi }$
, we may assume without loss of generality that
$\widetilde {\Psi }$
, we may assume without loss of generality that
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
contain the identity map and are closed under composition.
$\Psi $
contain the identity map and are closed under composition.
Now we set up the induction process. Let
![]() $\Lambda _0 := \Lambda $
. Suppose we have defined
$\Lambda _0 := \Lambda $
. Suppose we have defined
![]() $\Lambda _0 \subseteq \cdots \subseteq \Lambda _{2j}$
for some
$\Lambda _0 \subseteq \cdots \subseteq \Lambda _{2j}$
for some
![]() $j \ge 0$
. Let
$j \ge 0$
. Let
By the induction hypothesis,
![]() $\Lambda _{2j}$
is a countable group, so
$\Lambda _{2j}$
is a countable group, so
![]() $\Lambda _{2j+1}$
is also a countable group. Moreover, since
$\Lambda _{2j+1}$
is also a countable group. Moreover, since
![]() $\Phi $
is a semigroup,
$\Phi $
is a semigroup,
![]() $\Lambda _{2j+1}$
is
$\Lambda _{2j+1}$
is
![]() $\Phi $
-complete.
$\Phi $
-complete.
We now perform subinduction to define
![]() $\Lambda _{2j+2}$
. Put
$\Lambda _{2j+2}$
. Put
![]() $S_0 := \Lambda _{2j+1}$
. Suppose we have defined
$S_0 := \Lambda _{2j+1}$
. Suppose we have defined
![]() $S_k$
for some
$S_k$
for some
![]() $k \ge 0$
. For
$k \ge 0$
. For
![]() $\unicode{x3bb} \in S_k$
and
$\unicode{x3bb} \in S_k$
and
![]() $\psi \in \Psi $
, there exists
$\psi \in \Psi $
, there exists
![]() $\unicode{x3bb} ' \in \widehat {\Gamma }$
such that
$\unicode{x3bb} ' \in \widehat {\Gamma }$
such that
![]() $\unicode{x3bb} ' \circ \psi = \unicode{x3bb} $
. To see this, first define
$\unicode{x3bb} ' \circ \psi = \unicode{x3bb} $
. To see this, first define
![]() $\unicode{x3bb} ^{\prime }_0 : \psi (\Gamma ) \to S^1$
by
$\unicode{x3bb} ^{\prime }_0 : \psi (\Gamma ) \to S^1$
by
![]() $\unicode{x3bb} ^{\prime }_0(\psi (g)) = \unicode{x3bb} (g)$
. This is well defined since
$\unicode{x3bb} ^{\prime }_0(\psi (g)) = \unicode{x3bb} (g)$
. This is well defined since
![]() $\psi $
is injective. Then by [Reference Rudin30, Theorem 2.1.4],
$\psi $
is injective. Then by [Reference Rudin30, Theorem 2.1.4],
![]() $\unicode{x3bb} ^{\prime }_0$
extends to a character
$\unicode{x3bb} ^{\prime }_0$
extends to a character
![]() $\unicode{x3bb} ' \in \widehat {\Gamma }$
, and we have
$\unicode{x3bb} ' \in \widehat {\Gamma }$
, and we have
![]() $\unicode{x3bb} ' \circ \psi = \unicode{x3bb} $
. Define a choice function
$\unicode{x3bb} ' \circ \psi = \unicode{x3bb} $
. Define a choice function
![]() $\gamma _k : S_k \times \Psi \to \widehat {\Gamma }$
so that
$\gamma _k : S_k \times \Psi \to \widehat {\Gamma }$
so that
![]() $\gamma _k(\unicode{x3bb} , \psi ) \circ \psi = \unicode{x3bb} $
for every
$\gamma _k(\unicode{x3bb} , \psi ) \circ \psi = \unicode{x3bb} $
for every
![]() $\unicode{x3bb} \in S_k$
and
$\unicode{x3bb} \in S_k$
and
![]() $\psi \in \Psi $
. Then let
$\psi \in \Psi $
. Then let
By induction, the set
![]() $S_{k+1}$
is countable. Therefore,
$S_{k+1}$
is countable. Therefore,
![]() $S = \bigcup _{k \ge 0}{S_k}$
is countable and hence generates a countable group
$S = \bigcup _{k \ge 0}{S_k}$
is countable and hence generates a countable group
![]() $\Lambda _{2j+2} := \langle S \rangle $
.
$\Lambda _{2j+2} := \langle S \rangle $
.
We claim that
![]() $\Lambda _{2j+2}$
is
$\Lambda _{2j+2}$
is
![]() $\Psi $
-divisible. Let
$\Psi $
-divisible. Let
![]() $\unicode{x3bb} \in \Lambda _{2j+2}$
and let
$\unicode{x3bb} \in \Lambda _{2j+2}$
and let
![]() $\psi \in \Psi $
. We may write
$\psi \in \Psi $
. We may write
![]() $\unicode{x3bb}\hspace{-0.5pt} =\hspace{-0.5pt} \prod _{i=1}^r{\gamma _{k_i}^{{\varepsilon }_i}(\unicode{x3bb} _i, \psi _i)}$
with
$\unicode{x3bb}\hspace{-0.5pt} =\hspace{-0.5pt} \prod _{i=1}^r{\gamma _{k_i}^{{\varepsilon }_i}(\unicode{x3bb} _i, \psi _i)}$
with
![]() $\unicode{x3bb} _i\hspace{-0.5pt} \in\hspace{-0.5pt} S_{k_i}$
,
$\unicode{x3bb} _i\hspace{-0.5pt} \in\hspace{-0.5pt} S_{k_i}$
,
![]() $\psi _i \in \Psi $
, and
$\psi _i \in \Psi $
, and
![]() ${\varepsilon }_i \in \{-1,1\}$
. Let
${\varepsilon }_i \in \{-1,1\}$
. Let
![]() $\unicode{x3bb} ^{\prime }_i = \gamma _{k_i+1} ( \gamma _{k_i}(\unicode{x3bb} _i, \psi _i), \psi ) \in S$
and let
$\unicode{x3bb} ^{\prime }_i = \gamma _{k_i+1} ( \gamma _{k_i}(\unicode{x3bb} _i, \psi _i), \psi ) \in S$
and let
![]() $\unicode{x3bb} ' = \prod _{i=1}^r{(\unicode{x3bb} ^{\prime }_i)^{{\varepsilon }_i}} \in \Lambda _{2j+2}$
. Then
$\unicode{x3bb} ' = \prod _{i=1}^r{(\unicode{x3bb} ^{\prime }_i)^{{\varepsilon }_i}} \in \Lambda _{2j+2}$
. Then

Thus,
![]() $\Lambda _{2j+2}$
is
$\Lambda _{2j+2}$
is
![]() $\Psi $
-divisible as claimed.
$\Psi $
-divisible as claimed.
By induction, we have constructed an infinite sequence of countable groups
![]() $\Lambda _0 \subseteq \Lambda _1 \subseteq \Lambda _2 \subseteq \cdots $
such that
$\Lambda _0 \subseteq \Lambda _1 \subseteq \Lambda _2 \subseteq \cdots $
such that
![]() $\Lambda _{2j+1}$
is
$\Lambda _{2j+1}$
is
![]() $\Phi $
-complete and
$\Phi $
-complete and
![]() $\Lambda _{2j+2}$
is
$\Lambda _{2j+2}$
is
![]() $\Psi $
-divisible for
$\Psi $
-divisible for
![]() $j \ge 0$
. Let
$j \ge 0$
. Let
![]() $\Lambda _{\infty } := \bigcup _{j=0}^{\infty }{\Lambda _j}$
. Then
$\Lambda _{\infty } := \bigcup _{j=0}^{\infty }{\Lambda _j}$
. Then
![]() $\Lambda _{\infty }$
is a countable group that is
$\Lambda _{\infty }$
is a countable group that is
![]() $\Phi $
-complete and
$\Phi $
-complete and
![]() $\Psi $
-divisible.
$\Psi $
-divisible.
Finally, we apply Theorem 3.3 to obtain an ergodic extension
![]() $\widetilde {{\mathbf {X}}}$
of
$\widetilde {{\mathbf {X}}}$
of
![]() ${\mathbf {X}}$
such that the discrete spectrum
${\mathbf {X}}$
such that the discrete spectrum
![]() $\widetilde {\Lambda }$
of
$\widetilde {\Lambda }$
of
![]() $\widetilde {{\mathbf {X}}}$
is equal to
$\widetilde {{\mathbf {X}}}$
is equal to
![]() $\Lambda _{\infty }$
.
$\Lambda _{\infty }$
.
Remark 3.5. The subinduction and use of the choice functions
![]() $\gamma _k$
in the construction of the group
$\gamma _k$
in the construction of the group
![]() $\Lambda _{2j+2}$
is solely used to ensure that
$\Lambda _{2j+2}$
is solely used to ensure that
![]() $\Lambda _{2j+2}$
is countable. A
$\Lambda _{2j+2}$
is countable. A
![]() $\Psi $
-divisible group can be defined more directly, namely
$\Psi $
-divisible group can be defined more directly, namely
In general,
![]() $D_{2j+2}$
is uncountable. However, if
$D_{2j+2}$
is uncountable. However, if
![]() $\psi (\Gamma )$
is a finite index subgroup of
$\psi (\Gamma )$
is a finite index subgroup of
![]() $\Gamma $
for each
$\Gamma $
for each
![]() $\psi \in \Psi $
, then the set
$\psi \in \Psi $
, then the set
![]() $\{\unicode{x3bb} \in \widehat {\Gamma } : \unicode{x3bb} \circ \psi = \unicode{x3bb} _0\}$
has cardinality
$\{\unicode{x3bb} \in \widehat {\Gamma } : \unicode{x3bb} \circ \psi = \unicode{x3bb} _0\}$
has cardinality
![]() $[\Gamma : \psi (\Gamma )] < \infty $
for each
$[\Gamma : \psi (\Gamma )] < \infty $
for each
![]() $\unicode{x3bb} _0 \in \Lambda _{2j+1}$
and
$\unicode{x3bb} _0 \in \Lambda _{2j+1}$
and
![]() $\psi \in \Psi $
. Thus, in this case,
$\psi \in \Psi $
. Thus, in this case,
![]() $D_{2j+2}$
is countable, so one may take
$D_{2j+2}$
is countable, so one may take
![]() $\Lambda _{2j+2} = D_{2j+2}$
rather than using the more complicated construction appearing in the proof of Theorem 3.2. For the group
$\Lambda _{2j+2} = D_{2j+2}$
rather than using the more complicated construction appearing in the proof of Theorem 3.2. For the group
![]() $\Gamma = {\mathbb {Z}}^d$
, an endomorphism is injective if and only if it has finite index image if and only if the corresponding matrix is non-singular. Therefore, the simpler construction
$\Gamma = {\mathbb {Z}}^d$
, an endomorphism is injective if and only if it has finite index image if and only if the corresponding matrix is non-singular. Therefore, the simpler construction
![]() $\Lambda _{2j+2} = D_{2j+2}$
can always be used when dealing with the group
$\Lambda _{2j+2} = D_{2j+2}$
can always be used when dealing with the group
![]() $\Gamma = {\mathbb {Z}}^d$
.
$\Gamma = {\mathbb {Z}}^d$
.
4 Mackey group associated with
 $\{\varphi , \psi \}$
$\{\varphi , \psi \}$
Let
![]() $\varphi , \psi \in \mathrm {End}(\Gamma )$
such that
$\varphi , \psi \in \mathrm {End}(\Gamma )$
such that
![]() $(\psi - \varphi )(\Gamma )$
has finite index in
$(\psi - \varphi )(\Gamma )$
has finite index in
![]() $\Gamma $
, and suppose
$\Gamma $
, and suppose
![]() $\theta _1, \theta _2 \in \mathrm {End}(\Gamma )$
are such that
$\theta _1, \theta _2 \in \mathrm {End}(\Gamma )$
are such that
![]() $\theta _1 \circ \varphi + \theta _2 \circ \psi $
is injective.
$\theta _1 \circ \varphi + \theta _2 \circ \psi $
is injective.
Let
![]() ${\mathbf {X}}$
be an ergodic quasi-affine
${\mathbf {X}}$
be an ergodic quasi-affine
![]() $\Gamma $
-system, and write
$\Gamma $
-system, and write
![]() ${\mathbf {X}} = {\mathbf {Z}} \times _{\sigma } H$
. Assume that the discrete spectrum of
${\mathbf {X}} = {\mathbf {Z}} \times _{\sigma } H$
. Assume that the discrete spectrum of
![]() ${\mathbf {X}}$
is
${\mathbf {X}}$
is
![]() $\{\varphi , \psi , \theta _1, \theta _2\}$
-complete and
$\{\varphi , \psi , \theta _1, \theta _2\}$
-complete and
![]() $(\theta _1 \circ \varphi + \theta _2 \circ \psi )$
-divisible. In this section, we consider a variant of the notion of Mackey groups as discussed in §2.6 that is tailored to analyzing ergodic averages of the form
$(\theta _1 \circ \varphi + \theta _2 \circ \psi )$
-divisible. In this section, we consider a variant of the notion of Mackey groups as discussed in §2.6 that is tailored to analyzing ergodic averages of the form
for
![]() $f_1, f_2 \in L^{\infty }(Z \times H)$
.
$f_1, f_2 \in L^{\infty }(Z \times H)$
.
Since the discrete spectrum
![]() $\Lambda $
of
$\Lambda $
of
![]() ${\mathbf {X}}$
is
${\mathbf {X}}$
is
![]() $\{\varphi , \psi , \theta _1, \theta _2\}$
-complete, we have induced continuous endomorphisms of
$\{\varphi , \psi , \theta _1, \theta _2\}$
-complete, we have induced continuous endomorphisms of
![]() $Z = \widehat {\Lambda }$
, which we denote by
$Z = \widehat {\Lambda }$
, which we denote by
![]() $\widehat {\varphi }$
,
$\widehat {\varphi }$
,
![]() $\widehat {\psi }$
,
$\widehat {\psi }$
,
![]() $\widehat {\theta }_1$
, and
$\widehat {\theta }_1$
, and
![]() $\widehat {\theta }_2$
. To see this, view Z as the dual group, expressed additively as the group of homomorphisms
$\widehat {\theta }_2$
. To see this, view Z as the dual group, expressed additively as the group of homomorphisms
![]() $z : \Lambda \to {\mathbb {T}} = {\mathbb {R}}/{\mathbb {Z}}$
. For
$z : \Lambda \to {\mathbb {T}} = {\mathbb {R}}/{\mathbb {Z}}$
. For
![]() $f \in \{\varphi , \psi , \theta _1, \theta _2\}$
, the map
$f \in \{\varphi , \psi , \theta _1, \theta _2\}$
, the map
![]() $\widehat {f} : Z \to Z$
is then given by
$\widehat {f} : Z \to Z$
is then given by
Since
![]() $\Lambda $
is
$\Lambda $
is
![]() $(\theta _1 \circ \varphi + \theta _2 \circ \psi )$
-divisible, we claim that
$(\theta _1 \circ \varphi + \theta _2 \circ \psi )$
-divisible, we claim that
![]() $\widehat {\theta }_1 \circ \widehat {\varphi } + \widehat {\theta }_2 \circ \widehat {\psi }$
is injective. Indeed, suppose
$\widehat {\theta }_1 \circ \widehat {\varphi } + \widehat {\theta }_2 \circ \widehat {\psi }$
is injective. Indeed, suppose
![]() $(\widehat {\theta }_1 \circ \widehat {\varphi } + \widehat {\theta }_2 \circ \widehat {\psi })(z) = 0$
. Then for every
$(\widehat {\theta }_1 \circ \widehat {\varphi } + \widehat {\theta }_2 \circ \widehat {\psi })(z) = 0$
. Then for every
![]() $\unicode{x3bb} \in \Lambda $
,
$\unicode{x3bb} \in \Lambda $
,
However, for any
![]() $\unicode{x3bb} \in \Lambda $
, there exists
$\unicode{x3bb} \in \Lambda $
, there exists
![]() $\unicode{x3bb} ' \in \Lambda $
with
$\unicode{x3bb} ' \in \Lambda $
with
![]() $\unicode{x3bb} ' \circ (\theta _1 \circ \varphi + \theta _2 \circ \psi ) = \unicode{x3bb} $
, so
$\unicode{x3bb} ' \circ (\theta _1 \circ \varphi + \theta _2 \circ \psi ) = \unicode{x3bb} $
, so
That is,
![]() $z = 0$
.
$z = 0$
.
Let
and let
![]() $\widetilde {\alpha } : \Gamma \to W$
be the homomorphism
$\widetilde {\alpha } : \Gamma \to W$
be the homomorphism
Let
![]() $\widetilde {\sigma } : \Gamma \times W \to H^2$
be the cocycle
$\widetilde {\sigma } : \Gamma \times W \to H^2$
be the cocycle
Now we define the Mackey group to be the closed subgroup
![]() $M \le H^2$
with annihilator
$M \le H^2$
with annihilator
The Kronecker system
![]() ${\mathbf {W}} = (W, \widetilde {\alpha })$
is not necessarily ergodic. However, its ergodic decomposition is easy to describe and interacts well with the Mackey group M. Namely, we may express W as the union of the subsets
${\mathbf {W}} = (W, \widetilde {\alpha })$
is not necessarily ergodic. However, its ergodic decomposition is easy to describe and interacts well with the Mackey group M. Namely, we may express W as the union of the subsets
each supporting a Haar measure
![]() $m_z$
. The system
$m_z$
. The system
![]() $(W_0, \widetilde {\alpha })$
is uniquely ergodic, and each of the systems
$(W_0, \widetilde {\alpha })$
is uniquely ergodic, and each of the systems
![]() $(W_z, \widetilde {\alpha })$
for
$(W_z, \widetilde {\alpha })$
for
![]() $z \in Z$
is an isomorphic copy. It is easily verified that the Haar measure on W decomposes as
$z \in Z$
is an isomorphic copy. It is easily verified that the Haar measure on W decomposes as
![]() $m_W = \int _Z{m_z\,dz}$
. An important property of this ergodic decomposition is that, letting
$m_W = \int _Z{m_z\,dz}$
. An important property of this ergodic decomposition is that, letting
![]() $M_z$
denote the Mackey group corresponding to the ergodic component
$M_z$
denote the Mackey group corresponding to the ergodic component
![]() $(W_z, \widetilde {\alpha })$
, one has
$(W_z, \widetilde {\alpha })$
, one has
![]() $M_z = M$
for a.e.
$M_z = M$
for a.e.
![]() $z \in Z$
(see [Reference Ackelsberg, Bergelson and Best1, Proposition 7.9]).
$z \in Z$
(see [Reference Ackelsberg, Bergelson and Best1, Proposition 7.9]).
We now seek to describe the structure of the Mackey group M. A classical fact in ergodic theory is that, given two measure-preserving systems
![]() ${\mathbf {X}}_1$
and
${\mathbf {X}}_1$
and
![]() ${\mathbf {X}}_2$
, invariant functions for the product system
${\mathbf {X}}_2$
, invariant functions for the product system
![]() ${\mathbf {X}}_1 \times {\mathbf {X}}_2$
are formed from functions of the form
${\mathbf {X}}_1 \times {\mathbf {X}}_2$
are formed from functions of the form
![]() $f_1 \otimes f_2$
, where
$f_1 \otimes f_2$
, where
![]() $f_1$
is an eigenfunction of
$f_1$
is an eigenfunction of
![]() ${\mathbf {X}}_1$
,
${\mathbf {X}}_1$
,
![]() $f_2$
is an eigenfunction of
$f_2$
is an eigenfunction of
![]() ${\mathbf {X}}_2$
, and the corresponding eigenvalues are conjugates of one another. The following result describes the Mackey group M in an analogous manner.
${\mathbf {X}}_2$
, and the corresponding eigenvalues are conjugates of one another. The following result describes the Mackey group M in an analogous manner.
Theorem 4.1. Let M be the Mackey group as defined above. Then
 $$ \begin{align*} M^{\perp} = \{ \chi_1 &\otimes \chi_2 \in \widehat{H^2} : \text{ there exists } \gamma \in \widehat{\Gamma}, \chi_1(\sigma_{\varphi(g)}(w_1)) \\ &\sim \gamma(g)\text{ and } \chi_2(\sigma_{\psi(g)}(w_2)) \sim \overline{\gamma}(g) \text{ over } (W, \widetilde{\alpha}) \}. \end{align*} $$
$$ \begin{align*} M^{\perp} = \{ \chi_1 &\otimes \chi_2 \in \widehat{H^2} : \text{ there exists } \gamma \in \widehat{\Gamma}, \chi_1(\sigma_{\varphi(g)}(w_1)) \\ &\sim \gamma(g)\text{ and } \chi_2(\sigma_{\psi(g)}(w_2)) \sim \overline{\gamma}(g) \text{ over } (W, \widetilde{\alpha}) \}. \end{align*} $$
Remark 4.2. Throughout this section, we treat
![]() $g \in \Gamma $
and
$g \in \Gamma $
and
![]() $w = (w_1, w_2) \in W$
as variables, and write expressions of the form
$w = (w_1, w_2) \in W$
as variables, and write expressions of the form
![]() $\rho (g,w_1,w_2) \sim \tau (g,w_1,w_2)$
as shorthand for the statement that the cocycles
$\rho (g,w_1,w_2) \sim \tau (g,w_1,w_2)$
as shorthand for the statement that the cocycles
![]() $(g, (w_1,w_2)) \mapsto \rho (g, w_1, w_2)$
and
$(g, (w_1,w_2)) \mapsto \rho (g, w_1, w_2)$
and
![]() $(g, (w_1, w_2)) \mapsto \tau (g, w_1, w_2)$
are cohomologous. For example, the notation
$(g, (w_1, w_2)) \mapsto \tau (g, w_1, w_2)$
are cohomologous. For example, the notation
![]() $\chi _1(\sigma _{\varphi (g)}(w_1)) \sim \gamma (g)$
means that there is a measurable function
$\chi _1(\sigma _{\varphi (g)}(w_1)) \sim \gamma (g)$
means that there is a measurable function
![]() $F : W \to S^1$
such that
$F : W \to S^1$
such that
for every
![]() $g \in \Gamma $
and almost every
$g \in \Gamma $
and almost every
![]() $w = (w_1, w_2) \in W$
.
$w = (w_1, w_2) \in W$
.
Proof. Suppose
![]() $\chi _1, \chi _2 \in \widehat {H}$
and
$\chi _1, \chi _2 \in \widehat {H}$
and
![]() $\gamma \in \widehat {\Gamma }$
such that
$\gamma \in \widehat {\Gamma }$
such that
![]() $\chi _1(\sigma _{\varphi (g)}(w_1)) \sim \gamma (g)$
and
$\chi _1(\sigma _{\varphi (g)}(w_1)) \sim \gamma (g)$
and
![]() $\chi _2(\sigma _{\psi (g)} (w_2)) \sim \overline {\gamma }(g)$
. Then
$\chi _2(\sigma _{\psi (g)} (w_2)) \sim \overline {\gamma }(g)$
. Then
so
![]() $\chi _1 \otimes \chi _2 \in M^{\perp }$
.
$\chi _1 \otimes \chi _2 \in M^{\perp }$
.
Conversely, suppose
![]() $\chi _1 \otimes \chi _2 \in M^{\perp }$
. Let
$\chi _1 \otimes \chi _2 \in M^{\perp }$
. Let
![]() $(g_n)_{n \in {\mathbb {N}}}$
be a sequence in
$(g_n)_{n \in {\mathbb {N}}}$
be a sequence in
![]() $\Gamma $
such that
$\Gamma $
such that
![]() $\widetilde {\alpha }_{g_n} \to 0$
in W. By Lemma 2.8,
$\widetilde {\alpha }_{g_n} \to 0$
in W. By Lemma 2.8,
in
![]() $L^2(W)$
. That is,
$L^2(W)$
. That is,
in
![]() $L^2(Z \times Z)$
.
$L^2(Z \times Z)$
.
The cocycle
![]() $\sigma $
is quasi-affine, so by Lemma 2.14, there are sequences
$\sigma $
is quasi-affine, so by Lemma 2.14, there are sequences
![]() $(c_{i,n})_{n \in {\mathbb {N}}}$
in
$(c_{i,n})_{n \in {\mathbb {N}}}$
in
![]() $S^1$
and
$S^1$
and
![]() $(\unicode{x3bb} _{i,n})_{n \in {\mathbb {N}}}$
in
$(\unicode{x3bb} _{i,n})_{n \in {\mathbb {N}}}$
in
![]() $\widehat {Z}$
for
$\widehat {Z}$
for
![]() $i = 1, 2$
such that
$i = 1, 2$
such that
in
![]() $L^2(Z)$
. We will combine equations (4.1) and (4.2) to show that
$L^2(Z)$
. We will combine equations (4.1) and (4.2) to show that
![]() $\chi _1(\sigma _{\varphi (g)}(z)) \sim \gamma (g)$
and
$\chi _1(\sigma _{\varphi (g)}(z)) \sim \gamma (g)$
and
![]() $\chi _2(\sigma _{\psi (g)}(z)) \sim \overline {\gamma }(g)$
for some
$\chi _2(\sigma _{\psi (g)}(z)) \sim \overline {\gamma }(g)$
for some
![]() $\gamma \in \widehat {\Gamma }$
.
$\gamma \in \widehat {\Gamma }$
.
For convenience, let
![]() $\mu _n = \chi _1 \circ \sigma _{\varphi (g_n)}$
and
$\mu _n = \chi _1 \circ \sigma _{\varphi (g_n)}$
and
![]() $\nu _n = \chi _2 \circ \sigma _{\psi (g_n)}$
. Now we perform a change of coordinates. Define
$\nu _n = \chi _2 \circ \sigma _{\psi (g_n)}$
. Now we perform a change of coordinates. Define
![]() $\eta : Z^2 \to Z^2$
by
$\eta : Z^2 \to Z^2$
by
and, for
![]() $u \in Z$
, let
$u \in Z$
, let
![]() $\zeta _u : Z^2 \to Z^2$
be the map
$\zeta _u : Z^2 \to Z^2$
be the map
Note that equation (4.1) is equivalent to
in
![]() $L^2 ( Z^2 )$
.
$L^2 ( Z^2 )$
.
We claim
in
![]() $L^2 ( Z^2 )$
. Let
$L^2 ( Z^2 )$
. Let
![]() $\zeta := \zeta _0$
. Fix
$\zeta := \zeta _0$
. Fix
![]() $u \in Z$
and let
$u \in Z$
and let
![]() $f_n(z,t) = ( ( \mu _n \otimes \nu _n ) \circ \eta ) (z+u,t)$
. Then
$f_n(z,t) = ( ( \mu _n \otimes \nu _n ) \circ \eta ) (z+u,t)$
. Then
![]() $( \mu _n \otimes \nu _n ) \circ \eta \circ \zeta _u = f_n \circ \zeta $
. We then want to show
$( \mu _n \otimes \nu _n ) \circ \eta \circ \zeta _u = f_n \circ \zeta $
. We then want to show
![]() $f_n \circ \zeta \to 1$
in
$f_n \circ \zeta \to 1$
in
![]() $L^2 ( Z^2 )$
. Since the Haar measure on
$L^2 ( Z^2 )$
. Since the Haar measure on
![]() $Z^2$
is invariant under shifting by
$Z^2$
is invariant under shifting by
![]() $(u,0)$
, we have
$(u,0)$
, we have
![]() $f_n \to 1$
in
$f_n \to 1$
in
![]() $L^2 ( Z^2 )$
by equation (4.3). It therefore suffices to show that
$L^2 ( Z^2 )$
by equation (4.3). It therefore suffices to show that
![]() $\zeta ( Z^2 )$
has positive measure (equivalently, finite index) in
$\zeta ( Z^2 )$
has positive measure (equivalently, finite index) in
![]() $Z^2$
. By assumption,
$Z^2$
. By assumption,
![]() $(\psi - \varphi )(\Gamma )$
has finite index in
$(\psi - \varphi )(\Gamma )$
has finite index in
![]() $\Gamma $
. Hence,
$\Gamma $
. Hence,
![]() $[ Z : ( \widehat {\psi } - \widehat {\varphi } )(Z) ]\hspace{-0.5pt} \le\hspace{-0.5pt} [ \Gamma : (\psi - \varphi )(\Gamma ) ]\hspace{-0.5pt} <\hspace{-0.5pt} \infty $
. Let
$[ Z : ( \widehat {\psi } - \widehat {\varphi } )(Z) ]\hspace{-0.5pt} \le\hspace{-0.5pt} [ \Gamma : (\psi - \varphi )(\Gamma ) ]\hspace{-0.5pt} <\hspace{-0.5pt} \infty $
. Let
![]() $F\hspace{-1pt} \subseteq\hspace{-1pt} Z$
be a finite set such that
$F\hspace{-1pt} \subseteq\hspace{-1pt} Z$
be a finite set such that
![]() $( \widehat {\psi }\hspace{-0.5pt} -\hspace{-0.5pt} \widehat {\varphi } )(Z)\hspace{-0.5pt} +\hspace{-0.5pt} F\hspace{-1pt} =\hspace{-1pt} Z$
. Let
$( \widehat {\psi }\hspace{-0.5pt} -\hspace{-0.5pt} \widehat {\varphi } )(Z)\hspace{-0.5pt} +\hspace{-0.5pt} F\hspace{-1pt} =\hspace{-1pt} Z$
. Let
![]() $(z,t) \in Z^2$
be given. Choose
$(z,t) \in Z^2$
be given. Choose
![]() $x \in Z$
and
$x \in Z$
and
![]() $s \in F$
such that
$s \in F$
such that
![]() $( \widehat {\psi } - \widehat {\varphi } )(x) + s = z + \widehat {\varphi }(t)$
. Put
$( \widehat {\psi } - \widehat {\varphi } )(x) + s = z + \widehat {\varphi }(t)$
. Put
![]() $y = x + t$
. Then
$y = x + t$
. Then
This shows that
![]() $\zeta ( Z^2 ) + ( F \times \{0\} ) = Z^2$
, so
$\zeta ( Z^2 ) + ( F \times \{0\} ) = Z^2$
, so
Thus, equation (4.4) holds.
However,
We therefore deduce from equation (4.4) that
in
![]() $L^2 ( ( u + ( \widehat {\psi } - \widehat {\varphi } )(Z) )^2 )$
. Taking a conjugate and multiplying by equation (4.2), we deduce
$L^2 ( ( u + ( \widehat {\psi } - \widehat {\varphi } )(Z) )^2 )$
. Taking a conjugate and multiplying by equation (4.2), we deduce
in
![]() $L^2 ( ( u + ( \widehat {\psi } - \widehat {\varphi } )(Z) )^2 )$
. That is,
$L^2 ( ( u + ( \widehat {\psi } - \widehat {\varphi } )(Z) )^2 )$
. That is,
Multiplying by
![]() $\overline {\unicode{x3bb} }_{2,n}$
in the integrand and using the fact that each
$\overline {\unicode{x3bb} }_{2,n}$
in the integrand and using the fact that each
![]() $\unicode{x3bb} _{i,n}$
is a homomorphism,
$\unicode{x3bb} _{i,n}$
is a homomorphism,
It follows that for all sufficiently large n, we have
![]() $\unicode{x3bb} _{1,n}, \unicode{x3bb} _{2,n} \in ( ( \widehat {\psi } - \widehat {\varphi } )(Z) )^{\perp }$
.
$\unicode{x3bb} _{1,n}, \unicode{x3bb} _{2,n} \in ( ( \widehat {\psi } - \widehat {\varphi } )(Z) )^{\perp }$
.
Let
![]() $A = ( \widehat {\psi } - \widehat {\varphi } )(Z)$
and put
$A = ( \widehat {\psi } - \widehat {\varphi } )(Z)$
and put
![]() $A_1 = \{ (w_1, w_2) \in W : w_1 \in A \}$
. Note that
$A_1 = \{ (w_1, w_2) \in W : w_1 \in A \}$
. Note that
![]() $A_1$
is a Borel set and
$A_1$
is a Borel set and
![]() $m_W(A_1) = m_Z(A)> 0$
. Fix
$m_W(A_1) = m_Z(A)> 0$
. Fix
![]() $t = (t_1, t_2) \in A_1$
and let
$t = (t_1, t_2) \in A_1$
and let
 $$ \begin{align*} \rho_g(w) = \frac{\chi_1( \sigma_{\varphi(g)}(w_1 + t_1) )}{\chi_1 ( \sigma_{\varphi(g)}(w_1))}. \end{align*} $$
$$ \begin{align*} \rho_g(w) = \frac{\chi_1( \sigma_{\varphi(g)}(w_1 + t_1) )}{\chi_1 ( \sigma_{\varphi(g)}(w_1))}. \end{align*} $$
By Lemma 2.13, our goal is to show that
![]() $\rho $
is a coboundary. Since
$\rho $
is a coboundary. Since
![]() $(g_n)_{n \in {\mathbb {N}}}$
is an arbitrary sequence in
$(g_n)_{n \in {\mathbb {N}}}$
is an arbitrary sequence in
![]() $\Gamma $
with
$\Gamma $
with
![]() $\widetilde {\alpha }_{g_n} \to 0$
, it suffices, by Lemma 2.8, to show
$\widetilde {\alpha }_{g_n} \to 0$
, it suffices, by Lemma 2.8, to show
![]() $\rho _{g_n} \to 1$
in
$\rho _{g_n} \to 1$
in
![]() $L^2(W)$
. We have already seen that
$L^2(W)$
. We have already seen that
in
![]() $L^2(Z)$
and
$L^2(Z)$
and
![]() $\unicode{x3bb} _{1,n} \in A^{\perp }$
. In particular,
$\unicode{x3bb} _{1,n} \in A^{\perp }$
. In particular,
![]() $\unicode{x3bb} _{1,n}(z+t_1) = \unicode{x3bb} _{1,n}(z)$
, since
$\unicode{x3bb} _{1,n}(z+t_1) = \unicode{x3bb} _{1,n}(z)$
, since
![]() $t_1 \in A$
. Therefore,
$t_1 \in A$
. Therefore,

in
![]() $L^2(W)$
. This proves that
$L^2(W)$
. This proves that
![]() $\chi _1 ( \sigma _{\varphi (g)}(w_1) )$
is cohomologous to a character. The same argument applies to
$\chi _1 ( \sigma _{\varphi (g)}(w_1) )$
is cohomologous to a character. The same argument applies to
![]() $\chi _2 ( \sigma _{\psi (g)}(w_2) )$
, taking the set
$\chi _2 ( \sigma _{\psi (g)}(w_2) )$
, taking the set
![]() $A_2 = \{ (w_1, w_2) \in W : w_2 \in A \}$
.
$A_2 = \{ (w_1, w_2) \in W : w_2 \in A \}$
.
Therefore, we may assume in the above that
![]() $\unicode{x3bb} _{i,n} = 1$
for every
$\unicode{x3bb} _{i,n} = 1$
for every
![]() $n \in {\mathbb {N}}$
and
$n \in {\mathbb {N}}$
and
![]() $i = 1, 2$
. We may also assume
$i = 1, 2$
. We may also assume
![]() $c_{i,n}\hspace{-1pt} =\hspace{-1pt} \gamma _i(g_n)$
, where
$c_{i,n}\hspace{-1pt} =\hspace{-1pt} \gamma _i(g_n)$
, where
![]() $\chi _1 ( \sigma _{\varphi (g)}(w_1) ) \sim \gamma _1(g)$
and
$\chi _1 ( \sigma _{\varphi (g)}(w_1) ) \sim \gamma _1(g)$
and
![]() $\chi _2 ( \sigma _{\psi (g)}(w_2) ) \sim \gamma _2(g)$
. We have thus shown that for any sequence
$\chi _2 ( \sigma _{\psi (g)}(w_2) ) \sim \gamma _2(g)$
. We have thus shown that for any sequence
![]() $(g_n)_{n \in {\mathbb {N}}}$
with
$(g_n)_{n \in {\mathbb {N}}}$
with
![]() $\widetilde {\alpha }_{g_n} \to 0$
, we have
$\widetilde {\alpha }_{g_n} \to 0$
, we have
Hence, by Lemma 2.8,
![]() $\gamma _1 \gamma _2 \sim 1$
. By tweaking
$\gamma _1 \gamma _2 \sim 1$
. By tweaking
![]() $\gamma _2$
up to cohomology, we may assume
$\gamma _2$
up to cohomology, we may assume
![]() $\gamma _2 = \overline {\gamma }_1$
, completing the proof.
$\gamma _2 = \overline {\gamma }_1$
, completing the proof.
By passing to an extension of the original system, we will show that the Mackey group M associated with
![]() $\{\varphi , \psi \}$
decomposes into the Cartesian product of Mackey groups associated with
$\{\varphi , \psi \}$
decomposes into the Cartesian product of Mackey groups associated with
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
, respectively.
$\psi $
, respectively.
Theorem 4.3. Let
![]() $\varphi , \psi \in \mathrm {End}(\Gamma )$
such that
$\varphi , \psi \in \mathrm {End}(\Gamma )$
such that
![]() $(\psi - \varphi )(\Gamma )$
has finite index in
$(\psi - \varphi )(\Gamma )$
has finite index in
![]() $\Gamma $
, and suppose
$\Gamma $
, and suppose
![]() $\theta _1, \theta _2 \in \mathrm {End}(\Gamma )$
such that
$\theta _1, \theta _2 \in \mathrm {End}(\Gamma )$
such that
![]() $\theta _1 \circ \varphi + \theta _2 \circ \psi $
is injective. Let
$\theta _1 \circ \varphi + \theta _2 \circ \psi $
is injective. Let
![]() ${\mathbf {X}} = {\mathbf {Z}} \times _{\sigma } H$
be an ergodic quasi-affine
${\mathbf {X}} = {\mathbf {Z}} \times _{\sigma } H$
be an ergodic quasi-affine
![]() $\Gamma $
system such that the discrete spectrum
$\Gamma $
system such that the discrete spectrum
![]() $\widehat {Z}$
is
$\widehat {Z}$
is
![]() $\{\varphi , \psi , \theta _1, \theta _2\}$
-complete and
$\{\varphi , \psi , \theta _1, \theta _2\}$
-complete and
![]() $(\theta _1 \circ \varphi + \theta _2 \circ \psi )$
-divisible. There is an ergodic quasi-affine extension
$(\theta _1 \circ \varphi + \theta _2 \circ \psi )$
-divisible. There is an ergodic quasi-affine extension
![]() ${\mathbf {X}}' = {\mathbf {Z}}' \times _{\sigma '} H$
of
${\mathbf {X}}' = {\mathbf {Z}}' \times _{\sigma '} H$
of
![]() ${\mathbf {X}}$
such that the Mackey group
${\mathbf {X}}$
such that the Mackey group
![]() $M'$
decomposes as
$M'$
decomposes as
![]() $M' = M^{\prime }_{\varphi } \times M^{\prime }_{\psi }$
, where
$M' = M^{\prime }_{\varphi } \times M^{\prime }_{\psi }$
, where
and
Proof. Let
and
Then let
![]() $C = C_{\varphi } \cap C_{\psi }$
. Note that a character
$C = C_{\varphi } \cap C_{\psi }$
. Note that a character
![]() $\gamma \in \widehat {\Gamma }$
is cohomologous to another character
$\gamma \in \widehat {\Gamma }$
is cohomologous to another character
![]() $\gamma ' \in \widehat {\Gamma }$
if and only if
$\gamma ' \in \widehat {\Gamma }$
if and only if
![]() $\overline {\gamma } \gamma '$
is an eigenvalue for the system
$\overline {\gamma } \gamma '$
is an eigenvalue for the system
![]() $(W, \widetilde {\alpha })$
. That is,
$(W, \widetilde {\alpha })$
. That is,
Moreover, the groups
![]() $\widehat {Z}$
and
$\widehat {Z}$
and
![]() $\widehat {H}$
are countable, so C is a countable set of characters.
$\widehat {H}$
are countable, so C is a countable set of characters.
By Theorem 3.2, let
![]() $\Lambda '$
be a countable subgroup of
$\Lambda '$
be a countable subgroup of
![]() $\widehat {\Gamma }$
that is
$\widehat {\Gamma }$
that is
![]() $\{\varphi , \psi , \theta _1, \theta _2\}$
-complete,
$\{\varphi , \psi , \theta _1, \theta _2\}$
-complete,
![]() $(\theta _1 \circ \varphi + \theta _2 \circ \psi )$
-divisible, and contains the group generated by
$(\theta _1 \circ \varphi + \theta _2 \circ \psi )$
-divisible, and contains the group generated by
![]() $\Lambda = \widehat {Z}$
and C, and let
$\Lambda = \widehat {Z}$
and C, and let
![]() $Z' = \widehat {\Lambda }'$
. For
$Z' = \widehat {\Lambda }'$
. For
![]() $g \in \Gamma $
, let
$g \in \Gamma $
, let
![]() $\alpha ^{\prime }_g \in Z'$
be the element such that
$\alpha ^{\prime }_g \in Z'$
be the element such that
![]() $\alpha ^{\prime }_g(\unicode{x3bb} ) = \unicode{x3bb} (g)$
for every
$\alpha ^{\prime }_g(\unicode{x3bb} ) = \unicode{x3bb} (g)$
for every
![]() $\unicode{x3bb} \in \Lambda '$
. Since
$\unicode{x3bb} \in \Lambda '$
. Since
![]() $\Lambda \subseteq \Lambda '$
, there is a surjective homomorphism
$\Lambda \subseteq \Lambda '$
, there is a surjective homomorphism
![]() $\pi : Z' \to Z$
such that
$\pi : Z' \to Z$
such that
![]() $\pi (\alpha ^{\prime }_g) = \alpha _g$
. Define
$\pi (\alpha ^{\prime }_g) = \alpha _g$
. Define
![]() $\sigma ' : \Gamma \times Z' \to H$
by
$\sigma ' : \Gamma \times Z' \to H$
by
![]() $\sigma ^{\prime }_g(z) = \sigma _g(\pi (z))$
.
$\sigma ^{\prime }_g(z) = \sigma _g(\pi (z))$
.
Claim 1.
![]() $\sigma '$
is a cocycle.
$\sigma '$
is a cocycle.
Proof. Indeed, for any
![]() $g, h \in \Gamma $
and
$g, h \in \Gamma $
and
![]() $z \in Z'$
,
$z \in Z'$
,
 $$ \begin{align*} \sigma^{\prime}_{g+h}(z) & = \sigma_{g+h}(\pi(z)) \quad (\text{definition of } \sigma') \\ & = \sigma_g(\pi(z) + \alpha_h) + \sigma_h(\pi(z)) \quad (\sigma \text{ is a cocycle}) \\ & = \sigma_g(\pi(z + \alpha^{\prime}_h)) + \sigma_h(\pi(z)) \quad (\pi \text{ is a factor map}) \\ & = \sigma^{\prime}_g(z + \alpha^{\prime}_h) + \sigma^{\prime}_h(z). \end{align*} $$
$$ \begin{align*} \sigma^{\prime}_{g+h}(z) & = \sigma_{g+h}(\pi(z)) \quad (\text{definition of } \sigma') \\ & = \sigma_g(\pi(z) + \alpha_h) + \sigma_h(\pi(z)) \quad (\sigma \text{ is a cocycle}) \\ & = \sigma_g(\pi(z + \alpha^{\prime}_h)) + \sigma_h(\pi(z)) \quad (\pi \text{ is a factor map}) \\ & = \sigma^{\prime}_g(z + \alpha^{\prime}_h) + \sigma^{\prime}_h(z). \end{align*} $$
This proves the claim.
Claim 2.
![]() $\sigma '$
is quasi-affine.
$\sigma '$
is quasi-affine.
Proof. The cocycle
![]() $\sigma $
is quasi-affine, so there exist measurable functions
$\sigma $
is quasi-affine, so there exist measurable functions
![]() $F : Z \times Z \to S^1$
and
$F : Z \times Z \to S^1$
and
![]() $\gamma : Z \to \widehat {\Gamma }$
such that
$\gamma : Z \to \widehat {\Gamma }$
such that
 $$ \begin{align*} \frac{\sigma_g(z + t)}{\sigma_g(z)} = \gamma(t,g) \frac{F(t,z + \alpha_g)}{F(t,z)}. \end{align*} $$
$$ \begin{align*} \frac{\sigma_g(z + t)}{\sigma_g(z)} = \gamma(t,g) \frac{F(t,z + \alpha_g)}{F(t,z)}. \end{align*} $$
Define
![]() $F' : Z' \times Z' \to S^1$
by
$F' : Z' \times Z' \to S^1$
by
![]() $F'(t,z) = F(\pi (t), \pi (z))$
and
$F'(t,z) = F(\pi (t), \pi (z))$
and
![]() $\gamma ' : Z' \to \widehat {\Gamma }$
by
$\gamma ' : Z' \to \widehat {\Gamma }$
by
![]() $\gamma '(t, \cdot ) = \gamma (\pi (t), \cdot )$
. Then
$\gamma '(t, \cdot ) = \gamma (\pi (t), \cdot )$
. Then
 $$ \begin{align*} \frac{\sigma^{\prime}_g(z + t)}{\sigma^{\prime}_g(z)} = \frac{\sigma_g(\pi(z) + \pi(t))}{\sigma_g(\pi(z))} = \gamma(\pi(t),g) \frac{F(\pi(t), \pi(z) + \alpha_g)}{F(\pi(t), \pi(z))} = \gamma'(t,g) \frac{F'(t, z+\alpha^{\prime}_g)}{F'(z)}, \end{align*} $$
$$ \begin{align*} \frac{\sigma^{\prime}_g(z + t)}{\sigma^{\prime}_g(z)} = \frac{\sigma_g(\pi(z) + \pi(t))}{\sigma_g(\pi(z))} = \gamma(\pi(t),g) \frac{F(\pi(t), \pi(z) + \alpha_g)}{F(\pi(t), \pi(z))} = \gamma'(t,g) \frac{F'(t, z+\alpha^{\prime}_g)}{F'(z)}, \end{align*} $$
so
![]() $\sigma '$
is quasi-affine as claimed.
$\sigma '$
is quasi-affine as claimed.
Claim 3. The quasi-affine system
![]() ${\mathbf {Z}}' \times _{\sigma '} H$
is an ergodic system with Kronecker factor
${\mathbf {Z}}' \times _{\sigma '} H$
is an ergodic system with Kronecker factor
![]() ${\mathbf {Z}}' = (Z', \alpha ')$
.
${\mathbf {Z}}' = (Z', \alpha ')$
.
Proof
We need to check that
![]() $\sigma '$
is a weakly mixing cocycle. That is, for any
$\sigma '$
is a weakly mixing cocycle. That is, for any
![]() $\chi \in \widehat {H}$
, if
$\chi \in \widehat {H}$
, if
![]() $\chi \circ \sigma '$
is cohomologous to a character, then
$\chi \circ \sigma '$
is cohomologous to a character, then
![]() $\chi = 1$
(see [Reference Ackelsberg, Bergelson and Best1, Proposition 7.5]). Suppose
$\chi = 1$
(see [Reference Ackelsberg, Bergelson and Best1, Proposition 7.5]). Suppose
![]() $\chi \in \widehat {H}$
and
$\chi \in \widehat {H}$
and
![]() $\chi \circ \sigma ' \sim \gamma \in \widehat {\Gamma }$
over
$\chi \circ \sigma ' \sim \gamma \in \widehat {\Gamma }$
over
![]() ${\mathbf {Z}}'$
. Let
${\mathbf {Z}}'$
. Let
![]() $F : Z' \to S^1$
such that
$F : Z' \to S^1$
such that
 $$ \begin{align*} \chi(\sigma^{\prime}_g(z)) = \gamma(g) \frac{F(z + \alpha^{\prime}_g)}{F(z)} \end{align*} $$
$$ \begin{align*} \chi(\sigma^{\prime}_g(z)) = \gamma(g) \frac{F(z + \alpha^{\prime}_g)}{F(z)} \end{align*} $$
for every
![]() $g \in \Gamma $
and almost every
$g \in \Gamma $
and almost every
![]() $z \in Z'$
. Define
$z \in Z'$
. Define
![]() $G : Z \times H \to S^1$
by
$G : Z \times H \to S^1$
by
![]() $G(z,x) = \overline {F}(z) \chi (x)$
. Then
$G(z,x) = \overline {F}(z) \chi (x)$
. Then
Hence, G is an eigenfunction for the system
![]() ${\mathbf {Z}}' \times _{\sigma '} H$
(with eigenvalue
${\mathbf {Z}}' \times _{\sigma '} H$
(with eigenvalue
![]() $\gamma $
). The function
$\gamma $
). The function ![]() is measurable with respect to the Kronecker factor of
is measurable with respect to the Kronecker factor of
![]() ${\mathbf {Z}}' \times _{\sigma '} H$
, since
${\mathbf {Z}}' \times _{\sigma '} H$
, since
![]() ${\mathbf {Z}}'$
is a Kronecker system and therefore contained in the Kronecker factor. Therefore,
${\mathbf {Z}}'$
is a Kronecker system and therefore contained in the Kronecker factor. Therefore, ![]() is measurable with respect to the Kronecker factor.
is measurable with respect to the Kronecker factor.
Now, the projection of ![]() under the factor map
under the factor map
![]() ${\mathbf {Z}}' \times _{\sigma '} H \to {\mathbf {Z}} \times _{\sigma } H$
is the function
${\mathbf {Z}}' \times _{\sigma '} H \to {\mathbf {Z}} \times _{\sigma } H$
is the function ![]() . Thus,
. Thus, ![]() is measurable with respect to the Kronecker factor of
is measurable with respect to the Kronecker factor of
![]() ${\mathbf {Z}} \times _{\sigma } H$
, but by assumption, the Kronecker factor of
${\mathbf {Z}} \times _{\sigma } H$
, but by assumption, the Kronecker factor of
![]() ${\mathbf {Z}} \times _{\sigma } H$
is
${\mathbf {Z}} \times _{\sigma } H$
is
![]() ${\mathbf {Z}}$
. It follows that the function
${\mathbf {Z}}$
. It follows that the function ![]() does not depend on x. That is,
does not depend on x. That is,
![]() $\chi = 1$
.
$\chi = 1$
.
As a brief aside, it is worth remarking that the system
![]() ${\mathbf {Z}}' \times _{\sigma '} H$
is (isomorphic to) the relatively independent joining of
${\mathbf {Z}}' \times _{\sigma '} H$
is (isomorphic to) the relatively independent joining of
![]() ${\mathbf {Z}} \times _{\sigma } H$
and
${\mathbf {Z}} \times _{\sigma } H$
and
![]() ${\mathbf {Z}}'$
with respect to the common factor
${\mathbf {Z}}'$
with respect to the common factor
![]() ${\mathbf {Z}}$
. We therefore could have shown the previous three claims by establishing this isomorphism and referring to Theorem 2.5. However, to prove that
${\mathbf {Z}}$
. We therefore could have shown the previous three claims by establishing this isomorphism and referring to Theorem 2.5. However, to prove that
![]() ${\mathbf {X}}' = {\mathbf {Z}}' \times _{\sigma '} H$
is the desired extension of
${\mathbf {X}}' = {\mathbf {Z}}' \times _{\sigma '} H$
is the desired extension of
![]() ${\mathbf {X}}$
, it is more convenient to work with the system written explicitly as a group extension over its Kronecker factor rather than appealing to general abstract statements about Host–Kra factors.
${\mathbf {X}}$
, it is more convenient to work with the system written explicitly as a group extension over its Kronecker factor rather than appealing to general abstract statements about Host–Kra factors.
It remains to show that the ergodic quasi-affine system
![]() ${\mathbf {Z}}' \times _{\sigma '} H$
is the desired extension. Let us introduce some notation. We define a system
${\mathbf {Z}}' \times _{\sigma '} H$
is the desired extension. Let us introduce some notation. We define a system
![]() $(W', \widetilde {\alpha }')$
by
$(W', \widetilde {\alpha }')$
by
and
We then define the cocycle
![]() $\widetilde {\sigma }' : \Gamma \times W' \to H^2$
by
$\widetilde {\sigma }' : \Gamma \times W' \to H^2$
by
and associate a Mackey group
![]() $M'$
with annihilator
$M'$
with annihilator
We want to show
![]() $M' = M^{\prime }_{\varphi } \times M^{\prime }_{\psi }$
. To this end, we prove one more claim.
$M' = M^{\prime }_{\varphi } \times M^{\prime }_{\psi }$
. To this end, we prove one more claim.
Claim 4. Let
![]() $\chi \in \widehat {H}$
and
$\chi \in \widehat {H}$
and
![]() $\gamma \in \widehat {\Gamma }$
.
$\gamma \in \widehat {\Gamma }$
.
-
(a) If
 $\chi ( \sigma ^{\prime }_{\varphi (g)}(w_1) ) \sim \gamma (g)$
over
$\chi ( \sigma ^{\prime }_{\varphi (g)}(w_1) ) \sim \gamma (g)$
over
 $(W', \widetilde {\alpha }')$
, then there exists
$(W', \widetilde {\alpha }')$
, then there exists
 $\gamma ' \in C_{\varphi }$
such that
$\gamma ' \in C_{\varphi }$
such that
 $\gamma \sim \gamma '$
.
$\gamma \sim \gamma '$
. -
(b) If
 $\chi ( \sigma ^{\prime }_{\psi (g)}(w_2) ) \sim \gamma (g)$
over
$\chi ( \sigma ^{\prime }_{\psi (g)}(w_2) ) \sim \gamma (g)$
over
 $(W', \widetilde {\alpha }')$
, then there exists
$(W', \widetilde {\alpha }')$
, then there exists
 $\gamma ' \in C_{\psi }$
such that
$\gamma ' \in C_{\psi }$
such that
 $\gamma \sim \gamma '$
.
$\gamma \sim \gamma '$
.
Proof. The proofs of items (a) and (b) are the same, so we prove only item (a). Suppose
![]() $\chi ( \sigma ^{\prime }_{\varphi (g)}(w_1) ) \sim \gamma (g)$
over
$\chi ( \sigma ^{\prime }_{\varphi (g)}(w_1) ) \sim \gamma (g)$
over
![]() ${\mathbf {W}}' = (W', \widetilde {\alpha }')$
. Arguing as in the proof of Claim 3 above, the function
${\mathbf {W}}' = (W', \widetilde {\alpha }')$
. Arguing as in the proof of Claim 3 above, the function ![]() is measurable with respect to the Kronecker factor of
is measurable with respect to the Kronecker factor of
![]() ${\mathbf {W}}' \times _{\widetilde {\sigma }'} H^2$
. Projecting onto the factor
${\mathbf {W}}' \times _{\widetilde {\sigma }'} H^2$
. Projecting onto the factor
![]() ${\mathbf {W}} \times _{\widetilde {\sigma }} H^2$
, it follows that
${\mathbf {W}} \times _{\widetilde {\sigma }} H^2$
, it follows that ![]() is measurable with respect to the Kronecker factor of
is measurable with respect to the Kronecker factor of
![]() ${\mathbf {W}} \times _{\widetilde {\sigma }} H^2$
. We then project again to the factor
${\mathbf {W}} \times _{\widetilde {\sigma }} H^2$
. We then project again to the factor
![]() $(Z, \alpha \circ \varphi ) \times _{\sigma _{\varphi }} H$
(with the action of
$(Z, \alpha \circ \varphi ) \times _{\sigma _{\varphi }} H$
(with the action of
![]() $\Gamma $
given by
$\Gamma $
given by
![]() $g \cdot (z,x) = ( z + \alpha _{\varphi (g)}, x + \sigma _{\varphi (g)}(z) )$
) to conclude that
$g \cdot (z,x) = ( z + \alpha _{\varphi (g)}, x + \sigma _{\varphi (g)}(z) )$
) to conclude that ![]() is measurable with respect to the Kronecker factor
is measurable with respect to the Kronecker factor
![]() ${\mathbf {Z}}_{\varphi }$
of
${\mathbf {Z}}_{\varphi }$
of
![]() $(Z, \alpha \circ \varphi ) \times _{\sigma _{\varphi }} H$
. Noting that
$(Z, \alpha \circ \varphi ) \times _{\sigma _{\varphi }} H$
. Noting that
![]() $L^2({\mathcal {Z}}_{\varphi })$
is spanned by functions of the form
$L^2({\mathcal {Z}}_{\varphi })$
is spanned by functions of the form
![]() $F(z) \zeta (x)$
with
$F(z) \zeta (x)$
with
![]() $\zeta \in \widehat {H}$
such that
$\zeta \in \widehat {H}$
such that
![]() $\zeta \circ \sigma _{\varphi }$
is cohomologous to a character (see the proof of [Reference Ackelsberg, Bergelson and Best1, Proposition 7.5(2)]), it follows that
$\zeta \circ \sigma _{\varphi }$
is cohomologous to a character (see the proof of [Reference Ackelsberg, Bergelson and Best1, Proposition 7.5(2)]), it follows that
![]() $\chi \circ \sigma _{\varphi }$
is cohomologous to a character
$\chi \circ \sigma _{\varphi }$
is cohomologous to a character
![]() $\gamma ' \in \widehat {\Gamma }$
over
$\gamma ' \in \widehat {\Gamma }$
over
![]() $(Z, \alpha \circ \varphi )$
. Therefore,
$(Z, \alpha \circ \varphi )$
. Therefore,
![]() $\gamma ' \in C_{\varphi }$
and
$\gamma ' \in C_{\varphi }$
and
![]() $\gamma \sim \gamma '$
.
$\gamma \sim \gamma '$
.
Let
![]() $\chi _1 \otimes \chi _2 \in (M')^{\perp }$
. By Theorem 4.1, there exists
$\chi _1 \otimes \chi _2 \in (M')^{\perp }$
. By Theorem 4.1, there exists
![]() $\gamma \in \widehat {\Gamma }$
such that
$\gamma \in \widehat {\Gamma }$
such that
![]() $\chi _1(\sigma ^{\prime }_{\varphi (g)}(w_1)) \sim \gamma (g)$
and
$\chi _1(\sigma ^{\prime }_{\varphi (g)}(w_1)) \sim \gamma (g)$
and
![]() $\chi _2(\sigma ^{\prime }_{\psi (g)}(w_2)) \sim \overline {\gamma }(g)$
over
$\chi _2(\sigma ^{\prime }_{\psi (g)}(w_2)) \sim \overline {\gamma }(g)$
over
![]() $(W', \widetilde {\alpha }')$
. By Claim 4, we may assume
$(W', \widetilde {\alpha }')$
. By Claim 4, we may assume
![]() $\gamma \in C_{\varphi } \cap C_{\psi } = C$
. We constructed the extension
$\gamma \in C_{\varphi } \cap C_{\psi } = C$
. We constructed the extension
![]() ${\mathbf {Z}}' \times _{\sigma '} H$
so that
${\mathbf {Z}}' \times _{\sigma '} H$
so that
![]() $\Lambda ' \supseteq C$
. Therefore,
$\Lambda ' \supseteq C$
. Therefore,
![]() $\gamma \in \Lambda '$
. Also by construction,
$\gamma \in \Lambda '$
. Also by construction,
![]() $\Lambda '$
is
$\Lambda '$
is
![]() $\{\varphi , \psi , \theta _1, \theta _2\}$
-complete and (
$\{\varphi , \psi , \theta _1, \theta _2\}$
-complete and (
![]() $\theta _1 \circ \varphi + \theta _2 \circ \psi )$
-divisible. Using the divisibility condition, let
$\theta _1 \circ \varphi + \theta _2 \circ \psi )$
-divisible. Using the divisibility condition, let
![]() $\unicode{x3bb} \in \Lambda '$
such that
$\unicode{x3bb} \in \Lambda '$
such that
![]() $\unicode{x3bb} \circ (\theta _1 \circ \varphi + \theta _2 \circ \psi ) = \gamma $
. Let
$\unicode{x3bb} \circ (\theta _1 \circ \varphi + \theta _2 \circ \psi ) = \gamma $
. Let
![]() $\unicode{x3bb} _1 = \unicode{x3bb} \circ \theta _1$
and
$\unicode{x3bb} _1 = \unicode{x3bb} \circ \theta _1$
and
![]() $\unicode{x3bb} _2\hspace{-1pt} =\hspace{-1pt} \unicode{x3bb} \circ \theta _2$
. By the completeness condition,
$\unicode{x3bb} _2\hspace{-1pt} =\hspace{-1pt} \unicode{x3bb} \circ \theta _2$
. By the completeness condition,
![]() $\unicode{x3bb} _1, \unicode{x3bb} _2\hspace{-1pt} \in\hspace{-1pt} \Lambda '$
. Moreover,
$\unicode{x3bb} _1, \unicode{x3bb} _2\hspace{-1pt} \in\hspace{-1pt} \Lambda '$
. Moreover,
![]() $(\unicode{x3bb} _1 \circ \varphi )(\unicode{x3bb} _2 \circ \psi )\hspace{-1pt} =\hspace{-1pt} \gamma $
. So, taking
$(\unicode{x3bb} _1 \circ \varphi )(\unicode{x3bb} _2 \circ \psi )\hspace{-1pt} =\hspace{-1pt} \gamma $
. So, taking
![]() $F = ( \unicode{x3bb} _1 \otimes \unicode{x3bb} _2 ) |_{W'} : W' \to S^1$
, we have
$F = ( \unicode{x3bb} _1 \otimes \unicode{x3bb} _2 ) |_{W'} : W' \to S^1$
, we have
![]() $\gamma (g) = \Delta _gF$
, so
$\gamma (g) = \Delta _gF$
, so
![]() $\gamma \sim 1$
. Thus,
$\gamma \sim 1$
. Thus,
That is,
![]() $\chi _1 \otimes \chi _2 \in ( M^{\prime }_{\varphi } )^{\perp } \times ( M^{\prime }_{\psi } )^{\perp }$
as desired.
$\chi _1 \otimes \chi _2 \in ( M^{\prime }_{\varphi } )^{\perp } \times ( M^{\prime }_{\psi } )^{\perp }$
as desired.
5 Limit formula
In this section, we use the Mackey group M defined in §4 to derive a limit formula for double ergodic averages over quasi-affine systems.
Theorem 5.1. Let
![]() $\varphi , \psi , \theta _1, \theta _2 \in \mathrm {End}(\Gamma )$
such that
$\varphi , \psi , \theta _1, \theta _2 \in \mathrm {End}(\Gamma )$
such that
![]() $\psi - \varphi $
has finite index image in
$\psi - \varphi $
has finite index image in
![]() $\Gamma $
and
$\Gamma $
and
![]() $\theta _1 \circ \varphi + \theta _2 \circ \psi $
is injective. Let
$\theta _1 \circ \varphi + \theta _2 \circ \psi $
is injective. Let
![]() ${\mathbf {X}} = {\mathbf {Z}} \times _{\sigma } H$
be an ergodic quasi-affine
${\mathbf {X}} = {\mathbf {Z}} \times _{\sigma } H$
be an ergodic quasi-affine
![]() $\Gamma $
-system whose discrete spectrum is
$\Gamma $
-system whose discrete spectrum is
![]() $\{\varphi , \psi , \theta _1, \theta _2\}$
-complete and
$\{\varphi , \psi , \theta _1, \theta _2\}$
-complete and
![]() $(\theta _1 \circ \varphi + \theta _2 \circ \psi )$
-divisible. Let
$(\theta _1 \circ \varphi + \theta _2 \circ \psi )$
-divisible. Let
![]() $M \le H^2$
be the Mackey group associated with
$M \le H^2$
be the Mackey group associated with
![]() $\{\varphi , \psi \}$
. Then there is a measurable function
$\{\varphi , \psi \}$
. Then there is a measurable function
![]() $\omega : Z \times Z \to H^2$
such that:
$\omega : Z \times Z \to H^2$
such that:
-
(1)
 $\omega (0,z) \in M$
for all
$\omega (0,z) \in M$
for all
 $z \in Z$
and
$z \in Z$
and
 $t \mapsto \omega (t,\cdot ) + M$
is a continuous function from Z to
$t \mapsto \omega (t,\cdot ) + M$
is a continuous function from Z to
 ${\mathcal {M}}(Z, H^2/M)$
; and
${\mathcal {M}}(Z, H^2/M)$
; and -
(2) for any
 $f_1, f_2 \in L^{\infty }(Z \times H)$
, we have (5.1)in
$f_1, f_2 \in L^{\infty }(Z \times H)$
, we have (5.1)in $$ \begin{align} &\hspace{-22pt}\mathrm{UC}\text{-}\lim_{g \in \Gamma}~{f_1(T_{\varphi(g)}(z,x)) f_2(T_{\psi(g)}(z,x))}\nonumber\\ &\hspace{-10pt}= \!\int_{Z \times M}\!f_1 ( z + \widehat{\varphi}(t), x + u + \omega_1(t,z) ) f_2 ( z + \widehat{\psi}(t), x + v + \omega_2(t,z))\,dm_Z(t)\,dm_M(u,v) \end{align} $$
$$ \begin{align} &\hspace{-22pt}\mathrm{UC}\text{-}\lim_{g \in \Gamma}~{f_1(T_{\varphi(g)}(z,x)) f_2(T_{\psi(g)}(z,x))}\nonumber\\ &\hspace{-10pt}= \!\int_{Z \times M}\!f_1 ( z + \widehat{\varphi}(t), x + u + \omega_1(t,z) ) f_2 ( z + \widehat{\psi}(t), x + v + \omega_2(t,z))\,dm_Z(t)\,dm_M(u,v) \end{align} $$
 $L^2(Z \times H)$
, where
$L^2(Z \times H)$
, where
 $\omega = (\omega _1, \omega _2)$
.
$\omega = (\omega _1, \omega _2)$
.
Before proving Theorem 5.1, we note an immediate corollary.
Corollary 5.2. In the setup of Theorem 5.1, for any
![]() $f_0, f_1, f_2 \in L^{\infty }(Z \times H)$
and any continuous function
$f_0, f_1, f_2 \in L^{\infty }(Z \times H)$
and any continuous function
![]() $\kappa : Z \to {\mathbb {C}}$
, one has
$\kappa : Z \to {\mathbb {C}}$
, one has
 $$ \begin{align} \nonumber &\mathrm{UC}\text{-}\lim_{g \in \Gamma}~{\kappa(\alpha_g) \int_{Z \times H}{f_0 \cdot T_{\varphi(g)} f_1 \cdot T_{\psi(g)} f_2\,d(m_Z \times m_H)}} \\ \nonumber &\quad = \int_{Z^2 \times H \times M}{\kappa(t)~f_0(z,x)~f_1 ( z + \widehat{\varphi}(t), x + u + \omega_1(t,z) )} \\ &\quad\qquad \times{f_2 ( z + \widehat{\psi}(t), x + v +\omega_2(t,z))\,dm_Z(z)\,dm_Z(t)\,dm_H(x)\,dm_M(u,v)}. \end{align} $$
$$ \begin{align} \nonumber &\mathrm{UC}\text{-}\lim_{g \in \Gamma}~{\kappa(\alpha_g) \int_{Z \times H}{f_0 \cdot T_{\varphi(g)} f_1 \cdot T_{\psi(g)} f_2\,d(m_Z \times m_H)}} \\ \nonumber &\quad = \int_{Z^2 \times H \times M}{\kappa(t)~f_0(z,x)~f_1 ( z + \widehat{\varphi}(t), x + u + \omega_1(t,z) )} \\ &\quad\qquad \times{f_2 ( z + \widehat{\psi}(t), x + v +\omega_2(t,z))\,dm_Z(z)\,dm_Z(t)\,dm_H(x)\,dm_M(u,v)}. \end{align} $$
Proof. By the Stone–Weierstrass theorem, we may assume
![]() $\kappa $
is a character on Z. Since the discrete spectrum
$\kappa $
is a character on Z. Since the discrete spectrum
![]() $\Lambda \cong \widehat {Z}$
is
$\Lambda \cong \widehat {Z}$
is
![]() $(\theta _1 \circ \varphi + \theta _2 \circ \psi )$
-divisible, there exists
$(\theta _1 \circ \varphi + \theta _2 \circ \psi )$
-divisible, there exists
![]() $\kappa ' \in \widehat {Z}$
such that
$\kappa ' \in \widehat {Z}$
such that
![]() $\kappa ' \circ ( \widehat {\theta }_1 \circ \widehat {\varphi } + \widehat {\theta }_2 \circ \widehat {\psi } ) = \kappa $
. Define functions
$\kappa ' \circ ( \widehat {\theta }_1 \circ \widehat {\varphi } + \widehat {\theta }_2 \circ \widehat {\psi } ) = \kappa $
. Define functions
![]() $\widetilde {f}_i \in L^{\infty }(Z \times H)$
by
$\widetilde {f}_i \in L^{\infty }(Z \times H)$
by
 $$ \begin{align*} \widetilde{f}_0(z,x) & = \overline{\kappa' ( \widehat{\theta}_1(z) + \widehat{\theta}_2(z))} f_0(z,x), \\ \widetilde{f}_1(z,x) & = \kappa' ( \widehat{\theta}_1(z)) f_1(z,x), \\ \widetilde{f}_2(z,x) & = \kappa' ( \widehat{\theta}_2(z)) f_2(z,x). \end{align*} $$
$$ \begin{align*} \widetilde{f}_0(z,x) & = \overline{\kappa' ( \widehat{\theta}_1(z) + \widehat{\theta}_2(z))} f_0(z,x), \\ \widetilde{f}_1(z,x) & = \kappa' ( \widehat{\theta}_1(z)) f_1(z,x), \\ \widetilde{f}_2(z,x) & = \kappa' ( \widehat{\theta}_2(z)) f_2(z,x). \end{align*} $$
The left-hand side of equation (5.2) is equal to
while the right-hand side of equation (5.2) is equal to
 $$ \begin{align} \nonumber &\int_{Z^2 \times H \times M}{\widetilde{f}_0(z,x)~\widetilde{f}_1 ( z + \widehat{\varphi}(t), x + u + \omega_1(t,z))} \\ &\quad \times{\widetilde{f}_2 ( z + \widehat{\psi}(t), x + v + \omega_2(t,z))\,dm_Z(z)\,dm_Z(t)\,dm_H(x)\,dm_M(u,v)}. \end{align} $$
$$ \begin{align} \nonumber &\int_{Z^2 \times H \times M}{\widetilde{f}_0(z,x)~\widetilde{f}_1 ( z + \widehat{\varphi}(t), x + u + \omega_1(t,z))} \\ &\quad \times{\widetilde{f}_2 ( z + \widehat{\psi}(t), x + v + \omega_2(t,z))\,dm_Z(z)\,dm_Z(t)\,dm_H(x)\,dm_M(u,v)}. \end{align} $$
The quantities in equations (5.3) and (5.4) are equal by Theorem 5.1.
The first step in the proof of Theorem 5.1 is the following enhancement of Proposition 2.19.
Proposition 5.3. Let
![]() $f_1, f_2 \in L^{\infty }(Z \times H)$
. Suppose that for every
$f_1, f_2 \in L^{\infty }(Z \times H)$
. Suppose that for every
![]() $\widetilde {\chi } \in M^{\perp }$
, one has
$\widetilde {\chi } \in M^{\perp }$
, one has
for a.e.
![]() $w = (w_1, w_2) \in W$
. Then
$w = (w_1, w_2) \in W$
. Then
in
![]() $L^2(Z \times H)$
.
$L^2(Z \times H)$
.
Proof. The proof is very much in the spirit of [Reference Ackelsberg, Bergelson and Best1, Proposition 7.10]. Define
![]() $\widetilde {T}_g : W \times H^2 \to W \times H^2$
by
$\widetilde {T}_g : W \times H^2 \to W \times H^2$
by
Set
![]() $F(w, x) := f_1(w_1, x_1) f_2(w_2, x_2)$
for
$F(w, x) := f_1(w_1, x_1) f_2(w_2, x_2)$
for
![]() $w = (w_1, w_2) \in W$
and
$w = (w_1, w_2) \in W$
and
![]() $x = (x_1, x_2) \in H^2$
. We claim F is orthogonal to the space of
$x = (x_1, x_2) \in H^2$
. We claim F is orthogonal to the space of
![]() $(\widetilde {T}_g)_{g \in \Gamma }$
-invariant functions in
$(\widetilde {T}_g)_{g \in \Gamma }$
-invariant functions in
![]() $L^2(W \times H^2)$
.
$L^2(W \times H^2)$
.
Let
![]() $E_1 := \{z \in Z : M_z = M\}$
. As discussed in §4,
$E_1 := \{z \in Z : M_z = M\}$
. As discussed in §4,
![]() $E_1$
has full measure. Let
$E_1$
has full measure. Let
![]() $E_2 := \{z \in Z : \text {equation }(5.8) \text { holds for a.e. } w = (w_1, w_2) \in W_z\}$
, and let
$E_2 := \{z \in Z : \text {equation }(5.8) \text { holds for a.e. } w = (w_1, w_2) \in W_z\}$
, and let
![]() $E_3 := \{z \in Z : F \in L^{\infty }( W_z \times H^2 )\}$
. By Fubini’s theorem, both of the sets
$E_3 := \{z \in Z : F \in L^{\infty }( W_z \times H^2 )\}$
. By Fubini’s theorem, both of the sets
![]() $E_2$
and
$E_2$
and
![]() $E_3$
have full measure in Z. Put
$E_3$
have full measure in Z. Put
![]() $E := E_1 \cap E_2 \cap E_3$
.
$E := E_1 \cap E_2 \cap E_3$
.
Suppose
![]() $z \in E$
and let
$z \in E$
and let
![]() $\widetilde {\chi } \in M_z^{\perp } = M^{\perp }$
. Then
$\widetilde {\chi } \in M_z^{\perp } = M^{\perp }$
. Then
for a.e.
![]() $w \in W_z$
. Therefore,
$w \in W_z$
. Therefore,
in
![]() $L^2 ( W_z \times H^2 )$
by Proposition 2.19.
$L^2 ( W_z \times H^2 )$
by Proposition 2.19.
Fix a Følner sequence
![]() $(\Phi _N)_{N \in {\mathbb {N}}}$
in
$(\Phi _N)_{N \in {\mathbb {N}}}$
in
![]() $\Gamma $
, and define the average
$\Gamma $
, and define the average
 $$ \begin{align*} A_N := \frac{1}{|\Phi_N|} \sum_{g \in \Phi_N}{\widetilde{T}_g F} \in L^2 ( W \times H^2). \end{align*} $$
$$ \begin{align*} A_N := \frac{1}{|\Phi_N|} \sum_{g \in \Phi_N}{\widetilde{T}_g F} \in L^2 ( W \times H^2). \end{align*} $$
We want to show
![]() $A_N \to 0$
in
$A_N \to 0$
in
![]() $L^2 ( W \times H^2 )$
. Decompose the Haar measure on W as
$L^2 ( W \times H^2 )$
. Decompose the Haar measure on W as
![]() $m_W = \int _Z{m_z\,dz}$
. Then
$m_W = \int _Z{m_z\,dz}$
. Then
 $$ \begin{align*} {\| A_N \|_{{L^2 ( W \times H^2)}}}^2 & = \int_W{\int_{H^2}{|A_N(w,x)|^2\,dx}\,dw} \\ & = \int_Z{\bigg( \int_{W_z}{\int_{H^2}{|A_N(w,x)|^2\,dx}\,dm_z} \bigg)\,dz} \\ & = \int_Z{{\| A_N \|_{{L^2 ( W_z \times H^2 )}}}^2\,dz} \\ & {\xrightarrow[{N \to \infty}]{}}\, 0. \end{align*} $$
$$ \begin{align*} {\| A_N \|_{{L^2 ( W \times H^2)}}}^2 & = \int_W{\int_{H^2}{|A_N(w,x)|^2\,dx}\,dw} \\ & = \int_Z{\bigg( \int_{W_z}{\int_{H^2}{|A_N(w,x)|^2\,dx}\,dm_z} \bigg)\,dz} \\ & = \int_Z{{\| A_N \|_{{L^2 ( W_z \times H^2 )}}}^2\,dz} \\ & {\xrightarrow[{N \to \infty}]{}}\, 0. \end{align*} $$
To complete the proof, we apply the van der Corput trick. Let
![]() $u_g := T_{\varphi (g)}f_1 \cdot T_{\psi (g)}f_2 \in L^2(Z \times H)$
. Then
$u_g := T_{\varphi (g)}f_1 \cdot T_{\psi (g)}f_2 \in L^2(Z \times H)$
. Then
Since
![]() $(\psi - \varphi )(\Gamma )$
has finite index in
$(\psi - \varphi )(\Gamma )$
has finite index in
![]() $\Gamma $
, we have
$\Gamma $
, we have
![]() ${\mathcal {I}}_{\psi - \varphi } \subseteq {\mathcal {Z}}$
, so by the mean ergodic theorem,
${\mathcal {I}}_{\psi - \varphi } \subseteq {\mathcal {Z}}$
, so by the mean ergodic theorem,
 $$ \begin{align*} \xi_h & := \text{UC-}\lim_{g \in \Gamma}{{\langle {u_{g+h}}, {u_g} \rangle}} \\ & = \int_{Z \times H}{(\overline{f}_1 \cdot T_{\varphi(h)}f_1)(z,x) \cdot \bigg( \int_Z{{\mathbb{E} [ {\overline{f}_2 \cdot T_{\psi(h)}f_2} \mid {{\mathcal{Z}}} ]} ( z + ( \widehat{\psi} - \widehat{\varphi})(t))}\,dt \bigg)\,dz\,dx} \\ & = \int_W{{\mathbb{E} [ {\overline{f}_1 \cdot T_{\varphi(h)}f_1} \mid {{\mathcal{Z}}}]}(w_1) \cdot {\mathbb{E}[ {\overline{f}_2 \cdot T_{\psi(h)}f_2} \mid {{\mathcal{Z}}}]}(w_2)\,dw} \\ & = \int_{W \times H^2}{( \overline{f}_1 \cdot T_{\varphi(h)}f_1 )(w_1, x_1) ( \overline{f}_2 \cdot T_{\psi(h)}f_2)(w_2, x_2)\,dw\,dx} \\ & = {\langle {\widetilde{T}_hF}, {F} \rangle}_{L^2 ( W \times H^2)}. \end{align*} $$
$$ \begin{align*} \xi_h & := \text{UC-}\lim_{g \in \Gamma}{{\langle {u_{g+h}}, {u_g} \rangle}} \\ & = \int_{Z \times H}{(\overline{f}_1 \cdot T_{\varphi(h)}f_1)(z,x) \cdot \bigg( \int_Z{{\mathbb{E} [ {\overline{f}_2 \cdot T_{\psi(h)}f_2} \mid {{\mathcal{Z}}} ]} ( z + ( \widehat{\psi} - \widehat{\varphi})(t))}\,dt \bigg)\,dz\,dx} \\ & = \int_W{{\mathbb{E} [ {\overline{f}_1 \cdot T_{\varphi(h)}f_1} \mid {{\mathcal{Z}}}]}(w_1) \cdot {\mathbb{E}[ {\overline{f}_2 \cdot T_{\psi(h)}f_2} \mid {{\mathcal{Z}}}]}(w_2)\,dw} \\ & = \int_{W \times H^2}{( \overline{f}_1 \cdot T_{\varphi(h)}f_1 )(w_1, x_1) ( \overline{f}_2 \cdot T_{\psi(h)}f_2)(w_2, x_2)\,dw\,dx} \\ & = {\langle {\widetilde{T}_hF}, {F} \rangle}_{L^2 ( W \times H^2)}. \end{align*} $$
Now since
![]() $\text {UC-}\lim \nolimits _{h \in \Gamma }{\widetilde {T}_hF} = 0$
in
$\text {UC-}\lim \nolimits _{h \in \Gamma }{\widetilde {T}_hF} = 0$
in
![]() $L^2(W \times H^2)$
, we have
$L^2(W \times H^2)$
, we have
![]() $\text {UC-}\lim \nolimits _{h \in \Gamma }{\xi _h} = 0$
. By the van der Corput lemma (Lemma 2.1), it follows that
$\text {UC-}\lim \nolimits _{h \in \Gamma }{\xi _h} = 0$
. By the van der Corput lemma (Lemma 2.1), it follows that
![]() $\text {UC-}\lim \nolimits _{g \in \Gamma }{u_g} = 0$
in
$\text {UC-}\lim \nolimits _{g \in \Gamma }{u_g} = 0$
in
![]() $L^2(Z \times H)$
as desired.
$L^2(Z \times H)$
as desired.
The next step is to construct the function
![]() $\omega $
appearing in Theorem 5.1. Fix
$\omega $
appearing in Theorem 5.1. Fix
![]() $z \in Z$
such that
$z \in Z$
such that
![]() $M_z = M$
. Note that our assumptions on the discrete spectrum of
$M_z = M$
. Note that our assumptions on the discrete spectrum of
![]() ${\mathbf {X}}$
ensure that
${\mathbf {X}}$
ensure that
![]() $(W_z, \widetilde {\alpha })$
is isomorphic to
$(W_z, \widetilde {\alpha })$
is isomorphic to
![]() $(Z, \alpha )$
under the map
$(Z, \alpha )$
under the map
![]() $(w_1, w_2) \mapsto \widehat {\theta }_1(w_1 - z) + \widehat {\theta }_2(w_2 - z)$
. Hence, by Proposition 2.17, there is a function
$(w_1, w_2) \mapsto \widehat {\theta }_1(w_1 - z) + \widehat {\theta }_2(w_2 - z)$
. Hence, by Proposition 2.17, there is a function
![]() $\widetilde {\omega } : Z \times Z \to H^2/M$
such that
$\widetilde {\omega } : Z \times Z \to H^2/M$
such that
![]() $t \mapsto \widetilde {\omega }(t, \cdot )$
is a continuous map
$t \mapsto \widetilde {\omega }(t, \cdot )$
is a continuous map
![]() $Z \to {\mathcal {M}}(Z, H^2/M)$
and
$Z \to {\mathcal {M}}(Z, H^2/M)$
and
By the Kuratowski and Ryll-Nardewski measurable selection theorem (see [Reference Srivastava32, §5.2]), we can lift
![]() $\widetilde {\omega }$
to a function
$\widetilde {\omega }$
to a function
![]() $\omega : Z \times Z \to H^2$
such that
$\omega : Z \times Z \to H^2$
such that
![]() $\omega + M = \widetilde {\omega }$
.
$\omega + M = \widetilde {\omega }$
.
Now we put everything together to prove Theorem 5.1.
Proof of Theorem 5.1
By linearity, we may assume
![]() $f_i = h_i \otimes \chi _i$
with
$f_i = h_i \otimes \chi _i$
with
![]() $\chi _i \in \widehat {H}$
for
$\chi _i \in \widehat {H}$
for
![]() $i = 1, 2$
. Let
$i = 1, 2$
. Let
![]() $\widetilde {\chi } = \chi _1 \otimes \chi _2 \in \widehat {H^2}$
. Then the right-hand side of equation (5.1) is equal to
$\widetilde {\chi } = \chi _1 \otimes \chi _2 \in \widehat {H^2}$
. Then the right-hand side of equation (5.1) is equal to
 $$ \begin{align} \chi_1(x) \chi_2(x) \bigg( \int_Z{h_1 ( z + \widehat{\varphi}(t)) h_2 ( z + \widehat{\psi}(t)) \widetilde{\chi} ( \omega(t,z))\,dt}\bigg) \bigg( \int_M{\widetilde{\chi}\,dm_M} \bigg). \end{align} $$
$$ \begin{align} \chi_1(x) \chi_2(x) \bigg( \int_Z{h_1 ( z + \widehat{\varphi}(t)) h_2 ( z + \widehat{\psi}(t)) \widetilde{\chi} ( \omega(t,z))\,dt}\bigg) \bigg( \int_M{\widetilde{\chi}\,dm_M} \bigg). \end{align} $$
We break the proof into two cases depending on whether or not
![]() $\widetilde {\chi }$
belongs to
$\widetilde {\chi }$
belongs to
![]() $M^{\perp }$
.
$M^{\perp }$
.
Case 1:
![]() $\widetilde {\chi } \notin M^{\perp }$
. In this case, the expression in equation (5.6) is equal to 0. Proposition 5.3 guarantees that the left-hand side of equation (5.1) is also equal to zero.
$\widetilde {\chi } \notin M^{\perp }$
. In this case, the expression in equation (5.6) is equal to 0. Proposition 5.3 guarantees that the left-hand side of equation (5.1) is also equal to zero.
Case 2:
![]() $\widetilde {\chi } \in M^{\perp }$
. Let
$\widetilde {\chi } \in M^{\perp }$
. Let
![]() $F : Z \times Z \to {\mathbb {C}}$
be given by
$F : Z \times Z \to {\mathbb {C}}$
be given by
Note that
![]() $t \mapsto F(t, \cdot )$
is a continuous function from Z to
$t \mapsto F(t, \cdot )$
is a continuous function from Z to
![]() $L^2(Z)$
, and the expression in equation (5.6) simplifies to
$L^2(Z)$
, and the expression in equation (5.6) simplifies to
![]() $\chi _1(x) \chi _2(x) \int _Z{F(t,z)\,dt}$
.
$\chi _1(x) \chi _2(x) \int _Z{F(t,z)\,dt}$
.
Moving to the left-hand side of equation (5.1), for
![]() $g \in \Gamma $
, we have
$g \in \Gamma $
, we have
Therefore, since
![]() $(Z, \alpha )$
is uniquely ergodic, we have
$(Z, \alpha )$
is uniquely ergodic, we have
in
![]() $L^2(Z)$
by Lemma 2.6. This completes the proof.
$L^2(Z)$
by Lemma 2.6. This completes the proof.
6 Khintchine-type recurrence
In this section, we prove Theorem 1.16. We will first prove the following statement (corresponding to the case
![]() $\eta = \text {id}_{\Gamma }$
), from which Theorem 1.16 can be quickly deduced.
$\eta = \text {id}_{\Gamma }$
), from which Theorem 1.16 can be quickly deduced.
Theorem 6.1. Let
![]() $\Gamma $
be a countable discrete abelian group. Let
$\Gamma $
be a countable discrete abelian group. Let
![]() $\varphi , \psi \in \mathrm {End}(\Gamma )$
such that
$\varphi , \psi \in \mathrm {End}(\Gamma )$
such that
![]() $(\psi - \varphi )(\Gamma )$
is a finite index subgroup of
$(\psi - \varphi )(\Gamma )$
is a finite index subgroup of
![]() $\Gamma $
. Suppose there exist
$\Gamma $
. Suppose there exist
![]() $\theta _1, \theta _2 \in \mathrm {End}(\Gamma )$
such that
$\theta _1, \theta _2 \in \mathrm {End}(\Gamma )$
such that
![]() $\theta _1 \circ \varphi + \theta _2 \circ \psi $
is injective. Then for any ergodic measure-preserving
$\theta _1 \circ \varphi + \theta _2 \circ \psi $
is injective. Then for any ergodic measure-preserving
![]() $\Gamma $
-system
$\Gamma $
-system
![]() $( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
with Kronecker factor
$( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
with Kronecker factor
![]() ${\mathbf {Z}} = (Z, \alpha )$
, any
${\mathbf {Z}} = (Z, \alpha )$
, any
![]() $A \in {\mathcal {X}}$
, and any
$A \in {\mathcal {X}}$
, and any
![]() ${\varepsilon }> 0$
, there is a continuous function
${\varepsilon }> 0$
, there is a continuous function
![]() $\kappa : Z \to [0, \infty )$
with
$\kappa : Z \to [0, \infty )$
with
![]() $\int _Z{\kappa (z)\,dz} = 1$
such that
$\int _Z{\kappa (z)\,dz} = 1$
such that
Proof. Let
![]() ${\mathbf {X}} = ( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
be an ergodic
${\mathbf {X}} = ( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
be an ergodic
![]() $\Gamma $
-system with Kronecker factor
$\Gamma $
-system with Kronecker factor
![]() ${\mathbf {Z}} = (Z, \alpha )$
, let
${\mathbf {Z}} = (Z, \alpha )$
, let
![]() $A \in {\mathcal {X}}$
, and let
$A \in {\mathcal {X}}$
, and let
![]() ${\varepsilon }> 0$
. Put
${\varepsilon }> 0$
. Put ![]() . Let
. Let
![]() $\kappa : Z \to [0, \infty )$
be a continuous function (to be specified later) with
$\kappa : Z \to [0, \infty )$
be a continuous function (to be specified later) with
![]() $\int _Z{\kappa (z)\,dz} = 1$
. By [Reference Ackelsberg, Bergelson and Shalom2, Theorem 4.10], we may assume without loss of generality (by passing to an extension if necessary) that
$\int _Z{\kappa (z)\,dz} = 1$
. By [Reference Ackelsberg, Bergelson and Shalom2, Theorem 4.10], we may assume without loss of generality (by passing to an extension if necessary) that
 $$ \begin{align*} &\text{UC-}\lim_{g \in \Gamma}{~\kappa(\alpha_g)~\int_X{f \cdot T_{\varphi(g)} f \cdot T_{\psi(g)} f\,d\mu}} \\ &\quad = \text{UC-}\lim_{g \in \Gamma}{\kappa(\alpha_g)~\int_X{f \cdot T_{\varphi(g)} {\mathbb{E} [ {f} \mid {{\mathcal{Z}}^2 \lor {\mathcal{I}}_{\varphi}} ]} \cdot T_{\psi(g)} {\mathbb{E} [ {f} \mid {{\mathcal{Z}}^2 \lor {\mathcal{I}}_{\psi}}]}\,d\mu}}. \end{align*} $$
$$ \begin{align*} &\text{UC-}\lim_{g \in \Gamma}{~\kappa(\alpha_g)~\int_X{f \cdot T_{\varphi(g)} f \cdot T_{\psi(g)} f\,d\mu}} \\ &\quad = \text{UC-}\lim_{g \in \Gamma}{\kappa(\alpha_g)~\int_X{f \cdot T_{\varphi(g)} {\mathbb{E} [ {f} \mid {{\mathcal{Z}}^2 \lor {\mathcal{I}}_{\varphi}} ]} \cdot T_{\psi(g)} {\mathbb{E} [ {f} \mid {{\mathcal{Z}}^2 \lor {\mathcal{I}}_{\psi}}]}\,d\mu}}. \end{align*} $$
We may further assume that the discrete spectrum of
![]() ${\mathbf {X}}$
is
${\mathbf {X}}$
is
![]() $\{\varphi , \psi , \theta _1, \theta _2\}$
-complete and
$\{\varphi , \psi , \theta _1, \theta _2\}$
-complete and
![]() $(\theta _1 \circ \varphi + \theta _2 \circ \psi )$
-divisible by passing to another extension if necessary with the help of Theorem 3.2.
$(\theta _1 \circ \varphi + \theta _2 \circ \psi )$
-divisible by passing to another extension if necessary with the help of Theorem 3.2.
Let
![]() $f_{\varphi } = {\mathbb {E}[ {f} \mid {{\mathcal {Z}}^2 \lor {\mathcal {I}}_{\varphi }}]}$
and
$f_{\varphi } = {\mathbb {E}[ {f} \mid {{\mathcal {Z}}^2 \lor {\mathcal {I}}_{\varphi }}]}$
and
![]() $f_{\psi } = {\mathbb {E} [ {f} \mid {{\mathcal {Z}}^2 \lor {\mathcal {I}}_{\psi }} ]}$
. We may expand
$f_{\psi } = {\mathbb {E} [ {f} \mid {{\mathcal {Z}}^2 \lor {\mathcal {I}}_{\psi }} ]}$
. We may expand
 $$ \begin{align*} f_{\varphi} = \sum_{i}{c_i h_i} \quad\text{and}\quad f_{\psi} = \sum_{j}{d_j k_j}, \end{align*} $$
$$ \begin{align*} f_{\varphi} = \sum_{i}{c_i h_i} \quad\text{and}\quad f_{\psi} = \sum_{j}{d_j k_j}, \end{align*} $$
where
![]() $c_i$
is
$c_i$
is
![]() $\varphi (\Gamma )$
-invariant,
$\varphi (\Gamma )$
-invariant,
![]() $d_j$
is
$d_j$
is
![]() $\psi (\Gamma )$
-invariant, and
$\psi (\Gamma )$
-invariant, and
![]() $h_i$
,
$h_i$
,
![]() $k_j$
are
$k_j$
are
![]() ${\mathcal {Z}}^2$
-measurable. Write
${\mathcal {Z}}^2$
-measurable. Write
![]() ${\mathbf {Z}}^2 = {\mathbf {Z}} \times _{\sigma } H$
and apply Corollary 5.2:
${\mathbf {Z}}^2 = {\mathbf {Z}} \times _{\sigma } H$
and apply Corollary 5.2:
 $$ \begin{align*} &\text{UC-}\lim_{g \in \Gamma}{~\kappa(\alpha_g)~\mu ( A \cap T_{\varphi(g)}^{-1}A \cap T_{\psi(g)}^{-1}A)} \\&\quad = \text{UC-}\lim_{g \in \Gamma}{\kappa(\alpha_g)~\sum_{i,j} {\int_X{f c_i d_j \cdot T_{\varphi(g)} h_i \cdot T_{\psi(g)} k_j\,d\mu}}} \\&\quad = \sum_{i,j}{\int_{X \times Z \times M}{f(x) c_i(x) d_j(x) \cdot \kappa(t) \cdot h_i ( \pi_Z(x) + \widehat{\varphi}(t), \pi_H(x) + u + \omega_1 ( t, \pi_Z(x) ))}} \\& \qquad\times {{ k_j ( \pi_Z(x) + \widehat{\psi}(t), \pi_H(x) + v + \omega_2 ( t, \pi_Z(x) ) )\,d\mu(x)\,dm_Z(t)\,dm_M(u,v)}}. \end{align*} $$
$$ \begin{align*} &\text{UC-}\lim_{g \in \Gamma}{~\kappa(\alpha_g)~\mu ( A \cap T_{\varphi(g)}^{-1}A \cap T_{\psi(g)}^{-1}A)} \\&\quad = \text{UC-}\lim_{g \in \Gamma}{\kappa(\alpha_g)~\sum_{i,j} {\int_X{f c_i d_j \cdot T_{\varphi(g)} h_i \cdot T_{\psi(g)} k_j\,d\mu}}} \\&\quad = \sum_{i,j}{\int_{X \times Z \times M}{f(x) c_i(x) d_j(x) \cdot \kappa(t) \cdot h_i ( \pi_Z(x) + \widehat{\varphi}(t), \pi_H(x) + u + \omega_1 ( t, \pi_Z(x) ))}} \\& \qquad\times {{ k_j ( \pi_Z(x) + \widehat{\psi}(t), \pi_H(x) + v + \omega_2 ( t, \pi_Z(x) ) )\,d\mu(x)\,dm_Z(t)\,dm_M(u,v)}}. \end{align*} $$
Taking
![]() $\kappa $
supported on a sufficiently small neighborhood of
$\kappa $
supported on a sufficiently small neighborhood of
![]() $0$
in Z, it suffices to establish the inequality
$0$
in Z, it suffices to establish the inequality
 $$ \begin{align} &\sum_{i,j}\int_{X \times M} f(x) c_i(x) d_j(x) h_i ( \pi_Z(x),\pi_H(x) + u )\nonumber\\ & \quad \times k_j ( \pi_Z(x), \pi_H(x) + v)\,d\mu(x)\,dm_M(u,v) \ge \mu(A)^3. \end{align} $$
$$ \begin{align} &\sum_{i,j}\int_{X \times M} f(x) c_i(x) d_j(x) h_i ( \pi_Z(x),\pi_H(x) + u )\nonumber\\ & \quad \times k_j ( \pi_Z(x), \pi_H(x) + v)\,d\mu(x)\,dm_M(u,v) \ge \mu(A)^3. \end{align} $$
By applying Theorem 4.3 together with Theorem 2.5 and passing to yet another extension, we may assume the Mackey group M decomposes as
![]() $M = M_{\varphi } \times M_{\psi }$
. Let
$M = M_{\varphi } \times M_{\psi }$
. Let
![]() ${\mathcal {W}}_{\varphi }$
be the
${\mathcal {W}}_{\varphi }$
be the
![]() $\sigma $
-algebra generated by functions
$\sigma $
-algebra generated by functions
![]() $f : Z \times H \to {\mathbb {C}}$
satisfying
$f : Z \times H \to {\mathbb {C}}$
satisfying
![]() $f(z,x) = f(z,x+y)$
for
$f(z,x) = f(z,x+y)$
for
![]() $y \in M_{\varphi }$
, and let
$y \in M_{\varphi }$
, and let
![]() ${\mathcal {W}}_{\psi }$
be defined similarly. Then the left-hand side of equation (6.1) is equal to
${\mathcal {W}}_{\psi }$
be defined similarly. Then the left-hand side of equation (6.1) is equal to
which is bounded below by
![]() $( \int _X{f\,d\mu } )^3 = \mu (A)^3$
by [Reference Chu11, Lemma 1.6].
$( \int _X{f\,d\mu } )^3 = \mu (A)^3$
by [Reference Chu11, Lemma 1.6].
Now we complete the proof of Theorem 1.16.
Proof of Theorem 1.16
Let
![]() ${\mathbf {X}} = ( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
be an ergodic measure-preserving
${\mathbf {X}} = ( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$
be an ergodic measure-preserving
![]() $\Gamma $
-system, let
$\Gamma $
-system, let
![]() $A \in {\mathcal {X}}$
, and let
$A \in {\mathcal {X}}$
, and let
![]() ${\varepsilon }> 0$
.
${\varepsilon }> 0$
.
The
![]() $\Gamma $
-system
$\Gamma $
-system
![]() $( X, {\mathcal {X}}, \mu , ( T_{\eta (g)} )_{g \in \Gamma } )$
has finitely many ergodic components (at most the index of
$( X, {\mathcal {X}}, \mu , ( T_{\eta (g)} )_{g \in \Gamma } )$
has finitely many ergodic components (at most the index of
![]() $\eta (\Gamma )$
in
$\eta (\Gamma )$
in
![]() $\Gamma $
). Let
$\Gamma $
). Let
![]() $\mu = \sum _{i=1}^l{\mu _i}$
be the ergodic decomposition. Then each of the systems
$\mu = \sum _{i=1}^l{\mu _i}$
be the ergodic decomposition. Then each of the systems
![]() ${\mathbf {X}}_i = ( X, {\mathcal {X}}, \mu _i, ( T_{\eta (g)} )_{g \in \Gamma } )$
is ergodic, and they all have the same Kronecker factor
${\mathbf {X}}_i = ( X, {\mathcal {X}}, \mu _i, ( T_{\eta (g)} )_{g \in \Gamma } )$
is ergodic, and they all have the same Kronecker factor
![]() ${\mathbf {Z}}_{\eta } = (Z_{\eta }, \alpha \circ \eta )$
, where
${\mathbf {Z}}_{\eta } = (Z_{\eta }, \alpha \circ \eta )$
, where
![]() $Z_{\eta } = \overline {\{ \alpha _{\eta (g)} : g \in \Gamma \}}$
. By Theorem 6.1, we may therefore find a continuous function
$Z_{\eta } = \overline {\{ \alpha _{\eta (g)} : g \in \Gamma \}}$
. By Theorem 6.1, we may therefore find a continuous function
![]() $\kappa : Z_{\eta } \to [0, \infty )$
such that
$\kappa : Z_{\eta } \to [0, \infty )$
such that
![]() $\int _{Z_{\eta }}{\kappa (t)\,dt} = 1$
and
$\int _{Z_{\eta }}{\kappa (t)\,dt} = 1$
and
for each
![]() $i \in \{1, \ldots , l\}$
. Then by Jensen’s inequality,
$i \in \{1, \ldots , l\}$
. Then by Jensen’s inequality,
It follows that
is syndetic in
![]() $\eta (\Gamma )$
: if not, then by [Reference Ackelsberg, Bergelson and Best1, Lemma 1.9], there exists a Følner sequence
$\eta (\Gamma )$
: if not, then by [Reference Ackelsberg, Bergelson and Best1, Lemma 1.9], there exists a Følner sequence
![]() $(\Phi _N)_{N \in {\mathbb {N}}}$
in
$(\Phi _N)_{N \in {\mathbb {N}}}$
in
![]() $\eta (\Gamma )$
such that
$\eta (\Gamma )$
such that
for every
![]() $h \in \bigcup _{N \in {\mathbb {N}}}{\Phi _N}$
, whence
$h \in \bigcup _{N \in {\mathbb {N}}}{\Phi _N}$
, whence
 $$ \begin{align*} \lim_{N \to \infty}{\frac{1}{|\Phi_N|} \sum_{h \in \Phi_N}{\kappa ( \alpha_h ) \mu ( A \cap T_{\varphi'(h)}^{-1} A \cap T_{\psi'(h)}^{-1} A)}} \le ( \mu(A)^3 - {\varepsilon})\! \int_{Z_{\eta}}{\kappa(t)\,dt}\!\! =\! \mu(A)^3 - {\varepsilon}, \end{align*} $$
$$ \begin{align*} \lim_{N \to \infty}{\frac{1}{|\Phi_N|} \sum_{h \in \Phi_N}{\kappa ( \alpha_h ) \mu ( A \cap T_{\varphi'(h)}^{-1} A \cap T_{\psi'(h)}^{-1} A)}} \le ( \mu(A)^3 - {\varepsilon})\! \int_{Z_{\eta}}{\kappa(t)\,dt}\!\! =\! \mu(A)^3 - {\varepsilon}, \end{align*} $$
which is a contradiction. However,
![]() $\eta (\Gamma )$
has finite index in
$\eta (\Gamma )$
has finite index in
![]() $\Gamma $
, so
$\Gamma $
, so
is syndetic in
![]() $\Gamma $
.
$\Gamma $
.
Acknowledgements
This material is based upon work supported by the National Science Foundation under Grant No. DMS-1926686. We thank Vitaly Bergelson for helpful comments on the introduction and to Or Shalom for several useful discussions.