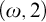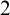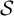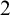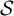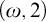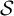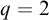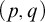1 Introduction
Given a family of sets
![]() $\mathcal {S}$
, a Boolean atom is a maximal nonempty intersection of sets in the closure of
$\mathcal {S}$
, a Boolean atom is a maximal nonempty intersection of sets in the closure of
![]() $\mathcal {S}$
under complements. The dual shatter function
$\mathcal {S}$
under complements. The dual shatter function
![]() $\pi ^*_{\mathcal {S}}:\omega \rightarrow \omega $
of
$\pi ^*_{\mathcal {S}}:\omega \rightarrow \omega $
of
![]() $\mathcal {S}$
sends each n to the maximum number of Boolean atoms of any subfamily of
$\mathcal {S}$
sends each n to the maximum number of Boolean atoms of any subfamily of
![]() $\mathcal {S}$
of size n.
$\mathcal {S}$
of size n.
For cardinals
![]() $p\geq q>1$
, a family of sets
$p\geq q>1$
, a family of sets
![]() $\mathcal {S}$
has the
$\mathcal {S}$
has the
![]() $(p,q)$
-property if it does not contain the empty set and, for any p sets in
$(p,q)$
-property if it does not contain the empty set and, for any p sets in
![]() $\mathcal {S}$
, there exists a subfamily among them of size q with nonempty intersection.
$\mathcal {S}$
, there exists a subfamily among them of size q with nonempty intersection.
Using ideas from Alon and Kleitman [Reference Alon and Kleitman1], Matoušek proved the following in [Reference Matoušek6, Theorem 4].
Theorem A (Alon–Kleitman–Matoušek
 $(p,q)$
-theoremFootnote
1
).
$(p,q)$
-theoremFootnote
1
).
Let
![]() $q\geq 2$
be an integer and let
$q\geq 2$
be an integer and let
![]() $\mathcal {S}$
be a family of sets whose dual shatter function satisfies
$\mathcal {S}$
be a family of sets whose dual shatter function satisfies
![]() $\pi _{\mathcal {S}}^*(n)\in o(n^q)$
(that is,
$\pi _{\mathcal {S}}^*(n)\in o(n^q)$
(that is,
![]() $\lim _{n\rightarrow \infty } \pi _{\mathcal {S}}^*(n)/n^q =0$
). For any integer
$\lim _{n\rightarrow \infty } \pi _{\mathcal {S}}^*(n)/n^q =0$
). For any integer
![]() $p\geq q$
, there exists some
$p\geq q$
, there exists some
![]() $m<\omega $
such that, if
$m<\omega $
such that, if
![]() $\mathcal {F}$
is a subfamily of
$\mathcal {F}$
is a subfamily of
![]() $\mathcal {S}$
with the
$\mathcal {S}$
with the
![]() $(p,q)$
-property, then
$(p,q)$
-property, then
![]() $\mathcal {F}$
can be partitioned into at most m subfamilies, each with the finite intersection property.
$\mathcal {F}$
can be partitioned into at most m subfamilies, each with the finite intersection property.
For notational conventions and some model theoretic definitions in this paper we refer the reader to Section 2.1 and to [Reference Simon8].
Chernikov and Simon [Reference Chernikov and Simon4] used Theorem A to study NIP theories. In [Reference Chernikov and Simon4, Problem 29] they asked whether a definable version of it holds in this setting. This has evolved to be known as the definable
![]() $(p,q)$
-conjecture [Reference Simon9, Conjecture 2.15]. Specifically, the conjecture (which was put forward before the connection with the
$(p,q)$
-conjecture [Reference Simon9, Conjecture 2.15]. Specifically, the conjecture (which was put forward before the connection with the
![]() $(p,q)$
-theorem was established) states that any NIP formula which is non-dividing over a model M belongs to a (finitely) consistent M-definable family. By means of first-order logic compactness, as well as Theorem A, this can be restated as follows.
$(p,q)$
-theorem was established) states that any NIP formula which is non-dividing over a model M belongs to a (finitely) consistent M-definable family. By means of first-order logic compactness, as well as Theorem A, this can be restated as follows.
Conjecture B (Definable
 $(p,q)$
-conjectureFootnote
2
).
$(p,q)$
-conjectureFootnote
2
).
Let
![]() $q\geq 2$
be an integer, let M be an L-structure, and let
$q\geq 2$
be an integer, let M be an L-structure, and let
![]() $\varphi (x,y)$
be an
$\varphi (x,y)$
be an
![]() $L(M)$
-formula (which we identify with the family of sets
$L(M)$
-formula (which we identify with the family of sets
![]() $\{\varphi (M,a) : a\in M^{|y|}\}$
) with dual shatter function
$\{\varphi (M,a) : a\in M^{|y|}\}$
) with dual shatter function
![]() $\pi _{\varphi }^*(n)\in o(n^q)$
. If there exists an integer
$\pi _{\varphi }^*(n)\in o(n^q)$
. If there exists an integer
![]() $p\geq q$
such that
$p\geq q$
such that
![]() $\varphi (x,y)$
has the
$\varphi (x,y)$
has the
![]() $(p,q)$
-property, then there exist some
$(p,q)$
-property, then there exist some
![]() $m<\omega $
and
$m<\omega $
and
![]() $L(M)$
-formulas
$L(M)$
-formulas
![]() $\sigma _1(y),\ldots , \sigma _m(y)$
such that
$\sigma _1(y),\ldots , \sigma _m(y)$
such that
![]() $\cup _i \sigma _i(M) = M^{|y|}$
and, for every
$\cup _i \sigma _i(M) = M^{|y|}$
and, for every
![]() $i\leq m$
, the family
$i\leq m$
, the family
![]() $\{\varphi (x,a) : a\in \sigma _i(M)\}$
is consistent.
$\{\varphi (x,a) : a\in \sigma _i(M)\}$
is consistent.
Conjecture B, which can be seen as a definable non-uniform version of Theorem A, is known to hold in certain cases. Simon [Reference Simon7] proved it in dp-minimal theories for formulas
![]() $\varphi (x,y)$
with
$\varphi (x,y)$
with
![]() $|x|\leq 2$
, and in any theory for formulas that extend to an invariant type of dp-rank
$|x|\leq 2$
, and in any theory for formulas that extend to an invariant type of dp-rank
![]() $1$
. In [Reference Simon9], he proved it in NIP theories of small or medium directionality. Simon and Starchenko [Reference Simon and Starchenko10, Theorem 5] proved a stronger version of the conjecture for a class of dp-minimal theories that includes those that are linearly ordered, unpackable VC-minimal, or have definable Skolem functions. Recently, Boxall and Kestner [Reference Boxall and Kestner2] proved, using Theorem A and the work on NIP forking of Chernikov and Kaplan [Reference Chernikov and Kaplan3], Conjecture B in distal NIP theories. While this paper was under review, Kaplan [Reference Kaplan5] presented a proof of a uniform version of Conjecture B for formulas in NIP theories.
$1$
. In [Reference Simon9], he proved it in NIP theories of small or medium directionality. Simon and Starchenko [Reference Simon and Starchenko10, Theorem 5] proved a stronger version of the conjecture for a class of dp-minimal theories that includes those that are linearly ordered, unpackable VC-minimal, or have definable Skolem functions. Recently, Boxall and Kestner [Reference Boxall and Kestner2] proved, using Theorem A and the work on NIP forking of Chernikov and Kaplan [Reference Chernikov and Kaplan3], Conjecture B in distal NIP theories. While this paper was under review, Kaplan [Reference Kaplan5] presented a proof of a uniform version of Conjecture B for formulas in NIP theories.
In this paper we prove a strengthening of both Conjecture B and (the non-uniform version of) Theorem A in the case where
![]() $q=2$
. In particular, we show that Conjecture B holds when
$q=2$
. In particular, we show that Conjecture B holds when
![]() $q=2$
, and that we may furthermore weaken the
$q=2$
, and that we may furthermore weaken the
![]() $(p,2)$
-property to the
$(p,2)$
-property to the
![]() $(\omega ,2)$
-property in the statements of Conjecture B and the case
$(\omega ,2)$
-property in the statements of Conjecture B and the case
![]() $\mathcal {S}=\mathcal {F}$
of Theorem A.
$\mathcal {S}=\mathcal {F}$
of Theorem A.
Theorem C (Definable
 $(\omega ,2)$
-theorem).
$(\omega ,2)$
-theorem).
Let M be an L-structure and let
![]() $\varphi (x,y)$
be an
$\varphi (x,y)$
be an
![]() $L(M)$
-formula with dual shatter function
$L(M)$
-formula with dual shatter function
![]() $\pi _{\varphi }^*(n)\in o(n^2)$
(e.g.,
$\pi _{\varphi }^*(n)\in o(n^2)$
(e.g.,
![]() $VC$
-codensity of
$VC$
-codensity of
![]() $\varphi (x,y)$
is less than
$\varphi (x,y)$
is less than
![]() $2$
). If
$2$
). If
![]() $\varphi (x,y)$
has the
$\varphi (x,y)$
has the
![]() $(\omega ,2)$
-property, then there exist some
$(\omega ,2)$
-property, then there exist some
![]() $m<\omega $
and
$m<\omega $
and
![]() $L(M)$
-formulas
$L(M)$
-formulas
![]() $\sigma _1(y),\ldots , \sigma _m(y)$
such that
$\sigma _1(y),\ldots , \sigma _m(y)$
such that
![]() $\cup _i \sigma _i(M) = M^{|y|}$
and, for every
$\cup _i \sigma _i(M) = M^{|y|}$
and, for every
![]() $i\leq m$
, the family
$i\leq m$
, the family
![]() $\{ \varphi (x,a) : a\in \sigma _i(M)\}$
is consistent.
$\{ \varphi (x,a) : a\in \sigma _i(M)\}$
is consistent.
Since any family of sets can be witnessed as a definable family in some structure, the following corollary is immediate.
Corollary D (
 $(\omega ,2)$
-theorem).
$(\omega ,2)$
-theorem).
Let
![]() $\mathcal {S}$
be a family of sets with
$\mathcal {S}$
be a family of sets with
![]() $\pi _{\mathcal {S}}^*(n)\in o(n^2)$
. If
$\pi _{\mathcal {S}}^*(n)\in o(n^2)$
. If
![]() $\mathcal {S}$
has the
$\mathcal {S}$
has the
![]() $(\omega ,2)$
-property, then it can be partitioned into finitely many subfamilies, each with the finite intersection property.
$(\omega ,2)$
-property, then it can be partitioned into finitely many subfamilies, each with the finite intersection property.
Our proof of Theorem C is elementary in that it avoids the use of both the Alon–Kleitman–Matoušek
![]() $(p,q)$
-theorem (as well as its related fractional Helly theorem) and the work of Shelah, Simon, and others on NIP theories.
$(p,q)$
-theorem (as well as its related fractional Helly theorem) and the work of Shelah, Simon, and others on NIP theories.
2 Preliminaries
2.1 Notation
Throughout we fix two structures
![]() $M\preccurlyeq U$
in some language L, where U realizes every type over M. For any
$M\preccurlyeq U$
in some language L, where U realizes every type over M. For any
![]() $A\subseteq U$
, let
$A\subseteq U$
, let
![]() $L(A)$
denote the expansion of L by formulas with parameters in A.
$L(A)$
denote the expansion of L by formulas with parameters in A.
Given a (partitioned) formula
![]() $\varphi (x,y)$
, some
$\varphi (x,y)$
, some
![]() $b\in U^{|y|}$
, and
$b\in U^{|y|}$
, and
![]() $A\subseteq U^{|x|}$
, let
$A\subseteq U^{|x|}$
, let
![]() $\varphi (A,b)=\{a\in A : U\models \varphi (a,b)\}$
. For
$\varphi (A,b)=\{a\in A : U\models \varphi (a,b)\}$
. For
![]() $A\subseteq U$
, we write
$A\subseteq U$
, we write
![]() $\varphi (A,b)$
instead of
$\varphi (A,b)$
instead of
![]() $\varphi (A^{|x|}, b)$
. By “definable set” we mean “definable set in M possibly with parameters”, i.e., a set of the form
$\varphi (A^{|x|}, b)$
. By “definable set” we mean “definable set in M possibly with parameters”, i.e., a set of the form
![]() $\varphi (M)$
for some
$\varphi (M)$
for some
![]() $L(M)$
-formula
$L(M)$
-formula
![]() $\varphi (x)$
.
$\varphi (x)$
.
We apply notions such as the
![]() $(p,q)$
-property and dual shatter function to formulas
$(p,q)$
-property and dual shatter function to formulas
![]() $\varphi (x,y)$
by adopting the usual convention of identifying them with the family of sets
$\varphi (x,y)$
by adopting the usual convention of identifying them with the family of sets
![]() $\{\varphi (M,a) : a\in M^{|y|}\}$
. In the context of formulas, we refer to the finite intersection property as being (finitely) consistent, and to being pairwise disjoint as being pairwise inconsistent.
$\{\varphi (M,a) : a\in M^{|y|}\}$
. In the context of formulas, we refer to the finite intersection property as being (finitely) consistent, and to being pairwise disjoint as being pairwise inconsistent.
Given a formula
![]() $\varphi (x,y)$
and
$\varphi (x,y)$
and
![]() $A\subseteq U^{|y|}$
, by a
$A\subseteq U^{|y|}$
, by a
![]() $\varphi $
-type over A we mean a maximal consistent collection
$\varphi $
-type over A we mean a maximal consistent collection
![]() $p(x)$
of formulas in
$p(x)$
of formulas in
![]() $\{ \varphi (x,a), \neg \varphi (x,a) : a\in A\}$
.
$\{ \varphi (x,a), \neg \varphi (x,a) : a\in A\}$
.
Throughout, n,m, i, j, k, and l are positive integers.
2.2 Preliminary results
We present some preliminary lemmas on
![]() $\varphi $
-types for formulas
$\varphi $
-types for formulas
![]() $\varphi (x,y)$
with
$\varphi (x,y)$
with
![]() $\pi ^*_\varphi (n)\in o(n^2)$
.
$\pi ^*_\varphi (n)\in o(n^2)$
.
Lemma 2.1. Let
![]() $\varphi (x,y)$
be an
$\varphi (x,y)$
be an
![]() $L(M)$
-formula such that
$L(M)$
-formula such that
![]() $\pi ^*_\varphi (n)\in o(n^2)$
. Suppose that there exists some
$\pi ^*_\varphi (n)\in o(n^2)$
. Suppose that there exists some
![]() $b\in U^{|y|}$
such that
$b\in U^{|y|}$
such that
![]() $\varphi (M,b)=\emptyset $
. Then there exists
$\varphi (M,b)=\emptyset $
. Then there exists
![]() $\theta (y)\in \operatorname {tp}(b/M)$
such that the elements of
$\theta (y)\in \operatorname {tp}(b/M)$
such that the elements of
![]() $\varphi (U,b)$
realize only finitely many
$\varphi (U,b)$
realize only finitely many
![]() $\varphi $
-types over
$\varphi $
-types over
![]() $\theta (M)$
.
$\theta (M)$
.
Proof Let
![]() $\varphi (x,y)$
and
$\varphi (x,y)$
and
![]() $b\in U^{|y|}$
be as in the lemma. We assume that, for any
$b\in U^{|y|}$
be as in the lemma. We assume that, for any
![]() $\theta (y)\in \operatorname {tp}(b/M)$
, the elements of
$\theta (y)\in \operatorname {tp}(b/M)$
, the elements of
![]() $\varphi (U,b)$
realize infinitely many
$\varphi (U,b)$
realize infinitely many
![]() $\varphi $
-types over
$\varphi $
-types over
![]() $\theta (M)$
. We prove the lemma by showing that, for every n,
$\theta (M)$
. We prove the lemma by showing that, for every n,
 $$ \begin{align} \pi^*_\varphi(n) \geq \sum_{i=1}^{n} i = \frac{n^2+n}{2}. \end{align} $$
$$ \begin{align} \pi^*_\varphi(n) \geq \sum_{i=1}^{n} i = \frac{n^2+n}{2}. \end{align} $$
In particular, it follows that
![]() $\pi ^*_\varphi (n)\notin o(n^2)$
.
$\pi ^*_\varphi (n)\notin o(n^2)$
.
We construct a sequence
![]() $(a_n : 1 \leq n<\omega )$
in
$(a_n : 1 \leq n<\omega )$
in
![]() $M^{|y|}$
and a set
$M^{|y|}$
and a set
![]() $\{ c_{i,j}:\, 1 \leq i<\omega ,\, 1 \leq j \leq i\}$
in
$\{ c_{i,j}:\, 1 \leq i<\omega ,\, 1 \leq j \leq i\}$
in
![]() $M^{|x|}$
with the following property. For every n and distinct pairs
$M^{|x|}$
with the following property. For every n and distinct pairs
![]() $(i,j)$
,
$(i,j)$
,
![]() $(i',j')$
, with
$(i',j')$
, with
![]() $i, i'\leq n$
,
$i, i'\leq n$
,
![]() $j\leq i$
and
$j\leq i$
and
![]() $j'\leq i'$
, it holds that
$j'\leq i'$
, it holds that
That is, for every n, the set
![]() $\{ c_{i,j}: 1 \leq i\leq n, \, 1 \leq j\leq i\}$
witnesses that
$\{ c_{i,j}: 1 \leq i\leq n, \, 1 \leq j\leq i\}$
witnesses that
 $$\begin{align*}|\{\varphi(c, \{a_1,\ldots, a_n\}) : c\in M^{|x|}\}|\geq \sum_{i=1}^{n} i, \end{align*}$$
$$\begin{align*}|\{\varphi(c, \{a_1,\ldots, a_n\}) : c\in M^{|x|}\}|\geq \sum_{i=1}^{n} i, \end{align*}$$
which in turn shows that the elements
![]() $\{a_1,\ldots , a_n\}$
witness Equation (1). Specifically, the set
$\{a_1,\ldots , a_n\}$
witness Equation (1). Specifically, the set
![]() $\{c_{i,j} : 1 \leq i<\omega , 1 \leq j\leq i\}$
will have the following two properties:
$\{c_{i,j} : 1 \leq i<\omega , 1 \leq j\leq i\}$
will have the following two properties:
-
(i)
 $\neg \varphi (c_{i',j'}, a_i) \text { and } \varphi (c_{i,j}, a_i) \text { hold for all } i'<i, \, j'\leq i',\, j\leq i.$
$\neg \varphi (c_{i',j'}, a_i) \text { and } \varphi (c_{i,j}, a_i) \text { hold for all } i'<i, \, j'\leq i',\, j\leq i.$
-
(ii)
 $\varphi (c_{i,j}, \{a_1,\ldots , a_{i-1}\})\neq \varphi (c_{i,j'}, \{a_1,\ldots , a_{i-1}\}) \text { for all } i\geq 2,\, j<j'\leq i.$
$\varphi (c_{i,j}, \{a_1,\ldots , a_{i-1}\})\neq \varphi (c_{i,j'}, \{a_1,\ldots , a_{i-1}\}) \text { for all } i\geq 2,\, j<j'\leq i.$
It is easy to see that condition (2) follows from (i) and (ii).
For every n and
![]() $a_1,\ldots , a_n$
in
$a_1,\ldots , a_n$
in
![]() $M^{|y|}$
, let
$M^{|y|}$
, let
![]() $s(a_1,\ldots , a_n)$
denote the number of Boolean atoms C of
$s(a_1,\ldots , a_n)$
denote the number of Boolean atoms C of
![]() $\{\varphi (U,a_1),\ldots , \varphi (U,a_n)\}$
satisfying that
$\{\varphi (U,a_1),\ldots , \varphi (U,a_n)\}$
satisfying that
![]() $\varphi (C,b)\neq \emptyset $
. We construct our sequence in such a way that
$\varphi (C,b)\neq \emptyset $
. We construct our sequence in such a way that
![]() $s(a_1,\ldots , a_n)\geq n+1$
for every n.
$s(a_1,\ldots , a_n)\geq n+1$
for every n.
We proceed to build sets
![]() $\{ a_i : 1 \leq i\leq n\}$
and
$\{ a_i : 1 \leq i\leq n\}$
and
![]() $\{c_{i,j} : 1 \leq i\leq n,\, 1 \leq j\leq i\}$
by induction on n.
$\{c_{i,j} : 1 \leq i\leq n,\, 1 \leq j\leq i\}$
by induction on n.
Case
![]() $n=1$
.
$n=1$
.
Since, by assumption, the elements of
![]() $\varphi (U,b)$
realize infinitely many
$\varphi (U,b)$
realize infinitely many
![]() $\varphi $
-types over M, there must be some
$\varphi $
-types over M, there must be some
![]() $a\in M^{|y|}$
such that
$a\in M^{|y|}$
such that
Let
![]() $a_1$
be any such a. Let
$a_1$
be any such a. Let
![]() $c_{1,1}$
be any element in
$c_{1,1}$
be any element in
![]() $\varphi (M,a_1)$
. Observe that
$\varphi (M,a_1)$
. Observe that
![]() $s(a_1)=2$
.
$s(a_1)=2$
.
Induction
![]() $n>1$
.
$n>1$
.
Suppose we have a sequence
![]() $(a_1,\ldots , a_{n-1})$
in
$(a_1,\ldots , a_{n-1})$
in
![]() $M^{|y|}$
as desired. Since
$M^{|y|}$
as desired. Since
![]() $s(a_1,\ldots , a_{n-1})\geq n$
, there are n distinct Boolean atoms
$s(a_1,\ldots , a_{n-1})\geq n$
, there are n distinct Boolean atoms
![]() $C_1,\ldots , C_n$
of the family
$C_1,\ldots , C_n$
of the family
![]() $\{\varphi (U,a_1),\ldots , \varphi (U,a_{n-1})\}$
containing each elements from
$\{\varphi (U,a_1),\ldots , \varphi (U,a_{n-1})\}$
containing each elements from
![]() $\varphi (U,b)$
. Let
$\varphi (U,b)$
. Let
Since
![]() $\varphi (M,b)=\emptyset $
, note that
$\varphi (M,b)=\emptyset $
, note that
![]() $b\in \theta (U)$
. Consequently, by assumption, the elements of
$b\in \theta (U)$
. Consequently, by assumption, the elements of
![]() $\varphi (U,b)$
realize infinitely many
$\varphi (U,b)$
realize infinitely many
![]() $\varphi $
-types over
$\varphi $
-types over
![]() $\theta (M)$
. In particular, there must exist some Boolean atom C of
$\theta (M)$
. In particular, there must exist some Boolean atom C of
![]() $\{\varphi (U,a_1),\ldots , \varphi (U,a_{n-1})\}$
satisfying that the elements of
$\{\varphi (U,a_1),\ldots , \varphi (U,a_{n-1})\}$
satisfying that the elements of
![]() $\varphi (C,b)$
realize more than one
$\varphi (C,b)$
realize more than one
![]() $\varphi $
-type over
$\varphi $
-type over
![]() $\theta (M)$
. Let
$\theta (M)$
. Let
![]() $a_n \in \theta (M)$
witness this, i.e.,
$a_n \in \theta (M)$
witness this, i.e.,
![]() $\varphi (C,b)\cap \varphi (U,a_n)\neq \emptyset $
and
$\varphi (C,b)\cap \varphi (U,a_n)\neq \emptyset $
and
![]() $\varphi (C,b) \setminus \varphi (U,a_n)\neq \emptyset $
. It then follows that
$\varphi (C,b) \setminus \varphi (U,a_n)\neq \emptyset $
. It then follows that
![]() $s(a_1,\ldots , a_n)\geq n+1$
.
$s(a_1,\ldots , a_n)\geq n+1$
.
Finally, by definition of
![]() $\theta (M)$
, we have that
$\theta (M)$
, we have that
![]() $\varphi (C_j, a_n)\neq \emptyset $
for every
$\varphi (C_j, a_n)\neq \emptyset $
for every
![]() $j\leq n$
. For any
$j\leq n$
. For any
![]() $j \leq n$
, let
$j \leq n$
, let
![]() $c_{n,j}$
be an element in
$c_{n,j}$
be an element in
![]() $\varphi (C_j, a_n) \cap M^{|x|}$
. Then clearly
$\varphi (C_j, a_n) \cap M^{|x|}$
. Then clearly
![]() $\{c_{i,j}: 1 \leq i\leq n,\, 1\leq j\leq i\}$
satisfies condition (ii). By definition of
$\{c_{i,j}: 1 \leq i\leq n,\, 1\leq j\leq i\}$
satisfies condition (ii). By definition of
![]() $\theta (M)$
, note that it also satisfies condition (i).
$\theta (M)$
, note that it also satisfies condition (i).
Lemma 2.2. Let
![]() $\varphi (x,y)$
be an
$\varphi (x,y)$
be an
![]() $L(M)$
-formula such that
$L(M)$
-formula such that
![]() $\pi ^*_\varphi (n)\in o(n^2)$
. Suppose that there exists some
$\pi ^*_\varphi (n)\in o(n^2)$
. Suppose that there exists some
![]() $b\in U^{|y|}$
such that, for any
$b\in U^{|y|}$
such that, for any
![]() $\sigma (y) \in \operatorname {tp}(b/M)$
, the family
$\sigma (y) \in \operatorname {tp}(b/M)$
, the family
![]() $\{\varphi (x,a) : a\in \sigma (M)\}$
fails to be consistent. Then there exists
$\{\varphi (x,a) : a\in \sigma (M)\}$
fails to be consistent. Then there exists
![]() $\theta (y)\in \operatorname {tp}(b/M)$
such that the elements of
$\theta (y)\in \operatorname {tp}(b/M)$
such that the elements of
![]() $\varphi (U,b)$
realize only finitely many
$\varphi (U,b)$
realize only finitely many
![]() $\varphi $
-types over
$\varphi $
-types over
![]() $\theta (M)$
and, moreover, for any such type
$\theta (M)$
and, moreover, for any such type
![]() $p(x)$
exactly one of the following two conditions holds.
$p(x)$
exactly one of the following two conditions holds.
-
(a)
 $\{ a\in \theta (M) : \varphi (x,a)\in p(x)\}=\emptyset $
.
$\{ a\in \theta (M) : \varphi (x,a)\in p(x)\}=\emptyset $
. -
(b) For every
 $\theta '(y)\in \operatorname {tp}(b/M)$
, the set
$\theta '(y)\in \operatorname {tp}(b/M)$
, the set
 $\{ a \in \theta '(M) : \varphi (x,a)\in p(x) \}$
is not definable (in M).
$\{ a \in \theta '(M) : \varphi (x,a)\in p(x) \}$
is not definable (in M).
Proof Note that, by definition of b, for any
![]() $c\in M^{|x|}$
we have
$c\in M^{|x|}$
we have
![]() $\varphi (c,y)\notin \operatorname {tp}(b/M)$
. So
$\varphi (c,y)\notin \operatorname {tp}(b/M)$
. So
![]() $\varphi (M,b)=\emptyset $
. We apply Lemma 2.1. Hence let
$\varphi (M,b)=\emptyset $
. We apply Lemma 2.1. Hence let
![]() $\theta _0(y)\in \operatorname {tp}(b/M)$
be such that the elements of
$\theta _0(y)\in \operatorname {tp}(b/M)$
be such that the elements of
![]() $\varphi (U,b)$
realize only finitely many
$\varphi (U,b)$
realize only finitely many
![]() $\varphi $
-types over
$\varphi $
-types over
![]() $\theta _0(M)$
. Since otherwise the lemma is trivial we may assume that
$\theta _0(M)$
. Since otherwise the lemma is trivial we may assume that
![]() $\varphi (U,b)\neq \emptyset $
. We denote these types by
$\varphi (U,b)\neq \emptyset $
. We denote these types by
![]() $p_1(x),\ldots ,p_m(x)$
.
$p_1(x),\ldots ,p_m(x)$
.
Let
![]() $F\subseteq \{1,\ldots , m\}$
be the set of i satisfying that there exists a formula
$F\subseteq \{1,\ldots , m\}$
be the set of i satisfying that there exists a formula
![]() $\theta _i(y)\in \operatorname {tp}(b/M)$
such that the set
$\theta _i(y)\in \operatorname {tp}(b/M)$
such that the set
![]() $\sigma _i(M)=\{ a\in \theta _i(M) : \varphi (x,a) \in p_i(x)\}$
is definable. Observe that, for any
$\sigma _i(M)=\{ a\in \theta _i(M) : \varphi (x,a) \in p_i(x)\}$
is definable. Observe that, for any
![]() $i\in F$
, since
$i\in F$
, since
![]() $\{\varphi (x,a) : a\in \sigma _i(M)\}$
is consistent, by definition of b it holds that
$\{\varphi (x,a) : a\in \sigma _i(M)\}$
is consistent, by definition of b it holds that
![]() $b\notin \sigma _i(M)$
. Finally let
$b\notin \sigma _i(M)$
. Finally let
![]() $\theta (y)$
be given by
$\theta (y)$
be given by
Since
![]() $\theta (M)\subseteq \theta _0(M)$
, the
$\theta (M)\subseteq \theta _0(M)$
, the
![]() $\varphi $
-types over
$\varphi $
-types over
![]() $\theta (M)$
realized in
$\theta (M)$
realized in
![]() $\varphi (U,b)$
are exactly the restrictions
$\varphi (U,b)$
are exactly the restrictions
![]() $p_i(x)|_{\theta (M)}$
of the types
$p_i(x)|_{\theta (M)}$
of the types
![]() $p_i(x)$
to
$p_i(x)$
to
![]() $\theta (M)$
, for
$\theta (M)$
, for
![]() $i\leq m$
. We have ensured that, for any
$i\leq m$
. We have ensured that, for any
![]() $i\in F$
, the type
$i\in F$
, the type
![]() $p_i(x)|_{\theta (M)}$
is the (necessarily unique) type described by condition (a). On the other hand, by definition of F, for any
$p_i(x)|_{\theta (M)}$
is the (necessarily unique) type described by condition (a). On the other hand, by definition of F, for any
![]() $j \in \{1,\ldots ,m\}\setminus F$
the type
$j \in \{1,\ldots ,m\}\setminus F$
the type
![]() $p_j(x)|_{\theta (M)}$
satisfies condition (b).
$p_j(x)|_{\theta (M)}$
satisfies condition (b).
Lemma 2.3. Let
![]() $\varphi (x,y)$
,
$\varphi (x,y)$
,
![]() $b\in U^{|y|}$
,
$b\in U^{|y|}$
,
![]() $\theta (y)\in \operatorname {tp}(b/M)$
, and
$\theta (y)\in \operatorname {tp}(b/M)$
, and
![]() $p(x)$
be such that they satisfy condition (b) in Lemma 2.2. Then, for any
$p(x)$
be such that they satisfy condition (b) in Lemma 2.2. Then, for any
![]() $L(M)$
-formula
$L(M)$
-formula
![]() $\lambda (x)$
satisfying that
$\lambda (x)$
satisfying that
![]() $\varphi (U,b)\subseteq \lambda (U)$
, there exists some
$\varphi (U,b)\subseteq \lambda (U)$
, there exists some
![]() $a\in \theta (M)$
such that
$a\in \theta (M)$
such that
Proof Let
![]() $\theta '(M)$
be the set of
$\theta '(M)$
be the set of
![]() $a\in \theta (M)$
with
$a\in \theta (M)$
with
![]() $\varphi (U,a)\subseteq \lambda (U)$
. Observe that
$\varphi (U,a)\subseteq \lambda (U)$
. Observe that
![]() $\theta '(y)\in \operatorname {tp}(b/M)$
. Then, by condition (b) in Lemma 2.2, the set
$\theta '(y)\in \operatorname {tp}(b/M)$
. Then, by condition (b) in Lemma 2.2, the set
![]() $\{ a \in \theta '(M) : \varphi (x,a)\in p(x) \}$
is nonempty. Let a be any element in the set.
$\{ a \in \theta '(M) : \varphi (x,a)\in p(x) \}$
is nonempty. Let a be any element in the set.
3 Proof of the main result
We prove Theorem C through the next proposition.
Proposition 3.1. Let
![]() $\varphi (x,y)$
be an
$\varphi (x,y)$
be an
![]() $L(M)$
-formula with
$L(M)$
-formula with
![]() $\pi ^*_\varphi (n)\in o(n^2)$
and suppose that there exists
$\pi ^*_\varphi (n)\in o(n^2)$
and suppose that there exists
![]() $b\in U^{|y|}$
such that, for any
$b\in U^{|y|}$
such that, for any
![]() $\sigma (y) \in \operatorname {tp}(b/M)$
, the family
$\sigma (y) \in \operatorname {tp}(b/M)$
, the family
![]() $\{\varphi (x,a) : a\in \sigma (M)\}$
fails to be consistent. Let
$\{\varphi (x,a) : a\in \sigma (M)\}$
fails to be consistent. Let
![]() $\chi (x)$
be an
$\chi (x)$
be an
![]() $L(M)$
-formula such that
$L(M)$
-formula such that
![]() $\varphi (U,b)\subseteq \chi (U)$
. Then there exists some
$\varphi (U,b)\subseteq \chi (U)$
. Then there exists some
![]() $a\in M^{|y|}$
such that
$a\in M^{|y|}$
such that
and moreover
Proof By Lemma 2.2, there exists some
![]() $\theta (y)\in \operatorname {tp}(b/M)$
such that the elements of
$\theta (y)\in \operatorname {tp}(b/M)$
such that the elements of
![]() $\varphi (U,b)$
realize only finitely many
$\varphi (U,b)$
realize only finitely many
![]() $\varphi $
-types over
$\varphi $
-types over
![]() $\theta (M)$
, and furthermore for any such type condition (a) or condition (b) in the lemma holds. By passing from
$\theta (M)$
, and furthermore for any such type condition (a) or condition (b) in the lemma holds. By passing from
![]() $\theta (M)$
to
$\theta (M)$
to
![]() $\theta (M) \cap \{ a \in M^{|y|} : \varphi (U,a)\subseteq \chi (U)\}$
if necessary, we may also assume that every
$\theta (M) \cap \{ a \in M^{|y|} : \varphi (U,a)\subseteq \chi (U)\}$
if necessary, we may also assume that every
![]() $a\in \theta (M)$
satisfies that
$a\in \theta (M)$
satisfies that
![]() $\varphi (U,a)\subseteq \chi (U)$
. In particular, to prove Proposition 3.1 it suffices to find some
$\varphi (U,a)\subseteq \chi (U)$
. In particular, to prove Proposition 3.1 it suffices to find some
![]() $a\in \theta (M)$
such that
$a\in \theta (M)$
such that
![]() $\varphi (U,a)\cap \varphi (U,b)=\emptyset $
. Since otherwise the result is trivial we may assume that
$\varphi (U,a)\cap \varphi (U,b)=\emptyset $
. Since otherwise the result is trivial we may assume that
![]() $\varphi (U,b)\neq \emptyset $
.
$\varphi (U,b)\neq \emptyset $
.
Let
![]() $p_1(x), \ldots , p_l(x)$
denote the distinct
$p_1(x), \ldots , p_l(x)$
denote the distinct
![]() $\varphi $
-types over
$\varphi $
-types over
![]() $\theta (M)$
realized by elements of
$\theta (M)$
realized by elements of
![]() $\varphi (U,b)$
. We prove Proposition 3.1 by finding some
$\varphi (U,b)$
. We prove Proposition 3.1 by finding some
![]() $a\in \theta (M)$
such that
$a\in \theta (M)$
such that
![]() $\varphi (x,a)\notin p_i(x)$
for every
$\varphi (x,a)\notin p_i(x)$
for every
![]() $i\leq l$
. If
$i\leq l$
. If
![]() $l=1$
and
$l=1$
and
![]() $p_1(x)$
is the (unique) type described by condition (a) in Lemma 2.2, then clearly it suffices to take any
$p_1(x)$
is the (unique) type described by condition (a) in Lemma 2.2, then clearly it suffices to take any
![]() $a\in \theta (M)$
and we are done. We assume this is not the case.
$a\in \theta (M)$
and we are done. We assume this is not the case.
Let the numbering of the types
![]() $p_i(x)$
be such that, for some fixed
$p_i(x)$
be such that, for some fixed
![]() $k \in \{l-1, l\}$
, the types
$k \in \{l-1, l\}$
, the types
![]() $p_i(x)$
for
$p_i(x)$
for
![]() $1\leq i \leq k$
satisfy condition (b) and the possibly remaining type
$1\leq i \leq k$
satisfy condition (b) and the possibly remaining type
![]() $p_{i}(x)$
for
$p_{i}(x)$
for
![]() $k<i\leq l$
satisfies condition (a) in Lemma 2.2. Hence, either
$k<i\leq l$
satisfies condition (a) in Lemma 2.2. Hence, either
![]() $k=l$
or otherwise
$k=l$
or otherwise
![]() $1\leq k=l-1$
and the type
$1\leq k=l-1$
and the type
![]() $p_l(x)$
satisfies that
$p_l(x)$
satisfies that
![]() $\varphi (x,a)\notin p_l(x)$
for every
$\varphi (x,a)\notin p_l(x)$
for every
![]() $a\in \theta (M)$
. In either case it suffices to find some
$a\in \theta (M)$
. In either case it suffices to find some
![]() $a\in \theta (M)$
with
$a\in \theta (M)$
with
![]() $\varphi (x,a)\notin p_i(x)$
for every
$\varphi (x,a)\notin p_i(x)$
for every
![]() $1\leq i \leq k$
.
$1\leq i \leq k$
.
Now let us fix, for every
![]() $1 \leq i \leq k$
, an
$1 \leq i \leq k$
, an
![]() $L(M)$
-formula
$L(M)$
-formula
![]() $\chi _i(x)$
satisfying the following conditions:
$\chi _i(x)$
satisfying the following conditions:
-
•
 $p_i(x)\models \chi _i(x)$
for every
$p_i(x)\models \chi _i(x)$
for every
 $i < k$
.
$i < k$
. -
•
 $p_j(x) \models \chi _{k}(x)$
for all
$p_j(x) \models \chi _{k}(x)$
for all
 $k \leq j \leq l$
.
$k \leq j \leq l$
. -
•
 $\chi _i(U)\cap \chi _j(U)=\emptyset $
for every
$\chi _i(U)\cap \chi _j(U)=\emptyset $
for every
 $i<j\leq k$
.
$i<j\leq k$
.
We define, for any
![]() $1\leq m \leq k$
and elements
$1\leq m \leq k$
and elements
![]() $a_1,\ldots , a_{m-1} \in M^{|y|}$
, a set
$a_1,\ldots , a_{m-1} \in M^{|y|}$
, a set
![]() $\psi _{m}(M, a_1,\ldots , a_{m-1}) \subseteq \theta (M)$
as follows.
$\psi _{m}(M, a_1,\ldots , a_{m-1}) \subseteq \theta (M)$
as follows.
For
![]() $m=k$
, let
$m=k$
, let
![]() $\psi _k(M, a_1,\ldots , a_{k-1})$
denote the set of all
$\psi _k(M, a_1,\ldots , a_{k-1})$
denote the set of all
![]() $a\in \theta (M)$
such that
$a\in \theta (M)$
such that
 $$\begin{align*}\varphi(U,a)\subseteq \bigcup_{i=1}^{k-1} (\varphi(U, a_i)\cap \chi_i(U))\cup \chi_k(U). \end{align*}$$
$$\begin{align*}\varphi(U,a)\subseteq \bigcup_{i=1}^{k-1} (\varphi(U, a_i)\cap \chi_i(U))\cup \chi_k(U). \end{align*}$$
For
![]() $m < k$
, let
$m < k$
, let
![]() $\psi _{m}(M, a_1,\ldots , a_{m-1})$
denote the set of all
$\psi _{m}(M, a_1,\ldots , a_{m-1})$
denote the set of all
![]() $a\in \theta (M)$
such that
$a\in \theta (M)$
such that
 $$\begin{align*}\varphi(U,a)\subseteq \bigcup_{i=1}^{m-1} (\varphi(U,a_i)\cap \chi_i(U)) \cup \bigcup_{i=m}^k \chi_i(U) \end{align*}$$
$$\begin{align*}\varphi(U,a)\subseteq \bigcup_{i=1}^{m-1} (\varphi(U,a_i)\cap \chi_i(U)) \cup \bigcup_{i=m}^k \chi_i(U) \end{align*}$$
and moreover there exists two elements
![]() $a', a"\in \psi _{m+1}(M, a_1,\ldots , a_{m-1}, a)$
, with
$a', a"\in \psi _{m+1}(M, a_1,\ldots , a_{m-1}, a)$
, with
Claim 3.2 For any
![]() $m \leq k$
, the sets
$m \leq k$
, the sets
![]() $ \psi _{m}(M, a_1,\ldots , a_{m-1}) $
are definable uniformly (in M) over the parameters
$ \psi _{m}(M, a_1,\ldots , a_{m-1}) $
are definable uniformly (in M) over the parameters
![]() $a_i \in M^{|y|}$
,
$a_i \in M^{|y|}$
,
![]() $i<m$
.
$i<m$
.
Proof
For any given
![]() $m\leq k$
, let
$m\leq k$
, let
![]() $(\text {A}_m)$
be the statement that the sets
$(\text {A}_m)$
be the statement that the sets
![]() $\psi _{m}(M, a_1,\ldots , a_{m-1})$
are definable uniformly over the parameters
$\psi _{m}(M, a_1,\ldots , a_{m-1})$
are definable uniformly over the parameters
![]() $a_i \in M^{|y|}$
,
$a_i \in M^{|y|}$
,
![]() $i<m$
. Statement
$i<m$
. Statement
![]() $(\text {A}_k)$
clearly holds by definition. Then, for any
$(\text {A}_k)$
clearly holds by definition. Then, for any
![]() $m<k$
,
$m<k$
,
![]() $(\text {A}_m)$
follows easily from
$(\text {A}_m)$
follows easily from
![]() $(\text {A}_{m+1})$
and the definition of sets
$(\text {A}_{m+1})$
and the definition of sets
![]() $\psi _m(M, a_1,\ldots , a_{m-1})$
.
$\psi _m(M, a_1,\ldots , a_{m-1})$
.
We now prove two claims regarding the set
![]() $\psi _{1}(M)$
that will yield Proposition 3.1, by showing the existence of some
$\psi _{1}(M)$
that will yield Proposition 3.1, by showing the existence of some
![]() $a\in \theta (M)$
with
$a\in \theta (M)$
with
![]() $\varphi (x,a)\notin p_i(x)$
for every
$\varphi (x,a)\notin p_i(x)$
for every
![]() $i\leq k$
.
$i\leq k$
.
Claim 3.3 There exist
![]() $a, a'\in \psi _1(M)$
such that
$a, a'\in \psi _1(M)$
such that
Proof
For any
![]() $m \leq k$
consider the following two statements
$m \leq k$
consider the following two statements
![]() $(\text {I}_m)$
and
$(\text {I}_m)$
and
![]() $(\text {II}_m)$
:
$(\text {II}_m)$
:
-
(I m) Let
 $a_i \in M^{|y|}$
be such that
$a_i \in M^{|y|}$
be such that
 $\varphi (x,a_i) \in p_i(x)$
, for
$\varphi (x,a_i) \in p_i(x)$
, for
 $i < m$
, and let
$i < m$
, and let
 $a\in \theta (M)$
. Suppose that and
$a\in \theta (M)$
. Suppose that and $$\begin{align*}\varphi(U,a)\subseteq \bigcup_{i=1}^{m-1} (\varphi(U, a_i)\cap \chi_i(U)) \cup \bigcup_{i=m}^k \chi_i(U) \end{align*}$$
Then
$$\begin{align*}\varphi(U,a)\subseteq \bigcup_{i=1}^{m-1} (\varphi(U, a_i)\cap \chi_i(U)) \cup \bigcup_{i=m}^k \chi_i(U) \end{align*}$$
Then $$\begin{align*}\varphi(x,a)\in p_m(x). \end{align*}$$
$$\begin{align*}\varphi(x,a)\in p_m(x). \end{align*}$$
 $$\begin{align*}a\in \psi_m(M, a_1,\ldots, a_{m-1}). \end{align*}$$
$$\begin{align*}a\in \psi_m(M, a_1,\ldots, a_{m-1}). \end{align*}$$
-
(II m) Let
 $a_i \in M^{|y|}$
be such that
$a_i \in M^{|y|}$
be such that
 $\varphi (x,a_i) \in p_i(x)$
, for
$\varphi (x,a_i) \in p_i(x)$
, for
 $i < m$
. Then there exist such that
$i < m$
. Then there exist such that $$\begin{align*}a, a'\in \psi_m(M, a_1,\ldots, a_{m-1}) \end{align*}$$
$$\begin{align*}a, a'\in \psi_m(M, a_1,\ldots, a_{m-1}) \end{align*}$$
 $$\begin{align*}\varphi(U,a)\cap \varphi(U,a')\cap \chi_{m}(U)=\emptyset. \end{align*}$$
$$\begin{align*}\varphi(U,a)\cap \varphi(U,a')\cap \chi_{m}(U)=\emptyset. \end{align*}$$
We prove
![]() $(\text {I}_m)$
and
$(\text {I}_m)$
and
![]() $(\text {II}_m)$
for every
$(\text {II}_m)$
for every
![]() $m\leq k$
using a reverse induction on m. Claim 3.3 is then given by
$m\leq k$
using a reverse induction on m. Claim 3.3 is then given by
![]() $(\text {II}_1)$
.
$(\text {II}_1)$
.
Trivially
![]() $(\text {I}_k)$
holds by definition of
$(\text {I}_k)$
holds by definition of
![]() $\psi _k(M, a_1,\ldots , a_{k-1})$
, even without the condition
$\psi _k(M, a_1,\ldots , a_{k-1})$
, even without the condition
![]() $\varphi (x,a)\in p_k(x)$
. We prove the remaining statements as follows. For
$\varphi (x,a)\in p_k(x)$
. We prove the remaining statements as follows. For
![]() $m\leq k$
, we derive
$m\leq k$
, we derive
![]() $(\text {II}_m)$
from
$(\text {II}_m)$
from
![]() $(\text {I}_m)$
using Claim 3.2. For
$(\text {I}_m)$
using Claim 3.2. For
![]() $m<k$
, we derive
$m<k$
, we derive
![]() $(\text {I}_m)$
from
$(\text {I}_m)$
from
![]() $(\text {II}_{m+1})$
.
$(\text {II}_{m+1})$
.
Proof of
![]() $(\text {I}_m)\Rightarrow (\text {II}_{m})$
for
$(\text {I}_m)\Rightarrow (\text {II}_{m})$
for
![]() $m\leq k$
.
$m\leq k$
.
Let
![]() $\varphi (x,a_i)\in p_i(x)$
for
$\varphi (x,a_i)\in p_i(x)$
for
![]() $i < m$
. Let
$i < m$
. Let
![]() $\theta '(M)$
be the set of all
$\theta '(M)$
be the set of all
![]() $a\in \theta (M)$
such that
$a\in \theta (M)$
such that
 $$\begin{align*}\varphi(U,a)\subseteq \bigcup_{i=1}^{m-1} (\varphi(U,a_i)\cap \chi_i(U)) \cup \bigcup_{i=m}^k \chi_i(U). \end{align*}$$
$$\begin{align*}\varphi(U,a)\subseteq \bigcup_{i=1}^{m-1} (\varphi(U,a_i)\cap \chi_i(U)) \cup \bigcup_{i=m}^k \chi_i(U). \end{align*}$$
Note that
![]() $\theta '(y)\in \operatorname {tp}(b/M)$
. By definition of
$\theta '(y)\in \operatorname {tp}(b/M)$
. By definition of
![]() $p_m(x)$
(see condition (b) in Lemma 2.2), the set A of all
$p_m(x)$
(see condition (b) in Lemma 2.2), the set A of all
![]() $a\in \theta '(M)$
with
$a\in \theta '(M)$
with
![]() $ \varphi (x,a)\in p_m(x) $
is not definable (in M). By
$ \varphi (x,a)\in p_m(x) $
is not definable (in M). By
![]() $(\text {I}_m)$
note that
$(\text {I}_m)$
note that
By Claim 3.2, the set
![]() $\psi _m(M, a_1,\ldots , a_{m-1})$
is definable. Since the subset A is not definable, there must exist some
$\psi _m(M, a_1,\ldots , a_{m-1})$
is definable. Since the subset A is not definable, there must exist some
![]() $a\in \psi _m(M, a_1,\ldots , a_{m-1})$
that is not in A, in particular
$a\in \psi _m(M, a_1,\ldots , a_{m-1})$
that is not in A, in particular
Now, by Lemma 2.3, there exists some
![]() $a'\in \theta (M)$
with
$a'\in \theta (M)$
with
 $$\begin{align*}\varphi(U,a')\subseteq \bigcup_{i=1}^{m-1} (\varphi(U,a_i) \cap \chi_i(U)) \cup (\chi_m(U)\setminus \varphi(U,a)) \cup \bigcup_{i=m+1}^k \chi_i(U) \end{align*}$$
$$\begin{align*}\varphi(U,a')\subseteq \bigcup_{i=1}^{m-1} (\varphi(U,a_i) \cap \chi_i(U)) \cup (\chi_m(U)\setminus \varphi(U,a)) \cup \bigcup_{i=m+1}^k \chi_i(U) \end{align*}$$
such that
(In the case
![]() $m=k=l-1$
Lemma 2.3 can still be applied because
$m=k=l-1$
Lemma 2.3 can still be applied because
![]() $\varphi (x,a)\notin p_l(x)$
by definition of the type
$\varphi (x,a)\notin p_l(x)$
by definition of the type
![]() $p_l(x)$
.) Once again by
$p_l(x)$
.) Once again by
![]() $(\text {I}_m)$
it follows that
$(\text {I}_m)$
it follows that
Finally, by construction note that
Proof of
![]() $(\text {II}_{m+1})\Rightarrow (\text {I}_{m})$
for
$(\text {II}_{m+1})\Rightarrow (\text {I}_{m})$
for
![]() $m<k$
.
$m<k$
.
Let
![]() $\varphi (x,a_i)\in p_i(x)$
for
$\varphi (x,a_i)\in p_i(x)$
for
![]() $i < m$
, and
$i < m$
, and
![]() $a\in \theta (M)$
be as described in
$a\in \theta (M)$
be as described in
![]() $(\text {I}_m)$
. In particular we have that
$(\text {I}_m)$
. In particular we have that
![]() $\varphi (x,a)\in p_m(x)$
.
$\varphi (x,a)\in p_m(x)$
.
By
![]() $(\text {II}_{m+1})$
, there exist
$(\text {II}_{m+1})$
, there exist
![]() $ a', a"\in \psi _{m+1}(M, a_1,\ldots , a_{m-1}, a) $
such that
$ a', a"\in \psi _{m+1}(M, a_1,\ldots , a_{m-1}, a) $
such that
But then by definition this means that
![]() $a\in \psi _m(M, a_1,\ldots , a_{m-1})$
.
$a\in \psi _m(M, a_1,\ldots , a_{m-1})$
.
Claim 3.4 Suppose that there exists some
![]() $a'\in \psi _1(M)$
with
$a'\in \psi _1(M)$
with
Then there exists some
![]() $a\in \theta (M)$
satisfying that
$a\in \theta (M)$
satisfying that
Proof
For any
![]() $m \leq k$
consider the following statement
$m \leq k$
consider the following statement
![]() $(\text {B}_m)$
:
$(\text {B}_m)$
:
-
(B m) Let
 $a_i \in M^{|y|}$
,
$a_i \in M^{|y|}$
,
 $i<m$
, be such that there exist
$i<m$
, be such that there exist
 $ a'\in \psi _m(M, a_1,\ldots , a_{m-1}), $
with
$ a'\in \psi _m(M, a_1,\ldots , a_{m-1}), $
with  $$\begin{align*}\varphi(x,a')\notin p_m(x). \end{align*}$$
$$\begin{align*}\varphi(x,a')\notin p_m(x). \end{align*}$$
Then there exists some
 $a\in \theta (M)$
with satisfying that
$a\in \theta (M)$
with satisfying that $$\begin{align*}\varphi(U,a)\subseteq \bigcup_{i=1}^{m-1} \left(\varphi(U,a_i)\cap \chi_i(U)\right) \cup \bigcup_{i=m}^k \chi_i(U) \end{align*}$$
$$\begin{align*}\varphi(U,a)\subseteq \bigcup_{i=1}^{m-1} \left(\varphi(U,a_i)\cap \chi_i(U)\right) \cup \bigcup_{i=m}^k \chi_i(U) \end{align*}$$
 $$\begin{align*}\varphi(x,a)\notin p_j(x) \text{ for every } m \leq j \leq k. \end{align*}$$
$$\begin{align*}\varphi(x,a)\notin p_j(x) \text{ for every } m \leq j \leq k. \end{align*}$$
We prove
![]() $(\text {B}_{m})$
for every
$(\text {B}_{m})$
for every
![]() $m \leq k$
by reverse induction on m. Claim 3.4 then immediately follows from
$m \leq k$
by reverse induction on m. Claim 3.4 then immediately follows from
![]() $(\text {B}_1)$
. Let
$(\text {B}_1)$
. Let
![]() $a_i$
, for
$a_i$
, for
![]() $i<m$
, and
$i<m$
, and
![]() $a'$
be as in
$a'$
be as in
![]() $(\text {B}_{m})$
.
$(\text {B}_{m})$
.
For the base case
![]() $m=k$
, it clearly suffices to take
$m=k$
, it clearly suffices to take
![]() $a=a'$
. We assume that
$a=a'$
. We assume that
![]() $m<k$
and show that
$m<k$
and show that
![]() $(\text {B}_{m+1}) \Rightarrow (\text {B}_{m})$
.
$(\text {B}_{m+1}) \Rightarrow (\text {B}_{m})$
.
By definition of
![]() $\psi _m(M, a_1,\ldots , a_{m-1})$
, there exist
$\psi _m(M, a_1,\ldots , a_{m-1})$
, there exist
![]() $a", a"' \in \psi _{m+1}(M, a_1,\ldots , a_{m-1}, a')$
with
$a", a"' \in \psi _{m+1}(M, a_1,\ldots , a_{m-1}, a')$
with
Without loss of generality we may assume that
![]() $\varphi (x,a")\notin p_{m+1}(x)$
. By
$\varphi (x,a")\notin p_{m+1}(x)$
. By
![]() $(\text {B}_{m+1})$
, we derive that there exists some
$(\text {B}_{m+1})$
, we derive that there exists some
![]() $a\in \theta (M)$
such that
$a\in \theta (M)$
such that
 $$ \begin{align} \varphi(U,a)\subseteq \bigcup_{i=1}^{m-1} \left(\varphi(U,a_i)\cap \chi_i(U)\right) \cup (\varphi(U,a')\cap \chi_m(U)) \cup \bigcup_{i=m+1}^k \chi_i(U) \end{align} $$
$$ \begin{align} \varphi(U,a)\subseteq \bigcup_{i=1}^{m-1} \left(\varphi(U,a_i)\cap \chi_i(U)\right) \cup (\varphi(U,a')\cap \chi_m(U)) \cup \bigcup_{i=m+1}^k \chi_i(U) \end{align} $$
and
However, since
![]() $\varphi (x,a')\notin p_m(x)$
, then by (3) it must also be that
$\varphi (x,a')\notin p_m(x)$
, then by (3) it must also be that
![]() $\varphi (x,a)\notin p_m(x)$
.
$\varphi (x,a)\notin p_m(x)$
.
We now complete the proof of the proposition. By Claim 3.3, let
![]() $a', a"\in \psi _1(M)$
be two elements such that
$a', a"\in \psi _1(M)$
be two elements such that
![]() $\varphi (U,a') \cap \varphi (U,a") \cap \chi _1(U)=\emptyset $
. Without loss of generality we may assume that
$\varphi (U,a') \cap \varphi (U,a") \cap \chi _1(U)=\emptyset $
. Without loss of generality we may assume that
![]() $a'$
is such that
$a'$
is such that
![]() $\varphi (x,a')\notin p_1(x)$
. By Claim 3.4 we conclude that there exists some
$\varphi (x,a')\notin p_1(x)$
. By Claim 3.4 we conclude that there exists some
![]() $a\in \theta (M)$
satisfying that
$a\in \theta (M)$
satisfying that
![]() $\varphi (x,a)\notin p_i$
for every
$\varphi (x,a)\notin p_i$
for every
![]() $i\leq k$
, as desired.
$i\leq k$
, as desired.
Proof of Theorem C
Let
![]() $\varphi (x,y)$
be an
$\varphi (x,y)$
be an
![]() $L(M)$
-formula with
$L(M)$
-formula with
![]() $\pi ^*_\varphi (n)\in o(n^2)$
. We assume that
$\pi ^*_\varphi (n)\in o(n^2)$
. We assume that
![]() $\varphi (x,y)$
does not partition into finitely many consistent families and derive that it does not have the
$\varphi (x,y)$
does not partition into finitely many consistent families and derive that it does not have the
![]() $(\omega ,2)$
-property, i.e., we build a sequence
$(\omega ,2)$
-property, i.e., we build a sequence
![]() $(a_n : 1\leq n<\omega )$
in
$(a_n : 1\leq n<\omega )$
in
![]() $M^{|y|}$
such that the family
$M^{|y|}$
such that the family
![]() $\{ \varphi (x,a_n) : 1 \leq n<\omega \}$
is pairwise inconsistent.
$\{ \varphi (x,a_n) : 1 \leq n<\omega \}$
is pairwise inconsistent.
Hence we assume that
![]() $\varphi (x,y)$
satisfies that, for any finite collection of
$\varphi (x,y)$
satisfies that, for any finite collection of
![]() $L(M)$
-formulas
$L(M)$
-formulas
![]() $\{ \sigma _i(y) : 1 \leq i\leq m\}$
, if the family
$\{ \sigma _i(y) : 1 \leq i\leq m\}$
, if the family
![]() $\{\varphi (x,a) : a\in \sigma _i(M)\}$
is consistent for every
$\{\varphi (x,a) : a\in \sigma _i(M)\}$
is consistent for every
![]() $i\leq m$
, then there exists some
$i\leq m$
, then there exists some
![]() $a\in M^{|y|}$
such that
$a\in M^{|y|}$
such that
![]() $a\notin \cup _i \sigma _i(M)$
. By model theoretic compactness we may fix some
$a\notin \cup _i \sigma _i(M)$
. By model theoretic compactness we may fix some
![]() $b\in U^{|y|}$
satisfying that, for any formula
$b\in U^{|y|}$
satisfying that, for any formula
![]() $\sigma (y)\in \operatorname {tp}(b/M)$
, the family
$\sigma (y)\in \operatorname {tp}(b/M)$
, the family
![]() $\{\varphi (x,a) : a\in \sigma (M)\}$
fails to be consistent. We build our sequence
$\{\varphi (x,a) : a\in \sigma (M)\}$
fails to be consistent. We build our sequence
![]() $(a_n : 1 \leq n<\omega )$
using Proposition 3.1. In particular it will satisfy that, for every
$(a_n : 1 \leq n<\omega )$
using Proposition 3.1. In particular it will satisfy that, for every
![]() $i<\omega $
, it holds that
$i<\omega $
, it holds that
We proceed inductively on n.
By Proposition 3.1 (with
![]() $\chi (x):="x=x"$
), let
$\chi (x):="x=x"$
), let
![]() $a_1\in M^{|y|}$
be any element satisfying (4). Then, for the inductive step, let
$a_1\in M^{|y|}$
be any element satisfying (4). Then, for the inductive step, let
![]() $(a_1,\ldots , a_{n-1})$
be elements each satisfying (4) and such that the formulas
$(a_1,\ldots , a_{n-1})$
be elements each satisfying (4) and such that the formulas
![]() $\varphi (x,a_i)$
, for
$\varphi (x,a_i)$
, for
![]() $i < n$
, are pairwise inconsistent. Let
$i < n$
, are pairwise inconsistent. Let
![]() $\chi (x)$
denote the formula
$\chi (x)$
denote the formula
 $$\begin{align*}\bigwedge_{i=1}^{n-1} \neg\varphi(x,a_i). \end{align*}$$
$$\begin{align*}\bigwedge_{i=1}^{n-1} \neg\varphi(x,a_i). \end{align*}$$
Note that
![]() $\varphi (U,b)\subseteq \chi (U)$
. Now, applying Proposition 3.1, let
$\varphi (U,b)\subseteq \chi (U)$
. Now, applying Proposition 3.1, let
![]() $a_n\in M^{|y|}$
be an element satisfying (4) and
$a_n\in M^{|y|}$
be an element satisfying (4) and
![]() $\varphi (U,a_n)\subseteq \chi (U)$
. The family
$\varphi (U,a_n)\subseteq \chi (U)$
. The family
![]() $\{ \varphi (x,a_i) : 1 \leq i\leq n\}$
is pairwise inconsistent as desired.
$\{ \varphi (x,a_i) : 1 \leq i\leq n\}$
is pairwise inconsistent as desired.
We end the paper with some questions. We note that, while this paper was under review, Kaplan [Reference Kaplan5] presented a positive answer to Question (2) for formulas in NIP theories.
-
(1) Definable
 $(\omega ,q)$
-conjecture: Let
$(\omega ,q)$
-conjecture: Let
 $\varphi (x,y)$
be a formula and let
$\varphi (x,y)$
be a formula and let
 $q \geq 2$
be an integer such that
$q \geq 2$
be an integer such that
 $\pi ^*_\varphi (n)\in o(n^q)$
. If
$\pi ^*_\varphi (n)\in o(n^q)$
. If
 $\varphi (x,y)$
has the
$\varphi (x,y)$
has the
 $(\omega ,q)$
-property, does it partition into finitely many consistent definable subfamilies?
$(\omega ,q)$
-property, does it partition into finitely many consistent definable subfamilies? -
(2) Uniform definable
 $(p,2)$
-conjecture 1: Let
$(p,2)$
-conjecture 1: Let
 $\varphi (x,y)$
and
$\varphi (x,y)$
and
 $\psi (y,z)$
be formulas where
$\psi (y,z)$
be formulas where
 $\pi ^*_\varphi (n)\in o(n^2)$
. Given any integer
$\pi ^*_\varphi (n)\in o(n^2)$
. Given any integer
 $p\geq 2$
, is there an m such that any family of the form
$p\geq 2$
, is there an m such that any family of the form
 $\{ \varphi (x,a) : M\models \psi (a,b) \}$
, for
$\{ \varphi (x,a) : M\models \psi (a,b) \}$
, for
 $b\in M^{|z|}$
, with the
$b\in M^{|z|}$
, with the
 $(p,2)$
-property partitions into at most m consistent definable subfamilies?
$(p,2)$
-property partitions into at most m consistent definable subfamilies? -
(3) Uniform definable
 $(p,2)$
-conjecture 2: Let
$(p,2)$
-conjecture 2: Let
 $\varphi (x,y)$
be a formula with
$\varphi (x,y)$
be a formula with
 $\pi ^*_\varphi (n)\in o(n^2)$
. Given any integer
$\pi ^*_\varphi (n)\in o(n^2)$
. Given any integer
 $p\geq 2$
, is there an m such that any definable subfamily of
$p\geq 2$
, is there an m such that any definable subfamily of
 $\varphi (x,y)$
with the
$\varphi (x,y)$
with the
 $(p,2)$
-property partitions into at most m consistent definable subfamilies?
$(p,2)$
-property partitions into at most m consistent definable subfamilies?
Acknowledgments
Pierre Simon provided some helpful comments regarding the main result of the paper. I moreover thank the anonymous referee for suggestions which greatly improved the presentation and for finding a mistake in an old version of Lemma 2.3. Lastly, I thank Pantelis Eleftheriou and Mervyn Tong for reading early versions of this paper and offering useful feedback.
Funding
This research was supported by the Fields Institute for Research in Mathematical Sciences, specifically by the 2021 Thematic Program on Trends in Pure and Applied Model Theory and the 2022 Thematic Program on Tame Geometry, Transseries and Applications to Analysis and Geometry. It was also supported by the EPSRC grant EP/V003291/1.