Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-12T23:04:55.617Z Has data issue: false hasContentIssue false
  • English
  • Français

ASPERÓ–MOTA ITERATION AND THE SIZE OF THE CONTINUUM

Part of: Set theory

Published online by Cambridge University Press:  02 May 2022

TERUYUKI YORIOKA
TERUYUKI YORIOKA*
Affiliation:
DEPARTMENT OF MATHEMATICS SHIZUOKA UNIVERSITY OHYA 836, SHIZUOKA 422-8529, JAPAN
*
E-mail: yorioka@shizuoka.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we build an Asperó–Mota iteration of length 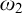$\omega _2$ that adds a family of 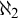$\aleph _2$ many club subsets of 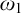$\omega _1$ which cannot be diagonalized while preserving 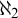$\aleph _2$. This result discloses a technical limitation of some types of Asperó–Mota iterations.

Keywords

Asperó–Mota iterationthe size of the continuumclub sets

MSC classification

Primary: 03E35: Consistency and independence results
Secondary: 03E50: Continuum hypothesis and Martin's axiom
Type
Article
Information
The Journal of Symbolic Logic , Volume 88 , Issue 4 , December 2023 , pp. 1387 - 1420
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author is supported by Grant-in-Aid for Scientific Research (C) 18K03393, Japan Society for the Promotion of Science.

References

Abraham, U. and Shelah, S., On the intersection of closed unbounded sets, Journal of Symbolic Logic, vol. 51 (1986), no. 1, pp. 180–189.Google Scholar
Asperó, D. and Mota, M. A., A generalization of Martin’s axiom . Israel Journal of Mathematics , vol. 210 (2015), no. 1, pp. 193–231.Google Scholar
Asperó, D. and Mota, M. A., Forcing consequences of PFA together with the continuum large . Transactions of the American Mathematical Society , vol. 367 (2015), no. 9, pp. 6103–6129.CrossRefGoogle Scholar
Asperó, D. and Mota, M.A., Separating club-guessing principles in the presence of fat forcing axioms . Annals of Pure and Applied Logic , vol. 167 (2016), no. 3, pp. 284–308.Google Scholar
Asperó, D. and Mota, M.A., Measuring club-sequences together with the continuum large, Journal of Symbolic Logic, vol. 82 (2017), no. 3, pp. 1066–1079. [Retracted]Google Scholar
Asperó, D. and Mota, M.A., Retraction: Measuring club-sequences together with the continuum large, Journal of Symbolic Logic, vol. 82 (2017), pp. 1066–1079.Google Scholar
Bartoszyński, T. and Judah, H., Set Theory: On the Structure of the Real Line , A K Peters, Wellesley, 1995.Google Scholar
Baumgartner, J. E., Hajnal, A., and Mate, A., Weak saturation properties of ideals , Infinite and Finite Sets , vol. I , Colloquia Mathematica Societatis Janos Boly, 10, North-Holland, Amsterdam, 1975, pp. 137–158.Google Scholar
Goldstern, M., Tools for your forcing construction , Set Theory of the Reals (Ramat Gan, 1991) , Israel Mathematical Conference Proceedings, vol. 6, Bar-Ilan University, Ramat Gan, 1993, pp. 305–360.Google Scholar
Miyamoto, T. and Yorioka, T., A fragment of Asperó–Mota’s finitely proper forcing axiom and entangled sets of reals . Fundamenta Mathematicae , vol. 251 (2020), no. 1, pp. 35–68.Google Scholar
Shelah, S., Proper and Improper Forcing , second ed., Perspectives in Mathematical Logic, Springer, Berlin, 1998.Google Scholar
Todorčević, S., Directed sets and cofinal types . Transactions of the American Mathematical Society , vol. 290 (1985), no. 2, pp. 711–723.CrossRefGoogle Scholar
Yorioka, T., Some consequences from Proper Forcing Axiom together with large continuum and the negation of Martin’s Axiom . Journal of the Mathematical Society of Japan , vol. 69 (2017), no. 3, pp. 913–943.Google Scholar