ALBANESE VARIETIES OF CYCLIC COVERS OF THE PROJECTIVE PLANE AND ORBIFOLD PENCILS

Abstract

The paper studies a relation between fundamental group of the complement to a plane singular curve and the orbifold pencils containing it. The main tool is the use of Albanese varieties of cyclic covers ramified along such curves. Our results give sufficient conditions for a plane singular curve to belong to an orbifold pencil, that is, a pencil of plane curves with multiple fibers inducing a map onto an orbifold curve whose orbifold fundamental group is nontrivial. We construct an example of a cyclic cover of the projective plane which is an abelian surface isomorphic to the Jacobian of a curve of genus 2 illustrating the extent to which these conditions are necessary.

Introduction

There is an interesting correspondence between the fundamental groups of the complement to plane algebraic curves and the structure of the pencils, possibly with multiple fibers which one can associate with such curves. For example, if a plane curve $C$ is composed of a pencil, that is, $C=\bigcup _{i=0}^{s}C_{i}$ where $C_{i}$ are zeros of sections $t_{i}$ in a 2-dimensional subspace $L$ of $H^{0}(\mathbb{P}^{2},{\mathcal{O}}(d))$ , then for each $P\in X_{C}:=\mathbb{P}^{2}\setminus C$ there is a well-defined element $t_{P}\in \mathbb{P}(L)$ such that $t_{P}(P)=0$ and the correspondence $P\rightarrow t_{P}$ gives a holomorphic map $X_{C}\rightarrow \mathbb{P}(L)\setminus \{T_{i}\}_{i=0}^{s}$ , where $T_{i}$ are the points of $\mathbb{P}(L)$ corresponding to the sections  $t_{i}$ . This map induces a surjection $\unicode[STIX]{x1D70B}_{1}(X_{C})\rightarrow \unicode[STIX]{x1D70B}_{1}(\mathbb{P}(L)\setminus \{T_{i}\}_{i=0}^{s})$ and hence $\unicode[STIX]{x1D70B}_{1}(X_{C})$ has a free group on $s$ generators as its quotient.

In a similar vein, the existence of pencils with multiple fibers containing $C$ (see Section 1.3) may have implications for the fundamental group even if $C$ is irreducible. For example, suppose that an irreducible curve $C\subset \mathbb{P}^{2}$ belongs in a pencil having two multiple fibers of multiplicities 2 and 3, that is, the equation $F$ of $C$ can be presented as $F=f^{2}+g^{3}$ where $f,g$ are homogeneous polynomials. Then the rational map $\unicode[STIX]{x1D70B}:\mathbb{P}^{2}{\dashrightarrow}\mathbb{P}^{1}$ given by $\unicode[STIX]{x1D70B}([x:y:z])=[f^{2}:g^{3}]$ induces a regular map of $X_{C}:=\mathbb{P}^{2}\setminus C$ onto $\mathbb{P}^{1}\setminus \{(1,-1)\}$ . This map can also be viewed as an orbifold map whose source is $X_{C}$ with a trivial orbifold structure and whose target is the orbifold $\mathbb{C}_{2,3}$ which is an affine line with two orbifold points with stabilizers of orders 2 and 3. Such a dominant map yields a surjection of the fundamental group $\unicode[STIX]{x1D70B}_{1}(X)$ onto the orbifold fundamental group (cf. [4], [12, Proposition 2.7]) for which one has $\unicode[STIX]{x1D70B}_{1}^{\text{orb}}(\mathbb{C}_{2,3})=\mathbb{Z}_{2}\ast \mathbb{Z}_{3}$ (isomorphic to $\text{PSL}_{2}(\mathbb{Z})$ ). In the rest of the paper we call a map between orbifolds having a one-dimensional target an orbifold pencil. The classically studied pencils (whether rational or irrational) are a special case of orbifold pencils.

Previous work [12, 5, 6] has shown that sometimes the relation between the fundamental group of a curve complement $X_{C}$ and its orbifold pencils can be reversed, namely, the structure of the fundamental group provides information on the existence of (rational) orbifold pencils on $X_{C}$ but the relation between fundamental groups and orbifold pencils has several aspects not appearing in the context of ordinary pencils. If a curve has only nodes and ordinary cusps as its singularities (or more generally, singularities called in [12] $\unicode[STIX]{x1D6FF}$ -essential) then the positivity of the rank of the abelianization of the commutator $\unicode[STIX]{x1D70B}_{1}(X_{C})^{\prime }/\unicode[STIX]{x1D70B}_{1}(X_{C})^{\prime \prime }$ implies the existence of orbifold maps on $X_{C}$ (see Section 1 for more precise statements).

In the present paper we consider the correspondence between orbifold pencils and fundamental groups of possibly reducible curves $C$ which may have singularities much more general than ordinary cusps and nodes. Our main result (see Theorem 4) describes a sufficient condition for the existence of orbifold pencils on $\mathbb{P}^{2}$ containing  $C$ in terms of the fundamental group $\unicode[STIX]{x1D70B}_{1}(X_{C})$ of its complement. Let us describe the results of the paper in more detail.

As in the case of curves with nodes and cusps only, it is convenient to state our results in terms of the Alexander invariants and the characters of the fundamental group. The statements also use the local Albanese varieties of singularities (cf. Section 1). Recall (see more details in Section 1.1) that there is a notion of Alexander polynomial $\unicode[STIX]{x1D6E5}_{C,\unicode[STIX]{x1D70B}}\in \mathbb{Z}[t,t^{-1}]$ associated with a given surjection $\unicode[STIX]{x1D70B}:\unicode[STIX]{x1D70B}_{1}(X_{C})\rightarrow \unicode[STIX]{x1D6E4}$ onto a cyclic group. Such a polynomial depends only on the quotient of $\unicode[STIX]{x1D70B}_{1}(X_{C})$ by the commutator of $\text{Ker}\unicode[STIX]{x1D70B}$ and it contains information about the cohomology of rank one local systems on $X_{C}$ , namely, for $\unicode[STIX]{x1D712}\in \text{Hom}(\unicode[STIX]{x1D6E4},\mathbb{C}^{\ast })$ one has $H^{1}(X_{C},\unicode[STIX]{x1D712})\neq 0$ if and only if, for a generator $\unicode[STIX]{x1D6FE}$ of $\unicode[STIX]{x1D6E4}$ , $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE})$ is a root of $\unicode[STIX]{x1D6E5}_{C,\unicode[STIX]{x1D70B}}$ . A root $\unicode[STIX]{x1D709}$ of the Alexander polynomial $\unicode[STIX]{x1D6E5}_{C,\unicode[STIX]{x1D70B}}$ can also be described as an eigenvalue of the covering transformation $\unicode[STIX]{x1D70F}_{C}$ acting on $H_{1}(V_{C},\mathbb{C})$ where $V_{C}$ is a smooth model of the cyclic cover of $\mathbb{P}^{2}$ of degree $\deg C$ branched over $C$ (cf. [17]). Note that since $H^{1}(V_{C},\mathbb{C})$ is a birational invariant, the eigenvalues of $\unicode[STIX]{x1D70F}_{C}$ are independent of a choice of the smooth model $V_{C}$ . An alternative description of the multiplicity of the root $\unicode[STIX]{x1D709}$ can be given as the superabundance of the linear system of plane curves described in terms of the degree and the local type of the singularities of $C$ . We refer to [18] for details.

The Alexander polynomial is affected by the local types of the singularities of $C$ as was shown in [17]. For the statement of our main results we will need the following more precise version of this relation which will be proved in Section 2.

Theorem 1. Let $C$ be a plane curve with arbitrary singularities and let $\unicode[STIX]{x1D712}$ be a character of finite order $N>0$ of the fundamental group $\unicode[STIX]{x1D70B}_{1}(X_{C})$ . Assume that $\unicode[STIX]{x1D712}$ is ramified along each irreducible component of $C$ . Assume also that $H^{1}(X_{C},\unicode[STIX]{x1D712})\neq 0$ . Then there exists a singularity $P\in C$ with local equation $f_{P}(x,y)=0$ for which the following property holds.

Denote by $B_{P}$ a Milnor ball about $P$ and let $\unicode[STIX]{x1D712}_{P}$ be the character of $\unicode[STIX]{x1D70B}_{1}(B_{P}\setminus C)$ which is the composition

$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{1}(B_{P}\setminus C)\rightarrow \unicode[STIX]{x1D70B}_{1}(X_{C})\overset{\unicode[STIX]{x1D712}}{\rightarrow }\mathbb{C}^{\ast }\end{eqnarray}$$

where the left map is induced by the inclusion $B_{P}\setminus C{\hookrightarrow}X_{C}$ . Then the corresponding map:

(T1) $$\begin{eqnarray}H^{1}(X_{C},\unicode[STIX]{x1D712})\rightarrow H^{1}(B_{P}\setminus C,\unicode[STIX]{x1D712}_{P})\end{eqnarray}$$

has a nontrivial image (in particular $H^{1}(B_{P}\setminus C,\unicode[STIX]{x1D712}_{P})\neq 0$ ).

The orbifold pencils on $\mathbb{P}^{2}$ which we attach to the curve $C$ are obtained from irrational pencils on $V_{C}$ and are constructed using the Albanese map $V_{C}\rightarrow \text{Alb}(V_{C})$ . Albanese varieties of cyclic covers of $\mathbb{P}^{2}$ were considered classically for covers of small degree (cf. [10, 7, 9] for a modern exposition). The work of Comessatti [10, 9] studies the irregular 3-cyclic coverings of the plane, and he finds examples both for Albanese dimensions 1 and 2. In the latter case, he constructs an example (also found in [7] and thoroughly explained in [9]) such that the cyclic cover is the product of two copies of a special elliptic curve. Bagnera and deFranchis take another viewpoint: they study rational cyclic quotients of abelian surfaces. However, as presented in Theorem 1, our focus is on $C$ and its algebraic/topological properties such as cohomology conditions on its complement.

Note that we obtain an explicit model of such quotients in Theorem 3.3; the ramification curve is described and we derived geometric properties of this curve from this fact. Our construction depends on the relation between $\text{Alb}(V_{C})$ and the invariants of singularities of $C$ described in [16]. There are also simple cases where such irrational orbifold pencils come up in a straightforward way. This is the case when $\text{Alb}(V_{C})$ is an elliptic curve, or analogously, for curves whose local Alexander polynomial equals $t^{2}-t+1$ . More generally we have the following corollary.

Corollary 2. (cf. Theorem 4)

Let $C$ , $\unicode[STIX]{x1D712}$ be as in Theorem 1 and let $V_{C}^{\unicode[STIX]{x1D712}}$ be a smooth projective model of the cyclic cover associated with the kernel of $\unicode[STIX]{x1D712}$ . Assume that the Albanese dimension of $V_{C}^{\unicode[STIX]{x1D712}}$ is equal to one (see Theorem 3.1 for explicit examples). Then $C$ is an element of a global quotient orbifold pencil such that $\unicode[STIX]{x1D712}$ is the pullback of a character of the orbifold fundamental group of the target of this orbifold pencil.

We want to relax the assumption on Albanese dimension in the Corollary 2 and assume only that one has a one-dimensional image in one of the isogeny $\unicode[STIX]{x1D712}$ -equivariant factor of $\text{Alb}(V_{C})$ . In what follows, we will describe how, under some restriction on the analytic type of the singularities of  $C$ , we may identify the abelian varieties which are the isogeny $\unicode[STIX]{x1D712}$ -equivariant factors of $\text{Alb}(V_{C})$ projection onto which may lead to construction of an orbifold pencil.

This restriction on the analytic type of singularities is given in terms of the local Albanese varieties, introduced in [12] associated with plane curve singularities (cf. Section 1 for definition). A local Albanese variety is equipped with an automorphism, that is, a $\mathbb{Z}$ -action coming from the action of the semisimple part of the local monodromy on the homology of the Milnor fiber. The relation between local Albanese varieties of singularities and global information about $C$ comes from canonical maps of each local Albanese variety into $\text{Alb}(V_{C})$ . The sum of these maps over all singularities of $C$ surjects onto $\text{Alb}(V_{C})$ (cf. [16]). These maps from the local Albanese varieties of the singularities of $C$ are $\mathbb{Z}$ -equivariant with respect to the just mentioned monodromy action and the action of the (cyclic) covering group of  $V_{C}$ .

Before stating the main result of this paper (Theorem 4) we shall give sufficient conditions for the existence of orbifold pencils in case $C$ has a $\mathbb{A}_{p-1}$ -singular point satisfying the conditions of Theorem 1, for which fewer technical assumptions need to be made.

Theorem 3. Let $C$ , $\unicode[STIX]{x1D712}$ , $P$ , and $V_{C}^{\unicode[STIX]{x1D712}}$ be as in Theorem 1 and Corollary 2 above. Assume that $C$ has at $P$ an $\mathbb{A}_{p-1}$ -singularity, $p$ an odd prime, and in particular, the local Albanese variety $\text{Alb}_{P}$ is the Jacobian of the curve $D$ of genus  $g:=\frac{p-1}{2}$ . Let $\text{alb}_{\unicode[STIX]{x1D712},D}:V_{C}^{\unicode[STIX]{x1D712}}\rightarrow \text{Jac}(D)$ be the composition of the Albanese map $V_{C}^{\unicode[STIX]{x1D712}}\rightarrow \text{Alb}(V_{C}^{\unicode[STIX]{x1D712}})$ with the projection on its isogeny component  $\text{Jac}(D)$ .

If the image of $\text{alb}_{\unicode[STIX]{x1D712},D}$ has dimension one, then there is a pencil $V_{C}^{\unicode[STIX]{x1D712}}\rightarrow D$ inducing an orbifold pencil

(T3) $$\begin{eqnarray}X_{C}\rightarrow D/\text{Im}\,\unicode[STIX]{x1D712}\end{eqnarray}$$

onto the global quotient of $D$ by the canonical action of $\text{Im}\,\unicode[STIX]{x1D712}$ on  $D$ .

Moreover the character $\unicode[STIX]{x1D712}$ is the pullback on $\unicode[STIX]{x1D70B}_{1}(X_{C})$ of a character of $\unicode[STIX]{x1D70B}_{1}^{\text{orb}}(D/\text{Im}\,\unicode[STIX]{x1D712})$ via the pencil (T3).

Now we are ready to state the main result of the paper with milder restrictions on the singularities of $C$ than those required in Theorem 3. The purpose is again to show the existence of global orbifold pencils.

Theorem 4. Let $C$ , $\unicode[STIX]{x1D712}$ , $N$ and $P$ be as in Theorem 1. Let $V_{C}^{\unicode[STIX]{x1D712}}$ be a smooth projective model of the cyclic branched cover of $\mathbb{P}^{2}$ associated with the kernel of $\unicode[STIX]{x1D712}$ and let $\unicode[STIX]{x1D70F}_{C}^{\unicode[STIX]{x1D712}}$ be the map induced by the deck transformation on $H_{1}(V_{C}^{\unicode[STIX]{x1D712}},\mathbb{C})$ .

1. (1) Assume that the local Albanese variety $\text{Alb}_{P}$ of the singularity $P$ has an isogeny component $J_{\unicode[STIX]{x1D712}}$ satisfying the following:

   1. (a) The action of $\text{Im}\,\unicode[STIX]{x1D712}$ on $\text{Alb}_{P}$ induces an action on $J_{\unicode[STIX]{x1D712}}$ and the map $J_{\unicode[STIX]{x1D712}}\rightarrow \text{Alb}(V_{C}^{\unicode[STIX]{x1D712}})$ induced by the $(\text{Im}\,\unicode[STIX]{x1D712})$ -equivariant map $\text{Alb}_{P}\rightarrow \text{Alb}(V_{C}^{\unicode[STIX]{x1D712}})$ has a finite kernel.

   2. (b) $J_{\unicode[STIX]{x1D712}}$ is the Jacobian of a curve $D$ such that $D$ is a quotient of an exceptional curve ${\mathcal{D}}$ of positive genus in a resolution of the singularity $z^{N}=f_{P}(x,y)$ , that is, $D={\mathcal{D}}/\unicode[STIX]{x1D6E5}({\mathcal{D}},\unicode[STIX]{x1D712})$ where $\unicode[STIX]{x1D6E5}({\mathcal{D}},\unicode[STIX]{x1D712})\subseteq \text{Im}\,\unicode[STIX]{x1D712}$ is a (possibly trivial) subgroup of the covering group $\text{Im}\,\unicode[STIX]{x1D712}$ , the latter being considered as an automorphism group of  ${\mathcal{D}}$ .

   Let $\text{alb}_{\unicode[STIX]{x1D712},D}$ be the composition of the Albanese map $V_{C}^{\unicode[STIX]{x1D712}}\rightarrow \text{Alb}(V_{C}^{\unicode[STIX]{x1D712}})$ with the projection on the factor $J_{\unicode[STIX]{x1D712}}=\text{Jac}(D)$ . If the dimension of the image of $\text{alb}_{\unicode[STIX]{x1D712},D}$ is one, then there exists a pencil

   $$\begin{eqnarray}V_{C}^{\unicode[STIX]{x1D712}}\rightarrow D\end{eqnarray}$$
   inducing an orbifold pencil
   (T4) $$\begin{eqnarray}X_{C}\rightarrow D_{\text{Im}\,\unicode[STIX]{x1D712}}^{\text{orb}}\end{eqnarray}$$
   where $D_{\text{Im}\,\unicode[STIX]{x1D712}}^{\text{orb}}=D/(\text{Im}\,\unicode[STIX]{x1D712}/\unicode[STIX]{x1D6E5}(D,\unicode[STIX]{x1D712}))$ is the global quotient orbifold obtained via the induced action of $(\text{Im}\,\unicode[STIX]{x1D712}/\unicode[STIX]{x1D6E5}(D,\unicode[STIX]{x1D712}))$ on $D$ . For such an orbifold pencil (T4) the character  $\unicode[STIX]{x1D712}$ is the pullback on $\unicode[STIX]{x1D70B}_{1}(X_{C})$ of a character of $\unicode[STIX]{x1D70B}_{1}^{\text{orb}}(D_{\text{Im}\,\unicode[STIX]{x1D712}}^{\text{orb}})$ via (T4).

2. (2) If $\text{Alb}_{P}$ is simple (i.e., is not isogenous to a product of abelian varieties of positive dimension) then the assumptions (a) and (b) in (1) are automatically satisfied.

Note that assumption (1) (a) means that $J_{\unicode[STIX]{x1D712}}$ is an $(\text{Im}\,\unicode[STIX]{x1D712})$ -equivariant isogeny component of $\text{Alb}(V_{C}^{\unicode[STIX]{x1D712}})$ . In particular, it implies that the tangent space to $J_{\unicode[STIX]{x1D712}}$ at the identity is contained in the $\unicode[STIX]{x1D712}$ -eigenspace of $\unicode[STIX]{x1D70F}_{C}^{\unicode[STIX]{x1D712}}$ acting on the tangent space of $\text{Alb}(V_{C}^{\unicode[STIX]{x1D712}})$ at the identity.

The conditions for the existence of orbifold pencils given by this theorem have the following converse showing that the existence of an orbifold pencil having the curve $C$ as a member, implies that the Albanese variety of the corresponding cyclic cover splits up to isogeny. Some factors of this splitting are the Jacobians of the curves with the orbifold associated with the pencils being the global quotients of these curves.

More precisely (see Section 1.3 for definitions related to orbifold pencils) one has the following theorem.

Theorem 5. Suppose that $C$ belongs to a global quotient orbifold pencil $\unicode[STIX]{x1D70B}$ (cf. Definition 1.7) of target $\mathbb{P}^{1}$ with orbifold points of multiplicities $\bar{m}=(m_{1},\ldots ,m_{s})$ so that $\unicode[STIX]{x1D70B}$ induces a homomorphism $\unicode[STIX]{x1D70B}_{1}(X_{C})\rightarrow \unicode[STIX]{x1D70B}_{1}^{\text{orb}}(\mathbb{P}_{\bar{m}}^{1})$ . Assume also that there is $\unicode[STIX]{x1D70C}\in \text{Char}\unicode[STIX]{x1D70B}_{1}^{\text{orb}}(\mathbb{P}_{\bar{m}}^{1})$ such that $\unicode[STIX]{x1D712}=\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D70C})$ and also that the orbifold $\mathbb{P}_{\bar{m}}^{1}$ is a global quotient of a curve $\unicode[STIX]{x1D6F4}$ . Then $\text{Alb}(V_{C}^{\unicode[STIX]{x1D712}})$ admits an $(\text{Im}\,\unicode[STIX]{x1D712})$ -equivariant surjection onto  $\text{Jac}(\unicode[STIX]{x1D6F4})$ and hence one has an $(\text{Im}\,\unicode[STIX]{x1D712})$ -equivariant isogeny $\text{Alb}(V_{C}^{\unicode[STIX]{x1D712}})\sim \text{Jac}(\unicode[STIX]{x1D6F4})\times A$ for an abelian $(\text{Im}\,\unicode[STIX]{x1D712})$ -variety  $A$ .

More generally, if there is a finite number $\unicode[STIX]{x1D719}_{1},\ldots ,\unicode[STIX]{x1D719}_{n}$ of global quotient orbifold pencils as above with targets $(\mathbb{P}_{\bar{m}}^{1},\unicode[STIX]{x1D70C})$ ( $\unicode[STIX]{x1D70C}\in \text{Char}\unicode[STIX]{x1D70B}_{1}^{\text{orb}}(\mathbb{P}_{\bar{m}}^{1})$ which are $\mathbb{Q}$ -strongly independent, then $\text{Alb}(V_{C}^{\unicode[STIX]{x1D712}})$ admits an $(\text{Im}\,\unicode[STIX]{x1D712})$ -surjection onto $\text{Jac}(\unicode[STIX]{x1D6F4})^{n}$ , that is there is an equivariant isogeny, $\text{Alb}(V_{C}^{\unicode[STIX]{x1D712}})\sim \text{Jac}(\unicode[STIX]{x1D6F4})^{n}\times A$ for an abelian $(\text{Im}\,\unicode[STIX]{x1D712})$ -variety  $A$ .

The proofs of Theorems 1, 3, 4 and 5 are presented in Section 2. In Section 3 we consider applications of Theorem 4. First we discuss an example of a curve $C$ with $\mathbb{A}_{2g}$ -singularities, that is, whose singularities are locally isomorphic to $u^{2}+v^{2g+1}=0$ , which belongs to an orbifold pencil. For the curves described in Theorem 3.1, all roots of the Alexander polynomial correspond to orbifold pencils on the complement. The Albanese variety of the canonical cyclic cover $V_{C}^{}$ is the Jacobian of a certain curve of genus  $g$ (described as a Belyi cover). In Theorem 3.3 we give an example of a curve for which the Albanese variety is the same as one of those in Theorem 3.1 (for the particular case of $g=2$ ), but whose characters corresponding to the roots of the Alexander polynomial cannot be obtained as pullback via orbifold maps. The difference between the curves in Theorems 3.1 and 3.3 comes from the difference in the Albanese maps of the corresponding cyclic covers, namely, the images of the Albanese maps have different dimensions. The curve given in explicit way described in Theorem 3.3 is particularly interesting, since its canonical cyclic cover has as a minimal model an abelian surface (specifically the Jacobian of a curve of genus 2 cf. also [9]). This construction of an abelian surface via cyclic coverings branched over curves given by explicit equation can be of independent interest. Finally, in Theorem 3.5 we present a family of curves contained in more than one orbifold pencil and for which the Albanese dimension is maximal, that is, two.

1 Preliminaries

1.1 Alexander polynomials (cf. [17])

Let $C$ be a plane curve with irreducible components $C_{0},C_{1},\ldots ,C_{r}$ where $F_{i}(x,y,z)=0$ is a reduced equation of  $C_{i}$ of degree  $d_{i}$ . Then $H_{1}(X_{C},\mathbb{Z})$ is an abelian group of rank  $r$ isomorphic to $\mathbb{Z}^{r+1}/(d_{0},\ldots ,d_{r})\mathbb{Z}$ . This isomorphism is given by

$$\begin{eqnarray}\unicode[STIX]{x1D6FE}\mapsto \left(\frac{1}{2\unicode[STIX]{x1D70B}\sqrt{-1}}\int _{\unicode[STIX]{x1D6FE}}\frac{dF_{i}}{F_{i}}\right)_{i=0}^{r}.\end{eqnarray}$$

Fix a surjection $\unicode[STIX]{x1D70B}:\unicode[STIX]{x1D70B}_{1}(X_{C})\rightarrow \unicode[STIX]{x1D6E4}$ onto a cyclic group $\unicode[STIX]{x1D6E4}$ . Note that $\unicode[STIX]{x1D70B}$ can be factored through $H_{1}(X_{C},\mathbb{Z})$ and hence induces a homomorphism $\mathbb{Z}^{r+1}/(d_{0},\ldots ,d_{r})\mathbb{Z}\rightarrow \unicode[STIX]{x1D6E4}$ . Let $K=\ker \unicode[STIX]{x1D70B}$ . Consider the exact sequence $0\rightarrow K/K^{\prime }\rightarrow \unicode[STIX]{x1D70B}_{1}(X_{C})/K^{\prime }\rightarrow \unicode[STIX]{x1D6E4}\rightarrow 0$ and the corresponding action of $\unicode[STIX]{x1D6E4}$ on $K/K^{\prime }\otimes \mathbb{C}$ . The Alexander polynomial $\unicode[STIX]{x1D6E5}_{C,\unicode[STIX]{x1D70B}}(t)$ of $C$ (relative to the surjection $\unicode[STIX]{x1D70B}$ ) is the characteristic polynomial associated with the action of $\unicode[STIX]{x1D6E4}$ on the vector space $K/K^{\prime }\otimes \mathbb{C}$ . Note that $\dim K/K^{\prime }\otimes \mathbb{C}<\infty$ (cf. [17]), $\unicode[STIX]{x1D6E5}_{C,\unicode[STIX]{x1D70B}}$ has integer coefficients and in the case of irreducible $C$ is independent, for all the previous choices, as an element in $\mathbb{C}[t,t^{-1}]$ modulo units. In the latter case, if $\unicode[STIX]{x1D6E4}=\mathbb{Z}/d\mathbb{Z}$ , then $K/K^{\prime }$ is the abelianization of the commutator of  $\unicode[STIX]{x1D70B}_{1}(X_{C})$ .

Zeros of the Alexander polynomial can be described in terms of the cohomology of local systems as follows. Note that, since $\unicode[STIX]{x1D70B}_{1}(X_{C})/K^{\prime }$ is abelian, $\unicode[STIX]{x1D70B}$ factors through a character, say $\unicode[STIX]{x1D712}$ . Let $\unicode[STIX]{x1D709}\in \mathbb{C}^{\ast },(1,\ldots ,1)\in \mathbb{Z}^{r+1}/(d_{0},\ldots ,d_{r})\mathbb{Z}=H_{1}(X_{C},\mathbb{Z})$ be a generator of $\text{Im}\,\unicode[STIX]{x1D712}\in \mathbb{C}^{\ast }$ ; one has:

(1.1) $$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{C,\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D709})=0\Longleftrightarrow \dim H^{1}(X_{C},\unicode[STIX]{x1D712})>0\quad \text{(cf. [14, 19]}.\end{eqnarray}$$

The Alexander polynomial is restricted by the local type of singularities and the degree of $C$ as follows. Each singularity $P\in C$ , has associated its local Alexander polynomial $\unicode[STIX]{x1D6E5}_{C}^{P}$ , or equivalently the characteristic polynomial of the local monodromy acting on the Milnor fiber of the singularity (cf. [21]). Then one has the divisibility relation (cf. [17])

(1.2) $$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{C}(t)|\mathop{\prod }_{P}\unicode[STIX]{x1D6E5}_{C}^{P}(t).\end{eqnarray}$$

Moreover the roots of the Alexander polynomial are roots of unity of the degree $\deg C$ .

Example 1.1. Let $C$ be a curve whose singularities are topologically equivalent to the $\mathbb{A}_{2g}$ -singularity with local equation $u^{2}=v^{2g+1}$ . Since the characteristic polynomial of the monodromy for such singularity is $\frac{t^{2g+1}+1}{t+1}$ the Alexander polynomial of $C$ is trivial unless $2(2g+1)|\deg C$ and moreover it is equal to $(\frac{t^{2g+1}+1}{t+1})^{s}$ for some $s\geqslant 0$ .

1.2 Local Albanese varieties and singularities of CM-type

Let $f=0$ be a germ of an isolated (i.e., reduced) plane curve singularity at the origin. Let $M_{f}$ be the Milnor fiber of $f$ , that is, the intersection of a sufficiently small ball $B_{\unicode[STIX]{x1D716}}$ about the origin and the hypersurface $f=t,0<|t|\ll \unicode[STIX]{x1D716}$ . The cohomology of $M_{f}$ (more generally, the cohomology of the Milnor fiber of an isolated hypersurface singularity) supports the limit mixed Hodge structure. It was constructed by Steenbrink and we refer to [24] for its study. Here we only note that it depends on the family of germs $f=t$ , rather than its specific member. We recall the following properties of this mixed Hodge structure used below:

1. (1) It has weight $2$ and the weight filtration is associated with the unipotent part of the monodromy $T_{u}$ in the decomposition into unipotent and semisimple parts of $T=T_{s}T_{u}$ , the monodromy operator acting on  $H^{1}(M_{f},\mathbb{C})$ .

2. (2) The size of Jordan blocks of the monodromy operator is at most 2 and equals $\text{rk}\,W_{0}$ . Moreover,

   $$\begin{eqnarray}\text{rk}\,\text{Gr}_{2}^{W}-\text{rk}\,W_{0}=r-1,\end{eqnarray}$$
   where $r$ is the number of branches of $f=0$ .

3. (3) The Hodge filtration is invariant under the action of the semisimple part of the monodromy. Note that by the Monodromy Theorem the order of $T_{s}$ is finite (cf. [24]).

4. (4) Let $L_{f}$ be the link of the singularity $z^{n}=f$ where $n$ is the order of the automorphism $T_{s}$ . Then

   (1.3) $$\begin{eqnarray}\text{Gr}_{1}^{W}H^{1}(M_{f})=\text{Gr}_{3}^{W}H^{2}(L_{f})(1)\end{eqnarray}$$
   (where $H(1)$ is the Tate twist of a Hodge structure $H$ , cf. [16, Proposition 3.1]).

Definition 1.2. The local Albanese variety of the germ $f$ is defined as the abelian variety $(\text{Gr}_{F}^{0}\,H^{1}(M_{f}))^{\ast }/H_{1}(M_{f},\mathbb{Z})$ , with polarization induced by the intersection form on $H_{1}(M_{f},\mathbb{Z})$ . Equivalently, the local Albanese is the abelian part of the semiabelian variety associated by Deligne (cf. [13]) to the 1-motif in the case of the mixed Hodge structure dual to the limit mixed Hodge structure discussed above.

The above definition is rather technical but it admits a simpler description in terms of the resolution of the singularity $z^{n}=f$ discussed above. Let $\tilde{B}\rightarrow B$ be an embedded log-resolution of the germ $f=0$ , $V_{n}\rightarrow B$ be the projection of the germ of the singularity $z^{n}=f$ onto $B$ . The singularities of the normalization of the fiber product $S=V_{n}\times _{B}\tilde{B}$ are cyclic quotient singularities and their (minimal) resolution $\widetilde{S}$ provides a resolution of the singularity of the germ $z^{n}=f$ (cf. [20]). In this resolution the boundary of the tubular neighborhood of the exceptional locus can be identified with the link $L_{f}$ in (1.3). Moreover $H^{1}(L_{f})$ (and by duality $H^{2}(L_{f})$ ) can be identified in an appropriate way with $\bigoplus H^{1}(E_{i})$ where $E_{i}$ runs through the set of exceptional curves in $\widetilde{S}$ having a positive genus. More precisely, we have the following theorem.

Theorem 1.3. (cf. [16, Theorem 3.11])

Let $f(x,y)=0$ be a singularity with a semisimple monodromy and let $N$ be the order of the monodromy operator. The Albanese variety of the germ $f(x,y)=0$ is isogenous to a product of Jacobians of the exceptional curves of positive genus for a resolution of

(1.4) $$\begin{eqnarray}z^{N}=f(x,y).\end{eqnarray}$$

The latter description suggests an approach to defining the local Albanese for the nonreduced case, that is, as the product of the Jacobians of curves of positive genus in the resolution of the singularities of the germ  $z^{n}=f$ .

Finally recall the following definition.

Definition 1.4. (cf. [16, Definition 3.4]) A plane curve singularity has a $\text{CM}$ -type if its local Albanese variety is isogenous to a product of simple abelian varieties of $\text{CM}$ -type.

We refer to [23] for basic information regarding abelian varieties of $\text{CM}$ -type. Unibranched singularities and singularities for which the characteristic polynomial of the monodromy operator has no multiple roots provide many examples of singularities of $\text{CM}$ -type (cf. [16]).

Example 1.5. Let $(C,P)$ be a simple curve singularity of type $\mathbb{A}_{2g}$ , with local equation $y^{2}-x^{2g+1}=0$ . The local Albanese variety is associated to the surface singularity $y^{2}-x^{2g+1}=z^{2(2g+1)}$ . For any resolution of this surface singularity, there is only one nonrational irreducible component $D_{\mathbb{A}_{2g}}$ of its exceptional divisor, which is a Belyi cover of the unique branching component of the minimal resolution of $(C,P)$ , ramified at the three intersection points with the other components, with ramification indices $2,2g+1,2(2g+1)$ , whose genus is  $g$ .

1.3 Orbifold pencils

Definition 1.6. Let $X$ be a quasi-projective manifold and $S$ be an orbicurve (one-dimensional orbifold). A holomorphic map $\unicode[STIX]{x1D719}$ between $X$ and the underlying $S$ complex curve we shall call an orbifold pencil if the index of each orbifold point $p$ divides the multiplicity of each connected component of the fiber $\unicode[STIX]{x1D719}^{\ast }(p)$ over  $p$ .

We will concentrate our attention on orbifold pencils of curve complements. Let $C\subset \mathbb{P}^{2}$ be a plane curve (not necessarily irreducible) and let $X_{C}$ denote its complement. Consider an orbifold pencil $\unicode[STIX]{x1D719}:X_{C}\rightarrow S$ , where $S$ is a rational orbifold curve (that is, its compactification is $\mathbb{P}^{1}$ ) given by a finite number of orbifold points, say $P_{i}$ , $i=1,\ldots ,s$ , with orbifold structure of order $m_{i}\in \mathbb{Z}_{{>}0}\cup \{\infty \}$ , $i=1,\ldots ,s$ (i.e., near which the orbifold chart is the chart given by a disk with the standard action of the cyclic group of order $m_{i}$ ). For convenience, $m_{i}=\infty$ means that $P_{i}$ has been removed from $S$ , namely, $S=\mathbb{P}^{1}\setminus \{P_{i}\mid m_{i}=\infty \}$ . In the future we will denote $S$ simply by  $\mathbb{P}_{\bar{m}}^{1}$ , where  $\bar{m}:=(m_{1},\ldots ,m_{s})$ .

Definition 1.7. In the situation as above, we say that $C$ belongs to an orbifold pencil of type $\bar{m}$ . Moreover, the orbifold pencil $\unicode[STIX]{x1D719}$ will be called a global quotient orbifold pencil if there exists a morphism $\unicode[STIX]{x1D6F7}:X_{G}\rightarrow \unicode[STIX]{x1D6F4}$ , where $X_{G}$ is a quasi-projective manifold endowed with an action of a finite group $G$ and $\unicode[STIX]{x1D6F4}$ a curve which makes the diagram

(1.5)

commutative, for which the vertical arrows are the models for the quotients by the action of $G$ .

If in addition, there is a character $\unicode[STIX]{x1D712}\in \text{Char}(X_{C})$ and a character $\unicode[STIX]{x1D70C}\in \text{Char}^{\text{orb}}(\mathbb{P}_{\bar{m}}^{1})$ such that $\unicode[STIX]{x1D712}=\unicode[STIX]{x1D70C}\circ \unicode[STIX]{x1D70B}$ , and $X_{G}$ (resp. $\unicode[STIX]{x1D6F4}$ ) is the covering of $X_{C}$ (resp. $\mathbb{P}_{\bar{m}}^{1}$ ) associated with the character $\unicode[STIX]{x1D712}$ (resp. $\unicode[STIX]{x1D70C}$ ), then we say $(C,\unicode[STIX]{x1D712})$ belongs to a global quotient orbifold pencil with target $(\mathbb{P}_{\bar{m}}^{1},\unicode[STIX]{x1D70C})$ .

Oftentimes, the set of global quotient orbifold pencils—up to the obvious equivalence by automorphisms of the target—is infinite (see [12, 5]). A very useful (cf. Theorem 3.5 below) property to determine the different nature of such orbifold pencils is given by the following.

Definition 1.8. Global quotient orbifold pencils $\unicode[STIX]{x1D719}_{i}:(X_{C},\unicode[STIX]{x1D712})\rightarrow (\mathbb{P}_{\bar{m}}^{1},\unicode[STIX]{x1D70C})$ , $i=1,\ldots ,n$ are called independent if the induced maps $\unicode[STIX]{x1D6F7}_{i}:X_{G}\rightarrow \unicode[STIX]{x1D6F4}$ define $\mathbb{Z}[G]$ -independent morphisms of modules

(1.6) $$\begin{eqnarray}{\unicode[STIX]{x1D6F7}_{i}}_{\ast }:H_{1}(X_{G},\mathbb{Z})\rightarrow H_{1}(\unicode[STIX]{x1D6F4},\mathbb{Z}),\end{eqnarray}$$

that is, independent elements of the $\mathbb{Z}[G]$ -module $\text{Hom}_{\mathbb{Z}[G]}$ ( $H_{1}(X_{G},\mathbb{Z})$ , $H_{1}(\unicode[STIX]{x1D6F4},\mathbb{Z})$ ).

In addition, if

(1.7) $$\begin{eqnarray}\bigoplus {\unicode[STIX]{x1D6F7}_{i}}_{\ast }:H_{1}(X_{G},\mathbb{Z})\rightarrow H_{1}(\unicode[STIX]{x1D6F4},\mathbb{Z})^{n}\end{eqnarray}$$

is surjective we say that the pencils $\unicode[STIX]{x1D719}_{i}$ are strongly independent. If the previous morphism (1.7) is considered with coefficients over $\mathbb{Q}$ , then we will use the term $\mathbb{Q}$ -strongly independent.

2 Proof of Theorems 1, 3, 4 and 5

Proof of Theorem 1.

We shall use notations set up in the Introduction and in Section 1 and consider the Alexander polynomial $\unicode[STIX]{x1D6E5}_{C,\unicode[STIX]{x1D712}}(t)$ of $C$ relative to the homomorphism $\unicode[STIX]{x1D712}:\unicode[STIX]{x1D70B}_{1}(X_{C})\rightarrow \unicode[STIX]{x1D6E4}\subset \mathbb{C}^{\ast }$ where $\unicode[STIX]{x1D6E4}=\text{Im}\,\unicode[STIX]{x1D712}$ is the group of $N$ th roots of unity by hypothesis. Let $\unicode[STIX]{x1D709}\in \mathbb{C}^{\ast }$ be a primitive $N$ th root of unity. Since $H^{1}(X_{C},\unicode[STIX]{x1D712})\neq 0$ one has $\unicode[STIX]{x1D6E5}_{C,\unicode[STIX]{x1D712}}(\unicode[STIX]{x1D709})=0$ (cf. (1.1)). Let $S_{\unicode[STIX]{x1D712}}:=\{P\in \text{Sing}(C)\mid H^{1}(B_{P}\setminus C,\unicode[STIX]{x1D712}_{P})\neq 0\}$ ; because of (1.2), this set is nonempty.

For each $P\in S_{\unicode[STIX]{x1D712}}$ , consider the unbranched covering of $E_{P}:=B_{P}\setminus C$ corresponding to the surjection $\unicode[STIX]{x1D70B}_{1}(E_{P})\rightarrow \unicode[STIX]{x1D6E4}$ and denote it by $(\widetilde{E}_{P})_{\unicode[STIX]{x1D6E4}}$ . Then the restriction of the cyclic cover of $B_{P}$ given by the equation (1.4) on $E_{P}$ is equivalent to $(\widetilde{E}_{P})_{\unicode[STIX]{x1D6E4}}\rightarrow E_{P}$ . The proof of the Divisibility Theorem (cf. [17, 16]) also shows that there is a surjection $\bigoplus _{P\in S_{\unicode[STIX]{x1D712}}}H_{1}((\widetilde{E}_{P})_{\unicode[STIX]{x1D6E4}},\mathbb{Q})_{\unicode[STIX]{x1D709}}\rightarrow H_{1}(V_{C}^{\unicode[STIX]{x1D712}},\mathbb{Q})_{\unicode[STIX]{x1D709}}$ , where the subindex $\unicode[STIX]{x1D709}$ stands for the $\unicode[STIX]{x1D709}$ -eigenspace of the corresponding deck transformations. Hence one can take as $P$ in (1) any singular point in $S_{\unicode[STIX]{x1D712}}$ for which the map $H_{1}((\widetilde{E}_{P})_{\unicode[STIX]{x1D6E4}},\mathbb{Q})_{\unicode[STIX]{x1D709}}\rightarrow H_{1}(V_{C}^{\unicode[STIX]{x1D712}},\mathbb{Q})_{\unicode[STIX]{x1D709}}$ has a nontrivial image.◻

Remark 2.1. In fact $H^{1}(B_{P}\setminus C,\unicode[STIX]{x1D712}_{P})\neq 0$ is not enough to ensure that the map (T1) in Theorem 1 has a nontrivial image. For instance, consider $C$ a sextic curve with seven ordinary cusps. It is well known (already to O. Zariski, cf. [3, 17, 12] for more recent discussions) that there is a conic passing through six out of the seven cusps. The Alexander polynomial of $C$ is $t^{2}-t+1$ , which coincides with the local Alexander polynomials of its singularities. However, if $\unicode[STIX]{x1D712}$ is a character of order 6, the map

$$\begin{eqnarray}H^{1}(X_{C},\unicode[STIX]{x1D712})\rightarrow H^{1}(B_{P}\setminus C,\unicode[STIX]{x1D712}_{P})\end{eqnarray}$$

is not trivial if and only if $P$ is one of the six cusps on the conic.

Proof of Theorem 4.

Now let us assume that $P$ is a singularity satisfying Theorem 4 and consider a resolution of the associated surface singularity $V_{P}=\{z^{N}=f_{P}(x,y)\}$ , where $N$ is the order of the character  $\unicode[STIX]{x1D712}$ and $f_{P}$ is a local equation of $C$ near $P$ . Recall that such a resolution can be obtained (Jung’s method cf. [20]) by normalizing a pullback of an embedded resolution of the singularity at  $P$ .

It follows from the A’Campo formula (cf. [1]), or from discussion in Section 1.2, that $\unicode[STIX]{x1D709}$ is the root of the characteristic polynomial of the transformation induced on homology by the action $z\mapsto \unicode[STIX]{x1D709}z$ on a resolution of singularities of the surface $V_{P}$ and restricted to one of the curves of positive genus in the resolution of the singularity  $V_{P}$ . Denote such a curve by  ${\mathcal{D}}$ . Jung’s procedure implies that, ${\mathcal{D}}$ is an irreducible component of a $\unicode[STIX]{x1D6E4}$ -cover of a rational curve (namely an exceptional divisor of the resolution of  $P$ ). By Theorem 1.3 (i.e., [16, Theorem 3.11]) there is an isogeny component of the Jacobian of ${\mathcal{D}}$ (possibly a direct sum of several simple components) which is also an isogeny component of $\text{Alb}(V_{C}^{\unicode[STIX]{x1D712}})$ . If this component is an $(\text{Im}\,\unicode[STIX]{x1D712})$ -invariant Jacobian of a curve $D$ , that is, if the assumption (b) in Theorem 4 is fulfilled, then by Torelli’s Theorem $\text{Im}\,\unicode[STIX]{x1D712}$ acts on $D$ as well (unfaithfully if ${\mathcal{D}}\neq D$ ). Note that Theorem 4 allows nonreduced curves $f=0$ , which are excluded in the statement of Theorem 1.3.

As a consequence of Jung’s method, the resolutions of $z^{n}=f$ and $z^{n}=f_{\text{red}}$ , where $f_{\text{red}}$ is the product of irreducible factors of $f$ , are both obtained by pullback and normalization of the same embedded resolution of the curve $f_{\text{red}}=0$ . In particular, the conclusions of Theorem 4 (1) still hold in the nonreduced case, whereas $D$ depends on the ramification data of the cyclic cover  $V_{P}$ .

Returning to the proof of the existence of an orbifold pencil satisfying (1), suppose that the composition of the Albanese map and the projection onto $\text{Jac}(D)$ has a 1-dimensional image  $W$ . Let $\unicode[STIX]{x1D70E}:{\mathcal{D}}\rightarrow D$ be the quotient map. Consider the diagram

(2.1)

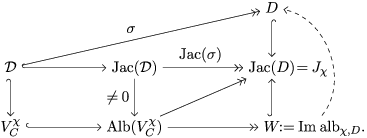
This diagram shows that the image of ${\mathcal{D}}$ in $\text{Jac}(D)$ coincides with the image of $D$ and hence it is contained in  $W$ . The assumption that $\dim \text{Im}\,\text{alb}_{\unicode[STIX]{x1D712},D}=1$ hence yields that $\text{Im}\,\text{alb}_{\unicode[STIX]{x1D712}}=D$ (up to a translation). Moreover the map $V_{C}^{\unicode[STIX]{x1D712}}\rightarrow D$ is $\unicode[STIX]{x1D6E4}$ -equivariant and hence it induces the orbifold pencil as described in Theorem 4 (1).

If $\text{Jac}(D)$ is a simple abelian variety, then $J_{\unicode[STIX]{x1D712}}=\text{Jac}(D)$ as it follows from the discussion above. This yields (2) which concludes the proof of Theorem 4.◻

Proof of Theorem 3.

To derive this proof from Theorem 4 we have to verify that its hypotheses are satisfied. For $\mathbb{A}_{2g}$ -singularities, one has $\text{Alb}_{P}=\text{Jac}({\mathcal{D}})$ , where ${\mathcal{D}}$ is a covering of the branching component of the minimal resolution of the singularity. Note that under the hypothesis $p=2g+1$ is prime, $\text{Jac}({\mathcal{D}})$ is simple (cf. [23, Example 4.8(1)]). Using Theorem 4 (2), the result follows.◻

Proof of Theorem 5.

Recall that $\unicode[STIX]{x1D70B}_{1}^{\text{orb}}(\mathbb{P}_{\bar{m}}^{1})=\unicode[STIX]{x1D70B}_{1}(\mathbb{P}^{1}\setminus \{P_{i}\}_{i=1}^{s})/\langle \unicode[STIX]{x1D6FE}_{i}^{m_{i}}\rangle _{i=1}^{s}$ where $\unicode[STIX]{x1D6FE}_{i}$ are meridians about the points $P_{i}$ in $\unicode[STIX]{x1D70B}_{1}(\mathbb{P}^{1}\setminus \{P_{i}\}_{i=1}^{s})$ . Consider the composition $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D70C}}$

$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{1}(\mathbb{P}^{1}\setminus \{P_{i}\}_{i=1}^{s})\overset{\unicode[STIX]{x1D706}}{\longrightarrow }\unicode[STIX]{x1D70B}_{1}^{\text{orb}}(\mathbb{P}_{\bar{m}}^{1})\overset{\unicode[STIX]{x1D70C}}{\longrightarrow }\mathbb{C}^{\ast }.\end{eqnarray}$$

Following the notation introduced in Definition 1.7, consider the natural surjection morphism $\unicode[STIX]{x1D6EC}:\unicode[STIX]{x1D70B}_{1}(\mathbb{P}^{2}\setminus (C\cup \bigcup _{i=1}^{s}D_{i}))\rightarrow \unicode[STIX]{x1D70B}_{1}(X_{C})$ . Note that the meridians about the components $D_{i}$ generate the normal subgroup $\ker \unicode[STIX]{x1D6EC}$ . Since they are taken by $\unicode[STIX]{x1D70B}$ onto $m_{i}$ th powers of (eventually powers of) meridians about $P_{i}$ , the surjection $\unicode[STIX]{x1D70B}$ is induced by $\unicode[STIX]{x1D70B}_{1}(\mathbb{P}^{2}\setminus (C\cup \bigcup _{i=1}^{s}D_{i}))\rightarrow \unicode[STIX]{x1D70B}_{1}(\mathbb{P}^{1}\setminus \{P_{i}\}_{i=1}^{s})$ . Hence we have the following commutative diagram:

(2.2)

Since $\unicode[STIX]{x1D712}=\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D70C})$ , the character $\unicode[STIX]{x1D712}$ is the composition $\unicode[STIX]{x1D70B}_{1}(X_{C})\overset{\unicode[STIX]{x1D70B}}{\longrightarrow }\unicode[STIX]{x1D70B}_{1}^{\text{orb}}(\mathbb{P}_{\bar{m}}^{1})\overset{\unicode[STIX]{x1D70C}}{\longrightarrow }\mathbb{C}^{\ast }$ , one has $\unicode[STIX]{x1D6F1}(\ker (\unicode[STIX]{x1D6EC}\circ \unicode[STIX]{x1D712}))\subseteq \ker (\unicode[STIX]{x1D706}\circ \unicode[STIX]{x1D70C})$ . Hence diagram (2.2) shows that $\unicode[STIX]{x1D70B}$ induces the map of covering spaces

(2.3) $$\begin{eqnarray}\mathop{\left(\mathbb{P}^{2}\setminus \left(C\cup \mathop{\bigcup }_{i=1}^{s}D_{i}\right)\right)}\nolimits_{\unicode[STIX]{x1D6EC}\circ \unicode[STIX]{x1D712}}\longrightarrow \left(\mathbb{P}^{1}\setminus \{P_{i}\}_{i=1}^{s}\right)_{\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D70C}}}\end{eqnarray}$$

corresponding to the subgroups $K:=\ker (\unicode[STIX]{x1D6EC}\circ \unicode[STIX]{x1D712})$ and $K_{\unicode[STIX]{x1D70C}}:=\ker (\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D70C}})$ respectively. The extension of the map (2.3) to a smooth compactification of $\left(\mathbb{P}^{2}\setminus (C\cup \bigcup _{i=1}^{s}D_{i})\right)_{\unicode[STIX]{x1D6EC}\circ \unicode[STIX]{x1D712}}$ and then to a resolution of its base points yields a map of a birational model of $V_{C}^{\unicode[STIX]{x1D712}}$ to $\unicode[STIX]{x1D6F4}$ ; recall that the orbifold $\mathbb{P}_{\bar{m}}^{1}$ is a global quotient of a Riemann surface  $\unicode[STIX]{x1D6F4}$ . And hence we have also a map $\text{Alb}(V_{C}^{\unicode[STIX]{x1D712}})\rightarrow \text{Jac}(\unicode[STIX]{x1D6F4})$ . The Poincaré Reducibility Theorem yields an isogeny between $\text{Alb}(V_{C}^{\unicode[STIX]{x1D712}})$ and $\text{Jac}(\unicode[STIX]{x1D6F4})\times A$ .

In the case of $n>1$ pencils $\unicode[STIX]{x1D719}_{1},\ldots ,\unicode[STIX]{x1D719}_{n}$ , we obtain a corresponding map for each $\unicode[STIX]{x1D719}_{i}$ and hence a map $\text{Alb}(V_{C}^{\unicode[STIX]{x1D712}})\rightarrow \text{Jac}(\unicode[STIX]{x1D6F4})^{n}$ . By Definition 1.8, the corresponding map of $H^{1}$ is surjective and hence, as above, the Poincaré Reducibility Theorem yields the claimed isogeny.◻

3 Curves with $\mathbb{A}_{2g}$ -singularities

The purpose of this section is to justify the lengthy statements of the main theorems by highlighting both their power and their subtleties through a series of examples. Simplifying the statements would only cause a more coarse description of the actual connection between characteristic varieties and orbifold pencils.

In what follows we present three essentially different types of situations: the pivotal example is shown in Theorem 3.3, where $\dim \text{Im}\,\text{alb}=2$ , $\text{Alb}(V_{C_{2}}^{\unicode[STIX]{x1D712}_{2}})$ is a simple abelian variety, which is the Jacobian of a curve, and hence the image $\text{alb}$ projected onto the isogeny factors of $\text{Alb}(V_{C_{2}}^{\unicode[STIX]{x1D712}_{2}})$ is never a curve. Therefore the conditions of Theorem 4 are not satisfied. Moreover, $(C_{2},\unicode[STIX]{x1D712}_{2})$ does not contain a global orbifold pencil (see [4]). Another remarkable fact is that $V_{C_{2}}^{\unicode[STIX]{x1D712}_{2}}$ is birational to an abelian surface of $\text{CM}$ -type corresponding to the cyclotomic field  $\mathbb{Q}(\unicode[STIX]{x1D701}_{5})$ . The cyclic quotients of these abelian surfaces have been studied by Bagnera and deFranchis [7]; this curve is the ramification divisor of one of such quotients.

On the other hand in Theorem 3.1 a curve $C_{1}$ is exhibited (for $k=1$ and $g=2$ ) whose $\text{Alb}(V_{C_{1}}^{\unicode[STIX]{x1D712}_{1}})$ coincides with $\text{Alb}(V_{C_{2}}^{\unicode[STIX]{x1D712}_{2}})$ , however $\dim \text{Im}\,\text{alb}=1$ , which implies, by Theorem 3, the existence of a global orbifold pencil containing $(C_{1},\unicode[STIX]{x1D712}_{1})$ . Finally, in Theorem 3.5, $\dim \text{Im}\,\text{alb}=2$ , as for $C_{2}$ . However $\text{Alb}(V_{C_{3}}^{\unicode[STIX]{x1D712}_{3}})$ decomposes (up to isogeny) as a product of three simple Jacobians of curves and the image $\text{alb}$ projected onto these factors is always 1-dimensional. By Theorem 3 this implies the existence of three independent global orbifold pencils containing  $(C_{3},\unicode[STIX]{x1D712}_{3})$ .

Theorem 3.1. Let $C_{1}$ be an irreducible curve in $\mathbb{P}^{2}$ given by the equation

(3.1) $$\begin{eqnarray}f_{2k}^{2g+1}+f_{(2g+1)k}^{2}=0,\end{eqnarray}$$

where $f_{i}$ is a generic homogeneous polynomial of degree  $i$ . Let $\unicode[STIX]{x1D712}_{1}$ be the character of $\unicode[STIX]{x1D70B}_{1}(\mathbb{P}^{2}\setminus C_{1})$ sending the generator of $H_{1}(\mathbb{P}^{2}\setminus C_{1})=\mathbb{Z}_{2k(2g+1)}$ to a primitive root of unity of degree $2(2g+1)$ . Consider $V_{C_{1}}^{\unicode[STIX]{x1D712}_{1}}$ the cyclic covering of order  $2(2g+1)$ of $\mathbb{P}^{2}$ ramified along  $C_{1}$ . Let $D_{\mathbb{A}_{2g}}$ be the curve of genus $g$ which is the cyclic Belyi cover of $\mathbb{P}_{(2,2g+1,2(2g+1))}^{1}$ of degree  $2(2g+1)$ . Then $\text{Alb}(V_{C_{1}}^{\unicode[STIX]{x1D712}_{1}})\sim \text{Jac}(D_{\mathbb{ A}_{2g}})$ and the Albanese dimension of $V_{C_{1}}^{\unicode[STIX]{x1D712}_{1}}$ is 1.

Remark 3.2. These curves were studied by Oka in [22] and the pencil provided by Theorem 3 is the one generated by $f_{2k}^{2g+1}$ and $f_{(2g+1)k}^{2}$ . Also note that $\text{Jac}(D_{\mathbb{A}_{2g}})$ is the local Albanese variety of any singularity of  $C_{1}$ , see Example 1.5.

Proof. The curve (3.1) has $2k^{2}(2g+1)$ singularities each locally equivalent to $u^{2}=v^{2g+1}$ forming scheme theoretical (for generic $f_{2k},f_{(2g+1)k}$ ) complete intersection ${\mathcal{B}}$ given by $f_{2k}=f_{(2g+1)k}=0$ . The Example 1.1 provides a general form of its Alexander polynomial and a calculation using [18] shows that $s=1$ , that is, it is $\frac{t^{2g+1}+1}{t+1}$ .

Consider the pencil of curves of degree $2k(2g+1)$ given by:

(3.2) $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{C_{1}}:[x_{0}:x_{1}:x_{2}]\mapsto [f_{2k}(x_{0},x_{1},x_{2})^{2g+1}:f_{2g+1}(x_{0},x_{1},x_{2})^{2k}]\end{eqnarray}$$

yielding a regular map $\mathbb{P}^{2}\setminus {\mathcal{B}}\rightarrow \mathbb{P}^{1}$ . We shall view this as an orbifold pencil with target $\mathbb{P}_{2,2g+1}^{1}$ . Since $\unicode[STIX]{x1D70B}_{C_{1}}(C_{1})=p\in \mathbb{P}^{1}$ , this map induces another orbifold map $\mathbb{P}^{2}\setminus C_{1}\rightarrow \mathbb{P}_{2,2g+1}^{1}\setminus \{p\}$ by restriction. Note that the inclusion $\mathbb{P}_{2,2g+1}^{1}\setminus \{p\}{\hookrightarrow}\mathbb{P}_{2,2g+1,2(2g+1)}^{1}$ is a dominant map. The latter orbifold is a global orbifold quotient by the action of cyclic group $\mathbb{Z}_{2(2g+1)}$ of a cyclic Belyi cover $\unicode[STIX]{x1D6F4}$ having genus $g$ (the value of the genus follows for example from the Riemann–Hurwitz formula). Moreover the pencil (3.2) lifts to the regular map $\tilde{\unicode[STIX]{x1D70B}}_{C_{1}}:V_{C_{1}}^{\unicode[STIX]{x1D712}_{1}}\rightarrow \unicode[STIX]{x1D6F4}$ . It follows from [17] that $\dim H_{1}(V_{C_{1}}^{\unicode[STIX]{x1D712}_{1}})=2g$ . Hence the induced map $\unicode[STIX]{x1D6F1}_{C_{1}}:\text{Alb}(V_{C_{1}}^{\unicode[STIX]{x1D712}_{1}})\rightarrow \text{Jac}(\unicode[STIX]{x1D6F4})$ is an isogeny and one has the commutative diagram:

(3.3)

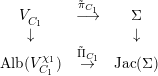
where the vertical arrows are the Albanese map and the canonical embedding of $\unicode[STIX]{x1D6F4}$ into its Jacobian. This implies that the Albanese image of $V_{C_{1}}^{\unicode[STIX]{x1D712}_{1}}$ is one-dimensional.◻

Theorem 3.3. Let $C_{2}$ be the union of a self-dual quintic $C_{0}$ with 3 $\mathbb{A}_{4}$ -singularities and the line $L$ which is tangent to $C_{0}$ at one of its singularities, say $P^{0}$ . Consider $\unicode[STIX]{x1D712}_{2}$ any character of order 10 that ramifies along $C_{0}+5L$ (the coefficients represent the ramification indices). Then

1. (1) The canonical class of the minimal model of $V_{C_{2}}^{\unicode[STIX]{x1D712}_{2}}$ is trivial.

2. (2) $\dim H_{1}(V_{C_{2}}^{\unicode[STIX]{x1D712}_{2}},\mathbb{C})=4$ . In particular, this minimal model is an abelian surface.

3. (3) This abelian surface is isomorphic to the $\text{Jac}(D_{\mathbb{A}_{4}})$ which is a simple abelian variety and hence its Albanese dimension is 2.

Proof. In order to prove part (1), we will construct the 10th-cyclic cover of $\mathbb{P}^{2}$ associated with $\unicode[STIX]{x1D712}_{2}$ . Note that $K_{\mathbb{P}^{2}}=-3H=-\frac{3}{5}C_{0}$ . Denote by $\hat{\mathbb{P}}^{2}$ the resulting surface (see Figure 2) after blowing up the singular points of $C_{0}$ to obtain a normal crossing divisor and then blowing down the preimage of  $L$ .

Figure 1. Local resolution at $P^{0}$ .

To understand this, we will briefly describe the local resolution of the singularity at $P^{0}$ shown in Figure 1. The subindices of $E_{i}^{0}$ indicate the order of appearance of the exceptional divisors. Since the first two blow-ups occur on infinitely near smooth points of $L$ , its self-intersection drops by  $2$ . However, these first two infinitely near points are not smooth on $C_{0}$ , but of multiplicity 2. Since two more blow-ups on infinitely near smooth points of $C_{0}$ are required to resolve the singularity, the self-intersection of $C_{0}$ drops by  $2\cdot (2)^{2}+2\cdot (1)^{2}=10$ .

We denote by $P^{\pm }$ the other singular points of type $\mathbb{A}_{4}$ . Note that Figure 1 (excluding the germ of $L$ ) also describes a resolution of $P^{\pm }$ in $C_{0}$ . For the corresponding exceptional divisors we replace the superscript $0$ by $\pm$ accordingly. Analogously as mentioned above, the self-intersection of $C_{0}$ drops by $10$ at each point.

By Bézout’s Theorem, $L$ intersects $C_{0}$ at another point. Since its self-intersection after the blow-ups is $-1$ and it intersects only $C_{0}$ and $E_{2}^{0}$ , we can blow it down keeping the normal crossing property. The self-intersection of both $E_{2}^{0}$ and $C_{0}$ increases by 1. The resulting surface is $\hat{\mathbb{P}}^{2}$ and the involved divisors are shown in Figure 2. By the Projection Formula we obtain

$$\begin{eqnarray}K_{\hat{\mathbb{P}}^{2}}=-{\textstyle \frac{3}{5}}C_{0}-{\textstyle \frac{1}{5}}(E_{1}^{+}+E_{1}^{-}+E_{1}^{0}+2E_{2}^{+}+2E_{2}^{-}+2E_{2}^{0}).\end{eqnarray}$$

Figure 2. Surface $\hat{\mathbb{P}}^{2}$ .

The self-intersections of the divisors are shown in parenthesis unless $(E_{i}^{\bullet })^{2}=(E_{i}^{+})^{2}$ . Since we have blown up 12 points and blown down one exceptional divisor, one can compute the Euler characteristic as follows:

$$\begin{eqnarray}\unicode[STIX]{x1D712}(\hat{\mathbb{P}}^{2})=\unicode[STIX]{x1D712}(\mathbb{P}^{2})+12-1=14.\end{eqnarray}$$

An alternative way to obtain a surface birationally equivalent to $V_{C_{2}}^{\unicode[STIX]{x1D712}_{2}}$ is to consider the 10th-cyclic cover of $\hat{\mathbb{P}}^{2}$ ramified along the total transform of $C_{0}+5L$ , that is,

$$\begin{eqnarray}\displaystyle R & := & \displaystyle C_{0}+7E_{1}^{0}+14E_{2}^{0}+15E_{3}^{0}+30E_{4}^{0}+2E_{1}^{\pm }+4E_{2}^{\pm }+5E_{3}^{\pm }+10E_{4}^{\pm }\nonumber\\ \displaystyle & \equiv & \displaystyle C_{0}+7E_{1}^{0}+4E_{2}^{0}+5E_{3}^{0}+2E_{1}^{\pm }+4E_{2}^{\pm }+5E_{3}^{\pm }\quad \hspace{0.6em}{\rm mod}\hspace{0.2em}10\text{Pic}(\hat{\mathbb{P}}^{2}),\nonumber\end{eqnarray}$$

where $E_{i}^{\pm }=E_{i}^{+}+E_{i}^{-}$ . It is easier to factor such covering as the composition of a double cover $\unicode[STIX]{x1D70B}_{2}$ and a 5th-fold cover  $\unicode[STIX]{x1D70B}_{5}$ .

The double cover of $\hat{\mathbb{P}}^{2}$ is ramified along

$$\begin{eqnarray}R_{2}:=C_{0}+E_{3}^{\pm }+E_{3}^{0}+E_{1}^{0}\equiv R\hspace{0.6em}{\rm mod}\hspace{0.2em}2\text{Pic}(\hat{\mathbb{P}}^{2})\end{eqnarray}$$

and will be denoted by $X$ . The dual graph of the total transform $\unicode[STIX]{x1D70B}_{2}^{\ast }(R)$ in $X$ is shown in Figure 3.

Figure 3. Surface $X$ .

In order to compute the self-intersection of each divisor one has to apply the intersection theory formulas for covers (cf. [8, Chapter II. Section 10]).

Note that

$$\begin{eqnarray}K_{X}=-{\textstyle \frac{1}{5}}c_{0}+{\textstyle \frac{3}{5}}e_{1}^{0}-{\textstyle \frac{2}{5}}e_{2}^{0}+e_{3}^{0}-{\textstyle \frac{1}{5}}e_{1}^{\pm \pm }-{\textstyle \frac{2}{5}}e_{2}^{\pm \pm }+e_{3}^{\pm },\end{eqnarray}$$

where $e_{i}^{\pm \pm }$ denotes the sum $e_{i}^{++}+e_{i}^{+-}+e_{i}^{-+}+e_{i}^{--}$ .

By Riemann–Hurwitz, the Euler characteristic of $X$ can be obtained as

$$\begin{eqnarray}\unicode[STIX]{x1D712}(X)=2(\unicode[STIX]{x1D712}(\hat{\mathbb{P}}^{2})-\unicode[STIX]{x1D712}(R_{2}))+\unicode[STIX]{x1D712}(\unicode[STIX]{x1D70B}_{2}^{\ast }(R_{2}))=2(14-10)+10=18.\end{eqnarray}$$

After blowing down the divisors $e_{1}^{0}$ , $e_{3}^{0}$ , $e_{3}^{+}$ , and $e_{3}^{-}$ one obtains the surface $Y$ , where

$$\begin{eqnarray}K_{Y}=-{\textstyle \frac{1}{5}}(c_{0}+2e_{2}^{0}+e_{1}^{\pm \pm }+2e_{2}^{\pm \pm })\quad \text{and}\quad \unicode[STIX]{x1D712}(Y)=14.\end{eqnarray}$$

Finally one needs to perform the 5:1 cover of $Y$ ramified along $R_{5}:=c_{0}+2e_{2}^{0}+e_{1}^{\pm \pm }+2e_{2}^{\pm \pm }$ , which incidentally is the support of  $K_{Y}$ . Note that this divisor has 5 connected components, namely, $e_{1}^{++}+2e_{2}^{++}$ , $e_{1}^{+-}+2e_{2}^{+-}$ , $e_{1}^{-+}+2e_{2}^{-+}$ , $e_{1}^{--}+2e_{2}^{--}$ , and $c_{0}+2e_{2}^{0}$ , each with the same combinatorial structure as shown at the bottom of Figure 4. The appropriate ramified cover on $e_{1}^{++}+2e_{2}^{++}$ is shown in Figure 4. Next to each irreducible component a list of numbers is shown: the first one being the self-intersection of the component, the second one being its multiplicity in the corresponding canonical $\mathbb{Q}$ -divisor ( $K_{Y}$ or $K_{Z}$ ), and the third one (where applicable) being the ramification index. The components $\unicode[STIX]{x1D700}_{i}^{++}$ are the strict transforms of $e_{i}^{++}$ by the 5:1 cover, while the remaining components $a^{++}$ and $b^{++}$ project onto the double point. Note that the support of $K_{Z}$ is in the preimage of $R_{5}$ . After blowing down all components, one obtains a smooth surface $\hat{Z}$ with trivial canonical divisor, which is in particular the minimal model of  $V_{C_{2}}^{\unicode[STIX]{x1D712}_{2}}$ . Using Riemann–Hurwitz once again, one obtains

$$\begin{eqnarray}\unicode[STIX]{x1D712}(\hat{Z})=5(\unicode[STIX]{x1D712}(Y)-\unicode[STIX]{x1D712}(R_{5}))+5=5(14-5\cdot 3)+5=0.\end{eqnarray}$$

Figure 4. Surface $Y$ .

From the Kodaira classification (see [8, Table 10]) the minimal model is a torus and hence it is an abelian surface.

For part (2), note that the degree of the Alexander polynomial of $C_{2}$ associated with $\unicode[STIX]{x1D712}_{2}$ (see [5, Section 2.2]) is $t^{4}-t^{3}+t^{2}-t+1$ [4, Theorem 4.5]. Since $\dim \text{Alb}(V_{C_{2}}^{\unicode[STIX]{x1D712}_{2}})=\frac{1}{2}\deg \unicode[STIX]{x1D6E5}_{C_{2},\unicode[STIX]{x1D712}_{2}}(t)=2$ , the result follows.◻

Remark 3.4. Note that $\text{Jac}(\mathbb{A}_{4})$ is a simple abelian variety. This follows from discussion in [16] yielding that $\text{CM}$ -field in this case is $\mathbb{Q}(\unicode[STIX]{x1D701}_{5})$ and explicit description of the $\text{CM}$ -type there. More generally, for the singularity type $x^{p}+y^{q}$ , where $p,q$ are different prime numbers, recall that Arnold–Steenbrink’s spectrum provides the $\text{CM}$ -type for the local Albanese variety (cf. [16]), whose explicit description is well known. One can apply Shimura–Taniyama conditions for primitivity of a $\text{CM}$ -type (cf. [23]) to verify that the local Albanese variety is simple in this case. In particular, Theorem 4 (2) can be applied to those plane curve singularities.

In general, however, local Albanese variety has several isogeny components. In the case of unibranched curves they all are Jacobians of Belyi cyclic covers (cf. [16]) and hence are the components of Jacobians of Fermat curves. We refer for additional information regarding these Jacobians to [15] and [2].

Theorem 3.5. Let $C_{3}$ be an irreducible curve in $\mathbb{P}^{2}$ given by the equation

(3.4) $$\begin{eqnarray}x_{0}^{2m}+x_{1}^{2m}+x_{2}^{2m}-2(x_{0}^{m}x_{1}^{m}+x_{1}^{m}x_{2}^{m}+x_{2}^{m}x_{0}^{m})=0,\end{eqnarray}$$

where $m$ is an odd number, say $m=2g+1$ . Consider $V_{C_{3}}^{\unicode[STIX]{x1D712}_{3}}$ the cyclic covering of order  $2m$ of $\mathbb{P}^{2}$ ramified along  $C_{3}$ . Let $D_{\mathbb{A}_{2g}}$ be as above. Then $\text{Alb}(V_{C_{3}}^{\unicode[STIX]{x1D712}_{3}})$ is isogenous to $\text{Jac}(D_{\mathbb{A}_{2g}}\!)^{3}$ and the Albanese dimension of $V_{C_{3}}^{\unicode[STIX]{x1D712}_{3}}$ is 2.

Proof. The pencils of curves

$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{i}=\{F_{i,[\unicode[STIX]{x1D6FC}:\unicode[STIX]{x1D6FD}]}\mid [\unicode[STIX]{x1D6FC}:\unicode[STIX]{x1D6FD}]\in \mathbb{P}^{1}\},\end{eqnarray}$$

(where $F_{i,[\unicode[STIX]{x1D6FC}:\unicode[STIX]{x1D6FD}]}=\{\unicode[STIX]{x1D6FC}(x_{j}x_{k})^{m}+\unicode[STIX]{x1D6FD}(x_{j}^{m}+x_{k}^{m}-x_{i}^{m})^{2}=0\}$ and $\{i,j,k\}=\{0,1,2\}$ ) induce orbifold morphisms from $\mathbb{P}^{2}$ onto the compact orbifold  $\mathbb{P}_{([1:0],2),([0:1],m)}^{1}$ . Since $C_{3}=F_{i,[-4:1]}$ they also define (by restriction) orbifold morphisms $\unicode[STIX]{x1D719}_{i}:\mathbb{P}^{2}\setminus C_{3}\rightarrow \mathbb{P}_{2,m,2m}^{1}$ defined as

$$\begin{eqnarray}[x_{0}:x_{1}:x_{2}]\stackrel{\unicode[STIX]{x1D719}_{i}~}{\mapsto }[x_{j}^{m}x_{k}^{m}:(x_{j}^{m}+x_{k}^{m}-x_{i}^{m})^{2}].\end{eqnarray}$$

If one shows that these morphisms are strongly independent, then by Theorem 5, they define a surjective morphism $\text{Alb}(V_{C_{3}}^{\unicode[STIX]{x1D712}_{3}})\rightarrow \text{Jac}(D_{\mathbb{ A}_{2g}})^{3}$ . Note that $D_{\mathbb{A}_{2g}}$ is a curve of genus $g$ . Moreover, the Alexander polynomial of $C_{3}$ associated with $\unicode[STIX]{x1D712}_{3}$ is the classical Alexander polynomial since $C_{3}$ is irreducible, which is $\unicode[STIX]{x1D6E5}_{C_{3}}(t)=(\frac{t^{2g}+1}{t+1})^{3}$ (see [11]). Thus

$$\begin{eqnarray}\dim \text{Alb}(V_{C_{3}}^{\unicode[STIX]{x1D712}_{3}})={\textstyle \frac{1}{2}}\deg \unicode[STIX]{x1D6E5}_{C_{3}}(t)=3g\end{eqnarray}$$

and then $\text{Alb}(V_{C_{3}}^{\unicode[STIX]{x1D712}_{3}})\sim \text{Jac}(D_{\mathbb{ A}_{2g}})^{3}$ by dimension reasons.

For the last part, consider $(\unicode[STIX]{x1D719}_{1}\times \unicode[STIX]{x1D719}_{2}):\mathbb{P}^{2}\setminus C_{3}\rightarrow (\mathbb{P}_{2,m,2m}^{1})^{2}$ . Note that the preimage of a generic point is the intersection of two generic members of the pencils $\unicode[STIX]{x1D6EC}_{1}$ and $\unicode[STIX]{x1D6EC}_{2}$ and hence the morphism is finite. The same applies to $(\unicode[STIX]{x1D6F7}_{1}\times \unicode[STIX]{x1D6F7}_{2}):V_{C_{3}}^{\unicode[STIX]{x1D712}_{3}}\rightarrow \unicode[STIX]{x1D6F4}^{2}$ . By the standard properties of the Albanese map, $\text{alb}(\unicode[STIX]{x1D6F7}_{1}\times \unicode[STIX]{x1D6F7}_{2}):\text{Alb}(V_{C_{3}}^{\unicode[STIX]{x1D712}_{3}})\rightarrow \text{Jac}(D_{\mathbb{ A}_{2g}})^{2}$ is surjective. Since the Albanese map of $V_{C_{3}}^{\unicode[STIX]{x1D712}_{3}}$ factors through $\text{alb}(\unicode[STIX]{x1D6F7}_{1}\times \unicode[STIX]{x1D6F7}_{2})$ , the result follows.

It remains to show that the global quotient orbifold pencils $\unicode[STIX]{x1D719}_{0}$ , $\unicode[STIX]{x1D719}_{1}$ , and $\unicode[STIX]{x1D719}_{2}$ are strongly independent, in other words, that the morphisms $\unicode[STIX]{x1D6F7}_{i,\ast }:H_{1}(V_{C_{3}}^{\unicode[STIX]{x1D712}_{3}})\rightarrow H_{1}(\unicode[STIX]{x1D6F4})$ , $i=0,1,2$ , obtained from (3.5),

(3.5)

are $\mathbb{Z}[\unicode[STIX]{x1D707}_{2m}]$ -independent ( $\unicode[STIX]{x1D707}_{2m}\subset \mathbb{C}^{\ast }$ the cyclic group of $2m$ -roots of unity) and that $\bigoplus _{i=0}^{2}\unicode[STIX]{x1D6F7}_{i,\ast }:H_{1}(V_{C_{3}}^{\unicode[STIX]{x1D712}_{3}})\rightarrow H_{1}(\unicode[STIX]{x1D6F4})^{3}$ is surjective (see Definition 1.8).

Note that the base points of the pencils can be described as follows: let $\{i,j,k\}=\{0,1,2\}$ and consider

$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{i}:=\{x_{i}=0\}\cap Q_{j}=\{x_{i}=0\}\cap Q_{k},\end{eqnarray}$$

$Q_{i}:=\{x_{j}^{m}+x_{k}^{m}-x_{i}^{m}=0\}$ . The $2m$ base points of $\unicode[STIX]{x1D6EC}_{i}$ are $\unicode[STIX]{x1D6E5}_{j}\cup \unicode[STIX]{x1D6E5}_{k}$ .

In order to understand $V_{C_{3}}^{\unicode[STIX]{x1D712}_{3}}$ we will first consider a resolution of the base points of the pencil $\unicode[STIX]{x1D6EC}_{i}$ . This is shown in Figure 5, where $\tilde{\ell }_{P}$ (resp. $\tilde{C}_{3}$ , and $\tilde{Q}_{i}$ ) represents the strict preimage of $\ell _{P}$ , the axis containing $P$ (resp. $C_{3}$ , and the Fermat curve $Q_{i}$ ). The notation $[k]$ next to an irreducible component $E$ indicates the image by $\unicode[STIX]{x1D712}_{3}$ of a meridian $\unicode[STIX]{x1D6FE}$ around the irreducible component $E$ as follows:

$$\begin{eqnarray}\unicode[STIX]{x1D712}_{3}(\unicode[STIX]{x1D6FE})=e^{\frac{k}{m}\unicode[STIX]{x1D70B}\sqrt{-1}}.\end{eqnarray}$$

Unbranched components, that is, $[k]=[0]$ , are shown in dashed lines.

Figure 5. Resolution of the base point of the pencil $\unicode[STIX]{x1D6EC}_{i}$ .

In other words $V_{C_{3}}^{\unicode[STIX]{x1D712}_{3}}$ is the cyclic covering of order $2m$ ramified along the locus

$$\begin{eqnarray}C_{3}+\mathop{\sum }_{P\in \unicode[STIX]{x1D6E5}}(2E_{1,P}+4E_{2,P}+\cdots +(2g-2)E_{g-1,P}+2gE_{g,P}+mE_{g+1,P}),\end{eqnarray}$$

where $\unicode[STIX]{x1D6E5}=\bigcup _{i=0}^{2}\unicode[STIX]{x1D6E5}_{i}$ . To resolve each $\unicode[STIX]{x1D6EC}_{i}$ it would be enough to blow up over $\unicode[STIX]{x1D6E5}_{j}\cup \unicode[STIX]{x1D6E5}_{k}$ , but this way the same surface works for the three pencils.

In particular, note that $V_{C_{3}}^{\unicode[STIX]{x1D712}_{3}}$ will contain curves $\unicode[STIX]{x1D6F4}_{P}$ which are the cyclic covering of $E_{g+2,P}$ ramified at 3 points of ramification indices $1$ , $m-1$ , and  $m$ . It is easy to check that the orders of $\unicode[STIX]{x1D712}_{3}$ at the meridians of these points are $2m$ , $m$ , and $2$ respectively. Hence $\unicode[STIX]{x1D6F4}_{P}=\unicode[STIX]{x1D6F4}$ is the curve of genus $g$ which is the Belyi cover $D_{\mathbb{A}_{2g}}$ of  $\mathbb{P}_{2,m,2m}^{1}$ .

Moreover, if $P\in \unicode[STIX]{x1D6E5}_{k}$ , then $\unicode[STIX]{x1D6F7}_{i}|_{\unicode[STIX]{x1D6F4}_{P}}:\unicode[STIX]{x1D6F4}_{P}\rightarrow \unicode[STIX]{x1D6F4}$ and $\unicode[STIX]{x1D6F7}_{j}|_{\unicode[STIX]{x1D6F4}_{P}}:\unicode[STIX]{x1D6F4}_{P}\rightarrow \unicode[STIX]{x1D6F4}$ are isomorphisms since $E_{g+2,P}$ in Figure 5 is a dicritical section of $\unicode[STIX]{x1D6EC}_{i}$ and $\unicode[STIX]{x1D6EC}_{j}$ , whereas $\unicode[STIX]{x1D6F7}_{k}|_{\unicode[STIX]{x1D6F4}_{P}}:\unicode[STIX]{x1D6F4}_{P}\rightarrow \unicode[STIX]{x1D6F4}$ is a constant map. This immediately implies the result as follows. Consider three indeterminacy points distributed among the axes, for instance $P_{0}:=[0:1:1]$ , $P_{1}:=[1:0:1]$ , and  $P_{2}:=[1:1:0]$ . By the previous considerations nontrivial meridians $\unicode[STIX]{x1D6FE}_{i}\in H_{1}(\unicode[STIX]{x1D6F4}_{P_{i}})\cong H_{1}(\unicode[STIX]{x1D6F4})$ exist considered as cycles in $H_{1}(V_{C_{3}}^{\unicode[STIX]{x1D712}_{3}})$ via the inclusion and such that

$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{j}(\unicode[STIX]{x1D6FE}_{i})=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D6FE}\quad & \text{if}\;i\neq j\\ 0\quad & \text{if}\;j=i,\end{array}\right.\end{eqnarray}$$

where $\unicode[STIX]{x1D6FE}\in H_{1}(\unicode[STIX]{x1D6F4})$ is a nontrivial cycle. If $\unicode[STIX]{x1D6F7}_{i,\ast }$ were dependent morphisms, then there should exist coefficients $\unicode[STIX]{x1D6FC}_{0},\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2}\in \mathbb{Z}[\unicode[STIX]{x1D707}_{2m}]$ such that

$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{0}\unicode[STIX]{x1D6F7}_{0,\ast }+\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6F7}_{1,\ast }+\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6F7}_{2,\ast }\equiv 0,\end{eqnarray}$$

but using the cycle $\unicode[STIX]{x1D6FE}_{0}$ one obtains that $\unicode[STIX]{x1D6FC}_{1}=-\unicode[STIX]{x1D6FC}_{2}$ , analogously, using $\unicode[STIX]{x1D6FE}_{1}$ (resp. $\unicode[STIX]{x1D6FE}_{2}$ ) one obtains $\unicode[STIX]{x1D6FC}_{0}=-\unicode[STIX]{x1D6FC}_{2}$ (resp. $\unicode[STIX]{x1D6FC}_{0}=-\unicode[STIX]{x1D6FC}_{1}$ ). Therefore $\unicode[STIX]{x1D6FC}_{1}=\unicode[STIX]{x1D6FC}_{0}=\unicode[STIX]{x1D6FC}_{2}=\unicode[STIX]{x1D6FC}$ and $2\unicode[STIX]{x1D6FC}=0$ in $\mathbb{Z}[\unicode[STIX]{x1D707}_{2m}]$ , which implies $\unicode[STIX]{x1D6FC}=0$ . The fact that the map $\bigoplus _{i=0}^{2}\unicode[STIX]{x1D6F7}_{i,\ast }:H_{1}(V_{C_{3}}^{\unicode[STIX]{x1D712}_{3}})\rightarrow H_{1}(\unicode[STIX]{x1D6F4})^{3}$ is surjective follows from the existence of the dicritical sections $E_{g+2,P_{i}}$ and the induced isomorphisms $\unicode[STIX]{x1D6F7}_{j}|_{\unicode[STIX]{x1D6F4}_{P_{i}}}:\unicode[STIX]{x1D6F4}_{P_{i}}\rightarrow \unicode[STIX]{x1D6F4}$ for $j\neq i$ described above.◻