1. Introduction
Wintertime atmosphere–ocean energy exchange in ice-covered regions is largest over leads and polynyas where open water and thin ice is abundant; it is particularly sensitive to the thickness of the thin ice. numerical models predict a decrease of the summer arctic ice extent due to a longer melt period (up to an almost complete loss), while it will remain nearly unchanged during winter (acia, 2004). consequently, the seasonal ice cover can be expected to become thinner, and an increase of the thin-ice fraction is likely to occur in the near future. sea-ice thickness observations were made with various methods (e.g. satellite altimetry, upward-looking sonar (uls) and in situ (e.g. Reference Kwok, Zwally and YiLaxon and others, 2003; Reference Rignot and DrinkwaterRothrock and others, 2003; Reference HaasHaas, 2004; Reference Kwok, Zwally and YiKwok and others, 2004)). but except for in situ measurements, quantities such as the snow depth have to be assumed in order to obtain the ice thickness from the observed draft or freeboard, a major limitation (Reference Kwok, Zwally and YiKwok and others, 2004). moreover, typical values of thin-ice draft (a few to about 25 cm) or freeboard (a few millimetres to centimetres) lie within the error range of the used sensors. an alternative is to combine satellite observations with numerical models. this requires a high accuracy of model input data (e.g. air temperature), good availability and high quality of satellite data (e.g. fine spatial resolution) and the ability to unambiguously identify thin ice (e.g. Reference Drucker, Martin and MoritzDrucker and others, 2003). another way is to use only remote-sensing data. attempts to obtain the thin-ice thickness from airborne radar imagery have been made, for example, by Reference Kwok, Nghiem, Yueh and HuynhKwok and others (1995) and Reference schauer and KattnerWakabayashi and others (2004). they utilize a neural network trained with fully polarimetric data (l- and c-band) and coincident infrared (ir) temperature observations, and a simple empirical relationship between uls-observed ice thickness and the radar backscatter co-polarization ratio (CPR; l-band), respectively. Reference Dierking, skriver and GudmandsenDierking and others (2003) mentioned that fully polarimetric data are indeed promising for thickness retrieval. however, although encouraging, these attempts reveal very different values for the maximum obtainable ice thickness: 10–100 cm. in this paper, synchronous measurements carried out by two helicopter-borne sensors, an electromagnetic (em) induction ice-thickness sounder (em-bird) and a multi-frequency, multi-polarization scattero-meter (heliscat) are combined to form a unique dataset (section 3) to estimate the thin-ice thickness (section 4), similar to the approach of Reference schauer and KattnerWakabayashi and others (2004).
2. Background
During the expedition ark XIX/1 of the R/v Polarstern (28 february–24 april 2003; Reference Rothrock, Zhang and YuSchauer and kattner, 2004), sea-ice and snow properties and distributions were observed north of svalbard in situ and by helicopter-borne laser altimetry, video imagery, em surveying and scatterometer measurements. on 19 april 2003, a tandem flight of em-bird and heliscat was carried out revealing a unique combination of data from both instruments. the synchronous flight was conducted using two helicopters, one towing the em-bird at 50 ft (15 m) height, immediately followed by the second one along the same track carrying the heliscat at 150–200 ft (46–61 m) altitude. ice conditions were characterized by vast multi-year ice floes, intersected by regions of first-year ice. thin and first-year ice formed in prominent, long and wide leads extending from the northwest towards the ice edge in the southeast, as a result of shear and divergence in the marginal ice zone.
The heliscat is a helicopter-based microwave scatter-ometer operating at frequencies of 1.0, 2.4, 5.3, 10.0 and 15.0 ghz (l, s, c, x and ku band, respectively). it permits measurement of radar backscatter quasi-simultaneously at the above frequencies at all like- and cross-polarizations from 50 to 150m altitude. the heliscat uses a single broadband 96cm parabolic dish antenna both for transmission and reception. the antenna is aft-looking and can be tilted during the flight from 23˚ to 65˚ nominal incidence angle (Reference Wakabayashi, Matsuoka, Nakamura and NishioWismann and others, 1998). heliscat data are complemented by the helicopter’s pitch and roll measured by a gyro, charge-coupled device (ccd) camera imagery of the antenna’s footprint on the ground, the global positioning system (GPs) and hand-held digital photography. data used in this paper were acquired at 65 m altitude at 40˚ incidence angle, resulting in a footprint size at l-band of 20 m×27m (±5–10m due to variations in altitude and incidence angle during the flight). the average flight speed was 30–35ms–1. the heliscat measurement time series of each frequency band were sampled at 10 khz. subsequently, doppler spectra were calculated and the integral of the spectral doppler peak was integrated within its 6 db limits with a sample rate of 10 hz (time-step of 0.1 s). the instrumental noise was calculated from a part of the spectrum well off the doppler peak with the same sample rate, and was used to obtain the signal-to-noise (snr) ratio. this paper focuses on observations at l-band, because its long wavelength promises the largest penetration depth into thin ice and therefore a maximum obtainable thickness.
The em-bird is a purpose-built, small, lightweight sea-ice thickness profiler in operation since 2001 at the alfred wegener institute, bremerhaven. it is a 3.5 m long, 100 kg towed sensor suspended 20m below a helicopter and operated at heights of 10–20m above the ice surface. in short, the em-bird consists of an assembly of coils for the transmission and reception of low-frequency em fields (3.69 and 112 khz) and a laser altimeter. while the em system is sensitive to the sensor’s height above the conductive sea water, the sensor’s altitude above the ice surface is determined with the laser altimeter. over sea ice, the water surface coincides with the ice underside. therefore, the difference of the height measurements of both components corresponds to the ice-plus-snow thickness. the method is calibrated over open water, where ice thickness is known to be zero. on a point-by-point basis, the estimates of the ice thickness agree within ±0.1m with drillhole data, whereas statistically determined level ice thickness can reach accuracies in the cm range (a. pfaffling, c. haas and j.e. reid, unpublished information). however, due to the diffusive nature of the low-frequency em induction field, its strength represents an average thickness of an area two to four times the instrument’s altitude above the ice surface, i.e. an area of 30–80m2 size. due to this ‘footprint’, maximum ridge thickness can be underestimated by as much as 50% in the worst cases, depending on the geometry and consolidation of the ridge keel (Reference Pfaffling, Haas and ReidReid and others, 2006).
In order to reduce the scatter inherent in the data due to small-scale sea-ice heterogeneities and instrument noise, both time series are smoothed spatially along the flight track with a running mean. different window widths (20, 50 and 100 data points, i.e. 65, 150 and 300 m) are applied in order to investigate their effectiveness in removing outliers and scatter. in a further step, only those heliscat l-band CPR data are used where the snr (smoothed with the same window) exceeds a threshold of 15 or 20 db.
figure 1 shows the location of the measurements (fig. 1a), the sea-ice thickness along the entire flight track measured by the em-bird (fig. 1b) and in figure 1c the sea-ice thickness along leg 1 (see fig. 1b) together with the heliscat l-band co-polarization ratio (CPR, vv/hh polarized backscatter). leg 1 crosses three multi-year ice floes separated by leads at 50 and 200–280 s flight time. subsequently, a heterogeneous ice-cover is crossed, predominantly covered by thin and first-year ice. the CPR is around 0 db over multi-year and first-year ice but takes values up to 5 db over the thin ice. like-polarized l-band radar backscatter (not shown) varied by up to 15 db between thin and multi-year ice, which agrees with earlier observations (e.g. Reference Reid, A. and VrbancichRignot and drinkwater, 1994).

Fig. 1. (a) Location of the tandem flight carried out on 19 April 2003, north of svalbard. (b) Zoom of the black box in (a) with the EM ice-thickness measurements. (c) EM ice thickness (white) and Heliscat L-band CPR (black) for leg 1 (see (b)) (time = 0 is upper right corner of triangle) averaged over 150 m. Gaps in the line of diamonds at the bottom indicate that the SNR is <20 dB.
3. Thin-Ice Thickness Estimation Method
Radar backscatter measurements carried out in the laboratory over thin saline ice (e.g. Reference Laxon, Peacock and smithNghiem and others, 1997) reveal low like-polarization radar backscatter values which increase with thickness during initial growth above a threshold thickness of about 3 cm (by about 6–10 db at l- and c-band). in order to observe such an increase under field conditions, the thin ice has to be tracked to ensure that an observed radar backscatter increase is caused by thin-ice growth and not by, for example, ice deformation. Reference NghiemOnstott (1992) and Reference schauer and KattnerWakabayashi and others (2004) showed a CPR decrease with increasing thin-ice thickness, and that this decrease is more pronounced at large incidence angles, i.e. above 40˚. this can be explained by changes in surface/near-surface backscattering characteristics of thin saline ice during its growth, causing radar backscatter to increase. this backscatter increase is much larger at horizontal than at vertical polarization. Reference schauer and KattnerWakabayashi and others (2004) utilized this approach to estimate the thin-ice thickness. our goal is to obtain a similar simple empirical relationship between em ice thickness and heliscat l-band CPR data obtained simultaneously along the same flight track (fig. 1c) to derive the thin-ice thickness solely from this CPR. for this purpose, both datasets are co-located using a cross-correlation analysis and subsequently compared for different snr thresholds and averaging windows.
figure 2 shows a sample set of scatter plots of em ice thickness vs heliscat l-band CPR for ice-thickness values between 0.0 and 1.0 m for leg 1 (see fig. 1b). two different snr values (15 and 20 db) and three different averaging windows are realized. all images of figure 2 indicate a constant CPR around 0 db at ice-thickness values above about 0.6 m (dashed horizontal line) up to the maximum ice thickness (not shown), and a tail of increasing CPR toward zero ice thickness; this is similar to the findings of Reference NghiemOnstott (1992) for c-band. two different fits, a linear and a logarithmic one, are applied to obtain an empirical relationship between the two datasets, which allows calculation of the thin-ice thickness from the CPR data. the fits are applied to data with a CPR above zero minus one standard deviation of the average CPR (hCPRi) of thick ice (>2.5m), calculated from em ice-thickness measurements averaged over 300m the em ice-thickness measurement range is 0.0–0.6m for the linear fit and 0.0–1.0m for the logarithmic fit. the fits are plotted in figure 2. their equations are:

Fig. 2. Em ice thickness vs Heliscat L-band CPR along leg 1 (see Fig. 1b) for different SNR values (only Heliscat data) and averaging windows (both datasets). (a) SNR > 20 dB, with 150m averaging; (b) SNR > 15 dB, with 150m averaging; (c) SNR > 20 dB, with 65m averaging; and (d) SNR > 20 dB, with 300m averaging. superposed are curves of a linear and a logarithmic fit. The rms differences (in metres) between the measured ice thickness and that estimated with the two fits are given in the upper right corner of each panel.
And
(logarithmic fit);
Cpr is the heliscat l-band CPR data, D H is the heliscat-derived ice thickness, a 0 = 0.503 and a 1 = –0.067 are the intercept and slope of the linear fit and b 0 = 1.0, b 1 = 0.7 and b 2 = maximum CPR value are the coefficients of the logarithmic fit. the larger CPR and thickness range used to establish the logarithmic fit was taken to ensure a realistic continuation of the fit for an ice thickness around the selected maximum value of 0.6 m
A larger snr threshold (20 db instead of 15 db) significantly reduces the number of outliers (circles in fig. 2a and b). their number is also determined by the width of the averaging window: 150, 65 and 300 m, in figure 2a, c and d, respectively. both have an influence on the quality of the fit. this is indicated by different rms differences between the measured ice thickness and the one estimated using one of the fits (see numbers in the upper right of fig. 2a–d). these differences as well as the heliscat-derived ice thickness (section 4) are obtained using only data where the measured (em) ice thickness is between 0.0 and 0.6 m and CPR values are larger than zero plus one standard deviation of hCPRi (see above). we decided to rely on CPR data with a snr above 20 db and to use an averaging window of 150 m. although the rms difference using this averaging window is slightly larger compared to using a window of 300m (see fig. 2a and d), a window of 150 mallows us to resolve thin-ice areas, which extend over 100–200m along the flight track, and to keep the entire thickness range starting right from 0 cm.
4. Results
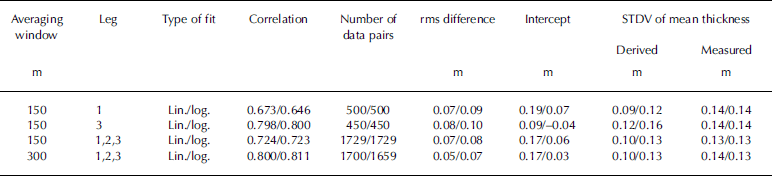
figure 3 shows the thin-ice thickness estimated from heliscat l-band CPR data (snr > 20 db) using the linear (fig. 3a and c) and the logarithmic (fig. 3b and d) fit obtained from the data of leg 1 (150m average; see fig. 2a). figure 3a and b show the results of the thickness estimation for leg 1, i.e. using dependent data. figure 3c and d show the results of this estimation for leg 3, i.e. using independent data. figure 3 reveals that the logarithmic fit yields lower ice-thickness values than the linear fit. table 1 summarizes the results of a regression analysis of heliscat-derived and em thin-ice thickness, together with the correlation between both datasets (assuming a linear relationship) and the standard deviation of the mean thin-ice thickness in the range 0.0– 0.6 m. these results are given separately for the dependent data of leg 1 (see fig. 3a and b) in the first data line, and for the independent data of leg 3 (see fig. 3c and d) in the second data line. the two bottom lines in table 1 show a comparison between mean results of regression analyses between heliscat-derived and em thin-ice thickness of all legs for two different averaging windows (150 and 300 m). it should be noted that, in case of using an averaging window of 300 m, the heliscat-derived thickness is derived from the fits plotted in figure 2d instead of those given in figure 2a.

Fig. 3. Heliscat-derived vs EM ice thickness using the fits obtained from data of leg 1 using SNR > 20 dB, with an averaging window of 150m (plotted in Fig. 2a). Thicknesses are (a) for leg 1 using the linear fit; (b) for leg 1 using the logarithmic fit; and (c, d) for the independent data of leg 3 using the linear (c) and the logarithmic fit (d). Thick grey lines denote the linear regression between each of the thickness datasets shown; results of these regressions are also given in the two upper lines of Table 1. Thin black diagonals denote perfect agreement. Note the different vertical scale compared to Figure 2.
Table 1. Comparison between Heliscat-derived and EM thin-ice thickness for ice-thickness values between 0.0 and 0.6 m Given are the leg numbers, the type of fit, the correlation between derived and measured thickness, the number of data pairs, the rms difference and intercept for the regression between the derived and measured thickness, and the standard deviation (sTDV) of the mean derived and mean measured thickness within the above-given thickness limits. Top two lines: results for leg 1 (see Fig. 3a and b) and for leg 3 (see Fig. 3c and d); bottom two lines: mean results (except number of data pairs) considering all legs (dependent and independent data) for two different averaging windows
5. Discussion
For the ice thickness and CPR used in this study (see sections 2 and 3), heliscat-derived and em thin-ice thickness are in reasonable agreement with each other within the uncertainties given by the two involved sensors: about ±0.05m for em measurements averaged over a reasonable number of single measurements, and ±0.14m for the CPR (see section 2 and fig. 2). in detail, correlations are similar for the linear (0.724) and the logarithmic fit (0.723). the rms difference of the regression (for thickness values of 0.0–0.6 m) between heliscat-derived and em thin-ice thickness is similar for both fits, while the intercept of the regression line is substantially higher for the linear fit: 0.17m compared to 0.06m the standard deviation of the mean heliscat-derived ice thickness is in closer agreement with the measured ice-thickness variability for the logarithmic fit. because of this and because the achieved intercepts are substantially lower (cf., e.g., fig. 3a andb), we suggest using the logarithmic fit. this agrees with earlier findings about the relationship between the CPR and the thickness of thin ice (e.g. Reference NghiemOnstott, 1992; Reference schauer and KattnerWakabayashi and others, 2004).
The maximum obtainable thickness is around 50–60 cm, which agrees to some extent with the findings of wakabaya-shi and others (2004; see fig. 11b). they used an airborne fully polarimetric l-band synthetic aperture radar (pi-sar; spatial resolution 3m) to observe sea-ice radar backscatter in the sea of okhotsk just north of hokkaido, japan. the CPR at l-band (calculated from the scattering matrix) was averaged over 20m×20m gridcells with 10m sampling distance along a track given by ice draft and drift observations made by moored sonar. these draft measurements were combined with the CPR observations (time difference <10 hours), both averaged along 100m intervals, in order to obtain the empirical fit used to map the ice thickness from pi-sar CPR observations (Reference schauer and KattnerWakabayashi and others, 2004). the main difference between their approach and ours, regarding instrumentation, is that we benefit from quasi-simultaneous (within seconds) measurements of ice thickness and radar backscatter along the same flight track.
A wider averaging window seems to improve our method (table 1, bottom two rows). but the width of this window together with the footprint size (a few tens of metres for both sensors) determines the minimum observable size of the thin-ice areas: the larger the averaging window, the larger the required along-track extent of a thin-ice area. moreover, the width of the averaging window influences the smallest observable thin-ice thickness and thereby the empirical fit, because open-water areas only a few tens of metres wide are smoothed out. the minimum observable ice thickness increases with the window width: 0 cm for 65 m, 2 cm for 150m and 10cm for 300m (fig. 2c, a and d). this would favour the use of a small averaging window. however, in order to sufficiently reduce instrument noise and noise inherent in the measurements due to small-scale sea-ice heterogeneities, the minimum size of the thin-ice areas to be observed should exceed two to three times the footprint size, i.e. at least 60–120m therefore, we regard the averaging window of 150m as a good compromise.
The heliscat measurements were carried out at 40˚ incidence angle. owing to the fact that the CPR change per unit change in thin-ice thickness (1 cm) is larger at higher incidence angles than at low ones (see section 3), our approach could benefit from radar backscatter measurements carried out at larger incidence angles. however, an important drawback of larger incidence angles is that the radar backscatter of level surfaces is closer to the noise level compared to smaller incidence angles. another improvement would be to improve the accuracy of the independent ice-thickness measurements, particularly for very thin ice, for which the accuracy of the em measurements decreases. such an improvement could be to additionally calculate the thin-ice thickness via the heat-flux method (Reference Drucker, Martin and MoritzDrucker and others, 2003) using simultaneous ir temperature measurements.
Reference Kwok, Nghiem, Yueh and HuynhKwok and others (1995) noted that a highly saline brine skim could be present, particularly on very thin ice (below 10 cm). such a skim is responsible for the high co-polarization values observed here. however, when the thin ice becomes covered even with a thin snow layer, this skim will vanish, the co-polarization ratio will decrease and the thin-ice thickness will be overestimated. a natural step to avoid this error source using our data would be to include the simultaneous video imagery in the analysis by classifying the thin ice into bare and snow-/slush-covered and develop the approach separately for different thin-ice classes.
6. Conclusions
The relationship between sea-ice thickness and like-polarized l-band radar backscatter has been investigated by synchronous helicopter-based measurements carried out north of svalbard in april 2003, during a tandem flight of an em induction ice-thickness sounder (em-bird) and a multi-frequency, multi-polarization scatterometer (heliscat). these are combined to derive a method for thin-ice thickness solely from l-band CPR data. co-located em ice-thickness and heliscat l-band CPR data are compared after smoothing with a running mean of different length along track. a linear and a logarithmic fit are applied to the data for em ice-thickness values between 0.0 and 0.6m and 0.0 and 1.0 m, respectively. the thin-ice thickness is derived by applying these fits to dependent (i.e. used to obtain the fits) and independent heliscat l-band CPR data. subsequently, heliscat-derived and em ice thickness are compared for ice-thickness values between 0.0 and 0.6m using a linear regression. the logarithmic fit gave the most reliable results: correlation 0.72; intercept of regression 6 cm; and rms difference 8 cm. it has to be stressed here, however, that the approach can only be applied to thin ice, i.e. below 50– 60 cm thickness, and that the role snow and/or slush has on the retrieval needs still to be investigated. consequently, the next step is to apply the method to data of other heliscat flights carried out during ark XIX/1 to further test the method, particularly with regard to the presence of snow or frost flowers on the surface because both can change the dielectric properties and roughness of the ice surface. the launch of alos–palsar (advanced land observing satellite–phased array-type l-band sar) in early 2006 will provide space-borne l-band data to which our method could be applied after some modification, provided that the CPR will be available from these data and that requirements regarding snr and incidence angle will be met. this might open the opportunity to obtain estimates of the thin-ice thickness on a regular basis independent of weather, daylight and limitations of numerical models.
Acknowledgements
This work was supported by the german science foundation (dfg): me-487/40-1, sfb 512 – e1, and the european union via evg1-ct-2000-00029 (marsais) and evk2-ct-2002-00146 (sithos). we thank the crew of the R/v Polarstern, the helicopter team and j. lieser, s. willmes and t. martin, as well as three anonymous reviewers.






