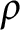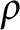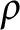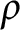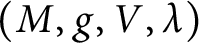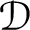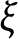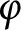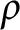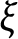1 Introduction
In recent years, the pioneering works of Hamilton [Reference Hamilton14] and Perelman [Reference Shaikh, Cunha and Mandal19] toward the solution of the Poincaré conjecture have produced a flourishing activity in the research of self-similar solutions, or solitons, of the Ricci flow. For more details on Ricci solitons, we refer to the reader to [Reference Barros and Ribeiro1, Reference Deshmukh, Al-sodais and Turki9, Reference Ghosh11–Reference Ghosh and Sharma13, Reference Perelman18, Reference Kumara and Venkatesha21]. In general, Bourguignon [Reference Bourguignon4] introduced a perturbed version of the Ricci flow on an n-dimensional Riemannian manifold
![]() $(M,g)$
, which satisfies the following evolution equation [Reference Bourguignon4] considered a geometric flow of the following type:
$(M,g)$
, which satisfies the following evolution equation [Reference Bourguignon4] considered a geometric flow of the following type:
 $$ \begin{align} \frac{\partial g}{\partial t}=-2\,({\operatorname{Ric_g}}-\rho\, r\,g), \end{align} $$
$$ \begin{align} \frac{\partial g}{\partial t}=-2\,({\operatorname{Ric_g}}-\rho\, r\,g), \end{align} $$
where
![]() ${\operatorname {Ric_g}}$
is the Ricci tensor, r is the scalar curvature of g and
${\operatorname {Ric_g}}$
is the Ricci tensor, r is the scalar curvature of g and
![]() $\rho \in \mathbb {R}$
. This flow is known as the Ricci-Bourguignon flow (or shortly RB flow) and the short time existence
$\rho \in \mathbb {R}$
. This flow is known as the Ricci-Bourguignon flow (or shortly RB flow) and the short time existence
 $\Big (\mbox {for }\rho <\frac {1}{2(n-1)}\Big )$
of this flow is provided in [Reference Catino, Cremaschi, Djadli, Mantegazza and Mazzieri7]. This family of geometric flows contains, as a special case, the Einstein flow
$\Big (\mbox {for }\rho <\frac {1}{2(n-1)}\Big )$
of this flow is provided in [Reference Catino, Cremaschi, Djadli, Mantegazza and Mazzieri7]. This family of geometric flows contains, as a special case, the Einstein flow
 $\big (\rho =\frac {1}{2}\big )$
, the traceless Ricci flow
$\big (\rho =\frac {1}{2}\big )$
, the traceless Ricci flow
 $\big (\rho =\frac {1}{n}\big )$
, the Schouten flow
$\big (\rho =\frac {1}{n}\big )$
, the Schouten flow
 $\Big (\rho =\frac {1}{2(n-1)}\Big )$
and the Ricci flow
$\Big (\rho =\frac {1}{2(n-1)}\Big )$
and the Ricci flow
 $\big (\rho =0\big )$
, and so on, see [Reference Catino, Cremaschi, Djadli, Mantegazza and Mazzieri7, Reference Huang15, Reference Shaikh, Cunha and Mandal19]. On the other hand, by choosing
$\big (\rho =0\big )$
, and so on, see [Reference Catino, Cremaschi, Djadli, Mantegazza and Mazzieri7, Reference Huang15, Reference Shaikh, Cunha and Mandal19]. On the other hand, by choosing
![]() $\rho \rightarrow -\infty $
, the RB flow behaves like a Yamabe flow. Recently, Ho [Reference Huang15] studied this flow on locally homogeneous
$\rho \rightarrow -\infty $
, the RB flow behaves like a Yamabe flow. Recently, Ho [Reference Huang15] studied this flow on locally homogeneous
![]() $3$
-manifolds. More examples of this flow were constructed on the product of an Anti de Sitter space with sphere in [Reference Biaso and Lüst2]. The self-similar solution associated to the flow (1.1) is described by the following definition:
$3$
-manifolds. More examples of this flow were constructed on the product of an Anti de Sitter space with sphere in [Reference Biaso and Lüst2]. The self-similar solution associated to the flow (1.1) is described by the following definition:
Definition 1.1 An n-dimensional Riemannian manifold
![]() $(M,g)$
,
$(M,g)$
,
![]() $n\geq 3$
, is said to be a Ricci–Bouguignon soliton (or RB soliton or
$n\geq 3$
, is said to be a Ricci–Bouguignon soliton (or RB soliton or
![]() $\rho $
-Einstein soliton) if there is a smooth vector field V (called potential vector field) satisfying
$\rho $
-Einstein soliton) if there is a smooth vector field V (called potential vector field) satisfying
 $$ \begin{align} \frac{1}{2}\,{\cal L}_{V}g + {\operatorname{Ric_g}} - \rho\, r\,g = \lambda\,g, \end{align} $$
$$ \begin{align} \frac{1}{2}\,{\cal L}_{V}g + {\operatorname{Ric_g}} - \rho\, r\,g = \lambda\,g, \end{align} $$
where
![]() $\rho ,\lambda \in \mathbb {R}$
and
$\rho ,\lambda \in \mathbb {R}$
and
![]() ${\cal L}_{V}$
denotes the Lie-derivative in the direction of V.
${\cal L}_{V}$
denotes the Lie-derivative in the direction of V.
It is a natural generalization of Einstein metrics and is a topic of current research in Riemannian geometry, see details [Reference Catino, Cremaschi, Djadli, Mantegazza and Mazzieri7, Reference Dwivedi10, Reference Ho16, Reference Huang15, Reference Sharma20]. It is denoted by
![]() $(M,g,V,\lambda )$
. A
$(M,g,V,\lambda )$
. A
![]() $\rho $
-Einstein soliton is called trivial if V is a Killing vector field, i.e.,
$\rho $
-Einstein soliton is called trivial if V is a Killing vector field, i.e.,
![]() ${\cal L}_{V}g=0$
. We say that a soliton is shrinking, steady, or expanding if
${\cal L}_{V}g=0$
. We say that a soliton is shrinking, steady, or expanding if
![]() $\lambda>0, \lambda =0$
, or
$\lambda>0, \lambda =0$
, or
![]() $\lambda <0$
, respectively. For particular value of the parameter
$\lambda <0$
, respectively. For particular value of the parameter
![]() $\rho $
, a
$\rho $
, a
![]() $\rho $
-Einstein soliton is called
$\rho $
-Einstein soliton is called
-
(I) Einstein soliton if
 $\rho =\frac {1}{2}$
,
$\rho =\frac {1}{2}$
, -
(II) traceless Ricci soliton if
 $\rho =\frac {1}{n}$
, and
$\rho =\frac {1}{n}$
, and -
(III) Schouten soliton if
 $\rho =\frac {1}{2(n-1)}$
.
$\rho =\frac {1}{2(n-1)}$
.
Recently, Dwivedi [Reference Dwivedi10] introduced the notion of Ricci–Bourguignon almost soliton (or RB almost soliton or
![]() $\rho $
-Einstein almost soliton) by allowing the soliton constant
$\rho $
-Einstein almost soliton) by allowing the soliton constant
![]() $\lambda $
to be a smooth function. If
$\lambda $
to be a smooth function. If
![]() $\nabla f$
is the gradient of a smooth function f on M, then the Hessian of f is defined by
$\nabla f$
is the gradient of a smooth function f on M, then the Hessian of f is defined by
 $$ \begin{align*} \nabla^2f(X_1,Y_1)={\textrm{Hess}}_f(X_1,Y_1) = g(\nabla_{X_1} \nabla f,Y_1) \end{align*} $$
$$ \begin{align*} \nabla^2f(X_1,Y_1)={\textrm{Hess}}_f(X_1,Y_1) = g(\nabla_{X_1} \nabla f,Y_1) \end{align*} $$
for all vector fields
![]() $X_1,Y_1$
on M. In particular, if
$X_1,Y_1$
on M. In particular, if
![]() $V=\nabla f$
for some smooth function f, then
$V=\nabla f$
for some smooth function f, then
 ${\cal L}_{\nabla f}=2\,\nabla ^2 f = \textrm{Hess}_\textrm{f}$
and the
${\cal L}_{\nabla f}=2\,\nabla ^2 f = \textrm{Hess}_\textrm{f}$
and the
![]() $\rho $
-Einstein soliton and
$\rho $
-Einstein soliton and
![]() $\rho $
-Einstein almost soliton is called the gradient
$\rho $
-Einstein almost soliton is called the gradient
![]() $\rho $
-Einstein soliton and gradient
$\rho $
-Einstein soliton and gradient
![]() $\rho $
-Einstein almost soliton, respectively, see details in [Reference Ho16, Reference Sharma20, Reference Venkatesha and Kumara22].
$\rho $
-Einstein almost soliton, respectively, see details in [Reference Ho16, Reference Sharma20, Reference Venkatesha and Kumara22].
In [Reference Catino, Cremaschi, Djadli, Mantegazza and Mazzieri7], Catino et al. studied the
![]() $\rho $
-Einstein solitons where they obtained important rigidity results and proved that every compact gradient Einstein, Schouten, or traceless Ricci soliton is trivial. Recently, Dwivedi [Reference Dwivedi10] studied
$\rho $
-Einstein solitons where they obtained important rigidity results and proved that every compact gradient Einstein, Schouten, or traceless Ricci soliton is trivial. Recently, Dwivedi [Reference Dwivedi10] studied
![]() $\rho $
-Einstein almost solitons and presented some nontrivial examples. He found some integral formulas for compact gradient
$\rho $
-Einstein almost solitons and presented some nontrivial examples. He found some integral formulas for compact gradient
![]() $\rho $
-Einstein solitons and compact gradient
$\rho $
-Einstein solitons and compact gradient
![]() $\rho $
-Einstein almost solitons. Using the integral formulas, he found some sufficient conditions under which a gradient
$\rho $
-Einstein almost solitons. Using the integral formulas, he found some sufficient conditions under which a gradient
![]() $\rho $
-Einstein almost solitons are isometric to a unit sphere or Einstein (trivial). On the other hand, Ho [Reference Huang15] studied gradient shrinking
$\rho $
-Einstein almost solitons are isometric to a unit sphere or Einstein (trivial). On the other hand, Ho [Reference Huang15] studied gradient shrinking
![]() $\rho $
-Einstein solitons under the assumption of Bach flatness, and Huang [Reference Ho16] found some integral pinching rigidity results for compact gradient shrinking
$\rho $
-Einstein solitons under the assumption of Bach flatness, and Huang [Reference Ho16] found some integral pinching rigidity results for compact gradient shrinking
![]() $\rho $
-Einstein solitons. Recently, Shaikh et al. [Reference Sharma20] found some geometric characterizations of gradient
$\rho $
-Einstein solitons. Recently, Shaikh et al. [Reference Sharma20] found some geometric characterizations of gradient
![]() $\rho $
-Einstein solitons.
$\rho $
-Einstein solitons.
In [Reference Ghosh and Sharma12], Ghosh-Sharma proved that if a Sasakian manifold of dimension
![]() $>3$
admits a nontrivial Ricci soliton, then M is
$>3$
admits a nontrivial Ricci soliton, then M is
![]() $\mathcal {D}$
-homothetically fixed null
$\mathcal {D}$
-homothetically fixed null
![]() $\eta $
-Einstein, and the potential vector field V leaves the structure tensor
$\eta $
-Einstein, and the potential vector field V leaves the structure tensor
![]() $\varphi $
invariant, and is an infinitesimal contact
$\varphi $
invariant, and is an infinitesimal contact
![]() $\mathcal {D}$
-homothetic transformation. It is well known that the scalar curvature on a Sasakian manifold is not a constant, and therefore,
$\mathcal {D}$
-homothetic transformation. It is well known that the scalar curvature on a Sasakian manifold is not a constant, and therefore,
![]() $\rho $
-Einstein solitons are an interesting generalization of Ricci solitons. In our first result, we generalize and improve the Theorem
$\rho $
-Einstein solitons are an interesting generalization of Ricci solitons. In our first result, we generalize and improve the Theorem
![]() $1$
of [Reference Ghosh and Sharma12] for
$1$
of [Reference Ghosh and Sharma12] for
![]() $\rho $
-Einstein soliton. Now, we recall the following definitions.
$\rho $
-Einstein soliton. Now, we recall the following definitions.
A contact metric manifold
![]() $(M^{2n+1},\varphi ,\xi ,\eta ,g)$
is said to be
$(M^{2n+1},\varphi ,\xi ,\eta ,g)$
is said to be
![]() $\eta $
-Einstein if its Ricci curvature tensor has the form
$\eta $
-Einstein if its Ricci curvature tensor has the form
where
![]() $\alpha $
,
$\alpha $
,
![]() $\beta $
are smooth functions on M. For a K-contact manifold of dimension
$\beta $
are smooth functions on M. For a K-contact manifold of dimension
![]() $>3$
,
$>3$
,
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are constants, see Yano and Kon [Reference Yano and Kon24, p. 286]. Moreover, under a
$\beta $
are constants, see Yano and Kon [Reference Yano and Kon24, p. 286]. Moreover, under a
![]() $\mathcal {D}$
-homothetic deformation:
$\mathcal {D}$
-homothetic deformation:
 $$ \begin{align*} \bar{\eta} = a\eta, \quad \bar{\xi}= \frac{1}{a}\xi, \quad \bar{\varphi} = \varphi, \quad \bar{g} = ag + a(a-1)\eta\otimes\eta \end{align*} $$
$$ \begin{align*} \bar{\eta} = a\eta, \quad \bar{\xi}= \frac{1}{a}\xi, \quad \bar{\varphi} = \varphi, \quad \bar{g} = ag + a(a-1)\eta\otimes\eta \end{align*} $$
for a positive real constant a, a K-contact
![]() $\eta $
-Einstein manifold transforms to another K-contact
$\eta $
-Einstein manifold transforms to another K-contact
![]() $\eta $
-Einstein manifold, in which
$\eta $
-Einstein manifold, in which
![]() $\bar {\alpha } = ({\alpha + 2 - 2a})/{a}$
and
$\bar {\alpha } = ({\alpha + 2 - 2a})/{a}$
and
![]() $\bar {\beta } = 2n - \bar {\alpha }$
. In particular, for
$\bar {\beta } = 2n - \bar {\alpha }$
. In particular, for
![]() $\alpha =-2$
remains fixed under a homothetic deformation, and as
$\alpha =-2$
remains fixed under a homothetic deformation, and as
![]() $\alpha +\beta =2n$
,
$\alpha +\beta =2n$
,
![]() $\beta $
also remains fixed, and therefore, we define: a K-contact
$\beta $
also remains fixed, and therefore, we define: a K-contact
![]() $\eta $
-Einstein manifold with
$\eta $
-Einstein manifold with
![]() $\alpha =-2$
is said to be
$\alpha =-2$
is said to be
![]() $\mathcal {D}$
-homothetically fixed.
$\mathcal {D}$
-homothetically fixed.
Let J denotes the restrictionof
![]() $\varphi $
to the contact sub-bundle
$\varphi $
to the contact sub-bundle
![]() $\mathcal {D} (\eta =0)$
. Then for a Sasakian manifold,
$\mathcal {D} (\eta =0)$
. Then for a Sasakian manifold,
![]() $(\mathcal {D}, J, d\eta )$
defines a Kähler metric on
$(\mathcal {D}, J, d\eta )$
defines a Kähler metric on
![]() $\mathcal {D}$
, with the transverse Kähler metric
$\mathcal {D}$
, with the transverse Kähler metric
![]() $g^{T}$
related to the Sasakian metric g as
$g^{T}$
related to the Sasakian metric g as
![]() $g = g^{T} + \eta \otimes \eta $
. One can easily compute the relation between the transverse Ricci tensor
$g = g^{T} + \eta \otimes \eta $
. One can easily compute the relation between the transverse Ricci tensor
 ${\operatorname {Ric_g}}^{T}$
of
${\operatorname {Ric_g}}^{T}$
of
![]() $g^{T}$
and the Ricci tensor
$g^{T}$
and the Ricci tensor
![]() ${\operatorname {Ric_g}}$
of g by
${\operatorname {Ric_g}}$
of g by
 $$ \begin{align*} {\operatorname{Ric_g}}^T (X_1,Y_1) = {\operatorname{Ric_g}}(X_1,Y_1) + 2\,g(X_1,Y_1), \quad X_1,Y_1\in\mathcal{D}. \end{align*} $$
$$ \begin{align*} {\operatorname{Ric_g}}^T (X_1,Y_1) = {\operatorname{Ric_g}}(X_1,Y_1) + 2\,g(X_1,Y_1), \quad X_1,Y_1\in\mathcal{D}. \end{align*} $$
The Ricci form
![]() $\tau $
and transverse Ricci form
$\tau $
and transverse Ricci form
![]() $\tau ^T$
are defined by
$\tau ^T$
are defined by
 $$ \begin{align*} \tau(X_1,Y_1)={\operatorname{Ric_g}} (X_1,\varphi Y_1), \qquad \tau^T(X_1,Y_1) = {\operatorname{Ric_g}}^T(X_1,\varphi Y_1), \quad \quad X_1,Y_1\in\mathcal{D}. \end{align*} $$
$$ \begin{align*} \tau(X_1,Y_1)={\operatorname{Ric_g}} (X_1,\varphi Y_1), \qquad \tau^T(X_1,Y_1) = {\operatorname{Ric_g}}^T(X_1,\varphi Y_1), \quad \quad X_1,Y_1\in\mathcal{D}. \end{align*} $$
The basic first Chern class
![]() $2\,\pi c_1^{B}$
of
$2\,\pi c_1^{B}$
of
![]() $\mathcal {D}$
is represented by
$\mathcal {D}$
is represented by
![]() $\tau ^T$
. A Sasakian structure is said to be null (transverse Calabi-Yau) if
$\tau ^T$
. A Sasakian structure is said to be null (transverse Calabi-Yau) if
![]() $c_1^{B}=0$
. An
$c_1^{B}=0$
. An
![]() $\eta $
-Einstein Sasakian manifold with
$\eta $
-Einstein Sasakian manifold with
![]() $\alpha = -2$
and
$\alpha = -2$
and
![]() $\beta = 2n+2$
is known as null-Sasakian, which is characterized by
$\beta = 2n+2$
is known as null-Sasakian, which is characterized by
![]() $c_{1}^B = 0$
. Further, an
$c_{1}^B = 0$
. Further, an
![]() $\eta $
-Einstein Sasakian manifold with
$\eta $
-Einstein Sasakian manifold with
![]() $\alpha> -2$
is called a positive-Sasakian manifold. We refer the reader to [Reference Boyer and Galicki6] for details of its importance, examples and geometrical characteristics.
$\alpha> -2$
is called a positive-Sasakian manifold. We refer the reader to [Reference Boyer and Galicki6] for details of its importance, examples and geometrical characteristics.
Theorem 1.1 If a Sasakian manifold
![]() $(M^{2n+1},\varphi ,\xi ,\eta ,g)$
,
$(M^{2n+1},\varphi ,\xi ,\eta ,g)$
,
![]() $n>1$
, admits a nontrivial
$n>1$
, admits a nontrivial
![]() $\rho $
-Einstein soliton
$\rho $
-Einstein soliton
![]() $(M,g,V,\lambda )$
, then
$(M,g,V,\lambda )$
, then
-
(i) the soliton vector field V is a Jacobi field along trajectories of the Reeb vector field
 $\xi $
,
$\xi $
, -
(ii) M is
 $\mathcal {D}$
-homothetically fixed null
$\mathcal {D}$
-homothetically fixed null
 $\eta $
-Einstein,
$\eta $
-Einstein, -
(iii) V is a non-strict infinitesimal contact transformation and is equal to
 $-\frac {1}{2}\,\varphi \,\nabla f+f\,\xi $
for a smooth function f on M such that
$-\frac {1}{2}\,\varphi \,\nabla f+f\,\xi $
for a smooth function f on M such that
 $\xi (f)=-4(n+1),$
and
$\xi (f)=-4(n+1),$
and -
(iv) Vleaves the structure tensor
 $\varphi $
invariant.
$\varphi $
invariant.
Remark 1.2 One may ask: under what conditions the above result holds for
![]() $\rho $
-Einstein almost soliton? Following Theorem
$\rho $
-Einstein almost soliton? Following Theorem
![]() $3.1$
of [Reference Ghosh11] and our Proposition 2.1, one can see that the above theorem also holds for
$3.1$
of [Reference Ghosh11] and our Proposition 2.1, one can see that the above theorem also holds for
![]() $\rho $
-Einstein almost soliton if V is a Jacobi field along trajectories of the Reeb vector field
$\rho $
-Einstein almost soliton if V is a Jacobi field along trajectories of the Reeb vector field
![]() $\xi $
.
$\xi $
.
In the geometry of a Ricci almost soliton, an important question is: under what conditions a Ricci almost soliton is trivial (Einstein)? Several results are proved in finding conditions under which a compact Ricci almost soliton is trivial, see details in [Reference Barros and Ribeiro1, Reference Deshmukh, Al-sodais and Turki9, Reference Deshmukh and Al-Sodais8, Reference Ghosh11, Reference Perelman18]. Note that a
![]() $\rho $
-Einstein almost soliton is a generalization of an Einstein manifold, Ricci soliton, Ricci almost soliton, as well as
$\rho $
-Einstein almost soliton is a generalization of an Einstein manifold, Ricci soliton, Ricci almost soliton, as well as
![]() $\rho $
-Einstein soliton; therefore, the following question arises:
$\rho $
-Einstein soliton; therefore, the following question arises:
Under what conditions a
![]() $\rho $
-Einstein almost soliton on a K-contact manifold is trivial (Einstein)?
$\rho $
-Einstein almost soliton on a K-contact manifold is trivial (Einstein)?
In [Reference Dwivedi10], Dwivedi obtained some sufficient conditions under which a compact
![]() $\rho $
-Einstein almost soliton is trivial (Einstein) on Riemannian manifold. Here, we find some sufficient conditions under which a
$\rho $
-Einstein almost soliton is trivial (Einstein) on Riemannian manifold. Here, we find some sufficient conditions under which a
![]() $\rho $
-Einstein almost soliton on K-contact manifold is trivial (Einstein). For this, in the next theorem, we consider the potential vector field as an infinitesimal contact transformation.
$\rho $
-Einstein almost soliton on K-contact manifold is trivial (Einstein). For this, in the next theorem, we consider the potential vector field as an infinitesimal contact transformation.
Theorem 1.3 If a compact K-contact manifold
![]() $(M^{2n+1},\varphi ,\xi ,\eta ,g)$
admits a
$(M^{2n+1},\varphi ,\xi ,\eta ,g)$
admits a
![]() $\rho $
-Einstein almost soliton
$\rho $
-Einstein almost soliton
![]() $(M,g,V,\lambda )$
with the potential vector field V is an infinitesimal contact transformation, then V is an infinitesimal automorphism and g is trivial
$(M,g,V,\lambda )$
with the potential vector field V is an infinitesimal contact transformation, then V is an infinitesimal automorphism and g is trivial
![]() $(Einstein)$
Sasakian and of constant scalar curvature
$(Einstein)$
Sasakian and of constant scalar curvature
![]() $2n(2n+1)$
. Moreover, the soliton is expanding, steady, or shrinking if
$2n(2n+1)$
. Moreover, the soliton is expanding, steady, or shrinking if
 $\rho>\frac {1}{2n+1}$
,
$\rho>\frac {1}{2n+1}$
,
 $\rho =\frac {1}{2n+1}$
, or
$\rho =\frac {1}{2n+1}$
, or
 $\rho <\frac {1}{2n+1}$
, respectively.
$\rho <\frac {1}{2n+1}$
, respectively.
Next, considering that the potential vector field V is parallel to the Reeb vector field
![]() $\xi $
, we find one more sufficient condition for trivial
$\xi $
, we find one more sufficient condition for trivial
![]() $\rho $
-Einstein almost soliton.
$\rho $
-Einstein almost soliton.
Theorem 1.4 If a K-contact manifold
![]() $(M^{2n+1},\varphi ,\xi ,\eta ,g)$
admits a
$(M^{2n+1},\varphi ,\xi ,\eta ,g)$
admits a
![]() $\rho $
-Einstein almost soliton
$\rho $
-Einstein almost soliton
![]() $(M,g,V,\lambda )$
, whose potential vector field V is parallel to the Reeb vector field
$(M,g,V,\lambda )$
, whose potential vector field V is parallel to the Reeb vector field
![]() $\xi $
, then V is a Killing vector field, g is trivial
$\xi $
, then V is a Killing vector field, g is trivial
![]() $(Einstein)$
and of constant scalar curvature
$(Einstein)$
and of constant scalar curvature
![]() $2n(2n+1)$
. Moreover, the soliton is expanding, steady, or shrinking if
$2n(2n+1)$
. Moreover, the soliton is expanding, steady, or shrinking if
 $\rho>\frac {1}{2n+1}$
,
$\rho>\frac {1}{2n+1}$
,
 $\rho =\frac {1}{2n+1}$
, or
$\rho =\frac {1}{2n+1}$
, or
 $\rho <\frac {1}{2n+1}$
, respectively.
$\rho <\frac {1}{2n+1}$
, respectively.
Finally, applying Boyer and Galicki’s result (see Theorem 11.1.7 of [Reference Boyer, Galicki and Matzeu5, p. 372]): “any compact K-contact Einstein manifold is Sasakian” in the previous result, we conclude the following.
Corollary 1.5 If a compact K-contact manifold
![]() $(M^{2n+1},\varphi ,\xi ,\eta ,g)$
admits a
$(M^{2n+1},\varphi ,\xi ,\eta ,g)$
admits a
![]() $\rho $
-Einstein almost soliton
$\rho $
-Einstein almost soliton
![]() $(M,g,V,\lambda )$
, whose potential vector field V is parallel to the Reeb vector field
$(M,g,V,\lambda )$
, whose potential vector field V is parallel to the Reeb vector field
![]() $\xi $
, then V is a Killing vector field, g is trivial
$\xi $
, then V is a Killing vector field, g is trivial
![]() $(Einstein)$
Sasakian and of constant scalar curvature
$(Einstein)$
Sasakian and of constant scalar curvature
![]() $2n(2n+1)$
. Moreover, the soliton is expanding, steady, or shrinking if
$2n(2n+1)$
. Moreover, the soliton is expanding, steady, or shrinking if
 $\rho>\frac {1}{2n+1}$
,
$\rho>\frac {1}{2n+1}$
,
 $\rho =\frac {1}{2n+1}$
, or
$\rho =\frac {1}{2n+1}$
, or
 $\rho <\frac {1}{2n+1}$
, respectively.
$\rho <\frac {1}{2n+1}$
, respectively.
Remark 1.6 We notice that Kumara et al. [Reference Patra17] studied K-contact manifold whose metric is a gradient Einstein-type. From their result (see Theorem
![]() $3.2$
in [Reference Patra17]) it follows that if a complete K-contact manifold admits a gradient
$3.2$
in [Reference Patra17]) it follows that if a complete K-contact manifold admits a gradient
![]() $\rho $
-Einstein almost soliton, then it is compact Einstein Sasakian and isometric to the unit sphere
$\rho $
-Einstein almost soliton, then it is compact Einstein Sasakian and isometric to the unit sphere
![]() $\mathbb {S}^{2n+1}$
.
$\mathbb {S}^{2n+1}$
.
2 Background
In this section, we recall some basic facts about Sasakian geometry and fixing the notation which will be adopted in the rest of the paper. All manifolds are assumed to be smooth and connected.
Let
![]() $\nabla $
be the Levi-Civita connection of a Riemannian manifold
$\nabla $
be the Levi-Civita connection of a Riemannian manifold
![]() $(M,g)$
and R the Riemann curvature tensor of g, given by
$(M,g)$
and R the Riemann curvature tensor of g, given by
where
![]() $\mathfrak {X}(M)$
is the Lie algebra of all vector fields on M. We recall that the Ricci operator Q is a symmetric
$\mathfrak {X}(M)$
is the Lie algebra of all vector fields on M. We recall that the Ricci operator Q is a symmetric
![]() $(1,1)$
-tensor field defined by
$(1,1)$
-tensor field defined by
 $$ \begin{align*} g(QX_1,Y_1)={\operatorname{Ric_g}} (X_1,Y_1)={\operatorname{Tr_g}}\big\{Z_1\rightarrow R(Z_1,X_1)Y_1\big\}, \quad X_1,Y_1,Z_1\in\mathfrak{X}(M), \end{align*} $$
$$ \begin{align*} g(QX_1,Y_1)={\operatorname{Ric_g}} (X_1,Y_1)={\operatorname{Tr_g}}\big\{Z_1\rightarrow R(Z_1,X_1)Y_1\big\}, \quad X_1,Y_1,Z_1\in\mathfrak{X}(M), \end{align*} $$
and the scalar curvature of g is the smooth function defined by
![]() $r={\operatorname {Tr_g}} Q$
. The gradient of the scalar curvature r is given by
$r={\operatorname {Tr_g}} Q$
. The gradient of the scalar curvature r is given by
 $$ \begin{align} \frac{1}{2}\,g(X_1,\nabla r) = ({\operatorname{div}} Q)(X_1)=\sum\nolimits_{\,i} g((\nabla_{E_i}Q)X_1,E_i), \quad X_1\in\mathfrak{X}(M), \end{align} $$
$$ \begin{align} \frac{1}{2}\,g(X_1,\nabla r) = ({\operatorname{div}} Q)(X_1)=\sum\nolimits_{\,i} g((\nabla_{E_i}Q)X_1,E_i), \quad X_1\in\mathfrak{X}(M), \end{align} $$
where
![]() $\{E_i\}$
is a local orthonormal frame on M.
$\{E_i\}$
is a local orthonormal frame on M.
A
![]() $(2n+1)$
-dimensional manifold M is said to be a contact manifold if it admits a global
$(2n+1)$
-dimensional manifold M is said to be a contact manifold if it admits a global
![]() $1$
-form
$1$
-form
![]() $\eta $
(called a contact form) such that
$\eta $
(called a contact form) such that
![]() $\eta \wedge (d\eta )^{n} \ne 0$
. For such a structure, there exists a unique vector field
$\eta \wedge (d\eta )^{n} \ne 0$
. For such a structure, there exists a unique vector field
![]() $\xi $
, called the Reeb vector field or characteristic vector field, satisfying
$\xi $
, called the Reeb vector field or characteristic vector field, satisfying
![]() $d\eta (\xi ,\,\cdot )=0$
and
$d\eta (\xi ,\,\cdot )=0$
and
![]() $\eta (\xi )=1$
. In addition, polarization of
$\eta (\xi )=1$
. In addition, polarization of
![]() $d\eta $
on the contact sub-bundle
$d\eta $
on the contact sub-bundle
![]() $\mathcal {D}$
(defined by
$\mathcal {D}$
(defined by
![]() $\eta =0$
) gives a
$\eta =0$
) gives a
![]() $(1,1)$
-tensor field
$(1,1)$
-tensor field
![]() $\varphi $
, and the Riemannian metric g satisfying
$\varphi $
, and the Riemannian metric g satisfying
where
![]() $id:TM\to TM$
is the identity operator. The above structure
$id:TM\to TM$
is the identity operator. The above structure
![]() $(\varphi ,\xi ,\eta ,g)$
is called a contact metric structure,
$(\varphi ,\xi ,\eta ,g)$
is called a contact metric structure,
![]() $(M^{2n+1},\varphi ,\xi ,\eta ,g)$
a contact metric manifold and g an associated metric. It follows from (2.3) that
$(M^{2n+1},\varphi ,\xi ,\eta ,g)$
a contact metric manifold and g an associated metric. It follows from (2.3) that
Moreover, a contact metric manifold
![]() $(M^{2n+1},\varphi ,\xi ,\eta ,g)$
is said to be Sasakian if the metric cone
$(M^{2n+1},\varphi ,\xi ,\eta ,g)$
is said to be Sasakian if the metric cone
![]() $(C(M),\bar {g})=(M\times \mathbb {R}^+, r^2g+dr^2)$
over M, is Kähler, or equivalently, a contact metric manifold is said to be Sasakian manifold (see [Reference Blair3, p. 86]) if
$(C(M),\bar {g})=(M\times \mathbb {R}^+, r^2g+dr^2)$
over M, is Kähler, or equivalently, a contact metric manifold is said to be Sasakian manifold (see [Reference Blair3, p. 86]) if
The curvature tensor R of a Sasakian manifold has the following property:
A vector field
![]() $X_1$
on a Riemannian manifold
$X_1$
on a Riemannian manifold
![]() $(M,g)$
is said to be Killing if
$(M,g)$
is said to be Killing if
![]() ${\cal L}\,_{X_1}\,g = 0$
. It is well known that if
${\cal L}\,_{X_1}\,g = 0$
. It is well known that if
![]() $\xi $
is a Killing vector field, then M is said to be a K-contact manifold. A Sasakian manifold is a K-contact manifold, but the converse is true only in dimension
$\xi $
is a Killing vector field, then M is said to be a K-contact manifold. A Sasakian manifold is a K-contact manifold, but the converse is true only in dimension
![]() $3$
(e.g., [Reference Blair3, p. 87]). On a K-contact manifold, the following formulae are valid (see Blair [Reference Blair3, p. 113]):
$3$
(e.g., [Reference Blair3, p. 87]). On a K-contact manifold, the following formulae are valid (see Blair [Reference Blair3, p. 113]):
Further, using (2.7), we find the covariant derivative of (2.8) along an arbitrary vector field
![]() $X_1\in \mathfrak {X}(M)$
,
$X_1\in \mathfrak {X}(M)$
,
According to Blair [Reference Blair3], a vector field V on a contact manifold
![]() $(M,\eta )$
is said to be an infinitesimal contact transformation (or a contact vector field) if it preserves the contact form
$(M,\eta )$
is said to be an infinitesimal contact transformation (or a contact vector field) if it preserves the contact form
![]() $\eta $
, i.e., there exists a smooth function
$\eta $
, i.e., there exists a smooth function
![]() $f : M \rightarrow \mathbb {R}$
satisfying
$f : M \rightarrow \mathbb {R}$
satisfying
and if
![]() $f=0$
, then the vector field V is said to be strict. A vector field V on a contact metric manifold is said to be an infinitesimal automorphism if it leaves
$f=0$
, then the vector field V is said to be strict. A vector field V on a contact metric manifold is said to be an infinitesimal automorphism if it leaves
![]() $\varphi ,\xi ,\eta $
and g invariant.
$\varphi ,\xi ,\eta $
and g invariant.
Proposition 2.1 Let a K-contact (Sasakian) metric g admits an
![]() $\rho $
-Einstein almost soliton. Then the following formula is valid:
$\rho $
-Einstein almost soliton. Then the following formula is valid:
 $$ \begin{align} ({\cal L}_{\,V} \nabla)(X_1,\xi) &+ 2\,Q\varphi X_1 = 4n\,\varphi X_1 + X_1(\lambda+\rho \,r)\xi \notag\\ &+ \xi (\lambda+\rho \,r)X_1 - \eta(X_1)\,\nabla(\lambda+\rho \,r), \quad X_1\in\mathfrak{X}(M). \end{align} $$
$$ \begin{align} ({\cal L}_{\,V} \nabla)(X_1,\xi) &+ 2\,Q\varphi X_1 = 4n\,\varphi X_1 + X_1(\lambda+\rho \,r)\xi \notag\\ &+ \xi (\lambda+\rho \,r)X_1 - \eta(X_1)\,\nabla(\lambda+\rho \,r), \quad X_1\in\mathfrak{X}(M). \end{align} $$
Proof Since the metric g is parallel, taking the covariant derivative of (1.2) along an arbitrary
![]() $Z_1\in \mathfrak {X}(M)$
, we get
$Z_1\in \mathfrak {X}(M)$
, we get
for all
![]() $X_1,Y_1\in \mathfrak {X}(M)$
. According to Yano (see [Reference Yano23, p. 23]), we write
$X_1,Y_1\in \mathfrak {X}(M)$
. According to Yano (see [Reference Yano23, p. 23]), we write
 $$ \begin{align*} &({\cal L}_{V}\nabla_{Z_1}\,g {-} \nabla_{Z_1}\,{\cal L}_{V}g {-} \nabla_{[V,Z_1]}g)(X_1,Y_1)\\ &\quad= -g(({\cal L}_{V}\nabla)(Z_1,X_1),Y_1) {-} g(({\cal L}_{V}\nabla)(Z_1,Y_1),X_1) \end{align*} $$
$$ \begin{align*} &({\cal L}_{V}\nabla_{Z_1}\,g {-} \nabla_{Z_1}\,{\cal L}_{V}g {-} \nabla_{[V,Z_1]}g)(X_1,Y_1)\\ &\quad= -g(({\cal L}_{V}\nabla)(Z_1,X_1),Y_1) {-} g(({\cal L}_{V}\nabla)(Z_1,Y_1),X_1) \end{align*} $$
for all
![]() $X_1,Y_1,Z_1\in \mathfrak {X}(M)$
. Since a Riemannian metric g is parallel, inserting (2.12) into the preceding equality yields the following:
$X_1,Y_1,Z_1\in \mathfrak {X}(M)$
. Since a Riemannian metric g is parallel, inserting (2.12) into the preceding equality yields the following:
 $$ \begin{align*} g(({\cal L}_{V}\nabla)(Z_1,X_1),Y_1) &+ g(({\cal L}_{V}\nabla)(Z_1,Y_1),X_1)\\ &+2\,(\nabla_{Z_1}{\operatorname{Ric_g}})(X_1,Y_1) = 2\,Z_1(\lambda+\rho \,r)\,g(X_1,Y_1). \end{align*} $$
$$ \begin{align*} g(({\cal L}_{V}\nabla)(Z_1,X_1),Y_1) &+ g(({\cal L}_{V}\nabla)(Z_1,Y_1),X_1)\\ &+2\,(\nabla_{Z_1}{\operatorname{Ric_g}})(X_1,Y_1) = 2\,Z_1(\lambda+\rho \,r)\,g(X_1,Y_1). \end{align*} $$
In view of symmetry
![]() $({\cal L}_{V}\nabla )(X_1,Y_1)=({\cal L}_{V}\nabla )(Y_1,X_1)$
of a
$({\cal L}_{V}\nabla )(X_1,Y_1)=({\cal L}_{V}\nabla )(Y_1,X_1)$
of a
![]() $(1,2)$
-type tensor field
$(1,2)$
-type tensor field
![]() ${\cal L}_{V}\nabla $
, interchanging cyclically the roles of
${\cal L}_{V}\nabla $
, interchanging cyclically the roles of
![]() $X_1$
,
$X_1$
,
![]() $Y_1$
,
$Y_1$
,
![]() $Z_1$
in the previous equality and by a direct calculation, we obtain
$Z_1$
in the previous equality and by a direct calculation, we obtain
 $$ \begin{align} g(({\cal L}_{V}\nabla)(X_1,Y_1),Z_1) =& g((\nabla_{Z_1}\,Q)X_1,Y_1)-g((\nabla_{X_1}Q)Y_1,Z_1)-g((\nabla_{Y_1}Q)Z_1,X_1)\nonumber\\ &+X_1(\lambda+\rho \,r)\,g(Y_1,Z_1)+Y_1(\lambda+\rho \,r)\,g(Z_1,X_1) \notag\\ &-Z_1(\lambda+\rho \,r)\,g(X_1,Y_1), \end{align} $$
$$ \begin{align} g(({\cal L}_{V}\nabla)(X_1,Y_1),Z_1) =& g((\nabla_{Z_1}\,Q)X_1,Y_1)-g((\nabla_{X_1}Q)Y_1,Z_1)-g((\nabla_{Y_1}Q)Z_1,X_1)\nonumber\\ &+X_1(\lambda+\rho \,r)\,g(Y_1,Z_1)+Y_1(\lambda+\rho \,r)\,g(Z_1,X_1) \notag\\ &-Z_1(\lambda+\rho \,r)\,g(X_1,Y_1), \end{align} $$
by using the notion
![]() $(\nabla _{Z_1}{\operatorname {Ric_g}})(X_1,Y_1)=g((\nabla _{Z_1}\,Q)X_1,Y_1)$
. As
$(\nabla _{Z_1}{\operatorname {Ric_g}})(X_1,Y_1)=g((\nabla _{Z_1}\,Q)X_1,Y_1)$
. As
![]() $\xi $
is killing, i.e.,
$\xi $
is killing, i.e.,
![]() ${\cal L}_{\xi }{\operatorname {Ric_g}}=0$
, and therefore,
${\cal L}_{\xi }{\operatorname {Ric_g}}=0$
, and therefore,
![]() $(\nabla _{\xi }Q)X_1 - \nabla _{QX_1}\xi + Q(\nabla _{X_1}\xi )=0$
for
$(\nabla _{\xi }Q)X_1 - \nabla _{QX_1}\xi + Q(\nabla _{X_1}\xi )=0$
for
![]() $X_1\in \mathfrak {X}(M)$
. It follows from (2.7) that
$X_1\in \mathfrak {X}(M)$
. It follows from (2.7) that
In view of this, the self-adjoint property of the Ricci operator Q and (2.9), taking
![]() $\xi $
instead of
$\xi $
instead of
![]() $Y_1$
in (2.13), one can deduce the required formula.▪
$Y_1$
in (2.13), one can deduce the required formula.▪
3 Proof of main results
Proof Proof of Theorem 1.1
Since
![]() $\xi $
is Killing on a Sasakian manifold,
$\xi $
is Killing on a Sasakian manifold,
![]() ${\cal L}_{\xi }{\operatorname {Ric_g}}=0$
, and therefore,
${\cal L}_{\xi }{\operatorname {Ric_g}}=0$
, and therefore,
![]() $\xi (r)=0$
. So, in case of
$\xi (r)=0$
. So, in case of
![]() $\rho $
-Einstein soliton, equation (2.11) reduces to
$\rho $
-Einstein soliton, equation (2.11) reduces to
 $$ \begin{align} ({\cal L}_{\,V} \nabla)(X_1,\xi) + 2\,Q\varphi X_1 =& 4n\,\varphi X_1 + \rho\,\Big\{ X_1(r)\xi - \eta(X_1)\,\nabla r\Big\}, \quad X_1\in\mathfrak{X}(M). \end{align} $$
$$ \begin{align} ({\cal L}_{\,V} \nabla)(X_1,\xi) + 2\,Q\varphi X_1 =& 4n\,\varphi X_1 + \rho\,\Big\{ X_1(r)\xi - \eta(X_1)\,\nabla r\Big\}, \quad X_1\in\mathfrak{X}(M). \end{align} $$
Since the Riemannian metric g is parallel and
![]() $\varphi (\xi )=0$
, from (2.7) and (3.1), we obtain
$\varphi (\xi )=0$
, from (2.7) and (3.1), we obtain
 $$ \begin{align} (\nabla_{\xi}{\cal L}_{\,V} \nabla)(X_1,\xi) &+ ({\cal L}_{\,V} \nabla)(\nabla_{\xi}X_1,\xi) + 2\,\Big\{(\nabla_{\xi}Q)\varphi X_1 + Q(\nabla_{\xi}\varphi)X_1 + Q\varphi(\nabla_{\xi}X_1)\Big\} \nonumber\\[-2pt] &= 4n\,\Big\{(\nabla_{\xi}\varphi) X_1 +\varphi(\nabla_{\xi}X_1)\Big\} + \rho\Big\{ g(\nabla_{\xi}X_1,\nabla r)\xi + g(X_1,\nabla_{\xi}\nabla r)\xi \nonumber \\[-2pt] &\quad- \eta(\nabla_{\xi}X_1)\,\nabla r - \eta(X_1)\,\nabla_{\xi}\nabla r\Big\}. \end{align} $$
$$ \begin{align} (\nabla_{\xi}{\cal L}_{\,V} \nabla)(X_1,\xi) &+ ({\cal L}_{\,V} \nabla)(\nabla_{\xi}X_1,\xi) + 2\,\Big\{(\nabla_{\xi}Q)\varphi X_1 + Q(\nabla_{\xi}\varphi)X_1 + Q\varphi(\nabla_{\xi}X_1)\Big\} \nonumber\\[-2pt] &= 4n\,\Big\{(\nabla_{\xi}\varphi) X_1 +\varphi(\nabla_{\xi}X_1)\Big\} + \rho\Big\{ g(\nabla_{\xi}X_1,\nabla r)\xi + g(X_1,\nabla_{\xi}\nabla r)\xi \nonumber \\[-2pt] &\quad- \eta(\nabla_{\xi}X_1)\,\nabla r - \eta(X_1)\,\nabla_{\xi}\nabla r\Big\}. \end{align} $$
On Sasakian manifold, the Ricci operator Q commutes with the contact metric structure
![]() $\varphi $
, see [Reference Blair3, p. 116], and therefore, (2.14) gives us
$\varphi $
, see [Reference Blair3, p. 116], and therefore, (2.14) gives us
![]() $\nabla _{\xi }Q=0$
. Thus, (3.1) and
$\nabla _{\xi }Q=0$
. Thus, (3.1) and
![]() $\nabla _{\xi }\varphi =0$
(follows from (2.5)) transform (3.2) into the following:
$\nabla _{\xi }\varphi =0$
(follows from (2.5)) transform (3.2) into the following:
 $$ \begin{align} (\nabla_{\xi}{\cal L}_{\,V} \nabla)(X_1,\xi) = \rho\Big\{ g(X_1,\nabla_{\xi}\nabla r)\xi - \eta(X_1)\,\nabla_{\xi}\nabla r\Big\}, \quad X_1\in\mathfrak{X}(M). \end{align} $$
$$ \begin{align} (\nabla_{\xi}{\cal L}_{\,V} \nabla)(X_1,\xi) = \rho\Big\{ g(X_1,\nabla_{\xi}\nabla r)\xi - \eta(X_1)\,\nabla_{\xi}\nabla r\Big\}, \quad X_1\in\mathfrak{X}(M). \end{align} $$
Now, setting
![]() $X_1=\xi $
in (3.1) and using
$X_1=\xi $
in (3.1) and using
![]() $\xi (r)=\varphi (\xi )=0$
, we get
$\xi (r)=\varphi (\xi )=0$
, we get
![]() $({\cal L}_{\,V} \nabla )(\xi ,\xi )=-\rho \,\nabla r$
, and therefore, by (2.7), one can find
$({\cal L}_{\,V} \nabla )(\xi ,\xi )=-\rho \,\nabla r$
, and therefore, by (2.7), one can find
Next, by the following commutation formulas on a Riemannian manifold, see Yano [Reference Yano23, p. 23],
by (3.1), (3.3), and (3.4), we obtain
 $$ \begin{align} &({\cal L}_{V}R)(X_1,\xi)\xi = (\nabla_{X_1}{\cal L}_{V}\nabla)(\xi,\xi) - (\nabla_{\xi}{\cal L}_{V}\nabla)(X_1,\xi) \nonumber\\[-2pt] &\quad= 2\, ({\cal L}_{\,V} \nabla)(\varphi X_1,\xi) - \rho \nabla_{X_1}\nabla r - \rho\Big\{g(X_1,\nabla_{\xi}\nabla r)\xi - \eta(X_1)\nabla_{\xi}\nabla r\Big\} \nonumber\\[-2pt] &\quad= 2\Big\{- 2Q(-X_1+\eta(X_1)\xi) + 4n(-X_1+\eta(X_1)\xi) +\rho\, (\varphi X_1)(r)\,\xi \Big\}\nonumber \\[-2pt] &\qquad- \rho \nabla_{X_1}\nabla r - \rho\Big\{ g(X_1,\nabla_{\xi}\nabla r)\xi - \eta(X_1)\,\nabla_{\xi}\nabla r\Big\} \nonumber\\[-2pt] &\quad= 4\,QX_1 - 8n\,X_1 + 2\rho\, (\varphi X_1)(r)\,\xi - \rho \nabla_{X_1}\nabla r \nonumber \\[-2pt] &\qquad - \rho\,\Big\{ g(X_1,\nabla_{\xi}\nabla r)\xi - \eta(X_1)\,\nabla_{\xi}\nabla r\Big\}, \end{align} $$
$$ \begin{align} &({\cal L}_{V}R)(X_1,\xi)\xi = (\nabla_{X_1}{\cal L}_{V}\nabla)(\xi,\xi) - (\nabla_{\xi}{\cal L}_{V}\nabla)(X_1,\xi) \nonumber\\[-2pt] &\quad= 2\, ({\cal L}_{\,V} \nabla)(\varphi X_1,\xi) - \rho \nabla_{X_1}\nabla r - \rho\Big\{g(X_1,\nabla_{\xi}\nabla r)\xi - \eta(X_1)\nabla_{\xi}\nabla r\Big\} \nonumber\\[-2pt] &\quad= 2\Big\{- 2Q(-X_1+\eta(X_1)\xi) + 4n(-X_1+\eta(X_1)\xi) +\rho\, (\varphi X_1)(r)\,\xi \Big\}\nonumber \\[-2pt] &\qquad- \rho \nabla_{X_1}\nabla r - \rho\Big\{ g(X_1,\nabla_{\xi}\nabla r)\xi - \eta(X_1)\,\nabla_{\xi}\nabla r\Big\} \nonumber\\[-2pt] &\quad= 4\,QX_1 - 8n\,X_1 + 2\rho\, (\varphi X_1)(r)\,\xi - \rho \nabla_{X_1}\nabla r \nonumber \\[-2pt] &\qquad - \rho\,\Big\{ g(X_1,\nabla_{\xi}\nabla r)\xi - \eta(X_1)\,\nabla_{\xi}\nabla r\Big\}, \end{align} $$
by using (2.3) and (2.8). On the other hand, taking the Lie derivative of the equation
![]() $R(X_1,\xi )\xi = X_1 - \eta (X_1)\xi $
(follows from (2.6)) along V and using (2.6), we compute
$R(X_1,\xi )\xi = X_1 - \eta (X_1)\xi $
(follows from (2.6)) along V and using (2.6), we compute
 $$ \begin{align} ({\cal L}_{\,V}R)(X_1, \xi)\xi =& R({\cal L}_{\,V}\xi,X_1)\xi - R(X_1, \xi){\cal L}_{\,V}\xi -({\cal L}_{\,V}g)(X_1,\xi)\xi \notag\\ &- g(X_1,{\cal L}_{\,V}\xi)\xi - \eta(X_1)\,{\cal L}_{V}\xi \notag\\ =& -2\, \eta({\cal L}_{V}\xi)X_1 - ({\cal L}_{\,V}g)(X_1,\xi)\xi, \quad X_1\in\mathfrak{X}(M). \end{align} $$
$$ \begin{align} ({\cal L}_{\,V}R)(X_1, \xi)\xi =& R({\cal L}_{\,V}\xi,X_1)\xi - R(X_1, \xi){\cal L}_{\,V}\xi -({\cal L}_{\,V}g)(X_1,\xi)\xi \notag\\ &- g(X_1,{\cal L}_{\,V}\xi)\xi - \eta(X_1)\,{\cal L}_{V}\xi \notag\\ =& -2\, \eta({\cal L}_{V}\xi)X_1 - ({\cal L}_{\,V}g)(X_1,\xi)\xi, \quad X_1\in\mathfrak{X}(M). \end{align} $$
Now, we deduce from (2.7) and
![]() $\xi (r)=0$
that
$\xi (r)=0$
that
![]() $(\varphi X_1)(r)=g(\xi ,\nabla _{X_1}\nabla r)$
, and therefore, combining (3.6) and (3.7), we acquire
$(\varphi X_1)(r)=g(\xi ,\nabla _{X_1}\nabla r)$
, and therefore, combining (3.6) and (3.7), we acquire
 $$ \begin{align} \rho \nabla_{X_1}\nabla r =& \rho\Big\{ g(\xi,\nabla_{X_1}\nabla r)\xi + \eta(X_1)\,\nabla_{\xi}\nabla r\Big\} \notag\\ &+ 4\,QX_1 - 8n\,X_1 + 2\, \eta({\cal L}_{V}\xi)X_1 + ({\cal L}_{\,V}g)(X_1,\xi)\xi, \end{align} $$
$$ \begin{align} \rho \nabla_{X_1}\nabla r =& \rho\Big\{ g(\xi,\nabla_{X_1}\nabla r)\xi + \eta(X_1)\,\nabla_{\xi}\nabla r\Big\} \notag\\ &+ 4\,QX_1 - 8n\,X_1 + 2\, \eta({\cal L}_{V}\xi)X_1 + ({\cal L}_{\,V}g)(X_1,\xi)\xi, \end{align} $$
by using the symmetric property of
![]() ${\textrm {Hess}}$
. Next, using (2.8) in (1.2), we achieve
${\textrm {Hess}}$
. Next, using (2.8) in (1.2), we achieve
and applying this in the Lie derivative of
![]() $\eta (\xi )=1$
leads to
$\eta (\xi )=1$
leads to
![]() $\eta ({\cal L}_{V}\xi ) = -(\lambda +\rho \,r-2n)$
. Further, making use of this and (3.8), the equality (3.9) transform into
$\eta ({\cal L}_{V}\xi ) = -(\lambda +\rho \,r-2n)$
. Further, making use of this and (3.8), the equality (3.9) transform into
 $$ \begin{align} \rho \nabla_{X_1}\nabla r =& \rho\Big\{ g(\xi,\nabla_{X_1}\nabla r)\xi + \eta(X_1)\,\nabla_{\xi}\nabla r\Big\} + 4\,QX_1 - 2(\lambda+\rho \,r+2n)X_1 \notag \\ &+ 2(\lambda+\rho \,r-2n)\,\eta(X_1)\xi, \quad X_1\in\mathfrak{X}(M). \end{align} $$
$$ \begin{align} \rho \nabla_{X_1}\nabla r =& \rho\Big\{ g(\xi,\nabla_{X_1}\nabla r)\xi + \eta(X_1)\,\nabla_{\xi}\nabla r\Big\} + 4\,QX_1 - 2(\lambda+\rho \,r+2n)X_1 \notag \\ &+ 2(\lambda+\rho \,r-2n)\,\eta(X_1)\xi, \quad X_1\in\mathfrak{X}(M). \end{align} $$
Now, taking its covariant derivative along an arbitrary
![]() $Y_1\in \mathfrak {X}(M)$
and using (2.7), we obtain
$Y_1\in \mathfrak {X}(M)$
and using (2.7), we obtain
 $$ \begin{align} \rho \nabla_{Y_1}\nabla_{X_1}\nabla r =& \rho\Big\{ g(\xi,\nabla_{Y_1}\nabla_{X_1}\nabla r)\xi - g(\varphi Y_1,\nabla_{X_1}\nabla r)\xi - g(\xi,\nabla_{X_1}\nabla r)\varphi Y_1 \notag\\ &+ \eta(\nabla_{Y_1}X_1)\,\nabla_{\xi}\nabla r - g(X_1,\varphi Y_1)\nabla_{\xi}\nabla r + \eta(X_1)\,\nabla_{Y_1}\nabla_{\xi}\nabla r \Big\} \notag\\ & + 4\Big\{(\nabla_{Y_1}Q)X_1{+}Q(\nabla_{Y_1}X_1)\Big\} \notag\\ &- 2(\lambda+\rho \,r+2n)\nabla_{Y_1}X_1 - 2\rho\, \big\{X_1-\eta(X_1)\xi\big\}\,Y_1(r)\notag \\ &+ 2(\lambda+\rho \,r-2n)\,\Big\{\eta(\nabla_{Y_1}X_1)\xi + g(\varphi X_1,Y_1)\xi - \eta(X_1)\varphi Y_1\Big\}, \end{align} $$
$$ \begin{align} \rho \nabla_{Y_1}\nabla_{X_1}\nabla r =& \rho\Big\{ g(\xi,\nabla_{Y_1}\nabla_{X_1}\nabla r)\xi - g(\varphi Y_1,\nabla_{X_1}\nabla r)\xi - g(\xi,\nabla_{X_1}\nabla r)\varphi Y_1 \notag\\ &+ \eta(\nabla_{Y_1}X_1)\,\nabla_{\xi}\nabla r - g(X_1,\varphi Y_1)\nabla_{\xi}\nabla r + \eta(X_1)\,\nabla_{Y_1}\nabla_{\xi}\nabla r \Big\} \notag\\ & + 4\Big\{(\nabla_{Y_1}Q)X_1{+}Q(\nabla_{Y_1}X_1)\Big\} \notag\\ &- 2(\lambda+\rho \,r+2n)\nabla_{Y_1}X_1 - 2\rho\, \big\{X_1-\eta(X_1)\xi\big\}\,Y_1(r)\notag \\ &+ 2(\lambda+\rho \,r-2n)\,\Big\{\eta(\nabla_{Y_1}X_1)\xi + g(\varphi X_1,Y_1)\xi - \eta(X_1)\varphi Y_1\Big\}, \end{align} $$
as the Rimannian metric g is parallel. Since
![]() ${\textrm {Hess}}$
is symmetric and
${\textrm {Hess}}$
is symmetric and
![]() $\varphi $
is anti-symmetric, equations (3.10), (3.11), and the curvature expression (2.1) gives us
$\varphi $
is anti-symmetric, equations (3.10), (3.11), and the curvature expression (2.1) gives us
 $$ \begin{align} \rho\,R(X_1,Y_1)\nabla r =& \rho\Big\{g(\varphi\,Y_1,\nabla_{X_1}\nabla r)\xi - g(\varphi X_1,\nabla_{Y_1}\nabla r)\xi + g(\xi, R(X_1,Y_1)\nabla r)\xi \notag\\ &+ g(\xi,\nabla_{X_1}\nabla r)\,\varphi\,Y_1 -g(\xi,\nabla_{Y_1}\nabla r)\,\varphi X_1 - 2\,g(\varphi X_1,Y_1)\,\nabla_{\xi}\nabla r \notag\\ &+ \eta(Y_1)\,\nabla_{X_1}\nabla_{\xi}\nabla r -\eta(X_1)\,\nabla_{Y_1}\nabla_{\xi}\nabla r\Big\} + 4\Big\{(\nabla_{X_1}Q)Y_1 - (\nabla_{Y_1}Q)X_1\Big\} \notag\\ &-2\rho\, \Big\{X_1(r)\,(Y_1-\eta(Y_1)\xi) - Y_1(r)\,(X_1 - \eta(X_1)\xi)\Big\} \notag\\ &- 2(\lambda+\rho \,r-2n)\,\Big\{2\, g(\varphi X_1,Y_1)\xi + \eta(Y_1)\,\varphi X_1 - \eta(X_1)\,\varphi Y_1\Big\}. \end{align} $$
$$ \begin{align} \rho\,R(X_1,Y_1)\nabla r =& \rho\Big\{g(\varphi\,Y_1,\nabla_{X_1}\nabla r)\xi - g(\varphi X_1,\nabla_{Y_1}\nabla r)\xi + g(\xi, R(X_1,Y_1)\nabla r)\xi \notag\\ &+ g(\xi,\nabla_{X_1}\nabla r)\,\varphi\,Y_1 -g(\xi,\nabla_{Y_1}\nabla r)\,\varphi X_1 - 2\,g(\varphi X_1,Y_1)\,\nabla_{\xi}\nabla r \notag\\ &+ \eta(Y_1)\,\nabla_{X_1}\nabla_{\xi}\nabla r -\eta(X_1)\,\nabla_{Y_1}\nabla_{\xi}\nabla r\Big\} + 4\Big\{(\nabla_{X_1}Q)Y_1 - (\nabla_{Y_1}Q)X_1\Big\} \notag\\ &-2\rho\, \Big\{X_1(r)\,(Y_1-\eta(Y_1)\xi) - Y_1(r)\,(X_1 - \eta(X_1)\xi)\Big\} \notag\\ &- 2(\lambda+\rho \,r-2n)\,\Big\{2\, g(\varphi X_1,Y_1)\xi + \eta(Y_1)\,\varphi X_1 - \eta(X_1)\,\varphi Y_1\Big\}. \end{align} $$
Now, consider a local orthonormal frame
![]() $\{E_i\}_{1\leq i \leq 2n+1}$
on M. By curvature properties and (2.6), one can compute the following formulae:
$\{E_i\}_{1\leq i \leq 2n+1}$
on M. By curvature properties and (2.6), one can compute the following formulae:
 $$ \begin{align*} &\sum_{i=1}^{2n+1} \,g(\varphi Y_1,\nabla_{E_i}\nabla r)\, g(\xi,E_{i}) = g(\xi,\nabla_{\varphi Y_1}\nabla r), \notag\\ &\sum_{i=1}^{2n+1} \,g(\xi,\nabla_{E_i}\nabla r)\, g(\varphi Y_1,E_{i}) = g(\varphi Y_1,\nabla_{\xi}\nabla r), \notag\\ &\sum_{i=1}^{2n+1} \, g(\xi,R(E_{i},Y_1)\nabla r) \, g(\xi,E_{i}) =Y_1(r) - \eta(\nabla r)\,\eta(Y_1) \end{align*} $$
$$ \begin{align*} &\sum_{i=1}^{2n+1} \,g(\varphi Y_1,\nabla_{E_i}\nabla r)\, g(\xi,E_{i}) = g(\xi,\nabla_{\varphi Y_1}\nabla r), \notag\\ &\sum_{i=1}^{2n+1} \,g(\xi,\nabla_{E_i}\nabla r)\, g(\varphi Y_1,E_{i}) = g(\varphi Y_1,\nabla_{\xi}\nabla r), \notag\\ &\sum_{i=1}^{2n+1} \, g(\xi,R(E_{i},Y_1)\nabla r) \, g(\xi,E_{i}) =Y_1(r) - \eta(\nabla r)\,\eta(Y_1) \end{align*} $$
for all
![]() $Y_1\in \mathfrak {X}(M)$
. Next, contracting (3.12) over
$Y_1\in \mathfrak {X}(M)$
. Next, contracting (3.12) over
![]() $X_1$
and using the antisymmetry of
$X_1$
and using the antisymmetry of
![]() $\varphi $
, the symmetry of
$\varphi $
, the symmetry of
![]() ${\textrm {Hess}}$
,
${\textrm {Hess}}$
,
![]() ${\operatorname {Tr_g}}\varphi =0=\varphi (\xi )$
and the above formulae, we obtain
${\operatorname {Tr_g}}\varphi =0=\varphi (\xi )$
and the above formulae, we obtain
 $$ \begin{align} \rho \, {\operatorname{Ric_g}}(Y_1,\nabla r) =& \rho\, \Big\{4\,g(\varphi Y_1,\nabla_{\xi}\nabla r) + (4n-1)\,Y_1(r) \notag\\[-2pt] &+ \eta(Y_1)\,{\operatorname{div}}(\nabla_{\xi}\nabla r) - g(\xi,\nabla_{Y_1}\nabla_{\xi}\nabla r)\Big\} - 2\, Y_1(r). \end{align} $$
$$ \begin{align} \rho \, {\operatorname{Ric_g}}(Y_1,\nabla r) =& \rho\, \Big\{4\,g(\varphi Y_1,\nabla_{\xi}\nabla r) + (4n-1)\,Y_1(r) \notag\\[-2pt] &+ \eta(Y_1)\,{\operatorname{div}}(\nabla_{\xi}\nabla r) - g(\xi,\nabla_{Y_1}\nabla_{\xi}\nabla r)\Big\} - 2\, Y_1(r). \end{align} $$
Further, replacing
![]() $X_1=\varphi \,X_1$
and
$X_1=\varphi \,X_1$
and
![]() $Y_1=\varphi \,Y_1$
in (3.12) and by using the formula for Sasakian manifold, see Blair [Reference Blair3, p. 137]:
$Y_1=\varphi \,Y_1$
in (3.12) and by using the formula for Sasakian manifold, see Blair [Reference Blair3, p. 137]:
 $$ \begin{align*} &R(\varphi X_1,\varphi Y_1)Z_1\\[-2pt] &\quad = R(X_1,Y_1)Z_1 +g(X_1,Z_1)Y_1 - g(Y_1,Z_1)X_1 - g(\varphi X_1,Z_1)\varphi Y_1 + g(\varphi Y_1,Z_1)\varphi X_1, \end{align*} $$
$$ \begin{align*} &R(\varphi X_1,\varphi Y_1)Z_1\\[-2pt] &\quad = R(X_1,Y_1)Z_1 +g(X_1,Z_1)Y_1 - g(Y_1,Z_1)X_1 - g(\varphi X_1,Z_1)\varphi Y_1 + g(\varphi Y_1,Z_1)\varphi X_1, \end{align*} $$
![]() $\varphi (\xi )=0=\eta \circ \varphi $
, symmetry of
$\varphi (\xi )=0=\eta \circ \varphi $
, symmetry of
![]() ${\textrm {Hess}}$
, antisymmetry of
${\textrm {Hess}}$
, antisymmetry of
![]() $\varphi $
and (2.3), we obtain
$\varphi $
and (2.3), we obtain
 $$ \begin{align} \hspace{2pc}&\rho\,\Big\{R(X_1,Y_1)\nabla r + X_1(r)Y_1 - Y_1(r)X_1\Big\} = \rho\, \Big\{g(X_1,\nabla_{\varphi Y_1}\nabla r)\xi - g(Y_1,\nabla_{\varphi X_1}\nabla r)\xi \notag\\[-2pt] &\quad+ 2\, \eta(Y_1)\,g(\xi,\nabla_{\varphi X_1}\nabla r)\xi - 2\, \eta(X_1)\,g(\xi,\nabla_{\varphi Y_1}\nabla r)\xi + g(\varphi Y_1,\nabla_{\xi}\nabla r)X_1 \notag\\[-2pt] &\quad- g(\varphi X_1,\nabla_{\xi}\nabla r)Y_1+ 2\, g(X_1,\varphi Y_1)\,\nabla_{\xi}\nabla r\Big\} \notag \\[-2pt] &\quad + 4\,\Big\{(\nabla_{\varphi X_1}Q)(\varphi Y_1)-(\nabla_{\varphi Y_1}Q)(\varphi X_1)\Big\}\notag\\[-2pt] &\quad- \rho\,\Big\{(\varphi X_1)(r)\, \varphi Y_1 - (\varphi Y_1)(r)\, \varphi X_1\Big\} - 4(\lambda+\rho\, r -2n)\, g(\varphi X_1,Y_1)\xi. \notag \\[-18pt] \end{align} $$
$$ \begin{align} \hspace{2pc}&\rho\,\Big\{R(X_1,Y_1)\nabla r + X_1(r)Y_1 - Y_1(r)X_1\Big\} = \rho\, \Big\{g(X_1,\nabla_{\varphi Y_1}\nabla r)\xi - g(Y_1,\nabla_{\varphi X_1}\nabla r)\xi \notag\\[-2pt] &\quad+ 2\, \eta(Y_1)\,g(\xi,\nabla_{\varphi X_1}\nabla r)\xi - 2\, \eta(X_1)\,g(\xi,\nabla_{\varphi Y_1}\nabla r)\xi + g(\varphi Y_1,\nabla_{\xi}\nabla r)X_1 \notag\\[-2pt] &\quad- g(\varphi X_1,\nabla_{\xi}\nabla r)Y_1+ 2\, g(X_1,\varphi Y_1)\,\nabla_{\xi}\nabla r\Big\} \notag \\[-2pt] &\quad + 4\,\Big\{(\nabla_{\varphi X_1}Q)(\varphi Y_1)-(\nabla_{\varphi Y_1}Q)(\varphi X_1)\Big\}\notag\\[-2pt] &\quad- \rho\,\Big\{(\varphi X_1)(r)\, \varphi Y_1 - (\varphi Y_1)(r)\, \varphi X_1\Big\} - 4(\lambda+\rho\, r -2n)\, g(\varphi X_1,Y_1)\xi. \notag \\[-18pt] \end{align} $$
Covariant derivative of
![]() $Q\varphi =\varphi Q$
and formula (2.2) provide the following formulae, see Lemma
$Q\varphi =\varphi Q$
and formula (2.2) provide the following formulae, see Lemma
![]() $5.1$
in [Reference Ghosh and Sharma13]:
$5.1$
in [Reference Ghosh and Sharma13]:
 $$ \begin{align*} &\sum_{i=1}^{2n+1}\, g\big((\nabla_{Y_1}Q)\,\varphi\, E_{i},E_{i}\big) =0, \quad \sum_{i=1}^{2n+1}\,g\big((\nabla_{\varphi\, E_{i}}Q)\,\varphi Y_1,E_{i}\big) =-\frac{1}{2}\,Y_1(r) \end{align*} $$
$$ \begin{align*} &\sum_{i=1}^{2n+1}\, g\big((\nabla_{Y_1}Q)\,\varphi\, E_{i},E_{i}\big) =0, \quad \sum_{i=1}^{2n+1}\,g\big((\nabla_{\varphi\, E_{i}}Q)\,\varphi Y_1,E_{i}\big) =-\frac{1}{2}\,Y_1(r) \end{align*} $$
for all
![]() $Y_1\in \mathfrak {X}(M)$
. Using
$Y_1\in \mathfrak {X}(M)$
. Using
![]() $\varphi (\xi )=0$
, one can easily compute that
$\varphi (\xi )=0$
, one can easily compute that
 $$ \begin{align*} &\sum_{i=1}^{2n+1} \,g(Y_1,\nabla_{\varphi E_i}\nabla r)\, g(\xi,E_{i}) = -g(\xi,\varphi(\nabla_{Y_1}\nabla r))=0, \quad Y_1\in\mathfrak{X}(M). \end{align*} $$
$$ \begin{align*} &\sum_{i=1}^{2n+1} \,g(Y_1,\nabla_{\varphi E_i}\nabla r)\, g(\xi,E_{i}) = -g(\xi,\varphi(\nabla_{Y_1}\nabla r))=0, \quad Y_1\in\mathfrak{X}(M). \end{align*} $$
Now, contracting (3.14) over
![]() $X_1$
and using the preceding formulae, we compute
$X_1$
and using the preceding formulae, we compute
 $$ \begin{align} \rho \, \Big\{{\operatorname{Ric_g}}(Y_1,\nabla r) - 2n\, Y_1(r)\Big\} =& \rho\, \Big\{2(n+1)\,g(\varphi Y_1,\nabla_{\xi}\nabla r) - g(\xi,\nabla_{\varphi Y_1}\nabla r)\Big\} - 2\, Y_1(r) \notag\\[-2pt] &+\rho\,\big\{Y_1(r) - \xi(r)\,\eta(Y_1)\}. \end{align} $$
$$ \begin{align} \rho \, \Big\{{\operatorname{Ric_g}}(Y_1,\nabla r) - 2n\, Y_1(r)\Big\} =& \rho\, \Big\{2(n+1)\,g(\varphi Y_1,\nabla_{\xi}\nabla r) - g(\xi,\nabla_{\varphi Y_1}\nabla r)\Big\} - 2\, Y_1(r) \notag\\[-2pt] &+\rho\,\big\{Y_1(r) - \xi(r)\,\eta(Y_1)\}. \end{align} $$
Since
![]() $\xi (r)=0$
and
$\xi (r)=0$
and
![]() $\nabla _{\xi }\xi =0$
, and therefore, we have
$\nabla _{\xi }\xi =0$
, and therefore, we have
![]() $g(\xi ,\nabla _{\xi }\nabla r)=\xi (\xi (r))=0$
. Differentiating it along
$g(\xi ,\nabla _{\xi }\nabla r)=\xi (\xi (r))=0$
. Differentiating it along
![]() $Y_1\in \mathfrak {X}(M)$
and recalling (2.7), we get
$Y_1\in \mathfrak {X}(M)$
and recalling (2.7), we get
In [Reference Ghosh and Sharma12], Ghosh-Sharma studied the case
![]() $\rho=0 $
. Here we consider
$\rho=0 $
. Here we consider
![]() $\rho $
is nonzero. Then combining (3.13) and (3.15) with the last equality, we reach
$\rho $
is nonzero. Then combining (3.13) and (3.15) with the last equality, we reach
 $$ \begin{align} \eta(Y_1)\,{\operatorname{div}}(\nabla_{\xi}\nabla r) = 2(n-1)\,\big\{ g(\varphi Y_1, \nabla_{\xi}\nabla r) - Y_1(r)\Big\}, \quad Y_1\in\mathfrak{X}(M). \end{align} $$
$$ \begin{align} \eta(Y_1)\,{\operatorname{div}}(\nabla_{\xi}\nabla r) = 2(n-1)\,\big\{ g(\varphi Y_1, \nabla_{\xi}\nabla r) - Y_1(r)\Big\}, \quad Y_1\in\mathfrak{X}(M). \end{align} $$
Next, replacing
![]() $Y_1$
by
$Y_1$
by
![]() $\varphi Y_1$
in (3.16) and using (2.3) and
$\varphi Y_1$
in (3.16) and using (2.3) and
![]() $\varphi (\xi )=0$
, we acquire
$\varphi (\xi )=0$
, we acquire
 $$ \begin{align} (n-1)\, \Big\{g(Y_1, \nabla_{\xi}\nabla r) - \eta(Y_1)\,g(\xi,\nabla_{\xi}\nabla r) + (\varphi Y_1)(r)\Big\} = 0 \end{align} $$
$$ \begin{align} (n-1)\, \Big\{g(Y_1, \nabla_{\xi}\nabla r) - \eta(Y_1)\,g(\xi,\nabla_{\xi}\nabla r) + (\varphi Y_1)(r)\Big\} = 0 \end{align} $$
and, in view of (2.3) and
![]() $\xi (r)=0$
, it is easily seen that
$\xi (r)=0$
, it is easily seen that
![]() $g(Y_1, \nabla _{\xi }\nabla r)=g(\xi ,\nabla _{Y_1}\nabla r) = (\varphi Y_1)(r)$
. Thus, the equality (3.17) becomes
$g(Y_1, \nabla _{\xi }\nabla r)=g(\xi ,\nabla _{Y_1}\nabla r) = (\varphi Y_1)(r)$
. Thus, the equality (3.17) becomes
![]() $(n-1)\,(\varphi Y_1)(r)=0$
, as
$(n-1)\,(\varphi Y_1)(r)=0$
, as
![]() $g(\xi ,\nabla _{\xi }\nabla r)=0$
; and therefore,
$g(\xi ,\nabla _{\xi }\nabla r)=0$
; and therefore,
![]() $\varphi \nabla r=0$
for
$\varphi \nabla r=0$
for
![]() $n>1$
. Operating this by
$n>1$
. Operating this by
![]() $\varphi $
and applying (2.3) yields that
$\varphi $
and applying (2.3) yields that
![]() $\nabla r = \xi (r)\xi = 0$
; hence, r is constant on
$\nabla r = \xi (r)\xi = 0$
; hence, r is constant on
![]() $M^{2n+1}$
for
$M^{2n+1}$
for
![]() $n>1$
. Thus, equation (3.1) and
$n>1$
. Thus, equation (3.1) and
![]() $\varphi (\xi )=0$
gives us
$\varphi (\xi )=0$
gives us
![]() $({\cal L}_{V}\nabla )(\xi ,\xi )=0$
. Applying this in the well known formula:
$({\cal L}_{V}\nabla )(\xi ,\xi )=0$
. Applying this in the well known formula:
see [Reference Yano23, p. 23], we acquire
![]() $R(\xi ,V)\xi =\nabla _{\xi }\nabla _{\xi }V$
, i.e., V is Jacobi along the geodesics determined by
$R(\xi ,V)\xi =\nabla _{\xi }\nabla _{\xi }V$
, i.e., V is Jacobi along the geodesics determined by
![]() $\xi $
, which proves part
$\xi $
, which proves part
![]() $(i)$
.
$(i)$
.
Next, we prove part
![]() ${\rm (ii)}$
. Since r is constant, equation (3.10) becomes
${\rm (ii)}$
. Since r is constant, equation (3.10) becomes
 $$ \begin{align} {\operatorname{Ric_g}}(X_1,Y_1) = \frac{1}{2}\Big\{(\lambda+\rho\, r+2n)\,g(X_1,Y_1) - (\lambda+\rho\, r-2n)\,\eta(X_1)\eta(Y_1)\Big\}, \end{align} $$
$$ \begin{align} {\operatorname{Ric_g}}(X_1,Y_1) = \frac{1}{2}\Big\{(\lambda+\rho\, r+2n)\,g(X_1,Y_1) - (\lambda+\rho\, r-2n)\,\eta(X_1)\eta(Y_1)\Big\}, \end{align} $$
and therefore, the scalar curvature is given by
which is constant, and the squared norm of the Ricci operator is given by
 $$ \begin{align} ||Q||^2 = \frac{n}{2}\,\Big\{(\lambda+\rho\,r+2n)^2 + 8n\Big\}. \end{align} $$
$$ \begin{align} ||Q||^2 = \frac{n}{2}\,\Big\{(\lambda+\rho\,r+2n)^2 + 8n\Big\}. \end{align} $$
Now, recalling the following integrability formula on
![]() $(2n+1)$
-dimensional contact metric manifold, see equation
$(2n+1)$
-dimensional contact metric manifold, see equation
![]() $(8)$
of [Reference Kumara and Venkatesha21]:
$(8)$
of [Reference Kumara and Venkatesha21]:
where we have used for convenience
![]() $\Delta r = - {\operatorname {div}} (\nabla r)$
. As
$\Delta r = - {\operatorname {div}} (\nabla r)$
. As
![]() $\lambda $
and r are constants, taking into account (3.19) as well as (3.20), the previous formula becomes
$\lambda $
and r are constants, taking into account (3.19) as well as (3.20), the previous formula becomes
 $$ \begin{align} 0 &= 2\,||Q||^2-2(\lambda+\rho\, r) r\notag\\ &= -n(\lambda+\rho\,r-2n)(\lambda+\rho\,r+2n+4). \end{align} $$
$$ \begin{align} 0 &= 2\,||Q||^2-2(\lambda+\rho\, r) r\notag\\ &= -n(\lambda+\rho\,r-2n)(\lambda+\rho\,r+2n+4). \end{align} $$
If
![]() $\lambda +\rho \,r-2n=0$
, then according to (3.18),
$\lambda +\rho \,r-2n=0$
, then according to (3.18),
![]() $(M,g)$
is an Einstein manifold, contradicting our hypothesis; and therefore, (3.22) implies that
$(M,g)$
is an Einstein manifold, contradicting our hypothesis; and therefore, (3.22) implies that
![]() $\lambda +\rho \,r+2n+4=0$
, which reduces (3.18) to the form
$\lambda +\rho \,r+2n+4=0$
, which reduces (3.18) to the form
 $$ \begin{align} {\operatorname{Ric_g}}(X_1,Y_1) = -2\,\big\{g(X_1,Y_1) - (n+1)\,\eta(X_1)\eta(Y_1)\big\}. \end{align} $$
$$ \begin{align} {\operatorname{Ric_g}}(X_1,Y_1) = -2\,\big\{g(X_1,Y_1) - (n+1)\,\eta(X_1)\eta(Y_1)\big\}. \end{align} $$
Hence,
![]() $(M,g)$
is
$(M,g)$
is
![]() $\mathcal {D}$
-homothetically fixed null
$\mathcal {D}$
-homothetically fixed null
![]() $\eta $
-Einstein manifold, which proves part
$\eta $
-Einstein manifold, which proves part
![]() ${\rm (ii)}$
.
${\rm (ii)}$
.
To prove part
![]() ${\rm (iii)}$
. Now, using (3.23) in the soliton equation (1.2), we get
${\rm (iii)}$
. Now, using (3.23) in the soliton equation (1.2), we get
 $$ \begin{align} \frac{1}{2}\,({\cal L}_{V}g)(X_1,Y_1) = -2(n+1)\,\Big\{g(X_1,Y_1) + \eta(X_1)\eta(Y_1)\Big\}, \quad X_1,Y_1\in\mathfrak{X}(M). \end{align} $$
$$ \begin{align} \frac{1}{2}\,({\cal L}_{V}g)(X_1,Y_1) = -2(n+1)\,\Big\{g(X_1,Y_1) + \eta(X_1)\eta(Y_1)\Big\}, \quad X_1,Y_1\in\mathfrak{X}(M). \end{align} $$
In view of (2.7) and (3.23), we deduce
 $$ \begin{align} (\nabla_{Z_1}{\operatorname{Ric_g}})(X_1,Y_1) = 2(n+1)\,\big\{g(\varphi X_1,Z_1)\,\eta(Y_1) + \eta(X_1)\,g(\varphi Y_1,Z_1)\big\}, \end{align} $$
$$ \begin{align} (\nabla_{Z_1}{\operatorname{Ric_g}})(X_1,Y_1) = 2(n+1)\,\big\{g(\varphi X_1,Z_1)\,\eta(Y_1) + \eta(X_1)\,g(\varphi Y_1,Z_1)\big\}, \end{align} $$
by using the parallelism of the Riemannian metric g. Repeated application of (3.25) and the antisymmetry of
![]() $\varphi $
in (2.13) gives us
$\varphi $
in (2.13) gives us
 $$ \begin{align} ({\cal L}_{V}\nabla)(X_1,Y_1) = 4(n+1)\,\big\{\eta(Y_1)\, \varphi X_1 + \eta(X_1)\, \varphi Y_1\big\}, \end{align} $$
$$ \begin{align} ({\cal L}_{V}\nabla)(X_1,Y_1) = 4(n+1)\,\big\{\eta(Y_1)\, \varphi X_1 + \eta(X_1)\, \varphi Y_1\big\}, \end{align} $$
and its covariant derivative along
![]() $Z_1\in \mathfrak {X}(M)$
yields that
$Z_1\in \mathfrak {X}(M)$
yields that
 $$ \begin{align} (\nabla_{Z_1}{\cal L}_{V}\nabla)(X_1,Y_1) =\,& 4(n+1)\,\Big\{g(\varphi Y_1, Z_1)\,\varphi X_1 + g(\varphi X_1, Z_1)\,\varphi Y_1 \notag\\ &+ \eta(Y_1)\, g(X_1,Z_1)\xi + \eta(X_1)\, g(Y_1,Z_1)\xi - 2\,\eta(X_1)\eta(Y_1)Z_1\Big\}, \end{align} $$
$$ \begin{align} (\nabla_{Z_1}{\cal L}_{V}\nabla)(X_1,Y_1) =\,& 4(n+1)\,\Big\{g(\varphi Y_1, Z_1)\,\varphi X_1 + g(\varphi X_1, Z_1)\,\varphi Y_1 \notag\\ &+ \eta(Y_1)\, g(X_1,Z_1)\xi + \eta(X_1)\, g(Y_1,Z_1)\xi - 2\,\eta(X_1)\eta(Y_1)Z_1\Big\}, \end{align} $$
by using (2.7). In view of this and the communication formula (3.5), we obtain
 $$ \begin{align} ({\cal L}_{V}R)(Z_1,X_1)Y_1 =& (\nabla_{Z_1}{\cal L}_{V}\nabla)(X_1,Y_1) - (\nabla_{X_1}{\cal L}_{V}\nabla)(Z_1,Y_1)\notag\\ =& 4(n+1)\,\Big\{g(\varphi Y_1, Z_1)\,\varphi X_1 + 2\, g(\varphi X_1, Z_1)\,\varphi Y_1 \notag\\ &-g(\varphi Y_1,X_1)\,\varphi Z_1 + \eta(X_1)\, g(Y_1,Z_1)\xi - \eta(Z_1)\, g(X_1,Y_1)\xi \notag\\ &- 2\,\eta(X_1)\eta(Y_1)Z_1 + 2\,\eta(Z_1)\eta(Y_1)X_1\Big\}, \end{align} $$
$$ \begin{align} ({\cal L}_{V}R)(Z_1,X_1)Y_1 =& (\nabla_{Z_1}{\cal L}_{V}\nabla)(X_1,Y_1) - (\nabla_{X_1}{\cal L}_{V}\nabla)(Z_1,Y_1)\notag\\ =& 4(n+1)\,\Big\{g(\varphi Y_1, Z_1)\,\varphi X_1 + 2\, g(\varphi X_1, Z_1)\,\varphi Y_1 \notag\\ &-g(\varphi Y_1,X_1)\,\varphi Z_1 + \eta(X_1)\, g(Y_1,Z_1)\xi - \eta(Z_1)\, g(X_1,Y_1)\xi \notag\\ &- 2\,\eta(X_1)\eta(Y_1)Z_1 + 2\,\eta(Z_1)\eta(Y_1)X_1\Big\}, \end{align} $$
by using the antisymmetry of
![]() $\varphi $
. Next, contracting it over
$\varphi $
. Next, contracting it over
![]() $Z_1$
and using
$Z_1$
and using
![]() ${\operatorname {Tr_g}} \varphi =0$
and (2.3), we obtain
${\operatorname {Tr_g}} \varphi =0$
and (2.3), we obtain
 $$ \begin{align} ({\cal L}_{V}{\operatorname{Ric_g}})(X_1,Y_1) = 8 (n+1)\,\Big\{g(X_1,Y_1) - 2(n+1)\, \eta(X_1)\eta(Y_1)\Big\}. \end{align} $$
$$ \begin{align} ({\cal L}_{V}{\operatorname{Ric_g}})(X_1,Y_1) = 8 (n+1)\,\Big\{g(X_1,Y_1) - 2(n+1)\, \eta(X_1)\eta(Y_1)\Big\}. \end{align} $$
On the other hand, taking into account (3.23) as well as (3.24), it suffices to show that
 $$ \begin{align} ({\cal L}_{V}{\operatorname{Ric_g}})(X_1,Y_1) =& 8(n+1)\,\Big\{g(X_1,Y_1) + \eta(X_1)\eta(Y_1)\Big\} \notag\\ &+ 2(n+1)\,\Big\{\eta(Y_1)\,({\cal L}_{V}\eta)(X_1) + \eta(X_1)\,({\cal L}_{V}\eta)(Y_1)\Big\}. \end{align} $$
$$ \begin{align} ({\cal L}_{V}{\operatorname{Ric_g}})(X_1,Y_1) =& 8(n+1)\,\Big\{g(X_1,Y_1) + \eta(X_1)\eta(Y_1)\Big\} \notag\\ &+ 2(n+1)\,\Big\{\eta(Y_1)\,({\cal L}_{V}\eta)(X_1) + \eta(X_1)\,({\cal L}_{V}\eta)(Y_1)\Big\}. \end{align} $$
In addition, it follows from
![]() $\eta (\xi )=1$
that
$\eta (\xi )=1$
that
![]() $({\cal L}_{V}\eta )(\xi )=-\eta ({\cal L}_{V}\xi )=(\lambda +\rho \,r-2n)=-4(n+1)$
. Thus, comparing (3.29) with (3.30) and then replacing
$({\cal L}_{V}\eta )(\xi )=-\eta ({\cal L}_{V}\xi )=(\lambda +\rho \,r-2n)=-4(n+1)$
. Thus, comparing (3.29) with (3.30) and then replacing
![]() $\xi $
instead of
$\xi $
instead of
![]() $Y_1$
, we have
$Y_1$
, we have
and therefore, V is a nonstrict infinitesimal contact transformation and is equal to
 $-\frac {1}{2}\,\varphi \,\nabla f+f\,\xi $
for a smooth function f on M such that
$-\frac {1}{2}\,\varphi \,\nabla f+f\,\xi $
for a smooth function f on M such that
![]() $\xi (f)=-4(n+1)$
, see [Reference Blair3, p. 72]. This proves part
$\xi (f)=-4(n+1)$
, see [Reference Blair3, p. 72]. This proves part
![]() ${\rm (iii)}$
.
${\rm (iii)}$
.
Furthermore, taking into account (3.24) as well as (3.31), it is easy to check that
![]() ${\cal L}_{V}\xi = 4(n+1)$
. Since the exterior derivative d commutes with the Lie derivative, i.e.,
${\cal L}_{V}\xi = 4(n+1)$
. Since the exterior derivative d commutes with the Lie derivative, i.e.,
![]() $d\circ {\cal L}_{\,V} = {\cal L}_{\,V}\circ d$
, applying d to (3.31), we acquire
$d\circ {\cal L}_{\,V} = {\cal L}_{\,V}\circ d$
, applying d to (3.31), we acquire
Therefore, applying this and (3.24) in the Lie-derivative of (2.4), we conclude that V leaves the structural tensor
![]() $\varphi $
invariant, which finishes the proof.
$\varphi $
invariant, which finishes the proof.
Proof Proof of Theorem 1.3
Operating (2.10) by d and since the exterior derivative d commutes with the Lie-derivative, i.e.,
![]() $d\circ {\cal L}_V = {\cal L}_V\circ d$
, we obtain
$d\circ {\cal L}_V = {\cal L}_V\circ d$
, we obtain
 $$ \begin{align} ({\cal L}_Vd\eta)(X_1,Y_1) = \frac{1}{2}\Big\{X_1(f)\,\eta(Y_1)-Y_1(f)\,\eta(X_1)\Big\}+f\,d\eta(X_1,Y_1) \end{align} $$
$$ \begin{align} ({\cal L}_Vd\eta)(X_1,Y_1) = \frac{1}{2}\Big\{X_1(f)\,\eta(Y_1)-Y_1(f)\,\eta(X_1)\Big\}+f\,d\eta(X_1,Y_1) \end{align} $$
for any
![]() $X_1,Y_1\in \mathfrak {X}(M)$
. On the other hand, Lie-derivative of (2.4) along V and making use of (1.2) yields that
$X_1,Y_1\in \mathfrak {X}(M)$
. On the other hand, Lie-derivative of (2.4) along V and making use of (1.2) yields that
 $$ \begin{align*} ({\cal L}_Vd\eta)(X_1,Y_1) &= ({\cal L}_Vg)(X_1, \varphi Y_1) + g(X_1, ({\cal L}_V \varphi)Y_1) \nonumber\\ &= - 2{\operatorname{Ric_g}}(X_1, \varphi Y_1) + 2(\lambda +\rho\, r)\,g(X_1, \varphi Y_1) + g(X_1, ({\cal L}_V \varphi)Y_1). \end{align*} $$
$$ \begin{align*} ({\cal L}_Vd\eta)(X_1,Y_1) &= ({\cal L}_Vg)(X_1, \varphi Y_1) + g(X_1, ({\cal L}_V \varphi)Y_1) \nonumber\\ &= - 2{\operatorname{Ric_g}}(X_1, \varphi Y_1) + 2(\lambda +\rho\, r)\,g(X_1, \varphi Y_1) + g(X_1, ({\cal L}_V \varphi)Y_1). \end{align*} $$
By virtue of this and (2.4), we deduce from (3.33) the relation
 $$ \begin{align} &({\cal L}_V\varphi)(X_1) = 2\,Q\varphi X_1 + (f-2\lambda-2\rho \,r)\varphi X_1 + \frac{1}{2}\Big\{\eta(X_1)\nabla f - X_1(f)\xi \Big\} \end{align} $$
$$ \begin{align} &({\cal L}_V\varphi)(X_1) = 2\,Q\varphi X_1 + (f-2\lambda-2\rho \,r)\varphi X_1 + \frac{1}{2}\Big\{\eta(X_1)\nabla f - X_1(f)\xi \Big\} \end{align} $$
for any
![]() $X_1\in \mathfrak {X}(M)$
. Next, taking into account (3.37) and (2.10) in the Lie-derivative of
$X_1\in \mathfrak {X}(M)$
. Next, taking into account (3.37) and (2.10) in the Lie-derivative of
![]() $\eta (X_1)=g(X_1,\xi )$
, we get
$\eta (X_1)=g(X_1,\xi )$
, we get
Further, taking Lie-derivative of
![]() $\varphi (\xi )=0$
along V and using (3.35),
$\varphi (\xi )=0$
along V and using (3.35),
![]() $\varphi (\xi )=0$
, we have
$\varphi (\xi )=0$
, we have
![]() $({\cal L}_V\varphi )\xi =0$
; thus, (3.34) gives us
$({\cal L}_V\varphi )\xi =0$
; thus, (3.34) gives us
![]() $\nabla f=\xi (f)\xi $
, or, in terms of the exterior derivation,
$\nabla f=\xi (f)\xi $
, or, in terms of the exterior derivation,
Now taking its exterior derivative and using Poincaré lemma (
![]() $d^2=0$
), and then applying the wedge product with
$d^2=0$
), and then applying the wedge product with
![]() $\eta $
, we obtain
$\eta $
, we obtain
![]() $\xi (f)\,\eta \wedge d\eta =0$
; thus,
$\xi (f)\,\eta \wedge d\eta =0$
; thus,
![]() $\xi (f)=0$
, as
$\xi (f)=0$
, as
![]() $\eta \wedge d\eta $
vanishes nowhere on a contact manifold M. It follows from (3.36) that
$\eta \wedge d\eta $
vanishes nowhere on a contact manifold M. It follows from (3.36) that
![]() $df=0$
; and hence, f is a constant on M. Further, using (2.8) in the soliton equation (1.2), we acquire
$df=0$
; and hence, f is a constant on M. Further, using (2.8) in the soliton equation (1.2), we acquire
At this point, taking Lie-derivative of
![]() $g(\xi ,\xi )=1$
and using (3.37), (3.35) yields
$g(\xi ,\xi )=1$
and using (3.37), (3.35) yields
![]() $\lambda +\rho \, r=f+2n$
, a constant, and therefore, g is a Ricci soliton.
$\lambda +\rho \, r=f+2n$
, a constant, and therefore, g is a Ricci soliton.
Let
![]() $\omega $
be the volume form of M, i.e.,
$\omega $
be the volume form of M, i.e.,
![]() $\omega = \eta \wedge (d\eta )^n\neq 0$
. Then taking Lie-derivative of
$\omega = \eta \wedge (d\eta )^n\neq 0$
. Then taking Lie-derivative of
![]() $\omega = \eta \wedge (d\eta )^n$
along V and using
$\omega = \eta \wedge (d\eta )^n$
along V and using
![]() ${\cal L}_{V}\,\omega =({\operatorname {div}} V)\omega $
and (3.33), we obtain
${\cal L}_{V}\,\omega =({\operatorname {div}} V)\omega $
and (3.33), we obtain
![]() ${\operatorname {div}} V = (n + 1)f$
. Integrating it over compact M and applying the divergence theorem, we get
${\operatorname {div}} V = (n + 1)f$
. Integrating it over compact M and applying the divergence theorem, we get
![]() $f = 0$
(as f is constant), and therefore,
$f = 0$
(as f is constant), and therefore,
![]() ${\operatorname {div}} V=0$
and
${\operatorname {div}} V=0$
and
![]() $\lambda +\rho \, r=2n$
. Hence (2.6) and (3.35) prove that V leaves
$\lambda +\rho \, r=2n$
. Hence (2.6) and (3.35) prove that V leaves
![]() $\eta $
invariant and
$\eta $
invariant and
![]() $\xi $
invariant, respectively. Using
$\xi $
invariant, respectively. Using
![]() ${\operatorname {div}} V=0$
and
${\operatorname {div}} V=0$
and
![]() $\lambda +\rho \, r=2n$
in the trace of (1.2), we have
$\lambda +\rho \, r=2n$
in the trace of (1.2), we have
![]() $r=(2n+1)(\lambda +\rho \,r)=2n(2n+1)$
. Therefore, using all these consequences in the integrability condition (3.12), we deduce
$r=(2n+1)(\lambda +\rho \,r)=2n(2n+1)$
. Therefore, using all these consequences in the integrability condition (3.12), we deduce
This is equivalent to
![]() $||Q - 2n\,I||^2 = 0$
, i.e.,
$||Q - 2n\,I||^2 = 0$
, i.e.,
![]() ${\operatorname {Ric_g}}=2n\,g$
. Hence
${\operatorname {Ric_g}}=2n\,g$
. Hence
![]() $(M,g)$
is Einstein with Einstein constant
$(M,g)$
is Einstein with Einstein constant
![]() $2n$
; thus, (3.34) and (1.2) imply that V leaves
$2n$
; thus, (3.34) and (1.2) imply that V leaves
![]() $\varphi $
and g invariant, respectively. Since M is compact, applying Boyer and Galicki’s result (see Theorem 11.1.7 of [Reference Boyer, Galicki and Matzeu5, p. 372]), we can conclude that M is Sasakian. Moreover, relations
$\varphi $
and g invariant, respectively. Since M is compact, applying Boyer and Galicki’s result (see Theorem 11.1.7 of [Reference Boyer, Galicki and Matzeu5, p. 372]), we can conclude that M is Sasakian. Moreover, relations
![]() $\lambda +\rho \, r=2n$
and
$\lambda +\rho \, r=2n$
and
![]() $r=2n(2n+1)$
gives
$r=2n(2n+1)$
gives
![]() $\lambda =2n(1-\rho (2n+1))$
, which states that the soliton is expanding, steady, or shrinking if
$\lambda =2n(1-\rho (2n+1))$
, which states that the soliton is expanding, steady, or shrinking if
 $\rho>\frac {1}{2n+1}$
,
$\rho>\frac {1}{2n+1}$
,
 $\rho =\frac {1}{2n+1}$
, or
$\rho =\frac {1}{2n+1}$
, or
 $\rho <\frac {1}{2n+1}$
, respectively. This completes the proof.
$\rho <\frac {1}{2n+1}$
, respectively. This completes the proof.
Proof Proof of Theorem 1.4
By conditions,
![]() $V = \sigma \,\xi $
for a nonzero smooth function
$V = \sigma \,\xi $
for a nonzero smooth function
![]() $\sigma $
on M. Using its covariant derivative, the antisymmetry of
$\sigma $
on M. Using its covariant derivative, the antisymmetry of
![]() $\varphi $
and (2.7), we find
$\varphi $
and (2.7), we find
In view of this, equation (1.2) becomes
At this point, replacing
![]() $Y_1$
by
$Y_1$
by
![]() $\xi $
in (3.39) and using (2.8), we achieve
$\xi $
in (3.39) and using (2.8), we achieve
 $$ \begin{align} X_1(\sigma)=\Big\{2(\lambda + \rho\,r - 2n)-\xi(\sigma)\Big\}\,\eta(X_1), \quad X_1\in\mathfrak{X}(M). \end{align} $$
$$ \begin{align} X_1(\sigma)=\Big\{2(\lambda + \rho\,r - 2n)-\xi(\sigma)\Big\}\,\eta(X_1), \quad X_1\in\mathfrak{X}(M). \end{align} $$
Again, substituting
![]() $\xi $
for both
$\xi $
for both
![]() $X_1$
and
$X_1$
and
![]() $Y_1$
in (3.39) and using (2.8), we get
$Y_1$
in (3.39) and using (2.8), we get
![]() $\xi (\sigma )=\lambda + \rho \,r - 2n$
, and therefore, equation (3.40) follows that
$\xi (\sigma )=\lambda + \rho \,r - 2n$
, and therefore, equation (3.40) follows that
![]() $\nabla \sigma =\xi (\sigma )\xi $
. Taking its covariant derivative along
$\nabla \sigma =\xi (\sigma )\xi $
. Taking its covariant derivative along
![]() $Y_1\in \mathfrak {X}(M)$
and using (2.7), we find
$Y_1\in \mathfrak {X}(M)$
and using (2.7), we find
By symmetry of
![]() ${\textrm {Hess}}_{\sigma }$
and antisymmetry of
${\textrm {Hess}}_{\sigma }$
and antisymmetry of
![]() $\varphi $
, (3.41) yields that
$\varphi $
, (3.41) yields that
Choosing
![]() $X_1,Y_1\perp \xi $
implies that
$X_1,Y_1\perp \xi $
implies that
![]() $\xi (\sigma )=0$
on M, as
$\xi (\sigma )=0$
on M, as
![]() $d\eta $
is non-zero on M; consequently,
$d\eta $
is non-zero on M; consequently,
![]() $\nabla \sigma =0$
on M. Therefore, we conclude that
$\nabla \sigma =0$
on M. Therefore, we conclude that
![]() $\sigma $
is constant on M. It follows from (3.38) and (3.40) that V is a Killing vector field and
$\sigma $
is constant on M. It follows from (3.38) and (3.40) that V is a Killing vector field and
![]() $\lambda +\rho \,r=2n$
, respectively; hence, rest of the proof follows from (3.39).▪
$\lambda +\rho \,r=2n$
, respectively; hence, rest of the proof follows from (3.39).▪
Acknowledgment
The author is thankful to the anonymous referee for many valuable comments that improves the paper. The author is grateful for the constant encouragement of Professor Vladimir Rovenski and would like to thank Professor Amalendu Ghosh for his helpful discussions and suggestions. The author is financially supported by the Council for Higher Education, Planning and Budgeting Committee, and the University of Haifa, Israel.