Coevolutionary strategies at the collective level for improved generalism

Abstract

In many complex practical optimization cases, the dominant characteristics of the problem are often not known prior. Therefore, there is a need to develop general solvers as it is not always possible to tailor a specialized approach to each application. The previously developed multilevel selection genetic algorithm (MLSGA) already shows good performance on a range of problems due to its diversity-first approach, which is rare among evolutionary algorithms. To increase the generality of its performance, this paper proposes utilization of multiple distinct evolutionary strategies simultaneously, similarly to algorithm selection, but with coevolutionary mechanisms between the subpopulations. This distinctive approach to coevolution provides less regular communication between subpopulations with competition between collectives rather than individuals. This encourages the collectives to act more independently creating a unique subregional search, leading to the development of coevolutionary MLSGA (cMLSGA). To test this methodology, nine genetic algorithms are selected to generate several variants of cMLSGA, which incorporates these approaches at the individual level. The mechanisms are tested on 100 different functions and benchmarked against the 9 state-of-the-art competitors to evaluate the generality of each approach. The results show that the diversity divergence in the principles of working of the selected coevolutionary approaches is more important than their individual performances. The proposed methodology has the most uniform performance on the divergent problem types, from across the tested state of the art, leading to an algorithm more likely to solve complex problems with limited knowledge about the search space, but is outperformed by more specialized solvers on simpler benchmarking studies.

Impact Statement

It is proposed in this paper that the uptake of many genetic algorithms is low as they are evaluated over a narrow range of problems. This means they have similar characteristics that do not properly reflect the complexity of real-world problems. The results show that those that perform across a range of problems are more likely to perform well on real applications. This explains how the leading algorithm presented in this benchmarking, cMLSGA, is now being implemented into a variety of different applications.

1. The Requirement for General Algorithms

There is a growing interest in computer-aided optimization of practical problems. This has driven the rapid development of a diverse range of evolutionary algorithms (EAs). Most of the current state-of-the-art algorithm development is driven by the benchmarking problems developed as part of the evolutionary computation literature to test their performance. Therefore, despite that the algorithms exhibit high performance on this range of problems, as they are designed for them, which can be seen in multiple competitive benchmarks (Zhang and Suganthan, 2009; Jiang and Yang, 2017; Liu et al., 2017), their general performance is reduced, as testing is often limited to a set of problems with similar characteristics. The overall result is that most of algorithms are specialists to these problems with a strong bias toward high convergence over diversity. However, high emphasis on convergence over diversity may lead to premature convergence on local optima, instead of finding the global one. This is especially prevalent on multiobjective problems with more complex search spaces such as heavily constrained, deceptive, or imbalanced problems, where the global optimum cannot be easily discovered. Here, a focus on convergence will often allow a limited region of the final Pareto optimal front to be reached, but without exploring it entirely as shown in multiple cases (Liu et al., 2014, 2017; Jiang et al., 2018). However, when they are applied to practical applications they can exhibit poor performance (Mutlu et al., 2017; Wang et al., 2018; Grudniewski and Sobey, 2019; Sobey and Grudniewski, 2019; Wang and Sobey, 2022). This is supported by the lack of uptake of most newer algorithms in the practical literature, despite their top performance in the evolutionary computation benchmarking exercises and the prevalence of second iteration of non-dominated sorting genetic algorithm (NSGA-II) (Deb et al., 2002) in many fields. Therefore despite its original development dating back to 2002 and many newer solvers having been developed since then, which are heavily outperforming the NSGA-II in the benchmarks, it is remaining as the most popular genetic algorithm (GA).

There are a number of factors for why these new algorithms may not have found success in the applied literature. Firstly, in many practical applications the characteristics of the search and objective spaces are often not well understood prior to performing the optimization. Therefore, it is not possible to select the most appropriate solvers in advance. Secondly, the benchmarking problems commonly utilized in the evolutionary literature are dominated by one main characteristic, whereas real-world problems may contain multiple dominant features. Lastly, the current state of the art focuses on unconstrained continuous problems, with few efficient algorithms specialized for problems with other characteristic types, while most of real-world applications tend to have discontinuous, multimodal, and imbalanced search spaces. This is reflected in Tables 1 and 2, where the red boxes indicate a lack of testing on a given problem set. It is possible to see a trend toward limited benchmarking during the development of an algorithm. The initial testing of algorithms is often limited to 2–3 problem sets with similar characteristics, usually not using all of the cases from the set. For example, dynamical multiobjective evolutionary algorithm with domain decomposition (DMOEA-DD) (Liu et al., 2009), MOEA/D-DE (Chen et al., 2009), and COEA (Goh and Tan, 2009) algorithms are only tested on two sets, and only three sets have been used for more popular algorithms such as multiple-trajectory search (MTS) (Tseng and Chen, 2007), NSGA-III (Deb and Jain, 2014), unified nondominated sorting genetic algorithm (U-NSGA-III) (Seada and Deb, 2015), and multiple multiobjective evolutionary algorithm based on decomposition (MOEA/D) variants (Jiang et al., 2018), despite the high diversity of available benchmarking sets. Furthermore, there is a prevalence toward testing on unconstrained problems, with all but the multi-pareto-ranking evolutionary algorithm (GAME) (Abdou et al., 2012a) and self-adaptive version of it (aGAME) (Abdou et al., 2012b) tested on these problems, with more limited testing on the constrained and imbalanced problems. In contrast, the only current algorithm that has been shown to have high performance across the range of current benchmarking problems is NSGA-II, which could explain its high popularity and utilization in practical optimization. Furthermore, it is known that convergence first algorithms struggle on a range of problems as they do not explore the entire decision variable and objective spaces due to their lack of diversity (Liu et al., 2014, 2017). This is supported by investigations on practical problems where algorithms with better diversity preservation show better performance as the complexity of the problem increases (Grudniewski and Sobey, 2019; Sobey and Grudniewski, 2019). This partly explains the success of NSGA-II, which has excellent diversity retention and can be classed as a general solver. Despite this, most of the currently developed EAs utilize a “convergence first, diversity second” approach (Liu et al., 2017) where the mechanisms that promote convergence are preferred, while diversity is obtained using secondary methods such as crowding distance calculations (Deb et al., 2002), external archive refining (Zitzler et al., 2001), problem decomposition (Zhang and Li, 2007; Liu and Li, 2009; Liu et al., 2009), or indicator-based solution selection (Zitzler and Simon, 2004; Beume et al., 2007; Priester et al., 2013).

Table 1. Summary of the literature on the unconstrained benchmarking sets used to test genetic algorithms.

Table 2. Summary of the literature on the constrained and imbalanced benchmarking sets used to test genetic algorithms.

A recent methodology developed by Grudniewski and Sobey (2018), Sobey and Grudniewski (2018), multilevel selection genetic algorithm (MLSGA), introduces a multilevel selection (MLS) mechanism, via subpopulations called collectives. The approach is based on distinct mechanisms at the individual and collective level, where the collective level utilizes reproduction of subgroups based on selection and elimination of collectives allowing information exchange between the groups. The “diversity first, convergence second” approach is generated by the unique region-based search, which is enhanced by separating the fitness function so that each level focuses its reproduction on different parts of the objective space. This approach has been shown to improve the diversity of the search and does not require extensive a priori knowledge about the problem.

In parallel to the development of MLSGA, a new range of coevolutionary algorithms, such as hybrid evolutionary immune algorithm (HEIA) (Lin et al., 2016) and bi-criterion evolutionary algorithm (BCE) (Li et al., 2016), have been shown to have strong general performance. They improve the generality of the search by merging multiple reproduction and/or improvement mechanisms which increases the chance that an effective approach will be available or by allowing the algorithm to self-adapt to the optimized problem during the process (Potter and De Jong, 1994; De Jong, 2006). However, in most cases the self-adapting algorithms have either high computational complexity or are sensitive to predefined hyperparameters (Zhou et al., 2011), making them impractical for real problems, and therefore, these approaches are not considered. Implementing these approaches without these complex mechanisms should allow a more general approach, with high diversity, without substantially reduced convergence.

To provide an algorithm that can be used practically without a priori knowledge, this paper creates a novel coevolutionary approach that works at the collective level, rather than between individuals, and combines multiple evolutionary strategies. In this case, the different collectives utilize separate reproduction mechanisms, and the information exchange is performed via the collective-level reproduction mechanisms. Due to the lack of characterization of complimentary mechanisms in coevolutionary algorithms, different state-of-the-art EAs are implemented as the individual-level reproduction mechanisms of cMLSGA: U-NSGA-III (Seada and Deb, 2015), indicator-based evolutionary algorithm (IBEA) (Zitzler and Simon, 2004), MOEA/D (Zhang and Li, 2007), BCE (Li et al., 2016), HEIA (Lin et al., 2016), MTS (Tseng and Chen, 2009), and the updated MOEA/D variants with different Scalarization Functions MOEA/D-PSF and MOEA/D-MSF (Jiang et al., 2018). The resulting algorithms are tested on a number of multiobjective test functions (Zitzler et al., 2000; Huband et al., 2005; Zhang et al., 2009; Liu et al., 2014, 2017), and the top performing variants are selected and compared to the current state of the art.

The remainder of this paper is organized as follows. In Section II, the mechanisms are compared to the related coevolutionary algorithm literature. In Section III, the proposed methodology and the benchmarking exercise are described in detail. Section IV presents the performance of cMLSGA, with a comparison to the current state of the art and is concluded in Section V.

2. Coevolutionary GAs

Coevolution is used to explain complex evolutionary dependencies between various groups of organisms (Nusimer, 2017) such as symbiosis (Currie et al., 2003), coadaptation (Potter and De Jong, 2000), host–parasite (Anderson and May, 1982), and hunter–prey (Downes and Shine, 1998) relations. The term coevolution is first introduced by Ehrlich and Raven (1964) to describe the coexistence of plants and butterflies where one group cannot survive without the other. However, the origins of this theory are older, and they are clearly described by Darwin (1859) when documenting the interactions between plants and insects. Coevolution can occur in two forms: cooperation (Potter and De Jong, 1994), where organisms coexist and “support” each other in various tasks or are mutually dependent for further benefits, or competition (Hill, 1990), where only the “strongest” may survive in the given environment, thus forcing a more effective evolution.

The idea of introducing coevolution into EAs is first presented by Potter and De Jong (1994). In the coevolutionary approach, multiple populations of species of individuals coexist and evolve in parallel, potentially utilizing distinct reproduction mechanisms, with data exchange introduced between them. Species are defined as subgroups of individuals where individuals have different “traits” assigned that determine their selection process such as sex (Raghuwanshi and Kakde, 2006); different focus on each variable (Li et al., 2003); or genotype structure and encoding (Potter and De Jong, 1994). Furthermore, the subpopulations can operate on the same search space (De Jong, 2006) or can be divided into several distinct regions by problem decomposition into multiple simpler subproblems (Jia et al., 2018). The form of data exchange between groups depends on the type of coevolution utilized: competitive or cooperative. In cooperative coevolution, the genetic information, usually the decision variables, is shared by distinct species to form a valid solution when the problem is decomposed (Potter and De Jong, 1994), or different subpopulations may cooperate to form the Pareto objective front with different subpopulations focusing on different regions (Coello Coello and Sierra, 2003). In competitive algorithms, diverse groups compete in the creation of new populations (Lin et al., 2016) or subpopulations (Goh and Tan, 2009), where fitter subpopulations gain a wider proportion of children in the next generation, by “survival of the fittest” rule or via an “arms race” approach where losing subpopulations try to counter the winning ones by changing their evolutionary approach (Rosin and Belew, 1997).

In the evolutionary computation literature, multiple algorithms can be found which are inspired by coevolution. These can be separated into two groups: approaches where all the subpopulations are subject to the same evolutionary strategies or those where different mechanisms are used to provide distinct searches. The first group implements additional mechanisms to increase the diversity while also maintaining the convergence, such as the “species” approach or problem decomposition (Goh and Tan, 2009) to split the complex problem into subproblems of a lower order. However, no increase in generality has been demonstrated for these methods. In the second approach, each group of individuals utilizes distinct evolutionary strategies, where each additional mechanism decreases the risk that every strategy will be ineffective on that particular problem at the same time leading to a more general approach. Here, only the top performing algorithms from the second group are considered and reviewed due to the interest in improving the general performance of MLSGA and similarity of approaches.

There are two recent examples of algorithms using distinct reproduction strategies, HEIA (Lin et al., 2016)and BCE (Li et al., 2016). In the BCE (Li et al., 2016), subpopulations operate on the same search spaces and instead the individuals within each group are selected for reproduction basing on two distinct fitness indicators: a Pareto-based criterion (PC) and a non-Pareto-based criterion. In the PC, standard Pareto dominance is utilized based on the objective functions, which rewards the convergence. The Non-Pareto based selection uses an additional fitness indicator that rewards diversity of solutions instead. Therefore, different subpopulation evaluation schemes are utilized, rather than fully distinct evolutionary strategies. This leads to an overall improvement in diversity for the entire population, especially on many-objective cases and problems with irregular search spaces and variable linkages. Furthermore, in the second BCE variant it has been shown that different methodologies can be utilized for both the Pareto and Non-Pareto criteria searches, without extensive parameter tuning. This shows the potential for algorithms that combine a range of mechanisms in the coevolutionary search. However, in this case the search is still convergence dominated and shows decreasing performance on practical problems of increasing complexity (Sobey and Grudniewski, 2019). A similar approach has been utilized in HEIA (Lin et al., 2016), but in this case two distinct evolutionary computation methods are used, immune algorithm and a GA, instead of separate quality indicators. In this method, the best individuals are moved to a shared pool at each generation and the subpopulations are then recreated from this. However, despite the potential of combining multiple distinct mechanisms, shown by BCE and HEIA, there is a lack of comprehensive documentation that would explain which combinations of mechanisms should be chosen for a particular problem to achieve a high performance. Therefore, the mechanisms appear to have been chosen arbitrarily, with the potential for improvements with a clearer documentation of how different mechanisms pair.

A similar approach to the coevolutionary algorithms can be found in the island-based methods (Whitley et al., 1999; Kurdi, 2016) and certain decomposition-based GAs, such as multiobjective to multiobjective (M2M) (Liu et al., 2014) and DMOEA-DD (Liu et al., 2009), which use subpopulations in a similar way to the coevolutionary approaches. For island-based methods, the subpopulation-based approach is introduced with information exchange in the form of migration of individuals. However, due to a lack of proper diversity preservation mechanisms, island-based methods are predominantly utilized for single-objective optimization and specific problems, such as scheduling (Kurdi, 2016). Both DMOEA-DD and M2M implement problem decomposition of the search spaces and then assign a separate subpopulation to each region. Therefore, the individuals are assigned to a specific subpopulation dependant on their current positions every generation. However, the combination of assigning subpopulations and the problem decomposition requires an extensive a priori knowledge about both the search and objective spaces (Trivedi et al., 2017). Furthermore, many problem decomposition methods are shown to be ineffective on problems with highly discontinuous areas, as the weight vectors cannot operate freely around the infeasible regions (Trivedi et al., 2017), and therefore application of these methods to real-life problems is limited.

The coevolutionary approaches are therefore preferred as they provide an additional diversity and generality of search, with minimal loss in convergence, and their performance is robust across a wide range of problems (Coello Coello and Sierra, 2003; Goh and Tan, 2009). However, none of these current approaches provide a fitness definition specific to the subpopulation or reproduction mechanisms for these subpopulations to allow them to evolve in combination with the individuals within them, unlike MLSGA (Sobey and Grudniewski, 2018).

3. Coevolutionary Multilevel Selection Genetic Algorithm

3.1. Multilevel selection genetic algorithm

A detailed explanation of the mechanisms and principles of working of MLSGA can be found in Sobey and Grudniewski (2018) and its extension to use other algorithms at the individual level to improve convergence can be found in Grudniewski and Sobey (2018). However, a brief review of the mechanisms is provided here for clarity. The high performance of MLSGA is based on two novel mechanisms: collective reproduction, which creates an additional selection pressure and enhances the convergence rate, and the separation of the fitness between levels, which encourages each collective to explore different areas and greatly increases the diversity of the obtained solutions. In MLSGA, the entire population is separated into a number of subgroups, called collectives, each operating on the same search and objective spaces. These collectives evolve in parallel using the same reproduction mechanism, but after a predefined, usually small, number of generations the worst collective is eliminated, based on its collective fitness value, and repopulated by individuals from the other collectives. Importantly, the collective has a specific fitness definition which can be different to the individuals inside of it. This is inspired by the evolutionary literature which demonstrates a split in how the fitness should be defined for each collective with two distinct options: multilevel selection 1 (MLS1) and multilevel selection 2 (MLS2). In the MLS1, the individual fitness is defined as the aggregate of all the objective functions for the individuals in the collective and in MLSGA this focuses the search toward the center of the Pareto front; MLS2 is defined as there being a different fitness between the individuals and the collective. Therefore, in MLSGA, using a bi-objective problem as an example, the collectives have one objective assigned to them and the individuals the other, with the result that the focus is on one extreme region of the Pareto front. By creating a reverse of this, MLS2R, the remaining collectives focus their search on the other extreme values. Therefore, each collective is “primed” to explore different regions of the objective space, leading to a subregional search strategy. As each collective’s survival and convergence is dependent on their ability to find diverse regions of the objective space, MLSGA follows a “diversity first, convergence second” principle.

3.2. Novel coevolutionary approach

In the previously developed hybrid approach, each collective utilizes the same mechanisms for the individual-level reproduction, taken from the current state of the art. In this paper, a novel method is suggested which combines multiple distinct evolutionary strategies within the multilevel structure of MLSGA to develop a distinct coevolutionary approach that is competitive through its collective-level reproduction mechanisms. In this case, different collectives utilize different mechanisms for individual offspring creation and the information exchange is less regular than in other approaches, encouraging collectives to act independently. All the original mechanisms, such as classification and collective reproduction, are copied from the previous algorithm iteration (Grudniewski and Sobey, 2018), and the same principle applies to the reproduced state-of-the-art evolutionary strategies. The methodology for cMLSGA is presented in Figure 1, where darker circles indicate fitter individuals and darker yellow rectangles indicate higher collective fitness. Only two collectives are shown for illustrative purposes of using two distinct evolutionary strategies. In the cMLSGA, multiple collectives of each type are used. The new algorithm, competitor algorithms, and benchmarking are coded in C++¹ with pseudocode detailed below.

Figure 1. cMLSGA methodology. Only two collectives are shown to illustrate how two distinct evolutionary strategies work in combination; in the cMLSGA eight collectives are used.

Inputs:

• • Multiobjective problem;

• • Np: Population size;

• • Nc: Number of collectives;

• • Fc: Frequency of collective elimination;

• • Fitness function definitions for each level;

• • Evolutionary Strategy 1 (ES1), for example, MTS;

• • Evolutionary Strategy 2 (ES2), for example, MOEA/D;

• • Individual-level specific parameters for ES1 and ES2;

• • Stopping criterion;

Output: External nondominated population (EP).

Step 1: Initialization:

Step 1.1: Set $ EP= NULL $ .

Step 1.2: Generate an initial population $ P $ of $ {N}_p $ individuals $ \left\{{x}_j,\dots, {x}_{Np}\right\} $ with randomly assigned genotypes.

Step 2: Classification:

Step 2.1: Classify the individuals from the initial population $ P $ into $ {N}_c $ collectives in total by using SVM basing on decision variable space. Each resulting collective, $ \left\{{C}_i,\dots, {C}_{Nc}\right\} $ , contains a separate population of individuals $ \left\{{P}_i,\dots, {P}_{Nc}\right\} $ .

Step 2.2: Assign the evolutionary strategy to each collective, where ES1 to first $ {N}_c/2 $ collectives and ES2 to the rest.

Step 2.3: Assign the fitness definitions from types {MLS1, MLS2, MLS2R} to each collective in the following order $ MLS1\to MLS2\to MLS2R\to MLS1\dots etc. $

Step 2.4: For each collective, perform the individual-level initialization operations according to assigned evolutionary strategy. For example, assigning weights to each individual within MOEA/D algorithm.

Step 3: Individual-level operations:

$$ Foreachcollective\hskip1em i=1,\dots, {N}_c\hskip1em do $$

Step 3.1: Individual-level GA’s operations: Perform the selection, crossover, mutation and update steps within the corresponding subpopulation $ {P}_i $ , according to assigned strategy {either ES1 or ES2}.

Step 3.2: Update external population:

Remove from the EP all solutions dominated by individuals from subpopulation $ {P}_i $ . Copy all nondominated solutions from subpopulation $ {P}_i $ to EP.

Step 4: Collective-level operations:

Step 4.1: Calculate collective fitness:

$$ Foreachcollective\hskip1em i=1,\dots, {N}_c\hskip1em do $$

Calculate the fitness of the collective $ {C}_i $ as the average of the fitnesses within the population $ {P}_i $ based on the collective-level fitness definition.

Step 4.2: Collective elimination:

Find the collective $ {C}_i $ with the worst fitness value, and store the index of that collective, $ z $ .

Store the size of the eliminated collective $ \mid {P}_z\mid $ as the variable $ s $ .

Erase the subpopulation $ {P}_z $ of the eliminated collective $ {C}_z $ .

Step 4.3: Collective reproduction:

$$ For\hskip1em i=1,\dots, {N}_c\hskip1em do $$

$ if\hskip1em \left(i\hskip1em !=\hskip1em z\right) $

Copy the best $ \frac{s}{\left({N}_c-1\right)} $ individuals, according to the collective-level fitness definition, from population $ {P}_i $ to $ {P}_z $ .

then.

Copy all individual-level parameters, specific to the assigned evolutionary strategy from eliminated collective $ {C}_z $ to the new collective, for example. In the case of the MOEA/D strategy: assign the weight vector $ {\lambda}_z $ randomly to population $ {P}_z $ .

Step 5: Termination: If the stopping criteria is met, stop and give EP as output. Otherwise, return to Step 3.

Similarly to MLSGA, the randomly generated initial population is firstly classified into a predefined number of collectives using a support vector machine (SVM) based on the decision variable space. This classification step occurs only once and is not repeated over the course of the optimization. Here, the multiclass classification SVM with C parameter and linear function (C-SVC) is being used. The utilized code has been directly taken from the LIBSVM open library (Chang and Lin, 2011 along with the training parameters. Furthermore, each collective has a separate fitness definition assigned to it, as detailed in Grudniewski and Sobey (2018).

In cMLSGA, there is an additional substep where half of the collectives utilize the selected “ES1” subroutine, and the other half the “ES2”. The type of evolution is assigned randomly to the collectives during the classification step and does not change over the run. In each subpopulation, the individuals evolve separately using the assigned strategy. After a predefined number of generations, the collective with the worst fitness value is eliminated; all individuals are being removed from it and then it is repopulated by copying the best individuals from among the rest of the collectives. The offspring collective inherits the individual reproduction methodology from the eliminated collective, as demonstrated in Figure 1 where the left collective retains MTS evolutionary strategy and the right MOEA/D strategy. Therefore, cMLSGA utilizes the multilevel approach to generate a distinct competitive coevolutionary approach, but this occurs via elimination and repopulation of one group by other subpopulations, rather than migration of individuals (Li et al., 2016), competition in each group (Goh and Tan, 2009), or recreation of all groups (Lin et al., 2016). In addition, unlike in other coevolutionary GAs, the subpopulations are not allowed to exchange information every generation but only during the collective reproduction steps. This leads to a higher diversity of the search, as each subpopulation can properly develop and maintain its independent front, thus preserving the search characteristic of the utilized evolutionary strategy, while the collective-level mechanisms allow exchange of information about the best solution leading to a higher generality and a lack of smaller bias toward specific problem types. Therefore, the cMLSGA is taking advantage of multiple distinct search strategies, similarly to algorithm selection approaches like GuRoBi, SATzilla (Xu et al., 2007), or SNNAP (Collautti et al., 2013). However, unlike in the algorithm selection, the optimization does not stop when a single methodology converges nor are the strategies separated. Instead, all of the strategies actively contribute toward the common goal and are sharing information in a coevolutionary manner.

3.3. Computational complexity and constraint handling

In cMLSGA, no computationally expensive mechanisms are added to the original MLSGA. The overall computational complexity of cMLSGA is the highest of three distinct operations:

• • Individual reproduction via ES1 with $ {X}_1 $ complexity.

• • Individual reproduction via ES2 with $ {X}_2 $ complexity.

• • Collective-level operations with $ O\left({mC}^2\right) $ complexity.

The first two are fully bound by the selection of evolutionary strategy, which is, for example, $ O\left({mN}^2\right) $ in case of U-NSGA-III, where $ m $ is the number of objectives and $ N $ is the population size, or $ O(mNT) $ in case of MOEA/D, where $ T $ is number of solutions in the neighborhood and is typically 0.2 N. The collective-level operations complexity is bound by external population nondominated sorting with $ O\left({mC}^2\right) $ complexity, where $ C $ is the size of the biggest collective with maximum size of 0.5 N, due to utilization of fast nondominated sorting approach as further detailed in Grudniewski and Sobey (2018). Therefore, the computational complexity of one generation of cMLSGA is the same as MLSGA and is bounded by $ O\left({mC}^2\right) $ , or $ X $ , which is the complexity of the most complex embedded algorithm. For constraint handling, the constraint-domination principle is adopted from NSGA-II (Deb et al., 2002), which is implemented at the individual level and describes that an individual $ {x}_1 $ dominates individual $ {x}_2 $ if:

• • $ {x}_1 $ is within constraints and $ {x}_2 $ is not OR

• • both are infeasible, but $ {x}_1 $ is violating constraints to a smaller extent OR

• • if both are feasible, then fitness domination principle is being used.

This applies whenever two individuals are compared and similarly to the original MLSGA no constraint handling is introduced for the collective-level comparison and selection.

4. Benchmarking cMLSGA Performance

4.1. Test problems

To investigate the performance over cases with different dominate characteristics, the proposed methodology is verified over 60 state-of-the-art bi-objective and 40 three-objective test functions (Zitzler et al., 2000; Huband et al., 2005; Zhang et al., 2009; Liu et al., 2014, 2017; Fan et al., 2019). These problems are divided into 12 categories for the 2-objective problems and 9 for the 3-objective problems, with the justification for the selection given in the Supplementary Material of Tables 7 and 8. Due to the variety of the problems in the test set, two- and three-objective problems are preferred as they allow a simpler interpretation of the results, without issues of scaling, while providing enough complexity to resemble a number of real-world problems. However, like most benchmarking problems in evolutionary computation, they are dominated by a single characteristic, which is less common in real-world problems.

4.2. Competitor algorithms and individual reproduction mechanisms

In this study, a variety of reproduction mechanisms are replicated from the original papers and combined through the cMLSGA methodology: IBEA (Zitzler and Simon, 2004) as the most commonly utilized indicator-based GA; BCE (Li et al., 2016) and HEIA (Lin et al., 2016) as the most highly performing coevolutionary approaches, demonstrating the difference in performance with the proposed methodology; MOEA/D-TCH (Zhang and Li, 2007) and MOEA/D-(PSF/MSF) (Jiang et al., 2018) as different variants of the top performing solver for unconstrained and imbalanced problems, respectively; MTS (Tseng and Chen, 2009) as a proficient constrained and unconstrained solver that utilizes local search strategies instead of typical evolutionary mechanisms; and U-NSGA-III (Seada and Deb, 2015) as the universal two/many-objective variant of the most commonly utilized general-solver NSGA-II (Deb et al., 2002).

Every possible pair of mechanisms is combined in the coevolutionary approach and tested. However, the combinations between U-NSGA-III, MOEA/D-TCH, MOEA/D-PSF, and MOEA/D-MSF are discarded from further evaluations. This is because every MOEA/D variant is based on the same framework while U-NSGA-III and MOEA/D are both based on developing a constant Pareto front at each generation. The concluded prebenchmarks demonstrate that such a high similarity in mechanisms and principles of working result in no performance gains within the coevolutionary approaches; thus, the results for these variants are not reported as part of this work. According to that, 22 variants in total are developed and evaluated with the results attached as Supplementary Material to this paper.

The tests are performed over 30 separate runs, with 300,000 function evaluations for each run, following CEC’ 09 recommendations, which is a commonly used standard for fair comparison of performance (Zhang et al., 2009). The results are compared using two performance indicators: inverted generational distance (IGD) and hypervolume (HV), as they provide information on the convergence and diversity of the obtained solutions. IGD measures the average Euclidean distance between any point in a uniformly distributed Pareto front and the closest solution in the obtained set. Low scores for this metric emphasize convergence and uniformity of the points (Zitzler et al., 2002). HV is the measure of volume of the objective space between a predefined reference point and the obtained solutions with a stronger focus on the diversity and edge points. For the IGD calculations, 1,000,000 reference points in total are generated in this paper and the HV score is calculated according to While et al. (2012), which is the fastest and most widely used method.

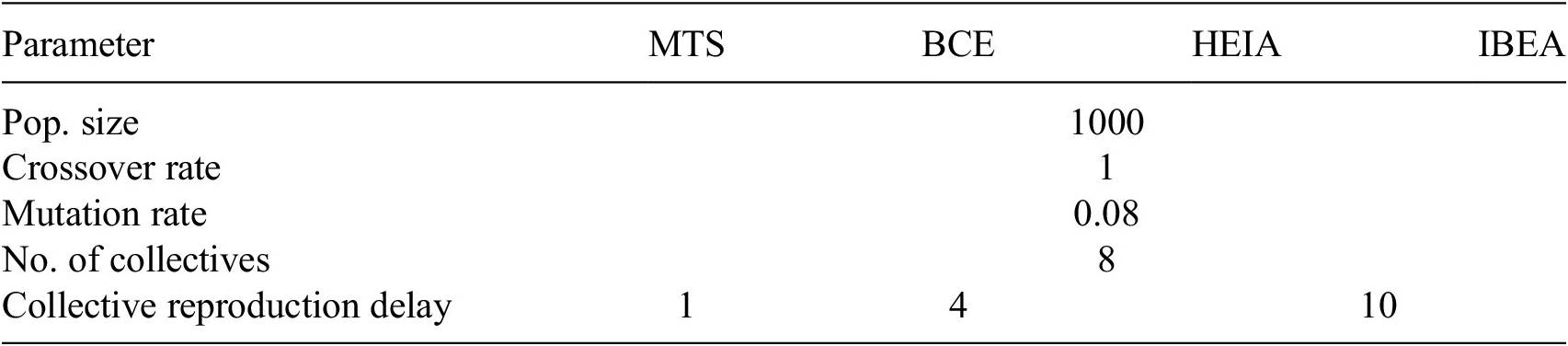
4.3. Hyperparameters

Different operational parameters, population size, number of collectives, and collective reproduction delay, were tested and the best performing values are summarized in Table 3. However, it has been concluded that the algorithm is insensitive to hyperparameters, as they do not have a significant impact on the overall performance within a reasonable variation and do not need changing between different problems or while utilizing divergent evolutionary strategies. Between different groups of mechanisms, the only parameter that is different is the collective reproduction delay. The variance is caused by BCE, HEIA, and IBEA developing fronts at different paces, and therefore, low values of collective elimination led to premature removal of these underdeveloped fronts. MTS requires significantly more iterations per generation, as it utilizes multiple local search methods, and therefore, the elimination has to occur more frequently to have an impact on the search. The number of collectives is 8 in all cases leading to 4 collectives using the first evolutionary strategy and the other 4 using the second one. All other GA-specific parameters, for example, MOEA/D neighborhood size, are taken directly from the original publications to create a more realistic scenario where a priori knowledge cannot be utilized.

Table 3. The GA parameters utilized for benchmarking.

4.4. Determining the characteristics of complementary coevolutionary mechanisms

The performances of the selected cMLSGA variants are compared to the original algorithms with the data attached as a Supplementary Material. Due to the large quantity of data, only the most interesting 4 representative cases of the 22 methods trialled are described further in this section: IBEA_BCE, which shows the highest improvement over the original algorithms; MOEA/D-MSF_HEIA as the combination of a convergence solver and a more general solver; MOEA/D-MSF_U-NSGA-III as the combination of a convergence solver and the top algorithm for problems with many objectives; and MTS_MOEA/D, which combines two convergence first methodologies, MTS with high performance on constrained cases and MOEA/D the top unconstrained GA. This is summarized in Table 4. It can be observed that the cMLSGA approach does not improve the performance of the original algorithms in all cases and for most of them the performance is in between the effectiveness of both implemented methodologies. This shows that cMLSGA is often limited by the performance of the worst of the utilized strategies but leads to a more robust, “general solver,” with a lower chance of poor performance.

Table 4. Comparison of selected cMLSGA variants to the implemented algorithms according to IGD/HV indicator.

Comparing the 22 variants of cMLSGA against the original algorithms, the highest improvement is exhibited by the cMLSGA _IBEA_BCE variant. In this case, the performance is improved on 67 out of 100 problems for the IGD indicator and 62 cases for the HV indicator; it only exhibits worse performance in 5 and 6 cases for IGD and HV, respectively. cMLSGA _MOEA/D-MSF_HEIA is the best performer on the two-objective test set, where it is better than both methodologies in 38 cases for IGD and 40 cases for HV but worse in 16 cases for each indicator, whereas cMLSGA _MOEA/D-MSF_U-NSGA-III is the top performer for the three-objective problems. It performs better on 33 problems but is worse for 10 problems for IGD and is better for 31 problems and worse for 17 problems when evaluating using the HV metric. For the high convergence solver, cMLSGA _MTS_MOEA/D better results are obtained in 29 and 23 cases for IGD and HV indicators but worse on 19 and 21 of them, respectively. This indicates that if two methodologies with strong diversity mechanisms, such as IBEA and BCE, are used then cMLSGA is able to successfully combine the methodologies and preserve the diversity mechanisms, while providing stronger convergence. It not only supports the previous findings that the MLSGA mechanisms promote diversity (Sobey and Grudniewski, 2018) but also indicates that if sufficient diversity is obtained the MLS-U collectives will focus the search, improving convergence. The reduced performance of the other two presented variants, which combine strong convergence-based mechanisms, may be caused by the inability of MLSGA to properly maintain a search pattern during the collective elimination and reproduction steps, as indicated previously in Grudniewski and Sobey (2018). In the case of the MTS and MOEA/D variants, the performance of the cMLSGA approach resembles the results of MTS, especially for the IGD indicator. This is due to the local searches that require a substantial number of iterations per generation, the MTS mechanisms “dominate” the search, and the secondary mechanisms, MLSGA and MOEA/D, do not have a sufficient influence. Therefore, if a method is combined with a significantly stronger convergence-first methodology than the other method, such as MTS, the weaker method will have negligible impact on the search. The result is that there is an improvement in the uniformity of the points, but no new areas of the Pareto optimal front are found and so diversity is not increased. A similar principle applies to the MOEA/D-MSF_HEIA and MOEA/D-MSF_U-NSGA-III variants, where the specialist convergence-based methodology is combined with a general diversity-based one. This indicates that cMLSGA maintains distinct searches for both algorithms if two methodologies with contrasting mechanisms are combined, rather than one method outperforming the other. It can be concluded that the selection of methodologies within cMLSGA is subject to how divergent the behavior of the chosen methods is. The poor performance of MOEA/D, MOEA/D-MSF, MOEA/D-PSF, and MTS combinations, compared to the original algorithms, shows that implementing methodologies that are too similar, strong convergence based in this case, is not at all beneficial, due to the noncomplementary nature of the searches. Therefore, the diversity of the methodologies, such as different principles of working with convergence vs. diversity-based search with the MOEA/D-MSF_HEIA and MOEA/D-MSF_U-NSGA-III variants, or different preferred areas of applications with IBEA_BCE variant, is more important than their individual performances.

4.5. Behavior of cMLSGA: Increased generality

The performance of the best-developed cMLSGA variant is compared with previous version of MLSGA algorithm, as well as to 8 selected current state-of-the-art algorithms, to evaluate the potential of the cMLSGA approach as a general solver. In the case of two objectives, the cMLSGA _HEIA_MOEA/D-MSF variant is utilized, whereas for more objectives the cMLSGA _MOEA/D-MSF_U-NSGA-III is compared, due to the outstanding performance of U-NSGA-III on three-objective problems, and the lower effectiveness of HEIA on them. This is presented in the form of an average ranking on each category of problem in Table 5 for two-objective problems and 6 for three-objective problems. From the two-objective ranking, it can be observed that the best solver on average is cMLSGA, 3.60/3.82 for the IGD/HV metrics, while MLSGA comes second with 4.33/4.15 for the IGD/HV indicators and the HEIA is third with 4.40/4.58, respectively. Higher differences in the HV scores indicate that cMLSGA is more likely to promote high diversity than HEIA but less likely than MLSGA. In addition, cMLSGA is showing a more general solver approach than both of those algorithms, as it has a lower deviation in performance with smaller standard deviations of its positions in the rankings presented in Table 5, 1.57/1.58 for IGD/HV compared to MLSGA and HEIA, 1.93/1.98 and 2.59/2.59, respectively. Those differences in robustness are further illustrated in Figure 2, where the occurrence of each rank is presented for the MLSGA-hybrid, cMLSGA, and HEIA algorithms. All three algorithms are often the top performers, rank 1 and 2, with HEIA and MLSGA-hybrid being the first more regularly, 11 times for IGD and 10 for HV for HEIA, and 8/5 for MLSGA, compared to 4/7 for cMLSGA. However, when HEIA and MLSGA show low performance on a problem they perform very poorly with rank 8 eight times for both indicators for HEIA, and 1/2 for MLSGA-hybrid; rank 9 one time for both algorithms according to HV and once according to IGD for MLSGA-hybrid; and rank 9 two times for IGD and one time for HV for HEIA only, whereas the lowest rank for cMLSGA is 7 and it has a high occurrence in the 3 $ {}^{rd} $ , 4 $ {}^{th} $ , and 5 $ {}^{th} $ positions, demonstrating that cMLSGA is the best general solver while showing a higher specialization of the previous version of it, MLSGA.

Table 5. The rankings for the 10 genetic algorithms according to the average performance on different two-objective problem categories for IGD/HV indicator.

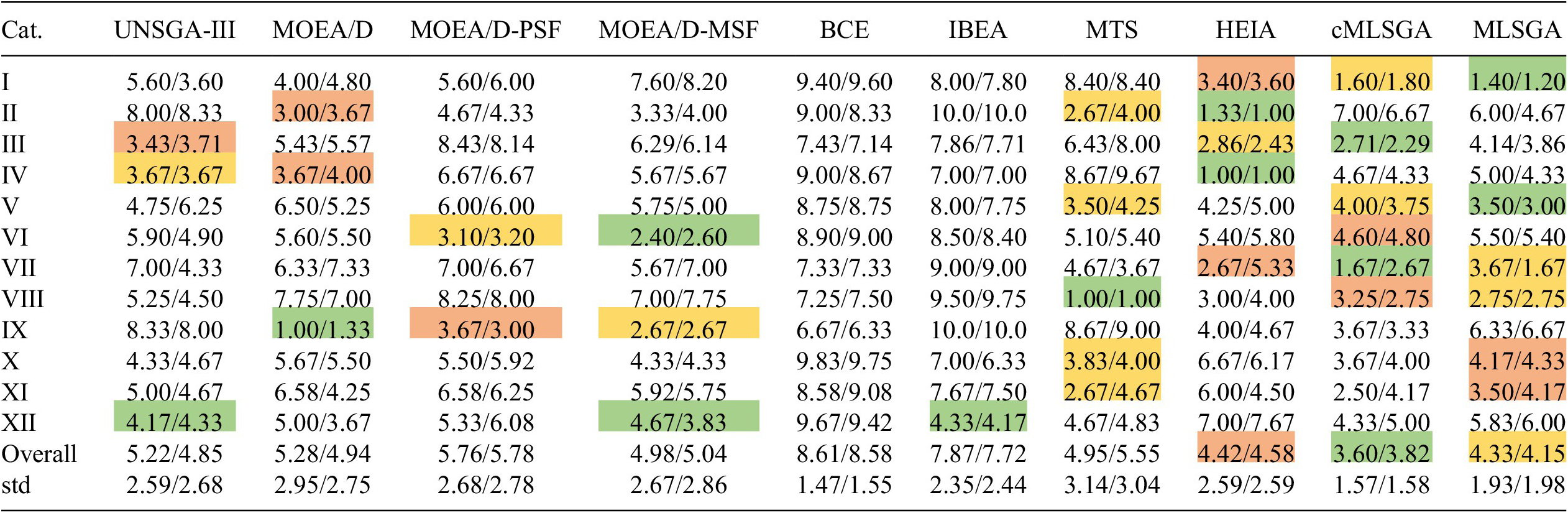
Note. The best algorithm in each category is highlighted in green, and the second and the third best solvers are highlighted in orange and red, respectively.

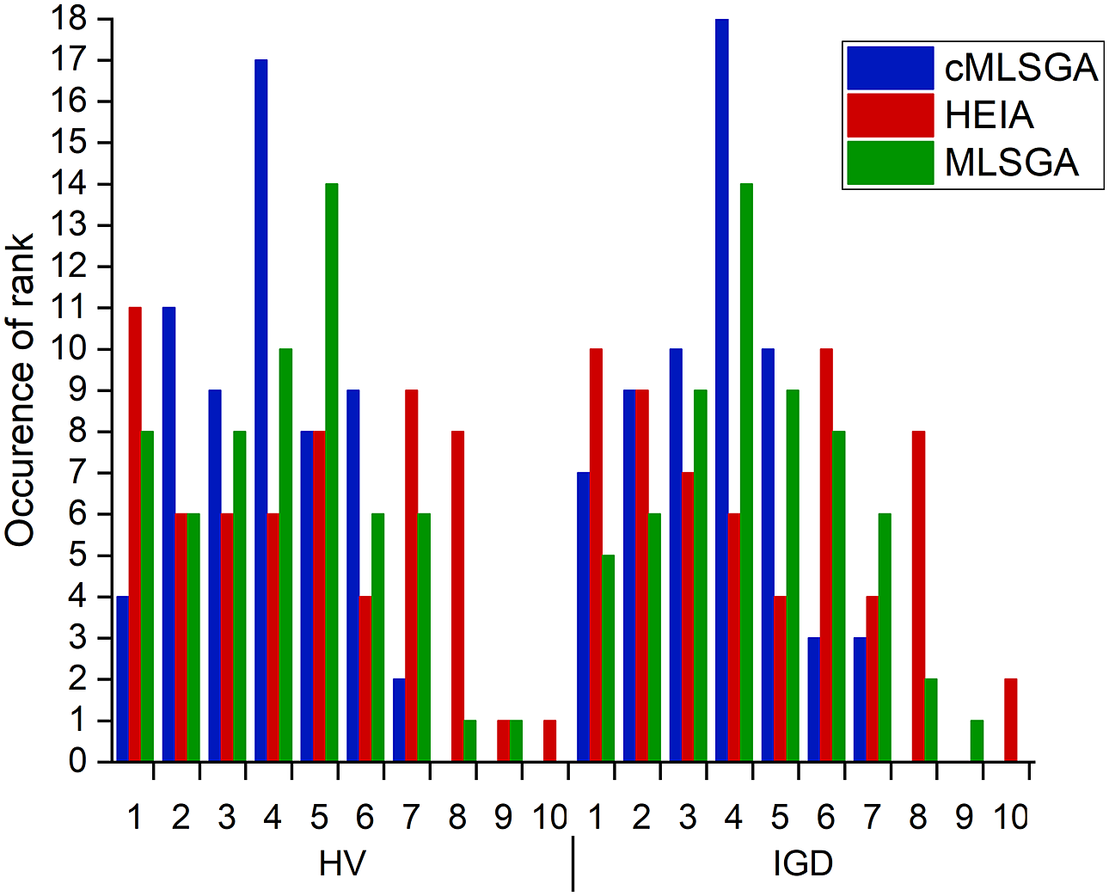
Figure 2. Occurrence of ranks for HEIA, cMLSGA, and MLSGA algorithms on two-objective problems.

Similar behavior can be observed for the three-objective problems. From the corresponding ranking, Table 6, it can be observed that the best solver on average is cMLSGA and U-NSGA-III comes second. The IGD rankings are 3.525 for cMLSGA and 4.100 for U-NSGA-III, and 3.175 and 4.550 according to HV, showing significantly better performance of cMLSGA over its predecessor, MLSGA, with scores 4.875 and 4.775 for IGD and HV, respectively. Similarly to the bi-objective cases, cMLSGA also shows lower standard deviations than the second best-on-average algorithm, U-NSGA-III, further proving its high generality. Comparing the occurrence of each rank for U-NSGA-III, cMLSGA, and MLSGA, illustrated in Figure 3, it can be seen that cMLSGA is again more likely to avoid poor performance. In this case, cMLSGA is less likely to exhibit the highest performance according to the IGD metric but is more likely to be top performer according to HV, in comparison to U-NSGA-III and MLSGA. Furthermore, cMLSGA is significantly more likely to have third-best performance, 13 times with both IGD and HV compared to 8 and 4 times for U-NSGA-III with HV and IGD, respectively. In contrast, U-NSGA-III is significantly more likely to perform poorly, as in the worst-case scenario it is 10 $ {}^{th} $ for IGD and 9 $ {}^{th} $ for HV, whereas for cMLSGA lowest position is 7 $ {}^{th} $ for both indicators. Furthermore, U-NSGA-III is more likely than cMLSGA to achieve ranks 6 and 7. Interestingly, both algorithms are more likely to be in the middle positions 2 $ {}^{nd} $ to 5 $ {}^{th} $ , showing a distribution reflecting a general performance. This indicates a high generality and universality of both solutions which are often outperformed by specialist solvers on their preferred cases. Furthermore, this shows that non-coevolutionary MLS-based strategy used in original MLSGA is less effective with more than two objectives. The resulting methodology is unlikely to outperform the individual algorithms on their preferred cases, as the cMLSGA is still bounded by the performance of the implemented algorithms. However, by combining the advantages of the two methodologies selected at the individual level and utilizing diversity-first approaches, derived from the MLS mechanisms, the chance of success of cMLSGA is still significantly higher than other algorithms, especially in cases where there is no knowledge about the optimization space. If a single evolutionary strategy fails, then the optimization continues through the second strategy, minimizing the risks of premature convergence on local optima, similarly to algorithm selection solutions. However, due to unique collective reproduction mechanisms within the cMLSGA, the initially ineffective strategy is still providing potential solutions which may be beneficial during the optimization, especially its later stages. This further enhances the effectiveness in avoiding infeasible or deceptive regions and thus finding the global optimum. The resulting overall profile is similar to that of U-NSGA-III than the rest of the state of the art, as this algorithm also shows a strong general performance and especially high performance on the HV diversity metric. This combination provides confidence that cMLSGA will provide satisfactory results on cases where there is no a priori knowledge of the problem characteristic or where there are multiple dominating characteristics, the case for many real-world problems. In cases where there is a priori knowledge of the problem, the provided supporting data, showing the results for all the variants of cMLSGA, will allow determination of the strongest variant for a given problem type. As performance of cMLSGA depends on the quality of the implemented evolutionary strategies, their selection remains important. A self-adaptive variant may be considered in the future, but currently the HEIA_MEOA/D-MSF combination is suggested for two-objective problems and MOEA/D-MSF_U-NSGA-III for more objectives, as these methodologies are the most distinct and show the most “general” behavior on the corresponding cases. Regarding the individual performance, the cMLSGA predominantly exhibits good results on problems that require high diversity in comparison to the original algorithms. It operates significantly better on cases with discontinuous search spaces, categories V, VII, and VIII, rather than continuous problems, and on diversity- and feasibility-hard functions, categories X and XI. The lower impact on the performance of the continuous functions is caused by the additional region searches provided by cMLSGA, which are not necessary as convergence is more important for these problems. Therefore, the presented methodology does not lead to performance improvements on the cases where the results from at least one of the original algorithms are close to the ideal Pareto optimal front. This is caused by there being little room for improvement, indicating that these mechanisms are well tuned to these problems and any changes reduce their effectiveness or that even more specialist mechanisms are required to improve the performance. Therefore, adding additional mechanisms that are created to enhance the overall diversity makes the search less focused and leads to worse overall performance if the algorithm is already able to obtain excellent results. Unsurprisingly, this indicates that cMLSGA will underperform convergence specialized GA methodologies on their preferred cases. This is demonstrated on the category XII problems, which are difficult convergence problems, with all the cMLSGA variants performing relatively poorly. In contrast to the results on the convergence-based problems, high performance is achieved on categories X–XI, which belong to the same test set (Fan et al., 2019) but focuses on providing hard diversity and feasibility problems.

Table 6. The rankings for the 10 genetic algorithms according to the average performance on different three-objective problem categories for IGD/HV indicator.

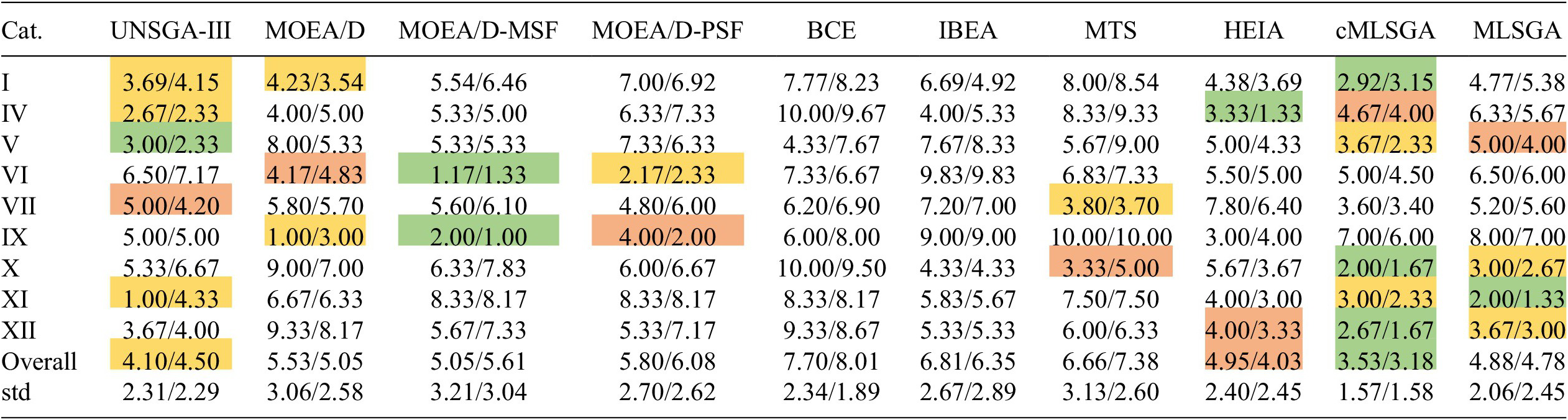
Note. The best algorithm in each category is highlighted in green, and the second and the third best solvers are highlighted in orange and red, respectively.

Figure 3. Occurrence of ranks for U-NSGA-III, cMLSGA, and MLSGA algorithms on three-objective problems.

5. Conclusions

Current real-world problems have been shown to be more complex than the available evolutionary computation benchmarking problems, requiring algorithms evaluated on constrained and imbalanced problems that require high diversity. In addition, when solving practical optimization problems, there is often no a priori knowledge about the problem set, meaning that specialist algorithms cannot be selected in advance. To develop an algorithm with both high diversity and general properties, this paper presents a novel coevolutionary approach. The novel approach is the first to develop an approach dependant on competition between collectives, and the additional mechanisms are added to the MLSGA, designated cMLSGA. A lower communication rate between subpopulations than in other coevolutionary approaches and a split in the fitness definition between individual and collective levels allow an independence of search between the different collectives. The new methodology promotes a diversity first, convergence second behavior seen in previous iterations of this algorithm, improving performance on highly discontinuous, constrained, and irregular problems. An investigation into the optimum pairing of algorithms in the coevolutionary approach provides general guidance for developers of algorithms using these approaches, showing that the diversity of the coevolutionary mechanisms is more important than their individual performance. Based on this pairing, the resulting cMLSGA is shown to have the best general performance over 100 test problems from among the 10 tested GAs selected for their high performance in the literature. This greatly increases cMLSGA’s applicability to real-world problems, especially on cases where the problem characteristics are not known or where they are dominated by more than one characteristic.