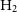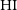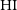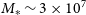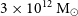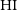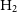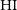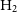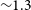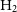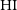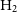1. Introduction
The determination of the matter–energy content of the Universe is one of the most important achievements from the recent advances in observational cosmology (e.g., Planck Collaboration et al. 2016; 2018). Current determinations are fully consistent with the spatially flat  $\Lambda$
Cold Dark Matter (
$\Lambda$
Cold Dark Matter ( $\Lambda\mbox{CDM}$
) cosmology, with a present-day matter–energy content dominated by the cosmological constant,
$\Lambda\mbox{CDM}$
) cosmology, with a present-day matter–energy content dominated by the cosmological constant,  $\Omega_{\Lambda} = 0.689$
, and contributions of cold dark matter and baryon matter of
$\Omega_{\Lambda} = 0.689$
, and contributions of cold dark matter and baryon matter of  $\Omega_{\rm cdm} \approx 0.262$
and
$\Omega_{\rm cdm} \approx 0.262$
and  $\Omega_{\rm bar} = 0.049$
, respectively (for a value of the normalised Hubble constant of
$\Omega_{\rm bar} = 0.049$
, respectively (for a value of the normalised Hubble constant of  $h=0.674$
, Aver et al. Reference Aver, Olive and Skillman2015; Cooke, Pettini, & Steidel Reference Cooke, Pettini and Steidel2018; Planck Collaboration et al. 2018). Therefore, the universal baryon mass density fraction is
$h=0.674$
, Aver et al. Reference Aver, Olive and Skillman2015; Cooke, Pettini, & Steidel Reference Cooke, Pettini and Steidel2018; Planck Collaboration et al. 2018). Therefore, the universal baryon mass density fraction is  $f_{\rm bar,U} \equiv \Omega_{\rm bar} / \Omega_{\rm m} = 0.158$
, where
$f_{\rm bar,U} \equiv \Omega_{\rm bar} / \Omega_{\rm m} = 0.158$
, where  $\Omega_{\rm m}= \Omega_{\rm cdm} + \Omega_{\rm bar}$
. How much of these baryons, and their different components, are locked inside galaxies? This paper addresses this question by quantifying the contribution from stars, atomic, and molecular gas in galaxies of different masses and morphological types.
$\Omega_{\rm m}= \Omega_{\rm cdm} + \Omega_{\rm bar}$
. How much of these baryons, and their different components, are locked inside galaxies? This paper addresses this question by quantifying the contribution from stars, atomic, and molecular gas in galaxies of different masses and morphological types.
According to the current paradigm of structure formation, non-baryonic dark matter played a major role in the evolution of the non-linear structures that we see today. Particularly, galaxies are believed to form and evolve within extended dark matter haloes, where multiple physical mechanisms are responsible for self-regulating star formation and thus setting up their observed properties (for reviews see, Mo, van den Bosch, & White Reference Mo, van den Bosch and White2010; Frenk & White Reference Frenk and White2012; Somerville & Davé Reference Somerville and Davé2015). As dark matter structures and galaxies evolve, baryons are redistributed from an initial smooth distribution to a more complex variety of structures. Of primordial importance for galaxy evolution is the amount of neutral hydrogen available for the formation of stars. Gas radiative cooling within the haloes regulates the inflow of cold gas to galaxies. The subsequent formation of stars is regulated by a complex interaction between cold gas inflows and the gas heating/outflows produced by the stars, a process that depends on halo mass. In low-mass halos, the stellar feedback, mostly form Supernova (SN) explosions, is able not only to heat the interstellar medium (ISM) but also to expel large gas fractions from the galaxy. In high-mass haloes, the long cooling time of shock-heated gas and the powerful feedback from rapidly accreting supermassive black holes that heats and/or expels the gas tend to suppress the star formation. Thus, it is not surprising that the expected fraction of baryons inside galaxies will differ from the universal baryon fraction,  $f_{\rm bar,U}$
. Therefore, constraining the fraction of baryons and their different components in galaxies (mainly stars, atomic, and molecular gas) is essential to constrain the processes that have taken place during the evolution of the galaxies.
$f_{\rm bar,U}$
. Therefore, constraining the fraction of baryons and their different components in galaxies (mainly stars, atomic, and molecular gas) is essential to constrain the processes that have taken place during the evolution of the galaxies.
One of the main properties of galaxies are their stellar masses  $M_{*}$
. Indeed, the abundance of galaxies as a function of
$M_{*}$
. Indeed, the abundance of galaxies as a function of  $M_{*}$
provides important clues regarding the evolution of the galaxy population (e.g., Peng et al. Reference Peng2010, Reference Peng, Lilly, Renzini and Carollo2012; Yang et al. Reference Yang, Mo, van den Bosch, Zhang and Han2012; Rodríguez-Puebla et al. 2017). Over the last two decades, there has been a remarkable progress in assembling large galaxy samples from multi-wavelength sky surveys that have led to robust determinations of the galaxy stellar mass function (GSMF; for recent discussions, and compilations of observations up to high redshifts see, Conselice et al. Reference Conselice, Wilkinson, Duncan and Mortlock2016; Rodríguez-Puebla et al. 2017). While there have been similar efforts in assembling galaxy samples for atomic gas mass,
$M_{*}$
provides important clues regarding the evolution of the galaxy population (e.g., Peng et al. Reference Peng2010, Reference Peng, Lilly, Renzini and Carollo2012; Yang et al. Reference Yang, Mo, van den Bosch, Zhang and Han2012; Rodríguez-Puebla et al. 2017). Over the last two decades, there has been a remarkable progress in assembling large galaxy samples from multi-wavelength sky surveys that have led to robust determinations of the galaxy stellar mass function (GSMF; for recent discussions, and compilations of observations up to high redshifts see, Conselice et al. Reference Conselice, Wilkinson, Duncan and Mortlock2016; Rodríguez-Puebla et al. 2017). While there have been similar efforts in assembling galaxy samples for atomic gas mass,  $M_{\rm HI}$
, based on radio blind observations (e.g., Zwaan et al. Reference Zwaan2003; Meyer et al. Reference Meyer2004; Koribalski et al. Reference Koribalski2004; Kovac et al. Reference Kovac, Oosterloo, van der Hulst, Jerjen and Binggeli2005; Martin et al. Reference Martin, Papastergis, Giovanelli, Haynes, Springob and Stierwalt2010; Haynes et al. Reference Haynes2011; Hoppmann et al. Reference Hoppmann, Staveley-Smith, Freudling, Zwaan, Minchin and Calabretta2015; Haynes et al. Reference Haynes2018) or from follow-up subsamples based on optical/infrared surveys (e.g., Springob et al. Reference Springob, Haynes, Giovanelli and Kent2005; van Driel et al. Reference van Driel2016), these are relatively shallow and/or in small volumes compared to the optical/infrared sky surveys, as well as strongly affected by selection effects. Therefore, the demographical analysis of
$M_{\rm HI}$
, based on radio blind observations (e.g., Zwaan et al. Reference Zwaan2003; Meyer et al. Reference Meyer2004; Koribalski et al. Reference Koribalski2004; Kovac et al. Reference Kovac, Oosterloo, van der Hulst, Jerjen and Binggeli2005; Martin et al. Reference Martin, Papastergis, Giovanelli, Haynes, Springob and Stierwalt2010; Haynes et al. Reference Haynes2011; Hoppmann et al. Reference Hoppmann, Staveley-Smith, Freudling, Zwaan, Minchin and Calabretta2015; Haynes et al. Reference Haynes2018) or from follow-up subsamples based on optical/infrared surveys (e.g., Springob et al. Reference Springob, Haynes, Giovanelli and Kent2005; van Driel et al. Reference van Driel2016), these are relatively shallow and/or in small volumes compared to the optical/infrared sky surveys, as well as strongly affected by selection effects. Therefore, the demographical analysis of  $M_{\rm HI}$
is challenging especially when determining the low- and high-mass ends of the
$M_{\rm HI}$
is challenging especially when determining the low- and high-mass ends of the  $\rm HI$
mass function (
$\rm HI$
mass function ( $\rm HI$
MF) (for a more detailed discussion, see Jones et al. Reference Jones, Haynes, Giovanelli and Moorman2018)Footnote a, as well as other statistics like the
$\rm HI$
MF) (for a more detailed discussion, see Jones et al. Reference Jones, Haynes, Giovanelli and Moorman2018)Footnote a, as well as other statistics like the  $\rm HI$
two-point correlation functionsFootnote b. The situation is not that different and even more challenging for the molecular gas as there are not blind galaxy samples in
$\rm HI$
two-point correlation functionsFootnote b. The situation is not that different and even more challenging for the molecular gas as there are not blind galaxy samples in  $\rm H_{2}$
. Nonetheless, there are some notable efforts to use optically selected samples combined with small and shallow CO surveys to indirectly derive, from the (uncertain) CO-to-
$\rm H_{2}$
. Nonetheless, there are some notable efforts to use optically selected samples combined with small and shallow CO surveys to indirectly derive, from the (uncertain) CO-to- $\rm H_{2}$
mass conversion factor, the galaxy MF in
$\rm H_{2}$
mass conversion factor, the galaxy MF in  $\rm H_{2}$
,
$\rm H_{2}$
,  $\rm H_{2}$
MF (e.g., Keres, Yun, & Young Reference Keres, Yun and Young2003; Lagos et al. Reference Lagos, Davis, Lacey, Zwaan, Baugh, Gonzalez-Perez and Padilla2014; Saintonge et al. Reference Saintonge2017; Andreani et al. Reference Andreani, Boselli, Ciesla, Vio, Cortese, Buat and Miyamoto2018). Unfortunately, these CO surveys are also subject to incompleteness and selection effects or subject to a large fraction of galaxies with upper limits reported due to flux detection limits.
$\rm H_{2}$
MF (e.g., Keres, Yun, & Young Reference Keres, Yun and Young2003; Lagos et al. Reference Lagos, Davis, Lacey, Zwaan, Baugh, Gonzalez-Perez and Padilla2014; Saintonge et al. Reference Saintonge2017; Andreani et al. Reference Andreani, Boselli, Ciesla, Vio, Cortese, Buat and Miyamoto2018). Unfortunately, these CO surveys are also subject to incompleteness and selection effects or subject to a large fraction of galaxies with upper limits reported due to flux detection limits.
As mentioned above, galaxy formation is a non-linear and complex process. Remarkably, well-defined correlations (usually power laws) are, however, found from the observations. Among these are the correlations between the  $\rm HI$
and stellar mass,
$\rm HI$
and stellar mass,  $M_{\rm HI}$
–
$M_{\rm HI}$
– $M_{*}$
, and the
$M_{*}$
, and the  $\rm H_{2}$
and stellar mass,
$\rm H_{2}$
and stellar mass,  $M_{\rm H2}$
–
$M_{\rm H2}$
– $M_{*}$
. While both correlations present large scatters, when divided into early- and late-type galaxies they tend to show different and tighter correlations (e.g., Calette et al. Reference Calette, Avila-Reese, Rodrguez-Puebla, Hernández-Toledo and Papastergis2018, and more references therein). This is not surprising given that the formation histories of early- and late-type galaxies were different. Thus, understanding the contribution of these two populations to the abundance of galaxies traced by
$M_{*}$
. While both correlations present large scatters, when divided into early- and late-type galaxies they tend to show different and tighter correlations (e.g., Calette et al. Reference Calette, Avila-Reese, Rodrguez-Puebla, Hernández-Toledo and Papastergis2018, and more references therein). This is not surprising given that the formation histories of early- and late-type galaxies were different. Thus, understanding the contribution of these two populations to the abundance of galaxies traced by  $\rm HI$
and
$\rm HI$
and  $\rm H_{2}$
provides further key constrains to galaxy formation theory models.
$\rm H_{2}$
provides further key constrains to galaxy formation theory models.
In a recent work, (Calette et al. Reference Calette, Avila-Reese, Rodrguez-Puebla, Hernández-Toledo and Papastergis2018, hereafter Paper I) were able to determine empirically not only the mean  $M_{\rm HI}$
–
$M_{\rm HI}$
– $M_{*}$
and
$M_{*}$
and  $M_{H_{2}}$
–
$M_{H_{2}}$
– $M_{*}$
relations and their scatters for early- and late-type galaxies but also the full conditional probability distribution functions (CPDFs) of
$M_{*}$
relations and their scatters for early- and late-type galaxies but also the full conditional probability distribution functions (CPDFs) of  $M_{\rm HI}$
and
$M_{\rm HI}$
and  $M_{H_{2}}$
given
$M_{H_{2}}$
given  $M_{*}$
, hereafter
$M_{*}$
, hereafter  $\rm HI$
-CPDF and
$\rm HI$
-CPDF and  $\rm H_{2}$
-CPDF, respectively. In this paper, we combine the empirical CPDFs with the
$\rm H_{2}$
-CPDF, respectively. In this paper, we combine the empirical CPDFs with the  $z=0$
GSMF to derive the bivariate gas-to-stellar mass distributions and the MFs for the
$z=0$
GSMF to derive the bivariate gas-to-stellar mass distributions and the MFs for the  $\rm HI$
,
$\rm HI$
,  $\rm H_{2}$
, cold gas, and baryon components, for all galaxies as well as for early and late types. Thus, the present paper represent a natural continuation of Paper I with some updates. These updates include new constraints on the best-fitting parameters to the observed CPDFs from Paper I.
$\rm H_{2}$
, cold gas, and baryon components, for all galaxies as well as for early and late types. Thus, the present paper represent a natural continuation of Paper I with some updates. These updates include new constraints on the best-fitting parameters to the observed CPDFs from Paper I.
In this paper, we compute the GSMF and its decomposition into early- and late-type galaxies. While there are many studies that have determined the GSMF in the past, they do not typically report systematic errors or do not deconvolve it from random errors (with a few exceptions, e.g., Bernardi et al. Reference Bernardi, Shankar, Hyde, Mei, Marulli and Sheth2010, Reference Bernardi, Meert, Sheth, Fischer, Huertas-Company, Maraston, Shankar and Vikram2017; Obreschkow et al. Reference Obreschkow, Murray, Robotham and Westmeier2018) or they are limited in the dynamical range of  $M_{*}$
due to the limited depth of the sample and/or the cosmic variance in the galaxy sample (but see Wright et al. Reference Wright2017). We combine here two large galaxy samples, the low-redshift sample, low-z, from the NYU Sloan Digital Sky Survey (SDSS) DR4 (Blanton et al. Reference Blanton2005a; b), and the new photometry pipeline for the SDSS DR7 from Meert et al. (Reference Meert, Vikram and Bernardi2015, Reference Meert, Vikram and Bernardi2016). The low-z sample suffers from surface brightness incompleteness, but here we estimate and correct for the fraction of missing galaxies due to this selection effect. As for the SDSS DR7, the new photometry from Meert et al. (Reference Meert, Vikram and Bernardi2015) shows that galaxy magnitudes were previously underestimated due to sky subtraction problems (see also, Simard et al. Reference Simard, Mendel, Patton, Ellison and McConnachie2011); the impact of these new determinations has been studied previously in Bernardi et al. (Reference Bernardi, Meert, Sheth, Fischer, Huertas-Company, Maraston, Shankar and Vikram2017). We extend the Bernardi et al. (Reference Bernardi, Meert, Sheth, Fischer, Huertas-Company, Maraston, Shankar and Vikram2017) analysis using not only different definitions of galaxy stellar masses but by dividing into two morphology groups, early- and late-type galaxies.
$M_{*}$
due to the limited depth of the sample and/or the cosmic variance in the galaxy sample (but see Wright et al. Reference Wright2017). We combine here two large galaxy samples, the low-redshift sample, low-z, from the NYU Sloan Digital Sky Survey (SDSS) DR4 (Blanton et al. Reference Blanton2005a; b), and the new photometry pipeline for the SDSS DR7 from Meert et al. (Reference Meert, Vikram and Bernardi2015, Reference Meert, Vikram and Bernardi2016). The low-z sample suffers from surface brightness incompleteness, but here we estimate and correct for the fraction of missing galaxies due to this selection effect. As for the SDSS DR7, the new photometry from Meert et al. (Reference Meert, Vikram and Bernardi2015) shows that galaxy magnitudes were previously underestimated due to sky subtraction problems (see also, Simard et al. Reference Simard, Mendel, Patton, Ellison and McConnachie2011); the impact of these new determinations has been studied previously in Bernardi et al. (Reference Bernardi, Meert, Sheth, Fischer, Huertas-Company, Maraston, Shankar and Vikram2017). We extend the Bernardi et al. (Reference Bernardi, Meert, Sheth, Fischer, Huertas-Company, Maraston, Shankar and Vikram2017) analysis using not only different definitions of galaxy stellar masses but by dividing into two morphology groups, early- and late-type galaxies.
The results reported in this paper integrate the  $\rm HI$
- and
$\rm HI$
- and  $\rm H_{2}$
-CPDFs with new determinations for the GSMF to offer a full statistical description of the local galaxy demographics traced by the stellar,
$\rm H_{2}$
-CPDFs with new determinations for the GSMF to offer a full statistical description of the local galaxy demographics traced by the stellar,  $\rm HI$
,
$\rm HI$
,  $\rm H_{2}$
, total cold gas, and baryon mass components. This statistical description of the local galaxy demographics is much more complete than the typically employed GSMF for constraining models and simulations of galaxy formation. The new generation of semi-analytic models (e.g., Croton et al. Reference Croton2016; Lagos et al. Reference Lagos, Tobar, Robotham, Obreschkow, Mitchell, Power and Elahi2018; Henriques et al. Reference Henriques, White, Lilly, Bell, Bluck and Terrazas2019; Yung et al. Reference Yung, Somerville, Finkelstein, Popping and Davé2019) and cosmological hydrodynamics simulations (e.g., Hirschmann et al. Reference Hirschmann, Dolag, Saro, Bachmann, Borgani and Burkert2014; Vogelsberger et al. Reference Vogelsberger2014; Schaye et al. Reference Schaye2015; Pillepich et al. Reference Pillepich2018; Davé et al. Reference Davé, Anglés-Alcázar, Narayanan, Li, Rafieferantsoa and Appleby2019), and their post-processing outcomes, are now able to predict stellar,
$\rm H_{2}$
, total cold gas, and baryon mass components. This statistical description of the local galaxy demographics is much more complete than the typically employed GSMF for constraining models and simulations of galaxy formation. The new generation of semi-analytic models (e.g., Croton et al. Reference Croton2016; Lagos et al. Reference Lagos, Tobar, Robotham, Obreschkow, Mitchell, Power and Elahi2018; Henriques et al. Reference Henriques, White, Lilly, Bell, Bluck and Terrazas2019; Yung et al. Reference Yung, Somerville, Finkelstein, Popping and Davé2019) and cosmological hydrodynamics simulations (e.g., Hirschmann et al. Reference Hirschmann, Dolag, Saro, Bachmann, Borgani and Burkert2014; Vogelsberger et al. Reference Vogelsberger2014; Schaye et al. Reference Schaye2015; Pillepich et al. Reference Pillepich2018; Davé et al. Reference Davé, Anglés-Alcázar, Narayanan, Li, Rafieferantsoa and Appleby2019), and their post-processing outcomes, are now able to predict stellar,  $\rm HI$
, and
$\rm HI$
, and  $\rm H_{2}$
masses for large galaxy populations in cosmological boxes (see e.g., Lagos et al. Reference Lagos2015; Diemer et al. Reference Diemer2018, Reference Diemer2019; Popping et al. Reference Popping2019). The empirically based results presented here are optimal for comparing with these predictions as well as for calibrating theoretical models of galaxy evolution (see e.g. Romeo Reference Romeo2020). The results to be presented in this paper are the basis for further studies as the inference of the galaxy–halo connection extended to
$\rm H_{2}$
masses for large galaxy populations in cosmological boxes (see e.g., Lagos et al. Reference Lagos2015; Diemer et al. Reference Diemer2018, Reference Diemer2019; Popping et al. Reference Popping2019). The empirically based results presented here are optimal for comparing with these predictions as well as for calibrating theoretical models of galaxy evolution (see e.g. Romeo Reference Romeo2020). The results to be presented in this paper are the basis for further studies as the inference of the galaxy–halo connection extended to  $\rm HI$
,
$\rm HI$
,  $\rm H_{2}$
, cold gas, and baryon masses.
$\rm H_{2}$
, cold gas, and baryon masses.
The present paper is organised as follows. In Section 2, we describe our method of using CPDFs in order to derive galaxy MFs traced by atomic, molecular, and cold gas masses as well as by the baryonic mass. In Section 3, we describe the samples we use to derive our local GSMF divided into early- and late-type galaxies. In Section 4, we present the results for our inventory of galaxy MFs and compare them with direct observational results. We also present our estimates for the cosmic density parameters related to the different baryonic components in galaxies. Section 5 discusses the impact of systematics and random errors. In Section 6, we present a summary and our main conclusions.
In this paper, we adopt cosmological parameter values that are close to the Planck mission:  $\Omega_{\Lambda} = 0.693$
,
$\Omega_{\Lambda} = 0.693$
,  $\Omega_{\rm m} = 0.307$
,
$\Omega_{\rm m} = 0.307$
,  $\Omega_{\rm bar} = 0.048$
, and
$\Omega_{\rm bar} = 0.048$
, and  $h = 0.678$
. All stellar masses are normalised to a Chabrier (Reference Chabrier2003) initial mass function (IMF).
$h = 0.678$
. All stellar masses are normalised to a Chabrier (Reference Chabrier2003) initial mass function (IMF).
2. Modelling the bivariate distributions and MFS from the conditional distribution functions
In this section, we describe the statistical method for deriving the  $\rm HI$
and
$\rm HI$
and  $\rm H_{2}\,$
MFs (as well as the total cold gas and baryon MFs), from the GSMF and the respective correlations of
$\rm H_{2}\,$
MFs (as well as the total cold gas and baryon MFs), from the GSMF and the respective correlations of  $M_{\rm HI}$
and
$M_{\rm HI}$
and  $M_{H_{2}}$
with
$M_{H_{2}}$
with  $M_{*}$
, or more generally, the respective full mass conditional distribution functions, CPDFs. In general, our approach allows to calculate bivariate distribution functions of the
$M_{*}$
, or more generally, the respective full mass conditional distribution functions, CPDFs. In general, our approach allows to calculate bivariate distribution functions of the  $\rm HI$
or
$\rm HI$
or  $\rm H_{2}$
mass and the stellar mass. One can imagine that our methodology is equivalent to an optically selected volume-limited sample that it is complete in stellar mass, with HI and
$\rm H_{2}$
mass and the stellar mass. One can imagine that our methodology is equivalent to an optically selected volume-limited sample that it is complete in stellar mass, with HI and  ${\rm H_{2}}$
gas masses determined for every galaxy in the sample, and for which any MF can be determined. When information about morphology is available, the CPDFs are useful for deriving the corresponding MFs into different morphological components. Here, we consider that the galaxy population is divided into two main morphological groups: early- and late-type galaxies. Following Paper I, our definition of early-type galaxies includes morphological types that comprise E and S0 galaxies or equivalently
${\rm H_{2}}$
gas masses determined for every galaxy in the sample, and for which any MF can be determined. When information about morphology is available, the CPDFs are useful for deriving the corresponding MFs into different morphological components. Here, we consider that the galaxy population is divided into two main morphological groups: early- and late-type galaxies. Following Paper I, our definition of early-type galaxies includes morphological types that comprise E and S0 galaxies or equivalently  $T\leq 0$
from the Nair & Abraham (Reference Nair and Abraham2010) morphology classification. Late-type galaxies are just the complement, from Sa to Irr. Below, we briefly describe the basic ingredients for calculating the MFs:
$T\leq 0$
from the Nair & Abraham (Reference Nair and Abraham2010) morphology classification. Late-type galaxies are just the complement, from Sa to Irr. Below, we briefly describe the basic ingredients for calculating the MFs:
Conditional Distribution Functions: For a fixed morphology, a galaxy of mass
 $M_{*}$
has the chance of having either a
$M_{*}$
has the chance of having either a  $\rm HI$
or
$\rm HI$
or  $\rm H_{2}$
mass described by their corresponding CPDFs. We denote the CPDFs of early and late types by
$\rm H_{2}$
mass described by their corresponding CPDFs. We denote the CPDFs of early and late types by  $P_{E} (M_j| M_{*}$
) and
$P_{E} (M_j| M_{*}$
) and  $P_{L} (M_j| M_{*}$
), respectively, where
$P_{L} (M_j| M_{*}$
), respectively, where  $ j = {\rm HI}$
or
$ j = {\rm HI}$
or  $\rm H_{2}$
. The HI-CPDF and H2-CPDF contain information about all the moments of the HI- and
$\rm H_{2}$
. The HI-CPDF and H2-CPDF contain information about all the moments of the HI- and  ${\rm H_{2}}$
-to-stellar mass correlations. We use the observed HI-CPDF and H2-CPDF from Paper I. In Section 2.2, we describe the functional forms for the CPDFs proposed in Paper I.
${\rm H_{2}}$
-to-stellar mass correlations. We use the observed HI-CPDF and H2-CPDF from Paper I. In Section 2.2, we describe the functional forms for the CPDFs proposed in Paper I.Galaxy Stellar Mass Function: The GSMF is an important input since it allows us to project the CPDFs into their corresponding MFs. We derive the GSMF for all galaxies, as well for the early and late type, based on the SDSS. Section 3 describes our methodology to compute the observed GSMF over
 $\sim\!5$
decades in
$\sim\!5$
decades in  $M_{*}$
, as well as its decomposition into early- and late-type galaxies.
$M_{*}$
, as well as its decomposition into early- and late-type galaxies.
The reader interested in our resulting MFs and bivariate distributions may skip to Section 4.
2.1. Generalities
As discussed above, a CPDF,  $P_j\text{(M}_j| M_{*}\text{)}$
, determines the chances that a galaxy of mass
$P_j\text{(M}_j| M_{*}\text{)}$
, determines the chances that a galaxy of mass  $M_{*}$
possess a specific galaxy property
$M_{*}$
possess a specific galaxy property  $M_j$
, with
$M_j$
, with  $ j = {\rm HI}$
,
$ j = {\rm HI}$
,  $\rm H_{2}$
, cold gas, or baryonic mass. Note that the units of
$\rm H_{2}$
, cold gas, or baryonic mass. Note that the units of  $P_j$
is per
$P_j$
is per  $\text{M}_{\odot}$
. The relation between the distribution
$\text{M}_{\odot}$
. The relation between the distribution  $P_j$
in bins per
$P_j$
in bins per  $\text{M}_{\odot}$
to dex-1,
$\text{M}_{\odot}$
to dex-1,  $\mathcal{P}_{j} $
, is given by
$\mathcal{P}_{j} $
, is given by
 \begin{equation}\mathcal{P}_{j} \text{(}M_j| M_{*}\text{)} = P_{j}\text{(}M_j| M_{*}\text{)} \times \frac{M_j}{\log e}.\end{equation}
\begin{equation}\mathcal{P}_{j} \text{(}M_j| M_{*}\text{)} = P_{j}\text{(}M_j| M_{*}\text{)} \times \frac{M_j}{\log e}.\end{equation}
The advantage of using  $P_j\text{(}M_j|M_{*}\text{)}$
is that it contains information about all the moments of the distribution, in particular the mean
$P_j\text{(}M_j|M_{*}\text{)}$
is that it contains information about all the moments of the distribution, in particular the mean  $M_j-M_{*}$
relation and its standard deviation.
$M_j-M_{*}$
relation and its standard deviation.
The joint distribution function of  $M_{*}$
and
$M_{*}$
and  $M_j$
, hereafter referred as the bivariate distribution function, is defined as:
$M_j$
, hereafter referred as the bivariate distribution function, is defined as:
 \begin{equation}\Phi(M_{j},M_{*}) = \frac{d^2 N\text{(}M_{j}| M_{*}\text{)}} {V d\log M_{j} d\log {M_{*}}}=\mathcal{P}_{j}\text{(}M_{j}| M_{*}\text{)} \phi_* \text{(}M_{*}\text{)},\end{equation}
\begin{equation}\Phi(M_{j},M_{*}) = \frac{d^2 N\text{(}M_{j}| M_{*}\text{)}} {V d\log M_{j} d\log {M_{*}}}=\mathcal{P}_{j}\text{(}M_{j}| M_{*}\text{)} \phi_* \text{(}M_{*}\text{)},\end{equation}
where  $d^2 N$
is the bivariate number of galaxies within the mass range
$d^2 N$
is the bivariate number of galaxies within the mass range  $\log {M_{*}}\pm d\log{M_{*}}/2$
and
$\log {M_{*}}\pm d\log{M_{*}}/2$
and  $\log M_{j}\pm d\log M_{j}/2$
in a given volume V, and
$\log M_{j}\pm d\log M_{j}/2$
in a given volume V, and  $\phi_* \text{(}M_{*}\text{)}$
is the GSMF in units of
$\phi_* \text{(}M_{*}\text{)}$
is the GSMF in units of  ${\rm Mpc}^{-3} {\rm dex}^{-1}$
. The integration (marginalisation) of
${\rm Mpc}^{-3} {\rm dex}^{-1}$
. The integration (marginalisation) of  $\Phi(M_{j},{M_{*}})$
over
$\Phi(M_{j},{M_{*}})$
over  $M_{*}$
results in the total MF for
$M_{*}$
results in the total MF for  $M_j$
,
$M_j$
,  $\phi_j(M_j)$
, that is,
$\phi_j(M_j)$
, that is,
 \begin{align}\phi_{j} (M_j) &=\int \Phi(M_{j},{M_{*}})d\log{M_{*}}\nonumber\\ &= \int \mathcal {P}_{j}(M_j|{M_{*}}) \phi_* \text{(}M_{*}\text{)} d\log{M_{*}}.\end{align}
\begin{align}\phi_{j} (M_j) &=\int \Phi(M_{j},{M_{*}})d\log{M_{*}}\nonumber\\ &= \int \mathcal {P}_{j}(M_j|{M_{*}}) \phi_* \text{(}M_{*}\text{)} d\log{M_{*}}.\end{align}
The above equation shows how the CPDFs are projected into a number density function via the GSMF. Note that integration of  $\Phi(M_{j},{M_{*}})$
over
$\Phi(M_{j},{M_{*}})$
over  $M_j$
gives the total GSMFFootnote c.
$M_j$
gives the total GSMFFootnote c.
As discussed previously, when studying the properties of galaxies, it is useful to separate them into, at least, two morphological components such as early types, or spheroid-dominated galaxies, and late types, or disc-dominated galaxies. Thus, the total GSMF can be formally represented as the contribution of these two types
 \begin{equation}\phi_*\text{(}M_{*}\text{)} = \phi_{*,E}\text{(}M_{*}\text{)} + \phi_{*,L}\text{(}M_{*}\text{)},\end{equation}
\begin{equation}\phi_*\text{(}M_{*}\text{)} = \phi_{*,E}\text{(}M_{*}\text{)} + \phi_{*,L}\text{(}M_{*}\text{)},\end{equation}
denoted respectively by  $\phi_{*,E}$
, and
$\phi_{*,E}$
, and  $\phi_{*,L}$
. In terms of the fraction of early- and late-type galaxies (
$\phi_{*,L}$
. In terms of the fraction of early- and late-type galaxies ( $f_E$
and
$f_E$
and  $f_L$
), their corresponding galaxy stellar MFs are given respectively by
$f_L$
), their corresponding galaxy stellar MFs are given respectively by  $\phi_{*,E} = f_E\times\phi_*$
, and
$\phi_{*,E} = f_E\times\phi_*$
, and  $\phi_{*,L} = f_L\times\phi_*$
, with
$\phi_{*,L} = f_L\times\phi_*$
, with  $f_E+f_L = 1$
.
$f_E+f_L = 1$
.
Early- and late-type galaxies are different in their HI- and  ${\rm H_{2}}$
-to-stellar mass distributions. Thereby, Equation (3) can be generalised in terms of the distribution
${\rm H_{2}}$
-to-stellar mass distributions. Thereby, Equation (3) can be generalised in terms of the distribution  $\mathcal {P}_{i,j}(M_j|{M_{*}})$
, where the subscripts indicate
$\mathcal {P}_{i,j}(M_j|{M_{*}})$
, where the subscripts indicate  $i = $
early or late type, and
$i = $
early or late type, and  $ j = $
$ j = $
 $\rm HI$
,
$\rm HI$
,  $\rm H_{2}$
, cold gas, or baryonic mass. Then, the generalisation of Equation (3) to galaxies with morphological type i and mass component j is
$\rm H_{2}$
, cold gas, or baryonic mass. Then, the generalisation of Equation (3) to galaxies with morphological type i and mass component j is
 \begin{equation}\phi_{j, i} (M_j) = \int f_i\text{(}M_{*}\text{)} \mathcal {P}_{i,j}(M_j|{M_{*}}) \phi_* \text{(}M_{*}\text{)} d\log{M_{*}}.\end{equation}
\begin{equation}\phi_{j, i} (M_j) = \int f_i\text{(}M_{*}\text{)} \mathcal {P}_{i,j}(M_j|{M_{*}}) \phi_* \text{(}M_{*}\text{)} d\log{M_{*}}.\end{equation}
Finally, the total CPDFs are calculated from the respective conditional distributions of early- and late-type galaxies as:
 \begin{align}\mathcal {P}_{j}\text{(}M_{j}| M_{*}\text{)} &= f_{E}\text{(}M_{*}\text{)}\times \mathcal {P}_{E,j} \text{(}M_{j}| M_{*}\text{)}\nonumber\\& \quad +f_{L}\text{(}M_{*}\text{)}\times \mathcal {P}_{L,j} \text{(}M_J| M_{*}\text{)},\end{align}
\begin{align}\mathcal {P}_{j}\text{(}M_{j}| M_{*}\text{)} &= f_{E}\text{(}M_{*}\text{)}\times \mathcal {P}_{E,j} \text{(}M_{j}| M_{*}\text{)}\nonumber\\& \quad +f_{L}\text{(}M_{*}\text{)}\times \mathcal {P}_{L,j} \text{(}M_J| M_{*}\text{)},\end{align}
with  $ j = {\rm HI}, {\rm H_{2}},$
cold gas, or baryonic mass.
$ j = {\rm HI}, {\rm H_{2}},$
cold gas, or baryonic mass.
2.2. The  $\text{\em HI}$
and
$\text{\em HI}$
and  $\text{\em H}_{\text{\em 2}}$
conditional distribution functions
$\text{\em H}_{\text{\em 2}}$
conditional distribution functions
As shown in Equations (2) and (5), the conditional or bivariate distribution functions are useful to statistically determine the MFs. Evidently, in the case of atomic and molecular gas, we are assuming that for every galaxy that is optically selected, there must exist  $\rm HI$
and
$\rm HI$
and  $\rm H_{2}$
counterparts. The discussion on the possible existence of pure
$\rm H_{2}$
counterparts. The discussion on the possible existence of pure  $\rm HI$
or
$\rm HI$
or  $\rm H_{2}$
galaxies, those that will not be observed in optically selected samples but rather in radio blind surveys, is out of the scope of this paper. Note that if they exist, the chance of observing those galaxies is very low over the mass ranges that we will derive the MFs. For example, in the case of pure
$\rm H_{2}$
galaxies, those that will not be observed in optically selected samples but rather in radio blind surveys, is out of the scope of this paper. Note that if they exist, the chance of observing those galaxies is very low over the mass ranges that we will derive the MFs. For example, in the case of pure  $\rm HI$
galaxies, the Arecibo Legacy Fast ALFA (ALFALFA) survey has found
$\rm HI$
galaxies, the Arecibo Legacy Fast ALFA (ALFALFA) survey has found  $\sim\!1.5\%$
of
$\sim\!1.5\%$
of  $\rm HI$
sources that were not clearly associated with an optical counterpart. Of those,
$\rm HI$
sources that were not clearly associated with an optical counterpart. Of those,  $\sim\!75\%$
are likely tidal in origin (Haynes et al. Reference Haynes2011). Thus,
$\sim\!75\%$
are likely tidal in origin (Haynes et al. Reference Haynes2011). Thus,  $\sim\!0.4\%$
of HI source observed in the ALFALFA survey are purely gaseous galaxies candidates, most of them at the mass range
$\sim\!0.4\%$
of HI source observed in the ALFALFA survey are purely gaseous galaxies candidates, most of them at the mass range  $10^{7}<M_{\rm HI}/\text{M}_{\odot}< 10^{10}$
(Cannon et al. Reference Cannon2015). As we will show, our completeness limit for the
$10^{7}<M_{\rm HI}/\text{M}_{\odot}< 10^{10}$
(Cannon et al. Reference Cannon2015). As we will show, our completeness limit for the  $\rm HI$
MF is
$\rm HI$
MF is  $M_{\rm HI}\sim 10^{8}\text{M}_{\odot}$
. The above fraction could be considered as an upper limit as some of these sources have already detected optical counterparts revealing unusual high HI mass-to-light ratios (Cannon et al. Reference Cannon2015). Thus, we conclude that our results are unlikely to be affected by excluding pure gas galaxies in our analysis.
$M_{\rm HI}\sim 10^{8}\text{M}_{\odot}$
. The above fraction could be considered as an upper limit as some of these sources have already detected optical counterparts revealing unusual high HI mass-to-light ratios (Cannon et al. Reference Cannon2015). Thus, we conclude that our results are unlikely to be affected by excluding pure gas galaxies in our analysis.
2.2.1. The Calette et al. (Reference Calette, Avila-Reese, Rodrguez-Puebla, Hernández-Toledo and Papastergis2018)  $\text{\em HI}$
and
$\text{\em HI}$
and  $\text{\em H}_{\text{\em 2}}$
conditional distribution functions
$\text{\em H}_{\text{\em 2}}$
conditional distribution functions
Here, we use the results from Paper I (Calette et al. Reference Calette, Avila-Reese, Rodrguez-Puebla, Hernández-Toledo and Papastergis2018) who determined the  $\rm HI$
- and
$\rm HI$
- and  $\rm H_{2}$
-to-stellar mass ratio distributions (CPDFs) as a function of
$\rm H_{2}$
-to-stellar mass ratio distributions (CPDFs) as a function of  $M_{*}$
from a large compilation of optically selected samples with radio observations. Next, we briefly describe the steps taken in Paper I to derive the
$M_{*}$
from a large compilation of optically selected samples with radio observations. Next, we briefly describe the steps taken in Paper I to derive the  $\rm HI$
and
$\rm HI$
and  $\rm H_{2}$
CPDFs. The reader is referred to that paper for details.
$\rm H_{2}$
CPDFs. The reader is referred to that paper for details.
The compiled data described in Paper I consist of a set of incomplete and inhomogeneous samples. We first homogenised all these samples to a common IMF, cosmology, radio telescope configuration and sensitivity, and CO-to-luminosity conversion factor. Then, we selected only those samples without obvious biases due to selection effects such as environment. Radio non-detections, reported in the literature as upper limits, are an important source of uncertainty when deriving distributions or correlations. In Paper I, we included non-detections to derive the  $\rm HI$
and
$\rm HI$
and  $\rm H_{2}$
CPDFs. Below, we briefly describe the treatment that we employed for radio non-detections.
$\rm H_{2}$
CPDFs. Below, we briefly describe the treatment that we employed for radio non-detections.
In our compiled samples, most of radio non-detections are early-type galaxies representing a non-negligible fraction of intermediate and massive galaxies, which are (typically) gas poor. An important fraction of those galaxies are from the GASS (Catinella et al. Reference Catinella2013) and the CO Legacy Database for the GALEX Arecibo SDSS survey (COLD-GASS) (Saintonge et al. Reference Saintonge2011) surveys at distance of  $109<D/{\rm Mpc}<222$
. Compared to other more nearby samples of intermediate and massive early-type galaxies with measurements of
$109<D/{\rm Mpc}<222$
. Compared to other more nearby samples of intermediate and massive early-type galaxies with measurements of  $\rm HI$
and
$\rm HI$
and  $\rm H_{2}$
mass, such as the ATLAS 3D (Serra et al. Reference Serra2012) at
$\rm H_{2}$
mass, such as the ATLAS 3D (Serra et al. Reference Serra2012) at  $\bar{D}\,{\sim}\,25\, {\rm Mpc}$
, we noted that the upper limits of the GASS/COLD-GASS samples are
$\bar{D}\,{\sim}\,25\, {\rm Mpc}$
, we noted that the upper limits of the GASS/COLD-GASS samples are  $\sim\!1-2$
orders of magnitude larger than nearby samples (Paper I). The above lead us to first introduce a correction for the upper limits of the GASS/COLD-GASS surveys by a distance effect. Recall that radio non-detections or upper limits depend not only on the sensitivity of the radio telescope or integration time but also on the distance to the object. In Paper I, we corrected the upper limits of the GASS/COLD-GASS samples by a distance effect using nearby samples such as the ATLAS 3D survey. Briefly, our correction consists in using the distances and upper limits from nearby samples to estimate the upper limits in the GASS and COLD-GASS as if these two samples were at the same distance as the nearby ones. We validated our procedure using a mock galaxy survey by applying similardistance sensitivity effects as GASS/COLD-GASS surveys, for details see Paper I. For late-type galaxies, notice that most of them are detected in radio due to their large fractions of gas and it is not necessary to introduce the above corrections. Next, we describe the treatment of the upper limits to derive the
$\sim\!1-2$
orders of magnitude larger than nearby samples (Paper I). The above lead us to first introduce a correction for the upper limits of the GASS/COLD-GASS surveys by a distance effect. Recall that radio non-detections or upper limits depend not only on the sensitivity of the radio telescope or integration time but also on the distance to the object. In Paper I, we corrected the upper limits of the GASS/COLD-GASS samples by a distance effect using nearby samples such as the ATLAS 3D survey. Briefly, our correction consists in using the distances and upper limits from nearby samples to estimate the upper limits in the GASS and COLD-GASS as if these two samples were at the same distance as the nearby ones. We validated our procedure using a mock galaxy survey by applying similardistance sensitivity effects as GASS/COLD-GASS surveys, for details see Paper I. For late-type galaxies, notice that most of them are detected in radio due to their large fractions of gas and it is not necessary to introduce the above corrections. Next, we describe the treatment of the upper limits to derive the  $\rm HI$
and
$\rm HI$
and  $\rm H_{2}$
CPDFs.
$\rm H_{2}$
CPDFs.
In our analysis from Paper I, we included upper limits, or left-censored data, using the Kaplan & Meier (Reference Kaplan and Meier1958) non-parametric estimator. This estimator provides a reconstruction of information lost by censoring. Feigelson & Nelson (Reference Feigelson and Nelson1985) adapted this estimator for astronomical samples. We used the Astronomical SURVival statistics (ASURV) package based on Feigelson & Nelson (Reference Feigelson and Nelson1985) to derive the  $\rm HI$
and
$\rm HI$
and  $\rm H_{2}$
CPDFs from our compiled samples. We have also applied the censoring Buckley & James (Reference Buckley and James1979) regression method to derive the relationship and standard deviations between the
$\rm H_{2}$
CPDFs from our compiled samples. We have also applied the censoring Buckley & James (Reference Buckley and James1979) regression method to derive the relationship and standard deviations between the  $\rm HI$
- and
$\rm HI$
- and  $\rm H_{2}$
-to-stellar mass ratio and
$\rm H_{2}$
-to-stellar mass ratio and  $M_{*}$
. We note that the regression results are consistent with the (logarithmic) mean and standard deviation values obtained from the CPDFs based on the Kaplan & Meier (Reference Kaplan and Meier1958) estimator.
$M_{*}$
. We note that the regression results are consistent with the (logarithmic) mean and standard deviation values obtained from the CPDFs based on the Kaplan & Meier (Reference Kaplan and Meier1958) estimator.
2.2.2. The functional forms of the  $\text{\em HI}$
and
$\text{\em HI}$
and  $\text{\em H}_{\text{\em 2}}$
conditional distribution functions
$\text{\em H}_{\text{\em 2}}$
conditional distribution functions
For the  $\rm HI$
and
$\rm HI$
and  $\rm H_{2}$
CPDFs of late-type galaxies, in Paper I, we found that they are described by a Schechter function. In the case of early-type galaxies, the CPDFs are better described by a (broken) Schechter function plus a uniform distribution at the low
$\rm H_{2}$
CPDFs of late-type galaxies, in Paper I, we found that they are described by a Schechter function. In the case of early-type galaxies, the CPDFs are better described by a (broken) Schechter function plus a uniform distribution at the low $-\mathcal{R}_j$
values. Following, we describe in more detail these functional forms.
$-\mathcal{R}_j$
values. Following, we describe in more detail these functional forms.
We begin by introducing the following Schechter-type probability distribution function for the  $\rm HI$
- or
$\rm HI$
- or  $\rm H_{2}$
-to-stellar mass ratios,
$\rm H_{2}$
-to-stellar mass ratios,  $ \mathcal{R}_j=M_j/M_{*}$
, in the range
$ \mathcal{R}_j=M_j/M_{*}$
, in the range  $\log \mathcal{R}_j \pm d \log \mathcal{R}_j / 2$
:
$\log \mathcal{R}_j \pm d \log \mathcal{R}_j / 2$
:
 \begin{equation}\mathcal{S}_{i,j} (\mathcal{R}_j) = \frac{\ln(10)}{\mathcal{N}_{i,j}}\left(\frac{\mathcal{R}_{j}}{\mathcal{R}^*_{i,j}}\right)^{\alpha_{i,j} + 1}\exp\left({-}\frac{\mathcal{R}_{j}}{\mathcal{R}^*_{i,j}}\right),\end{equation}
\begin{equation}\mathcal{S}_{i,j} (\mathcal{R}_j) = \frac{\ln(10)}{\mathcal{N}_{i,j}}\left(\frac{\mathcal{R}_{j}}{\mathcal{R}^*_{i,j}}\right)^{\alpha_{i,j} + 1}\exp\left({-}\frac{\mathcal{R}_{j}}{\mathcal{R}^*_{i,j}}\right),\end{equation}
where the morphology is represented with  $i = $
early or late type, and the galaxy property is represented with
$i = $
early or late type, and the galaxy property is represented with  $ j = $
$ j = $
 $\rm HI$
or
$\rm HI$
or  $\rm H_{2}$
. The parameters are the characteristic gas-to-stellar mass ratio,
$\rm H_{2}$
. The parameters are the characteristic gas-to-stellar mass ratio,  $\mathcal{R}^*_{i,j}$
, the normalisation parameter,
$\mathcal{R}^*_{i,j}$
, the normalisation parameter,  $\mathcal{N}_{i,j}$
, which constrains the probability to be between zero and one,Footnote d and the power law slope
$\mathcal{N}_{i,j}$
, which constrains the probability to be between zero and one,Footnote d and the power law slope  $\alpha_{i,j}$
for the part of the distribution of galaxies with low gas-to-stellar mass ratio.
$\alpha_{i,j}$
for the part of the distribution of galaxies with low gas-to-stellar mass ratio.
Late-type galaxies:
For late-type galaxies, that is  $i = L$
, in Paper I, we found that the HI-CPDF and H2-CPDF are described by the Schechter-type distribution function given by (7) with the parameters
$i = L$
, in Paper I, we found that the HI-CPDF and H2-CPDF are described by the Schechter-type distribution function given by (7) with the parameters  $\alpha_{L,j}$
and
$\alpha_{L,j}$
and  $\mathcal{R}^*_{L,j}$
functions of
$\mathcal{R}^*_{L,j}$
functions of  $M_{*}$
as follows:
$M_{*}$
as follows:
 \begin{equation}\alpha_{L,j} = \alpha_{0;L,j} \log {M_{*}} + \alpha_{1;L,j} ,\end{equation}
\begin{equation}\alpha_{L,j} = \alpha_{0;L,j} \log {M_{*}} + \alpha_{1;L,j} ,\end{equation}
and
 \begin{equation}\mathcal{R}^*_{L,j} = \frac{\mathcal{R}^*_{0;L,j}}{\left(\frac{{M_{*}}}{\mathcal{M}^*_{L,j}} \right)^{\beta_{L,j}} + \left(\frac{{M_{*}}}{\mathcal{M}^*_{L,j}} \right)^{\gamma_{L,j}}}.\end{equation}
\begin{equation}\mathcal{R}^*_{L,j} = \frac{\mathcal{R}^*_{0;L,j}}{\left(\frac{{M_{*}}}{\mathcal{M}^*_{L,j}} \right)^{\beta_{L,j}} + \left(\frac{{M_{*}}}{\mathcal{M}^*_{L,j}} \right)^{\gamma_{L,j}}}.\end{equation}
Consider that  $\mathcal{S}_{L,j} (\log\mathcal{R}_j) d\log \mathcal{R}_j = \mathcal{S}_{L,j} (\log M_j - \log{M_{*}}) d\log (M_j / {M_{*}})$
. By definition
$\mathcal{S}_{L,j} (\log\mathcal{R}_j) d\log \mathcal{R}_j = \mathcal{S}_{L,j} (\log M_j - \log{M_{*}}) d\log (M_j / {M_{*}})$
. By definition  $M_{*}$
is fixed, thus the
$M_{*}$
is fixed, thus the  $\rm HI$
and
$\rm HI$
and  $\rm H_{2}$
CPDFs of late-type galaxies are given by:
$\rm H_{2}$
CPDFs of late-type galaxies are given by:
 \begin{equation}\mathcal {P}_{L,j}(M_j | {M_{*}}) d\log M_j = \mathcal{S}_{L,j} (\log M_j - \log{M_{*}}) d\log M_j.\end{equation}
\begin{equation}\mathcal {P}_{L,j}(M_j | {M_{*}}) d\log M_j = \mathcal{S}_{L,j} (\log M_j - \log{M_{*}}) d\log M_j.\end{equation}
The above explicitly shows that the integration over conditional distribution functions can also be interpret as convolutions in Equation (3).
Early-type galaxies:
In the case of early-type galaxies,  $i = E $
, we showed in Paper I that both for the HI-CPDF and H2-CPDF are described as the sum of two distribution functions; the Schechter-type distribution function,
$i = E $
, we showed in Paper I that both for the HI-CPDF and H2-CPDF are described as the sum of two distribution functions; the Schechter-type distribution function,  $\mathcal{S}_{E,j}$
, and a uniform function,
$\mathcal{S}_{E,j}$
, and a uniform function,  $\mathcal {U}_{0,j}$
, are
$\mathcal {U}_{0,j}$
, are
 \begin{equation}\mathcal {E}_{j} (\mathcal{R}_j) = \left\{\begin{array}{l@{\quad}l}\mathcal {U}_{0,j} & \mathcal{R}_{0,j} \le\mathcal{R}_j
< \mathcal{R}_{1,j} \\A \times \mathcal{S}_{E,j} (\mathcal{R}_j) & \mathcal{R}_{1,j} \le \mathcal{R}_j\end{array},\right.\end{equation}
\begin{equation}\mathcal {E}_{j} (\mathcal{R}_j) = \left\{\begin{array}{l@{\quad}l}\mathcal {U}_{0,j} & \mathcal{R}_{0,j} \le\mathcal{R}_j
< \mathcal{R}_{1,j} \\A \times \mathcal{S}_{E,j} (\mathcal{R}_j) & \mathcal{R}_{1,j} \le \mathcal{R}_j\end{array},\right.\end{equation}
where  $\mathcal{R}_{0,j} = \mathcal{R}_{1,j} / 10,$
Footnote e and
$\mathcal{R}_{0,j} = \mathcal{R}_{1,j} / 10,$
Footnote e and  $ \log \mathcal{R}_{1,j} = r_{0,j} \log{M_{*}} + r_{1,j}$
, while the uniform distribution is given by
$ \log \mathcal{R}_{1,j} = r_{0,j} \log{M_{*}} + r_{1,j}$
, while the uniform distribution is given by
 \begin{equation}\mathcal {U}_{0,j} \text{(}M_{*}\text{)} = \frac{p_{0,j} \log{M_{*}} + p_{1,j}}{\Delta},\end{equation}
\begin{equation}\mathcal {U}_{0,j} \text{(}M_{*}\text{)} = \frac{p_{0,j} \log{M_{*}} + p_{1,j}}{\Delta},\end{equation}
and
 \begin{equation}A = \left( 1 - \mathcal {U}_{0,j} \times \Delta\right) \times \frac{\mathcal{N}_{i,j}}{\eta_{i,j}(\mathcal{R}_{1,j})},\end{equation}
\begin{equation}A = \left( 1 - \mathcal {U}_{0,j} \times \Delta\right) \times \frac{\mathcal{N}_{i,j}}{\eta_{i,j}(\mathcal{R}_{1,j})},\end{equation}
where in Paper I we assumed that  $\Delta = \log_{10} = 1$
dex, the symbol
$\Delta = \log_{10} = 1$
dex, the symbol  $\eta_{i,j}(\mathcal{R}_{1,j})$
takes into account the fraction of galaxies in the Schechter-type mode for galaxies with gas ratio above
$\eta_{i,j}(\mathcal{R}_{1,j})$
takes into account the fraction of galaxies in the Schechter-type mode for galaxies with gas ratio above  $\mathcal{R}_{1,j}$
.Footnote f The HI-CPDF and
$\mathcal{R}_{1,j}$
.Footnote f The HI-CPDF and  $\rm H_{2}$
-CPDF of early-type galaxies are
$\rm H_{2}$
-CPDF of early-type galaxies are
 \begin{equation}\mathcal {P}_{E,j}(M_j | {M_{*}}) d\log M_j = \mathcal{E}_{j}(\log M_j - \log{M_{*}}) d\log M_j.\end{equation}
\begin{equation}\mathcal {P}_{E,j}(M_j | {M_{*}}) d\log M_j = \mathcal{E}_{j}(\log M_j - \log{M_{*}}) d\log M_j.\end{equation}
2.2.3. Constraints on the best-fitting parameters
In Paper I, the best-fit parameters for late-type galaxies, Equations (8)–(9), and for early-type galaxies, Equations (11)–(13), were constrained using the observed  $\rm HI$
- and
$\rm HI$
- and  $\rm H_{2}$
-CPDFs on various stellar mass bins. Computing CPDFs over
$\rm H_{2}$
-CPDFs on various stellar mass bins. Computing CPDFs over  $M_{*}$
bins requires the GSMF in addition of the fraction of early- and late-type galaxies (see Section 4.1 for more details). Since we are using slightly different inputs, namely the GSMF and the fractions of early- and late-type galaxies, than in Paper I, we prefer to perform our own fits to the same data, for consistency. The results are presented in Section 4.1. The differences with the parameters reported in Paper I are actually small.
$M_{*}$
bins requires the GSMF in addition of the fraction of early- and late-type galaxies (see Section 4.1 for more details). Since we are using slightly different inputs, namely the GSMF and the fractions of early- and late-type galaxies, than in Paper I, we prefer to perform our own fits to the same data, for consistency. The results are presented in Section 4.1. The differences with the parameters reported in Paper I are actually small.
2.3. The cold gas and baryonic conditional distribution functions
Once we have constructed the HI-CPDF and  $\rm H_{2}$
-CPDF, we can now define the conditional distributions for the cold gas and baryon masses,
$\rm H_{2}$
-CPDF, we can now define the conditional distributions for the cold gas and baryon masses,  $M_{\rm gas}$
and
$M_{\rm gas}$
and  $M_{\rm bar}$
.
$M_{\rm bar}$
.
The total cold gas content in a galaxy is composed of  $\rm HI$
,
$\rm HI$
,  $\rm H_{2}$
, helium, and metals; helium and metals account for roughly 30% of the cold gas,
$\rm H_{2}$
, helium, and metals; helium and metals account for roughly 30% of the cold gas,  $M_{\rm He} + M_{\rm Z}\approx0.3 M_{\rm gas}$
Therefore,
$M_{\rm He} + M_{\rm Z}\approx0.3 M_{\rm gas}$
Therefore,  $M_{\rm gas} = M_{\rm HI} + M_{H_{2}} + M_{\rm He} + M_{\rm Z} = 1.4 \times (M_{\rm HI} + M_{H_{2}}\text{)}$
. For simplicity, let
$M_{\rm gas} = M_{\rm HI} + M_{H_{2}} + M_{\rm He} + M_{\rm Z} = 1.4 \times (M_{\rm HI} + M_{H_{2}}\text{)}$
. For simplicity, let  $M_{\rm HI}$
and
$M_{\rm HI}$
and  $M_{H_{2}}$
be two independent random variables. Section 5 discusses the validity of this assumption. Then,
$M_{H_{2}}$
be two independent random variables. Section 5 discusses the validity of this assumption. Then,  $M_{\rm gas}$
is a random variable with the conditional distribution function:
$M_{\rm gas}$
is a random variable with the conditional distribution function:
 \begin{align}P_{\rm gas}(M_{\rm gas}|{M_{*}}) &=\frac{1}{1.4} \int P_{\rm HI}\left(0.71 M_{\rm gas} - M_{H_{2}}|{M_{*}}\right) \nonumber\\[2pt] & \quad \times P_{\rm H_2}(M_{H_{2}}|{M_{*}}) d M_{H_{2}}, \nonumber\\[2pt] &=\frac{1}{1.4} \int P_{\rm HI}(M_{\rm HI}|{M_{*}}) \nonumber\\[2pt] & \quad \times P_{\rm H_2}(0.71 M_{\rm gas} - M_{\rm HI}|{M_{*}}) d M_{\rm HI},\end{align}
\begin{align}P_{\rm gas}(M_{\rm gas}|{M_{*}}) &=\frac{1}{1.4} \int P_{\rm HI}\left(0.71 M_{\rm gas} - M_{H_{2}}|{M_{*}}\right) \nonumber\\[2pt] & \quad \times P_{\rm H_2}(M_{H_{2}}|{M_{*}}) d M_{H_{2}}, \nonumber\\[2pt] &=\frac{1}{1.4} \int P_{\rm HI}(M_{\rm HI}|{M_{*}}) \nonumber\\[2pt] & \quad \times P_{\rm H_2}(0.71 M_{\rm gas} - M_{\rm HI}|{M_{*}}) d M_{\rm HI},\end{align}
or after some algebra, the same distribution function but per bin in log space is:
 \begin{align}\mathcal{P}_{\rm gas}({M_{\rm gas}}|{M_{*}}) &= \int \frac{\mathcal{P}_{\rm HI}(0.71{M_{\rm gas}} - {M_{H_{2}}}|{M_{*}})}{1 - 1.4\ {M_{H_{2}}}/{M_{\rm gas}}} \nonumber\\[2pt] & \quad \times \mathcal{P}_{\rm H_2}({M_{H_{2}}}|{M_{*}}) d \log {M_{H_{2}}}, \nonumber\\[3pt] &= \int \mathcal{P}_{\rm HI}({M_{\rm HI}}|{M_{*}}) \nonumber\\[3pt] &\quad\times \frac{\mathcal{P}_{\rm H_2}(0.71 {M_{\rm gas}} -{M_{\rm HI}}|{M_{*}})}{1 - 1.4\ {M_{\rm HI}}/{M_{\rm gas}}} d \log {M_{\rm HI}}.\end{align}
\begin{align}\mathcal{P}_{\rm gas}({M_{\rm gas}}|{M_{*}}) &= \int \frac{\mathcal{P}_{\rm HI}(0.71{M_{\rm gas}} - {M_{H_{2}}}|{M_{*}})}{1 - 1.4\ {M_{H_{2}}}/{M_{\rm gas}}} \nonumber\\[2pt] & \quad \times \mathcal{P}_{\rm H_2}({M_{H_{2}}}|{M_{*}}) d \log {M_{H_{2}}}, \nonumber\\[3pt] &= \int \mathcal{P}_{\rm HI}({M_{\rm HI}}|{M_{*}}) \nonumber\\[3pt] &\quad\times \frac{\mathcal{P}_{\rm H_2}(0.71 {M_{\rm gas}} -{M_{\rm HI}}|{M_{*}})}{1 - 1.4\ {M_{\rm HI}}/{M_{\rm gas}}} d \log {M_{\rm HI}}.\end{align}
For the baryonic conditional distribution functions, we again assume that  $M_{\rm gas}$
and
$M_{\rm gas}$
and  $M_{*}$
are two independent random variables. Thus,
$M_{*}$
are two independent random variables. Thus,  $M_{\rm bar} = M_{\rm gas} + M_{*}$
is a random variable with a distribution function given by
$M_{\rm bar} = M_{\rm gas} + M_{*}$
is a random variable with a distribution function given by
 \begin{align}P_{\rm bar}(M_{\rm bar}|{M_{*}}) &= \int P_{\rm gas} (M_{\rm bar} - \mathcal{M}_*|{M_{*}}) \nonumber \\[2pt] &\quad\times \delta(\mathcal{M}_* - {M_{*}}) d \mathcal{M}_*\\[3pt] &= P_{\rm gas} (M_{\rm bar} - {M_{*}}|{M_{*}}),\nonumber\end{align}
\begin{align}P_{\rm bar}(M_{\rm bar}|{M_{*}}) &= \int P_{\rm gas} (M_{\rm bar} - \mathcal{M}_*|{M_{*}}) \nonumber \\[2pt] &\quad\times \delta(\mathcal{M}_* - {M_{*}}) d \mathcal{M}_*\\[3pt] &= P_{\rm gas} (M_{\rm bar} - {M_{*}}|{M_{*}}),\nonumber\end{align}
where  $P_{\rm gas}$
is the conditional distribution function for gas, Equation (15), and the Dirac-
$P_{\rm gas}$
is the conditional distribution function for gas, Equation (15), and the Dirac- $\delta$
function appears explicitly for the
$\delta$
function appears explicitly for the  $M_{*}$
term. Similarly as above, we find that
$M_{*}$
term. Similarly as above, we find that
 \begin{equation}\mathcal{P}_{\rm bar}(M_{\rm bar}|{M_{*}}) = \frac{\mathcal{P}_{\rm gas}(M_{\rm bar} - {M_{*}}|{M_{*}})}{1 - {M_{*}} / M_{\rm bar}}.\end{equation}
\begin{equation}\mathcal{P}_{\rm bar}(M_{\rm bar}|{M_{*}}) = \frac{\mathcal{P}_{\rm gas}(M_{\rm bar} - {M_{*}}|{M_{*}})}{1 - {M_{*}} / M_{\rm bar}}.\end{equation}
Finally, we derive the gas and baryon MFs using Equations (5), (16), and (18), the last two valid for early- and late-type galaxies.
3. The GSMF of all, early-, and late-type galaxies
The preceding section described a methodology to use the GSMF as an interphase that transforms galaxy CPDFs into MFs, see Equation (5). In this section, we briefly describe how we determine the local GSMF for masses above  $M_{*}\,{\sim}\,3\times10^{7} \text{M}_{\odot}$
, as well as the GSMF s for early- and late-type galaxies. For a more detailed description of the galaxy samples utilised here and the different corrections we apply, the reader is referred to Appendices A–C.
$M_{*}\,{\sim}\,3\times10^{7} \text{M}_{\odot}$
, as well as the GSMF s for early- and late-type galaxies. For a more detailed description of the galaxy samples utilised here and the different corrections we apply, the reader is referred to Appendices A–C.
3.1. The galaxy samples and the GSMF
To estimate the GSMF over a large dynamical range, we use two galaxy samples. Next, we shortly describe the procedure and our determinations.
(1) For masses above  $M_{*} = 10^9\ \text{M}_{\odot}$
, we use the SDSS DR7 based on the photometric catalogue from Meert et al. (Reference Meert, Vikram and Bernardi2015) and Meert et al. (Reference Meert, Vikram and Bernardi2016)Footnote g at the redshift interval
$M_{*} = 10^9\ \text{M}_{\odot}$
, we use the SDSS DR7 based on the photometric catalogue from Meert et al. (Reference Meert, Vikram and Bernardi2015) and Meert et al. (Reference Meert, Vikram and Bernardi2016)Footnote g at the redshift interval  $0.005<z<0.2$
. Previous studies have concluded that the measurements of the apparent brightnesses based on the standard SDSS pipeline photometry are underestimated due to sky subtraction problems, particularly, in crowded fields (Bernardi et al. Reference Bernardi, Shankar, Hyde, Mei, Marulli and Sheth2010; Blanton et al. Reference Blanton, Kazin, Muna, Weaver and Price-Whelan2011; Simard et al. Reference Simard, Mendel, Patton, Ellison and McConnachie2011; Bernardi et al. Reference Bernardi, Meert, Sheth, Vikram, Huertas-Company, Mei and Shankar2013; He et al. Reference He, Xia, Hao, Jing, Mao and Li2013; Mendel et al. Reference Mendel, Simard, Palmer, Ellison and Patton2014; Kravtsov, Vikhlinin, & Meshscheryakov Reference Kravtsov, Vikhlinin and Meshscheryakov2014; Meert et al. Reference Meert, Vikram and Bernardi2015; D’Souza, Vegetti, & Kauffmann Reference D’Souza, Vegetti and Kauffmann2015; Bernardi et al. Reference Bernardi, Meert, Sheth, Huertas-Company, Maraston, Shankar and Vikram2016; Meert et al. Reference Meert, Vikram and Bernardi2016. New determinations of the GSMF based on the new algorithms for obtaining more precise measurements of the sky subtraction, and thus to improve the photometry, have concluded that the bright end of the luminosity/MF has been systematically underestimated (Bernardi et al. Reference Bernardi, Meert, Sheth, Fischer, Huertas-Company, Maraston, Shankar and Vikram2017). While there are various groups working in improving the determination of galaxy apparent brightnesses, see references above, Bernardi et al. (Reference Bernardi, Meert, Sheth, Fischer, Huertas-Company, Maraston, Shankar and Vikram2017) showed that all those studies agreed up to 0.1 dex in the GSMF. In this paper, we use the apparent Sérsic r, g, and i band luminosities reported in Meert et al. (Reference Meert, Vikram and Bernardi2015) and (2016) derived for the SDSS DR7 based on the PyMorph software pipeline (Vikram et al. Reference Vikram, Wadadekar, Kembhavi and Vijayagovindan2010; Meert, Vikram, & Bernardi Reference Meert, Vikram and Bernardi2013). This software has been extensively tested in Meert et al. (Reference Meert, Vikram and Bernardi2013) and shows that it does not suffer from sky subtraction problems. All magnitudes and colours are K+E corrected at a redshift rest frame
$0.005<z<0.2$
. Previous studies have concluded that the measurements of the apparent brightnesses based on the standard SDSS pipeline photometry are underestimated due to sky subtraction problems, particularly, in crowded fields (Bernardi et al. Reference Bernardi, Shankar, Hyde, Mei, Marulli and Sheth2010; Blanton et al. Reference Blanton, Kazin, Muna, Weaver and Price-Whelan2011; Simard et al. Reference Simard, Mendel, Patton, Ellison and McConnachie2011; Bernardi et al. Reference Bernardi, Meert, Sheth, Vikram, Huertas-Company, Mei and Shankar2013; He et al. Reference He, Xia, Hao, Jing, Mao and Li2013; Mendel et al. Reference Mendel, Simard, Palmer, Ellison and Patton2014; Kravtsov, Vikhlinin, & Meshscheryakov Reference Kravtsov, Vikhlinin and Meshscheryakov2014; Meert et al. Reference Meert, Vikram and Bernardi2015; D’Souza, Vegetti, & Kauffmann Reference D’Souza, Vegetti and Kauffmann2015; Bernardi et al. Reference Bernardi, Meert, Sheth, Huertas-Company, Maraston, Shankar and Vikram2016; Meert et al. Reference Meert, Vikram and Bernardi2016. New determinations of the GSMF based on the new algorithms for obtaining more precise measurements of the sky subtraction, and thus to improve the photometry, have concluded that the bright end of the luminosity/MF has been systematically underestimated (Bernardi et al. Reference Bernardi, Meert, Sheth, Fischer, Huertas-Company, Maraston, Shankar and Vikram2017). While there are various groups working in improving the determination of galaxy apparent brightnesses, see references above, Bernardi et al. (Reference Bernardi, Meert, Sheth, Fischer, Huertas-Company, Maraston, Shankar and Vikram2017) showed that all those studies agreed up to 0.1 dex in the GSMF. In this paper, we use the apparent Sérsic r, g, and i band luminosities reported in Meert et al. (Reference Meert, Vikram and Bernardi2015) and (2016) derived for the SDSS DR7 based on the PyMorph software pipeline (Vikram et al. Reference Vikram, Wadadekar, Kembhavi and Vijayagovindan2010; Meert, Vikram, & Bernardi Reference Meert, Vikram and Bernardi2013). This software has been extensively tested in Meert et al. (Reference Meert, Vikram and Bernardi2013) and shows that it does not suffer from sky subtraction problems. All magnitudes and colours are K+E corrected at a redshift rest frame  $z=0$
, see Appendixes A and B. As described in Appendix A, for every galaxy, we estimate
$z=0$
, see Appendixes A and B. As described in Appendix A, for every galaxy, we estimate  $M_{*}$
from five colour-dependent mass-to-light ratios but we define as our fiducial
$M_{*}$
from five colour-dependent mass-to-light ratios but we define as our fiducial  $M_{*}$
the geometric mean of all the determinations. Using the
$M_{*}$
the geometric mean of all the determinations. Using the  $1/{V}_{\rm max}$
method, we derive six
$1/{V}_{\rm max}$
method, we derive six  $\mbox{GSMF}$
s based on the mass definitions described above. Consistent with Bernardi et al. (Reference Bernardi, Meert, Sheth, Fischer, Huertas-Company, Maraston, Shankar and Vikram2017), we find that the differences in mass-to-light ratios introduce large discrepancies in the GSMF, especially at the high-mass end. In Figure 11 from Appendix A, we find that a shift of
$\mbox{GSMF}$
s based on the mass definitions described above. Consistent with Bernardi et al. (Reference Bernardi, Meert, Sheth, Fischer, Huertas-Company, Maraston, Shankar and Vikram2017), we find that the differences in mass-to-light ratios introduce large discrepancies in the GSMF, especially at the high-mass end. In Figure 11 from Appendix A, we find that a shift of  $\sim\pm0.15$
dex in the
$\sim\pm0.15$
dex in the  $M_{*}$
axis recovers systematic errors in the GSMF due to different mass-to-light ratios.
$M_{*}$
axis recovers systematic errors in the GSMF due to different mass-to-light ratios.
(2) For masses below  $M_{*} =10^9\ \text{M}_{\odot}$
, we use the SDSS DR4 NUY-VAGC low-z sample,Footnote h at the redshift interval
$M_{*} =10^9\ \text{M}_{\odot}$
, we use the SDSS DR4 NUY-VAGC low-z sample,Footnote h at the redshift interval  $0.0033<z<0.005$
, and ideal to study the low mass/luminosity galaxies (Blanton et al. Reference Blanton2005a; Blanton et al. Reference Blanton, Lupton, Schlegel, Strauss, Brinkmann, Fukugita and Loveday2005b). As before, all absolute magnitudes and colours were K+E corrected at a redshift rest frame
$0.0033<z<0.005$
, and ideal to study the low mass/luminosity galaxies (Blanton et al. Reference Blanton2005a; Blanton et al. Reference Blanton, Lupton, Schlegel, Strauss, Brinkmann, Fukugita and Loveday2005b). As before, all absolute magnitudes and colours were K+E corrected at a redshift rest frame  $z=0$
. Also, we derive
$z=0$
. Also, we derive  $M_{*}$
from five colour-dependent mass-to-light ratios and, again, we define our fiducial
$M_{*}$
from five colour-dependent mass-to-light ratios and, again, we define our fiducial  $M_{*}$
as the geometric mean of all the determinations. We construct the GSMF using the
$M_{*}$
as the geometric mean of all the determinations. We construct the GSMF using the  $1/V_{\rm max}$
method and include missing galaxies due to surface brightness incompleteness, as described in Appendix C. For surface brightness incompleteness, we follow closely the methodology described in Blanton et al. (Reference Blanton, Lupton, Schlegel, Strauss, Brinkmann, Fukugita and Loveday2005b). The latter correction is relevant for the low-mass end. Based on the conclusions from Baldry et al. (Reference Baldry2012), we use a simple correction for the low-mass end in order to correct for the local flow model distances from Willick et al. (Reference Willick, Courteau, Faber, Burstein, Dekel and Strauss1997) to the one by Tonry et al. (Reference Tonry, Blakeslee, Ajhar and Dressler2000).
$1/V_{\rm max}$
method and include missing galaxies due to surface brightness incompleteness, as described in Appendix C. For surface brightness incompleteness, we follow closely the methodology described in Blanton et al. (Reference Blanton, Lupton, Schlegel, Strauss, Brinkmann, Fukugita and Loveday2005b). The latter correction is relevant for the low-mass end. Based on the conclusions from Baldry et al. (Reference Baldry2012), we use a simple correction for the low-mass end in order to correct for the local flow model distances from Willick et al. (Reference Willick, Courteau, Faber, Burstein, Dekel and Strauss1997) to the one by Tonry et al. (Reference Tonry, Blakeslee, Ajhar and Dressler2000).
Our final GSMF is the result of combining the SDSS NUY-VAGC low-z sample, for galaxies with masses  $M_{*}\approx 3\times 10^{7}\text{M}_{\odot}$
to
$M_{*}\approx 3\times 10^{7}\text{M}_{\odot}$
to  $M_{*}\approx10^{9}\text{M}_{\odot}$
, and the SDSS DR7 sample for galaxies with
$M_{*}\approx10^{9}\text{M}_{\odot}$
, and the SDSS DR7 sample for galaxies with  $M_{*}\gtrsim 10^{9}\text{M}_{\odot}$
, based on our fiducial
$M_{*}\gtrsim 10^{9}\text{M}_{\odot}$
, based on our fiducial  $M_{*}$
determination. Figure 1 presents our final GSMF with the black solid circles and error bars. The black solid line shows the best fit to the data (described below), and the grey shaded area shows a shift in the
$M_{*}$
determination. Figure 1 presents our final GSMF with the black solid circles and error bars. The black solid line shows the best fit to the data (described below), and the grey shaded area shows a shift in the  $M_{*}$
axis of
$M_{*}$
axis of  $\pm 0.15$
dex. As discussed above, in Appendix A, we find that this is a good approximation to the systematic errors in the GSMF due to differences in the mass-to-light ratios. In the same figure, we include comparisons to previous works. In order to account for differences in cosmologies, we scale previous studies to our cosmology using the following relations:
$\pm 0.15$
dex. As discussed above, in Appendix A, we find that this is a good approximation to the systematic errors in the GSMF due to differences in the mass-to-light ratios. In the same figure, we include comparisons to previous works. In order to account for differences in cosmologies, we scale previous studies to our cosmology using the following relations:
 \begin{equation}\phi_{*, {\rm us}} = \phi_{*, {\rm lit}}\left(\frac{h_{\rm us}}{h_{\rm lit}}\right)^3,\end{equation}
\begin{equation}\phi_{*, {\rm us}} = \phi_{*, {\rm lit}}\left(\frac{h_{\rm us}}{h_{\rm lit}}\right)^3,\end{equation}
and
 \begin{equation}M_{*, {\rm us}} = M_{*, {\rm lit}}\left(\frac{h_{\rm lit}}{h_{\rm us}}\right)^2,\end{equation}
\begin{equation}M_{*, {\rm us}} = M_{*, {\rm lit}}\left(\frac{h_{\rm lit}}{h_{\rm us}}\right)^2,\end{equation}
where  $h_{\rm us} = 0.678$
and
$h_{\rm us} = 0.678$
and  $h_{\rm lit}$
is the respective value reported in the literature. Nonetheless, the impact of accounting for different cosmologies is small.
$h_{\rm lit}$
is the respective value reported in the literature. Nonetheless, the impact of accounting for different cosmologies is small.

Figure 1. Observed GSMF when combining the SDSS NYU-VAGC low-redshift sample and the SDSS DR7 sample, black filled circles with error bars. We reproduce our results in the upper and the middle panels. The best-fit model composed of a Schechter function with a sub-exponential slope and a double power law function is shown as the black solid line. The shaded area shows an estimate of the systematic errors with respect to the best-fitting model. The bottom panel shows the residuals for our best-fitting model as a function of  $M_{*}$
. We include comparisons to some previous observational determinations of the GSMF: in the upper panel we show determinations that are complete down to
$M_{*}$
. We include comparisons to some previous observational determinations of the GSMF: in the upper panel we show determinations that are complete down to  $\sim\! 10^9\ \text{M}_{\odot}$
, mostly based on the SDSS DR7, while in the middle panel we show determinations based on the GAMA survey, which are complete down to
$\sim\! 10^9\ \text{M}_{\odot}$
, mostly based on the SDSS DR7, while in the middle panel we show determinations based on the GAMA survey, which are complete down to  $\sim\! 3{-}5\times 10^7\ \text{M}_{\odot}$
, but suffer from cosmic variance at high masses due to the small volume.
$\sim\! 3{-}5\times 10^7\ \text{M}_{\odot}$
, but suffer from cosmic variance at high masses due to the small volume.
In the upper panel of Figure 1, we reproduce the  $\mbox{GSMF}$
s from previous determinations with stellar mass completeness above
$\mbox{GSMF}$
s from previous determinations with stellar mass completeness above  $M_{*}\,{\sim}\,10^9\ \text{M}_{\odot}$
. The violet triangles with error bars are the determinations from Moustakas et al. (Reference Moustakas2013), who used a spectroscopic sample of SDSS DR7 galaxies from the New York University Value Added Galaxy Catalog (NYU-VAGC) with redshifts
$M_{*}\,{\sim}\,10^9\ \text{M}_{\odot}$
. The violet triangles with error bars are the determinations from Moustakas et al. (Reference Moustakas2013), who used a spectroscopic sample of SDSS DR7 galaxies from the New York University Value Added Galaxy Catalog (NYU-VAGC) with redshifts  $0.01<z<0.2$
combined with observations from GALEX. The red squares with error bars are the estimation obtained in Bernardi et al. (Reference Bernardi, Meert, Sheth, Vikram, Huertas-Company, Mei and Shankar2013) from a sample of SDSS DR7 galaxies with photometry based on the PyMorph software pipeline at
$0.01<z<0.2$
combined with observations from GALEX. The red squares with error bars are the estimation obtained in Bernardi et al. (Reference Bernardi, Meert, Sheth, Vikram, Huertas-Company, Mei and Shankar2013) from a sample of SDSS DR7 galaxies with photometry based on the PyMorph software pipeline at  $z\,{\sim}\,0.1$
. Here, we reproduce their result based on Sérsic luminosities. Additionally, we compute the GSMF using the stellar mass estimates from Sérsic photometry from Mendel et al. (Reference Mendel, Simard, Palmer, Ellison and Patton2014) who used the Simard et al. (Reference Simard, Mendel, Patton, Ellison and McConnachie2011) SDSS DR7 sample of g and r band photometry and extended to u, i, and z bands, blue filled circles with error bars. We show the best-fitting model from D’Souza et al. (Reference D’Souza, Vegetti and Kauffmann2015), who estimated the GSMF by stacking images of galaxies with similar stellar masses and concentrations to correct Model magnitudes from the SDSS DR7, dark green solid line. Finally, we compare our result to Thanjavur et al. (Reference Thanjavur, Simard, Bluck and Mendel2016), who derived the GSMF using the analysis from Mendel et al. (Reference Mendel, Simard, Palmer, Ellison and Patton2014).
$z\,{\sim}\,0.1$
. Here, we reproduce their result based on Sérsic luminosities. Additionally, we compute the GSMF using the stellar mass estimates from Sérsic photometry from Mendel et al. (Reference Mendel, Simard, Palmer, Ellison and Patton2014) who used the Simard et al. (Reference Simard, Mendel, Patton, Ellison and McConnachie2011) SDSS DR7 sample of g and r band photometry and extended to u, i, and z bands, blue filled circles with error bars. We show the best-fitting model from D’Souza et al. (Reference D’Souza, Vegetti and Kauffmann2015), who estimated the GSMF by stacking images of galaxies with similar stellar masses and concentrations to correct Model magnitudes from the SDSS DR7, dark green solid line. Finally, we compare our result to Thanjavur et al. (Reference Thanjavur, Simard, Bluck and Mendel2016), who derived the GSMF using the analysis from Mendel et al. (Reference Mendel, Simard, Palmer, Ellison and Patton2014).
Our GSMF agrees well with previous determinations at the  $\sim 10^{9.3}-10^{11}\ \text{M}_{\odot}$
range. At the high-mass end, it is shallower than previous determinations (e.g., Moustakas et al. Reference Moustakas2013) except to Bernardi et al. (Reference Bernardi, Meert, Sheth, Vikram, Huertas-Company, Mei and Shankar2013), who use Sérsic photometry from the SDSS DR7. As extensively discussed in Bernardi et al. (Reference Bernardi, Meert, Sheth, Fischer, Huertas-Company, Maraston, Shankar and Vikram2017), there are two systematic effects that could lead to differences when comparing to previous determinations from the literature; assumptions on mass-to-light ratios and estimations of galaxy surface brightness. In the case of Moustakas et al. (Reference Moustakas2013) and D’Souza et al. (Reference D’Souza, Vegetti and Kauffmann2015), who used cmodel and Model magnitudes, the comparison is not obvious due to systematic effects in both mass-to-light ratios and photometry (Bernardi et al. Reference Bernardi, Meert, Sheth, Fischer, Huertas-Company, Maraston, Shankar and Vikram2017). In the case of Mendel et al. (Reference Mendel, Simard, Palmer, Ellison and Patton2014) and Bernardi et al. (Reference Bernardi, Meert, Sheth, Vikram, Huertas-Company, Mei and Shankar2013), effects on photometry are not the dominant ones but mass-to-light ratios. Nonetheless, those differences are within the expected systematic effect, especially at the massive end, (Bernardi et al. Reference Bernardi, Meert, Sheth, Fischer, Huertas-Company, Maraston, Shankar and Vikram2017, see also Figure 11). We therefore conclude that when comparing to other previous determinations, the differences that we observe are consistent with the differences expected from systematic effects. Indeed, Figure 1 shows that most of the previous determinations are within our region of systematic errors. Thus, hereafter we will assume that our shift of
$\sim 10^{9.3}-10^{11}\ \text{M}_{\odot}$
range. At the high-mass end, it is shallower than previous determinations (e.g., Moustakas et al. Reference Moustakas2013) except to Bernardi et al. (Reference Bernardi, Meert, Sheth, Vikram, Huertas-Company, Mei and Shankar2013), who use Sérsic photometry from the SDSS DR7. As extensively discussed in Bernardi et al. (Reference Bernardi, Meert, Sheth, Fischer, Huertas-Company, Maraston, Shankar and Vikram2017), there are two systematic effects that could lead to differences when comparing to previous determinations from the literature; assumptions on mass-to-light ratios and estimations of galaxy surface brightness. In the case of Moustakas et al. (Reference Moustakas2013) and D’Souza et al. (Reference D’Souza, Vegetti and Kauffmann2015), who used cmodel and Model magnitudes, the comparison is not obvious due to systematic effects in both mass-to-light ratios and photometry (Bernardi et al. Reference Bernardi, Meert, Sheth, Fischer, Huertas-Company, Maraston, Shankar and Vikram2017). In the case of Mendel et al. (Reference Mendel, Simard, Palmer, Ellison and Patton2014) and Bernardi et al. (Reference Bernardi, Meert, Sheth, Vikram, Huertas-Company, Mei and Shankar2013), effects on photometry are not the dominant ones but mass-to-light ratios. Nonetheless, those differences are within the expected systematic effect, especially at the massive end, (Bernardi et al. Reference Bernardi, Meert, Sheth, Fischer, Huertas-Company, Maraston, Shankar and Vikram2017, see also Figure 11). We therefore conclude that when comparing to other previous determinations, the differences that we observe are consistent with the differences expected from systematic effects. Indeed, Figure 1 shows that most of the previous determinations are within our region of systematic errors. Thus, hereafter we will assume that our shift of  $\pm0.15$
dex in the
$\pm0.15$
dex in the  $M_{*}$
axis approximately captures systematics not only from stellar population models but also from photometry.
$M_{*}$
axis approximately captures systematics not only from stellar population models but also from photometry.
The middle panel of Figure 1 presents comparisons to some previous determinations from deep but small-volume samples. The purple dots with error bars are from Baldry et al. (Reference Baldry, Glazebrook and Driver2008), who used the SDSS NYU-VAGC low-z sample but did not include missing galaxies due to surface brightness incompleteness. In addition, we compare to Baldry et al. (Reference Baldry2012), who used the Galaxy And Mass Assembly (GAMA) survey for galaxies at  $z<0.06$
, and complete down to
$z<0.06$
, and complete down to  $r=19.4$
mag for two-thirds of the galaxy sample and to
$r=19.4$
mag for two-thirds of the galaxy sample and to  $r=19.8$
for one-third of the sample. Finally, we reproduce the observed GSMF from Wright et al. (Reference Wright2017), who also used the GAMA survey to estimate the GSMF.
$r=19.8$
for one-third of the sample. Finally, we reproduce the observed GSMF from Wright et al. (Reference Wright2017), who also used the GAMA survey to estimate the GSMF.
At low masses, our results are in excellent agreement with the GAMA  $\mbox{GSMF}$
s. This is encouraging since the GAMA survey does not suffer from surface brightness incompleteness, at least within the stellar mass range that we are comparing our results. This is an indication that the surface brightness corrections described in Appendix C are able to recover the slope of the GSMF at low masses. Consistent with the values reported in Baldry et al. (Reference Baldry2012) and Wright et al. (Reference Wright2017), we find that the faint-end slope of the GSMF is
$\mbox{GSMF}$
s. This is encouraging since the GAMA survey does not suffer from surface brightness incompleteness, at least within the stellar mass range that we are comparing our results. This is an indication that the surface brightness corrections described in Appendix C are able to recover the slope of the GSMF at low masses. Consistent with the values reported in Baldry et al. (Reference Baldry2012) and Wright et al. (Reference Wright2017), we find that the faint-end slope of the GSMF is  $\alpha \approx -1.4$
, below we describe in more detail the fitting model for the GSMF. The above is also in good agreement with Sedgwick et al. (Reference Sedgwick, Baldry, James and Kelvin2019) who recently determined the low-mass end of the GSMF by identifying low surface brightness galaxies based on data of core-collapse supernovae. The authors used the IAC Stripe 82 legacy project (Fliri & Trujillo Reference Fliri and Trujillo2016) and the SDSS-II Supernovae Survey (Frieman et al. Reference Frieman2008).
$\alpha \approx -1.4$
, below we describe in more detail the fitting model for the GSMF. The above is also in good agreement with Sedgwick et al. (Reference Sedgwick, Baldry, James and Kelvin2019) who recently determined the low-mass end of the GSMF by identifying low surface brightness galaxies based on data of core-collapse supernovae. The authors used the IAC Stripe 82 legacy project (Fliri & Trujillo Reference Fliri and Trujillo2016) and the SDSS-II Supernovae Survey (Frieman et al. Reference Frieman2008).
At the massive end we notice, however, some apparent tension between our and the GAMA results. Effects due to cosmic variance (due to the small redshift and angular coverage of the GAMA sample) could explain those differences as well as systematics in the mass-to-light ratios. Indeed, we see that some of the data are within the systematic errors. In addition, note that Figure C5 from Appendix C shows that using the mass-to-light ratios from Taylor et al. (Reference Taylor2011), utilised in the Baldry et al. (Reference Baldry2012) GSMF, tend to underestimate the high-mass end of the GSMF.
3.2. Best-fitting model to the GSMF
To provide an analytic form to our GSMF, we choose to use a function composed of a Schechter function with a sub-exponential decreasing slope and a double power law function. Note that the resulting high-mass end of our GSMF is shallower than an exponential function, and, thus, better fitted to a power law (see also Tempel et al. Reference Tempel2014). The Schechter sub-exponential function is given by:
 \begin{equation}\phi_{*, {\rm S}}(M_{*})=\phi^{*}_S\ln 10 \left(\frac{M_{*}}{\mathcal {M}_S}\right)^{1+\alpha_S} \exp\left[{-\left(\frac{M_{*}}{\mathcal {M}_S}\right)^{\beta}}\right],\end{equation}
\begin{equation}\phi_{*, {\rm S}}(M_{*})=\phi^{*}_S\ln 10 \left(\frac{M_{*}}{\mathcal {M}_S}\right)^{1+\alpha_S} \exp\left[{-\left(\frac{M_{*}}{\mathcal {M}_S}\right)^{\beta}}\right],\end{equation}
where  $\phi^{*}_S$
is the normalisation parameter in units of Mpc–3 dex–1,
$\phi^{*}_S$
is the normalisation parameter in units of Mpc–3 dex–1,  $\alpha$
is the slope at the low-mass end,
$\alpha$
is the slope at the low-mass end,  $\mathcal {M}_S$
is the characteristic mass, and
$\mathcal {M}_S$
is the characteristic mass, and  $\beta$
is the parameter that controls the slope at the massive end; note that
$\beta$
is the parameter that controls the slope at the massive end; note that  $\beta=1$
corresponds to a Schechter function. The double power law function is given by:
$\beta=1$
corresponds to a Schechter function. The double power law function is given by:
 \begin{equation}\phi_{*, {\rm D}}(M_{*}) =\phi^{*}_D\ln 10\left(\frac{M_{*}}{\mathcal {M}_D}\right)^{1+\alpha_D}\left[1 + \left(\frac{M_{*}}{\mathcal {M}_D}\right)^{\gamma}\right]^{\frac{\delta-\alpha_D}{\gamma}},\end{equation}
\begin{equation}\phi_{*, {\rm D}}(M_{*}) =\phi^{*}_D\ln 10\left(\frac{M_{*}}{\mathcal {M}_D}\right)^{1+\alpha_D}\left[1 + \left(\frac{M_{*}}{\mathcal {M}_D}\right)^{\gamma}\right]^{\frac{\delta-\alpha_D}{\gamma}},\end{equation}
where  $\phi^{*}_D$
is the normalisation parameter in units of Mpc–3 dex–1,
$\phi^{*}_D$
is the normalisation parameter in units of Mpc–3 dex–1,  $\alpha$
and
$\alpha$
and  $\delta$
control the slope at low and high masses, respectively, while
$\delta$
control the slope at low and high masses, respectively, while  $\gamma$
determines the speed of the transition between the low- and high-mass regimes; and
$\gamma$
determines the speed of the transition between the low- and high-mass regimes; and  $\mathcal {M}_D$
is the characteristic mass of the transition. Finally, the analytic form for fitting the observed GSMF is given by
$\mathcal {M}_D$
is the characteristic mass of the transition. Finally, the analytic form for fitting the observed GSMF is given by
 \begin{equation}\phi_{*, {\rm model}}(M_{*}) = \phi_{*, {\rm S}}(M_{*}) + \phi_{*, {\rm D}}(M_{*}),\end{equation}
\begin{equation}\phi_{*, {\rm model}}(M_{*}) = \phi_{*, {\rm S}}(M_{*}) + \phi_{*, {\rm D}}(M_{*}),\end{equation}
where we assumed that  $\mathcal {M}_S =\mathcal {M}_D $
.
$\mathcal {M}_S =\mathcal {M}_D $
.
We find the best-fit parameters  $\vec{p}_{\rm GSMF} = (\phi_{S}^{*}, \alpha_{S}, \mathcal{M}_{S}, \beta, \phi_{D}^{*}, \alpha_{D}, \delta,\gamma)$
that maximise the likelihood function
$\vec{p}_{\rm GSMF} = (\phi_{S}^{*}, \alpha_{S}, \mathcal{M}_{S}, \beta, \phi_{D}^{*}, \alpha_{D}, \delta,\gamma)$
that maximise the likelihood function  $\mathcal{L}\propto \exp({-\chi^2/2})$
using the Markov chain Monte Carlo (MCMC) method algorithm described in Rodríguez-Puebla et al. (2013). Here
$\mathcal{L}\propto \exp({-\chi^2/2})$
using the Markov chain Monte Carlo (MCMC) method algorithm described in Rodríguez-Puebla et al. (2013). Here
 \begin{equation}\chi^2 = \sum_{i=1}^{N_{\rm obs}}\left(\frac{\phi^{i}_{*,{\rm SDSS}} - \phi_{*, {\rm model}}^i }{\sigma^{i}_{\rm SDSS}}\right)^2,\end{equation}
\begin{equation}\chi^2 = \sum_{i=1}^{N_{\rm obs}}\left(\frac{\phi^{i}_{*,{\rm SDSS}} - \phi_{*, {\rm model}}^i }{\sigma^{i}_{\rm SDSS}}\right)^2,\end{equation}
with  $N_{\rm obs} $
as the number of observational data points of the GSMF each with an ith value of
$N_{\rm obs} $
as the number of observational data points of the GSMF each with an ith value of  $\phi^{i}_{*,{\rm SDSS}}$
and an error of
$\phi^{i}_{*,{\rm SDSS}}$
and an error of  $\sigma^{i}_{\rm SDSS}$
. The ith value of our model is given by
$\sigma^{i}_{\rm SDSS}$
. The ith value of our model is given by  $\phi_{*, {\rm model}}^i$
.
$\phi_{*, {\rm model}}^i$
.
We sample the best-fit parameters by running a set of 10 chains with  $1\times 10^{5}$
MCMC models each. Table 1 lists the best-fit parameters. For our best-fitting model, we find that
$1\times 10^{5}$
MCMC models each. Table 1 lists the best-fit parameters. For our best-fitting model, we find that  $\chi^2=85.42$
from a number of
$\chi^2=85.42$
from a number of  $N_{\rm obs} = 50$
observational data points. Our model consist of
$N_{\rm obs} = 50$
observational data points. Our model consist of  $N_{\rm p} = 8$
free parameters, thus the reduced
$N_{\rm p} = 8$
free parameters, thus the reduced  $\chi^2$
is
$\chi^2$
is  $\chi^2 / {\rm d.o.f.} = 2.03$
. The upper and middle panels of Figure 1 show our best-fitting model as the black solid line and the bottom panel shows the residuals as a function of
$\chi^2 / {\rm d.o.f.} = 2.03$
. The upper and middle panels of Figure 1 show our best-fitting model as the black solid line and the bottom panel shows the residuals as a function of  $M_{*}$
. Our best-fitting model has an error of
$M_{*}$
. Our best-fitting model has an error of  $\sim\!2\%$
at the range
$\sim\!2\%$
at the range  $M_{*}\sim\!2\times10^{9}-5\times10^{11}\text{M}_{\odot}$
and an error lower than
$M_{*}\sim\!2\times10^{9}-5\times10^{11}\text{M}_{\odot}$
and an error lower than  $\sim\!10\%$
at the mass range
$\sim\!10\%$
at the mass range  $M_{*}\sim\!7\times10^{8}-1\times10^{12}\text{M}_{\odot}$
. For lower masses, errors can be up to
$M_{*}\sim\!7\times10^{8}-1\times10^{12}\text{M}_{\odot}$
. For lower masses, errors can be up to  $\sim\!20\%$
.
$\sim\!20\%$
.
A valid question is how much we improve the analytic prescription when using a Schechter sub-exponential plus a double power law function model confronted to a double Schechter function model, commonly employed by previous authors (see e.g., Baldry et al. Reference Baldry2012; Wright et al. Reference Wright2017). We have explored this possibility but assuming a Schechter function,  $\beta=1$
in Equation (21), and a Schechter sub-exponential function, that is, we are adding a extra degree of freedom due to the shallow decay at the high-mass end. Based on this alternative, we repeat our fitting procedure but this time finding that
$\beta=1$
in Equation (21), and a Schechter sub-exponential function, that is, we are adding a extra degree of freedom due to the shallow decay at the high-mass end. Based on this alternative, we repeat our fitting procedure but this time finding that  $\chi^2=662.817$
from a number of
$\chi^2=662.817$
from a number of  $N_{\rm obs} = 50$
observational data points. Now, our model consists of
$N_{\rm obs} = 50$
observational data points. Now, our model consists of  $N_{\rm p} = 6$
free parameters resulting in a reduced
$N_{\rm p} = 6$
free parameters resulting in a reduced  $\chi^2$
of
$\chi^2$
of  $\chi^2 / {\rm d.o.f.} = 15.06$
. This is considerably worse when combining Schechter sub-exponential and double power law functions. Thus, hereafter, we will consider only the latter model.
$\chi^2 / {\rm d.o.f.} = 15.06$
. This is considerably worse when combining Schechter sub-exponential and double power law functions. Thus, hereafter, we will consider only the latter model.
3.3. The GSMFs of early- and late-type galaxies
Our main goal for this paper is to construct bivariate distributions as well as MF based on the observed gas mass CPDFs and the  $\mbox{GSMF}$
s of early- and late-type galaxies. In this section, we determine the GSMF of early- and late-type galaxies from the SDSS DR7 spectroscopic sample with the public automated morphological galaxy classification by Huertas-Company et al. (Reference Huertas-Company, Aguerri, Bernardi, Mei and Sánchez Almeida2011).Footnote i The morphological classification in Huertas-Company et al. (Reference Huertas-Company, Aguerri, Bernardi, Mei and Sánchez Almeida2011) was determined based on support vector machine algorithms. Here we use their tabulated probabilities for each SDSS galaxy as being classified as an early type, P(E). For masses below the completeness of the SDSS DR7 sample, we use an extrapolation of the observed fraction of early-type galaxies. We will come back to this point later in this section.
$\mbox{GSMF}$
s of early- and late-type galaxies. In this section, we determine the GSMF of early- and late-type galaxies from the SDSS DR7 spectroscopic sample with the public automated morphological galaxy classification by Huertas-Company et al. (Reference Huertas-Company, Aguerri, Bernardi, Mei and Sánchez Almeida2011).Footnote i The morphological classification in Huertas-Company et al. (Reference Huertas-Company, Aguerri, Bernardi, Mei and Sánchez Almeida2011) was determined based on support vector machine algorithms. Here we use their tabulated probabilities for each SDSS galaxy as being classified as an early type, P(E). For masses below the completeness of the SDSS DR7 sample, we use an extrapolation of the observed fraction of early-type galaxies. We will come back to this point later in this section.
From a catalogue of galaxies with visual morphological classification (UNAM-KIAS; Hernández-Toledo et al. Reference Hernández-Toledo, Vázquez-Mata, Martínez-Vázquez, Choi and Park2010), we find that galaxies with types  $T\le0$
are mostly those with
$T\le0$
are mostly those with  $P(E)>0.65$
, and those with
$P(E)>0.65$
, and those with  $P(E)\le0.65$
correspond mostly to
$P(E)\le0.65$
correspond mostly to  $T>0$
; here T is the Fukugita et al. (Reference Fukugita2007) notation.Footnote j Based on the above, we consider as early-type galaxies those with a probability
$T>0$
; here T is the Fukugita et al. (Reference Fukugita2007) notation.Footnote j Based on the above, we consider as early-type galaxies those with a probability  $P(E)>0.65$
, while late-type galaxies those with
$P(E)>0.65$
, while late-type galaxies those with  $P(E)\le0.65$
. We checked that our morphology definition between early- and late-type galaxies is consistent with the morphological classification based on the concentration parameter
$P(E)\le0.65$
. We checked that our morphology definition between early- and late-type galaxies is consistent with the morphological classification based on the concentration parameter  $c=R_{90}/R_{50}$
. That is, the division between early- and late-types is approximately at
$c=R_{90}/R_{50}$
. That is, the division between early- and late-types is approximately at  $c=2.85$
(see below and also, Hyde & Bernardi Reference Hyde and Bernardi2009; Bernardi et al. Reference Bernardi, Shankar, Hyde, Mei, Marulli and Sheth2010).
$c=2.85$
(see below and also, Hyde & Bernardi Reference Hyde and Bernardi2009; Bernardi et al. Reference Bernardi, Shankar, Hyde, Mei, Marulli and Sheth2010).
We calculate the SDSS DR7 GSMF of early- and late-type galaxies using the  $1/\text{V}_{\rm max}$
method described in Appendix A. Figure 2 shows the corresponding
$1/\text{V}_{\rm max}$
method described in Appendix A. Figure 2 shows the corresponding  $\mbox{GSMF}$
s of early and late types in the upper left and right panels, respectively. For comparison, we show the
$\mbox{GSMF}$
s of early and late types in the upper left and right panels, respectively. For comparison, we show the  $\mbox{GSMF}$
s for red and blue galaxies based on a colour cut limit in the
$\mbox{GSMF}$
s for red and blue galaxies based on a colour cut limit in the  ${(g-r)^{0.0}-M_{*}}$
diagram. In this diagram, we find that a rough division criteria from blue to red galaxies is given by the colour limit of
${(g-r)^{0.0}-M_{*}}$
diagram. In this diagram, we find that a rough division criteria from blue to red galaxies is given by the colour limit of  ${(g-r)^{0.0}=0.66}$
.Footnote k In the same figure, we compare our results to different determinations from the literature as we describe below. All the data in this figure have been renormalised to our cosmology.
${(g-r)^{0.0}=0.66}$
.Footnote k In the same figure, we compare our results to different determinations from the literature as we describe below. All the data in this figure have been renormalised to our cosmology.

Figure 2. SDSS DR7 GSMFs for early- and late-type galaxies, left and right upper panels, respectively. Early- and late-type galaxies are defined as those with  $P(E)>0.65$
(
$P(E)>0.65$
( $P(E)\le0.65$
) from the tabulated probabilities of Huertas-Company et al. (Reference Huertas-Company, Aguerri, Bernardi, Mei and Sánchez Almeida2011). This is equivalent to morphological types that comprises E and S0 galaxies or
$P(E)\le0.65$
) from the tabulated probabilities of Huertas-Company et al. (Reference Huertas-Company, Aguerri, Bernardi, Mei and Sánchez Almeida2011). This is equivalent to morphological types that comprises E and S0 galaxies or  $T\le0$
(Sa to Irr galaxies or
$T\le0$
(Sa to Irr galaxies or  $T>0$
). We compare to various previous determinations from the literature as indicated by the legends, see also the text for details. Our determinations are in general in good agreement with previous determinations from SDSS spectroscopic samples, while a tension is evident with determinations from the GAMA survey. We also present our resulting GSMFs for blue and red galaxies. These GSMFs follow closely those by morphology from the GAMA survey. The bottom panel shows our number density-weighted fractions of early-type and red galaxies as a function of
$T>0$
). We compare to various previous determinations from the literature as indicated by the legends, see also the text for details. Our determinations are in general in good agreement with previous determinations from SDSS spectroscopic samples, while a tension is evident with determinations from the GAMA survey. We also present our resulting GSMFs for blue and red galaxies. These GSMFs follow closely those by morphology from the GAMA survey. The bottom panel shows our number density-weighted fractions of early-type and red galaxies as a function of  $M_{*}$
. Their corresponding best-fit models Equation (25) are shown with solid and dashed lines, respectively.
$M_{*}$
. Their corresponding best-fit models Equation (25) are shown with solid and dashed lines, respectively.
Recently, Moffett et al. (Reference Moffett2016a) visually classified morphologies in the GAMA survey and reported the GSMF for different morphologies. Here, we reproduce their GSMF from E to Sa galaxies as early types and the complement as late types. Contrary to our definition, Sa galaxies are included in the early-type group; this is because the authors report S0 and Sa galaxies as one morphology group. As shown in Figure 2, the GSMF of early-type galaxies from Moffett et al. (Reference Moffett2016a) results in an overabundance of low-mass galaxies compared to other studies. We reproduce the results from Thanjavur et al. (Reference Thanjavur, Simard, Bluck and Mendel2016) with bulge-to-total ratios of  $B/T>0.8$
as early types and
$B/T>0.8$
as early types and  $B/T\leq0.8$
as late types. Thanjavur et al. (Reference Thanjavur, Simard, Bluck and Mendel2016) used the bulge-to-disc decomposition from Simard et al. (Reference Simard, Mendel, Patton, Ellison and McConnachie2011) SDSS DR7 spectroscopic sample, and stellar masses derived from Mendel et al. (Reference Mendel, Simard, Palmer, Ellison and Patton2014). We also include results from Kelvin et al. (Reference Kelvin2014). Similarly to Moffett et al. (Reference Moffett2016a), Kelvin et al. (Reference Kelvin2014) visually classified morphologies in the GAMA survey. We again use their GSMF from E to Sa galaxies for early types since the authors combined S0–Sa galaxies as in Moffett et al. (Reference Moffett2016a). The filled triangles with error bars show the GSMF from Bernardi et al. (Reference Bernardi, Shankar, Hyde, Mei, Marulli and Sheth2010) for galaxies with concentration parameter
$B/T\leq0.8$
as late types. Thanjavur et al. (Reference Thanjavur, Simard, Bluck and Mendel2016) used the bulge-to-disc decomposition from Simard et al. (Reference Simard, Mendel, Patton, Ellison and McConnachie2011) SDSS DR7 spectroscopic sample, and stellar masses derived from Mendel et al. (Reference Mendel, Simard, Palmer, Ellison and Patton2014). We also include results from Kelvin et al. (Reference Kelvin2014). Similarly to Moffett et al. (Reference Moffett2016a), Kelvin et al. (Reference Kelvin2014) visually classified morphologies in the GAMA survey. We again use their GSMF from E to Sa galaxies for early types since the authors combined S0–Sa galaxies as in Moffett et al. (Reference Moffett2016a). The filled triangles with error bars show the GSMF from Bernardi et al. (Reference Bernardi, Shankar, Hyde, Mei, Marulli and Sheth2010) for galaxies with concentration parameter  $c>2.86$
for early types and
$c>2.86$
for early types and  $c\leq2.86$
for late types.Footnote l
$c\leq2.86$
for late types.Footnote l
Finally, using the Nair & Abraham (Reference Nair and Abraham2010) morphology catalogue, who visually classified 14,034 spectroscopic galaxies from the SDSS DR4, we derive the GSMF for early-type galaxies.Footnote m We utilise their morphological notation and define early-type galaxies as those objects with  $-5\le T\le0$
(E-S0s), equivalent to
$-5\le T\le0$
(E-S0s), equivalent to  $T\le1$
in the Fukugita et al. (Reference Fukugita2007) notation. We additionally derive the GSMF with morphologies between
$T\le1$
in the Fukugita et al. (Reference Fukugita2007) notation. We additionally derive the GSMF with morphologies between  $-5\le T\le1$
in the Nair & Abraham (Reference Nair and Abraham2010) notation, which include Sa galaxies.
$-5\le T\le1$
in the Nair & Abraham (Reference Nair and Abraham2010) notation, which include Sa galaxies.
In general, our results agree with previous determinations, especially with those from the SDSS spectroscopic samples. In contrast, the GSMF of early-type galaxies from the visual classification of the GAMA survey are systematically above our results at the low-mass end,  $M_{*}\lesssim2\times10^{10}\text{M}_{\odot}$
, but closer to our classification based on galaxy colour. While it is not clear the reason of the differences outlined above (the inclusion of Sa galaxies as early types, environment, etc.), in Appendix C.4, we will discuss the impact of using galaxy colour instead of morphology when deriving the
$M_{*}\lesssim2\times10^{10}\text{M}_{\odot}$
, but closer to our classification based on galaxy colour. While it is not clear the reason of the differences outlined above (the inclusion of Sa galaxies as early types, environment, etc.), in Appendix C.4, we will discuss the impact of using galaxy colour instead of morphology when deriving the  $\rm HI$
,
$\rm HI$
,  $\rm H_{2}$
, cold gas, and baryonic MFs separated into two main galaxy populations.
$\rm H_{2}$
, cold gas, and baryonic MFs separated into two main galaxy populations.
Finally, the bottom panel of Figure 2 shows the resulting fraction of early-type galaxies as a function of stellar mass,  $f_E\text{(}M_{*}\text{)}$
. In addition, we show the fraction of red galaxies when using our
$f_E\text{(}M_{*}\text{)}$
. In addition, we show the fraction of red galaxies when using our  $g-r$
colour cut limit,
$g-r$
colour cut limit,  $f_r\text{(}M_{*}\text{)}$
. We find that the fraction at which early-type galaxies is 50% is at
$f_r\text{(}M_{*}\text{)}$
. We find that the fraction at which early-type galaxies is 50% is at  $M_{*}\sim\!10^{11}\text{M}_{\odot}$
, while at
$M_{*}\sim\!10^{11}\text{M}_{\odot}$
, while at  $M_{*}\sim\!1.6\times10^{10}\text{M}_{\odot}$
and
$M_{*}\sim\!1.6\times10^{10}\text{M}_{\odot}$
and  $M_{*}\sim\!8\times10^{11}\text{M}_{\odot}$
the fractions are 16% and 84%, respectively. For red galaxies, the fraction of 50% is at
$M_{*}\sim\!8\times10^{11}\text{M}_{\odot}$
the fractions are 16% and 84%, respectively. For red galaxies, the fraction of 50% is at  $M_{*}\sim\! 10^{10}\text{M}_{\odot}$
, while at
$M_{*}\sim\! 10^{10}\text{M}_{\odot}$
, while at  $M_{*}\sim\!3\times10^{9}\text{M}_{\odot}$
and
$M_{*}\sim\!3\times10^{9}\text{M}_{\odot}$
and  $M_{*}\sim\!10^{11}\text{M}_{\odot}$
the fractions are 16% and 84%, respectively. Note that the characteristic mass at which the fraction of early-type galaxies is 50% is a factor of
$M_{*}\sim\!10^{11}\text{M}_{\odot}$
the fractions are 16% and 84%, respectively. Note that the characteristic mass at which the fraction of early-type galaxies is 50% is a factor of  $\sim\!10$
larger than for red galaxies. In general,
$\sim\!10$
larger than for red galaxies. In general,  $f_E\text{(}M_{*}\text{)}$
rises slower than the fraction
$f_E\text{(}M_{*}\text{)}$
rises slower than the fraction  $f_r\text{(}M_{*}\text{)}$
. In the same figure, we present the best-fit model to the data. After exploring different functions, we find that two sigmoid functions accurately describe the functionality of
$f_r\text{(}M_{*}\text{)}$
. In the same figure, we present the best-fit model to the data. After exploring different functions, we find that two sigmoid functions accurately describe the functionality of  $f_E\text{(}M_{*}\text{)}$
or
$f_E\text{(}M_{*}\text{)}$
or  $f_r\text{(}M_{*}\text{)}$
:
$f_r\text{(}M_{*}\text{)}$
:
 \begin{equation}f_{k}\text{(}M_{*}\text{)} = \frac{1-A}{1+e^{-\gamma_1(x_{C,1}+x_{0,1})}}+ \frac{A}{1+e^{-\gamma_2(x_{C,2}-x_{0,2})}},\end{equation}
\begin{equation}f_{k}\text{(}M_{*}\text{)} = \frac{1-A}{1+e^{-\gamma_1(x_{C,1}+x_{0,1})}}+ \frac{A}{1+e^{-\gamma_2(x_{C,2}-x_{0,2})}},\end{equation}
where  $k=E$
or r,
$k=E$
or r,  $x_{C,i} = {M_{*}} / \mathcal{M}_{C,i}$
, with
$x_{C,i} = {M_{*}} / \mathcal{M}_{C,i}$
, with  $i = 1,2$
. The best-fit parameters for the two fractions are listed in Table 2.
$i = 1,2$
. The best-fit parameters for the two fractions are listed in Table 2.
To derive the analytic model for the GSMF of early- and late-type galaxies, we use the best-fit model to our GSMF, Section 3.2, and the best-fit model for  $f_E\text{(}M_{*}\text{)}$
. For masses below
$f_E\text{(}M_{*}\text{)}$
. For masses below  $5\times 10^8\ \text{M}_{\odot}$
we extrapolate
$5\times 10^8\ \text{M}_{\odot}$
we extrapolate  $f_E\text{(}M_{*}\text{)}$
. This is an acceptable approximation since as seen in Figure 2, the fraction
$f_E\text{(}M_{*}\text{)}$
. This is an acceptable approximation since as seen in Figure 2, the fraction  $f_E\text{(}M_{*}\text{)}$
tends to
$f_E\text{(}M_{*}\text{)}$
tends to  $\sim\!0$
below
$\sim\!0$
below  $M_{*}=10^9\ \text{M}_{\odot}$
. Recall that our main goal in this paper is to derive the MFs for
$M_{*}=10^9\ \text{M}_{\odot}$
. Recall that our main goal in this paper is to derive the MFs for  $\rm HI$
,
$\rm HI$
,  $\rm H_{2}$
, cold gas, and baryons by combining the observed
$\rm H_{2}$
, cold gas, and baryons by combining the observed  $\rm HI$
and
$\rm HI$
and  $\rm H_{2}$
CPDFs with the GSMF, both for early- and late-type galaxies, over a large mass range. Thus, at this point, we are in a position to determine these MFs.
$\rm H_{2}$
CPDFs with the GSMF, both for early- and late-type galaxies, over a large mass range. Thus, at this point, we are in a position to determine these MFs.
4. Results
In this section, we present our fits to the  $\rm HI$
- and
$\rm HI$
- and  $\rm H_{2}$
-CPDFs for early- and late-type galaxies from Paper I, the corresponding correlations (first and second moments), the bivariate
$\rm H_{2}$
-CPDFs for early- and late-type galaxies from Paper I, the corresponding correlations (first and second moments), the bivariate  $\rm HI$
- and
$\rm HI$
- and  $\rm H_{2}$
-stellar mass distributions, and the
$\rm H_{2}$
-stellar mass distributions, and the  $\rm HI$
and
$\rm HI$
and  $\rm H_{2}\,$
MFs. We also present the total cold gas and baryonic MFs. We will show that our empirically inferred
$\rm H_{2}\,$
MFs. We also present the total cold gas and baryonic MFs. We will show that our empirically inferred  $\rm HI$
and
$\rm HI$
and  $\rm H_{2}\,$
MFs agree with direct determinations from blind or optically/infrared (selected) radio galaxy surveys. Previous works related to our approach are Obreschkow & Rawlings (Reference Obreschkow and Rawlings2009), Lemonias et al. (Reference Lemonias, Schiminovich, Catinella, Heckman and Moran2013), and Butcher et al. (Reference Butcher, Schneider, van Driel and Lehnert2018).
$\rm H_{2}\,$
MFs agree with direct determinations from blind or optically/infrared (selected) radio galaxy surveys. Previous works related to our approach are Obreschkow & Rawlings (Reference Obreschkow and Rawlings2009), Lemonias et al. (Reference Lemonias, Schiminovich, Catinella, Heckman and Moran2013), and Butcher et al. (Reference Butcher, Schneider, van Driel and Lehnert2018).
Table 2. Best-fit parameters to the fraction of early-type and red galaxies

Table 3. Best-fit parameters of the  $\rm HI$
and
$\rm HI$
and  $\rm H_{2}$
mass CPDFs for late- and early-type galaxies
$\rm H_{2}$
mass CPDFs for late- and early-type galaxies

For those interested in using our results, we provide a Python code containing all the necessary information to reproduce the results presented here, for details see Section 6.
4.1. The  $\text{\em HI}$
and
$\text{\em HI}$
and  $\text{\em H}_{\text{\em 2}}$
conditional distribution functions
$\text{\em H}_{\text{\em 2}}$
conditional distribution functions
Section 2.2 describes the functional forms for the  $\rm HI$
- and
$\rm HI$
- and  $\rm H_{2}$
-CPDFs of early- and late-type galaxies proposed in Paper I. Here, using the determinations of the CPDFs for early- and late-type galaxies from Paper I, we find the best-fit parameters of the proposed functional forms: a Schechter-type function and a Schechter-type + Uniform function, respectively (see Section 2.2). While Paper I reported their corresponding best-fit parameters, here we opt for an update based on our own determinations of the GSMFs, for consistency. There are two reasons for doing this: (i) when fitting a CPDF that is determined over stellar mass bins, one should take into account contributions to this CPDF from the different masses. Weighting the conditional distributions by the GSMF takes care on that, see Equations (6) and (8) of Section 5 from Paper I; and (ii) Paper I used the fraction of bulge-dominated galaxies from Moffett et al. (Reference Moffett2016b) as a proxy to the fraction of early-type galaxies. As discussed in Section 3.3, the results from Moffett et al. (Reference Moffett2016a), and thus Moffett et al. (Reference Moffett2016b), overestimate the fraction of early-type galaxies compared to the SDSS morphological catalogues. The above could be due to the inclusion of Sa galaxies into the group of early types. We used the above to argue in favour of our derived fraction of early-type galaxies based on the automated morphological classification from Huertas-Company et al. (Reference Huertas-Company, Aguerri, Bernardi, Mei and Sánchez Almeida2011).
$\rm H_{2}$
-CPDFs of early- and late-type galaxies proposed in Paper I. Here, using the determinations of the CPDFs for early- and late-type galaxies from Paper I, we find the best-fit parameters of the proposed functional forms: a Schechter-type function and a Schechter-type + Uniform function, respectively (see Section 2.2). While Paper I reported their corresponding best-fit parameters, here we opt for an update based on our own determinations of the GSMFs, for consistency. There are two reasons for doing this: (i) when fitting a CPDF that is determined over stellar mass bins, one should take into account contributions to this CPDF from the different masses. Weighting the conditional distributions by the GSMF takes care on that, see Equations (6) and (8) of Section 5 from Paper I; and (ii) Paper I used the fraction of bulge-dominated galaxies from Moffett et al. (Reference Moffett2016b) as a proxy to the fraction of early-type galaxies. As discussed in Section 3.3, the results from Moffett et al. (Reference Moffett2016a), and thus Moffett et al. (Reference Moffett2016b), overestimate the fraction of early-type galaxies compared to the SDSS morphological catalogues. The above could be due to the inclusion of Sa galaxies into the group of early types. We used the above to argue in favour of our derived fraction of early-type galaxies based on the automated morphological classification from Huertas-Company et al. (Reference Huertas-Company, Aguerri, Bernardi, Mei and Sánchez Almeida2011).
Following Paper I, we use the Bayesian approach described previously through a MCMC method applied jointly to all the data (the CPDFs in different  $M_{*}$
bins) to find the best-fit parameters of the proposed functions. These are listed in Table 3. Figure 3 shows our best-fitting models for late-type galaxies compared to the CPDFs from Paper I. Figure 4 shows the same but for early-type galaxies. We notice that our best-fit parameters are very similar to those determined in Paper I.
$M_{*}$
bins) to find the best-fit parameters of the proposed functions. These are listed in Table 3. Figure 3 shows our best-fitting models for late-type galaxies compared to the CPDFs from Paper I. Figure 4 shows the same but for early-type galaxies. We notice that our best-fit parameters are very similar to those determined in Paper I.

Figure 3.  $\text{HI}$
and
$\text{HI}$
and  $\text{H}_{\text{2}}$
mass CPDFs for late-type galaxies. The results for the compilation sample from Paper I are shown as filled circles with error bars. Note that the above results include non-detections since the authors used the Kaplan & Meier (Reference Kaplan and Meier1958) estimator for uncensored data in their analysis. Our best-fitting models are shown as the solid lines.
$\text{H}_{\text{2}}$
mass CPDFs for late-type galaxies. The results for the compilation sample from Paper I are shown as filled circles with error bars. Note that the above results include non-detections since the authors used the Kaplan & Meier (Reference Kaplan and Meier1958) estimator for uncensored data in their analysis. Our best-fitting models are shown as the solid lines.

Figure 4. Same as Figure 3 but for early-type galaxies. Note that the CPDFs of early-type galaxies reported in Paper I account for upper limits corrected by distance selection effects when necessary and the treated with the Kaplan & Meier (Reference Kaplan and Meier1958) estimator, see Section 2.2.1.

Figure 5. Logarithmic, left panels, and arithmetic, right panels, averaged mass ratios  $\mathcal{R}_j$
as a function of
$\mathcal{R}_j$
as a function of  $M_{*}$
from our analysis, with
$M_{*}$
from our analysis, with  $j={\text{HI}}$
,
$j={\text{HI}}$
,  ${\text{H}_{\text{2}}}$
. Blue and red lines are for early- and late-type galaxies, respectively, while the black lines correspond to all galaxies. The shaded areas show the respective standard deviations. Notice that
${\text{H}_{\text{2}}}$
. Blue and red lines are for early- and late-type galaxies, respectively, while the black lines correspond to all galaxies. The shaded areas show the respective standard deviations. Notice that  $\log \langle \mathcal{R}_j (M_{*})\rangle \geq \langle \log \mathcal{R}_j (M_{*})\rangle$
and the dispersion reduces for the arithmetic mean. The open circles with error bars in the upper left panel correspond to the data from ALFALFA galaxies with SDSS spectral and stellar mass counterparts according to Maddox et al. (Reference Maddox, Hess, Obreschkow, Jarvis and Blyth2015).
$\log \langle \mathcal{R}_j (M_{*})\rangle \geq \langle \log \mathcal{R}_j (M_{*})\rangle$
and the dispersion reduces for the arithmetic mean. The open circles with error bars in the upper left panel correspond to the data from ALFALFA galaxies with SDSS spectral and stellar mass counterparts according to Maddox et al. (Reference Maddox, Hess, Obreschkow, Jarvis and Blyth2015).
4.2. The  $\text{\em HI}$
- and
$\text{\em HI}$
- and  $\text{\em H}_{\text{\em 2}}$
-to-stellar mass correlations
$\text{\em H}_{\text{\em 2}}$
-to-stellar mass correlations
Next, we explore the resulting first and second moments from our best-fitting models to the observed  $\rm HI$
- and
$\rm HI$
- and  $\rm H_{2}$
-CPDFs, shown in Figure 5. The left panels of the figure present the logarithmic mean
$\rm H_{2}$
-CPDFs, shown in Figure 5. The left panels of the figure present the logarithmic mean  $\langle \log \mathcal{R}_j\rangle$
and its corresponding standard deviation,
$\langle \log \mathcal{R}_j\rangle$
and its corresponding standard deviation,  $\sigma_{\log \mathcal{R}_j}$
,
$\sigma_{\log \mathcal{R}_j}$
,  $j=$
$j=$
 $\rm HI$
or
$\rm HI$
or  $\rm H_{2}$
, as a function of
$\rm H_{2}$
, as a function of  $M_{*}$
for early- and late-type galaxies as well as for all the galaxies. At low masses, the correlation of all galaxies approaches the one of the late-type galaxies, while at high-mass end it approaches early types. The above trends are just the consequence of the observed fraction of early and late types. Figure 5 shows that early- and late-type galaxies follow different
$M_{*}$
for early- and late-type galaxies as well as for all the galaxies. At low masses, the correlation of all galaxies approaches the one of the late-type galaxies, while at high-mass end it approaches early types. The above trends are just the consequence of the observed fraction of early and late types. Figure 5 shows that early- and late-type galaxies follow different  $\langle \log \mathcal{R}_j\rangle-M_{*}$
correlations. Therefore, due to the strong bimodality of these correlations, conclusions based on some subset of galaxies as representative of all galaxies would lead to incorrect results.
$\langle \log \mathcal{R}_j\rangle-M_{*}$
correlations. Therefore, due to the strong bimodality of these correlations, conclusions based on some subset of galaxies as representative of all galaxies would lead to incorrect results.
In the literature, sometimes the gas-to-stellar mass relations are reported using the arithmetic mean (though the results are plotted in logarithmic diagrams). The right panel of Figure 5 shows  $\log \langle \mathcal{R}_j\rangle$
versus
$\log \langle \mathcal{R}_j\rangle$
versus  $M_{*}$
from our empirical CPDFs. As is clearly seen, there are notable differences when computing different ways of averaging the distributions: (i)
$M_{*}$
from our empirical CPDFs. As is clearly seen, there are notable differences when computing different ways of averaging the distributions: (i)  $\log \langle \mathcal{R}_j\text{(}M_{*}\text{)}\rangle > \langle \log\mathcal{R}_j\text{(}M_{*}\text{)}\rangle$
, being larger the difference for the early-type galaxies;Footnote n and (ii) the standard deviations from the arithmetic mean is smaller than from the logarithmic mean.
$\log \langle \mathcal{R}_j\text{(}M_{*}\text{)}\rangle > \langle \log\mathcal{R}_j\text{(}M_{*}\text{)}\rangle$
, being larger the difference for the early-type galaxies;Footnote n and (ii) the standard deviations from the arithmetic mean is smaller than from the logarithmic mean.
In the left upper panel of Figure 4, we reproduce the results from (Maddox et al. Reference Maddox, Hess, Obreschkow, Jarvis and Blyth2015) for the ALFALFA galaxies with SDSS spectral and stellar mass counterparts. It is clear that the ALFALFA survey is biased towards galaxies with high  $\rm HI$
-to–
$\rm HI$
-to– $M_{*}$
ratios. In other words, the ALFALFA survey mainly detects galaxies in the upper envelope of the full distribution of
$M_{*}$
ratios. In other words, the ALFALFA survey mainly detects galaxies in the upper envelope of the full distribution of  $\mathcal{R}_{{\rm HI}}$
(see also Maddox et al. Reference Maddox, Hess, Obreschkow, Jarvis and Blyth2015) and is dominated mostly by late types (see also e.g., Haynes et al. Reference Haynes2011).
$\mathcal{R}_{{\rm HI}}$
(see also Maddox et al. Reference Maddox, Hess, Obreschkow, Jarvis and Blyth2015) and is dominated mostly by late types (see also e.g., Haynes et al. Reference Haynes2011).
4.3. The bivariate mass distribution functions
Figure 6 shows the resulting bivariate stellar- $\rm HI$
mass distribution function,
$\rm HI$
mass distribution function,  $\Phi(M_{\rm HI},{M_{*}})$
, see Equation (2). The colour code shows various number density levels for
$\Phi(M_{\rm HI},{M_{*}})$
, see Equation (2). The colour code shows various number density levels for  $\Phi(M_{\rm HI},{M_{*}})$
. Notice that
$\Phi(M_{\rm HI},{M_{*}})$
. Notice that  $\Phi(M_{\rm HI},{M_{*}})$
is for all galaxies, that is, it includes the contribution from early- and late-type galaxies. The discontinuity in the number density isocontours at the bottom right of the diagrams is related to contributions from the non-detections from early types. Recall that for the CPDFs of early types, we assumed an uniform function (or top-hat) for the lowest values of the gas-to-stellar mass ratios
$\Phi(M_{\rm HI},{M_{*}})$
is for all galaxies, that is, it includes the contribution from early- and late-type galaxies. The discontinuity in the number density isocontours at the bottom right of the diagrams is related to contributions from the non-detections from early types. Recall that for the CPDFs of early types, we assumed an uniform function (or top-hat) for the lowest values of the gas-to-stellar mass ratios  $\mathcal{R}_{\rm HI}$
, where the non-detection piled up,Footnote o see Section 2.2.2 and Figure 4. In the bottom right and upper panels of the same figure, we present respectively our measurements of the
$\mathcal{R}_{\rm HI}$
, where the non-detection piled up,Footnote o see Section 2.2.2 and Figure 4. In the bottom right and upper panels of the same figure, we present respectively our measurements of the  $\rm HI$
MF and GSMF with the solid black lines. We compare the
$\rm HI$
MF and GSMF with the solid black lines. We compare the  $\rm HI$
MF with blind
$\rm HI$
MF with blind  $\rm HI$
galaxy surveys based on ALFALFA (Jones et al. Reference Jones, Haynes, Giovanelli and Moorman2018; Papastergis et al. Reference Papastergis, Cattaneo, Huang, Giovanelli and Haynes2012; Martin et al. Reference Martin, Papastergis, Giovanelli, Haynes, Springob and Stierwalt2010) and on
$\rm HI$
galaxy surveys based on ALFALFA (Jones et al. Reference Jones, Haynes, Giovanelli and Moorman2018; Papastergis et al. Reference Papastergis, Cattaneo, Huang, Giovanelli and Haynes2012; Martin et al. Reference Martin, Papastergis, Giovanelli, Haynes, Springob and Stierwalt2010) and on  $\rm HI$
Parkes All Sky Survey (HIPASS) (Zwaan et al. Reference Zwaan, Meyer, Staveley-Smith and Webster2005). While in the next subsection, we discuss in more detail the comparison with previous works, for the moment we note that our total
$\rm HI$
Parkes All Sky Survey (HIPASS) (Zwaan et al. Reference Zwaan, Meyer, Staveley-Smith and Webster2005). While in the next subsection, we discuss in more detail the comparison with previous works, for the moment we note that our total  $\rm HI$
MF is in good agreement with the above direct observations. In the case of ALFALFA, this is a revealing result given the strong selection bias of this survey towards
$\rm HI$
MF is in good agreement with the above direct observations. In the case of ALFALFA, this is a revealing result given the strong selection bias of this survey towards  $\rm HI$
-rich and late-type galaxies as seen in Figure 6 (open circles reproduce the results from Maddox et al. Reference Maddox, Hess, Obreschkow, Jarvis and Blyth2015, see also the discussion of the previous subsection and Figure 4). As we will discuss in the next section, the above reflects that the total
$\rm HI$
-rich and late-type galaxies as seen in Figure 6 (open circles reproduce the results from Maddox et al. Reference Maddox, Hess, Obreschkow, Jarvis and Blyth2015, see also the discussion of the previous subsection and Figure 4). As we will discuss in the next section, the above reflects that the total  $\rm HI$
MF is dominated by late-type galaxies.
$\rm HI$
MF is dominated by late-type galaxies.

Figure 6. Atomic gas–stellar mass bivariate (joint) distribution function. The colour code shows various number density levels as indicated by the legends. Due to the rising slope of the MFs at low masses, most of the galaxies are located at small  $\text{HI}$
and stellar masses. Note that the discontinuity seen at the low-
$\text{HI}$
and stellar masses. Note that the discontinuity seen at the low- $\text{HI}$
and high-stellar masses is due to the assumption of an uniform function for the lowest values of gas-to-stellar mass ratios of early-type galaxies where non-detections piled up. Recall that in our analysis, non-detections (upper limits) are included using the non-parametric estimator Kaplan & Meier (Reference Kaplan and Meier1958) for censored data in Paper I. The solid lines show the mean
$\text{HI}$
and high-stellar masses is due to the assumption of an uniform function for the lowest values of gas-to-stellar mass ratios of early-type galaxies where non-detections piled up. Recall that in our analysis, non-detections (upper limits) are included using the non-parametric estimator Kaplan & Meier (Reference Kaplan and Meier1958) for censored data in Paper I. The solid lines show the mean  $\langle\log M_{\rm HI}\rangle$
as a function of
$\langle\log M_{\rm HI}\rangle$
as a function of  $M_{*}$
, both for early- and late-type galaxies. The upper panel shows the GSMF which is the result of integrating the bivariate distribution function along the
$M_{*}$
, both for early- and late-type galaxies. The upper panel shows the GSMF which is the result of integrating the bivariate distribution function along the  $M_{\rm HI}$
axis, while the bottom right panel shows the same but for the
$M_{\rm HI}$
axis, while the bottom right panel shows the same but for the  $\text{HI}$
MF which results from integrating along the
$\text{HI}$
MF which results from integrating along the  $M_{*}$
axis. We compare to some previous observational determinations of the MFs and the relationship between
$M_{*}$
axis. We compare to some previous observational determinations of the MFs and the relationship between  $M_{\text{HI}}$
and
$M_{\text{HI}}$
and  $M_{*}$
derived in Maddox et al. (Reference Maddox, Hess, Obreschkow, Jarvis and Blyth2015) for the ALFALFA survey with SDSS spectral and stellar mass counterparts.
$M_{*}$
derived in Maddox et al. (Reference Maddox, Hess, Obreschkow, Jarvis and Blyth2015) for the ALFALFA survey with SDSS spectral and stellar mass counterparts.
Figure 6 explicitly shows the contribution of galaxies of different stellar masses to the  $\rm HI$
MF. Particularly, we observe that the low-mass end of the
$\rm HI$
MF. Particularly, we observe that the low-mass end of the  $\rm HI$
MF is composed mainly by low
$\rm HI$
MF is composed mainly by low  $M_{*}$
galaxies but there is also a non-negligible contribution from a population of high
$M_{*}$
galaxies but there is also a non-negligible contribution from a population of high  $M_{*}$
galaxies. Most of these high
$M_{*}$
galaxies. Most of these high  $M_{*}$
galaxies are early-type (quenched) galaxies for which there is a significant fraction of non-detections (
$M_{*}$
galaxies are early-type (quenched) galaxies for which there is a significant fraction of non-detections ( $\sim\! 55\%$
). In Paper I, we included non-detections for the determination of the HI-CPDF based on methods of censored data (Kaplan & Meier Reference Kaplan and Meier1958). Nonetheless, the contribution of non-detections is only marginal because the fraction of early-type galaxies at those masses is low, see the bottom panel of Figure 2. In addition, Figure 6 shows that the completeness limit in the
$\sim\! 55\%$
). In Paper I, we included non-detections for the determination of the HI-CPDF based on methods of censored data (Kaplan & Meier Reference Kaplan and Meier1958). Nonetheless, the contribution of non-detections is only marginal because the fraction of early-type galaxies at those masses is low, see the bottom panel of Figure 2. In addition, Figure 6 shows that the completeness limit in the  $\rm HI$
MF, due to our stellar mass limit of
$\rm HI$
MF, due to our stellar mass limit of  $M_{*}=10^{7}\text{M}_{\odot}$
, is at
$M_{*}=10^{7}\text{M}_{\odot}$
, is at  $M_{\rm HI}\sim\! 10^{8}\text{M}_{\odot}$
(see below), which excludes a large region of galaxies with non-detections.
$M_{\rm HI}\sim\! 10^{8}\text{M}_{\odot}$
(see below), which excludes a large region of galaxies with non-detections.

Figure 7. Same as Figure 6 but for molecular gas. Note that while there are more non-detections for  $\text{H}_{\text{2}}$
observations, these are mostly from early-type galaxies that represent only a small fraction overall in the
$\text{H}_{\text{2}}$
observations, these are mostly from early-type galaxies that represent only a small fraction overall in the  $\text{H}_{\text{2}}$
mass bivariate distribution function. We also compared to previous determinations from Keres et al. (Reference Keres, Yun and Young2003).
$\text{H}_{\text{2}}$
mass bivariate distribution function. We also compared to previous determinations from Keres et al. (Reference Keres, Yun and Young2003).
Similarly to Figure 6, Figure 7 presents the resulting bivariate stellar– $\rm H_{2}$
mass distribution function for all galaxies and the mean
$\rm H_{2}$
mass distribution function for all galaxies and the mean  $\langle\log M_{\rm H2}\rangle$
for early- and late-type galaxies. The resulting total
$\langle\log M_{\rm H2}\rangle$
for early- and late-type galaxies. The resulting total  $\rm H_{2}$
MF is shown with the solid line in the bottom right panel and compared to the Keres et al. (Reference Keres, Yun and Young2003)
$\rm H_{2}$
MF is shown with the solid line in the bottom right panel and compared to the Keres et al. (Reference Keres, Yun and Young2003)  $\rm H_{2}$
MF based on the CO luminosity function. At the low-mass end, there is a substantial population of galaxies with non-detections, roughly
$\rm H_{2}$
MF based on the CO luminosity function. At the low-mass end, there is a substantial population of galaxies with non-detections, roughly  $\sim\! 78\%$
, which are mostly early-type galaxies. As above, non-detections have been included in the statistical analysis of the H2-CPDFs, for details see Paper I. Nevertheless, from the contour density level, their contribution is marginal. Finally, we can conclude that our
$\sim\! 78\%$
, which are mostly early-type galaxies. As above, non-detections have been included in the statistical analysis of the H2-CPDFs, for details see Paper I. Nevertheless, from the contour density level, their contribution is marginal. Finally, we can conclude that our  $\rm H_{2}$
MF is complete for
$\rm H_{2}$
MF is complete for  $M_{\rm H2}\gtrsim10^{7}\text{M}_{\odot}$
.
$M_{\rm H2}\gtrsim10^{7}\text{M}_{\odot}$
.
4.4. The mass functions
Next, we discuss in detail the MFs presented above. In particular, we focus on the determinations separately for early- and late-type galaxies based on the morphology classification described in Section 3.3. The various panels in Figure 8 present the MFs for atomic and molecular gas, total cold gas, and baryons, as indicated by the labels. In all the panels, the MFs for late-type galaxies are shown as blue filled circles with error bars, while for early-type galaxies are shown as red circles with error bars. These symbols are for a stellar mass limit of  $M_{*}>10^{7}\ \text{M}_{\odot}$
. Instead, we use blue/red open circles when the MFs is incomplete. We also calculate the MFs in the hypothetical case of a mass limit of
$M_{*}>10^{7}\ \text{M}_{\odot}$
. Instead, we use blue/red open circles when the MFs is incomplete. We also calculate the MFs in the hypothetical case of a mass limit of  $M_{*}=0$
shown with the blue/red dashed lines. Note that the total MFs for
$M_{*}=0$
shown with the blue/red dashed lines. Note that the total MFs for  $\rm HI$
and cold gas are not plotted. This is because in these cases the MFs of late-type galaxies are hardly distinguishable from the total one at all masses. We also omit the total
$\rm HI$
and cold gas are not plotted. This is because in these cases the MFs of late-type galaxies are hardly distinguishable from the total one at all masses. We also omit the total  $\rm H_{2}$
MF. This is because it is hardly distinguishable from the MF of late-type galaxies at
$\rm H_{2}$
MF. This is because it is hardly distinguishable from the MF of late-type galaxies at  $M_{\rm H2}\lesssim 2\times 10^{10}\ \text{M}_{\odot}$
while for larger masses it is indistinguishable from the MF of the early-type galaxies. In the case of the baryon masses, the total MF is plotted with black filled circles.
$M_{\rm H2}\lesssim 2\times 10^{10}\ \text{M}_{\odot}$
while for larger masses it is indistinguishable from the MF of the early-type galaxies. In the case of the baryon masses, the total MF is plotted with black filled circles.

Figure 8. Results on the galaxy MFs of early- and late-type galaxies for atomic gas, left upper panel, molecular gas, right upper panel, cold gas, bottom left, and baryons, bottom right panel. In all the panels, late-type galaxies are shown as the blue circles with error bars, while early-type galaxies are shown as the red circles with error bars, when using a stellar mass limit of  $M_{*}=10^{7}\text{M}_{\odot}$
. Filled blue/red circles indicate when the MFs are complete, while open circles clearly show that the MFs became incomplete. The dashed lines are for MFs when using a stellar mass limit of
$M_{*}=10^{7}\text{M}_{\odot}$
. Filled blue/red circles indicate when the MFs are complete, while open circles clearly show that the MFs became incomplete. The dashed lines are for MFs when using a stellar mass limit of  $M_{*}=0$
. The total MFs for
$M_{*}=0$
. The total MFs for  $\text{HI}$
and cold gas are not shown because they are practically indistinguishable from the respective MFs of late-type galaxies. Our results are in good agreement with observational determinations of the total MFs. For only early-type galaxies, we compare our results with those from the ATLAS 3D sample (red triangles). While we observe some tension, we suspect that selection effects are more likely to artificially increase the amplitude of their MF at low masses.
$\text{HI}$
and cold gas are not shown because they are practically indistinguishable from the respective MFs of late-type galaxies. Our results are in good agreement with observational determinations of the total MFs. For only early-type galaxies, we compare our results with those from the ATLAS 3D sample (red triangles). While we observe some tension, we suspect that selection effects are more likely to artificially increase the amplitude of their MF at low masses.
We note that our determinations for the MFs are the result of the convolution between random errors and the intrinsic MFs, similarly as it happens with the direct observational determinations of MFs. In Section 5.1, we discuss the impact from random errors and present the intrinsic MFs, after deconvolving by these errors.
4.4.1. The  $\text{\em HI}$
MF
$\text{\em HI}$
MF
We compare our results with previous direct observational determinations of the total  $\rm HI\,$
MFs. According to our results, late-type galaxies dominate the
$\rm HI\,$
MFs. According to our results, late-type galaxies dominate the  $\rm HI$
MF, even at the highest masses, so that it is practically equivalent to the total
$\rm HI$
MF, even at the highest masses, so that it is practically equivalent to the total  $\rm HI$
MF. In Figure 8, we reproduce the best fit to the
$\rm HI$
MF. In Figure 8, we reproduce the best fit to the  $\rm HI$
MF from Jones et al. (Reference Jones, Haynes, Giovanelli and Moorman2018) based on the final catalogue of the blind
$\rm HI$
MF from Jones et al. (Reference Jones, Haynes, Giovanelli and Moorman2018) based on the final catalogue of the blind  $\rm HI$
ALFALFA Survey, dark grey solid line. The violet solid line shows the best-fit model reported in Butcher et al. (Reference Butcher, Schneider, van Driel and Lehnert2018) to the
$\rm HI$
ALFALFA Survey, dark grey solid line. The violet solid line shows the best-fit model reported in Butcher et al. (Reference Butcher, Schneider, van Driel and Lehnert2018) to the  $\rm HI$
MF from the Nançay Interstellar Baryons Legacy Extragalactic Survey, which is a project that complemented recent and/or ongoing large blind
$\rm HI$
MF from the Nançay Interstellar Baryons Legacy Extragalactic Survey, which is a project that complemented recent and/or ongoing large blind  $\rm HI$
surveys. Results from Papastergis et al. (Reference Papastergis, Cattaneo, Huang, Giovanelli and Haynes2012) and Martin et al. (Reference Martin, Papastergis, Giovanelli, Haynes, Springob and Stierwalt2010) based on the 40% sample of the ALFALFA Survey are shown respectively with black open circles and squares. The skeletal symbols with error bars show the results from Zwaan et al. (Reference Zwaan, Meyer, Staveley-Smith and Webster2005), who used the HIPASS. Note that our
$\rm HI$
surveys. Results from Papastergis et al. (Reference Papastergis, Cattaneo, Huang, Giovanelli and Haynes2012) and Martin et al. (Reference Martin, Papastergis, Giovanelli, Haynes, Springob and Stierwalt2010) based on the 40% sample of the ALFALFA Survey are shown respectively with black open circles and squares. The skeletal symbols with error bars show the results from Zwaan et al. (Reference Zwaan, Meyer, Staveley-Smith and Webster2005), who used the HIPASS. Note that our  $\rm HI$
MF for late-type galaxies, which dominates the total MF, is in good agreement with direct inferences from
$\rm HI$
MF for late-type galaxies, which dominates the total MF, is in good agreement with direct inferences from  $\rm HI$
blind surveys, particularly those based on ALFALFA as discussed in Figure 6. As for the
$\rm HI$
blind surveys, particularly those based on ALFALFA as discussed in Figure 6. As for the  $\rm HI$
MF of early-type galaxies, we plot the determinations from the ATLAS 3D (Serra et al. Reference Serra2012) and HIPASS (Lagos et al. Reference Lagos, Davis, Lacey, Zwaan, Baugh, Gonzalez-Perez and Padilla2014) samples shown as the red solid triangles and skeletal symbols, respectively.
$\rm HI$
MF of early-type galaxies, we plot the determinations from the ATLAS 3D (Serra et al. Reference Serra2012) and HIPASS (Lagos et al. Reference Lagos, Davis, Lacey, Zwaan, Baugh, Gonzalez-Perez and Padilla2014) samples shown as the red solid triangles and skeletal symbols, respectively.
Our resulting  $\rm HI\,$
MFs are in good agreement with direct determinations from radio observations. This is particularly true for
$\rm HI\,$
MFs are in good agreement with direct determinations from radio observations. This is particularly true for  $\rm HI$
masses above the completeness limit corresponding to our
$\rm HI$
masses above the completeness limit corresponding to our  $M_{*}$
limit for the GSMF. These masses are
$M_{*}$
limit for the GSMF. These masses are  $M_{\rm HI} \sim\! 10^{8}\text{M}_{\odot}$
for late-type galaxies and
$M_{\rm HI} \sim\! 10^{8}\text{M}_{\odot}$
for late-type galaxies and  $M_{\rm HI} \sim 10^{7}\text{M}_{\odot}$
for early-type galaxies. Even when extrapolating to a limit mass of
$M_{\rm HI} \sim 10^{7}\text{M}_{\odot}$
for early-type galaxies. Even when extrapolating to a limit mass of  $M_{*}=0$
, at the low-mass end, we find a good agreement with direct determinations, though the early-type galaxies from the ATLAS 3D sample present a higher amplitude for masses below
$M_{*}=0$
, at the low-mass end, we find a good agreement with direct determinations, though the early-type galaxies from the ATLAS 3D sample present a higher amplitude for masses below  $10^{7}\text{M}_{\odot}$
. However, those extrapolations should be taken with caution as it is not clear whether we can extrapolate our bivariate distribution functions to such low masses. In conclusion, we consider that the remarkable consistency between our
$10^{7}\text{M}_{\odot}$
. However, those extrapolations should be taken with caution as it is not clear whether we can extrapolate our bivariate distribution functions to such low masses. In conclusion, we consider that the remarkable consistency between our  $\rm HI$
MFs and radio blind surveys above
$\rm HI$
MFs and radio blind surveys above  $M_{\rm HI}\,{\sim}\,10^{8}\text{M}_{\odot}$
is reassuring and validates the HI-CPDFs determined in Paper I. Recall that the observational data used in that paper were derived from various heterogeneous samples, affected by many selection effects, including those related to the non-radio detections. Therefore, the agreement between the
$M_{\rm HI}\,{\sim}\,10^{8}\text{M}_{\odot}$
is reassuring and validates the HI-CPDFs determined in Paper I. Recall that the observational data used in that paper were derived from various heterogeneous samples, affected by many selection effects, including those related to the non-radio detections. Therefore, the agreement between the  $\rm HI$
MF with that of the blind radio observations is far from trivial, unless adequate corrections are introduced and the data are adequately analysed from the statistical point of view.
$\rm HI$
MF with that of the blind radio observations is far from trivial, unless adequate corrections are introduced and the data are adequately analysed from the statistical point of view.
4.4.2. The  $\text{\em H}_{\text{\em 2}}$
MF
$\text{\em H}_{\text{\em 2}}$
MF
In the upper right panel of Figure 8, we present the results for the  $\rm H_{2}$
MF. The
$\rm H_{2}$
MF. The  $\rm H_{2}$
MF is largely dominated by late-type galaxies below
$\rm H_{2}$
MF is largely dominated by late-type galaxies below  $M_{H_{2}}\,{\sim}\,2\times10^{10}\text{M}_{\odot}$
, but for larger masses, early-type galaxies are more abundant. In the same panel, we reproduce the total
$M_{H_{2}}\,{\sim}\,2\times10^{10}\text{M}_{\odot}$
, but for larger masses, early-type galaxies are more abundant. In the same panel, we reproduce the total  $\rm H_{2}$
MF from Keres et al. (Reference Keres, Yun and Young2003), who used a CO luminosity function from FIR and
$\rm H_{2}$
MF from Keres et al. (Reference Keres, Yun and Young2003), who used a CO luminosity function from FIR and  $B-$
band limited galaxy samples and adopting a constant CO-to-
$B-$
band limited galaxy samples and adopting a constant CO-to- $\rm H_{2}$
conversion factor of
$\rm H_{2}$
conversion factor of  $\alpha_{\rm CO} = 4.76$
, open black circles with error bars. The dashed line shows the best fit to a Schechter function derived in Obreschkow & Rawlings (Reference Obreschkow and Rawlings2009). Additionally, we show the results from the ATLAS 3D sample for early-type galaxies (Lagos et al. Reference Lagos, Davis, Lacey, Zwaan, Baugh, Gonzalez-Perez and Padilla2014) with the filled triangles. The magenta solid line shows the results from Obreschkow & Rawlings (Reference Obreschkow and Rawlings2009), who derived the
$\alpha_{\rm CO} = 4.76$
, open black circles with error bars. The dashed line shows the best fit to a Schechter function derived in Obreschkow & Rawlings (Reference Obreschkow and Rawlings2009). Additionally, we show the results from the ATLAS 3D sample for early-type galaxies (Lagos et al. Reference Lagos, Davis, Lacey, Zwaan, Baugh, Gonzalez-Perez and Padilla2014) with the filled triangles. The magenta solid line shows the results from Obreschkow & Rawlings (Reference Obreschkow and Rawlings2009), who derived the  $\rm H_{2}$
MF by introducing a phenomenological model for the
$\rm H_{2}$
MF by introducing a phenomenological model for the  $\rm H_{2}$
-to-
$\rm H_{2}$
-to- $\rm HI$
mass ratio that depends on the galaxy morphological type and its total cold gas mass.
$\rm HI$
mass ratio that depends on the galaxy morphological type and its total cold gas mass.
When comparing to the  $\rm H_{2}$
MF from Keres et al. (Reference Keres, Yun and Young2003), we observe a good agreement with our results. At the low-mass end, though, the Keres et al. (Reference Keres, Yun and Young2003) MF seems to be slightly shallower than ours. It is not clear the origin for this discrepancy. One possibility is due the constant
$\rm H_{2}$
MF from Keres et al. (Reference Keres, Yun and Young2003), we observe a good agreement with our results. At the low-mass end, though, the Keres et al. (Reference Keres, Yun and Young2003) MF seems to be slightly shallower than ours. It is not clear the origin for this discrepancy. One possibility is due the constant  $\alpha_{\rm CO}$
factor employed by the authors. Based on previous empirical studies, Paper I showed that ignoring the dependence of
$\alpha_{\rm CO}$
factor employed by the authors. Based on previous empirical studies, Paper I showed that ignoring the dependence of  $\alpha_{\rm CO}$
with
$\alpha_{\rm CO}$
with  $M_{*}$
Footnote p flattens the low-mass end of the
$M_{*}$
Footnote p flattens the low-mass end of the  $\rm H_{2}$
MF, consistent with the results from Keres et al. (Reference Keres, Yun and Young2003). Another possibility is an effect of the incompleteness of the CO luminosity function. As for Obreschkow & Rawlings (Reference Obreschkow and Rawlings2009), our results are consistent for masses below
$\rm H_{2}$
MF, consistent with the results from Keres et al. (Reference Keres, Yun and Young2003). Another possibility is an effect of the incompleteness of the CO luminosity function. As for Obreschkow & Rawlings (Reference Obreschkow and Rawlings2009), our results are consistent for masses below  $M_{H_{2}}\,{\sim}\,3\times10^{9}\text{M}_{\odot}$
. For larger masses, the Obreschkow & Rawlings (Reference Obreschkow and Rawlings2009) MF falls much stepper than ours. Similar to our analysis, Obreschkow & Rawlings (Reference Obreschkow and Rawlings2009) used the relationships between galaxy properties to derive their MF. As mentioned above, their phenomenological model employed the dependence of the
$M_{H_{2}}\,{\sim}\,3\times10^{9}\text{M}_{\odot}$
. For larger masses, the Obreschkow & Rawlings (Reference Obreschkow and Rawlings2009) MF falls much stepper than ours. Similar to our analysis, Obreschkow & Rawlings (Reference Obreschkow and Rawlings2009) used the relationships between galaxy properties to derive their MF. As mentioned above, their phenomenological model employed the dependence of the  $\rm H_{2}$
-to-
$\rm H_{2}$
-to- $\rm HI$
mass ratio with morphology and cold gas mass. While the above differences could be arguably referred to the use of different estimators for the
$\rm HI$
mass ratio with morphology and cold gas mass. While the above differences could be arguably referred to the use of different estimators for the  $\rm H_{2}$
gas masses, it could be also an indication that random errors are larger when using only one galaxy parameter. Recall that in this paper, we are using
$\rm H_{2}$
gas masses, it could be also an indication that random errors are larger when using only one galaxy parameter. Recall that in this paper, we are using  $M_{*}$
. In Section 5.1, we will show that after deconvolving from random errors, our intrinsic
$M_{*}$
. In Section 5.1, we will show that after deconvolving from random errors, our intrinsic  $\rm H_{2}$
MF becomes steeper at the high-mass end and more consistent with the derivation from Obreschkow & Rawlings (Reference Obreschkow and Rawlings2009). Nonetheless, it is difficult to conclude the origin of the above differences given the different nature of the models employed in both studies.
$\rm H_{2}$
MF becomes steeper at the high-mass end and more consistent with the derivation from Obreschkow & Rawlings (Reference Obreschkow and Rawlings2009). Nonetheless, it is difficult to conclude the origin of the above differences given the different nature of the models employed in both studies.
As for early-type galaxies, our results are consistent with those from the ATLAS 3D (Lagos et al. Reference Lagos, Davis, Lacey, Zwaan, Baugh, Gonzalez-Perez and Padilla2014) at the high-mass end but they lie slightly below at the low-mass end. It is unclear the reason of the above discrepancy for low- $M_{\rm H_2}$
early-type galaxies, though large-scale and environmental selection effects could boost the inferences of the MF when using the 1/V
$M_{\rm H_2}$
early-type galaxies, though large-scale and environmental selection effects could boost the inferences of the MF when using the 1/V $_{\rm max}$
estimator, see for example, Appendix C and Baldry et al. (Reference Baldry, Glazebrook and Driver2008). Recall that in the case of
$_{\rm max}$
estimator, see for example, Appendix C and Baldry et al. (Reference Baldry, Glazebrook and Driver2008). Recall that in the case of  $\rm HI$
, the ATLAS 3D also presents an slightly enhancement at the low-mass end of the
$\rm HI$
, the ATLAS 3D also presents an slightly enhancement at the low-mass end of the  $\rm HI$
MF. Thus, selection effects are more likely to artificially increase the amplitude of the MF for low-mass galaxies in the ATLAS 3D sample.
$\rm HI$
MF. Thus, selection effects are more likely to artificially increase the amplitude of the MF for low-mass galaxies in the ATLAS 3D sample.
4.4.3. The gas and baryonic MFs
Similarly to the  $\rm HI$
MF, the cold gas MF is completely dominated by late-type galaxies, even at the high-mass end. In Figure 8, we compare our results with the phenomenological determination from Obreschkow & Rawlings (Reference Obreschkow and Rawlings2009, pink solid line). These authors combined their inference of the
$\rm HI$
MF, the cold gas MF is completely dominated by late-type galaxies, even at the high-mass end. In Figure 8, we compare our results with the phenomenological determination from Obreschkow & Rawlings (Reference Obreschkow and Rawlings2009, pink solid line). These authors combined their inference of the  $\rm H_{2}$
MF with the
$\rm H_{2}$
MF with the  $\rm HI$
MF from Zwaan et al. (Reference Zwaan, Meyer, Staveley-Smith and Webster2005) to derive the gas MF. Despite the differences mentioned above for the Obreschkow & Rawlings (Reference Obreschkow and Rawlings2009)
$\rm HI$
MF from Zwaan et al. (Reference Zwaan, Meyer, Staveley-Smith and Webster2005) to derive the gas MF. Despite the differences mentioned above for the Obreschkow & Rawlings (Reference Obreschkow and Rawlings2009)  $\rm H_{2}$
MF, their total cold gas MF is in excellent agreement with our one. This is not surprising as it is just reflecting that
$\rm H_{2}$
MF, their total cold gas MF is in excellent agreement with our one. This is not surprising as it is just reflecting that  $\rm HI$
is much more abundant than
$\rm HI$
is much more abundant than  $\rm H_{2}$
.
$\rm H_{2}$
.
Finally, we show our results for the baryonic MFs in the bottom right panel of Figure 8. The baryonic MF is very similar to the GSMF at the high-mass end but at the low-mass end, it is steeper as the contribution of cold gas becomes more relevant. On the other hand, late-type galaxies dominate the baryonic MF for  $M_{\rm bar}<10^{11}\ \text{M}_{\odot}$
, while at the high-mass end, early-type galaxies are more abundant than the late-type ones. We reproduce with the green solid line the baryonic MF from Baldry et al. (Reference Baldry, Glazebrook and Driver2008). These authors combined the GSMF from the low-z survey of the SDSS DR4, the same galaxy survey used here for low masses, with a closed-box model and the mass–metallicity relation to derive cold gas masses for their baryonic MF. The open black circles show the MF from Papastergis et al. (Reference Papastergis, Cattaneo, Huang, Giovanelli and Haynes2012), who defined baryonic mass as
$M_{\rm bar}<10^{11}\ \text{M}_{\odot}$
, while at the high-mass end, early-type galaxies are more abundant than the late-type ones. We reproduce with the green solid line the baryonic MF from Baldry et al. (Reference Baldry, Glazebrook and Driver2008). These authors combined the GSMF from the low-z survey of the SDSS DR4, the same galaxy survey used here for low masses, with a closed-box model and the mass–metallicity relation to derive cold gas masses for their baryonic MF. The open black circles show the MF from Papastergis et al. (Reference Papastergis, Cattaneo, Huang, Giovanelli and Haynes2012), who defined baryonic mass as  $M_{\rm bar}=1.4 \times M_{\rm HI}+M_{*}$
. We notice that these previous baryonic MF determinations are in good agreement with our results at the mass range
$M_{\rm bar}=1.4 \times M_{\rm HI}+M_{*}$
. We notice that these previous baryonic MF determinations are in good agreement with our results at the mass range  $\sim\! 2\times 10^9-2\times 10^{11}\ \text{M}_{\odot}$
, while for lower and higher masses there are some differences, which are easy to understand.
$\sim\! 2\times 10^9-2\times 10^{11}\ \text{M}_{\odot}$
, while for lower and higher masses there are some differences, which are easy to understand.
The MF from Baldry et al. (Reference Baldry, Glazebrook and Driver2008) is steeper than our MF at low masses. This might be a consequence of the fact that the Baldry et al. (Reference Baldry, Glazebrook and Driver2008) GSMF itself is steeper compared to other determinations, for example, Baldry et al. (Reference Baldry2012). As these authors discuss, the disagreement between the Baldry et al. (Reference Baldry, Glazebrook and Driver2008) and Baldry et al. (Reference Baldry2012)  $\mbox{GSMF}$
s is just the result of different flow models for distances, which affect significantly to nearby low-mass galaxies. Recall that our GSMF has been corrected to be consistent with the flow model of Tonry et al. (Reference Tonry, Blakeslee, Ajhar and Dressler2000). Additionally, the gas masses in Baldry et al. (Reference Baldry, Glazebrook and Driver2008) were actually obtained from a close-box model constrained with the empirical mass–metallicity relation. The combination of these two assumptions are likely the result of a steep baryonic MF at low masses, which differs from our results and those of Papastergis et al. (Reference Papastergis, Cattaneo, Huang, Giovanelli and Haynes2012).
$\mbox{GSMF}$
s is just the result of different flow models for distances, which affect significantly to nearby low-mass galaxies. Recall that our GSMF has been corrected to be consistent with the flow model of Tonry et al. (Reference Tonry, Blakeslee, Ajhar and Dressler2000). Additionally, the gas masses in Baldry et al. (Reference Baldry, Glazebrook and Driver2008) were actually obtained from a close-box model constrained with the empirical mass–metallicity relation. The combination of these two assumptions are likely the result of a steep baryonic MF at low masses, which differs from our results and those of Papastergis et al. (Reference Papastergis, Cattaneo, Huang, Giovanelli and Haynes2012).
Regarding the high-mass end, our baryonic MF falls shallower than those of Papastergis et al. (Reference Papastergis, Cattaneo, Huang, Giovanelli and Haynes2012) and Baldry et al. (Reference Baldry, Glazebrook and Driver2008). This is because, our GSMF is shallower. As discussed in Section 3, there are two main systematic effects that could lead to different GSMFs, mass-to-light ratios, and the determination of galaxy surface brightness (especially due to sky subtraction problems). Both effects are likely to affect the high-mass end of the baryonic MF. In addition, due to the small volumes of the surveys used in Baldry et al. (Reference Baldry, Glazebrook and Driver2008) and Papastergis et al. (Reference Papastergis, Cattaneo, Huang, Giovanelli and Haynes2012), cosmic variance enhances the differences.
Table 4. Cosmic density of  $\text{HI}$
,
$\text{HI}$
,  $\text{H}_{\text{2}}$
, gas, stars, and baryons for all, LTGs and ETGs. The fraction of each component is denoted as
$\text{H}_{\text{2}}$
, gas, stars, and baryons for all, LTGs and ETGs. The fraction of each component is denoted as  $f_j = \Omega_j / \Omega_{\rm bar,U}$
with
$f_j = \Omega_j / \Omega_{\rm bar,U}$
with  $\Omega_{\rm bar,U} = 0.048$
.
$\Omega_{\rm bar,U} = 0.048$
.

LTG = late-type galaxies; ETG = Early-type galaxies

Figure 9. Density parameter  $\Omega$
of
$\Omega$
of  $\rm HI$
,
$\rm HI$
,  $\rm H_{2}$
, cold gas, and baryonic mass locked in all galaxies as well as in early- and late-type galaxies (coloured filled circles; the errors are smaller than the circle size). The
$\rm H_{2}$
, cold gas, and baryonic mass locked in all galaxies as well as in early- and late-type galaxies (coloured filled circles; the errors are smaller than the circle size). The  $\Omega$
parameter values are reported as fractions in per cent of the universal matter (left axis) and baryonic (right axis) densities. The grey boxes show the range of values from previous determinations and the horizontal lines correspond to the mean of these values.
$\Omega$
parameter values are reported as fractions in per cent of the universal matter (left axis) and baryonic (right axis) densities. The grey boxes show the range of values from previous determinations and the horizontal lines correspond to the mean of these values.
4.5. Cosmic density parameters and relevant timescales
4.5.1. Cosmic density parameters
The cosmic density parameter measures the average mass density of some matter species with respect to the critical density,  $\rho_c$
. Here, we determine the mass density in stars,
$\rho_c$
. Here, we determine the mass density in stars,  $\rm HI$
,
$\rm HI$
,  $\rm H_{2}$
, cold gas, and baryons that are locked inside galaxies using their MFs. The differential mass density function
$\rm H_{2}$
, cold gas, and baryons that are locked inside galaxies using their MFs. The differential mass density function  $d\rho_j(M_j)$
for some galaxy mass component
$d\rho_j(M_j)$
for some galaxy mass component  $M_{j}$
in the mass range
$M_{j}$
in the mass range  $\log M_j\pm d\log M_j /2$
is
$\log M_j\pm d\log M_j /2$
is  $d\rho_j(M_j ) = M_{j} \times \phi_j (M_j ) d\log M_j$
, where
$d\rho_j(M_j ) = M_{j} \times \phi_j (M_j ) d\log M_j$
, where  $\phi_{j}$
is in units of Mpc-3 dex-1. Thus, the cosmic mass density is given by:
$\phi_{j}$
is in units of Mpc-3 dex-1. Thus, the cosmic mass density is given by:
 \begin{equation}\rho_j = \int_{-\infty}^{\infty} d\rho_j(M_j ),\end{equation}
\begin{equation}\rho_j = \int_{-\infty}^{\infty} d\rho_j(M_j ),\end{equation}
with the cosmic density parameter
 \begin{equation}\Omega_j = \frac{\rho_j}{\rho_c},\end{equation}
\begin{equation}\Omega_j = \frac{\rho_j}{\rho_c},\end{equation}
where the critical density is  $\rho_c = 2.775\times 10^{11} h^{-1}\text{M}_{\odot}/ (h^{-1}{\rm Mpc})^3 = 1.2756 \times 10^{11} \text{M}_{\odot}/ {\rm Mpc}^3 h_{67.8}^{2}$
.Footnote q The limits of integration in Equation (26) reflect that we are considering all the spectrum of masses from galaxies. In reality, this is not possible, due to completeness limits in galaxy samples. Here, we consider the following mass limits for all our components:
$\rho_c = 2.775\times 10^{11} h^{-1}\text{M}_{\odot}/ (h^{-1}{\rm Mpc})^3 = 1.2756 \times 10^{11} \text{M}_{\odot}/ {\rm Mpc}^3 h_{67.8}^{2}$
.Footnote q The limits of integration in Equation (26) reflect that we are considering all the spectrum of masses from galaxies. In reality, this is not possible, due to completeness limits in galaxy samples. Here, we consider the following mass limits for all our components:  $M_{\rm inf} = 10^7\ \text{M}_{\odot}$
and
$M_{\rm inf} = 10^7\ \text{M}_{\odot}$
and  $M_{\rm upper} = 10^{12.6}\ \text{M}_{\odot}$
. We notice that using values smaller than
$M_{\rm upper} = 10^{12.6}\ \text{M}_{\odot}$
. We notice that using values smaller than  $M_{\rm inf}$
and/or larger than
$M_{\rm inf}$
and/or larger than  $M_{\rm upper}$
do not substantially change our results. This is because the multiplicity functions,
$M_{\rm upper}$
do not substantially change our results. This is because the multiplicity functions,  $\propto M_{j} \times \phi_j (M_j )$
, have a maximum around the knee of the MFs.
$\propto M_{j} \times \phi_j (M_j )$
, have a maximum around the knee of the MFs.
Figure 9 shows the different values of each  $\Omega_{j}$
corresponding to all galaxies and separately for early- and late-type galaxies, listed in Table 4. The
$\Omega_{j}$
corresponding to all galaxies and separately for early- and late-type galaxies, listed in Table 4. The  $\Omega_j$
values are presented as the fractions in per cent with respect to the universal matter density (
$\Omega_j$
values are presented as the fractions in per cent with respect to the universal matter density ( $\Omega_{\rm m}=0.307$
, left axis) and the universal baryonic density (
$\Omega_{\rm m}=0.307$
, left axis) and the universal baryonic density ( $\Omega_{\rm bar,U}=0.048$
, right axis). To estimate errors in our cosmic density parameters, we use all our MCMC models for the HI-CPDF and H2-CPDF in addition of all our MCMC models to the fit of the GSMFs. We found that the largest uncertainties arise from the uncertainties in the CPDFs.
$\Omega_{\rm bar,U}=0.048$
, right axis). To estimate errors in our cosmic density parameters, we use all our MCMC models for the HI-CPDF and H2-CPDF in addition of all our MCMC models to the fit of the GSMFs. We found that the largest uncertainties arise from the uncertainties in the CPDFs.
In the past, there have been some assessments of the cosmic density parameters at  $z\,{\sim}\,0$
. Usually, these studies do not report cosmic density parameters for different populations and for different components at the same time. As mentioned in the Introduction, it is important to distinguish between different populations given that late- and early-type galaxies follow different formation histories. Studies close to ours are the ones by Fukugita, Hogan, & Peebles (Reference Fukugita, Hogan and Peebles1998), Fukugita & Peebles (Reference Fukugita and Peebles2004), and Read & Trentham (Reference Read and Trentham2005). Below, we present and compare our results with many previous determinations from the literature.
$z\,{\sim}\,0$
. Usually, these studies do not report cosmic density parameters for different populations and for different components at the same time. As mentioned in the Introduction, it is important to distinguish between different populations given that late- and early-type galaxies follow different formation histories. Studies close to ours are the ones by Fukugita, Hogan, & Peebles (Reference Fukugita, Hogan and Peebles1998), Fukugita & Peebles (Reference Fukugita and Peebles2004), and Read & Trentham (Reference Read and Trentham2005). Below, we present and compare our results with many previous determinations from the literature.
 $\rm HI$
cosmic density: The atomic hydrogen in late-type galaxies is
$\rm HI$
cosmic density: The atomic hydrogen in late-type galaxies is  $\sim\! 27$
times larger than in early-type galaxies, which means that
$\sim\! 27$
times larger than in early-type galaxies, which means that  $\sim\!96\%$
of
$\sim\!96\%$
of  $\rm HI$
mass is in late-type galaxies. Previously, Zwaan et al. (Reference Zwaan, Meyer, Staveley-Smith and Webster2005), Read & Trentham (Reference Read and Trentham2005), Martin et al. (Reference Martin, Papastergis, Giovanelli, Haynes, Springob and Stierwalt2010), Braun (Reference Braun2012), Delhaize et al. (Reference Delhaize, Meyer, Staveley-Smith and Boyle2013), Hoppmann et al. (Reference Hoppmann, Staveley-Smith, Freudling, Zwaan, Minchin and Calabretta2015), Butcher et al. (Reference Butcher, Schneider, van Driel and Lehnert2018), and Jones et al. (Reference Jones, Haynes, Giovanelli and Moorman2018) have derived the
$\rm HI$
mass is in late-type galaxies. Previously, Zwaan et al. (Reference Zwaan, Meyer, Staveley-Smith and Webster2005), Read & Trentham (Reference Read and Trentham2005), Martin et al. (Reference Martin, Papastergis, Giovanelli, Haynes, Springob and Stierwalt2010), Braun (Reference Braun2012), Delhaize et al. (Reference Delhaize, Meyer, Staveley-Smith and Boyle2013), Hoppmann et al. (Reference Hoppmann, Staveley-Smith, Freudling, Zwaan, Minchin and Calabretta2015), Butcher et al. (Reference Butcher, Schneider, van Driel and Lehnert2018), and Jones et al. (Reference Jones, Haynes, Giovanelli and Moorman2018) have derived the  $\rm HI$
cosmic density parameter using either blind
$\rm HI$
cosmic density parameter using either blind  $\rm HI$
galaxy surveys (HIPASS and ALFALFA) or indirect techniques. The mean value from these determinations is
$\rm HI$
galaxy surveys (HIPASS and ALFALFA) or indirect techniques. The mean value from these determinations is  $\Omega_{\rm HI} = 4.2\times10^{-4}$
with a lower bound of
$\Omega_{\rm HI} = 4.2\times10^{-4}$
with a lower bound of  $\Omega_{\rm HI}^- = 3\times10^{-4}$
and an upper bound of
$\Omega_{\rm HI}^- = 3\times10^{-4}$
and an upper bound of  $\Omega_{\rm HI}^+ = 6.2\times10^{-4}$
, shown as the grey box in Figure 9Footnote r. Recently, using a spectral stacking technique and from Westerbrook Synthesis Radio Telescope observations of 1895 galaxies crossed with the SDSS, Hu et al. (Reference Hu2019) found
$\Omega_{\rm HI}^+ = 6.2\times10^{-4}$
, shown as the grey box in Figure 9Footnote r. Recently, using a spectral stacking technique and from Westerbrook Synthesis Radio Telescope observations of 1895 galaxies crossed with the SDSS, Hu et al. (Reference Hu2019) found  $\Omega_{\rm HI} = (4.15\pm 0.26)\times10^{-4}$
. Our determined value is in good agreement with these previous determinations, in particular with the latter one.
$\Omega_{\rm HI} = (4.15\pm 0.26)\times10^{-4}$
. Our determined value is in good agreement with these previous determinations, in particular with the latter one. $\rm H_{2}$
cosmic density: The molecular hydrogen cosmic density in late-type galaxies is
$\rm H_{2}$
cosmic density: The molecular hydrogen cosmic density in late-type galaxies is  $\sim\!21$
times larger than in early-type galaxies. This implies that
$\sim\!21$
times larger than in early-type galaxies. This implies that  $\sim\!95\%$
of
$\sim\!95\%$
of  $\rm H_{2}$
mass is in late-type galaxies. Using the CO surveys from Young et al. (Reference Young1995), Keres et al. (Reference Keres, Yun and Young2003) determined that
$\rm H_{2}$
mass is in late-type galaxies. Using the CO surveys from Young et al. (Reference Young1995), Keres et al. (Reference Keres, Yun and Young2003) determined that  $\Omega_{\rm H2}=(1.64\pm0.63)\times10^{-4}$
, while from the observations in CO from Maeda, Ohta, & Seko (Reference Maeda, Ohta and Seko2017) they report
$\Omega_{\rm H2}=(1.64\pm0.63)\times10^{-4}$
, while from the observations in CO from Maeda, Ohta, & Seko (Reference Maeda, Ohta and Seko2017) they report  $\Omega_{\rm H2}=0.51\times10^{-4}$
. Obreschkow & Rawlings (Reference Obreschkow and Rawlings2009) used a phenomenological model to derive
$\Omega_{\rm H2}=0.51\times10^{-4}$
. Obreschkow & Rawlings (Reference Obreschkow and Rawlings2009) used a phenomenological model to derive  $\Omega_{\rm H2}= (1.01\pm0.39)\times10^{-4}$
. Read & Trentham (Reference Read and Trentham2005) find that
$\Omega_{\rm H2}= (1.01\pm0.39)\times10^{-4}$
. Read & Trentham (Reference Read and Trentham2005) find that  $\Omega_{\rm H2}=2.68\times10^{-4}$
. The above ranges of values are shown with grey box in Figure 9. As can be seen, our results are consistent with the range of determinations described above, especially with the results from Obreschkow & Rawlings (Reference Obreschkow and Rawlings2009).
$\Omega_{\rm H2}=2.68\times10^{-4}$
. The above ranges of values are shown with grey box in Figure 9. As can be seen, our results are consistent with the range of determinations described above, especially with the results from Obreschkow & Rawlings (Reference Obreschkow and Rawlings2009).Cold gas cosmic density: Most of the cold gas is located in late-type galaxies,
 $\sim\!96\%$
. Keres et al. (Reference Keres, Yun and Young2003) found that
$\sim\!96\%$
. Keres et al. (Reference Keres, Yun and Young2003) found that  $\Omega_{\rm gas}=(6.34\pm1.62)\times 10^{-4}$
, which includes the resulting abundance of
$\Omega_{\rm gas}=(6.34\pm1.62)\times 10^{-4}$
, which includes the resulting abundance of  $\rm HI$
from Zwaan et al. (Reference Zwaan, Briggs, Sprayberry and Sorar1997). Obreschkow & Rawlings (Reference Obreschkow and Rawlings2009) used their best phenomenological model to the
$\rm HI$
from Zwaan et al. (Reference Zwaan, Briggs, Sprayberry and Sorar1997). Obreschkow & Rawlings (Reference Obreschkow and Rawlings2009) used their best phenomenological model to the  $\rm H_{2}$
-to-
$\rm H_{2}$
-to- $\rm HI$
ratio with the HIPASS results from the Zwaan et al. (Reference Zwaan, Meyer, Staveley-Smith and Webster2005) sample to derive
$\rm HI$
ratio with the HIPASS results from the Zwaan et al. (Reference Zwaan, Meyer, Staveley-Smith and Webster2005) sample to derive  $\Omega_{\rm gas}=(6.49\pm 1.18)\times 10^{-4}$
, while using the values for
$\Omega_{\rm gas}=(6.49\pm 1.18)\times 10^{-4}$
, while using the values for  $\rm HI$
and
$\rm HI$
and  $\rm H_{2}$
masses from Read & Trentham (Reference Read and Trentham2005), we calculate that
$\rm H_{2}$
masses from Read & Trentham (Reference Read and Trentham2005), we calculate that  $\Omega_{\rm gas}=7.95\times 10^{-4}$
after correcting from helium and heavier metals. Our value of
$\Omega_{\rm gas}=7.95\times 10^{-4}$
after correcting from helium and heavier metals. Our value of  $\Omega_{\rm gas}=(6.85\pm 0.92)\times 10^{-4}$
is consistent with the above results.
$\Omega_{\rm gas}=(6.85\pm 0.92)\times 10^{-4}$
is consistent with the above results.Stellar cosmic density: The stellar cosmic density in late-type galaxies that we derive from the SDSS is approximately
 $\sim\!1.8$
larger than in early-type galaxies. Thus,
$\sim\!1.8$
larger than in early-type galaxies. Thus,  $\sim\!64\%$
of the mass in stars at
$\sim\!64\%$
of the mass in stars at  $z\,{\sim}\,0.1$
is in late-type galaxies. From the compilation by Madau & Dickinson (Reference Madau and Dickinson2014), the stellar cosmic density lies within
$z\,{\sim}\,0.1$
is in late-type galaxies. From the compilation by Madau & Dickinson (Reference Madau and Dickinson2014), the stellar cosmic density lies within  $\Omega_{\ast}=(28.06-17.71)\times 10^{-4}$
, while the derivations from Wright et al. (Reference Wright2017) and Baldry et al. (Reference Baldry, Glazebrook and Driver2008) are respectively
$\Omega_{\ast}=(28.06-17.71)\times 10^{-4}$
, while the derivations from Wright et al. (Reference Wright2017) and Baldry et al. (Reference Baldry, Glazebrook and Driver2008) are respectively  $\Omega_{\ast}=17.14\times 10^{-4}$
and
$\Omega_{\ast}=17.14\times 10^{-4}$
and  $\Omega_{\ast}=29.73\times 10^{-4}$
. Our result for the cosmic density for all galaxies,
$\Omega_{\ast}=29.73\times 10^{-4}$
. Our result for the cosmic density for all galaxies,  $\Omega_{\ast}=(20.20\pm0.08)\times 10^{-4}$
, is consistent with the above values.
$\Omega_{\ast}=(20.20\pm0.08)\times 10^{-4}$
, is consistent with the above values.Baryonic cosmic density: Finally, we find that there is a factor of
 $\sim\!2.4$
more baryons in late-type galaxies than in early types, and thus,
$\sim\!2.4$
more baryons in late-type galaxies than in early types, and thus,  $\sim\!71\%$
of the baryons are in late-type galaxies. Read & Trentham (Reference Read and Trentham2005) found that
$\sim\!71\%$
of the baryons are in late-type galaxies. Read & Trentham (Reference Read and Trentham2005) found that  $\Omega_{\rm bar} = 35\times10^{-4}$
which is a factor of
$\Omega_{\rm bar} = 35\times10^{-4}$
which is a factor of  $\sim\!1.3$
larger than our results. We find a cosmic density parameters ratio of
$\sim\!1.3$
larger than our results. We find a cosmic density parameters ratio of  $\Omega_{\ast} / \Omega_{\rm bar} \approx 1.3$
. Finally, our baryon density parameter is
$\Omega_{\ast} / \Omega_{\rm bar} \approx 1.3$
. Finally, our baryon density parameter is  $\approx 5.4\%$
of the universal baryon fraction,
$\approx 5.4\%$
of the universal baryon fraction,  $f_{\rm bar,U}=0.156$
, or equivalently
$f_{\rm bar,U}=0.156$
, or equivalently  $\sim\! 18$
times lower than
$\sim\! 18$
times lower than  $f_{\rm bar,U}$
. Most of the baryons are definitively not locked inside galaxies.
$f_{\rm bar,U}$
. Most of the baryons are definitively not locked inside galaxies.
4.5.2. Cosmic timescales
We are now in a position to derive some relevant cosmic timescales, such as the mean galaxy depletion times. We focus on late-type galaxies because most of the star formation occurs in those galaxies. To do so, we use the observed cosmic star formation rate (CSFR) at  $z\,{\sim}\,0.1$
. According to Madau & Dickinson (Reference Madau and Dickinson2014), who derived the CSFR from far-UV and IR rest frame luminosities, the CSFR is
$z\,{\sim}\,0.1$
. According to Madau & Dickinson (Reference Madau and Dickinson2014), who derived the CSFR from far-UV and IR rest frame luminosities, the CSFR is  $\dot{\rho}_\ast \sim\! 90\times10^{-4}\ \text{M}_{\odot}$
$\dot{\rho}_\ast \sim\! 90\times10^{-4}\ \text{M}_{\odot}$
 $\textrm{yr}^{-1}\ \textrm{Mpc}^{-3}$
after correcting to a Chabrier (Reference Chabrier2003) IMF. Unfortunately, the authors report the CSFR for all galaxies but not divided into different groups. The recent study by Sánchez et al. (Reference Sánchez2019), based on the fossil record analysis of a sample of more than
$\textrm{yr}^{-1}\ \textrm{Mpc}^{-3}$
after correcting to a Chabrier (Reference Chabrier2003) IMF. Unfortunately, the authors report the CSFR for all galaxies but not divided into different groups. The recent study by Sánchez et al. (Reference Sánchez2019), based on the fossil record analysis of a sample of more than  $4\times10^{4}$
galaxies from the SDSS MaNGA survey, report similar values to the the total CSFR of
$4\times10^{4}$
galaxies from the SDSS MaNGA survey, report similar values to the the total CSFR of  $\dot{\rho}_\ast = 114.82\pm67.61\times10^{-4}\ \text{M}_{\odot}$
$\dot{\rho}_\ast = 114.82\pm67.61\times10^{-4}\ \text{M}_{\odot}$
 $\textrm{yr}^{-1}\ \textrm{Mpc}^{-3}$
or
$\textrm{yr}^{-1}\ \textrm{Mpc}^{-3}$
or  $\dot{\Omega}_\ast = \dot{\rho}_\ast/\rho_{\rm crit} = (9\pm 5)\times10^{-14}$
yr–1 corrected to a Chabrier (Reference Chabrier2003) IMF. The authors also derived the CSFRs for star-forming galaxies;
$\dot{\Omega}_\ast = \dot{\rho}_\ast/\rho_{\rm crit} = (9\pm 5)\times10^{-14}$
yr–1 corrected to a Chabrier (Reference Chabrier2003) IMF. The authors also derived the CSFRs for star-forming galaxies;  $\dot{\Omega}_{\ast, \rm SFG} = (6.5\pm 3.8)\times10^{-14}$
yr–1. In the following, we use their value for star-forming galaxies as a representative determination for late-type morphologies, that is,
$\dot{\Omega}_{\ast, \rm SFG} = (6.5\pm 3.8)\times10^{-14}$
yr–1. In the following, we use their value for star-forming galaxies as a representative determination for late-type morphologies, that is,  $\dot{\Omega}_{\ast, \rm L}\approx \dot{\Omega}_{\ast, \rm SFG}$
.
$\dot{\Omega}_{\ast, \rm L}\approx \dot{\Omega}_{\ast, \rm SFG}$
.
We begin our discussion by estimating the mean molecular hydrogen depletion time of late-type galaxies,  $\bar{t}_{\rm dep,L}({\rm H_{2}})=\Omega_{\rm H_2, L}/\dot{\Omega}_{\rm \ast,L}$
. The
$\bar{t}_{\rm dep,L}({\rm H_{2}})=\Omega_{\rm H_2, L}/\dot{\Omega}_{\rm \ast,L}$
. The  $\rm H_{2}$
depletion timescale is defined as the time at which a galaxy (or a molecular cloud) would consume its
$\rm H_{2}$
depletion timescale is defined as the time at which a galaxy (or a molecular cloud) would consume its  $\rm H_{2}$
gas reservoir by forming stars at the current SFR. From our cosmic density parameters, we find that
$\rm H_{2}$
gas reservoir by forming stars at the current SFR. From our cosmic density parameters, we find that  $\bar{t}_{\rm dep,L}\text{(}{\rm H_{2}}\text{)}\approx 1.3$
Gyrs. This is consistent with the mean depletion time
$\bar{t}_{\rm dep,L}\text{(}{\rm H_{2}}\text{)}\approx 1.3$
Gyrs. This is consistent with the mean depletion time  $\bar{t}_{\rm dep}\text{(}{\rm H_{2}}\text{)}=0.96$
Gyr reported in Saintonge et al. (Reference Saintonge2017) for star-forming galaxies in a volume complete sample. Note, however, that for local individual galaxies the molecular depletion time could vary from
$\bar{t}_{\rm dep}\text{(}{\rm H_{2}}\text{)}=0.96$
Gyr reported in Saintonge et al. (Reference Saintonge2017) for star-forming galaxies in a volume complete sample. Note, however, that for local individual galaxies the molecular depletion time could vary from  $\sim\! 0.9$
to 3 Gyrs (e.g., Kennicutt Reference Kennicutt1998; Bigiel et al. Reference Bigiel, Leroy, Walter, Brinks, de Blok, Madore and Thornley2008; Leroy et al. Reference Leroy, Walter, Brinks, Bigiel, de Blok, Madore and Thornley2008; Reference Leroy2013). Also, we estimate the mean total cold gas depletion time of late-type galaxies,
$\sim\! 0.9$
to 3 Gyrs (e.g., Kennicutt Reference Kennicutt1998; Bigiel et al. Reference Bigiel, Leroy, Walter, Brinks, de Blok, Madore and Thornley2008; Leroy et al. Reference Leroy, Walter, Brinks, Bigiel, de Blok, Madore and Thornley2008; Reference Leroy2013). Also, we estimate the mean total cold gas depletion time of late-type galaxies,  $\bar{t}_{\rm dep,L}({\rm gas})=\Omega_{\rm gas,L} / \dot{\Omega}_{\rm \ast,L}$
, and find
$\bar{t}_{\rm dep,L}({\rm gas})=\Omega_{\rm gas,L} / \dot{\Omega}_{\rm \ast,L}$
, and find  $\bar{t}_{\rm dep,L}({\rm gas})\approx 10.14$
Gyrs, that is,
$\bar{t}_{\rm dep,L}({\rm gas})\approx 10.14$
Gyrs, that is,  $\sim\!8$
times larger than for the molecular gas component. The values we find for these two timescales are consistent with the proposal that, on average, for local late-type galaxies, (i) the global conversion of molecular gas into stars is inefficient (recall that the
$\sim\!8$
times larger than for the molecular gas component. The values we find for these two timescales are consistent with the proposal that, on average, for local late-type galaxies, (i) the global conversion of molecular gas into stars is inefficient (recall that the  $\rm H_{2}$
depletion times of observed local star-forming regions are actually 40–500 Myr, for example, Lada, Lombardi, & Alves Reference Lada, Lombardi and Alves2010; Lada et al. Reference Lada, Forbrich, Lombardi and Alves2012); and (ii) the global conversion of atomic to molecular hydrogen gas is also inefficient, or equivalently, the molecular cloud formation efficiency is low. Thus, the mean star formation efficiency, SFE, of local late-type/star-forming galaxies is low despite the fact that they contain a considerable amount of interstellar gas; according to Table 4, on average approximately 36% of the baryons in these galaxies are in form of cold gas.
$\rm H_{2}$
depletion times of observed local star-forming regions are actually 40–500 Myr, for example, Lada, Lombardi, & Alves Reference Lada, Lombardi and Alves2010; Lada et al. Reference Lada, Forbrich, Lombardi and Alves2012); and (ii) the global conversion of atomic to molecular hydrogen gas is also inefficient, or equivalently, the molecular cloud formation efficiency is low. Thus, the mean star formation efficiency, SFE, of local late-type/star-forming galaxies is low despite the fact that they contain a considerable amount of interstellar gas; according to Table 4, on average approximately 36% of the baryons in these galaxies are in form of cold gas.
According to Leroy et al. (Reference Leroy, Walter, Brinks, Bigiel, de Blok, Madore and Thornley2008), the SFE of a galaxy is the inverse of the neutral H gas depletion time, that is, the time required for current star formation to consume the neutral H reservoir. The SFE can be estimated as the product of the net efficiency of converting  $\rm H_{2}$
gas into stars,
$\rm H_{2}$
gas into stars,  ${\rm SFE}\text{(}{\rm H_{2}}\text{)} =1 / {t}_{\rm dep}\text{(}{\rm H_{2}}\text{)}$
, and the net efficiency of molecular cloud formation given by the mass fraction of
${\rm SFE}\text{(}{\rm H_{2}}\text{)} =1 / {t}_{\rm dep}\text{(}{\rm H_{2}}\text{)}$
, and the net efficiency of molecular cloud formation given by the mass fraction of  $\rm H_{2}$
with respect to the total neutral H mass in the galaxy, that is,
$\rm H_{2}$
with respect to the total neutral H mass in the galaxy, that is,  $M_{H_{2}}/\text{(}M_{\rm HI} + M_{H_{2}}\text{)}$
. Thus, using our estimations of the cosmic parameters for late-type galaxies, we calculate the cosmic (mean) SFE of late-type galaxies as:
$M_{H_{2}}/\text{(}M_{\rm HI} + M_{H_{2}}\text{)}$
. Thus, using our estimations of the cosmic parameters for late-type galaxies, we calculate the cosmic (mean) SFE of late-type galaxies as:
 \begin{align}{\rm SFE}_L({\rm H}) &= {\rm SFE}_L\text{(}{\rm H_{2}}\text{)} \times \frac{\Omega_{\rm H_2,L}}{\Omega_{\rm HI,L}+\Omega_{\rm H_2,L}}\nonumber\\[3pt]
&= \frac{1}{\bar{t}_{\rm dep,L}\text{(}{\rm H_{2}}\text{)}} \times \frac{\Omega_{\rm H_2,L}}{\Omega_{\rm gas,L}/1.4} = 1.4 \times \frac{\dot{\Omega}_{\ast, \rm SF}}{\Omega_{\rm gas,L}} \nonumber\\[5pt]
& =\frac{1.4}{\bar{t}_{\rm dep,L}({\rm gas})} = 1.38\times 10^{-10} {\rm yr^{-1}}. \end{align}
\begin{align}{\rm SFE}_L({\rm H}) &= {\rm SFE}_L\text{(}{\rm H_{2}}\text{)} \times \frac{\Omega_{\rm H_2,L}}{\Omega_{\rm HI,L}+\Omega_{\rm H_2,L}}\nonumber\\[3pt]
&= \frac{1}{\bar{t}_{\rm dep,L}\text{(}{\rm H_{2}}\text{)}} \times \frac{\Omega_{\rm H_2,L}}{\Omega_{\rm gas,L}/1.4} = 1.4 \times \frac{\dot{\Omega}_{\ast, \rm SF}}{\Omega_{\rm gas,L}} \nonumber\\[5pt]
& =\frac{1.4}{\bar{t}_{\rm dep,L}({\rm gas})} = 1.38\times 10^{-10} {\rm yr^{-1}}. \end{align}
The inverse of this efficiency is the cosmic neutral H depletion time,  $\bar{t}_{\rm dep,L}({\rm H})\approx7.25$
Gyrs. Note that the relationship between the SFE based on the neutral H gas reservoir and the SFE based on the total cold gas reservoir is
$\bar{t}_{\rm dep,L}({\rm H})\approx7.25$
Gyrs. Note that the relationship between the SFE based on the neutral H gas reservoir and the SFE based on the total cold gas reservoir is  ${\rm SFE}_L({\rm H}) = 1.4\times {\rm SFE}_L({\rm gas})$
, or equivalently,
${\rm SFE}_L({\rm H}) = 1.4\times {\rm SFE}_L({\rm gas})$
, or equivalently,  $\bar{t}_{\rm dep,L}({\rm H})= \bar{t}_{\rm dep,L}({\rm gas})/1.4$
. The factor 1.4 takes into account He and metals.
$\bar{t}_{\rm dep,L}({\rm H})= \bar{t}_{\rm dep,L}({\rm gas})/1.4$
. The factor 1.4 takes into account He and metals.
We calculate also the cosmic SF timescale of late-type galaxies, which is given by the inverse of the cosmic-specific SFR,  $\bar{t}_{\rm SF,L}= \Omega_{\rm \ast,L}/\dot{\Omega}_{\rm \ast,L}\approx 20.3$
Gyrs; this is a factor of
$\bar{t}_{\rm SF,L}= \Omega_{\rm \ast,L}/\dot{\Omega}_{\rm \ast,L}\approx 20.3$
Gyrs; this is a factor of  $\sim\!1.5$
larger than the present age of the Universe. The cosmic SF timescale can be understood as the time required for the current cosmic SFR density to double the current cosmic stellar mass content. Interestingly enough, the ratio
$\sim\!1.5$
larger than the present age of the Universe. The cosmic SF timescale can be understood as the time required for the current cosmic SFR density to double the current cosmic stellar mass content. Interestingly enough, the ratio  $\bar{t}_{\rm dep,L}({\rm H})/\bar{t}_{\rm SF,L} = (\Omega_{\rm H2} + \Omega_{\rm HI}) / \Omega_{\ast} = 0.36$
, that is, the gas reservoir of late-type galaxies has not yet been dramatically consumed by star formation. Including He and metals in the gas reservoir, this ratio increases to
$\bar{t}_{\rm dep,L}({\rm H})/\bar{t}_{\rm SF,L} = (\Omega_{\rm H2} + \Omega_{\rm HI}) / \Omega_{\ast} = 0.36$
, that is, the gas reservoir of late-type galaxies has not yet been dramatically consumed by star formation. Including He and metals in the gas reservoir, this ratio increases to  $\sim\! 0.5$
.
$\sim\! 0.5$
.
5. Discussion
In this paper, we employed a statistical approach that allows to project the observed  $\rm HI$
- and
$\rm HI$
- and  $\rm H_{2}$
-CPDFs into their corresponding MFs, when using the GSMF as an interface or pivotal function, Section 2. Additionally, the cold gas and baryon MFs are obtained from the above. Our empirical approach makes use of the following observational data as input:
$\rm H_{2}$
-CPDFs into their corresponding MFs, when using the GSMF as an interface or pivotal function, Section 2. Additionally, the cold gas and baryon MFs are obtained from the above. Our empirical approach makes use of the following observational data as input:
1. The local GSMF over a large dynamical range and separated into early- and late-type galaxies.
2. The observed CPDFs of
 $\rm HI$
and
$\rm HI$
and  $\rm H_{2}$
as a function of
$\rm H_{2}$
as a function of  $M_{*}$
, both for early- and late-type galaxies.
$M_{*}$
, both for early- and late-type galaxies.
As a result, our approach provides a fully self-consistent and complete empirical description of the demographics of the local population of early- and late-type galaxies for a broad mass range. Furthermore, by construction, our MFs are derived separately for early- and late-type galaxies. As discussed in Section 4.4, our  $\rm HI$
and
$\rm HI$
and  $\rm H_{2}\,$
MFs are actually consistent with several previous determinations from radio blind or optically/infrared (selected) galaxy samples. Actually, the above level of agreement is not trivial due to the chain of assumptions and corrections for the data sets we used here and in Paper I, and it reinforces the robustness of the observational information employed. Note, however, that the above agreement is only valid above our completeness limit for the GSMF of
$\rm H_{2}\,$
MFs are actually consistent with several previous determinations from radio blind or optically/infrared (selected) galaxy samples. Actually, the above level of agreement is not trivial due to the chain of assumptions and corrections for the data sets we used here and in Paper I, and it reinforces the robustness of the observational information employed. Note, however, that the above agreement is only valid above our completeness limit for the GSMF of  $M_{*}=10^{7}\text{M}_{\odot}$
, which corresponds to a completeness limit of
$M_{*}=10^{7}\text{M}_{\odot}$
, which corresponds to a completeness limit of  $M_{\rm HI}\sim 10^{8}\text{M}_{\odot}$
and
$M_{\rm HI}\sim 10^{8}\text{M}_{\odot}$
and  $M_{H_{2}}\,{\sim}\,10^{7}\text{M}_{\odot}$
, respectively, for the
$M_{H_{2}}\,{\sim}\,10^{7}\text{M}_{\odot}$
, respectively, for the  $\rm HI$
and
$\rm HI$
and  $\rm H_{2}\,$
MFs. In that regards, we are unable to constraint the very low-mass end of the
$\rm H_{2}\,$
MFs. In that regards, we are unable to constraint the very low-mass end of the  $\rm HI$
and
$\rm HI$
and  $\rm H_{2}\,$
MFs.
$\rm H_{2}\,$
MFs.
Below, we highlight aspects that we consider are relevant for the success of our empirical approach:
The
 $\rm HI$
and
$\rm HI$
and  $\rm H_{2}$
CPDFs for early- and late-type galaxies. We used the CPDFs from Paper I, where we derived the CPDFs from a compilation of many incomplete and inhomogeneous samples, carefully homogenised to a common IMF, cosmology, CO-to-luminosity conversion factor, and accounting for selection biases.
$\rm H_{2}$
CPDFs for early- and late-type galaxies. We used the CPDFs from Paper I, where we derived the CPDFs from a compilation of many incomplete and inhomogeneous samples, carefully homogenised to a common IMF, cosmology, CO-to-luminosity conversion factor, and accounting for selection biases.The effect from upper limits in radio surveys. In addition to the above-mentioned homogenisation and corrections, it was important to take into account the upper limits reported in the original sources, when radio detections were not achieved. The fraction of non-detections in the compilation from Paper I was non negligible, especially for early-type galaxies. Non-detections were corrected by distance-sensitivity effects. Instead of ignoring radio non-detection or using the upper limits as the true values, as is commonly done in the literature, we derived the CPDFs by including them in our statistical analysis based on the non-parametric Kaplan–Meier estimator for censored data.
Next, we briefly discuss below some potential caveats on our approach. Over the next subsections, we will discuss them in more detail and show that they do not affect our main conclusions.
The assumption that the
 $\rm HI$
and
$\rm HI$
and  $\rm H_{2}$
masses are two independent random variables. In reality, this is not true, for example, Obreschkow & Rawlings (Reference Obreschkow and Rawlings2009) showed that the
$\rm H_{2}$
masses are two independent random variables. In reality, this is not true, for example, Obreschkow & Rawlings (Reference Obreschkow and Rawlings2009) showed that the  $\rm H_{2}$
-to-
$\rm H_{2}$
-to- $\rm HI$
mass ratio depends on the morphological type. Note, however, that this was partially taken into account in our approach in a statistical sense. Recall that we use the observed mass CPDFs separately for early- and late-type galaxies, that is, the dependence with morphology is roughly included, as shown in Paper I, see Figure C3 from that paper and Figure 5.
$\rm HI$
mass ratio depends on the morphological type. Note, however, that this was partially taken into account in our approach in a statistical sense. Recall that we use the observed mass CPDFs separately for early- and late-type galaxies, that is, the dependence with morphology is roughly included, as shown in Paper I, see Figure C3 from that paper and Figure 5.Differences on the mass-to-light ratios. Figure A1 in Appendix A shows that the different mass-to-light ratios used to estimate
 $M_{*}$
lead to different
$M_{*}$
lead to different  $\mbox{GSMF}$
s, with differences up to
$\mbox{GSMF}$
s, with differences up to  $0.5--1$
dex in number densities at the high-mass end (see also Bernardi et al. Reference Bernardi, Meert, Sheth, Fischer, Huertas-Company, Maraston, Shankar and Vikram2017). While we choose to use the geometric mean over the five mass-to-light ratios described in Appendix A, one could naturally question that the agreement of our
$0.5--1$
dex in number densities at the high-mass end (see also Bernardi et al. Reference Bernardi, Meert, Sheth, Fischer, Huertas-Company, Maraston, Shankar and Vikram2017). While we choose to use the geometric mean over the five mass-to-light ratios described in Appendix A, one could naturally question that the agreement of our  $\rm HI$
and
$\rm HI$
and  $\rm H_{2}\,$
MFs with the observed ones is relative because using a different GSMF could result in different MFs. In Section 5.1, we explore and quantify the impact of systematics from varying mass-to-light ratios and show that its effect is marginal in the obtained
$\rm H_{2}\,$
MFs with the observed ones is relative because using a different GSMF could result in different MFs. In Section 5.1, we explore and quantify the impact of systematics from varying mass-to-light ratios and show that its effect is marginal in the obtained  $\rm HI$
and
$\rm HI$
and  $\rm H_{2}\,$
MFs.
$\rm H_{2}\,$
MFs.Random errors from stellar mass estimates. Inevitably, random errors propagate to our MFs resulting in a Eddington (1940) bias effect. Thus, the comparison with the results based on radio surveys is not trivial as they do not suffer of an Eddington (1940) bias effect due to
 $M_{*}$
errors. Nonetheless, measurements of the
$M_{*}$
errors. Nonetheless, measurements of the  $\rm HI$
and
$\rm HI$
and  $\rm H_{2}$
masses are also subject to random errors. In Subsection 5.1.1, we deconvolve our MFs with the random errors, not only as a method to compare with results from radio surveys but also for obtaining the intrinsic MFs to be used to constrain the predictions from galaxy formation models.
$\rm H_{2}$
masses are also subject to random errors. In Subsection 5.1.1, we deconvolve our MFs with the random errors, not only as a method to compare with results from radio surveys but also for obtaining the intrinsic MFs to be used to constrain the predictions from galaxy formation models.The morphological classification from the SDSS DR7. To derive our GSMF separated into early- and late-type galaxies, we used the morphological classification based on the Huertas-Company et al. (Reference Huertas-Company, Aguerri, Bernardi, Mei and Sánchez Almeida2011) vector machine analysis of the SDSS DR7. As shown in Figure 2, we find that the obtained early- and late-type GSMFs using this classification are consistent with other determinations for the SDSS but disagree with those based on the visual classification from the GAMA survey. While we explore in detail this effect in Appendix C.4, we do not include it as one of the main sources of uncertainty.
We conclude this section by emphasising the robustness of the MFs derived when combining observational gas-to-stellar mass correlations from small data sets with the GSMF, (see also, Lemonias et al. Reference Lemonias, Schiminovich, Catinella, Heckman and Moran2013; Butcher et al. Reference Butcher, Schneider, van Driel and Lehnert2018). While this is an indirect method to study the demographics of the galaxy distribution, it is a valid and valuable approach that gives results that are comparable to direct observations and generalise them into a full bivariate distribution.

Figure 10. Impact of random and systematics errors in the baryonic, stellar, cold gas, atomic, and molecular gas MFs for all and separately for early- and late-type galaxies. The dashed lines show the ‘observational’ MF from Section 4.4, while the solid lines show the MF after deconvolving from random errors, i.e., the intrinsic MFs. Systematic errors are shown with the shaded areas. While the impact of random errors affects notably the total cold, atomic, and molecular gas MFs, the impact of systematic uncertainty on  $M_{*}$
is apparently marginal on them. However, the systematic uncertainties on
$M_{*}$
is apparently marginal on them. However, the systematic uncertainties on  $M_{*}$
are noticeable in the stellar and baryonic MFs.
$M_{*}$
are noticeable in the stellar and baryonic MFs.
5.1. The impact of random and systematics errors
When deriving stellar,  $\rm HI$
and
$\rm HI$
and  $\rm H_{2}$
masses, there are two sources of errors that will inevitably propagate over the MFs: the random and systematic errors. In this Section, we discuss the impact of both sources of errors on our results.
$\rm H_{2}$
masses, there are two sources of errors that will inevitably propagate over the MFs: the random and systematic errors. In this Section, we discuss the impact of both sources of errors on our results.
5.1.1. Random errors
The estimation of masses from both photometric and radio observations is subject to random errors. Here, we determine their impact on our resulting MFs. For simplicity, we assume that random errors follow lognormal distributions with a constant dispersion and independent of galaxy morphology. For the stellar masses, we assume a dispersion of  $\sigma = 0.1$
dex following Behroozi, Conroy, & Wechsler (Reference Behroozi, Conroy and Wechsler2010), Mendel et al. (Reference Mendel, Simard, Palmer, Ellison and Patton2014), and Rodríguez-Puebla et al. (2017). For HI masses,
$\sigma = 0.1$
dex following Behroozi, Conroy, & Wechsler (Reference Behroozi, Conroy and Wechsler2010), Mendel et al. (Reference Mendel, Simard, Palmer, Ellison and Patton2014), and Rodríguez-Puebla et al. (2017). For HI masses,  $\sigma = 0.14$
dex, and for
$\sigma = 0.14$
dex, and for  $\rm H_{2}$
masses,
$\rm H_{2}$
masses,  $\sigma = 0.22$
dex, following Calette et al. (Reference Calette, Avila-Reese, Rodrguez-Puebla, Hernández-Toledo and Papastergis2018, and more references therein). As for the gas and baryonic masses, we assume errors of respectively
$\sigma = 0.22$
dex, following Calette et al. (Reference Calette, Avila-Reese, Rodrguez-Puebla, Hernández-Toledo and Papastergis2018, and more references therein). As for the gas and baryonic masses, we assume errors of respectively  $\sigma = 0.14$
dex and
$\sigma = 0.14$
dex and  $\sigma = 0.1$
dex as they are dominated by HI and
$\sigma = 0.1$
dex as they are dominated by HI and  $M_{*}$
components, respectively, especially at high masses, where random errors have a larger impact. Thus, our ‘observational’ MFsFootnote s are the result of the convolution of the distribution of random errors and the respective intrinsic MFs. That is, our ‘observational’ MFs are given by
$M_{*}$
components, respectively, especially at high masses, where random errors have a larger impact. Thus, our ‘observational’ MFsFootnote s are the result of the convolution of the distribution of random errors and the respective intrinsic MFs. That is, our ‘observational’ MFs are given by  $\phi_{\rm obs} = \mathcal{G}\ast \phi_{\rm int}$
, where the symbol
$\phi_{\rm obs} = \mathcal{G}\ast \phi_{\rm int}$
, where the symbol  $\ast$
denotes the convolution operation,
$\ast$
denotes the convolution operation,  $\mathcal{G}$
is the distribution of random errors, and
$\mathcal{G}$
is the distribution of random errors, and  $\phi_{\rm int}$
is the intrinsic MF. For more details, the reader is referred to Appendix D. There we describe our numerical algorithm for deconvolving the intrinsic MF,
$\phi_{\rm int}$
is the intrinsic MF. For more details, the reader is referred to Appendix D. There we describe our numerical algorithm for deconvolving the intrinsic MF,  $\phi_{\rm int}$
.
$\phi_{\rm int}$
.
In Figure 10, we reproduce with dashed lines the ‘observational’ MFs derived in Section 4.4. Their corresponding intrinsic MFs are shown with solid lines. In the same figure, we present the ratios  $\phi_{\rm obs}/\phi_{\rm int}$
to show the effect of the deconvolution. The effect of deconvolving from random errors is small at low-intermediate masses but it increases at the massive end since the MFs are steeper (Eddington 1940). This is simply because the convolution depends on the logarithmic slope of the intrinsic MF (e.g., Cattaneo et al. Reference Cattaneo, Dekel, Faber and Guiderdoni2008); the steeper the slope, the larger the effect on the MFs. This is also the reason why we observe a lower impact in the baryonic and stellar MFs compared to the
$\phi_{\rm obs}/\phi_{\rm int}$
to show the effect of the deconvolution. The effect of deconvolving from random errors is small at low-intermediate masses but it increases at the massive end since the MFs are steeper (Eddington 1940). This is simply because the convolution depends on the logarithmic slope of the intrinsic MF (e.g., Cattaneo et al. Reference Cattaneo, Dekel, Faber and Guiderdoni2008); the steeper the slope, the larger the effect on the MFs. This is also the reason why we observe a lower impact in the baryonic and stellar MFs compared to the  $\rm HI$
,
$\rm HI$
,  $\rm H_{2}$
, and cold gas MFs; the latter fall steeply at the high-mass end. For example, the intrinsic
$\rm H_{2}$
, and cold gas MFs; the latter fall steeply at the high-mass end. For example, the intrinsic  $\rm HI$
MF is a factor of
$\rm HI$
MF is a factor of  $\sim\!4$
lower than the ‘observational’ one at
$\sim\!4$
lower than the ‘observational’ one at  $M_{\rm HI}\,{\sim}\,6\times10^{10}\ \text{M}_{\odot}$
, while the intrinsic
$M_{\rm HI}\,{\sim}\,6\times10^{10}\ \text{M}_{\odot}$
, while the intrinsic  $\rm H_{2}$
MF is an order of magnitude lower than the ‘observational’ MF at
$\rm H_{2}$
MF is an order of magnitude lower than the ‘observational’ MF at  $M_{\rm H2}\sim\!2\times10^{10}\ \text{M}_{\odot}$
. The intrinsic gas MF is an order of magnitude lower than the ‘observational’ MF at
$M_{\rm H2}\sim\!2\times10^{10}\ \text{M}_{\odot}$
. The intrinsic gas MF is an order of magnitude lower than the ‘observational’ MF at  $M_{\rm gas}\sim\!10^{11}\ \text{M}_{\odot}$
. Note that for the
$M_{\rm gas}\sim\!10^{11}\ \text{M}_{\odot}$
. Note that for the  $\rm HI$
,
$\rm HI$
,  $\rm H_{2}$
, and cold gas MFs the impact of random errors is more noticeable in late-type galaxies than in early-type ones.
$\rm H_{2}$
, and cold gas MFs the impact of random errors is more noticeable in late-type galaxies than in early-type ones.
5.1.2. Systematic errors
In addition to random errors, systematic errors have an impact when determining the MFs. The IMF is one of the most important sources of systematic errors for the GSMF. In this paper, we assumed an universal IMF given by the Chabrier (Reference Chabrier2003) function. While there is much debate on the IMF (see e.g., Bastian, Covey, & Meyer Reference Bastian, Covey and Meyer2010; Conroy et al. Reference Conroy2013; Bernardi et al. Reference Bernardi, Sheth, Dominguez-Sanchez, Fischer, Chae, Huertas-Company and Shankar2018), exploring the different alternatives is beyond the scope of this paper.
The stellar masses are calculated typically using colour-dependent mass-to-light ratios based on results from stellar population synthesis (SPS) models (for a recent review, see Conroy Reference Conroy2013). Thus, the calculated stellar masses depend on the used SPS model. This introduces a systematic uncertainty in  $M_{*}$
. Indeed, systematics in
$M_{*}$
. Indeed, systematics in  $M_{*}$
from SPS can be as large as
$M_{*}$
from SPS can be as large as  $\sim\!0.25$
dex, see for example, Pérez-González et al. (Reference Pérez-González2008); Muzzin et al. (Reference Muzzin, Marchesini, van Dokkum, Labbé, Kriek and Franx2009); Moustakas et al. (Reference Moustakas2013); Rodríguez-Puebla et al. (2017) and references therein. Recently, Bernardi et al. (Reference Bernardi, Meert, Sheth, Fischer, Huertas-Company, Maraston, Shankar and Vikram2017) showed that systematics from SPS introduces errors that are as large as
$\sim\!0.25$
dex, see for example, Pérez-González et al. (Reference Pérez-González2008); Muzzin et al. (Reference Muzzin, Marchesini, van Dokkum, Labbé, Kriek and Franx2009); Moustakas et al. (Reference Moustakas2013); Rodríguez-Puebla et al. (2017) and references therein. Recently, Bernardi et al. (Reference Bernardi, Meert, Sheth, Fischer, Huertas-Company, Maraston, Shankar and Vikram2017) showed that systematics from SPS introduces errors that are as large as  $\sim\!0.5$
dex in the normalisation of the GSMF at the high-mass end. In Appendix A, we found similar differences using various recipes of colour-dependent mass-to-light ratios. While in this paper, we calculate five different stellar masses for every galaxy and decided to use the geometric mean of the five as our fiducial definition of
$\sim\!0.5$
dex in the normalisation of the GSMF at the high-mass end. In Appendix A, we found similar differences using various recipes of colour-dependent mass-to-light ratios. While in this paper, we calculate five different stellar masses for every galaxy and decided to use the geometric mean of the five as our fiducial definition of  $M_{*}$
, the above inevitable introduces the question of which stellar mass definition shall we use when deriving our MFs. Additionally, Bernardi et al. (Reference Bernardi, Meert, Sheth, Fischer, Huertas-Company, Maraston, Shankar and Vikram2017) determined that systematics in photometry are of
$M_{*}$
, the above inevitable introduces the question of which stellar mass definition shall we use when deriving our MFs. Additionally, Bernardi et al. (Reference Bernardi, Meert, Sheth, Fischer, Huertas-Company, Maraston, Shankar and Vikram2017) determined that systematics in photometry are of  $\sim\!0.1$
dex. In order to quantify the impact of stellar populations in our MFs, in Appendix A, we noted that a constant shift of
$\sim\!0.1$
dex. In order to quantify the impact of stellar populations in our MFs, in Appendix A, we noted that a constant shift of  $\sim\!\pm0.15$
dex in the stellar mass axis reproduces systematic errors in the GSMF. In addition, Figure 1 shows that the same shift in the stellar mass axis could also explain differences from photometry. Thus, hereafter, we will use a shift of
$\sim\!\pm0.15$
dex in the stellar mass axis reproduces systematic errors in the GSMF. In addition, Figure 1 shows that the same shift in the stellar mass axis could also explain differences from photometry. Thus, hereafter, we will use a shift of  $\pm0.15$
dex in the stellar mass axis as our fiducial model for systematic errors in the GSMF. Note that we are assuming that this shift will be independent of morphology and we are ignoring systematic errors in the atomic and molecular gas components.
$\pm0.15$
dex in the stellar mass axis as our fiducial model for systematic errors in the GSMF. Note that we are assuming that this shift will be independent of morphology and we are ignoring systematic errors in the atomic and molecular gas components.
Figure 10 shows the impact of systematic errors from SPS models and photometry as the shaded areas around their corresponding  $\phi_{\rm int}$
(solid lines). The effects of systematics is non-negligible at the massive end of the stellar and baryonic MFs; we observe differences up to
$\phi_{\rm int}$
(solid lines). The effects of systematics is non-negligible at the massive end of the stellar and baryonic MFs; we observe differences up to  $\sim\! 0.6 $
dex in their normalisations. This is approximately the same both for early- and late-type galaxies. The impact of systematic errors in the gas,
$\sim\! 0.6 $
dex in their normalisations. This is approximately the same both for early- and late-type galaxies. The impact of systematic errors in the gas,  $\rm HI$
, and
$\rm HI$
, and  $\rm H_{2}\,{\rm{MFs}}$
is marginal; we notice a shift in their normalisations of
$\rm H_{2}\,{\rm{MFs}}$
is marginal; we notice a shift in their normalisations of  $\sim\!0.07$
at their low-mass ends but they increases respectively to
$\sim\!0.07$
at their low-mass ends but they increases respectively to  $\sim\!0.4$
,
$\sim\!0.4$
,  $\sim\!0.4$
, and
$\sim\!0.4$
, and  $\sim\!0.3$
dex at their massive ends. The above is due to the steeper slopes observed at the high-mass end from these MFs. In conclusion, the impact of systematic uncertainties in
$\sim\!0.3$
dex at their massive ends. The above is due to the steeper slopes observed at the high-mass end from these MFs. In conclusion, the impact of systematic uncertainties in  $M_{*}$
is only marginal for the derived
$M_{*}$
is only marginal for the derived  $\rm HI$
,
$\rm HI$
,  $\rm H_{2}$
, and cold gas MFs, making our results robust against this source of uncertainties.
$\rm H_{2}$
, and cold gas MFs, making our results robust against this source of uncertainties.
As mentioned in the Introduction, the value of deriving robust MFs is that they can be used as key tools for constraining the processes that govern the evolution of the galaxies. However, using direct measurements from observations to constrain galaxy formation models is not trivial due to random and systematic errors, as discussed here. We end this subsection by emphasising the importance of deconvolving from random errors and understanding the impact of systematic errors when reporting results on galaxy demographics.
6. Summary and conclusions
We present a self-consistent empirical approach that unifies local galaxy gas-to-stellar mass correlations and the MFs of galaxies traced by their different baryonic components. We make available a Python code that displays tables and figures with all the relevant statistical distributions and correlations discussed in this paper.Footnote t Next, we summarise our main results which can be used for comparing with theoretical predictions or as input for modelling galaxy mock catalogues:
Conditional probability distribution functions (CPDFs): Section 2.2 presents the functional forms for the
 $\rm HI$
and
$\rm HI$
and  $\rm H_{2}$
mass conditional distributions given
$\rm H_{2}$
mass conditional distributions given  $M_{*}$
(the CPDFs), which are described by Equations (7)–(12). Our best-fit parameters to the empirical information presented in Paper I are listed in Table 3, while Figures 3 and 4 show the data with their corresponding best fits in various stellar mass bins. Theoretical predictions for the
$M_{*}$
(the CPDFs), which are described by Equations (7)–(12). Our best-fit parameters to the empirical information presented in Paper I are listed in Table 3, while Figures 3 and 4 show the data with their corresponding best fits in various stellar mass bins. Theoretical predictions for the  $\rm HI$
,
$\rm HI$
,  $\rm H_{2}$
, and cold gas CPDFs can be confronted with our empirically constrained distributions, for all galaxies as well as for early and late types in case the morphological classifications are available. If these predictions are limited in stellar and/or gas masses, then our (analytical)
$\rm H_{2}$
, and cold gas CPDFs can be confronted with our empirically constrained distributions, for all galaxies as well as for early and late types in case the morphological classifications are available. If these predictions are limited in stellar and/or gas masses, then our (analytical)  $\rm HI$
-CPDFs and
$\rm HI$
-CPDFs and  $\rm H_{2}$
-CPDFs and their moments can be easily calculated over the same mass ranges as the theoretical predictions for a comparison. The
$\rm H_{2}$
-CPDFs and their moments can be easily calculated over the same mass ranges as the theoretical predictions for a comparison. The  $\rm HI$
- and
$\rm HI$
- and  $\rm H_{2}$
-CPDFs combined with the GSMF allowed us to calculate the respective bivariate mass distributions for all the galaxy population as plotted in Figures 6 and 7.
$\rm H_{2}$
-CPDFs combined with the GSMF allowed us to calculate the respective bivariate mass distributions for all the galaxy population as plotted in Figures 6 and 7.Moments of the CPDFs: The (analytical)
 $\rm HI$
- and
$\rm HI$
- and  $\rm H_{2}$
-CPDFs contain the information about any moment of the distributions. Figure 4 (see also Figures 6 and 7) shows the
$\rm H_{2}$
-CPDFs contain the information about any moment of the distributions. Figure 4 (see also Figures 6 and 7) shows the  $\langle \log M_j \rangle+-\log M_{*}$
relationships, with
$\langle \log M_j \rangle+-\log M_{*}$
relationships, with  $j={\rm HI}$
,
$j={\rm HI}$
,  $\rm H_{2}$
, for early- and late-type galaxies as well as for all galaxies. In addition, we present these relationships using the arithmetic mean,
$\rm H_{2}$
, for early- and late-type galaxies as well as for all galaxies. In addition, we present these relationships using the arithmetic mean,  $\langle M_j\rangle$
. As expected, these relationships lie above from those calculated with the logarithmic mean,
$\langle M_j\rangle$
. As expected, these relationships lie above from those calculated with the logarithmic mean,  $\langle\log M_j\rangle$
. Moreover standard deviations can vary significantly if they are computed with respect to the arithmetic or logarithmic mean, which also depends on the shape of the distributions. Other statistical measures that can be used to characterise the population distributions are medians and percentiles, for example. As mentioned above, any statistical quantity can be computed with our CPDFs and confronted with both theoretical and/or observational results.
$\langle\log M_j\rangle$
. Moreover standard deviations can vary significantly if they are computed with respect to the arithmetic or logarithmic mean, which also depends on the shape of the distributions. Other statistical measures that can be used to characterise the population distributions are medians and percentiles, for example. As mentioned above, any statistical quantity can be computed with our CPDFs and confronted with both theoretical and/or observational results.The Galaxy Stellar Mass Functions: In Section 3.1, we determined the GSMF from the SDSS DR7 based on the photometric catalogue from Meert et al. (Reference Meert, Vikram and Bernardi2015) and (Reference Mendel, Simard, Palmer, Ellison and Patton2016) for masses above
 $M_{*}=10^9\ \text{M}_{\odot}$
. For masses down to
$M_{*}=10^9\ \text{M}_{\odot}$
. For masses down to  $\sim\!3\times10^{7}\text{M}_{\odot}$
, we used the low-z SDSS DR4 (Blanton et al. Reference Blanton2005a; b), and corrected it from surface brightness incompleteness and fluctuations due to large-scale structures. We determined also the fractions of early- and late-type galaxies using the SDSS DR7 morphological classification of Huertas-Company et al. (Reference Huertas-Company, Aguerri, Bernardi, Mei and Sánchez Almeida2011). Stellar masses were derived from five colour-dependent mass-to-light ratios. We used as our fiducial definition the geometric mean of these five stellar masses derived for each galaxy. We also determined the impact of systematic errors in
$\sim\!3\times10^{7}\text{M}_{\odot}$
, we used the low-z SDSS DR4 (Blanton et al. Reference Blanton2005a; b), and corrected it from surface brightness incompleteness and fluctuations due to large-scale structures. We determined also the fractions of early- and late-type galaxies using the SDSS DR7 morphological classification of Huertas-Company et al. (Reference Huertas-Company, Aguerri, Bernardi, Mei and Sánchez Almeida2011). Stellar masses were derived from five colour-dependent mass-to-light ratios. We used as our fiducial definition the geometric mean of these five stellar masses derived for each galaxy. We also determined the impact of systematic errors in  $M_{*}$
due to mass-to-light ratio uncertainties in our MFs.
$M_{*}$
due to mass-to-light ratio uncertainties in our MFs.Calculated MFs: Section 4.4 presents the results of calculating with our approach the MFs for atomic, molecular, cold gas, and baryons for early- and late-type galaxies, as well as for all galaxies. As discussed in Section 5.1, random errors in mass determinations artificially decrease the slope of the ‘observational’ MFs, an effect that affects especially the high-mass end, and that would lead to incorrect conclusions when comparing to theoretical predictions. Figure 10 presents our MFs deconvolved from random errors, that is, the intrinsic MFs, for different baryon matter components, and separately for early- and late-type galaxies. In the same section, we studied the effects on the MFs from systematic errors in
 $M_{*}$
, also shown in Figure 10. In Appendix A and Figure 1, we showed explicitly that systematic errors in the GSMF due to mass-to-luminosity ratios and photometric uncertainties are well represented by a shift in the
$M_{*}$
, also shown in Figure 10. In Appendix A and Figure 1, we showed explicitly that systematic errors in the GSMF due to mass-to-luminosity ratios and photometric uncertainties are well represented by a shift in the  $M_{*}$
-axis of
$M_{*}$
-axis of  $\pm 0.15$
dex. The effect of random errors in the baryonic MF is of the same order, while for the gas MFs the propagated systematic errors in
$\pm 0.15$
dex. The effect of random errors in the baryonic MF is of the same order, while for the gas MFs the propagated systematic errors in  $M_{*}$
have a negligible effect. Note that our MFs are complete only above a given mass limit,
$M_{*}$
have a negligible effect. Note that our MFs are complete only above a given mass limit,  $\sim\! 3\times 10^7\ \text{M}_{\odot}$
for the GSMF,
$\sim\! 3\times 10^7\ \text{M}_{\odot}$
for the GSMF,  $\sim\! 10^7\ \text{M}_{\odot}$
for the
$\sim\! 10^7\ \text{M}_{\odot}$
for the  $\rm H_{2}$
MF, and
$\rm H_{2}$
MF, and  $\sim\! 10^8\ \text{M}_{\odot}$
for the
$\sim\! 10^8\ \text{M}_{\odot}$
for the  $\rm HI$
, cold gas, and baryonic MFs.
$\rm HI$
, cold gas, and baryonic MFs.
From the results summarised above, we highlight the following conclusions:
The low-mass slope of our GSMF, corrected for surface brightness incompleteness, is
 $\alpha \approx -1.4$
, consistent with recent determinations based on the deeper surveys such as GAMA (Wright et al. Reference Wright2017), and estimations based on the search of low surface brightness galaxies from core-collapse supernovae (Sedgwick et al. Reference Sedgwick, Baldry, James and Kelvin2019). The slope for the high-mass end is shallower than previous determination most likely as the result of the new photometric catalogue employed in this paper (Meert et al. Reference Meert, Vikram and Bernardi2015). Similar results have been reported in Bernardi et al. (Reference Bernardi, Meert, Sheth, Fischer, Huertas-Company, Maraston, Shankar and Vikram2017).
$\alpha \approx -1.4$
, consistent with recent determinations based on the deeper surveys such as GAMA (Wright et al. Reference Wright2017), and estimations based on the search of low surface brightness galaxies from core-collapse supernovae (Sedgwick et al. Reference Sedgwick, Baldry, James and Kelvin2019). The slope for the high-mass end is shallower than previous determination most likely as the result of the new photometric catalogue employed in this paper (Meert et al. Reference Meert, Vikram and Bernardi2015). Similar results have been reported in Bernardi et al. (Reference Bernardi, Meert, Sheth, Fischer, Huertas-Company, Maraston, Shankar and Vikram2017).The total GSMF is well fitted by a function composed of a sub-exponential Schechter function and a double power law function. This fitting model has an error of less than
 $\sim\! 2\%$
in the mass range
$\sim\! 2\%$
in the mass range  $2\times 10^9-5\times 10^{11}\ \text{M}_{\odot}$
. At the smallest and largest masses, the deviations increase to values above
$2\times 10^9-5\times 10^{11}\ \text{M}_{\odot}$
. At the smallest and largest masses, the deviations increase to values above  $\sim\!20\%$
. In contrast, the commonly employed double Schechter function model performs considerably worse.
$\sim\!20\%$
. In contrast, the commonly employed double Schechter function model performs considerably worse.Systematic errors due to SPS models, that affect results on mass-to-light ratios, introduce a systematic effect on the normalisation of the GSMF, especially at the massive end. We find differences between
 $\sim\! 0.5- 1$
dex, consistent with the result discussed in Bernardi et al. (Reference Bernardi, Meert, Sheth, Fischer, Huertas-Company, Maraston, Shankar and Vikram2017).
$\sim\! 0.5- 1$
dex, consistent with the result discussed in Bernardi et al. (Reference Bernardi, Meert, Sheth, Fischer, Huertas-Company, Maraston, Shankar and Vikram2017).The
 $\rm HI$
,
$\rm HI$
,  $\rm H_{2}$
, and cold gas MFs are mostly dominated by late-type galaxies. In general, we notice that our
$\rm H_{2}$
, and cold gas MFs are mostly dominated by late-type galaxies. In general, we notice that our  $\rm HI$
MF is in good agreement with previous determinations from blind surveys. Similarly, the
$\rm HI$
MF is in good agreement with previous determinations from blind surveys. Similarly, the  $\rm H_{2}$
MF is consistent with previous determinations based on CO follow-up optically selected samples. When we compare to the HIPASS and ATLAS 3D surveys for early-type galaxies, our
$\rm H_{2}$
MF is consistent with previous determinations based on CO follow-up optically selected samples. When we compare to the HIPASS and ATLAS 3D surveys for early-type galaxies, our  $\rm HI$
MF is consistent with those observations. However, our
$\rm HI$
MF is consistent with those observations. However, our  $\rm H_{2}$
MF for early-type galaxies is in tension at the low-mass side with the MF derived from the ATLAS 3D survey.
$\rm H_{2}$
MF for early-type galaxies is in tension at the low-mass side with the MF derived from the ATLAS 3D survey.Our ‘observational’ MFs were deconvolved from random errors to obtain the intrinsic MFs. The effect of random errors is small at the low-mass end but larger at the high-mass end of our MFs. This is because the convolution depends on the logarithmic slope of the intrinsic MFs. Because the baryonic and stellar MFs are shallower at the massive end, the effects are relatively small, but the atomic, molecular, and cold gas MFs have steeper slopes resulting in a larger effect.
While for the stellar (and hence baryonic) MF systematic errors due to mass-to-light ratio uncertainties introduce a non-negligible effect, especially at the high-mass end, for the atomic, molecular, and gas MFs, the effects of systematics are small. We thus conclude that our determinations for the gas MFs are robust against systematic errors in the the
 $M_{*}$
determination.
$M_{*}$
determination.We determined the
 $z\,{\sim}\,0$
cosmic densities of
$z\,{\sim}\,0$
cosmic densities of  $\rm HI$
,
$\rm HI$
,  $\rm H_{2}$
, cold gas, stars, and baryons locked in galaxies calculated from the respective MFs. Our results are in good agreement with previous determinations from different local censuses. Most of the atomic and molecular H gas is in late-type galaxies,
$\rm H_{2}$
, cold gas, stars, and baryons locked in galaxies calculated from the respective MFs. Our results are in good agreement with previous determinations from different local censuses. Most of the atomic and molecular H gas is in late-type galaxies,  $\sim\!96\%$
of the mass density, while this fraction decreases to
$\sim\!96\%$
of the mass density, while this fraction decreases to  $\sim\!70\%$
and
$\sim\!70\%$
and  $\sim\! 65\%$
for baryons and stars. We find that the fraction of
$\sim\! 65\%$
for baryons and stars. We find that the fraction of  $\rm HI$
and
$\rm HI$
and  $\rm H_{2}$
in galaxies with respect to the universal baryon fraction is respectively
$\rm H_{2}$
in galaxies with respect to the universal baryon fraction is respectively  $\sim\! 1 \%$
and
$\sim\! 1 \%$
and  $\sim\! 0.2\%$
, while the respective fractions for mass in stars is
$\sim\! 0.2\%$
, while the respective fractions for mass in stars is  $\sim\! 4\%$
. Baryons in galaxies (the ionised and hot gas were not included) are
$\sim\! 4\%$
. Baryons in galaxies (the ionised and hot gas were not included) are  $\sim\! 5.4\%$
of the universal baryon fraction.
$\sim\! 5.4\%$
of the universal baryon fraction.Based on the values reported in the literature for the local CSFR of star-forming (late-type) galaxies, we estimated the cosmic
 $\rm H_{2}$
and total gas depletion times of late-type galaxies. These timescales,
$\rm H_{2}$
and total gas depletion times of late-type galaxies. These timescales,  $t_{\rm dep}\text{(}{\rm H_{2}}\text{)}\approx 1.3\ \text{Gyr}$
and
$t_{\rm dep}\text{(}{\rm H_{2}}\text{)}\approx 1.3\ \text{Gyr}$
and  $\bar{t}_{\rm dep,L}({\rm gas})\approx 10.14\ \text{Gyr}$
, respectively, imply that galaxies, on average, are inefficient to convert their molecular gas into stars, and are inefficient to transform their atomic gas into molecular gas. The depletion time for the total neutral hydrogen is
$\bar{t}_{\rm dep,L}({\rm gas})\approx 10.14\ \text{Gyr}$
, respectively, imply that galaxies, on average, are inefficient to convert their molecular gas into stars, and are inefficient to transform their atomic gas into molecular gas. The depletion time for the total neutral hydrogen is  $\bar{t}_{\rm dep,L}({\rm H}) = \bar{t}_{\rm dep,L}({\rm gas}) / 1.4\sim\! 7.25$
Gyrs. On the other hand, the average cosmic SF timescale (the inverse of the cosmic sSFR) is
$\bar{t}_{\rm dep,L}({\rm H}) = \bar{t}_{\rm dep,L}({\rm gas}) / 1.4\sim\! 7.25$
Gyrs. On the other hand, the average cosmic SF timescale (the inverse of the cosmic sSFR) is  $\bar{t}_{\rm SF,L}\approx 20.3$
Gyrs, which implies that the ratio
$\bar{t}_{\rm SF,L}\approx 20.3$
Gyrs, which implies that the ratio  $\bar{t}_{\rm dep,L}({\rm H})/\bar{t}_{\rm SF,L} = 0.38$
. This shows that the gas reservoir of late-type galaxies has not yet been dramatically consumed by star formation.
$\bar{t}_{\rm dep,L}({\rm H})/\bar{t}_{\rm SF,L} = 0.38$
. This shows that the gas reservoir of late-type galaxies has not yet been dramatically consumed by star formation.
Here, we provided a statistical description for calculating any moment to characterise the gas-to-stellar mass correlations, the  $\rm HI$
- and
$\rm HI$
- and  $\rm H_{2}$
-stellar mass bivariate distributions as well as all the respective MFs. One of our motivations for this paper is to provide the community with a full self-consistent phenomenological description of the local galaxy population for various properties and divided into the two main morphological types in order to be confronted with theoretical results, both from semi-analytical models and cosmological hydrodynamical simulations. The next generation of sensitive radio telescopes will be able to survey large samples of extragalactic sources in
$\rm H_{2}$
-stellar mass bivariate distributions as well as all the respective MFs. One of our motivations for this paper is to provide the community with a full self-consistent phenomenological description of the local galaxy population for various properties and divided into the two main morphological types in order to be confronted with theoretical results, both from semi-analytical models and cosmological hydrodynamical simulations. The next generation of sensitive radio telescopes will be able to survey large samples of extragalactic sources in  $\rm HI$
and
$\rm HI$
and  $\rm H_{2}$
gas, something that is a common practice with current optical surveys. Thus, robust and unbiased bivariate distributions and MFs of
$\rm H_{2}$
gas, something that is a common practice with current optical surveys. Thus, robust and unbiased bivariate distributions and MFs of  $\rm HI$
and
$\rm HI$
and  $\rm H_{2}$
gas over large mass ranges will be routinely derived in the future along with the relationships of the gas contents with their optical/IR properties. Preparatory to that, and to pave the road to these surveys, studies based on radio follow-up observations of (relative small) optically selected galaxy samples provide valuable information that can be used for the gas demographics of galaxies. In this work, we have exploited the results from many of these studies, and by means of the conditional (or bivariate) approach we were able to derive the abundances of local galaxies as traced by different baryonic components and separated into the two main groups of galaxies, early, and late types.
$\rm H_{2}$
gas over large mass ranges will be routinely derived in the future along with the relationships of the gas contents with their optical/IR properties. Preparatory to that, and to pave the road to these surveys, studies based on radio follow-up observations of (relative small) optically selected galaxy samples provide valuable information that can be used for the gas demographics of galaxies. In this work, we have exploited the results from many of these studies, and by means of the conditional (or bivariate) approach we were able to derive the abundances of local galaxies as traced by different baryonic components and separated into the two main groups of galaxies, early, and late types.
The present work is the second paper of a series. In Paper I, we derived the CPDFs of  $\rm HI$
and
$\rm HI$
and  $\rm H_{2}$
as a function of
$\rm H_{2}$
as a function of  $M_{*}$
, separately for early- and late-type galaxies, for an extensive compilation and homogenisation of radio data from the literature. In the present work, we made extensive use of these data. In the future, we will use the MFs derived here to extend the galaxy–halo connection for different baryonic components, and we will show that not only the
$M_{*}$
, separately for early- and late-type galaxies, for an extensive compilation and homogenisation of radio data from the literature. In the present work, we made extensive use of these data. In the future, we will use the MFs derived here to extend the galaxy–halo connection for different baryonic components, and we will show that not only the  $\rm HI$
and
$\rm HI$
and  $\rm H_{2}\,$
MFs derived here are in good agreement with radio blind or optically selected surveys but also with the observed galaxy spatial clustering as a function of
$\rm H_{2}\,$
MFs derived here are in good agreement with radio blind or optically selected surveys but also with the observed galaxy spatial clustering as a function of  $\rm HI$
gas mass.
$\rm HI$
gas mass.
Acknowledgements
ARP and VAR acknowledges support from UNAM PAPIIT grant IA104118 and from the CONACyT ‘Ciencia Basica’ grant 285721. ARC acknowledges support from CONACyT graduate fellowship. We thank to the referee Tsutomu T. Takeuchi for a constructive report that helped to improve this paper.
A. Derivation of the SDSS DR7 GSMF
In this paper, we derive the GSMF from a spectroscopic sample of 670,722 galaxies from the SDSS DR7 based on the photometric estimates of the apparent brightnesses in the g, r, and i band from Meert et al. (Reference Meert, Vikram and Bernardi2015) and (Reference Meert, Vikram and Bernardi2016). In those papers, the authors selected galaxies with extinction-corrected  $r-$
band Petrosian magnitude between magnitude 14 and 17.77 to derive de Vacouleurs, Sérsic, de Vacoulers+Exponential, and Sérsic+Exponential fits to the observed surface brightness profiles of each galaxies in their SDSS DR7 catalogue. Surface brightness profiles were obtained via the PyMorph pipeline (Vikram et al. Reference Vikram, Wadadekar, Kembhavi and Vijayagovindan2010; Meert et al. Reference Meert, Vikram and Bernardi2013). PyMorph is a python software that uses Sextractor (Bertin & Arnouts Reference Bertin and Arnouts1996) and Galfit (Peng et al. Reference Peng, Ho, Impey and Rix2002) to fit both one- and two-component to the seeing convolved surface brightness profiles from the spectroscopic sample of SDSS DR7 galaxies. PyMorph has been extensively tested in (Meert et al. Reference Meert, Vikram and Bernardi2013, see also, Meert et al. Reference Meert, Vikram and Bernardi2015) showning that the algorithm does not suffer from the sky subtraction problems that has been detected in previous studies based on the SDSS, in particular in crowded fieldsFootnote u.
$r-$
band Petrosian magnitude between magnitude 14 and 17.77 to derive de Vacouleurs, Sérsic, de Vacoulers+Exponential, and Sérsic+Exponential fits to the observed surface brightness profiles of each galaxies in their SDSS DR7 catalogue. Surface brightness profiles were obtained via the PyMorph pipeline (Vikram et al. Reference Vikram, Wadadekar, Kembhavi and Vijayagovindan2010; Meert et al. Reference Meert, Vikram and Bernardi2013). PyMorph is a python software that uses Sextractor (Bertin & Arnouts Reference Bertin and Arnouts1996) and Galfit (Peng et al. Reference Peng, Ho, Impey and Rix2002) to fit both one- and two-component to the seeing convolved surface brightness profiles from the spectroscopic sample of SDSS DR7 galaxies. PyMorph has been extensively tested in (Meert et al. Reference Meert, Vikram and Bernardi2013, see also, Meert et al. Reference Meert, Vikram and Bernardi2015) showning that the algorithm does not suffer from the sky subtraction problems that has been detected in previous studies based on the SDSS, in particular in crowded fieldsFootnote u.
We estimate the GSMF at the redshift interval between  $z = 0.005$
and
$z = 0.005$
and  $z = 0.2$
using the standard
$z = 0.2$
using the standard  $1/V_{\rm max}$
method (Schmidt Reference Schmidt1968):
$1/V_{\rm max}$
method (Schmidt Reference Schmidt1968):
 \begin{equation} \phi_{\ast}\text{(}M_{*}\text{)} = \frac{1}{\Delta\log{M_{*}}}\sum_{i=1}^N\frac{\omega_i(\log{M_{*}}\pm\Delta\log{M_{*}})}{V_{{\rm max},i}}, \end{equation}
\begin{equation} \phi_{\ast}\text{(}M_{*}\text{)} = \frac{1}{\Delta\log{M_{*}}}\sum_{i=1}^N\frac{\omega_i(\log{M_{*}}\pm\Delta\log{M_{*}})}{V_{{\rm max},i}}, \end{equation}
where  $\omega_i$
is a weight factor correction that depends on the position in the sky for galaxies within the interval
$\omega_i$
is a weight factor correction that depends on the position in the sky for galaxies within the interval  $\log{M_{*}}\pm\Delta\log{M_{*}}/2$
, following Bernardi et al. (see also Reference Bernardi, Shankar, Hyde, Mei, Marulli and Sheth2010) we assume that
$\log{M_{*}}\pm\Delta\log{M_{*}}/2$
, following Bernardi et al. (see also Reference Bernardi, Shankar, Hyde, Mei, Marulli and Sheth2010) we assume that  $\omega_i = 1.1$
; and
$\omega_i = 1.1$
; and
 \begin{equation} V_{{\rm max},i} = \int_{\Omega}\int^{z_{u,i}}_{z_{l,i}}\frac{d^2V_c}{dzd\Omega} dzd\Omega. \end{equation}
\begin{equation} V_{{\rm max},i} = \int_{\Omega}\int^{z_{u,i}}_{z_{l,i}}\frac{d^2V_c}{dzd\Omega} dzd\Omega. \end{equation}
We denote the solid angle of the SDSS DR7 with  $\Omega$
, while
$\Omega$
, while  $V_c$
refers to the comoving volume enclosed within the redshift interval
$V_c$
refers to the comoving volume enclosed within the redshift interval  $[z_{l,i}, z_{u,i}]$
. The redshift limits are defined as
$[z_{l,i}, z_{u,i}]$
. The redshift limits are defined as  $z_{l,i} = {\rm max}(0.005, z_{{\rm min},i})$
and
$z_{l,i} = {\rm max}(0.005, z_{{\rm min},i})$
and  $z_{u,i} = {\rm min}(z_{{\rm max},i}, 0.2)$
; where
$z_{u,i} = {\rm min}(z_{{\rm max},i}, 0.2)$
; where  $z_{{\rm min},i}$
and
$z_{{\rm min},i}$
and  $z_{{\rm max},i}$
are, respectively, the minimum and maximum at which each galaxy can be observed in the SDSS DR7 sample. We estimate
$z_{{\rm max},i}$
are, respectively, the minimum and maximum at which each galaxy can be observed in the SDSS DR7 sample. We estimate  $z_{{\rm max},i}$
for every galaxy in the sample by solving iteratively the distance modulus equation:
$z_{{\rm max},i}$
for every galaxy in the sample by solving iteratively the distance modulus equation:
 \begin{eqnarray} m_{\rm lim,r} - M_{r,i}^{0.0} = 5 \log D_{L,i}(z_{{\rm max},i}) + 25\end{eqnarray}
\begin{eqnarray} m_{\rm lim,r} - M_{r,i}^{0.0} = 5 \log D_{L,i}(z_{{\rm max},i}) + 25\end{eqnarray}
 \begin{eqnarray} \hspace*{8pt}{+}\, K_{gr,i}(z_{{\rm max},i}) - E_{r,i}(z_{{\rm max},i}), \end{eqnarray}
\begin{eqnarray} \hspace*{8pt}{+}\, K_{gr,i}(z_{{\rm max},i}) - E_{r,i}(z_{{\rm max},i}), \end{eqnarray}
where  $M_{r,i}^{0.0}$
is the Petrosian magnitude K+E-corrected at a rest frame
$M_{r,i}^{0.0}$
is the Petrosian magnitude K+E-corrected at a rest frame  $z=0$
,
$z=0$
,  $K_{gr,i}(z)$
is the K-correction (see Appendix B) and
$K_{gr,i}(z)$
is the K-correction (see Appendix B) and  $E_{r,i} = 1.1 z$
(following Dragomir et al. Reference Dragomir, Rodrguez-Puebla, Primack and Lee2018) for the ith galaxy in the sample. For the completeness limits, we use the limiting apparent magnitude in the r-band of
$E_{r,i} = 1.1 z$
(following Dragomir et al. Reference Dragomir, Rodrguez-Puebla, Primack and Lee2018) for the ith galaxy in the sample. For the completeness limits, we use the limiting apparent magnitude in the r-band of  $m_{\rm lim,r}=17.77$
. Similarly, we estimate
$m_{\rm lim,r}=17.77$
. Similarly, we estimate  $z_{{\rm min},i}$
by solving iteratively the distance modulus equation but this time using the limiting apparent magnitude
$z_{{\rm min},i}$
by solving iteratively the distance modulus equation but this time using the limiting apparent magnitude  $m_{\rm lim,r}=14$
.
$m_{\rm lim,r}=14$
.
Errors are estimated using the jackknife technique by diving the galaxy sample into  $n=300$
subsamples of approximately equal size and estimating a
$n=300$
subsamples of approximately equal size and estimating a  $\phi_{*,i}\text{(}M_{*}\text{)}$
each time. Thus, errors are then given by:
$\phi_{*,i}\text{(}M_{*}\text{)}$
each time. Thus, errors are then given by:
 \begin{equation} \sigma^2 = \frac{n-1}{n} \sum_{i=1}^n\left(\phi_{*,i} - \langle\phi_{*}\rangle\right)^2, \end{equation}
\begin{equation} \sigma^2 = \frac{n-1}{n} \sum_{i=1}^n\left(\phi_{*,i} - \langle\phi_{*}\rangle\right)^2, \end{equation}
with  $\langle\phi_{*}\rangle$
as the average of the ensemble.
$\langle\phi_{*}\rangle$
as the average of the ensemble.
Stellar masses were derived from several colour-dependent mass-to-light ratios as listed below:
 \begin{equation} {M_{*}} = \left\{ \begin{array}{c l} \Upsilon^{\rm B03}_r(g-r)\cdot L_r & \mbox{{{{Bell} et al.}} ({2003})}\\ \Upsilon^{\rm B03}_i(g-i)\cdot L_i & \mbox{{{{Bell} et al.}} ({2003})}\\ \Upsilon^{\rm Z09}_r(g-r)\cdot L_r & \mbox{{{Zibetti, Charlot, \& Rix et al.}} ({2009})}\\ \Upsilon^{\rm Z09}_i(g-i)\cdot L_i & \mbox{{{{Zibetti} et al.}} ({2009})}\\ \Upsilon^{\rm T11}_i(g-i)\cdot L_i & \mbox{{{{Taylor} et al.}} ({2011})}\\ \end{array},\right. \end{equation}
\begin{equation} {M_{*}} = \left\{ \begin{array}{c l} \Upsilon^{\rm B03}_r(g-r)\cdot L_r & \mbox{{{{Bell} et al.}} ({2003})}\\ \Upsilon^{\rm B03}_i(g-i)\cdot L_i & \mbox{{{{Bell} et al.}} ({2003})}\\ \Upsilon^{\rm Z09}_r(g-r)\cdot L_r & \mbox{{{Zibetti, Charlot, \& Rix et al.}} ({2009})}\\ \Upsilon^{\rm Z09}_i(g-i)\cdot L_i & \mbox{{{{Zibetti} et al.}} ({2009})}\\ \Upsilon^{\rm T11}_i(g-i)\cdot L_i & \mbox{{{{Taylor} et al.}} ({2011})}\\ \end{array},\right. \end{equation}
and we define our fiducial  $M_{*}$
as the geometrical mean of all the determinations in 34:
$M_{*}$
as the geometrical mean of all the determinations in 34:
 \begin{eqnarray} M_*= [M_*(\Upsilon^{\rm B03}_r) \times M_*(\Upsilon^{\rm B03}_i) \times M_*(\Upsilon^{\rm Z09}_r) \times &\end{eqnarray}
\begin{eqnarray} M_*= [M_*(\Upsilon^{\rm B03}_r) \times M_*(\Upsilon^{\rm B03}_i) \times M_*(\Upsilon^{\rm Z09}_r) \times &\end{eqnarray}
 \begin{eqnarray} \nonumber M_*(\Upsilon^{\rm Z09}_i) \times M_*(\Upsilon^{\rm T11}_i)]^{1/5} \end{eqnarray}
\begin{eqnarray} \nonumber M_*(\Upsilon^{\rm Z09}_i) \times M_*(\Upsilon^{\rm T11}_i)]^{1/5} \end{eqnarray}
We use Sérsic apparent magnitudes to derive colours and magnitudes. We apply K+E-corrections at a rest frame  $z=0$
. We use the values reported in Dragomir et al. (Reference Dragomir, Rodrguez-Puebla, Primack and Lee2018) for g and i bands given, respectively, by
$z=0$
. We use the values reported in Dragomir et al. (Reference Dragomir, Rodrguez-Puebla, Primack and Lee2018) for g and i bands given, respectively, by  $E_{g} = 1.3\times z$
and
$E_{g} = 1.3\times z$
and  $E_{i} = 1.09\times z$
. K-corrections are discuss in Appendix B. We applied a shift of
$E_{i} = 1.09\times z$
. K-corrections are discuss in Appendix B. We applied a shift of  $-0.1$
dex to the resulting masses from the colour-dependent mass-to-light ratios of Bell et al. (Reference Bell, McIntosh, Katz and Weinberg2003) to be consistent with the Chabrier (Reference Chabrier2003) IMF adopted in this paper.
$-0.1$
dex to the resulting masses from the colour-dependent mass-to-light ratios of Bell et al. (Reference Bell, McIntosh, Katz and Weinberg2003) to be consistent with the Chabrier (Reference Chabrier2003) IMF adopted in this paper.
Figure 11 shows the resulting  $\mbox{GSMF}$
s as described above. The figure shows that using different recipes of deriving stellar masses yield to differences of
$\mbox{GSMF}$
s as described above. The figure shows that using different recipes of deriving stellar masses yield to differences of  $\sim\!0.1$
dex at low masses and between
$\sim\!0.1$
dex at low masses and between  $\sim\!0.5-1$
dex at the high-mass end. This is consistent with the recent study by (Bernardi et al. Reference Bernardi, Meert, Sheth, Fischer, Huertas-Company, Maraston, Shankar and Vikram2017) which showed that differences in mass-to-light ratios introduce discrepancies in the GSMF around
$\sim\!0.5-1$
dex at the high-mass end. This is consistent with the recent study by (Bernardi et al. Reference Bernardi, Meert, Sheth, Fischer, Huertas-Company, Maraston, Shankar and Vikram2017) which showed that differences in mass-to-light ratios introduce discrepancies in the GSMF around  $\sim\!0.5$
dex. As a fiducial estimation of the GSMF in this paper, we opt to utilise the geometric mean of all the masses derived based on the colour-dependent mass-to-light ratios listed in Equation (34), filled circles with error bars. The black solid line shows a shift of
$\sim\!0.5$
dex. As a fiducial estimation of the GSMF in this paper, we opt to utilise the geometric mean of all the masses derived based on the colour-dependent mass-to-light ratios listed in Equation (34), filled circles with error bars. The black solid line shows a shift of  $\pm 0.15$
dex in the stellar mass axis of our fiducial GSMF. Note that these shifts recover most of the differences observed due to systematics in mass-to-light ratios.
$\pm 0.15$
dex in the stellar mass axis of our fiducial GSMF. Note that these shifts recover most of the differences observed due to systematics in mass-to-light ratios.

Figure A1. The GSMF from our six stellar mass definitions, Equation A6. Using different stellar masses yield to differences of  $\sim\!0.1$
dex at low masses and as high as
$\sim\!0.1$
dex at low masses and as high as  $\sim\!1$
dex at the high-mass end. In this paper, we opted to use as our fiducial GSMF as the one derived from the geometric mean of five different stellar masses. The solid lines show a shift of
$\sim\!1$
dex at the high-mass end. In this paper, we opted to use as our fiducial GSMF as the one derived from the geometric mean of five different stellar masses. The solid lines show a shift of  $\pm0.15$
dex in the stellar mass axis of the our fiducial GSMF, note that it recovers systematics from mass-to-light ratios.
$\pm0.15$
dex in the stellar mass axis of the our fiducial GSMF, note that it recovers systematics from mass-to-light ratios.
B. K-corrections
Figure C1 shows the colour and redshift dependence of the K-corrections at a rest frame  $z=0$
for the r (upper left), g (upper right), and i (bottom left) bands, shown as the dashed lines, from the NYU-VAGC SDSS DR7 and calculated from the k-correct algorithm (v4_1_4 Blanton & Roweis Reference Blanton and Roweis2007). In the same figure, the solid lines show the best fit according to the following relations:
$z=0$
for the r (upper left), g (upper right), and i (bottom left) bands, shown as the dashed lines, from the NYU-VAGC SDSS DR7 and calculated from the k-correct algorithm (v4_1_4 Blanton & Roweis Reference Blanton and Roweis2007). In the same figure, the solid lines show the best fit according to the following relations:
 \begin{equation} K_j(z|\mathcal{C}) = \textbf{Z} \textbf{K}_j^{\mathcal{C}} \textbf{C,} \end{equation}
\begin{equation} K_j(z|\mathcal{C}) = \textbf{Z} \textbf{K}_j^{\mathcal{C}} \textbf{C,} \end{equation}
where j denotes the r, g, and i bands, while  $\mathcal{C}$
denotes the uncorrected
$\mathcal{C}$
denotes the uncorrected  $g-r$
and
$g-r$
and  $g-i$
galaxy colours. A similar approach has been done in Chilingarian, Melchior, & Zolotukhin (Reference Chilingarian, Melchior and Zolotukhin2010). The
$g-i$
galaxy colours. A similar approach has been done in Chilingarian, Melchior, & Zolotukhin (Reference Chilingarian, Melchior and Zolotukhin2010). The  $\textbf{C}$
and
$\textbf{C}$
and  $\textbf{Z}$
matrices are respectively given by
$\textbf{Z}$
matrices are respectively given by
 \begin{equation} \textbf{C} = \left( \begin{array}{c} 1\\ C\\ C^2\\ C^3\\ C^4\\ C^5\\ \end{array}\right), \end{equation}
\begin{equation} \textbf{C} = \left( \begin{array}{c} 1\\ C\\ C^2\\ C^3\\ C^4\\ C^5\\ \end{array}\right), \end{equation}
 \begin{equation} \textbf{Z} = \left( \begin{array}{c c c c c} z & z^2 & z^3 & z^4 & z^5\\ \end{array}\right), \end{equation}
\begin{equation} \textbf{Z} = \left( \begin{array}{c c c c c} z & z^2 & z^3 & z^4 & z^5\\ \end{array}\right), \end{equation}
while the  $\textbf{K}_j^{\mathcal{C}}$
matrices for the r, g, and i bands are respectively given by Equations (B4), (B5), and (B6). Note that our K-corrections are polynomials of degree 5 in both colour and redshift and that in the above set of Equation
$\textbf{K}_j^{\mathcal{C}}$
matrices for the r, g, and i bands are respectively given by Equations (B4), (B5), and (B6). Note that our K-corrections are polynomials of degree 5 in both colour and redshift and that in the above set of Equation  $K_j(z=0|\mathcal{C})=0$
.
$K_j(z=0|\mathcal{C})=0$
.
 {\fontsize{7.5}{9}\selectfont\begin{align} K_r^{g-r} = \left( \begin{array}{c c c c c c} 0.894302 & 2.32866 & -0.787673 & 0.324352 & -0.239774 & 0.0444971\\ -15.5648 & 1.544 & -2.70992 & 3.42484 & -0.280197 & -0.0221534\\ 49.7443 & -4.64543 & -8.72852 & 1.14138 & -1.76882 & 0.0702624\\ -48.9173 & -4.95549 & 2.06966 & 14.5241 & -2.48092 & -0.322153\\ 3.65716 & 21.3194 & -0.593275 & -6.04982 & -0.157727 & 0.731093\\ \end{array}\right) \end{align}}
{\fontsize{7.5}{9}\selectfont\begin{align} K_r^{g-r} = \left( \begin{array}{c c c c c c} 0.894302 & 2.32866 & -0.787673 & 0.324352 & -0.239774 & 0.0444971\\ -15.5648 & 1.544 & -2.70992 & 3.42484 & -0.280197 & -0.0221534\\ 49.7443 & -4.64543 & -8.72852 & 1.14138 & -1.76882 & 0.0702624\\ -48.9173 & -4.95549 & 2.06966 & 14.5241 & -2.48092 & -0.322153\\ 3.65716 & 21.3194 & -0.593275 & -6.04982 & -0.157727 & 0.731093\\ \end{array}\right) \end{align}}
 {\fontsize{7.5}{9}\selectfont\begin{align} K_g^{g-r} = \left( \begin{array}{c c c c c c} 0.0786144 & 4.01535 & -0.883155 & 0.707471 & -2.05303 & 0.793141\\ -6.81272 & 12.0599 & -10.7157 & 22.086 & -5.46384 & -1.34602\\ -7.17353 & -52.5682 & -13.5845 & 11.2634 & -6.25812 & 2.61254\\ 86.1835 & 96.7938 & -72.2792 & -1.44621 & -5.6531 & 9.09575\\ -106.868 & -23.5461 & 101.815 & -43.5146 & 40.8195 & -21.677\\ \end{array}\right) \end{align}}
{\fontsize{7.5}{9}\selectfont\begin{align} K_g^{g-r} = \left( \begin{array}{c c c c c c} 0.0786144 & 4.01535 & -0.883155 & 0.707471 & -2.05303 & 0.793141\\ -6.81272 & 12.0599 & -10.7157 & 22.086 & -5.46384 & -1.34602\\ -7.17353 & -52.5682 & -13.5845 & 11.2634 & -6.25812 & 2.61254\\ 86.1835 & 96.7938 & -72.2792 & -1.44621 & -5.6531 & 9.09575\\ -106.868 & -23.5461 & 101.815 & -43.5146 & 40.8195 & -21.677\\ \end{array}\right) \end{align}}
 {\fontsize{7.5}{9}\selectfont\begin{align} K_i^{g-i} = \left( \begin{array}{c c c c c c} -3.01597 & 3.287 & -0.455067 & 0.426496 & -0.242669 & 0.0283777\\ -1.11123 & -3.04641 & -5.2804 & 2.60911 & 0.134077 & -0.0813698\\ 68.4078 & -14.6203 & -5.06879 & 0.904234 & -1.82776 & 0.47701\\ -145.044 & 45.4714 & 8.75605 & 5.9425 & -1.32215 & -0.211679\\ 59.2903 & -12.387 & -10.8653 & -1.84054 & 0.843326 & -0.0248045\\ \end{array}\right) \end{align}}
{\fontsize{7.5}{9}\selectfont\begin{align} K_i^{g-i} = \left( \begin{array}{c c c c c c} -3.01597 & 3.287 & -0.455067 & 0.426496 & -0.242669 & 0.0283777\\ -1.11123 & -3.04641 & -5.2804 & 2.60911 & 0.134077 & -0.0813698\\ 68.4078 & -14.6203 & -5.06879 & 0.904234 & -1.82776 & 0.47701\\ -145.044 & 45.4714 & 8.75605 & 5.9425 & -1.32215 & -0.211679\\ 59.2903 & -12.387 & -10.8653 & -1.84054 & 0.843326 & -0.0248045\\ \end{array}\right) \end{align}}
C. GSMF for low-mass galaxies
C.1. Surface brightness correction completeness
In this paper, we are interested in deriving the GSMF over a wide dynamical mass range, that is, from dwarf galaxies to massive elliptical galaxies. In Appendix A, we describe that based on the SDSS DR7 galaxy sample, we determined the GSMF for galaxies above  $M_{*}\sim\!10^{9}\text{M}_{\odot}$
. In this section, we determine the GSMF for galaxies above
$M_{*}\sim\!10^{9}\text{M}_{\odot}$
. In this section, we determine the GSMF for galaxies above  $M_{*}\sim\!10^{7}\text{M}_{\odot}$
. Deriving the GSMF could be very challenging since the fraction of galaxies of missing galaxies due to surface brightness limits becomes very relevant at the faint end of the GSMF. Here, we follow a very simple statistical approach in order to quantify the number of galaxies missed due to surface brightness incompleteness limits as described in Blanton et al. (Reference Blanton, Lupton, Schlegel, Strauss, Brinkmann, Fukugita and Loveday2005b). Our galaxy sample consist of a small volume (
$M_{*}\sim\!10^{7}\text{M}_{\odot}$
. Deriving the GSMF could be very challenging since the fraction of galaxies of missing galaxies due to surface brightness limits becomes very relevant at the faint end of the GSMF. Here, we follow a very simple statistical approach in order to quantify the number of galaxies missed due to surface brightness incompleteness limits as described in Blanton et al. (Reference Blanton, Lupton, Schlegel, Strauss, Brinkmann, Fukugita and Loveday2005b). Our galaxy sample consist of a small volume ( $0.0033 < z < 0.05$
) carefully constructed to study very low-mass/luminosity galaxies from the SDSS NYU-VAGC with a total of 49968 galaxies (Blanton et al. Reference Blanton2005a; b)Footnote v. Hereafter, we will refer to this galaxy sample as the low-z SDSS.
$0.0033 < z < 0.05$
) carefully constructed to study very low-mass/luminosity galaxies from the SDSS NYU-VAGC with a total of 49968 galaxies (Blanton et al. Reference Blanton2005a; b)Footnote v. Hereafter, we will refer to this galaxy sample as the low-z SDSS.

Figure B1. Colour and redshift dependence of the K-corrections at a rest frame  $z=0$
for the r (upper left), g (upper right), and i (bottom left) bands from the k-correct algorithm (Blanton & Roweis Reference Blanton and Roweis2007), dashed lines. Solid lines show our best-fit models as described in the text.
$z=0$
for the r (upper left), g (upper right), and i (bottom left) bands from the k-correct algorithm (Blanton & Roweis Reference Blanton and Roweis2007), dashed lines. Solid lines show our best-fit models as described in the text.
Blanton et al. (Reference Blanton, Lupton, Schlegel, Strauss, Brinkmann, Fukugita and Loveday2005b) estimated that the low-z SDSS galaxy sample has a completeness  ${>}70\%$
for galaxies in the effective surface brightness range of
${>}70\%$
for galaxies in the effective surface brightness range of  $18<\mu_{50,r}< 24$
mag arcsec–2 and we consider galaxies only within this range. We assign to each galaxy a weight,
$18<\mu_{50,r}< 24$
mag arcsec–2 and we consider galaxies only within this range. We assign to each galaxy a weight,  $w_{\mu,j}$
, which is a function of their central surface brightness and it takes into account the spectroscopic incompleteness (
$w_{\mu,j}$
, which is a function of their central surface brightness and it takes into account the spectroscopic incompleteness ( $1 / w_{s,j}$
), photometric incompleteness (
$1 / w_{s,j}$
), photometric incompleteness ( $1 / w_{p,j}$
), and tiling catalogue incompleteness (
$1 / w_{p,j}$
), and tiling catalogue incompleteness ( $1 / w_{t,j}$
) in the sample. Thus,
$1 / w_{t,j}$
) in the sample. Thus,  $w_{\mu,j}=w_{s,j}\times w_{p,j} \times w_{t,j}$
. These weights were studied in detail in Blanton et al. (Reference Blanton, Lupton, Schlegel, Strauss, Brinkmann, Fukugita and Loveday2005b) and provide the correlation between
$w_{\mu,j}=w_{s,j}\times w_{p,j} \times w_{t,j}$
. These weights were studied in detail in Blanton et al. (Reference Blanton, Lupton, Schlegel, Strauss, Brinkmann, Fukugita and Loveday2005b) and provide the correlation between  $w_{\mu,j}$
and effective surface brightness,
$w_{\mu,j}$
and effective surface brightness,  $\mu_{50,r}$
, in a tabulated form, see their Table 1. We use cubic spline interpolations of this table in order to assign weight
$\mu_{50,r}$
, in a tabulated form, see their Table 1. We use cubic spline interpolations of this table in order to assign weight  $w_{\mu,j}$
to each galaxy in the sample.
$w_{\mu,j}$
to each galaxy in the sample.
The next step in our programme is to estimate the number of missed galaxies brighter than  $\mu_{50,r} = 24$
mag arcsec-2. To that end, we introduce a model for the distribution of
$\mu_{50,r} = 24$
mag arcsec-2. To that end, we introduce a model for the distribution of  $\mu_{50,r}$
as a function of
$\mu_{50,r}$
as a function of  $M_{*}$
. We define the fraction of missing galaxies brighter than
$M_{*}$
. We define the fraction of missing galaxies brighter than  $\mu_{50,r} = 24$
mag arcsec-2 as a function of stellar mass as:
$\mu_{50,r} = 24$
mag arcsec-2 as a function of stellar mass as:
 \begin{equation} f_{\rm loss} \text{(}M_{*}\text{)} = \frac {\sum\limits_{j} N_{\rm obs} (\mu_{50,j}|{M_{*}}) }{\sum\limits_{j} N_{\rm real} (\mu_{50,j}|{M_{*}}) }, \end{equation}
\begin{equation} f_{\rm loss} \text{(}M_{*}\text{)} = \frac {\sum\limits_{j} N_{\rm obs} (\mu_{50,j}|{M_{*}}) }{\sum\limits_{j} N_{\rm real} (\mu_{50,j}|{M_{*}}) }, \end{equation}
where  $N_{\rm real} (\mu_{50,j}|{M_{*}})$
and
$N_{\rm real} (\mu_{50,j}|{M_{*}})$
and  $N_{\rm obs} (\mu_{50,j}|{M_{*}})$
are the real and observed number galaxies with surface brightness (SB) between
$N_{\rm obs} (\mu_{50,j}|{M_{*}})$
are the real and observed number galaxies with surface brightness (SB) between  $\mu_{50,j} \pm d\mu_{50,j} $
and stellar masses between
$\mu_{50,j} \pm d\mu_{50,j} $
and stellar masses between  $\log{M_{*}}\pm d\log{M_{*}}/2$
, respectively. Thus, our problem reduces to estimate
$\log{M_{*}}\pm d\log{M_{*}}/2$
, respectively. Thus, our problem reduces to estimate  $N_{\rm real}$
. Let us now define
$N_{\rm real}$
. Let us now define  $P(\mu_{50,r}|{M_{*}})$
as the conditional probability distribution of galaxies with SB
$P(\mu_{50,r}|{M_{*}})$
as the conditional probability distribution of galaxies with SB  $\mu_{50,r}\pm d\mu_{50,r}/2$
at a stellar mass bin
$\mu_{50,r}\pm d\mu_{50,r}/2$
at a stellar mass bin  $\log{M_{*}}\pm d\log{M_{*}}/2$
. We calculate
$\log{M_{*}}\pm d\log{M_{*}}/2$
. We calculate  $P(\mu_{50,r}|{M_{*}})$
directly from our galaxy sample by dividing it into stellar mass bins of 0.5 dex. This is done only for galaxies with Sérsic index
$P(\mu_{50,r}|{M_{*}})$
directly from our galaxy sample by dividing it into stellar mass bins of 0.5 dex. This is done only for galaxies with Sérsic index  $n_s\leq2$
(galaxies with
$n_s\leq2$
(galaxies with  $n_s>2$
are mostly of high SB,
$n_s>2$
are mostly of high SB,  $\mu_{50,r} < 24$
mag arcsec–2, so that it is not necessary to correct them for missing galaxies). For each stellar mass bin, we perform an extra binning of 0.05 dex in SB. We carry out the mentioned binning in
$\mu_{50,r} < 24$
mag arcsec–2, so that it is not necessary to correct them for missing galaxies). For each stellar mass bin, we perform an extra binning of 0.05 dex in SB. We carry out the mentioned binning in  $M_{*}$
and
$M_{*}$
and  $\mu_{50,r}$
for each of the six different stellar mass estimators described above. As an example, the upper panel in Figure C2 show the distributions
$\mu_{50,r}$
for each of the six different stellar mass estimators described above. As an example, the upper panel in Figure C2 show the distributions  $P(\mu_{50,r}|{M_{*}})$
for one of our stellar mass estimators (empty circles). For each
$P(\mu_{50,r}|{M_{*}})$
for one of our stellar mass estimators (empty circles). For each  $M_{*}$
bin, we fit
$M_{*}$
bin, we fit  $P(\mu_{50,r}|{M_{*}})$
assuming that it is described by a lognormal distribution,
$P(\mu_{50,r}|{M_{*}})$
assuming that it is described by a lognormal distribution,
 \begin{equation} P(\mu_{50,r}|{M_{*}}) = \frac{1}{\sqrt{2\pi\sigma_\mu^2}} \exp\left[-\frac{\left(\mu_{50,r}-\langle\mu_{50,r}\text{(}M_{*}\text{)}\rangle\right)^2}{2\sigma_\mu^2}\right], \end{equation}
\begin{equation} P(\mu_{50,r}|{M_{*}}) = \frac{1}{\sqrt{2\pi\sigma_\mu^2}} \exp\left[-\frac{\left(\mu_{50,r}-\langle\mu_{50,r}\text{(}M_{*}\text{)}\rangle\right)^2}{2\sigma_\mu^2}\right], \end{equation}

Figure C1. Left panels: Conditional probability distribution  $P(\mu_{50,r}|{M_{*}})$
when using stellar mass estimations based on the fits to
$P(\mu_{50,r}|{M_{*}})$
when using stellar mass estimations based on the fits to  $g-i$
colours and absolute magnitudes
$g-i$
colours and absolute magnitudes  $M_i$
from Zibetti et al. (Reference Zibetti, Charlot and Rix2009). Empty circles show the resulting distribution from observations of galaxies with Sersic index
$M_i$
from Zibetti et al. (Reference Zibetti, Charlot and Rix2009). Empty circles show the resulting distribution from observations of galaxies with Sersic index  $n_s\leq2$
only. Solid lines show the fit to observations when assuming a lognormal model distribution as described in the text. Right panels: SB-to-galaxy stellar mass relation for three different stellar mass estimators used in this paper. Solid circles show the mean values of
$n_s\leq2$
only. Solid lines show the fit to observations when assuming a lognormal model distribution as described in the text. Right panels: SB-to-galaxy stellar mass relation for three different stellar mass estimators used in this paper. Solid circles show the mean values of  $\mu_{50}$
that are affected by SB incompleteness while empty circles show that are complete according Blanton et al. (Reference Blanton, Lupton, Schlegel, Strauss, Brinkmann, Fukugita and Loveday2005b).
$\mu_{50}$
that are affected by SB incompleteness while empty circles show that are complete according Blanton et al. (Reference Blanton, Lupton, Schlegel, Strauss, Brinkmann, Fukugita and Loveday2005b).
where  $\langle\mu_{50,r}\text{(}M_{*}\text{)}\rangle$
and
$\langle\mu_{50,r}\text{(}M_{*}\text{)}\rangle$
and  $\sigma_\mu$
are the mean SB at a given stellar mass and the dispersion around it. We fit these two free parameters for each stellar mass bin. The best fits are plotted with solid lines. This operation is carried out for each of the stellar mass estimators used here. In the bottom panels of Figure C2, we show an example of the resulting best fits to observations as circles with error bars in the bivariate (
$\sigma_\mu$
are the mean SB at a given stellar mass and the dispersion around it. We fit these two free parameters for each stellar mass bin. The best fits are plotted with solid lines. This operation is carried out for each of the stellar mass estimators used here. In the bottom panels of Figure C2, we show an example of the resulting best fits to observations as circles with error bars in the bivariate ( $\mu_{50,r}, M_{*}$
) distribution plane (grey iso-contours) for three of our stellar mass estimators. The dashed lines show our SB magnitudes limits. Similarly to Baldry et al. (Reference Baldry, Glazebrook and Driver2008), we find that the relation between
$\mu_{50,r}, M_{*}$
) distribution plane (grey iso-contours) for three of our stellar mass estimators. The dashed lines show our SB magnitudes limits. Similarly to Baldry et al. (Reference Baldry, Glazebrook and Driver2008), we find that the relation between  $\langle\mu_{50,r}\rangle$
and
$\langle\mu_{50,r}\rangle$
and  $\log M_{*}$
is linear for galaxies above
$\log M_{*}$
is linear for galaxies above  $M_{*}\sim\!10^{9}\text{M}_{\odot}$
Footnote w (filled circles) in the right panels of Figure C2. Departures from this linearity for galaxies below
$M_{*}\sim\!10^{9}\text{M}_{\odot}$
Footnote w (filled circles) in the right panels of Figure C2. Departures from this linearity for galaxies below  $M_{*}\sim\!10^{9}\text{M}_{\odot}$
(filled circles) is an indication that the relation between
$M_{*}\sim\!10^{9}\text{M}_{\odot}$
(filled circles) is an indication that the relation between  $\langle\mu_{50,r}\rangle$
and
$\langle\mu_{50,r}\rangle$
and  $\log M_{*}$
is affected by SB incompleteness. We fit the relationship between
$\log M_{*}$
is affected by SB incompleteness. We fit the relationship between  $\langle\mu_{50,r}\rangle$
and
$\langle\mu_{50,r}\rangle$
and  $\log M_{*}$
for galaxies above
$\log M_{*}$
for galaxies above  $M_{*} = 10^{9}\text{M}_{\odot}$
(where the missing number of low SB galaxies is negligible) as
$M_{*} = 10^{9}\text{M}_{\odot}$
(where the missing number of low SB galaxies is negligible) as
 \begin{equation} \langle\mu_{50,r}\rangle = \alpha \log M_{*} +\beta. \end{equation}
\begin{equation} \langle\mu_{50,r}\rangle = \alpha \log M_{*} +\beta. \end{equation}
For simplicity, we assume that the dispersion around this relation,  $\sigma_\mu$
, is independent of mass and has the same value for all the mass estimators; we assign a value of 0.75 dex, which is close to most of the values determined by fitting Equation (10) to the data from our galaxy sample for the three methods of assigning stellar masses. Note that the values of
$\sigma_\mu$
, is independent of mass and has the same value for all the mass estimators; we assign a value of 0.75 dex, which is close to most of the values determined by fitting Equation (10) to the data from our galaxy sample for the three methods of assigning stellar masses. Note that the values of  $\alpha$
and
$\alpha$
and  $\beta$
depend on each stellar mass estimator implying that SB corrections are susceptive to systematics due to stellar masses estimators. The next step is to assume that the distribution of real galaxies,
$\beta$
depend on each stellar mass estimator implying that SB corrections are susceptive to systematics due to stellar masses estimators. The next step is to assume that the distribution of real galaxies,  $N_{\rm real}$
, can be generated from the probability distribution
$N_{\rm real}$
, can be generated from the probability distribution  $P(\mu_{50}|{M_{*}})$
by simply extrapolating Equations (11) and (10) up to
$P(\mu_{50}|{M_{*}})$
by simply extrapolating Equations (11) and (10) up to  $M_{*}\sim\!10^{7}\ \text{M}_{\odot}$
. Using the definition of
$M_{*}\sim\!10^{7}\ \text{M}_{\odot}$
. Using the definition of  $w_{\mu,j}$
(the SB completeness factor), the observed distribution of galaxies,
$w_{\mu,j}$
(the SB completeness factor), the observed distribution of galaxies,  $N_{\rm obs}$
, is thus generated from the probability distribution
$N_{\rm obs}$
, is thus generated from the probability distribution  $P_{\rm obs}(\mu_{50,r}|{M_{*}}) = (1/ w_{\mu}) \times P(\mu_{50,r}|{M_{*}})$
. The factor of missing galaxies below the SB
$P_{\rm obs}(\mu_{50,r}|{M_{*}}) = (1/ w_{\mu}) \times P(\mu_{50,r}|{M_{*}})$
. The factor of missing galaxies below the SB  $\mu_{50} = 24$
mag arcsec–2 at a given stellar mass is then
$\mu_{50} = 24$
mag arcsec–2 at a given stellar mass is then
 \begin{equation} f_{\rm loss} \text{(}M_{*}\text{)} = \int \left(1/ w_{\mu}\right) P(\mu_{50,r}|{M_{*}}) d\mu_{50,r} \Big/ \int P(\mu_{50,r}|{M_{*}}) d\mu_{50,r}. \end{equation}
\begin{equation} f_{\rm loss} \text{(}M_{*}\text{)} = \int \left(1/ w_{\mu}\right) P(\mu_{50,r}|{M_{*}}) d\mu_{50,r} \Big/ \int P(\mu_{50,r}|{M_{*}}) d\mu_{50,r}. \end{equation}
Thus, we weight every galaxy in the sample with:
 \begin{equation} w_{{\rm SB},j} = w_{\mu,j} \times w_{\rm loss}, \end{equation}
\begin{equation} w_{{\rm SB},j} = w_{\mu,j} \times w_{\rm loss}, \end{equation}
where
 \begin{equation} w_{\rm loss} = \left\{ \begin{array}{rcl} 1 / f_{\rm loss} & \quad\mbox{for} & \quad n_s\leq2 \\
1 & \quad\mbox{for} & \quad\mbox{else}. \end{array}\right. \end{equation}
\begin{equation} w_{\rm loss} = \left\{ \begin{array}{rcl} 1 / f_{\rm loss} & \quad\mbox{for} & \quad n_s\leq2 \\
1 & \quad\mbox{for} & \quad\mbox{else}. \end{array}\right. \end{equation}
We are now in position to estimate the GSMF corrected by SB incompleteness.
C.2. The dependence of a stellar mass limit sample with redshift
In order to calculate the GSMF, we start by determining how the apparent magnitude limit of the SDSS transforms into a stellar mass limit. In other words, given that the apparent magnitude limit of the SDSS is  $m_{r, {\rm lim}} = 17.77$
, we compute the equivalent in terms of stellar mass,
$m_{r, {\rm lim}} = 17.77$
, we compute the equivalent in terms of stellar mass,  $M_{*, \rm lim}$
. Following van den Bosch et al. (Reference van den Bosch, Aquino, Yang, Mo, Pasquali, McIntosh, Weinmann and Kang2008), we determined the redshift-dependent absolute magnitude limit
$M_{*, \rm lim}$
. Following van den Bosch et al. (Reference van den Bosch, Aquino, Yang, Mo, Pasquali, McIntosh, Weinmann and Kang2008), we determined the redshift-dependent absolute magnitude limit  $M_{r, {\rm lim}}^{0.0}$
given the apparent magnitude limit from the SDSS
$M_{r, {\rm lim}}^{0.0}$
given the apparent magnitude limit from the SDSS  $m_{r, {\rm lim}} = 17.77$
$m_{r, {\rm lim}} = 17.77$
 \begin{equation} M_{r, {\rm lim}}^{0.0} = m_{r, {\rm lim}} - 5 \log D_{L}(z) - 25 - K_{\langle gr \rangle }(z) + E_{r}(z), \end{equation}
\begin{equation} M_{r, {\rm lim}}^{0.0} = m_{r, {\rm lim}} - 5 \log D_{L}(z) - 25 - K_{\langle gr \rangle }(z) + E_{r}(z), \end{equation}
where  $D_{L}$
,
$D_{L}$
,  $K_{\langle gr \rangle}$
, and
$K_{\langle gr \rangle}$
, and  $E_{r}$
are functions described in Appendix A. Note that we have emphasised the use of average colours for the
$E_{r}$
are functions described in Appendix A. Note that we have emphasised the use of average colours for the  $K-$
correction because we are interested in the stellar mass limit for all the galaxies. Thus, the above absolute magnitude limit depends both on redshift and colour (van den Bosch et al. Reference van den Bosch, Aquino, Yang, Mo, Pasquali, McIntosh, Weinmann and Kang2008). Using the colour-dependent mass-to-light ratio
$K-$
correction because we are interested in the stellar mass limit for all the galaxies. Thus, the above absolute magnitude limit depends both on redshift and colour (van den Bosch et al. Reference van den Bosch, Aquino, Yang, Mo, Pasquali, McIntosh, Weinmann and Kang2008). Using the colour-dependent mass-to-light ratio  $\Upsilon^{\rm Z09}_r(g-r)$
from Zibetti et al. (Reference Zibetti, Charlot and Rix2009), we transform
$\Upsilon^{\rm Z09}_r(g-r)$
from Zibetti et al. (Reference Zibetti, Charlot and Rix2009), we transform  $M_{r, {\rm lim}}^{0.0}$
into a stellar mass limit
$M_{r, {\rm lim}}^{0.0}$
into a stellar mass limit
 \begin{equation} M_{*, \rm lim} = -0.84 + 1.654\times \langle g-r \rangle^{0.0} - 0.4 \times \left( M_{r, {\rm lim}}^{0.0} - 4.64 \right). \end{equation}
\begin{equation} M_{*, \rm lim} = -0.84 + 1.654\times \langle g-r \rangle^{0.0} - 0.4 \times \left( M_{r, {\rm lim}}^{0.0} - 4.64 \right). \end{equation}
Finally, we use the mean relationship between colour and stellar mass for blue and red galaxies as well as the fraction of red,  $f_{\rm R}$
, and blue galaxies,
$f_{\rm R}$
, and blue galaxies,  $f_{\rm B}$
, to compute the average colour–stellar mass relationship as
$f_{\rm B}$
, to compute the average colour–stellar mass relationship as
 \begin{equation} \langle g-r \rangle^{0.0} = f_{\rm B} (g-r)_{\rm B}^{0.0} + f_{\rm Q} (g-r)_{\rm Q}^{0.0}, \end{equation}
\begin{equation} \langle g-r \rangle^{0.0} = f_{\rm B} (g-r)_{\rm B}^{0.0} + f_{\rm Q} (g-r)_{\rm Q}^{0.0}, \end{equation}
where  $(g-r)_{\rm B}^{0.0}$
and
$(g-r)_{\rm B}^{0.0}$
and  $(g-r)_{\rm Q}^{0.0}$
are the best-fit models to the mean colour–stellar mass relationships of blue and red galaxies.
$(g-r)_{\rm Q}^{0.0}$
are the best-fit models to the mean colour–stellar mass relationships of blue and red galaxies.
We paused here for a moment and described our method to derive  ${(g-r)_{\rm B}^{0.0}}$
and
${(g-r)_{\rm B}^{0.0}}$
and  ${(g-r)_{\rm Q}^{0.0}}$
. To do so, we use the SDSS DR7 based on the photometric catalogue from Meert et al. (Reference Meert, Vikram and Bernardi2016). We choose to use this catalogue as contains many more galaxies than the SDSS DR4 and one could derive robust colour distributions. We derived the observed distribution function of galaxy colours as a function of stellar mass,
${(g-r)_{\rm Q}^{0.0}}$
. To do so, we use the SDSS DR7 based on the photometric catalogue from Meert et al. (Reference Meert, Vikram and Bernardi2016). We choose to use this catalogue as contains many more galaxies than the SDSS DR4 and one could derive robust colour distributions. We derived the observed distribution function of galaxy colours as a function of stellar mass,  ${P_{gr}(g-r|{M_{*}})}$
, that is the observed distribution of galaxy colours at the range between
${P_{gr}(g-r|{M_{*}})}$
, that is the observed distribution of galaxy colours at the range between  ${(g-r)^{0.0}\pm\Delta (g-r)^{0.0}/2}$
and
${(g-r)^{0.0}\pm\Delta (g-r)^{0.0}/2}$
and  $\log{M_{*}}\pm\Delta\log{M_{*}} /2$
. We divide our space into 20 bins equally spaced for
$\log{M_{*}}\pm\Delta\log{M_{*}} /2$
. We divide our space into 20 bins equally spaced for  ${(g-r)^{0.0}}$
between
${(g-r)^{0.0}}$
between  ${(g-r)^{0.0} = 0}$
and
${(g-r)^{0.0} = 0}$
and  ${(g-r)^{0.0} = 1.4}$
and into 25 bins equally spaced between
${(g-r)^{0.0} = 1.4}$
and into 25 bins equally spaced between  $\log {M_{*}} = 8.5 - 12$
. For galaxy stellar masses, we use our fiducial definition from Appendix A.
$\log {M_{*}} = 8.5 - 12$
. For galaxy stellar masses, we use our fiducial definition from Appendix A.
We assume that the distribution  ${P_{gr}(g-r|{M_{*}})}$
is bimodal and composed of two Gaussian distributions, this is a good approximation as shown by previous studies (e.g., Baldry et al. Reference Baldry, Glazebrook, Brinkmann, Ivezić, Lupton, Nichol and Szalay2004, Reference Baldry, Balogh, Bower, Glazebrook, Nichol, Bamford and Budavari2006). We associate one of the modes of
${P_{gr}(g-r|{M_{*}})}$
is bimodal and composed of two Gaussian distributions, this is a good approximation as shown by previous studies (e.g., Baldry et al. Reference Baldry, Glazebrook, Brinkmann, Ivezić, Lupton, Nichol and Szalay2004, Reference Baldry, Balogh, Bower, Glazebrook, Nichol, Bamford and Budavari2006). We associate one of the modes of  ${P_{gr}(g-r|{M_{*}})}$
with the distribution of blue galaxies, denoted by
${P_{gr}(g-r|{M_{*}})}$
with the distribution of blue galaxies, denoted by  ${P_{gr,{\rm B}}(g-r|{M_{*}})}$
, while the remaining one with the distribution of red galaxies, denoted by
${P_{gr,{\rm B}}(g-r|{M_{*}})}$
, while the remaining one with the distribution of red galaxies, denoted by  ${P_{gr,{\rm R}}(g-r|{M_{*}})}$
. The relation between these distributions is given by:
${P_{gr,{\rm R}}(g-r|{M_{*}})}$
. The relation between these distributions is given by:
 \begin{align} P_{gr,{\rm B}}(g-r|{M_{*}}) &= f_{\rm B} \text{(}M_{*}\text{)} P_{gr,{\rm B}}(g-r|{M_{*}}) \nonumber\\[2pt]
&\quad + f_{\rm R} \text{(}M_{*}\text{)} P_{gr,{\rm R}}(g-r|{M_{*}}). \end{align}
\begin{align} P_{gr,{\rm B}}(g-r|{M_{*}}) &= f_{\rm B} \text{(}M_{*}\text{)} P_{gr,{\rm B}}(g-r|{M_{*}}) \nonumber\\[2pt]
&\quad + f_{\rm R} \text{(}M_{*}\text{)} P_{gr,{\rm R}}(g-r|{M_{*}}). \end{align}
We assume that  ${P_{gr,j}(g-r|{M_{*}})}$
, with
${P_{gr,j}(g-r|{M_{*}})}$
, with  $ j = $
B or R, is a Gaussian distribution given by:
$ j = $
B or R, is a Gaussian distribution given by:
 \begin{equation} \begin{split} P_{gr,j}(g-r|{M_{*}}) = \frac{1}{\sqrt{2\pi\sigma_j^2\text{(}M_{*}\text{)}}} \times \\
\exp\left[-\frac{((g-r)^{0.0} - (g-r)_{j}^{0.0}\text{(}M_{*}\text{)})^2}{2\sigma_j^2\text{(}M_{*}\text{)}}\right], \end{split} \end{equation}
\begin{equation} \begin{split} P_{gr,j}(g-r|{M_{*}}) = \frac{1}{\sqrt{2\pi\sigma_j^2\text{(}M_{*}\text{)}}} \times \\
\exp\left[-\frac{((g-r)^{0.0} - (g-r)_{j}^{0.0}\text{(}M_{*}\text{)})^2}{2\sigma_j^2\text{(}M_{*}\text{)}}\right], \end{split} \end{equation}
where  ${(g-r)_{j}^{0.0}\text{(}M_{*}\text{)}}$
, with
${(g-r)_{j}^{0.0}\text{(}M_{*}\text{)}}$
, with  $ j = $
B or R, is the mean colour–stellar mass relationship used in Equation (17) and
$ j = $
B or R, is the mean colour–stellar mass relationship used in Equation (17) and  $\sigma_j\text{(}M_{*}\text{)}$
is the standard deviation that depends on
$\sigma_j\text{(}M_{*}\text{)}$
is the standard deviation that depends on  $M_{*}$
. The functional forms for
$M_{*}$
. The functional forms for  ${(g-r)_{j}^{0.0}\text{(}M_{*}\text{)}}$
and
${(g-r)_{j}^{0.0}\text{(}M_{*}\text{)}}$
and  $\sigma_j\text{(}M_{*}\text{)}$
are given by
$\sigma_j\text{(}M_{*}\text{)}$
are given by
 \begin{equation} (g-r)_{j}^{0.0}\text{(}M_{*}) = \alpha_j + \beta_j\times\log\left(\frac{M_{*}}{10^{11}\text{M}_{\odot}} \right), \end{equation}
\begin{equation} (g-r)_{j}^{0.0}\text{(}M_{*}) = \alpha_j + \beta_j\times\log\left(\frac{M_{*}}{10^{11}\text{M}_{\odot}} \right), \end{equation}
and
 \begin{equation} \sigma_j\text{(}M_{*}\text{)} = \lambda_j + \kappa_j\times\log\text{(}M_{*}\text{)}, \end{equation}
\begin{equation} \sigma_j\text{(}M_{*}\text{)} = \lambda_j + \kappa_j\times\log\text{(}M_{*}\text{)}, \end{equation}
for  $ j = $
B, R. Finally, for the fraction of red galaxies, we assume that
$ j = $
B, R. Finally, for the fraction of red galaxies, we assume that
 \begin{equation} f_{\rm R} \text{(}M_{*}\text{)} = \frac{1}{1+ \left[ a + b\left( M_{*} / M_{\rm C} \right) \right]^{\gamma}}. \end{equation}
\begin{equation} f_{\rm R} \text{(}M_{*}\text{)} = \frac{1}{1+ \left[ a + b\left( M_{*} / M_{\rm C} \right) \right]^{\gamma}}. \end{equation}
We performed a  $\chi^2$
minimisation procedure to the observed galaxy colour bimodality in order to find the best-fitting parameters to the functional forms described above. Our best-fitting parameters are:
$\chi^2$
minimisation procedure to the observed galaxy colour bimodality in order to find the best-fitting parameters to the functional forms described above. Our best-fitting parameters are:  $(\alpha_{\rm B}, \beta_{\rm B}, \lambda_{\rm B}, \kappa_{\rm B},\alpha_{\rm R}, \beta_{\rm R}, \lambda_{\rm R}, \kappa_{\rm R}, a,b,\log M_{\rm C},\gamma) = (0.514,\, 0.086,\, 0.240,\, -0.015,\, 0.720,\, 0.064,\, -0.068,\, 0.014,\, 0.001, 1.390, 10.586, -1.001)$
.
$(\alpha_{\rm B}, \beta_{\rm B}, \lambda_{\rm B}, \kappa_{\rm B},\alpha_{\rm R}, \beta_{\rm R}, \lambda_{\rm R}, \kappa_{\rm R}, a,b,\log M_{\rm C},\gamma) = (0.514,\, 0.086,\, 0.240,\, -0.015,\, 0.720,\, 0.064,\, -0.068,\, 0.014,\, 0.001, 1.390, 10.586, -1.001)$
.
The upper panel of Figure C3 shows the dependence of  $M_{*, \rm lim}$
with redshift. The region above
$M_{*, \rm lim}$
with redshift. The region above  $M_{*, \rm lim}$
is the area above which the NYU-VAGC galaxy sample is a volume-limited sample that is complete in stellar mass. The small grey dots show individual galaxies from the NYU-VAGC sample in the case that stellar masses were determined using the geometric mean of all our stellar mass estimators.
$M_{*, \rm lim}$
is the area above which the NYU-VAGC galaxy sample is a volume-limited sample that is complete in stellar mass. The small grey dots show individual galaxies from the NYU-VAGC sample in the case that stellar masses were determined using the geometric mean of all our stellar mass estimators.
C.3. Volume and large-scale structure corrections
In a volume-limited sample that is complete in stellar mass, we can derive the GSMF as the number of observed galaxies,  $N_{\rm gals}$
, per unit of comoving volume V with stellar masses between
$N_{\rm gals}$
, per unit of comoving volume V with stellar masses between  $\log {M_{*}}\pm \Delta \log{M_{*}}/2$
, that is,
$\log {M_{*}}\pm \Delta \log{M_{*}}/2$
, that is,  $\phi_{\ast}\text{(}M_{*}\text{)} \Delta \log{M_{*}} = N_{\rm gals} / V$
. Once we determined the dependence of the stellar mass limit with redshift,
$\phi_{\ast}\text{(}M_{*}\text{)} \Delta \log{M_{*}} = N_{\rm gals} / V$
. Once we determined the dependence of the stellar mass limit with redshift,  $M_{*, \rm lim}$
, from the SDSS NYU VAGC sample, we can use the above idea by defining various volume-limited subsamples that are complete in stellar mass. These subsamples were defined by dividing the galaxy redshift range covered by the NYU VAGC,
$M_{*, \rm lim}$
, from the SDSS NYU VAGC sample, we can use the above idea by defining various volume-limited subsamples that are complete in stellar mass. These subsamples were defined by dividing the galaxy redshift range covered by the NYU VAGC,  $0.0033<z<0.005$
, into 20 bins. Therefore, the GSMF for the jth volume-limited subsample at the redshift range
$0.0033<z<0.005$
, into 20 bins. Therefore, the GSMF for the jth volume-limited subsample at the redshift range  $z\pm\Delta z/2$
that is complete in stellar mass can be estimated for the mass bin
$z\pm\Delta z/2$
that is complete in stellar mass can be estimated for the mass bin  $\log {M_{*}} \pm \Delta \log {M_{*}}/2$
as
$\log {M_{*}} \pm \Delta \log {M_{*}}/2$
as
 \begin{equation} \phi_j(M_{\ast},z) \Delta \log {M_{*}}= \frac{N_{{\rm gals},j}(M_{\ast},z)}{V(z-\Delta z/2) - V(z+\Delta z/2)}. \end{equation}
\begin{equation} \phi_j(M_{\ast},z) \Delta \log {M_{*}}= \frac{N_{{\rm gals},j}(M_{\ast},z)}{V(z-\Delta z/2) - V(z+\Delta z/2)}. \end{equation}
We tested the above methodology with realistic mock galaxy catalogues. To do so, we use the N-body Bolshoi–Planck simulation (Klypin et al. Reference Klypin, Yepes, Gottlöber, Prada and Heß2016) and halo catalogues described in Rodríguez-Puebla et al. (Reference Rodríguez-Puebla, Behroozi, Primack, Klypin, Lee and Hellinger2016). We use the semi-emperical modelling from (Rodríguez-Puebla et al. Reference Rodríguez-Puebla, Primack, Avila-Reese and Faber2017) in order to assign galaxies to dark matter halos/subhalos. The galaxies in the catalogue were projected into the redshift space through a lightcone. We use the dependence of the stellar mass limit with redshift described in Appendix C.2 and include galaxies only within the same redshift range as the NYU VAGC in order to reproduce the observed distribution of galaxies in the  $M_{*}$
and redshift plane for the low-z-SDSS sample. Our results show that the above methodology recovered the original GSMF with differences not larger than
$M_{*}$
and redshift plane for the low-z-SDSS sample. Our results show that the above methodology recovered the original GSMF with differences not larger than  $\sim\!5\%$
. In addition, we have calculated the GSMF using the stepwise maximum likelihood method (Efstathiou, Ellis, & Peterson Reference Efstathiou, Ellis and Peterson1988) and found very similar similar results (not shown) as those reported based on our methodology.
$\sim\!5\%$
. In addition, we have calculated the GSMF using the stepwise maximum likelihood method (Efstathiou, Ellis, & Peterson Reference Efstathiou, Ellis and Peterson1988) and found very similar similar results (not shown) as those reported based on our methodology.

Figure C2. Upper Panel: Distribution of galaxies in the  $M_{*}$
and redshift plane for the lowz-SDSS galaxy sample, grey dots. The solid lines shows the dependence of the stellar mass completeness limit as a function of redshift for our galaxy sample. Bottom Panel: The dependence of the GSMF with redshift for three different stellar masses. Note that the increase and decreases in the amplitudes is due the large-scale structure fluctuations. The solid lines show our corrections due to large-scale structures as described in the text.
$M_{*}$
and redshift plane for the lowz-SDSS galaxy sample, grey dots. The solid lines shows the dependence of the stellar mass completeness limit as a function of redshift for our galaxy sample. Bottom Panel: The dependence of the GSMF with redshift for three different stellar masses. Note that the increase and decreases in the amplitudes is due the large-scale structure fluctuations. The solid lines show our corrections due to large-scale structures as described in the text.

Figure C3. Corrected GSMF for surface brightness incompleteness, red filled circles with error bars. Blue filled circles with error bars show the uncorrected GSMF. Grey skeletal symbols and filled circles show the GSMF from Baldry et al. (Reference Baldry2012) and Baldry et al. (Reference Baldry, Glazebrook and Driver2008), respectively. The black filled circles show the GSMF from the SDSS DR7 derived from Appendix A. The different panels show the various stellar mass estimators used for this paper. Note that the at  $M_{*}\sim\! 10^9\ \text{M}_{\odot}$
there is a smooth transition between the low-z NYU-VAGC sample and the SDSS DR7 GSMFs.
$M_{*}\sim\! 10^9\ \text{M}_{\odot}$
there is a smooth transition between the low-z NYU-VAGC sample and the SDSS DR7 GSMFs.
Finally, we calculate the GSMF corrected by surface brightness incompleteness by
 \begin{equation} \phi_{{\rm SB},j}({M_{*}},z) \Delta \log {M_{*}}= \frac{N_{{\rm SB,gals},j}(M_{\ast},z)}{V(z-\Delta z/2) - V(z+\Delta z/2)}, \end{equation}
\begin{equation} \phi_{{\rm SB},j}({M_{*}},z) \Delta \log {M_{*}}= \frac{N_{{\rm SB,gals},j}(M_{\ast},z)}{V(z-\Delta z/2) - V(z+\Delta z/2)}, \end{equation}
where
 \begin{equation} N_{{\rm SB,gals},j} = \sum _{i=1}^{N_{{\rm gals},j}} w_{{\rm SB},i}, \end{equation}
\begin{equation} N_{{\rm SB,gals},j} = \sum _{i=1}^{N_{{\rm gals},j}} w_{{\rm SB},i}, \end{equation}
and  $w_{{\rm SB},i}$
is our SB incompleteness correction given by Equation (13).
$w_{{\rm SB},i}$
is our SB incompleteness correction given by Equation (13).
The bottom panel of Figure C3 shows  $\phi_{{\rm SB},j}(M_{\ast},z_j)$
for three different stellar masses,
$\phi_{{\rm SB},j}(M_{\ast},z_j)$
for three different stellar masses,  $M_{*}=10^{8.4}\text{M}_{\odot}$
,
$M_{*}=10^{8.4}\text{M}_{\odot}$
,  $10^{9.5}\text{M}_{\odot}$
, and
$10^{9.5}\text{M}_{\odot}$
, and  $10^{10.2}\text{M}_{\odot}$
. Fluctuations in the amplitude of the GSMF shows that the distributions of galaxies is not uniform across the redshift distribution because of environmental effects arising from large-scale structures. In order to minimise the above effect, we compute the weighted mean of the GSMF. In other words, we derive the total GSMF as
$10^{10.2}\text{M}_{\odot}$
. Fluctuations in the amplitude of the GSMF shows that the distributions of galaxies is not uniform across the redshift distribution because of environmental effects arising from large-scale structures. In order to minimise the above effect, we compute the weighted mean of the GSMF. In other words, we derive the total GSMF as
 \begin{equation} \langle \phi_{\rm SB}(M_{\ast}) \rangle = \sum_{j=1}^{N=20} \phi_{{\rm SB},j}(M_{\ast},z_j) \times w_j, \end{equation}
\begin{equation} \langle \phi_{\rm SB}(M_{\ast}) \rangle = \sum_{j=1}^{N=20} \phi_{{\rm SB},j}(M_{\ast},z_j) \times w_j, \end{equation}
where  $w_j = N_{{\rm gals},j} / \sum_j N_{{\rm gals},j} $
the fraction of galaxies at the jth volume-limited subsample centred at the redshift bin
$w_j = N_{{\rm gals},j} / \sum_j N_{{\rm gals},j} $
the fraction of galaxies at the jth volume-limited subsample centred at the redshift bin  $z\pm\Delta z/2$
for the mass bin
$z\pm\Delta z/2$
for the mass bin  $\log {M_{*}} \pm \Delta \log {M_{*}}/2$
. The solid line in Figure C3 shows the resulting value of
$\log {M_{*}} \pm \Delta \log {M_{*}}/2$
. The solid line in Figure C3 shows the resulting value of  $\langle \phi_{\rm SB} \rangle$
for the masses discussed above.
$\langle \phi_{\rm SB} \rangle$
for the masses discussed above.
Figure C4 compares the resulting GSMFs when SB corrections are applied  $\phi_{{\rm SB},*}$
(red filled circles) and when we ignore SB corrections
$\phi_{{\rm SB},*}$
(red filled circles) and when we ignore SB corrections  $\phi_{*}$
(blue filled circles) for each of the six stellar mass definitions used here. As expected, the SB correction increases the number density of low-mass galaxies. For higher masses than
$\phi_{*}$
(blue filled circles) for each of the six stellar mass definitions used here. As expected, the SB correction increases the number density of low-mass galaxies. For higher masses than  $\sim\! 3\times 10^9\ \text{M}_{\odot}$
, this correction is negligible. For comparison, we reproduce with grey filled circles the GSMF reported in Baldry et al. (Reference Baldry, Glazebrook and Driver2008), who used also the low-z NYU-VAGC sample but for the DR4 as well as the Baldry et al. (Reference Baldry2012) from the GAMA survey with the skeletal symbols. In none of them, SB corrections were applied. Finally, in all the panels of Figure C4, we reproduce the GSMF from the main SDSS DR7 derived in Appendix A. Observe how the GSMFs constructed from the low-z NYU-VAGC sample and the ones constructed from the main SDSS DR7 samples match extremely well at
$\sim\! 3\times 10^9\ \text{M}_{\odot}$
, this correction is negligible. For comparison, we reproduce with grey filled circles the GSMF reported in Baldry et al. (Reference Baldry, Glazebrook and Driver2008), who used also the low-z NYU-VAGC sample but for the DR4 as well as the Baldry et al. (Reference Baldry2012) from the GAMA survey with the skeletal symbols. In none of them, SB corrections were applied. Finally, in all the panels of Figure C4, we reproduce the GSMF from the main SDSS DR7 derived in Appendix A. Observe how the GSMFs constructed from the low-z NYU-VAGC sample and the ones constructed from the main SDSS DR7 samples match extremely well at  $M_{*}\sim\! 10^9\ \text{M}_{\odot}$
, but the latter overcomes the former at high stellar masses due to the larger volume covered by the SDSS DR7.
$M_{*}\sim\! 10^9\ \text{M}_{\odot}$
, but the latter overcomes the former at high stellar masses due to the larger volume covered by the SDSS DR7.
Finally, we briefly describe our final GSMF. For galaxies below  $M_{*}=10^{9}\text{M}_{\odot}$
, we use the GSMF derived from the low-z NYU-VAGC sample, while for galaxies above
$M_{*}=10^{9}\text{M}_{\odot}$
, we use the GSMF derived from the low-z NYU-VAGC sample, while for galaxies above  $M_{*}=10^{9}\text{M}_{\odot}$
, we use the GSMF from the SDSS DR7 based on the photometric catalogue from Meert et al. (Reference Meert, Vikram and Bernardi2015). We apply a simply correction in our GSMF for passing from the Willick et al. (Reference Willick, Courteau, Faber, Burstein, Dekel and Strauss1997) distance flow model to the Tonry et al. (Reference Tonry, Blakeslee, Ajhar and Dressler2000) one. Figure C1 from Baldry et al. (Reference Baldry2012) shows that after adjusting the Baldry et al. (Reference Baldry, Glazebrook and Driver2008) GSMF to the Tonry et al. (Reference Tonry, Blakeslee, Ajhar and Dressler2000) distances, both MFs are in excellent agreement. With that information, we first note that our fiducial (uncorrected) GSMF (bottom right panel from Figure C3) is very similar to the Baldry et al. (Reference Baldry, Glazebrook and Driver2008) GSMF, and thus we assume that the impact of correcting by Tonry et al. (Reference Tonry, Blakeslee, Ajhar and Dressler2000) distances is equivalent to rescale it to the Baldry et al. (Reference Baldry2012) GSMF. Based on the above, we rescale our SB-corrected GSMF as
$M_{*}=10^{9}\text{M}_{\odot}$
, we use the GSMF from the SDSS DR7 based on the photometric catalogue from Meert et al. (Reference Meert, Vikram and Bernardi2015). We apply a simply correction in our GSMF for passing from the Willick et al. (Reference Willick, Courteau, Faber, Burstein, Dekel and Strauss1997) distance flow model to the Tonry et al. (Reference Tonry, Blakeslee, Ajhar and Dressler2000) one. Figure C1 from Baldry et al. (Reference Baldry2012) shows that after adjusting the Baldry et al. (Reference Baldry, Glazebrook and Driver2008) GSMF to the Tonry et al. (Reference Tonry, Blakeslee, Ajhar and Dressler2000) distances, both MFs are in excellent agreement. With that information, we first note that our fiducial (uncorrected) GSMF (bottom right panel from Figure C3) is very similar to the Baldry et al. (Reference Baldry, Glazebrook and Driver2008) GSMF, and thus we assume that the impact of correcting by Tonry et al. (Reference Tonry, Blakeslee, Ajhar and Dressler2000) distances is equivalent to rescale it to the Baldry et al. (Reference Baldry2012) GSMF. Based on the above, we rescale our SB-corrected GSMF as  $ \phi_{\rm SB, T00} = \langle \phi_{\rm SB} \rangle\times \phi_{\rm B08} / \phi_{\rm B12} $
. Recall that our fiducial GSMF uses stellar masses from the geometric mean of all stellar masses described by Equation (A6).
$ \phi_{\rm SB, T00} = \langle \phi_{\rm SB} \rangle\times \phi_{\rm B08} / \phi_{\rm B12} $
. Recall that our fiducial GSMF uses stellar masses from the geometric mean of all stellar masses described by Equation (A6).
Figure C5 shows our final GSMF,  $\phi_{\rm SB, T00}$
, as the black filled circles with error bars. The filled grey symbols show the GSMF,
$\phi_{\rm SB, T00}$
, as the black filled circles with error bars. The filled grey symbols show the GSMF,  $\langle \phi_{\rm SB} \rangle$
, in which the Willick et al. (Reference Willick, Courteau, Faber, Burstein, Dekel and Strauss1997) model flow is utilised. We also compare to Baldry et al. (Reference Baldry2012) and Wright et al. (Reference Wright2017) determinations. Note that after distance and SB corrections, our fiducial GSMF is in good agreement with the observed low-mass end slope of the GAMA survey. For comparison, we present our corrected GSMF but when using the Taylor et al. (Reference Taylor2011) mass-to-light ratios. Note that in this case our GSMF is consistent with the Baldry et al. (Reference Baldry2012) GSMF.
$\langle \phi_{\rm SB} \rangle$
, in which the Willick et al. (Reference Willick, Courteau, Faber, Burstein, Dekel and Strauss1997) model flow is utilised. We also compare to Baldry et al. (Reference Baldry2012) and Wright et al. (Reference Wright2017) determinations. Note that after distance and SB corrections, our fiducial GSMF is in good agreement with the observed low-mass end slope of the GAMA survey. For comparison, we present our corrected GSMF but when using the Taylor et al. (Reference Taylor2011) mass-to-light ratios. Note that in this case our GSMF is consistent with the Baldry et al. (Reference Baldry2012) GSMF.
C.4. The impact of galaxy classification: the criteria for separating the galaxy population into two groups
For our goal of projecting gas scaling correlations (more precisely, the gas CPDFs) into gas MFs separately for early- and late-type galaxies, the derivation of the fraction of early-type galaxies as a function of  $M_{*}$
,
$M_{*}$
,  $f_E\text{(}M_{*}\text{)}$
, was an important step. As discussed in Section 3.3, based on the morphological classification from Huertas-Company et al. (Reference Huertas-Company, Aguerri, Bernardi, Mei and Sánchez Almeida2011), we found the GSMFs of early- and late-type galaxies that are in good agreement with the results based on the visual classification from Nair & Abraham (Reference Nair and Abraham2010) and with the classification based on concentration utilised in Bernardi et al. (Reference Bernardi, Shankar, Hyde, Mei, Marulli and Sheth2010). In contrast, we found that our GSMFs of early- and late-type galaxies are in tension when comparing to those from the GAMA survey with their visual morphological classification, but interestingly enough, they agree with the GAMA GSMFs when we use a
$f_E\text{(}M_{*}\text{)}$
, was an important step. As discussed in Section 3.3, based on the morphological classification from Huertas-Company et al. (Reference Huertas-Company, Aguerri, Bernardi, Mei and Sánchez Almeida2011), we found the GSMFs of early- and late-type galaxies that are in good agreement with the results based on the visual classification from Nair & Abraham (Reference Nair and Abraham2010) and with the classification based on concentration utilised in Bernardi et al. (Reference Bernardi, Shankar, Hyde, Mei, Marulli and Sheth2010). In contrast, we found that our GSMFs of early- and late-type galaxies are in tension when comparing to those from the GAMA survey with their visual morphological classification, but interestingly enough, they agree with the GAMA GSMFs when we use a  $g-r$
colour criterion to separate our galaxies into the two populations. Recall that for the GAMA classification, Sa galaxies are included into their early-type group since their visual classifications combines S0 and Sa galaxies (Kelvin et al. Reference Kelvin2014; Moffett et al. Reference Moffett2016a), contrary to our definition; see Section 3.3 for more details. Thus, understanding the impact of using different criteria to separate the galaxy population into two main groups is of great importance in our study. Following, we study the impact of using galaxy colour instead of morphology in order to give a rough idea of what would it be the result of using a very different proxy to galaxy morphology (a one close to the GAMA survey, for instance).
$g-r$
colour criterion to separate our galaxies into the two populations. Recall that for the GAMA classification, Sa galaxies are included into their early-type group since their visual classifications combines S0 and Sa galaxies (Kelvin et al. Reference Kelvin2014; Moffett et al. Reference Moffett2016a), contrary to our definition; see Section 3.3 for more details. Thus, understanding the impact of using different criteria to separate the galaxy population into two main groups is of great importance in our study. Following, we study the impact of using galaxy colour instead of morphology in order to give a rough idea of what would it be the result of using a very different proxy to galaxy morphology (a one close to the GAMA survey, for instance).
The lower panel of Figure 2 presented the fractions of early-type galaxies as well as of red galaxies as a function of  $M_{*}$
. The fraction of red galaxies is clearly larger than the one of early-type galaxies at all masses. Based on the SDSS DR7 sample described in Section 3, we found that the great majority of the galaxies that are classified as early type are actually red; the fraction of early-type galaxies with blue colours has a maximum at
$M_{*}$
. The fraction of red galaxies is clearly larger than the one of early-type galaxies at all masses. Based on the SDSS DR7 sample described in Section 3, we found that the great majority of the galaxies that are classified as early type are actually red; the fraction of early-type galaxies with blue colours has a maximum at  $M_{*}\sim\! 8\times10^{10}\text{M}_{\odot}$
representing only
$M_{*}\sim\! 8\times10^{10}\text{M}_{\odot}$
representing only  $\sim\!5\%$
of the population. In contrast, the fraction of red galaxies classified as late types is larger than
$\sim\!5\%$
of the population. In contrast, the fraction of red galaxies classified as late types is larger than  $\sim\!10\%$
at practically all masses and it peaks at
$\sim\!10\%$
at practically all masses and it peaks at  $M_{*}\sim\! 2\times10^{10}\text{M}_{\odot}$
with a contribution of
$M_{*}\sim\! 2\times10^{10}\text{M}_{\odot}$
with a contribution of  $\sim\! 50\%$
(we also observe a second peak at the massive end
$\sim\! 50\%$
(we also observe a second peak at the massive end  $M_{*}\sim\! 4\times10^{11}\text{M}_{\odot}$
). Similar results have been reported in previous studies (see e.g., Masters et al. Reference Masters2010b). Additionally, note that we ignored the effects of reddening due to extinction from the galaxy inclination, which would misclassify galaxies based on their colours (see e.g., Masters et al. Reference Masters2010a). Therefore, from the physical point of view, the separation of the galaxy population by colour is, perhaps, not as ‘clean or reliable as morphology.
$M_{*}\sim\! 4\times10^{11}\text{M}_{\odot}$
). Similar results have been reported in previous studies (see e.g., Masters et al. Reference Masters2010b). Additionally, note that we ignored the effects of reddening due to extinction from the galaxy inclination, which would misclassify galaxies based on their colours (see e.g., Masters et al. Reference Masters2010a). Therefore, from the physical point of view, the separation of the galaxy population by colour is, perhaps, not as ‘clean or reliable as morphology.
Figure C6 presents the resulting MFs when using the fraction of red galaxies,  $f_r\text{(}M_{*}\text{)}$
, as a proxy for early-type galaxies, dashed lines. The solid lines reproduce the results from Figure 8, where our morphology-based fraction,
$f_r\text{(}M_{*}\text{)}$
, as a proxy for early-type galaxies, dashed lines. The solid lines reproduce the results from Figure 8, where our morphology-based fraction,  $f_E\text{(}M_{*}\text{)}$
, was used. Notice that for
$f_E\text{(}M_{*}\text{)}$
, was used. Notice that for  $\rm HI$
,
$\rm HI$
,  $\rm H_{2}$
, and cold gas mass, not only the MFs of blue and red galaxies are different to their morphological counterparts but also the total MFs. The above can be understood in the following terms. Using the fraction of red galaxies as a proxy of early-type galaxies results in a large fraction of red galaxies misclassified as late-types as discussed above. However, the above has a lager impact for early-type galaxies with low to intermediate masses than at high masses, while for late-type galaxies, the major impact is from intermediate to high masses. As a consequence, on one hand, the resulting
$\rm H_{2}$
, and cold gas mass, not only the MFs of blue and red galaxies are different to their morphological counterparts but also the total MFs. The above can be understood in the following terms. Using the fraction of red galaxies as a proxy of early-type galaxies results in a large fraction of red galaxies misclassified as late-types as discussed above. However, the above has a lager impact for early-type galaxies with low to intermediate masses than at high masses, while for late-type galaxies, the major impact is from intermediate to high masses. As a consequence, on one hand, the resulting  $\rm HI$
and
$\rm HI$
and  $\rm H_{2}\,$
MFs see an increase in early-type galaxies at their low-mass ends. Interestingly enough, the use of
$\rm H_{2}\,$
MFs see an increase in early-type galaxies at their low-mass ends. Interestingly enough, the use of  $f_r$
instead of
$f_r$
instead of  $f_E$
would produce
$f_E$
would produce $\rm HI$
and
$\rm HI$
and  $\rm H_{2}$
MF of early-type galaxies in better agreement with the inferences of the ATLAS 3D sample. On the other hand, lowering the fraction of late-type galaxies at intermediate-high masses, which have significantly larger gas fractions than early-type galaxies, affects the projected total
$\rm H_{2}$
MF of early-type galaxies in better agreement with the inferences of the ATLAS 3D sample. On the other hand, lowering the fraction of late-type galaxies at intermediate-high masses, which have significantly larger gas fractions than early-type galaxies, affects the projected total  $\rm HI$
and
$\rm HI$
and  $\rm H_{2}\,$
MFs, and they would be in tension with direct observations, especially with the
$\rm H_{2}\,$
MFs, and they would be in tension with direct observations, especially with the  $\rm HI$
MF from the ALFALFA and HIPASS surveys.
$\rm HI$
MF from the ALFALFA and HIPASS surveys.

Figure C4. Corrected GSMF for SB and for the flow model, filled circles with error bars. This is our fiducial GSMF. The corresponding best-fit model is shown with the solid line, see Section 3.2. Grey filled circles shows when using the flow model from Willick et al. (Reference Willick, Courteau, Faber, Burstein, Dekel and Strauss1997). We also show our results when using the mass-to-light ration from Taylor et al. (Reference Taylor2011) and compared to Baldry et al. (Reference Baldry2012) who used the same mass estimator. Notice that both mass functions are consistent between each other. For completeness, we compared to Wright et al. (Reference Wright2017).
Finally, we emphasise that the above does not imply that using galaxy colours will lead to incorrect inferences of the gas MFs but that combining two different criteria for dividing the galaxy population will lead to a very different results that, perhaps, will be in tension with the observations. Thus, the success of our determinations is in part that we are using data sets that are consistent between each other in that regards the morphological separation into two galaxy subpopulations.

Figure C5. Impact on the MFs due to the use of two different criteria for the division of the galaxy population. The solid lines show the original MF from Section 4.4, based on galaxy morphology, while the dashed lines show the results when using galaxy colour. The classification according to galaxy colours results in a overabundance of red galaxies compared to early types, especially at intermediate and low masses.
D. Deconvolution algorithm
Individual mass estimates are subject to random errors. Thus, every MF that is inferred from observations through indirect estimations of any type of mass (we will denote this as  $\phi_{\rm obs}$
) is the result of the random errors over the intrinsic mass (it will be denoted by
$\phi_{\rm obs}$
) is the result of the random errors over the intrinsic mass (it will be denoted by  $\phi_{\rm int}$
). Formally, we can represent the observed
$\phi_{\rm int}$
). Formally, we can represent the observed  $\phi_{\rm obs}$
as the convolution of
$\phi_{\rm obs}$
as the convolution of  $\phi_{\rm int}$
:
$\phi_{\rm int}$
:
 \begin{equation} \phi_{\rm obs}(M)=\int \mathcal{G}(\log M-\log x)\phi_{{\rm int}}(x)d\log x. \end{equation}
\begin{equation} \phi_{\rm obs}(M)=\int \mathcal{G}(\log M-\log x)\phi_{{\rm int}}(x)d\log x. \end{equation}
We will assume that random errors have a lognormal distribution, denoted by  $\mathcal{G}(\log M-\log x )$
:
$\mathcal{G}(\log M-\log x )$
:
 \begin{equation} \mathcal{G}(\log M -\log x)=\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left[-\frac{1}{2\sigma^2}\log^2\left(\frac{M}{x}\right)\right], \end{equation}
\begin{equation} \mathcal{G}(\log M -\log x)=\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left[-\frac{1}{2\sigma^2}\log^2\left(\frac{M}{x}\right)\right], \end{equation}
where  $\sigma$
are the 1-
$\sigma$
are the 1- $\sigma$
statistical fluctuations, in either directions, in the inferred galaxy masses. Note that in Equation (27), the units for
$\sigma$
statistical fluctuations, in either directions, in the inferred galaxy masses. Note that in Equation (27), the units for  $\phi_{\rm obs}$
and
$\phi_{\rm obs}$
and  $\phi_{\rm int}$
are in Mpc–3dex–1.
$\phi_{\rm int}$
are in Mpc–3dex–1.
The basic idea of our algorithm is simple. We start by defining the following relation:
 \begin{equation} \phi_{ {\rm int}}^j(M) = \phi_{ {\rm int}}^{j-1}(M) \int \mathcal{G}(\log M -\log x)\frac{\phi_{\rm obs}}{\phi_{ {\rm conv}}^{j-1}} (x)d\log x, \end{equation}
\begin{equation} \phi_{ {\rm int}}^j(M) = \phi_{ {\rm int}}^{j-1}(M) \int \mathcal{G}(\log M -\log x)\frac{\phi_{\rm obs}}{\phi_{ {\rm conv}}^{j-1}} (x)d\log x, \end{equation}
where
 \begin{equation} \phi_{ {\rm conv}}^{j-1}(x) = \int \mathcal{G}(\log x-\log y)\phi_{ {\rm int}}^{j-1}(y)d\log y, \end{equation}
\begin{equation} \phi_{ {\rm conv}}^{j-1}(x) = \int \mathcal{G}(\log x-\log y)\phi_{ {\rm int}}^{j-1}(y)d\log y, \end{equation}
with  $\phi_{ {\rm int}}^{j-1}$
denoting the jth iterated intrinsic MF. Note that as
$\phi_{ {\rm int}}^{j-1}$
denoting the jth iterated intrinsic MF. Note that as  $\phi_{ {\rm conv}}^{j-1}$
approaches to
$\phi_{ {\rm conv}}^{j-1}$
approaches to  $\phi_{{\rm obs}}$
the above equation converges to the maximum likelihood solution for
$\phi_{{\rm obs}}$
the above equation converges to the maximum likelihood solution for  $\phi_{ {\rm int}}^{j-1}$
, in other words, we have found the numerical solution to the intrinsic MF,
$\phi_{ {\rm int}}^{j-1}$
, in other words, we have found the numerical solution to the intrinsic MF,  $\phi_{{\rm int}}$
. The zero-th iteration is defined as convolution of the observed MF with the lognormal distribution
$\phi_{{\rm int}}$
. The zero-th iteration is defined as convolution of the observed MF with the lognormal distribution  $\mathcal{G}$
described above:
$\mathcal{G}$
described above:
 \begin{equation} \phi_{ {\rm int}}^0\text{(}M_{*}\text{)}=\int \mathcal{G}(\log{M_{*}}-\log x)\phi_{\rm obs}(x)d\log x. \end{equation}
\begin{equation} \phi_{ {\rm int}}^0\text{(}M_{*}\text{)}=\int \mathcal{G}(\log{M_{*}}-\log x)\phi_{\rm obs}(x)d\log x. \end{equation}
We declare that the  $\phi_{{\rm int}}^{j}$
has converged when the parameter
$\phi_{{\rm int}}^{j}$
has converged when the parameter  $\Delta \leq 7\%$
defined as the relative error between the observed MF and the j-th iterated intrinsic MF convolved with the random error distribution:
$\Delta \leq 7\%$
defined as the relative error between the observed MF and the j-th iterated intrinsic MF convolved with the random error distribution:
 \begin{equation} \Delta = \frac{100\%}{N}\sum_i\left| 1 - \frac{\int \mathcal{G}(\log{M_{*}}-\log x)\phi_{ {\rm int},i}^{j}d\log x}{\phi_{ {\rm obs},i}}\right|. \end{equation}
\begin{equation} \Delta = \frac{100\%}{N}\sum_i\left| 1 - \frac{\int \mathcal{G}(\log{M_{*}}-\log x)\phi_{ {\rm int},i}^{j}d\log x}{\phi_{ {\rm obs},i}}\right|. \end{equation}
The summation in the above definition goes over all the tabulated values of individual reports of the observed MF  $\phi_{{\rm obs}}$
. By trial and error, we found that the value of
$\phi_{{\rm obs}}$
. By trial and error, we found that the value of  $\Delta = 7\%$
is a compromise between accuracy and efficiency. Typically,
$\Delta = 7\%$
is a compromise between accuracy and efficiency. Typically,  $\Delta = 7\%$
was reached in less than 10 iterations.
$\Delta = 7\%$
was reached in less than 10 iterations.