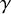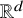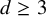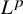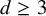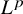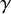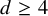1 Introduction
The regularity property of integral transforms defined by averages over submanifolds is a fundamental subject in harmonic analysis, which has been extensively studied since the 1970s. There is an immense body of literature devoted to the subject (see, for example, [Reference Stein and Wainger33, Reference Phong and Stein21, Reference Stein32, Reference Christ, Nagel, Stein and Wainger8] and references therein). However, numerous problems remain wide open. The regularity property is typically addressed in the frameworks of
![]() $L^p$
improving,
$L^p$
improving,
![]() $L^p$
Sobolev regularity, and local smoothing estimates, to which
$L^p$
Sobolev regularity, and local smoothing estimates, to which
![]() $L^p$
boundedness of the maximal average is also closely related. In this paper, we study the smoothing estimates for the averaging operator given by convolution with a measure supported on a curve.
$L^p$
boundedness of the maximal average is also closely related. In this paper, we study the smoothing estimates for the averaging operator given by convolution with a measure supported on a curve.
Let
![]() $I=[-1,1]$
and
$I=[-1,1]$
and
![]() $\gamma $
be a smooth curve from I to
$\gamma $
be a smooth curve from I to
![]() $\mathbb R^d$
. We define a measure
$\mathbb R^d$
. We define a measure
![]() $\mathfrak m_t$
supported on
$\mathfrak m_t$
supported on
![]() $t\gamma $
by
$t\gamma $
by
where
![]() $\psi \in \mathrm C_c^\infty ((-1,1))$
. We are concerned with
$\psi \in \mathrm C_c^\infty ((-1,1))$
. We are concerned with
![]() $d\ge 3$
since all the problems we address in the current paper are well understood when
$d\ge 3$
since all the problems we address in the current paper are well understood when
![]() $d=2$
. We consider the averaging operator
$d=2$
. We consider the averaging operator
and study the above-mentioned regularity problems on
![]() $\mathcal A_t $
under the assumption that
$\mathcal A_t $
under the assumption that
![]() $\gamma $
is nondegenerate, that is to say,
$\gamma $
is nondegenerate, that is to say,
The
![]() $L^p$
improving property of
$L^p$
improving property of
![]() $ \mathcal A_t$
for a fixed
$ \mathcal A_t$
for a fixed
![]() $t\neq 0$
now has a complete characterization; see [Reference Christ7, Reference Stovall34] (also, see [Reference Tao and Wright36] for generalizations to variable coefficient settings). However,
$t\neq 0$
now has a complete characterization; see [Reference Christ7, Reference Stovall34] (also, see [Reference Tao and Wright36] for generalizations to variable coefficient settings). However,
![]() $L^p$
Sobolev and local smoothing estimates for
$L^p$
Sobolev and local smoothing estimates for
![]() $\mathcal A_t$
turned out to be more involved and are far less well understood. Recently, there has been progress in low dimensions
$\mathcal A_t$
turned out to be more involved and are far less well understood. Recently, there has been progress in low dimensions
![]() $d= 3, 4$
([Reference Pramanik and Seeger24, Reference Ko, Lee and Oh14, Reference Beltran, Guo, Hickman and Seeger1, Reference Beltran, Guo, Hickman and Seeger2]), but it does not seem feasible to extend the approaches in the recent works to higher dimensions. We discuss this matter in detail near the end of the introduction. By devising an inductive strategy, we prove the optimal
$d= 3, 4$
([Reference Pramanik and Seeger24, Reference Ko, Lee and Oh14, Reference Beltran, Guo, Hickman and Seeger1, Reference Beltran, Guo, Hickman and Seeger2]), but it does not seem feasible to extend the approaches in the recent works to higher dimensions. We discuss this matter in detail near the end of the introduction. By devising an inductive strategy, we prove the optimal
![]() $L^p$
Sobolev regularity and sharp local smoothing estimates in any dimension
$L^p$
Sobolev regularity and sharp local smoothing estimates in any dimension
![]() $d\ge 3$
. As a result, we also obtain
$d\ge 3$
. As a result, we also obtain
![]() $L^p$
boundedness of the associated maximal function which was unknown for
$L^p$
boundedness of the associated maximal function which was unknown for
![]() $d\ge 4$
.
$d\ge 4$
.
 $L^p$
Sobolev regularity
$L^p$
Sobolev regularity
Let
![]() $2\le p\le \infty $
. We set
$2\le p\le \infty $
. We set
![]() $ \mathcal A f=\mathcal A_1 f $
and consider the
$ \mathcal A f=\mathcal A_1 f $
and consider the
![]() $L^p$
Sobolev regularity estimate
$L^p$
Sobolev regularity estimate
When
![]() $d=2$
, the estimate holds if and only if
$d=2$
, the estimate holds if and only if
![]() $\alpha \le 1/p$
(e.g., see [Reference Christ6]). In higher dimensions, however, the problem of obtaining (1.2) with the sharp smoothing order
$\alpha \le 1/p$
(e.g., see [Reference Christ6]). In higher dimensions, however, the problem of obtaining (1.2) with the sharp smoothing order
![]() $\alpha $
becomes highly nontrivial except for the
$\alpha $
becomes highly nontrivial except for the
![]() $L^2\to L^2_{1/d}$
estimate which is an easy consequence of the decay property of the Fourier transform of
$L^2\to L^2_{1/d}$
estimate which is an easy consequence of the decay property of the Fourier transform of
![]() ${\mathfrak m}_t$
:
${\mathfrak m}_t$
:
It was conjectured by Beltran, Guo, Hickman and Seeger [Reference Beltran, Guo, Hickman and Seeger2, Conjecture 1] that the estimate (1.2) holds for
![]() $\alpha \le 1/p$
if
$\alpha \le 1/p$
if
![]() $2d-2<p<\infty $
. When
$2d-2<p<\infty $
. When
![]() $d=3$
, the conjecture was verified by the conditional result of Pramanik and Seeger [Reference Pramanik and Seeger24] and the decoupling inequality due to Bourgain and Demeter [Reference Bourgain and Demeter4] (see [Reference Oberlin, Smith and Sogge20, Reference Tao and Vargas35] for earlier results). The case
$d=3$
, the conjecture was verified by the conditional result of Pramanik and Seeger [Reference Pramanik and Seeger24] and the decoupling inequality due to Bourgain and Demeter [Reference Bourgain and Demeter4] (see [Reference Oberlin, Smith and Sogge20, Reference Tao and Vargas35] for earlier results). The case
![]() $d=4$
was recently obtained by Beltran et al. [Reference Beltran, Guo, Hickman and Seeger2]. Our first result proves the conjecture for every
$d=4$
was recently obtained by Beltran et al. [Reference Beltran, Guo, Hickman and Seeger2]. Our first result proves the conjecture for every
![]() $d\ge 5$
.
$d\ge 5$
.
Theorem 1.1. Let
![]() $d\ge 3$
. Suppose
$d\ge 3$
. Suppose
![]() $\gamma $
is a smooth nondegenerate curve. Then, the estimate (1.2) holds for
$\gamma $
is a smooth nondegenerate curve. Then, the estimate (1.2) holds for
![]() $\alpha \le 1/p$
if
$\alpha \le 1/p$
if
![]() $p> 2(d-1)$
.
$p> 2(d-1)$
.
Interpolation with the
![]() $L^2\to L^2_{1/d}$
estimate gives (1.2) for
$L^2\to L^2_{1/d}$
estimate gives (1.2) for
![]() $\alpha <(p+2)/(2dp)$
when
$\alpha <(p+2)/(2dp)$
when
![]() $2< p \le 2(d-1)$
. It is also known that (1.2) fails if
$2< p \le 2(d-1)$
. It is also known that (1.2) fails if
![]() $\alpha> \alpha (p):=\min (1/p, (p+2)/(2dp)) $
(see [Reference Beltran, Guo, Hickman and Seeger2, Proposition 1.2]). Thus, only the estimate (1.2) with
$\alpha> \alpha (p):=\min (1/p, (p+2)/(2dp)) $
(see [Reference Beltran, Guo, Hickman and Seeger2, Proposition 1.2]). Thus, only the estimate (1.2) with
![]() $\alpha =\alpha (p) $
remains open for
$\alpha =\alpha (p) $
remains open for
![]() $2< p \le 2(d-1)$
. Those endpoint estimates seem to be a subtle problem. The argument in this paper provides simpler alternative proofs of the previous results for
$2< p \le 2(d-1)$
. Those endpoint estimates seem to be a subtle problem. The argument in this paper provides simpler alternative proofs of the previous results for
![]() $d=3,4$
. Theorem 1.1 remains valid as long as
$d=3,4$
. Theorem 1.1 remains valid as long as
![]() $\gamma \in \mathrm C^{2d}(I)$
(see Theorem 4.1). However, we do not try to optimize the regularity assumption.
$\gamma \in \mathrm C^{2d}(I)$
(see Theorem 4.1). However, we do not try to optimize the regularity assumption.
The result in Theorem 1.1 can be easily generalized to curves of different types. We say a smooth curve
![]() $\gamma $
from I to
$\gamma $
from I to
![]() $\mathbb R^d$
is of finite type if there is an
$\mathbb R^d$
is of finite type if there is an
![]() $ \ell $
such that
$ \ell $
such that
![]() $\operatorname {\mathrm {span}} \{ \gamma ^{(1)}(s), \dots , \gamma ^{( \ell )}(s)\}=\mathbb R^d$
for each
$\operatorname {\mathrm {span}} \{ \gamma ^{(1)}(s), \dots , \gamma ^{( \ell )}(s)\}=\mathbb R^d$
for each
![]() $s\in I$
. The type at s is defined to be the smallest of such
$s\in I$
. The type at s is defined to be the smallest of such
![]() $ \ell $
and the maximal type is the supremum over
$ \ell $
and the maximal type is the supremum over
![]() $s \in I$
of the type at s. (See, e.g., [Reference Pramanik and Seeger24, Reference Ham and Lee12].) Using Theorem 1.1 and a rescaling argument ([Reference Pramanik and Seeger24, Reference Ham and Lee12]), one can obtain the following, which proves the Conjecture 2 in [Reference Beltran, Guo, Hickman and Seeger2].
$s \in I$
of the type at s. (See, e.g., [Reference Pramanik and Seeger24, Reference Ham and Lee12].) Using Theorem 1.1 and a rescaling argument ([Reference Pramanik and Seeger24, Reference Ham and Lee12]), one can obtain the following, which proves the Conjecture 2 in [Reference Beltran, Guo, Hickman and Seeger2].
Corollary 1.2. Let
![]() $d\ge 3$
,
$d\ge 3$
,
![]() $ \ell> d$
and
$ \ell> d$
and
![]() $2 \le p <\infty $
. Suppose
$2 \le p <\infty $
. Suppose
![]() $\gamma $
is a curve of maximal type
$\gamma $
is a curve of maximal type
![]() $ \ell $
. Then the estimate (1.2) holds for
$ \ell $
. Then the estimate (1.2) holds for
![]() $\alpha \le \min \big (\alpha (p) , \,1/ \ell \big )$
if
$\alpha \le \min \big (\alpha (p) , \,1/ \ell \big )$
if
![]() $p\neq \ell $
when
$p\neq \ell $
when
![]() $ \ell \ge 2d-2$
, and if
$ \ell \ge 2d-2$
, and if
![]() $p\in [2, 2\ell /(2d-\ell ))\cup ( 2d-2, \infty )$
when
$p\in [2, 2\ell /(2d-\ell ))\cup ( 2d-2, \infty )$
when
![]() $d< \ell < 2d-2$
.
$d< \ell < 2d-2$
.
By interpolation, (1.2) holds for
![]() $\alpha < \min \big (\alpha (p) , \,1/ \ell \big )$
if
$\alpha < \min \big (\alpha (p) , \,1/ \ell \big )$
if
![]() $p= \ell $
when
$p= \ell $
when
![]() $ \ell \ge 2d-2$
, and if
$ \ell \ge 2d-2$
, and if
![]() ${2 \ell }/{(2d- \ell )} \le p \le 2d-2$
when
${2 \ell }/{(2d- \ell )} \le p \le 2d-2$
when
![]() $d< \ell < 2d-2$
. These estimates are sharp. Since a finite type curve contains a nondegenerate subcurve and the
$d< \ell < 2d-2$
. These estimates are sharp. Since a finite type curve contains a nondegenerate subcurve and the
![]() $L^2\to L^2_{1/ \ell }$
estimate is optimal, (1.2) fails if
$L^2\to L^2_{1/ \ell }$
estimate is optimal, (1.2) fails if
![]() $\alpha> \min \big (\alpha (p) , \,1/ \ell \big )$
. In particular, when
$\alpha> \min \big (\alpha (p) , \,1/ \ell \big )$
. In particular, when
![]() $ \ell \ge 2d-2$
, Corollary 1.2 resolves the problem of the Sobolev regularity estimate (1.2). In fact, failure of the
$ \ell \ge 2d-2$
, Corollary 1.2 resolves the problem of the Sobolev regularity estimate (1.2). In fact, failure of the
![]() $L^ \ell \to L^ \ell _{1/ \ell }$
bound was shown in [Reference Beltran, Guo, Hickman and Seeger2] using Christ’s example [Reference Christ6]. By [Reference Seeger and Wright28, Theorem 1.1], Corollary 1.2 also gives
$L^ \ell \to L^ \ell _{1/ \ell }$
bound was shown in [Reference Beltran, Guo, Hickman and Seeger2] using Christ’s example [Reference Christ6]. By [Reference Seeger and Wright28, Theorem 1.1], Corollary 1.2 also gives
![]() $H^1(\mathbb R^d)\to L^{1,\infty }(\mathbb R^d)$
bound on the lacunary maximal function
$H^1(\mathbb R^d)\to L^{1,\infty }(\mathbb R^d)$
bound on the lacunary maximal function
![]() $f\to \sup _{k\in \mathbb Z} |f\ast \mathfrak m_{2^k}|$
whenever
$f\to \sup _{k\in \mathbb Z} |f\ast \mathfrak m_{2^k}|$
whenever
![]() $\gamma $
is of finite type.
$\gamma $
is of finite type.
Sharp local smoothing
We now consider the estimate
where
![]() $\chi $
is a smooth function supported in
$\chi $
is a smooth function supported in
![]() $(1/2,4)$
. Compared with the
$(1/2,4)$
. Compared with the
![]() $L^p$
Sobolev estimate (1.2), the additional integration in t is expected to yield extra smoothing. Such a phenomenon is called local smoothing, which has been studied for the dispersive equations to a great extent (e.g., see [Reference Sjölin29, Reference Constantin and Saut9]). However, the local smoothing for the averaging operators exhibits considerably different nature.
$L^p$
Sobolev estimate (1.2), the additional integration in t is expected to yield extra smoothing. Such a phenomenon is called local smoothing, which has been studied for the dispersive equations to a great extent (e.g., see [Reference Sjölin29, Reference Constantin and Saut9]). However, the local smoothing for the averaging operators exhibits considerably different nature.
In particular, there is no local smoothing when
![]() $p=2$
. Besides, a bump function example shows (1.4) holds only if
$p=2$
. Besides, a bump function example shows (1.4) holds only if
![]() $\alpha \le 1/d$
. As we shall see, the estimate (1.4) fails unless
$\alpha \le 1/d$
. As we shall see, the estimate (1.4) fails unless
![]() $\alpha \le 2/p$
(Proposition 3.9 below). So, it seems to be plausible to conjecture that (1.4) holds for
$\alpha \le 2/p$
(Proposition 3.9 below). So, it seems to be plausible to conjecture that (1.4) holds for
![]() $\alpha <\min (2/p, 1/d)$
if
$\alpha <\min (2/p, 1/d)$
if
![]() $2<p<\infty $
. For
$2<p<\infty $
. For
![]() $d=2$
, the conjecture follows by the recent result on Sogge’s local smoothing conjecture for the wave operator ([Reference Sogge30, Reference Wolff38, Reference Lee and Vargas16, Reference Bourgain and Demeter4]), which is due to Guth, Wang and Zhang [Reference Guth, Wang and Zhang11]. When
$d=2$
, the conjecture follows by the recent result on Sogge’s local smoothing conjecture for the wave operator ([Reference Sogge30, Reference Wolff38, Reference Lee and Vargas16, Reference Bourgain and Demeter4]), which is due to Guth, Wang and Zhang [Reference Guth, Wang and Zhang11]. When
![]() $d=3$
, some local smoothing estimates were utilized by Pramanik and Seeger [Reference Pramanik and Seeger24] and Beltran et al. [Reference Beltran, Guo, Hickman and Seeger1] to prove
$d=3$
, some local smoothing estimates were utilized by Pramanik and Seeger [Reference Pramanik and Seeger24] and Beltran et al. [Reference Beltran, Guo, Hickman and Seeger1] to prove
![]() $L^p$
maximal bound.
$L^p$
maximal bound.
Nevertheless, for
![]() $d\ge 3$
, no local smoothing estimate up to the sharp order
$d\ge 3$
, no local smoothing estimate up to the sharp order
![]() $2/p$
has been known previously.
$2/p$
has been known previously.
Theorem 1.3. Let
![]() $d\ge 3$
. Suppose
$d\ge 3$
. Suppose
![]() $\gamma $
is a smooth nondegenerate curve. Then, if
$\gamma $
is a smooth nondegenerate curve. Then, if
![]() $p\ge 4d-2$
, the estimate (1.4) holds true for
$p\ge 4d-2$
, the estimate (1.4) holds true for
![]() $\alpha <2/p$
.
$\alpha <2/p$
.
Theorem 1.3 remains valid as far as
![]() $\gamma \in \mathrm C^{3d+1}(I)$
(see Theorem 2.2 below).
$\gamma \in \mathrm C^{3d+1}(I)$
(see Theorem 2.2 below).
Maximal estimate
The local smoothing estimate (1.4) has been of particular interest in connection to
![]() $L^p$
boundedness of the maximal operator
$L^p$
boundedness of the maximal operator
([Reference Mockenhaupt, Seeger and Sogge19, Reference Schlag and Sogge27, Reference Pramanik and Seeger24, Reference Beltran, Guo, Hickman and Seeger1]) and problems in geometric measure theory (see, e.g., [Reference Wolff38] and Corollary 1.6 below). If the estimate (1.4) holds for some
![]() $\alpha>1/p$
,
$\alpha>1/p$
,
![]() $L^p$
boundedness of M follows by a standard argument relying on the Sobolev embedding ([Reference Pramanik and Seeger24]).
$L^p$
boundedness of M follows by a standard argument relying on the Sobolev embedding ([Reference Pramanik and Seeger24]).
The study of the maximal functions generated by dilations of submanifolds goes back to Stein’s spherical maximal theorem [Reference Stein31] (see, also, [Reference Stein32, Ch.10] and [Reference Ikromov, Kempe and Müller13]). The circular maximal theorem was later proved by Bourgain [Reference Bourgain3] (also, see [Reference Sogge30, Reference Mockenhaupt, Seeger and Sogge19, Reference Schlag26, Reference Schlag and Sogge27, Reference Lee15]). Afterwards, a natural question was whether the maximal operator M under consideration in the current paper is bounded on
![]() $L^p$
for some
$L^p$
for some
![]() $p\neq \infty $
when
$p\neq \infty $
when
![]() $d\ge 3$
. In view of Stein’s interpolation argument based on
$d\ge 3$
. In view of Stein’s interpolation argument based on
![]() $L^2$
estimate [Reference Stein31], proving
$L^2$
estimate [Reference Stein31], proving
![]() $L^p$
boundedness of M becomes more challenging as d increases since the decay of the Fourier transform of
$L^p$
boundedness of M becomes more challenging as d increases since the decay of the Fourier transform of
![]() $\mathfrak m_t$
gets weaker (see (1.3)). Though the question was raised as early as in the late 1980s, it remained open for any
$\mathfrak m_t$
gets weaker (see (1.3)). Though the question was raised as early as in the late 1980s, it remained open for any
![]() $d\ge 3$
until recently. In
$d\ge 3$
until recently. In
![]() $\mathbb R^3$
, the first positive result was obtained by Pramanik and Seeger [Reference Pramanik and Seeger24] and the range of p was further extended to
$\mathbb R^3$
, the first positive result was obtained by Pramanik and Seeger [Reference Pramanik and Seeger24] and the range of p was further extended to
![]() $p>4$
thanks to the decoupling inequality for the cone [Reference Bourgain and Demeter4]. Very recently, the authors [Reference Ko, Lee and Oh14] proved
$p>4$
thanks to the decoupling inequality for the cone [Reference Bourgain and Demeter4]. Very recently, the authors [Reference Ko, Lee and Oh14] proved
![]() $L^p$
boundedness of M on the optimal range, that is, M is bounded on
$L^p$
boundedness of M on the optimal range, that is, M is bounded on
![]() $L^p$
if and only if
$L^p$
if and only if
![]() $p>3$
. The same result was independently obtained by Beltran et al. [Reference Beltran, Guo, Hickman and Seeger1].
$p>3$
. The same result was independently obtained by Beltran et al. [Reference Beltran, Guo, Hickman and Seeger1].
However, no nontrival
![]() $L^p$
bound on M has been known in higher dimensions. The following establishes existence of such maximal bounds for every
$L^p$
bound on M has been known in higher dimensions. The following establishes existence of such maximal bounds for every
![]() $d\ge 4$
.
$d\ge 4$
.
Theorem 1.4. Let
![]() $d\ge 4$
. Suppose
$d\ge 4$
. Suppose
![]() $\gamma $
is a smooth nondegenerate curve. Then, for
$\gamma $
is a smooth nondegenerate curve. Then, for
![]() $p>2(d-1)$
we have
$p>2(d-1)$
we have
The result is a consequence of Theorem 1.3. Since the estimate (1.4) holds for
![]() $p=2$
and
$p=2$
and
![]() $\alpha =1/d$
, interpolation gives (1.4) for some
$\alpha =1/d$
, interpolation gives (1.4) for some
![]() $\alpha>1/p$
when
$\alpha>1/p$
when
![]() $2d-2<p<\infty $
. So, the maximal estimate (1.5) follows, as mentioned before, by a standard argument. A natural conjecture is that M is bounded on
$2d-2<p<\infty $
. So, the maximal estimate (1.5) follows, as mentioned before, by a standard argument. A natural conjecture is that M is bounded on
![]() $L^p$
if and only if
$L^p$
if and only if
![]() $p>d$
. M cannot be bounded on
$p>d$
. M cannot be bounded on
![]() $L^p$
if
$L^p$
if
![]() $p\le d$
, as can be seen by a simple adaptation of the argument in [Reference Ko, Lee and Oh14, Proposition 4.4]. Theorem 1.4 also extends to the finite type curves by the rescaling argument. The following result is sharp when
$p\le d$
, as can be seen by a simple adaptation of the argument in [Reference Ko, Lee and Oh14, Proposition 4.4]. Theorem 1.4 also extends to the finite type curves by the rescaling argument. The following result is sharp when
![]() $\ell \ge 2(d-1)$
.
$\ell \ge 2(d-1)$
.
Corollary 1.5. Let
![]() $d\ge 4$
and
$d\ge 4$
and
![]() $\ell> d$
. Suppose
$\ell> d$
. Suppose
![]() $\gamma $
is a curve of maximal type
$\gamma $
is a curve of maximal type
![]() $\ell $
. Then the estimate (1.5) holds if
$\ell $
. Then the estimate (1.5) holds if
![]() $p>\max (\ell ,2(d-1))$
.
$p>\max (\ell ,2(d-1))$
.
Packing of curves in
 $\mathbb R^d$
$\mathbb R^d$
The sharp local smoothing estimate (1.4) in Theorem 1.3 has interesting measure theoretic consequences concerning unions of curves generated by translation and dilation of a nondegenerate curve. The following generalizes Wolff’s result [Reference Wolff38, Corollary 3], where unions of circles in
![]() $\mathbb R^2$
were considered (see also [Reference Marstrand17, Reference Mitsis18, Reference Wolff37] for earlier results).
$\mathbb R^2$
were considered (see also [Reference Marstrand17, Reference Mitsis18, Reference Wolff37] for earlier results).
Corollary 1.6. Let
![]() $\gamma $
be a smooth nondegenerate curve in
$\gamma $
be a smooth nondegenerate curve in
![]() $\mathbb R^d$
,
$\mathbb R^d$
,
![]() $d\ge 3$
, and let
$d\ge 3$
, and let
![]() $E \subset \mathbb R^{d+1}$
be a set of Hausdorff dimension greater than
$E \subset \mathbb R^{d+1}$
be a set of Hausdorff dimension greater than
![]() $d-1$
. Suppose F is a set in
$d-1$
. Suppose F is a set in
![]() $\mathbb R^d$
such that
$\mathbb R^d$
such that
![]() $(x+t\gamma (I))\cap F$
has positive one-dimensional outer measure for all
$(x+t\gamma (I))\cap F$
has positive one-dimensional outer measure for all
![]() $(x,t) \in E$
. Then F has positive outer measure.
$(x,t) \in E$
. Then F has positive outer measure.
Corollary 1.6 follows by Theorem 1.3 and the argument in [Reference Wolff38]. The result does not hold in general without the nondegeneracy assumption on
![]() $\gamma $
as one can easily see considering a curve contained in a lower dimensional vector space. The same result continues to be valid for the finite type curves. Consequently, Corollary 1.6 implies the following.
$\gamma $
as one can easily see considering a curve contained in a lower dimensional vector space. The same result continues to be valid for the finite type curves. Consequently, Corollary 1.6 implies the following.
Corollary 1.6′. Let
![]() $\gamma $
be a smooth finite type curve in
$\gamma $
be a smooth finite type curve in
![]() $\mathbb R^d$
,
$\mathbb R^d$
,
![]() $d\ge 3$
, and let E and F be compact subsets in
$d\ge 3$
, and let E and F be compact subsets in
![]() $\mathbb R^d$
. Suppose E has Hausdorff dimension greater than
$\mathbb R^d$
. Suppose E has Hausdorff dimension greater than
![]() $d-1$
and for each
$d-1$
and for each
![]() $x \in E$
there is
$x \in E$
there is
![]() $t(x)> 0$
such that
$t(x)> 0$
such that
![]() $x+t(x)\gamma (I)\subset F$
. Then, F has positive measure.
$x+t(x)\gamma (I)\subset F$
. Then, F has positive measure.
Our approach
To prove
![]() $L^p$
(
$L^p$
(
![]() $p\neq 2$
) smoothing properties of
$p\neq 2$
) smoothing properties of
![]() $\mathcal A_t$
, we need more than the decay of
$\mathcal A_t$
, we need more than the decay of
![]() $\widehat {\mathfrak m}_t$
, that is, (1.3). When
$\widehat {\mathfrak m}_t$
, that is, (1.3). When
![]() $d=2$
, we have rather a precise asymptotic expansion of
$d=2$
, we have rather a precise asymptotic expansion of
![]() $\widehat {\mathfrak m}_t$
, which makes it possible to relate
$\widehat {\mathfrak m}_t$
, which makes it possible to relate
![]() $\mathcal A_t$
to other forms of operators. In fact, one can use the estimate for the wave operator (e.g., [Reference Schlag and Sogge27, Reference Tao and Vargas35, Reference Lee15]) to obtain local smoothing estimate. However, in higher dimensions
$\mathcal A_t$
to other forms of operators. In fact, one can use the estimate for the wave operator (e.g., [Reference Schlag and Sogge27, Reference Tao and Vargas35, Reference Lee15]) to obtain local smoothing estimate. However, in higher dimensions
![]() $d\ge 3$
, to compute
$d\ge 3$
, to compute
![]() $\widehat {\mathfrak m}_t$
explicitly is not a simple matter. Even worse, this becomes much more complicated as d increases since one has to take into account the derivatives
$\widehat {\mathfrak m}_t$
explicitly is not a simple matter. Even worse, this becomes much more complicated as d increases since one has to take into account the derivatives
![]() $\gamma ^{(k)}(s)\cdot \xi $
,
$\gamma ^{(k)}(s)\cdot \xi $
,
![]() $k=2,\dots , d$
. The common approach in the previous works ([Reference Pramanik and Seeger24, Reference Beltran, Guo, Hickman and Seeger1, Reference Beltran, Guo, Hickman and Seeger2]) to get around this difficulty was to use detailed decompositions (of various scales) on the Fourier side away from the conic sets where
$k=2,\dots , d$
. The common approach in the previous works ([Reference Pramanik and Seeger24, Reference Beltran, Guo, Hickman and Seeger1, Reference Beltran, Guo, Hickman and Seeger2]) to get around this difficulty was to use detailed decompositions (of various scales) on the Fourier side away from the conic sets where
![]() $\widehat {\mathfrak m}_t$
decays slowly. The consequent decompositions were then combined with the decoupling or square function estimate ([Reference Oberlin, Smith and Sogge20, Reference Pramanik and Seeger23, Reference Pramanik and Seeger24, Reference Pramanik and Seeger25, Reference Beltran, Guo, Hickman and Seeger1, Reference Beltran, Guo, Hickman and Seeger2]). However, this type of approach based on fine scale decomposition becomes exceedingly difficult to manage as the dimension d gets larger and, consequently, does not seem to be tractable in higher dimensions.
$\widehat {\mathfrak m}_t$
decays slowly. The consequent decompositions were then combined with the decoupling or square function estimate ([Reference Oberlin, Smith and Sogge20, Reference Pramanik and Seeger23, Reference Pramanik and Seeger24, Reference Pramanik and Seeger25, Reference Beltran, Guo, Hickman and Seeger1, Reference Beltran, Guo, Hickman and Seeger2]). However, this type of approach based on fine scale decomposition becomes exceedingly difficult to manage as the dimension d gets larger and, consequently, does not seem to be tractable in higher dimensions.
To overcome the difficulty, we develop a new strategy which allows us to dispense with such sophisticated decomposition. Before closing the introduction, we briefly discuss the key ingredients of our approach.
-
• The main novelty of this paper lies in an induction argument which we build on the local nondegeneracy assumption:
(𝔑(L,B))for a constant $$\begin{align} \sum_{\ell=1}^L |\langle \gamma^{(\ell)}(s), \xi\rangle| \ge B^{-1}|\xi| \end{align} $$
$$\begin{align} \sum_{\ell=1}^L |\langle \gamma^{(\ell)}(s), \xi\rangle| \ge B^{-1}|\xi| \end{align} $$
 $B\ge 1$
. To prove our results, we consider the operator
$B\ge 1$
. To prove our results, we consider the operator
 $\mathcal A_t[\gamma , a]$
(see (2.2) below for its definition). Clearly,
$\mathcal A_t[\gamma , a]$
(see (2.2) below for its definition). Clearly,
 ${\mathfrak N({d}, {B'})}$
holds for a constant
${\mathfrak N({d}, {B'})}$
holds for a constant
 $B'>0$
if
$B'>0$
if
 $\gamma $
satisfies the condition (1.1). However, instead of considering the case
$\gamma $
satisfies the condition (1.1). However, instead of considering the case
 $L=d$
alone, we prove the estimate for all
$L=d$
alone, we prove the estimate for all
 $L=2,\dots , d$
under the assumption that
$L=2,\dots , d$
under the assumption that
 $\mathfrak N(L, B)$
holds on the support of a. See Theorem 2.2 and 4.1. A trivial (yet, important) observation is that
$\mathfrak N(L, B)$
holds on the support of a. See Theorem 2.2 and 4.1. A trivial (yet, important) observation is that
 ${\mathfrak N({L-1}, B)}$
implies
${\mathfrak N({L-1}, B)}$
implies
 ${\mathfrak N(L, B)}, $
so we may think of
${\mathfrak N(L, B)}, $
so we may think of
 $\mathcal A_t[\gamma , a]$
as being more degenerate as L gets larger. Thanks to this hierarchical structure, we may use an inductive strategy along the number L. See Proposition 2.3 and 4.2 below.
$\mathcal A_t[\gamma , a]$
as being more degenerate as L gets larger. Thanks to this hierarchical structure, we may use an inductive strategy along the number L. See Proposition 2.3 and 4.2 below.
-
• We extend the rescaling [Reference Ham and Lee12, Reference Ko, Lee and Oh14] and iteration [Reference Pramanik and Seeger24] arguments. Roughly speaking, we combine the first with the induction assumption in Proposition 2.3 (or 4.2) to handle the less degenerate parts, and use the latter to deal with the remaining part. In order to generalize those arguments, we introduce a class of symbols which are naturally adjusted to a small subcurve (Definition 2.4). We also use the decoupling inequalities for the nondegenerate curves obtained by Beltran et al. [Reference Beltran, Guo, Hickman and Seeger2] (Corollary 2.15). Their inequalities were deduced from those due to Bourgain, Demeter and Guth [Reference Bourgain, Demeter and Guth5]. Instead of applying the inequalities directly, we use modified forms which are adjusted to the sharp smoothing orders of the specific estimates (see (2.40) and (2.41) below). This makes it possible to obtain the sharp estimates on extended ranges.
Organization of the paper. We first prove Theorem 1.3 whose proof is more involved than that of Theorem 1.1. In Section 2, the proof of Theorem 1.3 is reduced to that of Proposition 2.9, which we prove while assuming Proposition 2.10. The proof of Proposition 2.10 is given in Section 3. We prove Theorem 1.1 in Section 4.
2 Smoothing estimates with localized frequency
In this section, we consider an extension of Theorem 1.3 via microlocalization (see Theorem 2.2 below) so that we can prove it in an inductive manner. We then reduce the matter to proving Proposition 2.9, which we show by applying Proposition 2.10. We also obtain some preparatory results.
Let
![]() $1\le L \le d$
be a positive integer and
$1\le L \le d$
be a positive integer and
![]() $B\ge 1$
be a large number. For quantitative control of estimates we consider the following two conditions:
$B\ge 1$
be a large number. For quantitative control of estimates we consider the following two conditions:
where
![]() $ \operatorname {\mathrm {Vol}} (v_1,\dots ,v_L)$
denotes the L-dimensional volume of the parallelepiped generated by
$ \operatorname {\mathrm {Vol}} (v_1,\dots ,v_L)$
denotes the L-dimensional volume of the parallelepiped generated by
![]() $v_1,\dots , v_L$
. By finite decomposition and a standard reduction using rescaling and a change of variables, the constant B can be taken to be close to
$v_1,\dots , v_L$
. By finite decomposition and a standard reduction using rescaling and a change of variables, the constant B can be taken to be close to
![]() $1$
(see Section 2.2).
$1$
(see Section 2.2).
Notation. For nonnegative quantities A and
![]() $ D$
, we denote
$ D$
, we denote
![]() $A\lesssim D$
if there exists an independent positive constant C such that
$A\lesssim D$
if there exists an independent positive constant C such that
![]() $A\le CD$
, but the constant C may differ at each occurrence depending on the context, and
$A\le CD$
, but the constant C may differ at each occurrence depending on the context, and
![]() $A \lesssim _{B}\! D$
means the inequality holds with an implicit constant depending on B. Throughout the paper, the constant C mostly depends on B. However, we do not make it explicit every time since it is clear in the context. By
$A \lesssim _{B}\! D$
means the inequality holds with an implicit constant depending on B. Throughout the paper, the constant C mostly depends on B. However, we do not make it explicit every time since it is clear in the context. By
![]() $A=O(D)$
we denote
$A=O(D)$
we denote
![]() $|A|\lesssim D$
.
$|A|\lesssim D$
.
Definition 2.1. For
![]() $k\ge 0$
, let
$k\ge 0$
, let
![]() $ \mathbb A_k=\{ \xi \in \mathbb R^d: 2^{k-1} \le |\xi | \le 2^{k+1}\}.$
We say
$ \mathbb A_k=\{ \xi \in \mathbb R^d: 2^{k-1} \le |\xi | \le 2^{k+1}\}.$
We say
![]() $a\in \mathrm C^{d+L+2}(\mathbb R^{d+2})$
is a symbol of type
$a\in \mathrm C^{d+L+2}(\mathbb R^{d+2})$
is a symbol of type
![]() $(k, L, B)$
relative to
$(k, L, B)$
relative to
![]() $\gamma $
if
$\gamma $
if
![]() $\operatorname {\mathrm {supp}} a \subset I \times [2^{-1},4] \times \mathbb A_k$
,
$\operatorname {\mathrm {supp}} a \subset I \times [2^{-1},4] \times \mathbb A_k$
,
![]() $\mathfrak N(L, B)$
holds for
$\mathfrak N(L, B)$
holds for
![]() $\gamma $
whenever
$\gamma $
whenever
![]() $(s,t,\xi )\in \operatorname {\mathrm {supp}} a$
for some t, and
$(s,t,\xi )\in \operatorname {\mathrm {supp}} a$
for some t, and
for
![]() $(j,l,\alpha )\in \mathcal I_L:=\{(j,l,\alpha ): 0\le j\le 1,\, 0\le l\le 2L,\, |\alpha |\le d+L+2\}$
.
$(j,l,\alpha )\in \mathcal I_L:=\{(j,l,\alpha ): 0\le j\le 1,\, 0\le l\le 2L,\, |\alpha |\le d+L+2\}$
.
We define an integral operator by
Note
![]() $\mathcal A_t f=\mathcal A_t[\gamma , \psi ]f$
. Theorem 1.3 is a consequence of the following.
$\mathcal A_t f=\mathcal A_t[\gamma , \psi ]f$
. Theorem 1.3 is a consequence of the following.
Theorem 2.2. Let
![]() $\gamma \in \mathrm C^{3d+1}(I)$
satisfy (2.1) and
$\gamma \in \mathrm C^{3d+1}(I)$
satisfy (2.1) and
![]() $\mathfrak V(L,B)$
for some
$\mathfrak V(L,B)$
for some
![]() $B\ge 1$
. Suppose a is a symbol of type
$B\ge 1$
. Suppose a is a symbol of type
![]() $(k, L, B)$
relative to
$(k, L, B)$
relative to
![]() $\gamma $
. Then, if
$\gamma $
. Then, if
![]() $p\ge 4L-2$
, for
$p\ge 4L-2$
, for
![]() $\epsilon>0$
there is a constant
$\epsilon>0$
there is a constant
![]() $C_\epsilon =C_\epsilon (B)$
such that
$C_\epsilon =C_\epsilon (B)$
such that
Theorem 2.2 is easy to prove when
![]() $L=1$
. Indeed, (2.3) follows from the estimate
$L=1$
. Indeed, (2.3) follows from the estimate
where
![]() $K(x)= 2^{(d-1)k}(1+ |2^{k}x|)^{-d-3}.$
Note
$K(x)= 2^{(d-1)k}(1+ |2^{k}x|)^{-d-3}.$
Note
![]() $|\gamma '(s)\cdot \xi |\sim 2^k$
if
$|\gamma '(s)\cdot \xi |\sim 2^k$
if
![]() $(s,t,\xi )\in \operatorname {\mathrm {supp}} a$
for some t. By integration by parts in s,
$(s,t,\xi )\in \operatorname {\mathrm {supp}} a$
for some t. By integration by parts in s,
![]() $\mathcal A_t[\gamma , a]=t^{-1}\mathcal A_t[\gamma , \tilde a]$
, where
$\mathcal A_t[\gamma , a]=t^{-1}\mathcal A_t[\gamma , \tilde a]$
, where
![]() $\tilde a=i(\gamma '(s)\cdot \xi \, \partial _s a -\gamma "(s)\cdot \xi \, a)/(\gamma '(s)\cdot \xi )^2$
. Since
$\tilde a=i(\gamma '(s)\cdot \xi \, \partial _s a -\gamma "(s)\cdot \xi \, a)/(\gamma '(s)\cdot \xi )^2$
. Since
![]() $|\partial _\xi ^{\alpha } \tilde a|\lesssim |\xi |^{-|\alpha |-1}$
for
$|\partial _\xi ^{\alpha } \tilde a|\lesssim |\xi |^{-|\alpha |-1}$
for
![]() $|\alpha |\le d+3$
, routine integration by parts in
$|\alpha |\le d+3$
, routine integration by parts in
![]() $\xi $
gives the desired estimate (e.g., see Proof of Lemma 2.7
below). When
$\xi $
gives the desired estimate (e.g., see Proof of Lemma 2.7
below). When
![]() $L=2$
, Theorem 2.2 follows by the result in [24, Theorem 4.1] and the decoupling inequality in [Reference Bourgain and Demeter4].
$L=2$
, Theorem 2.2 follows by the result in [24, Theorem 4.1] and the decoupling inequality in [Reference Bourgain and Demeter4].
Once we have Theorem 2.2, the proof of Theorem 1.3 is straightforward. By the Littlewood–Paley decomposition it is sufficient to show the estimate (2.3) for
![]() $p\ge 4d-2$
with
$p\ge 4d-2$
with
![]() $a_k(s,t,\xi )=\psi (s) \chi (t) \beta (2^{-k}|\xi |)$
, where
$a_k(s,t,\xi )=\psi (s) \chi (t) \beta (2^{-k}|\xi |)$
, where
![]() $\beta \in \mathrm C_c^\infty ((1/2,2))$
. This can be made rigorous using
$\beta \in \mathrm C_c^\infty ((1/2,2))$
. This can be made rigorous using
![]() $\iint e^{-i t(\tau +\gamma (s)\cdot \xi )} \psi (s) \chi (t) dsdt =O((1+|\tau |)^{-N})$
for any N if
$\iint e^{-i t(\tau +\gamma (s)\cdot \xi )} \psi (s) \chi (t) dsdt =O((1+|\tau |)^{-N})$
for any N if
![]() $|\tau |\ge (1+\max _{s\in \operatorname {\mathrm {supp}} \psi } |\gamma (s)|)|\xi |$
. Since
$|\tau |\ge (1+\max _{s\in \operatorname {\mathrm {supp}} \psi } |\gamma (s)|)|\xi |$
. Since
![]() $\gamma $
satisfies the condition (1.1),
$\gamma $
satisfies the condition (1.1),
![]() $a_k$
is of type
$a_k$
is of type
![]() $(k, d, B)$
relative to
$(k, d, B)$
relative to
![]() $\gamma $
for a large B. Therefore, Theorem 1.3 follows from Theorem 2.2.
$\gamma $
for a large B. Therefore, Theorem 1.3 follows from Theorem 2.2.
Theorem 2.2 is immediate from the next proposition, which places Theorem 2.2 in an inductive framework.
Proposition 2.3. Let
![]() $2 \le N \le d$
. Suppose Theorem 2.2 holds for
$2 \le N \le d$
. Suppose Theorem 2.2 holds for
![]() $L=N-1$
. Then, Theorem 2.2 holds true with
$L=N-1$
. Then, Theorem 2.2 holds true with
![]() $L=N$
.
$L=N$
.
To prove Proposition 2.3, from this section to Section 3 we fix
![]() $N\in [2, d]$
,
$N\in [2, d]$
,
![]() $\gamma $
satisfying
$\gamma $
satisfying
![]() ${\mathfrak V(N, B)}$
, and a symbol
${\mathfrak V(N, B)}$
, and a symbol
![]() $ a$
of type
$ a$
of type
![]() $(k, N, B)$
relative to
$(k, N, B)$
relative to
![]() $\gamma $
.
$\gamma $
.
One of the main ideas is that by a suitable decomposition of the symbol we can separate from
![]() $\mathcal A_t[\gamma ,a]$
the less degenerate part which corresponds to
$\mathcal A_t[\gamma ,a]$
the less degenerate part which corresponds to
![]() $L=N-1$
. To this part we apply the assumption combined with a rescaling argument. To do this, we introduce a class of symbols which are adjusted to short subcurves of
$L=N-1$
. To this part we apply the assumption combined with a rescaling argument. To do this, we introduce a class of symbols which are adjusted to short subcurves of
![]() $\gamma $
.
$\gamma $
.
2.1 Symbols associated to subcurves
We begin with some notations. Let
![]() $N\ge 2$
, and let
$N\ge 2$
, and let
![]() $\delta $
and
$\delta $
and
![]() $B'$
denote numbers such that
$B'$
denote numbers such that
for a large constant
![]() $C\ge 3d+1$
. We note that
$C\ge 3d+1$
. We note that
![]() ${\mathfrak V({N-1}, {B'})}$
holds for some
${\mathfrak V({N-1}, {B'})}$
holds for some
![]() $B'$
. In fact,
$B'$
. In fact,
![]() ${\mathfrak V({N-1}, {B^2})}$
follows by (2.1) and
${\mathfrak V({N-1}, {B^2})}$
follows by (2.1) and
![]() ${\mathfrak V(N, B)}$
.
${\mathfrak V(N, B)}$
.
For
![]() $s\in I$
, we define a linear map
$s\in I$
, we define a linear map
![]() $ \widetilde {\mathcal L}^\delta _s:\mathbb R^{d}\mapsto \mathbb R^{d}$
as follows:
$ \widetilde {\mathcal L}^\delta _s:\mathbb R^{d}\mapsto \mathbb R^{d}$
as follows:
 $$ \begin{align} \begin{aligned} (\widetilde{\mathcal L}_{s}^\delta)^\intercal \gamma^{(j)}(s) &=\delta^{N-j}\gamma^{(j)}(s), \qquad && j=1,\dots,N-1, \\ (\widetilde{\mathcal L}_{s}^\delta)^\intercal v &=v, \qquad \qquad \quad~ && v\in \big(\mathrm V_s^{\gamma,N-1}\big)^{\perp}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} (\widetilde{\mathcal L}_{s}^\delta)^\intercal \gamma^{(j)}(s) &=\delta^{N-j}\gamma^{(j)}(s), \qquad && j=1,\dots,N-1, \\ (\widetilde{\mathcal L}_{s}^\delta)^\intercal v &=v, \qquad \qquad \quad~ && v\in \big(\mathrm V_s^{\gamma,N-1}\big)^{\perp}, \end{aligned} \end{align} $$
where
![]() $\mathrm V_s^{\gamma ,\ell } = \operatorname {\mathrm {span}} \big \{ \gamma ^{(j)}(s) : j=1,\dots ,\ell \big \}$
.
$\mathrm V_s^{\gamma ,\ell } = \operatorname {\mathrm {span}} \big \{ \gamma ^{(j)}(s) : j=1,\dots ,\ell \big \}$
.
![]() $\widetilde {\mathcal L}_{s}^\delta $
is well defined since
$\widetilde {\mathcal L}_{s}^\delta $
is well defined since
![]() ${\mathfrak V({N-1}, {B^2})}$
holds for
${\mathfrak V({N-1}, {B^2})}$
holds for
![]() $\gamma $
. The linear map
$\gamma $
. The linear map
![]() $\widetilde {\mathcal L}_{s}^\delta $
naturally appears when we rescale a subcurve of length about
$\widetilde {\mathcal L}_{s}^\delta $
naturally appears when we rescale a subcurve of length about
![]() $\delta $
(see the proofs of Lemma 2.7 and 2.8). We denote
$\delta $
(see the proofs of Lemma 2.7 and 2.8). We denote
We set
![]() $G(s)=(1,\gamma (s))$
and define
$G(s)=(1,\gamma (s))$
and define
 $$ \begin{align*} \Lambda_k(s,\delta, B')= \bigcap_{0\le j\le N-1} \big\{(\tau,\xi) \in \mathbb R \times \mathbb A_k & : |\langle G^{(j)}(s),(\tau,\xi)\rangle| \le B'2^{k+5} \delta^{N-j} \big \}. \end{align*} $$
$$ \begin{align*} \Lambda_k(s,\delta, B')= \bigcap_{0\le j\le N-1} \big\{(\tau,\xi) \in \mathbb R \times \mathbb A_k & : |\langle G^{(j)}(s),(\tau,\xi)\rangle| \le B'2^{k+5} \delta^{N-j} \big \}. \end{align*} $$
Definition 2.4. Let
![]() such that
such that
![]() . Then, by
. Then, by
![]() we denote the set of
we denote the set of
![]() $\mathfrak a \in \mathrm C^{d+N+2}(\mathbb R^{d+3})$
such that
$\mathfrak a \in \mathrm C^{d+N+2}(\mathbb R^{d+3})$
such that
We define
![]() $\operatorname {\mathrm {supp}}_{\xi } \mathfrak a=\bigcup _{s,t,\tau } \operatorname {\mathrm {supp}} \mathfrak a(s,t,\tau ,\cdot )$
and
$\operatorname {\mathrm {supp}}_{\xi } \mathfrak a=\bigcup _{s,t,\tau } \operatorname {\mathrm {supp}} \mathfrak a(s,t,\tau ,\cdot )$
and
![]() $\operatorname {\mathrm {supp}}_{s, \xi } \mathfrak a=\bigcup _{t,\tau } \operatorname {\mathrm {supp}} \mathfrak a(\cdot ,t,\tau ,\cdot )$
, and
$\operatorname {\mathrm {supp}}_{s, \xi } \mathfrak a=\bigcup _{t,\tau } \operatorname {\mathrm {supp}} \mathfrak a(\cdot ,t,\tau ,\cdot )$
, and
![]() $\operatorname {\mathrm {supp}}_{s} \mathfrak a$
and
$\operatorname {\mathrm {supp}}_{s} \mathfrak a$
and
![]() $\operatorname {\mathrm {supp}}_{\tau , \xi } \mathfrak a$
are defined likewise. Note that a statement
$\operatorname {\mathrm {supp}}_{\tau , \xi } \mathfrak a$
are defined likewise. Note that a statement
![]() $S(s, \xi )$
, depending on
$S(s, \xi )$
, depending on
![]() $(s, \xi )$
, holds on
$(s, \xi )$
, holds on
![]() $\operatorname {\mathrm {supp}}_{s,\xi } \mathfrak a$
if and only if
$\operatorname {\mathrm {supp}}_{s,\xi } \mathfrak a$
if and only if
![]() $S(s,\xi )$
holds whenever
$S(s,\xi )$
holds whenever
![]() $(s,t, \tau ,\xi ) \in \operatorname {\mathrm {supp}} \mathfrak a$
for some t,
$(s,t, \tau ,\xi ) \in \operatorname {\mathrm {supp}} \mathfrak a$
for some t,
![]() $\tau $
.
$\tau $
.
Denote
![]() $\mathrm V_s^{G,\ell } = \operatorname {\mathrm {span}} \{(1,0), G'(s), \dots , G^{(\ell )}(s) \}.$
We take a close look at the map
$\mathrm V_s^{G,\ell } = \operatorname {\mathrm {span}} \{(1,0), G'(s), \dots , G^{(\ell )}(s) \}.$
We take a close look at the map
![]() ${\mathcal L}_s^\delta $
. By the equations (2.4) and (2.5) we have
${\mathcal L}_s^\delta $
. By the equations (2.4) and (2.5) we have
 $$ \begin{align} \begin{cases} \begin{aligned} (\mathcal L_s^\delta)^\intercal G(s) &= \delta^{N}(1,0), \\[2pt] (\mathcal L_s^\delta)^\intercal G^{(j)}(s) &= \delta^{N-j}G^{(j)}(s), \qquad &&j=1,\dots, N-1, \\ ({\mathcal L}_s^\delta)^\intercal v &=v, \qquad&& v\in (\mathrm V_s^{G,N-1} )^\perp. \end{aligned} \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \begin{aligned} (\mathcal L_s^\delta)^\intercal G(s) &= \delta^{N}(1,0), \\[2pt] (\mathcal L_s^\delta)^\intercal G^{(j)}(s) &= \delta^{N-j}G^{(j)}(s), \qquad &&j=1,\dots, N-1, \\ ({\mathcal L}_s^\delta)^\intercal v &=v, \qquad&& v\in (\mathrm V_s^{G,N-1} )^\perp. \end{aligned} \end{cases} \end{align} $$
The first identity is clear since
![]() $(\mathcal L_s^\delta )^\intercal (\tau , \xi )=(\delta ^N \tau , (\widetilde {\mathcal L}_s^\delta )^\intercal \xi -\tau (\widetilde {\mathcal L}_s^\delta )^\intercal \gamma (s))$
. The second and the third follow from (2.4) since
$(\mathcal L_s^\delta )^\intercal (\tau , \xi )=(\delta ^N \tau , (\widetilde {\mathcal L}_s^\delta )^\intercal \xi -\tau (\widetilde {\mathcal L}_s^\delta )^\intercal \gamma (s))$
. The second and the third follow from (2.4) since
![]() $G^{(j)}\in \{0\} \times \mathbb R^d$
,
$G^{(j)}\in \{0\} \times \mathbb R^d$
,
![]() $1 \le j \le N-1$
,
$1 \le j \le N-1$
,
![]() $\big ( \mathrm V_s^{G,N-1} \big )^\perp \subset \{0\} \times \mathbb R^d$
, and
$\big ( \mathrm V_s^{G,N-1} \big )^\perp \subset \{0\} \times \mathbb R^d$
, and
![]() $(\mathcal L_s^\delta )^\intercal (0,\xi )=(0,(\widetilde {\mathcal L}_s^\delta )^\intercal \xi )$
. Furthermore, there is a constant
$(\mathcal L_s^\delta )^\intercal (0,\xi )=(0,(\widetilde {\mathcal L}_s^\delta )^\intercal \xi )$
. Furthermore, there is a constant
![]() $C=C(B)$
, independent of s and
$C=C(B)$
, independent of s and
![]() $\delta $
, such that
$\delta $
, such that
Note that (2.9) is equivalent to
![]() $ |( \mathcal L_{s}^{\delta })^\intercal (\tau , \xi )| \le C|(\tau ,\xi )|$
. The inequality is clear from (2.4) because
$ |( \mathcal L_{s}^{\delta })^\intercal (\tau , \xi )| \le C|(\tau ,\xi )|$
. The inequality is clear from (2.4) because
![]() ${\mathfrak V({N-1}, {B^2})}$
holds and all the eigenvalues of
${\mathfrak V({N-1}, {B^2})}$
holds and all the eigenvalues of
![]() $(\widetilde {\mathcal L}_{s}^\delta )^\intercal $
are contained in the interval
$(\widetilde {\mathcal L}_{s}^\delta )^\intercal $
are contained in the interval
![]() $(0,1]$
.
$(0,1]$
.
Lemma 2.5. Let
![]() $ \mathcal L_{s}^\delta (\tau ,\xi )\in \Lambda _k(s,\delta , B')$
and
$ \mathcal L_{s}^\delta (\tau ,\xi )\in \Lambda _k(s,\delta , B')$
and
![]() ${\mathfrak V({N-1}, {B'})}$
hold for
${\mathfrak V({N-1}, {B'})}$
hold for
![]() $\gamma $
. Then, there exists a constant
$\gamma $
. Then, there exists a constant
![]() $C=C(B')$
such that
$C=C(B')$
such that
Proof. Since
![]() $ \mathcal L_{s}^\delta (\tau ,\xi )\in \Lambda _k(s,\delta , B')$
, by (2.5) we have
$ \mathcal L_{s}^\delta (\tau ,\xi )\in \Lambda _k(s,\delta , B')$
, by (2.5) we have
![]() $2^{k-1}\le |\widetilde {\mathcal L}_{s}^\delta \xi |\le 2^{k+1}$
. So, the second inequality in (2.10) is clear from (2.9) if we take
$2^{k-1}\le |\widetilde {\mathcal L}_{s}^\delta \xi |\le 2^{k+1}$
. So, the second inequality in (2.10) is clear from (2.9) if we take
![]() $\tau =0$
.
$\tau =0$
.
To show the first inequality, from (2.8) we have
![]() $| \langle (1,0),(\tau ,\xi ) \rangle | \le B'2^{k+5}$
and
$| \langle (1,0),(\tau ,\xi ) \rangle | \le B'2^{k+5}$
and
![]() $|\langle G^{(j)}(s),(\tau , \xi ) \rangle | \le B' 2^{k+5}$
,
$|\langle G^{(j)}(s),(\tau , \xi ) \rangle | \le B' 2^{k+5}$
,
![]() $1\le j\le N-1$
, because
$1\le j\le N-1$
, because
![]() $\mathcal L_{s}^\delta (\tau ,\xi )\in \Lambda _k(s,\delta , B').$
Also, if
$\mathcal L_{s}^\delta (\tau ,\xi )\in \Lambda _k(s,\delta , B').$
Also, if
![]() $v \in ( \mathrm V_s^{G,N-1} )^\perp $
and
$v \in ( \mathrm V_s^{G,N-1} )^\perp $
and
![]() $|v|=1$
, by (2.8) we see
$|v|=1$
, by (2.8) we see
![]() $ |\langle v,(\tau ,\xi ) \rangle | =|\langle v, \mathcal L_{s}^\delta (\tau ,\xi ) \rangle |\le 2^{k+1}$
. Therefore, we get
$ |\langle v,(\tau ,\xi ) \rangle | =|\langle v, \mathcal L_{s}^\delta (\tau ,\xi ) \rangle |\le 2^{k+1}$
. Therefore, we get
![]() $|(\tau ,\xi )| \le C2^k$
for some
$|(\tau ,\xi )| \le C2^k$
for some
![]() $C=C(B')$
since
$C=C(B')$
since
![]() ${\mathfrak V({N-1}, {B'})}$
holds and
${\mathfrak V({N-1}, {B'})}$
holds and
![]() $\mathrm V_s^{G,N-1}\oplus ( \mathrm V_s^{G,N-1} )^\perp =\mathbb R^{d+1}$
.
$\mathrm V_s^{G,N-1}\oplus ( \mathrm V_s^{G,N-1} )^\perp =\mathbb R^{d+1}$
.
The following shows the matrices
![]() $ \mathcal L_{s}^{\delta }$
,
$ \mathcal L_{s}^{\delta }$
,
![]() are close to each other if so are
are close to each other if so are
![]() .
.
Lemma 2.6. Let
![]() and
and
![]() $\gamma $
satisfy
$\gamma $
satisfy
![]() ${\mathfrak V({N-1}, {B'})}$
. If
${\mathfrak V({N-1}, {B'})}$
. If
![]() , then there exists a constant
, then there exists a constant
![]() $C=C(B')\ge 1$
such that
$C=C(B')\ge 1$
such that
Proof. It suffices to prove that (2.11) holds if
![]() for a constant
for a constant
![]() $c>0$
, independent of s and
$c>0$
, independent of s and
![]() . Applying this finitely many times, we can remove the additional assumption. Moreover, it is enough to show
. Applying this finitely many times, we can remove the additional assumption. Moreover, it is enough to show
when
![]() . Here,
. Here,
![]() $\| \cdot \|$
denotes a matrix norm. Taking
$\| \cdot \|$
denotes a matrix norm. Taking
![]() $c>0$
sufficiently small, we get (2.11).
$c>0$
sufficiently small, we get (2.11).
By (2.8),
for
![]() $j=1,\dots ,N-1$
. Let
$j=1,\dots ,N-1$
. Let
,
![]() $|c'|\le c$
. Expanding
$|c'|\le c$
. Expanding
![]() $G^{(j)}$
in Taylor series at s, by the condition (2.1) we have
$G^{(j)}$
in Taylor series at s, by the condition (2.1) we have

for
![]() $j=1,\dots ,N-1$
. By (2.8) and the mean value theorem, we get
$j=1,\dots ,N-1$
. By (2.8) and the mean value theorem, we get
From (2.8), we also have
. A similar argument also shows
.
Let
![]() $\{ v_N,\dots , v_d\}$
denote an orthonormal basis of
$\{ v_N,\dots , v_d\}$
denote an orthonormal basis of
![]() . By
. By
![]() ${\mathfrak V({N-1}, {B'})}$
and (2.1), it follows that
${\mathfrak V({N-1}, {B'})}$
and (2.1), it follows that
![]() ,
,
![]() $j=1, \dots , N-1$
. Since
$j=1, \dots , N-1$
. Since
![]() , there is an orthonormal basis
, there is an orthonormal basis
![]() $\{v_N(s),\dots ,v_d(s)\}$
of
$\{v_N(s),\dots ,v_d(s)\}$
of
![]() $( \mathrm V_s^{G,N-1})^\perp $
such that
$( \mathrm V_s^{G,N-1})^\perp $
such that
![]() $|v_j(s)-v_j| \lesssim _{B'}\! c\delta $
,
$|v_j(s)-v_j| \lesssim _{B'}\! c\delta $
,
![]() $j=N,\dots ,d$
. So, we have
$j=N,\dots ,d$
. So, we have
![]() $|(\mathcal L_{s}^\delta )^\intercal v_j -v_j|\lesssim _{B'}\! c\delta $
by (2.9). Since
$|(\mathcal L_{s}^\delta )^\intercal v_j -v_j|\lesssim _{B'}\! c\delta $
by (2.9). Since
![]() , it follows that
, it follows that
![]() ,
,
![]() $j=N,\dots ,d$
.
$j=N,\dots ,d$
.
We denote by
![]() $\mathrm M$
the matrix
$\mathrm M$
the matrix
![]() . Then, combining all together, we have
. Then, combining all together, we have
![]() . Note that
. Note that
![]() ${\mathfrak V({N-1}, {B'})}$
gives
${\mathfrak V({N-1}, {B'})}$
gives
![]() $|\mathrm M^{-1} v| \lesssim _{B'}\! |v|$
for
$|\mathrm M^{-1} v| \lesssim _{B'}\! |v|$
for
![]() $v\in \mathbb R^{d+1}$
. Therefore, we obtain (2.12).
$v\in \mathbb R^{d+1}$
. Therefore, we obtain (2.12).
For a continuous function
![]() $\mathfrak a$
supported in
$\mathfrak a$
supported in
![]() $I\times [1/2, 4]\times \mathbb R\times \mathbb A_k$
, we set
$I\times [1/2, 4]\times \mathbb R\times \mathbb A_k$
, we set
Lemma 2.7. Suppose
![]() $\mathfrak a\in \mathrm{C}^{d+3}(\mathbb R^{d+3})$
satisfies (2.6) and (2.7) for
$\mathfrak a\in \mathrm{C}^{d+3}(\mathbb R^{d+3})$
satisfies (2.6) and (2.7) for
![]() $j=l=0$
and
$j=l=0$
and
![]() $|\alpha | \le d+3$
. Then, there is a constant
$|\alpha | \le d+3$
. Then, there is a constant
![]() $C=C(B)$
such that
$C=C(B)$
such that
where
![]() $\tilde \chi \in \mathrm C_c^\infty ((2^{-2},2^3))$
such that
$\tilde \chi \in \mathrm C_c^\infty ((2^{-2},2^3))$
such that
![]() $\tilde \chi =1$
on
$\tilde \chi =1$
on
![]() $[3^{-1},6]$
.
$[3^{-1},6]$
.
Proof. We first note
where
Since
![]() , to prove the estimate (2.15) we need only to show
, to prove the estimate (2.15) we need only to show
for some
![]() $C=C(B)>0$
. To this end, changing variables
$C=C(B)>0$
. To this end, changing variables
![]() $(\tau ,\xi ) \rightarrow 2^k \mathcal L_{s}^{\delta }(\tau ,\xi )$
in the right-hand side of (2.18) and noting
$(\tau ,\xi ) \rightarrow 2^k \mathcal L_{s}^{\delta }(\tau ,\xi )$
in the right-hand side of (2.18) and noting
![]() $|\!\det \mathcal L_{s}^{\delta }|= \delta ^N |\!\det \widetilde {\mathcal L}_{s}^\delta | =\delta ^{{N(N+1)}/2}$
, we get
$|\!\det \mathcal L_{s}^{\delta }|= \delta ^N |\!\det \widetilde {\mathcal L}_{s}^\delta | =\delta ^{{N(N+1)}/2}$
, we get
where
![]() $C_\ast =(2\pi )^{-d-1} \delta ^{{N(N+1)}/2} 2^{k(d+1)}$
. Since
$C_\ast =(2\pi )^{-d-1} \delta ^{{N(N+1)}/2} 2^{k(d+1)}$
. Since
![]() $\mathfrak a$
satisfies (2.6), by (2.11) and Lemma 2.5 we have
$\mathfrak a$
satisfies (2.6), by (2.11) and Lemma 2.5 we have
![]() $\operatorname {\mathrm {supp}}\, \mathfrak a(s,t,2^k\mathcal L_{s}^\delta \cdot )\subset \{(\tau , \xi ): |(\tau ,\xi )| \lesssim _B\! 1\}$
. Besides, by (2.7) and (2.11) it follows that
$\operatorname {\mathrm {supp}}\, \mathfrak a(s,t,2^k\mathcal L_{s}^\delta \cdot )\subset \{(\tau , \xi ): |(\tau ,\xi )| \lesssim _B\! 1\}$
. Besides, by (2.7) and (2.11) it follows that
![]() $|\partial _{\tau ,\xi }^{\alpha } \big (\mathfrak a(s,t, 2^k\mathcal L_{s}^\delta (\tau ,\xi ))\big )| \lesssim _B \!1 $
for
$|\partial _{\tau ,\xi }^{\alpha } \big (\mathfrak a(s,t, 2^k\mathcal L_{s}^\delta (\tau ,\xi ))\big )| \lesssim _B \!1 $
for
![]() $|\alpha |\le d+3$
. Thus, repeated integration by parts in
$|\alpha |\le d+3$
. Thus, repeated integration by parts in
![]() $\tau ,\xi $
yields
$\tau ,\xi $
yields
 $$\begin{align*}|K[\mathfrak a](s,t,x)| \lesssim C_\ast \int_{1/2}^{4} \Big(1+2^k \big|\big (\delta^N(t-t'), (\widetilde{\mathcal L}_{s}^\delta)^\intercal(x-t\gamma(s))\big)\big| \Big)^{-d-3}\,dt',\end{align*}$$
$$\begin{align*}|K[\mathfrak a](s,t,x)| \lesssim C_\ast \int_{1/2}^{4} \Big(1+2^k \big|\big (\delta^N(t-t'), (\widetilde{\mathcal L}_{s}^\delta)^\intercal(x-t\gamma(s))\big)\big| \Big)^{-d-3}\,dt',\end{align*}$$
by which we obtain (2.19) as desired.
It is easy to show the estimate (2.16). The above estimate for
![]() $K[\mathfrak a]$
gives
$K[\mathfrak a]$
gives
Since
![]() , (2.16) for
, (2.16) for
![]() $p>1$
follows by (2.17) and Minkowski’s and Young’s convolution inequalities.
$p>1$
follows by (2.17) and Minkowski’s and Young’s convolution inequalities.
2.2 Rescaling
Let
![]() . Suppose that
. Suppose that
 $$ \begin{align} \sum_{j=1}^{N-1} \delta^{j} |\langle \gamma^{(j)}(s), \xi \rangle |\ge {2^k \delta^N}/{B'} \end{align} $$
$$ \begin{align} \sum_{j=1}^{N-1} \delta^{j} |\langle \gamma^{(j)}(s), \xi \rangle |\ge {2^k \delta^N}/{B'} \end{align} $$
holds on
![]() $\operatorname {\mathrm {supp}}_{s,\xi } \mathfrak a$
for some
$\operatorname {\mathrm {supp}}_{s,\xi } \mathfrak a$
for some
![]() $B'>0$
. Then, via decomposition and rescaling, we can bound the
$B'>0$
. Then, via decomposition and rescaling, we can bound the
![]() $L^p$
norm of
$L^p$
norm of
![]() $\mathcal T[\mathfrak a]f$
by those of the operators given by symbols of type
$\mathcal T[\mathfrak a]f$
by those of the operators given by symbols of type
![]() $(j, N-1, \tilde B)$
relative to a curve for some
$(j, N-1, \tilde B)$
relative to a curve for some
![]() $\tilde B$
and j (see Lemma 2.8 below).
$\tilde B$
and j (see Lemma 2.8 below).
To do so, we define a rescaled curve
![]() by
by
As
![]() $\delta \to 0$
, the curves
$\delta \to 0$
, the curves
![]() get close to a nondegenerate curve in an N-dimensional vector space, so the curves behave in a uniform manner. In particular, (2.1) and
get close to a nondegenerate curve in an N-dimensional vector space, so the curves behave in a uniform manner. In particular, (2.1) and
![]() ${\mathfrak V(N, B)}$
hold for some B for
${\mathfrak V(N, B)}$
hold for some B for
![]() if
if
![]() $\delta <\delta '$
for a constant
$\delta <\delta '$
for a constant
![]() $\delta '=\delta '(B)$
small enough.
$\delta '=\delta '(B)$
small enough.
Note
,
![]() $1\le j\le N-1$
, and
$1\le j\le N-1$
, and
,
![]() $N+1\le j\le 3d+1$
. Thus, Taylor series expansion and (2.4) give
$N+1\le j\le 3d+1$
. Thus, Taylor series expansion and (2.4) give

for
![]() $j=1, \dots , N-1$
. By (2.21), we have
$j=1, \dots , N-1$
. By (2.21), we have
. We write
, where
and
So,
. Since
and
![]() $|v'|\le B$
,
$|v'|\le B$
,
for some
![]() $C=C(B)$
. Thus,
$C=C(B)$
. Thus,
satisfies (2.1) with B replaced by
![]() $3B$
if
$3B$
if
![]() $\delta <\delta '$
.
$\delta <\delta '$
.
An elementary argument (elimination) shows
since
and
. Taking
![]() $\delta '$
small enough, from
$\delta '$
small enough, from
![]() ${\mathfrak V(N, B)}$
for
${\mathfrak V(N, B)}$
for
![]() $\gamma $
we see that
$\gamma $
we see that
![]() ${\mathfrak V({N}, {3B})}$
holds for
${\mathfrak V({N}, {3B})}$
holds for
if
![]() $0<\delta <\delta '$
.
$0<\delta <\delta '$
.
The next lemma (cf. [Reference Ko, Lee and Oh14, Lemma 2.9]) plays a crucial role in what follows.
Lemma 2.8. Let
![]() $2\le N\le d$
,
$2\le N\le d$
,
, and
![]() $j_\ast =\log (2^k \delta ^N)$
. Suppose (2.20) holds on
$j_\ast =\log (2^k \delta ^N)$
. Suppose (2.20) holds on
![]() $\operatorname {\mathrm {supp}}_{s,\xi } \mathfrak a$
. Then, there exist constants
$\operatorname {\mathrm {supp}}_{s,\xi } \mathfrak a$
. Then, there exist constants
![]() $C, l_\ast $
,
$C, l_\ast $
,
![]() $\tilde B\ge 1$
and
$\tilde B\ge 1$
and
![]() $\delta '>0$
depending on B, and symbols
$\delta '>0$
depending on B, and symbols
![]() $a_{1}, \dots , a_{l_\ast }$
of type
$a_{1}, \dots , a_{l_\ast }$
of type
![]() $(j, N-1, \tilde B)$
relative to
$(j, N-1, \tilde B)$
relative to
such that
![]() $\|\tilde f_l\|_p= \|f\|_p$
, and
$\|\tilde f_l\|_p= \|f\|_p$
, and
![]() $j\in [j_\ast -C, j_\ast +C]$
as long as
$j\in [j_\ast -C, j_\ast +C]$
as long as
![]() $0<\delta <\delta '$
.
$0<\delta <\delta '$
.
Proof. We set
Combining the identities (2.13) and (2.14), we write
![]() $\mathcal T[\mathfrak a] f$
as an integral (e.g., see (2.17) and (2.18)). Subsequently, the change of variables
$\mathcal T[\mathfrak a] f$
as an integral (e.g., see (2.17) and (2.18)). Subsequently, the change of variables
and
gives
where
Let
![]() $\tilde f$
be given by
$\tilde f$
be given by
where
![]() $\mathcal F( \tilde f\,)$
denotes the Fourier transform of
$\mathcal F( \tilde f\,)$
denotes the Fourier transform of
![]() $ \tilde f.$
Then,
$ \tilde f.$
Then,
![]() $ \|\tilde f\|_p=\|f\|_p$
. Changing variables
$ \|\tilde f\|_p=\|f\|_p$
. Changing variables
gives
where
. This leads us to set
It is easy to check
![]() $\tilde a\in \mathrm{C}^{d+N+2}(\mathbb R^{d+2})$
, since so is
$\tilde a\in \mathrm{C}^{d+N+2}(\mathbb R^{d+2})$
, since so is
![]() $\mathfrak a$
and
$\mathfrak a$
and
![]() $\gamma \in \mathrm C^{3d+1}$
. By (2.21) and (2.5), we note
$\gamma \in \mathrm C^{3d+1}$
. By (2.21) and (2.5), we note
. Therefore,
and a change of variables gives
We shall obtain symbols of type
![]() $(j, N-1,\tilde B)$
from
$(j, N-1,\tilde B)$
from
![]() $\tilde a$
via decomposition and rescaling. To this end, we first note
$\tilde a$
via decomposition and rescaling. To this end, we first note
for a constant
![]() $C=C(B)\ge 1$
. This follows by Lemma 2.5 since there exists
$C=C(B)\ge 1$
. This follows by Lemma 2.5 since there exists
![]() $\tau $
such that
$\tau $
such that
![]() if
if
![]() $\xi \in \operatorname {\mathrm {supp}}_\xi \tilde a$
. We claim
$\xi \in \operatorname {\mathrm {supp}}_\xi \tilde a$
. We claim
To show (2.25), let us set
Note that
![]() $0\le j\le 1$
. Taking derivatives on both sides of the equation (2.22), we have
$0\le j\le 1$
. Taking derivatives on both sides of the equation (2.22), we have
where

with
![]() $0 \le u_1 \le 1$
,
$0 \le u_1 \le 1$
,
![]() $0 \le |\alpha _1| \le u_1$
, and constants
$0 \le |\alpha _1| \le u_1$
, and constants
![]() $C_{\alpha , u}$
satisfying
$C_{\alpha , u}$
satisfying
![]() $|C_{\alpha , u}|=1$
. Integration by parts
$|C_{\alpha , u}|=1$
. Integration by parts
![]() $u_1+|\alpha _2|$
times in
$u_1+|\alpha _2|$
times in
![]() $\tau $
gives
$\tau $
gives
![]() $\partial _s^{j}\partial ^{l}_t\partial _\xi ^\alpha \tilde a=\mathcal I[\mathfrak b_2]$
, where
$\partial _s^{j}\partial ^{l}_t\partial _\xi ^\alpha \tilde a=\mathcal I[\mathfrak b_2]$
, where

with constants
![]() $C_{\alpha , u}'$
satisfying
$C_{\alpha , u}'$
satisfying
![]() $|C_{\alpha , u}'|=1$
. We decompose
$|C_{\alpha , u}'|=1$
. We decompose
![]() $\mathcal I[\mathfrak b_2]= \mathcal I[\chi _E \mathfrak b_2]+ \mathcal I[\chi _{E^c}\mathfrak b_2]$
, where
$\mathcal I[\mathfrak b_2]= \mathcal I[\chi _E \mathfrak b_2]+ \mathcal I[\chi _{E^c}\mathfrak b_2]$
, where
. Then, integrating by parts in
![]() $t'$
for
$t'$
for
![]() $ \mathcal I[\chi _{E^c}\mathfrak b_2]$
, we obtain
$ \mathcal I[\chi _{E^c}\mathfrak b_2]$
, we obtain

Since
,
![]() $ |\partial _s^{j'} \partial _t^{l'} \partial _{\tau ,\xi }^{\alpha '} \mathfrak b| \lesssim _B\! |\xi |^{-|\alpha '|} $
for
$ |\partial _s^{j'} \partial _t^{l'} \partial _{\tau ,\xi }^{\alpha '} \mathfrak b| \lesssim _B\! |\xi |^{-|\alpha '|} $
for
![]() $(j', l', \alpha ')\in \mathcal I_N$
. It is also clear that
$(j', l', \alpha ')\in \mathcal I_N$
. It is also clear that
if
![]() $\delta < \delta ' $
. Thus,
$\delta < \delta ' $
. Thus,
![]() $|\mathfrak b_2|=O(|\xi |^{-|\alpha |})$
, and
$|\mathfrak b_2|=O(|\xi |^{-|\alpha |})$
, and
![]() $|\partial _{t'}^2\mathfrak b_2|=O(|\xi |^{-|\alpha |})$
for
$|\partial _{t'}^2\mathfrak b_2|=O(|\xi |^{-|\alpha |})$
for
![]() $l\le 2(N-1) $
. Since
$l\le 2(N-1) $
. Since
![]() $\partial _s^{j}\partial ^{l}_t\partial _\xi ^\alpha \tilde a=\mathcal I[\mathfrak b_2]$
, we obtain the inequality (2.25).
$\partial _s^{j}\partial ^{l}_t\partial _\xi ^\alpha \tilde a=\mathcal I[\mathfrak b_2]$
, we obtain the inequality (2.25).
Now, we decompose
![]() $\tilde a$
. Let
$\tilde a$
. Let
![]() $\tilde \chi _1, \tilde \chi _2$
and
$\tilde \chi _1, \tilde \chi _2$
and
![]() $\tilde \chi _3\in \mathrm{C}_c^\infty (\mathbb R)$
such that
$\tilde \chi _3\in \mathrm{C}_c^\infty (\mathbb R)$
such that
![]() $\tilde \chi _1 +\tilde \chi _2+\tilde \chi _3 =1 $
on
$\tilde \chi _1 +\tilde \chi _2+\tilde \chi _3 =1 $
on
![]() $\operatorname {\mathrm {supp}} \tilde \chi $
and
$\operatorname {\mathrm {supp}} \tilde \chi $
and
![]() $\operatorname {\mathrm {supp}}\tilde \chi _\ell \subset [2^{\ell -3}, 2^{\ell }]$
for
$\operatorname {\mathrm {supp}}\tilde \chi _\ell \subset [2^{\ell -3}, 2^{\ell }]$
for
![]() $\ell =1,2,3$
. Also, let
$\ell =1,2,3$
. Also, let
![]() $\beta \in \mathrm C_c^\infty ((2^{-1}, 2))$
such that
$\beta \in \mathrm C_c^\infty ((2^{-1}, 2))$
such that
![]() $\sum \beta (2^{-k}\cdot ) =1$
on
$\sum \beta (2^{-k}\cdot ) =1$
on
![]() $\mathbb R_{+}$
. We set
$\mathbb R_{+}$
. We set
so
![]() $\sum _{\ell , j} a_{\ell , j}= \tilde a$
. By (2.24),
$\sum _{\ell , j} a_{\ell , j}= \tilde a$
. By (2.24),
![]() $a_{\ell , j} =0$
if
$a_{\ell , j} =0$
if
![]() $|j-j_\ast |> C$
for some
$|j-j_\ast |> C$
for some
![]() $C>0$
.
$C>0$
.
Denoting
![]() $(a)_\rho (s,t,\xi )=a(s,\rho t,\rho ^{-1}\xi )$
, via rescaling we observe
$(a)_\rho (s,t,\xi )=a(s,\rho t,\rho ^{-1}\xi )$
, via rescaling we observe
Thus, changes of variables yield
where
![]() $\tilde f_\ell = 2^{(\ell -2)d/p } \tilde f(2^{\ell -2}\cdot )$
. Since
$\tilde f_\ell = 2^{(\ell -2)d/p } \tilde f(2^{\ell -2}\cdot )$
. Since
, by (2.23) we get
To complete the proof, we only have to relabel
![]() $(a_{\ell , j})_{2^{\ell -2}}$
,
$(a_{\ell , j})_{2^{\ell -2}}$
,
![]() $\ell =1,2,3$
,
$\ell =1,2,3$
,
![]() $j_\ast -C\le j\le j_\ast +C$
. Indeed, since
$j_\ast -C\le j\le j_\ast +C$
. Indeed, since
![]() $\tilde a\in \mathrm{C}^{d+N+2}$
,
$\tilde a\in \mathrm{C}^{d+N+2}$
,
![]() $(a_{\ell , j})_{2^{\ell -2}}\in \mathrm{C}^{d+N+2}$
, which is supported in
$(a_{\ell , j})_{2^{\ell -2}}\in \mathrm{C}^{d+N+2}$
, which is supported in
![]() $I \times [2^{-1},4] \times \mathbb A_{j+\ell -2}$
. Obviously, (2.25) holds for
$I \times [2^{-1},4] \times \mathbb A_{j+\ell -2}$
. Obviously, (2.25) holds for
![]() $\tilde a=(a_{\ell , j})_{2^{\ell -2}}$
because
$\tilde a=(a_{\ell , j})_{2^{\ell -2}}$
because
![]() $\ell =1,2,3$
. Changing variables
$\ell =1,2,3$
. Changing variables
![]() and
and
![]() in (2.20), by the identity (2.21) we see that (2.20) on
in (2.20), by the identity (2.21) we see that (2.20) on
![]() $\operatorname {\mathrm {supp}}_{s,\xi } \mathfrak a$
is equivalent to
$\operatorname {\mathrm {supp}}_{s,\xi } \mathfrak a$
is equivalent to
![]() for
for
![]() . Note that
. Note that
![]() . So, the same holds on
. So, the same holds on
![]() $\operatorname {\mathrm {supp}}_{s,\xi } \tilde a$
and hence on
$\operatorname {\mathrm {supp}}_{s,\xi } \tilde a$
and hence on
![]() $\operatorname {\mathrm {supp}}_{s,\xi } (a_{\ell , j})_{2^{\ell -2}}$
if
$\operatorname {\mathrm {supp}}_{s,\xi } (a_{\ell , j})_{2^{\ell -2}}$
if
![]() $B'$
replaced by
$B'$
replaced by
![]() $2B'$
. Therefore,
$2B'$
. Therefore,
![]() $ C^{-1}(a_{\ell , j})_{2^{\ell -2}}$
is of type
$ C^{-1}(a_{\ell , j})_{2^{\ell -2}}$
is of type
![]() $(j+\ell -2, N-1, \tilde B)$
relative to
$(j+\ell -2, N-1, \tilde B)$
relative to
![]() for a large constant
for a large constant
![]() $C=C(B)$
.
$C=C(B)$
.
2.3 Preliminary decomposition and reduction
For the proof of Proposition 2.3, we make some reductions by decomposing the symbol a. We fix a sufficiently small positive constant
which is to be specified in what follows. Here,
![]() $\delta '$
is the number given in Lemma 2.8.
$\delta '$
is the number given in Lemma 2.8.
Recall
![]() $\gamma $
satisfies the condition (2.1),
$\gamma $
satisfies the condition (2.1),
![]() ${\mathfrak V(N, B)}$
and
${\mathfrak V(N, B)}$
and
![]() $ a$
is of type
$ a$
is of type
![]() $(k, N, B)$
relative to
$(k, N, B)$
relative to
![]() $\gamma $
. We set
$\gamma $
. We set
 $$ \begin{align} \eta_N(s,\xi)=\prod_{1\le j\le N-1} \beta_0 \Big( B2^{-k-1}\delta_*^{j-N} \langle\gamma^{(j)}(s),\, \xi \rangle \Big), \end{align} $$
$$ \begin{align} \eta_N(s,\xi)=\prod_{1\le j\le N-1} \beta_0 \Big( B2^{-k-1}\delta_*^{j-N} \langle\gamma^{(j)}(s),\, \xi \rangle \Big), \end{align} $$
where
![]() $\beta _0\in \mathrm C_c^\infty ((-1,1))$
such that
$\beta _0\in \mathrm C_c^\infty ((-1,1))$
such that
![]() $\beta _0= 1$
on
$\beta _0= 1$
on
![]() $[-1/2,1/2]$
. It is easy to see
$[-1/2,1/2]$
. It is easy to see
![]() $|\partial _s^{j} \partial ^{l}_t \partial _{\xi }^{\alpha } (a\eta _N)| \le C |\xi |^{-|\alpha |}$
for
$|\partial _s^{j} \partial ^{l}_t \partial _{\xi }^{\alpha } (a\eta _N)| \le C |\xi |^{-|\alpha |}$
for
![]() $(j,l,\alpha )\in \mathcal I_N$
, and the same holds for
$(j,l,\alpha )\in \mathcal I_N$
, and the same holds for
![]() $a(1-\eta _N)$
.
$a(1-\eta _N)$
.
Note
![]() $\sum _{j=1}^{N-1}|\gamma ^{(j)}(s)\cdot \xi |\ge (2B)^{-1} \delta _*^N|\xi |$
on
$\sum _{j=1}^{N-1}|\gamma ^{(j)}(s)\cdot \xi |\ge (2B)^{-1} \delta _*^N|\xi |$
on
![]() $\operatorname {\mathrm {supp}}_{s,\xi }(a(1-\eta _N))$
. So, we see
$\operatorname {\mathrm {supp}}_{s,\xi }(a(1-\eta _N))$
. So, we see
![]() $a(1-\eta _N)$
is a symbol of type
$a(1-\eta _N)$
is a symbol of type
![]() $(k, N-1, B')$
for
$(k, N-1, B')$
for
![]() $B'=CB^2 \delta _*^{-C}$
with a large C. Applying the assumption (Theorem 2.2 with
$B'=CB^2 \delta _*^{-C}$
with a large C. Applying the assumption (Theorem 2.2 with
![]() $L=N-1$
and
$L=N-1$
and
![]() $B=B'$
), we obtain
$B=B'$
), we obtain
Thus, it suffices to consider
![]() $\mathcal A_t[\gamma , a\eta _N]$
. Since
$\mathcal A_t[\gamma , a\eta _N]$
. Since
![]() ${\mathfrak N({N}, B)}$
holds on
${\mathfrak N({N}, B)}$
holds on
![]() $\operatorname {\mathrm {supp}}_{s,\xi } a$
,
$\operatorname {\mathrm {supp}}_{s,\xi } a$
,
holds whenever
![]() $(s,t,\xi )\in \operatorname {\mathrm {supp}} a\eta _N$
for some t.
$(s,t,\xi )\in \operatorname {\mathrm {supp}} a\eta _N$
for some t.
Basic assumption.
Before we continue to prove the estimate for
![]() $\mathcal A_t[\gamma , a\eta _N]$
, we make several assumptions which are clearly permissible by elementary decompositions.
$\mathcal A_t[\gamma , a\eta _N]$
, we make several assumptions which are clearly permissible by elementary decompositions.
Decomposing a, we may assume that
![]() $\operatorname {\mathrm {supp}}_\xi a$
is contained in a narrow conic neighborhood and
$\operatorname {\mathrm {supp}}_\xi a$
is contained in a narrow conic neighborhood and
![]() for some
for some
![]() . Let us set
. Let us set
We may also assume
![]() $\gamma ^{(N-1)}(s') \cdot \xi '=0$
for some
$\gamma ^{(N-1)}(s') \cdot \xi '=0$
for some
![]() . Otherwise,
. Otherwise,
![]() $|\gamma ^{(N-1)}(s) \cdot \xi |\gtrsim |\xi |$
on
$|\gamma ^{(N-1)}(s) \cdot \xi |\gtrsim |\xi |$
on
![]() $\operatorname {\mathrm {supp}}_{s,\xi } a\eta _N$
and hence
$\operatorname {\mathrm {supp}}_{s,\xi } a\eta _N$
and hence
![]() $a\eta _N=0$
if we take B large enough. By (2.28) and the implicit function theorem, there exists
$a\eta _N=0$
if we take B large enough. By (2.28) and the implicit function theorem, there exists
![]() $\sigma $
such that
$\sigma $
such that
on a narrow conic neighborhood of
![]() $\xi '$
where
$\xi '$
where
![]() $\sigma \in \mathrm{C}^{2d+2}$
, since
$\sigma \in \mathrm{C}^{2d+2}$
, since
![]() $\gamma \in \mathrm C^{3d+1}(I)$
. So, decomposing a further and taking
$\gamma \in \mathrm C^{3d+1}(I)$
. So, decomposing a further and taking
![]() $\delta _\ast $
small enough, we may assume that
$\delta _\ast $
small enough, we may assume that
![]() $\sigma \in \mathrm C^{2d+2}(\Gamma _k)$
and
$\sigma \in \mathrm C^{2d+2}(\Gamma _k)$
and
![]() for
for
![]() $\xi \in \Gamma _k$
. Moreover, since
$\xi \in \Gamma _k$
. Moreover, since
![]() $\sigma $
is homogeneous of degree zero, we have
$\sigma $
is homogeneous of degree zero, we have
for a constant
![]() $C=C(B)$
if
$C=C(B)$
if
![]() $|\alpha |\le 2d+2$
. Any symbol which appears in what follows is to be given by decomposing the symbol a with appropriate cutoff functions. So, the
$|\alpha |\le 2d+2$
. Any symbol which appears in what follows is to be given by decomposing the symbol a with appropriate cutoff functions. So, the
![]() $s,\xi $
-supports of the symbols are assumed to be contained in
$s,\xi $
-supports of the symbols are assumed to be contained in
![]() .
.
We break a to have further localization on the Fourier side. Let
and
![]() $\mathfrak a_0=a\eta _N-\mathfrak a_1$
. Then, by Fourier inversion
$\mathfrak a_0=a\eta _N-\mathfrak a_1$
. Then, by Fourier inversion
It is easy to show
![]() $ \| \mathcal T[ \mathfrak a_0]f \|_{p} \lesssim _B\! 2^{-2k} \|f\|_{p}$
for
$ \| \mathcal T[ \mathfrak a_0]f \|_{p} \lesssim _B\! 2^{-2k} \|f\|_{p}$
for
![]() $1 \le p \le \infty .$
Indeed, we consider
$1 \le p \le \infty .$
Indeed, we consider
![]() $ \tilde {\mathfrak a}_0 = -(\tau +\gamma (s)\cdot \xi )^{-2} {\partial _{t}^2\mathfrak a_0}. $
By (2.13) and integration by parts in
$ \tilde {\mathfrak a}_0 = -(\tau +\gamma (s)\cdot \xi )^{-2} {\partial _{t}^2\mathfrak a_0}. $
By (2.13) and integration by parts in
![]() $t'$
,
$t'$
,
![]() $m[\mathfrak a_0]=m[\tilde {\mathfrak a}_0]$
and hence
$m[\mathfrak a_0]=m[\tilde {\mathfrak a}_0]$
and hence
![]() $\mathcal T [ \mathfrak a_0 ]= \mathcal T [\tilde {\mathfrak a}_0]$
. Thanks to (2.17), it is sufficient to show
$\mathcal T [ \mathfrak a_0 ]= \mathcal T [\tilde {\mathfrak a}_0]$
. Thanks to (2.17), it is sufficient to show
for a constant
![]() $C=C(B, \delta _\ast )$
. Note
$C=C(B, \delta _\ast )$
. Note
![]() $|\tau +\langle \gamma (s),\xi \rangle |\gtrsim 2^k$
on
$|\tau +\langle \gamma (s),\xi \rangle |\gtrsim 2^k$
on
![]() $\operatorname {\mathrm {supp}} \tilde {\mathfrak a}_0$
, and recall (2.18). Rescaling and integration by parts in
$\operatorname {\mathrm {supp}} \tilde {\mathfrak a}_0$
, and recall (2.18). Rescaling and integration by parts in
![]() $\tau ,\xi $
, as in the proof of Lemma 2.7, show the estimate.
$\tau ,\xi $
, as in the proof of Lemma 2.7, show the estimate.
The difficult part is to obtain the estimate for
![]() $\mathcal T[\mathfrak a_1]$
. Since
$\mathcal T[\mathfrak a_1]$
. Since
![]() $\delta _*$
is a fixed constant, it is obvious that
$\delta _*$
is a fixed constant, it is obvious that
![]() for some
for some
![]() $C=C(B,\delta _\ast )$
. So, the desired estimate for
$C=C(B,\delta _\ast )$
. So, the desired estimate for
![]() $\mathcal T[\mathfrak a_1]$
follows once we have the next proposition.
$\mathcal T[\mathfrak a_1]$
follows once we have the next proposition.
Proposition 2.9. Let
![]() with
with
![]() $\operatorname {\mathrm {supp}}_{\xi } \mathfrak a \subset \Gamma _k$
. Suppose Theorem 2.2 holds for
$\operatorname {\mathrm {supp}}_{\xi } \mathfrak a \subset \Gamma _k$
. Suppose Theorem 2.2 holds for
![]() $L=N-1$
. Then, if
$L=N-1$
. Then, if
![]() $p\ge 4N-2$
, for
$p\ge 4N-2$
, for
![]() $\epsilon>0$
, we have
$\epsilon>0$
, we have
Therefore, the proof of Proposition 2.3 is completed if we prove Proposition 2.9. For the purpose, we use Proposition 2.10 below, which allows us to decompose
![]() $ \mathcal T[\mathfrak a]$
into the operators given by symbols with smaller s-supports while the consequent minor parts have acceptable bounds. A similar argument was used in [Reference Pramanik and Seeger24] when
$ \mathcal T[\mathfrak a]$
into the operators given by symbols with smaller s-supports while the consequent minor parts have acceptable bounds. A similar argument was used in [Reference Pramanik and Seeger24] when
![]() $L=2$
.
$L=2$
.
Let
![]() $\delta _0$
and
$\delta _0$
and
![]() $\delta _1$
be positive numbers such that
$\delta _1$
be positive numbers such that
Then, it is clear that
For
![]() $n\ge 0$
, we denote
$n\ge 0$
, we denote
![]() $ \mathfrak J_n^\mu =\{ \nu \in \mathbb Z: |2^n\delta _1 \nu - \delta _0 \mu | \le \delta _0\}. $
$ \mathfrak J_n^\mu =\{ \nu \in \mathbb Z: |2^n\delta _1 \nu - \delta _0 \mu | \le \delta _0\}. $
Proposition 2.10. For
![]() $\mu $
such that
$\mu $
such that
![]() , let
, let
![]() $\mathfrak a^\mu \in \mathfrak A_k(\delta _0\mu ,\delta _0)$
with
$\mathfrak a^\mu \in \mathfrak A_k(\delta _0\mu ,\delta _0)$
with
![]() . Suppose Theorem 2.2 holds for
. Suppose Theorem 2.2 holds for
![]() $L=N-1$
. Then, if
$L=N-1$
. Then, if
![]() $p\ge 4N-2$
, for
$p\ge 4N-2$
, for
![]() $\epsilon>0$
there exist a constant
$\epsilon>0$
there exist a constant
![]() $C_\epsilon =C_\epsilon (B) \ge 2$
and symbols
$C_\epsilon =C_\epsilon (B) \ge 2$
and symbols
![]() $\mathfrak a_{\nu } \in \mathfrak A_k(\delta _1\nu ,\delta _1)$
with
$\mathfrak a_{\nu } \in \mathfrak A_k(\delta _1\nu ,\delta _1)$
with
![]() ,
,
![]() $\nu \in \cup _\mu \mathfrak J_0^\mu $
, such that
$\nu \in \cup _\mu \mathfrak J_0^\mu $
, such that
 $$ \begin{align*} \!\!\left( \sum_\mu \| \mathcal T[ \mathfrak a^\mu]f\|_p^p\right)^{\frac1p}\! \le C_\epsilon & \big({\delta_1}/{\delta_0} \big)^{\frac {2N}{p}-1-\epsilon} \left( \sum_\nu \| \mathcal T[\mathfrak a_{\nu}]f\|_p^p \right)^{\frac1p} \!+C_\epsilon \delta_0^{-\frac {2N}p +1+\epsilon } 2^{-\frac{2}pk+2\epsilon k}\|f\|_p. \end{align*} $$
$$ \begin{align*} \!\!\left( \sum_\mu \| \mathcal T[ \mathfrak a^\mu]f\|_p^p\right)^{\frac1p}\! \le C_\epsilon & \big({\delta_1}/{\delta_0} \big)^{\frac {2N}{p}-1-\epsilon} \left( \sum_\nu \| \mathcal T[\mathfrak a_{\nu}]f\|_p^p \right)^{\frac1p} \!+C_\epsilon \delta_0^{-\frac {2N}p +1+\epsilon } 2^{-\frac{2}pk+2\epsilon k}\|f\|_p. \end{align*} $$
2.4 Proof of Proposition 2.9
Let
![]() . We may assume
. We may assume
![]() for some
for some
![]() $\mu \in \mathbb Z$
. To apply Proposition 2.10 iteratively, we need to choose an appropriate decreasing sequence of positive numbers since the decomposition is subject to the condition (2.31).
$\mu \in \mathbb Z$
. To apply Proposition 2.10 iteratively, we need to choose an appropriate decreasing sequence of positive numbers since the decomposition is subject to the condition (2.31).
Let
![]() $\delta _0=\delta _*$
, so
$\delta _0=\delta _*$
, so
![]() $(2^{7d}B^6)^{N}\delta _0< 1$
. Let J be the largest integer such that
$(2^{7d}B^6)^{N}\delta _0< 1$
. Let J be the largest integer such that
So,
![]() $ J \le C_1 \log k$
for a constant
$ J \le C_1 \log k$
for a constant
![]() $C_1\ge 1$
. We set
$C_1\ge 1$
. We set
for
![]() $j=J-1,\dots ,1$
. Thus, it follows that
$j=J-1,\dots ,1$
. Thus, it follows that
For a given
![]() $\epsilon>0$
, let
$\epsilon>0$
, let
![]() $\tilde \epsilon =\epsilon /4$
. Since
$\tilde \epsilon =\epsilon /4$
. Since
![]() $\mathfrak a\in \mathfrak A_k( \delta _0\mu ,\delta _0)$
and (2.31) holds for
$\mathfrak a\in \mathfrak A_k( \delta _0\mu ,\delta _0)$
and (2.31) holds for
![]() $\delta _0$
and
$\delta _0$
and
![]() $\delta _1$
, applying Proposition 2.10 to
$\delta _1$
, applying Proposition 2.10 to
![]() $\mathcal T[\mathfrak a]$
, we have
$\mathcal T[\mathfrak a]$
, we have
 $$ \begin{align*} \| \mathcal T[\mathfrak a]f\|_p \le C_{\tilde \epsilon} & \big({\delta_1}/{\delta_0}\big)^{\frac {2N}{p}-1-\tilde \epsilon} \left(\sum_{\nu_1} \| \mathcal T[ \mathfrak a_{\nu_1}]f\|_p^p\,\right)^{\frac1p} +C_{\tilde \epsilon} \delta_0^{-\frac {2N}p+1 +\tilde \epsilon } 2^{-\frac{2}pk+2\tilde \epsilon k}\|f\|_p, \end{align*} $$
$$ \begin{align*} \| \mathcal T[\mathfrak a]f\|_p \le C_{\tilde \epsilon} & \big({\delta_1}/{\delta_0}\big)^{\frac {2N}{p}-1-\tilde \epsilon} \left(\sum_{\nu_1} \| \mathcal T[ \mathfrak a_{\nu_1}]f\|_p^p\,\right)^{\frac1p} +C_{\tilde \epsilon} \delta_0^{-\frac {2N}p+1 +\tilde \epsilon } 2^{-\frac{2}pk+2\tilde \epsilon k}\|f\|_p, \end{align*} $$
where
![]() $ \mathfrak a_{\nu _1} \in \mathfrak A_k(\delta _1\nu _1,\delta _1)$
,
$ \mathfrak a_{\nu _1} \in \mathfrak A_k(\delta _1\nu _1,\delta _1)$
,
![]() $\nu _1 \in \mathfrak J_0^\mu $
. Thanks to (2.34), we may again apply Proposition 2.10 to
$\nu _1 \in \mathfrak J_0^\mu $
. Thanks to (2.34), we may again apply Proposition 2.10 to
![]() $\mathcal T[\mathfrak a_{\nu _1}]$
while
$\mathcal T[\mathfrak a_{\nu _1}]$
while
![]() $\delta _0$
,
$\delta _0$
,
![]() $\delta _1$
replaced by
$\delta _1$
replaced by
![]() $\delta _1, \delta _2$
, respectively. Repeating this procedure up to J-th step yields symbols
$\delta _1, \delta _2$
, respectively. Repeating this procedure up to J-th step yields symbols
![]() $\mathfrak a_\nu \in \mathfrak A_k(\delta _{\!J}\nu , \delta _{\!J})$
,
$\mathfrak a_\nu \in \mathfrak A_k(\delta _{\!J}\nu , \delta _{\!J})$
,
![]() $\delta _{\!J} \nu \in \delta _{\!J}\mathbb Z\cap I(\delta _0\mu , \delta _0)$
, such that
$\delta _{\!J} \nu \in \delta _{\!J}\mathbb Z\cap I(\delta _0\mu , \delta _0)$
, such that
 $$\begin{align*}\| \mathcal T[\mathfrak a]f\|_p \le C_{\tilde \epsilon}^J \delta_{\!J}^{\frac {2N}{p} -1-\tilde \epsilon} \left(\sum_\nu \|\mathcal T[\mathfrak a_\nu]f\|_p^p \,\right)^{\frac1p} +\sum_{0\le j\le J-1} C_{\tilde \epsilon}^{j+1} \delta_{0}^{-\frac{2N}p+1+\tilde \epsilon} 2^{-\frac{2} pk+ 2\tilde \epsilon k} \|f\|_p \end{align*}$$
$$\begin{align*}\| \mathcal T[\mathfrak a]f\|_p \le C_{\tilde \epsilon}^J \delta_{\!J}^{\frac {2N}{p} -1-\tilde \epsilon} \left(\sum_\nu \|\mathcal T[\mathfrak a_\nu]f\|_p^p \,\right)^{\frac1p} +\sum_{0\le j\le J-1} C_{\tilde \epsilon}^{j+1} \delta_{0}^{-\frac{2N}p+1+\tilde \epsilon} 2^{-\frac{2} pk+ 2\tilde \epsilon k} \|f\|_p \end{align*}$$
for
![]() $p \ge 4N-2$
. Now, assuming
$p \ge 4N-2$
. Now, assuming
 $$ \begin{align} \left( \sum_\nu\| \mathcal T[ \mathfrak a_{\nu} ]f\|_p^p \,\right)^{1/p} \lesssim_B 2^{-k/N} \|f\|_p, \qquad 2\le p\le \infty \end{align} $$
$$ \begin{align} \left( \sum_\nu\| \mathcal T[ \mathfrak a_{\nu} ]f\|_p^p \,\right)^{1/p} \lesssim_B 2^{-k/N} \|f\|_p, \qquad 2\le p\le \infty \end{align} $$
for the moment, we can finish the proof of Proposition 2.9. Since
![]() $C_{\tilde \epsilon }\ge 2$
, combining the above inequalities, we get
$C_{\tilde \epsilon }\ge 2$
, combining the above inequalities, we get
Since
![]() $J \le C_1 \log k$
,
$J \le C_1 \log k$
,
![]() $C_{\tilde \epsilon }^{J+1} \le C' 2^{\epsilon k/2}$
for some
$C_{\tilde \epsilon }^{J+1} \le C' 2^{\epsilon k/2}$
for some
![]() $C'$
if k is sufficiently large. Therefore, the right-hand side is bounded by
$C'$
if k is sufficiently large. Therefore, the right-hand side is bounded by
![]() $C 2^{- 2k/p+\epsilon k} \|f\|_p$
.
$C 2^{- 2k/p+\epsilon k} \|f\|_p$
.
It remains to show the estimate (2.35) for
![]() $2\le p\le \infty $
. By interpolation, it is enough to obtain (2.35) for
$2\le p\le \infty $
. By interpolation, it is enough to obtain (2.35) for
![]() $p=\infty $
and
$p=\infty $
and
![]() $p=2$
. The case
$p=2$
. The case
![]() $p=\infty $
follows by (2.15) since
$p=\infty $
follows by (2.15) since
![]() $\mathfrak a_\nu \in \mathfrak A_k(\delta _{\!J}\nu ,\delta _{\!J})$
. So, we need only to prove the estimate (2.35) for
$\mathfrak a_\nu \in \mathfrak A_k(\delta _{\!J}\nu ,\delta _{\!J})$
. So, we need only to prove the estimate (2.35) for
![]() $p=2$
. To do this, we first observe the following, which shows
$p=2$
. To do this, we first observe the following, which shows
![]() $\operatorname {\mathrm {supp}}_\xi \mathfrak a_{\nu }$
are finitely overlapping.
$\operatorname {\mathrm {supp}}_\xi \mathfrak a_{\nu }$
are finitely overlapping.
Lemma 2.11. For
![]() $b\ge 1$
,
$b\ge 1$
,
![]() and
and
![]() $0<\delta \le \delta _*$
, let us set
$0<\delta \le \delta _*$
, let us set
 $$ \begin{align} {\Lambda}^{\prime}_k(s,\delta, b) = \bigcap_{1\le j\le N-1} \big\{ \xi \in \Gamma_k : | \langle \gamma^{(j)}(s), \xi \rangle| \le b 2^{k} \delta^{N-j} \big \}. \end{align} $$
$$ \begin{align} {\Lambda}^{\prime}_k(s,\delta, b) = \bigcap_{1\le j\le N-1} \big\{ \xi \in \Gamma_k : | \langle \gamma^{(j)}(s), \xi \rangle| \le b 2^{k} \delta^{N-j} \big \}. \end{align} $$
If
![]() ${\Lambda }^{\prime}_k(s_1, \delta , b) \cap {\Lambda }^{\prime}_k(s_2, \delta , b)\neq \emptyset $
for some
${\Lambda }^{\prime}_k(s_1, \delta , b) \cap {\Lambda }^{\prime}_k(s_2, \delta , b)\neq \emptyset $
for some
![]() , then there is a constant
, then there is a constant
![]() $C=C(B)$
such that
$C=C(B)$
such that
![]() $|s_1-s_2|\le Cb\delta $
.
$|s_1-s_2|\le Cb\delta $
.
Proof. Let
![]() $\xi \in \Lambda _k'(s_1,\delta ,b) \cap \Lambda _k'(s_2,\delta ,b)$
. Since
$\xi \in \Lambda _k'(s_1,\delta ,b) \cap \Lambda _k'(s_2,\delta ,b)$
. Since
![]() $|\gamma ^{(N-1)}(s_j) \cdot \xi |\le b 2^k\delta $
,
$|\gamma ^{(N-1)}(s_j) \cdot \xi |\le b 2^k\delta $
,
![]() $j=1,2$
, by (2.29) and (2.28) we see
$j=1,2$
, by (2.29) and (2.28) we see
![]() $|s_j-\sigma (\xi )|\le 2^2bB \delta $
,
$|s_j-\sigma (\xi )|\le 2^2bB \delta $
,
![]() $j=1,2$
, using the mean value theorem. This implies
$j=1,2$
, using the mean value theorem. This implies
![]() $|s_1-s_2|\le 2^3bB \delta $
.
$|s_1-s_2|\le 2^3bB \delta $
.
We recall (2.13). Since (2.28) holds on
![]() $\operatorname {\mathrm {supp}}_{s,\xi } \mathfrak a_\nu $
, by van der Corput’s lemma (e.g., see [Reference Stein32, p. 334]) we have
$\operatorname {\mathrm {supp}}_{s,\xi } \mathfrak a_\nu $
, by van der Corput’s lemma (e.g., see [Reference Stein32, p. 334]) we have
The second inequality is clear since
![]() $\mathfrak a_{\nu } \in \mathfrak A_k(\delta _{\!J}\nu , \delta _{\!J})$
. From (2.14), note
$\mathfrak a_{\nu } \in \mathfrak A_k(\delta _{\!J}\nu , \delta _{\!J})$
. From (2.14), note
![]() $\mathcal F(\mathcal T[\mathfrak a_{\nu }] f)= m[\mathfrak a_{\nu }]\widehat f$
. Since
$\mathcal F(\mathcal T[\mathfrak a_{\nu }] f)= m[\mathfrak a_{\nu }]\widehat f$
. Since
![]() $\operatorname {\mathrm {supp}} \mathfrak a_{\nu }\subset \Lambda _k(\delta _{\!J}\nu , \delta _{\!J}, B)$
,
$\operatorname {\mathrm {supp}} \mathfrak a_{\nu }\subset \Lambda _k(\delta _{\!J}\nu , \delta _{\!J}, B)$
,
![]() $\operatorname {\mathrm {supp}}_\xi \mathfrak a_{\nu }\subset S_\nu := {\Lambda }^{\prime}_k(\delta _{\!J}\nu , \delta _{\!J}, 2^5 B)$
. So,
$\operatorname {\mathrm {supp}}_\xi \mathfrak a_{\nu }\subset S_\nu := {\Lambda }^{\prime}_k(\delta _{\!J}\nu , \delta _{\!J}, 2^5 B)$
. So,
![]() $\operatorname {\mathrm {supp}}_\xi \mathcal F(\mathcal T[\mathfrak a_{\nu }] f)\subset S_\nu $
(see (2.13)). By Lemma 2.11, it follows that the sets
$\operatorname {\mathrm {supp}}_\xi \mathcal F(\mathcal T[\mathfrak a_{\nu }] f)\subset S_\nu $
(see (2.13)). By Lemma 2.11, it follows that the sets
![]() $S_\nu $
overlap at most
$S_\nu $
overlap at most
![]() $C=C(B)$
times. Therefore, Plancherel’s theorem and the estimate above give
$C=C(B)$
times. Therefore, Plancherel’s theorem and the estimate above give
 $$\begin{align*}\| \sum_\nu \mathcal T[\mathfrak a_{\nu}] f\|_2^2 \lesssim_B\! 2^{-2k/N} \sum_\nu \int_{S_\nu}\int_{\{\tau: | \tau + \gamma(\delta_{\!J}\nu)\cdot \xi|\le 2^5 B\}} \,d\tau\, |\widehat f(\xi)|^2 \,d\xi, \end{align*}$$
$$\begin{align*}\| \sum_\nu \mathcal T[\mathfrak a_{\nu}] f\|_2^2 \lesssim_B\! 2^{-2k/N} \sum_\nu \int_{S_\nu}\int_{\{\tau: | \tau + \gamma(\delta_{\!J}\nu)\cdot \xi|\le 2^5 B\}} \,d\tau\, |\widehat f(\xi)|^2 \,d\xi, \end{align*}$$
by which we get (2.35) for
![]() $p=2$
.
$p=2$
.
2.5 Decoupling inequalities
We denote
![]() $\mathbf r_\circ ^N(s)=(s,s^2/2!,\,\dots, \, s^N/N!)$
and consider a collection of curves from I to
$\mathbf r_\circ ^N(s)=(s,s^2/2!,\,\dots, \, s^N/N!)$
and consider a collection of curves from I to
![]() $\mathbb R^N$
which are small perturbations of
$\mathbb R^N$
which are small perturbations of
![]() $\mathbf r_\circ ^N$
:
$\mathbf r_\circ ^N$
:
For
![]() $\mathbf r\in \mathfrak C(\epsilon _\circ ;N) $
and
$\mathbf r\in \mathfrak C(\epsilon _\circ ;N) $
and
![]() $s\in I$
, we define an anisotropic neighborhood by
$s\in I$
, we define an anisotropic neighborhood by
 $$\begin{align*}{\mathcal N}_{\mathbf r}(s,\delta)= \Big\{ \mathbf r(s)+ \sum_{1\le j\le N} u_j {{\mathbf r}^{(j)}(s)}: |u_j|\le \delta^j, \quad~j=1,\dots,N \Big\}. \end{align*}$$
$$\begin{align*}{\mathcal N}_{\mathbf r}(s,\delta)= \Big\{ \mathbf r(s)+ \sum_{1\le j\le N} u_j {{\mathbf r}^{(j)}(s)}: |u_j|\le \delta^j, \quad~j=1,\dots,N \Big\}. \end{align*}$$
Let
![]() $s_1, \dots , s_l\in I$
be
$s_1, \dots , s_l\in I$
be
![]() $\delta $
-separated points, that is,
$\delta $
-separated points, that is,
![]() $|s_n-s_j|\ge \delta $
if
$|s_n-s_j|\ge \delta $
if
![]() $n\neq j$
such that
$n\neq j$
such that
![]() $\bigcup _{j=1}^l(s_j-\delta , s_j+\delta )\supset I$
. Then, we set
$\bigcup _{j=1}^l(s_j-\delta , s_j+\delta )\supset I$
. Then, we set
The following is due to Bourgain, Demeter and Guth [Reference Bourgain, Demeter and Guth5] (also see [Reference Guo, Li, Yung and Zorin-Kranich10]).
Theorem 2.12. Let
![]() $0<\delta \ll 1$
. Suppose
$0<\delta \ll 1$
. Suppose
![]() $\mathbf r\in \mathfrak C(\epsilon _\circ ;N) $
for a small enough
$\mathbf r\in \mathfrak C(\epsilon _\circ ;N) $
for a small enough
![]() $\epsilon _\circ>0$
. Then, if
$\epsilon _\circ>0$
. Then, if
![]() $2 \le p\le N(N+1)$
, for
$2 \le p\le N(N+1)$
, for
![]() $\epsilon>0$
we have
$\epsilon>0$
we have
 $$ \begin{align} \big\| \sum_{1\le j\le l} f_j \big\|_{L^p(\mathbb R^{N})}\le C_\epsilon \delta^{-\epsilon} \left( \sum_{1\le j\le l}\|f_j \|_{L^p(\mathbb R^{N})}^2 \right)^{1/2} \end{align} $$
$$ \begin{align} \big\| \sum_{1\le j\le l} f_j \big\|_{L^p(\mathbb R^{N})}\le C_\epsilon \delta^{-\epsilon} \left( \sum_{1\le j\le l}\|f_j \|_{L^p(\mathbb R^{N})}^2 \right)^{1/2} \end{align} $$
whenever
![]() $\operatorname {\mathrm {supp}} \widehat f_j \subset \theta _j$
for
$\operatorname {\mathrm {supp}} \widehat f_j \subset \theta _j$
for
![]() $1\le j\le l$
.
$1\le j\le l$
.
The constant
![]() $C_\epsilon $
can be taken to be independent of particular choices of the
$C_\epsilon $
can be taken to be independent of particular choices of the
![]() $\delta $
-separated points
$\delta $
-separated points
![]() $s_1, \dots , s_l$
. One can obtain a conical extension of the inequality (2.37) by modifying the argument in [Reference Bourgain and Demeter4] which deduces the decoupling inequality for the cone from that for the paraboloid (see [Reference Beltran, Guo, Hickman and Seeger2, Proposition 7.7]). Let us consider the conical sets
$s_1, \dots , s_l$
. One can obtain a conical extension of the inequality (2.37) by modifying the argument in [Reference Bourgain and Demeter4] which deduces the decoupling inequality for the cone from that for the paraboloid (see [Reference Beltran, Guo, Hickman and Seeger2, Proposition 7.7]). Let us consider the conical sets
Corollary 2.13. Let
![]() $0<\delta \le 1$
, and let
$0<\delta \le 1$
, and let
![]() $\mathbf r\in \mathfrak C(\epsilon _\circ ;N) $
for a small enough
$\mathbf r\in \mathfrak C(\epsilon _\circ ;N) $
for a small enough
![]() $\epsilon _\circ>0$
. Then, if
$\epsilon _\circ>0$
. Then, if
![]() $2 \le p\le N(N+1)$
, for
$2 \le p\le N(N+1)$
, for
![]() $\epsilon>0$
we have
$\epsilon>0$
we have
 $$ \begin{align} \big\|\sum_{1\le j\le l} F_j \big\|_{L^p(\mathbb R^{N+1})}\le C_\epsilon \delta^{-\epsilon} \left(\sum_{1\le j\le l} \| F_j\|_{L^p(\mathbb R^{N+1})}^2 \,\right)^{1/2} \end{align} $$
$$ \begin{align} \big\|\sum_{1\le j\le l} F_j \big\|_{L^p(\mathbb R^{N+1})}\le C_\epsilon \delta^{-\epsilon} \left(\sum_{1\le j\le l} \| F_j\|_{L^p(\mathbb R^{N+1})}^2 \,\right)^{1/2} \end{align} $$
whenever
![]() $\operatorname {\mathrm {supp}} \widehat F_j \subset {\bar {\theta }}_j$
for
$\operatorname {\mathrm {supp}} \widehat F_j \subset {\bar {\theta }}_j$
for
![]() $1\le j\le l$
.
$1\le j\le l$
.
The inequality (2.38) does not fit with the symbols to appear when we decompose
![]() $\mathfrak a$
(see Section 3.1 and Section 4.2). As to be seen, those symbols are associated with the slabs of the following form.
$\mathfrak a$
(see Section 3.1 and Section 4.2). As to be seen, those symbols are associated with the slabs of the following form.
Definition 2.14. Let
![]() $N\ge 2$
and
$N\ge 2$
and
![]() $\tilde {\mathbf r}\in \mathfrak C(\epsilon _\circ ;N+1)$
. For
$\tilde {\mathbf r}\in \mathfrak C(\epsilon _\circ ;N+1)$
. For
![]() $s\in I$
, we denote by
$s\in I$
, we denote by
![]() $\mathbf S(s,\delta , \rho ;\tilde {\mathbf r})$
the set of
$\mathbf S(s,\delta , \rho ;\tilde {\mathbf r})$
the set of
![]() $(\tau ,\eta ) \in \mathbb R\times \mathbb R^{N}$
which satisfies
$(\tau ,\eta ) \in \mathbb R\times \mathbb R^{N}$
which satisfies
 $$ \begin{align*} & \rho^{-1}\le|\langle \tilde{\mathbf r}^{(N+1)}(s), (\tau,\eta) \rangle|\le 2\rho, \\[3pt] &\quad |\langle \tilde{\mathbf r}^{(j)}(s), (\tau,\eta) \rangle| \le \delta^{N+1-j}, \qquad \ \ j=N,\dots,1. \end{align*} $$
$$ \begin{align*} & \rho^{-1}\le|\langle \tilde{\mathbf r}^{(N+1)}(s), (\tau,\eta) \rangle|\le 2\rho, \\[3pt] &\quad |\langle \tilde{\mathbf r}^{(j)}(s), (\tau,\eta) \rangle| \le \delta^{N+1-j}, \qquad \ \ j=N,\dots,1. \end{align*} $$
The same form of decoupling inequality remains valid for the slabs
![]() $\mathbf S(s_1,\delta ,1; \tilde {\mathbf r}), \dots , \mathbf S(s_l,\delta ,1; \tilde {\mathbf r})$
. Beltran et al. [Reference Beltran, Guo, Hickman and Seeger2, Theroem 4.4] showed, using the Frenet–Serret formulas, that those slabs can be generated by conical extensions of the anisotropic neighborhoods given by a nondegenerate curve in
$\mathbf S(s_1,\delta ,1; \tilde {\mathbf r}), \dots , \mathbf S(s_l,\delta ,1; \tilde {\mathbf r})$
. Beltran et al. [Reference Beltran, Guo, Hickman and Seeger2, Theroem 4.4] showed, using the Frenet–Serret formulas, that those slabs can be generated by conical extensions of the anisotropic neighborhoods given by a nondegenerate curve in
![]() $\mathbb R^N$
. Therefore, the following is a consequence of Corollary 2.13 and a simple manipulation using decomposition and rescaling.
$\mathbb R^N$
. Therefore, the following is a consequence of Corollary 2.13 and a simple manipulation using decomposition and rescaling.
Corollary 2.15. Let
![]() $0<\delta \le 1$
,
$0<\delta \le 1$
,
![]() $\rho \ge 1$
and
$\rho \ge 1$
and
![]() $\tilde {\mathbf r} \in \mathfrak C(\epsilon _\circ ;N+1)$
for a small enough
$\tilde {\mathbf r} \in \mathfrak C(\epsilon _\circ ;N+1)$
for a small enough
![]() $\epsilon _\circ>0$
. Denote
$\epsilon _\circ>0$
. Denote
![]() $\mathbf S_j=\mathbf S(s_j,\delta , \rho ;\tilde {\mathbf r})$
for
$\mathbf S_j=\mathbf S(s_j,\delta , \rho ;\tilde {\mathbf r})$
for
![]() $1\le j\le l$
. Then, if
$1\le j\le l$
. Then, if
![]() $2 \le p\le N(N+1)$
, for
$2 \le p\le N(N+1)$
, for
![]() $\epsilon>0$
there is a constant
$\epsilon>0$
there is a constant
![]() $C_\epsilon =C_\epsilon (\rho )$
such that
$C_\epsilon =C_\epsilon (\rho )$
such that
 $$ \begin{align} \big\| \sum_{1\le j\le l} F_j \big\|_{L^p(\mathbb R^{N+1})}\le C_\epsilon \delta^{-\epsilon} \left( \sum_{1\le j\le l} \|F_j \|_{L^p(\mathbb R^{N+1})}^2 \right)^{1/2} \end{align} $$
$$ \begin{align} \big\| \sum_{1\le j\le l} F_j \big\|_{L^p(\mathbb R^{N+1})}\le C_\epsilon \delta^{-\epsilon} \left( \sum_{1\le j\le l} \|F_j \|_{L^p(\mathbb R^{N+1})}^2 \right)^{1/2} \end{align} $$
whenever
![]() $\operatorname {\mathrm {supp}} \widehat {F_j} \subset \mathbf S_j$
for
$\operatorname {\mathrm {supp}} \widehat {F_j} \subset \mathbf S_j$
for
![]() $1\le j\le l$
.
$1\le j\le l$
.
For our purpose of proving Proposition 2.10, we use a modified form. If
![]() $p_\ast \in [2 , N(N+1)] $
, then we have
$p_\ast \in [2 , N(N+1)] $
, then we have
 $$\begin{align*}\big\| \sum_{1\le j\le l} F_j \big\|_{L^p(\mathbb R^{N+1})}\le C_\epsilon \delta^{-1+\frac{2+p_\ast}{2p}-\epsilon} \left( \sum_{1\le j\le l} \|F_j \|_{L^p(\mathbb R^{N+1})}^p \right)^{1/p} \end{align*}$$
$$\begin{align*}\big\| \sum_{1\le j\le l} F_j \big\|_{L^p(\mathbb R^{N+1})}\le C_\epsilon \delta^{-1+\frac{2+p_\ast}{2p}-\epsilon} \left( \sum_{1\le j\le l} \|F_j \|_{L^p(\mathbb R^{N+1})}^p \right)^{1/p} \end{align*}$$
for
![]() $p\ge p_\ast $
. The case
$p\ge p_\ast $
. The case
![]() $p=p_\ast $
follows by the inequality (2.39) and Hölder’s inequality. Interpolation with the trivial
$p=p_\ast $
follows by the inequality (2.39) and Hölder’s inequality. Interpolation with the trivial
![]() $\ell ^\infty L^\infty $
–
$\ell ^\infty L^\infty $
–
![]() $L^\infty $
estimate gives the estimate for
$L^\infty $
estimate gives the estimate for
![]() $p> p_\ast $
. One may choose different
$p> p_\ast $
. One may choose different
![]() $p_\ast $
for the particular purposes. In fact, for the local smoothing estimate we take
$p_\ast $
for the particular purposes. In fact, for the local smoothing estimate we take
![]() $p_\ast = 4N-2$
to get
$p_\ast = 4N-2$
to get
 $$ \begin{align} \big\| \sum_{1\le j\le l} F_j \big\|_{L^p(\mathbb R^{N+1})}\le C_\epsilon \delta^{-1+\frac{2N}{p}-\epsilon} \left( \sum_{1\le j\le l} \|F_j \|_{L^p(\mathbb R^{N+1})}^p \right)^{1/p} \end{align} $$
$$ \begin{align} \big\| \sum_{1\le j\le l} F_j \big\|_{L^p(\mathbb R^{N+1})}\le C_\epsilon \delta^{-1+\frac{2N}{p}-\epsilon} \left( \sum_{1\le j\le l} \|F_j \|_{L^p(\mathbb R^{N+1})}^p \right)^{1/p} \end{align} $$
for
![]() $p\ge 4N-2$
(see Section 3.2). For the
$p\ge 4N-2$
(see Section 3.2). For the
![]() $L^p$
Sobolev regularity estimate, we observe that
$L^p$
Sobolev regularity estimate, we observe that
 $$ \begin{align} \big\| \sum_{1\le j\le l} F_j \big\|_{L^p(\mathbb R^{N+1})}\le C_{\epsilon_0} \delta^{-1+\frac{N+1}{p}+\epsilon_0} \left( \sum_{1\le j\le l} \|F_j \|_{L^p(\mathbb R^{N+1})}^p \right)^{1/p} \end{align} $$
$$ \begin{align} \big\| \sum_{1\le j\le l} F_j \big\|_{L^p(\mathbb R^{N+1})}\le C_{\epsilon_0} \delta^{-1+\frac{N+1}{p}+\epsilon_0} \left( \sum_{1\le j\le l} \|F_j \|_{L^p(\mathbb R^{N+1})}^p \right)^{1/p} \end{align} $$
holds for some
![]() $\epsilon _0= \epsilon _0(p)>0$
if
$\epsilon _0= \epsilon _0(p)>0$
if
![]() $2N<p<\infty $
. Indeed, we need only to take
$2N<p<\infty $
. Indeed, we need only to take
![]() $p_\ast> 2N$
close enough to
$p_\ast> 2N$
close enough to
![]() $2N$
. The presence of
$2N$
. The presence of
![]() $\epsilon _0$
in (2.41) is crucial for proving the optimal Sobolev regularity estimate (see Proposition 4.5).
$\epsilon _0$
in (2.41) is crucial for proving the optimal Sobolev regularity estimate (see Proposition 4.5).
The inequalities (2.40) and (2.41) obviously extend to cylindrical forms via the Minkowski inequality. For example, set
![]() $ \tilde {\mathbf S}_j=\big \{ (\xi ,\eta )\in \mathbb R^{N+1}\times \mathbb R^M: \xi \in \mathbf S_j \big \}$
for
$ \tilde {\mathbf S}_j=\big \{ (\xi ,\eta )\in \mathbb R^{N+1}\times \mathbb R^M: \xi \in \mathbf S_j \big \}$
for
![]() $1\le j\le l$
. Using (2.40), we have
$1\le j\le l$
. Using (2.40), we have
 $$ \begin{align} \big\| \sum_{1\le j\le l} G_j \big\|_{L^p(\mathbb R^{N+M+1})}\le C_\epsilon \delta^{-1+\frac{2N}{p}-\epsilon} \left( \sum_{1\le j\le l} \| G_j \|_{L^p(\mathbb R^{N+M+1})}^2 \right)^{1/2} \end{align} $$
$$ \begin{align} \big\| \sum_{1\le j\le l} G_j \big\|_{L^p(\mathbb R^{N+M+1})}\le C_\epsilon \delta^{-1+\frac{2N}{p}-\epsilon} \left( \sum_{1\le j\le l} \| G_j \|_{L^p(\mathbb R^{N+M+1})}^2 \right)^{1/2} \end{align} $$
whenever
![]() $\widehat {G}_j$
is supported in
$\widehat {G}_j$
is supported in
![]() $\tilde {\mathbf S}_j$
. Clearly, we also have a similar extension of the inequality (2.41).
$\tilde {\mathbf S}_j$
. Clearly, we also have a similar extension of the inequality (2.41).
3 Decomposition of the symbols
In this section, we prove Proposition 2.10 by applying the decoupling inequality. Meanwhile, the induction assumption (Theorem 2.2 with
![]() $L=N-1$
) plays an important role. We decompose a given symbol
$L=N-1$
) plays an important role. We decompose a given symbol
![]() $\mathfrak a^\mu \in \mathfrak A_k(\delta _0\mu ,\delta _0)$
into the symbols with their s-supports contained in intervals of length about
$\mathfrak a^\mu \in \mathfrak A_k(\delta _0\mu ,\delta _0)$
into the symbols with their s-supports contained in intervals of length about
![]() $\delta _1$
while the consequent minor contribution is controlled within an acceptable bound. To achieve it up to
$\delta _1$
while the consequent minor contribution is controlled within an acceptable bound. To achieve it up to
![]() $\delta _1$
satisfying the condition (2.31), we approximate
$\delta _1$
satisfying the condition (2.31), we approximate
![]() $\langle G(s), (\tau ,\xi ) \rangle $
in a local coordinate system near the set
$\langle G(s), (\tau ,\xi ) \rangle $
in a local coordinate system near the set
![]() $\{(s,\xi ):\langle \gamma ^{(N-1)}(s),\xi \rangle =0\}$
.
$\{(s,\xi ):\langle \gamma ^{(N-1)}(s),\xi \rangle =0\}$
.
3.1 Decomposition of the symbol
 $\mathfrak a^\mu $
$\mathfrak a^\mu $
We begin by introducing some notations.
Fixing
![]() $\mu \in \mathbb Z$
such that
$\mu \in \mathbb Z$
such that
![]() , we consider the linear maps
, we consider the linear maps
In particular,
![]() $y_\mu ^j(\tau ,\xi )=\langle \gamma ^{(j)}(\delta _0\mu ),\xi \rangle $
if
$y_\mu ^j(\tau ,\xi )=\langle \gamma ^{(j)}(\delta _0\mu ),\xi \rangle $
if
![]() $1\le j\le N.$
By (2.28), it follows that
$1\le j\le N.$
By (2.28), it follows that
We denote
 $$\begin{align*}\omega_\mu(\xi)=\frac{y_\mu^{N-1}(\tau,\xi)}{y_\mu^{N}(\tau,\xi)}, \end{align*}$$
$$\begin{align*}\omega_\mu(\xi)=\frac{y_\mu^{N-1}(\tau,\xi)}{y_\mu^{N}(\tau,\xi)}, \end{align*}$$
which is close to
![]() $\delta _0\mu -\sigma (\xi )$
(see (3.5) below). Then, we define
$\delta _0\mu -\sigma (\xi )$
(see (3.5) below). Then, we define
![]() $\mathfrak g_\mu ^N, \mathfrak g_\mu ^{N-1},\dots , \mathfrak g_\mu ^{0}$
recursively, by setting
$\mathfrak g_\mu ^N, \mathfrak g_\mu ^{N-1},\dots , \mathfrak g_\mu ^{0}$
recursively, by setting
![]() $ \mathfrak g_\mu ^N=y_\mu ^N,$
and
$ \mathfrak g_\mu ^N=y_\mu ^N,$
and
 $$ \begin{align} \mathfrak g_\mu^{j}(\tau,\xi)=y^{j}_\mu(\tau,\xi)-\sum_{\ell=j+1}^{N}\frac{\mathfrak g^{\ell}_\mu(\tau,\xi)}{(\ell-j)!} (\omega_\mu(\xi))^{\ell-j}, \quad j=N-1, \dots, 0. \end{align} $$
$$ \begin{align} \mathfrak g_\mu^{j}(\tau,\xi)=y^{j}_\mu(\tau,\xi)-\sum_{\ell=j+1}^{N}\frac{\mathfrak g^{\ell}_\mu(\tau,\xi)}{(\ell-j)!} (\omega_\mu(\xi))^{\ell-j}, \quad j=N-1, \dots, 0. \end{align} $$
Note that
![]() $\mathfrak g_\mu ^{N-1}=0$
and (3.2) can be rewritten as follows:
$\mathfrak g_\mu ^{N-1}=0$
and (3.2) can be rewritten as follows:
 $$ \begin{align} y^{m}_\mu(\tau,\xi) =\sum_{\ell=m}^{N}\frac{\mathfrak g^{\ell}_\mu(\tau,\xi)}{(\ell-m)!} (\omega_\mu(\xi))^{\ell-m}, \quad m=0,\dots,N. \end{align} $$
$$ \begin{align} y^{m}_\mu(\tau,\xi) =\sum_{\ell=m}^{N}\frac{\mathfrak g^{\ell}_\mu(\tau,\xi)}{(\ell-m)!} (\omega_\mu(\xi))^{\ell-m}, \quad m=0,\dots,N. \end{align} $$
The identity continues to hold for
![]() $m=N$
since
$m=N$
since
![]() $\mathfrak g_\mu ^N=y_\mu ^N$
. Apparently,
$\mathfrak g_\mu ^N=y_\mu ^N$
. Apparently,
![]() $\mathfrak g_\mu ^1,\dots , \mathfrak g_\mu ^N$
are independent of
$\mathfrak g_\mu ^1,\dots , \mathfrak g_\mu ^N$
are independent of
![]() $\tau $
since so are
$\tau $
since so are
![]() $y_\mu ^1, \dots , y_\mu ^N$
.
$y_\mu ^1, \dots , y_\mu ^N$
.
For
![]() $j=1,\dots ,N$
, set
$j=1,\dots ,N$
, set
 $$ \begin{align} \mathcal E_j(\xi):=(y_\mu^N(\tau,\xi))^{-1}\int_{\sigma(\xi)}^{\delta_0\mu}\frac{\langle\gamma^{(N+1)}(r),\xi\rangle}{j!}(\sigma(\xi) -r)^{j}dr. \end{align} $$
$$ \begin{align} \mathcal E_j(\xi):=(y_\mu^N(\tau,\xi))^{-1}\int_{\sigma(\xi)}^{\delta_0\mu}\frac{\langle\gamma^{(N+1)}(r),\xi\rangle}{j!}(\sigma(\xi) -r)^{j}dr. \end{align} $$
By (3.4) with
![]() $j=1$
and integration by parts, we have
$j=1$
and integration by parts, we have
Lemma 3.1. Let
![]() $0\le j\le N-1$
. Then, we have
$0\le j\le N-1$
. Then, we have
 $$ \begin{align} \langle G^{(j)}(\sigma(\xi)),(\tau,&\xi) \rangle = \sum_{\ell=j}^{N}\frac{\,\, \mathfrak g^{\ell}_\mu\,\,(\mathcal E_1)^{\ell-j}}{(\ell-j)!} -y^N_\mu\mathcal E_{N-j}. \end{align} $$
$$ \begin{align} \langle G^{(j)}(\sigma(\xi)),(\tau,&\xi) \rangle = \sum_{\ell=j}^{N}\frac{\,\, \mathfrak g^{\ell}_\mu\,\,(\mathcal E_1)^{\ell-j}}{(\ell-j)!} -y^N_\mu\mathcal E_{N-j}. \end{align} $$
Proof. When
![]() $j=N-1$
, the equation (3.6) is clear. To show (3.6) for
$j=N-1$
, the equation (3.6) is clear. To show (3.6) for
![]() $j=0,1,\dots ,N-2$
, by Taylor’s theorem with integral remainder we have
$j=0,1,\dots ,N-2$
, by Taylor’s theorem with integral remainder we have
 $$\begin{align*}\langle G^{(j)}(\sigma(\xi)),(\tau,\xi)\rangle =\sum_{m=j}^{N}y^{m}_\mu (\tau,\xi) \frac{(\sigma(\xi)-\delta_0\mu)^{m-j}}{(m-j)!}-y^N_\mu(\tau,\xi)\mathcal E_{N-j}(\xi).\end{align*}$$
$$\begin{align*}\langle G^{(j)}(\sigma(\xi)),(\tau,\xi)\rangle =\sum_{m=j}^{N}y^{m}_\mu (\tau,\xi) \frac{(\sigma(\xi)-\delta_0\mu)^{m-j}}{(m-j)!}-y^N_\mu(\tau,\xi)\mathcal E_{N-j}(\xi).\end{align*}$$
Using (3.3) and then changing the order of the sums, we see
 $$\begin{align*}\langle G^{(j)}(\sigma(\xi)),(\tau,\xi)\rangle= \sum_{\ell=j}^{N} \mathfrak g^{\ell}_\mu \left(\sum_{m=j}^{\ell} \frac{(\sigma(\xi)-\delta_0\mu)^{m-j}}{(\ell-m)!(m-j)!} (\omega_\mu)^{\ell-m} \right) -y^N_\mu\,\mathcal E_{N-j}. \end{align*}$$
$$\begin{align*}\langle G^{(j)}(\sigma(\xi)),(\tau,\xi)\rangle= \sum_{\ell=j}^{N} \mathfrak g^{\ell}_\mu \left(\sum_{m=j}^{\ell} \frac{(\sigma(\xi)-\delta_0\mu)^{m-j}}{(\ell-m)!(m-j)!} (\omega_\mu)^{\ell-m} \right) -y^N_\mu\,\mathcal E_{N-j}. \end{align*}$$
The sum over m equals
![]() $(\sigma (\xi )-\delta _0\mu + \omega _\mu )^{\ell -j} /(\ell -j)!$
. So, (3.6) follows by (3.5).
$(\sigma (\xi )-\delta _0\mu + \omega _\mu )^{\ell -j} /(\ell -j)!$
. So, (3.6) follows by (3.5).
We now decompose the symbol
![]() $\mathfrak a^\mu \in \mathfrak A_k(\delta _0\mu ,\delta _0)$
by making use of
$\mathfrak a^\mu \in \mathfrak A_k(\delta _0\mu ,\delta _0)$
by making use of
![]() $\mathfrak g_\mu ^j$
,
$\mathfrak g_\mu ^j$
,
![]() $j=0,\dots ,N-2$
. We define
$j=0,\dots ,N-2$
. We define
 $$\begin{align*}\mathfrak G_N^\mu(s,\tau,\xi)=\sum_{j=0}^{N-2}\big(2^{-k} \mathfrak g^{j}_\mu(\tau,\xi)\big)^{\frac{2N!}{N-j}}+(s-\sigma(\xi))^{2N!}. \end{align*}$$
$$\begin{align*}\mathfrak G_N^\mu(s,\tau,\xi)=\sum_{j=0}^{N-2}\big(2^{-k} \mathfrak g^{j}_\mu(\tau,\xi)\big)^{\frac{2N!}{N-j}}+(s-\sigma(\xi))^{2N!}. \end{align*}$$
Let
![]() $ \beta _N=\beta _0-\beta _0(2^{2N!}\cdot )$
, so we have
$ \beta _N=\beta _0-\beta _0(2^{2N!}\cdot )$
, so we have
![]() $\sum _{\ell \in \mathbb Z}\beta _N(2^{2N!\ell }\cdot )=1$
on
$\sum _{\ell \in \mathbb Z}\beta _N(2^{2N!\ell }\cdot )=1$
on
![]() $\mathbb R_+$
. We also take
$\mathbb R_+$
. We also take
![]() $\zeta \in \mathrm C_c^\infty ((-1,1))$
such that
$\zeta \in \mathrm C_c^\infty ((-1,1))$
such that
![]() $\sum _{\nu \in \mathbb Z} \zeta (\cdot -\nu )=1$
. For
$\sum _{\nu \in \mathbb Z} \zeta (\cdot -\nu )=1$
. For
![]() $n\ge 0$
and
$n\ge 0$
and
![]() $\nu \in \mathfrak J_n^\mu $
, we set
$\nu \in \mathfrak J_n^\mu $
, we set
 $$\begin{align*}\mathfrak a_{\nu}^{\mu,n} = \mathfrak a^\mu \times \begin{cases} \beta_0 \big( \delta_1^{-2N!} \, \mathfrak G_N^\mu \big) \, \zeta(\delta_1^{-1}s-\nu), \quad & n=0, \\[4pt] \beta_N \big( (2^{n}\delta_1)^{-2N!} \, \mathfrak G_N^\mu \big) \, \zeta(2^{-n}\delta_1^{-1}s-\nu), \quad & n\ge 1. \end{cases} \end{align*}$$
$$\begin{align*}\mathfrak a_{\nu}^{\mu,n} = \mathfrak a^\mu \times \begin{cases} \beta_0 \big( \delta_1^{-2N!} \, \mathfrak G_N^\mu \big) \, \zeta(\delta_1^{-1}s-\nu), \quad & n=0, \\[4pt] \beta_N \big( (2^{n}\delta_1)^{-2N!} \, \mathfrak G_N^\mu \big) \, \zeta(2^{-n}\delta_1^{-1}s-\nu), \quad & n\ge 1. \end{cases} \end{align*}$$
Then, it follows that
 $$ \begin{align} \mathfrak a^\mu = \sum_{n\ge 0} \sum_{\nu \in \mathfrak J_n^\mu} \mathfrak a^{\mu,n}_{\nu}. \end{align} $$
$$ \begin{align} \mathfrak a^\mu = \sum_{n\ge 0} \sum_{\nu \in \mathfrak J_n^\mu} \mathfrak a^{\mu,n}_{\nu}. \end{align} $$
Lemma 3.2. There is a constant
![]() $C=C(B)$
such that
$C=C(B)$
such that
![]() $C^{-1}\mathfrak a_{\nu }^{\mu ,n}\in \mathfrak A_k(2^n\delta _1\nu , 2^n\delta _1)$
for
$C^{-1}\mathfrak a_{\nu }^{\mu ,n}\in \mathfrak A_k(2^n\delta _1\nu , 2^n\delta _1)$
for
![]() $n\ge 0$
,
$n\ge 0$
,
![]() $\mu $
and
$\mu $
and
![]() $\nu $
.
$\nu $
.
The proof of Lemma 3.2 is elementary though it is somewhat involved. We postpone the proof until Section 3.3.
We collect some elementary facts regarding
![]() $\mathfrak a_{\nu }^{\mu ,n}$
. First, we may assume
$\mathfrak a_{\nu }^{\mu ,n}$
. First, we may assume
since, otherwise,
![]() $\mathfrak a_{\nu }^{\mu ,n}=0$
. To show this, we note
$\mathfrak a_{\nu }^{\mu ,n}=0$
. To show this, we note
![]() $|\langle \gamma ^{(N-1)}(\delta _0\mu ),\xi \rangle |\le B2^{k+5}\delta _0$
if
$|\langle \gamma ^{(N-1)}(\delta _0\mu ),\xi \rangle |\le B2^{k+5}\delta _0$
if
![]() $\xi \in \operatorname {\mathrm {supp}}_{\xi } \mathfrak a^\mu $
. Thus, (2.28), (2.29), and the mean value theorem show that
$\xi \in \operatorname {\mathrm {supp}}_{\xi } \mathfrak a^\mu $
. Thus, (2.28), (2.29), and the mean value theorem show that
for
![]() $\xi \in \operatorname {\mathrm {supp}}_{\xi } \mathfrak a^\mu .$
If
$\xi \in \operatorname {\mathrm {supp}}_{\xi } \mathfrak a^\mu .$
If
![]() $(\tau , \xi )\in \operatorname {\mathrm {supp}}_{\tau , \xi } \mathfrak a^\mu \subset \Lambda _k(\delta _0\mu , \delta _0, B)$
,
$(\tau , \xi )\in \operatorname {\mathrm {supp}}_{\tau , \xi } \mathfrak a^\mu \subset \Lambda _k(\delta _0\mu , \delta _0, B)$
,
![]() $|y_\mu ^j(\tau ,\xi )|\le B2^{k+5}\delta _0^{N-j} $
for
$|y_\mu ^j(\tau ,\xi )|\le B2^{k+5}\delta _0^{N-j} $
for
![]() $0\le j\le N-1$
. Note
$0\le j\le N-1$
. Note
![]() $|\omega _\mu | \le B^22^7\delta _0$
and
$|\omega _\mu | \le B^22^7\delta _0$
and
![]() $|\mathfrak g_\mu ^N| \le B2^{k+1}$
. A routine computation using (3.2) gives
$|\mathfrak g_\mu ^N| \le B2^{k+1}$
. A routine computation using (3.2) gives
![]() $|\mathfrak g_\mu ^{j}| \le B2^{k-1}(B^22^8\delta _0)^{N-j} $
for
$|\mathfrak g_\mu ^{j}| \le B2^{k-1}(B^22^8\delta _0)^{N-j} $
for
![]() $j=N-2, \dots , 0$
. Since
$j=N-2, \dots , 0$
. Since
![]() $|s-\sigma (\xi )|\le (B^22^{7}+1)\delta _0$
, we have
$|s-\sigma (\xi )|\le (B^22^{7}+1)\delta _0$
, we have
![]() $ \mathfrak G_N^\mu \le 2(B^32^8)^{2N!} \delta _0^{2N!}$
on
$ \mathfrak G_N^\mu \le 2(B^32^8)^{2N!} \delta _0^{2N!}$
on
![]() $\operatorname {\mathrm {supp}} \mathfrak a_{\nu }^{\mu ,n}$
, and (3.8) follows.
$\operatorname {\mathrm {supp}} \mathfrak a_{\nu }^{\mu ,n}$
, and (3.8) follows.
Since
![]() $\mathfrak G_N^\mu \le (2^n\delta _1)^{2N!}$
on
$\mathfrak G_N^\mu \le (2^n\delta _1)^{2N!}$
on
![]() $\operatorname {\mathrm {supp}} \mathfrak a_{\nu }^{\mu ,n}$
, the following hold:
$\operatorname {\mathrm {supp}} \mathfrak a_{\nu }^{\mu ,n}$
, the following hold:
Obviously, (3.11) holds true for
![]() $j=N-1$
since
$j=N-1$
since
![]() $\mathfrak g^{N-1}_\mu =0$
. We also have
$\mathfrak g^{N-1}_\mu =0$
. We also have
on
![]() $\operatorname {\mathrm {supp}}_\xi \mathfrak a_{\nu }^{\mu ,n}$
. By using (3.4), (3.9) and (3.1), it is easy to show (3.12). Since
$\operatorname {\mathrm {supp}}_\xi \mathfrak a_{\nu }^{\mu ,n}$
. By using (3.4), (3.9) and (3.1), it is easy to show (3.12). Since
![]() $|s-2^n\delta _1\nu | \le 2^n\delta _1$
on
$|s-2^n\delta _1\nu | \le 2^n\delta _1$
on
![]() $\operatorname {\mathrm {supp}}_s \mathfrak a_{\nu }^{\mu ,n}$
, (3.13) follows by (3.10).
$\operatorname {\mathrm {supp}}_s \mathfrak a_{\nu }^{\mu ,n}$
, (3.13) follows by (3.10).
3.2 Proof of Proposition 2.10
By (3.7) and the Minkowski inequality, we have
 $$ \begin{align} \begin{aligned} \left( \sum_\mu \big\| \mathcal T [\mathfrak a^\mu]f \big\|_p^p \,\right)^{1/p} \le \sum_{n\ge0} \left(\sum_{\mu} \big\| \sum_{\nu \in \mathfrak J_n^\mu} \mathcal T [ \mathfrak a^{\mu,n}_{\nu}]f \big\|_p^p\,\right)^{1/p}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left( \sum_\mu \big\| \mathcal T [\mathfrak a^\mu]f \big\|_p^p \,\right)^{1/p} \le \sum_{n\ge0} \left(\sum_{\mu} \big\| \sum_{\nu \in \mathfrak J_n^\mu} \mathcal T [ \mathfrak a^{\mu,n}_{\nu}]f \big\|_p^p\,\right)^{1/p}. \end{aligned} \end{align} $$
We use the inequality (2.40) for
![]() after a suitable linear change of variables. The symbols
after a suitable linear change of variables. The symbols
![]() $\mathfrak a_{\nu }^{\mu ,0}$
are to constitute the set
$\mathfrak a_{\nu }^{\mu ,0}$
are to constitute the set
![]() $\{\mathfrak a_\nu \}$
while the operators associated to
$\{\mathfrak a_\nu \}$
while the operators associated to
![]() $\mathfrak a_{\nu }^{\mu ,n}$
,
$\mathfrak a_{\nu }^{\mu ,n}$
,
![]() $n\ge 1$
are to be handled similarly as in Section 2.
$n\ge 1$
are to be handled similarly as in Section 2.
Applying the inequality (2.40). To prove Proposition 2.10, we first show
 $$ \begin{align} \big\| \sum_{\nu\in \mathfrak J_{n}^\mu} \mathcal T [\mathfrak a_{\nu}^{\mu,n}]f \big\|_p \le C_\epsilon \big({2^n\delta_1}/{\delta_0} \big)^{\frac {2N} {p}-1-\epsilon} \left(\sum_{\nu\in \mathfrak J_{n}^\mu} \big\| \mathcal T [\mathfrak a_{\nu}^{\mu,n}]f \big\|_p^p \,\right)^{1/p} \end{align} $$
$$ \begin{align} \big\| \sum_{\nu\in \mathfrak J_{n}^\mu} \mathcal T [\mathfrak a_{\nu}^{\mu,n}]f \big\|_p \le C_\epsilon \big({2^n\delta_1}/{\delta_0} \big)^{\frac {2N} {p}-1-\epsilon} \left(\sum_{\nu\in \mathfrak J_{n}^\mu} \big\| \mathcal T [\mathfrak a_{\nu}^{\mu,n}]f \big\|_p^p \,\right)^{1/p} \end{align} $$
for
![]() $p \ge 4N-2$
. To use (2.40), we consider
$p \ge 4N-2$
. To use (2.40), we consider
![]() $\operatorname {\mathrm {supp}}_{\tau ,\xi } \mathfrak a_{\nu }^{\mu ,n}$
, which contains the Fourier support of
$\operatorname {\mathrm {supp}}_{\tau ,\xi } \mathfrak a_{\nu }^{\mu ,n}$
, which contains the Fourier support of
![]() $ \mathcal T [\mathfrak a_{\nu }^{\mu ,n}]f$
as is clear from (2.13) and (2.14).
$ \mathcal T [\mathfrak a_{\nu }^{\mu ,n}]f$
as is clear from (2.13) and (2.14).
We set
Lemma 3.3. Let
![]() $\mathbf r =\mathbf r_{\circ }^{N+1}$
and
$\mathbf r =\mathbf r_{\circ }^{N+1}$
and
![]() $\mathcal D_\delta $
denote the matrix
$\mathcal D_\delta $
denote the matrix
![]() $ (\delta ^{-N} e_1, \delta ^{1-N} e_2, \dots , \delta ^0 e_{N+1})$
, where
$ (\delta ^{-N} e_1, \delta ^{1-N} e_2, \dots , \delta ^0 e_{N+1})$
, where
![]() $e_j$
denotes the j-th standard unit vector in
$e_j$
denotes the j-th standard unit vector in
![]() $\mathbb R^{N+1}$
. On
$\mathbb R^{N+1}$
. On
![]() $\operatorname {\mathrm {supp}}_{\tau ,\xi } \mathfrak a^{\mu ,n}_{\nu }$
, we have
$\operatorname {\mathrm {supp}}_{\tau ,\xi } \mathfrak a^{\mu ,n}_{\nu }$
, we have
Proof. We write
![]() $\mathbf r=(\mathbf r_1,\dots ,\mathbf r_{N+1})$
. Note
$\mathbf r=(\mathbf r_1,\dots ,\mathbf r_{N+1})$
. Note
![]() $\mathbf r^{(j)}_m(s)=s^{m-j}/(m-j)!$
for
$\mathbf r^{(j)}_m(s)=s^{m-j}/(m-j)!$
for
![]() $m\ge j$
. By the equation (3.3), we have
$m\ge j$
. By the equation (3.3), we have
 $$ \begin{align*} y^{m-1}_\mu \mathbf r^{(j)}_m(2^n\delta_1\nu-\delta_0\mu) &=\sum_{\ell=m-1}^{N}\mathfrak g^{\ell}_\mu\frac{(2^n\delta_1\nu-\delta_0\mu)^{m-j}}{(\ell+1-m)!(m-j)!}\,\omega_\mu^{\ell+1-m} \end{align*} $$
$$ \begin{align*} y^{m-1}_\mu \mathbf r^{(j)}_m(2^n\delta_1\nu-\delta_0\mu) &=\sum_{\ell=m-1}^{N}\mathfrak g^{\ell}_\mu\frac{(2^n\delta_1\nu-\delta_0\mu)^{m-j}}{(\ell+1-m)!(m-j)!}\,\omega_\mu^{\ell+1-m} \end{align*} $$
for
![]() $m\ge j$
. Since
$m\ge j$
. Since
![]() $\mathbf r^{(j)}_m(s)=0$
for
$\mathbf r^{(j)}_m(s)=0$
for
![]() $j>m$
, taking sum over m gives
$j>m$
, taking sum over m gives
 $$ \begin{align*} \big\langle \mathbf y_\mu, \mathbf r^{(j)}(2^n\delta_1\nu-\delta_0\mu)\big\rangle =\sum_{\ell=j-1}^{N}\mathfrak g^{\ell}_\mu\frac{( 2^n\delta_1\nu-\delta_0\mu+ \omega_\mu)^{\ell+1-j}}{(\ell+1-j)!}. \end{align*} $$
$$ \begin{align*} \big\langle \mathbf y_\mu, \mathbf r^{(j)}(2^n\delta_1\nu-\delta_0\mu)\big\rangle =\sum_{\ell=j-1}^{N}\mathfrak g^{\ell}_\mu\frac{( 2^n\delta_1\nu-\delta_0\mu+ \omega_\mu)^{\ell+1-j}}{(\ell+1-j)!}. \end{align*} $$
From the equation (3.5), we note
![]() $2^n\delta _1\nu -\delta _0\mu +\omega _\mu =2^n\delta _1\nu -\sigma (\xi )+\mathcal E_1$
. Thus, (3.13), (3.12) with
$2^n\delta _1\nu -\delta _0\mu +\omega _\mu =2^n\delta _1\nu -\sigma (\xi )+\mathcal E_1$
. Thus, (3.13), (3.12) with
![]() $j=1$
and (2.32) with
$j=1$
and (2.32) with
![]() $j=1$
show
$j=1$
show
![]() $|2^n\delta _1\nu -\delta _0\mu +\omega _\mu |\lesssim 2^n\delta _1$
. By (3.11), we obtain
$|2^n\delta _1\nu -\delta _0\mu +\omega _\mu |\lesssim 2^n\delta _1$
. By (3.11), we obtain
By homogeneity, it follows that
![]() $\langle \eta , \mathbf r^{(j)}(\delta _0 s)\rangle =\delta _0^{N+1-j}\langle \mathcal D_{\delta _0} \eta , \mathbf r^{(j)}( s)\rangle $
for
$\langle \eta , \mathbf r^{(j)}(\delta _0 s)\rangle =\delta _0^{N+1-j}\langle \mathcal D_{\delta _0} \eta , \mathbf r^{(j)}( s)\rangle $
for
![]() $\eta \in \mathbb R^{N+1}$
. Therefore, we get (3.16). For the inequality (3.17), note that
$\eta \in \mathbb R^{N+1}$
. Therefore, we get (3.16). For the inequality (3.17), note that
![]() $\mathbf r^{(N+1)}=(0,\dots , 0, 1)$
. Thus,
$\mathbf r^{(N+1)}=(0,\dots , 0, 1)$
. Thus,
![]() $\langle \mathbf y_\mu , \mathbf r^{(N+1)}\rangle =y^{N}_\mu $
and (3.17) follows by (3.1).
$\langle \mathbf y_\mu , \mathbf r^{(N+1)}\rangle =y^{N}_\mu $
and (3.17) follows by (3.1).
Let
![]() $\mathrm V= \operatorname {\mathrm {span}}\{\gamma '(\delta _0\mu ),\dots ,\gamma ^{(N)}(\delta _0\mu )\}$
and
$\mathrm V= \operatorname {\mathrm {span}}\{\gamma '(\delta _0\mu ),\dots ,\gamma ^{(N)}(\delta _0\mu )\}$
and
![]() $\{v_{N+1},\dots , v_d\}$
be an orthonormal basis of
$\{v_{N+1},\dots , v_d\}$
be an orthonormal basis of
![]() $\mathrm V^\perp $
. Since
$\mathrm V^\perp $
. Since
![]() $\gamma $
satisfies
$\gamma $
satisfies
![]() ${\mathfrak V({N}, B)}$
, for each
${\mathfrak V({N}, B)}$
, for each
![]() $\xi \in \mathbb R^d$
we can write
$\xi \in \mathbb R^d$
we can write
 $$ \begin{align} \xi= \overline \xi+\sum_{N+1\le j\le d}y_j(\xi) v_j, \end{align} $$
$$ \begin{align} \xi= \overline \xi+\sum_{N+1\le j\le d}y_j(\xi) v_j, \end{align} $$
where
![]() $\overline \xi \in \mathrm V$
and
$\overline \xi \in \mathrm V$
and
![]() $y_j(\xi ) \in \mathbb R$
,
$y_j(\xi ) \in \mathbb R$
,
![]() $N+1\le j\le d$
. We define a linear map by
$N+1\le j\le d$
. We define a linear map by
From (3.16) and (3.17), we see
for some
![]() $C>1$
. We now have the inequality (2.40) for
$C>1$
. We now have the inequality (2.40) for
![]() $\delta =C{2^n\delta _1}/{\delta _0}$
and the slabs
$\delta =C{2^n\delta _1}/{\delta _0}$
and the slabs
![]() $\mathbf S(2^n\delta _1\nu /\delta _0-\mu , C2^{n}\delta _1/\delta _0, 2^2B; \mathbf r_\circ ^{N+1}), \nu \in \mathfrak J_{n}^\mu $
. Therefore, by cylindrical extension in
$\mathbf S(2^n\delta _1\nu /\delta _0-\mu , C2^{n}\delta _1/\delta _0, 2^2B; \mathbf r_\circ ^{N+1}), \nu \in \mathfrak J_{n}^\mu $
. Therefore, by cylindrical extension in
![]() $y_{N+1},\dots ,y_d$
(see (2.42)) and the change of variables
$y_{N+1},\dots ,y_d$
(see (2.42)) and the change of variables
![]() $(\tau ,\xi )\to \mathrm Y_\mu ^{\delta _0}(\tau ,\xi )$
, we obtain (3.15) since the decoupling inequality is not affected by an affine change of variables in the Fourier side.
$(\tau ,\xi )\to \mathrm Y_\mu ^{\delta _0}(\tau ,\xi )$
, we obtain (3.15) since the decoupling inequality is not affected by an affine change of variables in the Fourier side.
Combining the inequalites (3.14) and (3.15), we obtain
 $$ \begin{align*} \left(\sum_\mu \| \mathcal T[\mathfrak a^\mu]f\|_p^p\,\right)^{1/p} \le \sum_{n\ge 0}\, \mathbf E_n \end{align*} $$
$$ \begin{align*} \left(\sum_\mu \| \mathcal T[\mathfrak a^\mu]f\|_p^p\,\right)^{1/p} \le \sum_{n\ge 0}\, \mathbf E_n \end{align*} $$
for
![]() $p \ge 4N-2$
, where
$p \ge 4N-2$
, where
 $$ \begin{align*} \mathbf E_n= C_\epsilon \big({2^n\delta_1}/\delta_0\big)^{\frac {2N} {p}-1-\epsilon} \left(\sum_{\mu} \sum_{\nu\in \mathfrak J_n^\mu} \| \mathcal T[\mathfrak a^{\mu, n}_\nu]f\|_p^p\,\right)^{1/p}. \end{align*} $$
$$ \begin{align*} \mathbf E_n= C_\epsilon \big({2^n\delta_1}/\delta_0\big)^{\frac {2N} {p}-1-\epsilon} \left(\sum_{\mu} \sum_{\nu\in \mathfrak J_n^\mu} \| \mathcal T[\mathfrak a^{\mu, n}_\nu]f\|_p^p\,\right)^{1/p}. \end{align*} $$
Since the intervals
![]() $I(\delta _0\mu ,\delta _0)$
overlap, there are at most three nonzero
$I(\delta _0\mu ,\delta _0)$
overlap, there are at most three nonzero
![]() $\mathfrak a^{\mu , 0}_{\nu }$
for each
$\mathfrak a^{\mu , 0}_{\nu }$
for each
![]() $\nu $
. We take
$\nu $
. We take
![]() $\mathfrak a_\nu =\mathfrak a^{\mu , 0}_\nu $
which maximizes
$\mathfrak a_\nu =\mathfrak a^{\mu , 0}_\nu $
which maximizes
![]() $\| \mathcal T[\mathfrak a^{\mu , 0}_\nu ]f\|_p$
. Then, it is clear that
$\| \mathcal T[\mathfrak a^{\mu , 0}_\nu ]f\|_p$
. Then, it is clear that
![]() $\mathbf E_0\le 3^{1/p} C_\epsilon (\delta _1/\delta _0)^{\frac {2N} {p}-1-\epsilon } \left(\sum _{\nu } \| \mathcal T[\mathfrak a_\nu ]f\|_p^p\right)^{1/p}.$
By Lemma 3.2,
$\mathbf E_0\le 3^{1/p} C_\epsilon (\delta _1/\delta _0)^{\frac {2N} {p}-1-\epsilon } \left(\sum _{\nu } \| \mathcal T[\mathfrak a_\nu ]f\|_p^p\right)^{1/p}.$
By Lemma 3.2,
![]() $C^{-1}\mathfrak a_\nu \in \mathfrak A_k(\delta _1\nu , \delta _1)$
for a constant C. Thus, the proof of Proposition 2.10 is now reduced to showing
$C^{-1}\mathfrak a_\nu \in \mathfrak A_k(\delta _1\nu , \delta _1)$
for a constant C. Thus, the proof of Proposition 2.10 is now reduced to showing
 $$ \begin{align} \sum_{n\ge1}\, \mathbf E_n \lesssim_B\! \delta_0^{-\frac{2N}p+1+\epsilon} 2^{-\frac 2pk +2\epsilon k} \|f\|_p, \quad p\ge 4N-2. \end{align} $$
$$ \begin{align} \sum_{n\ge1}\, \mathbf E_n \lesssim_B\! \delta_0^{-\frac{2N}p+1+\epsilon} 2^{-\frac 2pk +2\epsilon k} \|f\|_p, \quad p\ge 4N-2. \end{align} $$
Estimates for
![]() $\mathbf E_n$
when
$\mathbf E_n$
when
![]() $n\ge 1$
. To prove the estimate (3.20), we decompose
$n\ge 1$
. To prove the estimate (3.20), we decompose
![]() $\mathfrak a^{\mu , n}_\nu $
so that the inequalites (3.25) or (3.26) (see Lemma 3.5 below) holds on the
$\mathfrak a^{\mu , n}_\nu $
so that the inequalites (3.25) or (3.26) (see Lemma 3.5 below) holds on the
![]() $s,\xi $
-supports of the resulting symbols. If (3.25) holds, we use the assumption after rescaling, whereas we handle the other case using estimates for the kernels of the operators.
$s,\xi $
-supports of the resulting symbols. If (3.25) holds, we use the assumption after rescaling, whereas we handle the other case using estimates for the kernels of the operators.
Let
 $$ \begin{align} \bar{\mathfrak G}_N^{\mu}(s,\xi) =\sum_{1\le j\le N-2}\big(2^{-k}\mathfrak g^{j}_\mu\big)^{\frac{2N!}{N-j}}+\big(s-\sigma(\xi)\big)^{2N!}. \end{align} $$
$$ \begin{align} \bar{\mathfrak G}_N^{\mu}(s,\xi) =\sum_{1\le j\le N-2}\big(2^{-k}\mathfrak g^{j}_\mu\big)^{\frac{2N!}{N-j}}+\big(s-\sigma(\xi)\big)^{2N!}. \end{align} $$
Note that the right-hand side is independent of
![]() $\tau $
since so are
$\tau $
since so are
![]() $\mathfrak g^{j}_\mu $
,
$\mathfrak g^{j}_\mu $
,
![]() $1\le j\le N-2$
.
$1\le j\le N-2$
.
Let
![]() $C_0=2^{2d}B$
. We set
$C_0=2^{2d}B$
. We set
and
![]() $\mathfrak a_{\nu ,2}^{\mu ,n}=\mathfrak a_{\nu }^{\mu ,n} -\mathfrak a_{\nu ,1}^{\mu ,n},$
so we have
$\mathfrak a_{\nu ,2}^{\mu ,n}=\mathfrak a_{\nu }^{\mu ,n} -\mathfrak a_{\nu ,1}^{\mu ,n},$
so we have
![]() $ \mathfrak a_{\nu }^{\mu ,n} =\mathfrak a_{\nu ,1}^{\mu ,n}+\mathfrak a_{\nu ,2}^{\mu ,n}. $
Similarly as before, we have the following, which we prove in Section 3.4.
$ \mathfrak a_{\nu }^{\mu ,n} =\mathfrak a_{\nu ,1}^{\mu ,n}+\mathfrak a_{\nu ,2}^{\mu ,n}. $
Similarly as before, we have the following, which we prove in Section 3.4.
Lemma 3.4. There exists a constant
![]() $C=C(B)$
such that
$C=C(B)$
such that
![]() $C^{-1}\mathfrak a_{\nu ,1}^{\mu ,n}$
and
$C^{-1}\mathfrak a_{\nu ,1}^{\mu ,n}$
and
![]() $C^{-1} \mathfrak a_{\nu ,2}^{\mu ,n}$
are contained in
$C^{-1} \mathfrak a_{\nu ,2}^{\mu ,n}$
are contained in
![]() $\mathfrak A_k(2^n\delta _1\nu , 2^n\delta _1)$
for
$\mathfrak A_k(2^n\delta _1\nu , 2^n\delta _1)$
for
![]() $n\ge 1$
.
$n\ge 1$
.
The estimate (3.20) follows if we show
 $$ \begin{align} \left( \sum_{\mu} \sum_{\nu \in \mathfrak J_n^\mu} \|\mathcal T[\mathfrak a_{\nu,1}^{\mu,n}]f\|_p^p \right)^{1/p} \le C_\epsilon 2^{-\frac 2pk+\epsilon k} (2^n\delta_1)^{-\frac{2N}p+1+\epsilon} \|f\|_p, \, \quad p\ge 4N-6 \hspace{-4pt} \end{align} $$
$$ \begin{align} \left( \sum_{\mu} \sum_{\nu \in \mathfrak J_n^\mu} \|\mathcal T[\mathfrak a_{\nu,1}^{\mu,n}]f\|_p^p \right)^{1/p} \le C_\epsilon 2^{-\frac 2pk+\epsilon k} (2^n\delta_1)^{-\frac{2N}p+1+\epsilon} \|f\|_p, \, \quad p\ge 4N-6 \hspace{-4pt} \end{align} $$
for any
![]() $\epsilon>0$
, and
$\epsilon>0$
, and
 $$ \begin{align} \left( \sum_\mu\sum_{\nu\in \mathfrak J_{n}^{\mu}}\| \mathcal T[\mathfrak a_{\nu,2}^{\mu,n}]f\|_p^p \right)^{1/p} \lesssim_B\! 2^{-\frac {(N+2)k} {2N}}(2^n\delta_1)^{-\frac N2}\|f\|_p, \quad 2\le p\le \infty \end{align} $$
$$ \begin{align} \left( \sum_\mu\sum_{\nu\in \mathfrak J_{n}^{\mu}}\| \mathcal T[\mathfrak a_{\nu,2}^{\mu,n}]f\|_p^p \right)^{1/p} \lesssim_B\! 2^{-\frac {(N+2)k} {2N}}(2^n\delta_1)^{-\frac N2}\|f\|_p, \quad 2\le p\le \infty \end{align} $$
when
![]() $n\ge 1$
. Thanks to the inequality (3.8), those estimates give
$n\ge 1$
. Thanks to the inequality (3.8), those estimates give
 $$\begin{align*}\sum_{n\ge1} \mathbf E_n\,\le C_\epsilon \delta_0^{-\frac{2N}p+1+\epsilon} \! \sum_{1\le n\le \log_2 (C\delta_0/\delta_1)} \!\!\big(2^{-\frac {2}pk + \epsilon k} + 2^{-\frac {(N+2)k} {2N}}(2^n\delta_1)^{\frac{2N}p-\frac {N+2}2-\epsilon}\big) \|f\|_p \end{align*}$$
$$\begin{align*}\sum_{n\ge1} \mathbf E_n\,\le C_\epsilon \delta_0^{-\frac{2N}p+1+\epsilon} \! \sum_{1\le n\le \log_2 (C\delta_0/\delta_1)} \!\!\big(2^{-\frac {2}pk + \epsilon k} + 2^{-\frac {(N+2)k} {2N}}(2^n\delta_1)^{\frac{2N}p-\frac {N+2}2-\epsilon}\big) \|f\|_p \end{align*}$$
for
![]() $p\ge 4N-2$
. Note
$p\ge 4N-2$
. Note
![]() $ \log _2 (\delta _0/\delta _1)\le Ck $
from (2.31). So, the estimate (3.20) follows since
$ \log _2 (\delta _0/\delta _1)\le Ck $
from (2.31). So, the estimate (3.20) follows since
![]() $4N-2> 4N/(N+2)$
and
$4N-2> 4N/(N+2)$
and
![]() $\delta _1\ge 2^{-k/N}$
.
$\delta _1\ge 2^{-k/N}$
.
In order to prove the estimates (3.23) and (3.24), we start with the next lemma.
Lemma 3.5. Let
![]() $n\ge 1$
. For a constant
$n\ge 1$
. For a constant
![]() $C=C(B)>0$
, we have the following
$C=C(B)>0$
, we have the following
![]() $:$
$:$
 $$ \begin{align} \sum_{1\le j\le N-1} (2^n\delta_1)^{-(N-j)} |\langle\gamma^{(j)}(s),\xi\rangle| \ge C 2^k, \qquad (s,\xi)\in \operatorname{\mathrm{supp}}_{s,\xi} \mathfrak a_{\nu,1}^{\mu,n}, \end{align} $$
$$ \begin{align} \sum_{1\le j\le N-1} (2^n\delta_1)^{-(N-j)} |\langle\gamma^{(j)}(s),\xi\rangle| \ge C 2^k, \qquad (s,\xi)\in \operatorname{\mathrm{supp}}_{s,\xi} \mathfrak a_{\nu,1}^{\mu,n}, \end{align} $$
Proof. We first prove (3.25). Since
![]() $\mathfrak G_N^\mu \ge 2^{-2N!-1}(2^n\delta _1)^{2N!}$
on
$\mathfrak G_N^\mu \ge 2^{-2N!-1}(2^n\delta _1)^{2N!}$
on
![]() $\operatorname {\mathrm {supp}}_{s,\xi } \mathfrak a_{\nu }^{\mu ,n}$
, one of the following holds on
$\operatorname {\mathrm {supp}}_{s,\xi } \mathfrak a_{\nu }^{\mu ,n}$
, one of the following holds on
![]() $\operatorname {\mathrm {supp}} \mathfrak a_{\nu ,1}^{\mu ,n}$
:
$\operatorname {\mathrm {supp}} \mathfrak a_{\nu ,1}^{\mu ,n}$
:
for some
![]() $1\le j \le N-2$
, where
$1\le j \le N-2$
, where
![]() $C_0=2^{2d}B$
(see (3.22)). If (3.27) holds, by (2.28) and (2.29) it follows that
$C_0=2^{2d}B$
(see (3.22)). If (3.27) holds, by (2.28) and (2.29) it follows that
![]() $ (2^n\delta _1)^{-1}|\langle \gamma ^{(N-1)}(s),\xi \rangle | \gtrsim 2^{k}.$
Thus, to show (3.25) we may assume the inequality (3.27) fails, that is, (3.28) holds for some
$ (2^n\delta _1)^{-1}|\langle \gamma ^{(N-1)}(s),\xi \rangle | \gtrsim 2^{k}.$
Thus, to show (3.25) we may assume the inequality (3.27) fails, that is, (3.28) holds for some
![]() $1\le j \le N-2$
. So, there is an integer
$1\le j \le N-2$
. So, there is an integer
![]() $\ell \in [0, N-2]$
such that (3.28) fails for
$\ell \in [0, N-2]$
such that (3.28) fails for
![]() $\ell +1\le j \le N-2$
, whereas (3.28) holds for
$\ell +1\le j \le N-2$
, whereas (3.28) holds for
![]() $j=\ell $
. By (3.6) and (3.12), we have
$j=\ell $
. By (3.6) and (3.12), we have
 $$ \begin{align} |\langle G^{(\ell)}(\sigma(\xi)),(\tau,\xi) \rangle| \ge |\mathfrak g_\mu^\ell| -\!\!\sum_{j=\ell+1}^N|\mathfrak g_\mu^j| \frac{(B^6 2^{14}\delta_0^2)^{j-\ell}}{(j-\ell)!} -2B^3 (B^2 2^7\delta_0)^{N+1-\ell}|\xi|. \end{align} $$
$$ \begin{align} |\langle G^{(\ell)}(\sigma(\xi)),(\tau,\xi) \rangle| \ge |\mathfrak g_\mu^\ell| -\!\!\sum_{j=\ell+1}^N|\mathfrak g_\mu^j| \frac{(B^6 2^{14}\delta_0^2)^{j-\ell}}{(j-\ell)!} -2B^3 (B^2 2^7\delta_0)^{N+1-\ell}|\xi|. \end{align} $$
Thus, (2.32) gives
![]() $|\langle G^{(\ell )}(\sigma (\xi )),(\tau ,\xi ) \rangle | \ge (2^3C_0)^{-(N-\ell )} 2^k (2^n\delta _1)^{N-\ell }$
. Also, the equation (3.6) and our choice of
$|\langle G^{(\ell )}(\sigma (\xi )),(\tau ,\xi ) \rangle | \ge (2^3C_0)^{-(N-\ell )} 2^k (2^n\delta _1)^{N-\ell }$
. Also, the equation (3.6) and our choice of
![]() $\ell $
yield
$\ell $
yield
![]() $|\langle G^{(j)}(\sigma (\xi )),(\tau ,\xi ) \rangle | \le (2C_0)^{-(N-j)} 2^k (2^n\delta _1)^{N-j}$
for
$|\langle G^{(j)}(\sigma (\xi )),(\tau ,\xi ) \rangle | \le (2C_0)^{-(N-j)} 2^k (2^n\delta _1)^{N-j}$
for
![]() $\ell +1 \le j \le N-2$
. Combining this with
$\ell +1 \le j \le N-2$
. Combining this with
![]() $|s-\sigma (\xi )|< (2^3 C_0B)^{-1} 2^n\delta _1$
and expanding
$|s-\sigma (\xi )|< (2^3 C_0B)^{-1} 2^n\delta _1$
and expanding
![]() $G^{(\ell )}$
in Taylor series at
$G^{(\ell )}$
in Taylor series at
![]() $\sigma (\xi )$
, we see that
$\sigma (\xi )$
, we see that
![]() $ |\langle G^{(\ell )}(s), (\tau ,\xi ) \rangle |\ge C 2^k (2^n\delta _1)^{N-\ell }$
for some
$ |\langle G^{(\ell )}(s), (\tau ,\xi ) \rangle |\ge C 2^k (2^n\delta _1)^{N-\ell }$
for some
![]() $C=C(B)>0$
. This proves (3.25).
$C=C(B)>0$
. This proves (3.25).
We now show (3.26), which is easier. On
![]() $\operatorname {\mathrm {supp}} \mathfrak a_{\nu ,2}^{\mu ,n}$
,
$\operatorname {\mathrm {supp}} \mathfrak a_{\nu ,2}^{\mu ,n}$
,
![]() $2^{-k}|\mathfrak g_\mu ^0|\ge 2^{-N-1}(2^n\delta _1)^N$
and
$2^{-k}|\mathfrak g_\mu ^0|\ge 2^{-N-1}(2^n\delta _1)^N$
and
![]() $2^{-k}|\mathfrak g_\mu ^j| \le 2C_0^{-(N-j)}(2^n\delta _1)^{N-j}$
for
$2^{-k}|\mathfrak g_\mu ^j| \le 2C_0^{-(N-j)}(2^n\delta _1)^{N-j}$
for
![]() $j=1, \dots , N-2$
. Using (3.29) with
$j=1, \dots , N-2$
. Using (3.29) with
![]() $\ell =0$
, by (2.32) and (2.31) we get
$\ell =0$
, by (2.32) and (2.31) we get
![]() $ (2^n\delta _1)^{-N} |\tau +\langle \gamma (\sigma (\xi )),\xi \rangle | \ge 2^{-N-2}2^k$
. We also note that
$ (2^n\delta _1)^{-N} |\tau +\langle \gamma (\sigma (\xi )),\xi \rangle | \ge 2^{-N-2}2^k$
. We also note that
![]() $|s-\sigma (\xi )| \le 2C_0^{-1} 2^n\delta _1$
and
$|s-\sigma (\xi )| \le 2C_0^{-1} 2^n\delta _1$
and
![]() $|\langle G^{(j)}(\sigma (\xi )),(\tau ,\xi ) \rangle | \le C_0^{-1}2^k (2^n\delta _1)^{N-j}$
for
$|\langle G^{(j)}(\sigma (\xi )),(\tau ,\xi ) \rangle | \le C_0^{-1}2^k (2^n\delta _1)^{N-j}$
for
![]() $1 \le j \le N-2$
on
$1 \le j \le N-2$
on
![]() $\operatorname {\mathrm {supp}} \mathfrak a_{\nu ,2}^{\mu ,n}$
. Since
$\operatorname {\mathrm {supp}} \mathfrak a_{\nu ,2}^{\mu ,n}$
. Since
![]() $|\langle G^{(N)}(s),(\tau ,\xi ) \rangle | \le B2^{k+1}$
, using Taylor series expansion at
$|\langle G^{(N)}(s),(\tau ,\xi ) \rangle | \le B2^{k+1}$
, using Taylor series expansion at
![]() $\sigma (\xi )$
as above, we see (3.26) holds true for some
$\sigma (\xi )$
as above, we see (3.26) holds true for some
![]() $C=C(B)>0$
.
$C=C(B)>0$
.
Additionally, we make use of disjointness of
![]() $\operatorname {\mathrm {supp}}_\xi \mathfrak a_{\nu }^{\mu ,n}$
by combining Lemma 2.11 and the next.
$\operatorname {\mathrm {supp}}_\xi \mathfrak a_{\nu }^{\mu ,n}$
by combining Lemma 2.11 and the next.
Lemma 3.6. There is a positive constant
![]() $C=C(B)$
such that
$C=C(B)$
such that
whenever
![]() $\xi \in {\Lambda }^{\prime}_k(s,\delta ,b) ($
see (2.36)
$\xi \in {\Lambda }^{\prime}_k(s,\delta ,b) ($
see (2.36)
![]() $)$
. If
$)$
. If
![]() $\xi \in \Gamma _k$
and (3.30) holds with
$\xi \in \Gamma _k$
and (3.30) holds with
![]() $C=1$
, then
$C=1$
, then
![]() $\xi \in {\Lambda }^{\prime}_k(s,\delta , C_1b)$
for some
$\xi \in {\Lambda }^{\prime}_k(s,\delta , C_1b)$
for some
![]() $C_1=C_1(B)>0$
.
$C_1=C_1(B)>0$
.
Proof. Let
![]() $\eta \in \mathbb R^d$
and
$\eta \in \mathbb R^d$
and
![]() $\{ v_{N}, \dots , v_d\}$
be an orthonormal basis of
$\{ v_{N}, \dots , v_d\}$
be an orthonormal basis of
![]() $(\operatorname {\mathrm {span}}\{ \gamma ^{(j)}(s): 1\le j\le N-1\})^\perp $
. We write
$(\operatorname {\mathrm {span}}\{ \gamma ^{(j)}(s): 1\le j\le N-1\})^\perp $
. We write
![]() $ \eta =\sum _{j=1}^{N-1} \mathbf c_j \gamma ^{(j)}(s) + \sum _{j=N}^d \mathbf c_j v_j.$
Since
$ \eta =\sum _{j=1}^{N-1} \mathbf c_j \gamma ^{(j)}(s) + \sum _{j=N}^d \mathbf c_j v_j.$
Since
![]() ${\mathfrak V(N, B)}$
holds for
${\mathfrak V(N, B)}$
holds for
![]() $\gamma $
,
$\gamma $
,
![]() $|\eta |\sim |(\mathbf c_1, \cdots ,\mathbf c_d )|$
. Let
$|\eta |\sim |(\mathbf c_1, \cdots ,\mathbf c_d )|$
. Let
![]() $\xi \in {\Lambda }^{\prime}_k(s,\delta ,b) $
. Then, (2.4) gives
$\xi \in {\Lambda }^{\prime}_k(s,\delta ,b) $
. Then, (2.4) gives
 $$\begin{align*}\langle \eta, ( \widetilde{\mathcal L}_s^\delta)^{-1}\xi \rangle= \langle ( \widetilde{\mathcal L}_s^\delta)^{-\intercal} \eta, \xi \rangle= \sum_{j=1}^{N-1} \delta^{j-N} \mathbf c_j \langle\gamma^{(j)}(s), \xi\rangle + \sum_{j=N}^d \mathbf c_j \langle v_j,\xi\rangle. \end{align*}$$
$$\begin{align*}\langle \eta, ( \widetilde{\mathcal L}_s^\delta)^{-1}\xi \rangle= \langle ( \widetilde{\mathcal L}_s^\delta)^{-\intercal} \eta, \xi \rangle= \sum_{j=1}^{N-1} \delta^{j-N} \mathbf c_j \langle\gamma^{(j)}(s), \xi\rangle + \sum_{j=N}^d \mathbf c_j \langle v_j,\xi\rangle. \end{align*}$$
Thus, by (2.36) we get
![]() $|\langle \eta , ( \widetilde {\mathcal L}_s^\delta )^{-1}\xi \rangle |\le Cb|\eta | 2^k $
, which shows (3.30).
$|\langle \eta , ( \widetilde {\mathcal L}_s^\delta )^{-1}\xi \rangle |\le Cb|\eta | 2^k $
, which shows (3.30).
By (2.4),
![]() $\langle \gamma ^{(j)}(s),\xi \rangle = \delta ^{N-j} \langle \gamma ^{(j)}(s), (\widetilde {\mathcal L}_s^\delta )^{-1}\xi \rangle $
for
$\langle \gamma ^{(j)}(s),\xi \rangle = \delta ^{N-j} \langle \gamma ^{(j)}(s), (\widetilde {\mathcal L}_s^\delta )^{-1}\xi \rangle $
for
![]() $1\le j\le N-1$
. Therefore, (3.30) with
$1\le j\le N-1$
. Therefore, (3.30) with
![]() $C=1$
gives
$C=1$
gives
![]() $|\langle \gamma ^{(j)}(s),\xi \rangle | \le C_1 b \delta ^{N-j} 2^k$
for a constant
$|\langle \gamma ^{(j)}(s),\xi \rangle | \le C_1 b \delta ^{N-j} 2^k$
for a constant
![]() $C_1>0$
when
$C_1>0$
when
![]() $1\le j\le N-1$
. This proves the second statement.
$1\le j\le N-1$
. This proves the second statement.
Now, we are ready to prove the estimates (3.23) and (3.24).
Proof of (3.23).
By Lemma 3.4,
![]() $C^{-1}\mathfrak a_{\nu ,1}^{\mu ,n}\in \mathfrak A_k(2^n\delta _1\nu , 2^n\delta _1)$
for some
$C^{-1}\mathfrak a_{\nu ,1}^{\mu ,n}\in \mathfrak A_k(2^n\delta _1\nu , 2^n\delta _1)$
for some
![]() $C>0$
. Besides, (3.25) holds on
$C>0$
. Besides, (3.25) holds on
![]() $\operatorname {\mathrm {supp}}_{s,\xi } \mathfrak a_{\nu ,1}^{\mu ,n}$
, and we note
$\operatorname {\mathrm {supp}}_{s,\xi } \mathfrak a_{\nu ,1}^{\mu ,n}$
, and we note
![]() $2^n\delta _1<\delta '$
from (3.8), (2.26), and (2.31). Thus, taking
$2^n\delta _1<\delta '$
from (3.8), (2.26), and (2.31). Thus, taking
![]() $\delta =2^n\delta _1$
and
$\delta =2^n\delta _1$
and
, we may use Lemma 2.8 for
![]() $\tilde \chi \mathcal T [\mathfrak a_{\nu ,1}^{\mu ,n}] f$
to get
$\tilde \chi \mathcal T [\mathfrak a_{\nu ,1}^{\mu ,n}] f$
to get
where
![]() $ \|\tilde f_l\|_p= \|f\|_p$
,
$ \|\tilde f_l\|_p= \|f\|_p$
,
![]() $a_{l}$
are of type
$a_{l}$
are of type
![]() $(j, N-1, B')$
relative to
$(j, N-1, B')$
relative to
for some
![]() $B'>0$
, and
$B'>0$
, and
![]() $2^j\sim (2^n\delta _1)^N 2^k$
. As seen before,
$2^j\sim (2^n\delta _1)^N 2^k$
. As seen before,
satisfies
![]() ${\mathfrak V({N}, {3B})}$
and (2.1) with B replaced by
${\mathfrak V({N}, {3B})}$
and (2.1) with B replaced by
![]() $3B$
for
$3B$
for
![]() $\delta \le \delta _*$
. So,
$\delta \le \delta _*$
. So,
![]() ${\mathfrak V({N-1}, {B'})}$
with a large
${\mathfrak V({N-1}, {B'})}$
with a large
![]() $B'$
holds for
$B'$
holds for
.
Therefore, we may apply the assumption (Theorem 2.2 with
![]() $L=N-1$
) to
$L=N-1$
) to
![]() , which gives
, which gives
![]() for a constant
for a constant
![]() $C_\epsilon =C_\epsilon (B')$
. Consequently, we obtain
$C_\epsilon =C_\epsilon (B')$
. Consequently, we obtain
for
![]() $p\ge 4(N-1)-2$
. Besides, since
$p\ge 4(N-1)-2$
. Besides, since
![]() $C^{-1}\mathfrak a_{\nu ,1}^{\mu ,n}\in \mathfrak A_k(2^n\delta _1\nu , 2^n\delta _1)$
, by (2.16) we have
$C^{-1}\mathfrak a_{\nu ,1}^{\mu ,n}\in \mathfrak A_k(2^n\delta _1\nu , 2^n\delta _1)$
, by (2.16) we have
![]() $\| (1-\tilde \chi )\mathcal T[\mathfrak a_{\nu ,1}^{\mu ,n}]f\|_{L^p(\mathbb R^{d+1})} \lesssim _ B\!2^{-k}(2^n\delta _1)^{1-N} \|f\|_{L^p(\mathbb R^d)}$
for
$\| (1-\tilde \chi )\mathcal T[\mathfrak a_{\nu ,1}^{\mu ,n}]f\|_{L^p(\mathbb R^{d+1})} \lesssim _ B\!2^{-k}(2^n\delta _1)^{1-N} \|f\|_{L^p(\mathbb R^d)}$
for
![]() $p>1$
. Note
$p>1$
. Note
![]() $2^n\delta _1\gtrsim 2^{-k/N}$
. Combining those two estimates yields
$2^n\delta _1\gtrsim 2^{-k/N}$
. Combining those two estimates yields
To exploit disjointness of
![]() $\operatorname {\mathrm {supp}}_\xi \mathfrak a_{\nu ,1}^{\mu ,n}$
, we define a multiplier operator by
$\operatorname {\mathrm {supp}}_\xi \mathfrak a_{\nu ,1}^{\mu ,n}$
, we define a multiplier operator by
for a constant
![]() $C_1>0$
. Since
$C_1>0$
. Since
![]() $\operatorname {\mathrm {supp}}_\xi \mathfrak a_{\nu ,1}^{\mu ,n}\subset {\Lambda }^{\prime}_k (2^n\delta _1\nu , 2^n\delta _1, 2^5B)$
, by Lemma 3.6 we may choose
$\operatorname {\mathrm {supp}}_\xi \mathfrak a_{\nu ,1}^{\mu ,n}\subset {\Lambda }^{\prime}_k (2^n\delta _1\nu , 2^n\delta _1, 2^5B)$
, by Lemma 3.6 we may choose
![]() $C_1$
large enough so that
$C_1$
large enough so that
![]() $\beta _0\big (| (\widetilde {\mathcal L}_{2^n\delta _1\nu }^{2^n\delta _1})^{-1}\cdot |/(C_12^k) \big )=1 $
on
$\beta _0\big (| (\widetilde {\mathcal L}_{2^n\delta _1\nu }^{2^n\delta _1})^{-1}\cdot |/(C_12^k) \big )=1 $
on
![]() $\operatorname {\mathrm {supp}}_\xi \mathfrak a_{\nu ,1}^{\mu ,n}$
. Thus,
$\operatorname {\mathrm {supp}}_\xi \mathfrak a_{\nu ,1}^{\mu ,n}$
. Thus,
![]() $\mathcal T[\mathfrak a_{\nu ,1}^{\mu ,n}]f= \mathcal T[\mathfrak a_{\nu ,1}^{\mu ,n}] P_{2^n\delta _1\nu }^{2^n\delta _1} f $
. Combining this and (3.31), we obtain
$\mathcal T[\mathfrak a_{\nu ,1}^{\mu ,n}]f= \mathcal T[\mathfrak a_{\nu ,1}^{\mu ,n}] P_{2^n\delta _1\nu }^{2^n\delta _1} f $
. Combining this and (3.31), we obtain
 $$\begin{align*}\left(\sum_{\mu}\sum_{ \nu \in \mathfrak J_n^\mu} \| \mathcal T[\mathfrak a_{\nu,1}^{\mu,n}]f\|_p^p \,\right)^{1/p} \le C_\epsilon 2^{-\frac 2pk+\epsilon k} (2^n\delta_1)^{1-\frac{2N}p+\epsilon} \left( \sum_{\mu}\sum_{ \nu \in \mathfrak J_n^\mu} \|P_{2^n\delta_1\nu}^{2^n\delta_1} f\|_p^p\, \right)^{1/p} \end{align*}$$
$$\begin{align*}\left(\sum_{\mu}\sum_{ \nu \in \mathfrak J_n^\mu} \| \mathcal T[\mathfrak a_{\nu,1}^{\mu,n}]f\|_p^p \,\right)^{1/p} \le C_\epsilon 2^{-\frac 2pk+\epsilon k} (2^n\delta_1)^{1-\frac{2N}p+\epsilon} \left( \sum_{\mu}\sum_{ \nu \in \mathfrak J_n^\mu} \|P_{2^n\delta_1\nu}^{2^n\delta_1} f\|_p^p\, \right)^{1/p} \end{align*}$$
for a constant
![]() $C_\epsilon =C_\epsilon (B)$
if
$C_\epsilon =C_\epsilon (B)$
if
![]() $p\ge 4N-6$
. Therefore, the estimate (3.23) follows if we show
$p\ge 4N-6$
. Therefore, the estimate (3.23) follows if we show
 $$ \begin{align} \left( \sum_{\mu}\sum_{ \nu \in \mathfrak J_n^\mu} \|P_{2^n\delta_1\nu}^{2^n\delta_1} f\|_p^p\,\right)^{1/p}\lesssim_B\! \|f\|_p, \qquad 2\le p\le\infty. \end{align} $$
$$ \begin{align} \left( \sum_{\mu}\sum_{ \nu \in \mathfrak J_n^\mu} \|P_{2^n\delta_1\nu}^{2^n\delta_1} f\|_p^p\,\right)^{1/p}\lesssim_B\! \|f\|_p, \qquad 2\le p\le\infty. \end{align} $$
By interpolation, it suffices to obtain (3.32) for
![]() $p=2, \infty $
. The case
$p=2, \infty $
. The case
![]() $p=\infty $
is trivial since
$p=\infty $
is trivial since
![]() $\|P_{2^n\delta _1\nu }^{2^n\delta _1} f\|_\infty \lesssim \|f\|_\infty $
. For
$\|P_{2^n\delta _1\nu }^{2^n\delta _1} f\|_\infty \lesssim \|f\|_\infty $
. For
![]() $p=2$
, (3.32) follows by Plancherel’s theorem since
$p=2$
, (3.32) follows by Plancherel’s theorem since
![]() $\operatorname {\mathrm {supp}} \beta _0\big (| (\widetilde {\mathcal L}_{2^n\delta _1\nu }^{2^n\delta _1})^{-1}\cdot |/(C_12^k) \big )\widehat f$
,
$\operatorname {\mathrm {supp}} \beta _0\big (| (\widetilde {\mathcal L}_{2^n\delta _1\nu }^{2^n\delta _1})^{-1}\cdot |/(C_12^k) \big )\widehat f$
,
![]() $\nu \in \mathfrak J_n^\mu $
are finitely overlapping. Indeed, by Lemma 3.6 we have
$\nu \in \mathfrak J_n^\mu $
are finitely overlapping. Indeed, by Lemma 3.6 we have
![]() $\operatorname {\mathrm {supp}} \beta _0\big (| (\widetilde {\mathcal L}_{2^n\delta _1\nu }^{2^n\delta _1})^{-1}\cdot |/(C_12^k) \big )\widehat f\subset {\Lambda }^{\prime}_k (2^n\delta _1\nu , 2^n\delta _1, CB)$
for a constant C. It is clear from Lemma 2.11 that
$\operatorname {\mathrm {supp}} \beta _0\big (| (\widetilde {\mathcal L}_{2^n\delta _1\nu }^{2^n\delta _1})^{-1}\cdot |/(C_12^k) \big )\widehat f\subset {\Lambda }^{\prime}_k (2^n\delta _1\nu , 2^n\delta _1, CB)$
for a constant C. It is clear from Lemma 2.11 that
![]() ${\Lambda }^{\prime}_k (2^n\delta _1\nu , 2^n\delta _1, C B)$
,
${\Lambda }^{\prime}_k (2^n\delta _1\nu , 2^n\delta _1, C B)$
,
![]() $\nu \in \mathfrak J_n^\mu $
overlap at most
$\nu \in \mathfrak J_n^\mu $
overlap at most
![]() $C(B)$
times.
$C(B)$
times.
The proof of the estimate (3.24) is much easier since we have a favorable estimate for the kernel of
![]() $\mathcal T[\mathfrak a_{\nu ,2}^{\mu ,n}]$
thanks to the inequality (3.26).
$\mathcal T[\mathfrak a_{\nu ,2}^{\mu ,n}]$
thanks to the inequality (3.26).
Proof of (3.24).
Let
Then, integration by parts in t shows
![]() $m[\mathfrak a_{\nu ,2}^{\mu ,n}]=m[\mathfrak b]$
. Note that (3.26) holds and
$m[\mathfrak a_{\nu ,2}^{\mu ,n}]=m[\mathfrak b]$
. Note that (3.26) holds and
![]() $C^{-1}\mathfrak a_{\nu ,2}^{\mu ,n} \in \mathfrak A_k(2^n\delta _1\nu , 2^n\delta _1)$
for a constant
$C^{-1}\mathfrak a_{\nu ,2}^{\mu ,n} \in \mathfrak A_k(2^n\delta _1\nu , 2^n\delta _1)$
for a constant
![]() $C\ge 1$
. Thus,
$C\ge 1$
. Thus,
![]() $\mathfrak a:=C^{-1}2^k (2^n\delta _1)^N \mathfrak b$
satisfies, with
$\mathfrak a:=C^{-1}2^k (2^n\delta _1)^N \mathfrak b$
satisfies, with
![]() $\delta =2^n\delta _1$
and
$\delta =2^n\delta _1$
and
![]() , (2.6) and (2.7) for
, (2.6) and (2.7) for
![]() $0\le j\le 1$
,
$0\le j\le 1$
,
![]() $0\le l\le 2N-1$
, and
$0\le l\le 2N-1$
, and
![]() $|\alpha |\le d+N+2$
. Applying the estimate (2.15), we obtain
$|\alpha |\le d+N+2$
. Applying the estimate (2.15), we obtain
![]() $ \|\mathcal T[\mathfrak a_{\nu ,2}^{\mu ,n}]f\|_\infty \lesssim _B\! 2^{-k}(2^n\delta _1)^{1-N}\|f\|_\infty. $
Since
$ \|\mathcal T[\mathfrak a_{\nu ,2}^{\mu ,n}]f\|_\infty \lesssim _B\! 2^{-k}(2^n\delta _1)^{1-N}\|f\|_\infty. $
Since
![]() $\delta _1\ge 2^{-k/ N}$
, this gives
$\delta _1\ge 2^{-k/ N}$
, this gives
By interpolation it is sufficient to show (3.24) for
![]() $p=2$
. Note that
$p=2$
. Note that
![]() $\|b(\cdot ,t,\tau ,\xi )\|_\infty + \|\partial _s b(\cdot ,t,\tau ,\xi )\|_1\lesssim 2^{-k} (2^n\delta _1)^{-N}.$
Thus, (2.28) and using van der Corput’s lemma in s give
$\|b(\cdot ,t,\tau ,\xi )\|_\infty + \|\partial _s b(\cdot ,t,\tau ,\xi )\|_1\lesssim 2^{-k} (2^n\delta _1)^{-N}.$
Thus, (2.28) and using van der Corput’s lemma in s give
![]() $ |m[\mathfrak a_{\nu ,2}^{\mu ,n}](\tau ,\xi )| \lesssim 2^{-k(1+N)/N} (2^n\delta _1)^{-N}. $
Since
$ |m[\mathfrak a_{\nu ,2}^{\mu ,n}](\tau ,\xi )| \lesssim 2^{-k(1+N)/N} (2^n\delta _1)^{-N}. $
Since
![]() $\operatorname {\mathrm {supp}}_\xi \mathfrak a_{\nu ,2}^{\mu ,n} \subset {\Lambda }^{\prime}_k ( 2^n\delta _1\nu , 2^n\delta _1, 2^5B)$
, as before, we have
$\operatorname {\mathrm {supp}}_\xi \mathfrak a_{\nu ,2}^{\mu ,n} \subset {\Lambda }^{\prime}_k ( 2^n\delta _1\nu , 2^n\delta _1, 2^5B)$
, as before, we have
![]() $\mathcal T[\mathfrak a^{\mu ,n}_{2,\nu }]f= \mathcal T[\mathfrak a^{\mu ,n}_{2,\nu }] P_{2^n\delta _1\nu }^{2^n\delta _1} f $
with a positive constant
$\mathcal T[\mathfrak a^{\mu ,n}_{2,\nu }]f= \mathcal T[\mathfrak a^{\mu ,n}_{2,\nu }] P_{2^n\delta _1\nu }^{2^n\delta _1} f $
with a positive constant
![]() $C_1$
large enough. Thus, by Plancherel’s theorem
$C_1$
large enough. Thus, by Plancherel’s theorem
 $$ \begin{align*} \| \mathcal T[\mathfrak a_{\nu,2}^{\mu,n}] f \|_{L^2}^2 \lesssim_B\! 2^{-\frac{2(1+N)}N k} (2^n\delta_1)^{-2N}\!\!\!\iint_{\{ \tau: |\mathfrak g_\mu^0(\tau,\xi)| \le 2^{k+1}(2^n\delta_1)^N \}}\!\!\!\!\! d\tau\, |\mathcal F(P_{2^n\delta_1\nu}^{2^n\delta_1} f)(\xi)|^2\, d\xi. \end{align*} $$
$$ \begin{align*} \| \mathcal T[\mathfrak a_{\nu,2}^{\mu,n}] f \|_{L^2}^2 \lesssim_B\! 2^{-\frac{2(1+N)}N k} (2^n\delta_1)^{-2N}\!\!\!\iint_{\{ \tau: |\mathfrak g_\mu^0(\tau,\xi)| \le 2^{k+1}(2^n\delta_1)^N \}}\!\!\!\!\! d\tau\, |\mathcal F(P_{2^n\delta_1\nu}^{2^n\delta_1} f)(\xi)|^2\, d\xi. \end{align*} $$
3.3 Proof of Lemma 3.2
To simplify notations, we denote
for the rest of this section. To prove Lemma 3.2, we verify the conditions (2.6) and (2.7) with
![]() $\mathfrak a=\mathfrak a_{\nu }^{\mu ,n}$
,
$\mathfrak a=\mathfrak a_{\nu }^{\mu ,n}$
,
and
. The first is easy. In fact, since
![]() $\mathfrak a^\mu \in \mathfrak A_k(\delta _0\mu ,\delta _0)$
and
$\mathfrak a^\mu \in \mathfrak A_k(\delta _0\mu ,\delta _0)$
and
, we only need to show
on
![]() $\operatorname {\mathrm {supp}}_{\tau , \xi } \mathfrak a_{\nu }^{\mu ,n}$
. Using (3.6) and (3.11) together with (2.32) and (3.12), one can easily obtain
$\operatorname {\mathrm {supp}}_{\tau , \xi } \mathfrak a_{\nu }^{\mu ,n}$
. Using (3.6) and (3.11) together with (2.32) and (3.12), one can easily obtain
on
![]() $\operatorname {\mathrm {supp}}_{\tau , \xi } \mathfrak a_{\nu }^{\mu ,n}$
. Expanding
$\operatorname {\mathrm {supp}}_{\tau , \xi } \mathfrak a_{\nu }^{\mu ,n}$
. Expanding
![]() $\langle G^{(j)}(s),(\tau ,\xi )\rangle $
in Taylor’s series at
$\langle G^{(j)}(s),(\tau ,\xi )\rangle $
in Taylor’s series at
![]() $\sigma (\xi )$
gives (3.33) since (3.13) holds.
$\sigma (\xi )$
gives (3.33) since (3.13) holds.
We now proceed to show (2.7) with
![]() $\mathfrak a=\mathfrak a_{\nu }^{\mu ,n}$
,
$\mathfrak a=\mathfrak a_{\nu }^{\mu ,n}$
,
and
. Since
![]() $\mathfrak a_{\nu }^{\mu ,n}$
consists of three factors
$\mathfrak a_{\nu }^{\mu ,n}$
consists of three factors
![]() $\mathfrak a^\mu $
,
$\mathfrak a^\mu $
,
, and
, by Leibniz’s rule it is sufficient to consider the derivatives of each of them. The bounds on the derivatives of
are clear. So, it is enough to show (2.7) for
with
and
whenever
.
We handle
![]() $\mathfrak a^\mu $
first. That is to say, we show
$\mathfrak a^\mu $
first. That is to say, we show
for
. Since
![]() $\mathfrak a^\mu \in \mathfrak A_k(\delta _0\mu , \delta _0)$
and
$\mathfrak a^\mu \in \mathfrak A_k(\delta _0\mu , \delta _0)$
and
, we have
One can show this using (2.11). We consider
By (2.8), we have
![]() $|\,\mathcal U^\intercal z|\lesssim _B\! |z|$
because
$|\,\mathcal U^\intercal z|\lesssim _B\! |z|$
because
![]() $|\delta _0^{-1} 2^n \delta _1| \lesssim _B 1$
. Thus, (3.36) gives
$|\delta _0^{-1} 2^n \delta _1| \lesssim _B 1$
. Thus, (3.36) gives
for
.
Let
. Then,
, so
by Lemma 2.5. This and (2.9) give
for
. Therefore, we obtain (3.35) since
.
We continue to show (2.7) for
. Note that
![]() $\delta _\ast ^{-2N!} \mathfrak G_N^\mu $
is a sum of
$\delta _\ast ^{-2N!} \mathfrak G_N^\mu $
is a sum of
and
,
![]() $0\le j\le N-2$
. Since the exponents
$0\le j\le N-2$
. Since the exponents
![]() ${2N!}/{(N-j)}$
are even integers, for the desired bounds on
${2N!}/{(N-j)}$
are even integers, for the desired bounds on
it suffices to show the same bounds on the derivatives of
The bound on
is a consequence of (2.10) and the following lemma. For simplicity, we denote
Lemma 3.7. If
![]() $\Xi \in \operatorname {\mathrm {supp}}_{\tau ,\xi } \mathfrak a_{\nu }^{\mu ,n}$
, then we have
$\Xi \in \operatorname {\mathrm {supp}}_{\tau ,\xi } \mathfrak a_{\nu }^{\mu ,n}$
, then we have
Proof. By (2.29),
![]() $\gamma ^{(N-1)} ( \sigma (\tilde \Xi ) ) \cdot \tilde \Xi =0$
. Differentiation gives
$\gamma ^{(N-1)} ( \sigma (\tilde \Xi ) ) \cdot \tilde \Xi =0$
. Differentiation gives
Denote
![]() $s=\sigma (\tilde \Xi )$
. By (2.4),
$s=\sigma (\tilde \Xi )$
. By (2.4),
. Since
, that is, (3.10), by Lemma 2.6 we have
. Besides,
![]() $|\gamma ^{(N)}(\sigma (\tilde \Xi )) \cdot \tilde \Xi | \gtrsim |\tilde \Xi | \sim 2^k$
(see (2.28)). Thus, (3.38) and (2.10) give
$|\gamma ^{(N)}(\sigma (\tilde \Xi )) \cdot \tilde \Xi | \gtrsim |\tilde \Xi | \sim 2^k$
(see (2.28)). Thus, (3.38) and (2.10) give
which proves (3.37) with
![]() $|\alpha |=1$
.
$|\alpha |=1$
.
We show the bounds on the derivatives of higher orders by induction. Assume that (3.37) holds true for
![]() $|\alpha |\le L$
. Let
$|\alpha |\le L$
. Let
![]() $\alpha '$
be a multi-index such that
$\alpha '$
be a multi-index such that
![]() $|\alpha '|=L+1$
. Then, differentiating the equation (3.38) and using the induction assumption, one can easily see
$|\alpha '|=L+1$
. Then, differentiating the equation (3.38) and using the induction assumption, one can easily see
![]() , by which we get (3.37) for
, by which we get (3.37) for
![]() $|\alpha |=L+1$
. Since
$|\alpha |=L+1$
. Since
![]() $\sigma \in \mathrm{C}^{2d+2}$
, one can continue this as far as
$\sigma \in \mathrm{C}^{2d+2}$
, one can continue this as far as
![]() $L\le 2d+1$
.
$L\le 2d+1$
.
The proof of Lemma 3.2 is now completed if we show
for
![]() $0\le \ell \le N-2$
whenever
$0\le \ell \le N-2$
whenever
![]() $\Xi \in \operatorname {\mathrm {supp}} \mathfrak a_{\nu }^{\mu ,n} (s,t,\cdot )$
. To this end, we use the following.
$\Xi \in \operatorname {\mathrm {supp}} \mathfrak a_{\nu }^{\mu ,n} (s,t,\cdot )$
. To this end, we use the following.
Lemma 3.8. For
![]() $ j=0,\dots ,N$
, set
$ j=0,\dots ,N$
, set
If
, then for
![]() $ j=0,\dots ,N$
we have
$ j=0,\dots ,N$
we have
Proof. When
![]() $j=N$
, the estimate (3.40) follows by Lemma 3.7 and (2.10). So, we may assume
$j=N$
, the estimate (3.40) follows by Lemma 3.7 and (2.10). So, we may assume
![]() $j\le N-1$
. Differentiating
$j\le N-1$
. Differentiating
![]() $A_j$
, we have
$A_j$
, we have
where
Note that
for
![]() $0\le j\le N-1$
. Since
$0\le j\le N-1$
. Since
, similarly as before, Lemma 2.6 and (2.8) give
By Lemma 3.7 and (3.34),
![]() $| B_j|\lesssim |\xi |^{-1}$
. Thus, for
$| B_j|\lesssim |\xi |^{-1}$
. Thus, for
, we have
For the second inequality we use (2.10). This gives the inequality (3.40) when
![]() $|\alpha |=1$
.
$|\alpha |=1$
.
To show (3.40) for
![]() $2\le |\alpha |\le 2d+2$
, we use backward induction. By (2.29), we note
$2\le |\alpha |\le 2d+2$
, we use backward induction. By (2.29), we note
![]() $A_{N-1}=0$
, so (3.40) trivially holds when
$A_{N-1}=0$
, so (3.40) trivially holds when
![]() $j=N-1$
. We now assume that (3.40) holds true if
$j=N-1$
. We now assume that (3.40) holds true if
![]() $j_0+1\le j\le N-1$
for some
$j_0+1\le j\le N-1$
for some
![]() $j_0\le N-2$
. Lemma 3.7, (2.10) and the induction assumption show
$j_0\le N-2$
. Lemma 3.7, (2.10) and the induction assumption show
![]() $\partial ^{\alpha '}_{\tau , \xi } B_{j_0}=O(|(\tau ,\xi )|^{-1-|\alpha '|})$
for
$\partial ^{\alpha '}_{\tau , \xi } B_{j_0}=O(|(\tau ,\xi )|^{-1-|\alpha '|})$
for
![]() $1\le |\alpha '|\le 2d+1$
. Concerning
$1\le |\alpha '|\le 2d+1$
. Concerning
![]() $ D_{j_0}$
, observe that
$ D_{j_0}$
, observe that
![]() $\partial ^{\alpha '}_{\xi } ( G^{(j_0)}(\sigma (\tilde \Xi )))$
is given by a sum of the terms
$\partial ^{\alpha '}_{\xi } ( G^{(j_0)}(\sigma (\tilde \Xi )))$
is given by a sum of the terms
 $$\begin{align*}G^{(j)}(\sigma(\tilde \Xi ))\prod_{n=1}^{j-j_0}\partial^{\alpha^{\prime}_{n}}_{\xi}(\sigma(\tilde \Xi )), \end{align*}$$
$$\begin{align*}G^{(j)}(\sigma(\tilde \Xi ))\prod_{n=1}^{j-j_0}\partial^{\alpha^{\prime}_{n}}_{\xi}(\sigma(\tilde \Xi )), \end{align*}$$
where
![]() $j\ge j_0$
and
$j\ge j_0$
and
![]() $\alpha ^{\prime}_1+\cdots +\alpha ^{\prime}_{j-j_0}=\alpha '$
. Hence, Lemma 3.7, (3.41) and (2.10) give
$\alpha ^{\prime}_1+\cdots +\alpha ^{\prime}_{j-j_0}=\alpha '$
. Hence, Lemma 3.7, (3.41) and (2.10) give
![]() $\partial ^{\alpha '}_{ \xi } D_{j_0} =O(|(\tau ,\xi )|^{-1-|\alpha '|})$
for
$\partial ^{\alpha '}_{ \xi } D_{j_0} =O(|(\tau ,\xi )|^{-1-|\alpha '|})$
for
![]() $1\le |\alpha '|\le 2d+1$
. Therefore, combining the estimates for
$1\le |\alpha '|\le 2d+1$
. Therefore, combining the estimates for
![]() $B_{j_0}$
and
$B_{j_0}$
and
![]() $D_{j_0}$
, we get
$D_{j_0}$
, we get
![]() $\partial ^{\alpha '}_{\tau , \xi } \nabla _{\tau ,\xi }A_{j_0}= O(|(\tau ,\xi )|^{-1-|\alpha '|})$
. This proves (3.40) for
$\partial ^{\alpha '}_{\tau , \xi } \nabla _{\tau ,\xi }A_{j_0}= O(|(\tau ,\xi )|^{-1-|\alpha '|})$
. This proves (3.40) for
![]() $j=j_0$
.
$j=j_0$
.
Before proving (3.39), we first note that
for
![]() $j=1, \dots , N$
. This can be shown by a routine computation. Indeed, differentiating (3.4) and using Lemma 3.7 and (2.32), one can easily see (3.42) holds since
$j=1, \dots , N$
. This can be shown by a routine computation. Indeed, differentiating (3.4) and using Lemma 3.7 and (2.32), one can easily see (3.42) holds since
![]() $|\sigma (\tilde \Xi )-\delta _0\mu |\lesssim \delta _0$
.
$|\sigma (\tilde \Xi )-\delta _0\mu |\lesssim \delta _0$
.
To show (3.39) for
![]() $0\le \ell \le N-2$
, we again use backward induction. Observe that (3.39) holds for
$0\le \ell \le N-2$
, we again use backward induction. Observe that (3.39) holds for
![]() $\ell =N,N-1$
. Then, we assume that (3.39) holds for
$\ell =N,N-1$
. Then, we assume that (3.39) holds for
![]() $j+1\le \ell \le N$
for some
$j+1\le \ell \le N$
for some
![]() $j\le N-2$
. By (3.6), we have
$j\le N-2$
. By (3.6), we have

Thus, by Lemma 3.8 and (3.42), we get (3.39) with
![]() $\ell =j$
. This completes the proof of Lemma 3.2.
$\ell =j$
. This completes the proof of Lemma 3.2.
3.4 Proof of Lemma 3.4
Lemma 3.4 can be shown in the same manner as Lemma 3.2. So, we shall be brief.
By Lemma 3.2, we have
for a constant
![]() $C\ge 1$
, so it suffices to show
$C\ge 1$
, so it suffices to show
for some
![]() $C\ge 1$
. The support condition (2.6) is obvious, so we need only to show (2.7) with
$C\ge 1$
. The support condition (2.6) is obvious, so we need only to show (2.7) with
![]() $\mathfrak a=\mathfrak a_{\nu ,1}^{\mu ,n}$
,
$\mathfrak a=\mathfrak a_{\nu ,1}^{\mu ,n}$
,
, and
. Moreover, by recalling (3.22), it is enough to consider the additional factor only, that is, to show

for
. Since
on
![]() $\operatorname {\mathrm {supp}}_{s,\xi }\mathfrak a_{\nu ,1}^{\mu ,n}$
, one can obtain the estimate in the same way as in the proof of Lemma 3.2.
$\operatorname {\mathrm {supp}}_{s,\xi }\mathfrak a_{\nu ,1}^{\mu ,n}$
, one can obtain the estimate in the same way as in the proof of Lemma 3.2.
3.5 Sharpness of Theorem 1.3
Before closing this section, we show optimality of the regularity exponent
![]() $\alpha $
in Theorem 1.3.
$\alpha $
in Theorem 1.3.
Proposition 3.9. Suppose the estimate (1.4) holds for
![]() $\psi $
satisfying
$\psi $
satisfying
![]() $\psi (0)\neq 0$
. Then
$\psi (0)\neq 0$
. Then
![]() $\alpha \le 2/p$
.
$\alpha \le 2/p$
.
Proof. We write
![]() $\gamma =(\gamma _1, \dots , \gamma _d)$
. Via an affine change of variables, we may assume
$\gamma =(\gamma _1, \dots , \gamma _d)$
. Via an affine change of variables, we may assume
![]() $\gamma _1(0)=0$
and
$\gamma _1(0)=0$
and
![]() $\gamma _1'(s) \neq 0$
on an interval
$\gamma _1'(s) \neq 0$
on an interval
![]() $J=[-\delta _0,\delta _0] $
for
$J=[-\delta _0,\delta _0] $
for
![]() $0<\delta _0\ll 1$
. Since
$0<\delta _0\ll 1$
. Since
![]() $\psi (0)\neq 0$
, we may also assume
$\psi (0)\neq 0$
, we may also assume
![]() $\psi \ge 1$
on J.
$\psi \ge 1$
on J.
We choose
![]() $\zeta _0 \in \mathcal S(\mathbb R)$
such that
$\zeta _0 \in \mathcal S(\mathbb R)$
such that
![]() $\operatorname {\mathrm {supp}} \widehat \zeta _0 \subset [-1,1]$
and
$\operatorname {\mathrm {supp}} \widehat \zeta _0 \subset [-1,1]$
and
![]() $ \zeta _0 \ge 1$
on
$ \zeta _0 \ge 1$
on
![]() $[-r_1,r_1]$
, where
$[-r_1,r_1]$
, where
![]() $r_1=1+2\max \{ |\gamma (s)| : s \in J\}$
. Denoting
$r_1=1+2\max \{ |\gamma (s)| : s \in J\}$
. Denoting
![]() $\bar x = (x_1,\dots ,x_{d-1})$
and
$\bar x = (x_1,\dots ,x_{d-1})$
and
![]() $\bar \gamma (t)=(\gamma _1(t),\dots ,\gamma _{d-1}(t))$
, we define
$\bar \gamma (t)=(\gamma _1(t),\dots ,\gamma _{d-1}(t))$
, we define
Let
![]() $\zeta \in \mathrm C_c^\infty ((-2,2))$
be a positive function such that
$\zeta \in \mathrm C_c^\infty ((-2,2))$
be a positive function such that
![]() $\zeta =1$
on
$\zeta =1$
on
![]() $[-1,1]$
. For a positive constant
$[-1,1]$
. For a positive constant
![]() $c\ll \delta _0$
, let
$c\ll \delta _0$
, let
![]() $g_1(\bar x)=\sum _{\nu \in \lambda ^{-1}\mathbb Z \cap [-c,c]} \zeta (\lambda |\bar x+\bar \gamma (\nu )|)$
. We consider
$g_1(\bar x)=\sum _{\nu \in \lambda ^{-1}\mathbb Z \cap [-c,c]} \zeta (\lambda |\bar x+\bar \gamma (\nu )|)$
. We consider
where
![]() $\varphi (s)= \gamma _d \circ (- \gamma _1)^{-1}(s)$
. We claim that, if c is small enough,
$\varphi (s)= \gamma _d \circ (- \gamma _1)^{-1}(s)$
. We claim that, if c is small enough,
where
![]() $S_c= \{ (x,t): |\bar x| \le c \lambda ^{-1}, \, |x_d| \le c, \, |t-1| \le c \lambda ^{-1}\}$
. To show this, note
$S_c= \{ (x,t): |\bar x| \le c \lambda ^{-1}, \, |x_d| \le c, \, |t-1| \le c \lambda ^{-1}\}$
. To show this, note
Let
![]() $(x,t)\in S_c $
. Then,
$(x,t)\in S_c $
. Then,
![]() $\operatorname {\mathrm {supp}} g_1(\bar x - t \bar \gamma (\cdot )) \subset [-C_1c, C_1c]$
for some
$\operatorname {\mathrm {supp}} g_1(\bar x - t \bar \gamma (\cdot )) \subset [-C_1c, C_1c]$
for some
![]() $C_1>0$
. Since
$C_1>0$
. Since
![]() $\varphi (s)= \gamma _d \circ (- \gamma _1)^{-1}(s)$
, by the mean value theorem we see
$\varphi (s)= \gamma _d \circ (- \gamma _1)^{-1}(s)$
, by the mean value theorem we see
![]() $ |\varphi (x_1-t\gamma _1(s)) -\gamma _d(s)|\le 2r_0c\lambda ^{-1}, $
where
$ |\varphi (x_1-t\gamma _1(s)) -\gamma _d(s)|\le 2r_0c\lambda ^{-1}, $
where
![]() $r_0=10 r_1\max \{ |\partial _s \varphi (s)| : \, s \in (-\gamma _1)(J_\ast )\} $
and
$r_0=10 r_1\max \{ |\partial _s \varphi (s)| : \, s \in (-\gamma _1)(J_\ast )\} $
and
![]() $J_\ast =[-(C_1+1)c, (C_1+1)c]$
. Thus, we have
$J_\ast =[-(C_1+1)c, (C_1+1)c]$
. Thus, we have
Besides, if
![]() $\lambda $
is sufficiently large,
$\lambda $
is sufficiently large,
![]() $ g_1(\bar x-t\bar \gamma (s))=\sum _{\nu \in \lambda ^{-1}\mathbb Z \cap [-c,c]} \zeta (\lambda |\bar x-(t-1) \bar \gamma (s)+\bar \gamma (\nu )-\bar \gamma (s)|) \gtrsim 1 $
if
$ g_1(\bar x-t\bar \gamma (s))=\sum _{\nu \in \lambda ^{-1}\mathbb Z \cap [-c,c]} \zeta (\lambda |\bar x-(t-1) \bar \gamma (s)+\bar \gamma (\nu )-\bar \gamma (s)|) \gtrsim 1 $
if
![]() $s \in [-c/2, c/2]$
. Since
$s \in [-c/2, c/2]$
. Since
![]() $ \operatorname {\mathrm {supp}} g_1(\bar x - t \bar \gamma (\cdot ))\subset J$
with c small enough and
$ \operatorname {\mathrm {supp}} g_1(\bar x - t \bar \gamma (\cdot ))\subset J$
with c small enough and
![]() $\zeta _0 (x_d-t\gamma _d(s))\ge 1$
, we get
$\zeta _0 (x_d-t\gamma _d(s))\ge 1$
, we get
![]() $\int \zeta _0 (x_d-t\gamma _d(s)) g_1(\bar x-t\bar \gamma (s)) \psi (s)\,ds \gtrsim 1. $
Therefore, (3.43) follows by (3.44) if c is small enough, that is,
$\int \zeta _0 (x_d-t\gamma _d(s)) g_1(\bar x-t\bar \gamma (s)) \psi (s)\,ds \gtrsim 1. $
Therefore, (3.43) follows by (3.44) if c is small enough, that is,
![]() $c\ll 1/(3r_0)$
.
$c\ll 1/(3r_0)$
.
We set
![]() $f(x)=e^{-i\lambda x_d} \zeta _0(x_d) g(\bar x).$
Then,
$f(x)=e^{-i\lambda x_d} \zeta _0(x_d) g(\bar x).$
Then,
![]() $ \chi (t) \mathcal A_t f(x)= e^{-i\lambda x_d} \chi (t) \bar {\mathcal A}_t g(x). $
By our choice of
$ \chi (t) \mathcal A_t f(x)= e^{-i\lambda x_d} \chi (t) \bar {\mathcal A}_t g(x). $
By our choice of
![]() $\zeta _0$
,
$\zeta _0$
,
![]() $\operatorname {\mathrm {supp}} \widehat f\subset \{\xi : |\xi _d+\lambda |\le 1\}$
, so
$\operatorname {\mathrm {supp}} \widehat f\subset \{\xi : |\xi _d+\lambda |\le 1\}$
, so
![]() $\operatorname {\mathrm {supp}} \mathcal F(\chi (t)\mathcal A_t f)\subset \{(\tau , \xi ): |\xi _d+\lambda |\le 1\}$
. This gives
$\operatorname {\mathrm {supp}} \mathcal F(\chi (t)\mathcal A_t f)\subset \{(\tau , \xi ): |\xi _d+\lambda |\le 1\}$
. This gives
Indeed,
![]() $ \lambda ^\alpha \| \chi (t) \mathcal A_t f \|_{L^p(\mathbb R^{d+1})} \lesssim \| \chi (t) \mathcal A_t f \|_{L^p( \mathbb R_{t,\bar x}; L_\alpha ^p(\mathbb R_{x_d}))}$
by Mihlin’s multiplier theorem in
$ \lambda ^\alpha \| \chi (t) \mathcal A_t f \|_{L^p(\mathbb R^{d+1})} \lesssim \| \chi (t) \mathcal A_t f \|_{L^p( \mathbb R_{t,\bar x}; L_\alpha ^p(\mathbb R_{x_d}))}$
by Mihlin’s multiplier theorem in
![]() $x_d$
. Similarly, one also sees
$x_d$
. Similarly, one also sees
![]() $ \|F \|_{L^p( \mathbb R_{t,\bar x}; L_\alpha ^p(\mathbb R_{x_d}))} \le C \|F \|_{L_\alpha ^p(\mathbb R^{d+1})} $
for
$ \|F \|_{L^p( \mathbb R_{t,\bar x}; L_\alpha ^p(\mathbb R_{x_d}))} \le C \|F \|_{L_\alpha ^p(\mathbb R^{d+1})} $
for
![]() $\alpha \ge 0$
and any F. Combining those inequalities gives (3.45).
$\alpha \ge 0$
and any F. Combining those inequalities gives (3.45).
From (3.43), we have
![]() $\|\chi (t) \mathcal A_t f\|_p= \| \chi (t) \bar {\mathcal A}_t g \|_{p} \ge C\lambda ^{-d/p}.$
Note that
$\|\chi (t) \mathcal A_t f\|_p= \| \chi (t) \bar {\mathcal A}_t g \|_{p} \ge C\lambda ^{-d/p}.$
Note that
![]() $\operatorname {\mathrm {supp}} g$
is contained in a
$\operatorname {\mathrm {supp}} g$
is contained in a
![]() $O(\lambda ^{-1})$
-neighborhood of
$O(\lambda ^{-1})$
-neighborhood of
![]() $-\bar {\gamma }$
, so it follows that
$-\bar {\gamma }$
, so it follows that
![]() $\|f\|_p \lesssim \lambda ^{-(d-2)/p}$
. Therefore, by (3.45) the inequality (1.4) implies
$\|f\|_p \lesssim \lambda ^{-(d-2)/p}$
. Therefore, by (3.45) the inequality (1.4) implies
![]() $\lambda ^\alpha \lambda ^{-d/p} \lesssim \lambda ^{-(d-2)/p}$
. Taking
$\lambda ^\alpha \lambda ^{-d/p} \lesssim \lambda ^{-(d-2)/p}$
. Taking
![]() $\lambda \to \infty $
gives
$\lambda \to \infty $
gives
![]() $\alpha \le 2/p$
.
$\alpha \le 2/p$
.
4
 $L^p$
Sobolev regularity
$L^p$
Sobolev regularity
In this section, we prove Theorem 1.1, whose proof proceeds in a similar way as that of Theorem 1.3. However, we provide some details to make it clear how the optimal bounds are achieved. There are no t,
![]() $\tau $
variables appearing in the symbols, so the proof is consequently simpler but some modifications are necessary.
$\tau $
variables appearing in the symbols, so the proof is consequently simpler but some modifications are necessary.
For a large
![]() $B\ge 1$
, we assume
$B\ge 1$
, we assume
Let
![]() $2 \le L \le d$
. For
$2 \le L \le d$
. For
![]() $\gamma $
satisfying
$\gamma $
satisfying
![]() $\mathfrak V(L,B)$
, we say
$\mathfrak V(L,B)$
, we say
![]() $ \bar a \in \mathrm C^{d+1}(\mathbb R^{d+1})$
is a symbol of type
$ \bar a \in \mathrm C^{d+1}(\mathbb R^{d+1})$
is a symbol of type
![]() $(k,L, B)$
relative to
$(k,L, B)$
relative to
![]() $\gamma $
if
$\gamma $
if
![]() $ \operatorname {\mathrm {supp}} \bar a \subset I\times \mathbb A_k$
,
$ \operatorname {\mathrm {supp}} \bar a \subset I\times \mathbb A_k$
,
![]() $\mathfrak N(L, B)$
holds for
$\mathfrak N(L, B)$
holds for
![]() $\gamma $
on
$\gamma $
on
![]() $\operatorname {\mathrm {supp}} \bar a$
, and
$\operatorname {\mathrm {supp}} \bar a$
, and
for
![]() $0 \le j \le 1$
and
$0 \le j \le 1$
and
![]() $|\alpha | \le d+1$
. As before, Theorem 1.1 is a straightforward consequence of the following. We denote
$|\alpha | \le d+1$
. As before, Theorem 1.1 is a straightforward consequence of the following. We denote
![]() $\mathcal A[\gamma , \bar a ]=\mathcal A_1[\gamma , \bar a ]$
.
$\mathcal A[\gamma , \bar a ]=\mathcal A_1[\gamma , \bar a ]$
.
Theorem 4.1. Suppose
![]() $\gamma \in \mathrm C^{2d}(I)$
satisfies (4.1) and
$\gamma \in \mathrm C^{2d}(I)$
satisfies (4.1) and
![]() $\mathfrak V(L,B)$
for some
$\mathfrak V(L,B)$
for some
![]() $B\ge 1$
. Suppose
$B\ge 1$
. Suppose
![]() $ \bar a $
is a symbol of type
$ \bar a $
is a symbol of type
![]() $(k,L,B)$
relative to
$(k,L,B)$
relative to
![]() $\gamma $
for some
$\gamma $
for some
![]() $B\ge 1$
. Then, if
$B\ge 1$
. Then, if
![]() $p> 2(L-1)$
, for a constant
$p> 2(L-1)$
, for a constant
![]() $C=C(B)$
$C=C(B)$
In order to prove Theorem 1.1, we consider
![]() $ \bar a_k (s,\xi ):=\psi (s)\beta (2^{-k}|\xi |)$
, where
$ \bar a_k (s,\xi ):=\psi (s)\beta (2^{-k}|\xi |)$
, where
![]() $\beta \in \mathrm C_c^\infty ((1/2,4))$
. By the condition (1.1),
$\beta \in \mathrm C_c^\infty ((1/2,4))$
. By the condition (1.1),
![]() $ \bar a_k $
is a symbol of type
$ \bar a_k $
is a symbol of type
![]() $(k,d, B)$
relative to
$(k,d, B)$
relative to
![]() $\gamma $
for some B, thus Theorem 4.1 gives (4.3) for
$\gamma $
for some B, thus Theorem 4.1 gives (4.3) for
![]() $p> 2(d-1)$
. The estimate (4.3) for each dyadic pieces can be put together by the result in [Reference Pramanik, Rogers and Seeger22]. So, we get the estimate (1.2) for
$p> 2(d-1)$
. The estimate (4.3) for each dyadic pieces can be put together by the result in [Reference Pramanik, Rogers and Seeger22]. So, we get the estimate (1.2) for
![]() $\alpha =\alpha (p)$
if
$\alpha =\alpha (p)$
if
![]() $p> 2(d-1)$
(e.g., see [Reference Beltran, Guo, Hickman and Seeger2]).
$p> 2(d-1)$
(e.g., see [Reference Beltran, Guo, Hickman and Seeger2]).
Interpolation with
![]() $\| \mathcal A[\gamma , \bar a _k ] f\|_{2} \lesssim 2^{-k/d} \|f\|_{2}$
which follows from (1.3) gives
$\| \mathcal A[\gamma , \bar a _k ] f\|_{2} \lesssim 2^{-k/d} \|f\|_{2}$
which follows from (1.3) gives
![]() $\| \mathcal A[\gamma ,\bar a _k ] f\|_{p} \lesssim _B\! 2^{-\alpha k } \|f\|_{p}$
for
$\| \mathcal A[\gamma ,\bar a _k ] f\|_{p} \lesssim _B\! 2^{-\alpha k } \|f\|_{p}$
for
![]() $\alpha \le \alpha (p)$
with strict inequality when
$\alpha \le \alpha (p)$
with strict inequality when
![]() $p\in (2, 2(d-1)]$
. Using those estimates, we can prove Corollary 1.2. Indeed, if
$p\in (2, 2(d-1)]$
. Using those estimates, we can prove Corollary 1.2. Indeed, if
![]() $\gamma $
is a curve of maximal type
$\gamma $
is a curve of maximal type
![]() $\ell>d$
, a typical anisotropic scaling argument gives
$\ell>d$
, a typical anisotropic scaling argument gives
![]() $\| \mathcal A[\gamma ,\bar a _k ] f\|_{p} \lesssim _B\! 2^{-\min (\alpha (p), 1/\ell )k } \|f\|_{p}$
for
$\| \mathcal A[\gamma ,\bar a _k ] f\|_{p} \lesssim _B\! 2^{-\min (\alpha (p), 1/\ell )k } \|f\|_{p}$
for
![]() $p\neq \ell $
when
$p\neq \ell $
when
![]() $ \ell \ge 2d-2$
, and for
$ \ell \ge 2d-2$
, and for
![]() $p\in [2, 2\ell /(2d-\ell ))\cup ( 2d-2, \infty )$
when
$p\in [2, 2\ell /(2d-\ell ))\cup ( 2d-2, \infty )$
when
![]() $d< \ell < 2d-2$
. As in the above, one can combine those estimates to get the estimate (1.2) ([Reference Pramanik, Rogers and Seeger22]).
$d< \ell < 2d-2$
. As in the above, one can combine those estimates to get the estimate (1.2) ([Reference Pramanik, Rogers and Seeger22]).
4.1 Proof of Theorem 4.1
The case
![]() $L=2$
is easy. Since
$L=2$
is easy. Since
![]() $ \bar a $
is a symbol of type
$ \bar a $
is a symbol of type
![]() $(k,2,B)$
relative to
$(k,2,B)$
relative to
![]() $\gamma $
, van der Corput’s lemma and Plancherel’s theorem give (4.3) for
$\gamma $
, van der Corput’s lemma and Plancherel’s theorem give (4.3) for
![]() $p=2$
. Interpolation with the
$p=2$
. Interpolation with the
![]() $L^\infty $
estimate shows (4.3) for
$L^\infty $
estimate shows (4.3) for
![]() $p\ge 2$
. When
$p\ge 2$
. When
![]() $L\ge 3$
, we have the following, which immediately yields Theorem 4.1.
$L\ge 3$
, we have the following, which immediately yields Theorem 4.1.
Proposition 4.2. Let
![]() $3 \le N \le d$
. Suppose Theorem 4.1 holds for
$3 \le N \le d$
. Suppose Theorem 4.1 holds for
![]() $L=N-1$
. Then, Theorem 4.1 holds true with
$L=N-1$
. Then, Theorem 4.1 holds true with
![]() $L=N$
.
$L=N$
.
To prove the proposition, we fix
![]() $N\in [3, d]$
and
$N\in [3, d]$
and
![]() $\gamma $
satisfying
$\gamma $
satisfying
![]() ${\mathfrak V(N, B)}$
, and
${\mathfrak V(N, B)}$
, and
![]() $\bar a$
of type
$\bar a$
of type
![]() $(k, N, B)$
relative to
$(k, N, B)$
relative to
![]() $\gamma $
. For
$\gamma $
. For
and
![]() $\delta>0$
such that
$\delta>0$
such that
, let

By
we denote the collection of
![]() $ \bar {\mathfrak a} \in \mathrm C^{d+1}(\mathbb R^{d+1}) $
satisfying
$ \bar {\mathfrak a} \in \mathrm C^{d+1}(\mathbb R^{d+1}) $
satisfying
and
for
![]() $0 \le j \le 1$
,
$0 \le j \le 1$
,
![]() $|\alpha | \le d+1$
.
$|\alpha | \le d+1$
.
The next lemma which plays the same role as Lemma 2.8 can be shown by routinely following the proof of Lemma 2.8.
Lemma 4.3. Let
and
![]() $j_\ast =\log (2^k \delta ^N)$
. Suppose (2.20) holds on
$j_\ast =\log (2^k \delta ^N)$
. Suppose (2.20) holds on
![]() $\operatorname {\mathrm {supp}} \bar {\mathfrak a}$
. Then, there exist constants
$\operatorname {\mathrm {supp}} \bar {\mathfrak a}$
. Then, there exist constants
![]() $C, l_\ast $
,
$C, l_\ast $
,
![]() $\tilde B\ge 1$
, and
$\tilde B\ge 1$
, and
![]() $\delta '>0$
depending on B, and symbols
$\delta '>0$
depending on B, and symbols
![]() $\bar {\mathfrak a}_{1}, \dots , \bar {\mathfrak a}_{l_\ast }$
of type
$\bar {\mathfrak a}_{1}, \dots , \bar {\mathfrak a}_{l_\ast }$
of type
![]() $(j, N-1, \tilde B)$
relative to
$(j, N-1, \tilde B)$
relative to
such that
![]() $ \|\tilde f_l\|_p= \|f\|_p$
, and
$ \|\tilde f_l\|_p= \|f\|_p$
, and
![]() $j\in [j_\ast -C, j_\ast +C]$
as long as
$j\in [j_\ast -C, j_\ast +C]$
as long as
![]() $0<\delta <\delta '$
.
$0<\delta <\delta '$
.
The required regularity order for
![]() $\gamma $
is reduced thanks to the fact that
$\gamma $
is reduced thanks to the fact that
![]() $\bar {\mathfrak a}$
is independent of
$\bar {\mathfrak a}$
is independent of
![]() $\tau , t$
. Actually, one may take
$\tau , t$
. Actually, one may take
![]() when following the Proof of Lemma 2.8, since (4.2) clearly holds for
when following the Proof of Lemma 2.8, since (4.2) clearly holds for
![]() $\bar a=\tilde a$
.
$\bar a=\tilde a$
.
Using
![]() $\eta _N$
(see (2.27)), we break
$\eta _N$
(see (2.27)), we break
Note that
![]() $C^{-1} \bar a(1-\eta _N)$
is of type
$C^{-1} \bar a(1-\eta _N)$
is of type
![]() $(k, N-1, B')$
relative to
$(k, N-1, B')$
relative to
![]() $\gamma $
for some large constants
$\gamma $
for some large constants
![]() $B'$
and C, so we may apply the assumption to
$B'$
and C, so we may apply the assumption to
![]() $\mathcal A[\gamma , \bar a(1-\eta _N)]f$
. Consequently, we have the estimate (4.3) for
$\mathcal A[\gamma , \bar a(1-\eta _N)]f$
. Consequently, we have the estimate (4.3) for
![]() $\bar a=\bar a(1-\eta _N)$
if
$\bar a=\bar a(1-\eta _N)$
if
![]() $ p> 2N-4$
.
$ p> 2N-4$
.
To handle
![]() $\mathcal A[\gamma , \bar a\eta _N]$
, as before, we may assume that
$\mathcal A[\gamma , \bar a\eta _N]$
, as before, we may assume that
![]() for some
for some
![]() and a small
and a small
![]() $\delta _\ast $
. Here,
$\delta _\ast $
. Here,
![]() $\bar \Gamma _k$
is defined in the same way as
$\bar \Gamma _k$
is defined in the same way as
![]() $\Gamma _k$
by replacing
$\Gamma _k$
by replacing
![]() $a\eta _N$
by
$a\eta _N$
by
![]() $\bar a\eta _N$
(see Section 2.3). Since (2.28) holds on
$\bar a\eta _N$
(see Section 2.3). Since (2.28) holds on
![]() $\operatorname {\mathrm {supp}} (\bar a\eta _N)$
, we may work under the same
Basic assumption
as in Section 2.3. That is to say, we have
$\operatorname {\mathrm {supp}} (\bar a\eta _N)$
, we may work under the same
Basic assumption
as in Section 2.3. That is to say, we have
![]() $\sigma $
on
$\sigma $
on
![]() $\bar \Gamma _k$
satisfying (2.29) and
$\bar \Gamma _k$
satisfying (2.29) and
![]() for
for
![]() $\xi \in \bar \Gamma _k$
. Moreover,
$\xi \in \bar \Gamma _k$
. Moreover,
![]() $\sigma \in \mathrm C^{d+1}$
since
$\sigma \in \mathrm C^{d+1}$
since
![]() $\gamma \in \mathrm C^{2d}(I)$
, and (2.30) holds for
$\gamma \in \mathrm C^{2d}(I)$
, and (2.30) holds for
![]() $\xi \in \bar \Gamma _k$
and
$\xi \in \bar \Gamma _k$
and
![]() $|\alpha |\le d+1$
. Thus, (4.2) remains valid for the symbols to be given by decomposing
$|\alpha |\le d+1$
. Thus, (4.2) remains valid for the symbols to be given by decomposing
![]() $\bar a$
with cutoff functions associated with
$\bar a$
with cutoff functions associated with
![]() $\sigma $
and
$\sigma $
and
![]() $\bar {\mathfrak G}_N^{\mu }.$
$\bar {\mathfrak G}_N^{\mu }.$
Apparently,
![]() for a constant
for a constant
![]() $C=C(B, \delta _\ast )$
. Therefore, the proof of Proposition 4.2 is completed if we show the following.
$C=C(B, \delta _\ast )$
. Therefore, the proof of Proposition 4.2 is completed if we show the following.
Proposition 4.4. Let
![]() $3 \le N \le d$
and
$3 \le N \le d$
and
![]() with
with
![]() $ \operatorname {\mathrm {supp}}_\xi \bar {\mathfrak a}\subset \bar \Gamma _k$
. Suppose Theorem 4.1 holds for
$ \operatorname {\mathrm {supp}}_\xi \bar {\mathfrak a}\subset \bar \Gamma _k$
. Suppose Theorem 4.1 holds for
![]() $L=N-1$
. Then, if
$L=N-1$
. Then, if
![]() $p> 2(N-1)$
, we have the estimate (4.3).
$p> 2(N-1)$
, we have the estimate (4.3).
We prove Proposition 4.4 using the next, which corresponds to Proposition 2.10. In what follows, we denote
![]() $\mathcal A[\bar {\mathfrak a}]=\mathcal A[\gamma , \bar {\mathfrak a}]$
.
$\mathcal A[\bar {\mathfrak a}]=\mathcal A[\gamma , \bar {\mathfrak a}]$
.
Proposition 4.5. Let
![]() $\delta _0$
and
$\delta _0$
and
![]() $\delta _1$
satisfy (2.31). For
$\delta _1$
satisfy (2.31). For
![]() $\mu $
such that
$\mu $
such that
![]() , let
, let
![]() $ \bar {\mathfrak a}^\mu \in \bar {\mathfrak A}_k(\delta _0\mu , \delta _0)$
with
$ \bar {\mathfrak a}^\mu \in \bar {\mathfrak A}_k(\delta _0\mu , \delta _0)$
with
![]() . Suppose Theorem 4.1 holds for
. Suppose Theorem 4.1 holds for
![]() $L=N-1$
. Then, if
$L=N-1$
. Then, if
![]() $p\in (2N-2, \infty )$
, there are constants
$p\in (2N-2, \infty )$
, there are constants
![]() $\epsilon _0>0$
,
$\epsilon _0>0$
,
![]() $C_0=C_0(\epsilon _0, B)\ge 2$
, and symbols
$C_0=C_0(\epsilon _0, B)\ge 2$
, and symbols
![]() $ \bar {\mathfrak a}_\nu \in \bar {\mathfrak A}_k( \delta _1\nu ,\delta _1)$
with
$ \bar {\mathfrak a}_\nu \in \bar {\mathfrak A}_k( \delta _1\nu ,\delta _1)$
with
![]() ,
,
![]() $\nu \in \cup _\mu \mathfrak J_0^\mu $
such that
$\nu \in \cup _\mu \mathfrak J_0^\mu $
such that
 $$ \begin{align*} \left(\sum_\mu \| \mathcal A[\bar{\mathfrak a} ^\mu] f \|_{p}^p \right)^{\frac1p} \le C_0 \big({\delta_1} / {\delta_0}\big)^{\frac Np-1+\epsilon_0} \left(\sum_{\nu} \| \mathcal A[\bar{\mathfrak a} _\nu]f \|_{p}^p \right)^{\frac1p} +C_0 \delta_0^{-\frac Np+1} 2^{-\frac kp}\|f\|_p. \end{align*} $$
$$ \begin{align*} \left(\sum_\mu \| \mathcal A[\bar{\mathfrak a} ^\mu] f \|_{p}^p \right)^{\frac1p} \le C_0 \big({\delta_1} / {\delta_0}\big)^{\frac Np-1+\epsilon_0} \left(\sum_{\nu} \| \mathcal A[\bar{\mathfrak a} _\nu]f \|_{p}^p \right)^{\frac1p} +C_0 \delta_0^{-\frac Np+1} 2^{-\frac kp}\|f\|_p. \end{align*} $$
Let
![]() $\delta '$
be the number given in Lemma 4.3. We choose a positive constant
$\delta '$
be the number given in Lemma 4.3. We choose a positive constant
![]() $\delta _\circ $
(cf. (2.26)) such that
$\delta _\circ $
(cf. (2.26)) such that
Proof of Proposition 4.4.
Set
![]() $\delta _0=\delta _\circ $
, and let
$\delta _0=\delta _\circ $
, and let
![]() $\delta _1,\dots , \delta _J$
be given by (2.33). Then, applying Proposition 4.5 iteratively up to J-th step (cf. Section 2.4), we have symbols
$\delta _1,\dots , \delta _J$
be given by (2.33). Then, applying Proposition 4.5 iteratively up to J-th step (cf. Section 2.4), we have symbols
![]() $ \bar {\mathfrak a}_\nu \in \bar {\mathfrak A}_k( \delta _{\!J}\nu , \delta _{\!J})$
,
$ \bar {\mathfrak a}_\nu \in \bar {\mathfrak A}_k( \delta _{\!J}\nu , \delta _{\!J})$
,
![]() , such that
, such that
 $$\begin{align*}\big\| \mathcal A[\bar{\mathfrak a} ]f \big\|_{p} \le C_0^J\delta_{\!J}^{\frac {N}{p}-1+\epsilon_0} \left(\sum_\nu \| \mathcal A[\bar{\mathfrak a} _{\nu}]f\|_p^p \right)^{1/p} \!+ 2^{-\frac{k}p} \delta_0^{-\frac Np+1-\epsilon_0}\! \sum_{0\le j\le J-1}C_0^{j+1} \delta_j^{\epsilon_0} \|f\|_p. \end{align*}$$
$$\begin{align*}\big\| \mathcal A[\bar{\mathfrak a} ]f \big\|_{p} \le C_0^J\delta_{\!J}^{\frac {N}{p}-1+\epsilon_0} \left(\sum_\nu \| \mathcal A[\bar{\mathfrak a} _{\nu}]f\|_p^p \right)^{1/p} \!+ 2^{-\frac{k}p} \delta_0^{-\frac Np+1-\epsilon_0}\! \sum_{0\le j\le J-1}C_0^{j+1} \delta_j^{\epsilon_0} \|f\|_p. \end{align*}$$
By (4.4) and (2.33),
![]() $ \delta _j \le C_0^{-2((N+1)/N)^jN/{\epsilon _0} }$
for
$ \delta _j \le C_0^{-2((N+1)/N)^jN/{\epsilon _0} }$
for
![]() $0 \le j \le J-1.$
So,
$0 \le j \le J-1.$
So,
![]() $\sum _{j=0}^{J-1} C_0^{j+1} \delta _j^{\epsilon _0} \le C_1$
for a constant
$\sum _{j=0}^{J-1} C_0^{j+1} \delta _j^{\epsilon _0} \le C_1$
for a constant
![]() $C_1$
, and
$C_1$
, and
![]() $C_0^J\delta _J^{\epsilon _0} \le C_1$
. Thus, the matter is now reduced to showing
$C_0^J\delta _J^{\epsilon _0} \le C_1$
. Thus, the matter is now reduced to showing
 $$\begin{align*}\left(\sum_{\nu} \| \mathcal A[\bar{\mathfrak a}_\nu] f\|_{L^p(\mathbb R^d)}^p \right)^{1/p} \lesssim_B\! 2^{-\frac kN}\|f\|_{L^p(\mathbb R^d)}, \qquad 2\le p\le \infty, \end{align*}$$
$$\begin{align*}\left(\sum_{\nu} \| \mathcal A[\bar{\mathfrak a}_\nu] f\|_{L^p(\mathbb R^d)}^p \right)^{1/p} \lesssim_B\! 2^{-\frac kN}\|f\|_{L^p(\mathbb R^d)}, \qquad 2\le p\le \infty, \end{align*}$$
which corresponds to the estimate (2.35). The case
![]() $p=\infty $
follows from the estimate
$p=\infty $
follows from the estimate
![]() $\| \mathcal A[\bar {\mathfrak a} ]f\|_{L^\infty } \le C\delta \|f\|_{L^\infty }$
when
$\| \mathcal A[\bar {\mathfrak a} ]f\|_{L^\infty } \le C\delta \|f\|_{L^\infty }$
when
![]() for some
for some
![]() (cf. (2.15)). One can obtain this in the same manner as in the proof of Lemma 2.7. The case
(cf. (2.15)). One can obtain this in the same manner as in the proof of Lemma 2.7. The case
![]() $p=2$
can be handled similarly as before, using Plancherel’s theorem and van der Corput’s lemma combined with Lemma 2.11 and (2.28).
$p=2$
can be handled similarly as before, using Plancherel’s theorem and van der Corput’s lemma combined with Lemma 2.11 and (2.28).
The proof of Proposition 4.5 is similar to that of Proposition 2.10. Instead of (2.40), we use the estimate (2.41), in which the exponent is adjusted to the sharp Sobolev regularity estimate. However, a similar approach breaks down if one tries to obtain the local smoothing estimate (1.4) with the optimal regularity
![]() $\alpha =2/p$
. To do so, we need the inequality (2.39) for
$\alpha =2/p$
. To do so, we need the inequality (2.39) for
![]() $4N-2<p \le N(N+1)$
. However, there is no such estimate available when
$4N-2<p \le N(N+1)$
. However, there is no such estimate available when
![]() $N=2$
.
$N=2$
.
4.2 Proof of Proposition 4.5
Let
![]() $ \bar {\mathfrak a}^\mu \in \bar {\mathfrak A}_k(\delta _0\mu ,\delta _0)$
. For
$ \bar {\mathfrak a}^\mu \in \bar {\mathfrak A}_k(\delta _0\mu ,\delta _0)$
. For
![]() $\nu \in \mathfrak J_n^\mu $
, set
$\nu \in \mathfrak J_n^\mu $
, set
 $$\begin{align*}\bar{\mathfrak a}_{\nu}^{\mu,n} = \bar{\mathfrak a}^\mu \times \begin{cases} \beta_0 \big( \delta_1^{-2N!} \, \bar{\mathfrak G}_N^{\mu} \big) \, \zeta(\delta_1^{-1}s-\nu), & \ n=0, \\[2pt] \beta_N \big( (2^{n}\delta_1)^{-2N!} \, \bar{\mathfrak G}_N^{\mu} \big) \, \zeta(2^{-n}\delta_1^{-1}s-\nu), & \ n\ge 1. \end{cases} \end{align*}$$
$$\begin{align*}\bar{\mathfrak a}_{\nu}^{\mu,n} = \bar{\mathfrak a}^\mu \times \begin{cases} \beta_0 \big( \delta_1^{-2N!} \, \bar{\mathfrak G}_N^{\mu} \big) \, \zeta(\delta_1^{-1}s-\nu), & \ n=0, \\[2pt] \beta_N \big( (2^{n}\delta_1)^{-2N!} \, \bar{\mathfrak G}_N^{\mu} \big) \, \zeta(2^{-n}\delta_1^{-1}s-\nu), & \ n\ge 1. \end{cases} \end{align*}$$
(See (3.21)). Let
![]() $\bar {\mathbf y}_\mu = (y_\mu ^1,\dots ,y^{N}_\mu )$
, and let
$\bar {\mathbf y}_\mu = (y_\mu ^1,\dots ,y^{N}_\mu )$
, and let
![]() $\bar {\mathcal D}_\delta $
denote the
$\bar {\mathcal D}_\delta $
denote the
![]() $N\times N$
matrix
$N\times N$
matrix
![]() $(\delta ^{1-N} \bar e_1, \delta ^{2-N} \bar e_2, \dots , \delta ^0 \bar e_{N})$
where
$(\delta ^{1-N} \bar e_1, \delta ^{2-N} \bar e_2, \dots , \delta ^0 \bar e_{N})$
where
![]() $\bar e_j$
is the j-th standard unit vector in
$\bar e_j$
is the j-th standard unit vector in
![]() $\mathbb R^{N}$
. Recalling (3.18), we consider a linear map
$\mathbb R^{N}$
. Recalling (3.18), we consider a linear map
Let
![]() $\mathbf r$
denote the curve
$\mathbf r$
denote the curve
![]() $\mathbf r_\circ ^N$
. Note that (3.10) and (3.11) hold on
$\mathbf r_\circ ^N$
. Note that (3.10) and (3.11) hold on
![]() $\operatorname {\mathrm {supp}} \bar {\mathfrak a}_{\nu }^{\mu ,n}$
. Similarly as in Proof of Lemma 3.3
, we see
$\operatorname {\mathrm {supp}} \bar {\mathfrak a}_{\nu }^{\mu ,n}$
. Similarly as in Proof of Lemma 3.3
, we see
![]() $ | \langle \bar {\mathbf y}_\mu , \mathbf r^{(j)}((2^n\delta _1/\delta _0)\nu -\mu ) \rangle | \lesssim 2^k (2^{n}\delta _1/\delta _0)^{N-j} $
for
$ | \langle \bar {\mathbf y}_\mu , \mathbf r^{(j)}((2^n\delta _1/\delta _0)\nu -\mu ) \rangle | \lesssim 2^k (2^{n}\delta _1/\delta _0)^{N-j} $
for
![]() $1 \le j \le N-1$
and
$1 \le j \le N-1$
and
![]() $2^{k-2}/B \le \big |\big \langle \bar {\mathbf y}_\mu , \mathbf r^{(N)} \big \rangle \big |\le CB 2^k$
on
$2^{k-2}/B \le \big |\big \langle \bar {\mathbf y}_\mu , \mathbf r^{(N)} \big \rangle \big |\le CB 2^k$
on
![]() $\operatorname {\mathrm {supp}}_\xi \bar {\mathfrak a}_{\nu }^{\mu ,n}$
. Thus, as before (cf. (3.19)), we have
$\operatorname {\mathrm {supp}}_\xi \bar {\mathfrak a}_{\nu }^{\mu ,n}$
. Thus, as before (cf. (3.19)), we have
for some
![]() $C>0$
. Note
$C>0$
. Note
![]() $\operatorname {\mathrm {supp}} \mathcal F( \mathcal A[\bar {\mathfrak a} _{\nu }^{\mu ,n}]f)\subset \operatorname {\mathrm {supp}}_{\xi } \bar {\mathfrak a}_{\nu }^{\mu ,n}$
. Therefore, using the change of variables
$\operatorname {\mathrm {supp}} \mathcal F( \mathcal A[\bar {\mathfrak a} _{\nu }^{\mu ,n}]f)\subset \operatorname {\mathrm {supp}}_{\xi } \bar {\mathfrak a}_{\nu }^{\mu ,n}$
. Therefore, using the change of variables
![]() $\xi \to \bar {\mathrm Y}_\mu ^{\delta _0} (\xi )$
, (2.41) with N replaced by
$\xi \to \bar {\mathrm Y}_\mu ^{\delta _0} (\xi )$
, (2.41) with N replaced by
![]() $N-1$
and its cylindrical extension (e.g., (2.42)), we get
$N-1$
and its cylindrical extension (e.g., (2.42)), we get
 $$ \begin{align} \big\| \sum_{\nu\in \mathfrak J_{n}^\mu} \mathcal A[\bar{\mathfrak a}_{\nu}^{\mu,n}]f \big\|_p \le C_0 \big( {2^n\delta_1} /{\delta_0}\big)^{\frac {N} {p}-1+\epsilon_0} \left(\sum_{\nu\in \mathfrak J_{n}^\mu} \big\|\mathcal A[\bar{\mathfrak a} _{\nu}^{\mu,n}]f \big\|_p^p\right)^{1/p} \end{align} $$
$$ \begin{align} \big\| \sum_{\nu\in \mathfrak J_{n}^\mu} \mathcal A[\bar{\mathfrak a}_{\nu}^{\mu,n}]f \big\|_p \le C_0 \big( {2^n\delta_1} /{\delta_0}\big)^{\frac {N} {p}-1+\epsilon_0} \left(\sum_{\nu\in \mathfrak J_{n}^\mu} \big\|\mathcal A[\bar{\mathfrak a} _{\nu}^{\mu,n}]f \big\|_p^p\right)^{1/p} \end{align} $$
for
![]() $2N-2<p <\infty $
(cf. (3.15)). Since
$2N-2<p <\infty $
(cf. (3.15)). Since
![]() $\mathcal A [\bar {\mathfrak a}^\mu ]f=\sum _n \sum _{\nu \in \mathfrak J_n^\mu } \mathcal A[\bar {\mathfrak a}_{\nu }^{\mu ,n}]f$
, by Minkowski’s inequality and (4.5), we have
$\mathcal A [\bar {\mathfrak a}^\mu ]f=\sum _n \sum _{\nu \in \mathfrak J_n^\mu } \mathcal A[\bar {\mathfrak a}_{\nu }^{\mu ,n}]f$
, by Minkowski’s inequality and (4.5), we have
![]() $(\sum _\mu \| \mathcal A[\bar {\mathfrak a} ^\mu ]f\|_p^p\,)^{1/p}$
bounded by
$(\sum _\mu \| \mathcal A[\bar {\mathfrak a} ^\mu ]f\|_p^p\,)^{1/p}$
bounded by
 $$ \begin{align*} \begin{aligned} \sum_{n\ge 0} \bar {\mathbf E}_n:= C_0 \sum_{n\ge 0} \big( {2^n\delta_1}/{\delta_0} \big)^{{\frac {N} {p}-1+\epsilon_0}} \left(\sum_{\mu} \sum_{\nu\in \mathfrak J_n^\mu} \| \mathcal A[\bar{\mathfrak a} ^{\mu,n}_{\nu}]f\|_p^p\right)^{1/p}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \sum_{n\ge 0} \bar {\mathbf E}_n:= C_0 \sum_{n\ge 0} \big( {2^n\delta_1}/{\delta_0} \big)^{{\frac {N} {p}-1+\epsilon_0}} \left(\sum_{\mu} \sum_{\nu\in \mathfrak J_n^\mu} \| \mathcal A[\bar{\mathfrak a} ^{\mu,n}_{\nu}]f\|_p^p\right)^{1/p}. \end{aligned} \end{align*} $$
The proof of Lemma 3.2 also shows
![]() $C^{-1} \bar {\mathfrak a}_{\nu }^{\mu ,n}\in \bar {\mathfrak A}_k(2^n\delta _1\nu , 2^n\delta _1)$
for a positive constant C. The matter is reduced to obtaining
$C^{-1} \bar {\mathfrak a}_{\nu }^{\mu ,n}\in \bar {\mathfrak A}_k(2^n\delta _1\nu , 2^n\delta _1)$
for a positive constant C. The matter is reduced to obtaining
 $$ \begin{align} \left(\sum_{\mu} \sum_{\nu \in \mathfrak J_n^\mu} \|\mathcal A[\bar{\mathfrak a}_{\nu}^{\mu,n}] f\|_{L^p(\mathbb R^d)}^p \right)^{1/p} \lesssim_B\! (2^n\delta_1)^{1-\frac Np} 2^{-\frac kp} \|f\|_{L^p(\mathbb R^d)}, \qquad n\ge 1 \end{align} $$
$$ \begin{align} \left(\sum_{\mu} \sum_{\nu \in \mathfrak J_n^\mu} \|\mathcal A[\bar{\mathfrak a}_{\nu}^{\mu,n}] f\|_{L^p(\mathbb R^d)}^p \right)^{1/p} \lesssim_B\! (2^n\delta_1)^{1-\frac Np} 2^{-\frac kp} \|f\|_{L^p(\mathbb R^d)}, \qquad n\ge 1 \end{align} $$
for
![]() $p>2(N-2)$
. This gives
$p>2(N-2)$
. This gives
![]() $\sum _{n\ge 1} \bar {\mathbf E}_n \lesssim _B\! \delta _0^{-N/p+1} 2^{-k/p}\|f\|_p$
since
$\sum _{n\ge 1} \bar {\mathbf E}_n \lesssim _B\! \delta _0^{-N/p+1} 2^{-k/p}\|f\|_p$
since
![]() $2^n\delta _1\le C\delta _0$
.
$2^n\delta _1\le C\delta _0$
.
The proof of (4.6) is similar with that of (3.23). Since
![]() $C^{-1} \bar {\mathfrak a}_{\nu }^{\mu ,n}\in \bar {\mathfrak A}_k(2^n\delta _1\nu , 2^n\delta _1)$
, we have
$C^{-1} \bar {\mathfrak a}_{\nu }^{\mu ,n}\in \bar {\mathfrak A}_k(2^n\delta _1\nu , 2^n\delta _1)$
, we have
![]() $\mathcal A[\bar {\mathfrak a} ^{\mu , n}_{\nu }]f= \mathcal A[\bar {\mathfrak a} ^{\mu , n}_{\nu }] P_{2^n\delta _1\nu }^{2^n\delta _1} f $
. Besides, (3.27) or (3.28) for some
$\mathcal A[\bar {\mathfrak a} ^{\mu , n}_{\nu }]f= \mathcal A[\bar {\mathfrak a} ^{\mu , n}_{\nu }] P_{2^n\delta _1\nu }^{2^n\delta _1} f $
. Besides, (3.27) or (3.28) for some
![]() $1\le j\le N-2$
holds on
$1\le j\le N-2$
holds on
![]() $\operatorname {\mathrm {supp}} \bar {\mathfrak a}_{\nu }^{\mu ,n}$
. Thus, we have (2.20) with
$\operatorname {\mathrm {supp}} \bar {\mathfrak a}_{\nu }^{\mu ,n}$
. Thus, we have (2.20) with
![]() $\delta =2^n\delta _1$
for some
$\delta =2^n\delta _1$
for some
![]() $B'$
on
$B'$
on
![]() $\operatorname {\mathrm {supp}} \bar {\mathfrak a}_{\nu }^{\mu ,n}$
for
$\operatorname {\mathrm {supp}} \bar {\mathfrak a}_{\nu }^{\mu ,n}$
for
![]() $n\ge 1$
(see Proof of Lemma 3.5
). Therefore, applying Lemma 4.3 to
$n\ge 1$
(see Proof of Lemma 3.5
). Therefore, applying Lemma 4.3 to
![]() $\mathcal A[\bar {\mathfrak a}_{\nu }^{\mu ,n}] f$
and then the assumption (Theorem 4.1 with
$\mathcal A[\bar {\mathfrak a}_{\nu }^{\mu ,n}] f$
and then the assumption (Theorem 4.1 with
![]() $L=N-1$
), we obtain
$L=N-1$
), we obtain
Acknowledgments
This research was supported by the National Research Foundation of Korea (grant 2022R1A4A1018904). We would like to thank N. Bez, A. Seeger and J. Wright for their valuable comments.
Conflict of Interest
The authors have no conflict of interest to declare.