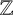1. Introduction
The aim of the present paper is to explain how the number of spanning trees in a
![]() $\mathbb {Z}$
-cover of finite graphs evolves, by providing an explicit recipe to compute the invariants that describe this evolution in terms of a polynomial that can be associated to the cover in question.
$\mathbb {Z}$
-cover of finite graphs evolves, by providing an explicit recipe to compute the invariants that describe this evolution in terms of a polynomial that can be associated to the cover in question.
1.1. Historical remarks
Before describing in detail the main results of this paper, let us provide an overview of the main questions that motivated the present paper.
Iwasawa theory is concerned with the study of the evolution of certain invariants within a tower of objects (see [Reference Greenberg and Miyake18] for a comprehensive survey). The first example of this is provided by the evolution, as
![]() $n \to +\infty $
, of the group of
$n \to +\infty $
, of the group of
![]() $\mathbb {F}_n$
-rational points of the Jacobian of a curve defined over a finite field
$\mathbb {F}_n$
-rational points of the Jacobian of a curve defined over a finite field
![]() $\mathbb {F}$
, where
$\mathbb {F}$
, where
![]() $\mathbb {F}_n \supseteq \mathbb {F}$
is the unique extension (up to isomorphism) of
$\mathbb {F}_n \supseteq \mathbb {F}$
is the unique extension (up to isomorphism) of
![]() $\mathbb {F}$
having degree n. This example was studied by Weil and led him to formulate his celebrated conjectures concerning the properties of the zeta functions associated to varieties defined over a finite field. Iwasawa pursued analogous investigations concerning the evolution of class groups of number fields in a tower of cyclotomic extensions, which are akin to the extensions of a function field that are obtained by increasing the field of constants, as explained in [Reference Rosen47, page 188]. This initiated a large series of works that study the evolution of different invariants along a tower of number fields whose Galois group is a p-adic Lie group (see [Reference Kakde, Pop, Coates, Kim, Saïdi and Schneider25] for a survey). Moreover, Iwasawa theory has been extended to the study of the evolution of invariants of many different arithmetic objects, such as elliptic curves or even general motives (see [Reference Fukaya and Kato14] for one of the most general frameworks available at present).
$\mathbb {F}$
having degree n. This example was studied by Weil and led him to formulate his celebrated conjectures concerning the properties of the zeta functions associated to varieties defined over a finite field. Iwasawa pursued analogous investigations concerning the evolution of class groups of number fields in a tower of cyclotomic extensions, which are akin to the extensions of a function field that are obtained by increasing the field of constants, as explained in [Reference Rosen47, page 188]. This initiated a large series of works that study the evolution of different invariants along a tower of number fields whose Galois group is a p-adic Lie group (see [Reference Kakde, Pop, Coates, Kim, Saïdi and Schneider25] for a survey). Moreover, Iwasawa theory has been extended to the study of the evolution of invariants of many different arithmetic objects, such as elliptic curves or even general motives (see [Reference Fukaya and Kato14] for one of the most general frameworks available at present).
In a somehow different direction, ideas from Iwasawa theory have found applications also outside number theory and algebraic geometry. More precisely, the torsion subgroups of the first homology groups of a tower of hyperbolic
![]() $3$
-manifolds whose base is the complement of a knot or a link have been shown to evolve according to a pattern that is very similar to the one appearing in Iwasawa theory (see [Reference Hillman, Matei and Morishita21, Reference Kadokami and Mizusawa24, Reference Ueki55]). Considering hyperbolic manifolds allows one to study towers whose groups of deck transformations are not necessarily profinite, which is not possible when one studies towers of number fields. For instance, one can consider a
$3$
-manifolds whose base is the complement of a knot or a link have been shown to evolve according to a pattern that is very similar to the one appearing in Iwasawa theory (see [Reference Hillman, Matei and Morishita21, Reference Kadokami and Mizusawa24, Reference Ueki55]). Considering hyperbolic manifolds allows one to study towers whose groups of deck transformations are not necessarily profinite, which is not possible when one studies towers of number fields. For instance, one can consider a
![]() $\mathbb {Z}$
-cover of hyperbolic manifolds. In this case, when the base of the tower consists of the complement of a knot in the three-dimensional sphere, the Alexander polynomial of the knot in question can be used to describe explicitly the growth of the torsion inside the first homology groups of the manifolds in question, as proven by Ueki [Reference Ueki56] in the p-adic case, and by González-Acuña and Short [Reference González-Acuña and Short17] and Riley [Reference Riley46] in the Archimedean case. These results are particularly interesting in view of the widely explored analogy between number fields and knots (see [Reference Morishita43] for a survey).
$\mathbb {Z}$
-cover of hyperbolic manifolds. In this case, when the base of the tower consists of the complement of a knot in the three-dimensional sphere, the Alexander polynomial of the knot in question can be used to describe explicitly the growth of the torsion inside the first homology groups of the manifolds in question, as proven by Ueki [Reference Ueki56] in the p-adic case, and by González-Acuña and Short [Reference González-Acuña and Short17] and Riley [Reference Riley46] in the Archimedean case. These results are particularly interesting in view of the widely explored analogy between number fields and knots (see [Reference Morishita43] for a survey).
Finally, an analogue of Iwasawa theory has also been developed to study the evolution of the so-called Picard group of degree zero of a finite connected graph X, as one moves along a tower. This finite group, defined for instance in [Reference Corry and Perkinson6, Section 1.3], is analogous to the class group of a number field, or to the Picard group of degree zero of a curve defined over a finite field. Its cardinality, usually denoted by
![]() $\kappa (X)$
, is given by the number of spanning trees of the graph in question. The evolution of this number when the finite graph in question varies along a tower has been the subject of a series of papers written by several authors in collaboration with the second author of the present paper [Reference DuBose and Vallières9, Reference Lei and Vallières35, Reference McGown and Vallières39, Reference McGown and Vallières40, Reference Vallières57]. More precisely, if
$\kappa (X)$
, is given by the number of spanning trees of the graph in question. The evolution of this number when the finite graph in question varies along a tower has been the subject of a series of papers written by several authors in collaboration with the second author of the present paper [Reference DuBose and Vallières9, Reference Lei and Vallières35, Reference McGown and Vallières39, Reference McGown and Vallières40, Reference Vallières57]. More precisely, if
![]() $\ell \in \mathbb {N}$
is a rational prime and
$\ell \in \mathbb {N}$
is a rational prime and
is a tower of finite graphs, such that each
![]() $X_{\ell ^n}/X$
is a Galois cover with Galois group
$X_{\ell ^n}/X$
is a Galois cover with Galois group
![]() $\mathbb {Z}/\ell ^n \mathbb {Z}$
, it was shown in [Reference McGown and Vallières39, Reference McGown and Vallières40, Reference Vallières57] that there exist nonnegative integers
$\mathbb {Z}/\ell ^n \mathbb {Z}$
, it was shown in [Reference McGown and Vallières39, Reference McGown and Vallières40, Reference Vallières57] that there exist nonnegative integers
![]() $\mu _{\ell },\lambda _{\ell }$
and an integer
$\mu _{\ell },\lambda _{\ell }$
and an integer
![]() $\nu _{\ell }$
such that
$\nu _{\ell }$
such that
for n large enough, where
![]() ${\mathrm {ord}}_\ell $
denotes the usual
${\mathrm {ord}}_\ell $
denotes the usual
![]() $\ell $
-adic valuation on
$\ell $
-adic valuation on
![]() $\mathbb {Q}$
. Moreover, it was shown in [Reference Lei and Vallières35] that if p is another rational prime different than
$\mathbb {Q}$
. Moreover, it was shown in [Reference Lei and Vallières35] that if p is another rational prime different than
![]() $\ell $
, then there exist a nonnegative integer
$\ell $
, then there exist a nonnegative integer
![]() $\mu _{p}$
and an integer
$\mu _{p}$
and an integer
![]() $\nu _{p}$
such that
$\nu _{p}$
such that
for n large enough. Furthermore, given an integer
![]() $d \geq 1$
, and a tower of finite graphs
$d \geq 1$
, and a tower of finite graphs
such that each
![]() $X_{\ell ^n}^{(d)}/X$
is a Galois cover with Galois group
$X_{\ell ^n}^{(d)}/X$
is a Galois cover with Galois group
![]() $(\mathbb {Z}/\ell ^n \mathbb {Z})^d$
, it was shown in [Reference DuBose and Vallières9] that there exists a polynomial
$(\mathbb {Z}/\ell ^n \mathbb {Z})^d$
, it was shown in [Reference DuBose and Vallières9] that there exists a polynomial
![]() $P \in \mathbb {Q}[t_1,t_2]$
of total degree at most d, and linear in
$P \in \mathbb {Q}[t_1,t_2]$
of total degree at most d, and linear in
![]() $t_2$
, such that
$t_2$
, such that
for every n that is large enough. These advances in the Iwasawa theory of finite graphs can be seen as being analogous to more classical theorems and conjectures in the Iwasawa theory of number fields. More precisely, (1-2) is analogous to a classical theorem of Iwasawa [Reference Iwasawa22] for
![]() $\mathbb {Z}_\ell $
-extensions of number fields, whereas (1-3) is analogous to a result of Washington for the cyclotomic
$\mathbb {Z}_\ell $
-extensions of number fields, whereas (1-3) is analogous to a result of Washington for the cyclotomic
![]() $\mathbb {Z}_\ell $
-extension of an abelian number field, proved in [Reference Washington58], and (1-4) is akin to a conjecture of Greenberg, which is discussed by Cuoco and Monsky in [Reference Cuoco and Monsky7, Section 7].
$\mathbb {Z}_\ell $
-extension of an abelian number field, proved in [Reference Washington58], and (1-4) is akin to a conjecture of Greenberg, which is discussed by Cuoco and Monsky in [Reference Cuoco and Monsky7, Section 7].
The results (1-2) and (1-4) were originally proven by working on the ‘analytic side’ of Iwasawa theory, that is, by constructing appropriate elements of the Iwasawa algebra
However, Gonet [Reference Gonet15, Reference Gonet16] reproved (1-2) using a module theoretical approach, which was recently shown to be closely related to the analytic approach in the work of Kleine and Müller [Reference Kleine and Müller27]. More precisely, this work proves an analogue of the Iwasawa main conjecture in the setting of graphs, which allows Kleine and Müller to prove (1-4) in an algebraic way. Moreover, Kataoka’s recent work [Reference Kataoka26] studies the Fitting ideals that appear in this setting, and Kleine and Müller’s more recent work [Reference Kleine and Müller28] shows how to adapt some of these ideas to the nonabelian setting.
To conclude this overview, let us mention that the recent work of Lei and Müller [Reference Lei and Müller33, Reference Lei and Müller34] shows how one can obtain natural towers of finite graphs by looking at the isogeny graphs associated to elliptic curves defined over a finite field
![]() $\mathbb {F}$
. More precisely, in [Reference Lei and Müller33], the authors consider
$\mathbb {F}$
. More precisely, in [Reference Lei and Müller33], the authors consider
![]() $\ell $
-isogeny graphs
$\ell $
-isogeny graphs
![]() $\tilde {G}_N^m$
of ordinary elliptic curves with a
$\tilde {G}_N^m$
of ordinary elliptic curves with a
![]() $\Gamma _1(N p^m)$
-level structure, where p is the characteristic of
$\Gamma _1(N p^m)$
-level structure, where p is the characteristic of
![]() $\mathbb {F}$
, while
$\mathbb {F}$
, while
![]() $\ell $
is a prime different from p and N is a fixed integer coprime to p. In particular, they fix an ordinary elliptic curve E defined over
$\ell $
is a prime different from p and N is a fixed integer coprime to p. In particular, they fix an ordinary elliptic curve E defined over
![]() $\mathbb {F}$
, which also admits a nontrivial
$\mathbb {F}$
, which also admits a nontrivial
![]() $\ell $
-isogeny defined over
$\ell $
-isogeny defined over
![]() $\mathbb {F}$
, and they prove that there exists an integer
$\mathbb {F}$
, and they prove that there exists an integer
![]() $m_0$
such that the connected components
$m_0$
such that the connected components
![]() $(\tilde {\mathcal {G}}_N^m)_{m = m_0}^{+\infty }$
of the graphs
$(\tilde {\mathcal {G}}_N^m)_{m = m_0}^{+\infty }$
of the graphs
![]() $(\tilde {G}_N^m)_{m = m_0}^{+\infty }$
that contain a vertex corresponding to E give rise to a
$(\tilde {G}_N^m)_{m = m_0}^{+\infty }$
that contain a vertex corresponding to E give rise to a
![]() $\mathbb {Z}_p$
-tower. These graphs generalise the celebrated isogeny volcanoes, which are vastly used in cryptography, and have been classified in recent work of Bambury et al. [Reference Bambury, Campagna and Pazuki1]. In a subsequent paper [Reference Lei and Müller34], Lei and Müller considered
$\mathbb {Z}_p$
-tower. These graphs generalise the celebrated isogeny volcanoes, which are vastly used in cryptography, and have been classified in recent work of Bambury et al. [Reference Bambury, Campagna and Pazuki1]. In a subsequent paper [Reference Lei and Müller34], Lei and Müller considered
![]() $\ell $
-isogeny graphs of elliptic curves with full
$\ell $
-isogeny graphs of elliptic curves with full
![]() $\Gamma (N p^n)$
-level structures, and they showed that their ordinary connected components do not give rise to Galois covers, while their supersingular ones do, at least when
$\Gamma (N p^n)$
-level structures, and they showed that their ordinary connected components do not give rise to Galois covers, while their supersingular ones do, at least when
![]() $N \leq 2$
and for a positive proportion of primes p. In this case, the resulting tower has a nonabelian Galois group, isomorphic to
$N \leq 2$
and for a positive proportion of primes p. In this case, the resulting tower has a nonabelian Galois group, isomorphic to
![]() $\mathrm {GL}_2(\mathbb {Z}_p)$
, which therefore fits into the framework developed by Kleine and Müller in [Reference Kleine and Müller28].
$\mathrm {GL}_2(\mathbb {Z}_p)$
, which therefore fits into the framework developed by Kleine and Müller in [Reference Kleine and Müller28].
1.2. Main results
Inspired by the results mentioned in the previous section, we show in the present paper how the invariants appearing in (1-2) and (1-3) can be explicitly computed when (1-1) comes from a
![]() $\mathbb {Z}$
-cover of finite graphs. More precisely, every Galois cover of graphs
$\mathbb {Z}$
-cover of finite graphs. More precisely, every Galois cover of graphs
![]() $Y/X$
with Galois group G can be constructed from a voltage assignment, which is a function
$Y/X$
with Galois group G can be constructed from a voltage assignment, which is a function
![]() $\alpha \colon \mathbf {E}_X \to G$
such that
$\alpha \colon \mathbf {E}_X \to G$
such that
![]() $\alpha (\overline {e}) = \alpha (e)^{-1}$
for every
$\alpha (\overline {e}) = \alpha (e)^{-1}$
for every
![]() $e \in \mathbf {E}_X$
, where
$e \in \mathbf {E}_X$
, where
![]() $\mathbf {E}_X$
denotes the set of directed edges of X, and
$\mathbf {E}_X$
denotes the set of directed edges of X, and
![]() $\overline {e}$
denotes the inverse of an edge (see Section 3.1 for further details). Indeed, if G is an arbitrary group and
$\overline {e}$
denotes the inverse of an edge (see Section 3.1 for further details). Indeed, if G is an arbitrary group and
![]() $\alpha \colon \mathbf {E}_X \to G$
is a voltage assignment, one can construct a graph
$\alpha \colon \mathbf {E}_X \to G$
is a voltage assignment, one can construct a graph
![]() $X(G,\alpha )$
, introduced by Gross in [Reference Gross19], which generalises the usual notion of a Cayley graph, and is endowed with a canonical map
$X(G,\alpha )$
, introduced by Gross in [Reference Gross19], which generalises the usual notion of a Cayley graph, and is endowed with a canonical map
![]() $X(G,\alpha ) \to X$
, which is a Galois cover if and only if
$X(G,\alpha ) \to X$
, which is a Galois cover if and only if
![]() $X(G,\alpha )$
is connected, in which case,
$X(G,\alpha )$
is connected, in which case,
![]() $\mathrm {Gal}(X(G,\alpha )/X) \cong G$
. Moreover, if
$\mathrm {Gal}(X(G,\alpha )/X) \cong G$
. Moreover, if
![]() $Y/X$
is a Galois cover of finite graphs, with Galois group G, there exists a voltage assignment
$Y/X$
is a Galois cover of finite graphs, with Galois group G, there exists a voltage assignment
![]() $\alpha \colon \mathbf {E}_X \to G$
and an isomorphism of covers
$\alpha \colon \mathbf {E}_X \to G$
and an isomorphism of covers
![]() $Y/X \cong X(G,\alpha )/X$
, as outlined in [Reference DuBose and Vallières9, Section 3].
$Y/X \cong X(G,\alpha )/X$
, as outlined in [Reference DuBose and Vallières9, Section 3].
Now, let G be an arbitrary group and
![]() $\alpha \colon \mathbf {E}_X \to G$
be a voltage assignment. Then, for every normal subgroup
$\alpha \colon \mathbf {E}_X \to G$
be a voltage assignment. Then, for every normal subgroup
![]() $H \trianglelefteq G$
that has finite index, one has a finite graph
$H \trianglelefteq G$
that has finite index, one has a finite graph
![]() $X_H := X(G/H,\alpha _H)$
, where
$X_H := X(G/H,\alpha _H)$
, where
![]() $\alpha _H \colon \mathbf {E}_X \to G/H$
denotes the voltage assignment obtained by composing
$\alpha _H \colon \mathbf {E}_X \to G/H$
denotes the voltage assignment obtained by composing
![]() $\alpha $
with the natural projection map
$\alpha $
with the natural projection map
![]() $\pi \colon G \twoheadrightarrow G/H$
. If each of the finite graphs
$\pi \colon G \twoheadrightarrow G/H$
. If each of the finite graphs
![]() $X_H$
is connected, then it is a Galois cover of X, whose Galois group is canonically isomorphic to
$X_H$
is connected, then it is a Galois cover of X, whose Galois group is canonically isomorphic to
![]() $G/H$
. In this setting, one of the main goals, which is related to the results mentioned above, is to describe how the number of spanning trees
$G/H$
. In this setting, one of the main goals, which is related to the results mentioned above, is to describe how the number of spanning trees
![]() $\kappa (X_H)$
depends on H. When
$\kappa (X_H)$
depends on H. When
![]() $G = \mathbb {Z}_\ell ^d$
for some
$G = \mathbb {Z}_\ell ^d$
for some
![]() $d \geq 1$
, this is the content of the results that we recalled in the previous section, that lead to (1-2), (1-3) and (1-4).
$d \geq 1$
, this is the content of the results that we recalled in the previous section, that lead to (1-2), (1-3) and (1-4).
As we mentioned above, in this paper, we focus on the case
![]() $G = \mathbb {Z}$
, and we provide a global analogue of the results obtained in (1-2) and (1-3). More precisely, for every finite graph X and every voltage assignment
$G = \mathbb {Z}$
, and we provide a global analogue of the results obtained in (1-2) and (1-3). More precisely, for every finite graph X and every voltage assignment
![]() $\alpha \colon \mathbf {E}_X \to \mathbb {Z}$
such that each finite graph
$\alpha \colon \mathbf {E}_X \to \mathbb {Z}$
such that each finite graph
![]() $X_n := X(\mathbb {Z}/n \mathbb {Z},\alpha _n)$
is connected, where
$X_n := X(\mathbb {Z}/n \mathbb {Z},\alpha _n)$
is connected, where
![]() $\alpha _n := \alpha _{n \mathbb {Z}}$
, we show in Theorem 3.6 that the number of spanning trees
$\alpha _n := \alpha _{n \mathbb {Z}}$
, we show in Theorem 3.6 that the number of spanning trees
![]() $\kappa (X_n)$
of the graph
$\kappa (X_n)$
of the graph
![]() $X_n$
is intimately related to the Pierce–Lehmer sequence
$X_n$
is intimately related to the Pierce–Lehmer sequence
![]() $\{ \Delta _n(J_\alpha ) \}_{n=1}^{+\infty }$
associated to a factor
$\{ \Delta _n(J_\alpha ) \}_{n=1}^{+\infty }$
associated to a factor
![]() $J_\alpha \in \mathbb {Z}[t]$
of the Ihara polynomial
$J_\alpha \in \mathbb {Z}[t]$
of the Ihara polynomial
![]() $\mathcal {I}_\alpha \in \mathbb {Z}[t^{\pm 1}]$
, which is a Laurent polynomial that can be explicitly constructed from the voltage assignment
$\mathcal {I}_\alpha \in \mathbb {Z}[t^{\pm 1}]$
, which is a Laurent polynomial that can be explicitly constructed from the voltage assignment
![]() $\alpha $
, as we explain in Section 3.3. The Archimedean and p-adic absolute values of the aforementioned Pierce–Lehmer sequence, introduced by Pierce [Reference Pierce44] and Lehmer [Reference Lehmer32], turn out to be related to the Archimedean and p-adic Mahler measures of the polynomial
$\alpha $
, as we explain in Section 3.3. The Archimedean and p-adic absolute values of the aforementioned Pierce–Lehmer sequence, introduced by Pierce [Reference Pierce44] and Lehmer [Reference Lehmer32], turn out to be related to the Archimedean and p-adic Mahler measures of the polynomial
![]() $\mathcal {I}_\alpha $
, as we explain in Section 2.3. In particular, these Mahler measures provide the main term that explains the order of growth of the different absolute values of the Pierce–Lehmer sequence
$\mathcal {I}_\alpha $
, as we explain in Section 2.3. In particular, these Mahler measures provide the main term that explains the order of growth of the different absolute values of the Pierce–Lehmer sequence
![]() $\{ \Delta _n(J_\alpha ) \}_{n=1}^{+\infty }$
. This suffices to describe the asymptotic behaviour of the Archimedean (respectively p-adic) absolute value of the number of spanning trees
$\{ \Delta _n(J_\alpha ) \}_{n=1}^{+\infty }$
. This suffices to describe the asymptotic behaviour of the Archimedean (respectively p-adic) absolute value of the number of spanning trees
![]() $\kappa (X_n)$
whenever no root of
$\kappa (X_n)$
whenever no root of
![]() $\mathcal {I}_\alpha $
lies on the unit circle of
$\mathcal {I}_\alpha $
lies on the unit circle of
![]() $\mathbb {C}$
(respectively
$\mathbb {C}$
(respectively
![]() $\mathbb {C}_p$
), as we explain in Corollaries 3.10 and 3.15. In particular, we show in Examples 3.13 and 3.14 that our Archimedean result generalises previous work of Mednykh and Mednykh [Reference Mednykh and Mednykh41, Reference Mednykh42].
$\mathbb {C}_p$
), as we explain in Corollaries 3.10 and 3.15. In particular, we show in Examples 3.13 and 3.14 that our Archimedean result generalises previous work of Mednykh and Mednykh [Reference Mednykh and Mednykh41, Reference Mednykh42].
One may of course wonder about the behaviour of the Archimedean or p-adic absolute value of
![]() $\kappa (X_n)$
when
$\kappa (X_n)$
when
![]() $\mathcal {I}_\alpha $
has some of its roots on the Archimedean (or p-adic) unit circle. In fact, this question is central to understanding the behaviour of the sequence
$\mathcal {I}_\alpha $
has some of its roots on the Archimedean (or p-adic) unit circle. In fact, this question is central to understanding the behaviour of the sequence
![]() $\kappa (X_n)$
, as for almost every prime p, all the roots of
$\kappa (X_n)$
, as for almost every prime p, all the roots of
![]() $\mathcal {I}_\alpha $
will lie on the p-adic unit circle. In the case of the Archimedean absolute value, one can only get some upper and lower bounds for
$\mathcal {I}_\alpha $
will lie on the p-adic unit circle. In the case of the Archimedean absolute value, one can only get some upper and lower bounds for
![]() $\kappa (X_n)$
, but not an exact asymptotic, as follows from Weyl’s equidistribution theorem (see Remark 3.12). In the p-adic case, to understand the absolute value of
$\kappa (X_n)$
, but not an exact asymptotic, as follows from Weyl’s equidistribution theorem (see Remark 3.12). In the p-adic case, to understand the absolute value of
![]() $\kappa (X_n)$
, one needs to take into account a correcting factor, which is described in Theorem 2.3. Doing so, we arrive at the following result, which we now present in a simplified version. For the precise formulation, see Theorem 3.17.
$\kappa (X_n)$
, one needs to take into account a correcting factor, which is described in Theorem 2.3. Doing so, we arrive at the following result, which we now present in a simplified version. For the precise formulation, see Theorem 3.17.
Theorem 1.1. Let X be a finite connected graph whose Euler characteristic
![]() $\chi (X)$
does not vanish, and
$\chi (X)$
does not vanish, and
![]() $\alpha \colon \mathbf {E}_X \to \mathbb {Z}$
be a voltage assignment such that for every
$\alpha \colon \mathbf {E}_X \to \mathbb {Z}$
be a voltage assignment such that for every
![]() $n \geq 1$
, the finite graph
$n \geq 1$
, the finite graph
![]() $X_n := X(\mathbb {Z}/n \mathbb {Z},\alpha _n)$
is connected (which can be checked using Theorem 3.2). Let
$X_n := X(\mathbb {Z}/n \mathbb {Z},\alpha _n)$
is connected (which can be checked using Theorem 3.2). Let
![]() $\mathcal {I}_\alpha \in \mathbb {Z}[t^{\pm 1}]$
be the Ihara polynomial associated to
$\mathcal {I}_\alpha \in \mathbb {Z}[t^{\pm 1}]$
be the Ihara polynomial associated to
![]() $\alpha $
, and set
$\alpha $
, and set
where
![]() $b := -{\mathrm {ord}}_{t=0}(\mathcal {I}_\alpha )$
, and
$b := -{\mathrm {ord}}_{t=0}(\mathcal {I}_\alpha )$
, and
![]() $e := {\mathrm {ord}}_{t=1}(\mathcal {I}_\alpha )$
. Fix a rational prime
$e := {\mathrm {ord}}_{t=1}(\mathcal {I}_\alpha )$
. Fix a rational prime
![]() $p \in \mathbb {N}$
and let
$p \in \mathbb {N}$
and let
where
![]() $m_p(J_\alpha )$
denotes the logarithmic p-adic Mahler measure of
$m_p(J_\alpha )$
denotes the logarithmic p-adic Mahler measure of
![]() $J_\alpha $
, defined as in (2-3). Then, there exist two explicit functions
$J_\alpha $
, defined as in (2-3). Then, there exist two explicit functions
 $$ \begin{align*} \begin{aligned} {\mathbb{N}} &\to {\mathbb{Z}}_{\geq 0} \\ n &\mapsto \lambda_{p,n}(X,\alpha) \end{aligned} \quad \text{and} \quad \begin{aligned} {\mathbb{N}} &\to {\mathbb{Z}} \\ n &\mapsto \nu_{p,n}(X,\alpha) \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} {\mathbb{N}} &\to {\mathbb{Z}}_{\geq 0} \\ n &\mapsto \lambda_{p,n}(X,\alpha) \end{aligned} \quad \text{and} \quad \begin{aligned} {\mathbb{N}} &\to {\mathbb{Z}} \\ n &\mapsto \nu_{p,n}(X,\alpha) \end{aligned} \end{align*} $$
whose images are finite, and an integer
![]() $c_{p}(X,\alpha )$
, such that
$c_{p}(X,\alpha )$
, such that
for all
![]() $n \in \mathbb {N}$
.
$n \in \mathbb {N}$
.
Specialising (1-5) to the subsequence
![]() $\{\kappa (X_{p^{k}}) \}_{k=1}^{\infty }$
gives
$\{\kappa (X_{p^{k}}) \}_{k=1}^{\infty }$
gives
and specialising to the subsequence
![]() $\{\kappa (X_{\ell ^{k}}) \}_{k=1}^{\infty }$
, where
$\{\kappa (X_{\ell ^{k}}) \}_{k=1}^{\infty }$
, where
![]() $\ell $
is another rational prime different from p, gives
$\ell $
is another rational prime different from p, gives
After studying the dependency on k of the constants
![]() $\lambda _{p,p^{k}}(X,\alpha ), \nu _{p,p^{k}}(X,\alpha )$
and
$\lambda _{p,p^{k}}(X,\alpha ), \nu _{p,p^{k}}(X,\alpha )$
and
![]() $\nu _{p,\ell ^{k}}(X,\alpha )$
, one gets back (1-2) and (1-3), as we explain in Remark 3.8. Moreover, we obtain similar results by specialising Theorem 1.1 to sequences of integers divisible only by a finite number of primes, as we explain in Corollary 2.10. These identities can be seen as analogous to a result proven by Friedman [Reference Friedman13] for cyclotomic
$\nu _{p,\ell ^{k}}(X,\alpha )$
, one gets back (1-2) and (1-3), as we explain in Remark 3.8. Moreover, we obtain similar results by specialising Theorem 1.1 to sequences of integers divisible only by a finite number of primes, as we explain in Corollary 2.10. These identities can be seen as analogous to a result proven by Friedman [Reference Friedman13] for cyclotomic
![]() $\mathbb{Z}_{p_{1}}\times \cdots \times \mathbb{Z}_{p_{s}}$
-extensions of number fields that are abelian over
$\mathbb{Z}_{p_{1}}\times \cdots \times \mathbb{Z}_{p_{s}}$
-extensions of number fields that are abelian over
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
To conclude, we show in Section 3.7 that Theorem 1.1 allows one to recover a well-known formula that computes the p-adic valuations of Fibonacci numbers, which is due to Lengyel [Reference Lengyel36].
1.3. Notation and conventions
Let p be a rational prime. We let
![]() $\mathbb {C}_{p}$
denote a fixed completion of an algebraic closure of the p-adic rational numbers
$\mathbb {C}_{p}$
denote a fixed completion of an algebraic closure of the p-adic rational numbers
![]() $\mathbb {Q}_{p}$
. As usual,
$\mathbb {Q}_{p}$
. As usual,
![]() $\lvert \cdot \rvert _{p}$
and
$\lvert \cdot \rvert _{p}$
and
![]() $\mathrm {ord}_{p}$
denote the p-adic absolute value and the p-adic valuation on
$\mathrm {ord}_{p}$
denote the p-adic absolute value and the p-adic valuation on
![]() $\mathbb {C}_{p}$
, respectively. They are related via
$\mathbb {C}_{p}$
, respectively. They are related via
 $$ \begin{align*}\mathrm{ord}_{p}(x) = -\frac{\log |x|_{p}}{\log p} \end{align*} $$
$$ \begin{align*}\mathrm{ord}_{p}(x) = -\frac{\log |x|_{p}}{\log p} \end{align*} $$
for all
![]() $x \in \mathbb {C}_{p}$
, and they are normalised so that
$x \in \mathbb {C}_{p}$
, and they are normalised so that
![]() $\mathrm {ord}_{p}(p) = 1$
. We also denote by
$\mathrm {ord}_{p}(p) = 1$
. We also denote by
![]() $\mathbb {C}$
the field of complex numbers, endowed with the usual Archimedean absolute value
$\mathbb {C}$
the field of complex numbers, endowed with the usual Archimedean absolute value
![]() $\lvert \cdot \rvert _\infty $
.
$\lvert \cdot \rvert _\infty $
.
If G is an abelian group, not necessarily finite, we let
![]() $G^{\vee } = \mathrm {Hom}_{\mathbb {Z}}(G,W_{\infty })$
, where
$G^{\vee } = \mathrm {Hom}_{\mathbb {Z}}(G,W_{\infty })$
, where
![]() $W_{\infty }$
denotes the group of roots of unity in an algebraic closure
$W_{\infty }$
denotes the group of roots of unity in an algebraic closure
![]() $\overline {\mathbb {Q}} \subseteq \mathbb {C}$
of
$\overline {\mathbb {Q}} \subseteq \mathbb {C}$
of
![]() $\mathbb {Q}$
. An element of
$\mathbb {Q}$
. An element of
![]() $G^{\vee }$
will be called a character of finite order. Here, we depart from the usual notation, since
$G^{\vee }$
will be called a character of finite order. Here, we depart from the usual notation, since
![]() $G^{\vee }$
is not necessarily the Pontryagin dual of G. For each rational prime p, we fix once and for all an embedding
$G^{\vee }$
is not necessarily the Pontryagin dual of G. For each rational prime p, we fix once and for all an embedding
![]() $\overline {\mathbb {Q}} \hookrightarrow \mathbb {C}_{p}$
. Via these embeddings, we view the characters in
$\overline {\mathbb {Q}} \hookrightarrow \mathbb {C}_{p}$
. Via these embeddings, we view the characters in
![]() $G^{\vee }$
as taking values in
$G^{\vee }$
as taking values in
![]() $\mathbb {C}_{p}$
once a rational prime p has been fixed. If n is a positive integer, then we let
$\mathbb {C}_{p}$
once a rational prime p has been fixed. If n is a positive integer, then we let
![]() $W_{n}$
denote the group of n th roots of unity. The symbol
$W_{n}$
denote the group of n th roots of unity. The symbol
![]() $\mathbb {N} = \{1,2,\ldots \}$
refers to the collection of all positive integers.
$\mathbb {N} = \{1,2,\ldots \}$
refers to the collection of all positive integers.
2. Mahler measures and Pierce–Lehmer sequences
In this section, we remind the reader about the resultant of two polynomials, which appears in Section 2.1, and about the p-adic and Archimedean Mahler measures of polynomials, which we treat in Section 2.2. Moreover, we devote Section 2.3 to collecting some results about Pierce–Lehmer sequences. In particular, Theorems 2.2 and 2.3 provide explicit formulae to compute the p-adic valuations of Pierce–Lehmer sequences.
2.1. Resultant
Let F be a field and let
 $$ \begin{align*}p(t) = a_{m}t^{m} + \cdots + a_{0} = a_{m} \prod_{i=1}^{m}(t - \alpha_{i}) \end{align*} $$
$$ \begin{align*}p(t) = a_{m}t^{m} + \cdots + a_{0} = a_{m} \prod_{i=1}^{m}(t - \alpha_{i}) \end{align*} $$
and
 $$ \begin{align*}q(t) = b_{n}t^{n} + \cdots + b_{0} = b_{n} \prod_{j=1}^{n}(t - \beta_{i})\end{align*} $$
$$ \begin{align*}q(t) = b_{n}t^{n} + \cdots + b_{0} = b_{n} \prod_{j=1}^{n}(t - \beta_{i})\end{align*} $$
be two polynomials in
![]() $F[t]$
of degrees m and n, respectively. Here, the roots
$F[t]$
of degrees m and n, respectively. Here, the roots
![]() $\alpha _{i}$
and
$\alpha _{i}$
and
![]() $\beta _{i}$
are assumed to be in a fixed algebraic closure of F. The resultant
$\beta _{i}$
are assumed to be in a fixed algebraic closure of F. The resultant
![]() $\mathrm {Res}(p,q)$
of p and q is defined to be
$\mathrm {Res}(p,q)$
of p and q is defined to be
 $$ \begin{align} \mathrm{Res}(p,q) = a_{m}^{n}b_{n}^{m} \prod_{i=1}^{m}\prod_{j=1}^{n}(\alpha_{i} - \beta_{j}) \end{align} $$
$$ \begin{align} \mathrm{Res}(p,q) = a_{m}^{n}b_{n}^{m} \prod_{i=1}^{m}\prod_{j=1}^{n}(\alpha_{i} - \beta_{j}) \end{align} $$
and is easily seen to be an element of F. Let
![]() $r(t)$
be another polynomial with coefficients in F. From the definition in (2-1), the two properties
$r(t)$
be another polynomial with coefficients in F. From the definition in (2-1), the two properties
follow immediately. Furthermore, one has
 $$ \begin{align*}a_{m}^{n}\prod_{i=1}^{m}q(\alpha_{i})=\mathrm{Res}(p,q)= (-1)^{mn}b_{n}^{m}\prod_{j=1}^{n}p(\beta_{j}),\end{align*} $$
$$ \begin{align*}a_{m}^{n}\prod_{i=1}^{m}q(\alpha_{i})=\mathrm{Res}(p,q)= (-1)^{mn}b_{n}^{m}\prod_{j=1}^{n}p(\beta_{j}),\end{align*} $$
which can be seen as an instance of Weil’s reciprocity law for the projective line over F. Finally, the resultant can also be defined as the determinant of the Sylvester matrix of p and q, as shown for instance in [Reference Cohen5, Lemma 3.3.4]. This allows one to define the resultant
![]() $\mathrm {Res}(f,g) \in R$
of any pair of polynomials
$\mathrm {Res}(f,g) \in R$
of any pair of polynomials
![]() $f, g \in R[t]$
that have coefficients in an arbitrary commutative ring with unity R.
$f, g \in R[t]$
that have coefficients in an arbitrary commutative ring with unity R.
2.2. Mahler measure
Recall that if
is a nonzero polynomial of degree d, which can be factorised as
 $$ \begin{align*}f(t) = a_{d} \prod_{i=1}^{d}(t - \alpha_{i}) \end{align*} $$
$$ \begin{align*}f(t) = a_{d} \prod_{i=1}^{d}(t - \alpha_{i}) \end{align*} $$
for some
![]() $\alpha _1,\ldots ,\alpha _d \in \mathbb {C}$
, then one defines its Archimedean Mahler measure to be
$\alpha _1,\ldots ,\alpha _d \in \mathbb {C}$
, then one defines its Archimedean Mahler measure to be
 $$ \begin{align} M_{\infty}(f) := |a_{d}|_\infty \prod_{i=1}^{d} \mathrm{\max}\{1,|\alpha_{i}|_\infty \} \in \mathbb{R}_{>0}. \end{align} $$
$$ \begin{align} M_{\infty}(f) := |a_{d}|_\infty \prod_{i=1}^{d} \mathrm{\max}\{1,|\alpha_{i}|_\infty \} \in \mathbb{R}_{>0}. \end{align} $$
This invariant, originally studied by Lehmer [Reference Lehmer32], was generalised by Mahler [Reference Mahler38] to polynomials with any number of variables.
Now, let p be a rational prime and let
be a nonzero polynomial of degree d, which factors as
 $$ \begin{align*}g(t) = b_{d} \prod_{i=1}^{d}(t - \beta_{i}) \end{align*} $$
$$ \begin{align*}g(t) = b_{d} \prod_{i=1}^{d}(t - \beta_{i}) \end{align*} $$
for some
![]() $\beta _1,\ldots ,\beta _d \in \mathbb {C}_{p}$
. Following [Reference Ueki56], we define similarly the p-adic Mahler measure of
$\beta _1,\ldots ,\beta _d \in \mathbb {C}_{p}$
. Following [Reference Ueki56], we define similarly the p-adic Mahler measure of
![]() $g(t)$
to be
$g(t)$
to be
 $$ \begin{align*}M_{p}(g) := \lvert b_{d} \rvert_{p} \prod_{i=1}^{d} \mathrm{\max}\{1,\lvert \beta_{i} \rvert_{p} \} \in \mathbb{R}_{>0}. \end{align*} $$
$$ \begin{align*}M_{p}(g) := \lvert b_{d} \rvert_{p} \prod_{i=1}^{d} \mathrm{\max}\{1,\lvert \beta_{i} \rvert_{p} \} \in \mathbb{R}_{>0}. \end{align*} $$
This invariant and its Archimedean analogue are clearly multiplicative. Furthermore, the p-adic Mahler measure of a polynomial
 $$ \begin{align*}g(t) = \sum_{i = 0}^d b_i t^i \in \mathbb{C}_p[t]\end{align*} $$
$$ \begin{align*}g(t) = \sum_{i = 0}^d b_i t^i \in \mathbb{C}_p[t]\end{align*} $$
can be easily computed from its coefficients, thanks to the formula
which was proved by Ueki in [Reference Ueki56, Proposition 2.7]. Finally, we introduce the logarithmic Archimedean Mahler measure
of a polynomial
![]() $f(t) \in \mathbb {C}[t]$
, and analogously the logarithmic p-adic Mahler measure
$f(t) \in \mathbb {C}[t]$
, and analogously the logarithmic p-adic Mahler measure
of a polynomial
![]() $g(t) \in \mathbb {C}_p[t]$
.
$g(t) \in \mathbb {C}_p[t]$
.
Remark 2.1. We note in passing that the logarithmic p-adic Mahler measure introduced in (2-3) does not coincide with the p-adic logarithmic Mahler measure introduced by Besser and Deninger in [Reference Besser and Deninger3], which is a p-adic number.
2.3. Pierce–Lehmer sequences
Let
with
![]() $a_{d} \neq 0$
and write
$a_{d} \neq 0$
and write
 $$ \begin{align*}f(t) = a_{d}\prod_{i=1}^{d}(t - \alpha_{i}) \end{align*} $$
$$ \begin{align*}f(t) = a_{d}\prod_{i=1}^{d}(t - \alpha_{i}) \end{align*} $$
for some
![]() $\alpha _1,\ldots ,\alpha _d \in \overline {\mathbb {Q}}$
. The associated Pierce–Lehmer sequence is defined to be
$\alpha _1,\ldots ,\alpha _d \in \overline {\mathbb {Q}}$
. The associated Pierce–Lehmer sequence is defined to be
 $$ \begin{align} \Delta_{n}(f) = a_{d}^{n}\prod_{i=1}^{d}(\alpha_{i}^{n} - 1) = \mathrm{Res}(f(t),t^{n}-1) \in \mathbb{Z}. \end{align} $$
$$ \begin{align} \Delta_{n}(f) = a_{d}^{n}\prod_{i=1}^{d}(\alpha_{i}^{n} - 1) = \mathrm{Res}(f(t),t^{n}-1) \in \mathbb{Z}. \end{align} $$
Fix now a rational prime p and an embedding
![]() $\overline {\mathbb {Q}} \hookrightarrow \mathbb {C}_{p}$
, as we did in Section 1.3, and view all the algebraic numbers
$\overline {\mathbb {Q}} \hookrightarrow \mathbb {C}_{p}$
, as we did in Section 1.3, and view all the algebraic numbers
![]() $\alpha _1,\ldots ,\alpha _d$
as lying in
$\alpha _1,\ldots ,\alpha _d$
as lying in
![]() $\mathbb {C}_{p}$
via this embedding.
$\mathbb {C}_{p}$
via this embedding.
Theorem 2.2. With the notation as above, one has
 $$ \begin{align*}|\Delta_{n}(f)|_{p} = M_{p}(f)^{n} \prod_{\substack{i=1 \\ |\alpha_{i}|_{p} = 1}}^{d} |\alpha_{i}^{n}-1|_{p}. \end{align*} $$
$$ \begin{align*}|\Delta_{n}(f)|_{p} = M_{p}(f)^{n} \prod_{\substack{i=1 \\ |\alpha_{i}|_{p} = 1}}^{d} |\alpha_{i}^{n}-1|_{p}. \end{align*} $$
Proof. Noting that for
![]() $\alpha \in \mathbb {C}_{p}$
and
$\alpha \in \mathbb {C}_{p}$
and
![]() $n \in \mathbb {N}$
, one has
$n \in \mathbb {N}$
, one has
 $$ \begin{align*} |\alpha^{n} - 1|_{p} = \begin{cases} |\alpha|_{p}^{n} &\text{if } |\alpha|_{p}> 1,\\ 1 & \text{if } |\alpha|_{p} < 1, \end{cases} \end{align*} $$
$$ \begin{align*} |\alpha^{n} - 1|_{p} = \begin{cases} |\alpha|_{p}^{n} &\text{if } |\alpha|_{p}> 1,\\ 1 & \text{if } |\alpha|_{p} < 1, \end{cases} \end{align*} $$
one calculates
 $$ \begin{align*} \begin{aligned} |\Delta_{n}(f)|_{p} &= |a_{d}|_{p}^{n} \prod_{\substack{i=1 \\ |\alpha_{i}|_{p}> 1}}^{d}|\alpha_{i}|_{p}^{n} \prod_{\substack{i=1 \\ |\alpha_{i}|_{p} = 1}}^{d}|\alpha_{i}^{n} - 1|_{p}\\ &= M_{p}(f)^{n} \prod_{\substack{i=1 \\ |\alpha_{i}|_{p} = 1}}^{d}|\alpha_{i}^{n} - 1|_{p}. \end{aligned}\\[-54pt] \end{align*} $$
$$ \begin{align*} \begin{aligned} |\Delta_{n}(f)|_{p} &= |a_{d}|_{p}^{n} \prod_{\substack{i=1 \\ |\alpha_{i}|_{p}> 1}}^{d}|\alpha_{i}|_{p}^{n} \prod_{\substack{i=1 \\ |\alpha_{i}|_{p} = 1}}^{d}|\alpha_{i}^{n} - 1|_{p}\\ &= M_{p}(f)^{n} \prod_{\substack{i=1 \\ |\alpha_{i}|_{p} = 1}}^{d}|\alpha_{i}^{n} - 1|_{p}. \end{aligned}\\[-54pt] \end{align*} $$
It follows that, to determine the p-adic valuation of the numbers
![]() $\Delta _{n}(f)$
, one needs to understand the p-adic valuation of numbers of the form
$\Delta _{n}(f)$
, one needs to understand the p-adic valuation of numbers of the form
![]() $\alpha ^n - 1$
, where
$\alpha ^n - 1$
, where
![]() $n \in \mathbb {N}$
and
$n \in \mathbb {N}$
and
![]() $\alpha \in \overline {\mathbb {Q}}_{p} \subseteq \mathbb {C}_{p}$
is a p-adic number such that
$\alpha \in \overline {\mathbb {Q}}_{p} \subseteq \mathbb {C}_{p}$
is a p-adic number such that
![]() $\lvert \alpha \rvert _p = 1$
. The following theorem, which is inspired by [Reference Ueki56, Lemma 2.11], provides a first step in this direction.
$\lvert \alpha \rvert _p = 1$
. The following theorem, which is inspired by [Reference Ueki56, Lemma 2.11], provides a first step in this direction.
Theorem 2.3. Let
![]() $\alpha \in \overline {\mathbb {Q}}_{p}$
be such that
$\alpha \in \overline {\mathbb {Q}}_{p}$
be such that
![]() $\lvert \alpha \rvert _p = 1$
, and assume that
$\lvert \alpha \rvert _p = 1$
, and assume that
![]() $\alpha $
is not a root of unity. Let
$\alpha $
is not a root of unity. Let
![]() $\mathfrak {m}$
be the maximal ideal of the valuation ring
$\mathfrak {m}$
be the maximal ideal of the valuation ring
![]() $\mathcal {O}$
of
$\mathcal {O}$
of
![]() $\overline {\mathbb {Q}}_{p}$
and let
$\overline {\mathbb {Q}}_{p}$
and let
![]() $N(\alpha )$
be the multiplicative order of
$N(\alpha )$
be the multiplicative order of
![]() $\alpha $
modulo
$\alpha $
modulo
![]() $\mathfrak {m}$
. Then, there exists a function
$\mathfrak {m}$
. Then, there exists a function
![]() $c:\mathbb {N} \rightarrow \mathbb {Q}$
such that
$c:\mathbb {N} \rightarrow \mathbb {Q}$
such that
![]() $c(m)$
is constant for m large and for which
$c(m)$
is constant for m large and for which
 $$ \begin{align} \mathrm{ord}_{p}(\alpha^{n}-1) = \begin{cases} 0 &\text{if } N(\alpha) \nmid n, \\ \mathrm{ord}_{p}(n) + c(\mathrm{ord}_{p}(n)) &\text{if } N(\alpha) \,\, |\, \, n. \end{cases} \end{align} $$
$$ \begin{align} \mathrm{ord}_{p}(\alpha^{n}-1) = \begin{cases} 0 &\text{if } N(\alpha) \nmid n, \\ \mathrm{ord}_{p}(n) + c(\mathrm{ord}_{p}(n)) &\text{if } N(\alpha) \,\, |\, \, n. \end{cases} \end{align} $$
Proof. First of all, let us write
 $$ \begin{align} \lvert \alpha^n - 1 \rvert_p = \prod_{\zeta \in W_n} \lvert \alpha - \zeta \rvert_p, \end{align} $$
$$ \begin{align} \lvert \alpha^n - 1 \rvert_p = \prod_{\zeta \in W_n} \lvert \alpha - \zeta \rvert_p, \end{align} $$
where
![]() $W_n \subseteq \mathcal {O}^\times $
denotes the group of roots of unity of order dividing n. Now, the natural embedding of the ring of Witt vectors of
$W_n \subseteq \mathcal {O}^\times $
denotes the group of roots of unity of order dividing n. Now, the natural embedding of the ring of Witt vectors of
![]() $\overline {\mathbb {F}}_p$
inside
$\overline {\mathbb {F}}_p$
inside
![]() $\mathcal {O}$
gives rise to the Teichmüller lift
$\mathcal {O}$
gives rise to the Teichmüller lift
which is a morphism of groups that sends any
![]() $\beta \in \overline {\mathbb {F}}_p^\times $
to a root of unity whose order coincides with the multiplicative order of
$\beta \in \overline {\mathbb {F}}_p^\times $
to a root of unity whose order coincides with the multiplicative order of
![]() $\beta $
in
$\beta $
in
![]() $\overline {\mathbb {F}}_p^\times $
. Therefore, if
$\overline {\mathbb {F}}_p^\times $
. Therefore, if
is the natural projection map, the root of unity
![]() $\xi = \tau ( \pi (\alpha )) \in \mathcal {O}^\times $
has order
$\xi = \tau ( \pi (\alpha )) \in \mathcal {O}^\times $
has order
![]() $N = N(\alpha )$
, and we have that
$N = N(\alpha )$
, and we have that
![]() $\lvert \alpha - \xi \rvert _{p} < 1 $
because
$\lvert \alpha - \xi \rvert _{p} < 1 $
because
![]() $\tau $
is a section of
$\tau $
is a section of
![]() $\pi $
.
$\pi $
.
We can then use this root of unity
![]() $\xi $
to write the following formula:
$\xi $
to write the following formula:
 $$ \begin{align} |\alpha^{n} - 1|_{p} = \prod_{\zeta \in W_{n}} |\alpha - \xi + \xi - \zeta|_{p}, \end{align} $$
$$ \begin{align} |\alpha^{n} - 1|_{p} = \prod_{\zeta \in W_{n}} |\alpha - \xi + \xi - \zeta|_{p}, \end{align} $$
which follows from (2-6). Using this formula, we can prove immediately the first part of (2-5). Indeed, if
![]() $N \nmid n$
, then for every
$N \nmid n$
, then for every
![]() $\zeta \in W_n$
, the order of the root of unity
$\zeta \in W_n$
, the order of the root of unity
![]() $\zeta /\xi $
is not a power of p, because otherwise there would exist some
$\zeta /\xi $
is not a power of p, because otherwise there would exist some
![]() $r \in \mathbb {N}$
such that
$r \in \mathbb {N}$
such that
![]() $\zeta ^{p^{r}} = \xi ^{p^{r}}$
, from which it would follow that
$\zeta ^{p^{r}} = \xi ^{p^{r}}$
, from which it would follow that
![]() $\xi ^{np^{r}} = 1$
, and thus that
$\xi ^{np^{r}} = 1$
, and thus that
![]() $N \, | \, np^{r}$
. Since we know that
$N \, | \, np^{r}$
. Since we know that
![]() $(N,p) = 1$
, this would imply that
$(N,p) = 1$
, this would imply that
![]() $N \, | \, n$
, contradicting our assumption. Therefore, [Reference Ueki56, Lemma 2.9] implies that
$N \, | \, n$
, contradicting our assumption. Therefore, [Reference Ueki56, Lemma 2.9] implies that
for all
![]() $\zeta \in W_{n}$
, which entails that
$\zeta \in W_{n}$
, which entails that
![]() $\lvert \alpha - \xi + \xi - \zeta \rvert _p = 1$
for every
$\lvert \alpha - \xi + \xi - \zeta \rvert _p = 1$
for every
![]() $\zeta \in W_n$
, because
$\zeta \in W_n$
, because
![]() $\lvert \alpha - \xi \rvert _p < 1$
by construction. Finally, we see thanks to (2-7) that
$\lvert \alpha - \xi \rvert _p < 1$
by construction. Finally, we see thanks to (2-7) that
![]() $|\alpha ^{n} - 1|_{p} = 1$
, which proves the first part of the statement (2-5).
$|\alpha ^{n} - 1|_{p} = 1$
, which proves the first part of the statement (2-5).
Suppose now that
![]() $N \, | \, n$
. As before, we have that
$N \, | \, n$
. As before, we have that
![]() $\lvert \xi - \zeta \rvert _p = 1$
unless the order of
$\lvert \xi - \zeta \rvert _p = 1$
unless the order of
![]() $\mu := \zeta /\xi $
is a power of p. Therefore,
$\mu := \zeta /\xi $
is a power of p. Therefore,
 $$ \begin{align} \lvert \alpha^n - 1 \rvert_p = \prod_{\mu \in W_{p^m}} \lvert \alpha - \xi \mu \rvert_p = \prod_{\mu \in W_{p^m}} \lvert \alpha - \xi + \xi(1-\mu) \rvert_p, \end{align} $$
$$ \begin{align} \lvert \alpha^n - 1 \rvert_p = \prod_{\mu \in W_{p^m}} \lvert \alpha - \xi \mu \rvert_p = \prod_{\mu \in W_{p^m}} \lvert \alpha - \xi + \xi(1-\mu) \rvert_p, \end{align} $$
where
![]() $m := {\mathrm {ord}}_p(n)$
. Moreover, if
$m := {\mathrm {ord}}_p(n)$
. Moreover, if
![]() $\mu $
has order
$\mu $
has order
![]() $p^k$
, for some
$p^k$
, for some
![]() $k \in \mathbb {N} \cup \{0\}$
such that
$k \in \mathbb {N} \cup \{0\}$
such that
we have that
![]() $\lvert \xi (1-\mu ) \rvert _p = \lvert 1 - \mu \rvert _p> \lvert \alpha -\xi \rvert _p$
, as follows from the classical fact that
$\lvert \xi (1-\mu ) \rvert _p = \lvert 1 - \mu \rvert _p> \lvert \alpha -\xi \rvert _p$
, as follows from the classical fact that
 $$ \begin{align*}{\mathrm{ord}}_p(1-\mu) = \frac{1}{p^{k-1} (p-1)}\end{align*} $$
$$ \begin{align*}{\mathrm{ord}}_p(1-\mu) = \frac{1}{p^{k-1} (p-1)}\end{align*} $$
for every root of unity
![]() $\mu \in W_{p^m} \setminus \{1\}$
of order
$\mu \in W_{p^m} \setminus \{1\}$
of order
![]() $p^k$
, whose proof can be found for example in [Reference Ueki56, Lemma 2.9].
$p^k$
, whose proof can be found for example in [Reference Ueki56, Lemma 2.9].
Hence, if we define
![]() $s \in \mathbb {N} \cup \{0\}$
to be the minimal nonnegative integer such that
$s \in \mathbb {N} \cup \{0\}$
to be the minimal nonnegative integer such that
and we set
![]() $r := \min (s,m)$
, we see from (2-8) that
$r := \min (s,m)$
, we see from (2-8) that
 $$ \begin{align*} \begin{aligned} |\alpha^{n} - 1|_{p} &= \bigg( \prod_{\mu \in W_{p^r}} \lvert \alpha - \xi \mu \rvert_p \bigg) \bigg( \prod_{\mu \in W_{p^m} \setminus W_{p^r}} \lvert \alpha - \xi + \xi (1 - \mu) \rvert_p \bigg) \\ &= |\alpha - \xi|_{p} \bigg( \prod_{\mu \in W_{p^r} \setminus \{1\}} \frac{\lvert \alpha - \xi \mu \rvert_p}{|1 - \mu|_{p}} \, |1 - \mu|_{p} \bigg) \bigg( \prod_{\mu \in W_{p^m} \setminus W_{p^r}}|1 - \mu|_{p} \bigg) \\ &= |\alpha - \xi|_{p} \bigg( \prod_{\mu \in W_{p^r} \setminus \{1\}} \frac{\lvert \alpha - \xi \mu \rvert_p}{\lvert 1 - \mu \rvert_p} \bigg) \bigg( \prod_{\mu \in W_{p^m} \setminus \{1\}} |1 - \mu|_{p} \bigg) \\ &= |\alpha - \xi|_{p} \bigg( \prod_{\mu \in W_{p^r} \setminus \{1\}} \frac{\lvert \alpha - \xi \mu \rvert_p}{\lvert 1 - \mu \rvert_p} \bigg) |n|_{p}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} |\alpha^{n} - 1|_{p} &= \bigg( \prod_{\mu \in W_{p^r}} \lvert \alpha - \xi \mu \rvert_p \bigg) \bigg( \prod_{\mu \in W_{p^m} \setminus W_{p^r}} \lvert \alpha - \xi + \xi (1 - \mu) \rvert_p \bigg) \\ &= |\alpha - \xi|_{p} \bigg( \prod_{\mu \in W_{p^r} \setminus \{1\}} \frac{\lvert \alpha - \xi \mu \rvert_p}{|1 - \mu|_{p}} \, |1 - \mu|_{p} \bigg) \bigg( \prod_{\mu \in W_{p^m} \setminus W_{p^r}}|1 - \mu|_{p} \bigg) \\ &= |\alpha - \xi|_{p} \bigg( \prod_{\mu \in W_{p^r} \setminus \{1\}} \frac{\lvert \alpha - \xi \mu \rvert_p}{\lvert 1 - \mu \rvert_p} \bigg) \bigg( \prod_{\mu \in W_{p^m} \setminus \{1\}} |1 - \mu|_{p} \bigg) \\ &= |\alpha - \xi|_{p} \bigg( \prod_{\mu \in W_{p^r} \setminus \{1\}} \frac{\lvert \alpha - \xi \mu \rvert_p}{\lvert 1 - \mu \rvert_p} \bigg) |n|_{p}, \end{aligned} \end{align*} $$
where the last equality follows from the fact that
 $$ \begin{align*} \prod_{\mu \in W_{p^m} \setminus \{1\}} |1 - \mu|_{p} = \prod_{\mu \in W_n \setminus \{1\}} \lvert 1 - \mu \rvert_p = \bigg\lvert \mathrm{Res}\bigg( \frac{t^n - 1}{t-1}, t-1 \bigg) \bigg\rvert_p = \lvert n \rvert_p. \end{align*} $$
$$ \begin{align*} \prod_{\mu \in W_{p^m} \setminus \{1\}} |1 - \mu|_{p} = \prod_{\mu \in W_n \setminus \{1\}} \lvert 1 - \mu \rvert_p = \bigg\lvert \mathrm{Res}\bigg( \frac{t^n - 1}{t-1}, t-1 \bigg) \bigg\rvert_p = \lvert n \rvert_p. \end{align*} $$
Therefore, we see that
![]() $\mathrm {ord}_p(\alpha ^n - 1) = {\mathrm {ord}}_p(n) + c(\mathrm {ord}_p(n))$
, where the expression
$\mathrm {ord}_p(\alpha ^n - 1) = {\mathrm {ord}}_p(n) + c(\mathrm {ord}_p(n))$
, where the expression
 $$ \begin{align*} \begin{aligned} c(m) &:= \mathrm{ord}_p(\alpha - \xi) + \sum_{\mu \in W_{p^r} \setminus \{1\}} ({\mathrm{ord}}_p(\alpha - \xi \mu) - {\mathrm{ord}}_p(1 - \mu))\\ &= {\mathrm{ord}}_p(\alpha^{p^r} - \xi^{p^r}) - r \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} c(m) &:= \mathrm{ord}_p(\alpha - \xi) + \sum_{\mu \in W_{p^r} \setminus \{1\}} ({\mathrm{ord}}_p(\alpha - \xi \mu) - {\mathrm{ord}}_p(1 - \mu))\\ &= {\mathrm{ord}}_p(\alpha^{p^r} - \xi^{p^r}) - r \end{aligned} \end{align*} $$
depends only on m and
![]() $\alpha $
, and is evidently constant when m becomes sufficiently large. This proves the second part of (2-5), and concludes the proof.
$\alpha $
, and is evidently constant when m becomes sufficiently large. This proves the second part of (2-5), and concludes the proof.
Remark 2.4. Let
![]() $\alpha \in \overline {\mathbb {Q}}$
. Then, there exists a finite subset
$\alpha \in \overline {\mathbb {Q}}$
. Then, there exists a finite subset
![]() $S \subseteq \mathbb {N}$
such that for every rational prime
$S \subseteq \mathbb {N}$
such that for every rational prime
![]() $p \in \mathbb {N} \setminus S$
and every embedding
$p \in \mathbb {N} \setminus S$
and every embedding
![]() $\iota \colon \mathbb {Q}(\alpha ) \hookrightarrow \overline {\mathbb {Q}}_p$
, we have that
$\iota \colon \mathbb {Q}(\alpha ) \hookrightarrow \overline {\mathbb {Q}}_p$
, we have that
![]() $\lvert \iota (\alpha ) \rvert _p = 1$
and
$\lvert \iota (\alpha ) \rvert _p = 1$
and
Therefore, for every rational prime
![]() $p \in \mathbb {N} \setminus (S \cup \{2\})$
, we see that
$p \in \mathbb {N} \setminus (S \cup \{2\})$
, we see that
![]() $s = 0$
is the minimal nonnegative integer such that (2-9) holds true.
$s = 0$
is the minimal nonnegative integer such that (2-9) holds true.
From Theorems 2.2 and 2.3, we obtain several corollaries. First of all, one can obtain an explicit formula for the p-adic valuation of the elements of the Pierce–Lehmer sequence associated to a polynomial
![]() $f \in \mathbb {Z}[t]$
.
$f \in \mathbb {Z}[t]$
.
Corollary 2.5. Let
![]() $f \in \mathbb {Z}[t] \setminus \{0\}$
be a polynomial that does not vanish at any root of unity, and fix a prime p. Let
$f \in \mathbb {Z}[t] \setminus \{0\}$
be a polynomial that does not vanish at any root of unity, and fix a prime p. Let
![]() $\beta _1,\ldots ,\beta _d \in \overline {\mathbb {Q}}_p$
denote the p-adic roots of f, counted with multiplicities. Then, for every
$\beta _1,\ldots ,\beta _d \in \overline {\mathbb {Q}}_p$
denote the p-adic roots of f, counted with multiplicities. Then, for every
![]() $n \in \mathbb {N}$
, we define
$n \in \mathbb {N}$
, we define
and for every
![]() $\beta \in \overline {\mathbb {Q}}_p$
such that
$\beta \in \overline {\mathbb {Q}}_p$
such that
![]() $\lvert \beta \rvert _p = 1$
,
$\lvert \beta \rvert _p = 1$
,
and we write
![]() $r_{p,n}(\beta ) := \min ({\mathrm {ord}}_p(n),s_p(\beta ))$
. Using this notation,
$r_{p,n}(\beta ) := \min ({\mathrm {ord}}_p(n),s_p(\beta ))$
. Using this notation,
where
 $\nu _{p,n}(f) := \sum _{\substack {j \in \{1,\ldots ,d\} \\ \beta _j \in B_{p,n}(f)}} ( {\mathrm {ord}}_p(\beta _j^{p^{r_{p,n}(\beta _j)}} - \tau _p(\pi _p(\beta _j))^{p^{r_{p,n}(\beta _j)}}) - r_{p,n}(\beta _j) )$
.
$\nu _{p,n}(f) := \sum _{\substack {j \in \{1,\ldots ,d\} \\ \beta _j \in B_{p,n}(f)}} ( {\mathrm {ord}}_p(\beta _j^{p^{r_{p,n}(\beta _j)}} - \tau _p(\pi _p(\beta _j))^{p^{r_{p,n}(\beta _j)}}) - r_{p,n}(\beta _j) )$
.
Proof. We see from Theorem 2.2 that
 $$ \begin{align*} {\mathrm{ord}}_p(\Delta_n(f)) = \mu_p(f) \cdot n + \sum_{\substack{j \in \{1,\ldots,d\} \\ \beta_j \in B_{p,n}(f)}} {\mathrm{ord}}_p(\beta_j^n - 1), \end{align*} $$
$$ \begin{align*} {\mathrm{ord}}_p(\Delta_n(f)) = \mu_p(f) \cdot n + \sum_{\substack{j \in \{1,\ldots,d\} \\ \beta_j \in B_{p,n}(f)}} {\mathrm{ord}}_p(\beta_j^n - 1), \end{align*} $$
and Theorem 2.3 implies that
for every
![]() $\beta \in B_{p,n}(f)$
, which allows us to conclude the proof.
$\beta \in B_{p,n}(f)$
, which allows us to conclude the proof.
Moreover, we can use Theorems 2.2 and 2.3 to pin down the asymptotic behaviour of the p-adic valuation of the Pierce–Lehmer sequence associated to an integral polynomial that does not vanish on the p-adic unit circle or on roots of unity.
Corollary 2.6. Let
![]() $f(t) \in \mathbb {Z}[t] \setminus \{0\}$
and assume that
$f(t) \in \mathbb {Z}[t] \setminus \{0\}$
and assume that
![]() $f(\alpha ) \neq 0$
for every
$f(\alpha ) \neq 0$
for every
![]() $\alpha \in \mathbb {C}_p$
such that
$\alpha \in \mathbb {C}_p$
such that
![]() $\lvert \alpha \rvert _p = 1$
. Then,
$\lvert \alpha \rvert _p = 1$
. Then,
for all
![]() $n \in \mathbb {N}$
. If one only assumes that
$n \in \mathbb {N}$
. If one only assumes that
![]() $f(\zeta ) \neq 0$
for every
$f(\zeta ) \neq 0$
for every
![]() $\zeta \in W_\infty $
,
$\zeta \in W_\infty $
,
as
![]() $n \to \infty $
.
$n \to \infty $
.
Remark 2.7. A similar result holds true for the Archimedean Mahler measure. More precisely, we see directly from the definition given in (2-2) that for every polynomial
![]() $f \in \mathbb {Z}[t] \setminus \{0\}$
that does not vanish on the unit circle of
$f \in \mathbb {Z}[t] \setminus \{0\}$
that does not vanish on the unit circle of
![]() $\mathbb {C}$
, the asymptotic
$\mathbb {C}$
, the asymptotic
holds true as
![]() $n \to +\infty $
. If one only assumes that the roots of f are not roots of unity, then one sees that
$n \to +\infty $
. If one only assumes that the roots of f are not roots of unity, then one sees that
as
![]() $n \to \infty $
. This follows from an inequality originally proved by Gelfand, as explained for instance in [Reference Everest and Ward11, Lemma 1.10]. However, if f has some root on the unit circle of
$n \to \infty $
. This follows from an inequality originally proved by Gelfand, as explained for instance in [Reference Everest and Ward11, Lemma 1.10]. However, if f has some root on the unit circle of
![]() $\mathbb {C}$
, the behaviour of the absolute values
$\mathbb {C}$
, the behaviour of the absolute values
![]() $\lvert \Delta _n(f) \rvert _\infty $
is quite chaotic, as exemplified for instance by [Reference Everest and Ward11, Theorem 2.16], which shows that the sequence of ratios
$\lvert \Delta _n(f) \rvert _\infty $
is quite chaotic, as exemplified for instance by [Reference Everest and Ward11, Theorem 2.16], which shows that the sequence of ratios
![]() $\lvert \Delta _n(f)/\Delta _{n-1}(f) \rvert _\infty $
converges if and only if f has no roots on the unit circle of
$\lvert \Delta _n(f)/\Delta _{n-1}(f) \rvert _\infty $
converges if and only if f has no roots on the unit circle of
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
The p-adic valuation of various subsequences of a Pierce–Lehmer sequence can be understood from Theorems 2.2 and 2.3. For instance, the following corollary shows that such a p-adic valuation of the sub-sequence
![]() $\{ \Delta _{p^n}(f) \}_{n=0}^{+\infty }$
associated to a polynomial
$\{ \Delta _{p^n}(f) \}_{n=0}^{+\infty }$
associated to a polynomial
![]() $f \in \mathbb {Z}[t]$
that does not vanish at roots of unity exhibits a behaviour similar to the p-adic valuation of the class number in
$f \in \mathbb {Z}[t]$
that does not vanish at roots of unity exhibits a behaviour similar to the p-adic valuation of the class number in
![]() $\mathbb {Z}_{p}$
-extensions of number fields, which was already studied in the seminal work of Iwasawa [Reference Iwasawa22].
$\mathbb {Z}_{p}$
-extensions of number fields, which was already studied in the seminal work of Iwasawa [Reference Iwasawa22].
Corollary 2.8. Let
![]() $f(t) \in \mathbb {Z}[t]$
be a polynomial that does not vanish at roots of unity, p be a rational prime and
$f(t) \in \mathbb {Z}[t]$
be a polynomial that does not vanish at roots of unity, p be a rational prime and
![]() $\beta _1,\ldots ,\beta _d$
denote the p-adic roots of f, counted with multiplicities. Then, there exist two constants
$\beta _1,\ldots ,\beta _d$
denote the p-adic roots of f, counted with multiplicities. Then, there exist two constants
![]() $k_0(f,p) \in \mathbb {N}$
and
$k_0(f,p) \in \mathbb {N}$
and
![]() $\nu _p(f) \in \mathbb {Z}$
, depending on p and f, such that the following equality:
$\nu _p(f) \in \mathbb {Z}$
, depending on p and f, such that the following equality:
holds true for every
![]() $k \geq k_0(f,p)$
, where
$k \geq k_0(f,p)$
, where
![]() $\mu _{p}(f) := -m_{p}(f)/{\log} (p)$
and
$\mu _{p}(f) := -m_{p}(f)/{\log} (p)$
and
Proof. This follows directly from Corollary 2.5. Indeed, the invariant
![]() $\mu _p(f)$
coincides with the one introduced in (2-10). Moreover, let us note that
$\mu _p(f)$
coincides with the one introduced in (2-10). Moreover, let us note that
![]() $B_{p,p^k}(f) = B_{p,1}(f)$
for every
$B_{p,p^k}(f) = B_{p,1}(f)$
for every
![]() $k \geq 1$
. To see this, fix any
$k \geq 1$
. To see this, fix any
![]() $\beta \in \overline {\mathbb {Q}}_p$
such that
$\beta \in \overline {\mathbb {Q}}_p$
such that
![]() $\lvert \beta \rvert _p = 1$
. Then, we have that
$\lvert \beta \rvert _p = 1$
. Then, we have that
![]() $\lvert \beta ^{p^k} - 1 \rvert _p < 1$
if and only if the multiplicative order of
$\lvert \beta ^{p^k} - 1 \rvert _p < 1$
if and only if the multiplicative order of
![]() $\pi _p(\beta ) \in \overline {\mathbb {F}}_p^\times $
is a multiple of
$\pi _p(\beta ) \in \overline {\mathbb {F}}_p^\times $
is a multiple of
![]() $p^k$
. However, the aforementioned multiplicative order is coprime to p. Therefore,
$p^k$
. However, the aforementioned multiplicative order is coprime to p. Therefore,
![]() $\lvert \beta ^{p^k} - 1 \rvert _p < 1$
if and only if
$\lvert \beta ^{p^k} - 1 \rvert _p < 1$
if and only if
![]() $\pi _p(\beta ) = 1$
, which is equivalent to saying that
$\pi _p(\beta ) = 1$
, which is equivalent to saying that
![]() $\lvert \beta - 1 \rvert _p < 1$
. Hence, we see immediately from the definition of the sets
$\lvert \beta - 1 \rvert _p < 1$
. Hence, we see immediately from the definition of the sets
![]() $B_{p,n}(f)$
given in (2-11) that
$B_{p,n}(f)$
given in (2-11) that
![]() $B_{p,p^k}(f) = B_{p,1}(f)$
for every
$B_{p,p^k}(f) = B_{p,1}(f)$
for every
![]() $k \geq 1$
, as we wanted to show. This shows in particular that
$k \geq 1$
, as we wanted to show. This shows in particular that
![]() $\lambda _{p,p^k}(f) = \lambda _p(f)$
for every
$\lambda _{p,p^k}(f) = \lambda _p(f)$
for every
![]() $k \geq 1$
, where
$k \geq 1$
, where
![]() $\lambda _{p,p^k}(f)$
is the invariant defined in (2-12).
$\lambda _{p,p^k}(f)$
is the invariant defined in (2-12).
To conclude, it suffices to define
where
![]() $s_p(\beta )$
is the invariant defined in (2-13). Then, for every
$s_p(\beta )$
is the invariant defined in (2-13). Then, for every
![]() $k \geq k_0(f,p)$
and every
$k \geq k_0(f,p)$
and every
![]() $\beta \in \overline {\mathbb {Q}}_p$
, such that
$\beta \in \overline {\mathbb {Q}}_p$
, such that
![]() $\lvert \beta \rvert _p = 1$
and
$\lvert \beta \rvert _p = 1$
and
![]() $f(\beta ) = 0$
, we have that
$f(\beta ) = 0$
, we have that
![]() $r_{p,p^k}(\beta ) = s_p(\beta )$
, as follows immediately from the fact that
$r_{p,p^k}(\beta ) = s_p(\beta )$
, as follows immediately from the fact that
![]() $r_{p,p^k}(\beta ) = \min (k,s_p(\beta ))$
. Therefore, using the definition of
$r_{p,p^k}(\beta ) = \min (k,s_p(\beta ))$
. Therefore, using the definition of
![]() $\nu _{p,n}(f)$
given in Corollary 2.5, we see that for every integer
$\nu _{p,n}(f)$
given in Corollary 2.5, we see that for every integer
![]() $k \geq k_0(f,p)$
, the invariant
$k \geq k_0(f,p)$
, the invariant
 $$ \begin{align*} \begin{aligned} \nu_{p,p^k}(f) &= \sum_{\substack{j \in \{1,\ldots,d\} \\ \beta_j \in B_{p,p^k}(f)}} ( {\mathrm{ord}}_p(\beta_j^{p^{r_{p,p^k}(\beta_j)}} - \tau_p(\pi_p(\beta_j))^{p^{r_{p,p^k}(\beta_j)}}) - r_{p,p^k}(\beta_j) ) \\ &= \sum_{\substack{j \in \{1,\ldots,d\} \\ \beta_j \in B_{p,1}(f)}} ( {\mathrm{ord}}_p(\beta_j^{p^{s_p(\beta_j)}} - \tau_p(\pi_p(\beta_j))^{p^{s_p(\beta_j)}}) - s_p(\beta_j) ) \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \nu_{p,p^k}(f) &= \sum_{\substack{j \in \{1,\ldots,d\} \\ \beta_j \in B_{p,p^k}(f)}} ( {\mathrm{ord}}_p(\beta_j^{p^{r_{p,p^k}(\beta_j)}} - \tau_p(\pi_p(\beta_j))^{p^{r_{p,p^k}(\beta_j)}}) - r_{p,p^k}(\beta_j) ) \\ &= \sum_{\substack{j \in \{1,\ldots,d\} \\ \beta_j \in B_{p,1}(f)}} ( {\mathrm{ord}}_p(\beta_j^{p^{s_p(\beta_j)}} - \tau_p(\pi_p(\beta_j))^{p^{s_p(\beta_j)}}) - s_p(\beta_j) ) \end{aligned} \end{align*} $$
is independent of k. This allows us to set
 $$ \begin{align*} \nu_p(f) := \sum_{\substack{j \in \{1,\ldots,d\} \\ \beta_j \in B_{p,1}(f)}} ( {\mathrm{ord}}_p(\beta_j^{p^{s_p(\beta_j)}} - \tau_p(\pi_p(\beta_j))^{p^{s_p(\beta_j)}}) - s_p(\beta_j) ), \end{align*} $$
$$ \begin{align*} \nu_p(f) := \sum_{\substack{j \in \{1,\ldots,d\} \\ \beta_j \in B_{p,1}(f)}} ( {\mathrm{ord}}_p(\beta_j^{p^{s_p(\beta_j)}} - \tau_p(\pi_p(\beta_j))^{p^{s_p(\beta_j)}}) - s_p(\beta_j) ), \end{align*} $$
and to conclude our proof.
Moreover, if
![]() $\ell , p \in \mathbb {N}$
are two distinct rational primes, the
$\ell , p \in \mathbb {N}$
are two distinct rational primes, the
![]() $\ell $
-adic valuation of the sub-sequence
$\ell $
-adic valuation of the sub-sequence
![]() $\{ \Delta _{p^n}(P) \}_{n=0}^{+\infty }$
exhibits a behaviour that is similar to that observed by Washington [Reference Washington58] in the case of
$\{ \Delta _{p^n}(P) \}_{n=0}^{+\infty }$
exhibits a behaviour that is similar to that observed by Washington [Reference Washington58] in the case of
![]() $\mathbb {Z}_p$
-towers of number fields.
$\mathbb {Z}_p$
-towers of number fields.
Corollary 2.9. Let
![]() $f(t) \in \mathbb {Z}[t]$
be a polynomial that does not vanish at roots of unity. Let p and
$f(t) \in \mathbb {Z}[t]$
be a polynomial that does not vanish at roots of unity. Let p and
![]() $\ell $
be two distinct rational primes. Then, there exist two constants
$\ell $
be two distinct rational primes. Then, there exist two constants
![]() $k_0(f,p,\ell ) \in \mathbb {N}$
and
$k_0(f,p,\ell ) \in \mathbb {N}$
and
![]() $\nu _p(f,\ell ) \in \mathbb {Z}$
, depending on p,
$\nu _p(f,\ell ) \in \mathbb {Z}$
, depending on p,
![]() $\ell $
and f, such that the equality
$\ell $
and f, such that the equality
holds true for every
![]() $k \geq k_0(f,p,\ell )$
, where again
$k \geq k_0(f,p,\ell )$
, where again
![]() $\mu _{p}(f) = -m_{p}(f)/{\log} (p)$
.
$\mu _{p}(f) = -m_{p}(f)/{\log} (p)$
.
Proof. This follows once again from Corollary 2.5. Indeed,
![]() $\mu _p(f)$
is once again identical to the invariant defined in (2-10). Moreover,
$\mu _p(f)$
is once again identical to the invariant defined in (2-10). Moreover,
![]() $\mathrm {ord}_p(\ell ^k) = 0$
for every
$\mathrm {ord}_p(\ell ^k) = 0$
for every
![]() $k \geq 0$
, which shows that the part of the equality (2-14) involving the invariant
$k \geq 0$
, which shows that the part of the equality (2-14) involving the invariant
![]() $\lambda _{p,n}(f)$
does not appear when
$\lambda _{p,n}(f)$
does not appear when
![]() $n = \ell ^k$
.
$n = \ell ^k$
.
To conclude, let
![]() $\beta _1,\ldots ,\beta _d \in \overline {\mathbb {Q}}_p$
be the p-adic roots of
$\beta _1,\ldots ,\beta _d \in \overline {\mathbb {Q}}_p$
be the p-adic roots of
![]() $f(t)$
, counted with multiplicities, that lie on the p-adic unit circle, and
$f(t)$
, counted with multiplicities, that lie on the p-adic unit circle, and
![]() $N_1,\ldots ,N_d$
be the multiplicative orders of their reductions
$N_1,\ldots ,N_d$
be the multiplicative orders of their reductions
![]() $\pi _p(\beta _1),\ldots ,\pi _p(\beta _d) \in \overline {\mathbb {F}}_p^\times $
. Then, for every
$\pi _p(\beta _1),\ldots ,\pi _p(\beta _d) \in \overline {\mathbb {F}}_p^\times $
. Then, for every
![]() $j \in \{1,\ldots ,d\}$
, we have that
$j \in \{1,\ldots ,d\}$
, we have that
![]() $\lvert \beta _j^{\ell ^k} - 1 \rvert _p < 1$
if and only if there exists some nonnegative integer
$\lvert \beta _j^{\ell ^k} - 1 \rvert _p < 1$
if and only if there exists some nonnegative integer
![]() $a_j \le k$
such that
$a_j \le k$
such that
![]() $N_j = \ell ^{a_j}$
. Moreover,
$N_j = \ell ^{a_j}$
. Moreover,
for every
![]() $j \in \{1,\ldots ,d\}$
and every
$j \in \{1,\ldots ,d\}$
and every
![]() $k \geq 0$
. Therefore, if we set
$k \geq 0$
. Therefore, if we set
 $$ \begin{align*} \begin{aligned} k_0(f,p,\ell) &:= \max\{\mathrm{ord}_\ell(N_j) \colon j \in \{ 1,\ldots,d \} \} \\ \nu_p(f,\ell) &:= \sum_{\substack{ j \in \{1,\ldots,d\} \\ \beta_j \in B_{p,\ell^{k_0}}(f)}} \mathrm{ord}_p(\beta_j - \tau_p(\pi_p(\beta_j))), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} k_0(f,p,\ell) &:= \max\{\mathrm{ord}_\ell(N_j) \colon j \in \{ 1,\ldots,d \} \} \\ \nu_p(f,\ell) &:= \sum_{\substack{ j \in \{1,\ldots,d\} \\ \beta_j \in B_{p,\ell^{k_0}}(f)}} \mathrm{ord}_p(\beta_j - \tau_p(\pi_p(\beta_j))), \end{aligned} \end{align*} $$
where we write
![]() $k_0$
instead of
$k_0$
instead of
![]() $k_0(f,p,\ell )$
, then, we see from the definition of
$k_0(f,p,\ell )$
, then, we see from the definition of
![]() $\nu _{p,n}(f)$
given in Corollary 2.5 that
$\nu _{p,n}(f)$
given in Corollary 2.5 that
![]() $\nu _{p,\ell ^k}(f) = \nu _p(f,\ell )$
for every
$\nu _{p,\ell ^k}(f) = \nu _p(f,\ell )$
for every
![]() $k \geq k_0(f,p,\ell )$
, and this allows us to conclude our proof.
$k \geq k_0(f,p,\ell )$
, and this allows us to conclude our proof.
In fact, Corollaries 2.8 and 2.9 can be generalised by looking at sequences of integers that are divisible only by a finite number of primes, as done by Friedman [Reference Friedman13] for cyclotomic
![]() $\mathbb{Z}_{p_{1}}\times \cdots \times \mathbb{Z}_{p_{s}}$
-extensions of number fields that are abelian over
$\mathbb{Z}_{p_{1}}\times \cdots \times \mathbb{Z}_{p_{s}}$
-extensions of number fields that are abelian over
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
Corollary 2.10. Let
![]() $f(t) \in \mathbb {Z}[t]$
be a polynomial that does not vanish at roots of unity. Let
$f(t) \in \mathbb {Z}[t]$
be a polynomial that does not vanish at roots of unity. Let
![]() $\ell _1,\ldots ,\ell _r$
be distinct prime numbers, and let
$\ell _1,\ldots ,\ell _r$
be distinct prime numbers, and let
![]() $\mathcal {S} \subseteq \mathbb {N}$
be the set of those integers whose prime divisors are contained in
$\mathcal {S} \subseteq \mathbb {N}$
be the set of those integers whose prime divisors are contained in
![]() $\{\ell _1,\ldots ,\ell _r\}$
. Then:
$\{\ell _1,\ldots ,\ell _r\}$
. Then:
-
• for every
 $j \in \{1,\ldots ,r\}$
, there exist a nonnegative integer
$j \in \{1,\ldots ,r\}$
, there exist a nonnegative integer
 $\lambda _j(f)$
and an integer
$\lambda _j(f)$
and an integer
 $\nu _j(f)$
such that for every
$\nu _j(f)$
such that for every
 $n = \ell _1^{k_1} \cdots \ell _j^{k_j} \cdots \ell _r^{k_r} \in \mathcal {S}$
, as long as n is big enough, where again
$n = \ell _1^{k_1} \cdots \ell _j^{k_j} \cdots \ell _r^{k_r} \in \mathcal {S}$
, as long as n is big enough, where again $$ \begin{align*} \mathrm{ord}_{\ell_j}(\kappa(X_n)) = \mu_{\ell_j}(f) \cdot n + \lambda_j(f) \cdot k_j + \nu_j(f) \end{align*} $$
$$ \begin{align*} \mathrm{ord}_{\ell_j}(\kappa(X_n)) = \mu_{\ell_j}(f) \cdot n + \lambda_j(f) \cdot k_j + \nu_j(f) \end{align*} $$
 $\mu _{\ell _j}(f) = -m_{\ell _j}(f)/{\log}(\ell _j)$
;
$\mu _{\ell _j}(f) = -m_{\ell _j}(f)/{\log}(\ell _j)$
;
-
• for every prime
 $p \not \in \{\ell _1,\ldots ,\ell _r\}$
, there exists an integer
$p \not \in \{\ell _1,\ldots ,\ell _r\}$
, there exists an integer
 $\nu (f)$
such that for every
$\nu (f)$
such that for every $$ \begin{align*} \mathrm{ord}_p(\kappa(X_n)) = \mu_p(f) \cdot n + \nu(f) \end{align*} $$
$$ \begin{align*} \mathrm{ord}_p(\kappa(X_n)) = \mu_p(f) \cdot n + \nu(f) \end{align*} $$
 $n \in \mathcal {S}$
that is big enough.
$n \in \mathcal {S}$
that is big enough.
Proof. The proof is similar to the proofs of the two previous corollaries, and we leave it to the reader.
Remark 2.11. In the situation where the polynomial
![]() $f(t)$
is monic, the p-adic valuation of a Pierce–Lehmer sequence was also studied in [Reference Ji and Qin23]. In this situation, there is no p-adic Mahler measure appearing in the formulae.
$f(t)$
is monic, the p-adic valuation of a Pierce–Lehmer sequence was also studied in [Reference Ji and Qin23]. In this situation, there is no p-adic Mahler measure appearing in the formulae.
Remark 2.12. Note that the Pierce–Lehmer sequence
![]() $\{ \Delta _n(f) \}_{n \in \mathbb {N}}$
associated to any polynomial
$\{ \Delta _n(f) \}_{n \in \mathbb {N}}$
associated to any polynomial
![]() $f \in \mathbb {Z}[t]$
satisfies a linear recurrence, as explained in [Reference Lehmer32, Section 8]. Therefore, studying the p-adic valuation of Pierce–Lehmer sequences can be seen as a special case of the more general problem of studying the p-adic valuation of linearly recurrent sequences, which has been the subject of great attention (see for instance [Reference Bilu, Luca, Nieuwveld, Ouaknine and Worrell4]). We also refer the interested reader to the works [Reference Einsiedler, Everest and Ward10, Reference Flatters12], which treat problems related to the p-adic valuation of Pierce–Lehmer sequences.
$f \in \mathbb {Z}[t]$
satisfies a linear recurrence, as explained in [Reference Lehmer32, Section 8]. Therefore, studying the p-adic valuation of Pierce–Lehmer sequences can be seen as a special case of the more general problem of studying the p-adic valuation of linearly recurrent sequences, which has been the subject of great attention (see for instance [Reference Bilu, Luca, Nieuwveld, Ouaknine and Worrell4]). We also refer the interested reader to the works [Reference Einsiedler, Everest and Ward10, Reference Flatters12], which treat problems related to the p-adic valuation of Pierce–Lehmer sequences.
3. Graph theory
The aim of this section is to prove Theorem 3.17, which provides an explicit expression for the p-adic valuation of the number of spanning trees in a
![]() $\mathbb {Z}$
-tower of graphs in terms of a polynomial naturally associated to this tower, which we call the Ihara polynomial and which we define in Section 3.3. In particular, Theorem 1.1 is a simplified version of Theorem 3.17, as we explain in Section 3.6. To do so, we first recall some fundamentals about graphs and their covers in Sections 3.1 and 3.2. Then, we devote Section 3.3 to the proof of Theorem 3.6, which provides an explicit formula relating the number of spanning trees of the members of a
$\mathbb {Z}$
-tower of graphs in terms of a polynomial naturally associated to this tower, which we call the Ihara polynomial and which we define in Section 3.3. In particular, Theorem 1.1 is a simplified version of Theorem 3.17, as we explain in Section 3.6. To do so, we first recall some fundamentals about graphs and their covers in Sections 3.1 and 3.2. Then, we devote Section 3.3 to the proof of Theorem 3.6, which provides an explicit formula relating the number of spanning trees of the members of a
![]() $\mathbb {Z}$
-cover of graphs to the Pierce–Lehmer sequence associated to the Ihara polynomial of this tower. We provide an explicit example that verifies this relation in Section 3.4. Moreover, Section 3.5 shows how to combine Theorem 3.6 with the results proven in Section 2.3, to provide some asymptotic expressions for the growth of the number of spanning trees in a
$\mathbb {Z}$
-cover of graphs to the Pierce–Lehmer sequence associated to the Ihara polynomial of this tower. We provide an explicit example that verifies this relation in Section 3.4. Moreover, Section 3.5 shows how to combine Theorem 3.6 with the results proven in Section 2.3, to provide some asymptotic expressions for the growth of the number of spanning trees in a
![]() $\mathbb {Z}$
-tower. In particular, this generalises two previous results of Mednykh and Mednykh [Reference Mednykh and Mednykh41, Reference Mednykh42].
$\mathbb {Z}$
-tower. In particular, this generalises two previous results of Mednykh and Mednykh [Reference Mednykh and Mednykh41, Reference Mednykh42].
3.1. Galois covers of locally finite graphs
The aim of this subsection is to formally introduce the kinds of graphs that are considered in this article and their Galois theory.
3.1.1. Locally finite graphs
Let
![]() $X = (V_{X},\mathbf {E}_{X})$
be a graph in the sense of Serre (see [Reference Serre48] and also [Reference Sunada52]), where
$X = (V_{X},\mathbf {E}_{X})$
be a graph in the sense of Serre (see [Reference Serre48] and also [Reference Sunada52]), where
![]() $V_X$
and
$V_X$
and
![]() $\mathbf {E}_X$
are two sets, to be interpreted as the sets of vertices and (directed) edges of X. In particular, each edge
$\mathbf {E}_X$
are two sets, to be interpreted as the sets of vertices and (directed) edges of X. In particular, each edge
![]() $e \in \mathbf {E}_X$
has an origin
$e \in \mathbf {E}_X$
has an origin
![]() $o(e) \in V_X$
and a terminus
$o(e) \in V_X$
and a terminus
![]() $t(e) \in V_X$
, giving rise to the incidence map
$t(e) \in V_X$
, giving rise to the incidence map
 $$ \begin{align*} \begin{aligned} \mathrm{inc} \colon &\mathbf{E}_{X} \to V_{X} \times V_{X} \\ &e \mapsto (o(e),t(e)) \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathrm{inc} \colon &\mathbf{E}_{X} \to V_{X} \times V_{X} \\ &e \mapsto (o(e),t(e)) \end{aligned} \end{align*} $$
and to the inversion map
![]() $\mathbf {E}_{X} \rightarrow \mathbf {E}_{X}$
, denoted by
$\mathbf {E}_{X} \rightarrow \mathbf {E}_{X}$
, denoted by
![]() $e \mapsto \bar {e}$
, such that
$e \mapsto \bar {e}$
, such that
and
![]() $\overline {\overline {e}} = e \neq \overline {e}$
for every
$\overline {\overline {e}} = e \neq \overline {e}$
for every
![]() $e \in \mathbf {E}_X$
.
$e \in \mathbf {E}_X$
.
A graph X is called finite if both
![]() $V_{X}$
and
$V_{X}$
and
![]() $\mathbf {E}_{X}$
are finite sets. Moreover, a graph X is called locally finite if for each vertex
$\mathbf {E}_{X}$
are finite sets. Moreover, a graph X is called locally finite if for each vertex
![]() $v \in V_{X}$
, the set of edges with origin at v, defined as
$v \in V_{X}$
, the set of edges with origin at v, defined as
is finite. In this case, one defines the valency (or degree) of a vertex
![]() $v \in V_{X}$
to be
$v \in V_{X}$
to be
Any finite graph is in particular locally finite.
Assumption 3.1. In this paper, all graphs will be locally finite.
3.1.2. Paths and loops
Let us recall that a path
![]() $c = e_{1} \cdot \cdots \cdot e_{m}$
in a graph X consists of a sequence of directed edges
$c = e_{1} \cdot \cdots \cdot e_{m}$
in a graph X consists of a sequence of directed edges
![]() $e_{i} \in \mathbf {E}_{X}$
such that
$e_{i} \in \mathbf {E}_{X}$
such that
![]() $t(e_{i}) = o(e_{i+1})$
for each index
$t(e_{i}) = o(e_{i+1})$
for each index
![]() $i \in \{1,\ldots ,m-1\}$
. The origin and the terminus of the path
$i \in \{1,\ldots ,m-1\}$
. The origin and the terminus of the path
![]() $c = e_1 \cdot \cdots \cdot e_m$
are defined as
$c = e_1 \cdot \cdots \cdot e_m$
are defined as
![]() $o(c) = o(e_{1})$
and
$o(c) = o(e_{1})$
and
![]() $t(c) = t(e_{m})$
, respectively.
$t(c) = t(e_{m})$
, respectively.
A graph X is called connected if given any two vertices
![]() $v_{1}, v_{2} \in V_{X}$
, there exists a path c in X such that
$v_{1}, v_{2} \in V_{X}$
, there exists a path c in X such that
![]() $o(c) = v_{1}$
and
$o(c) = v_{1}$
and
![]() $t(c) = v_{2}$
. Finally, a loop based at a vertex
$t(c) = v_{2}$
. Finally, a loop based at a vertex
![]() $v_0 \in X$
is a path c in X such that
$v_0 \in X$
is a path c in X such that
![]() $o(c) = t(c) = v_0$
.
$o(c) = t(c) = v_0$
.
This allows one to define the fundamental group of X based at a vertex
![]() $v_0 \in V_X$
, which is denoted by
$v_0 \in V_X$
, which is denoted by
![]() $\pi _1(X,v_0)$
, as the set of loops based at
$\pi _1(X,v_0)$
, as the set of loops based at
![]() $v_0$
, considered modulo homotopy (see [Reference Sunada52, Section 3.5] for the precise definition of this equivalence relation in the context of graphs), endowed with the group operation given by the concatenation of paths (see [Reference Sunada52, Section 5.3] for details).
$v_0$
, considered modulo homotopy (see [Reference Sunada52, Section 3.5] for the precise definition of this equivalence relation in the context of graphs), endowed with the group operation given by the concatenation of paths (see [Reference Sunada52, Section 5.3] for details).
3.1.3. Galois covers of graphs
Let Y and X be two graphs. A morphism of graphs
![]() $f:Y \rightarrow X$
is called a cover (or a covering map) if the following two conditions are satisfied:
$f:Y \rightarrow X$
is called a cover (or a covering map) if the following two conditions are satisfied:
-
(1)
 $f:V_{Y} \rightarrow V_{X}$
is surjective;
$f:V_{Y} \rightarrow V_{X}$
is surjective; -
(2) for all
 $w \in V_{Y}$
, the restriction
$w \in V_{Y}$
, the restriction
 $f|_{\mathbf {E}_{Y,w}}$
induces a bijection
$f|_{\mathbf {E}_{Y,w}}$
induces a bijection  $$ \begin{align*}f|_{\mathbf{E}_{Y,w}}:\mathbf{E}_{Y,w} \stackrel{\approx}{\rightarrow} \mathbf{E}_{X,f(w)}. \end{align*} $$
$$ \begin{align*}f|_{\mathbf{E}_{Y,w}}:\mathbf{E}_{Y,w} \stackrel{\approx}{\rightarrow} \mathbf{E}_{X,f(w)}. \end{align*} $$
We will often refer to
![]() $Y/X$
as a cover if the covering map is understood from the context. Given a cover
$Y/X$
as a cover if the covering map is understood from the context. Given a cover
![]() $f:Y \rightarrow X$
, one defines as usual
$f:Y \rightarrow X$
, one defines as usual
![]() $\mathrm {Aut}_{f}(Y/X)$
to be the subgroup of
$\mathrm {Aut}_{f}(Y/X)$
to be the subgroup of
![]() $\mathrm {Aut}(Y)$
consisting of the automorphisms
$\mathrm {Aut}(Y)$
consisting of the automorphisms
![]() $\iota \in \mathrm {Aut}(Y)$
satisfying
$\iota \in \mathrm {Aut}(Y)$
satisfying
![]() $f \circ \iota = f$
. Again, we will often write
$f \circ \iota = f$
. Again, we will often write
![]() $\mathrm {Aut}(Y/X)$
instead of
$\mathrm {Aut}(Y/X)$
instead of
![]() $\mathrm {Aut}_{f}(Y/X)$
if f is understood.
$\mathrm {Aut}_{f}(Y/X)$
if f is understood.
Let us also recall that a cover
![]() $f:Y \rightarrow X$
is called Galois if the following two conditions are satisfied:
$f:Y \rightarrow X$
is called Galois if the following two conditions are satisfied:
-
(1) the graph Y is connected (and hence also X);
-
(2) the group
 $\mathrm {Aut}(Y/X)$
acts transitively on the fibre
$\mathrm {Aut}(Y/X)$
acts transitively on the fibre
 $f^{-1}(v)$
for all
$f^{-1}(v)$
for all
 $v \in V_{X}$
.
$v \in V_{X}$
.
If
![]() $Y/X$
is a Galois cover, we write
$Y/X$
is a Galois cover, we write
![]() $\mathrm {Gal}(Y/X)$
instead of
$\mathrm {Gal}(Y/X)$
instead of
![]() $\mathrm {Aut}(Y/X)$
. In this case, one has the usual Galois correspondence between subgroups of
$\mathrm {Aut}(Y/X)$
. In this case, one has the usual Galois correspondence between subgroups of
![]() $\mathrm {Aut}(Y/X)$
and equivalence classes of intermediate covers of
$\mathrm {Aut}(Y/X)$
and equivalence classes of intermediate covers of
![]() $Y/X$
.
$Y/X$
.
3.1.4. Voltage assignments
Let X be a graph and let G be a group. A voltage assignment on X with values in G is defined to be a function
![]() $\alpha :\mathbf {E}_{X} \rightarrow G$
satisfying
$\alpha :\mathbf {E}_{X} \rightarrow G$
satisfying
for every
![]() $e \in \mathbf {E}_{X}$
. Each such voltage assignment can be defined starting from an orientation of X, which is a subset
$e \in \mathbf {E}_{X}$
. Each such voltage assignment can be defined starting from an orientation of X, which is a subset
![]() $S \subseteq \mathbf {E}_X$
such that for each edge
$S \subseteq \mathbf {E}_X$
such that for each edge
![]() $e \in \mathbf {E}_X$
, either e or
$e \in \mathbf {E}_X$
, either e or
![]() $\overline {e}$
belong to S, but not both. Then, to get a voltage assignment as above, it suffices to define it on any orientation S and set
$\overline {e}$
belong to S, but not both. Then, to get a voltage assignment as above, it suffices to define it on any orientation S and set
![]() $\alpha (\overline {s}) := \alpha (s)^{-1}$
for every
$\alpha (\overline {s}) := \alpha (s)^{-1}$
for every
![]() $s \in S$
.
$s \in S$
.
3.1.5. Covers from voltage assignments
Given a graph X, a group G and a voltage assignment
one can construct a new graph
![]() $X(G,\alpha )$
as follows:
$X(G,\alpha )$
as follows:
-
• the vertices of
 $X(G,\alpha )$
are given by
$X(G,\alpha )$
are given by
 $V_X \times G$
;
$V_X \times G$
; -
• the (directed) edges of
 $X(G,\alpha )$
are given by
$X(G,\alpha )$
are given by
 $\mathbf {E}_X \times G$
;
$\mathbf {E}_X \times G$
; -
• the origin, terminus and inverse maps are defined as
for each edge $$ \begin{align*} \begin{aligned} o(e,\sigma) &= (o(e),\sigma), \\ t(e,\sigma) &= (t(e),\sigma \cdot \alpha(e)), \\ \overline{(e,\sigma)} &= (\bar{e},\sigma \cdot \alpha(e)) \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} o(e,\sigma) &= (o(e),\sigma), \\ t(e,\sigma) &= (t(e),\sigma \cdot \alpha(e)), \\ \overline{(e,\sigma)} &= (\bar{e},\sigma \cdot \alpha(e)) \end{aligned} \end{align*} $$
 $(e,\sigma ) \in \mathbf {E}_X \times G$
.
$(e,\sigma ) \in \mathbf {E}_X \times G$
.
It is easy to see that if X is locally finite, then so is
![]() $X(G,\alpha )$
, and that the map of graphs
$X(G,\alpha )$
, and that the map of graphs
defined as
![]() $p(v,\sigma ) := v$
on each vertex
$p(v,\sigma ) := v$
on each vertex
![]() $(v,\sigma ) \in V_X \times G$
, and as
$(v,\sigma ) \in V_X \times G$
, and as
![]() $p(e,\sigma ) := e$
on each edge
$p(e,\sigma ) := e$
on each edge
![]() $(e,\sigma ) \in \mathbf {E}_X \times G$
, is actually a covering map. Moreover, this covering map is Galois whenever
$(e,\sigma ) \in \mathbf {E}_X \times G$
, is actually a covering map. Moreover, this covering map is Galois whenever
![]() $X(G,\alpha )$
is connected and, in this case,
$X(G,\alpha )$
is connected and, in this case,
![]() $\operatorname {Gal}(X(G,\alpha )/X) \cong G$
canonically.
$\operatorname {Gal}(X(G,\alpha )/X) \cong G$
canonically.
To conclude, let us observe that the construction of
![]() $X(G,\alpha )$
is functorial with respect to
$X(G,\alpha )$
is functorial with respect to
![]() $\alpha $
. More precisely, for each morphism of groups
$\alpha $
. More precisely, for each morphism of groups
![]() $f \colon G \to H$
, one gets a new voltage assignment
$f \colon G \to H$
, one gets a new voltage assignment
![]() $\beta := f \circ \alpha $
with values in H, and a natural map of graphs
$\beta := f \circ \alpha $
with values in H, and a natural map of graphs
which is defined on each vertex
![]() $(v,\sigma ) \in V_X \times G$
as
$(v,\sigma ) \in V_X \times G$
as
![]() $f_{\ast }(v,\sigma ) := (v,f(\sigma ))$
, and on each edge
$f_{\ast }(v,\sigma ) := (v,f(\sigma ))$
, and on each edge
![]() $(e,\sigma ) \in \mathbf {E}_X \times G$
as
$(e,\sigma ) \in \mathbf {E}_X \times G$
as
![]() $f_\ast (e,\sigma ) := (e,f(\sigma ))$
. Finally, it is easy to see that this morphism
$f_\ast (e,\sigma ) := (e,f(\sigma ))$
. Finally, it is easy to see that this morphism
![]() $f_\ast $
is a covering map whenever f is surjective.
$f_\ast $
is a covering map whenever f is surjective.
3.1.6. Monodromy representations
Let X be a graph and
![]() $\alpha \colon \mathbf {E}_X \to G$
be a voltage assignment with values in a group G. Then, the monodromy representation attached to
$\alpha \colon \mathbf {E}_X \to G$
be a voltage assignment with values in a group G. Then, the monodromy representation attached to
![]() $\alpha $
at a vertex
$\alpha $
at a vertex
![]() $v_0 \in V_X$
is given by the following map:
$v_0 \in V_X$
is given by the following map:
 $$ \begin{align*} \begin{aligned} \rho_{\alpha,v_0} \colon \pi_{1}(X,v_{0}) &\to G \\ [e_1 \cdot \cdots \cdot e_n] &\mapsto \alpha(e_1) \cdot \cdots \cdot \alpha(e_n), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \rho_{\alpha,v_0} \colon \pi_{1}(X,v_{0}) &\to G \\ [e_1 \cdot \cdots \cdot e_n] &\mapsto \alpha(e_1) \cdot \cdots \cdot \alpha(e_n), \end{aligned} \end{align*} $$
which is easily seen to be a well-defined morphism of groups. Moreover, this map can be used to detect when the graph
![]() $X(G,\alpha )$
is connected, and thus when the natural covering map
$X(G,\alpha )$
is connected, and thus when the natural covering map
![]() $p \colon X(G,\alpha ) \to X$
is Galois, as we recall in the following theorem, which is proven in [Reference Ray and Vallières45, Section 2.3.1].
$p \colon X(G,\alpha ) \to X$
is Galois, as we recall in the following theorem, which is proven in [Reference Ray and Vallières45, Section 2.3.1].
Theorem 3.2. Let X be a connected graph and
![]() $\alpha \colon \mathbf {E}_X \to G$
be a voltage assignment. Then, the graph
$\alpha \colon \mathbf {E}_X \to G$
be a voltage assignment. Then, the graph
![]() $X(G,\alpha )$
is connected if and only if the monodromy representation
$X(G,\alpha )$
is connected if and only if the monodromy representation
![]() $\rho _{\alpha ,v_0}$
attached to
$\rho _{\alpha ,v_0}$
attached to
![]() $\alpha $
at some (equivalently, any) vertex
$\alpha $
at some (equivalently, any) vertex
![]() $v_0 \in V_X$
is surjective.
$v_0 \in V_X$
is surjective.
Remark 3.3. Let X be a connected graph,
![]() $v_0 \in V_X$
a vertex of X, and
$v_0 \in V_X$
a vertex of X, and
![]() $\alpha \colon \mathbf {E}_X \to G$
a voltage assignment such that
$\alpha \colon \mathbf {E}_X \to G$
a voltage assignment such that
![]() $\rho _{\alpha ,v_0}$
is surjective. Fix moreover a universal cover
$\rho _{\alpha ,v_0}$
is surjective. Fix moreover a universal cover
![]() $\pi \colon \widetilde {X} \twoheadrightarrow X$
and a vertex
$\pi \colon \widetilde {X} \twoheadrightarrow X$
and a vertex
![]() $w_0 \in \widetilde {X}$
such that
$w_0 \in \widetilde {X}$
such that
![]() $\pi (w_0) = v_0$
. Thanks to the universal property of the universal cover, proved for example in [Reference Sunada52, Theorem 5.10], it can be shown that the intermediate Galois cover of
$\pi (w_0) = v_0$
. Thanks to the universal property of the universal cover, proved for example in [Reference Sunada52, Theorem 5.10], it can be shown that the intermediate Galois cover of
![]() $\widetilde {X} \to X$
given by
$\widetilde {X} \to X$
given by
![]() $X(G,\alpha )$
corresponds to the subgroup
$X(G,\alpha )$
corresponds to the subgroup
![]() $\varphi _{w_0}(\ker (\rho _{\alpha ,v_0})) \trianglelefteq \mathrm {Gal}(\widetilde {X}/X)$
, where
$\varphi _{w_0}(\ker (\rho _{\alpha ,v_0})) \trianglelefteq \mathrm {Gal}(\widetilde {X}/X)$
, where
is the usual group isomorphism.
3.1.7. Systems of Galois covers
Let X be a graph and
![]() $\alpha \colon \mathbf {E}_X \to G$
a voltage assignment taking values in a group G. Given a group homomorphism
$\alpha \colon \mathbf {E}_X \to G$
a voltage assignment taking values in a group G. Given a group homomorphism
![]() $f \colon G \to H$
and a vertex
$f \colon G \to H$
and a vertex
![]() $v_0 \in V_X$
, the monodromy representation attached at
$v_0 \in V_X$
, the monodromy representation attached at
![]() $v_0$
to the Galois cover
$v_0$
to the Galois cover
![]() $f_\ast $
defined in (3-1) is given by
$f_\ast $
defined in (3-1) is given by
![]() $f \circ \rho _{\alpha ,v_0}$
. This shows in particular that if the graph
$f \circ \rho _{\alpha ,v_0}$
. This shows in particular that if the graph
![]() $X(G,\alpha )$
is connected, the graph
$X(G,\alpha )$
is connected, the graph
![]() $X(H,f \circ \alpha )$
will be connected whenever f is surjective. Moreover, any morphism of groups
$X(H,f \circ \alpha )$
will be connected whenever f is surjective. Moreover, any morphism of groups
![]() $f \colon G \to H$
induces another morphism of groups
$f \colon G \to H$
induces another morphism of groups
which sends each
![]() $\tau \in \ker (f)$
to the automorphism
$\tau \in \ker (f)$
to the automorphism
![]() $\phi _\tau \colon X(G,\alpha ) \to X(G,\alpha )$
defined by setting
$\phi _\tau \colon X(G,\alpha ) \to X(G,\alpha )$
defined by setting
![]() $\phi _\tau (v,\sigma ) := (v,\tau \cdot \sigma )$
for each vertex
$\phi _\tau (v,\sigma ) := (v,\tau \cdot \sigma )$
for each vertex
![]() $(v,\sigma ) \in V_X \times G$
, and
$(v,\sigma ) \in V_X \times G$
, and
![]() $\phi _\tau (e,\sigma ) := ({e,\tau \cdot \sigma })$
for each edge
$\phi _\tau (e,\sigma ) := ({e,\tau \cdot \sigma })$
for each edge
![]() $(e,\sigma ) \in \mathbf {E}_X \times G$
. The morphism of groups (3-2) is actually an isomorphism whenever f is surjective, as follows from the unique lifting theorem [Reference Sunada52, Theorem 5.1].
$(e,\sigma ) \in \mathbf {E}_X \times G$
. The morphism of groups (3-2) is actually an isomorphism whenever f is surjective, as follows from the unique lifting theorem [Reference Sunada52, Theorem 5.1].
In particular, the previous discussion shows that any voltage assignment
for which
![]() $X(G,\alpha)$
is connected induces a system of Galois covers indexed by the lattice of quotients of the group G. As we will see in the upcoming sections of this paper, it is interesting to study how various graph invariants evolve when moving across this system.
$X(G,\alpha)$
is connected induces a system of Galois covers indexed by the lattice of quotients of the group G. As we will see in the upcoming sections of this paper, it is interesting to study how various graph invariants evolve when moving across this system.
3.2. The number of spanning trees in finite abelian covers of finite graphs
One particularly interesting kind of invariant of a connected finite graph X is given by its Picard group
![]() $\mathrm {Pic}^{0}(X)$
, also known as the Jacobian, sandpile or class group of X. Its cardinality, denoted by
$\mathrm {Pic}^{0}(X)$
, also known as the Jacobian, sandpile or class group of X. Its cardinality, denoted by
![]() $\kappa (X)$
, is given by the number of spanning trees of the graph X. The aim of this section is to recall, following [Reference Vallières57, Section 3], how this number changes in an abelian cover of a finite graph, using Ihara’s determinant formula.
$\kappa (X)$
, is given by the number of spanning trees of the graph X. The aim of this section is to recall, following [Reference Vallières57, Section 3], how this number changes in an abelian cover of a finite graph, using Ihara’s determinant formula.
3.2.1. Ihara zeta functions
To do so, we will make use of another invariant of a finite connected graph X, namely its Ihara zeta function, which we denote by
![]() $Z_X(u)$
. This is a rational function of u, which can be explicitly computed thanks to the Ihara determinant formula, which we recall below in (3-3), and is proven in [Reference Bass2, Reference Kotani and Sunada29]. More precisely, given an ordering
$Z_X(u)$
. This is a rational function of u, which can be explicitly computed thanks to the Ihara determinant formula, which we recall below in (3-3), and is proven in [Reference Bass2, Reference Kotani and Sunada29]. More precisely, given an ordering
![]() $V_X = \{v_1,\ldots ,v_g\}$
of the vertices of X, we let
$V_X = \{v_1,\ldots ,v_g\}$
of the vertices of X, we let
![]() $A_X := (a_{i,j}) \in \mathbb {Z}^{g \times g}$
denote the adjacency matrix of X, which is defined by setting
$A_X := (a_{i,j}) \in \mathbb {Z}^{g \times g}$
denote the adjacency matrix of X, which is defined by setting
![]() $a_{i,j} := \# \{ e \in \mathbf {E}_X \colon o(e) = v_i, \ t(e) = v_j \}$
. Moreover, we let
$a_{i,j} := \# \{ e \in \mathbf {E}_X \colon o(e) = v_i, \ t(e) = v_j \}$
. Moreover, we let
![]() $D_X := (d_{i,j}) \in \mathbb {Z}^{g \times g}$
denote the valency (or degree) matrix of X, which is a diagonal matrix defined by setting
$D_X := (d_{i,j}) \in \mathbb {Z}^{g \times g}$
denote the valency (or degree) matrix of X, which is a diagonal matrix defined by setting
![]() $d_{i,i} := \mathrm {val}_X(v_i)$
for each
$d_{i,i} := \mathrm {val}_X(v_i)$
for each
![]() $i \in \{1,\ldots ,g\}$
. Then, we can write the Ihara zeta function
$i \in \{1,\ldots ,g\}$
. Then, we can write the Ihara zeta function
![]() $Z_X(u)$
using the following explicit formula:
$Z_X(u)$
using the following explicit formula:
 $$ \begin{align} Z_{X}(u) = \frac{1}{(1-u^{2})^{-\chi(X)} \cdot \mathrm{det}(\mathrm{Id}_g - A_X u + (D_X - \mathrm{Id}_g)u^{2})}, \end{align} $$
$$ \begin{align} Z_{X}(u) = \frac{1}{(1-u^{2})^{-\chi(X)} \cdot \mathrm{det}(\mathrm{Id}_g - A_X u + (D_X - \mathrm{Id}_g)u^{2})}, \end{align} $$
where
![]() $\mathrm {Id}_g$
denotes the
$\mathrm {Id}_g$
denotes the
![]() $g \times g$
identity matrix and
$g \times g$
identity matrix and
![]() $\chi (X) := \lvert V_X \rvert - \lvert \mathbf {E}_X \rvert /2$
is the Euler characteristic of X. In particular, we have that
$\chi (X) := \lvert V_X \rvert - \lvert \mathbf {E}_X \rvert /2$
is the Euler characteristic of X. In particular, we have that
![]() $Z_X(u)^{-1} = (1-u^2)^{-\chi (X)} \cdot h_X(u)$
, where
$Z_X(u)^{-1} = (1-u^2)^{-\chi (X)} \cdot h_X(u)$
, where
is a polynomial.
3.2.2. Hashimoto’s formula
This explicit formula can be used to relate the Ihara zeta function to the number of spanning trees of X. More precisely, given a finite connected graph X, one has
as was proven by Hashimoto in [Reference Hashimoto20, Theorem B] (see also [Reference Bass2, Part II, Sections 5 and 6]). Such a formula, which can be considered as an analogue of the class number formula in the context of graph theory, admits an equivariant generalisation.
3.2.3. Artin–Ihara L-functions
Given a Galois cover of finite connected graphs
![]() $Y/X$
, one can associate to any linear complex representation
$Y/X$
, one can associate to any linear complex representation
![]() $\rho \colon \mathrm {Gal}(Y/X) \to \mathrm {GL}_n(\mathbb {C})$
an Artin–Ihara L-function
$\rho \colon \mathrm {Gal}(Y/X) \to \mathrm {GL}_n(\mathbb {C})$
an Artin–Ihara L-function
![]() $L_{Y/X}(u,\rho )$
. This admits an explicit description analogous to (3-3). More precisely, let
$L_{Y/X}(u,\rho )$
. This admits an explicit description analogous to (3-3). More precisely, let
![]() $d_\rho \in \mathbb {N}$
denote the degree of the representation
$d_\rho \in \mathbb {N}$
denote the degree of the representation
![]() $\rho $
, and fix an ordering
$\rho $
, and fix an ordering
![]() $V_X = \{v_1,\ldots ,v_g\}$
of the vertices of X and a section
$V_X = \{v_1,\ldots ,v_g\}$
of the vertices of X and a section
![]() $\iota \colon V_{X} \rightarrow V_{Y}$
of the projection
$\iota \colon V_{X} \rightarrow V_{Y}$
of the projection
![]() $V_{Y} \to V_{X}$
. Then, [Reference Terras53, Theorem 18.15] shows that the Artin–Ihara L-function
$V_{Y} \to V_{X}$
. Then, [Reference Terras53, Theorem 18.15] shows that the Artin–Ihara L-function
![]() $L_{Y/X}(u,\rho )$
can be explicitly computed thanks to the following formula:
$L_{Y/X}(u,\rho )$
can be explicitly computed thanks to the following formula:
 $$ \begin{align*} L_{Y/X}(u,\rho) = \frac{1}{(1-u^2)^{- \chi(X) \cdot d_\rho} \cdot \det(\mathrm{Id}_{gd_{\rho}} - A_\rho u + Q_\rho u^2)}, \end{align*} $$
$$ \begin{align*} L_{Y/X}(u,\rho) = \frac{1}{(1-u^2)^{- \chi(X) \cdot d_\rho} \cdot \det(\mathrm{Id}_{gd_{\rho}} - A_\rho u + Q_\rho u^2)}, \end{align*} $$
where
![]() $A_\rho , Q_\rho \in \mathbb {C}^{g d_\rho \times g d_\rho }$
are two explicit matrices, whose definitions we now recall. Given
$A_\rho , Q_\rho \in \mathbb {C}^{g d_\rho \times g d_\rho }$
are two explicit matrices, whose definitions we now recall. Given
![]() $\sigma \in G$
,
$\sigma \in G$
,
and we define
where
![]() $\otimes $
denotes the Kronecker product of matrices. For more details, we refer the interested reader to [Reference Terras53, Definition 18.13]. As before, this explicit formula allows one to write
$\otimes $
denotes the Kronecker product of matrices. For more details, we refer the interested reader to [Reference Terras53, Definition 18.13]. As before, this explicit formula allows one to write
![]() $L_{Y/X}(u,\rho )^{-1} = (1-u^2)^{- \chi (X) \cdot d_\rho } \cdot h_{Y/X}(u,\rho )$
, where
$L_{Y/X}(u,\rho )^{-1} = (1-u^2)^{- \chi (X) \cdot d_\rho } \cdot h_{Y/X}(u,\rho )$
, where
is a polynomial. In particular, if
![]() $\mathrm {Gal}(Y/X)$
is abelian and
$\mathrm {Gal}(Y/X)$
is abelian and
![]() $\psi $
is a character of
$\psi $
is a character of
![]() $\mathrm {Gal}(Y/X)$
, we have that
$\mathrm {Gal}(Y/X)$
, we have that
![]() $L_{Y/X}(u,\psi )^{-1} = (1-u^2)^{-\chi (X)} \cdot h_{Y/X}(u,\psi )$
, where
$L_{Y/X}(u,\psi )^{-1} = (1-u^2)^{-\chi (X)} \cdot h_{Y/X}(u,\psi )$
, where
because
![]() $d_\psi = 1$
and
$d_\psi = 1$
and
![]() $Q_\psi = D_X - \mathrm {Id}_g$
, as follows easily from [Reference Terras53, Definition 18.13].
$Q_\psi = D_X - \mathrm {Id}_g$
, as follows easily from [Reference Terras53, Definition 18.13].
3.2.4. Spanning trees and abelian covers
To conclude this subsection, let us recall that the Artin–Ihara L-functions satisfy the Artin formalism (see [Reference Bass2, Reference Stark and Terras51]). This implies that for every Galois cover of finite graphs
![]() $Y/X$
, with Galois group
$Y/X$
, with Galois group
![]() $G := \mathrm {Gal}(Y/X)$
, the Ihara zeta function
$G := \mathrm {Gal}(Y/X)$
, the Ihara zeta function
![]() $Z_Y(u)$
admits the following factorisation:
$Z_Y(u)$
admits the following factorisation:
 $$ \begin{align*} Z_Y(u) = \prod_{\rho \in \mathrm{Irr}(G)} L_{Y/X}(u,\rho)^{d_\rho}, \end{align*} $$
$$ \begin{align*} Z_Y(u) = \prod_{\rho \in \mathrm{Irr}(G)} L_{Y/X}(u,\rho)^{d_\rho}, \end{align*} $$
where
![]() $\mathrm {Irr}(G)$
denotes the set of equivalence classes of complex irreducible representations of a finite group G (see [Reference Terras53, Corollary 18.11]). Therefore, we see easily that
$\mathrm {Irr}(G)$
denotes the set of equivalence classes of complex irreducible representations of a finite group G (see [Reference Terras53, Corollary 18.11]). Therefore, we see easily that
 $$ \begin{align} h_{Y}(u) = \prod_{\rho \in \mathrm{Irr}(G)} h_{Y/X}(u,\rho)^{d_\rho}, \end{align} $$
$$ \begin{align} h_{Y}(u) = \prod_{\rho \in \mathrm{Irr}(G)} h_{Y/X}(u,\rho)^{d_\rho}, \end{align} $$
using the relation
![]() $\chi (Y) = \lvert G \rvert \cdot \chi (X)$
between the Euler characteristics of Y and X, which is explained at the end of [Reference Sunada52, Section 5.1], and the classical identity
$\chi (Y) = \lvert G \rvert \cdot \chi (X)$
between the Euler characteristics of Y and X, which is explained at the end of [Reference Sunada52, Section 5.1], and the classical identity
![]() $\lvert G \rvert = \sum _{\rho \in \mathrm {Irr}(G)} d_\rho ^2$
, proven for example in [Reference Serre49, Section 2.4, Corollary 2]. Finally, if
$\lvert G \rvert = \sum _{\rho \in \mathrm {Irr}(G)} d_\rho ^2$
, proven for example in [Reference Serre49, Section 2.4, Corollary 2]. Finally, if
![]() $\rho _0$
denotes the trivial representation of G and
$\rho _0$
denotes the trivial representation of G and
![]() $\chi (X) \neq 0$
,
$\chi (X) \neq 0$
,
 $$ \begin{align*} \lvert G \rvert \cdot \kappa(Y) = \kappa(X) \cdot \prod_{\rho \neq \rho_0} h_{Y/X}(1,\rho)^{d_\rho}, \end{align*} $$
$$ \begin{align*} \lvert G \rvert \cdot \kappa(Y) = \kappa(X) \cdot \prod_{\rho \neq \rho_0} h_{Y/X}(1,\rho)^{d_\rho}, \end{align*} $$
thanks to (3-4) and (3-6), combined with the fact that
which holds because the Laplacian matrix
![]() $D_X - A_X$
is singular (as explained in [Reference Corry and Perkinson6, Proposition 2.8]). In particular, if
$D_X - A_X$
is singular (as explained in [Reference Corry and Perkinson6, Proposition 2.8]). In particular, if
![]() $Y/X$
is a Galois cover of finite graphs such that
$Y/X$
is a Galois cover of finite graphs such that
![]() $\chi (X) \neq 0$
and
$\chi (X) \neq 0$
and
![]() $G := \mathrm {Gal}(Y/X)$
is abelian,
$G := \mathrm {Gal}(Y/X)$
is abelian,
 $$ \begin{align} |G| \cdot \kappa(Y) = \kappa(X) \prod_{\psi \neq \psi_{0}}h_{Y/X}(1,\psi), \end{align} $$
$$ \begin{align} |G| \cdot \kappa(Y) = \kappa(X) \prod_{\psi \neq \psi_{0}}h_{Y/X}(1,\psi), \end{align} $$
where
![]() $\psi _0$
denotes the trivial character of G and
$\psi _0$
denotes the trivial character of G and
![]() $\psi \in G^\vee $
runs over all nontrivial characters of G.
$\psi \in G^\vee $
runs over all nontrivial characters of G.
3.3. Exact formulae for the number of spanning trees
In this subsection, we introduce what we take the liberty to call the Ihara polynomial
![]() $\mathcal {I}_{\alpha }$
associated to a voltage assignment
$\mathcal {I}_{\alpha }$
associated to a voltage assignment
![]() $\alpha :\mathbf {E}_{X} \rightarrow G$
. When
$\alpha :\mathbf {E}_{X} \rightarrow G$
. When
![]() $G = \mathbb {Z}^d$
for some
$G = \mathbb {Z}^d$
for some
![]() $d \in \mathbb {N}$
, this polynomial was introduced, with a slightly different terminology, in the work of Silver and Williams [Reference Silver and Williams50] (see Remark 3.4 for a comparison between the two definitions). Moreover, when
$d \in \mathbb {N}$
, this polynomial was introduced, with a slightly different terminology, in the work of Silver and Williams [Reference Silver and Williams50] (see Remark 3.4 for a comparison between the two definitions). Moreover, when
![]() $G \in \{ \mathbb {Z}, \mathbb {Z}_\ell \}$
, for some rational prime
$G \in \{ \mathbb {Z}, \mathbb {Z}_\ell \}$
, for some rational prime
![]() $\ell $
, this polynomial was considered by Lei and the second author of the present paper [Reference Lei and Vallières35]. In the general case, this invariant consists of an element of the group ring
$\ell $
, this polynomial was considered by Lei and the second author of the present paper [Reference Lei and Vallières35]. In the general case, this invariant consists of an element of the group ring
![]() $\mathbb {Z}[G]$
, which we write as a generalised polynomial ring
$\mathbb {Z}[G]$
, which we write as a generalised polynomial ring
![]() $\mathbb {Z}[t^G]$
by adding a formal variable t.
$\mathbb {Z}[t^G]$
by adding a formal variable t.
3.3.1. The Ihara polynomial
More precisely, let X be a finite connected graph such that
![]() $\chi (X) \neq 0$
, and let us start with a voltage assignment
$\chi (X) \neq 0$
, and let us start with a voltage assignment
![]() $\alpha :\mathbf {E}_{X} \rightarrow G$
. As before, let us fix an ordering of the vertices of X, given by
$\alpha :\mathbf {E}_{X} \rightarrow G$
. As before, let us fix an ordering of the vertices of X, given by
![]() $V_{X} = \{v_{1},\ldots ,v_{g}\}$
. Then, we can define the matrix
$V_{X} = \{v_{1},\ldots ,v_{g}\}$
. Then, we can define the matrix
 $$ \begin{align*} A_{\alpha}(t) := \bigg(\sum_{\substack{e \in \mathbf{E}_{X} \\ \mathrm{inc}(e) = (v_{i},v_{j})}} t^{\alpha(e)}\bigg) \in \mathbb{Z}[t^G]^{g \times g}, \end{align*} $$
$$ \begin{align*} A_{\alpha}(t) := \bigg(\sum_{\substack{e \in \mathbf{E}_{X} \\ \mathrm{inc}(e) = (v_{i},v_{j})}} t^{\alpha(e)}\bigg) \in \mathbb{Z}[t^G]^{g \times g}, \end{align*} $$
which we use to introduce the Ihara polynomial
where
![]() $D_X$
denotes, as before, the valency (or degree) matrix of X. When no confusion seems to occur, we will just write
$D_X$
denotes, as before, the valency (or degree) matrix of X. When no confusion seems to occur, we will just write
![]() $\mathcal {I}_\alpha $
instead of
$\mathcal {I}_\alpha $
instead of
![]() $\mathcal {I}_\alpha (t)$
.
$\mathcal {I}_\alpha (t)$
.
We note in particular that the Ihara polynomial is self-reciprocal. In other words, we have the following identity:
which comes from the fact that the transpose of the matrix
![]() $A_\alpha (t)$
equals the matrix
$A_\alpha (t)$
equals the matrix
![]() $A_\alpha (t^{-1})$
by definition. Moreover, for every morphism of groups
$A_\alpha (t^{-1})$
by definition. Moreover, for every morphism of groups
![]() $f \colon G \to H$
, we have by definition that
$f \colon G \to H$
, we have by definition that
where
![]() $\beta := f \circ \alpha $
and
$\beta := f \circ \alpha $
and
![]() $f_\ast \colon \mathbb {Z}[t^G] \to \mathbb {Z}[t^H]$
denotes the morphism of rings induced by f.
$f_\ast \colon \mathbb {Z}[t^G] \to \mathbb {Z}[t^H]$
denotes the morphism of rings induced by f.
Remark 3.4. For
![]() $G = \mathbb {Z}^d$
with
$G = \mathbb {Z}^d$
with
![]() $d \in \mathbb {N}$
, this polynomial was introduced in [Reference Silver and Williams50] under the name of Laplacian polynomial. In particular, an unsigned d-periodic graph
$d \in \mathbb {N}$
, this polynomial was introduced in [Reference Silver and Williams50] under the name of Laplacian polynomial. In particular, an unsigned d-periodic graph
![]() $\mathfrak {X}$
in the sense of [Reference Silver and Williams50, Section 6] can be obtained as
$\mathfrak {X}$
in the sense of [Reference Silver and Williams50, Section 6] can be obtained as
![]() $\mathfrak {X} = X(\mathbb {Z}^d,\alpha )$
, where X is a finite graph and
$\mathfrak {X} = X(\mathbb {Z}^d,\alpha )$
, where X is a finite graph and
![]() $\alpha \colon \mathbf {E}_X \to \mathbb {Z}^d$
is a voltage assignment.
$\alpha \colon \mathbf {E}_X \to \mathbb {Z}^d$
is a voltage assignment.
3.3.2. The Ihara polynomial and the number of spanning trees
Suppose now that X is a finite connected graph such that
![]() $\chi (X) \neq 0$
, and fix a voltage assignment
$\chi (X) \neq 0$
, and fix a voltage assignment
with values in some finite abelian group G, such that the induced graph
![]() $X(G,\alpha )$
is connected. The following result expresses how the number of spanning trees changes from X to
$X(G,\alpha )$
is connected. The following result expresses how the number of spanning trees changes from X to
![]() $X(G,\alpha )$
, using the Ihara polynomial
$X(G,\alpha )$
, using the Ihara polynomial
![]() $\mathcal {I}_\alpha $
.
$\mathcal {I}_\alpha $
.
Proposition 3.5. For every finite connected graph X, such that
![]() $\chi (X) \neq 0$
, and every voltage assignment
$\chi (X) \neq 0$
, and every voltage assignment
![]() $\alpha \colon \mathbf {E}_X \to G$
with values in a finite abelian group G, such that the associated graph
$\alpha \colon \mathbf {E}_X \to G$
with values in a finite abelian group G, such that the associated graph
![]() $X(G,\alpha )$
is connected,
$X(G,\alpha )$
is connected,
 $$ \begin{align*} \lvert G \rvert \cdot \kappa(X(G,\alpha)) = \kappa(X) \cdot \prod_{\psi \neq \psi_0} \mathcal{I}_\alpha(\psi(1)), \end{align*} $$
$$ \begin{align*} \lvert G \rvert \cdot \kappa(X(G,\alpha)) = \kappa(X) \cdot \prod_{\psi \neq \psi_0} \mathcal{I}_\alpha(\psi(1)), \end{align*} $$
where
![]() $\mathcal {I}_\alpha (\psi (1)) := \psi (\mathcal {I}_\alpha ) \in \mathbb {C}$
is obtained by applying to
$\mathcal {I}_\alpha (\psi (1)) := \psi (\mathcal {I}_\alpha ) \in \mathbb {C}$
is obtained by applying to
![]() $\mathcal {I}_\alpha $
the natural linear extension of the character
$\mathcal {I}_\alpha $
the natural linear extension of the character
![]() $\psi $
to the group ring
$\psi $
to the group ring
![]() $\mathbb {Z}[t^G]$
.
$\mathbb {Z}[t^G]$
.
Proof. First of all, observe that
![]() $\mathcal {I}_\alpha (\psi (1)) = \det (D_X - \widetilde {A}_\psi )$
, where we define
$\mathcal {I}_\alpha (\psi (1)) = \det (D_X - \widetilde {A}_\psi )$
, where we define
 $$ \begin{align*} \widetilde{A}_{\psi} := \bigg(\sum_{\substack{e \in \mathbf{E}_{X} \\ \mathrm{inc}(e) = (v_{i},v_{j})}} \psi(\alpha(e)) \bigg) \in \mathbb{C}^{g \times g} \end{align*} $$
$$ \begin{align*} \widetilde{A}_{\psi} := \bigg(\sum_{\substack{e \in \mathbf{E}_{X} \\ \mathrm{inc}(e) = (v_{i},v_{j})}} \psi(\alpha(e)) \bigg) \in \mathbb{C}^{g \times g} \end{align*} $$
for every character
![]() $\psi \in G^\vee $
. In particular, one can prove that
$\psi \in G^\vee $
. In particular, one can prove that
![]() $\widetilde {A}_\psi = A_\psi $
, as explained in [Reference McGown and Vallières40, Corollary 5.3]. Therefore, we see from the definition of the polynomial
$\widetilde {A}_\psi = A_\psi $
, as explained in [Reference McGown and Vallières40, Corollary 5.3]. Therefore, we see from the definition of the polynomial
![]() $h_{Y/X}(u,\psi )$
, which was given in (3-5), that
$h_{Y/X}(u,\psi )$
, which was given in (3-5), that
![]() $\mathcal {I}_\alpha (\psi (1)) = h_{Y/X}(1,\psi )$
for every character
$\mathcal {I}_\alpha (\psi (1)) = h_{Y/X}(1,\psi )$
for every character
![]() $\psi \in G^\vee $
. To conclude the proof, it is just sufficient to substitute this equality in the explicit expression
$\psi \in G^\vee $
. To conclude the proof, it is just sufficient to substitute this equality in the explicit expression
 $$ \begin{align*} |G| \cdot \kappa(Y) = \kappa(X) \prod_{\psi \neq \psi_{0}}h_{Y/X}(1,\psi), \end{align*} $$
$$ \begin{align*} |G| \cdot \kappa(Y) = \kappa(X) \prod_{\psi \neq \psi_{0}}h_{Y/X}(1,\psi), \end{align*} $$
which was recalled in (3-7).
3.3.3.
 $\mathbb {Z}$
-towers of graphs and Pierce–Lehmer sequences
$\mathbb {Z}$
-towers of graphs and Pierce–Lehmer sequences
From now on, we will specialise to the case of
![]() $\mathbb {Z}$
-towers of graphs. More precisely, we will consider a finite connected graph X such that
$\mathbb {Z}$
-towers of graphs. More precisely, we will consider a finite connected graph X such that
![]() $\chi (X) \neq 0$
, endowed with a voltage assignment
$\chi (X) \neq 0$
, endowed with a voltage assignment
![]() ${\alpha \colon \mathbf {E}_X \to \mathbb {Z}}$
with values in the additive group of the integers, such that the derived graph
${\alpha \colon \mathbf {E}_X \to \mathbb {Z}}$
with values in the additive group of the integers, such that the derived graph
![]() $X_\infty := X(\mathbb {Z},\alpha )$
is connected, which is equivalent to saying that there exists a vertex
$X_\infty := X(\mathbb {Z},\alpha )$
is connected, which is equivalent to saying that there exists a vertex
![]() $v_0 \in V_X$
such that the monodromy representation
$v_0 \in V_X$
such that the monodromy representation
![]() $\rho _{\alpha ,v_0} \colon \pi _1(X,v_0) \to \mathbb {Z}$
is surjective, as explained in Theorem 3.2. In this case, we have a natural isomorphism
$\rho _{\alpha ,v_0} \colon \pi _1(X,v_0) \to \mathbb {Z}$
is surjective, as explained in Theorem 3.2. In this case, we have a natural isomorphism
![]() $\mathbb {Z}[t^{\mathbb {Z}}] \cong \mathbb {Z}[t^{\pm 1}]$
. Therefore, we see from (3-9) that the Ihara polynomial can be written as
$\mathbb {Z}[t^{\mathbb {Z}}] \cong \mathbb {Z}[t^{\pm 1}]$
. Therefore, we see from (3-9) that the Ihara polynomial can be written as
for some
![]() $c_0,\ldots ,c_b \in \mathbb {Z}$
such that
$c_0,\ldots ,c_b \in \mathbb {Z}$
such that
![]() $c_b \neq 0$
. Clearing denominators, we can define
$c_b \neq 0$
. Clearing denominators, we can define
which is a polynomial of degree
![]() $2 b$
such that
$2 b$
such that
![]() $I_\alpha (0) \neq 0$
. Finally, we define
$I_\alpha (0) \neq 0$
. Finally, we define
![]() $e := \mathrm {ord}_{t = 1}(I_\alpha )$
, and we write
$e := \mathrm {ord}_{t = 1}(I_\alpha )$
, and we write
for some polynomial
![]() $J_\alpha \in \mathbb {Z}[t]$
such that
$J_\alpha \in \mathbb {Z}[t]$
such that
![]() $J_\alpha (0) \cdot J_\alpha (1) \neq 0$
.
$J_\alpha (0) \cdot J_\alpha (1) \neq 0$
.
Now, one can associate to the voltage assignment
![]() $\alpha \colon \mathbf {E}_X \to \mathbb {Z}$
a system of finite graphs
$\alpha \colon \mathbf {E}_X \to \mathbb {Z}$
a system of finite graphs
![]() $X_n := X(\mathbb {Z}/n \mathbb {Z},\pi _n \circ \alpha )$
, where
$X_n := X(\mathbb {Z}/n \mathbb {Z},\pi _n \circ \alpha )$
, where
![]() $\pi _n \colon \mathbb {Z} \twoheadrightarrow \mathbb {Z}/n \mathbb {Z}$
is the natural quotient map. In particular, each of these graphs will be connected, because
$\pi _n \colon \mathbb {Z} \twoheadrightarrow \mathbb {Z}/n \mathbb {Z}$
is the natural quotient map. In particular, each of these graphs will be connected, because
![]() $X_\infty $
is assumed to be connected, and the maps
$X_\infty $
is assumed to be connected, and the maps
![]() $\pi _n$
are surjective. Moreover, the number of spanning trees of each graph
$\pi _n$
are surjective. Moreover, the number of spanning trees of each graph
![]() $X_n$
can be computed in terms of a Pierce–Lehmer sequence associated to the polynomial
$X_n$
can be computed in terms of a Pierce–Lehmer sequence associated to the polynomial
![]() $J_\alpha $
, as the following result shows.
$J_\alpha $
, as the following result shows.
Theorem 3.6. Let X be a finite connected graph such that
![]() $\chi (X) \neq 0$
and fix a voltage assignment
$\chi (X) \neq 0$
and fix a voltage assignment
![]() $\alpha \colon \mathbf {E}_X \to \mathbb {Z}$
such that the graph
$\alpha \colon \mathbf {E}_X \to \mathbb {Z}$
such that the graph
![]() $X_\infty := X(\mathbb {Z},\alpha )$
is connected. Moreover, for every
$X_\infty := X(\mathbb {Z},\alpha )$
is connected. Moreover, for every
![]() $n \in \mathbb {N}$
, we let
$n \in \mathbb {N}$
, we let
![]() $X_n := X(\mathbb {Z}/n \mathbb {Z},\pi _n \circ \alpha )$
, where
$X_n := X(\mathbb {Z}/n \mathbb {Z},\pi _n \circ \alpha )$
, where
![]() $\pi _n \colon \mathbb {Z} \twoheadrightarrow \mathbb {Z}/n \mathbb {Z}$
is the natural quotient map. Then, the number of spanning trees of
$\pi _n \colon \mathbb {Z} \twoheadrightarrow \mathbb {Z}/n \mathbb {Z}$
is the natural quotient map. Then, the number of spanning trees of
![]() $X_n$
can be computed as
$X_n$
can be computed as
where the integers
![]() $b := -{\mathrm {ord}}_{t = 0}(\mathcal {I}_\alpha ) \geq 0$
and
$b := -{\mathrm {ord}}_{t = 0}(\mathcal {I}_\alpha ) \geq 0$
and
![]() $e := {\mathrm {ord}}_{t = 1}(\mathcal {I}_\alpha ) \geq 1$
are defined in terms of the Ihara polynomial
$e := {\mathrm {ord}}_{t = 1}(\mathcal {I}_\alpha ) \geq 1$
are defined in terms of the Ihara polynomial
![]() $\mathcal {I}_\alpha \in \mathbb {Z}[t^{\pm 1}]$
, whose definition was recalled in (3-8). Moreover,
$\mathcal {I}_\alpha \in \mathbb {Z}[t^{\pm 1}]$
, whose definition was recalled in (3-8). Moreover,
![]() $\{ \Delta _n(J_\alpha ) \}_{n \in \mathbb {N}}$
is the Pierce–Lehmer sequence, defined as in (2-4), which is associated to the polynomial
$\{ \Delta _n(J_\alpha ) \}_{n \in \mathbb {N}}$
is the Pierce–Lehmer sequence, defined as in (2-4), which is associated to the polynomial
![]() $J_\alpha (t) := t^b \cdot (t-1)^{-e} \cdot \mathcal {I}_\alpha (t) \in \mathbb {Z}[t]$
.
$J_\alpha (t) := t^b \cdot (t-1)^{-e} \cdot \mathcal {I}_\alpha (t) \in \mathbb {Z}[t]$
.
Proof. First of all, observe that
![]() $e \geq 1$
because
$e \geq 1$
because
![]() $\mathcal {I}_\alpha (1) = \det (D_X - A_X)$
, where
$\mathcal {I}_\alpha (1) = \det (D_X - A_X)$
, where
![]() $D_X$
and
$D_X$
and
![]() $A_X$
are respectively the degree and adjacency matrices associated to X, whose difference
$A_X$
are respectively the degree and adjacency matrices associated to X, whose difference
![]() $D_X - A_X$
is singular, as explained in [Reference Corry and Perkinson6, Proposition 2.8]. Now, applying Proposition 3.5 to the Galois cover
$D_X - A_X$
is singular, as explained in [Reference Corry and Perkinson6, Proposition 2.8]. Now, applying Proposition 3.5 to the Galois cover
![]() $X_n/X$
,
$X_n/X$
,
 $$ \begin{align} n \cdot \kappa(X_n) = \kappa(X) \cdot \prod_{\psi \neq \psi_0} \mathcal{I}_{\alpha_n}(\psi(1)), \end{align} $$
$$ \begin{align} n \cdot \kappa(X_n) = \kappa(X) \cdot \prod_{\psi \neq \psi_0} \mathcal{I}_{\alpha_n}(\psi(1)), \end{align} $$
where
![]() $\alpha _n := \pi _n \circ \alpha $
for every
$\alpha _n := \pi _n \circ \alpha $
for every
![]() $n \in \mathbb {N}$
. Moreover, it is easy to see using (3-10) that
$n \in \mathbb {N}$
. Moreover, it is easy to see using (3-10) that
 $$ \begin{align} \prod_{\psi \neq \psi_0} \mathcal{I}_{\alpha_n}(\psi(1)) = \prod_{\psi \neq \psi_0} \mathcal{I}_\alpha(\psi(1)) = \prod_{\zeta \in W_n^\ast} \mathcal{I}_\alpha(\zeta), \end{align} $$
$$ \begin{align} \prod_{\psi \neq \psi_0} \mathcal{I}_{\alpha_n}(\psi(1)) = \prod_{\psi \neq \psi_0} \mathcal{I}_\alpha(\psi(1)) = \prod_{\zeta \in W_n^\ast} \mathcal{I}_\alpha(\zeta), \end{align} $$
where
![]() $W_n^\ast := W_n \setminus \{1\}$
denotes the set of nontrivial roots of unity whose order divides n. Now, let us observe that
$W_n^\ast := W_n \setminus \{1\}$
denotes the set of nontrivial roots of unity whose order divides n. Now, let us observe that
 $$ \begin{align} \prod_{\zeta \in W_n^\ast} \mathcal{I}_\alpha(\zeta) &= \prod_{\zeta \in W_n^\ast} (\zeta^{-b} \cdot I_\alpha(\zeta)) = (-1)^{b (n-1)} \prod_{\zeta \in W_n^\ast} I_\alpha(\zeta) \nonumber\\ &= (-1)^{b (n-1)} \mathrm{Res}\bigg( I_\alpha(t), \frac{t^n-1}{t-1} \bigg) \end{align} $$
$$ \begin{align} \prod_{\zeta \in W_n^\ast} \mathcal{I}_\alpha(\zeta) &= \prod_{\zeta \in W_n^\ast} (\zeta^{-b} \cdot I_\alpha(\zeta)) = (-1)^{b (n-1)} \prod_{\zeta \in W_n^\ast} I_\alpha(\zeta) \nonumber\\ &= (-1)^{b (n-1)} \mathrm{Res}\bigg( I_\alpha(t), \frac{t^n-1}{t-1} \bigg) \end{align} $$
as follows from the definition of resultant recalled in Section 2.1. Thus,
by combining (3-13) with (3-14) and (3-15). To conclude, it suffices to observe that
 $$ \begin{align*} \begin{aligned} \mathrm{Res} \bigg(I_{\alpha}(t),\frac{t^{n} - 1}{t-1} \bigg) &= \mathrm{Res} \bigg(t-1,\frac{t^{n} - 1}{t-1} \bigg)^e \cdot \mathrm{Res} \bigg(J_{\alpha}(t),\frac{t^{n} - 1}{t-1} \bigg) \\ &= n^e \cdot \mathrm{Res} \bigg(J_{\alpha}(t),\frac{t^{n} - 1}{t-1} \bigg) = n^e \cdot \frac{\Delta_n(J_\alpha)}{\Delta_1(J_\alpha)}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathrm{Res} \bigg(I_{\alpha}(t),\frac{t^{n} - 1}{t-1} \bigg) &= \mathrm{Res} \bigg(t-1,\frac{t^{n} - 1}{t-1} \bigg)^e \cdot \mathrm{Res} \bigg(J_{\alpha}(t),\frac{t^{n} - 1}{t-1} \bigg) \\ &= n^e \cdot \mathrm{Res} \bigg(J_{\alpha}(t),\frac{t^{n} - 1}{t-1} \bigg) = n^e \cdot \frac{\Delta_n(J_\alpha)}{\Delta_1(J_\alpha)}, \end{aligned} \end{align*} $$
thanks to the multiplicative property of resultants.
Remark 3.7. Formulae such as (3-16) appear also in the theory of curves over finite fields and in knot theory. Indeed:
-
• if C is a nonsingular, geometrically irreducible projective curve over a finite field
 $\mathbb {F}_{q}$
with at least one rational point over
$\mathbb {F}_{q}$
with at least one rational point over
 $\mathbb {F}_{q}$
, and J is its Jacobian variety, then [Reference Rosen47, Corollary, page 110] implies that where
$\mathbb {F}_{q}$
, and J is its Jacobian variety, then [Reference Rosen47, Corollary, page 110] implies that where $$ \begin{align*}\#J(\mathbb{F}_{q^{n}}) = |\mathrm{Res}(P_{C}(t),t^{n}-1 )|, \end{align*} $$
$$ \begin{align*}\#J(\mathbb{F}_{q^{n}}) = |\mathrm{Res}(P_{C}(t),t^{n}-1 )|, \end{align*} $$
 $P_{C}(t)$
is the Weil polynomial of C, defined as the reverse of the L-polynomial
$P_{C}(t)$
is the Weil polynomial of C, defined as the reverse of the L-polynomial
 $L_{C}(t)$
;
$L_{C}(t)$
;
-
• if
 $K \subseteq S^3$
is a knot and
$K \subseteq S^3$
is a knot and
 $M_n$
is a Galois cover of
$M_n$
is a Galois cover of
 $M := S^3 \setminus K$
, with Galois group
$M := S^3 \setminus K$
, with Galois group
 $\mathbb {Z}/n \mathbb {Z}$
, Fox’s formula (see [Reference Weber59]) implies that where
$\mathbb {Z}/n \mathbb {Z}$
, Fox’s formula (see [Reference Weber59]) implies that where $$ \begin{align*}\#H_{1}(X_{n},\mathbb{Z})_{\text{tors}} = |\mathrm{Res}(A_{K}(t), t^{n}-1)|,\end{align*} $$
$$ \begin{align*}\#H_{1}(X_{n},\mathbb{Z})_{\text{tors}} = |\mathrm{Res}(A_{K}(t), t^{n}-1)|,\end{align*} $$
 $A_{K}(t)$
is the Alexander polynomial associated to the knot K.
$A_{K}(t)$
is the Alexander polynomial associated to the knot K.
Remark 3.8. Let us note that, in the setting of Theorem 3.6, the explicit formula (3-12) implies that
![]() $J_\alpha $
does not vanish at roots of unity. Indeed, if this was the case, we would have
$J_\alpha $
does not vanish at roots of unity. Indeed, if this was the case, we would have
![]() $\kappa (X_n) = 0$
for some
$\kappa (X_n) = 0$
for some
![]() $n \geq 2$
, which is absurd because
$n \geq 2$
, which is absurd because
![]() $X_n$
is not empty. Therefore, combining Theorem 3.6 with Corollaries 2.8 and 2.9, one can recover (1-2) and (1-3) for the
$X_n$
is not empty. Therefore, combining Theorem 3.6 with Corollaries 2.8 and 2.9, one can recover (1-2) and (1-3) for the
![]() $\mathbb {Z}_\ell $
-towers
$\mathbb {Z}_\ell $
-towers
![]() $\{X_{\ell ^n}\}_{n = 0}^{+\infty }$
induced from a
$\{X_{\ell ^n}\}_{n = 0}^{+\infty }$
induced from a
![]() $\mathbb {Z}$
-tower
$\mathbb {Z}$
-tower
![]() $\{X_n\}_{n = 1}^{+\infty }$
. More generally, combining Theorem 3.6 with Corollary 2.5 will allow us to prove Theorem 1.1, as we will explain in Theorem 3.17.
$\{X_n\}_{n = 1}^{+\infty }$
. More generally, combining Theorem 3.6 with Corollary 2.5 will allow us to prove Theorem 1.1, as we will explain in Theorem 3.17.
Remark 3.9. Since the polynomial
![]() $J_{\alpha }$
is a reciprocal polynomial, it is known that the quantity
$J_{\alpha }$
is a reciprocal polynomial, it is known that the quantity
![]() $\lvert \Delta _{n}(J_{\alpha })/\Delta _{1}(J_{\alpha }) \rvert $
is a square when n is odd and
$\lvert \Delta _{n}(J_{\alpha })/\Delta _{1}(J_{\alpha }) \rvert $
is a square when n is odd and
![]() $J_{\alpha }$
is a monic polynomial, as explained for instance in [Reference Einsiedler, Everest and Ward10, Section 2]. It follows that if p and
$J_{\alpha }$
is a monic polynomial, as explained for instance in [Reference Einsiedler, Everest and Ward10, Section 2]. It follows that if p and
![]() $\ell $
are two distinct rational primes with
$\ell $
are two distinct rational primes with
![]() $\ell $
odd and
$\ell $
odd and
![]() $J_{\alpha }$
is monic, then
$J_{\alpha }$
is monic, then
and the parity of the number
![]() $\mathrm {ord}_{p}(\kappa (X_{\ell ^{k}}))$
, for all
$\mathrm {ord}_{p}(\kappa (X_{\ell ^{k}}))$
, for all
![]() $k \ge 1$
, depends only on the parity of
$k \ge 1$
, depends only on the parity of
![]() $\mathrm {ord}_{p}(\kappa (X))$
. This remark explains the parity of the p-adic valuation of the number of spanning trees in various
$\mathrm {ord}_{p}(\kappa (X))$
. This remark explains the parity of the p-adic valuation of the number of spanning trees in various
![]() $\mathbb {Z}_{\ell }$
-towers appearing in [Reference McGown and Vallières39, Reference McGown and Vallières40, Reference Vallières57] and [Reference Lei and Vallières35], since in each case, the tower in question is constructed from a voltage assignment
$\mathbb {Z}_{\ell }$
-towers appearing in [Reference McGown and Vallières39, Reference McGown and Vallières40, Reference Vallières57] and [Reference Lei and Vallières35], since in each case, the tower in question is constructed from a voltage assignment
![]() $\alpha \colon \mathbf {E}_X \to \mathbb {Z}_\ell $
such that
$\alpha \colon \mathbf {E}_X \to \mathbb {Z}_\ell $
such that
![]() $\alpha (\mathbf {E}_X) \subseteq \mathbb {Z}$
. We point out as well that (3-12) is compatible with various results in the literature, such as [Reference Kwon, Mednykh and Mednykh31, Theorem 5.5], [Reference Mednykh42, Theorem 5.5] and [Reference Mednykh and Mednykh41, Theorem 3].
$\alpha (\mathbf {E}_X) \subseteq \mathbb {Z}$
. We point out as well that (3-12) is compatible with various results in the literature, such as [Reference Kwon, Mednykh and Mednykh31, Theorem 5.5], [Reference Mednykh42, Theorem 5.5] and [Reference Mednykh and Mednykh41, Theorem 3].
3.4. An explicit example
Let us revisit [Reference Vallières57, Example 2] using the results proven in the present paper. Consider the bouquet graph
![]() $X = B_{2}$
on two loops and pick an orientation
$X = B_{2}$
on two loops and pick an orientation
![]() $S = \{s_{1},s_{2} \}$
. Consider the function
$S = \{s_{1},s_{2} \}$
. Consider the function
![]() $\alpha :S \rightarrow \mathbb {Z}$
given by
$\alpha :S \rightarrow \mathbb {Z}$
given by
![]() $\alpha (s_{1}) = 3$
and
$\alpha (s_{1}) = 3$
and
![]() $\alpha (s_{2}) = 5$
. Note that
$\alpha (s_{2}) = 5$
. Note that
![]() $\alpha (s_{1}^{2} \cdot \bar {s}_{2})=1$
, and thus Theorem 3.2 implies that
$\alpha (s_{1}^{2} \cdot \bar {s}_{2})=1$
, and thus Theorem 3.2 implies that
![]() $X(\mathbb {Z},\alpha )$
is connected. Therefore, so are all the finite graphs
$X(\mathbb {Z},\alpha )$
is connected. Therefore, so are all the finite graphs
where
![]() $\pi _n \colon \mathbb {Z} \twoheadrightarrow \mathbb {Z}/n \mathbb {Z}$
denotes the canonical projection map. The infinite graph
$\pi _n \colon \mathbb {Z} \twoheadrightarrow \mathbb {Z}/n \mathbb {Z}$
denotes the canonical projection map. The infinite graph
![]() $X(\mathbb {Z},\alpha )$
is a connected
$X(\mathbb {Z},\alpha )$
is a connected
![]() $4$
-regular graph that is not a tree, but it is a quotient of the infinite
$4$
-regular graph that is not a tree, but it is a quotient of the infinite
![]() $4$
-regular tree. All the finite graphs
$4$
-regular tree. All the finite graphs
![]() $X_{n}$
are finite quotients of
$X_{n}$
are finite quotients of
![]() $X(\mathbb {Z},\alpha )$
. Moreover, one can draw each of these graphs
$X(\mathbb {Z},\alpha )$
. Moreover, one can draw each of these graphs
![]() $X_n$
, using their definition, and we did so for
$X_n$
, using their definition, and we did so for
![]() $n \in \{ 1,\ldots ,10,25,27 \}$
in Figure 1, where we also drew a line
$n \in \{ 1,\ldots ,10,25,27 \}$
in Figure 1, where we also drew a line
![]() $X_n \to X_m$
whenever
$X_n \to X_m$
whenever
![]() $m \mid n$
.
$m \mid n$
.

Figure 1 The
![]() $\mathbb{Z}$
-tower of graphs described in Section 3.4.
$\mathbb{Z}$
-tower of graphs described in Section 3.4.
Note in particular that the
![]() $\mathbb {Z}_2$
-tower considered in [Reference Vallières57, Example 2] corresponds to the leftmost column of the previous figure. For the
$\mathbb {Z}_2$
-tower considered in [Reference Vallières57, Example 2] corresponds to the leftmost column of the previous figure. For the
![]() $\mathbb {Z}$
-tower considered in the present example, the Ihara polynomial is given by
$\mathbb {Z}$
-tower considered in the present example, the Ihara polynomial is given by
with
![]() $J_{\alpha }(t) = -(t^{8} + 2t^{7} + 4t^{6} + 6t^{5}+8t^{4} + 6t^{3} + 4t^{2} + 2t + 1)$
. Using SageMath [54], for each
$J_{\alpha }(t) = -(t^{8} + 2t^{7} + 4t^{6} + 6t^{5}+8t^{4} + 6t^{3} + 4t^{2} + 2t + 1)$
. Using SageMath [54], for each
![]() $n\in \{1,\dots,10\}$
we computed the number of spanning trees
$n\in \{1,\dots,10\}$
we computed the number of spanning trees
![]() $\kappa (X_{n})$
, the resultants
$\kappa (X_{n})$
, the resultants
![]() $\mathrm {Res}(I_\alpha (t),({t^n-1})/({t-1}))$
and the values of the Pierce–Lehmer sequence
$\mathrm {Res}(I_\alpha (t),({t^n-1})/({t-1}))$
and the values of the Pierce–Lehmer sequence
![]() $\Delta _n(J_\alpha )$
. Doing so, we obtained the values that are tabulated in the following table, which shows in particular that the relationship between these invariants is the one predicted by (3-12):
$\Delta _n(J_\alpha )$
. Doing so, we obtained the values that are tabulated in the following table, which shows in particular that the relationship between these invariants is the one predicted by (3-12):

3.5. Asymptotics for the number of spanning trees
The aim of this subsection is to obtain some asymptotic results for the number of spanning trees in a
![]() $\mathbb {Z}$
-tower of graphs, using the relation between the number of spanning trees and Pierce–Lehmer sequences, provided by Theorem 3.6, in combination with the asymptotic results for Pierce–Lehmer sequences, which we explored in Section 2.3.
$\mathbb {Z}$
-tower of graphs, using the relation between the number of spanning trees and Pierce–Lehmer sequences, provided by Theorem 3.6, in combination with the asymptotic results for Pierce–Lehmer sequences, which we explored in Section 2.3.
3.5.1. Archimedean asymptotics
We will start from the Archimedean asymptotics of the number of spanning trees, which are provided by the following corollary of Theorem 3.6.
Corollary 3.10. Let X be a finite connected graph such that
![]() $\chi (X) \neq 0$
and fix a voltage assignment
$\chi (X) \neq 0$
and fix a voltage assignment
![]() $\alpha \colon \mathbf {E}_X \to \mathbb {Z}$
such that
$\alpha \colon \mathbf {E}_X \to \mathbb {Z}$
such that
![]() $X(\mathbb {Z},\alpha )$
is connected. Then, if the polynomial
$X(\mathbb {Z},\alpha )$
is connected. Then, if the polynomial
![]() $J_{\alpha }$
defined by (3-11) does not have any root on the unit circle of
$J_{\alpha }$
defined by (3-11) does not have any root on the unit circle of
![]() $\mathbb {C}$
,
$\mathbb {C}$
,
as
![]() $n \to +\infty $
.
$n \to +\infty $
.
Remark 3.11. Let us note that given an Ihara polynomial
![]() $\mathcal {I}_\alpha $
associated to some voltage assignment
$\mathcal {I}_\alpha $
associated to some voltage assignment
![]() $\alpha $
, either
$\alpha $
, either
![]() $M_\infty (\mathcal {I}_\alpha ) = 1$
or
$M_\infty (\mathcal {I}_\alpha ) = 1$
or
![]() $M_\infty (\mathcal {I}_\alpha ) \geq 2$
, as was proved in [Reference Silver and Williams50, Proposition 12.7].
$M_\infty (\mathcal {I}_\alpha ) \geq 2$
, as was proved in [Reference Silver and Williams50, Proposition 12.7].
Remark 3.12. It is reasonable to ask what happens when the Ihara polynomial
![]() $\mathcal {I}_\alpha $
has some roots on the Archimedean unit circle. In this case, it is easy to see that these roots will prevent one from getting a precise asymptotic for the growth of
$\mathcal {I}_\alpha $
has some roots on the Archimedean unit circle. In this case, it is easy to see that these roots will prevent one from getting a precise asymptotic for the growth of
![]() $\kappa (X_n)$
. To see this, fix some
$\kappa (X_n)$
. To see this, fix some
![]() $\alpha = e^{2 \pi i \theta } \in \mathbb {C}$
with
$\alpha = e^{2 \pi i \theta } \in \mathbb {C}$
with
![]() $\theta \in \mathbb {R} \setminus \mathbb {Q}$
. Then, the sequence
$\theta \in \mathbb {R} \setminus \mathbb {Q}$
. Then, the sequence
is distributed on the interval
![]() $[0,4]$
according to the probability density function
$[0,4]$
according to the probability density function
![]() $({2}/\pi) {\sqrt {4 x-x^2}}$
, thanks to Weyl’s equidistribution theorem [Reference Kuipers and Niederreiter30, Ch. 1, Example 2.1], and to the explicit computation of the probability density function of the random variable
$({2}/\pi) {\sqrt {4 x-x^2}}$
, thanks to Weyl’s equidistribution theorem [Reference Kuipers and Niederreiter30, Ch. 1, Example 2.1], and to the explicit computation of the probability density function of the random variable
![]() $2 (1-\cos (2 \pi U))$
, where U is a random variable that is uniformly distributed in the interval
$2 (1-\cos (2 \pi U))$
, where U is a random variable that is uniformly distributed in the interval
![]() $[0,1]$
, which follows from the general transformation formula for probability density functions (see [Reference DeGroot and Schervish8, Theorem 3.8.4]). Therefore, we see that any asymptotic expansion for the growth of
$[0,1]$
, which follows from the general transformation formula for probability density functions (see [Reference DeGroot and Schervish8, Theorem 3.8.4]). Therefore, we see that any asymptotic expansion for the growth of
![]() $\kappa (X_n)$
would have to feature some oscillating term, which takes into account this equidistribution phenomenon.
$\kappa (X_n)$
would have to feature some oscillating term, which takes into account this equidistribution phenomenon.
The previous Corollary 3.10 allows us to recover the asymptotics for the number of spanning trees of two particular examples of
![]() $\mathbb {Z}$
-towers, which were thoroughly studied in [Reference Mednykh and Mednykh41, Reference Mednykh42].
$\mathbb {Z}$
-towers, which were thoroughly studied in [Reference Mednykh and Mednykh41, Reference Mednykh42].
Example 3.13. Consider the following orientation
![]() $S = \{s_1,s_2,s_3\}$
on the dumbbell graph:
$S = \{s_1,s_2,s_3\}$
on the dumbbell graph:
and fix a function
![]() $\alpha :S \rightarrow \mathbb {Z}$
such that
$\alpha :S \rightarrow \mathbb {Z}$
such that
![]() $\alpha (s_2) = 0$
. This defines a voltage assignment on the dumbbell graph X, with values in
$\alpha (s_2) = 0$
. This defines a voltage assignment on the dumbbell graph X, with values in
![]() $\mathbb {Z}$
. Moreover, the derived covers
$\mathbb {Z}$
. Moreover, the derived covers
![]() $X_n := X(\mathbb {Z}/n \mathbb {Z},\pi _n \circ \alpha )$
, where
$X_n := X(\mathbb {Z}/n \mathbb {Z},\pi _n \circ \alpha )$
, where
![]() $\pi _n \colon \mathbb {Z} \twoheadrightarrow \mathbb {Z}/n \mathbb {Z}$
denotes the canonical projection, are given by the I-graphs
$\pi _n \colon \mathbb {Z} \twoheadrightarrow \mathbb {Z}/n \mathbb {Z}$
denotes the canonical projection, are given by the I-graphs
![]() $I(n,k,l)$
, where
$I(n,k,l)$
, where
![]() $k := \alpha (s_1)$
and
$k := \alpha (s_1)$
and
![]() $l := \alpha (s_3)$
. In particular, if
$l := \alpha (s_3)$
. In particular, if
![]() $k = 1$
, one gets the family of generalised Petersen graphs
$k = 1$
, one gets the family of generalised Petersen graphs
![]() $\mathrm {GP}(n,l)$
.
$\mathrm {GP}(n,l)$
.
Now, one sees from Theorem 3.2 that the graph
![]() $X(\mathbb {Z},\alpha )$
is connected if and only if
$X(\mathbb {Z},\alpha )$
is connected if and only if
![]() $(k,l) = 1$
, which we will assume for the rest of this example. Then, we can compute the Ihara polynomial associated to the voltage assignment
$(k,l) = 1$
, which we will assume for the rest of this example. Then, we can compute the Ihara polynomial associated to the voltage assignment
![]() $\alpha $
, which is given by
$\alpha $
, which is given by
where
![]() $I_{\alpha }(t) = (3 t^k - t^{2 k} - 1) \cdot (3 t^l - t^{2 l} - 1) - t^{k+l}$
. Since
$I_{\alpha }(t) = (3 t^k - t^{2 k} - 1) \cdot (3 t^l - t^{2 l} - 1) - t^{k+l}$
. Since
![]() $I_\alpha (1) = I^{\prime }_\alpha (1) = 0$
, while
$I_\alpha (1) = I^{\prime }_\alpha (1) = 0$
, while
![]() $I^{\prime \prime }_\alpha (1) \neq 0$
, we see that
$I^{\prime \prime }_\alpha (1) \neq 0$
, we see that
![]() $e := {\mathrm {ord}}_{t=1}(\mathcal {I}_\alpha ) = 2$
, which allows us to write
$e := {\mathrm {ord}}_{t=1}(\mathcal {I}_\alpha ) = 2$
, which allows us to write
for some
![]() $J_\alpha \in \mathbb {Z}[t]$
such that
$J_\alpha \in \mathbb {Z}[t]$
such that
![]() $J_\alpha (1) \neq 0$
. A simple calculation shows that
$J_\alpha (1) \neq 0$
. A simple calculation shows that
![]() $J_\alpha $
has no roots on the unit circle, as explained for instance in [Reference Mednykh42, Lemma 5.2]. Moreover, it is easy to see that
$J_\alpha $
has no roots on the unit circle, as explained for instance in [Reference Mednykh42, Lemma 5.2]. Moreover, it is easy to see that
and that
![]() $\kappa (X) = 1$
. Therefore, Corollary 3.10 shows that
$\kappa (X) = 1$
. Therefore, Corollary 3.10 shows that
as
![]() $n \to \infty $
, which is precisely [Reference Mednykh42, Theorem 6.1].
$n \to \infty $
, which is precisely [Reference Mednykh42, Theorem 6.1].
Example 3.14. Consider the graph X consisting of a bouquet with k loops for some
![]() $k \in \mathbb {N}$
, and take an orientation
$k \in \mathbb {N}$
, and take an orientation
![]() $S = \{s_{1},\ldots ,s_{k} \}$
of X. Moreover, fix any function
$S = \{s_{1},\ldots ,s_{k} \}$
of X. Moreover, fix any function
![]() $\alpha :S \rightarrow \mathbb {Z}$
such that
$\alpha :S \rightarrow \mathbb {Z}$
such that
and write
![]() $a_i := \alpha (s_i)$
for every
$a_i := \alpha (s_i)$
for every
![]() $i \in \{1,\ldots ,k\}$
. Then, for n large enough, the derived graph
$i \in \{1,\ldots ,k\}$
. Then, for n large enough, the derived graph
![]() $X_n := X(\mathbb {Z}/n\mathbb {Z},\pi _n \circ \alpha )$
is the circulant graph
$X_n := X(\mathbb {Z}/n\mathbb {Z},\pi _n \circ \alpha )$
is the circulant graph
![]() $C_{n}(a_{1},\ldots ,a_{k})$
. Note in particular that the example described in Section 3.4 belongs to this more general family.
$C_{n}(a_{1},\ldots ,a_{k})$
. Note in particular that the example described in Section 3.4 belongs to this more general family.
Once again, it is easy to see by Theorem 3.2 that the graph
![]() $X(\mathbb {Z},\alpha )$
is connected if and only if
$X(\mathbb {Z},\alpha )$
is connected if and only if
![]() $(a_{1},\ldots ,a_{k}) = 1$
, which we will assume for the rest of this example. Then, we can compute the Ihara polynomial associated to the voltage assignment
$(a_{1},\ldots ,a_{k}) = 1$
, which we will assume for the rest of this example. Then, we can compute the Ihara polynomial associated to the voltage assignment
![]() $\alpha $
, and we obtain
$\alpha $
, and we obtain
 $$ \begin{align*} \mathcal{I}_{\alpha}(t) = 2k - \sum_{i=1}^{k}(t^{a_{i}} + t^{-a_{i}}) = t^{-a_k} I_\alpha(t), \end{align*} $$
$$ \begin{align*} \mathcal{I}_{\alpha}(t) = 2k - \sum_{i=1}^{k}(t^{a_{i}} + t^{-a_{i}}) = t^{-a_k} I_\alpha(t), \end{align*} $$
where
![]() $I_\alpha (t) := 2 k t^{a_k} - \sum _{i=1}^k (t^{a_k+a_i} + t^{a_k-a_i}) \in \mathbb {Z}[t]$
. In particular, we easily see that
$I_\alpha (t) := 2 k t^{a_k} - \sum _{i=1}^k (t^{a_k+a_i} + t^{a_k-a_i}) \in \mathbb {Z}[t]$
. In particular, we easily see that
which implies that
![]() $e := {\mathrm {ord}}_{t = 1}(\mathcal {I}_\alpha ) = 2$
, and that
$e := {\mathrm {ord}}_{t = 1}(\mathcal {I}_\alpha ) = 2$
, and that
![]() $I_{\alpha }(t) = (t-1)^{2} \cdot J_{\alpha }(t)$
for some
$I_{\alpha }(t) = (t-1)^{2} \cdot J_{\alpha }(t)$
for some
![]() $J_{\alpha } \in \mathbb {Z}[t]$
satisfying
$J_{\alpha } \in \mathbb {Z}[t]$
satisfying
![]() $J_{\alpha }(1) \neq 0$
. Moreover, one can easily show that
$J_{\alpha }(1) \neq 0$
. Moreover, one can easily show that
![]() $J_\alpha $
does not have any root on the unit circle of
$J_\alpha $
does not have any root on the unit circle of
![]() $\mathbb {C}$
, as explained in [Reference Mednykh and Mednykh41, Lemma 2]. Finally, we see that
$\mathbb {C}$
, as explained in [Reference Mednykh and Mednykh41, Lemma 2]. Finally, we see that
![]() $\kappa (X) = 1$
and
$\kappa (X) = 1$
and
 $$ \begin{align*}\lvert \Delta_1(J_{\alpha}) \rvert = \lvert J_{\alpha}(1) \rvert = \lvert I_{\alpha}^{"}(1) \rvert/2 = \sum_{i=1}^{k}a_{i}^{2} \end{align*} $$
$$ \begin{align*}\lvert \Delta_1(J_{\alpha}) \rvert = \lvert J_{\alpha}(1) \rvert = \lvert I_{\alpha}^{"}(1) \rvert/2 = \sum_{i=1}^{k}a_{i}^{2} \end{align*} $$
which, thanks to Corollary 3.10, implies that
 $$ \begin{align*} \kappa(C_{n}(a_{1},\ldots,a_{k})) \sim \frac{n}{\sum_{i=1}^{k}a_{i}^{2}} \cdot M_\infty(I_{\alpha})^n \end{align*} $$
$$ \begin{align*} \kappa(C_{n}(a_{1},\ldots,a_{k})) \sim \frac{n}{\sum_{i=1}^{k}a_{i}^{2}} \cdot M_\infty(I_{\alpha})^n \end{align*} $$
as
![]() $n \to \infty $
, which is [Reference Mednykh and Mednykh41, Theorem 5] in the particular case when
$n \to \infty $
, which is [Reference Mednykh and Mednykh41, Theorem 5] in the particular case when
![]() $d=1$
.
$d=1$
.
3.5.2. p-adic asymptotics
Let us look at the asymptotics of the p-adic valuations of the number of spanning trees in a
![]() $\mathbb {Z}$
-tower, for a fixed prime p. As in the Archimedean setting, we start from the case when the Ihara polynomial
$\mathbb {Z}$
-tower, for a fixed prime p. As in the Archimedean setting, we start from the case when the Ihara polynomial
![]() $\mathcal {I}_\alpha $
does not have any nontrivial root lying on the unit circle of
$\mathcal {I}_\alpha $
does not have any nontrivial root lying on the unit circle of
![]() $\mathbb {C}_p$
.
$\mathbb {C}_p$
.
Corollary 3.15. Let X be a finite connected graph such that
![]() $\chi (X) \neq 0$
, and fix a voltage assignment
$\chi (X) \neq 0$
, and fix a voltage assignment
![]() $\alpha \colon \mathbf {E}_X \to \mathbb {Z}$
such that
$\alpha \colon \mathbf {E}_X \to \mathbb {Z}$
such that
![]() $X(\mathbb {Z},\alpha )$
is connected. Fix moreover a rational prime
$X(\mathbb {Z},\alpha )$
is connected. Fix moreover a rational prime
![]() $p \in \mathbb {N}$
. Then, if the polynomial
$p \in \mathbb {N}$
. Then, if the polynomial
![]() $J_{\alpha }$
defined by (3-11) has no root on the unit circle of
$J_{\alpha }$
defined by (3-11) has no root on the unit circle of
![]() $\mathbb {C}_{p}$
,
$\mathbb {C}_{p}$
,
 $$ \begin{align*}|\kappa(X_{n})|_{p} = |n|_{p}^{e-1} \frac{|\kappa(X)|_{p}}{|\Delta_{1}(J_{\alpha})|_{p}} M_{p}(I_{\alpha})^{n} \end{align*} $$
$$ \begin{align*}|\kappa(X_{n})|_{p} = |n|_{p}^{e-1} \frac{|\kappa(X)|_{p}}{|\Delta_{1}(J_{\alpha})|_{p}} M_{p}(I_{\alpha})^{n} \end{align*} $$
for every
![]() $n \in \mathbb {N}$
, where
$n \in \mathbb {N}$
, where
![]() $e := \mathrm {ord}_{t = 1}(\mathcal {I}_\alpha )$
is the order of vanishing at
$e := \mathrm {ord}_{t = 1}(\mathcal {I}_\alpha )$
is the order of vanishing at
![]() $t = 1$
of the Ihara polynomial associated to
$t = 1$
of the Ihara polynomial associated to
![]() $\alpha $
.
$\alpha $
.
Remark 3.16. Let
![]() $f(t) = \sum _{j = 0}^d c_j t^j \in \mathbb {Z}[t]$
be any polynomial. Then, every root of f lies in the unit circle of
$f(t) = \sum _{j = 0}^d c_j t^j \in \mathbb {Z}[t]$
be any polynomial. Then, every root of f lies in the unit circle of
![]() $\mathbb {C}_p$
whenever
$\mathbb {C}_p$
whenever
![]() $p \nmid c_0 \cdot c_d$
. Therefore, we see that, for every given
$p \nmid c_0 \cdot c_d$
. Therefore, we see that, for every given
![]() $\mathbb {Z}$
-tower of graphs, Corollary 3.15 can be applied only for finitely many primes p.
$\mathbb {Z}$
-tower of graphs, Corollary 3.15 can be applied only for finitely many primes p.
3.6. Exact formulae for the p-adic valuation of the number of spanning trees
The previous remark prompts us to study the case when
![]() $J_\alpha $
has some roots on the unit circle of
$J_\alpha $
has some roots on the unit circle of
![]() $\mathbb {C}_p$
. In this case, we can prove the following result (which is the more precise version of Theorem 1.1 from §1), which gives a partial analogue of Iwasawa’s theorem for
$\mathbb {C}_p$
. In this case, we can prove the following result (which is the more precise version of Theorem 1.1 from §1), which gives a partial analogue of Iwasawa’s theorem for
![]() $\mathbb {Z}$
-towers.
$\mathbb {Z}$
-towers.
Theorem 3.17. Let X be a finite connected graph whose Euler characteristic
![]() $\chi (X)$
does not vanish, and let
$\chi (X)$
does not vanish, and let
![]() $\alpha \colon \mathbf {E}_X \to \mathbb {Z}$
be a voltage assignment such that
$\alpha \colon \mathbf {E}_X \to \mathbb {Z}$
be a voltage assignment such that
![]() $X(\mathbb {Z},\alpha )$
is connected. Let
$X(\mathbb {Z},\alpha )$
is connected. Let
![]() $\mathcal {I}_\alpha \in \mathbb {Z}[t]$
be the Ihara polynomial associated to
$\mathcal {I}_\alpha \in \mathbb {Z}[t]$
be the Ihara polynomial associated to
![]() $\alpha $
, and set
$\alpha $
, and set
where
![]() $b := -{\mathrm {ord}}_{t=0}(\mathcal {I}_\alpha )$
, and
$b := -{\mathrm {ord}}_{t=0}(\mathcal {I}_\alpha )$
, and
![]() $e := {\mathrm {ord}}_{t=1}(\mathcal {I}_\alpha )$
.
$e := {\mathrm {ord}}_{t=1}(\mathcal {I}_\alpha )$
.
Fix now a rational prime
![]() $p \in \mathbb {N}$
, an algebraic closure
$p \in \mathbb {N}$
, an algebraic closure
![]() $\overline {\mathbb {Q}}_p$
of the field of p-adic numbers, and let
$\overline {\mathbb {Q}}_p$
of the field of p-adic numbers, and let
![]() $\mathcal {O}_p$
be the ring of integers of
$\mathcal {O}_p$
be the ring of integers of
![]() $\overline {\mathbb {Q}}_p$
. Using this notation, we can define the quantities
$\overline {\mathbb {Q}}_p$
. Using this notation, we can define the quantities
 $$ \begin{align*} \begin{aligned} \mu_p(X,\alpha) &:= -m_p(J_\alpha)/{\log}(p), \\ c_p(X,\alpha) &:= \mathrm{ord}_{p}(\kappa(X)) - \mathrm{ord}_{p}(\Delta_{1}(J_{\alpha}) ), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mu_p(X,\alpha) &:= -m_p(J_\alpha)/{\log}(p), \\ c_p(X,\alpha) &:= \mathrm{ord}_{p}(\kappa(X)) - \mathrm{ord}_{p}(\Delta_{1}(J_{\alpha}) ), \end{aligned} \end{align*} $$
where
![]() $m_p(J_\alpha )$
denotes the logarithmic p-adic Mahler measure of
$m_p(J_\alpha )$
denotes the logarithmic p-adic Mahler measure of
![]() $J_\alpha $
, defined as in (2-3).
$J_\alpha $
, defined as in (2-3).
Moreover, let
![]() $\beta _1,\ldots ,\beta _d \in \overline {\mathbb {Q}}_p$
be the p-adic roots of
$\beta _1,\ldots ,\beta _d \in \overline {\mathbb {Q}}_p$
be the p-adic roots of
![]() $J_\alpha $
, counted with multiplicity. Then, for every
$J_\alpha $
, counted with multiplicity. Then, for every
![]() $n \in \mathbb {N}$
, we introduce the set
$n \in \mathbb {N}$
, we introduce the set
which can be used to define the quantity
Finally, for every
![]() $\beta \in \mathcal {O}_p$
such that
$\beta \in \mathcal {O}_p$
such that
![]() $\lvert \beta \rvert _p = 1$
,
$\lvert \beta \rvert _p = 1$
,
and for every
![]() $n \in \mathbb {N}$
, we set
$n \in \mathbb {N}$
, we set
![]() $r_{p,n}(\beta ) := \min ({\mathrm {ord}}_p(n),s_p(\beta ))$
, where
$r_{p,n}(\beta ) := \min ({\mathrm {ord}}_p(n),s_p(\beta ))$
, where
![]() $\tau _p(\pi _p(\beta ))$
denotes the Teichmüller lift of the reduction
$\tau _p(\pi _p(\beta ))$
denotes the Teichmüller lift of the reduction
![]() $\pi _p(\beta )$
of
$\pi _p(\beta )$
of
![]() $\beta $
modulo the maximal ideal of
$\beta $
modulo the maximal ideal of
![]() $\mathcal {O}_p$
. This can be used to define the quantity
$\mathcal {O}_p$
. This can be used to define the quantity
 $$ \begin{align*} \nu_{p,n}(X,\alpha) := \sum_{\substack{j \in \{1,\ldots,d\} \\ \beta_j \in B_{p,n}(X,\alpha)}} ( {\mathrm{ord}}_p(\beta_j^{p^{r_{p,n}(\beta_j)}} - \tau_p(\pi_p(\beta_j))^{p^{r_{p,n}(\beta_j)}}) - r_{p,n}(\beta_j) ). \end{align*} $$
$$ \begin{align*} \nu_{p,n}(X,\alpha) := \sum_{\substack{j \in \{1,\ldots,d\} \\ \beta_j \in B_{p,n}(X,\alpha)}} ( {\mathrm{ord}}_p(\beta_j^{p^{r_{p,n}(\beta_j)}} - \tau_p(\pi_p(\beta_j))^{p^{r_{p,n}(\beta_j)}}) - r_{p,n}(\beta_j) ). \end{align*} $$
Then,
for every
![]() $n \in \mathbb {N}$
.
$n \in \mathbb {N}$
.
Proof. From Theorem 3.6, one has the identity
Moreover, Corollary 2.5 implies that
where
![]() $A_{p,n}(X,\alpha ) := \# \{ j \in \{1,\ldots ,d\} \colon \beta _j \in B_{p,n}(X,\alpha ) \}$
, because we have that
$A_{p,n}(X,\alpha ) := \# \{ j \in \{1,\ldots ,d\} \colon \beta _j \in B_{p,n}(X,\alpha ) \}$
, because we have that
![]() $B_{p,n}(X,\alpha ) = B_{p,n}(J_\alpha )$
and
$B_{p,n}(X,\alpha ) = B_{p,n}(J_\alpha )$
and
![]() $\nu _{p,n}(X,\alpha ) = \nu _{p,n}(J_\alpha )$
by definition. Therefore, we can conclude the proof by combining (3-20) with (3-19).
$\nu _{p,n}(X,\alpha ) = \nu _{p,n}(J_\alpha )$
by definition. Therefore, we can conclude the proof by combining (3-20) with (3-19).
Using Theorem 3.17, one can easily show that once we fix the base graph X, the voltage assignment
![]() $\alpha \colon \mathbf {E}_X \to \mathbb {Z}$
and the prime number p, we can subdivide
$\alpha \colon \mathbf {E}_X \to \mathbb {Z}$
and the prime number p, we can subdivide
![]() $\mathbb {N}$
in a finite number of sequences, given by imposing certain divisibility conditions. Along each of these sequences, the invariant
$\mathbb {N}$
in a finite number of sequences, given by imposing certain divisibility conditions. Along each of these sequences, the invariant
![]() ${\mathrm {ord}}_p(\kappa (X_n))$
can be computed as a linear form in n and
${\mathrm {ord}}_p(\kappa (X_n))$
can be computed as a linear form in n and
![]() ${\mathrm {ord}}_p(n)$
, as we show more precisely in the following theorem.
${\mathrm {ord}}_p(n)$
, as we show more precisely in the following theorem.
Theorem 3.18. Let X be a finite connected graph whose Euler characteristic
![]() $\chi (X)$
does not vanish, and
$\chi (X)$
does not vanish, and
![]() $\alpha \colon \mathbf {E}_X \to \mathbb {Z}$
be a voltage assignment such that for every
$\alpha \colon \mathbf {E}_X \to \mathbb {Z}$
be a voltage assignment such that for every
![]() $n \geq 1$
, the finite graph
$n \geq 1$
, the finite graph
![]() $X_n := X(\mathbb {Z}/n \mathbb {Z},\alpha _n)$
is connected (which can be checked using Theorem 3.2). Moreover, for every prime
$X_n := X(\mathbb {Z}/n \mathbb {Z},\alpha _n)$
is connected (which can be checked using Theorem 3.2). Moreover, for every prime
![]() $p \in \mathbb {Z}$
,
$p \in \mathbb {Z}$
,
where
![]() $m_p(\mathcal {I}_\alpha )$
denotes the logarithmic p-adic Mahler measure of the Ihara polynomial
$m_p(\mathcal {I}_\alpha )$
denotes the logarithmic p-adic Mahler measure of the Ihara polynomial
![]() $\mathcal {I}_\alpha $
. Then, for every rational prime p, there exist a finite set
$\mathcal {I}_\alpha $
. Then, for every rational prime p, there exist a finite set
![]() $\mathcal {N}_p(X,\alpha ) \subseteq \mathbb {N}$
of integers coprime to p, and an integer
$\mathcal {N}_p(X,\alpha ) \subseteq \mathbb {N}$
of integers coprime to p, and an integer
![]() $R_p(X,\alpha ) \geq 0$
such that for every
$R_p(X,\alpha ) \geq 0$
such that for every
![]() $\mathfrak {n} \subseteq \mathcal {N}_p(X,\alpha )$
and every
$\mathfrak {n} \subseteq \mathcal {N}_p(X,\alpha )$
and every
![]() $r \in \{0,\ldots ,R_p(X,\alpha )\}$
, there exist two integers
$r \in \{0,\ldots ,R_p(X,\alpha )\}$
, there exist two integers
![]() $\lambda _p(X,\alpha ,\mathfrak {n}) \geq 0$
and
$\lambda _p(X,\alpha ,\mathfrak {n}) \geq 0$
and
![]() $\nu _p(X,\alpha ,\mathfrak {n},r)$
such that
$\nu _p(X,\alpha ,\mathfrak {n},r)$
such that
for every
![]() $n \in \mathcal {S}_p(X,\alpha ,\mathfrak {n},r)$
, where
$n \in \mathcal {S}_p(X,\alpha ,\mathfrak {n},r)$
, where
![]() $\mathcal {S}_p(X,\alpha ,\mathfrak {n},r)$
consists of those
$\mathcal {S}_p(X,\alpha ,\mathfrak {n},r)$
consists of those
![]() $n \in \mathbb {N}$
such that:
$n \in \mathbb {N}$
such that:
-
•
 $N \mid n$
for each
$N \mid n$
for each
 $N \in \mathfrak {n}$
;
$N \in \mathfrak {n}$
; -
•
 $N' \nmid n$
for each
$N' \nmid n$
for each
 $N' \in \mathcal {N}_p(X,\alpha ) \setminus \mathfrak {n}$
;
$N' \in \mathcal {N}_p(X,\alpha ) \setminus \mathfrak {n}$
; -
•
 ${\mathrm {ord}}_p(n) = r$
if
${\mathrm {ord}}_p(n) = r$
if
 $r < R_p(X,\alpha )$
, or
$r < R_p(X,\alpha )$
, or
 ${\mathrm {ord}}_p(n) \geq R_p(X,\alpha )$
if
${\mathrm {ord}}_p(n) \geq R_p(X,\alpha )$
if
 $r = R_p(X,\alpha )$
.
$r = R_p(X,\alpha )$
.
Moreover, the finite set
![]() $\mathcal {N}_p(X,\alpha )$
, the integer
$\mathcal {N}_p(X,\alpha )$
, the integer
![]() $R_p(X,\alpha )$
, and the two invariants
$R_p(X,\alpha )$
, and the two invariants
![]() $\lambda _p(X,\alpha ,\mathfrak {n})$
and
$\lambda _p(X,\alpha ,\mathfrak {n})$
and
![]() $\nu _p(X,\alpha ,\mathfrak {n},r)$
can be explicitly computed in terms of the polynomial
$\nu _p(X,\alpha ,\mathfrak {n},r)$
can be explicitly computed in terms of the polynomial
![]() $\mathcal {I}_\alpha $
.
$\mathcal {I}_\alpha $
.
Proof. Fix a finite connected graph X and a voltage assignment
![]() $\alpha \colon \mathbf {E}_X \to \mathbb {Z}$
. Moreover, fix a rational prime p and let
$\alpha \colon \mathbf {E}_X \to \mathbb {Z}$
. Moreover, fix a rational prime p and let
![]() $\beta _1,\ldots ,\beta _d$
denote the roots of
$\beta _1,\ldots ,\beta _d$
denote the roots of
![]() $J_\alpha $
, counted with multiplicities, that lie on the unit circle of
$J_\alpha $
, counted with multiplicities, that lie on the unit circle of
![]() $\mathbb {C}_p$
, and let
$\mathbb {C}_p$
, and let
![]() $N_1,\ldots ,N_d$
denote the multiplicative orders of
$N_1,\ldots ,N_d$
denote the multiplicative orders of
![]() $\pi _p(\beta _1),\ldots ,\pi _p(\beta _d)$
in
$\pi _p(\beta _1),\ldots ,\pi _p(\beta _d)$
in
![]() $\overline {\mathbb {F}}_p^\times $
. Then,
$\overline {\mathbb {F}}_p^\times $
. Then,
 $$ \begin{align*} \begin{aligned} \mathcal{N}_p(X,\alpha) &:= \{N_1,\ldots,N_d\}, \\ R_p(X,\alpha) &:= \max_{j=1,\ldots,d} s_p(\beta_j), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathcal{N}_p(X,\alpha) &:= \{N_1,\ldots,N_d\}, \\ R_p(X,\alpha) &:= \max_{j=1,\ldots,d} s_p(\beta_j), \end{aligned} \end{align*} $$
where
![]() $s_p(\beta _j)$
is defined as in (2-13). Moreover, for every subset
$s_p(\beta _j)$
is defined as in (2-13). Moreover, for every subset
![]() $\mathfrak {n} \subseteq \mathcal {N}_p(X,\alpha )$
,
$\mathfrak {n} \subseteq \mathcal {N}_p(X,\alpha )$
,
as we will now show.
First of all, suppose that
![]() $\mathfrak {n} = \emptyset $
. In other words, let us take an integer
$\mathfrak {n} = \emptyset $
. In other words, let us take an integer
![]() $n \in \mathbb {N}$
such that
$n \in \mathbb {N}$
such that
![]() $N_1 \nmid n, \ldots , N_d \nmid n$
. Then, the set
$N_1 \nmid n, \ldots , N_d \nmid n$
. Then, the set
![]() $B_{p,n}(X,\alpha )$
defined in (3-17) is empty. Therefore, Theorem 3.17 shows that for every
$B_{p,n}(X,\alpha )$
defined in (3-17) is empty. Therefore, Theorem 3.17 shows that for every
![]() $r \in \{0,\ldots ,R_p(X,\alpha )\}$
,
$r \in \{0,\ldots ,R_p(X,\alpha )\}$
,
and (3-21) will hold true.
Now let us suppose that
![]() $\mathfrak {n} \neq \emptyset $
and let
$\mathfrak {n} \neq \emptyset $
and let
![]() $J \subseteq \{1,\ldots ,d\}$
be the unique nonempty subset such that
$J \subseteq \{1,\ldots ,d\}$
be the unique nonempty subset such that
![]() $\mathfrak {n} = \{N_j \colon j \in J \}$
. Then, if we suppose in addition that
$\mathfrak {n} = \{N_j \colon j \in J \}$
. Then, if we suppose in addition that
![]() $p \neq 2$
and
$p \neq 2$
and
![]() $p \nmid \mathrm {Disc}(J_\alpha )$
, we have that
$p \nmid \mathrm {Disc}(J_\alpha )$
, we have that
![]() $B_{p,n}(X,\alpha ) = \{ \beta _j \colon j \in J \}$
. Moreover, the quantity
$B_{p,n}(X,\alpha ) = \{ \beta _j \colon j \in J \}$
. Moreover, the quantity
![]() $r_{p,n}(\beta )$
, which was defined in (3-18), vanishes whenever
$r_{p,n}(\beta )$
, which was defined in (3-18), vanishes whenever
![]() $\beta \in B_{p,n}(X,\alpha )$
, because
$\beta \in B_{p,n}(X,\alpha )$
, because
![]() ${\mathrm {ord}}_p(\beta - \tau _p(\pi _p(\beta ))) \in \mathbb {N}$
and
${\mathrm {ord}}_p(\beta - \tau _p(\pi _p(\beta ))) \in \mathbb {N}$
and
![]() $p-1> 1$
in this case. Therefore, Theorem 3.17 shows that for every prime
$p-1> 1$
in this case. Therefore, Theorem 3.17 shows that for every prime
![]() $p \neq 2$
such that
$p \neq 2$
such that
![]() $p \nmid \mathrm {Disc}(J_\alpha )$
and every
$p \nmid \mathrm {Disc}(J_\alpha )$
and every
![]() $r \in \{0,\ldots ,R_p(X,\alpha )\}$
,
$r \in \{0,\ldots ,R_p(X,\alpha )\}$
,
 $$ \begin{align*} \nu_p(X,\alpha,\mathfrak{n},r) := c_p(X,\alpha) + \sum_{j \in J} {\mathrm{ord}}_p(\beta_j - \tau_p(\pi_p(\beta_j))), \end{align*} $$
$$ \begin{align*} \nu_p(X,\alpha,\mathfrak{n},r) := c_p(X,\alpha) + \sum_{j \in J} {\mathrm{ord}}_p(\beta_j - \tau_p(\pi_p(\beta_j))), \end{align*} $$
and (3-21) will hold true. However, if
![]() $p = 2$
and
$p = 2$
and
![]() $\mathrm {Disc}(J_\alpha )$
is odd, we still have that
$\mathrm {Disc}(J_\alpha )$
is odd, we still have that
![]() $B_{p,n}(X,\alpha ) = \{\beta _j \colon j \in J\}$
and
$B_{p,n}(X,\alpha ) = \{\beta _j \colon j \in J\}$
and
![]() ${\mathrm {ord}}_p(\beta - \tau _p(\pi _p(\beta ))) \in \mathbb {N}$
for every
${\mathrm {ord}}_p(\beta - \tau _p(\pi _p(\beta ))) \in \mathbb {N}$
for every
![]() $\beta \in B_{p,n}(X,\alpha )$
. Therefore, we see that for every
$\beta \in B_{p,n}(X,\alpha )$
. Therefore, we see that for every
![]() $\beta \in B_{p,n}(X,\alpha )$
, we have
$\beta \in B_{p,n}(X,\alpha )$
, we have
![]() $r_{p,n}(\beta ) = 0$
if
$r_{p,n}(\beta ) = 0$
if
![]() $2 \nmid n$
, and
$2 \nmid n$
, and
![]() $r_{p,n}(\beta ) \leq 1$
otherwise, because
$r_{p,n}(\beta ) \leq 1$
otherwise, because
![]() $\mathrm {Disc}(J_\alpha )$
is assumed to be odd. In other words, if
$\mathrm {Disc}(J_\alpha )$
is assumed to be odd. In other words, if
![]() $r = 0$
,
$r = 0$
,
 $$ \begin{align*} \nu_2(X,\alpha,\mathfrak{n},0) := c_2(X,\alpha) + \sum_{j \in J} {\mathrm{ord}}_2(\beta_j - \tau_2(\pi_2(\beta_j))), \end{align*} $$
$$ \begin{align*} \nu_2(X,\alpha,\mathfrak{n},0) := c_2(X,\alpha) + \sum_{j \in J} {\mathrm{ord}}_2(\beta_j - \tau_2(\pi_2(\beta_j))), \end{align*} $$
while if
![]() $r \geq 1$
,
$r \geq 1$
,
 $$ \begin{align*} \begin{aligned} \nu_2(X,\alpha,\mathfrak{n},r) &:= c_2(X,\alpha) \\ & \quad + \sum_{\substack{j \in J \\ \mathrm{ord}_2(\beta_j - \tau_2(\pi_2(\beta_j))) = 1}} ({\mathrm{ord}}_2(\beta_j^2 - \tau_2(\pi_2(\beta_j))^2) - 1) \\ & \quad + \sum_{\substack{j \in J \\ \mathrm{ord}_2(\beta_j - \tau_2(\pi_2(\beta_j))) \geq 2}} {\mathrm{ord}}_2(\beta_j - \tau_2(\pi_2(\beta_j))) \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \nu_2(X,\alpha,\mathfrak{n},r) &:= c_2(X,\alpha) \\ & \quad + \sum_{\substack{j \in J \\ \mathrm{ord}_2(\beta_j - \tau_2(\pi_2(\beta_j))) = 1}} ({\mathrm{ord}}_2(\beta_j^2 - \tau_2(\pi_2(\beta_j))^2) - 1) \\ & \quad + \sum_{\substack{j \in J \\ \mathrm{ord}_2(\beta_j - \tau_2(\pi_2(\beta_j))) \geq 2}} {\mathrm{ord}}_2(\beta_j - \tau_2(\pi_2(\beta_j))) \end{aligned} \end{align*} $$
and Theorem 3.17 will ensure that (3-21) holds true when
![]() $p = 2$
.
$p = 2$
.
To conclude, let us assume that
![]() $p \mid \mathrm {Disc}(J_\alpha )$
and let again
$p \mid \mathrm {Disc}(J_\alpha )$
and let again
![]() $\mathfrak {n} = \{N_j \colon j \in J\}$
for some nonempty
$\mathfrak {n} = \{N_j \colon j \in J\}$
for some nonempty
![]() $J \subseteq \{1,\ldots ,d\}$
, so that
$J \subseteq \{1,\ldots ,d\}$
, so that
![]() $B_{p,n}(X,\alpha ) = \{\beta _j \colon j \in J\}$
. Then, if
$B_{p,n}(X,\alpha ) = \{\beta _j \colon j \in J\}$
. Then, if
![]() $r = R_p(X,\alpha )$
, which implies that
$r = R_p(X,\alpha )$
, which implies that
![]() ${\mathrm {ord}}_p(n) \geq R_{p}(X,\alpha )$
,
${\mathrm {ord}}_p(n) \geq R_{p}(X,\alpha )$
,
for every
![]() $\beta \in B_{p,n}(X,\alpha )$
. Therefore, Theorem 3.17 guarantees that if we take
$\beta \in B_{p,n}(X,\alpha )$
. Therefore, Theorem 3.17 guarantees that if we take
![]() $\nu _p(X,\alpha ,\mathfrak {n},R_p(X,\alpha ))$
to be
$\nu _p(X,\alpha ,\mathfrak {n},R_p(X,\alpha ))$
to be
 $$ \begin{align*} c_p(X,\alpha) + \sum_{j \in J} ( {\mathrm{ord}}_p( \beta_j^{p^{s_p(\beta_j)}} - \tau_p(\pi_p(\beta_j))^{p^{s_p(\beta_j)}} ) - s_p(\beta_j) ), \end{align*} $$
$$ \begin{align*} c_p(X,\alpha) + \sum_{j \in J} ( {\mathrm{ord}}_p( \beta_j^{p^{s_p(\beta_j)}} - \tau_p(\pi_p(\beta_j))^{p^{s_p(\beta_j)}} ) - s_p(\beta_j) ), \end{align*} $$
the identity (3-21) will hold true. Finally, if we fix
![]() $r \in \{0,\ldots ,R_p(X,\alpha ) - 1\}$
, we can take
$r \in \{0,\ldots ,R_p(X,\alpha ) - 1\}$
, we can take
![]() $\nu _p(X,\alpha ,\mathfrak {n},r)$
to be
$\nu _p(X,\alpha ,\mathfrak {n},r)$
to be
 $$ \begin{align*} c_p(X,\alpha) + \sum_{j \in J} ( {\mathrm{ord}}_p( \beta_j^{p^{\min(r,s_p(\beta_j))}} - \tau_p(\pi_p(\beta_j))^{p^{\min(r,s_p(\beta_j))}} ) - \min(r,s_p(\beta_j)) ) \end{align*} $$
$$ \begin{align*} c_p(X,\alpha) + \sum_{j \in J} ( {\mathrm{ord}}_p( \beta_j^{p^{\min(r,s_p(\beta_j))}} - \tau_p(\pi_p(\beta_j))^{p^{\min(r,s_p(\beta_j))}} ) - \min(r,s_p(\beta_j)) ) \end{align*} $$
Remark 3.19. The previous proof shows that the p-adic valuation of the number of spanning trees is actually constant along many of the sequences
![]() $\mathcal {S}_p(X,\alpha ,\mathfrak {n},r)$
. More precisely, let
$\mathcal {S}_p(X,\alpha ,\mathfrak {n},r)$
. More precisely, let
![]() $\lVert J_\alpha \rVert $
be the greatest common divisor of the coefficients of
$\lVert J_\alpha \rVert $
be the greatest common divisor of the coefficients of
![]() $J_\alpha $
. Then, if p is a prime such that
$J_\alpha $
. Then, if p is a prime such that
for every
![]() $\mathfrak {n} = \{N_j \colon j \in J\} \subseteq \mathcal {N}_p(X,\alpha )$
,
$\mathfrak {n} = \{N_j \colon j \in J\} \subseteq \mathcal {N}_p(X,\alpha )$
,
 $$ \begin{align*} {\mathrm{ord}}_p(\kappa(X_n)) = c_p(X,\alpha) + \sum_{j \in J} {\mathrm{ord}}_p(\beta_j - \tau_p(\pi_p(\beta_j))) \end{align*} $$
$$ \begin{align*} {\mathrm{ord}}_p(\kappa(X_n)) = c_p(X,\alpha) + \sum_{j \in J} {\mathrm{ord}}_p(\beta_j - \tau_p(\pi_p(\beta_j))) \end{align*} $$
whenever
![]() $n \in \mathcal {S}_p(X,\alpha ,\mathfrak {n},0)$
.
$n \in \mathcal {S}_p(X,\alpha ,\mathfrak {n},0)$
.
Remark 3.20. It is clear from the proof of Theorem 1.1 that the multiplicative orders
![]() $N_1,\ldots ,N_d$
play a crucial role in the understanding of the evolution of the p-adic valuation of the number of spanning trees along a
$N_1,\ldots ,N_d$
play a crucial role in the understanding of the evolution of the p-adic valuation of the number of spanning trees along a
![]() $\mathbb {Z}$
-tower. Therefore, it would be nice to know how these orders vary with the prime number p. This can be understood in terms of a far reaching generalisation of Artin’s primitive root conjecture, due to Lenstra [Reference Lenstra37], which is known to hold under the assumption of the generalised Riemann hypothesis.
$\mathbb {Z}$
-tower. Therefore, it would be nice to know how these orders vary with the prime number p. This can be understood in terms of a far reaching generalisation of Artin’s primitive root conjecture, due to Lenstra [Reference Lenstra37], which is known to hold under the assumption of the generalised Riemann hypothesis.

Figure 2 The
![]() $\mathbb{Z}$
-tower of graphs described in Section 3.7.
$\mathbb{Z}$
-tower of graphs described in Section 3.7.
3.7. The Fibonacci tower
To conclude this paper, let us note how the formula provided by Theorem 3.17 generalises a famous formula for the p-adic valuation of the Fibonacci numbers, due to Lengyel [Reference Lengyel36]. More precisely, if in Example 3.14 we take the bouquet on two loops X, with an orientation
![]() $S = \{s_1,s_2\}$
, and we let
$S = \{s_1,s_2\}$
, and we let
![]() $\alpha $
be the unique voltage assignment
$\alpha $
be the unique voltage assignment
![]() $\alpha :\mathbf {E}_{X} \rightarrow \mathbb {Z}$
such that
$\alpha :\mathbf {E}_{X} \rightarrow \mathbb {Z}$
such that
![]() $\alpha (s_1) = 1$
and
$\alpha (s_1) = 1$
and
![]() $\alpha (s_2) = 2$
, then we obtain the
$\alpha (s_2) = 2$
, then we obtain the
![]() $\mathbb {Z}$
-tower portrayed in Figure 2.
$\mathbb {Z}$
-tower portrayed in Figure 2.
It turns out that the number of spanning trees of the finite layers of this tower is intimately related to the sequence of Fibonacci numbers. To show this, let us observe that
![]() $\kappa (X) = 1$
and
$\kappa (X) = 1$
and
which implies that
![]() $e = 2$
and
$e = 2$
and
![]() $J_\alpha (t) = -(t^2 + 3 t + 1)$
. We denote by
$J_\alpha (t) = -(t^2 + 3 t + 1)$
. We denote by
![]() $\beta _1 = ({-3 - \!\sqrt {5}})/{2}$
and
$\beta _1 = ({-3 - \!\sqrt {5}})/{2}$
and
![]() $\beta _2 = ({-3+\!\sqrt {5}})/{2}$
the roots of
$\beta _2 = ({-3+\!\sqrt {5}})/{2}$
the roots of
![]() $J_\alpha $
, and we observe that
$J_\alpha $
, and we observe that
![]() $\Delta _1(J_\alpha ) = -5$
.
$\Delta _1(J_\alpha ) = -5$
.
Then, Theorem 3.6 can be combined with a simple computation to show that
 $$ \begin{align*} \kappa(X_{n}) = n \frac{\Delta_{n}(J_{\alpha})}{\Delta_{1}(J_{\alpha})} = n \frac{(-1)^{n}(\beta_{1}^{n} - 1)(\beta_{2}^{n} - 1)}{-5} = n F_{n}^{2}, \end{align*} $$
$$ \begin{align*} \kappa(X_{n}) = n \frac{\Delta_{n}(J_{\alpha})}{\Delta_{1}(J_{\alpha})} = n \frac{(-1)^{n}(\beta_{1}^{n} - 1)(\beta_{2}^{n} - 1)}{-5} = n F_{n}^{2}, \end{align*} $$
where
![]() $F_{n}$
is the n th Fibonacci number. Therefore, Theorem 3.17 implies that
$F_{n}$
is the n th Fibonacci number. Therefore, Theorem 3.17 implies that
for every prime
![]() $p \neq 5$
and every
$p \neq 5$
and every
![]() $n \in \mathbb {N}$
, because
$n \in \mathbb {N}$
, because
![]() $m_p(J_\alpha ) = 0$
for every prime
$m_p(J_\alpha ) = 0$
for every prime
![]() $p \in \mathbb {N}$
.
$p \in \mathbb {N}$
.
Now, let us note that the two roots
![]() $\beta _1$
and
$\beta _1$
and
![]() $\beta _2$
of the polynomial
$\beta _2$
of the polynomial
![]() $J_\alpha $
are both reciprocal units, which implies that the set
$J_\alpha $
are both reciprocal units, which implies that the set
![]() $B_{p,n}(X,\alpha )$
is either empty or consists of the two roots
$B_{p,n}(X,\alpha )$
is either empty or consists of the two roots
![]() $\{\beta _1,\beta _2\}$
. The latter scenario occurs if and only if n is a multiple of the multiplicative order
$\{\beta _1,\beta _2\}$
. The latter scenario occurs if and only if n is a multiple of the multiplicative order
![]() $N_p$
of
$N_p$
of
![]() $\beta _1$
(and
$\beta _1$
(and
![]() $\beta _2$
) in
$\beta _2$
) in
![]() $\overline {\mathbb {F}}_p^\times $
. Therefore, Theorem 3.17 shows that
$\overline {\mathbb {F}}_p^\times $
. Therefore, Theorem 3.17 shows that
![]() $N_p$
coincides with the so called rank of apparition of the prime p, that is, with the smallest index n such that
$N_p$
coincides with the so called rank of apparition of the prime p, that is, with the smallest index n such that
![]() $p \mid F_n$
. Since there exists
$p \mid F_n$
. Since there exists
![]() $k \in \mathbb {N}$
such that
$k \in \mathbb {N}$
such that
![]() $N_p \mid p^k - 1$
, we see that
$N_p \mid p^k - 1$
, we see that
![]() ${\mathrm {ord}}_p(N_p) = 0$
and thus that
${\mathrm {ord}}_p(N_p) = 0$
and thus that
![]() $\sum _{j=1}^2 {\mathrm {ord}}_p(\beta _j - \tau _p(\pi _p(\beta _j))) = 2 \cdot {\mathrm {ord}}_p(F_{N_p})$
, provided one assumes moreover that
$\sum _{j=1}^2 {\mathrm {ord}}_p(\beta _j - \tau _p(\pi _p(\beta _j))) = 2 \cdot {\mathrm {ord}}_p(F_{N_p})$
, provided one assumes moreover that
![]() $p \neq 2$
. Hence, these considerations entail that
$p \neq 2$
. Hence, these considerations entail that
 $$ \begin{align*} {\mathrm{ord}}_p(F_n) = \begin{cases} {\mathrm{ord}}_p(n) + {\mathrm{ord}}_p(F_{N_p}) & \text{if} \ N_p \mid n, \\ 0 & \text{otherwise}, \end{cases} \end{align*} $$
$$ \begin{align*} {\mathrm{ord}}_p(F_n) = \begin{cases} {\mathrm{ord}}_p(n) + {\mathrm{ord}}_p(F_{N_p}) & \text{if} \ N_p \mid n, \\ 0 & \text{otherwise}, \end{cases} \end{align*} $$
for every
![]() $p \neq 2,5$
, as was proven in [Reference Lengyel36, Section 3].
$p \neq 2,5$
, as was proven in [Reference Lengyel36, Section 3].
To conclude this example, and this paper, let us see what happens when
![]() $p = 2$
and
$p = 2$
and
![]() $p = 5$
. In the first case, when
$p = 5$
. In the first case, when
![]() $p=2$
, we can observe that
$p=2$
, we can observe that
![]() $J_\alpha $
has no roots in
$J_\alpha $
has no roots in
![]() $\mathbb {F}_2$
, which implies necessarily that
$\mathbb {F}_2$
, which implies necessarily that
![]() $N_2 = 3$
. Moreover, to compute the Teichmüller representatives
$N_2 = 3$
. Moreover, to compute the Teichmüller representatives
![]() $\tau _2(\pi _2(\beta _j))$
, for
$\tau _2(\pi _2(\beta _j))$
, for
![]() $j \in \{1,2\}$
, we can work globally and consider the number field
$j \in \{1,2\}$
, we can work globally and consider the number field
![]() $K = \mathbb {Q}(\!\sqrt {5},\zeta _3)$
, where
$K = \mathbb {Q}(\!\sqrt {5},\zeta _3)$
, where
![]() $\zeta _3$
is a primitive third root of unity. A simple calculation shows that
$\zeta _3$
is a primitive third root of unity. A simple calculation shows that
![]() $2$
decomposes as a product of two primes in K both with inertia degree
$2$
decomposes as a product of two primes in K both with inertia degree
![]() $2$
and ramification degree
$2$
and ramification degree
![]() $1$
. Using SageMath [54], or by hand, one calculates that
$1$
. Using SageMath [54], or by hand, one calculates that
![]() $(\beta _1 - \zeta _{3}) = \mathfrak {p}$
, where
$(\beta _1 - \zeta _{3}) = \mathfrak {p}$
, where
![]() $\mathfrak {p}$
is one of the two primes lying above
$\mathfrak {p}$
is one of the two primes lying above
![]() $2$
. If we denote the other prime lying above
$2$
. If we denote the other prime lying above
![]() $2$
by
$2$
by
![]() $\mathfrak {q}$
, then we also have
$\mathfrak {q}$
, then we also have
![]() $(\beta _1 - \zeta _{3}^{2}) = \mathfrak {q}$
. Moreover, we have
$(\beta _1 - \zeta _{3}^{2}) = \mathfrak {q}$
. Moreover, we have
![]() $(\beta _1^{2} - \zeta _{3}^{2}) = \mathfrak {p}^{3}$
and
$(\beta _1^{2} - \zeta _{3}^{2}) = \mathfrak {p}^{3}$
and
![]() $(\beta _1^{2} - \zeta _{3}^{4}) = \mathfrak {q}^{3}$
. A similar calculation can be performed for
$(\beta _1^{2} - \zeta _{3}^{4}) = \mathfrak {q}^{3}$
. A similar calculation can be performed for
![]() $\beta _{2}$
. After embedding K into
$\beta _{2}$
. After embedding K into
![]() $\overline {\mathbb {Q}}_{2}$
with any embedding, these calculations show that
$\overline {\mathbb {Q}}_{2}$
with any embedding, these calculations show that
![]() $N_{2} = 3$
and
$N_{2} = 3$
and
for every
![]() $j \in \{1,2\}$
. Finally, one can check easily that
$j \in \{1,2\}$
. Finally, one can check easily that
![]() ${\mathrm {ord}}_2(F_3) = 1$
. Thus, (3-18) implies that
${\mathrm {ord}}_2(F_3) = 1$
. Thus, (3-18) implies that
 $$ \begin{align*} {\mathrm{ord}}_2(F_n) = \begin{cases} 0 \ & \text{if} \ n \equiv 1,2 \ \pmod {\ 3}, \\ 1 \ & \text{if} \ n \equiv 3 \ \pmod {\ 6}, \\ {\mathrm{ord}}_2(n) + 2 \ & \text{if} \ n \equiv 0 \ \pmod {\ 6}, \end{cases} \end{align*} $$
$$ \begin{align*} {\mathrm{ord}}_2(F_n) = \begin{cases} 0 \ & \text{if} \ n \equiv 1,2 \ \pmod {\ 3}, \\ 1 \ & \text{if} \ n \equiv 3 \ \pmod {\ 6}, \\ {\mathrm{ord}}_2(n) + 2 \ & \text{if} \ n \equiv 0 \ \pmod {\ 6}, \end{cases} \end{align*} $$
which was proven in [Reference Lengyel36, Lemma 2].
Let us now suppose that
![]() $p = 5$
. Since
$p = 5$
. Since
![]() $-J_\alpha \equiv (t-1)^2 \ (\text {mod} \ 5)$
, we see that the multiplicative order of
$-J_\alpha \equiv (t-1)^2 \ (\text {mod} \ 5)$
, we see that the multiplicative order of
![]() $\beta _{1}$
and
$\beta _{1}$
and
![]() $\beta _{2}$
in
$\beta _{2}$
in
![]() $\overline {\mathbb {F}}_{5}^{\times }$
is
$\overline {\mathbb {F}}_{5}^{\times }$
is
![]() $1$
, which is not the rank of apparition of the prime
$1$
, which is not the rank of apparition of the prime
![]() $5$
. Moreover, one has that
$5$
. Moreover, one has that
![]() ${\mathrm {ord}}_5(\beta _j - \tau _5(\pi _5(\beta _j))) = 1/2$
. Indeed,
${\mathrm {ord}}_5(\beta _j - \tau _5(\pi _5(\beta _j))) = 1/2$
. Indeed,
![]() $\tau _5(\pi _5(\beta _j)) = \tau _5(1) = 1$
. Hence,
$\tau _5(\pi _5(\beta _j)) = \tau _5(1) = 1$
. Hence,
![]() ${\mathrm {ord}}_5(\beta _j - \tau _5(\pi _5(\beta _j))) = \mathrm {ord}_5(\!\sqrt {5}) = 1/2$
for every
${\mathrm {ord}}_5(\beta _j - \tau _5(\pi _5(\beta _j))) = \mathrm {ord}_5(\!\sqrt {5}) = 1/2$
for every
![]() $j \in \{1,2\}$
, as we wanted to show. Finally, let us observe that
$j \in \{1,2\}$
, as we wanted to show. Finally, let us observe that
![]() $s_5(\beta _j) = 0$
for every
$s_5(\beta _j) = 0$
for every
![]() $j \in \{1,2\}$
. Combining this with the fact that
$j \in \{1,2\}$
. Combining this with the fact that
![]() $c_5(X,\alpha ) = -1$
,
$c_5(X,\alpha ) = -1$
,
for every
![]() $n \in \mathbb {N}$
, as was proven in [Reference Lengyel36, Lemma 1]. This shows that Theorem 3.17 can be seen as a generalisation of Lengyel’s theorem to sequences that arise as the number of spanning trees in a
$n \in \mathbb {N}$
, as was proven in [Reference Lengyel36, Lemma 1]. This shows that Theorem 3.17 can be seen as a generalisation of Lengyel’s theorem to sequences that arise as the number of spanning trees in a
![]() $\mathbb {Z}$
-cover of finite graphs.
$\mathbb {Z}$
-cover of finite graphs.
Acknowledgements
We thank Sören Kleine, Matilde Lalín, Katharina Müller and Antonio Lei for some comments on an earlier version of the present paper. Moreover, the first author thanks Francesco Campagna, Roberto Gualdi, Pieter Moree and Fabien Pazuki for useful discussions and remarks. We would also like to thank the anonymous referee for thoroughly going through the paper and making many valuable comments, remarks and suggestions.