1. Introduction
When a scientist is introduced to the mechanics of polycrystalline ice, the first two lessons learned are (Reference HobbsHobbs, 1974; Reference Budd and JackaBudd and Jacka, 1989):
1. under normal temperature and pressure conditions, ice crystals possess a hexagonal lattice whose main axis of symmetry is the c axis, normal to the basal planes of the lattice;
2. in glaciers and ice sheets, the (visco-)plastic deformation (creep) of polycrystalline ice is predominantly promoted by slip on the basal planes, in a process called basal or easy glide, in such a way that the individual grains deform as transversally isotropic media.
Diverse consequences of these two lessons can be inferred from theoretical and/or experimental arguments. In particular, the restrictive mechanism of crystalline deformation by easy glide may generate torques on the ice lattice during straining, promoting a reorientation of c axes (in a process called lattice rotation) and consequent strain-induced anisotropy in a polycrystalline sample which might have been originally isotropic. This means, for instance, that ice compressed vertically (either by unconfined compression or by pure shear) tends to develop, via lattice rotation, a clustering of c axes oriented towards the vertical, the so-called ‘single-maximum fabric’. Such a fabric has been
observed in the upper 1300m of the Dome Concordia (Dome C, East Antarctica) ice core, in a region where the upper part of the ice sheet is expected to be subjected to vertical compression in a regime of pure shear.
Nevertheless, fabric analysis alone clearly does not suffice to determine the kind of stress to which an ice sample has been submitted. Further hints may arise from other microstructural features. In this work, we combine fabric analysis with the optical determination of the orientational distribution of slip bands (also called gliding layers or slip lines), which are planes of high slip activity, usually made of basal planes spaced by several micrometers.
Theoretically (see section 3), most slip bands of a polycrystalline ice sample subjected to homogeneous deformation should be inclined at 45˚ with respect to the principal directions of compression and extension, since basal planes so inclined would be submitted to the largest shear stresses, and consequently should glide more easily. In practice, however, the situation seems to be a little more complicated. Slip bands observed in samples from different depths of the Dome C ice core (204–1291m depth) are often nearly horizontal, so that >60% of the detected slip bands have an inclination of <30˚ with respect to the horizontal. This feature is not consistent with the predicted slip activity induced by vertical compression.
In this paper, we present evidence for this unexpected orientational distribution of slip bands and discuss the possible causes. Additionally, we show the occurrence of bent slip bands, which represent an early stage of polygonization and highlight the strong inhomogeneity of deformation at the crystal level.
2. Materials and Methods
Microstructural features of polar ice, such as grain boundaries, subgrain boundaries, slip bands and air inclusions, were mapped in the field (austral season 2000/01) generally a few days to 2 weeks after drilling. To map a thick section of ice, we used a charge-coupled device (CCD) video camera system and a computer-controlled X-Y stage attached to a microscope. About 1500 images, each covering 2.5 mm×1.6 mm, are needed to reconstruct a complete image of a thick section in microscopic resolution. The details of this method will be presented elsewhere. These observations were carried out in increments of 11 m between 150 and 600m depth, and at irregular intervals down to 1300 m. The dimensions of a vertical thick section are 4.5 cm ×9 cm, with a thickness of 5 mm.
From five sections the orientations of slip bands were determined using image-processing software (the public domain NIH Image program, developed at the US National Institutes of Health and available at http://rsb.info.nih.gov/nih-image/). Due to hardware and software limitations, we were not able to reconstruct digital images of the full sections. We therefore had to determine the orientations of slip bands by going through all the individual images of a section. Because this method includes multiple counts of the same grain or slip band in two images, we compared the distribution of slip bands of one sample by excluding multiple counts. The comparison showed that the character of the distribution remains basically unchanged. This makes us confident that the present distributions are not artifacts of the method employed to derive the statistics.
Studies of slip bands are rare. There have been no systematic studies performed on a deep ice core, most likely because the tenuous slip bands of polar ice are very difficult to observe by standard microscopic techniques, i.e. with the naked eye it is extremely demanding to detect slip bands using a ‘normal’ microscope (with no video camera). CCD video cameras with automatic gain control produce clear images with high contrast and sufficient quality to recognize weak slip bands. To prove that slip bands and their angular distribution are not observational artifacts, the sections were rotated, slightly inclined and illuminated using different light sources and paths. Slip bands become visible only when the slip plane (parallel to the basal plane) is orthogonal to the plane of view.
Dome C ice-core texture and fabrics were determined through the automatic ice-fabric analyzer (AIFA; Reference Wang, Kipfstuhl, Azuma, Thorsteinsson and MillerWang and others, 2003). The procedure to derive the c-axis distribution using this analyzer can be found in detail in Reference Y. and AzumaWang and Azuma (1999) and Reference WangWang and others (2002).
3. Theoretical Basis
The mathematical prediction of the most active gliding layers in the ice polycrystal proceeds from the general theory of homogeneous strain, through the fundamental result (cf. Reference LoveLove, 1944; Reference Truesdell, Toupin and FlüggeTruesdell and Toupin, 1960): the pairs of orthogonal directions in which the shears are extreme are normal to one principal axis of strain and bisect the angles between the other two.
Hence, where vertical compression is active (as in the upper part of an ice-sheet dome), we conclude that the maximum shears should occur on certain planes inclined at 45˚ with respect to the vertical. Notice that this reasoning is independent of the stress configuration or its intensity: for instance, in the case of pure shear just two families of inclined planes (whose normal vectors are orthogonal to the axis of the smallest principal strain) would correspond to surfaces of largest shear, whereas during unconfined compression any plane inclined at 45˚ with respect to the compressive axis would correspond to a plane of maximum shear (owing to the symmetry of this particular stress configuration). In any case, however, the shears will be extreme in the directions bisecting the angles between two principal axes of strain.
Consequently, if the deformation could be assumed homogeneous throughout the ice polycrystal, the most frequent and intense slip bands in samples from the Dome C ice core would theoretically be found about that inclination angle of 45˚ with respect to the vertical.
However, the deformation of an ice polycrystal is not homogeneous. Stress is transmitted from grain to grain of the aggregate in a complex, almost unpredictable, way. This means that the strain experienced by a particular crystallite may differ significantly from that observed in the polycrystal. Furthermore, the grain itself may deform inhomogeneously, through either bending, shear band formation or other intracrystalline processes (see, e.g., Reference Mansuy, Philip and MeyssonnierMansuy and others, 2000).
The question is therefore whether such deformation inhomogeneities are effectively indiscriminate, in the sense that they produce simply a ‘spreading’ of the predicted orientational distribution of slip bands within the ice core, or if they are influenced by particular mesoscale factors (e.g. the seasonal stratification of ice layers or the aspect ratio of the grains) capable of modifying the orientational distribution of slip bands in some definite manner.
4. Slip Bands in Dome C Ice Core
Figure 1a shows the orientational distribution of slip bands determined from samples taken from five different depths of the Dome C ice core. The respective fabric diagrams of these samples are presented in Figure 1b. Figure 1b clearly indicates a slight clustering tendency of c axes towards the vertical, which gradually enhances with depth from an initially isotropic orientational distribution of c axes at the free surface of the ice sheet. Such a strain-induced anisotropy is compatible with the expected macroscale stress state in the upper part of a dome, i.e. dominated by vertical compression in a regime of pure shear.
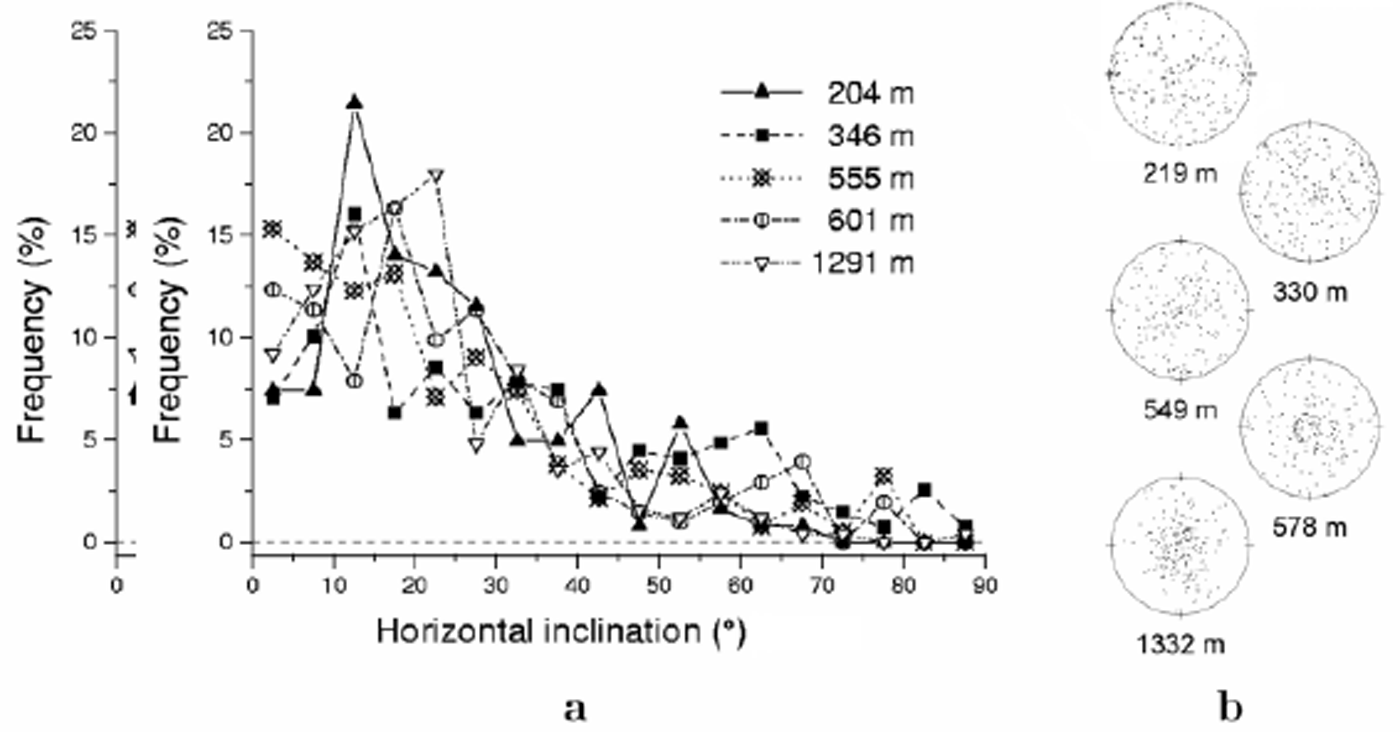
Fig. 1. Data from Dome C: (a) orientational distributions of slip bands for five different depths; (b) respective fabric diagrams from Reference Wang, Kipfstuhl, Azuma, Thorsteinsson and MillerWang and others (2003).
The orientational distributions of slip bands plotted in Figure 1a have several intriguing features. First, in each of the five samples, >60% of the detected slip bands have inclinations of <30˚ with respect to the horizontal. Second, four out of five orientational distributions have maxima at inclinations within the interval 10–25˚, while the other exhibits a maximum at 0˚, i.e. horizontal planes. Third, all distributions have approximately the same shape, which seems therefore to be roughly independent of depth. Finally, the slip activity is not symmetric, i.e. the number of slip bands discerned at 20˚, say, in a given sample differs from the number found at 160˚ (symmetry about vertical) or 110˚ (symmetry about some hypothetical principal axis of strain).
Such features are not consistent with the theoretically expected slip activity induced by vertical compression and/or horizontal extension, suggesting that the majority of the grains in the ice-core samples may experience a similar kind of deformation, which is nevertheless different from that of the aggregate at a much larger scale. Indeed, owing to the lack of symmetry in the orientational distribution of slip bands, one may conjecture that the simplest sort of deformation compatible with the above distributions would be some kind of nearly horizontal simple shearing. Now, before ice-sheet modelers become alarmed, it must be emphasized that the results discussed here may actually represent one of several different possibilities, among them:
-
1. the strange distributions might be artifacts of the methods of observation employed and/or preparation of the samples;
-
2. they might represent the regime of deformation to which the samples have been exposed prior to extraction from the ice sheet;
-
3. they might correspond neither to a real description of the deformation of the ice samples in the field nor to experimental artifacts, but rather to a mishandling of the ice cores during the processes of extraction, manipulation, transport and/or storage.
The question is which of these possibilities is the most probable cause of the distributions shown in Figure 1a.
The hypothesis of artifactual results is discarded here, on account of the various methods of observation described in section 2. On the other hand, one could imagine that the data plotted in Figure 1a describe a deformation regime experienced by the ice samples in the past, by supposing that the summit of Dome C has recently migrated to its present location. Although this supposition cannot be completely discarded, it seems unlikely according to findings from shallow depths of the ice core, which suggest that nearly the same kind of orientational distribution of slip bands can be found even close to the ice-sheet surface, requiring unattainable migration rates of the summit, of the order of many meters per year.
Now, if the orientational distributions of slip bands depicted in Figure 1a do really describe the current physics of the deformation of ice samples in situ, we are forced to conclude that at the ice-core scale the deformation may not be characterized by the same principal axes of strain which define the deformation at a larger scale. In other words, we must introduce the concept of a mesoscale strain, which lies between the crystalline (sometimes also called ‘microscopic’) strain, representing the deformation of individual crystallites, and the macroscale (also called homogenized or ‘macroscopic’) strain, related to material regions much larger than that comprised by a single ice-core sample. The mesoscale strain should therefore be associated with polycrystalline regions of many centimeters, i.e. approximately the size of an ice-core sample.
But why would such mesoscale strains so contrasting with macroscale deformations arise? One explanation could be the existence of structural heterogeneities in an ice sheet, which are larger than those related to the crystalline structure but still sufficiently small to become homogenized during the passage to the macroscale.
Precisely which kind of structural heterogeneity is responsible for such phenomena remains to be identified. It is still impossible to give a definitive answer, but some conjectures may be discussed. One potential candidate is the characteristic stratification of ice sheets in seasonal layers, whose thicknesses typically range from tens of centimeters to a few millimeters, depending on depth (Reference Hodgkins, Siegert and DowdeswellHodgkins and others, 2000). The stratified structure of ice sheets fulfills four important requirements for an effective mesoscopic heterogeneity: it has the correct dimensions, the correct geometry, it seems to persist through the depth (according to airborne radar data; see, e.g., Reference Siegert and KwokSiegert and Kwok, 2000), and it is peculiar to ice sheets, i.e. it cannot be found in artificial ice samples deformed in the laboratory.
Whether such layers really affect the mechanics of the ice sheet at a mesoscale is certainly questionable. The combination of low strain rates and the layered structure of ice sheets may eventually enhance shearing in nearly horizontal planes. One could imagine several possible causes of such an enhancement: for instance, from a continuum point of view it is well known that, for steady slow flows of a vertically stratified fluid, the effect of stratification is to inhibit vertical motion and horizontal inhomogeneities as much as possible (Reference YihYih, 1959). On the other hand, by reckoning the polycrystalline structure of the material we can conceive a process of horizontal shearing enhancement through shear localization by cluster gliding. Such a process somewhat resembles a mechanism observed in polydisperse granular media called ‘block sliding’, when localized regions of high shear are produced by the sliding of elongated blocks of grains (Reference Drescher and de Josselin de JongDrescher and de Josselin de Jong, 1972). Whereas in granular media such a localized shearing is evidently intergranular, in the case of polycrystalline media it would be more appropriate to think of an intragranular process, since grain boundary sliding is not expected to be effective in polar ice. Hence, in the ice polycrystal, one can conjecture that the seasonal stratification might favor the formation of oblate polycrystalline clusters, which may move horizontally like ‘stiff blocks’ under the influence of nearest-neighbor interactions through the formation of force chains (Reference Veje, Howell, Behringer, Schöllmann, Luding, Herrmann, Hovi and LudingVeje and others, 1997), shearing simultaneously several surrounding grains, provided that grain boundary sliding is not active. The process of cluster gliding may enhance the mesoscale horizontal simple shearing very effectively, without compromising the pure shear deformation at the larger macroscale.
It is too early to say whether the above surmises are correct, and certainly too early to discuss their consequences for ice-sheet modeling. Indeed, the supposition that the orientational distributions of slip bands shown in Figure 1a do really represent the deformation of ice samples in situ is just one of the three possibilities mentioned above. Another possibility not discussed yet is that those distributions may actually express some problem in the process of extraction, handling, transport and/or storage of the ice cores. In fact, it is well known that slip bands are produced very readily in ice crystals, appearing after strains of <1% (Reference HobbsHobbs, 1974). Therefore, it is not surprising that a slight bending or torsion of the slender ice cores during processing can induce enough shear to generate transversal (‘horizontal’) slip bands. Furthermore, although this is less likely, such slip bands might be created by some complex process of stress relaxation, initiated after the core is retrieved from the borehole.
From the above discussion, one thing is certain: both ice-core processing and ice-sheet modeling will be affected by the results scrutinized here. In particular, the present analysis suggests that the effects of structural heterogeneities upon the mechanics of ice sheets may be much more severe than previously expected.
5. Bent Slip Bands
Another interesting manifestation of the inhomogeneity of strain at the crystalline level comes from the observation of bent slip bands. Such a bending represents an early stage of the process of fragmentation of crystallites which is called polygonization: during deformation, ice polycrystals often develop very inhomogeneous stress fields, which eventually produce (by intercrystalline interaction) concentrated bending moments upon specific grains. Some of these grains might have c axes which are orthogonal to the applied moments, consequently suffering the bending of their respective basal planes, when the twisting stresses are large enough. Such a flexure can often be visualized in the form of slightly curved slip bands. As time passes, the curvature of the bent basal planes tends to increase and to become concentrated in smaller regions, so that the curved slip bands finally converge, in the simplest case, into a V-shaped set of surfaces, from which two well-defined regions with slightly different c-axis orientations can be discerned. The frontier between these two regions is called a subgrain boundary, and may evolve with the increasing c-axis misorientation into a real grain boundary, when the crystallite is finally split into two.
From the above description, it is clear that polygonization is defined by a continuous process of c-axis rotation, which can only be correctly modelled (from the physical point of view) by reckoning a field of c-axis orientations within every crystallite. Mathematically, this can be accomplished through the introduction of the transition-rate vector u*(x ,t,n) (where x denotes a position within the crystallite, t is a time instant and n (with n . n = 1) represents an orientation in space), which measures the rate at which c axes transit through different orientations (Reference Faria, Kremer and HutterFaria and others, 2003). Doing so, polygonization can be modeled mathematically as the orientational divergence of the transition rate in a point of the grain, i.e. (i,j = 1,2,3, Einstein’s summation convention adopted)
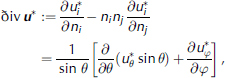
where the last expression in the second line of Equation 1 is written in terms of spherical coordinates. Considering that a perfect grain possesses just one c-axis orientation, if the orientational divergence of u* within a given crystallite is larger than zero (i.e., ðiv u* > 0), then the latter is polygonizing. (Actually, Equation 1 is a direct counterpart of the concept of volume expansion in ordinary continuum mechanics, expressed by the divergence of velocity, ðiv v. Therefore, it follows that polygonization can also be interpreted as a kind of ‘expansion of orientations’, since the range of c-axis orientations within a crystallite is increased during bending.)
Unfortunately, virtually all ice-sheet models have been based on the assumption of homogeneous crystallite deformation (Reference Azuma and Goto-AzumaAzuma and Goto-Azuma, 1996; Reference Castelnau, Thorsteinsson, Kipfstuhl, Duval and CanovaCastelnau and others, 1996; Reference Meyssonnier and PhilipMeyssonnier and Philip, 1996; Gödert and Hutter, 1998), so that a unique c-axis orientation can be related to each grain. Even those very few models which account for polygonization (e.g. Reference MontagnatMontagnat and Duval, 2000; Reference Faria, Ktitarev and HutterFaria and others, 2002) often do so in a somewhat artificial manner, by considering a sudden split of one grain into two. This artificial modeling of polygonization as a discontinuous process is partially justified by the usual observation of polygonization by interference analysis in thin sections. In such a method, polygonization is detected when a grain is already split into two or more portions with different interference colors. Hence, subgrains can easily be detected, but not bent crystallites. In contrast, the direct observation of curved slip bands, although much more laborious, permits the detection of polygonization at a very early stage. In fact, it has served to show that, at least in Dome C, ice crystallites start to bend at much shallower depths than previously expected. Curved slip bands similar to those shown in Figure 2 have been observed in samples of ice from <100m depth.

Fig. 2. Bent slip bands in an ice sample from Dome C (767m depth). The superposed white line serves as reference to the inclination of the slip bands
6. Conclusion
Unexpected features of the orientational distribution of slip bands observed in ice-core samples from Dome C have shown the need for a reappraisal of the polycrystalline deformation of ice sheets, as well as of our methods of ice-core processing. Two conjectures have been discussed:
-
1. the combination of very low strain rates with the typical stratified structure of ice sheets may induce the occurrence of an intermediate mesoscale deformation regime, which might be very different from the extremal micro- and macroscale strainings;
-
2. during processing and/or storage of an ice core, some slight torsion, bending or stress relaxation may be sufficient to generate additional slip bands, that are confused with the original slip bands produced by the natural deformation of the ice sample.
In order to corroborate the first conjecture, we need further analyses of slip bands in other naturally and artificially deformed samples of ice. The identification of slip-band distributions similar to those presented in Figure 1a solely in the naturally deformed samples will support this first hypothesis. On the other hand, the analysis of slip bands in situ, minutes after the core retrieval, is now essential to reveal the effects of storage, intensive handling and stress relaxation upon the microstructure of the ice core.
Acknowledgements
We are grateful to N. Azuma for his interest and for useful discussions. We also thank two anonymous referees for valuable comments. This work is a contribution to the ‘European Project for Ice Coring in Antarctica’ (EPICA), a joint European Science Foundation (ESF)/European Commission (EC) scientific program, funded by the EC under the Environment and Climate Program contract ENV4-CT95-0074 and by national contributions from Belgium, Denmark, France, Germany, Italy, the Netherlands, Norway, Sweden, Switzerland and the United Kingdom. This is EPICA publication No. 119.




