INTRODUCTION
Incident solar radiation is partly reflected at a snow surface, but also penetrates and is absorbed within the snow cover. It therefore has an influence on thermal conditions in the surface layer, including temperature profile and snow melting processes. To explain thermal conditions it is necessary to clarify the extinction and absorption of solar radiation within the snow cover.
Extinction is due both to absorption and to scattering of the radiation by snow particles. Saito (1948), Dunkel and Bevance (1956), Liljequist (1956), etc treated this problem by considering two fluxes, a downward flux A and an upward flux B; at a depth X from the snow surface these are expressed by:
where A0 and Bo are respectively the downward and the upward flux at the internal side of the snow surface, and μ is the extinction coefficient of solar radiation within the snow cover. Values of Ao and Bo differ according to boundary conditions at the snow surface. But q, the amount of solar radiation absorbed by a unit volume of snow at a depth X from the snow surface, is expressed as

Where I0 is the incident solar radiation, and r the albedo of snow.
Various investigators have measured μ, and obtained differing values. The authors have developed an optical device capable of measuring μ accurately, and used it to measure values on natural snow covers in the field. The accuracy of the measurements was checked thermally by laboratory experiments of local temperature increases in snow cover, which were closely related to absorption of solar radiation within it.
MEASURING DEVICE

Fig. 1. Block diagram of the measuring device. R represents variable loading resistance (0-2 kΩ). r’ - 1.6 kfl; kΩ = 43 kΩ.
The principle of the measuring device is shown by block diagram in Figure I (Aburakawa and Fukami 1978). It consists mainly of 4 parts; sensor, amplifier, divider, and indicator. The sensors used are small silicone photocells, each 5 mm x 5 mm: nine photocells, each attached to the end of an arm 4 mm in diameter and 0.15-0.20 m in length, can be placed horizontally at various depths within the snow cover. Usually five are used to measure the downward fluxes, four for the upward ones. The output of one photocell, which is modulated by the loading resistance R, is proportional to the intensity of light. Modulated output is amplified by an operational amplifier. A photocell is placed on the snow surface horizontally as the control for measuring the value of the incident solar radiation, its output being amplified in the same manner. To reduce the influence of fluctuations in solar radiation, the ratio of the output of the photocell within the cover to that on the surface is calculated by the divider (Teledyne Philbrick, 4452). R is modulated to satisfy the condition that the amplified output of the photocell on the surface does not exceed the maximum input (10 volts) of the divider. The output of the divider from 0 to 10 volts indicates the ratio from 0 to 1.0. Thus, the output of the photocell within the cover is normalized by the incident solar radiation, and is indicated on a voltmeter.

Fig. 2. Photograph of the measuring device.
Figure 2 shows a photograph of the device; (a) is the photocell for insertion into the snow cover, (b) the one on the snow surface; (a) is inserted horizontally more than 0.1 m from the south vertical wall of a snow pit, through the holes of the support guide (c).
CALIBRATION OF THE SENSOR
Two types of photocells (Hamamatsu, S642 and S642B), differing in wavelength sensitivity, were used for checking the dependence of extinction coefficient on wavelength. The spectral sensitivity of each photocell is shown in Figure 3. Plots of the downward flux of light obtained from two sensors are shown in Figure 4, Though the downward flux within the snow cover decreased exponentially, the extinction coefficient measured by S642 was larger than that measured by S642B. Considering the difference in spectral sensitivity between photocells, Figure 4 suggests that the extinction coefficient increased with an increase in wavelength.
In order to obtain μ, the extinction coefficent of solar radiation, the amplified output of each photocell (S642 and S642B) was related to the intensity of solar radiation (Fukami and Kojima 1980a). From the result, the flux of solar radiation within the snow cover, A and/or B, was expressed as follows: when S642 was used as the sensor,
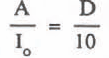

Fig. 3. :.pectral characteristics of photocells (S642 and S642B).

Fig. 4. Downward flux of light within the snow cover. (A) is obtained from S642, and (B) from S642B. The slope of fitting line shows the extinction coefficient’ (A) = 54 m-1 (B) = 32 m-1.
and when S642B was used as the sensor,

where D (volt) is the output of the divider.
Using Equations 4 and 5, the extinction of solar radition was obtained from the measurements. Figure 5 shows the comparison of u between those obtained from S642 and S642B. There is little difference of u between them. Though the extinction coefficient depended on the wavelength, the device was capable of measuring the extinction of solar radiation accurately.
How placement of the photocells into the snow cover affected the measured result was checked by an optical fiber 0.5 mm in diameter, which minimized the disturbance of the solar radiation field within the snow cover (O’Neill and Gray 1973). Details of this calibration appear in Fukami and Kojima (1980a). As a result, influence of placement was found to be negligibly small.
The calibrations mentioned above revealed the capability of the device for making accurate measurements of extinction of solar radiation within the snow cover. The sensor used mainly was S642B instead of S642, for the former’s wavelength sensitivity is nearer to the spectrum characteristics of solar radiation than the latter’s.

Fig. 5. Comparison of extinction coefficient of solar radiation obtained from S642 to that from S642B

Fig. 6. Downward and upward flux of solar radiation within the snow cover, where μ is the extinction coefficient, ρ the density, G.S. the average grain size, and W the water content, (a) = dry new snow; (b) = wet granular snow.
RESULT OF MEASUREMENT
Each of the snow layers subjected to field measurements seemed to be homogeneous throughout more than 0.1 m in thickness. Figure ó shows two examples of extinction measurements in the field. Here downward and upward flux within the snow cover are normalized by the incident solar radiation. The downward and the upward flux decreased exponentially as expressed by Equations 1 and 2 respectively.
Variation of the extinction coefficient, μ
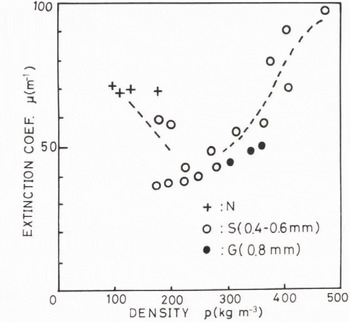
Fig. 7. Plots of extinction coefficient vs snow density for dry snow. N = new snow; S - slightly compacted snow or compacted snow; G = granular snow. () shows average grain size.
Figure 7 shows the relation between μ and the snow density p in the case of dry snow. Values of μ were found to be 37-97 m-1 in snow density ranging from 90-470 kg m-3. A minimum value was obtained in slightly compacted snow; μ decreased during metamorphosis from new snow to slightly compacted snow, and increased during settlement from slightly compacted snow to compacted snow. It seemed that μ decreased with an increase in average grain size when the density was the same.

Fig. 8. Plots of extinction coeffcient vs water content of wet snow with average grain size as parameter. Density of wet snow observed here was 430-530 kg m-3.
Figure 8 shows the relation between μ and the water content W of wet snow with average grain size as a parameter. The density of wet snow observed here was 430-530 kg m-3. Values of μ were 23-58 m-1 l, which were smaller than those of dry snow for the same density. A decrease in μ with increase in average grain size was clearly shown in Figure 8. The tendency for μ to decrease with an increase in W was slight.
Absorption of the solar radiation
From measurements of downward and upward flux, and albedo of the snow cover, it was found that the absorption of solar radiation within the snow cover was expressed approximately as Equation 3.
Shown in Figure 9 is the variation of q with depth for different values of μ. An increase in μ indicates an increase in q at the layer near the snow surface, and a rapid decrease in q with depth. Figure 9 also show that the thermal influence of solar radiation occurs almost entirely above a depth of 0.1 m in natural snow cover, because μ ranges then from 20-100 m-1.

Fig. 9. Variation of absorption of solar radiation with depth for different extinction coefficients. The value of (l-r)I is constant.
EXPERIMENT OF LOCAL TEMPERATURE INCREASE
As a result of absorption of solar radiation within a snow cover, the temperature of its surface layer increases locally and may lead to internal melting. Qualitative conditions of local temperature increase or internal melting are fine weather, wind, and air temperature close above 0°C. By simulating these conditions, an experiment was carried out to examine local temperature increase so that the accuracy of the extinction measurements could be checked thermally.
Experimental apparatus
The experimental apparatus is shown in Figure 10. The sides of a 0.15 m cube of snow were covered with insulating material. The temperature at the bottom of the block was adjusted by a temperature controller. A photoflood tamp (daylight type) was used as the light source. Since the color temperature of the lamp was 5500°K, the short-wave radiation from the light source had a spectrum similar to solar radiation. Water was used as a filter to cut off long-wave radiation from the light source.
Temperatures at various depths were measured by inserting copper-constantan thermocouples 0.23 mm in diameter into the sample block at adequate time intervals, supplying short-wave radiation and wind on the upper surface of the block. The intensity of incident short-wave radiation, measured by a pyranometer at the start and end of each run of the experiment, was found to be constant.
Calculation o I a temperature profile within the snow cover
The temperature profile within the snow cover is calculated by solving the following equation of heat conduction, which includes the term of absorption of the radiative energy, q (Yosida I960):

Fig. 10. Schematic diagram of the experimental apparatus for local temperature increase.

where U is the temperature of snow, T is the time elapsing after the beginning of insolation, X is the depth from the snow surface, c (2100 J kg-1 °C_1) is the specific heat of ice, p is the density of snow, and k is the thermal conductivity of snow. As mentioned previously, u, r, and I are the extinction coefficient, albedo, and incident short-wave radiation at the snow surface respectively. Values of u and r were measured by using the developed device.
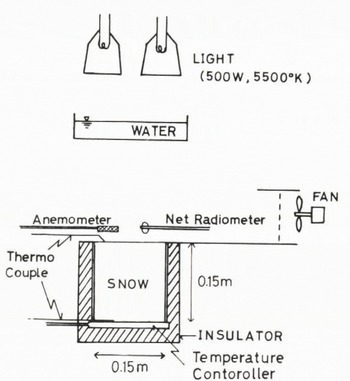
Fig. 11. Temperature profiles within the snow cover for different elapsing times. Plots = measured temperatures; solid line = calculated temperature profiles.
during each run of the experiment, ρ, k, μ, r, and Io were constant; all were measured except k. Fukami and Kojima (1980b) solved Equation 6 with initial and boundary conditions derived from the experimental result. They also showed that the value of k calculated from the experimental formula presented by Akitaya (1974) was suitable.
Figure 11 shows an example of a comparison of the measured temperatures with calculated temperature profiles at various elapsing times. In this run, p was 340 kg m-3, μ was 52 m-1, r was 0.70, 10 was 390 W m-2 (9.2 x 10-3 cal cm-1 sec-1), and k was 0.42 W m-1 °C-1 (1.0 x 10-1‘ cal cm-1 sec-1 °C-1). A local temperature increase occurred in this run. The calculated depth of the maximal value of the local temperature increase almost agreed with the measured depth. Shown in Figure 12 are the plots of the measured temperature increase, U-U0 (°C), against calculated increases for various depths and elapsing times. Both agree well. In turn, when a smaller value of μ was used in the calculation, the calculated depth of the maximal value of the local temperature increase became deeper, and the calculated temperatures disagreed with the measured ones. These results, and those from other runs of the experiment, indicate the accuracy of the extinction measurements.

Fig. 12. Plots of measured temperature increase, U-Uo, against calculated ones at various depths and for elapsing times.
CONCLUSION
Extinction and absorption of solar radiation within the snow cover were studied, using a device developed to make accurate measurements of the extinction coefficient. Extinction was measured for various snow covers in the field. Values of extinction coefficient, which ranged from 20-100 m-1, were found to vary according to structure of snow. Another experiment of the local temperature increase of the snow cover due to absorption of solar radiation indicated the accuracy of the extinction measurements. The results indicated that the extinction and absorption of solar radiation within the snow cover was explained sufficiently by the two-flux model.
ACKNOWLEDGMENTS
This work was conducted in the Institute of Low Temperature Science, Hokkaido University (ILTS). The authors thank Drs D Kobayashi and N Ishikawa of ILTS for their helpful suggestions.














