Hostname: page-component-669899f699-7xsfk Total loading time: 0 Render date: 2025-04-26T20:37:14.475Z Has data issue: false hasContentIssue false
  • English
  • Français

Pointwise convergence in nilmanifolds along smooth functions of polynomial growth

Part of: Noncompact transformation groups Ergodic theory

Published online by Cambridge University Press:  25 September 2023

KONSTANTINOS TSINAS
KONSTANTINOS TSINAS*
Affiliation:
University of Crete, Department of Mathematics and Applied Mathematics, Voutes University Campus, Heraklion 71003, Greece
*
e-mail: kon.tsinas@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the equidistribution of orbits of the form 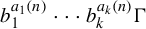$b_1^{a_1(n)}\cdots b_k^{a_k(n)}\Gamma $ in a nilmanifold X, where the sequences $a_i(n)$ arise from smooth functions of polynomial growth belonging to a Hardy field. We show that under certain assumptions on the growth rates of the functions $a_1,\ldots ,a_k$, these orbits are equidistributed on some subnilmanifold of the space X. As an application of these results and in combination with the Host–Kra structure theorem for measure-preserving systems, as well as some recent seminorm estimates of the author for ergodic averages concerning Hardy field functions, we deduce a norm convergence result for multiple ergodic averages. Our method mainly relies on an equidistribution result of Green and Tao on finite segments of polynomial orbits on a nilmanifold [The quantitative behaviour of polynomial orbits on nilmanifolds. Ann. of Math. (2) 175 (2012), 465–540].

Keywords

ergodic averagesequidistributionnilmanifoldsHardy fields

MSC classification

Primary: 22F30: Homogeneous spaces
Secondary: 37A17: Homogeneous flows
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 44 , Issue 7 , July 2024 , pp. 1963 - 2008
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bergelson, V., Moreira, J. and Richter, F.. Multiple ergodic averages along functions from a Hardy field: convergence, recurrence and combinatorial applications. Preprint, 2020, arXiv:2006.03558.Google Scholar
Boshernitzan, M.. Uniform distribution and Hardy fields. J. Anal. Math. 62 (1994), 225–240.CrossRefGoogle Scholar
Corwin, L. and Greenleaf, F. P.. Representations of Nilpotent Lie Groups and their Applications. Part 1: Basic Theory and Examples (Cambridge Studies in Advanced Mathematics, 18). Cambridge University Press, Cambridge, 1990.Google Scholar
Frantzikinakis, N.. Equidistribution of sparse sequences on nilmanifolds. J. Anal. Math. 109 (2009), 353–395.CrossRefGoogle Scholar
Frantzikinakis, N.. Some open problems on multiple ergodic averages. Bull. Hellenic Math. Soc. 60 (2016), 41–90.Google Scholar
Frantzikinakis, N.. Joint ergodicity of sequences. Adv. Math. 417 (2023), 63pp.CrossRefGoogle Scholar
Frantzikinakis, N., Lesigne, E. and Wierdl, M.. Sets of $k$ -recurrence but not $\left(k+1\right)$ -recurrence. Ann. Inst. Fourier (Grenoble) 56(4) (2006), 839–849.CrossRefGoogle Scholar
Furstenberg, H.. Ergodic behavior of diagonal measures and a theorem of Szemerédi on arithmetic progressions. J. Anal. Math. 71 (1977), 204–256.CrossRefGoogle Scholar
Green, B. and Tao, T.. The quantitative behaviour of polynomial orbits on nilmanifolds. Ann. of Math. (2) 175 (2012), 465–540.CrossRefGoogle Scholar
Hardy, G. H.. Properties of logarithmico-exponential functions. Proc. Lond. Math. Soc. (2) 10 (1912), 54–90.CrossRefGoogle Scholar
Host, B. and Kra, B.. Non-conventional ergodic averages and nilmanifolds. Ann. of Math. (2) 161(2) (2005), 397–488.CrossRefGoogle Scholar
Host, B. and Kra, B.. Nilpotent Structures in Ergodic Theory (Mathematical Surveys and Monographs, 236). American Mathematical Society, Providence, RI, 2018.CrossRefGoogle Scholar
Leibman, A.. Pointwise convergence of ergodic averages for polynomial sequences of rotations of a nilmanifold. Ergod. Th. & Dynam. Sys. 25(1) (2005), 201–213.CrossRefGoogle Scholar
Mal’cev, A.. On a class of homogeneous spaces. Izvestiya Akad. Nauk SSSR, Ser Mat. 13 (1949), 9–32.Google Scholar
Parry, W.. Dynamical systems on nilmanifolds. Bull. Lond. Math. Soc. 2 (1970), 37–40.CrossRefGoogle Scholar
Ratner, M.. Raghunatan’s topological conjecture and distribution of unipotent flows. Duke Math. J. 61(1) (1991), 235–280.Google Scholar
Richter, F. K.. Uniform distribution in nilmanifolds along functions from a Hardy field. J. Anal. Math. 149 (2023), 421–483.CrossRefGoogle Scholar
Tsinas, K.. Joint ergodicity of Hardy field sequences. Trans. Amer. Math. Soc. 376 (2023), 3191–3263.CrossRefGoogle Scholar