1. Introduction
For hard-bedded glaciers, basal water pressure and bed connectivity are a major control on glacier behaviour (e.g. Reference KambKamb, 1987; Reference Harper, Humphrey, Pfeffer and LazarHarper and others, 2007; Reference Howat, Tulaczyk, Waddington and BjörnssonHowat and others, 2008; Reference SchoofSchoof, 2010). The development of the subglacial drainage system causes basal pressure to vary throughout the melt season. These changes comprise a reorganization of the water pathways through changes in efficiency and connections, which influences pressurization at the glacier bed and ice flow (Reference Iken and TrufferIken and Truffer, 1997; Reference Bartholomew, Nienow, Sole, Mair, Cowton and KingBartholomew and others, 2012; Reference Hoffman and PriceHoffman and Price, 2014). Observations of water pressure have revealed complex spatial patterns even for boreholes located close together (Reference Hubbard, Sharp, Willis, Nielsen and SmartHubbard and others, 1995; Reference Murray and ClarkeMurray and Clarke, 1995; Reference Gordon, Sharp, Hubbard, Smart, Ketterling and WillisGordon and others, 1998; Reference Harper, Humphrey, Pfeffer, Fudge and O’NeelHarper and others, 2005; Reference Fudge, Humphrey, Harper and PfefferFudge and others, 2008; Reference Schoof, Rada, Wilson, Flowers and HaseloffSchoof and others, 2014). However, synchronous pressure variations across multiple boreholes were identified as a common feature indicating the effect of basal water pressure on ice flow (Reference Iken and BindschadlerIken and Bindschadler, 1986; Reference Harper, Humphrey, Pfeffer and LazarHarper and others, 2007).
At the Svartisen Subglacial Laboratory (SSL), northern Norway, a unique 20 year long record of basal pressure from direct observations (as opposed to water pressure from boreholes) is used to investigate synchronous pressure variations. This approach, where sensors are fixed at the ice–rock interface underneath ~200m of ice, avoids the effect of borehole transport on pressure and disturbance of the glacier bed when drilling (Reference Boulton, Morris, Armstrong and ThomasBoulton and others, 1979; Reference Hagen, Sollid, Wold and ØstremHagen and others, 1993). The load cells measure normal stress, which depends on the local overburden pressure and is also affected by the presence of water and basal debris/clasts at the ice–rock interface.
This study builds on previous work by Reference Lappegard, Kohler, Jackson and HagenLappegard and others (2006). They characterized conditions at the bed of the same glacier for the period 1993–2003 from the same sensors installed at the glacier base. They identified pressure events that show rapid fluctuations (days to weeks) associated with rising subglacial discharge in response to surface meltwater input. The seasonal variation in frequency and distribution in amplitude of these events differentiates the winter and summer regimes. The winter regime is dominated by stable pressure. On a few occasions in the record, this is disturbed by a delayed input of surface melt, which triggers pressure events seen by all sensors (‘global events’). The summer regime is characterized instead by numerous daily pressure events, which show little lag with the timing of surface melt. The sensor response is also heterogeneous within the network, exhibiting local pressure events at some sensors only (‘local events’), periods of low to atmospheric pressure and anticorrelation between sensors.
In this work, we investigate the same time series, but extended by 10 years and using a more automated, objective and qualitative method based on a running Pearson correlation. Our aim is to identify similar responses among the basal pressure sensors over the 20 year record to evaluate the annual and seasonal variability. A Pearson correlation is used to identify when synchronous fluctuations occur and determine their temporal variation. With this technique, we quantify the similarity in response at the glacier base for a ‘normal’ year, study in more detail two years that show anomalies relative to the ‘normal’ year and consider the glaciological implications.
2 Cause of Correlated Versus Anticorrelated Behaviour: Previous Work
The existence and type of spatial correlation observed in borehole studies on glaciers can identify the predominant processes at the glacier base (Reference Hubbard, Sharp, Willis, Nielsen and SmartHubbard and others, 1995; Reference Harper, Humphrey, Pfeffer and LazarHarper and others, 2007; Reference Schoof, Rada, Wilson, Flowers and HaseloffSchoof and others, 2014). This is possible without necessarily considering differences in local overburden pressure and magnitude of the changes, but by considering such factors as correlation versus anticorrelation of the borehole pressure data (Reference Gordon, Sharp, Hubbard, Smart, Ketterling and WillisGordon and others, 1998; Reference Dow, Kavanaugh, Sanders, Cuffey and MacGregorDow and others, 2011). By identifying the character of the synchronous pressure variations, we can distinguish between hydrological connection at the glacier base (Reference Hubbard, Sharp, Willis, Nielsen and SmartHubbard and others, 1995; Reference Iken and TrufferIken and Truffer, 1997; Reference Fudge, Humphrey, Harper and PfefferFudge and others, 2008) and mechanical processes related to stress redistribution (Reference WeertmanWeertman, 1972; Reference Murray and ClarkeMurray and Clarke, 1995; Reference AndrewsAndrews and others, 2014).
The existence of a hydrological drainage system establishes connections at the glacier bed that then lead to synchronous pressure variations, and hence correlated reponse. The cause of the connections will differ over the melting season. In spring and autumn, a sudden impulse of water (e.g. surface melt or rainfall) in a poorly developed drainage system causes cavities to open and development of a linked-cavity drainage system (Reference Iken and BindschadlerIken and Bindschadler, 1986; Reference Iken and TrufferIken and Truffer, 1997; Reference Fudge, Harper, Humphrey and PfefferFudge and others, 2009). Eventually, the cavities can grow unstable, leading to cavity collapse and flooding of the glacier base as seen at Bench Glacier, Alaska, USA (Reference Harper, Humphrey, Pfeffer and LazarHarper and others, 2007). The parts of the bed affected by these changes in hydrological regime will show a correlated response. In summer, diurnal melt stimulates bed connectivity in direct link with the efficient drainage system either when multiple small channels are connected to a major conduit (Reference Fudge, Humphrey, Harper and PfefferFudge and others, 2008) or at soft-bedded glaciers when water flows from the channel through a sediment layer (Reference Hubbard, Sharp, Willis, Nielsen and SmartHubbard and others, 1995).
The pattern of mechanical stresses can explain a synchronous response across the sensor network. This differs from the response for hydrological connections because although both are synchronous, the mechanical stresses may be anticorrelated, rather than correlated. Anticorrelation was first inferred to be due to load transfer (Reference Murray and ClarkeMurray and Clarke, 1995). Because a pressurized channel redistributes stresses at the bed, basal pressure can display an anticorrelated signal between the forcing connected to the efficient drainage system, the pressurized channel, and the response in the ice immediately surrounding the channel that is isolated from the hydrological system. Anticorrelation between sensors can also be due to stress bridging (Reference WeertmanWeertman, 1972; Reference LappegardLappegard, 2006), which occurs when a subglacial channel or cavity is at low pressure. The lateral wall of this channel/cavity supports, in addition to the overlying column of ice, the channel/cavity roof, which increases the normal stress at the base of the walls. A third mechanism is the direct effect of changes in sliding speed on the normal stress on an undulating bed (Reference Iken and TrufferIken and Truffer, 1997; Reference AndrewsAndrews and others, 2014). Pressure at a sensor located on the upstream part of a bump will be anticorrelated with pressure at a sensor placed on the downstream side. This can lead to passive opening of cavities as seen in Greenland (Reference AndrewsAndrews and others, 2014). All three mechanisms produce anticorrelation, which is a feature commonly seen in borehole studies (Reference Murray and ClarkeMurray and Clarke, 1995; Reference Gordon, Sharp, Hubbard, Smart, Ketterling and WillisGordon and others, 1998; Reference Dow, Kavanaugh, Sanders, Cuffey and MacGregorDow and others, 2011; Reference AndrewsAndrews and others, 2014; Reference Schoof, Rada, Wilson, Flowers and HaseloffSchoof and others, 2014). A possible approach to distinguish between them is to look at the distance at which normal stress is perturbed. Compared to load transfer that can affect the bed at a distance of 20m (Reference Murray and ClarkeMurray and Clarke, 1995), stress bridging increases normal stress at the metre scale for a channel with a 1m diameter (Reference LappegardLappegard, 2006), and non-locally generated sliding was observed to affect the bed at several hundreds of metres in Greenland (Reference AndrewsAndrews and others, 2014). The distance will vary with glacier or ice-sheet thickness. It is important to note that the anticorrelation will depend on the initial spatial variation in bed connectivity, which causes the formation of isolated regions of the bed (Reference Iken and TrufferIken and Truffer, 1997). Furthermore, these mechanical processes can produce correlated synchronous pressure variations if the sensors measure only isolated parts of the bed or only the connected drainage system.
3. Field Site and The Svartisen Subglacial Laboratory
3.1. Engabreen
Engabreen is a maritime outlet glacier of western Svartisen, the second largest ice cap in Norway (Fig. 1). This hard-bedded temperate glacier has an elevation range of 1567 m and an area of 36 km2 (Reference Andreassen and WinsvoldAndreassen and others, 2012). The ice cap drains onto a large highly crevassed plateau around 1175 m a.s.l. and then flows into an icefall from ~900 m a.s.l. The glacier tongue is currently at 114 m a.s.l., but reached 9 m a.s.l. in 1999 because of an advance in the 1990s. Since 2000, the glacier front has continuously retreated.

Fig. 1. Satellite image of Engabreen with elevation contours superimposed, showing the locations of tunnels, discharge stations and the SSL (‘Research shaft’), and Svartisen ice cap (inset). Air temperature and precipitation are measured at Synkhøyden (800ma.s.l.) and Glomfjord (30ma.s.l.) weather stations respectively (inset).
Mass-balance measurements conducted annually since 1970 give a winter balance of 1.5–4.6mw.e. and a summer balance from –4.0 to –1.2mw.e. (Reference Kjøllmoen, Andreassen, Elvehøy, Jackson and GiesenKjøllmoen and others, 2011). Interpolation from stake measurement gives a mean equilibrium-line altitude of 108 m a.s.l.
Surface velocity on the plateau is an average of 5 cm d−1, and >60 cm d−1 in the steepest part (Reference Cohen, Iverson, Hooyer, Fischer, Jackson and MooreJackson and others, 2005). Drag-spool measurements performed at the glacier base give a sliding speed of 15 ± 7 cm d−1 (Reference Cohen, Iverson, Hooyer, Fischer, Jackson and MooreCohen and others, 2005), which represents <25% of the glacier surface velocity.
3.2. Svartisen Subglacial Laboratory
The SSL is a unique site for glacier research. Two other subglacial laboratories have been used for glaciological studies: at Glacier d’Argentière, France, under 60m of ice (Reference Vivian and BocquetVivian and Bocquet, 1973; Reference Boulton, Morris, Armstrong and ThomasBoulton and others, 1979) and at Bondhusbreen, Norway, under 160m of ice (Reference Hagen, Sollid, Wold and ØstremHagen and others, 1993). However, the SSL is still accessible and in operation, and is suited to a wide range of glacier experimentation.
A rock tunnel located directly beneath Engabreen’s icefall (200m ice thickness) provides direct access to the glacier base (Fig. 1). Within the tunnel network, the SSL offers living and working facilities including two research shafts, horizontal and vertical, that were excavated from the main tunnel to access the ice–rock interface (Figs 1 and 2). From these entrances, an ice cave can be melted by spraying hot water provided by a hot-water drilling system of 600 kW. This artificial cavity enables the installation of sensors at the glacier base as well as other studies, such as analysis of basal ice. Once melted out, an ice cave will contract at a mean rate of 25 cm d−1, leading to complete closure over 3–5 days (Reference LappegardLappegard, 2006).

Fig. 2. Load-cell location and digital elevation model of bedrock surrounding the research shafts. The pressure sensor network consists of eight load cells drilled into the bedrock. The coordinates are in NGO 1948 (Oslo) zone IV. From Reference Lappegard, Kohler, Jackson and HagenLappegard and others (2006).
4. Data Collection
4.1. Basal pressure
Figure 2 shows the location of the eight load cells and the two research shafts. The load cells are in a zone that is 22m long and 5m wide, orientated approximately perpendicular to the prevailing direction of basal sliding, which is ~240° (Reference LappegardLappegard, 2006).
The load cells were drilled and cemented flush with the bedrock. Each sensor consists of an encased plate of 15 cm diameter, under which a wire under tension is attached to two vertical pins. The applied normal load causes the plate to bend, and the distance between the pins increases, changing the frequency at which the wire vibrates. The measured frequency has been calibrated to record pressure up to 9 MPa with an error <1% for the total range (GEONOR AS, Oslo; Reference DiBiagio and MyrvollDiBiagio, 2003). Each sensor has its own individual calibration. Orientation of the sensors is given in Table 1.
Table 1. Load-cell description adapted from Reference Lappegard, Kohler, Jackson and HagenLappegard and others (2006). North is defined as 0° for the azimuth. The LC6 coordinates in UTM 33W are 446801E 7395463N

The sampling frequency is usually 15 min, but is sometimes changed to 2 min during field campaigns (<2 weeks) and for the years 2012 and 2013. The major data gaps were caused by battery or data-logger issues, and affected all sensors as they are wired to the same data logger as seen in Figure 3.
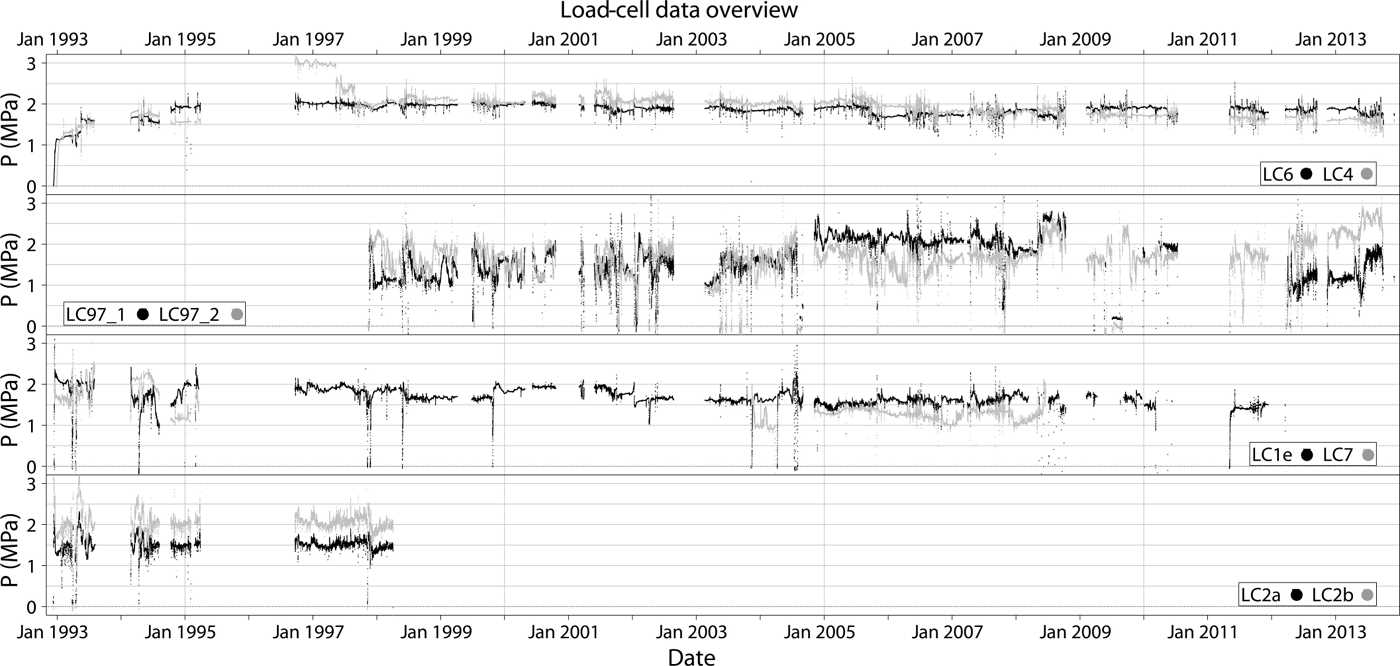
Fig. 3. Pressure records from 1993 to 2013 plotted by pair: from top down, LC6 (black) and LC4 (grey); LC97_1 (black) and LC97_2 (grey); LC1e (black) and LC7 (grey); and LC2a (black) and LC2b (grey). Data have a frequency of 15 min.
When pressure measured at the load cells is stable and approximately equal to the local overburden pressure, the load cells are assumed to measure the normal stress of the ice. Pressure variations sometimes vary rapidly and can reach twice the overburden pressure, then return to the background pressure level following an exponential-like curve (Fig. 4). Due to the magnitude, timing and exponential decay of the signal of these events at the load cells, this is also assumed to be a measure of the normal stress, which can vary rapidly due to stress redistribution within the ice (occurring because of channel or cavity opening or closure) (Reference Cohen, Iverson, Hooyer, Fischer, Jackson and MooreCohen and others, 2005; Reference LappegardLappegard, 2006). The load cells are assumed to measure water pressure, when pressure decreases from the background level and fluctuates in phase with meltwater input. Water is likely to be over the load cell in this condition, as water will be redirected from highpressure to low-pressure areas. Rocks dragged along the bed also disturb the normal stress. The effect of a clast will depend on such factors as its proximity to the bed and transport direction relative to the load cell (Reference Boulton, Morris, Armstrong and ThomasBoulton and others, 1979; Reference Hagen, Sollid, Wold and ØstremHagen and others, 1993). However, this is not observed except on rare occasions in winter (not correlated to hydrological changes).
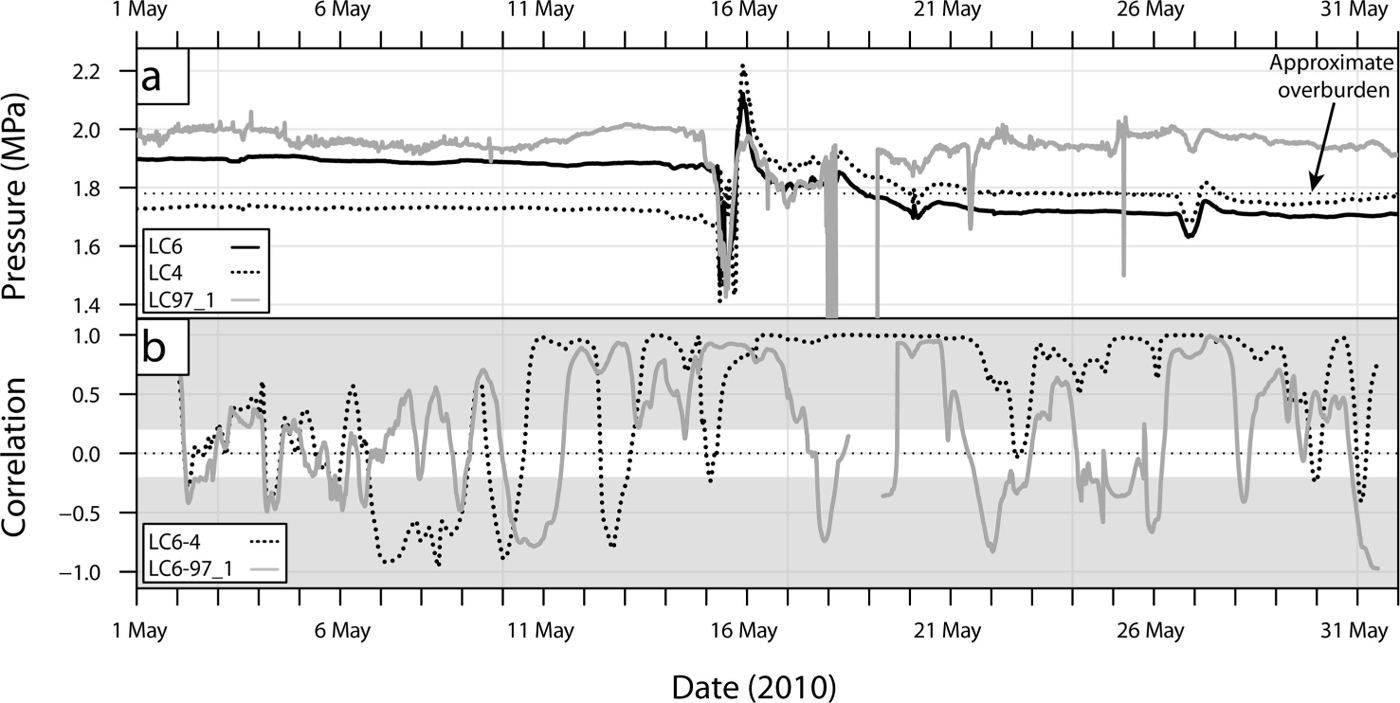
Fig. 4. Correlation test: (a) LC4, LC6 and LC97_1 and (b) the correlation for each pair of load cells LC6–LC4 (grey) and LC6–LC97_1 (dashed). The shaded grey covers correlations within the 95% confidence interval. In (b), the value at time t represents the correlation for a window between t 12 hours and t + 12 hours.
4.2. Hydrometeorological data
The Svartisen hydropower project includes an extensive tunnel network, which leads water to Storglomvatnet, the reservoir. Two of these tunnels are subglacial. They lie at ~600ma.s.l. and collect water from subglacial intakes at the glacier base and from subaerial intakes near the glacier (station 4; Fig. 1). The tunnels join close to the laboratory at an underground sedimentation chamber (station 3). At station 4 (subaerial source) and station 3 (mixed subaerial and subglacial sources), discharge has been recorded since 1998 at an hourly interval. The difference in discharge between stations 3 and 4 provides an approximation for water at the glacier base, mainly of supraglacial origin. In order to compare discharge with the pressure data on an annual timescale, only mean daily values are used. The result covers the period 1998–2013 except for the years 2002, 2004 and 2005, for which data were missing.
Air temperature measurements are from a meteorological station at Synkhøyden, installed in 1997 and maintained by the hydropower company Statkraft. The station is located at 800ma.s.l., 18 km inland (northeast) of the SSL. The sampling frequency is hourly, and only mean daily values starting at midnight were provided. Where gaps occurred in the records (usually a few days in a year and maximum 2–3 months), they were filled based on spatial extrapolation using nearby stations.
Precipitation data are from Glomfjord meteorological station, located 18 km northeast of the SSL and at 30 m a.s.l. They are accessible via eKlima.no, a climate database of the Norwegian Meteorological Institute, and cover the period 1992–2005. The daily value corresponds to precipitation that has fallen over the previous 24 hours starting at midnight.
5. Methods
5.1. Correlation method
We identify synchronous pressure variations between two load-cell time series from a Pearson correlation coefficient, which determines the strength of the relationship between two pressure records assuming it is linear. If a load cell varies in/out-of-phase with a second load cell, the expected result will be a positive/negative correlation and the Pearson correlation coefficient is 1/–1, respectively. The coefficient is zero, indicating no correlation, when the response of the load cells is not related or the relationship is nonlinear.
Periods with a higher sampling frequency are averaged such that all records are studied using a 15 min interval. The Pearson correlation coefficient is then calculated between a reference load cell and each of the other sensors with a centred running window of 24 hours (Figs 4 and 5; Reference Gordon, Sharp, Hubbard, Smart, Ketterling and WillisGordon and others, 1998; Reference Webster and OliverWebster and Oliver, 2007, p. 20). The choice of LC6 as reference is motivated by the length and stability of the record. The procedure is then repeated at each time step and computed for each pair (i.e. LC6–LC1e, LC6–LC4, LC6–LC97_1, etc.). Applying a moving correlation means that for a time window of 24 hours centred at t 0, the obtained correlation value indicates how the two time series behave between t 0 12 hours and t 0 + 12 hours. The running correlation will go from t 0 to tn , where n is the number of observations. The overlap of the time window will yield redundant data, but will reduce the effect of the starting time of the window on the correlation. As a result, the overlap will emphasize the major signals. To prevent correlations with too few points, computation is allowed only when the number of missing values is <25% of the time window. The Pearson correlation is sensitive to outliers, so a Spearman’s rank correlation that reduces this effect was also tested, but both techniques yielded comparable results.
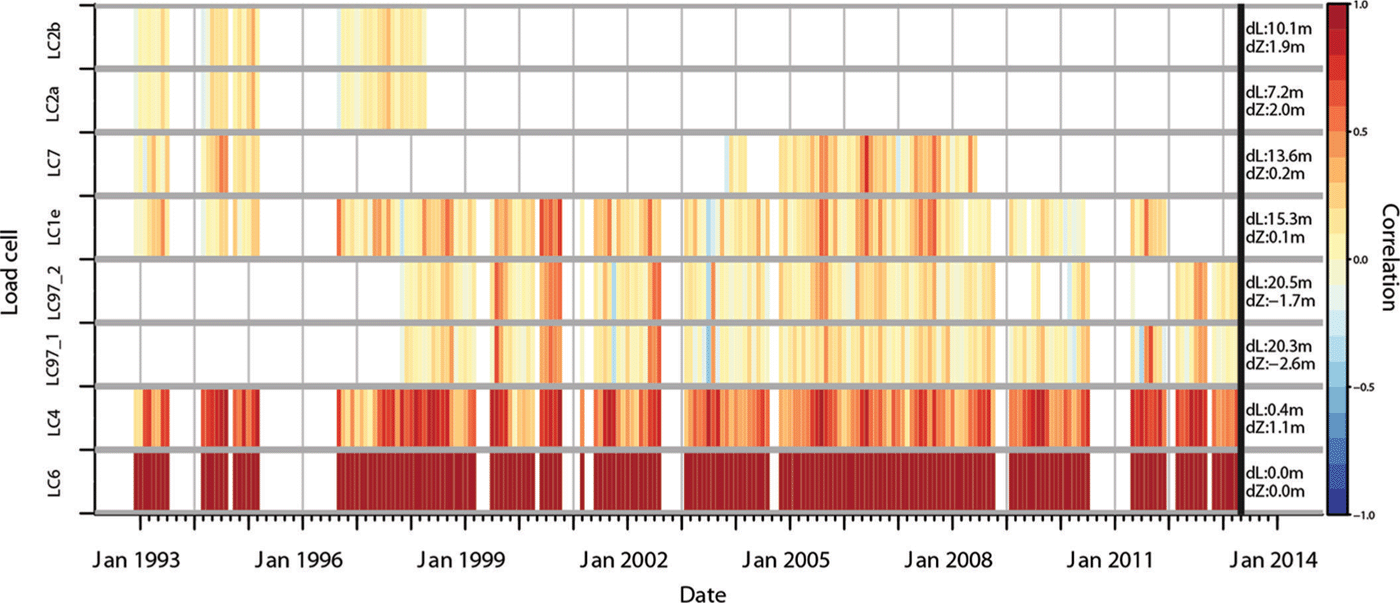
Fig. 5. Monthly averaged correlation between reference load cell LC6 and the other load cells. The positive correlation, no correlation and negative correlation are shown in red, yellow and blue respectively, with values given by scale at right. The distance and elevation difference between the reference load cell and the other load cells are shown on the right margin, as indicated by dL and dZ.
In order to extract seasonal and annual patterns in connectivity, the fluctuation in correlation obtained from the raw data with a sampling frequency of 15 min (Fig. 4) is averaged for each day and month. Because a running 24 hour correlation is used before the averaging, 25% of the total number of pressure points included in the daily mean correlation are from the preceding or the following day (for the monthly mean the percentage used is only 0.01%). As discussed in Section 6, this emphasizes the predominant correlation at the expense of the daily resolution. Figures 5 and 6 show annual variability through monthly averages, whereas Figures 7 and 8 highlight seasonal changes in correlation from daily values.

Fig. 6. Monthly correlation, with seasonal colour-coding, between two pairs of load cells (a) LC6–LC4 and (d) LC97_1–LC97_2 for the past 20 years, density distribution (c, f) and location of the sensors (b, e). In the box-plot graph, the thick black line, the bottom/top edge of the box and the lower/upper whisker edge represent the median, first/third quartile and minimum/maximum within the interquartile range respectively. Outliers are points outside the whiskers, but cannot be distinguished due to their high density. To highlight seasons, summer months are coloured in red, transition in orange and winter months in blue. Pictures are from Reference Lappegard, Kohler, Jackson and HagenLappegard and others (2006): (b) vertical cross section of LC4 and LC6; (e) photos of LC97_1 and LC97_2 placed on a gently sloping bed.
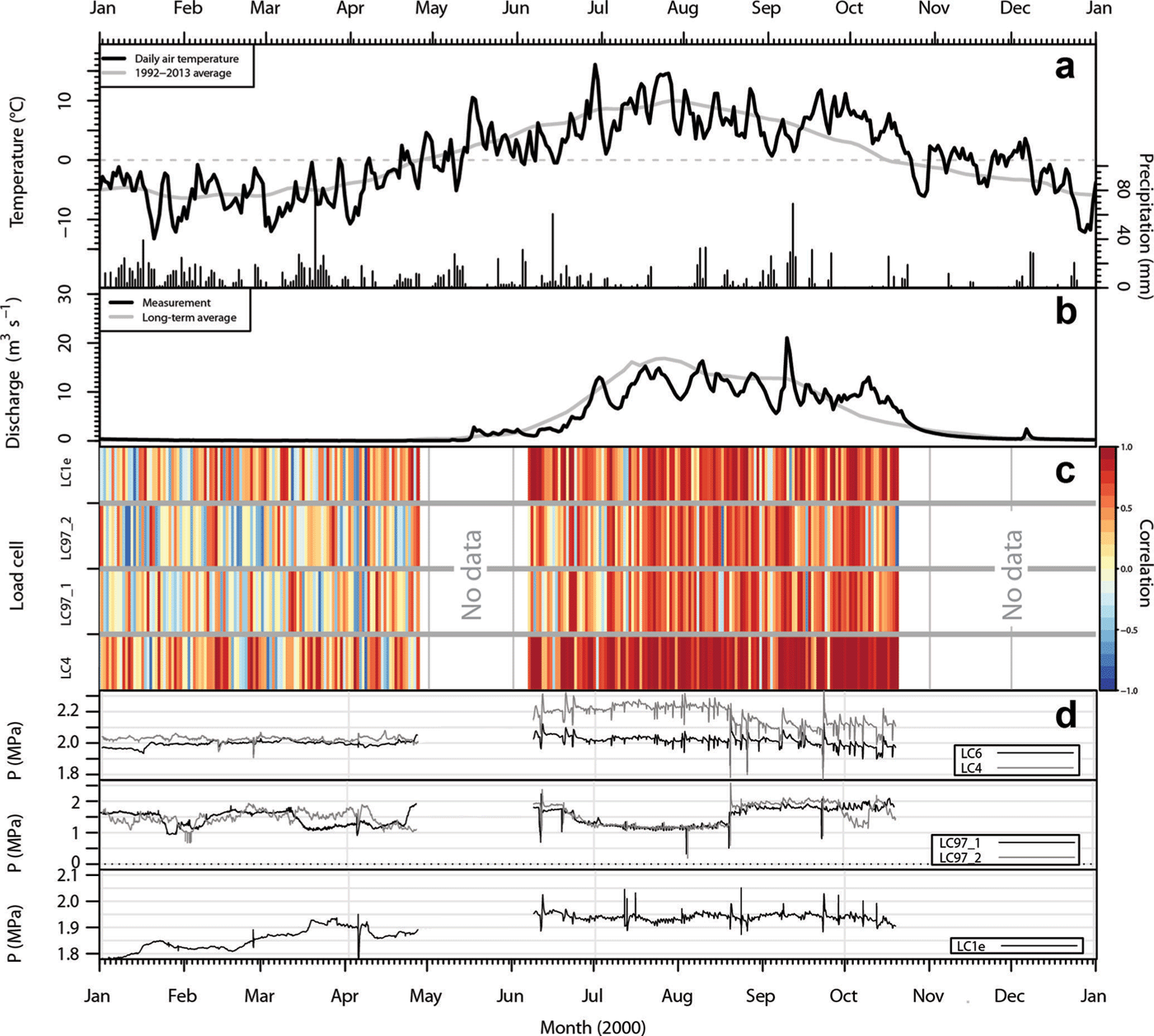
Fig. 7. Year 2000 data: (a) daily air temperature from Synkhøyden (800ma.s.l.) and daily precipitation from Glomfjord station (30ma.s.l.); (b) daily subglacial discharge from the SSL (~600ma.s.l.); (c) daily averaged correlation between LC6 (reference) and LC4, LC97_1, LC97_2 and LC1e; and (d) the original load-cell records.
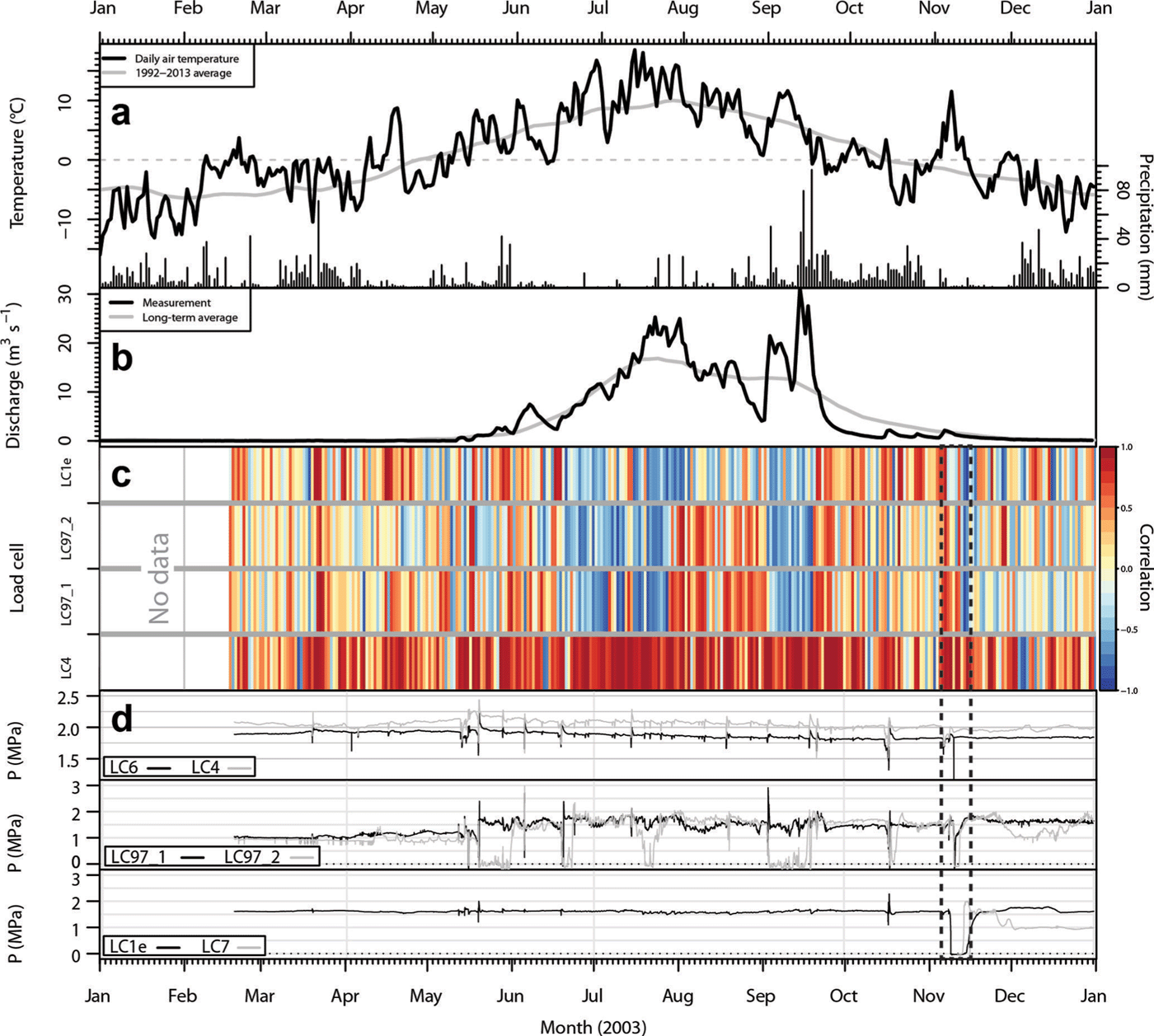
Fig. 8. Same as Figure 7, but 2003 data. Dashed frame shows melting of an artificial cavity.
5.2. Sensitivity test
To assess the effect of the time window length, a sensitivity test was conducted for window lengths of 1, 2, 4, 8, 12, 24, 48, 96 and 144 hours. The running correlation was computed with the 15 min data product for the entire period. The evaluation was performed using the monthly distribution of this correlation for each time window. Figure 6 shows the result when using a 24 hour window. The main result is that the observed seasonal variation is maintained for each time window. The longer time window favours a reduction in variability and more positive correlation, although a slight decrease is observed for periods >1 day. These features are assumed to be due to noise reduction. From this analysis, a running window of 1 day was chosen, as the effect of instrumental noise is reduced and the window still captures seasonal variations.
6. Method Assessment
The performance of the moving correlation is tested against synchronous pressure fluctuations between 1 and 31 May 2010, when a spring speed-up event occurred (Reference ChristiansonChristianson, 2011). As shown in Figure 4, correlations between LC6 and LC4 as well as LC6 and LC97_1 identify periods of correlated pressure signal, as on 16 and 27 May. Furthermore, the correlation is significant as it is within the 95% confidence interval (shaded area in Fig. 4). This correlation signal is hypothesized to indicate strong basal connectivity during this period (Reference Lappegard, Kohler, Jackson and HagenLappegard and others, 2006). In contrast, quieter periods that at first glance appear correlated, tend to produce inconsistent correlation (e.g. 1–15 May). A closer look at the records reveals distinct pressure variations at each sensor. Detrending, i.e. the removal of the seasonal trend (1 month running mean) from the pressure records to analyse the variance only, does not change the correlation (quartile range of the error for the difference in correlations is 0.02) since the load cells have a pressure close to overburden and the long-term changes in mean are small relative to the short-term variations. The high variability in correlation is assumed to indicate a loss in basal connectivity. Thus, in addition to correctly identifying correlated periods, the method reveals periods of low fluctuations in pressure, unique to each sensor, from a decrease in coherence of the correlation signal.
7. Results
7.1. Annual variation in correlation from 1993 to 2013
A moving correlation is applied to the 20 year long basal pressure records. To investigate annual variability in connectivity, monthly averages were calculated for each pair of load cells (i.e. LC6–LC6, LC6–LC4, LC6–LC97_1, etc.) and are presented as a temporal ‘heat map’ in Figure 5. In this figure, patterns of temporal changes (along horizontal axis) and connectivity (along vertical axis) are visually determined. The plot primarily highlights:
-
A seasonal variation notably marked for the pair LC6– LC4 as a gradual change from correlation close to zero in winter (pale yellow) to positive correlation (red) in summer.
-
A strong correlation pattern seen by five load cells during the summer months in 2000 and to some extent in 2002 and 2012.
-
An anticorrelation period between the groups LC6–LC4 and LC97_1–LC97_2–LC1e in 2003 as well as in 1999 and 2010, but with a weaker correlation.
A consequence of averaging correlations fluctuating above and below zero is that they cancel out and only a long positive or negative signal will be highlighted. This will cause an overestimate of periods of no correlation. Indeed, they can also indicate periods of equally distributed positive and negative correlations. When averaging absolute values instead, the general monthly no-correlation (~0–0.25) increases to 0.4–0.6. Therefore, in Figure 5, no correlation (pale yellow) preferentially represents short-term variations that fluctuate in sign, and thus high signal variability.
7.2. Seasonal variation
The seasonality is emphasized through the monthly distribution in correlation as shown in Figure 6. It gives a statistical estimate of the connectivity characteristics for a typical year. The load-cell pair LC6–LC4 displays a strong seasonal variation and high correlation values, which is supported by the similarity in response seen in Figures 3 and 4. The mean correlation for May–October is 0.70, whereas it is equal to 0.45 for November–April. This pattern seems to be a consistent variation, even though Figure 5 does not feature it as clearly for the other sensors, notably for LC97_1 and LC97_2. This discrepancy could be due to the 22m that separates LC6 and LC97_1 and LC97_2 (Fig. 2). Comparing LC97_1 with LC97_2 demonstrates that this pair, too, exhibits higher summer (0.39) than winter (0.14) correlation (Fig. 6d). Another interesting characteristic is the asymmetrical shape of the seasonal variation. The spring transition is characterized by a progressive increase in subglacial connectivity, whereas the onset of winter is more abrupt, as discussed further below.
7.3. High monthly correlation
Some interannual variations overlie this seasonal pattern (Fig. 5). One of the observed features is an unusually high summer correlation between LC6 and all other sensors in 2000. To understand this variation, the connectivity in 2000 was subject to further analysis (Fig. 7). The year 2000 is characterized by rather low and stable discharge, which was due to a relatively dry and cold summer, 1–2°C cooler than the 1992–2013 mean. The correlation in winter is similar to other years with no coherent patterns, whereas the summer shows a general high connectivity between the load cells. According to the load-cell records, 2000 is different from the other years in terms of the number and frequency of pressure events, shown as peaks in Figure 7d. These are observed to occur for >51 days and even continue into late summer. Additionally, the strong stability of the subglacial system is highlighted by the stability of the pressure signal and the absence of low-pressure channels, indicated by drops in pressure down to 0 MPa (Reference Lappegard, Kohler, Jackson and HagenLappegard and others, 2006).
7.4. Anticorrelated pressure variation
In contrast to 2000 when basal pressure records were highly correlated, summer 2003 displays two significant periods of anticorrelation (Fig. 8). The first occurs at the same time as the rising limb of daily discharge, which is associated with an increase in surface melt (mid-June to August; Fig. 9), and the second occurs during heavy rainfall in September. They are interrupted by a period of high correlation that coincides with a drop in discharge. During the remainder of the year, the daily correlation, particularly for LC4, shows the same pattern of no coherence as seen in 2000, which is associated with the seasonal variation in discharge. Indeed, the coherence of the correlation signal increases in spring when surface melt starts, and is lost in autumn at the end of the melting season. The pressure records show evidence of a highly active subglacial environment in 2003. Sensor LC97_2 has six periods when the basal pressure dropped to zero, with duration ranging from 2 days to 2 weeks. Five events of low pressure between 0 and 0.5 MPa that lasted <1 day are identifed in the LC97_1 record. These events occur mostly during long periods of negative correlation. A similar feature is also observed during the melting of an artificial water-free cavity in November (dashed frame in Fig. 8), which suggests the existence of water-free channels or drained cavities at atmospheric pressure.
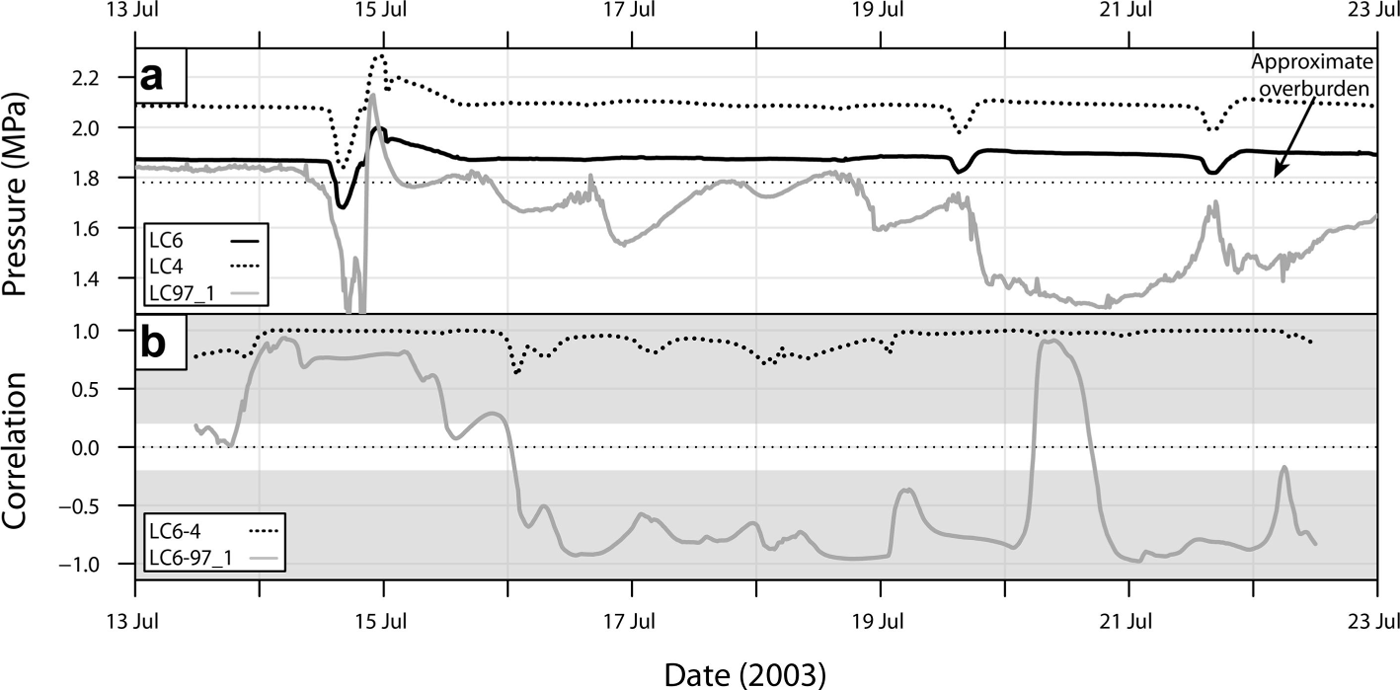
Fig. 9. Anticorrelated pressure: (a) LC4, LC6 and LC97_1 and (b) the correlation for each pair of load cells LC6–LC4 (grey) and LC6–LC97_1 (dashed). The shaded grey covers correlations that are within the 95% confidence interval. Because of the scale, the diurnal variation in pressure for LC6 and LC4 is difficult to see between 16 and 19 July, but is of the order of 0.01 MPa.
8. Interpretation and Discussion
The results of the statistical analysis over the 20 year period show two things. The seasonal changes of the pressure signals are consistent with what is commonly agreed on the behaviour of glacier hydrological systems. This suggests first that the use of the load cells is a reliable method for studying the subglacial hydrology, despite any uncertainty in the nature of the local forcing controlling the pressure signal. The results also give us pointers for further work in interpreting departures from a theoretical well-behaved glacier hydrological system that always goes through the same annual cycle according to schedule.
8.1. Load-cell environment
The load-cell network covers a small area of the bed, with dimensions of 22m × 5 m. Although the area is small, it is large enough to see variations in pressure that exist at the bed. For example, when a subglacial channel at the bed or a cavity exists at the base of the glacier, its size will probably not encompass the whole network. Individual load cells thus can sense different parts of the system and will respond according to where they are in relation to a channel or cavity, possibly showing opposite responses to what is apparently the same forcing. Hence, the network is able to capture both temporal and spatial changes in pressure.
The load cells are located in subtly different environments in terms of the immediate subglacial topography, and this affects their exposure to the subglacial hydrological system and their response. Two of the load cells, LC4 and LC6, are installed in an overhanging cliff (Fig. 6a), with the difference in orientation between them being ~115° (Table 1) such that one load cell faces approximately down, and the other approximately up. The protected environment of these two load cells is responsible for their general stability at high pressure. There is a pronounced correlation in signal between them, and usually a small difference in the pressure (0.1 MPa), which suggests that they are connected by a thin water film (TWF) (Reference WeertmanWeertman, 1972; Reference Lappegard, Kohler, Jackson and HagenLappegard and others, 2006). The pressure variations that these load cells record are thus variations in the pressure of the TWF when the hydrological system is relatively undisturbed.
Load cells LC97_1 and LC97_2 are in a more exposed location. They are situated on the lee side of a bedrock bump and in a more hydrologically active part of the bed. The in concert response of all the load cells, including the sheltered pair and the exposed pair, over much of the record implies that a continuous TWF connects the response of all the load cells. However, this is often disrupted, either when cavities exist and pathways and linkages are forming between them or when the subglacial hydrology becomes more developed over the spring and summer. The bedrock topography is not known in detail, and Figure 2 is based on measurements made using traditional land-surveying instruments when the load cells were first installed. However, based on this map as well as direct observations of five of the load cells (LC97_1, 97_2, 1e, 2b and 7), none of them is located on the stoss side of bedrock bumps.
That the load cells are occasionally in the same channels or cavities is observed several times in the record. An example from 2003 is shown in Figure 8d for LC97_1 and LC97_2. The load cells are at atmospheric pressure, indicating the presence of an open channel or drained basal cavity. This is corroborated by the presence of a similar signal when an artificial cavity is melted, as seen in November 2003 (Fig. 8d) when fieldwork and melting of an ice cave took place. Such an artificial cavity is open to the tunnel system so is at atmospheric pressure.
8.2. Seasonal variation in synchronous pressure variation
The correlation signal (Figs 5–8) reveals a strong seasonality defined by a shutdown of the subglacial channelized system in winter, and reactivation of synchronous pressure variations in summer.
Winter is characterized by a decrease in correlation coherence, which denotes unique fluctuations in pressure at each sensor despite maintaining more or less similar magnitude. We associate this pattern with the shutdown of the subglacial hydrological system, which increases the importance of local processes in the creation of pressure fluctuations. For example, pressure may vary due to local ice flow or to reorganization of the drainage system (Reference Fudge, Humphrey, Harper and PfefferFudge and others, 2008; Reference Schoof, Rada, Wilson, Flowers and HaseloffSchoof and others, 2014). These factors may also play a role in summer during episodes of decrease in surface meltwater input, absence of rain and when channel closure dominates. Transport of rocks at the glacier base can also cause pressure variation at single load cells as discussed in Section 4. The disturbance of basal pressure from clasts occurs throughout the year; however, this effect may only become important in winter as hydrological changes in summer dominate the pressure signal.
The transition to a summer regime of high correlation (either positive or negative) occurs in May with the development of the subglacial drainage system. Synchronous variations seem to respond to changes in meltwater input because seasonal variations in the coherence of correlation can be linked to seasonal changes in subglacial discharge (Fig. 8b and c). Reference Lappegard, Kohler, Jackson and HagenLappegard and others (2006) determined that peaks in discharge gradient coincide with the start of the daily pressure events, suggesting that isolated parts of the bed react when the efficient drainage system becomes pressurized. Bed separation and cavity formation are presumed to enhance the connection at the glacier base (Reference Harper, Humphrey, Pfeffer and LazarHarper and others, 2007), thus explaining the change in correlation regime from no coherent correlation to high correlation.
The seasonal pattern in correlation for the whole data period (Fig. 5) displays a slow transition from winter to summer, especially for LC97_1 and LC97_2 and to some extent for LC6 and LC4, perhaps indicating the importance of water retention within the snowpack (Reference Nienow, Sharp and WillisNienow and others, 1998), water storage within the glacier or development of englacial pathways (Reference Lappegard, Kohler, Jackson and HagenLappegard and others, 2006). Retention would delay meltwater transfer to the glacier base up to 6 days (Reference Lappegard, Kohler, Jackson and HagenLappegard and others, 2006), thus slowing the activation and connection of the drainage system. At the onset of winter (October), correlation drops rapidly to winter levels. Lower temperatures and reduced meltwater input lead to rapid closure of the subglacial drainage system, as channels swiftly contract and close due to the weight of the overlying ice.
8.3. Strong correlation patterns in summer
Despite showing similar high summer correlation, the signals for 2000 and 2003 differ from each other due to the anti-correlation observed in 2003 between LC6–LC4 and the rest of the sensors (Fig. 8c and 9). Anticorrelation is a consistent feature of the subglacial system (Reference Murray and ClarkeMurray and Clarke, 1995; Reference Gordon, Sharp, Hubbard, Smart, Ketterling and WillisGordon and others, 1998; Reference Dow, Kavanaugh, Sanders, Cuffey and MacGregorDow and others, 2011; Reference Schoof, Rada, Wilson, Flowers and HaseloffSchoof and others, 2014). As previously discussed, this out-of-phase signal is due to mechanical load transfer (Reference Murray and ClarkeMurray and Clarke, 1995), stress bridging (Reference WeertmanWeertman, 1972; Reference LappegardLappegard, 2006) or passive cavity opening (Reference AndrewsAndrews and others, 2014). We consider that either load transfer or passive cavity opening is likely to cause the observed anticorrelation because they affect larger areas of the glacier bed than stress bridging.
The two anticorrelation periods shown in Figure 8c for 2013 occurred during an abnormally warm June–July and during heavy rainfall in September that caused large surface water input to flood the subglacial system. Continuous and/or rapid increase in surface input is thought to exceed the capacity of the drainage system and cause water pressure to rise in the channels (LC97_1 in Fig. 9). This is accompanied by rising subglacial discharge until the system can accommodate the melt. Some of the load cells (LC97_1 and LC97_2) then measure atmospheric pressure as shown in Figures 8d and 9. As melt and discharge start to decrease, the anticorrelation stops, confirming the effect of input rate on bed pressurization. These events can last for weeks as seen in early summer 2003. Over-pressurization of channels depends on the initial state of the drainage system and its capacity, as seen for the heavy rainfall in September 2003. Prior to the event, reduced melt input enhances closure of the subglacial drainage system. The contracting channels force flooding of the glacier base and reactivation of the hydrological system (i.e. melting of channels and opening of cavities) during the precipitation event (Reference Howat, Tulaczyk, Waddington and BjörnssonHowat and others, 2008), creating an anticorrelated signal.
In contrast, summer 2000 showed high positive monthly correlations for nearly all load cells. The high degree of correlation is mainly due to the number of diurnal signals and their recurrence (Fig. 7d). The load cells also record modest diurnal variations with an amplitude difference as small as 0.01 MPa. Reference Lappegard, Kohler, Jackson and HagenLappegard and others (2006) describe these as ‘global events’. In general, the diurnal signals consist of a pressure drop followed by a high or more gradual peak before returning to the original background pressure (Figs 4 and 9; Reference Lappegard, Kohler, Jackson and HagenLappegard and others, 2006). The diurnal periodicity of the events and their increasing number in summer suggest control by surface melting, similar to what is seen in 2003, but only the response from the distributed drainage system is measured. The year 2000 had one of the lowest summer mass balances since 1970, at –1.8 m w.e. (mean is –2.4 m w.e.; Reference Kjøllmoen, Andreassen, Elvehøy, Jackson and GiesenKjøllmoen and others, 2011), caused by lower summer air temperatures than the long-term average by 0.8°C. A colder year reduces the extent of the melt season and decreases the likelihood of melt events and daily melt variability. The standard deviation in air temperature for summer 2000 is 3.8°C, whereas it is 5.0°C for 2003. Rainfall events are also less common and less intense than in 2003 (Figs 7a and 8a). For the period June–September, there are 39 and 25 rain-free days for 2000 and 2003, respectively. There was 732mm of rain in summer 2000, with most of it falling in June (231 mm) and September (278 mm). Precipitation in summer 2003 is of the same order (828 mm), but nearly 70% fell in September (565 mm). From these observations, we infer that surface melt was relatively constant over summer 2000, which is supported by stable subglacial discharge (Fig. 7b). Thus, diurnal melt cycles dominate and the subglacial hydrological system was not disturbed by the sudden input of water coming from major melt episodes or precipitation events. The observations of high correlation and stable meteorological conditions in 2000 suggest that constant surface meltwater favours steady-state conditions at the glacier base. In this case, a more persistent meltwater input enhances channelized flow at stable locations and maintains a channel size in balance with the input, which promotes frequent over-pressurization (Reference Bartholomaus, Anderson and AndersonBartholomaus and others, 2008; Reference SchoofSchoof, 2010). This is consistent with the absence of low-pressure channels (Fig. 7d), indicating that the load cells are in a less hydrologically active zone in 2000 than in 2003. Nevertheless, a subglacial channel is likely to cause the pressure events, as was observed in 2003. The existence of subglacial intakes (black cross in Fig. 1) within 250–500m of the load cells creates a low-pressure area at the glacier bed and could favour the development of a channelized drainage in the vicinity. This channel may then affect an area changing with the intensity of the over-pressurization, which causes the load cells to respond synchronously. The potential of point measurements for extrapolation would then be possible for larger areas considering their variation and amplitude correction for bedrock geometry and ice flow.
9. Conclusion
A study of the correlation of the basal pressure records shows the seasonal variation in pressure over a load-cell network and the importance of meltwater input to basal connectivity. The connectivity is highly responsive to meltwater input on a seasonal scale. A typical year consists of poor connectivity in winter (loss in correlation coherence) and high connectivity in summer (high correlation, generally positive). This pattern is more obvious for closely located sensors (<1 m) as expected.
Two years were studied in detail, one with negatively correlated sensors during summer whereas the other was characterized by positively correlated sensors during summer. The variability in meltwater production is the direct or indirect cause of bed connectivity stability (Reference Iken and TrufferIken and Truffer, 1997; Reference Harper, Humphrey, Pfeffer and LazarHarper and others, 2007; Reference Bartholomaus, Anderson and AndersonBartholomaus and others, 2008). In 2003, continuously increasing melt and rainfall favour over-pressurization of channels and flooding of new parts of the bed (Reference Harper, Humphrey, Pfeffer and LazarHarper and others, 2007). In 2000, constant melt and discharge lead to steady-state conditions for channels that would be spatially more stable. The connectivity is therefore less influenced by the volume of meltwater than its variability (Reference Harper, Humphrey, Pfeffer and LazarHarper and others, 2007; Reference Bartholomaus, Anderson and AndersonBartholomaus and others, 2008; Reference SchoofSchoof, 2010).
This study further highlights the difficulty of inferring basal conditions based on single borehole measurements, and caution is needed when drawing conclusions from one location. As shown in this work, widespread bed connectivity is rarely the case over the entire sensor network and occurs only during particularly stable meteorological conditions (Fig. 7). In most cases, pressure records from sensors located even <1m apart can be very different and reveal extreme pressure gradients. The research community should be sceptical of inferring general basal conditions from results of a single borehole. These results are coherent over the studied two decades, and give an overall picture consistent with borehole studies (Reference Murray and ClarkeMurray and Clarke, 1995; Reference Schoof, Rada, Wilson, Flowers and HaseloffSchoof and others, 2014). However, long-term direct observations show that bed conditions can differ significantly between years, displaying contrasting pressure variations either positively or negatively correlated over long periods. These results agree with Reference AndrewsAndrews and others (2014), who showed that mechanical processes occurring at the glacier base are important in understanding how the hydrological system affects glacier dynamics.
Author Contribution Statement
P-.M.L. performed time-series analysis and plotting. P.-M.L. and M.J. designed the method and wrote the paper with input and discussion from G.L. and J.O.H. M.J. and G.L. collected load-cell data.
Acknowledgements
This publication is contribution No. 41 of the Nordic Centre of Excellence SVALI (Stability and Variations of Arctic Land Ice), funded by the Nordic Top-level Research Initiative (TRI). We are grateful to Statkraft for providing access to the SSL as well as air temperature data, and to the Norwegian Water Resources and Energy Directorate for maintaining and funding the laboratory over the past 20 years. We also thank T.V. Schuler, A. Sinisalo, C. Nuth and T. Johanesson for discussions, S.H. Winsvold for help with maps, and two anonymous referees, whose comments substantially improved the manuscript.












