1 Introduction
Let
![]() $(X,T)$
be a dynamical system, that is, let X be a compact metric space and T a homeomorphism of X to itself. An automorphism of
$(X,T)$
be a dynamical system, that is, let X be a compact metric space and T a homeomorphism of X to itself. An automorphism of
![]() $(X,T)$
is a homeomorphism
$(X,T)$
is a homeomorphism
![]() $\varphi \colon X\to X$
that commutes with T. The set of all automorphisms of
$\varphi \colon X\to X$
that commutes with T. The set of all automorphisms of
![]() $(X,T)$
is a group under composition called the automorphism group of
$(X,T)$
is a group under composition called the automorphism group of
![]() $(X,T)$
, and we denote it by
$(X,T)$
, and we denote it by
![]() $\operatorname {Aut}(X,T)$
.
$\operatorname {Aut}(X,T)$
.
The automorphism groups of symbolic systems have been studied since the 1960s, starting with the works of Hedlund in [Reference Hedlund9]. These groups continue to be studied extensively, see, for example, [Reference Boyle, Lind and Rudolph2–Reference Donoso, Durand, Maass and Petite5, Reference Kim and Roush11, Reference Ryan14]. In particular, the automorphism group of Toeplitz subshifts has been studied by Donoso et al [Reference Donoso, Durand, Maass and Petite6] and Salo [Reference Salo15]. In this work, we study a larger group of symmetries called the stabilized automorphism group for odometers and Toeplitz shifts.
The stabilized automorphism group was introduced in 2021 by Hartman, Kra, and Schmieding [Reference Hartman, Kra and Schmieding8]. Given
![]() $(X, T)$
a dynamical system, the stabilized automorphism group is the subgroup of
$(X, T)$
a dynamical system, the stabilized automorphism group is the subgroup of
![]() $\operatorname {Homeo}(X)$
given by
$\operatorname {Homeo}(X)$
given by
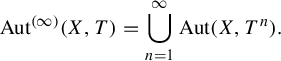 $$ \begin{align*}\operatorname{Aut}^{(\infty)}(X,T) = \bigcup_{n=1}^\infty \operatorname{Aut}(X,T^n).\end{align*} $$
$$ \begin{align*}\operatorname{Aut}^{(\infty)}(X,T) = \bigcup_{n=1}^\infty \operatorname{Aut}(X,T^n).\end{align*} $$
Building on partial results from [Reference Hartman, Kra and Schmieding8], Schmieding gave a full characterization of the stabilized automorphism group for shifts of finite type [Reference Schmieding16]. Given natural numbers
![]() $m, n \geq 2$
, the stabilized groups of the full m-shift and the full n-shift are isomorphic if and only if
$m, n \geq 2$
, the stabilized groups of the full m-shift and the full n-shift are isomorphic if and only if
![]() $m^k = n^j$
for some
$m^k = n^j$
for some
![]() $k, j \in \mathbb {N}$
.
$k, j \in \mathbb {N}$
.
We study the stabilized automorphism group of a class of dynamical systems with contrasting behavior to that studied by Schmieding. While mixing shifts of finite type have high complexity, we study odometer systems which have zero entropy. An important technique introduced in [Reference Schmieding16] is the notion of local
![]() $\mathcal {P}$
-entropy, a quantity that captures the exponential growth rate of certain classes of finite subgroups in the limit that defines the stabilized automorphism group. These techniques however cannot be applied directly to our case since all odometers exhibit the same growth rate of finite groups in their stabilized automorphism group. Hence, local
$\mathcal {P}$
-entropy, a quantity that captures the exponential growth rate of certain classes of finite subgroups in the limit that defines the stabilized automorphism group. These techniques however cannot be applied directly to our case since all odometers exhibit the same growth rate of finite groups in their stabilized automorphism group. Hence, local
![]() $\mathcal {P}$
-entropy alone is not enough to distinguish two odometers by analyzing their stabilized automorphism group. However, we draw inspiration from this method to develop a new approach to the study of the growth of finite subgroups of the automorphism groups that define the stabilized automorphism group. In a similar way as to how the complexity function is a sequence that provides more information about a symbolic system than its limit, that is, the topological entropy, by pinpointing the finite stages of the definition of the stabilized automorphism group where we see growth, we can recover the primes for which the p-adic valuation of the scale of the odometer tends to infinity. In particular, we show that for torsion-free odometers, the stabilized automorphism group is a full isomorphism invariant.
$\mathcal {P}$
-entropy alone is not enough to distinguish two odometers by analyzing their stabilized automorphism group. However, we draw inspiration from this method to develop a new approach to the study of the growth of finite subgroups of the automorphism groups that define the stabilized automorphism group. In a similar way as to how the complexity function is a sequence that provides more information about a symbolic system than its limit, that is, the topological entropy, by pinpointing the finite stages of the definition of the stabilized automorphism group where we see growth, we can recover the primes for which the p-adic valuation of the scale of the odometer tends to infinity. In particular, we show that for torsion-free odometers, the stabilized automorphism group is a full isomorphism invariant.
We use our results about odometers to study a class of subshifts called Toeplitz subshifts that have odometers as their maximal equicontinuous factor. These subshifts were first studied by Jacobs and Keane [Reference Jacobs and Keane10] and have no restrictions in terms of their complexity. However, since they carry a lot of the same rigid structure of an odometer, we are able to use the results on odometers to conclude similar results about Toeplitz subshifts.
We defer the precise definitions and notation to §2. In §3, we study the stabilized automorphism group for odometers. The main result of this section is the following theorem. We use the notation
![]() $\operatorname {Sym}(n)$
to represent the symmetric group on n symbols.
$\operatorname {Sym}(n)$
to represent the symmetric group on n symbols.
Theorem 1.1. The stabilized automorphism group of an odometer
![]() $\mathbb {Z}_{(p_n)}$
with scale
$\mathbb {Z}_{(p_n)}$
with scale
![]() $(p_n)$
is isomorphic to the direct limit of a sequence of monomorphisms of groups of the form
$(p_n)$
is isomorphic to the direct limit of a sequence of monomorphisms of groups of the form
![]() $(\mathbb {Z}_{(q_n)})^{p_k}\rtimes \operatorname {Sym}(p_k)$
, where
$(\mathbb {Z}_{(q_n)})^{p_k}\rtimes \operatorname {Sym}(p_k)$
, where
![]() $\mathbb {Z}_{(q_n)}$
is an odometer that is a factor of
$\mathbb {Z}_{(q_n)}$
is an odometer that is a factor of
![]() $\mathbb {Z}_{(p_n)}$
and
$\mathbb {Z}_{(p_n)}$
and
![]() $p_k$
is an element of the scale
$p_k$
is an element of the scale
![]() $(p_n)$
.
$(p_n)$
.
A more precise description of the stabilized automorphism group of odometers including a characterization of the monomorphisms defining the limit is given in Theorem 3.5. The main technical difficulty to overcome for proving this theorem is characterizing
![]() $\operatorname {Aut}(\mathbb {Z}_{(p_n)},+ \textbf {m})$
for all
$\operatorname {Aut}(\mathbb {Z}_{(p_n)},+ \textbf {m})$
for all
![]() $m\in \mathbb {Z}$
. We do so in Proposition 3.1. This characterization is different from characterizing
$m\in \mathbb {Z}$
. We do so in Proposition 3.1. This characterization is different from characterizing
![]() $\operatorname {Aut}(\mathbb {Z}_{(p_n)},+\mathbf {1})$
for any odometer
$\operatorname {Aut}(\mathbb {Z}_{(p_n)},+\mathbf {1})$
for any odometer
![]() $\mathbb {Z}_{(p_n)}$
as that proof relies heavily on the fact that
$\mathbb {Z}_{(p_n)}$
as that proof relies heavily on the fact that
![]() $(\mathbb {Z}_{(p_n)},+\mathbf {1})$
is minimal. However, when m divides an element of the sequence
$(\mathbb {Z}_{(p_n)},+\mathbf {1})$
is minimal. However, when m divides an element of the sequence
![]() $(p_n)$
, the system
$(p_n)$
, the system
![]() $(\mathbb {Z}_{(p_n)},+\mathbf {1})$
fails to be minimal, as we show in Proposition 3.1.
$(\mathbb {Z}_{(p_n)},+\mathbf {1})$
fails to be minimal, as we show in Proposition 3.1.
In §4, we study the stabilized automorphism group of Toeplitz subshifts and prove a similar result.
Theorem 1.2. Let
![]() $(X,\sigma )$
be a Toeplitz subshift with period structure
$(X,\sigma )$
be a Toeplitz subshift with period structure
![]() $(p_n)$
. Then, the stabilized automorphism group of
$(p_n)$
. Then, the stabilized automorphism group of
![]() $(X,\sigma )$
is isomorphic to the direct limit of a sequence of monomorphisms of groups of the form
$(X,\sigma )$
is isomorphic to the direct limit of a sequence of monomorphisms of groups of the form
![]() $\operatorname {Aut}(T,\tau )^{p_k}\rtimes \operatorname {Sym}(p_k)$
, where
$\operatorname {Aut}(T,\tau )^{p_k}\rtimes \operatorname {Sym}(p_k)$
, where
![]() $(T,\tau )$
is a Toeplitz shift and
$(T,\tau )$
is a Toeplitz shift and
![]() $p_k$
is an element of the sequence
$p_k$
is an element of the sequence
![]() $(p_n)$
.
$(p_n)$
.
A more precise description of the stabilized automorphism group of Toeplitz subshifts including a characterization of the monomorphisms defining the limit is given in Theorem 4.4. Similarly to the theorem about odometers, the main technical difficulty is characterizing
![]() $\operatorname {Aut}(X,\sigma ^m)$
for all
$\operatorname {Aut}(X,\sigma ^m)$
for all
![]() $m\in \mathbb {Z}$
. We do so in Proposition 4.1.
$m\in \mathbb {Z}$
. We do so in Proposition 4.1.
As an immediate corollary to the previous theorems, since amenable groups are preserved under direct limits, we have the following corollary.
Corollary 1.3. Both the stabilized automorphism group of an odometer and the stabilized automorphism of a Toeplitz subshift are amenable.
Odometers are completely classified by an equivalence relation on their scale (see [Reference Downarowicz, Kolyada, Manin and Ward7]). Let
![]() $(p_n)$
be the scale of an odometer. For each prime number p, denote by
$(p_n)$
be the scale of an odometer. For each prime number p, denote by
![]() $\nu _p(n)$
the p-adic valuation of the integer n, that is,
$\nu _p(n)$
the p-adic valuation of the integer n, that is,
![]() $\nu _p(n)=\max \{k\geq 0: p^k \text { divides } n\}.$
For each prime, the multiplicity function at p of the scale
$\nu _p(n)=\max \{k\geq 0: p^k \text { divides } n\}.$
For each prime, the multiplicity function at p of the scale
![]() $(p_n)$
is given by
$(p_n)$
is given by
![]() $\operatorname {\mathbf {v}}_p(p_n)=\lim _{n\to \infty }\nu _p(p_n).$
Two scales
$\operatorname {\mathbf {v}}_p(p_n)=\lim _{n\to \infty }\nu _p(p_n).$
Two scales
![]() $(p_n)$
and
$(p_n)$
and
![]() $(s_n)$
are equivalent if and only if
$(s_n)$
are equivalent if and only if
![]() $ \operatorname {\mathbf {v}}_p(p_n)=\operatorname {\mathbf {v}}_p(s_n) \text { for all primes } p$
. Two odometers are isomorphic if and only if their scales are equivalent. In §5, we study the finite subgroups at each level of the sequences in Theorems 1.1 and 1.2 to prove the isomorphism invariance of the primes for which the multiplicity function at p is infinite. We use this to derive our main invariance results.
$ \operatorname {\mathbf {v}}_p(p_n)=\operatorname {\mathbf {v}}_p(s_n) \text { for all primes } p$
. Two odometers are isomorphic if and only if their scales are equivalent. In §5, we study the finite subgroups at each level of the sequences in Theorems 1.1 and 1.2 to prove the isomorphism invariance of the primes for which the multiplicity function at p is infinite. We use this to derive our main invariance results.
Theorem 1.4. Let
![]() $(\mathbb {Z}_{(p_n)},+\mathbf {1})$
and
$(\mathbb {Z}_{(p_n)},+\mathbf {1})$
and
![]() $(\mathbb {Z}_{(q_n)},+\mathbf {1})$
be torsion-free odometers with scales
$(\mathbb {Z}_{(q_n)},+\mathbf {1})$
be torsion-free odometers with scales
![]() $(p_n)$
and
$(p_n)$
and
![]() $(q_n)$
, respectively. If
$(q_n)$
, respectively. If
![]() $\operatorname {Aut}^{(\infty )}(\mathbb {Z}_{(p_n)},+\mathbf {1})$
and
$\operatorname {Aut}^{(\infty )}(\mathbb {Z}_{(p_n)},+\mathbf {1})$
and
![]() $\operatorname {Aut}^{(\infty )}(\mathbb {Z}_{(q_n)},+\mathbf {1})$
are isomorphic as groups, then
$\operatorname {Aut}^{(\infty )}(\mathbb {Z}_{(q_n)},+\mathbf {1})$
are isomorphic as groups, then
![]() $\mathbb {Z}_{(p_n)}$
and
$\mathbb {Z}_{(p_n)}$
and
![]() $\mathbb {Z}_{(q_n)}$
are isomorphic as groups.
$\mathbb {Z}_{(q_n)}$
are isomorphic as groups.
Theorem 1.5. Let
![]() $(X,\sigma )$
and
$(X,\sigma )$
and
![]() $(T,\tau )$
be torsion-free Toeplitz subshifts with scales
$(T,\tau )$
be torsion-free Toeplitz subshifts with scales
![]() $(p_n)$
and
$(p_n)$
and
![]() $(q_n)$
, respectively. If
$(q_n)$
, respectively. If
![]() $\operatorname {Aut}^{(\infty )}(X,\sigma )$
and
$\operatorname {Aut}^{(\infty )}(X,\sigma )$
and
![]() $\operatorname {Aut}^{(\infty )}(T,\tau )$
are isomorphic as groups, then
$\operatorname {Aut}^{(\infty )}(T,\tau )$
are isomorphic as groups, then
![]() $(p_n)$
is equivalent to
$(p_n)$
is equivalent to
![]() $(q_n)$
.
$(q_n)$
.
2 Preliminaries
2.1 Background
A topological dynamical system (or simply a system) is a pair
![]() $(X,T)$
, where X is a compact metric space with metric
$(X,T)$
, where X is a compact metric space with metric
![]() $\operatorname {d}\colon X\times X\to \mathbb {R}$
and
$\operatorname {d}\colon X\times X\to \mathbb {R}$
and
![]() $T\colon X\to X$
is a homeomorphism. In the particular case when X is a compact topological group and T acts by group translation by a fixed element in X, we call the dynamical system
$T\colon X\to X$
is a homeomorphism. In the particular case when X is a compact topological group and T acts by group translation by a fixed element in X, we call the dynamical system
![]() $(X,T)$
a group rotation. The orbit of a point
$(X,T)$
a group rotation. The orbit of a point
![]() $x\in X$
is denoted by
$x\in X$
is denoted by
![]() $\mathcal {O}_T(x)=\{T^n(x): n\in \mathbb {Z}\}$
. Given a subset
$\mathcal {O}_T(x)=\{T^n(x): n\in \mathbb {Z}\}$
. Given a subset
![]() $U\subseteq X$
, we define
$U\subseteq X$
, we define
![]() $\mathcal {O}_T(U)=\bigcup \nolimits _{x\in U}\mathcal {O}_T(x)$
. A system is minimal if the orbit of every point
$\mathcal {O}_T(U)=\bigcup \nolimits _{x\in U}\mathcal {O}_T(x)$
. A system is minimal if the orbit of every point
![]() $x\in X$
is dense in X. A subset
$x\in X$
is dense in X. A subset
![]() $U\subseteq X$
is called a minimal component of
$U\subseteq X$
is called a minimal component of
![]() $(X,T)$
if U is closed, T-invariant, and the restriction of T to U makes
$(X,T)$
if U is closed, T-invariant, and the restriction of T to U makes
![]() $(U,T|_U)$
a minimal system.
$(U,T|_U)$
a minimal system.
Given two topological dynamical systems
![]() $(X,T)$
,
$(X,T)$
,
![]() $(Y,S)$
, a continuous surjection
$(Y,S)$
, a continuous surjection
![]() $\pi \colon X\to Y$
such that
$\pi \colon X\to Y$
such that
![]() $\pi \circ T=S\circ \pi $
is called a factor map. If such a map exists, we say
$\pi \circ T=S\circ \pi $
is called a factor map. If such a map exists, we say
![]() $(Y,S)$
is a factor of
$(Y,S)$
is a factor of
![]() $(X,T)$
. If in addition
$(X,T)$
. If in addition
![]() $\pi $
is a bijection, we say
$\pi $
is a bijection, we say
![]() $(X,T)$
and
$(X,T)$
and
![]() $(Y,S)$
are conjugate systems.
$(Y,S)$
are conjugate systems.
Let G and H be two topological groups. We say that G and H are isomorphic as topological groups if there exists a group isomorphism
![]() $\phi \colon G \to H$
that is also a homeomorphism. Not all group isomorphisms are necessarily topological isomorphisms and to avoid confusion, we refer to a usual group isomorphism as an algebraic isomorphism and denote it with the symbol
$\phi \colon G \to H$
that is also a homeomorphism. Not all group isomorphisms are necessarily topological isomorphisms and to avoid confusion, we refer to a usual group isomorphism as an algebraic isomorphism and denote it with the symbol
![]() $\cong $
. Moreover, two group rotations
$\cong $
. Moreover, two group rotations
![]() $(G,g)$
and
$(G,g)$
and
![]() $(H,h)$
are conjugate if and only if there exists a topological isomorphism
$(H,h)$
are conjugate if and only if there exists a topological isomorphism
![]() $\phi \colon G \to H$
such that
$\phi \colon G \to H$
such that
![]() $\phi (g)=\phi (h)$
.
$\phi (g)=\phi (h)$
.
We say the system
![]() $(X,T)$
is equicontinuous if for any
$(X,T)$
is equicontinuous if for any
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $\delta>0$
such that if
$\delta>0$
such that if
![]() $\operatorname {d}(x,y)\leq \delta $
for
$\operatorname {d}(x,y)\leq \delta $
for
![]() $x,y\in X$
, then for any
$x,y\in X$
, then for any
![]() $n\in \mathbb {Z}$
, we have
$n\in \mathbb {Z}$
, we have
![]() $\operatorname {d}(T^n(x),T^n(y))\leq \varepsilon $
. Every minimal equicontinuous system is conjugate to a group rotation (see, for example, [Reference Kurka12]).
$\operatorname {d}(T^n(x),T^n(y))\leq \varepsilon $
. Every minimal equicontinuous system is conjugate to a group rotation (see, for example, [Reference Kurka12]).
2.2 Automorphism group and stabilized automorphism group
An automorphism of a system
![]() $(X,T)$
is a homeomorphism
$(X,T)$
is a homeomorphism
![]() $\varphi $
of X such that
$\varphi $
of X such that
![]() $\varphi \circ T=T\circ \varphi $
. The set of all automorphisms of X forms a group under composition which we denote by
$\varphi \circ T=T\circ \varphi $
. The set of all automorphisms of X forms a group under composition which we denote by
![]() $\operatorname {Aut}(X,T)$
and call the automorphism group of
$\operatorname {Aut}(X,T)$
and call the automorphism group of
![]() $(X,T)$
. A commonly used result in the literature is the following lemma. We include the proof for completeness.
$(X,T)$
. A commonly used result in the literature is the following lemma. We include the proof for completeness.
Lemma 2.1. Let
![]() $(X,T)$
be a dynamical system and
$(X,T)$
be a dynamical system and
![]() $\varphi \in \operatorname {Aut}(X,T)$
. Then,
$\varphi \in \operatorname {Aut}(X,T)$
. Then,
![]() $U\subseteq X$
is a minimal component of
$U\subseteq X$
is a minimal component of
![]() $(X,T)$
if and only if
$(X,T)$
if and only if
![]() $\varphi (U)$
is a minimal component.
$\varphi (U)$
is a minimal component.
Proof. Let
![]() $U\subseteq X$
be a minimal component of
$U\subseteq X$
be a minimal component of
![]() $(X,T)$
and let
$(X,T)$
and let
![]() $\varphi \in \operatorname {Aut}(X,T)$
. Since
$\varphi \in \operatorname {Aut}(X,T)$
. Since
![]() $\varphi $
is a homeomorphism of X,
$\varphi $
is a homeomorphism of X,
![]() $\varphi (U)$
is closed. Additionally, since U is T-invariant, we have that
$\varphi (U)$
is closed. Additionally, since U is T-invariant, we have that
![]() $T(\varphi (U))=\varphi (T(U))\subseteq \varphi (U)$
. Hence,
$T(\varphi (U))=\varphi (T(U))\subseteq \varphi (U)$
. Hence,
![]() $\varphi (U)$
is T-invariant. Take
$\varphi (U)$
is T-invariant. Take
![]() $y\in \varphi (U)$
. Since
$y\in \varphi (U)$
. Since
![]() $\varphi $
is a bijection, there exists
$\varphi $
is a bijection, there exists
![]() $x\in U$
with
$x\in U$
with
![]() $\varphi (x)=y$
and since U is a minimal component,
$\varphi (x)=y$
and since U is a minimal component,
![]() ${\overline {\mathcal {O}}_T(x)=U}$
. Because
${\overline {\mathcal {O}}_T(x)=U}$
. Because
![]() $\varphi $
is an automorphism of
$\varphi $
is an automorphism of
![]() $(X,T)$
, we have that
$(X,T)$
, we have that
![]() $\overline {\mathcal {O}}_T(y)=\overline {\mathcal {O}}_T(\varphi (x))=\varphi (U)$
. We conclude
$\overline {\mathcal {O}}_T(y)=\overline {\mathcal {O}}_T(\varphi (x))=\varphi (U)$
. We conclude
![]() $\varphi (U)$
is a minimal component. To show that
$\varphi (U)$
is a minimal component. To show that
![]() $\varphi ^{-1}(U)$
is a minimal component, we repeat the proof with
$\varphi ^{-1}(U)$
is a minimal component, we repeat the proof with
![]() $\varphi ^{-1}$
instead of
$\varphi ^{-1}$
instead of
![]() $\varphi $
.
$\varphi $
.
As introduced by Hartman, Kra, and Shmieding in [Reference Hartman, Kra and Schmieding8], for
![]() $(X,T)$
a dynamical system, we define the stabilized automorphism group of
$(X,T)$
a dynamical system, we define the stabilized automorphism group of
![]() $(X,T)$
to be the subgroup of
$(X,T)$
to be the subgroup of
![]() $\operatorname {Homeo}(X)$
given by
$\operatorname {Homeo}(X)$
given by
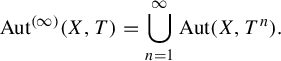 $$ \begin{align*}\operatorname{Aut}^{(\infty)}(X,T)=\bigcup_{n=1}^\infty\operatorname{Aut}(X,T^n).\end{align*} $$
$$ \begin{align*}\operatorname{Aut}^{(\infty)}(X,T)=\bigcup_{n=1}^\infty\operatorname{Aut}(X,T^n).\end{align*} $$
Remark 2.2. It is obvious that if i divides j, then
![]() $\operatorname {Aut}(X,T^i)\subseteq \operatorname {Aut}(X,T^j)$
. The stabilized automorphism group is equivalently defined as the direct limit (colimit in the categorical sense) of the following diagram in Figure 1 where the arrows represent inclusions.
$\operatorname {Aut}(X,T^i)\subseteq \operatorname {Aut}(X,T^j)$
. The stabilized automorphism group is equivalently defined as the direct limit (colimit in the categorical sense) of the following diagram in Figure 1 where the arrows represent inclusions.

Figure 1 The stabilized automorphism group viewed as a direct limit.
Proposition 2.3. Let
![]() $(X,T)$
be a minimal dynamical system. Assume that for
$(X,T)$
be a minimal dynamical system. Assume that for
![]() ${k>1}$
, we have that
${k>1}$
, we have that
![]() $(X,T^k)$
has
$(X,T^k)$
has
![]() $n>1$
minimal components
$n>1$
minimal components
![]() $U_1, U_2,\ldots , U_n$
such that
$U_1, U_2,\ldots , U_n$
such that
![]() ${X=\bigcup _{i=1}^n U_i}$
. If the dynamical systems
${X=\bigcup _{i=1}^n U_i}$
. If the dynamical systems
![]() $(U_i, T^k|_{U_i})$
are conjugate for
$(U_i, T^k|_{U_i})$
are conjugate for
![]() $i=1,2,\ldots ,n$
, then there exists an algebraic group isomorphism
$i=1,2,\ldots ,n$
, then there exists an algebraic group isomorphism
where
![]() $\operatorname {Sym}(n)$
is the symmetric group on n symbols, satisfying for all
$\operatorname {Sym}(n)$
is the symmetric group on n symbols, satisfying for all
![]() $\varphi ,\phi \in \operatorname {Aut}(X,T^k)$
with
$\varphi ,\phi \in \operatorname {Aut}(X,T^k)$
with
![]() $\chi (\varphi )=((a_1,a_2,\ldots ,a_n),\pi _1)$
and
$\chi (\varphi )=((a_1,a_2,\ldots ,a_n),\pi _1)$
and
![]() $\chi (\phi )=((b_1,b_2,\ldots ,b_n),\pi _2) $
,
$\chi (\phi )=((b_1,b_2,\ldots ,b_n),\pi _2) $
,
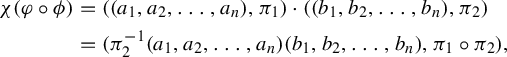 $$ \begin{align} \begin{aligned} \chi(\varphi\circ\phi)&=((a_1,a_2,\ldots,a_n),\pi_1)\cdot((b_1,b_2,\ldots,b_n),\pi_2) \\ &=(\pi_2^{-1}(a_1,a_2,\ldots,a_n)(b_1,b_2,\ldots,b_n),\pi_1\circ\pi_2), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \chi(\varphi\circ\phi)&=((a_1,a_2,\ldots,a_n),\pi_1)\cdot((b_1,b_2,\ldots,b_n),\pi_2) \\ &=(\pi_2^{-1}(a_1,a_2,\ldots,a_n)(b_1,b_2,\ldots,b_n),\pi_1\circ\pi_2), \end{aligned} \end{align} $$
where
![]() $\pi _2^{-1}(a_1,a_2,\ldots ,a_n)=(a_{\pi _2^{-1}(1)},a_{\pi _2^{-1}(2)},\ldots ,a_{\pi _2^{-1}(n)})$
and
$\pi _2^{-1}(a_1,a_2,\ldots ,a_n)=(a_{\pi _2^{-1}(1)},a_{\pi _2^{-1}(2)},\ldots ,a_{\pi _2^{-1}(n)})$
and
![]() $\pi _1\circ \pi _2$
denotes the composition of the composition of functions (as opposed to cycle concatenation).
$\pi _1\circ \pi _2$
denotes the composition of the composition of functions (as opposed to cycle concatenation).
We point out that the isomorphism
![]() $\chi $
is not canonical. It requires making a choice of isomorphism between
$\chi $
is not canonical. It requires making a choice of isomorphism between
![]() $\operatorname {Aut}(U_i, T^k|_{U_i})$
and
$\operatorname {Aut}(U_i, T^k|_{U_i})$
and
![]() $\operatorname {Aut}(U_1, T^k|_{U_1})$
for all
$\operatorname {Aut}(U_1, T^k|_{U_1})$
for all
![]() $i=1,\ldots ,n$
.
$i=1,\ldots ,n$
.
Proof. The minimal components of
![]() $(X,T^k)$
form a partition of X into closed sets. Since
$(X,T^k)$
form a partition of X into closed sets. Since
![]() $(U_i, T^k|_{U_i})$
are conjugate for
$(U_i, T^k|_{U_i})$
are conjugate for
![]() $i=1,2,\ldots ,n$
, define
$i=1,2,\ldots ,n$
, define
![]() $\varphi _{i,i+1}$
for
$\varphi _{i,i+1}$
for
![]() $i=1,2,\ldots ,n-1$
to be a conjugacy between
$i=1,2,\ldots ,n-1$
to be a conjugacy between
![]() $(U_i, T^k|_{U_i})$
and
$(U_i, T^k|_{U_i})$
and
![]() $(U_{i+1}, T^k|_{U_{i+1}})$
, and define
$(U_{i+1}, T^k|_{U_{i+1}})$
, and define
![]() $\varphi _{n,1}=\varphi _{1,2}^{-1}\circ \varphi _{2,3}^{-1}\circ \cdots \circ \varphi _{n-2,n-1}^{-1}\circ \varphi _{n-1,n}^{-1}$
. Hence, we have the following commutative diagram in Figure 2:
$\varphi _{n,1}=\varphi _{1,2}^{-1}\circ \varphi _{2,3}^{-1}\circ \cdots \circ \varphi _{n-2,n-1}^{-1}\circ \varphi _{n-1,n}^{-1}$
. Hence, we have the following commutative diagram in Figure 2:
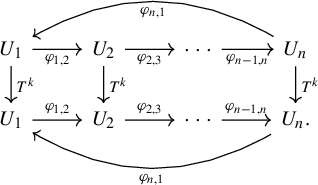
Figure 2 Commutative diagram used in the proof of Proposition 2.3.
Additionally, for
![]() $i,j\in \{1,2,\ldots ,n\}$
with
$i,j\in \{1,2,\ldots ,n\}$
with
![]() $i\leq j$
, define
$i\leq j$
, define
![]() $\varphi _{i,j}=\varphi _{j-1,j}\circ \varphi _{j-2,j-1}\circ \cdots \circ \varphi _{i+1,i+2}\circ \varphi _{i,i+1}$
and
$\varphi _{i,j}=\varphi _{j-1,j}\circ \varphi _{j-2,j-1}\circ \cdots \circ \varphi _{i+1,i+2}\circ \varphi _{i,i+1}$
and
![]() $\varphi _{j,i}=\varphi _{ij}^{-1}$
.
$\varphi _{j,i}=\varphi _{ij}^{-1}$
.
By Lemma 2.1, an automorphism of
![]() $(X, T^k)$
defines a permutation on the set of minimal components of
$(X, T^k)$
defines a permutation on the set of minimal components of
![]() $(X, T^k)$
. So we can define a map
$(X, T^k)$
. So we can define a map
![]() $\rho \colon \operatorname {Aut} (X, T^k) \to \operatorname {Sym}(n)$
by sending each automorphism to its corresponding permutation on the set of minimal components.
$\rho \colon \operatorname {Aut} (X, T^k) \to \operatorname {Sym}(n)$
by sending each automorphism to its corresponding permutation on the set of minimal components.
Let
![]() $\pi \in \operatorname {Sym}(n)$
. Define
$\pi \in \operatorname {Sym}(n)$
. Define
![]() $\Phi _\pi $
such that
$\Phi _\pi $
such that
![]() $U_i$
is mapped to
$U_i$
is mapped to
![]() $U_{\pi (i)}$
via
$U_{\pi (i)}$
via
![]() $\varphi _{i,\pi (i)}$
. Since minimal components are closed and disjoint,
$\varphi _{i,\pi (i)}$
. Since minimal components are closed and disjoint,
![]() $\Phi _\pi $
is continuous and since it commutes with
$\Phi _\pi $
is continuous and since it commutes with
![]() $T^k$
on each minimal component, we can conclude that
$T^k$
on each minimal component, we can conclude that
![]() $\Phi _\pi $
is an automorphism of
$\Phi _\pi $
is an automorphism of
![]() $(X,T)$
. Notice
$(X,T)$
. Notice
![]() $\rho (\Phi _\pi )=\pi $
. Thus,
$\rho (\Phi _\pi )=\pi $
. Thus,
![]() $\rho $
is surjective.
$\rho $
is surjective.
We can construct an automorphism
![]() $\Psi $
of
$\Psi $
of
![]() $(X,T)$
by choosing a particular automorphism
$(X,T)$
by choosing a particular automorphism
![]() $f_i$
of each minimal component
$f_i$
of each minimal component
![]() $(U_i, T^k|U_{i})$
and defining
$(U_i, T^k|U_{i})$
and defining
![]() $\Psi \equiv f_i$
on
$\Psi \equiv f_i$
on
![]() $U_i$
. That is,
$U_i$
. That is,
![]() $\Psi $
does not permute the minimal components and only acts on each one by their specified automorphism. Since minimal components are closed and disjoint,
$\Psi $
does not permute the minimal components and only acts on each one by their specified automorphism. Since minimal components are closed and disjoint,
![]() $\Psi $
is continuous and since it commutes with
$\Psi $
is continuous and since it commutes with
![]() $T^k$
on each minimal component, we can conclude that
$T^k$
on each minimal component, we can conclude that
![]() $\Psi $
is an automorphism of
$\Psi $
is an automorphism of
![]() $(X,T^k)$
. Hence, we can define a group monomorphism
$(X,T^k)$
. Hence, we can define a group monomorphism
![]() $\iota \colon \operatorname {Aut}(U_1, T^k|_{U_1})^n\to \operatorname {Aut}(X,T^k)$
, since
$\iota \colon \operatorname {Aut}(U_1, T^k|_{U_1})^n\to \operatorname {Aut}(X,T^k)$
, since
![]() $\operatorname {Aut}(U_i, T^k|_{U_i})$
is isomorphic to
$\operatorname {Aut}(U_i, T^k|_{U_i})$
is isomorphic to
![]() $\operatorname {Aut}(U_1, T^k|_{U_1})$
for
$\operatorname {Aut}(U_1, T^k|_{U_1})$
for
![]() $i=1,\ldots ,n$
. Notice
$i=1,\ldots ,n$
. Notice
![]() $\Psi \in {\operatorname {Aut}(U_1, T^k|_{U_1})}^n $
and
$\Psi \in {\operatorname {Aut}(U_1, T^k|_{U_1})}^n $
and
![]() $\rho (\iota (\Psi ))= e$
, where e is the identity in
$\rho (\iota (\Psi ))= e$
, where e is the identity in
![]() $\operatorname {Sym}(n)$
. Therefore, we have the following short exact sequence:
$\operatorname {Sym}(n)$
. Therefore, we have the following short exact sequence:
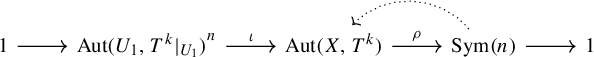
Using the fact that the diagram in Figure 2 commutes, we can define a splitting of this sequence as the map from
![]() $\operatorname {Sym}(n)$
to
$\operatorname {Sym}(n)$
to
![]() $\operatorname {Aut}(X, T^k)$
by sending each permutation
$\operatorname {Aut}(X, T^k)$
by sending each permutation
![]() ${\pi \in \operatorname {Sym}(n)}$
to
${\pi \in \operatorname {Sym}(n)}$
to
![]() $\Phi _\pi $
as defined above. Hence,
$\Phi _\pi $
as defined above. Hence,
The formula for the multiplication in equation (2.1) follows immediately.
2.3 Odometers
We give a brief review of odometers. For a more complete exposition, see [Reference Downarowicz, Kolyada, Manin and Ward7].
Let
![]() $(p_n)$
be a sequence of natural numbers such that
$(p_n)$
be a sequence of natural numbers such that
![]() $p_n$
divides
$p_n$
divides
![]() $p_{n+1}$
. We call any such sequence a scale. We define the odometer with scale
$p_{n+1}$
. We call any such sequence a scale. We define the odometer with scale
![]() $(p_n)$
as the subgroup of
$(p_n)$
as the subgroup of ![]() given by
given by
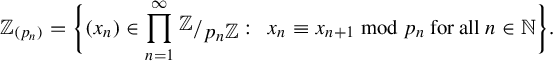
The odometer
![]() $\mathbb {Z}_{(p_n)}$
can also be defined as the inverse limit
$\mathbb {Z}_{(p_n)}$
can also be defined as the inverse limit ![]() of the canonical homomorphisms
of the canonical homomorphisms ![]() . The natural dynamics on an odometer
. The natural dynamics on an odometer
![]() $\mathbb {Z}_{(p_n)}$
is given by the addition of
$\mathbb {Z}_{(p_n)}$
is given by the addition of
![]() $\operatorname {\mathbf {1}}=(1,1,1,\ldots )$
. It is not difficult to see that it is a minimal equicontinuous topological dynamical system called an odometer and denote by
$\operatorname {\mathbf {1}}=(1,1,1,\ldots )$
. It is not difficult to see that it is a minimal equicontinuous topological dynamical system called an odometer and denote by
![]() $(Z_{(p_n)},+\operatorname {\mathbf {1}})$
. We call both the group
$(Z_{(p_n)},+\operatorname {\mathbf {1}})$
. We call both the group
![]() $\mathbb {Z}_{(p_n)}$
and the system
$\mathbb {Z}_{(p_n)}$
and the system
![]() $(\mathbb {Z}_{(p_m)},+\mathbf {1})$
an odometer, and to which one we are referring is clear from the context. In particular, the subgroup
$(\mathbb {Z}_{(p_m)},+\mathbf {1})$
an odometer, and to which one we are referring is clear from the context. In particular, the subgroup
![]() $\langle \operatorname {\mathbf {1}}\rangle $
is dense in
$\langle \operatorname {\mathbf {1}}\rangle $
is dense in
![]() $\mathbb {Z}_{(p_n)}$
and is isomorphic to
$\mathbb {Z}_{(p_n)}$
and is isomorphic to
![]() $\mathbb {Z}$
. We denote the multiples of
$\mathbb {Z}$
. We denote the multiples of
![]() $\mathbf {1}$
by
$\mathbf {1}$
by
![]() $\textbf {m}=m\operatorname {\mathbf {1}}=(m \,\mod {p_1},m\,\mod {p_2},m\,\mod {p_3},\ldots )$
for all
$\textbf {m}=m\operatorname {\mathbf {1}}=(m \,\mod {p_1},m\,\mod {p_2},m\,\mod {p_3},\ldots )$
for all
![]() $m\in \mathbb {N}$
.
$m\in \mathbb {N}$
.
For each prime number p, denote by
![]() $\nu _p(n)$
the p-adic valuation of the integer n, that is,
$\nu _p(n)$
the p-adic valuation of the integer n, that is,
Given an odometer
![]() $\mathbb {Z}_{(p_n)}$
, the sequence
$\mathbb {Z}_{(p_n)}$
, the sequence
![]() $(\nu _p(p_n))_{n\geq 1}$
is non-decreasing and we can define for each prime the multiplicity function at p as
$(\nu _p(p_n))_{n\geq 1}$
is non-decreasing and we can define for each prime the multiplicity function at p as
We can endow an odometer
![]() $\mathbb {Z}_{(p_n)}$
with the metric
$\mathbb {Z}_{(p_n)}$
with the metric
for any
![]() $x=(x_n)$
and
$x=(x_n)$
and
![]() $y=(y_n)\in \mathbb {Z}_{(p_n)}$
. With this metric,
$y=(y_n)\in \mathbb {Z}_{(p_n)}$
. With this metric,
![]() $\mathbb {Z}_{(p_n)}$
is a compact topological group.
$\mathbb {Z}_{(p_n)}$
is a compact topological group.
The question of when two odometers are isomorphic (as topological groups or simply algebraically) is completely understood by the following theorem.
Theorem 2.4. (See, for example, [Reference Downarowicz, Kolyada, Manin and Ward7])
Two odometers
![]() $\mathbb {Z}_{(p_n)}$
and
$\mathbb {Z}_{(p_n)}$
and
![]() $\mathbb {Z}_{(s_n)}$
are isomorphic both algebraically and as topological groups if and only if
$\mathbb {Z}_{(s_n)}$
are isomorphic both algebraically and as topological groups if and only if
![]() $\operatorname {\mathbf {v}}_q(p_n)=\operatorname {\mathbf {v}}_q(s_n)$
for all primes q. Moreover, for an odometer
$\operatorname {\mathbf {v}}_q(p_n)=\operatorname {\mathbf {v}}_q(s_n)$
for all primes q. Moreover, for an odometer
![]() $\mathbb {Z}_{(p_n)}$
, we have the following group isomorphism:
$\mathbb {Z}_{(p_n)}$
, we have the following group isomorphism:
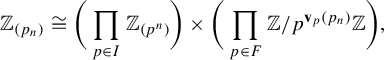 $$ \begin{align} \mathbb{Z}_{(p_n)}\cong\bigg(\prod_{p\in I}\mathbb{Z}_{(p^n)}\bigg)\times\bigg( \prod_{p \in F}\mathbb{Z}/{p^{\textbf{v}_p(p_n)}}\mathbb{Z}\bigg), \end{align} $$
$$ \begin{align} \mathbb{Z}_{(p_n)}\cong\bigg(\prod_{p\in I}\mathbb{Z}_{(p^n)}\bigg)\times\bigg( \prod_{p \in F}\mathbb{Z}/{p^{\textbf{v}_p(p_n)}}\mathbb{Z}\bigg), \end{align} $$
where
![]() $I=\{ p \text { prime}:\operatorname {\mathbf {v}}_p(p_n)=\infty \}$
and
$I=\{ p \text { prime}:\operatorname {\mathbf {v}}_p(p_n)=\infty \}$
and
![]() $F=\{ p \text { prime}:1<\operatorname {\mathbf {v}}_p(p_n)<\infty \}$
. The image of
$F=\{ p \text { prime}:1<\operatorname {\mathbf {v}}_p(p_n)<\infty \}$
. The image of
![]() $\operatorname {\mathbf {1}}$
under this isomorphism is
$\operatorname {\mathbf {1}}$
under this isomorphism is
![]() $((\operatorname {\mathbf {1}}, \operatorname {\mathbf {1}},\ldots ),(1,1,1,\ldots )).$
$((\operatorname {\mathbf {1}}, \operatorname {\mathbf {1}},\ldots ),(1,1,1,\ldots )).$
An immediate consequence of the previous theorem is that the torsion subgroup of an odometer can be written explicitly as
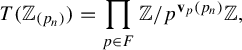 $$ \begin{align*}T(\mathbb{Z}_{(p_n)})=\prod_{p \in F}\mathbb{Z}/{p^{\textbf{v}_p(p_n)}}\mathbb{Z},\end{align*} $$
$$ \begin{align*}T(\mathbb{Z}_{(p_n)})=\prod_{p \in F}\mathbb{Z}/{p^{\textbf{v}_p(p_n)}}\mathbb{Z},\end{align*} $$
where
![]() $F=\{ p \text { prime}:1<\operatorname {\mathbf {v}}_p(p_n)<\infty \}$
.
$F=\{ p \text { prime}:1<\operatorname {\mathbf {v}}_p(p_n)<\infty \}$
.
This theorem leads us to define the following equivalence relation on scales. Two scales
![]() $(p_n)$
and
$(p_n)$
and
![]() $(s_n)$
are equivalent, denoted by
$(s_n)$
are equivalent, denoted by
![]() $(p_n)\sim (s_n)$
, if and only if
$(p_n)\sim (s_n)$
, if and only if
![]() $ \operatorname {\mathbf {v}}_p(p_n)\,{=}\,\operatorname {\mathbf {v}}_p(s_n) \text { for all primes } p$
. It is easy to check that this is an equivalence relation. Two odometers
$ \operatorname {\mathbf {v}}_p(p_n)\,{=}\,\operatorname {\mathbf {v}}_p(s_n) \text { for all primes } p$
. It is easy to check that this is an equivalence relation. Two odometers
![]() $\mathbb {Z}_{(p_n)}$
and
$\mathbb {Z}_{(p_n)}$
and
![]() $\mathbb {Z}_{(s_n)}$
are isomorphic if and only if
$\mathbb {Z}_{(s_n)}$
are isomorphic if and only if
![]() $(p_n)\sim (s_n)$
.
$(p_n)\sim (s_n)$
.
As stated in [Reference Downarowicz, Kolyada, Manin and Ward7], an odometer
![]() $\mathbb {Z}_{(p_n)}$
is a factor of another odometer
$\mathbb {Z}_{(p_n)}$
is a factor of another odometer
![]() $\mathbb {Z}_{(q_n)}$
if and only if for all
$\mathbb {Z}_{(q_n)}$
if and only if for all
![]() $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
,
![]() $p_k$
divides
$p_k$
divides
![]() $q_\ell $
for some
$q_\ell $
for some
![]() $\ell \in \mathbb {N}$
. This allows us to define the partial ordering
$\ell \in \mathbb {N}$
. This allows us to define the partial ordering
![]() $(p_n)\preccurlyeq (s_n)$
if and only if all the following hold.
$(p_n)\preccurlyeq (s_n)$
if and only if all the following hold.
-
(1) For all primes p,
 $\operatorname {\mathbf {v}}_p(p_n)=\infty $
if and only if
$\operatorname {\mathbf {v}}_p(p_n)=\infty $
if and only if
 $\operatorname {\mathbf {v}}_p(s_n)=\infty $
.
$\operatorname {\mathbf {v}}_p(s_n)=\infty $
. -
(2) For all primes p such that
 $\operatorname {\mathbf {v}}_p(s_n)<\infty $
, we have that
$\operatorname {\mathbf {v}}_p(s_n)<\infty $
, we have that
 $\operatorname {\mathbf {v}}_p(p_n)\leq \operatorname {\mathbf {v}}_p(s_n)$
.
$\operatorname {\mathbf {v}}_p(p_n)\leq \operatorname {\mathbf {v}}_p(s_n)$
.
Remark 2.5. By Theorem 2.4, two scales
![]() $(p_n)$
and
$(p_n)$
and
![]() $(s_n)$
define isomorphic odometers if and only if
$(s_n)$
define isomorphic odometers if and only if
![]() $(p_n)\sim (s_n)$
. That is, an odometer is completely determined by the sequence
$(p_n)\sim (s_n)$
. That is, an odometer is completely determined by the sequence
![]() $(\operatorname {\mathbf {{v}}_q(p_n))}_{q\text { a prime}}\in (\mathbb {N}\cup \{\infty \})^\infty $
. Additionally, if
$(\operatorname {\mathbf {{v}}_q(p_n))}_{q\text { a prime}}\in (\mathbb {N}\cup \{\infty \})^\infty $
. Additionally, if
![]() $(p_n)\preccurlyeq (q_n)$
, then the odometer
$(p_n)\preccurlyeq (q_n)$
, then the odometer
![]() $\mathbb {Z}_{(p_n)}$
is a factor of the odometer
$\mathbb {Z}_{(p_n)}$
is a factor of the odometer
![]() $\mathbb {Z}_{q_n}$
.
$\mathbb {Z}_{q_n}$
.
We say a scale
![]() $(p_n)$
is a prime scale if
$(p_n)$
is a prime scale if
![]() $p_{n+1}/p_{n}$
is prime for all
$p_{n+1}/p_{n}$
is prime for all
![]() $n\in \mathbb {N}$
. Notice that for any scale
$n\in \mathbb {N}$
. Notice that for any scale
![]() $(p_n)$
, there exists a prime scale
$(p_n)$
, there exists a prime scale ![]() such that
such that ![]() .
.
We say an odometer
![]() $\mathbb {Z}_{(p_n)}$
or equivalently a scale
$\mathbb {Z}_{(p_n)}$
or equivalently a scale
![]() $(p_n)$
is:
$(p_n)$
is:
-
(i) finite if there exits
 $N\in \mathbb {N}$
such that
$N\in \mathbb {N}$
such that
 $p_m=p_N$
for all
$p_m=p_N$
for all
 $m\geq N$
;
$m\geq N$
; -
(ii) torsion free if
 $\operatorname {\mathbf {v}}_p(p_n)\in \{0,\infty \}$
for all primes p.
$\operatorname {\mathbf {v}}_p(p_n)\in \{0,\infty \}$
for all primes p.
For a more detailed classification of odometers, see [Reference Downarowicz, Kolyada, Manin and Ward7].
Remark 2.6. From now on, we assume any scale
![]() $(p_n)$
is not finite as otherwise, the group
$(p_n)$
is not finite as otherwise, the group
![]() $\mathbb {Z}_{(p_n)}$
is finite and the dynamical system
$\mathbb {Z}_{(p_n)}$
is finite and the dynamical system
![]() $(\mathbb {Z}_{(p_n)},+\mathbf {1})$
is periodic.
$(\mathbb {Z}_{(p_n)},+\mathbf {1})$
is periodic.
Odometers classify all equicontinuous dynamical systems on a totally disconnected infinite space.
Theorem 2.7. (See, for example, [Reference Kurka12])
Let
![]() $(X,T)$
be a minimal equicontinuous dynamical system on a totally disconnected infinite space X. Then
$(X,T)$
be a minimal equicontinuous dynamical system on a totally disconnected infinite space X. Then
![]() $(X,F)$
is conjugate to an odometer.
$(X,F)$
is conjugate to an odometer.
The automorphism groups of odometers are completely classified.
Proposition 2.8. (See, for example, [Reference Donoso, Durand, Maass and Petite6])
Let
![]() $\mathbb {Z}_{(p_n)}$
be an odometer, then
$\mathbb {Z}_{(p_n)}$
be an odometer, then
![]() $\operatorname {Aut}(\mathbb {Z}_{(p_n)}, +\operatorname{\mathbf{1}})\cong \mathbb {Z}_{(p_n)}$
as groups.
$\operatorname {Aut}(\mathbb {Z}_{(p_n)}, +\operatorname{\mathbf{1}})\cong \mathbb {Z}_{(p_n)}$
as groups.
This theorem establishes the full isomorphism invariance of the automorphism group for odometers.
Corollary 2.9. If
![]() $\mathbb {Z}_{(p_n)}$
and
$\mathbb {Z}_{(p_n)}$
and
![]() $\mathbb {Z}_{(s_n)}$
are two odometers, then
$\mathbb {Z}_{(s_n)}$
are two odometers, then
![]() $\mathbb {Z}_{(p_n)}\cong \mathbb {Z}_{(s_n)}$
if and only if
$\mathbb {Z}_{(p_n)}\cong \mathbb {Z}_{(s_n)}$
if and only if
![]() $\operatorname {Aut}(\mathbb {Z}_{(p_n)},+\mathbf {1})\cong \operatorname {Aut}(\mathbb {Z}_{(s_n)},+\mathbf {1})$
.
$\operatorname {Aut}(\mathbb {Z}_{(p_n)},+\mathbf {1})\cong \operatorname {Aut}(\mathbb {Z}_{(s_n)},+\mathbf {1})$
.
2.4 Symbolic systems
Let
![]() $\mathcal {A}$
be a finite set. We define
$\mathcal {A}$
be a finite set. We define
![]() $\mathcal {A}^{\mathbb {Z}}$
to be the set of bi-infinite sequences
$\mathcal {A}^{\mathbb {Z}}$
to be the set of bi-infinite sequences
![]() $(x_i)_{i\in \mathbb {Z}}$
with
$(x_i)_{i\in \mathbb {Z}}$
with
![]() $x_i\in \mathcal {A}$
for all
$x_i\in \mathcal {A}$
for all
![]() $i\in \mathbb {Z}$
. When endowed with the metric
$i\in \mathbb {Z}$
. When endowed with the metric
![]() $\mathcal {A}^{\mathbb {Z}}$
is a compact metric space. We define the left shift
$\mathcal {A}^{\mathbb {Z}}$
is a compact metric space. We define the left shift
![]() $\sigma \colon \mathcal {A}^{\mathbb {Z}}\to \mathcal {A}^{\mathbb {Z}}$
by
$\sigma \colon \mathcal {A}^{\mathbb {Z}}\to \mathcal {A}^{\mathbb {Z}}$
by
![]() $(\sigma x)_i = x_{i+1}$
for all
$(\sigma x)_i = x_{i+1}$
for all
![]() $i\in \mathbb {Z}$
. If
$i\in \mathbb {Z}$
. If
![]() $X \subseteq \mathcal {A}^{\mathbb {Z}}$
is closed and
$X \subseteq \mathcal {A}^{\mathbb {Z}}$
is closed and
![]() $\sigma $
-invariant, then the dynamical system
$\sigma $
-invariant, then the dynamical system
![]() $(X,\sigma |_X)$
is called a subshift. We omit the notation
$(X,\sigma |_X)$
is called a subshift. We omit the notation
![]() $\sigma |_X$
and just denote a subshift by
$\sigma |_X$
and just denote a subshift by
![]() $(X,\sigma )$
.
$(X,\sigma )$
.
For
![]() $w = (w_1,\ldots , w_{n})\in \mathcal {A}^n$
, we define the cylinder set as
$w = (w_1,\ldots , w_{n})\in \mathcal {A}^n$
, we define the cylinder set as
The collection of cylinder sets
![]() $\{\sigma ^i([w]) : w \in \mathcal {A}^\ast , i \in \mathbb {Z}\}$
where
$\{\sigma ^i([w]) : w \in \mathcal {A}^\ast , i \in \mathbb {Z}\}$
where
![]() $ \mathcal {A}^\ast =\bigcup \nolimits _{j=1}^{\infty }\mathcal {A}^j$
is a basis for the topology of
$ \mathcal {A}^\ast =\bigcup \nolimits _{j=1}^{\infty }\mathcal {A}^j$
is a basis for the topology of
![]() $\mathcal {A}^{\mathbb {Z}}$
.
$\mathcal {A}^{\mathbb {Z}}$
.
The language of a subshift
![]() $(X, \sigma )$
is
$(X, \sigma )$
is
and any
![]() $w \in \mathcal {L}(X)$
is called a word in the language. For all
$w \in \mathcal {L}(X)$
is called a word in the language. For all
![]() $n\in \mathbb {N}$
, define
$n\in \mathbb {N}$
, define
![]() $\mathcal {L}_n(X)$
to be set of words of length n in
$\mathcal {L}_n(X)$
to be set of words of length n in
![]() $\mathcal {L}(X)$
. The complexity of a subshift is
$\mathcal {L}(X)$
. The complexity of a subshift is
![]() $P_X\colon \mathbb {N}\to \mathbb {N}$
defined as
$P_X\colon \mathbb {N}\to \mathbb {N}$
defined as
![]() $P_X(n)=\# \mathcal {L}_n(X)$
.
$P_X(n)=\# \mathcal {L}_n(X)$
.
2.5 Toeplitz subshifts
A sequence
![]() $u=\{u_t\}_{t\in \mathbb {Z}}$
is a Toeplitz sequence if for all
$u=\{u_t\}_{t\in \mathbb {Z}}$
is a Toeplitz sequence if for all
![]() $ n\,{\in}\, \mathbb {Z}, \text {there exists } m\in \mathbb {N} \text { such that for all } k\in \mathbb {Z}\text {, we have } u_{n}=u_{n+km}.$
For any
$ n\,{\in}\, \mathbb {Z}, \text {there exists } m\in \mathbb {N} \text { such that for all } k\in \mathbb {Z}\text {, we have } u_{n}=u_{n+km}.$
For any
![]() $p\in \mathbb {N}$
, define
$p\in \mathbb {N}$
, define
Then u is a Toeplitz sequence if there exists a sequence of integers
![]() $(p_n)$
such that
$(p_n)$
such that
![]() $p_n$
divides
$p_n$
divides
![]() $ p_{n+1}$
for all
$ p_{n+1}$
for all
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
We call the sequence
![]() $(p_n)$
a scale of u. Similarly to odometers, we say a scale
$(p_n)$
a scale of u. Similarly to odometers, we say a scale
![]() $(p_n)$
is a prime scale if
$(p_n)$
is a prime scale if
![]() $p_{n+1}/p_{n}$
is prime for all
$p_{n+1}/p_{n}$
is prime for all
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
We say that
![]() $p_n$
is an essential period of u if for any
$p_n$
is an essential period of u if for any
![]() $1 \leq p < p_n$
, the sets
$1 \leq p < p_n$
, the sets
![]() $\operatorname {per}_p(u)$
and
$\operatorname {per}_p(u)$
and
![]() $\operatorname {per}_{p_n}(u)$
do not coincide. If the sequence
$\operatorname {per}_{p_n}(u)$
do not coincide. If the sequence
![]() ${p_n}$
is formed by essential periods, we call it a period structure of u.
${p_n}$
is formed by essential periods, we call it a period structure of u.
If u is a Toeplitz sequence, we define the Toeplitz subshift given by u to be
![]() $(X_u,\sigma _u)$
, where
$(X_u,\sigma _u)$
, where
![]() $X_u=\overline {\mathcal {O}_{\sigma }(u)}$
and
$X_u=\overline {\mathcal {O}_{\sigma }(u)}$
and
![]() $\sigma _u=\sigma |_{X_u}$
. We omit the sub-index to simplify the notation and denote by
$\sigma _u=\sigma |_{X_u}$
. We omit the sub-index to simplify the notation and denote by
![]() $(X, \sigma )$
the respective Toeplitz subshift. Toeplitz subshifts were defined by Jacobs and Keane who also showed that every Toeplitz shift is minimal [Reference Jacobs and Keane10].
$(X, \sigma )$
the respective Toeplitz subshift. Toeplitz subshifts were defined by Jacobs and Keane who also showed that every Toeplitz shift is minimal [Reference Jacobs and Keane10].
Let
![]() $(X,\sigma )$
be a Toeplitz subshift given by the Toeplitz sequence u. From now on, we assume u is not periodic as otherwise, the system
$(X,\sigma )$
be a Toeplitz subshift given by the Toeplitz sequence u. From now on, we assume u is not periodic as otherwise, the system
![]() $(X,\sigma )$
is periodic. An element
$(X,\sigma )$
is periodic. An element
![]() $x\in X$
is called a Toeplitz orbital. It is important to note that a Toeplitz orbital may not be a Toeplitz sequence as some of its coordinates may not be periodic. Since u is not a periodic sequence, points in X that are not Toeplitz sequences necessarily exist (compare to [Reference Baake and Grimm1, Corollary 4.2]). If x is a Toeplitz sequence in X, we call it a regular point. We denote by R the set of all regular points in X. The singleton fibers of the map
$x\in X$
is called a Toeplitz orbital. It is important to note that a Toeplitz orbital may not be a Toeplitz sequence as some of its coordinates may not be periodic. Since u is not a periodic sequence, points in X that are not Toeplitz sequences necessarily exist (compare to [Reference Baake and Grimm1, Corollary 4.2]). If x is a Toeplitz sequence in X, we call it a regular point. We denote by R the set of all regular points in X. The singleton fibers of the map
![]() $\pi \colon X\to \mathbb {Z}_{(p_n)}$
from X to its maximal equicontinuous factor
$\pi \colon X\to \mathbb {Z}_{(p_n)}$
from X to its maximal equicontinuous factor
![]() $(\mathbb {Z}_{(p_n)},+1)$
correspond to the regular points in X and form a dense
$(\mathbb {Z}_{(p_n)},+1)$
correspond to the regular points in X and form a dense
![]() $G_\delta $
subset of X (see, for example, [Reference Downarowicz, Kolyada, Manin and Ward7]). It is clear that any period that occurs in x is also a period that occurs in u. We define the periodic part of x as
$G_\delta $
subset of X (see, for example, [Reference Downarowicz, Kolyada, Manin and Ward7]). It is clear that any period that occurs in x is also a period that occurs in u. We define the periodic part of x as
and the aperiodic part of x as
We call the p-skeleton of
![]() $x=(x_i)\in X$
the part of x which is periodic with period p. To make this precise, we define the p-skeleton to be the sequence obtained from x by replacing
$x=(x_i)\in X$
the part of x which is periodic with period p. To make this precise, we define the p-skeleton to be the sequence obtained from x by replacing
![]() $x_i$
by a new symbol ‘?’ for all
$x_i$
by a new symbol ‘?’ for all
![]() $i{\not \in } {\operatorname {per}}_{p}(x)$
.
$i{\not \in } {\operatorname {per}}_{p}(x)$
.
Regarding the aperiodic part, we have the following useful properties.
Lemma 2.10. (See, for example, [Reference Downarowicz, Kolyada, Manin and Ward7])
Let
![]() $(X,\sigma )$
be a Toeplitz subshift and
$(X,\sigma )$
be a Toeplitz subshift and
![]() $x\in X$
.
$x\in X$
.
-
(a) For any
 $n\in \operatorname {A}(x)$
, there is no
$n\in \operatorname {A}(x)$
, there is no
 $l>0$
such that
$l>0$
such that
 $x_{n+kl}=x_{n}$
for all
$x_{n+kl}=x_{n}$
for all
 $k\in \mathbb {Z}$
.
$k\in \mathbb {Z}$
. -
(b) Every finite pattern occurring along the aperiodic part of x also occurs along some periodic part.
The following key lemma about Toeplitz subshifts was proved by Williams.
Lemma 2.11. (Williams [Reference Williams17])
Let
![]() $(X,\sigma )$
be a Toeplitz subshift given by the Toeplitz word u with period structure
$(X,\sigma )$
be a Toeplitz subshift given by the Toeplitz word u with period structure
![]() $(p_n)$
. For each
$(p_n)$
. For each
![]() $i\in \mathbb {N}$
,
$i\in \mathbb {N}$
,
![]() $n\in \mathbb {Z}/p_i\mathbb {Z}$
, define
$n\in \mathbb {Z}/p_i\mathbb {Z}$
, define
![]() $A_n^i=\{\sigma ^m(u):m\equiv n \mod p_i\}$
. Then:
$A_n^i=\{\sigma ^m(u):m\equiv n \mod p_i\}$
. Then:
-
(i)
 $\{\overline {A_n^i}:n\in \mathbb {Z}/p_i\mathbb {Z}\}$
is a partition of
$\{\overline {A_n^i}:n\in \mathbb {Z}/p_i\mathbb {Z}\}$
is a partition of
 $X=\overline {\mathcal {O}}_\sigma (u)$
into relatively open (and closed) sets;
$X=\overline {\mathcal {O}}_\sigma (u)$
into relatively open (and closed) sets; -
(ii)
 $\overline {A_m^j}\subseteq \overline {A_n^i}$
for
$\overline {A_m^j}\subseteq \overline {A_n^i}$
for
 $i<j$
and
$i<j$
and
 $m\equiv n \,\mod p_i$
;
$m\equiv n \,\mod p_i$
; -
(iii)
 $\sigma (\overline {A_n^i})=\overline {A_{n+1}^i}$
.
$\sigma (\overline {A_n^i})=\overline {A_{n+1}^i}$
.
Toeplitz subshifts have been fully characterized up to topological conjugacy by the following theorem.
Theorem 2.12. (See, for example, [Reference Downarowicz, Kolyada, Manin and Ward7])
A dynamical system
![]() $(X,\sigma )$
is conjugate to a Toeplitz subshift if and only if it satisfies the following three properties:
$(X,\sigma )$
is conjugate to a Toeplitz subshift if and only if it satisfies the following three properties:
-
(i)
 $(X,T)$
is minimal;
$(X,T)$
is minimal; -
(ii)
 $(X,T)$
is an almost one-to-one extension of an odometer;
$(X,T)$
is an almost one-to-one extension of an odometer; -
(iii)
 $(X,T)$
is symbolic.
$(X,T)$
is symbolic.
Remark 2.13. (See, for example, [Reference Williams17])
The map that gives rise to property (ii) of the previous lemma is constructed as follows. Let
![]() $(X,\sigma )$
be a Toeplitz subshift with period structure
$(X,\sigma )$
be a Toeplitz subshift with period structure
![]() $(p_n)$
. For
$(p_n)$
. For
![]() $g=(x_i)\in \mathbb {Z}_{(p_n)}$
, we set
$g=(x_i)\in \mathbb {Z}_{(p_n)}$
, we set
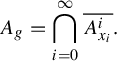 $$ \begin{align*}A_g=\bigcap_{i=0}^\infty \overline{A_{x_i}^i}.\end{align*} $$
$$ \begin{align*}A_g=\bigcap_{i=0}^\infty \overline{A_{x_i}^i}.\end{align*} $$
We define the factor map
![]() $\pi \colon (X,\sigma )\to (\mathbb {Z}_{(p_n)},+\mathbf {1})$
by
$\pi \colon (X,\sigma )\to (\mathbb {Z}_{(p_n)},+\mathbf {1})$
by
![]() $\pi ^{-1}(g)=A_g$
. Then
$\pi ^{-1}(g)=A_g$
. Then
![]() ${\pi (y)=\pi (y')}$
for
${\pi (y)=\pi (y')}$
for
![]() $y,y'\in X$
if and only if y and
$y,y'\in X$
if and only if y and
![]() $y'$
have the same
$y'$
have the same
![]() $p_i$
-skeleton for all
$p_i$
-skeleton for all
![]() $i\in \mathbb {N}$
. In particular,
$i\in \mathbb {N}$
. In particular,
![]() $\pi $
is one-to-one on the set of Toeplitz sequences in X.
$\pi $
is one-to-one on the set of Toeplitz sequences in X.
As a consequence of property (ii) of the previous theorem, if
![]() $(X, \sigma )$
is a the Toeplitz subshift given by the Toeplitz sequence u with period structure
$(X, \sigma )$
is a the Toeplitz subshift given by the Toeplitz sequence u with period structure
![]() $(p_n)$
, then
$(p_n)$
, then
![]() $(\mathbb {Z}_{(p_n)}, +\operatorname {\mathbf {1}})$
is its maximal equicontinuous factor (see, for example, [Reference Williams17]). Another consequence of this is the following result.
$(\mathbb {Z}_{(p_n)}, +\operatorname {\mathbf {1}})$
is its maximal equicontinuous factor (see, for example, [Reference Williams17]). Another consequence of this is the following result.
Lemma 2.14. (See, for example, [Reference Donoso, Durand, Maass and Petite5])
The automorphism group of a Toeplitz subshift is isomorphic to a subgroup of its corresponding odometer maximal equicontinuous factor.
Remark 2.15. As a consequence of the previous lemma, the automorphism group of a Toeplitz subshift is abelian.
We use some similar terminology for Toeplitz subshifts as for odometers. We say a Toeplitz subshift given by the Toeplitz word u with period structure
![]() $(p_n)$
is torsion free if its corresponding odometer maximal equicontinuous factor is torsion free.
$(p_n)$
is torsion free if its corresponding odometer maximal equicontinuous factor is torsion free.
3 The stabilized automorphism group of an odometer
This section is dedicated to characterizing the stabilized automorphism group of odometers. To study the stabilized automorphism group of odometers, we first analyze
![]() $\operatorname {Aut}(\mathbb {Z}_{(p_n)}, + \textbf {m})$
for all
$\operatorname {Aut}(\mathbb {Z}_{(p_n)}, + \textbf {m})$
for all
![]() $m\in \mathbb {N}$
. We start by proving the following proposition.
$m\in \mathbb {N}$
. We start by proving the following proposition.
Proposition 3.1. Let
![]() $\mathbb {Z}_{(p_n)}$
be an odometer with scale
$\mathbb {Z}_{(p_n)}$
be an odometer with scale
![]() $(p_n)$
and set
$(p_n)$
and set
![]() $m\in \mathbb {N}$
. Let
$m\in \mathbb {N}$
. Let
![]() ${d\geq 0}$
be such that for some
${d\geq 0}$
be such that for some
![]() $k_0\in \mathbb {N}$
, we have that
$k_0\in \mathbb {N}$
, we have that
![]() $(p_k,m)=d$
for
$(p_k,m)=d$
for
![]() $k\geq k_0$
and
$k\geq k_0$
and
![]() $k_0$
is the smallest integer with this property. Then
$k_0$
is the smallest integer with this property. Then
![]() $(\mathbb {Z}_{(p_n)},+\textbf {m})$
has d minimal components each of them conjugate to the odometer with scale
$(\mathbb {Z}_{(p_n)},+\textbf {m})$
has d minimal components each of them conjugate to the odometer with scale
![]() $({p_n}/{d})_{n\geq k_0}$
. Furthermore,
$({p_n}/{d})_{n\geq k_0}$
. Furthermore,
![]() $\operatorname {Aut}(\mathbb {Z}_{(p_n)},+\textbf {m})\cong \mathbb {Z}_{(p_{n}/d)_{n\geq k_0}}^d {\rtimes} \operatorname {Sym}(d)$
and is isomorphic to a subgroup of
$\operatorname {Aut}(\mathbb {Z}_{(p_n)},+\textbf {m})\cong \mathbb {Z}_{(p_{n}/d)_{n\geq k_0}}^d {\rtimes} \operatorname {Sym}(d)$
and is isomorphic to a subgroup of
![]() $\operatorname {Aut}(\mathbb {Z}_{(p_n)},+\textbf {p}_{k_0})$
.
$\operatorname {Aut}(\mathbb {Z}_{(p_n)},+\textbf {p}_{k_0})$
.
Proof. We will first assume
![]() $d=1$
. We know
$d=1$
. We know
![]() $(\mathbb {Z}_{(p_n)},+\textbf {m})$
is minimal by [Reference Donoso, Durand, Maass and Petite6, Lemma 2.1]. Since
$(\mathbb {Z}_{(p_n)},+\textbf {m})$
is minimal by [Reference Donoso, Durand, Maass and Petite6, Lemma 2.1]. Since
![]() $(\mathbb {Z}_{(p_n)}, +\mathbf {m})$
is a minimal equicontinuous dynamical system on a totally disconnected space by Proposition 2.8 and Theorem 2.7,
$(\mathbb {Z}_{(p_n)}, +\mathbf {m})$
is a minimal equicontinuous dynamical system on a totally disconnected space by Proposition 2.8 and Theorem 2.7,
![]() $(\mathbb {Z}_{(p_n)}, +\mathbf {m})$
is conjugate to the odometer
$(\mathbb {Z}_{(p_n)}, +\mathbf {m})$
is conjugate to the odometer
![]() $(\mathbb {Z}_{(p_n)}, +\mathbf {1})$
and
$(\mathbb {Z}_{(p_n)}, +\mathbf {1})$
and
![]() $\operatorname {Aut}(\mathbb {Z}_{(p_n)}, +\mathbf {m})\cong \mathbb {Z}_{(p_n)}$
. However, since many groups have subgroups isomorphic to themselves, including some odometers, this is not enough to conclude
$\operatorname {Aut}(\mathbb {Z}_{(p_n)}, +\mathbf {m})\cong \mathbb {Z}_{(p_n)}$
. However, since many groups have subgroups isomorphic to themselves, including some odometers, this is not enough to conclude
![]() $\operatorname {Aut}(\mathbb {Z}_{(p_n)},+\textbf {m})=(\mathbb {Z}_{(p_n)},+\mathbf {1})$
. We show this next.
$\operatorname {Aut}(\mathbb {Z}_{(p_n)},+\textbf {m})=(\mathbb {Z}_{(p_n)},+\mathbf {1})$
. We show this next.
It is obvious that
![]() $\operatorname {Aut}(\mathbb {Z}_{(p_n)}, +\mathbf {1})\subseteq \operatorname {Aut}(\mathbb {Z}_{(p_n)}, +\mathbf {m})$
. We are left with proving the other inclusion. Take
$\operatorname {Aut}(\mathbb {Z}_{(p_n)}, +\mathbf {1})\subseteq \operatorname {Aut}(\mathbb {Z}_{(p_n)}, +\mathbf {m})$
. We are left with proving the other inclusion. Take
![]() $\varphi \in \operatorname {Aut}(\mathbb {Z}_{(p_n)}, +\mathbf {m})$
and
$\varphi \in \operatorname {Aut}(\mathbb {Z}_{(p_n)}, +\mathbf {m})$
and
![]() $\varepsilon>0$
. Since
$\varepsilon>0$
. Since
![]() $\varphi $
is continuous, by our definition of the metric in
$\varphi $
is continuous, by our definition of the metric in
![]() $\mathbb {Z}_{(p_n)}$
, there exists
$\mathbb {Z}_{(p_n)}$
, there exists
![]() $N\in \mathbb {N}$
such that for all
$N\in \mathbb {N}$
such that for all
![]() $(x_i),(y_i)\in \mathbb {Z}_{(p_n)}$
, if
$(x_i),(y_i)\in \mathbb {Z}_{(p_n)}$
, if
![]() $x_j=y_j$
for all
$x_j=y_j$
for all
![]() $j\leq N$
, then
$j\leq N$
, then
![]() $\operatorname {d}(\varphi (x_i),\varphi (y_i))<\varepsilon /2$
. Pick
$\operatorname {d}(\varphi (x_i),\varphi (y_i))<\varepsilon /2$
. Pick
![]() $M\in \mathbb {N}$
such that for all
$M\in \mathbb {N}$
such that for all
![]() $(x_i),(y_i)\in \mathbb {Z}_{(p_n)}$
, if
$(x_i),(y_i)\in \mathbb {Z}_{(p_n)}$
, if
![]() $x_j=y_j$
for all
$x_j=y_j$
for all
![]() $j\leq M$
, then
$j\leq M$
, then
![]() $\operatorname {d}((x_i),(y_i))<\varepsilon /2$
. Define
$\operatorname {d}((x_i),(y_i))<\varepsilon /2$
. Define
![]() $K=\max \{N,M\}$
. By Bézout’s identity, since
$K=\max \{N,M\}$
. By Bézout’s identity, since
![]() $(p_K,m)=1$
, there exist
$(p_K,m)=1$
, there exist
![]() $a,b\in \mathbb {N}$
such that
$a,b\in \mathbb {N}$
such that
Because
![]() $+\textbf {m}$
commutes with
$+\textbf {m}$
commutes with
![]() $\phi $
and by our choice of K we have that for all
$\phi $
and by our choice of K we have that for all
![]() $x=(x_i)\in \mathbb {Z}_{(p_n)}$
,
$x=(x_i)\in \mathbb {Z}_{(p_n)}$
,
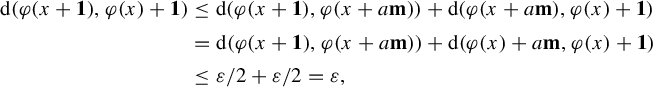 $$ \begin{align*} \operatorname{d}(\varphi(x+\mathbf{1}),\varphi (x)+\mathbf{1})&\leq\operatorname{d}(\varphi(x+\mathbf{1}),\varphi(x+a\textbf{m}))+\operatorname{d}(\varphi(x+a\textbf{m}),\varphi (x)+\mathbf{1}) \\&=\operatorname{d}(\varphi(x+\mathbf{1}),\varphi(x+a\textbf{m}))+\operatorname{d}(\varphi(x)+a\textbf{m},\varphi(x)+\mathbf{1}) \\&\leq \varepsilon/2+\varepsilon/2 =\varepsilon, \end{align*} $$
$$ \begin{align*} \operatorname{d}(\varphi(x+\mathbf{1}),\varphi (x)+\mathbf{1})&\leq\operatorname{d}(\varphi(x+\mathbf{1}),\varphi(x+a\textbf{m}))+\operatorname{d}(\varphi(x+a\textbf{m}),\varphi (x)+\mathbf{1}) \\&=\operatorname{d}(\varphi(x+\mathbf{1}),\varphi(x+a\textbf{m}))+\operatorname{d}(\varphi(x)+a\textbf{m},\varphi(x)+\mathbf{1}) \\&\leq \varepsilon/2+\varepsilon/2 =\varepsilon, \end{align*} $$
where the last inequality follows from the fact that
![]() $x+a\textbf {m}$
and
$x+a\textbf {m}$
and
![]() $x+a\mathbf {1}$
agree on the first K coordinates. We conclude
$x+a\mathbf {1}$
agree on the first K coordinates. We conclude
![]() $\varphi (x+\mathbf {1})=\varphi x+\mathbf {1}$
, and hence
$\varphi (x+\mathbf {1})=\varphi x+\mathbf {1}$
, and hence
![]() $\varphi \in \operatorname {Aut}(\mathbb {Z}_{(p_n)},+\mathbf {1})$
. This proves
$\varphi \in \operatorname {Aut}(\mathbb {Z}_{(p_n)},+\mathbf {1})$
. This proves
![]() $\operatorname {Aut}(\mathbb {Z}_{(p_n)},+\textbf {m})=\operatorname {Aut}(\mathbb {Z}_{(p_n)},+\mathbf {1})\cong \mathbb {Z}{(p_n)}$
.
$\operatorname {Aut}(\mathbb {Z}_{(p_n)},+\textbf {m})=\operatorname {Aut}(\mathbb {Z}_{(p_n)},+\mathbf {1})\cong \mathbb {Z}{(p_n)}$
.
Assume now that
![]() $d>1$
. By Theorem 2.4,
$d>1$
. By Theorem 2.4,
![]() $(\mathbb {Z}_{(p_n)}, +\mathbf {1})$
is conjugate to an odometer
$(\mathbb {Z}_{(p_n)}, +\mathbf {1})$
is conjugate to an odometer
![]() $(\mathbb {Z}_{(p^{\prime }_n)}, +\mathbf {1})$
with period structure
$(\mathbb {Z}_{(p^{\prime }_n)}, +\mathbf {1})$
with period structure
![]() $(p^{\prime }_n)$
such that
$(p^{\prime }_n)$
such that
![]() $p^{\prime }_1=d$
and
$p^{\prime }_1=d$
and
![]() $\operatorname {\textbf {v}}_q(p_n)=\operatorname {\textbf {v}}_q(p^{\prime }_n)$
. Without loss of generality, we assume
$\operatorname {\textbf {v}}_q(p_n)=\operatorname {\textbf {v}}_q(p^{\prime }_n)$
. Without loss of generality, we assume
![]() $p_1=d$
. Since the first coordinate of elements in
$p_1=d$
. Since the first coordinate of elements in
![]() $\mathbb {Z}_{(p_n)}$
belongs to
$\mathbb {Z}_{(p_n)}$
belongs to
![]() $\mathbb {Z}/d\mathbb {Z}$
, the addition
$\mathbb {Z}/d\mathbb {Z}$
, the addition
![]() $+\textbf {m}$
fixes the first coordinate. For
$+\textbf {m}$
fixes the first coordinate. For
![]() $j=0,1,\ldots ,d-1$
, we define the subsets of
$j=0,1,\ldots ,d-1$
, we define the subsets of
![]() $\mathbb {Z}_{(p_n)}$
$\mathbb {Z}_{(p_n)}$
Notice that these are clopen sets invariant under the action
![]() $+\textbf {m}$
. Define the map
$+\textbf {m}$
. Define the map
![]() $\varphi \colon {U_j}\to \mathbb {Z}_{(p_{n+1}/d)_{n\in \mathbb {N}}}$
by
$\varphi \colon {U_j}\to \mathbb {Z}_{(p_{n+1}/d)_{n\in \mathbb {N}}}$
by
 $$ \begin{align*}\varphi((x_i)_{i\in \mathbb{N}})=\bigg(\frac{x_{i+1}-j}{d}\bigg)_{i\in \mathbb{N}}.\end{align*} $$
$$ \begin{align*}\varphi((x_i)_{i\in \mathbb{N}})=\bigg(\frac{x_{i+1}-j}{d}\bigg)_{i\in \mathbb{N}}.\end{align*} $$
Then
![]() $\varphi $
is a homeomorphism and the following diagram commutes:
$\varphi $
is a homeomorphism and the following diagram commutes:
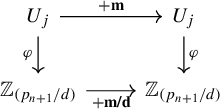
This implies the action of
![]() $+\textbf {m}$
restricted to
$+\textbf {m}$
restricted to
![]() $U_j$
is conjugate to
$U_j$
is conjugate to
![]() $(\mathbb {Z}_{(p_{n+1}/d)}, +\textbf {s})$
, where
$(\mathbb {Z}_{(p_{n+1}/d)}, +\textbf {s})$
, where
![]() $s=m/d$
. By the case
$s=m/d$
. By the case
![]() $d=1$
,
$d=1$
,
![]() $U_j$
is a minimal component. Hence, the number of minimal components of
$U_j$
is a minimal component. Hence, the number of minimal components of
![]() $(\mathbb {Z}_{(p_n)}, +\mathbf {m})$
is d. Moreover, we have that each minimal component is conjugate to
$(\mathbb {Z}_{(p_n)}, +\mathbf {m})$
is d. Moreover, we have that each minimal component is conjugate to
![]() $(\mathbb {Z}_{(p_{n+1}/d)}, +\mathbf {1})$
and we have the identity
$(\mathbb {Z}_{(p_{n+1}/d)}, +\mathbf {1})$
and we have the identity
![]() $\operatorname {Aut}(U_j,+\textbf {m})=\operatorname {Aut}(U_j,+\textbf {s}).$
$\operatorname {Aut}(U_j,+\textbf {m})=\operatorname {Aut}(U_j,+\textbf {s}).$
By the case
![]() $d=1$
, we have that the automorphism group of each minimal component under the action
$d=1$
, we have that the automorphism group of each minimal component under the action
![]() $+\mathbf {s}$
is isomorphic to
$+\mathbf {s}$
is isomorphic to
![]() $\mathbb {Z}_{(p_{n+1})/d}$
. Moreover, as a consequence of Proposition 2.3, we have
$\mathbb {Z}_{(p_{n+1})/d}$
. Moreover, as a consequence of Proposition 2.3, we have
Given
![]() $(q_n)$
any equivalent period structure, we have shown the inclusion
$(q_n)$
any equivalent period structure, we have shown the inclusion
where
![]() $k_0\in \mathbb {N}$
is such that
$k_0\in \mathbb {N}$
is such that
![]() $(q_k,m)=d$
for
$(q_k,m)=d$
for
![]() $k\geq k_0$
.
$k\geq k_0$
.
Remark 3.2. One can translate the previous proof to one relying on the Bratelli–Vershik representation of odometers. To do this, for
![]() $k\in \mathbb {N}$
and
$k\in \mathbb {N}$
and
![]() $0\leq i<p_k$
, consider the sets
$0\leq i<p_k$
, consider the sets
The sets
![]() $\{U_{k,0},U_{k,1},\ldots ,U_{k,p_k-1}\}$
correspond to the floors of the kth Kakutani–Rokhlin partition of the odometer. The action
$\{U_{k,0},U_{k,1},\ldots ,U_{k,p_k-1}\}$
correspond to the floors of the kth Kakutani–Rokhlin partition of the odometer. The action
![]() $+\textbf {m}$
on the collection of sets
$+\textbf {m}$
on the collection of sets
![]() $\{U_{k,0},\kern-0.5pt U_{k,1},\ldots ,\kern-0.5pt U_{k,p_k-1}\kern-0.5pt\}$
works like addition by m in
$\{U_{k,0},\kern-0.5pt U_{k,1},\ldots ,\kern-0.5pt U_{k,p_k-1}\kern-0.5pt\}$
works like addition by m in
![]() $\mathbb {Z}/p_k\mathbb {Z}$
by identifying
$\mathbb {Z}/p_k\mathbb {Z}$
by identifying
![]() $U_{k,i}$
with
$U_{k,i}$
with
![]() $i\in \mathbb {Z}/p_k\mathbb {Z}$
. Thus,
$i\in \mathbb {Z}/p_k\mathbb {Z}$
. Thus,
![]() $U_{k,i}+\textbf {m}=U_{k,i+m \,\mod p_k}$
and
$U_{k,i}+\textbf {m}=U_{k,i+m \,\mod p_k}$
and
![]() $U_{k,i}+r\textbf {m}=U_{k,i}$
if and only if
$U_{k,i}+r\textbf {m}=U_{k,i}$
if and only if
![]() $rm\in p_k\mathbb {Z}$
. Take
$rm\in p_k\mathbb {Z}$
. Take
![]() $r_k$
the smallest number such that
$r_k$
the smallest number such that
![]() $U_{k,i}+r\textbf {m}=U_{k,i}$
. For a large enough k, a minimal component of
$U_{k,i}+r\textbf {m}=U_{k,i}$
. For a large enough k, a minimal component of
![]() $(\mathbb {Z}_{p_n},+\textbf {m})$
is a union of elements in
$(\mathbb {Z}_{p_n},+\textbf {m})$
is a union of elements in
![]() $\{U_{k,0},U_{k,1},\ldots ,U_{k,p_k-1}\}$
that form a single orbit under the action
$\{U_{k,0},U_{k,1},\ldots ,U_{k,p_k-1}\}$
that form a single orbit under the action
![]() $+\textbf {m}$
. In the language of Bratelli–Vershik diagrams, a minimal component of
$+\textbf {m}$
. In the language of Bratelli–Vershik diagrams, a minimal component of
![]() $(\mathbb {Z}_{p_n},+\textbf {m})$
is the induced system given by the r-paths that correspond to the sets
$(\mathbb {Z}_{p_n},+\textbf {m})$
is the induced system given by the r-paths that correspond to the sets
![]() $U_{k,i}$
of the level k which are in the same orbit under the action
$U_{k,i}$
of the level k which are in the same orbit under the action
![]() $+\textbf {m}$
. This becomes more apparent after the proof of Proposition 4.1 using the map
$+\textbf {m}$
. This becomes more apparent after the proof of Proposition 4.1 using the map
![]() $\pi $
in Remark 2.13.
$\pi $
in Remark 2.13.
Corollary 3.3. The stabilized automorphism group of an odometer is
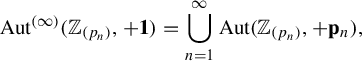 $$ \begin{align*}\operatorname{Aut}^{(\infty)}(\mathbb{Z}_{(p_n)},+\mathbf{1})=\bigcup_{n=1}^\infty \operatorname{Aut}(\mathbb{Z}_{(p_n)},+ {\mathbf{p}_n}),\end{align*} $$
$$ \begin{align*}\operatorname{Aut}^{(\infty)}(\mathbb{Z}_{(p_n)},+\mathbf{1})=\bigcup_{n=1}^\infty \operatorname{Aut}(\mathbb{Z}_{(p_n)},+ {\mathbf{p}_n}),\end{align*} $$
where the union is taken inside
![]() $\operatorname {Homeo}(\mathbb {Z}_{(p_n)})$
. Additionally, this statement is true for all scales equivalent to
$\operatorname {Homeo}(\mathbb {Z}_{(p_n)})$
. Additionally, this statement is true for all scales equivalent to
![]() $(p_n)$
.
$(p_n)$
.
Proof. By Proposition 3.1, we have that
![]() $\operatorname {Aut}(\mathbb {Z}_{(p_n)},+\textbf {m})\subseteq \bigcup \nolimits _{n=1}^\infty \operatorname {Aut}(\mathbb {Z}_{(p_n)},+{\mathbf {p}_n})$
for all
$\operatorname {Aut}(\mathbb {Z}_{(p_n)},+\textbf {m})\subseteq \bigcup \nolimits _{n=1}^\infty \operatorname {Aut}(\mathbb {Z}_{(p_n)},+{\mathbf {p}_n})$
for all
![]() $m\in \mathbb {N}$
. Moreover, by Theorem 2.4, this is true for all scales equivalent to
$m\in \mathbb {N}$
. Moreover, by Theorem 2.4, this is true for all scales equivalent to
![]() $(p_n)$
.
$(p_n)$
.
The last ingredient we need before proving our characterization of the stabilized automorphism group of odometers is the following algebraic lemma. This is a basic fact about direct limits; for a proof see, for example, [Reference Lang13, Proposition 10.3].
Lemma 3.4. Let
![]() $\{G_i\}_{i\in \mathbb {N}}$
and
$\{G_i\}_{i\in \mathbb {N}}$
and
![]() $\{H_i\}_{i\in \mathbb {N}}$
be groups and
$\{H_i\}_{i\in \mathbb {N}}$
be groups and
![]() $f_{i}\colon G_i\to G_{i+1}$
,
$f_{i}\colon G_i\to G_{i+1}$
,
![]() $k_{i}\colon H_i\to H_{i+1}$
group homomorphisms for all
$k_{i}\colon H_i\to H_{i+1}$
group homomorphisms for all
![]() $i\in \mathbb {N}$
. Define
$i\in \mathbb {N}$
. Define
![]() $\hat {G}$
to be the direct limit
$\hat {G}$
to be the direct limit
![]() $\lim _{\to }G_i$
and
$\lim _{\to }G_i$
and
![]() $\hat {H}$
to be the direct limit
$\hat {H}$
to be the direct limit
![]() $\lim _{\to }H_i$
. If there exist group isomorphisms
$\lim _{\to }H_i$
. If there exist group isomorphisms
![]() $\varphi _i\colon G_i\to H_i$
, for all
$\varphi _i\colon G_i\to H_i$
, for all
![]() $i\in \mathbb {N}$
such that the following diagram commutes:
$i\in \mathbb {N}$
such that the following diagram commutes:
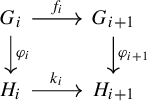
then
![]() $\hat {G}$
and
$\hat {G}$
and
![]() $\hat {H}$
are isomorphic as groups.
$\hat {H}$
are isomorphic as groups.
Theorem 3.5. The stabilized automorphism group of an odometer
![]() $\mathbb {Z}_{(p_n)}$
with scale
$\mathbb {Z}_{(p_n)}$
with scale
![]() $(p_n)$
is isomorphic to the direct limit of the following sequence:
$(p_n)$
is isomorphic to the direct limit of the following sequence:
where
![]() $j_k$
are injective maps.
$j_k$
are injective maps.
The injective maps
![]() $j_k$
from the previous theorem are constructed explicitly as follows. Let
$j_k$
from the previous theorem are constructed explicitly as follows. Let
![]() $\varphi \colon \operatorname {Aut}(\mathbb {Z}_{(p_n)},+{p_k})\to \mathbb {Z}_{(p_{n+k})}^{p_k} \rtimes \operatorname {Sym}(p_k)$
for all
$\varphi \colon \operatorname {Aut}(\mathbb {Z}_{(p_n)},+{p_k})\to \mathbb {Z}_{(p_{n+k})}^{p_k} \rtimes \operatorname {Sym}(p_k)$
for all
![]() $k\in \mathbb {N}\cup \{0\}$
be the isomorphisms described in Proposition 3.1, define
$k\in \mathbb {N}\cup \{0\}$
be the isomorphisms described in Proposition 3.1, define
![]() $j_k=\varphi _{k+1}\circ i_k\circ \varphi _k^{-1}$
, where
$j_k=\varphi _{k+1}\circ i_k\circ \varphi _k^{-1}$
, where
![]() $i_k:\operatorname {Aut}(X,\sigma ^k)\mapsto \operatorname {Aut}(X,\sigma ^{k+1})$
is the natural inclusion.
$i_k:\operatorname {Aut}(X,\sigma ^k)\mapsto \operatorname {Aut}(X,\sigma ^{k+1})$
is the natural inclusion.
Proof. By Corollary 3.3, the stabilized automorphism group of
![]() $\mathbb {Z}_{p_n}$
is
$\mathbb {Z}_{p_n}$
is
![]() $\operatorname {Aut}^{(\infty )}(\mathbb {Z}_{(p_n)},\hspace{-1pt} +\mathbf {1})\hspace{-1pt}= \bigcup _{n=1}^\infty \operatorname {Aut}(\mathbb {Z}_{(p_n)},+{\mathbf {p}_n})$
, where the union is taken inside
$\operatorname {Aut}^{(\infty )}(\mathbb {Z}_{(p_n)},\hspace{-1pt} +\mathbf {1})\hspace{-1pt}= \bigcup _{n=1}^\infty \operatorname {Aut}(\mathbb {Z}_{(p_n)},+{\mathbf {p}_n})$
, where the union is taken inside
![]() $\operatorname {Homeo}(\mathbb {Z}_{(p_n)})$
. This is equivalent to taking the direct limit of the following diagram:
$\operatorname {Homeo}(\mathbb {Z}_{(p_n)})$
. This is equivalent to taking the direct limit of the following diagram:
So, we have the following commutative diagram:

where the direct limit of the top row defines the stabilized automorphism group of
![]() $\mathbb {Z}_{(p_n)}$
. By Lemma 3.4, we conclude that this direct limit is equal to the direct limit of the bottom row which is what we wanted to prove.
$\mathbb {Z}_{(p_n)}$
. By Lemma 3.4, we conclude that this direct limit is equal to the direct limit of the bottom row which is what we wanted to prove.
As a direct corollary of Theorem 3.5, since amenability is preserved under direct limits, we conclude Corollary 1.3 for the case of odometers.
4 The stabilized automorphism group of a Toeplitz subshift
This section is devoted to the proof of Theorem 1.2. We begin our study of the stabilized automorphism group of Toeplitz subshifts by proving the following proposition.
Proposition 4.1. Let
![]() $(X,\sigma )$
be a Toeplitz subshift with period structure
$(X,\sigma )$
be a Toeplitz subshift with period structure
![]() $(p_n)$
and set
$(p_n)$
and set
![]() $m\in \mathbb {N}$
. Let
$m\in \mathbb {N}$
. Let
![]() $d> 0$
be such that for some
$d> 0$
be such that for some
![]() $k_0\in \mathbb {N}$
, we have that
$k_0\in \mathbb {N}$
, we have that
![]() $(p_k,m)=d$
for
$(p_k,m)=d$
for
![]() $k\geq k_0$
and
$k\geq k_0$
and
![]() $k_0$
is the smallest integer with this property. Then, there exists a Toeplitz subshift
$k_0$
is the smallest integer with this property. Then, there exists a Toeplitz subshift
![]() $(T,\tau )$
with period structure
$(T,\tau )$
with period structure
![]() $({p_n}/{d})_{n\geq k_0}$
such that
$({p_n}/{d})_{n\geq k_0}$
such that
![]() $(X,\sigma ^m)$
has d minimal components, each of them conjugate to
$(X,\sigma ^m)$
has d minimal components, each of them conjugate to
![]() $(T,\tau )$
. Furthermore,
$(T,\tau )$
. Furthermore,
![]() $\operatorname {Aut}(X,\sigma ^m)\cong \operatorname {Aut}(T,\tau )^d\rtimes \operatorname {Sym}(d)$
and is isomorphic to a subgroup of
$\operatorname {Aut}(X,\sigma ^m)\cong \operatorname {Aut}(T,\tau )^d\rtimes \operatorname {Sym}(d)$
and is isomorphic to a subgroup of
![]() $\operatorname {Aut}(\mathbb {Z}_{(p_n/d)_{n\geq k_0}},+\textbf {d})$
.
$\operatorname {Aut}(\mathbb {Z}_{(p_n/d)_{n\geq k_0}},+\textbf {d})$
.
Proof. Define
![]() $A_j^i$
as in Lemma 2.11. By property (iii) of this lemma, we have that
$A_j^i$
as in Lemma 2.11. By property (iii) of this lemma, we have that
![]() $\sigma ^m$
permutes the elements in
$\sigma ^m$
permutes the elements in
![]() $\{\overline {A_0^{i}},\overline {A_{1}^i},\ldots ,\overline {A_{p_{i-1}}^{i}}\}$
as
$\{\overline {A_0^{i}},\overline {A_{1}^i},\ldots ,\overline {A_{p_{i-1}}^{i}}\}$
as
![]() $\sigma ^m(\overline {A_j^{i}})=\overline {A_{j+m\,\mod p_{i}}^{i}}$
. Hence, for each
$\sigma ^m(\overline {A_j^{i}})=\overline {A_{j+m\,\mod p_{i}}^{i}}$
. Hence, for each
![]() $i\in \mathbb {N}$
, the smallest integer
$i\in \mathbb {N}$
, the smallest integer
![]() $r_i$
such that
$r_i$
such that
![]() $\sigma ^{r_im}(\overline {A_j^{i}})=\overline {A_j^{i}}$
is
$\sigma ^{r_im}(\overline {A_j^{i}})=\overline {A_j^{i}}$
is
![]() $r_i$
such that
$r_i$
such that
Since
![]() $k_0$
is the smallest integer such that we have that
$k_0$
is the smallest integer such that we have that
![]() $(p_k,m)=d$
for
$(p_k,m)=d$
for
![]() $k\geq k_0$
, by property (ii) in Lemma 2.11, we have that for any
$k\geq k_0$
, by property (ii) in Lemma 2.11, we have that for any
![]() $i,j$
, the orbit of
$i,j$
, the orbit of
![]() $\overline {A_j^i}$
under
$\overline {A_j^i}$
under
![]() $\sigma ^m$
can be expressed as the union of
$\sigma ^m$
can be expressed as the union of
![]() $r_{k_0}$
elements in
$r_{k_0}$
elements in
![]() $\{\overline {A_0^{k_0}},\overline {A_{1}^{k_0}},\ldots ,\overline {A_{p_{{k_0}-1}}^{k_0}}\}$
.
$\{\overline {A_0^{k_0}},\overline {A_{1}^{k_0}},\ldots ,\overline {A_{p_{{k_0}-1}}^{k_0}}\}$
.
Define
![]() $U_i=\mathcal {O}_{\sigma ^m}(\overline {A_i^{k_0}})$
for
$U_i=\mathcal {O}_{\sigma ^m}(\overline {A_i^{k_0}})$
for
![]() $i=1,\ldots ,d$
. (Notice that
$i=1,\ldots ,d$
. (Notice that
![]() $d=(p_{k_0},m)=p_{k_0}/r_{k_0}$
.) Since
$d=(p_{k_0},m)=p_{k_0}/r_{k_0}$
.) Since
![]() $(X,\sigma )$
is minimal, using property (ii) of Lemma 2.11, we can show that every orbit in
$(X,\sigma )$
is minimal, using property (ii) of Lemma 2.11, we can show that every orbit in
![]() $(U_i,\sigma |_{U_i})$
is dense for
$(U_i,\sigma |_{U_i})$
is dense for
![]() $i=1,\ldots ,d$
, i.e.
$i=1,\ldots ,d$
, i.e.
![]() $(U_i,\sigma |_{U_i})$
is minimal. Hence,
$(U_i,\sigma |_{U_i})$
is minimal. Hence,
![]() $(X,\sigma )$
has d minimal components. In particular, if
$(X,\sigma )$
has d minimal components. In particular, if
![]() $(m,p_n)=1$
for all
$(m,p_n)=1$
for all
![]() $n\in \mathbb {N}$
, then
$n\in \mathbb {N}$
, then
![]() $(X,\sigma ^m)$
is minimal.
$(X,\sigma ^m)$
is minimal.
By Proposition 3.1, since
![]() $(X,\sigma )$
is an almost one-to-one extension of
$(X,\sigma )$
is an almost one-to-one extension of
![]() $(\mathbb {Z}_{(p_n)},+\mathbf {1})$
and since
$(\mathbb {Z}_{(p_n)},+\mathbf {1})$
and since
![]() $(\mathbb {Z}_{(p_n)},+\mathbf {1})$
has exactly d minimal components, we conclude that every
$(\mathbb {Z}_{(p_n)},+\mathbf {1})$
has exactly d minimal components, we conclude that every
![]() $U_i$
is the inverse image under the almost one-to-one extension map from X to
$U_i$
is the inverse image under the almost one-to-one extension map from X to
![]() $\mathbb {Z}_{(p_n)}$
of a minimal component of
$\mathbb {Z}_{(p_n)}$
of a minimal component of
![]() $(\mathbb {Z}_{(p_n)},+\textbf {m})$
. Since every minimal component on
$(\mathbb {Z}_{(p_n)},+\textbf {m})$
. Since every minimal component on
![]() $(\mathbb {Z}_{(p_n)},+\textbf {m})$
is conjugate to the odometer with scale
$(\mathbb {Z}_{(p_n)},+\textbf {m})$
is conjugate to the odometer with scale
![]() $({p_n}/{d})_{n\geq k_0}$
, we have that
$({p_n}/{d})_{n\geq k_0}$
, we have that
![]() $(U_i,\sigma |_{U_i})$
is an almost one-to-one extension of the odometer
$(U_i,\sigma |_{U_i})$
is an almost one-to-one extension of the odometer
![]() $\mathbb {Z}_{{p_n}/{d})_{n\geq k_0}}$
. Since
$\mathbb {Z}_{{p_n}/{d})_{n\geq k_0}}$
. Since
![]() $(X,\sigma )$
is a symbolic system, so is
$(X,\sigma )$
is a symbolic system, so is
![]() $(X,\sigma ^m)$
. Hence, since
$(X,\sigma ^m)$
. Hence, since
![]() $\sigma $
is a conjugacy between the minimal components of
$\sigma $
is a conjugacy between the minimal components of
![]() $(X,\sigma ^m)$
, by Theorem 2.12, we conclude that there exists a Toeplitz subshift
$(X,\sigma ^m)$
, by Theorem 2.12, we conclude that there exists a Toeplitz subshift
![]() $(T,\tau )$
with period structure
$(T,\tau )$
with period structure
![]() $({{p_n}/{d})_{n\geq k_0}}$
such that
$({{p_n}/{d})_{n\geq k_0}}$
such that
![]() $(U_i,\sigma |_{U_i})$
is conjugate to
$(U_i,\sigma |_{U_i})$
is conjugate to
![]() $(T,\tau )$
for
$(T,\tau )$
for
![]() $i=1,\ldots ,d$
. By Proposition 2.3, we conclude
$i=1,\ldots ,d$
. By Proposition 2.3, we conclude
Remark 4.2. As stated in Remark 3.2, one can use the map
![]() $\pi $
in Remark 2.13 to construct an explicit representation of the minimal components of
$\pi $
in Remark 2.13 to construct an explicit representation of the minimal components of
![]() $(\mathbb {Z}_{p_n},+\textbf {m})$
without modifying the period structure by taking
$(\mathbb {Z}_{p_n},+\textbf {m})$
without modifying the period structure by taking
![]() $\pi ^{-1}(U_i)$
for
$\pi ^{-1}(U_i)$
for
![]() $i=1,\ldots ,d$
.
$i=1,\ldots ,d$
.
So far, we have shown that if
![]() $(X,\sigma )$
be a Toeplitz subshift with period structure
$(X,\sigma )$
be a Toeplitz subshift with period structure
![]() $(p_n)$
and
$(p_n)$
and
![]() $(m,p_n)=1$
for all
$(m,p_n)=1$
for all
![]() $n\in \mathbb {N}$
, then
$n\in \mathbb {N}$
, then
![]() $\operatorname {Aut}(X,\sigma )\cong \operatorname {Aut}(X,\sigma ^m).$
We will turn this statement into an equality in the following proposition.
$\operatorname {Aut}(X,\sigma )\cong \operatorname {Aut}(X,\sigma ^m).$
We will turn this statement into an equality in the following proposition.
Proposition 4.3. Let
![]() $(X,\sigma )$
be a Toeplitz subshift with period structure
$(X,\sigma )$
be a Toeplitz subshift with period structure
![]() $(p_n)$
. If
$(p_n)$
. If
![]() $(m,p_n)=1$
for all
$(m,p_n)=1$
for all
![]() $n\in \mathbb {N}$
, then
$n\in \mathbb {N}$
, then
Proof. We know
![]() $\operatorname {Aut}(X,\sigma )\subseteq \operatorname {Aut}(X,\sigma ^m).$
We now prove the other inclusion. Let
$\operatorname {Aut}(X,\sigma )\subseteq \operatorname {Aut}(X,\sigma ^m).$
We now prove the other inclusion. Let
![]() $\varphi \in \operatorname {Aut}(X,\sigma ^m)$
. We must show
$\varphi \in \operatorname {Aut}(X,\sigma ^m)$
. We must show
![]() $\phi \circ \sigma (x)=\sigma \circ \varphi (x)$
for all
$\phi \circ \sigma (x)=\sigma \circ \varphi (x)$
for all
![]() $x\in X$
. Let R be the set of regular points in X defined as in §2.5. Since R is a dense
$x\in X$
. Let R be the set of regular points in X defined as in §2.5. Since R is a dense
![]() $G_\delta $
subset of X and
$G_\delta $
subset of X and
![]() $\varphi $
is a homeomorphism,
$\varphi $
is a homeomorphism,
![]() $\varphi ^{-1}(R)\cap R$
is a dense
$\varphi ^{-1}(R)\cap R$
is a dense
![]() $G_\delta $
set by Baire’s category theorem. Hence, it is enough to prove this statement for
$G_\delta $
set by Baire’s category theorem. Hence, it is enough to prove this statement for
![]() $x\in \varphi ^{-1}(R)\cap R$
by continuity of
$x\in \varphi ^{-1}(R)\cap R$
by continuity of
![]() $\varphi $
and
$\varphi $
and
![]() $\sigma $
.
$\sigma $
.
Let
![]() $x\in \varphi ^{-1}(R)\cap R$
. Notice x and
$x\in \varphi ^{-1}(R)\cap R$
. Notice x and
![]() $\varphi (x)$
are both Toeplitz sequences. We show
$\varphi (x)$
are both Toeplitz sequences. We show
![]() $|\varphi \circ \sigma (x)-\sigma \circ \varphi (x)|=0$
. Let
$|\varphi \circ \sigma (x)-\sigma \circ \varphi (x)|=0$
. Let
![]() $\varepsilon _i$
be a decreasing sequence of positive numbers such that
$\varepsilon _i$
be a decreasing sequence of positive numbers such that
![]() $\varepsilon _i\to 0$
. For each
$\varepsilon _i\to 0$
. For each
![]() $\varepsilon _i$
, define
$\varepsilon _i$
, define
![]() $M_i\in \mathbb {N}$
to be an integer such that for any two elements
$M_i\in \mathbb {N}$
to be an integer such that for any two elements
![]() $z,y\in X$
, if
$z,y\in X$
, if
![]() $z_i=y_i$
for all
$z_i=y_i$
for all
![]() $|i|\leq M$
, then
$|i|\leq M$
, then
![]() $|z-y|\leq \varepsilon _i.$
Let
$|z-y|\leq \varepsilon _i.$
Let
![]() $p_s$
be the largest period of the coordinates
$p_s$
be the largest period of the coordinates
![]() $x_j$
with
$x_j$
with
![]() $|j|\leq M_i+1$
of x. Let
$|j|\leq M_i+1$
of x. Let
![]() $p_\ell $
be the largest period of the coordinates
$p_\ell $
be the largest period of the coordinates
![]() $\varphi (x)_j$
with
$\varphi (x)_j$
with
![]() $|j|\leq M_i+1$
of
$|j|\leq M_i+1$
of
![]() $\varphi (x)$
. Notice that
$\varphi (x)$
. Notice that
![]() $p_s$
divides
$p_s$
divides
![]() $ p_\ell $
or
$ p_\ell $
or
![]() $p_\ell $
divides
$p_\ell $
divides
![]() $ p_s$
, so fix
$ p_s$
, so fix
![]() $\hat p_i$
the larger of the two. Since
$\hat p_i$
the larger of the two. Since
![]() $(m,\hat p_i)=1$
, there exist integers
$(m,\hat p_i)=1$
, there exist integers
![]() $a_i, b_i$
such that
$a_i, b_i$
such that
![]() $a_i=1+b\hat p_i$
. Then we have that
$a_i=1+b\hat p_i$
. Then we have that
by our construction of the
![]() $a_i$
terms. Notice we have the following inequality:
$a_i$
terms. Notice we have the following inequality:
 $$ \begin{align*} d(\varphi\circ\sigma(x),\sigma\circ\varphi(x))&\leq d (\sigma\circ\varphi(x),\sigma^{a_im}(\varphi(x)))+d(\sigma^{a_im}(\varphi(x)),\varphi\circ\sigma(x))\\&= d(\sigma(\varphi(x)),\sigma^{a_im}(\varphi(x)))+d(\varphi(\sigma^{a_im}(x)),\varphi(\sigma(x))). \end{align*} $$
$$ \begin{align*} d(\varphi\circ\sigma(x),\sigma\circ\varphi(x))&\leq d (\sigma\circ\varphi(x),\sigma^{a_im}(\varphi(x)))+d(\sigma^{a_im}(\varphi(x)),\varphi\circ\sigma(x))\\&= d(\sigma(\varphi(x)),\sigma^{a_im}(\varphi(x)))+d(\varphi(\sigma^{a_im}(x)),\varphi(\sigma(x))). \end{align*} $$
By equations (4.1) and (4.2) and since
![]() $\varphi $
is continuous, the right-hand side goes to
$\varphi $
is continuous, the right-hand side goes to
![]() $0$
as
$0$
as
![]() $i\to \infty $
. Thus,
$i\to \infty $
. Thus,
![]() $|\varphi \circ \sigma (x)-\sigma \circ \varphi (x)|=0$
. Since
$|\varphi \circ \sigma (x)-\sigma \circ \varphi (x)|=0$
. Since
![]() $\varphi ^{-1}(R)\cap R$
is a
$\varphi ^{-1}(R)\cap R$
is a
![]() $G_\delta $
subset of X and
$G_\delta $
subset of X and
![]() $\varphi $
is continuous, we can conclude that
$\varphi $
is continuous, we can conclude that
![]() $\varphi \circ \sigma (x)=\sigma \circ \varphi (x)$
for all
$\varphi \circ \sigma (x)=\sigma \circ \varphi (x)$
for all
![]() $x\in X$
. Hence,
$x\in X$
. Hence,
![]() $\varphi \in \operatorname {Aut}(X,\sigma )$
.
$\varphi \in \operatorname {Aut}(X,\sigma )$
.
Theorem 4.4. Let
![]() $(X, \sigma )$
be a Toeplitz subshift with period structure
$(X, \sigma )$
be a Toeplitz subshift with period structure
![]() $(p_n)$
. Then, the stabilized automorphism group of
$(p_n)$
. Then, the stabilized automorphism group of
![]() $(X, \sigma )$
is the direct limit of the sequence
$(X, \sigma )$
is the direct limit of the sequence
where the maps are the natural inclusion of each automorphism group into the next.
Observe that in Proposition 4.1, we described
![]() $\operatorname {Aut}(X,\sigma ^{p_n})$
for all n.
$\operatorname {Aut}(X,\sigma ^{p_n})$
for all n.
Proof. Let
![]() $m\in \mathbb {N}$
. If
$m\in \mathbb {N}$
. If
![]() $(m,p_n)=1$
for all
$(m,p_n)=1$
for all
![]() $n\in \mathbb {N}$
, by part (i) of Proposition 4.1,
$n\in \mathbb {N}$
, by part (i) of Proposition 4.1,
![]() $\operatorname {Aut}(X,\sigma ^m)=\operatorname {Aut}(X,\sigma )$
. Hence,
$\operatorname {Aut}(X,\sigma ^m)=\operatorname {Aut}(X,\sigma )$
. Hence,
![]() $\operatorname {Aut}(X,\sigma ^m)\subseteq \bigcup \nolimits _{n=1}^\infty \operatorname {Aut}(X,\sigma ^{p_n})$
. If
$\operatorname {Aut}(X,\sigma ^m)\subseteq \bigcup \nolimits _{n=1}^\infty \operatorname {Aut}(X,\sigma ^{p_n})$
. If
![]() $(m,p_n)\neq 1$
, take
$(m,p_n)\neq 1$
, take
![]() $M=\lim _{k\to \infty }\operatorname {lcm}(m,p_k)$
. By Proposition 4.1,
$M=\lim _{k\to \infty }\operatorname {lcm}(m,p_k)$
. By Proposition 4.1,
![]() $\operatorname {Aut}(X,\sigma ^{m})=\operatorname {Aut}(X,\sigma ^{M})$
. By our construction of M, there exists
$\operatorname {Aut}(X,\sigma ^{m})=\operatorname {Aut}(X,\sigma ^{M})$
. By our construction of M, there exists
![]() $k\in \mathbb {N}$
such that M divides
$k\in \mathbb {N}$
such that M divides
![]() $ p_k$
. Hence,
$ p_k$
. Hence,
![]() $\operatorname {Aut}(X,\sigma ^{m})=\operatorname {Aut}(X,\sigma ^{M})\subseteq \operatorname {Aut}(X,\sigma ^{p_k})$
. This implies
$\operatorname {Aut}(X,\sigma ^{m})=\operatorname {Aut}(X,\sigma ^{M})\subseteq \operatorname {Aut}(X,\sigma ^{p_k})$
. This implies
![]() $\operatorname {Aut}(X,\sigma ^m)\subseteq \bigcup \nolimits _{n=1}^\infty \operatorname {Aut}(X,\sigma ^{p_n})$
.
$\operatorname {Aut}(X,\sigma ^m)\subseteq \bigcup \nolimits _{n=1}^\infty \operatorname {Aut}(X,\sigma ^{p_n})$
.
As a direct corollary of Theorem 4.4, since amenability is preserved under direct limits and Toeplitz subshifts have abelian automorphism groups, we conclude Corollary 1.3 for the case of Toeplitz subshifts.
5 Invariance of the stabilized automorphism group for odometers and Toeplitz subshifts up to scale equivalence
This section is dedicated to proving Theorem 5.3.
5.1 Invariance
Lemma 5.1. Let
![]() $(\mathbb {Z}_{(p_n)},+\mathbf {1})$
be an odometer with scale
$(\mathbb {Z}_{(p_n)},+\mathbf {1})$
be an odometer with scale
![]() ${(p_n)}$
and q be a prime such that
${(p_n)}$
and q be a prime such that
![]() $\operatorname {\textbf {v}}_q(p_n)=\infty $
. If
$\operatorname {\textbf {v}}_q(p_n)=\infty $
. If
![]() $\textbf {x}\in \mathbb {Z}_{(p_n)}$
is an element of infinite order, then there exists
$\textbf {x}\in \mathbb {Z}_{(p_n)}$
is an element of infinite order, then there exists
![]() ${\unicode{x3bb} \in \operatorname {Aut}^\infty (\mathbb {Z}_{(p_n)},+\mathbf {1})}$
such that for some
${\unicode{x3bb} \in \operatorname {Aut}^\infty (\mathbb {Z}_{(p_n)},+\mathbf {1})}$
such that for some
![]() $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
,
![]() $\unicode{x3bb} $
commutes with
$\unicode{x3bb} $
commutes with
![]() $+q^k\textbf {x}$
but not with
$+q^k\textbf {x}$
but not with
![]() $+\textbf {x}$
.
$+\textbf {x}$
.
Proof. Let
![]() $\textbf {x}=(x_i) \in \mathbb {Z}_{(p_n)}$
be an element of infinite order and let
$\textbf {x}=(x_i) \in \mathbb {Z}_{(p_n)}$
be an element of infinite order and let
![]() $N\in \mathbb {N}$
be the first integer such that q divides
$N\in \mathbb {N}$
be the first integer such that q divides
![]() $p_N$
and
$p_N$
and
![]() $x_N\neq 0$
. We can always find such an integer since
$x_N\neq 0$
. We can always find such an integer since
![]() $\textbf {x}$
is not a torsion element and
$\textbf {x}$
is not a torsion element and
![]() $\textbf {v}_q(p_n)=\infty $
. Set
$\textbf {v}_q(p_n)=\infty $
. Set
![]() $k=\nu _q(x_N)+1$
.
$k=\nu _q(x_N)+1$
.
Define
![]() $p^{\prime }_n=p_{n+N-1}$
, then
$p^{\prime }_n=p_{n+N-1}$
, then
![]() $\mathbb {Z}_{(p_n)}\cong \mathbb {Z}_{(p^{\prime }_n)}$
via the isomorphism
$\mathbb {Z}_{(p_n)}\cong \mathbb {Z}_{(p^{\prime }_n)}$
via the isomorphism
![]() $(y_i)\mapsto (y_{i+N-1})$
. Take
$(y_i)\mapsto (y_{i+N-1})$
. Take
![]() $\textbf {x}'=(x_{i+N-1})$
. By Proposition 3.1,
$\textbf {x}'=(x_{i+N-1})$
. By Proposition 3.1,
![]() $(\mathbb {Z}_{p^{\prime }_n},+\textbf {q}^k)$
has
$(\mathbb {Z}_{p^{\prime }_n},+\textbf {q}^k)$
has
![]() $q^k$
minimal components, denote them by
$q^k$
minimal components, denote them by
![]() $V_1, V_2,\ldots ,V_{q^k}$
, each a union of sets of the form
$V_1, V_2,\ldots ,V_{q^k}$
, each a union of sets of the form
![]() $U_i=\{(y_i)\in \mathbb {Z}_{(p^{\prime }_n)}:x_1=j\}$
for
$U_i=\{(y_i)\in \mathbb {Z}_{(p^{\prime }_n)}:x_1=j\}$
for
![]() ${j=0,1,\ldots ,p_N-1}$
, and
${j=0,1,\ldots ,p_N-1}$
, and
![]() $(U_j,+\textbf {q}|_{U_j})$
is conjugate to an odometer. Let
$(U_j,+\textbf {q}|_{U_j})$
is conjugate to an odometer. Let
![]() $\varphi $
be a non-trivial element in
$\varphi $
be a non-trivial element in
![]() $\operatorname {Aut}(U_j,+\textbf {q}|_{U_j})$
. Let
$\operatorname {Aut}(U_j,+\textbf {q}|_{U_j})$
. Let
![]() $\unicode{x3bb} $
be the image under the map
$\unicode{x3bb} $
be the image under the map
![]() $\iota $
described in Proposition 2.3 of the map that acts via
$\iota $
described in Proposition 2.3 of the map that acts via
![]() $\varphi $
on
$\varphi $
on
![]() $V_1$
and the identity on all other minimal components.
$V_1$
and the identity on all other minimal components.
Notice that
![]() $U_j+\textbf {x}=U_{j+x^{\prime }_1 \,\mod p^{\prime }_1}$
. Since
$U_j+\textbf {x}=U_{j+x^{\prime }_1 \,\mod p^{\prime }_1}$
. Since ![]() and by our choice of k,
and by our choice of k,
![]() $+\textbf {x}$
permutes the minimal components
$+\textbf {x}$
permutes the minimal components
![]() $V_j$
in a non-trivial permutation corresponding to an element of the subgroup isomorphic to
$V_j$
in a non-trivial permutation corresponding to an element of the subgroup isomorphic to
![]() $\mathbb {Z}/q^k\mathbb {Z}$
of the group of permutations of the
$\mathbb {Z}/q^k\mathbb {Z}$
of the group of permutations of the
![]() $V_j$
terms identified with
$V_j$
terms identified with
![]() $\operatorname {Sym}(q^k).$
However,
$\operatorname {Sym}(q^k).$
However,
![]() $+q^k\textbf {x}$
leaves all of the minimal components
$+q^k\textbf {x}$
leaves all of the minimal components
![]() $V_j$
invariant. Since odometers are abelian, one can easily see that
$V_j$
invariant. Since odometers are abelian, one can easily see that
![]() $+q^k\textbf {x}$
commutes with
$+q^k\textbf {x}$
commutes with
![]() $\unicode{x3bb} $
but
$\unicode{x3bb} $
but
![]() $+\textbf {x}$
does not.
$+\textbf {x}$
does not.
Corollary 5.2. Let
![]() $(X,\sigma )$
be a Toeplitz subshift with scale
$(X,\sigma )$
be a Toeplitz subshift with scale
![]() ${(p_n)}$
and let q be a prime such that
${(p_n)}$
and let q be a prime such that
![]() $\textbf {v}_q(p_n)=\infty $
. If
$\textbf {v}_q(p_n)=\infty $
. If
![]() $x\in \operatorname {Aut}(X,\sigma )$
is an element of infinite order, then there exists
$x\in \operatorname {Aut}(X,\sigma )$
is an element of infinite order, then there exists
![]() $\unicode{x3bb} \in \operatorname {Aut}^\infty (X,\sigma )$
such that
$\unicode{x3bb} \in \operatorname {Aut}^\infty (X,\sigma )$
such that
![]() $\unicode{x3bb} $
commutes with
$\unicode{x3bb} $
commutes with
![]() $x^q$
but not with x.
$x^q$
but not with x.
Proof. This proof is identical to the last proof since
![]() $\operatorname {Aut}(X,\sigma )$
is isomorphic to a subgroup of an odometer and in the proof of Lemma 5.1, we only used the existence of a non-trivial element in the automorphism group of the minimal components of
$\operatorname {Aut}(X,\sigma )$
is isomorphic to a subgroup of an odometer and in the proof of Lemma 5.1, we only used the existence of a non-trivial element in the automorphism group of the minimal components of
![]() $(X,T^{k})$
for all
$(X,T^{k})$
for all
![]() ${k\in \mathbb {N}}$
.
${k\in \mathbb {N}}$
.
Theorem 5.3. Let
![]() $(\mathbb {Z}_{(p_n)},+\mathbf {1})$
and
$(\mathbb {Z}_{(p_n)},+\mathbf {1})$
and
![]() $(\mathbb {Z}_{(q_n)},+\mathbf {1})$
be two odometers with scales
$(\mathbb {Z}_{(q_n)},+\mathbf {1})$
be two odometers with scales
![]() $(p_n)$
and
$(p_n)$
and
![]() $(q_n)$
, respectively, and let s be a prime. If
$(q_n)$
, respectively, and let s be a prime. If
![]() $\textbf {v}_s(p_n)=\infty $
and
$\textbf {v}_s(p_n)=\infty $
and
![]() $\operatorname {Aut}^{(\infty )}(\mathbb {Z}_{(p_n)},+\mathbf {1})\cong \operatorname {Aut}^{(\infty )}(\mathbb {Z}_{q_n},+\mathbf {1})$
, then
$\operatorname {Aut}^{(\infty )}(\mathbb {Z}_{(p_n)},+\mathbf {1})\cong \operatorname {Aut}^{(\infty )}(\mathbb {Z}_{q_n},+\mathbf {1})$
, then
![]() $\textbf {v}_s(p_n)=\infty $
.
$\textbf {v}_s(p_n)=\infty $
.
Proof. Proceeding by contradiction, assume
![]() $\varphi \colon \operatorname {Aut}^{(\infty )}(\mathbb {Z}_{(p_n)},+\mathbf {1}) \to \operatorname {Aut}^{(\infty )}(\mathbb {Z}_{(q_n)},+\mathbf {1})$
is a group isomorphism and
$\varphi \colon \operatorname {Aut}^{(\infty )}(\mathbb {Z}_{(p_n)},+\mathbf {1}) \to \operatorname {Aut}^{(\infty )}(\mathbb {Z}_{(q_n)},+\mathbf {1})$
is a group isomorphism and
![]() $\ell =\textbf {v}_s(p_n)<\infty $
. Take
$\ell =\textbf {v}_s(p_n)<\infty $
. Take
![]() $j=s^\ell $
and
$j=s^\ell $
and
![]() $\gamma =\varphi (+\mathbf {1})$
. We can assume there exists
$\gamma =\varphi (+\mathbf {1})$
. We can assume there exists
![]() $k>0$
such that
$k>0$
such that
![]() $\gamma ^j\in \operatorname {Aut}(\mathbb {Z}_{(q_n)},+\textbf {q}_k)\cong \mathbb {Z}_{(q_{n+k}/q_k)}^{q_k}\rtimes \operatorname {Sym}(q_k)$
. With some abuse of notation, we assume
$\gamma ^j\in \operatorname {Aut}(\mathbb {Z}_{(q_n)},+\textbf {q}_k)\cong \mathbb {Z}_{(q_{n+k}/q_k)}^{q_k}\rtimes \operatorname {Sym}(q_k)$
. With some abuse of notation, we assume
![]() $\gamma ^j \in \mathbb {Z}_{(q_{n+k}/q_k)}^{q_k}\rtimes \operatorname {Sym}(q_k)$
as opposed to taking the image of
$\gamma ^j \in \mathbb {Z}_{(q_{n+k}/q_k)}^{q_k}\rtimes \operatorname {Sym}(q_k)$
as opposed to taking the image of
![]() $\gamma ^j$
under the appropriate isomorphism. We also use
$\gamma ^j$
under the appropriate isomorphism. We also use
![]() $\operatorname {Aut}(\mathbb {Z}_{(q_n)},+\textbf {q}_k)$
and
$\operatorname {Aut}(\mathbb {Z}_{(q_n)},+\textbf {q}_k)$
and
![]() $\mathbb {Z}_{(q_{n+k}/q_k)}^{q_k}\rtimes \operatorname {Sym}(q_k)$
interchangeably (as they are isomorphic) according to the best interpretation required for our reasoning. Define
$\mathbb {Z}_{(q_{n+k}/q_k)}^{q_k}\rtimes \operatorname {Sym}(q_k)$
interchangeably (as they are isomorphic) according to the best interpretation required for our reasoning. Define
![]() $\pi \colon \mathbb {Z}_{(q_{n+k}/q_k)}^{q_k}\rtimes \operatorname {Sym}(q_k)\to \operatorname {Sym}(q_k)$
to be the canonical projection.
$\pi \colon \mathbb {Z}_{(q_{n+k}/q_k)}^{q_k}\rtimes \operatorname {Sym}(q_k)\to \operatorname {Sym}(q_k)$
to be the canonical projection.
Let
![]() $y\in \mathbb {N}$
be such that
$y\in \mathbb {N}$
be such that
![]() $\pi (\gamma ^{j\cdot y})=e$
. Write
$\pi (\gamma ^{j\cdot y})=e$
. Write
![]() $\gamma ^{j\cdot y}=((\gamma _1,\gamma _2,\ldots ,\gamma _{q_k}),e)$
. Since
$\gamma ^{j\cdot y}=((\gamma _1,\gamma _2,\ldots ,\gamma _{q_k}),e)$
. Since
![]() $+\mathbf {1}$
is an infinite order element and
$+\mathbf {1}$
is an infinite order element and
![]() $\varphi $
is an isomorphism, so is
$\varphi $
is an isomorphism, so is
![]() $\gamma $
. Hence, there exists
$\gamma $
. Hence, there exists
![]() $\gamma _i\in \mathbb {Z}_{(q_{n+k}/q_k)}$
such that
$\gamma _i\in \mathbb {Z}_{(q_{n+k}/q_k)}$
such that
![]() $\gamma _i$
is an infinite order element in
$\gamma _i$
is an infinite order element in
![]() $\mathbb {Z}_{(q_{n+k}/q_k)}$
.
$\mathbb {Z}_{(q_{n+k}/q_k)}$
.
Let us restrict our attention to the action of
![]() $\gamma _i$
on the ith minimal component of
$\gamma _i$
on the ith minimal component of
![]() $+\textbf {q}_k$
. Since
$+\textbf {q}_k$
. Since
![]() $\textbf {v}_s(p_n)=\infty $
, by Lemma 5.1, there exists an element in
$\textbf {v}_s(p_n)=\infty $
, by Lemma 5.1, there exists an element in
![]() $\operatorname {Aut}^\infty (\mathbb {Z}_{(q_n)},+\mathbf {1})$
that commutes with
$\operatorname {Aut}^\infty (\mathbb {Z}_{(q_n)},+\mathbf {1})$
that commutes with
![]() $\gamma _i^{y\cdot s}$
but not with
$\gamma _i^{y\cdot s}$
but not with
![]() $\gamma ^y$
. By Proposition 2.3 and equation (2.1),
$\gamma ^y$
. By Proposition 2.3 and equation (2.1),
![]() $\gamma ^{j\cdot y\cdot s}=((\gamma _1^s,\gamma _2^s,\ldots ,\gamma _{q_k}^s),e)$
. We conclude, there exists
$\gamma ^{j\cdot y\cdot s}=((\gamma _1^s,\gamma _2^s,\ldots ,\gamma _{q_k}^s),e)$
. We conclude, there exists
![]() $\unicode{x3bb} $
that commutes with
$\unicode{x3bb} $
that commutes with
![]() $\gamma ^{j\cdot y\cdot s}$
but not with
$\gamma ^{j\cdot y\cdot s}$
but not with
![]() $\gamma ^{j\cdot y}$
. This is a contradiction to Proposition 3.1 because it implies
$\gamma ^{j\cdot y}$
. This is a contradiction to Proposition 3.1 because it implies
![]() $\operatorname {Aut}(\mathbb {Z}_{(p_n)},+{\textbf {j}\cdot \textbf {y}\cdot \textbf {s}})\neq \operatorname {Aut}(\mathbb {Z}_{(p_n)},+{\textbf {j}\cdot \textbf {y}})$
. We conclude
$\operatorname {Aut}(\mathbb {Z}_{(p_n)},+{\textbf {j}\cdot \textbf {y}\cdot \textbf {s}})\neq \operatorname {Aut}(\mathbb {Z}_{(p_n)},+{\textbf {j}\cdot \textbf {y}})$
. We conclude
![]() $\textbf {v}_s(p_n)=\infty $
.
$\textbf {v}_s(p_n)=\infty $
.
Corollary 5.4. Let
![]() $(X,\sigma )$
and
$(X,\sigma )$
and
![]() $(Y,\tau )$
be two Toeplitz subshifts with scales
$(Y,\tau )$
be two Toeplitz subshifts with scales
![]() $(p_n)$
and
$(p_n)$
and
![]() $(q_n)$
, respectively, and let s be a prime. If
$(q_n)$
, respectively, and let s be a prime. If
![]() $\textbf {v}_s(p_n)=\infty $
and
$\textbf {v}_s(p_n)=\infty $
and
![]() $\operatorname {Aut}^{(\infty )}(X,\sigma )\cong \operatorname {Aut}^{(\infty )}(Y,\tau )$
, then
$\operatorname {Aut}^{(\infty )}(X,\sigma )\cong \operatorname {Aut}^{(\infty )}(Y,\tau )$
, then
![]() $\textbf {v}_s(p_n)=\infty $
.
$\textbf {v}_s(p_n)=\infty $
.
Proof. Proceeding by contradiction, assume
![]() $\varphi \colon \operatorname {Aut}^{(\infty )}(X,\sigma ) \to \operatorname {Aut}^{(\infty )}(Y,\tau )$
is a group isomorphism and
$\varphi \colon \operatorname {Aut}^{(\infty )}(X,\sigma ) \to \operatorname {Aut}^{(\infty )}(Y,\tau )$
is a group isomorphism and
![]() $j=\textbf {v}_s(p_n)<\infty $
. Take
$j=\textbf {v}_s(p_n)<\infty $
. Take
![]() $\gamma =\varphi (\sigma )$
. We can assume there exists
$\gamma =\varphi (\sigma )$
. We can assume there exists
![]() $k>0$
such that
$k>0$
such that
![]() $\gamma ^j\in \operatorname {Aut}(Y,\tau ^{q_k})\cong \operatorname {Aut}(\hat Y,\hat \tau )^{q_k}\rtimes \operatorname {Sym}(q_k)$
, where
$\gamma ^j\in \operatorname {Aut}(Y,\tau ^{q_k})\cong \operatorname {Aut}(\hat Y,\hat \tau )^{q_k}\rtimes \operatorname {Sym}(q_k)$
, where
![]() $(\hat Y,\hat S )$
is a Toeplitz subshift with scale
$(\hat Y,\hat S )$
is a Toeplitz subshift with scale
![]() $(q_{n+k}/q_k)$
. The rest proceeds identically to that of Theorem 5.3, using Corollary 5.2 to reach a contradiction to Theorem 1.2.
$(q_{n+k}/q_k)$
. The rest proceeds identically to that of Theorem 5.3, using Corollary 5.2 to reach a contradiction to Theorem 1.2.
Corollary 5.5. Let
![]() $(\mathbb {Z}_{(p_n)},+\mathbf {1})$
and
$(\mathbb {Z}_{(p_n)},+\mathbf {1})$
and
![]() $(\mathbb {Z}_{(q_n)},+\mathbf {1})$
be torsion-free odometers with scales
$(\mathbb {Z}_{(q_n)},+\mathbf {1})$
be torsion-free odometers with scales
![]() $(p_n)$
and
$(p_n)$
and
![]() $(q_n)$
, respectively. If
$(q_n)$
, respectively. If
![]() $\operatorname {Aut}^{(\infty )}(\mathbb {Z}_{(p_n)},+\mathbf {1})$
and
$\operatorname {Aut}^{(\infty )}(\mathbb {Z}_{(p_n)},+\mathbf {1})$
and
![]() $\operatorname {Aut}^{(\infty )}(\mathbb {Z}_{(q_n)},+\mathbf {1})$
are isomorphic as groups, then
$\operatorname {Aut}^{(\infty )}(\mathbb {Z}_{(q_n)},+\mathbf {1})$
are isomorphic as groups, then
![]() $(p_n)\sim (q_n)$
and
$(p_n)\sim (q_n)$
and
![]() $\mathbb {Z}_{(p_n)}\cong \mathbb {Z}_{(q_n)}$
.
$\mathbb {Z}_{(p_n)}\cong \mathbb {Z}_{(q_n)}$
.
We have proved Theorems 1.4 and 1.5 by proving Corollaries 5.4 and 5.5.
5.2 Limitations
For the case of torsion-free odometers, we have established a full automorphism invariance of the stabilized automorphism group. However, in the case of Toeplitz subshifts, we do not get such a strong result. To illustrate this, we present the following example of two Toeplitz sequences that admit
![]() $(2^n)$
as a scale (not an essential period structure for the second example) that are not conjugate but our methods fail to identify them as different systems. These examples can be found in [Reference Downarowicz, Kolyada, Manin and Ward7].
$(2^n)$
as a scale (not an essential period structure for the second example) that are not conjugate but our methods fail to identify them as different systems. These examples can be found in [Reference Downarowicz, Kolyada, Manin and Ward7].
Example 5.6. Consider the Toeplitz sequence
![]() $u=(u_i)$
with symbols
$u=(u_i)$
with symbols
![]() $0$
and
$0$
and
![]() $1$
constructed in the following iterative process. First consider the sequence
$1$
constructed in the following iterative process. First consider the sequence
![]() $x^0=(x_i)$
where every entry
$x^0=(x_i)$
where every entry
![]() $x_i=?$
, where
$x_i=?$
, where
![]() $?$
indicates a place-holder for the entries that have not yet been determined. We define
$?$
indicates a place-holder for the entries that have not yet been determined. We define
![]() $x^{j}$
as follows: if j is odd, we fill every second available position in
$x^{j}$
as follows: if j is odd, we fill every second available position in
![]() $x^{j-1}$
with
$x^{j-1}$
with
![]() $0$
; if j is even, we fill every second available position in
$0$
; if j is even, we fill every second available position in
![]() $x^{j-1}$
with
$x^{j-1}$
with
![]() $1$
. We define u to be the limit of this process. The following chart depicts the construction of each
$1$
. We define u to be the limit of this process. The following chart depicts the construction of each
![]() $x^j$
:
$x^j$
:
 $$ \begin{align*}\begin{array}{l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}} x^0=&\ldots&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&\ldots\\ x^1=&\ldots&?&0&?&0&?&0&?&0&?&0&?&0&?&0&?&0&?&0&?&0&?&0&?&0&?&0&?&\ldots\\ x^2=&\ldots&1&0&?&0&1&0&?&0&1&0&?&0&1&0&?&0&1&0&?&0&1&0&?&0&1&0&?&\ldots\\ x^3=&\ldots&1&0&0&0&1&0&?&0&1&0&0&0&1&0&?&0&1&0&0&0&1&0&?&0&1&0&0&\ldots\\ x^4=&\ldots&1&0&0&0&1&0&1&0&1&0&0&0&1&0&?&0&1&0&0&0&1&0&1&0&1&0&0&\ldots\\ \quad\vdots\\ u=&\ldots&1&0&0&0&1&0&1&0&1&0&0&0&1&0&0&0&1&0&0&0&1&0&1&0&1&0&0&\ldots \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}} x^0=&\ldots&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&\ldots\\ x^1=&\ldots&?&0&?&0&?&0&?&0&?&0&?&0&?&0&?&0&?&0&?&0&?&0&?&0&?&0&?&\ldots\\ x^2=&\ldots&1&0&?&0&1&0&?&0&1&0&?&0&1&0&?&0&1&0&?&0&1&0&?&0&1&0&?&\ldots\\ x^3=&\ldots&1&0&0&0&1&0&?&0&1&0&0&0&1&0&?&0&1&0&0&0&1&0&?&0&1&0&0&\ldots\\ x^4=&\ldots&1&0&0&0&1&0&1&0&1&0&0&0&1&0&?&0&1&0&0&0&1&0&1&0&1&0&0&\ldots\\ \quad\vdots\\ u=&\ldots&1&0&0&0&1&0&1&0&1&0&0&0&1&0&0&0&1&0&0&0&1&0&1&0&1&0&0&\ldots \end{array} \end{align*} $$
Example 5.7. For this example, consider the Toeplitz sequence
![]() $w=(u_i)$
with symbols
$w=(u_i)$
with symbols
![]() $0$
and
$0$
and
![]() $1$
constructed in a similar iterative process. First consider the sequence
$1$
constructed in a similar iterative process. First consider the sequence
![]() $y^0=(y_i)$
where every entry
$y^0=(y_i)$
where every entry
![]() $y_i=?$
. Define
$y_i=?$
. Define
![]() $y^{j}$
as we fill every second available position in
$y^{j}$
as we fill every second available position in
![]() $y^{j-1}$
by alternating between
$y^{j-1}$
by alternating between
![]() $0$
and
$0$
and
![]() $1$
. We define w to be the limit of this process. The following chart depicts the construction of each
$1$
. We define w to be the limit of this process. The following chart depicts the construction of each
![]() $y^j$
:
$y^j$
:
 $$ \begin{align*} \begin{array}{l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}} y^0=&\ldots&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&\ldots\\y^1=&\ldots&?&0&?&1&?&0&?&1&?&0&?&1&?&0&?&1&?&0&?&1&?&0&?&1&?&0&?&\ldots\\ y^2=&\ldots&0&0&?&1&1&0&?&1&0&0&?&1&1&0&?&1&0&0&?&1&1&0&?&1&0&0&?&\ldots \\ y^2=&\ldots&0&0&0&1&1&0&?&1&0&0&1&1&1&0&?&1&0&0&0&1&1&0&?&1&0&0&1&\ldots \\ y^3=&\ldots&0&0&0&1&1&0&0&1&0&0&1&1&1&0&?&1&0&0&0&1&1&0&1&1&0&0&1&\ldots \\\quad\vdots \\w=&\ldots&0&0&0&1&1&0&0&1&0&0&1&1&1&0&0&1&0&0&0&1&1&0&1&1&0&0&1&\ldots \end{array}\end{align*} $$
$$ \begin{align*} \begin{array}{l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}l@{\ \ \kern0.7pt}} y^0=&\ldots&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&?&\ldots\\y^1=&\ldots&?&0&?&1&?&0&?&1&?&0&?&1&?&0&?&1&?&0&?&1&?&0&?&1&?&0&?&\ldots\\ y^2=&\ldots&0&0&?&1&1&0&?&1&0&0&?&1&1&0&?&1&0&0&?&1&1&0&?&1&0&0&?&\ldots \\ y^2=&\ldots&0&0&0&1&1&0&?&1&0&0&1&1&1&0&?&1&0&0&0&1&1&0&?&1&0&0&1&\ldots \\ y^3=&\ldots&0&0&0&1&1&0&0&1&0&0&1&1&1&0&?&1&0&0&0&1&1&0&1&1&0&0&1&\ldots \\\quad\vdots \\w=&\ldots&0&0&0&1&1&0&0&1&0&0&1&1&1&0&0&1&0&0&0&1&1&0&1&1&0&0&1&\ldots \end{array}\end{align*} $$
The Toeplitz subshift in Example 5.6 has
![]() $(2^n)$
as a period structure and the one in Example 5.7 has period structure
$(2^n)$
as a period structure and the one in Example 5.7 has period structure
![]() $(4^n)$
. Hence, both examples have
$(4^n)$
. Hence, both examples have
![]() $(2^n)$
as a prime scale. These two systems are not conjugate and neither is a factor of the other (see [Reference Downarowicz, Kolyada, Manin and Ward7]). Our methods consist on finding the highest order of finite subgroups and how this number increases along different sequences of contentions of the form
$(2^n)$
as a prime scale. These two systems are not conjugate and neither is a factor of the other (see [Reference Downarowicz, Kolyada, Manin and Ward7]). Our methods consist on finding the highest order of finite subgroups and how this number increases along different sequences of contentions of the form
for all primes p. Because the Toeplitz subshift in Example 5.7 has period structure
![]() $(4^n)$
, when we consider
$(4^n)$
, when we consider
![]() $\operatorname {Aut}(X_{w},\sigma ^{2^j})$
for j odd, since
$\operatorname {Aut}(X_{w},\sigma ^{2^j})$
for j odd, since
![]() $2^j$
divides a period,
$2^j$
divides a period,
![]() $\operatorname {Aut}(X_{w},\sigma ^{2^j})$
contains a subgroup of order
$\operatorname {Aut}(X_{w},\sigma ^{2^j})$
contains a subgroup of order
![]() $2^j!$
. Notice
$2^j!$
. Notice
![]() $\operatorname {Aut}(X_{u},\sigma ^{2^j})$
also contains a subgroup of order
$\operatorname {Aut}(X_{u},\sigma ^{2^j})$
also contains a subgroup of order
![]() $2^j!$
and in this case,
$2^j!$
and in this case,
![]() $2^j$
is an essential period. The methods we have developed so far cannot distinguish between these two scenarios.
$2^j$
is an essential period. The methods we have developed so far cannot distinguish between these two scenarios.
Acknowledgments
This material is based upon work supported by the National Science Foundation Graduate Research Fellowship under Grant No. DGE-1842165. The author is also grateful for the helpful discussions and feedback received throughout this project from Bryna Kra and Scott Schmieding. They would also like to thank the referee for their careful and insightful review of this paper and for the comments, corrections, and suggestions they made that greatly improved this work. Additionally, they would like to thank Kaitlyn Loyd, Nick Lohr, Nir Avni, Stephan Snegirov, Bastián Espinoza, and Adam Holeman for their helpful comments.





