Rheology of subglacial till

The Editor,

Journal of Glaciology

Sir,

It is not so long since theoreticians awoke from their clean studies of ice sliding over hard bedrock, and realized that life at the subglacial bed was less pristine than they had thought; that metres-thick layers of subglacial till sometimes exist (Boulton and Jones, 1979; Clarke and others, 1984; Blankenship and others, 1987), and that this material deforms. Since then, many studies have tried to incorporate the deformation of subglacial till into models of glacier and ice-sheet dynamics, by proposing a functional form for the rheology of till (e.g. Alley and others, 1987; Hindmarsh, 1998; Fowler, 2000; Ng, 2000).

Many of these studies assume a viscous rheology of till, in which the viscosity η may be taken to depend on shear stress τ and effective pressure N, as first advocated by Boulton and Hindmarsh (1987). While Boulton and Hindmarsh’s law has the appeal of simplicity and common sense, it can hardly be said to be rooted in experiment, since only seven data points were used by Boulton and Hindmarsh to constrain the form of η, and the way in which the stress was computed was not reported (but was unlikely to be correct). In fact, a growing body of work (Clarke, 1987; Kamb, 1991, 2001; Hooke and others, 1997; Iverson and others, 1997; Tulaczyk and others, 2000) clearly indicates that till (like soils and other granular materials) behaves plastically, having a yield surface (in stress space) which is well described by a Coulomb failure criterion relating the maximum shear stress at a point to the effective stress acting normal to the corresponding shear plane.

A possible implication is that theoretical studies which assume a viscous rheology for till are simply wrong, and should not be supported. The reason I write is that I sense that this attitude is becoming something of a matter of faith, and I want to confront it before it becomes written in stone.

The first thing to say is that a rheological constitutive law is not determined by simply defining a yield surface; so simply saying that till is plastic is not in itself enough to describe strain or strain rate. The simplest kind of flow rule in plasticity theory uses the Levy–Mises relation for large strain (Hill, 1950), and if we take a Von Mises yield criterion (as an example), we find that a rigid/perfectly plastic material deforms as if viscous, but with an effective viscosity which adapts itself so that the stress remains on the yield surface. This does not mean that it is a viscous material, but it behaves in the same way, in the sense that the material responds to an applied shear stress by undergoing spatially distributed deformation.

Despite this, I do not want to give the impression that such a description of finite plastic strain provides an excuse for Hindmarsh’s (1997) optimistic assessment that a plastic rheology may appear viscous at large scales — yet. But I do want to raise a further worry about plastic rheology. The simplest type of problem that we might study is a simple shear flow in which the yield stress is constant; this approximates the situation in subglacial till. The shear stress is then constant (at the yield stress k), but the velocity profile is unconstrained, if we use the Levy–Mises assumption mentioned above. If u is the velocity and z is the vertical coordinate, then we simply have η(∂u/∂z) = k, where η is the “viscosity”, and no further uncoupling of η and u is possible. This is worrying, but is not generally discussed by soil engineering texts (Chen and Mizuno, 1990; Khan and Huang, 1995). It suggests that the normal flow rule (Hill, 1950) may not provide a complete constitutive recipe for finite plastic strain.

There may be other problems in assessing what the yield stress is. Laboratory ring shear tests (e.g. Kamb, 2001) routinely remove clasts which may jam the device by formation of grain bridges (Iverson and others, 1996). It is arguable that the removal of clasts changes the nature of the material, and therefore potentially also changes the very properties which are of concern. In addition, it is likely that effective pressure, and thus also yield stress, will vary with depth as well as with time, and this makes the rheological interpretation of field observations awkward. A minimal expectation of time-varying water pressures would be stick–slip behaviour, as is observed in the field (Kavanaugh and Clarke, 2001) and in the laboratory (Moore and Iverson, 2002), but what this means for an effective rheology is unknown.

In the absence of suitable experimental results on the flow law (as opposed to the yield stress) for tills, one has to rely on models. Iverson and Iverson (2001) provide such a model based on the effect of short-term pressure fluctuations and consequent local slip events. Algebraic simplification of their result (equation (13)) in terms of an effective strain rate leads to the effective flow law

(1)

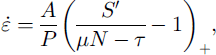
where A = gT² S′/2δΔt is a constant, μ is the coefficient of friction, τ is shear stress, N is effective pressure, and P is overburden ice pressure.

Whether one chooses to call such a flow law plastic or viscous is a matter of semantics. It does, however, point toward my conclusion: the Coulomb yield behaviour of fine-grained sediment mixtures does not necessarily imply that the effective rheology of clastic tills in the field is the same.

6 December 2002