Nomenclature
a slope of the icicle’s lateral surface, Equation (17)
A lateral surface area (m2)
Β dimensionless number, Equation (7)
C dimensionless number, Equation (11)
h convective heat transfer coefficient (W m −2 Κ−1)
k coefficient, Equation (2)
l icicle length (m)
L dimensionless icicle length, Equation (7)
LF latent heat of freezing (J kg−1)
mI icicle mass (kg)
mT total delivered water mass (kg)
M dimensionless mass, Equations (14) and (15)
ṁD drip rate (kg s−1)
ṁo supply rate (kg s−1)
ṀD dimensionless drip rate, Equation (11)
r icicle radius (m)
ro radius of liquid core = radius of pendant drop
(assumed constant) (m)
R dimensionless icicle radius, Equation (4)
Τ dimensionless time, Equation (4)
Q heat loss from the lateral surface of the icicle (W)
X dimensionless horizontal distance (radius) from icicle axis, Equation (19)
Y dimensionless downward distance from the icicle root, Equation (20)
ΔT the difference between the surface and air temperature (K)
δ thickness of dendritic cylinder at tip (assumed constant) (m)
ρ icicle density (kg m−3)
Subscripts
C refers to the critical moment when dripping stops
D refers to the pendant drop
o refers to the liquid core
R refers to the icicle root
Introduction
Icicles occur most commonly when water flows from an overhang and the heat loss from the water is large enough for freezing to occur. The existence of icicles may be undesirable because they represent an additional load on a structure. They can also be dangerous when they fall. The modelling of icicle formation is challenging since the water flow is three-dimensional, and the heat transfer determines not only the amount of freezing but also the shape of the forming icicles.
Numerical models of fresh water icicles (Reference MakkonenMakkonen, 1988) and brine icicles (Reference Chung and LozowskiChung and Lozowski, 1990) have been developed. These models are comparatively complex, the governing equations were solved numerically, and consequently the results lack generality. Recently, Reference Szilder and LozowskiSzilder and Lozowski (1993) developed a stochastic computer model of icicle formation, based on a conceptual model in which the water drops supplied to the icicle root move randomly downwards along the icicle’s surface. During the downward motion of the drops, some freeze along the way and others drip from the icicle’s tip. This model predicts the details of the icicle’s shape including the random occurrence of ribs on the icicle’s surface.
In this paper, an analytical approach to modelling icicle formation is taken which provides additional insight into the growth process. Simple differential forms of the heat and mass balance equations are solved analytically, and the results are presented in a general, time-dependent, dimensionless form.
Model Description and Results
In the model there are two stages of icicle growth if the liquid supply rate is constant with time (Reference MakkonenMakkonen, 1988). In the first stage, some of the supplied water freezes on the icicle’s lateral surface and at the tip. Any unfrozen water drips from the tip. When the icicle reaches a critical length, all the supplied water freezes on the icicle’s lateral surface, and there is no water available at the tip either to freeze or to drip. After this critical point, in the second stage, the icicle’s length remains constant and the icicle grows only radially.
Based on observations (e.g.Reference Maeno and Takahashi Maeno and Takahashi, 1984) it is assumed that the icicle elongates as a hollow conical tube of ice with unfrozen water trapped in a cylindrical core. The radius of the liquid core corresponds to the radius of the pendant drop and is 2.5 mm. It is observed that the water eventually freezes in the liquid core, possibly through heat conduction towards the icicle’s root (Reference MakkonenMakkonen, 1988). This aspect of the freezing process is not considered in the present paper.
In the model the total heat loss from the icicle’s surface to the cold air is expressed as the product of the heat transfer coefficient (which includes heat loss by convection and evaporation) and the temperature difference between the icicle’s surface and the air. The heat lost from the lateral surface of a horizontal slice of thickness dl and radius r is proportional to the amount of ice which forms. Thus:
The relationship between the Nusselt number and the Reynolds number gives the variation of the convective heat-transfer coefficient with icicle radius:
The coefficient k increases with increasing Reynolds number from 0.33 (0.4 < Re < 4) to 0.80 (4 × 104 < Re < 4 × 105) (Reference Incropera and DeWittIncropera and DeWitt, 1985). If k is unity, the convective heat transfer coefficient is independent of radius. Integration of Equation (1), using Equation (2), leads to an expression for the dimensionless icicle radius as a function of the dimensionless time:
where:
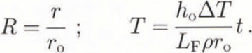
The icicle’s radial growth rate decreases with time for any realistic value of the coefficient k (0 < k < 1). Equation (3) may be applied for any horizontal section of the icicle, provided the time is measured from the moment when the icicle tip reaches that section.
The length growth of the icicle is calculated assuming that heat is lost from a hemispherical pendant drop of radius ro. The details of the dripping process are thus ignored in favour of a time-independent average geometry. This heat transfer leads to the downward growth of a hollow dendritic cylinder of thickness δ and radius ro:
For simplicity, the influence of water supercooling on the freezing process has been neglected. There is also some-question as to the magnitude of the supercooling and how it arises. The dimensionless icicle length as a function of dimensionless time is obtained by integrating Equation (5):
where:

Using Equations (3) and (6), the changing profiles of an icicle are shown in Figure 1 for two values of the coefficient k. For simplicity, we have assumed in drawing the figures that the heat flux from the icicle tip is equal to the lateral heat flux from the icicle at radius ro (i.e. hDΔTD = hoΔT). In addition, the thickness of the dendrite wall has been taken to be 75μm (Reference MakkonenMakkonen, 1988). With these values and a liquid core radius of 2.5 mm, the value of Β is 33. As a result of the decreasing heat loss from the growing icicle when k < 1, the radial rate of growth decreases with time. However, the icicle shape, even for low values of the coefficient k (e.g. k = 0.33), does not deviate substantially from simple conical geometry. Nevertheless, the ratio of icicle length to icicle radius at the root increases with time if the convective heat transfer coefficient is a function of radius.
The rate of change of the icicle’s mass is the difference between the supply rate and the drip rate. It is also the ratio of the heat loss from the entire icicle surface to the latent heat of freezing:
We assume here that the icicle loses heat only from its lateral surface. Integration over this area, Equations (3)
and (6), leads to the following expression for the heat loss:
Using Equations (8) and (9), the dimensionless drip rate may be obtained as a function of dimensionless time:
where:

The drip rate decreases with time because more of the constant water supply freezes on the increasing lateral surface of the icicle. For small values of the coefficient k, the rate of freezing decreases rapidly with radius, and consequently the drip rate decreases slowly with time (Fig. 2). If the magnitude of the heat flux increases or the supply rate decreases, the dimensionless product of Β and C increases and the dimensionless drip rate decreases faster with time. Since the heat flux expression is also included in the definition of the dimensionless time, Equation (4), even for a constant dimensionless time, an increase of the heat flux leads to a decrease in the actual time to achieve a certain drip rate.

Fig. 2. Dimensionless drip rate as a function of dimensionless time, Equation (10), for two values of the product BC, 0.005 and 0.010, and two values of the coefficient k, 0.33 and 1.0.
When the drip rate reaches zero, the icicle ceases to grow in length because there is no more water available at the icicle tip to freeze. The critical dimensionless time at which dripping just stops may be calculated from Equation (10), by setting ṀD = 0:

If the supply rate increases or the heat flux decreases, the time required to reach the critical state increases (Fig. 3).

Fig. 3. Dimensionless critical time as a function of the product BC, Equation (12), for three values of the coefficient k.
If the heat transfer decreases slowly with increasing radius, the critical time is shorter. However, if BC is large, the critical time is independent of k, and is simply 0.5/BC. At this critical moment, the icicle radius at the root has a certain critical value and the icicle length reaches a maximum:

Interestingly, the critical radius of the icicle root is independent of k, that is, it is independent of the way the heat flux changes with radius.
The icicle mass as a function of time may also be calculated. Integrating Equation (8) and using Equation (9), the temporal variation of the dimensionless icicle mass during the first stage when dripping occurs is given by:

where :

It can readily be seen that the dimensionless icicle mass is simply the number of drops of radius ro forming the icicle. The rate of icicle mass growth increases with time and is greater for larger values of the coefficient k (Fig. 4). The mass growth rate reaches a maximum when dripping stops and it is equal to the supply rate.
The cumulative mass of water delivered to the icicle root is a linear function of time since the supply rate is assumed to be constant. Hence:

Since the definition of dimensionless time involves the external heat flux, the dimensionless number C must also appear in Equation (15) in order to eliminate any

Fig. 4. Dimensionless icicle mass as a function of dimensionless time. The icicle mass ΜI, Equation (14), is depicted by solid lines for two values of k, 0.33 and 1.0. The critical state at which dripping stops is represented by the dots. The cumulative delivered water mass MT, Equation (15), is represented by dashed tine. The dimensionless number Β is 33 and C is 0.001.
influence of the heal flux on the delivered water mass. The variation of the dimensionless total delivered mass, which may be interpreted as the number of drops delivered to the icicle root, is shown for C ecjtial to 0.001 in Figure 4.
The ratio of the icicle mass to the total delivered water mass at the critical time is:

Thus the icicle mass represents 33.3 to 50% of the total delivered water mass when dripping stops (Fig. 5). A

Fig. 5. The ratio of icicle mass to cumulative delivered liquid mass at the critical time. Equation (16), as a function of the dimensionless product BC, for three values of the coefficient k.
more efficient heat loss from the icicle surface or a smaller supply rate leads to an increase of this relative critical icicle mass. In addition, if the convective heat flux decreases rapidly with radius, the relative icicle mass also increases. This occurs because smaller values of the coefficient k mean more lime is needed to reach the critical root radius, which is independent of k. During this greater time, the icicle length and icicle mass increase. We can see therefore that icicles are quite efficient in converting liquid water to ice, provided that they grow until they stop dripping.
The evolution of the icicle’s shape after dripping stops and all the incoming water freezes on the icicle surface has also been investigated. To simplify the ensuing calcul-ations, it is assumed that the vertical cross-section of the growing portion of the lateral icicle surface can be approximated by a straight line, for any value of the coefficient k. Figure 1 shows that this assumption is reasonable even for a k of 0.33. It is further assumed thai the heat flux is constant, and hence that the extent of the area on which the water freezes is independent of time. Thus the water freezes in uniform layers, and the lateral surface of the growing icicle remains parallel to the surface at the critical time. In the other words, the slope of an icicle surface close to the root remains constant.
At the critical time, water freezes on the entire lateral icicle surface. This area can be approximated as the difference between the lateral surface of a cone of radius rRC and height arRC (a is the slope of the icicle’s lateral surface) and the area of a cone of radius ro and length aro:

This constant area AC is expressed as a function of the radius of the icicle’s root rR and the distance x from the icicle’s axis to the freezing front, assuming a constant slope of the icicle’s surface. The freezing front is the location along the icicle wall beyond which there is no flow of liquid water. Thus AC is given by:
Comparing Equations (17) and (18), the dimensionless distance from the icicle axis to its retreating (ascending) freezing front is given by:
It may easily be shown that the dimensionless vertical coordinate of the freezing front is given by:
Equations (19) and (20) yield the variation of the dimensionless location of the freezing front with dimensionless icicle root radius, which in turn is a function of time, Equation (3).
Elimination of the icicle root radius leads to a time-independent function describing the final shape of the icicle:

Figure 6 shows the icicle shape when dripping stops and thereafter for two values of the coefficient k and constant values of Β = 33 and C = 0.002. Since the critical dimensionless root radius docs not depend on the value of k, Equation (13), but a longer time interval is needed to reach this critical size for smaller k, the critical icicle length is larger for k = 0.33. The critical lime is 5.513 and 3.012 for k of 0.33 and 1, respectively. The shapes for TC,…,5TC are plotted for the two cases. Note that the scale is not the same for X and Y.
Some qualitative comparisons of the present model results with experiments and other models have been accomplished. Experiments show (Reference Maeno and TakahashiMaeno and Takahashi, 1984) that with a constant supply rate, the icicle-length growth rate is almost constant and that the radial growth rate has a tendency to decrease with time. In addition, the numerical model of Reference MakkonenMakkonen (1988) shows that the rate of icicle mass growth increases gradually with time and reaches a maximum when dripping stops. A similar time-dependent behaviour is predicted by the present analytical model. The experiments also show (Reference Maeno and TakahashiMaeno and Takahashi, 1984) that changes of the supply rate may influence the icicle length, but that the diameter is independent of the supply rate. The present model predicts insensitivity of the icicle diameter to the supply rate; however, as a result of neglecting supercooling, the length growth rate in the model is also insensitive to the supply rate. Both experimental results and our model show that an increase in the heat transfer from the icicle leads to an increase of both the icicle diameter and length.
Conclusions
A simple analytical model has been proposed which successfully emulates some of the main features of the icicle growth process. The model predicts the time-dependent evolution of the dimensionless icicle shape, size, drip rate and mass. It provides some general insight which would be hard to obtain from experiments or numerical models. The analytical solution shows, for example, that at the moment when dripping stops, 33 to 50% of the water delivered to the icicle actually forms the icicle, the rest of the water having dripped from the tip. In spite of its simplicity, the model predicts realistic icicle shapes, and the variation of some icicle parameters agrees qualitatively with experimental results and with other icicle models.
Acknowledgements
This research was financially supported through an NSERC strategic research grant. One of the authors (EPL) thanks his son Alex, whose youthful enthusiasm for glowing icicles has provided numerous insights into the simplicity and elegance of the process.










